BR112019020898B1 - Método de codificação e decodificação, aparelho, terminal, estação base, sistema de comunicações e meio de armazenamento legível por computador - Google Patents

Abstract

este pedido revela um método de codificação, um aparelho, um dispositivo de comunicações e um sistema de comunicações. o método inclui: codificar (502, 603) uma sequência de bits de entrada ao usar uma matriz de verificação de paridade de baixa densidade ldpc, onde a matriz ldpc é obtida com base em um fator de elevação z e em uma matriz de base, a matriz de base inclui a linha 0 à linha 4 e a coluna 0 à coluna 26 em uma das matrizes mostradas na figura 3b-1 à figura 3b-10, ou a matriz de base inclui a linha 0 à linha 4 e algumas de a coluna 0 à coluna 26 em uma das matrizes mostradas na figura 3b-1 à figura 3b-10. o método de codificação, o aparelho, o dispositivo de comunicações e o sistema de comunicações neste pedido podem satisfazer uma exigência de codificação de canal.

Description

CAMPO TÉCNICO

[001] Modalidades do presente pedido dizem respeito ao campo de comunicações, e em particular a um método de processamento de informação e a um aparelho de comunicações.

ANTECEDENTES

[002] Código de verificação de paridade de baixa densidade (low density parity check, LDPC) é um tipo de código de bloco linear com uma matriz de verificação de paridade esparsa, e é caracterizado por uma estrutura flexível e baixa complexidade de decodificação. Porque decodificação do código LDPC usa um algoritmo de decodificação iterativo parcialmente paralelo, o código LDPC tem uma taxa de transferência maior que a de um código turbo convencional. O código LDPC pode ser usado como um código de correção de erro em um sistema de comunicações, a fim de aumentar confiabilidade de transmissão de canal e utilização de potência. Código LDPC também pode ser aplicado amplamente para comunicação espacial, comunicação por fibra ótica, sistemas de comunicações pessoais, ADSL, dispositivos de gravação magnéticos e outros mais. Correntemente, esquema de código LDPC tem sido considerado como um dos esquemas de codificação de canal na comunicação móvel de quinta geração.

[003] Em aplicações práticas, matrizes LDPC caracterizadas por estruturas especiais diferentes podem ser usadas. Uma matriz LDPC H, tendo uma estrutura especial, pode ser obtida ao expandir uma matriz de base LDPC tendo uma estrutura quase cíclica (quasi cycle, QC). Um esquema de codificação usando matrizes QC-LDPC é adequado para hardware com um alto grau de paralelismo, e fornece uma taxa de transferência maior.

[004] QC-LDPC é adequada para hardware com um alto grau de paralelismo, e fornece uma taxa de transferência maior. A matriz LDPC pode ser projetada para ser aplicável à codificação de canal.

SUMÁRIO

[005] Modalidades do presente pedido fornecem um método de processamento de informação e um aparelho e sistema de comunicações, para dar suporte para codificação e decodificação de sequências de bits de informação de uma pluralidade de comprimentos.

[006] De acordo com um primeiro aspecto, um método de codificação e um codificador são fornecidos. O codificador codifica uma sequência de entrada ao usar uma matriz de verificação de paridade de baixa densidade LDPC.

[007] De acordo com um segundo aspecto, um método de decodificação e um decodificador são fornecidos. O decodificador decodifica uma sequência de entrada ao usar uma matriz de verificação de paridade de baixa densidade LDPC.

[008] Em uma primeira implementação do primeiro aspecto ou do segundo aspecto, a matriz LDPC é obtida com base em um fator de elevação Z e em uma matriz de base.

[009] Com base na implementação indicada anteriormente, uma matriz de base de um gráfico de base 30a pode incluir a linha 0 à linha 4 e a coluna 0 à coluna 26 em uma das matrizes 30b-10, 30b-11, 30b-20, 30b-21, 30b-30, 30b-40, 30b-50, 30b60, 30b-70 e 30b-80, ou a matriz de base inclui a linha 0 à linha 4 e algumas de a coluna 0 à coluna 26 em uma das matrizes 30b-10, 30b-11, 30b-20, 30b-21, 30b-30, 30b-40, 30b-50, 30b-60, 30b-70 e 30b-80, ou a matriz de base pode ser uma matriz obtida ao executar permutação de linha/coluna em uma matriz incluindo a linha 0 à linha 4 e a coluna 0 à coluna 26 em uma das matrizes 30b-10 a 30b-80, ou a matriz de base pode ser uma matriz obtida ao executar permutação de linha/coluna em uma matriz incluindo a linha 0 à linha 4 e algumas de a coluna 0 à coluna 26 em uma das matrizes 30b10, 30b-11, 30b-20, 30b-21, 30b-30, 30b-40, 30b-50, 30b-60, 30b- 70 e 30b-80.

[010] Adicionalmente, a matriz de base do gráfico de base 30a pode incluir também a linha 0 à linha (m-1) e a coluna 0 à coluna (n-1) na uma das matrizes 30b-10, 30b-11, 30b-20, 30b-21, 30b-30, 30b-40, 30b-50, 30b-60, 30b-70 e 30b-80, ou a matriz de base pode ser uma matriz obtida ao executar permutação de linha/coluna em uma matriz incluindo a linha 0 à linha (m-1) e a coluna 0 à coluna (n-1) na uma das matrizes 30b-10, 30b-11, 30b-20, 30b-21, 30b-30, 30b-40, 30b-50, 30b-60, 30b-70 e 30b-80, onde 5 < m < 46, e 27 < n < 68.

[011] Para suportar comprimentos de blocos de códigos diferentes, um código LDPC precisa de fatores de elevação Z diferentes. Com base na implementação indicada anteriormente, em uma implementação possível, com base nos fatores de elevação Z diferentes, matrizes de base correspondendo a fatores de elevação Z diferentes são usadas. Por exemplo, Z=a*2j, 0<j<7, e ae{2,3,5,7,9,11,13,15}.

[012] Se a=2, a matriz de base pode incluir a linha 0 à linha 4 e a coluna 0 à coluna 26 na matriz 30b-10 ou 30b-11, ou a matriz de base inclui a linha 0 à linha 4 e algumas de a coluna 0 à coluna 26 na matriz 30b-10 ou 30b-11. Adicionalmente, a matriz de base inclui também a linha 0 à linha (m-1) e a coluna 0 à coluna (n-1) na matriz 30b-10 ou 30b-11.

[013] Se a=3, a matriz de base pode incluir a linha 0 à linha 4 e a coluna 0 à coluna 26 na matriz 30b-20 ou 30b-21, ou a matriz de base inclui a linha 0 à linha 4 e algumas de a coluna 0 à coluna 26 na matriz 30b-20 ou 30b-21. Adicionalmente, a matriz de base inclui também a linha 0 à linha (m-1) e a coluna 0 à coluna (n-1) na matriz 30b-20 ou 30b-21.

[014] Se a=5, a matriz de base pode incluir a linha 0 à linha 4 e a coluna 0 à coluna 26 na matriz 30b-30, ou a matriz de base inclui a linha 0 à linha 4 e algumas de a coluna 0 à coluna 26 na matriz 30b-30. Adicionalmente, a matriz de base inclui também a linha 0 à linha (m-1) e a coluna 0 à coluna (n-1) na matriz 30b-30.

[015] Se a=7, a matriz de base pode incluir a linha 0 à linha 4 e a coluna 0 à coluna 26 na matriz 30b-40, ou a matriz de base inclui a linha 0 à linha 4 e algumas de a coluna 0 à coluna 26 na matriz 30b-40. Adicionalmente, a matriz de base inclui também a linha 0 à linha (m-1) e a coluna 0 à coluna (n-1) na matriz 30b-40.

[016] Se a=9, a matriz de base pode incluir a linha 0 à linha 4 e a coluna 0 à coluna 26 na matriz 30b-50, ou a matriz de base inclui a linha 0 à linha 4 e algumas de a coluna 0 à coluna 26 na matriz 30b-50. Adicionalmente, a matriz de base inclui também a linha 0 à linha (m-1) e a coluna 0 à coluna (n-1) na matriz 30b-50.

[017] Se a=11, a matriz de base pode incluir a linha 0 à linha 4 e a coluna 0 à coluna 26 na matriz 30b-60, ou a matriz de base inclui a linha 0 à linha 4 e algumas de a coluna 0 à coluna 26 na matriz 30b-60. Adicionalmente, a matriz de base inclui também a linha 0 à linha (m-1) e a coluna 0 à coluna (n-1) na matriz 30b-60.

[018] Se a=13, a matriz de base pode incluir a linha 0 à linha 4 e a coluna 0 à coluna 26 na matriz 30b-70, ou a matriz de base inclui a linha 0 à linha 4 e algumas de a coluna 0 à coluna 26 na matriz 30b-70. Adicionalmente, a matriz de base inclui também a linha 0 à linha (m-1) e a coluna 0 à coluna (n-1) na matriz 30b-70.

[019] Se a=15, a matriz de base pode incluir a linha 0 à linha 4 e a coluna 0 à coluna 26 na matriz 30b-80, ou a matriz de base inclui a linha 0 à linha 4 e algumas de a coluna 0 à coluna 26 na matriz 30b-80. Adicionalmente, a matriz de base inclui também a linha 0 à linha (m-1) e a coluna 0 à coluna (n-1) na matriz 30b-80.

[020] A matriz de base pode ser uma matriz obtida ao executar permutação de linha/coluna nas matrizes de base mencionadas anteriormente.

[021] Adicionalmente, de forma alternativa, com base nas implementações indicadas anteriormente, a matriz LDPC pode ser obtida com base no fator de elevação Z e em uma matriz Hs obtida ao deslocar cada uma das matrizes de base indicadas anteriormente, ou pode ser obtida com base no fator de elevação Z e em uma matriz obtida ao executar permutação de linha/coluna em uma matriz Hs obtida ao deslocar cada uma das matrizes de base indicadas anteriormente. O deslocamento de cada uma das matrizes de base indicadas anteriormente pode compreender: aumentar ou diminuir valores de mudança iguais ou maiores que 0 em uma ou mais colunas por meio de um deslocamento.

[022] O gráfico de base e as matrizes de base da matriz LDPC nas implementações indicadas anteriormente podem satisfazer exigências de desempenho de blocos de código de uma pluralidade de comprimentos de blocos.

[023] Com base em qualquer um dos aspectos indicados anteriormente ou nas implementações possíveis dos aspectos, em uma outra implementação possível, o método inclui adicionalmente: determinar o fator de elevação Z. Por exemplo, um valor do fator de elevação Z é determinado com base em um comprimento K da sequência de entrada. Um valor mínimo Zo que satisfaz Kb • Zo > K pode ser determinado de um conjunto de fatores de elevação suportado como um valor do fator de elevação Z. Em um projeto possível, Kb pode ser uma contagem de colunas correspondendo a bits de informação em uma matriz de base do código LDPC. Por exemplo, para o gráfico de base 3oa, Kb=22. Em um outro projeto possível, um valor de Kb pode variar com um valor de K, mas não excede a contagem de colunas correspondendo a bits de informação em uma matriz de base do código LDPC. Por exemplo, quando K é maior que um primeiro limiar, Kb=22; quando K é igual ou menor que um primeiro limiar, Kb=21. Alternativamente, quando K é maior que um primeiro limiar, Kb=22; quando K é igual ou menor que um primeiro limiar e é maior que um segundo limiar, Kb=21; quando K é igual ou menor que um segundo limiar, Kb=20.

[024] O fator de elevação Z pode ser determinado pelo codificador ou pelo decodificador com base no comprimento K da sequência de entrada, ou pode ser determinado por um outro componente e fornecido para o codificador ou para o decodificador como um parâmetro de entrada.

[025] Opcionalmente, a matriz LDPC pode ser obtida com base no fator de elevação Z obtido e em uma matriz de base correspondendo ao fator de elevação Z.

[026] Em uma segunda implementação do primeiro aspecto ou do segundo aspecto, a matriz LDPC é obtida com base no fator de elevação Z e em parâmetros da matriz LDPC.

[027] Os parâmetros da matriz LDPC podem incluir um índice de linha, uma posição de coluna na qual um elemento diferente de zero está localizado e um valor de mudança do elemento diferente de zero, e são armazenados em termos da Tabela 310, Tabela 3-11, Tabela 3-20, Tabela 3-21, Tabela 3-30, Tabela 3-40, Tabela 3-50, Tabela 3-60, Tabela 3-70 e da Tabela 3-80. Os parâmetros podem incluir adicionalmente um peso de linha. Posições de colunas nas quais o elemento diferente de zero está localizado estão em correspondência de um para um com valores de mudança do elemento diferente de zero.

[028] Portanto, o codificador codifica a sequência de entrada com base no fator de elevação Z e nos parâmetros da matriz LDPC. Parâmetros armazenados com base na Tabela 3-10 estão correspondendo à matriz 30b-10, parâmetros armazenados com base na Tabela 3-11 estão correspondendo à matriz 30b11, parâmetros armazenados com base na Tabela 3-20 estão correspondendo à matriz 30b-20, parâmetros armazenados com base na Tabela 3-21 estão correspondendo à matriz 30b-21, parâmetros armazenados com base na Tabela 3-30 estão correspondendo à matriz 30b-30, parâmetros armazenados com base na Tabela 3-40 estão correspondendo à matriz 30b-40, parâmetros armazenados com base na Tabela 3-50 estão correspondendo à matriz 30b-50, parâmetros armazenados com base na Tabela 3-60 estão correspondendo à matriz 30b-60, parâmetros armazenados com base na Tabela 3-70 estão correspondendo à matriz 30b-70 e parâmetros armazenados com base na Tabela 3-80 estão correspondendo à matriz 30b-80.

[029] Para um dispositivo de comunicações em uma extremidade de transmissão, codificar uma sequência de entrada ao usar uma matriz LDPC pode incluir: codificar a sequência de entrada ao usar a matriz LDPC correspondendo ao fator de elevação Z; ou codificar a sequência de entrada ao usar uma matriz, em que a matriz é obtida ao executar permutação de linha/coluna na matriz LDPC correspondendo ao fator de elevação Z. Nesta aplicação, a permutação de linha/coluna se refere a permutação de linha, permutação de coluna ou permutação de linha e permutação de coluna.

[030] Para um dispositivo de comunicações em uma extremidade de recebimento, decodificar uma sequência de entrada ao usar uma matriz LDPC inclui: decodificar a sequência de entrada ao usar a matriz LDPC correspondendo ao fator de elevação Z; ou decodificar a sequência de entrada ao usar uma matriz, em que a matriz é obtida ao executar permutação de linha/coluna na matriz LDPC correspondendo ao fator de elevação Z. Nesta aplicação, a permutação de linha/coluna se refere a permutação de linha, permutação de coluna ou permutação de linha e permutação de coluna.

[031] Em uma implementação possível, a matriz LDPC pode ser armazenada em uma memória, e a sequência de entrada é codificada ao usar a matriz LDPC, ou permutação (permutação de linha/coluna) ou elevação é executada com base na matriz LDPC, para obter uma matriz LDPC que pode ser usada para codificação.

[032] Em uma outra implementação possível, um ou mais parâmetros podem ser armazenados, uma matriz LDPC usada para codificar ou decodificar pode ser obtida com base no um ou mais parâmetros, e por esta razão a sequência de entrada pode ser codificada ou decodificada com base na matriz LDPC. O um ou mais parâmetros incluem pelo menos um do seguinte: um gráfico de base, uma matriz de base, uma matriz permutada obtida ao executar permutação de linha/coluna com base em um gráfico de base ou em uma matriz de base, uma matriz elevada com base em um gráfico de base ou em uma matriz de base, um valor de mudança de um elemento diferente de zero em uma matriz de base, ou qualquer parâmetro relacionado com obtenção da matriz LDPC.

[033] Ainda em uma outra implementação possível, a matriz de base da matriz LDPC pode ser armazenada em uma memória.

[034] Ainda em uma outra implementação possível, o gráfico de base da matriz LDPC pode ser armazenado em uma memória, e valores de mudança dos elementos diferentes de zero na matriz de base da matriz LDPC podem ser armazenados na memória.

[035] Ainda em uma outra implementação possível, os parâmetros da matriz LDPC são armazenados em uma memória em termos da Tabela 3-10 à Tabela 3-80.

[036] Com base nas implementações possíveis indicadas anteriormente, em um projeto possível, pelo menos um de um gráfico de base e uma matriz de base que são usados para codificar ou decodificar LDPC é obtido ao executar permutação de linha, ou permutação de coluna, ou permutação de linha e permutação de coluna em pelo menos um de o gráfico de base e a matriz de base da matriz LDPC indicada anteriormente.

[037] De acordo com um terceiro aspecto, um aparelho de comunicações é fornecido. O aparelho de comunicações pode incluir um módulo correspondente configurado para executar os projetos de método indicados anteriormente. O módulo pode ser software e/ou hardware.

[038] Em um projeto possível, o aparelho de comunicações fornecido no terceiro aspecto inclui um processador e um componente transceptor. O processador e o componente transceptor podem ser configurados para implementar funções do método de codificação ou de decodificação indicado anteriormente. No projeto, se o aparelho de comunicações for um terminal, uma estação base ou um outro dispositivo de rede, o componente transceptor do aparelho de comunicações pode ser um transceptor; se o aparelho de comunicações for um chip de banda base ou uma placa de processamento de banda base, o componente transceptor do aparelho de comunicações pode ser um circuito de entrada/saída do chip de banda base ou da placa de processamento de banda base, e é configurado para receber/enviar um sinal de entrada/saída. Opcionalmente, o aparelho de comunicações pode incluir adicionalmente uma memória, configurada para armazenar dados e/ou uma instrução.

[039] Em uma implementação, o processador pode incluir o codificador de acordo com o primeiro aspecto e uma unidade de determinação. A unidade de determinação é configurada para determinar um fator de elevação Z exigido para codificar uma sequência de entrada. O codificador é configurado para codificar a sequência de entrada ao usar uma matriz LDPC correspondendo ao fator de elevação Z.

[040] Em uma outra implementação, o processador pode incluir o decodificador de acordo com o segundo aspecto e uma unidade de obtenção. A unidade de obtenção é configurada para obter valores suaves do código LDPC e um fator de elevação Z. O decodificador é configurado para decodificar os valores suaves do código LDPC com base em uma matriz de base HB correspondendo ao fator de elevação Z, para obter uma sequência de bits de informação.

[041] De acordo com um quarto aspecto, um aparelho de comunicações é fornecido, incluindo um ou mais processadores.

[042] Em um projeto possível, o um ou mais processadores podem implementar funções do codificador no primeiro aspecto. Em um outro projeto possível, o codificador no primeiro aspecto pode ser uma parte do processador. O processador pode implementar outras funções além de funções do codificador no primeiro aspecto.

[043] Em um projeto possível, o um ou mais processadores podem implementar funções do decodificador descrito no segundo aspecto. Em um outro projeto possível, o decodificador no segundo aspecto pode ser uma parte do processador.

[044] Opcionalmente, o aparelho de comunicações pode incluir adicionalmente um transceptor e uma antena.

[045] Opcionalmente, o aparelho de comunicações pode incluir adicionalmente um componente configurado para gerar uma CRC de bloco de transporte, um componente configurado para executar segmentação de bloco de código e anexação de CRC, um intercalador configurado para executar intercalação, um modulador configurado para executar processamento de modulação ou coisa parecida.

[046] Opcionalmente, o aparelho de comunicações pode incluir adicionalmente um demodulador configurado para executar demodulação, um desintercalador configurado para executar desintercalação, um componente configurado para executar descasamento de taxas ou coisa parecida. Funções destes componentes podem ser implementadas ao usar o um ou mais processadores.

[047] Em um projeto possível, funções destes componentes podem ser implementadas ao usar o um ou mais processadores.

[048] De acordo com um quinto aspecto, uma modalidade do presente pedido fornece um sistema de comunicações. O sistema inclui o aparelho de comunicações descrito no terceiro aspecto.

[049] De acordo com um sexto aspecto, uma modalidade do presente pedido fornece um sistema de comunicações. O sistema inclui um ou mais aparelhos de comunicações descritos no quarto aspecto.

[050] De acordo com um outro aspecto, uma modalidade do presente pedido fornece um meio de armazenamento de computador. O meio de armazenamento de computador armazena um programa, e quando o programa é executado em um computador, o computador executa um método de acordo com qualquer um dos aspectos indicados anteriormente.

[051] De acordo ainda com um outro aspecto deste pedido, um produto de programa de computador incluindo instruções é fornecido. Quando o produto de programa de computador é executado em um computador, o computador executa um método de acordo com qualquer um dos aspectos indicados anteriormente.

[052] De acordo com o método de processamento de informação, o aparelho, o dispositivo de comunicações e o sistema de comunicações nas modalidades do presente pedido, comprimento de código flexível e exigências de taxa de código de um sistema podem ser satisfeitos em termos de desempenho de codificação e um piso de erro.

BREVE DESCRIÇÃO DOS DESENHOS

[053] A figura 1 é um diagrama esquemático de um gráfico de base, de uma matriz de base e de matrizes de permutações circulares da matriz de base em um esquema de código LDPC;

[054] A figura 2 é um diagrama estrutural esquemático de um gráfico de base de um código LDPC;

[055] A figura 3a é um diagrama esquemático de um gráfico de base de um código LDPC de acordo com uma modalidade do presente pedido;

[056] A figura 3b-1 é um diagrama esquemático de uma matriz de base de acordo com uma modalidade do presente pedido;

[057] A figura 3b-2 é um diagrama esquemático de uma outra matriz de base de acordo com uma modalidade do presente pedido;

[058] A figura 3b-3 é um diagrama esquemático de uma outra matriz de base de acordo com uma modalidade do presente pedido;

[059] A figura 3b-4 é um diagrama esquemático de uma outra matriz de base de acordo com uma modalidade do presente pedido;

[060] A figura 3b-5 é um diagrama esquemático de uma outra matriz de base de acordo com uma modalidade do presente pedido;

[061] A figura 3b-6 é um diagrama esquemático de uma outra matriz de base de acordo com uma modalidade do presente pedido;

[062] A figura 3b-7 é um diagrama esquemático de uma outra matriz de base de acordo com uma modalidade do presente pedido;

[063] A figura 3b-8 é um diagrama esquemático de uma outra matriz de base de acordo com uma modalidade do presente pedido;

[064] A figura 3b-9 é um diagrama esquemático de uma outra matriz de base de acordo com uma modalidade do presente pedido;

[065] A figura 3b-10 é um diagrama esquemático de uma outra matriz de base de acordo com uma modalidade do presente pedido;

[066] A figura 4 é um diagrama esquemático de desempenho de acordo com uma modalidade do presente pedido;

[067] A figura 5 é um fluxograma de um método de processamento de informação de acordo com uma outra modalidade do presente pedido;

[068] A figura 6 é um fluxograma de um método de processamento de informação de acordo com uma outra modalidade do presente pedido;

[069] A figura 7 é um diagrama estrutural esquemático de um aparelho de processamento de informação de acordo com uma outra modalidade do presente pedido;

[070] A figura 8 é um diagrama esquemático de um sistema de comunicações de acordo com uma outra modalidade do presente pedido; e

[071] A figura 9 é um diagrama esquemático de valores de mudança de uma matriz de base de acordo com uma outra modalidade do presente pedido.

DESCRIÇÃO DE MODALIDADES

[072] Para facilitar entendimento, alguns termos usados neste pedido são descritos a seguir.

[073] Neste pedido, os termos “rede” e “sistema” são usados normalmente de modo permutável, e os termos “aparelho” e “dispositivo” também são usados normalmente de modo permutável. Uma pessoa versada na técnica pode entender os significados dos termos. Um “aparelho de comunicações” pode ser um chip (tal como um chip de banda base, um chip de processamento de sinais digitais ou um chip de uso geral), um terminal, uma estação base ou um outro dispositivo de rede. O terminal é um dispositivo tendo uma função de comunicação, e pode incluir um dispositivo portátil, um dispositivo em veículo, um dispositivo usável, um dispositivo de computação, um outro dispositivo de processamento conectado a um modem sem fio, ou coisa parecida que tenha uma função de comunicação sem fio. O terminal pode ter nomes diferentes em redes diferentes; por exemplo, equipamento de usuário, uma estação móvel, uma unidade assinante, uma estação, um telefone celular, um assistente digital pessoal, um modem sem fio, um dispositivo de comunicações sem fio, um dispositivo portátil, um laptop, um telefone sem fio e uma estação de circuito local sem fio. Para facilidade de descrição, estes dispositivos são referidos resumidamente como um terminal neste pedido. Uma estação base (base station, BS) também pode ser referida como um dispositivo de estação base, e é um dispositivo implementado em uma rede de acesso via rádio para fornecer uma função de comunicação sem fio. A estação base pode ter nomes diferentes em sistemas de acesso sem fio diferentes. Por exemplo, uma estação base em uma rede de Sistema Universal de Telecomunicações Móveis (Universal Mobile Telecommunications System, UMTS) é referida como um NodeB (NodeB), uma estação base em uma rede LTE é referida como um NodeB evoluído (evolved NodeB, eNB ou eNodeB), uma estação base em uma rede de novo rádio (new radio, NR) é referida como um ponto de transmissão e recepção (transmission reception point, TRP) ou um NodeB de próxima geração (generation nodeB, gNB), ou uma estação base em uma outra rede evoluída pode ter um outro nome. Isto não está limitado no presente pedido.

[074] O exposto a seguir descreve as soluções técnicas nas modalidades do presente pedido com referência para os desenhos anexos nas modalidades do presente pedido.

[075] Um código LDPC pode ser definido ao usar uma matriz de verificação de paridade H. A matriz de verificação de paridade H para o código LDPC pode ser obtida ao usar um gráfico de base (base graph) e valores de mudança. O gráfico de base usualmente pode incluir mxn entradas de matriz (entry), e pode ser representado ao usar uma matriz de m linhas e n colunas. Um valor de um elemento de matriz é 0 ou 1. Um elemento cujo valor é 0 algumas vezes é referido como um elemento igual a zero, o qual pode ser substituído por uma matriz toda de zeros (zero matrix) de tamanho ZxZ. Um elemento cujo valor é 1 algumas vezes é referido como um elemento diferente de zero, o qual pode ser substituído por uma matriz de permutação circular de tamanho ZxZ. Em outras palavras, cada elemento de matriz representa uma matriz toda de zeros ou uma matriz de permutação circular. A figura 1 mostra um exemplo 10a de um gráfico de base de um código LDPC em que m=5 e n=27 e que tem uma estrutura QC. Deve ser notado que, neste relatório descritivo, meramente para facilidade de descrição, índices de linhas e índices de colunas de um gráfico de base e de uma matriz são todos numerados começando de 0. Por exemplo, a coluna 0 representa uma primeira coluna do gráfico de base e da matriz, e uma primeira coluna representa uma segunda coluna do gráfico de base e da matriz, a linha 0 representa uma primeira linha do gráfico de base e da matriz, a linha 1 representa uma segunda linha do gráfico de base e da matriz e assim por diante.

[076] Pode ser entendido que índices de linhas e índices de colunas alternativamente podem ser numerados começando de 1, e neste caso os índices de linhas e índices de colunas mostrados neste relatório descritivo são aumentados por 1 para obter índices de linhas e índices de colunas correspondentes. Por exemplo, se os índices de linhas ou índices de colunas forem numerados começando de 1, a coluna 1 representa uma primeira coluna do gráfico de base e da matriz, a coluna 2 representa uma segunda coluna do gráfico de base e da matriz, a linha 1 representa uma primeira linha do gráfico de base e da matriz, a linha 2 representa uma segunda linha do gráfico de base e a matriz e assim por diante. Deve ser entendido que as linhas e as colunas do gráfico de base ou da matriz de base podem ser numeradas por modos diferentes, e o presente pedido não está limitado por nenhum modo particular de numeração.

[077] Se um valor de um elemento na linha i e na coluna j no gráfico de base for 1, e um valor de mudança do elemento for Pi,j, onde Pi,j é um número inteiro igual ou maior que 0, ele indica que o elemento pode ser substituído por uma matriz de permutação circular de tamanho Z*Z correspondendo a Pi,j. A matriz de permutação circular pode ser obtida ao deslocar de forma circular uma matriz de identidade de tamanho ZxZ para a direita por Pi,j vezes. Pode ser aprendido que cada elemento cujo valor é 0 no gráfico de base é substituído por uma matriz toda de zeros de tamanho ZxZ, e cada elemento cujo valor é 1 é substituído por uma matriz de permutação circular de tamanho Z*Z correspondendo a um valor de mudança do elemento, para obter a matriz de verificação de paridade do código LDPC. O gráfico de base pode ser usado para indicar posições de valores de mudança, e cada elemento diferente de zero no gráfico de base está correspondendo a um valor de mudança. Z é um número inteiro positivo, e também pode ser referido como um fator de elevação, ou algumas vezes pode ser referido como um tamanho de elevação, um fator de elevação ou coisa parecida. Z pode ser determinado com base em um tamanho de bloco de código suportado por um sistema e tamanho de dados de informação. Pode ser aprendido que a matriz de verificação de paridade H tem um tamanho de (mxZ)*(nxZ). Por exemplo, se o fator de elevação Z for 4, cada elemento igual a zero é substituído por uma matriz toda de zeros de tamanho 4x4 11a. Se P2,3 for 2, um elemento diferente de zero na linha 2 e na coluna 3 é substituído por uma matriz de permutação circular 4x4 11d, e a matriz 11d é obtida ao deslocar de forma circular uma matriz de identidade 4x4 11b para a direita duas vezes. Se P2,4 for 0, um elemento diferente de zero na linha 2 e na coluna 4 é substituído pela matriz de identidade 11b. Deve ser notado que somente exemplos são descritos neste documento, e os exemplos não constituem uma limitação.

[078] O valor de Pi,j pode depender do fator de elevação Z, para um elemento de 1 (um elemento diferente de zero) na linha i e na coluna j do gráfico de base, e Pi,j pode ser diferente para fatores de elevação Z diferentes. Para facilidade de implementação, uma matriz de base (base matrix) de m linhas e n colunas, a qual algumas vezes é referida como uma matriz de verificação de paridade (PCM), pode ser definida no sistema. Elementos na matriz de base estão em correspondência de um para um com elementos no gráfico de base. Um elemento igual a zero no gráfico de base tem uma mesma posição na matriz de base. Na matriz, um elemento igual a zero é representado por um valor -1 ou por um valor nulo. Um elemento diferente de zero na linha i e na coluna j, cujo valor é 1 no gráfico de base, corresponde a um elemento diferente de zero em uma mesma posição na matriz de base. O elemento diferente de zero é representado por um valor Pi,j, onde Pi,j pode ser um valor de mudança definido em relação a um fator de elevação Z predefinido ou particular. Nas modalidades deste pedido, a matriz de base algumas vezes também é referida como uma matriz de mudança de um gráfico de base.

[079] Tal como mostrado na figura 1, 10b é uma matriz de base correspondendo ao gráfico de base 10a.

[080] De uma maneira geral, o gráfico de base ou a matriz de base do código LDPC pode incluir adicionalmente p colunas correspondendo a bits de perfuração incorporados (perfuração incorporada), e p pode ser um número inteiro variando de 0 a 2. Estas colunas podem ser usadas em codificação, mas bits de sistema correspondendo à codificação usando as colunas correspondendo a bits de perfuração incorporados não são enviados. Uma taxa de código da matriz de base do código LDPC satisfaz R=(n-m)/(n-p). Usando o gráfico de base 10a como um exemplo, se existirem duas colunas correspondendo a bits de perfuração incorporados, uma taxa de código é (275)/(27-2)=0,88, a qual está próxima de 8/9.

[081] Um código LDPC usado em um sistema de comunicações sem fio é um código QC-LDPC, e uma parte de matriz que está correspondendo a bits de paridade do código QC-LDPC tem uma estrutura bidiagonal ou uma estrutura tal como raptor. Isto pode simplificar codificação e suportar repetição híbrida incremental de redundância. Em um decodificador para o código QC-LDPC, uma rede de mudança QC-LDPC (QC-LDPC shift network, QSN), uma rede de Banyan ou uma rede de Benes é usada comumente para implementar deslocamento de forma circular de informação.

[082] Um gráfico de base do código QC-LDPC com a estrutura tal como raptor é uma matriz de m linhas e n colunas. O gráfico de base pode incluir cinco submatrizes: A, B, C, D e E, onde um peso de uma matriz é determinado por uma quantidade de elementos diferentes de zero, um peso de uma linha (peso de linha) se refere a uma quantidade de elementos diferentes de zero em uma linha, um peso de uma coluna (peso de coluna) se refere a uma quantidade de elementos diferentes de zero em uma coluna. Tal como mostrado em 200 na figura 2.

[083] A submatriz A é uma matriz incluindo mA linhas e nA colunas, e um tamanho da submatriz A é mA x nA. Cada coluna está correspondendo a Z bits sistemáticos no código LDPC, e um bit sistemático algumas vezes é referido como um bit de informação.

[084] A submatriz B é uma matriz incluindo mA linhas e mA colunas, e um tamanho da submatriz B é mA x mA. Cada coluna está correspondendo a Z bits de paridade no código LDPC. A submatriz B inclui uma submatriz B’ com uma estrutura bidiagonal e uma matriz coluna cujo peso de coluna é 3 (para abreviar, coluna de peso 3), e a coluna de peso 3 pode ficar localizada no lado esquerdo da submatriz B’, tal como mostrado em 20a na figura 2. A submatriz B pode incluir adicionalmente uma ou mais matrizes colunas cujos pesos de colunas são 1 (para abreviar, coluna de peso 1). Por exemplo, uma implementação possível está mostrada em 20b ou 20c na figura 2.

[085] Usualmente, uma matriz gerada com base na submatriz A e na submatriz B pode ser referida como uma matriz núcleo, e pode ser usada para suportar codificação de taxa de código alta.

[086] A submatriz C é uma matriz toda de zeros, e tem um tamanho de mA x mD.

[087] A submatriz E é uma matriz de identidade, e tem um tamanho de mD x mD.

[088] A submatriz D tem um tamanho de mD x (nA + mA), e usualmente pode ser usada para gerar bits de paridade para taxa de código baixa.

[089] Pode ser entendido que o gráfico de base foi descrito anteriormente a partir de uma perspectiva de definição matemática. Por causa de a submatriz C ser uma matriz toda de zeros e E ser uma matriz de identidade, em uma implementação possível, uma matriz incluindo a submatriz A e a submatriz B, ou uma matriz incluindo a submatriz A, a submatriz B e a submatriz D pode ser usada para representar simplesmente um gráfico de base de uma matriz em codificação ou decodificação.

[090] Por causa de a submatriz C e a submatriz E terem estruturas relativamente definidas, estruturas da submatriz A, da submatriz B e da submatriz D são um dos fatores afetando desempenho de codificação e de decodificação do código LDPC.

[091] Quando uma matriz LDPC com uma estrutura tal como raptor é usada para codificação, em uma implementação possível, a matriz incluindo a submatriz A e a submatriz B, em outras palavras, a matriz núcleo, pode ser usada primeiro para codificação para obter um ou mais bits de paridade correspondendo à submatriz B, e então a matriz total é usada para codificação para obter um ou mais bits de paridade correspondendo à submatriz E. Por causa de a submatriz B poder incluir uma submatriz B’ com a estrutura bidiagonal e uma ou mais colunas de peso 1, durante codificação, bits de paridade correspondendo à estrutura bidiagonal podem ser obtidos primeiro, e então bits de paridade correspondendo às colunas de peso 1 podem ser obtidos.

[092] O exposto a seguir fornece uma implementação de codificação exemplar. É assumido que a matriz núcleo incluindo a submatriz A e a submatriz B é Hnúcleo. Uma última linha e uma última coluna na Hnúcleo são removidas da Hnúcleo, em outras palavras, uma coluna de peso 1 e uma linha em que um elemento diferente de zero na coluna de peso 1 está localizado na Hnúcleo são removidas da Hnúcleo, para obter uma matriz Hnúcleo-duplo. Parte de bits de paridade da Hnúcleo-duplo é representada por He=[He1 He2]. He1 é uma coluna de peso 3, e He2 tem uma estrutura bidiagonal. De acordo com uma definição da matriz LDPC, Hnúcl eo-duplo •[S Pe]T=0, onde S é uma sequência de entrada e é representada por um vetor de bits de informação, Pe é um vetor incluindo bits de paridade, e [S Pe]T representa uma matriz transposta formada pela sequência de entrada S e Pe. Portanto, bits de paridade correspondendo à Hnúcleo-duplo podem ser calculados primeiro com base na sequência de entrada S e em Hnúcl eo-duplo, onde a sequência de entrada S inclui todos os bits de informação. Então bits de paridade correspondendo a uma ou mais colunas de peso 1 na submatriz B são calculados com base nos bits de paridade obtidos correspondendo à Hnúcleo-duplo e à sequência de entrada S. Neste caso, todos os bits de paridade correspondendo à submatriz B podem ser obtidos. Então bits de paridade correspondendo à submatriz E são obtidos ao codificar a submatriz D e com base na sequência de entrada S e nos bits de paridade correspondendo à submatriz B. Assim todos os bits de informação e todos os bits de paridade são obtidos. Estes bits formam uma sequência codificada, em outras palavras, palavra(s) código de LDPC.

[093] Opcionalmente, codificação de código LDPC pode incluir adicionalmente uma operação de encurtamento (shortening) e uma operação de perfuração (puncturing). Os bits encurtados e bits perfurados não são enviados.

[094] O encurtamento usualmente é executado iniciando doúltimo bit de bits de informação, e pode ser executado em modos diferentes. Por exemplo, para uma quantidade de bits encurtados ser s0, os s0 últimos bits na sequência de entrada S podem ser estabelecidos como bits conhecidos, por exemplo, estabelecidos para 0 ou nulos ou outro valor, para obter uma sequência de entrada S’, e então a sequência de entrada S’ é codificada ao usar uma matriz LDPC. Como um outro exemplo, os últimos (s0 mód Z) bits na sequência de entrada S podem ser estabelecidos como bits conhecidos, por exemplo, estabelecidos para 0 ou nulos ou outro valor, para obter uma sequência de entrada S’, e as

últimas colunas na submatriz A são eliminadas para obter uma matriz LDPC H’, e a sequência de entrada S’ é codificada ao usar a matriz LDPC H’, ou as

últimas colunas na submatriz A não participam na codificação da sequência de entrada S’. Após a codificação, os bits encurtados não são enviados.

[095] A perfuração pode ser executada em bit(s) de perfuração incorporado(s) ou em bit(s) de paridade em uma sequência de entrada. Perfuração de bit(s) de paridade é executada usualmente iniciando do último bit em bits de paridade. Alternativamente, perfuração de bit(s) de paridade pode ser executada de acordo com uma ordem de perfuração predefinida do sistema. Em uma implementação possível, uma sequência de entrada é primeiro codificada, e então com base em uma quantidade p de bits que precisam ser perfurados, o(s) p último(s) bit(s) em bits de paridade é/são selecionados ou p bit(s) é/são selecionado(s) com base na sequência de perfuração predefinida no sistema, onde o(s) p bit(s) é(não são) enviado(s). Em uma outra implementação possível, p colunas correspondendo a bits perfurados em uma matriz e p linhas em que elementos diferentes de zero nestas colunas estão localizados podem ser determinadas, e as linhas e as colunas não participam em codificação, e por esta razão bits de paridade correspondentes não são gerados.

[096] Deve ser notado que a implementação de codificação é usada meramente como um exemplo neste documento, e uma outra implementação de codificação conhecida para os versados na técnica pode ser usada com base no gráfico de base e/ou nas matrizes de base fornecidas neste pedido, e nenhuma limitação não é imposta neste pedido. Decodificação neste pedido pode ser executada usando uma pluralidade de métodos de decodificação, por exemplo, um método de decodificação de soma de mínimos (MS) ou um método de decodificação propagação de crença. O método de decodificação MS algumas vezes é também referido como um método de decodificação MS de inundação. Por exemplo, uma sequência de entrada é inicializada e uma iteração é executada na sequência de entrada inicializada. Detecção de decisão rígida é executada após a iteração, e um resultado de decisão rígida é verificado. Se o resultado de decodificação satisfizer uma equação de verificação de paridade, decodificação é bem sucedida, processamento de iteração termina e o resultado de decisão é produzido. Se um resultado de decodificação não satisfizer uma equação de verificação de paridade, uma iteração é executada de novo dentro de uma quantidade máxima de vezes de iteração. Se a verificação ainda falhar quando a quantidade máxima de vezes de iteração é alcançada, a decodificação falha. Pode ser entendido que uma pessoa versada na técnica pode entender que um princípio da decodificação MS é conhecido convencionalmente, e detalhes não são descritos aqui.

[097] Deve ser notado que o método de decodificação é usado meramente como um exemplo neste documento, e outro método de decodificação conhecido para os versados na técnica pode ser usado com base no gráfico de base e/ou na matriz de base fornecida neste pedido, e nenhuma limitação não é imposta neste pedido.

[098] Um código LDPC usualmente pode ser obtido com base em um projeto de um gráfico de base ou de uma matriz de base. Por exemplo, um limite superior de desempenho do código LDPC pode ser determinado ao executar evolução de densidade no gráfico de base ou na matriz de base, e um piso de erro do código LDPC é determinado com base em valores de mudança na matriz de base. Melhorar desempenho de codificação ou de decodificação e diminuição do piso de erro são alguns objetivos de projetar o gráfico de base e a matriz de base. Comprimentos de códigos são amplamente variados em um sistema de comunicações sem fio. Por exemplo, um comprimento de código pode ser de 2.560 bits, 38.400 bits ou coisa parecida. A figura 3a mostra um exemplo de um gráfico de base 30a de um código LDPC. A figura 3b-1 à figura 3b-10 são exemplos de matrizes de base do gráfico de base 30a, e exigências de desempenho de vários comprimentos de blocos podem ser satisfeitas. Para facilidade de descrição e entendimento, índices de linhas e índices de colunas estão mostrados separadamente no lado mais alto e no lado mais à esquerda na figura 3a, e nas figuras 3b-1 a 3b-10.

[099] A figura 3a mostra um exemplo de um gráfico de base 30a de um código LDPC. Na figura, 0 a 67 (isto é, a coluna 0 à coluna 67) na linha mais alta indicam índices de colunas, e 0 a 45 (isto é, a linha 0 à linha 45) na coluna mais à esquerda indicam índices de linhas. Isto é, o gráfico de base tem um tamanho de 46 linhas e 68 colunas.

[0100] Em uma implementação, a submatriz A e a submatriz B podem ser consideradas como uma matriz núcleo do gráfico de base do código LDPC, e podem ser usadas para codificação de taxa de código alta. Uma matriz incluindo 5 linhas e 27 colunas tal como mostrado no gráfico de base 10a pode ser uma matriz núcleo do gráfico de base, a qual é uma matriz incluindo 5 linhas e 27 colunas.

[0101] Em uma implementação, a submatriz A pode incluir uma ou mais colunas correspondendo a bits de perfuração incorporados, por exemplo, pode incluir duas colunas correspondendo a bits de perfuração incorporados. Após a perfuração, uma taxa de código que pode ser suportada pela matriz núcleo é de 0,88.

[0102] A submatriz B pode incluir uma coluna de peso 3, isto é, um peso de coluna da coluna 0 da submatriz B (coluna 22 da matriz núcleo) é 3. A submatriz B tem uma estrutura bidiagonal que inclui a coluna 1 à coluna 3 (coluna 23 à coluna 25 da matriz núcleo) e a linha 0 à linha 3 da submatriz, e a submatriz B inclui adicionalmente uma coluna de peso 1 (coluna 26 da matriz núcleo).

[0103] Em uma implementação, a submatriz A pode corresponder a bits sistemáticos. Os bits sistemáticos algumas vezes são referidos como bits de informação. A submatriz A tem um tamanho de mA linhas e 22 colunas, se mA =5, e a submatriz A inclui elementos na linha 0 à linha 4 e na coluna 0 à coluna 21 no gráfico de base 30a.

[0104] Em uma implementação, a submatriz B pode corresponder a bits de paridade, a submatriz B tem um tamanho de mA linhas e mA colunas, e inclui elementos na linha 0 à linha 4 e na coluna 22 à coluna 26 no gráfico de base 30a.

[0105] Para obter taxas de códigos flexíveis, uma submatriz C, uma submatriz D e uma submatriz E de tamanhos correspondentes podem ser adicionadas com base na matriz núcleo, para obter taxas de códigos diferentes. A submatriz C é uma matriz toda de zeros. A submatriz E é uma matriz de identidade, tamanhos das matrizes são determinados de acordo com uma taxa de código, e estruturas das matrizes são fixadas relativamente. Portanto, desempenho de codificação e desempenho de decodificação são afetados principalmente pela matriz núcleo e pela submatriz D. Linhas e colunas são adicionadas com base na matriz núcleo para formar C, D e E correspondentes, de maneira que taxas de códigos diferentes podem ser obtidas.

[0106] Uma contagem de colunas mD da submatriz D é uma soma de uma contagem de colunas da submatriz A e uma contagem de colunas da submatriz B, e uma contagem de linhas da submatriz D está relacionada principalmente com uma taxa de código. O gráfico de base 30a é usado como um exemplo. Uma contagem de colunas da submatriz D é de 27 colunas. Se uma taxa de código suportada por um código LDPC for Rm, um gráfico de base ou uma matriz de base do código LDPC tem um tamanho de m linhas e n colunas, onde

. Se uma taxa de código mínima Rm for 1/3, e uma quantidade p de colunas correspondendo a bits de perfuração incorporados for 2, no exemplo do gráfico de base 30a, n=68, m=46, uma contagem de linhas mD da submatriz D pode ser de até m-mA = 46-5=41, e 0<mD<41.

[0107] O gráfico de base 30a é usado como um exemplo. A submatriz D pode incluir mD linhas na linha 5 à linha 41 no gráfico de base 30a.

[0108] Nesta aplicação, se existir no máximo um elemento diferente de zero em uma mesma coluna para duas linhas adjacentes em um gráfico de base, as duas linhas são mutuamente ortogonais. Em outras colunas diferentes de algumas colunas para duas linhas adjacentes no gráfico de base, se existir no máximo um elemento diferente de zero em uma mesma coluna das outras colunas para duas linhas adjacentes, as duas linhas são quase ortogonais. Por exemplo, para duas linhas adjacentes, se existir somente um elemento diferente de zero em uma coluna a não ser colunas correspondendo a bits de perfuração incorporados, as duas linhas adjacentes são quase ortogonais.

[0109] A linha 5 à linha 41 no gráfico de base 30a podem incluir uma pluralidade de linhas com uma estrutura quase ortogonal e pelo menos duas linhas com uma estrutura ortogonal. Por exemplo, a linha 5 à linha 41 no gráfico de base 30a incluem pelo menos 15 linhas que satisfazem a estrutura quase ortogonal. Existe no máximo um elemento diferente de zero em uma mesma coluna nas colunas a não ser colunas correspondendo a bits de perfuração incorporados em quaisquer duas linhas adjacentes das 15 linhas. A linha 5 à linha 41 no gráfico de base 30a podem incluir adicionalmente 10 a 26 linhas que satisfazem a estrutura ortogonal. Em outras palavras, nestas linhas, existe no máximo um elemento diferente de zero em uma mesma coluna para quaisquer duas linhas adjacentes. Em outras palavras, também existe no máximo um elemento diferente de zero em uma coluna correspondendo aos bits de perfuração incorporados.

[0110] Se mD=15, a submatriz D no gráfico de base do código LDPC tem um tamanho de 15 linhas e 27 colunas. A submatriz D pode ser uma matriz constituída pela linha 5 à linha 19 e pela coluna 0 à coluna 26 no gráfico de base 30a. Uma taxa de código correspondente suportada pelo código LDPC é de 22/40=0,55. Nesta taxa de código, o gráfico de base do código LDPC está correspondendo a uma matriz constituída pela linha 0 à linha 19 e pela coluna 0 à coluna 41 no gráfico de base 30a. A submatriz E é uma matriz de identidade de 15 linhas e 15 colunas, e a submatriz C é uma matriz toda de zeros de 5 linhas e 15 colunas.

[0111] Se mD=19, a submatriz D no gráfico de base do código LDPC tem um tamanho de 19 linhas e 27 colunas. A submatriz D pode ser uma matriz constituída pela linha 5 à linha 23 e pela coluna 0 à coluna 26 no gráfico de base 30a. Uma taxa de código correspondente suportada pelo código LDPC é de 22/44=1/2. Nesta taxa de código, o gráfico de base do código LDPC está correspondendo a uma matriz formada pela linha 0 à linha 23 e pela coluna 0 à coluna 45 no gráfico de base 30a. A submatriz E é uma matriz de identidade de 19 linhas e 19 colunas, e a submatriz C é uma matriz toda de zeros de 5 linhas e 19 colunas.

[0112] O mesmo é verdadeiro se mD for outro valor, e detalhes não são descritos.

[0113] Em um projeto, permutação de linha/coluna pode ser executada no gráfico de base e/ou na matriz de base. Em outras palavras, permutação de linha, ou permutação de coluna ou permutação de linha e permutação de coluna pode ser executada. A operação de permutação de linha/coluna não muda um peso de linha ou um peso de coluna, e também não muda uma quantidade de elementos diferentes de zero. Portanto, um gráfico de base e/ou uma matriz de base obtida por meio de permutação de linha/coluna tem impacto limitado em desempenho de sistema. Como um todo, o impacto no desempenho de sistema por causa da permutação de linha/coluna é aceitável e está dentro de uma faixa tolerável. Por exemplo, em alguns cenários ou em algumas faixas o desempenho é diminuído em uma faixa admissível, enquanto que em alguns cenários ou em algumas faixas o desempenho é aperfeiçoado. No conjunto, desempenho geral não é afetado significativamente.

[0114] Por exemplo, a linha 34 e a linha 36 no gráfico de base 30a podem ser permutadas, e a coluna 44 e a coluna 45 podem ser permutadas. Como um outro exemplo, a submatriz D inclui mD linhas em uma matriz F, permutação de linha não pode ser executada nas mD linhas, ou permutação de linha pode ser executada em uma ou mais linhas das mD linhas; e a submatriz E ainda tem uma estrutura de diagonal, e permutação de linha ou permutação de coluna não é executada na submatriz E. Por exemplo, a linha 27 e a linha 29 na matriz F são permutadas, a submatriz D inclui mD linhas na submatriz F, e a submatriz E ainda tem uma estrutura de diagonal. Pode ser entendido que, se o gráfico de base ou a matriz de base incluir a submatriz D, quando intercâmbio de colunas é executado nas colunas na matriz núcleo, intercâmbio de colunas precisa ser executado correspondentemente na submatriz D.

[0115] As matrizes 30b-10 a 30b-80 mostradas na figura 3b-1 à figura 3b-10 são respectivamente projetos de uma pluralidade de matrizes de base do gráfico de base 30a. Uma posição de um elemento diferente de zero na linha i e na coluna j, no gráfico de base 30a, em cada uma das matrizes 30b-10 a 30b-80 não é mudada, e um valor do elemento diferente de zero na linha i e na coluna j em cada uma das matrizes é um valor de mudança Vi,j, e um elemento igual a zero é representado por -1 ou nulo na matriz de base. Uma parte correspondente da submatriz D nas matrizes de base pode incluir mD linhas na linha 5 à linha 45 de qualquer uma das matrizes de base, e um valor de mD pode ser selecionado com base em taxas de códigos diferentes. Pode ser entendido que, se o gráfico de base for uma matriz obtida ao executar transformação de linha/coluna no gráfico de base 30a, a matriz de base é também uma matriz obtida ao executar transformação de linha/coluna em qualquer uma das matrizes 30b-10 a 30b-80.

[0116] Em um projeto possível, a matriz de base do código LDPC pode incluir a linha 0 à linha 4 e a coluna 0 à coluna 26 em qualquer uma das matrizes 30b-10 a 30b-80 mostradas na figura 3b-1 à figura 3b-10. Neste caso, uma matriz incluindo a linha 0 à linha 4 e a coluna 0 à coluna 26 da matriz mostrada na figura 3b-1 à figura 3b-10 pode ser usada como uma parte de matriz núcleo da matriz de base. Neste projeto, uma estrutura de outra parte da matriz de base do código LDPC, por exemplo, a matriz C, a matriz D ou a matriz E, não está limitada. Por exemplo, qualquer estrutura mostrada na figura 3b-1 à figura 3b-10 pode ser usada, ou outros projetos de matrizes podem ser usados.

[0117] Em um outro projeto possível, a matriz de base do código LDPC pode incluir: uma matriz incluindo a linha 0 à linha (m-1) e a coluna 0 à coluna (n-1) em qualquer uma das matrizes 30b-10 a 30b-80 mostradas na figura 3b-1 à figura 3b-10, onde 5 < m < 46, m é um número inteiro, 27 < n < 68, e n é um número inteiro.

[0118] Neste projeto, uma estrutura de outra parte da matriz de base do código LDPC não está limitada. Por exemplo, qualquer estrutura mostrada na figura 3b-1 à figura 3b-10 pode ser usada, ou outros projetos de matrizes podem ser usados.

[0119] Em um outro projeto possível, a matriz de base do código LDPC pode incluir: a linha 0 à linha 4 e algumas de a coluna 0 à coluna 26 em qualquer uma das matrizes 30b10 a 30b-80 mostradas na figura 3b-1 à figura 3b-10. Por exemplo, encurtamento (shortening) e/ou perfuração (puncturing) pode ser executada em uma parte de matriz núcleo (linha 0 à linha 4 e coluna 0 à coluna 26) de uma matriz mostrada na figura 3b-1 à figura 3b-10. Em uma implementação, a matriz de base do código LDPC pode não incluir uma coluna correspondendo a bits encurtados e/ou perfurados.

[0120] Neste projeto, outra parte da matriz de base do código LDPC não está limitada. Por exemplo, estruturas mostradas na figura 3b-1 à figura 3b-10 podem ser referenciadas, ou outras estruturas podem ser usadas.

[0121] Em um outro projeto possível, a matriz de base do código LDPC pode incluir: uma matriz incluindo a linha 0 à linha (m-1) e algumas de a coluna 0 à coluna (n-1) em qualquer uma das matrizes 30b-10 a 30b-80 mostradas na figura 3b-1 à figura 3b-10, onde 5 < m < 46, m é um número inteiro, 27 < n ^ 68, e n é um número inteiro. Por exemplo, encurtamento (shortening) e/ou perfuração (puncturing) pode ser executada na linha 0 à linha (m-1) e na coluna 0 à coluna (n-1) em qualquer uma das matrizes 30b-10 a 30b-80 mostradas na figura 3b-1 à figura 3b-10. Em uma implementação, a matriz de base do código LDPC pode não incluir coluna(s) correspondendo a bit(s) encurtado(s) e/ou perfurado(s). Neste projeto, uma outra parte da matriz de base do código LDPC não está limitada. Por exemplo, estruturas mostradas na figura 3b-1 à figura 3b-10 podem ser referenciadas, ou uma outra estrutura pode ser usada.

[0122] Em uma implementação, a operação de encurtamento pode ser executada em bits de informação. Por exemplo, qualquer matriz mostrada na figura 3b-1 à figura 3b-10 é usada como um exemplo. Se uma ou mais colunas de a coluna 0 à coluna 21 forem encurtadas, a matriz de base do código LDPC pode não incluir a uma ou mais colunas encurtadas das matrizes mostradas na figura 3b-1 à figura 3b-10. Por exemplo, se a coluna 21 for encurtada, a matriz de base do código LDPC pode incluir: a coluna 0 à coluna 20 e a coluna 22 à coluna 26 em qualquer uma das matrizes 30b-10 a 30b-80. Para uma matriz incluindo a linha 0 à linha 4, coluna 0 à coluna 20 e a coluna 22 à coluna 26 em qualquer uma das matrizes 30b 10 a 30b-80, uma taxa de código suportada pela matriz neste caso é de 7/8.

[0123] Em uma outra implementação, a perfuração pode ser executada em bits de paridade. Por exemplo, qualquer matriz mostrada na figura 3b-1 à figura 3b-10 é usada como um exemplo, e uma ou mais colunas da coluna 22 à coluna 26 são perfuradas. A matriz de base do código LDPC pode não incluir a uma ou mais colunas perfuradas nas matrizes mostradas na figura 3b-1 à figura 3b-10. Por exemplo, se coluna a 26 for perfurada, a matriz de base do código LDPC pode incluir: a coluna 0 à coluna 25 em qualquer uma das matrizes 30b-10 a 30b-80.

[0124] Fatores de elevação Z diferentes são projetados para o código LDPC, para suportar sequências de bits de informação de comprimentos diferentes. Em um projeto possível, matrizes de base diferentes podem ser usadas para fatores de elevação diferentes, para obter desempenho relativamente alto. Por exemplo, fatores de elevação Z = a x 2j, onde 0 < j < 7, e ae {2,3,5,7,9,11,13,15}. A Tabela 1 é um conjunto de fatores de elevação {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 18, 20, 22, 24, 26, 28, 30, 32, 36, 40, 44, 48, 52, 56, 60, 64, 72, 80, 88, 96, 104, 112, 120, 128, 144, 160, 176, 192, 208, 224, 240, 256, 288, 320, 352, 384} que é possivelmente suportado. Cada uma das células exceto para a linha mais alta e para a coluna mais à esquerda representa um valor de Z correspondendo a valores de a e j correspondentes. Por exemplo, para uma coluna em que a=2 e uma linha em que j=1, Z=4. Como um outro exemplo, para a=11 e j=3, Z=88. Por analogia, detalhes não são descritos. Tabela 1

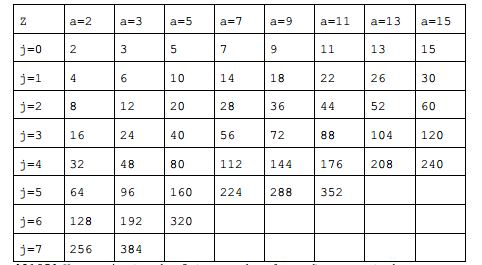
[0125] Um conjunto de fatores de elevação suportados por um gráfico de base podem ser todos ou alguns dos fatores de elevação na Tabela 1; por exemplo, pode ser {24, 26, 28, 30, 32, 36, 40, 44, 48, 52, 56, 60, 64, 72, 80, 88, 96, 104, 112, 120, 128, 144, 160, 176, 192, 208, 224, 240, 256, 288, 320, 352, 384}, em que Z é igual ou maior que 24. Como um outro exemplo, o conjunto de fatores de elevação pode ser um conjunto união de um ou mais de {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 18, 20, 22} e {24, 26, 28, 30, 32, 36, 40, 44, 48, 52, 56, 60, 64, 72, 80, 88, 96, 104, 112, 120, 128, 144, 160, 176, 192, 208, 224, 240, 256, 288, 320, 352, 384}. Deve ser notado que somente exemplos são fornecidos neste documento. O conjunto de fatores de elevação suportado pelo gráfico de base pode ser dividido em subconjuntos diferentes com base em um valor de a. Por exemplo, se a=2, um subconjunto do fator de elevação Z pode incluir um ou mais de {2, 4, 8, 16, 32, 64, 128, 256}. Como um outro exemplo, se a=3, um subconjunto do fator de elevação Z pode incluir um ou mais de {3, 6, 12, 24, 48, 96, 192, 384} e assim por diante.

[0126] O conjunto de fatores de elevação suportado pelo gráfico de base pode ser dividido com base em valores diferentes de a, e uma matriz de base correspondente é determinada.

[0127] Se a=2, ou um valor do fator de elevação Z for um de {2, 4, 8, 16, 32, 64, 128, 256}, a matriz de base pode incluir a linha 0 à linha 4 e a coluna 0 à coluna 26 na matriz 30b-10 ou 30b-11; ou a matriz de base inclui a linha 0 à linha (m-1) e a coluna 0 à coluna (n-1) na matriz 30b10 ou 30b-11, onde 5 < m < 46, m é um número inteiro, 27 < n < 68, e n é um número inteiro; ou a matriz de base inclui a linha 0 à linha (m-1) e algumas de a coluna 0 à coluna (n1) na matriz 30b-10 ou 30b-11, onde 5 < m < 46, m é um número inteiro, 27 ^ n ^ 68, e n é um número inteiro.

[0128] Se a=3, ou um valor do fator de elevação Z é um de {3, 6, 12, 24, 48, 96, 192, 384}, a matriz de base pode incluir a linha 0 à linha 4 e a coluna 0 à coluna 26 na matriz 30b 20 ou 30b-21; ou a matriz de base inclui a linha 0 à linha (m-1) e a coluna 0 à coluna (n-1) na matriz 30b20 ou 30b-21, onde 5 < m < 46, m é um número inteiro, 27 < n < 68, e n é um número inteiro; ou a matriz de base inclui a linha 0 à linha (m-1) e algumas de a coluna 0 à coluna (n1) na matriz 30b-20 ou 30b-21, onde 5 ^ m ^ 46, m é um número inteiro, 27 < n < 68, e n é um número inteiro.

[0129] Se a=5, ou um valor do fator de elevação Z é um de {5, 10, 20, 40, 80, 160, 320}, a matriz de base pode incluir a linha 0 à linha 4 e a coluna 0 à coluna 26 na matriz 30b-30; ou a matriz de base inclui a linha 0 à linha (m-1) e a coluna 0 à coluna (n-1) na matriz 30b-30, onde 5 < m < 46, m é número inteiro, 27 < n < 68, e n é um número inteiro; ou a matriz de base inclui a linha 0 à linha (m-1) e algumas de a coluna 0 à coluna (n-1) na matriz 30b-30, onde 5 ^ m < 46, m é um número inteiro, 27 < n < 68, e n é um número inteiro.

[0130] Se a=7, ou um valor do fator de elevação Z é um de {7, 14, 28, 56, 112, 224}, a matriz de base pode incluir a linha 0 à linha 4 e a coluna 0 à coluna 26 na matriz 30b-40; ou a matriz de base inclui a linha 0 à linha (m-1) e a coluna 0 à coluna (n-1) na matriz 30b-40, onde 5 ^ m < 46, m é número inteiro, 27 < n < 68, e n é um número inteiro; ou a matriz de base inclui a linha 0 à linha (m-1) e algumas de a coluna 0 à coluna (n-1) na matriz 30b-40, onde 5 ^ m < 46, m é um número inteiro, 27 < n < 68, e n é um número inteiro.

[0131] Se a=9, ou um valor do fator de elevação Z é um de {9, 18, 36, 72, 144, 288}, a matriz de base pode incluir a linha 0 à linha 4 e a coluna 0 à coluna 26 na matriz 30b-50; ou a matriz de base inclui a linha 0 à linha (m-1) e a coluna 0 à coluna (n-1) na matriz 30b-50, onde 5 ^ m < 46, m é número inteiro, 27 < n < 68, e n é um número inteiro; ou a matriz de base inclui a linha 0 à linha (m-1) e algumas de a coluna 0 à coluna (n-1) na matriz 30b-50, onde 5 < m < 46, m é um número inteiro, 27 < n < 68, e n é um número inteiro.

[0132] Se a=11, ou um valor do fator de elevação Z é um de {11, 22, 44, 88, 176, 352}, a matriz de base pode incluir a linha 0 à linha 4 e a coluna 0 à coluna 26 na matriz 30b-60; ou a matriz de base inclui a linha 0 à linha (m-1) e a coluna 0 à coluna (n-1) na matriz 30b-60, onde 5 < m < 46, m é número inteiro, 27 < n < 68, e n é um número inteiro; ou a matriz de base inclui a linha 0 à linha (m-1) e algumas de a coluna 0 à coluna (n-1) na matriz 30b-60, onde 5 < m < 46, m é um número inteiro, 27 ^ n < 68, e n é um número inteiro.

[0133] Se a=13, ou um valor do fator de elevação Z é um de {13, 26, 52, 104, 208}, a matriz de base pode incluir a linha 0 à linha 4 e a coluna 0 à coluna 26 na matriz 30b70; ou a matriz de base inclui a linha 0 à linha (m-1) e a coluna 0 à coluna (n-1) na matriz 30b-70, onde 5 ^ m < 46, m é número inteiro, 27 ^ n < 68, e n é um número inteiro; ou a matriz de base inclui a linha 0 à linha (m-1) e algumas de a coluna 0 à coluna (n-1) na matriz 30b-70, onde 5 ^ m < 46, m é um número inteiro, 27 ^ n < 68, e n é um número inteiro.

[0134] Se a=15, ou um valor do fator de elevação Z é um de {15, 30, 60, 120, 240}, a matriz de base pode incluir a linha 0 à linha 4 e a coluna 0 à coluna 26 na matriz 30b80; ou a matriz de base inclui a linha 0 à linha (m-1) e a coluna 0 à coluna (n-1) na matriz 30b-80, onde 5 ^ m < 46, m é número inteiro, 27 ^ n < 68, e n é um número inteiro; ou a matriz de base inclui a linha 0 à linha (m-1) e algumas de a coluna 0 à coluna (n-1) na matriz 30b-80, onde 5 ^ m < 46, m é um número inteiro, 27 ^ n < 68, e n é um número inteiro.

[0135] Opcionalmente, para uma matriz de base para um código LDPC, valores de mudança de elementos diferentes de zero em uma ou mais colunas na matriz podem ser aumentados ou diminuídos por meio de um Deslocamentos, sem afetar significativamente o desempenho de sistema. Deslocamentos de elementos diferentes de zero em colunas diferentes podem ser os mesmos ou podem ser diferentes. Por exemplo, para compensar uma ou mais colunas na matriz, valores de compensação para colunas diferentes podem ser os mesmos ou podem ser diferentes. Isto não está limitado neste pedido.

[0136] Sem afetar significativamente o desempenho de sistema significa que o impacto no desempenho de sistema é aceitável e está dentro de uma faixa tolerável como um todo. Por exemplo, o desempenho diminui dentro de uma faixa de tolerância em alguns cenários ou em algumas faixas. Entretanto, em alguns cenários ou em algumas faixas, o desempenho melhora de certa forma. Desempenho total não é afetado significativamente.

[0137] Por exemplo, cada valor de mudança igual ou maior que 0 na coluna s em qualquer uma das matrizes 30b-10 a 30b-80 é aumentado ou diminuído por um Deslocamentos, de maneira que uma matriz de deslocamento Hs da matriz pode ser obtida, onde Deslocamentos é um número inteiro igual ou maior que 0, e 0 < s < 23. Os deslocamentos Deslocamentos de uma ou mais colunas pode ser os mesmos ou podem ser diferentes.

[0138] Em um diagrama de desempenho mostrado na figura 4, curvas de desempenho de códigos LDPC codificados com base nas matrizes 30b-10 a 30b-80 estão mostradas. Uma coordenada horizontal representa um comprimento de uma sequência de bits de informação, e uma unidade do comprimento é bit. Uma coordenada vertical é uma razão de sinal para ruído de símbolo (Es/N0) exigida para alcançar um BLER correspondente. Duas linhas de cada taxa de código estão correspondendo respectivamente a dois casos quando BLERs são 0,01 e 0,0001. Em uma mesma taxa de código, o caso em que o BLER é 0,01 está correspondendo a uma curva superior, e o caso em que o BLER é 0,0001 está correspondendo a uma curva inferior. Se cada curva for suave, ela indica que a matriz tem desempenho relativamente bom nos casos de comprimentos de códigos diferentes.

[0139] A figura 1 à figura 3a e a figura 3b-1 à figura 3b-10 mostram estruturas de um gráfico de base e de uma matriz de base de um código LDPC. Para descrever projetos do gráfico de base e/ou das matrizes de base nas implementações do presente pedido, os projetos podem ser descritos adicionalmente na Tabela 2-10 e na Tabela 2-11.

[0140] Em um projeto, o gráfico de base 10a na figura 1 é uma matriz de 5 linhas e 27 colunas, e parâmetros relacionados podem ser expressados na Tabela 2-10. Tabela 2-10

[0141] Em um projeto, a matriz de base mostrada em 10b na figura 1 é uma matriz de 5 linhas e 27 colunas, e parâmetros relacionados podem ser expressados na Tabela 211. Tabela 2-11

[0142] Em um projeto, a matriz 30b-10 na figura 3b-1 pode ser expressada na Tabela 3-10. Tabela 3-10

[0143] Em um projeto, a matriz 30b-11 na figura 3b-1 pode ser expressada na Tabela 3-11. Tabela 3-11

[0144] Em um projeto, a matriz 30b-20 na figura 3b-1 pode ser expressada na Tabela 3-20. Tabela 3-20

[0145] Em um projeto, a matriz 30b-21 na figura 3b-1 pode ser expressada na Tabela 3-21. Tabela 3-21

[0146] Em um projeto, a matriz 30b-30 na figura 3b-1 pode ser expressada na Tabela 3-30. Tabela 3-30

[0147] Em um projeto, a matriz 30b-40 na figura 3b-1 pode ser expressada na Tabela 3-40. Tabela 3-40

[0148] Em um projeto, a matriz 30b-50 na figura 3b-1 pode ser expressada na Tabela 3-50. Tabela 3-50

[0149] Em um projeto, a matriz 30b-60 na figura 3b-1 pode ser expressada na Tabela 3-60. Tabela 3-60

[0150] Em um projeto, a matriz 30b-70 na figura 3b-1 pode ser expressada na Tabela 3-70. Tabela 3-70

[0151] Em um projeto, a matriz 30b-80 na figura 3b-1 pode ser expressada na Tabela 3-80. Tabela 3-80

[0152] Pode ser entendido que a figura 1 à figura 3a, figura 3b-1 à figura 3b-10, Tabela 2-10, Tabela 2-11 e a Tabela 310 à Tabela 3-80 são para ajudar a entender os projetos do gráfico de base e da matriz, e formas de expressão dos projetos não estão limitadas às formas de expressão na figura 1 à figura 3a, figura 3b-1 à figura 3b10, ou na Tabela 2-10, Tabela 2-11 e na Tabela 3-10 à Tabela 3-80. Uma outra variação possível pode ser incluída.

[0153] Em uma implementação, o parâmetro “peso de linha” na Tabela 2-10, Tabela 2-11 e na Tabela 3-10 à Tabela 3-80 alternativamente pode ser omitido. Uma quantidade de elementos diferentes de zero em uma linha pode ser aprendida de acordo com posições de colunas dos elementos diferentes de zero na linha. Portanto, um peso de linha é também aprendido.

[0154] Em uma implementação, valores de parâmetros em “índice de coluna de elemento diferente de zero” na Tabela 2-10, Tabela 2-11 e na Tabela 3-10 à Tabela 3-80 podem não ser classificados em ordem crescente desde que uma posição de coluna de um elemento diferente de zero possa ser recuperada ao usar os valores de parâmetros. Além disso, valores de parâmetros em “valor de mudança de elemento diferente de zero” na Tabela 2-10, Tabela 2-11 e na Tabela 3-10 à Tabela 3-80 podem não ser classificados com base em uma ordem de colunas desde que os valores de parâmetros em “valor de mudança de elemento diferente de zero” estejam em correspondência de um para um com os valores de parâmetros em “índice de coluna de elemento diferente de zero”.

[0155] Em um projeto, para economizar espaço de armazenamento, uma posição de um elemento diferente de zero em uma parte com uma estrutura relativamente definida em um gráfico de base ou em uma matriz de base pode ser calculada com base em uma posição de linha ou em uma posição de coluna, e pode não ser armazenada.

[0156] Por exemplo, a submatriz E é uma matriz diagonal, e inclui elementos diferentes de zero somente em uma diagonal da matriz. Valores de mudança destes elementos diferentes de zero na diagonal são 0. Um índice de coluna de um elemento diferente de zero na submatriz E pode ser calculado com base em um índice de linha, ou um índice de linha de um elemento diferente de zero pode ser calculado com base em um índice de coluna. Usando a matriz 30b-50 na figura 3b-7 como um exemplo, um índice de coluna de um elemento diferente de zero na linha mθ é a coluna (mθ+Kb), onde mθ^4, e Kb=22. Por exemplo, um índice de coluna de um elemento diferente de zero na linha 7 é a coluna 29, e um valor de mudança do elemento diferente de zero é 0.

[0157] Como um outro exemplo, uma estrutura bidiagonal B’ em uma submatriz B está localizada na linha 0 à linha 3 e na coluna 23 à coluna 25 na matriz 30b-50. Um índice de coluna de um elemento diferente de zero na estrutura bidiagonal B’ pode ser calculado com base em um índice de linha, ou uma posição de linha de um elemento diferente de zero pode ser calculada com base em um índice de coluna. Índices de colunas de elementos diferentes de zero na linha mB incluem a coluna (mB+Kb) e a coluna (mB+Kb+1), onde 0<mB<3. Um índice de coluna de um elemento diferente de zero na linha mB inclui a coluna (mB+Kb), onde mB=0 ou mB=3. Um valor de mudança de um elemento diferente de zero na estrutura bidiagonal da submatriz B é também 0. Também pode ser aprendido que, em uma parte de matriz incluindo a coluna 23 à coluna 25 que pertence a uma submatriz D, índices de colunas de elementos diferentes de zero na linha 5 à linha 47 não são fixados, valores de mudança dos elementos diferentes de zero não são 0, e as posições e os valores de mudança dos elementos diferentes de zero ainda precisam ser armazenados.

[0158] Como um outro exemplo, para uma coluna de peso 1 em uma submatriz B, em outras palavras, para a coluna 26 na matriz 30b-50, um índice de coluna de um elemento diferente de zero na linha mB inclui a coluna (mB+Kb), onde mB=4, e um valor de mudança do elemento diferente de zero é também 0.

[0159] A Tabela 3-90 mostra parâmetros relacionados com as linhas na matriz 30b-50. Índices de colunas de elementos diferentes de zero na coluna 0 à coluna 25 podem ser armazenados, enquanto que índices de colunas de elementos diferentes de zero na coluna 26 à coluna 68 não são armazenados. Em outras palavras, índices de colunas de elementos diferentes de zero em colunas de peso 1 na submatriz E e na submatriz B não são armazenados. Tabela 3-90

[0160] A Tabela 3-91 mostra parâmetros relacionados com as linhas na matriz 30b-50. Posições de colunas de elementos diferentes de zero na coluna 0 à coluna 26 podem ser armazenadas, enquanto que posições de colunas de elementos diferentes de zero na coluna 27 à coluna 68 não são armazenadas. Em outras palavras, posições de colunas de elementos diferentes de zero na submatriz E não são armazenadas. Tabela 3-91

[0161] Na Tabela 3-10 à Tabela 3-91 , um peso de linha é opcional, e um índice de linha e índices de colunas de elementos diferentes de zero indicam posições de colunas de elementos diferentes de zero em cada linha, o que é também referido como informação a respeito de um gráfico de base de uma matriz LDPC. Em um projeto, informação a respeito de um gráfico de base e valores de mudança de uma matriz LDPC podem ser armazenados com base nos modos na Tabela 3-10 à Tabela 3-91.

[0162] Em um outro projeto, o gráfico de base da matriz LDPC e os valores de mudança da matriz LDPC podem ser armazenados separadamente. A informação a respeito dos valores de mudança da matriz LDPC pode ser armazenada ao usar índices de linhas e valores de mudança de elementos diferentes de zero na Tabela 3-10 à Tabela 3-91. O gráfico de base da matriz LDPC pode ser armazenado em uma pluralidade de modos; por exemplo, pode ser armazenado em uma forma de matriz do gráfico de base 30a mostrado na figura 3a, ou pode ser armazenado com base nos índices de linhas e em posições dos elementos diferentes de zero na Tabela 3-10 à Tabela 391, ou pode ser armazenado em um modo no qual 1 e 0 em cada linha ou em cada coluna em um gráfico de base podem ser considerados como números binários, e o gráfico de base é armazenado em uma forma de números decimais ou de números hexadecimais para economizar espaço de armazenamento. O gráfico de base 30a é usado como um exemplo. Em cada linha, posições de elementos diferentes de zero nas 26 primeiras colunas ou nas 27 primeiras colunas podem ser armazenadas em quatro números hexadecimais. Por exemplo, se as 26 primeiras colunas na linha 0 forem 11110110 01111101 10111111 00, posições de elementos diferentes de zero na linha 0 podem ser denotadas como 0xF6, 0x7D, 0xBF e 0x00. Para ser específico, cada oito colunas formam um número hexadecimal. 0 pode ser colocado como enchimento nas duas ou três últimas colunas para obter oito dígitos, de maneira que um número hexadecimal correspondente é obtido. O mesmo é verdadeiro para outra linha, e detalhes não são descritos aqui novamente.

[0163] Opcionalmente, nos vários projetos indicados anteriormente, os valores de mudança do LDPC podem ser armazenados em uma outra transformação. Por exemplo, para facilitar processamento de deslocamento de forma circular, uma diferença entre um valor de mudança e um valor de mudança anterior em uma coluna na qual o valor de mudança está localizado pode ser armazenada. A figura 9 mostra valores de mudança da linha 0 à linha 4 e da coluna 0 à coluna 26 na matriz 3b-50 após transformação. No exemplo mostrado na figura 9, a linha 0 é uma linha de início, e valores de mudança na linha 0 não mudam. Elementos iguais a zero em cada linha não mudam, e um valor de mudança de um elemento diferente de zero em cada linha é uma diferença entre um valor de mudança em uma mesma posição na matriz 30b-50 e um elemento diferente de zero anterior na matriz 30b-50 em uma coluna na qual o valor de mudança está localizado. Se não existir elemento diferente de zero antes de uma linha na qual o valor de mudança está localizado e em uma coluna na qual o valor de mudança está localizado, o valor de mudança não muda. Por exemplo, um valor de mudança na linha 1 e na coluna 0 da matriz 30b-50 é 179, e um valor de mudança na linha 1 e na coluna 0 na figura 9 é uma diferença -32 entre 179 e um valor de mudança anterior 211 na coluna 0. Por causa de um elemento na linha 0 e na coluna 4 na figura 9 ser um elemento igual a zero, um valor de mudança na linha 1 e na coluna 4 na figura 9 é o mesmo valor de mudança na linha 1 e na coluna 4 na matriz 30b-50. Um elemento na linha 2 e na coluna 3 na figura 9 é um elemento igual a zero, e um elemento na linha 1 e na coluna 3 é um elemento diferente de zero, e por esta razão um valor de mudança na linha 3 e na coluna 3 é uma diferença -57 entre um valor de mudança 166 na linha 3 e na coluna 3 na matriz 30b-50 e um valor de mudança 223 na linha 1 e na coluna 3 e assim por diante. Por causa de espaço limitado, outras linhas da matriz 30b-50 não estão mostradas na figura 9. O mesmo é verdadeiro para as outras linhas, e detalhes não são descritos aqui novamente. Quando uma diferença de um valor de mudança neste documento é um número positivo, deslocamento de forma circular para a direita é executado em uma matriz de identidade; quando uma diferença é um número negativo, deslocamento de forma circular para a esquerda é executado em uma matriz de identidade. Correspondentemente, um valor de mudança obtido após permutação, em outras palavras, uma diferença de um valor de mudança, pode ser armazenado em “valores de mudança de elementos diferentes de zero” na Tabela 3-10 à Tabela 391. Somente exemplos são fornecidos acima, e os exemplos não constituem uma limitação.

[0164] A figura 5 é um projeto de um processo de processamento de dados. O processo de processamento de dados pode ser implementado ao usar um aparelho de comunicações. O aparelho de comunicações pode ser uma estação base, um terminal ou uma outra entidade tal como um chip de comunicações ou um codificador/um decodificador.

[0165] Parte 501: Obter uma sequência de entrada.

[0166] Em uma implementação, uma sequência de entrada para codificação pode ser uma sequência de bits de informação. A sequência de bits de informação algumas vezes é referida como um bloco de código (code block); por exemplo, pode ser uma sequência de saída obtida após segmentação de bloco de código ser executada em um bloco de transporte. Opcionalmente, a sequência de entrada pode incluir pelo menos um do seguinte: bits de enchimento ou bits de verificação de redundância cíclica (CRC). Em um projeto possível, uma sequência de bits de informação pode ser inserida em bits de enchimento para obter uma sequência de entrada, de maneira que um comprimento da sequência de entrada é K=Kb^Z, e Z=K/Kb. A sequência de bits de informação pode ser inserida em bits de enchimento durante segmentação de bloco de código, ou pode ser inserida após segmentação de bloco de código.

[0167] Em um projeto possível, valores de bits de enchimento podem ser nulo, 0, ou outros valores combinados em um sistema. Deste modo, após codificação, estes bits de enchimento podem ser identificados e não são enviados. O presente pedido não está limitado a isto.

[0168] Em uma implementação, uma sequência de entrada para decodificação pode ser uma sequência de valores suaves de um código LDPC.

[0169] Parte 502: Codificar/decodificar a sequência de entrada com base em uma matriz LDPC, onde uma matriz de base da matriz LDPC pode ser qualquer matriz de base nos exemplos indicados anteriormente.

[0170] Em uma implementação, a matriz LDPC H pode ser obtida com base em um fator de elevação Z e em uma matriz de base.

[0171] Em uma implementação, parâmetros relacionados com a matriz LDPC H podem ser armazenados, e os parâmetros incluem um ou mais dos seguintes: (a) parâmetro usado para obter qualquer matriz de base descrita nas implementações indicadas anteriormente. A matriz de base pode ser obtida com base nos parâmetros, e, por exemplo, os parâmetros podem ser um ou mais dos seguintes: índice de linha, peso de linha, índice de coluna, peso de coluna, posições de um elemento diferente de zero (tais como índices de linhas de elementos diferentes de zero ou índices de colunas de elementos diferentes de zero), valores de mudança de uma matriz de base, valores de mudança dos elementos diferentes de zero e posições correspondentes, um deslocamento, um fator de elevação, um gráfico de base, uma taxa de código e outros mais; (b) uma matriz de base, a qual é uma de quaisquer matrizes de base descritas nas implementações indicadas anteriormente; (c) uma matriz de deslocamento Hs obtida ao deslocar pelo menos uma coluna de qualquer matriz de base listada nas implementações indicadas anteriormente; (d) uma matriz obtida por meio de elevação da matriz de base ou por meio de elevação de uma matriz de deslocamento Hs da matriz de base; (e) uma matriz de base obtida ao executar transformação de linha/coluna em qualquer matriz de base listada nas implementações indicadas anteriormente ou em uma matriz de deslocamento Hs; (f) uma matriz obtida por meio de elevação de uma matriz de base transformada de linha/coluna ou uma matriz de deslocamento transformada de linha/coluna Hs da matriz de base; e (g) uma matriz obtida ao encurtar ou perfurar qualquer matriz de base ou uma matriz de deslocamento Hs da matriz de base descrita nas implementações indicadas anteriormente.

[0172] Em uma implementação possível, a sequência de entrada pode ser codificada/decodificada com base na matriz de verificação de paridade de baixa densidade LDPC em um processo de codificação/decodificação em um ou mais dos seguintes modos: i. Obter a matriz de base com base em (a); e executar codificação/decodificação com base na matriz de base obtida, ou executar permutação de linha/coluna com base na matriz de base obtida, e executar codificação/decodificação com base em uma matriz de base obtida ao executar permutação de linha/coluna, ou executar codificação/decodificação com base em uma matriz de deslocamento da matriz de base obtida, ou executar codificação/decodificação em uma matriz obtida ao executar permutação de linha/coluna com base em uma matriz de deslocamento Hs da matriz de base obtida. Opcionalmente, executar codificação/decodificação com base na matriz de base ou na matriz de deslocamento Hs aqui pode incluir adicionalmente: executar codificação/decodificação com base em uma matriz elevada da matriz de base ou em uma matriz elevada da matriz de deslocamento Hs, ou executar codificação/decodificação com base em uma matriz obtida ao encurtar ou perfurar a matriz de base ou a matriz de deslocamento. ii. Executar codificação/decodificação com base na matriz de base (a matriz de base armazenada H ou Hs, ou a matriz de base armazenada obtida ao executar permutação de linha/coluna na matriz de base H ou Hs) armazenada em (b), (c), (d) ou (e); ou executar permutação de linha/coluna com base na matriz de base armazenada, e executar codificação/decodificação com base em uma matriz de base obtida ao executar permutação de linha/coluna. Opcionalmente, executar codificação/decodificação com base na matriz de base ou na matriz de deslocamento Hs aqui pode incluir adicionalmente: executar codificação/decodificação com base em uma matriz elevada da matriz de base ou em uma matriz elevada da matriz de deslocamento Hs, ou executar codificação/decodificação com base em uma matriz obtida ao encurtar ou perfurar a matriz de base ou a matriz de deslocamento. iii. Executar codificação/decodificação com base em (d), (f) ou (g).

[0173] Parte 503: Produzir uma sequência de bits obtida após a codificação/decodificação.

[0174] A figura 6 é um projeto de obter um processo de processamento de dados, e o projeto pode ser aplicado para a parte 502 na figura 5.

[0175] Parte 601: Obter um fator de elevação Z.

[0176] Em uma implementação, o fator de elevação Z pode ser determinado com base em um comprimento K de uma sequência de entrada. Por exemplo, um valor mínimo Z0 pode ser descoberto em um conjunto de fatores de elevação suportados, e é usado como o valor do fator de elevação Z, onde Kb^Zo > K é satisfeita. Em um projeto possível, Kb pode ser uma contagem de colunas de bits de informação em uma matriz de base de um código LDPC. Para um gráfico de base 30a, uma contagem de colunas de bits de informação é Kbmáx=22, e é assumido que um conjunto de fatores de elevação suportado pelo gráfico de base 30a é {24, 26, 28, 30, 32, 36, 40, 44, 48, 52, 56, 60, 64, 72, 80, 88, 96, 104, 112, 120, 128, 144, 160, 176, 192, 208, 224, 240, 256, 288, 320, 352, 384}.

[0177] Se o comprimento K da sequência de entrada for de 529 bits, então Z é 26; se o comprimento K da sequência de entrada for de 5.000 bits, então Z é 240. Deve ser notado que somente exemplos são fornecidos neste documento, e os exemplos não constituem uma limitação.

[0178] Como um outro exemplo, um valor de Kb pode variar com base em um valor de K, mas não excede uma contagem de colunas de bits de informação em uma matriz de base de um código LDPC. Por exemplo, quando K é maior que um primeiro limiar, Kb=22; quando K é igual ou menor que um primeiro limiar, Kb=21. Alternativamente, quando K é maior que um primeiro limiar, Kb=22; quando K é igual ou menor que um primeiro limiar e é maior que um segundo limiar, Kb=21; quando K é igual ou menor que um segundo limiar, Kb=20. Deve ser notado que somente exemplos são fornecidos neste documento, e os exemplos não constituem uma limitação.

[0179] Além disso, com base em qualquer uma das implementações indicadas anteriormente, para um comprimento de informação especificado K, por exemplo, quando 104<K<512, Z pode ser selecionado com base em uma regra definida por sistema. Quando K é um comprimento a não ser 104<K<512, Z ainda é selecionado com base em qualquer uma das implementações indicadas anteriormente; por exemplo, um valor mínimo Zo que satisfaz Kb^Zo > K é selecionado, onde o valor de Kb é 22 ou é determinado com base em um limiar.

[0180] Em um projeto, quando 104<K<512, um valor de Z está mostrado na Tabela 4-1. Para outro comprimento, Z é selecionado com base em qualquer uma das implementações indicadas anteriormente. Tabela 4-1

[0181] Em um outro projeto possível, um valor mínimo Z0 que satisfaz Kb^Zo > K é selecionado. Quando 104<K<512, o valor de Kb pode variar com base no valor de K, por exemplo, tal como mostrado na Tabela 4-2. Quando K é um comprimento a não ser 104<K<512, Kb é selecionado com base em qualquer uma das implementações indicadas anteriormente, por exemplo, Kb=22 ou Kb é determinado com base em um limiar. Tabela 4-2

[0182] O fator de elevação Z pode ser determinado por um aparelho de comunicações com base no comprimento K da sequência de entrada, ou pode ser obtido por um aparelho de comunicações de uma outra entidade (por exemplo, um processador).

[0183] Parte 602: Obter uma matriz LDPC com base no fator de elevação e em uma matriz de base.

[0184] A matriz de base é qualquer matriz de base descrita nas implementações indicadas anteriormente, ou uma matriz de deslocamento obtida ao deslocar pelo menos uma coluna em qualquer matriz de base descrita anteriormente, ou uma matriz de base obtida ao executar permutação de linha, ou permutação de coluna, ou permutação de linha e permutação de coluna em qualquer matriz de base ou matriz de deslocamento descrita anteriormente. Um gráfico de base da matriz de base inclui pelo menos uma submatriz A e uma submatriz B. Opcionalmente, o gráfico de base da matriz de base pode incluir adicionalmente uma submatriz C, uma submatriz D e uma submatriz E. Para a submatrizes, consultar as descrições nas modalidades expostas anteriormente, e detalhes não são descritos aqui novamente.

[0185] Em uma implementação possível, uma matriz de base correspondente é determinada com base no fator de elevação Z, e a matriz de base é permutada com base no fator de elevação Z para obter a matriz LDPC.

[0186] Em uma implementação, uma correspondência entre um fator de elevação e uma matriz de base pode ser armazenada, e uma matriz de base correspondente é determinada com base no fator de elevação Z obtido na parte 601.

[0187] Por exemplo, quando Z é 26, e a=13, a matriz de base pode incluir a linha 0 à linha 4 e a coluna 0 à coluna 26 em uma matriz 30b-70; ou a matriz de base inclui a linha 0 à linha 4 e algumas de a coluna 0 à coluna 26 em uma matriz 30b-70. Alternativamente, a matriz de base pode incluir a linha 0 à linha (m-1) e a coluna 0 à coluna (n-1) em uma matriz 30b-70, onde 5 < m < 46, m é um número inteiro, 27 < n ^ 68, e n é um número inteiro; ou a matriz de base inclui a linha 0 à linha (m-1) e a coluna 0 à coluna (n-1) em uma matriz 30b-70, onde 5 < m < 46, m é número inteiro, 27 < n < 68, e n é um número inteiro. Adicionalmente, a matriz de base pode incluir um ou mais linhas na linha 5 à linha 45 e uma ou mais colunas na coluna 27 à coluna 67 na matriz 30b- 70. A matriz LDPC é obtida ao permutar a matriz de base com base no fator de elevação Z.

[0188] Deve ser notado que Z=26, a=13 e a matriz mostrada na figura 3b-7 são usados meramente como um exemplo neste documento. Somente exemplos são fornecidos neste documento, e o presente pedido não está limitado a isto. Pode ser entendido que, se fatores de elevação forem diferentes, matrizes de base também são diferentes.

[0189] Em uma implementação possível, a correspondência entre um fator de elevação e uma matriz de base pode ser mostrada na Tabela 5. Um índice de uma matriz de base correspondendo a um fator de elevação é determinado com base na Tabela 5. Em um projeto possível, PCM1 pode ser uma matriz 30b-10 mostrada na figura 3b-1, ou é uma matriz 30b-11 mostrada na figura 3b-2; PCM2 pode ser uma matriz 30b-20 mostrada na figura 3b-3, ou é uma matriz 30b-21 mostrada na figura 3b-4; PCM3 pode ser uma matriz 30b-30 mostrada na figura 3b-5; PCM4 pode ser uma matriz 30b-40 mostrada na figura 3b-6; PCM5 pode ser uma matriz 30b-50 mostrada na figura 3b-7; PCM6 pode ser uma matriz 30b-60 mostrada na figura 3b-8; PCM7 pode ser uma matriz 30b-70 mostrada na figura 3b-9; e PCM8 pode ser uma matriz 30b-80 mostrada na figura 3b-80. Somente exemplos são fornecidos neste documento, e os exemplos não constituem uma limitação. Tabela 5

[0190] Em um projeto possível, tal como mostrado na Tabela 6, índices de conjuntos são estabelecidos para os oito conjuntos de fatores de elevação na Tabela 5. Tabela 6

[0191] Cada índice de conjunto está correspondendo a uma PCM. Por exemplo, 1 está correspondendo à PCM1, 2 está correspondendo à PCM2, 3 está correspondendo à PCM3, ..., e 8 está correspondendo à PCM8 e assim por diante.

[0192] Opcionalmente, em um projeto possível, para o fator de elevação Z, um elemento Pi,j na linha i e na coluna j na matriz de base pode satisfazer a seguinte relação:

onde Vi,j é um valor de mudança de um elemento na linha i e na coluna j em uma matriz de base de um conjunto ao qual o fator de elevação Z pertence, ou um valor de mudança de um elemento diferente de zero na linha i e na coluna j em uma matriz de base de um fator de elevação máximo em um conjunto ao qual o fator de elevação Z pertence.

[0193] Por exemplo, para Z igual a 13, um elemento Vi,j na linha i e na coluna j em uma matriz de base de Z satisfaz a seguinte relação:

onde Vi,j é um valor de mudança de um elemento diferente de zero na linha i e na coluna j em PCM7; em outras palavras, na matriz 30b-70, onde, quando Z=13, uma operação de módulo precisa ser executada ao pegar o valor de mudança Vi,j do elemento diferente de zero na linha i e na coluna j na matriz 30b-70 e Z, onde Z=13.

[0194] Deve ser notado que somente exemplos são fornecidos neste documento, e o presente pedido não está limitado a isto.

[0195] Parte 603: Codificar/decodificar uma sequência de entrada com base na matriz LDPC.

[0196] Em uma implementação, uma sequência de entrada para codificação pode ser uma sequência de bits de informação. Em uma outra implementação, uma sequência de entrada para decodificação pode ser uma sequência de valores suaves do código LDPC. Para detalhes, consultar as descrições relacionadas com a figura 5.

[0197] Em uma implementação possível, uma sequência de entrada para codificação é c = {c0,c1,c2,...,ck-1}, um comprimento da sequência de entrada c é K, e uma sequência de saída obtida após a sequência de entrada c ser codificada é d = {d0,d1,d2,...,dN-1}. K é um número inteiro maior que 0, e K pode ser um múltiplo inteiro do fator de elevação Z.

[0198] A sequência de saída d inclui K0 bits na sequência de entrada c e bits de paridade em uma sequência de bits de paridade w, onde K0 é um número inteiro maior que 0 e igual ou menor que K, um comprimento da sequência de verificação de paridade w é N - K0, e w = {w0, w1, w2, . . . , wN - K0 - 1}.

[0199] A sequência de bits de paridade w e a sequência de entrada c satisfazem a fórmula (1):

onde cT = [c0,c1,c2,...,ck-1]T, cT é um vetor transposto de um vetor incluindo bits na sequência de entrada, w- = [w!, w", w#, . . . , w%&’ &"]-, wT é um vetor transposto de um vetor incluindo bits na sequência de bits de paridade, 0T é um vetor coluna, e valores de todos os elementos de 0T são 0.

[0200] H é uma matriz LDPC obtida com base em qualquer gráfico de base ou matriz de base descrita nas modalidades expostas anteriormente. Um gráfico de base de H tem m linhas e n colunas, e pode ser qualquer gráfico descrito nas modalidades expostas anteriormente, por exemplo, o gráfico de base 30a.

[0201] Em um projeto, o gráfico de base de H inclui p colunas correspondendo a bits de perfuração incorporados, p é um número inteiro igual ou maior que 0, bits de informação correspondendo às p colunas correspondendo a bits de perfuração incorporados não são produzidos, e a sequência de saída não inclui os bits de informação correspondendo às p colunas correspondendo a bits de perfuração incorporados. Neste caso, Ko = K - p-Z. Por exemplo, se p=2, Ko = K - 2-Z, e o comprimento da sequência de bits de paridade w é N + 2-Z - K. Se as p colunas correspondendo a bits de perfuração incorporados participarem em codificação, K0 = K, e o comprimento da sequência de bits de paridade w é N - K.

[0202] Correspondentemente, H pode ter M linhas e (N + p-Z) colunas ou M linhas e N colunas, e um tamanho do gráfico de base de H é: m=M/Z e

[0203] O gráfico de base da matriz LDPC H pode ser representado por [HBG HBG,EXT], onde

0m xn representa uma matriz toda de zeros de tamanho mpnc, e IncXnc representa uma matriz de identidade de tamanho ncxnc.

[0204] Em um projeto possível, se 0m xn for a submatriz C no gráfico de base nas modalidades expostas anteriormente, e 𝐼𝑛𝑐×𝑛𝑐 for a submatriz E nas modalidades expostas

, onde A, B e D são respectivamentea submatriz B e a submatriz D no gráfico de base nas modalidades expostas anteriormente, mc=5, 0≤nc≤41, uma contagem de linhas de HBG é igual ou menor que 46 e igual ou maior que 5, e uma contagem de colunas de HBG é igual a 27.

[0205] Em um outro projeto possível, porque a coluna 26 é uma coluna de peso 1, e um elemento diferente de zero na coluna 26 está localizado na linha 5, 0m xn também pode incluir as quatro primeiras linhas na coluna 26 no gráfico de base nas modalidades expostas anteriormente e as quatro primeiras linhas na submatriz C nas modalidades expostas anteriormente, e X também pode incluir a submatriz E no gráfico de base nas modalidades expostas anteriormente, a linha 5 à linha 46 na coluna 26, e uma última linha na submatriz C, onde mc=4, 0<nc<42, HBG é uma matriz obtida após a última coluna ser removida de uma parte incluindo a submatriz A, a submatriz B e a submatriz D no gráfico de base nas modalidades expostas anteriormente, uma contagem de linhas de HBG é igual ou menor que 46 e igual ou maior que 5, e uma contagem de colunas de HBG é igual a 26. Opcionalmente, se uma taxa de código precisar ser aumentada adicionalmente, HBG pode ter quatro linhas: linha 0 à linha 3.

[0206] Correspondentemente, a matriz LDPC H pode ser representada por H=[H1 H2].

[0207] H1 pode ser obtida ao substituir cada elemento igual a zero em HBG por uma matriz toda de zeros de tamanho ZxZ e substituir cada elemento diferente de zero por uma matriz de permutação circular hi,j de tamanho ZxZ. A matriz de permutação circular hi,j é obtida ao deslocar de forma circular uma matriz de identidade de tamanho Z*Z para a direita Pi,j vezes, e algumas vezes é representada por I(Pi,j), onde i é um índice de linha, e j é um índice de coluna. Em um projeto possível, Pi,j = mód (Vi,j,Z), e Vi,j é um elemento diferente de zero na linha i e na coluna em uma matriz de base correspondendo a um índice de conjunto de fatores de elevação iLS correspondendo a Z.

[0208] H2 pode ser obtida ao substituir cada elemento igual a zero em HBG,EXT por uma matriz toda de zeros de tamanho ZxZ e substituir cada elemento diferente de zero por uma matriz de identidade de tamanho ZxZ.

[0209] Um codificador pode executar codificação e enviar em uma pluralidade de modos. O gráfico de base 30a e a matriz de base 30b-50 descritos na modalidade exposta anteriormente são usados como um exemplo para descrição a seguir. Cada um de o gráfico de base e a matriz de base tem um máximo de 46 linhas e um máximo de 68 colunas e cada um inclui duas colunas correspondendo a bits de perfuração incorporados. Para facilidade de descrição, no presente pedido, um gráfico de base que tem uma quantidade máxima de linhas e uma quantidade máxima de colunas algumas vezes é referido como um gráfico de base completo, e uma matriz de base que tem uma quantidade máxima de linhas e uma quantidade máxima de colunas algumas vezes é referida como uma matriz de base completa.

[0210] Modo 1:

[0211] Codificação é executada com base no gráfico de base completo ou na matriz de base completa, de maneira que tanto bits de paridade quanto possível podem ser obtidos. Neste caso, m=46, e n=68, os quais estão correspondendo à linha 0 à linha 45 e à coluna 0 à coluna 67 no gráfico de base 30a, ou aos valores de mudança na linha 0 à linha 45 e na coluna 0 à coluna 67 na matriz de base 30b-50.

[0212] Correspondentemente, M=46^Z para a matriz LDPC H. Se uma sequência de saída incluir bits de informação correspondendo às colunas correspondendo a bits de perfuração incorporados, N=68^Z; ou se uma sequência de saída não incluir 2-Z bits de informação que são bits de perfuração incorporados, N=66^Z.

[0213] Durante processamento subsequente, bits de informação e bits de paridade que precisam ser enviados podem ser determinados da sequência de saída gerada pelo codificador.

[0214] Modo 2:

[0215] Codificação é executada com base em algumas linhas e em algumas colunas no gráfico de base completo ou na matriz de base completa. Linhas e colunas podem ser selecionadas, com base em uma taxa de código para uma transmissão, ou em uma quantidade de bits de informação e em uma quantidade de bits de paridade ou coisa parecida, do gráfico de base completo ou da matriz de base completa para codificação.

[0216] Por exemplo, a taxa de código é 8/9, m=5 e n=27. Em outras palavras, codificação é executada com base na linha 0 à linha 4 e na coluna 0 à coluna 26 no gráfico de base 30a, ou codificação é executada com base em valores de mudança da linha 0 à linha 4 e da coluna 0 à coluna 26 na matriz de base 30b-50.

[0217] Correspondentemente, M=5^Z para a matriz LDPC H. Se uma sequência de saída incluir bits de informação correspondendo às colunas correspondendo a bits de perfuração incorporados, N=27^Z; ou se uma sequência de saída não incluir bits de informação correspondendo às colunas correspondendo a bits de perfuração incorporados, N=25^Z.

[0218] Como um outro exemplo, a taxa de código é 1/3, m=46 e n=68.

[0219] Pode ser aprendido que, neste modo, tamanhos do gráfico de base de H ou da matriz de base satisfazem 5 < m < 46 e 27 < n < 68, e correspondentemente, para a matriz LDPC H, 5-Z < M < 46^Z e 27^Z < N < 68-Z.

[0220] Em um projeto possível, a coluna 26 no gráfico de base 30a é uma coluna de peso 1, e perfuração pode ser executada na coluna de peso 1 em uma matriz núcleo, de maneira que uma linha e uma coluna são removidas da matriz núcleo de modo correspondente, e m=4 e n=26. Em outras palavras, codificação é executada com base na linha 0 à linha 3 e na coluna 0 à coluna 25 no gráfico de base 30a ou na matriz de base 30b- 50. Uma taxa de código maior pode ser obtida neste modo. Portanto, tamanhos do gráfico de base ou da matriz de base satisfazer 4 < m < 46 e 26 < n < 68, e correspondentemente, para a matriz LDPC H, 4-Z < M < 46^Z e 26^Z < N < 68-Z.

[0221] Por causa de decodificação ser um processo inverso de codificação, para descrições da matriz LDPC H e do gráfico de base e da matriz de base da matriz LDPC H, consultar o método de codificação indicado anteriormente. Decodificação pode ser executada com base em um gráfico de base completo ou em uma matriz de base completa, ou decodificação pode ser executada com base em algumas linhas ou em algumas colunas em um gráfico de base completo ou em uma matriz de base completa.

[0222] Quando a sequência de entrada é para ser codificada/decodificada, a matriz de base pode ser elevada com base em Z para obter a matriz LDPC H. Uma matriz de permutação circular hi,j de tamanho Z*Z é determinada para cada elemento diferente de zero Pi,j na matriz de base, onde hi,j é uma matriz de permutação circular obtida ao deslocar de forma circular uma matriz de identidade Pi,j vezes. Um elemento diferente de zero Pi,j é substituído por hi,j, e um elemento igual a zero em uma matriz de base HB é substituído por uma matriz toda de zeros de tamanho ZxZ, para obter a matriz de verificação de paridade H.

[0223] Em uma implementação possível, a matriz de base do código LDPC pode ser armazenada em uma memória, e o aparelho de comunicações obtém a matriz LDPC correspondendo ao fator de elevação Z, para codificar/decodificar a sequência de entrada.

[0224] Em uma implementação possível, porque existe uma pluralidade de matrizes de base do código LDPC, e espaço de armazenamento relativamente grande é ocupado se as matrizes de base são armazenadas com base em uma estrutura de matriz, um gráfico de base do código LDPC pode ser armazenado em uma memória, valores de mudança de elementos diferentes de zero em cada matriz de base podem ser armazenados por linha ou por coluna, e então a matriz LDPC pode ser obtida com base no gráfico de base e em valores de mudança da matriz de base correspondendo ao fator de elevação Z.

[0225] Um gráfico de base pode indicar posições de elementos diferentes de zero de cada matriz de base. Obter a matriz LDPC com base no gráfico de base e em valores de mudança da matriz de base correspondendo ao fator de elevação Z também pode ser: obter a matriz LDPC com base em posições de elemento diferente de zero e em valores de mudança da matriz de base correspondendo ao fator de elevação Z.

[0226] Em uma outra implementação possível, armazenar um gráfico de base pode ser armazenar posições de elementos diferentes de zero no gráfico de base. Uma posição de um elemento diferente de zero pode ser indicada por um índice de linha e um índice de coluna em que o elemento diferente de zero está localizado. Por exemplo, posições de elementos diferentes de zero podem ser posições de colunas de elementos diferentes de zero em cada linha, ou posições de linhas de elementos diferentes de zero em cada coluna. Em uma outra implementação possível, armazenar um gráfico de base pode ser armazenar posições de elementos iguais a zero no gráfico de base. Igualmente, uma posição de um elemento igual a zero também pode ser indicada por um índice de linha e um índice de coluna em que o elemento igual a zero está localizado. Por exemplo, posições de elementos iguais a zero podem ser posições de colunas de elementos iguais a zero em cada linha, ou posições de linhas de elementos iguais a zero em cada coluna em que o elemento igual a zero está localizado, e posições correspondentes de elementos diferentes de zero podem ser obtidas ao excluir as posições dos elementos iguais a zero. Deve ser notado que somente exemplos são fornecidos neste documento, e o presente pedido não está limitado a isto.

[0227] Em uma implementação possível, valores de mudança de elementos diferentes de zero de cada matriz de base podem ser armazenados nos modos da Tabela 2-10, Tabela 2-11, Tabela 3-10 à Tabela 3-80, Tabela 3-90 e da Tabela 391, e usados como parâmetros da matriz LDPC. Uma coluna de “peso de linha” na Tabela 2-10, Tabela 2-11, Tabela 3-10 à Tabela 3-80, Tabela 3-90 e na Tabela 3-91 é opcional. Em outras palavras, opcionalmente, a coluna de “peso de linha” pode ser armazenada ou não armazenada. Uma quantidade de elementos diferentes de zero em uma linha pode ser conhecida ao usar posições de colunas dos elementos diferentes de zero na linha. Portanto, um peso de linha pode ser conhecido. Em uma implementação possível, valores de parâmetros em “índice de coluna de elemento diferente de zero” na Tabela 2-10, Tabela 2-11, Tabela 3-10 à Tabela 3-80, Tabela 3-90 e na Tabela 391 podem não ser classificados em ordem crescente desde que posições de colunas de elementos diferentes de zero possam ser recuperadas ao usar os valores de parâmetros. Além disso, valores de parâmetros em “valores de mudança de elementos diferentes de zero” na Tabela 2-10, Tabela 2-11, Tabela 310 à Tabela 3-80, Tabela 3-90 e na Tabela 3-91 não são necessariamente classificados com base em uma ordem de coluna desde que os valores de parâmetros em “valores de mudança de elementos diferentes de zero” fiquem em correspondência de um para um com os valores de parâmetros em “posições de colunas de elementos diferentes de zero” e desde que o aparelho de comunicações possa ficar sabendo em qual linha e em qual coluna um elemento diferente de zero está com base em um valor de mudança do elemento diferente de zero. Por exemplo:

[0228] Em uma implementação possível, os parâmetros relacionados da matriz LDPC podem ser armazenados com referência para descrições relacionadas com a figura 5.

[0229] Em uma implementação possível, quando os parâmetros relacionados da matriz LDPC são armazenados, os parâmetros armazenados podem não compreender todas as linhas das matrizes mostradas na figura 1 à figura 3a, figura 3b-1 à figura 3b-10, ou na Tabela 2-10, Tabela 2-11, Tabela 3-10 à Tabela 3-80, Tabela 3-90 e na Tabela 3-91, e um parâmetro indicado por uma linha correspondente em uma tabela pode ser armazenado com base em linhas incluídas na matriz de base. Por exemplo, uma matriz incluindo linhas e colunas incluídas na matriz de base da matriz LDPC descrita na modalidade exposta anteriormente pode ser armazenada, ou parâmetros relacionados com a matriz incluindo as linhas e colunas são armazenados.

[0230] Por exemplo, se a matriz de base incluir a linha 0 à linha 4 e a coluna 0 à coluna 26 em qualquer uma das matrizes 30b-10 a 30b-80 e das matrizes mostradas na Tabela 3-90 e na Tabela 3-91, uma matriz incluindo a linha 0 à linha 4 e a coluna 0 à coluna 26 pode ser armazenada, e/ou parâmetros relacionados com a matriz incluindo a linha 0 à linha 4 e a coluna 0 à coluna 26 são armazenados. Para detalhes, consultar os parâmetros mostrados na Tabela 3-10 à Tabela 3-80, Tabela 3-90 e na Tabela 3-91 e descrições na parte indicada anteriormente.

[0231] Se a matriz de base incluir a linha 0 à linha (m-1) e a coluna 0 à coluna (n-1) em qualquer uma das matrizes 30b- 10 a 30b-80 e das matrizes mostradas na Tabela 3-90 e na Tabela 3-91, onde 5 < m < 46, m é um número inteiro, 27 < n < 68, n é um número inteiro, uma matriz incluindo a linha 0 à linha (m-1) e a coluna 0 à coluna (n-1) pode ser armazenada, e/ou parâmetros relacionados com a matriz incluindo a linha 0 à linha (m-1) e a coluna 0 à coluna (n-1) são armazenados. Para detalhes, consultar os parâmetros mostrados na Tabela 3-10 à Tabela 3-80, Tabela 3-90 e na Tabela 3-91 e descrições na parte indicada anteriormente.

[0232] Em uma implementação possível, cada valor de mudança igual ou maior que 0 e indicado por pelo menos uma posição s de “índice de coluna de elemento diferente de zero” em qualquer uma de a Tabela 3-10 à Tabela 3-80, Tabela 3-90 e a Tabela 3-91 pode ser aumentado ou diminuído por um Deslocamentos.

[0233] Em uma implementação possível, um ou mais valores de mudança transformados descritos na modalidade exposta anteriormente podem ser armazenados em “valor de mudança de elemento diferente de zero” em qualquer uma de a Tabela 310 à Tabela 3-80, Tabela 3-90 e a Tabela 3-91; por exemplo, um ou mais valores de mudança mostrados na figura 9.

[0234] Em um outro projeto, o gráfico de base da matriz LDPC e os valores de mudança da matriz LDPC podem ser armazenados separadamente. Informação a respeito dos valores de mudança da matriz LDPC pode ser armazenada ao usar índices de linhas e valores de mudança de elementos diferentes de zero na Tabela 3-10 à Tabela 3-91. O gráfico de base da matriz LDPC pode ser armazenado em uma pluralidade de modos; por exemplo, pode ser armazenado em uma forma de matriz do gráfico de base 30a mostrado na figura 3a, ou pode ser armazenado com base nos índices de linhas e em posições dos elementos diferentes de zero na Tabela 3-10 à Tabela 3-91, ou pode ser armazenado em um modo no qual 1 e 0 em cada linha ou em cada coluna em um gráfico de base podem ser considerados como dígitos binários, e o gráfico de base é armazenado em uma forma de números decimais ou números hexadecimais para economizar espaço de armazenamento. O gráfico de base 30a é usado como um exemplo. Posições de elementos diferentes de zero nas 26 primeiras colunas ou nas 27 primeiras colunas podem ser armazenadas em quatro números hexadecimais em cada linha. Por exemplo, se as 26 primeiras colunas na linha 0 forem 11110110 01111101 10111111 00, posições de elementos diferentes de zero na linha 0 podem ser denotadas como 0xF6, 0x7D, 0xBF e 0x00. Para ser específico, cada oito colunas formam um número hexadecimal. 0 pode ser colocado como enchimento nas duas ou três últimas colunas para obter oito dígitos, de maneira que um número hexadecimal correspondente é obtido. O mesmo é verdadeiro para uma outra linha, e detalhes não são descritos aqui novamente. Deve ser notado que somente exemplos são fornecidos neste documento, e os exemplos não constituem uma limitação.

[0235] A figura 1 é usada como um exemplo. Após a matriz de base HB ser determinada, bits de paridade correspondendo à coluna 22 à coluna 25 podem ser primeiro obtidos ao usar a sequência de entrada e a linha 0 à linha 3 e a coluna 0 à coluna 25 na matriz de base, em outras palavras, Hnúcleo-duplo. Então, bits de paridade correspondendo à coluna 26, em outras palavras, uma coluna de peso 1, podem ser obtidos com base na sequência de entrada e em bits de paridade correspondendo à Hnúcleo-duplo, e então codificação pode ser executada com base na sequência de entrada, nos bits de paridade correspondendo à coluna 22 à coluna 26 e na submatriz D, para obter bits de paridade correspondendo à submatriz E. Deste modo, codificação é completada. Para um processo de codificação do código LDPC, consultar as descrições nas implementações indicadas anteriormente, e detalhes não são descritos aqui novamente.

[0236] Em uma implementação possível, a matriz LDPC H pode ser elevada em relação ao fator de elevação com base no fator de elevação Z antes de codificação; em outras palavras, cada valor de mudança é substituído por uma matriz de permutação circular correspondente com base em cada valor de mudança.

[0237] Em uma outra implementação possível, um valor de mudança correspondendo a um elemento diferente de zero é obtido com base em uma posição do elemento diferente de zero correspondendo a bits a ser codificados durante codificação, e o elemento diferente de zero é substituído por uma matriz de permutação circular correspondente e processamento é executado.

[0238] Em uma outra implementação possível, a matriz LDPC H não é elevada diretamente durante o uso, e bits em uma sequência de entrada são processados com base em uma relação de conexão que existe entre linhas e colunas de uma matriz equivalente e que é calculada com base em valores de mudança.

[0239] Em uma outra implementação possível, codificação pode ser executada ao usar um método QSN. Para cada elemento diferente de zero a ser processado, com base em um valor de mudança do elemento diferente de zero, uma operação de mudança é executada em um segmento de bits a ser codificado correspondendo ao elemento diferente de zero; e então, uma operação de codificação é executada em todos os segmentos de bits nos quais a operação de mudança é executada.

[0240] Em uma outra implementação possível, uma matriz geradora G da matriz LDPC H também pode ser armazenada, e a sequência de entrada c e a sequência de saída d satisfazem a fórmula (2): D = c • G (2)

[0241] Se permutação de linha/coluna for executada na matriz LDPC H para obter H’, onde o lado direito de H’ é uma matriz de identidade I, e um lado esquerdo matriz é P, H’=[P I], e a matriz geradora G satisfaz a fórmula (3) seguinte: G = [I PT] (3)

[0242] Deve ser notado que a descrição anterior é um exemplo, e o presente pedido não está limitado a isto.

[0243] Opcionalmente, em um sistema de comunicações, o código LDPC pode ser obtido após codificação ser executada ao usar o método indicado anteriormente. Após o código LDPC ser obtido, o aparelho de comunicações pode executar adicionalmente uma ou mais das seguintes operações: executar casamento de taxas no código LDPC; executar, com base em um esquema de intercalação, intercalação em um código LDPC de taxa casada; modular, com base em um esquema de modulação, um código LDPC intercalado, para obter uma sequência de bits X; e enviar a sequência de bits X.

[0244] Decodificação é um processo inverso de codificação, e a matriz de base usada durante decodificação e a matriz de base usada durante codificação têm uma mesma característica. Para o processo de codificação do código LDPC, consultar as descrições nas implementações indicadas anteriormente, e detalhes não são descritos aqui novamente. Em uma implementação, antes de decodificar, o aparelho de comunicações pode executar adicionalmente uma ou mais das seguintes operações: receber um sinal obtido após codificação de código LDPC; e executar demodulação, desintercalação e descasamento de taxas no sinal para obter uma sequência de valores suaves de um código LDPC; e decodificar a sequência de valores suaves do código LDPC.

[0245] O armazenamento neste pedido pode ser armazenamento em uma ou mais memórias. A uma ou mais memórias podem ser dispostas separadamente, ou podem ser integradas ao codificador, ao decodificador, a um processador, a um chip, ao aparelho de comunicações ou a um terminal. Parte de a uma ou mais memórias pode ser disposta separadamente, e as outras podem ser integradas ao decodificador, ao processador, ao chip, ao aparelho de comunicações ou ao terminal. Um tipo da memória pode ser qualquer forma de meio de armazenamento, e esta aplicação não está limitada a isto.

[0246] Correspondendo aos projetos dos processos de processamento de dados na figura 5 e na figura 6, uma modalidade do presente pedido fornece adicionalmente um aparelho de comunicações correspondente. O aparelho de comunicações inclui módulos configurados para executar cada parte na figura 5 ou na figura 6. O módulo pode ser software, ou pode ser hardware, ou pode ser uma combinação de software e hardware. Por exemplo, os módulos podem incluir uma memória, um dispositivo eletrônico, um componente eletrônico, um circuito lógico, ou coisa parecida ou qualquer combinação dos mesmos. A figura 7 é um diagrama estrutural esquemático de um aparelho de comunicações 700. O aparelho 700 pode ser configurado para implementar o método descrito na modalidade de método exposta anteriormente. Para detalhes, consultar as descrições na modalidade de método exposta anteriormente. O aparelho de comunicações 700 pode ser um chip, uma estação base, um terminal ou um outro dispositivo de rede.

[0247] O aparelho de comunicações 700 inclui um ou mais processadores 701. O processador 701 pode ser um processador de uso geral, um processador de uso especial ou coisa parecida. Por exemplo, o processador 701 pode ser um processador de banda base ou uma unidade central de processamento. O processador de banda base pode ser configurado para processar um protocolo de comunicação e dados de comunicação. A unidade central de processamento pode ser configurada para controlar o aparelho de comunicações (tal como a estação base, o terminal ou o chip), executar um programa de software, e processar dados do programa de software.

[0248] Em um projeto possível, o um ou mais módulos na figura 5 e na figura 6 podem ser implementados ao usar um ou mais processadores, ou podem ser implementados ao usar um ou mais processadores e uma ou mais memórias.

[0249] Em um projeto possível, o aparelho de comunicações 700 inclui o um ou mais processadores 701. O um ou mais processadores 701 podem implementar funções de codificação/decodificação. Por exemplo, o aparelho de comunicações pode ser um codificador ou um decodificador. Em um outro projeto possível, o processador 701 pode implementar outras funções além das funções de codificação/decodificação.

[0250] O aparelho de comunicações 700 codifica/decodifica uma sequência de entrada com base em uma matriz LDPC. Uma matriz de base da matriz LDPC pode ser qualquer matriz de base nos exemplos indicados anteriormente, ou uma matriz de base obtida ao executar permutação de linha, ou permutação de coluna, ou permutação de linha e permutação de coluna em qualquer matriz de base nos exemplos indicados anteriormente, ou uma matriz de base obtida ao executar encurtamento ou perfuração em qualquer matriz de base nos exemplos indicados anteriormente, ou uma matriz obtida ao elevar qualquer matriz de base nos exemplos indicados anteriormente. Para processamento de codificação/decodificação, consultar as descrições de partes relacionadas na figura 5 e na figura 6, e detalhes não são descritos aqui novamente.

[0251] Opcionalmente, em um projeto, o processador 701 pode incluir uma instrução 703 (algumas vezes referida também como código ou um programa). A instrução pode ser executada no processador, de maneira que o aparelho de comunicações 700 executa o método descrito na modalidade de método exposta anteriormente. Em um outro projeto possível, o aparelho de comunicações 700 pode incluir também um circuito, e o circuito pode implementar as funções de codificação/decodificação na modalidade exposta anteriormente.

[0252] Opcionalmente, em um projeto, o aparelho de comunicações 700 pode incluir uma ou mais memórias 702. A memória armazena uma instrução 704, e a instrução pode ser executada no processador, de maneira que o aparelho de comunicações 700 executa o método descrito na modalidade de método exposta anteriormente.

[0253] Opcionalmente, a memória pode armazenar adicionalmente dados. Opcionalmente, o processador pode armazenar adicionalmente uma instrução e/ou dados. O processador e a memória podem ser dispostos separadamente, ou podem ser integrados conjuntamente.

[0254] Opcionalmente, o “armazenamento” na modalidade exposta anteriormente pode ser armazenar dados na memória 702, ou pode ser armazenar dados em uma outra memória ou dispositivo de armazenamento periférico.

[0255] Por exemplo, a uma ou mais memórias 702 podem armazenar um ou mais parâmetros relacionados com a matriz LDPC no exemplo indicado anteriormente; por exemplo, o um ou mais parâmetros relacionados com uma matriz de base tais como valores de mudança, um gráfico de base, uma matriz elevada com base em um gráfico de base, linhas na matriz de base, um fator de elevação, a matriz de base ou uma matriz elevada com base na matriz de base. Para detalhes, consultar as descrições relacionadas com a figura 5.

[0256] Opcionalmente, o aparelho de comunicações 700 pode incluir adicionalmente um transceptor 705 e uma antena 706. O processador 701 pode ser referido como uma unidade de processamento, e pode controlar o aparelho de comunicações (o terminal ou a estação base). O transceptor 705 pode ser referido como uma unidade transceptora ou um circuito transceptor, e é configurado para implementar uma função de transcepção do aparelho de comunicações ao usar a antena 706.

[0257] Opcionalmente, o aparelho de comunicações 700 pode incluir adicionalmente um componente configurado para gerar uma CRC de bloco de transporte, um componente configurado para executar segmentação de bloco de código e verificação CRC, um intercalador configurado para executar intercalação, um componente configurado para executar casamento de taxa, um modulador configurado para executar processamento de modulação ou coisa parecida. Funções destes componentes podem ser implementadas pelo um ou mais processadores 701.

[0258] Opcionalmente, o aparelho de comunicações 700 pode incluir adicionalmente um demodulador configurado para executar demodulação, um desintercalador configurado para executar desintercalação, um componente configurado para executar descasamento de taxas, um componente configurado para executar concatenação de bloco de código e verificação CRC ou coisa parecida. Funções destes componentes podem ser implementadas pelo um ou mais processadores 701.

[0259] A figura 8 é um diagrama esquemático de um sistema de comunicações 800. O sistema de comunicações 800 inclui um dispositivo de comunicações 80 e um dispositivo de comunicações 81. O dispositivo de comunicações 80 e o dispositivo de comunicações 81 recebem dados de informação um do outro e enviam dados de informação um para o outro. O dispositivo de comunicações 80 e o dispositivo de comunicações 81 podem ser o aparelho de comunicações 700, ou cada um de o dispositivo de comunicações 80 e o dispositivo de comunicações 81 inclui o aparelho de comunicações 700, e recebe e/ou envia dados de informação. Por exemplo, o dispositivo de comunicações 80 pode ser um terminal, e correspondentemente o dispositivo de comunicações 81 pode ser uma estação base. Como um outro exemplo, o dispositivo de comunicações 80 é uma estação base, e correspondentemente o dispositivo de comunicações 81 pode ser um terminal.

[0260] Uma pessoa versada na técnica pode entender adicionalmente que vários blocos lógicos ilustrativos (bloco lógico ilustrativo) e etapas (etapa) que estão listados nas modalidades do presente pedido podem ser implementados ao usar hardware eletrônico, software de computador ou uma combinação dos mesmos. Se as funções são implementadas ao usar hardware ou software depende de aplicações particulares e de uma exigência de projeto do sistema total. Uma pessoa versada na técnica pode usar vários métodos para implementar as funções descritas para cada aplicação particular, mas não deve ser considerado que a implementação vai além do escopo das modalidades do presente pedido.

[0261] As tecnologias descritas neste pedido podem ser implementadas de várias maneiras. Por exemplo, estas tecnologias podem ser implementadas ao usar hardware, software ou uma combinação dos mesmos. Para implementação por meio de hardware, uma unidade de processamento configurada para executar estas tecnologias em um aparelho de comunicações (por exemplo, uma estação base, um terminal, uma entidade de rede ou um chip) pode ser implementada em um ou mais processadores de uso geral, processadores de sinais digitais (DSP), dispositivos de processamento de sinais digitais (DSPD), circuitos integrados de aplicação específica (ASIC), Dispositivos Lógicos Programáveis (PLD), matrizes de portas programáveis em campo (FPGA) ou outros aparelhos lógicos programáveis, portas distintas ou lógica de transistor, componentes de hardware distintos ou qualquer combinação dos mesmos. O processador de uso geral pode ser um microprocessador. Opcionalmente, o processador de uso geral pode ser qualquer processador, controlador, microcontrolador ou máquina de estados convencional. O processador pode ser implementado por meio de uma combinação de aparelhos de computação, tais como um processador de sinais digitais e um microprocessador, uma pluralidade de microprocessadores, um ou mais microprocessadores com um núcleo de processador de sinais digitais ou qualquer outra configuração similar.

[0262] Etapas dos métodos ou algoritmos descritos nas modalidades do presente pedido podem ser incorporados diretamente em hardware, uma instrução executada por um processador ou em uma combinação dos mesmos. A memória pode ser uma memória RAM, uma memória flash, uma memória ROM, uma memória EPROM, uma memória EEPROM, um registrador, um disco rígido, um disco magnético removível, um CD-ROM, ou um meio de armazenamento de qualquer outra forma na técnica. Por exemplo, a memória pode ser conectada ao processador, de maneira que o processador pode ler informação na memória e gravar informação na memória. Opcionalmente, a memória pode ser integrada ao processador. O processador e a memória podem ser dispostos em um ASIC, e o ASIC pode ser disposto em UE. Opcionalmente, o processador e a memória podem ser dispostos em componentes diferentes de UE.

[0263] Com base em descrições das implementações indicadas anteriormente, uma pessoa versada na técnica pode entender claramente que as tecnologias podem ser implementadas por meio de hardware, firmware ou por uma combinação dos mesmos. Para implementação por meio de um programa de software, a implementação pode ser totalmente ou parcialmente em uma forma de um produto de programa de computador. O produto de programa de computador inclui uma ou mais instruções de computador. Quando as instruções de computador são carregadas e executadas no computador, as funções ou procedimentos de acordo com as modalidades do presente pedido são gerados totalmente ou parcialmente. Quando o presente pedido é implementado por meio de um programa de software, as funções indicadas anteriormente podem ser armazenadas em um meio legível por computador ou transmitidas como uma ou mais instruções ou código no meio legível por computador. O computador pode ser um computador de uso geral, um computador dedicado, uma rede de computadores ou um outro aparelho programável. A instrução de computador pode ser armazenada em um meio de armazenamento legível por computador, ou pode ser transmitida de um meio de armazenamento legível por computador para outra. O meio legível por computador inclui um meio de armazenamento de computador e um meio de comunicações. O meio de comunicações inclui qualquer meio que faz com que um programa de computador seja transmitido de um lugar para outro. O meio de armazenamento pode ser qualquer meio disponível acessível para um computador. O exposto a seguir fornece um exemplo, mas não impõe uma limitação: O meio legível por computador pode incluir uma RAM, uma ROM, uma EEPROM, um CD-ROM ou um outro armazenamento de disco ótico, um meio de armazenamento de disco ou um outro dispositivo de armazenamento magnético, ou qualquer outro meio que possa carregar ou armazenar código de programa esperado em uma forma de uma instrução ou uma estrutura de dados e que possa ser acessada por um computador. Além disso, qualquer conexão pode ser definida de modo apropriado como um meio legível por computador. Por exemplo, se software for transmitido de um sítio de rede, um servidor ou de uma outra fonte remota ao usar um cabo coaxial, uma fibra ótica/cabo, um par trançado, uma linha de assinante digital (DSL), ou tecnologias sem fio tais como raio infravermelho, rádio e micro-onda, o cabo coaxial, fibra ótica/cabo, par trançado, DSL, ou tecnologias sem fio tais como raio infravermelho, rádio e micro-onda estão incluídos em uma definição de um meio à qual eles pertencem. Por exemplo, um disco usado no presente pedido inclui um disco compacto (CD), um disco laser, um disco ótico, um disco versátil digital (DVD), um disquete e um disco Blu-ray, onde de uma maneira geral os dados são copiados por meio de um dispositivo magnético ou oticamente por meio de um dispositivo a laser. A combinação indicada anteriormente também deve ser incluída no escopo de proteção do meio legível por computador.

[0264] Deve ser notado que, neste pedido, “/” indica “e/ou”. Por exemplo, “codificação/decodificação (encoding e/ou decoding)” indica codificação, ou decodificação, ou codificação e decodificação.

[0265] Em conclusão, o que foi descrito anteriormente representa meramente modalidades preferidas das soluções técnicas do presente pedido, e não é proposto para limitar o escopo de proteção do presente pedido. Qualquer modificação, substituição equivalente ou melhoramento feito sem divergir do espírito e princípio do presente pedido deverá estar incluído no escopo de proteção do presente pedido.

Claims (28)

1. Método de codificação, caracterizado pelo fato de que o método compreende: codificar (502, 603) uma sequência de entrada com base em um fator de elevação Z e em parâmetros de uma matriz de verificação de paridade de baixa densidade LDPC, em que os parâmetros da matriz LDPC compreendem parâmetros correspondendo às linhas cujos índices de linhas são de 0 a 4 tais como a seguir:

2. Método de decodificação, caracterizado pelo fato de que compreende: decodificar (502, 603) uma sequência de entrada com base em um fator de elevação Z e em parâmetros de uma matriz de verificação de paridade de baixa densidade LDPC, em que os parâmetros da matriz LDPC compreendem parâmetros correspondendo às linhas cujos índices de linhas são de 0 a 4 tais como a seguir:

3. Método, de acordo com a reivindicação 1 ou 2, caracterizado pelo fato de que os parâmetros da matriz LDPC compreendem adicionalmente parâmetros correspondendo a mD linhas em linhas cujos índices de linhas são de 5 a 45 tais como a seguir, em que 0≤mD≤41:

4. Método de codificação, caracterizado pelo fato de que compreende: codificar (502, 603) uma sequência de entrada c com base em uma matriz de verificação de paridade de baixa densidade LDPC H, para obter uma sequência codificada, em que a sequência de entrada compreende K bits, em que uma matriz de base da matriz LDPC H compreende m linhas e n colunas, m e n são números inteiros, e 5<m<46, e n é um número inteiro, 27<n<68, e a matriz de base compreende uma pluralidade de elementos diferentes de zero (i, j), em que i é um índice de linha, j é um índice de coluna, 0<i<m, 0<j<n, cada elemento diferente de zero (i, j) corresponde a uma matriz de permutação circular de tamanho ZxZ, e a matriz de permutação circular é igual a uma matriz obtida ao deslocar de forma circular uma matriz de identidade de tamanho Z*Z para a direita por Pi,j vezes, em que Pi,j = mód (Vi,j,Z), Z é um fator de elevação, e cada um dos elementos diferentes de zero (i, j) e Vi,j correspondente são tais como a seguir: i=0, j=0, 1, 2, 3, 5, 6, 9, 10, 11, 12, 13, 15, 16, 18, 19, 20, 21, 22, 23, e Vi,j é respectivamente 211, 198, 188, 186, 219, 4, 29, 144, 116, 216, 115, 233, 144, 95, 216, 73, 261, 1, 0; i=1, j=0, 2, 3, 4, 5, 7, 8, 9, 11, 12, 14, 15, 16, 17, 19, 21, 22, 23, 24, e Vi,j é respectivamente 179, 162, 223, 256, 160, 76, 202, 117, 109, 15, 72, 152, 158, 147, 156, 119, 0, 0, 0; i=2, j=0, 1, 2, 4, 5, 6, 7, 8, 9, 10, 13, 14, 15, 17, 18, 19, 20, 24, 25, e Vi,j é respectivamente 258, 167, 220, 133, 243, 202, 218, 63, 0, 3, 74, 229, 0, 216, 269, 200, 234, 0, 0; i=3, j=0, 1, 3, 4, 6, 7, 8, 10, 11, 12, 13, 14, 16, 17, 18, 20, 21, 22, 25, e Vi,j é respectivamente 187, 145, 166, 108, 82, 132, 197, 41, 162, 57, 36, 115, 242, 165, 0, 113, 108, 1, 0; e i=4, j=0, 1, 26, e Vi,j é respectivamente 246, 235, 0.

5. Método, de acordo com a reivindicação 1 ou 4, caracterizado pelo fato de que a sequência de entrada é c ={c0, c1, c2, ..., cK-1}, a sequência codificada é d ={d0, d1, d2, ..., dN-1}, em que K e N são ambos números inteiros positivos, e N = 66’Z.

6. Método, de acordo com a reivindicação 5, caracterizado pelo fato de que a sequência codificada d compreende K0 bits da sequência de entrada c e N - K0 bits de paridade em uma sequência de paridade w={wo, wi, W2, ..., WN-KO-I}, em que K0 é um número inteiro maior que 0 e igual ou menor que K, em que a sequência de paridade w e a sequência de entrada c satisfazem:

é um vetor coluna, e valores de todos os elementos de 0T são 0.

7. Método, de aCordo Com a reivindiCação 6, caracterizado pelo fato de que Ko = K - 2*Z.

8. Método de decodificação, caracterizado pelo fato de que Compreende: decodificar (502, 603) uma sequência de valores suaves com base em uma matriz de verificação de paridade de baixa densidade LDPC H para obter uma sequência de informação, em que uma matriz de base da H compreende m linhas e n colunas, m e n são números inteiros, e 5<m<46, e n é um número inteiro, 27<n<68, e a matriz de base compreende elementos diferentes de zero (i, j), em que i é um índice de linha, j é um índice de coluna, 0<i<m, 0<j<n, cada elemento diferente de zero (i, j) corresponde a uma matriz de permutação circular de tamanho ZxZ, e a matriz de permutação circular é igual a uma matriz obtida ao deslocar de forma circular uma matriz de identidade de tamanho ZxZ para a direita Pi,j vezes, em que Pi,j = mód (Vi,j,Z), Z é um fator de elevação, e cada elemento diferente de zero (i, j) e um valor correspondente Vi,j do elemento diferente de zero (i, j) são tais como a seguir: i=0, j=0, 1, 2, 3, 5, 6, 9, 10, 11, 12, 13, 15, 16, 18, 19, 20, 21, 22, 23, e Vi,j é respectivamente 211, 198, 188, 186, 219, 4, 29, 144, 116, 216, 115, 233, 144, 95, 216, 73, 261, 1, 0; i=1, j=0, 2, 3, 4, 5, 7, 8, 9, 11, 12, 14, 15, 16, 17, 19, 21, 22, 23, 24, e Vi,j é respectivamente 179, 162, 223, 256, 160, 76, 202, 117, 109, 15, 72, 152, 158, 147, 156, 119, 0, 0, 0; i=2, j=0, 1, 2, 4, 5, 6, 7, 8, 9, 10, 13, 14, 15, 17, 18, 19, 20, 24, 25, e Vi,j é respectivamente 258, 167, 220, 133, 243, 202, 218, 63, 0, 3, 74, 229, 0, 216, 269, 200, 234, 0, 0; i=3, j=0, 1, 3, 4, 6, 7, 8, 10, 11, 12, 13, 14, 16, 17, 18, 20, 21, 22, 25, e Vi,j é respectivamente 187, 145, 166, 108, 82, 132, 197, 41, 162, 57, 36, 115, 242, 165, 0, 113, 108, 1, 0; e i=4, j=0, 1, 26, e Vi,j é respectivamente 246, 235, 0.

9. Método, de acordo com qualquer uma das reivindicações 4 a 8, caracterizado pelo fato de que a matriz de base da H compreende adicionalmente os elementos diferentes de zero (i, j) seguintes, e valores correspondentes Vi,j dos elementos diferentes de zero (i, j) são tais como a seguir: i=5, j=0, 1, 3, 12, 16, 21, 22, 27, e Vi,j é respectivamente 261, 181, 72, 283, 254, 79, 144, 0; i=6, j=0, 6, 10, 11, 13, 17, 18, 20, 28, e Vi,j é respectivamente 80, 144, 169, 90, 59, 177, 151, 108, 0; i=7, j=0, 1, 4, 7, 8, 14, 29, e Vi,j é respectivamente 169, 189, 154, 184, 104, 164, 0; i=8, j=0, 1, 3, 12, 16, 19, 21, 22, 24, 30, e Vi,j é respectivamente 54, 0, 252, 41, 98, 46, 15, 230, 54, 0; i=9, j=0, 1, 10, 11, 13, 17, 18, 20, 31, e Vi,j é respectivamente 162, 159, 93, 134, 45, 132, 76, 209, 0; i=10, j=1, 2, 4, 7, 8, 14, 32, e Vi,j é respectivamente 178, 1, 28, 267, 234, 201, 0; i=11, j=0, 1, 12, 16, 21, 22, 23, 33, e Vi,j é respectivamente 55, 23, 274, 181, 273, 39, 26, 0; i=12, j=0, 1, 10, 11, 13, 18, 34, e Vi,j é respectivamente 225, 162, 244, 151, 238, 243, 0; i=13, j=0, 3, 7, 20, 23, 35, e Vi,j é respectivamente 231, 0, 216, 47, 36, 0; i=14, j=0, 12, 15, 16, 17, 21, 36, e Vi,j é respectivamente 0, 186, 253, 16, 0, 79, 0; i=15, j=0, 1, 10, 13, 18, 25, 37, e Vi,j é respectivamente 170, 0, 183, 108, 68, 64, 0; i=16, j=1, 3, 11, 20, 22, 38, e Vi,j é respectivamente 270, 13, 99, 54, 0, 0; i=17, j=0, 14, 16, 17, 21, 39, e Vi,j é respectivamente 153, 137, 0, 0, 162, 0; i=18, j=1, 12, 13, 18, 19, 40, e Vi,j é respectivamente 161, 151, 0, 241, 144, 0; i=19, j=0, 1, 7, 8, 10, 41, e Vi,j é respectivamente 0, 0, 118, 144, 0, 0; i=20, j=0, 3, 9, 11, 22, 42, e Vi,j é respectivamente 265, 81, 90, 144, 228, 0; i=21, j=1, 5, 16, 20, 21, 43, e Vi,j é respectivamente 64, 46, 266, 9, 18, 0; i=22, j=0, 12, 13, 17, 44, e Vi,j é respectivamente 72, 189, 72, 257, 0; i=23, j=1, 2, 10, 18, 45, e Vi,j é respectivamente 180, 0, 0, 165, 0; i=24, j=0, 3, 4, 11, 22, 46, e Vi,j é respectivamente 236, 199, 0, 266, 0, 0; i=25, j=1, 6, 7, 14, 47, e Vi,j é respectivamente 205, 0, 0, 183, 0; i=26, j=0, 2, 4, 15, 48, e Vi,j é respectivamente 0, 0, 0, 277, 0; i=27, j=1, 6, 8, 49, e Vi,j é respectivamente 45, 36, 72, 0; i=28, j=0, 4, 19, 21, 50, e Vi,j é respectivamente 275, 0, 155, 62, 0; i=29, j=1, 14, 18, 25, 51, e Vi,j é respectivamente 0, 180, 0, 42, 0; i=30, j=0, 10, 13, 24, 52, e Vi,j é respectivamente 0, 90, 252, 173, 0; i=31, j=1, 7, 22, 25, 53, e Vi,j é respectivamente 144, 144, 166, 19, 0; i=32, j=0, 12, 14, 24, 54, e Vi,j é respectivamente 0, 211, 36, 162, 0; i=33, j=1, 2, 11, 21, 55, e Vi,j é respectivamente 0, 0, 76, 18, 0; i=34, j=0, 7, 15, 17, 56, e Vi,j é respectivamente 197, 0, 108, 0, 0; i=35, j=1, 6, 12, 22, 57, e Vi,j é respectivamente 199, 278, 0, 205, 0; i=36, j=0, 14, 15, 18, 58, e Vi,j é respectivamente 216, 16, 0, 0, 0; i=37, j=1, 13, 23, 59, e Vi,j é respectivamente 72, 144, 0, 0; i=38, j=0, 9, 10, 12, 60, e Vi,j é respectivamente 190, 0, 0, 0, 0; i=39, j=1, 3, 7, 19, 61, e Vi,j é respectivamente 153, 0, 165, 117, 0; i=40, j=0, 8, 17, 62, e Vi,j é respectivamente 216, 144, 2, 0; i=41, j=1, 3, 9, 18, 63, e Vi,j é respectivamente 0, 0, 0, 183, 0; i=42, j=0, 4, 24, 64, e Vi,j é respectivamente 27, 0, 35, 0; i=43, j=1, 16, 18, 25, 65, e Vi,j é respectivamente 52, 243, 0, 270, 0; i=44, j=0, 7, 9, 22, 66, e Vi,j é respectivamente 18, 0, 0, 57, 0; e i=45, j=1, 6, 10, 67, e Vi,j é respectivamente 168, 0, 144, 0.

10. Método, de acordo com qualquer uma das reivindicações 1 a 9, caracterizado pelo fato de que Z é um de 9, 18, 36, 72, 144 e 288.

11. Método, de acordo com qualquer uma das reivindicações 1 a 10, caracterizado pelo fato de que, na matriz de base, elementos que não são elementos diferentes de zero são elementos iguais a zero; em que cada elemento igual a zero corresponde a uma matriz toda de zeros de tamanho Z*Z na matriz LDPC H.

12. Método, de acordo com qualquer uma das reivindicações 1 a 11, caracterizado pelo fato de que a codificação ou a decodificação com base na matriz LDPC H compreende: codificar ou decodificar com base em uma matriz transformada; em que uma matriz de base da matriz transformada é obtida ao executar transformação de linha, ou transformação de coluna, ou transformação de linha e transformação de coluna na matriz de base da matriz LDPC H.

13. Aparelho, caracterizado pelo fato de que compreende um codificador e uma unidade de determinação, em que a unidade de determinação é configurada para determinar um fator de elevação Z; e o codificador é configurado para codificar uma sequência de entrada com base em uma matriz de verificação de paridade de baixa densidade LDPC H para obter uma sequência codificada, em que uma matriz de base da H compreende m linhas e n colunas, m e n são números inteiros, e 5<m<46, e n é um número inteiro, 27<n<68, e a matriz de base compreende uma pluralidade de elementos diferentes de zero (i, j), em que i é um índice de linha, j é um índice de coluna, 0<i<m, 0<j<n, cada elemento diferente de zero (i, j) corresponde a uma matriz de permutação circulante de tamanho ZxZ, e a matriz de permutação circulante é igual a uma matriz obtida ao deslocar de forma circular uma matriz de identidade de tamanho Z*Z para a direita por Pi,j vezes, em que Pi,j = mód (Vi,j,Z), e cada elemento diferente de zero (i, j) e um valor correspondente Vi,j do elemento diferente de zero (i, j) são tais como a seguir: i=0, j=0, 1, 2, 3, 5, 6, 9, 10, 11, 12, 13, 15, 16, 18, 19, 20, 21, 22, 23, e Vi,j é respectivamente 211, 198, 188, 186, 219, 4, 29, 144, 116, 216, 115, 233, 144, 95, 216, 73, 261, 1, 0; i=1, j=0, 2, 3, 4, 5, 7, 8, 9, 11, 12, 14, 15, 16, 17, 19, 21, 22, 23, 24, e Vi,j é respectivamente 179, 162, 223, 256, 160, 76, 202, 117, 109, 15, 72, 152, 158, 147, 156, 119, 0, 0, 0; i=2, j=0, 1, 2, 4, 5, 6, 7, 8, 9, 10, 13, 14, 15, 17, 18, 19, 20, 24, 25, e Vi,j é respectivamente 258, 167, 220, 133, 243, 202, 218, 63, 0, 3, 74, 229, 0, 216, 269, 200, 234, 0, 0; i=3, j=0, 1, 3, 4, 6, 7, 8, 10, 11, 12, 13, 14, 16, 17, 18, 20, 21, 22, 25, e Vi,j é respectivamente 187, 145, 166, 108, 82, 132, 197, 41, 162, 57, 36, 115, 242, 165, 0, 113, 108, 1, 0; e i=4, j=0, 1, 26, e Vi,j é respectivamente 246, 235, 0.

14. Aparelho, de acordo com a reivindicação 13, caracterizado pelo fato de que: a sequência de entrada é c ={c0, c1, c2, ..., cK-1}, a sequência codificada é d ={d0, d1, d2, ..., dN-1}, em que tanto K quanto N são números inteiros positivos, e N = 66*Z.

15. Aparelho, de acordo com a reivindicação 14, caracterizado pelo fato de que a sequência codificada d compreende K0 bits na sequência de entrada c e N - K0 bits de paridade em uma sequência de paridade w = {w , w , w , . . . , w }, em que Ko é um número inteiro e O<Ko<K; e a sequência de paridade w e a sequência de entrada c satisfazem:

em que cT=[co, ci, C2, ..., CK-I]T, wT=[ w0, w1, w2, ..., wN-K ]T, OT é um vetor coluna, e valores de todos os elementos de oT são o.

16. Aparelho, de acordo com a reivindicação i5, caracterizado pelo fato de que Ko = K - 2*Z.

17. Aparelho, caracterizado pelo fato de que compreende um decodificador e uma unidade de obtenção, em que a unidade de obtenção é configurada para obter uma sequência de valores suaves e um fator de elevação Z; e o decodificador é configurado para decodificar a sequência de valores suaves com base em uma matriz LDPC H, para obter uma sequência de bits de informação, em que uma matriz de base da H compreende m linhas e n colunas, m e n são números inteiros, e 5<m<46, e n é um número inteiro, 27<n<68, e a matriz de base compreende elementos diferentes de zero (i, j), em que i é um índice de linha, j é um índice de coluna, 0<i<m, 0<j<n, cada elemento diferente de zero (i, j) corresponde a uma matriz de permutação circulante de tamanho ZxZ, e a matriz de permutação circulante é igual a uma matriz obtida ao deslocar de forma circular uma matriz de identidade de tamanho ZxZ para a direita Pi,j vezes, em que Pi,j = mód (Vi,j,Z), e cada elemento diferente de zero (i, j) e um valor correspondente Vi,j do elemento diferente de zero (i, j) são tais como a seguir: i=0, j=0, 1, 2, 3, 5, 6, 9, 10, 11, 12, 13, 15, 16, 18, 19, 20, 21, 22, 23, e Vi,j é respectivamente 211, 198, 188, 186, 219, 4, 29, 144, 116, 216, 115, 233, 144, 95, 216, 73, 261, 1, 0; i=1, j=0, 2, 3, 4, 5, 7, 8, 9, 11, 12, 14, 15, 16, 17, 19, 21, 22, 23, 24, e Vi,j é respectivamente 179, 162, 223, 256, 160, 76, 202, 117, 109, 15, 72, 152, 158, 147, 156, 119, 0, 0; i=2, j=0, 1, 2, 4, 5, 6, 7, 8, 9, 10, 13, 14, 15, 17, 18, 19, 20, 24, 25, e Vi,j é respectivamente 258, 167, 220, 133, 243, 202, 218, 63, 0, 3, 74, 229, 0, 216, 269, 200, 234, 0, 0; i=3, j=0, 1, 3, 4, 6, 7, 8, 10, 11, 12, 13, 14, 16, 17, 18, 20, 21, 22, 25, e Vi,j é respectivamente 187, 145, 166, 108, 82, 132, 197, 41, 162, 57, 36, 115, 242, 165, 0, 113, 108, 1, 0; e i=4, j=0, 1, 26, e Vi,j é respectivamente 246, 235, 0.

18. Aparelho, de acordo com qualquer uma das reivindicações 13 a 17, caracterizado pelo fato de que a matriz de base da H compreende adicionalmente os elementos diferentes de zero (i, j) seguintes, e valores correspondentes Vi,j dos elementos diferentes de zero (i, j) são tais como a seguir: i=5, j=0, 1, 3, 12, 16, 21, 22, 27, e Vi,j é respectivamente 261, 181, 72, 283, 254, 79, 144, 0; i=6, j=0, 6, 10, 11, 13, 17, 18, 20, 28, e Vi,j é respectivamente 80, 144, 169, 90, 59, 177, 151, 108, 0; i=7, j=0, 1, 4, 7, 8, 14, 29, e Vi,j é respectivamente 169, 189, 154, 184, 104, 164, 0; i=8, j=0, 1, 3, 12, 16, 19, 21, 22, 24, 30, e Vi,j é respectivamente 54, 0, 252, 41, 98, 46, 15, 230, 54, 0; i=9, j=0, 1, 10, 11, 13, 17, 18, 20, 31, e Vi,j é respectivamente 162, 159, 93, 134, 45, 132, 76, 209, 0; i=10, j=1, 2, 4, 7, 8, 14, 32, e Vi,j é respectivamente 178, 1, 28, 267, 234, 201, 0; i=11, j=0, 1, 12, 16, 21, 22, 23, 33, e Vi,j é respectivamente 55, 23, 274, 181, 273, 39, 26, 0; i=12, j=0, 1, 10, 11, 13, 18, 34, e Vi,j é respectivamente 225, 162, 244, 151, 238, 243, 0; i=13, j=0, 3, 7, 20, 23, 35, e Vi,j é respectivamente 231, 0, 216, 47, 36, 0; i=14, j=0, 12, 15, 16, 17, 21, 36, e Vi,j é respectivamente 0, 186, 253, 16, 0, 79, 0; i=15, j=0, 1, 10, 13, 18, 25, 37, e Vi,j é respectivamente 170, 0, 183, 108, 68, 64, 0; i=16, j=1, 3, 11, 20, 22, 38, e Vi,j é respectivamente 270, 13, 99, 54, 0, 0; i=17, j=0, 14, 16, 17, 21, 39, e Vi,j é respectivamente 153, 137, 0, 0, 162, 0; i=18, j=1, 12, 13, 18, 19, 40, e Vi,j é respectivamente 161, 151, 0, 241, 144, 0; i=19, j=0, 1, 7, 8, 10, 41, e Vi,j é respectivamente 0, 0, 118, 144, 0, 0; i=20, j=0, 3, 9, 11, 22, 42, e Vi,j é respectivamente 265, 81, 90, 144, 228, 0; i=21, j=1, 5, 16, 20, 21, 43, e Vi,j é respectivamente 64, 46, 266, 9, 18, 0; i=22, j=0, 12, 13, 17, 44, e Vi,j é respectivamente 72, 189, 72, 257, 0; i=23, j=1, 2, 10, 18, 45, e Vi,j é respectivamente 180, 0, 0, 165, 0; i=24, j=0, 3, 4, 11, 22, 46, e Vi,j é respectivamente 236, 199, 0, 266, 0, 0; i=25, j=1, 6, 7, 14, 47, e Vi,j é respectivamente 205, 0, 0, 183, 0; i=26, j=0, 2, 4, 15, 48, e Vi,j é respectivamente 0, 0, 0, 277, 0; i=27, j=1, 6, 8, 49, e Vi,j é respectivamente 45, 36, 72, 0; i=28, j=0, 4, 19, 21, 50, e Vi,j é respectivamente 275, 0, 155, 62, 0; i=29, j=1, 14, 18, 25, 51, e Vi,j é respectivamente 0, 180, 0, 42, 0; i=30, j=0, 10, 13, 24, 52, e Vi,j é respectivamente 0, 90, 252, 173, 0; i=31, j=1, 7, 22, 25, 53, e Vi,j é respectivamente 144, 144, 166, 19, 0; i=32, j=0, 12, 14, 24, 54, e Vi,j é respectivamente 0, 211, 36, 162, 0; i=33, j=1, 2, 11, 21, 55, e Vi,j é respectivamente 0, 0, 76, 18, 0; i=34, j=0, 7, 15, 17, 56, e Vi,j é respectivamente 197, 0, 108, 0, 0; i=35, j=1, 6, 12, 22, 57, e Vi,j é respectivamente 199, 278, 0, 205, 0; i=36, j=0, 14, 15, 18, 58, e Vi,j é respectivamente 216, 16, 0, 0, 0; i=37, j=1, 13, 23, 59, e Vi,j é respectivamente 72, 144, 0, 0; i=38, j=0, 9, 10, 12, 60, e Vi,j é respectivamente 190, 0, 0, 0, 0; i=39, j=1, 3, 7, 19, 61, e Vi,j é respectivamente 153, 0, 165, 117, 0; i=40, j=0, 8, 17, 62, e Vi,j é respectivamente 216, 144, 2, 0; i=41, j=1, 3, 9, 18, 63, e Vi,j é respectivamente 0, 0, 0, 183, 0; i=42, j=0, 4, 24, 64, e Vi,j é respectivamente 27, 0, 35, 0; i=43, j=1, 16, 18, 25, 65, e Vi,j é respectivamente 52, 243, 0, 270, 0; i=44, j=0, 7, 9, 22, 66, e Vi,j é respectivamente 18, 0, 0, 57, 0; e i=45, j=1, 6, 10, 67, e Vi,j é respectivamente 168, 0, 144, 0.

19. Aparelho, de acordo com qualquer uma das reivindicações 13 a 18, caracterizado pelo fato de que Z é um de 9, 18, 36, 72, 144 e 288.

20. Aparelho, de acordo com qualquer uma das reivindicações 13 a 19, caracterizado pelo fato de que, na matriz de base, elementos que não são elementos diferentes de zero são elementos iguais a zero; em que cada elemento igual a zero corresponde a uma matriz toda de zeros de tamanho Z*Z na matriz LDPC H.

21. Aparelho, de acordo com qualquer uma das reivindicações 13 a 20, caracterizado pelo fato de que a codificação ou a decodificação com base na matriz LDPC H compreende: codificar ou decodificar com base em uma matriz transformada; em que uma matriz de base da matriz transformada é obtida ao executar transformação de linha, ou transformação de coluna, ou transformação de linha e transformação de coluna na matriz de base da matriz LDPC H.

22. Aparelho, de acordo com qualquer uma das reivindicações 13 a 21, caracterizado pelo fato de que a matriz de base, ou a matriz transformada ou o fator de elevação Z é recuperado de uma ou mais memórias.

23. Aparelho, de acordo com qualquer uma das reivindicações 13 a 16 e 18 a 22, caracterizado pelo fato de que compreende adicionalmente: um componente configurado para executar casamento de taxa na sequência codificada para obter uma sequência de taxa casada; um componente configurado para executar intercalação na sequência de taxa casada para obter uma sequência intercalada; e um componente configurado para modular a sequência intercalada.

24. Aparelho, de acordo com qualquer uma das reivindicações 17 a 22, caracterizado pelo fato de que compreende adicionalmente: um demodulador, configurado para demodular um sinal para obter uma sequência demodulada; um desintercalador, configurado para executar desintercalação na sequência demodulada para obter uma sequência desintercalada; e um componente de descasamento de taxa, configurado para executar descasamento taxa na sequência desintercalada, para obter a sequência de valores suaves.

25. Terminal, caracterizado pelo fato de que compreende o aparelho conforme definido em qualquer uma das reivindicações 13 a 24 e um transceptor.

26. Estação base, caracterizada pelo fato de que compreende o aparelho conforme definido em qualquer uma das reivindicações 13 a 24 e um transceptor.

27. Sistema de comunicações, caracterizado pelo fato de que compreende o terminal conforme definido na reivindicação 25 e a estação base conforme definido na reivindicação 26.

28. Meio de armazenamento legível por computador, caracterizado pelo fato de que compreende uma ou mais instruções, em que, quando executadas em um computador, a uma ou mais instruções induzem o computador para executar o método conforme definido em qualquer uma das reivindicações 1 a 12.

Images