JP4542889B2 - パラメトリックモデリングユニットとポリゴンベースレンダリングシステム間のインターフェースをとるインターフェース及びその方法 - Google Patents

Description

本発明は、パラメトリックモデリングユニット及びポリゴンベースレンダリングシステムを備える３次元グラフィックシステムで使用するためのインターフェースに関する。

従来の３次元レンダリングシステムは、ポリゴン（通常は三角形）のメッシュを使用してシーン内のオブジェクトをモデリングする。三角形は、形状が単純であり、従って、表示用画像を生成するために変換、ライティング、テクスチャリング、及びラスタライゼーションなどの演算を実行するのが比較的容易である利点がある。

ポリゴンメッシュを使用してオブジェクトをモデリングする既知の別の方法は、オブジェクトを領域にセグメント化して、モデリングされるオブジェクトの異なる領域に多数の湾曲した高次サーフェス（多くの場合パッチと呼ばれる）を適合させる。これらのパッチは一般に、制御ポイントのグリッドによって規定されたサーフェス形状を有するパラメトリックサーフェスとして定義される。高次サーフェスを用いる利点は、一般的に、特定のモデルを表示するために必要としているデータ量が、相当するポリゴンメッシュと比較して制御ポイントの集合の方がはるかに少ないという点である。また一般的に、高次サーフェスは、形状が変化するオブジェクトをアニメ化する際の操作が比較的簡単である。高次サーフェスを使用するモデリングの主な欠点は、レンダリングシステムのラスタライゼーション段階で、複雑さが付加的に導入されることである。

また、ラスタライゼーションなどの処理段階を実行する前に、モデリング段階用に高次サーフェスを使用すること、及びサーフェスを一連のテセレーション三角形に変換することが知られている。この組み合わされた方法は、ラスタライゼーション段階に複雑さを付加することなく湾曲サーフェスを用いることができる利点が得られるが、サーフェスパッチデータを処理してポリゴンベースデータを形成するために好適なインターフェースを必要とする。湾曲平面を一連のポリゴンに変換するテセレーション過程では、２つの方法が通常良く使用され、すなわち、前方差分又は再帰細分割のいずれかである。本発明は再帰細分割法から導出される。

組み合わされた３次元グラフィックシステムのパラメトリックモデリング段階（すなわち、後のレンダリング段階に対してポリゴンを生成するためにテセレーション段階を組み合わせたもの）では、複数の湾曲サーフェスのパッチをオブジェクトのサーフェスに適合させてオブジェクトの領域を定義する。このようなパッチの作用を定義するための、これらの定義する制御ポイントに対する幾つかの異なる規格が知られている。このような規格の１つはベジェパッチであり、例えば、Ｗａｔｔ ＆ Ｗａｔｔによる「Ａｄｖａｎｃｅｄ Ａｎｉｍａｔｉｏｎ ａｎｄ Ｒｅｎｄｅｒｉｎｇ Ｔｅｃｈｎｉｑｕｅｓ」ｐｐ６６−６８、又はＦｏｒｅｙ Ｖａｎ Ｄａｍらによる「Ｃｏｍｐｕｔｅｒ Ｇｒａｐｈｉｃｓ Ｐｒｉｎｃｉｐｌｅｓ ａｎｄ Ｐｒａｃｔｉｃｅ」ｐｐ４７１−５３０を参照されたい。また、１つのフォーマットのパッチに対応した制御ポイントを異なるパッチ形式に対応した新しい位置に、最終サーフェスが等しくなるように変換する方法も知られている。これらのパッチは双３次数である場合が多い。

共通のパラメトリックパッチには要に２つのバリエーションがある。第１のバリエーションは「標準の」ｍｐｍ有理サーフェスパッチ群であり、一方、第２のバリエーションは有理パッチの拡張集合である。有理パッチは、特定のモデリングがより単純な非有理的変化において利点を有しているといえるが、幾つかの点では処理が幾分複雑になる可能性がある。両方のタイプのパッチは前述の２つの引用文献で十分に説明されるが、しかしながら、本実施形態の説明を簡略化するために、次の要約が示される。非有理的パラメトリックサーフェスに対して、３次元位置は以下のように記述することができる。

ここで、ｘ（ｓ，ｔ）、ｙ（ｓ，ｔ）、及びｚ（ｓ，ｔ）の各々は、同次数のスカラパラメータの多項式であり、０≦ｓ，ｔ≦１である。双三次（すなわち２つの３次式の積）のベジェサーフェスの場合、多項式の次数は６である。ベジェ方程式とサーフェスの制御ポイントの各ｘ、ｙ、ｚ成分とがサーフェスの形状を定義する。

非有理的サーフェスは、制御ポイントの各々に対応した正の値「ｗ」をさらに有する第４の多項式ｗ（ｓ，ｔ）を導入することによって定義を拡張する。この場合、サーフェス位置は次のように定義される。

また、一般によく使用されている種類のパラメトリックサーフェスパッチが行列形式で表現可能であることは、当該技術分野ではよく知られている（前述の引用を参照）。例えば、双三次ベジェパッチ

は、次のように表すことができる。

ここでＱはスカラー定数行列、Ｐはサーフェスに対する制御ポイントの行列である。

ＰはＰ_STとして番号付けられる点に留意されたい。

再帰細分割手法によるパッチのテセレーション三角形への変換は、最初に各パッチをその２つのパラメータ次元（すなわちｓ又はｔ）のいずれか１つにわたって２つのサブパッチに分割することよって達成される。これは図１ａ及び１ｂに示され、ここでは制御ポイントを有するパッチがパラメータ空間に表現されている。サブパッチの各々は、的確な細分割レベルが達成されるまでさらに細分割される。これが達成されると、結果として得られるサブパッチはそれぞれ同一平面上にない四辺形として扱われ、三角形の規定のパターンが、サブパッチ、計算された三角形の頂点、及び出力された三角形に重畳される。

図２は、３つのレベルの細分割が適用された、細分割によるパッチの概念的処理を示す概略図である。図２から、処理は、オリジナルパッチ、すなわち「ルート」パッチから中間レベルのパッチを介して、「リーフ」パッチと呼ばれるエンドポイントパッチまで進む２分木の形態をとることが分かる。各リーフパッチは、レンダリングのラスタライゼーション段階のために必要とされる、テセレーション三角形を定義する頂点を生成するために使用される。

再帰細分割の既知のシステムにおいて、テセレーションは、各段階に対して多数の計算が必要とされるので従来からＣＰＵ上で実行される。これに伴う一連の計算を検討すると、ＣＰＵ使用時には、リーフパッチに対する多くのパスに関して同じ中間結果が使用されるので、この中間結果をスタック上に格納することが効率的であることが分かる。従って、スタックを使用することにより、実行される計算の数が最小となる。ハードウェアの実装の面からすると、内部（すなわちオンチップの）記憶装置がコスト高であること、及び外部に格納された多大な量のデータを検索することがシステム性能の面でボトルネックとなる可能性があるということは実際的ではないということに留意されたい。

Ｗａｔｔ ＆ Ｗａｔｔによる「Ａｄｖａｎｃｅｄ Ａｎｉｍａｔｉｏｎ ａｎｄ Ｒｅｎｄｅｒｉｎｇ Ｔｅｃｈｎｉｑｕｅｓ」ｐｐ６６−６８ Ｆｏｒｅｙ Ｖａｎ Ｄａｍらによる「Ｃｏｍｐｕｔｅｒ Ｇｒａｐｈｉｃｓ Ｐｒｉｎｃｉｐｌｅｓ ａｎｄ Ｐｒａｃｔｉｃｅ」ｐｐ４７１−５３０ Ｃｌａｒｋによる「Ａ Ｆａｓｔ Ｓｃａｎ Ｌｉｎｅ Ａｌｇｏｒｉｔｈｍ ｆｏｒ Ｒｅｎｄｅｒｉｎｇ Ｐａｒａｍｅｔｒｉｃ Ｓｕｒｆａｃｅｓ」、Ｃｏｍｐｕｔｅｒ Ｇｒａｐｈｉｃｓ １３（２）、２８９−９９ Ｗａｔｔ ＆ Ｗａｔｔ、Ｆｏｒｌｅｙ他、及びＦａｋｉｎによる「Ｃｕｒｖｅｓ ａｎｄ Ｓｕｒｆａｃｅｓ ｆｏｒ ＧＡＧＤ． Ａ Ｐｒａｃｔｉｃａｌ Ｇｕｉｄｅ， ４ｔｈ Ｅｄｉｔｉｏｎ， Ａｃａｄｅｍｉｃ Ｐｒｅｓｓ， ＩＳＢＮ−０−１２−２４９０５４−１， ｐｐ２４４−２４７ Ｗａｔｔ ＆ Ｗａｔｔの「Ａｄｖａｎｃｅｄ Ａｎｉｍａｔｉｏｎ ａｎｄ Ｒｅｎｄｅｒｉｎｇ Ｔｅｃｈｎｉｑｕｅｓ． Ｔｈｅｏｒｙ ａｎｄ Ｐｒａｃｔｉｃｅ」， ＡＣＭ Ｐｒｅｓｓ． ＩＳＢＮ ０−２０１−５４４１２−１

本発明の第１の態様は、これらの問題を改善することを目的としている。これは、メモリ及びメモリ帯域幅の使用を最小にしながら高度な計算能力をもたらす方法で再帰細分割を使用して、パラメトリックモデリングデータをポリゴンベースデータに変換するためのインターフェースを提供する。
本発明の第１の態様によれば、請求項１２によるインターフェースが提供される。本発明の第１の態様の好適な特徴は、従属請求項１３から１６で定義される。

また、請求項１６により、パラメトリックモデリングユニットとポリゴンベースレンダリングシステムとの間でインターフェースをとる方法が提供される。好適な方法の各段階は、従属請求項１６から１９で定義される。

組み合わされたグラフィックシステムにおいて、パラメトリックモデリングユニットとポリゴンベースのデータとの間でインターフェースをとるときに発生する第２の問題は、モデリングされるオブジェクトの隣接する領域を示す第１と第２のパッチにおいて、第１のパッチに関係するパラメータデータと第２のパッチに関係するパラメータデータとを変換するために、細分割の異なるレベルが要求される場合があることである。高度に湾曲したサーフェスを定義するパッチは、パラメトリックモデリングの利点が失われることがない場合には、パラメータデータをポリゴンベースのデータに変換するときに、平坦なサーフェスを示すパッチよりも高度に細分割されなければならない。隣接するパッチの変換が同じレベルの細分割を各パッチに適用するように制約されない場合には、モデリングされたオブジェクトにクラックが生じる恐れがあり、これは細分割のより高度なレベルのサーフェスが余分なサンプル点を有しており、要するに形状が僅かに異なることに起因する。クラックの問題は図４に示される。

クラックの問題に対する１つの解決方法は、すべてのパッチに対して同じレベルの細分割を使用ことである。しかしながら、これは、幾つかのパッチがより小さく分割されたレベルで適切にテセレーションされるときには過度に細分割される結果となり、適切な結果をもたらすのに必要な領域に対しての処理になっていない。

別の解決方法は、サーフェスを適切に表すのに十分な細分割レベルまで各パッチを処理し、次いで、細分割のレベルが異なる隣接するサーフェスパッチ間にいわゆる「ステッチメッシュ」を挿入することである。従って、図５ａに示されるように、ステッチメッシュは可能性のある任意のクラックをカバーする。図において、２つの隣接パッチは異なるレベルまで細分割されており、すなわち一方は２×４のサブパッチを使用し、他方は細分割されず、すなわち単一の四辺形で示される。２×４パッチ上に「隣接する」輪郭は頂点Ａ、Ｂ、Ｃ、Ｄ、及びＥから成り、一方、１×１細分割に相当するものはエッジＡＥから成る。サーフェスにギャップが出現するのを回避するために、三角形ＡＢＣ、ＡＣＥ、及びＣＤＥがさらに生成される。

残念なことに、このようなメッシュの接続はサーフェス方向に急激な変化が生じる可能性がある。隣接するパッチのエッジを共にステッチすることは、計算集約的であり、且つ細分割レベルが変化するときにステッチメッシュの再生成が必要となることは同様に理解される。

Ｃｌａｒｋは、「Ａ Ｆａｓｔ Ｓｃａｎ Ｌｉｎｅ Ａｌｇｏｒｉｔｈｍ ｆｏｒ Ｒｅｎｄｅｒｉｎｇ Ｐａｒａｍｅｔｒｉｃ Ｓｕｒｆａｃｅｓ」、Ｃｏｍｐｕｔｅｒ Ｇｒａｐｈｉｃｓ １３（２）、２８９−９９により、各パッチ内で細分割が異なるレベルであっても可能な別の技法を提案した。この方法の一部として、クラック問題が「解決」されなければならなかった。Ｃｌａｒｋの解決方法は、より高い細分割の領域のエッジがより低い細分割の領域に適合する場合に、これを意図的に「平坦化する」ことである。これは図５ｂに示される。高い細分割領域と低い細分割領域間で「共有された」境界は、低細分割領域の境界に数学的に適合するように高細分割領域上で「平坦化」されていた。これを図５ａの方法と比較すると、頂点Ｂ、Ｃ、及びＤが線ＡＥ上にあることが分かる。

この手法は数式的には正しいが、僅かな欠点がある。コンピュータグラフィックスハードウエアの精度は限界があり、正確なポリゴン頂点位置を表示することができない。従って、共有境界上の平坦化された頂点を正しく配置することが不可能である場合が多い。これは、当該技術分野でよく知られている「Ｔ−ジョイント」によって引き起こされる問題につながる。これは図５ｃに示されており、ここでは不正確さによって極めて狭いギャップが現われる。このギャップは極めて小さいのが典型的であるが、それでも尚、他の場合では、隣接する三角形のエッジに沿って位置するセミランダムピクセルホールの集合としてレンダリングされた画像において見ることができる。画像がアニメ化されると、これらは断続して「輝き」、容易に見られるようになる。

これらのＴ−ジョイントは、ステッチポリゴンを再度導入することによって固定することができることは理解されるが、しかしながらこのようなポリゴンは極めて小さく、ポリゴンのレンダリングに伴う「設定」コストがより有意に大きなサイズのポリゴンに対して良好に役立つことから、これはむしろ非効率な方法である。

さらに別の手法は、Ｐｉｘａｒ’ｓ Ｒｅｎｄｅｒｍａｎシステムで使用されるように、結果として得られるポリゴンが画素よりも小さくなるまでパッチを細分割することである。そのため、これらのマイクロポリゴンは「点」として取り扱うことができる。この方法は膨大な量のデータを生成し、リアルタイムのレンダリングには実際には適していない。

従って、現在の技術におけるクラックのない細分割のための選択肢としては、以下のように要約することができる。
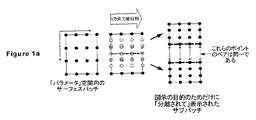
（１）モデルのすべてのパッチを同一の細分割レベルまで細分割する。これは単純であるがリソースを浪費する。
（２）各パッチ内で一様に細分割し、次いでステッチポリゴンを使用して非一様に分割されたパッチ間のギャップを隠す。これは、ステッチポリゴンが追加コストとなり、（図５ａに見られるように）方向の急激な変化を誘導する可能性があるので理想的ではない。
（３）Ｃｌａｒｋの方法を使用することにより、パッチ内でも非一様な細分割が可能となるが、Ｔ−ジョイント問題を欠点として有する。
（４）Ｃｌａｒｋの方法にさらなるステッチポリゴンを適用する。
（５）メッシュをマイクロポリゴンに細分割する。

パッチのエッジに沿って非一様な細分割をできるようにすることは、結合部にクラックが発生することなく異なるパッチを結合することができるので望ましいことが理解される。また、Ｃｌａｒｋの方法を用いて可能なように、パッチ内で非一様な細分割をできるようにすることは、パッチの１つの側面上の高細分割のエッジから反対側面上の低細分割のエッジまでの漸次的移行が、パッチが内部的に一様に細分割されるシステムにおけるよりも少ないポリゴンしか必要とせず、より効率的なポリゴンの使用を可能にするので望ましいことである。また、内部的又は境界上でステッチポリゴンを必要としないシステム、及び同様にＴ−ジョイントを導入しないシステムは非常に望ましいことが理解される。

従って、本発明は第２の態様において、パッチ内でパッチデータを異なる細分割方向に異なる細分割レベルまで処理し、Ｃｌａｒｋの方法による問題を回避する、「不規則なパッチ」の処理をサポートする。異なる数の頂点を「不規則なパッチ」の異なるエッジ上に形成することによって、オブジェクトの隣接領域をモデリングするテセレーションパッチ間のクラックを防止するステッチメッシュが不必要となる。不規則なテセレーションに対応することにより、隣接するパッチの隣接エッジが、残りのエッジについてパッチの細分割のレベルに影響を与えることなく、同じ数のポリゴンの頂点を保持できるようになる。２つの均等に細分割されたパッチの境界を示す実施例が図１３ｂに与えられる。

本発明の第２の態様によれば、請求項８によるインターフェースが提供される。本発明の第２の態様の好適な特徴は、従属請求項９に詳細に記載される。また、請求項１０により、パラメトリックモデリングユニットとポリゴンベースレンダリングシステムとの間でインターフェースをとる方法が提供される。

細分割の不規則なレベルは、最終のサブパッチから四辺形の各エッジに沿って適切な数の頂点を有するメッシュを自動的に生成することによって対応される。これによりクラックの発生なしにポリゴン化されたパッチを簡単に結合することが可能になる。

既知のインターフェース技法に関する別の問題は、いわゆるポリゴンポッピングである。異なるパッチのインターフェースにおいて、すべてのパッチの各エッジは自己細分割制御値を有すると仮定する。細分割変化の手段としてオブジェクトの平滑なアニメ化を可能にするために、これらの値は、浮動小数点を取るか、又は少なくとも小数点部分を包含すると仮定する。ポリゴンポッピングは、テセレーションポリゴンにおいて急激に点が移動するときの説明に使用される用語であり、細分割制御値の小さな小数部分の変化により処理の追加段階（パッチの追加の２元細分割）を実行させる場合に生じる可能性がある。エッジの細分割制御値は任意の値を取ることができるが、好適なテセレーション手法は、次の直近の２の累乗にまで２元パッチ細分割を実行するように制約される。従って、細分割比率が僅かでも増加すると、細分割の実際のレベルが大幅に増加する可能性がある。例えば、各エッジに対して規定された細分割の値が４の場合、細分割は１６のリーフパッチをもたらす。各エッジに対して規定された細分割の値が４から４．１に増加すると、次のより大きな２の累乗は８であり、結果として得られる細分割は６４のリーフパッチを生じる。従って、多くの新しい三角形がオブジェクト内に現われる。このプロセスが適切に制御されない場合には、図３に示されるように、アニメーションに望ましくない視覚的な影響が引き起こされる。

図３ａにおいて、湾曲サーフェスは既に２つの四辺形領域に細分割されている。従って、パッチの「最前部」の湾曲エッジは線分ＡＢ及びＢＣによって近似される。図３ｂでは、前エッジに沿って２つの新しいポイントＤ及びＥが生成されるように、細分割のレベルは増加（１次元だけにおいて）されている。従って、パッチの前エッジは線分ＡＤ、ＤＢ、ＢＥ、及びＥＣによって表される。ＡＢＣからＡＤＢＥＣへの形状の変化は比較的大きく、新しいポイントＤ及びＥはジャンプ、又は「ポップ」して見えるようになったと言うことができる。これは、位置Ｅ’からジャンプして出現したポイントＥを有するこの実施例において最も容易に分かる。

本発明は第３の態様において、ポリゴンポッピングに関連する視覚の問題を改善することを意図している。

本発明による第３の態様では、請求項１によるインターフェースが提供される。本発明の第３の態様の好適な特徴は、従属請求項２及び３で定められる。また、請求項４により、パラメトリックモデリングユニットとポリゴンベースレンダリングシステムとの間でインターフェースをとる方法が提供される。好適な方法の段階は従属請求項５から７で定められる。

本発明は第３の態様において、高次サーフェスを使用するモデルの詳細レベルを変えるときに、よりスムーズに見えるアニメ化された画像を生成する。これは、最終的にテセレーションリーフパッチの線形細分割と３次細分割の間で重み付けされた混合を好適に使用する。この混合に対する重み付け因子は、必要とされる細分割値と次のより小さな２の累乗との比率によって好適に決定される。

ライティング及びシェーディング演算が３次元グラフィックのサーフェスに適用されるときには、通常は１つの点におけるサーフェスの法線、すなわちその位置でのサーフェスに垂直なベクトルが、既知であることが要件である。テセレーションされたサーフェスをシェーディングするために、サーフェス法線は計算された三角形の頂点のみにおいて計算される必要がある。

Ｗａｔｔ ＆ Ｗａｔｔ、Ｆｏｒｌｅｙ他、及びＦａｋｉｎによる「Ｃｕｒｖｅｓ ａｎｄ Ｓｕｒｆａｃｅｓ ｆｏｒ ＧＡＧＤ． Ａ Ｐｒａｃｔｉｃａｌ Ｇｕｉｄｅ， ４ｔｈ Ｅｄｉｔｉｏｎ， Ａｃａｄｅｍｉｃ Ｐｒｅｓｓ， ＩＳＢＮ−０−１２−２４９０５４−１， ｐｐ２４４−２４７」で述べられているように、１つの点で法線を得るための標準的な方法は、その点で２つの（１次独立の）接線ベクトルを計算して、これらの外積を取ることである。必要であれば、その結果を後に、ｓ及びｔのパラメータに関係するサーフェスの１次偏導関数を計算するユニットに変換することができる。

普遍性を損なうこと無く、サーフェス法線の計算がパッチのコーナー点においてのみ行われるように制限した場合、非有理的ベジェサーフェスは、コーナーの制御点とその２つの直近のエッジ制御点との間の差が、それぞれの１次偏導関数のスカラー積であるという極めて好都合な特性を有することになる。これは図１９に示され、ここで「正接Ｓ」はコーナー点Ｐ₀₀とその隣接する制御点Ｐ₁₀間の差と一致し、一方、「正接Ｔ」はコーナーと制御点Ｐ₀₁間の差と一致する。

幾つかのシステムは、この事実（繰り返される細分割に加えて）を使用してパッチ上の種々の位置において法線を計算する。

残念なことにこの計算は成功しない場合が多い。正接ベクトルが１次独立で、ベジェパッチの制御点が、特にこれらの隣接するコーナー点と一致していることが要求される場合がある。これは１次偏導関数の１つ又は両方が０とすることができ、不正確な法線が得られることを意味する。このようなサーフェスパッチは多くの場合「縮退」と呼ばれ、幾つかのシステムはこれらを「不正」であると見なす。これは、このような制御点でのサーフェス構成が完全に有効である形状をモデリングする必要性が高く、モデリングソフトウエアパッケージによって容易に生成することができるので、むしろ残念なことである。

より実用的な既知の１つの解決方法は、ｓ及びｔ方向のパラメータにおいてコーナーから僅かにオフセットした２つのポイントでサーフェスの数値を求めることである。従って、２つの接線ベクトルはこれらの計算されたポイントとパッチコーナーとの間の差を取ることによって近似される。これは通常は適切な結果を与えるが、追加の計算の観点から言えばコスト高である。

接線ベクトルの定義を再度参照して微積分計算を適用すると、１次が０である場合、２次偏導関数を用いることができるのが分かる。Ｗａｔｔ ＆ Ｗａｔｔの「Ａｄｖａｎｃｅｄ Ａｎｉｍａｔｉｏｎ ａｎｄ Ｒｅｎｄｅｒｉｎｇ Ｔｅｃｈｎｉｑｕｅｓ． Ｔｈｅｏｒｙ ａｎｄ Ｐｒａｃｔｉｃｅ」， ＡＣＭ Ｐｒｅｓｓ． ＩＳＢＮ ０−２０１−５４４１２−１は、同様に非有理的ベジェパッチに関して、この状況におけるコーナー制御点と後続の２次偏導関数の積との間の差を論証している。図１９を再度参照すると、例えばＰ₀₁とＰ₀₀が一致する場合、Ｐ₀₂とＰ₀₀の差は潜在的正接をもたらす。同様にこれも０である場合、Ｐ₀₃との差を取ることによって、３次偏導関数に対して同様のプロセスを用いることができる。

残念なことに、この方法でも尚成功しない可能性がある。パッチのエッジに沿ったすべての点は一致する場合があり、パッチが球体の８分空間をモデリングしている際に起きるように、パッチは「三角形」になっている。この特定の状況では、２次偏導関数を選択することができる。Ｆａｒｉｎはまた、さらにより微妙な問題、すなわちｓ及びｔ方向に０でない偏導関数が存在できるが、幾つかの状況においてこれらが平行とすることができることを述べている。その結果、外積は０を与え、従って無効な法線である。Ｆａｒｉｎは１つの特定の場合に対する解決方法を述べている。

本発明は第４の態様において、有理的ベジェサーフェスに対する法線をロバストであるばかりでなく効率よくサーフェス法線を計算する計算方法を示している。

本発明の実施形態を添付図面を参照してより詳細に説明する。

本インターフェースは、パラメトリックモデリングユニット及びポリゴンベースのレンダリングシステムを使用した３次元グラフィックシステムでの使用を目的とするものであり、オブジェクトをモデリングするパラメトリックデータが、ポリゴンベースレンダリングシステムによって、該データを表示用に処理するために使用可能なフォーマットに変換されることができるようになる。

図６はインターフェースのブロック図である。インターフェース１０は、入力バッファ１２、フォーマット変換器１４、再帰バッファ１６、細分割ユニット１８、重み付けプロセッサ２０、方向プロセッサ２４、出力バッファ２６、及び制御ユニット２２を含む。

パラメトリックモデリングユニットにおいて、パッチを用いてサーフェスを定義する。典型的な双三次パッチは、１６個の制御点によって定義される。各制御点は、幾つかの要素（通常は（ｘｙｚｗ）位置、色、及びテクスチャマッピング情報を含む）を定義するＮ次元のベクトルである。典型的な３次元グラフィックシステムにおいては、各パッチのデータは制御点によってグループ化され、入力バッファ１２を介してインターフェース１０に入力されるのは、この制御点グループ化データである。細分割ユニットは、制御点ではなく要素によってデータをグループ化することを要求する。

入力バッファ１２は、制御点グループ化データを取り入れ、該データを細分割ユニット１８によって要求される要素的なフォーマットに再配置して、これをフォーマット変換器に出力する。

インターフェース１０の細分割ユニットは、ベジェ双三次パッチとして知られる特別な標準のパッチを処理するように設計される。同様に、例えば、Ｃａｔｍｕｌｌ−Ｒｏｍ及びＢ−スプラインに基づく他のパッチのフォーマットも３次元モデリングで使用される。インターフェース１０が他のパッチフォーマットを処理できるようにするために、フォーマット変換器１４を設ける。入力バッファ１２が出力する要素的データで表示されたパッチのフォーマットが決定される。データのフォーマットがベジェ双三次フォーマットではない場合には、フォーマット変換器１４は、最適化された一連の行列乗算によりデータをベジェ双三次フォーマットに変換する。種々のパッチフォーマット間の変換方法は、３次元グラフィックの分野で公知であるので本明細書では説明しない。フォーマット変換器１４は、変換アルゴリズムのライブラリを維持し、データに対して適切な変換アルゴリズムを適用して、ベジェ双三次フォーマットに変換する。

再帰バッファ又はストア１６は、２つのパッチ、すなわちルートパッチと中間パッチに対応するデータの記憶領域を与える。ルートパッチは各中間パッチに対する出発点であるので、細分割処理中に複数回アクセスする必要がある。中間パッチデータを再帰バッファ１６内に格納すると、インターフェース内でのデータ転送が減少し、効率が改善されて処理時間が短縮される。再帰バッファ１６のこの領域は中間結果用の作業領域を効果的に与える。

要求レベルに対するパッチの細分割は、細分割ユニット１８によって実行される。細分割ユニット１８への入力は再帰バッファ１６から供給される。細分割は４つのカテゴリ、すなわち、パッチの上半分を取り込むｔの細分割、パッチの下半分を取り込むｔの細分割、パッチの左半分を取り込むｓの細分割、及びパッチの右半分を取り込むｓの細分割に分けられる。

ベジェパッチは１６個の制御点を有し、制御点のデータは４×４行列で配列される。任意のカテゴリにおける第１レベルのパッチｎ−１から次のレベルのパッチｎまでの細分割は、パッチデータに対して次の再帰方程式を適用することによって実現される。

ここで、Ａｉ、Ｂｉ、Ｃｉ、及びＤｉは、細分割のカテゴリによる４×４制御点の行列の適切な要素を表す。要素の索引付けが制御される方法は、細分割の各カテゴリに関して以下で説明する。

細分割の計算は、図７に示され且つ以下に説明されるように、演算をパイプライン形式にすることによって効率よく実行される。

図７は下位計算ユニットを示す。下位計算ユニットに対する入力は、ｎ−１番目レベルのパッチの４つの制御点値Ａ^n-1、Ｂ^n-1、Ｃ^n-1、及びＤ^n-1である。第１の計算段階は、並列に配置され各々が入力と第２の計算段階に結合された３つの加算器４６、４８、及び５０を有する。加算器４６の１つはまた第４の計算段階にも結合される。

第２の計算段階は並列に配置された２つの加算器５２及び５４を含む。各加算器は、第１の計算段階の３つの加算器の２つの出力に結合される。１つの加算器５２は第４の計算段階に直接結合される。加算器５２及び５４は両方とも第３の計算段階に結合される。

第３の計算段階は、その入力として第２の計算段階の加算器５２及び５４の両方からの出力を取り込む単一の加算器５６を含む。加算器５６の出力は、第４の計算段階に結合される。

第４の計算段階は、並列に配置された３つの除算器５８、６０、及び６２を含み、これらはそれぞれ、加算器４６の出力を２で除算し、加算器５２の出力を４で除算し、加算器５６の出力を８で除算する。

下位計算ユニットが出力する出力は、ｎ番目レベルのパッチ、すなわちＡⁿ＝Ａ^n-1の制御点の値であり、３つの除算器５８、６０、及び６２の出力はそれぞれＢⁿ、Ｃⁿ、及びＤⁿである。

パイプライン形式のシステムは、高速なシステムクロックを実現する。

サブパッチにおける制御点値Ａⁿ、Ｂⁿ、Ｃⁿ、及びＤⁿの計算は、細分されているパッチ内の対応する制御点値、Ａ^n-1、Ｂ^n-1、Ｃ^n-1、及びＤ^n-1からの一連の加算において下位計算ユニットにより実行される。計算の第１の段階は、該第１の段階における中間値Ｐ、Ｑ、及びＲの並列計算であり、ここで、
Ｐ＝Ａ^n-1＋Ｂ^n-1
Ｑ＝Ｂ^n-1＋Ｃ^n-1
Ｒ＝Ｃ^n-1＋Ｄ^n-1
である。

第２の段階は、該第２の段階における中間値Ｓ及びＴの並列計算であり、ここで、
Ｓ＝Ｐ＋Ｑ
Ｔ＝Ｑ＋Ｒ
である。

第３の段階は、該第３の段階における中間値Ｕの計算であり、ここで、
Ｕ＝Ｓ＋Ｔ
である。

第４の段階において、値Ｖ＝Ｐ／２、Ｗ＝Ｓ／４、及びＸ＝Ｕ／８が並列計算され、値Ａⁿ＝Ａ^n-1、Ｂⁿ＝Ｖ、Ｃⁿ＝Ｗ、及びＤⁿ＝Ｘが下位計算ユニットから出力される。

各下位計算ユニットは、ｎ番目レベルでのサブパッチ内の４つの新しい制御点の値を計算する。４つの新しい制御点の各セットの計算は、他の１２個の制御点の計算とは独立している。このように、４つの下位計算ユニットを並列使用することによって、最小数のクロックサイクルでｎ番目レベルでのサブパッチの１６個の新しい制御点を計算することが可能となり、高いスループットを達成することができる。４つの下位計算ユニットの出力は、出力マルチプレクサ（ｍｕｘ）４４において組み立てられて、ｎ番目レベルのサブパッチの制御点行列を生成する。

下位計算ユニットは、細分割のどのカテゴリが実行されているかに応じて４×４の制御点行列の様々な要素上で動作することが要求される。しかしながら、細分割ユニットに入力及び出力マルチプレクサを組み込むことによって、４つの同一な細分割ユニットを使用して新しい制御点を計算することができる。入力及び出力マルチプレクサの機能について以下に説明する。

＜入力マルチプレクサ＞
入力マルチプレクサの機能は、ｎ−１番目レベルのパッチ制御点行列の行と列とを入れ替え、下位計算ユニットによって実行される細分割のカテゴリを制御できるようにすることである。

ｔ方向の細分割において、制御点行列の行はＡからＤまで索引付けられ、制御点行列の列は左から右に１から４まで索引付けられる。行における索引付けの方向は、上半分のパッチ又は下半分のパッチが生成されることになるかどうかによって決まる。上半分のパッチを生成するために、行は、行列の最上行としてＡから始まって行列の最下行としてＤで終了するように索引付けられる。このように、ｎ番目レベルの上半分のサブパッチの制御点の最上行は、ｎ−１番目レベルのパッチの制御点の最上行と同一である。ｎ番目の上半分のサブパッチの残りの３つの行は、上の式１で定義されたｎ番目レベルのパッチの制御点の行に関係している。同様に、ｎ番目レベルの下半分のサブパッチの制御点の最下行は、ｎ−１番目レベルのサブパッチの制御点の最下行と同一であり、残りの行は式１と対応してｎ−１番目レベルの行列の行に関係する。

図８ａ及び８ｂはそれぞれ、上半分のサブパッチを取り込むｔ方向の分割と、下半分のサブパッチを取り込むｔ方向の分割とを実行するための、ｎ−１番目レベルのパッチの適切な索引付けを示す。このように、ｔ方向の細分割から下半分を生成するためには、最初に行が反転されて、次に暫定的なデータを形成する上半分のサブパッチの生成に対して処理され、該データは次いで、必要とされるサブパッチデータを形成するように配列されなければならない。

ｓ方向の細分割においては、パッチの列はＡからＤに索引付けられ、行は上から下まで１から４に索引付けされる。列の索引付けの方向は、左のサブパッチ又は右のサブパッチのいずれかが生成されることになるかによって決まる。左半分のサブパッチを生成するためには、列はパッチの左側の列としてＡから始まり、右側の列としてＤで終わるように索引付けされる。従って、レベルの左半分のサブパッチの制御点の左側の列は、ｎ−１番目レベルのパッチの制御点の左側の列と同一である。左半分のサブパッチの残り３つの列は、上の式１で定義されたようにｎ−１番目レベルのパッチの制御点の列に関係する。同様に、ｎ番目レベルの右半分のサブパッチの制御点の右側の列は、ｎ−１番目レベルのパッチの制御点の右側の列と同一であり、残りの列は式１と対応してｎ−１番目レベルのパッチの制御点の列に関係する。

図８ｃ及び８ｄは、左半分のサブパッチを取り込むｓ方向の分割と、右半分のサブパッチを取り込むｓ方向の分割とを実行するためのｎ−１番目レベルのパッチの適切な索引付けをそれぞれ示す。このように、ｓ方向の細分割から左半分のサブパッチを生成するためには、最初にパッチの行と列を入れ替えて、再配置されたパッチを上半分のサブパッチの生成に対して処理することができる。同様にｓ方向の細分割から右半分のサブパッチを生成するためには、行を反転させて、次に行と列を入れ替える。ｔ方向に分割された上半分のサブパッチの処理が実行され、結果として得られる制御点は出力マルチプレクサによって要求された右半分のサブパッチに対応するように再配置される。

＜出力マルチプレクサ＞
出力マルチプレクサの機能は入力マルチプレクサの機能に類似している。該マルチプレクサは細分割のカテゴリに応じて、細分割ユニットによる暫定的なデータ出力を配置して、要求されたサブパッチ制御点行列を形成する。下位計算ユニットがｔ方向の上半分の細分割を実行するように設定されたと仮定すると、ｔ方向の下半分の細分割とｓ方向の左及び右半分の細分割を生成するよう下位計算ユニットの出力を再配置する必要がある。出力マルチプレクサは下位計算ユニットの４つの出力を組み立てて単一の行列にし、入力マルチプレクサによって実行された再配置を反転させて、要求されたサブパッチ制御点行列を生成する。

ｎ番目レベルのサブパッチに対する要素的な制御データが、図７ａ、７ｂ、７ｃ、及び７ｄに示されるように細分割のカテゴリに従って適切な順序に組み立てられると、該データは、リーフパッチに関係する場合には重み付けプロセッサ２０と方向プロセッサ２４に出力され、或いは中間パッチに関係する場合には再帰バッファ１６に戻される。

インターフェースでは、図９に示されるように下位計算が実行される。この細分割のアーキテクチャの実行は、極めて効率的であることが分かっている。Ｗａｔｔ ＆ Ｗａｔｔで示された従来技術の方法はより多くの「計算」段階を必要とし、ハードウェア浮動小数点の実装の点で著しくコスト高になる可能性がある。細分割ユニット１８は幾つかの段階を含む。各段階は１つのレベルの細分割を実行する。第２段階の細分割は、第１段階による処理の後に細分割の要求レベルが達成される場合にバイパスさせることができる。現在のところ好ましいとされる実施形態においては、２つの段階、すなわち第１の段階３０と第２の段階３２は、細分割ユニット１８において実行される。２つの細分割段階を含むと、再帰バッファからの所定量のデータ帯域幅に対してシステムの原計算効率が向上するという利点がある。多くの段階は、最終のシステムにおいて要求されるサイズ／性能のトレードオフを与えるように変更することができる。各段階は、入力マルチプレクサ３４、４つの下位計算プロセッサ３６、３８、４０、４２、及び出力マルチプレクサ４４から成る。

第１の段階では、パッチの要素のデータは再帰バッファ１６から読み取られる。入力及び出力マルチプレクサ３４及び４４それぞれにより、要素の行列の行と列を再配置して実行される計算を制御することができるようになる。計算のオプションは以下の通りである。
ｓ方向に細分割、左半分を出力，
ｓ方向に細分割、右半分を出力，
ｔ方向に細分割、上半分を出力，
ｔ方向に細分割、下半分を出力，
バイパス

入力マルチプレクサ３４は、要求された細分割のカテゴリに応じて行列を再配置し、ｎ−１番目レベルのパッチの４つの制御点を処理のために各下位計算ユニットに送る。各下位計算ユニットの出力はマルチプレクサ４４に供給され、該マルチプレクサは下位計算ユニットの出力を組み立てて、要求された細分割のカテゴリに応じて必要とされたサブパッチに行列を再配置する。段階１の出力マルチプレクサ４４からの出力は、段階２の入力マルチプレクサ３４に対する入力として処理される。段階２の出力は、再帰バッファ１６に送り返されるか、又はリーフパッチが達成された場合には次の計算段階に供給される。

入力及び出力マルチプレクサを使用すると、下位計算ユニットの４つの別々のブロックの必要が無くなるので、湾曲サーフェス細分割システムの要素部品の数が最小になる。

細分割ユニット１８の演算は制御ユニット２２から示される一連の命令によって制御される。制御ユニット２２は、図１０のフローチャートに示されるアルゴリズム上で動作する。制御ユニット２２により、再帰バッファ１６からルートパッチが取り込まれて、第１段階の入力マルチプレクサ３４に送られる。

パッチの４つのエッジに対応する４つのパッチの細分割レベルの割り当てが、ソフトウエア又はハードウェアのいずれかにおいて外部的に計算されていたと仮定する。

制御ユニット２２は、ルートパッチ制御行列の左エッジ及び右エッジの細分割値を調べることによって、ｔ次元の細分割が必要とされるかどうかを判断する。左エッジ値及び右エッジ値のどちらも１．０と２．０の間の値にない場合は、ｔ方向のパッチの細分割が必要とされる。左エッジ値及び右エッジ値は２で除算される。ｔ方向に分割するコマンドは、制御ユニット２２によって細分割ユニット１８に送られ、これにより入力マルチプレクサによるデータの適切な再配置と、出力マルチプレクサによる暫定的なデータの配置とが行われる。ｔ方向に分割されると、次に、上エッジ及び下エッジの新しい細分割値の計算が必要になる。上半分の細分割が実行される場合、制御行列の最上行は変化せず、上半分のサブパッチにおける最上部の値は、分割されていない行列から繰り越される。しかしながら、上半分の細分割は、分割されていない行列のものとは異なるサブパッチの最下行が得られる。従って最下部の値は更新されなければならない。新しい値は、分割されていない行列の上部値及び下部値の平均値又は好ましくは相乗平均値のいずれかとして計算される。相乗平均は、細分割のレベルをパッチ全体にわたってより有用に分布するので好ましい。下半分の細分割については、計算される必要があるのは細分割された行列の最上部の値であり、一方、最下エッジの値は分割されていない行列から繰り越される。最上エッジの値は上半分の細分割における最下エッジ部の値と同じ方法で計算される。

制御ユニット２２は、点の処理がｓ次元に進む終了条件に適合するまでｔ方向の細分割を継続する。パッチ全体のｔ方向のこれ以上の細分割が必要でないことを示す、左エッジ又は右エッジのいずれかの値が１．０と２．０の間にある時に終了条件は満たされる。しかしながら、結果としてのパッチが不規則な場合にはパッチの追加処理を必要とすることができる。不規則なパッチの処理は後で説明される。

ｓ方向の細分割が必要かどうかを判定するために試験される最上エッジ及び最下エッジの値を除いて、ｓ方向の処理は同様にして進められる。新しい右エッジ及び左エッジの値が、左半分の細分割及び右半分の細分割のそれぞれに対して計算される。新しい右エッジ及び左エッジの値は、分割されていない行列の右エッジ及び左エッジの値の平均値又は好適には幾何平均値のいずれかとして計算される。ｓ次元終了条件が満たされると、ｔが再チェックされて要求に合わせて処理が繰り替えされる。ｓの細分割に対する終了条件は、左エッジ及び右エッジのいずれかの値が１．０と２．０の間にある時に満たされる。ｔの細分割と同様に、パッチが不規則な場合には生じたパッチをさらに処理されるよう要求できる。

ｓ及びｔの終了条件が両方とも満たされると、ルートパッチ又は中間パッチは、細分割の第１レベルに進んでおり、エンド点、リーフパッチを表すデータを生成している。次にコマンドは、制御ユニット２２から細分割ユニット１８に送られ、該リーフパッチデータを出力する。

制御ユニット２２は完成されたアルゴリズムを介してパスの数をモニタする。第１のパスでは、制御ユニット２２は下位計算ユニット１８に制御信号を送り、上半分のサブパッチにｔ方向の分割の計算を行わせ、左半分のサブパッチにｓ方向の分割の計算を行わせる。制御ユニット２２から細分割ユニット１８に送られたコマンドの履歴は記録される。次にこのコマンドの履歴は、他のすべてのシーケンスが確実に機能するよう後続のパスで使用される。制御ユニットアルゴリズムの最終のパスは、ｔ方向への分割が常に下半分のサブパッチを出力として取り込み、ｓ方向への分割が常に右半分のサブパッチを出力として取り込むときに実行されている。

＜規則的なリーフパッチの処理＞
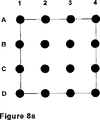
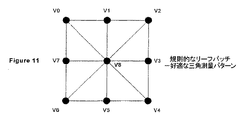
リーフパッチの最終エッジの値の各々が１．０と２．０の間である場合、リーフパッチは規則的であると言える。規則的なリーフパッチが処理されて、変換器により、図１１に示されるようなパッチをカバーするように配置された三角形のグリッドの９つの頂点を生成する。好適には変換器はプロセッサ２０を組み込む。三角形のテセレーションは、正方形の各辺に規則的配列で並べられた３つの頂点と、正方形の中心に配置された９番目の頂点とを有する正方形をカバーする。三角形は正方形を回転しながら扇形に配置され、その結果８つの三角形の各々は正方形の中心の頂点を共有する。図１２に示され、従来技術でよく見られるような別のパターンもまた使用することができる。

図１２の構成に優る図１１の構成の１つの利点は、生成される三角形が元のパッチの制御点の順序とは無関係になることである。すなわち、元のパッチのＳとＴの定義を入れ替えること、又は制御点の順序を反転させることは、同じ結果をもたらすことになる。第２の利点は、パターンが「不規則な」リーフパッチを処理するときに生成されたものに、より近いということである。

リーフパッチから９つの出力頂点位置への変換は、「リーフパッチテセレーションユニット」２０において実行される。これらの頂点に対応するサーフェス法線は、「サーフェス法線生成ユニット」２４において同様に計算される。処理演算のこの段階において、ポリゴンポッピングを最小にするアルゴリズムが実行される。

図１６は規則的なパッチの制御点データからテセレーション三角形の９つの頂点への変換を概略的に示している。パッチの１６の制御点は、該点がＰｉｊで索引付けられた４×４の行列で配列され、ここでｊは０から３まで変わる行列の行を示し、且つ制御点は行０が最上行であるように配置されており、ｉは０から３まで変わる行列の列を示し、制御点は列０が左列であるように配置されていると仮定する。また、テセレーション三角形の９つの頂点が３×３の正方形で配列され、左上の頂点がＶ０に索引付けられ、索引付けは３×３の正方形を時計回りに左中央の頂点Ｖ７まで増分し、中央の頂点がＶ８に索引付けられると仮定する。

テセレーション三角形の４つの外側の頂点は、規則的なリーフパッチの外側の制御点から直接導出される。左上の頂点Ｖ０は左上の制御点の値Ｐ００を取り込み、右上の頂点Ｖ２は右上の制御点の値Ｐ３０を取り込み、左下の頂点Ｖ６は左下の制御点の値Ｐ０３を取り込み、及び右下の頂点Ｖ４は右下の制御点の値Ｐ３３を取り込む。

残りの５つの頂点Ｖ１、Ｖ３、Ｖ５、Ｖ７、及びＶ８の取り込みは多少複雑である。

図１７の線図を考察すると、曲線は、コーナーの頂点の２つ（例えばＶ０及びＶ２）である点ＡとＢを有するリーフパッチのエッジの１つであると考えることができる。さらに細分割が実行された場合には、これは、曲線Ｃ上に新しい点を生成することになり、該点は中間の頂点Ｖ１の可能な位置に対応する。反対に、細分割の数が同じままであった場合には、曲線は線ＡＢで近似され、Ｖ１は点Ｄの線上に存在することになる。細分割のレベルが変化するときに点ＣとＤの間で平滑な転移を実現するために、線分ＣＤに沿って新しい点Ｅが計算され、これがＶ１の値として使用される。これは次の式で表される。
Ｅ＝ｗＣ＋（１−ｗ）Ｄ …式２
ここでｗは、エッジ細分割比率の小数部分から導出された重み付け因子、Ｄはリーフパッチの細分割レベルで導出された第１の頂点の値、及びＣはサブリーフパッチの細分割レベルで導出された第２の頂点の値である。（エッジ比率の小数部分は、その値の２進浮動小数点表示の仮数部を調べることによって自明に得られる点に留意されたい）。

Ｄは２つのコーナーの頂点、すなわち図１６の場合では点Ａ及びＢにそれぞれ相当するＶ０及びＶ２の平均を取ることによって計算される。Ｃを計算するために、ｓ方向の左半分の細分割が実行され、Ｃは左半分の細分割パッチの右上の制御点の値を取る。左（右）エッジに対するＣの値を計算するために、リーフパッチの左（右）エッジに沿ったベジェ曲線をｔ＝１／２において求める。これは、まさしく図７でのＤｎの計算に等しい点に留意されたい。最上エッジ及び最下エッジの「Ｃ」点の計算は類似している。Ｃの値（第２の値）とＤの値（第１の値）が計算されると、頂点Ｖ１は式２に基づいて計算される。この計算は結合器によって実行される。結合器は、テセレーションユニット２０の整数部分とすることができる。

この計算はリーフパッチの四辺形の各エッジについて繰り返される。中央の点は同様の方法で計算されるが、しかしながらＶ８の点Ｃの計算はｓ及びｔ次元の両方で細分割を必要とする。これは、つまり最上エッジ及び最下エッジから計算された「Ｃ」の値を使用し、制御点の２つの中央の行から２つの追加の「Ｃ」値を計算して、次いでこれら４つの値の方法を再適用することにより効率的に行うことができる。

Ｖ８のＤの計算では、図１１に示されたテセレーションパターンが好適であることから、頂点の対角線ペアの１つである、（Ｖ０、Ｖ４）又は（Ｖ２、Ｖ６）のいずれかが使用される。いずれの対角線ペアを選択するかは、ルートパッチに対するリーフパッチの相対的位置に基づく。図１８ａは１６のリーフパッチについてルートパッチに対するリーフパッチの相対位置を表すチェッカーボード構成を示している。リーフパッチの正方形は、４行及び４列で配列され、ルートパッチをカバーする。交互配置パターンで正方形の半分には陰影が付けられ、残りの正方形には陰影が付けられていない。左上の正方形には陰影が付けられている。図１８を参照すると、シェーディングされたリーフパッチは点Ｄの計算で（Ｖ０、Ｖ４）を使用し、一方、陰影が付けられていないリーフパッチのＤの計算には（Ｖ２、Ｖ６）を使用する。リーフパッチの他の数については、同様のパターン化手法を適用する同様の線図を構成することができる。

この好適なパターン化手法は、細分割レベルが「２つの境界のパワーをクロスさせる」ときに、三角形構成が急には変わらないことを保証する。細分割レベルが増大すると、生成された任意の新しい三角形は親の三角形に「内在する」ことが保証される。これは図１８ｂに示される。例えば、より高度にテセレーションされた領域（右側に示される）の左上のリーフパッチ内に導入された中央の点は、「親」リーフ（左側）から中央の半対角線までの左上に依存することになる。これは図１２に示された三角測量パターンには必要ではない代替の演算である点に留意されたい。

＜不規則パッチ処理＞
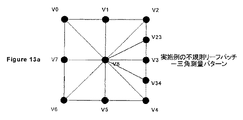
細分割は、関連するエッジのいずれか１つの値が１．０と２．０との間にある場合に、ｓ又はｔの任意の方向で終了する。不規則である場合、すなわち１つ又はそれ以上のエッジの値が１．０から２．０の範囲の外にある場合には、リーフパッチのさらなる処理が必要とされる。不規則リーフパッチは、細分割値が隣接するパッチに結合させることが可能な範囲の外にあるエッジ上に追加の頂点を必要とする、規則的なリーフパッチと考えることができる。不規則リーフパッチは最初に規則的なリーフパッチとして取り扱われ、パッチの９つの頂点は上述のようにして計算される。追加の頂点を計算するために、さらなる細分割を実行する。さらなる細分割は、リーフパッチを形成するための細分割と同一の細分割ユニット内で実行することができ、制御ユニット２２によって制御することができる。追加の頂点を得るための扇状パッチの変換は、リーフパッチ用の変換器内か、又は別の変換器内で実行することができる。

右エッジの値が１．０から２．０の範囲外にある不規則リーフパッチに対する細分割処理の実施例は、図１３ａ及び１４に示される。この実施例では、右エッジの細分割値は２．０と４．０の間にあり、細分割の付加的レベルの１つは、クラッキングを防止するために、右エッジ上に必要な２つの余分の頂点（Ｖ２３とＶ３４）を生成することが求められることを示している。追加の頂点は、エッジの値が１．０から２．０の範囲外であるリーフパッチのエッジ上に設けられ、この場合は右エッジ上にある。追加の頂点によって記述された三角形はパッチの中央の頂点から扇状に広がり、このエッジにまたがる元の三角形を２つに分割する。このように、実施例では不規則パッチの右エッジは５つの頂点（３つではなく）、すなわち反時計回りにＶ２、Ｖ２３、Ｖ３、Ｖ３４、及びＶ４を有し、すべてがＶ８において共通の頂点を有する、Ｖ８−Ｖ２−Ｖ２３、Ｖ８−Ｖ２３−Ｖ３、Ｖ８−Ｖ３−Ｖ３４、及びＶ８−Ｖ３４−Ｖ４の４つの三角形を定義する。

Ｖ２３及びＶ３４は、右エッジの値が１．０と２．０の間になるまで、ｔ方向にさらなる細分割を実行することによって計算され、及び追加の細分割の出力を使用して新しい頂点Ｖ２３とＶ３４とを生成するのに使用される一連の扇状パッチを形成することによって計算される。扇状のパッチは、規則的なリーフパッチにおける頂点に相当する、９つの標準的な頂点であるＶ０からＶ８までの計算には使用されない。

図１３ａ及び１４の不規則リーフパッチの追加の頂点を生成するために必要とされる処理を実施例を用いて説明する。以下の実施例により、当業者であれば、他の種類の不規則パッチの追加の頂点を生成する方法は明らかであろう。

実施例では右エッジの値が２．０から４．０の範囲にあるときに、右エッジの値を１．０から２．０の範囲に入れるためには、細分割の１つだけのレベルが必要とされることが分かるであろう。不規則パッチの処理ステップは、図１５のフローチャートに要約される。不規則パッチのエッジの値が試験され、どのエッジの値が１．０から２．０の範囲の外にあるかが判定される。処理はエッジ関係を基に進められる。図１３ａ及び１４に示された実施例の場合、右エッジの値だけが範囲外である。これはｔ方向の細分割だけが必要であることを示す。制御ユニット２２は細分割ユニット１８に適切なコマンド信号を送出し、不規則パッチをｔ方向に分割する。扇状パッチのエッジの値は、適切な一般的形態の細分割に関して前述のように計算される。１８によって戻された上半分及び下半分のサブパッチは、追加の頂点Ｖ２３及びＶ３４を計算するために使用することができる上部及び下部扇状パッチを定義する。制御ユニット２２は扇状パッチ形成の履歴を保持して、すべての適切な扇状パッチの形成を保証する。この場合、上半分の扇状パッチと下半分の扇状パッチの形成後、すべてのエッジの値は１．０と２．０の範囲内にあり、扇状パッチを形成するさらなる細分割は必要とされない。

追加の頂点Ｖ２３は、上述の式２に従って上部扇状パッチの中央右の頂点を計算することによって得られる。追加の頂点Ｖ２４は、上の式２に従って下部扇状パッチの中央右側の頂点を見積もることによって計算される。

扇状のパッチの他の頂点のいずれもテセレーションプロセスでは必要とされない。不規則なリーフポリゴンデータは、通常の細分割プロセスによって形成された頂点を結合して、リーフパッチ、「第１の複数の頂点」、及び扇状パッチから計算された追加の頂点、並びに「扇状パッチの値」を形成することによって生成される。

＜頂点のサーフェス法線の方向の計算に対する背景＞
サーフェス法線生成ユニット２４は、細分割ユニット１８の出力を取り込み、各頂点に関係するサーフェス法線を計算する。（好適な実施形態では、ユニット２０及び２４は別個のものであるが、別の実施形態では、これらは共通している幾つかの計算値を共有することができることに留意されたい）。サーフェス法線は、サンプルの点においてモデリングされているサーフェスが面している方向を示すのに使用され、後続のライティングとテクスチャの計算のために必要とされる。方向プロセッサ２４は、不規則パッチから計算された任意の追加の頂点を含むリーフパッチの各々の頂点に対する法線を計算する。ポリゴンポッピングのシェーディングされた相似形を最小にするために、式２による前述のような線形補間法が、内部頂点の法線に対して適用され、すなわち出力法線は隣接する頂点の法線と「正しい」法線の混合とすることができる。

理想的には該出力法線は実際には「混合」されるべき最終のシェーディング及びテクスチャ値である点に留意されたい。好適な実施形態では、外部グラフィックス標準（例えば、ＭｉｃｒｏｓｏｆｔのＤｉｒｅｃｔＸ）によって制約を受けているためにこれは行われない。頂点のシェーディングが計算された後でこれらの制約は取り除かれるべきである場合には、呈示された「ポリゴンポッピングの減少」法を容易に適用できることは同業者には明らかである。

従来技術において知られているように、非有理的ベジェパッチのコーナーに配置された４つの頂点については、サーフェス法線の計算はより簡単なはずである。この実施例は図１９に示されている。本発明はこの原理を有理パッチを用いる用途に適合させる。

最初は４つの点だけがリーフパッチのコーナーに存在するので、本発明ではリーフの追加の「部分的な」細分割が実行される。この処理は図２０に示される。規則的なリーフパッチの９つの頂点の場合（番号付けは図１１で使用されているもの）、３つの追加の部分的細分割（１つはＳ方向（図２０（ｉｉｉ））、１つはＴ方向（図２０（ｉｉ））、及び追加の細分割（図２０（ｉｖ））は、Ｖ１、Ｖ３、Ｖ５、Ｖ７、及びＶ８の位置が少なくとも１つのサブパッチのコーナーであるように、子のサブパッチを生成するのに十分である。頂点の法線を生成するためには各サブパッチのすべての制御点が必要ではなく、好適な実施形態では必要最小限の制御点だけが計算されることに留意されたい。図２０では、（コーナーの法線の計算のため、又は必要な子のパッチの制御点を生成のためのいずれかが直接的に）必要とされる制御点は灰色又は黒で示され、一方、必要とされないものは白で示される。

上記のように、本発明は有理ベジェパッチの法線を効率的な方法で計算するが、その方法及び背景理由を以下に示す。
パラメータ位置（ｓ、ｔ）（ｓ、ｔ）における有理サーフェスの位置は以下の式で与えられる。

一方、（０，０）における（ａ，ｂ）方向の単位長さの接線ベクトルの定義は次式で与えられる。

式中の「差分」項を考察すると、次式が得られる。

これは、以下のことを意味する。

スカラー値ｗ（ｅａ，ｅｂ）ｗ（０，０）が正でありゼロではないので、これは上の制約式の上部と下部の両方に適用することができ、次式で与えられる。

有理的なベジェパラメトリックサーフェスに限定して注目し、ベジェパッチの（０，０）（０，０）点が

の制御点に相当する点に留意すると、次式の挙動を調べる必要がある。

便宜上、以下のように定義する。

好適な実施形態では、ベジェ関数は双三次である。より高次のサーフェスを使用する実施形態に対するこの手法の拡張は、当業者に容易なものでなければならない。

取得される行列形式の（ｅａ，ｅｂ）において（すなわちｗ成分によるｘ、ｙ、及びｚ成分の除法の前に）双三次の均質なベジェサーフェスを表す。

従って、これは次のように表し得ることが分かる。

Ｑ行列の特定の特性に留意すると、これは次のように簡略化される。

これは以下のように変形される。

本発明の方法は、「Ｓ」、「Ｔ」、及び「対角線」の接線候補である最大３つまでの可能性のある接線候補を計算する。

＜「Ｓ」方向の候補接線ベクトルの導出＞

「Ｓ」方向の接線ベクトルを生成する場合を考えると、式３と４はそれぞれ次のように変形される。

を考察すると、次の式が求められる。

ここで次の３つの場合が考えられる
１．

２．

３．

上のケースの各々に関して、ｅ→０のような極限値が分子と分母の両方に存在すると（及び極限値がゼロでない）場合、式全体の極限値が存在することが計算から分かる。

ケース１：
分子／分母の「内容」から始めると、次式が得られる。

の場合に限り、極限値は明らかに存在し且つゼロではない。
この条件が成り立つ場合は、Ｓ方向の接線ベクトルは次の式で与えられる。

この点ではベクトルの長さは重要ではないことに留意されたい。

ケース２：
ケース１の条件が当てはまらない場合、

は、ケース２の極限値が調べられ、次式が与えられる。

であることに留意すると、上式の和の第２の部分は、０と仮定されたケース１の結果と同じであることが分かる。従って次式が得られる。

同様に、

と仮定していたので、これは次式になる。

従って、選択された条件が成り立つ場合、これが０でなければ次のような有効な「Ｓ」正接が存在する。

ケース３：
ケース２及び３が両方とも成り立たない場合には、示されたのと同じ引数を使用して、０でないという前提で次式によって「Ｓ」を計算することができる。

＜「Ｔ」方向の候補接線ベクトルの導出＞
これはまさしく「Ｓ」正接と同じ論証に従うので、ここでは説明しない。

上述の方法では、特定のコーナーの頂点の法線を計算するために、最大９つまでの制御点が必要とされる可能性があることは明らかである。図２１は、Ｖ０（すなわち、（ｓ、ｔ）＝（０，０））のコーナー頂点の場合における組を示す。制御点の選択は、計算される頂点の法線に応じて変わるので、残りの説明では別の命名法が適用されることになろう。特定の頂点の法線を計算するために使用される制御点は、Ｃ、Ｓ₁、Ｓ₂、Ｓ₃、Ｔ₁、Ｔ₂、Ｔ₃、及びＤと呼ばれる。また、実施例として、この命名法と頂点Ｖ０に必要な制御頂点の間の相関性は図２１に示される。

＜「サーフェス法線生成ユニット」の好適な実施形態＞
ここでサーフェス法線生成ユニット２４を図２２ａに関連して説明する。

リーフパッチの制御点が提供され（２００）、頂点Ｖ０、Ｖ２、Ｖ４、及びＶ６の各々に対して正しい８つの制御点（Ｃ、Ｓ₁、Ｓ₂、Ｓ₃、Ｔ₁、Ｔ₂、Ｔ₃、Ｄ）の組が選択され（２０１）、次にコーナー法線ユニットに供給される（２０２）。サーフェス法線生成ユニットにおいては、制御点の成分Ｘ、Ｙ、Ｚ、及びＷだけが必要とされる点に留意されたい。

ユニット２０１は、元のリーフパッチ制御点のどれが８つの点の４つの組の各々に対応するかを選択するＭＵＸである。好適な実施形態では、４つの選択は以下の通りである。
頂点Ｖ０：これは図２１に示されている。

好適な実施形態では、「仮想の」Ｓ、Ｔ及び対角線の正接候補の方向は、後続のコーナー頂点に対して９０°だけ回転している点に留意されたい。

代替の実施形態では、実在する軸方向のミラーリングによる制御点の選択を使用することができるが、外積の結果が相殺されるべきかどうかを示すために、これはユニット「２０２」に供給されるべきフラッグの追加を必要とする。このような相殺は少なくとも頂点Ｖ２とＶ６に対して示されるべきであった。（頂点Ｖ４は両方の軸が反転されるので相殺を必要としないであろう）。

ユニット２０３は、頂点Ｖ１及びＶ５のサーフェス法線を生成するのに適した新しい制御点を計算するために、リーフパッチの部分的な細分割を実行する。必要とされるセットは図２０（ｉｉｉ）に示されている。ユニット２０４は、Ｖ１とＶ５の各々に対してそれぞれ必要とされる点を選択する別のマルチプレクサであり、該点をコーナー法線ユニット２０２に供給する。選択プロセスはユニット２０１のプロセスに類似しており、事前の説明があれば当業者にとっては明らかなはずである。

同様な方法で、ユニット２０５及び２０６は、頂点Ｖ３及びＶ７の法線のために必要な２セットの制御点を生成する（図２０（ｉｉｉ）参照）。

ユニット２０７及び２０８は、Ｖ８のサーフェス法線を生成するのに必要な８つの制御点のセットを生成する。この組は図２０（ｉｖ）に示される。図２０（ｉｖ）の右エッジに示された４つの制御点は、図２０（ｉｉ）の右エッジの１回の細分割によって得ることができ、一方、下エッジの制御点は、図２０（ｉｉｉ）の下エッジの１回の細分割から計算される点に留意すべきである。「Ｄ」に対応する制御点は、図２０（ｉｉｉ）の下から２番目の行か、又は代替として２０（ｉｉ）の右から２番目の列のいずれかから得ることができる。

性能的に、好適な実施形態は、複数のユニットとパイプライン形式のアーキテクチャとを組み合わせることにより、幾つかの頂点法線の計算が部分的に重なる。代替の実施形態では、並列処理のレベルはコスト／性能のトレードオフに応じて変えることができる。

次に「コーナー法線ユニット」２０２を図２２ｂと関連して説明する。この図は、理解しやすいように単一の法線の計算だけを説明している点に留意すべきである。８つの選択された制御点が入力される（２２０）。Ｃ点と３つのＳ点は「Ｓ候補」計算ユニット（２２１）に送られ、Ｃ点及び３つのＴ点は「Ｔ候補」計算ユニット（２２２）に送られると共に、Ｃ及びＤは「対角線候補」ユニットに送られる。次に、３つの計算された正接候補Ｔ_S、Ｔ_T、及びＴ_Diagは「候補選択及び法線計算」ユニット（２２４）に入力される。

別の実施形態では、追加の「最適化」を組み込んで、任意選択的に乗算を実行する前に、ｗすなわち「重み付け」要素の値が同一であるかどうかを最初に調べる。これはパッチが非有理的である場合、すなわちｗの値が一定である場合の計算遅延を潜在的に低減することができる。

従って、１つのベクトル減算ユニットだけが必要とされ、好適な実施形態ではこれはパイプライン形式である点に留意されたい。別の実施形態では、減算ユニットはまた、ユニット２２２及び２２３と共有することが可能である。
ユニット２２２はＴ_Tを計算すること以外はユニット２２１と同一であり、一方、ユニット２２３は単にＴ_Diag＝Ｄ_XYZＣ_W−Ｃ_XYZＤ_Wを計算するだけである。

次にユニット２２４を図２４に関連して説明する。試験２５０及び２５２は、Ｔ_S又はＴ_Tのいずれかを０ベクトルとすることができる特別な場合をチェックし、それぞれ−Ｔ_T（２５１）又はＴ_S（２５３）のいずれかである中間ベクトルＴ_NZに設定する。両方のベクトルが０でない場合には、Ｔ_S及びＴ_Tのベクトルの外積を取ることによって、ステップ２５４で候補サーフェス法線が生成される。次いで、候補法線は０に対して比較される（２５５）。０でない場合には、サーフェス法線として使用される（２５６）。０である場合には、ステップ２５３で中間ベクトルが設定される。

中間ベクトルが必要とされた場合には、別の法線の計算が使用される（２５７）。これは中間ベクトルの外積と対角線の正接候補を計算する。ステップ２５１でＴ_NZがマイナスのＴ_Tとして送られたことに留意すべきである。これは法線の方向の整合性を保つために行われる。浮動小数点の相殺が自明であることは理解されたい。

前述のように、このようにして頂点Ｖ１、Ｖ３、Ｖ５、Ｖ７、及びＶ８について計算された法線は、これらの頂点をリーフパッチ内における最大の小数部分の細分割レベルで表示する。より小さな小数部分レベルについては、ポリゴンポッピングを除去するために使用された同じブレンディングプロセスが同様に適用され、最終的な法線ベクトルの結果を生成する。同様に不規則パッチの法線の計算は、前述したものと類似した追加のレベルの細分割を受けなければならない。

このように本発明では、費用のかかる分割演算を必要とせずに有理ベジェサーフェスに対するサーフェス法線を計算することを理解されたい。これは有意な節約である。好適な実施形態では、出力される法線は単位ベクトルではなく、すなわち、好適な実施形態では、後続のシェーディング及び変換ユニット（本明細書には記載されていない）は、必要に応じてこの簡単なタスクを実行することが可能であると仮定する。

図６を参照すると、パイプライン形式のテセレーション処理の最終段階は出力バッファ２６内で実行される。入力バッファ１２は、制御点（ポイント）を取得し、データをグループ化して、データを要素毎に再配置した。出力バッファ２６は、頂点毎に計算段階からのデータをグループ化する反転タスクを実行することが必要とされる。出力バッファ２６は、重み付けプロセッサ２４によって計算された頂点と、サーフェス法線プロセッサ２４によって計算された法線とを取り込み、各要素のデータを頂点毎に共にグループ化してこれを出力し、ディスプレー用に画像の変換、ライティング、テクスチャリング、及びラスタライゼーションで続いて使用する。

特定の図に関連して説明され且つ説明の様々な点で説明された特徴は、特に説明又は図示されたもの以外を組み合わせて使用することができることに留意されたい。このような変更はすべて、以下の請求項に記載の本発明の範囲内に包含される。

上記説明に関して、当業者であれば均等な装置及び方法を容易に思いつくことができ、且つ図面に示され本明細書に記載されたものに均等なすべての装置及び方法は、本発明に包含されることが意図されるものであることは理解されるべきである。従って、前述のものは本発明の原理のみを示すものと考えるべきである。さらに、当業者には多くの修正及び変更を容易に行うことができるので、本発明を図示及び説明された厳密な構成及び実施に限定することは望ましいものではなく、従ってすべての適切な修正及び均等物は本発明の範囲として行使され且つ包含されることになる。

例えば、テセレーション三角形の代替のパターンは本発明の範囲内に包含されると考えられる。

上半分のｎ番目のレベルのサブパッチと下半分のｎ番目のレベルのサブパッチとを形成するためのｔ方向のｎ−１番目のレベルのパッチの細分割を示す概略図である（理解しやすいように、これらは図中物理的に分けて示されている）。 左半分のｎ番目のレベルのサブパッチと右半分のｎ番目のレベルのサブパッチとを形成するためのｓ方向のｎ−１番目のレベルのパッチの細分割を示す概略図である。 各々の段階におけるＳ又はＴの細分割方向の選択肢が供給される細分割のパラメータによって決定される、中間パッチと最終的に８つのリーフサブパッチに分割されるパッチのためのリーフパッチとに対するルートパッチの細分割の可能性のある選択肢を示す概略線図である。 「前エッジ」に沿って頂点ＡＢＣを生成する、第1のテセレーションプロセスによって近似された湾曲サーフェスを示す線図である。 ポリゴンポッピングを生じるテセレーションプロセス間の比較的大きな形状の変化を示す、「前エッジ」に沿って頂点ＡＢＣＤＥを生成する第２のテセレーションプロセスによって近似された同じサーフェスを示す図である。 隣接するパッチが別々の細分割比率に細分割されるときのクラックの問題を示す図である。 クラックの問題を克服するための既知のポリゴン生成システムによって使用されるステッチメッシュである。 クラックの問題を解消するためのＣｌａｒｋの手法を示す。 コンピュータグラフィックにおける「Ｔ−継ぎ手」の問題を示す。 インターフェースの好適な実施形態を示す概略図である。 下位計算ユニットの計算段階を示す概略図である。 図７の計算を使用したｔ方向の上半分の細分割に関するパッチデータの行及び列の索引付けを示す。 図７の計算を使用したｔ方向の下半分の細分割に関するパッチデータの行及び列の索引付けを示す。 図７の計算を使用したＳ方向の左半分の細分割に関するパッチデータの行及び列の索引付けを示す。 図７の計算を使用したＳ方向の右半分の細分割に関するパッチデータの行及び列の索引付けを示す。 ２段階細分割ユニットの概略図である。 制御ユニットの演算を示すフローチャートである。 好適なテセレーションパターンである。 別のテセレーションパターンである。 右エッジの不規則リーフパッチのテセレーションパターンである。 １３ａの不規則なパッチと高レベルの細分割パッチの結合を示す。 図１３ａの不規則パッチの追加の頂点を推定するための扇状パッチの生成を示す概略図である。 扇状パッチ処理中の制御ユニットの演算を示すフローチャートである。 リーフパッチの制御点Ｐ００、Ｐ３０、及びＰ３３と、テセレーション三角形の頂点Ｖ０、Ｖ２、Ｖ６、及びＶ４との間の対応を示す概略図である。 頂点Ｖ１、Ｖ３、Ｖ５、Ｖ７、及びＶ８の結合値の生成を示す概略図である。 異なるリーフパッチのための中心の頂点Ｖ８の計算でどの頂点が使用されるかに関する線図である。 非有理双三次ベジェパッチのコーナーにおける接線ベクトルの挙動の１つの実施例を示す。 ９つの「テセレーション」頂点（すなわち図１１に示されるような）においてサーフェス法線を構成するのに好適な制御点を生成するために（規則的な）リーフパッチに適用された追加の部分細分割段階を示す。 パッチの特定のコーナー点に対するサーフェス法線を生成するために本発明によって使用される有理双三次ベジェパッチの制御点のサブセットを示す。 テセレーションリーフパッチに対する９つの頂点法線を生成するため必要とされる制御点を生成するために取られる段階を説明する。 この法線生成プロセスの一部をさらに説明する。 有理ベジェパッチのコーナーで１つのパラメータ次元の候補接線ベクトルの導出で使用される段階／装置を説明する。 サーフェス法線を生成するためにパッチのコーナーにおいて３つの候補接線ベクトルを結合するために使用される段階／装置を説明する。

符号の説明

１０ インターフェース
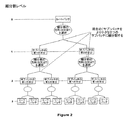
１２ 入力バッファ
１４ フォーマット変換器
１６ 再帰バッファ
１８ 細分割ユニット
２０ リーフパッチテセレーションユニット
２２ 制御ユニット
２４ サーフェス法線生成ユニット
２６ 出力バッファ

Claims (19)

1. オブジェクトを高次サーフェスとしてモデリングするためのパラメトリックモデリングユニットと表示用にポリゴンにモデリングされたオブジェクトをレンダリングするためのポリゴンベースレンダリングシステムとを備えた３次元グラフィックシステムで使用するためのインターフェースであって、
   ａ）少なくとも１つの高次サーフェスパッチを表すデータを受け取るための入力装置と、
   ｂ）前記データを処理して第１のレベルの細分割で前記パッチを表すリーフパッチデータを形成するため、及び前記データをさらに処理して第２のレベルの細分割で前記パッチを表すサブリーフパッチデータを形成するための、前記入力装置に結合された細分割ユニットと、
   ｃ）前記リーフパッチを記述するテセレーションポリゴンの頂点を表す第１の複数の値を前記リーフパッチデータから求めるため、及び前記サブパッチを記述するテセレーションポリゴンの頂点を表す第２の複数の値を前記サブリーフパッチデータから求めるための、前記細分割ユニットに結合された変換器と、
   ｄ）前記第１及び第２の複数の値を結合して前記第１の細分割レベルで前記ポリゴンの頂点を定義するリーフポリゴンデータを形成するための前記変換器に結合された結合器と、
   ｅ）前記リーフポリゴンデータを出力するための、前記結合器に結合された出力装置と、
   を備えることを特徴とするインターフェース。
2. 前記結合器は前記第１及び第２の複数の値を重み付け平均を行うための重み付けプロセッサであることを特徴とする請求項１に記載のインターフェース。
3. 前記細分割ユニットによる前記データの処理を制御するため、並びに前記第１及び第２の複数の値の重み付け平均値において重み付けプロセッサによって使用するための小数値ｗを生成するために、前記細分割ユニット及び前記重み付けプロセッサに結合された制御ユニットをさらに備えることを特徴とする請求項２に記載のインターフェース。
4. ３次元グラフィックシステムにおいてパラメトリックモデリングユニットとポリゴンベースのレンダリングシステムとの間でインターフェースをとる方法であって、
   ａ）少なくとも１つの高次サーフェスパッチを表すデータを受け取り、
   ｂ）前記データを処理して第１のレベルの細分割で前記パッチを表すリーフパッチデータを形成し、
   ｃ）前記リーフパッチを記述する複数のテセレーションポリゴンの頂点を表す第１の複数の値を前記リーフパッチデータから求め、
   ｄ）前記データをさらに処理して第２のレベルの細分割で前記パッチを表すサブリーフパッチデータを形成し、
   ｅ）前記サブリーフパッチを記述する前記複数のテセレーションポリゴンの頂点を表す第２の複数の値を前記サブリーフパッチデータから求め、
   ｆ）前記第１及び第２の複数の値を組み合わせて前記第１のレベルの細分割で前記ポリゴンの頂点を定義するリーフポリゴンデータを形成し、
   ｇ）前記リーフポリゴンデータを出力する、
   各段階を含む方法。
5. 前記データを処理する段階（ｄ）は、前記リーフパッチデータの単一レベルの細分割を必要とすることを特徴とする請求項４に記載の方法。
6. 前記第１及び第２の複数の値を組み合わせる段階（ｆ）は、重み付け平均であることを特徴とする請求項４又は５に記載の方法。
7. 前記細分割ユニットによる前記データ処理を制御する段階と、前記重み付け平均で使用するための小数値ｗを生成する段階とをさらに含む請求項６に記載の方法。
8. パラメトリックモデリングユニットとポリゴンベースのレンダリングシステムとを備える３次元グラフィックシステム用のインターフェースであって、
   ａ）少なくとも１つの高次サーフェスパッチを表すデータと、前記パッチのために必要とされる第１のレベルの細分割を表すパッチ細分割データと、前記パッチの少なくとも１つのエッジのために必要とされる第２のレベルの細分割を表すエッジ細分割データとを受け取るための入力装置と、
   ｂ）前記データを処理して前記第１のレベルの細分割で前記パッチを表すリーフパッチデータを形成するため、及び前記データをさらに処理して前記第２のレベルの細分割で前記パッチを表す扇状パッチデータを形成するために前記入力装置に結合された細分割ユニットと、
   ｃ）前記リーフパッチを記述するテセレーションポリゴンの頂点を表す第１の複数の値を前記リーフパッチデータから決定し、及び前記リーフパッチをさらに記述する前記第１の複数の値によって表されたポリゴンに対して追加のテセレーションポリゴンの頂点を表す扇状パッチの値を前記扇状パッチデータから決定するために前記細分割ユニットに結合された変換器と、
   ｄ）前記第１の複数の値と前記扇状パッチの値とを結合して前記第１の細分割レベルでテセレーションポリゴンの不規則なパターンの頂点を定義する不規則なリーフポリゴンデータを形成する前記変換器に結合された結合器と、
   ｅ）前記不規則なリーフポリゴンデータを出力するための前記結合器に結合された出力装置と、
   を備えることを特徴とするインターフェース。
9. 前記細分割ユニットによって前記データの処理を制御して前記パッチを第１の方向に前記第１の方向の必要とされるレベルまで細分割し、続いて前記パッチを第２の方向に前記第２の方向の必要とされるレベルまで細分割する、前記細分割ユニットに結合された制御ユニットをさらに備えることを特徴とする請求項８に記載のインターフェース。
10. ３次元グラフィックシステムにおいてパラメトリックモデリングユニットとポリゴンベースのレンダリングシステムとの間でインターフェースをとる方法であって、
    ａ）少なくとも１つの高次サーフェスパッチを表すデータと、前記パッチに必要とされる第１のレベルの細分割を表すパッチ細分割データと、前記パッチの少なくとも１つのエッジに必要とされる第２のレベルの細分割を表すエッジ細分割データとを受け取り、
    ｂ）第１のレベルの細分割で前記パッチを表すリーフパッチデータを形成するよう前記データを処理し、
    ｃ）前記リーフパッチを記述するテセレーションポリゴンの頂点を表す第１の複数の値を前記リーフパッチデータから求め、
    ｄ）前記第２のレベルの細分割で前記パッチを表す扇状パッチデータを形成するよう前記データをさらに処理し、
    ｅ）前記第１の複数の値によって表されたポリゴンに対して、前記リーフパッチをさらに記述する追加のテセレーションポリゴンの頂点を表す扇状パッチの値を前記扇状パッチデータから求め、
    ｆ）前記第１の複数の値と前記扇状パッチの値を組み合わせて、テセレーションポリゴンの不規則なパターンの頂点を前記第１の細分割レベルで定義する不規則なリーフポリゴンデータを形成し、
    ｇ）前記不規則なリーフポリゴンデータを出力する、
    各段階を含む方法。
11. 前記細分割ユニットによって前記データの処理を制御して前記パッチを第１の方向に前記第１の方向の必要とされるレベルまで細分割し、続いて前記パッチを第２の方向に前記第２の方向の必要とされるレベルまで細分割する段階をさらに含む請求項１０に記載の方法。
12. パラメトリックモデリングユニットとポリゴンベースのレンダリングシステムとを備えた３次元グラフィックシステム用のインターフェースであって、
    ａ）少なくとも１つの高次サーフェスパッチを表すデータを受け取るための入力装置と、
    ｂ）前記データを再配置するための前記入力装置に結合された入力マルチプレクサと、
    ｃ）前記データを処理して第１の細分割方向の細分割レベルで前記パッチの一部分を表す暫定的なデータを形成するための、前記入力マルチプレクサに結合された細分割ユニットと、
    ｄ）前記暫定的なデータを配列して前記パッチの必要とされる部分を前記細分割レベルで表すリーフパッチデータを形成するために、前記細分割ユニットに結合された出力マルチプレクサと、
    ｅ）前記データの再配置と前記暫定的なデータの配置を制御し、前記細分割ユニットの前記第１の細分割方向を用いて必要とされる方向に前記パッチの必要とされる部分の生成を可能にするために、前記入力マルチプレクサ及び前記出力マルチプレクサに結合された制御ユニットと、
    ｆ）前記必要とされる方向に前記細分割レベルで前記パッチの必要とされる部分を記述するテセレーションポリゴンの頂点を表すリーフポリゴンデータを求めるための、前記出力マルチプレクサに結合されたポリゴニゼーションプロセッサと、
    ｇ）前記リーフポリゴンデータを出力するために前記ポリゴニゼーションプロセッサに結合された出力装置と、
    を備えることを特徴とするインターフェース。
13. 前記細分割ユニットは、前記入力及び出力マルチプレクサ並びに前記制御ユニットに並列に結合された４つの下位計算ユニットを備え、各下位計算ユニットが１／４のデータを処理して暫定的なデータの１／４を形成し、前記制御ユニットは、各下位計算ユニットが処理するための１／４のデータを前記データから選択することを特徴とする請求項１２に記載のインターフェース。
14. 各細分割ユニットが、
    ａ）４つの値Ａ^n-1、Ｂ^n-1、Ｃ^n-1、及びＤ^n-1を含むデータを受け取るための入力マルチプレクサに結合され且つ第２及び第４の計算段階に結合された、加算：Ｐ＝Ａ^n-1＋Ｂ^n-1、Ｑ＝Ｂ^n-1＋Ｃ^n-1、Ｒ＝Ｃ^n-1＋Ｄ^n-1を並列に実行するため、並びに前記第４の計算段階にＰを出力し且つ前記第２の計算段階にＰ、Ｑ、及びＲを出力するための３つの加算器を備える第１の計算段階と、
    ｂ）前記第１及び第４の計算段階に結合され並びに第３の計算段階に結合された、加算：Ｓ＝Ｐ＋Ｑ、Ｔ＝Ｑ＋Ｒを並列に実行するため、並びに前記第４の計算段階にＳを出力し且つ前記第３の計算段階にＳとＴとを出力するための２つの加算器を備える第２の計算段階と、
    ｃ）前記第２及び第４の計算段階に結合された、加算：Ｕ＝Ｓ＋Ｔを実行するため、並びに前記第４の計算段階にＵを出力するための１つの加算器を備える第３の計算段階と、
    ｄ）除算：Ｖ＝Ｐ／２、Ｗ＝Ｓ／４、Ｘ＝Ｕ／８を並列に実行するため、並びに出力装置にＶ、Ｗ、及びＸを出力するための３つの除算器を備える第４の計算段階と、
    ｅ）前記第１及び第４の計算段階並びに前記細分割ユニットの出力マルチプレクサに結合された、１／４の暫定的データ：Ａⁿ＝Ａ^n-1、Ｂⁿ＝Ｖ、Ｃⁿ＝Ｗ、及びＤⁿ＝Ｘを出力するための出力装置と、
    を備えることを特徴とする請求項１３に記載のインターフェース。
15. ルートパッチを表示するデータと処理されたデータとを格納するための、前記入力マルチプレクサ及び前記出力マルチプレクサに結合された再帰バッファをさらに備えることを特徴とする請求項１２から請求項１４のいずれか１項に記載のインターフェース。
16. ３次元グラフィックシステムにおいてパラメトリックモデリングユニットとポリゴンベースのレンダリングシステムとの間でインターフェースをとる方法であって、
    ａ）少なくとも１つの高次サーフェスパッチを表すデータを受け取り、
    ｂ）前記データを再配置し、
    ｃ）前記再配置されたデータを処理して前記パッチの一部分を第１の細分割方向に細分割レベルで表す暫定的なデータを形成し、
    ｄ）前記の暫定的なデータを配置して前記パッチの必要とされる部分を前記細分割レベルで表すリーフパッチデータを形成し、
    ｅ）前記データを再配置する段階と前記暫定的なデータを配置する段階を制御し、前記細分割ユニットの前記第１の細分割方向を用いて前記パッチの必要とされる部分を前記必要とされる方向に生成し、
    ｆ）前記必要とされる方向に前記必要とされる細分割レベルで前記パッチの必要とされる部分を記述するテセレーションポリゴンの頂点を表すリーフポリゴンデータを求め、
    ｇ）前記リーフポリゴンデータを出力する、
    各段階を含む方法。
17. 前記データを１／４に分割し、該１／４の４つのデータを並列に処理し、１／４の暫定的なデータを組み立てる段階をさらに含む請求項１６に記載の方法。
18. 各細分割ユニットの前記処理が、
    ａ）４つの値：Ａ^n-1、Ｂ^n-1、Ｃ^n-1、及びＤ^n-1を含むデータを受け取り、加算：Ｐ＝Ａ^n-1＋Ｂ^n-1、Ｑ＝Ｂ^n-1＋Ｃ^n-1、Ｒ＝Ｃ^n-1＋Ｄ^n-1を並列に実行し、
    ｂ）加算：Ｓ＝Ｐ＋Ｑ、Ｔ＝Ｑ＋Ｒを並列に実行し、
    ｃ）加算：Ｕ＝Ｓ＋Ｔを実行し、
    ｄ）除算：Ｖ＝Ｐ／２、Ｗ＝Ｓ／４、Ｘ＝Ｕ／８を並列に実行し、
    ｅ）前記１／４の暫定的なデータ：Ａⁿ＝Ａ^n-1、Ｂⁿ＝Ｖ、Ｃⁿ＝Ｗ、及びＤⁿ＝Ｘを出力する、
    各段階を含む請求項１７に記載の方法。
19. ルートパッチを表すデータと処理時間を短縮するための処理されたデータとを格納する段階をさらに含む請求項１８に記載の方法。

Images