WO2014061660A1 - 図形板セット - Google Patents
図形板セット Download PDFInfo
- Publication number
- WO2014061660A1 WO2014061660A1 PCT/JP2013/077967 JP2013077967W WO2014061660A1 WO 2014061660 A1 WO2014061660 A1 WO 2014061660A1 JP 2013077967 W JP2013077967 W JP 2013077967W WO 2014061660 A1 WO2014061660 A1 WO 2014061660A1
- Authority
- WO
- WIPO (PCT)
- Prior art keywords
- triangular
- triangular plate
- plate
- triangle
- regular
- Prior art date
- Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
- Ceased
Links
Images
Classifications
-
- G—PHYSICS
- G09—EDUCATION; CRYPTOGRAPHY; DISPLAY; ADVERTISING; SEALS
- G09B—EDUCATIONAL OR DEMONSTRATION APPLIANCES; APPLIANCES FOR TEACHING, OR COMMUNICATING WITH, THE BLIND, DEAF OR MUTE; MODELS; PLANETARIA; GLOBES; MAPS; DIAGRAMS
- G09B1/00—Manually or mechanically operated educational appliances using elements forming, or bearing, symbols, signs, pictures, or the like which are arranged or adapted to be arranged in one or more particular ways
- G09B1/32—Manually or mechanically operated educational appliances using elements forming, or bearing, symbols, signs, pictures, or the like which are arranged or adapted to be arranged in one or more particular ways comprising elements to be used without a special support
- G09B1/34—Manually or mechanically operated educational appliances using elements forming, or bearing, symbols, signs, pictures, or the like which are arranged or adapted to be arranged in one or more particular ways comprising elements to be used without a special support the elements to be placed loosely in adjacent relationship
-
- A—HUMAN NECESSITIES
- A63—SPORTS; GAMES; AMUSEMENTS
- A63F—CARD, BOARD, OR ROULETTE GAMES; INDOOR GAMES USING SMALL MOVING PLAYING BODIES; VIDEO GAMES; GAMES NOT OTHERWISE PROVIDED FOR
- A63F9/00—Games not otherwise provided for
- A63F9/06—Patience; Other games for self-amusement
- A63F9/0669—Tesselation
-
- G—PHYSICS
- G09—EDUCATION; CRYPTOGRAPHY; DISPLAY; ADVERTISING; SEALS
- G09B—EDUCATIONAL OR DEMONSTRATION APPLIANCES; APPLIANCES FOR TEACHING, OR COMMUNICATING WITH, THE BLIND, DEAF OR MUTE; MODELS; PLANETARIA; GLOBES; MAPS; DIAGRAMS
- G09B1/00—Manually or mechanically operated educational appliances using elements forming, or bearing, symbols, signs, pictures, or the like which are arranged or adapted to be arranged in one or more particular ways
- G09B1/02—Manually or mechanically operated educational appliances using elements forming, or bearing, symbols, signs, pictures, or the like which are arranged or adapted to be arranged in one or more particular ways and having a support carrying or adapted to carry the elements
- G09B1/30—Manually or mechanically operated educational appliances using elements forming, or bearing, symbols, signs, pictures, or the like which are arranged or adapted to be arranged in one or more particular ways and having a support carrying or adapted to carry the elements wherein the elements are adapted to be arranged in co-operation with the support to form symbols
-
- G—PHYSICS
- G09—EDUCATION; CRYPTOGRAPHY; DISPLAY; ADVERTISING; SEALS
- G09B—EDUCATIONAL OR DEMONSTRATION APPLIANCES; APPLIANCES FOR TEACHING, OR COMMUNICATING WITH, THE BLIND, DEAF OR MUTE; MODELS; PLANETARIA; GLOBES; MAPS; DIAGRAMS
- G09B19/00—Teaching not covered by other main groups of this subclass
-
- G—PHYSICS
- G09—EDUCATION; CRYPTOGRAPHY; DISPLAY; ADVERTISING; SEALS
- G09B—EDUCATIONAL OR DEMONSTRATION APPLIANCES; APPLIANCES FOR TEACHING, OR COMMUNICATING WITH, THE BLIND, DEAF OR MUTE; MODELS; PLANETARIA; GLOBES; MAPS; DIAGRAMS
- G09B23/00—Models for scientific, medical, or mathematical purposes, e.g. full-sized devices for demonstration purposes
- G09B23/02—Models for scientific, medical, or mathematical purposes, e.g. full-sized devices for demonstration purposes for mathematics
- G09B23/04—Models for scientific, medical, or mathematical purposes, e.g. full-sized devices for demonstration purposes for mathematics for geometry, trigonometry, projection or perspective
-
- A—HUMAN NECESSITIES
- A63—SPORTS; GAMES; AMUSEMENTS
- A63F—CARD, BOARD, OR ROULETTE GAMES; INDOOR GAMES USING SMALL MOVING PLAYING BODIES; VIDEO GAMES; GAMES NOT OTHERWISE PROVIDED FOR
- A63F9/00—Games not otherwise provided for
- A63F9/06—Patience; Other games for self-amusement
- A63F9/0669—Tesselation
- A63F2009/067—Tesselation using a particular shape of tile
- A63F2009/0694—Tesselation using a particular shape of tile triangular
-
- A—HUMAN NECESSITIES
- A63—SPORTS; GAMES; AMUSEMENTS
- A63F—CARD, BOARD, OR ROULETTE GAMES; INDOOR GAMES USING SMALL MOVING PLAYING BODIES; VIDEO GAMES; GAMES NOT OTHERWISE PROVIDED FOR
- A63F9/00—Games not otherwise provided for
- A63F9/06—Patience; Other games for self-amusement
- A63F9/0669—Tesselation
- A63F2009/0695—Tesselation using different types of tiles
- A63F2009/0697—Tesselation using different types of tiles of polygonal shapes
-
- A—HUMAN NECESSITIES
- A63—SPORTS; GAMES; AMUSEMENTS
- A63F—CARD, BOARD, OR ROULETTE GAMES; INDOOR GAMES USING SMALL MOVING PLAYING BODIES; VIDEO GAMES; GAMES NOT OTHERWISE PROVIDED FOR
- A63F9/00—Games not otherwise provided for
- A63F9/06—Patience; Other games for self-amusement
- A63F9/10—Two-dimensional jig-saw puzzles
- A63F9/1044—Display boards therefor
Definitions
- the present invention relates to a learning graphic board set.
- the graphic board can also be used as a learning material for understanding figures and geometry. By preparing a plurality of graphic boards and changing the combination of arrangements on the plane, various figures with different external shapes can be created. This can be used to understand the nature of the figure.
- the flat figure quadrature guidance blackboard disclosed in Patent Document 1 below includes a plurality of triangular figure boards.
- the outer shape formed by the plurality of graphic boards can be made into various triangles, rectangular or parallelogram. This not only helps to understand various basic figures, but also helps to understand how to determine the area of each figure.
- the figure puzzle disclosed in Patent Document 2 below includes four triangular cards.
- Combinations of triangle cards can form shapes such as squares, rectangles, parallelograms, rhombuses, trapezoids, and triangles, which are basic shapes of figures. According to this configuration, the understanding of the basic shape of the figure is deepened by operation and vision.
- An object of the present invention is to solve the conventional problems as described above, and to provide a graphic board set that can deepen geometrical considerations related to a regular pentagon that is a basic shape of a planar graphic. To do.
- the inventor of the present application creates a graphic board for two types of isosceles triangles constituting a regular pentagon, and understands the relationship between the similarities and the relationship between the angle at the vertex and the interior angle of the regular pentagon by combining these. It has been found that geometrical considerations related to regular pentagons can be deepened by deepening.
- the graphic board set of the present invention is a learning graphic board set comprising a first triangular plate of an isosceles triangle having an apex angle of 108 degrees and a base angle of 36 degrees.
- the bases have the same length, and a new triangle can be formed by combining the first triangular plate and the second triangular plate.
- the first triangle plate and the second triangle plate are configured such that the lengths of the equal sides of the first triangular plate coincide with the lengths of the equal sides of the second triangular plate.
- This isosceles triangle is similar to the triangle of the second triangular plate. If the length of the equal sides of the first triangular plate and the length of the bottom side of the second triangular plate are made to coincide, the first triangular plate and the second triangular plate are combined, and the apex angle is 108 degrees. Thus, an isosceles triangle having a base angle of 36 degrees can be newly formed (see FIG. 3). This triangle is similar to the triangle of the first triangular plate.
- the regular pentagon is composed of two isosceles triangles, an isosceles triangle having an apex angle of 108 degrees and a base angle of 36 degrees, and an isosceles triangle having an apex angle of 36 degrees and a base angle of 72 degrees.
- the triangle plate in the graphic board set of the present invention is an isosceles triangle as a regular pentagonal component, regardless of whether it is a single triangle or a triangle formed in combination.
- the triangle formed by combination is similar to any of the single triangles to be combined.
- the graphic board set of the present invention preferably has the following configurations.
- a triangle plate set including the first triangle plate and the second triangle plate is provided, and a regular pentagon or a regular decagon can be formed by combining the triangle plates constituting the triangle plate set.
- a regular pentagon or a regular decagon can be formed by combining the triangle plates constituting the triangle plate set.
- an experiential understanding of a regular pentagon or a regular decagon is deepened, and a regular pentagon or a regular decagon is obtained. Helps improve related geometrical considerations.
- a plate member having a recess, and a set of triangular plates including the first triangular plate and the second triangular plate, and the triangular plate constituting the triangular plate set has sides or vertices. It is preferable that it can arrange
- a plate member formed with a circular recess and a set of triangular plates including the first triangular plate and the second triangular plate, and combining the triangular plates constituting the triangular plate set, It is preferable that a regular pentagon or a regular decagon inscribed in the circular recess can be formed.
- the triangular plate is placed in the concave portion while the apex of the triangular plate is brought into contact with the inner peripheral wall surface of the concave portion that forms a circumscribed circle of a regular pentagon or a regular decagon.
- the regular pentagon or regular decagon formed of a triangular plate is rotatable along the concave portion, and forms a regular pentagon or regular decagon inscribed in a circle in the mounting operation of the triangular plate.
- the relationship between the circumscribed circle and a regular pentagon or a regular decagon can be understood through experience.
- the recess is circular, a gap is generated between the side of the placed triangular plate and the inner peripheral wall surface of the recess.
- the clearance makes it easy to take out the placed triangular plate and eliminates the need for a separate recess for taking out.
- the triangular plate can be held in a regular pentagonal shape or a regular decagonal shape by the concave portion, and therefore, for example, if a storage case is added, it is convenient to carry the graphic board set.
- a plate member having a regular decagonal recess and a set of triangular plates including the first triangular plate and the second triangular plate are provided, and the triangular plates constituting the triangular plate set are combined.
- a regular pentagon inscribed in the circular concave portion can be formed.
- the triangular plate is placed in the concave portion while the apex of the triangular plate is brought into contact with the inner peripheral wall surface of the regular decagonal concave portion, thereby completing the regular pentagon.
- a regular pentagon or a regular decagon can be formed by combining triangular plates constituting one set, and the plurality of triangular plates can be stacked and stored in the recess.
- a set of triangular plates to be used can be selected as necessary, and the learning range can be expanded.
- the triangular plate can be held in a regular pentagonal shape or a regular decagonal shape by the concave portion, for example, if a storage case is added, it becomes convenient to carry the graphic board set.
- the triangular plate can be placed while being aware of the display, and the learning effect is enhanced.
- a display for recognizing a similar triangle or a display of a regular pentagon is attached to at least one of the first triangular plate and the second triangular plate. According to this configuration, a sufficient learning effect can be obtained even if the first triangular plate and the second triangular plate are used alone.
- the regular pentagonal display is preferably a regular pentagonal hole. According to this configuration, the regular pentagon can be easily recognized and the learning effect can be further enhanced. Further, if a regular pentagonal hole is provided in both the first triangular plate and the second triangular plate, a connecting means such as a clip is passed through the hole portion, and the first triangular plate and the second triangular plate are passed through. The triangular plate can be held together, making it convenient to carry.
- a display for recognizing a similar triangle and a display for a regular pentagon are added to the inside of the regular pentagon display. According to this configuration, the learning effect when the first triangular plate and the second triangular plate are used alone is further enhanced.
- a number of marks corresponding to the angles of the vertices are displayed near the vertices of the first triangular plate and the second triangular plate. According to this structure, an angle can be recognized visually and a learning effect increases.
- At least some of the vertices of the first triangular plate and the second triangular plate are chamfered. According to this configuration, sharp corners are not formed at the apex, and injury during handling can be prevented.
- a plurality of triangular plates included in the graphic plate set are color-coded according to the type of triangle. According to this configuration, the visual understanding is deepened, and also when using a combination of triangles, Color and angle can be considered in association with each other, and the learning effect is enhanced.
- At least one of the plurality of triangular plates included in the graphic plate set is color-coded so that a single triangular plate can recognize a similar triangle. This configuration is useful for visual understanding.
- FIG. 4 is a plan view showing another combination of the triangular plate 1 and the triangular plate 2 shown in FIG. 3.
- the figure explaining the property of the figure of a regular pentagon The figure explaining the property of the figure of a regular pentagon.
- the figure explaining the property of the figure of a regular pentagon The figure explaining the property of the figure of a regular pentagon.
- FIG. 13 is a plan view showing a state in which a set of triangular plates 30 is placed in the recess of the plate member 25 of FIG. 12.
- the top view which shows the example which chamfered the vertex of the triangular board of FIG. The figure which shows the exercise example of the geometrical consideration of a regular pentagon.
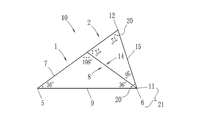
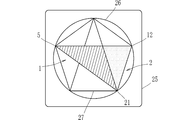
- FIG. 1 is a plan view of a graphic board set 10 according to the first embodiment of the present invention.
- the graphic board set 10 includes a triangular board 1 and a triangular board 2.
- the triangular plate 1 is an isosceles triangle having an apex angle at the vertex 4 of 108 degrees and a base angle at the vertices 5 and 6 of 36 degrees.
- the triangular plate 2 is an isosceles triangle having an apex angle at the apex 11 of 36 degrees and a base angle at the apexes 12 and 13 of 72 degrees.
- the triangle plate 1 and the triangle plate 2 in FIG. 1 display the angle at each vertex.
- a mark 20 is displayed at each vertex.
- One mark 20 represents an angle of 36 degrees. Since the angle 108 of the vertex 4 is three times 36 degrees, the number of marks 20 is three. Since the mark 20 is displayed, the angle can be visually recognized, and in particular, the sum of the angles when the triangular plates are combined can be easily recognized.
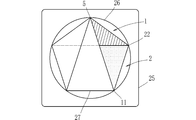
- FIG. 2 shows a state in which the side 8 of the triangular plate 1 and the side 14 of the triangular plate 2 are abutted to form a new triangle.
- FIG. 3 shows another example of the graphic board set 10.
- the side 16 that is the base side of the triangular plate 2 is matched with the side 7 and the side 8 that are equal sides of the triangular plate 1.
- the side 8 of the triangular plate 1 and the side 16 of the triangular plate 2 can be brought into contact with each other to form a new triangle.
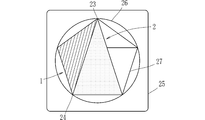
- the combined triangle shown in FIG. 3 is an isosceles triangle having a vertex angle of 108 degrees that is the sum of 36 degrees and 72 degrees at the vertex 22. For this reason, each length of the side 14 and the side 15 and the length of the side 9 are equal. For this reason, as shown in FIG. 4, the side 9 of the triangle 1 can be abutted against the side 14 of the triangle 2 to form a quadrangle. As will be described later, this quadrangle is a quadrangle related to a regular pentagon (see FIGS. 7 and 11).
- FIGS. 1 to 4 are diagrams for explaining the properties of a regular pentagonal figure.
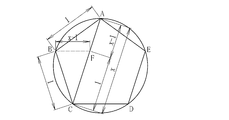
- FIG. 5 is a diagram in which a regular pentagon is divided into three triangles by adding a line AC and a line AD to the regular pentagon.
- regular pentagons there are two types: an isosceles triangle BCA and an isosceles triangle EAD having an apex angle of 108 degrees and a base angle of 36 degrees, and an isosceles triangle ACD having an apex angle of 36 degrees and a base angle of 72 degrees. It can be divided into isosceles triangles.
- FIG. 6 is obtained by adding a line CF to the figure of FIG.
- the isosceles triangle ACD is divided into an isosceles triangle FAC having an apex angle of 108 degrees and a base angle of 36 degrees, and an isosceles triangle CDF having an apex angle of 36 degrees and a base angle of 72 degrees.
- One isosceles triangle FAC obtained by the division is congruent with the isosceles triangle BCA.
- the other isosceles triangle CDF obtained by the division is similar to the isosceles triangle ACD before the division.
- FIG. 7 is obtained by adding a line EF to the figure of FIG.
- the isosceles triangle EAD is divided into an isosceles triangle FEA having an apex angle of 108 degrees and a base angle of 36 degrees, and an isosceles triangle DEF having an apex angle of 36 degrees and a base angle of 72 degrees.
- One isosceles triangle FEA obtained by the division is similar to the isosceles triangle EAD before the division.
- the other isosceles triangle DEF obtained by the division is similar to the isosceles triangle ACD.
- the regular pentagon has two types of isosceles triangles: an isosceles triangle having an apex angle of 108 degrees and a base angle of 36 degrees, and an isosceles triangle having an apex angle of 36 degrees and a base angle of 72 degrees.
- the dividing lines shown in FIGS. 6 and 7 are examples, and by adding dividing lines, isosceles triangles that are congruent or similar to the isosceles triangles shown in FIGS. 5 to 7 can be added.
- a regular pentagon is geometrically related to two types of isosceles triangles, an isosceles triangle having an apex angle of 108 degrees and a base angle of 36 degrees, and an isosceles triangle having an apex angle of 36 degrees and a base angle of 72 degrees.
- the triangle set 10 is derived from the above viewpoint.
- the combination triangle shown in FIG. 2 corresponds to an isosceles triangle ACD in which the isosceles triangle FAC and the isosceles triangle CDF are combined in the regular pentagon of FIG.
- the combination triangle shown in FIG. 3 corresponds to an isosceles triangle EAD that combines the isosceles triangle FEA and the isosceles triangle DEF in the regular pentagon of FIG.
- the combination polygon shown in FIG. 4 corresponds to a quadrangle combining the isosceles triangle BCA and the isosceles triangle ACD in the regular pentagon of FIG.
- the guide In order to effectively advance learning using the graphic board set 10, it is preferable to create a guide that describes the learning procedure using the graphic board set 10.
- information useful for geometrical consideration using the triangular plate 1 and the triangular plate 2 is described.
- the correspondence between the triangular plate 1 and the triangular plate 2 and the regular pentagon and the relationship between the angle at the apex of the triangular plate 1 and the triangular plate 2 and the internal angle of the regular pentagon are described.
- a similar relationship between a new triangle formed by combining the triangular plate 1 and the triangular plate 2, and the triangular plate 1 and the triangular plate 2 is also described.
- the learner is aware that the triangular plate 1 and the triangular plate 2 are constituent elements of a regular pentagon, and has an angle of 36 degrees, an angle of 72 degrees, and an angle of 108 degrees. You can understand the correspondence with regular pentagons through experience. Similarly, by using the triangular plate 1 and the triangular plate 2 in combination, the relationship between the internal angle of the regular pentagon of 108 degrees, the angle of 36 degrees, and the angle of 72 degrees can be understood through experience.
- a quadratic equation can be formed based on an understanding of the similarity relationship, and the length of a side of a new triangle formed by combining the triangular plate 1 and the triangular plate 2 Can also be derived.
- the triangular plate 1 and the triangular plate 2 can be combined to form a regular decagon.
- the triangular plate 1 and the triangular plate 2 are regarded as regular decagonal components, and learning associated with the regular decagon using the triangular plate 1 and the triangular plate 2 is also possible. This learning example will be described later with reference to FIG.
- the triangular plate 1 and the triangular plate 2 are plate-like members, they can be easily reversed. This prevents a fixed understanding of the triangle shape and allows a flexible understanding. Further, the graphic board set 10 can be rotated on a plane, which is also useful for a flexible understanding.
- the combined triangle shown in FIG. 2 is formed by combining a triangular plate 1 and a triangular plate 2. Since the triangle plate 1 and the triangle plate 2 are provided with an angle display, it can be understood that the angle of the combined vertex of the new triangle 21 is the sum of 36 degrees and 36 degrees, that is, 72 degrees. In addition, it can be understood that the combination triangle is an isosceles triangle having an apex angle of 36 degrees and a base angle of 72 degrees, that is, a triangle similar to the triangle of the triangle plate 2.
- a triangle having an angle of 36 degrees, an angle of 72 degrees, and an angle of 108 degrees is geometrically related to a regular pentagon. Therefore, an understanding by the combination described above is an understanding of the nature of a regular pentagon. Also useful.
- the example of the graphic board set 10 in FIG. 2 has been described.
- the same learning effect can be obtained by using the graphic board set 10 in FIG.
- the graphic board set 10 of FIG. 3 can be combined to form a quadrangle as shown in FIG.
- the quadrangle in FIG. 4 corresponds to the quadrangle ABCD in FIG. 7 and is geometrically related to the regular pentagon. Therefore, the learner can obtain a learning effect while performing the two combinations of FIGS. 3 and 4.
- the graphic board set 10 is provided with a number of marks 20 in the vicinity of each vertex corresponding to the angle of each vertex.
- One mark 20 corresponds to an angle of 36 degrees. Since the mark 20 is attached, the angle can be visually recognized and the learning effect is enhanced.
- the angle of 108 degrees is an interior angle of a regular pentagon and is three times the angle of 36 degrees.
- the angles of the corners of the triangle plate 1 and the triangle plate 2 are 36 degrees, 72 degrees (twice 36 degrees), and 108 degrees (3 times 36 degrees and an internal angle of a regular pentagon), and 36 degrees or a multiple thereof. is there. From this, one mark 20 corresponds to an angle of 36 degrees. Since the mark 20 is added, the angle of each vertex can be visually recognized in association with 36 degrees, and the learning effect is enhanced.
- the vertex 6 and the vertex 11 are combined to form a new vertex 21.
- the angle at the vertex 21 is twice 36 degrees, that is, 72 degrees.
- the number of marks 20 at the vertex 21 and the vertex 12 are both two, and it can be easily recognized that the number of marks 20 at the vertex 5 is one. Therefore, it can be visually understood that the combined triangle shown in FIG. 2 is an isosceles triangle having a vertex angle of 36 degrees and a base angle of 72 degrees.
- FIG. 8 shows an exploded perspective view of the graphic board set according to the second embodiment of the present invention.
- the graphic board set 10 shown in FIG. 8 includes a plate member 25 in addition to the triangular board 1 and the triangular board 2.
- a circular recess 26 is formed in the plate member 25.
- the bottom surface of the recess 26 is provided with a regular pentagon and various triangles 27 inscribed in the circumference of the recess 26, and the triangular plate 1 and the triangular plate 2 can be placed while being aware of the display 27. , Learning effect will increase.
- the concave portion 26 is circular
- a triangular plate can be placed in the concave portion 26, and the concave portion 26 is not limited to a circular shape.
- the concave portion 26 may be a regular pentagon or a regular decagon. This will be described later with reference to FIG. Further, the triangle plate may be displayed with an angle or a mark 20 as in FIGS.
- FIG. 9 is a plan view showing a state in which the triangular plate 1 and the triangular plate 2 are placed in the concave portion 26 of the plate member 25.
- the triangular plate 1 and the triangular plate 2 correspond to those shown in FIGS.
- a diagonal line is added to the triangular plate 1 and a point is added to the triangular plate 2.
- FIGS. 10, 11, 13, and 18 The same applies to FIGS. 10, 11, 13, and 18 below.
- the triangle plate 1 and the triangle plate 2 may be color-coded so that both can be identified. According to this configuration, the understanding is deepened visually, and when the triangular plate 1 and the triangular plate 2 are used in combination, the color and the angle can be considered in association with each other, and the learning effect is enhanced. In addition, the learning effect is enhanced even if the colors are divided so that similar triangles are recognized within a single triangle plate 1 or triangle plate 2. This configuration is particularly effective when a display for recognizing a similar triangle is added to the triangular plate 1 or the triangular plate 2 as in the configuration of FIGS. 14 to 16 described later.
- the color-coded structure may be a colored part and a colorless part (transparent).
- the color coding is also effective when three or more triangular plates are used as shown in FIGS. 12 to 13 and FIGS. In this case, for example, the colors may be classified according to the type of triangle (a triangle similar to the triangular plate 1 in FIG. 1 and a triangle similar to the triangular plate 2 in FIG. 2).
- the concave portion 26 is circular, an inner peripheral wall surface is formed in the concave portion 26 in a circumferential shape.
- the vertexes 5, 12, and 21 of the triangle formed by the triangular plate 1 and the triangular plate 2 are in point contact with the inner peripheral wall surface of the recess 26.
- the triangular plate 1 and the triangular plate 2 are mounted on the concave portion 26 while the apexes of the triangular plate 1 and the triangular plate 2 are brought into contact with the inner peripheral wall surface of the concave portion 26 that forms a regular pentagonal circumscribed circle. Will be placed. Accordingly, through this placement operation, the correspondence between the regular pentagon or the pentagon circumscribed circle and the triangular plate 1 and the triangular plate 2 is conscious, and the learning effect is enhanced.
- FIG. 10 is a plan view showing another example of the state in which the triangular plate 1 and the triangular plate 2 are placed in the concave portion 26 of the plate member 25.
- the new triangle formed by the triangle plate 1 and the triangle plate 2 corresponds to the triangle shown in FIG.
- FIG. 11 is a plan view showing still another example of the state in which the triangular plate 1 and the triangular plate 2 are placed in the concave portion 26 of the plate member 25.
- the quadrangle formed by the triangular plate 1 and the triangular plate 2 corresponds to the quadrangle shown in FIG. 10 and 11, similarly to the configuration shown in FIG. 9, through the placement work of the triangular plate 1 and the triangular plate 2, a regular pentagon or a regular pentagon circumscribed circle, and the triangular plate 1
- the correspondence with the triangular plate 2 is conscious, and the learning effect is enhanced.
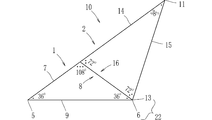
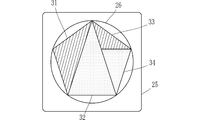
- the graphic board set 10 shown in FIG. 12 includes a triangular board set 30 composed of a total of four triangular boards 31 to 34 that can form a regular pentagon.
- the graphic board set 10 in this figure includes a plate member 25 similar to the plate member 25 shown in FIG. 8, and triangular plates 31 to 34 can be placed on the plate member 25.
- FIG. 13 is a plan view showing a state in which the triangular plates 31 to 34 are placed on the plate member 25. Since the recess 26 is circular, the apexes of the triangular plates 31 to 34 are in point contact with the inner peripheral wall surface of the recess 26 in the state shown in FIG. According to this configuration, the triangular plates 31 to 34 are placed on the concave portion 26 while the apexes of the triangular plates 31 to 34 are brought into contact with the inner peripheral wall surface of the concave portion 26 constituting a regular pentagonal circumscribed circle. The pentagon will be completed. Accordingly, through this placement operation, the correspondence between the regular pentagon or the regular pentagon circumscribed circle and the triangular plates 31 to 34 is conscious, and the learning effect is enhanced.
- each side is not in contact with the inner peripheral wall surface of the concave portion 26, but the concave portion 26 is circular. Is in contact with the inner peripheral wall surface.
- the regular pentagon formed by the triangular plates 31 to 34 in the recess 26 is not completely fixed in position, and can rotate along the recess 26. For this reason, in placing the triangular plates 31 to 34, it is easy to be aware that a regular pentagon inscribed in the circle is formed, and the relationship between the circumscribed circle and the regular pentagon can be understood through experience.
- the concave portion 26 is circular, a gap is generated between the sides of the placed triangular plates 31 to 34 and the inner peripheral wall surface of the concave portion 26.
- the clearance makes it easy to take out the placed triangular plates 31 to 34 and eliminates the need for a separate recess for taking out.
- each vertex is positioned on the inner peripheral wall surface of the concave portion 26, and the triangular plates 31 to 34 are held in the concave portion 26. .
- the graphic board set 10 is arranged and is in a collective state. For this reason, for example, if a storage case is added, it will be convenient to carry the graphic board set 10.
- the pair of triangular plates shown in FIG. 2 or 3 may be included.
- the remaining other triangular plates do not necessarily have to be the pair of triangular plates shown in FIG. 2 or FIG. 3, and may not be the triangular plates having the angles shown in FIG.
- the triangular plate 33 and the triangular plate 34 may be integrated.
- the triangular plate 31 and the triangular plate 32 may be further divided. In this case, the divided triangles do not have to be triangular plates having the angles shown in FIG.
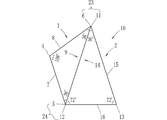
- FIG. 14 shows an example in which various displays are added to the triangular plate 2.
- the outer shape is a regular pentagon, and a line connecting vertices of the regular pentagon is added.
- a triangle similar to the triangle of the triangular plate 2 can be recognized inside the regular pentagon, and a triangle similar to the triangular plate 1 shown in FIG. 1 can also be recognized.
- another regular pentagon 41 can be recognized inside the regular pentagon.
- the indications 42 to 45 are triangles similar to the triangular plate 2.
- a display 43 is added to the display 42, a display 44 is added to the display 43, and a display 45 is added to the display 44.
- smaller similar triangles can be recognized sequentially, and triangles similar to the triangular plate 1 shown in FIG. 1 can also be recognized.
- the triangular plate 2 shown in FIG. 14 it is possible to learn using the triangular plate 2 alone while referring to the displays 40, 42 to 45 of the triangular plate 2.
- the display 40 and the displays 42 to 45 are attached, but any one of them may be attached.
- the thing without a scale may be sufficient.
- FIG. 15 shows an example in which various displays are added to the triangular plate 1.
- the display 50 is the same display as the display 40 of FIG. 14, and the displays 52 to 55 are the same displays as the displays 42 to 45 of FIG.
- the triangular plate 1 shown in FIG. 15 can be learned by using the triangular plate 1 alone while referring to the displays 50 and 52 to 55 of the triangular plate 1. Become.
- the display 50 and the displays 52 to 55 may be provided with any one of them, or may have no scale.
- the regular pentagon 41 in FIG. 14 and the regular pentagon 51 in FIG. 15 may be formed as holes. According to this configuration, the regular pentagon can be easily recognized and the learning effect can be further enhanced. 14 and the triangular plate 1 of FIG. 15 constitute a graphic board set, if the hole of the regular pentagon 41 and the hole of the regular pentagon 51 are overlapped, this hole The triangular plate 1 and the triangular plate 2 can be held together by passing connecting means such as a clip through the portion. According to this configuration, it is convenient to carry.
- FIG. 16 is a diagram showing another embodiment of a triangular plate.
- the triangular plate 2 shown in this figure has chamfered vertices 11 to 13 of the triangular plate 2 shown in FIG.
- the chamfering in this embodiment is to round a vertex, that is, a corner. According to this configuration, sharp corners are not formed at the vertices 11 to 13, and injury during handling can be prevented.
- the example which chamfered the triangular plate 2 shown in FIG. 14 was demonstrated, it is not restricted to this, What is necessary is just to be a triangular plate contained in a graphic board set. Further, all the three vertices may be chamfered, but the present invention is not limited to this.
- the crest may be chamfered only on a vertex having an angle of 36 degrees that is the sharpest.
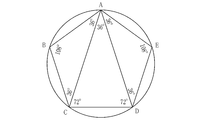
- FIG. 17 is a diagram showing an example of an exercise related to geometrical consideration of a regular pentagon.
- the regular pentagon shown in FIG. In this practice example, the length x of the diagonal AC is obtained by geometric consideration. From the given conditions, it can be directly derived that the length of the side AB and the side BC is 1, and that the angle at the vertex B is an internal angle of a regular pentagon of 108 degrees. Therefore, this practice example is the same as obtaining the length of the base AC of the isosceles triangle BCA having an apex angle of 108 degrees.
- the isosceles triangle BCA is divided into two to create a triangle FAB.
- the auxiliary line BF is a part of a line connecting the vertex B and the vertex E of a regular pentagon.
- the isosceles triangle BCA corresponds to a new triangle formed by combining the triangular plate 1 and the triangular plate 2 in FIG.
- the triangle FAB corresponds to the triangle of the triangular plate 1 in FIG.
- the triangle board 1 and the triangle in FIG. Similar to the fact that the boundary line is formed by combining with the plate 2, the association with drawing the auxiliary line BF works in FIG. That is, the learning effect by the graphic board set 10 is also exhibited in an exercise example in which the geometrical consideration of the regular pentagon as shown in FIG. If the auxiliary line BF is drawn and it is derived that the isosceles triangle BAC and the triangle FAB are similar, then the quadratic equation can be formulated for the ratio of the lengths of the sides of the triangle, and by solving this equation The length x of the diagonal line AC is obtained.
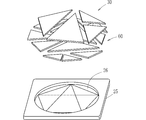
- FIG. 18 shows an example in which the number of triangular plates included in the graphic plate set is increased.
- the set 60 of triangular plates is composed of 12 triangular plates. These triangular plates are triangular plates (shaded portions) similar to the triangular plate 1 in FIG. 1, or triangular plates (dotted portions) similar to the triangular plate 2 in FIG.
- a polygonal regular decagon is formed rather than a regular pentagon. This makes it possible to expand the range of learning using the graphic board set.
- FIG. 19 shows an example in which the number of triangular plates included in the graphic plate set is further increased.
- the graphic board set shown in this figure includes both a triangular plate set 30 capable of forming a regular pentagon and a triangular plate set 60 capable of forming a regular decagon. According to this configuration, a set of triangular plates to be used can be selected as necessary, and the learning range can be expanded.
- the triangular plate set 30 and the triangular plate set 60 can be placed on the plate member 25 in a two-tiered manner. For this reason, as in the case of the configuration of FIG. 12, the graphic board set 10 can be organized in a collective state. For example, if a storage case is added, the graphic board set 10 can be easily carried.
- the concave portion 26 of the plate member 25 has been described as being circular. However, as described above, the present invention is not limited to this. If the recess 26 is a regular decagon, not only a regular decagonal combination plate but also a regular pentagonal combination plate can be placed along the inner peripheral wall surface of the recess 26.
- FIG. 20 is a plan view showing an example in which the concave portion 26 is a regular decagon, and corresponds to a configuration in which the concave portion 26 is a regular decagon in FIG. As shown in the figure, each vertex of the regular pentagon formed by the triangular plates 31 to 34 is in contact with the recess 26.
- the triangular plates 31 to 34 are placed on the concave portion 26 while the apexes of the triangular plates 31 to 34 are brought into contact with the inner peripheral wall surface of the regular decagonal concave portion 26 to complete a regular pentagon. It will be. Therefore, through this placement work, the user is aware of the correspondence between the regular decagon and the regular pentagon inscribed therein, and the learning effect is enhanced.
- the concave portion 26 is a regular decagon and is placed on a regular pentagonal combination plate, a gap is generated between the sides of the placed triangular plates 31 to 34 and the inner peripheral wall surface of the concave portion 26. .
- the clearance makes it easy to take out the placed triangular plates 31 to 34 and eliminates the need for a separate recess for taking out.
- a regular decagonal combination plate and a regular pentagonal combination plate can be stacked in two steps on the regular decagonal recess 26. That is, in the configuration of FIG.
- the triangular plate is fitted into the plate member 25, but a protractor, a straight plate, a compass, etc. are provided at a location different from the fitting location of the triangular plate. May be further fitted.
- the material of the triangular plate is not particularly limited, and is, for example, a resin material or a paper material.
- both the angle and the mark 20 are attached as the display regarding the angle, but a configuration in which one or both of these are not provided may be used. There is no need to display the angle. For example, if the guidance as described above is used in combination, learning that is conscious of the angle becomes possible.
Landscapes
- Engineering & Computer Science (AREA)
- General Physics & Mathematics (AREA)
- Physics & Mathematics (AREA)
- Business, Economics & Management (AREA)
- Theoretical Computer Science (AREA)
- Educational Technology (AREA)
- Educational Administration (AREA)
- Mathematical Analysis (AREA)
- Pure & Applied Mathematics (AREA)
- Mathematical Optimization (AREA)
- Computational Mathematics (AREA)
- Mathematical Physics (AREA)
- Algebra (AREA)
- Geometry (AREA)
- Multimedia (AREA)
- Entrepreneurship & Innovation (AREA)
- Instructional Devices (AREA)
Priority Applications (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| US14/656,715 US9443440B2 (en) | 2012-10-17 | 2015-03-13 | Figure plate set |
Applications Claiming Priority (2)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| JP2012-229989 | 2012-10-17 | ||
| JP2012229989A JP5614690B2 (ja) | 2012-10-17 | 2012-10-17 | 図形板セット |
Related Child Applications (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| US14/656,715 Continuation US9443440B2 (en) | 2012-10-17 | 2015-03-13 | Figure plate set |
Publications (1)
| Publication Number | Publication Date |
|---|---|
| WO2014061660A1 true WO2014061660A1 (ja) | 2014-04-24 |
Family
ID=50488221
Family Applications (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| PCT/JP2013/077967 Ceased WO2014061660A1 (ja) | 2012-10-17 | 2013-10-15 | 図形板セット |
Country Status (3)
| Country | Link |
|---|---|
| US (1) | US9443440B2 (enExample) |
| JP (1) | JP5614690B2 (enExample) |
| WO (1) | WO2014061660A1 (enExample) |
Cited By (1)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN104282199A (zh) * | 2014-10-17 | 2015-01-14 | 南丹县青少年学生校外活动中心 | 平移和旋转演示教具 |
Families Citing this family (4)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US20160303472A1 (en) * | 2014-01-28 | 2016-10-20 | Rebecca Klemm | Polygon puzzle and related methods |
| KR101641459B1 (ko) * | 2015-03-23 | 2016-07-20 | 차동식 | 십이교놀이 세트 |
| US20180286281A1 (en) * | 2017-03-31 | 2018-10-04 | Carl Abdullah Islam Muhammad | Universal mathematical scale A1. and A2. set |
| CN109147499A (zh) * | 2018-11-12 | 2019-01-04 | 扈少飞 | 几何拼接装置 |
Citations (3)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| JPH074660U (ja) * | 1993-06-13 | 1995-01-24 | 節 宇治 | 複数の正多角形が構成可能な四角形の形状 |
| JPH09285642A (ja) * | 1996-04-22 | 1997-11-04 | Kazuaki Tani | パズル |
| JP3149263U (ja) * | 2009-01-06 | 2009-03-19 | 晋 奥村 | 形態把握演習器 |
Family Cites Families (21)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US143835A (en) * | 1873-10-21 | Improvement in toy blocks for object-teaching | ||
| US342651A (en) * | 1886-05-25 | Means for teaching fractions | ||
| US1173298A (en) * | 1913-03-18 | 1916-02-29 | Maria Montessori | Cut-out geometrical figure for didactical purposes. |
| US1261710A (en) * | 1917-05-12 | 1918-04-02 | John Henry Coyle | Right-triangle puzzle. |
| US2611193A (en) * | 1949-07-05 | 1952-09-23 | Kenneth V Davis | Arithmetic fraction trainer |
| US2885207A (en) * | 1951-12-11 | 1959-05-05 | Wormser Arthur | Geometrical puzzle game |
| US3614835A (en) * | 1969-09-02 | 1971-10-26 | Macon D Rice | Educational toy construction kit |
| JPS4815175Y1 (enExample) | 1969-12-29 | 1973-04-26 | ||
| US3637217A (en) * | 1970-02-13 | 1972-01-25 | Sherman Kent | Puzzle with pieces in the form of subdivided rhombuses |
| JPS5534859U (enExample) | 1978-08-29 | 1980-03-06 | ||
| US4343471A (en) * | 1981-06-22 | 1982-08-10 | Calvert Murray B | Pentagonal puzzle |
| US4723382A (en) * | 1986-08-15 | 1988-02-09 | Haresh Lalvani | Building structures based on polygonal members and icosahedral |
| US4913436A (en) * | 1988-11-25 | 1990-04-03 | Li Shuo Yen R | Puzzles and game based on geometric shapes |
| US5281145A (en) * | 1989-10-02 | 1994-01-25 | Sidrak Fahim R | Pictorial image transforming manipulatives |
| US5215467A (en) * | 1992-01-27 | 1993-06-01 | Brischke Donald A | Mathematical instruction board and method of use |
| US5470234A (en) * | 1993-06-16 | 1995-11-28 | Sher; Louis Y. | Circular, piece-matching math educational aid |
| US5873729A (en) * | 1997-02-19 | 1999-02-23 | Aghevli; Behrouz B. | Mathematical triangle kit and method of use |
| US6145837A (en) * | 1998-08-28 | 2000-11-14 | A. Daigger And Company, Inc. | Three-dimensional geometric puzzle |
| US6575755B2 (en) * | 2000-04-13 | 2003-06-10 | Ricardo Dreyfous | Fraction circle |
| US20060076732A1 (en) * | 2004-10-13 | 2006-04-13 | Jean-Hwa Chiou | Multi-functional geometric puzzle system |
| US8834167B2 (en) * | 2010-07-06 | 2014-09-16 | Barbara Spotts | Manipulative for modeling quantitative concepts |
-
2012
- 2012-10-17 JP JP2012229989A patent/JP5614690B2/ja active Active
-
2013
- 2013-10-15 WO PCT/JP2013/077967 patent/WO2014061660A1/ja not_active Ceased
-
2015
- 2015-03-13 US US14/656,715 patent/US9443440B2/en active Active
Patent Citations (3)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| JPH074660U (ja) * | 1993-06-13 | 1995-01-24 | 節 宇治 | 複数の正多角形が構成可能な四角形の形状 |
| JPH09285642A (ja) * | 1996-04-22 | 1997-11-04 | Kazuaki Tani | パズル |
| JP3149263U (ja) * | 2009-01-06 | 2009-03-19 | 晋 奥村 | 形態把握演習器 |
Non-Patent Citations (2)
| Title |
|---|
| KEI SHINDO: "8. Daigaku Nyushi Mondai Kenkyu Seijikkakukei", KYOMU ESSAY (SANSU) -SANSUGAKU NYUMON, February 2011 (2011-02-01), Retrieved from the Internet <URL:http://www.nichinoken.co.jp/column/essay/sansu/2011_m02.html> [retrieved on 20140110] * |
| NOZOMU TANAKA: "Enshukaku to Chushinkaku", CHUGAKU KARA SUGAKU DAISUKI!, 12 April 2011 (2011-04-12), Retrieved from the Internet <URL:http://mtf.z-abc.com/?eid=1414480> [retrieved on 20140110] * |
Cited By (1)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN104282199A (zh) * | 2014-10-17 | 2015-01-14 | 南丹县青少年学生校外活动中心 | 平移和旋转演示教具 |
Also Published As
| Publication number | Publication date |
|---|---|
| US9443440B2 (en) | 2016-09-13 |
| US20150194061A1 (en) | 2015-07-09 |
| JP5614690B2 (ja) | 2014-10-29 |
| JP2014081530A (ja) | 2014-05-08 |
Similar Documents
| Publication | Publication Date | Title |
|---|---|---|
| JP5614690B2 (ja) | 図形板セット | |
| JP5565710B2 (ja) | 図形板セット | |
| US5732474A (en) | Visual aid and manipulative for demonstrating geometric and trigonmetric functions | |
| CN102737263B (zh) | 应用于编码的图案标志 | |
| CN202748987U (zh) | 一种带有投影功能的空间几何演示器 | |
| US11279167B2 (en) | Combinational template and scale ruler for drawing parallel 3-dimensions | |
| US6132217A (en) | Method and apparatus for teaching relationship of trigonometric functions between unit circle and rectangular coordinate system | |
| JP2014081530A5 (enExample) | ||
| US5215467A (en) | Mathematical instruction board and method of use | |
| JP5506881B2 (ja) | 図形板セット | |
| JP3153143U (ja) | 多角形描画用定規 | |
| JP6083095B2 (ja) | 図形板セット | |
| CN213958366U (zh) | 多功能几何图形教学用具 | |
| JP3222911U (ja) | マルチスケール製図補助具 | |
| Rathnam | A First Course in Engineering Drawing | |
| KR20110103156A (ko) | 수학 학습용 교구 | |
| KR20160003397U (ko) | 수학 교구 | |
| JP3208390U (ja) | 三角定規 | |
| AU2017101889A4 (en) | A space efficient template | |
| TWI597135B (zh) | 具有標示結構之指示型扭力扳手 | |
| CN202986540U (zh) | 一种数学课专用绘图工具 | |
| KR102840493B1 (ko) | 구면 디자인 학습 교구, 이의 이용 및 제조방법 | |
| CN204406797U (zh) | 一种二元函数及二重积分教学模具 | |
| JP3194689U (ja) | 知育用積木 | |
| JP2014070291A (ja) | パッチワーク用作業用具 |
Legal Events
| Date | Code | Title | Description |
|---|---|---|---|
| 121 | Ep: the epo has been informed by wipo that ep was designated in this application |
Ref document number: 13846694 Country of ref document: EP Kind code of ref document: A1 |
|
| NENP | Non-entry into the national phase |
Ref country code: DE |
|
| 122 | Ep: pct application non-entry in european phase |
Ref document number: 13846694 Country of ref document: EP Kind code of ref document: A1 |