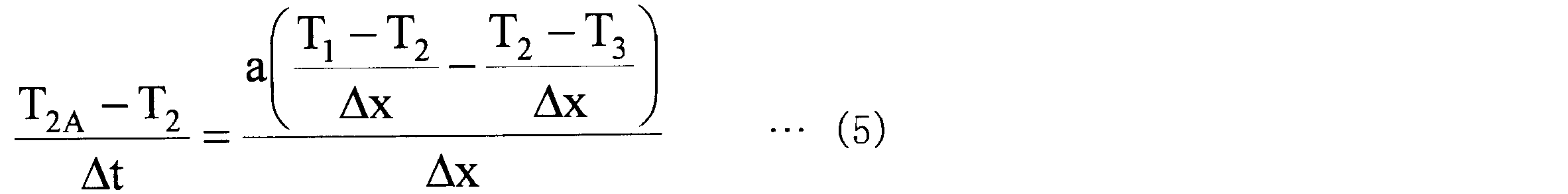JP6996440B2 - ダイスの温度計算方法及びダイスの温度計算システム - Google Patents

Description

本発明は、金属又は合金の押出技術、特に押出加工に用いられるダイスの温度分布の把握に関するものである。

金属又は合金の押出加工において高精度と高品質の押出を実現するには、押出の金型（ダイス）が押出形材におよぼす影響の特定が不可欠である。

ダイスの温度分布は、押出形材の精度、特に肉厚に影響を与えることが知られている。よって、ダイスの温度分布の把握が重要となる。従来より、有限要素法（ＦＥＭ：Finite Element Method）解析を行ってダイスの温度分布をシミュレートする方法が知られている（例えば、非特許文献１）。

林沛征著「アルミニウム合金押出形材の肉厚変動に関する検討」、アルトピア、日本国、カロス出版、２０１７年７月１５日発行、第４７巻、２０１７年７月号、ｐ．９－１６

しかしながら、ＦＥＭ解析は、高度な技術と専用の設備（ソフトウェア含む）を必要とするため、実施可能な環境が極めて限定されていた。このため、より容易にダイスの温度分布をシミュレート可能な方法等が求められていた。

本発明はかかる問題にかんがみてなされたものであり、より容易にダイスの温度分布をシミュレート可能なダイスの温度計算方法及びダイスの温度計算システムを提供することを目的とする。

本発明の態様に係るダイスの温度計算方法は、金属又は合金である押出対象の押出加工に用いられるダイスの温度分布をシミュレートするダイスの温度計算方法であって、前記ダイスにおける前記押出対象の押出方向を列方向とし、前記押出方向に直交する方向を行方向として、前記押出対象の押出口が配置される前記ダイスの中央部に対する行方向断面の仮想モデルを設定する工程と、前記仮想モデルにおいて、前記行方向及び前記列方向に複数の部分領域を含む２次元マトリクス状の分割モデルを設定する工程と、前記ダイスに対して前記押出方向に押し当てられる前記押出対象が存する第１箇所と、前記ダイスから押し出される前記押出対象が存する第２箇所と、前記第２箇所に対して前記押出方向側であって前記ダイスの内側の空間である第３箇所と、前記ダイスの前記押出方向側の端部側の空間である第４箇所と、前記第２箇所及び前記第３箇所の反対側に位置する前記ダイスの外周側の空間である第５箇所と、の温度を取得する工程と、前記第１箇所及び前記第２箇所における前記ダイスに対する入熱量と、前記第３箇所、前記第４箇所及び前記第５箇所における前記ダイスからの放熱量と、を算出する工程と、前記分割モデルに含まれる各部分領域の温度を算出する温度分布算出工程と、を含み、前記温度分布算出工程は、前記ダイスの内周側における前記第２箇所からの入熱量及び前記ダイスの内周側における前記第３箇所への放熱量と、前記ダイスの外周側から前記第５箇所への放熱量と、予め定められた各部分領域の初期温度とに基づいて、１行分に含まれる各部分領域の温度を算出する第１算出工程と、前記ダイスの一端側における前記第１箇所からの入熱量と、前記ダイスの他端側から前記第４箇所への放熱量と、予め定められた各部分領域の初期温度とに基づいて、１列分に含まれる各部分領域の温度を算出する第２算出工程と、を含み、前記第１算出工程と前記第２算出工程はそれぞれ複数回行われ、前記第１算出工程と前記第２算出工程は交互に行われ、２回目以降の前記第１算出工程では、温度を算出する１行分の各部分領域の温度のうち、それ以前の前記第２算出工程で算出された部分領域の温度を当該部分領域の前記初期温度とし、２回目以降の前記第２算出工程では、温度を算出する１列分の各部分領域の温度のうち、それ以前の前記第１算出工程で算出された部分領域の温度を当該部分領域の前記初期温度とすることを特徴とする。

本発明の一態様として、１回目の前記第１算出工程と１回目の前記第２算出工程のうち、後に行われる工程では、先に行われる工程で算出された部分領域の温度を当該部分領域の前記初期温度とすることが好ましい。

本発明の一態様として、所定時間が経過することが想定された前記所定時間前後の異なる２タイミングの各々における前記温度分布算出工程において、後のタイミングにおける各部分領域の前記初期温度は、前のタイミングの前記温度分布算出工程で算出された各部分領域の温度であることが好ましい。

本発明の態様に係るダイスの温度計算システムは、金属又は合金である押出対象の押出加工に用いられるダイスの温度情報を取得する温度情報取得装置と、金属又は合金である押出対象の押出加工に用いられるダイスの温度分布をシミュレートする情報処理装置とを備えるダイスの温度計算システムであって、前記温度情報取得装置は、前記ダイスに対して前記押出対象の押出方向に押し当てられる前記押出対象が存する第１箇所の温度情報を取得する第１温度情報取得部と、前記ダイスから押し出される前記押出対象が存する第２箇所の温度情報を取得する第２温度情報取得部と、前記第２箇所に対して前記押出方向側であって前記ダイスの内側の空間である第３箇所の温度情報を取得する第３温度情報取得部と、前記ダイスの前記押出方向側の端部側の空間である第４箇所の温度情報を取得する第４温度情報取得部と、前記第２箇所及び前記第３箇所の反対側に位置する前記ダイスの外周側の空間である第５箇所の温度情報を取得する第５温度情報取得部とを有し、前記情報処理装置は、前記ダイスにおける前記押出対象の押出方向を列方向とし、前記押出方向に直交する方向を行方向として、前記押出対象の押出口が配置される前記ダイスの中央部に対する行方向断面の仮想モデルを設定し、前記仮想モデルにおいて、前記行方向及び前記列方向に複数の部分領域を含む２次元マトリクス状の分割モデルを設定し、前記ダイスの内周側における前記第２箇所からの入熱量及び前記ダイスの内周側における前記第３箇所への放熱量と、前記ダイスの外周側から前記第５箇所への放熱量とを算出し、前記分割モデルに含まれる各部分領域の温度を算出する演算部を有し、前記演算部は、前記第２箇所及び前記第３箇所を含む前記ダイスの内周側からの入熱量及び放熱量と、前記第５箇所を含む前記ダイスの外周側からの放熱量と、予め定められた各部分領域の初期温度とに基づいて、１行分に含まれる各部分領域の温度を算出する第１算出工程と、前記第１箇所を含む前記ダイスの一端側からの入熱量と、前記第４箇所を含む前記ダイスの他端側からの放熱量と、予め定められた各部分領域の初期温度とに基づいて、１列分に含まれる各部分領域の温度を算出する第２算出工程と、をそれぞれ複数回行い、前記第１算出工程と前記第２算出工程を交互に行い、２回目以降の前記第１算出工程では、温度を算出する１行分の各部分領域の温度のうち、それ以前の前記第２算出工程で算出された部分領域の温度を当該部分領域の前記初期温度とし、２回目以降の前記第２算出工程では、温度を算出する１列分の各部分領域の温度のうち、それ以前の前記第１算出工程で算出された部分領域の温度を当該部分領域の前記初期温度とすることを特徴とすることを特徴とする。

本発明に係る態様によれば、より容易にダイスの温度分布をシミュレートすることができる。

図１は、実施形態に係る温度計算システムの主要構成を示すブロック図である。 図２は、押出装置による金属又は合金の直接押出加工のイメージ図を示す。 図３は、広幅チャンネル形状形材のダイスとその温度測定点（Ｐ１～Ｐ４）を示す図である。 図４は、図３に示す温度測定点に対する温度センサの進入方法を説明するためのダイスの概略断面図である。 図５は、ビレット３本連続押出の各測定点の温度履歴の測定結果とＦＥＭ解析結果を示す図である。 図６は、ビレット１０本連続押出における押出先端材と後端材のＡ，Ｂ，Ｃ部の肉厚測定値を示す図である。 図７は、２次元の熱伝導の模式図を示す図である。 図８は、１次元の外部熱と固体の非定常熱伝導の図式解法を示す図である。 図９は、フーリエ理論式と差分法によるダイスの熱伝導計算のモデルを示す図である。 図１０は、１次元の場合における入熱と放熱に基づいた差分法の計算モデルを示す図である。 図１１は、Ｆ１とＦ４の境界条件である熱伝達係数と雰囲気温度および熱伝達を熱伝導に直した場合の相当距離を示す表図である。 図１２は、ＦＥＭ解析モデルを示す図である。 図１３は、３００秒経過後のＦＥＭ解析結果の温度分布図を示す図である。 図１４は、に３００秒経過後の差分法計算結果とＦＥＭ解析結果の比較を示す図である。 図１５は、図９の５つの境界条件である熱伝達係数と雰囲気温度、熱伝達を熱伝導に直した場合の相当距離を示す表図である。 図１６は、３００秒経過後のＦＥＭ解析結果の温度分布図を示す図である。 図１７は、ＦＥＭ解析結果の各行要素のＸ方向の温度分布を示す。 図１８は、３００秒経過後の差分法による各行要素のＸ方向の温度分布の結果を示す図である。 図１９は、１行要素と５行要素の差分法計算結果とＦＥＭ解析結果の比較を示す図である。 図２０は、考案した左右、上下の伝熱の計算方法を示す図である。 図２１は、考案した左右、上下の伝熱の計算方法を示す図である。 図２２は、考案した左右、上下の伝熱の計算方法を示す図である。 図２３は、考案した左右、上下の伝熱の計算方法を示す図である。 図２４は、考案した差分法計算方法による各行要素のＸ方向の温度分布を示す図である。 図２５は、考案した差分法の１行要素と５行要素の計算結果とＦＥＭ解析結果の比較を示す図である。 図２６は、差分法計算による押出加工中のダイスのベアリング付近要素Ｅ１１と外周側要素Ｅ１５の経過時間と温度履歴の関係を示す図である。

以下、本発明に係る実施形態について図面を参照しながら説明するが、本発明はこれに限定されない。以下で説明する実施形態の構成要素は、適宜組み合わせることができる。また、一部の構成要素を用いない場合もある。また、以下で説明する実施形態における構成要素には、当業者が容易に想定できるもの、実質的に同一のもの、いわゆる均等の範囲のものが含まれる。

図１は、実施形態に係る温度計算システム１の主要構成を示すブロック図である。温度計算システム１は、温度情報取得装置６０と、情報処理装置７０と、を含む。温度情報取得装置６０は、押出装置１００の各所の温度情報を取得する。温度情報取得装置６０は、第１温度情報取得部６１、第２温度情報取得部６２、第３温度情報取得部６３、第４温度情報取得部６４及び第５温度情報取得部６５を含む。

図２に押出装置１００による金属又は合金の直接押出加工のイメージを示す。なお、図２に示すイメージは、外周形状が円筒状のダイス２を、当該円筒の中心軸に沿って切断した場合の断面のイメージである。図２では、ビレット３を押出加工中の押出装置１００を図示している。ダイス２は、金属又は合金の押出加工に用いられる金型である。ビレット３は、ダイス２を用いて加工される押出形材３ａのもとになる金属又は合金であり、例えばアルミニウム又はアルミニウムを含む合金である。ステム４は、ビレット３をダイス２に押し付ける。ダミブロック５は、ビレット３とステム４との間に設けられる。コンテナ６は、ダイス２に押し付けられるビレット３を、ビレット３の外周側から支持する。コンテナ６の内側の空間の形状及び大きさは、ビレット３、ステム４及びダミブロックの形状及び大きさに対応する。

第１温度情報取得部６１は、第１ポイントＦＰ１の温度を検知する。第２温度情報取得部６２は、第２ポイントＦＰ２の温度を検知する。第３温度情報取得部６３は、第３ポイントＦＰ３の温度を検知する。第４温度情報取得部６４は、第４ポイントＦＰ４の温度を検知する。第５温度情報取得部６５は、第５ポイントＦＰ５の温度を検知する。

第１温度情報取得部６１、第２温度情報取得部６２、第３温度情報取得部６３、第４温度情報取得部６４及び第５温度情報取得部６５は、少なくとも１００［℃］～５５０［℃］の範囲内の温度を検知可能な温度センサである。第１温度情報取得部６１、第２温度情報取得部６２、第３温度情報取得部６３、第４温度情報取得部６４及び第５温度情報取得部６５の具体的構成例として、熱電対を用いた温度センサが挙げられるが、これに限られるものでなく、機能的に上述の要件を満たす温度センサであればよい。

第１ポイントＦＰ１は、ダイス２に対して押出方向に押し当てられる押出対象が存する第１箇所に相当する。第２ポイントＦＰ２は、ダイス２から押し出される押出対象が存する第２箇所に相当する。第３ポイントＦＰ３は、第２箇所に対して押出方向側であってダイス２の内側の空間である第３箇所に相当する。第４ポイントＦＰ４は、ダイス２の押出方向側の端部側の空間である第４箇所に相当する。第５ポイントＦＰ５は、第２部分及び第３部分の反対側に位置するダイス２の外周側の空間である第５箇所に相当する。言い換えれば、第２ポイントＦＰ２及び第３ポイントＦＰ３は、押出対象である押出形材３ａと対向するダイス２の内周側に位置する。

第１ポイントＦＰ１の温度は、ダイスチャンバー内のメタル加工熱からの入熱Ｆ０の算出に用いられる。第２ポイントＦＰ２の温度は、ダイス２のベアリングのメタル摩擦熱からの入熱Ｆ１の算出に用いられる。第３ポイントＦＰ３の温度は、ダイス逃げ部の空気との界面からの放熱Ｆ２の算出に用いられる。第４ポイントＦＰ４の温度は、ダイス後部の工具系との接触からの放熱Ｆ３の算出に用いられる。第５ポイントＦＰ５の温度は、ダイスタックとの接触からの放熱Ｆ４の算出に用いられる。入熱Ｆ０、入熱Ｆ１、放熱Ｆ２、放熱Ｆ３及び放熱Ｆ４については後述する。

情報処理装置７０は、演算部７１、記憶部７２、入力部７３、出力部７４、インタフェース７５等を備える。演算部７１は、ＣＰＵ（Central Processing Unit）等の演算装置を有し、記憶部７２から処理内容に応じたソフトウェア・プログラム及びデータを読み出して実行処理することで、情報処理装置７０が実現する各種の機能に対応する演算処理を行う。記憶部７２は、主記憶装置及び補助記憶装置を有し、演算部７１により読み出されるソフトウェア・プログラム及びデータを記憶する。主記憶装置の具体的構成例として、ＲＡＭ（Random Access Memory）として機能する半導体メモリが挙げられる。補助記憶装置の具体的構成例として、ＨＤＤ（Hard Disk Drive）、ＳＳＤ（Solid State Drive）、フラッシュメモリー、ＲＯＭ（Read Only Memory）等が挙げられる。

入力部７３は、キーボード、マウス、マイクその他の入力装置を１つ以上含み、情報処理装置７０を操作するユーザからの入力を受け付ける。出力部７４は、液晶ディスプレイ等の表示装置、スピーカ等の音声出力装置のうち少なくとも１つを含み、情報処理装置７０の処理内容に応じた出力を行う。インタフェース７５は、情報処理装置７０に対して温度情報取得装置６０を接続可能にするインタフェースである。インタフェース７５は、例えば、ＵＳＢ（Universal Serial Bus）等のバスインタフェースであるが、温度情報取得装置６０の出力インタフェースに対応したインタフェースであればよい。言い換えれば、温度情報取得装置６０の出力インタフェースとインタフェース７５との関係は、相互接続及びデータ伝送可能なインタフェースの関係になるよう設けられる。

なお、実施形態で温度情報取得装置６０からインタフェース７５に入力されるデータは、デジタルデータである。第１温度情報取得部６１、第２温度情報取得部６２、第３温度情報取得部６３、第４温度情報取得部６４及び第５温度情報取得部６５がデジタルデータを出力可能なセンサであってもよいし、第１温度情報取得部６１、第２温度情報取得部６２、第３温度情報取得部６３、第４温度情報取得部６４及び第５温度情報取得部６５から出力されるアナログの温度情報を温度情報取得装置６０に設けられたアナログ／デジタル変換回路でデジタルデータ化して出力する構成であってもよい。

実施形態の記憶部７２は、シミュレート用プログラム７２Ｐを記憶する。シミュレート用プログラム７２Ｐは、例えば表計算ソフトウェア・プログラムと、当該ソフトウェア・プログラムで利用可能な表計算データとを含む。当該表計算データは、当該表計算ソフトウェア・プログラムを実行中の演算部７１が後述するダイス２の温度計算方法を実行処理するためのアルゴリズムに則った計算式及びデータを含む。

以下、ダイス２の温度計算方法及び当該温度計算方法に関連する事項について、図２から図２６を参照して説明する。

押出加工プロセスにおいては、ダイス２の温度分布の変化が直にダイス開口部寸法、形材の肉厚に影響を及ぼすため、検討が重要となる。本稿では、フーリエの理論式と差分法計算によるダイス２の非定常熱伝導解析、ダイス温度分布の計算方法を紹介する。２次元の熱伝導解析には、２方向からの熱伝導の影響が考慮されることによって、計算精度が高い差分法計算方法が開発された。

（１．はじめに）
近年、車両軽量化による燃費向上のため、アルミニウム押出形材は、自動車、車両などの分野への適用が広がりつつある。これにともない、押出形材３ａに求められる要求性能、精度、品質も年々高度化している。高精度と高品質の押出を実現するには、形材形状寸法と肉厚におよぼす影響因子の究明・対策が不可欠である。

押出形材３ａの精度、特に肉厚の変動は、押出加工中の力の変化、ダイス２と工具系の温度変化によるものが多い。押出加工プロセスにおいて、ダイス２の温度分布の変化は、直にダイス開口部（形材の肉厚）に影響を及ぼす。よって、ダイス２の温度分布の検討が重要となる。

本稿では、フーリエの理論式と差分法計算による押出加工プロセスのダイス２の非定常熱伝導解析およびダイス温度分布の計算方法を紹介する。

（２．押出加工の肉厚変動問題）
押出中、力の因子であるコンテナシール力７（図２参照）、ダイス２内のメタル圧力８（図２参照）、および熱的因子であるダイス２内の温度分布は時間とともに変化する。

例として、広幅チャンネル形状形材のダイス２の温度変化と肉厚変動結果を説明する。

図３及び図４に広幅チャンネル形状形材のダイス２とその温度測定点（Ｐ１～Ｐ４）を示す。図５にビレット３本連続押出の各測定点の温度履歴の測定結果とＦＥＭ解析結果を示す。図５に示すように、押出中、塑性加工の発熱により、ダイス２のベアリング付近部のＰ３とＰ４の温度は高くなる。一方、ダイスタックへの伝熱などにより、ダイス２の外周のＰ１とＰ２の温度は低くなる。押出先端から押出後端にかけて、ベアリング付近部と外周部の温度差が広がっている。さらに、押出ビレット本数が増えるにつれて、その温度差が大きくなる。

なお、図４は、図３に示す温度測定点Ｐ１，Ｐ３に対する温度センサの進入方法を説明するためのダイス２の概略断面図である。また、図４におけるｉ１は、８［ｍｍ］である。また、図４におけるｉ２は、１０［ｍｍ］である。図４では、温度測定点Ｐ１，Ｐ３の温度を測定するため、ダイス２に穴Ｈ１，Ｈ２を設けて温度センサを進入させている。図示しないが、温度測定点Ｐ２，Ｐ４の温度測定の仕組みも温度測定点Ｐ１，Ｐ３と同様である。また、第１温度情報取得部６１を用いた第１ポイントＦＰ１の温度測定及び第２温度情報取得部６２を用いた第２ポイントＦＰ２の温度測定においても、温度測定点Ｐ１，Ｐ３の温度測定のためにダイス２に穴をあけているのと同様、ダイス２及びビレット３の少なくとも一方に穴をあけて温度センサを進入させる。

図６にビレット１０本連続押出における押出先端材と後端材のＡ，Ｂ，Ｃ部の肉厚測定値を示す。各押出ビレットの先端材から後端材にかけて、肉厚が薄くなる傾向にある。ビレット間においても、押出本数が増えるにつれて、肉厚が薄くなっていく。このように、押出先後端、ビレット間の肉厚変動は、負荷とダイス２内の温度変化によるものと考えられる。

（３．フーリエ理論式と差分法の計算）
前述のように、押出加工中に、時間とともに変化するダイス２の温度は、ダイス２の開口に影響を及ぼし、形材肉厚変動の原因となる。定量的にダイス２内部の温度分布と温度変化を検討するため、ここでは、フーリエ理論式と差分法による計算を試みた。

図７に２次元の熱伝導の模式図を示す。時間ｄｔの間に、Ｘ方向の左から右への熱伝導とＹ方向の上から下への熱伝導による直方体内部に蓄えられた熱量ｄＱ_１の方程式を式（１）のように書ける。

ここで、Ｔは温度、λは熱伝導率である。

なお、温度（Ｔ）は、測定又は設定により定められる。熱伝導率（λ）は、例えばダイス２の組成により決定される定数である。また、∂は、偏微分を表す符号である。また、Ｘ方向は、行方向に相当する。また、Ｙ方向は、列方向に相当する。

一方、時間ｄｔの間に、内部温度変化に必要な熱量ｄＱ_２は式（２）となる。ここで、Ｃは比熱、ρは密度である。

なお、比熱（Ｃ）及び密度（ρ）は、例えばダイス２の組成により決定される定数である。

式（１）と式（２）から、熱伝導による内部温度変化は式（３）となる。

ここで、ａ＝λ／Cρとすると、式（３）は式（４）となる。

式（４）はフーリエの微分式である。この２重偏微分方程式を解くには、差分法が有効な手法である。

図８に１次元の外部熱と固体の非定常熱伝導の図式解法を示す。ここで、非定常熱伝導の図式解法と差分法計算を説明する。

まず、固体内部の熱伝導計算については、内部のある時間ｔの温度計算点（Ｔ_１，Ｔ_２，Ｔ_３・・・）を等間隔Δｘで分割する。図８に示すように、時間ｔの温度Ｔ_２が時間Δｘを経過した後、Ｔ_１，Ｔ_３との熱伝導により、Ｔ_２Ａとなる。その温度変化の差分法の計算は式（５）となる。

従って、時間ｔ＋Δｔの温度Ｔ_２Ａと時間ｔの温度Ｔ_１，Ｔ_２，Ｔ_３の関係は式（６）となる。ここで、Ｍ＝（Δｘ）^２／ａΔｔ とする。

次に、外部熱から固体への熱伝達計算を説明する。外部熱から固体への熱伝達計算を熱伝導計算に直して検討する。この時、熱伝導計算は熱伝達係数と熱伝導率から算出される相当距離を用いて、計算する。

図８に示すように外部熱の温度をＴ_ｆ、外部熱と固体表面の熱伝達係数をα、固体表面の初期温度をＴ_０、固体の熱伝導率をλとする。

熱伝達により、外部熱から固体表面への熱流束ｑの計算式は式（７）となる。

一方、熱伝導と考えた場合、外部熱から固体表面への熱流束ｑの計算式は式（８）となる。

式（７）と式（８）から、式（９）の等式を書ける。

式（９）により、外部熱から固体表面への熱伝達を熱伝導に直した場合、外部熱と固体表面の相当距離ｄｘは、熱伝達係数と熱伝導率から、式（１０）で求められる。

差分法を利用して外部からの熱伝達を計算するときに、図８に示すように、外部に固体表面から相当距離λ／αの位置に外部雰囲気温度点Ｔ_ｆ、固体表面からΔｘ／２位置にＴ_－１点を設ける必要がある。Ｔ_－１の値は、固体表面点Ｔ_０と外部点Ｔ_ｆのｘ座標の線形関係から計算できる。Ｔ_－１の値が求めれば、ｔ＋Δｔ時間のＴ_１Ａは式（６）のように、ｔ時間のＴ_－１，Ｔ_１，Ｔ_２から計算できる。Ｔ_１Ａが決まれば、Ｔ_１ＡとＴ_－１の線形関係から、表面Ｔ_０Ａ（Ｔ_０のｔ＋Δｔ時間の温度）が計算できる。

このように、設定された時間ステップで、固体内部の各計算点の温度が計算される。また、各計算点の温度結果を次の時間ステップの伝熱計算の初期温度として定義し、温度変化を計算する。時間ステップの繰り返し計算により、外部熱と固体、固体内部の非定常伝熱解析を行う。繰り返し計算は表計算ソフトウェア・プログラムを利用した演算部７１による演算等で実施可能である。

なお、ダイス２の外部の雰囲気温度（Ｔ_ｆ）は、第１温度情報取得部６１、第２温度情報取得部６２、第３温度情報取得部６３、第４温度情報取得部６４又は第５温度情報取得部６５によって取得される。初期のダイス２の表面の温度（Ｔ_０）は、予め定められたダイス２の初期温度（例えば、４５０［℃］）である。ダイス２は、押出加工の開始前に初期温度になるよう加熱される。

（４．押出加工中のダイスの熱伝導計算）
（４．１ ダイスの熱伝導計算）
図９にフーリエ理論式と差分法によるダイス２の熱伝導計算のモデルを示す。押出加工中のダイス２の入熱と放熱は、ダイスチャンバー内のメタル加工熱からの入熱Ｆ０、ダイス２のベアリングのメタル摩擦熱からの入熱Ｆ１、ダイス逃げ部の空気との界面からの放熱Ｆ２、ダイス後部の工具系との接触からの放熱Ｆ３、ダイスタックとの接触からの放熱Ｆ４と定義する。

以下、単にＦ０と記載した場合、入熱Ｆ０をさす。また、単にＦ１と記載した場合、入熱Ｆ１をさす。また、単にＦ２と記載した場合、放熱Ｆ２をさす。また、単にＦ３と記載した場合、放熱Ｆ３をさす。また、単にＦ４と記載した場合、放熱Ｆ４をさす。

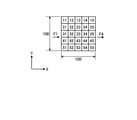
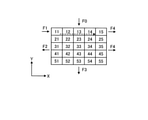
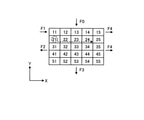
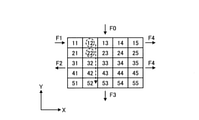
図９では、ダイスの仮想モデルとして、行列方向（Ｘ方向×Ｙ方向）に５×５の部分領域が設定された分割モデルを例示している。図９及び後述する図２０、図２１、図２２及び図２３等に示すダイスの仮想モデルは、例えば図２に示すダイス２の断面２Ｖの仮想モデルである。また、各部分領域を区別する目的で、それぞれ異なる番号（１１～１５，２１～２５，３１～３５，４１～４５，５１～５５）を付している。この番号の１０の位がＸ方向の位置を示し、１の位がＹ方向の位置を示す。

図９及び後述する図２０、図２１、図２２及び図２３等に示す入熱Ｆ０は、Ｙ方向の一端に配置された部分領域に「１１」、「１２」、「１３」、「１４」、「１５」が付されている５列分の部分領域に対する入熱として機能する。図９に示す放熱Ｆ３は、Ｙ方向の一端に配置された部分領域に「５１」、「５２」、「５３」、「５４」、「５５」が付されている５列分の部分領域からの放熱として機能する。図９に示す入熱Ｆ１は、Ｘ方向の一端に配置された部分領域に「１１」が付されている１行分の部分領域に対する入熱として機能する。図９に示す放熱Ｆ２は、Ｘ方向の一端に配置された部分領域に「２１」、「３１」、「４１」、「５１」が付された１行分の部分領域からの放熱として機能する。図９に示す放熱Ｆ４は、Ｘ方向の他端に配置された部分領域に「１５」、「２５」、「３５」、「４５」、「５５」が付されている１行分の部分領域からの放熱として機能する。

また、入熱Ｆ０は、第１箇所におけるダイス２への入熱に相当する。また、入熱Ｆ１は、第２箇所におけるダイス２への入熱に相当する。また、放熱Ｆ２は、第３箇所におけるダイス２からの放熱に相当する。また、放熱Ｆ３は、第４箇所におけるダイス２からの放熱に相当する。また、放熱Ｆ４は、第５箇所におけるダイス２からの放熱に相当する。

例示する解析モデルは５行×５列に分けられて、計２５要素である。

（４．２ １次元の左右方向の熱伝導計算）
まず、図１０に示す１次元の場合、左からのＦ１の入熱と右へのＦ４の放熱の計算を検討する。モデルの形状は正方形の１００×１００ｍｍである。

ダイス２の初期温度は４５０℃、熱伝導率は３０Ｗ／（ｍ・℃）、比熱は４６０Ｊ／（ｋｇ・℃）、密度は７８００ｋｇ／ｍ^３である。モデルは平面モデルである。

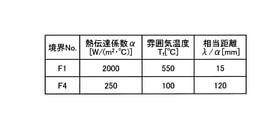
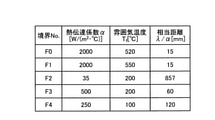
Ｆ１とＦ４の境界条件である熱伝達係数と雰囲気温度および熱伝達を熱伝導に直した場合の相当距離を図１１に示す。計算時間は３００ｓである。差分法の計算時間間隔を６ｓとし、計算ステップは５０である。

なお、３００ｓは、３００秒（ｓ：second）をさす。６ｓは、６秒（ｓ）をさす。

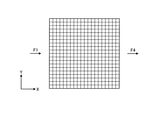
差分法の計算精度を検討するため、非定常伝熱のＦＥＭ解析を行った。非定常伝熱のＦＥＭ解析は汎用ＦＥＭ解析ソフトＡｎｓｙｓ１８.０（登録商標）を用いた。図１２にＦＥＭ解析モデルを示す。要素は分割サイズが５ｍｍで、計４００個である。

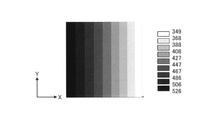
図１３に３００ｓ経過後のＦＥＭ解析結果の温度分布図を示す。左から右に向かって、温度が低くなる。図１４に３００ｓ経過後の差分法計算結果とＦＥＭ解析結果の比較を示す。両者は一致していることが分かる。従って、１次元の場合、左右からの２つの熱境界条件の伝熱解析において、差分法の計算精度が高いことが分かる。

［４．３ ２次元の左右、上下方向の熱伝導解析］
図９に示すようにダイス２の熱伝導は左右、上下方向である。ここで、同様に正方形の１００×１００ｍｍのモデルを用いて、図９の５つの境界条件の伝熱解析を検討する。ベアリング部の長さは２０ｍｍとする。

図９の５つの境界条件である熱伝達係数と雰囲気温度、熱伝達を熱伝導に直した場合の相当距離を図１５に示す。計算時間は３００ｓである。差分法の計算時間間隔を６ｓとし、計算ステップは５０である。同様に、差分法の計算精度を検討するため、非定常伝熱のＦＥＭ解析を行った。

図１５に示す雰囲気温度（Ｔ_ｆ）は、温度情報取得装置６０により取得される温度である。境界Ｎｏ．「Ｆ０」の雰囲気温度（Ｔ_ｆ＝５２０［℃］）は、第１温度情報取得部６１により取得される。境界Ｎｏ．「Ｆ１」の雰囲気温度（Ｔ_ｆ＝５５０［℃］）は、第２温度情報取得部６２により取得される。境界Ｎｏ．「Ｆ２」の雰囲気温度（Ｔ_ｆ＝２００［℃］）は、第３温度情報取得部６３により取得される。境界Ｎｏ．「Ｆ３」の雰囲気温度（Ｔ_ｆ＝２００［℃］）は、第４温度情報取得部６４により取得される。境界Ｎｏ．「Ｆ４」の雰囲気温度（Ｔ_ｆ＝１００［℃］）は、第５温度情報取得部６５により取得される。すなわち、実施形態における入熱Ｆ０は、第１箇所で検知された温度により生じるダイス２に対する熱伝導である。また、入熱Ｆ１は、第２箇所で検知された温度により生じるダイス２に対する熱伝導である。また、放熱Ｆ２は、第３箇所で検知された温度により生じるダイス２に対する熱伝導である。また、放熱Ｆ３は、第４箇所で検知された温度により生じるダイス２に対する熱伝導である。また、放熱Ｆ４は、第５箇所で検知された温度により生じるダイス２に対する熱伝導である。

図１６に３００ｓ経過後のＦＥＭ解析結果の温度分布図を示す。図１７にＦＥＭ解析結果の各行要素のＸ方向の温度分布を示す。チャンバー内のメタルのＦ０とベアリング部のＦ１からの入熱により、ベアリング付近の温度が高くなる。一方、ダイス２外周のＦ４、逃げ部のＦ２とバックダイ部のＦ３の放熱により、ダイス２の内部から外部へ向かって、ダイス２の上面から下面に向かって、温度が低下する。

図１８に３００ｓ経過後の差分法による各行要素のＸ方向の温度分布の結果を示す。２次元の差分法による各時間ステップの温度計算値は、Ｘ方向とＹ方向の温度計算結果の重ね合わせの値である。

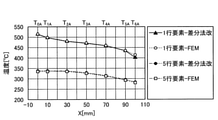
図１８の差分法による各行要素の温度計算結果と図１７のＦＥＭ解析結果を比較すると、両者に差があることが分かる。図１９に１行要素と５行要素の差分法計算結果とＦＥＭ解析結果の比較を示す。図１９から、１行の右側要素の差分法計算結果はＦＥＭ解析結果より約３６℃低い。一方、５行の右側要素の差分法計算結果はＦＥＭ解析結果より全体的に約２５℃高い。このように、２次元の場合、単純にＸ，Ｙ方向の温度計算結果を重ね合わせただけでは、精度が良くないことが分かる。

前述の差分法計算結果とＦＥＭ解析結果の不一致の原因は、計算の初期温度の設定によるものと考えられ、ここで、差分法の計算方法を再考案した。本実施形態の方法は、この再考案された差分法の計算方法による。

図２０から図２３に考案した左右、上下の伝熱の計算方法を示す。時間ステップのダイス温度を計算する際、まず、第１ステップは、図２０に示すように１行目の要素１１と要素１５の間に境界条件Ｆ１とＦ４による熱伝導を計算する。次に、第２ステップは、図２１の１列目の要素１１と要素５１の間に境界条件Ｆ０とＦ３による熱伝導を計算する。その際、要素１１の初期温度値を第１ステップでの計算後の温度値とする。その後、図２２の第３ステップの２行目要素の熱伝導を計算する際、要素２１の初期温度値を第２ステップでの１列目計算後の温度値とする。その後、図２３の第４ステップの２列目要素の熱伝導を計算する際、要素１２と２２の初期温度値をそれぞれ第１ステップと第３ステップでの計算後の温度値とする。同じように、３行～５行要素、３列～５列要素の熱伝導を計算する際は、上記の方法で、前の行と列で計算した値を初期温度と定義し、計算する。この計算方法とすれば、Ｘ，Ｙ方向の熱伝導の温度変化の影響が考慮され、計算精度の向上につながると考えられる。

なお、「１行目の要素１１と要素１５の間に境界条件Ｆ１とＦ４による熱伝導」とは、「ダイスのベアリングのメタル摩擦熱からの入熱Ｆ１と、ダイスタックとの接触からの放熱Ｆ４との影響によって、ダイスの仮想モデルに設定された１行目の部分領域（要素１１、要素１２、要素１３、要素１４、要素１５）に生じる熱伝導」をさす。また、「１列目の要素１１と要素５１の間に境界条件Ｆ０とＦ３による熱伝導」とは、「ダイスチャンバー内のメタル加工熱からの入熱Ｆ０と、ダイス後部の工具系との接触からの放熱Ｆ３との影響によって、ダイスの仮想モデルに設定された１列目の部分領域（要素１１、要素２１、要素３１、要素４１、要素５１）に生じる熱伝導」をさす。

例えば、図１５に示す相当距離（λ／α［ｍｍ］）を図８に示す「λ／α」にあてはめる。図１５に示す雰囲気温度（Ｔ_ｆ［℃］）を図８に示す「Ｔ_ｆ」にあてはめる。なお、熱伝達係数α［（Ｗ／ｍ２・℃）］は、相当距離（λ／α［ｍｍ］）を導出するために用いられている。熱伝達係数α［（Ｗ／ｍ２・℃）］及び相当距離（λ／α［ｍｍ］）の少なくとも一方は、押出装置１００の具体的構成、押出装置１００が置かれる環境等の条件に応じて導出される既定の値として与えられる。

なお、ダイスの仮想モデルが正方形の１００×１００ｍｍのモデルである場合、図８に示すΔｘは、２０ｍｍである。Δｘ／２は、１０ｍｍである。すなわち、Δｘは、仮想モデルのＸ方向（又はＹ方向）の寸法の１／５である。

具体例として、図２０において「１１」、「１２」、「１３」、「１４」、「１５」が付されている部分領域がＸ方向に並ぶ１行分の部分領域における初期温度及び算出される温度について説明する。境界Ｎｏ．「Ｆ１」の雰囲気温度Ｔ_ｆが「５５０」であるため、図８のＴ_ｆに「５５０」が代入される。また、図８のＴ_０の初期値は、上述の通り、ダイス２の初期温度（例えば、４５０［℃］）である。従って、ここではＴ_０に「４５０」が代入される。また、図８の「λ／α」に境界Ｎｏ．「Ｆ１」の相当距離λ／αの「１５」が代入される。また、ダイスの仮想モデルが正方形の１００×１００ｍｍのモデルであるので、「Δｘ／２」に、「１０」が代入される。これらの値が代入されたＴ_ｆ，Ｔ_０，λ／α，Δｘ／２によって、演算部７１は、図１５の「Ｆ１」に対応するＴ_－１を算出する。このＴ_－１が、「１１」、「１２」、「１３」、「１４」、「１５」が付されている部分領域がＸ方向に並ぶ１行分の部分領域における、「１１」側からの入熱Ｆ１に相当する。

図８のＴ_１，Ｔ_２，Ｔ_３はそれぞれ、図２０において「１１」、「１２」、「１３」が付されている部分領域の初期温度である。この初期温度は、ダイス２の初期温度である。この具体例では、Ｔ_１，Ｔ_２，Ｔ_３にはそれぞれ「４５０」が代入される。図示しないが、実際には、「１４」、「１５」が付されている部分領域の初期温度として、Ｔ_４，Ｔ_５が設定されている。この具体例では、Ｔ_４，Ｔ_５にも「４５０」が代入される。

さらに、図８では図示しないが、「１５」側からの放熱Ｆ４に相当するＴ_７が設定される。Ｔ_７は、上述の入熱Ｆ１に相当するＴ_－１の算出と同様の仕組みで算出される。すなわち、境界Ｎｏ．「Ｆ４」の雰囲気温度Ｔ_ｆが「１００」であるため、図８のＴ_ｆに「１００」が代入される。また、図８のＴ_０の初期値は、上述の通り、ダイス２の初期温度（例えば、４５０［℃］）である。従って、ここではＴ_０に「４５０」が代入される。また、図８の「λ／α」に境界Ｎｏ．「Ｆ４」の相当距離λ／αの「１２０」が代入される。また、ダイスの仮想モデルが正方形の１００×１００ｍｍのモデルであるので、「Δｘ／２」に、「１０」が代入される。これらの値が代入されたＴ_ｆ，Ｔ_０，λ／α，Δｘ／２によって、演算部７１は、図１５の「Ｆ４」に対応するＴ_－１を算出する。この「Ｆ４」に対応するＴ_－１が、Ｔ_７として扱われる。また、Ｔ_５とＴ_７との間のＴ_６の初期値は、Ｔ_０の初期値と同一である。

このようにして定められたＴ_－１，Ｔ_０，Ｔ_１，Ｔ_２，Ｔ_３，Ｔ_４，Ｔ_５，Ｔ_６，Ｔ_７と、上述の式（６）に基づいて、Ｔ_－１Ａ，Ｔ_０Ａ，Ｔ_１Ａ，Ｔ_２Ａ，Ｔ_３Ａ，Ｔ_４Ａ，Ｔ_５Ａ，Ｔ_６Ａ及びＴ_７Ａが算出される。なお、実施形態では、図１５のＴ_ｆは一定であるものとする。なお、式（６）でＴ２Ａの算出に用いられる３つの値を（Ｔ_１，Ｔ_２，Ｔ_３）と表すことができるとする。この場合、Ｔ_１Ａの算出に用いられる３つの値は、（Ｔ_－１，Ｔ_１，Ｔ_２）であり、Ｔ_０を含まない。Ｔ_０Ａは、Ｔ_１ＡとＴ_－１の線性関係に基づいて求められる。また、Ｔ_－１Ａは、Ｔ_－１の算出に用いられるＴ_ｆとＴ_０Ａとを結ぶ線分の傾き（Ｔ_ｆとＴ_０Ａとの差）と、λ／αとΔｘ／２との比に基づいて求められる。Ｔ_ｆは、「Ｆ１」の雰囲気温度Ｔ_ｆである。

以上、説明した最初の演算（最初の第１算出工程）で、演算部７１は、図２０において「１１」、「１２」、「１３」、「１４」、「１５」が付されている部分領域がＸ方向に並ぶ１行分の部分領域に対応するＴ_－１Ａ，Ｔ_０Ａ，Ｔ_１Ａ，Ｔ_２Ａ，Ｔ_３Ａ，Ｔ_４Ａ，Ｔ_５Ａ，Ｔ_６Ａ及びＴ_７Ａを算出する。ここで、Ｔ_１Ａが「１１」の部分領域のｔ［ｓ］経過後の温度である。Ｔ_２Ａが「１２」の部分領域のｔ［ｓ］経過後の温度である。Ｔ_３Ａが「１３」の部分領域のｔ［ｓ］経過後の温度である。Ｔ_４Ａが「１４」の部分領域のｔ［ｓ］経過後の温度である。Ｔ_５Ａが「１５」の部分領域のｔ［ｓ］経過後の温度である。

次に、演算部７１は、図２１において「１１」、「２１」、「３１」、「４１」、「５１」が付されている部分領域がＹ方向に並ぶ１列分の部分領域に対応するＴ_－１Ａ，Ｔ_０Ａ，Ｔ_１Ａ，Ｔ_２Ａ，Ｔ_３Ａ，Ｔ_４Ａ，Ｔ_５Ａ，Ｔ_６Ａ及びＴ_７Ａを算出するための処理を行う。ここで、「１１」側からの入熱は、入熱Ｆ０である。従って、上述の説明で代入された境界Ｎｏ．「Ｆ１」の雰囲気温度Ｔ_ｆ及び境界Ｎｏ．「Ｆ１」の相当距離λ／αを境界Ｎｏ．「Ｆ０」の雰囲気温度Ｔ_ｆ及び境界Ｎｏ．「Ｆ０」の相当距離λ／αに置換して値を代入し、これらの値が代入されたＴ_ｆ，Ｔ_０，λ／α，Δｘ／２によって、演算部７１は、図１５の「Ｆ０」に対応するＴ_－１を算出する。このＴ_－１が、「１１」、「２１」、「３１」、「４１」、「５１」が付されている部分領域がＹ方向に並ぶ１列分の部分領域における、「１１」側からの入熱Ｆ０に相当する。

同様の仕組みで、「５１」側からの放熱Ｆ３に相当するＴ_６は、上述の説明で代入された境界Ｎｏ．「Ｆ４」の雰囲気温度Ｔ_ｆ及び境界Ｎｏ．「Ｆ４」の相当距離λ／αを境界Ｎｏ．「Ｆ３」の雰囲気温度Ｔ_ｆ及び境界Ｎｏ．「Ｆ３」の相当距離λ／αに置換して値を代入し、これらの値が代入されたＴ_ｆ，Ｔ_０，λ／α，Δｘ／２によって、演算部７１は、図１５の「Ｆ０」に対応するＴ_－１を算出する。この「Ｆ３」に対応するＴ_－１が、「５１」側からの放熱Ｆ３に相当するＴ_７として扱われる。

このようにして定まったＴ_－１，Ｔ_７と、図２１において「２１」、「３１」、「４１」、「５１」が付されている部分領域がＹ方向に並ぶ１列分の部分領域の初期値Ｔ_２，Ｔ_３，Ｔ_４，Ｔ_５と、「最初の第１算出工程」で算出された「１１」の温度Ｔ_１Ａとに基づいて、演算部７１は、「最初の第１算出工程」の後に行われる「最初の第２算出工程」を行う。具体的には、演算部７１は、「最初の第２算出工程」において、Ｔ_１を「最初の第１算出工程」で算出された「１１」の温度Ｔ_１Ａで置換する。すなわち、演算部７１は、図８に示すＴ_－１，Ｔ_７に、入熱Ｆ０に相当するＴ_－１、放熱Ｆ３に相当するＴ_７を代入する。また、演算部７１は、Ｔ_０，Ｔ_２，Ｔ_３，Ｔ_４，Ｔ_５に、ダイス２の初期温度を代入する。また、演算部７１は、Ｔ_１に、「最初の第１算出工程」で算出された「１１」の温度Ｔ_１Ａを代入する。このようにして定められたＴ_－１，Ｔ_１，Ｔ_２，Ｔ_３，Ｔ_４，Ｔ_５，Ｔ_６と、上述の式（６）に基づいて、Ｔ_－１Ａ，Ｔ_０Ａ，Ｔ_１Ａ，Ｔ_２Ａ，Ｔ_３Ａ，Ｔ_４Ａ，Ｔ_５Ａ，Ｔ_６Ａ及びＴ_７Ａが算出される。ここで、「１１」の温度Ｔ_１Ａが再計算される。すなわち、第１算出工程と第２算出工程で同じ部分領域の値が算出される場合、後に行われた工程の値が採用される。

次に、演算部７１は、図２２において「２１」、「２２」、「２３」、「２４」、「２５」が付されている部分領域がＸ方向に並ぶ１行分の部分領域に対応するＴ_－１Ａ，Ｔ_０Ａ，Ｔ_１Ａ，Ｔ_２Ａ，Ｔ_３Ａ，Ｔ_４Ａ，Ｔ_５Ａ，Ｔ_６Ａ及びＴ_７Ａを算出するための処理を行う。ここで、「１２」側からの放熱は、放熱Ｆ２である。従って、上述の説明で代入された境界Ｎｏ．「Ｆ１」の雰囲気温度Ｔ_ｆ及び境界Ｎｏ．「Ｆ１」の相当距離λ／αを境界Ｎｏ．「Ｆ２」の雰囲気温度Ｔ_ｆ及び境界Ｎｏ．「Ｆ２」の相当距離λ／αに置換して値を代入し、これらの値が代入されたＴ_ｆ，Ｔ_０，λ／α，Δｘ／２によって、演算部７１は、図１５の「Ｆ２」に対応するＴ_－１を算出する。このＴ_－１が、「２１」、「２２」、「２３」、「２４」、「２５」が付されている部分領域がＸ方向に並ぶ１行分の部分領域における、「２１」側からの放熱Ｆ２に相当する。なお、放熱Ｆ４に相当するＴ_７は、既に算出済みである最初の演算（最初の第１算出処理）におけるＴ_７と同一である。

このようにして定まったＴ_－１，Ｔ_７と、図２２において「２２」、「２３」、「２４」、「２５」が付されている部分領域がｘ方向に並ぶ１行分の部分領域の初期値Ｔ_２，Ｔ_３，Ｔ_４，Ｔ_５と、「最初の第２算出工程」で算出された「２１」の温度Ｔ_２Ａとに基づいて、演算部７１は、「最初の第２算出工程」の後に行われる「２回目の第１算出工程」を行う。具体的には、演算部７１は、「２回目の第１算出工程」において、Ｔ_１を「最初の第２算出工程」で算出された「２１」の温度Ｔ_２Ａで置換する。すなわち、演算部７１は、図８に示すＴ_－１，Ｔ_７に、放熱Ｆ２に相当するＴ_－１、放熱Ｆ４に相当するＴ_７を代入する。また、演算部７１は、Ｔ_０，Ｔ_２，Ｔ_３，Ｔ_４，Ｔ_５に、ダイス２の初期温度を代入する。また、演算部７１は、Ｔ_１に、「最初の第２算出工程」で算出された「２１」の温度Ｔ_２Ａを代入する。このようにして定められたＴ_－１，Ｔ_０，Ｔ_１，Ｔ_２，Ｔ_３，Ｔ_４，Ｔ_５，Ｔ_６，Ｔ_７と、上述の式（６）に基づいて、Ｔ_－１Ａ，Ｔ_０Ａ，Ｔ_２Ａ，Ｔ_３Ａ，Ｔ_４Ａ，Ｔ_５Ａ，Ｔ_６Ａ及びＴ_７Ａが算出される。

次に、演算部７１は、図２３において「１２」、「２２」、「３２」、「４２」、「５２」が付されている部分領域がＹ方向に並ぶ１列分の部分領域に対応するＴ_－１Ａ，Ｔ_１Ａ，Ｔ_２Ａ，Ｔ_３Ａ，Ｔ_４Ａ，Ｔ_５Ａ，Ｔ_６Ａ及びＴ_０Ａを算出するための処理を行う。ここで、「１２」側からの入熱は、既に算出済みの入熱Ｆ０である。また、「５２」側からの放熱は、既に算出済みの放熱Ｆ３である。

このようにして定まったＴ_－１，Ｔ_６と、図２３において「３２」、「４２」、「５２」が付されている部分領域がＹ方向に並ぶ１列分の部分領域の初期値Ｔ_３，Ｔ_４，Ｔ_５と、「最初の第１算出工程」で算出された「１２」の温度Ｔ_２Ａ及び「２回目の第１算出工程」で算出された「２２」の温度Ｔ_２Ａとに基づいて、演算部７１は、「２回目の第２算出工程」を行う。すなわち、演算部７１は、図８に示すＴ_－１，Ｔ_７に、入熱Ｆ３に相当するＴ_－１、放熱Ｆ３に相当するＴ_６を代入する。また、演算部７１は、Ｔ_３，Ｔ_４，Ｔ_５に、ダイス２の初期温度を代入する。また、演算部７１は、Ｔ_０，Ｔ_１に、「最初の第１算出工程」で算出された「１２」の温度Ｔ_２Ａを代入する。また、演算部７１は、Ｔ_２に、「２回目の第１算出工程」で算出された「２２」の温度Ｔ_２Ａを代入する。このようにして定められたＴ_－１，Ｔ_０，Ｔ_１，Ｔ_２，Ｔ_３，Ｔ_４，Ｔ_５，Ｔ_６，Ｔ_７と、上述の式（６）に基づいて、Ｔ_－１Ａ，Ｔ_０Ａ，Ｔ_２Ａ，Ｔ_３Ａ，Ｔ_４Ａ，Ｔ_５Ａ，Ｔ_６Ａ及びＴ_７Ａが算出される。

以後、図示しないが、５番目の演算（３回目の第１算出工程）では、それ以前の第２算出工程で算出済みの「３１」、「３２」が付されている部分領域の温度Ｔ_３Ａ，Ｔ_３Ａを初期値Ｔ_１，Ｔ_２に代入する。６番目の演算（３回目の第２算出工程）では、それ以前の第１算出工程で算出済みの「１３」、「２３」、「３３」が付されている部分領域の温度Ｔ_３Ａ，Ｔ_３Ａ，Ｔ_３Ａを初期値Ｔ_１，Ｔ_２，Ｔ_３に代入する。７番目の演算（４回目の第１算出工程）では、それ以前の第２算出工程で算出済みの「４１」、「４２」、「４３」が付されている部分領域の温度Ｔ_４Ａ，Ｔ_４Ａ，Ｔ_４Ａを初期値Ｔ_１，Ｔ_２，Ｔ_３に代入する。８番目の演算（４回目の第２算出工程）では、それ以前の第１算出工程で算出済みの「１４」、「２４」、「３４」、「４４」が付されている部分領域の温度Ｔ_４Ａ，Ｔ_４Ａ，Ｔ_４Ａ，Ｔ_４Ａを初期値Ｔ_１，Ｔ_２，Ｔ_３，Ｔ_４に代入する。９番目の演算（５回目の第１算出工程）では、それ以前の第２算出工程で算出済みの「５１」、「５２」、「５３」、「５４」が付されている部分領域の温度Ｔ_５Ａ，Ｔ_５Ａ，Ｔ_５Ａ，Ｔ_５Ａを初期値Ｔ_１，Ｔ_２，Ｔ_３，Ｔ_４に代入する。１０番目の演算（５回目の第２算出工程）では、それ以前の第１算出工程で算出済みの「１５」、「２５」、「３５」、「４５」、「５５」が付されている部分領域の温度Ｔ_５Ａ，Ｔ_５Ａ，Ｔ_５Ａ，Ｔ_５Ａ，Ｔ_５Ａを初期値Ｔ_１，Ｔ_２，Ｔ_３，Ｔ_４，Ｔ_５に代入する。

以上、特筆した「それ以前の算出工程の値を参照した置換」を除いた各部分領域の初期値は、ダイス２の初期温度である。また、２回目以降の第１算出工程における一端側からの放熱（Ｔ_－１）と他端側からの放熱（Ｔ_７）は、既に算出済みの放熱Ｆ２と放熱Ｆ４である。また、第２算出工程における一端側からの入熱（Ｔ_－１）と他端側からの放熱（Ｔ_７）は、既に算出済みの入熱Ｆ１と放熱Ｆ３である。

このように、演算部７１は、ダイス２の内周側における第２箇所からの入熱量Ｆ１及びダイス２の内周側における第３箇所への放熱量Ｆ２と、ダイス２の外周側から第５箇所への放熱量Ｆ４と、予め定められた各部分領域の初期温度とに基づいて、１行分に含まれる各部分領域の温度を算出する第１算出工程と、ダイス２の一端側における第１箇所からの入熱量Ｆ０と、ダイス２の他端側から第４箇所への放熱量Ｆ３と、予め定められた各部分領域の初期温度とに基づいて、１列分に含まれる各部分領域の温度を算出する第２算出工程と、を行う。また、第１算出工程と第２算出工程は、ｔを同一の値として、それぞれ複数回行われる。また、第１算出工程と第２算出工程は交互に行われる。また、２回目以降の第１算出工程では、温度を算出する１行分の各部分領域の温度のうち、それ以前の第２算出工程で算出された部分領域の温度を当該部分領域の初期温度とする。また、２回目以降の第２算出工程では、温度を算出する１列分の各部分領域の温度のうち、それ以前の第１算出工程で算出された部分領域の温度を当該部分領域の初期温度とする。

また、１回目の第１算出工程と１回目の第２算出工程のうち、後に行われる工程では、先に行われる工程で算出された部分領域の温度を当該部分領域の初期温度とする。なお、上述の説明では、第１算出工程が先に行われているが、第２算出工程を先に行ってもよい、その場合、最初（１回目の第２算出工程）で算出された「１１」の部分領域の温度Ｔ_１Ａを、２番目（１回目の第１算出工程）の「１１」の部分領域の初期値Ｔ_１に代入する。

実施形態では、上述のように、計算時間は３００ｓである。また、差分法の計算時間間隔を６ｓとし、計算ステップは５０である。具体的には、初期温度４５０［℃］であるタイミングを開始時点（０ｓ）とする。このタイミングにおける全ての部分領域のダイス２の温度は、初期温度（４５０［℃］）である。演算部７１は、ｔ＝６を設定し、上述の式（６）に基づいて、上述のように第１算出工程と第２算出工程を繰り返して開始時点から６ｓ経過後の各部分領域の温度を算出する。

次に、演算部７１は、ｔ＝６を設定して開始時点（０ｓ）の初期温度に基づいて算出された各部分領域の温度を初期温度（Ｔ_１，Ｔ_２，…）とし、改めてｔ＝６を設定し、上述の式（６）に基づいて、上述のように第１算出工程と第２算出工程を繰り返す。これによって、開始時点から１２ｓ経過後の各部分領域の温度が算出される。以下、算出された温度を初期温度とした処理を計算ステップの回数だけ繰り返すことで、計算時間（３００ｓ）後の各部分領域の温度及びそれまでの６秒間隔での各部分領域の温度が算出される。

このように、所定時間が経過することが想定された所定時間前後の異なる２タイミングの各々における温度分布算出工程において、後のタイミングにおける各部分領域の初期温度は、前のタイミングの温度分布算出工程で算出された各部分領域の温度である。

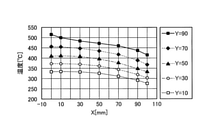
図２４に考案した差分法計算方法による各行要素のＸ方向の温度分布を示す。図２４の差分法の温度計算結果と図１７のＦＥＭ解析結果を比較すると、全体的に一致していることが分かる。

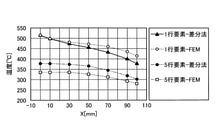
図２５に考案した差分法の１行要素と５行要素の計算結果とＦＥＭ解析結果の比較を示す。両者は一致する。このように、２次元の熱伝導解析においても、２方向からの熱伝導の影響が考慮されることによって、計算精度が高い差分法計算方法が得られた。

なお、図２４及び図２５では、実施形態によるダイス２の温度計算方法によって導出された３００ｓ後のダイス２の温度分布と、ＦＥＭ解析によって導出された３００ｓ後のダイス２の温度分布とを比較している。図２４及び図２５では、３００ｓ後の各部分領域の温度を、上述の第１算出工程及び第２算出工程で算出されるＴ_０Ａ，Ｔ_１Ａ，Ｔ_２Ａ，Ｔ_３Ａ，Ｔ_４Ａ，Ｔ_５Ａ，Ｔ_６Ａで表している。

また、図２４における「１行Ｙ＝９０」は、図９等において「１１」、「１２」、「１３」、「１４」、「１５」が付されている部分領域がＸ方向に並ぶ１行分の部分領域に対応する。また、図２４における「２行Ｙ＝７０」は、図９等において「２１」、「２２」、「２３」、「２４」、「２５」が付されている部分領域がＸ方向に並ぶ１行分の部分領域に対応する。また、図２４における「３行Ｙ＝５０」は、図９等において「３１」、「３２」、「３３」、「３４」、「３５」が付されている部分領域がＸ方向に並ぶ１行分の部分領域に対応する。また、図２４における「４行Ｙ＝３０」は、図９等において「４１」、「４２」、「４３」、「４４」、「４５」が付されている部分領域がＸ方向に並ぶ１行分の部分領域に対応する。また、図２４における「５行Ｙ＝１０」は、図９等において「５１」、「５２」、「５３」、「５４」、「５５」が付されている部分領域がＸ方向に並ぶ１行分の部分領域に対応する。

また、図２５における「１行要素」は、図９等において「１１」、「１２」、「１３」、「１４」、「１５」が付されている部分領域がＸ方向に並ぶ１行分の部分領域に対応する。また、図２５における「５行要素」は、図９等において「５１」、「５２」、「５３」、「５４」、「５５」が付されている部分領域がＸ方向に並ぶ１行分の部分領域に対応する。また、図２５における「差分法改」は、実施形態によるダイス２の温度計算方法であることを示す。また、図２５における「ＦＥＭ」は、ＦＥＭ解析による演算結果であることを示す。

図２６に差分法計算による押出加工中のダイス２のベアリング付近要素Ｅ１１と外周側要素Ｅ１５の経過時間と温度履歴の関係を示す。今回考案した計算方法を用いることにより、押出先後端におけるダイス２の内部と外部の温度差を定量的に検討できる。

なお、図２６におけるＥ１１は、図９等において「１１」が付されている部分領域に対応する。また、図２６におけるＥ１５は、図９等において「１５」が付されている部分領域に対応する。図２６は、差分法の計算時間間隔を６ｓとし、計算ステップを５０とした０ｓ～３００ｓまでの各タイミングの部分領域の温度を結ぶ線を描くグラフである。

［作用効果］
以上、本実施形態によれば、ＦＥＭ解析により近似する各部分領域の温度を算出することができる。すなわち、ＦＥＭ解析と同等の高精度な演算を、ＦＥＭ解析を実施可能な環境によらず得ることができる。このように、実施形態によれば、より容易にダイス２の温度分布をシミュレートすることができ、しかも、ＦＥＭ解析と同等の高精度な演算結果を得られる。

［その他］
なお、金属はアルミニウムに限られない。また、合金はアルミニウムを含む合金に限られない。金属又は合金は、ダイス２を用いた押出加工を適用可能な金属又は合金であればよい。

上述した「モデルの形状（正方形、１００ｍｍ×１００ｍｍ）」、「ベアリング部の長さ（２０ｍｍ）」、「計算時間（３００ｓ）」、「差分法の計算時間間隔（６ｓ）」、「計算ステップ（５０）」はあくまで一例であり、これに限られるものでなく、適宜変更可能である。また、解析モデルは２５要素に限られない。解析モデルは、行列方向にｈ×ｖであればよい。ｈ及びｖは、２以上の自然数である。

上述の実施形態における仮想モデルは、ダイス２の断面の平面モデルであるが、ダイス２の軸対称モデルであってもよい。

以上、本願発明の種々の有用な実施例を示し、かつ、説明を施した。本願発明は、上述した種々の実施例や変形例に限定されること無く、この発明の要旨や添付する特許請求の範囲に記載された内容を逸脱しない範囲で種々変形可能であることは言うまでも無い。

１ 温度計算システム
２ ダイス
２Ｖ 断面
３ ビレット
６０ 温度情報取得装置
６１ 第１温度情報取得部
６２ 第２温度情報取得部
６３ 第３温度情報取得部
６４ 第４温度情報取得部
６５ 第５温度情報取得部
７０ 情報処理装置
７１ 演算部

Claims (4)

1. 金属又は合金である押出対象の押出加工に用いられるダイスの温度分布をシミュレートするダイスの温度計算方法であって、
   前記ダイスにおける前記押出対象の押出方向を列方向とし、前記押出方向に直交する方向を行方向として、前記押出対象の押出口が配置される前記ダイスの中央部に対する行方向断面の仮想モデルを設定する工程と、
   前記仮想モデルにおいて、前記行方向及び前記列方向に複数の部分領域を含む２次元マトリクス状の分割モデルを設定する工程と、
   前記ダイスに対して前記押出方向に押し当てられる前記押出対象が存する第１箇所と、前記ダイスから押し出される前記押出対象が存する第２箇所と、前記第２箇所に対して前記押出方向側であって前記ダイスの内側の空間である第３箇所と、前記ダイスの前記押出方向側の端部側の空間である第４箇所と、前記第２箇所及び前記第３箇所の反対側に位置する前記ダイスの外周側の空間である第５箇所と、の温度を取得する工程と、
   前記第１箇所及び前記第２箇所における前記ダイスに対する入熱量と、前記第３箇所、前記第４箇所及び前記第５箇所における前記ダイスからの放熱量と、を算出する工程と、
   前記分割モデルに含まれる各部分領域の温度を算出する温度分布算出工程と、を含み、
   前記温度分布算出工程は、
   前記ダイスの内周側における前記第２箇所からの入熱量及び前記ダイスの内周側における前記第３箇所への放熱量と、前記ダイスの外周側から前記第５箇所への放熱量と、予め定められた各部分領域の初期温度とに基づいて、１行分に含まれる各部分領域の温度を算出する第１算出工程と、
   前記ダイスの一端側における前記第１箇所からの入熱量と、前記ダイスの他端側から前記第４箇所への放熱量と、予め定められた各部分領域の初期温度とに基づいて、１列分に含まれる各部分領域の温度を算出する第２算出工程と、
   を含み、
   前記第１算出工程と前記第２算出工程はそれぞれ複数回行われ、
   前記第１算出工程と前記第２算出工程は交互に行われ、
   ２回目以降の前記第１算出工程では、温度を算出する１行分の各部分領域の温度のうち、それ以前の前記第２算出工程で算出された部分領域の温度を当該部分領域の前記初期温度とし、
   ２回目以降の前記第２算出工程では、温度を算出する１列分の各部分領域の温度のうち、それ以前の前記第１算出工程で算出された部分領域の温度を当該部分領域の前記初期温度とすることを特徴とする、
   ダイスの温度計算方法。
2. １回目の前記第１算出工程と１回目の前記第２算出工程のうち、後に行われる工程では、先に行われる工程で算出された部分領域の温度を当該部分領域の前記初期温度とすることを特徴とする、
   請求項１に記載のダイスの温度計算方法。
3. 所定時間が経過することが想定された前記所定時間前後の異なる２タイミングの各々における前記温度分布算出工程において、後のタイミングにおける各部分領域の前記初期温度は、前のタイミングの前記温度分布算出工程で算出された各部分領域の温度であることを特徴とする、
   請求項１又は２に記載のダイスの温度計算方法。
4. 金属又は合金である押出対象の押出加工に用いられるダイスの温度情報を取得する温度情報取得装置と、金属又は合金である押出対象の押出加工に用いられるダイスの温度分布をシミュレートする情報処理装置とを備えるダイスの温度計算システムであって、
   前記温度情報取得装置は、
   前記ダイスに対して前記押出対象の押出方向に押し当てられる前記押出対象が存する第１箇所の温度情報を取得する第１温度情報取得部と、前記ダイスから押し出される前記押出対象が存する第２箇所の温度情報を取得する第２温度情報取得部と、前記第２箇所に対して前記押出方向側であって前記ダイスの内側の空間である第３箇所の温度情報を取得する第３温度情報取得部と、前記ダイスの前記押出方向側の端部側の空間である第４箇所の温度情報を取得する第４温度情報取得部と、前記第２箇所及び前記第３箇所の反対側に位置する前記ダイスの外周側の空間である第５箇所の温度情報を取得する第５温度情報取得部とを有し、
   前記情報処理装置は、
   前記ダイスにおける前記押出対象の押出方向を列方向とし、前記押出方向に直交する方向を行方向として、前記押出対象の押出口が配置される前記ダイスの中央部に対する行方向断面の仮想モデルを設定し、
   前記仮想モデルにおいて、前記行方向及び前記列方向に複数の部分領域を含む２次元マトリクス状の分割モデルを設定し、
   前記ダイスの内周側における前記第２箇所からの入熱量及び前記ダイスの内周側における前記第３箇所への放熱量と、前記ダイスの外周側から前記第５箇所への放熱量とを算出し、
   前記分割モデルに含まれる各部分領域の温度を算出する演算部を有し、
   前記演算部は、
   前記第２箇所及び前記第３箇所を含む前記ダイスの内周側からの入熱量及び放熱量と、前記第５箇所を含む前記ダイスの外周側からの放熱量と、予め定められた各部分領域の初期温度とに基づいて、１行分に含まれる各部分領域の温度を算出する第１算出工程と、前記第１箇所を含む前記ダイスの一端側からの入熱量と、前記第４箇所を含む前記ダイスの他端側からの放熱量と、予め定められた各部分領域の初期温度とに基づいて、１列分に含まれる各部分領域の温度を算出する第２算出工程と、をそれぞれ複数回行い、
   前記第１算出工程と前記第２算出工程を交互に行い、
   ２回目以降の前記第１算出工程では、温度を算出する１行分の各部分領域の温度のうち、それ以前の前記第２算出工程で算出された部分領域の温度を当該部分領域の前記初期温度とし、
   ２回目以降の前記第２算出工程では、温度を算出する１列分の各部分領域の温度のうち、それ以前の前記第１算出工程で算出された部分領域の温度を当該部分領域の前記初期温度とすることを特徴とすることを特徴とする、
   ダイスの温度計算システム。

Images