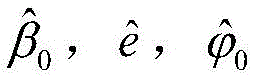CN115077458B - 回转零件截面弯曲偏心的杠杆球式通用精密测量方法 - Google Patents

回转零件截面弯曲偏心的杠杆球式通用精密测量方法 Download PDF

Info

Publication number
CN115077458B
CN115077458B CN202210670591.8A CN202210670591A CN115077458B CN 115077458 B CN115077458 B CN 115077458B CN 202210670591 A CN202210670591 A CN 202210670591A CN 115077458 B CN115077458 B CN 115077458B
Authority
CN
China
Prior art keywords
eccentricity
measured
lever
section
model
Prior art date
Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
Active
Application number
CN202210670591.8A
Other languages
English (en)
Other versions
CN115077458A (zh
Inventor
裴永臣
辛清源
刘建尧
张贺龙
王斌
罗梦演
Current Assignee (The listed assignees may be inaccurate. Google has not performed a legal analysis and makes no representation or warranty as to the accuracy of the list.)
Jilin University
Original Assignee
Jilin University
Priority date (The priority date is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the date listed.)
Filing date
Publication date
Application filed by Jilin University filed Critical Jilin University
Priority to CN202210670591.8A priority Critical patent/CN115077458B/zh
Publication of CN115077458A publication Critical patent/CN115077458A/zh
Application granted granted Critical
Publication of CN115077458B publication Critical patent/CN115077458B/zh
Active legal-status Critical Current
Anticipated expiration legal-status Critical

Links

Images

Classifications

    • G—PHYSICS
    • G01—MEASURING; TESTING
    • G01B—MEASURING LENGTH, THICKNESS OR SIMILAR LINEAR DIMENSIONS; MEASURING ANGLES; MEASURING AREAS; MEASURING IRREGULARITIES OF SURFACES OR CONTOURS
    • G01B21/00—Measuring arrangements or details thereof, where the measuring technique is not covered by the other groups of this subclass, unspecified or not relevant
    • G01B21/20—Measuring arrangements or details thereof, where the measuring technique is not covered by the other groups of this subclass, unspecified or not relevant for measuring contours or curvatures, e.g. determining profile
    • G—PHYSICS
    • G01—MEASURING; TESTING
    • G01B—MEASURING LENGTH, THICKNESS OR SIMILAR LINEAR DIMENSIONS; MEASURING ANGLES; MEASURING AREAS; MEASURING IRREGULARITIES OF SURFACES OR CONTOURS
    • G01B21/00—Measuring arrangements or details thereof, where the measuring technique is not covered by the other groups of this subclass, unspecified or not relevant
    • G01B21/22—Measuring arrangements or details thereof, where the measuring technique is not covered by the other groups of this subclass, unspecified or not relevant for measuring angles or tapers; for testing the alignment of axes
    • G01B21/24—Measuring arrangements or details thereof, where the measuring technique is not covered by the other groups of this subclass, unspecified or not relevant for measuring angles or tapers; for testing the alignment of axes for testing alignment of axes
    • G—PHYSICS
    • G01—MEASURING; TESTING
    • G01B—MEASURING LENGTH, THICKNESS OR SIMILAR LINEAR DIMENSIONS; MEASURING ANGLES; MEASURING AREAS; MEASURING IRREGULARITIES OF SURFACES OR CONTOURS
    • G01B21/00—Measuring arrangements or details thereof, where the measuring technique is not covered by the other groups of this subclass, unspecified or not relevant
    • G01B21/32—Measuring arrangements or details thereof, where the measuring technique is not covered by the other groups of this subclass, unspecified or not relevant for measuring the deformation in a solid
    • G—PHYSICS
    • G06—COMPUTING OR CALCULATING; COUNTING
    • G06F—ELECTRIC DIGITAL DATA PROCESSING
    • G06F17/00—Digital computing or data processing equipment or methods, specially adapted for specific functions
    • G06F17/10—Complex mathematical operations
    • G—PHYSICS
    • G06—COMPUTING OR CALCULATING; COUNTING
    • G06F—ELECTRIC DIGITAL DATA PROCESSING
    • G06F17/00—Digital computing or data processing equipment or methods, specially adapted for specific functions
    • G06F17/10—Complex mathematical operations
    • G06F17/14—Fourier, Walsh or analogous domain transformations, e.g. Laplace, Hilbert, Karhunen-Loeve, transforms
    • G—PHYSICS
    • G06—COMPUTING OR CALCULATING; COUNTING
    • G06F—ELECTRIC DIGITAL DATA PROCESSING
    • G06F17/00—Digital computing or data processing equipment or methods, specially adapted for specific functions
    • G06F17/10—Complex mathematical operations
    • G06F17/16—Matrix or vector computation, e.g. matrix-matrix or matrix-vector multiplication, matrix factorization
    • G—PHYSICS
    • G06—COMPUTING OR CALCULATING; COUNTING
    • G06F—ELECTRIC DIGITAL DATA PROCESSING
    • G06F30/00—Computer-aided design [CAD]
    • G06F30/20—Design optimisation, verification or simulation

Landscapes

  • Physics & Mathematics (AREA)
  • Engineering & Computer Science (AREA)
  • General Physics & Mathematics (AREA)
  • Mathematical Physics (AREA)
  • Theoretical Computer Science (AREA)
  • Data Mining & Analysis (AREA)
  • Computational Mathematics (AREA)
  • Mathematical Analysis (AREA)
  • Mathematical Optimization (AREA)
  • Pure & Applied Mathematics (AREA)
  • General Engineering & Computer Science (AREA)
  • Software Systems (AREA)
  • Databases & Information Systems (AREA)
  • Algebra (AREA)
  • Computer Hardware Design (AREA)
  • Evolutionary Computation (AREA)
  • Geometry (AREA)
  • Computing Systems (AREA)
  • Length Measuring Devices With Unspecified Measuring Means (AREA)

Abstract

回转零件截面弯曲偏心的杠杆球式通用精密测量方法属于回转零件截面弯曲偏心检测领域，由测量参数预处理模型和实测数据处理模型两部分组成。首先，将杠杆球式测量机构的结构尺寸和被测截面标准轮廓信息输入参数预处理模型，计算测量机构的杠杆比；进行无偏心工件的回转测量过程仿真，获得形状项参量的傅里叶系数矩阵。之后，将被测截面的实测信号代入实测数据处理模型，求取被测截面初始解的估计值；采用循环迭代方式，获得被测截面偏心的精确解。通过设置测量机构的结构尺寸，本方法可拟合计算任意形状、任意尺寸回转工件的偏心量、偏心角和初始姿态角，本方法应用领域广，通用性强，检测效率高，适宜大范围推广应用。

Description

回转零件截面弯曲偏心的杠杆球式通用精密测量方法
技术领域
本发明属于回转零件截面弯曲偏心检测领域，尤其涉及一种通过杠杆球式测量机构接触式检测回转零件截面弯曲偏心的通用精密测量方法。
背景技术
回转零件包含标准几何零件和异性回转体零件，其被广泛应用于旋转机械和生产设备中，是现代传动装置中重要的组成部分。随着工业技术的快速发展，制造结构更精密、装配更紧凑，传动更稳定的回转零件成为工业生产领域的重要需求，而零件的精密检测是确保零件几何精度的基础和手段。
在零件的制造和装配过程中，回转零件的截面形状和轴线的直线度尤为重要，其决定了零件的安装精度和设备的稳定性；而在零件的安装和运行过程中，回转零件的弯曲变形和径向偏心是难以避免的。零件弯曲一方面会导致传动不平稳，传动比不精确；另一方面也会使机械系统发生明显的振动、噪声乃至破坏。当前常规的回转零件形位误差检测主要有两种：光学非接触式测量和平折杠杆式接触测量，前者检测时受周围环境状况的影响较为明显，测量区域内的油污、灰尘、杂质等干扰因素均会导致测量结果不准，同时由于非接触式测量设备往往成本较高，电子元器件有寿命限制，不适于大范围推广；而后者受限于测杆的结构，只能测量截面为凸多变形的回转零件而无法测量凹表面，且在测量正多边形棱柱时，只能采用部分段数据或个别关键点，精度低，重复性差；另外，现有的回转零件测量方法仅适用于测量截面为规则形状的零件，而对于截面形状复杂或形状任意的零件尚缺少有效的测量方法。
综上所述，回转零件截面弯曲偏心检测技术的发展迫切需要一种结构简洁、测试高效、价格低廉和精度可控的杠杆球式通用精密测量方法。
发明内容
本发明的目的在于提供一种回转零件截面弯曲偏心的杠杆球式通用精密测量方法，该测量方法利用测球的圆弧状结构，使零件在旋转过程中，始终与测球有且仅有一个接触点，从而增加有效测试信息，快速准确获取回转零件截面弯曲偏心。
为实现上述目的，本发明包括测量参数预处理和实测数据处理两部分，其中测量参数预处理包括使用杠杆比求解模型和无偏心零件回转测量模型，实测数据处理包括使用测试信号成分分析模型和循环迭代模型，其具体操作步骤为：
(1)根据采集设备的调试及运行状况，准确获取零件回转中心O的坐标(A,B)和杠杆球式测量机构(2)的基本结构尺寸，包括主动臂长度D、从动臂长度r、球形测头直径s、测头球心与杠杆的距离E和传感器探头与杠杆的距离C；
(2)将参数A、B、C、D、E、r、s输入杠杆比求解模型，计算杠杆球式测量机构2的杠杆比Kb；
(3)根据被测零件3的轮廓函数表达式或实测数据，计算被测截面在无偏心时的标准轮廓数据(xP,yP)；
(4)将标准轮廓数据(xP,yP)带入无偏心零件的回转测量模型，模拟仿真无偏心零件的回转测量过程，获得仿真测试信号zm并计算形状项参量的傅里叶系数矩阵A；至此，测量参数预处理完成；
(5)利用带有杠杆球式测量机构2的测量设备获取被测截面的实测信号Z；
(6)将实测信号Z输入到测试信号成分分析模型，计算被测截面偏心参数的估计值
Figure GDA0004222350890000021
Figure GDA0004222350890000022
(7)将估计值
Figure GDA0004222350890000023
代入循环迭代模型，采用循环迭代方式进行迭代求解，循环收敛后获得被测截面偏心参数的精确解，循环迭代模型的迭代量为姿态角β0、偏心量e和偏心角/>
Figure GDA0004222350890000024
收敛评价指标为拟合信号与原始信号的计算误差；
其中，步骤(2)、步骤(4)分别对应测量参数预处理使用的杠杆比求解模型和无偏心零件回转测量模型，步骤(6)、步骤(7)分别对应实测数据处理使用的测试信号成分分析模型和循环迭代模型。
所述步骤(1)中的杠杆球式测量机构2的基本结构尺寸C、r、D、E、s及零件回转中心O点的坐标(A,B)需根据实际测量设备的安装调试状态确定，测试前需要首先对试验台标定，以获得结构尺寸的精确值，测球可选用整球也可选用半球。
所述步骤(3)中，在计算被测截面在无偏心时的标准轮廓数据过程中，若零件截面轮廓的函数表达式已知，可通过函数计算直接获得零件轮廓数据信息；若被测零件3为非标准件或截面轮廓函数未知，可以通过图像识别、零件试测的方式获取轮廓数据信息。
所述步骤(4)中，用于仿真分析的零件的结合中心与回转中心重合，且截面姿态初始相位角为0，获得信号为仿真测试信号zm。
所述步骤(5)中，实测信号Z为工程应用中利用杠杆球式测量机构2测量被测零件3时，获得的工程测试信号，实测信号Z与步骤(4)中的仿真测试信号zm在数值上通常不相等。
本发明的优势在于：
1)本测量方法可以在线检测任意形状、任意尺寸的回转零件，应用领域广，检测效率高，迭代精确高，极大地提升了回转零件的检测精度。通过更改杠杆球式测量机构的结构尺寸，本测量方法可以实现对任意形状、任意尺寸零件的测量处理，方法通用性强；
2)相较于传统的平折式杠杆测量方法，本测量方法可以保证在零件旋转过程中有且仅有一个点与被测零件接触，避免了被测截面为凹多边形时引起的测量信息丢失的问题，为后续的数据处理提供了准确的轮廓测量信息；
3)相较于光学非接触式测量方法，本测量方法不受周围环境状况的影响，测量结果准确，成本较低，一次标定即可长期使用，操作简便。
附图说明
图1为本发明具体实施流程图
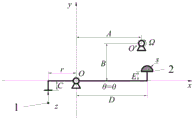
图2为本发明杠杆球式测量机构2处于平衡位置的测量原理图
图3为本发明杠杆球式测量机构2测量任意截面时的原理图
图4为本发明被测零件3在无偏心时的测试原理图
图5为本发明被测零件3在有偏心时的测试原理图
图6为本发明计算误差随迭代次数增加的变化曲线图
图7为本发明迭代项β0，e，
Figure GDA0004222350890000031
随迭代次数增加的变化曲线图
其中：1：接触式位移传感器，2：杠杆球式测量机构，3：被测零件
具体实施方式
本发明提供了一种回转零件截面弯曲偏心的杠杆球式通用精密测量方法，为使本发明目的、技术方案及效果更佳明晰，本实施方案附图中以凸轮和摆线轮为例对方案进行进一步说明。本发明描述的具体实例仅用于解释本发明，不用于限定本发明。以下结合附图对本发明进行进一步说明：
如图1所示，其包括测量参数预处理和实测数据处理两部分，其中测量参数预处理包括使用杠杆比求解模型和无偏心零件回转测量模型，实测数据处理包括使用测试信号成分分析模型和循环迭代模型，具体操作步骤为：
(1)根据采集设备的调试及运行状况，准确获取零件回转中心O的坐标(A,B)和杠杆球式测量机构2的基本结构尺寸，包括主动臂长度D、从动臂长度r、球形测头直径
s、测头球心与杠杆的距离E和传感器探头与杠杆的距离C；
(2)将参数A、B、C、D、E、r、s输入杠杆比求解模型，计算杠杆球式测量机构2的杠杆比Kb；
(3)根据被测零件3的轮廓函数表达式或实测数据，计算被测截面在无偏心时的标准
轮廓数据(xP,yP)；
(4)将标准轮廓数据(xP,yP)带入无偏心零件的回转测量模型，模拟仿真无偏心零件的回
转测量过程，获得仿真测试信号zm并计算形状项参量的傅里叶系数矩阵A；至此，测量参数预处理完成；
(5)利用带有杠杆球式测量机构2的测量设备获取被测截面的实测信号Z；
(6)将实测信号Z输入到测试信号成分分析模型，计算被测截面偏心参数的估计值
Figure GDA0004222350890000041
Figure GDA0004222350890000042
(7)将估计值
Figure GDA0004222350890000043
代入循环迭代模型，采用循环迭代方式进行迭代求解，循环
收敛后获得被测截面偏心参数的精确解，循环迭代模型的迭代量为姿态角β0、偏
心量e和偏心角
Figure GDA0004222350890000044
收敛评价指标为拟合信号与原始信号的计算误差；
其中，步骤(2)、步骤(4)分别对应测量参数预处理使用的杠杆比求解模型和无偏心零件回转测量模型，步骤(6)、步骤(7)分别对应实测数据处理使用的测试信号成分分析模型和循环迭代模型。
如图2、图3所示，杠杆球式通用精密测量装置由接触式位移传感器1和杠杆球式测量机构2两部分组成，以杠杆球式测量机构2的回转中心O为原点，杠杆球式测量机构2下侧折杆水平位置所在直线为x轴，其垂直方向为y轴建立杠杆球式测量机构2的全局坐标系。杠杆球式测量机构2基本结构尺寸分别为C，r，D，E，s。若被测零件3为非圆截面或者回转中心与几何中心不重合，当被测零件3旋转时，杠杆球式测量机构2将围绕回转中心O上下摆动。设定杠杆球式测量机构2与x轴夹角为θ，回转中心O的坐标为(0,0)，位移位移传感器1示值为z。被测零件3外接圆半径为Rm，被测截面几何中心O″坐标(A0,B0)，该截面实际回转中心O′坐标为(A,B)，e和
Figure GDA0004222350890000045
分别为被测零件3被测截面偏心量(挠度)和偏心角。
接触式位移传感器1和杠杆球式测量机构2的两折杆所在直线方程分别为：
L0:x＝-r (1)
L1:y＝xtan(θ)-C/cos(θ) (2)
L2:y＝xtan(θ)+E/cos(θ) (3)
将式(1)代入式(2)，并去除接触式位移传感器1在θ＝0时的初始位置-C，获得接触式位移传感器1的绝对示值为：
z＝C-rtan(θ)-C/cos(θ) (4)
根据平面解析几何原理和三角函数关系，零件被测截面几何中心O″(A0,B0)与实际回转中心O′(A,B)的坐标转换关系为：
Figure GDA0004222350890000051
式中，
Figure GDA0004222350890000052
为安装时初始偏心角，/>
Figure GDA0004222350890000053
为测量过程中零件截面转过的角度。
当杠杆球式测量机构2处于水平位置时，测量球的球心坐标为(D,E)，当杠杆球式测量机构2与x轴夹角为θ时，测量球的球心坐标(xs,ys)为
Figure GDA0004222350890000058
无论零件旋转任意角度，零件表面始终与杠杆球式测量机构2的测球接触，当截面无偏心时，杠杆测量倾角θ估计值为
Figure GDA0004222350890000054
被测零件3以其几何中心为坐标原点的轮廓数据点向量为(xP,yP)，将它们视为截面相角γ的极坐标函数，0<γ<2π。截面姿态初始相位角为β0，那么当测量转动
Figure GDA0004222350890000055
角后，零件截面坐标变为
Figure GDA0004222350890000056
那么零件截面任意点到球心距离
Figure GDA0004222350890000057
以θm作为初始值，当dNs(θ)＝0时，通过数值迭代精确确定θ解。
如图3所示，步骤(2)中杠杆比求解模型建立和杠杆比Kb的求解过程如下所述：
设Kb为杠杆球式测量机构2的杠杆比，其能够用于实现传感器示数z与偏心量间的折算，在被测截面的外接圆半径Rm上施加小扰动ε，则公式(4)(7)转化为
zε(ε)＝C-rtan(θε)-C/tan(θε) (10)
Figure GDA0004222350890000061
将(11)带入(10)中，并对(10)求关于ε的偏导，化简后得
Figure GDA0004222350890000062
如图4所示，步骤(4)中无偏心零件的回转测量模型建立、仿真测试信号zm的获取过程，及形状项参量的傅里叶系数矩阵A的求取过程如下所述：
当零件回转过程中无偏心时，获得的信号全部来自零件自身形状引起的信号波动，其反映了零件的形状项参量。无偏心e＝0，无姿态初始相位角β0＝0，测量过程仿真测试信号zm随转角
Figure GDA0004222350890000063
的变化关系为
Figure GDA0004222350890000064
对其进行Fourier级数展开
Figure GDA0004222350890000065
其中，
Figure GDA0004222350890000066
A＝[a0,a1,b1,a2,b2,...,ak,bk,...]T。
同时，形状项参量的傅里叶系数矩阵A化为，
Figure GDA0004222350890000067
如图5所示，步骤(6)中截面存在回转偏心的测试信号成分分析模型建立过程及被测截面初始解估计值
Figure GDA0004222350890000068
求取过程如下所述：
在被测截面存在小偏心量e的情况下，仿真测试信号zm本质上是形状项与偏心项的叠加，
Figure GDA0004222350890000069
对形状项与偏心项分别进行Fourier展开
Figure GDA0004222350890000071
形状项：
Figure GDA0004222350890000072
其中，
Figure GDA0004222350890000073
偏心项：
Figure GDA0004222350890000074
其中，/>
Figure GDA0004222350890000075
因此式(16)的Fourier展开形式为，
Figure GDA0004222350890000076
通过对公式(19)化简求解，获得姿态角β0的最小值和变量c的求解公式，
Figure GDA0004222350890000077
Figure GDA0004222350890000078
公式(20)(21)的离散化形式为，
Figure GDA0004222350890000079
Figure GDA00042223508900000710
其中，
Figure GDA00042223508900000715
为接触式位移传感器1的测量值，/>
Figure GDA00042223508900000711
为转角采样间隔，/>
Figure GDA00042223508900000712
为转角向量，
Figure GDA00042223508900000713
零件被测截面的偏心量和偏心角的估计公式为，
Figure GDA00042223508900000714
Figure GDA0004222350890000081
其中，
Figure GDA0004222350890000082
至此，获得初始解的估计值
Figure GDA0004222350890000083
如图5，图6所示，循环迭代模型的迭代量为姿态角β0、偏心量e和偏心角
Figure GDA0004222350890000084
收敛评价指标为拟合信号与原始信号的计算误差。迭代求解过程中计算误差随迭代次数增加逐渐减小，通过一定次数的迭代获得被测截面的精确解β0，e，/>
Figure GDA0004222350890000085
图6展示了计算误差随迭代次数增加的变化曲线，图7(a)(b)(c)分别展示了β0，e，/>
Figure GDA0004222350890000086
随迭代次数增加的变化曲线。
依据步骤(6)中获得的初始解估计值
Figure GDA0004222350890000087
采用循环迭代方式，对β0，e，/>
Figure GDA0004222350890000088
进行迭代求解，循环收敛后获得精确解，迭代函数为
Figure GDA0004222350890000089
迭代函数的离散化形式为
Figure GDA00042223508900000810

Claims (5)

1.回转零件截面弯曲偏心的杠杆球式通用精密测量方法，其包括测量参数预处理和实测数据处理两部分，其中测量参数预处理包括使用杠杆比求解模型和无偏心零件回转测量模型，实测数据处理包括使用测试信号成分分析模型和循环迭代模型，具体操作步骤为：
(1)根据采集设备的调试及运行状况，准确获取零件回转中心O的坐标(A,B)和杠杆球式测量机构(2)的基本结构尺寸，包括主动臂长度D、从动臂长度r、球形测头直径s、测头球心与杠杆的距离E和传感器探头与杠杆的距离C；
(2)将参数A、B、C、D、E、r、s输入杠杆比求解模型，计算杠杆球式测量机构(2)的杠杆比Kb；
(3)根据被测零件(3)的轮廓函数表达式或实测数据，计算被测截面在无偏心时的标准轮廓数据(xP,yP)；
(4)将标准轮廓数据(xP,yP)带入无偏心零件的回转测量模型，模拟仿真无偏心零件的回转测量过程，获得仿真测试信号zm并计算形状项参量的傅里叶系数矩阵A，至此，测量参数预处理完成；
(5)利用带有杠杆球式测量机构(2)的测量设备获取被测截面的实测信号Z；
(6)将实测信号Z输入到测试信号成分分析模型，计算被测截面偏心参数的估计值
Figure FDA0004222350870000011
Figure FDA0004222350870000012
(7)将估计值
Figure FDA0004222350870000013
代入循环迭代模型，采用循环迭代方式进行迭代求解，循环收敛后获得被测截面偏心参数的精确解，循环迭代模型的迭代量为姿态角β0、偏心量e和偏心角/>
Figure FDA0004222350870000014
收敛评价指标为拟合信号与原始信号的计算误差；
其中，步骤(2)、步骤(4)分别对应测量参数预处理使用的杠杆比求解模型和无偏心零件回转测量模型，步骤(6)、步骤(7)分别对应实测数据处理使用的测试信号成分分析模型和循环迭代模型。
2.根据权利要求1所述的回转零件截面弯曲偏心的杠杆球式通用精密测量方法，其特征在于：步骤(2)中杠杆比求解模型建立和杠杆比Kb的求解过程如下所述：
设Kb为杠杆球式测量机构(2)的杠杆比，其能够用于实现传感器示数z与偏心量间的折算，在被测截面的外接圆半径Rm上施加小扰动ε，传感器示值信号zε及杠杆测量倾角的估计值θε表示为，
zε(ε)＝C-r tan(θε)-C/tan(θε) (10)
Figure FDA0004222350870000021
将(11)带入(10)中，并对(10)求关于ε的偏导，化简后得，
Figure FDA0004222350870000022
3.根据权利要求1所述的回转零件截面弯曲偏心的杠杆球式通用精密测量方法，其特征在于：步骤(4)中无偏心零件的回转测量模型建立，仿真测试信号zm的获取过程，及形状项参量的傅里叶系数矩阵A的求取过程如下所述：
当零件回转过程中无偏心时，获得的信号全部来自零件自身形状引起的信号波动，其反映了零件的形状项参量，无偏心e＝0，无姿态初始相位角β0＝0，测量过程仿真测试信号zm随转角
Figure FDA0004222350870000023
的变化关系为，
Figure FDA0004222350870000024
对其进行Fourier级数展开，
Figure FDA0004222350870000025
其中，
Figure FDA0004222350870000026
A＝[a0,a1,b1,a2,b2,...,ak,bk,...]T；
同时，形状项参量的傅里叶系数矩阵A化为，
Figure FDA0004222350870000027
4.根据权利要求1所述的回转零件截面弯曲偏心的杠杆球式通用精密测量方法，其特征在于：步骤(6)中，截面存在回转偏心的测试信号成分分析模型建立过程及被测截面初始解估计值
Figure FDA0004222350870000028
求取过程如下所述：
在被测截面存在小偏心量e的情况下，仿真测试信号zm本质上是形状项与偏心项的叠加，
Figure FDA0004222350870000029
对形状项与偏心项分别进行Fourier展开，
形状项：
Figure FDA0004222350870000031
其中，
Figure FDA0004222350870000032
偏心项：
Figure FDA0004222350870000033
其中，/>
Figure FDA0004222350870000034
c＝[xe,ye,z0]T；
因此，式(16)的Fourier展开形式为，
Figure FDA0004222350870000035
通过对公式(19)化简求解，获得姿态角β0的最小值和变量c的求解公式，
Figure FDA0004222350870000036
Figure FDA0004222350870000037
公式(20)(21)的离散化形式为，
Figure FDA0004222350870000038
Figure FDA0004222350870000039
其中，
Figure FDA00042223508700000310
为接触式位移传感器(1)的测量值，/>
Figure FDA00042223508700000311
为转角采样间隔，/>
Figure FDA00042223508700000312
为转角向量，
Figure FDA00042223508700000313
零件被测截面的偏心量和偏心角的估计公式为，
Figure FDA00042223508700000314
Figure FDA00042223508700000315
其中，
Figure FDA00042223508700000316
至此，获得初始解的估计值
Figure FDA0004222350870000041
5.根据权利要求1所述的回转零件截面弯曲偏心的杠杆球式通用精密测量方法，其特征在于：依据步骤(6)中获得的初始解估计值
Figure FDA0004222350870000042
采用循环迭代方式，对β0，e，/>
Figure FDA0004222350870000043
进行迭代求解，循环收敛后获得精确解，迭代函数为，
Figure FDA0004222350870000044
迭代函数的离散化形式为，
Figure FDA0004222350870000045
CN202210670591.8A 2022-06-14 2022-06-14 回转零件截面弯曲偏心的杠杆球式通用精密测量方法 Active CN115077458B (zh)

Priority Applications (1)

Application Number Priority Date Filing Date Title
CN202210670591.8A CN115077458B (zh) 2022-06-14 2022-06-14 回转零件截面弯曲偏心的杠杆球式通用精密测量方法

Applications Claiming Priority (1)

Application Number Priority Date Filing Date Title
CN202210670591.8A CN115077458B (zh) 2022-06-14 2022-06-14 回转零件截面弯曲偏心的杠杆球式通用精密测量方法

Publications (2)

Publication Number Publication Date
CN115077458A CN115077458A (zh) 2022-09-20
CN115077458B true CN115077458B (zh) 2023-06-16

Family

ID=83251047

Family Applications (1)

Application Number Title Priority Date Filing Date
CN202210670591.8A Active CN115077458B (zh) 2022-06-14 2022-06-14 回转零件截面弯曲偏心的杠杆球式通用精密测量方法

Country Status (1)

Country Link
CN (1) CN115077458B (zh)

Families Citing this family (2)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
CN117804401B (zh) * 2023-12-28 2025-04-04 河北华伦线缆有限公司 电缆用绝缘层偏心度校对方法
CN119533326B (zh) * 2024-11-08 2025-09-16 吉林大学 一种圆截面轮廓及其周向谐波分量的精确测量和测定方法

Family Cites Families (5)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
JP3722288B2 (ja) * 2003-03-03 2005-11-30 福島県 円筒体の形状測定方法
CN105136099B (zh) * 2015-05-18 2017-09-26 长春理工大学 一种回转体偏心检验方法
CN110906901B (zh) * 2018-09-14 2020-11-24 吉林大学 一种正六棱截面轴类偏心测量方法
CN109855590B (zh) * 2019-01-12 2021-03-23 吉林大学 一种圆柱类零件弯曲变形轴线杠杆式连续测量方法
CN111043960B (zh) * 2019-12-26 2021-04-30 哈尔滨工业大学 一种基于激光传感的大型高速回转装备误差测量及分离方法

Also Published As

Publication number Publication date
CN115077458A (zh) 2022-09-20

Similar Documents

Publication Publication Date Title
CN107588742B (zh) 一种基于线结构光的圆柱齿轮齿廓偏差测量方法
CN109141225B (zh) 基于圆光栅的轴系五、六自由度误差测量方法及测量系统
CN109032070B (zh) 一种采用电涡流位移传感器的非接触式R-test测量仪标定方法
CN115077458B (zh) 回转零件截面弯曲偏心的杠杆球式通用精密测量方法
CN109115095B (zh) 一种非接触式R-test测量仪的结构参数优化方法
CN115682917B (zh) 一种圆光栅编码器主轴偏心误差补偿方法及系统
CN114782513B (zh) 一种基于平面的点激光传感器安装位姿标定方法
CN108827190B (zh) 基于双自准直仪的高精度测角误差检测装置及其检测方法
CN106643613A (zh) 一种非球面在位检测中的位置误差标定方法
CN106940175A (zh) 用于内孔参数测量装置测头长度校准的球面环规及测头长度校准方法
CN107860313A (zh) 一种基于线结构光的斜齿轮齿向偏差测量方法
CN105333828A (zh) 一种四轴联动跟踪式曲轴测量方法
CN108317985A (zh) 高精度工业机器人重复定位精度的测量装置和测量方法
CN103862327A (zh) 一种球头球心位置检测方法
CN101750031B (zh) 一种二维轮廓形状的测量方法及测量装置
CN106989670A (zh) 一种机器人协同的非接触式高精度大型工件跟踪测量方法
CN112344895B (zh) 一种关节臂坐标测量机多参数模型的建立及标定方法
Liu et al. Online approach to measuring relative location of spatial geometric features of long rotating parts
CN102095366A (zh) 一种大梯度非球面的轮廓测量方法
CN113137943A (zh) 一种位移传感器标定装置及其测定方法
CN113962932A (zh) 一种基于三维立体建模的螺纹检测方法
CN208269868U (zh) 高精度工业机器人重复定位精度的测量装置
CN117781805A (zh) 活塞空间角度孔系位置度检测方法
CN110906901B (zh) 一种正六棱截面轴类偏心测量方法
CN114777607A (zh) 一种回转体同轴度误差检测装置及方法

Legal Events

Date Code Title Description
PB01 Publication
PB01 Publication
SE01 Entry into force of request for substantive examination
SE01 Entry into force of request for substantive examination
GR01 Patent grant
GR01 Patent grant