JP3972784B2 - 画像処理装置およびその方法 - Google Patents
画像処理装置およびその方法 Download PDFInfo
- Publication number
- JP3972784B2 JP3972784B2 JP2002286326A JP2002286326A JP3972784B2 JP 3972784 B2 JP3972784 B2 JP 3972784B2 JP 2002286326 A JP2002286326 A JP 2002286326A JP 2002286326 A JP2002286326 A JP 2002286326A JP 3972784 B2 JP3972784 B2 JP 3972784B2
- Authority
- JP
- Japan
- Prior art keywords
- brdf
- unit
- matrix
- vector
- model
- Prior art date
- Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
- Expired - Fee Related
Links
Images
Classifications
-
- G—PHYSICS
- G06—COMPUTING; CALCULATING OR COUNTING
- G06T—IMAGE DATA PROCESSING OR GENERATION, IN GENERAL
- G06T15/00—3D [Three Dimensional] image rendering
- G06T15/50—Lighting effects
- G06T15/506—Illumination models
-
- G—PHYSICS
- G06—COMPUTING; CALCULATING OR COUNTING
- G06T—IMAGE DATA PROCESSING OR GENERATION, IN GENERAL
- G06T15/00—3D [Three Dimensional] image rendering
- G06T15/50—Lighting effects
Landscapes
- Engineering & Computer Science (AREA)
- Computer Graphics (AREA)
- Physics & Mathematics (AREA)
- General Physics & Mathematics (AREA)
- Theoretical Computer Science (AREA)
- Image Generation (AREA)
Description
【発明の属する技術分野】
本発明は、3次元コンピュータグラフィックスを実現するための画像処理装置およびその方法に係り、特に、よりリアリスティックな画像を生成するコンピュータグラフィックス装置の構成と方法に関するものである。
【0002】
【従来の技術】
昨今のコンピュータシステムにおける演算速度の向上や描画機能の強化とも相俟って、コンピュータ資源を用いて図形や画像の作成や処理を行う「コンピュータグラフィックス(CG)」技術が盛んに研究・開発され、さらに実用化されている。
【0003】
たとえば、3次元グラフィックスは、3次元オブジェクトが所定の光源によって照らされたときの光学現象を数学モデルで表現して、このモデルに基づいてオブジェクト表面に陰影や濃淡を付けたり、さらには模様を貼り付けたりして、よりリアルで3次元的な2次元高精細画像を生成するものである。
このようなコンピュータグラフィックスは、科学、工学、製造などの開発分
野でのCAD/CAM、その他の各種応用分野においてますます盛んに利用されるようになってきている。
【0004】
3次元グラフィックスは、一般には、フロントエンドとして位置づけられる「ジオメトリ・サブシステム」と、バックエンドとして位置づけられる「ラスタ・サブシステム」とにより構成される。
【0005】
ジオメトリ・サブシステムとは、ディスプレイ・スクリーン上に表示する3次元オブジェクトの位置や姿勢などの幾何学的な演算処理を行う過程のことである。
ジオメトリ・サブシステムでは、一般にオブジェクトは多数のポリゴンの集合体として扱われ、ポリゴン単位で、「座標変換」、「クリッピング」、「光源計算」などの幾何学的な演算処理が行われる。
【0006】
一方、ラスタ・サブシステムは、オブジェクトを構成する各ピクセル(pixel)を塗りつぶす過程のことである。
ラスタライズ処理は、たとえばポリゴンの頂点毎に求められた画像パラメータを基にして、ポリゴン内部に含まれるすべてのピクセルの画像パラメータを補間することによって実現される。
ここで言う画像パラメータには、いわゆるRGB形式などで表される色(描画色)データ、奥行き方向の距離を表すz値などがある。
また、最近の高精細な3次元グラフィックス処理では、遠近感を醸し出すためのf(fog:霧)や、物体表面の素材感や模様を表現してリアリティを与えるテクスチャt(texture)なども、画像パラメータの1つとして含まれている。
【0007】
ここで、ポリゴンの頂点情報からポリゴン内部のピクセルを発生する処理では、よくDDA(Digital Differential Analyzer)と呼ばれる線形補間手法を用いて実行される。
DDAプロセスでは、頂点情報からポリゴンの辺方向へのデータの傾きを求め、この傾きを用いて辺上のデータを算出した後、続いてラスタ走査方向(X方向)の傾きを算出し、この傾きから求めたパラメータの変化分を走査の開始点のパラメータ値に加えていくことで、内部のピクセルを発生していく。
【0008】
このような3次元グラフィックスにおいて、近年、リアリスティックなコンピュータグラフィックス画像を生成するため、イルミネーションモデルの改良が行われている。一方、リアルタイムな描画性能を追求するハードウェアアーキテクチャの研究開発が行われている。
一般的に、リアルティを向上させようとすると、演算量が増加しリアルタイム性が損なわれ、リアルタイム性を向上させようとするとアルゴリズムの簡略化が要求されリアリティが犠牲になる。これらの相反する要求をできるだけ同時に実現しようとする研究開発も行われている。
【0009】
リアルタイムな描画性能を追求する最新のハードウェア技術の中で、プログラマブルピクセルシェーダという技術がある。
プログラマブルピクセルシェーダは、ポリゴンを構成するピクセル毎に行うシェーディングの工程にプログラマビリティの機能を与えた。
このプログラマビリティによって、BRDF(Bi−directional Reflection Distribution Function)という一般的な反射モデルが実装され始め、リアルタイムでかつリアリスティックな画像生成の可能性がでてきた。また、テクスチャマッピングがポリゴン表面の色彩に変化を与えるように、BRDFの性質を変化させることも考えられる。このようなポリゴンの表面上の位置によって異なる性質を持つBRDFをシフトバリアント(Shifts−variant)BRDFという。
以下に、プログラマブルピクセルシェーダ、BRDF、およびシフトバリアントBRDFについて詳細に説明する。
【0010】
プログラマブルピクセルシェーダ
プログラマブルピクセルシェーダは、ピクセル毎に行う輝度計算の工程にプログラマビリティの機能を与えるものである。
NVIDIA社のGForce3,GForce4やATI社のRADEON8500などのグラフィックスLSIにプログラマブルピクセルシェーダの技術が採用されている。
ユーザは、ピクセルシェーダプログラムを工夫して書くことにより、従来のグーローシェーディングのみをサポートした固定的なハードウェアではなし得なかったリアリティのあるシェーディングモデルを、リアルタイムな実行環境で実現できるようになった。
たとえば、従来の固定的なハードウェアでも実装されていたグーローシェーディングやテクスチャマッピングなどの技術だけでなく、プログラマブルピクセルシェーダを使えばフォンシェーディング、バンプマッピング、トゥーンシェーディング、環境マッピングなども実装できる。さらに異法性反射モデルや一部のBRDFも利用できる。
【0011】
プログラマブルピクセルシェーダを使えば、ポリゴン上にマップ化したシェーディイングパラメータの記憶場所としてテクスチャメモリを使用することができる。
たとえば、法線方向を利用するシェーダプログラムがあるとき、テクスチャメモリの各テクセルに法線方向にデータを格納しておき、ランタイム時にテクセル値から得られた法線を使ってシェーディング計算をすることができる。バンプマッピングや一部のBRDFモデルがこの方法で実現されている。
【0012】
NVIDIA社のGForce3,GForce4のプログラマブルピクセルシェーダの仕組みは、図15に示すようになっている。
基本的には、このプログラマブルピクセルシェーダは、テクスチャルックアップユニット1とALUユニット2から構成されている。
上流のプログラマブル頂点シェーダからテクスチャルックアップユニット1に4つのテクスチャアドレスTEX0〜TEX3が供給される。テクスチャルックアップユニット1は、最大4つのテクスチャアドレスに対応したRGBAの4要素のテクセルをルックアップできる。ルックアップは4並列に実行できる。ルックアップした結果はピクセルALUユニット2に出力される。
また、プログラマブル頂点シェーダは、ピクセルALUユニット2に2つのRGBAの4要素を供給する。ピクセルALUユニット2は、図16に示すように、レジスタコンバイナ2−1,2−2,2−3という特殊な演算器を有する。
レジスタコンバイナ2−1,2−2は内積と乗算を実行し、レジスタコンバイナ2−3は加算を実行する。ピクセルALUユニット2では、入力マップ2−4,2−5を通してレジスタコンバイナ2−1にデータを入力し、入力マップ2−6,2−7を通してレジスタコンバイナ2−2にデータを入力する。これにより、乗算と内積を2並列で実行できる。ただし、内積は3次元×3次元のみである。内積演算は、たとえばフォン反射モデルやディフューズ反射モデルのベクトルの内積に利用できる。
【0013】
ピクセルシェーダプログラムは、ユーザが定義できる数ステップのプログラムで、ピクセル毎に先頭から実行される。このプログラムが上記テクスチャルックアップユニット1およびALUユニット2を制御する。
【0014】
BRDF
BRDFは、表面上の一点に入射する光が物体表面で反射される割合を表す関数である。それは、次式のように、光源と視点の方向からなる4次元の関数として表される。
【0015】
【数1】
【0016】
BRDFは、従来良く知られてきたシェーディングモデルの上位概念として扱うことができる。たとえば次の3つのライティング効果は、視点と光源の向きをパラメータとするBRDFのサブセットとして考えることができる。
アンビエントライティングモデルは、視点、光源の方向とは独立に決まるライティング効果の一つである。
ディフューズ反射モデルは、光源の方向によって決まるライティング効果の一つである。
スペキュラー反射モデルは、光源と視点の方向によって決まるライティング効果の一つである。
上記の他にBRDFは、異方性を持つシェーディングモデルや光源の方向に反射するレトロリフレクションモデルなどを表現することができる。
【0017】
汎用のBRDFも最も単純に表現するには、4次元のデータを用いればよい。しかし、産業的に利用しようとするとこのままでは実現コストが高く現実的ではない。BRDFの表現形式は大きく分けて、以下に示すように、物理的な式、経験的な式、近似式などがある。
【0018】
物理的な式
物理的な原理から導き出した式であり、演算が複雑なことが多い。たとえばRorrance−Sparrowモデル、Pren−Nayarモデルなどである。
【0019】
経験的な式
人間が知覚できる顕著な特徴を再現するコンパクトな表現による式であり、見た目上確からしい結果が得られ、演算コストも低い。たとえばフォンシェーディングモデル、ポリノミナルテクスチャマップ(Polynominal Texture Maps:非特許文献1)、LafortuneBRDF(非特許文献2)モデルなどである。
【0020】
近似値、近似式
各種の基底関数を使うものや、テーブル化したデータを使う式である。汎用のBRDFが持つ4次元テーブルをデータ圧縮したと考えられる方法である。たとえばKauztBRDF(非特許文献3)モデル、WaveletはSphrical−Harmonicsを用いたBRDFなどである。
【0021】
LafortuneBRDFモデルは、Generalized Cosine Lobeを用いて定義されるBRDFである。
【0022】
【数2】
【0023】
異方性スペキュラー効果、レトロリフレクション、オフスペキュラー効果などを再現できる。
【0024】
ポリノミナルテクスチャマップは、セルフシャドウ効果が得意なシェーディングモデルである。
【0025】
【数3】
【0026】
専用の測定器を使って撮影した複数枚の画像からモデルのパラメータを得ることができる。
【0027】
Kauzt−BRDFモデルは、Normalized Decompositionを使って4次元のテーブルを2枚の2次元テーブルの乗算で近似したBRDFモデルである。NVIDIA社のプログラマブルピクセルシェーダを使った実装が存在する。金属やプラスティックの質感の再現性は良い。しかし、テーブルを2枚使うため、必要なデータ量は大きい。
【0028】
シフトバリアントBRDF
表面上の位置によって変化するBRDFをシフト−バリアントBRDFまたはBTFという(以下、シフトバリアントBRDFに統一する。)。シフトバリアントBRDFは6次元の関数である。ポリゴンの表面上の位置を表す2次元のパラメータをBRDFに使用したものと考えても良い。
表面上の各位置に異なるBRDFを持つため、一様ではないテクスチャを持つ材質をリアルに表現できる。たとえば、衣服や生地や皮膚を表現するのに適している。
プログラマブルピクセルシェーダでは、BRDFモデルのパラメータをテクスチャマッピングと同様の回路に保持し、そのパラメータをルックアップすることによりBRDFをピクセル単位で変化させることができる。すなわち、シフトバリアントBRDFを実現できる。
【0029】
たとえば、DaubertBRDF(非特許文献4)は、LafortuneBRDFモデルのシフトバリアントBRDF化を試みたものである。
しかし、改良が安易であり、優れた方法とは言えない。シフトバリアント化に関しては、LafortuneBRDFの式のパラメータをテクセルに格納したに過ぎない。LafortuneBRDFの式を評価する座標系がシフトバリアント化されていないため、バンプマップのような表現ができない。視線方向に依存する効果をキューブマップを用いて実現している。しかし、キューブマップを使った実装では、この効果をシフトバリアント化できない。また、セルフシャドウ効果は全く考慮されていない。
【0030】
ポリノミナルテクスチャマップは、上記数3のように6つの項からなる2次元式を使って輝度を計算する。
従来のテクスチャマッピング技術を置き換えることを目指した技術である。各項の6係数をテクセルに格納したテーブルを使えば良い。セルフシャドウ効果が特徴的である。
【0031】
【非特許文献1】
Tom Malzbender, et al., "Polynomial Texture Maps", ComputerGraphics (SIGGAPH2001 Proceedings), pp.519-528 .
【非特許文献2】
E.P.F.Lafortune, et al., "Non-Linear Approximation of Reflectance Functions", ComputerGraphics (SIGGAPH1997 Proceedings), August 1997, pp.117-126 .
【非特許文献3】
J. Kautz, et al., "Interactive Rendering with Arbitrary BRDFsusing Separable Approximations", Proceedings of the 10th Eurographics Workshop on Rendering, pages 281-292, June 1999.
【非特許文献4】
Katja Daubert, et al., "Efficient Cloth Modeling and Rendering", in Rendering Techniques '01 proceedings of the 12th Eurographics Workshop on Rendering 2001, Springer Verlag, Berlin .
【0032】
【発明が解決しようとする課題】
以上述べたような、プログラマブルピクセルシェーダ、BRDF、およびシフトバリアントBRDFについては、以下のような不利益がある。
【0033】
プログラマブルピクセルシェーダは、従来固定的なハードウェア回路だったピクセルシェーダにプログラマビリティを与えて、汎用演算器が持つ柔軟性を与えたものである。
しかし、グラフィックスハードウェアのセールスポイントである演算効率を損なわせないために、効率を優先した汎用化が行われている。
たとえば分岐命令は使えない、命令セットに直交性が無い、データタイプが8ビットに限られる、などの制約を持つ。
【0034】
NVIDIA社のGForceシリーズに実装されたプログラマブルピクセルシェーダでは、ピクセル毎に最大4つのテクスチャマップから4要素からなるテクセルのルックアップと数回の内積や乗算によって計算できるシェーディングモデルを想定した回路構成となっている。
各種のシェーディングモデルを実装できる一方で、実装の効率が悪かったり実装が不可能なシェーディングモデルもある。特に、行列演算を多く含むシェーディングモデルの演算効率は悪い。また、最大4つのテクスチャマップからは最大16要素しか得られず、行列の十分な供給には不十分である。
つまり、将来利用されるであろうシェーディングモデルをできるだけ正確に予測して、効率性と汎用性のバランスが良いハードウェアアーキテクチャを考える必要がある。
【0035】
BRDFの表現形式は多様で、それぞれが特徴を持つ。アプリケーションは、目的に応じたBRDFの表現形式を選択すれば良い。
しかし、効率を優先し、最小限の汎用化を考慮して設計されるグラフィックスハードウェアにとっては、対応するBRDFモデルは最小限でそれによって最大限の効果が得られることが望ましい。この背反する要求をうまく満たす、都合の良いBRDFモデルが必要とされる。
【0036】
また、良いシフトバリアントBRDFを実現するには、高い表現力を持ちかつコンパクトなBRDFの表現モデルが必要にある。
パラメータの少ないBRDFの表現形式は、シフトバリアントBRDF化に向いている。一つのテクセルに割り当てられたパラメータが少ないと、それだけテーブルのサイズが小さくなる。逆に、パラメータが多いと、テーブルサイズが大きくなり、KauztBRDFなどのテーブルを組み合わせたタイプのBRDFはシフトバリアントBRDF化には向かない。
【0037】
本発明は、かかる事情に鑑みてなされたものであり、その目的は、BRDFの演算方式に適し、プログラマブルピクセルシェーダに実装した場合に、多様な表現力と良好な演算効率とを両立させことができ、さらに、シフトバリアントBRDF化に容易に対応するできるコンパクトさを持った画像処理装置およびその方法を提供することにある。
【0038】
【課題を解決するための手段】
上記目的を達成するため、本発明の第1の観点は、描画対象の表面上の一点に入射する光が物体表面で反射される割合を表す関数であるBRDFモデルを適用した処理を行う画像処理装置であって、表面座標系での光源方向を表す光源方向ベクトルと表面座標系での視点方向を表す視点方向ベクトルと表面座標系での法線方向を表す法線方向ベクトルの各ベクトルと、BRDFモデルの特性を決めるパラメータを表す行列を含む2次形式の行列表現で上記BRDFモデルを計算する演算手段を有し、上記演算手段は、上記2次形式の行列表現で計算されるBRDFモデルの特性を決めるパラメータを表す行列を少なくとも1つの要素が0でない小行列に分割して、分割した小行列の2次形式からなる多項式を用いて評価演算する。
【0039】
本発明の第2の観点は、描画対象の表面上の一点に入射する光が物体表面で反射される割合を表す関数であるBRDFモデルを適用した処理を行う画像処理方法であって、演算手段が、表面座標系での光源方向を表す光源方向ベクトルと表面座標系での視点方向を表す視点方向ベクトルと表面座標系での法線方向を表す法線方向ベクトルの各ベクトルと、BRDFモデルの特性を決めるパラメータを表す行列を含む2次形式の行列表現で上記BRDFモデルを計算し、上記計算に際し、演算手段が、上記2次形式の行列表現で計算されるBRDFモデルの特性を決めるパラメータを表す行列を少なくとも1つの要素が0でない小行列に分割して、分割した小行列の2次形式からなる多項式を用いて評価演算する。
【0040】
本発明では、上記光源方向と視点方向と法線方向からなるベクトルは、方向を表す3次元ベクトル、クオータニオン、極座標のいずれかである。
【0041】
また、本発明では、上記光源方向と視点方向と法線方向からなるベクトルは、所定の線形変換を用いて次数を高い次数から低い次数に退化させたものである。
【0042】
また、本発明では、上記光源方向と視点方向と法線方向からなるベクトルは、任意の初等演算、テーブル参照、またはその組み合わせによって、それらのベクトルを変換したものである。
【0044】
また、好適には、上記2次形式を行列とベクトルの乗算後、ベクトル同士の乗算をする手順で計算する。
【0045】
また、単数または複数の上記BRDFモデルの評価結果を加減算、乗算、除算、累乗算、2次形式を選択的に使用して合成する。
【0046】
本発明では、上記BRDFモデルは、2つの異なるベクトルからなる行列演算式と、三角行列を含む2次形式行列とベクトル乗算との和との2つの演算モードを持つ複合演算器によって計算する。
【0050】
また、上記BRDFモデルの特性を決める行列を、あらかじめマテリアルの特性を観測して、またはシミュレーションを行って得た複数のBRDF生データを上記BRDFモデルに代入して得られる複数の多項式からなる方程式を解くことによって得る。
【0051】
また、好適には、光源方向に対応したディフューズ(拡散)の反射率分布が、ハーフベクターの方向に対応したスペキュラーの反射率分布と同じ分布であると仮定することによって得られる対応関係より、ポリノミナルテクスチャマップ(Polynomial Texture Maps )のパラメータから、上記BRDFモデルの特性を決める行列を作る。
【0052】
本発明によれば、たとえば演算手段において、光源方向ベクトルと視点方向ベクトルと法線方向ベクトルからなるベクトルと、BRDFモデルの特性を決める行列を含む2次形式の行列表現で計算されるBRDFモデルに基づいて反射率が計算される。
【0053】
【発明の実施の形態】
以下、図面に関連付けて本発明の実施の形態を詳細に説明する。
本実施形態においては、本発明に係るBRDFモデル評価演算を採用した画像処理装置の構成および機能を説明した後、本発明に係るBRDFモデル、およびその評価演算などについて順を追って詳細に説明する。
【0054】
図1は、本発明に係る画像処理装置の一実施形態を示すブロック図である。
【0055】
本画像処理装置10は、図1に示すように、インプットデバイス部11、ディスプレイ部12、ネットワーク部13、およびコンピュータ部14を有する。
【0056】
インプットデバイス部11は、キーボードやマウス、ジョイスティックなどの入力装置を含み、ユーザがコンピュータ部12に指示したり、情報を入力するために使用する。
【0057】
ディスプレイ部12は、CRT(Cathod Ray Tube)やLCD(Liquid Crystal Device)などの画像表示装置からなり、コンピュータ部14で生成された画像データに応じた画像表示を行う。
【0058】
ネットワーク部13は、LANやインターネットなど多数のコンピュータが相互に接続されている。ネットワーク部13を介してコンピュータ部14は、外部とデータのやり取りを行う。
【0059】
コンピュータ部14は、図1に示すように、CPU部141、メモリ部142、ブリッジ部143、外部入出力部144、外部記憶部145、LANデバイス部146、フレームバッファ部147、およびグラフィックスプロセッサユニット(以下、GPU部という)148を有している。
【0060】
CPU部141は、メモリ部142に格納されたプログラムに従ってコンピュータ全体を制御する。
【0061】
メモリ部142は、CPU部141が高速に読み書きするためのDRAMやSRAMなどの記憶装置で、プログラムやデータを格納する。
【0062】
ブリッジ部143は、CPU部141、GPU部148がメモリ部142や外部入出力部144とデータをやり取りするための接続回路である。
【0063】
外部入出力部144は、インプットデバイス11や外部記憶部145とデータのやり取りをするためのインタフェースであり、USBインタフェースやIDEインタフェース、PCIインタフェースなどを有する。
【0064】
外部記憶部145は、プログラムやデータを格納するハードディスクドライブやCDROMドライブ、MOドライブ、メモリカードなどの大容量の記憶装置である。
【0065】
LANデバイス部146は、外部のネットワークとコンピュータ部14を接続するためのインタフェースである。たとえばLANデバイス部146は、モデムやイーサネット(Ethernet)(登録商標)デバイス等を含む。
【0066】
フレームバッファ部147は、GPU部148が画像などのデータを一時的に記憶するための高速なメモリを有する。
【0067】
GPU部148は、コンピュータグラフィックスの高速描画を支援する装置である。また、GPU部148は、フレームバッファ部147に描画された画像データを外部のディスプレイデバイス142に出力する作業も行う。
【0068】
図2は、図1のGPU部148の具体的な構成例を示すブロック図である。
このGPU部148は、図2に示すように、プロセッサ部1481、RAMDAC1482、インターコネクト部1483、作業メモリ部1484、および算術演算部1485を有する。
【0069】
プロセッサ部1481は、CPU部1451から受け取った手順に従ってレンダリング処理を行う。
【0070】
RAMDAC1482は、フレームバッファ部147に記憶された画像データをディスプレイ12で表示するためにデジタルデータからアナログデータに変換し、変換後のアナログデータをディスプレイ12に出力する。
【0071】
インターコネクト部1483は、GPU部148の内部(プロセッサ部1481、RAMDAC1482、作業メモリ部1484、および算術演算部1485)および外部にある各ブロック(フレームバッファ149やブリッジ部143)間でデータをやり取りするための接続回路である。
【0072】
作業メモリ部1484は、プロセッサ部1481や算術演算部が使用するメモリで、プログラムや一時的な計算結果が記憶される。
【0073】
算術演算部1485は、プロセッサ部1481がBRDFの評価計算を効率良く行うための演算器を有し、複合演算器などを実装する。
【0074】
以上の構成を有するコンピュータ部14は、コンピュータ部14内に格納されたプログラムによって、たとえば図3に示すように、コンピュータ部14の内部、特にCPU部141、GPU部148に論理的な構成が構築される。
この論理ブロック200は、図3に示すように、大きく3段から構成され、幾何演算部201、イメージ合成部202、およびピクセル毎演算部203により構成される。
【0075】
幾何演算部201は、図3に示すように、アプリケーション部2011、カメラ座標変換部2012、透視変換部2013、およびラスタライズ部2014を含む。
【0076】
アプリケーション部2011は、インプットデバイス11からの操作情報に従って所定の情報処理を行い、複数のポリゴンから構成されるシーングラフを生成し、カメラ座標変換部2012、およびイメージ合成部202に出力する。
カメラ座標変換部2012は、各ポリゴンの座標を仮想カメラの座標を基点とした座標系に変換し、透視変換部2013に出力する。
透視変換部2013は、各ポリゴンの座標を仮想カメラの2次元の投影面に投影する。
ラスタライズ部2014は、各ポリゴンをディスプレイ部12の解像度特性に合ったピクセルに分解し、ピクセル毎計算部203に出力する。
【0077】
イメージ合成部202は、図3に示すように、イメージバッファ部2021およびイメージ合成演算部2022を含む。
【0078】
イメージバッファ部2021は、一般的にフレームバッファといわれる画像を記憶保持するために使用されるメモリで、ピクセル毎計算部203の演算結果やイメージ合成演算部2022に演算結果のデータ、ディスプレイ部12に表示するデータを一時的に保持する。
イメージ合成演算部2022は、イメージバッファ部2021に格納された画像データに対して、画像の重み付け合成などのイメージコンポジティング処理を行う(たとえば Foley,COMPUTER GRAPGHICS principles and practice,pp.835,Section17.6 Image Compositing 参照)。
【0079】
ピクセル毎計算部203は、ポリゴンよりも小さい単位のピクセル毎に実行される演算装置で、ラスタライズ部2014で用意した情報に基づいて各ピクセルのライティング計算を行う。
【0080】
ピクセル毎計算部203は、図3に示すように、BRDF演算部2031、ルックアップ部2032、べき乗演算部2033、スケール演算部2034、およびテクスチャマップ2035を含む。
【0081】
BRDF演算部2031は、後で詳述する2次形式を使って定義された本発明に係るBRDFモデルを次のように評価演算する。
【0082】
【数4】
【0083】
ここで、L,Vはラスタライズ部2014から入力した光源と視点の方向を表すベクトルを示す。Nは法線の方向を表す(0,0,1)のベクトルを示す。Mはルックアップ部2032から入力した本発明に係るBRDFの性質を表すパラメータを示す。
【0084】
小行列の全ての要素が0の場合は、その項の値は明らかに0になる、そのときは、その項の演算を省略することができる。
また、複合演算器を使うと、LM21Vと(LM11L+LM31N)と(VM22V+VM32N)が同程度の計算コストを計算できる。これにより、ハードウェア資源の利用効率の向上を図っている。
【0085】
ルックアップ部2032は、ラスタライズ部2014から入力したアドレスに従って各ピクセルに対応したパラメータをテクスチャマップ2035からルックアップする。得られたパラメータはBRDF演算部2031、べき乗演算部2033、およびスケール演算部2034で行い関数演算のパラメータとして使用される。
【0086】
本実施形態においては、後で詳述するように、単一の本発明に係るBRDFで再現しずらい表現を持つBRDFに対応するために、BRDF演算部2031の評価値をべき乗演算部2033やスケール演算部2034で変化させている。
【0087】
べき乗演算部2033は、次式のように、BRDF演算部2031から入力した評価値を累乗する。
【0088】
【数5】
【0089】
スケール演算部2034は、次式のように、べき乗演算部2033から入力した値Powerとラスタライズ部2014から入力した光源の強度LightIntensityとルックアップ部2032から入力したRGB別の反射率Reflectivityを掛け合わせる演算を行う。
【0090】
【数6】
【0091】
スケール演算部2034は、数6に基づいて得られたResultIntensityをイメージバッファ2021に書き込む。
イメージバッファ2021に書き込まれたデータは、イメージ合成演算部2022においてイメージコンポジティング処理により合成される。これの処理により、1ポリゴンをマルチパスレンダリングの手法でシェーディングパラメータを変えながら複数回描画し、それらを合成することで目的のシェーディング結果画像を得ることができる。
【0092】
次に、イメージ合成部を利用した場合の動作例について、図4および図5のフローチャートに関連付けて説明する。
【0093】
本実施形態がイメージ合成部を利用して、一般的にマルチパスレンダリングと称される手法によって、1つのポリゴンに対して複数回のレンダリングを行い、各レンダリング結果をイメージコンポジティング技術の要領で合成し、1つのポリゴンを描画することができる。
この手順を、図4のフローチャートを参照して説明する。
【0094】
ステップST1:マルチパスレンダリング初期化
まず、ステップST1において、マルチパスレンダリングを行うために必要な初期化を行う。たとえば、ポリゴンの描画先のイメージバッファのデータの消去、描画手順や作業内容を表すイメージグラフをセットなどを行う。
【0095】
ステップST2:トラバース
ステップST2において、イメージグラフをトラバースして、1パス分の描画のためのセットアップをする。
【0096】
ステップST3:1パス描画
ステップST3において、幾何演算部201、ピクセル毎演算部203が協調して1パス分のポリゴンをイメージバッファ2021に描画する。
【0097】
ステップST4:イメージ合成
ステップST4において、今ステップや前ステップで描画したポリゴンを合成したり必要な画像処理を行う。
【0098】
ステップST5:マルチパス完了判定
ステップST5において、全てのパス分の描画が完了したかどうかを判定する。マルチパス完了判定で、まだ途中であればステップST2からの処理に戻って、次のパスのセットアップを行い処理を継続し、最後にマルチパスレンダリングを完了させる。
【0099】
上記の手順中、ステップST3における1パス描画のための詳細な手順は図5に示すようになる。
【0100】
ステップST11:カメラ座標変換
まず、ステップST11において、カメラ座標変換部2012によりモデル座標系のポリゴンをカメラ座標系に変換する。
【0101】
ステップST12:透視変換
ステップST12において、透視変換部2013によりポリゴンをスクリーン座標に投影する。
【0102】
ステップST13:内挿パラメータ初期化
ステップST13において、ラスタライズ部2014によりテクスチャアドレス、光源方向、視点方向などポリゴン内の各ピクセルについて内挿補間して求める値の初期化をする。
【0103】
ステップST14:内挿パラメータ補間
次に、ステップST14において、ラスタライズ部2014によりテクスチャアドレス、光源方向、視点方向などを各ピクセル毎に補間して求める。
【0104】
ステップST15:テクスチャルックアップ
ステップST15において、ルックアップ部2032によりテクスチャアドレスに従って、テクスチャデータからテクセルの値をルックアップする。
【0105】
ステップST16:BRDF計算
次に、ステップST16において、BRDF演算部2031で本発明に係るBRDFモデルを評価演算する。
【0106】
ステップST17:べき乗計算
ステップST17において、べき乗演算部2033で、前ステップST16で得られた評価結果をべき乗する。
【0107】
ステップST18:スケール計算
ステップST18において、スケール演算部2034で前ステップST17で得られた結果をスケーリングする。
【0108】
ステップST19:イメージバッファに書き込み
ステップST19において、前ステップST18で得られた結果をイメージバッファ2021に書き込む。
【0109】
ステップST20:ラスタライズ完了判定
ステップST20において、ラスタライズが完了したか否かの判定を行い、全てのポリゴン内の全てのピクセルを描画するまでステップST14からの処理を繰り返す。
【0110】
次に、本発明に係るBRDFモデル、およびその評価演算などについて順を追って詳細に説明する。
【0111】
2次形式を用いたBRDFモデル化
本実施形態においては、BRDFを2次形式(Quadratic-form)を使い次のようにモデル化する(以下、このモデルを、本発明BRDFモデルと呼ぶ。)。
【0112】
【数7】
【0113】
ここで、行列Mは本発明BRDFモデルの特性を決めるパラメータである。式の性質上、任意のMは対称行列または三角行列に簡略化できる。また、Lは表面座標系での光源方向を表すベクトルを示す。Vは表面座標系での視点方向を表すベクトルを示す。Nは表面座標系での法線方向を表すベクトルを示す。
本発明BRDFモデルは、上記L,V,Nを並べて構成されるベクトル〔LVN〕を用いる。
たとえば、各L,V,Nは、それぞれの方向を表した3次元の単位ベクトルで良い。これを具体的に書くと以下のようになる。
【0114】
【数8】
【0115】
また、各L,V,Nは、他のベクトル空間を用いて表したベクトルでも良い。たとえば、極座標系やクオータニオン(Quaternion)など一般的な座標系を用いても良いし、他の特殊な座標系を使っても良い。
また、適当な線形変換を用いて次数を退化させても良い。その他、任意の初等演算やテーブル参照、またはその組み合わせによって、それらのベクトルを変換したものであってもよい。以下の例は、3次元ベクトルのL,Vを2次元に退化させたものと、Nを定数1に変換したものを使用している。
【0116】
【数9】
【0117】
計算方法の詳細
本発明BRDFモデルは、以下のようにモデルのパラメータを表す行列を小行列に分割して、それらの小行列からなる多項式を用いて評価演算することもできる。
【0118】
【数10】
【0119】
小行列Mnnが零行列なら、その項は明らかに値が0となる。つまり、その項の計算を省略することができる。実際の実装では、必要な項だけ実装するほうが効率がよい。
次の行列表現は以下のように計算すると、必要な乗算器の数が軽減できる。
【0120】
【数11】
【0121】
行列とベクトルの乗算の後、ベクトル同士の乗算をする手順で計算でき、乗算12回と加算8回となる。
一方、同式は以下のように各項を展開した形式にもなるが、この場合、乗算18回と加算8回が必要となる。
【0122】
【数12】
【0123】
結果、前者(数11)の方法で計算したほうが、効率が良い。
以上のように、本発明BRDFは積和演算だけで構成される。また、ベクトルや行列により構成される式なので、効率の良い演算が可能である。
【0124】
本発明BRDFのシェーディング効果
本発明BRDFのシェーディング効果はパラメータMによって決まる。以下、シェーディング効果とパラメータの対応関係を説明する。
パラメータMの中の0は零行列、Mnnは少なくとも1つの要素が0でない小行列である。
【0125】
アンビエントライティング効果は、光源方向と視点方向に非依存の効果を意味する。ディフューズ反射効果は光源方向に依存で視点方向には非依存の効果を意味する。スペキュラー反射効果は、光源方向と視点方向に依存の効果を意味する。それぞれ、以下のように一つ以上の零行列ではない小行列をもつパラメータMで表現できる。
【0126】
アンビエントライティング効果パラメータ:
【0127】
【数13】
【0128】
ディフューズ反射効果パラメータ:
【0129】
【数14】
【0130】
スペキュラー反射効果パラメータ:
【0131】
【数15】
【0132】
光源方向依存効果パラメータ:
【0133】
【数16】
【0134】
視点方向依存効果パラメータ:
【0135】
【数17】
【0136】
全効果パラメータ:
【0137】
【数18】
【0138】
従来モデルとの対応
本発明BRDFは、従来から良く知られているシェーディングモデルを包含する効果をもつ。
以下に、従来のモデルの表記と本発明BRDFにおけるパラメータの詳細との対応を記す。
【0139】
アンビエントライティングモデル k a :
【0140】
【数19】
【0141】
ディフュー反射モデル k a (N・L):
【0142】
【数20】
【0143】
フォン反射モデル k s (V・L) n :
(フォンモデルのn乗にあわせて、本発明BRDFの評価結果もn乗する。)
【0144】
【数21】
【0145】
LafortuneBRDF
ρ s 〔C x u x v x +C y u y v y +C z u z v z 〕 n :
(Lafortune BRDFのn乗とρs 倍にあわせて、本発明BRDFの評価結果もn乗、ρs 倍する。)
【0146】
【数22】
【0147】
ポリノミナルテクスチャマップ
a 0 l u 2 +a 1 l v 2 +a 1 l u l v +a 3 l u +a 4 l v +a 5 :
【0148】
【数23】
【0149】
以上のように、本発明BRDFを用いると、従来の各種シェーディングモデルと同等のモデルをパラメータの適切な設定で実現し、それらの効果を表現できる。さらにこれらの設定を組み合わせて複合した効果や、これらの効果を包含した効果を発現させることもできる。
【0150】
視点方向依存効果が不要な場合
視点方向依存効果が不要なとき、本発明BRDFを以下のように変形してもよい。
【0151】
【数24】
【0152】
上記の式は、従来法のLafortuneBRDFとポリノミナルテクスチャマップ(Polynomial Texture Maps )の2つのモデルにより表現できる効果を少なくとも含んでいる。M21がLafortuneBRDFに対応し、M11,M31,M33がポリノミナルテクスチャマップに対応することは以前に説明したが、これらの2つのモデルの小行列のセットからパラメータ行列Mが成り立っていることがわかる。
しかも、これらのモデルに対応する小行列が互いに排他的な位置を占めるため、お互いの効果は独立していると考えられる。つまり、この変形型本発明BRDFは、ポリノミナルテクスチャマップ(Polynomial Texture Maps )とLafortuneBRDFとが持つ相補的な効果を包含した効果を少なくとも持ち、かつそれぞれの効果を独立にコントロールできる特徴をもつ。
【0153】
単一の本発明BRDFで再現しづらい表現をもつBRDFに対応するための方法単一の本発明BRDFで再現しづらい表現をもつBRDFに対しては、単数または複数の本発明BRDFの評価結果を各種演算によって合成し、目的のBRDFを作り出せばよい。
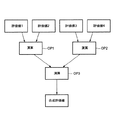
たとえば、各本発明BRDFの出力を末端ノードにして、図6に示すように、各種演算器OP1〜OP3を中間ノードとしたツリーを作り、ルートノードの出力を目的のBRDFの値とする。各種演算器OP1〜OP3は、加減算、乗算、除算、累乗算、2次形式などの演算器を選択的に使用する。
【0154】
たとえば、PhongシェーディングやLafortuneのBRDFで使うスペキュラー反射の指向性を制御したい場合は、以下のように本発明BRDFの評価結果をn-1乗(またはn乗)すると良い。
【0155】
【数25】
【0156】
セルフシャドウやビューディペンデント効果をよりはっきり出したいときは、以下のように異なるパラメータを持つ本発明BRDFモデルの評価結果を掛け合わせると良い。
【0157】
【数26】
【0158】
また、本発明BRDFモデルの評価で使用する22 次形式の行列演算器を流用してもよい。以下の式のように、異なる本発明BRDFモデルの評価結果を合成することもできる。
【0159】
【数27】
【0160】
ここで、quadBRDF2 ,quadBRDF3 は、それぞれ異なる本発明BRDFモデルの評価結果を示し、BRDF1 はその合成結果を示している。
【0161】
三角行列と行列の同時計算
本発明BRDFの評価演算を効率よく行うため、次のように、本発明BRDFを小行列からなる複数の項に分解した形式を用いることができることは既に述べた。
【0162】
【数28】
【0163】
このうち、LM21Vと(LM11L+LM31N)と(VM22V+VM32N)は、同量の演算器の組み合わせによって計算できるため、これら3種の演算を選択的に演算できる複合演算器を作ると実装効率が良い。
上記3種の演算を詳しく見てみる。
【0164】
まず、次の2つの異なるベクトルから成る行列演算式LM21Vは、乗算12回と加算8回から構成される。
【0165】
【数29】
【0166】
次に、次の三角行列から成る2次形式行列とベクトル乗算との和(LM21L+LM31N)は、それぞれ乗算9回と加算5回、乗算3回と加算2回、からなる2項を足し合わせた、乗算12回と加算8回の演算となる。
【0167】
【数30】
【0168】
また、演算(VM22V+VM32N)についても、上記と同様に乗算12回と加算8回の演算とからなる。
つまり3種の演算、LM21Vと(LM11L+LM31N)と(VM22V+VM32N)は、同量の計算器の組み合わせを使う2種の第1モードおよび第2モードを持った図7に示すような複合演算器COP1,COP2によって、これら3種からどれか一つを選択して演算すれば良い。
【0169】
図8は、図7を実現するための演算回路例を示す図である。
この演算回路300は、図8に示すように、乗算器301〜311、加算器312〜317、およびレジスタ318〜322をツリー状に接続して構成されている。
この演算回路300は、第1モード、第2モードで動作可能である。
第1モードでは、加算器313,317、レジスタ318,320,322を除く回路構成で演算を行う。
第2モードでは、乗算器304の加算器314への出力、乗算器308の加算器3154への出力、およびレジスタ321を除く回路構成で演算を行う。
このように、演算回路300は、一部の配線を変更するだけ、第1モードと第2モードの演算を同じ演算回路を用いて実現できる。
【0170】
シフトバリアント( Shift-variant )BRDF
図9に示すように、行列Mをテクセルとするテクスチャマップをつくる。実行時にテクスチャマップから行列Mをルックアップして、本発明BRDFのパラメータとして使用する。
この場合、BRDF評価演算部401に対してテクスチャマップ402から行列MをMを供給し、インタポレータ403からベクトルL,V,Nを供給する。そして、BRDF評価演算部401の演算結果をフレームバッファ404に格納する。
【0171】
描画しようとする表面がビュー座標系に対してスケーリングするために生じるテクスチャマップのサンプリング問題は、従来の方法と同様に本発明BRDFのパラメータをMIPMAP(複数解像度テクスチャ)化すればよい。
下式は、パラメータm11-99 を表面上のパッチΩについてnサンプルするとき、そのパッチ領域について計算した本発明BRDFを平均化した値と、同じパッチ領域について平均化したパラメータを用いて本発明BRDFを計算した結果が等しいことを表している。
【0172】
【数31】
【0173】
つまり、従来のMIPMAP技術やBi−Linear,Tri−Linearフィルタリング技術を使えば上記のサンプリング問題は解決できる。
【0174】
インデックスマップを利用したパラメータの取得とべき乗計算の方法
従来のテクスチャマッピングで使われてきたインデックスカラーの技術を応用して、本発明BRDFモデルのパラメータとべき乗計算のための変換テーブルをインデックス化したテーブルに持ち、それを参照することも考えられる。
【0175】
図10は、インデックスマップを利用した場合の論理回路構成を示す図である。図10は、上述した具体的な実施形態において説明した図3の論理ブロック200に対応し、さらに一般化した構成を有する。
図10において、500がインデックスマップを、501がラスタライズ部を、502がルックアップ部を、503がパラメータリストを、504がBRDF演算部を、505がべき乗リスト部を、506がべき乗処理部を、507がスケール処理部をそれぞれ示している。
【0176】
描画オブジェクトの表面上の位置に対応するインデックスをインデックスマップ500からルックアップ部502でルックアップし、そのインデックスに対応したパラメータとべき乗リストを得る。得られたパラメータは、本発明BRDFの計算に使われる。本発明BRDFの評価結果のべき乗値は、その評価結果値に対応した値をべき乗リストから参照し、適当な補間を行った結果が目的のべき乗値となる。
【0177】
本発明BRDFのパラメータ算出方法
図11に示すように、実世界にある布や皮膚など対象となるマテリアルの特性を特別な装置で観測して得たBRDF生データや、それらのマテリアルの反射特性をシミュレーションによって計算した結果得たBRDF生データから、本発明BRDFで使用するパラメータを得ることができる。
【0178】
以下に、BRDF生データから本発明BRDFで使用するパラメータを求める方法を説明する。
光源方向L(k) 、視点方向V(k) に対応した生BRDFデータである反射率r(k) が分かっているとき、パラメータMを未知数として本発明BRDFモデルに当てはめる。
【0179】
【数32】
【0180】
この式を展開すると次のような多項式が得られる。
【数33】
【0181】
ここで、w(k),11-99 はL(k) 、V(k) 、Nから得られる未知数m11-99 に対応する乗数である。
【0182】
観測データがn通り存在するとき、n通りの上式からなる方程式が得られる。これらのn通りの式をもっとも良く満たす係数m11-99 を求めれば、すなわちパラメータMが求められる。
これを求めるには、上記式の両辺の値の差の2乗の平均ができるだけ小さくなるようにする最小二乗近似法などを使えばよい。
【0183】
ポリノミナルテクスチャマップ( Polynomial Texture Maps )用パラメータから簡易的にスペキュラー成分を作り出す方法
ポリノミナルテクスチャマップのパラメータから、本発明BRDFで使えるスペキュラー成分の効果を簡易的に作り出すことができる。
まず、以下の2つの分布が同一だと仮定する(図12参照)。
すなわち、光源方向に対応しディフューズの反射率分布およびハーフベクターの方向に対応したスペキュラーの反射率分布の2つである。
この仮定より、スペキュラー成分を持つ効果は以下の式で作り出せる。
【0184】
【数34】
【0185】
ここで、PTMはポリノミナルテクスチャマップモデルの評価式である。
【0186】
上記式の右辺第2 項を詳しく書くと以下のようになる。
【0187】
【数35】
【0188】
この式を本発明BRDFのパラメータ行列に当てはめると以下のようになる。
【0189】
【数36】
【0190】
上記のままではポリノミナルテクスチャマップにハーフベクターを与えた効果と同一である。
しかし、上記パラメータから得られる擬似的な法線方向などを利用して適当な変化をパラメータに与えると異方性などの効果が得られる可能性がある。この点で本発明BRDFモデルの方が今後の効果拡張に有利である。
以上をまとめて、簡易スペキュラー効果を使った評価結果は以下のような式で求められる。
【0191】
【数37】
【0192】
以上説明したように、本発明BRDFモデルは従来のシェーディングモデルが持つ効果を組み合わせても得られない効果を持つ。
「従来モデルとの対応」節において、従来のシェーディングアルゴリズムであるLafortuneBRDFやポリノミナルテクスチャマップ(Polynomial Texture Maps )等と本発明BRDFモデルとの対応関係を説明している。ここの説明に従って適当なパラメータMを決定すれば、従来のシェーディング技術と同等の効果を本発明BRDFモデルで表現できる。
色工学において、異なる光の効果を重ね合わせるためには個々の光の効果を加算すればよいことが一般的に知られている。本発明BRDFモデルは線形性を有し、異なるパラメータMを足し合わせることで効果を重ね合わせることができる。
しかし、従来のシェーディングアルゴリズムに対応したパラメータMを重み付け加算していかに合成しても、本発明BRDFモデルのパラメータMの空間をすべて満たすことはできない。
したがって、本発明BRDFモデルは従来のシェーディングモデルにはない、新しい効果を持つ。
【0193】
また、本発明のアルゴリズムを従来回路に基づいて設計した場合について考察する。
汎用の演算器と比較すると、図7の演算器(具体的には図8)は本発明BRDFに特有の2つの演算モードを効率よく処理できるよう特化されている。したがって汎用の演算器でこれを処理するよりも効率よく処理できる。
また、特殊演算器であるNVIDIAのグラフィックスプロセッサがもつ特殊な演算器であるレジスタコンバイナと比較する。
図16よりも詳細なレジスタコンバイナ内部の構成は不明である。しかし、図16の詳細度で考察しても、レジスタコンバイナの非効率さは明らかである。
図13は、図16のレジスタコンバイナを用いて、図7の第1モードの機能を実現したものである。
また、図14は図16のレジスタコンバイナを用いて、図7の第2モードの機能を実現したものである。この場合3つのレジスタコンバイナCMB1〜CMB3を3段に組み合わせる必要がある。
3段のうち最初の2段の演算は同時刻に演算できるにもかかわらず、2段に分けて演算せざるを得ないため計算の遅延が大きい。また、第1モードでは3つのうち2つのレジスタコンバイナ内の演算回路の利用効率が半減している。
第2モードでも3つのうち1つのレジスタコンバイナ内の演算回路の利用効率が半減している。
よって、本発明BRDFモデルを従来技術であるレジスタコンバイナで演算することは非効率である。
【0194】
以上のように、本実施形態によれば、本発明BRDFは、従来からリアルタイム用途で使われる多くのシェーディングモデルを一般化したモデルなので、従来モデルと同等の効果を表現できる。さらに、このモデルが持つ独自効果を表現することができる。
また、衣服や皮膚などのリアルな素材を観測、またはシミュレーションによって求めたBRDF生データから、本発明BRDFモデル用のパラメータを生成することができる。また、ポリノミナルテクスチャマップ(Polynomial Texture Maps )などの従来モデルのパラメータを材料にして本発明BRDFのパラメータを得ることもできる。
また、本発明BRDFは、BRDFを2次形式行列表現でモデル化したものである。モデルの評価は積和計算だけで行える。本発明BRDFを小行列からなる多項式の形式に分解すると、不要な項の計算は省略できる。こうすることで、表現力と計算効率のトレードオフの関係を調整することができる。
また、ベクトルや行列により構成されるモデルなので、ベクトル演算器を使用して効率よく演算できる。
【0195】
さらに、従来のテーブル参照を多用したBRDF表現などに比べるとコンパクトな表現形式をもつ。また、表現力と計算効率のトレードオフの関係は調節できるため、さらにコンパクトな表現形式で計算することもできる。
このようなコンパクトさを持つため、テクスチャマッピング技術と組み合わせて、シフト−バリアント(Shift-variant )化することが容易である。モデルのパラメータMをテーブルに格納し、実行時にルックアップすれば良い。
【0196】
BRDFを2次形式行列表現でモデル化したため、一般的なベクトル・行列演算に特化したハードウェアであれば、このモデルを効率よく評価することができる。本発明BRDFはモデルの評価に特殊な回路を必要としないことも特徴である。しかし、既に説明した複合演算器があれば、この本発明BRDFをさらに効率よく演算できる。
【0197】
【発明の効果】
以上説明したように、本発明によれば、従来からリアルタイム用途で使われているシェーディングモデルを一般化したモデルを採用していることから、従来モデルと同等の効果を発現できる。さらに、このモデルが持つ独自効果を表現することができる。
衣服や皮膚などのリアルな素材を観測、またはシミュレーションによって求めたBRDF生データから、本発明に係るBRDFモデル用のパラメータを生成することができる。また、ポリノミナルテクスチャマップ(Polynominal Texture Maps)などの従来モデルのパラメータを材料にして本発明に係るBRDFのパラメータを得ることもできる。
【0198】
本発明に係るBRDFは、BRDFを2次形式行列表現でモデル化したものであり、モデルの評価は積和演算だけで行える。本発明に係るBRDFを小行列からなる多項式の形式に分解すると、不要な項の計算は省略できる。これにより、表現力と演算効率のトレードオフの関係を調整することができる。
ベクトルや行列により構成されるモデルであることから、ベクトル演算器を使用して効率良く演算することができる。
【0199】
従来のテーブル参照を多用したBRDF表現などに比べるとコンパクトな表現形式を持つ。また、表現力と演算効率のトレードオフの関係は調整できるため、さらにコンパクトな表現形式で演算することもできる。
上記のようなコンパクトさを持つため、テクスチャマッピング技術と組み合わせてシフトバリアント(Shifts−variant)化することが容易である。モデルのパラメータMをテーブルに格納し、実行時にルックアップすれば良い。
【0200】
BRDFを2次形式行列表現でモデル化したため、一般的なベクトル・行列演算に特化したハードウェアであれば、このモデルを効率良く評価することができる。本発明に係るBRDFはモデルの評価に特殊な回路を必要としない。しかし、既に説明した複合演算器があれば、本発明に係るBRDFをさらに効率良く演算することができる。
【図面の簡単な説明】
【図1】 本発明に係る画像処理装置の一実施形態を示すブロック図である。
【図2】 図1のGPU部の具体的な構成例を示すブロック図である。
【図3】 本実施形態に係るコンピュータ部に格納されたプログラムによって、構築された論理ブロックの構成例を示す図である。
【図4】 イメージ合成部を利用した場合の動作例について説明するためのフローチャートである。
【図5】 図4のステップST3における1パス描画のための詳細な手順を説明するためのフローチャートである。
【図6】 単一の本発明BRDFで再現しづらい表現をもつBRDFに対応するための方法を説明するための図である。
【図7】 本発明BRDFの評価演算を効率よく行うための好適な演算器例を説明するための図である。
【図8】 図7を実現するための演算回路例を示す図である。
【図9】 行列Mをテクセルとするテクスチャマップをつくり、実行時にテクスチャマップから行列Mをルックアップして、本発明BRDFのパラメータとして使用する例を説明するための図である。
【図10】 インデックスマップを利用した場合の論理回路構成を示す図である。
【図11】 本発明BRDFのパラメータ算出方法を説明するための図である。
【図12】 光源方向に対応しディフューズの反射率分布およびハーフベクターの方向に対応したスペキュラーの反射率分布の2つが同一であるという仮定を説明するための図である。
【図13】 図16のレジスタコンバイナを用いて、図7の第1モードの機能を実現した場合の構成例を示す図である。
【図14】 図16のレジスタコンバイナを用いて、図7の第2モードの機能を実現した場合の構成例を示す図である。
【図15】 従来のプログラマブルピクセルシェーダの仕組みを説明するための図である。
【図16】 図15のピクセルALUの具体的な構成を示す図である。
【符号の説明】
10…画像処理装置、11…インプットデバイス部、12…ディスプレイ部、13…ネットワーク部、14…コンピュータ部、141…CPU部、142…メモリ部、143…ブリッジ部、144…外部入出力部、145…外部記憶部、146…LANデバイス部、147…フレームバッファ部、148…グラフィックスプロセッサユニット(GPU部),1481…プロセッサ部、1482…RAMDAC、1483…インターコネクト部、1484…作業メモリ部、1485…算術演算部、200…論理ブロック、201…幾何演算部、幾何演算部2011…アプリケーション部、2012…カメラ座標変換部、2013…透視変換部、2014…ラスタライズ部、202…イメージ合成部、2021…イメージバッファ部、2022…イメージ合成演算部、203…ピクセル毎演算部、2031…BRDF演算部、2032…ルックアップ部、2033…べき乗演算部、2034…スケール演算部、2035…テクスチャマップ。
Claims (10)
- 描画対象の表面上の一点に入射する光が物体表面で反射される割合を表す関数であるBRDFモデルを適用した処理を行う画像処理装置であって、
表面座標系での光源方向を表す光源方向ベクトルと表面座標系での視点方向を表す視点方向ベクトルと表面座標系での法線方向を表す法線方向ベクトルの各ベクトルと、BRDFモデルの特性を決めるパラメータを表す行列を含む2次形式の行列表現で上記BRDFモデルを計算する演算手段を有し、
上記演算手段は、
上記2次形式の行列表現で計算されるBRDFモデルの特性を決めるパラメータを表す行列を少なくとも1つの要素が0でない小行列に分割して、分割した小行列の2次形式からなる多項式を用いて評価演算する
画像処理装置。 - 上記光源方向と視点方向と法線方向からなるベクトルは、方向を表す3次元ベクトル、クオータニオン、極座標のいずれかである
請求項1記載の画像処理装置。 - 上記光源方向と視点方向と法線方向からなるベクトルは、所定の線形変換を用いて次数を高い次数から低い次数に退化させたものである
請求項1記載の画像処理装置。 - 上記光源方向と視点方向と法線方向からなるベクトルは、任意の初等演算、テーブル参照、またはその組み合わせによって、それらのベクトルを変換したものである
請求項1記載の画像処理装置。 - 上記演算手段は、上記2次形式は行列とベクトルの乗算後、ベクトル同士の乗算をする手順で計算する
請求項1記載の画像処理装置。 - 単数または複数の上記BRDFモデルの評価結果を加減算、乗算、除算、累乗算、2次形式を選択的に使用して合成する
請求項1記載の画像処理装置。 - 上記演算手段は、2つの異なるベクトルからなる行列演算式と、三角行列を含む2次形式行列とベクトル乗算との和との2つの演算モードを持ち、上記BRDFモデルを計算する複合演算器を有する
請求項1記載の画像処理装置。 - 上記演算手段は、上記BRDFモデルの特性を決める行列を、あらかじめマテリアルの特性を観測して、またはシミュレーションを行って得た複数のBRDF生データを上記BRDFモデルに代入して得られる複数の多項式からなる方程式を解くことによって得る
請求項1記載の画像処理装置。 - 上記演算手段は、光源方向に対応したディフューズ(拡散)の反射率分布が、ハーフベクターの方向に対応したスペキュラーの反射率分布と同じ分布であると仮定することによって得られる対応関係より、ポリノミナルテクスチャマップ(Polynomial Texture Maps)のパラメータから、上記BRDFモデルの特性を決める行列を作る
請求項1記載の画像処理装置。 - 描画対象の表面上の一点に入射する光が物体表面で反射される割合を表す関数であるBRDFモデルを適用した処理を行う画像処理方法であって、
演算手段が、表面座標系での光源方向を表す光源方向ベクトルと表面座標系での視点方向を表す視点方向ベクトルと表面座標系での法線方向を表す法線方向ベクトルの各ベクトルと、BRDFモデルの特性を決めるパラメータを表す行列を含む2次形式の行列表現で上記BRDFモデルを計算し、
上記計算に際し、演算手段が、
上記2次形式の行列表現で計算されるBRDFモデルの特性を決めるパラメータを表 す行列を少なくとも1つの要素が0でない小行列に分割して、分割した小行列の2次形式からなる多項式を用いて評価演算する
画像処理方法。
Priority Applications (2)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| JP2002286326A JP3972784B2 (ja) | 2002-09-30 | 2002-09-30 | 画像処理装置およびその方法 |
| US10/672,381 US7256781B2 (en) | 2002-09-30 | 2003-09-26 | Image processing apparatus and method of same |
Applications Claiming Priority (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| JP2002286326A JP3972784B2 (ja) | 2002-09-30 | 2002-09-30 | 画像処理装置およびその方法 |
Publications (3)
| Publication Number | Publication Date |
|---|---|
| JP2004126692A JP2004126692A (ja) | 2004-04-22 |
| JP2004126692A5 JP2004126692A5 (ja) | 2005-04-07 |
| JP3972784B2 true JP3972784B2 (ja) | 2007-09-05 |
Family
ID=32025368
Family Applications (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| JP2002286326A Expired - Fee Related JP3972784B2 (ja) | 2002-09-30 | 2002-09-30 | 画像処理装置およびその方法 |
Country Status (2)
| Country | Link |
|---|---|
| US (1) | US7256781B2 (ja) |
| JP (1) | JP3972784B2 (ja) |
Families Citing this family (31)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| JP2004152015A (ja) * | 2002-10-30 | 2004-05-27 | Digital Fashion Ltd | 画像処理装置、画像処理プログラム、そのプログラムを記録する記録媒体、画像処理方法、シェーディング情報取得装置及びデータ構造 |
| US20040169656A1 (en) * | 2002-11-15 | 2004-09-02 | David Piponi Daniele Paolo | Method for motion simulation of an articulated figure using animation input |
| US20060017729A1 (en) * | 2004-07-22 | 2006-01-26 | International Business Machines Corporation | Method to improve photorealistic 3D rendering of dynamic viewing angle by embedding shading results into the model surface representation |
| US7324106B1 (en) * | 2004-07-27 | 2008-01-29 | Nvidia Corporation | Translation of register-combiner state into shader microcode |
| JP4162245B2 (ja) * | 2005-02-23 | 2008-10-08 | ニチハ株式会社 | 建築材設計支援システム、建築材及びプログラム |
| JP2006279227A (ja) * | 2005-03-28 | 2006-10-12 | Fuji Xerox Co Ltd | 撮像装置 |
| JP4462132B2 (ja) | 2005-07-04 | 2010-05-12 | ソニー株式会社 | 画像特殊効果装置,グラフィックスプロセッサ,プログラム |
| WO2007063586A1 (ja) * | 2005-11-30 | 2007-06-07 | Fujitsu Limited | 3次元グラフィック装置、3次元グラフィック方法、3次元グラフィックプログラム、および記録媒体 |
| JP4782583B2 (ja) * | 2006-02-23 | 2011-09-28 | 株式会社バンダイナムコゲームス | プログラム、情報記憶媒体及び画像生成システム |
| JP4734137B2 (ja) * | 2006-02-23 | 2011-07-27 | 株式会社バンダイナムコゲームス | プログラム、情報記憶媒体及び画像生成システム |
| JP4734138B2 (ja) * | 2006-02-23 | 2011-07-27 | 株式会社バンダイナムコゲームス | プログラム、情報記憶媒体及び画像生成システム |
| JP4031509B1 (ja) * | 2006-09-21 | 2008-01-09 | 株式会社コナミデジタルエンタテインメント | 画像処理装置、画像処理装置の制御方法及びプログラム |
| JP4808600B2 (ja) * | 2006-11-22 | 2011-11-02 | デジタルファッション株式会社 | レンダリングプログラム、レンダリング装置、及びレンダリング方法 |
| US7979814B1 (en) * | 2007-03-12 | 2011-07-12 | ProPlus Design Solutions, Inc. | Model implementation on GPU |
| US20080236014A1 (en) * | 2007-03-29 | 2008-10-02 | Kinpo Electronics, Inc. | Autorotative digital photo frame |
| US20080252652A1 (en) * | 2007-04-13 | 2008-10-16 | Guofang Jiao | Programmable graphics processing element |
| US8306367B2 (en) * | 2007-06-08 | 2012-11-06 | Apple Inc. | Method and apparatus for managing image-processing operations |
| US8325184B2 (en) * | 2007-09-14 | 2012-12-04 | Qualcomm Incorporated | Fragment shader bypass in a graphics processing unit, and apparatus and method thereof |
| KR101582607B1 (ko) * | 2009-04-30 | 2016-01-19 | 삼성전자주식회사 | 반도체 메모리 장치 |
| US9098945B2 (en) * | 2009-05-01 | 2015-08-04 | Microsoft Technology Licensing, Llc | Modeling anisotropic surface reflectance with microfacet synthesis |
| US8248613B2 (en) | 2010-04-29 | 2012-08-21 | Microsoft Corporation | Capturing reflected light from a sampling surface |
| JP5591017B2 (ja) | 2010-08-09 | 2014-09-17 | キヤノン株式会社 | 画像処理装置および画像処理方法 |
| KR101871222B1 (ko) | 2013-02-01 | 2018-06-27 | 삼성전자주식회사 | 영상 처리 장치 및 방법 |
| JP5898109B2 (ja) * | 2013-02-25 | 2016-04-06 | 日本電信電話株式会社 | 画像合成装置、画像合成方法及び画像合成プログラム |
| EP3057067B1 (en) * | 2015-02-16 | 2017-08-23 | Thomson Licensing | Device and method for estimating a glossy part of radiation |
| JP6617432B2 (ja) * | 2015-04-13 | 2019-12-11 | 富士ゼロックス株式会社 | 画像処理装置及びプログラム |
| US11373272B2 (en) | 2015-06-05 | 2022-06-28 | MindAptiv, LLC | Digital gradient signal processing system and method for signals comprising at least three dimensions |
| US10037592B2 (en) | 2015-06-05 | 2018-07-31 | Mindaptiv LLC | Digital quaternion logarithm signal processing system and method for images and other data types |
| US10740957B1 (en) * | 2018-06-14 | 2020-08-11 | Kilburn Live, Llc | Dynamic split screen |
| US10573060B1 (en) * | 2018-06-14 | 2020-02-25 | Kilburn Live, Llc | Controller binding in virtual domes |
| CN111489448B (zh) * | 2019-01-24 | 2024-08-20 | 宏达国际电子股份有限公司 | 检测真实世界光源的方法、混合实境系统及记录介质 |
Family Cites Families (2)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US6858826B2 (en) * | 1996-10-25 | 2005-02-22 | Waveworx Inc. | Method and apparatus for scanning three-dimensional objects |
| GB2367471B (en) * | 2000-09-29 | 2002-08-14 | Pixelfusion Ltd | Graphics system |
-
2002
- 2002-09-30 JP JP2002286326A patent/JP3972784B2/ja not_active Expired - Fee Related
-
2003
- 2003-09-26 US US10/672,381 patent/US7256781B2/en not_active Expired - Fee Related
Also Published As
| Publication number | Publication date |
|---|---|
| JP2004126692A (ja) | 2004-04-22 |
| US7256781B2 (en) | 2007-08-14 |
| US20040061700A1 (en) | 2004-04-01 |
Similar Documents
| Publication | Publication Date | Title |
|---|---|---|
| JP3972784B2 (ja) | 画像処理装置およびその方法 | |
| US6417858B1 (en) | Processor for geometry transformations and lighting calculations | |
| JP3294149B2 (ja) | 立体テクスチャマッピング処理装置及びそれを用いた3次元画像生成装置 | |
| JP3021368B2 (ja) | 画素の法線ベクトルを用いたバンプマッピングレンダリング方法及びそれを具現するレンダリング装置 | |
| US8648856B2 (en) | Omnidirectional shadow texture mapping | |
| US6825851B1 (en) | Method and apparatus for environment-mapped bump-mapping in a graphics system | |
| US7088362B2 (en) | Graphic computing apparatus | |
| US6275235B1 (en) | High precision texture wrapping method and device | |
| US7212206B2 (en) | Method and apparatus for self shadowing and self interreflection light capture | |
| Welsh | Parallax mapping with offset limiting: A per-pixel approximation of uneven surfaces | |
| US20050237337A1 (en) | Method and apparatus for interleaved processing of direct and indirect texture coordinates in a graphics system | |
| US7843463B1 (en) | System and method for bump mapping setup | |
| JP2000227966A (ja) | 3dコンピュ―タ・グラフィックス処理装置及び方法 | |
| Li et al. | Chameleon: An interactive texture-based rendering framework for visualizing three-dimensional vector fields | |
| US7576746B1 (en) | Methods and systems for rendering computer graphics | |
| US7071937B1 (en) | Dirt map method and apparatus for graphic display system | |
| JP2003296750A (ja) | 低周波数ライティング環境の放射輝度自己伝達を用いたグラフィック画像レンダリング | |
| WO1996028794A1 (fr) | Dispositif d'affichage graphique tridimensionnel | |
| Nijasure et al. | Real-time global illumination on gpus | |
| US20090284524A1 (en) | Optimized Graphical Calculation Performance by Removing Divide Requirements | |
| JP2006517705A (ja) | コンピュータグラフィックスシステム及びコンピュータグラフィクイメージのレンダリング方法 | |
| US6924805B2 (en) | System and method for image-based rendering with proxy surface animation | |
| Green | Efficient self-shadowed radiosity normal mapping | |
| JP3066035B2 (ja) | 計算機図形処理表示装置制御システムのためのテクスチャマッピング技法 | |
| KR100848687B1 (ko) | 3차원 그래픽 처리 장치 및 그것의 동작 방법 |
Legal Events
| Date | Code | Title | Description |
|---|---|---|---|
| A521 | Written amendment |
Free format text: JAPANESE INTERMEDIATE CODE: A523 Effective date: 20040512 |
|
| A621 | Written request for application examination |
Free format text: JAPANESE INTERMEDIATE CODE: A621 Effective date: 20040512 |
|
| A131 | Notification of reasons for refusal |
Free format text: JAPANESE INTERMEDIATE CODE: A131 Effective date: 20070220 |
|
| A521 | Written amendment |
Free format text: JAPANESE INTERMEDIATE CODE: A523 Effective date: 20070423 |
|
| TRDD | Decision of grant or rejection written | ||
| A01 | Written decision to grant a patent or to grant a registration (utility model) |
Free format text: JAPANESE INTERMEDIATE CODE: A01 Effective date: 20070522 |
|
| A61 | First payment of annual fees (during grant procedure) |
Free format text: JAPANESE INTERMEDIATE CODE: A61 Effective date: 20070604 |
|
| FPAY | Renewal fee payment (event date is renewal date of database) |
Free format text: PAYMENT UNTIL: 20100622 Year of fee payment: 3 |
|
| FPAY | Renewal fee payment (event date is renewal date of database) |
Free format text: PAYMENT UNTIL: 20100622 Year of fee payment: 3 |
|
| FPAY | Renewal fee payment (event date is renewal date of database) |
Free format text: PAYMENT UNTIL: 20110622 Year of fee payment: 4 |
|
| FPAY | Renewal fee payment (event date is renewal date of database) |
Free format text: PAYMENT UNTIL: 20120622 Year of fee payment: 5 |
|
| LAPS | Cancellation because of no payment of annual fees |