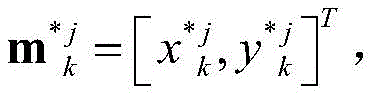CN114545968A - 基于纯方位定位的无人机集群多目标跟踪轨迹规划方法 - Google Patents

基于纯方位定位的无人机集群多目标跟踪轨迹规划方法 Download PDF

Info

Publication number
CN114545968A
CN114545968A CN202210153407.2A CN202210153407A CN114545968A CN 114545968 A CN114545968 A CN 114545968A CN 202210153407 A CN202210153407 A CN 202210153407A CN 114545968 A CN114545968 A CN 114545968A
Authority
CN
China
Prior art keywords
unmanned aerial
aerial vehicle
target
target tracking
positioning
Prior art date
Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
Granted
Application number
CN202210153407.2A
Other languages
English (en)
Other versions
CN114545968B (zh
Inventor
孙本
李银伢
戚国庆
盛安冬
Current Assignee (The listed assignees may be inaccurate. Google has not performed a legal analysis and makes no representation or warranty as to the accuracy of the list.)
Nanjing University of Science and Technology
Original Assignee
Nanjing University of Science and Technology
Priority date (The priority date is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the date listed.)
Filing date
Publication date
Application filed by Nanjing University of Science and Technology filed Critical Nanjing University of Science and Technology
Priority to CN202210153407.2A priority Critical patent/CN114545968B/zh
Publication of CN114545968A publication Critical patent/CN114545968A/zh
Application granted granted Critical
Publication of CN114545968B publication Critical patent/CN114545968B/zh
Active legal-status Critical Current
Anticipated expiration legal-status Critical

Links

Images

Classifications

    • G—PHYSICS
    • G05—CONTROLLING; REGULATING
    • G05D—SYSTEMS FOR CONTROLLING OR REGULATING NON-ELECTRIC VARIABLES
    • G05D1/00—Control of position, course, altitude or attitude of land, water, air or space vehicles, e.g. using automatic pilots
    • G05D1/10—Simultaneous control of position or course in three dimensions
    • G05D1/101—Simultaneous control of position or course in three dimensions specially adapted for aircraft
    • G05D1/104—Simultaneous control of position or course in three dimensions specially adapted for aircraft involving a plurality of aircrafts, e.g. formation flying
    • Y—GENERAL TAGGING OF NEW TECHNOLOGICAL DEVELOPMENTS; GENERAL TAGGING OF CROSS-SECTIONAL TECHNOLOGIES SPANNING OVER SEVERAL SECTIONS OF THE IPC; TECHNICAL SUBJECTS COVERED BY FORMER USPC CROSS-REFERENCE ART COLLECTIONS [XRACs] AND DIGESTS
    • Y02—TECHNOLOGIES OR APPLICATIONS FOR MITIGATION OR ADAPTATION AGAINST CLIMATE CHANGE
    • Y02T—CLIMATE CHANGE MITIGATION TECHNOLOGIES RELATED TO TRANSPORTATION
    • Y02T10/00—Road transport of goods or passengers
    • Y02T10/10—Internal combustion engine [ICE] based vehicles
    • Y02T10/40—Engine management systems

Landscapes

  • Engineering & Computer Science (AREA)
  • Aviation & Aerospace Engineering (AREA)
  • Radar, Positioning & Navigation (AREA)
  • Remote Sensing (AREA)
  • Physics & Mathematics (AREA)
  • General Physics & Mathematics (AREA)
  • Automation & Control Theory (AREA)
  • Control Of Position, Course, Altitude, Or Attitude Of Moving Bodies (AREA)

Abstract

本发明公开了一种基于纯方位定位的无人机集群多目标跟踪轨迹规划方法，方法为：首先建立无人机集群目标跟踪系统模型；其次分析传感器‑目标最优几何构型；然后对目标进行无人机数量分配；接着进行基于UKF的目标跟踪滤波，确认目标估计位置；随后进行无人机任务规划，确认无人机期望部署点；然后确认无人机的机动策略，进行轨迹规划；最后根据克拉美罗下界与均方根误差对于滤波进行评估。本发明采用最小化无人机移动距离之和的准则来规划基于传感器‑目标最优几何构型的无人机机动轨迹，在确保了高定位精度的同时缩短了无人机部署时间，大大提高无人机集群目标定位与跟踪以及后续围捕攻击、追逃对抗等任务的效率。

Description

基于纯方位定位的无人机集群多目标跟踪轨迹规划方法
技术领域
本发明涉及目标跟踪技术领域，特别是一种基于纯方位定位的无人机集群多目标跟踪机动轨迹规划方法。
背景技术
在目标跟踪领域中，纯方位跟踪作为经典的被动式无源定位跟踪技术，具有强隐蔽性和高战场生存能力，同时无人机凭借其易部署、低代价的特点，在搜索救援、侦查监视和跟踪打击等方面都有诸多应用。在军用场景下，随着现代战场环境的复杂化与信息化，单一无人机的作战能力日显不足，而无人机集群具有大规模、多功能等特点，能够以成体系的作战方式引领未来战争的导向。因此，无人机集群目标定位与跟踪的相关研究有着极为重要的实用价值。
众所周知，传感器与目标之间的相对几何构型会对最终的定位精度有着极其重要的影响，因此良好的目标-传感器几何构型，可以从根本上保证最佳的可达目标定位精度。因此本发明将研究一种基于传感器-目标最优几何构型的定位方式，并在此基础上研究多目标跟踪下的传感器分配问题、分配后传感器的任务规划问题以及无人机的最优机动问题，最终给出无人机集群多目标跟踪机动轨迹规划方法。现有的大部分轨迹规划方法都是基于提高目标状态估计精度而设置的，如最大化信息矩阵行列式(FIM)、最小化几何精度因子(GDOP)等，它们通常只考虑提高理想状态下的定位精度而忽略工程应用中的部署时间等实际因素。
发明内容
本发明的目的在于提供一种跟踪精度高、部署速度快的基于纯方位定位的无人机集群多目标跟踪机动轨迹规划方法。
实现本发明的技术解决方案为：一种基于纯方位定位的无人机集群多目标跟踪机动轨迹规划方法，包括如下步骤：
建立无人机集群目标跟踪系统模型；
初始化无人机集群目标跟踪系统参数；
对目标进行无人机数量分配；
根据传感器-目标最优几何构型获取目标初始位置估计值，初始化UKF；
进行基于UKF的目标跟踪滤波，确认目标估计位置；
进行无人机任务规划，确认无人机期望部署点；
确认无人机的机动策略，进行轨迹规划；
时刻、位置更新，获取更新后无人机的位置；
判断判断跟踪过程是否结束；
根据克拉美罗下界与均方根误差对滤波进行评估。
本发明与现有技术相比，其显著优点为：
(1)本发明采用了基于传感器-目标最优几何构型的定位方式，保证无人机在移动跟踪过程中逐渐逼近最优的部署位置，达到最优的跟踪精度；
(2)本发明构建了一种基于最小化GDOP差值平方和的无人机目标分配非线性整数规划数学模型，保证对于每个目标的跟踪精度相近，满足跟踪系统一致性的分配理念，从而实现整体跟踪系统效益的最大化；
(3)本发明采用了基于最小化无人机移动距离之和的无人机最优部署方案和轨迹规划方案，在无人机集群最终能够达到最优定位精度的情况下，给出无人机集群快速部署的单步最优机动策略，提高无人机集群进行目标跟踪以及后续任务的效率。
附图说明
图1为本发明基于纯方位定位的无人机集群多目标跟踪机动轨迹规划方法的流程图。
图2为本发明中纯方位定位下传感器-目标几何构型的示意图。
图3为本发明中无人机轨迹规划示意图。
图4为本发明实施例中目标与无人机初始位置分布示意图。
图5为本发明实施例中目标跟踪中途轨迹示意图。
图6为本发明实施例中目标跟踪终点轨迹示意图。
图7为本发明实施例中无人机与最优部署点间剩余距离之和曲线图。
图8为本发明实施例中目标真实轨迹与估计轨迹对比图。
图9为本发明实施例中目标位置x，y通道滤波误差示意图。
图10为本发明实施例中目标x，y通道位置CRLB与RMSE的对比图。
图11为本发明实施例中目标x，y通道速度CRLB与RMSE的对比图。
具体实施方式
如图1所示，本发明的一种基于纯方位定位的无人机集群多目标跟踪机动轨迹规划方法，包括如下步骤：
步骤1：建立无人机集群目标跟踪系统模型
对目标进行运动学分析，建立目标的运动模型。分析纯方位定位下多传感器测量的量测方程，建立多无人机目标跟踪系统的数学模型；
步骤2：初始化无人机集群目标跟踪系统
1.初始化目标数量U和每个目标l的状态向量
Figure BDA0003511330440000031
l∈{1,2,…,U}。其中
Figure BDA0003511330440000032
代表第l个目标在0时刻x，y通道上的位置，
Figure BDA0003511330440000033
代表第l个目标在0时刻x，y通道上的速度。
2.初始化无人机数量n，每个无人机的位置向量
Figure BDA0003511330440000034
及其速度vs，i∈{1,2,…,n}。
3.确认每个目标l的观测半径rl，最优部署偏移角
Figure BDA0003511330440000035
和决定具体最优几何构型的kl。
步骤3：获取目标位置初值
使用n个传感器对目标初值进行一步估计。
步骤4：对每个目标进行无人机数量分配
利用非线性整数规划工具对无人机数量分配的优化问题进行计算，求取每个目标应该分配的无人机数量nl。
步骤5：初始最优部署点计算
根据当前每个目标位置的估计值
Figure BDA0003511330440000036
计算所有初始最优部署点的位置
Figure BDA0003511330440000037
j∈{1,2,…,n}。
步骤6：初始无人机任务规划
根据计算出的初始最优部署点的位置
Figure BDA0003511330440000038
和无人机初始位置
Figure BDA0003511330440000039
进行任务规划，得到部署的决策结果xij，并以此确定无人机i在下个时刻要进行测量跟踪的目标l。
步骤7：初始化UKF滤波
设置UKF中的协方差矩阵P0，与目标状态向量的估计初值
Figure BDA00035113304400000310
共同初始化UKF滤波。
步骤8：进行基于UKF的目标跟踪滤波
使用UKF算法计算出k时刻每个目标状态向量的估计值
Figure BDA0003511330440000041
步骤9：最优部署点计算
根据当前每个目标位置的估计值
Figure BDA0003511330440000042
计算所有最优部署点的位置
Figure BDA0003511330440000043
步骤10：无人机任务规划
根据计算出的最优部署点的位置
Figure BDA0003511330440000044
和无人机当前位置
Figure BDA0003511330440000045
进行任务规划，得到部署的决策结果xij，确定每个无人机具体的期望部署点
Figure BDA0003511330440000046
同时确定无人机i在下个时刻要进行测量跟踪的目标l。
步骤11：无人机轨迹规划
1.判断无人机位置和期望部署点间的距离，若
Figure BDA0003511330440000047
则根据每个无人机的期望部署点确定此时刻无人机运动的方向角
Figure BDA0003511330440000048
保持速率不变，朝向此期望部署点运动，其中D为设定值。
2.判断无人机位置和期望部署点间的距离，若
Figure BDA0003511330440000049
则直接在下个时刻将无人机部署到期望部署点
Figure BDA00035113304400000410
的位置。
步骤12：时刻、位置更新
k＝k+1，按照步骤11的规则更新无人机的位置
Figure BDA00035113304400000411
步骤13：判断跟踪过程是否结束
判断k是否达到设定值，是则退出；否则返回步骤8。
步骤14：根据克拉美罗下界与均方根误差对于滤波进行评估
结合目标运动模型和纯方位定位下无人机集群多目标跟踪模型，推导并计算克拉美罗下界与均方根误差公式，评估UKF算法的性能。
本发明提出一种在纯方位定位下基于最小化无人机移动距离之和的轨迹规划方案，在无人机集群最终能够达到最优定位精度的情况下，给出无人机集群快速部署的方案，大大提高无人机集群目标定位与跟踪以及后续围捕攻击、追逃对抗等任务的效率。
下面结合附图及具体实施例对本发明作进一步详细说明。
实施例
结合图1，基于纯方位定位的无人机集群多目标跟踪机动轨迹规划方法，包括以下步骤：
步骤1：建立无人机集群目标跟踪系统模型：
为了表示跟踪系统模型具体形式，需要搭建目标的状态方程和量测方程，其离散化形式如下所示：
Figure BDA0003511330440000051
式中，X(k)表示系统在k时刻的状态向量真值，二维目标的状态向量由x，y两个方向上的位移和速度组成：
Figure BDA0003511330440000052
f(·)表示系统的状态转移函数。Γ表示噪声驱动矩阵。W(k)表示过程噪声矢量，通常假设其是满足均值为零且协方差矩阵为Q的高斯白噪声，即E[W(k)]=0,E[W(k)WT(k)]=Q(k)。Z(k)代表传感器的测量信号。h(·)表示测量转换函数。V(k)表示的是观测噪声，通常假设其为均值为零，协方差矩阵为R的高斯白噪声，即E[V(k)]=0,E[V(k)VT(k)]=R(k)。
纯方位定位指的是仅通过测量目标相对传感器的方位角信息实施目标定位。那么针对共有n个无人机的纯方位定位目标跟踪系统，具体量测方程如下：
Figure BDA0003511330440000053
式中，
Figure BDA0003511330440000054
为第i个传感器在k时刻的测量方位角，
Figure BDA0003511330440000055
分别为目标在k时刻x，y方向上的位置坐标，
Figure BDA0003511330440000056
分别为第i个传感器在k时刻x，y方向上的位置坐标。
步骤2：确认纯方位目标定位最优几何构型：
二维场景下纯方位定位系统的目标-传感器几何构型见图2，其中有n(n≥2)架搭载纯方位传感器的无人机围绕目标分布，用黑色方块表示，目标节点用三角表示，其中
Figure BDA0003511330440000061
分别是目标和无人机的位置向量，且i∈{1,2,…,n}。
GDOP表征了观测节点和目标位置之间的几何关系对定位误差的影响，是衡量一个跟踪系统定位精度的标准，GDOP越大，代表定位精度越差。对于图2所示的基于纯方位传感器定位的n(n≥2)个无人机跟踪系统，本发明考虑一种规则的部署情况。在此定义Δθl＝θl+1-θl，l∈{1,2,…,n-1}，并设置无人机到目标的观察半径r。在这种情况下，相邻传感器之间角度增量、所有传感器到目标的距离、所有传感器的测量误差都相等，用公式表示即为Δθ1＝Δθ2＝…＝Δθn-1，di=r，
Figure BDA0003511330440000062
此时关于目标的最优几何构型即可表示为
Figure BDA0003511330440000063
GDOP的显式公式为：
Figure BDA0003511330440000064
其中θij＝θj-θi，i，j∈{1,2,…,n}，GDOP的全局最小值
Figure BDA0003511330440000065
当且仅当
Figure BDA0003511330440000066
其中
Figure BDA0003511330440000067
k∈Φ且
Figure BDA0003511330440000068
考虑到实际工程应用中，每个传感器的角度θi通常定义在[0,2π]的区间内，因此Φ可压缩为
Figure BDA0003511330440000069
θ1为最优部署偏移角，可任意选择，k的取值决定了相邻传感器间夹角的值，
步骤3：对每个目标的初始位置进行估计：
使用n个传感器对U个目标初次测量，获取每个目标的量测值Zl(0)，根据Zl(0)和n个无人机的位置向量
Figure BDA00035113304400000610
使用最小二乘法对目标初值进行一步估计，得到每个目标状态向量的估计初值
Figure BDA00035113304400000611
步骤4：对每个目标进行无人机最优个数分配：
考虑一共有U个目标，U≥2，每个目标规定一个观察半径rl，l∈{1,2,…,U}，共有n(n≥2U)个拥有相同量测噪声方差
Figure BDA0003511330440000071
的无人机对目标进行定位跟踪，将所有目标的GDOP差值的平方和设置为最优个数分配的代价函数，其公式为：
Figure BDA0003511330440000072
其中
Figure BDA0003511330440000073
且nl≥2。以上最优个数分配问题就可以归纳为一个非线性整数规划(NLIP)问题，用公式表示即为：
Figure BDA0003511330440000074
其中
Figure BDA0003511330440000075
关于此非线性整数规划问题的解决方案，可以使用MATLAB工具箱内的fmincon函数进行处理，也可以使用LINGO(Linear Interactive and General Optimizer)处理此问题，得到每个目标分配的无人机数量nl。
步骤5：最优部署点计算：
确定了目标的位置估计值后，根据其观测半径r和无人机分配数量n，可以计算出目标周围的最优部署点为：
Figure BDA0003511330440000076
其中
Figure BDA0003511330440000077
即从式(11)中的获得的最优几何构型点中的
Figure BDA0003511330440000078
Figure BDA0003511330440000079
和
Figure BDA00035113304400000710
分别代表目标x通道和y通道位置的估计值。由此计算出n个最优部署点的位置
Figure BDA00035113304400000711
步骤6：进行无人机任务规划：
采用基于最小化无人机移动距离之和的部署准则，将n个无人机si＝[xi,yi]T部署到n个最优部署点
Figure BDA0003511330440000081
去，此问题可归纳为0-1规划问题，用公式表达即为：
Figure BDA0003511330440000082
其中dij＝||si-mj||代表第i个无人机到第j个最优部署点的二维平面距离。xij代表决策的选择，xij=1即意味着把第i个无人机部署到第j个最优部署点，γ即为每种决策下的无人机移动距离之和。对此0-1规划问题可采用多种智能算法解决，如含罚函数的粒子群算法。
步骤7：进行基于UKF的目标跟踪滤波：
步骤7.1：设置初始状态统计特性：设置UKF中的协方差矩阵P0，与目标状态向量的估计初值
Figure BDA0003511330440000083
共同初始化UKF滤波。
步骤7.2：进行循环递归滤波：根据前一个采样时刻k-1(k≥1)下，每个目标状态向量的估计值
Figure BDA0003511330440000084
协方差矩阵Pk-1和当前时刻nl个无人机的测量量Zl(k)，使用UKF滤波算法得到k时刻每个目标状态向量的估计值
Figure BDA0003511330440000085
步骤8：如图3所示，确定无人机机动策略，进行轨迹规划：
其中
Figure BDA0003511330440000086
是无人机i在k时刻的位置，
Figure BDA0003511330440000087
是目标在k时刻的状态估计值，
Figure BDA0003511330440000088
是根据目标k时刻的状态估计值计算出的最优部署点j的位置。假设在k时刻任务规划进行完之后，将无人机i分配到了最优部署点j，那么无人机的机动策略可以表示为：
Figure BDA0003511330440000089
其中
Figure BDA0003511330440000091
若无人机当前位置与期望部署点间距离大于设定值D=5m，则以固定速率vs向期望部署点移动；若小于设定值，则在下个时刻直接部署到期望部署点。以此确定无人机集群的单步最优机动策略，最终将这些单步最优的机动轨迹连结起来就获得了无人机集群目标跟踪的最优机动轨迹。
步骤9：根据克拉美罗下界与均方根误差对于滤波进行评估：
步骤9.1：克拉美罗下界CRLB：设定P为一未知变量无偏估计器的估计误差协方差矩阵，则如下不等式成立：
Figure BDA0003511330440000092
其中，FIM为Fisher信息矩阵，其推导公式为：
Figure BDA0003511330440000093
其中，
Figure BDA0003511330440000094
初始Fisher矩阵为FIM0＝(P0)-1，各通道在k时刻的CRLB值为
Figure BDA0003511330440000095
的对角线上的值。对于式(13)中的Hk，采用求取一阶偏导的方法来对角度信息进行离散化处理，经过线性化后得到Hk如下：
Figure BDA0003511330440000096
步骤9.2：均方根误差RMSE：
Figure BDA0003511330440000097
式中，X(k)、
Figure BDA0003511330440000098
表示第i次蒙特卡洛仿真中k时刻的目标真值和状态估计值。
设置采样时间间隔T为0.5s，采样次数为150次，蒙特卡洛仿真次数为100次。长度单位为m，速度单位为m/s，角度单位为rad。过程噪声强度设置为Q=diag[0.52 0.52 12 12]，每个传感器的方位角量测误差标准差都相等设置为4mil，初始协方差P0=diag[1000010000 1000 1000]。
设置目标参数如下表所示：
Figure BDA0003511330440000101
对于进行匀速转弯运动的目标，目标状态方程中各参数的如下所示：
Figure BDA0003511330440000102
其中ω为运动角速度，T为采样时间间隔。
无人机速度设置为vs=20m/s，数量设置为n＝10，初始位置随机分布在目标周围，具体位置可参考图4，其中三角代表目标，圆点代表无人机，圆圈是目标的观测半径所构成的圆，浅色方块是根据目标状态估计值计算出的最优部署点位置，深色方块是据目标状态真值计算出的最优部署点位置。
跟踪中途与跟踪终点轨迹如图5、图6所示，无人机与最优部署点间剩余距离之和曲线图如图7所示，目标真实轨迹与估计轨迹对比图如图8所示，x、y通道滤波误差曲线图如图9所示，x、y通道位置CRLB与RMSE对比图如图10所示，x、y通道速度CRLB与RMSE对比图如图11所示，由图5～图11可知，本发明中无人机达到期望部署点的速度较快，目标跟踪精度较高，滤波算法收敛速度较快。
以上内容详细描述了本发明的基本原理、主要特征及优点。本行业的技术人员应该了解，本发明不受上述实施例的限制，上述实施例和说明书中描述的只是说明本发明的原理，在不脱离本发明精神和范围的前提下，本发明还会有各种变化和改进，这些变化和改进都落入要求保护的本发明范围内。本发明要求保护范围由所附的权利要求书及其等效物界定。

Claims (10)

1.一种基于纯方位定位的无人机集群多目标跟踪轨迹规划方法，其特征在于，包括如下步骤：
建立无人机集群目标跟踪系统模型；
初始化无人机集群目标跟踪系统参数；
对目标进行无人机数量分配；
根据传感器-目标最优几何构型获取目标初始位置估计值，初始化UKF；
进行基于UKF的目标跟踪滤波，确认目标估计位置；
进行无人机任务规划，确认无人机期望部署点；
确认无人机的机动策略，进行轨迹规划；
时刻、位置更新，获取更新后无人机的位置；
判断判断跟踪过程是否结束；
根据克拉美罗下界与均方根误差对滤波进行评估。
2.根据权利要求1所述的基于纯方位定位的无人机集群多目标跟踪轨迹规划方法，其特征在于，所述的建立无人机集群目标跟踪系统模型，具体如下：
对目标进行运动学分析，建立目标的运动模型；分析纯方位定位下多传感器测量的量测方程，建立多无人机目标跟踪系统的数学模型。
3.根据权利要求2所述的基于纯方位定位的无人机集群多目标跟踪轨迹规划方法，其特征在于，搭建目标的状态方程和量测方程，其离散化形式如下所示：
Figure FDA0003511330430000011
式中，X(k)表示系统在k时刻的状态向量真值，二维目标的状态向量由x，y两个方向上的位移和速度组成：
Figure FDA0003511330430000012
f(·)表示系统的状态转移函数；Γ表示噪声驱动矩阵；W(k)表示过程噪声矢量，假设其是满足均值为零且协方差矩阵为Q的高斯白噪声，即E[W(k)]＝0,E[W(k)WT(k)]＝Q(k)；Z(k)代表传感器的测量信号；h(·)表示测量转换函数；V(k)表示观测噪声，假设其为均值为零，协方差矩阵为R的高斯白噪声，即E[V(k)]＝0,E[V(k)VT(k)]＝R(k)；
纯方位定位指的是仅通过测量目标相对传感器的方位角信息实施目标定位；针对共有n个无人机的纯方位定位目标跟踪系统，具体量测方程如下：
Figure FDA0003511330430000021
式中，
Figure FDA0003511330430000022
为第i个传感器在k时刻的测量方位角，
Figure FDA0003511330430000023
分别为目标在k时刻x，y方向上的位置坐标，
Figure FDA0003511330430000024
分别为第i个传感器在k时刻x，y方向上的位置坐标。
4.根据权利要求1所述的基于纯方位定位的无人机集群多目标跟踪轨迹规划方法，其特征在于，所述初始化无人机集群目标跟踪系统参数，具有如下；
初始化目标数量U和每个目标l的状态向量
Figure FDA0003511330430000025
其中
Figure FDA0003511330430000026
代表第l个目标在0时刻x，y通道上的位置，
Figure FDA0003511330430000027
代表第l个目标在0时刻x，y通道上的速度；
初始化无人机数量n，每个无人机的位置向量
Figure FDA0003511330430000028
及其速度vs，i∈{1,2,…,n}；
确认每个目标l的观测半径rl，最优部署偏移角
Figure FDA0003511330430000029
和决定具体最优几何构型的kl。
5.根据权利要求4所述的基于纯方位定位的无人机集群多目标跟踪轨迹规划方法，其特征在于，所述对目标进行无人机数量分配，根据传感器-目标最优几何构型获取目标初始位置估计值，初始化UKF，具有如下；
使用n个传感器对目标初值进行一步估计；
利用非线性整数规划工具对无人机数量分配的优化问题进行计算，求取每个目标应该分配的无人机数量nl；
根据当前每个目标位置的估计值
Figure FDA00035113304300000210
计算所有初始最优部署点的位置
Figure FDA00035113304300000211
根据计算出的初始最优部署点的位置
Figure FDA0003511330430000031
和无人机初始位置
Figure FDA0003511330430000032
进行任务规划，得到部署的决策结果xij，并以此确定无人机i在下个时刻要进行测量跟踪的目标l；
设置UKF中的协方差矩阵P0，与目标状态向量的估计初值
Figure FDA0003511330430000033
共同初始化UKF滤波。
6.根据权利要求5所述的基于纯方位定位的无人机集群多目标跟踪轨迹规划方法，其特征在于，进行基于UKF的目标跟踪滤波，具有如下；使用UKF算法计算出k时刻每个目标状态向量的估计值
Figure FDA0003511330430000034
7.根据权利要求6所述的基于纯方位定位的无人机集群多目标跟踪轨迹规划方法，其特征在于，根据当前每个目标位置的估计值
Figure FDA0003511330430000035
计算所有最优部署点的位置
Figure FDA0003511330430000036
8.根据权利要求7所述的基于纯方位定位的无人机集群多目标跟踪轨迹规划方法，其特征在于，根据计算出的最优部署点的位置
Figure FDA0003511330430000037
和无人机当前位置
Figure FDA0003511330430000038
进行任务规划，得到部署的决策结果xij，确定每个无人机具体的期望部署点
Figure FDA0003511330430000039
同时确定无人机i在下个时刻要进行测量跟踪的目标l。
9.根据权利要求8所述的基于纯方位定位的无人机集群多目标跟踪轨迹规划方法，其特征在于，无人机轨迹规划方法如下：
判断无人机位置和期望部署点间的距离，若
Figure FDA00035113304300000310
则根据每个无人机的期望部署点确定此时刻无人机运动的方向角
Figure FDA00035113304300000311
保持速率不变，朝向此期望部署点运动，其中D为设定值；
判断无人机位置和期望部署点间的距离，若
Figure FDA00035113304300000312
则直接在下个时刻将无人机部署到期望部署点
Figure FDA00035113304300000313
的位置。
10.根据权利要求9所述的基于纯方位定位的无人机集群多目标跟踪轨迹规划方法，其特征在于，进行时刻、位置更新：k＝k+1，更新无人机的位置
Figure FDA00035113304300000314
判断跟踪过程是否结束：判断k是否达到设定值，是则退出；否则返回进行基于UKF的目标跟踪滤波。
CN202210153407.2A 2022-02-18 2022-02-18 基于纯方位定位的无人机集群多目标跟踪轨迹规划方法 Active CN114545968B (zh)

Priority Applications (1)

Application Number Priority Date Filing Date Title
CN202210153407.2A CN114545968B (zh) 2022-02-18 2022-02-18 基于纯方位定位的无人机集群多目标跟踪轨迹规划方法

Applications Claiming Priority (1)

Application Number Priority Date Filing Date Title
CN202210153407.2A CN114545968B (zh) 2022-02-18 2022-02-18 基于纯方位定位的无人机集群多目标跟踪轨迹规划方法

Publications (2)

Publication Number Publication Date
CN114545968A true CN114545968A (zh) 2022-05-27
CN114545968B CN114545968B (zh) 2023-09-26

Family

ID=81675593

Family Applications (1)

Application Number Title Priority Date Filing Date
CN202210153407.2A Active CN114545968B (zh) 2022-02-18 2022-02-18 基于纯方位定位的无人机集群多目标跟踪轨迹规划方法

Country Status (1)

Country Link
CN (1) CN114545968B (zh)

Cited By (1)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
CN114840028A (zh) * 2022-07-04 2022-08-02 中国科学院自动化研究所 目标监视方法、装置、电子设备及存储介质

Citations (8)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
CN106873628A (zh) * 2017-04-12 2017-06-20 北京理工大学 一种多无人机跟踪多机动目标的协同路径规划方法
CN107238388A (zh) * 2017-05-27 2017-10-10 合肥工业大学 多无人机任务分配与航迹规划联合优化方法及装置
CN108388270A (zh) * 2018-03-21 2018-08-10 天津大学 面向安全域的集群无人机轨迹姿态协同控制方法
CN108536171A (zh) * 2018-03-21 2018-09-14 电子科技大学 一种多约束下多无人机协同跟踪的路径规划方法
CN109613931A (zh) * 2019-01-07 2019-04-12 北京航空航天大学 基于生物社会力的异构无人机集群目标跟踪系统及方法
US20190244378A1 (en) * 2018-02-08 2019-08-08 Haiwei DONG Group optimization depth information method and system for constructing a 3d feature map
CN110262543A (zh) * 2019-05-23 2019-09-20 北京航空航天大学 多目标点同时到达约束下的集群四维轨迹规划设计方法
CN111460636A (zh) * 2020-03-20 2020-07-28 南京理工大学 不完全量测数据驱动下的机动扩展目标混合交互式强跟踪滤波方法

Patent Citations (8)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
CN106873628A (zh) * 2017-04-12 2017-06-20 北京理工大学 一种多无人机跟踪多机动目标的协同路径规划方法
CN107238388A (zh) * 2017-05-27 2017-10-10 合肥工业大学 多无人机任务分配与航迹规划联合优化方法及装置
US20190244378A1 (en) * 2018-02-08 2019-08-08 Haiwei DONG Group optimization depth information method and system for constructing a 3d feature map
CN108388270A (zh) * 2018-03-21 2018-08-10 天津大学 面向安全域的集群无人机轨迹姿态协同控制方法
CN108536171A (zh) * 2018-03-21 2018-09-14 电子科技大学 一种多约束下多无人机协同跟踪的路径规划方法
CN109613931A (zh) * 2019-01-07 2019-04-12 北京航空航天大学 基于生物社会力的异构无人机集群目标跟踪系统及方法
CN110262543A (zh) * 2019-05-23 2019-09-20 北京航空航天大学 多目标点同时到达约束下的集群四维轨迹规划设计方法
CN111460636A (zh) * 2020-03-20 2020-07-28 南京理工大学 不完全量测数据驱动下的机动扩展目标混合交互式强跟踪滤波方法

Non-Patent Citations (1)

* Cited by examiner, † Cited by third party
Title
王晶: "基于leader-follower的多无人机编队轨迹跟踪设计" *

Cited By (1)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
CN114840028A (zh) * 2022-07-04 2022-08-02 中国科学院自动化研究所 目标监视方法、装置、电子设备及存储介质

Also Published As

Publication number Publication date
CN114545968B (zh) 2023-09-26

Similar Documents

Publication Publication Date Title
CN109885883B (zh) 一种基于gk聚类算法模型预测的无人车横向运动的控制方法
CN101943916B (zh) 一种基于卡尔曼滤波器预测的机器人避障方法
CN109597864B (zh) 椭球边界卡尔曼滤波的即时定位与地图构建方法及系统
CN109947136B (zh) 一种面向无人机群体快速目标搜索的协同主动感知方法
CN112762957B (zh) 一种基于多传感器融合的环境建模及路径规划方法
CN105785359B (zh) 一种多约束机动目标跟踪方法
CN108152812B (zh) 一种调整网格间距的改进agimm跟踪方法
CN116337045A (zh) 一种基于karto和teb的高速建图导航方法
CN111189454A (zh) 基于秩卡尔曼滤波的无人车slam导航方法
CN114545968A (zh) 基于纯方位定位的无人机集群多目标跟踪轨迹规划方法
CN114219022B (zh) 结合聚类分析和粒子群优化算法的多传感器多目标跟踪方法
Huang et al. A novel route planning method of fixed-wing unmanned aerial vehicle based on improved QPSO
CN107391446A (zh) 基于随机矩阵的不规则形状多扩展目标形状和状态估计方法
CN117249829A (zh) 一种测向交叉定位体制下的无人机平台的航迹规划方法
CN116225053A (zh) 一种面向任务分级目标运动特性的跟踪轨迹优化方法
CN113503891B (zh) 一种sinsdvl对准校正方法、系统、介质及设备
CN114815899A (zh) 基于3d激光雷达传感器的无人机三维空间路径规划方法
Goswami et al. Design of an interactive multiple model based two-stage multi-vehicle tracking algorithm for autonomous navigation
CN113189578A (zh) 一种扩展目标跟踪方法
CN113064154A (zh) 一种空中目标跟踪方法
Zheng et al. A method for UAV tracking target in obstacle environment
CN107590509B (zh) 基于最大期望近似的切尔诺夫融合方法
Rao et al. A comparison of SLAM prediction densities using the Kolmogorov smirnov statistic
CN112904854B (zh) 多机器人多目标实时动态避障方法、系统及存储介质
CN115758060A (zh) 一种基于optics的高机动目标无源雷达跟踪方法

Legal Events

Date Code Title Description
PB01 Publication
PB01 Publication
SE01 Entry into force of request for substantive examination
SE01 Entry into force of request for substantive examination
GR01 Patent grant
GR01 Patent grant