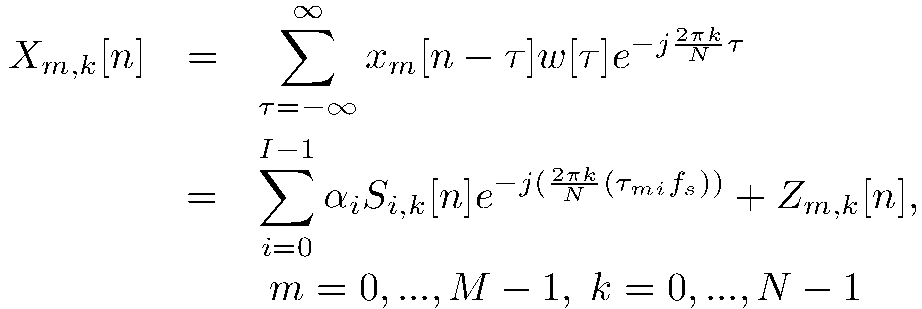KR101413229B1 - 방향 추정 장치 및 방법 - Google Patents
방향 추정 장치 및 방법 Download PDFInfo
- Publication number
- KR101413229B1 KR101413229B1 KR20130053828A KR20130053828A KR101413229B1 KR 101413229 B1 KR101413229 B1 KR 101413229B1 KR 20130053828 A KR20130053828 A KR 20130053828A KR 20130053828 A KR20130053828 A KR 20130053828A KR 101413229 B1 KR101413229 B1 KR 101413229B1
- Authority
- KR
- South Korea
- Prior art keywords
- signal
- sound source
- statistical distribution
- calculated
- music
- Prior art date
Links
Images
Classifications
-
- G—PHYSICS
- G01—MEASURING; TESTING
- G01S—RADIO DIRECTION-FINDING; RADIO NAVIGATION; DETERMINING DISTANCE OR VELOCITY BY USE OF RADIO WAVES; LOCATING OR PRESENCE-DETECTING BY USE OF THE REFLECTION OR RERADIATION OF RADIO WAVES; ANALOGOUS ARRANGEMENTS USING OTHER WAVES
- G01S3/00—Direction-finders for determining the direction from which infrasonic, sonic, ultrasonic, or electromagnetic waves, or particle emission, not having a directional significance, are being received
- G01S3/02—Direction-finders for determining the direction from which infrasonic, sonic, ultrasonic, or electromagnetic waves, or particle emission, not having a directional significance, are being received using radio waves
- G01S3/14—Systems for determining direction or deviation from predetermined direction
-
- G—PHYSICS
- G01—MEASURING; TESTING
- G01S—RADIO DIRECTION-FINDING; RADIO NAVIGATION; DETERMINING DISTANCE OR VELOCITY BY USE OF RADIO WAVES; LOCATING OR PRESENCE-DETECTING BY USE OF THE REFLECTION OR RERADIATION OF RADIO WAVES; ANALOGOUS ARRANGEMENTS USING OTHER WAVES
- G01S3/00—Direction-finders for determining the direction from which infrasonic, sonic, ultrasonic, or electromagnetic waves, or particle emission, not having a directional significance, are being received
- G01S3/80—Direction-finders for determining the direction from which infrasonic, sonic, ultrasonic, or electromagnetic waves, or particle emission, not having a directional significance, are being received using ultrasonic, sonic or infrasonic waves
- G01S3/8006—Multi-channel systems specially adapted for direction-finding, i.e. having a single aerial system capable of giving simultaneous indications of the directions of different signals
-
- G—PHYSICS
- G01—MEASURING; TESTING
- G01S—RADIO DIRECTION-FINDING; RADIO NAVIGATION; DETERMINING DISTANCE OR VELOCITY BY USE OF RADIO WAVES; LOCATING OR PRESENCE-DETECTING BY USE OF THE REFLECTION OR RERADIATION OF RADIO WAVES; ANALOGOUS ARRANGEMENTS USING OTHER WAVES
- G01S3/00—Direction-finders for determining the direction from which infrasonic, sonic, ultrasonic, or electromagnetic waves, or particle emission, not having a directional significance, are being received
- G01S3/02—Direction-finders for determining the direction from which infrasonic, sonic, ultrasonic, or electromagnetic waves, or particle emission, not having a directional significance, are being received using radio waves
- G01S3/04—Details
- G01S3/12—Means for determining sense of direction, e.g. by combining signals from directional antenna or goniometer search coil with those from non-directional antenna
Landscapes
- Physics & Mathematics (AREA)
- Engineering & Computer Science (AREA)
- General Physics & Mathematics (AREA)
- Radar, Positioning & Navigation (AREA)
- Remote Sensing (AREA)
- Measurement Of Velocity Or Position Using Acoustic Or Ultrasonic Waves (AREA)
Abstract
방향 추정 장치 및 방법을 개시한다. 신호를 감지하고, 상기 감지한 신호에 대한 감지 신호인 센서 신호를 출력하는 적어도 두 개의 센서를 포함하는 센서부, 상기 적어도 두 개의 센서가 각각 출력한 센서 신호별로 상기 센서 신호의 통계학적 분포를 지시하는 통계학적 분포 데이터를 산출하고, 상기 산출된 통계학적 분포 데이터에서 상기 신호에 포함된 비고정(non-stationary) 신호인 음원 신호의 통계학적 분포를 지시하는 통계학적 분포 데이터를 추출하며, 상기 추출된 통계학적 분포 데이터를 기초로 상기 음원 신호를 출력한 음원의 방향을 추정하는 제어부를 포함할 수 있다.
Description
본 발명은 음원 방향 추정 장치에 관한 것으로서, 더 상세하게는 언더디터민트 상황에서 고해상도를 가지는 2p 차원의 신호 및 잡음 신호 부공간 제약 최적화에 기반한 방향 추정 장치 및 방법에 관한 것이다.
전자 , 통신, 기계 등 다양한 분야의 기술이 발달함에 따라 인간의 생활은 더욱 편리하게 되었고, 많은 부분에 있어서 인간을 대신하여 움직이고 주어진 일을 처리하는 자동 시스템이 개발되고 있다. 이러한 자동 시스템은 인간, 비행기, 새, 잠수함 등과 같은 음원이 출력하는 신호를 인식하고, 인식된 음성 데이터에 따라 적절한 행동을 취할 수 있게 구현되고 있다. 특히, 음원의 신호를 인식하여 음원이 발생하는 위치를 추정할 수도 있다.
음원 방향 검출장치는 장치에 장착된 수신기를 통해 음향 신호가 출력되는 순서를 이용하여 음원의 방향을 검출하며, 이러한 음원에서 출력되는 신호는 비젼(vision)보다 데이터량이 적고, 단조로운 데이터 형태를 가지는 단점이 있다. 하지만 조명이 없는 곳이나 장애물이 있어 시야를 벗어나 보이지 않는 곳 등의 환경에서도 유용하다는 점에서 신호는 비젼이 인식하지 못하는 것들을 보완해줄 수 있는 중요한 데이터이다.
한편, 로봇에 마이크로폰과 같은 수신기를 부착시키고 사용자의 호출 음성이나 박수소리를 입력받아 인식함으로서 카메라나 키보드와 같은 입력 시스템 대용으로 활용할 수 있도록 하는 자동 인터페이스 기능 구현을 위한 연구가 수행되고 있으며, 로봇 스스로가 소비자의 목소리를 포함하는 음원에 반응하여 그 방향을 정확하게 추정하는 기술에 대한 관심이 높아지고 있는 실정이다.
이를 위해 대한 특허공개공부(A) 제10-2011-0057661호에서는 음원 방향 추정기술로 음원과의 거리를 계산하여 이동하는 이동체 및 그 제어방법을 제시하고 있다. 따라서 이동체가 음원의 방향을 추정하는데 있어서 오차 및 시간이 오래 걸리는 어려움이 있다.
특허공개공보(A) 제10-20006-0000064호에서는 음성 신호를 발생시킨 화자의 위치를 추정하는 것으로 비고정 잡음(non-stationary noise) 환경에서의 화자 위치 추정 시스템을 제시하고 있다. 따라서 고정 잡음(stationary noise) 환경에서는 음원의 방향 추적의 어려움이 있다.
IEEE 논문인 W. J. Zeng and X. L. Li, "High-resolution multiple wideband and nonstationary source localization with unknown number of sources", IEEE Trans. Signal Process., vol. 58, pp. 3125-3136, Jun. 2010.는 비고정 음원 신호에 대한 방향 추정 방법을 제시하고 있다. 하지만 음원의 개수를 알지 못할 경우에는 음원 신호를 추정의 해상도 및 정확도가 높지 않은 어려움이 있다.
본 발명이 이루고자 하는 기술적인 과제는 언더디터민트 상황에서 신호가 출력되는 음원의 방향에 대한 공간적 고해상도를 가지는데 목적이 있다.
본 발명이 이루고자 하는 다른 기술적인 과제는 언더디터민트 상황에서 신호가 출력되는 음원의 방향에 대한 높은 정확도를 가는데 목적이 있다.
본 발명이 이루고자 하는 또 다른 기술적인 과제는 언더디터민트 상황에서 음원의 개수를 더 많이 추출하는데 목적이 있다.
신호를 감지하고, 상기 감지한 신호에 대한 감지 신호인 센서 신호를 출력하는 적어도 두 개의 센서를 포함하는 센서부, 상기 적어도 두 개의 센서가 각각 출력한 센서 신호별로 상기 센서 신호의 통계학적 분포를 지시하는 통계학적 분포 데이터를 산출하고, 상기 산출된 통계학적 분포 데이터에서 상기 신호에 포함된 비고정(non-stationary) 신호인 음원 신호의 통계학적 분포를 지시하는 통계학적 분포 데이터를 추출하며, 상기 추출된 통계학적 분포 데이터를 기초로 상기 음원 신호를 출력한 음원의 방향을 추정하는 제어부를 포함할 수 있다.
상기 센서부에 포함된 센서의 개수는 상기 음원의 개수보다 같거나 적을 수 있다.
상기 통계학적 분포 데이터는 상기 음원 신호의 시간에 따른 변화 및 특성 변화를 지시하는 데이터를 포함할 수 있다.
상기 산출된 통계학적 분포는 가우시안 분포, 비 가우시안 분포, 라플라스 분포 및 빔포밍 분포 중 적어도 하나일 수 있다.
상기 제어부는 상기 산출된 통계학적 분포 데이터로 커뮬런트(cumulant) 행렬을 산출하고, 상기 커뮬런트 행렬을 하기 수학식을 이용하여 산출할 수 있다:
[수학식]
여기서, 는 k 번째 주파수 빈(frequency bin)의 2p차원 커뮬런트 행렬을 나타내고, 는 k 번째 주파수 빈의 가상 배열 매니폴드(manifold) 벡터를 나타내며, 는 고정 신호인 잡음 신호를 나타낸다.
상기 제어부는 상기 센서 신호를 디지털 신호로 변환하는 전처리부, 상기 변환된 디지털 신호의 통계학적 분포를 지시하는 통계학적 분포 데이터를 산출하고, 상기 산출된 통계학적 분포 데이터에서 상기 신호에 포함된 잡음 신호에 대한 데이터를 제거하여 상기 음원 신호의 통계학적 분포를 지시하는 통계학적 분포 데이터를 추출하며, 상기 추출된 통계학적 분포 데이터를 이용하여 상기 디지털 신호의 음원의 개수 및 방향에 대한 공간 스펙트럼(spatial spectrum)을 산출하는 신호 분석부 및 상기 산출된 디지털 신호의 공간 스펙트럼의 피크(peak)를 상기 음원의 방향인 것으로 추정하는 방향 추정부를 포함할 수 있다.
상기 신호 분석부는 상기 공간 스펙트럼을 하기에 기재된 수학식 및 조건식을 이용하여 산출할 수 있다:
[수학식]
[조건식]
여기서, 는 k 번째 주파수 빈의 가중치 벡터를 나타내고, 는 k 번째 주파수 빈에서 의 가상 배열 매니폴드(manifold) 벡터를 나타낸다. 또한 는 비특이 행렬을 나타내고, 은 임의의 0이 아닌 실제 상수이다.
[수학식]
는 고유벡터 이고, 영이 아닌 고유값에 해당하는 고유벡터이다. 는 고유벡터 이고, 영인 고유값에 해당하는 고유벡터이다. 는 음원의 개수이고, 는 단위 행렬이다.는 음원 신호를 나타내는 고유벡터 및 잡음 신호를 나타내는 고유벡터 에 모두 해당하는 고유값에 관련된 고유벡터이고, 는 잡음 신호 제거 및 치수 조정된 2p차원 커뮬런트 행렬이다.
상기 신호 분석부는 상기 음원의 개수가 사전에 정해진 경우에는 상기 비특이 행렬 를 상기 고유벡터 및 상기 고유벡터 를 이용하여 산출하고, 상기 산출된 비특이 행렬 를 이용하여 라그랑주 승수 를 산출하며, 상기 산출된 를 이용하여 최적의 가중치 벡터 를 산출하고, 상기 산출된 및 상기 고유 벡터 를 이용하여 고유벡터 를 산출할 수 있다.
상기 신호 분석부는 상기 음원의 개수가 사전에 정해지지 않은 경우에는,
상기 비특이 행렬 를 2p차원 커뮬런트 행렬 를 이용하여 산출하고, 상기 산출된 비특이 행렬 를 이용하여 라그랑주 승수 를 산출하며, 상기 산출된 를 이용하여 최적의 가중치 벡터 를 산출하고, 상기 산출된 및 상기 2p차원 커뮬런트 행렬 를 이용하여 고유벡터 를 산출할 수 있다.
상기 방향 추정부는 상기 2p차원 커뮬런트 행렬 를 이용하여 산출된 비특이값들 중 가장 큰 비특이 값을 가지는 상기 고유벡터 에 해당하는 상기 음원 신호의 방향각을 음원의 방향으로 추정할 수 있다.
신호를 감지하고, 상기 감지한 신호에 대한 감지 신호인 센서 신호를 출력하는 단계, 상기 출력한 센서 신호별로 상기 센서 신호의 통계학적 분포를 지시하는 통계학적 분포 데이터를 산출하고, 상기 산출된 통계학적 분포 데이터에서 상기 신호에 포함된 비고정(non-stationary) 신호인 음원 신호의 통계학적 분포를 지시하는 통계학적 분포 데이터를 추출하는 단계, 상기 추출된 통계학적 분포 데이터를 기초로 상기 음원 신호를 출력한 음원의 방향을 추정하는 단계를 포함할 수 있다.
본 발명에 따른 방향 추정 장치 및 방법에 의하면 언더디터민트 상황에서 신호가 출력되는 음원의 방향에 대한 공간적 고해상도를 가질 수 있다.
또한 언더디터민트 상황에서 신호가 출력되는 음원의 방향에 대한 높은 정확도를 가질 수 있다.
또한 언더디터민트 상황에서 음원의 개수를 더 많이 추출할 수 있다.
도 1은 본 발명의 일 실시예에 따른 방향 추정 장치를 도시한 구성도이다.
도 2은 본 발명의 일 실시에에 따른 방향 추정 장치를 도시한 블록도이다.
도 3은 본 발명의 일 실시예에 따른 방향 추정 장치의 제어부를 도시한 블록도이다.
도 4는 본 발명의 일 실시예에 따른 방향 추정 장치의 고해상도를 도시한 그래프이다.
도 5는 본 발명의 다른 실시예에 따른 방향 추정 장치의 고해상도를 도시한 그래프이다.
도 6은 본 발명의 또 다른 실시예에 따른 방향 추정 장치의 고해상도를 도시한 그래프이다.
도 7은 본 발명의 또 다른 실시예에 따른 방향 추정 장치의 고해상도를 도시한 그래프이다.
도 8은 본 발명의 일 실시예에 따른 방향 추정 장치의 정확도를 도시한 그래프이다.
도 9는 본 발명의 다른 실시예에 따른 방향 추정 장치의 정확도를 도시한 그래프이다.
도 10은 본 발명의 또 다른 실시예에 따른 방향 추정 장치의 정확도를 도시한 그래프이다.
도 11은 본 발명의 또 다른 실시예에 따른 방향 추정 장치의 정확도를 도시한 그래프이다.
도 12는 본 발명의 또 다른 실시예에 따른 방향 추정 장치의 정확도를 도시한 그래프이다.
도 13은 본 발명의 또 다른 실시예에 따른 방향 추정 장치의 정확도를 도시한 그래프이다.
도 14는 본 발명의 또 다른 실시예에 따른 방향 추정 장치의 정확도를 도시한 그래프이다.
도 15는 본 발명의 또 다른 실시예에 따른 방향 추정 장치의 정확도를 도시한 그래프이다.
도 16은 본 발명의 일 실시예에 따른 방향 추정 장치의 음원 추출 개수를 도시한 그래프이다.
도 17은 본 발명의 다른 실시예에 따른 방향 추정 장치의 음원 추출 개수를 도시한 그래프이다.
도 18은 본 발명의 또 다른 실시예에 따른 방향 추정 장치의 음원 추출 개수를 도시한 그래프이다.
도 19는 본 발명의 일 실시예 따른 방향 추정 방법을 도시한 순서도이다.
도 20은 도 19의 S140을 더 상세하게 도시한 순서도이다.
도 21은 도 19의 S150을 더 상세하게 도시한 순서도이다.
도 2은 본 발명의 일 실시에에 따른 방향 추정 장치를 도시한 블록도이다.
도 3은 본 발명의 일 실시예에 따른 방향 추정 장치의 제어부를 도시한 블록도이다.
도 4는 본 발명의 일 실시예에 따른 방향 추정 장치의 고해상도를 도시한 그래프이다.
도 5는 본 발명의 다른 실시예에 따른 방향 추정 장치의 고해상도를 도시한 그래프이다.
도 6은 본 발명의 또 다른 실시예에 따른 방향 추정 장치의 고해상도를 도시한 그래프이다.
도 7은 본 발명의 또 다른 실시예에 따른 방향 추정 장치의 고해상도를 도시한 그래프이다.
도 8은 본 발명의 일 실시예에 따른 방향 추정 장치의 정확도를 도시한 그래프이다.
도 9는 본 발명의 다른 실시예에 따른 방향 추정 장치의 정확도를 도시한 그래프이다.
도 10은 본 발명의 또 다른 실시예에 따른 방향 추정 장치의 정확도를 도시한 그래프이다.
도 11은 본 발명의 또 다른 실시예에 따른 방향 추정 장치의 정확도를 도시한 그래프이다.
도 12는 본 발명의 또 다른 실시예에 따른 방향 추정 장치의 정확도를 도시한 그래프이다.
도 13은 본 발명의 또 다른 실시예에 따른 방향 추정 장치의 정확도를 도시한 그래프이다.
도 14는 본 발명의 또 다른 실시예에 따른 방향 추정 장치의 정확도를 도시한 그래프이다.
도 15는 본 발명의 또 다른 실시예에 따른 방향 추정 장치의 정확도를 도시한 그래프이다.
도 16은 본 발명의 일 실시예에 따른 방향 추정 장치의 음원 추출 개수를 도시한 그래프이다.
도 17은 본 발명의 다른 실시예에 따른 방향 추정 장치의 음원 추출 개수를 도시한 그래프이다.
도 18은 본 발명의 또 다른 실시예에 따른 방향 추정 장치의 음원 추출 개수를 도시한 그래프이다.
도 19는 본 발명의 일 실시예 따른 방향 추정 방법을 도시한 순서도이다.
도 20은 도 19의 S140을 더 상세하게 도시한 순서도이다.
도 21은 도 19의 S150을 더 상세하게 도시한 순서도이다.
도 1은 본 발명의 일 실시예에 따른 방향 추정 장치를 도시한 구성도이다.
도 1을 참조하면, 방향 추정 장치(1)는 신호가 출력되는 방향(DOA: Direction of arrival)을 추정하는 장치이다. 방향 추정 장치(1)는 음원에서 출력하는 신호를 감지할 수 있다. 방향 추정 장치(1)는 감지된 신호로부터 비고정(non-stationary) 신호인 음원 신호를 추출하고, 추출된 음원 신호의 통계학적 분포를 산출할 수 있다. 방향 추정 장치(1)는 산출된 통계학적 분포를 기초로 음원 신호를 출력된 음원의 방향을 추정할 수 있다. 방향 추정 장치(1)는 레이더(radar), 소나(sonar) 및 생물의학(biomedical) 신호 추출 중 적어도 하나에 이용될 수 있다.
음원은 신호가 발생하는 근원일 수 있다. 음원은 자동차, 새, 비행기, 잠수함, 미사일, 및 사람 중 적어도 하나일 수 있다. 음원은 레이더 및 소나 시스템에서 자동차, 새, 비행기, 잠수함 및 미사일 중 적어도 하나일 수 있다. 또한 음원은 소리 인식 시스템에서 방 안에 있는 말하는 사람일 수 있다. 또한 음원은 소스(source)로 명명될 수 있다.
신호는 음원에서 출력하는 소리일 수 있다. 신호는 전자기파 신호, 생체 신호, 레이더 신호, 소나 신호 및 음파 중 적어도 하나일 수 있다. 신호는 소스 신호로 명명될 수 있다.
또한 음원 신호는 센서를 통해 들어온 센서 신호 중 잡음 신호를 제거한 신호일 수 있다.
방향 추정 장치(1)는 음원의 개수가 음원의 신호를 감지하는 센서의 개수보다 많을 경우에 동작할 수 있다. 상기 음원의 신호는 음원 신호 및 잡음 신호를 포함할 수 있다. 방향 추정 장치(1)는 비고정 신호인 음원 신호 및 고정(stationary) 신호인 잡음 신호(noise)를 수신할 수 있다.
음원 신호 및 잡음 신호는 평균이 0인 정규분포일 수 있다. 또한 음원 신호 및 잡음 신호는 가우시안(Gaussian) 분포, 비 가우시안(non-Gaussian) 분포, 라플라스(Laplace) 분포 및 빔포밍(beamforming) 분포 중 적어도 하나의 통계학적 분포를 포함할 수 있다.
통계학적 분포는 가우시안 분포, 비 가우시안 분포, 라플라스 분포 및 빔포밍 분포와 같은 신호 특성일 수 있다.
방향 추정 장치(1)는 음원(110), 음원(120), 음원(130) 및 음원(140)에서 출력하는 신호를 감지하고 분석하여 음원의 방향을 추정할 수 있다.
방향 추정 장치(1)는 음원(110), 음원(120), 음원(130) 및 음원(140)에서 출력하는 신호를 센서로 감지할 수 있다. 방향 추정 장치(1)는 센서의 개수가 음원의 개수보다 적을 수 있다. 센서는 레이더, 마이크로 폰(Microphone) 및 초음파 센서 중 적어도 하나일 수 있다.
방향 추정 장치(1)는 감지된 신호를 디지털 신호로 변환할 수 있다. 방향 추정 장치(1)는 변환된 신호에 포함된 잡음 신호를 필터링할 수 있다. 방향 추정 장치(1)는 필터링된 신호인 음원 신호가 포함하고 있는 통계학적 분포를 분석하여 신호의 방향을 추정할 수 있다.
방향 추정 장치(1)는 센서의 개수가 음원의 개수보다 적을 경우에도 음원 신호에 대한 공간적 해상도가 높을 수 있고, 방향의 추정 정확도가 높을 수 있다.
공간적 해상도는 여러 개의 음원이 비슷한 방향각을 가질 경우, 얼마나 정확하게 음원의 방향각을 판단하는지를 말한다. 즉, 음원(110)이 30°에서 출력하고 음원(120)이 32°에서 출력했다고 가정할 때, 공간적 해상도가 높은 방향 추정 장치는 음원(110)과 음원(120)을 두 개의 음원으로 감지할 수 있다. 하지만 공간적 해상도가 낮은 방향 추정 장치는 음원(110)과 음원(120)을 하나의 음원으로 감지할 수 있다.
도 2는 본 발명의 일 실시예에 따른 방향 추정 장치를 도시한 블록도이다.
도 2를 참조하면, 방향 추정 장치(1)는 신호가 포함하는 비고정 신호인 음원 신호 및 고정 신호인 잡음 신호를 감지하고, 감지된 신호의 방향을 추정할 수 있다. 방향 추정 장치(1)는 언더디터민드(underdetermined) 상황 즉, 음원의 개수가 센서의 개수보다 많은 상황에서 비고정 신호인 음원 신호를 방향 추정할 수 있다.
방향 추정 장치(1)는 센서부(220), 제어부(240), 출력부(260) 및 저장부(280)를 포함할 수 있다.
센서부(220)는 음원에서 발생된 신호를 감지할 수 있다. 즉, 센서부(220)는 비고정 신호인 음원 신호 및 고정 신호인 잡음 신호를 감지할 수 있다. 센서부(220)에서 감지하여 수신된 신호는 센서 신호라고 명명할 수 있다. 센서 신호는 음원 신호 및 잡음 신호를 포함한 신호일 수 있다.
센서부(220)는 신호를 0°~ 180°범위에서 감지할 수 있다. 또한 센서부(220)는 움직이지않고 고정될 수 있다. 센서부는 적어도 2개의 센서를 포함할 수 있다. 또한 센서부(220)는 음원의 개수보다 센서의 개수가 같거나 적을 수 있다. 센서부(220)에서 감지한 신호는 각각의 센서들의 위치에 따라 시간 딜레이(delay)가 생길 수 있다. 센서부(220)는 레이더, 마이크로 폰 및 초음파 센서 중 적어도 하나의 센서를 포함할 수 있다.
제어부(240)는 센서부(220)의 센서가 각각 감지한 신호로부터 비고정 신호인 음원 신호를 추출하고, 추출된 음원 신호의 통계학적 분포를 산출할 수 있다. 제어부(240)는 상기 음원 신호별로 산출된 통계학적 분포 데이터들을 기초로 음원 신호를 출력한 음원의 방향을 추정할 수 있다.
제어부(240)는 아날로그 신호인 음원 신호 및 잡음 신호를 디지털 신호로 변환할 수 있다. 제어부(240)는 변환된 신호에 포함된 잡음 신호를 필터링할 수 있다. 제어부(240)는 필터링된 신호를 분석할 수 있다. 이때, 제어부(240)가 음원의 개수가 정해져 있을 경우와 정해지지 않은 경우에 따라 서로 다른 알고리즘을 이용할 수 있다.
음원의 개수가 정해진 경우, 제어부(240)는 c-2p-KR-MUSIC 알고리즘을 이용할 수 있다. c-2p-KR-MUSIC 알고리즘은 2p-KR-MUSIC 알고리즘을 변형시켜서 공간적인 해상도를 높이고, 정확도를 높인 알고리즘일 수 있다.
음원의 개수가 정해지지 않은 경우, 제어부(240)는 c-2p-KR-Capon 알고리즘을 이용할 수 있다. c-2p-KR-Capon 알고리즘은 2p-KR-Capon 알고리즘을 변형시켜서 공간적인 해상도를 높이고, 정확도를 높인 알고리즘일 수 있다.
제어부(240)는 산출된 통계학적 분포 데이터들을 기초로 음원의 방향을 추정할 수 있다.
통계학적 분포 데이터는 상기 음원 신호의 시간에 따른 변화 및 특성 변화를 포함하는 데이터일 수 있다. 특성 변화는 신호의 증폭, 주기 및 센서 간의 딜레이(delay)에 따른 오차 중 적어도 하나일 수 있다.
출력부(260)는 제어부(240)에서 추정된 음원 방향의 데이터를 출력할 수 있다. 출력부(260)는 모니터, 프로젝터, 액정 및 전방 유리에 화면을 출력하는 헤드 업 디스플레이(head-up display) 중 적어도 하나일 수 있다.
저장부(280)는 제어부(240)에서 사용되는 음원 방향 추정 알고리즘이 저장될 수 있다. 또한 저장부(280)는 신호의 2p차원의 통계학적 특성에 대한 데이터가 저장될 수 있다.
따라서, 음원 방향 장치(1)는 센서부(220)의 각각의 센서로 감지한 신호를 제어부(240)에서 통계학적인 분포 데이터를 이용하여 상기 센서들의 데이터를 비교 분석할 수 있다. 음원 방향 장치(1)는 상기 비교 분석된 데이터를 이용하여 음원의 방향을 추정할 수 있다.
도 3은 본 발명의 일 실시예에 따른 방향 추정 장치의 제어부를 도시한 블록도이다.
도 3을 참조하면, 제어부(240)는 신호를 디지털 신호로 변환하고, 변환된 디지털 신호의 잡음 신호를 제거할 수 있다. 제어부(240)는 제거된 디지털 신호의 통계학적 분포를 이용하여 디지털 신호의 음원 개수 및 방향에 대한 공간 스펙트럼을 산출할 수 있다. 제어부(240)는 산출된 디지털 신호의 공간 스펙트럼의 피크를 음원의 방향인 것으로 추정할 수 있다.
전처리부(320)는 아날로그 신호를 디지털 신호로 변환할 수 있다. 전처리부(320)는 아날로그 디지털 변환기(ADC: Analog-to-Digital Conversion)를 포함할 수 있다. ADC는 음원 신호 및 잡음 신호를 디지털 신호로 변환할 수 있다.
전처리부(320)는 균일하게 떨어진 거리 에 이격된 센서 과 균일 선형 배열(ULA: Uniform Linear Array)을 고려할 수 있다. 전처리부(320)는 광대역 음원 가 인 경우, m 번째 센서에서 수신된 센서 신호 로 [수학식 1]처럼 모델링을 할 수 있다.
와 는 미시간 전파 효과에 의한 감쇠 계수이다. 전처리부(320)는 m 번째 센서에서 i 번째 음원 신호의 첫 번째 센서로부터 전파 시간 지연을 할 수 있다. 는 m 번째 센서에서의 잡음 신호다. 전처리부(320)는 짧은 시간 이산 푸리에 변환(STDFT: Shot-Time Discrete Fourier Transform)을 이용하여 의 샘플링 속도를 로 만들 수 있다. 전처리부(320)는 k번째 주파수 빈(frequency bin) 및 시간 n에서 m센서의 주파수 요소를 [수학식 2]로 표현할 수 있다.
는 의 이산 시간 수신 센서 신호이다. 는 윈도우(window) 순서이고, 는 DFT(Discrete Fourier Transform) 지점의 개수이다. 및 는 각각 및 의 STDFT이다. 전처리부(320)는 센서 배열 구멍의 크기가 신호부터 센서 배열까지의 거리에 비해 훨씬 작고 멀어지면 [수학식3]과 같이 를 정의할 수 있다.
음원 신호는 평균이 0인 정규분포이고 비고정 신호이며, 가우시안 분포 또는 비 가우시안 분포가 될 수 있다. 음원 신호는 서로 독립적일 수 있다. 잡음 신호는 평균이 0인 정규분포이고 고정 신호이며, 가우스 분포 또는 비 가우시안 분포가 될 수 있다. 잡음 신호는 공간적인 상관성(correlated) 또는 비 상관성(uncorrelated)이 있을 수 있다. 음원 신호 및 잡음 신호는 서로 독립적일 수 있다.
전처리부(320)는 변환된 신호의 잡음 신호를 필터링할 수 있다. 전처리부(320)는 저역 통과 필터(low pass filter) 및 대역 통과 필터(band pass filter) 중 적어도 하나를 포함할 수 있다.
는 L차원의 복잡한 임의의 벡터이다. 는 L-길이 벡터의 원소의 지수인 2p의 길이 벡터이다. 는 이다. 의 는 의 차원이다. 전처리부(320)는 의 2p 차원 커뮬런트(cumulant)를 Leonov - Shiryaev에 기반으로 [수학식 5]로 정의할 수 있다.
전처리부(320)는 를 의 집합에서 모든 분할(partitions)이라고 설명할 수 있다. 또한 전처리부(320)는 를 예상을 나타내는데 사용할 수 있다. 는 이고, 그렇지 않으면 및 와 같이 이고, 가 될 수 있다. *는 결합 연산자를 나타낼 수 있다. 의 총 차원 집합은 이고, 집합의 원소의 개수인 는 일 수 있다. 의 각 원소는 의 지수를 생성할 수 있습니다. 는 이고, 일 수 있다. 의 번째 원소는 로 나타낼 수 있다. 는 의 2p 길이 L항을 나타낼 수 있다. 전처리부(320)는 시간 n에서 와 함께 k 번째 주파수 빈인 의 수신 센서 신호 벡터는 [수학식 6]으로 나타낼 수 있다.
전처리부(320)는 를 모든 요소 것들의 2p-길이 벡터로 할 수 있다. 및 는 각각 시간 에서 번째 주파수 빈의 음원 신호 벡터의 2p차원 커뮬런트 행렬 및 잡음 신호 벡터일 수 있다. 번째 주파수 빈의 음원 신호 벡터의 2p차원 커뮬런트 행렬인 는 이다. 번째 주파수 빈의 잡음 신호 벡터인 는 이다.
전처리부(320)는 가 일 때, 라고 할 수 있다. 전처리부(320)는 비고정 음원 신호의 경우에는 배열 을 시간 에서 열(column)같이 [수학식 6]에서 정의할 수 있다. 지수 는 0부터 까지 오름차순이고, 고정부분 를 위해 시간 에 열을 스택(stack)할 수 있다.
신호 분석부(340)는 전처리부(320)에서 변환된 음원 신호의 통계학적 분포를 산출할 수 있다. 또한 신호 분석부(340)는 2차원 통계학적 분포 데이터를 포함한 높은 2p 차원의 통계학적 분포 데이터를 이용하여 음원 신호가 포함하고 있는 통계학적 분포 데이터를 분석하여 산출할 수 있다.
신호 분석부(340)는 음원의 개수가 정해지고, 정해지지 않은 경우에 따라 다른 알고리즘을 이용하여 신호 분석을 할 수 있다. 신호 분석부(340)는 음원의 개수가 정해진 경우에는 MUSIC 알고리즘 기반의 c-2p-MUSIC 알고리즘을 이용할 수 있다. 신호 분석부(340)는 음원의 개수가 정해지지 않은 경우에는 Capon 알고리즘 기반의 c-2p-Canpon 알고리즘을 이용할 수 있다.
신호 분석부(340)는 번째 주파수 빈의 2p차원 커뮬런트 행렬을 [수학식 7]로 정의할 수 있다. [수학식 7]의 신호는 통계학적 분포를 나타내고 있고, 잡음 신호를 포함할 수 있다.
신호 분석부(340)는 감지된 센서 신호의 를 고정 부분을 포함하고 있다고 가정한다. 신호 분석부(340)는 및 에 의해 지수로 주어진 의 고정 부분을 위해 을 모든 고정 부분에서 고정 길이로 설정할 수 있다. 신호 분석부(340)는 를 번째 부분의 에서 로컬(로컬 고정) 2차원 커뮬런트 행렬로 나타낼 수 있다. 신호 분석부(340)는 [수학식 7]에서 는 k 번째 주파수 빈의 가상 배열 매니폴드(manifold) 벡터를 나타낼 수 있다. 또한 및 의 i번째 열은 k 번째 주파수 빈에서 의 가상 배열는 매니폴드 벡터일 수 있고, p차원의 함수일 수 있다.
신호 분석부(340)는 p = 1일 때, 의 차원 감소 절차를 직교 열행렬 및 반데르몬데(Vandermonde) 행렬의 곱으로 표현할 수 있고, KR 부공간 기반의 알고리즘에 사용할 수 있다. KR 부공간 기반의 알고리즘은 방향을 추정하는 차원 감소 절차를 제안 알고리즘의 복잡성을 줄여줄 수 있다.
신호 분석부(340)는 의 켤레전치(conjugate transpose)로 를 곱할 수 있다. 이를 통해, 신호 분석부(340)는 잡음 신호 제거 및 치수 조정된 2차원 커뮬런트 행렬을 [수학식 11]과 같이 정의할 수 있다.
신호 분석부(340)는 [수학식11]에서 는 반드시 대각선이 아니지만 대칭이고, 에 충족할 수 있다. [수학식 12] 및 [수학식 13]은 [수학식 11]을 적용하여 순위 및 범위를 나타낼 수 있다.
신호 분석부(340)는 한계 최적화 문제(COP: constrained optimization problem)에 대해 [수학식 11]의 를 이용할 수 있다. 신호 분석부(340)는 COP의 해결책(solution)을 방향각(look direction)에서 가중치 벡터 이득의 제곱을 극대화하는 것으로 할 수 있다.
신호 분석부(340)는 COP에 대한 제약 조건을 해결책 사이의 내적의 제곱의 합을 제한할 수 있다. 신호 분석부(340)는 각각의 고유 벡터인 및 는 2p 차원 음원 신호의 부공간 및 2p 차원 잡음 신호의 부공간에 참조할 수 있다. 신호 분석부(340)는 을 널(NULL) 공간으로 나타낼 수 있다. 신호 분석부(340)는 제약 조건에서 음원의 개수에 대한 가용성을 조절하고, 제약 조건의 특정 매개 변수 설정에 따라 해결책을 세 가지 공간 중 하나에 걸쳐 제한할 수 있다. 상기 세 가지 공간은 , 및 와 일 수 있다.
신호 분석부(340)는 COP를 [수학식 14]로 나타낼 수 있다.
[수학식 15]는 [수학식 14]의 조건을 나타낼 수 있다.
신호 분석부(340)는 및 은 각각 및 를 영이 아닌 고유값과 영인 고유값에 해당하는 고유 벡터로 구성할 수 있다. 신호 분석부(340)는 를 대각선을 따라 영이 아닌 고유값을 가질 수 있다. 는 이고 이면, 이다. 는 k 번째 주파수의 가중치 벡터이고, 는 임의의 영 아닌 실제 상수이다.
신호 분석부(340)는 제약된 [수학식 15]를 음원 개수의 가용성을 조건으로 할 수 있다. 신호 분석부(340)는 [수학식 16] 또는 [수학식 17]의 를 비특이(non-singular)로 나타낼 수 있다. 신호 분석부(340)는 의 EVD에서 변수를 및 에 모두 해당하는 강점(고유값) 관련된 고유 벡터로 결정할 수 있다. 신호 분석부(340)는 COP를 라그랑주 승수(Lagrange multiplier)인 를 이용하여 해결할 수 있다. [수학식 18]은 COP의 해결책을 보여줄 수 있다.
신호 분석부(340)는 음원 수의 가용성 조건에 따라 두 가지 분석으로 나누어 분석할 수 있다. 상기 가용성 조건은 음원(I)의 개수가 정해진 경우와 정해지지 않을 경우일 수 있다.
[수학식 24]의 은 이고, 은 이다. 또한 는 M 행령의 i번째 열을 나타낸다. [수학식 23] 및 [수학식 24]을 이용하면, [수학식 22]에서 주어진 는 다시 정의될 수 있다.
[수학식 26]는 2차원 음원 신호 부공간 행렬이고, [수학식 27]은 2차원 잡음 신호 부공간 행렬이다.
인 경우, 신호 분석부(340)는 [수학식 24]의 오른쪽에서 첫 번째 항과 두 번째 항인 및 를 이용하여 을 추정할 수 있다. 신호 분석부(340)는 를 [수학식 30]와 같이 추정할 수 있다.
는 [수학식 25]에서 주어질 수 있다. [수학식 26] 및 [수학식 27]에서 정의된 및 의 는 을 정의할 수 있는 또는 및 를 방향각 으로 나타낼 수 있다. 의 범위 조건은 두 가지 속성을 가질 수 있다.
첫 번째 속성은 의 고해상도 DOA 추정을 달성하기 위해 [수학식 25]에서 및 와 한 것 같이 로 할 수 있다. 여기서 는 공집합이다. 따라서, [수학식 27]에서 정의된 의 각각의 대각선 값이 더 커질 수 있다.
두 번째 속성은 은 2p-KR-MUSIC에 동등한 기능을 달성하기 위해 및 를 조정된 일 수 있다. 따라서, [수학식 26] 및 [수학식 27]에서 정의된 모든 대각선 값인 및 이 동시에 커질 수 있다.
신호 분석부(340)가 음원의 개수가 정해지지 않고 을 분석할 경우에는, [수학식 17]를 이용할 수 있다. [수학식 17]의 는 [수학식 25]에서 주어진 를 산출하기 위해 이용될 수 있다. 그러나 [수학식 25]의 및 은 알지 못한다. 신호 분석부(340)는 를 인 경우와 아닌 경우로 나눌 수 있다.
인 경우, 는 [수학식 25]에서 주어진 와 함께 [수학식 30]를 충족을 시킬 수 있다. 또한 신호 분석부(340)는 의 두 가지 속성 범위 조건으로 의 스판(spans)인 또는 와 을 걸쳐 만들 수 있다.
첫 번째 조건은 의 고해상도 DOA 추정을 달성하기 위해, [수학식 25]의 은 및 이고, 일 수 있다. 따라서, [수학식 26]에서 정의된 의 각 대각선 값은 더 작아질 수 있다.
신호 분석부(340)는 음원(I)의 개수가 정해지거나 정해지지 않을 경우에는 서로 다른 공간 스펙트럼 알고리즘을 이용할 수 있다.
음원의 개수가 정해져 있을 경우에는 신호 분석부(340)는 공간 스펙트럼 알고리즘을 [수학식 31]과 같이 제안할 수 있다. 신호 분석부(340)는 [수학식 16] 및 에 해당하는 를 이용하여 산출된 를 제약된 2p차원 공간 스펙트럼인 c-2p-KR-MUSIC을 [수학식 31]과 같이 제안할 수 있다.
음원의 개수가 정해지지 않은 경우에는 신호 분석부(340)는 공간 스펙트럼 알고리즘을 [수학식 33]과 같이 제안할 수 있다. 신호 분석부(340)는 [수학식 17] 및 에 해당하는 를 이용하여 산출된 를 제약된 2p차원 공간 스펙트럼인 c-2p-KR-Capon을 [수학식 33]와 같이 제안할 수 있다.
신호 분석부(340)는 c-2p-KR-MUSIC 및 c-2p-KR-Capon에서 [수학식 21]의 해결책 을 특이값분해(SVD: singular value decomposition)로 의 가장 큰 비특이값(non-singular value)을 고려한 비특이벡터를 제공할 수 있다. 또한 신호 분석부(340)는 방향각 을 검색하면 DOA가 제안하는 C-2P-KR-MUSIC과 C-2P-KR-Capon의 로컬 피크(peak)를 산출할 수 있다.
방향 추정부(360)는 신호 분석부(340)에서 분석된 신호의 데이터를 이용하여 음원 신호의 방향을 추정할 수 있다. 방향 추정부(360)는 특이값 분해에서 산출한 가장 큰 비특이값을 가지는 비특이벡터의 방향각을 음원 신호의 방향으로 추정할 수 있다.
실제로, 방향 추정부(360)는 를 이용할 수 없기 때문에 를 추정하는 것은 쉽지 않을 수 있고, [수학식 13]이 충족되지 않은 것 같이 상기 추정치에 특정 오류가 있을 수 있다. 즉, 는 의 추정한 것을 나타내고, 및 일 수 있다. 또한 의 오류를 고려하면, 는 2P-KR-MUSIC와 2P-KR-Capon과 같이 고해상도 DOA 추정과 기능의 균형을 결정될 수 있다.
방향 추정부(360)는 [수학식 11]에서 주어진 및 를 이용하여 시간 평균을 추정할 수 있다. 그러나 방향 추정부(360)는 신호가 오디오 같은 비고정 신호일 때만 가능할 수 있다. 은 알고 있지 않고 결정하는 것은 불가능하다. 또한 고정값 및 은 정확한 DOA추정으로 이어지지 않을 수 있다. 이러한 이유로, 방향 추정부(360)는 의 추정값을 모든 것이 가능한 를 이용하여 [수학식 37]처럼 산출할 수 있다.
제어부(240)는 [수학식 4]의 정의된 실제 센서 지역의 집합인 은 거리 와 함께 를 산출한다. 제어부(240)는 [수학식 7]의 에서 실제 및 가상 센서 지역의 집합을 [수학식 38]과 같이 설정할 수 있다.
제어부(240)는 가상 배열 프레임워크(virtual array framework)의 관점에서 공간만의 다양성을 고려하여 p차원의 가상 센서의 좌표를 이용할 수 있다. 제어부(240)는 [수학식 38]에서 실제 및 가상의 센서의 수는 이고, 따라서 C-2P-KR-MUSIC,의 식별 가능성은 p 및 M의 함수로 [수학식 39]과 같이 구성할 수 있다.
[수학식 39]은 c-2p-KR-MUSIC 및 c-2p-KR-Capon의 센서의 식별 가능성을 나타낼 수 있다.
결론적으로, 제어부(240)는 하기의 순서대로 구동하여 동작할 수 있다.
제 2단계는 방향각 를 산출하기 위해[수학식 22]을 이용하여 의 SVD에서 산출된 가장 큰 비특이값에 해당하는 비특이벡터인 을 [수학식 31]에서 또는 [수학식 33]에서 로 산출한다. 음원의 개수가 정해진 경우에는 를 [수학식 16]를 이용하여 산출하고, 는 [수학식 35]를 이용하여 산출한다. 음원의 개수가 정해지지 않은 경우에는 를 [수학식 17]를 이용하여 산출하고, 는 [수학식 36]를 이용하여 산출한다.
제 3단계는 제안된 공간 스펙트럼의 로컬 최대값에 해당하는 방향으로 추정한다.
제어부(240)는 일 때, 하기 알고리즘을 제안할 수 있다. c-2p-KR-MUSIC 및 c-2-KR-Capon 알고리즘은 을 이용한 COP에서 파생된 알고리즘일 수 있다. c-2-KR-MUSIC-M 및 c-2-KR-Capon-M 알고리즘은 을 이용한 c-2p-KR-MUSIC 및 2p-KR-Capon 알고리즘일 수 있다. 4-KR-MUSIC 및 4-KR-Capon 알고리즘은 을 이용한 간단하게 확장된 KR-MUSIC 및 KR-Capon 알고리즘일 수 있다. c-4-KR-MUSIC 및 c-4-KR-Capon은 을 이용한 COP에서 파생된 알고리즘일 수 있다. c-4-KR-MUSIC-M 및 c-4-KR-Capon-M은 을 이용한 c-4-KR-MUSIC 및 c-4-KR-Capon 알고리즘일 수 있다.
도 4는 본 발명의 일 실시예에 따른 방향 추정 장치의 고해상도를 도시한 그래프이고, 도 5는 본 발명의 다른 실시예에 따른 방향 추정 장치의 고해상도를 도시한 그래프이며, 도 6은 본 발명의 또 다른 실시예에 따른 방향 추정 장치의 고해상도를 도시한 그래프이고, 도 7은 본 발명의 또 다른 실시예에 따른 방향 추정 장치의 고해상도를 도시한 그래프이다.
도 4 내지 도 7을 참조하면, 방향 추정 장치(1)은 공간적 고해상도가 높을 수 있다.
도 4는 일반화된 가우시안 분포에서 생성된 협대역 비고정 음원 신호의 그래프이다. 도 4는 KR-Capon, c-2-KR-Capon, 4-KR-Capon 및 c-4-KR-Capon의 공간 스펙트럼을 나타낸다. 도 4는 , , 및 인 그래프이다.
도 4(a)는 KR-Capon과 c-2-KR-Capon을 비교한 그래프이다. 도 4(a)는 c-2-KR-Capon가 KR-Capon보다 더 높은 공간 해상도를 나타내는 것을 보여주고 있다. c-2-KR-Capon의 공간 스펙트럼은 KR-Capon의 공간 스펙트럼보다 더 깊은 곡선을 보여주면서 과 의 구분을 명확하게 하여 공간 해상도가 높다는 것을 보여준다.
도 4(b)는 4-KR-Capon과 c-4-KR-Capon을 비교한 그래프이다. 도 4(b)는 c-4-KR-Capon가 4-KR-Capon보다 더 높은 공간 해상도를 나타내는 것을 보여주고 있다. c-4-KR-Capon의 공간 스펙트럼은 4-KR-Capon의 공간 스펙트럼보다 더 깊은 곡선을 보여주면서 과 의 구분을 명확하게 하여 공간 해상도가 높다는 것을 보여준다.
도 5는 일반화된 가우시안 분포에서 생성된 협대역 비고정 음원 신호의 그래프이다. 도 5는 KR-MUSIC, c-2-KR-MUSIC, 4-KR-MUSIC 및 c-4-KR-MUSIC의 공간 스펙트럼을 나타낸다. 도 5는 , , 및 인 그래프이다.
도 5(a)는 KR-MUSIC과 c-2-KR-MUSIC을 비교한 그래프이다. 도 5(a)는 c-2-KR-MUSIC가 KR-MUSIC보다 더 높은 공간 해상도를 나타내는 것을 보여주고 있다. c-2-KR-MUSIC의 공간 스펙트럼은 KR-MUSIC의 공간 스펙트럼보다 더 깊은 곡선을 보여주면서 과 의 구분을 명확하게 하여 공간 해상도가 높다는 것을 보여준다.
도 5(b)는 4-KR-MUSIC과 c-4-KR-MUSIC을 비교한 그래프이다. 도 5(b)는 c-4-KR-MUSIC가 4-KR-MUSIC보다 더 높은 공간 해상도를 나타내는 것을 보여주고 있다. c-4-KR-MUSIC의 공간 스펙트럼은 4-KR-MUSIC의 공간 스펙트럼보다 더 깊은 곡선을 보여주면서 과 의 구분을 명확하게 하여 공간 해상도가 높다는 것을 보여준다.
도 6은 일반화된 가우시안 분포에서 생성된 협대역 비고정 음원 신호의 그래프이다. 도 6는 4-KR-MUSIC, c-4-KR-MUSIC, 4-KR-Capon 및 c-4-KR-Capon의 공간 스펙트럼을 보여주고 있다. 도 6는 , ,, 및 인 그래프이다.
도 6(a)는 4-KR-MUSIC과 c-4-KR-MUSIC을 비교한 그래프이다. 도 6(a)는 c-4-KR-MUSIC가 4-KR-MUSIC보다 더 높은 공간 해상도를 나타낸다. c-4-KR-MUSIC의 공간 스펙트럼은 4-KR-MUSIC의 공간 스펙트럼보다 더 깊은 곡선을 보여주면서 , 및 의 구분을 명확하게 하여 공간 해상도가 높다는 것을 보여준다.
도 6(b)는 4-KR-Capon과 c-4-KR-Capon을 비교한 그래프이다. 도 6(b)는 c-4-KR-Capon가 4-KR-Capon보다 더 높은 공간 해상도를 나타내는 것을 보여주고 있다. c-4-KR-Capon의 공간 스펙트럼은 4-KR-Capon의 공간 스펙트럼보다 더 깊은 곡선을 보여주면서 , 및 의 구분을 명확하게 하여 공간 해상도가 높다는 것을 보여준다.
도 7은 광대역 비고정 음원 신호인 음성 및 오디오의 그래프이다. 도 7은 4-KR-MUSIC, c-4-KR-MUSIC, 4-KR-Capon 및 c-4-KR-Capon의 공간 스펙트럼을 나타낸다. 도 7는 , , , 및 인 그래프이다.
도 7(a)는 4-KR-MUSIC과 c-4-KR-MUSIC을 비교한 그래프이다. 도 7(a)는 c-4-KR-MUSIC가 4-KR-MUSIC보다 더 높은 공간 해상도를 나타내는 것을 보여주고 있다. c-4-KR-MUSIC의 공간 스펙트럼은 4-KR-MUSIC의 공간 스펙트럼보다 해당 방향각에서 뚜렷한 곡선을 보여주면서 , 및 의 구분을 명확하게 하여 공간 해상도가 높다는 것을 보여준다.
도 7(b)는 4-KR-Capon과 c-4-KR-Capon을 비교한 그래프이다. 도 6(b)는 c-4-KR-Capon가 4-KR-Capon보다 더 높은 공간 해상도를 나타내는 것을 보여주고 있다. c-4-KR-Capon의 공간 스펙트럼은 4-KR-Capon의 공간 스펙트럼보다 해당 방향각에서 뚜렷한 곡선을 보여주면서 , 및 의 구분을 명확하게 하여 공간 해상도가 높다는 것을 보여준다.
도 8은 본 발명의 일 실시예에 따른 방향 추정 장치의 정확도를 도시한 그래프이고, 도 9는 본 발명의 다른 실시예에 따른 방향 추정 장치의 정확도를 도시한 그래프이며, 도 10은 본 발명의 또 다른 실시예에 따른 방향 추정 장치의 정확도를 도시한 그래프이고, 도 11은 본 발명의 또 다른 실시예에 따른 방향 추정 장치의 정확도를 도시한 그래프이며, 도 12는 본 발명의 또 다른 실시예에 따른 방향 추정 장치의 정확도를 도시한 그래프이고, 도 13은 본 발명의 또 다른 실시예에 따른 방향 추정 장치의 정확도를 도시한 그래프이며, 도 14는 본 발명의 또 다른 실시예에 따른 방향 추정 장치의 정확도를 도시한 그래프이고, 도 15는 본 발명의 또 다른 실시예에 따른 방향 추정 장치의 정확도를 도시한 그래프이다.
도 8 내지 도 15를 참조하면, 방향 추정 장치(1)은 성공 가능성(PoS: Probability of Success)이 높고 평균 제곱근 각도 오차(RMSE: root-mean-squared-angle-error)가 낮을 수 있다.
도 8은 일반화된 가우시안 분포에서 생성된 협대역 비고정 음원 신호의 그래프이다. 도 8은 KR-MUSIC, c-2-KR-MUSIC, KR-Capon, c-2-KR-Capon, 4-KR-MUSIC, c-4-KR-MUSIC, 4-KR-Capon, c-4-KR-Capon 및 4-MUSIC의 신호대잡음 신호비(SNR: Signal to noise ratio)에 대한 RMSE를 나타낸다. 도 8은 , , 및 PoS=1 인 그래프이다.
도 8은 KR-MUSIC, KR-Capon, 4-KR-MUSIC 및 4-KR-Capon 에 대응하는 c-2-KR-MUSIC, c-2-KR-Capon, c-4-KR-MUSIC 및 c-4-KR-Capon이 RMSE가 낮은 것을 보여준다. 즉, c-2-KR-MUSIC, c-2-KR-Capon, c-4-KR-MUSIC 및 c-4-KR-Capon이 KR-MUSIC, KR-Capon, 4-KR-MUSIC 및 4-KR-Capon 보다 오차가 작다는 것을 의미한다.
도 9는 일반화된 가우시안 분포에서 생성된 협대역 비고정 음원 신호의 그래프이다. 도 9는 KR-MUSIC, c-2-KR-MUSIC-M, KR-Capon, c-2-KR-Capon-M, 4-KR-MUSIC, c-4-KR-MUSIC-M, 4-KR-Capon, c-4-KR-Capon-M 및 4-MUSIC의 신호대잡음 신호비(SNR: Signal to noise ratio)에 대한 RMSE를 나타낸다. 도 8은 , , 및 PoS=1 인 그래프이다.
도 9는 KR-MUSIC, KR-Capon, 4-KR-MUSIC 및 4-KR-Capon 에 대응하는 c-2-KR-MUSIC-M, c-2-KR-Capon-M, c-4-KR-MUSIC-M 및 c-4-KR-Capon-M이 RMSE가 낮은 것을 보여준다. 즉, c-2-KR-MUSIC-M, c-2-KR-Capon-M, c-4-KR-MUSIC-M 및 c-4-KR-Capon-M이 KR-MUSIC, KR-Capon, 4-KR-MUSIC 및 4-KR-Capon 보다 오차가 작다는 것을 의미한다. 또한 도 9는 [수학식 37]의 을 이용하여 점선과 RMSE의 차를 늘려준다. 따라서, 는 더 정확한 DOA를 제공해주는 효과가 있다.
도 10은 일반화된 가우시안 분포에서 생성된 협대역 비고정 음원 신호의 그래프이다. 도 10은 4-KR-MUSIC, c-4-KR-MUSIC, 4-KR-Capon 및 c-4-KR-Capon의 신호대잡음 신호비(SNR: Signal to noise ratio)에 대한 RMSE를 나타낸다. 도 10은 , , , 및 PoS=1 인 그래프이다.
도 10은 4-KR-MUSIC 및 4-KR-Capon에 대응하는 c-4-KR-MUSIC 및 c-4-KR-Capon이 RMSE가 낮은 것을 보여준다. 즉, c-4-KR-MUSIC 및 c-4-KR-Capon이 4-KR-MUSIC 및 4-KR-Capon보다 오차가 작다는 것을 의미한다.
도 11은 일반화된 가우시안 분포에서 생성된 협대역 비고정 음원 신호의 그래프이다. 도 11은 4-KR-MUSIC, c-4-KR-MUSIC-M, 4-KR-Capon 및 c-4-KR-Capon-M의 SNR에 대한 RMSE를 나타낸다. 도 11은 , , , 및 PoS=1 인 그래프이다.
도 11은 4-KR-MUSIC 및 4-KR-Capon 에 대응하는 c-4-KR-MUSIC-M 및 c-4-KR-Capon-M이 RMSE가 낮은 것을 보여준다. 즉, c-4-KR-MUSIC 및 c-4-KR-Capon이 4-KR-MUSIC 및 4-KR-Capon 보다 오차가 작다는 것을 의미한다. 또한 도 11은 을 이용하여 점선과 RMSE의 차를 늘려준다. 따라서, 는 더 정확한 DOA를 제공해주는 효과가 있다.
도 12는 광대역 비고정 음원 신호인 음성 및 오디오의 그래프이다. 도 12는 KR-MUSIC, c-2-KR-MUSIC-M, KR-Capon, c-2-KR-Capon-M, 4-KR-MUSIC, c-4-KR-MUSIC-M, 4-KR-Capon 및 c-4-KR-Capon-M의 SNR에 대한 PoS를 나타낸다. 도 12는 , 및 인 그래프이다.
도 12는 p=1, 2일 때, c-2p-KR-MUSIC-M 및 c-2p-Capon-M이 2p-KR-MUSIC 및 2p-KR-Capon보다 높은 PoS를 보여준다. 도 12는 SNR이 낮고 p=2일 때, PoS가 특히 높은 것을 보여준다.
도 13는 광대역 비고정 음원 신호인 음성 및 오디오의 그래프이다. 도 13는 KR-MUSIC, c-2-KR-MUSIC-M, KR-Capon, c-2-KR-Capon-M, 4-KR-MUSIC, c-4-KR-MUSIC-M, 4-KR-Capon 및 c-4-KR-Capon-M의 SNR에 대한 RMSE를 나타낸다. 도 12는 , , 및 PoS=0인 그래프이다.
도 13는 p=1, 2일 때, c-2p-KR-MUSIC-M 및 c-2p-Capon-M이 2p-KR-MUSIC 및 2p-KR-Capon보다 더 좋은 결과를 보여준다.
도 14는 광대역 비고정 음원 신호인 음성 및 오디오의 그래프이다. 도 14는 4-KR-MUSIC, c-4-KR-MUSIC-M, 4-KR-Capon 및 c-4-KR-Capon-M의 SNR에 대한 PoS를 나타낸다. 도 14는 , , 및 인 그래프이다.
도 14는 c-4-KR-MUSIC-M 및 c-4-KR-Capon-M은 4-KR-MUSIC 및 4-KR-Capon보다 높은 PoS를 보여준다. 도 14는 특히 SNR이 낮을 때, PoS가 특히 높은 것을 보여준다.
도 15는 광대역 비고정 음원 신호인 음성 및 오디오의 그래프이다. 도 14는 4-KR-MUSIC, c-4-KR-MUSIC-M, 4-KR-Capon 및 c-4-KR-Capon-M의 SNR에 대한 RMSE를 나타낸다. 도 15는 , , 및 인 그래프이다.
도 15는 c-4-KR-MUSIC-M 및 c-4-KR-Capon-M은 4-KR-MUSIC 및 4-KR-Capon보다 더 좋은 결과를 보여준다. 도 15는 특히 SNR이 낮을 때, PoS가 특히 높은 것을 보여준다.
도 16은 본 발명의 일 실시예에 따른 방향 추정 장치의 음원 추출 개수를 도시한 그래프이고, 도 17은 본 발명의 다른 실시예에 따른 방향 추정 장치의 음원 추출 개수를 도시한 그래프이며, 도 18은 본 발명의 또 다른 실시예에 따른 방향 추정 장치의 음원 추출 개수를 도시한 그래프이다.
도 16 내지 도 18은 방향 추정 장치(1)은 음원 신호의 개수를 더 많이 추출할 수 있다.
도 16은 일반화된 가우시안 분포에서 생성된 협대역 비고정 음원 신호의 그래프이다. 도 16은 4-KR-MUSIC, c-4-KR-MUSIC, 4-KR-Capon 및 c-4-KR-Capon의 음원 신호의 개수 추출을 나타낸다. 도 16은 , , , , 및 인 그래프이다.
도 16(a)은 4-KR-MUSIC과 c-4-KR-MUSIC을 비교한 그래프이다. 도 16(a)는 c-4-KR-MUSIC의 4개 피크(peak)가 4-KR-MUSIC의 4개 피크보다 더 명확하게 보여준다. 따라서, 도 16(a)는 c-4-KR-MUSIC가 4-KR-MUSIC보다 더 많은 음원 신호를 추출할 수 있다는 것을 보여준다.
도 16(b)은 4-KR-Capon과 c-4-KR-Capon을 비교한 그래프이다. 도 16(b)는 c-4-KR-Capon의 4개 피크가 4-KR-Capon의 4개 피크보다 더 명확하게 보여준다. 따라서, 도 16(b)는 c-4-KR-Capon가 4-KR-Capon보다 더 많은 음원 신호를 추출할 수 있다는 것을 보여준다.
도 17은 광대역 비고정 음원 신호인 음성 및 오디오의 그래프이다. 도 17은 KR-Capon, c-2-KR-Capon, 4-KR-Capon 및 c-4-KR-Capon의 음원 신호의 개수 추출을 나타낸다. 도 17은 , , 및 인 그래프이다.
도 17(a)은 KR-Capon과 c-2-KR-Capon을 비교한 그래프이다. 도 17(a)은 방향 추정 장치(1)이 c-2-KR-Capon을 이용하여 2개 피크가 추출하지만 KR-Capon을 이용해서는 1개 피크만 추출되는 것을 보여준다. 따라서, 도 17(a)은 c-2-KR-Capon이 KR-Capon보다 더 많은 음원 신호를 추출할 수 있다는 것을 보여준다.
도 17(b)은 4-KR-Capon과 c-4-KR-Capon을 비교한 그래프이다. 도 17(b)는 c-4-KR-Capon을 이용하여 2개 피크를 추출하지만 4-KR-Capon을 이용해서는 1개 피크밖에 추출되는 것을 보여준다. 따라서, 도 17(b)은 c-4-KR-Capon이 4-KR-Capon보다 더 많은 음원 신호를 추출할 수 있다는 것을 보여준다.
도 18은 광대역 비고정 음원 신호인 음성 및 오디오의 그래프이다. 도 18은 KR-MUSIC, c-2-KR-MUSIC, 4-KR-MUSIC 및 c-4-KR-MUSIC의 음원 신호의 개수 추출을 나타낸다. 도 18(a)은 , , 및 인 그래프이고, 도 18(b)은 , , 및 인 그래프이다.
도 18(a)은 KR-MUSIC 및 c-2-KR-MUSIC을 비교한 그래프이다. 도 18(a)은 c-4-KR-MUSIC의 2개 피크가 4-KR-MUSIC의 2개 피크보다 더 명확하게 보여준다. 따라서, 도 18(a)은 c-4-KR-MUSIC이 4-KR-MUSIC보다 더 많은 음원 신호를 추출할 수 있다는 것을 보여준다.
도 18(b)은 4-KR-MUSIC 및 c-4-KR-MUSIC을 비교한 그래프이다. 도 18(b)은 c-4-KR-MUSIC의 2개 피크가 4-KR-MUSIC의 2개 피크보다 더 명확하게 보여준다. 따라서, 도 18(b)은 c-4-KR-MUSIC이 4-KR-MUSIC보다 더 많은 음원 신호를 추출할 수 있다는 것을 보여준다.
도 19는 본 발명의 일 실시예 따른 방향 추정 방법을 도시한 순서도이다.
도 19를 참조하면, 방향 추정 장치(1)는 음원의 신호를 분석하여 음원이 출력되는 방향을 추정하는 장치일 수 있다.
센서부(220)는 신호를 감지한다(S100). 상기 감지된 신호는 음원으로부터 출력된 음원 신호 및 잡음 신호 중 적어도 하나를 포함할 수 있다. 상기 음원 신호는 비고정 신호이고, 상기 잡음 신호은 고정 신호일 수 있다.
센서부(220)는 음원(110), 음원(120), 음원(130) 및 음원(140) 중 적어도 하나의 음원에서 출력하는 신호를 감지할 수 있다. 또한 센서부(220)는 센서의 개수가 음원의 개수보다 적을 수 있다.
전처리부(320)는 아날로그 신호인 신호를 디지털 신호인 센서 신호로 ADC 변환을 한다(S110). 전처리부(320)는 신호를 샘플링하여 디지털 신호인 센서 신호로 변환할 수 있다.
신호 분석부(340)는 변환된 센서 신호에 포함되어 있는 잡음 신호를 필터링한다(S120). 신호 분석부(340)는 전처리부(320)에서 변화된 신호의 통계학적 분포 데이터를 산출할 수 있다. 또한 신호 분석부(340)는 고정 신호인 잡음 신호를 제거하고 비고정 신호인 음원 신호의 통계학적 분포 데이터만 추출할 수 있다. 신호 분석부(340)는 저역 통과 필터 및 대역 통과 필터 중 적어도 하나를 포함할 수 있다.
신호 분석부(340)는 음원의 개수가 정해져 있는지 확인한다(S130). 신호 분석부(340)는 음원의 개수가 정해져 있는지 확인하고, 정해져 있을 경우와 정해지지 않은 경우에 따라 다른 알고리즘을 이용할 수 있다.
신호 분석부(340)는 음원의 개수가 정해져 있는 경우, c-2p-KR-MUSIC 알고리즘을 실행한다(S140). 신호 분석부(340)는 MUSIC 알고리즘 기반의 c-2p-KR-MUSIC 알고리즘을 이용하여 비특이 값을 산출할 수 있다.
신호 분석부(340)는 음원의 개수가 정해지지 않은 경우, c-2p-KR-Capon 알고리즘을 실행한다(S150). 신호 분석부(340)는 Capon 알고리즘 기반의 c-2p-KR-Capon 알고리즘을 이용하여 비특이 값을 산출할 수 있다.
방향 추정부(360)는 산출된 비특이값을 이용하여 음원 방향을 추정한다(S160). 방향 추정부(360)는 단계 S140 및 단계 S150에서 산출된 비특이값의 가장 큰 값에 해당하는 음원 신호를 음원의 방향으로 추정할 수 있다.
도 20은 도 19의 S140을 더 상세하게 도시한 순서도이다.
도 20을 참조하면, 신호 분석부(340)는 음원 개수가 정해져 있는 경우에는 c-2p-KR-MUSIC 알고리즘을 실행할 수 있다.
신호 분석부(340)는 를 산출한다(S210). 신호 분석부(340)는 [수학식 22]를 이용하여 라그랑주 승수 을 산출할 수 있다. 신호 분석부(340)는 단계 S200에서 산출된 를 이용하여 을 산출할 수 있다.
신호 분석부(340)는 를 산출한다(S220). 신호 분석부(340)는 [수학식 28] 또는 [수학식 29]을 이용하여 최적의 가중치 벡터 을 산출할 수 있다. 신호 분석부(340)는 단계 S210에서 산출된 을 이용하여 을 산출할 수 있다.
신호 분석부(340)는 를 산출한다(S230). 신호 분석부(340)는 [수학식 35]를 이용하여 음원 신호를 나타내는 고유벡터 및 잡음 신호를 나타내는 고유벡터 에 모두 해당하는 고유값에 관련된 고유벡터 을 산출할 수 있다. 신호 분석부(340)는 단계 S220에서 산출된 를 이용하여 를 산출할 수 있다.
도 21은 도 19의 S150을 더 상세하게 도시한 순서도이다.
도 21을 참조하면, 신호 분석부(340)는 음원의 개수가 정해져 있지 않은 경우에는 c-2p-KR-Capon 알고리즘을 실행할 수 있다.
신호 분석부(340)는 를 산출한다(S310). 신호 분석부(340)는 [수학식 22]를 이용하여 라그랑주 승수 을 산출할 수 있다. 신호 분석부(340)는 단계 S300에서 산출된 를 이용하여 을 산출할 수 있다.
신호 분석부(340)는 를 산출한다(S320). 신호 분석부(340)는 [수학식 28] 또는 [수학식 29]을 이용하여 최적의 가중치 벡터 을 산출할 수 있다. 신호 분석부(340)는 단계 S310에서 산출된 을 이용하여 을 산출할 수 있다.
신호 분석부(340)는 를 산출한다(S330). 신호 분석부(340)는 [수학식 36]를 이용하여 음원 신호를 나타내는 고유벡터 및 잡음 신호를 나타내는 고유벡터 에 모두 해당하는 고유값에 관련된 고유벡터 을 산출할 수 있다. 신호 분석부(340)는 단계 S320에서 산출된 를 이용하여 를 산출할 수 있다.
본 발명은 또한 컴퓨터로 읽을 수 있는 기록매체에 컴퓨터가 읽을 수 있는 코드로서 구현하는 것이 가능하다. 컴퓨터가 읽을 수 있는 기록매체는 컴퓨터 장치에 의하여 읽혀질 수 있는 데이터가 저장되는 모든 종류의 기록장치를 포함한다. 컴퓨터가 읽을 수 있는 기록매체의 예로는 ROM, RAM, CD-ROM, 자기 테이프, 플로피디스크, 광데이터 저장장치 등이 있으며, 또한 캐리어 웨이브(예를 들어 인터넷을 통한 전송)의 형태로 구현되는 것도 포함한다. 또한 컴퓨터가 읽을 수 있는 기록매체는 네트워크로 연결된 컴퓨터 장치에 분산되어 분산방식으로 컴퓨터가 읽을 수 있는 코드가 저장되고 실행될 수 있다.
이상에서 본 발명의 바람직한 실시예에 대해 도시하고 설명하였으나, 본 발명은 상술한 특정의 바람직한 실시예에 한정되지 아니하며, 청구범위에서 청구하는 본 발명의 요지를 벗어남이 없이 당해 발명이 속하는 기술분야에서 통상의 지식을 가진 자라면 누구든지 다양한 변형 실시가 가능한 것은 물론이고, 그와 같은 변경은 청구범위 기재의 범위 내에 있게 된다.
1: 방향 추정 장치 220: 센서부
240: 제어부 260: 출력부
280: 저장부 320: 전처리부
340: 신호 분석부 360: 방향 추정부
240: 제어부 260: 출력부
280: 저장부 320: 전처리부
340: 신호 분석부 360: 방향 추정부
Claims (12)
- 신호를 감지하고, 상기 감지한 신호에 대한 감지 신호인 센서 신호를 출력하는 적어도 두 개의 센서를 포함하는 센서부;
상기 적어도 두 개의 센서가 각각 출력한 센서 신호별로 상기 센서 신호의 통계학적 분포를 지시하는 통계학적 분포 데이터를 산출하고, 상기 산출된 통계학적 분포 데이터에서 상기 신호에 포함된 비고정(non-stationary) 신호인 음원 신호의 통계학적 분포를 지시하는 통계학적 분포 데이터를 추출하며, 상기 추출된 통계학적 분포 데이터를 기초로 상기 음원 신호를 출력한 음원의 방향을 추정하는 제어부를 포함하되,
상기 제어부는 상기 산출된 통계학적 분포 데이터로 커뮬런트(cumulant) 행렬을 산출하고, 상기 커뮬런트 행렬을 하기 수학식을 이용하여 산출하는 것을 특징으로 하는 방향 추정 장치.
[수학식]
(여기서, 는 k 번째 주파수 빈(frequency bin)의 2p차원 커뮬런트 행렬을 나타내고, 는 k 번째 주파수 빈의 가상 배열 매니폴드(manifold) 벡터를 나타내며, 는 고정 신호인 잡음 신호를 나타냄)
- 제 1항에 있어서,
상기 센서부에 포함된 센서의 개수는 상기 음원의 개수보다 같거나 적은 것을 특징으로 하는 방향 추정 장치.
- 제 1항에 있어서,
상기 통계학적 분포 데이터는 상기 음원 신호의 시간에 따른 변화 및 특성 변화를 지시하는 데이터를 포함하는 것을 특징으로 하는 방향 추정 장치.
- 제 1항에 있어서,
상기 산출된 통계학적 분포는 가우시안 분포, 비 가우시안 분포, 라플라스 분포 및 빔포밍 분포 중 적어도 하나인 것을 특징으로 하는 방향 추정 장치.
- 삭제
- 제 1항에 있어서,
상기 제어부는,
상기 센서 신호를 디지털 신호로 변환하는 전처리부;
상기 변환된 디지털 신호의 통계학적 분포를 지시하는 통계학적 분포 데이터를 산출하고, 상기 산출된 통계학적 분포 데이터에서 상기 신호에 포함된 잡음 신호에 대한 데이터를 제거하여 상기 음원 신호의 통계학적 분포를 지시하는 통계학적 분포 데이터를 추출하며, 상기 추출된 통계학적 분포 데이터를 이용하여 상기 디지털 신호의 음원의 개수 및 방향에 대한 공간 스펙트럼(spatial spectrum)을 산출하는 신호 분석부; 및
상기 산출된 디지털 신호의 공간 스펙트럼의 피크(peak)를 상기 음원의 방향인 것으로 추정하는 방향 추정부를 포함하는 것을 특징으로 하는 방향 추정 장치.
- 제 6항 또는 제 7항에 있어서,
상기 신호 분석부는 음원(I)가 정해져있는 경우 및 정해지지 않은 경우에 따라 하기에 기재된 수학식을 이용하여, 상기 비특이 행렬 을 산출하는 것을 특징으로 하는 방향 추정 장치:
[수학식]
는 고유벡터 이고, 영이 아닌 고유값에 해당하는 고유벡터이다. 는 고유벡터 이고, 영인 고유값에 해당하는 고유벡터이다. 는 음원의 개수이고, 는 단위 행렬이다.는 음원 신호를 나타내는 고유벡터 및 잡음 신호를 나타내는 고유벡터 에 모두 해당하는 고유값에 관련된 고유벡터이고, 는 잡음 신호 제거 및 치수 조정된 2p차원 커뮬런트 행렬이다.
- 신호를 감지하고, 상기 감지한 신호에 대한 감지 신호인 센서 신호를 출력하는 단계;
상기 출력한 센서 신호별로 상기 센서 신호의 통계학적 분포를 지시하는 통계학적 분포 데이터를 산출하고, 상기 산출된 통계학적 분포 데이터에서 상기 신호에 포함된 비고정(non-stationary) 신호인 음원 신호의 통계학적 분포를 지시하는 통계학적 분포 데이터를 추출하는 단계;
상기 추출된 통계학적 분포 데이터를 기초로 상기 음원 신호를 출력한 음원의 방향을 추정하는 단계를 포함하되,
상기 산출된 센서 신호의 통계학적 분포를 지시하는 통계학적 분포 데이터로 커뮬런트(cumulant) 행렬을 산출하고, 상기 커뮬런트 행렬을 하기 수학식을 이용하여 산출하는 것을 특징으로 하는 방향 추정 방법.
[수학식]
(여기서, 는 k 번째 주파수 빈(frequency bin)의 2p차원 커뮬런트 행렬을 나타내고, 는 k 번째 주파수 빈의 가상 배열 매니폴드(manifold) 벡터를 나타내며, 는 고정 신호인 잡음 신호를 나타냄)
Priority Applications (2)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| KR20130053828A KR101413229B1 (ko) | 2013-05-13 | 2013-05-13 | 방향 추정 장치 및 방법 |
| US14/070,716 US20140334265A1 (en) | 2013-05-13 | 2013-11-04 | Direction of Arrival (DOA) Estimation Device and Method |
Applications Claiming Priority (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| KR20130053828A KR101413229B1 (ko) | 2013-05-13 | 2013-05-13 | 방향 추정 장치 및 방법 |
Publications (1)
| Publication Number | Publication Date |
|---|---|
| KR101413229B1 true KR101413229B1 (ko) | 2014-08-06 |
Family
ID=51748601
Family Applications (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| KR20130053828A KR101413229B1 (ko) | 2013-05-13 | 2013-05-13 | 방향 추정 장치 및 방법 |
Country Status (2)
| Country | Link |
|---|---|
| US (1) | US20140334265A1 (ko) |
| KR (1) | KR101413229B1 (ko) |
Cited By (5)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN105301557A (zh) * | 2015-11-06 | 2016-02-03 | 中国石油大学(华东) | 波达方位估计架构方法 |
| KR20180056391A (ko) * | 2016-11-16 | 2018-05-28 | 고려대학교 산학협력단 | 초음파 센서를 대상으로 하는 공격 탐지 장치 및 방법 |
| KR20190023463A (ko) | 2017-08-29 | 2019-03-08 | 현대오트론 주식회사 | 차량용 물체 식별 장치 및 그것의 동작 방법 |
| CN109959891A (zh) * | 2019-04-11 | 2019-07-02 | 南京航空航天大学 | 电磁矢量l阵中空间角与极化参数的降维谱峰搜索方法 |
| CN112379327A (zh) * | 2020-12-01 | 2021-02-19 | 北京工业大学 | 一种基于秩损估计的二维doa估计与互耦校正方法 |
Families Citing this family (18)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN105676168B (zh) * | 2015-12-02 | 2018-03-06 | 江苏科技大学 | 一种声矢量阵方位估计方法 |
| CN106526565B (zh) * | 2016-12-06 | 2019-02-22 | 哈尔滨工业大学 | 一种基于支持向量机的单比特空间谱估计方法 |
| US11079462B2 (en) | 2017-10-24 | 2021-08-03 | International Business Machines Corporation | Facilitation of efficient signal source location employing a coarse algorithm and high-resolution computation |
| KR102323655B1 (ko) * | 2018-01-08 | 2021-11-09 | 현대모비스 주식회사 | 가상 수신신호 생성을 이용한 도래각 추정 방법 및 장치 |
| CN108713323B (zh) * | 2018-05-30 | 2019-11-15 | 歌尔股份有限公司 | 估计到达方向的方法和装置 |
| CN109188345B (zh) * | 2018-08-27 | 2023-03-10 | 电子科技大学 | 基于去预延迟空时结构的相干信号源doa估计方法 |
| CN109781791A (zh) * | 2019-02-22 | 2019-05-21 | 广西大学 | 基于空间谱估计算法的电阻抗成像方法 |
| CN109932679B (zh) * | 2019-02-28 | 2020-11-06 | 南京航空航天大学 | 一种传感器列系统最大似然角度分辨率估计方法 |
| CN110161452B (zh) * | 2019-04-28 | 2023-03-21 | 西安电子科技大学 | 基于互质式l型电磁矢量传感器阵列的波达方向估计方法 |
| CN110927662A (zh) * | 2019-05-16 | 2020-03-27 | 陕西理工大学 | 基于声矢量传感器的近场多参数估计四阶累积量方法 |
| CN110927663A (zh) * | 2019-05-16 | 2020-03-27 | 陕西理工大学 | 近场声源参数估计的三维压缩感知降维方法 |
| CN110927664B (zh) * | 2019-05-16 | 2023-07-11 | 陕西理工大学 | 基于循环三阶矩与压缩感知的近场声源参数估计 |
| KR20210093550A (ko) * | 2020-01-20 | 2021-07-28 | 삼성전자주식회사 | 객체 검출 장치 및 이를 포함하는 차량 제어 시스템 |
| CN111665469B (zh) * | 2020-06-11 | 2022-08-23 | 浙江大学 | 一种基于空间时频分布的水下多径信号参数估计方法 |
| CN112363109B (zh) * | 2020-11-12 | 2023-06-23 | 西安科技大学 | 一种基于宽带强弱临近信号的加权波达方向估计方法 |
| CN112363110B (zh) * | 2020-11-30 | 2021-12-21 | 海南大学 | 一种基于嵌套交叉偶极子阵列的无网格单比特doa估计方法 |
| CN116054909B (zh) * | 2022-12-16 | 2023-08-08 | 广东工业大学 | 一种基于改进型传播算子的卫星通信抗干扰方法 |
| CN116299150B (zh) * | 2022-12-27 | 2023-12-01 | 南京航空航天大学 | 一种均匀面阵中降维传播算子的二维doa估计方法 |
Citations (3)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| KR20030087373A (ko) * | 2002-05-08 | 2003-11-14 | 삼성전자주식회사 | 음성신호에 대한 벡터 양자화 및 역 벡터 양자화 장치와그 방법 |
| KR20100065811A (ko) * | 2008-12-09 | 2010-06-17 | 한국전자통신연구원 | 음원분리 및 음원식별을 이용한 음성인식 장치 및 방법 |
| KR20110002533A (ko) * | 2009-07-02 | 2011-01-10 | 세종대학교산학협력단 | 음성신호 양자화 장치 및 방법 |
-
2013
- 2013-05-13 KR KR20130053828A patent/KR101413229B1/ko active IP Right Grant
- 2013-11-04 US US14/070,716 patent/US20140334265A1/en not_active Abandoned
Patent Citations (3)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| KR20030087373A (ko) * | 2002-05-08 | 2003-11-14 | 삼성전자주식회사 | 음성신호에 대한 벡터 양자화 및 역 벡터 양자화 장치와그 방법 |
| KR20100065811A (ko) * | 2008-12-09 | 2010-06-17 | 한국전자통신연구원 | 음원분리 및 음원식별을 이용한 음성인식 장치 및 방법 |
| KR20110002533A (ko) * | 2009-07-02 | 2011-01-10 | 세종대학교산학협력단 | 음성신호 양자화 장치 및 방법 |
Cited By (6)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN105301557A (zh) * | 2015-11-06 | 2016-02-03 | 中国石油大学(华东) | 波达方位估计架构方法 |
| KR20180056391A (ko) * | 2016-11-16 | 2018-05-28 | 고려대학교 산학협력단 | 초음파 센서를 대상으로 하는 공격 탐지 장치 및 방법 |
| KR102045286B1 (ko) * | 2016-11-16 | 2019-11-18 | 고려대학교 산학협력단 | 초음파 센서를 대상으로 하는 공격 탐지 장치 및 방법 |
| KR20190023463A (ko) | 2017-08-29 | 2019-03-08 | 현대오트론 주식회사 | 차량용 물체 식별 장치 및 그것의 동작 방법 |
| CN109959891A (zh) * | 2019-04-11 | 2019-07-02 | 南京航空航天大学 | 电磁矢量l阵中空间角与极化参数的降维谱峰搜索方法 |
| CN112379327A (zh) * | 2020-12-01 | 2021-02-19 | 北京工业大学 | 一种基于秩损估计的二维doa估计与互耦校正方法 |
Also Published As
| Publication number | Publication date |
|---|---|
| US20140334265A1 (en) | 2014-11-13 |
Similar Documents
| Publication | Publication Date | Title |
|---|---|---|
| KR101413229B1 (ko) | 방향 추정 장치 및 방법 | |
| Mao et al. | Rnn-based room scale hand motion tracking | |
| KR101238362B1 (ko) | 음원 거리에 따라 음원 신호를 여과하는 방법 및 장치 | |
| US10127922B2 (en) | Sound source identification apparatus and sound source identification method | |
| US20170140771A1 (en) | Information processing apparatus, information processing method, and computer program product | |
| US9420368B2 (en) | Time-frequency directional processing of audio signals | |
| CN111418012B (zh) | 用于处理音频信号的方法和音频处理设备 | |
| WO2016100460A1 (en) | Systems and methods for source localization and separation | |
| EP2530484B1 (en) | Sound source localization apparatus and method | |
| JP2004334218A (ja) | マイクロホンアレイ方法及びシステム、並びにこれを用いた音声認識方法及び装置 | |
| US9971012B2 (en) | Sound direction estimation device, sound direction estimation method, and sound direction estimation program | |
| CN105409241A (zh) | 麦克风校准 | |
| JP2019117055A (ja) | 推定方法、推定装置およびプログラム | |
| CN106031196B (zh) | 信号处理装置、方法以及程序 | |
| US11646009B1 (en) | Autonomously motile device with noise suppression | |
| US20150172842A1 (en) | Sound processing apparatus, sound processing method, and sound processing program | |
| CN114661142A (zh) | 一种手势识别方法以及装置 | |
| EP3050056B1 (en) | Time-frequency directional processing of audio signals | |
| CN114830686A (zh) | 声源的改进定位 | |
| CN112034433A (zh) | 一种基于干扰信号重构的穿墙无源移动目标检测方法 | |
| KR100621076B1 (ko) | 마이크로폰 어레이 방법 및 시스템 및 이를 이용한 음성인식 방법 및 장치 | |
| Candy et al. | Anomaly detection for a vibrating structure: A subspace identification/tracking approach | |
| CN108713323B (zh) | 估计到达方向的方法和装置 | |
| Kumar et al. | Self-Noise Cancellation in Underwater Acoustics Using Deep Neural Network-Based Eigencomponent Transformation | |
| Gannot | Speech processing utilizing the Kalman filter |
Legal Events
| Date | Code | Title | Description |
|---|---|---|---|
| E701 | Decision to grant or registration of patent right | ||
| GRNT | Written decision to grant | ||
| FPAY | Annual fee payment |
Payment date: 20170530 Year of fee payment: 4 |
|
| FPAY | Annual fee payment |
Payment date: 20180525 Year of fee payment: 5 |
|
| FPAY | Annual fee payment |
Payment date: 20191230 Year of fee payment: 6 |
|
| R401 | Registration of restoration |