JP2015231663A - 多数の要素システムを制御調節する装置および方法 - Google Patents

Abstract

【課題】少なくとも１つが駆動装置により移動される運動学的に協働する複数の個別要素を有するシステムの動作の動的特性を改善する。
【解決手段】
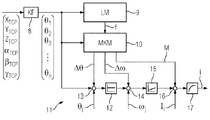
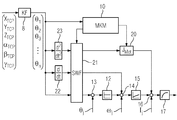
予め決められた基準座標（Ｘ_TCP，Ｙ_TCP，Ｚ_TCP，α_TCP，β_TCP，γ_TCP）に依存して、システムの動作中に連続的に、各個別要素についてそれぞれ１つの力ベクトルを算定する負荷計算装置（９）と、前記基準座標および前記力ベクトルに基づいて、運動中に連続的に、前記力ベクトルを補償する少なくとも１つの補償量（Ｍ）を算定するトルク計算装置（１０）とが設けられている。さらに、制御調節装置は、前記基準座標および前記少なくとも１つの補償回転トルクに依存して、運動中に連続的に、前記少なくとも１つの駆動装置のための力形成量（ｉ）を調節する調節ユニット（１１）を持つ。
【選択図】図２

Description

本発明は、少なくとも１つが駆動装置によって駆動可能である運動学的に協働する複数の個別要素を有するシステムの動作を制御および調節する装置に関する。さらに、本発明は、このようなシステムの動作を制御および調節する方法に関する。この種のシステムは、例えば設備、加工機械、処理機械および特にロボット又は工作機械である。駆動装置は、例えば電動機、又は液圧駆動装置、又は空気圧駆動装置である。

この種の機械システムは製造分野で広く使用される。高品質の結果を達成するための重要な前提はこの製造工具の絶対精度にある。しかし、機械的な構造物に外乱力（例えば、重力、加工力、摩擦、負荷変動）が作用し、これらの外乱力は関節および構造部分（以下において個別要素とも称する）の弾性に基づいて、所謂「ＴＣＰ」（＝Tool Center Point、工具中心点）に誤差をもたらし得る。場合によっては外乱力に起因するＴＣＰの誤差の位置依存性が非常に激しい。例えば、ロボットアームの自由端が、アームを伸ばした状態では、アームを引っ込めた又は曲げた状態よりもさらに下に向かって引っ張られる。これに関する尺度は絶対的な静的精度である。

従来においては軸が調節される場合に第２の直接測定システムを負荷側に、即ちＴＣＰ近くに設けることによって、この絶対的な静的精度の問題に対処された。必要な補償力が伝動機構ばねを介して構造体に伝達されるように、位置調節ループを介して電動機もしくは駆動装置の位置が十分に調整される。第２の測定システムの使用は、ハードウェアの著しい追加コストにつながり、測定システムを取り付けるための高価な構造的調整を必要とする。

そのほかに、絶対的な静的精度を改善するために、基準位置に関して作業空間の多数の点においてＴＣＰの誤差を測定して、補償値として基準値チャンネルに加算する、もしくは実際値チャンネルから減算することが試みられた。この方法の欠点は、必要な費用および作業空間もしくはロボット／機械の測定コストにある。誤差の測定は、設備に外部の測定手段を必要とする。測定パターンは個々のケースにおいて定められる。解析は、構造的に等しいどの設備においても繰り返されなければならない。そのうえ、表形式にて記憶された補正値は負荷に依存し、即ちそれらの補正値は厳密に１つの負荷条件に適用される。例えば、負荷が変化すると、それらの値はもはや通用しない。

これに対して、産業用ロボットを制御するために絶対的に正確なモデルが記憶されているロボット制御が、特許文献１から公知である。従って、運動の始点および終点では、その都度制定したシステムにおいて、位置決めのために外乱力が考慮される。

他の重要な特徴は、所謂「準静的精度」である。加速段階中に、関節において電動力および反力が等しく作用する。反力が無限に堅くはない構造物上で作用し、ＴＣＰにおいて寄生運動を確実に引き起こし得る。ロボットアームが、例えば、それぞれ１つの電動機と共に互いに移動可能である複数の要素を有する場合に（付属の駆動装置もしくは電動機を有する１つの要素は１つの運動軸を意味し、以下では運動軸を略して「軸」と呼ぶ。）、１つの要素の運動、特に加速度が他の要素に作用を及ぼし、それによって準静的精度が影響を及ぼされる。このために、従来、工作機械では、制御軸の加速度に基づいて生じた寄生運動が、位置基準値として印加される補償値により補償される。

１つの軸の回転運動の際に、しばしばトルクが所謂トルクフィードフォワード方式によって制御される。トルクフィードフォワード制御のパラメータ設定は電動機に関する軸慣性トルクの入力を必要とする。しかし、産業用ロボットにおいて、このデータは、その構造ゆえに、作業空間にわたって一定でない。電動機から見た全体慣性は関節位置の関数である。従来では、トルク基準値を算定するために、電動機加速度が軸慣性の予め決められた値と乗算される。

最大の軸加速度のパラメータ設定は、電動機および出力部の設計の結果として生じ、軸ごとに最大の許容電流および軸慣性から導き出される。その最大の加速度は一定値として登録すべきであるので、その最大の加速度のパラメータ設定のためには、電動機に関する軸慣性が最大値に達する位置のみが重要である。それゆえ、この値が達せられない範囲内では電流予備が十分に利用されないで、もっと高い加速度限界が理論的には可能であろうと結論される。従って、場合によっては、電流限界のより良い利用のために、各位置についての予備の加速度を算定し、限界加速度を適用することが望ましいであろう。従来においては軌道計画時に位置依存性の加速度限界は考慮されていなかった。

特に、産業用ロボットの場合には、作業工具の可動性およびフレキシビリティが非常に重宝される。しかし、このことが構造上の境界条件を必要とし、当該境界条件がロボットを非常に振動しやすい構造物にする。測定可能性が十分でないために、この振動の電気的な制動は可能でない。振動励起の一部は指令量から直接にもたらされる。従って、振動に関して指令特性が適切に調整されるべきである。可能な対処方法は、固有共振がもはや励起されないように急激な動きを低減することによって運動波形に含まれる周波数を緩和することにある。この方法の欠点は、軸の動特性の部分的に強い必要不可欠な制限にある。

部分的に複雑な運動変換およびそれによりもたらされる補償運動に基づいて、事前に衝突の危険を確認することは、平凡な課題ではない。負荷が部分的に激しく変化するために、測定信号（例えば、電動機電流）の監視もできない。従って、改善された衝突監視は追及するに値する。このために、従来において知られている解決策では、モデルによって算定された電動機電流が実際に測定された電動機電流と比較され、偏差が許容できないほど大きい場合に、機械／ロボットが停止される。このようなシステムは、例えば特許文献２から公知である。

特許文献３から、少なくとも１つが駆動装置により移動可能である運動学的に協働する複数の個別要素の運動を制御および調節する装置および方法が公知である。ロボットの特徴を示す力値がシステムの動作中に連続的に算定される。さらに、補償する補償量が基準座標に基づいて同様にシステムの動作中に連続的に算定される。少なくとも１つの駆動装置のための力形成量が、基準座標および少なくとも１つの補償量に基づいて運動中に連続的に調節される。

欧州特許出願公開第１９８０３７４号明細書 欧州特許第１４０３７４６号明細書 独国特許出願公開第１０２００７０２４１４３号明細書

従って、本発明の課題は、運動学的に協働する複数の個別要素を有するシステムの動作の制御調節装置、ならびにそれに対応する方法において、そのような装置および方法としてシステムの動作を正確に実施することを可能にすることにある。

この課題は、本発明によれば、請求項１記載の装置によって解決される。

さらに、本発明によれば、請求項１１記載の方法が提供される。

駆動装置が電動機である場合には力形成量が電流であり、これに対して液圧駆動装置又は空気圧駆動装置の場合には力形成量が圧力である。

従って、有利なやり方では、システムの動作が連続的に動的に調節される。従って、予め決められた運動軌道をより良好に維持できるように、運動中に絶え間なく、力ベクトルおよび適切な補償量が新たに算定される。運動軌道の正確な維持は、多くの製造課題において必要不可欠であるが、しかし、大部分のピックアンドプレースの課題の場合には必要不可欠というわけではなく、特許文献１による公知の解決法で十分である。

補償量は、補償回転トルク、補償力、補償速度又は補償位置であってよい。従って、これらの量のそれぞれは、補償のために個別に又は組み合わせで使用することができる。カスケード接続された調節系の場合に、補償量として補償回転トルクを用いる制御は、より迅速な外乱力補償をもたらす。補償量として補償位置を用いる制御は、より正確な補償をもたらす。

各力ベクトルを算定するための負荷計算装置は、個別要素の１つへの力導入の位置および／又は方向および／又は振幅が考慮されている負荷モデルを使用することが好ましい。このようにして、それらの全てのパラメータを有する力導入が動的に運動中に考慮されるとよい。

さらに、調節ユニットがカスケード接続された位置調節系、速度調節系および電流調節系（もしくは力形成量の調節系）を有すると格別に有利である。これによって、システムの動作をあらゆる細部において正確に調節することができる。

少なくとも１つの補償トルクを算定するトルク計算装置は、各個別要素の質量および／又は弾性および／又は減衰および／又は自由度の線形依存性が考慮されているマルチ要素モデルを使用するとよい。このようにして、システムのモデル化の際に、全ての又は最も重要な機械的量を考慮することができる。

特に、マルチ要素モデルは線形の微分方程式系に基づいているとよい。これは、大きな計算費用なしに解決できるという利点を有する。

特に、微分方程式系が、それぞれ個別要素に関する質量行列、減衰行列および剛性行列に基づいていると有利である。従って、質量、減衰および剛性のような基本的な機械的量がマルチ要素モデルに取り込まれている。

さらに、マルチ要素モデルにおいて、それぞれ個別要素に作用する慣性力（場合によってはコリオリの力）および／又はジャイロ力が考慮されるとよい。それによって、特に運動の準静的精度を高くすることができる。

他の実施形態では、トルク計算装置により、１つの個別要素又は複数の個別要素の複合体の最大加速度を運動中に連続的に算定することができる。これは、各位置において、電流限界もしくは圧力限界の改善された利用のために、加速度限界を調整することができるという利点を有する。

他の実施形態では、トルク計算装置および調節ユニットが、運動中に連続的にシステムの少なくとも１つの固有振動数の励起を低減するように設計されている。これは、固有振動数の励起が少ないこと、そしてそのことが改善されたシステムの動作特性をもたらすことを意味する。

制御調節装置がシステムの制御対象のモデルを有し、そのモデルにより、駆動装置のための少なくとも１つの最適指令量が算定可能であるとよい。それにより、軸に対して所定の動特性を予め与えることができる。

他の実施形態では、制御調節装置がシステムの制御対象モデルを有し、駆動装置の実際回転トルクを監視するために、そのモデルにより駆動装置の最適回転トルクが算定可能である。このような制御対象モデルにより、例えば実際のシステムの駆動トルクを監視することができ、これによって衝突の推定をすることができる。

上述の発展的に構成された本発明による制御調節装置は、本発明による方法に、方法ステップとして組み込むこともできる。

本発明を添付図面に基づいてさらに詳細に説明する。

図１は産業用ロボットの１つのモデルを概略的に示す斜視図である。 図２は外乱力補償の構造的概要を示すブロック図である。 図３は準静的力に基づいて生じる寄生運動の補償の構造的概要を示すブロック図である。 図４はトルクフィードフォワード制御の構造的概要を示すブロック図である。 図５は基準値フィルタを有するフィードフォワード制御の構造的概要を示すブロック図である。 図６はモデルに基づく状態調節系のフィードフォワード制御の構造的概要を示すブロック図である。 図７は２Ｄロボットを有するシミュレーション例を概略的に示す斜視図である。 図８は従来技術による図７のロボットの変位を示すダイアグラムである。 図９は本発明によるモデルに基づく力補償を有する図７のロボットの変位を示す図である。

以下においてさらに詳細に説明する実施例は、本発明の好ましい実施形態である。

冒頭に述べた種類の任意に構成されたシステム（機械、設備等）、特にロボット又は工作機械のために、該システムの動作学的に協働する複数の個別要素の運動を制御および調節する装置が使用される。このようなマルチ要素システムの一例が図１に示されている。そこには象徴的に１つのロボットの複数の構成要素が示されている。このロボットは、例えば台板１の上に設置されている。ロボット本体２は垂直軸において台板１の上方で回転することができる。その回転は電動機３により行われる。たとえ、次の個々の例において駆動装置として電動機を使用していても、それぞれにおいて他の駆動装置を使用してもよい。液圧駆動装置および空気圧駆動装置の場合には、電流の代わりに、圧力が重要な量である。

ロボット本体２は、電動機３とともに１つの運動軸（以下、略して単に軸ともいう）をなす。ロボット本体２には、第１アーム４が電動機５により回転可能に支持されている。この第１アーム４の末端には、第２アーム６が他の電動機７により同様に回転可能に支持されている。従って、そのロボットはここでは３つの軸を有し、それらの軸のうち、第１軸が個別要素２（場合によっては電動機３を含む）により形成され、第２軸が個別要素４（場合によっては電動機５を含む）により形成され、第３軸が個別要素６（場合によっては電動機７を含む）により形成されている。

これらの軸のうち少なくとも１つが運動する場合に、それをここではシステムの動作という。各軸もしくは各個別要素は、それぞれ個別の質量、減衰、剛性等を有する。これは、軸同士が互いにどの位置にあるかに応じて、例えば重力又はプロセス力がシステムにさまざまの作用を及ぼす。例えば、図１に水平方向に描かれた第２アーム６の先端において力が下方に向いている場合に、これは、第２アーム６の先端の絶対位置に対して、第２アーム６が例えば垂直に上方に向けられている場合とは異なる作用を及ぼす。従って、システムに作用する各力は、全ての軸の位置に依存した作用を及ぼす。

システムの挙動は、３次元の機械的なＭＩＭＯモデル（ＭＩＭＯ＝Multi Input, Multi Output、多入力多出力）であるマルチ要素モデルで記述されている。

制御調節装置は、本発明に従ってシステムの動作を調節するために図１のロボットの如く、このようなマルチ要素モデルに基づいている（このことおよび以下のことが本装置に対応した方法にも当てはまる）。このモデルは、好ましくは３次元の線形マルチ要素モデルである。このモデルの構成要素は、次に挙げる物理学的および幾何学的な量である。
・個別要素の質量特性および空間内の質量挙動
・関節および動力伝達系の弾性（場合によっては要素の弾性も含む）
・ばね要素の線形減衰特性
・個々の自由度の間の幾何学的な強制条件もしくは線形依存性
・関節の定義（タイプ、位置および方向性）

入出力間の静的および動的な伝達特性は、次の線形微分方程式系により記述することができる。

上式において、Ｍは質量行列、Ｄは減衰行列、Ｋは弾性行列、Ｔはモデルの全ての自由度と状態量Ｘとの間の関係を再現する矩形変換行列である。システムの各個別要素（図１の符号１，２，４，６参照）自体は剛体であり、丁度６個の自由度（３個の並進および３個の回転）を有する。ベクトルｆは、各個別要素の重心における外力である。従って、この力ベクトルは、例えば、個別要素ごとに重心および場合によってはプロセス力等（例えば、被工作物に対する工具の押圧によって生じさせられる力）を含む。状態量Ｘは、当初の動作点の周りにおける小さな運動を記述する。従って、行列Ｍ，Ｄ，ＫおよびＴは、状態量に依存しない。関節位置は状態量ではなく、行列Ｍ，Ｄ，ＫおよびＴを算定するための他のパラメータである。

モデルは、システム挙動の位置依存性が考慮される線形マルチ要素システムであるとよい。というのは、改善された絶対精度は、各時点で電動機力を全ての外乱力を補償するために導入することによって達成することができるからである。それにより、ＴＣＰにおける小さな誤差が０である平衡状態がもたらされる。

電動機トルク（モーメント）を算定するための重要な条件は、負荷状態を正確に認識することである。負荷状態の記述は、力導入の１つ以上の位置、１つ以上の方向および１つ以上の振幅に関する情報を含む。力として、前述の外乱力のほかに、例えばフライス加工又はボーリング加工の際に生じる加工力も導入される。

電動機トルクおよび個別要素（ロボットアーム）の位置は、次の定常状態の方程式系の解である。

ただし、状態ベクトルＸおよび電動機力ｆ_Motは既知でない。この方程式系は過少決定系であるために、ＴＣＰの座標に関する強制条件を補足されなければならない。つまり、

である。

行列Ｔ_TCPは、行列Ｔからの抜粋であり、ＴＣＰの座標と状態量との間の線形依存性を記述する。問題の可解性のための重要な条件は、０に指定される全てのＴＣＰ座標が電動機によって移動可能であることである。しかし、ここで考察される全ての機械およびロボットの運動学の場合がそうしたケースである。従って、ロボットは、各工具を所望の方向にも移動することができなければならない。

機械構造体への電動機トルクの伝達は、電動機での角度ずれによる伝動機構ばねの付勢を必要とする。この角度ずれは状態ベクトルＸから導き出され、基準値生成時に考慮されなければならない。

図２は、外乱力の補償を行うための制御および調節をする方法もしくはこれに対応する装置の構成を示す。上位ユニットから、ＴＣＰのための基準座標、即ちＸ_TCP，Ｙ_TCP，Ｚ_TCPおよびＸα_TCP，β_TCP，γ_TCPが予め与えられる。変換ユニット８において、関節座標θ₁〜θ_nへの座標変換が行われ、ｎは自然数、例えばｎ＝６である。負荷モデル９（ＬＭ；場合によっては負荷計算装置として実現されている）において、各関節座標について、１つの力ベクトルｆが力導入の個所、方向および大きさに関して算定される。これは、システムの各個別要素について行われることが好ましい。

マルチ要素モデル１０（ＭＫＭ；トルク計算装置として実現されている）が、複数の力ベクトルもしくは１つの力ベクトルｆをさらに処理する。力ベクトルｆと関節座標とに基づいて、各軸のそれぞれの電動機について、それぞれ１つの電動機トルクもしくはそれに対応した等価電流が算定される。さらに、マルチ要素モデル１０において、角度ずれΔθが算定される。この算定時に、各軸もしくは各個別要素の質量特性、弾性、減衰および自由度の線形依存性が考慮される。マルチ要素モデル１０は、上述の２次線形微分方程式系に基づいていることが好ましい。

マルチ要素モデル１０に後続接続された調節ユニット１１は、関節座標θ₁，θ₂，θ₃，…，θ_i，…，θ_nと、角度ずれΔθと、電動機トルクＭとから、システムの軸の１つの図２に示されていない電動機を制御するための電流ｉを求め、それによって外乱力に起因する寄生運動が低減もしくは補償されている。この調節ユニットは、カスケード接続された位置調節系、速度調節系および電流調節系を有するとよい。位置調節系のために位置調節器１２（好ましくはＰ調節器）が設けられ、この位置調節器１２は、入力量として、関節座標θ₁〜θ_nと角度ずれΔθと実際座標θ_jとの極性正しい加算値を受け取る。

位置調節器１２の操作量は後続の速度調節系のための入力量として使用され、この入力量には加算器１４において実際角速度ω_jが極性正しく加算される。その加算信号が速度調節器１５（好ましくはＰＩ調節器）に導かれる。

速度調節系もしくは速度調節器１５の出力信号は電流調節系のための入力量として使用される。この入力量には、各電動機トルクＭもしくは対応する等価量と実際電流Ｉ_Jとが極性正しく加算器１６において加算される。この加算器１６および他の２つの加算器１３，１４（一般的には結合要素）は、例えば乗算によってそれぞれ所望の量を得るために換算もしくは増幅機能を有する。加算器１６の出力信号は電流調節器１７に導かれ、電流調節器１７は電動機のための操作量、即ち電流ｉを出力する。

図を見やすくするために、図２では、外乱力補償が唯一の軸に対してしか示されていない。しかし、相応の算定および調節がシステムの全ての軸に対して行われることが好ましい。最も簡単な場合には、各軸について固有の電流値が算定され、該電流値によりそれぞれの電動機が制御される。従って、マルチ要素モデル１０は、既知の負荷状態からの静的な外乱力を電動機力によって全ての運動の期間中に、即ち常に現在の座標および現在の実際値に関して補償するために使用することができる。

さらに、準静的負荷状態および加速過程を補償するために、マルチ要素モデルを使用することができる。１つの軸の加速と、それによって関節内で生じる反力が、場合によっては構造物の弾性に基づいてＴＣＰにおける寄生運動をもたらすことがある。例えば加速される第１の軸が第２の軸に支えられている場合に、第２の軸の位置又は傾斜がそれの有限の剛性のために変化する。このような寄生運動および類似の寄生運動は、残りの軸の補償運動により補償することができる。このケースでは、算定された補償運動が回転数および回転トルクとしてフィードフォワード制御される。このようなフィードフォワード制御が、ｎ個の軸Ａ１，Ａ２，…，Ａｉ，…，Ａｎについて、図３に示されている。その調節構造は、図２の調節構造を基礎にしている。同一の要素には同一の符号が付されている。以下においては相違点だけを強調する。

図２には、既に述べたように図を見やすくするために唯一の軸についての調節ユニット１１だけが示されている。図３には、軸Ａ１〜Ａｎのうち２つの選択された直交軸Ａ１およびＡｉについて、調節ユニット１１₁〜１１_nのうちそれぞれの調節ユニット１１₁および１１_iが示されている。調節ユニット１１₁は、入力量として、変換ユニット８から関節座標θ₁を受け取ると共に、マルチ要素モデル１０から角度ずれΔθ₁と速度ずれΔω₁と補償トルクＭ₁とを受け取る。同じようにして、調節ユニット１１_iは、変換ユニット８から関節座標θ_iを受け取ると共に、マルチ要素モデル１０から角度ずれΔθ_iと速度ずれΔω_iと補償トルクＭ_iとを受け取る。

ｎ個の全ての調節ユニット１１₁〜１１_nは構造的に同一に構成されている。従って、ここでは第１の調節ユニット１１₁だけを詳細に説明する。第１の調節ユニット１１₁は図２の調節ユニット１１を基礎にしており、それの説明をもう一度参照されたい。それゆえ、位置調節器１２₁と、速度調節器１５₁と、電流調節器１７₁と、加算器１３₁，１４₁，１６₁とがもたらされる。調節ユニット１１₁内に、ここでは付加的に第１微分器１８₁が設けられており、この第１微分器により角度ずれΔθ₁から速度調節用の付加的な指令量が速度ずれΔω₁の考慮下で算定され、この付加的な指令量は加算器１４₁において考慮される。この付加的な指令量は第２微分器１９₁によって加速度量に変換され、引き続いて乗算器２０₁において軸全体慣性Ｊ_Mot1と乗算される。最後に、その結果として生じた値が加算器１６₁において補償トルクＭ₁に加算される。最終的な結果として、第１軸を制御するための電流信号ｉ₁が生じる。同様にして調節ユニット１１_iにおいて電流信号ｉ_iが生成される。このようにして、準静的力に起因して生じる寄生運動を適切な補償運動によって補償することができる。

さらに、マルチ要素モデル１０から各位置について各電動機に関する軸慣性が算定される。軸慣性は剛体モード（固有振動数０Ｈｚ）と関連するモード質量から算定される。この剛体モードは、純粋に理論上の性質であり、どんな振動もない運動と呼ばれている。従って、その算定のためには、その都度１つ電動機のみが自由に運動するのが許容されていなければならない。残りの軸はそれぞれ固定されている。モード質量の算定のためには、剛体モードに関連する固有ベクトルのみを認識することで十分である。固有ベクトルの疑似反転は普通のことであり、計算プロセスにとって複素行列の反転よりも負担が少ない。

剛体モードに関連する固有ベクトルの決定は、残りの固有値および固有ベクトルの考察なしに簡単な方法で行うことができる。その方法を任意の正方形行列Ａの例で説明する。その行列Ａに関しては、固有値λおよびそれに付属する固有ベクトルＸλが次の方程式系の解である。

上記の解を求める問題定義付けは、行列Ａが唯一の剛体モードのみを有することを前提とする必要がある。これは、λ＝０については解空間が１次元のベクトル空間であることを意味する。基底ベクトルの決定は単純な方程式系の解を必要とする。

線形方程式系の解は、例えばそのアルゴリズムにより「固有に」最適化することができる。その結果は求められた固有ベクトルＸλである。

モード質量の算定のためには疑似逆ベクトルＸ_iλが必要とされる。ベクトルはエレメントごとに構成するとよい。疑似逆ベクトルＸ_iλは次の条件、即ち、Ｘ_iλ^TＸλ＝１を満たす。

であり、そしてｎ₀は０に等しくないベクトルＸλのエレメント個数である。

モード質量を決定するために、剛体モードを求めようとする行列が、次の微分方程式系、即ち、

から導き出される。ここに、ＭおよびＫは自由な電動機を有するシステムの質量行列および剛性行列である。Ｔ_jは、ｊ番目を除く全ての電動機もしくは軸が固定されるという強制条件に対応する変換行列である。状態ベクトルＸは全ての自由度を有するのに対して、縮小されたベクトルＸ_redは、関節に基づいて構造体が有する自由度の状態量しか含んでいない。剛体モードにはモード減衰が割り当てられないので、その方程式系から減衰行列を取り除くことができる。

固有ベクトルを決定するための方程式系は、このケースでは、

である。

全体慣性は、その算定された量から導き出される。

これに加えて図４はトルク制御構造の原理図を示す。係数Ｊ_Motは該当軸について電動機に関係する軸全体の慣性である。その係数Ｊ_Motは、構造的に図３の調節ユニット１１₁に対応する調節ユニット１１内で、加算器１６のための付加的な指令量を形成する乗算器２０において使用される。調節ユニット１１の残りのエレメントも、図３の調節ユニット１１₁の残りのエレメントに対応し、図４ではインデックス「１」なしで示されているにすぎない。図を見やすくするために、さらに図４では負荷モデル９の表示が当然存在しているにもかかわらず省略されている。同じことが、次の図５および図６についても当てはまる。

従って、マルチ要素モデルは、各位置についてトルクフィードフォワード制御のパラメータ設定をするために電動機に関係する軸慣性Ｊ_Motを算定するのに使用することができる。従って、図４におけるマルチ要素モデル１０は、軸慣性Ｊ_Motを調整するために乗算器２０に信号を供給する特別な出力を有する。

とりわけ前述の線形微分方程式系に基づく上記マルチ要素モデルは、上述の如く、各位置について各電動機に関係する軸慣性を算定するために使用することができる。それにより、場合によっては拡張されたモデルにおいて、最大の軸加速度を決定することができる。システムの動作中におけるその都度現在の最大の軸加速度が運動経過に十分に影響を及ぼす。

モデルによって記述される動特性に基づいて、固有振動数の励起が回避されるように、指令量が調整されるとよい。そのために種々の方法を使用することができる。
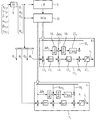
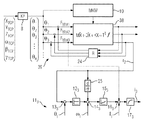
・モデル（即ち、マルチ要素モデル）から導き出される特性を有する位置基準値フィルタ（ゼロ設定、図５参照）
・モデルのための多次元の状態調節の構想およびそれによって生じる操作量のフィードフォワード制御（図６参照）

基準値フィルタを有するフィードフォワード制御の概略構成を示す図５の描写は、図を見やすくするために、ここでも１つの軸に限定されている。図４におけると同様に、負荷モデル９の表示が省略されている。図５において前出図におけると同一の符号で示された残りの構成要素はそこにおけると同一の機能を有する。従って、それぞれそこでの説明を参照されたい。

前出の実施形態と違って、ここでは基準値フィルタ（ＳＷＦ）２１が設けられている。この基準値フィルタ２１は、入力信号として、関節座標θ₁〜θ_nに関する位置情報を直接的に得るだけでなく、微分器２２により形成された速度信号および２階微分器２３により形成された加速度信号を得る。これらの３つの信号から基準値フィルタ２１がフィルタ処理された加速度信号を形成し、その加速度信号が結合ユニット２０に供給される。その結合ユニット２０は、フィルタ処理された加速度信号と、マルチ要素モデル１０から供給される軸全体の慣性Ｊ_Motとを乗算し、その結果を加算器１６に電流調節のために指令量として自由に使わせる。電流調節のための電流のこのフィードフォワード制御のほかに、１階微分された関節座標から基準値フィルタ２１が得るフィルタ処理された速度信号により速度調節がフィードフォワード制御される。このために、フィルタ処理された速度信号が加算器１４に入力される。

最終的に、関節座標θ₁〜θ_nから基準値フィルタ２１が取得するフィルタ処理された位置信号によって位置調節のフィードフォワード制御もしくは指令制御が行われる。このフィルタ処理された位置信号は加算器１３に指令量として供給される。

基準値フィルタ２１により、位置に依存して、即ちその都度時間的に実際に加速中に、システムの特別な固有振動数が除去される。従って、例えば、ロボットがアーム位置を変える際に、ロボットの固有振動数が変化する。即ち、アームを伸ばした状態においては、アームを引っ込めた状態においてよりも固有振動が遅い。それにより運動中にもロボットの固有振動数に応答させることができる。従って、例えば、ロボットがアームを伸ばしている時には１５Ｈｚ付近の振動数が除去され、アームが中間位置にある時には１７Ｈｚ付近の振動数が除去され、アームが引っ込められている時には２０Ｈｚ付近の振動数が除去される。

指令量を調整するための他の可能性が図６の実施例において示されている。ここでも、システムが図５におけると同様に簡単化されている。ここでは、指令量の調整のために、制御対象モデル３８がシステム内に導入されている。モデル３８は、例えばマルチ要素モデル１０と同じ線形微分方程式系に基づいている。この制御対象モデル３８は１つの調節ループ３９内に挿入されており、この調節ループはここでは３つの全ての軸に対して描かれ、フィードバック分岐内に１つの調節器２４を有する。調節ループ３９によって理想的に調節される制御対象がもたらされ、その制御対象の調節量ｒ₃（図６にはｎ個の軸のうち３番目の軸の調節量のみが描かれている）が調節ユニット１１₃のための指令量として使用される。このために調節量ｒ₃が加算器１３₃に位置調節のために入力される。加算器１３₃の結果がＰＩ調節器１２₃に導かれ、その調節器１２₃の結果が速度調節の加算器１４₃に導かれる。微分器２５が調節量ｒ₃から速度信号を生成し、その速度信号が同様に加算器１４₃に導かれる。極性正しい加算形成後に、その加算信号が速度調節のＰＩ調節器１５₃に導かれ、そのＰＩ調節器の出力信号が電流調節の加算器１６₃に導かれる。この加算器１６₃には付加的に最適制御対象もしくはモデル３８の操作量Ｆ_Mot3が導かれる。さらに加算器１３₃，１４₃，１６₃には軸特有の実際値θ_j，ω_j，Ｉ_jが供給される。最終的には加算器１６₃の加算信号が電流調節器１７₃に供給され、その電流調節器から、結果として生じる３番目の軸のための電流信号がもたらされる。構造的には、調節ユニット１１₃と同じ調節ユニットが残りのｎ−１個の軸のために設けられている。しかし、図を見やすくするために、図６にはそれらが示されていない。

さらに注目すべきは、マルチ要素モデル１０が現在有効な行列Ｍ，ＤおよびＫをそれぞれモデル３８に引き渡すことである。

さらに、最適調節系３９にフィードバックされる量が、関節座標とともに結合されて、それぞれ力である制御対象の操作量Ｆ_Mot1，Ｆ_Mot2，Ｆ_Mot3となる。

従って、固有振動数の励起を低減するために実際の調節ユニットの指令量の調整を行うべく、実際の制御対象のモデルを使用するとよい。

あらゆる想定される負荷状態を考慮して正しいトルクフィードフォワード制御を使用するならば、各時点で電動機トルクの適切な評価を得ることができる。制御対象もしくはモデル３８によって出力される算定された電動機トルクからの測定された電動機トルクもしくは実際電流値Ｉ_iの著しい偏差は、予期しない事象（例えば衝突）を示唆することになるであろう。従って、モデル３８は、指令量の調整に使用できるほか、電動機トルクの監視にも使用できる。

図７は、本発明の実現性および有利性を具体的に示すことのできる２Ｄロボットの具体例を示す。概略的に示された２Ｄロボットが、ここでは２つのアーム２６および２７を有し、これらのアームがそれぞれ１つの電動機２８，２９によって運動させられる。

一般的には４つの要素２６〜２９のそれぞれが６つの自由度を有する。これは２次元の機械的な問題であるので、完全な記述のためには要素当たり３つの座標で十分である。さらに、その運動学は次の強制条件の支配下にある。
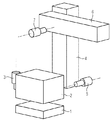
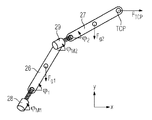
・アーム２６は基台上に回転可能に支持されている。
・アーム２７はアーム２６に対して回転可能に支持されている
・電動機２８は基台に対して相対的に回転のみできる。
・電動機２９はアーム２６と一緒に移動させられ、アーム２６に対して相対的に回転のみできる。

位置条件は運動可能性を制限し、自由度間の線形依存性として定式化される。従って、２Ｄロボットは４つの独立な運動量だけを有する。このことは、電動機２８および２９の角度位置φ_M1，φ_M2と、アーム２６および２７の角度位置φ₁，φ₂とを予め与える場合に、図７で直観的に明白である。

ＴＣＰ（工具中心点）は運動にとって重要な基準点である。直交座標系でのＴＣＰの位置とアームの位置との間の座標変換は次のとおりである。

同様に、その他の予定された点、例えば要素の重心又は運動させられる回転関節のための運動学的関係式を立てることができる。線形化表示（ヤコビ行列）においては、これが座標変換のための変換行列Ｔの入力を形成する。

力学方程式の線形化は与えられた動作点で行われる。この基準位置は、トルクに対して「固定」されている。状態ベクトルＸは、今やこの動作点からの構造体の変位を含んでいる。

電動機およびアームは理想的に堅く結合されているのではなくて、伝動機構の弾力性をモデル化する弾性ばねを介して結合されている。従って、動作点ごとに、ばねの復帰トルクを変位Ｘに対する線形応答として記述する剛性行列Ｋを定めることができる。

構造に対して、電動機の駆動トルク、要素の重力および場合によってＴＣＰにおける付加的な力が作用する。従って、上述の方程式系は完全である。それは運動と力の間の関係を記述する。

外力が作用しない場合には、ばねが定常的に解放されており、電動機およびアームの角度位置はそれぞれ等しい。力（例えば重力Ｆ_g1およびＦ_g2又は外力Ｆ_TCP）が作用する場合には、ばねが変位させられ、電動機８および２９の角度位置φ_M1，φ_M2と、アーム２６および２７の角度位置φ₁，φ₂とは等しくない。

図８は、従来技術に基づく制御方法（電動機位置の調節、補償なし）によって図７のロボットの位置関係がどのようになるかのシミュレーション計算の結果を示す。基準位置はそれぞれφ₁＝６０°およびφ₂＝−３０°である。ロボットは、ＴＣＰにおいて重力も外力も作用しない場合に、線３０に従ってｙ方向への傾きが最も少ない。線３１，３２，３３，３４は、（負のｙ方向における）重力と、ＴＣＰでの外力Ｆ_TCPの異なる値（尺度＝それぞれの力矢印の長さ）とのもとでの２Ｄロボットの位置関係を示す。

外力の影響時にロボットの構造体がどのようにたわむかを明確に認識することができる。両電動機はそれぞれ同じ位置のままであるのに対して、アームは移動する。

図９は本発明による方法によって図７のロボットの位置関係がどのようになるかのシミュレーション計算の結果を示す。基準位置は再びφ₁＝６０°およびφ₂＝−３０°である。線３５は、重力と、ＴＣＰにおける外力の異なる値とのもとでの２Ｄロボットの位置関係を示す。本発明による動的調節によって、ロボット自体の位置は変化せず、しかも外力Ｆ_TCPが変化しても変化しない。

運動および力のための開発された上述の方程式系は、選択的に、（運動が与えられた場合）力を求めるように、又は（力およびトルクが与えられた場合）移動を求めるように転用される。しかし、独立量の個数はあらゆる場合において同じである（ここでは、４個）。本発明による方法は、好ましくは方程式系を次のように評価する。即ち、運動座標の一部（ここではＴＣＰの位置）と作用する力の一部とが予め与えられて、残りの自由量（ここでは回転トルクおよび電動機の変位）を求めることを目指して方程式系が解かれる。

既に明らかにしたように、図９は、構造体が外力作用下で動かないことを明確に示している。両電動機は、必要な程度に弾力性のある伝動機構を締め付けることによって、変位を補償する（線形に広げられた矢印３６および３７）。両アームは、それぞれ同じ位置のままである。

１ 台板
２ ロボット本体
３ 電動機
４ 第１アーム
５ 電動機
６ 第２アーム
７ 電動機
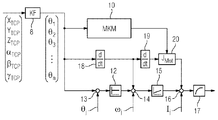
８ 変換ユニット
９ 負荷モデル（負荷計算装置）
１０ マルチ要素モデル（トルク計算装置）
１１ 調節ユニット
１２ 位置調節ユニット
１３ 加算器
１４ 加算器
１５ 速度調節器
１６ 加算器
１７ 電流調節器
１８ 微分器
１９ 微分器
２０ 乗算器
２１ 基準値フィルタ
２２ 微分器
２３ ２階微分器
２４ 調節器
２５ 微分器
２６，２７ アーム
２８，２９ 電動機
３０〜３５ 線
３６，３７ 矢印

モード質量の算定のためには疑似逆ベクトルＸ_ｉλが必要とされる。ベクトルはエレメントごとに構成するとよい。疑似逆ベクトルＸ_ｉλは次の条件、即ち、Ｘ_ｉλ^ＴＸλ＝１を満たす。

であり、そしてｎ_０は０に等しくないベクトルＸλのエレメント個数である。

Claims (11)

1. 運動学的に協働する複数の個別要素（１，２，４，６，２６，２７）を有し、そのうち少なくとも１つが駆動装置（３，５，７，２８，２９）により移動可能であるシステムの動作を制御調節装置であって、
   予め決められた基準座標（Ｘ_TCP，Ｙ_TCP，Ｚ_TCP，α_TCP，β_TCP，γ_TCP）に依存して、前記システムの動作中に連続的に、各個別要素についてそれぞれ１つの力ベクトルを算定する負荷計算装置（９）と、
   前記基準座標（Ｘ_TCP，Ｙ_TCP，Ｚ_TCP，α_TCP，β_TCP，γ_TCP）および前記力ベクトルに基づいて、運動中に連続的に、前記力ベクトルを補償する少なくとも１つの補償量を算定するトルク計算装置（１０）と、
   前記基準座標（Ｘ_TCP，Ｙ_TCP，Ｚ_TCP，α_TCP，β_TCP，γ_TCP）および前記少なくとも１つの補償量に依存して、運動中に連続的に、前記少なくとも１つの駆動装置のための力形成量を調節する調節ユニット（１１）と、
   前記駆動装置の実際回転トルクを監視するために、前記駆動装置のための少なくとも１つの最適指令量又は前記駆動装置の少なくとも１つの最適回転トルクを算定することを可能にするシステムの制御軌道のモデル（３８）と、
   を備えた制御調節装置。
2. 前記補償量が、補償回転トルク、補償力、補償速度又は補償位置である、請求項１記載の制御調節装置。
3. 前記負荷計算装置（９）が、各力ベクトルを算定するために、前記個別要素（１，２，４，６，２６，２７）の１つにおける力を導入する個所および／又は方向および／又は大きさを考慮した負荷モデルを使用する、請求項１又は２記載の制御調節装置。
4. 前記調節ユニット（１１）が、カスケード接続された位置調節系、速度調節系、および、圧力調節系又は電流調節系を有する、請求項１乃至３の１つに記載の制御調節装置。
5. 前記トルク計算装置（１０）が、少なくとも１つの補償トルクを算定するために、前記個別要素（１，２，４，６，２６，２７）のそれぞれの質量および／又は弾性および／又は減衰および／又は自由度の線形依存性を考慮したマルチ要素モデルを使用する、請求項１乃至４の１つに記載の制御調節装置。
6. 前記マルチ要素モデルが、線形微分方程式系に基づいている、請求項５記載の制御調節装置。
7. 前記線形微分方程式系が、前記個別要素（１，２，４，６，２６，２７）のそれぞれに関する質量行列、減衰行列および剛性行列に基づいている、請求項６記載の制御調節装置。
8. 前記マルチ要素モデルにおいて、前記個別要素（１，２，４，６，２６，２７）にそれぞれ作用する慣性力および／又はジャイロ力が考慮されている、請求項１乃至７の１つに記載の制御調節装置。
9. 前記トルク計算装置（１０）により、前記個別要素（１，２，４，６，２６，２７）の１つの最大加速度又は複数の前記個別要素の複合体の最大加速度が運動中に連続的に算定可能である、請求項１乃至８の１つに記載の制御調節装置。
10. 前記トルク計算装置（１０）および前記調節ユニット（１１）が、運動中に連続的にシステムの少なくとも１つの固有振動数の励起を低減するように構成されている、請求項１乃至９の１つに記載の制御調節装置。
11. 運動学的に協働する複数の個別要素（１，２，４，６，２６，２７）を有し、そのうち少なくとも１つが駆動装置（３，５，７，２８，２９）により移動されるシステムの動作を制御調節方法であって、
    予め決められた基準座標（Ｘ_TCP，Ｙ_TCP，Ｚ_TCP，α_TCP，β_TCP，γ_TCP）に依存して、システムの動作中に連続的に、前記個別要素（１，２，４，６，２６，２７）のそれぞれについて１つの力ベクトルを算定し、
    前記基準座標（Ｘ_TCP，Ｙ_TCP，Ｚ_TCP，α_TCP，β_TCP，γ_TCP）および前記力ベクトルに基づいて、運動中に連続的に、前記力ベクトルを補償する少なくとも１つの補償量を算定し、
    前記基準座標（Ｘ_TCP，Ｙ_TCP，Ｚ_TCP，α_TCP，β_TCP，γ_TCP）および前記少なくとも１つの補償量に依存して、運動中に連続的に、前記少なくとも１つの駆動装置のための力形成量を調節し、
    前記駆動装置の実際回転トルクを監視するために、システムの制御軌道のモデル（３８）により、前記駆動装置のための少なくとも１つの最適指令量又は前記駆動装置の少なくとも１つの最適回転トルクを算定する、
    制御調節方法。

Images