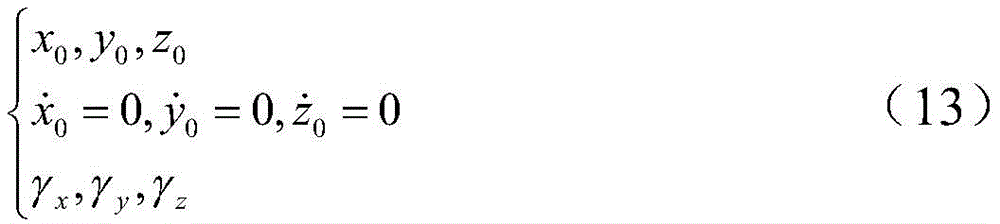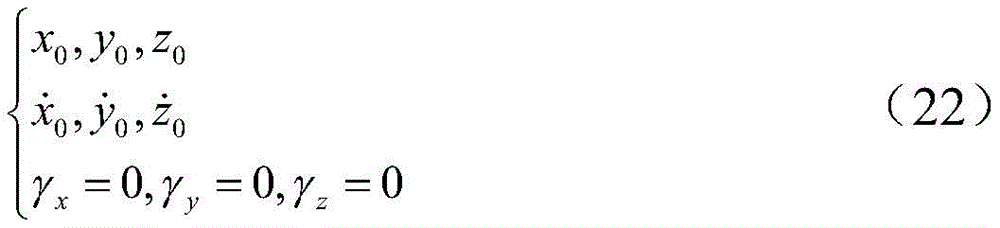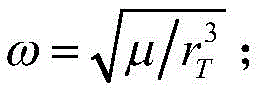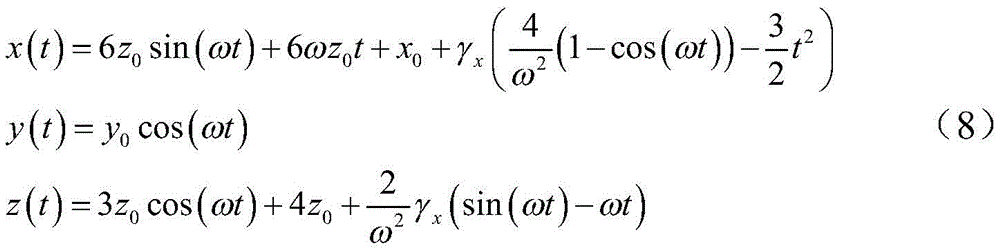CN109159923B - 一种航天器追踪目标丢失段的相对可达区域计算方法 - Google Patents

一种航天器追踪目标丢失段的相对可达区域计算方法 Download PDF

Info

Publication number
CN109159923B
CN109159923B CN201810837425.6A CN201810837425A CN109159923B CN 109159923 B CN109159923 B CN 109159923B CN 201810837425 A CN201810837425 A CN 201810837425A CN 109159923 B CN109159923 B CN 109159923B
Authority
CN
China
Prior art keywords
spacecraft
target spacecraft
equation
target
thrust
Prior art date
Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
Expired - Fee Related
Application number
CN201810837425.6A
Other languages
English (en)
Other versions
CN109159923A (zh
Inventor
袁建平
张军华
岳晓奎
李琪
王伟
高琛
Current Assignee (The listed assignees may be inaccurate. Google has not performed a legal analysis and makes no representation or warranty as to the accuracy of the list.)
Northwestern Polytechnical University
Original Assignee
Northwestern Polytechnical University
Priority date (The priority date is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the date listed.)
Filing date
Publication date
Application filed by Northwestern Polytechnical University filed Critical Northwestern Polytechnical University
Priority to CN201810837425.6A priority Critical patent/CN109159923B/zh
Publication of CN109159923A publication Critical patent/CN109159923A/zh
Application granted granted Critical
Publication of CN109159923B publication Critical patent/CN109159923B/zh
Expired - Fee Related legal-status Critical Current
Anticipated expiration legal-status Critical

Links

Images

Classifications

    • B—PERFORMING OPERATIONS; TRANSPORTING
    • B64—AIRCRAFT; AVIATION; COSMONAUTICS
    • B64G—COSMONAUTICS; VEHICLES OR EQUIPMENT THEREFOR
    • B64G1/00—Cosmonautic vehicles
    • B64G1/22—Parts of, or equipment specially adapted for fitting in or to, cosmonautic vehicles
    • B64G1/24—Guiding or controlling apparatus, e.g. for attitude control
    • B64G1/242—Orbits and trajectories
    • G—PHYSICS
    • G06—COMPUTING; CALCULATING OR COUNTING
    • G06F—ELECTRIC DIGITAL DATA PROCESSING
    • G06F17/00—Digital computing or data processing equipment or methods, specially adapted for specific functions
    • G06F17/10—Complex mathematical operations
    • G06F17/11—Complex mathematical operations for solving equations, e.g. nonlinear equations, general mathematical optimization problems

Landscapes

  • Engineering & Computer Science (AREA)
  • Physics & Mathematics (AREA)
  • Mathematical Physics (AREA)
  • General Physics & Mathematics (AREA)
  • Data Mining & Analysis (AREA)
  • Mathematical Optimization (AREA)
  • Mathematical Analysis (AREA)
  • Remote Sensing (AREA)
  • Pure & Applied Mathematics (AREA)
  • Theoretical Computer Science (AREA)
  • Computational Mathematics (AREA)
  • General Engineering & Computer Science (AREA)
  • Software Systems (AREA)
  • Databases & Information Systems (AREA)
  • Algebra (AREA)
  • Chemical & Material Sciences (AREA)
  • Combustion & Propulsion (AREA)
  • Radar, Positioning & Navigation (AREA)
  • Operations Research (AREA)
  • Aviation & Aerospace Engineering (AREA)
  • Control Of Position, Course, Altitude, Or Attitude Of Moving Bodies (AREA)
  • Navigation (AREA)

Abstract

本发明公开了一种航天器追踪目标丢失段的相对可达区域计算方法，包括以下步骤：1)建立地球惯性坐标系EXYZ及目标航天器轨道坐标系Txyz，并构建航天器相对运动轨道模型，求解航天器相对运动轨道模型的解；2)根据航天器相对运动轨道模型，在任一时刻加入目标航天器施加的机动力，以构造新的航天器相对运动轨道模型；3)求解新的航天器相对运动轨道模型的解析解，然后将求解得到的解析解作为目标航天器丢失段的相对可达区域的方程，该方法能够计算得到航天器追踪目标丢失段的相对可达区域。

Description

一种航天器追踪目标丢失段的相对可达区域计算方法
技术领域
本发明属于空间航天器相对运动技术领域，涉及一种航天器追踪目标丢失段的相对可达区域计算方法。
背景技术
近几年，随着在轨服务任务的需求，对目标航天器的轨道预测变得越来越重要。追踪航天器时时掌握目标航天器在轨信息，是进一步对目标进行任务的前提。但当追踪航天器对目标进行观测过程中，由于太阳光、地球遮蔽等因素，在一段时间内是无法观测到目标的，如果在该时间段内，目标航天器实施机动时，追踪航天器将无法成功预测目标航天器下一时段的位置信息，这将导致目标的丢失。因此利用相对可达区域的概念，对目标丢失段进行相对可达区域的计算，对目标在该时间段可能到达的区域进行描述，有利于追踪航天器对目标位置信息的把握。
对可达区域的研究是对航天器机动能力的解析表征，“Reachable Domain forInterception at Hyperbolic Speeds”首次将提出了可达区域的概念，用于洲际弹道导弹的拦截问题，研究了施加单脉冲后具有双曲线速度的拦截器的可达区域。“ReachableDomain for Spacecraft with a Single Impulse”将可达区域用于航天器的脉冲机动问题，研究了航天器单脉冲后的可达区域问题，考虑了三种情况：1)施加机动的位置固定，脉冲方向任意；2)脉冲方向固定，施加机动的位置任意；3)施加机动的位置和脉冲方向均为任意。但他们都没有研究相对可达区域的概念，这样无法将可达区域的概念运用到相对运动中，另外，对于丢失段的相对可达区域问题，也很少有文献进行研究。
发明内容
本发明的目的在于克服上述现有技术的缺点，提供了一种航天器追踪目标丢失段的相对可达区域计算方法，该方法能够计算得到航天器追踪目标丢失段的相对可达区域。
为达到上述目的，本发明所述的航天器追踪目标丢失段的相对可达区域计算方法包括以下步骤：
1)建立地球惯性坐标系EXYZ及目标航天器轨道坐标系Txyz，并构建航天器相对运动轨道模型，求解航天器相对运动轨道模型的解；
2)根据航天器相对运动轨道模型，在任一时刻加入目标航天器施加的机动力，以构造新的航天器相对运动轨道模型；
3)求解新的航天器相对运动轨道模型的解析解，然后将求解得到的解析解作为目标航天器丢失段的相对可达区域的方程。
步骤1)的具体操作为：
建立地球惯性坐标系EXYZ及目标航天器轨道坐标系Txyz，其中，地球惯性坐标系EXYZ的原点在地心E，地球惯性坐标系EXYZ的X轴指向春分点，地球惯性坐标系EXYZ的Z轴垂直于地球赤道平面向上，地球惯性坐标系EXYZ的Y轴满足右手法则；
目标航天器轨道坐标系Txyz的原点在目标航天器的质心T，目标航天器轨道坐标系Txyz的z轴沿目标航天器的矢径方向并指向地心，目标航天器轨道坐标系Txyz的y轴垂直于轨道平面，目标航天器轨道坐标系Txyz的x轴沿目标航天器的速度方向，且遵循右手法则；
当追踪航天器与目标航天器沿近圆轨道运行时，其相对运动方程能够用C-W方程表示，则在作用力为零的情况下的自由相对运动方程，即：
Figure BDA0001744765890000031
其中，ω为平均角速度，对于圆轨道
Figure BDA0001744765890000032
设初始条件为
Figure BDA0001744765890000033
得到式(1)的解析解为：
Figure BDA0001744765890000034
式(2)内x(t)中的
Figure BDA0001744765890000035
为漂移项，将漂移项消除，则式(2)可以简化为：
Figure BDA0001744765890000036
常值力下C-W方程存在漂移项的解为：
Figure BDA0001744765890000037
其中，
Figure BDA0001744765890000041
目标航天器在t0时刻在太阳阴影区内施加机动力，其中，机动方式为连续推力或脉冲推力。
当目标航天器在t0时刻在太阳阴影区内施加连续推力时，设目标航天器施加的连续推力为F，则将连续推力F分解到轨道坐标系下为：
Figure BDA0001744765890000042
单位质量下的连续推力在轨道坐标系下的分量为：
Figure BDA0001744765890000043
设目标航天器只施加x轴方向的连续推力，则初始条件为：
Figure BDA0001744765890000044
根据式(7)，目标航天器只施加x轴方向连续推力的相对可达区域方程为：
Figure BDA0001744765890000045
设目标航天器只施加y轴方向的连续推力，则初始条件为：
Figure BDA0001744765890000046
根据式(9)，目标航天器只施加y轴方向连续推力的相对可达区域方程为：
Figure BDA0001744765890000051
设目标航天器只施加z轴方向的连续推力，则初始条件为：
Figure BDA0001744765890000052
根据式(11)，目标航天器只施加z轴方向连续推力的相对可达区域方程为：
Figure BDA0001744765890000053
设目标航天器施加连续推力的方向任意，则初始条件为：
Figure BDA0001744765890000054
根据式(13)，目标航天器施加任意方向连续推力的相对可达区域方程为：
Figure BDA0001744765890000055
当目标航天器在t0时刻在太阳阴影区内施加脉冲推力时，设目标航天器施加的脉冲推力为ΔV，将脉冲推力ΔV分解到轨道坐标系下为：
Figure BDA0001744765890000061
设目标航天器只施加x轴方向的脉冲推力，则初始条件为：
Figure BDA0001744765890000062
根据式(16)，目标航天器只施加x轴方向脉冲推力的相对可达区域方程为：
Figure BDA0001744765890000063
设目标航天器只施加y轴方向的脉冲推力，则初始条件为：
Figure BDA0001744765890000064
根据式(18)，目标航天器只施加y方向脉冲推力的相对可达区域方程为：
Figure BDA0001744765890000065
设目标航天器只施加z轴方向的脉冲推力，则初始条件为：
Figure BDA0001744765890000066
根据式(20)，目标航天器只施加z方向脉冲推力的相对可达区域方程为：
Figure BDA0001744765890000071
设目标航天器施加脉冲推力的方向任意，则初始条件为：
Figure BDA0001744765890000072
根据式(22)，目标航天器施加任意方向脉冲推力的相对可达区域方程为：
Figure BDA0001744765890000073
本发明具有以下有益效果：
本发明所述的航天器追踪目标丢失段的相对可达区域计算方法在具体操作时，根据航天器相对运动轨迹模型在任一时刻加入目标航天器施加的机动力，从而构建出新的航天器相对运动轨道模型，再求解该新的航天器相对运动轨道模型，以得到目标航天器丢失段的相对可达区域的方程，从而确定出目标航天器丢失段的相对可达区域，在实际应用时，追踪航天器即使在没有观测到目标的情况下，同样能够充分把握目标航天器的位置信息，实现追踪航天器对目标航天器可能出现的相对位置区域的掌握。
附图说明
图1为本发明中目标航天器丢失段的示意图；
图2为本发明中构建的地球惯性坐标系EXYZ示意图；
图3为本发明中构建的目标航天器轨道坐标系Txyz示意图。
具体实施方式
下面结合附图对本发明做进一步详细描述：
如图1所示，由于地球围绕太阳转动的缘故，在地球轨道运行的航天器，受到的太阳光照总会有一段时间被地球遮挡，这种情况下，当目标航天器进入阴影区后，利用相机作为传感器的追踪航天器就会失去对目标航天器的观测，因此在该丢失段目标可能实施的机动，利用相对可达区域的概念对目标航天器与追踪航天器之间相对运动进行刻画，使得追踪航天器对目标航天器的位置信息有全面的把握。
本发明所述的航天器追踪目标丢失段的相对可达区域计算方法包括以下步骤：
1)建立地球惯性坐标系EXYZ及目标航天器轨道坐标系Txyz，并构建航天器相对运动轨道模型，求解航天器相对运动轨道模型的解；
2)根据航天器相对运动轨道模型，在任一时刻加入目标航天器施加的机动力，以构造新的航天器相对运动轨道模型；
3)求解新的航天器相对运动轨道模型的解析解，然后将求解得到的解析解作为目标航天器丢失段的相对可达区域的方程。
步骤1)的具体操作为：
建立地球惯性坐标系EXYZ及目标航天器轨道坐标系Txyz，其中，地球惯性坐标系EXYZ的原点在地心E，地球惯性坐标系EXYZ的X轴指向春分点，地球惯性坐标系EXYZ的Z轴垂直于地球赤道平面向上，地球惯性坐标系EXYZ的Y轴满足右手法则；
目标航天器轨道坐标系Txyz的原点在目标航天器的质心T，目标航天器轨道坐标系Txyz的z轴沿目标航天器的矢径方向并指向地心，目标航天器轨道坐标系Txyz的y轴垂直于轨道平面，目标航天器轨道坐标系Txyz的x轴沿目标航天器的速度方向，且遵循右手法则；
当追踪航天器与目标航天器沿近圆轨道运行时，其相对运动方程能够用C-W方程表示，则在作用力为零的情况下的自由相对运动方程，即：
Figure BDA0001744765890000091
其中，ω为平均角速度，对于圆轨道
Figure BDA0001744765890000092
设初始条件为
Figure BDA0001744765890000093
得到式(1)的解析解为：
Figure BDA0001744765890000094
式(2)内x(t)中的
Figure BDA0001744765890000095
为漂移项，将漂移项消除，则式(2)可以简化为：
Figure BDA0001744765890000096
常值力下C-W方程存在漂移项的解为：
Figure BDA0001744765890000101
其中，
Figure BDA0001744765890000102
目标航天器在t0时刻在太阳阴影区内施加机动力，其中，机动方式为连续推力或脉冲推力。
当目标航天器在t0时刻在太阳阴影区内施加连续推力时，设目标航天器施加的连续推力为F，则将连续推力F分解到轨道坐标系下为：
Figure BDA0001744765890000103
单位质量下的连续推力在轨道坐标系下的分量为：
Figure BDA0001744765890000104
设目标航天器只施加x轴方向的连续推力，则初始条件为：
Figure BDA0001744765890000105
根据式(7)，目标航天器只施加x轴方向连续推力的相对可达区域方程为：
Figure BDA0001744765890000111
设目标航天器只施加y轴方向的连续推力，则初始条件为：
Figure BDA0001744765890000112
根据式(9)，目标航天器只施加y轴方向连续推力的相对可达区域方程为：
Figure BDA0001744765890000113
设目标航天器只施加z轴方向的连续推力，则初始条件为：
Figure BDA0001744765890000114
根据式(11)，目标航天器只施加z轴方向连续推力的相对可达区域方程为：
Figure BDA0001744765890000115
设目标航天器施加连续推力的方向任意，则初始条件为：
Figure BDA0001744765890000116
根据式(13)，目标航天器施加任意方向连续推力的相对可达区域方程为：
Figure BDA0001744765890000121
当目标航天器在t0时刻在太阳阴影区内施加脉冲推力时，设目标航天器施加的脉冲推力为ΔV，将脉冲推力ΔV分解到轨道坐标系下为：
Figure BDA0001744765890000122
设目标航天器只施加x轴方向的脉冲推力，则初始条件为：
Figure BDA0001744765890000123
根据式(16)，目标航天器只施加x轴方向脉冲推力的相对可达区域方程为：
Figure BDA0001744765890000124
设目标航天器只施加y轴方向的脉冲推力，则初始条件为：
Figure BDA0001744765890000125
根据式(18)，目标航天器只施加y方向脉冲推力的相对可达区域方程为：
Figure BDA0001744765890000131
设目标航天器只施加z轴方向的脉冲推力，则初始条件为：
Figure BDA0001744765890000132
根据式(20)，目标航天器只施加z方向脉冲推力的相对可达区域方程为：
Figure BDA0001744765890000135
设目标航天器施加脉冲推力的方向任意，则初始条件为：
Figure BDA0001744765890000133
根据式(22)，目标航天器施加任意方向脉冲推力的相对可达区域方程为：
Figure BDA0001744765890000134
以上内容仅为说明本发明的技术思想，不能以此限定本发明的保护范围，凡是按照本发明提出的技术思想，在技术方案基础上所做的任何改动，均落入本发明权利要求书的保护范围之内。

Claims (3)

1.一种航天器追踪目标丢失段的相对可达区域计算方法，其特征在于，包括以下步骤：
1)建立地球惯性坐标系EXYZ及目标航天器轨道坐标系Txyz，并构建航天器相对运动轨道模型，求解航天器相对运动轨道模型的解；
2)根据航天器相对运动轨道模型，在任一时刻加入目标航天器施加的机动力，以构造新的航天器相对运动轨道模型；
3)求解新的航天器相对运动轨道模型的解析解，然后将求解得到的解析解作为目标航天器丢失段的相对可达区域的方程；
步骤1)的具体操作为：
建立地球惯性坐标系EXYZ及目标航天器轨道坐标系Txyz，其中，地球惯性坐标系EXYZ的原点在地心E，地球惯性坐标系EXYZ的X轴指向春分点，地球惯性坐标系EXYZ的Z轴垂直于地球赤道平面向上，地球惯性坐标系EXYZ的Y轴满足右手法则；
目标航天器轨道坐标系Txyz的原点在目标航天器的质心T，目标航天器轨道坐标系Txyz的z轴沿目标航天器的矢径方向并指向地心，目标航天器轨道坐标系Txyz的y轴垂直于轨道平面，目标航天器轨道坐标系Txyz的x轴沿目标航天器的速度方向，且遵循右手法则；
当追踪航天器与目标航天器沿近圆轨道运行时，其相对运动方程能够用C-W方程表示，得在作用力为零的情况下的自由相对运动方程，即：
Figure FDA0003497600350000011
其中，ω为平均角速度，对于圆轨道
Figure FDA0003497600350000012
μ是地球引力常数，rT表示目标航天器在轨道坐标系下位置矢量的大小；
设初始条件为x0,y0,z0,
Figure FDA0003497600350000021
得到式(1)的解析解为：
Figure FDA0003497600350000022
式(2)内x(t)中的
Figure FDA0003497600350000023
为漂移项，将漂移项消除，则式(2)可以简化为：
Figure FDA0003497600350000024
常值力下C-W方程存在漂移项的解为：
Figure FDA0003497600350000025
其中，
Figure FDA0003497600350000026
mc表示追踪航天器的质量，目标航天器在t0时刻在太阳阴影区内施加机动力，其中，机动方式为连续推力或脉冲推力；
当目标航天器在t0时刻在太阳阴影区内施加连续推力时，设目标航天器施加的连续推力为F，则将连续推力F分解到轨道坐标系下为：
Figure FDA0003497600350000031
单位质量下的连续推力在轨道坐标系下的分量为：
Figure FDA0003497600350000032
2.根据权利要求1所述的航天器追踪目标丢失段的相对可达区域计算方法，其特征在于，设目标航天器只施加x轴方向的连续推力，则初始条件为：
Figure FDA0003497600350000033
根据式(7)，目标航天器只施加x轴方向连续推力的相对可达区域方程为：
Figure FDA0003497600350000034
设目标航天器只施加y轴方向的连续推力，则初始条件为：
Figure FDA0003497600350000035
根据式(9)，目标航天器只施加y轴方向连续推力的相对可达区域方程为：
Figure FDA0003497600350000036
设目标航天器只施加z轴方向的连续推力，则初始条件为：
Figure FDA0003497600350000041
根据式(11)，目标航天器只施加z轴方向连续推力的相对可达区域方程为：
Figure FDA0003497600350000042
设目标航天器施加连续推力的方向任意，则初始条件为：
Figure FDA0003497600350000043
根据式(13)，目标航天器施加任意方向连续推力的相对可达区域方程为：
Figure FDA0003497600350000044
3.根据权利要求2所述的航天器追踪目标丢失段的相对可达区域计算方法，其特征在于，当目标航天器在t0时刻在太阳阴影区内施加脉冲推力时，设目标航天器施加的脉冲推力为△V，将脉冲推力△V分解到轨道坐标系下为：
Figure FDA0003497600350000045
设目标航天器只施加x轴方向的脉冲推力，则初始条件为：
Figure FDA0003497600350000051
根据式(16)，目标航天器只施加x轴方向脉冲推力的相对可达区域方程为：
Figure FDA0003497600350000052
设目标航天器只施加y轴方向的脉冲推力，则初始条件为：
Figure FDA0003497600350000053
根据式(18)，目标航天器只施加y方向脉冲推力的相对可达区域方程为：
Figure FDA0003497600350000054
设目标航天器只施加z轴方向的脉冲推力，则初始条件为：
Figure FDA0003497600350000055
根据式(20)，目标航天器只施加z方向脉冲推力的相对可达区域方程为：
Figure FDA0003497600350000056
设目标航天器施加脉冲推力的方向任意，则初始条件为：
Figure FDA0003497600350000061
根据式(22)，目标航天器施加任意方向脉冲推力的相对可达区域方程为：
Figure FDA0003497600350000062
CN201810837425.6A 2018-07-26 2018-07-26 一种航天器追踪目标丢失段的相对可达区域计算方法 Expired - Fee Related CN109159923B (zh)

Priority Applications (1)

Application Number Priority Date Filing Date Title
CN201810837425.6A CN109159923B (zh) 2018-07-26 2018-07-26 一种航天器追踪目标丢失段的相对可达区域计算方法

Applications Claiming Priority (1)

Application Number Priority Date Filing Date Title
CN201810837425.6A CN109159923B (zh) 2018-07-26 2018-07-26 一种航天器追踪目标丢失段的相对可达区域计算方法

Publications (2)

Publication Number Publication Date
CN109159923A CN109159923A (zh) 2019-01-08
CN109159923B true CN109159923B (zh) 2022-05-13

Family

ID=64898327

Family Applications (1)

Application Number Title Priority Date Filing Date
CN201810837425.6A Expired - Fee Related CN109159923B (zh) 2018-07-26 2018-07-26 一种航天器追踪目标丢失段的相对可达区域计算方法

Country Status (1)

Country Link
CN (1) CN109159923B (zh)

Families Citing this family (2)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
CN111324137B (zh) * 2020-03-05 2022-08-05 中国工程物理研究院总体工程研究所 一种基于常值连续推力的区域悬停轨道控制方法
CN113401364B (zh) * 2021-06-07 2022-06-14 中国人民解放军国防科技大学 基于日食效应的空间攻防方法

Citations (7)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
EP0628899A1 (en) * 1990-04-16 1994-12-14 Space Systems / Loral Inc. Method and apparatus for inclined orbit attitude control for momentum bias spacecraft
EP0992429A2 (de) * 1998-10-06 2000-04-12 SEL Verteidigungssysteme GmbH Satellitengestütztes Verteidigungssystem und Verfahren zur satellitengestützten Verteidigung
CN103455707A (zh) * 2013-07-22 2013-12-18 西北工业大学 基于凸优化技术的有限推力航天器自主交会轨迹规划方法
CN103950555A (zh) * 2014-04-22 2014-07-30 北京控制工程研究所 超近距离的高精度相对位置保持控制方法
CN107529376B (zh) * 2013-08-01 2015-12-30 上海新跃仪表厂 多模融合的微小卫星非合作目标相对导航的方法
CN106970530A (zh) * 2017-04-28 2017-07-21 西北工业大学 空间非合作目标自主视线交会的无模型预设性能控制方法
CN107168345A (zh) * 2017-04-07 2017-09-15 西北工业大学 一种针对空间翻滚目标上任意点的交会方法

Patent Citations (7)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
EP0628899A1 (en) * 1990-04-16 1994-12-14 Space Systems / Loral Inc. Method and apparatus for inclined orbit attitude control for momentum bias spacecraft
EP0992429A2 (de) * 1998-10-06 2000-04-12 SEL Verteidigungssysteme GmbH Satellitengestütztes Verteidigungssystem und Verfahren zur satellitengestützten Verteidigung
CN103455707A (zh) * 2013-07-22 2013-12-18 西北工业大学 基于凸优化技术的有限推力航天器自主交会轨迹规划方法
CN107529376B (zh) * 2013-08-01 2015-12-30 上海新跃仪表厂 多模融合的微小卫星非合作目标相对导航的方法
CN103950555A (zh) * 2014-04-22 2014-07-30 北京控制工程研究所 超近距离的高精度相对位置保持控制方法
CN107168345A (zh) * 2017-04-07 2017-09-15 西北工业大学 一种针对空间翻滚目标上任意点的交会方法
CN106970530A (zh) * 2017-04-28 2017-07-21 西北工业大学 空间非合作目标自主视线交会的无模型预设性能控制方法

Also Published As

Publication number Publication date
CN109159923A (zh) 2019-01-08

Similar Documents

Publication Publication Date Title
CN103991559B (zh) 一种洛伦兹航天器悬停控制方法
CN104570742B (zh) 基于前馈pid控制的异面交叉快变轨道快速高精度相对指向控制方法
CN103112603B (zh) 欠驱动高速自旋卫星建立正常姿态的方法
CN112607065B (zh) 一种基于电推进系统的高精度相位控制方法
CN106096148A (zh) 一种简单姿态控制下的大倾角轨道卫星太阳帆板指向方法
CN106931967B (zh) 一种助推-滑翔式临近空间飞行器的捷联惯性导航方法
CN102878995A (zh) 一种静止轨道卫星自主导航方法
CN109911249B (zh) 低推重比飞行器的星际转移有限推力入轨迭代制导方法
CN103092209A (zh) 一种基于动量轮控制的全姿态捕获方法
Sun et al. Roto-translational spacecraft formation control using aerodynamic forces
CN112572835B (zh) 一种具有姿态切换的卫星在轨角动量管理及控制方法
CN109190158B (zh) 一种考虑非合作目标禁飞区约束的最优轨道设计方法
CN106055810A (zh) 用于在轨快速抓捕的姿轨臂一体化运动规划方法
CN112407336B (zh) 一种利用姿态旋转进行干扰角动量自平衡的轨道控制方法
CN109159923B (zh) 一种航天器追踪目标丢失段的相对可达区域计算方法
CN104730506A (zh) 一种合成孔径雷达卫星的全零多普勒姿态导引方法
CN109212970A (zh) 一种欠驱动绳系复合体系统的神经网络动态面控制方法
CN115837989A (zh) 一种基于姿轨耦合控制策略的在轨目标接近导引方法
CN108427429B (zh) 一种考虑动态指向约束的航天器视轴机动控制方法
CN105527974B (zh) 一种缺失径向控制的欠驱动航天器悬停渐近控制方法
CN105739511A (zh) 一种缺失迹向控制的欠驱动航天器悬停渐近控制方法
CN114019794B (zh) 一种固定轨位电推分时卸载的整轨角动量估计和管理方法
CN110466803A (zh) 基于等倾角姿态控制的自旋稳定卫星姿态预测方法
CN107704424B (zh) 基于被动推扫成像模式下距离与所需时间的精确计算方法
CN112389679B (zh) 一种考虑多种摄动力的小卫星常值推力轨道递推方法

Legal Events

Date Code Title Description
PB01 Publication
PB01 Publication
SE01 Entry into force of request for substantive examination
SE01 Entry into force of request for substantive examination
GR01 Patent grant
GR01 Patent grant
CF01 Termination of patent right due to non-payment of annual fee
CF01 Termination of patent right due to non-payment of annual fee

Granted publication date: 20220513