JP5393461B2 - 多軸機械の数値制御方法及び該方法を用いた処理システム - Google Patents
多軸機械の数値制御方法及び該方法を用いた処理システム Download PDFInfo
- Publication number
- JP5393461B2 JP5393461B2 JP2009526668A JP2009526668A JP5393461B2 JP 5393461 B2 JP5393461 B2 JP 5393461B2 JP 2009526668 A JP2009526668 A JP 2009526668A JP 2009526668 A JP2009526668 A JP 2009526668A JP 5393461 B2 JP5393461 B2 JP 5393461B2
- Authority
- JP
- Japan
- Prior art keywords
- singular
- joints
- vector
- jacobian matrix
- value
- Prior art date
- Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
- Expired - Fee Related
Links
- 238000000034 method Methods 0.000 title claims description 22
- 238000012545 processing Methods 0.000 title claims description 7
- 239000013598 vector Substances 0.000 claims description 41
- 239000011159 matrix material Substances 0.000 claims description 40
- 230000007246 mechanism Effects 0.000 claims description 21
- 238000000354 decomposition reaction Methods 0.000 claims description 9
- 230000008859 change Effects 0.000 claims description 5
- 238000013459 approach Methods 0.000 claims description 4
- 238000012544 monitoring process Methods 0.000 claims description 4
- 238000010586 diagram Methods 0.000 description 6
- 230000008901 benefit Effects 0.000 description 2
- 238000004422 calculation algorithm Methods 0.000 description 2
- 238000004364 calculation method Methods 0.000 description 2
- 230000001143 conditioned effect Effects 0.000 description 2
- 238000012937 correction Methods 0.000 description 2
- 230000000694 effects Effects 0.000 description 2
- 230000006870 function Effects 0.000 description 2
- 238000003754 machining Methods 0.000 description 2
- 238000012423 maintenance Methods 0.000 description 2
- 238000004519 manufacturing process Methods 0.000 description 2
- 230000008569 process Effects 0.000 description 2
- 238000012897 Levenberg–Marquardt algorithm Methods 0.000 description 1
- 238000004891 communication Methods 0.000 description 1
- 238000005520 cutting process Methods 0.000 description 1
- 238000009434 installation Methods 0.000 description 1
- 239000000463 material Substances 0.000 description 1
- 238000012986 modification Methods 0.000 description 1
- 230000004048 modification Effects 0.000 description 1
- 230000009467 reduction Effects 0.000 description 1
- 230000009466 transformation Effects 0.000 description 1
- 239000002699 waste material Substances 0.000 description 1
Images
Classifications
-
- B—PERFORMING OPERATIONS; TRANSPORTING
- B25—HAND TOOLS; PORTABLE POWER-DRIVEN TOOLS; MANIPULATORS
- B25J—MANIPULATORS; CHAMBERS PROVIDED WITH MANIPULATION DEVICES
- B25J9/00—Programme-controlled manipulators
- B25J9/16—Programme controls
- B25J9/1602—Programme controls characterised by the control system, structure, architecture
- B25J9/1607—Calculation of inertia, jacobian matrixes and inverses
Landscapes
- Engineering & Computer Science (AREA)
- Physics & Mathematics (AREA)
- Mathematical Physics (AREA)
- Automation & Control Theory (AREA)
- Robotics (AREA)
- Mechanical Engineering (AREA)
- Numerical Control (AREA)
- Manipulator (AREA)
Description
この開示は、多軸機械に関し、より具体的には、機械操作中に運動学的特異点に対処するためのシステムおよび方法に関する。この項における記述は、この開示に関連する背景情報を提供するのみであって、先行技術を構成するものではない。
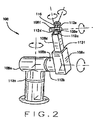
この開示は、1つの実現例においては、多軸機械の操作方法に関する。この機械の運動学的リンク機構が監視される。リンク機構は、複数のジョイントおよびリンクを含む。リンク機構は、リンク機構の1つ以上のジョイントによる特異点への接近を検出するために監視される。この監視は、ヤコビ行列を用いて行なわれる。接近される特異点の度数nが求められる。特異点に接近している1つ以上のジョイントが識別される。この方法は、n個の仮想ジョイントを得るステップと、識別される1つ以上のジョイントを、ヤコビ行列中の仮想ジョイントと置き換え、ヤコビ行列を修正するステップと、修正されたヤコビ行列を用いてリンク機構のリンクの位置変更を決定するステップとを含む。
以下の説明は、本質的に単に例示的なものであり、この開示、説明、または使用を限定することを意図しない。図面全体を通して、対応する参照番号は、同様のまたは対応する部品または特徴を示すことが理解されるべきである。
またはより多い、より少ないおよび/または異なる自由度および/または自由度の種類を提供してもよい。
させる手段を提供する。精度を向上させることができると、新しい資本設備の取得費用および既存設備の維持費用を少なくすることができる。さらに、この開示のさまざまな実現例は、いくつかの異なる機械形状に対して有効な単一の方法を提供することができ、これにより新たな機械形状に対処するためのソフトウェア開発およびメンテナンスの必要性が低減される。
Claims (4)
- 複数のリンク(108)と前記リンクを接続する複数のジョイント(112)とを有する運動学的リンク機構(100)を含む多軸機械(24)をヤコビ行列J(200)を用いて数値制御(NC)する方法であって、
前記リンク機構の1つ以上のジョイントによる特異点への接近を検出するために前記リンク機構を監視するステップであって、
(a)ヤコビ行列J(200)の特異値分解J=U*S*V T を求めるステップ(UおよびVは正規直交行列であり、Uの列は左特異ベクトル(208)を、Vの列は右特異ベクトル(228)を構成し、Sは対角行列であり特異値(236)が降順に対角に配置される)(312)と、
(b)特異値分解から求められる特異値のうち最大特異値を求め、各特異値を該最大特異値で除した値を条件数の逆数として求め(316)、所定のしきい値以下(320)となる条件数の逆数の数を接近される特異点の度数nとして求める(324)ステップと、
(c)最後のn個の右特異ベクトル(228)の最大成分の位置を特定することにより特異であるまたは特異に近いn個のジョイント(112)を決定し(328)、最後のn個の左特異ベクトル(208)を最大特異値(236)で乗算し、n個の仮想ジョイントを得(332)、前記n個のジョイント(112)と関連付けられるヤコビ行列Jの列(204)を該仮想ジョイントと置き換えることにより、修正されたヤコビ行列を求めるステップ(336)と、
(d)最初のリンク位置ベクトルQ(i)を求めるステップ(340)と、
(e)前記修正されたヤコビ行列を用いてリンクの位置ベクトルの変化ΔQを計算し(352)、ΔQとQ(i)から、新しいリンク位置ベクトルQ(i+1)を求める(356)ステップと、
(f)Q(i+1)によりQ(i)を更新し、更新後のQ(i)を用いて前記(e)を収斂に達するまで繰り返すステップとを備える、方法。 - (g) (f)のステップの後に、前記リンク機構が特異点に接近しているかどうかを判定し(364)接近していると判定された場合、前記n個の仮想ジョイントを表わす1つ以上の値を、前記リンク位置ベクトルQ(i+1)から取り除く(368)ステップと、
(h)前記Q(i+1)を用いて、非特異ジョイント(112)を補正するステップ(372)とをさらに含む、請求項1に記載された方法。 - 数値制御(NC)される処理システムであって、前記NC処理システムは、
複数のリンク(108)と前記リンクを接続する複数のジョイント(112)とを有する運動学的リンク機構(100)を含む多軸機械(24)と、
プロセッサ(32)とを備え、前記プロセッサは、
前記リンク機構の1つ以上のジョイントによる特異点への接近を検出するために前記リンク機構を監視し、前記監視は、ヤコビ行列(200)を用いて行なわれ、
(a)ヤコビ行列J(200)の特異値分解J=U*S*V T を求め(UおよびVは正規直交行列であり、Uの列は左特異ベクトル(208)を、Vの列は右特異ベクトル(228)を構成し、Sは対角行列であり特異値(236)が降順に対角に配置される)(312)、
(b)特異値分解から求められる特異値のうち最大特異値を求め、各特異値を該最大特異値で除した値を条件数の逆数として求め(316)、所定のしきい値以下(320)となる条件数の逆数の数を接近される特異点の度数nとして求め(324)、
(c)最後のn個の右特異ベクトル(228)の最大成分の位置を特定することにより特異であるまたは特異に近いn個のジョイント(112)を決定し(328)、最後のn個の左特異ベクトル(208)を最大特異値(236)で乗算し、n個の仮想ジョイントを得(332)、前記n個のジョイント(112)と関連付けられるヤコビ行列Jの列(204)を該仮想ジョイントと置き換えることにより、修正されたヤコビ行列を求め(336)、
(d)最初のリンク位置ベクトルQ(i)を求め(340)、
(e)前記修正されたヤコビ行列を用いてリンクの位置ベクトルの変化ΔQを決定し(352)、ΔQとQ(i)から、新しいリンク位置ベクトルQ(i+1)を求め(356)、
(f)Q(i+1)によりQ(i)を更新し、更新後のQ(i)を用いて前記(e)を収斂に達するまで繰り返すように構成される、システム。 - 前記プロセッサはさらに、
(g) (f)の後に、前記リンク機構が特異点に接近しているかどうかを判定し(364)、接近していると判定された場合、前記n個の仮想ジョイントを表わす1つ以上の値を、前記リンク位置ベクトルQ(i+1)から取り除き(368)、
(h)前記Q(i+1)を用いて、非特異ジョイント(112)を補正することを含むように構成される、請求項3に記載されたシステム。
Applications Claiming Priority (3)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| US11/514,072 | 2006-08-31 | ||
| US11/514,072 US8010235B2 (en) | 2005-05-31 | 2006-08-31 | Approaching and compensating for machine kinematic singularities |
| PCT/US2007/018820 WO2008027334A2 (en) | 2006-08-31 | 2007-08-27 | Approaching and compensating for machine kinematic singularities |
Publications (3)
| Publication Number | Publication Date |
|---|---|
| JP2010502454A JP2010502454A (ja) | 2010-01-28 |
| JP2010502454A5 JP2010502454A5 (ja) | 2013-09-12 |
| JP5393461B2 true JP5393461B2 (ja) | 2014-01-22 |
Family
ID=39136516
Family Applications (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| JP2009526668A Expired - Fee Related JP5393461B2 (ja) | 2006-08-31 | 2007-08-27 | 多軸機械の数値制御方法及び該方法を用いた処理システム |
Country Status (5)
| Country | Link |
|---|---|
| US (1) | US8010235B2 (ja) |
| EP (1) | EP2073959B1 (ja) |
| JP (1) | JP5393461B2 (ja) |
| CN (1) | CN101505925B (ja) |
| WO (1) | WO2008027334A2 (ja) |
Families Citing this family (12)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| JP4692488B2 (ja) * | 2005-12-26 | 2011-06-01 | 三菱電機株式会社 | 数値制御装置及び数値制御工作機械 |
| JP2008073830A (ja) * | 2006-09-25 | 2008-04-03 | Fanuc Ltd | ロボット制御装置 |
| FR2960074B1 (fr) * | 2010-05-14 | 2012-06-15 | Staubli Sa Ets | Procede de commande d'une cellule de travail automatisee |
| CA2801163A1 (en) | 2010-06-03 | 2011-12-08 | Delaval Holding Ab | A milking robot, and a milking arrangement |
| DE102010032917A1 (de) * | 2010-07-30 | 2012-04-19 | Brötje-Automation GmbH | Verfahren zur Offline-Programmierung eines NC-gesteuerten Manipulators |
| US8532825B1 (en) * | 2010-08-25 | 2013-09-10 | The Boeing Company | Software compensation for kinematically singular machines |
| CN104965517B (zh) * | 2015-07-07 | 2018-01-26 | 张耀伦 | 一种机器人笛卡尔空间轨迹的规划方法 |
| CN105415363B (zh) * | 2015-12-23 | 2017-11-17 | 珠海格力电器股份有限公司 | 机器人奇异点处理方法 |
| US10065311B1 (en) * | 2016-06-08 | 2018-09-04 | X Development Llc | Singularity handling for robot jogging |
| JP7222898B2 (ja) * | 2017-06-12 | 2023-02-15 | ジーメンス インダストリー ソフトウェア リミテッド | ロボット製造での所定のターゲットへの到達をロボットにティーチングするための方法およびシステム |
| CN113263496B (zh) * | 2021-04-01 | 2022-09-23 | 北京无线电测量研究所 | 一种六自由度机械臂优化路径的方法和计算机设备 |
| CN114549352A (zh) * | 2022-02-21 | 2022-05-27 | 中国第一汽车股份有限公司 | 图像处理方法、装置、电子设备和存储介质 |
Family Cites Families (18)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US4680519A (en) * | 1985-09-23 | 1987-07-14 | General Electric Co. | Recursive methods for world-to-joint transformation for a robot manipulator |
| US4937759A (en) * | 1986-02-18 | 1990-06-26 | Robotics Research Corporation | Industrial robot with controller |
| US5038089A (en) * | 1988-03-23 | 1991-08-06 | The United States Of America As Represented By The Administrator Of The National Aeronautics And Space Administration | Synchronized computational architecture for generalized bilateral control of robot arms |
| US4967126A (en) * | 1990-01-30 | 1990-10-30 | Ford Aerospace Corporation | Method of controlling a seven degree of freedom manipulator arm |
| SE9400579L (sv) * | 1994-02-21 | 1995-08-22 | Asea Brown Boveri | Förfarande för att styra en industrirobots rörelse i och i närheten av singulariteter |
| US5793795A (en) * | 1996-12-04 | 1998-08-11 | Motorola, Inc. | Method for correcting errors from a jamming signal in a frequency hopped spread spectrum communication system |
| JPH10329066A (ja) * | 1997-05-26 | 1998-12-15 | Mitsubishi Heavy Ind Ltd | 冗長マニピュレータの特異姿勢検知方法および特異姿勢回避方法 |
| US6208949B1 (en) * | 1998-07-01 | 2001-03-27 | Adaptive Audio, Inc. | Method and apparatus for dynamical system analysis |
| US6493608B1 (en) * | 1999-04-07 | 2002-12-10 | Intuitive Surgical, Inc. | Aspects of a control system of a minimally invasive surgical apparatus |
| US8004229B2 (en) * | 2005-05-19 | 2011-08-23 | Intuitive Surgical Operations, Inc. | Software center and highly configurable robotic systems for surgery and other uses |
| US6847925B2 (en) * | 2000-06-21 | 2005-01-25 | Hrl Laboratories, Llc | Method and apparatus for modeling three-dimensional electromagnetic scattering from arbitrarily shaped three-dimensional objects |
| US6603281B2 (en) * | 2000-10-16 | 2003-08-05 | Xerox Corporation | High mechanical advantage ratcheting apparatus |
| US6845295B2 (en) * | 2002-03-07 | 2005-01-18 | Fanuc Robotics America, Inc. | Method of controlling a robot through a singularity |
| JP3997405B2 (ja) * | 2002-07-26 | 2007-10-24 | 株式会社安川電機 | 移動マニピュレータの制御装置および移動マニピュレータ |
| US6952657B2 (en) * | 2003-09-10 | 2005-10-04 | Peak Sensor Systems Llc | Industrial process fault detection using principal component analysis |
| GB0507618D0 (en) * | 2005-04-15 | 2005-05-25 | Lms Internat Nv | Method and system for dynamic analysis of complex systems |
| US7571027B2 (en) * | 2005-05-31 | 2009-08-04 | The Boeing Company | Kinematic singular point compensation systems and methods |
| US8725283B2 (en) * | 2006-08-04 | 2014-05-13 | Hurco Companies, Inc. | Generalized kinematics system |
-
2006
- 2006-08-31 US US11/514,072 patent/US8010235B2/en not_active Expired - Fee Related
-
2007
- 2007-08-27 EP EP07837375.0A patent/EP2073959B1/en not_active Not-in-force
- 2007-08-27 CN CN2007800306231A patent/CN101505925B/zh not_active Expired - Fee Related
- 2007-08-27 WO PCT/US2007/018820 patent/WO2008027334A2/en active Application Filing
- 2007-08-27 JP JP2009526668A patent/JP5393461B2/ja not_active Expired - Fee Related
Also Published As
| Publication number | Publication date |
|---|---|
| JP2010502454A (ja) | 2010-01-28 |
| WO2008027334A2 (en) | 2008-03-06 |
| EP2073959A2 (en) | 2009-07-01 |
| CN101505925A (zh) | 2009-08-12 |
| CN101505925B (zh) | 2012-07-18 |
| WO2008027334A3 (en) | 2008-10-02 |
| US8010235B2 (en) | 2011-08-30 |
| EP2073959B1 (en) | 2018-01-10 |
| US20070112468A1 (en) | 2007-05-17 |
Similar Documents
| Publication | Publication Date | Title |
|---|---|---|
| JP5393461B2 (ja) | 多軸機械の数値制御方法及び該方法を用いた処理システム | |
| EP1885524B1 (en) | Kinematic singular point compensation systems and methods | |
| Zhu et al. | An off-line programming system for robotic drilling in aerospace manufacturing | |
| Liao et al. | Region-based toolpath generation for robotic milling of freeform surfaces with stiffness optimization | |
| Peng et al. | Smoothness-oriented path optimization for robotic milling processes | |
| CN110722576B (zh) | 工业机器人铣削加工路径全局光顺方法及系统 | |
| Lee et al. | A robust trajectory tracking control of a polishing robot system based on CAM data | |
| US20130013110A1 (en) | Method of finding feasible joint trajectories for an n-dof robot with rotation in-variant process (n>5) | |
| Liu et al. | An engineering-oriented motion accuracy fluctuation suppression method of a hybrid spray-painting robot considering dynamics | |
| CN110989490B (zh) | 一种基于轮廓误差的工件最优安装位置的获取方法 | |
| Celikag et al. | Cartesian stiffness optimization for serial arm robots | |
| EP2523786B1 (en) | Method of finding feasible joint trajectories for an n-dof robot with rotation invariant process (n>5) | |
| Huang et al. | A new method of inverse kinematics solution for industrial 7DOF robot | |
| CN115502984A (zh) | 六自由度机器人侧铣运动规划方法及系统 | |
| CN118438449A (zh) | 适用于移动工业机器加工大型回转类构件的站位优化方法 | |
| US8532825B1 (en) | Software compensation for kinematically singular machines | |
| Zhu et al. | Inverse kinematics solution of a new circumferential drilling machine for aircraft assembly | |
| Gao et al. | Robotic milling stability optimization based on robot functional redundancy | |
| Ledesma et al. | A non‐recursive Lagrangian solution of the non‐causal inverse dynamics of flexible multibody systems: The planar case | |
| JP2021186929A (ja) | 多軸ロボットの制御方法 | |
| CN112847441A (zh) | 基于梯度下降法的六轴机器人坐标偏移检测方法和装置 | |
| Wang et al. | The trajectory planning of 9 degree-of-freedom manipulator based on model predictive control method | |
| Tong et al. | Automatic Tool Path Planning Strategy Based on Feature Extraction of 3D Models | |
| Sapmaz et al. | Tool axis optimization for robotic 5-axis milling considering kinematics | |
| Walther et al. | Trajectory planning for kinematically redundant robots using jacobi matrix–an industrial implementation |
Legal Events
| Date | Code | Title | Description |
|---|---|---|---|
| RD03 | Notification of appointment of power of attorney |
Free format text: JAPANESE INTERMEDIATE CODE: A7423 Effective date: 20091111 |
|
| A521 | Request for written amendment filed |
Free format text: JAPANESE INTERMEDIATE CODE: A821 Effective date: 20100303 |
|
| RD04 | Notification of resignation of power of attorney |
Free format text: JAPANESE INTERMEDIATE CODE: A7424 Effective date: 20100303 |
|
| A621 | Written request for application examination |
Free format text: JAPANESE INTERMEDIATE CODE: A621 Effective date: 20100820 |
|
| A131 | Notification of reasons for refusal |
Free format text: JAPANESE INTERMEDIATE CODE: A131 Effective date: 20120306 |
|
| A601 | Written request for extension of time |
Free format text: JAPANESE INTERMEDIATE CODE: A601 Effective date: 20120604 |
|
| A602 | Written permission of extension of time |
Free format text: JAPANESE INTERMEDIATE CODE: A602 Effective date: 20120613 |
|
| A601 | Written request for extension of time |
Free format text: JAPANESE INTERMEDIATE CODE: A601 Effective date: 20120705 |
|
| A602 | Written permission of extension of time |
Free format text: JAPANESE INTERMEDIATE CODE: A602 Effective date: 20120712 |
|
| A521 | Request for written amendment filed |
Free format text: JAPANESE INTERMEDIATE CODE: A523 Effective date: 20120904 |
|
| A521 | Request for written amendment filed |
Free format text: JAPANESE INTERMEDIATE CODE: A523 Effective date: 20120906 |
|
| A131 | Notification of reasons for refusal |
Free format text: JAPANESE INTERMEDIATE CODE: A131 Effective date: 20130402 |
|
| A601 | Written request for extension of time |
Free format text: JAPANESE INTERMEDIATE CODE: A601 Effective date: 20130702 |
|
| A602 | Written permission of extension of time |
Free format text: JAPANESE INTERMEDIATE CODE: A602 Effective date: 20130709 |
|
| A524 | Written submission of copy of amendment under article 19 pct |
Free format text: JAPANESE INTERMEDIATE CODE: A524 Effective date: 20130731 |
|
| TRDD | Decision of grant or rejection written | ||
| A01 | Written decision to grant a patent or to grant a registration (utility model) |
Free format text: JAPANESE INTERMEDIATE CODE: A01 Effective date: 20130917 |
|
| A61 | First payment of annual fees (during grant procedure) |
Free format text: JAPANESE INTERMEDIATE CODE: A61 Effective date: 20131015 |
|
| R150 | Certificate of patent or registration of utility model |
Ref document number: 5393461 Country of ref document: JP Free format text: JAPANESE INTERMEDIATE CODE: R150 Free format text: JAPANESE INTERMEDIATE CODE: R150 |
|
| R250 | Receipt of annual fees |
Free format text: JAPANESE INTERMEDIATE CODE: R250 |
|
| R250 | Receipt of annual fees |
Free format text: JAPANESE INTERMEDIATE CODE: R250 |
|
| R250 | Receipt of annual fees |
Free format text: JAPANESE INTERMEDIATE CODE: R250 |
|
| R250 | Receipt of annual fees |
Free format text: JAPANESE INTERMEDIATE CODE: R250 |
|
| LAPS | Cancellation because of no payment of annual fees |