JP2005516458A - 復号器内構成要素ブロックによるメッセージ処理 - Google Patents

Abstract

符号語からシンドローム生成器（４１０）でシンドロームが計算され、シンドロームに基づいて誤り多項式生成器（４２０）で誤り多項式が生成され、誤り多項式から誤り位置生成器（４３０）で誤り位置が決定され、誤り多項式から誤り度合生成器（４４０）で誤り度合が計算され、位置および誤り度合に応答して誤り訂正符号語生成器（４５０）により符号語が訂正される復号器および復号方法を説明する。１つまたは複数の構成要素（４１０、４２０、４３０、４４０、４５０）が不活動メッセージ（６４０、６５０）を生成して、次の符号語に対応するデータを処理する機能を知らせる復号器内ブロック・メッセージ処理方式を説明する。チェン・ブロック（９３０）を用いて、チェン／フォーニー・ブロック（９４０）により実施される誤り位置および度合の計算とは別に、指定された符号語に対応する誤りの数を決定する二重チェン・サーチ・ブロック（９３０、９４０）の実施形態を説明する。追加のガロア体加算器（１１４０）を使用して符号語と誤りベクトルの同期をとり、それにより、ＬＩＦＯレジスタ（９５２）と共に実施される誤り訂正ブロック（９５０）に伴う遅延およびコストを低減する、強化型チェン・サーチ・セル・アーキテクチャを説明する。

Description

本発明は、ディジタル通信システムの誤り検出および訂正に関する。

本特許出願は、２００２年１月２３日に本願と同時出願の「ＤＵＡＬ ＣＨＩＥＮ ＳＥＡＲＣＨ ＢＬＯＣＫＳ ＩＮ ＡＮ ＥＲＲＯＲ−ＣＯＲＲＥＣＴＩＮＧ ＤＥＣＯＤＥＲ」という名称の米国特許出願第１０／０５５，０７６号（整理番号ＰＵ０２０００３）および２００２年１月２３日に本願と同時出願の「ＣＨＩＥＮ ＳＥＡＲＣＨ ＣＥＬＬ ＦＯＲ ＡＮ ＥＲＲＯＲ−ＣＯＲＲＥＣＴＩＮＧ ＤＥＣＯＤＥＲ」という名称の米国特許出願第１０／０５５，４７０号（整理番号ＰＵ０２０００１）に関連する。

現在のディジタル通信システムの重要な機能は、誤り制御符号化処理（ｅｒｒｏｒ ｃｏｎｔｒｏｌ ｃｏｄｉｎｇ）である。誤り制御符号化処理は、ディジタル・システムにおける誤りの検出（ｄｅｔｅｃｔｉｎｇ）および訂正（ｃｏｒｒｅｃｔｉｎｇ）に関する技術を扱う通信の分野である。一般に、誤り検出／訂正方式は、ディジタル・データの送信時またはディジタル・データの記憶により、データに誤りが生じないようにするか、或いは、データに誤りが生じた場合には、生じた誤りの訂正が行われるようにすることが望まれるときに必ず用いられる。データの誤り検出および／または訂正を行う機能は、データに冗長性を付加することにより実現される。送信または記憶するデータ中に冗長ビットを含めると、元の符号化していない信号またはフィールドよりも多くのビットからなる符号化された信号またはフィールドが得られる。

誤り検出／訂正に頻繁に用いられる１つの方式は、いわゆるリード・ソロモン（ＲＳ：Ｒｅｅｄ−Ｓｏｌｏｍｏｎ）符号の使用によるものである。リード・ソロモン符号は、非２値組織的線形ブロック符号である。非２値符号は、幾つかのビットからなるシンボルを扱う。リード・ソロモン符号などの非２値符号は、これらの符号による訂正がシンボル・レベルで行われるので、バースト誤りを訂正するのに適している。リード・ソロモン符号などの組織的符号は、不変形式のメッセージ・シンボルを含む符号語を生成する。符号器は、これらのメッセージ・シンボルに可逆的な数学関数を適用して、冗長またはパリティ・シンボルを生成する。次いで、このパリティ・シンボルをメッセージ・シンボルに付加することにより符号語を形成する。リード・ソロモン符号は、任意の有効符号語を巡回シフトしても別の有効符号語が生成されるので、巡回符号とみなされる。巡回符号は、それを実施する効率的で安価な復号技術が存在するので一般に普及している。最後に、リード・ソロモン符号は、任意の２つの有効符号語を追加すると、別の有効符号語が得られるので線形とみなされる。

典型的なリード・ソロモン復号器は、（ｉ）シンドローム（ｓｙｎｄｒｏｍｅ）生成ブロック、（ｉｉ）誤り多項式ブロック、（ｉｉｉ）誤り位置ブロック、（ｉｖ）誤り度合ブロック、（ｖ）誤り訂正ブロック、および（ｖｉ）遅延ブロックという主要な構成要素ブロックからなる。シンドローム生成ブロックは、符号語を受信し、この符号語からシンドロームを生成するのに用いる。このシンドロームを用いて、誤り多項式ブロックで誤り多項式を生成する。この誤り多項式を誤り位置ブロックおよび誤り度合ブロックに渡し、そこで符号語の誤りの位置および大きさがそれぞれ決まる。この誤りの位置および大きさから誤りベクトルを生成する。特定の符号語に対応する誤りベクトルを用いて、誤り訂正ブロックで、受信し遅延させたバージョンの符号語を訂正する。遅延ブロックは、誤りベクトルを生成する復号プロセスが実施される間、受信した符号語を記憶するメモリからなる。

従来技術の復号器は、これらのブロックを用いて「伝送パイプライン」を形成する。即ち、ある１つのブロックへの入力は前のブロックの出力のみによって決まり、１つの構成要素ブロックから前のブロックまたは後続のブロックへのフィードバックはない。従って、一度に１つの符号語しか処理することができず、前の符号語の処理が完了するまで、処理すべき次の符号語には取りかからない。

（発明の概要）
符号語中のデータの誤り検出を実施する方法および装置である本発明では、従来技術の効率の悪さが解決される。データの誤り検出を実施する復号器は、符号語からシンドロームを計算するシンドローム生成器、シンドロームから誤り多項式を生成する誤り多項式生成器、誤り多項式から誤り位置を決定する誤り位置生成器、および誤り多項式から誤り度合を計算する誤り度合生成器からなる。この復号器は、シンドローム生成器、誤り多項式生成器、誤り位置生成器および誤り度合生成器を含む群から選択された少なくとも１つの構成要素から復号器内非活動メッセージを送信するように適合されることを特徴とする。

添付の図面と併せて本発明の以下の説明を参照されたい。

図１を参照すると、本発明で実施する原理による誤り検出／訂正方式を組み込んだディジタル・データ伝送システム１００を示すブロック図が示されている。一般に、誤り検出／訂正方式は、ディジタル・データの送信時またはディジタル・データの記憶により、データに誤りが生じないようにするか、或いは、データに誤りが生じた場合には、生じた誤りの訂正が行われるようにすることが望まれるときに必ず用いられる。データの誤り検出および／または訂正を行う機能は、データに冗長性を付加することにより実現される。送信または記憶するデータ中に冗長ビットを含めると、元の符号化していない信号またはフィールドよりも多くのビットからなる符号化された信号またはフィールドが得られる。この追加のオーバーヘッドを許容する見返りとして、誤りを検出する機能、或いは、誤りを検出し訂正する機能が得られる。誤り制御符号化処理を用いて得られる性能の改善は、符号化利得について評価されることが多い。符号化処理を行わない通信システムで、３０ｄＢのＳＮＲ（Ｓｉｇｎａｌ−ｔｏ−Ｎｏｉｓｅ Ｒａｔｉｏｎ：信号対雑音比）で所定のＢＥＲ（Ｂｉｔ Ｅｒｒｏｒ Ｒａｔｅ：ビット誤り率）が実現されるとする。このシステムに３ｄＢの符号化利得の誤り制御符号化方式を加える場合、この符号化処理を行うシステムは、２７ｄＢという更に低いＳＮＲでこのＢＥＲを実現することができる。或いは、このシステムを３０ｄＢのＳＮＲで稼働させる場合、符号化処理を行うシステムにより実現されるＢＥＲは、符号化処理を行わないシステムが３３ｄＢのＳＮＲで実現するものと同じＢＥＲとなる。符号化利得の威力は、通信システムが、（ｉ）符号化処理を行わずに所望のＢＥＲを維持することが可能であったＳＮＲよりも低いＳＮＲでそのＢＥＲを維持できるか、或いは、（ｉｉ）符号化処理を行わないシステムが所定のＳＮＲで得ることができるはずのものよりも高いＢＥＲを実現できることである。

例として、符号器１１０の機能は、データ源からディジタル・データを受信し、チャネルを介してデータを送信するか、または記憶媒体にデータを記憶するか（図には、全体としてチャネルまたは記憶装置１１５として示す）、或いは、他の方法でこのデータを操作または処理することである。データの処理、送信または記憶時に、データにノイズまたは誤り１２５が導入され、そのためしばしば、データが破損するか、或いは元のディジタル・データから変質した形式になる。復号器１２０は、ディジタル・データの規定部分が破損したかどうかを検出し訂正するか、或いは、単に検出するように機能する。

図２を参照すると、送信機／チャネル／受信機環境の状況で利用可能な様々な誤り検出／訂正プロセスを示す流れ図が示されている。このような状況で説明するが、当業者には、このような誤り検出／訂正プロセスが、ブロードキャスト送信、ディジタル・データ記憶、または（データ・フィールド、パケット、ストリームなどの形態にあろうが）ディジタル・データを処理または操作する任意の他のプロセスにも同様に適用されることが明らかであろう。網羅的または排他的ではなく単なる例として、（ｉ）テープ、ＣＤ（コンパクト・ディスク）、ＤＶＤ（ディジタル多用途ディスク）、バーコードなどの様々な記憶装置（ただし、これらに限定されるものではない）、（ｉｉ）（携帯電話、双方向トランシーバ、マイクロ波リンクなどの）無線または携帯通信、（ｉｉｉ）、衛星通信、（ｉｖ）ディジタル・ラジオ、ＤＴＶ（ディジタル・テレビジョン）、ＤＶＢ（ディジタル・ビデオ放送）など、（ｖ）ケーブル、Ｖ．ｐｃｍ、ＡＤＳＬ、ｘＤＳＬなどに用いるモデム（ただし、これらに限定されるものではない）という技術／装置が、誤り検出／訂正方式を用いて、それらの性能、完全性および信頼性を改善させることができる。

ステップ２１０によれば、最初にリンクを確立し、送信チャネル・パラメータを調停した後で、送信元は、送信に適当な形式でディジタル・データを処理する。ステップ２１５によれば、送信元は送信を行う前に、少なくとも部分的に送信ディジタル・データの値に基づいて、ある程度のデータ冗長度が得られる誤り符号を生成する。ステップ２２０によれば、この生成された誤り符号を、添付、付加、多重化その他の方法でディジタル・データと共に含め、送信機から受信機に送信する。ステップ２２５によれば、このディジタル・データおよび誤り符号を受信機で受信する。ステップ２３０によれば、必要な場合には、受信機で初期信号処理を実施する。ステップ２３５によれば、受信機は、用いられている誤り制御符号化方式に従って誤り符号の冗長ビットにアクセスし、その中に含まれる情報を処理する。ステップ２４０によれば、受信したディジタル・データと処理された冗長ビットの照合が肯定的であった場合、このデータは破損していないとみなされる。ステップ２４５によれば、受信機において、このディジタル・データの更なる信号処理を（それがある場合には）継続して行う。

しかし、処理された冗長ビットが、受信したディジタル・データが破損していることを示す（少なくとも１つのビット誤りを含む）場合、ステップ２５０によれば、このデータ誤りの値を求めて、この誤りが、用いられている誤り制御方式で訂正可能かどうかを判定する。即ち、幾つかの誤り制御方式は、誤り検出しか行うことができず、これらの誤りを訂正することができる特質およびタイプの冗長データは含んでいない。他の誤り制御方式は、検出および訂正機能を共に有し得るにも関わらず、誤り検出機能しか利用しないことがある。これは、個々のデータ信号、メッセージまたはパケットの正確さがさほど重要ではなく、一貫し時宜を得たデータの配信が最も重要であるときにしばしば用いられる方式である。このような応用例は、会話、音声およびビデオ用途の同期ストリーム・データである。或いは、誤り訂正方式を用いて誤りを検出し訂正するときでも、検出された誤りの数または連続して生じた誤りが、誤り訂正機能を上回る場合（即ち、誤り符号ビットにより提供される冗長情報では不足の場合）、このデータは絶対に復元不可能である。ステップ２５５によれば、データが訂正可能な場合、受信機でデータ誤りを訂正し、更なる信号処理を（それがある場合には）継続する。しかし、データが訂正不可能な場合、ステップ２６０によれば、データの正確さが本質的なことであるかどうかを決める評価を実施する。純粋なデータ・システムではそうであるように、データの正確さが本質的なことである場合、単一のビット誤りが決定的なものである可能性が大きく、ステップ２６５によれば、送信元に再送要求を送り返す。しかし、（会話、音声またはビデオなどの）同期的な性質のデータ・メッセージの場合がそうであるように、訂正不可能なデータの正確さが本質的なことではない場合、ステップ２７０によれば、破損し訂正不可能なデータを単に破棄し、次の連続したデータ・メッセージを処理する。

図３を参照すると、様々な誤り符号の分類および方式の階層図が示されている。誤り符号３１０は、（ｉ）自動再送要求（ＡＲＱ：Ａｕｔｏｍａｔｉｃ Ｒｅｔｒａｎｓｍｉｓｓｉｏｎ Ｒｅｑｕｅｓｔ）または検出符号３１５、および（ｉｉ）前方誤り訂正（ＦＥＣ：Ｆｏｒｗａｒｄ Ｅｒｒｏｒ Ｃｏｒｒｅｃｔｉｏｎ）符号３２０という２つの基本的な分類に分けることができる。ＡＲＱは、検出だけを行うタイプの符号であり、受信機により送信時の誤りを検出することができるが、誤りを訂正することはできない。受信機は、受信されたデータを調べ、誤りが検出された受信データを送信し直す要求を出さなければならない。このような再送は、貴重な帯域を横取りすることになるので、一般に、ＡＲＱ符号は「クリーン」な（誤りの可能性がより低い）送信媒体に用いられる。最も一般的な例の１つは、単純なパリティ・チェック３２５であり、ＲＡＭ中のデータ誤りを検出するのにしばしば用いられる。別の例は、ＣＲＣ（巡回冗長検査）３３０であり、例えば、イーサネット（登録商標）上の送信における誤りを検出するのに用いられる。誤りが検出された場合、そのメッセージが再送されることになる。イーサネット（登録商標）は主に電線上を送信されるので、誤りの確率は他の幾つかの媒体よりも少ない。ＣＲＣおよびＡＲＱは、誤り検出符号方式の単なる２つの例であり、当業者には他の誤り検出符号方式が知られている。単に誤りを検出するだけでそれらを訂正しない誤り符号は、加えられる冗長度が誤り訂正符号よりもかなり少ない。更に、誤り検出用の復号器は、誤り訂正用の復号器よりもはるかに簡単である。一般に、誤り検出符号方式を利用するシステムは、データの再送で生じるオーバーヘッドに関して帯域許容性が高い。即ち、データを再送しても、全体的なシステムのスループットに大きく影響しない。

ノイズの多い媒体では、所定の送信中に誤りが生じる確率が高いので、自動再送要求（ＡＲＱ）法を用いると常時データの再送が生じることになり、それにより、システムのスループットが許容できないレベルまで落ちる。このような例では、誤り訂正符号により、その名前が示すとおり、受信側で誤りを検出するだけでなく、誤りの訂正を行うこともできる。こうすると、データを再送する必要が減り、用いられる誤り訂正方法により訂正することができる数よりも誤りの数が多いときだけデータの再送が必要になる。誤り訂正は、受信機が送信元に再送を要求する機会がない一方向通信にも用いられる。このような一方向経路の例には、一部の衛星送信および磁気テープ記憶媒体が含まれる。

誤り訂正符号は、２つの主要な副分類に分けることができる。第１はブロック符号３３５であり、第２は畳込み符号３４０である。ブロック符号３３５は、定義された有限長のメッセージ・ブロックを扱う誤り訂正符号であり、しばしば用いられている。ブロック符号３３５は、この副分類では、ブロック単位のメッセージ・シンボルを処理し、次いで、ブロック単位の符号語シンボルを出力する符号器を利用するのでこの名前がついている。一般に、ブロック符号は、２値符号３４５および非２値符号３５５の２つのタイプに分類することができる。２値符号３４５の一例はハミング符号３５０であり、１文字当たり４つの情報ビットおよび３つの検査ビットを有するという特徴がある。非２値符号の例は、リード・ソロモン符号３６０である。

対照的に、畳込み符号３４０用の符号器は、連続したストリームのメッセージ・シンボルを扱い、同時に、符号化された連続出力ストリームを生成する。これらの符号は、その符号化プロセスを、メッセージ・シンボルと符号器のインパルス応答の畳込み処理とみなすことができることからこの名前がついている。畳込み符号３４０の例には、ＴＣＭ（トレリス（Ｔｒｅｌｌｉｓ）符号化変調）３６５および２値畳込み符号化処理３７０の２つがある。

図４は、ＲＳ（リード・ソロモン）復号器の例を示すブロック図である。前に説明したように、リード・ソロモン符号は、非２値組織的線形ブロック符号である。非２値符号は、幾つかのビットからなるシンボルを扱う。非２値符号用の一般的なシンボル・サイズは、８ビット即ち１バイトである。リード・ソロモン符号などの非２値符号は、これらの符号の訂正がシンボル・レベルで行われるので、バースト誤りを訂正するのに適している。復号プロセスでシンボルを扱うことにより、これらの符号は、１個のビット誤りを伴うシンボルを訂正することができるのと同じように簡単に、８個の誤りのバーストを伴うシンボルを訂正する。リード・ソロモン符号などの組織的符号は、不変形式のメッセージ・シンボルを含む符号語を生成する。符号器は、これらのメッセージ・シンボルに可逆的な数学関数を適用して、冗長またはパリティ・シンボルを生成する。次いで、このパリティ・シンボルをメッセージ・シンボルに付加することにより符号語を形成する。リード・ソロモン符号は、任意の有効符号語を巡回シフトしても別の有効符号語が生成されるので、巡回符号とみなされる。巡回符号は、それを実施する効率的で安価な復号技術が存在するので一般に普及している。最後に、リード・ソロモン符号は、任意の２つの有効符号語を追加すると、別の有効符号語が得られるので線形とみなされる。

誤り制御符号の理論では、有限体またはガロア体として知られている数学的な構造体を用いる。ガロア体は、有限個の元を含む１つの組である。この組に対する加算および乗算演算が定義される。これらの演算は、通常の算術から予想されるように動作する。例えば、加算の単位元はゼロであり、乗算の単位元は１である。リード・ソロモン符号は、この符号の巡回且つ線形な性質を司るガロア体の数学的処理を用いて実施され、ｑ＝ｐ^ｍ次のガロア体上で演算が行われる。ただし、ｐは正の素数であり、ｍは正の整数である。ｑ次のガロア体はＧＦ（ｑ）で表し、ｑ個の別個の元を含んでいる。

所定のリード・ソロモン符号は、それを（ｎ，ｋ）符号と称することにより示す。パラメータｎは、符号語中のシンボルの数で表した符号語長を示す。パラメータｋは、符号語中のメッセージ・シンボルの数を示す。従って、加えられるパリティ・シンボルの数はｎ−ｋ個になる。この符号の誤り訂正機能は、ｔ＝（ｎ−ｋ）／２である。この符号は、Ｔ個の誤りを検出し訂正する。ただし、０≦Ｔ≦ｔである。この符号語は、メッセージ・シンボルに基づくものであり、リード・ソロモン符号器により生成される。リード・ソロモンは組織的符号（ｓｙｓｔｅｍａｔｉｃ ｃｏｄｅ：システマティック・コード）なので、ｎ個のメッセージ・シンボルはそのまま送信され、これらのメッセージ・シンボルにｎ−ｋ個のパリティ・シンボルが付加されて符号語が形成される。送信される符号語に冗長度を加えるこのパリティ・シンボルの値は、メッセージ・シンボルにより決まる。受信機の復号器はこの冗長度を利用して、誤りを検出し訂正する。

受信機の復号器で、シンドローム生成ブロック４１０への入力として符号語を受信する。復号器により実施される最初のステップはシンドローム計算であり、（しばしばシンドローム生成モジュールまたは単にシンドローム生成器とも称する）シンドローム生成ブロック４１０により実施される。このシンドロームはｎ−ｋ個のシンボルからなり、これらの値は受信した符号語から計算する。このシンドロームは、誤りベクトルのみにより決まり、送信された符号語とは無関係である。即ち、各誤りベクトルは固有のシンドローム・ベクトルを有するが、受信された多くの異なる符号語は、それらの誤りパターンが同じ場合には同じシンドロームを有することになる。最初にシンドロームを計算する理由は、そうすると誤りベクトルの探索範囲が狭まるからである。まず、シンドロームが分かると、妥当な誤りベクトルの数が、全部で２^ｎ個の可能な誤りベクトルから２^ｎ−ｋ個の誤りベクトルに減る。

シンドローム生成ブロック４１０がシンドロームを計算する１つの方法は、ガロア体代数を用いて、受信した符号語を生成多項式で割ることによるものである。この除算の剰余をシンドローム多項式ｓ（ｘ）と呼ぶ。実際のシンドローム・ベクトルＳ（ｘ）は、α〜α^ｎ−ｋでｓ（ｘ）の値を求めることにより計算する。ただし、この方法は、ハードウエアの観点から最も効率的でないことがあり、ハードウエア内で頻繁に用いられる代替方法では、直接α〜α^ｎ−ｋで受信済み符号語Ｒ（ｘ）の値を求める。シンドローム生成ブロック４１０は、α〜α^ｎ−ｋで受信した符号語Ｒの値を求めることにより、即ちＲ（α）〜Ｒ（α^ｎ−ｋ）によりシンドロームＳを計算する。リード・ソロモン符号では、ｎ−ｋ＝２ｔであり、従って、計算しようとする２ｔ個のシンドローム値［Ｓ１ Ｓ２ Ｓ３．．．Ｓ（２ｔ）］がある。一般に、これらの値は、第１シンドローム生成器がαで受信済み符号語の値を求めてＳ１を形成し、次のシンドローム生成器がα^２で受信済み符号語の値を求めてＳ２を形成し、以下同様に行って、並列に計算する。

シンドローム生成ブロック４１０によりシンドロームが計算されると、この値は、誤り多項式ブロック４２０に渡される。そこで、このシンドロームを用いて誤り位置多項式を生成する。このプロセスでは、ｔ個の未知数の連立方程式を解くことが必要である。これらの計算を行うのに、バーレカンプ・マッシィ（Ｂｅｒｌｅｋａｍｐ−Ｍａｓｓａｙ）アルゴリズムまたはユークリッド・アルゴリズムを含めて、幾つかの高速アルゴリズムが利用可能である。これらのアルゴリズムは、リード・ソロモン符号の特別な行列構造を利用し、必要な計算の労力を大きく減らす。

誤り多項式ブロック４２０は、誤り位置多項式を（それが決定された後で）誤り位置ブロック４３０および誤り度合ブロック４４０に渡す。誤り位置ブロック４３０は、この誤り位置多項式の根を見つけて誤り位置を決定する。一般に、これは、チェン・サーチ・アルゴリズムまたはチェン・セルを利用して行われる。誤り位置ブロック４３０により決定された誤り位置は、前に決定された誤り位置多項式と共に誤り度合ブロック４４０に渡される。誤り度合ブロック４４０は、ｔ個の未知数を有する連立方程式を解くことにより誤り度合を決定する。誤り度合ブロック４４０を実施する際に用いる高速で広く用いられているアルゴリズムは、フォーニー（Ｆｏｒｎｅｙ）アルゴリズムである。

計算された誤り位置および誤り度合は、誤り訂正ブロック４５０に転送されて、符号語が破損している場合には、符号語が訂正されて復元される。誤り位置および誤り度合の組合せを、しばしば誤りベクトルと称する。この誤りベクトルは、符号語と同じサイズであり、誤りに対応する位置で非ゼロ値を含んでいる。他の全ての位置にはゼロが入る。誤り訂正ブロック４５０への別の入力は遅延ブロック４６０の出力である。遅延ブロック４６０は、受信した符号語を取り込み、この受信した同じ符号語を遅延させて出力する。一実施形態では、誤り訂正ブロック４５０は、（最後に入力されたものが最初に出力される）ＬＩＦＯブロック４５４と共にガロア体加算器４５２を使用して実施する。受信した符号語中の誤りは、ガロア体加算器４５２を使用して、この受信した符号語に誤りベクトルを加えることにより訂正される。ＬＩＦＯブロック４５４を使用するのは、誤りベクトルが受信した符号語とは逆の順序で生成され、従って、受信した符号語または誤りベクトルの何れかにＬＩＦＯ演算を適用して、両方のベクトル中のバイトの順序を整合させなければならないからである。誤り訂正ブロック４５０の出力は、復号器による元の符号語の推定値である。

図５は、ＲＳ（リード・ソロモン）復号器の実施形態の例を示すブロック図である。入力は受信した符号語であり、それをシンドローム生成ブロック５１０に転送する。シンドローム生成ブロック５１０によりシンドロームＳ（ｘ）が計算されると、その値は、ユークリッド・アルゴリズム・ブロック５２０に渡される。ユークリッド・アルゴリズムによりシンドロームＳ（ｘ）が処理され、それにより、誤り位置多項式Λ（ｘ）および誤り度合多項式Ω（ｘ）が生成される。即ち、ユークリッド・アルゴリズムにより、キー（Ｋｅｙ）方程式と称する以下の方程式が解かれる。

リード・ソロモン復号処理で用いるアルゴリズムは、２つの多項式の最大公約数（ＧＣＤ）を求めるのにユークリッド・アルゴリズムに基づいている。ユークリッド・アルゴリズムは、周知の反復多項式除算アルゴリズムである。

誤り位置多項式Λ（ｘ）が計算されると、この多項式の値を求めてその根を見つける必要がある。チェン・サーチ・アルゴリズムを用いて、これらの根を見つける。チェン・サーチは、全ての可能な入力値に対して多項式の値を求める総当たり式アルゴリズムであり、次いで、どの出力がゼロに等しいかを決める。位置ｉで誤りが生じる場合、次式がゼロに等しくなる。

チェン・サーチにより、全てのｉおよびｊの値について式２の値が求まり、この式がゼロに等しくなる回数が数えられる。ゼロの位置は誤りの位置であり、ゼロの数は誤りのあるシンボルの数である。

ある実施形態の例では、（ｔ＋１）個のチェン・サーチ・ステージがあり、これらはハードウエアで実施される。これらのステージ（ステージは、乗算器、マルチプレクサおよびレジスタからなる）はそれぞれ、上記チェン・サーチ方程式中のｊについて異なる値を示す。このサーチは、ｎクロック・サイクルに亘って実行され（上記方程式中の異なるｉの値が、各クロック・サイクルを表す）、加算器出力がゼロに等しいかどうか検査される。加算器出力がゼロに等しい場合、ゼロ検出ブロックが１を出力することになり、そうでない場合には、ゼロが出力されることになる。このように、チェン・サーチ・ブロックの出力は、「０」または「１」の何れかの値をとるｎ個のビット列になる。「１」はそれぞれ、誤りのあるシンボルの位置を表す。

第１クロック・サイクルで、マルチプレクサが、誤り位置多項式の係数をレジスタに送る。残りの（ｎ−１）個のクロック・サイクルに亘って、乗算器出力は、マルチプレクサを介してレジスタに送られることになる。これらの乗算器のベキ指数は負の値を有する。ただし、これらの値は、モジュロ演算子を用いてあらかじめ計算することができる。α^−ｉのベキ指数は、（−ｉ ｍｏｄｕｌｏ ｎ）＝（−ｉ ｍｏｄｕｌｏ ２５５）に等しい。例えば、α^−１はα^２５４に等しく、α^−２はα^２５３に等しい。以下同様である。

フォーニー・アルゴリズムを用いて、誤りの値Ｙ_ｉを計算する。これらの値を計算するために、フォーニー・アルゴリズムでは、誤り位置多項式Λ（ｘ）および誤り度合多項式Ω（ｘ）を用いる。誤りの値を求める式は次のようになる。

形式的導関数Λ′（ｘ）の計算は、実際には極めて簡単である。例えば、Λ（ｘ）＝α^４Ｘ^３＋α^３Ｘ^２＋αＸ＋α^２と仮定する。こうすると、Λ′（ｘ）は次式のようになる。

Ｘの奇数の指数の係数をとり、それらを次に低い指数（偶数）のＸに割り当てることにより導関数を形成する。

次いで、チェン・サーチに用いたのと同じタイプのハードウエアを用いて、Λ′（ｘ）多項式と共にΩ（ｘ）多項式の値を求める。Ω（ｘ）の値を求めるには、Ω_０の係数にΩ_１の係数にα^−１を掛けたものを加え、続けて、Ω_２の係数にα^−２を掛けたもの、以下同様に、Ω_ｔの係数にα^−ｔを掛けたものまで加える。次いで、これらの乗算器の出力を合計する。

次いで、逆数の乗算器を用いて分子に分母を掛ける。この逆数の乗算器は、分母の逆数を見つけ出すルックアップ・テーブルを含んでいる。例えば、分母がα^３の場合、逆数はα^−３になる。次いで、これを次式のように表すことができる。

チェン・サーチおよびフォーニー・アルゴリズムには共に同じタイプのハードウエアが必要なので、チェン／フォーニー・ブロック５３０として示すように、これら２つの機能を同じブロック内で組み合わせることができる。この実施形態では、チェン・サーチの出力のところで２つの加算器を用いる。第１加算器は偶数ステージの値を合計し、他方の加算器は奇数ステージの値を合計する。最終的なチェン・サーチ出力を形成するには、次いで、これら２つの加算器の出力を合計し、ゼロ検出ブロックが根の位置を検出する。フォーニー・アルゴリズムでは、奇数ステージ用加算器の出力も用いる。奇数ステージの合計は、フォーニー方程式の分母を表す。この合計値の逆数をとり、次いで、誤り度合多項式の値を求めることにより形成された分子の値を掛ける。この出力とゼロ検出出力のアンド（ＡＮＤ）演算を行う。というのは、これらの誤りの値は、実際の誤り位置でしか有効でないからである（そうでない場合には、誤りの値はゼロにしようとするである）。

このように、チェン／フォーニー・ブロック５３０は、誤り位置多項式および誤り度合多項式を用いて誤りベクトルを生成し、それを誤り訂正ブロック５４０に転送する。この誤りベクトルは、符号語と同じサイズであり、誤りに対応する位置で非ゼロ値を含んでいる。他の全ての位置にはゼロが入る。誤り訂正ブロック５４０への別の入力は遅延ブロック５５０の出力である。遅延ブロック５５０は、受信した符号語を取り込み、この受信した同じ符号語を遅延させて出力する。この実施形態では、誤り訂正ブロック５４０は、ＬＩＦＯブロック５４２と共にガロア体加算器５４４を使用して実施する。受信した符号語中の誤りは、ガロア体加算器５４４を使用して、この受信した符号語に誤りベクトルを加えることにより訂正される。ＬＩＦＯブロック５４２を使用するのは、誤りベクトルが受信した符号語とは逆の順序で生成され、従って、受信した符号語または誤りベクトルの何れかにＬＩＦＯ演算を適用して、両方のベクトルについてバイトの順序を同期させなければならないからである。誤り訂正ブロック５４０の出力は、復号器による元の符号語の推定値である。

復号器内構成要素ブロック・メッセージ処理
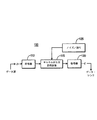
前に説明したように、リード・ソロモン復号器は、少なくとも４つの主要な構成要素即ち機能ブロックを有する。それらは、シンドローム生成器、誤り多項式ブロック、誤り位置ブロックおよび誤り度合ブロックである。復号器が誤りを検出するのに加えてそれを訂正する場合、復号器は誤り訂正ブロックも含んでいる。従来技術の復号器では、これらのブロックにより、ある１つのブロックへの入力は前のブロックの出力によりのみ決まる「伝送パイプライン」が形成される。即ち、１つのブロックから前のブロックへのフィードバックはない。リード・ソロモン復号器は、（図４および図５の遅延ブロックにより示す）個々の符号語に対する復号プロセスを実施する間に、受信した符号語を記憶するためのメモリまたはバッファ・ブロックを実現することも必要である。誤り位置／度合ブロックは、復号プロセスの完了時に誤りベクトルを生成し、この誤りベクトルとメモリ中に記憶させた受信済み符号語のＸＯＲ演算を行って復号器出力を形成する。一般に、使用するメモリのサイズは１符号語に等しく、そのため、この復号器は、一度に１つの符号語しか処理することができない。

図６は、本発明の原理による復号器内ハンドシェイク・プロトコルの実施形態の例を示すブロック図である。復号器内ブロックＡ ６１０および復号器内ブロックＢ ６２０は、（上記で説明した機能ブロックから選択した）リード・ソロモン復号器内の任意の２つのブロックを表し、これらのブロック間でフィードバックまたは通信を利用する。復号処理用「伝送パイプライン（ｄｅｌｉｖｅｒｙ ｐｉｐｅｌｉｎｅ）」はデータ・チャネル６３０であり、これは、リード・ソロモン復号器の機能ブロック間の従来技術による任意の一方向チャネルを表す。それに加えて、本発明によれば、フィードバック・チャネルも示されている。このフィードバック・チャネルは、ある１つの機能ブロックが、その機能ブロックの現在または今後の非活動状態を上流側または下流側の機能ブロックに伝えるための手段とみなすことができる。例えば、復号器内ブロックＡ ６１０が、ある特定の符号語に対してその処理機能を完了したと仮定する。復号器内ブロックＡ ６１０は、指定された符号語に対するその計算機能の結果を復号器内ブロックＢ ６２０に転送する準備ができていることを示す非活動メッセージを復号器内ブロックＢ ６２０に送る。そのため、このタイプの非活動メッセージをＲＴＳ（Ｒｅａｄｙ−Ｔｏ−Ｓｅｎｄ：送信準備完了）メッセージ６５０と呼ぶ。逆に、復号器内ブロックＢ ６２０が、ある特定の符号語に対してその処理機能を完了したと仮定する。復号器内ブロックＢ ６２０は、それが受信する準備ができていることを示す非活動メッセージを復号器内ブロックＡ ６１０に送る。そのため、このタイプの非活動メッセージをＲＴＲ（Ｒｅａｄｙ−Ｔｏ−Ｒｅｃｅｉｖｅ：受信準備完了）メッセージ６４０と呼ぶ。

機能ブロック間のフィードバックまたはハンドシェイク処理を伴う復号器の実施形態である本発明のこの実施形態は、こうすると、ユーザが構成可能な、ＩＰ（知的財産）コアに適当なアーキテクチャが可能になり、それにより、実現して使用したいメモリ・サイズに基づいて、ユーザが復号器の性能をカスタマイズすることができるという点で有利である。

図７は、ＲＳ（リード・ソロモン）復号器の実施形態の例の機能ブロック間のハンドシェイク・プロトコルを示すブロック図である。シンドローム生成ブロック４１０、誤り多項式ブロック４２０、誤り位置ブロック４３０、誤り度合ブロック４４０、（ガロア体加算器４５２およびＬＩＦＯブロック４５４を含む）誤り訂正ブロック４５０および遅延ブロック４６０の機能、目的および動作は、図４に関して十分に説明されており、従ってここでは繰り返さない。図７に新たに含めた上記非活動メッセージ（またはハンドシェイク信号）が示されている。これらの処理ブロックは、ハンドシェイク信号（例えば、ＲＴＳおよびＲＴＲメッセージ）を用いて、これらの処理ブロックが送信データをもっている時点、および／またはそれらがデータを受信する準備が整っている時点を示す。こうすると、シンドローム生成ブロック４１０と誤り多項式ブロック４２０は、ＲＴＳチャネル７１０を介してＲＴＳメッセージを、或いは、ＲＴＲチャネル７１２を介してＲＴＲメッセージを交換する。誤り多項式ブロック４２０と誤り位置ブロック４３０は、ＲＴＳチャネル７１８を介してＲＴＳメッセージを、或いは、ＲＴＲチャネル７２０を介してＲＴＲメッセージを交換する。誤り多項式ブロック４２０と誤り度合ブロック４４０は、ＲＴＳチャネル７２４を介してＲＴＳメッセージを、或いは、ＲＴＲチャネル７２６を介してＲＴＲメッセージを交換する。誤り度合ブロック４４０と誤り訂正ブロック４５０は、ＲＴＳチャネル７３０を介してＲＴＳメッセージを、或いは、ＲＴＲチャネル７３２を介してＲＴＲメッセージを交換する。シンドローム生成ブロック４１０は、ＲＴＲチャネル７４０を介してＲＴＲメッセージを送信することにより次に受信する符号語を要求するようにも適合される。誤り訂正ブロック４５０は、ＲＴＳチャネル７６０を介して出力処理ステージにＲＴＳメッセージを送信するようにも適合される。更に、本発明の選択した実施形態により、遅延を適切に調整して、誤り訂正ブロック４５０において受信した符号語が誤りベクトルに同期して検査され、正しく訂正されるように、（メッセージ・チャネル７５０を介して）遅延ブロック４６０にＲＴＲまたはＲＴＳメッセージを送信することが必要になることがある。

本発明から得られる有利な有用性は、復号器内機能ブロック間のハンドシェイク処理を可能にすることにより、機能ブロックが非活動状態になったときに（即ち、機能ブロックがその最後の手順を完了したときに）、機能ブロックがより多くの処理データの受信を要求できることである。同様に、機能ブロックは、その機能ブロックがその手順を完了しており、且つ下流側の機能ブロックがその結果を受信することができるときにはいつでもその結果を転送することができることを下流側の機能ブロックに示すことができる。例えば、一般に、シンドローム生成ブロック４１０は、特定の長さの受信した符号語に対して固定された（既知の）数のクロック・サイクルを用いてシンドロームを生成することになるが、誤り多項式ブロック４２０は、その実行時間が変化し得る反復プロセスである。更に、一般に、誤り位置ブロック４３０および誤り度合ブロック４４０は、固定された（既知の）数のクロック・サイクルの時間が掛かることになるが、符号語中に存在する誤りの数が多すぎて符号語が訂正不可能と判定された場合には、その符号語に対する更なる処理を中断することができ、誤り位置ブロック４３０および誤り度合ブロック４４０は、適切なＲＴＲチャネル７２０、７２６を介して誤り多項式ブロック４２０にＲＴＲメッセージを送信することにより、次の符号語に対する処理を開始するように要求する。従って、誤り位置ブロック４３０および誤り度合ブロック４４０も、その処理を完了するのにかけるクロック・サイクルを可変にする。

ただし、図７に示す本発明の実施形態は、本発明の趣旨および範囲から逸脱することなく実施することができる幾つかの実施形態の１つであることに留意されたい。例えば、復号器の各機能ブロックがＲＴＳおよびＲＴＲメッセージを送信するように構成される必要はない。そうではなくて、設計上の選択事項として、シンドローム生成ブロック４１０と誤り多項式ブロック４２０の間だけでハンドシェイク処理を行うことができることが望ましいことがある。多くの他の変形形態も可能である。更に、ＲＴＳおよびＲＴＲチャネルを介して通信されるようにＲＴＳおよびＲＴＲメッセージを示し説明するが、このような説明は単なる論理上の説明であり、メッセージ・チャネルは、データ・チャネルとは別の１つの共通物理層メッセージ・チャネル上に組み込むこともできるし、或いは、データ・チャネル自体と同じ物理層上に組み込むこともできる。

本発明の原理によれば、ユーザは、メモリ割当てサイズを変更することにより復号器の性能をカスタマイズする。従って、１符号語長に等しいメモリ・サイズを割り当てた実施形態は、ハードウエアおよび電力が効率的に使用される設計になるが、一度に１つの符号語しか処理することができなくなる。１符号語長よりも長いメモリ・サイズを割り当てられた実施形態は、１つの符号語を処理しながら、第２の符号語の取込みを開始する。２つの符号語のメモリ・サイズを割り当てられた実施形態は、２つの符号語を同時に処理する。以下同様である。もちろん、組み込まれるメモリのサイズを増やすと、それに対応して、ハードウエアおよび電力の点でより高価になるが、所定の時間内により多くの数の符号語を処理することができるので、それに対応して復号プロセスのスピードが速くなり、且つ待ち時間が少なくなるという利益が得られる。ハンドシェイク信号によりプロセスが完全に自動化され、それにより、ユーザは、復号器が使用するメモリ・サイズを入力するだけでよい。この単一のパラメータを制御することにより、ユーザは、スピード、電力およびサイズ（ゲート数）の点で復号器の性能をカスタマイズする。

図８は、本発明の原理によるブロック内ハンドシェイク処理を用いた復号器に関する効率を示す、ＲＳ（リード・ソロモン）復号器の例のタイミング図である。タイミング図の上側部分８１０に、ブロック内ハンドシェイク処理を用いない典型的な復号器における処理に必要な時間を示す。この方式では、ＣＷ１（ＣｏｄｅＷｏｒｄ １：符号語１）の処理は時間ｔ_０から始まる。ＣＷ１のシンドロームは時間ｔ_１で生成され、その結果は誤り多項式ブロックに渡される。誤り多項式ブロックは時間ｔ_２でＣＷ１の処理を完了し、以下同様に行われ、最後に時間ｔ_４でＣＷ１の処理が完了する。従って、ＣＷ２（ＣｏｄｅＷｏｒｄ ２：符号語２）の処理は時間ｔ_４から始まる。ＣＷ２に対するこの単一機能逐次処理は、ＣＷ２に対する誤り位置および誤り度合計算が完了する時間ｔ_８まで続く。ブロック内ハンドシェイク処理を用いないと、２つの符号語を処理するのに、全部で（ｔ_８−ｔ_０）単位の時間が掛かることに留意されたい。

タイミング図の下側部分８２０に、ブロック内ハンドシェイク処理を用いた復号器における処理時間を示す。３つの符号語に用いるのに十分な大きさのメモリを実現することにより、この復号器は、一度に３つの符号語を同時に処理できることに留意されたい。各ブロックは、準備が整っていることを前のブロックに伝えるので、各ブロックは処理を終了した時点でより多くのデータを受信することができるため、このように効率的に行われる。図に示した例では、ＣＷ３（ＣｏｄｅＷｏｒｄ ３：符号語３）の処理は、ｔ_６〜ｔ_７の間のどこかの時点で完了する。

誤り訂正復号器内の二重チェン・サーチ・ブロック
本発明の実施形態の一例では、二重チェン・サーチ・ブロックを用いて誤り訂正プロセスを実施する。本発明のこの実施形態の原理を利用する復号器により、復号器の待ち時間および復号器の記憶／メモリ要件が共に低減する。

図９は、本発明の原理による二重チェン・サーチ・ブロックを使用するＲＳ（リード・ソロモン）復号器の実施形態の例を示すブロック図である。入力は受信した符号語であり、これをシンドローム生成ブロック９１０に転送する。シンドローム生成ブロック９１０によりシンドロームＳ（ｘ）が計算されると、このシンドロームは、ユークリッド・アルゴリズム・ブロック９２０に転送される。ユークリッド・アルゴリズムを用いて、シンドロームＳ（ｘ）を処理して、誤り位置多項式Λ（ｘ）および誤り度合多項式Ω（ｘ）を生成する。

本発明のこの実施形態では、符号語中の誤りの数を決定するために新しいチェン・ブロック９３０が組み込まれる。誤り位置多項式Λ（ｘ）が計算されると、チェン・ブロック９３０は、チェン・サーチ・アルゴリズムを適用して根の値を求める。チェン・サーチは、全ての可能な入力値に対して多項式の値を求める総当たり式アルゴリズムであり、次いで、どの出力がゼロに等しいかを決める。位置ｉで誤りが生じる場合、次式がゼロに等しくなる。

チェン・ブロック９３０により、全てのｉおよびｊの値について上式の値が求まり、この式がゼロに等しくなる回数が数えられる。得られた数は、検出された誤りの数である。

前に説明したように、誤り位置および誤り度合の両方についてこの誤り多項式の値を求めなければならない。チェン・サーチおよびフォーニー・アルゴリズムを共に実施するには同じタイプのハードウエアが必要なので、チェン／フォーニー・ブロック９４０として示すように、これら２つの機能を同じブロック内で組み合わせることができる。この実施形態では、チェン・サーチの出力のところで２つの加算器を用いる。第１加算器は偶数ステージの値を合計し、他方の加算器は奇数ステージの値を合計する。最終的なチェン・サーチ出力を形成するには、次いで、これら２つの加算器の出力を合計し、ゼロ検出ブロックが根の位置を検出する。フォーニー・アルゴリズムでは、奇数ステージ用加算器の出力も用いる。奇数ステージの合計は、フォーニー方程式の分母を表す。この合計値の逆数をとり、次いで、誤り度合多項式の値を求めることにより形成された分子の値を掛ける。この出力とゼロ検出出力のアンド（ＡＮＤ）演算を行う。というのは、これらの誤りの値は、実際の誤り位置でしか有効でないからである（そうでない場合には、誤りの値はゼロにすべきである）。

このように、チェン／フォーニー・ブロック９４０は、誤り位置多項式および誤り度合多項式を用いて誤りベクトルを生成し、それを誤り訂正ブロック９５０に転送する。この誤りベクトルは、符号語と同じサイズであり、誤りに対応する位置で非ゼロ値を含んでいる。他の全ての位置にはゼロが入る。誤り訂正ブロック９５０への別の入力は遅延ブロック９６０の出力である。遅延ブロック９６０は、受信した符号語を取り込み、この受信した同じ符号語を遅延させて出力する。この実施形態では、誤り訂正ブロック９５０は、ＬＩＦＯブロック９５２と共にガロア体加算器９５４を使用して実施する。受信した符号語中の誤りは、ガロア体加算器９５４を使用して、この受信した符号語に誤りベクトルを加えることにより訂正される。ＬＩＦＯブロック９５２を使用するのは、誤りベクトルが受信した符号語とは逆の順序で生成され、従って、受信した符号語または誤りベクトルの何れかにＬＩＦＯ演算を適用して、両方のベクトル中のバイトの順序を整合させなければならないからである。誤り訂正ブロック９５０の出力は、復号器による元の符号語の推定値である。

リード・ソロモン復号器は、ｔ個の誤りまでしか訂正することができない。ただし、含まれるパリティ・バイトの数は２ｔである。検出された誤りの数がｔ個よりも多い場合には、一般に、この受信した符号語を変更せず且つ訂正せずに復号器の出力に転送することが望ましい。というのは、検出された誤りの数がｔ個よりも多い場合、この符号語は訂正不可能だからである。従来技術のチェン／フォーニーの実施形態では、誤りの数を決定することが可能になる前に、符号語全体を処理しなければならない。そのため、この操作にはＮクロック・サイクルが掛かる。ただし、Ｎは符号語の長さである。チェン／フォーニーの計算が完了すると、誤りの数が決定され、値ｔと比較される。誤りの数がｔ以下の場合、チェン／フォーニー・ブロックからの誤りの値は、受信した符号語とのＸＯＲ（排他的論理和）演算にかけられて誤りが訂正され、それにより最終的な復号器出力が生成される。しかし、誤りの数がｔよりも多い場合、受信した符号語は、変更されずに復号器出力として転送される。従って、従来技術の方法では、チェン／フォーニー・ブロックによる処理が完了するまで、受信した符号語全体を記憶する必要がある。このような方式では、待ち時間による遅延も生じる。というのは、このブロックのＮクロック・サイクル全体が完了するまで、復号器の出力を転送することができないからである。

対照的に、本発明のこの実施形態では、符号語をチェン・アルゴリズムに２回かける。１回目で誤りの数を決定し、２回目で誤りの位置を決定する。従って、チェン・ブロック９３０が、誤りの数が閾値ｔよりも多いことを検出すると、この受信した符号語は復号器出力として渡され、メモリが解放される。逆に、誤りの数が閾値ｔ以下であるときには、このデータは、チェン／フォーニー・ブロックに渡されて、実際の誤り位置および度合が決定される。このような実施形態は、図６〜図８に示す本発明のハンドシェイク処理の実施形態と共に用いると最適であろう。このような組合せにより、チェン／フォーニー・ブロック９４０が誤りを計算しながら、チェン・ブロック９３０が次の符号語の誤りの数を決定する。従って、チェン／フォーニー・ブロック９４０の出力を直ちに送出し、それに対応するメモリを解放する。

誤り訂正復号器用に強化されたチェン・サーチ・セル
前に説明したように、チェン／フォーニー・ブロックは、入力として、誤り位置および誤り度合多項式という２つの多項式を受信し、出力として誤りベクトルを生成する。この誤りベクトルは、受信した符号語中の誤りの復号器の推定値を表すＮバイトのベクトルである。この誤りベクトルを、受信した符号語とのＸＯＲ（排他的論理和）演算にかけて誤りを訂正し、それにより復号器による元の符号語の推定値が形成される。誤りベクトルを決定するためにチェン／フォーニー・ブロックを使用する従来型復号器は、符号語ベクトルに対して逆の順序で誤りベクトルを生成する。即ち、符号語および誤りベクトルは、誤りベクトルに（または逆に符号語に）更なる処理をかけずにＸＯＲ演算にかけることができない。一般に、この更なる処理は、誤りベクトルまたは受信した符号語の何れかに対する（最後に入力されたものが最初に出力される）ＬＩＦＯ操作の形式をとる。これは、入力の順序を逆にして、符号語および誤りベクトルをＸＯＲ演算にかけることができるようにするためである。残念ながら、このために、Ｎクロック・サイクルの遅延が生じる。ただし、Ｎは符号語のバイト数である。更に、一部の従来方式の実施形態では、１符号語長よりも大きいメモリ・サイズを用いるので、このメモリを２つ以上の別々のＬＩＦＯブロックに分割する必要がある。そうすると、アドレス指定が複雑になり得て、メモリ・サイズも符号語長の整数倍に制限される。

本発明の実施形態の一例は、符号語に対して正しく同期がとれている出力を生成する新しいチェン・サーチ・セルである。即ち、誤りベクトルも符号語ベクトルもＸＯＲ演算にかける前に逆にする必要がなく、そのため、ＬＩＦＯブロックその他の反転手段が不要になる。従って、Ｎクロック・サイクルの遅延の必要がないので、待ち時間がより短くなる。更に、本発明のこの実施形態では、（従来技術に比べて）アドレス指定方式が簡略化され、符号語長の単なる整数倍以外のメモリ・サイズがサポートされる。例えば、符号語長の２．５倍のメモリを使用することができ、それにより、復号器が２つの符号語を処理する間に、次の符号語の一部を取り込むことができる。

図１０は、チェン・サーチおよびチェン／フォーニー・ブロックの基本的な構成単位である典型的な従来技術のチェン・サーチ・セル１０００を示すブロック図である。このチェン・サーチ・ブロックを用いて、誤り位置多項式Λの値を求め、それによりその根を見つける。この根の位置は、受信した符号語中の誤りのある位置に対応する。図１０のチェン・サーチ・セルを用いて次式を実施する。

式７を計算すると、符号語中の誤りに対応するバイト位置でヌル（ゼロ）値が得られる。チェン・サーチ・セル１０００は、上記の式の１つのステージを実施するのに用いるハードウエア・アーキテクチャである。各ステージでは、誤り位置多項式Λの１つの係数を処理するので、全部で（ｔ＋１）個のステージがある（というは、誤り位置多項式の最大次数はｔであり得、次数ｔの多項式は（ｔ＋１）個の係数を有するからである）。

チェン・サーチ・セル１０００は、誤り位置多項式の係数を反復して処理する。最初の反復で、マルチプレクサ１０２０は、処理中の符号語に対応する適切な多項式係数１０１０を受信し、この多項式の係数をレジスタ１０３０に送る。後続のクロック・サイクルで、このレジスタの出力は、まず乗算器１０４０に転送され、そこでα^−ｊが掛けられ、次いで、マルチプレクサ１０２０によりレジスタに戻されて記憶される。このプロセスを全部でＮクロック・サイクルに亘って実施する。再度、式７を参照すると、指数ｉは反復数を示し、指数ｊはチェン・サーチ・セルのステージを示す。即ち、ｊの値はゼロからｔまで増え、そのため、ハードウエア内で実施されるチェン・サーチ・セル・ステージは全部で（ｔ＋１）個ある。

例として、このセルは、第２ステージ（ｊ＝１）を表すものと仮定する。即ち、各クロック・サイクルで、レジスタ出力にはα^−１が掛けられ、その結果をレジスタに戻して記憶する。こうすると、以下の数列が生成される。
λ＋λα^−１Ｘ＋（λα^−１）α^−１Ｘ^２＋（（λα^−１）α^−１）α^−１Ｘ^３＋
．．．
ただし、Ｘ^ｎはｎクロック・サイクルの遅延を表す。

各項を合成することにより、最終的な数列は次式のようになる。
λ＋λα^−１Ｘ＋λα^−２Ｘ^２＋λα^−３Ｘ^３＋．．．＋λα^{−（Ｎ−１）}Ｘ^Ｎ−１

この実施形態に関連する問題は、誤り位置が、対応する符号語のバイトと逆の順序で生成され、そのため、誤り位置を符号語に加えて訂正が行われる前に、ＬＩＦＯブロックにより逆にする必要があることである。ＬＩＦＯブロックは、複数のレジスタを含むハードウエア記憶要素である。全てのレジスタが一杯になると、ＬＩＦＯブロックはその出力を送出する。入力時の最後の要素が出力時には最初の要素になり、以下同様に続く。ＬＩＦＯブロックを用いると２つの問題が生じる。１つは、ＬＩＦＯブロックが大規模な記憶／メモリ素子であり、そのため、ＩＣのゲート数および電力消費量が増えることである。別の問題は、ＬＩＦＯブロックによりＮクロック・サイクルの待ち時間が生じることである。この待ち時間が生じるのは、ＬＩＦＯブロックが最初に一杯になるのにＮクロック・サイクル掛かり、最後の要素がＬＩＦＯに読み込まれるまで出力を生成することができないからである。

図１１は、本発明の原理に従ってメモリ要件および遅延が共に低減された改良型チェン・サーチ・セル１１００を示すブロック図である。本発明のこの実施形態の基礎となる原理は、チェン・サーチ・ブロックに、係数が逆の順序（以下では、「正規化された順序」と称する）で生成されるにも関わらず、標準チェン・サーチにより生成されるものと数学的に等価な数列を生成させることができることである。この実施形態では、正規化された順序で誤り位置を生成して符号語を訂正するのに用いる以下の２つの式（式８および式９）を実施する。

図１０の従来技術のチェン・サーチ・セル１０００では、誤り位置多項式の係数を、各クロック・サイクル毎に減らすαのベキ指数を「ゼロ」から始め、−ｊ（Ｎ−１）の値まで減らして反復的に処理することを想起されたい。図１１のチェン・サーチ・セル１１００の実施形態では、αのベキ指数の値を−ｊ（Ｎ−１）から始めて、ベキ指数がゼロに達するまで各クロック・サイクル毎に増やす。

従って、最初のクロック・サイクルの際に、前段乗算器１１５０により多項式の係数１１１０にα^{−ｊ（Ｎ−１）}が掛けられ（ただし、ｊはステージ番号）、それがマルチプレクサ１１２０に転送され、レジスタ１１３０に送られて記憶される。後続のクロック・サイクルで、レジスタ１１３０の出力は乗算器１１４０に転送され、そこでα^ｊが掛けられ、次いで、マルチプレクサ１１２０によりレジスタに戻される。

例として、このセルは、第２ステージ（ｊ＝１）を表すものと仮定する。こうすると、以下の数列が生成される。
λα^{−（Ｎ−１）}Ｘ＋（λα^{−（Ｎ−１）}）αＸ^２＋（（λα^{−（Ｎ−１）}）α）αＸ^３＋．．．
各項を合成すると、以下の数列が生成される。
λα^{−（Ｎ−１）}＋λα^{−（Ｎ−２）}Ｘ＋λα^{−（Ｎ−３）}Ｘ^２＋．．．＋λα^−１Ｘ^Ｎ−２＋λＸ^Ｎ−１

この数列中で生成される係数は、図１０の標準チェン・サーチ・セル１０００により生成されるものと、それらがこの時点では（遅延係数が逆の順序で示されるように）逆の順序である点を除いて同じであることに留意されたい。図１１のチェン・サーチ・セル１１００は、追加のガロア体乗算器（１つではなく２つ）を用いるが、これらは、ハードウエアで実施するのに小規模且つ安価なものである。反転させるのにＬＩＦＯブロックがもはや不要であることと、ＬＩＦＯを一杯にするのに必要とされる遅延が回避されることから得られる利点および有用性は、各チェン・サーチ・セル毎に追加のガロア体乗算器を供給することの欠点を補って余りあるものである。

単一ブロック内でチェン・サーチをフォーニー・アルゴリズムと組み合わせることは、これらのアルゴリズムが共に類似の機能の実行を必要とすることから、一般の設計実務慣行となっている。図１１に即して示し説明される本発明のこの実施形態の原理は、フォーニー・ブロック・セルにも同様に適用される。というのは、フォーニー・アルゴリズムが極めて類似したハードウエアを使用して誤り度合多項式を処理するからである。本発明の原理を、フォーニー・ブロック・セルおよびチェン／フォーニー・ブロック・セルの設計に拡張することができることは当業者には周知のことであろう。

多くの既存のシステムは、リード・ソロモン符号を符号化し復号する「既成」の集積回路を使用する。これらのＩＣは、ある分量のプログラム可能性（例えば、ＲＳ（２５５，ｋ）。ただし、ｔは１〜１６個のシンボルを表す）をサポートする傾向がある。最近の傾向は、ＶＨＤＬ即ちベリログ（Ｖｅｒｉｌｏｇ）設計（論理コアまたは知的財産コア）に向かいつつある。こうすると、標準ＩＣに比べて多くの利点がある。論理コアを、他のＶＨＤＬ即ちベリログ・コンポーネントと一体化し、ＦＰＧＡ（現場で書込み可能なゲート・アレイ）またはＡＳＩＣ（特定用途向け集積回路）に統合することができ、これにより、複数のモジュールを単一ＩＣに組み合わせることができるいわゆる「システム・オン・チップ」設計が可能になる。生産量によりは、論理コアにより、「標準」ＩＣよりもシステム・コストをしばしば大きく下げることができる。

ハードウエアによる実施形態の状況で本発明を説明しているが、本発明の原理をそのように限定されると解釈すべきではない。最近まで、「リアルタイム」でのソフトウエアによる実施形態は、最も簡単なリード・ソロモン符号（即ち、ｔの値が小さい符号）以外は全てあまりにも多くの計算能力を必要とした。ソフトウエアでリード・ソロモン符号を実施する際の主要な難点は、汎用プロセッサが、ガロア体算術演算をサポートしていないことである。例えば、ソフトウエアでガロア体乗算を実施するには、ゼロの検査、２つの対数テーブル索引、モジュロ加算および真数テーブル索引を必要とする。しかし、注意深く設計するとプロセッサ性能の増加とあいまって、ソフトウエアによる実施形態は、比較的高速なデータ・レートで動作し得る。

例示の実施形態および／または構成に関して本発明を説明してきたが、本発明は、この開示の趣旨および範囲内で更に改変することができる。従って、本出願は、本発明の一般原理を用いた本発明の任意の変形形態、使用形態または適応形態を包含するためのものである。更に、本出願は、本発明に関連し、の特許請求の範囲の制限に含まれる、当技術分野において周知の、または実務上の慣行に収まるようなこの開示からの派生物を包含するためのものである。

誤り訂正方式を組み込んだディジタル・データ伝送システムを示すブロック図である。 典型的な誤り訂正方式の方法を示す流れ図である。 様々な誤り訂正方式を示す階層図である。 ＲＳ（リード・ソロモン）復号器を示すブロック図である。 本発明の原理に従って用いられるＲＳ（リード・ソロモン）復号器の実施形態の例を示すブロック図である。 本発明の原理による復号器内ハンドシェイク・プロトコルの例を示すブロック図である。 本発明の原理によるＲＳ（リード・ソロモン）復号器の実施形態の例の機能ブロック間のハンドシェイク・プロトコルを示すブロック図である。 本発明の原理によるブロック内ハンドシェイク処理を用いた復号器に関する効率を示す、ＲＳ（リード・ソロモン）復号器の例のタイミング図である。 本発明の原理によるチェン／フォーニー・ブロックに加えて、チェン・ブロックを使用するＲＳ（リード・ソロモン）復号器の実施形態の例を示すブロック図である。 ＲＳ（リード・ソロモン）復号器で実施する典型的な従来技術のチェン・サーチ・セルを示すブロック図である。 本発明の原理に従ってメモリ要件および遅延が共に低減されたＲＳ（リード・ソロモン）復号器で実施する改良型チェン・サーチ・セルを示すブロック図である。

Claims (20)

1. シンドローム生成ブロック（４１０）、誤り多項式ブロック（４２０）、誤り位置ブロック（４３０）および誤り度合ブロック（４４０）を含めて、少なくとも４つのブロックを有する巡回線形ブロック符号誤り訂正復号器において、符号語のデータの誤り訂正を実施する方法であって、
   前記シンドローム生成ブロック（４１０）で、前記符号語からシンドロームを計算する動作と、
   前記誤り多項式ブロック（４２０）で、前記シンドロームから誤り多項式を生成する動作と、
   前記誤り位置ブロック（４３０）で、前記誤り多項式から誤り位置を決定する動作と、
   前記誤り度合ブロック（４４０）で、前記誤り多項式から誤り度合を計算する動作とを含み、
   前記少なくとも４つのブロックの少なくとも１つのブロックが、前記少なくとも４つのブロックの他のブロックに非活動メッセージ（６４０、６５０）を送信するように適合されることを特徴とする、方法。
2. 前記誤り位置および前記誤り度合に応答して、前記符号語を訂正する動作を更に含む、請求項１に記載の方法。
3. 前記非活動メッセージが受信準備完了メッセージ（６４０）である、請求項１に記載の方法。
4. 前記非活動メッセージが送信準備完了メッセージ（６５０）である、請求項１に記載の方法。
5. 前記誤り多項式ブロックがユークリッド・アルゴリズム・ブロックである、請求項１に記載の方法。
6. 前記誤り多項式ブロックがバーレカンプ・マッシィ・アルゴリズム・ブロックである、請求項１に記載の方法。
7. 前記誤り位置ブロックがチェン・サーチ・ブロックである、請求項１に記載の方法。
8. 前記誤り度合ブロックがフォーニー・アルゴリズム・ブロックである、請求項１に記載の方法。
9. 前記誤り位置ブロックおよび前記誤り度合ブロックに関連する前記動作が、チェン／フォーニー組合せブロック内で実施される、請求項１に記載の方法。
10. 前記巡回線形ブロック符号誤り訂正復号器がリード・ソロモン復号器である、請求項１に記載の方法。
11. 符号語中のデータの誤り検出を実施する復号器であって、
    前記符号語からシンドロームを計算する手段（４１０）と、
    前記シンドロームから誤り多項式を生成する手段（４２０）と、
    前記誤り多項式から誤り位置を決定する手段（４３０）と、
    前記誤り多項式から誤り度合を計算する手段（４４０）とを備え、
    前記シンドロームを計算する前記手段（４１０）、前記誤り多項式を生成する前記手段（４２０）、前記誤り位置を決定する前記手段（４３０）および前記誤り度合を計算する前記手段（４４０）を含む群から選択される少なくとも１つの構成要素内に、復号器内非活動メッセージ（６４０、６５０）を送信するように適合させることが組み込まれることを特徴とする、復号器。
12. 前記符号語、前記誤り位置および前記誤り度合を入力として受信することに応答して、前記符号語を訂正する手段（４５０）を更に備える、請求項１１に記載の復号器。
13. 前記復号器がリード・ソロモン復号器である、請求項１１に記載の復号器。
14. 前記復号器内非活動メッセージが受信準備完了メッセージ（６４０）である、請求項１１に記載の復号器。
15. 前記復号器内非活動メッセージが送信準備完了メッセージ（６５０）である、請求項１１に記載の復号器。
16. 誤り多項式を生成する前記手段（４２０）がユークリッド・アルゴリズム・ブロックである、請求項１１に記載の復号器。
17. 誤り位置を生成する前記手段（４３０）がチェン・サーチ・ブロックである、請求項１１に記載の復号器。
18. 誤り度合を計算する前記手段（４４０）がフォーニー・アルゴリズム・ブロックである、請求項１１に記載の復号器。
19. 符号語中のデータの誤り検出を実施する復号器であって、
    前記符号語からシンドロームを計算するシンドローム生成器（４１０）と、
    前記シンドロームから誤り多項式を生成する誤り多項式生成器（４２０）と、
    前記誤り多項式から誤り位置を決定する誤り位置生成器（４３０）と、
    前記誤り多項式から誤り度合を計算する誤り度合生成器（４４０）とを備え、
    前記シンドローム生成器（４１０）、前記誤り多項式生成器（４２０）、前記誤り位置生成器（４３０）および前記誤り度合生成器（４４０）を含む群から選択される少なくとも１つの構成要素内に、復号器内非活動メッセージ（６４０、６５０）を送信するように適合させることが組み込まれることを特徴とする、復号器。
20. 前記符号語、前記誤り位置および前記誤り度合を入力として受信することに応答して、前記符号語を訂正する誤り訂正符号語生成器（４５０）を更に備える、請求項１９に記載の復号器。

Images