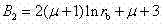CN103246789A - Computing method of deformation of annular sandwich valve plates of vibration absorber under non-uniform pressure - Google Patents

Computing method of deformation of annular sandwich valve plates of vibration absorber under non-uniform pressure Download PDF

Info

Publication number
CN103246789A
CN103246789A CN2013102122738A CN201310212273A CN103246789A CN 103246789 A CN103246789 A CN 103246789A CN 2013102122738 A CN2013102122738 A CN 2013102122738A CN 201310212273 A CN201310212273 A CN 201310212273A CN 103246789 A CN103246789 A CN 103246789A
Authority
CN
China
Prior art keywords
valve plate
deformation
radius
annular
uniform pressure
Prior art date
Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
Pending
Application number
CN2013102122738A
Other languages
Chinese (zh)
Inventor
周长城
赵雷雷
孔艳玲
Current Assignee (The listed assignees may be inaccurate. Google has not performed a legal analysis and makes no representation or warranty as to the accuracy of the list.)
Shandong University of Technology
Original Assignee
Shandong University of Technology
Priority date (The priority date is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the date listed.)
Filing date
Publication date
Application filed by Shandong University of Technology filed Critical Shandong University of Technology
Priority to CN2013102122738A priority Critical patent/CN103246789A/en
Publication of CN103246789A publication Critical patent/CN103246789A/en
Pending legal-status Critical Current

Links

Images

Landscapes

  • Testing Of Devices, Machine Parts, Or Other Structures Thereof (AREA)

Abstract

本发明涉及减振器环形叠加阀片在非均布压力下变形的计算方法，属于减振器技术领域，其特征在于：首先计算出环形叠加阀片的等效厚度，在非均布压力下的环形阀片在任意半径处的变形系数；然后，根据等效厚度、变形系数及非均布压力最大值，对减振器环形叠加阀片在非均布压力下的在任意半径处的变形进行计算。通过计算实例及ANSYS仿真验证结果可知，该方法可对减振器环形叠加阀片在非均布压力下任意半径位置变形进行精确计算，利用该方法可建立精确的减振器参数设计及特性仿真模型，可得到准确、可靠的减振器节流阀参数设计值及减振器特性仿真值，从而降低减振器设计及试验费用，提高设计水平、质量和性能及车辆行驶平顺性。

Figure 201310212273

The invention relates to a calculation method for the deformation of an annular superimposed valve plate of a shock absorber under non-uniform pressure, and belongs to the technical field of shock absorbers. The deformation coefficient of the annular valve plate at any radius; then, according to the equivalent thickness, deformation coefficient and the maximum value of non-uniform pressure, the deformation of the annular superimposed valve plate of the shock absorber at any radius under non-uniform pressure Calculation. Through calculation examples and ANSYS simulation verification results, it can be seen that this method can accurately calculate the deformation of the annular superimposed valve plate of the shock absorber at any radial position under non-uniform pressure, and use this method to establish accurate shock absorber parameter design and characteristic simulation The model can obtain accurate and reliable shock absorber throttle valve parameter design values and shock absorber characteristic simulation values, thereby reducing shock absorber design and test costs, improving design level, quality and performance, and vehicle ride comfort.

Figure 201310212273

Description

减振器环形叠加阀片在非均布压力下变形的计算方法Calculation method of deformation of annular superimposed valve plate of shock absorber under non-uniform pressure

技术领域 technical field

本发明涉及减振器，特别是减振器环形叠加阀片在非均布压力下变形的计算方法。 The invention relates to a shock absorber, in particular to a calculation method for deformation of an annular superimposed valve plate of the shock absorber under non-uniform pressure.

背景技术 Background technique

复原阀和压缩阀的环形叠加阀片是减振器中最为关键性的精密元件，在阀口半径位置的阀片变形对减振器阻尼特性具有重要影响，因此，能否实现对环形叠加阀片变形的精确计算，决定着能否建立精确的减振器阀参数设计及减振器特性仿真数学模型,得到准确的减振器节流阀参数设计值及特性仿真值,并且决定着能否真正实现汽车减振器的现代化CAD设计及计算机特性仿真。由于减振器常通节流孔和节流缝隙的存在，减振器阀片实际所受的压力并不是均布的而实际是非均布的, 尽管国内、外很多学者已对此进行了大量研究,但是对于在非均布载荷下的阀片变形计算至今还没有给出精确的解析计算式及计算方法。目前国内外大都是利用有限元仿真软件，对给定压力下的阀片通过建立实体模型进行数值仿真，尽管可得到近似的数值解，但是不能满足减振器阀参数精确设计及特性仿真的要求。我国在减振器环形叠加阀片变形计算方面的研究取得了重要突破，但只能对均布压力下的环形叠加阀片变形精确解析计算，但是由于减振器环形叠加阀片所受压力为非均布的，要建立精确的减振器设计及特性仿真数学模型，必须解决减振器环形叠加阀片在非均布压力下的变形精确解析计算问题。随着汽车工业的快速发展及车辆行驶速度的不断提高，对减振器设计提出了更高的要求，要实现减振器现代化CAD设计及特性计算仿真，必须建立一种精确的减振器环形叠加阀片在非均布压力下的变形计算方法，满足减振器设计及特性仿真精确建模的要求，使减振器参数设计值更加准确，特性仿真值更加可靠，提高减振器设计水平和产品性能,满足车辆行驶平顺性对减振器特性不断提高的要求。 The annular superimposed valve plate of the recovery valve and the compression valve is the most critical precision component in the shock absorber. The deformation of the valve plate at the radial position of the valve port has an important impact on the damping characteristics of the shock absorber. Therefore, whether the annular superimposed valve can be realized The accurate calculation of sheet deformation determines whether the accurate shock absorber valve parameter design and shock absorber characteristic simulation mathematical model can be established, and the accurate shock absorber throttle valve parameter design value and characteristic simulation value can be obtained, and whether it can be determined Realize the modern CAD design and computer characteristic simulation of automobile shock absorber. Due to the existence of the normally open orifice and the throttling gap of the shock absorber, the actual pressure on the shock absorber valve plate is not uniform but actually non-uniform, although many domestic and foreign scholars have done a lot of research on this However, there is no accurate analytical calculation formula and calculation method for the deformation calculation of valve plate under non-uniform load. At present, finite element simulation software is mostly used at home and abroad to conduct numerical simulation of the valve plate under a given pressure by establishing a solid model. Although an approximate numerical solution can be obtained, it cannot meet the requirements of accurate design of shock absorber valve parameters and characteristic simulation. . Our country has made an important breakthrough in the research on the deformation calculation of the annular superimposed valve plate of the shock absorber, but it can only accurately calculate the deformation of the annular superimposed valve plate under uniform pressure, but because the pressure on the annular superimposed valve plate of the shock absorber is Non-uniform distribution, in order to establish an accurate shock absorber design and characteristic simulation mathematical model, it is necessary to solve the problem of accurate analytical calculation of the deformation of the annular superimposed valve plate of the shock absorber under non-uniform pressure. With the rapid development of the automobile industry and the continuous improvement of vehicle speed, higher requirements are put forward for the design of shock absorbers. To realize the modern CAD design and characteristic calculation and simulation of shock absorbers, it is necessary to establish an accurate shock absorber ring The deformation calculation method of superimposed valve plates under non-uniform pressure meets the requirements of shock absorber design and accurate modeling of characteristic simulation, making the design value of shock absorber parameters more accurate, the characteristic simulation value more reliable, and improving the design level of shock absorber And product performance, to meet the continuous improvement of vehicle ride comfort on the characteristics of shock absorbers.

发明内容 Contents of the invention

针对上述现有技术中存在的缺陷，本发明所要解决的技术问题是提供一种精确、可靠的减振器环形叠加阀片在非均布压力下变形的计算方法。 In view of the above-mentioned defects in the prior art, the technical problem to be solved by the present invention is to provide an accurate and reliable calculation method for the deformation of the annular superimposed valve plate of the shock absorber under non-uniform pressure.

为了解决上述技术问题，本发明所提供的减振器环形叠加阀片在非均布压力下变形的计算方法，其技术方案实施步骤如下： In order to solve the above-mentioned technical problems, the method for calculating the deformation of the ring-shaped superimposed valve plate of the shock absorber under non-uniform pressure provided by the present invention, the implementation steps of the technical solution are as follows:

（1）确定减振器环形叠加阀片的等效厚度h e: (1) Determine the equivalent thickness h e of the annular superimposed valve plate of the shock absorber:

对于材料特性相同、内圆半径                                                

Figure 522090DEST_PATH_IMAGE001
和外圆半径
Figure 697856DEST_PATH_IMAGE002
相等的环形叠加阀片，根据叠加阀片各片的厚度和片数（h 1，n 1；h 2，n 2；…；h n ，n n），确定减振器环形叠加阀片的等效厚度h e为： For the same material properties, inner circle radius
Figure 522090DEST_PATH_IMAGE001
and outer circle radius
Figure 697856DEST_PATH_IMAGE002
For equal annular stacked valve slices, according to the thickness and number of stacked valve slices ( h 1 , n 1 ; h 2 , n 2 ;…; h n , n n ), determine the equivalent The effective thickness h e is:

Figure 436136DEST_PATH_IMAGE003
；
Figure 436136DEST_PATH_IMAGE003
;

（2）均布压力下p 0下叠加阀片在任意半径r位置的变形系数G r1的计算: (2) Calculation of the deformation coefficient G r 1 of the superimposed valve plate at any radius r position under p 0 under uniform pressure:

根据减振器环形叠加阀片的内圆半径r a，外圆半径r b，弹性模量E和泊松比μ，计算在均布压力下的环形阀片在任意半径r（r a ≤r≤ r b ）位置的变形系数G r1，即： According to the inner circle radius r a , outer circle radius r b , elastic modulus E and Poisson's ratio μ of the annular superimposed valve plate of the shock absorber, calculate the annular valve plate under uniform pressure at any radius r ( r a ≤ r ≤ r b ) the deformation coefficient G r 1 at the position, namely:

              

Figure 535810DEST_PATH_IMAGE004
              
Figure 535810DEST_PATH_IMAGE004

式中,

Figure 925204DEST_PATH_IMAGE005
,      
Figure 757024DEST_PATH_IMAGE006
, ,            
Figure 72916DEST_PATH_IMAGE008
； 
Figure 316816DEST_PATH_IMAGE009
，
Figure 635715DEST_PATH_IMAGE010
，
Figure 83008DEST_PATH_IMAGE011
， In the formula,
Figure 925204DEST_PATH_IMAGE005
,
Figure 757024DEST_PATH_IMAGE006
, ,
Figure 72916DEST_PATH_IMAGE008
;
Figure 316816DEST_PATH_IMAGE009
,
Figure 635715DEST_PATH_IMAGE010
,
Figure 83008DEST_PATH_IMAGE011
,

Figure 711436DEST_PATH_IMAGE012
；，
Figure 389990DEST_PATH_IMAGE014
，
Figure 324579DEST_PATH_IMAGE015
，
Figure 756697DEST_PATH_IMAGE016
；
Figure 711436DEST_PATH_IMAGE012
; ,
Figure 389990DEST_PATH_IMAGE014
,
Figure 324579DEST_PATH_IMAGE015
,
Figure 756697DEST_PATH_IMAGE016
;

（3）反向线性非均布压力

Figure 788238DEST_PATH_IMAGE017
下的阀片在任意半径r位置的变形系数G r2的计算: (3) Reverse linear non-uniform pressure
Figure 788238DEST_PATH_IMAGE017
The calculation of the deformation coefficient G r 2 of the valve plate at any radius r position:

根据环形阀片的内圆半径r a，外圆半径r b，弹性模量E，泊松比μ，非均布压力的起始作用位置半径r k，计算在反向线性非均布压力下的环形叠加阀片变形系数,即： According to the radius r a of the inner circle of the ring valve, the radius r b of the outer circle, the elastic modulus E , Poisson's ratio μ , and the radius r k of the initial action position of the non-uniform pressure, it is calculated under the reverse linear non-uniform pressure The deformation coefficient of the annular superimposed valve plate, that is:

                    

Figure 398342DEST_PATH_IMAGE018
；
Figure 398342DEST_PATH_IMAGE018
;

式中, In the formula,

Figure 665824DEST_PATH_IMAGE020
Figure 665824DEST_PATH_IMAGE020

Figure 738822DEST_PATH_IMAGE021
，
Figure 738822DEST_PATH_IMAGE021
,

Figure 582144DEST_PATH_IMAGE022
，
Figure 582144DEST_PATH_IMAGE022
,

Figure 491326DEST_PATH_IMAGE023
Figure 265247DEST_PATH_IMAGE024
Figure 491326DEST_PATH_IMAGE023
Figure 265247DEST_PATH_IMAGE024

Figure 5801DEST_PATH_IMAGE025
Figure 5801DEST_PATH_IMAGE025

Figure 957707DEST_PATH_IMAGE026
，
Figure 957707DEST_PATH_IMAGE026
,

Figure 416502DEST_PATH_IMAGE027
Figure 416502DEST_PATH_IMAGE027

Figure 994113DEST_PATH_IMAGE028
Figure 994113DEST_PATH_IMAGE028

Figure 526857DEST_PATH_IMAGE029
Figure 526857DEST_PATH_IMAGE029

Figure 782706DEST_PATH_IMAGE031
Figure 782706DEST_PATH_IMAGE031

Figure 898430DEST_PATH_IMAGE032
Figure 898430DEST_PATH_IMAGE032

Figure 738210DEST_PATH_IMAGE033
，
Figure 738210DEST_PATH_IMAGE033
,

Figure 43638DEST_PATH_IMAGE034
Figure 43638DEST_PATH_IMAGE034

Figure 663975DEST_PATH_IMAGE035
Figure 663975DEST_PATH_IMAGE035

Figure 68542DEST_PATH_IMAGE036
Figure 68542DEST_PATH_IMAGE036

Figure 825146DEST_PATH_IMAGE037
，
Figure 825146DEST_PATH_IMAGE037
,

Figure 555336DEST_PATH_IMAGE038
，
Figure 555336DEST_PATH_IMAGE038
,

Figure 397390DEST_PATH_IMAGE039
Figure 397390DEST_PATH_IMAGE039

Figure 605648DEST_PATH_IMAGE040
Figure 605648DEST_PATH_IMAGE040

Figure 482337DEST_PATH_IMAGE041
Figure 482337DEST_PATH_IMAGE041

Figure 304800DEST_PATH_IMAGE042
，
Figure 304800DEST_PATH_IMAGE042
,

Figure 384883DEST_PATH_IMAGE043
Figure 384883DEST_PATH_IMAGE043

Figure 646100DEST_PATH_IMAGE044
Figure 646100DEST_PATH_IMAGE044

Figure 190345DEST_PATH_IMAGE045
Figure 190345DEST_PATH_IMAGE045

Figure 183708DEST_PATH_IMAGE046
Figure 183708DEST_PATH_IMAGE046

Figure 550416DEST_PATH_IMAGE048
Figure 550416DEST_PATH_IMAGE048

Figure 73801DEST_PATH_IMAGE049
Figure 73801DEST_PATH_IMAGE049

Figure 316695DEST_PATH_IMAGE050
Figure 316695DEST_PATH_IMAGE050

Figure 558320DEST_PATH_IMAGE051
Figure 558320DEST_PATH_IMAGE051

Figure 895761DEST_PATH_IMAGE052
，
Figure 895761DEST_PATH_IMAGE052
,

其中，

Figure 352281DEST_PATH_IMAGE053
； in,
Figure 352281DEST_PATH_IMAGE053
;

（4）减振器环形叠加阀片在任意半径r位置的变形系数G r 计算： (4) Calculation of the deformation coefficient G r of the annular superimposed valve plate of the shock absorber at any position of radius r :

根据步骤（2）中的G r1和步骤（3）中的G r2，通过叠加运算确定环形阀片在任意半径r（r a ≤r≤ r b ）位置的总叠加变形系数G r ，即 According to G r 1 in step (2) and G r 2 in step (3), the total superimposed deformation coefficient G r of the annular valve plate at any radius r ( r a ≤ r ≤ r b ) position is determined by superposition operation, Right now

； ;

（5）减振器环形叠加阀片在任意半径r位置的变形f r 计算： (5) Calculation of the deformation f r of the annular superimposed valve plate of the shock absorber at any position of radius r :

根据环形叠加阀片所受的最大非均布压力p 0，步骤（1）中的等效厚度h e，及步骤（3）中的变形系数G r ，对非均布压力下的减振器环形叠加阀片在半径r位置的变形量f r 进行计算，即： According to the maximum non-uniform pressure p 0 of the annular superimposed valve plate, the equivalent thickness he in step (1), and the deformation coefficient G r in step (3), the shock absorber under non-uniform pressure The deformation amount f r of the annular superimposed valve plate at the position of radius r is calculated, namely:

                                                       

Figure 478686DEST_PATH_IMAGE056
。
Figure 478686DEST_PATH_IMAGE056
.

本发明比现有技术具有的优点： The present invention has the advantage over prior art:

由于实际减振器大多采用环形叠加节流阀片,且所受压力为非均布的，先前尽管已给出了在均布压力下的变形计算方法，但计算得到阀口半径处变形量与实际阀片变形量相差较大，因此，所建立的减振器节流阀参数设计及特性仿真模型不够精确，参数设计值及特性仿真值还不够可靠。对于减振器环形叠加阀片在非均布压力下的变形，先前国内、外均无给出精确、可靠的计算方法，大都是利用有限元仿真软件，对给定压力下的阀片通过建立实体模型进行数值仿真得到近似的数值解，不能满足减振器节流阀参数设计及特性仿真精确建模要求。本发明所建立的减振器环形叠加阀片在非均布压力下变形的计算方法，首先，根据环形叠加阀片的厚度和片数，计算出环形叠加阀片的等效厚度；然后，将减振器环形叠加阀片在非均布压力下的力学模型，看作为均布压力与反向线性非均布压力的叠加，利用均布压力下的环形阀片在任意半径r位置的变形系数G r1，及反向线性非均布压力下的环形阀片在任意半径r位置的变形系数G r2，通过叠加计算得到环形阀片在非均布压力下的叠加变形系数G r =G r2+G r1；随后，根据叠加阀片等效厚度、叠加变形系数G r 和最大非均布压力值，对减振器环形叠加阀片在非均布压力下的变形进行计算。通过计算实例与ANSYS仿真验证结果比较可知，该减振器环形叠加阀片在非均布压力下变形的计算方法准确、可靠，并且可对阀片在任意半径r位置处的变形量进行精确计算，因此，为建立精确的减振器节流阀参数设计及特性仿真模型，提供了精确的环形叠加阀片在非均布压力下变形的计算方法，确保减振器节流阀参数设计及特性仿真值准确可靠，从而降低减振器设计及试验费用，提高减振器的设计水平、质量和性能。 Since most of the actual shock absorbers use annular superimposed throttle valve plates, and the pressure is not uniform, although the deformation calculation method under uniform pressure has been given before, the calculated deformation at the radius of the valve port is the same as The actual deformation of the valve plate is quite different. Therefore, the established parameter design and characteristic simulation model of the shock absorber throttle valve is not accurate enough, and the parameter design value and characteristic simulation value are not reliable enough. For the deformation of the annular superimposed valve plate of the shock absorber under non-uniform pressure, no accurate and reliable calculation method has been given before at home and abroad. Most of them use finite element simulation software to establish Numerical simulation of the solid model can obtain an approximate numerical solution, which cannot meet the requirements of accurate modeling of shock absorber throttle valve parameter design and characteristic simulation. The method for calculating the deformation of the annular superimposed valve plate of the shock absorber under non-uniform pressure, first, calculates the equivalent thickness of the annular superimposed valve plate according to the thickness and the number of the annular superimposed valve plate; then, the The mechanical model of the annular superimposed valve plate of the shock absorber under the non-uniform pressure is regarded as the superposition of the uniform pressure and the reverse linear non-uniform pressure, and the deformation coefficient of the annular valve plate under the uniform pressure at any radius r position is used G r 1 , and the deformation coefficient G r 2 of the annular valve plate at any radius r position under the reverse linear non-uniform pressure, and the superimposed deformation coefficient G r = G of the annular valve plate under non-uniform pressure through superposition calculation r 2 + G r 1 ; then, according to the equivalent thickness of the superimposed valve plate, the superimposed deformation coefficient G r and the maximum non-uniform pressure value, the deformation of the annular superimposed valve plate of the shock absorber under the non-uniform pressure is calculated. Through the comparison of the calculation example and the ANSYS simulation verification results, it can be seen that the calculation method of the deformation of the annular superimposed valve plate of the shock absorber under non-uniform pressure is accurate and reliable, and the deformation amount of the valve plate at any radius r position can be accurately calculated , therefore, in order to establish an accurate shock absorber throttle valve parameter design and characteristic simulation model, an accurate calculation method for the deformation of the annular superimposed valve plate under non-uniform pressure is provided to ensure that the shock absorber throttle valve parameter design and characteristic The simulation value is accurate and reliable, thereby reducing the design and test costs of the shock absorber, and improving the design level, quality and performance of the shock absorber.

为了更好地理解本发明下面结合附图作进一步的说明。 In order to better understand the present invention, the following will be further described in conjunction with the accompanying drawings.

图1 是减振器环形叠加阀片在非均布压力下变形的计算流程图； Figure 1 is a calculation flow chart of the deformation of the annular superimposed valve plate of the shock absorber under non-uniform pressure;

图2 是减振器环形叠加阀片非均布压力的力学模型； Figure 2 is the mechanical model of the non-uniform pressure distribution of the annular superimposed valve plate of the shock absorber;

图3 是实施例一的环形叠加阀片在均布压力下的变形系数G r1； Fig. 3 is the deformation coefficient G r 1 of the annular stacked valve plate in the first embodiment under uniform pressure;

图4 是实施例一的环形叠加阀片在反向线性非均布压力下的变形系数G r2； Fig. 4 is the deformation coefficient G r 2 of the annular stacked valve plate in the first embodiment under the reverse linear non-uniform pressure;

图5 是实施例一的减振器环形叠加阀片在非均布压力下的变形系数G r ； Fig. 5 is the deformation coefficient G r of the annular stacked valve plate of the shock absorber under non-uniform pressure in the first embodiment;

图6 是实施例一的减振器环形叠加阀片在非均布压力下的变形曲线； Fig. 6 is the deformation curve of the annular stacked valve plate of the shock absorber under non-uniform pressure of embodiment one;

图7 是实施例一的减振器环形叠加阀片在非均布压力下的变形仿真云图； Fig. 7 is the simulation cloud diagram of the deformation of the annular superimposed valve plate of the shock absorber under the non-uniform pressure of the first embodiment;

图8 是实施例二的环形叠加阀片在反向线性非均布压力下的变形系数G r2； Fig. 8 is the deformation coefficient G r 2 of the annular stacked valve plate of the second embodiment under the reverse linear non-uniform pressure;

图9 是实施例二的减振器环形叠加阀片在非均布压力下的变形系数G r ； Fig. 9 is the deformation coefficient G r of the annular stacked valve plate of the shock absorber under non-uniform pressure in the second embodiment;

图10 是实施例二的减振器环形叠加阀片在非均布压力下的变形曲线； Fig. 10 is the deformation curve of the annular stacked valve plate of the shock absorber under non-uniform pressure of embodiment two;

图11是实施例二的减振器环形叠加阀片在非均布压力下的变形仿真云图； Fig. 11 is the simulation cloud diagram of the deformation of the annular superimposed valve plate of the shock absorber under non-uniform pressure in the second embodiment;

图12是实施例三的环形叠加阀片在均布压力下的变形系数G r1； Fig. 12 is the deformation coefficient G r 1 of the annular stacked valve plate in the third embodiment under uniform pressure;

图13 是实施例三的环形叠加阀片在反向线性非均布压力下的变形系数G r2； Fig. 13 is the deformation coefficient G r 2 of the annular stacked valve plate in the third embodiment under the reverse linear non-uniform pressure;

图14 是实施例三的减振器环形叠加阀片在非均布压力下的变形系数G r ； Fig. 14 is the deformation coefficient G r of the annular superimposed valve plate of the shock absorber under non-uniform pressure in the third embodiment;

图15 是实施例三的减振器环形叠加阀片在非均布压力下的变形曲线； Fig. 15 is the deformation curve of the annular superimposed valve plate of the shock absorber under the non-uniform pressure of the third embodiment;

图16是实施例三的减振器环形叠加阀片在非均布压力下的变形仿真云图。 Fig. 16 is a simulation cloud diagram of the deformation of the annular superimposed valve plate of the shock absorber under non-uniform pressure in the third embodiment.

具体实施方案 specific implementation plan

下面通过实施例对本发明作进一步详细说明。 The present invention will be described in further detail below by way of examples.

实施例一：某减振器等构环形叠加阀片的内圆半径r a＝5.0mm，外圆半径r b＝8.5mm，阀口半径r k=8.0mm；弹性模量E=200GPa，泊松比μ＝0.3；叠加阀片的厚度和片数，分别为h 1=0.1mm，n 1=3；h 2=0.15mm，n 2=2；h 3=0.2mm，n 3=1；非均布最大压力p 0=3.0MPa。 Example 1: The inner circle radius r a = 5.0mm, the outer circle radius r b = 8.5mm, the valve port radius r k = 8.0mm; the modulus of elasticity E = 200GPa, poise Loose ratio μ = 0.3; the thickness and number of stacked valve plates are h 1 =0.1mm, n 1 =3; h 2 =0.15mm, n 2 =2; h 3 =0.2mm, n 3 =1; Non-uniform maximum pressure p 0 =3.0MPa.

本发明实例所提供的减振器环形叠加阀片变形的计算方法，其计算流程如图1所示，减振器环形叠加阀片的力学模型如图2所示,具体步骤如下： The calculation method for the deformation of the annular superimposed valve plate of the shock absorber provided by the example of the present invention, its calculation process is shown in Figure 1, and the mechanical model of the annular superimposed valve plate of the shock absorber is shown in Figure 2, and the specific steps are as follows:

（1）确定环形叠加阀片的等效厚度h e: (1) Determine the equivalent thickness h e of the annular stacked valve plate:

根据某减振器等构环形叠加阀片的厚度和片数h 1=0.1mm，n 1=3；h 2=0.15mm，n 2=2； h 3=0.2mm，n 3=1，等构环形叠加阀片的等效厚度h e为： According to the thickness and number of isostructured annular superimposed valve plates of a certain shock absorber h 1 =0.1mm, n 1 =3; h 2 =0.15mm, n 2 =2; h 3 =0.2mm, n 3 =1, etc. The equivalent thickness h e of the ring-shaped superimposed valve plate is:

Figure 370549DEST_PATH_IMAGE057
=0.260855mm；
Figure 370549DEST_PATH_IMAGE057
=0.260855mm;

（2）均布压力下环形叠加阀片在任意半径r位置变形系数G r1的计算: (2) Calculation of the deformation coefficient G r 1 of the annular superimposed valve plate at any radius r position under uniform pressure:

根据减振器环形叠加阀片的E=2.0

Figure 868527DEST_PATH_IMAGE058
和泊松比μ=0.3，内圆半径r a=5.0mm，外圆半径r b=8.5mm，计算均布压力下的阀片在任意半径r（r a ≤r≤ r b ）位置的变形系数G r1，即： E = 2.0 according to the shock absorber annular superimposed valve plate
Figure 868527DEST_PATH_IMAGE058
And Poisson's ratio μ = 0.3, inner radius r a = 5.0mm, outer radius r b = 8.5mm, calculate the deformation coefficient of the valve plate at any radius r ( r a ≤ r ≤ r b ) under uniform pressure G r 1 , namely:

                    

Figure 702491DEST_PATH_IMAGE004
,
Figure 702491DEST_PATH_IMAGE004
,

式中, 

Figure 653129DEST_PATH_IMAGE059
，
Figure 348684DEST_PATH_IMAGE060
， In the formula,
Figure 653129DEST_PATH_IMAGE059
,
Figure 348684DEST_PATH_IMAGE060
,

 , ,

Figure 706033DEST_PATH_IMAGE008
=
Figure 957017DEST_PATH_IMAGE062
；  
Figure 706033DEST_PATH_IMAGE008
=
Figure 957017DEST_PATH_IMAGE062
;

Figure 377634DEST_PATH_IMAGE009
，
Figure 912520DEST_PATH_IMAGE010
，
Figure 839019DEST_PATH_IMAGE011
，
Figure 826567DEST_PATH_IMAGE012
，
Figure 50875DEST_PATH_IMAGE013
，
Figure 925421DEST_PATH_IMAGE014
，，
Figure 684615DEST_PATH_IMAGE016
； 
Figure 377634DEST_PATH_IMAGE009
,
Figure 912520DEST_PATH_IMAGE010
,
Figure 839019DEST_PATH_IMAGE011
,
Figure 826567DEST_PATH_IMAGE012
,
Figure 50875DEST_PATH_IMAGE013
,
Figure 925421DEST_PATH_IMAGE014
, ,
Figure 684615DEST_PATH_IMAGE016
;

       计算得到变形系数G r1随半径r（r a ≤r≤ r b ）的变化曲线，如图3所示； Calculate the variation curve of the deformation coefficient G r 1 with the radius r ( r a ≤ r ≤ r b ), as shown in Figure 3;

（3）反向线性非均布压力下的阀片在任意半径r位置变形系数G r2 的计算: (3) Calculation of the deformation coefficient G r 2 of the valve plate at any radius r position under reverse linear non-uniform pressure:

根据环形阀片的内圆半径r a=5.0mm，外圆半径r b=8.5mm，弹性模量E=2.0

Figure 712614DEST_PATH_IMAGE058
，泊松比μ=0.3、非均布压力的起始作用位置半径r k=8.0mm，计算在反向线性非均布压力下的阀片在任意半径r（r a ≤r≤ r b ）位置的变形系数G r2，即： According to the inner radius r a =5.0mm of the ring valve, the outer radius r b =8.5mm, the modulus of elasticity E =2.0
Figure 712614DEST_PATH_IMAGE058
, Poisson's ratio μ = 0.3, the radius of the starting position of the non-uniform pressure r k =8.0mm, calculate the valve plate under the reverse linear non-uniform pressure at any radius r ( r a ≤ r ≤ r b ) The deformation coefficient G r 2 of the position, namely:

 

Figure 707246DEST_PATH_IMAGE063
；
Figure 707246DEST_PATH_IMAGE063
;

式中, 

Figure 959236DEST_PATH_IMAGE064
，，
Figure 238219DEST_PATH_IMAGE066
，
Figure 539887DEST_PATH_IMAGE067
及 In the formula,
Figure 959236DEST_PATH_IMAGE064
, ,
Figure 238219DEST_PATH_IMAGE066
,
Figure 539887DEST_PATH_IMAGE067
and

，

Figure 349897DEST_PATH_IMAGE069
，
Figure 521029DEST_PATH_IMAGE070
，
Figure 473942DEST_PATH_IMAGE071
； ,
Figure 349897DEST_PATH_IMAGE069
,
Figure 521029DEST_PATH_IMAGE070
,
Figure 473942DEST_PATH_IMAGE071
;

       计算得到在反向线性非均布压力下的阀片在任意半径r位置变形系数G r2随半径r （r a ≤r≤ r b ）的变化曲线，如图4所示； Calculate the change curve of the deformation coefficient G r 2 of the valve plate at any radius r position with the radius r ( r a ≤ r ≤ r b ) under the reverse linear non-uniform pressure, as shown in Figure 4;

（4）减振器环形叠加阀片在任意半径r位置的叠加变形系数G r 计算: (4) Calculation of the superimposed deformation coefficient G r of the annular superimposed valve plate of the shock absorber at any radius r position:

根据步骤（2）中的G r1和步骤（3）中的G r2，通过叠加运算得减振器环形叠加阀片的变形系数G r 随半径r（r a ≤r≤ r b ）的变化曲线，如图5所示； According to G r 1 in step (2) and G r 2 in step (3), the deformation coefficient G r of the annular superimposed valve plate of the shock absorber varies with the radius r ( r a ≤ r ≤ r b ) through superposition calculation Variation curve, as shown in Figure 5;

其中，在阀口半径r k位置的变形系数G rk=m6/N，在外圆半径r b位置的变形系数G rb=

Figure 692882DEST_PATH_IMAGE073
m6/N； Among them, the deformation coefficient G r k at the valve port radius r k = m 6 /N, the deformation coefficient G r b at the position of outer circle radius r b =
Figure 692882DEST_PATH_IMAGE073
m 6 /N;

（5）阀片在任意半径r位置的叠加变形f r 计算： (5) Calculation of the superimposed deformation f r of the valve plate at any radius r position:

根据步骤(1)中的叠加阀片等效厚度h e=0.260855mm，在区间r a ≤r≤r b的分布压力p 0=3.0MPa，在区间r k <r≤r b 的分布的压力p=

Figure 866374DEST_PATH_IMAGE074
MPa，及步骤（4）中的变形系数G r ，对减振器环形叠加阀片非均布压力下在任意半径r位置的变形进行计算，即 According to the equivalent thickness of the superimposed valve plate h e =0.260855mm in step (1), the distribution pressure p 0 =3.0MPa in the interval r a ≤ r ≤ r b , the distribution pressure in the interval r k < r ≤ r b p =
Figure 866374DEST_PATH_IMAGE074
MPa, and the deformation coefficient G r in step (4), the deformation of the annular superimposed valve plate of the shock absorber at any radius r under the non-uniform pressure to calculate, that is

Figure 720378DEST_PATH_IMAGE076
;
Figure 720378DEST_PATH_IMAGE076
;

计算所得到的减振器环形叠加阀片变形曲线，如图6所示；  The calculated deformation curve of the annular superimposed valve plate of the shock absorber is shown in Figure 6;

其中,叠加阀片在阀口半径位置的变形量为

Figure 816510DEST_PATH_IMAGE077
=0.127226mm，在外半径位置的最大变形量为= 0.154026mm。 Among them, the deformation of the superimposed valve plate at the radial position of the valve port is
Figure 816510DEST_PATH_IMAGE077
=0.127226mm, the maximum deformation at the outer radius is = 0.154026mm.

根据减振器环形叠加阀片的内圆半径r a＝5.0mm，外圆半径r b＝8.5mm，弹性模型E＝200GPa，泊松比μ＝0.3，叠加阀片的厚度和片数分别为h 1=0.1mm，n 1=3；h 2=0.15mm，n 2=2；h 3=0.2mm，n 3=1；利用ANSYS建立叠加阀片仿真模型，网格划分单位为0.1mm，在区间r a ≤r≤ r b 的分布压力p 0=3.0MPa，在区间r k <r≤ r b 的分布的压力p=

Figure 455618DEST_PATH_IMAGE074
MPa，仿真所得到的减振器环形叠加阀片变形仿真云图，如图7所示。 According to the inner circle radius r a =5.0mm of the annular stacked valve plate of the shock absorber, the outer circle radius r b =8.5mm, the elastic model E =200GPa, and the Poisson’s ratio μ =0.3, the thickness and the number of the stacked valve plates are respectively h 1 =0.1mm, n 1 =3; h 2 =0.15mm, n 2 =2; h 3 =0.2mm, n 3 =1; use ANSYS to establish a simulation model of superimposed valve slices, the grid division unit is 0.1mm, The distribution pressure p 0 =3.0MPa in the interval r a ≤ r≤ r b , the distribution pressure p = in the interval r k <r≤ r b
Figure 455618DEST_PATH_IMAGE074
MPa, the deformation simulation cloud image of the annular superimposed valve plate of the shock absorber obtained by simulation, as shown in Figure 7.

由图7可知，减振器环形叠加阀片最大变形仿真值为0.154293mm，与利用该计算方法所得到的0.154023mm之间的偏差为0.00027mm，相对偏差仅为0.17%，表明本发明所建立的减振器环形叠加阀片在非均布压力下变形的计算方法是正确的。 It can be seen from Fig. 7 that the simulation value of the maximum deformation of the annular superimposed valve plate of the shock absorber is 0.154293mm, and the deviation between the 0.154023mm obtained by using the calculation method is 0.00027mm, and the relative deviation is only 0.17%, which shows that the present invention establishes The calculation method for the deformation of the annular superimposed valve plate of the shock absorber under non-uniform pressure is correct.

实施例二：某减振器环形叠加阀片的内圆半径、外圆半径、厚度和片数及材料特性参数和与非均布最大压力p 0实施例一的完全相同, 只是阀口位置半径r k=7.0mm。 Embodiment 2: The inner circle radius, outer circle radius, thickness, number of slices and material characteristic parameters of a shock absorber annular superimposed valve plate are exactly the same as those of the non-uniform maximum pressure p 0 embodiment 1, except that the radius of the valve port position r k =7.0mm.

采用实施例一的计算步骤，即： The calculation steps of Embodiment 1 are adopted, namely:

（1）确定等构环形叠加阀片的等效厚度h e： (1) Determine the equivalent thickness h e of the isomorphic annular superimposed valve plate:

由于叠加阀片的厚度和片数与实施例一相同，计算因此，减振器环形叠加阀片的等效厚度h e=0.260855mm； Since the thickness and number of superimposed valve plates are the same as those in Embodiment 1, the calculation results in that the equivalent thickness of the annular superimposed valve plate of the shock absorber h e =0.260855mm;

（2）均布压力下环形叠加阀片在任意半径r位置变形系数G r1计算： (2) Calculation of the deformation coefficient G r 1 of the annular superimposed valve plate at any radius r position under uniform pressure:

减振器环形叠加阀片的内圆半径、外圆半径及材料特性参数与实施例一相同，因此，环形叠加阀片均布压力下在任意半径r位置变形系数G r1与实施例一相同，如图3所示： The inner radius, outer radius and material characteristic parameters of the annular superimposed valve plate of the shock absorber are the same as those in the first embodiment, therefore, the deformation coefficient G r 1 of the annular superimposed valve plate at any position of radius r under uniform pressure is the same as that in the first embodiment ,As shown in Figure 3:

（3） 反向线性非均布压力下的阀片在任意半径r位置变形系数G r2的计算: (3) Reverse linear non-uniform pressure Calculation of the deformation coefficient G r 2 of the valve plate at any radius r position:

根据环形阀片的内圆半径r a=5.0mm，外圆半径r b=8.5mm，弹性模量E=2.0

Figure 990953DEST_PATH_IMAGE058
，泊松比μ=0.3、阀口位置半径r k=7.0mm，计算在反向线性非均布压力下的阀片在任意半径r （r k <r≤ r b ）位置的变形系数G r2，即： According to the inner radius r a =5.0mm of the ring valve, the outer radius r b =8.5mm, the modulus of elasticity E =2.0
Figure 990953DEST_PATH_IMAGE058
, Poisson's ratio μ =0.3, valve port position radius r k =7.0mm, calculate the deformation coefficient G r of the valve plate at any radius r ( r k <r≤ r b ) position under the reverse linear non-uniform pressure 2 , namely:

 

Figure 302986DEST_PATH_IMAGE063
；
Figure 302986DEST_PATH_IMAGE063
;

式中, 

Figure 101309DEST_PATH_IMAGE079
，，
Figure 544108DEST_PATH_IMAGE081
，及 In the formula,
Figure 101309DEST_PATH_IMAGE079
, ,
Figure 544108DEST_PATH_IMAGE081
, and

Figure 250344DEST_PATH_IMAGE083
，
Figure 793321DEST_PATH_IMAGE084
，
Figure 85762DEST_PATH_IMAGE085
，
Figure 755909DEST_PATH_IMAGE086
；
Figure 250344DEST_PATH_IMAGE083
,
Figure 793321DEST_PATH_IMAGE084
,
Figure 85762DEST_PATH_IMAGE085
,
Figure 755909DEST_PATH_IMAGE086
;

计算得到在反向线性非均布压力下的阀片在任意半径r位置变形系数G r2随半径r（

Figure 450195DEST_PATH_IMAGE087
）的变化曲线，如图8所示； Calculated under the reverse linear non-uniform pressure, the deformation coefficient G r 2 of the valve plate at any radius r position increases with the radius r (
Figure 450195DEST_PATH_IMAGE087
) change curve, as shown in Figure 8;

（4）减振器环形叠加阀片在任意半径r位置的叠加变形系数G r 计算: (4) Calculation of the superimposed deformation coefficient G r of the annular superimposed valve plate of the shock absorber at any radius r position:

根据步骤（2）中的G r1和步骤（3）中的G r2，通过叠加运算得减振器环形叠加阀片的变形系数G r 随半径r（r a ≤r≤ r b ）的变化曲线，如图9所示； According to G r 1 in step (2) and G r 2 in step (3), the deformation coefficient G r of the annular superimposed valve plate of the shock absorber varies with the radius r ( r a ≤ r ≤ r b ) through superposition calculation Variation curve, as shown in Figure 9;

其中，在阀口半径

Figure 164074DEST_PATH_IMAGE088
位置的变形系数G rk=
Figure 22439DEST_PATH_IMAGE089
m6/N，在外圆半径
Figure 417649DEST_PATH_IMAGE002
位置的变形系数G rb=
Figure 28758DEST_PATH_IMAGE090
m6/N； where, in the valve port radius
Figure 164074DEST_PATH_IMAGE088
The deformation coefficient G r k =
Figure 22439DEST_PATH_IMAGE089
m 6 /N, at outer circle radius
Figure 417649DEST_PATH_IMAGE002
Deformation coefficient G r b =
Figure 28758DEST_PATH_IMAGE090
m 6 /N;

（5）阀片在任意半径r位置的叠加变形f r 计算： (5) Calculation of the superimposed deformation f r of the valve plate at any radius r position:

根据步骤(1)中的叠加阀片等效厚度h e=0.260855mm，在区间r a ≤r≤r b的分布压力p 0=3.0MPa，在区间r k <r≤ r b 的分布的压力p=

Figure 116800DEST_PATH_IMAGE074
MPa，及步骤（4）中的变形系数G r ，对减振器环形叠加阀片非均布压力下在任意半径r位置的变形
Figure 196883DEST_PATH_IMAGE075
进行计算，即 According to the equivalent thickness of the superimposed valve plate h e =0.260855mm in step (1), the distribution pressure p 0 =3.0MPa in the interval r a ≤ r ≤ r b , the distribution pressure in the interval r k < r ≤ r b p =
Figure 116800DEST_PATH_IMAGE074
MPa, and the deformation coefficient G r in step (4), the deformation of the annular superimposed valve plate of the shock absorber at any radius r under the non-uniform pressure
Figure 196883DEST_PATH_IMAGE075
to calculate, that is

Figure 395783DEST_PATH_IMAGE076
;
Figure 395783DEST_PATH_IMAGE076
;

计算所得到的减振器环形叠加阀片变形曲线，如图10所示；  The calculated deformation curve of the annular superimposed valve plate of the shock absorber is shown in Figure 10;

其中, 减振器环形叠加阀片在阀口半径位置的变形量为

Figure 861399DEST_PATH_IMAGE077
=0.08353mm，在外半径位置的最大变形量为
Figure 933392DEST_PATH_IMAGE078
= 0.100478mm。 Among them, the deformation of the annular superimposed valve plate of the shock absorber at the radial position of the valve port is
Figure 861399DEST_PATH_IMAGE077
=0.08353mm, the maximum deformation at the outer radius is
Figure 933392DEST_PATH_IMAGE078
= 0.100478mm.

根据减振器环形叠加阀片的内圆半径r a＝5.0mm，外圆半径r b＝8.5mm，阀口半径r k=7.0mm弹性模型E＝200GPa，泊松比μ＝0.3，叠加阀片的厚度和片数分别为h 1=0.1mm，n 1=3；h 2=0.15mm，n 2=2；h 3=0.2mm，n 3=1；利用ANSYS建立叠加阀片仿真模型，网格划分单位为0.1mm，在区间r a ≤r≤ r b 的分布压力p 0=3.0MPa，在区间r k  <r≤ r b 的分布的压力p=

Figure 687721DEST_PATH_IMAGE074
MPa，仿真所得到的减振器环形叠加阀片变形仿真云图，如图11所示。 According to the inner circle radius r a = 5.0mm, outer circle radius r b = 8.5mm, valve port radius r k = 7.0mm elastic model E = 200GPa, Poisson's ratio μ = 0.3, stacked valve The thickness and number of slices are respectively h 1 =0.1mm, n 1 =3; h 2 =0.15mm, n 2 =2; h 3 =0.2mm, n 3 =1; using ANSYS to establish a simulation model of stacked valve slices, The grid division unit is 0.1mm, the distribution pressure p 0 =3.0MPa in the interval r a ≤ r ≤ r b , the distribution pressure p = in the interval r k <r≤ r b
Figure 687721DEST_PATH_IMAGE074
MPa, the deformation simulation cloud image of the ring-shaped superimposed valve plate of the shock absorber obtained by simulation, as shown in Fig. 11.

由图11可知，减振器环形叠加阀片最大变形仿真值为0.100618mm，与利用该计算方法所得到的0.100478mm之间的偏差为0.000144mm，相对偏差仅为0.14%，表明本发明所建立的减振器环形叠加阀片在非均布压力下变形的计算方法是正确的。 It can be seen from Fig. 11 that the simulation value of the maximum deformation of the annular superimposed valve plate of the shock absorber is 0.100618mm, and the deviation from the 0.100478mm obtained by this calculation method is 0.000144mm, and the relative deviation is only 0.14%, which shows that the present invention establishes The calculation method for the deformation of the annular superimposed valve plate of the shock absorber under non-uniform pressure is correct.

实施例三：某减振器等构环形叠加阀片的材料特性参数与实施例一的相同，内圆半径r a=5.0mm，外圆半径r b=8.75mm，阀口半径r k=8.0mm；叠加阀片的厚度和片数分别为h 1=0.15mm，n 1=1；h 2=0.2mm，n 2=3；非均布最大压力p 0=3.0MPa。 Embodiment 3: The material characteristic parameters of a shock absorber isomorphic annular superimposed valve plate are the same as those in Embodiment 1, the inner circle radius r a =5.0mm, the outer circle radius r b =8.75mm, and the valve port radius r k =8.0 mm; the thickness and number of stacked valve plates are h 1 =0.15mm, n 1 =1; h 2 =0.2mm, n 2 =3; non-uniform maximum pressure p 0 =3.0MPa.

采用实施例一的计算步骤，即： The calculation steps of Embodiment 1 are adopted, namely:

（1）确定等构环形叠加阀片的等效厚度h e: (1) Determine the equivalent thickness h e of the isomorphic annular superimposed valve plate:

根据叠加阀片的厚度和片数，h 1=0.15mm，n 1=1；h 2=0.2mm，n 2=3，确定减振器环形叠加阀片的等效厚度h e=0.3013mm； According to the thickness and number of superimposed valve plates, h 1 =0.15mm, n 1 =1; h 2 =0.2mm, n 2 =3, determine the equivalent thickness h e =0.3013mm of the annular superimposed valve plate of the shock absorber;

（2）均布压力下环形叠加阀片在任意半径r位置变形系数G r1的计算: (2) Calculation of the deformation coefficient G r 1 of the annular superimposed valve plate at any radius r position under uniform pressure:

根据减振器环形叠加阀片的E=2.0和泊松比μ=0.3，阀片的内圆半径r a=5.0mm，外圆半径r b=8.75mm，计算均布压力下的阀片在任意半径r（r a ≤r≤ r b ）位置的变形系数G r1，即： E = 2.0 according to the shock absorber annular superimposed valve plate And Poisson's ratio μ =0.3, the inner radius of the valve plate r a =5.0mm, the outer circle radius r b =8.75mm, calculate the position of the valve plate under uniform pressure at any radius r ( r a ≤ r≤ r b ) The deformation coefficient G r 1 , namely:

              

Figure 10435DEST_PATH_IMAGE004
；
Figure 10435DEST_PATH_IMAGE004
;

式中，，

Figure 291692DEST_PATH_IMAGE092
=， In the formula, ,
Figure 291692DEST_PATH_IMAGE092
= ,

 

Figure 288915DEST_PATH_IMAGE094
,
Figure 288915DEST_PATH_IMAGE094
,

Figure 686398DEST_PATH_IMAGE008
=
Figure 415320DEST_PATH_IMAGE095
；
Figure 686398DEST_PATH_IMAGE008
=
Figure 415320DEST_PATH_IMAGE095
;

Figure 307184DEST_PATH_IMAGE009
，
Figure 867478DEST_PATH_IMAGE010
，
Figure 186595DEST_PATH_IMAGE011
，
Figure 402813DEST_PATH_IMAGE012
；
Figure 347635DEST_PATH_IMAGE013
，
Figure 700119DEST_PATH_IMAGE014
，
Figure 455716DEST_PATH_IMAGE015
，
Figure 955968DEST_PATH_IMAGE016
；
Figure 307184DEST_PATH_IMAGE009
,
Figure 867478DEST_PATH_IMAGE010
,
Figure 186595DEST_PATH_IMAGE011
,
Figure 402813DEST_PATH_IMAGE012
;
Figure 347635DEST_PATH_IMAGE013
,
Figure 700119DEST_PATH_IMAGE014
,
Figure 455716DEST_PATH_IMAGE015
,
Figure 955968DEST_PATH_IMAGE016
;

       计算得到变形系数G r1随半径r（r a ≤r≤ r b ）的变化曲线，如图12所示； Calculate the variation curve of the deformation coefficient G r 1 with the radius r ( r a ≤ r ≤ r b ), as shown in Figure 12;

（3）反向线性非均布压力下的阀片在任意半径r位置变形系数G r2 的计算: (3) Calculation of the deformation coefficient G r 2 of the valve plate at any radius r position under reverse linear non-uniform pressure:

根据环形阀片的内圆半径r a=5.0mm，外圆半径r b=8.75mm，弹性模量E=2.0

Figure 376585DEST_PATH_IMAGE058
，泊松比μ=0.3、非均布压力的起始作用位置半径r k=8.0mm，计算在反向线性非均布压力下的阀片在任意半径r（r a ≤r≤ r b ）位置的变形系数G r2，即： According to the inner radius r a =5.0mm of the ring valve, the outer radius r b =8.75mm, the modulus of elasticity E =2.0
Figure 376585DEST_PATH_IMAGE058
, Poisson's ratio μ = 0.3, the radius of the starting position of the non-uniform pressure r k =8.0mm, calculate the valve plate under the reverse linear non-uniform pressure at any radius r ( r a ≤ r ≤ r b ) The deformation coefficient G r 2 of the position, namely:

 

Figure 662204DEST_PATH_IMAGE063
；
Figure 662204DEST_PATH_IMAGE063
;

式中, 

Figure 510074DEST_PATH_IMAGE096
，
Figure 497622DEST_PATH_IMAGE097
，
Figure 546698DEST_PATH_IMAGE098
，
Figure 936091DEST_PATH_IMAGE099
； In the formula,
Figure 510074DEST_PATH_IMAGE096
,
Figure 497622DEST_PATH_IMAGE097
,
Figure 546698DEST_PATH_IMAGE098
,
Figure 936091DEST_PATH_IMAGE099
;

，，

Figure 270754DEST_PATH_IMAGE102
，； , ,
Figure 270754DEST_PATH_IMAGE102
, ;

       计算得到在反向线性非均布压力下的阀片在任意半径r位置变形系数G r2随半径r（r a ≤r≤ r b ）的变化曲线，如图13所示； Calculate the change curve of the deformation coefficient G r 2 of the valve plate at any radius r position with the radius r ( r a ≤ r ≤ r b ) under the reverse linear non-uniform pressure, as shown in Figure 13;

（4）减振器环形叠加阀片在任意半径r位置的叠加变形系数G r 计算: (4) Calculation of the superimposed deformation coefficient G r of the annular superimposed valve plate of the shock absorber at any radius r position:

根据步骤（2）中的G r1和步骤（3）中的G r2，通过叠加运算得减振器环形叠加阀片的变形系数G r 随半径r（r a ≤r≤ r b ）的变化曲线，如图14所示； According to G r 1 in step (2) and G r 2 in step (3), the deformation coefficient G r of the annular superimposed valve plate of the shock absorber varies with the radius r ( r a ≤ r ≤ r b ) through superposition calculation Variation curve, as shown in Figure 14;

其中，在阀口半径位置的变形系数G rk=m6/N，在外圆半径

Figure 248888DEST_PATH_IMAGE002
位置的变形系数G rb=
Figure 284978DEST_PATH_IMAGE105
m6/N； where, in the valve port radius The deformation coefficient G r k = m 6 /N, at outer circle radius
Figure 248888DEST_PATH_IMAGE002
Deformation coefficient G r b =
Figure 284978DEST_PATH_IMAGE105
m 6 /N;

（5）减振器环形叠加阀片在任意半径r位置的叠加变形f r 计算： (5) Calculation of the superimposed deformation f r of the annular superimposed valve plate of the shock absorber at any radius r position:

根据步骤(1)中的叠加阀片等效厚度h e=0.260855mm，最大非均布压力p 0=3.0MPa及步骤（4）中的变形系数G r ，对减振器环形叠加阀片非均布压力下在任意半径r位置的变形

Figure 724180DEST_PATH_IMAGE075
进行计算，即： According to the equivalent thickness of the stacked valve plate h e =0.260855mm in step (1), the maximum non-uniform pressure p 0 =3.0MPa and the deformation coefficient G r in step (4), the shock absorber annular stacked valve plate is not Deformation at any radius r under uniform pressure
Figure 724180DEST_PATH_IMAGE075
Do the calculation, that is:

Figure 111299DEST_PATH_IMAGE076
;
Figure 111299DEST_PATH_IMAGE076
;

计算所得到的减振器环形叠加阀片变形曲线，如图15所示；  The calculated deformation curve of the annular superimposed valve plate of the shock absorber is shown in Figure 15;

其中, 在阀口半径位置的变形量为

Figure 277838DEST_PATH_IMAGE077
=0.101585mm，在外半径位置的最大变形量为
Figure 434013DEST_PATH_IMAGE078
=0.1209876mm。 Among them, the deformation at the radial position of the valve port is
Figure 277838DEST_PATH_IMAGE077
=0.101585mm, the maximum deformation at the outer radius is
Figure 434013DEST_PATH_IMAGE078
=0.1209876mm.

根据减振器环形叠加阀片的内圆半径r a＝5.0mm，外圆半径r b＝8.75mm，阀口半径r k＝8.0mm，叠加阀片的厚度和片数分别为h 1=0.15mm，n 1=1；h 2=0.2mm，n 2=3，均布压力p=3.0MPa，弹性模型E＝200GPa，泊松比μ＝0.3，利用ANSYS建立叠加阀片仿真模型，网格划分单位为0.1mm，在区间r a ≤r≤r b的分布压力p 0=3.0MPa，在区间r k <r≤r b 的分布的压力p=

Figure 44117DEST_PATH_IMAGE074
MPa，仿真所得到的减振器环形叠加阀片变形仿真云图，如图16所示。 According to the inner circle radius r a = 5.0mm, the outer circle radius r b = 8.75mm, the valve port radius r k = 8.0mm, the thickness and the number of stacked valve plates are respectively h 1 =0.15 mm, n 1 =1; h 2 =0.2mm, n 2 =3, uniform pressure p =3.0MPa, elastic model E =200GPa, Poisson's ratio μ =0.3, using ANSYS to establish a simulation model of superimposed valve slices, grid The division unit is 0.1mm, the distribution pressure p 0 =3.0MPa in the interval r a ≤ r ≤ r b , the distribution pressure p = in the interval r k <r≤r b
Figure 44117DEST_PATH_IMAGE074
MPa, the deformation simulation cloud image of the annular superimposed valve plate of the shock absorber obtained by simulation, as shown in Figure 16.

由图16可知，减振器环形叠加阀片最大变形仿真值为0.120777mm，与利用该计算方法所得到的0.1209876mm之间的偏差为0.000213mm，相对偏差仅为0.0213%，表明本发明所建立的减振器环形叠加阀片在非均布压力下变形的计算方法是精确，为建立精确的减振器节流阀参数设计及特性仿真数学模型，提供了可靠的非均布压力下的阀片变形计算方法。 It can be seen from Fig. 16 that the simulation value of the maximum deformation of the annular superimposed valve plate of the shock absorber is 0.120777mm, and the deviation from the 0.1209876mm obtained by this calculation method is 0.000213mm, and the relative deviation is only 0.0213%, which shows that the present invention establishes The calculation method for the deformation of the annular superimposed valve plate of the shock absorber under non-uniform pressure is accurate, which provides a reliable valve under non-uniform pressure for the establishment of accurate shock absorber throttle valve parameter design and characteristic simulation mathematical model. Calculation method of sheet deformation.

Claims (4)

1. The method for calculating the deformation of the annular sandwich valve plate of the shock absorber under the nonuniform pressure comprises the following specific calculation steps:
(1) determining equivalent thickness of annular sandwich valve plate of shock absorberh e:
For same material characteristics and inner circle radius
Figure 177123DEST_PATH_IMAGE001
And the outer circleRadius of
Figure 102354DEST_PATH_IMAGE002
Equal annular sandwich valve plates according to the thickness and the number of the sandwich valve plates (h 1，n 1；h 2，n 2；…；h n ，n n) Determining the equivalent thickness of the annular sandwich valve plate of the damperh eComprises the following steps:
Figure 388979DEST_PATH_IMAGE003
；
(2) under uniform pressurep 0The lower superposed valve plate is at any radiusrCoefficient of deformation of positionG r1The calculation of (2):
according to the inner circle radius of the annular superposed valve plate of the shock absorberr aOuter radius of circler bModulus of elasticityEAnd poisson's ratioμCalculating the random radius of the annular valve plate under the uniform pressurer（r a ≤r≤ r b ) Coefficient of deformation of positionG r1Namely:
Figure 325842DEST_PATH_IMAGE004
in the formula,
Figure 423242DEST_PATH_IMAGE005
,
Figure 898086DEST_PATH_IMAGE006
,
Figure 739134DEST_PATH_IMAGE007
,
Figure 983034DEST_PATH_IMAGE008
；
Figure 172706DEST_PATH_IMAGE009
，
Figure 885579DEST_PATH_IMAGE010
，
Figure 514006DEST_PATH_IMAGE011
，
Figure 628724DEST_PATH_IMAGE012
；
Figure 989298DEST_PATH_IMAGE013
，
Figure 438734DEST_PATH_IMAGE014
，，
Figure 574497DEST_PATH_IMAGE016
；
(3) reverse linear non-uniform pressure
Figure 371552DEST_PATH_IMAGE017
Lower valve plate at any radiusrCoefficient of deformation of positionG r2The calculation of (2):
according to the inner circle radius of the annular valve plater aOuter radius of circler bModulus of elasticityEPoisson ratioμRadius of initial action position of non-uniform pressurer kAnd calculating the deformation coefficient of the annular superposed valve plate under the reverse linear non-uniform pressure, namely:
Figure 793437DEST_PATH_IMAGE018
；
in the formula,
Figure 966929DEST_PATH_IMAGE019
Figure 39928DEST_PATH_IMAGE020
Figure 820933DEST_PATH_IMAGE021
，
Figure 917065DEST_PATH_IMAGE022
，
Figure 690986DEST_PATH_IMAGE023
Figure 357504DEST_PATH_IMAGE024
Figure 496362DEST_PATH_IMAGE025
Figure 142107DEST_PATH_IMAGE026
，
Figure 204872DEST_PATH_IMAGE027
Figure 562221DEST_PATH_IMAGE029
Figure 561718DEST_PATH_IMAGE031
Figure 401498DEST_PATH_IMAGE032
Figure 695207DEST_PATH_IMAGE033
，
Figure 49965DEST_PATH_IMAGE034
Figure 907063DEST_PATH_IMAGE035
Figure 414398DEST_PATH_IMAGE036
Figure 65960DEST_PATH_IMAGE037
，
Figure 173593DEST_PATH_IMAGE039
，
Figure 381851DEST_PATH_IMAGE040
Figure 930644DEST_PATH_IMAGE041
Figure 81003DEST_PATH_IMAGE042
，
Figure 359986DEST_PATH_IMAGE044
Figure 825602DEST_PATH_IMAGE045
Figure 897595DEST_PATH_IMAGE046
Figure 451253DEST_PATH_IMAGE048
Figure 974638DEST_PATH_IMAGE049
Figure 217532DEST_PATH_IMAGE050
Figure 255895DEST_PATH_IMAGE051
Figure 796597DEST_PATH_IMAGE052
Figure 253118DEST_PATH_IMAGE053
，
wherein,
Figure 650601DEST_PATH_IMAGE054
；
(4) annular sandwich valve plate of shock absorber in any radiusrCoefficient of deformation of positionG r And (3) calculating:
according to step (2)G r1And in step (3)G r2Determining the radius of the annular valve plate at any radius through superposition operationr（r a ≤r≤ r b ) Total superimposed deformation coefficient of positionG r I.e. by
Figure 379523DEST_PATH_IMAGE055
；
(5) Annular sandwich valve plate of shock absorber in any radiusrDeformation of positionf r And (3) calculating:
according to the maximum non-uniform pressure borne by the annular superposed valve platep 0Equivalent thickness in step (1)h eAnd the deformation coefficient in step (3)G r For the annular superposed valve plates of the shock absorber under non-uniform pressure with the radiusrAmount of deformation of positionf r Perform calculations, i.e.
Figure 271386DEST_PATH_IMAGE057
。
2. Step (3) of the method according to claim 1, characterized in that: determining reverse linear non-uniform pressure to be applied according to a non-uniform pressure mechanical model borne by an annular superposed valve plate of an actual shock absorber, and determining the reverse linear non-uniform pressure according to the inner circle radius of the annular valve plate of the annular superposed valve plater aOuter radius of circler bModulus of elasticityEPoisson ratioμRadius of initial action position of non-uniform pressurer kCalculating the deformation coefficient under the reverse linear non-uniform pressureG r2Namely:
Figure DEST_PATH_IMAGE059
。
3. step (4) of the method according to claim 1, characterized in that: according to the deformation coefficient of the annular valve plate under uniform pressureG r1And coefficient of deformation under reverse linear non-uniform pressureG r2The superposition operation of the two-way valve is carried out to obtain the random radius of the annular valve plate of the shock absorber under the actual non-uniform pressurer（r a ≤r≤ r b ) Coefficient of deformation ofG r 。
4. Step (5) of the method according to claim 1, characterized in that: according to the equivalent thickness of the annular superposed valve plateh eMaximum non-uniform pressure to be appliedp 0And at any radiusr（r a ≤r≤ r b ) Coefficient of deformation ofG r By using
Figure 831681DEST_PATH_IMAGE057
Any radius of annular superposed valve plate of damper under non-uniform pressurerDeformation of (b)
Figure DEST_PATH_IMAGE061
And (6) performing calculation.
CN2013102122738A 2013-05-31 2013-05-31 Computing method of deformation of annular sandwich valve plates of vibration absorber under non-uniform pressure Pending CN103246789A (en)

Priority Applications (1)

Application Number Priority Date Filing Date Title
CN2013102122738A CN103246789A (en) 2013-05-31 2013-05-31 Computing method of deformation of annular sandwich valve plates of vibration absorber under non-uniform pressure

Applications Claiming Priority (1)

Application Number Priority Date Filing Date Title
CN2013102122738A CN103246789A (en) 2013-05-31 2013-05-31 Computing method of deformation of annular sandwich valve plates of vibration absorber under non-uniform pressure

Publications (1)

Publication Number Publication Date
CN103246789A true CN103246789A (en) 2013-08-14

Family

ID=48926307

Family Applications (1)

Application Number Title Priority Date Filing Date
CN2013102122738A Pending CN103246789A (en) 2013-05-31 2013-05-31 Computing method of deformation of annular sandwich valve plates of vibration absorber under non-uniform pressure

Country Status (1)

Country Link
CN (1) CN103246789A (en)

Cited By (3)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
CN103678945A (en) * 2014-01-02 2014-03-26 山东理工大学 Method for calculating deformation of non-equal structure superposed valve plates of vehicle shock absorber
CN103678833A (en) * 2014-01-02 2014-03-26 山东理工大学 Method for calculating radial stress of non-equal structure superposed valve plates of vehicle shock absorber
CN105260533A (en) * 2015-10-08 2016-01-20 山东理工大学 Method for calculating deformation of unequal thickness annular valve block of hydro-pneumatic spring

Citations (3)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
US20020022948A1 (en) * 2000-07-19 2002-02-21 Murata Manufacturing Co., Ltd. Method of adjusting characteristics of electronic part
CN103106312A (en) * 2013-03-08 2013-05-15 山东理工大学 Calculation method for vibration absorber isodesmic annular superposed valve plate deformation
CN103116683A (en) * 2013-03-15 2013-05-22 山东理工大学 Superposition computing method for deformation of absorber annular valve sheet under unevenly distributed pressure

Patent Citations (3)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
US20020022948A1 (en) * 2000-07-19 2002-02-21 Murata Manufacturing Co., Ltd. Method of adjusting characteristics of electronic part
CN103106312A (en) * 2013-03-08 2013-05-15 山东理工大学 Calculation method for vibration absorber isodesmic annular superposed valve plate deformation
CN103116683A (en) * 2013-03-15 2013-05-22 山东理工大学 Superposition computing method for deformation of absorber annular valve sheet under unevenly distributed pressure

Cited By (6)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
CN103678945A (en) * 2014-01-02 2014-03-26 山东理工大学 Method for calculating deformation of non-equal structure superposed valve plates of vehicle shock absorber
CN103678833A (en) * 2014-01-02 2014-03-26 山东理工大学 Method for calculating radial stress of non-equal structure superposed valve plates of vehicle shock absorber
CN103678945B (en) * 2014-01-02 2016-06-15 山东理工大学 The non-defining method waiting the distortion of structure superposition valve block of a kind of vehicle vibration damping device
CN103678833B (en) * 2014-01-02 2016-09-07 山东理工大学 The non-computational methods waiting structure superposition valve block radial stress of vehicle shock absorber
CN105260533A (en) * 2015-10-08 2016-01-20 山东理工大学 Method for calculating deformation of unequal thickness annular valve block of hydro-pneumatic spring
CN105260533B (en) * 2015-10-08 2018-01-05 山东理工大学 The hydro-pneumatic spring computational methods that uniform thickness annular valve block does not deform

Similar Documents

Publication Publication Date Title
CN105550487B (en) Few main spring of piece bias type variable cross-section is in the design method in oblique line section Yu auxiliary spring gap
CN102748418B (en) Method for designing stiffness of helical spring of combined valve for shock absorbers
CN107908917B (en) A method for predicting springback in stamping forming of high-strength plates
CN105697625B (en) The design method of few piece parabolic type iso-stress leaf spring of the non-equal structures in end
CN112733406B (en) Establishment of a prediction model for friction stir welding structure defects using finite element method
CN103106312A (en) Calculation method for vibration absorber isodesmic annular superposed valve plate deformation
CN103294919A (en) Method for calculating radial stress of annular superposed valve slices of shock absorber under nonuniform pressure
CN103116683A (en) Superposition computing method for deformation of absorber annular valve sheet under unevenly distributed pressure
CN103246789A (en) Computing method of deformation of annular sandwich valve plates of vibration absorber under non-uniform pressure
CN103150434A (en) Method for calculating combined stress of annular valve sheet of shock absorber
CN103678832B (en) The non-computational methods waiting structure superposition valve block combined stress of vehicle shock absorber
CN105138806B (en) The strength check methods of hydro-pneumatic spring not uniform thickness annular valve block
CN103116709A (en) Computing method for circumferential stress of absorber annular valve sheet
CN103324824A (en) Computing method for equivalent thickness of hydraulic buffer isomorphic annular sandwich valve plates
CN103177158A (en) Computing method for circumferential stress of equivalent structure circular sandwich valve plate of absorber
CN103632011B (en) The computational methods of shock absorber valve block deformation arbitrarily under axial symmetry non-uniform distributed pressure
CN103148148A (en) Method for checking strength of rebound sandwich valve sheet of shock absorber
CN103246791A (en) Computing method of circumferential stress of annular sandwich valve plates of vibration absorber under non-uniform pressure
CN103617334B (en) Strength check methods under vibroshock valve block meaning in office non-uniform distributed pressure
CN103150478B (en) The computing method of absorber annular valve sheet circumferential stress under non-uniform distributed pressure
CN103177157A (en) Computing method for radial stress of equivalent structure circular sandwich valve plate of absorber
CN103440354A (en) Calculation method for deformation of annular elastic valve plate of shock absorber
CN105279319B (en) The computational methods of hydro-pneumatic spring not uniform thickness annular valve block Maximum circumferential stress
CN103678833B (en) The non-computational methods waiting structure superposition valve block radial stress of vehicle shock absorber
CN114880904A (en) Large-scale finite element analysis method for rubber bushing

Legal Events

Date Code Title Description
C06 Publication
PB01 Publication
C10 Entry into substantive examination
SE01 Entry into force of request for substantive examination
C02 Deemed withdrawal of patent application after publication (patent law 2001)
WD01 Invention patent application deemed withdrawn after publication

Application publication date: 20130814