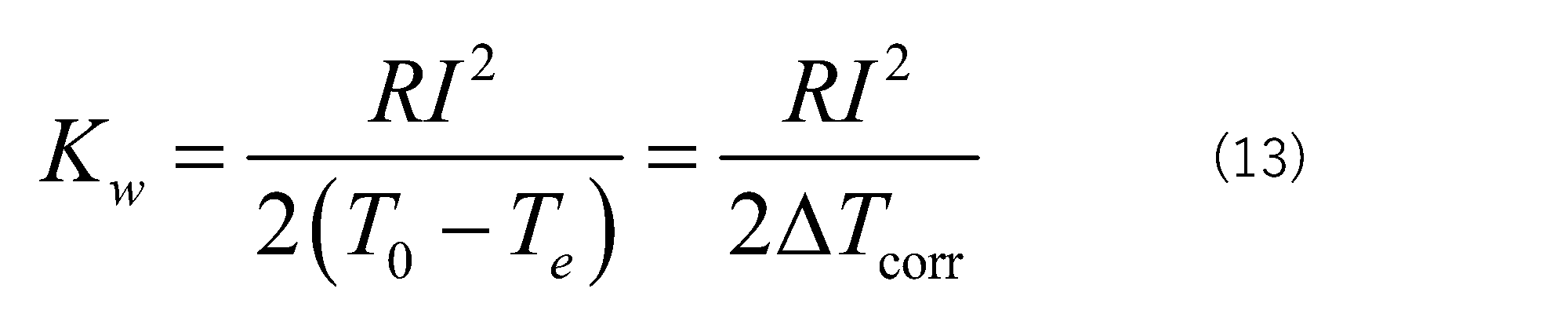WO2024116508A1 - Peltier coefficient calculation method, program, and measurement system - Google Patents
Peltier coefficient calculation method, program, and measurement system Download PDFInfo
- Publication number
- WO2024116508A1 WO2024116508A1 PCT/JP2023/031251 JP2023031251W WO2024116508A1 WO 2024116508 A1 WO2024116508 A1 WO 2024116508A1 JP 2023031251 W JP2023031251 W JP 2023031251W WO 2024116508 A1 WO2024116508 A1 WO 2024116508A1
- Authority
- WO
- WIPO (PCT)
- Prior art keywords
- conductor sample
- sample
- current
- temperature
- conductor
- Prior art date
Links
- 238000004364 calculation method Methods 0.000 title claims abstract description 16
- 238000005259 measurement Methods 0.000 title claims description 55
- 239000004020 conductor Substances 0.000 claims abstract description 168
- 238000000034 method Methods 0.000 claims description 22
- 238000009529 body temperature measurement Methods 0.000 claims description 15
- 230000007246 mechanism Effects 0.000 claims description 4
- 238000012937 correction Methods 0.000 description 18
- 230000005679 Peltier effect Effects 0.000 description 13
- 238000010586 diagram Methods 0.000 description 10
- 230000005678 Seebeck effect Effects 0.000 description 9
- WABPQHHGFIMREM-UHFFFAOYSA-N lead(0) Chemical compound [Pb] WABPQHHGFIMREM-UHFFFAOYSA-N 0.000 description 7
- 230000000694 effects Effects 0.000 description 6
- 238000005516 engineering process Methods 0.000 description 6
- 239000000463 material Substances 0.000 description 5
- 238000004458 analytical method Methods 0.000 description 4
- 230000020169 heat generation Effects 0.000 description 4
- XEEYBQQBJWHFJM-UHFFFAOYSA-N Iron Chemical compound [Fe] XEEYBQQBJWHFJM-UHFFFAOYSA-N 0.000 description 3
- 238000000576 coating method Methods 0.000 description 3
- 238000004891 communication Methods 0.000 description 3
- 230000006870 function Effects 0.000 description 3
- 238000000691 measurement method Methods 0.000 description 3
- 230000000704 physical effect Effects 0.000 description 3
- 238000012545 processing Methods 0.000 description 3
- 230000008901 benefit Effects 0.000 description 2
- 230000008859 change Effects 0.000 description 2
- 238000006243 chemical reaction Methods 0.000 description 2
- 239000011248 coating agent Substances 0.000 description 2
- 238000007796 conventional method Methods 0.000 description 2
- 238000009792 diffusion process Methods 0.000 description 2
- 230000005611 electricity Effects 0.000 description 2
- 238000011156 evaluation Methods 0.000 description 2
- 230000005855 radiation Effects 0.000 description 2
- 239000012925 reference material Substances 0.000 description 2
- 238000012795 verification Methods 0.000 description 2
- 229910002899 Bi2Te3 Inorganic materials 0.000 description 1
- RYGMFSIKBFXOCR-UHFFFAOYSA-N Copper Chemical compound [Cu] RYGMFSIKBFXOCR-UHFFFAOYSA-N 0.000 description 1
- 238000010521 absorption reaction Methods 0.000 description 1
- 239000002131 composite material Substances 0.000 description 1
- 238000001816 cooling Methods 0.000 description 1
- 229910052802 copper Inorganic materials 0.000 description 1
- 239000010949 copper Substances 0.000 description 1
- 230000001419 dependent effect Effects 0.000 description 1
- 238000002474 experimental method Methods 0.000 description 1
- 230000010365 information processing Effects 0.000 description 1
- 229910052742 iron Inorganic materials 0.000 description 1
- 239000002184 metal Substances 0.000 description 1
- 229910052751 metal Inorganic materials 0.000 description 1
- 230000003071 parasitic effect Effects 0.000 description 1
- 238000002360 preparation method Methods 0.000 description 1
- 230000008569 process Effects 0.000 description 1
- 238000012827 research and development Methods 0.000 description 1
- 230000004044 response Effects 0.000 description 1
- 239000004065 semiconductor Substances 0.000 description 1
- 239000007787 solid Substances 0.000 description 1
- 230000009897 systematic effect Effects 0.000 description 1
- 238000002076 thermal analysis method Methods 0.000 description 1
- 239000002918 waste heat Substances 0.000 description 1
Images
Classifications
-
- G—PHYSICS
- G01—MEASURING; TESTING
- G01N—INVESTIGATING OR ANALYSING MATERIALS BY DETERMINING THEIR CHEMICAL OR PHYSICAL PROPERTIES
- G01N25/00—Investigating or analyzing materials by the use of thermal means
-
- H—ELECTRICITY
- H10—SEMICONDUCTOR DEVICES; ELECTRIC SOLID-STATE DEVICES NOT OTHERWISE PROVIDED FOR
- H10N—ELECTRIC SOLID-STATE DEVICES NOT OTHERWISE PROVIDED FOR
- H10N10/00—Thermoelectric devices comprising a junction of dissimilar materials, i.e. devices exhibiting Seebeck or Peltier effects
- H10N10/01—Manufacture or treatment
Definitions
- the present invention relates to a technique for calculating the Peltier coefficient.
- thermoelectric conversion The mutual conversion of heat and electricity through the movement of electrons in a solid is called thermoelectric conversion, and research and development is being conducted on power supplies and electronic cooling components that use this principle to recycle waste heat as electricity.
- These technologies use the Seebeck effect, in which a voltage is generated according to the temperature difference applied to an object, and the Peltier effect, in which a heat flow is generated according to the direction of the voltage.
- the proportionality coefficient linking the temperature difference and voltage is called the Seebeck coefficient, and conversely, the proportionality coefficient linking voltage and heat flow is called the Peltier coefficient.
- thermoelectric materials There has been great progress in the measurement technology of thermoelectric materials over the past 20 years.
- the reference material for the Seebeck effect has been supplied by NIST (National Institute of Standards and Technology) as high-purity iron (i.e., electrolytic iron) as part of its thermal property standards.
- NIST National Institute of Standards and Technology
- electrolytic iron high-purity iron
- the supply of a more sophisticated semiconductor-type reference material began. This is because, in the race to develop highly efficient thermoelectric materials, data with poor reproducibility has become more common, and measurement technology has become increasingly important.
- Non-Patent Document 1 discloses a method for determining the Peltier coefficient from the heat flow of a sample when a temperature difference is applied and when it is electrically shorted and opened, and the current value flowing through the sample at that time.
- the advantage of this method is that it does not require measurement of the thermal conductivity or dimensions of the sample.
- it has a disadvantage in that it requires measurement of the heat flow flowing through the sample, which is more difficult to measure accurately than temperature measurement.
- the heater part of the measurement device generally has a complex and large-scale mechanism to prevent heat leakage.
- the temperature difference is measured to measure the heat flow, but multiple temperature measurements are performed with multiple thermometers, which is time-consuming for general physical property and device evaluation.
- Non-Patent Document 2 also discloses a technology that derives a more general relationship between the Peltier coefficient and temperature, taking into account the parasitic thermal resistance of the electrodes, from thermal conduction analysis, making it possible to accurately determine the Peltier coefficient from temperature measurement.
- This method has the advantage of being able to determine the Peltier coefficient by temperature measurement rather than heat flow.
- the temperature is measured at two locations on both ends of the sample, the information that can be obtained from the temperature measurement is limited, and the thermal conductivity and dimensions of the sample and current lead wire are included as unknowns in the measurement equation. Therefore, in order to measure the Peltier coefficient, not only is the temperature generated by the Peltier effect measured, but multiple measurement systems (synonymous with multiple measurement devices) with different measurement principles and boundary conditions are used. In particular, since the measurement of thermal conductivity requires the measurement of heat flow, problems similar to those in Non-Patent Document 1 may occur.
- an object of the present invention is to provide a technique for easily measuring the Peltier coefficient of a sample.
- the method for calculating the Peltier coefficient includes the steps of: (A) bringing a conductor sample, the object of which is to measure the Peltier coefficient, to a constant temperature, and then passing a direct current through the conductor sample to measure the temperature at both ends of the conductor sample; (B) passing an alternating current, the effective value of which is equal to the direct current, through the conductor sample to measure the temperature at the ends and center of the conductor sample; and (C) calculating the Peltier coefficient using the temperatures at both ends of the conductor sample measured by passing a direct current through the conductor sample, the temperatures at the ends and center of the conductor sample measured by passing an alternating current through the conductor sample, the electrical resistance value of the conductor sample, and the value of the current passed through the conductor sample.
- FIG. 1 is a diagram for explaining the measurement principle.
- FIG. 2 is a diagram for explaining a temperature change when a direct current is passed through a conductor sample.
- FIG. 3 is a diagram for explaining a temperature change when an AC current is applied to a conductor sample.
- FIG. 4 is a diagram for explaining the configuration of the measurement system according to the embodiment.
- FIG. 5 is a diagram showing the measurement procedure.
- FIG. 6 is a diagram for explaining a preferred frequency band of an alternating current.
- FIG. 7 is a diagram for explaining a preferable range of the direct current.
- FIG. 8 is a diagram for explaining the effect of the correction term.
- FIG. 9 is a diagram for explaining the relationship between the correction value and the theoretical value of the correction value.
- FIG. 10 is a diagram illustrating an example of the configuration of the calculation unit.
- an AC current and a DC current are applied to the sample to distinguish between Peltier heat and Joule heat, and the Peltier coefficient is calculated by measuring at least the temperature difference at both ends of the sample caused by the Peltier heat generated at the ends of the sample and the temperature rise at the center of the sample caused by the Joule heat.
- FIG. 1 shows a thermal analysis model for deriving the Peltier coefficient.
- the heat bath block is held at temperature Te.
- the length of the left current lead is Lc
- the length of the right current lead is Lh .
- a represents the cross-sectional area of the sample
- Q [W] represents the heat flow
- ⁇ [V] represents the Peltier coefficient of the sample
- T [K] represents the temperature of the sample
- I [A] represents the current density
- ⁇ [W/(mK)] represents the thermal conductivity of the sample
- ⁇ [ ⁇ m] represents the electrical resistivity of the sample
- the variable x [m] represents the coordinates of the sample.
- the left side represents heat generation due to the Peltier effect.
- the right side represents heat diffusion due to thermal conduction in the sample, Joule heat, and heat loss through the lead wires. In other words, it represents that the Peltier heat generated at both ends of the sample and the Joule heat generated inside the sample are equal to the heat flow due to thermal conduction in the sample and thermal conduction in the lead wires.
- ⁇ T dc T L - T 0
- the DC current I the thermal conductance K of the sample
- Kw the thermal conductance Kw of the current lead wire
- T 0 and T L can be obtained as follows:
- RI ⁇ T dc /(8 ⁇ T ac ) in equation (14) represents the Peltier coefficient when there is no heat loss
- RI ⁇ T dc /(8 ⁇ T ac ) ⁇ (2 ⁇ T ac )/ ⁇ T corr represents a correction term, which represents the Peltier heat lost due to heat loss
- K ⁇ T ac /I represents the Peltier coefficient when there is no heat loss
- K ⁇ T ac /I ⁇ K w /(2K) represents a theoretical correction term, which represents the Peltier coefficient lost due to heat loss
- the measurement system according to the present embodiment includes a DC power source 11, an AC power source 12, a switch 13 for switching the current flowing through the conductor sample 100 between DC and AC, heat bath blocks 31 and 32 for maintaining the conductor sample 100 and the like at a constant temperature Te, a current lead wire 14 connecting the DC power source 11 and the AC power source 12 to one end of the conductor sample 100, a current lead wire 15 connecting the switch 13 to the other end of the conductor sample 100, a voltmeter 21 for measuring the voltage generated between both ends of the conductor sample 100, a temperature measurement unit 40 for measuring the temperatures of both ends and the center of the conductor sample 100, and a calculation unit 50 for calculating the Peltier coefficient based on the measurement results of the temperature measurement unit 40 and the like.
- Heaters and thermometers are attached to the heat bath blocks 31 and 32, and the temperature is controlled to be kept constant at Te.
- the calculation unit 50 may be used for this control.
- the heat bath blocks 31 and 32 ensure that the temperatures of at least a part of the current leads 14 and 15 and the conductor sample 100 are also in thermal equilibrium at temperature Te.
- Heat bath blocks 31 and 32 are made of a metal such as copper.
- the temperature measuring unit 40 includes a thermocouple 42 for measuring the temperature of one end of the conductor sample 100, a thermocouple 44 for measuring the temperature of the center of the conductor sample 100, and a thermocouple 46 for measuring the temperature of the other end of the conductor sample 100.
- the voltmeter 21 is used to measure the voltage generated across both ends of the conductor sample 100 when an alternating current is passed through it, and to obtain the electrical resistance R of the conductor sample 100.
- the calculation unit 50 is a calculation device such as a personal computer, and the main function is realized by a processor executing a program that calculates the Peltier coefficient using the entire formula (14) or the first term of formula (14).
- thermocouples are attached to both ends and the center of the conductor sample 100, and current leads 14 and 15 are connected to both ends of the conductor sample 100.
- the current leads 14 and 15 are in contact with the heat bath blocks 31 and 32 via the electrical insulating coatings 16 and 17.
- the conductor sample 100 and the like are placed in a vacuum environment, the heat bath blocks 31 and 32 are kept at a temperature Te, and the temperature of the conductor sample 100 is also kept at a temperature Te until it reaches thermal equilibrium. That is, even at this stage, the temperatures of the ends and center of the conductor sample 100 are measured to confirm whether they have reached temperature Te.
- the switch 13 is connected to the DC power source 11 to pass a DC current through the conductor sample 100, and the temperature measuring unit 40 measures the temperatures at both ends of the conductor sample 100 (step S3).
- the switch 13 is used to stop current from flowing through the conductor sample 100 from either power source, so that the conductor sample 100 returns to the temperature Te of the heat bath blocks 31 and 32.
- the switch 13 is connected to the AC power source 12 to pass an AC current (the effective value of the AC current is the same as the DC current passed in step S3) through the conductor sample 100, and the temperature (T 0 , T L ) of the end portion of the conductor sample 100 and the temperature (T L/2 ) of the center portion are measured by the temperature measuring unit 40 (step S5).
- the end portion of the conductor sample 100 may be both ends or one end.
- an AC current (the effective value of the AC current is set to be the same as the DC current passed in step S3) is passed through conductor sample 100, i.e., in the same manner as in step S5, the voltage at the end of conductor sample 100 is measured by voltmeter 21 (step S7).
- the electrical resistance R of conductor sample 100 is obtained by dividing the measured voltage V by the passed current I.
- the calculation unit 50 calculates the Peltier coefficient based on the measurement results and outputs it to, for example, a display device or other output device (step S9). Since ⁇ T dc is obtained in step S3, ⁇ T ac and T corr are obtained in step S5, and the electrical resistance R is obtained in step S7, the Peltier coefficient ⁇ is calculated by equation (14) by further using the flowing current I. Note that if the correction term is ignored, the Peltier coefficient ⁇ is calculated as RI ⁇ T dc /(8 ⁇ T ac ), so it is not necessary to calculate ⁇ T corr .
- the Peltier coefficient can be easily calculated by measuring the temperature at three points on the conductor sample 100.
- major uncertain factors such as the measurement of the dimensions of the conductor sample 100, thermal conductivity, and heat loss can be eliminated from the measurement system, so high accuracy is achieved from this perspective as well.
- Example 10 The measurement system shown in FIG. 4 was used, and a polycrystalline sample of Bi2Te3 , an n-type semiconductor material, was used as the conductor sample 100.
- the conductor sample 100 measuring 30 mm x 3 mm x 2 mm, was thermally connected to the heat bath blocks 31 and 32 by current leads 14 and 15 having a thermal conductance Kw.
- a vacuum environment was used to prevent heat loss due to convection.
- the entire conductor sample 100 was covered with a heat shield to suppress heat exchange between the conductor sample 100 and the outside due to radiation.
- the effective value of the AC current was 25 mA, and the AC frequency was 62.5 Hz.
- the temperature difference in the conductor sample 100 caused by the Peltier effect at both ends of the conductor sample 100 is measured at an appropriate range of frequencies, and the frequency for measurement is determined within a range in which the temperature difference is independent of frequency.
- Figure 6 shows an example of measurement. That is, the horizontal axis represents frequency, and the vertical axis represents the temperature difference [K] at both ends of the conductor sample 100.
- a frequency of 1 Hz or higher should be selected. Integer values such as 10 Hz and 100 Hz are also acceptable, but to avoid power supply frequency noise, selecting 62.5 Hz allows for more accurate measurement.
- FIG. 7 shows an example of a measurement.
- the horizontal axis represents the DC current [mA]
- the vertical axis represents the temperature difference [K] between both ends of the conductor sample 100. It can be seen that if the range is between -60 mA and +60 mA, the temperature difference changes in full proportion to the DC current.
- Figure 8 shows the results of calculating the Peltier coefficient while intentionally changing the amount of heat loss from the conductor sample 100 by changing the length of the current leads 14 and 15.
- the horizontal axis of Figure 8 represents the thermal conductance [mW/K] of the current leads, the vertical axis represents the Peltier coefficient [mV], the black circles represent the Peltier coefficient calculated without the correction term, and the black squares represent the Peltier coefficient calculated using equation (14). Since the Peltier coefficient is a value specific to the sample, it is constant regardless of heat loss. However, as shown by the black circles, if the correction term is not taken into account, the Peltier coefficient increases as the thermal conductance of the current leads 14 and 15 increases.
- the voltmeter 21 may also be connected to the calculation unit 50.
- the switching control of the switch 13 and the temperature control of the heat bath blocks 31 and 32 may also be performed by the calculation unit 50.
- the procedure shown in FIG. 4 may also be modified so as not to affect the measurement results.
- the order in which the AC current and the DC current are passed may be interchanged.
- the AC method in which the AC current is passed through the conductor sample 100 is used, but the method may be modified so as not to affect the measurement results.
- a time-resolved measurement method in which a step-like current is passed through the conductor sample 100 and the voltage is measured before the Peltier heat is distributed throughout the sample may be used.
- the calculation unit 50 described above is, for example, a computer device as shown in FIG. 10, in which the memory 2501, the CPU 2503, the hard disk drive (HDD) 2505, the display control unit 2507 connected to the display device 2509, the drive device 2513 for the removable disk 2511, the input device 2515, and the communication control unit 2517 for connecting to the network are connected by a bus 2519.
- the operating system (OS) and the application program for implementing the processing in this embodiment are stored in the HDD 2505, and when executed by the CPU 2503, are read from the HDD 2505 to the memory 2501.
- the CPU 2503 controls the display control unit 2507, the communication control unit 2517, and the drive device 2513 according to the processing contents of the application program to perform a predetermined operation.
- Data during processing is mainly stored in the memory 2501, but may be stored in the HDD 2505.
- an application program for carrying out the above-mentioned processes is distributed stored on a computer-readable removable disk 2511, and is installed from the drive device 2513 to the HDD 2505. It may also be installed to the HDD 2505 via a network such as the Internet and a communication control unit 2517.
- Such a computer device realizes the various functions described above by organic cooperation between the above-mentioned hardware such as the CPU 2503 and memory 2501, and programs such as the OS and application programs.
- the method for calculating the Peltier coefficient includes the steps of: (A) bringing the conductor sample, the object of which is to measure the Peltier coefficient, to a constant temperature, and then passing a direct current through the conductor sample to measure the temperature at both ends of the conductor sample; (B) passing an alternating current, the effective value of which is equal to the direct current, through the conductor sample to measure the temperature at the ends and center of the conductor sample; and (C) calculating the Peltier coefficient using the temperatures at both ends of the conductor sample measured by passing a direct current through the conductor sample, the temperatures at the ends and center of the conductor sample measured by passing an alternating current through the conductor sample, the electrical resistance value of the conductor sample, and the value of the current passed through the conductor sample.
- the Peltier coefficient can also be obtained with high accuracy.
- the above method may further include a step of measuring the temperature at the end of the conductor sample when no current is flowing through the conductor sample.
- the temperature at the end of the conductor sample when no current is flowing may be further used to calculate the Peltier coefficient.
- the difference in temperature at both ends of the conductor sample measured by passing a direct current through the conductor sample, and the difference in temperature between the center of the conductor sample measured by passing an alternating current and the end of the conductor sample measured by passing an alternating current may be calculated. Since ⁇ T dc and ⁇ T ac are obtained, at least the first term of formula (14) can be calculated.
- the step of calculating the Peltier coefficient if the electrical resistance value of the conductor sample is represented as R, the value of the current passed through the conductor sample is represented as I, the temperature difference at both ends of the conductor sample measured by passing a direct current through the conductor sample is represented as ⁇ T dc , and the temperature difference between the center of the conductor sample measured by passing an alternating current and the temperature at both ends of the conductor sample measured by passing an alternating current is represented as ⁇ T ac , then:
- the Peltier coefficient is RI ⁇ T dc /(8 ⁇ T ac ) In this way, if the thermal resistance of the current lead wire is high, the Peltier coefficient may be calculated with sufficient accuracy using only the first term of equation (14).
- the method may further include a step of measuring a temperature at an end of the conductive sample when no current is flowing through the conductive sample.
- a step of measuring a temperature at an end of the conductive sample when no current is flowing through the conductive sample when the difference between the temperature at the end of the conductive sample measured by flowing an AC current and the temperature at the end of the conductive sample when no current is flowing in the step of calculating the Peltier coefficient is expressed as ⁇ T corr , 2 ⁇ T ac / ⁇ T corr In this way, the Peltier coefficient can be calculated with higher accuracy by correcting the heat loss.
- the program according to this embodiment causes a computer (or processor) to execute the steps of: (A) bringing the conductor sample, the object of which is to measure the Peltier coefficient, to a constant temperature, and then passing a direct current through the conductor sample to obtain the temperatures at both ends of the conductor sample; (B) passing an alternating current, the effective value of which is equal to the direct current, through the conductor sample to obtain the temperatures at the ends and center of the conductor sample; and (C) calculating the Peltier coefficient using the temperatures at both ends of the conductor sample measured by passing a direct current through the conductor sample, the temperatures at the ends and center of the conductor sample measured by passing an alternating current through the conductor sample, the electrical resistance value of the conductor sample, and the value of the current passed through the conductor sample.
- the measurement system also includes: (A) a heat bath mechanism (e.g., heat bath blocks 31 and 32) for maintaining a constant temperature of the conductor sample for which the Peltier coefficient is to be measured; (B) a temperature measurement unit (which may include, for example, a thermocouple) for measuring the temperature at both ends and the center of the conductor sample; (C) a DC power supply for passing a DC current through the conductor sample; (D) an AC power supply for passing an AC current through the conductor sample; and (E) a calculation unit (e.g., a computer or other information processing device) for calculating the Peltier coefficient using the temperatures at both ends of the conductor sample measured by the temperature measurement unit when a DC current is passed from the DC power supply to the conductor sample, the temperatures at the ends and the center of the conductor sample measured by the temperature measurement unit when an AC current having an effective value equal to the DC current is passed from the AC power supply to the conductor sample, the electrical resistance value of the conductor sample, and the value of the current
Landscapes
- Engineering & Computer Science (AREA)
- Manufacturing & Machinery (AREA)
- Physics & Mathematics (AREA)
- Health & Medical Sciences (AREA)
- Life Sciences & Earth Sciences (AREA)
- Chemical & Material Sciences (AREA)
- Analytical Chemistry (AREA)
- Biochemistry (AREA)
- General Health & Medical Sciences (AREA)
- General Physics & Mathematics (AREA)
- Immunology (AREA)
- Pathology (AREA)
- Investigating Or Analyzing Materials Using Thermal Means (AREA)
Abstract
In order to easily measure the Peltier coefficient of a sample, this Peltier coefficient calculation method comprises: (A) a step for measuring the temperature at both ends of a conductor sample of which a Peltier coefficient is to be measured by passing a direct current through the conductor sample, after making the conductor sample have a constant temperature; (B) a step for measuring the temperature at the end portions and the center of the conductor sample by passing an alternating current having an effective value equal to the direct current through the conductor sample; and (C) a step for calculating the Peltier coefficient by using the temperature at both ends of the conductor sample measured by passing the direct current through the conductor sample, the temperature at the end portions and the center of the conductor sample measured by passing the alternating current, an electrical resistance value of the conductor sample, and a value of the current passed through conductor sample.
Description
本発明は、ペルチェ係数を算出する技術に関する。
The present invention relates to a technique for calculating the Peltier coefficient.
固体中の電子の運動による熱と電気の相互変換は熱電変換と呼ばれ、この原理を利用し、廃熱を電気として再利用する電源や電子冷却部品の研究開発が行われている。これらの技術は、物体に与えた温度差に応じ電圧が生じるゼーベック効果や、電圧の向きに応じ熱流が生じるペルチェ効果を利用している。そして、温度差と電圧を結ぶ比例係数をゼーベック係数といい、逆に電圧と熱流を結ぶ比例係数をペルチェ係数という。
The mutual conversion of heat and electricity through the movement of electrons in a solid is called thermoelectric conversion, and research and development is being conducted on power supplies and electronic cooling components that use this principle to recycle waste heat as electricity. These technologies use the Seebeck effect, in which a voltage is generated according to the temperature difference applied to an object, and the Peltier effect, in which a heat flow is generated according to the direction of the voltage. The proportionality coefficient linking the temperature difference and voltage is called the Seebeck coefficient, and conversely, the proportionality coefficient linking voltage and heat flow is called the Peltier coefficient.
過去20年間に熱電材料の計測技術においては大きな進展があった。これまでゼーベック効果の基準となる標準物質は、熱物性標準の一部としてNIST(National Institute of Standards and Technology)から高純度の鉄(すなわち電界鉄)として供給されていたが、約半世紀ぶりに、より洗練された半導体型の標準物質の供給が2012年から開始された。これは、高効率な熱電材料の開発競争において、再現性に乏しいデータが報告されることが多くなり、計測技術の重要性が高まったためである。
There has been great progress in the measurement technology of thermoelectric materials over the past 20 years. Until now, the reference material for the Seebeck effect has been supplied by NIST (National Institute of Standards and Technology) as high-purity iron (i.e., electrolytic iron) as part of its thermal property standards. However, in 2012, for the first time in about half a century, the supply of a more sophisticated semiconductor-type reference material began. This is because, in the race to develop highly efficient thermoelectric materials, data with poor reproducibility has become more common, and measurement technology has become increasingly important.
しかしながら、材料の効率評価や物性評価で極めて頻繁に測定されるゼーベック効果に対し、ペルチェ効果が測定されることはほとんどない。これは温度差と電圧を測定すれば良いゼーベック効果に対し、ペルチェ効果の測定には熱流の測定が要求されるからである。幸い、温度差が電流を駆動するとき(ゼーベック効果)と電圧が熱流を駆動するとき(ペルチェ効果)で応答係数が等しくなる相反性が理論的に示されているので、多くの場合、ゼーベック効果から間接的にペルチェ効果を定める。すなわち、これまで報告されてきたペルチェ効果の正確さは、ゼーベック効果の測定の正確さに強く依存していると言える。しかし、近年になり、計測方式や材質の違いでゼーベック効果に系統的な乖離が生じ得ることが明らかになり、問題となっている。また、相反関係のより精密な実験検証も論文などで繰り返し訴えられている。この問題を解決するには、ゼーベック係数とは独立にペルチェ効果を測定することが好ましい。
However, while the Seebeck effect is very frequently measured in the evaluation of the efficiency and physical properties of materials, the Peltier effect is rarely measured. This is because the measurement of the Seebeck effect requires the measurement of heat flow, whereas the temperature difference and voltage are sufficient to measure the Seebeck effect. Fortunately, a reciprocity has been theoretically shown in which the response coefficient is equal when the temperature difference drives the current (Seebeck effect) and when the voltage drives the heat flow (Peltier effect), so in many cases the Peltier effect is indirectly determined from the Seebeck effect. In other words, the accuracy of the Peltier effect reported so far is strongly dependent on the accuracy of the measurement of the Seebeck effect. However, in recent years, it has become clear that differences in measurement methods and materials can cause systematic deviations in the Seebeck effect, which has become a problem. In addition, more precise experimental verification of the reciprocity has been repeatedly called for in papers and other publications. To solve this problem, it is preferable to measure the Peltier effect independently of the Seebeck coefficient.
このような背景を踏まえて、ペルチェ係数を測定する様々な技術が開発されてきた。例えば、非特許文献1は、温度差を与えた試料を電気的に短絡させた場合と、開放にした場合に流れる試料の熱流と、その際に試料を流れる電流値から、ペルチェ係数を求める方法を開示している。この方法の利点は、試料の熱伝導率測定や寸法の測定値を要さない点である。しかしながら、温度測定よりも正確な測定が難しい、試料を流れる熱流の測定を要するという欠点がある。すなわち、ヒータで生成した熱流を周囲に漏らすことなくすべて試料に流し込むことになるため、一般に、測定装置のうちヒータ部分は熱が漏れないように複雑で大がかりな機構となる。また、熱流測定のため温度差を測定することになるが、複数の温度計で多数の温度測定を行うことになり、一般的な物性及びデバイス評価では測定の手間になる。
In light of this background, various techniques for measuring the Peltier coefficient have been developed. For example, Non-Patent Document 1 discloses a method for determining the Peltier coefficient from the heat flow of a sample when a temperature difference is applied and when it is electrically shorted and opened, and the current value flowing through the sample at that time. The advantage of this method is that it does not require measurement of the thermal conductivity or dimensions of the sample. However, it has a disadvantage in that it requires measurement of the heat flow flowing through the sample, which is more difficult to measure accurately than temperature measurement. In other words, since the heat flow generated by the heater is all flowed into the sample without leaking to the surroundings, the heater part of the measurement device generally has a complex and large-scale mechanism to prevent heat leakage. In addition, the temperature difference is measured to measure the heat flow, but multiple temperature measurements are performed with multiple thermometers, which is time-consuming for general physical property and device evaluation.
また、非特許文献2は、電極の寄生的な熱抵抗を考慮したペルチェ係数と温度のより一般的な関係を熱伝導解析より導出し、温度測定からペルチェ係数を正確に求めることを可能とする技術を開示している。この方法では、熱流ではなく温度測定によりペルチェ係数を求めることができることが利点である。しかし、試料両端の2か所の温度測定のため、温度測定から得られる情報が限られ、計測方程式には、試料と電流リード線の熱伝導率及び寸法が未知数として含まれる。そのため、ペルチェ係数を測定するために、ペルチェ効果により生じた温度測定だけではなく、測定原理及び境界条件の異なる複数の測定系(複数の測定装置と同義)を用いることになる。特に、熱伝導率の測定では熱流の測定を要するために、非特許文献1と同じような問題が生じ得る。
Non-Patent Document 2 also discloses a technology that derives a more general relationship between the Peltier coefficient and temperature, taking into account the parasitic thermal resistance of the electrodes, from thermal conduction analysis, making it possible to accurately determine the Peltier coefficient from temperature measurement. This method has the advantage of being able to determine the Peltier coefficient by temperature measurement rather than heat flow. However, since the temperature is measured at two locations on both ends of the sample, the information that can be obtained from the temperature measurement is limited, and the thermal conductivity and dimensions of the sample and current lead wire are included as unknowns in the measurement equation. Therefore, in order to measure the Peltier coefficient, not only is the temperature generated by the Peltier effect measured, but multiple measurement systems (synonymous with multiple measurement devices) with different measurement principles and boundary conditions are used. In particular, since the measurement of thermal conductivity requires the measurement of heat flow, problems similar to those in Non-Patent Document 1 may occur.
このように、従来技術では、熱流測定のために大がかりな計測装置を用いることになるだけではなく、異なる原理の系を持ち込むことにより、計測系に影響を及ぼす未知量とそれに伴う不確かさも付け加えてしまうという問題も加わる。例えば、熱伝導率を測定する場合、熱流量値、試料から周囲への熱損失量などが新たに考慮する要因となり、その不確かさがペルチェ係数の測定全体に占める主要な要因となってしまう。
As such, conventional technology not only requires the use of large-scale measurement equipment to measure heat flow, but also introduces a system based on a different principle, which adds unknown quantities that affect the measurement system and the associated uncertainties. For example, when measuring thermal conductivity, the heat flow value and the amount of heat loss from the sample to the surroundings become new factors that must be considered, and the uncertainty involved becomes a major factor in the overall measurement of the Peltier coefficient.
従って、本発明の目的は、一側面によれば、試料のペルチェ係数を簡便に測定できるようにするための技術を提供することである。
Therefore, in one aspect, an object of the present invention is to provide a technique for easily measuring the Peltier coefficient of a sample.
本発明に係るペルチェ係数算出方法は、(A)ペルチェ係数を測定する対象となる導体試料を一定温度にした後、導体試料に直流電流を流して導体試料の両端における温度を測定するステップと、(B)直流電流と実効値が等しい交流電流を導体試料に流して導体試料の端部及び中央部における温度を測定するステップと、(C)導体試料に直流電流を流して測定した導体試料の両端における温度と、交流電流を流して測定した導体試料の端部及び中央部における温度と、導体試料の電気抵抗値と、導体試料に流した電流の値とを用いて、ペルチェ係数を算出するステップとを含む。
The method for calculating the Peltier coefficient according to the present invention includes the steps of: (A) bringing a conductor sample, the object of which is to measure the Peltier coefficient, to a constant temperature, and then passing a direct current through the conductor sample to measure the temperature at both ends of the conductor sample; (B) passing an alternating current, the effective value of which is equal to the direct current, through the conductor sample to measure the temperature at the ends and center of the conductor sample; and (C) calculating the Peltier coefficient using the temperatures at both ends of the conductor sample measured by passing a direct current through the conductor sample, the temperatures at the ends and center of the conductor sample measured by passing an alternating current through the conductor sample, the electrical resistance value of the conductor sample, and the value of the current passed through the conductor sample.
[本発明の実施の形態に係る測定原理]
本実施の形態では、交流電流と直流電流を試料に加えてペルチェ熱とジュール熱を峻別し、試料端部で発生するペルチェ熱により作られる試料両端における温度差、ジュール熱により生じる試料中央部における温度上昇値を少なくとも測定することで、ペルチェ係数を算出する。このように試料の中央部の温度測定を1点追加することで、従来の計測方程式に含まれる未知数から熱伝導率や試料サイズ値を排除でき、同一の計測系で対応できる。これにより、異なる原理及び境界条件の計測系を複数用いる従来の方法と比べて簡便に測定できるようになる。さらに、熱伝導率や熱損失など主要な不確かな要因を計測系から排除できるので、高精度化も達成される。以下、その原理について、詳細に説明する。 [Measurement principle according to the embodiment of the present invention]
In this embodiment, an AC current and a DC current are applied to the sample to distinguish between Peltier heat and Joule heat, and the Peltier coefficient is calculated by measuring at least the temperature difference at both ends of the sample caused by the Peltier heat generated at the ends of the sample and the temperature rise at the center of the sample caused by the Joule heat. By adding one temperature measurement point at the center of the sample in this way, the thermal conductivity and sample size values can be eliminated from the unknowns included in the conventional measurement equation, and the same measurement system can be used. This makes it possible to perform measurements more easily than the conventional method using multiple measurement systems with different principles and boundary conditions. Furthermore, since major uncertain factors such as thermal conductivity and heat loss can be eliminated from the measurement system, high accuracy can be achieved. The principle will be described in detail below.
本実施の形態では、交流電流と直流電流を試料に加えてペルチェ熱とジュール熱を峻別し、試料端部で発生するペルチェ熱により作られる試料両端における温度差、ジュール熱により生じる試料中央部における温度上昇値を少なくとも測定することで、ペルチェ係数を算出する。このように試料の中央部の温度測定を1点追加することで、従来の計測方程式に含まれる未知数から熱伝導率や試料サイズ値を排除でき、同一の計測系で対応できる。これにより、異なる原理及び境界条件の計測系を複数用いる従来の方法と比べて簡便に測定できるようになる。さらに、熱伝導率や熱損失など主要な不確かな要因を計測系から排除できるので、高精度化も達成される。以下、その原理について、詳細に説明する。 [Measurement principle according to the embodiment of the present invention]
In this embodiment, an AC current and a DC current are applied to the sample to distinguish between Peltier heat and Joule heat, and the Peltier coefficient is calculated by measuring at least the temperature difference at both ends of the sample caused by the Peltier heat generated at the ends of the sample and the temperature rise at the center of the sample caused by the Joule heat. By adding one temperature measurement point at the center of the sample in this way, the thermal conductivity and sample size values can be eliminated from the unknowns included in the conventional measurement equation, and the same measurement system can be used. This makes it possible to perform measurements more easily than the conventional method using multiple measurement systems with different principles and boundary conditions. Furthermore, since major uncertain factors such as thermal conductivity and heat loss can be eliminated from the measurement system, high accuracy can be achieved. The principle will be described in detail below.
図1に、ペルチェ係数導出のための熱解析モデルを示す。図1に示すように、試料左端をx=0とし、長さLの試料の両端が、それぞれ熱コンダクタンスKwを有する電流リード線で熱浴ブロック(ヒートシンク)と熱的に繋がっている。なお、熱浴ブロックは、温度Teに保持されている。また、左側の電流リード線の長さはLcであり、右側の電流リード線の長さはLhとなっている。そして、直流電流を試料に流すと、ペルチェ効果により発生した熱流が、試料内で拡散により試料両端に流れ温度勾配が生じる。すなわち、図1に模式的に示すように、x=0付近で吸熱が生じて、x=L付近で発熱が生じるので、試料における温度勾配は、図2に示すようなものとなる。具体的には、x=0では、熱浴ブロックの温度Teよりも低い温度T0となり、x=L/2では、温度Teとなり、x=Lでは、温度Teよりも高い温度TLとなる。ここで、ペルチェ効果により生じた試料両端の温度差ΔTdcは、以下のように表される。
ΔTdc=TL-T0 FIG. 1 shows a thermal analysis model for deriving the Peltier coefficient. As shown in FIG. 1, the left end of the sample is x=0, and both ends of the sample with length L are thermally connected to a heat bath block (heat sink) by current leads having thermal conductance Kw. The heat bath block is held at temperature Te. The length of the left current lead is Lc , and the length of the right current lead is Lh . When a direct current is applied to the sample, a heat flow generated by the Peltier effect flows to both ends of the sample by diffusion within the sample, generating a temperature gradient. That is, as shown in FIG. 1, heat absorption occurs near x=0, and heat generation occurs near x=L, so the temperature gradient in the sample is as shown in FIG. 2. Specifically, at x=0, the temperature is T0 , which is lower than the temperature Te of the heat bath block, at x=L/2, the temperature is Te, and at x=L, the temperature is TL , which is higher than the temperature Te. Here, the temperature difference ΔT dc between both ends of the sample caused by the Peltier effect is expressed as follows:
ΔT dc = T L - T 0
ΔTdc=TL-T0 FIG. 1 shows a thermal analysis model for deriving the Peltier coefficient. As shown in FIG. 1, the left end of the sample is x=0, and both ends of the sample with length L are thermally connected to a heat bath block (heat sink) by current leads having thermal conductance Kw. The heat bath block is held at temperature Te. The length of the left current lead is Lc , and the length of the right current lead is Lh . When a direct current is applied to the sample, a heat flow generated by the Peltier effect flows to both ends of the sample by diffusion within the sample, generating a temperature gradient. That is, as shown in FIG. 1, heat absorption occurs near x=0, and heat generation occurs near x=L, so the temperature gradient in the sample is as shown in FIG. 2. Specifically, at x=0, the temperature is T0 , which is lower than the temperature Te of the heat bath block, at x=L/2, the temperature is Te, and at x=L, the temperature is TL , which is higher than the temperature Te. Here, the temperature difference ΔT dc between both ends of the sample caused by the Peltier effect is expressed as follows:
ΔT dc = T L - T 0
一方、交流電流を加えた場合にはペルチェ効果は相殺され、直線的な温度勾配はなくなり、ジュール効果による放物線状の温度分布が生じる。この場合における温度分布は、図3に示すようなものとなる。すなわち、x=0では、ジュール効果により温度上昇があるので、熱浴ブロックの温度TeからΔTcorr上昇して、この場合におけるT0となる。同様に、x=Lでも、温度TeからΔTcorr上昇して、この場合におけるTLとなる。一方、試料中では放物線状の温度分布が生じて、x=L/2において最も温度が高くなり、TL/2=T0+ΔTacとなる。なお、T0=TL=Te+ΔTcorrとなる。
On the other hand, when an AC current is applied, the Peltier effect is cancelled out, the linear temperature gradient disappears, and a parabolic temperature distribution occurs due to the Joule effect. The temperature distribution in this case is as shown in FIG. 3. That is, at x=0, the temperature rises due to the Joule effect, so the temperature rises from the temperature Te of the heat bath block by ΔT corr , which becomes T 0 in this case. Similarly, at x=L, the temperature rises from Te by ΔT corr , which becomes T L in this case. Meanwhile, a parabolic temperature distribution occurs in the sample, and the temperature is highest at x=L/2, where T L/2 =T 0 +ΔT ac . Note that T 0 =T L =Te+ΔT corr .
(a)直流電流の印加時における解析
直流電流を加えると試料を流れる熱流密度JQと試料の温度Tについては、以下の関係が成り立つ。
(a) Analysis when DC current is applied When DC current is applied, the following relationship holds for the heat flow density JQ flowing through the sample and the temperature T of the sample.
直流電流を加えると試料を流れる熱流密度JQと試料の温度Tについては、以下の関係が成り立つ。
ここで、aは試料の断面積を表し、Q[W]は熱流、π[V]は試料のペルチェ係数、T[K]は試料の温度、I[A]は電流密度、κ[W/(mK)]は試料の熱伝導率、ρ[Ωm]は試料の電気抵抗率、変数x[m]は試料座標である。図1のx=0及びx=Lでの熱的境界条件は、熱流が連続であることから、電流リード線の熱コンダクタンスKwを用いて次のように表すことができる。なお、物性値である熱伝導率、ペルチェ係数、電気抵抗率は、有限の温度係数を持つため、温度勾配や発熱がある導体においては、一般的に位置xの関数となるが、温度勾配やジュール発熱が十分に小さいとしてこの解析では無視している。但し、後に述べる実施例で示した検証実験もそのような条件で行っており、当業者であればこの前提条件は理解できると思われる。
Kw(Te-T0)=Q(0) (3)
Kw(TL-Te)=Q(L) (4) Here, a represents the cross-sectional area of the sample, Q [W] represents the heat flow, π [V] represents the Peltier coefficient of the sample, T [K] represents the temperature of the sample, I [A] represents the current density, κ [W/(mK)] represents the thermal conductivity of the sample, ρ [Ωm] represents the electrical resistivity of the sample, and the variable x [m] represents the coordinates of the sample. The thermal boundary conditions at x = 0 and x = L in FIG. 1 can be expressed as follows using the thermal conductance Kw of the current lead wire, since the heat flow is continuous. Note that the physical properties of thermal conductivity, Peltier coefficient, and electrical resistivity have finite temperature coefficients, and therefore generally become functions of position x in conductors with temperature gradients and heat generation, but are ignored in this analysis as the temperature gradient and Joule heat generation are sufficiently small. However, the verification experiments shown in the examples described later were also conducted under such conditions, and it is believed that those skilled in the art would understand this premise.
Kw(Te−T 0 )=Q(0) (3)
Kw(T L -Te)=Q(L) (4)
Kw(Te-T0)=Q(0) (3)
Kw(TL-Te)=Q(L) (4) Here, a represents the cross-sectional area of the sample, Q [W] represents the heat flow, π [V] represents the Peltier coefficient of the sample, T [K] represents the temperature of the sample, I [A] represents the current density, κ [W/(mK)] represents the thermal conductivity of the sample, ρ [Ωm] represents the electrical resistivity of the sample, and the variable x [m] represents the coordinates of the sample. The thermal boundary conditions at x = 0 and x = L in FIG. 1 can be expressed as follows using the thermal conductance Kw of the current lead wire, since the heat flow is continuous. Note that the physical properties of thermal conductivity, Peltier coefficient, and electrical resistivity have finite temperature coefficients, and therefore generally become functions of position x in conductors with temperature gradients and heat generation, but are ignored in this analysis as the temperature gradient and Joule heat generation are sufficiently small. However, the verification experiments shown in the examples described later were also conducted under such conditions, and it is believed that those skilled in the art would understand this premise.
Kw(Te−T 0 )=Q(0) (3)
Kw(T L -Te)=Q(L) (4)
次に、(2)式は簡単に積分できるのでxで積分し、(1)式の熱流密度の式を用いて変形すると、試料両端x=0及びx=Lの熱流Q(0)及びQ(L)について、以下の式が得られる。
ここで、試料の熱コンダクタンスK及び電気抵抗率Rを定義に従ってK=(κa)/L、電気抵抗率をR=(ρL)/aとした。(3)式及び(4)式の境界条件を用いると、(5)式及び(6)式は次のように表される。
Next, since equation (2) can be easily integrated, we integrate it with respect to x and transform it using the heat flow density equation (1), and obtain the following equations for the heat flows Q(0) and Q(L) at both ends of the sample, x = 0 and x = L.
Here, the thermal conductance K and electrical resistivity R of the sample are defined as K = (κa)/L and the electrical resistivity R = (ρL)/a. Using the boundary conditions of equations (3) and (4), equations (5) and (6) can be expressed as follows:
これは熱伝導方程式から導かれる厳密な電気エネルギーと熱エネルギーのバランスの式である。左辺はペルチェ効果による発熱を表す。右辺は試料の熱伝導による熱の拡散、ジュール発熱、リード線による熱損失を表す。すなわち、試料両端で発生したペルチェ熱および試料内部で発生したジュール熱が、試料の熱伝導とリード線の熱伝導による熱流と等しいことを表している。(7)式及び(8)式の両辺を足して、ペルチェ係数について解くと次の式が得られる。
This is a strict equation for the balance between electrical energy and thermal energy derived from the heat conduction equation. The left side represents heat generation due to the Peltier effect. The right side represents heat diffusion due to thermal conduction in the sample, Joule heat, and heat loss through the lead wires. In other words, it represents that the Peltier heat generated at both ends of the sample and the Joule heat generated inside the sample are equal to the heat flow due to thermal conduction in the sample and thermal conduction in the lead wires. Adding both sides of equations (7) and (8) and solving for the Peltier coefficient, we obtain the following equation.
よって、試料両端の温度差ΔTdc=TL-T0、直流電流I、試料の熱コンダクタンスK、電流リード線の熱コンダクタンスKwを求めればペルチェ係数πが得られることが分かる。このように、従来の計測方程式には、試料の温度勾配ΔTdc以外にも測定を要するパラメータが残ってしまう。
Therefore, it can be seen that the Peltier coefficient π can be obtained by calculating the temperature difference between both ends of the sample, ΔT dc = T L - T 0 , the DC current I, the thermal conductance K of the sample, and the thermal conductance Kw of the current lead wire. As such, in the conventional measurement equation, there are still other parameters that need to be measured in addition to the temperature gradient ΔT dc of the sample.
(b)交流電流の印加時における解析
(9)式についての問題は、試料に交流電流を加えた際、試料の中央と端部の温度差を測定することにより解決される。ここで試料内部で生じている温度分布について考察を行う。この温度分布は(2)式を解くことにより簡単に求めることができて、試料端部の温度をT0及びTLとして温度分布は次のとおりである。なお、ここでも電気抵抗率と熱伝導率の温度依存性は無視している。
(b) Analysis when AC current is applied The problem with equation (9) can be solved by measuring the temperature difference between the center and the end of the sample when AC current is applied to the sample. Here, we consider the temperature distribution occurring inside the sample. This temperature distribution can be easily obtained by solving equation (2), and the temperature distribution is as follows, with the temperatures at the ends of the sample being T0 and TL . Note that here too, the temperature dependence of electrical resistivity and thermal conductivity is ignored.
(9)式についての問題は、試料に交流電流を加えた際、試料の中央と端部の温度差を測定することにより解決される。ここで試料内部で生じている温度分布について考察を行う。この温度分布は(2)式を解くことにより簡単に求めることができて、試料端部の温度をT0及びTLとして温度分布は次のとおりである。なお、ここでも電気抵抗率と熱伝導率の温度依存性は無視している。
そして、境界条件である(3)式及び(4)式を例えば2元連立方程式を解くことでT0及びTLは、以下のように求まる。
Then, by solving the boundary conditions of equations (3) and (4) as simultaneous equations with two unknowns, T 0 and T L can be obtained as follows:
そして、(10)式に対してx=L/2及びx=0を代入すると、試料及び電流リード線の熱コンダクタンスK及びKwが、試料中央部及び端部の温度を用いて、以下のように表される。
Then, by substituting x=L/2 and x=0 into equation (10), the thermal conductances K and Kw of the sample and the current lead wire are expressed as follows using the temperatures of the center and ends of the sample.
よって、(9)式に(12)式及び(13)式を代入すると、以下の式が得られる。
このように、直流電流を加えた際に発生するペルチェ効果による試料両端の温度差ΔTdc、交流電流を加えた際にジュール効果により発生する試料中央部の温度と試料端部の温度との差ΔTacが得られれば、試料の熱伝導率値や寸法値を別途測定することなく簡便な方法にてペルチェ係数πを求めることができるようになる。さらに、熱伝導率や熱損失など主要な不確かな要因を計測系から排除できるので、この観点において高精度化が達成される。
Therefore, by substituting equations (12) and (13) into equation (9), the following equation is obtained.
In this way, if the temperature difference ΔT dc between both ends of the sample caused by the Peltier effect when a direct current is applied and the temperature difference ΔT ac between the temperature at the center of the sample and the temperature at the end of the sample caused by the Joule effect when an alternating current is applied can be obtained, the Peltier coefficient π can be obtained in a simple manner without separately measuring the thermal conductivity value or dimensional values of the sample. Furthermore, since major uncertain factors such as thermal conductivity and heat loss can be eliminated from the measurement system, high accuracy can be achieved in this respect.
なお、(14)式におけるRIΔTdc/(8ΔTac)は、熱損失がない場合におけるペルチェ係数を表しており、RIΔTdc/(8ΔTac)×(2ΔTac)/ΔTcorrは補正項を表しており、熱損失により失われたペルチェ熱を表す。
In addition, RIΔT dc /(8ΔT ac ) in equation (14) represents the Peltier coefficient when there is no heat loss, and RIΔT dc /(8ΔT ac )×(2ΔT ac )/ΔT corr represents a correction term, which represents the Peltier heat lost due to heat loss.
また、(9)式においても、KΔTac/Iについては熱損失がない場合におけるペルチェ係数を表しており、KΔTac/I×Kw/(2K)は、理論的な補正項を表しており、熱損失により失われたペルチェ係数を表す。
Also in equation (9), KΔT ac /I represents the Peltier coefficient when there is no heat loss, and KΔT ac /I×K w /(2K) represents a theoretical correction term, which represents the Peltier coefficient lost due to heat loss.
[実施の形態]
図4を用いて本実施の形態に係る測定システムの構成例を示す。本実施の形態に係る測定システムは、直流電源11と、交流電源12と、導体試料100に流す電流を直流と交流とで切り替えるためのスイッチ13と、導体試料100等を一定温度Teに保持するための熱浴ブロック31及び32と、直流電源11及び交流電源12と導体試料100の一端とを接続する電流リード線14と、スイッチ13と導体試料100の他端とを接続する電流リード線15と、導体試料100の両端間に生ずる電圧を測定するための電圧計21と、導体試料100の両端及び中央部の温度測定を行う温度測定部40と、温度測定部40の測定結果などに基づきペルチェ係数を算出する演算部50とを有する。 [Embodiment]
An example of the configuration of the measurement system according to the present embodiment is shown in Fig. 4. The measurement system according to the present embodiment includes aDC power source 11, an AC power source 12, a switch 13 for switching the current flowing through the conductor sample 100 between DC and AC, heat bath blocks 31 and 32 for maintaining the conductor sample 100 and the like at a constant temperature Te, a current lead wire 14 connecting the DC power source 11 and the AC power source 12 to one end of the conductor sample 100, a current lead wire 15 connecting the switch 13 to the other end of the conductor sample 100, a voltmeter 21 for measuring the voltage generated between both ends of the conductor sample 100, a temperature measurement unit 40 for measuring the temperatures of both ends and the center of the conductor sample 100, and a calculation unit 50 for calculating the Peltier coefficient based on the measurement results of the temperature measurement unit 40 and the like.
図4を用いて本実施の形態に係る測定システムの構成例を示す。本実施の形態に係る測定システムは、直流電源11と、交流電源12と、導体試料100に流す電流を直流と交流とで切り替えるためのスイッチ13と、導体試料100等を一定温度Teに保持するための熱浴ブロック31及び32と、直流電源11及び交流電源12と導体試料100の一端とを接続する電流リード線14と、スイッチ13と導体試料100の他端とを接続する電流リード線15と、導体試料100の両端間に生ずる電圧を測定するための電圧計21と、導体試料100の両端及び中央部の温度測定を行う温度測定部40と、温度測定部40の測定結果などに基づきペルチェ係数を算出する演算部50とを有する。 [Embodiment]
An example of the configuration of the measurement system according to the present embodiment is shown in Fig. 4. The measurement system according to the present embodiment includes a
熱浴ブロック31及び32には、図示しないヒータと温度計が取り付けられており、温度調節により一定温度Teに保つように制御する。演算部50は、この制御に用いられる場合もある。また、対流による熱損失を避けるため、電流リード線14及び15の少なくとも一部及び導体試料100と、熱浴ブロック31及び32とは、真空環境に置くことが好ましい。また、輻射による導体試料100と外部の熱交換を抑制するため、導体試料100全体は熱シールドで覆うことが好ましい。なお、熱浴ブロック31及び32により、電流リード線14及び15の少なくとも一部及び導体試料100の温度も温度Teで熱平衡となるようにする。そのため、電流リード線14は電気絶縁被覆16を介して熱浴ブロック32に接しており、電流リード線15は電気絶縁被覆17を介して熱浴ブロック31に接している。電流リード線14及び15に熱抵抗が高いものを用いることで、(14)式における補正項の値が小さくなるので、補正項なしでも高精度なペルチェ係数を得ることが出来るようになる。熱浴ブロック31及び32は、例えば銅などの金属からなる。
Heaters and thermometers (not shown) are attached to the heat bath blocks 31 and 32, and the temperature is controlled to be kept constant at Te. The calculation unit 50 may be used for this control. In order to avoid heat loss due to convection, it is preferable to place at least a part of the current leads 14 and 15, the conductor sample 100, and the heat bath blocks 31 and 32 in a vacuum environment. In order to suppress heat exchange between the conductor sample 100 and the outside due to radiation, it is preferable to cover the entire conductor sample 100 with a heat shield. The heat bath blocks 31 and 32 ensure that the temperatures of at least a part of the current leads 14 and 15 and the conductor sample 100 are also in thermal equilibrium at temperature Te. For this reason, the current lead 14 is in contact with the heat bath block 32 via the electrical insulating coating 16, and the current lead 15 is in contact with the heat bath block 31 via the electrical insulating coating 17. By using current leads 14 and 15 with high thermal resistance, the value of the correction term in equation (14) becomes small, making it possible to obtain a highly accurate Peltier coefficient without the correction term. Heat bath blocks 31 and 32 are made of a metal such as copper.
温度測定部40は、導体試料100の一端の温度を測定するための熱電対42と、導体試料100の中央部の温度を測定するための熱電対44と、導体試料100の他端の温度を測定するための熱電対46とを含む。電圧計21は、交流電流を流した際に導体試料100の両端に発生する電圧を測定して、導体試料100の電気抵抗Rを得るために用いられる。演算部50は、例えばパーソナルコンピュータなどの演算装置であり、(14)式全体又は(14)式の第1項によりペルチェ係数を算出するプログラムを、プロセッサが実行することで主たる機能が実現される。
The temperature measuring unit 40 includes a thermocouple 42 for measuring the temperature of one end of the conductor sample 100, a thermocouple 44 for measuring the temperature of the center of the conductor sample 100, and a thermocouple 46 for measuring the temperature of the other end of the conductor sample 100. The voltmeter 21 is used to measure the voltage generated across both ends of the conductor sample 100 when an alternating current is passed through it, and to obtain the electrical resistance R of the conductor sample 100. The calculation unit 50 is a calculation device such as a personal computer, and the main function is realized by a processor executing a program that calculates the Peltier coefficient using the entire formula (14) or the first term of formula (14).
次に、図5を用いて、本実施の形態に係る測定システムによるペルチェ係数の算出手順について説明する。まず、温度測定のための準備を実施する(ステップS1)。図4に示すように、導体試料100の両端及び中央部に熱電対を取り付けたり、導体試料100の両端に電流リード線14及び15を接続する。電流リード線14及び15は、電気絶縁被覆16及び17を介して熱浴ブロック31及び32に接するようにする。さらに、導体試料100等を真空環境に置き、熱浴ブロック31及び32を温度Teに保ち、導体試料100の温度についても温度Teとなる熱平衡となるまで待つ。すなわち、この段階でも、導体試料100の端部及び中央部の温度を測定して、温度Teとなっているか否かを確認する。
Next, the calculation procedure of the Peltier coefficient by the measurement system according to this embodiment will be described with reference to FIG. 5. First, preparations for temperature measurement are made (step S1). As shown in FIG. 4, thermocouples are attached to both ends and the center of the conductor sample 100, and current leads 14 and 15 are connected to both ends of the conductor sample 100. The current leads 14 and 15 are in contact with the heat bath blocks 31 and 32 via the electrical insulating coatings 16 and 17. Furthermore, the conductor sample 100 and the like are placed in a vacuum environment, the heat bath blocks 31 and 32 are kept at a temperature Te, and the temperature of the conductor sample 100 is also kept at a temperature Te until it reaches thermal equilibrium. That is, even at this stage, the temperatures of the ends and center of the conductor sample 100 are measured to confirm whether they have reached temperature Te.
その後、スイッチ13を直流電源11に接続させることで導体試料100に直流電流を流して、温度測定部40により導体試料100の両端の温度を測定する(ステップS3)。これにより、T0及びTLが得られて、ΔTdc=TL-T0が得られることになる。測定後には、スイッチ13により導体試料100にいずれの電源からも電流が流れない状態にして、導体試料100が熱浴ブロック31及び32の温度Teに戻るようにする。
Thereafter, the switch 13 is connected to the DC power source 11 to pass a DC current through the conductor sample 100, and the temperature measuring unit 40 measures the temperatures at both ends of the conductor sample 100 (step S3). As a result, T 0 and T L are obtained, and ΔT dc =T L -T 0 is obtained. After the measurement, the switch 13 is used to stop current from flowing through the conductor sample 100 from either power source, so that the conductor sample 100 returns to the temperature Te of the heat bath blocks 31 and 32.
その後、スイッチ13を交流電源12に接続させることで導体試料100に交流電流(交流電流の実効値は、ステップS3で流した直流電流と同じにする)を流して、温度測定部40により導体試料100の端部の温度(T0、TL)及び中央部の温度(TL/2)を測定する(ステップS5)。導体試料100の端部は、両端であっても良いが一方の端部であっても良い。図3を用いて説明したとおり、交流電流を流した際のx=0の温度T0とx=Lの温度TLは原理的には同じなのでいずれを用いても良い。場合によってはそれらの平均値を算出しても良い。この測定により、ΔTac(=TL/2-T0=TL/2-TL)と、ΔTcorr(=T0-Te=TL-Te)が得られることになる。
Thereafter, the switch 13 is connected to the AC power source 12 to pass an AC current (the effective value of the AC current is the same as the DC current passed in step S3) through the conductor sample 100, and the temperature (T 0 , T L ) of the end portion of the conductor sample 100 and the temperature (T L/2 ) of the center portion are measured by the temperature measuring unit 40 (step S5). The end portion of the conductor sample 100 may be both ends or one end. As described with reference to FIG. 3, the temperature T 0 at x=0 and the temperature T L at x=L when an AC current is passed are the same in principle, so either one may be used. In some cases, their average values may be calculated. This measurement provides ΔT ac (=T L/2 -T 0 =T L/2 -T L ) and ΔT corr (=T 0 -Te=T L -Te).
さらに、スイッチ13を交流電源12に接続させることで導体試料100に交流電流(交流電流の実効値は、ステップS3で流した直流電流と同じにする)を流して、すなわちステップS5と同じようにして、電圧計21により導体試料100の端部の電圧を測定する(ステップS7)。測定された電圧V/流した電流Iにより、導体試料100の電気抵抗Rが得られることになる。
Furthermore, by connecting switch 13 to AC power source 12, an AC current (the effective value of the AC current is set to be the same as the DC current passed in step S3) is passed through conductor sample 100, i.e., in the same manner as in step S5, the voltage at the end of conductor sample 100 is measured by voltmeter 21 (step S7). The electrical resistance R of conductor sample 100 is obtained by dividing the measured voltage V by the passed current I.
そして、演算部50により、測定結果に基づきペルチェ係数を算出して、例えば表示装置その他の出力装置に出力する(ステップS9)。ステップS3ではΔTdcが得られ、ステップS5ではΔTac及びTcorrが得られ、ステップS7では電気抵抗Rが得られるので、流した電流Iをさらに用いれば、(14)式によりペルチェ係数πが算出される。なお、補正項を無視する場合には、ペルチェ係数πはRIΔTdc/(8ΔTac)で算出されるので、ΔTcorrを算出せずとも良い。
Then, the calculation unit 50 calculates the Peltier coefficient based on the measurement results and outputs it to, for example, a display device or other output device (step S9). Since ΔT dc is obtained in step S3, ΔT ac and T corr are obtained in step S5, and the electrical resistance R is obtained in step S7, the Peltier coefficient π is calculated by equation (14) by further using the flowing current I. Note that if the correction term is ignored, the Peltier coefficient π is calculated as RIΔT dc /(8ΔT ac ), so it is not necessary to calculate ΔT corr .
以上のような手順にて、導体試料100の3カ所の温度測定により簡便にペルチェ係数を算出できるようになる。この際、導体試料100の寸法の測定や、熱伝導率や熱損失など主要な不確かな要因を計測系から排除できるので、この観点においても高精度化が達成される。
By following the above procedure, the Peltier coefficient can be easily calculated by measuring the temperature at three points on the conductor sample 100. In this case, major uncertain factors such as the measurement of the dimensions of the conductor sample 100, thermal conductivity, and heat loss can be eliminated from the measurement system, so high accuracy is achieved from this perspective as well.
[実施例]
図4に示した測定システムを用い、導体試料100にはn型半導体材料であるBi2Te3の多結晶試料を用いた。30mm×3mm×2mmの導体試料100が、熱コンダクタンスKwを有する電流リード線14及び15で熱浴ブロック31及び32と熱的に繋がれた。対流による熱損失を防ぐため、真空環境とした。輻射による導体試料100と外部の熱交換を抑制するため、導体試料100全体は熱シールドで覆った。この実施例における交流電流の実効値は25mA、交流周波数は62.5Hzとした。 [Example]
The measurement system shown in FIG. 4 was used, and a polycrystalline sample of Bi2Te3 , an n-type semiconductor material, was used as the conductor sample 100. Theconductor sample 100, measuring 30 mm x 3 mm x 2 mm, was thermally connected to the heat bath blocks 31 and 32 by current leads 14 and 15 having a thermal conductance Kw. A vacuum environment was used to prevent heat loss due to convection. The entire conductor sample 100 was covered with a heat shield to suppress heat exchange between the conductor sample 100 and the outside due to radiation. In this example, the effective value of the AC current was 25 mA, and the AC frequency was 62.5 Hz.
図4に示した測定システムを用い、導体試料100にはn型半導体材料であるBi2Te3の多結晶試料を用いた。30mm×3mm×2mmの導体試料100が、熱コンダクタンスKwを有する電流リード線14及び15で熱浴ブロック31及び32と熱的に繋がれた。対流による熱損失を防ぐため、真空環境とした。輻射による導体試料100と外部の熱交換を抑制するため、導体試料100全体は熱シールドで覆った。この実施例における交流電流の実効値は25mA、交流周波数は62.5Hzとした。 [Example]
The measurement system shown in FIG. 4 was used, and a polycrystalline sample of Bi2Te3 , an n-type semiconductor material, was used as the conductor sample 100. The
ペルチェ熱が減衰し、十分に小さくなる特性周波数があるので、正確に測定するためには、その特性周波数よりも十分に高い特定の周波数を選んで測定する。そのために、適当な範囲の周波数で、導体試料100の両端に発生する、ペルチェ効果による導体試料100の温度差を測定し、その温度差が周波数に依存しない範囲で、測定のための周波数を決める。図6には測定例を示す。すなわち、横軸は周波数を表し、縦軸は導体試料100の両端の温度差[K]を表している。この例では、1Hz以上で周波数に依存せず温度差が一定となることから、1Hz以上の周波数を選択すればよいことになる。10Hz、100Hzなど整数値でもよいが、電源周波数のノイズを避けるため、62.5Hzを選択するとより正確な測定ができる。
There is a characteristic frequency at which the Peltier heat decays and becomes sufficiently small, so in order to measure accurately, a specific frequency that is sufficiently higher than that characteristic frequency is selected. For this purpose, the temperature difference in the conductor sample 100 caused by the Peltier effect at both ends of the conductor sample 100 is measured at an appropriate range of frequencies, and the frequency for measurement is determined within a range in which the temperature difference is independent of frequency. Figure 6 shows an example of measurement. That is, the horizontal axis represents frequency, and the vertical axis represents the temperature difference [K] at both ends of the conductor sample 100. In this example, since the temperature difference is constant and independent of frequency at 1 Hz or higher, a frequency of 1 Hz or higher should be selected. Integer values such as 10 Hz and 100 Hz are also acceptable, but to avoid power supply frequency noise, selecting 62.5 Hz allows for more accurate measurement.
一方、電流値が大きすぎると、ジュール効果により吸発熱量のアンバランスを招き、温度差が電流に比例して増加しなくなる。従って、直線的に変化する電流の領域を見出し、その範囲で電流値を定める。図7には測定例を示す。図7において、横軸は直流電流[mA]を表しており、縦軸は導体試料100の両端の温度差[K]を表している。これを見ると-60mA以上+60mA以下の範囲であれば、直流電流に十分に比例して温度差が変化することが分かる。
On the other hand, if the current value is too large, the Joule effect will cause an imbalance in the amount of heat absorbed and the temperature difference will no longer increase in proportion to the current. Therefore, a region of current that changes linearly is found, and the current value is set within that range. Figure 7 shows an example of a measurement. In Figure 7, the horizontal axis represents the DC current [mA], and the vertical axis represents the temperature difference [K] between both ends of the conductor sample 100. It can be seen that if the range is between -60 mA and +60 mA, the temperature difference changes in full proportion to the DC current.
図8に、電流リード線14及び15の長さを変えて意図的に導体試料100からの熱の損失量を変えながら、ペルチェ係数を算出した結果を表す。図8の横軸は、電流リード線の熱コンダクタンス[mW/K]を表し、縦軸はペルチェ係数[mV]を表し、黒丸は補正項なしで算出したペルチェ係数を表し、黒四角は(14)式で算出したペルチェ係数を表す。ペルチェ係数は試料固有の値なので、熱損失にかかわらず一定である。しかしながら、黒丸で示したように、補正項を考慮しない場合、電流リード線14及び15の熱コンダクタンスが大きくなると、ペルチェ係数が増加する。これは、導体試料100の端部で発生したペルチェ熱が電流リード線14及び15を介して流出してしまい、導体試料100の両端の温度差が低下してしまうためである。一方、電流リード線14及び15の熱コンダクタンスの影響を補正すれば、黒四角で表すように、電流リード線14及び15からの熱損失にほぼ依存せず、一定になることがわかる。
Figure 8 shows the results of calculating the Peltier coefficient while intentionally changing the amount of heat loss from the conductor sample 100 by changing the length of the current leads 14 and 15. The horizontal axis of Figure 8 represents the thermal conductance [mW/K] of the current leads, the vertical axis represents the Peltier coefficient [mV], the black circles represent the Peltier coefficient calculated without the correction term, and the black squares represent the Peltier coefficient calculated using equation (14). Since the Peltier coefficient is a value specific to the sample, it is constant regardless of heat loss. However, as shown by the black circles, if the correction term is not taken into account, the Peltier coefficient increases as the thermal conductance of the current leads 14 and 15 increases. This is because the Peltier heat generated at the ends of the conductor sample 100 flows out through the current leads 14 and 15, reducing the temperature difference between both ends of the conductor sample 100. On the other hand, if the effect of the thermal conductance of the current leads 14 and 15 is corrected, it becomes almost independent of the heat loss from the current leads 14 and 15 and becomes constant, as shown by the black squares.
また、補正が正しく働いているか検証する。補正値の理論値は、(9)式の2項目であるKΔTac/I×Kw/(2K)で分かるように、電流リード線14及び15の熱コンダクタンスKwと導体試料100の熱コンダクタンスKとをさらに用いることで求めることが出来る。そこで、導体試料100と電流リード線14及び15の熱伝導率及び寸法を正確に計測し、これらの値から計算したペルチェ係数の補正値を図9における実線で示す。図9の横軸は、電流リード線14及び15の熱コンダクタンス[mW/K]を表し、縦軸は補正値[mV]を表す。(14)式の補正項から求めた補正値(すなわち測定値)と、補正値の理論値とは、略一致した。
Also, whether the correction works correctly is verified. As can be seen from the two terms of formula (9), KΔT ac /I×K w /(2K), the theoretical value of the correction value can be obtained by further using the thermal conductance Kw of the current leads 14 and 15 and the thermal conductance K of the conductor sample 100. Therefore, the thermal conductivity and dimensions of the conductor sample 100 and the current leads 14 and 15 are accurately measured, and the correction value of the Peltier coefficient calculated from these values is shown by a solid line in FIG. 9. The horizontal axis of FIG. 9 represents the thermal conductance [mW/K] of the current leads 14 and 15, and the vertical axis represents the correction value [mV]. The correction value (i.e., the measured value) obtained from the correction term of formula (14) and the theoretical value of the correction value were approximately equal.
このように、本実施の形態を用いれば、異なる原理及び境界条件の計測系を複数用意することになる従来の方法と異なり、ひとつの計測系で温度と電気抵抗値の複合的な測定をしてペルチェ係数を求めることができる。これは、導体試料の中央の温度測定を1点だけ追加し、従来の計測方程式に含まれる未知数から熱伝導率や試料サイズ値を排除することで実現できたものである。これにより、計測方程式から熱伝導率値や幾何形状値を排除できたので測定の高精度化が達成される。この際に、測定システムの構成及び測定方法は、簡素なものである。
In this way, by using this embodiment, unlike conventional methods in which multiple measurement systems with different principles and boundary conditions are prepared, it is possible to obtain the Peltier coefficient by performing a composite measurement of temperature and electrical resistance value with a single measurement system. This is achieved by adding a single temperature measurement point at the center of the conductive sample and eliminating thermal conductivity and sample size values from the unknowns included in the conventional measurement equation. This makes it possible to eliminate thermal conductivity values and geometric shape values from the measurement equation, thereby achieving high measurement accuracy. In this case, the configuration of the measurement system and the measurement method are simple.
以上本発明の実施の形態について説明したが、本発明はこれに限定されるものではない。例えば、電圧計21も演算部50に接続されるような形であっても良い。さらに、スイッチ13のスイッチング制御や熱浴ブロック31及び32の温度制御についても、演算部50により行うようにしても良い。また、図4に示した手順についても、測定結果に影響を与えないように変更するようにしても良い。例えばΔTcorrを測定するためには、交流電流を流す前における導体試料100の端部における温度T0=TL=Teを用いるが、ステップS1で測定したものを用いても良いし、他のタイミングで電流を流さずに温度を測定してその値を用いても良い。交流電流と直流電流とを流す順番を入れ替えても良い。さらに、ペルチェ熱による電気抵抗Rの過大評価を避けるため、交流電流を導体試料100に流す交流法を用いたが、測定結果に影響を与えないよう変更しても良い。例えば、ステップ状の電流を導体試料100に流し、試料全体にペルチェ熱が行きわたる前に電圧の測定を行う時間分解測定法を用いても良い。
Although the embodiment of the present invention has been described above, the present invention is not limited to this. For example, the voltmeter 21 may also be connected to the calculation unit 50. Furthermore, the switching control of the switch 13 and the temperature control of the heat bath blocks 31 and 32 may also be performed by the calculation unit 50. Furthermore, the procedure shown in FIG. 4 may also be modified so as not to affect the measurement results. For example, to measure ΔT corr , the temperature T 0 =T L =Te at the end of the conductor sample 100 before the AC current is passed is used, but the temperature measured in step S1 may be used, or the temperature may be measured at another timing without passing the current and the value may be used. The order in which the AC current and the DC current are passed may be interchanged. Furthermore, in order to avoid overestimating the electrical resistance R due to Peltier heat, the AC method in which the AC current is passed through the conductor sample 100 is used, but the method may be modified so as not to affect the measurement results. For example, a time-resolved measurement method in which a step-like current is passed through the conductor sample 100 and the voltage is measured before the Peltier heat is distributed throughout the sample may be used.
なお、上で述べた演算部50は、例えば図10に示すようなコンピュータ装置であって、メモリ2501とCPU2503とハードディスク・ドライブ(HDD)2505と表示装置2509に接続される表示制御部2507とリムーバブル・ディスク2511用のドライブ装置2513と入力装置2515とネットワークに接続するための通信制御部2517とがバス2519で接続されている。オペレーティング・システム(OS:Operating System)及び本実施の形態における処理を実施するためのアプリケーション・プログラムは、HDD2505に格納されており、CPU2503により実行される際にはHDD2505からメモリ2501に読み出される。CPU2503は、アプリケーション・プログラムの処理内容に応じて表示制御部2507、通信制御部2517、ドライブ装置2513を制御して、所定の動作を行わせる。また、処理途中のデータについては、主としてメモリ2501に格納されるが、HDD2505に格納されるようにしてもよい。本発明の実施例では、上で述べた処理を実施するためのアプリケーション・プログラムはコンピュータ読み取り可能なリムーバブル・ディスク2511に格納されて頒布され、ドライブ装置2513からHDD2505にインストールされる。インターネットなどのネットワーク及び通信制御部2517を経由して、HDD2505にインストールされる場合もある。このようなコンピュータ装置は、上で述べたCPU2503、メモリ2501などのハードウエアとOS及びアプリケーション・プログラムなどのプログラムとが有機的に協働することにより、上で述べたような各種機能を実現する。
The calculation unit 50 described above is, for example, a computer device as shown in FIG. 10, in which the memory 2501, the CPU 2503, the hard disk drive (HDD) 2505, the display control unit 2507 connected to the display device 2509, the drive device 2513 for the removable disk 2511, the input device 2515, and the communication control unit 2517 for connecting to the network are connected by a bus 2519. The operating system (OS) and the application program for implementing the processing in this embodiment are stored in the HDD 2505, and when executed by the CPU 2503, are read from the HDD 2505 to the memory 2501. The CPU 2503 controls the display control unit 2507, the communication control unit 2517, and the drive device 2513 according to the processing contents of the application program to perform a predetermined operation. Data during processing is mainly stored in the memory 2501, but may be stored in the HDD 2505. In an embodiment of the present invention, an application program for carrying out the above-mentioned processes is distributed stored on a computer-readable removable disk 2511, and is installed from the drive device 2513 to the HDD 2505. It may also be installed to the HDD 2505 via a network such as the Internet and a communication control unit 2517. Such a computer device realizes the various functions described above by organic cooperation between the above-mentioned hardware such as the CPU 2503 and memory 2501, and programs such as the OS and application programs.
以上述べた実施の形態をまとめると以下のようになる。
The above-mentioned embodiment can be summarized as follows:
本実施の形態に係るペルチェ係数算出方法は、(A)ペルチェ係数を測定する対象となる導体試料を一定温度にした後、導体試料に直流電流を流して導体試料の両端における温度を測定するステップと、(B)直流電流と実効値が等しい交流電流を導体試料に流して導体試料の端部及び中央部における温度を測定するステップと、(C)導体試料に直流電流を流して測定した導体試料の両端における温度と、交流電流を流して測定した導体試料の端部及び中央部における温度と、導体試料の電気抵抗値と、導体試料に流した電流の値とを用いて、ペルチェ係数を算出するステップとを含む。
The method for calculating the Peltier coefficient according to this embodiment includes the steps of: (A) bringing the conductor sample, the object of which is to measure the Peltier coefficient, to a constant temperature, and then passing a direct current through the conductor sample to measure the temperature at both ends of the conductor sample; (B) passing an alternating current, the effective value of which is equal to the direct current, through the conductor sample to measure the temperature at the ends and center of the conductor sample; and (C) calculating the Peltier coefficient using the temperatures at both ends of the conductor sample measured by passing a direct current through the conductor sample, the temperatures at the ends and center of the conductor sample measured by passing an alternating current through the conductor sample, the electrical resistance value of the conductor sample, and the value of the current passed through the conductor sample.
このように、導体試料のサイズや熱伝導率などを得ることなく温度測定によってペルチェ係数を算出できるようになるので、試料のペルチェ係数を簡便に得ることが出来るようになる。なお、熱伝導率などに基づく不確かな要因を計測系から排除できるので、この観点において、ペルチェ係数の高精度化も図られる。
In this way, it is possible to calculate the Peltier coefficient by measuring the temperature without obtaining the size or thermal conductivity of the conductor sample, making it possible to easily obtain the Peltier coefficient of the sample. Furthermore, since uncertain factors based on thermal conductivity, etc. can be eliminated from the measurement system, the Peltier coefficient can also be obtained with high accuracy.
上記方法は、導体試料に電流を流さない状態における導体試料の端部における温度を測定するステップをさらに含むようにしても良い。この場合、ペルチェ係数を算出するステップにおいて、電流を流さない状態における導体試料の端部における温度をさらに用いて、ペルチェ係数を算出するようにしても良い。電流を流さない状態における導体試料の端部における温度を用いることで、熱損失分を補正することが出来るようになる。具体的には(14)式の補正項でペルチェ係数を補正できるようになる。
The above method may further include a step of measuring the temperature at the end of the conductor sample when no current is flowing through the conductor sample. In this case, in the step of calculating the Peltier coefficient, the temperature at the end of the conductor sample when no current is flowing may be further used to calculate the Peltier coefficient. By using the temperature at the end of the conductor sample when no current is flowing, it becomes possible to correct for heat loss. Specifically, it becomes possible to correct the Peltier coefficient using the correction term in equation (14).
なお、ペルチェ係数を算出するステップにおいて、導体試料に直流電流を流して測定した導体試料の両端における温度の差と、交流電流を流して測定した導体試料の中央部における温度と交流電流を流して測定した導体試料の端部における温度との差とを算出するようにしても良い。ΔTdc及びΔTacが得られるので、少なくとも(14)式の第1項を算出できる。
In addition, in the step of calculating the Peltier coefficient, the difference in temperature at both ends of the conductor sample measured by passing a direct current through the conductor sample, and the difference in temperature between the center of the conductor sample measured by passing an alternating current and the end of the conductor sample measured by passing an alternating current may be calculated. Since ΔT dc and ΔT ac are obtained, at least the first term of formula (14) can be calculated.
また、ペルチェ係数を算出するステップにおいて、導体試料の電気抵抗値をRと表し、導体試料に流した電流の値をIと表し、導体試料に直流電流を流して測定した導体試料の両端における温度の差をΔTdcと表し、交流電流を流して測定した導体試料の中央部における温度と交流電流を流して測定した導体試料の端部における温度との差をΔTacと表した場合、
ペルチェ係数を、
RIΔTdc/(8ΔTac)
を用いて算出するようにしても良い。このように、(14)式の第1項だけでも、電流リード線の熱抵抗が高ければ、十分な精度にてペルチェ係数が算出できる場合もある。 Furthermore, in the step of calculating the Peltier coefficient, if the electrical resistance value of the conductor sample is represented as R, the value of the current passed through the conductor sample is represented as I, the temperature difference at both ends of the conductor sample measured by passing a direct current through the conductor sample is represented as ΔT dc , and the temperature difference between the center of the conductor sample measured by passing an alternating current and the temperature at both ends of the conductor sample measured by passing an alternating current is represented as ΔT ac , then:
The Peltier coefficient is
RIΔT dc /(8ΔT ac )
In this way, if the thermal resistance of the current lead wire is high, the Peltier coefficient may be calculated with sufficient accuracy using only the first term of equation (14).
ペルチェ係数を、
RIΔTdc/(8ΔTac)
を用いて算出するようにしても良い。このように、(14)式の第1項だけでも、電流リード線の熱抵抗が高ければ、十分な精度にてペルチェ係数が算出できる場合もある。 Furthermore, in the step of calculating the Peltier coefficient, if the electrical resistance value of the conductor sample is represented as R, the value of the current passed through the conductor sample is represented as I, the temperature difference at both ends of the conductor sample measured by passing a direct current through the conductor sample is represented as ΔT dc , and the temperature difference between the center of the conductor sample measured by passing an alternating current and the temperature at both ends of the conductor sample measured by passing an alternating current is represented as ΔT ac , then:
The Peltier coefficient is
RIΔT dc /(8ΔT ac )
In this way, if the thermal resistance of the current lead wire is high, the Peltier coefficient may be calculated with sufficient accuracy using only the first term of equation (14).
また、上記方法が、導体試料に電流を流さない状態における導体試料の端部における温度を測定するステップをさらに含むようにしても良い。この場合、ペルチェ係数を算出するステップにおいて、交流電流を流して測定した導体試料の端部における温度と電流を流さない状態における導体試料の端部における温度との差をΔTcorrと表す場合、
2ΔTac/ΔTcorr
をさらに用いて、ペルチェ係数を算出するようにしても良い。これにより、熱損失の補正をも行うことで、より精度良くペルチェ係数を算出できるようになる。 The method may further include a step of measuring a temperature at an end of the conductive sample when no current is flowing through the conductive sample. In this case, when the difference between the temperature at the end of the conductive sample measured by flowing an AC current and the temperature at the end of the conductive sample when no current is flowing in the step of calculating the Peltier coefficient is expressed as ΔT corr ,
2ΔT ac /ΔT corr
In this way, the Peltier coefficient can be calculated with higher accuracy by correcting the heat loss.
2ΔTac/ΔTcorr
をさらに用いて、ペルチェ係数を算出するようにしても良い。これにより、熱損失の補正をも行うことで、より精度良くペルチェ係数を算出できるようになる。 The method may further include a step of measuring a temperature at an end of the conductive sample when no current is flowing through the conductive sample. In this case, when the difference between the temperature at the end of the conductive sample measured by flowing an AC current and the temperature at the end of the conductive sample when no current is flowing in the step of calculating the Peltier coefficient is expressed as ΔT corr ,
2ΔT ac /ΔT corr
In this way, the Peltier coefficient can be calculated with higher accuracy by correcting the heat loss.
本実施の形態に係るプログラムは、(A)ペルチェ係数を測定する対象となる導体試料を一定温度にした後、導体試料に直流電流を流して導体試料の両端における温度を取得するステップと、(B)直流電流と実効値が等しい交流電流を導体試料に流して導体試料の端部及び中央部における温度を取得するステップと、(C)導体試料に直流電流を流して測定した導体試料の両端における温度と、交流電流を流して測定した導体試料の端部及び中央部における温度と、導体試料の電気抵抗値と、導体試料に流した電流の値とを用いて、ペルチェ係数を算出するステップとを、コンピュータ(又はプロセッサ)に実行させるものである。
The program according to this embodiment causes a computer (or processor) to execute the steps of: (A) bringing the conductor sample, the object of which is to measure the Peltier coefficient, to a constant temperature, and then passing a direct current through the conductor sample to obtain the temperatures at both ends of the conductor sample; (B) passing an alternating current, the effective value of which is equal to the direct current, through the conductor sample to obtain the temperatures at the ends and center of the conductor sample; and (C) calculating the Peltier coefficient using the temperatures at both ends of the conductor sample measured by passing a direct current through the conductor sample, the temperatures at the ends and center of the conductor sample measured by passing an alternating current through the conductor sample, the electrical resistance value of the conductor sample, and the value of the current passed through the conductor sample.
また、本実施の形態に係る測定システムは、(A)ペルチェ係数を測定する対象となる導体試料の温度を一定に保つための熱浴機構(例えば、熱浴ブロック31及び32)と、(B)導体試料の両端及び中央部における温度を測定する温度測定部(例えば、熱電対などを含む場合もある)と、(C)導体試料に対して直流電流を流す直流電源と、(D)導体試料に対して交流電流を流す交流電源と、(E)導体試料を熱浴機構により一定温度にした後、直流電源から導体試料に直流電流を流して温度測定部により測定された導体試料の両端における温度と、交流電源から直流電流と実効値が等しい交流電流を導体試料に流して温度測定部により測定された導体試料の端部及び中央部における温度と、導体試料の電気抵抗値と、導体試料に流した電流の値とを用いて、ペルチェ係数を算出する演算部(例えばコンピュータその他の情報処理装置)とを有する。
The measurement system according to this embodiment also includes: (A) a heat bath mechanism (e.g., heat bath blocks 31 and 32) for maintaining a constant temperature of the conductor sample for which the Peltier coefficient is to be measured; (B) a temperature measurement unit (which may include, for example, a thermocouple) for measuring the temperature at both ends and the center of the conductor sample; (C) a DC power supply for passing a DC current through the conductor sample; (D) an AC power supply for passing an AC current through the conductor sample; and (E) a calculation unit (e.g., a computer or other information processing device) for calculating the Peltier coefficient using the temperatures at both ends of the conductor sample measured by the temperature measurement unit when a DC current is passed from the DC power supply to the conductor sample, the temperatures at the ends and the center of the conductor sample measured by the temperature measurement unit when an AC current having an effective value equal to the DC current is passed from the AC power supply to the conductor sample, the electrical resistance value of the conductor sample, and the value of the current passed through the conductor sample.
Claims (8)
- ペルチェ係数を測定する対象となる導体試料を一定温度にした後、前記導体試料に直流電流を流して前記導体試料の両端における温度を測定するステップと、
前記直流電流と実効値が等しい交流電流を前記導体試料に流して前記導体試料の端部及び中央部における温度を測定するステップと、
前記導体試料に直流電流を流して測定した前記導体試料の両端における温度と、前記交流電流を流して測定した前記導体試料の端部及び中央部における温度と、前記導体試料の電気抵抗値と、前記導体試料に流した電流の値とを用いて、ペルチェ係数を算出するステップと、
を含む、ペルチェ係数算出方法。 a step of setting a conductor sample, the Peltier coefficient of which is to be measured, at a constant temperature, and then passing a direct current through the conductor sample to measure the temperature at both ends of the conductor sample;
a step of passing an AC current having an effective value equal to that of the DC current through the conductor sample and measuring temperatures at an end and a center of the conductor sample;
calculating a Peltier coefficient using temperatures at both ends of the conductor sample measured by passing a direct current through the conductor sample, temperatures at the ends and center of the conductor sample measured by passing an alternating current through the conductor sample, an electrical resistance value of the conductor sample, and a value of the current passed through the conductor sample;
A method for calculating a Peltier coefficient, comprising: - 前記導体試料に電流を流さない状態における前記導体試料の端部における温度を測定するステップをさらに含み、
前記ペルチェ係数を算出するステップにおいて、
前記電流を流さない状態における前記導体試料の端部における温度をさらに用いて、前記ペルチェ係数を算出する
請求項1記載のペルチェ係数算出方法。 The method further includes a step of measuring a temperature at the end of the conductor sample when no current is flowing through the conductor sample;
In the step of calculating the Peltier coefficient,
The method for calculating a Peltier coefficient according to claim 1 , further comprising the step of calculating the Peltier coefficient by further using a temperature at the end of the conductive sample in a state where no current is flowing. - 前記ペルチェ係数を算出するステップにおいて、
前記導体試料に直流電流を流して測定した前記導体試料の両端における温度の差と、前記交流電流を流して測定した前記導体試料の中央部における温度と前記交流電流を流して測定した前記導体試料の端部における温度との差とを算出する
請求項1記載のペルチェ係数算出方法。 In the step of calculating the Peltier coefficient,
2. The Peltier coefficient calculation method according to claim 1, further comprising the steps of: calculating a difference in temperature between both ends of the conductor sample measured by passing a direct current through the conductor sample; and a difference in temperature between a center portion of the conductor sample measured by passing the alternating current through the conductor sample and an end portion of the conductor sample measured by passing the alternating current through the conductor sample. - 前記ペルチェ係数を算出するステップにおいて、
前記交流電流を流して測定した前記導体試料の端部における温度と、前記電流を流さない状態における前記導体試料の端部における温度との差を算出する
請求項2記載のペルチェ係数算出方法。 In the step of calculating the Peltier coefficient,
3. The method for calculating a Peltier coefficient according to claim 2, further comprising the step of calculating a difference between a temperature at the end of the conductive sample measured while the AC current is being passed and a temperature at the end of the conductive sample measured while the current is not being passed. - 前記ペルチェ係数を算出するステップにおいて、
前記導体試料の電気抵抗値をRと表し、前記導体試料に流した電流の値をIと表し、前記導体試料に直流電流を流して測定した前記導体試料の両端における温度の差をΔTdcと表し、前記交流電流を流して測定した前記導体試料の中央部における温度と前記交流電流を流して測定した前記導体試料の端部における温度との差をΔTacと表した場合、
前記ペルチェ係数を、
RIΔTdc/(8ΔTac)
を用いて算出する
請求項3記載のペルチェ係数算出方法。 In the step of calculating the Peltier coefficient,
When the electrical resistance value of the conductor sample is represented as R, the value of the current passed through the conductor sample is represented as I, the temperature difference at both ends of the conductor sample measured by passing a direct current through the conductor sample is represented as ΔT dc , and the temperature difference between the center of the conductor sample measured by passing the alternating current and the temperature at both ends of the conductor sample measured by passing the alternating current is represented as ΔT ac ,
The Peltier coefficient is
RIΔT dc /(8ΔT ac )
The Peltier coefficient calculation method according to claim 3, wherein the Peltier coefficient is calculated using the following formula: - 前記導体試料に電流を流さない状態における前記導体試料の端部における温度を測定するステップをさらに含み、
前記ペルチェ係数を算出するステップにおいて、
前記交流電流を流して測定した前記導体試料の端部における温度と前記電流を流さない状態における前記導体試料の端部における温度との差をΔTcorrと表す場合、
2ΔTac/ΔTcorr
をさらに用いて、前記ペルチェ係数を算出する
請求項5記載のペルチェ係数算出方法。 measuring a temperature at the end of the conductor sample when no current is flowing through the conductor sample;
In the step of calculating the Peltier coefficient,
When the difference between the temperature at the end of the conductive sample measured by passing the AC current and the temperature at the end of the conductive sample measured without passing the AC current is represented as ΔT corr ,
2ΔT ac /ΔT corr
The method for calculating a Peltier coefficient according to claim 5 , further comprising the steps of: calculating the Peltier coefficient by using: - ペルチェ係数を測定する対象となる導体試料を一定温度にした後、前記導体試料に直流電流を流して前記導体試料の両端における温度を取得するステップと、
前記直流電流と実効値が等しい交流電流を前記導体試料に流して前記導体試料の端部及び中央部における温度を取得するステップと、
前記導体試料に直流電流を流して測定した前記導体試料の両端における温度と、前記交流電流を流して測定した前記導体試料の端部及び中央部における温度と、前記導体試料の電気抵抗値と、前記導体試料に流した電流の値とを用いて、ペルチェ係数を算出するステップと、
を、コンピュータに実行させるためのプログラム。 a step of setting a conductor sample, the Peltier coefficient of which is to be measured, at a constant temperature, and then passing a direct current through the conductor sample to obtain temperatures at both ends of the conductor sample;
a step of passing an AC current having an effective value equal to that of the DC current through the conductor sample to obtain temperatures at an end and a center of the conductor sample;
calculating a Peltier coefficient using temperatures at both ends of the conductor sample measured by passing a direct current through the conductor sample, temperatures at the ends and center of the conductor sample measured by passing an alternating current through the conductor sample, an electrical resistance value of the conductor sample, and a value of the current passed through the conductor sample;
A program for causing a computer to execute the above. - ペルチェ係数を測定する対象となる導体試料の温度を一定に保つための熱浴機構と、
前記導体試料の両端及び中央部における温度を測定する温度測定部と、
前記導体試料に対して直流電流を流す直流電源と、
前記導体試料に対して交流電流を流す交流電源と、
前記導体試料を前記熱浴機構により一定温度にした後、前記直流電源から前記導体試料に直流電流を流して前記温度測定部により測定された前記導体試料の両端における温度と、前記交流電源から前記直流電流と実効値が等しい交流電流を前記導体試料に流して前記温度測定部により測定された前記導体試料の端部及び中央部における温度と、前記導体試料の電気抵抗値と、前記導体試料に流した電流の値とを用いて、ペルチェ係数を算出する演算部と、
を有する測定システム。 a heat bath mechanism for keeping the temperature of the conductor sample to be measured constant;
a temperature measuring unit for measuring temperatures at both ends and a center of the conductor sample;
a DC power source for supplying a DC current to the conductor sample;
an AC power source that applies an AC current to the conductor sample;
a calculation unit which calculates a Peltier coefficient using the temperatures at both ends of the conductor sample measured by the temperature measurement unit when a DC current is passed through the conductor sample from the DC power source after the conductor sample has been kept at a constant temperature by the heat bath mechanism, the temperatures at the ends and center of the conductor sample measured by the temperature measurement unit when an AC current having an effective value equal to that of the DC current is passed through the conductor sample from the AC power source, an electrical resistance value of the conductor sample, and a value of the current passed through the conductor sample;
A measurement system having
Applications Claiming Priority (2)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| JP2022191172 | 2022-11-30 | ||
| JP2022-191172 | 2022-11-30 |
Publications (1)
| Publication Number | Publication Date |
|---|---|
| WO2024116508A1 true WO2024116508A1 (en) | 2024-06-06 |
Family
ID=91323342
Family Applications (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| PCT/JP2023/031251 WO2024116508A1 (en) | 2022-11-30 | 2023-08-29 | Peltier coefficient calculation method, program, and measurement system |
Country Status (1)
| Country | Link |
|---|---|
| WO (1) | WO2024116508A1 (en) |
Citations (5)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| JP2003014804A (en) * | 2001-06-28 | 2003-01-15 | Komatsu Ltd | Apparatus and method for measurement of figure of merit of thermoelectric element |
| JP2007024603A (en) * | 2005-07-13 | 2007-02-01 | Toyota Motor Corp | Measuring method of thin film like sample |
| CN102305807A (en) * | 2011-05-25 | 2012-01-04 | 清华大学 | Method for measuring Seebeck coefficient of micro/nano thermoelectric materials or devices |
| JP2019120531A (en) * | 2017-12-28 | 2019-07-22 | 国立研究開発法人産業技術総合研究所 | Thermophysical property measuring apparatus and thermophysical property measuring method |
| JP2022101744A (en) * | 2020-12-25 | 2022-07-07 | 国立研究開発法人物質・材料研究機構 | Thermoelectric conversion characteristic evaluation method, thermoelectric conversion characteristic analysis device and analysis program and thermoelectric conversion characteristic evaluation system |
-
2023
- 2023-08-29 WO PCT/JP2023/031251 patent/WO2024116508A1/en unknown
Patent Citations (5)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| JP2003014804A (en) * | 2001-06-28 | 2003-01-15 | Komatsu Ltd | Apparatus and method for measurement of figure of merit of thermoelectric element |
| JP2007024603A (en) * | 2005-07-13 | 2007-02-01 | Toyota Motor Corp | Measuring method of thin film like sample |
| CN102305807A (en) * | 2011-05-25 | 2012-01-04 | 清华大学 | Method for measuring Seebeck coefficient of micro/nano thermoelectric materials or devices |
| JP2019120531A (en) * | 2017-12-28 | 2019-07-22 | 国立研究開発法人産業技術総合研究所 | Thermophysical property measuring apparatus and thermophysical property measuring method |
| JP2022101744A (en) * | 2020-12-25 | 2022-07-07 | 国立研究開発法人物質・材料研究機構 | Thermoelectric conversion characteristic evaluation method, thermoelectric conversion characteristic analysis device and analysis program and thermoelectric conversion characteristic evaluation system |
Similar Documents
| Publication | Publication Date | Title |
|---|---|---|
| Högblom et al. | A simulation framework for prediction of thermoelectric generator system performance | |
| Deng et al. | Influence of temperature on the pressure distribution within press pack IGBTs | |
| Anatychuk et al. | Procedure and equipment for measuring parameters of thermoelectric generator modules | |
| Rauscher et al. | Efficiency determination and general characterization of thermoelectric generators using an absolute measurement of the heat flow | |
| He et al. | An approximate and efficient characterization method for temperature-dependent parameters of thermoelectric modules | |
| Ziolkowski et al. | Heat flow measurement as a key to standardization of thermoelectric generator module metrology: A comparison of reference and absolute techniques | |
| US10088439B2 (en) | Thermophysical property measurement method and thermophysical property measurement apparatus | |
| Amagai et al. | Precise measurement of absolute Seebeck coefficient from Thomson effect using ac-dc technique | |
| TWI467165B (en) | Measurement method, measurement apparatus, and computer program product | |
| WO2024116508A1 (en) | Peltier coefficient calculation method, program, and measurement system | |
| Amagai et al. | High-accuracy compensation of radiative heat loss in Thomson coefficient measurement | |
| CN117192266A (en) | Junction temperature online monitoring method for power device in new energy automobile inverter | |
| Amagai et al. | AC/DC transfer technique for measuring Thomson coefficient: Toward thermoelectric metrology | |
| CN109211963A (en) | System and method for detecting thermal resistance of heat-conducting material | |
| Dhawan et al. | Independent determination of Peltier coefficient in thermoelectric devices | |
| Amagai et al. | Improved electrothermal simulation for low-frequency characterization of a single-junction thermal converter | |
| TW201510519A (en) | System and method for measuring properties of thermoelectric module | |
| Bubanja et al. | Mathematical Modeling and Measurement of Low Frequency Characteristics of Single-Junction Thermal Converters | |
| Patel et al. | Automated instrumentation for the determination of the high-temperature thermoelectric figure-of-merit | |
| Sasaki et al. | A numerical simulation of thermoelectric effects in single-junction thermal converters | |
| JP2006040989A (en) | Thermoelectric characteristic measuring apparatus for semiconductor element | |
| Jeon et al. | Measurement of electrical resistance of thermoelectric materials with a temperature gradient using instant load-voltage analysis | |
| Gao et al. | A Method for testing the integrated thermal resistance of thermoelectric modules | |
| WO2024214475A1 (en) | Parameter acquisition method for thermoelectric conversion module, information provision method, current value list creation method, and computer program | |
| Nakamura et al. | Evaluation of thermal couple impedance model of power modules for accurate die temperature estimation up to 200° C |
Legal Events
| Date | Code | Title | Description |
|---|---|---|---|
| 121 | Ep: the epo has been informed by wipo that ep was designated in this application |
Ref document number: 23897168 Country of ref document: EP Kind code of ref document: A1 |