KR20140056276A - 접속된 컴포넌트의 오리엔테이션 벡터를 인코딩하기 위한 방법 및 디바이스, 대응하는 디코딩 방법 및 디바이스, 및 그 인코딩된 데이터를 전달하는 저장 매체 - Google Patents

접속된 컴포넌트의 오리엔테이션 벡터를 인코딩하기 위한 방법 및 디바이스, 대응하는 디코딩 방법 및 디바이스, 및 그 인코딩된 데이터를 전달하는 저장 매체 Download PDF

Info

Publication number
KR20140056276A
KR20140056276A KR1020147004053A KR20147004053A KR20140056276A KR 20140056276 A KR20140056276 A KR 20140056276A KR 1020147004053 A KR1020147004053 A KR 1020147004053A KR 20147004053 A KR20147004053 A KR 20147004053A KR 20140056276 A KR20140056276 A KR 20140056276A
Authority
KR
South Korea
Prior art keywords
component
additional
vector
components
absolute value
Prior art date
Application number
KR1020147004053A
Other languages
English (en)
Inventor
웬페이 지앙
캉잉 카이
지앙 티안
Original Assignee
톰슨 라이센싱
Priority date (The priority date is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the date listed.)
Filing date
Publication date
Application filed by 톰슨 라이센싱 filed Critical 톰슨 라이센싱
Publication of KR20140056276A publication Critical patent/KR20140056276A/ko

Links

Images

Classifications

    • G—PHYSICS
    • G06—COMPUTING; CALCULATING OR COUNTING
    • G06T—IMAGE DATA PROCESSING OR GENERATION, IN GENERAL
    • G06T9/00—Image coding
    • G06T9/008—Vector quantisation
    • G—PHYSICS
    • G06—COMPUTING; CALCULATING OR COUNTING
    • G06T—IMAGE DATA PROCESSING OR GENERATION, IN GENERAL
    • G06T9/00—Image coding
    • H—ELECTRICITY
    • H03—ELECTRONIC CIRCUITRY
    • H03M—CODING; DECODING; CODE CONVERSION IN GENERAL
    • H03M7/00—Conversion of a code where information is represented by a given sequence or number of digits to a code where the same, similar or subset of information is represented by a different sequence or number of digits
    • H03M7/30—Compression; Expansion; Suppression of unnecessary data, e.g. redundancy reduction
    • H03M7/3082—Vector coding

Landscapes

  • Engineering & Computer Science (AREA)
  • Theoretical Computer Science (AREA)
  • Multimedia (AREA)
  • Physics & Mathematics (AREA)
  • General Physics & Mathematics (AREA)
  • Compression, Expansion, Code Conversion, And Decoders (AREA)
  • Compression Or Coding Systems Of Tv Signals (AREA)
  • Processing Or Creating Images (AREA)

Abstract

본 발명은 접속된 컴포넌트의 적어도 하나의 오리엔테이션 벡터를 인코딩하고 디코딩하는 분야에서 이루어진다. 인코딩을 위해 벡터 컴포넌트들을 양자화할 때, 인코딩된 벡터 컴포넌트들의 수용가능한 양자화 편차는 때때로 계산된 벡터 컴포넌트들의 수용불가능한 편차들을 초래한다. 따라서, 벡터의 제1 및 제2 컴포넌트를 양자화 및 역양자화하고, 양자화된 제1 및 제2 컴포넌트 및 상기 벡터의 제3 컴포넌트의 부호를 시그널링하는 비트를 인코딩하는 것, 상기 벡터의 제3 컴포넌트의 근사화의 계산된 절대값이 제1 임계보다 더 작은지의 여부를 결정하기 위해 미리 결정된 길이 및 역양자화된 제1 및 제2 컴포넌트를 사용하는 것, 및 계산된 절대값이 제1 임계보다 더 작은 경우, 제3 컴포넌트의 계산된 절대값 및 제3 컴포넌트의 절대값 사이의 잔차를 결정하고, 양자화하고, 인코딩하는 것을 포함하는 방법이 제안된다.

Description

접속된 컴포넌트의 오리엔테이션 벡터를 인코딩하기 위한 방법 및 디바이스, 대응하는 디코딩 방법 및 디바이스, 및 그 인코딩된 데이터를 전달하는 저장 매체{METHOD AND DEVICE FOR ENCODING AN ORIENTATION VECTOR OF A CONNECTED COMPONENT, CORRESPONDING DECODING METHOD AND DEVICE AND STORAGE MEDIUM CARRYING SUCH ENCODED DATA}
본 발명은 벡터들의 컴포넌트들의 인코딩 분야에서 이루어진다. 특히, 본 발명은 접속된 컴포넌트의 오리엔테이션(orientation) 벡터의 인코딩에 관련되며, 상기 벡터는 미리 결정된 길이를 가지고 또한 3개의 컴포넌트들을 포함한다.
접속된 컴포넌트들의 오리엔테이션 벡터들은 컴포넌트의 템플릿의 컴포넌트의 인스턴스(instance)로의 회전 변환을 담당하며, 시청각 컨텐츠의 프로세싱에 있어서 많은 상이한 방식들로 사용된다. 예를 들어, 청각적 오브젝트들을 모델링할 때, 오브젝트는 사운드 소스를 나타낼 수 있다. 시각적 오브젝트들을 모델링할 때, 오브젝트는 강체를 나타낼 수 있다.
몇몇을 들자면 예를 들어, CAD 시스템, 3D 게임, 3D TV 또는 3D 영화에서 사용하기 위해 특히 삼차원(3D)으로 시각적 오브젝트들을 모델링할 때, 종종 반복적인 구조들에 당면하게 된다. 이러한 반복적인 구조들, 예를 들어, 여러번 발생하는 오브젝트들 또는 오브젝트-부분들은 구조의 템플릿을 한번 인코딩하고, 구조의 각각의 인스턴스에 대해 템플릿의 인스턴스로의 변환을 허용하는 데이터를 인코딩함으로써 압축 인코딩될 수 있다. 템플릿들은 또한 패턴들로서 명명되며 클러스터링으로부터 초래될 수 있다.
가장 일반적으로 말하자면, 이러한 변환은 회전, 스케일링, 전단(shear) 및/또는 변위로 분해될 수 있는 아핀(affine) 변환이다. 회전, 스케일링, 전단은 가환성의(commutative) 선형 변환들인데, 즉, 이들의 적용의 순서는 전체 변환 결과에 영향을 미치지 않으며, 선형 변환 각각을 허용하는 데이터는 독립적으로 인코딩될 수 있다.
선형 변환들 사이에서, 평범한 3차원 공간에서의 회전들이 3개의 상이한 축들 주위의 회전들로 추가로 분해될 수 있는데, 즉, 3D인 회전들의 회전 데이터는 일반적으로 3개 자유도들을 가진다.
즉, 아핀 변환의 회전 변환 부분은 서로에 대해 수직하는 한 쌍의 정규화된 오리엔테이션 벡터들을 특정하는 파라미터들에 의해 표현될 수 있다. 수직성 제한 및 정규성 제한들로 인해, 이러한 한 쌍의 오리엔테이션 벡터들은 3개의 자유도들을 가지는데, 즉, 다른 파라미터들이 인코딩된 파라미터들 및 제약들을 사용하여 계산될 수 있으므로, 2개의 벡터들의 모호하지 않은 결정을 허용하기 위해 3개의 파라미터들이 결정되어야 한다.
회전들의 특정 하나가 제로 또는 Π(또한, Pi라고 기록되며 180°에 대응함)인 소위 짐벌 락(gimbal lock)의 경우, 세차 회전 및 고유 회전이 동일한 축 주위에, 즉 동일한 면에서 발생한다. 이후, 세차 회전 및 고유 회전은 가환성이며, 연이은(cumulated) 회전에 의해 표현될 수 있다. 따라서, 이러한 경우, 자유도가 유실되고, 회전은 2개의 파라미터들에 의해 고유하게 특정된다.
M. Deering: 단위 노멀(unit normal)의 종단 포인트들이 놓여 있고, 각각의 8분의(octant)가 6개의 6분의(sextant)들로 추가로 분할되는, 8개의 8분의들로 분할되는 정상 구인, 오리엔테이션 벡터의 인코딩을 위해 제안된 1995년 ACM SIGGRAPH의 회의록 "Geometry Compression", pp. 13-20.
접속된 컴포넌트들의 오리엔테이션 축들이 일부 우세한 오리엔테이션들을 가지는 경우들에 대해, 김덕수, 조영성, 및 김현: 2002년, 컴퓨터 그래픽 및 응용예에 대한 태평양 컨퍼런스 IEEE, "Normal Compression Based on Clustering and Relative Indexing"은, 고정된 개수의 클러스터들을 가지는 k-평균 클러스터링에 기초한 방식들을 제안한다.
압축을 위해 반복적인 패턴들을 사용하는 것에 대한 또다른 방식은 Kangying Cai, Wencheng Wang, Zhibo Chen, Quqing Chen, Jun Teng: "Exploiting repeated patterns for efficient compression of massive models", 산업에서의 가상 현실 컨티넘 및 그 응용예들에 대한 제8차 국제 컨퍼런스의 회의록(VRCAI 2009) : 145-150, 2009에 기술되어 있다.
인코딩을 위한 벡터 컴포넌트들을 양자화(quantizing)할 때, 발명자들은 인코딩된 컴포넌트들의 양자화에 의해 유입된 수용가능한 편차(deviation)가 때때로 계산된 컴포넌트들의 수용불가능한 편차들을 초래한다는 점을 관측하였다. 발명자들은 이것이 제수가 제로에 가까운 경우 제수에 존재하는 에러의 수용불가능한 전파를 초래하는 계산에 포함된 나눔 단계로 인한 것임을 인지하였다.
따라서, 청구항 1에 따른 방법은 접속된 컴포넌트의 오리엔테이션 벡터를 인코딩하기 위해 제안되며, 상기 벡터는 미리 결정된 길이를 가지고 또한 3개의 컴포넌트들을 포함한다.
본 발명에 따른 방법들은 유리하게는 3D 모델에서 발생하는 반복적인 패턴의 인스턴스들에 대응하는 접속된 컴포넌트의 인코딩/디코딩에서 사용된다.
상기 방법은 벡터의 제1 및 제2 컴포넌트들을 양자화 및 역양자화(de-quantizing)하고, 양자화된 제1 및 제2 컴포넌트들 및 상기 벡터의 제3 컴포넌트의 부호를 시그널링하는 비트를 인코딩하는 단계, 상기 벡터의 제3 컴포넌트의 근사화의 계산된 절대값(absolute)이 제1 임계보다 더 작은지의 여부를 결정하기 위해 미리 결정된 길이 및 역양자화된 제1 및 제2 컴포넌트를 사용하는 단계, 및 계산된 절대값이 제1 임계보다 더 작은 경우, 제3 컴포넌트의 계산된 절대값 및 제3 컴포넌트의 절대값 사이의 잔차를 결정하고, 양자화하고, 인코딩하는 단계를 포함한다.
실시예에서, 상기 방법은, 상기 벡터에 대해 수직하는 상기 접속된 컴포넌트의 추가적인 오리엔테이션 벡터를 인코딩하는 단계 - 상기 추가적인 벡터는 상기 미리 결정된 길이를 가지고 또한 3개의 추가적인 컴포넌트들을 포함함 - 를 더 포함하고, 상기 인코딩하는 단계는, 청구항 1에 따라 인코딩된 데이터를 사용하여 재구성된 제3 컴포넌트를 결정하고, 재구성된 제3 컴포넌트가 제2 임계보다 더 작다고 결정하고, 역양자화된 제1 및 제2 컴포넌트들의 절대값들을 비교하고 - 여기서, 역양자화된 제1 컴포넌트의 절대값이 역양자화된 제2 컴포넌트의 절대값보다 더 큰 경우, 추가적인 컴포넌트들 중 제1 추가적인 컴포넌트의 부호를 시그널링하는 비트가 인코딩되고, 역양자화된 제1 컴포넌트의 절대값이 역양자화된 제2 컴포넌트의 절대값보다 더 크지 않은 경우, 추가적인 컴포넌트들 중 제2 추가적인 컴포넌트의 부호를 시그널링하는 비트가 인코딩됨 -, 제3 추가적인 컴포넌트를 양자화하고 인코딩함으로써 수행된다.
상이한 실시예에서, 상기 방법은, 벡터에 대해 수직하는 추가적인 벡터를 인코딩하는 단계 - 상기 추가적인 벡터는 상기 미리 결정된 길이를 가지고 또한 3개의 추가적인 컴포넌트들을 포함함 - 를 더 포함하고, 상기 인코딩하는 단계는, 청구항 1에 따라 인코딩된 데이터를 사용하여 재구성된 제3 컴포넌트를 결정하고, 재구성된 제3 컴포넌트가 제1 임계보다 더 작은 제2 임계보다 더 작지 않다고 결정하고, 추가적인 컴포넌트들의 제1 및 제2 추가적인 컴포넌트 중 하나의 추가적인 컴포넌트를 선택하고, 양자화하고, 역양자화하기 위해 역양자화된 제1 및 제2 컴포넌트들의 절대값들을 사용하고, 상기 추가적인 벡터의 제1 및 제2 추가적인 컴포넌트 중 선택되지 않은 하나의 추가적인 컴포넌트의 2개의 가능한 값들을 계산하기 위해 상기 벡터의 재구성, 미리 결정된 길이 및 역양자화된 선택된 추가적인 컴포넌트를 사용하고, 계산된 2개의 가능한 값들 중 어느 것이 선택되지 않은 추가적인 컴포넌트에 더 잘 근사화하는지에 대한 의존성에서의 플래그를 설정하고, 양자화된 선택된 추가적인 컴포넌트 및 플래그를 인코딩함으로써 수행된다.
상기 상이한 실시예에서, 상기 방법은 상기 추가적인 벡터의 제3 추가적인 컴포넌트의 근사화의 계산된 추가적인 절대값이 제1 임계보다 더 작은지의 여부를 결정하기 위해 미리 결정된 길이, 플래그 및 역양자화된 선택된 추가적인 컴포넌트를 사용하는 단계, 및 계산된 추가적인 절대값이 제1 미리 결정된 임계보다 더 작은 경우, 계산된 절대값 및 상기 추가적인 벡터의 제3 추가적인 컴포넌트의 절대값 사이의 추가적인 잔차를 결정하고, 양자화하고, 인코딩하는 단계를 더 포함할 수 있다.
그러나, 상기 방법은 비-일시적 저장 매체 상에 인코딩된 모든 데이터를 저장하는 단계를 포함할 필요가 없을 수 있다.
상기 방법의 실시예들 중 하나 또는 제안된 방법에 따라 저장된 데이터를 전달하는(carrying) 저장 매체가 추가로 제안되어 있다.
그리고, 접속된 컴포넌트의 오리엔테이션 벡터를 재구성하기 위한 청구항 7에 따른 방법이 제안되어 있으며, 상기 벡터는 미리 결정된 길이를 가지며 3개의 컴포넌트들을 포함한다.
상기 재구성 방법은 제3 컴포넌트의 부호를 시그널링하는 비트, 벡터의 제1 및 제2 컴포넌트를 디코딩하고 제1 및 제2 컴포넌트를 역양자화하는 단계, 상기 벡터의 제3 컴포넌트의 근사화의 계산된 절대값이 제1 임계보다 더 작은지의 여부를 결정하기 위해 미리 결정된 길이 및 역양자화된 제1 및 제2 컴포넌트를 사용하는 단계, 계산된 절대값이 제1 임계보다 더 작은 경우, 제3 컴포넌트의 계산된 절대값 및 제3 컴포넌트의 절대값 사이의 잔차를 결정하고, 디코딩하고, 역양자화하는 단계, 및 상기 벡터의 제3 컴포넌트를 재구성하기 위해 디코딩된 데이터를 사용하는 단계를 포함한다.
실시예에서, 상기 재구성 방법은, 상기 벡터에 대해 수직하는 상기 접속된 컴포넌트의 추가적인 오리엔테이션 벡터를 디코딩하는 단계 - 상기 추가적인 벡터는 상기 미리 결정된 길이를 가지고 또한 3개의 추가적인 컴포넌트들을 포함함 - 를 더 포함하고, 상기 디코딩하는 단계는, 재구성된 제3 컴포넌트가 제1 임계보다 더 작은 제2 임계보다 더 작다고 결정하고, 역양자화된 제1 및 제2 컴포넌트들의 절대값들을 비교하고 - 여기서, 역양자화된 제1 컴포넌트의 절대값이 역양자화된 제2 컴포넌트의 절대값보다 더 큰 경우, 추가적인 컴포넌트들 중 제1 추가적인 컴포넌트의 부호를 시그널링하는 비트가 인코딩되고, 역양자화된 제1 컴포넌트의 절대값이 역양자화된 제2 컴포넌트의 절대값보다 더 크지 않은 경우, 추가적인 컴포넌트들 중 제2 추가적인 컴포넌트의 부호를 시그널링하는 비트가 인코딩됨 -, 상기 벡터의 제3 추가적인 컴포넌트를 디코딩하고 역양자화함으로써 수행된다.
상이한 실시예에서, 상기 재구성 방법은, 상기 벡터에 대해 수직하는 상기 접속된 컴포넌트의 추가적인 오리엔테이션 벡터를 디코딩하는 단계 - 상기 추가적인 벡터는 상기 미리 결정된 길이를 가지고 또한 추가적인 3개의 추가적인 컴포넌트들을 포함함 - 를 더 포함하고, 상기 디코딩하는 단계는, 재구성된 제3 컴포넌트가 제2 임계보다 더 작지 않다고 결정하고, 플래그 및 추가적인 컴포넌트들 중 하나의 추가적인 컴포넌트를 디코딩하고 추가적인 컴포넌트 중 하나의 추가적인 컴포넌트를 역양자화하고, 추가적인 컴포넌트들 중 하나의 추가적인 컴포넌트가 상기 추가적인 벡터의 제1 또는 제2 추가적인 컴포넌트인지의 여부를 결정하기 위해 역양자화된 제1 및 제2 컴포넌트들의 절대값들을 사용하고, 추가적인 컴포넌트들 중 하나의 추가적인 컴포넌트가 아닌 것으로 결정되는 상기 추가적인 벡터의 그 추가적인 컴포넌트를 계산하기 위해 상기 벡터의 재구성, 미리 결정된 길이, 플래그 및 추가적인 컴포넌트들 중 역양자화된 하나의 추가적인 컴포넌트를 사용하고, 제3 추가적인 컴포넌트의 근사화를 결정하기 위해 미리 결정된 길이, 역양자화된 하나의 추가적인 컴포넌트 및 계산된 추가적인 컴포넌트들을 사용함으로써 수행된다.
상기 상이한 실시예에서, 상기 재구성 방법은 제3 추가적인 컴포넌트의 결정된 근사화의 절대값이 제1 임계보다 더 작다고 결정하는 단계, 추가적인 잔차를 디코딩하고 역양자화하는 단계, 및 역양자화된 추가적인 잔차를 사용하여 결정된 근사화를 업데이트하는 단계를 더 포함할 수 있다.
추가로, 제안된 방법들 중 하나를 수행하기 위한 프로세서를 포함하는 디바이스가 제안되어 있다. 또한, 발명은 접속된 컴포넌트의 오리엔테이션 벡터를 인코딩/디코딩하기 위한 인코더 또는 디코더를 포함하는 디바이스를 제공하며, 여기서, 접속된 컴포넌트는 3D 모델에서 반복적인 패턴의 인스턴스에 대응한다.
추가적인 유리한 실시예들의 특징들이 종속 청구항들에 특정되어 있다.
발명의 예시적인 실시예들이 도면들에 예시되며 후속하는 기재에서 더욱 상세하게 설명된다. 예시적인 실시예들은, 청구항들에 정의되어 있는 발명의 개시내용 또는 범위를 제한하기 위해서가 아니라, 오직 발명을 상술하기 위해서 설명된다.
도 1은 인코딩 방법의 실시예의 흐름도를 예시적으로 도시하는 도면이다.
도 2는 디코딩 방법의 실시예의 흐름도를 예시적으로 도시하는 도면이다.
도 3은 본 발명의 원리들에 따른 3D 모델들의 예시적인 인코더를 도시하는 도면이다.
도 4는 본 발명의 원리들에 따른 3D 모델들의 예시적인 디코더를 도시하는 도면이다.
발명은 대응적으로 적응되는 프로세싱 디바이스를 포함하는 임의의 전자 디바이스 상에서 달성될 수 있다. 발명이 달성될 수 있는 예시적인 디바이스들의 불완전한 리스트는 텔레비전, 모바일 폰, 개인용 컴퓨터, 디지털 스틸 카메라, 디지털 비디오 카메라, mp3 플레이어, 내비게이션 시스템 또는 카 오디오 시스템을 포함한다.
발명은 인코딩된 벡터가 사용될 수 있는 임의의 목적과는 독립적인 미리 결정된 길이의 벡터를 인코딩하기 위해 사용될 수 있다.
다음에서 기술되는 예시적인 실시예는 인코딩된 벡터가 오리엔테이션 벡터인 시각적 오브젝트들의 모델링에 관한 것이지만, 발명이 이에 제한되지는 않는다.
표 1에서, 본 발명의 실시예에 따라 인코딩된 수직하는 정규화된 벡터의 쌍이 전달될 수 있는 비트 스트림 포맷의 예가 제시되어 있다:
Figure pct00001
데카르트 모드(Cartesian mode)에서 제i 인스턴스의 오리엔테이션은 2개의 직교 축들(x0, y0, z0) 및 (x1, y1, z1)에 의해 표현된다.
compr_ith_insta_orient_x0: 제i 인스턴스의 오리엔테이션의 압축된 x0를 포함한다.
compr_ith_insta_orient_y0: 제i 인스턴스의 오리엔테이션의 압축된 y0를 포함한다.
compr_ith_insta_orient_z0_sgn: x0 및 y0를 사용하여 z0를 계산하기 위해 필요한 z0의 부호를 표시하는 1비트 무부호 정수. "-"에 대해서는 0이고 "+"에 대해서는 1임.
compr_ith_insta_orient_z0_res: (z0 - computer_z0 ( ))에 의해 계산된 z0의 압축된 잔차를 포함한다.
compr_ith_insta_orient_z1: 제i 인스턴스의 오리엔테이션의 압축된 z1을 포함한다.
ith_insta_orient_x1_sgn: x0, y0를 사용하여 x1을 계산하기 위해 필요한 x1의 부호를 표시하는 1비트 무부호 정수. "-"에 대해서는 0이고 "+"에 대해서는 1임.
ith_insta_orient_y1_sgn: x0, y0를 사용하여 y1을 계산하기 위해 필요한 y1의 부호를 표시하는 1비트 무부호 정수. "-"에 대해서는 0이고 "+"에 대해서는 1임.
compr_ith_insta_orient_x1: 제i 인스턴스의 오리엔테이션의 압축된 x1을 포함한다.
compr_ith_insta_orient_y1: 제i 인스턴스의 오리엔테이션의 압축된 y1을 포함한다.
ith_insta_orient_delta_sgn: x0, y0, z0 및 y1 또는 x1을 사용하여 x1 또는 y1을 계산하기 위해 필요한 부호를 표시하는 1비트 무부호 정수. "-"에 대해서는 0이고 "+"에 대해서는 1임.
compr_ith_insta_orient_z1_res: (z1 - computer_z1( ))에 의해 계산되는 z1의 압축된 잔차를 포함한다
threshold: 압축 필드에서 널리 수용되는 임계.
compute_z0() : x0, y0 및 z0 부호를 사용하여 제i 인스턴스의 z0를 계산한다.
bit_num_orient_cartesian( ): QP에 기초한 데카르트 좌표 시스템(cartesian coordinate system)에서 각각의 오리엔테이션 값에 대한 비트 수를 계산한다.
bit_num_orient_res_cartesian( ): QP에 기초한 데카르트 좌표 시스템에서 각각의 오리엔테이션 잔차 값에 대한 비트 수를 계산한다.
compute_z1() : x0, y0, z0, x1 및 y1를 사용하여 제i 인스턴스의 z1을 계산한다.
표 2에서, 비트 스트림 포맷의 또다른 예가 제시되어 있다:
Figure pct00002
구면 모드(spherical mode)에서 제i 인스턴스의 오리엔테이션은 3개의 각인 알파, 베타 & 감마에 의해 표현된다.
compr_ith_insta_orient_alpha: 제i 인스턴스의 오리엔테이션의 압축된 알파를 포함한다.
compr_ith_insta_orient_beta: 제i 인스턴스의 오리엔테이션의 압축된 베타를 포함한다.
compr_ith_insta_orient_gamma: 제i 인스턴스의 오리엔테이션의 압축된 감마를 포함한다.
compr_ith_insta_orient_res: 제i 인스턴스의 오리엔테이션의 데카르트 좌표 시스템에서 압축된 잔차를 포함한다.
bit_num_orient_alpha ( ): QP에 기초하여 각각의 알파 값에 대한 비트수를 계산한다.
bit_num_orient_beta ( ): QP에 기초하여 각각의 베타 값에 대한 비트수를 계산한다.
bit_num_orient_gamma ( ): QP에 기초하여 각각의 감마 값에 대한 비트수를 계산한다.
need_correction ( ): 오리엔테이션을 체크하여, 만약 그것이 큰 에러를 초래할 가능성이 있는 에지 조건에 있는 경우, 참을 리턴시키고, 그렇지 않은 경우, 거짓을 리턴시킨다.
정규화된 벡터의 인코딩에 대한 필요성이 발생하는 예는 3D 접속 컴포넌트의 오리엔테이션의 표현이다. 일반적으로, 방향들은, 데카르트 좌표 또는 구면 좌표(spherical coordinates) 중 어느 하나에서, 접속된 컴포넌트의 오리엔테이션 축들 중 2개에 대해 인코딩된다. 3D 접속된 컴포넌트의 3개의 오리엔테이션 축들이 서로 수직하므로, 제3 축은 처음 2개의 축들의 외적(cross product)을 계산함으로써 획득될 수 있다.
d0(x0, y0, z0), d1(x1, y1, z1), 및 d2 (x2, y2, z2)에 의해 3개의 축들을 나타내면,
Figure pct00003
및
Figure pct00004
가 되며, 이후 오리엔테이션 축들의 인코딩 방법은 다음을 포함할 수 있다:
1) x0 및 y0를 압축한다.
2) z0의 부호를 인코딩한다.
3) x1을 압축한다.
이후, y1, z0 및 z1는 다음을 사용하여 계산될 수 있다:
z1= sqrt (1-x12-y12),
z1= sqrt (1-x12-y12), 및
0= x0*x1 + y0*y1 + z0*z1.
오리엔테이션 축 d2는 d2=d0xd1를 사용하여 결정가능하다.
그러나, x0, y0 및 x1의 부동 값들(float values)이 코딩 이전에 양자화되므로, 계산들에서의 에러 전파(error propagation)로 인해 계산된 컴포넌트들에서 훨씬 더 큰 에러들을 초래하는 편차가 유입된다.
예를 들어, 12비트 양자화를 가지는 다음 오리엔테이션을 압축한 이후:
Figure pct00005
및
Figure pct00006
재구성은 다음이 될 것이다.
Figure pct00007
및
Figure pct00008
x0, y0 및 x1의 양자화 에러들은 수용가능하다:0.000182, 0.000216 및 0.000188. 그러나, 계산된 값들 z0, y1 및 z1의 에러들은 0.01471296, 0.052531 및 0.059042인데, 이는 완전히 수용불가능하다.
위의 주요 원인은 z0의 계산 에러이다. 1-x02-y02가 작고 따라서, z0가 작은 경우, z0가 1-x02-y02의 제곱근이므로, x 또는 y에 대한 미미한 에러들은 z0의 더 큰 에러들로 성장한다. 따라서 발명은 z0가 작은 경우, 즉, 그것의 절대값이 제1 임계 미만인 경우, 정정을 추가적으로 인코딩하는 것을 제안한다.
또한, z1을 재구성하는 것은 z0에 의한 나누기를 포함한다. 이러한 나누기는 또한 z0가 제로에 가까운 경우 수용불가능한 에러 전파를 초래한다. 유사하게, x1이 인코딩된 경우, y1을 재구성하는 것은 (1-x02)에 의한 나누기를 포함한다. 대안적으로, y1이 인코딩된 경우, x1은 (1-y02)에 의한 나누기를 사용하여 재구성될 수 있다.
발명의 압축 방법은 벡터의 재구성이 겨우 최대 편차만큼만 벡터로부터 벗어남을 보장한다.
언급한 바와 같이, 오리엔테이션 표현에서의 일부 값들은 코딩된다기보다는 계산될 수 있다. 불행히도, 이는 양자화로 인해 계산에 사용되는 인코딩된 값들 자체가 부정확하므로 수용불가능한 에러들을 초래할 수 있다. 본 발명은 이 문제점을 다루며, 그것이 상당히 작은 해당 계산된 컴포넌트들에 대한 잔차 데이터를 인코딩하는 것을 포함한다는 점에서 계산 에러를 최소화하는 압축 방법을 제안한다.
한쌍의 수직 벡터들이 인코딩되는 특정 실시예에서, 발명의 코딩 방법은 한쌍의 벡터들 중 하나의 제1 및 제2 양자화된 부동 컴포넌트 값들 및 한쌍의 벡터들 중 다른 하나의 제1 또는 제2 양자화된 부동 컴포넌트 값을 인코딩하는 단계를 포함한다. 상기 특정 실시예에서, 2개의 부호 비트들 또는 플래그 비트들은, 즉, 단일 비트들에 대해, 3D 컴포넌트의 오리엔테이션을 나타내도록 추가로 인코딩된다. 재구성 에러를 최소화하기 위해, 상기 특정 실시예의 인코딩 방식은 다음 포인트들에 기초하여 설계된다:
1. 계산시 분모(denominator)를 가능한 크게 둔다.
2. 분모가 극도로 작거나 제로인 경우들에 대한 특수 처리.
3. 가능하게는 수용불가능한 에러를 초래하는 경우들에 대해 자동 식별하고, 이러한 경우들에 대해 잔차 데이터를 전송한다.
도 1은 상기 특정 실시예에 따른 인코딩 프로세스를 예시적으로 제시한다.
하나의 벡터의 제1 컴포넌트 x0는 항상 양자화되고 인코딩된다. 적어도 제1 양자화 벡터 컴포넌트의 역양자화 값 x0r이 1과 같지 않은 한, 부호 비트가 추가로 인코딩되고 - 부호 비트는 하나의 벡터의 제3 컴포넌트 z0의 부호를 시그널링함 - , 하나의 벡터의 제2 컴포넌트 y0가 추가로 양자화되고 인코딩된다.
z0 유도 모듈(Derivation module)은 하나의 벡터의 미리 결정된 길이 및 인코딩된 데이터의 재구성들을 사용하여 하나의 벡터의 제3 컴포넌트의 근사화 z0a를 계산한다. 즉, 적어도, 제1 양자화된 벡터 컴포넌트의 역양자화 값 x0r의 절대값이 1과 같지 않은 한, 부호 비트 뿐만 아니라, 제1 및 제2 양자화된 벡터 컴포넌트의 역양자화 값들 x0r, y0r은 z0a를 결정하기 위해 사용된다. 제1 양자화된 벡터 컴포넌트의 역양자화 값 x0r의 절대값이 1과 같은 경우, z0a는 제로로서 결정될 수 있다.
에러 정정 모듈은 z0a에 대해 계산된 값이 매우 작은 경우, 즉, 제1 임계보다 더 작고 따라서 가능하게는 부정확할 수 있는 경우 인에이블된다. 이러한 경우들에서, 인코더는 원래 및 근사치 z0a 사이의 양자화된 잔차를 추가로 인코딩한다. 즉, z0의 재구성 z0r은 z0a와 같거나, 또는 역양자화된 잔차만큼 z0a와 상이하다.
다른 벡터의 제1 컴포넌트가 인코딩되는 경우, y1 유도 모듈은 하나의 벡터의 역양자화된 제1 및 제2 양자화된 부동 컴포넌트 값들 x0r, y0r 뿐만 아니라 다른 벡터의 역양자화된 제1 양자화된 부동 컴포넌트 값 x1r을 사용하여 다른 벡터의 제2 컴포넌트에 대한 2가지 가능한 해(solution)들을 계산한다:
Figure pct00009
또는
Figure pct00010
이들 방정식들에서, Δ는 z0r이 가능하게는 잔차 정정된 재구성인
Figure pct00011
과 같다.
유사하게, 다른 벡터의 제2 컴포넌트가 인코딩되는 경우, x1 유도 모듈은 하나의 벡터의 역양자화된 제1 및 제2 양자화 부동 컴포넌트 값들 x0r, y0r 뿐만 아니라 다른 벡터의 역양자화된 제2 양자화 부동 컴포넌트 값 y1r을 사용하여 다른 벡터의 제1 컴포넌트에 대한 2개의 가능한 해들을 계산한다:
Figure pct00012
또는
Figure pct00013
이들 방정식들에서, Δ는 z0r이 가능하게는 잔차 정정된 재구성인
Figure pct00014
와 같다.
z0r의 절대값이 매우 작은 경우, 즉, 제1 임계보다 훨씬 더 작은 제2 임계보다 더 작은 경우, x1 유도 모듈도 y1 유도 모듈도 활성화되지 않는다. 대신, z1이 양자화되고 인코딩된다. 추가로, 추가적인 부호 비트가 인코딩되는데, 추가적인 부호 비트는 더 작은 절대값을 가지는 다른 벡터의 재구성된 제1 및 제2 컴포넌트들 중 하나의 부호를 표시한다.
z0r의 절대값이 제2 임계보다 더 작지 않은 경우 x1 유도 모듈이 활성화되는지 또는 y1 유도 모듈이 활성화되는지의 여부는 하나의 벡터의 재구성된 제1 및 제2 컴포넌트들 x0r 및 y0r의 절대값들의 관계에 의존한다. abs(x0r) > abs(y0r)인 경우, x1이 양자화되고 인코딩되고, y1 유도 모듈이 활성화된다. abs(x0r)≤ abs(y0r)인 경우, y1이 양자화되고 인코딩되고, x1 유도 모듈이 활성화된다. x1 유도 모듈 및 y1 유도 모듈 각각이 가능한 해들을 제공하므로, 사용될 해를 디코더에 표시하기 위해 플래그 비트가 추가로 인코딩된다.
z1 유도 모듈은, z0가 상기 제1 임계 미만인 경우, 제곱근 함수
Figure pct00015
, 하나의 벡터의 미리 결정된 길이 뿐만 아니라 하나의 벡터의 역양자화된 제1 및 제2 양자화된 부동 컴포넌트 값들을 사용하여, z1의 절대값을 계산한다:
Figure pct00016
z0가 상기 제1 임계 미만이 아닌 경우, z1의 절대값은 절대값 함수
Figure pct00017
를 사용하여 다음과 같이 계산된다:
Figure pct00018
z1에 대한 계산된 값이 작고 따라서 가능하게는 부정확한 경우, 에러 정정 모듈이 또한 인에이블될 수 있다. z1에 대해 계산된 값이 작은 경우 에러 정정 모듈이 또한 인에이블된다면, 인코더는 z1의 원래 및 계산된 값 사이의 추가적인 양자화된 잔차를 추가로 인코딩한다.
도 2는 상기 특정 실시예에 따른 디코딩 프로세스를 예시적으로 제시한다.
하나의 벡터의 제1 x0r 부동 컴포넌트 값은 항상 디코딩되고 역양자화된다. 또한, 플래그 비트가 항상 디코딩된다. 적어도, 제1 양자화된 벡터 컴포넌트의 역양자화 값 x0r이 1과 같지 않은 한, 부호 비트가 추가로 디코딩되고 - 부호 비트는 하나의 벡터의 제3 컴포넌트 z0r의 부호를 시그널링함 - , 하나의 벡터의 제2 컴포넌트 y0가 추가로 디코딩되고 역양자화된다.
z0 유도 모듈은 하나의 벡터의 미리 결정된 길이 및 디코딩되고 역양자화된 데이터를 사용하여 하나의 벡터의 제3 컴포넌트의 근사화 z0a를 계산한다. 즉, 적어도, 제1 양자화된 벡터 컴포넌트의 역양자화 값 x0r의 절대값이 1과 같지 않은 한, 제1 및 제2 양자화된 벡터 컴포넌트의 부호 비트 뿐만 아니라 역양자화 값들 x0r, y0r은 z0a를 결정하기 위해 사용된다. 제1 양자화된 벡터 컴포넌트의 역양자화 값 x0r의 절대값이 1과 같은 경우, y0r 및 z0a 모두는 제로로서 결정될 수 있다.
z0a에 대해 계산된 값이 매우 작은 경우, 즉 제1 임계보다 더 작고, 따라서 가능하게는 부정확한 경우, 에러 정정 모듈이 인에이블된다. 이러한 경우들에서, 디코더는 원래 및 근사화 z0a 사이의 양자화된 잔차를 추가로 디코딩하고 역양자화한다. 즉, z0의 재구성 z0r은 z0a와 같거나 또는 역양자화 잔차만큼 z0a와 상이하다.
z0r이 제1 임계보다 더 작은 제2 임계보다 더 작지 않고, x0r의 절대값이 y0r의 절대값보다 더 작은 경우, 다른 벡터의 제2 양자화된 컴포넌트가 y1r을 획득하기 위해 디코딩되고 역양자화되며, 여기서 플래그 비트는 2개의 가능한 해들 중 어느 것이 다른 벡터의 제1 컴포넌트를 계산하기 위해 사용될 것인지를 표시한다. 이후, x1r 및 z1r이 계산된다.
z0r이 제1 임계보다 더 작은 제2 임계보다 더 작지 않고 x0r의 절대값이 y0r의 절대값보다 더 작은 경우, y1 유도 모듈은 다른 벡터의 제2 컴포넌트를 계산하기 위한 2개의 가능한 해들 중 하나를 선택하기 위한 플래그 비트를 사용한다:
Figure pct00019
또는
Figure pct00020
이들 방정식들에서, Δ는 z0r이 가능하게는 잔차 정정된 재구성인
Figure pct00021
과 같다.
z0r가 제1 임계보다 더 작은 제2 임계보다 더 작지 않고, x0r의 절대값이 y0r의 절대값보다 더 작지 않은 경우, 다른 벡터의 제1 양자화 컴포넌트는 x1r을 획득하기 위해 디코딩되고 역양자화되며, 여기서, 플래그 비트는 2개의 가능한 해들 중 어느 것이 다른 벡터의 제2 컴포넌트를 계산하기 위해 사용될지를 표시한다. 이후, y1r 및 z1r이 계산된다.
z0r이 제1 임계보다 더 작은 제2 임계보다 더 작지 않고 x0r의 절대값이 y0r의 절대값보다 더 작지 않은 경우, x1 유도 모듈은 다른 벡터의 제1 컴포넌트를 계산하기 위한 2개의 가능한 해들 중 하나를 선택하기 위한 플래그 비트를 사용한다:
Figure pct00022
또는
Figure pct00023
이들 방정식들에서, Δ는 z0r이 가능하게는 잔차 정정된 재구성인
Figure pct00024
과 같다.
z0r가 제1 임계보다 더 작은 제2 임계보다 더 작고, y0r의 절대값이 x0r의 절대값보다 더 작은 경우, 다른 벡터의 제3 양자화 컴포넌트는 z1r을 획득하기 위해 디코딩되고 역양자화되며, 플래그 비트는 ylr의 부호(ylr)를 결정하기 위해 사용되고, x1r 및 y1r는 다음과 같이 계산된다:
Figure pct00025
z0r가 제1 임계보다 더 작은 제2 임계보다 더 작고, y0r의 절대값이 x0r의 절대값보다 더 작지 않은 경우, 다른 벡터의 제3 양자화 컴포넌트는 z1r을 획득하기 위해 디코딩되고 역양자화되며, 플래그 비트는 x1r의 부호(x1r)를 결정하기 위해 사용되고, y1r는 다음과 같이 계산된다:
Figure pct00026
z1r이 디코딩 및 역양자화로부터가 아니라 계산으로부터 초래되고, 제1 임계 미만의 절대값을 가지는 경우, 에러 정정 모듈이 인에이블될 수 있다. 이러한 경우들에서, 디코더는 원래 및 z1r 사이의 추가적인 양자화된 잔차를 추가로 디코딩하고 역양자화하고, 역양자화된 추가 잔차에 따라 z1r을 정정한다.
특정 실시예가 데카르트 좌표의 견지에서 발명을 기술하지만, 발명은 이에 제한되지 않는다. 구면 좌표에서, 유사한 문제점이 또한 90°또는 PI/2로서 쓰여지는 Π/2에 가까운 각들에서 발생한다. 즉, 상기 계산된 각의 절대값이 임계만큼 Π/2와 상이하지 않은 경우, 정규화된 벡터의 계산된 각의 잔차를 인코딩하는 것이 제안된다.
이전에 논의된 바와 같이, 본 발명의 원리들은 3D 모델 반복적 구조들을 인코딩하는 견지에서 유리하게 적용될 수 있다. 3D 모델들을 효율적으로 인코딩하기 위해, 반복적 구조들은 패턴들 및 인스턴스들로 조직될 수 있고, 여기서 인스턴스는, 예를 들어, 번역(translation), 회전 및 스케일링에 대한 정보를 포함하는 변환 행렬 및 대응하는 패턴의 패턴 ID를 사용하여, 대응하는 패턴의 변환으로서 표현된다.
인스턴스가 패턴 ID 및 변환 행렬에 의해 표현되는 경우, 패턴 ID 및 변환 행렬은 인스턴스를 압축할 때 압축될 것이다. 결과적으로, 인스턴스는 패턴 ID 및 디코딩된 변환 행렬을 통해 재구성될 수 있는데, 즉, 인스턴스는 패턴 ID에 의해 인덱싱되는 디코딩된 패턴의 (디코딩된 변환 행렬로부터의) 변환으로서 재구성될 수 있다.
도 3은 예시적인 3D 모델 인코더(300)의 블록도를 도시한다. 장치(300)의 입력은 3D 모델, 3D 모델을 인코딩하기 위한 품질 파라미터 및 다른 메타데이터를 포함할 수 있다. 3D 모델은 먼저, 패턴들, 인스턴스들 및 고유 컴포넌트들의 견지에서 3D 모델을 출력하는 반복적인 구조 발견 모듈(310)을 통과한다. 패턴 인코더(320)는 패턴들을 압축하기 위해 사용되며, 고유 컴포넌트 인코더(350)는 고유 컴포넌트들을 인코딩하기 위해 사용된다. 예를 들어, 인스턴스 컴포넌트 정보는 사용자-선택 모드에 기초하여 인코딩된다. 인스턴스 정보 그룹 모드가 선택되는 경우, 인스턴스 정보는 그룹화된 인스턴스 정보 인코더(340)를 사용하여 인코딩되고, 그렇지 않은 경우, 그것은 기본(elementary) 인스턴스 정보 인코더(330)를 사용하여 인코딩된다. 인코딩된 컴포넌트들은 반복적인 구조 검증기(360)에서 추가로 검증된다. 인코딩된 컴포넌트가 그것의 품질 요건을 만족하지 않는 경우, 그것은 고유 컴포넌트 인코더(350)를 사용하여 인코딩될 것이다. 패턴들, 인스턴스들 및 고유 컴포넌트들에 대한 비트스트림들은 비트스트림 어셈블러(370)에서 조립된다.
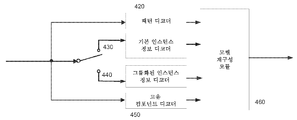
도 4는 예시적인 3D 모델 디코더(400)의 블록도를 도시한다. 장치(400)의 입력은 3D 모델의 비트스트림, 예를 들어, 인코더(300)에 의해 생성된 비트스트림을 포함할 수 있다. 압축된 비트스트림 내의 패턴들과 관련된 정보는 패턴 디코더(420)에 의해 디코딩된다. 고유 컴포넌트들에 관련된 정보는 고유 컴포넌트 디코더(450)에 의해 디코딩된다. 인스턴스 정보의 디코딩은 또한 사용자-선택 모드에 의존한다. 인스턴스 정보 그룹 모드가 선택되는 경우, 인스턴스 정보는 그룹화된 인스턴스 정보 디코더(440)를 사용하여 디코딩되고; 그렇지 않은 경우, 그것은 기본 인스턴스 정보 디코더(430)를 사용하여 디코딩된다. 디코딩된 패턴들, 인스턴스 정보 및 고유 컴포넌트들은 모델 재구성 모듈(460)에서 출력 3D 모델을 생성하도록 재구성된다.
여기서 기술된 구현예들은, 예를 들어, 방법 또는 프로세스, 장치, 소프트웨어 프로그램, 데이터 스트림, 또는 신호로 구현될 수 있다. 단지 단일 형태의 구현예의 상황에서 논의되었지만(예를 들어 오직 방법으로서 논의되었지만), 논의된 특징들의 구현예는 또한 다른 형태들(예를 들어, 장치 또는 프로그램)로 구현될 수 있다. 장치는 예를 들어, 적절한 하드웨어, 소프트웨어 및 펌웨어에서 구현될 수 있다. 예를 들어, 방법들은, 예를 들어, 컴퓨터, 마이크로프로세서, 집적 회로 또는 프로그램가능한 논리 디바이스를 포함하는 프로세싱 디바이스들을 일반적으로 지칭하는, 예를 들어 프로세서와 같은 장치에서 구현될 수 있다. 프로세서들은 또한 예를 들어, 컴퓨터들, 셀 폰들, 휴대용/개인 디지털 보조 단말("PDA")들, 및 최종 사용자들 사이의 정보의 통신을 용이하게 하는 다른 디바이스들과 같은 통신 디바이스들을 포함한다.
본 발명의 원리들의 "일 실시예" 또는 "실시예" 또는 "일 구현예" 또는 "구현예", 뿐만 아니라 이들의 다른 변형들에 대한 참조는, 실시예와 관련하여 기술된 특정 특징, 구조, 특성 등이 본 발명의 원리들의 적어도 일 실시예에 포함됨을 의미한다. 따라서, 구문 "일 실시예에서" 또는 "실시예에서" 또는 "일 구현예에서" 또는 "구현예에서"의 출현들, 뿐만 아니라 명세서 전반의 다양한 장소들에서 출현하는 임의의 다른 변형예들이 반드시 모두 동일한 실시예를 지칭하지는 않는다.
당업자에게 명백할 바와 같이, 구현예들은 예를 들어, 저장되거나 전송될 수 있는 정보를 전달(carry)하기 위해 포맷된 다양한 신호들을 생성할 수 있다. 정보는, 예를 들어, 방법을 수행하기 위한 명령들, 또는 설명된 구현예들 중 하나에 의해 생성되는 데이터를 포함할 수 있다. 예를 들어, 신호는 기술된 실시예의 비트스트림을 전달하기 위해 포맷될 수 있다. 이러한 신호는 예를 들어, 전자기파로서(예를 들어, 스펙트럼의 라디오 주파수 부분을 사용하여) 또는 베이스밴드 신호로서 포맷될 수 있다. 포맷팅은, 예를 들어, 데이터 스트림을 인코딩하는 것 및 인코딩된 데이터 스트림을 이용하여 캐리어를 변조하는 것을 포함할 수 있다. 신호가 전달하는 정보는, 예를 들어, 아날로그 또는 디지털 정보일 수 있다. 공지되어 있는 바와 같이, 신호는 다양한 상이한 유선 또는 무선 링크들을 통해 전송될 수 있다. 신호는 프로세서-판독가능한 매체 상에 저장될 수 있다.
원리상, 개시된 발명은 또한 다른 데이터 압축 영역들에도 적용될 수 있다. 발명은 고유한 비트스트림 포맷을 초래한다.
비트스트림이 모든 변환 데이터를 내장하고 있는 동안, 그것은 효율적이며, 대때로, 비트스트림 크기 또는 디코딩 효율성 또는 에러 회복력 중 어느 하나가 가장 크게 문제가 되는 몇몇 응용예들을 다룰 수 있다. 따라서, 하나의 인스턴스의 변환 데이터, 즉, 그것의 위치, 오리엔테이션 및 스케일링 인자를, 비트 스트림 내에 두는 방법에 대해 2개의 모드 옵션들이 개시된다. 제1 모드(옵션 A)에서, 하나의 인스턴스의 위치, 오리엔테이션 및 가능한 스케일링 인자는 비트스트림 내에 함께 패킹된다. 제2 모드(옵션 B)에서, 모든 인스턴스들의 위치들, 오리엔테이션들 또는 가능한 스케일링 인자들이 비트스트림 내에 함께 패킹된다.
본 발명이 순수하게 예시에 의해 기술되어 있으며, 상세항목의 수정들이 본 발명의 범위로부터의 이탈 없이 이루어질 수 있다는 점이 이해될 것이다.
설명 및 (적절한 경우) 청구항들 및 도면들에서 개시된 각각의 특징들은 독립적으로 또는 임의의 적절한 조합으로 제공될 수 있다. 특징들은, 적절한 경우, 하드웨어, 소프트웨어, 또는 이 둘의 조합에서 구현될 수 있다. 접속들은, 적절한 경우, 무선 접속들 또는, 반드시 직접적이거나 전용이 아닌, 유선 접속들로서 구현될 수 있다.
청구항들에서 나타나는 참조 번호들은 오직 예시에 의한 것이며, 청구항들의 범위에 대한 어떠한 제한적 효과도 가지지 않을 것이다.

Claims (15)

  1. 접속된 컴포넌트의 오리엔테이션(orientation) 벡터를 인코딩하기 위한 방법으로서,
    상기 벡터는 미리 결정된 길이를 가지고 또한 3개의 컴포넌트들을 포함하며, 상기 방법은:
    상기 벡터의 제1 및 제2 컴포넌트를 양자화 및 역양자화하고, 상기 양자화된 제1 및 제2 컴포넌트 및 상기 벡터의 제3 컴포넌트의 부호를 시그널링하는 비트를 인코딩하는 단계,
    상기 벡터의 제3 컴포넌트의 근사화의 계산된 절대값(absolute)이 제1 임계보다 더 작은지의 여부를 결정하기 위해 상기 미리 결정된 길이 및 상기 역양자화된 제1 및 제2 컴포넌트를 사용하는 단계, 및
    상기 계산된 절대값이 상기 제1 임계보다 더 작은 경우, 상기 제3 컴포넌트의 계산된 절대값 및 상기 제3 컴포넌트의 절대값 사이의 잔차(residual)를 결정하고, 양자화하고, 인코딩하는 단계
    를 포함하는 방법.
  2. 제1항에 있어서,
    상기 방법은,
    상기 벡터에 대해 수직하는 상기 접속된 컴포넌트의 추가적인 오리엔테이션 벡터를 인코딩하는 단계 - 상기 추가적인 벡터는 상기 미리 결정된 길이를 가지고 또한 3개의 추가적인 컴포넌트들을 포함함 -
    를 더 포함하고,
    상기 추가적인 오리엔테이션 벡터를 인코딩하는 단계는,
    제1항에 따라 인코딩된 데이터를 사용하여 재구성된 제3 컴포넌트를 결정하고,
    상기 재구성된 제3 컴포넌트가 제2 임계보다 더 작다고 결정하고,
    상기 역양자화된 제1 및 제2 컴포넌트들의 절대값들을 비교하고 - 상기 역양자화된 제1 컴포넌트의 절대값이 상기 역양자화된 제2 컴포넌트의 절대값보다 더 큰 경우, 상기 추가적인 컴포넌트들 중 제1 추가적인 컴포넌트의 부호를 시그널링하는 비트가 인코딩되고,
    상기 역양자화된 제1 컴포넌트의 절대값이 상기 역양자화된 제2 컴포넌트의 절대값보다 더 크지 않은 경우, 상기 추가적인 컴포넌트들 중 제2 추가적인 컴포넌트의 부호를 시그널링하는 비트가 인코딩됨 -,
    제3 추가적인 컴포넌트를 양자화하고 인코딩함으로써 수행되는, 방법.
  3. 제1항에 있어서,
    상기 방법은,
    상기 벡터에 대해 수직하는 추가적인 벡터를 인코딩하는 단계 - 상기 추가적인 벡터는 상기 미리 결정된 길이를 가지고 또한 3개의 추가적인 컴포넌트들을 포함함 -
    를 더 포함하고,
    상기 추가적인 벡터를 인코딩하는 단계는,
    제1항에 따라 인코딩된 데이터를 사용하여 재구성된 제3 컴포넌트를 결정하고,
    상기 재구성된 제3 컴포넌트가 상기 제1 임계보다 더 작은 제2 임계보다 더 작지 않다고 결정하고,
    상기 추가적인 컴포넌트들의 제1 및 제2 추가적인 컴포넌트 중 하나의 추가적인 컴포넌트를 선택하고 양자화하고 역양자화하기 위해 상기 역양자화된 제1 및 제2 컴포넌트들의 절대값들을 사용하고,
    상기 추가적인 벡터의 상기 제1 및 제2 추가적인 컴포넌트 중 선택되지 않은 추가적인 컴포넌트의 2개의 가능한 값들을 계산하기 위해 상기 벡터, 상기 미리 결정된 길이 및 상기 역양자화된 선택된 추가적인 컴포넌트를 사용하고,
    상기 계산된 2개의 가능한 값들 중 어느 것이 상기 선택되지 않은 추가적인 컴포넌트에 더 잘 근사화되는지에 대한 의존성에 있어서의 플래그를 설정하고,
    상기 양자화된 선택된 추가적인 컴포넌트 및 상기 플래그를 인코딩함으로써 수행되는 방법.
  4. 제3항에 있어서,
    상기 방법은,
    상기 추가적인 벡터의 제3 추가적인 컴포넌트의 근사화의 계산된 추가적인 절대값이 상기 제1 임계보다 더 작은지의 여부를 결정하기 위해 상기 미리 결정된 길이, 상기 플래그 및 상기 역양자화된 선택된 추가적인 컴포넌트를 사용하는 단계, 및
    상기 계산된 추가적인 절대값이 상기 제1 미리 결정된 임계보다 더 작은 경우, 상기 계산된 절대값 및 상기 추가적인 벡터의 제3 추가적인 컴포넌트의 절대값 사이의 추가적인 잔차를 결정하고, 양자화하고, 인코딩하는 단계
    를 더 포함하는 방법.
  5. 제1항 내지 제4항 중 어느 한 항에 있어서,
    비-일시적 저장 매체에 인코딩된 모든 데이터를 저장하는 단계를 더 포함하는 방법.
  6. 제5항의 방법에 따라 저장된 데이터를 전달하는(carry) 저장 매체.
  7. 접속된 컴포넌트의 오리엔테이션 벡터를 재구성하기 위한 방법으로서,
    상기 벡터는 미리 결정된 길이를 가지고 또한 3개의 컴포넌트들을 포함하며, 상기 방법은,
    상기 제3 컴포넌트의 부호를 시그널링하는 비트, 상기 벡터의 제1 및 제2 컴포넌트를 디코딩하고, 상기 제1 및 제2 컴포넌트를 역양자화하는 단계,
    상기 벡터의 제3 컴포넌트의 근사화의 계산된 절대값이 제1 임계보다 더 작은지의 여부를 결정하기 위해 상기 미리 결정된 길이 및 상기 역양자화된 제1 및 제2 컴포넌트를 사용하는 단계,
    상기 계산된 절대값이 상기 제1 임계보다 더 작은 경우, 상기 제3 컴포넌트의 계산된 절대값 및 상기 제3 컴포넌트의 절대값 사이의 잔차를 결정하고, 디코딩하고, 역양자화하는 단계, 및
    상기 벡터의 제3 컴포넌트를 재구성하기 위해 상기 디코딩된 데이터를 사용하는 단계
    를 포함하는 방법.
  8. 제7항에 있어서,
    상기 방법은,
    상기 벡터에 대해 수직하는 상기 접속된 컴포넌트의 추가적인 오리엔테이션 벡터를 재구성하는 단계 - 상기 추가적인 벡터는 상기 미리 결정된 길이를 가지고 또한 3개의 추가적인 컴포넌트들을 포함함 -
    를 더 포함하고,
    상기 재구성하는 단계는,
    상기 재구성된 제3 컴포넌트가 상기 제1 임계보다 더 작은 제2 임계보다 더 작다고 결정하고,
    상기 역양자화된 제1 및 제2 컴포넌트들의 절대값들을 비교하고 - 상기 역양자화된 제1 컴포넌트의 절대값이 상기 역양자화된 제2 컴포넌트의 절대값보다 더 큰 경우, 상기 추가적인 컴포넌트들 중 제1 추가적인 컴포넌트의 부호를 시그널링하는 비트가 인코딩되고,
    상기 역양자화된 제1 컴포넌트의 절대값이 상기 역양자화된 제2 컴포넌트의 절대값보다 더 크지 않은 경우, 상기 추가적인 컴포넌트들 중 제2 추가적인 컴포넌트의 부호를 시그널링하는 비트가 인코딩됨 -,
    상기 벡터의 제3 추가적인 컴포넌트를 디코딩하고 역양자화함으로써 수행되는 방법.
  9. 제7항에 있어서,
    상기 방법은,
    상기 벡터에 대해 수직하는 상기 접속된 컴포넌트의 추가적인 오리엔테이션 벡터를 재구성하는 단계 - 상기 추가적인 벡터는 상기 미리 결정된 길이를 가지고 또한 3개의 추가적인 컴포넌트들을 포함함 -
    를 더 포함하고,
    상기 재구성하는 단계는,
    상기 재구성된 제3 컴포넌트가 제2 임계보다 더 작지 않다고 결정하고,
    플래그 및 상기 추가적인 컴포넌트들 중 하나의 추가적인 컴포넌트를 디코딩하고 상기 추가적인 컴포넌트 중 하나의 추가적인 컴포넌트를 역양자화하고,
    상기 추가적인 컴포넌트들 중 하나의 추가적인 컴포넌트가 상기 추가적인 벡터의 제1 또는 제2 추가적인 컴포넌트인지의 여부를 결정하기 위해 상기 역양자화된 제1 및 제2 컴포넌트들의 절대값들을 사용하고,
    상기 추가적인 컴포넌트들 중 하나의 추가적인 컴포넌트가 아닌 것으로 결정되는 상기 추가적인 벡터의 그 추가적인 컴포넌트를 계산하기 위해 상기 벡터의 재구성, 상기 미리 결정된 길이, 상기 플래그, 및 상기 추가적인 컴포넌트들 중 역양자화된 추가적인 컴포넌트를 사용하고,
    제3 추가적인 컴포넌트의 근사화를 결정하기 위해 상기 미리 결정된 길이, 상기 역양자화된 하나의 추가적인 컴포넌트 및 상기 계산된 추가적인 컴포넌트들을 사용함으로써 수행되는 방법.
  10. 제9항에 있어서,
    상기 방법은,
    상기 제3 추가적인 컴포넌트의 결정된 근사화의 절대값이 상기 제1 임계보다 더 작다고 결정하는 단계,
    추가적인 잔차를 디코딩하고 역양자화하는 단계, 및
    상기 역양자화된 추가적인 잔차를 사용하여 상기 결정된 근사화를 업데이트하는 단계
    를 더 포함하는 방법.
  11. 제1항 내지 제5항 중 어느 한 항 또는 제7항 내지 제10항 중 어느 한 항의 방법을 수행하기 위한 프로세서를 포함하는 디바이스.
  12. 디바이스로서,
    접속된 컴포넌트와 연관된 오리엔테이션 벡터를 결정하는 반복적인 구조 발견 모듈 ― 상기 접속된 컴포넌트는 패턴의 인스턴스(instance)에 대응하고, 상기 패턴은 3D 모델에서 발생하는 반복적인 구조에 대응함 ― ; 및
    상기 오리엔테이션 벡터를 인코딩하기 위해 제1항 내지 제5항 중 한 항의 방법을 수행하는 인코더
    를 포함하는 디바이스.
  13. 디바이스로서,
    제7항 내지 제10항 중 어느 한 항의 방법에 따라 인코딩된 오리엔테이션 벡터를 디코딩하는 디코더 ― 상기 접속된 컴포넌트는 패턴의 인스턴스에 대응하고, 상기 패턴은 3D 모델에서 발생하는 반복적인 구조에 대응함 ― ; 및
    상기 접속된 컴포넌트를 포함하는 3D 모델을 생성하는 모델 재구성 모듈
    을 포함하는 디바이스.
  14. 제1항 내지 제5항 중 어느 한 항에 있어서,
    상기 접속된 컴포넌트는 패턴의 인스턴스에 대응하고, 상기 패턴은 3D 모델에서 발생하는 반복적인 구조에 대응하고,
    상기 접속된 컴포넌트와 연관된 상기 오리엔테이션 벡터를 결정하는 단계를 더 포함하는 방법.
  15. 제7항 내지 제10항 중 어느 한 항에 있어서,
    상기 접속된 컴포넌트는 패턴의 인스턴스에 대응하고, 상기 패턴은 3D 모델에서 발생하는 반복적인 구조에 대응하고, 상기 접속된 컴포넌트를 포함하는 상기 3D 모델을 생성하는 단계를 더 포함하는 방법.
KR1020147004053A 2011-07-18 2012-07-17 접속된 컴포넌트의 오리엔테이션 벡터를 인코딩하기 위한 방법 및 디바이스, 대응하는 디코딩 방법 및 디바이스, 및 그 인코딩된 데이터를 전달하는 저장 매체 KR20140056276A (ko)

Applications Claiming Priority (3)

Application Number Priority Date Filing Date Title
CNPCT/CN2011/077277 2011-07-18
CN2011077277 2011-07-18
PCT/CN2012/078750 WO2013010476A1 (en) 2011-07-18 2012-07-17 Method and device for encoding an orientation vector of a connected component, corresponding decoding method and device and storage medium carrying such encoded data

Publications (1)

Publication Number Publication Date
KR20140056276A true KR20140056276A (ko) 2014-05-09

Family

ID=47557669

Family Applications (1)

Application Number Title Priority Date Filing Date
KR1020147004053A KR20140056276A (ko) 2011-07-18 2012-07-17 접속된 컴포넌트의 오리엔테이션 벡터를 인코딩하기 위한 방법 및 디바이스, 대응하는 디코딩 방법 및 디바이스, 및 그 인코딩된 데이터를 전달하는 저장 매체

Country Status (6)

Country Link
US (1) US20140146043A1 (ko)
EP (1) EP2734979A4 (ko)
JP (1) JP2014527736A (ko)
KR (1) KR20140056276A (ko)
BR (1) BR112014001016A2 (ko)
WO (1) WO2013010476A1 (ko)

Families Citing this family (1)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
WO2021095242A1 (ja) * 2019-11-15 2021-05-20 日本電信電話株式会社 映像符号化方法、映像符号化装置及びコンピュータープログラム

Family Cites Families (8)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
US5010574A (en) * 1989-06-13 1991-04-23 At&T Bell Laboratories Vector quantizer search arrangement
JP3655451B2 (ja) * 1997-12-11 2005-06-02 富士通株式会社 紙葉鑑別装置
US6304275B1 (en) * 1998-10-31 2001-10-16 Hewlett-Packard Company Memory efficient surface normal decompression
JP4506039B2 (ja) * 2001-06-15 2010-07-21 ソニー株式会社 符号化装置及び方法、復号装置及び方法、並びに符号化プログラム及び復号プログラム
GB0216668D0 (en) * 2002-07-17 2002-08-28 Imagination Tech Ltd Method and apparatus for compressed data storage and retrieval
US8369406B2 (en) * 2005-07-18 2013-02-05 Electronics And Telecommunications Research Institute Apparatus of predictive coding/decoding using view-temporal reference picture buffers and method using the same
JP4787100B2 (ja) * 2006-07-27 2011-10-05 パナソニック株式会社 画像符号化装置
US8625911B2 (en) * 2009-06-23 2014-01-07 Thomson Licensing Compression of 3D meshes with repeated patterns

Also Published As

Publication number Publication date
JP2014527736A (ja) 2014-10-16
EP2734979A1 (en) 2014-05-28
WO2013010476A1 (en) 2013-01-24
US20140146043A1 (en) 2014-05-29
EP2734979A4 (en) 2015-09-09
BR112014001016A2 (pt) 2017-02-21

Similar Documents

Publication Publication Date Title
JP6246233B2 (ja) 頂点誤差訂正のための方法および装置
KR101654777B1 (ko) 3차원 메쉬 가변 부호화 장치 및 방법, 그리고 3차원 메쉬 가변 복호화 장치 및 방법
CN111386551A (zh) 点云的预测编码、解码的方法和设备
KR20050109413A (ko) 위치 인터폴레이터 복호화 방법 및 장치
KR102002654B1 (ko) 반복 구조를 갖는 3d 모델을 위한 비트스트림을 인코딩하고 디코딩하는 시스템 및 방법
EP4336835A1 (en) Encoding method and apparatus, decoding method and apparatus, device, storage medium, and computer program and product
AU2012283580A1 (en) System and method for encoding and decoding a bitstream for a 3D model having repetitive structure
JP6093847B2 (ja) 反復構造の発見に基づく３ｄモデル圧縮のための方法及び装置
KR20140056276A (ko) 접속된 컴포넌트의 오리엔테이션 벡터를 인코딩하기 위한 방법 및 디바이스, 대응하는 디코딩 방법 및 디바이스, 및 그 인코딩된 데이터를 전달하는 저장 매체
JP5933742B2 (ja) 反復構造発見ベースの３ｄモデル圧縮のビットストリームを生成する方法及び装置
EP2839439B1 (en) Vertex correction method and apparatus for rotated three-dimensional (3d) components
CN103748615A (zh) 用于对连接分量的取向向量进行编码的方法和设备、相应的解码方法和设备、以及携带这种已编码数据的存储介质
US20020122035A1 (en) Method and system for parameterized normal predictive encoding
WO2013010315A1 (en) Method and device for encoding rotational data, corresponding decoding method and device and storage medium carrying encoded rotational data
Wu et al. Joint watermarking and compression for Gaussian and Laplacian sources using uniform vector quantization
EP2783509B1 (en) Method and apparatus for generating a bitstream of repetitive structure discovery based 3d model compression
KR20240112902A (ko) 포인트 클라우드 코딩 방법, 장치 및 매체
WO2024132941A1 (en) Apparatus and method for predicting voxel coordinates for ar/vr systems
KR20240113803A (ko) 포인트 클라우드 코딩을 위한 방법, 장치 및 매체
CN104303210A (zh) 用于基于重复结构探索的三维模型压缩的方法及装置

Legal Events

Date Code Title Description
WITN Application deemed withdrawn, e.g. because no request for examination was filed or no examination fee was paid