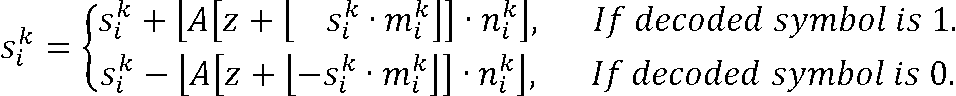JP7590397B2 - 算術エンコーダ、算術デコーダ、ビデオエンコーダ、ビデオデコーダ、符号化方法、復号方法、およびコンピュータプログラム - Google Patents

Description

本発明による実施形態は、算術エンコーダを作成する。
本発明によるさらなる実施形態は、算術デコーダを作成する。
本発明によるさらなる実施形態は、ビデオエンコーダを作成する。
本発明によるさらなる実施形態は、ビデオデコーダを作成する。
本発明によるさらなる実施形態は、複数のシンボルを符号化するための方法および複数のシンボルを復号するための方法を作成する。
本発明によるさらなる実施形態は、対応するコンピュータプログラムを作成する。
一般的に言えば、本発明による実施形態は、有限状態機械を使用したコンテキストモデル更新方法を作成する。

算術符号化および復号は、オーディオおよびビデオコンテンツの符号化および復号、ならびに画像、ニューラルネットワーク係数などの他のタイプの情報の符号化においても貴重な手段であることが証明されている。本発明の実施形態は、これらすべての用途に使用することができる。例えば、ビデオまたはオーディオコンテンツ（または他のタイプのコンテンツ）を表すバイナリシーケンス内のバイナリ値（例えば、シンボル）の既知の発生確率を利用して、符号化の効率を高めることが可能である。特に、算術符号化は、「０」と「１」の様々な確率を効率的に処理でき、微調整して確率の変化に適合できる。

ただし、算術符号化と復号で最適なコーディング効率を実現するには、実際の発生頻度をよく反映した「０」と「１」の確率に関する適切な情報を入手することが重要である。

「０」と「１」の確率に適合するために（または一般に、符号化されるシンボルの確率に適合するために）、概念は通常、値の合計（現在の）範囲内の間隔の境界を調整するために使用され、間隔の細分割を取得する（例えば、値の全範囲が、異なるバイナリ値またはバイナリ値群に関連付けられた間隔に細分割されるようにする）。

言い換えると、様々なシンボル（「０」や「１」など）の確率に関する情報を使用して、シンボルに関連付けられた間隔の幅を表す間隔サイズ情報（または同等に間隔サイズ値）を導出する（合計間隔幅は、例えば、間隔の再正規化のために、符号化または復号プロセスに応じて時間とともに変化する可能性がある）。

したがって、間隔の細分割（例えば、コーディング間隔の合計の細分割）のソース統計値（例えば、状態変数値）および／または範囲値（間隔サイズ値など）を決定するための概念が必要であり、これは、計算効率と責任の間の適切なトレードオフを提供する。

本発明による実施形態は、シンボル値（例えば、バイナリ値）を有する複数のシンボルを符号化するための算術エンコーダを作成し、算術エンコーダは、間隔サイズ情報（ｐ^ｋ、Ｒ＊ｐ^ｋ）を、１つまたは複数のシンボル値（例えば、バイナリ値）の算術符号化が複数の状態変数値（ｓ_ｉ ^ｋ）（例えば、インデックスｋによって表示される所与のコンテキストモードに関連付けられるもの）に基づいて符号化されるように導出するように構成され、これは、異なる適合時定数で以前に符号化された複数のシンボル値（例えば、バイナリ値０と１のシーケンス）の統計を表し、算術エンコーダは、ルックアップテーブル（ＬＵＴ１）を使用して、第１の状態変数値（ｓ^ｋ _１）、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ _１＊ａ^ｋ _１]）をマッピングし、ルックアップテーブル（ＬＵＴ１）を使用して、第２の状態変数値（ｓ^ｋ _２）、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ _２＊ａ^ｋ _２]）をマッピングするように構成され、符号化される１つまたは複数のシンボルの算術符号化のための間隔サイズを説明する間隔サイズ情報（例えば、ｐ_ｋまたはＲ＊ｐ_ｋ）を取得するようにする。

本発明によるこの実施形態は、ルックアップテーブルベースのマッピングが異なる適合時定数に関連付けられた状態変数値に適用される場合、間隔サイズ情報を特に良好な信頼性で取得できるという考えに基づいている。言い換えると、異なる時間スケールで統計（例えばシンボル確率）を記述する２つの状態変数値に同じルックアップテーブルを適用することにより、間隔サイズ情報を効率的な方法（１つのルックアップテーブルのみが必要なため）でありながらも、信頼性が高い（間隔サイズ情報の決定では、様々な時間スケールの統計が考慮されるため）様式で取得できる。ルックアップテーブルを使用した状態変数値のマッピングは、状態変数値に基づいて間隔サイズ情報を導出する際の重要かつ即時のステップと見なすことができる。任意選択で、１つまたは複数の追加のマッピングおよび／またはマッピング結果の結合は、間隔サイズ情報の導出における第１および第２の状態変数値のルックアップテーブルベースのマッピングに従うことができる。任意選択で、確率値は、第１の状態変数値および第２の状態変数値のルックアップテーブルベースのマッピングを使用して中間量として取得され得る。さらに、第１の状態変数値のルックアップテーブルベースのマッピングの結果から、および第２の状態変数値のルックアップテーブルベースのマッピングの結果から、間隔サイズ情報を導出するための異なる概念が可能である。

結論として、本発明によるこの実施形態は、（少なくとも）２つのルックアップテーブルベースのマッピングを使用する第１の状態変数値および第２の状態変数値に基づく間隔サイズ情報の導出を提供する。したがって、異なる適合時定数に関連付けられている状態変数値は、個別にマッピングできるが、同じマッピングルール（ルックアップテーブルで定義）を使用して、間隔サイズ情報を決定するためのリソースの要求を適度に少なく保つが、異なる適合時定数または統計計算時定数で取得された複数の以前に処理された（例えば、符号化または復号された）シンボルの統計（または統計情報）の考慮（例えば、重み付けの考慮）を依然として可能にする。

好ましい実施形態では、算術エンコーダは、ルックアップテーブルを使用して、第１の状態変数値、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ _１＊ａ^ｋ _１]）を第１の確率値（ｐ_ｋ ^１）にマッピングするように構成され、算術エンコーダは、ルックアップテーブルを使用して、第２の状態変数値、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ _２＊ａ^ｋ _２]）を第２の確率値（ｐ_ｋ ^２）にマッピングするように構成され、算術エンコーダは、第１の確率値および第２の確率値を使用して（例えば、加重和または加重平均を使用して）結合確率値（ｐｋ）を取得するように構成される。

このような概念を使用すると、シンボル確率（例えば、「１」シンボルの確率または「０」シンボルの確率）を表す結合確率値は、第１の状態変数値と第２の状態変数値に基づいて容易く導出できる。例えば、第１の敏捷性を有する以前に処理された（例えば、符号化または復号された）シンボルに続く第１の状態変数値は、第１の確率値にマッピングすることができ、また第２の敏捷性を有する以前に処理された（例えば、符号化または復号された）シンボルに続く第２の状態変数値は、第２の確率値に効率的にマッピングできる。したがって、異なる時間スケールで発生する以前に処理されたシンボルの傾向を考慮することができ、それでも非常に効率的な方法で結合確率値を導出することが可能である。第１および第２の状態変数値により、異なる適合時定数で以前に処理されたシンボルの傾向を追跡でき、状態変数値を「部分的な」確率値（第１の確率値および第２の確率値）にマッピングすることは、結合確率値に寄与し、上記の概念を使用して非常にリソース効率の高い方法で実行できる。

好ましい実施形態では、算術エンコーダは、符号化されるシンボルが第１の値（例えば「１」）をとる場合に状態変数値を第１の方向に変更する（例えばより正になる）ように構成され、また符号化されるシンボルが第１の値とは異なる第２の値（例えば「０」）をとる場合（例えば、状態変数値が正と負の値をとることができるように）に状態変数値を第２の方向に（例えば、より負になるもの）変更するように構成され、算術エンコーダは、それぞれの状態変数値の絶対値（ｓ_ｋ ^ｉ＞０の場合はｓ_ｋ ^ｉ、それ以外の場合は－ｓ_ｋ ^ｉ）に応じて（例えば、状態変数値の絶対値のスケーリングおよび丸められたバージョンに応じて）評価されるルックアップテーブルのエントリを決定するように構成される。

例えば、正と負の値をとることができる状態変数値を使用することによって（例えば、以前に処理されたシンボルの履歴に応じて、また例えば、以前に処理された反対のシンボルに対して対称的に）、それぞれの状態変数値の絶対値に依存するルックアップテーブルのエントリを選択することにより、概念の効率をさらに向上させることができる。例えば、状態変数値の可能な値（または量子化された値）ごとにルックアップテーブルの専用エントリを用意する必要は、もはやなくなった。むしろ、正の状態変数値と対応する負の状態変数値の両方（つまり、絶対値は等しいが符号が反対の「逆」状態変数値）に対してルックアップテーブルのエントリを二重に使用することができる。その結果、ルックアップテーブルのエントリの数を少なく保つことができ、以前に処理された反対のシンボルに関する間隔サイズ情報の決定の「対称性」を利用することができる。

好ましい実施形態では、算術エンコーダは、第１の状態変数値が第１の符号（例えば、正の符号）をとる場合に、第１の確率値（ｐ^ｋ _１）をルックアップテーブルによって提供される値（例えば、

）に設定するように構成され、算術エンコーダは、第１の状態変数値が第２の符号（例えば、負の符号）をとる場合、第１の確率値（ｐ^ｋ _１）を、所定の値（例えば、１）からルックアップテーブルによって提供される値（例えば、

）を減算することによって得られる値に設定するように構成される。

このようなメカニズムを使用すると、ルックアップテーブルのエントリの数を少なく保つことができ（例えば、ルックアップテーブルのエントリは、それぞれの状態変数値の絶対値に基づいてのみ選択されるため）、一方でそれぞれの状態変数値の反対の符号の「相補的な」確率値を取得することが依然として可能である。したがって、確率値を決定するために、高度なリソース効率と低い計算の複雑さが達成される。
好ましい実施形態では、算術エンコーダは、

ＬＵＴ１は確率値を含むルックアップテーブルであり、
[．]はフロア演算子であり、
ｓ^ｋ _ｉはｉ番目の状態変数値であり、
ａ^ｋ _ｉは、ｉ番目の状態変数値に関連付けられた重み付け値である（例えば、ｉ番目の状態変数値の数の範囲をルックアップテーブルのいくつかのエントリに適合させる重み付け値）ことにより、２つ以上の確率値ｐ^ｋ _ｉを決定するように構成される。
このような計算は計算効率が高く、リソース需要を適度に小さく保つことがわかっている。

好ましい実施形態では、算術エンコーダは、

ＬＵＴ１は確率値を含むルックアップテーブルであり、
[．]はフロア演算子であり、
ｓ^ｋ _ｉはｉ番目の状態変数値であり、
ａ^ｋ _ｉは、ｉ番目の状態変数値に関連付けられた重み付け値である（例えば、ｉ番目の状態変数値の数の範囲をルックアップテーブルのいくつかのエントリに適合させる重み付け値）ことにより、２つ以上の確率値ｐ^ｋ _ｉを決定するように構成される。
このような計算は、実際の数の表現に応じて、一部の状況においては有利であることがわかっている。特に、フロア演算子は、状態変数値の符号に関係なく、同じオペランドに適用される。特に、フロア演算子のオペランドの符号を削除する必要がないため、幾分かの計算の複雑さが軽減される。むしろ、否定は、通常は整数値であるフロア演算子の結果にのみ適用される。したがって、否定演算子を適用する複雑さは特に少程度である。言い換えれば、本明細書で説明される概念はまた、特に低度の複雑さをもたらす。

好ましい実施形態では、算術エンコーダは、

式中Ｎは考慮される確率値の数で（考慮される状態変数値の数に等しい場合がある）、ｂ^ｋ _ｉは、重み付け値（例えば、結合確率値に対する個々の状態変数値の影響を制御する重み付け係数）である（ｂ^ｋ _ｉは、好ましくは、ｖｏｎ ２の整数値の効力であり、２つの異なるｂ^ｋ _ｉ間の比は好ましくは、２の整数値の効力である）
ことに従って、複数の確率値ｐ^ｋ _ｉに基づいて結合確率値ｐ^ｋを取得するように構成される。
異なる状態変数値に基づいて取得された確率値に異なる重み付けを適用することにより、短期統計と長期統計の結合確率値への異なる影響を考慮することができ、特に意味のある結合確率値を取得できる。

好ましい実施形態では、算術エンコーダは、２次元ルックアップテーブルを使用して、第１の状態変数値、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ _１＊ａ^ｋ _１]）を第１のサブインターバル幅値（Ｒ＊ｐ^ｋ _１）にマッピングするように構成され、そのエントリは、第１の状態変数値に依存して（例えば、確率指数ｉを使用するなどして、第１のルックアップテーブルエントリ座標を決定するために）、およびシンボルの符号化前の算術符号化のコーディング間隔のサイズを記述するコーディング間隔サイズ情報（例えば、Ｒ、またはＲから導出される指数ｊ）に依存して（例えば、第２のルックアップテーブルエントリ座標を決定するために）アドレス指定され、算術エンコーダは、２次元ルックアップテーブルを使用して、第２の状態変数値、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ _２＊ａ^ｋ _２]）を第２のサブインターバル幅値（Ｒ＊ｐ^ｋ _２）にマッピングするように構成され、そのエントリは、第２の状態変数値に依存して（例えば、第１のルックアップテーブルエントリ座標を決定するために）、およびシンボルの符号化前の算術符号化のコーディング間隔のサイズを記述するコーディング間隔サイズ情報（例えば、Ｒ）に依存してアドレス指定され（例えば、第２のルックアップテーブルエントリ座標を決定するために）、算術エンコーダは、第１のサブインターバル幅値および第２のサブインターバル幅値を使用して（例えば、加重和または加重平均を使用して）、結合されたサブインターバル幅値を取得するように構成される。

複数の異なる確率値と複数の異なる間隔サイズ値との乗算を反映するこのような２次元ルックアップテーブルを使用することにより、乗算の演算を省けるため、計算の複雑さを軽減することができる。例えば、２次元ルックアップテーブルのエントリを指定する２つのインデックス（行インデックスと列インデックス）の１つは、それぞれの状態変数値（またはそのスケーリングおよび／または丸められたバージョン）によって定義され、第２のインデックスは、現在の（合計）コーディング間隔サイズによって決定される。したがって、第１のインデックスおよび第２のインデックスに基づいて、２次元ルックアップテーブルの要素（エントリ）を一意に識別することができ、識別された要素は、通常、それぞれの状態変数値に関連付けられた確率値と、第２のテーブルインデックスに関連付けられたコーディング間隔サイズとの積を反映する。その結果、場合によっては読み取り専用メモリである可能性があるメモリを２次元ルックアップテーブルに費やすことにより、乗算演算の実行を省ける。これは、計算リソースの観点からも、またエネルギー消費の観点からも有利な場合がある。

算術エンコーダの好ましい実施形態では、２次元ルックアップテーブルは、そのエントリが第１および第２の状態変数値の値ドメインの異なる値間隔の確率値、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]；

）を含む第１の１次元ベクトル（１次元ルックアップテーブルを形成する）、およびそのエントリがコーディング間隔サイズ情報の量子化レベルを含む第２の１次元ベクトル（

）の間の２項積として表すことができる。
このような３次元ルックアップテーブルを使用することにより、確率値とコーディング間隔サイズの異なるペア間の乗算演算をテーブルにより反映させることができる。したがって、２次元ルックアップテーブルの適切な要素を選択することにより、乗算演算の実行を省くことができる。さらに、このようなアプローチを使用すると、２次元ルックアップテーブルのエントリを非常に簡単な方法で取得できる。

算術エンコーダの好ましい実施形態では、２次元ルックアップテーブル（ＲａｎｇＴａｂＬＰＳ）の要素が、ベースルックアップテーブル（Ｂａｓｅ ＴａｂＬＰＳ）に基づいて定義され、２次元ルックアップテーブルの要素の第１のグループ（またはブロック、例えば、「上半分」）は、ベースルックアップテーブルの要素と同一であるか、ベースルックアップテーブルの要素の丸められたバージョンであり、２次元ルックアップテーブルの要素の第２のグループ（またはブロック、例えば「下半分」）は、ベースルックアップテーブルの要素のスケーリングおよび丸められたバージョンである。
このようなアプローチを使用することにより、２次元ルックアップテーブルの要素の概ね指数関数的である増加または減衰を取得できる。例えば、２次元ルックアップテーブルの要素を定義して、２次元ルックアップテーブルの要素の第２のグループが、実質的に（例えば、丸めによって引き起こされる偏差を除いて）２次元ルックアップテーブルの要素の第１のグループのスケーリングされたバージョンになるようにすることによって、非常に均一な２次元ルックアップテーブルを取得できる。また、このようなアプローチを使用して、２次元ルックアップテーブルの要素を簡単に取得できることに留意されたい。

算術エンコーダの好ましい実施形態では、２次元ルックアップテーブルの要素の第２のグループは、ベースルックアップテーブルの要素の右シフトバージョンである。
このようなアプローチを使用することにより、右シフト操作を非常に簡単に実行できるため、２次元ルックアップテーブルの要素を特に効率的な方法で取得できる。また、右シフト操作は適切なスケーリングを引き起こし、非常に効率的な方法で丸め操作を実行することもできる。

算術エンコーダの好ましい実施形態では、確率指数（Ｑｐ_２（ｐ_ＬＰＳ）；ｉ）は、２次元ルックアップテーブルの要素の第１のグループの要素または２次元ルックアップテーブルの要素の第２のグループの要素のどちらを評価するかを決定し、確率指数（例えば、確率値、例えばｐ_ＬＰＳを定量化することによって取得される）の第１の範囲（例えば、０～μ－１）は、要素の第１のグループの要素に関連付けられ、確率指数（例えば、確率値、例えばｐ_ＬＰＳを、例えば、量子化関数Ｑｐ２（．）を使用して定量化することによって取得される）の第２の範囲（例えば、μ以上）は、要素の第２のグループの要素に関連付けられている。そのような概念を使用することにより、要素の第１のグループの要素を使用すべきか、要素の第２のグループの要素を使用すべきかの違いが、確率指数に応じてできるようになり得、例えば、それぞれの状態変数値に基づき得る。例えば、確率指数（例えば、最も可能性の低いシンボルの確率によって、または整数の指数値によって定義され得る）は、例えば、マッピングを使用して、それぞれの状態変数値に基づいて導出され得る。例えば、第１の状態変数値のマッピングを使用して得られた第１の確率値、または第２の状態変数値のマッピングを使用して得られた第２の確率値を使用して、２次元ルックアップテーブルのどの要素を評価すべきかを決定することができる（特に、２次元ルックアップテーブルの要素の第１のグループの要素を評価するか、２次元ルックアップテーブルの要素の第２のグループの要素を評価するかを決定する）。
また、この概念を使用すると、ベースルックアップテーブルに基づいて「オンザフライ」で２次元ルックアップテーブルのそれぞれの要素を決定することができ、その要素の数は、確率指数とコーディング間隔サイズ指数によって対処されるテーブル要素の数よりも少なくなる。

算術エンコーダの好ましい実施形態では、確率指数（ｉ）と第１のサイズ値（例えば、μ、サイズ値は例えば、第１の方向のベースルックアップテーブルの拡張を説明する）および間隔サイズ指数（例えば量子化演算Ｑｒ２（．）、例えばｊを使用するなどして間隔サイズ情報Ｒに基づいて取得できる）との間の除算の除算残差（ｉ％μ）は、２次元ルックアップテーブルの要素を取得するためにベースルックアップテーブルのどの要素を使用するかを決定する。
このような概念を使用することにより、ベースルックアップテーブルの第１の方向への拡張が可能な確率指数値の数よりも小さい場合でも、ベースルックアップテーブルの適切な要素を選択できる。確率指数と第１のサイズ値の間の除算の分割残差を評価することにより、ベースルックアップテーブルの第１の方向への拡張を表すことができ、ベースルックアップテーブルの要素を２つ以上の異なる確率指数値に再利用できる（例えば、第１のサイズ値の分異なる場合がある）。その結果、ベースルックアップテーブルのエントリは、第１のサイズ値の分が異なる２つの確率指数値に対して、例えば異なるスケーリングを使用して２回使用できる。したがって、２次元ルックアップテーブルは通常、確率指数値の進化を記述し、確率指数値の第２の範囲の進化は、確率指数値の第１の範囲の進化と比較した場合に、スケーリングされたバージョン（例えば、丸め効果を受け入れる）であることが利用できる。

好ましい実施形態では、算術エンコーダは、
ＲａｎｇｅＴａｂＬＰＳ［ｉ］［ｊ］＝Ｓｃａｌ（ＢａｓｅＴａｂＬＰＳ［ｉ％μ］［ｊ）、[ｉ／μ]）；
ＢａｓｅＴａｂＬＰＳは、次元μｘλのベースルックアップテーブルであり、ｉは、確率情報に関連付けられたテーブルインデックスであり、ｊは、間隔サイズ情報に関連付けられたテーブルインデックスであり（例えば、現在のコーディング間隔サイズを記述する）、％は除算残差演算であり、／は除算演算であり、Ｓｃａｌ（ｘ，ｙ）はスケーリング関数であり（例えば、Ｓｃａｌ（ｘ，ｙ）＝[ｘ＊ａ^－ｂｙ]として定義され、[．]はフロア演算であり、ａは、好ましくは２以上の定数であり、またはｂは、好ましくは１以上の定数であり、スケーリング関数は、好ましくは、右シフトビットシフト演算を使用して実装され、ｙは、ｘの右側にシフトするかどうか、および何ビットシフトするかを決定する、
ことに従って２次元ルックアップテーブル（ＲａｎｇＴａｂＬＰＳ）の要素を取得するように構成される。
そのようなアプローチを使用することによって、スケーリング関数またはスケーリング操作の結果によって定義され得る間隔サイズ情報は、特にメモリ効率の良い方法で取得され得る。例えば、「ＢａｓｅＴａｂＬＰＳ」ルックアップテーブルは、その第１の次元μが、確率情報に関連付けられたテーブルインデックスiの値の範囲よりも通常小さいため、またその第２の次元λが間隔サイズ情報によって記述される可能な異なる間隔サイズに等しい可能性があるため、特に小さい場合がある。さらに、ｉとμの商のフロア演算によって定義される異なるスケーリング係数の数が比較的小さいため、スケーリング関数は特に効率的な方法で実装することができる。例えば、ｉとμの間の除算の範囲が０と２より小さい最大値との間である場合、２つの異なるスケーリング操作のみを実行できる。例えば、２つ、３つ、または４つの異なるスケーリングの任意の選択のみが存在する可能性があり（ｉとμの間の商に応じて）、これらのスケーリングの任意の選択は、少数の所定の値のみを使用した乗算を使用して、または単なるシフト演算さえをも使用して、効率的に実装できる。

算術エンコーダの好ましい実施形態では、２次元ルックアップテーブル（ＲａｎｇＴａｂＬＰＳ）の要素は、確率テーブル（ｐｒｏｂＴａｂＬＰＳ）に基づいて定義され、確率テーブルは、複数の確率値のセット（例えば、指数ｉによって表される）および所与のコーディング間隔サイズの間隔サイズを記述し、複数の確率値のセットにない確率値および／または所与の（参照）コーディング間隔サイズとは異なるコーディング間隔サイズの２次元ルックアップテーブルの要素は、スケーリングを使用して確率テーブルから導出される。
そのようなアプローチを使用して、異なる間隔サイズが、関連する確率値間の差異、および／または関連するコーディング間隔サイズ間の差異に依存するスケーリングによって互いに関連していることが多いことを利用することができる。別の言い方をすれば、２次元ルックアップテーブルが現在考慮されている確率値および／または現在考慮されているコーディング間隔サイズに適合する要素を含まない場合でも、適切な間隔サイズを依然として取得でき、２次元ルックアップテーブルの別の要素は相応してスケーリングされる（例えば、現在考慮されている確率値に依存して、および／または現在考慮されているコーディング間隔サイズに依存して）。

算術エンコーダの好ましい実施形態では、２次元ルックアップテーブルの要素が、コーディング間隔サイズ（Ｒ）に応じて、確率テーブルの選択された要素（ｐｒｏｂＴａｂＬＰＳ［ｉ％μ］）の（乗法の）第１のスケーリングを使用し、現在の確率値（指数ｉにより指定）に関連付けられた要素が確率値のセットに含まれるかどうかに応じて（例えば、現在の確率値は、確率テーブルでカバーされている確率値の範囲内にあるかどうかに応じて）、第１のスケーリングの結果の第２のスケーリングを使用して取得される。
したがって、２次元ルックアップテーブルの要素は、確率テーブルの適切なエントリを使用して、また適切なスケーリングを使用して「オンザフライ」で取得でき、評価される「確率テーブル」は、通常、２次元のルックアップテーブルよりも大幅に小さくなる。言い換えると、２次元ルックアップテーブルの要素をアドレス指定する２つのインデックスに基づいて、確率テーブルの適切な要素が選択され、スケーリングされる。ただし、多くの場合、このような概念により、メモリの要求と計算の複雑さの間のトレードオフが改善される。

算術エンコーダの好ましい実施形態では、確率指数（例えばｉ、例えば、現在の確率値を表す）、および第１のサイズ値（例えばμ、例えばサイズ値が確率テーブルの拡張について説明する）の間の除算の除算残差（ｉ％μ）は、確率テーブルのどの要素が第１のスケーリングでスケーリングされるかを決定する、および／または確率指数（ｉ）と第１のサイズ値との間の除算の整数除算結果（[ｉ／μ]）は、第２のスケーリングで使用されるスケーリング係数（２－[ｉ／μ]）を決定するおよび／またはコーディング間隔サイズは、第１のスケーリングの乗法スケーリング係数（Ｑｒ２（Ｒ））を決定する。
このような概念を使用すると、確率指数とコーディング間隔サイズ指数の２次元グリッドの（比較的小さい）部分の間隔サイズのみを表す小さな確率テーブルを使用でき、メモリスペースを省ける。次に、適切な間隔サイズ情報は、確率テーブルの要素の上記の選択によって、および確率テーブルの選択された要素の上記の２倍のスケーリングによっても取得することができる。

好ましい実施形態では、算術エンコーダは、

ｉは、確率情報に関連付けられたテーブルインデックスであり、ｊは間隔サイズ情報に関連付けられたテーブルインデックスであり、％は除算残差演算であり、／は除算演算であり、ｐｒｏｂＴａｂＬＰＳ ［］は確率テーブルであり、μは確率テーブルの要素の数であり（Ｉの値の範囲は通常μよりも大きくなる）、Ｒは間隔サイズ（または現在のコーディング間隔サイズ）であり、Ｑｒ２（Ｒ）はＲに依存するスケーリング係数であり、Ｓｃａｌ（ｘ，ｙ）はスケーリング関数であり（例えば、Ｓｃａｌ（ｘ，ｙ）＝[ｘ＊ａ^－ｂｙ]として定義され、[．]はフロア演算であり、ａは、好ましくは２以上の定数であり、ｂは、好ましくは１以上の定数であり、スケーリング関数は、好ましくは、右シフトビットシフト演算を使用して実装され、ｙは、ｘの右シフトをするかどうか、および何ビットシフトするかを決定する、
ことに従って２次元ルックアップテーブルの要素

を取得するように構成される。
間隔サイズ情報を表している可能性があるか、間隔サイズ情報に等しい可能性がある２次元ルックアップテーブルの適切な要素を取得するためにこのような概念を使用することにより、メモリの要件と計算の複雑さの間の非常に良いトレードオフを得ることができる。テーブル「ｐｒｏｂＴａｂＬＰＳ」は、例えば、１次元テーブルであり得、該テーブルの要素の数は、テーブルインデックスｉのいくつかの異なる可能な値よりも小さくてもよい。ただし、確率テーブルｐｒｏｂＴａｂＬＰＳの選択された要素と、間隔サイズＲに依存するスケーリング係数Ｑｒ_２（Ｒ）の積をスケーリングすることにより、良好な精度に到達でき、発生する可能性のある丸め誤差を適度に小さく保つことができる。さらに、スケーリングは「フロア」演算子によって取得される整数値について演算するため、効率的なスケーリングの概念を使用でき、これは、例えば、整数の乗算、整数の除算、またはビットシフト演算によって定義できる。したがって、計算の負荷は非常に小さい。

好ましい実施形態では、算術エンコーダは、

ｉは、確率情報に関連付けられたテーブルインデックスであり、ｊは間隔サイズ情報に関連付けられたテーブルインデックスであり、％は除算残差演算であり、／は除算演算であり、ｐｒｏｂＴａｂＬＰＳ ［］は確率テーブルであり、μは確率テーブルの要素の数であり（Ｉの値の範囲は通常μよりも大きくなる）、Ｒは間隔サイズ（または現在のコーディング間隔サイズ）であり、Ｑｒ２（Ｒ）はＲに依存するスケーリング係数であり、Ｓｃａｌ（ｘ，ｙ）はスケーリング関数であり（例えば、Ｓｃａｌ（ｘ，ｙ）＝[ｘ＊ａ^－ｂｙ]として定義され、[．]はフロア演算であり、ａは、好ましくは２以上の定数であり、ｂは、好ましくは１以上の定数であり、スケーリング関数は、好ましくは、右シフトビットシフト演算を使用して実装され、ｙは、ｘの右シフトをするかどうか、および何ビットシフトするかを決定する、
ことに従って２次元ルックアップテーブルの要素

を取得するように構成される。
また、間隔サイズ情報を取得するためのこのアプローチは特に効率的であり、間隔サイズ情報（第１のスケーリングと第２のスケーリングの結果として取得される）に対して質の高い結果をもたらすことがわかっている。

算術エンコーダの好ましい実施形態では、確率指数（例えばｉ、例えば、現在の確率値を表す）および第１のサイズ値（例えばμ、例えばサイズ値が確率テーブルの拡張について説明する）の間の除算の除算残差（ｉ％μ）は、確率テーブルのどの要素が第１のスケーリングでスケーリングされるかを決定する、および／または確率指数（ｉ）と第１のサイズ値との間の除算の整数除算結果（[ｉ／μ]）は、第１のスケーリングで使用されるスケーリング係数（２^{－[ｉ／μ]}）を決定する、および／またはコーディング間隔サイズ（Ｒ）は、第２のスケーリングの乗法スケーリング係数（Ｑｒ_２（Ｒ））を決定する。
上記の分割残差に依存して確率テーブルの要素（１次元の確率テーブルである可能性がある）を選択することにより、間隔サイズが、スケーリングを除いて、確率指数の異なる範囲で実質的に類似するという事実が利用され得る。したがって、確率テーブルは、確率指数の単一の範囲の値のみを反映し、確率指数の他の範囲の間隔サイズ値は、第１のスケーリングを使用して取得される。第２のスケーリングは、確率テーブルによって表される値、または第１のスケーリングを使用してそれに基づいて得られる値を、コーディング間隔サイズに適合させ、それによって適切な間隔サイズ情報を取得するようにする。
その結果、メモリ消費、計算の複雑さ、および精度の間の良好なトレードオフが得られ、例えば、第１のサイズ値が適切に選択された場合、除算残差と整数除算の結果は、計算上非常に簡単な方法で取得できる（例えば、２つの効力になる）。

好ましい実施形態では、算術エンコーダは、

ｉは、確率情報に関連付けられたテーブルインデックスであり、ｊは間隔サイズ情報に関連付けられたテーブルインデックスであり、％は除算残差演算であり、／は除算演算であり（例えば、整数の結果を提供する）、ｐｒｏｂＴａｂＬＰＳ ［］は確率テーブルであり、μは確率テーブルの要素の数であり（Ｉの値の範囲は通常μよりも大きくなる）、Ｒは間隔サイズであり、Ｑｒ_２（Ｒ）はＲに依存するスケーリング係数であり、Ｓｃａｌ（ｘ，ｙ）はスケーリング関数であり（例えば、Ｓｃａｌ（ｘ，ｙ）＝[ｘ＊ａ^－ｂｙ]として定義され、[．]はフロア演算であり、ａは、好ましくは２以上の定数であり、ｂは、好ましくは１以上の定数であり、スケーリング関数は、好ましくは、右シフトビットシフト演算を使用して実装され、ｙは、ｘの右シフトをするかどうか、および何ビットシフトするかを決定する、
ことに従って２次元ルックアップテーブルの要素

を取得するように構成される。
この計算ルールは、前述の概念を非常に効率的な方法で実装する。

算術エンコーダの好ましい実施形態では、２次元ルックアップテーブルは、そのエントリが第１および第２の状態変数値の値ドメインの異なる値間隔の確率値、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]；

）を含む第１の１次元ベクトル（１次元ルックアップテーブルを形成する）、およびそのエントリがコーディング間隔サイズ情報の量子化レベルを含む第２の１次元ベクトル（

）の間の２項積として、表すことができる。
このような２次元ルックアップテーブルは、状態変数値に基づいて、およびコーディング間隔サイズ情報に基づいて、間隔サイズ情報を効率的に導出するために十分に使用可能である。２次元ルックアップテーブル内のルックアップは、状態変数値の確率値へのマッピング、および取得された確率値とコーディング間隔サイズの乗算に対応する。したがって、２次元ルックアップテーブルの選択されたエントリに等しい可能性がある間隔サイズ情報を取得することは非常に容易に可能であり、２次元ルックアップテーブルのそれぞれの要素は、それぞれの状態変数値に応じて、またコーディング間隔サイズ情報の独立性で、選択され得る（それぞれの状態変数値が２次元ルックアップテーブルの要素の第１のインデックスを決定し得、コーディング間隔サイズ情報が第２のインデックスを決定し得る）。

好ましい実施形態では、算術エンコーダは、第１および第２の状態変数値、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]）からそれぞれ第１および第２のサブインターバル幅値（Ｒ＊ｐ^ｋ）を計算するよう構成され、この計算は、そのエントリが第１および第２の状態変数値の値ドメインの異なる値間隔の確率値、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ _２＊ａ^ｋ _２]）を含む１次元ルックアップテーブル（ＬＵＴ４）を使用して、第１および第２の状態変数値（ｓ_ｋ）、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]）を第１および第２の確率値にマッピングすること、およびシンボルを量子化レベルに符号化する前に、算術符号化のコーディング間隔のサイズを記述するコーディング間隔サイズ情報（例えば、Ｒ）を量子化することにより、これを行い、算術エンコーダは、さらに、第１および第２の確率値と、一方で量子化レベルの間の積を決定する（事前計算された積のルックアップまたは乗算によって）し、第１のサブインターバル幅値と第２のサブインターバル幅値を使用して（例えば、加重和または加重平均を使用して）結合されたサブインターバル幅値を取得するように構成される。
このようなアプローチを使用することはまた、特定の状況下で非常に効率的であることがわかっている。第１の状態値のみに基づいて（ただし、第２の状態変数値を考慮せずに）第１のサブインターバル幅の値を導出し、第２の状態変数値のみに基づいて（ただし、第１の状態変数値を考慮せずに）第２のサブインターバル幅の値を計算することにより、異なる適合時定数を使用して取得される状態変数値の実質的に別個の処理は、処理の大半を通じて維持される。最終段階でのみ、第１のサブインターバル幅の値と第２のサブインターバル幅の値を結合して、結合したサブインターバル幅の値を取得し、これは高い精度をもたらし、状況によっては、第１の状態変数値と第２の状態変数値が、あまりにも早い段階で組み合わされる場合に発生する劣化を回避する。

好ましい実施形態では、算術エンコーダは、コーディング間隔サイズ情報に論理右シフトを適用することによってコーディング間隔サイズ情報の量子化を実行するように構成される。
論理右シフトは最小限の計算リソースしか必要としないため、この概念は特に実装が簡単である。
好ましい実施形態では、算術エンコーダは、コーディング間隔サイズ情報

の量子化を

により実行するように構成され、式中、

、

および

はパラメータである。
このような量子化も非常に簡単に実装できることがわかった。特に、パラメータ

と

が整数の値（または１より大きい整数の値）になるように選択されている場合、計算の労力は非常に低くなる。

算術エンコーダの好ましい実施形態では、１次元ルックアップテーブルのエントリは、第１および第２の状態変数値、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]）の増加で単調に減少する。
１次元ルックアップテーブルの単調に減少するエントリを使用すると、間隔サイズ情報に良好な結果がもたらされることが示されている。

算術エンコーダの好ましい実施形態では、第１および第２の状態変数値の値ドメインの異なる値間隔、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]）は、等しいサイズになる。
値の間隔のこのような等しいサイズの使用により、単純な量子化が可能になる。さらに、値の間隔を同じサイズにすることで、ルックアップテーブルの要素を適度な労力でオンザフライで決定できる。

算術エンコーダの好ましい実施形態では、第１および第２の状態変数値の値ドメインの異なる値間隔、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]）は、等しいサイズになる。
１次元ルックアップテーブルのエントリのこのような単調な減少を使用すると、指数関数的減衰を高い精度で表すことができるようになる。

本発明による実施形態は、シンボル値（例えば、バイナリ値）を有する複数のシンボルを符号化するための算術エンコーダを作成し、算術エンコーダは、間隔サイズ情報（ｐ^ｋ、Ｒ＊ｐ^ｋ）を、１つまたは複数のシンボル値（例えば、バイナリ値）の算術符号化が複数の状態変数値（ｓ_ｉ ^ｋ）（例えば、インデックスｋによって表示される所与のコンテキストモードに関連付けられるもの）に基づいて符号化されるように導出するように構成され、これは、異なる適合時定数で以前に符号化された複数のシンボル値（例えば、バイナリ値０と１のシーケンス）の統計を表し、算術エンコーダは、結合状態変数値（ｓ_ｋ）（例えば、状態変数値の加重和であり得る）、複数の個々の状態変数値（ｓ_ｉ ^ｋ）の基礎となるものを導出するように構成され、算術エンコーダは、結合状態変数値（ｓ_ｋ）、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ _２＊ａ^ｋ _２]）を、ルックアップテーブルを使用してマッピングして、符号化される１つまたは複数のシンボルの算術符号化の間隔サイズを説明する間隔サイズ情報（例えば、ｐ_ｋまたはＲ＊ｐ_ｋ）を取得するように構成される。

本発明によるこの実施形態は、ルックアップテーブルを使用してマッピングが実行される前に結合状態変数値が決定される場合、間隔サイズ情報の決定において高い効率が得られるという考えに基づく。したがって、２つ（またはそれ以上）の状態変数値を使用して個別のルックアップテーブルルックアップを実行する必要がもはやなくなった。むしろ、間隔サイズ情報を決定するには、単一のテーブルルックアップで十分な場合がある。特に、ルックアップテーブルルックアップを実行する前の第１の状態変数値と第２の状態変数値の結合は、多くの状況下で間隔サイズ情報の質を著しく低下させないことがわかった。

好ましい実施形態では、算術エンコーダは、結合状態変数値を取得するために、状態変数値の加重和を決定するように構成される。
状態変数値の加重和の計算は、結合状態変数値を決定するための効率的な方法であり、また２つの状態変数値の異なる関連性を考慮するのにも適していることがわかっており、それは状態変数値を導出するときに使用される様々な適合時定数により引き起こされる。

好ましい実施形態では、算術エンコーダは、状態変数値（

）および関連する重み付け値（

結合状態変数値（ｓ_ｋ）を得るため）の積を丸めることによって得られる丸められた値（

）の合計を決定するように構成される。
合計を実行する前にスケーリングされた値の丸めを実行すると、特に意味のある結果が得られることがわかっている。状態変数値の１つの無視できる寄与は、丸めによって排除され、結合状態変数値に影響を与えない。したがって、信頼性の高い結果を得ることができ、結合状態変数値は通常整数の値をとり、これは、ルックアップテーブルの要素を選択するためのインデックスとして機能するのに非常に適している。

好ましい実施形態では、算術エンコーダは、

ｓ^ｋ _２は状態変数値であり、Ｎは考慮される状態変数値の数であり、
[．]はフロア演算子であり、ｄ^ｋ _ｉは状態変数値に関連付けられた重み付け値（例えば、結合状態変数値への個々の状態変数値の影響を制御する重み付け係数）（ｄ^ｋ _ｉは好ましくはフォン２の整数値の効力であり、２つの異なるｄ^ｋ _ｉ間の比率は好ましくは２の整数値の効力である）［２つの異なるｄ^ｋ _ｉ間の比率は、好ましくは８以上）であることに従って、結合状態変数値ｓ_ｋを決定するように構成される。
結合状態変数値を導出するためのこの概念は、前に説明したように、非常に意味のある結合状態変数値をもたらす。

好ましい実施形態では、算術エンコーダは、符号化されるシンボルが第１の値（例えば「１」）をとる場合に状態変数値を第１の方向に変更する（例えばより正になる）ように構成され、また符号化されるシンボルが第１の値とは異なる第２の値（例えば「０」）をとる場合（例えば、状態変数値が正と負の値をとることができるように）に状態変数値を第２の方向に（例えば、より負になるもの）変更するように構成され、算術エンコーダは、結合状態変数値の絶対値（ｓ_ｋ ^ｉ＞０の場合はｓ_ｋ、それ以外の場合は－ｓ_ｋ）に応じて（例えば、結合状態変数値の絶対値のスケーリングおよび丸められたバージョンに応じて）評価されるルックアップテーブルのエントリを決定するように構成される。
状態変数値の決定のためのこの概念（例えば、第１の状態変数値の決定および第２の状態変数値のため）は、第１の状態変数値および第２の状態変数値の別個のマッピングが使用される場合と同じ利点をもたらす。

好ましい実施形態では、算術エンコーダは、結合状態変数値が第１の符号（例えば、正の符号）をとる場合に、確率値（ｐ^ｋ）をルックアップテーブルによって提供される値（例えば、

）に設定するように構成され、算術エンコーダは、状態変数値が第２の符号（例えば、負の符号）をとる場合、確率値（ｐ^ｋ）を、所定の値（例えば、１）からルックアップテーブルによって提供される値（例えば、

）を減算することによって得られる値に設定するように構成される。
ルックアップテーブルのサイズを小さくできるため、結合状態変数値を確率値にマッピングすることに対するこの概念は効率的である。特に、ルックアップテーブルの同じ要素が、所与の正の結合状態変数値および所与の（正の）結合状態変数値の負のバージョンに関連付けられるため、ルックアップテーブルの要素の数を減らすことができる。言い換えると、所与の概念では、結合状態変数値の絶対値が、確率値の提供のためにルックアップテーブルのどの要素が評価されるかを決定する。
ただし、結合状態変数値の符号は、確率値をルックアップテーブルによって提供される値、またはルックアップテーブルによって提供される値を符号に応じて所定の値から減算することによって得られる値に設定することにより、適切かつ効率的な方法で依然として考慮される。したがって、計算の複雑さが低い程度の結合状態値に基づいて、意味のある確率値を取得することができる。

好ましい実施形態では、算術エンコーダは、

ＬＵＴ２は確率値を含むルックアップテーブルであり、[．]はフロア演算子であり、ｓ^ｋは結合変数値であり、ａ^ｋは、結合状態変数値に関連付けられた重み付け値である（例えば、ｉ番目の状態変数値の数の範囲をルックアップテーブルのいくつかのエントリに適合させる重み付け値）ことにより、結合確率値ｐ_ｋを決定するように構成される。
結合状態変数値ｓ_ｋに基づいて結合確率値を決定するためのこの概念は、計算上非常に効率的な方法で前に概説された概念を実装する。

好ましい実施形態では、算術エンコーダは、

ＬＵＴ２は確率値を含むルックアップテーブルであり、[．]はフロア演算子であり、ｓ^ｋは結合変数値であり、ａ^ｋは、結合状態変数値に関連付けられた重み付け値である（例えば、ｉ番目の状態変数値の数の範囲をルックアップテーブルのいくつかのエントリに適合させる重み付け値）ことにより、結合確率値ｐ_ｋを決定するように構成される。
この概念では、スケーリングされた結合状態変数値ｓ_ｋの絶対値の計算はない。むしろ、スケーリングされた（「重み付けされた」）結合状態変数値に適用される「フロア」の演算のみがあり、状況によっては、絶対値の形成よりも少ない労力で実装できる。否定は整数値にのみ適用される。整数値は、重み付けされた結合状態変数値の下方の丸め（フロア演算子）によって取得される。ただし、整数値の否定は、通常、小数値または浮動小数点表現の値の否定ほど複雑ではない。したがって、ここで説明する概念は、状況によっては複雑さを軽減するのに役立ち得る。

好ましい実施形態では、算術エンコーダは、結合状態変数値、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]）を、２次元ルックアップテーブルを使用してサブインターバル幅値（Ｒ＊ｐ^ｋ）にマッピングするように構成され、そのエントリは、結合状態変数値に依存して（例えば、第１のルックアップテーブルエントリの座標を決定するために）、およびシンボルの符号化前の算術符号化のコーディング間隔のサイズを記述するコーディング間隔サイズ情報（例えば、Ｒ）に依存して（例えば、第２のルックアップテーブルエントリの座標を決定するために）アドレス指定される。
この概念を使用して、結合状態変数値の結合確率値へのマッピング、および結合確率値とコーディング間隔サイズとの乗算を、単一のルックアップテーブルルックアップ演算に結合することができる。したがって、２次元のルックアップテーブルが必要だが、乗算の演算は省ける。２次元ルックアップテーブルのエントリは事前に計算されている場合があり、これにより、実行時の結合の負荷が非常に低く抑えられる。むしろ、第１のテーブルインデックスは、結合状態変数値、またはそのスケーリングおよび／または丸められたバージョンに基づいて決定され得、第２のテーブルインデックスは、コーディング間隔サイズ情報に基づいて決定され得る（例えば、丸めまたは量子化を使用）。第１のステップ指数および第２の状態指数は、２次元ルックアップテーブルの要素を一意に指定することができ、２次元ルックアップテーブルの指定された要素は、サブ間隔幅値として（または間隔サイズ情報として）使用することができる。したがって、非常に効率的な概念が得られ、ルックアップテーブルに十分なメモリが利用可能な場合の計算の複雑さが軽減される。

算術エンコーダの好ましい実施形態では、２次元ルックアップテーブルは、そのエントリが結合状態変数値の値ドメインの異なる値間隔の確率値、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]；

）を含む第１の１次元ベクトル（

、１次元ルックアップテーブルを形成する）、およびそのエントリがコーディング間隔サイズ情報の量子化レベルを含む第２の１次元ベクトル（

）の間の２項積として、表すことができる。
このような２次元ルックアップテーブルは、非常に良い結果をもたらす。特に、この２次元ルックアップテーブルのすべての要素は、結合状態変数値に関連付けられたそれぞれの確率値とコーディング間隔サイズの乗算を表す。したがって、本明細書で説明する２次元ルックアップテーブルは、乗算の必要性を排除し、これは、非常にリソース効率が高いと見なすことができる。

算術エンコーダの好ましい実施形態では、２次元ルックアップテーブル（ＲａｎｇＴａｂＬＰＳ）の要素が、ベースルックアップテーブル（Ｂａｓｅ ＴａｂＬＰＳ）に基づいて定義され、２次元ルックアップテーブルの要素の第１のグループ（またはブロック、例えば、「上半分」）は、ベースルックアップテーブルの要素と同一であるか、ベースルックアップテーブルの要素の丸められたバージョンであり、２次元ルックアップテーブルの要素の第２のグループ（またはブロック、例えば「下半分」）は、ベースルックアップテーブルの要素のスケーリングおよび丸められたバージョンである。
ベースルックアップテーブルに基づいて２次元ルックアップテーブルの要素を定義することにより、２次元ルックアップテーブルを非常に簡単な方法で生成できる。さらに、２次元ルックアップテーブルの要素の第２のグループは、ベースルックアップテーブルの要素のスケーリングおよび丸められたバージョンであるため（２次元ルックアップテーブルの要素の第１のグループの要素は、ベースルックアップテーブルの要素またはベースルックアップテーブルの要素の丸められたバージョンと同一）、２次元ルックアップテーブルの行または列の要素の指数関数的な展開がよく反映される。２次元ルックアップテーブルの要素の第２のブロックが実質的に（丸め効果を除く）２次元ルックアップテーブルの要素の第１のブロックのスケーリングされたバージョンであるという概念を使用することにより、結合状態変数値を間隔サイズ情報にマッピングすることに対する適切な特性を反映することができる。

算術エンコーダの好ましい実施形態では、２次元ルックアップテーブルの要素の第２のグループはベースルックアップテーブルの要素の右シフトバージョンである。
これにより、２次元ルックアップテーブルのエントリ（要素）を簡単に生成できる。
ベースルックアップテーブルの右シフト要素は、スケーリングと丸め操作を結合した非常に効率的な概念であることがわかっている。

算術エンコーダの好ましい実施形態では、確率指数（Ｑｐ_２（ｐ_ＬＰＳ）；ｉ）は、２次元ルックアップテーブルの要素の第１のグループの要素または２次元ルックアップテーブルの要素の第２のグループの要素のどちらを評価するかを決定し、確率指数（例えば、確率値、例えばｐ_ＬＰＳを定量化することによって取得される）の第１の範囲（例えば、０～μ－１）は、要素の第１のグループの要素に関連付けられ、確率指数（例えば、確率値、例えばｐ_ＬＰＳを、例えば、量子化関数Ｑｐ２（．）を使用して定量化することによって取得される）の第２の範囲（例えば、μ以上）は、要素の第２のグループの要素に関連付けられている。
（中間量として確率値を使用せずに）結合状態変数値から直接導出され得る、または結合状態変数値に基づく結合確率値を使用して導出され得る確率指数を使用することによって、２次元ルックアップテーブルの要素の選択は非常に効率的に行うことができる。また、確率指数は、要素の第１のグループの要素と要素の第２のグループの要素の使用を切り替えるために使用され、これにより、２次元ルックアップテーブルの要素をオンザフライで効率的に決定できる。

算術エンコーダの好ましい実施形態では、確率指数（ｉ）と第１のサイズ値（例えば、μ、サイズ値は例えば、第１の方向のベースルックアップテーブルの拡張を説明する）および間隔サイズ指数（例えば量子化演算Ｑｒ２（．）、例えばｊを使用するなどして間隔サイズ情報Ｒに基づいて取得できる）との間の除算の除算残差（ｉ％μ）は、２次元ルックアップテーブルの要素を取得するためにベースルックアップテーブルのどの要素を使用するかを決定する。

好ましい実施形態では、算術エンコーダは、
ＲａｎｇｅＴａｂＬＰＳ［ｉ］［ｊ］＝Ｓｃａｌ（ＢａｓｅＴａｂＬＰＳ［ｉ％μ］［ｊ）、[ｉ／μ]）
ＢａｓｅＴａｂＬＰＳは、次元μｘλのベースルックアップテーブルであり、ｉは、確率情報に関連付けられたテーブルインデックスであり、ｊは、間隔サイズ情報に関連付けられたテーブルインデックスであり（例えば、現在のコーディング間隔サイズを記述する）、％は除算残差演算であり、／は除算演算であり、Ｓｃａｌ（ｘ，ｙ）はスケーリング関数であり（例えば、Ｓｃａｌ（ｘ，ｙ）＝[ｘ＊ａ^－ｂｙ]として定義され、[．]はフロア演算であり、ａは、好ましくは２以上の定数であり、またはｂは、好ましくは１以上の定数であり、スケーリング関数は、好ましくは、右シフトビットシフト演算を使用して実装され、ｙは、ｘの右側にシフトするかどうか、および何ビットシフトするかを決定する、
ことに従って２次元ルックアップテーブル（ＲａｎｇＴａｂＬＰＳ）の要素を取得するように構成される。
該除算残差を評価して、ベースルックアップテーブルのどの要素を使用して２次元ルックアップテーブルの要素を取得するかを決定することにより、２次元ルックアップテーブルの要素のオンザフライの決定を、非常に高い効率で実行することができる。特に、２次元ルックアップテーブルが、ベースルックアップテーブルの同じ要素に基づく２つ以上の要素グループで構成されているという事実は、ベースルックアップテーブルのどの要素を２次元ルックアップテーブルの要素を取得するために使用するかを決定するための分割残差の使用によって反映され得る。言い換えれば、２次元ルックアップテーブルの要素とベースルックアップテーブルの要素との間の周期的関係は、除算残差がまた確率指数の増加に関して周期的であるため、該除算残差の考慮によってよく反映される。

算術エンコーダの好ましい実施形態では、２次元ルックアップテーブル（ＲａｎｇＴａｂＬＰＳ）の要素は、確率テーブル（ｐｒｏｂＴａｂＬＰＳ）に基づいて定義され、確率テーブルは、複数の確率値のセット（例えば、指数ｉによって表される）および所与のコーディング間隔サイズの間隔サイズを記述し、複数の確率値のセットにない確率値および／または所与の（参照）コーディング間隔サイズとは異なるコーディング間隔サイズの２次元ルックアップテーブルの要素は、スケーリングを使用して確率テーブルから導出される。
この概念は、状態変数値の個別のマッピングの場合について説明した対応する概念と同じ考慮事項に基づいている。

算術エンコーダの好ましい実施形態では、２次元ルックアップテーブル（ＲａｎｇＴａｂＬＰＳ）の要素は、確率テーブル（ｐｒｏｂＴａｂＬＰＳ）に基づいて定義され、確率テーブルは、複数の確率値のセット（例えば、指数ｉによって表される）および所与のコーディング間隔サイズの間隔サイズを記述し、複数の確率値のセットにない確率値および／または所与の（参照）コーディング間隔サイズとは異なるコーディング間隔サイズの２次元ルックアップテーブルの要素は、スケーリングを使用して確率テーブルから導出される。
２次元ルックアップテーブルの要素のそのようなオンザフライの決定は、特に高い資源効率を含むことがわかっている。さらにまた、第１の状態変数値および第２の状態変数値の別個のマッピングの文脈内で使用される対応するアルゴリズムに関してなされた上記のコメントが適用されることに留意されたい。２次元ルックアップテーブルの要素の決定の基礎として、典型的には２次元ルックアップテーブルよりも小さい（例えば、より少ない要素を含む）確率テーブルを使用することによって、非常に高い効率を得ることができる。例えば、確率テーブルは、重要な範囲にわたる様々な確率値と様々な（量子化された）コーディング間隔サイズのマッピングを表す場合があり、したがって、単純なスケーリングを超える乗算を回避するのに役立つ場合がある（「単純な」スケーリングでは、例えば、シフト演算を使用して実装する場合がある）。
複数の確率値のセットに含まれない１つまたは複数の確率値、および所与のコーディング間隔サイズとは異なる１つまたは複数のコーディング間隔サイズの２次元ルックアップテーブルの要素は、確率テーブルから、スケーリングを使用して導出される。したがって、例えば、１つの行または１つの列のみを含み得る非常に小さい確率テーブルを有することで十分である。したがって、確率テーブルの要素の数は、異なる可能性のある確率値の数よりも少ない場合さえもあり得る（つまり、２次元ルックアップテーブルの異なる可能な確率指数の数よりも少ない場合がある）。さらに、スケーリングは確率値に依存する、および／またはコーディング間隔サイズに依存することに留意されたい。スケーリングは、例えば、確率テーブルのサイズが適切に選択されている場合、ビットシフト演算などの非常に単純なメカニズムを使用して実行できる。ビットシフト演算に基づくこのような「単純な」スケーリング演算は、任意の可変オペランド（例えば、２の効力とは異なる）を使用した「通常の」乗算と比較すると、必要な計算リソースが大幅に少なくなる。

算術エンコーダの好ましい実施形態では、２次元ルックアップテーブルの要素が、コーディング間隔サイズ（Ｒ）に応じて、確率テーブルの選択された要素（ｐｒｏｂＴａｂＬＰＳ［ｉ％μ］）の（乗法の）第１のスケーリングを使用し、現在の確率値（指数ｉにより指定）に関連付けられた要素が確率値のセットに含まれるかどうかに応じて（例えば、現在の確率値は、確率テーブルでカバーされている確率値の範囲内にあるかどうかに応じて）、第１のスケーリングの結果の第２のスケーリングを使用して取得される。
２次元ルックアップテーブルの要素のそのような計算は特に効率的であることがわかっている。さらに、第１の状態変数値および第２の状態変数値の別個のマッピングの文脈で提供される、対応する機能の上記の議論も参照される。

算術エンコーダの好ましい実施形態では、確率指数（例えばｉ、例えば、現在の確率値を表す）、および第１のサイズ値（例えばμ、例えばサイズ値が確率テーブルの拡張について説明する）の間の除算の除算残差（ｉ％μ）は、確率テーブルのどの要素が第１のスケーリングでスケーリングされるかを決定する、および／または確率指数（ｉ）と第１のサイズ値との間の除算の整数除算結果（[ｉ／μ]）は、第２のスケーリングで使用されるスケーリング係数（２^{－[ｉ／μ]}）を決定するおよび／またはコーディング間隔サイズは、第１のスケーリングの乗法スケーリング係数（Ｑｒ２（Ｒ））を決定する。
この機能に関しては、第１の状態変数値および第２の状態変数値の別個のマッピングの文脈で提供される、対応する機能の上記の議論も参照される。

好ましい実施形態では、算術エンコーダは、

ｉは、確率情報に関連付けられたテーブルインデックスであり、ｊは間隔サイズ情報に関連付けられたテーブルインデックスであり、％は除算残差演算であり、／は除算演算であり、ｐｒｏｂＴａｂＬＰＳ ［］は確率テーブルであり、μは確率テーブルの要素の数であり（Ｉの値の範囲は通常μよりも大きくなる）、Ｒは間隔サイズ（または現在のコーディング間隔サイズ）であり、Ｑｒ２（Ｒ）はＲに依存するスケーリング係数であり、Ｓｃａｌ（ｘ，ｙ）はスケーリング関数であり（例えば、Ｓｃａｌ（ｘ，ｙ）＝[ｘ＊ａ^－ｂｙ]として定義され、[．]はフロア演算であり、ａは、好ましくは２以上の定数であり、ｂは、好ましくは１以上の定数であり、スケーリング関数は、好ましくは、右シフトビットシフト演算を使用して実装され、ｙは、ｘの右シフトをするかどうか、および何ビットシフトするかを決定する、
ことに従って
２次元ルックアップテーブルの要素

を取得するように構成される。
この機能に関しては、第１の状態変数値および第２の状態変数値の別個のマッピングの文脈で提供される、対応する機能の上記の議論も参照される。

算術エンコーダの好ましい実施形態では、２次元ルックアップテーブルの要素が、確率テーブルの選択された要素（ｐｒｏｂＴａｂＬＰＳ［ｉ％μ］）の（乗法の）第１のスケーリングを使用し、現在の確率値（指数ｉにより指定）に関連付けられた要素が確率値のセットに含まれるかどうかに応じて（例えば、現在の確率値は、確率テーブルでカバーされている確率値の範囲内にあるかどうかに応じて）、また、コーディング間隔サイズ（Ｒ）に応じて、第１のスケーリングの結果の第２のスケーリングを使用して取得される。
この機能に関しては、第１の状態変数値および第２の状態変数値の別個のマッピングの文脈で提供される、対応する機能の上記の議論も参照される。

算術エンコーダの好ましい実施形態では、確率指数（例えばｉ、例えば、現在の確率値を表す）、および第１のサイズ値（例えばμ、例えばサイズ値が確率テーブルの拡張について説明する）の間の除算の除算残差（[ｉ％μ]）は、確率テーブルのどの要素が第１のスケーリングでスケーリングされるかを決定する、および／または確率指数（ｉ）と第１のサイズ値との間の除算の整数除算結果（[ｉ／μ]）は、第１のスケーリングで使用されるスケーリング係数（２^{－[ｉ／μ]}）を決定する、および／またはコーディング間隔サイズ（Ｒ）は、第２のスケーリングの乗法スケーリング係数（Ｑｒ_２（Ｒ））を決定する。
この機能に関しては、第１の状態変数値と第２の状態変数値との別個のマッピングの文脈で提供される対応する機能の上記の議論も参照され、結合状態変数値または結合確率値は、それぞれの個々の状態変数値またはそれぞれの個々の確率値の代わりに使用される。

好ましい実施形態では、算術エンコーダは、

ｉは、確率情報に関連付けられたテーブルインデックスであり、ｊは間隔サイズ情報に関連付けられたテーブルインデックスであり、％は除算残差演算であり、／は除算演算であり（例えば、整数の結果を提供する）、ｐｒｏｂＴａｂＬＰＳ ［］は確率テーブルであり、μは確率テーブルの要素の数であり（Ｉの値の範囲は通常μよりも大きくなる）、Ｒは間隔サイズであり、Ｑｒ_２（Ｒ）はＲに依存するスケーリング係数であり、Ｓｃａｌ（ｘ，ｙ）はスケーリング関数であり（例えば、Ｓｃａｌ（ｘ，ｙ）＝[ｘ＊ａ^－ｂｙ]として定義され、[．]はフロア演算であり、ａは、好ましくは２以上の定数であり、ｂは、好ましくは１以上の定数であり、スケーリング関数は、好ましくは、右シフトビットシフト演算を使用して実装され、ｙは、ｘの右シフトをするかどうか、および何ビットシフトするかを決定する、
ことに従って、２次元ルックアップテーブルの要素

を取得するように構成される。
この機能に関しては、第１の状態変数値と第２の状態変数値との別個のマッピングの文脈で提供される対応する機能の上記の議論も参照され、結合状態変数値または結合確率値は、個々の状態変数値の代わりになり、結合確率値が個々の確率値の代わりになる。

好ましい実施形態では、算術エンコーダは、結合状態変数値、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]）からサブインターバル幅値（Ｒ＊ｐ^ｋ）を計算するよう構成され、この計算は、そのエントリが結合状態変数値の値ドメインの異なる値間隔の確率値、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]；

）を含む１次元ルックアップテーブル（ＬＵＴ４）を使用して、結合状態変数値（ｓ_ｋ）、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]；

）を結合確率値にマッピングすること、およびシンボルを量子化レベルに符号化する前に、算術符号化のコーディング間隔のサイズを記述するコーディング間隔サイズ情報（例えば、Ｒ）を量子化することにより、これを行い、算術エンコーダは、さらに、結合確率値と量子化レベルの間の積を計算する（事前に計算された積のルックアップまたは乗算によって）ように構成される。
この機能に関しては、第１の状態変数値と第２の状態変数値との別個のマッピングの文脈で提供される対応する機能の上記の議論も参照され、ここで結合状態変数値または結合確率値は、個々の状態変数値の代わりになり、ここで結合確率値が個々の確率値の代わりになる。

好ましい実施形態では、算術エンコーダは、コーディング間隔サイズ情報に論理右シフトを適用することによってコーディング間隔サイズ情報の量子化を実行するように構成される。
この機能に関しては、第１の状態変数値および第２の状態変数値の別個のマッピングの文脈で提供される、対応する機能の上記の議論も参照される。

好ましい実施形態では、算術エンコーダは、コーディング間隔サイズ情報

の量子化を

により実行するように構成され、式中、

、

および

はパラメータである。
この機能に関しては、第１の状態変数値および第２の状態変数値の別個のマッピングの文脈で提供される、対応する機能の上記の議論も参照される。

算術エンコーダの好ましい実施形態では、１次元ルックアップテーブルのエントリは、結合状態変数値、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]）の増加で単調に減少する。
この機能に関しては、第１の状態変数値および第２の状態変数値の別個のマッピングの文脈で提供される、対応する機能の上記の議論も参照される。

算術エンコーダの好ましい実施形態では、結合状態変数値の値ドメインの異なる値間隔、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]）は、等しいサイズである。
この機能に関しては、第１の状態変数値および第２の状態変数値の別個のマッピングの文脈で提供される、対応する機能の上記の議論も参照される。

算術エンコーダの好ましい実施形態では、１次元ルックアップテーブルのエントリは、結合状態変数値、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]）の増加で減少率を伴って単調に減少する。
この機能に関しては、第１の状態変数値および第２の状態変数値の別個のマッピングの文脈で提供される、対応する機能の上記の議論も参照される。

算術エンコーダの好ましい実施形態では、ルックアップテーブルは、指数関数的減衰（例えば、０．５からの低下）を（例えば、＋／－１０％または＋／－２０％の許容範囲内で）定義する。
指数関数的減衰は、状態変数値に基づいて間隔サイズ情報を導出するための適切な関係をよく反映していることがわかっている。また、指数関数的減衰は、ルックアップテーブルを使用して非常に効率的に表すことができ、ルックアップテーブルの要素のオンザフライでの決定でさえ、わずかな労力で可能である。

好ましい実施形態では、算術エンコーダは、

ｚは所定の（一定の）オフセット値であり、

は１つまたは複数の重み付け値であり、

は１つ以上の重み付け値であり、Ａは

であるか、ゼロ設定または大きさの縮小によって、引数の１つ以上の極値に対してのみ、それから逸脱して、更新された

を所定の値の範囲のままにすることを回避する（例えば、

は

より大きな値ドメインを持つ；つまり、

は

に準量子化される；

の極値の場合、

は上記の式に従って未修正のＡによって変更され、その値ドメインを離れることができる：これを回避するために、これらの極値に対応するエントリが削減またはゼロにされる場合があることを考慮されたい）、

、

、

、および

は所定のパラメータである（例は上記に記載されている）
ことに従って複数の可変状態値

を更新するように構成される。
状態変数のそのような更新は、高い計算効率で行うことができ、マッピングテーブルを事前に計算することができることがわかっている。例えば、状態変数値

が所定の範囲（例えば、所定の最小値と所定の最大値との間）を維持することを達成することができる。さらに、マッピングテーブルＡの適切な選択を使用して、状態変数値が、以前に処理された（例えば、符号化または復号された）シンボルの統計の記述にうまく適合されることが達成され得る。また、それぞれの状態変数値の適合時定数は、重み付け値ｍおよびｎを適切に選択することによって適合できることに留意されたい。したがって、ここで説明するアルゴリズムは、状態変数値

の更新に効率的に使用できる。

好ましい実施形態では、算術エンコーダは、テーブルルックアップまたは計算によって

を導出するように構成される。
したがって、更新された状態変数値を導出するために、様々な概念が可能である。

本発明による実施形態は、シンボル値（例えば、バイナリ値）を有する複数のシンボルを符号化するための算術エンコーダであって、算術エンコーダは、１つまたは複数の状態変数値（ｓ_１ ^ｋ、ｓ_２ ^ｋ）を決定するように構成され、これは、以前に符号化された複数のシンボル値（例えば、バイナリ値０および１のシーケンス）の統計（例えば、複数の状態変数値の場合、異なる適合時定数の統計）を表し、および
算術エンコーダは、１つまたは複数の状態変数値（ｓ_ｉ ^ｋ）（例えば、インデックスｋにより示される、所与のコンテキストモードに関連付けられている）に基づいて符号化される１つまたは複数のシンボル値の算術符号化の間隔サイズ情報（ｐ^ｋ、Ｒ＊ｐ^ｋ）を導出するように構成され、これは複数の以前に符号化されたシンボル値（例えば、バイナリ値０および１のシーケンス）の統計（例えば、複数の状態変数値の場合、異なる適合時定数の統計）を表し、算術エンコーダは、符号化されるシンボルに依存して、ルックアップテーブル（Ａ）を使用して（例えば、シンボルを符号化した後）、第１の状態変数値（ｓ^ｋ _１）を更新するように構成される。

本発明によるこの実施形態は、算術符号化（例えば、符号化または復号）のための間隔サイズ情報の導出に使用される状態変数値の更新が、ルックアップテーブルを使用しながら特に良好な結果を伴って実行され得るという発見に基づいており、その理由はルックアップテーブルを使用することが、符号化または復号される信号の特性に特によく適合した状態変数値の更新を可能にするためである。例えば、ルックアップテーブルを使用して、「古い」状態変数値と更新された状態変数値の間の微調整された関係を簡単に表すことができるが、大規模な計算（例えば、三角関数または指数関数または対数関数などの評価）を実行する必要はない。したがって、ルックアップテーブルを使用した状態変数値の更新の実装は、計算の複雑さを適度に小さく保つのに役立つ。理想的には、「古い」状態変数値に基づいて更新された状態変数値を取得するために、ルックアップテーブルルックアップの他に、乗算（または単純な乗算、例えばビットシフト演算）、丸め演算、および加算のみが使用される。例えば、現在処理されているシンボル（例えば、符号化されるシンボルまたは復号されるシンボル）は、更新された状態変数値を取得するために、例えばルックアップテーブルベースのマッピングルールのどの部分を評価するかを決定する。
結論として、ルックアップテーブルを使用して更新された状態変数値を提供すると、高い柔軟性と低い計算の複雑さの両方が提供されることがわかっている。

好ましい実施形態では、算術エンコーダは、符号化されるシンボルに依存して、ルックアップテーブル（Ａ）を使用して（例えば、符号化されるシンボルを符号化した後）第２の状態変数値（ｓ^ｋ _２）を更新するように構成される。
第１の状態変数値を更新するために使用されるのと同じルックアップテーブルを使用して、第２の状態変数値を更新することが有利であることがわかっている。例えば、第１の状態変数値および第２の状態変数値の適合時定数に関して考えられる差異は、例えば、１つまたは複数のスケーリング係数を使用して考慮することができ、これは、例えば、ルックアップテーブルの要素の選択、および／またはルックアップテーブルの選択された要素のスケーリングに適用され得る。結論として、２つ以上の状態変数値の導出に単一のルックアップテーブルのみが使用されている場合でも、２つ以上の状態変数値を適合させて、処理されたシンボル値の（つまり、以前に符号化されたシンボル値または復号されたシンボル値の）異なる統計特性を表すことができる。

好ましい実施形態では、算術エンコーダは、異なる適合時定数を使用して、第１の状態変数値および第２の状態変数値を更新するように構成される。
異なる適合時定数を使用して第１の状態変数値と第２の状態変数値を更新することにより、以前に処理されたシンボルの異なる統計特性を状態変数値に反映させることができる。異なる適合時定数で処理されたシンボルの統計を表す状態変数値の可用性は、シンボルの算術コーディング（符号化／復号）の間隔サイズの正確な調整に非常に役立つことがわかっている。また、状態変数値のルックアップテーブルベースの更新により、非常に高い信頼性と低い計算の複雑さが実現されることがわかっている。

好ましい実施形態では、算術エンコーダは、符号化されるシンボルが第１の値をとるか、第１の値とは異なる第２の値をとるかに応じて、ルックアップテーブルを使用して決定された値によって以前の状態変数値を選択的に増減するように構成される。
このようなアプローチを使用することにより、状態変数値を再帰的に適合させることができ、処理されたシンボル（例えば、符号化されるシンボル、または以前に符号化されたシンボル、または以前に復号されたシンボル）が、状態変数値の変化の方向（増加または減少）を決定する。他方、適合のサイズ（すなわち、増加または減少のサイズ）は、選択されたルックアップテーブルエントリによって決定され、スケーリングが適用され得る。その結果、状態変数値を更新するための効率的なメカニズムが存在し、これは、高度な柔軟性を実現し、それでも非常にリソース効率が高くなる。

好ましい実施形態では、算術エンコーダは、以前の状態変数値を、符号化されるシンボルが第１の値をとる場合に、以前の状態変数値が正である場合と比較して、以前の状態変数値が負である場合に、比較的大きい値だけ増加させるように構成され、算術エンコーダは、以前の状態変数値を、符号化されるシンボルが、第１の値とは異なる第２の値をとる場合に、以前の状態変数値が負である場合と比較して、以前の状態変数値が正である場合に、比較的大きい値だけ減少させるように構成される（それは、例えば、ルックアップテーブルを適切に選択することで到達する）。
このようなアプローチを使用すると、状態変数値が指数関数的に最大の正の値に向かって発展し、指数関数的に最小値に向かって発展するように到達できる。（正の）最大値および（負の）最小値に向かうこの近似は、ほぼ漸近的になる可能性がある。言い換えると、現在の状態変数値が（正の）最大値から離れるほど、（増加する）ステップが（正の）最大値に向かって大きくなり、現在の状態変数値が（負の）最大値から離れるほど、（負の）最小値に向かう（減少）ステップが大きくなる。したがって、指数漸近的挙動は、この概念を使用して近似できる。ただし、このような概念は、状態変数値の更新に非常に適していることがわかっている。特に、そのようなアプローチは、状態変数値を決定するための「無限インパルス応答」アプローチに非常に適していることがわかっている。

好ましい実施形態では、算術エンコーダは、符号化されるシンボルが第１の値をとる場合、所定（例えば、固定の）のオフセット値（ｚ）と以前に計算された第１の状態変数値（

）、またはそのスケーリングおよび／または丸められたバージョン（

）の合計に依存して、第１の状態変数値を更新するときに評価されるルックアップテーブルのエントリのインデックスを決定するように構成され、算術エンコーダは、符号化されるシンボルが第２の値をとる場合、所定（例えば、固定の）のオフセット値（ｚ）と以前に計算された第１の状態変数値の逆（－１を乗算する）バージョン（

）、またはそのスケーリングおよび／または丸められたバージョン（

）（例えば、以前に計算された第１の状態変数値の逆バージョン）の合計に依存して、第１の状態変数値を更新するときに評価されるルックアップテーブルのエントリのインデックスを決定するように構成される。
このようなアプローチを使用すると、現在処理されているシンボルを考慮して、適度な労力でルックアップテーブルの適切なエントリを選択できる。以前に計算された状態変数値と処理された（符号化または復号された）シンボルの両方がルックアップテーブルのエントリの選択を決定し、その結果、以前に計算された状態変数値と比較したときに更新された状態変数値がどれだけ増加または減少するかによって決定され得る。オフセット値は、例えば、オフセット値とスケーリングされた（処理されたシンボルによっては逆にされる可能性がある）以前計算された状態変数値の合計が、有効なルックアップテーブルインデックスになることを保証し得る。これは、有効なルックアップテーブルインデックスが通常負ではないためである。このような概念を使用すると、適切なルックアップテーブルインデックスを選択し、更新された状態変数値を効率的に提供することが簡単に可能になる。

好ましい実施形態では、算術エンコーダは、符号化されるシンボルが第１の値をとる場合、所定（例えば、固定の）のオフセット値（ｚ）と以前に計算された第２の状態変数値（

）、またはそのスケーリングおよび／または丸められたバージョン（

）の合計に依存して、第２の状態変数値を更新するときに評価されるルックアップテーブルのエントリのインデックスを決定するように構成され、算術エンコーダは、符号化されるシンボルが第２の値をとる場合、所定（例えば、固定の）のオフセット値（ｚ）と以前に計算された第２の状態変数値の逆（－１を乗算する）バージョン（

）、またはそのスケーリングおよび／または丸められたバージョン（

）（例えば、以前に計算された第２の状態変数値の逆バージョン）の合計に依存して、第２の状態変数値を更新するときに評価されるルックアップテーブルのエントリのインデックスを決定するように構成される。
第２の状態変数値の更新に関するこの概念は、第１の状態変数値の更新に関する概念と実質的に同一であり、例えば、同じルックアップテーブルを評価してメモリリソースを省くことができ、例えば、第１の状態変数値の更新と比較した場合の異なるスケーリング値を使用して、それにより、修正された状態変数値の更新特性を取得することができる。例えば、第１の状態変数値および状態変数値についての異なる適合時定数は、更新された第１の状態変数値および更新された第２の状態変数値の決定のために異なるスケーリング値を使用することによって取得され得る。

好ましい実施形態では、算術エンコーダは、第１の状態変数値の更新時に評価されるルックアップテーブルのエントリのインデックスを決定するときに、第１のスケーリング値（ｍ^ｋ _１）を適用して、以前に計算された第１の状態変数値（ｓ^ｋ _１）をスケーリングするように構成され、算術エンコーダは、第２の状態変数値の更新時に評価されるルックアップテーブルのエントリのインデックスを決定するときに、第２のスケーリング値（ｍ^ｋ _２）を適用して、以前に計算された第２の状態変数値（ｓ^ｋ _２）をスケーリングするように構成され、第１のスケーリング値が第２のスケーリング値とは異なる（また、第１および第２のスケーリング値は好ましくは２の整数効力であり、第１のスケーリング値と第２のスケーリング値との間の比は、２の場合、好ましくは整数効力であり、第１のスケーリング値および第２のスケーリング値は、好ましくは少なくとも８倍異なる）。
第１の状態変数値を更新するときに評価されるルックアップテーブルのエントリのインデックスを決定するときと、第２の状態変数値を更新するときに評価されるルックアップテーブルのエントリのインデックスを決定するときに異なるスケーリング値を使用することによって、異なる適合時定数が効率的に実装でき、基本的な状態変数値の更新アルゴリズムと、使用されるルックアップテーブルとは同一であり得、唯一の重要な違いはスケーリング値の選択であり得る。これにより、非常にリソースを省く実装が可能になる。

好ましい実施形態では、算術エンコーダは、第１の状態変数値を更新するときに第１のスケーリング値（例えば、ｎ^ｋ _１）を使用してルックアップテーブルの評価によって返される値をスケーリングするように構成され、算術エンコーダは、第２の状態変数値を更新するときに第２のスケーリング値（例えば、ｎ^ｋ _２）を使用してルックアップテーブルの評価によって返される値をスケーリングするように構成され、第１のスケーリング値は第２のスケーリング値とは異なる。
（例えば、選択されたルックアップテーブルエントリの）ルックアップテーブルの評価によって返される値の説明された異なるスケーリングは、第１の状態変数値および第２の状態変数値を更新するときに、異なる適合時定数の効率的な実装を可能にする。さらに、このようなスケーリングにより、第１の状態変数値の更新と第２の状態変数値の更新に同じルックアップテーブルを使用できるようになるため、メモリリソースの節約に役立つ。
好ましい実施形態では、算術エンコーダは、

Ａはルックアップテーブルであり（例えば、整数の値を含む）、ｚは所定の（一定の）オフセット値であり、

は１つまたは複数の重み付け値であり、

は１つまたは複数の重み付け値であることに従って、１つまたは複数の更新された状態変数値

を決定するように構成される。
状態変数値のこのような更新メカニズムは、高い計算効率で実装でき、信頼できる結果を提供することがわかっている。

好ましい実施形態では、算術エンコーダは、

Ａはルックアップテーブルであり（例えば、整数の値を含む）、ｚは所定の（一定の）オフセット値であり、

は１つまたは複数の重み付け値であり、

は１つまたは複数の重み付け値であることに従って、１つまたは複数の更新された状態変数値

を決定するように構成される。
状態変数値を更新するためのそのようなメカニズムはまた、状況によっては非常に有利である可能性があることがわかっている。特に、このようなアプローチを使用して、一部の実装では計算効率が悪い可能性がある浮動小数点値を反転する必要はない。したがって、本概念は、状況によっては非常に優れたリソース効率をもたらす可能性がある。

好ましい実施形態では、算術エンコーダは、

Ａはルックアップテーブルであり（例えば、整数の値を含む）、ｚは所定の（一定の）オフセット値であり、

は１つまたは複数の重み付け値であり、

は１つまたは複数の重み付け値であることに従って、１つまたは複数の更新された状態変数値

を決定するように構成される。
この概念はまた、一部の実装環境で特に高い計算効率と優れた精度をもたらすことがわかっている。

好ましい実施形態では、算術エンコーダは、

Ａはルックアップテーブルであり（例えば、整数の値を含む）、ｚは所定の（一定の）オフセット値であり、

は１つまたは複数の重み付け値であり、

は１つまたは複数の重み付け値であることに従って、１つまたは複数の更新された状態変数値

を決定するように構成される。
この概念はまた、状況によっては計算効率と信頼性の面で利点をもたらすことがわかっている。

算術エンコーダの好ましい実施形態では、Ａのエントリは、ルックアップテーブルインデックスの増加とともに単調に減少する。
このようなアプローチを使用すると、状態変数値の最大値または最小値への近似が単調および／または連続的および／または漸近的であることに到達する可能性がある。例えば、それぞれの最大値または最小値から遠く離れている状態変数は、それぞれの最大値または最小値に向かって比較的速く修正される一方で、それぞれの最大値または最小値に近い状態変数値は、該最大値または最小値に向かって比較的ゆっくりと修正されることに到達することができる。したがって、ルックアップテーブルのエントリの上記の選択により、最大値または最小値のスムーズな近似が可能になり、それはもう１つの状態変数値に基づいて間隔サイズ情報を導出するのに非常に役立つことがわかっている。

好ましい実施形態では、算術エンコーダは、Ａは

であるか、ゼロ設定または大きさの縮小によって、引数の１つ以上の極値に対してのみ、それから逸脱して、更新された

を所定の値の範囲のままにすることを回避する（例えば、

は

より大きな値ドメインを持つ；つまり、

は

に準量子化される；

の極値の場合、

は上記の式に従って未修正のＡによって変更され、その値ドメインを離れることができる：これを回避するために、これらの極値に対応するエントリが削減またはゼロにされる場合があることを考慮されたい）、

、

、

、および

は所定のパラメータである（例は上記に記載されている）。
ルックアップテーブルΑのそのような選択は、該ルックアップテーブルＡを使用して更新される状態変数値の特に有利な挙動をもたらすことがわかっている。

算術エンコーダの好ましい実施形態では、ルックアップテーブルの最後のエントリ（これは、第１の状態変数値が最大許容値まで及ぶ所定の値の範囲に達したとき、または第１の状態変数値が所定のしきい値を超えたときにアドレス指定される）はゼロに等しい。
ルックアップテーブルの最後のエントリ（０に等しい）を使用することにより、更新された状態変数値が最大値および／または最小値を超えることを簡単に回避できる。
好ましい実施形態では、算術エンコーダは、更新された状態変数値にクリッピング操作を適用して、更新されクリップされた状態変数値を所定の値の範囲内に保つように構成される。
このようなメカニズムを使用すると、状態変数値が最小値と最大値の間の所定の範囲を超えることを容易に防ぐことができる。したがって、状態変数値が「合理的な」値をとることを保証することができる。

好ましい実施形態では、算術エンコーダは、

によってクリッピング操作を
更新された状態変数値に適用するように構成され、

は

の最大許容値であり、

は

の最小許容値である。
このようなクリッピング操作は効率的な方法で実装でき、無効な状態変数値を回避できることがわかっている。

好ましい実施形態では、算術エンコーダは、異なるコンテキストモデルに異なるスケーリング値を適用するように構成される（例えば、スケーリング値の少なくとも１つが２つの異なるコンテキストモデル間で異なるようにする）。
異なるコンテキストモデルに対して異なるスケーリング値を使用して、異なるコンテキストモデルの異なる統計特性（異なるタイプの情報および／またはタイプのビットストリーム構文要素に関連付けられている可能性がある）を考慮することができる。異なるコンテキストモデルに異なるスケーリング値を使用することにより、状態変数値の更新手順を、基礎となるアルゴリズムを根本的に変更することなく、異なるコンテキストモデルに簡単に適合させることができる。したがって、適切なスケーリング値を非常に効率的な方法で取得できる。

好ましい実施形態では、算術エンコーダは、上記の実施形態の１つで定義された間隔サイズ情報を取得するように構成される。
状態変数値の更新の概念は、間隔サイズ情報の導出のための上記の概念と結合して十分に使用できることがわかっている。

本発明による実施形態は、シンボル値（例えば、バイナリ値）を有する複数のシンボルを符号化するための算術エンコーダを作成するものであり、算術エンコーダは、１つまたは複数の状態変数値（ｓ_ｉ ^ｋ）に基づいて符号化される１つまたは複数のシンボル値の算術符号化の間隔サイズ値（Ｒ_ＬＰＳ）（それは例えば、インデックスｋで示される所与のコンテキストモードに関連付けられている）を導出するように構成され、これは、以前に符号化された複数のシンボル値（例えば、バイナリ値０および１のシーケンス）の統計を表し（例えば、異なる適合時定数を使用）、算術エンコーダは、ベースルックアップテーブル（Ｂａｓｅ ＴａｂＬＰＳ）を使用して間隔サイズ値（Ｒ_ＬＰＳ）を決定するように構成され（その次元は、確率指数の観点から、可能な確率指数ｉの数よりも小さい）、算術エンコーダは、１つまたは複数の状態変数値（例えば、ｉ＝Ｑｐ（ｐ_ＬＰＳ）のように）を基にして得られる確率指数（ｉ）が第１の範囲（例えば、μ未満）内にある場合、決定された間隔サイズ値がベースルックアップテーブルの要素と同一であるか、またはベースルックアップテーブルの要素の丸めのバージョンであり、確率指数が第２の範囲（例えば、μ以上）内にある場合は、ベースルックアップテーブルの要素のスケーリングと丸めを使用して、決定された間隔サイズ値が取得されるように、間隔サイズ値（Ｒ_ＬＰＳ）が決定されるように構成され、算術エンコーダは、間隔サイズ値（Ｒ_ＬＰＳ）を使用して１つまたは複数のシンボルの算術符号化を実行するように構成される。

本発明によるこの実施形態は、算術エンコーダにおける間隔サイズ値の決定が「ベースルックアップテーブル」を使用して実行できるという考えに基づいており、その次元は、該ベースルックアップテーブルの要素を再利用することによる所与の現在のコーディング間隔サイズに関連するいくつかの異なる間隔サイズ値よりも小さく、１回はスケーリングなしで、もう１回はスケーリングがありである。したがって、異なる範囲の状態変数値に関連付けられている算術符号化（符号化／復号）の間隔サイズ値は、スケーリングによって実質的に異なる（例えば、いくつかの丸め効果を除いて）ことが利用可能である。したがって、比較的小さな「ベースルックアップテーブル」を使用することができ、そのエントリは、異なる確率指数に対して複数回使用される（確率指数は、それぞれの状態変数値に基づいて導出され得る）。
結論として、ここで説明する概念により、１つまたは複数の状態変数値に基づいて間隔サイズ値を非常に効率的に決定できる。

好ましい実施形態では、算術エンコーダは、間隔サイズ値を決定するように構成され、決定された間隔サイズ値（Ｒ_ＬＰＳ）は、確率指数が第２の範囲内にある場合、ベースルックアップテーブルの要素の右シフトバージョンである。
この概念は、右シフト演算が計算上非常に効率的であり、また、確率指数が第２の範囲内にある場合、信頼できる間隔サイズ値を提供するという考えに基づいている（一方、好ましくは、確率指数が第１の範囲内にある場合は、ベースルックアップテーブルの要素にシフト演算が適用されない）。その結果、第１の範囲内と第２の範囲内の「対応する」確率指数に提供される間隔サイズ値は、主にビットシフトによって異なる（可能な丸めを除く）。これは通常、確率指数値の範囲全体、または完全な「第１の範囲」（通常は３つ以上の異なる値で構成される）にも当てはまる。さらに、右シフト演算は通常、２の効力による除算に対応することに留意されたい。

好ましい実施形態では、確率指数（Ｑｐ２（ｐ_ＬＰＳ））は、ルックアップテーブルの要素が間隔サイズ値（Ｒ_ＬＰＳ）として提供されるかどうか、またはルックアップテーブルの要素が間隔サイズ値（Ｒ_ＬＰＳ）を得るようにスケーリングおよび丸められるかどうかを決定する。
確率指数（または、より具体的には、確率指数が第１の範囲内にあるか、第２の範囲内にあるかという質問）が、ルックアップテーブル（ベースルックアップテーブル）の要素に基づいて、スケーリング（および任意選択で丸め）を適用して間隔サイズ値を取得するかどうか決定するため、アルゴリズムは非常に単純に保つことができる。例えば、確率指数が第１の範囲内にあるか、第２の範囲内にあるかを確認することは、確率指数を所定の値で除算するか、確率指数を１つ以上のしきい値と比較することで簡単に実行できる。したがって、確率指数に基づいて、スケーリング（および任意選択の丸め）を実行するかどうかを簡単に決定できる。したがって、間隔サイズ値の導出の概念は非常に効率的である。

算術エンコーダの好ましい実施形態では、確率指数（ｉ）と第１のサイズ値（例えば、μ、サイズ値は例えば、第１の方向のベースルックアップテーブルの拡張を説明する）および間隔サイズ指数（例えば量子化演算Ｑｒ２（．）を使用するなどして間隔サイズ情報または合計間隔サイズ情報Ｒに基づいて取得できる）との間の除算の除算残差（ｉ％μ）は、間隔サイズ値を取得するためにベースルックアップテーブルのどの要素を使用するかを決定する。
分割残差と区間サイズ指数に依存してベースルックアップテーブルのエントリを選択することにより、２次元ベースルックアップテーブルを簡単に評価でき、２次元ベースルックアップテーブルの要素には、間隔サイズ値（間隔サイズ指数で表すことができる）を使用して乗算を組み込むことができる。したがって、２次元のベースルックアップテーブルを有することにより、間隔サイズ値を使用した乗算を省くことができる（分割残差を第１のテーブルインデックスとして使用でき、間隔サイズ指数を第２のテーブルインデックスとして使用できる）。さらに、第１のテーブルインデックスとしての除算残差の使用は、ベースルックアップテーブルの要素が確率指数の増加に伴って周期的に選択されるという事実によく適合している（確率指数の後続の範囲がベースルックアップテーブルの共通範囲を選択するため）。結論として、上記の実装は、ベースルックアップテーブルの要素への非常に簡単なアクセスを可能にし、ベースルックアップテーブルの２次元の性質により、間隔サイズ値との乗算を回避するのに役立つ。

好ましい実施形態では、算術エンコーダは、
Ｒ_ＸＰＳ＝Ｓｃａｌ（ＢａｓｅＴａｂＬＰＳ［ｉ％μ］［ｊ］、[ｉ／μ]）
ＢａｓｅＴａｂＬＰＳは、次元μｘλのベースルックアップテーブルであり、ｉは、確率情報に関連付けられたテーブルインデックスであり、ｊは、間隔サイズ情報に関連付けられたテーブルインデックスであり（例えば、合計間隔サイズ情報Ｒ）、％は除算残差演算であり、／は除算演算であり、Ｓｃａｌ（ｘ，ｙ）はスケーリング関数であり（例えば、Ｓｃａｌ（ｘ，ｙ）＝[ｘ＊ａ^－ｂｙ]として定義され、[．]はフロア演算であり、ａは、好ましくは２以上の定数であり、またはｂは、好ましくは１以上の定数であり、スケーリング関数は、好ましくは、右シフトビットシフト演算を使用して実装され、ｙは、ｘの右側にシフトするかどうか、および何ビットシフトするかを決定する、
ことに従って、間隔サイズ値Ｒ_ＸＰＳ（例えば、Ｒ_ＬＰＳ）を取得するように構成される。
間隔サイズ情報を構成する間隔サイズ値を決定するためのそのような概念は、計算効率が高く、比較的小さなベースルックアップテーブルの使用を可能にすることがわかっている。特に、乗算演算を回避できる。さらに、分割残差演算および除算演算は、例えば、次元μが２の効力である場合、非常に計算効率の高い方法で実施することもできる。したがって、間隔サイズ値の導出について説明した概念により、計算上非常に効率的な実装が可能になる。

好ましい実施形態では、算術エンコーダは、１つまたは複数の状態変数値（ｓ_ｉ ^ｋ）（これはインデックスｋによって示される所与のコンテキストモードに関連付けられる）に基づいて符号化される１つまたは複数のシンボル値の算術符号化の間隔サイズ値（Ｒ_ＬＰＳ）を導出するように構成され、これは、以前に符号化された複数のシンボル値の統計を表し（例えば、バイナリ値０と１のシーケンス）（例えば、異なる適合時定数で）；算術エンコーダは、１つまたは複数の状態変数値から導出された（現在の）確率値に基づいて、また（現在の）コーディング間隔サイズ（Ｒ）に基づいて、確率テーブル（Ｐｒｏｂ ＴａｂＬＰＳ）（確率指数という観点で次元が可能な確率指数ｉの数値より小さい）を使用して間隔サイズ値（Ｒ_ＬＰＳ）を決定するように構成され、確率テーブルは、複数の確率値のセット（例えば、０とμ－１の間の確率指数に対して）および（単一の）所与の（参照）コーディング間隔サイズの間隔サイズ（間隔サイズ値）を記述し、算術エンコーダは、現在の確率値が複数の確率値のセットにない（例えば、μ以上の現在の確率値と関連付けられた確率指数である）場合、および／または現在のコーディング間隔サイズ（Ｒ）が、所与（参照）のコーディング間隔サイズとは異なる場合、間隔サイズ値（Ｒ_ＬＰＳ）を取得するよう所与（参照）の確率テーブル（Ｐｒｏｂ＿ＴａｂＬＰＳ）の要素をスケーリングするように構成され、また、算術エンコーダは、間隔サイズ値（Ｒ_ＬＰＳ）を使用して１つまたは複数のシンボルの算術符号化を実行するように構成される。
この概念は、確率値（または確率指数）の異なる（重複しない）範囲に関連付けられた間隔サイズ値が、スケーリング操作によって実質的に（可能な丸め効果を除いて）関連付けられているという考えに基づいている。ルックアップテーブル（確率テーブル）のサイズが適切に選択されている場合、スケーリング演算は、例えば、ビットシフト演算を使用して、計算効率の高い方法で実装され得ることにも留意されたい。その結果、小さな計算労力で算術コーディング（符号化または復号）に使用され、メモリを省く小さなサイズのルックアップテーブルのみを使用する間隔サイズ値を導出することが可能である。

好ましい実施形態では、算術エンコーダは、（現在の）コーディング間隔サイズ（Ｒ）に応じて、確率テーブルの選択された要素（ｐｒｏｂＴａｂＬＰＳ［ｉ％μ］）の（乗法の）第１のスケーリングを使用し、現在の確率値（指数ｉにより指定）に関連付けられた要素が複数の確率値のセットに含まれるかどうかに応じて（例えば、現在の確率値は、確率テーブルでカバーされている確率値の範囲内にあるかどうかに応じて）、第１のスケーリングの結果の第２のスケーリングを使用して間隔サイズ値を取得されるように構成される。
２段階の乗算またはスケーリングを使用して、間隔サイズ情報を取得することにより、小さな確率テーブルを使用できる。例えば、確率テーブルは、単一のコーディング間隔サイズおよび所与の比較的狭い範囲の確率値（「複数の確率値のセット」によって表され得る）のみを「直接」カバーし得る。したがって、他のいずれかのコーディング間隔サイズ、および確率テーブルによって「直接」カバーされる複数の確率値のセットに含まれない任意の確率値について、意味のある信頼できる間隔サイズ値が取得されるように、スケーリングが実行される。

算術エンコーダの好ましい実施形態では、確率指数（例えばｉ、例えば、現在の確率値を表す）および第１のサイズ値（例えばμ、例えばサイズ値が確率テーブルの拡張について説明する）の間の除算の除算残差（ｉ％μ）は、確率テーブルのどの要素が第１のスケーリングでスケーリングされるかを決定する、および／または確率指数（ｉ）および第１のサイズ値間の除算の整数除算結果（[ｉ／μ]）は、第２のスケーリングで使用されるスケーリング係数（２－[ｉ／μ]）を決定する、および／またはコーディング間隔サイズ（Ｒ）は、第１のスケーリングの乗法スケーリング係数（Ｑｒ２（Ｒ））を決定する。
除算残差を使用して確率のどの要素がスケーリングされるかを決定することは、確率テーブルのエントリが確率指数の増加とともに定期的に再利用される（例えば、周期的に）という事実を活用するのに役立つ。除算残差の使用は、この事実を表している。また、除算残差は、状況によっては、特に除算が２の効力で行われる場合、非常に高い計算効率で計算できる。
さらに、整数除算の結果に基づいてスケーリング係数を決定することにより、スケーリング係数を確率指数値の異なる（隣接する）範囲に簡単に割り当てることができる。さらに、整数除算の結果は、状況によっては、特に除算が２の効力で行われる場合、計算上非常に効率的な方法で計算できる。
さらに、コーディング間隔サイズに依存して乗法スケーリング係数を決定することは、間隔サイズ値がコーディング間隔サイズに比例するという事実を反映している。したがって、間隔サイズ値を高い効率かつ精度で得ることができる。

好ましい実施形態では、算術エンコーダは、

ｉは、確率情報に関連付けられたテーブルインデックスであり、ｊは間隔サイズ情報に関連付けられたテーブルインデックスであり、％は除算残差演算であり、／は除算演算であり、ｐｒｏｂＴａｂＬＰＳ ［］は確率テーブルであり、μは確率テーブルの要素の数であり（ｉの値の範囲は通常μよりも大きくなる）、Ｒは間隔サイズ（または現在のコーディング間隔サイズ）であり、Ｑｒ_２（Ｒ）はＲに依存するスケーリング係数であり、Ｓｃａｌ（ｘ，ｙ）はスケーリング関数であり（例えば、Ｓｃａｌ（ｘ，ｙ）＝[ｘ＊ａ^－ｂｙ]として定義され、[．]はフロア演算であり、ａは、好ましくは２以上の定数であり、ｂは、好ましくは１以上の定数であり、スケーリング関数は、好ましくは、右シフトビットシフト演算を使用して実装され、ｙは、ｘの右シフトをするかどうか、および何ビットシフトするかを決定する、
ことに従って間隔サイズ値Ｒ_ＸＰＳ（例えば、Ｒ_ＬＰＳ）を取得するように構成される。
間隔サイズ値を決定するためのそのようなアルゴリズムは、計算上効率的であり、良質の結果を提供することがわかっている。確率テーブルは比較的小さくすることができ、スケーリング関数は、例えば、１つまたは複数のビットシフト演算を使用して、計算効率の良い方法で実装することができる。

好ましい実施形態では、算術エンコーダは、現在の確率値（指数ｉにより指定）に関連付けられた要素が確率値に含まれるかどうかに応じて（例えば、現在の確率値は、確率テーブルでカバーされている確率値の範囲内にあるかどうかに応じて）、確率テーブルの選択された要素（ｐｒｏｂＴａｂＬＰＳ［ｉ％μ］）の（乗法の）第１のスケーリングを使用し、また、コーディング間隔サイズ（Ｒ）に応じて、第１のスケーリングの結果の第２のスケーリングを使用して、間隔サイズ値を取得されるように構成される。
この概念では、上記の概念と比較すると、第１のスケーリングと第２のスケーリングの処理順序が逆になっている。ただし、基本的な考慮事項は同じままである。

好ましい実施形態では、確率指数（例えばｉ、例えば、現在の確率値を表す）、および第１のサイズ値（例えばμ、例えばサイズ値が確率テーブルの拡張について説明する）の間の除算の除算残差（ｉ％μ）は、確率テーブルのどの要素が第１のスケーリングでスケーリングされるかを決定する、および／または確率指数（ｉ）および第１のサイズ値間の除算の整数除算結果（[ｉ／μ]）は、第１のスケーリングで使用されるスケーリング係数（例えば、２－[ｉ／μ]またはａ－ｂ[ｉ／μ]）を決定する、および／または（現在の）コーディング間隔サイズ（Ｒ）は、第２のスケーリングの乗法スケーリング係数（Ｑｒ２（Ｒ））を決定する。
この概念では、上記の概念と比較すると、第１のスケーリングと第２のスケーリングの順序が逆になっている。ただし、基本的な考慮事項は変更されていない。

好ましい実施形態では、算術エンコーダは、

ｉは、確率情報に関連付けられたテーブルインデックスであり、ｊは（現在の）間隔サイズ情報に関連付けられたテーブルインデックスであり、％は除算残差演算であり、／は除算演算であり（例えば、整数の結果を提供する）、ｐｒｏｂＴａｂＬＰＳ ［］は確率テーブルであり、μは確率テーブルの要素の数であり（ｉの値の範囲は通常μよりも大きくなる）、Ｒは間隔サイズ（または現在のコーディング間隔サイズ）であり、Ｑｒ_２（Ｒ）はＲに依存するスケーリング係数であり、Ｓｃａｌ（ｘ，ｙ）はスケーリング関数であり（例えば、Ｓｃａｌ（ｘ，ｙ）＝[ｘ＊ａ^－ｂｙ]として定義され、[．]はフロア演算であり、ａは、好ましくは２以上の定数であり、ｂは、好ましくは１以上の定数であり、スケーリング関数は、好ましくは、右シフトビットシフト演算を使用して実装され、ｙは、ｘの右シフトをするかどうか、および何ビットシフトするかを決定する、
ことに従って間隔サイズ値Ｒ_ＸＰＳ（例えば、Ｒ_ＬＰＳ）を取得するように構成される。
この概念では、上記の実装と比較すると、第１のスケーリングおよび第２のスケーリングのスケーリング順序が逆になっている。ただし、基本的な基礎となる考え方は変わりない。

以下では、算術復号に関連するいくつかの実施形態について説明する。ただし、算術復号に関連する概念、考慮事項、およびこれらの概念の基礎となる詳細は、算術符号化の概念の基礎となる概念、考慮事項、および詳細と実質的に同じである。したがって、上記の説明も同様に当てはまる。ただし、符号化されるシンボル値は、復号されるシンボル値または以前に復号されたシンボルに対応し、以前に符号化されたシンボル値は、以前に復号されたシンボル値に対応する。さらに、符号化特徴と復号特徴との間の対応は、当業者には明らかであり、請求項の文言の比較からも明らかである。

本発明による実施形態は、シンボル値（例えば、バイナリ値）を有する複数のシンボルを復号するための算術デコーダを作成するものであり、算術デコーダは、１つまたは複数の状態変数値（ｓ_ｉ ^ｋ）に基づいて復号される１つまたは複数のシンボル値の算術復号の間隔サイズ値（Ｒ_ＬＰＳ）（それは例えば、インデックスｋで示される所与のコンテキストモードに関連付けられている）を導出するように構成され、これは、以前に復号された複数のシンボル値（例えば、バイナリ値０および１のシーケンス）の統計を表し（例えば、異なる適合時定数を使用）、算術デコーダは、ベースルックアップテーブル（Ｂａｓｅ ＴａｂＬＰＳ）を使用して間隔サイズ値（Ｒ_ＬＰＳ）を決定するように構成され（その次元は、確率指数の観点から、可能な確率指数ｉの数よりも小さい）、算術デコーダは、１つまたは複数の状態変数値（例えば、ｉ＝Ｑｐ（ｐ_ＬＰＳ）のように）を基にして得られる確率指数（ｉ）が第１の範囲（例えば、μ未満）内にある場合、決定された間隔サイズ値がベースルックアップテーブルの要素と同一であるか、またはベースルックアップテーブルの要素の丸めのバージョンであり、確率指数が第２の範囲（例えば、μ以上）内にある場合は、ベースルックアップテーブルの要素のスケーリングと丸めを使用して、決定された間隔サイズ値が取得されるように、間隔サイズ値（Ｒ_ＬＰＳ）が決定されるように構成され、算術デコーダは、間隔サイズ値（Ｒ_ＬＰＳ）を使用して１つまたは複数のシンボルの算術復号を実行するように構成される。

好ましい実施形態では、算術デコーダは、間隔サイズ値を決定するように構成され、決定された間隔サイズ値（Ｒ_ＬＰＳ）は、確率指数が第２の範囲内にある場合、ベースルックアップテーブルの要素の右シフトバージョンである。

算術デコーダの好ましい実施形態では、確率指数（Ｑｐ２（ｐ_ＬＰＳ））は、ルックアップテーブルの要素が間隔サイズ値（Ｒ_ＬＰＳ）として提供されるかどうか、またはルックアップテーブルの要素が間隔サイズ値（Ｒ_ＬＰＳ）を得るようにスケーリングおよび丸められるかどうかを決定する。

算術デコーダの好ましい実施形態では、確率指数（ｉ）と第１のサイズ値（例えば、μ、サイズ値は例えば、第１の方向のベースルックアップテーブルの拡張を説明する）および間隔サイズ指数（例えば量子化演算Ｑｒ２（．）を使用するなどして間隔サイズ情報または合計間隔サイズ情報Ｒに基づいて取得できる）との間の除算の除算残差（ｉ％μ）は、間隔サイズ値を取得するためにベースルックアップテーブルのどの要素を使用するかを決定する。

好ましい実施形態では、算術デコーダは、
Ｒ_ＸＰＳ＝Ｓｃａｌ（ＢａｓｅＴａｂＬＰＳ［ｉ％μ］［ｊ）、[ｉ／μ]）
ＢａｓｅＴａｂＬＰＳは、次元μｘλのベースルックアップテーブルであり、ｉは、確率情報に関連付けられたテーブルインデックスであり、ｊは、間隔サイズ情報に関連付けられたテーブルインデックスであり（例えば、合計間隔サイズ情報Ｒ）、％は除算残差演算であり、／は除算演算であり、Ｓｃａｌ（ｘ，ｙ）はスケーリング関数であり（例えば、Ｓｃａｌ（ｘ，ｙ）＝[ｘ＊ａ^－ｂｙ]として定義され、[．]はフロア演算であり、ａは、好ましくは２以上の定数であり、またはｂは、好ましくは１以上の定数であり、スケーリング関数は、好ましくは、右シフトビットシフト演算を使用して実装され、ｙは、ｘの右側にシフトするかどうか、および何ビットシフトするかを決定する、
ことに従って、間隔サイズ値Ｒ_ＸＰＳ（例えば、Ｒ_ＬＰＳ）を取得するように構成される。

本発明による実施形態は、シンボル値（例えば、バイナリ値）を有する複数のシンボルを復号するための算術デコーダを作成するものであり、算術デコーダは、１つまたは複数の状態変数値（ｓ_ｉ ^ｋ）（これは、例えば、インデックスｋによって示される所与のコンテキストモードに関連付けられる）に基づいて復号される１つまたは複数のシンボル値の算術復号の間隔サイズ値（Ｒ_ＬＰＳ）を導出するように構成され、これは、以前に復号された複数のシンボル値の統計を表し（例えば、バイナリ値０と１のシーケンス）（例えば、異なる適合時定数で）；算術デコーダは、１つまたは複数の状態変数値から導出された（現在の）確率値に基づいて、また（現在の）コーディング間隔サイズ（Ｒ）に基づいて、確率テーブル（Ｐｒｏｂ ＴａｂＬＰＳ）（確率指数という観点で次元が可能な確率指数ｉの数値より小さい）を使用して間隔サイズ値（Ｒ_ＬＰＳ）を決定するように構成され、確率テーブルは、複数の確率値のセット（例えば、０とμ－１の間の確率指数に対して）および（単一の）所与の（参照）コーディング間隔サイズの間隔サイズ（間隔サイズ値）を記述し、算術デコーダは、現在の確率値が複数の確率値のセットにない（例えば、μ以上の現在の確率値と関連付けられた確率指数である）場合、および／または現在のコーディング間隔サイズ（Ｒ）が、所与（参照）のコーディング間隔サイズとは異なる場合、間隔サイズ値（Ｒ_ＬＰＳ）を取得するよう確率テーブル（Ｐｒｏｂ＿ＴａｂＬＰＳ）の要素（例えば、現在の確率値に依存して選択された要素）をスケーリングするように構成され、また、算術デコーダは、間隔サイズ値（Ｒ_ＬＰＳ）を使用して１つまたは複数のシンボルの算術復号化を実行するように構成される。

好ましい実施形態では、算術デコーダは、（現在の）コーディング間隔サイズ（Ｒ）に応じて、確率テーブルの選択された要素（ｐｒｏｂＴａｂＬＰＳ［ｉ％μ］）の（乗法の）第１のスケーリングを使用し、現在の確率値（指数ｉにより指定）に関連付けられた要素が複数の確率値のセットに含まれるかどうかに応じて（例えば、現在の確率値は、確率テーブルでカバーされている確率値の範囲内にあるかどうかに応じて）、第１のスケーリングの結果の第２のスケーリングを使用して間隔サイズ値を取得されるように構成される。

算術デコーダの好ましい実施形態では、確率指数（例えばｉ、例えば、現在の確率値を表す）、および第１のサイズ値（例えばμ、例えばサイズ値が確率テーブルの拡張について説明する）の間の除算の除算残差（ｉ％μ）は、確率テーブルのどの要素が第１のスケーリングでスケーリングされるかを決定する、および／または確率指数（ｉ）および第１のサイズ値間の除算の整数除算結果（[ｉ／μ]）は、第２のスケーリングで使用されるスケーリング係数（２^{－[ｉ／μ]}）を決定する、および／またはコーディング間隔サイズ（Ｒ）は、第１のスケーリングの乗法スケーリング係数（Ｑｒ２（Ｒ））を決定する。

好ましい実施形態では、算術デコーダは、

ｉは、確率情報に関連付けられたテーブルインデックスであり、ｊは間隔サイズ情報に関連付けられたテーブルインデックスであり、％は除算残差演算であり、／は除算演算であり、ｐｒｏｂＴａｂＬＰＳ ［］は確率テーブルであり、μは確率テーブルの要素の数であり（ｉの値の範囲は通常μよりも大きくなる）、Ｒは間隔サイズ（または現在のコーディング間隔サイズ）であり、Ｑｒ_２（Ｒ）はＲに依存するスケーリング係数であり、Ｓｃａｌ（ｘ，ｙ）はスケーリング関数であり（例えば、Ｓｃａｌ（ｘ，ｙ）＝[ｘ＊ａ^－ｂｙ]として定義され、[．]はフロア演算であり、ａは、好ましくは２以上の定数であり、ｂは、好ましくは１以上の定数であり、スケーリング関数は、好ましくは、右シフトビットシフト演算を使用して実装され、ｙは、ｘの右シフトをするかどうか、および何ビットシフトするかを決定する、
ことに従って間隔サイズ値Ｒ_ＸＰＳ（例えば、Ｒ_ＬＰＳ）を取得するように構成される。

好ましい実施形態では、算術デコーダは、現在の確率値（指数ｉにより指定）に関連付けられた要素が確率値に含まれるかどうかに応じて（例えば、現在の確率値は、確率テーブルでカバーされている確率値の範囲内にあるかどうかに応じて）、確率テーブルの選択された要素（ｐｒｏｂＴａｂＬＰＳ［ｉ％μ］）の（乗法の）第１のスケーリングを使用し、また、コーディング間隔サイズ（Ｒ）に応じて、第１のスケーリングの結果の第２のスケーリングを使用して、間隔サイズ値を取得されるように構成される。

算術デコーダの好ましい実施形態では、確率指数（例えばｉ、例えば、現在の確率値を表す）、および第１のサイズ値（例えばμ、例えばサイズ値が確率テーブルの拡張について説明する）との間の除算の除算残差（ｉ％μ）は、確率テーブルのどの要素が第１のスケーリングでスケーリングされるかを決定する、および／または確率指数（ｉ）および第１のサイズ値間の除算の整数除算結果（[ｉ／μ]）は、第１のスケーリングで使用されるスケーリング係数（例えば、２^{－[ｉ／μ]}またはａ^{－ｂ[ｉ／μ]}）を決定する、および／または（現在の）コーディング間隔サイズ（Ｒ）は、第２のスケーリングの乗法スケーリング係数（Ｑｒ_２（Ｒ））を決定する。

好ましい実施形態では、算術デコーダは、

ｉは、確率情報に関連付けられたテーブルインデックスであり、ｊは（現在の）間隔サイズ情報に関連付けられたテーブルインデックスであり、％は除算残差演算であり、／は除算演算であり（例えば、整数の結果を提供する）、ｐｒｏｂＴａｂＬＰＳ ［］は確率テーブルであり、μは確率テーブルの要素の数であり（ｉの値の範囲は通常μよりも大きくなる）、Ｒは間隔サイズ（または現在のコーディング間隔サイズ）であり、Ｑｒ_２（Ｒ）はＲに依存するスケーリング係数であり、Ｓｃａｌ（ｘ，ｙ）はスケーリング関数であり（例えば、Ｓｃａｌ（ｘ，ｙ）＝[ｘ＊ａ^－ｂｙ]として定義され、[．]はフロア演算であり、ａは、好ましくは２以上の定数であり、ｂは、好ましくは１以上の定数であり、スケーリング関数は、好ましくは、右シフトビットシフト演算を使用して実装され、ｙは、ｘの右シフトをするかどうか、および何ビットシフトするかを決定する、
ことに従って間隔サイズ値Ｒ_ＸＰＳ（例えば、Ｒ_ＬＰＳ）を取得するように構成される。

以下では、算術符号化に関連するいくつかのさらなる実施形態について説明する。
本発明による実施形態は、シンボル値（例えば、バイナリ値）を有する複数のシンボルを符号化するための算術エンコーダを作成するものであり、算術エンコーダは、以前に符号化された複数のシンボル値の統計を表す１つの状態変数値（ｓ_ｋ）を決定するように構成され、算術エンコーダは、結合状態変数値、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]）から、符号化されるシンボル値の算術符号化のためのサブインターバル幅値（

）を計算するよう構成され、この計算は、そのエントリが結合状態変数値の値ドメインの異なる値間隔の確率値、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]；

）を含む１次元ルックアップテーブル（

）を使用して、１つの状態変数値（ｓ_ｋ）、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]；

）を確率値にマッピングすること、および量子化レベル（

）に符号化されるシンボル値の算術符号化の前に、算術符号化のコーディング間隔のサイズを記述するコーディング間隔サイズ情報（例えば、Ｒ）を量子化することにより、これを行い、算術エンコーダは、さらに、確率値と、量子化レベルの間の積を決定する（事前に計算された積のルックアップまたは乗算によって）ように構成され、算術エンコーダは、符号化されるシンボル値に依存して状態変数値の更新を実行するように構成される。

この実施形態は、非常に単純な一次元ルックアップテーブルを、結合状態変数値に基づくサブインターバル幅値の決定に使用できるという発見に基づいている。コーディング間隔サイズは、コーディング間隔サイズ情報の量子化、および確率値と量子化値（または量子化レベル）の間の積の決定によって考慮される。したがって、信頼できる結果は適度な努力で得られる。

好ましい実施形態では、算術エンコーダは、１つの状態変数値（ｓ_ｋ）として、結合状態変数値（例えば、状態変数値の加重和であり得る）、複数の状態変数値（ｓ_ｉ ^ｋ）（例えば、バイナリ値０および１のシーケンス）（例えば、複数の状態変数値の場合、異なる適合時定数の統計）の基礎となるものを導出するように構成され、これは、異なる適合時定数の複数の以前に符号化されたシンボル値（例えば、バイナリ値０および１のシーケンス）の統計を表す。
結合状態変数値を１つの状態変数値として使用すると、特に良好な結果が得られることがわかっている。様々な適合時定数を考慮すると、短時間の統計と長時間の統計の両方を考慮することができるため、サブインターバル幅の値の信頼性が特に高くなる。

好ましい実施形態では、算術エンコーダは、結合状態変数値を取得するために、状態変数値の加重和を決定するように構成される。
結合状態変数値のそのような計算は、計算の労力を適度に少なく保ちながら、結合状態変数値に対する短期統計と長期統計の異なる影響の考慮を可能にする。

好ましい実施形態では、算術エンコーダは、状態変数値（

）および関連する重み付け値（

結合状態変数値（ｓ_ｋ）を得るため）の積を丸めることによって得られる丸められた値（

）の合計を決定するように構成される。
合計の前に丸め演算を適用すると、計算の労力が軽減され、状態変数値と関連する重み付け値の非常に小さな積の影響も排除される。したがって、信頼性が向上する。
好ましい実施形態では、算術エンコーダは、

ｓ^ｋ _２は状態変数値であり、Ｎは考慮される状態変数値の数であり、[．]はフロア演算子であり、ｄ^ｋ _ｉは状態変数値に関連付けられた重み付け値（例えば、結合状態変数値への個々の状態変数値の影響を制御する重み付け係数）（ｄ^ｋ _ｉは好ましくはフォン２の整数値の効力であり、２つの異なるｄ^ｋ _ｉ間の比率は好ましくは２の整数値の効力である）［２つの異なるｄ^ｋ _ｉ間の比率は、好ましくは８以上）であることに従って、結合状態変数値ｓ_ｋを決定するように構成される。
結合状態変数値のそのような導出は特に有利であることがわかっている。結合状態変数値を決定するための対応する概念の上記の説明の言及もなされている。

好ましい実施形態では、算術エンコーダは、

ｚは所定の（一定の）オフセット値であり、

は１つまたは複数の重み付け値であり、

は１つ以上の重み付け値であり、Ａは

であるか、ゼロ設定または大きさの縮小によって、引数の１つ以上の極値に対してのみ、それから逸脱して、更新された

を所定の値の範囲のままにすることを回避する（例えば、

は

より大きな値ドメインを持つ；つまり、

は

に準量子化される；

の極値の場合、

は上記の式に従って未修正のＡによって変更され、その値ドメインを離れることができる：これを回避するために、これらの極値に対応するエントリが削減またはゼロにされる場合があることを考慮されたい）、

、

、

、および

は所定のパラメータである（例は上記に記載されている）
ことに従って、状態変数値の更新を行う際、複数の状態変数値

を更新するように構成される。
状態変数値のそのような更新は特に有利であることがわかっている。状態変数の更新については、この概念に関する上記の説明も参照される。

好ましい実施形態では、算術エンコーダは、テーブルルックアップまたは計算によって

を導出するように構成される。
この概念に関しては、上記の説明が参照される。

好ましい実施形態では、算術エンコーダは、

Ａはルックアップテーブルであり（例えば、整数の値を含む）、ｚは所定の（一定の）オフセット値であり、

は１つまたは複数の重み付け値であり、

は１つまたは複数の重み付け値であることに従って、１つまたは複数の更新された状態変数値

を決定するように構成される。
１つまたは複数の状態変数値を更新するためのこの概念の利点については、上記の説明が参照される。

好ましい実施形態では、算術エンコーダは、

Ａはルックアップテーブルであり（例えば、整数の値を含む）、ｚは所定の（一定の）オフセット値であり、

は１つまたは複数の重み付け値であり、

は１つまたは複数の重み付け値であることに従って、１つまたは複数の更新された状態変数値

を決定するように構成される。
１つまたは複数の状態変数値を更新するためのこの概念の利点について、上記の説明が参照される。

好ましい実施形態では、算術エンコーダは、

Ａはルックアップテーブルであり（例えば、整数の値を含む）、ｚは所定の（一定の）オフセット値であり、

は１つまたは複数の重み付け値であり、

は１つまたは複数の重み付け値であることに従って、１つまたは複数の更新された状態変数値

を決定するように構成される。
１つまたは複数の状態変数値を更新するためのこの概念の利点については、上記の説明が参照される。

好ましい実施形態では、算術エンコーダは、コーディング間隔サイズ情報に論理右シフトを適用することによってコーディング間隔サイズ情報の量子化を実行するように構成される。
コーディング間隔サイズ情報の論理的な右シフトは、計算上非常に効率的である。
好ましい実施形態では、算術エンコーダは、コーディング間隔サイズ情報

の量子化を

により実行するように構成され、式中、

、

および

はパラメータである。
コーディング間隔サイズ情報のこの量子化の利点に関しては、上記の論述が参照される。
算術エンコーダの好ましい実施形態では、１次元ルックアップテーブルのエントリは、１つの状態変数値、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]）の増加で単調に減少する。
１次元ルックアップテーブルのこの構造の利点については、上記の説明が参照される。
算術エンコーダの好ましい実施形態では、１つの状態変数値の値ドメインの異なる値間隔、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]）は、等しいサイズである。
この概念の利点については、上記の説明が参照される。

算術エンコーダの好ましい実施形態では、１次元ルックアップテーブルのエントリは、１つの状態変数値、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]）の増加で減少率を伴って単調に減少する。
この概念の利点については、上記の説明が参照される。
以下では、算術符号化についての上記の概念に対応する算術復号の概念について説明する。したがって、同じ説明が適用され、上記と同じ詳細を任意選択で使用できる。ただし、算術エンコーダは算術デコーダに対応することに留意されたい。さらに、以前に符号化されたシンボル値は、通常、以前に復号されたシンボル値に対応し、符号化されるシンボル値は、通常、以前に復号されたシンボル値（または復号されるシンボル値）に対応し得る。ただし、特徴の対応に関しては、関連する（または対応する）概念を定義する対応するクレームの比較も参照される。

本発明による実施形態は、シンボル値（例えば、バイナリ値）を有する複数のシンボルを復号するための算術デコーダを作成し、算術デコーダは、間隔サイズ情報（ｐ^ｋ、Ｒ＊ｐ^ｋ）を、１つまたは複数のシンボル値（例えば、バイナリ値）の算術復号が複数の状態変数値（ｓ_ｉ ^ｋ）（例えば、インデックスｋによって表示される所与のコンテキストモードに関連付けられるもの）に基づいて復号されるように導出するように構成され、これは、異なる適合時定数で以前に復号された複数のシンボル値（例えば、バイナリ値０と１のシーケンス）の統計（例えば、復号される１つまたは複数のシンボルが特定のシンボル値を含む確率の推定）を表し、算術デコーダは、ルックアップテーブル（ＬＵＴ１）を使用して、第１の状態変数値（ｓ^ｋ _１）、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ _１＊ａ^ｋ _１]）をマッピングし、ルックアップテーブル（ＬＵＴ１）を使用して、第２の状態変数値（ｓ^ｋ _２）、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ _２＊ａ^ｋ _２]）をマッピングするように構成され、復号される１つまたは複数のシンボルの算術復号のための間隔サイズを説明する間隔サイズ情報（例えば、ｐ_ｋまたはＲ＊ｐ_ｋ）を取得するようにする。

好ましい実施形態では、算術デコーダは、ルックアップテーブルを使用して、第１の状態変数値、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ _１＊ａ^ｋ _１]）を第１の確率値（ｐ_ｋ ^１）にマッピングするように構成され、算術デコーダは、ルックアップテーブルを使用して、第２の状態変数値、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ _２＊ａ^ｋ _２]）を第２の確率値（ｐ_ｋ ^２）にマッピングするように構成され、算術デコーダは、第１の確率値および第２の確率値を使用して（例えば、加重和または加重平均を使用して）結合確率値（ｐｋ）を取得するように構成される。
好ましい実施形態では、算術デコーダは、復号されるシンボルが第１の値（例えば「１」）をとる場合に状態変数値を第１の方向に変更する（例えばより正になる）ように構成され、また復号されるシンボルが第１の値とは異なる第２の値（例えば「０」）をとる場合（例えば、状態変数値が正と負の値をとることができるように）に状態変数値を第２の方向に（例えば、より負になるもの）変更するように構成され、算術デコーダは、それぞれの状態変数値の絶対値（ｓ_ｋ ^ｉ＞０の場合はｓ_ｋ ^ｉ、それ以外の場合は－ｓ_ｋ ^ｉ）に応じて（例えば、状態変数値の絶対値のスケーリングおよび丸められたバージョンに応じて）評価されるルックアップテーブルのエントリを決定するように構成される。

好ましい実施形態では、算術デコーダは、第１の状態変数値が第１の符号（例えば、正の符号）をとる場合に、第１の確率値（ｐ^ｋ _１）をルックアップテーブルによって提供される値（例えば、

）に設定するように構成され、算術デコーダは、第１の状態変数値が第２の符号（例えば、負の符号）をとる場合、第１の確率値（ｐ^ｋ _１）を、所定の値（例えば、１）からルックアップテーブルによって提供される値（例えば、

）を減算することによって得られる値に設定するように構成される。

好ましい実施形態では、算術デコーダは、

ＬＵＴ１は確率値を含むルックアップテーブルであり、[．]はフロア演算子であり、ｓ^ｋ _ｉはｉ番目の状態変数値であり、ａ^ｋ _ｉは、ｉ番目の状態変数値に関連付けられた重み付け値である（例えば、ｉ番目の状態変数値の数の範囲をルックアップテーブルのいくつかのエントリに適合させる重み付け値）ことにより、２つ以上の確率値ｐ^ｋ _ｉを決定するように構成される。

好ましい実施形態では、算術デコーダは、

ＬＵＴ１は確率値を含むルックアップテーブルであり、[．]はフロア演算子であり、ｓ^ｋ _ｉはｉ番目の状態変数値であり、ａ^ｋ _ｉは、ｉ番目の状態変数値に関連付けられた重み付け値である（例えば、ｉ番目の状態変数値の数の範囲をルックアップテーブルのいくつかのエントリに適合させる重み付け値）ことにより、２つ以上の確率値ｐ^ｋ _ｉを決定するように構成される。

好ましい実施形態では、算術デコーダは、

式中Ｎは考慮される確率値の数で（考慮される状態変数値の数に等しい場合がある）、ｂ^ｋ _ｉは、重み付け値（例えば、結合確率値に対する個々の状態変数値の影響を制御する重み付け係数）である［ｂ^ｋ _ｉは、好ましくは、ｖｏｎ ２の整数値の効力であり、２つの異なるｂ^ｋ _ｉ間の比は好ましくは、２の整数値の効力である）
ことに従って、複数の確率値ｐ^ｋ _ｉに基づいて結合確率値ｐ^ｋを取得するように構成される。

好ましい実施形態では、算術デコーダは、２次元ルックアップテーブルを使用して、第１の状態変数値、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ _１＊ａ^ｋ _１]）を第１のサブインターバル幅値（Ｒ＊ｐ^ｋ _１）にマッピングするように構成され、そのエントリは、第１の状態変数値に依存して（例えば、第１のルックアップテーブルエントリ座標を決定するために）、およびシンボルの復号前の算術復号のコーディング間隔のサイズを記述するコーディング間隔サイズ情報（例えば、Ｒ）に依存して（例えば、第２のルックアップテーブルエントリ座標を決定するために）アドレス指定され、算術デコーダは、２次元ルックアップテーブルを使用して、第２の状態変数値、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ _１＊ａ^ｋ _１]）を第２のサブインターバル幅値（Ｒ＊ｐ^ｋ _２）にマッピングするように構成され、そのエントリは、第２の状態変数値に依存して（例えば、第１のルックアップテーブルエントリ座標を決定するために）、およびシンボルの復号前の算術復号のコーディング間隔のサイズを記述するコーディング間隔サイズ情報（例えば、Ｒ）に依存してアドレス指定され（例えば、第２のルックアップテーブルエントリ座標を決定するために）、算術デコーダは、第１のサブインターバル幅値および第２のサブインターバル幅値を使用して（例えば、加重和または加重平均を使用して）、結合されたサブインターバル幅値を取得するように構成される。

算術デコーダの好ましい実施形態では、２次元ルックアップテーブルは、そのエントリが第１および第２の状態変数値の値ドメインの異なる値の確率値またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]；

）を含む第１の１次元ベクトル（１次元ルックアップテーブルを形成する）、およびそのエントリがコーディング間隔サイズ情報の量子化レベルを含む第２の１次元ベクトル（

）の間の二項積として表すことができる。

算術デコーダの好ましい実施形態では、２次元ルックアップテーブル（ＲａｎｇＴａｂＬＰＳ）の要素が、ベースルックアップテーブル（Ｂａｓｅ ＴａｂＬＰＳ）に基づいて定義され、２次元ルックアップテーブルの要素の第１のグループ（またはブロック、例えば、「上半分」）は、ベースルックアップテーブルの要素と同一であるか、ベースルックアップテーブルの要素の丸められたバージョンであり、２次元ルックアップテーブルの要素の第２のグループ（またはブロック、例えば「下半分」）は、ベースルックアップテーブルの要素のスケーリングおよび丸められたバージョンである。

算術デコーダの好ましい実施形態では、２次元ルックアップテーブルの要素の第２のグループはベースルックアップテーブルの要素の右シフトバージョンである。

算術デコーダの好ましい実施形態では、確率指数（Ｑｐ_２（ｐ_ＬＰＳ）；ｉ）は、２次元ルックアップテーブルの要素の第１のグループの要素または２次元ルックアップテーブルの要素の第２のグループの要素のどちらを評価するかを決定し、確率指数（例えば、確率値、例えばｐ_ＬＰＳを定量化することによって取得される）の第１の範囲（例えば、０～μ－１）は、要素の第１のグループの要素に関連付けられ、確率指数（例えば、確率値、例えばｐ_ＬＰＳを、例えば、量子化関数Ｑｐ２（．）を使用して定量化することによって取得される）の第２の範囲（例えば、μ以上）は、要素の第２のグループの要素に関連付けられている。

算術デコーダの好ましい実施形態では、確率指数（ｉ）と第１のサイズ値（例えば、μ、サイズ値は例えば、第１の方向のベースルックアップテーブルの拡張を説明する）および間隔サイズ指数（例えば量子化演算Ｑｒ２（．）、例えばｊを使用するなどして間隔サイズ情報Ｒに基づいて取得できる）との間の除算の除算残差（ｉ％μ）は、２次元ルックアップテーブルの要素を取得するためにベースルックアップテーブルのどの要素を使用するかを決定する。

好ましい実施形態では、算術デコーダは、
ＲａｎｇｅＴａｂＬＰＳ［ｉ］［ｊ］＝Ｓｃａｌ（ＢａｓｅＴａｂＬＰＳ［ｉ％μ］［ｊ）、[ｉ／μ]）
ＢａｓｅＴａｂＬＰＳは、次元μｘλのベースルックアップテーブルであり、ｉは、確率情報に関連付けられたテーブルインデックスであり、ｊは、間隔サイズ情報に関連付けられたテーブルインデックスであり（例えば、現在のコーディング間隔サイズを記述する）、％は除算残差演算であり、／は除算演算であり、Ｓｃａｌ（ｘ，ｙ）はスケーリング関数であり（例えば、Ｓｃａｌ（ｘ，ｙ）＝[ｘ＊ａ^－ｂｙ]として定義され、[．]はフロア演算であり、ａは、好ましくは２以上の定数であり、またはｂは、好ましくは１以上の定数であり、スケーリング関数は、好ましくは、右シフトビットシフト演算を使用して実装され、ｙは、ｘの右側にシフトするかどうか、および何ビットシフトするかを決定する、
ことに従って２次元ルックアップテーブル（ＲａｎｇＴａｂＬＰＳ）の要素を取得するように構成される。

算術デコーダの好ましい実施形態では、２次元ルックアップテーブル（ＲａｎｇＴａｂＬＰＳ）の要素は、確率テーブル（ｐｒｏｂＴａｂＬＰＳ）に基づいて定義され、確率テーブルは、複数の確率値のセット（例えば、指数ｉによって表される）および所与のコーディング間隔サイズの間隔サイズを記述し、複数の確率値のセットにない確率値および／または所与の（参照）コーディング間隔サイズとは異なるコーディング間隔サイズの２次元ルックアップテーブルの要素は、スケーリングを使用して確率テーブルから導出される。

算術デコーダの好ましい実施形態では、２次元ルックアップテーブルの要素が、コーディング間隔サイズ（Ｒ）に応じて、確率テーブルの選択された要素（ｐｒｏｂＴａｂＬＰＳ［ｉ％μ］）の（乗法の）第１のスケーリングを使用し、現在の確率値（指数ｉにより指定）に関連付けられた要素が確率値のセットに含まれるかどうかに応じて（例えば、現在の確率値は、確率テーブルでカバーされている確率値の範囲内にあるかどうかに応じて）、第１のスケーリングの結果の第２のスケーリングを使用して取得される。

算術デコーダの好ましい実施形態では、確率指数（例えばｉ、例えば、現在の確率値を表す）、および第１のサイズ値（例えばμ、例えばサイズ値が確率テーブルの拡張について説明する）の間の除算の除算残差（ｉ％μ）は、確率テーブルのどの要素が第１のスケーリングでスケーリングされるかを決定する、および／または確率指数（ｉ）および第１のサイズ値間の除算の整数除算結果（[ｉ／μ]）は、第２のスケーリングで使用されるスケーリング係数（２^{－[ｉ／μ]}）を決定する、および／またはコーディング間隔サイズは、第１のスケーリングの乗法スケーリング係数（Ｑｒ２（Ｒ））を決定する。

好ましい実施形態では、算術デコーダは、

ｉは、確率情報に関連付けられたテーブルインデックスであり、ｊは間隔サイズ情報に関連付けられたテーブルインデックスであり、％は除算残差演算であり、／は除算演算であり、ｐｒｏｂＴａｂＬＰＳ ［］は確率テーブルであり、μは確率テーブルの要素の数であり（Ｉの値の範囲は通常μよりも大きくなる）、Ｒは間隔サイズ（または現在のコーディング間隔サイズ）であり、Ｑｒ２（Ｒ）はＲに依存するスケーリング係数であり、Ｓｃａｌ（ｘ，ｙ）はスケーリング関数であり（例えば、Ｓｃａｌ（ｘ，ｙ）＝[ｘ＊ａ^－ｂｙ]として定義され、[．]はフロア演算であり、ａは、好ましくは２以上の定数であり、ｂは、好ましくは１以上の定数であり、スケーリング関数は、好ましくは、右シフトビットシフト演算を使用して実装され、ｙは、ｘの右シフトをするかどうか、および何ビットシフトするかを決定する、
ことに従って２次元ルックアップテーブルの要素

を取得するように構成される。

算術デコーダの好ましい実施形態では、現在の確率値（指数ｉにより指定）に関連付けられた要素が確率値に含まれるかどうかに応じて（例えば、現在の確率値は、確率テーブルでカバーされている確率値の範囲内にあるかどうかに応じて）、確率テーブルの選択された要素（ｐｒｏｂＴａｂＬＰＳ［ｉ％μ］）の（乗法の）第１のスケーリングを使用し、また、コーディング間隔サイズ（Ｒ）に応じて、第１のスケーリングの結果の第２のスケーリングを使用して、２次元ルックアップテーブルの要素を取得するように構成される。

算術デコーダの好ましい実施形態では、確率指数（例えばｉ、例えば、現在の確率値を表す）、および第１のサイズ値（例えばμ、例えばサイズ値が確率テーブルの拡張について説明する）の間の除算の除算残差（[ｉ％μ]）は、確率テーブルのどの要素が第１のスケーリングでスケーリングされるかを決定する、および／または確率指数（ｉ）と第１のサイズ値との間の除算の整数除算結果（[ｉ／μ]）は、第１のスケーリングで使用されるスケーリング係数（２^{－[ｉ／μ]}）を決定する、および／またはコーディング間隔サイズ（Ｒ）は、第２のスケーリングの乗法スケーリング係数（Ｑｒ_２（Ｒ））を決定する。

好ましい実施形態では、算術デコーダは、

ｉは、確率情報に関連付けられたテーブルインデックスであり、ｊは間隔サイズ情報に関連付けられたテーブルインデックスであり、％は除算残差演算であり、／は除算演算であり（例えば、整数の結果を提供する）、ｐｒｏｂＴａｂＬＰＳ ［］は確率テーブルであり、μは確率テーブルの要素の数であり（Ｉの値の範囲は通常μよりも大きくなる）、Ｒは間隔サイズであり、Ｑｒ_２（Ｒ）はＲに依存するスケーリング係数であり、Ｓｃａｌ（ｘ，ｙ）はスケーリング関数であり（例えば、Ｓｃａｌ（ｘ，ｙ）＝[ｘ＊ａ^－ｂｙ]として定義され、[．]はフロア演算であり、ａは、好ましくは２以上の定数であり、ｂは、好ましくは１以上の定数であり、スケーリング関数は、好ましくは、右シフトビットシフト演算を使用して実装され、ｙは、ｘの右シフトをするかどうか、および何ビットシフトするかを決定する、
ことに従って、２次元ルックアップテーブルの要素

を取得するように構成される。

好ましい実施形態では、算術デコーダは、第１および第２の状態変数値、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]）からそれぞれ第１および第２のサブインターバル幅値（Ｒ＊ｐ^ｋ）を計算するよう構成され、第１および第２の状態変数値の値ドメインの異なる値間隔の確率値、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ _２＊ａ^ｋ _２]）を含む１次元ルックアップテーブル（ＬＵＴ４）エントリを第１および第２の確率値へ使用して、第１および第２の状態変数値（ｓ_ｋ）、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]）にマッピングすること、およびシンボルを量子化レベルに符号化する前に、算術符号化のコーディング間隔のサイズを記述するコーディング間隔サイズ情報（例えば、Ｒ）を量子化すること、第１および第２の確率値と、一方で量子化レベルの間の積を決定する（事前計算された積のルックアップまたは乗算によって）こと、および第１のサブインターバル幅値と第２のサブインターバル幅値を使用して（例えば、加重和または加重平均を使用して）結合されたサブインターバル幅値を取得することによる。
好ましい実施形態では、算術デコーダは、コーディング間隔サイズ情報に論理右シフトを適用することによってコーディング間隔サイズ情報の量子化を実行するように構成される。

好ましい実施形態では、算術デコーダは、コーディング間隔サイズ情報

の量子化を

により実行するように構成され、式中、

、

および

はパラメータである。

算術デコーダの好ましい実施形態では、１次元ルックアップテーブルのエントリは、第１および第２の状態変数値、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]）の増加で単調に減少する。

算術デコーダの好ましい実施形態では、第１および第２の状態変数値の値ドメインの異なる値間隔、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]）は、等しいサイズになる。

算術デコーダの好ましい実施形態では、１次元ルックアップテーブルのエントリは、第１および第２の状態変数値、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]）の増加で減少率を伴って単調に減少する。
本発明による実施形態は、シンボル値（例えば、バイナリ値）を有する複数のシンボルを復号するための算術デコーダを作成し、算術デコーダは、間隔サイズ情報（ｐ^ｋ、Ｒ＊ｐ^ｋ）を、１つまたは複数のシンボル値（例えば、バイナリ値）の算術復号が複数の状態変数値（ｓ_ｉ ^ｋ）（例えば、インデックスｋによって表示される所与のコンテキストモードに関連付けられるもの）に基づいて復号されるように導出するように構成され、これは、異なる適合時定数で以前に復号された複数のシンボル値（例えば、バイナリ値０と１のシーケンス）（例えば、復号される１つまたは複数のシンボルが特定のシンボル値を含む確率の推定）の統計を表し、算術デコーダは、結合状態変数値（ｓ_ｋ）（例えば、状態変数値の加重和であり得る）、複数の個々の状態変数値（ｓ_ｉ ^ｋ）の基礎となるものを導出するように構成され、算術デコーダは、結合状態変数値（ｓ_ｋ）、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ _２＊ａ^ｋ _２]）を、ルックアップテーブルを使用してマッピングして、復号される１つまたは複数のシンボルの算術復号の間隔サイズを説明する間隔サイズ情報（例えば、ｐ_ｋまたはＲ＊ｐ_ｋ）を取得するように構成される。
好ましい実施形態では、算術デコーダは、結合状態変数値を取得するために、状態変数値の加重和を決定するように構成される。

好ましい実施形態では、算術デコーダは、状態変数値（

）および関連する重み付け値（

結合状態変数値（ｓ_ｋ）を得るため）の積を丸めることによって得られる丸められた値（

）の合計を決定するように構成される。

好ましい実施形態では、算術デコーダは、

ｓ^ｋ _２は状態変数値であり、Ｎは考慮される状態変数値の数であり、[．]はフロア演算子であり、ｄ^ｋ _ｉは状態変数値に関連付けられた重み付け値（例えば、結合状態変数値への個々の状態変数値の影響を制御する重み付け係数）（ｄ^ｋ _ｉは好ましくはフォン２の整数値の効力であり、２つの異なるｄ^ｋ _ｉ間の比率は好ましくは２の整数値の効力である）［２つの異なるｄ^ｋ _ｉ間の比率は、好ましくは８以上）であることに従って、結合状態変数値ｓ_ｋを決定するように構成される。

好ましい実施形態では、算術デコーダは、復号されるシンボルが第１の値（例えば「１」）をとる場合に状態変数値を第１の方向に変更する（例えばより正になる）ように構成され、また復号されるシンボルが第１の値とは異なる第２の値（例えば「０」）をとる場合（例えば、状態変数値が正と負の値をとることができるように）に状態変数値を第２の方向に（例えば、より負になるもの）変更するように構成され、算術デコーダは、結合状態変数値の絶対値（ｓ_ｋ ^ｉ＞０の場合はｓ_ｋ、それ以外の場合は－ｓ_ｋ）に応じて（例えば、結合状態変数値の絶対値のスケーリングおよび丸められたバージョンに応じて）評価されるルックアップテーブルのエントリを決定するように構成される。

好ましい実施形態では、算術デコーダは、結合状態変数値が第１の符号（例えば、正の符号）をとる場合に、確率値（ｐ^ｋ）をルックアップテーブルによって提供される値（例えば、

）に設定するように構成され、算術デコーダは、状態変数値が第２の符号（例えば、負の符号）をとる場合、確率値（ｐ^ｋ）を、所定の値（例えば、１）からルックアップテーブルによって提供される値（例えば、

）を減算することによって得られる値に設定するように構成される。

好ましい実施形態では、算術デコーダは、

ＬＵＴ２は確率値を含むルックアップテーブルであり、[．]はフロア演算子であり、ｓ^ｋは結合変数値であり、ａ^ｋは、結合状態変数値に関連付けられた重み付け値である（例えば、ｉ番目の状態変数値の数の範囲をルックアップテーブルのいくつかのエントリに適合させる重み付け値）ことにより、結合確率値ｐ_ｋを決定するように構成される。

好ましい実施形態では、算術デコーダは、

ＬＵＴ２は確率値を含むルックアップテーブルであり、[．]はフロア演算子であり、ｓ^ｋは結合変数値であり、ａ^ｋは、結合状態変数値に関連付けられた重み付け値である（例えば、ｉ番目の状態変数値の数の範囲をルックアップテーブルのいくつかのエントリに適合させる重み付け値）ことにより、結合確率値ｐ_ｋを決定するように構成される。

好ましい実施形態では、算術デコーダは、結合状態変数値、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]）を、２次元ルックアップテーブルを使用してサブインターバル幅値（Ｒ＊ｐ^ｋ）にマッピングするように構成され、そのエントリは、結合状態変数値に依存して（例えば、第１のルックアップテーブルエントリの座標を決定するために）、およびシンボルの復号前の算術復号のコーディング間隔のサイズを記述するコーディング間隔サイズ情報（例えば、Ｒ）に依存して（例えば、第２のルックアップテーブルエントリの座標を決定するために）アドレス指定される。

算術デコーダの好ましい実施形態では、２次元ルックアップテーブルは、そのエントリが結合状態変数値の値ドメインの異なる値間隔の確率値、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]；

）を含む第１の１次元ベクトル（

、１次元ルックアップテーブルを形成する）、およびそのエントリがコーディング間隔サイズ情報の量子化レベルを含む第２の１次元ベクトル（

）の間の２項積として、表すことができる。

算術デコーダの好ましい実施形態では、２次元ルックアップテーブル（ＲａｎｇＴａｂＬＰＳ）の要素が、ベースルックアップテーブル（Ｂａｓｅ ＴａｂＬＰＳ）に基づいて定義され、２次元ルックアップテーブルの要素の第１のグループ（またはブロック、例えば、「上半分」）は、ベースルックアップテーブルの要素と同一であるか、ベースルックアップテーブルの要素の丸められたバージョンであり、２次元ルックアップテーブルの要素の第２のグループ（またはブロック、例えば「下半分」）は、ベースルックアップテーブルの要素のスケーリングおよび丸められたバージョンである。

算術デコーダの好ましい実施形態では、２次元ルックアップテーブルの要素の第２のグループはベースルックアップテーブルの要素の右シフトバージョンである。

算術デコーダの好ましい実施形態では、確率指数（Ｑｐ_２（ｐ_ＬＰＳ）；ｉ）は、２次元ルックアップテーブルの要素の第１のグループの要素または２次元ルックアップテーブルの要素の第２のグループの要素のどちらを評価するかを決定し、確率指数（例えば、確率値、例えばｐ_ＬＰＳを定量化することによって取得される）の第１の範囲（例えば、０～μ－１）は、要素の第１のグループの要素に関連付けられ、確率指数（例えば、確率値、例えばｐ_ＬＰＳを、例えば、量子化関数Ｑｐ２（．）を使用して定量化することによって取得される）の第２の範囲（例えば、μ以上）は、要素の第２のグループの要素に関連付けられている。

算術デコーダの好ましい実施形態では、確率指数（ｉ）と第１のサイズ値（例えば、μ、サイズ値は例えば、第１の方向のベースルックアップテーブルの拡張を説明する）および間隔サイズ指数（例えば量子化演算Ｑｒ２（．）、例えばｊを使用するなどして間隔サイズ情報Ｒに基づいて取得できる）との間の除算の除算残差（ｉ％μ）は、２次元ルックアップテーブルの要素を取得するためにベースルックアップテーブルのどの要素を使用するかを決定する。

好ましい実施形態では、算術デコーダは、
ＲａｎｇｅＴａｂＬＰＳ［ｉ］［ｊ］＝Ｓｃａｌ（ＢａｓｅＴａｂＬＰＳ［ｉ％μ］［ｊ）、[ｉ／μ]）
ＢａｓｅＴａｂＬＰＳは、次元μｘλのベースルックアップテーブルであり、ｉは、確率情報に関連付けられたテーブルインデックスであり、ｊは、間隔サイズ情報に関連付けられたテーブルインデックスであり（例えば、現在のコーディング間隔サイズを記述する）、％は除算残差演算であり、／は除算演算であり、Ｓｃａｌ（ｘ，ｙ）はスケーリング関数であり（例えば、Ｓｃａｌ（ｘ，ｙ）＝[ｘ＊ａ^－ｂｙ]として定義され、[．]はフロア演算であり、ａは、好ましくは２以上の定数であり、またはｂは、好ましくは１以上の定数であり、スケーリング関数は、好ましくは、右シフトビットシフト演算を使用して実装され、ｙは、ｘの右側にシフトするかどうか、および何ビットシフトするかを決定する、
ことに従って、２次元ルックアップテーブル（ＲａｎｇＴａｂＬＰＳ）の要素を取得するように構成される。

算術デコーダの好ましい実施形態では、２次元ルックアップテーブル（ＲａｎｇＴａｂＬＰＳ）の要素は、確率テーブル（ｐｒｏｂＴａｂＬＰＳ）に基づいて定義され、確率テーブルは、複数の確率値のセット（例えば、指数ｉによって表される）および所与のコーディング間隔サイズの間隔サイズを記述し、複数の確率値のセットにない確率値および／または所与の（参照）コーディング間隔サイズとは異なるコーディング間隔サイズの２次元ルックアップテーブルの要素は、スケーリングを使用して確率テーブルから導出される。

算術デコーダの好ましい実施形態では、２次元ルックアップテーブルの要素が、コーディング間隔サイズ（Ｒ）に応じて、確率テーブルの選択された要素（ｐｒｏｂＴａｂＬＰＳ［ｉ％μ］）の（乗法の）第１のスケーリングを使用し、現在の確率値（指数ｉにより指定）に関連付けられた要素が確率値のセットに含まれるかどうかに応じて（例えば、現在の確率値は、確率テーブルでカバーされている確率値の範囲内にあるかどうかに応じて）、第１のスケーリングの結果の第２のスケーリングを使用して取得される。

算術デコーダの好ましい実施形態では、確率指数（例えばｉ、例えば、現在の確率値を表す）、および第１のサイズ値（例えばμ、例えばサイズ値が確率テーブルの拡張について説明する）の間の除算の除算残差（ｉ％μ）は、確率テーブルのどの要素が第１のスケーリングでスケーリングされるかを決定する、および／または確率指数（ｉ）および第１のサイズ値間の除算の整数除算結果（[ｉ／μ]）は、第２のスケーリングで使用されるスケーリング係数（２^{－[ｉ／μ]}）を決定する、および／またはコーディング間隔サイズは、第１のスケーリングの乗法スケーリング係数（Ｑｒ２（Ｒ））を決定する。

好ましい実施形態では、算術デコーダは、

ｉは、確率情報に関連付けられたテーブルインデックスであり、ｊは間隔サイズ情報に関連付けられたテーブルインデックスであり、％は除算残差演算であり、／は除算演算であり、ｐｒｏｂＴａｂＬＰＳ ［］は確率テーブルであり、μは確率テーブルの要素の数であり（Ｉの値の範囲は通常μよりも大きくなる）、Ｒは間隔サイズ（または現在のコーディング間隔サイズ）であり、Ｑｒ２（Ｒ）はＲに依存するスケーリング係数であり、Ｓｃａｌ（ｘ，ｙ）はスケーリング関数であり（例えば、Ｓｃａｌ（ｘ，ｙ）＝[ｘ＊ａ^－ｂｙ]として定義され、[．]はフロア演算であり、ａは、好ましくは２以上の定数であり、ｂは、好ましくは１以上の定数であり、スケーリング関数は、好ましくは、右シフトビットシフト演算を使用して実装され、ｙは、ｘの右シフトをするかどうか、および何ビットシフトするかを決定する、
ことに従って
２次元ルックアップテーブルの要素

を取得するように構成される。

算術デコーダの好ましい実施形態では、現在の確率値（指数ｉにより指定）に関連付けられた要素が確率値に含まれるかどうかに応じて（例えば、現在の確率値は、確率テーブルでカバーされている確率値の範囲内にあるかどうかに応じて）、確率テーブルの選択された要素（ｐｒｏｂＴａｂＬＰＳ［ｉ％μ］）の（乗法の）第１のスケーリングを使用し、また、コーディング間隔サイズ（Ｒ）に応じて、第１のスケーリングの結果の第２のスケーリングを使用して、２次元ルックアップテーブルの要素を取得するように構成される。

算術デコーダの好ましい実施形態では、確率指数（例えばｉ、例えば、現在の確率値を表す）、および第１のサイズ値（例えばμ、例えばサイズ値が確率テーブルの拡張について説明する）の間の除算の除算残差（ｉ％μ）は、確率テーブルのどの要素が第１のスケーリングでスケーリングされるかを決定する、および／または確率指数（ｉ）および第１のサイズ値間の除算の整数除算結果（[ｉ／μ]）は、第１のスケーリングで使用されるスケーリング係数（２^{－[ｉ／μ]}）を決定する、および／またはコーディング間隔サイズ（Ｒ）は、第２のスケーリングの乗法スケーリング係数（Ｑｒ_２（Ｒ））を決定する。

好ましい実施形態では、算術デコーダは、

ｉは、確率情報に関連付けられたテーブルインデックスであり、ｊは間隔サイズ情報に関連付けられたテーブルインデックスであり、％は除算残差演算であり、／は除算演算であり（例えば、整数の結果を提供する）、ｐｒｏｂＴａｂＬＰＳ ［］は確率テーブルであり、μは確率テーブルの要素の数であり（Ｉの値の範囲は通常μよりも大きくなる）、Ｒは間隔サイズであり、Ｑｒ_２（Ｒ）はＲに依存するスケーリング係数であり、Ｓｃａｌ（ｘ，ｙ）はスケーリング関数であり（例えば、Ｓｃａｌ（ｘ，ｙ）＝[ｘ＊ａ^－ｂｙ]として定義され、[．]はフロア演算であり、ａは、好ましくは２以上の定数であり、ｂは、好ましくは１以上の定数であり、スケーリング関数は、好ましくは、右シフトビットシフト演算を使用して実装され、ｙは、ｘの右シフトをするかどうか、および何ビットシフトするかを決定する、
ことに従って、２次元ルックアップテーブルの要素

を取得するように構成される。

好ましい実施形態では、算術デコーダは、結合状態変数値、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]）からサブインターバル幅値（Ｒ＊ｐ^ｋ）を計算するよう構成され、このことは、結合状態変数値の値ドメインの異なる値間隔の確率値、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]；

）を含む１次元ルックアップテーブル（ＬＵＴ４）エントリを使用して、結合状態変数値（ｓ_ｋ）、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]；

）を結合確率値にマッピングすること、およびシンボルを量子化レベルに符号化する前に、算術符号化のコーディング間隔のサイズを記述するコーディング間隔サイズ情報（例えば、Ｒ）を量子化すること、結合確率値と量子化レベルの間の積を決定することによる。

好ましい実施形態では、算術デコーダは、コーディング間隔サイズ情報に論理右シフトを適用することによってコーディング間隔サイズ情報の量子化を実行するように構成される。

好ましい実施形態では、算術デコーダは、コーディング間隔サイズ情報

の量子化を

により実行するように構成され、式中、

、

および

はパラメータである。

算術デコーダの好ましい実施形態では、１次元ルックアップテーブルのエントリは、結合状態変数値、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]）の増加で単調に減少する。

算術デコーダの好ましい実施形態では、結合状態変数値の値ドメインの異なる値間隔、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]）は、等しいサイズである。

算術デコーダの好ましい実施形態では、１次元ルックアップテーブルのエントリは、結合状態変数値、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]）の増加で減少率を伴って単調に減少する。

算術デコーダの好ましい実施形態では、ルックアップテーブルは、指数関数的減衰（例えば、０．５からの低下）を（例えば、＋／－１０％または＋／－２０％の許容範囲内で）定義する。

好ましい実施形態では、算術デコーダは、

ｚは所定の（一定の）オフセット値であり、

は１つまたは複数の重み付け値であり、

は１つ以上の重み付け値であり、Ａは

であるか、ゼロ設定または大きさの縮小によって、引数の１つ以上の極値に対してのみ、それから逸脱して、更新された

を所定の値の範囲のままにすることを回避する（例えば、

は

より大きな値ドメインを持つ；つまり、

は

に準量子化される；

の極値の場合、

は上記の式に従って未修正のＡによって変更され、その値ドメインを離れることができる：これを回避するために、これらの極値に対応するエントリが削減またはゼロにされる場合があることを考慮されたい）、

、

、

、および

は所定のパラメータである（例は上記に記載されている）
ことに従って複数の可変状態値

を更新するように構成される。。

好ましい実施形態では、算術デコーダは、テーブルルックアップまたは計算によって

を導出するように構成される。

本発明による実施形態は、シンボル値（例えば、バイナリ値）を有する複数のシンボルを符号化するための算術デコーダを作成するものであり、算術デコーダは、１つまたは複数の状態変数値（ｓ_１ ^ｋ、ｓ_２ ^ｋ）を決定するように構成され、これは、以前に復号された複数のシンボル値（例えば、バイナリ値０および１のシーケンス）の統計（例えば、復号される１つまたは複数のシンボルが特定のシンボル値を含む確率の推定値）（例えば、複数の状態変数値が決定される場合、異なる適合時定数の統計）を表し、また、算術デコーダは、１つまたは複数の状態変数値（ｓ_ｉ ^ｋ）（例えば、インデックスｋにより示される、所与のコンテキストモードに関連付けられている）に基づいて復号される１つまたは複数のシンボル値の算術復号の間隔サイズ情報（ｐ^ｋ、Ｒ＊ｐ^ｋ）を導出するように構成され、これは複数の以前に符号化されたシンボル値（例えば、バイナリ値０および１のシーケンス）の統計（例えば、複数の状態変数値が決定される場合、異なる適合時定数の統計）を表し、算術デコーダは、復号されるシンボルに依存して、ルックアップテーブル（Ａ）を使用して（例えば、復号されるシンボルを復号した後）、第１の状態変数値（ｓ^ｋ _１）を更新するように構成される。

好ましい実施形態では、算術デコーダは、復号されたるシンボルに依存し、ルックアップテーブル（Ａ）を使用して（例えば、復号されるシンボルを復号した後）、第２の状態変数値（ｓ^ｋ _２）を更新するように構成される。

好ましい実施形態では、算術デコーダは、異なる適合時定数を使用して、第１の状態変数値および第２の状態変数値を更新するように構成される。

好ましい実施形態では、算術デコーダは、復号されるシンボルが第１の値をとるか、第１の値とは異なる第２の値をとるかに応じて、ルックアップテーブルを使用して決定された値によって以前の状態変数値を選択的に増減するように構成される。

好ましい実施形態では、算術デコーダは、以前の状態変数値を、復号されるシンボルが第１の値をとる場合に、以前の状態変数値が正である場合と比較して、以前の状態変数値が負である場合に、比較的大きい値だけ増加させるように構成され、算術デコーダは、以前の状態変数値を、復号されるシンボルが、第１の値とは異なる第２の値をとる場合に、以前の状態変数値が負である場合と比較して、以前の状態変数値が正である場合に、比較的大きい値だけ減少させるように構成される（それは、例えば、ルックアップテーブルを適切に選択することで到達する）。

好ましい実施形態では、算術デコーダは、復号されるシンボルが第１の値をとる場合、所定（例えば、固定の）のオフセット値（ｚ）と以前に計算された第１の状態変数値（

）、またはそのスケーリングおよび／または丸められたバージョン（

）の合計に依存して、第１の状態変数値を更新するときに評価されるルックアップテーブルのエントリのインデックスを決定するように構成され、算術デコーダは、復号されるシンボルが第２の値をとる場合、所定（例えば、固定の）のオフセット値（ｚ）と以前に計算された第１の状態変数値の逆（－１を乗算する）バージョン（

）、またはそのスケーリングおよび／または丸められたバージョン（

）（例えば、以前に計算された第１の状態変数値の逆バージョン）の合計に依存して、第１の状態変数値を更新するときに評価されるルックアップテーブルのエントリのインデックスを決定するように構成される。

好ましい実施形態では、算術デコーダは、復号されるシンボルが第１の値をとる場合、所定（例えば、固定の）のオフセット値（ｚ）と以前に計算された第２の状態変数値（

）、またはそのスケーリングおよび／または丸められたバージョン（

）の合計に依存して、第２の状態変数値を更新するときに評価されるルックアップテーブルのエントリのインデックスを決定するように構成され、算術デコーダは、復号されるシンボルが第２の値をとる場合、所定（例えば、固定の）のオフセット値（ｚ）と以前に計算された第２の状態変数値の逆（－１を乗算する）バージョン（

）、またはそのスケーリングおよび／または丸められたバージョン（

）（例えば、以前に計算された第２の状態変数値の逆バージョン）の合計に依存して、第２の状態変数値を更新するときに評価されるルックアップテーブルのエントリのインデックスを決定するように構成される。

好ましい実施形態では、算術デコーダは、第１の状態変数値の更新時に評価されるルックアップテーブルのエントリのインデックスを決定するときに、第１のスケーリング値（ｍ^ｋ _１）を適用して、以前に計算された第１の状態変数値（ｓ^ｋ _１）をスケーリングするように構成され、算術デコーダは、第２の状態変数値の更新時に評価されるルックアップテーブルのエントリのインデックスを決定するときに、第２のスケーリング値（ｍ^ｋ _２）を適用して、以前に計算された第２の状態変数値（ｓ^ｋ _２）をスケーリングするように構成され、第１のスケーリング値が第２のスケーリング値とは異なる（また、第１および第２のスケーリング値は好ましくは２の整数効力であり、第１のスケーリング値と第２のスケーリング値との間の比は、２の場合、好ましくは整数効力であり、第１のスケーリング値および第２のスケーリング値は、好ましくは少なくとも８倍異なる）。

好ましい実施形態では、算術デコーダは、第１の状態変数値を更新するときに第１のスケーリング値（例えば、ｎ^ｋ _１）を使用してルックアップテーブルの評価によって返される値をスケーリングするように構成され、
算術デコーダは、第２の状態変数値を更新するときに第２のスケーリング値（例えば、ｎ^ｋ _２）を使用してルックアップテーブルの評価によって返される値をスケーリングするように構成され、第１のスケーリング値は第２のスケーリング値とは異なる。

好ましい実施形態では、算術デコーダは、

Ａはルックアップテーブルであり（例えば、整数の値を含む）、ｚは所定の（一定の）オフセット値であり、

は１つまたは複数の重み付け値であり、

は１つまたは複数の重み付け値であることに従って、１つまたは複数の更新された状態変数値

を決定するように構成される。

好ましい実施形態では、算術デコーダは、

Ａはルックアップテーブルであり（例えば、整数の値を含む）、ｚは所定の（一定の）オフセット値であり、

は１つまたは複数の重み付け値であり、

は１つまたは複数の重み付け値であることに従って、１つまたは複数の更新された状態変数値

を決定するように構成される。

好ましい実施形態では、算術デコーダは、

Ａはルックアップテーブルであり（例えば、整数の値を含む）、ｚは所定の（一定の）オフセット値であり、

は１つまたは複数の重み付け値であり、

は１つまたは複数の重み付け値であることに従って、１つまたは複数の更新された状態変数値

を決定するように構成される。

好ましい実施形態では、算術デコーダは、

Ａはルックアップテーブルであり（例えば、整数の値を含む）、ｚは所定の（一定の）オフセット値であり、

は１つまたは複数の重み付け値であり、

は１つまたは複数の重み付け値であることに従って、１つまたは複数の更新された状態変数値

を決定するように構成される。

算術デコーダの好ましい実施形態では、Ａのエントリは、ルックアップテーブルインデックスの増加とともに単調に減少する。

好ましい実施形態では、算術デコーダは、Ａは

であるか、ゼロ設定または大きさの縮小によって、引数の１つ以上の極値に対してのみ、それから逸脱して、更新された

を所定の値の範囲のままにすることを回避する（例えば、

は

より大きな値ドメインを持つ；つまり、

は

に準量子化される；

の極値の場合、

は上記の式に従って未修正のＡによって変更され、その値ドメインを離れることができる：これを回避するために、これらの極値に対応するエントリが削減またはゼロにされる場合があることを考慮されたい）、

、

、

、および

は所定のパラメータである（例は上記に記載されている）。

算術デコーダの好ましい実施形態では、ルックアップテーブルの最後のエントリ（これは、第１の状態変数値が最大許容値まで及ぶ所定の値の範囲に達したとき、または第１の状態変数値が所定のしきい値を超えたときにアドレス指定される）はゼロに等しい。

好ましい実施形態では、算術デコーダは、更新された状態変数値にクリッピング操作を適用して、更新されクリップされた状態変数値を所定の値の範囲内に保つように構成される。

好ましい実施形態では、算術デコーダは、更新された状態変数値に、

、に従ってクリッピング操作を適用するように構成され、

は、

の最大許容値であり、

は、

の最小許容値である。

好ましい実施形態では、算術デコーダは、異なるコンテキストモデルに異なるスケーリング値を適用するように構成される（例えば、スケーリング値の少なくとも１つが２つの異なるコンテキストモデル間で異なるようにする）。

好ましい実施形態では、算術デコーダは、上記の実施形態の１つで定義された間隔サイズ情報を取得するように構成される。

本発明による実施形態は、シンボル値（例えば、バイナリ値）を有する複数のシンボルを復号するための算術デコーダを作成するものであり、算術デコーダは、以前に復号された複数のシンボル値の統計を表す１つの状態変数値（ｓ_ｋ）を決定するように構成され、算術デコーダは、結合状態変数値、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]）から、復号されるシンボル値の算術復号のためのサブインターバル幅値（

）を計算するよう構成され、この計算は、そのエントリが結合状態変数値の値ドメインの異なる値間隔の確率値、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]；

）を含む１次元ルックアップテーブル（

）を使用して、１つの状態変数値（ｓ_ｋ）、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]；

）を結合確率値にマッピングすること、および量子化レベル（

）に符号化されるシンボル値の算術復号の前に、算術符号化のコーディング間隔のサイズを記述するコーディング間隔サイズ情報（例えば、Ｒ）を量子化することにより、これを行い、算術デコーダは、さらに、確率値と、量子化レベルの間の積を決定する（事前に計算された積のルックアップまたは乗算によって）ように構成され、算術デコーダは、（実際に復号される）復号されるシンボルに依存して状態変数値の更新を実行するように構成される。

好ましい実施形態では、算術デコーダは、１つの状態変数値（ｓ_ｋ）として、結合状態変数値（例えば、状態変数値の加重和であり得る）、複数の状態変数値（ｓ_ｉ ^ｋ）（例えば、バイナリ値０および１のシーケンス）（例えば、複数の状態変数値の場合、異なる適合時定数の統計）の基礎となるものを導出するように構成され、これは、異なる適合時定数の複数の以前に復号されたシンボル値（例えば、バイナリ値０および１のシーケンス）の統計を表す。

好ましい実施形態では、算術デコーダは、結合状態変数値を取得するために、状態変数値の加重和を決定するように構成される。

好ましい実施形態では、算術デコーダは、状態変数値（

）および関連する重み付け値（

結合状態変数値（ｓ_ｋ）を得るため）の積を丸めることによって得られる丸められた値（

）の合計を決定するように構成される。

好ましい実施形態では、算術デコーダは、

ｓ^ｋ _２は状態変数値であり、Ｎは考慮される状態変数値の数であり、[．]はフロア演算子であり、ｄ^ｋ _ｉは状態変数値に関連付けられた重み付け値（例えば、結合状態変数値への個々の状態変数値の影響を制御する重み付け係数）（ｄ^ｋ _ｉは好ましくはフォン２の整数値の効力であり、２つの異なるｄ^ｋ _ｉ間の比率は好ましくは２の整数値の効力である）［２つの異なるｄ^ｋ _ｉ間の比率は、好ましくは８以上）であることに従って、結合状態変数値ｓ_ｋを決定するよう構成される。

好ましい実施形態では、算術デコーダは、

ｚは所定の（一定の）オフセット値であり、

は１つまたは複数の重み付け値であり、

は１つ以上の重み付け値であり、Ａは

であるか、ゼロ設定または大きさの縮小によって、引数の１つ以上の極値に対してのみ、それから逸脱して、更新された

を所定の値の範囲のままにすることを回避する（例えば、

は

より大きな値ドメインを持つ；つまり、

は

に準量子化される；

の極値の場合、

は上記の式に従って未修正のＡによって変更され、その値ドメインを離れることができる：これを回避するために、これらの極値に対応するエントリが削減またはゼロにされる場合があることを考慮されたい）、

、

、

、および

は所定のパラメータである（例は上記に記載されている）
ことに従って、状態変数値の更新を行う際、複数の状態変数値

を更新するように構成される。

好ましい実施形態では、算術デコーダは、テーブルルックアップまたは計算によって

を導出するように構成される。

好ましい実施形態では、算術デコーダは、

Ａはルックアップテーブルであり（例えば、整数の値を含む）、ｚは所定の（一定の）オフセット値であり、

は１つまたは複数の重み付け値であり、

は１つまたは複数の重み付け値であることに従って、１つまたは複数の更新された状態変数値

を決定するように構成される。

好ましい実施形態では、算術デコーダは、

Ａはルックアップテーブルであり（例えば、整数の値を含む）、ｚは所定の（一定の）オフセット値であり、

は１つまたは複数の重み付け値であり、

は１つまたは複数の重み付け値であることに従って、１つまたは複数の更新された状態変数値

を決定するように構成される。

好ましい実施形態では、算術デコーダは、

Ａはルックアップテーブルであり（例えば、整数の値を含む）、ｚは所定の（一定の）オフセット値であり、

は１つまたは複数の重み付け値であり、

は１つまたは複数の重み付け値であることに従って、１つまたは複数の更新された状態変数値

を決定するように構成される。

好ましい実施形態では、算術デコーダは、コーディング間隔サイズ情報に論理右シフトを適用することによってコーディング間隔サイズ情報の量子化を実行するように構成される。

好ましい実施形態では、算術デコーダは、コーディング間隔サイズ情報

の量子化を

により実行するように構成され、式中、

、

および

はパラメータである。

算術デコーダの好ましい実施形態では、１次元ルックアップテーブルのエントリは、１つの状態変数値、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]）の増加で単調に減少する。

算術デコーダの好ましい実施形態では、１つの状態変数値の値ドメインの異なる値間隔、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]）は、等しいサイズである。

算術デコーダの好ましい実施形態では、１次元ルックアップテーブルのエントリは、１つの状態変数値、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ＊ａ^ｋ]）の増加で減少率を伴って単調に減少する。

本発明による実施形態は、ビデオエンコーダを作成するものであり、ビデオエンコーダは、複数のビデオフレームを符号化するように構成され、ビデオエンコーダは、上記の実施形態のいずれかに記載の、ビデオコンテンツを表すバイナリ値のシーケンスに基づいて符号化されたバイナリシーケンスを提供するための算術エンコーダを備える。

本明細書で論じられる算術エンコーダは、ビデオエンコーダ内部での使用に非常に適していることに留意されたい。この場合、符号化されるシンボルおよび／または以前に符号化されたシンボルは、ビデオビットストリームのシンボルであり得る。例えば、符号化されるシンボルおよび／または以前に符号化されたシンボルは、ビデオコンテンツを表すサイド情報または制御情報のビットおよび／または符号化された変換係数のビットを表すことができる。言い換えれば、符号化されるシンボルおよび／または以前に符号化されたシンボルは、ビデオコンテンツを表すためにビットストリームに含まれる情報のいずれかを表すことができる。ただし、状態変数値は、様々な「コンテキスト」、つまり様々なタイプの情報に対して個別に決定される場合があることに留意されたい。例えば、特定のタイプの情報（例えば、特定のタイプのサイド情報）に関連付けられたビットのみが、特定の結合状態変数値を取得するために使用される特定の状態変数値、または特定の状態変数値のセットに寄与することができる。したがって、間隔サイズ情報はまた、異なるコンテキストに対して、すなわち、異なるタイプの情報（例えば、サイド情報）に関連付けられたシンボル値の符号化のために、個別に導出され得る。

本発明による実施形態は、ビデオデコーダを作成するものであって、ビデオエンコーダは、複数のビデオフレームを復合するように構成され、ビデオデコーダは、上記の実施形態のいずれかに記載の、バイナリシーケンスの符号化表現（２１１）に基づいて復号されたバイナリシーケンス（例えば、復号されたシンボル値に基づく）を提供するための算術デコーダ（１２０；２２０）を備える。
ビデオデコーダは、ビデオエンコーダと同じ考慮事項に基づいている。したがって、上記の説明もまた、当てはまるものであり、符号化されたシンボルまたは符号化されるシンボルは、復号されたシンボルに対応する。

さらに、本発明によるさらなる実施形態は、それぞれの方法およびコンピュータプログラムを作成することに留意されたい。

本発明による実施形態は、シンボル値（例えば、バイナリ値）を有する複数のシンボルを符号化するための方法を作成し、方法は、間隔サイズ情報（ｐ^ｋ、Ｒ＊ｐ^ｋ）を、１つまたは複数のシンボル値（例えば、バイナリ値）の算術符号化が複数の状態変数値（ｓ_ｉ ^ｋ）（例えば、インデックスｋによって表示される所与のコンテキストモードに関連付けられるもの）に基づいて符号化されるように導出することを含み、これは、異なる適合時定数で以前に符号化された複数のシンボル値（例えば、バイナリ値０と１のシーケンス）の統計を表し、方法は、ルックアップテーブル（ＬＵＴ１）を使用して、第１の状態変数値（ｓ^ｋ _１）、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ _１＊ａ^ｋ _１]）をマッピングし、ルックアップテーブル（ＬＵＴ１）を使用して、第２の状態変数値（ｓ^ｋ _２）、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ _２＊ａ^ｋ _２]）をマッピングすることを含み、符号化される１つまたは複数のシンボルの算術符号化のための間隔サイズを説明する間隔サイズ情報（例えば、ｐ_ｋまたはＲ＊ｐ_ｋ）を取得するようにする。

本発明による実施形態は、シンボル値（例えば、バイナリ値）を有する複数のシンボルを符号化するための方法を作成し、方法は、間隔サイズ情報（ｐ^ｋ、Ｒ＊ｐ^ｋ）を、１つまたは複数のシンボル値（例えば、バイナリ値）の算術符号化が複数の状態変数値（ｓ_ｉ ^ｋ）（例えば、インデックスｋによって表示される所与のコンテキストモードに関連付けられるもの）に基づいて符号化されるように導出することを含み、これは、異なる適合時定数で以前に符号化された複数のシンボル値（例えば、バイナリ値０と１のシーケンス）の統計を表し、方法は、結合状態変数値（ｓ_ｋ）（例えば、状態変数値の加重和であり得る）、複数の個々の状態変数値（ｓ_ｉ ^ｋ）の基礎となるものを導出するように構成され、算術デコーダは、結合状態変数値（ｓ_ｋ）、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ _２＊ａ^ｋ _２]）を、ルックアップテーブルを使用してマッピングして、符号化される１つまたは複数のシンボルの算術符号化の間隔サイズを説明する間隔サイズ情報（例えば、ｐ_ｋまたはＲ＊ｐ_ｋ）を取得することを含む。

本発明による実施形態は、シンボル値（二進値）を有する複数のシンボルを符号化するための方法を作成し、この方法は、１つまたは複数の状態変数値（ｓ_１ ^ｋ、ｓ_２ ^ｋ）を決定することを含み、これは、以前に符号化された複数のシンボル値（例えば、バイナリ値０および１のシーケンス）の統計（例えば、複数の状態変数値の場合、異なる適合時定数の統計）を表し、また、方法は、１つまたは複数の状態変数値（ｓ_ｉ ^ｋ）（例えば、インデックスｋにより示される、所与のコンテキストモードに関連付けられている）に基づいて符号化される１つまたは複数のシンボル値の算術符号化の間隔サイズ情報（ｐ^ｋ、Ｒ＊ｐ^ｋ）を導出することを含み、これは複数の以前に符号化されたシンボル値（例えば、バイナリ値０および１のシーケンス）の統計（例えば、複数の状態変数値の場合、異なる適合時定数の統計）を表し、方法は、符号化されるシンボルに依存して、ルックアップテーブル（Ａ）を使用して（例えば、シンボルを符号化した後）、第１の状態変数値（ｓ^ｋ _１）を更新することを含む。

本発明による実施形態は、シンボル値（例えば、バイナリ値）を有する複数のシンボルを復号するための方法を作成し、方法は、間隔サイズ情報（ｐ^ｋ、Ｒ＊ｐ^ｋ）を、１つまたは複数のシンボル値（例えば、バイナリ値）の算術復号が複数の状態変数値（ｓ_ｉ ^ｋ）（例えば、インデックスｋによって表示される所与のコンテキストモードに関連付けられるもの）に基づいて復号されるように導出することを含み、これは、異なる適合時定数で以前に復号された複数のシンボル値（例えば、バイナリ値０と１のシーケンス）の統計（例えば、復号される１つまたは複数のシンボルが特定のシンボル値を含む確率の推定）を表し、方法は、ルックアップテーブル（ＬＵＴ１）を使用して、第１の状態変数値（ｓ^ｋ _１）、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ _１＊ａ^ｋ _１]）をマッピングし、ルックアップテーブル（ＬＵＴ１）を使用して、第２の状態変数値（ｓ^ｋ _２）、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ _２＊ａ^ｋ _２]）をマッピングすることを含み、復号される１つまたは複数のシンボルの算術復号のための間隔サイズを説明する間隔サイズ情報（例えば、ｐ_ｋまたはＲ＊ｐ_ｋ）を取得するようにする。

本発明による実施形態は、シンボル値（例えば、バイナリ値）を有する複数のシンボルを復号するための方法を作成し、方法は、間隔サイズ情報（ｐ^ｋ、Ｒ＊ｐ^ｋ）を、１つまたは複数のシンボル値（例えば、バイナリ値）の算術復号が複数の状態変数値（ｓ_ｉ ^ｋ）（例えば、インデックスｋによって表示される所与のコンテキストモードに関連付けられるもの）に基づいて復号されるように導出することを含み、これは、異なる適合時定数で以前に復号された複数のシンボル値（例えば、バイナリ値０と１のシーケンス）（例えば、復号される１つまたは複数のシンボルが特定のシンボル値を含む確率の推定）の統計を表し、方法は、結合状態変数値（ｓ_ｋ）（例えば、状態変数値の加重和であり得る）、複数の個々の状態変数値（ｓ_ｉ ^ｋ）の基礎となるものを導出することを含み、方法は、結合状態変数値（ｓ_ｋ）、またはそのスケーリングおよび／または丸められたバージョン（[ｓ^ｋ _２＊ａ^ｋ _２]）を、ルックアップテーブルを使用してマッピングして、復号される１つまたは複数のシンボルの算術復号の間隔サイズを説明する間隔サイズ情報（例えば、ｐ_ｋまたはＲ＊ｐ_ｋ）を取得することを含む。

本発明による実施形態は、シンボル値（例えば、バイナリ値）を有する複数のシンボルを符号化するための方法を作成するものであり、方法は、１つまたは複数の状態変数値（ｓ_１ ^ｋ、ｓ_２ ^ｋ）を決定することを含み、これは、以前に復号された複数のシンボル値（例えば、バイナリ値０および１のシーケンス）の統計（例えば、復号される１つまたは複数のシンボルが特定のシンボル値を含む確率の推定値）（例えば、複数の状態変数値が決定される場合、異なる適合時定数の統計）を表し、また、方法は、１つまたは複数の状態変数値（ｓ_ｉ ^ｋ）（例えば、インデックスｋにより示される、所与のコンテキストモードに関連付けられている）に基づいて復号される１つまたは複数のシンボル値の算術復号の間隔サイズ情報（ｐ^ｋ、Ｒ＊ｐ^ｋ）を導出することを含み、これは複数の以前に符号化されたシンボル値（例えば、バイナリ値０および１のシーケンス）の統計（例えば、複数の状態変数値が決定される場合、異なる適合時定数の統計）を表し、算術デコーダは、復号されるシンボルに依存して、ルックアップテーブル（Ａ）を使用して、第１の状態変数値（ｓ^ｋ _１）を更新することを含む。

本発明による実施形態は、上記の実施形態のうちの１つによるエンコーダおよびデコーダによって実行される方法を作成する。

本発明による実施形態は、コンピュータプログラムがコンピュータ上で実行されるときに、上記の実施形態のうちの１つによる方法を実行するためのコンピュータプログラムを作成する。

本発明による実施形態は、シンボル値（例えば、バイナリ値）を有する複数のシンボルを符号化するための方法を作成するものであり、方法は、１つまたは複数の状態変数値（ｓ_ｉ ^ｋ）に基づいて符号化される１つまたは複数のシンボル値の算術符号化の間隔サイズ値（Ｒ_ＬＰＳ）（それは例えば、インデックスｋで示される所与のコンテキストモードに関連付けられている）を導出することを含み、これは、以前に符号化された複数のシンボル値（例えば、バイナリ値０および１のシーケンス）の統計を表し（例えば、異なる適合時定数を使用）、方法は、ベースルックアップテーブル（Ｂａｓｅ ＴａｂＬＰＳ）を使用して間隔サイズ値（Ｒ_ＬＰＳ）を決定することを含み（その次元は、確率指数の観点から、可能な確率指数ｉの数よりも小さい）、方法は、１つまたは複数の状態変数値（例えば、ｉ＝Ｑｐ（ｐ_ＬＰＳ）のように）を基にして得られる確率指数（ｉ）が第１の範囲（例えば、μ未満）内にある場合、決定された間隔サイズ値がベースルックアップテーブルの要素と同一であるか、またはベースルックアップテーブルの要素の丸めのバージョンであり、確率指数が第２の範囲（例えば、μ以上）内にある場合は、ベースルックアップテーブルの要素のスケーリングと丸めを使用して、決定された間隔サイズ値が取得されるように、間隔サイズ値（Ｒ_ＬＰＳ）を決定することを含み、方法は、間隔サイズ値（Ｒ_ＬＰＳ）を使用して１つまたは複数のシンボルの算術符号化を実行することを含む。

本発明による実施形態は、シンボル値（例えば、バイナリ値）を有する複数のシンボルを符号化するための方法を作成するものであり、方法は、１つまたは複数の状態変数値（ｓ_ｉ ^ｋ）（これはインデックスｋによって示される所与のコンテキストモードに関連付けられる）に基づいて符号化される１つまたは複数のシンボル値の算術符号化の間隔サイズ値（Ｒ_ＬＰＳ）を導出することを含み、これは、以前に符号化された複数のシンボル値の統計を表し（例えば、バイナリ値０と１のシーケンス）（例えば、異なる適合時定数で）；算術デコーダは、１つまたは複数の状態変数値から導出された（現在の）確率値に基づいて、また（現在の）コーディング間隔サイズ（Ｒ）に基づいて、確率テーブル（Ｐｒｏｂ ＴａｂＬＰＳ）（確率指数という観点で次元が可能な確率指数ｉの数値より小さい）を使用して間隔サイズ値（Ｒ_ＬＰＳ）を決定することを含み、確率テーブルは、複数の確率値のセット（例えば、０とμ－１の間の確率指数に対して）および（単一の）所与の（参照）コーディング間隔サイズの間隔サイズ（間隔サイズ値）を記述し、方法は、現在の確率値が複数の確率値のセットにない（例えば、μ以上の現在の確率値と関連付けられた確率指数である）場合、および／または現在のコーディング間隔サイズ（Ｒ）が、所与（参照）のコーディング間隔サイズとは異なる場合、間隔サイズ値（Ｒ_ＬＰＳ）を取得するよう所与（参照）の確率テーブル（Ｐｒｏｂ＿ＴａｂＬＰＳ）の要素をスケーリングすることを含み、また、方法は、間隔サイズ値（Ｒ_ＬＰＳ）を使用して１つまたは複数のシンボルの算術符号化を実行することを含む。

本発明による実施形態は、シンボル値（例えば、バイナリ値）を有する複数のシンボルを復号するための方法を作成するものであり、方法は、１つまたは複数の状態変数値（ｓ_ｉ ^ｋ）に基づいて復号される１つまたは複数のシンボル値の算術復号の間隔サイズ値（Ｒ_ＬＰＳ）（それは例えば、インデックスｋで示される所与のコンテキストモードに関連付けられている）を導出することを含み、これは、以前に復号された複数のシンボル値（例えば、バイナリ値０および１のシーケンス）の統計を表し（例えば、異なる適合時定数を使用）、方法は、ベースルックアップテーブル（Ｂａｓｅ ＴａｂＬＰＳ）を使用して間隔サイズ値（Ｒ_ＬＰＳ）を決定することを含み（その次元は、確率指数の観点から、可能な確率指数ｉの数よりも小さい）、方法は、１つまたは複数の状態変数値（例えば、ｉ＝Ｑｐ（ｐ_ＬＰＳ）のように）を基にして得られる確率指数（ｉ）が第１の範囲（例えば、μ未満）内にある場合、決定された間隔サイズ値がベースルックアップテーブルの要素と同一であるか、またはベースルックアップテーブルの要素の丸めのバージョンであり、確率指数が第２の範囲（例えば、μ以上）内にある場合は、ベースルックアップテーブルの要素のスケーリングと丸めを使用して、決定された間隔サイズ値が取得されるように、間隔サイズ値（Ｒ_ＬＰＳ）を決定することを含み、方法は、間隔サイズ値（Ｒ_ＬＰＳ）を使用して１つまたは複数のシンボルの算術復号を実行するように構成される。

本発明による実施形態は、シンボル値（例えば、バイナリ値）を有する複数のシンボルを復号するための方法を作成するものであり、方法は、１つまたは複数の状態変数値（ｓ_ｉ ^ｋ）（これはインデックスｋによって示される所与のコンテキストモードに関連付けられる）に基づいて復号される１つまたは複数のシンボル値の算術復号の間隔サイズ値（Ｒ_ＬＰＳ）を導出することを含み、これは、以前に復号された複数のシンボル値の統計を表し（例えば、バイナリ値０と１のシーケンス）（例えば、異なる適合時定数で）；算術デコーダは、１つまたは複数の状態変数値から導出された（現在の）確率値に基づいて、また（現在の）コーディング間隔サイズ（Ｒ）に基づいて、確率テーブル（Ｐｒｏｂ ＴａｂＬＰＳ）（確率指数という観点で次元が可能な確率指数ｉの数値より小さい）を使用して間隔サイズ値（Ｒ_ＬＰＳ）を決定することを含み、確率テーブルは、複数の確率値のセット（例えば、０とμ－１の間の確率指数に対して）および（単一の）所与の（参照）コーディング間隔サイズの間隔サイズ（間隔サイズ値）を記述し、方法は、現在の確率値が複数の確率値のセットにない（例えば、μ以上の現在の確率値と関連付けられた確率指数である）場合、および／または現在のコーディング間隔サイズ（Ｒ）が、所与（参照）のコーディング間隔サイズとは異なる場合、間隔サイズ値（Ｒ_ＬＰＳ）を取得するよう所与（参照）の確率テーブル（Ｐｒｏｂ＿ＴａｂＬＰＳ）の要素をスケーリングすることを含み、また、方法は、間隔サイズ値（Ｒ_ＬＰＳ）を使用して１つまたは複数のシンボルの算術復号を実行することを含む。

本発明による実施形態は、コンピュータプログラムがコンピュータ上で実行されるときに、上記の実施形態のうちの１つによる方法を実行するためのコンピュータプログラムを作成する。

上記の方法は、上記の装置と同じ考慮事項に基づいている。しかし、この方法は、装置に関しても、本明細書に記載の特徴、機能、および詳細のいずれかによって任意選択で補足できることに留意されたい。これらの方法は、任意選択で、該特徴、機能、および詳細によって、個別および組み合わせの両方で、補足することができる。同じことがコンピュータプログラムにも当てはまる。

続いて、本発明による実施形態を、以下の付属の図面を参照して説明する。

本発明の実施形態による、データストリーム内の画像を予測的にコーディングするための装置のブロック概略図を示す。 本発明の実施形態による、デコーダのブロック概略図を示す。 再構成された信号と、予測残差および予測信号の結合との間の関係の概略図を示す。 本発明の実施形態による、算術エンコーダのブロック概略図を示す。 本発明の実施形態による、算術デコーダのブロック概略図を示す。 本発明の実施形態による、間隔サイズ情報を決定するための概念の概略図を示す。 発明の実施形態による、間隔サイズ情報を決定するための概念の概略図を示す。 発明の実施形態による、間隔サイズ情報を決定するための概念の概略図を示す。 発明の実施形態による、間隔サイズ情報を決定するための概念の概略図を示す。 本発明の実施形態による、間隔サイズ情報を決定するための概念の概略図を示す。 本発明の実施形態による、間隔サイズ情報を決定するための概念の概略図を示す。 発明の実施形態による、間隔サイズ情報を決定するための概念の概略図を示す。 発明の実施形態による、１つまたは複数の更新された状態変数を決定するための概念の概略図を示す。 発明の実施形態による、間隔サイズ値を決定するための概念の概略図を示す。 発明の実施形態による、間隔サイズ値を決定するための概念の概略図を示す。 発明の実施形態による、間隔サイズ値を決定するための概念の概略図を示す。 発明の実施形態による、間隔サイズ値を決定するための概念の概略図を示す。 発明の実施形態による、ビデオデコーダの概略図を示す。 発明の実施形態による、ビデオデコーダの概略図を示す。

１．図１によるエンコーダ
以下の図の説明は、コーディングフレームワークの例を形成するために、ビデオの画像をコーディングするためのブロックベースの予測コーデックのエンコーダ（図１）とデコーダ（図２）の説明から始まり、これに本発明の実施形態が組み込まれ得る。それぞれのエンコーダとデコーダは、図１から図３に関して説明されている。以下、本発明の概念の実施形態の説明は、そのような概念をそれぞれ図１および図２のエンコーダおよびデコーダに組み込むことができる方法に関する説明とともに提示されるが、後続の図４以降で説明される実施形態はまた、図１および図２のエンコーダおよびデコーダの基礎となるコーディングフレームワークに従って動作しないエンコーダおよびデコーダを形成するために使用され得る。

本発明による実施形態は、図１および図２に関して説明したように、ビデオエンコーダおよびビデオデコーダを含み得る。また、本明細書に開示される概念のいずれも、例えば、図１および図２を参照して説明されるように、エントロピーコーダ３４またはエントロピーデコーダ５０で使用され得る。

図１は、例示的に変換ベースの残差コーディングを使用して、画像１２をデータストリーム１４に予測的にコーディングするための装置を示す。装置またはエンコーダは、参照符号１０を使用して示されている。図２は、対応するデコーダ２０、すなわち、変換ベースの残差復号も使用してデータストリーム１４から画像１２’を予測的に復号するように構成される装置２０を示し、アポストロフィは、デコーダ２０によって再構成された画像１２’が、予測残差信号の量子化によって導入されたコーディング損失に関して、装置１０によって元々符号化されている画像１２から逸脱していることを示すために使用されている。図１および図２は、変換ベースの予測残差コーディングを例示的に使用するが、本出願の実施形態は、この種の予測残差コーディングに限定されない。これは、以下に概説されるように、図１および図２に関して説明される他の詳細にも当てはまる。

エンコーダ１０は、予測残差信号を空間からスペクトルへの変換にかけ、こうして得られた予測残差信号をデータストリーム１４に符号化するように構成される。同様に、デコーダ２０は、データストリーム１４からの予測残差信号を復号し、こうして得られた予測残差信号を、スペクトルから空間への変換にかけるように構成される。

内部的には、エンコーダ１０は、元の信号からの、すなわち画像１２からの予測信号２６の偏差を測定するために予測残差２４を生成する予測残差信号形成器２２を備えることができる。予測残差信号形成器２２は、例えば、元の信号から、すなわち画像１２から予測信号を減算する減算器であってもよい。次に、エンコーダ１０は、予測残差信号２４を空間対スペクトル変換にかけてスペクトル領域予測残差信号２４’を取得する変換器２８をさらに含み、これは次いで、同様にエンコーダ１０に含まれる量子化器３２によって量子化される。このように量子化された予測残差信号２４’’は、ビットストリーム１４にコード化される。この目的のために、エンコーダ１０は、任意選択として、データストリーム１４に変換および量子化され場合に予測残差信号をエントロピー符号化するエントロピーコーダ３４を備えることができる。予測信号２６は、データストリーム１４に符号化され、このストリームから復号可能な予測残差信号２４’に基づいて、エンコーダ１０の予測ステージ３６によって生成される。この目的のために、予測ステージ３６は、図１に示されるように、量子化損失を除いて信号２４’に対応するスペクトル領域予測残差信号２４’’’を得るように予測残差信号２４’’を逆量子化する逆量子化器３８を内部で含み得、その後に逆変換器４０が続き、これは後者の予測残差信号２４’’’を逆変換、すなわちスペクトルから空間への変換にかけ、量子化損失を除いて元の予測残差信号２４に対応する予測残差信号２４’’’’を取得する。次に、予測ステージ３６のコンバイナ４２は、加算などにより、予測信号２６と予測残差信号２４’’’とを再結合して、再構成された信号４６、すなわち元の信号１２の再構成を得る。再構成された信号４６は、信号１２’に対応し得る。次に、予測ステージ３６の予測モジュール４４は、例えば、空間予測、すなわち画像内予測、および／または時間予測、すなわち画像間予測を使用することによって、信号４６に基づいて予測信号２６を生成する。

２．図２によるデコーダ
同様に、図２に示されるように、デコーダ２０は、予測ステージ３６に対応し、それに対応する方法で相互接続されるコンポーネントから内部に構成されてもよい。特に、デコーダ２０のエントロピーデコーダ５０は、データストリームからの量子化されたスペクトル領域予測残差信号２４’’をエントロピー復号することができ、それにおいて、予測ステージ３６のモジュールに関して上述したように相互接続および協働される逆量子化器５２、逆変換器５４、コンバイナ５６および予測モジュール５８は、予測残差信号２４’’に基づいて再構成された信号を回復し、その結果、図２に示すように、コンバイナ５６の出力が再構成された信号、すなわち画像１２’をもたらすようにする。

上記で具体的に説明されていないが、エンコーダ１０が、例えば、いくつかのレートおよび歪みに関連する基準、つまりコーディングコストを最適化する方法などの、いくつかの最適化スキームに従って、例えば予測モード、動きパラメータなどを含むいくつかのコーディングパラメータを設定できることは容易に明らかである。例えば、エンコーダ１０およびデコーダ２０ならびに対応するモジュール４４、５８は、それぞれ、イントラコーディングモードおよびインターコーディングモードなどの異なる予測モードをサポートすることができる。エンコーダとデコーダがこれらの予測モードタイプを切り替える粒度は、それぞれ画像１２と１２’のコーディングセグメントまたはコーディングブロックへの細分に対応する。これらのコーディングセグメントの単位で、例えば、画像は、イントラコーディングされるブロックとインターコーディングされるブロックに細分され得る。以下でより詳細に概説するように、イントラコード化されたブロックは、それぞれのブロックの空間的な、すでにコード化／復号された近傍に基づいて予測される。いくつかのイントラコーディングモードが存在でき、方向または角度のイントラコーディングモードを含むそれぞれのイントラコーディングされたセグメントに対して選択され、これに従って、それぞれのイントラコーディングされたセグメントへ、それぞれの方向性イントラコーディングモードに特異的な特定の方向に沿って、近傍のサンプル値を外挿することにより、てそれぞれのセグメントが満たされる。イントラコーディングモードは、例えば、１つまたは複数のさらなるモードを含むこともでき、例えば、それぞれのイントラコーディングされたブロックの予測がそれぞれのイントラコーディングされたセグメント内のすべてのサンプルにＤＣ値を割り当てるＤＣコーディングモード、および／または、それぞれのブロックの予測が、隣接するサンプルに基づいて、２次元の線形関数によって定義される平面の駆動の傾きとオフセットを備える、それぞれのイントラコーディングブロックのサンプル位置にわたる２次元線形関数によって記述されるサンプル値の空間分布であると近似または決定される平面イントラコーディングモードが挙げられる。それと比較して、インターコーディングされたブロックは、例えば、時間的に予測され得る。インターコーディングされたブロックの場合、モーションベクトルはデータストリーム内で通知され得て、モーションベクトルは、以前にコーディング／復号された画像がサンプリングされる、画像１２が属するビデオの以前にコーディングされた画像の部分の空間変位を示し、それぞれのインターコーディングブロックの予測信号を取得するようにする。これは、量子化されたスペクトル領域予測残差信号２４’’を表すエントロピーコード化変換係数レベルなど、データストリーム１４に含まれる残差信号コーディングに加えて、データストリーム１４は、様々なブロックへのコーディングモード、インターコーディングされたセグメントのモーションパラメータなどの一部のブロックの予測パラメータ、および画像１２および１２’の各セグメントへの細分を制御およびシグナリングするためのパラメータなどの任意選択の追加パラメータを割り当てるためのコーディングモードパラメータを符号化した可能性があるということを意味する。デコーダ２０は、これらのパラメータを使用して、エンコーダが行ったのと同じ方法で画像を細分割し、同じ予測モードをセグメントに割り当て、同じ予測を実行して同じ予測信号を生成する。

３．図３による機能
図３は、再構成された信号、すなわち再構成された画像１２’と、一方でデータストリーム１４で信号が送られる予測残差信号２４’’’’と結合と、他方で予測信号２６との間の関係を示している。すでに上で示したように、結合は追加である場合がある。予測信号２６は、図３において、ハッチングを使用して例示的に示されるイントラコーディングブロック、およびハッチングなしで例示的に示されるインターコーディングブロックへの画像領域の細分として示される。細分は、画像領域を正方形ブロックまたは非正方形ブロックの行と列へと通常の細分をすること、または四分木細分割など画像１２をツリールートブロックから様々なサイズの複数のリーフブロックへとマルチツリー細分することなど、任意の細分にすることができ、それらの混合物が図３に示され、画像領域は最初にツリールートブロックの行および列に細分され、次に再帰的マルチツリー細分に従って１つ以上に細分化する。

再び、データストリーム１４は、いくつかのサポートされたイントラコーディングモードのうちの１つをそれぞれのイントラコーディングブロック８０に割り当てるイントラコーディングブロック８０のためにそこにコーディングイントラコーディングモードを有し得る。インターコーディングブロック８２の場合、データストリーム１４は、その中にコード化された１つまたは複数の運動パラメータを有することができる。一般的に言えば、インターコーディングブロック８２は、時間的にコード化されることに限定されない。あるいは、インターコーディングブロック８２は、現在の画像１２自体を超えて以前にコーディングされた部分から予測される任意のブロック、例えば、画像１２が属するビデオの以前にコーディングされた画像、または別のビューの画像、またはエンコーダとデコーダがそれぞれスケーラブルなエンコーダとデコーダである場合には、階層的に下位のレイヤであり得る。

図３の予測残差信号２４’’’’はまた、ブロック８４への画像領域の細分として示されている。これらのブロックは、コーディングブロック８０および８２と区別するために、変換ブロックと呼ばれる場合がある。事実上、図３は、エンコーダ１０およびデコーダ２０が、それぞれ、画像１２および画像１２’の２つの異なる細分割をブロックに、すなわち、１つはそれぞれコーディングブロック８０および８２に細分割し、別の細分割を変換ブロック８４に使用できることを示している。両方の細分割は同じであり得、すなわち、各コーディングブロック８０および８２は、同時に変換ブロック８４を形成し得るが、図３は、例えば、変換ブロック８４への細分割が、コーディングブロック８０、８２への細分割の拡張を形成する場合を示し、ブロック８０と８２の２つのブロック間の任意の境界が２つのブロック８４間の境界に重なるようにし、または代替的に言えば、各ブロック８０、８２は、変換ブロック８４の１つと一致するか、または変換ブロック８４のクラスターと一致するようにしている。しかし、細分割はまた、変換ブロック８４がブロック８０、８２の間のブロックの境界を交互に横切ることができるように、互いに独立して決定または選択され得る。したがって、変換ブロック８４への細分割に関する限り、ブロック８０、８２への細分割に関して提起されたものと同様のステートメントが当てはまる、すなわち、ブロック８４は、画像領域のブロックへの通常の細分の結果、画像領域の再帰的なマルチツリー細分、またはそれらの組み合わせ、またはその他の種類のブロックの結果である可能性がある（行と列への配置の有無にかかわらず）。余談だが、ブロック８０、８２、８４は２次、長方形、その他の形状に限定されないことに留意されたい。

図３はさらに、予測信号２６と予測残差信号２４’’’’の結合が直接再構成された信号１２’をもたらすことを示している。しかし、代替実施形態によれば、２つ以上の予測信号２６を予測残差信号２４’’’と結合して、結果として画像１２’を得ることができることに留意されたい。

図３において、変換ブロック８４は、以下の意味を有するものとする。変換器２８および逆変換器５４は、これらの変換ブロック８４のユニットでそれらの変換を実行する。例えば、多くのコーデックは、すべての変換ブロック８４にある種のＤＳＴまたはＤＣＴを使用する。いくつかのコーデックは、変換をスキップすることを可能にするので、いくつかの変換ブロック８４について、予測残差信号は、空間領域で直接コード化される。しかし、以下に説明する実施形態によれば、エンコーダ１０およびデコーダ２０は、それらがいくつかの変換をサポートするように構成される。例えば、エンコーダ１０およびデコーダ２０によってサポートされる変換は、以下を含むことができる。
ｏＤＣＴ－ＩＩ（またはＤＣＴ－ＩＩＩ）、ＤＣＴは離散コサイン変換の略
ｏＤＳＴ－ＩＶ、ＤＳＴはＤｉｓｃｒｅｔｅ Ｓｉｎｅ Ｔｒａｎｓｆｏｒｍの略
ｏＤＣＴ－ＩＶ
ｏＤＳＴ－ＶＩＩ
ｏアイデンティティ変換（ＩＴ）

当然、変換器２８はこれらの変換のすべての順方向変換バージョンをサポートするが、デコーダ２０または逆変換器５４はその対応する逆方向または逆バージョンをサポートする。
ｏ逆ＤＣＴ－ＩＩ（または逆ＤＣＴ－ＩＩＩ）
ｏ逆ＤＳＴ－ＩＶ
ｏ逆ＤＣＴ－ＩＶ
ｏ逆ＤＳＴ－ＶＩＩ
ｏアイデンティティ変換（ＩＴ）

以下の説明は、エンコーダ１０およびデコーダ２０によってサポートされ得る変換についてのさらなる詳細を提供する。いずれの場合でも、サポートされる変換のセットは、１つのスペクトルから空間への変換や空間からスペクトルへの変換など、１つの変換のみを含む場合があることに留意されたい。

すでに上で概説したように、図１から図３は、本出願によるエンコーダおよびデコーダの特定の例を形成するために、以下でさらに説明する本発明の概念を実施できる例として提示されている。これまでのところ、図１および図２のエンコーダおよびデコーダは、それぞれ、本明細書で以下に説明するエンコーダおよびデコーダの可能な実装を表すことができる。ただし、図１と図２は単なる例である。しかし、本出願の実施形態によるエンコーダは、画像１２のブロックベースの符号化を実行することができ、以下でより詳細に概説される概念を使用し、例えばビデオエンコーダはないが、依然画像エンコーダである点、相互予測をサポートしていない点、またはブロック８０への細分割が図３に例示されているのとは異なる方法で実行されるという点で、図１のエンコーダとは異なる。同様に、本出願の実施形態によるデコーダは、データストリーム１４からの画像１２’のブロックベースの復号を実行することができ、以下でより詳細に概説される概念を使用しているが、例えばビデオデコーダはないが、依然画像デコーダである点、相互予測をサポートしていない点、またはブロックへの画像１２’の細分割が図３に記載されているのとは異なる点、および／または変換ドメインではなく、空間ドメインのデータストリーム１４から予測残差を導出する点、などで、図２のデコーダ２０とは異なり得る。

４．図４による算術エンコーダ
図４は、本発明の一実施形態による、算術エンコーダのブロック概略図を示す。
図４による算術エンコーダ４００は、例えば、ビデオエンコーダで使用することができる。しかし、任意選択で、算術エンコーダ４００は、オーディオエンコーダ、画像エンコーダ、ニューラルネットワークの係数を符号化するためのエンコーダなどでも使用することができる。

算術エンコーダ４００は、符号化されるシンボル４１０を受信するように構成され、符号化されるシンボル４１０は、シンボル値によって表すことができる。さらに、エンコーダ４００は、典型的には、コンテキスト情報４１２も受信し、これは、例えば、どのタイプの情報が、符号化されるシンボル４１０によって表されるかを記述し得る。例えば、コンテキスト情報４１２は、例えば、符号化されるシンボル４１０がどのタイプのサイド情報を記述するか、またはシンボル４１０がどのタイプの変換係数を符号化するかを記述するコンテキストインデックスｋによって表すことができる。

さらに、算術エンコーダ４００は、符号化されるシンボル４１０を表す、または符号化されるシンボル４１０のシーケンスを表すビットストリーム４２０を提供するように構成される。

算術エンコーダ４００は、算術符号化コアまたは算術エンコーダコア４３０を備え、これは、符号化されるシンボル４１０を受け取り、それに基づいて、ビットストリーム４２０を提供する。算術符号化コアまたは算術エンコーダコア４３０は、通常、間隔サイズ情報を受信し、これは、例えば、シンボル（例えば、最も可能性の低いシンボル）がマップされるサブインターバル（全コーディング間隔のうち）のサイズを表すことができる。さらに、算術符号化コアまたは算術エンコーダコアはまた、現在のコーディング間隔サイズ（例えば、コーディング間隔の合計サイズ）を記述するコーディング間隔サイズ情報４３４を提供する。コーディング間隔サイズ４３４は、符号化されるシンボル４１０に応じて（または、より正確には、符号化されるシンボル４１０のシーケンスに応じて）、時間とともに変化し得ることに留意されたい。

コーディング間隔サイズは、例えば、算術符号化の過程で実行される再スケーリング操作のために変化する可能性がある。例えば、算術符号化コアは、例えば、Ｈｉｇｈ Ｅｆｆｉｃｉｅｎｃｙ Ｖｉｄｅｏ Ｃｏｄｉｎｇ（ＨＥＶＣ）の規格（Ｈ．２６５）に記載されている機能を実行することができる。

算術エンコーダ４００はまた、コーディング間隔サイズ決定またはコーディング間隔サイズ決定器４４０を備える。コーディング間隔サイズ決定４４０は、符号化されるシンボル４１０、または少なくとも１つまたは複数の以前に符号化されたシンボルを受信し、好ましくは（必ずしもではないが）コンテキスト情報４１２も受信する。さらに、間隔サイズ決定４４０は、コーディング間隔サイズ情報４３４を受信する。間隔サイズ決定４４０は、コーディング間隔サイズ情報に基づいて、符号化されるシンボル４１０（または少なくとも１つまたは複数の以前に符号化されたシンボル）、および任意選択で、算術符号化コア４３０によって使用される間隔サイズ情報４３２のコンテキスト情報４１２を提供する。

図４による概念の機能に関して、間隔サイズ決定４４０は、間隔サイズ情報４３２を更新するのに役立つことに留意されたい（継続的に、例えば、符号化される新しいシンボルごとに）。この更新では、以前に符号化されたシンボルの統計が考慮される。さらに、算術符号化４３０によって提供されるコーディング間隔サイズ情報４３４も考慮される。なぜなら、間隔サイズ情報４３２は、好ましくは、コーディング間隔サイズ情報４３４との適切な関係で提供されるべきものであるからである。この文脈において、コーディング間隔サイズ情報４３４は、例えば、（合計）コーディング間隔の現在のサイズを表すことができる（これは、時々発生するコーディング間隔の再正規化によって引き起こされ得る）が、一方で間隔サイズ情報４３２は、例えば、特定のシンボル（例えば、最も可能性の低いシンボル）に関連付けられた全体の（合計）コーディング間隔内の部分のサイズを記述し得る。したがって、間隔サイズ情報４３４は、コーディング間隔の合計サイズを表しながら、間隔サイズ情報４３４は、特定のシンボルに関連付けられているコーディング間隔の一部のサイズを表しているため、間隔サイズ情報は、通常、コーディング間隔サイズ情報４３４よりも小さい。その結果、間隔サイズ情報４３２は、通常、コーディング間隔サイズ情報４３４に合わせてスケーリングする（スケーリングは、コーディングが非常に非効率的である状況を回避するために、任意選択でいくらか非線形の振る舞いを含み得る）。

さらに結論として、適切な間隔サイズ情報４３２を決定することにより、コーディング間隔の合計サイズ（コーディング間隔サイズ情報４３４によって表される）および以前に符号化されたシンボル（ならびにコンテキスト）の統計を考慮して、算術符号化は効率的な方法で実行され、以前に符号化されたシンボルの統計を考慮することは、コーディング効率を改善するのに役立つ。

しかし、図４による算術エンコーダ４００は、本明細書に開示されるような信号エンコーダのいずれか（例えば、ビデオエンコーダ）で使用できることに留意されたい。さらに、図４による算術エンコーダ４００は、本明細書に記載の特徴、機能、および詳細のいずれかによって任意選択で補足できることに留意されたい。特に、間隔サイズ決定４４０は、本明細書に開示された概念のいずれかを、個別に、および組み合わせて使用することができる。

図４による算術エンコーダ４００を結論付けることは、任意選択で、個別におよび組み合わせて、本明細書に開示される特徴、機能および詳細のいずれかによって補足され得る。

５．図５による算術デコーダ
図５は、本発明の実施形態による、算術デコーダ５００のブロック概略図を示す。算術デコーダ５００は、ビットストリーム５１０（ビットストリーム４２０に対応し得る）を受信し、それに基づいて、復号されたシンボル５２０（または復号されたシンボル５２０のシーケンス）を提供するように構成される。典型的には、復号されたシンボル５２０は、符号化されるシンボル４１０に対応し得る。典型的には、算術エンコーダ４００および算術デコーダ５００は、一緒にされると、ロスレス符号化および復号を実行し得、その結果、算術エンコーダ４００によって符号化されたシンボル４１０は、算術デコーダ５００によって復号されたときに「完全な」再構成を可能にするビットストリーム４２０を提供し、復号されたシンボル５２０が符号化されたシンボル４１０に対応するようにする。

算術デコーダ５００は、ビットストリームを受信し、それに基づいて、復号されたシンボル５２０を提供する、算術復号コアまたは算術デコーダコア５３０を備える。算術復号コア５３０は、典型的には、コーディング間隔サイズ情報４３４に実質的に対応し得るコーディング間隔サイズ情報５３２を提供し、間隔サイズ情報４３２に対応し得る間隔サイズ情報５３４を受信する。算術デコーダ５００はまた、コーディング間隔サイズ情報５３２に基づいて、また、１つまたは複数の復号されたシンボル５２０に基づいて、算術復号コア５３０によって使用される、間隔サイズ情報５３４を提供するように構成された、コーディング間隔サイズ決定またはコーディング間隔サイズ決定器５４０を備える。さらに、コーディング間隔サイズ決定５４０は、任意選択で、コンテキスト情報５５０を使用することができ、これは、現在考慮されている復号されたシンボル５２０によって表される情報のタイプを記述し得る。したがって、コーディング間隔サイズ決定５４０は、複数の異なる「コンテキスト」、すなわち、複数の異なるタイプの復号された情報（または復号される異なるタイプの情報）の間隔サイズ情報５３４を決定することができる。

算術復号コア５３０は、例えば、全コーディング間隔（そのサイズはコーディング間隔サイズ情報によって記述される）のうち、ビットストリーム５１０によって表される値がどのサブ間隔にあるかを決定し、その結果、どのシンボルがビットストリームで表されているか決定することができる。総コーディング間隔のサブ間隔のサイズは、例えば、間隔サイズ情報５３４によって記述される。例えば、間隔サイズ情報５３４は、特定のシンボル（例えば、最も可能性の低いシンボル）に関連付けられた合計コーディング間隔のサブインターバルのサイズを記述し得る。さらに、再正規化のために、コーディング間隔サイズ（例えば、総コーディング間隔のサイズ）が時々（または復号されたシンボルごとにさえ）変化する可能性があることに留意されたい。

結論として、算術復号５００は、ビットストリーム５１０に基づいて復号されたシンボル５２０を提供するために使用され、以前に復号されたシンボルの履歴（またはより正確には、以前に復号されたシンボルの統計）は、復号されるシンボルに関連付けられた間隔サイズを（動的に）調整するために使用される（調整された間隔サイズは、間隔サイズ情報５３４によって記述される）。さらに、間隔サイズ決定５４０は、例えば、間隔サイズ決定４４０と実質的に同一であり得ることに留意されたい。また、間隔サイズ決定５４０は、本明細書に開示される機能のいずれかを含み得ることに留意されたい。したがって、間隔サイズを決定するための概念のいずれかを、間隔サイズ決定５４０で使用することができる。

本明細書に記載の算術デコーダ５００は、本明細書に記載のデコーダ（例えば、オーディオデコーダまたはビデオデコーダ）のいずれかで使用できることに留意されたい。しかし、算術デコーダ５００はまた、画像またはニューラルネットワークの係数の復号のために使用され得る。

一般的に言えば、本明細書に記載の算術デコーダ５００は、任意選択で、個別におよび組み合わせて、本明細書に開示される特徴、機能、および詳細のいずれかによって補足され得る。

６．図６による間隔サイズ情報の決定の概念
図６は、間隔サイズ情報を決定するための概念の概略図を示し、これは、例えば、図４による算術エンコーダ４００または図５による算術デコーダ５００で使用することができる。間隔サイズ決定の形で、または間隔サイズ決定器の形で実装され得る概念６００は、例えば、間隔サイズ決定または間隔サイズ決定器４４０を実現するために使用され得、および／または間隔サイズ決定または間隔サイズ決定器５４０を実現するために使用される。

間隔サイズ決定６００は、例えば、１つまたは複数のシンボル値６１０を受け取ることができ、これは、符号化されるシンボル４１０に対応すしても、以前に符号化されたシンボルに対応しても、または１つまたは複数の以前に復号されたシンボル５２０に対応してもよい。さらに、間隔サイズ決定６００は、任意選択で、コンテキスト情報６１２を受信することができ、これは、例えば、コンテキストモデルインデックスｋの形をとることができる。さらに、間隔サイズ決定６００は、間隔サイズ情報６２０を提供することができ、これは、例えば、間隔サイズ情報４３２に対応することができ、または間隔サイズ情報５３４に対応することができる。

間隔サイズ決定は、シンボル値６１０を考慮し、任意選択でコンテキスト情報６１２を考慮して、１つまたは複数の以前に決定された状態変数６４４に基づいて、１つまたは複数の更新された状態変数６４２を提供する状態変数更新６４０を含む。状態変数更新６４０はまた、１つまたは複数の他のパラメータを考慮することができ、これらは、例えば、静的であり得るか、または、例えば、コンテキスト情報に依存してそれぞれのコンテキストに適合され得る。例えば、状態変数更新６４０は、１つまたは複数の重み付け係数、すなわち、

および／または

を考慮することができる。状態変数更新６４０は、任意選択で、「オフセット」、例えば、ｚ、およびルックアップテーブル、例えば、Ａも考慮することができる。さらに、状態変数更新６４０は、任意選択で、状態変数の初期化を実行する必要がある情報信号に応答して、初期値に初期化され得る。状態変数の初期化の場合、以前に決定された状態変数値６４４は無視され得、「更新された」状態変数６４２は、例えば、事前に決定され得る初期値に設定され得る。

さらに、間隔サイズ決定６００は、更新された状態変数（または状態変数値）６２０に基づいて間隔サイズ情報６２０を決定する間隔サイズ決定コアを備える。さらに、間隔サイズ決定コア６５０は、例えば、コーディング間隔サイズ情報６５２を考慮することができ、これは、例えば、コーディング間隔サイズ情報４３２またはコーディング間隔サイズ情報５３２に対応し得る。

したがって、間隔サイズ決定コア６５０は、コーディング間隔の合計サイズを説明するコーディング間隔サイズ情報６５２に基づいて、また以前に符号化された、または以前に復号されたシンボルの統計に関する情報に基づいて、特定のシンボルに関連付けられたサブインターバルのサイズを説明する間隔サイズ情報を提供することができ、それは１つまたは複数の更新された状態変数６４２によって表される。

しかし、間隔サイズ決定６００は、本明細書で説明される算術エンコーダおよび算術デコーダで使用され得ることに留意されたい。さらに、間隔サイズ決定６００は、本明細書に開示される特徴、機能、および詳細のいずれかによって補足され得る。特に、状態変数の更新は、本明細書に開示された概念のいずれかを使用することができる。さらに、間隔サイズ決定コアはまた、本明細書に開示される概念のいずれかを使用することができる。

状態変数の更新について本明細書で説明されている概念のいずれかを、本明細書で開示されている間隔サイズ決定コアの概念のいずれかと任意選択に結合することができることに留意されたい。本明細書に開示される特徴、機能、および詳細のいずれかは、任意選択で、個別に、および組み合わせて、概念６００に導入することができる。１つまたは複数の更新された状態変数６４２に基づく間隔サイズ情報６２０の決定に関して開示された特徴、機能、および詳細のいずれも、状態変数の更新に関して説明する特徴、機能、および詳細のいずれかと独立して使用できることに留意されたい。

７．図７による間隔サイズ決定の概念
図７は、間隔サイズ決定概念７００の概略図を示す。特に、図７は、「間隔サイズ決定コア」の機能を利用できる概念を示している。言い換えれば、図７による概念７００は、更新された状態変数に基づいて、またコーディング間隔サイズ情報に基づいて、間隔サイズ情報を提供するのに適している。しかし、図７による概念７００は、間隔サイズ決定または間隔サイズ決定器で実装され得る。

「間隔サイズ決定コア」と見なすことができる間隔サイズ決定７００は、更新された状態変数７１０を受け取り、これは、例えば、更新された状態変数６４２に対応し得る。さらに、間隔サイズ決定７００は、コーディング間隔サイズ情報７１２を受信し、これは、例えば、コーディング間隔サイズ情報６５２に対応し得る。任意選択として、間隔サイズ決定７００の機能は、コンテキストに応じて調整され得るので、間隔サイズ決定７００はまた、コンテキスト情報を使用する。例えば、コンテキスト情報は、コンテキストモデルインデックスｋの形をとることができる。したがって、間隔サイズ決定７００で使用される特定の機能またはパラメータは、コンテキストモデルインデックスｋによって表されるように、実際のコンテキストに依存して適合され得る。

間隔サイズ決定７００は、間隔サイズ情報７２０を提供し、これは、間隔サイズ情報６２０に対応し得る。
したがって、間隔サイズ決定７００は、例えば、図６に記載された間隔サイズ決定コア６５０の代わりになり得る。

以下では、間隔サイズ決定コア７００のいくつかの詳細について説明する。
間隔サイズ決定コア７００は、第１の処理パス７３０および第２の処理パス７５０を含み、これらは代替案と見なされ得ることに留意されたい。第１の処理パス７３０は、（任意選択の）スケーリング／丸め７３２を含み、第１の更新された状態変数（例えば、

）がスケーリングおよび／または丸められる。例えば、第１の更新された状態変数（値）のスケーリングにスケーリング係数

を使用できる。例えば、スケーリングは、スケーリング係数との乗算であり得る。例えば、丸めは、隣の整数の値へ切り捨て、スケーリングの結果以下にする場合がある。同様に、第１の処理パス７３０は、第２の（任意選択の）スケーリング／丸め７３４を含み得、これは、例えば、それぞれのスケーリング係数（例えば、

）を有する第２の更新された状態変数（例えば、

）のスケーリングを含み得、それはまた、スケーリングの結果以下へと、隣り合う整数の値へ切り捨てることを含む場合もある。したがって、第１のスケーリングされ丸められた状態変数７３３および第２のスケーリングされ丸められた状態変数７３５を取得することができる。さらに、第１の処理パス７３０は、第１のスケーリングおよび／または丸められた更新状態変数７３３を受け取り、さらに量子化されたコーディング間隔サイズ情報７６２を受け取る、第１のルックアップテーブルベースのマッピング７３６を含み得る。例えば、第１のルックアップテーブルベースのマッピング７３６は、２次元ルックアップテーブルを使用して、第１の間隔サイズ寄与７３７を取得することができる。同様に、第１の信号処理パス７３０は、第２のルックアップテーブルベースのマッピング７３８を含み得、これは、第２のスケーリングおよび／または丸められた更新状態変数７３５および量子化されたコーディング間隔サイズ情報７６２を受け取れ、それに基づいて、第２の間隔サイズの寄与７３９を提供する。

例えば、第１のルックアップテーブルベースのマッピング７３６は、２次元ルックアップテーブルを使用することができ、第１のルックアップテーブルインデックスは、スケーリングおよび／または丸められた第１の更新された状態変数７３３によって決定され得、第２のルックアップテーブルインデックスは、量子化されたコーディング間隔サイズ情報７６２によって決定され得る。例えば、第１のスケーリングおよび／または丸められた更新状態変数７３３は、特定の範囲内（例えば、０から最大値、または１から最大値、または第１のテーブルインデックスとして許容可能な範囲内）の整数の値をとることができる。同様に、量子化された間隔サイズ情報７６２は、第２のテーブルインデックスとして機能することができる整数値の形式をとることができる。例えば、量子化されたコーディング間隔サイズ情報７６２は、０から最大値の間、または１から最大値の間の範囲（または第２のテーブルインデックスとして機能することができる任意の値の範囲内）の整数値の形式をとることができる。言い換えれば、第１のスケーリングおよび／または丸められた更新状態変数７３３および量子化されたコーディング間隔サイズ情報７６２の両方が、ルックアップテーブルベースのマッピング７３６で使用されるルックアップテーブルの要素を選択するためのテーブルインデックスとして使用される。したがって、使用されるルックアップテーブルのエントリは、第１の間隔サイズ寄与７３７として提供される。

しかし、第２のルックアップテーブルベースのマッピング７３８は、同じ方法で実行することができ、スケーリングおよび／または丸められた第２の更新された状態変数７３５および量子化されたコーディング間隔サイズ情報７６２が、第２のルックアップテーブルベースのマッピング７３８で使用されるルックアップテーブルのエントリの選択のため、２つのインデックス（例えば、ｉおよびｊ）として使用される。したがって、第２の間隔サイズ寄与７３９が得られる。

第１の間隔サイズ寄与７３７および第２の間隔サイズ寄与７３９は、結合７４０で結合され得、それにより、結合間隔サイズ寄与７４２が得られる。結合間隔サイズ寄与７４２は、間隔サイズ情報７２０として直接機能し得るか、または間隔サイズ情報７２０は、後処理（例えば、固定スケーリング、または丸めなど）を使用して結合間隔サイズ寄与７４２から導出され得る。

結論として、第１の処理パス７３０を使用する場合、間隔サイズ情報７２０は、２つ以上のルックアップテーブルベースのマッピング７３６、７３８の結果を結合することによって取得することができ、使用されるルックアップテーブルのそれぞれのエントリは、それぞれの更新された状態変数に基づいて、またコーディング間隔サイズ情報に基づいて、決定される。したがって、間隔サイズ情報７２０は、非常に効率的な方法で取得することができる。

しかし、あるいは、第２の信号処理パス７５０に示されるような処理を実行することができる。第２の信号処理パスによって実行される処理は、精度がわずかに低下するという代償を払って、かなり計算効率が高くなる。例えば、第２の信号処理パス７５０は、第１の更新された状態変数および第２の更新された状態変数（および任意選択で追加の更新された状態変数）が結合され、それによって結合された更新された状態変数７５１ａを取得する結合７５１を含む。第２の処理パス７５０はまた、任意選択のスケーリング／丸め７５２を含み、これは、例えば、スケーリング／丸め７３２、７３４に対応し得る。したがって、スケーリング／丸め７５０は、ルックアップテーブルベースのマッピング７５６内の要素を選択するために使用される、スケーリングおよび／または丸められた結合された更新された状態変数７３３を提供する。ルックアップテーブルベースのマッピング７５６は、好ましくは２次元マッピングであり、ルックアップテーブルの第１のインデックスは、結合された更新された状態変数７５１ａまたはそのスケーリングおよび／または丸められたバージョン７５３によって決定され、２次元ルックアップテーブルの第２のインデックスは、量子化されたコーディング間隔サイズ情報７６２によって決定される。したがって、ルックアップテーブルベースのマッピング７５６は、間隔サイズ寄与７５７を提供し、これは、間隔サイズ情報７５２として使用され得るか、または任意の後処理（例えば、スケーリング）によって間隔サイズ情報７２０から導出され得る。

結論として、間隔サイズ決定コア７００は、更新された状態変数７１０に基づいて、コーディング間隔サイズ情報７１２を考慮して、間隔サイズ情報７２０を取得するように構成される。ルックアップテーブルベースのマッピングは、間隔サイズ情報７２０を導出するために使用される２つ以上の間隔サイズ寄与７３７、７３９を決定するために、第１の信号処理パス７２０で使用される。ルックアップテーブルベースのマッピング７５６は、代替の第２の信号処理パス７５０で使用されて、間隔サイズ寄与７５７または間隔サイズ情報７２０を決定する。更新された状態変数とコーディング間隔サイズ情報７１２の両方を考慮してルックアップテーブルのインデックスを決定するルックアップテーブルベースのマッピングを使用することによって、特に効率的な計算を達成することができ、乗算の演算を省くことが可能になる。

図７による間隔サイズ決定コア７００は、本明細書に記載の算術エンコーダおよび算術デコーダのいずれかで使用できることに留意されたい。さらに、間隔サイズ決定コア７００は、任意選択で、本明細書に開示される特徴、機能、および詳細のいずれかによって、個別におよび組み合わせて、補足することができる。

８．図８による間隔サイズ決定コア
図８は、本発明の実施形態による、間隔サイズ決定コア８００のブロック概略図を示す。図８による間隔サイズ決定コア８００は、本明細書に開示されるオーディオエンコーダおよびオーディオデコーダのいずれかにおいて使用され得る。

間隔サイズ決定コア８００は、更新された状態変数８１０と、コーディング間隔サイズ情報８１２も受け取る。更新された状態変数８１０は、例えば、更新された状態変数７１０または更新された状態変数６４２に対応し得る。コーディング間隔サイズ情報８１２は、例えば、コーディング間隔サイズ情報７１２またはコーディング間隔サイズ情報６５２またはコーディング間隔サイズ情報５３２またはコーディング間隔サイズ情報４３４に対応し得る。さらに、間隔サイズ決定コア８００は、間隔サイズ情報８２０を提供し、これは、間隔サイズ情報７２０または間隔サイズ情報６２０または間隔サイズ情報５３４または間隔サイズ情報４３２に対応し得る。

間隔サイズ決定コア８００は、例えば、確率値８３２の決定８３０を含み得る。確率値８３２は、例えば、１つまたは複数の更新された状態変数８１０に基づいて取得され得、例えば、符号化されるシンボル（例えば、「０」または「１」）の確率を記述し得る。間隔サイズ決定コア８３０は、可能性の低いシンボル（または可能性の最も低いシンボル）の確率の決定８４０をさらに含み、これは、可能性の低いシンボルまたは最も可能性の低いシンボルの確率を説明する確率値８４２を提供し得る。間隔サイズ決定コア８００はまた、量子化８５０を含み、これは、確率値８４２を量子化して、量子化された確率値８５２を取得する。さらに、間隔サイズ決定コア８００はまた、量子化されたコーディング間隔サイズ情報８６２を得るために、コーディング間隔サイズ情報を量子化する量子化８６０を備える。間隔サイズ決定コア８００はまた、量子化確率値８５２および量子化コーディング間隔サイズ情報８６２を受け取り、量子化確率値８５２および量子化コーディング間隔サイズ情報８６２の両方を間隔サイズ情報８２０にマッピングするマッピング８７０を備える。

以下の間に、間隔サイズ決定コア８００の機能に関するいくつかの詳細が説明される。
確率値８３２の決定８３０は、例えば、第１の信号処理パス８８０または第２の信号処理パス８９０を含み得る。信号処理パス８８０、８９０が代替案として考慮され得ることに留意されたい。第１の信号処理パス８８０は、例えば、ルックアップテーブルを使用して、第１の更新された状態変数８１０を第１の確率値８８３にマッピングする第１のマッピング８８２を備える。第１の信号処理パス８８０はまた、第２のマッピング８８４を含み、これは、例えば、ルックアップテーブルを使用して、第２の更新された状態変数８１０を第２の確率値８８５にマッピングする。第１の信号処理パス８８０はまた、例えば、異なるスケーリングが第１の確率値８８３および第２の確率値８８５（および、任意選択で、量子化を使用することができる）に適用され得る線形の結合を使用するなどして、第１の確率値８８３および第２の確率値８８５を結合するように構成され得る結合８８６を含む。したがって、結合８８６は、確率値８３２を提供する。

あるいは、第２の信号処理パス８９０を使用することができる。第２の信号処理パス８９０は、結合８９２を含み、これは、２つ以上の更新された状態変数８１０を受け取り、それに基づいて、結合された更新された状態変数８９３を（例えば、線形結合を使用して）提供する。さらに、第２の信号処理パス８９０は、例えば、ルックアップテーブルを使用して、結合された更新された状態変数８９３を確率値８３２にマッピングするマッピング８９４を備える。

したがって、第１の信号処理パス８８０を使用するか、または第２の信号処理パス８９０を使用して、確率値８３２を取得することが可能であり、これは、２つの異なる代替案と見なすことができる。第１の信号処理パスは、２つのマッピング８８２、８８４があり、精度もわずかに向上しているため、複雑さがわずかに増加する。対照的に、第２の信号処理パス８９０は、単一のマッピングのみを含み、したがって、わずかに精度が低下するという犠牲を払い、わずかに複雑さが減少する。

可能性の低いシンボルの確率の決定８５０において、可能性の低いシンボルの確率は、例えば、確率値８３２および確率値の補数（１から確率値を引いたもの）からより小さな値を選択することによって決定され得る。したがって、可能性の低いシンボルの確率を表す確率値８４２が得られる。この確率値８４２は、例えば、量子化関数

（．）または

（．）を使用して、量子化８５０で量子化される。したがって、量子化された確率値または確率指数ｉ ８５２が取得され、マッピング８７０で使用される。

コーディング間隔サイズ情報８１２の量子化８６０は、例えば、量子化されたコーディング間隔サイズ値８６２または量子化されたコーディング間隔サイズ指数ｊを提供することができる。しかし、場合によっては、両方が量子化されたコーディング間隔サイズ値Ｑ_ｒ（Ｒ）であり、コーディング間隔サイズ指数ｊが取得され得、これは、例えば、両方ともマッピング８６０で使用され得る。マッピング８６０は、例えば、本明細書に記載のルックアップテーブルＲａｎｇｅＴａｂＬＰＳに基づく、および／または本明細書に記載のルックアップテーブルＢａｓｅＴａｂＬＰＳに基づくことができる、および／または本明細書に記載のルックアップテーブルＰｒｏｂＴａｂＬＰＳを使用することができるマッピングメカニズムを使用することができる。任意選択で、本明細書で説明されるスケーリング関数Ｓｃａｌ（．）もまた、マッピング８７０で使用され得る。

言い換えれば、量子化された確率値または確率指数８５２に基づいて、および量子化されたコーディング間隔サイズ８６２および／またはコーディング間隔サイズ指数ｊに基づいて、間隔サイズ情報８２０を導出するために使用することができるいくつかの異なるマッピングがあり得る。

追加の注意として、量子化８５０は、例えば、確率値８４２（あるいは、決定８４０が省略される場合、確率値８３２）を整数値にマッピングすることができることに留意されたい。あるいは、量子化８５０は、値８４２（あるいは、決定８４０が任意選択で省略される場合、値８３２）を、確率値８３２または確率値８４２よりも低い数値分解能を有する値にマッピングすることができる。しかし、量子化された確率値８５２は、確率指数（例えば、ｉ）の形式、すなわち整数の表現の形式をとることが好ましく、それはルックアップテーブル（例えば、ＲａｎｇｅＴａｂＬＰＳ）のエントリを指定するためのテーブルインデックスとして使用できる。

量子化８６０は、異なる結果をもたらす可能性がある。コーディング間隔サイズ情報８１２は、例えば、コーディング間隔サイズ情報８１２よりも低い解像度を含む量子化されたコーディング間隔サイズ情報８６２に量子化され得る。言い換えれば、コーディング間隔サイズ情報８１２の値の間隔は、量子化されたコーディング間隔サイズ情報８６２の個々の量子化された値にマッピングされ得、量子化は、例えば、線形または非線形であり得る。あるいは、またはさらに、コーディング間隔サイズ情報は、コーディング間隔サイズインデックスｊ、すなわち、ルックアップテーブルのエントリを選択するためのテーブルインデックスとして直接使用することができる整数値の連続範囲にマッピングされ得る。しかし、場合によっては、異なる値に量子化された量子化されたコーディング間隔サイズ情報と、異なる指数ｊ（すなわち、後続の整数値）に量子化された量子化されたコーディング間隔サイズ情報の両方が使用され得ることに留意されたい。
上記のように、マッピング８７０は、本明細書で説明される異なる概念を使用して作成することができる。

結論として、間隔サイズ決定コア８００は、本明細書に記載の算術エンコーダおよび算術デコーダのいずれかで使用することができる。さらに、間隔サイズ決定コア８００は、任意選択で、本明細書に開示される特徴、機能、および詳細のいずれかによって、個別におよび組み合わせて、補足することができる。

９．図９による間隔サイズ決定コア
図９は、本明細書に開示される算術エンコーダおよび算術デコーダのいずれかで使用可能な間隔サイズ決定コア９００のブロック概略図を示す。

間隔サイズ決定コア９００は、状態変数値９１０を受け取り、間隔サイズ情報９２０を提供するように構成される。一般的に言えば、間隔サイズ決定コア９００は、複数の状態変数値９１０に基づいて、符号化される１つまたは複数のシンボル値の算術符号化（または復号される１つまたは複数のシンボル値の算術復号）の間隔サイズ情報９２０を導出するように構成され、これは、異なる適合時定数で以前に符号化された複数のシンボル値の統計を表す。間隔サイズ決定コア９００は、任意選択の第１のスケーリングおよび／または丸め９３０を含み、第１の状態変数（更新された状態変数であり得る）がスケーリングおよび／または丸められる。間隔サイズ決定コア９００はまた、任意選択の第２のスケーリングおよび／または丸め９３４を含み、第２の状態変数がスケーリングおよび／または丸められる。したがって、任意選択の第１のスケーリングおよび／または丸めは、第１のスケーリングおよび／または丸められた状態変数９３２を提供し、任意選択の第２のスケーリングおよび／または丸め９３４は、第２のスケーリングおよび／または丸められた状態変数９３４を提供する。

間隔サイズ決定コア９００はまた、ルックアップテーブルを使用する第１のマッピング９４０を備える。第１のマッピング９４０は、ルックアップテーブル（例えば、ルックアップテーブルＬＵＴ１、または複数の異なる値Ｒに対するＲ・ＬＵＴ１を定義する２次元ルックアップテーブル）を使用して、第１の状態変数、または第１の状態変数のスケーリングおよび／または丸められたバージョン９３２をマッピングする。したがって、第１の確率値９４２は、第１のマッピング９４０によって得られる。間隔サイズ決定コア９００はまた、第２のマッピング９５０を備え、これはルックアップテーブル（例えば、ルックアップテーブルＬＵＴ１、または複数の異なる値Ｒに対するＲ・ＬＵＴ１を定義する２次元ルックアップテーブルを使用）を使用して、第２の状態変数、またはそのスケーリングおよび／または丸められたバージョン９３４をマッピングする。したがって、第２の確率値９５２は、第２の状態変数値に基づいて、またはそのスケーリングおよび／または丸められたバージョン９３４に基づいて、第２のマッピング９５０によって得られる。

最後に、間隔サイズ情報９２０は、第１の確率値９４２に基づいて、および第２の確率値９５２に基づいて取得される。
しかし、第１の確率値９４２および第２の確率値９５２の決定は、第１のマッピング９４０および第２のマッピング９５０を使用して取得できる量の例としてのみ考慮されるべきであることに留意されたい。対照的に、例えば、間隔サイズ情報９２０への寄与のように、第１のマッピング９４０および第２のマッピング９５０を使用して他の量を導出することも可能であろう。

しかし、図９に記載されている間隔サイズ決定コア９００は、本明細書に開示されている算術エンコーダまたは算術デコーダのいずれかで使用できることに留意されたい。さらに、間隔サイズ決定コア９００は、任意選択で、個別におよび組み合わせて、本明細書に記載の特徴、機能、および詳細のいずれかによって補足され得ることに留意されたい。

１０．図１０ａおよび１０ｂによる間隔サイズの決定
図１０ａは、例えば、間隔サイズ決定コアで使用することができる、間隔サイズ情報を決定するための概念の概略図を示している。

見てわかるように、図１０ａの概念は、状態変数値９１０に対応することができ、状態変数値を更新することができる複数の状態変数値１０１０ａ、１０１０ｂを受け取る。さらに、概念１０００は、間隔サイズ情報１０２０を提供し、これは、間隔サイズ情報９２０に対応し得る。概念１０００は、第１の状態変数値１０１０ａ（またはそのスケーリングおよび／または丸められたバージョン）を第１の確率値９４２に対応し得る第１の確率値１０４２にマッピングする第１のマッピング１０４０を備える。さらに、概念１０００は、第２の状態変数値１０１０ｂ（またはそのスケーリングおよび／または丸められたバージョン）を第２の確率値１０５２にマッピングする第２のマッピング１０５０を含む。さらに、概念１０００は、第１の確率値１０４２と第２の確率値１０５２との結合を含み、この結合は、例えば、式（７）を使用して実行され得る。したがって、結合１０６０は、結合確率値１０６２を提供する。さらに、概念１０００は、結合確率値１０６２の乗算１０７０を含み、乗算は、コーディング間隔サイズ値Ｒで行うことができる。したがって、間隔サイズ情報１０２０は、結合確率値１０６２ａおよびコーディング間隔サイズ値Ｒ間の乗算１０７０に基づいて得られる。間隔サイズ情報１０２０は、例えば、可能性の低いシンボルまたは可能性の最も低いシンボルに関連付けられているコーディング間隔のサイズ（または、あるいは、より可能性の高いシンボルまたは最も可能性の高いシンボルに関連付けられたコーディング間隔のサイズ）を記述し得る。任意選択で、概念１０００は、可能性の低いシンボルまたは可能性の低いシンボルの確率を導出するためのメカニズムを含み得（例えば、結合１０６０と乗算１０７０の間）、または乗算１０７０の結果に基づいて、より可能性の低いシンボルまたは最も可能性の低いシンボルに関連する間隔サイズ情報を導出するためのメカニズムを含み得る。
したがって、図１０ａによる概念１０００は、図９に関して説明したような機能を実装することができる。

概念１０００は、本明細書に開示される算術エンコーダまたは算術デコーダのいずれかで使用できることに留意されたい。
また、概念１０００は、任意選択で、個別におよび組み合わせて、本明細書に開示される特徴、機能、および詳細のいずれかによって補足され得る。

図１０ｂは、第１の状態変数値１０８２ａおよび第２の状態変数値１０８２ｂに基づいて間隔サイズ情報１０８４を提供するための概念１０８０のブロック概略図を示す。概念１０８０は、第１の状態変数値１０８２ａ、またはそのスケーリングおよび／または量子化されたバージョンの第１の間隔サイズ寄与１０８６ａに対するマッピング１０８５ａを含む。さらに、概念１０８０は、第２の状態変数値１０８２ｂ、またはそのスケーリングおよび／または量子化されたバージョンを第２の間隔サイズ寄与１０８６ｂにマッピングする、第２のマッピング１０８５ｂを含む。

第１のマッピング１０８５ａおよび第２のマッピング１０８５ｂは、例えば、２次元ルックアップテーブルを使用して、該マッピングを実行することができる。２次元ルックアップテーブルは、例えば、コーディング間隔サイズ情報Ｒの量子化された値と、Ｒの複数の異なる値に対する一次元ルックアップテーブル（例えば、ＬＵＴ１）との間の積を定義することができる。言い換えれば、マッピング１０８５ａで使用される２次元ルックアップテーブルの各行または各列は、本明細書で説明されるルックアップテーブルＬＵＴ１と、該行または列に関連するそれぞれのコーディング間隔サイズ値との間の積を定義することができる。同じことが、第２のマッピング１０８５ｂで使用される２次元ルックアップテーブルにも当てはまり得、該ルックアップテーブルは、第１のマッピング１０８５ａで使用されるルックアップテーブルと同一であり得るか、または該ルックアップテーブルとは異なり得る。さらに、コーディング間隔サイズ情報は、第１のマッピング１０８５ａおよび第２のマッピング１０８５ｂで使用されて、２次元ルックアップテーブルの適切な要素を選択することができることに留意されたい（例えば、第１のルックアップテーブルインデックスは、それぞれの状態変数値に基づくことができ、第２のルックアップテーブルインデックスは、コーディング間隔サイズ値（またはその量子化バージョンＱｒ（Ｒ）に基づくことができる）。

したがって、間隔サイズ情報１０８４は、非常に低い計算の複雑さで取得することができる。さらに、マッピング１０８５ａ、１０８５ｂと、間隔サイズ寄与１０８６ａ、１０８６ｂが結合された結合１０８８との間に適切な処理を挿入して、可能性の低いシンボルまたは可能性の最も低いシンボルに関連する間隔の間隔サイズへの寄与を決定できることに留意されたい。あるいは、しかし、後処理は、間隔サイズ寄与１０８６ａ、１０８６ｂの結合１０８８の結果に基づいて、最も可能性の低いシンボルまたはより可能性の低いシンボルの間隔サイズを決定するために、結合１０８８の後に任意選択で挿入され得る。

結論として、図１０ｂによる概念１０８０を使用して、状態変数値１０８２ａ、１０８２ｂに基づいて、またコーディング間隔サイズ情報またはコーディング間隔サイズ値に依存して、間隔サイズ情報１０８６を導出することができる。
さらに、概念１０８０は、本明細書に開示される算術エンコーダまたは算術デコーダのいずれかで使用できることに留意されたい。
さらに、図１０ｂの概念１０８０は、本明細書に開示される特徴、機能、および詳細のいずれかによって、個別におよび組み合わせて、任意に補足することができることに留意されたい。

１１．図１１による間隔サイズ決定コア
図１１は、本発明の実施形態による、間隔サイズ決定コア１１００のブロック概略図を示す。

間隔サイズ決定コアは、複数の（通常は更新される）状態変数値１１１０を受け取り、それに基づいて、間隔サイズ情報１１２０を提供する。一般的に言えば、間隔サイズ決定コア１１００は、複数の状態変数値１１１０に基づいて、符号化される１つまたは複数のシンボルの算術符号化（または復号される１つまたは複数のシンボル値の算術復号）の間隔サイズ情報を導出するように構成され、これは、異なる適合時定数で以前に符号化された（または、以前に復号された）複数のシンボル値の統計を表す。間隔サイズ決定コア１１００は、複数の状態変数値１１１０に基づいて結合状態変数値１１３２を導出するように構成される結合／コンバイナ１１３０を備える。任意選択で、間隔サイズ決定コア１１００は、スケーリングおよび／または丸められた結合状態変数値１１４２を得るために、結合状態変数値１１３２をスケーリングおよび／または丸める、スケーリングおよび／または丸め１１４０を備える。さらに、間隔サイズ決定コア１１００は、ルックアップテーブルに基づくマッピング１１５０を含み、これは、ルックアップテーブルを使用して、結合状態変数値１１３２、またはそのスケーリングおよび／または丸められたバージョン１１４２をマッピングし、算術符号化／復号のため、間隔サイズ（例えば、重要度の低いシンボルまたは重要度の高いシンボルなどの特定のシンボルに関連付けられた間隔のサイズ）を説明する間隔サイズ情報を取得するように構成される。しかし、任意選択で、後処理１１６０を使用して、ルックアップテーブルベースのマッピング１１５０の結果１１５２に基づいて間隔サイズ情報１１２０を導出することができる。

間隔サイズ決定コア１１００は、本明細書に開示される算術エンコーダおよび算術デコーダのいずれかで使用できることに留意されたい。さらに、間隔サイズ決定コア１１は、本明細書に開示される特徴、機能、および詳細のいずれかによって任意選択で補足され得ることに留意されたい。

１２．図１２による状態変数の更新
図１２は、本発明の実施形態による、状態変数更新のブロック概略図を示す。状態変数更新１２００（これは、状態変数アップデータと見なされてもよい）は、シンボル値１２１０を受信するように構成され、これは、符号化されるシンボルのシンボル値、または以前に復号されたシンボルのシンボル値（または以前に符号化されたシンボルのシンボル値）であり得る。さらに、状態変数更新１２００は、１つまたは複数の以前に決定された状態変数値１２１２を受け取り、１つまたは複数の更新された状態変数値１２２０を提供するように構成され得る。特に、状態変数更新１２００は、シンボル値に依存して（例えば、符号化されるシンボルまたは以前に符号化されたシンボルまたは以前に復号されたシンボルを表す）、ルックアップテーブルを使用して、第１の状態変数値を更新するように構成され得る。言い換えれば、状態変数更新１２１０は、ルックアップテーブルベースの状態変数更新またはルックアップテーブルベースの状態変数アップデータ１２３０を含み得る。したがって、更新された状態変数値は、対応する以前に決定された状態変数値に基づいて、符号化されるシンボルまたは以前に符号化されたシンボルまたは以前に復号されたシンボルに基づくシンボル値を考慮して提供され得る。

したがって、状態変数更新１２００は、１つまたは複数の更新された状態変数値を提供することができる。複数の更新された状態変数値が決定される場合、ルックアップテーブルベースの状態変数更新は、各状態変数値に対して個別に実行され得る（ただし、同じメカニズムおよび／または同じルックアップテーブルは、おそらく異なるスケーリングパラメータおよび／または量子化機能とともに使用される可能性がある）。
しかし、本明細書で説明される状態変数更新１２００は、本明細書で開示される算術エンコーダおよび算術デコーダのいずれかで使用することができる。しかし、状態変数更新１２００は、任意選択で、本明細書に開示される特徴、機能、および詳細のいずれかによって、個別におよび組み合わせて取られて補足され得ることに留意されたい。

１３．図１３による間隔サイズ決定コア
図１３は、本発明の実施形態による、間隔サイズ決定コア１３００のブロック概略図を示す。

間隔サイズ決定コアは、１つまたは複数の状態変数値１３１０を受け取り、これは、例えば、更新された状態変数値であり得る。さらに、間隔サイズ決定コアは、１つまたは複数の状態変数値１３１０に基づいて、間隔サイズ値１３２０を提供する。
間隔サイズ決定コアは、ルックアップテーブル評価メカニズム１３３０を含み、これは、１つまたは複数の状態変数値１３１０に基づくことができ、間隔サイズ値１３２０を提供する確率指数１３３２を受け取る。

例えば、確率指数１３３２は、確率指数導出１３４０（これは、スケーリングおよび／または丸めおよび／または量子化を含み得る）を使用して、１つまたは複数の（更新された）状態変数値から導出され得る。
例えば、１つまたは複数の更新された状態変数値１３１０は、本明細書に開示されるように、算術エンコーダまたは算術デコーダで決定され得、複数の以前に符号化されたシンボル値の統計を表すことができる。

一般的に言えば、間隔サイズ決定コア１３００は、ベースルックアップテーブル１３５０を使用して間隔サイズ値１３２０を決定するように構成される。ルックアップテーブル評価メカニズムは、間隔サイズ値１３２０を決定するように構成され得、１つまたは複数の状態変数値に基づいて取得される確率指数１３３２が第１の範囲内にある場合、決定された間隔サイズ値がベースルックアップテーブル１３５０の要素またはベースルックアップテーブル１３５０の要素の丸められたバージョンと同一であるようにし、確率指数１３３２が第２の範囲内にある場合、ベースルックアップテーブル１３５０の要素のスケーリング１３６０（および任意選択で丸め）を使用して、決定された間隔サイズ値が取得されるようにする。したがって、間隔サイズ値１３２０を使用して、１つまたは複数のシンボルの算術符号化または算術復号を実行することができる。

言い換えれば、例えば、図８に示されるように、１つまたは複数の（更新された）状態変数値から導出され得る確率指数１３３２（第１の信号処理パス８８０または第２の信号処理パス８９０、任意選択の決定８４０および量子化８５０との組み合わせ）は、ベースルックアップテーブルのエントリが「そのまま」使用されるか、またはスケーリング１３６０で使用されるかを決定するために使用され得る（確率指数１３３２によって決定され得る）。

言い換えれば、確率指数１３３２は、参照符号１３７０に概略的に示されているように、ベースルックアップテーブル１３５０のどの要素が選択されるか、およびベースルックアップテーブル１３５０のこの選択されたエントリのスケーリングが、参照符号１３８０に象徴的に示されるように、実行されるかどうかの両方を決定することができる。例えば、ベースルックアップテーブル１３７０のエントリの選択は、確率指数１３３２の１つまたは複数の最下位ビットによって決定され得、スケーリング１３６０が実行されるかどうかの決定は、確率指数１３３２の１つまたは複数の最上位ビットに基づいてなされ得る。しかし、ビットのグループを評価するのではなく、ベースルックアップテーブル１３５０のエントリを選択することは、所定の値を有する確率指数１３３２の除算の除算残差によって決定され得、スケーリング１３６０を実施するか否かを判断することは、複数の範囲のうち、現在考えられている確率指数値がどの範囲にあるかを判断することにより、なされ得る。

さらに、任意選択で、例えば、ベースルックアップテーブルが、２次元テーブルである場合、ベースルックアップテーブル１３５０のエントリの選択において、コーディング間隔サイズ情報（例えば、Ｒ）が考慮され得ることに留意されたい。別の任意選択の代替案では、コーディング間隔サイズ情報（例えば、Ｒ）を使用して、間隔サイズ値１３２０を取得するために、コーディング間隔サイズ情報に依存する追加のスケーリングを実行する必要があるかどうかを決定することができる（例えば、ベースルックアップテーブルの選択されたエントリに適用される）。

しかし、ここで説明する間隔サイズ決定コア１３００は、間隔サイズ値を導出するために、本明細書で開示される算術エンコーダおよび算術デコーダのいずれかで使用できることに留意されたい。
さらに、間隔サイズ決定コア１３００は、任意選択で、本明細書に開示される特徴、機能、および詳細のいずれかによって補足され得ることに留意されたい。

１４．間隔サイズ決定コア
図１４は、本発明の実施形態による、間隔サイズ決定コア１４００のブロック概略図を示す。

間隔サイズ決定コア１４００は、１つまたは複数の状態変数値１４１０を受け取り、これは、例えば、更新された状態変数値であり得る。さらに、間隔サイズ決定コア１４００は、１つまたは複数の状態変数値１４１０に基づいて、間隔サイズ値１４２０を提供する。
間隔サイズ決定コア１４００は、ルックアップテーブル評価メカニズム１４３０を含み、これは、１つまたは複数の状態変数値１４１０に基づくことができ、間隔サイズ情報または間隔サイズ値１４２０を提供する確率指数１４３２を受け取る。

例えば、確率指数１４３２は、１つまたは複数（確率指数導出１４４０を使用して更新された状態変数値）から導出され得る。
例えば、１つまたは複数の更新された状態変数値１４１０は、本明細書に開示されるように、算術エンコーダまたは算術デコーダで決定され得、複数の以前に符号化されたシンボル値および／または複数の以前に復号されたシンボル値の統計を表すことができる。

一般的に言えば、間隔サイズ決定コア１４００は、１つまたは複数の状態変数値１４１０から導出された確率値（例えば、確率指数１４３２）に基づいて、およびコーディング間隔サイズに基づいて（例えば、コーディング間隔サイズ情報１４１２によって記述される）、確率テーブル（例えば、ＰｒｏｂＴａｂＬＰＳ）を使用して間隔サイズ値１４２０を決定するように構成される。例えば、確率テーブル１４５０は、複数の異なる確率値（または確率指数１４３２）のセットおよび所与のコーディング間隔サイズ（例えば、単一の所与の参照コーディング間隔サイズ）の間隔サイズを説明する。図１４に見られるように、確率指数１４３２は、例えば、確率テーブルのどの要素を間隔サイズ値１４２０の提供の基礎として使用するべきか選択するために使用され得る。別の言い方をすれば、確率指数１４３２は、さらなる処理のための確率テーブルの要素の選択を決定する。さらに、確率指数１４３２が決定され、その値によって、確率テーブルの選択されたエントリがスケーリング１４６０でスケーリングされる。一般的に言えば、間隔サイズ決定コアは、現在の確率値が複数の確率値のセットでない場合、および／または現在のコーディング間隔サイズが所与の（参照）コーディング間隔サイズと異なる場合、確率テーブルの要素またはエントリ（例えば、現在の確率値または確率指数１４３２に依存して選択された要素）をスケーリングするように構成され得る。言い換えれば、間隔サイズ値１４２０は、スケーリング１４６０を使用して確率テーブル１４５０の選択されたエントリから導出され得、スケーリングは、確率値または確率指数１４３２およびコーディング間隔サイズ情報１４１２の両方に依存し得る。

例えば、確率テーブル１４５０のエントリは、単一のコーディング間隔サイズと、所与の範囲の確率値または確率指数（この範囲は、通常、３つ以上の異なる確率値または確率指数をカバーし得、確率テーブルのエントリの数は、計算操作を容易にするために、好ましくは２の効力であり得る）に関連付けられ得る。スケーリング１４６０は、例えば、コーディング間隔サイズ１４１２が、確率テーブル１４５０のエントリが関連付けられている参照コーディング間隔サイズと異なる場合、確率テーブル１４６０の選択されたエントリをスケーリングすることができる。言い換えれば、実際のコーディング間隔サイズ１４１２が参照コーディング間隔サイズ（例えば、確率テーブル１４５０のエントリが関連付けられるコーディング間隔サイズ）と異なる場合、スケーリング１４６０は、この偏差を考慮し得る（少なくとも、参照コーディング間隔サイズと実際のコーディング間隔サイズ１４１０との間の偏差は、コーディング間隔サイズを量子化するために使用される量子化間隔のサイズを超える）。さらに、スケーリング１４６０はまた、確率値または確率指数１４３２が、確率テーブル１４５０のエントリが関連付けられている確率値または確率指数の範囲外にあるかどうかを考慮し得る。例えば、確率テーブル１４５０のエントリが確率指数の第１の範囲に関連付けられているが、実際の確率指数１４３２が、確率指数の第１の範囲と重複しない指数の第２の範囲内にある場合、スケーリング１４６０はこの発見を考慮して追加のスケーリングを適用することができる（実際のコーディング間隔サイズの参照コーディング間隔サイズからの偏差に基づくスケーリングに加えて）。

結論として、間隔サイズ決定コア１４００は、確率値または確率指数１４３２が複数の確率値のセット内にある場合、および、実際のコーディング間隔サイズ１４１２が参照コーディング間隔サイズに等しい（または参照コーディング間隔サイズに等しい値に量子化される）場合、確率テーブル１４５０の選択されたエントリを間隔サイズ値１４２０として提供することができ、そのための確率テーブルエントリが提供される。他方、確率値または確率指数１４３２が、確率テーブルエントリが提供される「複数の確率値のセット」の外側にある場合、および／または実際のコーディング間隔サイズ１４１２が参照コーディング間隔サイズから逸脱する場合（例えば、実際のコーディング間隔サイズが異なる値に量子化される分だけ）、スケーリング１４６０は、間隔サイズ値１４２０を得るために、確率テーブル１４５０の選択されたエントリをスケーリングする。

したがって、間隔サイズ値１４２０は、比較的小さいルックアップテーブル１４５０を使用して取得することができ、これは、例えば、エントリの数がより少ない（例えば、少なくとも２倍）１次元確率テーブルであり得、次に、いくつかの異なる可能な確率値または確率指数値であり得る。
しかし、間隔サイズ決定コア１４００は、任意選択で、本明細書に記載の特徴、機能、および詳細のいずれかによって補足され得ることに留意されたい。さらに、間隔サイズ決定コア１４００は、本明細書に開示される算術エンコーダまたは算術デコーダのいずれか、および本明細書に開示されるビデオエンコーダまたはビデオデコーダのいずれかにおいて任意選択で使用できることに留意されたい。

１５．図１５による間隔サイズ決定コア
図１５は、本発明の実施形態による、間隔サイズ決定コア１５００のブロック概略図を示す。

間隔サイズ決定コア１５００は、１つまたは複数の状態変数値を受信するように構成され、これは、例えば、更新された状態変数値であり得る。例えば、１つまたは複数の状態変数値１５１０は、結合状態変数値を含み得る。さらに、間隔サイズ決定コア１５００は、間隔サイズ値１５２０を提供するように構成され、これは、例えば、サブインターバル幅値、例えば、Ｒ_ＬＰＳであり得る。

間隔サイズ決定コア１５００は、任意選択のマッピングおよび／または丸めを含み、これは、１つの状態変数値を決定するために使用され、これは、複数の以前に処理された（例えば、以前に符号化または以前に復号された）シンボル値の統計を表す。一般的に言えば、算術エンコーダは、結合状態変数値（例えば、１つの更新された結合状態変数値１５１０から）から、またはそのスケーリングおよび／または丸められたバージョンから、符号化または復号されるシンボル値の算術符号化または算術復号のためのサブインターバル幅値（例えば、間隔サイズ値１５２０）を計算するよう構成される。間隔サイズ決定コア１５００は、例えば、１つの状態変数値（例えば、結合状態変数値）、またはそのスケーリングおよび／または丸められたバージョンを確率値にマッピングするために使用される１次元ルックアップテーブル１５５０を備える。例えば、１次元ルックアップテーブル１５５０のエントリは、結合状態変数値の値ドメインの異なる値間隔の確率値を含む。さらに、間隔サイズ決定コアは、量子化レベルに、算術符号化または算術復号のコーディング間隔のサイズを記述するコーディング間隔サイズ情報１５１２を量子化するように構成される量子化１５６０を備える（例えば、符号化されるシンボル値の算術符号化の前に、または復号されるシンボル値の算術復号の前に）。したがって、量子化されたコーディング間隔サイズ情報１５６２が提供される。さらに、スケーリング／乗算１５７０があり、これは、確率値と量子化レベル（より正確には、量子化されたコーディング間隔サイズ情報１５６２）との間の積を決定する（例えば、事前計算された積のルックアップを使用する、または乗算を使用する）。例えば、確率値は、状態変数値またはそのスケーリングおよび／または丸められたバージョンに依存して、１次元ルックアップテーブル１５５０のエントリを選択することによって提供される。次に、この確率値１５５２は、（量子化された）コーディング間隔サイズ情報１５６２に依存して（すなわち、「量子化レベル」に依存して）スケーリングされ得、スケーリングは、確率値と量子化レベルの間の積の決定に対応し得る。したがって、間隔サイズ値１５２０は、効率的な方法で提供され、１次元ルックアップテーブルを使用することで十分である。

しかし、ここで説明される間隔サイズ決定コア１５００は、任意選択で、個別におよび組み合わせて、本明細書に開示される特徴、機能、および詳細のいずれかによって補足され得ることに留意されたい。さらに、間隔サイズ決定コア１５００は、本明細書に記載の算術エンコーダおよび算術デコーダのいずれか、また本明細書に記載のビデオエンコーダおよびビデオデコーダのいずれかにおいても使用できることに留意されたい。

１６．図１６によるビデオデコーダ
図１６は、本発明の一実施形態による、ビデオデコーダ１６００のブロック概略図を示す。

ビデオデコーダ１６００は、符号化されたビデオ情報を受信し、それに基づいて、復号されたビデオ情報（または復号されたビデオコンテンツ）を提供するように構成される。
符号化されたビデオ情報１６１０（これは、ビデオビットストリームと見なされ得る）は、例えば、スライスタイプの情報を含み得、また、バイナリシーケンスの符号化された表現を含み得る。任意選択で、符号化されたビデオ情報１６１０は、追加の情報を含み得るが、これは、本発明にとって必須ではない。

一般的に言えば、ビデオデコーダは、複数のビデオフレーム（例えば、ビデオフレームのシーケンス）を復号するように構成され、ビデオデコーダは、例えば、１つまたは複数のスライスのセットに細分されるビデオフレームを復号するように構成され得る（好ましくは、複数のスライスに）。ビデオデコーダは、例えば、符号化されたビデオ情報１６１０に含まれ、以前のフレームのビデオコンテンツに基づく現在のフレームのビデオコンテンツの予測がない、独立した符号化モードを使用するか、または以前のフレームのピクセルの１つのブロックに基づくピクセルのブロックの予測がある単一予測モードを使用するか、または１つまたは複数の以前のフレームのピクセルの２つ以上のブロックに基づくピクセルのブロックの予測が存在する二重予測モードを使用して、スライスが符号化されているかどうかを示すスライスタイプ情報を評価するように構成され得、スライスの復号のための動作モードを選択するようにする（例えば、「ビデオ再構成」ブロック１６８０によって実行され得る。

ビデオデコーダ１６００は、符号化されたビデオ情報１６１０に含まれる、バイナリシーケンスの符号化された表現に基づいて（「ビデオ再構成」ブロックによって使用するための）復号されたバイナリシーケンス１６２２を提供するように構成される算術デコーダ１６２０を備える。算術デコーダは、好ましくは、第１のソース静的値決定１６３０および第２のソース統計値決定１６４０を含む。したがって、算術デコーダ１６２０は、第１のウィンドウサイズを使用して（または第１の時定数を使用して）第１のソース統計値１６３２（例えば、第１の状態変数値）を決定し（例えば、本明細書に記載の状態変数更新が使用され得る）、第２のウィンドウサイズを使用して（または第２の時定数を使用して）第２のソース統計値１６４２（例えば、第２の状態変数値）を決定する（例えば、本明細書に記載の状態変数更新を使用することができる）ように構成される。算術デコーダはまた、任意選択でコンバイナ１６５０を備える。したがって、算術デコーダは、第１のソース静的値および第２のソース統計値に基づいて、結合ソース統計値１６５２（例えば、結合状態変数値）を決定するように構成され得る。

さらに、算術デコーダ１６２０は、好ましくは、範囲値決定１６６０を備える（これは、例えば、本明細書に記載の間隔サイズ決定コア、または本明細書に記載の間隔サイズ決定のいずれかを含むことができる）。したがって、算術デコーダは、バイナリシーケンス（符号化されたビデオ情報１６１０）の符号化された表現のマッピングに使用される間隔細分割のための１つまたは複数の範囲値（または本明細書で説明される間隔サイズ情報）を、結合されたソース統計値１６５２に基づいて（または第１および第２のソース統計値に基づいて）、復号されたバイナリシーケンス１６２２（ビデオ再構成ブロック１６８０によって使用される）に決定するように構成され得る。

好ましくは、算術デコーダ１６２０はまた、範囲値決定１６６０から１つまたは複数の範囲値１６６２を受け取り、符号化されたビデオ情報１６１０に含まれる符号化されたバイナリシーケンスから復号されたバイナリシーケンス１６２２を導出する範囲値を使用する算術復号コア１６７０（例えば、ブロックまたはユニットであり得る）を備える。
さらに、ビデオデコーダは、例えば、復号されたバイナリシーケンス１６２２を受信し、復号されたバイナリシーケンス１６２２に基づいて復号されたビデオコンテンツ１６１２を提供する（おそらくスライスタイプの情報などの追加の制御情報を考慮して）ビデオ再構成ブロック（またはユニット）１６８０を含み得る。

結論として、算術デコーダ１６００は、符号化されたビデオ情報１６１０を受信し、バイナリシーケンスの符号化された表現の算術復号を実行して、復号されたバイナリシーケンス１６２２を導出する。算術復号は、復号されたバイナリシーケンス１６２２におけるバイナリ値の確率に関する知識を利用する。復号されたバイナリシーケンス１６２２内のバイナリ値の確率（または推定確率）に関するこの知識は、間隔の細分割を定義する範囲値１６６２に依存することによって、算術復号コア１６７０によって考慮される。簡単に言えば、算術復号コアは、範囲値１６６２を使用して、異なる間隔を定義することができる（例えば、０から１の間、または整数値の範囲にわたって）。算術復号コアは、例えば、バイナリシーケンスの符号化された表現を、範囲値を使用して定義された間隔の１つにある数値の表現として解釈できる。バイナリシーケンスの符号化された表現によって表される数がどの間隔にあるかを認識することによって、算術復号コア１６７０は、バイナリシーケンスの符号化された表現を使用してどのビットまたはどのビットシーケンスが符号化されたかを結論付けることができる。

しかし、算術復号コア１６７０のこの説明は、非常に簡潔で一般的な説明としてのみ考慮されるべきであることに留意されたい。算術復号コアに関する詳細は、例えば、規格Ｈ．２６４およびＨ．２６５で確認できる。しかし、（算術復号コアの動作のための）異なる概念も文献に見ることができ、算術復号コアの詳細は、本発明にとって特に関連性がない。

しかし、（高いビットレート効率を可能にする）適切な範囲値を得るために、算術デコーダ１６２０（または、一般的に言えば、ビデオデコーダ）は、異なるウィンドウサイズを使用して２つのソース統計値１６３２、１６４２を決定する（「ウィンドウサイズ」は、復号されたバイナリシーケンス１６２２の複数の復号されたバイナリ値にわたる平滑化の程度を定義する）。さらに、算術復号コア１６７０に提供される範囲値の信頼性を高めるために、第１のソース統計値１６３２および第２のソース統計値１６４２は、いくつかの実施形態では、結合されたソース統計値１６５２に組み合わされる。

したがって、算術復号コア１６７０によって使用される範囲値は、ビット値の実際の確率（例えば、復号されたバイナリシーケンス１６２２内のビット値「０」および「１」のもの）によく適合しているので、ビデオデコーダ１６００は、高効率を提供すると言うことができる。

補足として、ビデオデコーダ１６００も変更可能であることに留意されたい。代替の実装形態では、第２のソース統計値決定１６４０は、固定値（復号されたバイナリシーケンスから独立していてもよいが、１つまたは複数のパラメータに依存し得る）の提供によって置き換えることができる。この場合、算術デコーダは、結合されたソース統計値１６５２を取得するために、第１のソース統計値１６３２を固定の非ゼロ値と結合するように任意選択で構成される。そのような単純化は、場合によっては良い結果をもたらし、例えば、結合されたソース統計値の不適切に強い変動を回避する可能性があることがわかっている。言い換えれば、結合されたソース統計値の決定に固定寄与を導入することによって、結合されたソース統計値がこの固定値から大きく逸脱することがもはやできなくなることを達成することができる。したがって、復号されたバイナリシーケンス１６２２内に同一のビット値のより長いシーケンスが偶然に存在する場合、復号されたバイナリシーケンスの統計に対するいくつかの「後知恵」を使用して、コーディング効率の大幅な低下を回避することができる。

補足として、算術デコーダ（および算術デコーダの個々のブロック）の機能は、一般に、ビデオデコーダ全体の機能と見なすこともできることに留意されたい。言い換えれば、算術デコーダの機能として本明細書に記載されている機能は、ビデオデコーダの他のブロックによっても実行することができる。
さらに、図１によるビデオデコーダ１６００は、個別におよび組み合わせて、本明細書に記載の特徴、機能、および詳細のいずれかによって補足され得ることに留意されたい。

１７．図１７によるビデオデコーダ
図１７は、本発明の実施形態による、ビデオデコーダ１７００のブロック概略図を示す。
ビデオデコーダ１７００は、符号化されたビデオ情報１７１０（例えば、ビデオビットストリーム）を受信し、それに基づいて、復号されたビデオコンテンツ１７１２（例えば、ビデオフレームのシーケンス）を提供するように構成される。符号化されたビデオ情報１７１０は、例えば、本明細書で説明されるように、スライスタイプ情報を含み得る。符号化されたビデオ情報１７１０は、構成情報をさらに含み得、これはまた、制御情報と見なすことができる。さらに、符号化されたビデオ情報１７１０は、バイナリシーケンスの符号化された表現を含み得る。

図１７には、ビデオデコーダ１７００の２つの主要なブロック、すなわち、算術デコーダ１７２０およびビデオ再構成１７８０が示されている。ただし、ビデオデコーダの機能の分布は、固定ブロック構造に拘束されるのではなく、広範囲にわたって変更される可能性があることに留意されたい。また、ビデオデコーダの実際の実装は、当業者によく知られている追加のブロックおよび／または機能を有する可能性があることに留意されたい。

算術デコーダ１７２０は、バイナリシーケンスの符号化された表現１７１１を受信する。しかし、算術デコーダ（または算術デコーダの外側にあり得る制御ブロック）は、任意選択で、スライスタイプ情報および構成情報（または制御情報）を受信することができる。特に、算術デコーダ１７２０は、任意選択でスライスタイプ情報および構成情報または制御情報の一部またはすべてを考慮に入れて、バイナリシーケンスの符号化表現１７１１に基づいて、復号されたバイナリシーケンス１７２２をビデオ再構成１７８０に提供する。

以下では、算術デコーダ１７２０の機能についてより詳細に説明する。算術デコーダは、算術復号コア１７７０を含み、これは、バイナリシーケンスの符号化された表現１７１１を受信し、復号されたバイナリシーケンス１７２２を提供する。算術復号コアは、復号されたバイナリシーケンス１７２２のどのビット値が、バイナリシーケンスの符号化された表現１７１１によって表されるかを決定する。この目的のために、算術復号コア１７７０は、バイナリシーケンスの符号化された表現１７１１によって表されるどの数値の範囲の間隔にあるかを確認する。複数の（少なくとも２つの）間隔のうち、バイナリシーケンスの符号化された表現１７１１によって表される数が存在する間隔の決定に応じて、復号されたバイナリシーケンス１７２２の特定のビット値、またはビット値のグループ、またはシンボル、が認識される。

復号されたバイナリシーケンス１７２２を導出する目的で、算術復号コアは、間隔に関する情報を受信し、これは通常、ビット値の確率にある程度対応する。この場合、算術復号コア１７７０は、間隔細分割に使用される「範囲値」または「間隔サイズ情報」１７６２（すなわち、算術復号コア１７７０によって使用される数範囲の間隔を定義するのに役立つ範囲値１７６２）を受け取る。特に、算術復号コア１７７０は、例えば、規格Ｈ．２６４によるビデオエンコーダ／デコーダまたは規格Ｈ．２６５によるビデオエンコーダ／デコーダで使用される算術復号コアと類似または同一であり得ることに留意されたい。しかし、算術復号コア１７７０を実現するための異なるアプローチも使用できることに留意されたい。

上記の議論を考慮すると、算術復号コア１７７０の間隔細分割を定義する範囲値または間隔サイズ情報１７６２を提供することが算術デコーダ１７２０の重要な機能であることが明らかになる。一般的に言えば、算術デコーダ１７２０は、復号されたバイナリシーケンス１７２２の以前に復号されたバイナリ値からこれらの範囲値１７６２を導出し、任意選択で、例えば、初期化値、「ウィンドウサイズ」、「ウィンドウサイズ適合」などのパラメータを定義するいくつかの制御情報を考慮に入れる。

算術デコーダ１７００では、２つのソース統計値決定ブロック（またはユニット）１７３０、１７４０が使用される（これは、例えば、本明細書で説明される状態変数の更新に対応し得る）。例えば、第１のソース統計値決定ブロック１７３０は、復号されたバイナリシーケンス１７２２（ｘ_ｔでも示される）の１つまたは複数の以前に復号されたバイナリ値（またはシンボル値）を受け取り、それに基づいて、第１のソース統計値１７３２（これは、本明細書で説明される第１の状態変数値に対応し得る）を提供する。第１のソース統計値決定ブロックは、例えば、ソース統計値１７３２を表すために使用されるビット数を定義する定数または変数ＢＩＴＳ_ａ、およびソース統計値決定ブロック１７３０が使用するために「ウィンドウサイズ」を定義する定数または変数ｎ_ａ、および／または本明細書に記載されている他の任意のパラメータなどのようないくつかの構成情報を受け取ることができる。例えば、第１のソース統計値決定ブロック１７３０は、第１のソース統計値１７３２を再帰的に決定することができ、ウィンドウサイズｎ_ａまたはパラメータｎ_ｉ ^ｋは、第１のソース統計値または第１の状態変数値１７３２の決定において、復号されたバイナリシーケンス１７２２の最後に復号されたバイナリ値の重み付けを決定する。

第１のソース統計値決定ブロック１７３０の機能は、例えば、いくつかの「無限インパルス応答」特性を導入する再帰的アルゴリズムが使用されるという事実を除いて、特定のウィンドウサイズを有するスライディングする平均の形成に類似している。したがって、第１のソース統計値１７３２は、スライディングウィンドウ合計操作またはスライディングウィンドウ平均化操作の結果を正確に表すのではなく、結果が非常に類似しているため、「仮想スライディングウィンドウ」操作と見なす必要がある。

さらに、第２のソース静的値決定ブロック１７４０は、第１のソース統計値決定ブロック１７３０と比較した場合、同様の操作を実行する。しかし、第２のソース統計値決定ブロック１７４０は、通常、異なるパラメータ（例えば、異なるウィンドウ長ｎ_ｂおよび／または異なるビット数パラメータＢＩＴＳ_ｂまたは異なるパラメータｎ_ｉ ^ｋ）を使用し、その結果、第２のソース統計値または第２の状態変数値１７４２を提供し、これは通常、第１のソース統計値または第１の状態変数値１７３２とは異なる。例えば、ソース統計値１７３２、１７４２の１つは、短期（または短めの期間）平均ソース統計値であり得、ソース統計値１７３２、１７４２の１つは、長期（または長めの期間）の平均ソース統計値であり得る。

ソース統計値決定ブロック１７３０、１７４０は、例えば、本明細書の状態変数更新について説明したような機能を実行することができることに留意されたい。さらに、いくつかの実施形態では、ソース統計値決定ブロック１７３０、１７４０において異なる計算規則を使用することもできることに留意されたい。

算術デコーダ１７２０は、任意選択で、第１のソース統計値１７３２および第２のソース統計値１７４２を受信するように構成された、結合されたソース統計値決定ブロック（またはユニット）２５０をさらに備える。ソース統計値結合ブロック１７５０は、それに基づいて、結合されたソース統計値１７５２を提供する。例えば、ソース統計値結合ブロック１７５０は、第１のソース統計値１７３２および第２のソース統計値１７４２の合計または平均を形成し、それによって、結合されたソース統計値１７５２を取得することができる。
しかし、ソース統計値結合ブロック１７５０は、結合されたソース統計値１７５２を導出するときに、第１のソース統計値１７３２および第２のソース統計値１７４２に異なる重みを適用することもでき、異なる重みは、スライス内または異なるスライス間でさえ変化し得る。

例えば、ソース統計値結合ブロック１７５０は、結合７５１または結合８９２の機能を実行することができる。ただし、この機能のバリエーションも可能である。
例えば、１つの（代替の）実施形態では、ソース統計値結合ブロック１７５０は、第１の統計値のうちの１つのみを固定値と結合し、それによって、結合されたソース統計値または結合状態変数値１７５２を取得する。そのような概念は、結合されたソース統計値１７５２が、復号されたバイナリシーケンス１７２２内のバイナリ値の期待される確率から大きく逸脱することを回避するために有利である可能性がある。

算術デコーダ１７２０は、結合されたソース統計値または結合状態変数値１７５２に基づいて、または代わりに、２つ以上の状態変数値に基づいて、間隔細分割（算術復号コア１７７０に提供される）の範囲値１７６２を導出するように構成される。
この処理ステップは、例えば、「範囲値の決定」と見なすことができる。例えば、範囲値の決定は、結合されたソース統計値１７５２を受け取り、それに基づいて、確率値または状態指数値を提供する、任意選択の値処理１７６６を含み得る。値処理１７６６は、例えば、結合されたソース統計値１７５２の値の範囲を、０から１の間の範囲、０から０．５の間の範囲、または整数の指数値にマッピングすることができる。

任意選択で、値処理１７６６は、情報１７６７を提供することができ、これは、次の復号された値（例えば、復号されたバイナリシーケンス１７２２の）が「１」の値をとるか、または「０」の値をとる可能性が高いかどうかを示すバイナリ情報であり得る。任意選択で、算術デコーダ（または範囲値決定）は、マッピングテーブル１７６９を含み得る。マッピングテーブル１７６９は、例えば、テーブルエントリを指定する指数値（例えば、ｐＳｔａｔｅＩｄｘ）を受け取ることができる。したがって、マッピングテーブル１７６９は、指数値（例えば、ｐＳｔａｔｅＩｄｘ）によって指定された該テーブルエントリに対応する１つまたは複数の範囲値１７６２を提供することができる。したがって、「状態指数値」（例えば、ｐＳｔａｔｅＩｄｘ）を導出し、状態指数値に基づいてマッピングテーブルを評価することによって、間隔細分割のための１つまたは複数の範囲値が、結合されたソース静的値１７５２に基づいて提供され得る。

マッピングテーブル１７６９は、例えば、規格Ｈ．２６４または規格Ｈ．２６５で説明されているマッピングテーブルと同じ構造を有することができる。しかし、任意選択で、マッピングテーブルのコンテンツは、ビデオデコーダの特定の詳細に適合させることができる。特に、マッピングテーブルのエントリは、特定のビデオデコーダで期待される統計プロパティに適合させることができる。

しかし、１つまたは複数の状態変数値に基づく、または結合状態変数値に基づく間隔サイズ情報の導出は、本明細書に開示される概念のいずれかに従って実行され得ることに留意されたい。例えば、間隔サイズ決定を使用するか、間隔サイズ決定コアを使用するか、または図４から図１５のいずれかを参照して説明された状態変数更新を使用することが挙げられる。
また、本明細書で言及される算術復号コアは、本明細書で開示される算術復号コアのいずれかに対応し得ることに留意されたい。

算術デコーダ（または、一般的に言えば、ビデオデコーダ）はまた、任意選択で、制御ブロック１７９０を含み、これは制御情報または構成情報を受信でき、それに基づいて範囲値の提供に使用されるパラメータ（および場合によっては他のパラメータも、例えば算術復号コア１７７０によって使用される追加のパラメータ）を調整できる。例えば、制御ブロック１７９０は、符号化されたビデオ情報１７１０に含まれ得る、「ｃａｂａｃ ｉｎｉｔ ｆｌａｇ」、「ｗｓ＿ｆｌａｇ」、および「ｃｔｕ＿ｗｓ＿ｆｌａｇ」という１つまたは複数のスライスタイプ情報を受信することができる。

さらに、制御１７９０は、例えば、制御情報に応じて、ウィンドウサイズパラメータｎ_ａ、ｎ_ｂまたはｎ_ｉ ^ｋおよび／またはビットサイズパラメータＢＩＴＳａ、ＢＩＴＳｂを調整することができる。特に、制御ブロック１７９０はまた、現在のコンテキストモデルを考慮し得る。この問題に関して、復号される復号されたバイナリシーケンス１７２２の各ビット（またはビットのグループ）について、どのコンテキストモデルを使用するかを決定できることに留意されたい。例えば、どのコンテキストモデルを使用するかの決定は、どのタイプの情報（復号パラメータ、変換係数など）がそれぞれのビット（またはビットのグループ）によって表されるかという事実に基づくことができる。例えば、制御ブロック１７９０は、復号されたバイナリシーケンス１７２２の構文を認識するように構成され得、それにより、どの構文要素（または構文要素のどの部分、例えば、最上位ビットまたは最下位ビットなど）が次に復号されるべきかを認識する。したがって、異なるコンテキストモデル間の選択を行うことができる。また、ウィンドウサイズパラメータおよび／またはビットサイズパラメータおよび／または他の任意のパラメータは、コンテキストモデルに応じて選択され得ることに留意されたい。さらに、ソース統計値１７３２、１７４２または結合されたソース統計値１７５２は、異なるソース統計値または結合されたソース統計（または状態変数値、または結合状態変数値）値が、様々なコンテキストモデルで使用できるように、特定のコンテキストモデルに関連付けられ得ることにも留意されたい。例えば、特定のコンテキストモデルに関連付けられたソース統計値は、それぞれのコンテキストモデルを使用して復号された復号されたバイナリシーケンス１７２２の復号されたバイナリ値に基づいて選択的に提供され得る。言い換えると、パラメータｎ_ａ、ｎ_ｂ、ｎ_ｉ ^ｋ、ＢＩＴＳ_ａ、ＢＩＴＳ_ｂなどに関する個別の独立した処理、および個別の（場合によっては独立した）決定を、異なるコンテキストモデルに対して行うことができる。

制御ユニット１７９０の機能に関して、制御ユニットは、例えば、以下に説明するメカニズムに従って、パラメータｎ_ａ、ｎ_ｂ、ｎ_ｉ ^ｋ、ＢＩＴＳ_ａ、ＢＩＴＳ_ｂを決定することができることに留意されたい。例えば、ウィンドウサイズパラメータｎ_ａ、ｎ_ｂ、ｎ_ｉ ^ｋは、スライスタイプ情報に依存して、および／またはｃａｂａｃ ｉｎｉｔ ｆｌａｇに依存して、および／またはｗｓ＿ｆｌａｇに依存して、および／またはｃｔｕ＿ｗｓ＿ｆｌａｇに依存して選択できる。また、ビットサイズパラメータＢＩＴＳａ、ＢＩＴＳｂは、いくつかの実施形態におけるいくつかの構成情報に依存して選択され得る。しかし、他の実施形態では、ビットサイズパラメータは固定され得る。パラメータの調整のメカニズムについては、例えば、以下の説明を参照されたい。

ここでビデオ再構成ブロック１７８０を参照すると、ビデオ再構成ブロック１７８０は、通常、復号されたバイナリシーケンス１７２２と、構成情報の少なくともいくつかの要素も受信することに留意されたい。例えば、ビデオ再構成１７８０は、復号されたバイナリシーケンス１７２２に基づいて、整数パラメータおよび／または浮動小数点パラメータおよび／または画像データを再構成することができる。例えば、復号されたバイナリシーケンスの特定のビットまたは部分をいかに整数パラメータ、浮動小数点パラメータ、または画像データ（例えば、変換係数など）にマッピングするべきかを定義するマッピングルールが存在する場合がある。したがって、ビデオ再構成ブロック１７８０は、復号されたバイナリシーケンス１７２２からビデオフレームの再構成に使用される情報を再構成する。次に、ビデオ再構成ブロックは、再構成された情報（復号されたバイナリシーケンス１７２２から導出された）に基づいて画像情報を生成することができる。

例えば、ビデオ再構成１７８０は、規格Ｈ．２６４または規格Ｈ．２６５に記載されているものと同じ機能を備え得る。しかし、復号されたバイナリシーケンス（および、場合によっては、追加の構成情報または制御情報）に基づいて、復号されたビデオコンテンツを提供するように適合された他のアプローチも、ビデオ再構成に使用され得る。したがって、ビデオ再構成１７８０は、復号されたビデオコンテンツ１７１２を提供し、これは、ビデオフレームのシーケンスとしての形態をとることができる。

結論として、本発明の実施形態によるビデオデコーダの概要が提供された。しかし、機能ブロックには異なる実装があることに留意されたい（例えば、ソース統計値決定ブロック１７３０、１７４０、ソース統計値結合ブロック１７５０、値処理ブロック１７６６、マッピングテーブル１７６９および算術復号コア１７７０用）。また、ビデオ再構成ブロック１７８０および制御ブロック１７９０に対して異なる実装が可能である。

しかし、本明細書に記載の機能ブロックは、本出願内にその全体が開示されている特徴、機能、および詳細のいずれかによって補足され得ることにも留意されたい。また、本出願内で開示される特徴、機能、および詳細は、個別に導入することも、組み合わせて使用することもでき、それによってビデオデコーダ１７００の機能を拡張できることに留意されたい。

１８．さらなる実施形態
以下では、本発明によるさらなる実施形態について説明する。
他の特徴、機能および詳細の中で、有限状態機械を使用するコンテキストモデル更新方法が説明され、これは、個別に、または本明細書に開示されるすべての特徴、機能および詳細と結合して使用することができる。

序論
以下では、異なる本発明の実施形態および態様が、例えば、「状態変数からの確率推定値の導出」および「状態変数の更新」および「好ましい実施形態」の章で説明される。
しかし、他のいずれかの章に記載されている特徴、機能、および詳細はまた、任意選択で、本発明による実施形態に導入することができる。

また、上記の章で説明された実施形態は、個別に使用することができ、また、別の章の特徴、機能、および詳細のいずれかによって補足することができる。
また、本明細書に記載の個々の態様は、個別にまたは組み合わせて使用できることに留意されたい。したがって、詳細は、該態様の別の１つに詳細を追加することなく、該個々の態様のそれぞれに追加することができる。

特に、実施形態はまた特許請求の範囲に記載されている。請求項に記載の実施形態は、任意選択で、個別におよび組み合わせて、本明細書に記載の特徴、機能、および詳細のいずれかによって補足することができる。

本開示は、明示的または暗黙的に、ビデオエンコーダ（入力ビデオ信号の符号化された表現を提供するための装置）およびビデオデコーダ（ビデオ信号の符号化された表現に基づいて、ビデオ信号の復号された表現を提供するための装置）で使用可能な機能を説明することにも留意されたい。したがって、本明細書に記載の特徴のいずれも、ビデオエンコーダのコンテキストおよびビデオデコーダのコンテキストで使用することができる。

さらに、方法に関連して本明細書に開示される特徴および機能は、（そのような機能を実行するように構成された）装置においても使用され得る。さらに、装置に関して本明細書に開示される任意の特徴および機能性もまた、対応する方法で使用することができる。言い換えれば、本明細書に開示される方法は、装置に関して説明された特徴および機能のいずれかによって補足され得る。

また、本明細書で説明する特徴および機能のいずれも、「実装の代替」のセクションで説明するように、ハードウェアまたはソフトウェアで、あるいはハードウェアとソフトウェアの組み合わせを使用して実装することができる。

緒言
コンテキストモデルの更新は、コーディングエンジンを基礎となるソース統計に適合させる可能性を提供することにより、効率的なバイナリ算術エントロピーコーダの重要な機能となる。

本発明では、各コンテキストモデルは、例えば、シンボルのシーケンスの各シンボルに対して、エントロピー符号化または復号のための確率推定を提供する独立した確率推定ステージを備えている。このコンテキストモデルの更新方法の基本的な概念は、現在の確率推定を共同で表すコンテキストモデルごとに１つ以上の状態変数を維持することである。シンボルシーケンスの統計に適合するために、コンテキストモデルの状態変数は頻繁に更新される（例えば、状態変数の更新）。例えば、各シンボルの符号化後である。

本発明は、他の態様の中でもとりわけ、２つの重要な態様を含む。第１の態様は、状態変数から確率推定（または間隔サイズ情報）を導出する方法に対処するものである。第２の態様は、シンボルの発生後に状態変数を更新する方法に対処するものである。態様は、任意選択で結合して使用できる。

本発明は、任意選択で、バイナリ算術コーディングエンジンと結合することができるが、符号化または復号されるバイナリシンボルの個々の確率推定を必要とする他のエントロピー符号化エンジンとも結合することができる。例えば、本発明はまた、ＰＩＰＥコーディング概念と結合することができる。

実装の詳細
例えば、

を伴う１つ以上のコンテキストモデル

を使用するビデオ圧縮アルゴリズムのようなエントロピーエンコーディングまたはデコーディングアプリケーションについて考察してみる。符号化または復号されるバイナリシンボルのほとんどは、コンテキストモデルの１つに明確に関連付けられている。このようなバイナリシンボルを符号化または復号するために、関連するコンテキストモデル

は、エントロピーコーディングステージに、「１」であるバイナリシンボルの確率推定値

を提供する。良好な圧縮効率を実現するには、バイナリシンボルを符号化するエントロピーによって生成されるビットストリームの部分を、「１」に対しては

に、「０」に対しては

に近づける必要がある。

コンテキストモデル

ごとに、１つ以上の状態変数（または状態変数値）

が

で維持される。各状態変数

は、例えば、符号付き整数値として実装され、確率値

を表す。コンテキストモデル

の確率推定値

は、例えば、コンテキストモデルのすべての状態変数の確率値

の加重和として定義する必要がある。

状態変数は、次のプロパティを有することが好ましいが、必ずしもゆうするものではない：
１．

の場合、

。
２．

のより大きい値はより大きい

に対応する。

。
したがって、負の状態変数は

に対応する可能性がある。一般に、各コンテキストモデルの状態変数ごとに異なる関数

を指定することができる。

総論１
本発明は、多くの状況でビットシフト演算の非常に効率的な使用を可能にする。式

は、

が整数で

が２の累乗の場合、単純なビットシフト演算で実装できる。これは、

が負の場合、２つの補数表現が

に使用されている場合にも機能する。

総論２
例えば確率値、重み付け係数、ルックアップテーブル要素などの非整数を格納するいずれかの変数は、予告なしに固定小数点または浮動小数点演算で実装される場合がある。これは、本発明の特定の実装ごとに異なる可能性がある丸め操作を導入する。
状態変数を確率値に関連付けるための例示的な構成
状態変数を確率値に関連付ける、つまり

を実装するための多くの便利な方法がある。例えば、ＨＥＶＣの確率推定量に匹敵する状態表現は、次の式

は重み付け係数である
で実現できる。

は重み付け係数である。

は

を伴うパラメータである。
ＨＥＶＣに匹敵する構成を実現するには、

および

をすべてのｉおよび

に対してを設定する。

この例示的な構成は、状態変数をどのように定義できるかについての何らかの洞察を与えるものとする。以下に示すように、一般的には直接使用されないため、

を定義する必要はない。代わりに、それはしばしば本発明の個々の部分の実際の実施から生じる。

状態変数の初期化
コンテキストモデルを使用して第１のシンボルを符号化または復号する前に、すべての状態変数は、圧縮アプリケーションに最適化できる正常な値で任意選択で初期化される。
状態変数からの確率推定値の導出
シンボルの符号化または復号の場合、確率推定値はコンテキストモデルの状態変数から導出される。以下に、２つの代替アプローチを示す。アプローチ１は、アプローチ２よりも正確な結果をもたらすが、計算の複雑さも高次になる。

アプローチ１
このアプローチは２つのステップからなる。まず、コンテキストモデルの各状態変数

が確率値

に変換される。次に、確率推定値

は、確率値の加重和

として導出される。

ステップ１：
ルックアップテーブル

は、例えば式（１）に従って、状態変数

を対応する確率値

に変換するために使用される。

（１）

は、確率値を含むルックアップテーブルである。

は、

を

のサイズに適合する重み付け係数である。
このステップは、例えば、ブロック８８２および８８４によって実行され得る。

ステップ２：
確率推定値

は、例えば次のように、確率値

から導出される。

（７）

は、個々の状態変数の影響を制御する重み付け係数である。
このステップは、例えば、ブロック８８６によって実行され得る。

アプローチ２
状態変数から確率推定値を導出するための代替アプローチを以下に示す。結果の精度が低くなり、計算の複雑さが軽減される。最初に、状態変数の加重和

が、例えば次のように導出される。

（１０）

は、各状態変数の影響を制御する重み付け係数である。
このステップは、例えば、ブロック８９２によって実行され得る。
次に、確率推定値

は、状態変数の加重和

から導出される。例えば、次のようになる。

（２）

は、確率推定を含むルックアップテーブルである。

は、

を

のサイズに適合する重み付け係数である。
このステップは、例えば、ブロック８９４によって実行され得る。

アプローチ１および２への任意選択の変更
ソフトウェア実装の場合、可能な限り多くの操作をルックアップテーブルにシフトできると、スループットが向上する可能性がある。式（１）を次のように置き換えると、アプローチ１ではこれが簡単になる。

アプローチ２の場合、式（２）は次のように置き換えられる。

どちらの方程式でも、この変更により、ケースの区別をルックアップテーブルに統合でき、これにより、要素数は以前のほんの２倍になる必要がある。ただし、高スループットを実現するには、演算の数を減らすと役立つ場合があるが、ルックアップテーブルのサイズを大きくすると関連性が低くなる場合がある。
さらに通知することなく、アプローチ１および２の任意の修正を、本発明のアプローチ１および２のすべての用途に任意選択で適用することができる。

ＣＡＢＡＣ（Ｍコーダー）のバイナリ算術コーディングエンジンとの結合（任意選択）
ＣＡＢＡＣのＭコーダーは、２Ｄルックアップテーブルを使用して、コーディング間隔の間隔細分割に必要な乗算を置き換える。

を、バイナリシンボルの算術符号化前のコーディング間隔とする。例えば、

は間隔

内にあるものとする。符号化されるシンボルは、バイナリ算術符号化または復号の確率推定

を導出するために使用されるコンテキストモデル

に関連付けられている。２つのサブインターバル

と

の幅をそれぞれ導出する必要がある。例えば、ＣＡＢＡＣのＭコーダー（例として機能する）は、２Ｄルックアップテーブルを使用することでこれらの乗算を回避する。確率推定値

は、シンボルが１である推定確率であることを思い返されたい。ただし、Ｍコーダーは、シンボル０または１の両方の確率が低い確率を使用して、そのサブインターバル幅

を導出する。次に、より可能性の高いシンボル

のサブインターバル幅は、

から

減算することで簡単に導き出すことができる。

はＭコーダーの実装に応じて、事前定義された最小許容値を下回らない場合があることに留意されたい。例えば、この最小許容値は２、３、または４になり得る。テキストの残りの部分では、

がＭコーダーに渡される前に、少なくとも事前定義された最小許容値と同じ大きさになるまで、（あるとしても）１ずつ繰り返し増加すると想定される。これはクリッピング操作に対応し、個別の計算ステップとして実装できる。以下に示すいくつかのアプローチ（ルックアップテーブル値の調整など）に直接組み込むことができる場合がある。

可能性の低いシンボルの確率

は

のように得られる。
例えば、ルックアップテーブル

に、８ｘ３２または８ｘ１６の要素を含めることができ、

の許容値は８セルに量子化され、

は３２セルまたは１６セルに量子化される。次に、

。

と

は、それぞれ

と

の量子化関数である。

代替案１：
あるいは、ルックアップテーブルｐｒｏｂＴａｂＬＰＳは３２または１６の要素を持つことができ、Ｒの許容値は８または１６セルに量子化され、

は３２または１６セルに量子化される。次に、

（１１）

と

は、それぞれ

と

の量子化関数である。
通常、両方の量子化関数を簡単に実装できることが望ましい。

の要素が適切に選択されている限り、任意の量子化関数を使用できる。

これは、本発明のために利用することができる。
ルックアップテーブル

または

を使用し、コンテキストモデルの確率推定値を導出する必要があったことを思い返されたい。これらのルックアップテーブルは、

に（または、一般的に言えば、Ｍコーダーのルックアップテーブルとは異なる２次元ルックアップテーブルに）組み込むことができる。

アプローチ１および２で確率推定値を計算する代わりに、サブインターバル幅は、例えば次のように、

の特定の値に対して直接計算される：
アプローチ１の場合、

が式（１）と式（７）の両側で乗算され、

になる。

次に、

は、必要な数の異なる量子化値

の事前計算された積

を含む２Ｄルックアップテーブルに置き換えられる。（実施形態の実際の実装の例）
結果として得られる２Ｄルックアップテーブルは、例えば、ブロック７３６および７３８で使用することができる。

アプローチ２の場合、

は式（２）の両側で乗算され、次のようになる。

（８）
次に、

は、所望の数の異なる量子化値

について事前に計算された積

を含む２Ｄルックアップテーブルに置き換えられる（実施形態の実際の実装の例）。

がこのような２Ｄルックアップテーブルであると、式（８）は次のようになる。

（９）
式（９）からわかるように、例えば、

を１つの単一のルックアップテーブルにおいて

と

に組み込む。

ＬＵＴ３、または式（９）は、例えば、ブロック７５６で使用することができる。
あるいは、ＬＵＴ３をＬＵＴ４（１Ｄ）に置き換え、代替案１として提示されたスキームに従って乗算演算を行うこともできる

関数

は、例えば

のように定義できる。

、

および

は圧縮アプリケーションによって異なる。
例えば、

、

、および

。
コンテキストモデル

に関連付けられたバイナリシンボルの算術符号化は、次いでサブインターバル幅

を導出するために、式（１０）に従って状態変数

の加重和を導出し、式（９）を実行することだけを必要とする。
同じ議論がアプローチ１にも当てはまる。

以下に、

を効率的に実装する（または間隔サイズ情報を導出する）ためのさらなる（任意選択の代替）方法を示す。ルックアップテーブル全体を格納する代わりに、要素は必要に応じてオンザフライで計算される。この目的のために、新しいルックアップテーブル

を定義する必要がある。これには、簡単な操作を使用して

の各要素を導出するために使用できる値が含まれている。

一般的に言えば、例えば、ＲａｎｇｅＴａｂＬＰＳ［ｉ］［ｊ］は、ブロック８７０で評価され得、ＲａｎｇｅＴａｂＬＰＳのエントリは、例えば、ＢａｓｅＴａｂＬＰＳおよび対応するスケーリング関数Ｓｃａｌ（ｘ，ｙ）（ＢａｓｅＴａｂＬＰＳを使用した実施形態）を使用するか、またはＰｒｏｂＴａｂＬＰＳと対応するスケーリング関数Ｓｃａｌ（ｘ，ｙ）（ＰｒｏｂＴａｂＬＰＳを使用した実施形態）を使用することで取得できる。

好ましい実施形態（例えば、ＢａｓｅＴａｂＬＰＳを使用する実施形態）では、

は、サイズ

であり、

サイズ

は以下のように

から生成されなければならない：

はスケーリング関数である。例えば、

、

、

、

、および

｛
｛１２５、１４０、１５６、１７１、１８７、２０３、２１８、２３４、｝、
｛１０８、１２１、１３５、１４８、１６２、１７５、１８９、２０２、｝、
｛９４、１０５、１１７、１２９、１４１、１５２、１６４、１７６、｝、
｛８１、９１、１０１、１１１、１２１、１３１、１４１、１５１、｝、
｛７１、７９、８８、９７、１０６、１１５、１２４、１３３、｝、
｛６１、６８、７６、８３、９１、９９、１０６、１１４、｝、
｛５３、５９、６６、７２、７９、８６、９２、９９、｝、
｛４６、５１、５７、６３、６９、７４、８０、８６、｝、
｛４０、４５、５０、５５、６０、６５、７０、７５、｝、
｛３５、３９、４３、４８、５２、５６、６１、６５、｝、
｛３１、３４、３８、４２、４６、５０、５４、５８、｝、
｛２７、３０、３３、３７、４０、４３、４７、５０、｝、
｛２４、２７、３０、３３、３６、３９、４２、４５、｝、
｛２１、２３、２６、２８、３１、３４、３６、３９、｝、
｛１８、２０、２２、２４、２７、２９、３１、３３、｝、
｛１６、１８、２０、２２、２４、２６、２８、３０、｝、
｝。（例）

言い換えると、例えば、

の上半分は、フロア操作が各要素に適用される

の値からなる（または構成される）。例えば、

の下半分は、各要素が８（または別の数値）で除算された

の値からなり（または構成され）、その後、フロア操作が続き、これは、例えば、３だけに右シフトに対応する。
このアプローチは、

よりも小さい値

を格納するだけでよく、例えば、

の行の値が行の増加に伴って指数関数的に減衰するという事実を利用する。指数関数的減衰はパラメータ

に依存する。

別の例（例えば、ＢａｓｅＴａｂＬＰＳを使用する別の実施形態）では、

、

、

、

、および

｛
｛１２１、１３６、１５１、１６６、１８１、１９６、２１１、２２６、｝、
｛１００、１１２、１２５、１３７、１５０、１６２、１７５、１８７、｝、
｛８３、９３、１０３、１１４、１２４、１３４、１４５、１５５、｝、
｛７０、７８、８７、９６、１０５、１１３、１２２、１３１、｝
｝。（例）
この構成は、

が

の行の値が４行ごとに半分になるように選択されている場合に、使用できる。

の値は、例えば、

に関連付けられたから簡単に抽出できることに留意されたい。

関与するアプローチ

は、（任意選択で）式（１１）および関連する好ましい実施形態で定義される代替案１と結合することができる。代替案１は、１つの定数からの

の行と計算演算（各行）を導出するためのアプローチと見なすことができる。例えば、

は、（丸めを無視して）

のスケーリングされた行が含まれているため、代替案１を適用して

を導出できる。

好ましい実施形態（例えば、別の実施形態、例えば、ＰｒｏｂＴａｂＬＰＳを使用する実施形態）では、サイズ

の

が定義される。サイズ

の

は、例えば、

から次のように生成される。

例えば、

、

、

、

、

、

および

｛
１２５、
１０８、
９４、
８１、
７１、
６１、
５３、
４６、
４０、
３５、
３１、
２７、
２４、
２１、
１８、
１６、
｝。（例）

次に、

は前述のアプローチに従って

から計算できる。

の各値は、例えば、

の関連する値を計算してからスケーリング関数

を適用することにより、オンザフライで計算できることに留意されたい：

このアプローチでは、

より、したがって

よりも小さい

を格納することだけを要する。

同じ議論に続いて、例えば、

の１つの列は、

および

のその他すべての列を単に無視することによって、

の１つの列のみを導出するために使用できる。次に、

の導出列などを使用して、式（１１）に従って代替１を使用することにより、

の残りの列を導出させることができる。

好ましい実施形態では、サイズ

の

が定義される。

サイズの

は、次のように

から生成される：

を留意されたい（例）
状態変数の更新（発明の態様）
シンボルの符号化または復号の後、シンボルシーケンスの統計的動作を追跡するために、コンテキストモデルの１つまたは複数の状態変数を更新することができる。これは、例えば、ブロック６４０で行うことができる。

更新は、例えば、次のように実行される：

（３）

は整数値を格納するルックアップテーブルである。

と

は、更新の「敏捷性」を制御する重み付け係数である。

はルックアップテーブル

が負でない値でのみアクセスされることを保証するオフセットである。

以下で説明するように、ルックアップテーブル

の値は、

が特定の所与の間隔にとどまるように選択できる。
あるいは、例えば、以下のように、式（３）の各実行後に実行されるクリッピング操作を導入することが可能である：

（６）

は

の最大許容値である

は

の最小許容値である

圧縮アプリケーションに関してルックアップテーブルＡを最適化するために、ルックアップテーブルＡの値で近似される想定される関数を計算操作に置き換えることもできる。例えば、

（７）

、

、および

は、確率更新の動作を制御するパラメータである。

ルックアップテーブルＡを作成するこの方法には、上記のようなクリッピング操作が含まれていないことに留意されたい。ルックアップテーブルＡは、式７の

の様々な結合の圧縮効率を評価し、続いて目的の値

で

をサンプリングすることによって最適化できる。

特定のエンコーダまたはデコーダアプリケーションは、計算操作を使用するか、同等のテーブル（計算操作によって導出された値を含む）を使用するかを選択できる。
ビデオ圧縮コンテキストのルックアップテーブルＡを最適化するために、次の範囲の可能な構成が使用される：

式（３）の任意選択の変更
最適化されたソフトウェア実装でより高いスループットを達成するために、２つの任意選択の変更を式（３）に適用できる。
第１の任意選択の変更では、式（３）は次のように置き換えられる：

式（３ａ）
第２の任意選択の変更では、式（３）は次のように置き換えられる：

式（３ｂ）
第１および第２の任意選択の変更の結合の場合、式（３）は次のように置き換えられる：

式（３ｃ）

第１および第２の任意選択の変更の結合を採用することにより、ケースの区別をルックアップテーブル

に統合することが可能になり、ルックアップテーブルは、以前の２倍の要素数しか必要としない。ただし、高スループットを実現するには、演算の数を減らすと役立つ場合があるが、ルックアップテーブルのサイズを大きくすると関連性が低くなる場合がある。
さらに通知することなく、２つの任意選択の変更（個別にまたは組み合わせて）を、本発明の式３のすべての適用例に適用することができる。

好ましい実施形態（詳細は任意選択である）
好ましい実施形態では、以下の構成が使用される：
コンテキストモデル

の数は、圧縮アプリケーションによって異なる。
アプローチ２は、状態変数から確率推定値を導出するために使用される。

式（３）は、状態変数の更新に使用される。
式（６）による任意選択のクリッピングは使用されない。

シンボルを符号化する前に、

は間隔

の値で初期化され、

は間隔

の値で初期化される。
この構成の場合、式（３）は次のように記述できる：

（４）

（５）

が間隔

内にある場合、式（４）は、符号化されるシンボルの値に関係なく、同じ間隔内にとどまる

に対する更新された値を生成する。

が間隔

内にある場合、式（５）は、符号化されるシンボルの値に関係なく、同じ間隔内にとどまる

に対する更新された値を生成する。

したがって、

は例えば、８ビットの符号付き整数値で実装でき、

は１２ビットの符号付き整数で実装できる。
どちらの式も、１を符号化した後に状態変数を（最大値まで）増加させ、０を符号化した後に状態変数を（最小値まで）減少させる。ただし、式（４）は、

に関して式（５）の場合よりも大幅に

を増減する傾向がある。言い換えると、

は以前に符号化されたシンボルに速く適合し、一方で

はゆっくりと適合する。

別の好ましい実施形態では、前の好ましい実施形態と同じ構成が使用されるが、第１および第２の任意の修正が式（３）に適用されて、以下が得られる：

ルックアップテーブル

と

は通常、特定の圧縮アプリケーションに最適化されていることに留意されたい。
ルックアップテーブルＡが最適化されると、次の構成が式（７）で使用される：

その結果、

Ａはすでにクリップされているため、最後の値は４ではなく０に等しいことに留意されたい。
別の好ましい実施形態では、構成は、以下の態様を除いて、前の好ましい実施形態と同一である：
式（６）に従ったクリッピングは、次のパラメータを使用して式（３）を実行するたびに使用される：

ルックアップテーブル

には、次の値が含まれている。

ルックアップテーブル

の最後の要素のみが変更され、現在、

の後半のすべての値に値

があり、効率的に実装できることに留意されたい。
ルックアップテーブルが最初の

の後に切り捨てられ、テーブルのアクセスインデックスが最後のテーブル要素にクリップされると想像されたい（実施形態の任意選択の変更）。
このトリックは、テーブルの最後にあるいくつかの要素が同じ値である限り、任意選択でルックアップテーブル

の様々なバージョンに使用できる。
別の好ましい実施形態では、構成は、以下の態様を除いて、前の好ましい実施形態と同一である：
サイズ３２の代替案１が使用される

別の好ましい実施形態では、構成は、前の好ましい実施形態と同一である：

別の好ましい実施形態では、構成は、以下の態様を除いて、前の好ましい実施形態と同一である。
サイズ１６の代替案１が使用される

別の好ましい実施形態では、構成は、前の好ましい実施形態と同一である：

別の好ましい実施形態では、以下の構成が使用される：
コンテキストモデル

の数は、圧縮アプリケーションによって異なる。
アプローチ２は、状態変数から確率推定値を導出するために使用される。
式（３）は、状態変数の更新に使用される。
式（６）による任意選択のクリッピングは使用されない。

シンボルを符号化する前に、

は任意選択で間隔

からの値で初期化する必要がある。

別の好ましい実施形態では、アプローチ２が使用され、パラメータ

、

、および

は、異なるコンテキストモデルに対して異なる確率更新動作を得るために、異なるコンテキストモデルに対して異なるように設定される。

別の好ましい実施形態では、アプローチ１が使用され、パラメータ

、

、および

は、異なるコンテキストモデルに対して異なる確率更新動作を得るために、異なるコンテキストモデルに対して異なるように設定される。別の好ましい実施形態では、アプローチ１またはアプローチ２が使用される場合、Ｎ＝１およびパラメータ

、

、および

は、異なるコンテキストモデルに対して異なる確率更新動作を得るために、異なるコンテキストモデルに対して異なるように設定され、

ルックアップテーブルＡが最適化されると、次の構成が式（７）で使用される：

その結果、

Ａはすでにクリップされているため、最後の値は４ではなく０に等しいことに留意されたい。

別の好ましい実施形態では、アプローチ１またはアプローチ２が使用される場合、Ｎ＝２およびパラメータ

、

、および

は、異なるコンテキストモデルに対して異なる確率更新動作を得るために、異なるコンテキストモデルに対して異なるように設定される。
ルックアップテーブルＡが最適化されると、次の構成が式（７）で使用される。

その結果、

あるいは、

はまた、

に至るこの実施形態における所望の構成である。Ａがすでにクリップされており、したがって、最後の値は４ではなく０に等しいことに留意されたい。

１９．実装の代替
いくつかの態様は、装置の文脈で説明されているが、これらの態様が、対応する方法の説明も表すことは明らかであり、ブロックまたはデバイスは、方法ステップまたは方法ステップの特徴に対応する。同様に、方法ステップの文脈で説明された態様は、対応する装置の対応するブロックまたはアイテムまたは特徴の説明も表す。方法ステップの一部またはすべては、例えば、マイクロプロセッサ、プログラム可能なコンピュータ、または電子回路などのハードウェア装置によって（または使用して）実行することができる。いくつかの実施形態では、最も重要な方法ステップの１つまたは複数は、そのような装置によって実行され得る。

特定の実装要件に応じて、本発明の実施形態は、ハードウェアまたはソフトウェアで実装することができる。実装は、フロッピーディスク、ＤＶＤ、ブルーレイ、ＣＤ、ＲＯＭ、ＰＲＯＭ、ＥＰＲＯＭ、ＥＥＰＲＯＭ、フラッシュメモリなどのデジタル記憶媒体を使用して実行でき、電子的に読み取り可能な制御信号が格納されて、それぞれの方法が実行されるように、プログラム可能なコンピュータシステムと協働する（または協働することができる）。したがって、デジタル記憶媒体は、コンピュータ可読であり得る。

本発明によるいくつかの実施形態は、本明細書に記載の方法の１つが実行されるように、プログラム可能なコンピュータシステムと協働することができる電子的に読み取り可能な制御信号を有するデータキャリアを含む。
一般に、本発明の実施形態は、プログラムコードを有するコンピュータプログラム製品として実装することができ、プログラムコードは、コンピュータプログラム製品がコンピュータ上で実行されるときに方法の１つを実行するように動作する。プログラムコードは、例えば、機械可読キャリアに格納されてもよい。

他の実施形態は、機械可読キャリアに記憶された、本明細書に記載された方法の１つを実行するためのコンピュータプログラムを含む。
言い換えれば、本発明の方法の実施形態は、したがって、コンピュータプログラムがコンピュータ上で実行されるときに、本明細書で説明される方法の１つを実行するためのプログラムコードを有するコンピュータプログラムである。

したがって、本発明の方法のさらなる実施形態は、本明細書に記載の方法の１つを実行するためのコンピュータプログラムを記録し含むデータキャリア（またはデジタル記憶媒体、またはコンピュータ可読媒体）である。データキャリア、デジタル記憶媒体、または記録された媒体は、通常、有形および／または非過渡的である。
したがって、本発明の方法のさらなる実施形態は、本明細書で説明される方法の１つを実行するためのコンピュータプログラムを表すデータストリームまたは信号のシーケンスである。データストリームまたは信号のシーケンスは、例えば、インターネットなどのデータ通信接続を介して転送されるように構成されてもよい。

さらなる実施形態は、本明細書に記載された方法の１つを実行するように構成または適合された処理手段、例えば、コンピュータまたはプログラム可能な論理デバイスを含む。
さらなる実施形態は、本明細書に記載される方法の１つを実行するためのコンピュータプログラムがインストールされているコンピュータを含む。

本発明によるさらなる実施形態は、本明細書に記載の方法の１つを実行するためのコンピュータプログラムを（例えば、電子的または光学的に）受信機に転送するように構成された装置またはシステムを含む。受信機は、例えば、コンピュータ、モバイルデバイス、メモリデバイスなどであり得る。装置またはシステムは、例えば、コンピュータプログラムを受信機に転送するためのファイルサーバを含み得る。

いくつかの実施形態では、プログラマブルロジックデバイス（例えば、フィールドプログラマブルゲートアレイ）を使用して、本明細書に記載されている方法の機能の一部またはすべてを実行することができる。いくつかの実施形態では、フィールドプログラマブルゲートアレイは、本明細書で説明される方法の１つを実行するために、マイクロプロセッサと協働し得る。一般に、方法は、好ましくは、任意のハードウェア装置によって実行される。

本明細書で説明する装置は、ハードウェア装置を使用して、またはコンピュータを使用して、またはハードウェア装置とコンピュータの組み合わせを使用して実装することができる。
本明細書で説明される装置、または本明細書で説明される装置の任意のコンポーネントは、少なくとも部分的にハードウェアおよび／またはソフトウェアで実装され得る。

本明細書で説明する方法は、ハードウェア装置を使用して、またはコンピュータを使用して、またはハードウェア装置とコンピュータの組み合わせを使用して実行することができる。
本明細書で説明される方法、または本明細書で説明される装置の任意のコンポーネントは、ハードウェアおよび／またはソフトウェアによって少なくとも部分的に実行され得る。

本明細書に記載の実施形態は、本発明の原理を単に例示するものである。本明細書に記載の配置および細部の修正および変形は、当業者には明らかであることが理解される。したがって、本明細書の実施形態の記載および説明として提示される特定の細部によってではなく、間近の特許請求の範囲によってのみ制限されることが意図されている。
算術エンコーダ、算術デコーダ、ビデオエンコーダ、ビデオデコーダ、符号化方法、復号方法、およびコンピュータプログラム

Claims (31)

1. シンボル値を有する複数のシンボル（２４’’；５２０；１６２２；１７２２）を復号するための算術デコーダ（５０；５００；１６２０；１７２０）であって、
   前記算術デコーダは、１つまたは複数の状態変数値（ｓ_１ ^ｋ、ｓ_２ ^ｋ；６４２、６４４；７１０；８１０；９１０；１０１０ａ、１０１０ｂ；１０８２ａ、１０８２ｂ；１１１０；１２１０；１３１０；１４１０；１５１０；１６３２，１６４２；１７３２、１７４２）を決定するように構成され、これは、以前に符号化された複数のシンボル値の統計を表し、および
   前記算術デコーダは、前記１つまたは複数の状態変数値（ｓ_ｉ ^ｋ）に基づいて復号される１つまたは複数のシンボル値の算術復号の間隔サイズ情報（ｐ^ｋ、Ｒ＊ｐ^ｋ）を導出するように構成され、これは複数の以前に復号されたシンボル値の統計を表し、
   前記算術デコーダは、復号されるシンボルに依存して、ルックアップテーブル（Ａ）を使用して、第１の状態変数値（ｓ^ｋ _１）を更新するように構成され、
   前記算術デコーダは、以前の状態変数値を、復号されるシンボルが第１の値をとる場合に、前記以前の状態変数値が正である場合と比較して、前記以前の状態変数値が負である場合に、比較的大きい値だけ増加させるように構成され、
   前記算術デコーダは、以前の状態変数値を、復号されるシンボルが、前記第１の値とは異なる第２の値をとる場合に、前記以前の状態変数値が負である場合と比較して、前記以前の状態変数値が正である場合に、比較的大きい値だけ減少させるように構成される、算術デコーダ。
2. 前記算術デコーダは、復号されるシンボルに依存して、前記ルックアップテーブル（Ａ）を使用して、第２の状態変数値（ｓ^ｋ _２）を更新するように構成される、請求項１に記載の算術デコーダ。
3. 前記算術デコーダは、異なる適合時定数を使用して、前記第１の状態変数値および第２の状態変数値を更新するように構成されている、請求項１または請求項２に記載の算術デコーダ。
4. 前記算術デコーダは、復号されるシンボルが第１の値をとるか、前記第１の値とは異なる第２の値をとるかに応じて、前記ルックアップテーブルを使用して決定された値によって以前の状態変数値を選択的に増減するように構成される、請求項１または請求項２または請求項３に記載の算術デコーダ。
5. 前記算術デコーダは、復号されるシンボルが第１の値をとる場合、所定のオフセット値（ｚ）と以前に計算された第１の状態変数値（
   

   

   ）、またはそのスケーリングおよび／または丸められたバージョン（
   

   

   ）の合計に依存して、前記第１の状態変数値を更新するときに評価される前記ルックアップテーブルのエントリのインデックスを決定するように構成され、
   前記算術デコーダは、復号されるシンボルが第２の値をとる場合、所定のオフセット値（ｚ）と以前に計算された第１の状態変数値の逆バージョン（
   

   

   ）、またはそのスケーリングおよび／または丸められたバージョン（
   

   

   ）の合計に依存して、前記第１の状態変数値を更新するときに評価される前記ルックアップテーブルのエントリのインデックスを決定するように構成される、請求項１から４のいずれか一項に記載の算術デコーダ。
6. 前記算術デコーダは、復号されるシンボルが第１の値をとる場合、所定のオフセット値（ｚ）と以前に計算された第２の状態変数値（
   

   

   ）、またはそのスケーリングおよび／または丸められたバージョン（
   

   

   ）の合計に依存して、第２の状態変数値を更新するときに評価される前記ルックアップテーブルのエントリのインデックスを決定するように構成され、
   前記算術デコーダは、復号されるシンボルが第２の値をとる場合、所定のオフセット値（ｚ）と以前に計算された第２の状態変数値の逆バージョン（
   

   

   ）、またはそのスケーリングおよび／または丸められたバージョン（
   

   

   ）の合計に依存して、前記第２の状態変数値を更新するときに評価される前記ルックアップテーブルのエントリのインデックスを決定するように構成される、請求項１から５のいずれか一項に記載の算術デコーダ。
7. 前記算術デコーダは、前記第１の状態変数値を更新するときに第１のスケーリング値を使用して前記ルックアップテーブルの評価によって返される値をスケーリングするように構成され、
   前記算術デコーダは、第２の状態変数値を更新するときに第２のスケーリング値を使用して前記ルックアップテーブルの評価によって返される値をスケーリングするように構成され、
   前記第１のスケーリング値は前記第２のスケーリング値とは異なる、請求項１から６のいずれか一項に記載の算術デコーダ。
8. 前記算術デコーダは、
   

   

   Ａはルックアップテーブルであり、
   ｚは所定のオフセット値であり、
   

   

   は１つまたは複数の重み付け値であり、
   

   

   は１つまたは複数の重み付け値である
   ことに従って、１つまたは複数の更新された状態変数値
   

   

   を決定するように構成される、請求項１から７のいずれか一項に記載の算術デコーダ。
9. 前記算術デコーダは、
   

   

   Ａはルックアップテーブルであり、
   ｚは所定のオフセット値であり、
   

   

   は１つまたは複数の重み付け値であり、
   

   

   は１つまたは複数の重み付け値である
   ことに従って、１つまたは複数の更新された状態変数値
   

   

   を決定するように構成される、請求項１から７のいずれか一項に記載の算術デコーダ。
10. 前記算術デコーダは、
    

    

    Ａはルックアップテーブルであり、
    ｚは所定のオフセット値であり、
    

    

    は１つまたは複数の重み付け値であり、
    

    

    は１つまたは複数の重み付け値である
    ことに従って、１つまたは複数の更新された状態変数値
    

    

    を決定するように構成される、請求項１から７のいずれか一項に記載の算術デコーダ。
11. 前記算術デコーダは、
    

    

    Ａはルックアップテーブルであり、
    ｚは所定のオフセット値であり、
    

    

    は１つまたは複数の重み付け値であり、
    

    

    は１つまたは複数の重み付け値である
    ことに従って、１つまたは複数の更新された状態変数値
    

    

    を決定するように構成される、請求項１から７のいずれか一項に記載の算術デコーダ。
12. Ａのエントリは、ルックアップテーブルインデックスの増加とともに単調に減少する、請求項８から１１のいずれか一項に記載の算術デコーダ。
13. Ａは
    

    

    または、ゼロ設定または大きさの減少によって、引数の１つまたは複数の極値についてのみそこから逸脱して、前記更新された
    

    

    が所定の値の範囲を残すのを回避し、
    

    

    、
    

    

    、
    

    

    、および
    

    

    は所定のパラメータである、請求項８から１２のいずれか一項に記載の算術デコーダ。
14. 前記ルックアップテーブルの最後のエントリはゼロに等しい、請求項１から１３のいずれか一項に記載の算術デコーダ。
15. 

    

    である、請求項８から１４のいずれか一項に記載の算術デコーダ。
16. 前記算術デコーダは、前記更新された状態変数値にクリッピング操作を適用して、前記更新されクリップされた状態変数値を所定の値の範囲内に保つように構成される、請求項１から１５のいずれか一項に記載の算術デコーダ。
17. 前記算術デコーダは、
    前記更新された状態変数値に、
    

    

    、に従ってクリッピング操作を適用するように構成され、
    

    

    は、
    

    

    の最大許容値であり、
    

    

    は、
    

    

    の最小許容値である、請求項１６に記載の算術デコーダ。
18. 前記算術デコーダは、異なるコンテキストに異なるスケーリング値を適用するように構成されており、前記異なるコンテキストは、異なる統計特性を有する、請求項１から１７のいずれか一項に記載の算術デコーダ。
19. シンボル値を有する複数のシンボル（２４’’、４１０）を符号化するための算術エンコーダ（３４；４００）であって、
    前記算術エンコーダは、１つまたは複数の状態変数値（ｓ_１ ^ｋ、ｓ_２ ^ｋ；６４２、６４４；７１０；８１０；９１０；１０１０ａ、１０１０ｂ；１０８２ａ、１０８２ｂ；１１１０；１２１０；１３１０；１４１０；１５１０；１６３２，１６４２；１７３２、１７４２）を決定するように構成され、これは、以前に符号化された複数のシンボル値の統計を表し、および
    前記算術エンコーダは、前記１つまたは複数の状態変数値（ｓ_ｉ ^ｋ）に基づいて符号化される１つまたは複数のシンボル値の算術符号化の間隔サイズ情報（ｐ^ｋ、Ｒ＊ｐ^ｋ；４３２；５３４；６２０；７２０；８２０；８２０；１０２０；１０８４；１１２０；１３２０；１４２０；１５２０；１６６２；１７６２）を導出するように構成され、これは複数の以前に符号化されたシンボル値の統計を表し、
    前記算術エンコーダは、符号化されるシンボルに依存して、ルックアップテーブル（Ａ）を使用して、第１の状態変数値（ｓ^ｋ _１）を更新するように構成され、
    前記算術エンコーダは、
    

    

    Ａはルックアップテーブルであり、
    ｚは所定のオフセット値であり、
    

    

    は１つまたは複数の重み付け値であり、
    

    

    は１つまたは複数の重み付け値である
    ことに従って、１つまたは複数の更新された状態変数値
    

    

    を決定するように構成される、算術エンコーダ。
20. シンボル値を有する複数のシンボル（２４’’、４１０）を符号化するための算術エンコーダ（３４；４００）であって、
    前記算術エンコーダは、１つまたは複数の状態変数値（ｓ_１ ^ｋ、ｓ_２ ^ｋ；６４２、６４４；７１０；８１０；９１０；１０１０ａ、１０１０ｂ；１０８２ａ、１０８２ｂ；１１１０；１２１０；１３１０；１４１０；１５１０；１６３２，１６４２；１７３２、１７４２）を決定するように構成され、これは、以前に符号化された複数のシンボル値の統計を表し、および
    前記算術エンコーダは、前記１つまたは複数の状態変数値（ｓ_ｉ ^ｋ）に基づいて符号化される１つまたは複数のシンボル値の算術符号化の間隔サイズ情報（ｐ^ｋ、Ｒ＊ｐ^ｋ；４３２；５３４；６２０；７２０；８２０；８２０；１０２０；１０８４；１１２０；１３２０；１４２０；１５２０；１６６２；１７６２）を導出するように構成され、これは複数の以前に符号化されたシンボル値の統計を表し、
    前記算術エンコーダは、符号化されるシンボルに依存して、ルックアップテーブル（Ａ）を使用して、第１の状態変数値（ｓ^ｋ _１）を更新するように構成され、
    前記算術エンコーダは、
    

    

    Ａはルックアップテーブルであり、
    ｚは所定のオフセット値であり、
    

    

    は１つまたは複数の重み付け値であり、
    

    

    は１つまたは複数の重み付け値である
    ことに従って、１つまたは複数の更新された状態変数値
    

    

    を決定するように構成される、算術エンコーダ。
21. シンボル値を有する複数のシンボル（２４’’、４１０）を符号化するための算術エンコーダ（３４；４００）であって、
    前記算術エンコーダは、１つまたは複数の状態変数値（ｓ_１ ^ｋ、ｓ_２ ^ｋ；６４２、６４４；７１０；８１０；９１０；１０１０ａ、１０１０ｂ；１０８２ａ、１０８２ｂ；１１１０；１２１０；１３１０；１４１０；１５１０；１６３２，１６４２；１７３２、１７４２）を決定するように構成され、これは、以前に符号化された複数のシンボル値の統計を表し、および
    前記算術エンコーダは、前記１つまたは複数の状態変数値（ｓ_ｉ ^ｋ）に基づいて符号化される１つまたは複数のシンボル値の算術符号化の間隔サイズ情報（ｐ^ｋ、Ｒ＊ｐ^ｋ；４３２；５３４；６２０；７２０；８２０；８２０；１０２０；１０８４；１１２０；１３２０；１４２０；１５２０；１６６２；１７６２）を導出するように構成され、これは複数の以前に符号化されたシンボル値の統計を表し、
    前記算術エンコーダは、符号化されるシンボルに依存して、ルックアップテーブル（Ａ）を使用して、第１の状態変数値（ｓ^ｋ _１）を更新するように構成され、
    前記算術エンコーダは、
    

    

    Ａはルックアップテーブルであり、
    ｚは所定のオフセット値であり、
    

    

    は１つまたは複数の重み付け値であり、
    

    

    は１つまたは複数の重み付け値である
    ことに従って、１つまたは複数の更新された状態変数値
    

    

    を決定するように構成される、算術エンコーダ。
22. シンボル値を有する複数のシンボル（２４’’、４１０）を符号化するための算術エンコーダ（３４；４００）であって、
    前記算術エンコーダは、１つまたは複数の状態変数値（ｓ_１ ^ｋ、ｓ_２ ^ｋ；６４２、６４４；７１０；８１０；９１０；１０１０ａ、１０１０ｂ；１０８２ａ、１０８２ｂ；１１１０；１２１０；１３１０；１４１０；１５１０；１６３２，１６４２；１７３２、１７４２）を決定するように構成され、これは、以前に符号化された複数のシンボル値の統計を表し、および
    前記算術エンコーダは、前記１つまたは複数の状態変数値（ｓ_ｉ ^ｋ）に基づいて符号化される１つまたは複数のシンボル値の算術符号化の間隔サイズ情報（ｐ^ｋ、Ｒ＊ｐ^ｋ；４３２；５３４；６２０；７２０；８２０；８２０；１０２０；１０８４；１１２０；１３２０；１４２０；１５２０；１６６２；１７６２）を導出するように構成され、これは複数の以前に符号化されたシンボル値の統計を表し、
    前記算術エンコーダは、符号化されるシンボルに依存して、ルックアップテーブル（Ａ）を使用して、第１の状態変数値（ｓ^ｋ _１）を更新するように構成され、
    前記算術エンコーダは、
    

    

    Ａはルックアップテーブルであり、
    ｚは所定のオフセット値であり、
    

    

    は１つまたは複数の重み付け値であり、
    

    

    は１つまたは複数の重み付け値である
    ことに従って、１つまたは複数の更新された状態変数値
    

    

    を決定するように構成される、算術エンコーダ。
23. 

    

    である、請求項１９から２２のいずれか一項に記載の算術エンコーダ。
24. ビデオデコーダ（２０；１６００；１７００）であって、
    前記ビデオデコーダは、複数のビデオフレーム（１２’）を復号するように構成され、
    前記ビデオデコーダは、請求項１に記載の、バイナリシーケンスの符号化表現（１４；５１０；１６１０；１７１０）に基づいて復号されたバイナリシーケンス（２４’’、５２０；１６２２；１７２２）を提供するための算術デコーダ（５０；５００；１６２０；１７２０）を備え、
    前記バイナリシーケンスは、前記複数のビデオフレームのビデオコンテンツを表す、ビデオデコーダ。
25. ビデオエンコーダ（１０）であって、
    前記ビデオエンコーダは、複数のビデオフレーム（１２）を符号化するように構成され、
    前記ビデオエンコーダは、請求項１８に記載の、前記複数のビデオフレームのビデオコンテンツを表すバイナリ値（４１０）のシーケンスに基づいて符号化されたバイナリシーケンス（４２０）を提供するための算術エンコーダ（３４；４００）を備える、ビデオエンコーダ。
26. シンボル値を有する複数のシンボルを復号するための方法であって、
    前記方法は、１つまたは複数の状態変数値（ｓ_１ ^ｋ、ｓ_２ ^ｋ）を決定することを含み、これは、以前に復号された複数のシンボル値の統計を表し、および
    前記方法は、前記１つまたは複数の状態変数値（ｓ_ｉ ^ｋ）に基づいて復号される１つまたは複数のシンボル値の算術復号の間隔サイズ情報（ｐ^ｋ、Ｒ＊ｐ^ｋ）を導出することを含み、これは複数の以前に復号されたシンボル値の統計を表し、
    前記方法は、復号されるシンボルに依存して、ルックアップテーブル（Ａ）を使用して、第１の状態変数値（ｓ^ｋ _１）を更新することを含み、
    前記方法は、以前の状態変数値を、復号されるシンボルが第１の値をとる場合に、前記以前の状態変数値が正である場合と比較して、前記以前の状態変数値が負である場合に、比較的大きい値だけ増加させることを含み、
    前記方法は、以前の状態変数値を、復号されるシンボルが、前記第１の値とは異なる第２の値をとる場合に、前記以前の状態変数値が負である場合と比較して、前記以前の状態変数値が正である場合に、比較的大きい値だけ減少させることを含む、方法。
27. シンボル値を有する複数のシンボルを符号化するための方法であって、
    前記方法は、１つまたは複数の状態変数値（ｓ_１ ^ｋ、ｓ_２ ^ｋ）を決定することを含み、これは、以前に符号化された複数のシンボル値の統計を表し、および
    前記方法は、前記１つまたは複数の状態変数値（ｓ_ｉ ^ｋ）に基づいて符号化される１つまたは複数のシンボル値の算術符号化の間隔サイズ情報（ｐ^ｋ、Ｒ＊ｐ^ｋ）を導出することを含み、これは複数の以前に符号化されたシンボル値の統計を表し、
    前記方法は、符号化されるシンボルに依存して、ルックアップテーブル（Ａ）を使用して、第１の状態変数値（ｓ^ｋ _１）を更新することを含み、
    前記方法は、
    

    

    Ａはルックアップテーブルであり、
    ｚは所定のオフセット値であり、
    

    

    は１つまたは複数の重み付け値であり、
    

    

    は１つまたは複数の重み付け値である
    ことに従って、１つまたは複数の更新された状態変数値
    

    

    を決定することを含む、方法。
28. シンボル値を有する複数のシンボルを符号化するための方法であって、
    前記方法は、１つまたは複数の状態変数値（ｓ_１ ^ｋ、ｓ_２ ^ｋ）を決定することを含み、これは、以前に符号化された複数のシンボル値の統計を表し、および
    前記方法は、前記１つまたは複数の状態変数値（ｓ_ｉ ^ｋ）に基づいて符号化される１つまたは複数のシンボル値の算術符号化の間隔サイズ情報（ｐ^ｋ、Ｒ＊ｐ^ｋ）を導出することを含み、これは複数の以前に符号化されたシンボル値の統計を表し、
    前記方法は、符号化されるシンボルに依存して、ルックアップテーブル（Ａ）を使用して、第１の状態変数値（ｓ^ｋ _１）を更新することを含み、
    前記方法は、
    

    

    Ａはルックアップテーブルであり、
    ｚは所定のオフセット値であり、
    

    

    は１つまたは複数の重み付け値であり、
    

    

    は１つまたは複数の重み付け値である
    ことに従って、１つまたは複数の更新された状態変数値
    

    

    を決定することを含む、方法。
29. シンボル値を有する複数のシンボルを符号化するための方法であって、
    前記方法は、１つまたは複数の状態変数値（ｓ_１ ^ｋ、ｓ_２ ^ｋ）を決定することを含み、これは、以前に符号化された複数のシンボル値の統計を表し、および
    前記方法は、前記１つまたは複数の状態変数値（ｓ_ｉ ^ｋ）に基づいて符号化される１つまたは複数のシンボル値の算術符号化の間隔サイズ情報（ｐ^ｋ、Ｒ＊ｐ^ｋ）を導出することを含み、これは複数の以前に符号化されたシンボル値の統計を表し、
    前記方法は、符号化されるシンボルに依存して、ルックアップテーブル（Ａ）を使用して、第１の状態変数値（ｓ^ｋ _１）を更新することを含み、
    前記方法は、
    

    

    Ａはルックアップテーブルであり、
    ｚは所定のオフセット値であり、
    

    

    は１つまたは複数の重み付け値であり、
    

    

    は１つまたは複数の重み付け値である
    ことに従って、１つまたは複数の更新された状態変数値
    

    

    を決定することを含む、方法。
30. シンボル値を有する複数のシンボルを符号化するための方法であって、
    前記方法は、１つまたは複数の状態変数値（ｓ_１ ^ｋ、ｓ_２ ^ｋ）を決定することを含み、これは、以前に符号化された複数のシンボル値の統計を表し、および
    前記方法は、前記１つまたは複数の状態変数値（ｓ_ｉ ^ｋ）に基づいて符号化される１つまたは複数のシンボル値の算術符号化の間隔サイズ情報（ｐ^ｋ、Ｒ＊ｐ^ｋ）を導出することを含み、これは複数の以前に符号化されたシンボル値の統計を表し、
    前記方法は、符号化されるシンボルに依存して、ルックアップテーブル（Ａ）を使用して、第１の状態変数値（ｓ^ｋ _１）を更新することを含み、
    前記方法は、
    

    

    Ａはルックアップテーブルであり、
    ｚは所定のオフセット値であり、
    

    

    は１つまたは複数の重み付け値であり、
    

    

    は１つまたは複数の重み付け値である
    ことに従って、１つまたは複数の更新された状態変数値
    

    

    を決定することを含む、方法。
31. コンピュータに方法を実行させるためのコンピュータプログラムであって、前記方法として、請求項２６から３０のいずれか一項に記載の方法を実行させるコンピュータプログラム。

Images