JP6341931B2 - 更新確率値を格納する共用確率的カウンタを実施するシステムおよび方法 - Google Patents

Description

背景
開示の分野
この開示は、共用統計カウンタに関し、より具体的には、共用統計カウンタへのアクセスを含むアプリケーションの性能を向上させる技術に関する。

関連技術の説明
マルチコアアーキテクチャ設計における現在の傾向は、シンプルなバスベースの設計から分散型不均一メモリアクセス（ＮＵＭＡ）およびキャッシュ干渉性ＮＵＭＡ（ＣＣ−ＮＵＭＡ）アーキテクチャへの移行が将来的に加速することを暗に示している。ＮＵＭＡにおいて、所与のアクセスについてのメモリアクセス時間は、プロセッサに対するアクセスされるメモリの位置に依存する。このようなアーキテクチャは、通常、速いローカルメモリ（たとえば、プロセッサに対して密接に結合される、および／または同じ単一マルチコアチップ上に位置するメモリ）を有する演算コアの集合から構成され、より遅い（チップ間）通信媒体を介して互いに通信する。このようなシステムにおいて、プロセッサは、通常、非ローカルメモリよりも速い、自己のキャッシュメモリなどの自己のローカルメモリにアクセスし得る。一部のシステムにおいて、非ローカルメモリは、プロセッサ間で共用されるメモリの１つ以上のバンク、および／または他のプロセッサのローカルのメモリを含み得る。多くのＮＵＭＡシステムを含む一部のシステムは、他のプロセッサコアのキャッシュに対するアクセス時間が要求側コアからの物理的距離に応じて変化する不均一通信アーキテクチャ（ＮＵＣＡ）特性を提供する。これらのシステムにおいて、コアによるローカルメモリへのアクセス、および特定的には共用ローカルキャッシュへのアクセスは、リモートメモリ（たとえば、他のチップ上に位置するキャッシュ）へのアクセスよりも数倍（またはそれ以上）速い。

大きなソフトウェアシステムの多くは、性能監視および診断のために統計カウンタを使用する。たとえば、統計カウンタは、過度に割合の高い様々なシステム事象の検知などの目的のために、または事象頻度に基づいて適応する機構のために、実際に重要である。シングルスレッド統計カウンタは問題とならない一方、一般に使用されるナイーブ同時実施は、特にスレッドカウントが大きくなと直ちに問題となる。たとえば、システムが大きくなり、不均一メモリアクセス（ＮＵＭＡ）システムにおいて統計カウンタが使用されると、一般に使用されるナイーブカウンタは、スケーラビリティのボトルネック、および／またはそれらが有用でなくなるような不正確性を課すこととなる。特に、これらのカウンタは、（スレッド間で共用されると）カウンタの変更のすべてにおいて無効化トラフィックを引き起こし得て、これはＮＵＭＡマシンにおいては特にコストがかかる。

並行してトランザクションを実行する能力は、スケーラブル性能の鍵となる。しかしながら、統計（たとえば、どのくらい頻度でコードが実行されるのか、ハッシュテーブルには要素がいくつあるのかなどについての統計）を収集するために共用カウンタを使用することは、トランザクション内でカウンタへのアクセスが発生した時にトランザクション成功率にマイナスの影響を与え得る（異なるトランザクションまたはスレッドによる共用カウンタに対する任意の２つの更新は、互いにコンフリクトする可能性があるため）。この問題を解決するための一部の以前の手法は、カウンタを更新する演算をトランザクションの外へ移動させてプログラムのセマンティクスを変更すること、またはすべての状況において適用できない複雑かつ高額な「トランザクションブースティング（transactional boosting）」の支持を実施することを含む。

これらおよびその他の理由から、アプリケーション設計者は、軽度に競合するカウンタに課されるレイテンシ、重度に競合するカウンタのスケーラビリティおよび（一部の場合において）正確性、ならびに様々なプローブ効果を含む、難しいトレードオフに直面する。

概要
ここに記載されるシステムおよび方法は、様々な実施形態において、スケーラブル統計カウンタを実施するために使用され得る。一部の実施形態において、標準的なカウンタではなくこれらのカウンタを使用することにより、ＮＵＭＡスタイルメモリアーキテクチャを採用する、および／またはＮＵＣＡ特性を示すシステムにおいて実行されるアプリケーションの性能が向上し得る。ここで使用される、「ＮＵＭＡ」および「ＮＵＭＡスタイルメモリアーキテクチャ」の用語は、ＮＵＭＡおよび／またはＮＵＣＡ特性を示す任意のシステムに関して使用され得る。一部の実施形態において、カウンタは、カウント値部分とノード識別子部分とを含むデータ構造として実施され得る。ノード識別子部分は、最も新しくカウンタをインクリメントしたスレッドが実行されていたノード、または共用カウンタをインクリメントするプライオリティを要求したスレッドが実行されていたノードを識別し得る。カウンタデータ構造のノード識別子部分によって識別されたノード上で実行されるスレッドは、カウンタをインクリメントさせる優先度が他のスレッドよりも高くなり得る。一部の実施形態において、カウンタデータ構造のノード識別子部分によって識別されたノード以外のノード上で実行されるスレッドは、リトライする前にカウンタをインクリメントする試みを遅らせ得る。これにより、単一のノード上のスレッドからの連続的な更新が促され得て、キャッシュミスが減少し、全体的な性能が向上する。一部の実施形態において、性急な（impatient）スレッドは、データ構造のノード識別子部分を更新するよう試み得て、または別個のアンチスタベーション変数（非枯渇変数：anti-starvation variable）を更新し得て（たとえば、スレッドが実行されているノードの識別子を書き込むことにより）、共用カウンタをインクリメントさせるプライオリティの要求を示す。

一部の実施形態において、ここに記載されるシステムおよび方法は、確率的カウンタを実施し得る。ここにより詳細に記載されるように、様々な実施形態において、これらの確率的カウンタは、更新確率値を直接的に格納し得る、または他のタイプの確率的カウンタ値を格納し得る（たとえば、更新確率値および／もしくは予測値を表わす１つ以上の値、または更新確率値および／もしくは予測値が計算される１つ以上の値を格納し得る）。一部の実施形態において、カウンタおよび／またはそれらの更新機構の実施は、構成可能な正確性パラメータの値に依存し得る。このような実施形態において、構成可能な正確性パラメータ値は、カウンタの正確性とカウンタにアクセスするアプリケーションの性能との間のトレードオフに対するきめ細かい制御を提供するように調整され得る。たとえば、カウンタは、集合的に更新確率値を表わす仮数部分と指数部分とを含むデータ構造として実施され得る。ここにより詳細に記載されるように、カウンタを更新する時に、構成可能な正確性パラメータの値は、仮数部分および／または指数部分の更新が行なわれるのか、いつ行なわれるか、どのくらいの頻度で行なわれるのか、および／またはどのくらいの量で行なわれるかに対して影響を与え得る。他の例において、確率的カウンタ値の更新は、その値と構成可能な正確性パラメータの値に依存する定数とを掛け合わせることを含み得る。

一部の実施形態において、ここに記載されるシステムおよび方法は、アプリケーションの複数のスレッドによるカウンタの競合の量に適応するスケーラブル統計カウンタを実施し得る。たとえば、インクリメント演算の開始に応答してカウンタをインクリメントさせるかを判定する方法、および／またはカウンタを更新する方法は、現在、最近、または過去の競合の量に応じて複数の利用可能な方法から選択され得る。一部の実施形態において、カウンタは、アトミックトランザクション内からアクセス可能であり得る。様々な実施形態において、異なる競合管理ポリシーおよび／またはリトライ条件が適用され、複数の方法間での選択がなされ得る。たとえば、一部の実施形態において、共用カウンタを更新するか、またはどのように更新するかを判定する方法は、カウンタの競合の増加または減少（たとえば、初期もしくはデフォルトの方法を使用してカウンタをインクリメントもしくは更新する試みの失敗の所定最大数の後）に応答して動的に（すなわち、実行中に）変更され得る。一部の実施形態において、共用カウンタは、競合が低い状態においてインクリメントされる正確カウンタ部分と競合が高い状態において更新される確率的カウンタ部分とを含み得る。一部の実施形態において、確率的カウンタがインクリメントされる量は、競合に依存し得る。他の実施形態において、カウンタは、カウンタが競合状態にある場合のみに単一ノード上のスレッドによる連続的なインクリメントを促すノード識別子部分を含み得る。さらに他の実施形態において、以下により詳細に記載するように、比較的シンプルなカウンタデータ構造がカウンタの競合に応答して拡張され得る。

ここに記載されるように、ＮＵＭＡアウェア（NUMA-aware）共用カウンタを実施する方法の一実施形態を示すフロー図である。 ＮＵＭＡスタイルメモリアーキテクチャを実施するコンピュータシステムの部分を示すブロック図である。 ここに記載される様々なカウンタ構造の例を示すブロック図である。 ここに記載される様々なカウンタ構造の例を示すブロック図である。 ここに記載される様々なカウンタ構造の例を示すブロック図である。 ここに記載される様々なカウンタ構造の例を示すブロック図である。 ここに記載される様々なカウンタ構造の例を示すブロック図である。 ここに記載される様々なカウンタ構造の例を示すブロック図である。 一実施形態に係る、ＮＵＭＡアウェア共用カウンタをインクリメントする方法を示すフロー図である。 一実施形態に係る、共用カウンタの競合に依存するＮＵＭＡアウェア共用カウンタをインクリメントする方法を示すフロー図である。 一実施形態に係る、競合に応答して共用カウンタを拡張する方法を示すフロー図である。 一実施形態に係る、浮動小数点値を格納する確率的カウンタをインクリメントする方法を示すフロー図である。 一実施形態に係る、カウンタの競合に依存するハイブリッドカウンタをインクリメントする方法を示すフロー図である。 一実施形態に係る、２進浮動小数点値を格納する確率的カウンタをインクリメントする方法を示すフロー図である。 一実施形態に係る、複数の更新オプションを含む確率的カウンタをインクリメントする方法を示すフロー図である。 一実施形態に係る、構成可能な正確性パラメータに依存する確率的カウンタをインクリメントする方法を示すフロー図である。 一実施形態に係る、共用カウンタの競合に依存する浮動小数点値を格納する確率的カウンタをインクリメントする方法を示すフロー図である。 一実施形態に係る、共用カウンタをインクリメントさせるかを判定する方法、および共用カウンタの競合に依存する共用カウンタをインクリメントする方法を示すフロー図である。 ここに記載される１つ以上の共用カウンタをインクリメントするように構成されたコンピューティングシステムの一実施形態を示すブロック図である。

いくつかの実施形態および例示的な図面によって本開示がここに記載されるが、当業者は、本開示が記載の実施形態または図面に限定されないことを認識するであろう。なお、図面および詳細な記載は、開示される特定の形態に本開示を限定する意図はなく、逆に、本開示は、添付の請求項によって定義される精神および範囲内のすべての変更、均等物、および代替物を包含するものである。ここで使用される標題は、編成のみを目的としており、明細書または請求項の範囲を限定する意図はない。ここで使用される、「し得る（may）」の単語は、強制的な意味（すなわち、不可欠であるという意味）ではなく、許容的な意味（すなわち、可能性があるという意味）で使用されている。同様に、「含む（include）」、「含んでいる（including）」、および「含む（includes）」の単語は含むことを意味しており、限定を意味するものではない。

実施形態の詳細な説明
上記のように、統計カウンタの使用は、多くの大きなソフトウェアシステムにおいて非常に一般的である。共用統計カウンタへのアクセスは、ハードウェアおよび／またはソフトウェアのトランザクションメモリを支持するシステムにおいて実行されるものを含む、マルチスレッドアプリケーションの同時スレッド間の競合の原因となり得る。マルチコアマシンは、サイズが大きくなっており、シンプルなバスベースの設計からＮＵＭＡおよびＣＣ−ＮＵＭＡスタイルのメモリアーキテクチャへ移行されている。この移行に伴い、スケーラブル統計カウンタの必要性が増している。ここに記載のシステムおよび方法は、一部の実施形態において、スケーラブル統計カウンタを実施するために使用され得る。異なる実施形態において、ここに記載されるスケーラブル統計カウンタは、カウンタを複数のコンポーネントに分割して各コンポーネントにおける競合を減少させることにより、またはより低い頻度でカウンタを更新する技術を採用することにより、このスケーラビリティを実現する。両方のクラスの技術は、それらを使用する同時に実行されるアトミックトランザクション間のコンフリクトを大きく減少させ、成功の機会を向上させるとともに、スケーラブル性能の実現を助ける。

異なる実施形態において、ここに記載される技術は、ノンブロッキング（non-blocking）であるとともに、一般的に使用されるナイーブカウンタと比較して劇的に良好なスケーラビリティおよび正確性特性を提供する、正確カウンタおよび／または確率的（統計的）カウンタを実施するために使用され得る。確率的カウンタは、完全に一致したカウントを提供し得ないが、たとえば構成可能な正確性パラメータにより、高い確率で正確なカウントから逸脱「しすぎない」ような統計的性質を有し得る。一部の実施形態において、ここに記載されるカウンタは、競合が低い場合であってもナイーブカウンタと競合し得る。概して、ここに記載される統計カウンタは、高頻度で起こる可能性の高い事象をカウントするためにこれらが使用されるアプリケーションに適し得る一方、性能監視および診断に共通するように、カウンタの値が読み取られる頻度は低くなり得る。ここに記載されるカウンタの多くは、１だけインクリメントされ、または全くデクリメントされないと仮定される一方で、他の実施形態において、ここに記載される技術は、これらの仮定を弱める、および／または回避するように一般化され得る。

一部の実施形態において、ここに記載される技術は、競合する統計カウンタの複数の連続的なインクリメントを、ＮＵＭＡシステムの１つのノードにおいて、他のノードでカウンタ更新が発生する前に促し得る。これらの連続的な更新間のノード間通信を回避することにより、一部の実施形態において、ＮＵＭＡノード間の高コストな通信トラフィックが劇的に減少し、処理能力およびスケーラビリティが向上する。一部の実施形態において、これらの技術は、スペースオーバーヘッドの追加をほぼ伴わず、一般に使用されるナイーブ手法よりも良好にスケールを変更する正確な統計カウンタを提供し得る。

概して、同期することなく共用カウンタをシンプルにインクリメントすることは、マルチスレッドアプリケーションにおいては功を奏さない。なぜなら、１つのスレッドによる更新は、他のスレッドによる更新によって上書きされ得て、これによってカウンタ上の１つ以上のインクリメントの効果が失われる。一部の場合において、このようなカウンタは、ロックを用いてそれらを保護することによってスレッドセーフとなり得る。しかしながら、最新の共用メモリマルチプロセッサにおいては、コンペア・アンド・スワップ（ＣＡＳ）型命令などのアトミック命令を使用してカウンタをインクリメントするほうが良い。カウンタをインクリメントするためにＣＡＳ型命令が使用される場合、インクリメントするスレッドがインクリメントの前にみることが見込まれる値をカウンタが保持し、演算がカウンタ値の更新に成功した時のみに成功が示される。それ以外に、場合によっては一部のバックオフ期間（back-off period）の後にインクリメント演算がリトライされ得る。この解決法は、シンプル、正確、およびノンブロッキングであるが、より大きく増大するＮＵＭＡシステムにスケールを変更するものではない。シングルスレッドのインクリメント演算を使用して（たとえば、カウンタを更新するために別個のロードおよび格納命令を使用して）ＣＡＳ型命令のオーバーヘッドをなくしてレイテンシを減少させること（たとえば、カウンタの正確な値を知ることが必要でない場合）は、ＮＵＭＡシステムにおいて多くのスレッドによって変数が変更された場合に起こる可能性が高いリモートキャッシュミスを解決する主要なコストを回避することにはならない。加えて、この手法は、単に競合時に更新の時々の損失につながるのではなく、多数のスレッド（たとえば、３２以上）によって共用された場合に更新の大部分の損失につながることが示されてきた。皮肉にも、この問題は競合がインクリメントするにつれて悪化し、これはカウンタが検知することが意図されるシナリオである場合が多い。

カウンタをスケーラブルにする１つの手法は、カウンタをスレッドごとのコンポーネントに分割することであり、各スレッドは同期することなく各自のコンポーネントをインクリメントする。しかしながら、この手法にはいくつかの欠点があり得る。たとえば、カウンタがスレッドの動的セットによって使用される場合、スレッドは登録および登録取消される必要があり得て、カウンタを読み取るためにスレッドのコンポーネントを繰り返す方法が必要となり得る。加えて、この手法は、カウンタを使用するスレッドの数の要因によってスペース要件を増加させ得る。様々な実施形態において、ここに記載される技術は、異なる程度にこれらの欠点を軽減し得る。

追加のスペースオーバーヘッドが望ましくない、または許容できないとともに、カウンタが正確でなければならない状況において、ランダムバックオフ（ＲＢＯ）技術が使用され、重度の競合における完全な崩壊が少なくとも回避され得る。一部の実施形態において、ＮＵＭＡロックアルゴリズムまたはコホートロック（これは、所与のＮＵＭＡノード内においてロックが他のノード上で取得される前にロックを複数回にわたって渡すことによって競合下で性能およびスケーラビリティを大きく向上させる）は、ＲＢＯを採用するカウンタの競合管理を向上させ得る。たとえば、ＣＡＳ型命令を使用してカウンタをインクリメントする試みにスレッドが失敗した時（たとえば、競合が生じた時）、スレッドは、コホートロックが取得された後のみにカウンタをインクリメントする試みをリトライし得て、他のノードにおける更新の前に１つのＮＵＭＡノード上における複数の更新を促し得る。この技術は、ＲＢＯの性能を向上させるのに効果的であることが示されてきた。しかしながら、コホートロックのスペースオーバーヘッドにより、この技術はここで記載する他の手法に対する利点をほとんどもたらし得ない。

一部の実施形態において、上記のＮＵＭＡロックに類似するが大きなスペースオーバーヘッドを加えない手法は、カウンタ値の数ビットを使用して、ＮＵＭＡスタイルメモリアーキテクチャにおけるノードのうちいずれのノードが現在プライオリティを有しているのかを識別する。このような実施形態において、カウンタがインクリメントされると、これらのビットの値は、（通常の演算の一部として）時間の経過とともに変化し、カウンタを更新するプライオリティを他のノードに与え得る。言い換えると、いくつかのインクリメント演算の後（優先ノードを示すビットの位置に応じて）、これらのインクリメント演算の結果としてのこれらのビットの値の変化により、他のノードが優先ノードとなり得る。このような実施形態において、他のノード上のスレッドは、それらの更新を遅らせ、優先ノード上のスレッドが連続的な更新を行なう可能性を高め得る。なお、概して、優先ノードを識別するために使用されるビットは、最低位ビット（すなわち、最も頻繁に変化するもの）を含み得ないが、不合理な遅れを回避するのに十分な頻度で優先度が変化するように選択され得る。この手法は、シンプルであり、スペースオーバーヘッドを加えず、すべてのノードにわたって比較的均等にインクリメント演算が広がる時に良好に行なわれることが示された。しかしながら、均一性の低い作業負荷には良好に適さないものとなり得る。

ＮＵＭＡアウェア共用カウンタ（たとえば、ＮＵＭＡアウェアＲＢＯ型カウンタまたは他のタイプのＮＵＭＡアウェアカウンタ）を実施する方法の一実施形態は、図１のフロー図によって示される。１１０に示されるように、この例において、方法は、ＮＵＭＡメモリアーキテクチャを実施するシステムの所与のノード上で実行されるスレッドが共用カウンタのインクリメントを開始することを含み得る。また、方法は、システムにおける他のノード上で実行されるスレッドがカウンタを更新するプライオリティを現在有しているか、またはカウンタを更新するプライオリティを要求したか否かをスレッドが判定することを含む（１２０のように）。たとえば、一部の実施形態において、カウンタの数ビットは、最も新しくカウンタを更新したスレッドが実行されたノードを識別するために使用され得る（したがって、ノードを優先ノードとして指定する）、または、カウンタの数ビットは、他の基準に基づいて優先ノードとして現在指定されているノードを識別し得る。一部の実施形態において、スレッドがカウンタを更新するプライオリティを有しているか（またはこのようなプライオリティを要求したか）を指定するために他の方法が使用され得て、この方法は、アンチスタベーション変数（ここでより詳細に記載される）の使用を含み得る。

この例において示されるように、方法は、１３０のように、少なくとも部分的に判定（システムにおける他のノード上で実行されるスレッドが、カウンタを更新するプライオリティを現在有しているか、またはカウンタを更新するプライオリティを要求したか）に依存し、スレッドが共用カウンタをインクリメントするように試みる、またはカウンタをインクリメントする試みを遅らせることを含み得る。たとえば、一部の実施形態において、（たとえば、カウンタにおける指定された数ビットの値に基づいて、または他の優先ノード指標に基づいて）他のノード上で実行されるスレッドがカウンタを更新するプライオリティを有している（または要求した）とスレッドが判定した場合、スレッドは、たとえば試みが成功するまで、または所定のリトライ限界に達するまで（様々な競合管理ポリシーに応じて）、カウンタをインクリメントする試みを遅らせ得る、および続いてカウンタをインクリメントする試みを１回以上リトライし得る。（たとえば、カウンタにおける指定された数ビットの値に基づいて、または他の優先ノード指標に基づいて）プライオリティが設定（または要求）されていない、またはスレッドが実行されるノードがカウンタを更新するプライオリティを現在有している（または要求している）とスレッドが判定した場合、スレッドは、カウンタをインクリメントする１つ以上の試みを進め得る（たとえば、試みのうちの１つが成功するまで、または所定のリトライ限界に達するまで）。なお、一部の実施形態において、優先ノードを識別するものとして指定されるカウンタビットの（または専用の優先ノード指標の）所定のデフォルトもしくは初期値は、プライオリティがまだ要求もしくは設定されていないことを示し得る。

ここに記載される例の多くにおいて、コンピュータシステムはプロセッサコアのクラスタに構成されるものと仮定され得て、その各々は、クラスタのローカルコア間で共用される１つ以上のキャッシュを有する。このような実施形態において、クラスタ間の通信は、クラスタ内通信よりもかなり高コストとなり得る。ここに記載の例の少なくとも一部において、「クラスタ」および「ノード」の用語は、プロセッサコアの集合を言うために使用され得て、このコアの集合は、システムにおいて実施されるＮＵＭＡマシンのサイズに応じて、単一のマルチコアチップ上のコア、または同じメモリもしくはキャッシング構造に近接するマルチコアチップの集合上のコアを含み得る。また、これらの例においては、クラスタ上のすべてのスレッドに知られる固有クラスタＩＤを各クラスタが有すると仮定され得る。

図２は、ＮＵＭＡスタイルメモリアーキテクチャを実施するコンピュータシステムの部分を示す。この例において、コンピュータシステムは、インターコネクト２５０を介して互いに通信する複数のＣＰＵボード２００（２００ａ〜２００ｎとして示される）を含む。これらのＣＰＵボードのうちの１つ（２００ａ）は、他よりも詳細に示される。一部の実施形態において、ＣＰＵボード２００の各々は、ＣＰＵボード２００ａについて示されたものと同じもしくは同様のアーキテクチャを含み得る。他の実施形態において、ＣＰＵボードの各々は、異なる数および／または配置のプロセッサチップ、プロセッサコア、キャッシュなどを含み得る。たとえば、一部の実施形態において、各プロセッサチップに密接に結合される１つ以上のメモリチップが設けられ得て、そのプロセッサコアのための「ローカルメモリ」として機能する（図示せず）。図２に示されるように、コンピュータシステムは、１つ以上のシステムメモリ２６０および／または他のコンポーネント２７０も含み得る。この例において、ＣＰＵボード２００ａは、インターコネクト２４０を介して互いに通信する４つのプロセッサチップ（プロセッサチップ２１０ａ〜２１０ｄとして示される）を含み、それらの内の１つはより詳細に示される。この例においては、プロセッサチップ２１０ｂ〜２１０ｄが、プロセッサチップ２１０ａと同様のメモリアーキテクチャを含むものとして仮定される。

図２に示される例において、プロセッサチップ２１０ａは、８つのプロセッサコア（２２０ａ〜２２０ｈとして示される）を含み、各プロセッサコアは、それぞれ（専用の）レベル１（Ｌ１）キャッシュ（２３０ａ〜２３０ｈとして示される）を有する。各プロセッサコアは、一部の実施形態において、マルチスレッドコアであり得る。たとえば、一実施形態において、各プロセッサコアは、８つのハードウェアスレッドを同時に実行することが可能であり得る。所与のプロセッサコア２２０上で実行されるスレッドは、そのプロセッサコア２２０のためのレベル１キャッシュ２３０を共用し得て、プロセッサコア２２０およびそのハードウェアスレッドのローカルであると考えられるこのレベル１キャッシュへのアクセスは、非常に速くなり得る。加えて、８つのプロセッサコア２２０は、プロセッサチップ２１０ａのためのレベル２（Ｌ２）キャッシュ２４０を共用し得て、各プロセッサコアのレベル１キャッシュへのアクセスほど速くはないが、このレベル２キャッシュへのアクセスも速くなり得る。この例において、同じＣＰＵボード２２０上の異なるプロセッサチップ２１０のキャッシュへのアクセス、異なるＣＰＵボード２００上のプロセッサチップ２１０のキャッシュへのアクセス、および様々なシステムメモリ２６０へのアクセス（これらすべては、プロセッサチップ２１０ａの特定のプロセッサコア２２０を実行するハードウェアスレッドに対するリモートアクセスであると考えられ得る）は、レベル１およびレベル２キャッシュならびに／またはハードウェアスレッドのローカルの他のメモリへのアクセスと比較すると、漸増的に高いレイテンシを示し得る。

上述のように、一部の実施形態において、カウンタを連続的にインクリメントするよう高い相互メモリ局所性を有するスレッド（たとえば、同じプロセッサチップ上のプロセッサコア上、または互いに近いプロセッサコア上で実行されるスレッド）を促す共用カウンタを採用することにより、ＮＵＭＡアーキテクチャにおいて性能の向上が得られ、複数のスレッドがこれらのカウンタをインクリメントする試みを開始した時に全体的なキャッシュミスのレベルが減少する。ＮＵＭＡアウェア共用カウンタ（たとえば、１つ以上のシステムメモリ２６０に常駐するカウンタデータ構造であって、その一部は、システムにおける対応のプロセッサコア上で実行されるスレッドによって更新および／または読み取られると様々なキャッシュに持ち込まれ得る）を実施するためのここに記載されるシステムおよび方法により、このような高いメモリ局所性がもたらされ得る。なぜなら、これらの技術は、単一のクラスタにおけるスレッド（たとえば、レベル１もしくはレベル２キャッシュを共用するスレッド）からのこのようなカウンタをインクリメントするよう要求のバッチを促すためである。

上記のようなＮＵＭＡアウェアＲＢＯカウンタの一実施形態は、以下の例示的な疑似コードによってさらに示され得る。

上記の例示的な疑似コードに示されるように、一部の実施形態において、カウンタは、カウンタを更新するプライオリティを現在有するスレッドのノードの表示を格納するために使用される数ビット分が増大され得る（または、代替的にカウンタから数ビットを抜き取り、その範囲を制限する）。この手法では、ＮＵＭＡノードの識別子（たとえば、ノードＩＤ）に１ビット加えたものを格納するのに十分な追加のビットのみを必要とする。

示される例において、技術は、Ｎビットを使用して０から

の範囲内の値を保持するカウンタを収容し得る。
たとえば、一実施形態において、カウンタは３２ビットを含み得て、そのうちの３つがＮＵＭＡノードＩＤを格納するために抜き取られ得て、カウンタの範囲が２^２９−１に制限される。この例において、これらの３つのビットは、カウンタが最後にインクリメントされたノードのＩＤをカウンタと合わせて格納するために使用され得て、識別されたノード上での連続的なインクリメントを促すために他のノード上のスレッドがカウンタをインクリメントする試みを控えることが許容および／または要求される。他の実施形態において、カウンタデータ構造の異なるビット数が使用され得て、カウンタを更新するプライオリティを現在有するスレッドのノードの識別子が格納される。

図３Ａ〜図３Ｆは、ここに記載される異なるカウンタデータ構造の一部の様々な実施形態を示すブロック図である。たとえば、図３Ａは、ノードＩＤを格納する追加のビット３１０の分だけカウンタ３０５が増大されたカウンタ構造３００を示す。図３Ｂは、格納されたカウント値３２０のビットの最高位部分集合（３２５として示される）がカウント値フィールドから「抜き取られ」、ノードＩＤを示すために使用された、カウンタ構造３１５を示す。一部の実施形態において、このビットの部分集合は、ノードＩＤを格納するために確保され得て、様々なノードＩＤ値がカウンタ構造３１５のこの部分に明示的に書き込まれ得る（たとえば、カウント値３２０が更新された場合）。他の実施形態において、これらのビットの値は、カウンタ構造３１５に格納されるカウント値３２０の対応するビット値をシンプルに反映し得る。図３Ｃは、カウント値３３５の最高位ビットを含まないビットの部分集合（３４０として示される）がノードＩＤを表わすカウンタ構造３３０を示す。この例において、これらのビットの値は、カウンタ構造３３０に格納されるカウント値３３５の対応するビット値をシンプルに反映し得る。概して、格納されたカウント値のビットの任意の部分集合は、異なる実施形態において、ノードＩＤを示すものとして指定され得て、ビットの部分集合の選択は、単一ノード上で実行されるスレッドによる連続的なインクリメント演算の数に影響を与え得る。

以下により詳細に記載されるように、図３Ｄ〜図３Ｅは、一部の実施形態において特定の条件に応答して拡張され得るカウンタ構造を示す。たとえば、図３Ｄは、カウンタ部分３５０がカウント値または他の構造に対するポインタを格納するかを確保されたビット３５５が示すカウンタ構造３４５を示す。この例において、確保されたビット３５５の値がゼロであることから、カウンタ部分３５０はカウント値を格納する。同様に、図３Ｅは、カウンタ部分３６５がカウント値または他の構造へのポインタを格納するかをカウンタ値３５０の確保されたビット３７０が示すカウンタ構造３６０を示す。この例において、確保されたビット３７０の値が１であることから、カウンタ部分３６５はポインタ値を格納しており、このポインタ値が追加のカウンタ構造３７５へポイントする。この例において、カウンタ構造３７５は、３８０ａ〜３８０ｎとして示される複数のカウント値を格納する。図３Ｆは、一部の実施形態において、確率的カウンタを実施するために使用され得るデータ構造を示す。この例において、図３Ｆは、仮数部分３９０と指数部分３９６とを含むカウンタ構造３８５を示す。

なお、上記の例示的な疑似コードによって表されるカウンタを含む上記のＮＵＭＡアウェアカウンタの一部の実施形態において、カウンタを更新する試みを長く待ち過ぎているスレッドは性急となり得て、この点において、そのノードＩＤをアンチスタベーション変数へ格納し得る。このような実施形態において、各共用カウンタはこのようなアンチスタベーション変数に関連付けられ得るが、カウンタごとに別個のアンチスタベーション変数を有する必要はない。たとえば、一部の実施形態において、単一のアンチスタベーション変数が採用され得て、アンチスタベーション変数に関連付けられた１つ以上の共用カウンタを更新する試みを待つように他のノード上のスレッドに対して要求し、これによって、性急なスレッドを有するノード上のスレッドが、カウンタを含むキャッシュラインをそのノードへ持ち込み、カウンタをインクリメントすることが可能となる。しかしながら、この手法は、他のスレッド（たとえば、同じノード上の他のスレッド）が性急なスレッドの前にカウンタをインクリメントすることを防止し得るものではない（したがって、カウンタのノンブロッキング特性を確保する）。上記の発見的方法（heuristic approach）は、重度の競合下であっても実際上は飢餓を防止するものとして示された。なお、上記の疑似コードに示される例を含む一部の実施形態において、単一のグローバルアンチスタベーション変数が採用され得て、マルチスレッドアプリケーションへアクセス可能な共用カウンタの一部またはすべてを更新する試みを待つように他のノード上のスレッドに要求する。

共用カウンタをインクリメントするこのＮＵＭＡアウェア手法を採用する一部の実施形態において、性急となったスレッドと同じノード上のスレッドは、性急なスレッドがアンチスタベーション変数を設定することに応答して遅れ（たとえば、遅いバックオフ）を中止し得るとともに、直ちにカウンタのインクリメントを試み得る。このような実施形態においては、ノード上のいずれのスレッドがカウンタをインクリメントするかに関わらず、適切なキャッシュラインをノードに持ち込むという結果を有し得て、これによってそのノード上のすべてのスレッドにカウンタをインクリメントする良好な機会が与えられ得る。このような実施形態においては、性急となるスレッドが確実に次にカウンタをインクリメントするように試みるのではなく、性急なスレッドを補助するであろうインクリメントを行なう近くのスレッドが性急なスレッドの前にカウンタをインクリメントすることが許容され得る。この手法は、他のより制限的な手法よりも良好な性能を得られることが分かった。

ＮＵＭＡアウェア共用カウンタをインクリメントする方法の一実施形態が、図４のフロー図によって示される。４１０に示されるように、この例において、方法は、ＮＵＭＡスタイルメモリアーキテクチャを実施するシステムの所与のノード上で実行されるスレッドが共用カウンタのインクリメントを開始することを含み得る。方法は、４１５のように、他のノード上で実行されるスレッドの代わりにカウンタを更新するプライオリティを他のノード上のスレッドが要求したことをグローバル変数が示したかを判定すること（たとえば、カウンタをインクリメントする試みの一部として）を含み得る。たとえば、様々な実施形態において、アンチスタベーション変数が設定される、特定の所定値を保持する、または他のノードの識別子を保持する場合、アンチスタベーション変数は、カウンタを更新するプライオリティを他のノード上のスレッドが要求したことを示し得る。他のノード上のスレッドが他のノード上のスレッドのためのプライオリティを要求したことをグローバル変数が示す場合（４１５からの肯定の出口として示される）、方法は、４２０のように、スレッドがカウンタをインクリメントする試みを遅らせることを含み得る。たとえば、異なる実施形態において、スレッドは、所定量またはランダムな量だけ試みを遅らせ得て、その後にスレッドは共用カウンタをインクリメントするとともに（たとえば、カウンタ構造に格納されるカウント値をインクリメントすることにともなってアトミックに）、スレッドが実行されるノードを反映するようにカウンタ構造のノードＩＤ部分を更新するよう試み得る（４２５のように）。なお、一部の実施形態において、試みを遅らせる時間を制御する１つ以上のパラメータは、異なるノード上のスレッドによって最後の更新が行なわれたことをノードＩＤフィールドが示す時とは異なる値を、同じノード上のスレッドによって最後の更新が行なわれたことをノードＩＤフィールドが示す時に有し得る。

この例において、他のノード上のスレッドがカウンタを更新するプライオリティを要求しなかったことをグローバル変数が示す場合（４１５からの否定の出口として示される）、方法は、共用カウンタをインクリメントするとともに（たとえば、カウンタ構造に格納されるカウンタ値をインクリメントすることにともなってアトミックに）スレッドが実行されるノードを反映するようにカウンタ構造のノードＩＤ部分を更新するようスレッドが試みることを含み得る（４２５のように）。一部の実施形態において、カウント値をインクリメントするとともにカウンタ構造のノードＩＤ部分を更新する試みは、単一のＣＡＳ型演算または同様の同期演算を使用して行なわれ得る。この例に示されるように、カウンタおよびノードＩＤをインクリメントする試みが成功した場合（４３０からの肯定の出口として示される）、４３５のように、インクリメント演算が完了し得る。他方、カウンタおよびノードＩＤをインクリメントする試みが成功しなかった場合（４３０からの否定の出口として示される）、および他のノード上のスレッドがカウンタを更新した最も新しいスレッドであることをカウンタ構造のノードＩＤ部分が示さない場合（４４０からの否定の出口として示される）、方法は、４６０のように、カウンタをインクリメントする試みをスレッドが遅らせることを含み得る。たとえば、異なる実施形態において、スレッドは、所定量またはランダムな量だけ試みを遅らせ得て、その後にスレッドは、共用カウンタをインクリメントするとともにカウンタ構造のノードＩＤ部分を更新する試みをリトライし、スレッドが実行されるノードを反映する（４６０から４２５へのフィードバックとして示される）。

この例に示されるように、カウンタおよびノードＩＤをインクリメントする試みが成功しなかった場合（４３０からの否定の出口として示される）、および他のノード上のスレッドがカウンタを更新した最も新しいスレッドであることをカウンタ構造のノードＩＤ部分が示す場合（４４０からの肯定の出口として示される）、方法は、他のノード上のスレッドがノードプライオリティを要求したことをグローバル変数が示すかを判定することを含む（４４５のように）。そうであれば（４４５からの肯定の出口として示される）、方法は、４６０のように、カウンタをインクリメントする試みをスレッドが遅れさせることを含み得る。たとえば、異なる実施形態において、スレッドは、試みを所定量またはランダムな量だけ遅らせ得て、その後に共用のカウンタをインクリメントするとともにカウンタ構造のノードＩＤ部分を更新する試みをリトライし得て、スレッドが実行されるノードを反映する（４６０から４２５へのフィードバックとして示される）。他のノード上のスレッドがノード優先を要求したことをグローバル変数が示さなかったが（４４５からの否定の出口として示される）、スレッドの忍耐が尽きた場合（４５０からの否定の出口として示される）、方法は、４６０のように、カウンタをインクリメントする試みをスレッドが遅らせることを含み得る。たとえば、異なる実施形態において、スレッドは試みを所定量またはランダムな量だけ遅らせ得て、その後にスレッドは共用カウンタをインクリメントするとともにカウンタ構造のノードＩＤ部分を更新する試みをリトライし得て、スレッドが実行されるノードを反映する（４６０から４２５へのフィードバックとして示される）。それ以外に、（４４５からの否定の出口および４５０からの否定の出口として示される）方法は、スレッドが、グローバル変数を更新してノードのための優先を要求して（４５５のように）、４６０のようにカウンタをインクリメントする試みを遅らせることを含み得る。

上記の共用カウンタをインクリメントするＮＵＭＡアウェア手法は、一部の実施形態において、重度の競合下において標準的なＲＢＯ手法よりも良好な処理能力をもたらし得るが、低競合シナリオにおいて大きなオーバーヘッドが課され得る。たとえば、これまで記載した手法は、カウンタをインクリメントする各試みの前にアンチスタベーションフラグをテストすることを含む。他の実施形態において、カウンタが経験した現在、最近、または過去の競合量にインクリメント演算が依存する適応ＮＵＭＡアウェア手法が採用され得る。たとえば、一部の実施形態において、適応ＮＵＭＡアウェア手法は、カウンタを最も新しくインクリメントしたスレッドのノードＩＤを記録しない標準カウンタをインクリメントすることによって、カウンタをインクリメントする要求に最初に応答する。たとえば、カウンタデータ構造は、カウンタのノードＩＤ部分への書き込みをすることなくカウンタをインクリメントするようスレッドが試み得ることを示す初期もしくはデフォルト値に初期化され得る（たとえば、マルチスレッドアプリケーションの初期化段階において）。このような実施形態において、ノードＩＤが記録されていないことから、アンチスタベーション変数をチェックする必要がなくなり得る。

この適応ＮＵＭＡアウェア手法において、カウンタのインクリメントに成功する前に所定回数より多く（たとえば、迅速かつ連続的に３回よりも多い回数のあと、ランダム化されたバックオフ期間を伴って１６回）カウンタをインクリメントする試みをリトライするスレッドは、（ひとたび最終的に成功すると）そのノードＩＤをカウンタに記録する。その後、カウンタをインクリメントする後続の要求に応答して、上記の遅いながらもよりスケーラブルなＮＵＭＡアウェア技術が適用され得る。一部の実施形態において、カウンタはたまに（たとえば、周期的または様々なポリシーに従い、共用カウンタの競合の減少を含む）通常のカウンタにリセットされ得る（または戻され得る）ことから、たまに起こる競合の効果は永久には続かない。たとえば、カウンタのノードＩＤ部分は、カウンタをインクリメントするプライオリティをいずれのノード上のスレッドも有していない（または要求しなかった）ことを示す初期もしくはデフォルト値にたまにリセットされ得て、カウンタのノードＩＤ部分にこの初期もしくはデフォルト値が格納された時にカウンタをインクリメントしようと試みるスレッドは、カウンタのノードＩＤ部分へ値を書き込むことなくカウンタをインクリメントしようと試み得る。この適応ＮＵＭＡアウェア手法は、すべての競合レベルにおいて、既存のＲＢＯ手法のうちの最高のものおよび上記の非適応ＮＵＭＡ手法と競合することが示されてきた。

共用カウンタの競合に依存するＮＵＭＡアウェア共用カウンタをインクリメントする方法の一実施形態は、図５のフロー図によって示される。５１０に示されるように、この例において、方法は、所与のノード上で実行されるスレッドが共用カウンタのインクリメントを開始することを含み得る。共用カウンタのノードＩＤ部分がプライオリティを有する（または要求した）ノードを識別した場合（５１５からの肯定の出口として示される）、方法は、要素４１５で始まる、図４に示される方法のように共用カウンタをインクリメントする試みを継続することを含み得る。共用カウンタのノードＩＤ部分がプライオリティを有する（または要求した）ノードを識別しなかった場合（５１５からの否定の出口として示される）、方法は、５２０のように、スレッドが共用のカウンタをインクリメントするよう試みることを含み得る。一部の実施形態において、共用カウンタをインクリメントする試みは、ＣＡＳ型演算または同様の同期演算を使用して行なわれ得る。

この例に示されるように、共用カウンタをインクリメントする試みが成功した場合（５３０からの肯定の出口として示される）、インクリメント演算は完了し得る（５３５のように）。他方、共用カウンタをインクリメントする試みが成功しなかった（５３０からの否定の出口として示される）がリトライ限界にまだ達していない場合（５４０からの否定の出口として示される）、方法は、５４５のように、遅れの有無に関わらず、スレッドが共用カウンタをインクリメントする試みを１回以上リトライすることを含み得る。たとえば、スレッドは、介在するバックオフ期間の有無に関わらず単一のＣＡＳ型演算または同様の同期演算を使用して共用カウンタをインクリメントする試みを繰り返し得る。これは、５４５から５３０へのフィードバックによって図５に示される。共用カウンタをインクリメントする試みが成功せず（５３０からの否定の出口として示される）、リトライ限界に達した場合（５４０からの肯定の出口として示される）、方法は、５５０のように、遅れの有無に関わらず、スレッドが共用カウンタをインクリメントするとともにカウンタ構造のノードＩＤ部分を更新するよう試みることを含み得て、スレッドが実行されるノードを反映する。この例に示されるように、この試みが成功しなかった場合（５５５からの肯定の出口として示される）、方法は、共用カウンタをインクリメントするとともにカウンタ構造のノードＩＤ部分を更新する試みを、成功するまで（または様々な適用可能なリトライもしくは競合管理ポリシーによって中止されるまで）１回以上繰り返すことを含み得る。これは、５５５から５５０へのフィードバックによって図５に示される。共用カウンタをインクリメントするとともにカウンタ構造のノードＩＤ部分を更新する試みがひとたび成功すると（５５５からの肯定の出口として示される）、５６０のように、インクリメント演算が完了し得る。

様々な実施形態において、これまで記載したカウンタは、重度の競合下において良好な単一スレッド性能およびスケーラビリティを実現し得る。しかしながら、シンプルなＲＢＯ型カウンタに対するこれらの利点は、適度な負荷がかかった状態において減少し得る。なぜなら、同一のノードに対して連続的なインクリメントを行なう機会がより少なくなり得るためである。加えて、これらのカウンタは、システム専用の調整に対して感度が高く、一部の他の手法よりも安定性が低くなり得る。他の実施形態において、一部が以下に記載される、少し大きなスペースを使用するカウンタは、これらの効果を減少または消滅させ得る。

一部の実施形態において、「マルチライン」手法と言われる手法が使用され、上記のスレッドごとのカウンタコンポーネントの欠点を招くことなく高コストなノード間通信が回避され得る。たとえば、一部の実施形態において、マルチライン手法は、ＮＵＭＡノードごとに別個のカウンタコンポーネントを採用し得る。このような実施形態において、カウンタをインクリメントする試み間のランダム化されたバックオフ期間の有無に関わらず、カウンタコンポーネントの各々をインクリメントするためにＣＡＳ型命令を使用してノードごとのコンポーネントの同期が実施され得る。なお、この場合において同期のためにＣＡＳ型命令を使用する場合、ノード間競合の心配はない。マルチライン手法を採用する場合、カウンタの読み取りには、同期することなく各コンポーネントを読み取ること、および読み取られた値の合計を返すことが含まれ得る。なお、この手法の正確さは、インクリメント演算によって１のみがカウントに加えられるという仮定に依存し得る。しかしながら、この仮定が適用されない実施形態において、同じ効果に対して他の技術が採用され得る。

マルチライン手法を採用した場合のスペースの増加はノードの数によって限定されるが、まれにのみインクリメントされるカウンタについては全体的にスペースの増加を回避することが好ましいものとなり得る。一部の実施形態において、ここでは「マルチライン適応」手法と言われる適応手法が採用され得る。この手法においては、インクリメント演算は、現在、最近、または過去のカウンタの競合量に依存する。たとえば、一部の実施形態において、マルチライン適応手法は、最初は標準的カウンタを採用およびインクリメントし得て、標準的カウンタをインクリメントする所定数の試み（たとえば、一実施形態においては４回）よりも多くの回数にわたって失敗した場合にのみ上記のマルチライン技術を使用するように「拡張」され得る。たとえば、リモートキャッシュミスが頻繁に起こる場合にカウンタを拡張するなど、他のポリシーが他の実施形態において適用され得る。一部の実施形態において、カウンタを拡張することは、ノードごとに１つのカウンタを含む追加の構造を割り当てること、および標準的カウンタをその構造へのポインタと置き換えることを含み得る。一部のこのような実施形態において、初期（標準）カウンタ構造の１つのビットが確保され、追加の構造もしくはカウンタ値へのポインタを初期構造が格納するかが区別され得る。このようなカウンタの一例は、図３Ｄ〜図３Ｅに示されるとともに上に記載されている。

一部の実施形態において、マルチライン適応手法を採用する低競合カウンタのためのスペースオーバーヘッドが単に確保されたビットであり得て（これは、実際上はカウンタの範囲を半減させる）、高いスペースオーバーヘッドは、高い競合を経験するカウンタのみに適用され得る（様々な所定の競合管理ポリシーによる）。一部の実施形態において、マルチライン適応手法は、競合したカウンタのために追加レベルの間接指定を導入し得て、これによってカウンタのためのインクリメント演算が遅くなり得る。しかしながら、実際上、これはカウンタが競合した場合に大きな性能上の問題とはなり得ない。なぜなら、初期カウンタ構造上のＣＡＳ型インクリメント試みが減少し得るためである（これ故に、マルチスレッドアプリケーションによって経験する全体的な競合が減少する）。

競合に応答して共用カウンタを拡張する方法の一実施形態が図６のフロー図によって示される。６１０に示されるように、この例において、方法は、所与のノード上で実行されるスレッドが共用カウンタのインクリメントを開始することを含み得る。一部の実施形態において、スレッドは、たとえば、介在するバックオフ期間の有無に関わらずＣＡＳ型演算を使用して、共用カウンタをインクリメントするよう試み得る（６２０のように）。共用カウンタをインクリメントする試みが成功した場合（６３０からの肯定の出口として示される）、インクリメント演算は完了し得る（６３５のように）。共用カウンタをインクリメントする試みが成功しなかったが（６３０からの否定の出口として示される）、適用可能なリトライ限界条件が満たされなかった場合（６４０からの否定の出口として示される）、方法は、成功するまで、またはリトライ限界条件が満たされるまで、スレッドがカウンタをインクリメントする試みを１回以上繰り返すことを含み得る。これは、６４０から６２０へのフィードバックによって図６に示される。様々な実施形態において、リトライ限界条件は、成功しなかった試みの数、キャッシュミスの数、または他の適用可能なリトライもしくは競合管理ポリシーに基づき得る。

この例において示されるように、共用カウンタをインクリメントする試みが成功せず（６３０からの否定の出口として示される）、適用可能なリトライ限界条件が満たされなかった場合（６４０からの肯定の出口として示される）、方法は、６５０のように、共用カウンタ（またはそのカウント部分）を、ノードごとに１つのカウンタ（すなわち、１つ以上のノードローカルカウンタ）を含む構造へのポインタと置き換えることを含み得る。たとえば、一部の実施形態において、カウンタの１ビットは、カウンタ部分の値が現在カウント値を表わす、または複数カウンタ構造へのポインタを表わすかを示すために使用され得る。方法は、６６０のように、成功するまでスレッドがノードローカルカウンタをインクリメントすることを１回以上試みることを含み得る。たとえば、スレッドは、介在するバックオフ期間の有無に関わらず、ＣＡＳ型演算または同様の同期演算を使用して、ノードローカルカウンタをインクリメントすることを試み得る。この例に示されるように、一部の実施形態において、ノードの１つにおけるスレッドが共用カウンタの値を読み取る後続の演算は、ノードローカルカウンタのすべてを読み取ってそのカウンタ値の合計を返すことによって行なわれ得る。

一部の実施形態において、ここに記載されるマルチライン適応手法は、低レベルの競合において、スペースオーバーヘッドおよび処理能力の両方が競合し得るカウンタに対し、上記の基本的なＲＢＯカウンタを提供し得て、これにより、増加する競合に対してスケールが良好に変更され、高い競合において基本的なＲＢＯカウンタよりもかなり高い処理能力がもたらされる（たとえば、一部の実験においては、７００倍よりも高い処理能力）。なお、一部の実施形態において、マルチラインおよびマルチライン適応手法を採用するカウンタは、単一のコンポーネントを使用する同じノード上のスレッド間での競合により、高い競合レベルとなり得る。一部のこのような実施形態において、このタイプの競合は、ノードごとのコンポーネントをより多く使用することによって緩和され得る。たとえば、ノード間のフォールスシェアリングを回避するためにノードごとのコンポーネントを別個のキャッシュラインに置かなければならないところ、１つより多いコンポーネントがノードごとに採用される場合、同じキャッシュラインにおいて単一のノードに対して複数のコンポーネントを置くことは不合理とはなり得ない。この場合においてフォールスシェアリングが幾分のオーバーヘッドを負わせ得るものであることから、１つのＮＵＭＡノード内のみとなり得る。加えて、この場合においてはＣＡＳ障害が少なくなることから、複数のコンポーネントを使用することの利益があり得る。したがって、一部の実施形態においては、この手法を使用することにより、スペース使用を増加させることなく性能を向上させることが可能となり得る。

なお、一部の実施形態において、マルチライン手法によって引き起こされる追加のスペースオーバーヘッドは、大部分が重度に競合していない多数の統計カウンタを有するシステムにおいては受け入れられ得ない。上記のマルチライン適応手法は競合するカウンタのみについてこのスペースオーバーヘッドを引き起こし得るところ、異なるカウンタが異なる回数にわたって競合した場合、これによって時間とともに過剰なオーバーヘッドが起こり得る。さらに、一部の実施形態において、これらの手法は、一部の状況において、カウンタを読み取る演算のレイテンシを増加させ得る、および／または動的に割り当てられたメモリの使用によって受け入れ不可能となり得る。以下により詳細に記載するように、一部の実施形態において、これらの問題の一部またはすべては、カウンタが正確である必要がない場合には回避され得る。

前述のように、シンプルな非同期カウンタは、通常、競合が適度なレベルにあったとしても、カウンタ更新の大部分を失う。カウンタは様々なシステム事象の過剰な割合を検知するために使用される場合が多いことから、これらのナイーブ実施は、（皮肉にも）提供すべきデータが最も重要である場合に有効性が最小となる。それにもかかわらず、一部の状況において、および一部の適用のために、正確なカウントは必要となり得ない。以下により詳細に記載するように、一部の実施形態において、カウンタは、この柔軟性を利用する一方、ナイーブカウンタ実施によって実現されない所定レベルの正確さを維持することを目的としている。

１つの既存の確率的カウンタ（「モーリス（Morris）カウンタ」と言われる場合もある）は、通常含まれるビット数（たとえば、８ビット）よりも大きな値の範囲を表わし得る。モーリスカウンタは、以下に基づいて、ここでｖ（ｎ）と言われるカウント値の確率的近似を格納することによってこれを行なう。ｎは正確なカウントである（すなわち、対応するインクリメント演算が何度呼び出されたか）。

v(n)=log(1+n/a)/log(1+1/a)
この例において、ａは、以下で説明するように、カウンタの正確性を制御する値のパラメータである。この例において、（分母にみられるように）ｎ／ａに１を加えることにより、関数が良好に定義され、ｎ＝０の時にゼロに等しくなることが保証される。加えて、ｌｏｇ（１＋１／ａ）で割ることにより、ｎ＝１の時に関数が１となることが保証される。言い換えると、この近似により、少なくとも０および１の値について正確な値をカウンタが含むことが保証される。この定義に続いて、カウンタに格納される値がｖである時、表わされる正確なカウントは以下のとおりとなる。

n(v)=a((1+1/a)^v-1)
ここでの様々な記載において、確率的カウンタに物理的に格納される値ｖは「格納値」と言われ得て、それが表わす値ｎ（ｖ）は、確率的カウンタによって「カウントされる」タイプの発生事象の数の「予測値」または「推測値」と言われ得る。言い換えると、モーリスカウンタは、確率的近似ｖ（ｎ）を格納し、ｎは正確なカウントである。この例において、この例が８ビットのみを使用するものと仮定されることから、格納値は整数でなければならない。結果として、格納値から正確なカウントを判定することはできない。このため、カウンタの値が高い格納値によって表されるように十分なインクリメントが発生したことを反映するためにカウンタに格納される値をいつインクリメントするかを知る確定的な方法はない。これらの問題に対処するために、モーリスカウンタアルゴリズムは、以下のように、カウンタが値ｖを含む時に、確率ｐ（ｖ）を用いて格納値をインクリメントする。

p(v)=1/(n(v+1)-n(v))
直観的に、これは、平均的に、モーリスカウンタに格納された値が、任意の値ｖが格納された後にｎ（ｖ＋１）−ｎ（ｖ）インクリメント演算からひとたび外れるとインクリメントされることを意味する。これにより、格納値によって予測される値が、正確なカウントに等しい期待値を有するランダム変数であることが保証される。各インクリメントに対する確率の演算を回避するために、この確率的カウンタを実施する既存のアルゴリズムは、所与の値ａについてのすべての２５６通りの確率を事前に演算し、それらをルックアップテーブルに格納する。この例において、ルックアップテーブルは、各カウンタについて複製される必要はなく、各正確性クラスのみについて複製される（すなわち、ａの各選択）。

この例において、パラメータａは、モーリスカウンタが表わすことのできる範囲、および予測値と実際のカウントとの間の期待誤差の両方を判定し得る。期待誤差は、予測値と実際のカウントとの間の標準偏差（ＳＴＤＶ）間の比率として測定される（相対ＳＴＤＶまたはＲＳＴＤＶという場合もある）。

正確なカウントがｎである時の予測値の変動は、σ²=n(n-1)/2aによって与えられ、これに続き、ＲＳＴＤＶは、nが大きくなるにつれおおよそ

となる。
１つの例において、ａ＝３０の正確性パラメータを選択することにより、約１／８のＲＳＴＤＶがもたらされる。この例において、このａの選択により、カウンタはｎ（２５５）を表わし、これは約１３０，０００である。８ビットのみを使用するカウンタ構造においてこれは強い効果を生むものとなり得るところ、これは近代のコンピュータシステムにおいて使用される統計カウンタの多くのタイプに対して（範囲および／または正確性の点において）満足なものとはなり得ない。以下により詳細に記載されるように、この手法は、一部の実施形態において、より大きな範囲および高い正確性を伴うスケーラブルカウンタを実施するために変更され得る。

なお、ｎ（ｖ）はｖにおける指数であることから、モーリスカウンタに対する更新は、正確なカウントが増えるにつれて頻度が下がる。一部の実施形態において、確率的カウンタは、期待誤差を制限しながら、頻繁に更新された共用カウンタの競合を減少させるために、この特性を活用し得る。一部の実施形態において、確率的カウンタが実施され得て、上記のモーリスカウンタ手法の使用によって可能な範囲および正確性よりも大きな範囲および高い正確性を提供する。なお、より多くのカウンタビットが使用されるにつれてすべての可能な格納値について更新確率値を事前に計算することは望ましくないものとなり得ることから、より多くのビットを使用するモーリスカウンタへ上記の手法をシンプルに拡張することは、一部の状況においては受け入れ可能となり得ない。一部の実施形態において、確率的カウンタおよび以下に記載の対応するインクリメント演算は、この要件を回避するように上記の技術を拡張し得る。たとえば、以下に示すように、格納カウントをｖからｖ＋１へインクリメントする可能性は、ａ/（ａ＋１）の関数を用いたｖにおける等比級数であることが認められている。

このため、一部の実施形態において、所与の値ｐ（ｙ）について、ｐ（ｖ+１）の値は、シンプルに値ｐ（ｖ）をａ／（ａ＋１）だけインクリメントすることによって計算され得る。一部の実施形態において、この定数は、この浮動小数点割り算演算を繰り返し行なうことを回避するために事前に計算され得る。また、（たとえば、上記の）ｎ（ｖ）＝ａ（１／ｐ（ｖ）−１）であることも認められた。このため、一部の実施形態において、確率的カウンタの格納カウンタ値ｖの予測値ｎ（ｖ）は、ｖを知ることなくｐ（ｙ）から直接的に計算され得る。実際には、これを行なう一部の実施形態は、ｎ（ｖ）をｖから直接的に計算するよりも約５倍の速さとなり得る。このため、一部の実施形態において、確率的カウンタにｖを格納するのではなく、上記のモーリスカウンタの例のように、確率的カウンタのためのカウンタ構造が浮動小数点値ｐ（ｖ）を代わりに格納し得る。１つの例において、このようなカウンタ構造は、ｐ（ｖ）の３２ビット浮動小数点表現を格納し得るが、他の実施形態においては、６４ビットの倍長語を使用してｐ（ｖ）の値を格納することによってさらに範囲および／または正確性が拡張され得る。一部の実施形態において、この手法を使用して、カウンタをターゲットとする各呼び出されたインクリメント演算については、カウンタに格納された値ｐが読み出され得て、確率ｐを用いてｐ＊ａ／（ａ＋１）に等しい値と置き換えられ得る。この手法は、上記のモーリスカウンタ手法と比較した場合、予測値のより速い評価を提供し得るとともに、カウンタを表わすためにｂビットが使用される場合にすべての２ｂビットについて事前に計算および格納する必要を回避し得る。代わりに、所望のＲＳＴＤＶをもたらすａの値および対応するａ（ａ＋１）の値のみを事前に計算する必要があり得る。

このような確率的カウンタの様々な実施形態において、カウンタをターゲットとする各インクリメント演算時において、格納値は、確率ｐを用いて更新され得て、これは格納された確率値（すなわち、最も新しく格納された値）に等しくなり得る（またはこれに依存して判定され得る）。たとえば、一実施形態において、インクリメント演算は、パラメータ（６、２１、７）を伴うスレッド−ローカルＸＯＲシフト擬似乱数生成部を採用し得て、１と最大正数値ＭａｘＩｎｔ（これは、たとえば、２^２３−１に等しい）との間の値を有する整数ｉを返し得る。この例において、格納値は、ｉ／ＭａｘＩｎｔ≦ｐの場合に更新され得る。一部の実施形態において、確率的カウンタ構造は、（ＭａｘＩｎｔ＊ｐ）（たとえば、浮動小数点数として）を格納し得て、インクリメント演算は、格納値を更新するかを判定するためにｉを格納値と比較することのみを必要とする。この格納値は、ここでは「閾値」と言われ得る。この例において、初期閾値Ｔ_０＝ＭａｘＩｎｔであって、格納値が更新される時、現在値Ｔ_ｉは、疑似乱数生成部によって返される数が最大でＴ_ｉである場合のみに値Ｔ_ｉ＋１＝Ｔ_ｉ＊ａ／（ａ＋１））と置き換えられ得る。一実施形態に従う、この技術を実施するために使用され得る例示的な疑似コードは、以下に示される。

浮動小数点値を格納する確率的カウンタをインクリメントする方法の一実施形態は、図７のフロー図によって示される。７１０に示されるように、この例において、方法は、所与のノード上で実行されるスレッドが、浮動小数点更新確率値（ここに記載されるようなもの）を格納する共用確率的カウンタのインクリメントを開始することを含み得る。また、方法は、７２０のように、格納された確率値および整数乱数の値に応じて、共用カウンタがインクリメントされるべきかをスレッドが判定することを含み得る。たとえば、一部の実施形態において、判定は、値が０と所定の最大値（たとえば、ｍａｘｉｎｔ）との間である整数乱数変数の値に依存し得る。なお、一部の実施形態において、判定には、更新確率値の浮動小数点表示をこの整数乱数と比較する浮動小数点演算の使用が含まれ得る。共用カウンタをインクリメントすべきでないとスレッドが判定した場合（７３０からの否定の出口として示される）、７５５のようにインクリメント演算は完了し得る（すなわち、共用カウンタをインクリメントすることなく）。

この例に示されるように、共用カウンタをインクリメントすべきとスレッドが判定した場合（７３０からの肯定の出口として示される）、方法は、７４０のように、所望の正確性パーセンテージに依存する確率要因と掛け合わされた格納された更新確率値に等しい共用カウンタにおける新しい値を格納する試みによってスレッドがカウンタをインクリメントするよう試みることを含む。たとえば、一部の実施形態において、スレッドは、介在するバックオフ期間の有無に関わらず、単一のＣＡＳ型演算（または同様の同期演算）を使用して共用カウンタに新しい値を格納しようと試み得る。共用カウンタをインクリメントする試みが成功しなかった場合（７５０からの否定の出口として示される）、方法は、試みが成功するまで（または、図示されていないが、様々な適用可能なリトライもしくは競合管理ポリシーによって試みが中止されるまで）共用カウンタをインクリメントする試みを１回以上繰り返すことを含み得る。これは、図７の７５０から７２０へのフィードバックによって示される。なお、この場合において、方法は、（更新確率値に基づいて）格納値を更新するか（否か）の判定を繰り返すことを含み得る。なぜなら、共用カウンタをインクリメントする試みがコンフリクトによって失敗した場合、これは、以前の判定が行なわれてから他の演算（たとえば、他のスレッドのインクリメント演算）によって更新確率値が変更されたことを示し得るためである。ひとたび共用カウンタをインクリメントする試みが成功すると（７５０からの肯定の出口として示される）、７５５のように、インクリメント演算が完了し得る。この例に示されるように、一部の実施形態において、７６０のように、共用カウンタを読み取るスレッドの後続の演算は、格納された更新確率値を読み取り、格納された更新確率値および所望の正確性パーセンテージに応じて共用カウンタの予測値を計算することによって行なわれ得る。

上記の確率的カウンタの一部の実施形態において、Ｔ_ｉが小さくなり過ぎた場合には更新を回避するよう注意する必要があり得る。これによってカウンタの特性が失われ得るためである。特に、この手法は整数乱数生成部を使用することから、格納された閾値の整数部が更新によって減少しない場合、これは実際には更新の確率に影響を与え得ない。

一部の実施形態において、少なくともＴ_ｉ≧ａ＋１である間はＴ_ｉ−Ｔ_ｉ＋１以上であることが観察された。このため、一部の実施形態において、確率的カウンタは、もはや真でない場合にはリセットされ得る。他の実施形態において、所与の状況において、および／または所与のマルチスレッドアプリケーションについてこれが好ましい場合は、この場合においてエラーが生じ得る。ａ＝５０００が選択され（たとえば、１％のＲＳＴＤＶを実現するために）、３２ビットカウンタが使用される例において、この閾値は、予測値がＭａｘＩｎｔ値よりも約０．０２％下回る場合には取り消され得る。したがって、ナイーブ３２ビットカウンタと比較した場合、確率的カウンタは、実施されたカウンタの範囲を大きく減少させることなく、低い相対誤差および良好なスケーラビリティを実現し得る。

一部の実施形態において、ここまで記載された確率的カウンタ手法は、カウンタが競合するとともに高い値に達した時に非常に良好に仕事を実行し得るが、競合が低く予測値が低い時は標準的なＣＡＳベースのカウンタよりもかなり遅くなり得る。一部の実施形態において、この確率的カウンタのハイブリッド版（ここでは「確率適応」カウンタと言われる）が採用され得て、インクリメント演算はカウンタの現在、最近、または過去の競合量に依存する。たとえば、一部の実施形態において、この適応確率的カウンタは、標準的な同時カウンタをインクリメントすることによって（たとえば、ＣＡＳ型命令を使用して）カウンタをインクリメントする要求に最初に応答し得るが、ＣＡＳ演算が複数回にわたって失敗した場合（たとえば、所定のリトライ限界または他の競合管理ポリシーに基づいて）、上記の確率的カウントスキームに切り換えられ得る。たとえば、一実施形態において、確率的カウンタ構造は、６４ビット語の半分を標準的カウンタに格納し、他の半分を確率的カウンタに格納する。競合に遭遇すると、インクリメント演算は、構造の標準的カウンタ部分の更新から、確率的カウンタ部分の更新へ切り換えられ得る。この例において、カウンタを読み取ることは、カウンタ構造の確率的カウンタ部分によって予測された値を構造の標準的カウンタ部分によって格納された値に加えることを含み得る。この適応手法は、特に、ごく少数のみが競合する場合が多い（または常に競合する）数千のカウンタにアクセスするマルチスレッドアプリケーションにおける使用に良好に適し得る。

カウンタの競合に応じてハイブリッドカウンタをインクリメントする方法の一実施形態は、図８のフロー図によって示される。８１０に示されるように、この例において、方法は、マルチスレッドアプリケーションのスレッドが、ハイブリッド共用カウンタ（たとえば、標準的カウンタ部分と確率的カウンタ部分とを含むもの）のインクリメントを開始することを含む。なお、この例および他の例において、共用カウンタのインクリメントを開始するスレッドは、複数の同時に実行されるアトミックトランザクションを集合的に表わす複数のスレッドのうちの１つであり得て、共用カウンタはこれらのトランザクションのうちの１つ以上からアクセスされ得る。また、方法は、８２０のように、共用カウンタの標準的カウンタ部分をインクリメントするようスレッドが試みることを含み得る（たとえば、ＣＡＳ型演算または同様の同期演算を使用する）。試みが成功した場合（８３０からの肯定の出口として示される）、８７０のように、インクリメント演算が完了し得る。ハイブリッド共用カウンタの標準的カウンタ部分をインクリメントする試みが成功しなかった（８３０からの否定の出口として示される）が、リトライ限界条件に到達しなかった場合（８４０からの否定の出口として示される）、方法は、８４５のように、スレッドが、遅れの有無に関わらず共用カウンタの標準的カウンタ部分をインクリメントする試みを１回以上リトライすること、およびこれらの試みが成功したかどうかを判定すること（８４５から８３０へのフィードバックとして示される）を含み得る。なお、様々な実施形態において、リトライ限界条件は、１つ以上の以前のＣＡＳ型演算がカウンタの標準的部分のインクリメントに失敗したこと、および／または共用カウンタ上の競合を示す１つ以上の他の要因であり得る。

ハイブリッド共用カウンタの標準的カウンタ部分をインクリメントする試みが成功せず（８３０からの否定の出口として示される）、リトライ限界条件に到達した場合（８４０からの肯定の出口として示される）、方法は、スレットが、共用カウンタの確率的カウンタ部分をインクリメントするよう試みることによってハイブリッド共用カウンタをインクリメントするよう試みることを含み得る（８５０のように）。この試みが成功しなかった場合（８６０からの否定の出口として示される）、方法は、試みが成功するまで（または、図示されないが、様々な適用可能なリトライもしくは競合管理ポリシーによって試みが中止されるまで）、ハイブリッド共用カウンタの確率的カウンタ部分をインクリメントする試みをスレッドが繰り返すことを含み得る。これは、８６０から８５０へのフィードバックによって図８に示される。ハイブリッド共用カウンタの確率的カウンタ部分をインクリメントする試みが成功した場合（８６０からの肯定の出口として示される）、８７０のように、インクリメント演算が完了し得る。この例に示されるように、一部の実施形態において、８８０のように、ハイブリッド共用カウンタを読み取るスレッドの後続の演算は、標準的カウンタ部分の値および確率的カウンタ部分の値を読み取り、合計を返すことによって行なわれ得る。

上記の確率的カウンタは、それらの正確性、低競合下における性能、高競合下におけるスケーラビリティ、およびスペース使用の点から、多くの状況における使用、および多くのタイプのマルチスレッドアプリケーションに適したものとなり得る。しかしながら、他の状況において、浮動小数点演算を使用することなく同様の特性を提供する確率的カウンタがより適したものとなり得る。このため、一部の実施形態において、更新確率値は、常に２の負数乗（non-positive powers of two）となるように制限され得る。これにより、カウンタを更新するかどうかについての判断（適切な確率を伴う）することが比較的容易となり、更新する場合、浮動小数点演算を使用することなく次の更新確率値を計算することが比較的容易となり得る。２つのこのようなカウンタは、以下に記載される（対応するインクリメントおよび読み取り演算とともに）。

更新確率値について２の負数乗のみが使用される実施形態において、カウンタをインクリメントする要求に応答して、インクリメント演算は、確率整数乱数の低位ｋビットがすべてゼロであるかどうかを判定することにより（浮動小数点計算を行なう必要なく）、１／２^ｋを用いてカウンタを更新するかを判断し得る。なお、この手法は、上記の手法よりもきめが粗い更新確率値を採用する。これは、ａ／（ａ＋１）の要因によって減少させることとは対照的に、各更新は更新確率値を半分にするのみであるためである。更新確率値を減少させることは、性能およびスケーラビリティのためには重要である（少なくともある程度までは）。しかしながら、更新ごとに更新確率値が半減する場合、小さくなるのが速すぎることから、カウンタの正確性を減少させ得る。このため、一部の実施形態において、ここに例が記載されるこのトレードオフを管理する様々なポリシーにより、実際に減少させる前に同じ更新確率値が繰り返し使用され得る。

以下に記載される例において、カウンタ値は、２進浮動小数点（ＢＦＰ）を使用して表わされ得る。たとえば、カウンタは、ペア（ｍ，ｅ）を格納し得て、これは予測値ｍ＊２^ｅを表わす（すなわち、ｍは仮数であり、ｅは指数である）。ｍおよびｅを格納するために、カウンタ変数における異なるビットフィールドが使用される。たとえば、ｅの値を格納するために４ビットが使用され、ｍの値を格納するために２８ビットが使用され、カウンタ構造は、（２^２８−１）＊２^１５までのカウンタ値、またはＭａｘＩｎｔの約２０００倍のカウンタ値を表わすことができる。

以下に記載される例において、指数がｅである場合、カウンタは確率２^−ｅを用いて更新され得る。以前の例のように、カウンタの期待される予測値を現在までに行なわれたインクリメントの合計数と等しく維持するために、確率２^−ｅを用いてカウンタをインクリメントする時に２^ｅが予測値に加えられ得る。なお、様々な実施形態において、２^ｅは、（ｍ，ｅ）で表わされるカウンタの予測値に対し、少なくとも２つの異なる方法によって加えられる。たとえば、１つの方法は、格納値を（ｍ＋１，ｅ）に更新することである。ｍが奇数であって指数フィールドが満たされていない時のみに適用される他の方法は、カウンタを（（ｍ＋１）／２，ｅ＋１）に更新することである。両方の場合において、予測値に加えられる量は、２^ｅとして容易にみられる。この一般的な手法に基づいた以下に記載される実施形態は、カウンタを更新する時にどの方法を使用するかについて制御する１つ以上のポリシーにおいて異なり得る。

２進浮動小数点値を格納する確率的カウンタをインクリメントする方法の一実施形態は、図９のフロー図によって示される。９１０に示されるように、この例において、方法は、所与のノード上で実行されるスレッドが、確率的カウンタ値を２進浮動小数点数として格納する共用確率的カウンタのインクリメントを開始することを含み得て、更新確率値は、確率的カウンタ値の指数部分から計算可能であり、２の負数乗に制限される。たとえば、一部の実施形態において、カウンタ構造は、仮数部分と指数部分とを含み得て、これらは合わせてｍ＊２^ｅの予測（または期待）値を表わすために使用される。また、方法は、共用確率的カウンタをインクリメントするべきかをスレッドが判定することを含み得る（９２０のように）。たとえば、共用確率的カウンタは、一部の実施形態において、１／２^ｅを用いて更新され得る。

この例において、共用確率的カウンタをインクリメントすべきでないとスレッドが判定した場合（９３０からの否定の出口として示される）、９５５のようにインクリメント演算は完了し得る（すなわち、共用確率的カウンタをインクリメントすることなく）。他方、共用確率的カウンタをインクリメントすべきとスレッドが判定した場合（９３０からの肯定の出口として示される）、方法は、９４０のように、新しい予測値が以前の予測値と２^ｅとの合計に等しくなるように、共用確率的カウンタに新しい値を格納するよう試みることにより、カウンタをインクリメントするようスレッドが試みることを含み得る。たとえば、カウンタをインクリメントする試みは、バックオフの有無に関わらずＣＡＳ型演算を使用して行なわれ得る。なお、この方法でカウンタをインクリメントすることにより（たとえば、（ｍ，ｅ）を（（ｍ＋１）／２，ｅ＋１）に置き換えることにより）、カウンタを更新する確率が半減する。共用確率的カウンタをインクリメントする試みが成功した場合（９５０からの肯定の出口として示される）、インクリメント演算は完了し得る（９５５のように）。共用確率的カウンタをインクリメントする試みが成功しなかった場合（９５０からの否定の出口として示される）、方法は、試みが成功するまで（または、図示されないが、様々な適用可能なリトライまたは競合管理ポリシーによって試みが中止されるまで）共用確率的カウンタをインクリメントする試みを１回以上繰り返すことを含み得る。なお、この例において、確率的カウンタをインクリメントする試みを繰り返すことは、インクリメントを行なうか（否か）についての決定を繰り返すことを含み得る。これは、９５０から９２０へのフィードバックによって図９に示される。この例に示されるように、一部の実施形態において、９６０のように、共用確率的カウンタを読み取るスレッドの後続の演算は、格納された確率的カウンタ値を読み取って予測値を計算する（すなわち、この例においては、指数値によってシフトされたままの仮数値を返す）ことによって行なわれ得る。なお、この例において、これはｍ＊２^ｅを演算することに等しい。

一部の実施形態において、確率的カウンタ値を２進浮動小数点数として格納する確率的カウンタは、決定的更新ポリシーを採用し得て、更新確率値は、確率的カウンタ値の指数部分から計算可能である。このようなカウンタ（ここではＢＦＰ−ＤＵＰカウンタと言われる）の一例は、上記の確率的カウンタの特性と同様の特性を示し得て、たとえば、ＲＳＴＤＶの所望の境界が指定され得て、所望のＲＳＴＤＶ境界を保証しながらスケーラビリティを向上させるために、対応する更新処理は、可能な限り速く更新確率値を減少させ得る。一部の実施形態において、指定された境界を保証することは、更新確率値の減少が速くなり過ぎないよう保証することを含み得る。一部の実施形態において、更新ポリシーにより、カウンタに対する更新は、デフォルトで仮数をインクリメントさせ得る。しかしながら、仮数をインクリメントすることによって、偶数となることが必要とされ得る所定の限界（ここでは「仮数閾値」という）に到達し得る場合、インクリメント演算は、代わりに仮数を半減させ（インクリメント後）、指数をインクリメントする。この手法を使用することにより、インクリメントの第１の仮数閾値数は、確率２^０＝１を用いてカウンタを更新し得て、誤差をもたらすことなくカウンタが仮数閾値に到達することを保証する。その後、カウンタが更新される仮数閾値／２回ごとに指数がインクリメントされ得る（および仮数が半分となり得る）。一部の実施形態において、仮数閾値の選択により、どのくらい速く指数が増加するか（およびどのくらい速く更新確率値が減少するか）が決定され得る。仮数閾値を選択する様々な方法がここに記載される。

上記のようなＢＦＰ−ＤＵＰカウンタの一実施形態は、以下に示される例示的な疑似コードによって示され得る。

複数の更新オプションを含む確率的カウンタをインクリメントする方法の一実施形態は、図１０のフロー図に示される。１０１０に示されるように、この例において、方法は、所与のノード上で実行されるスレッドが、確率的カウンタ値を２進浮動小数点数として格納する共用確率カウンタのインクリメントを開始することを含み得て、確率的カウンタ値の指数部分から計算可能な更新確率値は、２の負数乗に制限される。たとえば、一部の実施形態において、カウンタ構造は、仮数部分および指数部分が合わせてｍ＊２^ｅの予測（期待）値を表わすことを含み得る。また、方法は、格納された確率的カウンタ値および整数乱数の値に応じて、共用確率的カウンタをインクリメントすべきかをスレッドが判定することを含み得る（１０２０のように）。たとえば、一実施形態において、確率１／２^ｅを用いてカウンタを更新するために、方法は、整数乱数の低位ｅビットがすべてゼロであるかを判定することを含み得る（浮動小数点数値演算は不要）。そうである場合、ここに記載する方法でカウンタを更新することにより、カウンタを更新する確率が半分に減少し得る。一部の実施形態において、カウンタの更新を行なうために使用される方法は、カウンタの仮数部分がインクリメントされた場合にオーバーフローし得るか、および／またはカウンタの指数部分が満たされているかに依存し得る。

この例に示されるように、共用カウンタをインクリメントすべきでない（１０３０からの否定の出口として示される）とスレッドが判定した場合、１０８０のように、インクリメント演算は完了し得る（すなわち、共用確率的カウンタをインクリメントすることなく）。他方、共用確率的カウンタをインクリメントすべきとスレッドが判定した場合（１０３０からの肯定の出口として示される）、および仮数をインクリメントしても正確性依存閾値に等しくならない場合（１０４０からの否定の出口として示される）、方法は、共用カウンタの仮数部分をインクリメントするよう試みることによってカウンタをインクリメントするようスレッドが試み得て（１０７０のように）、この点においてインクリメント演算が完了し得る（１０８０のように）。一部の実施形態において、共用カウンタの仮数部分をインクリメントする試みは、介在するバックオフ期間（図示せず）の有無に関わらず、試みが成功するまで（または様々な適用可能なリトライまたは競合管理ポリシーによって中止されるまで）ＣＡＳ型演算（または同様の同期演算）を使用して１回以上行なうことであり得る。他の例のように、共用カウンタの仮数部分をインクリメントする試みが失敗すると、方法は、要素１０２０から始まる図１０に示される演算の少なくとも一部を繰り返すことを含み得る（図示せず）。

この例に示されるように、共用確率的カウンタをインクリメントすべきであるとスレッドが判定したが（１０３０からの肯定の出口として示される）、仮数をインクリメントすることによって正確性依存閾値に等しくなり（１０４０からの肯定の出口として示される）、共用確率的カウンタの指数部分が既に最大値にある場合（１０５０からの肯定の出口として示される）、方法は、スレッドがカウンタをゼロにリセットすることを含み得て（１０５５のように）、この点においてインクリメント演算が完了し得る（１０８０のように）。言い換えると、方法は、（仮数，指数）ペアを（０，０）の値にリセットすることを含み得る。仮数をインクリメントすることによって正確性依存閾値に等しくなるが（１０４０からの肯定の出口として示される）、共用確率的カウンタの指数部分が最大値でない場合（１０５０からの否定の出口として示される）、方法は、仮数をインクリメントし、インクリメントされた仮数を半減させ、指数をインクリメントするよう試みることによってスレッドがカウンタをインクリメントするよう試みることを含み得て（１０６０のように）、その後にインクリメント演算が完了し得る（１０８０のように）。一部の実施形態において、共用カウンタを更新する試みは、単一のＣＡＳ型演算または同様の同期演算を使用して行なわれ得て、これは、（必要であれば）成功するまで（または、図示されないが、様々な適用可能なリトライまたは競合管理ポリシーによって試みが中止されるまで）繰り返され得る。他の例のように、共用カウンタを更新する試みが失敗した場合、方法は、要素１０２０から始まる図１０に示される演算の少なくとも一部を繰り返すことを含み得る（図示せず）。

上記の例示的な疑似コードに示されるように、ＢＦＰカウンタクラスは、一部の実施形態において、（テンプレート引数として）ＲＳＴＶＤ上の所望の境界をパーセンテージとして受け入れ得る（たとえば、１の正確性パラメータ値は、１％のＲＳＴＤＶ上の所望の境界に対応し得る）。一部の実施形態において、以下で説明するように、仮数閾値パラメータの値が所望の正確性に基づいて判定され得る。この例において、インクリメント演算（Ｉｎｃとして示される）は、確率１−１／２^ｅを用いて、カウンタを更新しないように決定し得て、ここでｅはカウンタ内に現在格納されている指数値である（上記の疑似コードの３６〜４６行目のように）。この例において、カウンタを更新する決定がなされた場合、インクリメント演算は、まず、カウンタが既に最大値に達したかをみるためにチェックを行い（５２行目のように）、この場合においては、カウンタをゼロに更新するように試み得る。なお、他の実施形態において、インクリメント演算は、たとえば所与の状況において、または所与のアプリケーションのために好ましい場合は、この場合においてエラーを代わりに発信する。その他に、現在のペアに基づいて新しいペアが判定され得る（上記の５６〜６１行目に示されるように）。最後に、インクリメント演算は、たとえばＣＡＳ型命令を使用して新しいペアをカウンタに格納するよう試み得て、カウンタが既に変更されていないことを確認する（６３行目のように）。この例において、ＣＡＳ演算が失敗した場合、演算は、カウンタを更新するか（否か）についての判定から始まり、リトライされ得る。他の実施形態において、他の競合管理ポリシーが適用され得る。

一部の実施形態において、ここに記載されるインクリメント演算の様々な最適化により、全体的な性能が向上し得る。たとえば、一部の実施形態において、インクリメント演算を実施するコードは、共通の更新の場合（すなわち、カウンタを更新するＣＡＳ型演算が成功した場合）を「インライン化」し得るとともに、失敗したＣＡＳ型演算の戻値を使用し、インクリメント演算をリトライする前のカウンタデータ（たとえば、上記の例示的なコードにおけるｂｆｐＤａｔａ）を再び読み取る必要を回避し得る。一部の実施形態において、同時更新（たとえば、マルチスレッドアプリケーションの他のスレッドによって更新が試みられる）に伴うコンフリクトによってＣＡＳ型演算が失敗した場合、新しい値に基づいて更新を適用すべきかを判定するテストがバックオフ前に行なわれ得るが、常にそうではない。一部の実施形態において、カウンタについての上記のすべての計算は、ビットのシフトおよびマスク演算を使用して（すなわち、浮動小数点演算なしに）行なわれ得る。

なお、上記のものと類似の既存の連続的な近似カウントアルゴリズムは、同時更新を支持せず、上記の手法よりも柔軟性が小さい。この既存のアルゴリズムにおいては、カウンタが更新された時に仮数および指数を明示的に更新するのではなく、格納値を単にインクリメントすることによって更新が行なわれる。この既存のアルゴリズムにおいては、カウンタの仮数部分がその最大値を超えてインクリメントされる場合、オーバーフローによって自然に指数フィールドがインクリメントされ得る（これを保証するために適切に配置され得る）。この選択の結果として、既存のアルゴリズムにおいて使用される更新関数は、上記のものよりも幾分シンプルとなり得る。しかしながら、時間の経過とともにカウンタの更新頻度が下がることから、性能に対する影響は小さくなり得る。既存のアルゴリズムの他の暗示としては、更新が指数をインクリメントする（および後続の演算について更新確率値を減少させる）頻度は、２の乗数とする必要がある。さらに、既存のアルゴリズムは、カウンタに格納されるデータから予測値を計算する異なる方法を実施しなければならない。なぜなら、指数がインクリメントされると格納データの仮数部分がゼロになるためである。

一部の実施形態において、ここに記載されるＢＦＰ−ＤＵＰカウンタは、指数をインクリメントする前の仮数のインクリメントを後続の指数のインクリメント間に行なわれるインクリメントの２倍行ない得て、既存のアルゴリズムは、指数の各インクリメント前に同じ数の仮数に対するインクリメントを行なう。結果として、ＢＦＰ−ＤＵＰカウンタをモデル化するために使用されるマルコフ連鎖は、既存のアルゴリズムによって使用される連鎖と同様の連鎖の前に仮数閾値／２の長さの決定的連鎖を含む。しかしながら、これは限界における結果を変更し得るものではない。なぜなら、これらの仮数の決定的インクリメントは確率１で発生し、このため、カウンタの不正確性を増加させない。

上記の確率適応カウンタに関連する演算とは対照的に、このＢＦＰ−ＤＵＰカウンタにおいて、ＲＳＴＤＶの境界は、行なわれるインクリメント演算の数から独立し得ない。むしろ、これらの技術は、インクリメントの数ｎが無限大に近づくにつれて、限界における期待ＲＳＴＤＶの境界を提供し得る。より正確には、これは以下のとおり記載され得る。

この例において、Ａ_ｎは、インクリメント演算後の期待ＲＳＴＤＶを表わし、Ｍは、指数のインクリメント間の仮数（この例においては、仮数閾値／２に等しい）のインクリメントの数を表わす。一部の実施形態において、この式は、所望の境界を実現するためにＭの選択を判定するために使用され得る。たとえば、上記の疑似コードにおけるＢＦＰカウンタクラスはその正確性引数をパーセンテージとして受け入れることから（上記のとおり）、上記の式は以下を意味し得る。

M≦((30,000/正確性^２)+3)/8
この例において、仮数閾値について対応する式は、上記の疑似コード（および仮数閾値＝２Ｍ）の１８行目に見つけられる。なお、一部の実施形態において、ＢＦＰ−ＤＵＰカウンタは、指数のインクリメント間の仮数に対するインクリメントの数を２の乗数に制限しないことから、この手法を使用することにより、この計算に基づいて仮数閾値を選択する柔軟性が提供され得て、正確性と性能のトレードオフに対するよりきめ細かい制御が得られる。一部の実施形態において（ここに記載される様々な実験においてモデル化されたものを含む）、ＲＳＴＤＶに対する１％の制限を反映するように正確性パラメータ値が設定され、結果として仮数閾値が７５００に設定される。

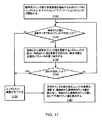
構成可能な正確性パラメータに応じて確率的カウンタをインクリメントする方法の一実施形態は、図１１のフロー図によって示される。１１１０に示され得るように、この例において、方法は、確率的カウンタの多値表現を格納する共用カウンタのインクリメントをマルチスレッドアプリケーションのスレッドが開始することを含み得て、予測値は、格納された確率的カウンタ値から計算され得る。格納された確率的カウンタ値を更新すべきであるとスレッドが判定した場合（１１２０からの肯定の出口として示される）、方法は、格納された確率的カウンタ値を更新するようスレッドが試みることを含み、格納された確率的カウンタ値を更新する試みは、構成可能な正確性パラメータの値に依存する（１１３０のように）。なお、一部の実施形態において、格納された確率的カウンタ値を更新する試み（および／またはそれを行なう判定）は、格納された確率的カウンタ値自体（すなわち、現在格納されている値）に基づき得る。

この例に示されるように、格納された確率的カウンタ値を更新する試みが成功した場合（１１４０からの肯定の出口として示される）、インクリメント演算が完了し得る（１１５０のように）。他方、格納された確率的カウンタ値を更新する試みが成功しなかった場合（１１４０からの否定の出口として示される）、方法は、試みが成功するまで、または様々な適用可能なリトライもしくは競合管理ポリシーによって試みが中止されるまで、格納された確率的カウンタ値を更新する試みを繰り返すことを含み得る。なお、この例において、格納された確率的カウンタを更新する試みを繰り返すことは、更新を行なうか（否か）の判定を繰り返すことを含み得る。これは、１１４０から１１２０へのフィードバックとして図１１に示される。この例に示されるように、一部の実施形態において、１１６０のように、共用カウンタを読み取るスレッドの後続の演算は、格納された確率的カウンタ値を読み取り、格納された確率的カウンタ値に応じて予測値を計算することによって行なわれ得る。

様々な実施形態において、ＢＦＰ−ＤＵＰカウンタによって使用される決定的更新ポリシーは、様々な状況において、および様々なマルチスレッドアプリケーションにおいて使用するのが好ましい。しかしながら、スケーラビリティおよび性能のために、カウンタが増加するにつれて更新確率値を減少させることが重要である一方、所与のシステムおよび作業負荷のための一部の点において、カウンタ変数の競合は実質的にゼロに減少され得て、カウンタの更新についてのオーバーヘッドは、重要でなくなる場合がある。この点を超えて、更新確率値をさらに減少させることは、カウンタの正確性を増加させるよう作用するのみとなり得る。このため、一部の実施形態は、競合感知更新ポリシーなど、適応性および／または競合感知更新ポリシーを採用する。たとえば、一部の実施形態において、インクリメント演算は、カウンタの競合がある（またはあった）場合にのみ指数を更新する（これにより、更新確率値を減少させる）ことを選択し得る。言い換えると、適応ＢＦＰカウンタは、カウンタについての現在、最近、または過去の競合量に応じたインクリメント演算を採用し得る。たとえば、一部の実施形態において、インクリメント演算は、ＣＡＳ型命令を使用して１回（または所定回数にわたって）仮数をインクリメントする（たとえば、無条件に、またはオーバーフローするまで）よう試み得て、それが失敗した場合にのみ、上記のＢＦＰ−ＤＵＰカウンタにおいて使用されるものと同様のポリシーを使用し、指数を更新して仮数を半減させるかを決定し得る。このような競合感知更新ポリシーを採用するＢＦＰカウンタは、ここではＢＦＰ−ＣＳＵＰカウンタと言われ得る。様々な実験において、ＢＦＰ−ＣＳＵＰカウンタは、実際に高い正確性を実現しながら、上記のＢＦＰ−ＤＵＰカウンタの性能と同様の性能をもたらし得ることが示された。

共用カウンタの競合に応じてカウンタ値を表わす２進浮動小数点値を格納する確率的カウンタをインクリメントする方法の一実施形態は、図１２のフロー図によって示される。１２１０に示されるように、この例において、方法は、所与のノード上で実行されるスレッドが確率的カウンタ値を２進浮動小数点数として格納する共用確率的カウンタのインクリメントを開始することを含み得て、確率的カウンタ値の指数部分から計算可能な更新確率値は、２の負数乗となるように制限される。たとえば、一部の実施形態において、カウンタ構造は仮数部分と指数部分とを含み得て、これらは合わせてｍ＊２^ｅの予測（期待）値を表わす。カウンタの仮数部分をインクリメントすることによって値が正確性依存閾値に等しくなる場合（１２２０からの肯定の出口として示される）、方法は、要素１０４０から始まる図１０に示される方法のように共用確率的カウンタをインクリメントする試みを継続することを含み得る。

この例に示されるように、カウンタの仮数部分をインクリメントしてもその値が正確性依存閾値に等しくならない場合（１２２０からの否定の出口として示される）、方法は、仮数をインクリメントする試みを１回以上行なうことによってスレッドが共用確率的カウンタをインクリメントするよう試みることが含まれ得る（１２３０のように）。様々な実施形態において、スレッドが試みをリトライし得る回数は、１つ以上の適用可能なリトライもしくは競合管理ポリシーに依存し得て、介在するバックオフ期間の有無に関わらず複数のリトライの試みが行なわれ得る。スレッドが共用確率的カウンタのインクリメントに成功した場合（１２４０からの肯定の出口として示される）、インクリメント演算は完了し得る（１２５０のように）。スレッドが共用確率的カウンタのインクリメントに成功しなかった場合（１２４０からの否定の出口として示される）、方法は、要素１０４０から始まる図１０に示される方法のように共用確率的カウンタをインクリメントする試みを継続することを含み得る。

異なる実施形態において、現在、最近、または過去の競合に基づき、統計カウンタを更新するか、いつ更新するか、および／またはどのように更新するかを判定するために、様々な競合感知法が適用され得る。共用カウンタの競合に応じて共用カウンタをインクリメントするか（および／またはいつインクリメントするか）を判定するとともに共用カウンタをインクリメントする方法の一実施形態は、図１３のフロー図によって示される。１３１０に示されるように、この例において、方法は、マルチスレッドアプリケーションの複数の同時に実行されるスレッドのうちの１つが共用カウンタのインクリメントを開始することを含み得る。一部の実施形態において、スレッドは、複数の同時に実行されるアトミックトランザクションを集合的に実施する複数のスレッドのうちの１つであり得る。方法は、スレッドが共用カウンタを更新するか、またはいつ更新するかを判定することを含み得て、共用カウンタを更新するか、またはいつ更新するかを判定する方法は、同時に実行されるスレッド間の共用カウンタの競合の量に依存する（１３２０のように）。たとえば、方法は、現在、最近、または過去の共用カウンタの競合に少なくとも部分的に依存し得る。

共用カウンタを更新すべきでないとスレッドが判定した場合（１３３０からの否定の出口として示される）、１３６０のように、インクリメント演算は完了し得る（すなわち、共用カウンタを更新することなく）。他方、共用カウンタを更新すべきとスレッドが判定した場合（１３３０からの肯定の出口として示される）、方法は、スレッドが共用カウンタを更新するよう試みることを含み得て、共用カウンタを更新するよう試みる方法は、同時に実行されるスレッド間における共用カウンタの競合の量に依存する（１３４０のように）。再び、方法は、現在、最近、または過去の共用カウンタの競合に少なくとも部分的に依存し得る。この例に示されるように、共用カウンタを更新する試みが成功した場合（１３５０からの肯定の出口として示される）、インクリメント演算は完了し得る（１３６０のように）。他方、共用カウンタを更新する試みが成功しなかった場合（１３５０からの否定の出口として示される）、方法は、試みが成功するまで（または、図示されないが、様々な適用可能なリトライまたは競合管理ポリシーによって試みが中止されるまで）共用カウンタを更新する試みをスレッドが１回以上リトライすることを含み得る。なお、この例において、共用カウンタを更新する試みを繰り返すことは、カウンタを更新するか（否か）、またはカウンタをいつ更新するかについての判定を繰り返すことを含み得る。これは、１３５０から１３２０へのフィードバックによって図１３に示される。なお、一部の実施形態において、試みのリトライの性能（および／または試みがリトライされ得る回数）は、カウンタの競合の量（この最も新しい失敗を引き起こした競合を含む）に依存し得る。なお、図１３に示される例においては、１３２０に示される演算および１３４０に示される演算は、カウンタの競合の量に依存するものとして記載されるが、他の実施形態において、これらの演算のうちの１つのみが、現在、最近、または過去のカウンタの競合の量に依存し得る。

ここに記載される例の大部分は、多くのカウンタがあって、そのうちの一部が頻繁にインクリメントされる状況における使用に統計カウンタを実施する技術に焦点を当ててきた。このため、例は、低いスペースオーバーヘッド、競合がない場合における低いオーバーヘッド、および重度の競合下における良好なスケーラビリティを示す技術を含む。これらの技術は必ずしも読み取り性能（たとえば、カウンタをターゲットとした読み取り動作）のために最適化されなかったが、一部の実施形態において、これらの読み取り動作に関連付けられたコストは、ここに記載される技術の多くにおいて合理的に低いものとなり得る。

なお、概して、カウンタの値を引き出すコストについては、２つの主な構成部分があり得る。１つの構成部分は、必要なデータを読み取るコストに関連付けられたコストであり、他の構成部分は、読み取られたデータから戻値を計算することに関連付けられたコストである。ここに記載されるシナリオの多くにおいて、まずこれらのコストが所与のカウンタに関連付けられたカウント値を引き出すコストを左右する可能性が高い。なぜなら、カウンタ下にあるデータは、読み取り演算を実行するスレッドのキャッシュにない可能性が高いためである。このため、データは、メモリから、または他のキャッシュから取ってくる必要があり得て、システムにおいて異なるＮＵＭＡノードにあり得る。

なお、既存のナイーブカウンタの値を読み取ることは、カウンタ自体に格納されたデータを読み取り、読み取られた値を返すことを単に含み得る。これ故に、読み取りコストは（最大でも）単一のキャッシュミスのコストである。一部の実施形態において、ここに記載されるＮＵＭＡアウェアＲＢＯ型カウンタもしくは適応ＮＵＭＡアウェアＲＢＯ型カウンタ、またはここでＢＦＰ−ＤＵＰおよびＢＦＰ−ＣＳＵＰと言われる手法を採用するカウンタは単一のキャッシュミスのコストも引き起こし得るが、これらのカウンタはカウンタ予測値を判定するための様々なマスクおよび／またはシフト動作のコストも引き起こし得る。ここに記載されるマルチラインカウンタを読み取ることは、カウンタ下のキャッシュラインの各々を読み取ることを必要とし得る。しかしながら、これらは独立した読み取りであり、ほとんどの最新のアーキテクチャにおいては並行して大きく解消され得る。ここに記載するマルチライン適応手法を採用するカウンタ上のリード演算は、拡張される更新の競合を十分にカウンタが経験しない限り既存のシンプルなカウンタのものと同様であり、この場合、リード演算は、カウンタに割り当てられた複数のキャッシュラインだけでなく、どこにあるかを判定するポインタも読み取らなければならない。割り当てられたキャッシュラインのリード演算は、ポインタの値に依存し、このため、リード演算のレイテンシは、すべての割り当てられたラインが平行に読み取りを行なう場合であっても、連続的に少なくとも２つのキャッシュミスのコストを含む可能性が高くなり得る。モーリスおよび「確率適応」カウンタをターゲットとしたリード演算は、両方とも、頻繁に実行された場合に顕著なオーバーヘッドを加える可能性の高い複数の浮動小数点演算を含み得る。このため、ＢＦＰベースのカウンタは、このようなシナリオにおいて好ましいものとなり得る。代替的に、（実質的に）カウンタの格納値が稀にのみ変更され得る（たとえば、更新確率値が十分に減少した後）と仮定すると、格納値から計算された予測値を記録する最適化は有益となり得る。

一部の実施形態において、ここに記載されるスケーラブル統計カウンタは、トランザクションメモリ支持がハードウェア、ソフトウェア、またはハードウェアおよびソフトウェアの両方の組み合わせのいずれを用いて実施されても、トランザクションメモリ支持を含むシステムにおいて使用された場合に特に価値あるものとなり得る。たとえば、統計カウンタは、ハッシュ表におけるエントリの数の記録、または特定のコードがどのくらい頻繁に実行されるかについての統計を維持するなど、このようなシステムにおける様々な目的に使用され得る。アトミックトランザクション内のカウンタの使用がすべてのトランザクションのペアがカウンタを更新することからコンフリクトさせるという共通の経験がある。ここに記述されるように、カウンタは、複数の更新が並行して発生し得るように分割する（上記のマルチライン手法のように）、または更新の頻度を減少させることで（ここに記載の確率的カウンタのように）競合を減少させることにより、よりスケーラブルものとなり得る。一部の実施形態において、これらの技術は、ナイーブ非スケーラブルカウンタを採用するトランザクションと比較し、これらのカウンタを使用したアトミックトランザクションが互いにコンフリクトする頻度を大きく減少させるという副作用を有し得て、これによって通常はスケールがとぼしくなる、および／または高度に不正確なカウントがもたらされる。

様々な実施形態において、様々なカウンタ技術（そのうちの一部は正確なカウントを提供し、そのうちの他の部分は合理的な相対誤差に向けられ、多数回にわたってインクリメントされるカウント値を検知する目的において有用である）は、ナイーブ同時カウンタよりもスケーラビリティおよび／または正確性の点において良好な結果をもたらし得る。ここに記載のカウンタのうちのいくつかは、特にＮＵＭＡシステムにおいて、スペースオーバーヘッドを低く保ちながら、処理能力および正確性の点において、一般に使用される統計カウンタよりも劇的に優れたものとなり得る。

ここに記載のカウンタ技術の多くは、ロックフリーであることが容易に分かる。さらに、ここに記載の確率的カウンタ技術を採用した場合、カウンタをインクリメントする試みをリトライする必要が時間の経過とともに下がり、これはカウンタの更新確率値が時間の経過とともに下がるためである（特に、上記のＢＦＰ−ＣＳＵＰ技術を採用するカウンタに競合がある場合）。一部の実施形態において、ここに記載されるカウンタは、待機フリーとなるように変更され得て、これは一部の場合においてオーバーヘッドおよび／または複雑性を加え得る。カウンタを待機フリーとなるように変更することにより、付加的な制約がもたらされ得る（事前にスレッドの最大値を知る必要があるなど）、またはこのような制約を回避するためにさらなるオーバーヘッドおよび複雑性が必要となり得る。しかしながら、実際上、ロックフリーとすることは、一部の実施形態において、マルチスレッドアプリケーションの同時スレッドの進行を保証するのに十分に強い特性となり得る。ただし、カウンタに競合がある場合には、一部のタイプのバックオフスキームが適用され得る。

図１４は、様々な実施形態による、ここに記載される方法を実施するように構成されたコンピューティングシステムを示す。コンピュータシステム１４００は、パーソナルコンピュータシステム、デスクトップコンピュータ、ラップトップもしくはノート型コンピュータ、メインフレームコンピュータシステム、ハンドヘルドコンピュータ、ワークステーション、ネットワークコンピュータ、消費者機器、アプリケーションサーバ、記憶装置、スイッチ、モデム、ルータなどの周辺機器、または一般の任意のタイプの計算装置を含む様々なタイプの装置であり得るが、これらに限定されない。一部の実施形態において、コンピュータシステム１４００は、ＮＵＭＡスタイルメモリアーキテクチャおよび／またはＮＵＣＡ特性を採用するシステムにおける複数のノードのうちの１つ、または概して一部のタイプのメモリ（たとえば、キャッシュ、ローカルメモリ、リモートメモリなど）に結合された少なくとも１つのプロセッサコアを含む任意のタイプの計算ノードであり得る。

ここに記載のスケーラブル統計カウンタのいずれかまたはすべてを実施する機構は、様々な実施形態に係る処理を行なうコンピュータシステム（または他の電子機器）をプログラミングするために使用され得る命令を格納する、非一時的コンピュータ読み取り可能記憶媒体を含み得る、コンピュータプログラム製品またはソフトウェアとして提供され得る。コンピュータ読み取り可能記憶媒体は、マシン（たとえば、コンピュータ）によって読み取り可能な形式の情報（たとえば、ソフトウェア、処理アプリケーション）を格納する任意の機構を含み得る。マシン読み取り可能記憶媒体は、磁気記憶媒体（たとえば、フロッピー（登録商標）ディスケット）、光記憶媒体（たとえば、ＣＤ−ＲＯＭ）、光磁気記憶媒体、読み取り専用メモリ（ＲＯＭ）、ランダムアクセスメモリ（ＲＡＭ）、消去およびプログラム可能メモリ（たとえば、ＥＰＲＯＭおよびＥＥＰＲＯＭ）、フラッシュメモリ、プログラム命令を格納するのに適した電気的もしくは他のタイプの媒体を含み得るが、これらに限定されない。加えて、プログラム命令は、光、音、または他の形式の伝播信号（たとえば、搬送波、赤外線信号、デジタル信号など）を使用して伝達され得る。

様々な実施形態において、コンピュータシステム１４００は、１つ以上のプロセッサ１４７０を含み得て、各々はマルチコアを含み得て、そのうちのいずれかはシングルもしくはマルチスレッドであり得る。たとえば、図２に示されるように、複数のプロセッサコアは、単一のプロセッサチップ（たとえば、単一のプロセッサ１４７０）に含まれ得て、複数のプロセッサチップはＣＰＵボード上に含まれ得て、そのうちの２つ以上はコンピュータシステム１４００に含まれ得る。プロセッサ１４７０の各々は、様々な実施形態において、キャッシュの階層を含み得る。たとえば、図２に示されるように、各プロセッサチップ１４７０は、複数のＬ１キャッシュ（たとえば、プロセッサコアごとに１つ）と、単一のＬ２キャッシュ（プロセッサチップ上でプロセッサコアによって共有され得る）とを含み得る。コンピュータシステム１４００は、１つ以上の持続的記憶装置１４５０（たとえば、光学記憶装置、磁気記憶装置、ハードドライブ、テープドライブ、ソリッドステートメモリなど）と、１つ以上のシステムメモリ１４１０（たとえば、キャッシュ、ＳＲＡＭ、ＤＲＡＭ、ＲＤＲＡＭ、ＥＤＯＲＡＭ、ＤＤＲ１０ＲＡＭ、ＳＤＲＡＭ、ラムバスＲＡＭ、ＥＥＰＲＯＭなどのうちの１つ以上）とを含み得る。様々な実施形態は、より少ないコンポーネント、または図１４に示されない付加的なコンポーネントを含み得る（たとえば、ビデオカード、音声カード、付加的なネットワークインターフェイス、周辺機器、ＡＴＭインターフェイス、イーサネット（登録商標）インターフェイス、フレームリレーインターフェイスなどのネットワークインターフェイス）。

１つ以上のプロセッサ１４７０、記憶装置１４５０、およびシステムメモリ１４１０は、システムインターコネクト１４４０に結合され得る。システムメモリ１４１０のうちの１つ以上は、プログラム命令１４２０を含み得る。プログラム命令１４２０は、１つ以上のアプリケーション１４２２（ここに記載されるように、共用統計カウンタへの１つ以上のアクセスを含み得る）、共有ライブラリ１４２４、またはオペレーティングシステム１４２６を実施するよう実行可能であり得る。一部の実施形態において、プログラム命令１４２０は、競合マネージャ（図示せず）を実施するよう実行可能であり得る。プログラム命令１４２０は、プラットフォームネイティブバイナリ、Ｊａｖａ（登録商標）バイトコードなどの任意のインタープリタ型言語、またはＣ／Ｃ＋＋やＪａｖａ（登録商標）などの他の言語、またはこれらの任意の組み合わせにコード化され得る。プログラム命令１４２０は、ここに記載されるように、スケーラブル統計カウンタおよび関連付けられた関数を実施する関数、演算、および／または他の処理（たとえば、スケーラブル統計カウンタをターゲットとしたインクリメント演算および／またはリード演算）を含み得る。このような支持および関数は、様々な実施形態において、共有ライブラリ１４２４、オペレーティングシステム１４２６、またはアプリケーション１４２２のうちの１つ以上に存在し得る。システムメモリ１４１０は、データが格納され得るプライベートメモリロケーション１４３０および／または共有メモリロケーション１４３５をさらに含み得る。たとえば、様々な実施形態において、共有メモリロケーション１４３５は、同時に実行されるスレッド、処理、またはアトミックトランザクションにアクセス可能なデータを格納し得て、共用統計カウンタ（たとえば、ここに記載される正確カウンタまたは確率的カウンタのうちの１つ）を実施する１つ以上の構造に格納されるデータを含み得る。

上記の実施形態は、かなり詳細に記載されたが、当業者が上記の開示をひとたび完全に理解すると、多くの変形および変更が明白となる。すべてのこのような変形および変更を含むように以下の請求項が解釈されることが意図される。

Claims (17)

1. 方法であって、
   １つ以上の計算ノードによって実行され、前記計算ノードの各々は少なくとも１つのプロセッサコアとメモリとを含み、方法は、
   共用カウンタをインクリメントする１つ以上の演算を含むマルチスレッドアプリケーションの実行を始めることを備え、前記共用カウンタは、前記１つ以上の計算ノード上で実行される前記マルチスレッドアプリケーションの複数のスレッドによってアクセス可能なデータ構造として実施され、前記データ構造は更新確率値の表現を格納し、前記更新確率値は、前記共用カウンタをターゲットとするインクリメント演算の開始に応答して前記更新確率値の前記表現が更新される確率を示し、前記共用カウンタの予測値は、前記更新確率値の前記表現に少なくとも部分的に基づいて計算可能であり、方法はさらに、
   前記マルチスレッドアプリケーションの所与のスレッドにより、前記共用カウンタをターゲットとしたインクリメント演算を開始することと、
   前記開始に応答し、前記インクリメント演算を行なうかを判定することとを備え、前記判定することは、前記データ構造に格納された前記更新確率値の前記表現に少なくとも部分的に依存し、方法はさらに、
   前記インクリメント演算が行なわれるという判定に応答して、前記データ構造に格納された前記更新確率値の前記表現を更新することを備え、前記更新された表現は、後続のインクリメント演算の開始に応答して前記データ構造に格納された前記更新確率値の前記更新された表現がさらに更新される確率を表わす、方法。
2. 前記複数のスレッドのうちの１つによって前記共用カウンタをターゲットとしたリード演算を行うことを備え、前記リード演算を行なうことは、
   前記データ構造に格納された前記更新確率値の前記表現を読み取ることと、
   前記データ構造に格納された前記更新確率値の前記表現から前記共用カウンタの前記予測値を計算することと、
   前記共用カウンタの前記予測値を返すこととを含む、請求項１に記載の方法。
3. 前記データ構造は前記更新確率値の浮動小数点表現を格納する、請求項１または２に記載の方法。
4. 前記更新することは、前記更新確率値の前記浮動小数点表現と構成可能な正確性パラメータの所定値に依存する定数とを掛け合わせることを含む、請求項３に記載の方法。
5. 前記データ構造は、仮数部分と指数部分とを含む前記更新確率値の二進浮動小数点表現を格納する、請求項１または２に記載の方法。
6. 前記更新することは、構成可能な正確性パラメータの所定値に応じて前記仮数部分または前記指数部分のうちの１つ以上を更新することを含む、請求項５に記載の方法。
7. 前記更新は、後続のインクリメント演算の開始に応答して前記データ構造に格納された前記更新確率値の前記更新された表現がさらに更新される前記確率を減少させる、請求項１〜６のいずれか１項に記載の方法。
8. 前記開始することに応答して、乱数を生成することを備え、
   前記判定することは、前記生成された乱数にさらに依存する、請求項１〜７のいずれか１項に記載の方法。
9. 前記マルチスレッドアプリケーションの前記複数のスレッドは、同時に実行されるトランザクションを表わし、前記開始することは、前記同時に実行されるトランザクションのうちの１つにおいてインクリメント演算を開始することを含む、請求項１〜８のいずれか１項に記載の方法。
10. 前記データ構造は、正確なカウント値をさらに格納し、
    前記データ構造に格納された前記更新確率値の前記表現の前記更新は、前記格納された正確なカウント値をインクリメントする試みが１回以上失敗したことに応答して行なわれる、請求項１〜９のいずれか１項に記載の方法。
11. 前記複数のスレッドのうちの１つにより、前記共用カウンタをターゲットとするリード演算を開始することと、
    前記複数のスレッドのうちの前記１つが前記リード演算を開始したことに応答して、
    前記データ構造に格納された前記更新確率値の前記表現を読み取ることと、
    前記データ構造に格納された前記更新確率値の前記表現から前記共用カウンタの前記予測値を計算することと、
    前記格納された正確なカウント値に前記予測値を加算することと、
    前記加算することの結果を返すこととをさらに備える、請求項１０に記載の方法。
12. システムであって、
    マルチスレッドを支持する１つ以上のプロセッサと、
    プログラム命令を格納するメモリとを備え、前記１つ以上のプロセッサ上で前記プログラム命令が実行されると、前記１つ以上のプロセッサは、
    共用カウンタをインクリメントする１つ以上の演算を含むマルチスレッドアプリケーションの実行を始め、前記共用カウンタは、前記１つ以上の計算ノード上で実行される前記マルチスレッドアプリケーションの複数のスレッドによってアクセス可能なデータ構造として実施され、前記データ構造は更新確率値の表現を格納し、前記更新確率値は、前記共用カウンタをターゲットとするインクリメント演算の開始に応答して前記更新確率値の前記表現が更新される確率を示し、前記共用カウンタの予測値は、前記更新確率値の前記表現に少なくとも部分的に基づいて計算可能であり、前記１つ以上のプロセッサはさらに、
    前記マルチスレッドアプリケーションの所与のスレッドにより、前記共用カウンタをターゲットとしたインクリメント演算を開始し、
    前記開始に応答し、前記インクリメント演算を行なうかを判定し、前記判定することは、前記データ構造に格納された前記更新確率値の前記表現に少なくとも部分的に依存し、前記１つ以上のプロセッサはさらに、
    前記インクリメント演算が行なわれるという判定に応答して、前記データ構造に格納された前記更新確率値の前記表現を更新し、前記更新された表現は、後続のインクリメント演算の開始に応答して前記データ構造に格納された前記更新確率値の前記更新された表現がさらに更新される確率を表わす、システム。
13. 前記データ構造は前記更新確率値の浮動小数点表現を格納し、
    前記更新することは、前記更新確率値の前記浮動小数点表現と構成可能な正確性パラメータの所定値に依存する定数とを掛け合わせることを含む、請求項１２に記載のシステム。
14. 前記データ構造は、仮数部分と指数部分とを含む前記更新確率値の二進浮動小数点表現を格納し、
    前記更新することは、構成可能な正確性パラメータの所定値に応じて前記仮数部分または前記指数部分のうちの１つ以上を更新することを含む、請求項１２に記載のシステム。
15. 前記プログラム命令が前記１つ以上のプロセッサ上で実行されると、前記１つ以上のプロセッサはさらに、
    前記開始することに応答して、乱数を生成し、
    前記判定することは、前記生成された乱数にさらに依存する、請求項１２〜１４のいずれか１項に記載のシステム。
16. 前記データ構造は、正確なカウント値をさらに格納し、
    前記正確なカウント値および前記予測値は前記共用カウンタの前記値を集合的に表わし、
    前記データ構造に格納された前記更新確率値の前記表現の前記更新は、前記格納された正確なカウント値をインクリメントする試みが１回以上失敗したことに応答して行なわれる、請求項１２〜１５のいずれか１項に記載のシステム。
17. コンピュータ読み取り可能プログラムであって、前記プログラムが１つ以上のコンピュータ上で実行されると、前記１つ以上のコンピュータは、
    共用カウンタをインクリメントする１つ以上の演算を含むマルチスレッドアプリケーションの実行を始め、前記共用カウンタは、前記１つ以上の計算ノード上で実行される前記マルチスレッドアプリケーションの複数のスレッドによってアクセス可能なデータ構造として実施され、前記データ構造は更新確率値の表現を格納し、前記更新確率値は、前記共用カウンタをターゲットとするインクリメント演算の開始に応答して前記更新確率値の前記表現が更新される確率を示し、前記共用カウンタの予測値は、前記更新確率値の前記表現に少なくとも部分的に基づいて計算可能であり、前記１つ以上のコンピュータはさらに
    、
    前記マルチスレッドアプリケーションの所与のスレッドにより、前記共用カウンタをターゲットとしたインクリメント演算を開始し、
    前記開始に応答し、前記インクリメント演算を行なうかを判定し、前記判定することは、前記データ構造に格納された前記更新確率値の前記表現に少なくとも部分的に依存し、前記１つ以上のコンピュータはさらに、
    前記インクリメント演算が行なわれるという判定に応答して、前記データ構造に格納された前記更新確率値の前記表現を更新し、前記更新された表現は、後続のインクリメント演算の開始に応答して前記データ構造に格納された前記更新確率値の前記更新された表現がさらに更新される確率を表わす、コンピュータ読み取り可能プログラム。

Images