JP6069918B2 - Simulation method and device simulator - Google Patents
Simulation method and device simulator Download PDFInfo
- Publication number
- JP6069918B2 JP6069918B2 JP2012153970A JP2012153970A JP6069918B2 JP 6069918 B2 JP6069918 B2 JP 6069918B2 JP 2012153970 A JP2012153970 A JP 2012153970A JP 2012153970 A JP2012153970 A JP 2012153970A JP 6069918 B2 JP6069918 B2 JP 6069918B2
- Authority
- JP
- Japan
- Prior art keywords
- gate
- potential
- current
- charge
- simulation method
- Prior art date
- Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
- Expired - Fee Related
Links
- 238000000034 method Methods 0.000 title claims description 39
- 238000004088 simulation Methods 0.000 title claims description 16
- 238000004364 calculation method Methods 0.000 claims description 48
- 230000000737 periodic effect Effects 0.000 claims description 12
- 238000004613 tight binding model Methods 0.000 claims description 9
- 238000010586 diagram Methods 0.000 description 19
- OKTJSMMVPCPJKN-UHFFFAOYSA-N Carbon Chemical group [C] OKTJSMMVPCPJKN-UHFFFAOYSA-N 0.000 description 17
- 238000012545 processing Methods 0.000 description 16
- 125000004429 atom Chemical group 0.000 description 15
- 230000005684 electric field Effects 0.000 description 7
- 238000005516 engineering process Methods 0.000 description 5
- 238000004891 communication Methods 0.000 description 4
- 230000006870 function Effects 0.000 description 4
- 229910052799 carbon Inorganic materials 0.000 description 3
- 125000004432 carbon atom Chemical group C* 0.000 description 3
- 150000001721 carbon Chemical group 0.000 description 2
- 238000002834 transmittance Methods 0.000 description 2
- 230000000694 effects Effects 0.000 description 1
- 239000000463 material Substances 0.000 description 1
- 238000012986 modification Methods 0.000 description 1
- 230000004048 modification Effects 0.000 description 1
- 230000005610 quantum mechanics Effects 0.000 description 1
- 238000012552 review Methods 0.000 description 1
- 239000004065 semiconductor Substances 0.000 description 1
Images
Landscapes
- Insulated Gate Type Field-Effect Transistor (AREA)
Description
本発明は、デバイスの電流電圧特性を計算するためのシミュレーション方法及びデバイスシミュレータに関する。 The present invention relates to a simulation method and a device simulator for calculating a current-voltage characteristic of a device.
ナノデバイスでは、その局所的な構造や界面がデバイス全体の特性に大きく影響するため、量子力学に基づき、原子の種類と位置の情報だけからデバイスの特性を計算することが可能な第一原理計算が重要である。 In nanodevices, the local structure and interface greatly affect the properties of the entire device. Based on quantum mechanics, first-principles calculations that allow device properties to be calculated based on atomic type and position information only. is important.
近年、第一原理計算に基づく非平衡グリーン関数法によるソース・ドレイン間の電流電圧特性の計算は盛んに行われるようになっている。しかし、第一原理計算の計算量は膨大であり、実際にゲート構造を原子構造模型に取り入れ、ゲート電圧をかける計算は非常にコストがかかる。このため、ゲート電圧を印加した際のデバイス特性を第一原理計算に基づく手法で調べることはほとんど行われていない。 In recent years, the calculation of the current-voltage characteristics between the source and the drain by the nonequilibrium Green function method based on the first principle calculation has been actively performed. However, the amount of calculations for first-principles calculations is enormous, and calculations that actually incorporate the gate structure into the atomic structure model and apply the gate voltage are very expensive. For this reason, device characteristics when a gate voltage is applied are hardly investigated by a method based on first-principles calculations.
このため、例えば、ソース・ドレイン間の電流電圧特性の計算において、ゲート電極が作るモデルポテンシャルを外場として加え、ゲート電界依存性を計算する試みがなされている。 For this reason, for example, in the calculation of the current-voltage characteristics between the source and the drain, an attempt has been made to calculate the gate electric field dependence by adding the model potential created by the gate electrode as an external field.
しかしながら、上述した外場として加えられるポテンシャルが作り出す誘起電荷は現実に対応したものではなく、ソース・ドレイン間の電流電圧特性を精度良く計算することができないと言った問題があった。 However, the induced charges generated by the potential applied as the external field described above do not correspond to reality, and there is a problem that the current-voltage characteristics between the source and the drain cannot be calculated with high accuracy.
よって、本発明の目的は、第一原理計算に基づく非平衡グリーン関数法によるソース・ドレイン電流電圧特性計算において、簡便かつ、現実に対応するゲート電界を取り入れ、ナノデバイスにおけるソース・ドレイン間の電流電圧特性を精度良く計算することである。 Therefore, an object of the present invention is to easily and practically incorporate a gate electric field corresponding to reality in the source-drain current-voltage characteristic calculation by the nonequilibrium Green function method based on the first-principles calculation. It is to calculate the voltage characteristics with high accuracy.
開示の技術は、コンピュータによって実行されるシミュレーション方法であって、記憶部に記憶されたデバイスの構造モデルを読み込み、非平衡グリーン関数法によるソースとドレイン間のチャネルを流れる電流の量子伝導計算において、伝導方向に垂直な2方向のうち1方向に無限長であって他方に垂直であり前記構造モデルで与えられるチャネルに対向するゲートのゲート幅で端を持つ面電荷がつくる解析的なポテンシャルを、該伝導方向に垂直な2方向に周期的な形で加えて、電流を計算する。 The disclosed technique is a computer-implemented simulation method that reads a structural model of a device stored in a storage unit, and calculates quantum current of a current flowing through a channel between a source and a drain by a nonequilibrium Green function method. An analytical potential produced by a surface charge having an end at the gate width of the gate that is infinitely long in one of the two directions perpendicular to the conduction direction and perpendicular to the other and opposite to the channel given by the structural model, The current is calculated by adding in a periodic manner in two directions perpendicular to the conduction direction.
また、上記課題を解決するための手段として、デバイスシミュレータ、プログラム、及び、そのプログラムを記録した記録媒体とすることもできる。 Further, as means for solving the above problems, a device simulator, a program, and a recording medium on which the program is recorded can be used.
開示の技術では、現実に対応するゲート電界を印加した場合の誘起電荷をモデル化することで、計算手法を大きく変更することなく、電流電圧特性のゲート電界依存性を計算することができる。 In the disclosed technique, the induced electric charge when a gate electric field corresponding to reality is applied is modeled, whereby the gate electric field dependence of the current-voltage characteristic can be calculated without greatly changing the calculation method.
以下、本発明の実施の形態を図面に基づいて説明する。発明者は、関連技術である非特許文献1の記載に基づくゲートのモデルポテンシャルによる誘起電荷を検証した。
Hereinafter, embodiments of the present invention will be described with reference to the drawings. The inventor verified the charge induced by the model potential of the gate based on the description of Non-Patent
先ず、図1のようなカーボンチェーン構造を例として説明する。図1は、カーボンチェーン構造模型を示す図である。図1に示すカーボン構造模型では、2aは炭素原子を表し、炭素4原子からなるReserver部分(領域3a及び3b)は、それぞれ半無限に同じ構造を繰り返している。この図では、炭素原子2aが12個あり、12個の炭素原子2aが1列に並んだこの構造をchain-12と呼ぶ。Center+Leadsの領域4は、モデルのサイズにより原子の個数が変わり、それに応じて呼び方の数字を変える。
First, a carbon chain structure as shown in FIG. 1 will be described as an example. FIG. 1 is a diagram showing a carbon chain structure model. In the carbon structural model shown in FIG. 1, 2a represents a carbon atom, and the Reserver portion (
非特許文献1によれば、この構造の電流電圧特性の計算において加えるポテンシャルは次式で与えられ、
According to
図2は、関連技術によるゲートのモデルポテンシャルを示す図である。図2において、chain-12、Vg (0)=10eVの場合を示す。このポテンシャルは伝導方向であるx方向にだけ依存性を持ち、それに垂直なy、z方向には一定であるため、y、z方向を周期境界条件で取り扱う第一原理計算に基づく非平衡グリーン関数法に容易に取り入れることができる。この2方向のポアッソン方程式を高速フーリエ変換を用いて計算することが可能となるからである。 FIG. 2 is a diagram showing the model potential of the gate according to the related art. FIG. 2 shows a case where chain-12 and V g (0) = 10 eV. Since this potential depends only on the x direction, which is the conduction direction, and is constant in the y and z directions perpendicular to it, it is a non-equilibrium Green function based on first-principles calculations that treat the y and z directions with periodic boundary conditions. Can be easily incorporated into the law. This is because the two-way Poisson equation can be calculated using the fast Fourier transform.
発明者は、このポテンシャルが作り出す誘起電荷を計算したところ、しかしながら、図3のようになった。図3は、関連技術におけるモデルポテンシャルによる誘起電荷を示す図である。横軸は各炭素原子、縦軸は各原子の電荷量で、ゲートポテンシャルがない時との差を表している。 The inventor calculated the induced charge created by this potential, however, it was as shown in FIG. FIG. 3 is a diagram showing the induced charge due to the model potential in the related art. The horizontal axis represents each carbon atom, and the vertical axis represents the charge amount of each atom, representing the difference from when there is no gate potential.
図3において、Center+Leadsの領域4の端に大きな誘起電荷5aがあり、そのすぐ外側には逆符号の大きな誘起電荷5bが存在する。電荷は誘起されているものの、現実との対応が難しいことが分かる。
In FIG. 3, there is a large induced
また、発明者は、Center+Leadsの領域4において、Centerの領域、また、Leadsの領域を長くした場合におけるポテンシャルが作り出す誘起電荷を検証した。図4は、Centerの領域を長くした場合の、関連技術におけるモデルポテンシャルによる誘起電荷を説明するための図である。図4(A)では、chain-28でCenterの領域を長くした場合のモデルポテンシャルを示し、図4(B)では、図4(A)に示すモデルポテンシャルに基づいて計算された誘起電荷を示している。
In addition, the inventor verified the induced charge generated by the potential when the Center region and the Leads region are lengthened in the Center +
Centerの領域を長くした場合では、図4(B)に示されるように、chain-28のカーボンチェーン構造において、Center+Leadsの領域4内の両端(Leads部分)で誘起電荷が大きく、Centerでは誘起電荷が小さいことが示され、更に、領域4のすぐ外側には負の誘起電荷が大きく発生する結果となった。
When the center region is lengthened, as shown in FIG. 4B, in the chain-28 carbon chain structure, the induced charge is large at both ends (Leads portion) in the center +
また、図5は、Leadsの領域を長くした場合の、関連技術におけるモデルポテンシャルによる誘起電荷を説明するための図である。図5(A)では、chain-28でLeadsの領域を長くした場合のモデルポテンシャルを示し、図5(B)では、図5(A)に示すモデルポテンシャルに基づいて計算された誘起電荷を示している。 FIG. 5 is a diagram for explaining the induced charges due to the model potential in the related art when the Leads region is lengthened. 5A shows the model potential when the Leads region is lengthened with chain-28, and FIG. 5B shows the induced charge calculated based on the model potential shown in FIG. 5A. ing.
Leadsの領域を長くした場合では、図5(B)に示されるように、chain-28のカーボンチェーン構造において、Center+Leadsの領域4内で、CenterとLeadsの境で大きな誘起電荷があり、そのすぐ外側には逆符号の大きな誘起電荷が発生する結果となった。
When the Leads region is lengthened, as shown in FIG. 5 (B), in the chain-28 carbon chain structure, there is a large induced charge at the boundary between Center and Leads in the Center + Leads
上述したように、Centerの領域を長くしても、また、Leadsの領域を長くすることでも改善されないことが分かった。 As described above, it has been found that even if the center area is lengthened or the leads area is lengthened, there is no improvement.
本実施の形態において、発明者は、伝導方向に垂直な2つの方向に周期的なゲート印加のためのモデルポテンシャルを導入することによって、より現実的な誘起電荷の発生をシミュレートすることを可能とし、ソース・ドレイン電流電圧特性の計算を精度良く行えるようにした。また、この実施の形態では、原子構造が伝導方向に垂直な方向に連続でなく真空層が存在する場合、ポテンシャルは周期的であれば連続でなくてもよく、ポテンシャルの飛びがちょうど真空層にあるようにすればよい。 In this embodiment, the inventor can simulate the generation of more realistic induced charges by introducing a model potential for periodic gate application in two directions perpendicular to the conduction direction. The source / drain current-voltage characteristics can be calculated with high accuracy. Further, in this embodiment, when the atomic structure is not continuous in the direction perpendicular to the conduction direction and a vacuum layer exists, the potential may not be continuous as long as the potential is periodic. You just have to be there.
図6は、一方向に無限長の面電荷の模式図である。図6に例示する面電荷は、現実に対応するゲート電界を印加した場合の誘起電荷をモデル化したものであり、aは面電荷の幅(ゲート長に相当)の半分を示す。また、Rはポテンシャルの基準点を示しており、どこにとってもかまわない。発明者は、このような一方向の無限長の単位電荷密度の面電荷がつくるポテンシャルが、次式で与えられることを解析的に示した。 FIG. 6 is a schematic diagram of an infinitely long surface charge in one direction. The surface charge illustrated in FIG. 6 is a model of the induced charge when a gate electric field corresponding to reality is applied, and a indicates half of the width of the surface charge (corresponding to the gate length). R represents a reference point of potential and may be used anywhere. The inventor has analytically shown that the potential generated by such a surface charge having an infinite unit charge density in one direction is given by the following equation.
ここでもカーボンチェーン構造を例として説明する。図1の構造の場合、a=1/6となり、Rを今、X=0、Z=0の点にとる。今、カーボンチェーンはy=0、z=0にあるものとしている。上式を図示すると図7のようになる。ここでは、面電荷の電荷密度は、1013cm−2とした。 Here, the carbon chain structure will be described as an example. In the case of the structure shown in FIG. 1, a = 1/6, and R is now set at the points X = 0 and Z = 0. It is assumed that the carbon chain is at y = 0 and z = 0. The above equation is illustrated in FIG. Here, the charge density of the surface charge was 10 13 cm −2 .
図7は、本実施の形態によるゲートのモデルポテンシャルを示す図である。図7では、chain-12の場合を示している。関連技術としての非特許文献1と異なり、z方向にも依存性を持つ。今、面電荷はz=−1のところにあるものとして図示しており、図7の領域には含まれていない。z方向にはこのポテンシャルを周期的に繰り返せばよく、y方向には今依存性がないので、周期的に取り扱うことができる。
FIG. 7 is a diagram showing the model potential of the gate according to the present embodiment. FIG. 7 shows the case of chain-12. Unlike
原子構造が伝導方向に垂直な方向に連続でなく真空層が存在する場合、ポテンシャルは周期的であれば連続でなくてもよく、ポテンシャルの飛びがちょうど真空層にあるようにすればよい。 When the atomic structure is not continuous in the direction perpendicular to the conduction direction and a vacuum layer is present, the potential may not be continuous as long as the potential is periodic, and the jump of the potential may be just in the vacuum layer.
原子列は、今、z=0の位置にあるため、これにより、z=−1の距離にある面電荷からの影響を取り入れたソース・ドレイン電流電圧特性の計算が可能となる。具体的には、このモデルでは1nmの真空を絶縁層としたゲート電極による、現実に近いナノデバイスのシミュレーションが可能となる。 Since the atomic column is now at the position of z = 0, this makes it possible to calculate the source / drain current voltage characteristics taking into account the influence from the surface charge at a distance of z = -1. Specifically, in this model, it is possible to simulate a realistic nanodevice using a gate electrode having a 1 nm vacuum as an insulating layer.
このポテンシャルに誘起される電荷は、図8のようになり、図3に類似している。図8は、本実施の形態のモデルポテンシャルによる誘起電荷を示す図である。図8では、chain-12の場合の各原子の誘起電荷を示している。しかしながら、本発明のモデルポテンシャルの場合は、現実同様Leadを十分の長さに取ることで、図9のように現実的な電荷分布を再現することが分かった。 The charge induced by this potential is as shown in FIG. 8 and is similar to FIG. FIG. 8 is a diagram showing the induced charges due to the model potential of the present embodiment. FIG. 8 shows the induced charges of each atom in the case of chain-12. However, in the case of the model potential of the present invention, it has been found that the realistic charge distribution can be reproduced as shown in FIG.
図9は、本実施の形態のモデルポテンシャルによる誘起電荷を示す図である。図9では、Lead部分を長くしたchain-28の場合の各原子の誘起電荷を示している。図9に示すように、chain-28の場合では、Center部分で、ゲートポテンシャルのない時との差が最も高く、両端(x=0及びx=1)に向かって差が小さくなる曲線を描く。 FIG. 9 is a diagram showing the induced charges due to the model potential of the present embodiment. FIG. 9 shows the induced charge of each atom in the case of chain-28 with a long lead portion. As shown in FIG. 9, in the case of chain-28, a curve is drawn with the highest difference in the center portion with no gate potential, and the difference becomes smaller toward both ends (x = 0 and x = 1). .
本実施の形態では、Lead部分を長くしたカーボンチェーン構造とするのみで、現実的な誘起電荷の計算結果を得ることができ、従って、より精度高く電流値を計算することが可能となる。 In the present embodiment, it is possible to obtain a realistic calculation result of induced charges only by using a carbon chain structure with a long lead portion, and therefore, it is possible to calculate a current value with higher accuracy.
本実施の形態に係るデバイスシミュレータについて説明する。図10は、デバイスシミュレータのハードウェア構成を示す図である。図10において、デバイスシミュレータ100は、コンピュータによって制御される端末であって、CPU(Central Processing Unit)11と、主記憶装置12と、補助記憶装置13と、入力装置14と、表示装置15と、出力装置16と、通信I/F(インターフェース)17と、ドライブ18とを有し、バスBに接続される。
A device simulator according to the present embodiment will be described. FIG. 10 is a diagram illustrating a hardware configuration of the device simulator. In FIG. 10, a
CPU11は、主記憶装置12に格納されたプログラムに従ってデバイスシミュレータ100を制御する。主記憶装置12には、RAM(Random Access Memory)等が用いられ、CPU11にて実行されるプログラム、CPU11での処理に必要なデータ、CPU11での処理にて得られたデータ等を格納する。また、主記憶装置12の一部の領域が、CPU11での処理に利用されるワークエリアとして割り付けられている。
The
補助記憶装置13には、ハードディスクドライブが用いられ、各種処理を実行するためのプログラム等のデータを格納する。補助記憶装置13に格納されているプログラムの一部が主記憶装置12にロードされ、CPU11に実行されることによって、各種処理が実現される。記憶部130は、主記憶装置12及び/又は補助記憶装置13を有する。
The
入力装置14は、マウス、キーボード等を有し、ユーザがデバイスシミュレータ100による処理に必要な各種情報を入力するために用いられる。表示装置15は、CPU11の制御のもとに必要な各種情報を表示する。出力装置16は、プリンタ等を有し、ユーザからの指示に応じて各種情報を出力するために用いられる。通信I/F17は、例えばインターネット、LAN(Local Area Network)等に接続し、外部装置との間の通信制御をするための装置である。
The
デバイスシミュレータ100によって行われる処理を実現するプログラムは、例えば、CD−ROM(Compact Disc Read-Only Memory)等の記憶媒体19によってデバイスシミュレータ100に提供される。即ち、プログラムが保存された記憶媒体19がドライブ18にセットされると、ドライブ18が記憶媒体19からプログラムを読み出し、その読み出されたプログラムがバスBを介して補助記憶装置13にインストールされる。そして、プログラムが起動されると、補助記憶装置13にインストールされたプログラムに従ってCPU11がその処理を開始する。尚、プログラムを格納する媒体としてCD−ROMに限定するものではなく、コンピュータが読み取り可能な媒体であればよい。コンピュータ読取可能な記憶媒体として、CD−ROMの他に、DVDディスク、USBメモリ等の可搬型記録媒体、フラッシュメモリ等の半導体メモリであっても良い。
A program that realizes processing performed by the
図11は、デバイスシミュレータの機能構成例を示す図である。図11において、デバイスシミュレータ100は、CPU11によって行われる処理部として、原子座標入力部21と、ゲートデータ入力部22と、電流電圧特性計算部23とを有する。各処理部21から23は、CPU11が対応するプログラムを実行することによって実現される。
FIG. 11 is a diagram illustrating a functional configuration example of the device simulator. In FIG. 11, the
記憶部130には、原子座標データ31と、ゲートデータ32と、計算結果33とが記憶される。原子座標データ31と、ゲートデータ32とによって、構造モデル7m(図12)が表現される。
The
原子座標入力部21は、記憶部130から原子座標データ31を入力する処理部である。ゲートデータ入力部22は、記憶部130からゲートデータ32を入力する処理部である。電流電圧特性計算部23は、原子座標データ31と、ゲートデータ32とによって得られる構造モデル7mに基づいて、電流電圧特性を計算する処理部である。電流電圧特性計算部23は、第一原理計算に基づく非平衡グリーン関数法による量子伝導計算において、1方向に無限長の面電荷(図6)がつくる解析的なポテンシャル(数2)を伝導方向(x方向)に垂直な2方向(y方向及びz方向)に周期的な形で加えて(y方向では∞に周期的)、電流電圧特性を求める。
The atomic coordinate
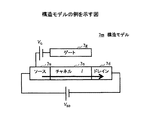
図12は、構造モデルの例を示す。図12において、構造モデル7は、ゲート7gと、ソース7sと、チャネル7cと、ドレイン7dと、ゲート電圧VGと、ソースドレイン電圧VSDとを有する。
FIG. 12 shows an example of a structural model. 12, the structural model 7 has a gate 7 g, and the
本実施の形態では、ゲート7gが図6で示される一方向の無限長の面電荷で表現され、面電荷がつくるポテンシャルを解析的に示した上記数2を用いて、面電荷がチャネル7cに与える影響を考慮したソース7sとドレイン7d間の電流Iを算出する。
In this embodiment, the gate 7g is expressed by an infinitely long surface charge in one direction shown in FIG. 6, and the surface charge is applied to the channel 7c by using the
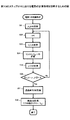
図13は、本実施の形態における電流電圧特性計算処理を説明するためのフローチャート図である。図11に示す電流電圧特性計算処理は、CPU11が対応するプログラムを実行することによって実現される。
FIG. 13 is a flowchart for explaining the current-voltage characteristic calculation processing in the present embodiment. The current-voltage characteristic calculation process shown in FIG. 11 is realized by the
図11において、CPU11の制御によって起動された原子座標入力部21は、記憶部130から原子座標データ31を読み込んで入力する(ステップS11)。原子座標入力部21は、予め記憶部130に記憶された原子座標データ31を読み込んでも良いし、原子座標データ31を取得するための所定のユーザインタフェースを表示装置15に表示して、ユーザから取得するようにしても良い。ユーザから取得した原子座標データ31は記憶部130に記憶される。原子座標データ31は、ソース、ドレイン、チャネルに係る原子座標を含む。
In FIG. 11, the atomic coordinate
次に、CPU11はゲートデータ入力部22を起動して、記憶部130からゲートデータ32を読み込んで入力する(ステップS12)。ゲートデータ入力部22は、予め記憶部130に記憶されたゲートデータ32を読み込んでも良いし、ゲートデータ32を取得するための所定のユーザインタフェースを表示装置15に表示して、ユーザから取得するようにしても良い。ユーザから取得したゲートデータ32は記憶部130に記憶される。ゲートデータ32は、ゲートの個数、位置、ゲート幅等の値を含む。leads部分の長さは、ゲート幅に基づく。
Next, the
そして、CPU11は電流電圧特性計算部23を起動する。電流電圧特性計算部23は、ゲート電圧VGO(r)を計算する(ステップS13)。ステップS13におけるゲート電圧VGO(r)の計算では、図6で示される一方向の無限長の面電荷でゲート7gを表現し、面電荷がつくるポテンシャルを解析的に示した上記数2に基づいて計算される。
Then, the
電流電圧特性計算部23は、ゲート電圧VG(r)毎にループして(ステップS14)、ソースドレイン電圧VSDに応じた電流Iを計算する(ステップS15及びS16)。電流電圧特性計算部23による計算結果33が記憶部130に記憶される。
The current-voltage
図14は、図13のステップS16における電流Iの計算処理を説明するための図である。図14において、電流電圧特性計算部23は、変数iを0に初期化し、電荷密度ρ0(r)を計算する(ステップS31)。
FIG. 14 is a diagram for explaining the calculation process of the current I in step S16 of FIG. In FIG. 14, the current-voltage
電流電圧特性計算部23は、変数iを1インクリメントして(ステップS32)、直前に計算された電荷密度ρに基づいてVi(r)を計算する(ステップS33)。そして、電流電圧特性計算部23は、Vi(r)+VGVG0(r)を計算する(ステップS34)。電流電圧特性計算部23は、ステップS34で計算された電圧に基づいて、ρi(r)を計算する(ステップS35)。
The current-voltage
ρi(r)とρi−1(r)との差が所定値Δ未満に収束したか否かを判断する(ステップS36)。収束していない場合、電圧特性計算部23は、ステップS32へと戻り、電荷密度の値が収束するまで、上記同様の処理を繰り返す。
It is determined whether or not the difference between ρ i (r) and ρ i-1 (r) has converged below a predetermined value Δ (step S36). If not converged, the voltage
一方、収束した場合、電圧特性計算部23は、透過率T(E)を計算し(ステップS37)、透過率T(E)を積分(E=0〜VSD)することにより電流Iを計算する(ステップS38)。
On the other hand, when the voltage converges, the voltage
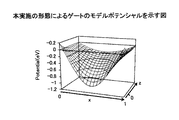
上述したような電流電圧特性計算処理によって得られるデバイスの電流電圧特性が、図15に例示される。図15は、デバイスの電流電圧特性の模式図である。図15において、ゲート電圧VG(1)、VG(2)、VG(3)を夫々印加したときの電流電圧特性が示されている。 FIG. 15 illustrates the current-voltage characteristic of the device obtained by the current-voltage characteristic calculation process as described above. FIG. 15 is a schematic diagram of the current-voltage characteristics of the device. FIG. 15 shows current-voltage characteristics when gate voltages V G (1), V G (2), and V G (3) are applied.
以下に、本実施の形態に係る電流電圧特性計算処理によるデバイスシミュレーションの実施例を示す。図9では、ゲート長(図6のaで表される長さ)が4原子分の長さの場合であったが、ゲート幅に応じてleads部分を長くすることで、種々のゲート長での計算が可能となる。
[実施例1]
図16は、ゲート長16原子、chainは32原子の場合を示す図である。図16において、ゲート長が16原子分の長さの場合を示している。ゲート長16原子、chainは32原子の場合における、モデルポテンシャルを図16(A)に示し、誘起電荷を図16(B)に示す。リード長は、これ以上長くてもよく、誘起電荷は、現実の誘起電荷に対応し、同じ結果を示す。
[実施例2]
図17は、ダブルゲート構造の場合を示す図である。図17では、カーボンチェーンの反対側にも面電荷があるものとし、上述した数2のポテンシャルを重ね合わせたもので、ダブルゲート構造を模している。このようなダブルゲート構造における、モデルポテンシャルを図17(A)に示し、誘起電荷を図17(B)に示す。ダブルゲートの効果により、図16と比較して2倍程度の電荷が誘起されていることが分かる。
[実施例3]
図17のダブルゲート構造の場合で、面電荷間の間隔をひろげ、カーボンチェーンを2本配置することもできる。2本のカーボンチェーンに同じ電荷が誘起されていることが分かり、チャネル層が厚みをもっていても、即ち、厚み方向に2以上のカーボンチェーンを持っていても、この方法が適用できる。
Hereinafter, examples of device simulation by the current-voltage characteristic calculation processing according to the present embodiment will be shown. In FIG. 9, the gate length (length represented by a in FIG. 6) is a length of 4 atoms, but by increasing the leads portion according to the gate width, various gate lengths can be obtained. Can be calculated.
[Example 1]
FIG. 16 shows a case where the gate length is 16 atoms and the chain is 32 atoms. FIG. 16 shows a case where the gate length is 16 atoms. FIG. 16A shows the model potential and FIG. 16B shows the induced charge when the gate length is 16 atoms and the chain is 32 atoms. The lead length may be longer than this, and the induced charge corresponds to the actual induced charge and shows the same result.
[Example 2]
FIG. 17 is a diagram showing a case of a double gate structure. In FIG. 17, it is assumed that there is a surface charge on the opposite side of the carbon chain, and the above-described potential of 2 is overlapped to simulate a double gate structure. FIG. 17A shows the model potential and FIG. 17B shows the induced charge in such a double gate structure. It can be seen that approximately twice as much charge is induced as compared with FIG. 16 due to the double gate effect.
[Example 3]
In the case of the double gate structure of FIG. 17, it is possible to widen the space between the surface charges and arrange two carbon chains. It can be seen that the same charge is induced in the two carbon chains, and this method can be applied even if the channel layer has a thickness, that is, has two or more carbon chains in the thickness direction.
図18は、ダブルゲート構造で、カーボンチェーンが2本の場合を示す図である。図18では、ダブルゲート構造であって、ゲート長16原子、chainは32原子が2本の場合を示している。このようなダブルゲート構造における、モデルポテンシャルを図18(A)に示し、誘起電荷を図18(B)に示す。図18(B)では、2本のchainの誘起電荷を示している。
[実施例4]
実施例2のダブルゲート構造の場合は、面電荷の電荷密度が1013cm−2であった。電荷密度を変化させることで、それに応じて誘起される電荷を制御することができる。図19は、図17のダブルゲート構造の場合で、面電荷の密度を変化させた場合の誘起電荷を示す図である。図19において、数値は、chainの中央の原子に誘起された電荷の量を示している。
FIG. 18 is a diagram showing a double gate structure and two carbon chains. FIG. 18 shows a double gate structure in which the gate length is 16 atoms and the chain has 2 32 atoms. FIG. 18A shows the model potential and FIG. 18B shows the induced charge in such a double gate structure. FIG. 18B shows induced charges of two chains.
[Example 4]
In the case of the double gate structure of Example 2, the surface charge density was 10 13 cm −2 . By changing the charge density, the charge induced accordingly can be controlled. FIG. 19 is a diagram showing the induced charges when the surface charge density is changed in the case of the double gate structure of FIG. In FIG. 19, the numerical value indicates the amount of charge induced in the central atom of the chain.
上述したように、本実施の形態に係る電流電圧特性計算処理を用いることによって、ゲート個数、ゲート長、カーボンチェーンの長さ及び本数等のデバイス構造に応じた電流電圧特性を計算することができる。 As described above, by using the current-voltage characteristic calculation processing according to the present embodiment, the current-voltage characteristics corresponding to the device structure such as the number of gates, the gate length, the length of the carbon chain, and the number of the gates can be calculated. .
ナノデバイスのソース・ドレイン間の電流電圧特性計算にて、一方向に無限長で他方向に端をもつ面電荷によってゲートをモデル化し、該面電荷がつくるポテンシャルによって現実的な電荷分布を再現するため、電流を精度良く計算することができる。 In the calculation of the current-voltage characteristics between the source and drain of a nanodevice, the gate is modeled by a surface charge with an infinite length in one direction and an edge in the other direction, and a realistic charge distribution is reproduced by the potential created by the surface charge. Therefore, the current can be calculated with high accuracy.
従って、本実施の形態によれば、第一原理計算に基づく非平衡グリーン関数法によるソース・ドレイン間の電流電圧特性の計算において、その手法を大きく変えることなく、また、計算量を大きく増大させることなく、簡便かつ、現実に対応するゲート電界を印加した場合の誘起電荷をモデル化することができ、電流電圧特性のゲート電界依存性を計算することができる。 Therefore, according to the present embodiment, in the calculation of the current-voltage characteristics between the source and the drain by the nonequilibrium green function method based on the first principle calculation, the calculation amount is greatly increased without largely changing the method. Therefore, it is possible to model the induced charge when a gate electric field corresponding to reality is applied simply and easily, and the gate electric field dependence of the current-voltage characteristics can be calculated.
本実施の形態において、電流電圧特性を計算する対象をカーボンチェーンとしたが、これに限定するものではない。 In the present embodiment, the target for calculating the current-voltage characteristics is the carbon chain, but the present invention is not limited to this.
本発明は、具体的に開示された実施例に限定されるものではなく、特許請求の範囲から逸脱することなく、種々の変形や変更が可能である。 The present invention is not limited to the specifically disclosed embodiments, and various modifications and changes can be made without departing from the scope of the claims.
以上の実施例を含む実施形態に関し、更に以下の付記を開示する。
(付記1)
コンピュータによって実行されるシミュレーション方法であって、
記憶部に記憶されたデバイスの構造モデルを読み込み、
非平衡グリーン関数法による量子伝導計算において、1方向に無限長であって他方に前記構造モデルで与えられるゲート幅で端を持つ面電荷がつくる解析的なポテンシャルを、伝導方向に垂直な2方向に周期的な形で加えて、電流を計算する
ことを特徴とするシミュレーション方法。
(付記2)
上記ポテンシャルは、周期的であるが連続でなく飛びがあることを特徴とする付記1記載のシミュレーション方法。
(付記3)
前記構造モデルによって表される原子構造に真空層を設け、該真空層において前記飛びをもつことを特徴とする付記2記載のシミュレーション方法。
(付記4)
2以上の面電荷によって前記ポテンシャルが重ねられることを特徴とする付記1乃至3のいずれか一項記載のシミュレーション方法。
(付記5)
前記構造モデルは、前記ポテンシャルの平坦な領域に厚みのある伝導層の原子構造を有することを特徴とする付記4記載のシミュレーション方法。
(付記6)
デバイスの構造モデルを記憶した記憶部と、
非平衡グリーン関数法による量子伝導計算を行う際に、1方向に無限長であって他方に前記記憶部に記憶された前記構造モデルで与えられるゲート幅で端を持つ面電荷がつくる解析的なポテンシャルを、伝導方向に垂直な2方向に周期的な形で加えて、電流を計算する特性計算部と
を有することを特徴とするデバイスシミュレータ。
(付記7)
記憶部に記憶されたデバイスの構造モデルを読み込み、
非平衡グリーン関数法による量子伝導計算において、1方向に無限長であって他方に前記構造モデルで与えられるゲート幅で端を持つ面電荷がつくる解析的なポテンシャルを、伝導方向に垂直な2方向に周期的な形で加えて、電流を計算する
ことを特徴とするシミュレーション方法。
The following additional notes are further disclosed with respect to the embodiment including the above examples.
(Appendix 1)
A simulation method executed by a computer,
Read the device structural model stored in the storage unit,
In the quantum conduction calculation by the nonequilibrium Green's function method, the analytical potential generated by the surface charge that is infinite in one direction and has an edge with the gate width given by the above structure model is expressed in two directions perpendicular to the conduction direction. A simulation method characterized by calculating a current in addition to a periodic form.
(Appendix 2)
The simulation method according to
(Appendix 3)
The simulation method according to
(Appendix 4)
4. The simulation method according to
(Appendix 5)
The simulation method according to
(Appendix 6)
A storage unit that stores a structural model of the device;
When performing quantum conduction calculation by the nonequilibrium Green's function method, an analytical charge is generated that has an infinite length in one direction and a surface charge having an edge at the gate width given by the structural model stored in the storage unit on the other side. A device simulator comprising: a characteristic calculation unit that calculates a current by adding a potential in two directions perpendicular to a conduction direction in a periodic manner.
(Appendix 7)
Read the device structural model stored in the storage unit,
In the quantum conduction calculation by the nonequilibrium Green's function method, the analytical potential generated by the surface charge that is infinite in one direction and has an edge with the gate width given by the above structure model is expressed in two directions perpendicular to the conduction direction. A simulation method characterized by calculating a current in addition to a periodic form.
7c チャネル
7d ドレイン
7g ゲート
7s ソース
7m 構造モデル
11 CPU
12 主記憶装置
13 補助記憶装置
14 入力装置
15 表示装置
16 出力装置
17 通信I/F
18 ドライブ
19 記憶媒体
21 原子座標入力部
22 ゲートデータ入力部
23 電流電圧特性計算部
31 原子座標データ
32 ゲートデータ
33 計算結果
100 デバイスシミュレータ
130 記憶部
12
18
Claims (5)
記憶部に記憶されたデバイスの構造モデルを読み込み、
非平衡グリーン関数法によるソースとドレイン間のチャネルを流れる電流の量子伝導計算において、伝導方向に垂直な2方向のうち1方向に無限長であって他方に垂直であり前記構造モデルで与えられるチャネルに対向するゲートのゲート幅で端を持つ面電荷がつくる解析的なポテンシャルを、該伝導方向に垂直な2方向に周期的な形で加えて、電流を計算する
ことを特徴とするシミュレーション方法。 A simulation method executed by a computer,
Read the device structural model stored in the storage unit,
In quantum conduction calculation of current flowing through the channel between the source and the drain by nonequilibrium Green function method is given by a vertical the structural model to the other The endless length in one direction of the two directions perpendicular to the conduction direction channel A simulation method characterized in that a current is calculated by adding an analytical potential generated by a surface charge having an edge with a gate width of a gate opposite to a gate in a periodic form in two directions perpendicular to the conduction direction.
非平衡グリーン関数法によるソースとドレイン間のチャネルを流れる電流の量子伝導計算を行う際に、伝導方向に垂直な2方向のうち1方向に無限長であって他方に前記記憶部に記憶された前記構造モデルで与えられるチャネルに対向するゲートのゲート幅で端を持つ面電荷がつくる解析的なポテンシャルを、該伝導方向に垂直な2方向に周期的な形で加えて、電流を計算する特性計算部と
を有することを特徴とするデバイスシミュレータ。 A storage unit that stores a structural model of the device;
When performing the quantum conduction calculation of the current flowing through the channel between the source and drain by the nonequilibrium Green function method , one of the two directions perpendicular to the conduction direction is infinitely long in one direction, and the other is stored in the storage unit. A characteristic for calculating a current by adding an analytical potential generated by a surface charge having an edge at the gate width of the gate facing the channel given by the structural model in two directions perpendicular to the conduction direction. A device simulator comprising a calculation unit.
Priority Applications (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| JP2012153970A JP6069918B2 (en) | 2012-07-09 | 2012-07-09 | Simulation method and device simulator |
Applications Claiming Priority (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| JP2012153970A JP6069918B2 (en) | 2012-07-09 | 2012-07-09 | Simulation method and device simulator |
Publications (2)
| Publication Number | Publication Date |
|---|---|
| JP2014017382A JP2014017382A (en) | 2014-01-30 |
| JP6069918B2 true JP6069918B2 (en) | 2017-02-01 |
Family
ID=50111819
Family Applications (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| JP2012153970A Expired - Fee Related JP6069918B2 (en) | 2012-07-09 | 2012-07-09 | Simulation method and device simulator |
Country Status (1)
| Country | Link |
|---|---|
| JP (1) | JP6069918B2 (en) |
Family Cites Families (1)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| JP3660137B2 (en) * | 1998-09-25 | 2005-06-15 | 株式会社東芝 | Simulation method, simulator, recording medium recording simulation program, and method for manufacturing semiconductor device |
-
2012
- 2012-07-09 JP JP2012153970A patent/JP6069918B2/en not_active Expired - Fee Related
Also Published As
| Publication number | Publication date |
|---|---|
| JP2014017382A (en) | 2014-01-30 |
Similar Documents
| Publication | Publication Date | Title |
|---|---|---|
| Nam et al. | Automated optimization of large quantum circuits with continuous parameters | |
| Nakagome et al. | Kernel approximate Bayesian computation in population genetic inferences | |
| Spiliopoulos et al. | Fluctuation analysis for the loss from default | |
| JP2006178907A (en) | Circuit simulation method and device | |
| KR101213268B1 (en) | Method of simulation and simulation device | |
| Sullivan et al. | Time-domain simulation of three dimensional quantum wires | |
| Marin et al. | Analytic drain current model for III–V cylindrical nanowire transistors | |
| US11023639B2 (en) | Systems and methods for providing approximate electronic-structure models from calculated band structure data | |
| JP6069918B2 (en) | Simulation method and device simulator | |
| US8122406B2 (en) | Generating models for integrated circuits with sensitivity-based minimum change to existing models | |
| Casagrande et al. | DG treatment of non-conforming interfaces in 3D Curl-Curl problems | |
| JP6992534B2 (en) | Data creation device, guidance model learning device, guidance estimation device, data creation method, guidance model learning method, guidance estimation method and program | |
| Lee et al. | Device simulations with A U-Net model predicting physical quantities in two-dimensional landscapes | |
| EP3850495A1 (en) | Computer-implemented method and electronic device for detecting influential components in a netlist representing an electrical circuit | |
| JP5839922B2 (en) | Surface potential simulation apparatus and surface potential simulation program | |
| Gerstenmayer et al. | Comparison of a finite-element and finite-volume scheme for a degenerate cross-diffusion system for ion transport | |
| JP2014045050A (en) | Simulation device of drain current and simulation program of drain current | |
| US20100125442A1 (en) | Model parameter extracting apparatus and model parameter extracting program for semiconductor device model | |
| Barrera et al. | Polynomial pattern finding in scattered data | |
| JPWO2006107025A1 (en) | Parameter adjustment device | |
| US20120323548A1 (en) | Method, system and program storage device for simulating electronic device performance as a function of process variations | |
| Vellasques et al. | A dual-purpose memory approach for dynamic particle swarm optimization of recurrent problems | |
| JP2007027390A (en) | Device simulation equipment, device simulation method, and device simulation program | |
| Li et al. | Fast inverse using nested dissection for NEGF | |
| JP2011205034A (en) | On implantation distribution generation method and simulator |
Legal Events
| Date | Code | Title | Description |
|---|---|---|---|
| A621 | Written request for application examination |
Free format text: JAPANESE INTERMEDIATE CODE: A621 Effective date: 20150406 |
|
| A131 | Notification of reasons for refusal |
Free format text: JAPANESE INTERMEDIATE CODE: A131 Effective date: 20160705 |
|
| A521 | Request for written amendment filed |
Free format text: JAPANESE INTERMEDIATE CODE: A523 Effective date: 20160902 |
|
| TRDD | Decision of grant or rejection written | ||
| A01 | Written decision to grant a patent or to grant a registration (utility model) |
Free format text: JAPANESE INTERMEDIATE CODE: A01 Effective date: 20161206 |
|
| A61 | First payment of annual fees (during grant procedure) |
Free format text: JAPANESE INTERMEDIATE CODE: A61 Effective date: 20161219 |
|
| R150 | Certificate of patent or registration of utility model |
Ref document number: 6069918 Country of ref document: JP Free format text: JAPANESE INTERMEDIATE CODE: R150 |
|
| LAPS | Cancellation because of no payment of annual fees |