JP2005292027A - 三次元形状計測・復元処理装置および方法 - Google Patents

Abstract

【課題】 本発明は、キャリブレーションを行う必要がなく、かつレーザなどの光を吸収または反射する材質に対しても計測が可能な三次元形状計測・復元装置および方法を提供する
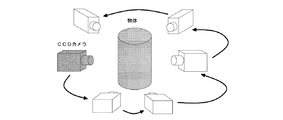
【解決手段】 本発明は、三次元位置と姿勢方向を検出できる三次元磁気センサをＣＣＤカメラに取り付けることにより、ＣＣＤカメラを自由に動かし多方向からのシルエット画像を得ることで計測物体形状を復元する。この計測法ではＣＣＤカメラ一台のみで計測を行うため画像間の対応をとる必要が無く、またレーザなどの光を吸収または反射する材質の物体に対しても計測が可能となる。
【選択図】 図１

Description

本発明は、物体の多方向シルエット画像のデータを取得して、このデータから物体の三次元形状を復元できるようにした三次元形状計測・復元装置および方法に関する。

近年、物体の形状を計測することは工業や医療、芸術など様々な分野において必須の技術である。一般に物体の形状計測法には触針による接触型とＣＣＤカメラを用いた非接触型があるが、接触型は測定する際、物体の表面に触れるため、柔らかいものや壊れやすいものには利用できない。一方、非接触型の計測法は対象を傷つけること無く計測できるため、多くの機関で活発に研究されている。

三次元画像計測の手法を大きく二つに分けるとＣＣＤカメラの他に音や光などの何らかのエネルギを用いる能動型と、それらエネルギを用いない受動型に分けられる。能動型計測ではスリットレーザを用いた光切断法や空間コード化された光パターンを投影するパターン光投影法があるが、光を吸収または反射する物体の計測は困難である。一方、受動型の代表的な計測法として、二台以上のＣＣＤカメラの視差を利用したステレオ法があるが計測点が多数存在する場合、画像間での対応がとりにくい欠点がある。さらに能動型または受動型どちらの計測法も三角測量の原理を利用しており、計測器と対象の配置は一度キャリブレーションを行うと変更できない。そのため対象の背面を計測したい場合や対象の大きさや計測範囲に合わせＣＣＤカメラを移動させる場合は、その都度ＣＣＤカメラのキャリブレーションを行わなければならない。

本発明は、キャリブレーションを行う必要がなく、かつレーザなどの光を吸収または反射する材質に対しても計測が可能な三次元形状計測・復元装置および方法を提供することを目的とする。

本発明の三次元形状計測・復元処理装置は、被計測体である物体に対して相対的に移動可能な撮像手段と、少なくとも該撮像手段と前記物体との相対的な三次元位置と撮像姿勢方向とのデータを取得できる位置センサと、前記撮像手段で得られた画像データと前記相対的な三次元位置と撮像姿勢方向とのデータを用いて前記物体の形状に関する復元可能なデータとして処理する画像処理手段と、を備えたことを特徴とする。
この特徴によれば、計測を行う前にキャリブレーションを行うことで計測時間の短縮と全ての輪郭計測において同条件での計測が可能になる。また一度キャリブレーションを行うことで、ＣＣＤカメラを動かした際もその動きは三次元磁気センサによって計測されるため、その都度、ＣＣＤカメラのキャリブレーションを行う必要がない。更に、この計測法ではＣＣＤカメラ一台のみで計測を行うため画像間の対応をとる必要が無く、またレーザなどの光を吸収または反射する材質の物体に対しても計測が可能となる。
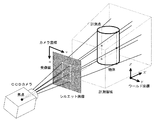
好適な実施態様としては、三次元位置と姿勢方向を検出できる三次元磁気センサ（3 SPACE FASTRACK Polhemus Inc.）をＣＣＤカメラに取り付けることにより、ＣＣＤカメラを自由に動かし多方向からのシルエット画像を得ることで計測物体形状を復元出来る。

本発明の実施例１を図１ないし図１０で説明する。

図１に第１実施例の基本的装置構成を示す。装置は、カメラユニットＡ、三次元磁気センサ２、制御を行う回路７およびＰＣ３（パーソナルコンピュータ）等で構成される。

三次元磁気センサ２（以下レシーバ）はトランスミッタ４から発信される半径80cm半球内の磁界ベクトルを検出している。また、三次元センサコントローラ５はレシーバ位置三成分と姿勢の三成分をサンプリング周波数120Hzで出力している。
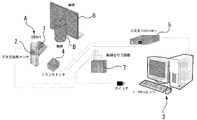
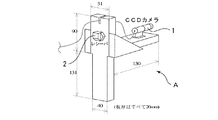
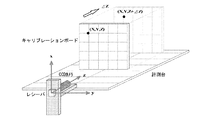
レシーバ２はＣＣＤカメラ１を固定したカメラユニットＡに取り付けてあり、カメラユニットＡを動かした際もその動きは三次元センサ２によって計測される。
シルエット画像の撮影に同期して、カメラユニットＡの位置と姿勢が計測される。これらの制御はＰＬＤによる回路およびＰＣで行われる。
物体Ｂ後方にある黒板６は対象のシルエット画像を撮りやすくするために使用する。

図２にカメラユニットの詳細が示され、カメラユニットＡはＣＣＤカメラ１が固定されており、その中心軸上にレシーバ２を取り付けてある。
レシーバ２はトランスミッタ４から発信される磁気を検出しており、周辺に金属などがあると計測結果にその影響を受ける。そのため、カメラユニットＡは木材やプラスチック、アルミ製の材料で作成している。

本実施例では、シルエット画像から計測対象輪郭の受像面上の座標を計測しており、
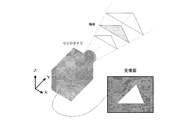
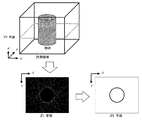
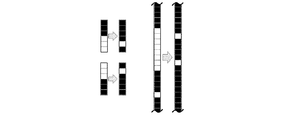
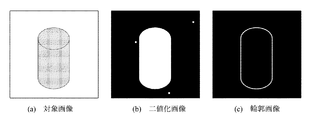
得られた画像に二値化、輪郭抽出などの画像処理を行い、シルエット画像Ｃを得る。

ここで、カメラ１とシルエット画像の関係を説明すると、図３にその遠近法の原理を示しており、計測対象が存在する候補領域は撮影されたシルエット影像を断面に持つとともに、遠近法の原理によりカメラ１から離れるほど、広い領域となる。

これらの関係は、図４、図５に座標関係で示されている。すなわち、(u、v)は受像面上の座標、(X、Y、Z)はワールド座標系であり、図４のようにカメラ１の焦点から受像上の対象の点を通る直線は、実際の対象上の点も通過する。そのため、受像面上の計測点座標がわかれば、実際の対象上にある計測点を通る直線を算出できる。

本実施例では、計測対象のシルエット画像Ｃより得られた受像面上の計測点とカメラの焦点を結ぶ直線をワールド座標系（物体に固定した座標系）上で、算出することで対象を含む領域を取り出す。

ここでシルエット画像からの形状復元イメージについて説明する。シルエット画像から計測対象の形状を復元する例として、人が彫刻などを行う際の技術をイメージして試作するような場合を想定し、図５のように立方体から四角錐を削り出していく場合を考える。

まず、図６のように、計測対象を正面、側面、上面方向からＣＣＤカメラ１で計測し、設定した領域で削り出す。つぎに、図６で削り出された立方体を重ね合わせると、図７のような計測形状の四角錐を削り出すことができる。

図７では目標となる図５の図形より形がいびつであるが、さらに別の方向からも計測を行い、削り出していくことで形状復元が可能である。この手法では、対象が複雑な形状であっても、より多くの方向から計測を行い全ての結果を重ねることで形状復元が可能である。この技術を応用し、図８のように計測対象の多方向からのシルエット画像を取得することで対象の形状を復元することができる。

まず、合成された領域上に水平なＺ＝Ｚ１平面を設定し、その断面形状を取り出す。図９のように円柱を多方向から計測し、合成された対象の断面形状イメージ図を示す。

そして、図９で得られた断面形状のデータより、輪郭形状のみを取り出す。更に、設定した水平なＺ＝Ｚ１平面を変更していき、各平面上における断面形状を取り出す。図１０のように各高さの断面形状をまとめ、計測対象の形状を復元する。

この計測手順は、
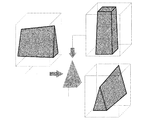
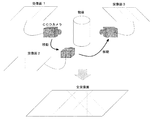
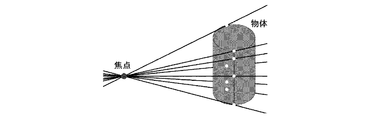
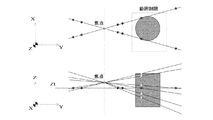
（１） カメラを移動させながら多方向からの撮影を行い、各方向からのシルエット画像を得る。
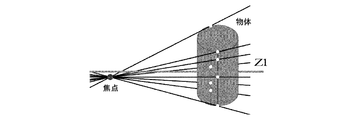
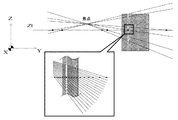
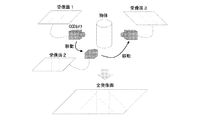
（２） 各シルエット画像を基にそれぞれの撮影方向において、計測対象を含む候補領域を抽出する。
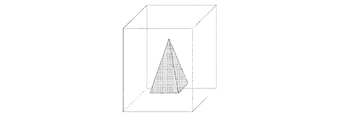
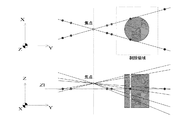
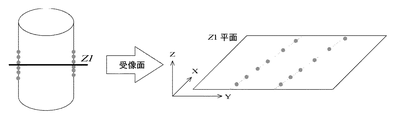
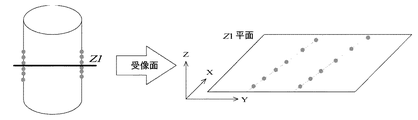
（３） 抽出された候補領域内に水平面と平行な面を設定し、その平面上で候補領域の断面形状を算出する。
（４） （３）の処理を異なる撮影方向から得られた候補領域に対し行う。
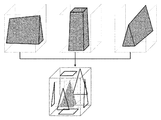
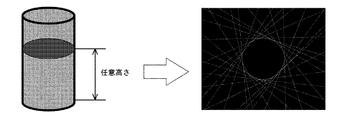
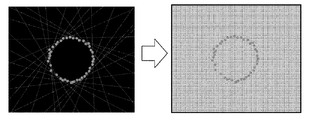
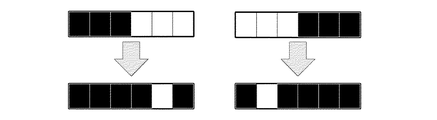
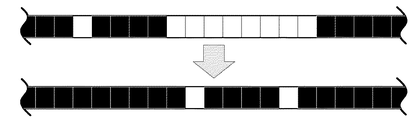
（５） 同一平面内で様々な撮影方向から得られた候補領域の断面形状を重ね合わせ
重複した部分を抽出することで、計測対象のその平面での断面形状が決定される。
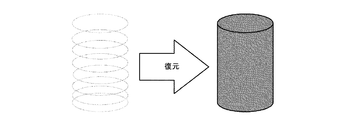
（６） （３）で設定した平面を上下に移動し、それぞれの平面上で対象の断面形状の算出を繰り返すことで，対象全体の形状を復元する。
という手順で説明を行っている。

第２実施例は、第１実施例と異なる手順で対象全体を復元する方法であり、図１１ないし図２０で説明する。

すなわち、第２実施例の計測手順は、
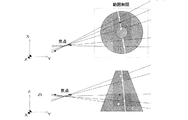
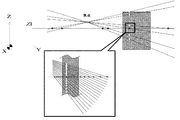
（１） 一方向から対象を撮影しシルエット画像を得る。
（２） 撮影されたシルエット画像を基に計測対象を含む候補領域を抽出する。
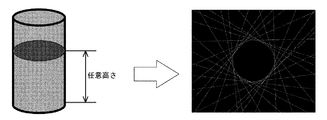
（３） 取り出した候補領域内に水平面と平行な面を設定し、その平面上の候補領域の断面形状を算出する。
（４） （３）で設定した平面の位置を上下方向に移動し、それぞれの平面上で候補領域の断面形状の算出を繰り返すことで，候補領域全体の形状を算出する。
（５） カメラを移動させながら多方向からの撮影を行い、それぞれの方向から算出された候補領域形状を重ね、重複した部分を抽出することで対象の形状を復元する。
という手順で行う。

すなわち、本実施例では、対象の断面形状より対象の形状を復元している。図１１のように円柱を計測した場合を例に説明する。

図１１は各座標系の関係を示しており、図１２は直線方程式イメージ図である。実際は輪郭全てに対して輪郭点が計測されており、それぞれの点に直線の方程式が算出されている。

図１２において水平面と平行な面Ｚ＝Ｚ１を設定し、各直線との交点Ｘ、Ｙを算出する。またＸ、Ｙについても領域を設定し、水平面と平行な面Ｚ＝Ｚ１近傍の形状をＺ１平面上に取り出す。

図１３に円柱を計測した場合の計測領域設定について示す。

図１４は、図１３を一部、拡大した図であり、全輪郭点について直線の方程式を算出すると、図１４のようにＺ＝Ｚ１平面上の対象形状候補を点群で取り出す事ができる。

図１５にはＺ＝Ｚ１平面上に抽出された輪郭のイメージ図が示されており、この図１５により、ある方向から計測されたＺ１平面上の対象形状を取り出すことができる。これはある一方向からのデータである。

つぎに、カメラを移動させながら各方向シルエット画像を計測し、任意高さＺ＝Ｚ１平面状の形状を算出していく。得られた全てのＺ１平面上の形状を重ねていく事で、任意高さＺ＝Ｚ１の断面形状を得ることができる。

図１６には多方向からの計測イメージ図が示されているが、実際の計測を行う際には、カメラの移動間隔を狭め、より多くのシルエット画像を得る事で良好な形状復元が行える。

多方向からの計測を行い、各方向の全ての輪郭形状を重ねると図１７のように水平面と平行な任意平面における断面形状が点群の曲線で計測できる。そして、各曲線の交点を求め、輪郭のみのデータを算出する。図１８のように得られた点群について交点を求めていくことで図１７のように対象形状のみのデータを得る事ができる。

つぎに任意に設定した平面Ｚ＝Ｚ１の高さを変えていき、各断面の形状を算出する。最後に図１９のように全ての結果より対象の形状を復元する。

図２０には計測の流れをフローチャートで示されており、具体的には、
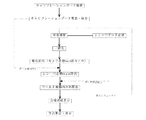
（１）計測を行う前にキャリブレーションを行う。先にキャリブレーションを行うことで計測時間の短縮と全ての輪郭計測において同条件での計測が可能になる。
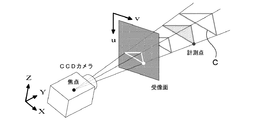
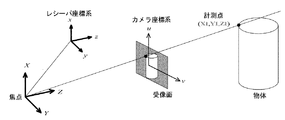
（２）対象をＣＣＤカメラで取り込み、同時にＣＣＤカメラの位置と姿勢をレシーバにより計測する。得られた画像に二値化、輪郭抽出などの処理を行い、カメラ座標を読み取る。
（３）キャリブレーションデータを元にカメラ座標をレシーバ座標に変換し、更にレシーバ座標を撮影時のカメラの位置と姿勢を元にワールド座標に変換する。
（４）カメラを移動させつぎのシルエットの撮影を行い、（２）〜（３）を繰り返す。
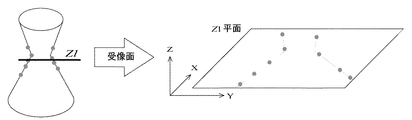
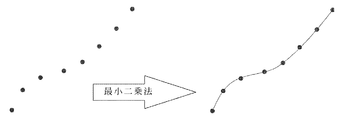
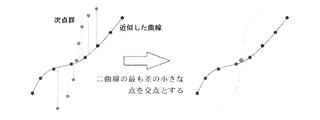
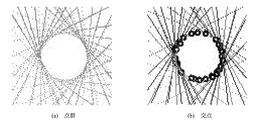
（５）全ての輪郭の計測が終了したら全輪郭を表示し、交点を算出する。
（６）全ての結果より対象の形状を復元する。
となる。

前記したフローの（２）における二値化について説明すると、本実施例で得られる画像は分解能512×512の濃淡画像であり、ピクセルごとに明るさレベル（輝度値）を持っている。輝度値に対し閾値を設定し、二値化を行う。二値化を行いやすくするため、対象の後ろに黒いボードを設置して撮影している。図２１に円柱の対象をある方向から撮影したイメージ図を示す。

図２２に図２１の対象周辺を拡大した図を示す。背景に黒いボードを設置した事で対象周辺は輝度値が高く、それ以外は輝度値が低くなる。図２２の対象左上と右下の点はノイズを示している。

図２１の濃淡画像に対し閾値を設定し、輝度値が閾値より高い場合は「１」、低い場合は「０」とし二値化を行う。本システムでは二値化の際「１」を白、「０」を黒で表している。二値化を行う事で、図２２は図２３のような対象のシルエット画像を得る事ができる。対象右下の点はノイズを示している。

同様に、フロー（２）における輪郭抽出について説明すると、二値化（白黒化）された画像より輪郭を抽出する場合、二値化画像は各ピクセルが「１（白）」と「０（黒）」、どちらかに処理されており、対象シルエットは、ある幅の「１」の塊を持っていると考えられる。そこで，図２４のようにピクセルを左から右へと横に走査していき、「０００１１１」の場合は「００００１０」、または「１１１０００」の場合は「０１００００」と処理する事で対象の右端、左端の輪郭が抽出される。またこの処理は同時にノイズ除去にもなる。このように、輪郭抽出を行う事で図２５のように対象の輪郭のみが抽出され、ノイズは除去される。

この工程を図２６のように上から下に対しても同様の処理を行い、二値化された画像を上下左右，全ピクセルに対し輪郭抽出を行う事で、図２３は図２７、図２８のようになる。すなわち、図２７の画像により対象輪郭が決定され各点のカメラ座標(u,v)が決まる。

本実施例では得られた対象の各輪郭カメラ座標(u,v)を座標変換することで実際の座標(X,Y,Z)を算出する。以下に座標変換について記述する。

前述したフロー（３）におけるカメラ座標系からレシーバ座標系（焦点と計測点を通る直線の算出方法）を説明すると、本実施例には、トランスミッタを基準にした実座標であるワールド座標系、カメラの焦点距離を基準にしたカメラ座標系、レシーバを基準としたレシーバ座標系が存在することになる。

ここでは、カメラで撮影した点をカメラ座標からレシーバ座標へ変換し、さらにレシーバ座標をワールド座標に変換する事で実座標を算出している。図２９にカメラ座標、レシーバ座標、ワールド座標の関係を示す。

計測対象をＣＣＤカメラで撮影し二値化・輪郭抽出などの画像処理を行った後，輪郭のカメラ座標上での位置(u,v)を読み取る。ＣＣＤカメラの焦点と計測点通る直線を算出し，レシーバを原点とした座標系(x,y,z)に変換する。同時にＣＣＤカメラの位置や姿勢をレシーバにより計測し，最後にレシーバ座標を三次元磁気センサからの位置と姿勢のデータを組み合わせることでワールド座標(X,Y,Z)に変換する。

まず，カメラ座標からレシーバ座標。への変換について説明する。図３０に図２９をX1-Z1(Y1-Z1)平面で二次元化したカメラ焦点と受像面及び計測点までの距離の関係を示す。

カメラの焦点から受像面までの距離をfとおくと，受像面上の座標（カメラ座標）はカメラの焦点を原点とした座標系において以下のように表せられる。

Z 1＝λとおき、線形化すると以下のように表せられる。

(4.2)式をレシーバを原点とした座標（レシーバ座標）で表すために回転と平行移動を行う。

カメラ座標原点からレシーバ座標原点への平行移動量は、ベクトルa=(x_r,y_r,z_r)となる。
これら回転と平行移動の変化を(4.2)式に導入すると、

となり、代数ｈ_１１〜ｈ_３４を設定すると、以下のような行列で表すことができる。

ここでx,y,zは三次元位置センサのレシーバ座標である。
また、(4.5)式をｈ_３４で両辺を割り、代数ｓ，ｋ_１１〜ｋ_３３で置き換えると次式で表すことができる。

ｋ_１１〜ｋ_３３のパラメータには、カメラの位置や姿勢などをはじめとする計測対象とカメラの関係を表すデータが全て含まれている。したがって、式(4.8)が、レシーバ座標(x,y,z)とカメラ座標(u,v)の関係式となる。
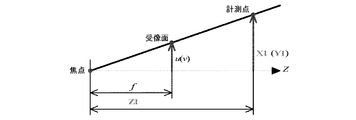
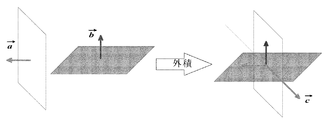
(4.8)式を展開すると、

更に変形させることで、

ここで未知数である１１個の係数ｋ_１１〜ｋ_３３は、4.5で述べる方法によって、既知の１１点以上のカメラ座標(u,v)とその点に対応するレシーバ座標(x,y,z)の組み合わせを(4.9)式に代入し、連立方程式を解くことで求められる。

(4.10)は２平面の方程式であり、これを満たすものは２平面の交線を示す。この交線は、カメラの焦点と計測点を通る直線の方程式である。ただし、ここで求まる直線はＣＣＤカメラに固定したレシーバ座標系であり、4.25、4.26で説明する方法で、ワールド座標系（計測物体に固定した座標系）に変換する。

前述した計測を行う前のキャリブレーションについて説明すると、初めにレシーバ座標とカメラ座標の校正をとるためにキャリブレーションを行う。ここで、図３１にはキャリブレーションの概要が示され、以下の手順で行われる。
（１） 50mmおきに目盛りの刻まれたキャリブレーションボードをＣＣＤカメラに固定されているレシーバのｘ−ｙ平面と平行に設置する。
（２） キャリブレーションボードを撮影し，ディスプレイ上に表示する。
（３） ディスプレイ上のキャリブレーションボード目盛りをマウスでクリックする（カメラ座標(u,v)の読み込み）。
（４） （３）でクリックした点と対応するレシーバ座標を入力する（レシーバ座標(x,y,z)の読み込み）。
（５） （３）〜（４）の処理を４回繰り返す。
（６） キャリブレーションボードをｚ軸方向に移動させながら（２）〜（５）の処理を４回繰り返す。

図３２と図３３は、レシーバを原点として、それぞれｚ＝400mmとｚ＝650mm時に撮影される画像である。奥行きを変えることで目盛りの大きさが変化するのがわかる。

以上の手続きにより得られたデータを式(4.11)に代入すると，以下のような式が導出される。

ここでT, k, cは、

また、

である。

１１個の未知数ｋ_１１〜ｋ_３３はＴの擬似逆行列Ｔ^＊を用いて以下の式より算出される。

キャリブレーションにより未知数ｋ_１１〜ｋ_３３を算出した事で，式(4.10)より計測点のカメラ座標(u , v)が得られたときの一般式が決定する。

また、式(4.15)は次式のように表される。

次に、ＣＣＤカメラと輪郭上の計測点を結ぶ直線を求めるために平面の交線を求める。
一般的な平面の式は、

または変形して、

と表される。

式(4.16)をそれぞれの平面の式と考えると、計測点はそれぞれの平面上に存在する。

ＣＣＤカメラと計測点を結ぶ直線は、二平面それぞれに垂直なベクトルの外積を求める事で、算出する。それぞれの式の平面に垂直なベクトルは、

と表される。

図３４に、それぞれの面に垂直なベクトルの外積を示す。
外積cはベクトルaとベクトルbにそれぞれ垂直なベクトルである。
ベクトルaとベクトルbの外積cを求めると、

となる。

これを媒介変数表示によって表すと以下のようになる。

α，β，γはこの直線がｚ＝０平面を通ることを考慮し、ｚ＝０とおき式(4.19)の連立方程式を解く事で求められる。

(4.23)はレシーバ座標なので4.25、4.26で述べる方法により、ワールド座標へ変換する。

また、レシーバ座標からワールド座標への変換について詳述する。

すなわち、カメラユニットの動きを考慮するためレシーバ座標をワールド座標に変換する必要があり、カメラユニットを動かした場合、その動きはレシーバによって計測されている。

レシーバによって得られる値はトランスミッタ座標を原点としたレシーバの三次元的位置(wx, wy, wz)と姿勢を表すロール角φ、ピッチ角θ、ヨー角ψである。

図３５にロール・ピッチ・ヨー角の座標変換を示す。
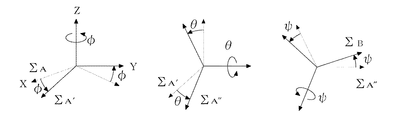
（ i ）まずΣ_ＡをＺ_Ａ軸回りに角度φ回転させた座標系をΣ_Ａ′とする。
（ ii ）つぎにΣ_Ａ′をＹ_Ａ′軸回りに角度θ回転させた座標系をΣ_Ａ″とする。
（ iii ）最後に，Σ_Ａ″をＸ_Ａ″軸回りに角度ψ回転させた座標系をΣ_Ｂとする。

ロール・ピッチ・ヨー角が与えられた場合の変換行列はC：Ｃｏｓ，S：Ｓｉｎとしたとき以下のようにして求まる。

レシーバを中心とした座標系であるレシーバ座標(x, y, z)から実座標であるワールド座標(X, Y, Z)への座標変換式は、(4.24)のロール・ピッチ・ヨー角が与えられた場合の回転の式にトランスミッタからレシーバまでの距離(wx, wy, wz)を足すことにより求められる。

したがって、以下のようになる。

これにより、ワールド座標における計測点を通る直線の方程式が求められる。

次に、求められた媒介変数表示の直線に対し平面Ｚ＝Z₁との交点を求めることでX_1，Y₁を算出する。

上式より、

t₁を(4.26)式に代入しその水平面Ｚ＝Ｚ１上におけるX_1，Y₁を算出する。

(4.29)は、ある輪郭点(u₁,v₁)のワールド座標(X_1，Y_1，Z₁)である。

次に、領域設定について説明すると、図３６は直線方程式イメージ図であり、実際は輪郭全てに対して輪郭点が計測されており、それぞれの点に直線の方程式が算出されている。これら直線を全てワールド座標に変換し、任意水平面Ｚ＝Ｚ１を設定することで、その水平面上での形状を得る。

ここで、(4.28)式より水平面と平行な面Ｚ＝Ｚ１を設定し、各直線との交点Ｘ，Ｙを算出する。ここで、ｎは輪郭点の数である。

( 4.30 )で求められたX_1〜n，Y_1〜nにおいてＸ，Ｙ方向においても範囲を設定することで任意の水平面Ｚ＝Ｚ１近傍の輪郭形状をＺ＝Ｚ１平面上に点群で取り出す。

図３７には、円柱を計測した場合の領域設定例が示されている。

また、図３８には、円錐台を計測した場合の領域設定例が示されている。ここでは、任意水平面Ｚ＝Ｚ１を設定し、領域を設定することで任意水平面Ｚ＝Ｚ１近傍のｍ個の形状座標(X_m, Y_m, Z_m)を得る。

図３９は、図３７の一部を拡大した図であり、全輪郭点について直線の方程式を算出すると、図３９のようにＺ＝Ｚ１平面上の対象形状候補を多数の点群で取り出す事が出来る。

図４０、図４１にＺ１平面上に抽出された輪郭のイメージ図が示されており、このように任意水平面Ｚ＝Ｚ１を設定し、Ｘ，Ｙについて範囲を制限することで任意水平面Ｚ＝Ｚ１近傍の形状をＺ＝Ｚ１平面上に取り出せる。

次に，カメラを移動させながら各方向シルエット画像を計測し、計測されたシルエット画像より前シルエット画像と同じ任意水平面Ｚ＝Ｚ１上の輪郭形状を算出していく。

図４２には、多方向からの計測イメージ図が示されており、各方向の全ての輪郭形状を重ねると図４３のように任意水平面Ｚ＝Ｚ１における断面形状が点群の曲線で計測できる。

図４４には、実際の計測の結果が示され、対象は円柱の木材であるが、図４４（ｂ）に示すとおり、円柱の断面形状点群で計測されているのが確認できる。

図４４の輪郭形状は全てのシルエット画像から算出された点群曲線の集合データにしか過ぎず，各輪郭の座標は算出されていない．輪郭の座標を求めるために点群を近似曲線で表し，曲線と曲線の交点を求める。

一つのシルエット画像から得られた候補点群に最小二乗法を行う事で近似曲線を求めることにより、Ｎ個の候補点の集合｛(x_i, y_i)|i=1,2,…,N｝が与えられた場合、点群は次式で近似することができる。

ここでa₀〜a₃のパラメータは変分法により、

として次式の行列演算を行うことにより求める。

図４５に曲線近似が示され、各交点は、近似した曲線とつぎのシルエット画像から得られた点群により求める。次点群全てに対し近似した曲線との差を算出し、差の最も少ない点を交点とする。

図４７のように得られた点群について交点を求めていくことで、図４３は対象形状の座標を得る事が出来る。図４８は実際に計測を行った図４４の点群に対し、交点を算出した結果であり、これにより、任意水平面における対象の断面形状を算出可能である。

これにより、設定した任意の水平面Ｚ＝Ｚ１における断面形状が算出され、つぎに設定した水平面Ｚ＝Ｚ１を変更し、同じ計測を繰り返し、全ての結果から対象の形状を図４９のように復元できることになる。

本実施例の場合、装置の精度評価を行うために大きさが既知である計測対象を５０回計測し、任意に２０回の結果によりRMS誤差を算出した。RMS誤差は系統的な対象となる値がその平均からどれだけ広い範囲に分布しているかを計算することで精度評価に用いられるものであり、

上式により本実施例の装置におけるRMS誤差は1.552mmであった。

図５０および図５１はそれぞれ木材円柱の画像と計測結果であり、図５１（ｂ）のように本システムにより円柱の断面形状が正確に計測されている事がわかる。
本発明の実施例では、位置センサとして三次元磁気センサを利用しているが、これに限らずＧＰＳ位置情報取得装置を利用しても良い。前記撮像手段としてＣＣＤカメラを利用しているが、ＣＭＯＳセンサその他の画像取得センサを利用することは自由である。

本発明の第１実施例の装置構成概要を示す図である。 カメラユニットの詳細を示す図である。 遠近法の原理を示す図である。 座標系表示を示す図である。 立方体から四角錐への削り出しの場合を示す図である。 各方面の形状の削り出しを示す図である。 削り出しの合成を示す図である。 多方向シルエットの取得について示す図である。 断面形状イメージ図である。 形状の復元を示す図である。 各座標系の関係を示す図である。 直線の方程式イメージ図である。 円柱を計測した場合の計測領域の設定を示す図である。 図１３の一部を拡大したイメージ図である。 輪郭形状抽出について示す図である。 多方向シルエットの取得について示す図である。 任意水平面上での輪郭イメージ図である。 交点の表示を示す図である。 形状の復元を示す図である。 計測の流れを示すフローチャートである。 濃淡画像イメージ図である。 図２１の濃淡画像拡大イメージ図である。 二値化シルエット画像イメージ図である。 輪郭抽出イメージ図である。 ノイズ除去イメージ図である。 輪郭抽出とノイズ除去イメージ図（縦）である。 輪郭画像イメージ図である。 各画像イメージ図である。 各座標系の関係を示す図である。 二次元での座標系相対関係を示す図である。 キャリブレーションの概要を示す図である。 レシーバを原点として、Z=400mm時に撮影される画像である。 レシーバを原点として、Z=650mm時に撮影される画像である。 それぞれの面に垂直なベクトルの外積を示す図である。 ロール・ピッチ・ヨー角による座標変換を示す図である。 直線の方程式イメージ図である。 円柱を計測した場合の領域設定例（円柱）を示す図である。 円錐台を計測した場合の領域設定例を示す図である。 図３７の拡大イメージ図である。 ＺＩ平面上に抽出された輪郭のイメージ図である。 同じく、ＺＩ平面上に抽出された輪郭のイメージ図である。 多方向からの計測イメージ図である。 任意水平面上での輪郭イメージ図である。 実際の計測結果例を示す図である。 曲線近似を示す図である。 交点の計算を示す図である。 交点の表示を示す図である。 実際の交点結果を示す図である。 形状復元を示す図である。 木材円柱の画像と計測結果を示す図である。 同じく、木材円柱の画像と計測結果を示す図である。

Claims (9)

1. 被計測体である物体に対して相対的に移動可能な撮像手段と、少なくとも該撮像手段と前記物体との相対的な三次元位置と撮像姿勢方向とのデータを取得できる位置センサと、前記撮像手段で得られた画像データと前記相対的な三次元位置と撮像姿勢方向とのデータを用いて前記物体の形状に関する復元可能なデータとして処理する画像処理手段と、を備えたことを特徴とする三次元形状計測・復元処理装置。
2. 前記位置センサは、前記撮像手段の移動に追従するように該撮像手段に固定された三次元磁気センサである請求項１に記載の三次元形状計測・復元処理装置。
3. 前記位置センサは、前記撮像手段の移動に追従するように該撮像手段に固定された超音波センサである請求項１に記載の三次元形状計測・復元処理装置。
4. 前記位置センサは、前記撮像手段の移動に追従するように該撮像手段に固定された方位センサとＧＰＳ位置情報取得装置である請求項１に記載の三次元形状計測・復元処理装置。
5. 前記撮像手段は、ＣＣＤカメラであり、画像データをデジタルデータで直接取得できるようになっている請求項１ないし４のいずれかに記載の三次元形状計測・復元処理装置。
6. 始めに撮像手段と被計測体である物体との相対的な三次元位置と撮像姿勢方向とに関して少なくとも一度のキャリブレーションを行い、前記撮像手段を前記物体に対して撮像を継続しながら相対的に移動させて撮像データを取得し、さらに位置センサによりこの撮像データとリンクする少なくとも前記撮像手段と前記物体との相対的な三次元位置と撮像姿勢方向とのデータを取得し、画像処理手段によりこれら撮像手段で得られた画像データと前記相対的な三次元位置と撮像姿勢方向との少なくとも３つのデータを用いて前記物体の形状に関する復元可能なデータを得ることを特徴とする三次元形状計測・復元処理方法。
7. 前記物体の一方向から前記撮像手段による画像取得である撮影を行い、計測対象の物
   体を含む領域のデータを取り出し、前記撮像手段を移動させて多方向からの画像取得
   である撮影を行い、その結果を重ね、取り出した領域に水平面と平行な面を設定し、
   その平面上で対象の断面形状を算出し、設定した水平面と平行な面の位置をその水平
   を保ちながら上下方向に変えて算出を繰り返し行い、対象全体の形状を復元する請求
   項６に記載の三次元形状計測・復元処理方法。
8. 前記物体の多方向から前記撮像手段による画像取得である撮影を行い、各方向において計測対象の物体を含む候補領域のデータを取り出し、取り出した各候補領域内に水平面と平行な面を設定し、その平面上で各候補領域の断面形状を算出し、同一平面内で各候補領域の断面形状を重ね合わせ重複した部分を抽出することで，その平面における計測対象の断面形状を決定し，水平面と平行な面の位置をその平行を保ちながら上下方向に移動させ，各水平面の位置において上記計測対象の断面形状の決定を繰り返し行って，対象全体である物体の形状を復元する請求項６に記載の三次元形状計測・復元処理方法。
9. 対象全体である物体をＣＣＤカメラで取り込み、同時にＣＣＤカメラの位置と姿勢を位置センサであるレシーバにより計測し、得られた画像に二値化、輪郭抽出などの処理を行ってカメラ座標を読み取り、前もって得たキャリブレーションデータを元にカメラ座標をレシーバ座標に変換し、更にレシーバ座標を撮影時のカメラの位置と姿勢を元にワールド座標に変換し、カメラを移動させて次のシルエットの撮影を行い、上記処理を繰り返し行って、全ての輪郭の計測が終了した後、全輪郭を表示し、交点を算出し、全ての結果より対象の形状を復元する請求項６に記載の三次元形状計測・復元処理方法。
   
   

Images