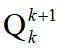CN115343734B - 一种基于双线性内插半球模型的gnss变形监测方法 - Google Patents

一种基于双线性内插半球模型的gnss变形监测方法 Download PDF

Info

Publication number
CN115343734B
CN115343734B CN202211253819.XA CN202211253819A CN115343734B CN 115343734 B CN115343734 B CN 115343734B CN 202211253819 A CN202211253819 A CN 202211253819A CN 115343734 B CN115343734 B CN 115343734B
Authority
CN
China
Prior art keywords
double
value
difference
monitoring
grid
Prior art date
Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
Active
Application number
CN202211253819.XA
Other languages
English (en)
Other versions
CN115343734A (zh
Inventor
李凯
谭冬梅
韩鹏
柳钧议
李绿洲
周强
吴屾
罗杰
甘沁霖
冀鹏阳
郭泰�
韩雷雷
李培杰
何雨琨
Current Assignee (The listed assignees may be inaccurate. Google has not performed a legal analysis and makes no representation or warranty as to the accuracy of the list.)
Wuhan Optics Valley Beidou Geo Spatial Information Industry Co ltd
Wuhan Metro Group Co Ltd
Original Assignee
Wuhan Optics Valley Beidou Geo Spatial Information Industry Co ltd
Wuhan Metro Group Co Ltd
Priority date (The priority date is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the date listed.)
Filing date
Publication date
Application filed by Wuhan Optics Valley Beidou Geo Spatial Information Industry Co ltd, Wuhan Metro Group Co Ltd filed Critical Wuhan Optics Valley Beidou Geo Spatial Information Industry Co ltd
Priority to CN202211253819.XA priority Critical patent/CN115343734B/zh
Publication of CN115343734A publication Critical patent/CN115343734A/zh
Application granted granted Critical
Publication of CN115343734B publication Critical patent/CN115343734B/zh
Active legal-status Critical Current
Anticipated expiration legal-status Critical

Links

Images

Classifications

    • G—PHYSICS
    • G01—MEASURING; TESTING
    • G01S—RADIO DIRECTION-FINDING; RADIO NAVIGATION; DETERMINING DISTANCE OR VELOCITY BY USE OF RADIO WAVES; LOCATING OR PRESENCE-DETECTING BY USE OF THE REFLECTION OR RERADIATION OF RADIO WAVES; ANALOGOUS ARRANGEMENTS USING OTHER WAVES
    • G01S19/00—Satellite radio beacon positioning systems; Determining position, velocity or attitude using signals transmitted by such systems
    • G01S19/01—Satellite radio beacon positioning systems transmitting time-stamped messages, e.g. GPS [Global Positioning System], GLONASS [Global Orbiting Navigation Satellite System] or GALILEO
    • G01S19/13—Receivers
    • G01S19/35—Constructional details or hardware or software details of the signal processing chain
    • G01S19/37—Hardware or software details of the signal processing chain
    • G—PHYSICS
    • G01—MEASURING; TESTING
    • G01B—MEASURING LENGTH, THICKNESS OR SIMILAR LINEAR DIMENSIONS; MEASURING ANGLES; MEASURING AREAS; MEASURING IRREGULARITIES OF SURFACES OR CONTOURS
    • G01B7/00—Measuring arrangements characterised by the use of electric or magnetic techniques
    • G01B7/16—Measuring arrangements characterised by the use of electric or magnetic techniques for measuring the deformation in a solid, e.g. by resistance strain gauge

Landscapes

  • Engineering & Computer Science (AREA)
  • Signal Processing (AREA)
  • Radar, Positioning & Navigation (AREA)
  • Remote Sensing (AREA)
  • Physics & Mathematics (AREA)
  • General Physics & Mathematics (AREA)
  • Computer Networks & Wireless Communication (AREA)
  • Position Fixing By Use Of Radio Waves (AREA)

Abstract

本发明公开了一种基于双线性内插半球模型的GNSS监测方法，包括获取观测数据，求解监测点约束坐标；根据监测点约束坐标获得载波与伪距双差观测值的残差值，并据此建立半球模型；判断当前卫星位置所对应半球模型中格网内多路径效应改正值是否为空，若否，则获取所建立的半球模型中当前卫星所处格网内的多路径效应改正值；若是，则通过双线性内插法估计出当前卫星所处格网内的多路径效应改正值；通过基站数据与监测站数据获得双差组合观测值，对双差组合观测值进行最优估计，得到变形监测点坐标，在估计过程的残差项中减去所述多路径效应改正值，对残差中包含的多路径误差进行修正。本发明有效解决了自动化监测过程中存在的监测结果不稳定的问题。

Description

一种基于双线性内插半球模型的GNSS变形监测方法
技术领域
本发明涉及全球导航卫星系统数据处理领域，尤其涉及一种基于双线性内插半球模型的GNSS变形监测方法。
背景技术
全球导航卫星系统 (GNSS) 定位服务于多种工程应用，日益增长的市场需求也将GNSS定位精度推到毫米级甚至更高。随着GNSS相关误差（如：电离层误差、对流层误差、卫星钟差等）的研究在高精度定位方面取得了重大进展，而多路径由于受具体环境的不同而不同，难以参数化且无法通过差分技术予以消除，因此，其目前仍然是主要误差源之一。
目前消除多路径影响的方法主要有以下三种：方法一，严格天线安装的现场环境，在周围反射物较少的环境中进行选址；方法二，基于硬件的方法，通过采用扼流圈天线改进天线的增益模式以对抗多路径；方法三，基于软件的方法，包括使用GPS观测中的信噪比（SNR）以及利用各种滤波技术抑制多路径主导频带，如小波分析、卡尔曼滤波和交叉验证的冯德拉克滤波器等。在所有基于软件的方法中，恒星日滤波方法和半球模型方法是基于静态环境下多路径的时空重复性而开展的，因此适用于实时多路径改进。恒星滤波（SF）方法基于每个GNSS卫星星座具有恒星日重复性的特点，通过在时间域观测恒星日滞后时间并进行建模改进来实现。半球模型方法是基于多路径仅依赖于天空中的轨道位置这一特征，在空间领域通过建立网格或球谐波来实现。
美国的全球定位系统（GPS）是目前在全球应用最为广泛的卫星导航定位系统。目前，随着美国GPS的现代化，俄罗斯GLONASS系统的恢复，欧洲GALILEO系统的建设，中国COMPASS系统的后来居上，以及美国的WAAS、欧洲的EGNOS、日本的MSAS、印度的GAGAN等广域差分增强系统的建立，多个频率多个卫星导航系统组合导航定位，不仅能够防止GPS系统对民用用户功能的限制，而且能够在作业环境较差的区域，提供稳定、可靠的定位结果,扩展作业范围。同时可以提高RTK的作业距离，提高系统的稳定性。多频多系统组合定位己成为国内外的热点研究方向。
随着传感器技术、数据处理技术、通信技术的迅速发展，变形监测行业也随之引入各类先进传感技术进行水平位移与沉降的实时监测，现有的方法主要是采用全站仪监测、激光雷达监测、视频监测以及北斗载波差分定位技术对目标物进行在线监测,但全站仪监测技术操作复杂，需要专业人员实时交互操作，效率低下；激光雷达存在监测成本高、数据处理量大的缺点；视频监测容易受空气可见度和供电的影响。北斗差分定位技术数学模型成熟，且数据处理自动化性强，因此目前较为广泛地被应用于变形监测中。然而，北斗定位技术存在受外界环境影响、监测结果不稳定的问题，尤其是在监测天线周围存在高反射性介质时，天线由于接收到直射信号与反射信号的叠加信号而导致监测结果中含有一定的系统误差，即为多路径效应的影响。
当前，国内行业内GNSS变形监测中针对并着手解决此问题的先例较少。在GNSS数据处理技术领域中已有针对多路径效应而提出的半球模型（Multipath-Hemispherical-Map, MHM），该模型基于GNSS中轨卫星轨道具有空间重复性的特征，利用GNSS中轨卫星在两次重访同一空间位置时信号的反射路径基本不变的特点，对不同空间位置的多路径效应误差值进行提取并记录，在后续监测过程中通过卫星方位角与高度角查询对应的多路径修正值并进行改正。然而该模型依赖于多次轨迹必须具有高重复性，当出现卫星轨道机动、卫星星历误差而导致两次重复轨迹出现在不同的格网内时，会导致当前格网内无多路径改正值，进而导致多路径效应无法正常改正。
发明内容
本发明的目的在于克服现有技术之缺陷，提供了一种基于双线性内插半球模型的GNSS变形监测方法，有效解决了自动化监测过程中存在的监测结果不稳定、监测曲线异常波动的问题，为自动化监测的不稳定性提供一种解决方案。
本发明的技术方案是这样实现的：本发明公开了一种基于双线性内插半球模型的GNSS变形监测方法，包括如下步骤：
获取观测数据，求解监测点约束坐标；
根据监测点约束坐标获得载波与伪距双差观测值的残差值，并据此建立半球模型；
判断当前卫星位置所对应半球模型中格网内多路径效应改正值是否为空，若否，则获取所建立的半球模型中当前卫星所处格网内的多路径效应改正值；若是，则通过双线性内插法估计出当前卫星所处格网内的多路径效应改正值；
通过基站数据与监测站数据获得双差组合观测值，对双差组合观测值进行最优估计，得到变形监测点坐标，在估计过程的残差项中减去所述多路径效应改正值，对残差中包含的多路径误差进行修正。
进一步地，获取观测数据，求解监测点约束坐标，具体包括：在GNSS基准站和GNSS监测站的静态观测环境下连续采集规定时间段内的特定赫兹的差分改正数据；
根据采集的差分改正数据进行传统静态基线解算，获取监测点长期坐标时间序列，然后进行求均，将求均值作为监测点约束坐标。
进一步地，根据监测点约束坐标获得载波与伪距双差观测值的残差值，具体包括：通过将获取的监测点约束坐标代入GNSS双差组合观测方程中，获得载波与伪距双差观测值的残差值。
进一步地，获得载波与伪距双差观测值的残差值后，对所述残差值进行求均值处理，得到多路径误差值。
进一步地，建立半球模型，具体包括：通过监测点坐标约束方法获取不同卫星的高度角、方位角以及多路径误差值之间的对应关系，并基于高度角与方位角建立多路径误差空间格网模型。
进一步地，根据方位角与高度角建立1°×1°的空间格网模型。
进一步地，通过双线性内插法估计出当前卫星所处格网内的多路径效应改正值，具体包括：
若当前卫星轨迹所在的格网四周仅有一个格网存在多路径效应改正值时，则将该多路径效应改正值作为当前卫星所处格网内的多路径效应改正值使用；
若当前卫星轨迹所在的格网四周有多个格网存在多路径效应改正值时，将多个格网存在的多路径效应改正值的平均值作为当前卫星所处格网内的多路径效应改正值使用。
进一步地，通过基站数据与监测站数据获得双差组合观测值，具体包括：
当GNSS观测数据为载波数据时，双差组合观测值表示为：
Figure 485501DEST_PATH_IMAGE001
，
其中，
Figure 543586DEST_PATH_IMAGE002
表示载波相位在t历元的双差观测值，
Figure 588903DEST_PATH_IMAGE003
表示实际载波 双差距离，
Figure 249691DEST_PATH_IMAGE004
表示双差整周模糊度；
Figure 329643DEST_PATH_IMAGE005
表示载波多路径效应的双差改正 值，
Figure 290121DEST_PATH_IMAGE006
为双差载波噪声。
进一步地，对双差组合观测值进行最优估计，具体表示为：
Figure 822733DEST_PATH_IMAGE007
，
Figure 287213DEST_PATH_IMAGE008
，
Figure 221671DEST_PATH_IMAGE009
，
Figure 355980DEST_PATH_IMAGE010
，
Figure 375889DEST_PATH_IMAGE011
，
其中，
Figure 378480DEST_PATH_IMAGE012
为多路径效应改正值，
Figure 167444DEST_PATH_IMAGE013
在此处指载波或伪距组成的双差观测值，
Figure 597288DEST_PATH_IMAGE014
指将实时待估参数（包括监测点三维坐标、整周模糊度）代入双差观测数学模型 而组成的双差观测值，则
Figure 979859DEST_PATH_IMAGE015
代表双差观测残差值；
Figure 520562DEST_PATH_IMAGE016
表示待估计的状态向 量，
Figure 429612DEST_PATH_IMAGE017
表示协方差矩阵，（-）表示滤波过程中测量更新前的状态，（+）表示卡尔曼滤波过程 中测量更新后的状态，
Figure 30358DEST_PATH_IMAGE018
表示双差测量模型向量，
Figure 900225DEST_PATH_IMAGE019
表示线性偏导数矩阵，
Figure 244619DEST_PATH_IMAGE020
表示测量误差协方差矩阵，
Figure 8175DEST_PATH_IMAGE021
表示系统噪声从k历元到k+1历元的过渡矩阵，
Figure 45401DEST_PATH_IMAGE022
表 示
Figure 996040DEST_PATH_IMAGE021
矩阵转置，
Figure 19491DEST_PATH_IMAGE023
表示系统噪声从k历元到k+1历元的协方差矩阵，I表示单位矩阵，
Figure 637554DEST_PATH_IMAGE024
表示卡尔曼增益系数。
本发明至少具有如下有益效果：本发明申请提出了一种基于双线性内插半球模型的GNSS变形监测方法，根据GNSS原始载波与伪距观测值，构建双差观测方程，并通过坐标约束的方法计算载波与伪距的残差，作为多路径效应误差值与噪声的叠加信号；以卫星方位角与高度角为基准建立不同类型定位卫星的半球格网模型；通过对多个卫星重复轨道周期同一格网内的残差值进行低通滤波处理，降低噪声的影响。本申请在传统半球模型改正多路径效应的基础上，针对卫星星空位置计算误差而引起的空格网改正的情况，提出了格网间双线性内插的技术思路，利用最邻近四个格网改正值对空白格网进行内插，用以修正双差观测值中的多路径。
本发明有效解决了自动化监测过程中存在的监测结果不稳定、监测曲线异常波动的问题，为自动化监测的不稳定性提供一种解决方案。
附图说明
为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其它的附图。
图1为本发明在电力铁塔监测环境下的应用场景图；
图2为本发明的一种实施例的MHM模型建立的流程图；
图3为本发明的一种实施例提供的一种基于双线性内插半球模型的GNSS变形监测方法的流程图；
图4为本发明当前轨迹点存在的格网四周存在1~4个格网存在模型改正值的示意图。
具体实施方式
下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其它实施例，都属于本发明保护的范围。
本发明针对各类静态监测环境提出一种基于双线性内插半球模型的GNSS监测方法。如图1所示为电力铁塔监测环境下的应用场景。所有满足短期内监测点不发生长距离位移，且周围地物反射特性不发生时空剧烈变化的监测环境均适用于本申请。
参见图2和图3，本发明公开了一种基于双线性内插半球模型的GNSS变形监测方法，包括如下步骤：
获取观测数据，求解监测点约束坐标；
根据监测点约束坐标获得载波与伪距双差观测值的残差值，并据此建立半球模型；
判断当前卫星位置所对应半球模型中格网内多路径效应改正值是否为空，若否，则获取所建立的半球模型中当前卫星所处格网内的多路径效应改正值；若是，则通过双线性内插法估计出当前卫星所处格网内的多路径效应改正值；
通过基站数据与监测站数据获得双差组合观测值，对双差组合观测值进行最优估计，得到变形监测点坐标，在估计过程的残差项中减去所述多路径效应改正值，对残差中包含的多路径误差进行修正。
进一步地，获取观测数据，求解监测点约束坐标，具体包括：在GNSS基准站和GNSS监测站的静态观测环境下连续采集规定时间段内的特定赫兹的差分改正数据；
根据采集的差分改正数据进行传统静态基线解算，获取监测点长期坐标时间序列，然后进行求均，将求均值作为监测点约束坐标。
GNSS观测数据积累要求在静态观测环境下连续采集多日（如3至7日）的频率为≤1/30HZ差分改正数据。由于本申请考虑到载波与伪距多路径误差的估算，在估算时需要一致基线矢量的准确值，因此需要首先利用采集的连续观测数据进行GNSS静态基线解算，获得监测点的长期静态坐标时间序列，即监测点坐标真值。之后，通过求均值作为本发明的监测点约束坐标。
进一步地，根据监测点约束坐标获得载波与伪距双差观测值的残差值，具体包括：通过将获取的监测点约束坐标代入GNSS双差组合观测方程中，获得载波与伪距双差观测值的残差值。
进一步地，获得载波与伪距双差观测值的残差值后，对所述残差值进行求均值处理，得到多路径误差值。双差残差中包含多路径误差与噪声两部分，求均值后等于将噪声消除，剩余的部分为多路径误差值。也即是将同一格网内不同频率、不同观测类型的双差残差分别进行求均值处理。
进一步地，建立半球模型，具体包括：通过监测点坐标约束方法获取不同卫星的高度角、方位角以及多路径误差值之间的对应关系，并基于高度角与方位角建立多路径误差空间格网模型。
将获取的监测点约束坐标代入GNSS双差组合观测方程中，即可获得双差载波或伪距对应的多路径误差值。由于在解算过程中采用单历元模糊度固定的策略，因此将固定好的模糊度参数也代入载波双差组合方程中，此时多路径误差值中仅含有额外的数值较小的噪声项，通过求均值处理即可减弱噪声项的影响。
通过监测点约束坐标获取不同卫星的高度角、方位角以及多路径误差值之间的对应关系，并基于高度角与方位角建立多路径误差空间格网模型。实验证明，建立1°×1°的空间格网模型在保持解算效率的基础上对于多路径改正效果最优。
因此，作为优先实施例，本发明根据方位角与高度角建立1°×1°的空间格网模型。如以监测站所在点位为中心，方位角0~360°、高度角0~90°，建立1°×1°的格网模型。每条轨迹都代表一颗卫星单日所经过的路线，而且同一颗卫星每次绕地飞行经过的轨迹是不变的，将每个格网内前七次周期内卫星的双差残差值求均值，就获得单个格网内的多路径改正值，在第八次卫星轨迹周期内，可算得卫星处在哪个格网内，即可将当前卫星双差残差值减去格网内对应的多路径改正值，即为v-mp，进而代入卡尔曼滤波过程中，进行最优估计，即可获得较为准确的监测点三维坐标值。
进一步地，通过双线性内插法估计出当前卫星所处格网内的多路径效应改正值，具体包括：
若当前卫星轨迹所在的格网四周仅有一个格网存在多路径效应改正值时，则将该多路径效应改正值作为当前卫星所处格网内的多路径效应改正值使用；
若当前卫星轨迹所在的格网四周有多个格网存在多路径效应改正值时，将多个格网存在的多路径效应改正值的平均值作为当前卫星所处格网内的多路径效应改正值使用。
针对卫星轨道非重复性问题提出双线性内插方案。由于卫星轨道机动或星历误差而可能导致当前卫星轨迹与MHM模型卫星轨迹不处于同一格网内，因此针对此类问题提出双线性插值的方案进行解决。参见图4，双线性内插方案面向两类可能的情况，第一种，当前轨迹点存在的格网四周仅有一个格网存在模型改正值，采用最邻近格网的方法，即用相邻格网改正值直接作为当前格网改正值使用；第二种，当前轨迹点存在的格网四周存在2~4个格网存在模型改正值，采用双线性内插的方法，即通过相邻格网改正值求平均的方法作为当前格网改正值使用。具体如下进行处理：
Figure 845681DEST_PATH_IMAGE025
，
其中，
Figure 549195DEST_PATH_IMAGE026
表示当前格网根据模型估计出的多路径效应改正值，
Figure 969812DEST_PATH_IMAGE027
表示所建立模型中与当前格网相邻的格网模型多路径改正值。
进一步地，通过基站数据与监测站数据获得双差组合观测值，具体包括：
当GNSS观测数据为载波数据时，双差组合观测值表示为：
Figure 583327DEST_PATH_IMAGE028
，
其中，
Figure 962356DEST_PATH_IMAGE029
表示载波相位在t历元的双差观测值，
Figure 153166DEST_PATH_IMAGE030
表示实际载波 双差距离，
Figure 643053DEST_PATH_IMAGE031
表示双差整周模糊度；
Figure 845495DEST_PATH_IMAGE032
表示载波多路径效应的双差改正 值，
Figure 129846DEST_PATH_IMAGE033
为双差载波噪声。双差整周模糊度由整周模糊度固定算法（LAMBDA算法）求得。
双差载波多路径误差值表示为：
Figure 807952DEST_PATH_IMAGE034
。
进一步地，对双差组合观测值进行最优估计，具体表示为：
Figure 101530DEST_PATH_IMAGE035
，
Figure 548692DEST_PATH_IMAGE036
，
Figure 879310DEST_PATH_IMAGE037
，
Figure 44713DEST_PATH_IMAGE038
，
Figure 610823DEST_PATH_IMAGE039
，
其中，
Figure 178071DEST_PATH_IMAGE040
表示为载波双差残差值减去多路径误差的影 响，
Figure 804224DEST_PATH_IMAGE041
为多路径效应改正值，
Figure 352796DEST_PATH_IMAGE042
在此处指载波或伪距组成的双差观测值，
Figure 988177DEST_PATH_IMAGE043
指 将实时待估参数（包括监测点三维坐标、整周模糊度）代入双差观测数学模型而组成的双差 观测值，则
Figure 144352DEST_PATH_IMAGE044
代表双差观测残差值；
Figure 941407DEST_PATH_IMAGE045
表示待估计的状态向量，
Figure 815822DEST_PATH_IMAGE046
表 示协方差矩阵，（-）表示滤波过程中测量更新前的状态，（+）表示卡尔曼滤波过程中测量更 新后的状态，
Figure 130260DEST_PATH_IMAGE047
表示双差测量模型向量，
Figure 406520DEST_PATH_IMAGE048
表示线性偏导数矩阵，
Figure 640055DEST_PATH_IMAGE049
表示测量 误差协方差矩阵，
Figure 736187DEST_PATH_IMAGE050
表示系统噪声从k历元到k+1历元的过渡矩阵，
Figure 713371DEST_PATH_IMAGE051
表示
Figure 719504DEST_PATH_IMAGE050
矩阵转置，
Figure 123940DEST_PATH_IMAGE052
表示系统噪声从k历元到k+1历元的协方差矩阵，I表示单位矩阵，
Figure 972948DEST_PATH_IMAGE053
表 示卡尔曼增益系数。
卡尔曼滤波过程是一个随时间迭代的过程，即当前时刻的估计依赖于上一个时刻的估计结果，k代表时刻，k+1代表下一个时刻，x代表待估状态向量，包含监测站三维坐标以及整周模糊度，（+）代表卡尔曼估计的最优值，（-）代表卡尔曼估计的一步预测值。如上式所示，在估计过程的残差项中减去多路径模型值用以对残差中包含的多路径误差进行修正，该模型值可通过在半球模型的模型参数中查表获得。
本发明通过GNSS基准站和GNSS监测站获取载波或伪距观测数据，后经粗差剔除、周跳探测等常规数据清洗处理得到双差组合观测值，再用MHM模型参数进行修正，而后进行格网匹配判断，当格网匹配时，直接采用卡尔曼滤波器的方式进行最优估计，如果格网不匹配，需要经过双线性内插方案处理后再采用卡尔曼滤波器进行最优估计。
以上所述仅为本发明的较佳实施例而已，并不用以限制本发明，凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。

Claims (3)

1.一种基于双线性内插半球模型的GNSS变形监测方法，其特征在于：包括如下步骤：
获取观测数据，求解监测点约束坐标，具体包括：在GNSS基准站和GNSS监测站的静态观测环境下连续采集规定时间段内的特定赫兹的差分改正数据；
根据采集的差分改正数据进行GNSS静态基线解算，获取监测点长期坐标时间序列，然后进行求均，将求均值作为监测点约束坐标；
根据监测点约束坐标获得载波与伪距双差观测值的残差值，并据此建立半球模型，具体包括：
通过将获取的监测点约束坐标代入GNSS双差组合观测方程中，获得载波与伪距双差观测值的残差值；
获得载波与伪距双差观测值的残差值后，对所述残差值进行求均值处理，得到多路径误差值；
建立半球模型通过监测点坐标约束方法获取不同卫星的高度角、方位角以及多路径误差值之间的对应关系，并基于高度角与方位角建立多路径误差空间格网模型；
判断当前卫星位置所对应半球模型中格网内多路径效应改正值是否为空，若否，则获取所建立的半球模型中当前卫星所处格网内的多路径效应改正值；若是，则通过双线性内插法估计出当前卫星所处格网内的多路径效应改正值，具体包括：
若当前卫星轨迹所在的格网四周仅有一个格网存在多路径效应改正值时，则将该多路径效应改正值作为当前卫星所处格网内的多路径效应改正值使用；
若当前卫星轨迹所在的格网四周有多个格网存在多路径效应改正值时，将多个格网存在的多路径效应改正值的平均值作为当前卫星所处格网内的多路径效应改正值使用；
通过基站数据与监测站数据获得双差组合观测值，对双差组合观测值进行最优估计，得到变形监测点坐标，在估计过程的残差项中减去所述多路径效应改正值，对残差中包含的多路径误差进行修正，具体表示为：
Figure DEST_PATH_IMAGE002
，
Figure DEST_PATH_IMAGE004
，
Figure DEST_PATH_IMAGE006
，
Figure DEST_PATH_IMAGE008
，
Figure DEST_PATH_IMAGE010
，
其中，
Figure DEST_PATH_IMAGE012
为多路径效应改正值，
Figure DEST_PATH_IMAGE014
在此处指载波或伪距组成的双差观测值，
Figure DEST_PATH_IMAGE016
指将实时待估参数代入双差观测数学模型而组成的双差观测值，则
Figure DEST_PATH_IMAGE018
代表双差观测残差值；
Figure DEST_PATH_IMAGE020
表示待估计的状态向量，
Figure DEST_PATH_IMAGE022
表示协方差矩阵，（-）表示滤波过程中测量更新前的状态，（+）表示卡尔曼滤波过程中测量更新后的状态，
Figure DEST_PATH_IMAGE024
表示双差测量模型向量，
Figure DEST_PATH_IMAGE026
表示线性偏导数矩阵，
Figure DEST_PATH_IMAGE028
表示测量误差协方差矩阵，
Figure DEST_PATH_IMAGE030
表示系统噪声从k历元到k+1历元的过渡矩阵，
Figure DEST_PATH_IMAGE032
表示
Figure DEST_PATH_IMAGE030A
矩阵转置，
Figure DEST_PATH_IMAGE034
表示系统噪声从k历元到k+1历元的协方差矩阵，I表示单位矩阵，
Figure DEST_PATH_IMAGE036
表示卡尔曼增益系数。
2.根据权利要求1所述的基于双线性内插半球模型的GNSS变形监测方法，其特征在于：根据方位角与高度角建立1°×1°的空间格网模型。
3.根据权利要求1所述的基于双线性内插半球模型的GNSS变形监测方法，其特征在于：通过基站数据与监测站数据获得双差组合观测值，具体包括：
当GNSS观测数据为载波数据时，双差组合观测值表示为：
Figure DEST_PATH_IMAGE038
，
其中，
Figure DEST_PATH_IMAGE040
表示载波相位在t历元的双差观测值，
Figure DEST_PATH_IMAGE042
表示实际载波双差距离，
Figure DEST_PATH_IMAGE044
表示双差整周模糊度；
Figure DEST_PATH_IMAGE046
表示载波多路径效应的双差改正值，
Figure DEST_PATH_IMAGE048
为双差载波噪声。
CN202211253819.XA 2022-10-13 2022-10-13 一种基于双线性内插半球模型的gnss变形监测方法 Active CN115343734B (zh)

Priority Applications (1)

Application Number Priority Date Filing Date Title
CN202211253819.XA CN115343734B (zh) 2022-10-13 2022-10-13 一种基于双线性内插半球模型的gnss变形监测方法

Applications Claiming Priority (1)

Application Number Priority Date Filing Date Title
CN202211253819.XA CN115343734B (zh) 2022-10-13 2022-10-13 一种基于双线性内插半球模型的gnss变形监测方法

Publications (2)

Publication Number Publication Date
CN115343734A CN115343734A (zh) 2022-11-15
CN115343734B true CN115343734B (zh) 2023-01-17

Family

ID=83957406

Family Applications (1)

Application Number Title Priority Date Filing Date
CN202211253819.XA Active CN115343734B (zh) 2022-10-13 2022-10-13 一种基于双线性内插半球模型的gnss变形监测方法

Country Status (1)

Country Link
CN (1) CN115343734B (zh)

Families Citing this family (2)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
CN116858085B (zh) * 2023-06-14 2024-04-02 广东省水利水电科学研究院 一种坝体表面变形监测系统及方法
CN117991303B (zh) * 2024-04-03 2024-06-14 武汉大学 一种天线环境变化情况下的多路径误差修正方法及装置

Citations (1)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
WO2021094753A1 (en) * 2019-11-11 2021-05-20 University Of Newcastle Upon Tyne Configuration of global satellite navigation system infrastructure

Family Cites Families (9)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
CN108195283B (zh) * 2017-12-04 2019-12-10 千寻位置网络有限公司 基于无缝变换的gnss实时变形监测方法及系统
CN108519614A (zh) * 2018-03-16 2018-09-11 东南大学 一种gps/bds紧组合载波差分定位方法
CN109541647B (zh) * 2018-12-13 2019-12-10 武汉大学 基于半天球格网点模型的gnss多路径效应修正方法
CN109738917B (zh) * 2018-12-30 2022-04-22 广州海达安控智能科技有限公司 一种北斗变形监测中的多路径误差削弱方法及装置
CN112433240B (zh) * 2020-10-13 2022-08-30 武汉理工大学 一种基于非差非组合ppp模型的相位多路径提取改正方法
CN114488227B (zh) * 2022-01-26 2023-10-20 西南交通大学 一种基于空间相关性的多路径误差改正方法
CN114488228B (zh) * 2022-04-11 2022-07-01 南京北斗创新应用科技研究院有限公司 一种适用于动态载体平台的gnss多路径误差削弱方法
CN114879222A (zh) * 2022-04-26 2022-08-09 同济大学 一种基于自适应随机模型的全球电离层建模方法
CN114757238B (zh) * 2022-06-15 2022-09-20 武汉地铁集团有限公司 地铁保护区变形监测的方法、系统、电子设备和存储介质

Patent Citations (1)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
WO2021094753A1 (en) * 2019-11-11 2021-05-20 University Of Newcastle Upon Tyne Configuration of global satellite navigation system infrastructure

Non-Patent Citations (1)

* Cited by examiner, † Cited by third party
Title
Correcting Position Error in Precipitation Data Using Image Morphing;Camille Le Coz et al.;《Remote Sensing》;20191231;第1-27页 *

Also Published As

Publication number Publication date
CN115343734A (zh) 2022-11-15

Similar Documents

Publication Publication Date Title
CN115343734B (zh) 一种基于双线性内插半球模型的gnss变形监测方法
CN109709591B (zh) 一种面向智能终端的gnss高精度定位方法
CN106842268B (zh) 双gnss接收机载波相位双差整周模糊度浮点解向量估计方法
Zangeneh-Nejad et al. Cycle slip detection and repair of undifferenced single-frequency GPS carrier phase observations
CA2681918A1 (en) Distance dependant error mitigation in real-time kinematic (rtk) positioning
CN111239787A (zh) 一种集群自主协同中的gnss动态卡尔曼滤波方法
CN111596321B (zh) 利用非差改正数的多gnss多路径误差恒星日滤波方法及系统
CN105116423B (zh) Araim地面监测站完好性监测方法和装置
CN112433240B (zh) 一种基于非差非组合ppp模型的相位多路径提取改正方法
CN110412638A (zh) 一种低成本三天线gnss rtk定位及测姿方法
CN108387912B (zh) 一种Multi-GNSS精密单点定位的解算方法
CN108919316B (zh) 一种基于局部球对称假设的单站多系统硬件延迟估计方法
CN109541647B (zh) 基于半天球格网点模型的gnss多路径效应修正方法
WO2023197714A1 (zh) 一种适用于动态载体平台的gnss多路径误差削弱方法
CN107544075A (zh) 基于精密单点定位与调和分析估计海潮负荷位移参数方法
CN110146904B (zh) 一种适用于区域电离层tec的精确建模方法
CN116755126B (zh) 一种基于三维模型映射匹配的北斗实时精准定位方法
CN116009042A (zh) 一种单站载波历元间差分实时探测相对形变的方法及系统
CN104991265B (zh) 一种北斗卫星导航系统用户统一性定位方法
Bahadur et al. Real-time single-frequency multi-GNSS positioning with ultra-rapid products
CN115980317B (zh) 基于修正相位的地基gnss-r数据土壤水分估算方法
Zou et al. Multipath error mitigation method considering NLOS signal for high-precision GNSS data processing
Bahadur Real-time single-frequency precise positioning with Galileo satellites
CN110764122A (zh) 一种单频gps接收机的精密单点定位方法
Li et al. Study on Precise Point Positioning based on combined GPS and GLONASS

Legal Events

Date Code Title Description
PB01 Publication
PB01 Publication
SE01 Entry into force of request for substantive examination
SE01 Entry into force of request for substantive examination
GR01 Patent grant
GR01 Patent grant