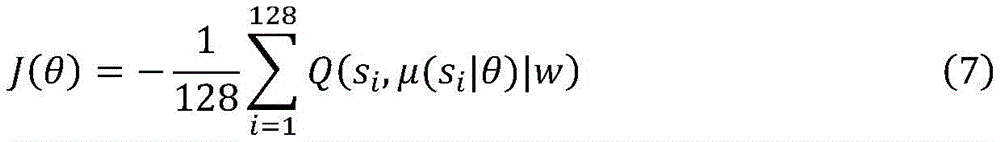CN113093526B - 一种基于强化学习的无超调pid控制器参数整定方法 - Google Patents
一种基于强化学习的无超调pid控制器参数整定方法 Download PDFInfo
- Publication number
- CN113093526B CN113093526B CN202110359952.2A CN202110359952A CN113093526B CN 113093526 B CN113093526 B CN 113093526B CN 202110359952 A CN202110359952 A CN 202110359952A CN 113093526 B CN113093526 B CN 113093526B
- Authority
- CN
- China
- Prior art keywords
- network
- action
- state
- value
- target
- Prior art date
- Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
- Active
Links
- 238000000034 method Methods 0.000 title claims abstract description 22
- 230000002787 reinforcement Effects 0.000 title claims abstract description 15
- 230000009471 action Effects 0.000 claims abstract description 85
- 238000011156 evaluation Methods 0.000 claims abstract description 38
- 230000007704 transition Effects 0.000 claims abstract description 26
- 238000013528 artificial neural network Methods 0.000 claims abstract description 21
- 238000012549 training Methods 0.000 claims abstract description 19
- 238000012546 transfer Methods 0.000 claims abstract description 9
- 239000000284 extract Substances 0.000 claims abstract description 4
- 230000006870 function Effects 0.000 claims description 54
- 239000003795 chemical substances by application Substances 0.000 claims description 20
- 230000004913 activation Effects 0.000 claims description 9
- 238000005457 optimization Methods 0.000 claims description 6
- 230000008569 process Effects 0.000 claims description 6
- 230000001419 dependent effect Effects 0.000 claims description 3
- 238000005728 strengthening Methods 0.000 claims description 3
- 239000013598 vector Substances 0.000 claims description 3
- 230000000977 initiatory effect Effects 0.000 claims description 2
- 238000012360 testing method Methods 0.000 claims 1
- 238000013461 design Methods 0.000 description 5
- 230000008859 change Effects 0.000 description 4
- 230000000694 effects Effects 0.000 description 4
- 241000282414 Homo sapiens Species 0.000 description 2
- 238000011217 control strategy Methods 0.000 description 2
- 238000011161 development Methods 0.000 description 2
- 230000002068 genetic effect Effects 0.000 description 2
- 238000004519 manufacturing process Methods 0.000 description 2
- 238000013473 artificial intelligence Methods 0.000 description 1
- 230000006399 behavior Effects 0.000 description 1
- 230000001149 cognitive effect Effects 0.000 description 1
- 238000013135 deep learning Methods 0.000 description 1
- 230000007547 defect Effects 0.000 description 1
- 238000010586 diagram Methods 0.000 description 1
- 230000004069 differentiation Effects 0.000 description 1
- 238000005516 engineering process Methods 0.000 description 1
- 230000010354 integration Effects 0.000 description 1
- 230000003993 interaction Effects 0.000 description 1
- 238000013178 mathematical model Methods 0.000 description 1
- 238000012544 monitoring process Methods 0.000 description 1
- 230000001537 neural effect Effects 0.000 description 1
- 210000002569 neuron Anatomy 0.000 description 1
- 230000010355 oscillation Effects 0.000 description 1
- 230000008447 perception Effects 0.000 description 1
- 230000002028 premature Effects 0.000 description 1
Images
Classifications
-
- G—PHYSICS
- G05—CONTROLLING; REGULATING
- G05B—CONTROL OR REGULATING SYSTEMS IN GENERAL; FUNCTIONAL ELEMENTS OF SUCH SYSTEMS; MONITORING OR TESTING ARRANGEMENTS FOR SUCH SYSTEMS OR ELEMENTS
- G05B11/00—Automatic controllers
- G05B11/01—Automatic controllers electric
- G05B11/36—Automatic controllers electric with provision for obtaining particular characteristics, e.g. proportional, integral, differential
- G05B11/42—Automatic controllers electric with provision for obtaining particular characteristics, e.g. proportional, integral, differential for obtaining a characteristic which is both proportional and time-dependent, e.g. P. I., P. I. D.
Landscapes
- Physics & Mathematics (AREA)
- General Physics & Mathematics (AREA)
- Engineering & Computer Science (AREA)
- Automation & Control Theory (AREA)
- Feedback Control In General (AREA)
Abstract
本申请涉及一种基于强化学习的无超调PID控制器参数整定方法。本申请通过构造学习智能体,观测当前状态数据输入到动作神经网络得到动作参数,之后再观测下一状态的数据以及奖励。当前状态,动作,转移后状态,奖励值,四个元素组成了状态转移元组,每一次被控对象执行动作时都会进行一次状态转移,并将状态转移元组存入经验池内。智能体抽取一定量的状态转移元组,用于训练动作网络和评价网络。重复训练动作网络和评价网络直到参数收敛,保存参数权重。最终智能体根据当前状态数据输出最优PID参数提供给PID控制器,使得被控对象的状态值在无超调的基础上以较快的速度达到设定值,进而实现对控制器PID参数无超调整定的方面改进。
Description
技术领域
本发明设计了一种基于强化学习的PID控制器调参方法。针对无超调的工程,通过对当前状态的判断,利用神经网络能够输出一组控制性能较好的PID参数,降低由超调引起安全事故的概率。
技术背景
随着工业的快速发展,机器人逐渐替代了人类,在分拣、装配以及生产等其他工作中成为了不可缺少的一个环节。如何让机器人能够快速而精准完成预先设定的目标成为了当前工业机器人领域所需要解决问题之一。比例积分微分控制(PID控制)作为最早发展起来的控制策略之一,由于其算法简单、鲁棒性好和适应性较强,被广泛应用于工业过程控制。但是,由于PID控制的性能高度依赖于PID控制的三个参数kp,ki,kd,而这些参数一般是通过经验调参法或者是试错调整法,高度依赖工程师的经验,所以存在效率低和控制效果不佳等问题。如果这些参数挑选不当,控制器输出的状态不可预测,在控制过程中可能发生震荡、过量超调等现象,严重影响控制的效果。
PID控制技术正处于不断发展与变化中,基于传统PID参数调整方法,模糊PID控制、神经网络PID控制、遗传算法PID控制等控制思想相继被提出。模糊PID控制将离线的模糊规则与PID相结合,提高了控制精度,但无法针对整个控制过程,且其性能过于依赖模糊规则的设定。神经网络PID控制通过迭代训练反向优化权值和阈值,对PID参数进行动态微调达到精确控制的目的,但需要大量的训练数据进行在线训练。遗传算法PID控制通过模拟自然进化过程搜索最优解,能够实现较好的动态性能和稳态性能,但是编码方式的选取依靠工程师的经验,且该算法存在过早收敛和低效率的问题。
在专利发明方面,中国专利文献CN102621883A和CN108227479A是本发明最接近的现有技术。专利CN102621883A介绍了一种基于数学模型误差判断的PID参数整定方法,而专利CN108227479A通过整体增益、比例增益、积分增益、微分增益的综合调节进行PID参数整定。但是这两种方法侧重于经验公式或在线学习的方法,在实际应用中专利CN102621883A需要监控人员根据误差判断进行调整,不能达到自动整定的效果,而专利CN108227479A中整体增益单元依赖于经验公式,过于繁琐。
近年来,在人工智能博弈取得了巨大成功的深度强化学习被引入以解决各类控制问题。深度强化学习通过一种通用的形式将深度学习的感知能力与强化学习的决策能力相结合,并能够通过端对端的学习方式实现从原始输入到输出的直接控制。该方法通常构造代理智能体,与环境的反复实验试错和交互,学习最佳行为而无需人参与其中。AndrewHynes等研究人员在2020年Irish Conference on Artificial Intelligence andCognitive Science期刊上发表了Optimising PID Control with Residual PolicyReinforcement,研究带残差策略的PID控制优化,通过强化学习实现PID参数的优化,得到了良好的PID参数自整定效果,但是此工作没有考虑到如何对超调量进行控制。在某些情况下,例如在机械臂控制或电机控制中,超调量过大可能造成机器本身的损坏甚至引起安全事故。在实际情况中,需要兼顾系统调节时间快慢以及超调量的大小获得最佳的控制策略。
发明内容
针对PID控制器的参数设定问题,本发明要克服传统PID参数设定中参数整定困难,性能依赖于工程师设计经验的缺点。本发明提供了一种基于强化学习的无超调PID控制器参数整定方法,旨在帮助实际应用场景中,PID控制器的参数整定更简便有效。控制方案如下所述:
步骤1,建立深度强化模型;
构建深度强化学习智能体,初始化动作网络和评价网络,分别用于选取PID控制器的参数以及评价当前状态下的动作选取。由于动作网络和评价网络的参数更新相互依赖,会造成不易收敛的结果。因此为每个神经网络都设置一个目标网络,对应的目标网络和当前的网络结构相同。动作网络和评价网络的结构相似,均由若干层全连接层组成,隐藏层的激活函数均为Relu函数。两个网络区别在于动作网络的最后一层的激活函数为Sigmoid函数,而评价网络的最后一层没有激活函数。初始化经验池D,用于存放状态转移元组。
步骤2,构建并存储状态转移元组;
智能体通过观测,或传感器得到当前状态的数据,与设定的目标值进行比较得到误差值δ,把其作为当前状态st输入到动作网络中。动作网络会根据当前状态st计算得到初始动作at′:
at′=μ(st|θ) (1)
其中μ为动作网络函数,at′为动作网络的输出结果,θ为动作网络的参数。
其中at为动作网络输出的最终动作。由于动作网络的输出维度是3,所以at为一组三维的向量,即PID控制器的最终参数kp,ki,kd,并用下述公式计算控制量:
其中u(t)为PID控制器输出的控制量。被控对象执行控制量所对应的动作,当前状态发生转移,得到改变后的状态st+1并计算奖励值rt。
具体奖励公式设计如下:
其中e表示自然常数。为了能够在避免超调的情况下尽量地兼顾调节时间,将奖励值设置为三个区间:当误差小于所允许的范围ε时的奖励值最大;当误差大于所允许的范围ε但没有发生超调时的奖励值次之;而误差大于所允许的范围ε且发生了超调时的奖励值最小。
当前状态st,动作at,转移后状态st+1,奖励值rt,四个元素组成了状态转移元组T。每一次被控对象执行动作时都会进行一次状态转移,并将状态转移元组T存入经验池D内。当经验池D的容量达到上限后,每存入一个新的状态转移元组,便会剔除一个原有的状态转移元组。
步骤3,抽取状态转移元组来训练神经网络;
智能体抽取一定量的状态转移元组,用于训练动作网络和评价网络。根据状态转移元组中的转移后状态st+1以及动作at,可以得到下一状态预测Q值,即目标值函数yi:
yi=ri+γQ′(si+1,μ′(si+1|θ)|w) (5)
其中Q′为目标评价网络函数,其结构与评价网络Q结构一致;μ′为目标动作网络函数,其结构与动作网络结构一致;w为评价网络的参数。目标网络函数的意义在于固定目标值函数,加快收敛速度。
对目标值函数yi和当前评价网络使用均方差损失函数进行更新:
式(6)中N表示训练所抽取的样本数量,Q(si,ai)表示评价网络的输出值,通过神经网络的反向传播来更新当前评价网络的所有参数。由于动作网络输出的是动作st,没有参数更新的梯度方向,所以根据评价网络的Q值提供梯度信息进行训练,损失函数如下:
同样采用通过神经网络的反向传播来更新当前动作网络的所有参数。
步骤4,更新目标网络的参数;
在步骤3中,下一状态预测Q值是通过目标神经网络获得。而目标网络需要进行更新,以确保目标值函数yi的正确性。通过下述公式,来对目标网络进行更新:
τ是更新系数,w是当前评价网络的参数,w′是目标评价网络的参数,θ是当前动作网络的参数,θ′是目标动作网络的参数。通过网络参数的缓慢滑动减少目标值的波动,增强了训练过程的稳定性。
步骤5,智能体通过动作网络生成PID控制器参数;
不断重复步骤2至步骤4,神经网络参数不断迭代直至收敛。将网络权重文件进行保存。智能体通过动作网络函数可以根据不同的误差值状态,输出相应的一组PID控制器的参数,最终使得被控对象的状态值在无超调的基础上以较快的速度达到设定值。由于智能体针对不同的控制任务,根据奖励值rt优化策略,即动作网络的参数,从而得到最大的奖励值。因此本发明面对不同的控制环境,均可适用,具有较好的泛化能力。
本发明与现有技术相比具有以下特点:
本发明提出了一种基于强化学习的无超调PID控制方法,其能够在无超调的基础上,以较快的速度将误差减小至零。并且是智能体自主探索动作空间,所以不需要训练集,也不依赖于工程师的设计经验,设计简便,实用性强。同时奖励值的设计使得被控对象不会产生超调现象,本发明可以广泛运用于各种对超调量敏感的控制任务中,避免安全事故的发生。
附图说明
图1为本发明的训练流程图。
图2为本发明实例中的动作网络结构。
图3为本发明实例中的评价网络结构。
图4为本发明实例中的仿真机械臂角度变化与固定PID参数角度变化的比较图(3号关节)。
图5为本发明实例中的仿真机械臂的PID控制器参数变化图(3号关节)。
具体实施方式
本发明提出了一种基于强化学习的无超调PID控制方法,下面结合附图和具体实施例中的附图对本发明进一步详细说明如下:
在本实施实例中采用了Universal Robots UR5机械臂。机械臂的任务设定为在一个长宽均为0.5m的正方形区间内,使得机械臂末端移动至正方形区间内5×5共计25个的格点。根据机器人逆运动学计算机械臂的各个关节所需的关节角,对各个关节进行控制。
步骤1,建立深度强化模型;
构建深度强化学习智能体,初始化动作网络和评价网络,具体网络构造如图2和图3所示,分别用于选取PID控制器的参数以及评价当前状态下的动作选取。由于动作网络和评价网络的参数更新相互依赖,会造成不容易收敛的结果。因此为每个神经网络都设置一个目标网络,目标网络分别和当前的动作网络与评价网络结构相同。动作网络和评价网络的结构相似,均由三层全连接层组成,隐藏层的神经元个数均为350,隐藏层的激活函数均为Relu函数,区别在于动作网络的最后一层的激活函数为Sigmoid函数,而评价网络的最后一层没有激活函数。同时初始化经验池D,容量为2000,用于存放状态转移元组。
步骤2,构建并存储状态转移元组;
智能体通过传感器得到当前各个关节实际角度的数据,与设定的目标角度进行比较得到误差值δ,把其作为当前状态st输入到动作网络中。而动作网络会根据当前状态st计算得到动作at′:
at′=μ(st|θ) (1)
其中μ为动作网络函数,at′为动作网络的输出结果。
由于动作网络的输出维度是3,所以μ′(st)为一组三维的向量,即PID控制器的最终参数kp,ki,kd,并用下述公式计算控制量:
其中u(t)为PID控制器输出的关节角转动的速度值。关节电机执行PID控制器输出的速度值,当前角度值发生变化,得到改变后的角度值st+1并计算奖励值rt。
具体奖励公式设计如下:
其中e表示自然常数。为了能够在避免超调的情况下能够尽量地兼顾调节时间。将奖励值设置为三个区间:当误差小于所允许的范围ε时的奖励值最大;当误差大于所允许的范围ε但没有发生超调时的奖励值次之;而误差大于所允许的范围ε且发生了超调时的奖励值最小。
当前角度st,动作at,变化后角度st+1,奖励值rt,四个元素组成了状态转移元组T。每一次被控对象执行动作时都会进行一次状态转移,并将状态转移元组T存入经验池D内。当经验池D的容量达到上限后,每存入一个新的状态转移元组,便会剔除一个原有的状态转移元组。
步骤3,抽取状态转移元组来训练神经网络;
智能体抽取128个状态转移元组,用于训练动作网络和评价网络。根据状态转移元组中的转移后角度st+1以及动作at,可以得到下一状态预测Q值,计算目标值函数yi:
yi=ri+γQ′(si+1,μ′(si+1|θ)|w) (5)
其中Q′为目标评价网络函数,其结构与评价网络Q结构一致;μ′为目标动作网络函数,其结构与动作网络结构一致。目标网络函数的意义在于固定目标值函数,加快收敛速度。
对目标值函数yi和当前评价网络使用均方差损失函数进行更新:
式(6)中训练所抽取的样本数量为128,Q(si,ai)表示评价网络的输出值,通过神经网络的反向传播来更新当前评价网络的所有参数。由于动作网络输出的是动作st,没有参数更新的梯度方向,所以根据评价网络的Q值提供梯度信息进行训练,优化函数如下:
同样采用通过神经网络的反向传播来更新当前动作网络的所有参数。
步骤4,更新目标网络的参数;
在步骤3中,下一状态预测Q值是通过目标神经网络获得。而目标网络需要进行更新,以确保目标值函数yi的正确性。通过下述公式,来对目标网络进行更新:
τ是更新系数为0.01,w是当前评价网络的参数,w′是目标评价网络的参数,θ是当前动作网络的参数,θ′是目标动作网络的参数。通过网络参数的缓慢滑动减少目标值的波动,增强了训练过程的稳定性。
步骤5,智能体通过动作网络生成PID控制器参数;
不断重复步骤2至步骤4,神经网络参数不断迭代直至收敛。将网络权重文件进行保存。智能体通过动作网络函数可以根据不同的误差值状态,输出相应的一组PID控制器的参数,最终使得被控对象的状态值在无超调的基础上以较快的速度达到设定值。由于智能体针对不同的控制任务,根据奖励值rt优化策略,即动作网络的参数,从而得到最大的奖励值。因此本发明面对不同的控制环境,均可适用,具有较好的泛化能力。
Claims (1)
1.基于强化学习的无超调PID控制器参数整定方法,具体步骤如下:
步骤1,建立深度强化模型;
构建深度强化学习智能体,初始化动作网络和评价网络,分别用于选取PID控制器的参数以及评价当前状态下的动作选取;由于动作网络和评价网络的参数更新相互依赖,会造成不易收敛的结果;因此为每个神经网络都设置一个目标网络,对应的目标网络和当前的网络结构相同;动作网络和评价网络的结构相似,均由若干层全连接层组成,隐藏层的激活函数均为Relu函数;两个网络区别在于动作网络的最后一层的激活函数为Sigmoid函数,而评价网络的最后一层没有激活函数;初始化经验池D,用于存放每一次的状态转移元组;
步骤2,构建并存储状态转移元组;
智能体通过观测,或传感器得到当前状态的数据,与设定的目标值进行比较得到误差值δ,把其作为当前状态st输入到动作网络中;动作网络会根据当前状态st计算得到初始动作at′:
a′t=μ(st|θ) (1)
其中μ为动作网络函数,at为动作网络的输出结果;
其中at为动作网络输出的最终动作;由于动作网络的输出维度是3,所以at为一组三维的向量,即PID控制器的最终参数kp,ki,kd,并用下述公式计算控制量:
其中u(t)为PID控制器输出的控制量;被控对象执行控制量所对应的动作,当前状态发生转移,得到改变后的状态st+1并计算奖励值rt;
具体奖励公式设计如下:
其中e表示自然常数;为了能够在避免超调的情况下能够尽量地兼顾调节时间;将奖励值设置为三个区间:当误差小于所允许的范围ε时的奖励值最大;当误差大于所允许的范围ε但没有发生超调时的奖励值次之;而误差大于所允许的范围ε且发生了超调时的奖励值最小;
当前状态st,动作at,转移后状态st+1,奖励值rt,四个元素组成了状态转移元组T;每一次被控对象执行动作时都会进行一次状态转移,并将状态转移元组T存入经验池D内;当经验池D的容量达到上限后,每存入一个新的状态转移元组,便会剔除一个原有的状态转移元组;
步骤3,抽取状态转移元组来训练神经网络;
智能体抽取一定量的状态转移元组,用于训练动作网络和评价网络;根据状态转移元组中的转移后状态st+1以及动作at,得到下一状态预测Q值,计算目标值函数yi:
yi=ri+γQ′(si+1,μ′(si+1|θ)|w) (5)
其中Q′为目标评价网络函数,其结构与评价网络Q结构一致;μ′为目标动作网络函数,其结构与动作网络结构一致;目标网络函数的意义在于固定目标值函数,加快收敛速度;
对目标值函数yi和当前评价网络使用均方差损失函数进行更新:
式(6)中N表示训练所抽取的样本数量,Q(si,ai)表示评价网络的输出值,通过神经网络的反向传播来更新当前评价网络的所有参数;由于动作网络输出的是动作st,没有参数更新的梯度方向,所以根据评价网络的Q值提供梯度信息进行训练,优化函数如下:
同样采用通过神经网络的反向传播来更新当前动作网络的所有参数;
步骤4,更新目标网络的参数;
在步骤3中,下一状态预测Q值是通过目标神经网络获得;而目标网络需要进行更新,以确保目标值函数yi的正确性;通过下述公式,来对目标网络进行更新:
τ是更新系数,w是当前评价网络的参数,w′是目标评价网络的参数,θ是当前动作网络的参数,θ′是目标动作网络的参数;通过网络参数的缓慢滑动减少目标值的波动,增强了训练过程的稳定性;
步骤5,智能体通过动作网络生成PID控制器参数;
不断重复步骤2至步骤4,神经网络参数不断迭代直至收敛;将网络权重文件进行保存;智能体通过动作网络函数根据不同的误差值状态,输出相应的一组PID控制器的参数,最终使得被控对象的状态值在无超调的基础上以较快的速度达到设定值。
Priority Applications (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| CN202110359952.2A CN113093526B (zh) | 2021-04-02 | 2021-04-02 | 一种基于强化学习的无超调pid控制器参数整定方法 |
Applications Claiming Priority (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| CN202110359952.2A CN113093526B (zh) | 2021-04-02 | 2021-04-02 | 一种基于强化学习的无超调pid控制器参数整定方法 |
Publications (2)
| Publication Number | Publication Date |
|---|---|
| CN113093526A CN113093526A (zh) | 2021-07-09 |
| CN113093526B true CN113093526B (zh) | 2022-05-24 |
Family
ID=76673104
Family Applications (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| CN202110359952.2A Active CN113093526B (zh) | 2021-04-02 | 2021-04-02 | 一种基于强化学习的无超调pid控制器参数整定方法 |
Country Status (1)
| Country | Link |
|---|---|
| CN (1) | CN113093526B (zh) |
Families Citing this family (3)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN114114896B (zh) * | 2021-11-08 | 2024-01-05 | 北京机电工程研究所 | 一种基于路径积分的pid参数设计方法 |
| CN114188955B (zh) * | 2021-12-01 | 2023-08-01 | 天津大学 | 基于自适应学习的互联微电网复合频率控制方法及装置 |
| CN114527642B (zh) * | 2022-03-03 | 2024-04-02 | 东北大学 | 一种基于深度强化学习的agv自动调整pid参数的方法 |
Citations (11)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN108363293A (zh) * | 2018-02-13 | 2018-08-03 | 台州学院 | 一种基于pid控制的交叉耦合控制算法和系统 |
| CN108629084A (zh) * | 2018-04-08 | 2018-10-09 | 陈光瑞 | 一种cmac和pid复合的智能车辆轨迹跟踪控制方法 |
| CN109739090A (zh) * | 2019-01-15 | 2019-05-10 | 哈尔滨工程大学 | 一种自主式水下机器人神经网络强化学习控制方法 |
| CN109919969A (zh) * | 2019-01-22 | 2019-06-21 | 广东工业大学 | 一种利用深度卷积神经网络实现视觉运动控制的方法 |
| CN110083057A (zh) * | 2019-06-12 | 2019-08-02 | 哈尔滨工程大学 | 基于水翼运动姿态的pid控制方法 |
| CN110502033A (zh) * | 2019-09-04 | 2019-11-26 | 中国人民解放军国防科技大学 | 一种基于强化学习的固定翼无人机群集控制方法 |
| CN111413981A (zh) * | 2020-04-07 | 2020-07-14 | 上海海事大学 | 一种船舶自动舵复合神经网络pid控制方法 |
| CN111458646A (zh) * | 2020-05-25 | 2020-07-28 | 安徽理工大学 | 一种基于pso-rbf神经网络的锂电池soc估算方法 |
| CN111812968A (zh) * | 2020-06-24 | 2020-10-23 | 合肥工业大学 | 基于模糊神经网络pid控制器的阀位串级控制方法 |
| CN111835261A (zh) * | 2020-07-22 | 2020-10-27 | 曲阜师范大学 | 基于自适应神经网络的磁悬浮垂直轴风电机组悬浮控制方法 |
| CN112488082A (zh) * | 2020-12-24 | 2021-03-12 | 刘强 | 基于深度学习的煤矸石智能分拣系统 |
-
2021
- 2021-04-02 CN CN202110359952.2A patent/CN113093526B/zh active Active
Patent Citations (11)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN108363293A (zh) * | 2018-02-13 | 2018-08-03 | 台州学院 | 一种基于pid控制的交叉耦合控制算法和系统 |
| CN108629084A (zh) * | 2018-04-08 | 2018-10-09 | 陈光瑞 | 一种cmac和pid复合的智能车辆轨迹跟踪控制方法 |
| CN109739090A (zh) * | 2019-01-15 | 2019-05-10 | 哈尔滨工程大学 | 一种自主式水下机器人神经网络强化学习控制方法 |
| CN109919969A (zh) * | 2019-01-22 | 2019-06-21 | 广东工业大学 | 一种利用深度卷积神经网络实现视觉运动控制的方法 |
| CN110083057A (zh) * | 2019-06-12 | 2019-08-02 | 哈尔滨工程大学 | 基于水翼运动姿态的pid控制方法 |
| CN110502033A (zh) * | 2019-09-04 | 2019-11-26 | 中国人民解放军国防科技大学 | 一种基于强化学习的固定翼无人机群集控制方法 |
| CN111413981A (zh) * | 2020-04-07 | 2020-07-14 | 上海海事大学 | 一种船舶自动舵复合神经网络pid控制方法 |
| CN111458646A (zh) * | 2020-05-25 | 2020-07-28 | 安徽理工大学 | 一种基于pso-rbf神经网络的锂电池soc估算方法 |
| CN111812968A (zh) * | 2020-06-24 | 2020-10-23 | 合肥工业大学 | 基于模糊神经网络pid控制器的阀位串级控制方法 |
| CN111835261A (zh) * | 2020-07-22 | 2020-10-27 | 曲阜师范大学 | 基于自适应神经网络的磁悬浮垂直轴风电机组悬浮控制方法 |
| CN112488082A (zh) * | 2020-12-24 | 2021-03-12 | 刘强 | 基于深度学习的煤矸石智能分拣系统 |
Also Published As
| Publication number | Publication date |
|---|---|
| CN113093526A (zh) | 2021-07-09 |
Similar Documents
| Publication | Publication Date | Title |
|---|---|---|
| CN113093526B (zh) | 一种基于强化学习的无超调pid控制器参数整定方法 | |
| CN109901403B (zh) | 一种自主水下机器人神经网络s面控制方法 | |
| CN108161934B (zh) | 一种利用深度强化学习实现机器人多轴孔装配的方法 | |
| CN110238839B (zh) | 一种利用环境预测优化非模型机器人多轴孔装配控制方法 | |
| Piltan et al. | Design Artificial Nonlinear Robust Controller Based on CTLC and FSMC with Tunable Gain | |
| CN110806759A (zh) | 一种基于深度强化学习的飞行器航线跟踪方法 | |
| Lian | Intelligent controller for robotic motion control | |
| CN113510704A (zh) | 一种基于强化学习算法的工业机械臂运动规划方法 | |
| Detiček et al. | An Intelligent Electro-Hydraulic Servo Drive Positioning. | |
| Lin et al. | Observer-based indirect adaptive fuzzy-neural tracking control for nonlinear SISO systems using VSS and H∞ approaches | |
| CN116460860B (zh) | 一种基于模型的机器人离线强化学习控制方法 | |
| CN115157238A (zh) | 一种多自由度机器人动力学建模和轨迹跟踪方法 | |
| CN111752151A (zh) | 一种工业叶片磨抛加工自适应力跟踪与补偿方法及系统 | |
| Precup et al. | A survey on fuzzy control for mechatronics applications | |
| van Kampen et al. | Continuous adaptive critic flight control aided with approximated plant dynamics | |
| Sathyan et al. | Collaborative control of multiple robots using genetic fuzzy systems approach | |
| CN117250853A (zh) | 一种分数阶pid的压力控制方法和装置 | |
| CN116755323A (zh) | 一种基于深度强化学习的多旋翼无人机pid自整定方法 | |
| Yao et al. | Research and comparison of automatic control algorithm for unmanned ship | |
| Belarbi et al. | Stable direct adaptive neural network controller with a fuzzy estimator of the control error for a class of perturbed nonlinear systems | |
| CN115327890A (zh) | 一种改进型人群搜索算法优化pid控制火电深度调峰机组的主汽压力的方法 | |
| Kamalasadan | A new generation of adaptive control: An intelligent supervisory loop approach | |
| Brasch et al. | Lateral control of a vehicle using reinforcement learning | |
| CN113805598B (zh) | 一种面向欠驱动auv的航行控制方法 | |
| Prabu et al. | Dynamic control of three-link SCARA manipulator using adaptive neuro fuzzy inference system |
Legal Events
| Date | Code | Title | Description |
|---|---|---|---|
| PB01 | Publication | ||
| PB01 | Publication | ||
| SE01 | Entry into force of request for substantive examination | ||
| SE01 | Entry into force of request for substantive examination | ||
| GR01 | Patent grant | ||
| GR01 | Patent grant |