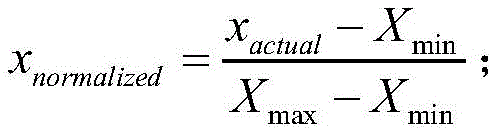CN112257337B - A GMDH neural network-based method for predicting material removal rate of wafer CMP - Google Patents

Abstract

The invention relates to a method for predicting the removal rate of a wafer CMP material of a GMDH neural network, which comprises the following steps: (1) acquiring a polishing sample data set after removing the abnormal value; (2) analyzing the samples in the polishing sample data set to determine b effective process variables; (3) extracting the mean value, standard deviation, skewness and kurtosis of each effective process variable to obtain 4 × b characteristic vectors; (4) screening the correlation between the 4 × b characteristic vectors and the corresponding MRR values, and determining m characteristic vectors as input characteristic vectors of the GMDH neural network model; (5) carrying out normalization processing on a data set formed by the m feature vectors to obtain a training feature set; (6) obtaining a trained GMDH network model by adopting a binary quadratic Volterra polynomial regression model and taking input characteristic values in the training characteristic set as input layers and corresponding output MRR values as output layers; (7) and inputting the m characteristic values serving as input in the sample to be predicted into the trained GMDH network model, and outputting the predicted MRR value.

Description

A GMDH neural network-based method for predicting material removal rate of wafer CMP

technical field

The invention belongs to the technical field of semiconductor material prediction methods, and relates to a GMDH neural network wafer CMP material removal rate prediction method.

Background technique

Chemical Mechanical Polishing (CMP) is the end-stream mainstream process for wafer fabrication; the process is designed to overcome the problem of multi-layer metallization of wafers. CMP is the passivation and etching of the wafer material by slurry chemicals, ie the wafer is flattened by sliding its surface over slurry particles under downward pressure. The wafer CMP process is very complex and involves multiple chemical and mechanical phenomena, such as surface dynamics, electrochemical interfaces, contact mechanics, stress mechanics, fluid dynamics, and tribochemistry.

In the CMP process of wafers, MRR is an important indicator to measure the performance in the process (MRR value is the material removal rate). However, the quality of all wafers is controlled based on the measurement of process variables, requiring expensive metrology tools and production cycles; and demanding experimental work procedures in the laboratory. The main influencing factors that affect MRR are: down pressure, rotating speed of polishing disc and polishing head, temperature, type and flow rate of polishing liquid, etc. Currently, to simulate the physical mechanism of CMP, several models have been proposed: a typical model is the Preston equation, which describes the MRR as a function of pressure and the relative velocity V between the pad and the wafer, and the prediction accuracy of this physical model is The mean squared error MSE is 870.25. There are also improvements based on the aforementioned Preston equation, such as adding slurry flow rate, contact stress and chemical reaction rate to the original Preston equation; only considering the general process parameters of the deep belief network DBN, the test set prediction accuracy of the model is average The squared error MSE is 7.29. But current research efforts have been focused on the development of physics-based and model-based predictive modeling techniques for CMP.

There are many factors that affect the MRR of a wafer. In addition to the factors involved in the above model, there are also the rotational speed, temperature, and type of polishing liquid of the polishing disc and polishing head. The above approach is limited to considering only common process parameters. According to the experimental research on the influencing factors of MRR in the existing CMP process, the above-mentioned general process optimal parameters have been basically determined: such as pressure, rotation speed and slurry flow rate, etc., these basic parameters are strictly controlled. However, in the actual polishing process, the wear (i.e., consumption) of wearable components such as polishing pads and dressers over time also has an irreversible effect on the MRR value. Existing methods only consider few general process variables, and ignore the critical influence defect of important consumption variables on MRR value.

In a CMP process system, a large number of process variables are collected for process control purposes. Therefore, usually the input dimension of modeling methods is very high, sometimes involving hundreds of input variables, where the existence of redundant features can significantly affect the performance of virtual metric models.

Therefore, it is of great significance to study a model that can introduce important consumption variables, simplify feature selection and model selection, and have high measurement accuracy.

SUMMARY OF THE INVENTION

In order to solve the problem that the material removal rate in the CMP technology cannot be accurately obtained in the prior art, the present invention provides a GMDH neural network wafer CMP material removal rate prediction method, which is based on a complex system construction combining physical knowledge and statistics. Modulo method; specifically, the adaptive model method of the GMDH neural network is used to ensure that the MRR value is within the normal range to improve the removal rate accuracy through accurate prediction of the MRR value. The MRR value ranges from 140 to 170 nm/min and 50 to 110 nm/min. If the predicted value does not meet this range, adjust the process parameters in time, for example, replace the wearable materials such as new dressers and polishing pads in time. The accurate prediction of the model provides a decision-making analysis basis for evaluating the performance and health status of each component of the CMP.

For achieving the above object, the scheme that the present invention adopts is as follows:

A method for predicting the removal rate of wafer CMP material by GMDH neural network, comprising the following steps:

(1) Obtain a polishing sample data set after removing outliers; the number of samples is n, and each sample contains a process variable and corresponding MRR value (ie, material removal rate);

(2) Statistically analyze the main process variables generated by several wafer polishing in the polishing sample data set, comprehensively consider the uniformity and distribution range of the distribution of each variable, and determine b effective process variables with uniform distribution and wide range; among them, b < a;

(3) Extract the mean, standard deviation, skewness and kurtosis of each effective process variable, and obtain 4*b eigenvectors;

(4) The regression correlation analysis method is used to screen the 4*b eigenvectors and the corresponding MRR values, and after setting the correlation coefficient threshold, m eigenvectors can be determined as the input eigenvectors of the GMDH neural network model; wherein, m <(4*b);

Then, the input dimension of the GMDH neural network model is determined to be m, and y is the MRR value of the corresponding output. (The input feature dimension m is proportional to the total number of samples n. The specific data is determined to improve the training accuracy. The more features, the better the accuracy. High, but the accuracy tends to be stable as the feature dimension increases, or even decreases; in order to improve the training accuracy and reduce the model complexity, the input feature dimension is within 10);

(5) Normalize the data set A formed by m feature vectors to obtain a training feature set A' and a test feature set, wherein the sample size of the training feature set is n ₁ , and the sample size of the test feature set is n ₂ , n=n ₁ +n ₂ . The purpose of normalization processing is to reduce the impact of the unit dimension inconsistency of the input data on the prediction accuracy.

(6) Using the binary quadratic Volterra polynomial regression model, the m feature vectors in the training feature set A' with a sample size of n ₁ are used as the input layer, the corresponding MRR value in the training feature set is the output layer, and the GMDH neural network model is trained. ;which is:

为训练特征集A′中的第b个特征向量，x_a′_,b为训练特征集 A′中的第a个样本中第b个特征向量中对应的特征值，y_a为训练特征集A′中第a个样本对应的实际MRR值，n₁为训练样本量，a∈{1,2,…,n₁},b∈{1,2, …,m}；in,

is the b-th feature vector in the training feature set A', x _a ' _{, b} is the corresponding feature value in the b-th feature vector in the a-th sample in the training feature set A', y _a is the training feature set A The actual MRR value corresponding to the a-th sample in ', n ₁ is the training sample size, a∈{1,2,...,n ₁ },b∈{1,2,...,m};

(7) input the m eigenvalues as input in the test feature set (sample set to be tested) into the trained GMDH network model, then output the predicted MRR value;

(8) Compare the predicted MRR value with the MRR value corresponding to the input m eigenvalues in the test feature set, and obtain the prediction accuracy of the model.

In the rough throwing working mode, the accuracy of the prediction results: the mean square error MSE is 3.95, and the root mean square error RMSE is 1.99;

In the fine polishing working mode, the accuracy of the prediction results: the mean square error MSE is 9.82, and the root mean square error RMSE is 3.31.

As the preferred technical solution:

In the above-mentioned method for predicting the removal rate of wafer CMP material by GMDH neural network, in step (1), the polishing sample data set is collected by the sensor on the CMP equipment, and when the MRR value is 140-170 nm/min, The polishing sample data set refers to the rough polishing sample data set; when the MRR value is 50-110 nm/min, the polishing sample data set refers to the fine polishing sample data set;

In step (1), a is 25, and the process variables include chamber pressure, main external pressure, center pressure, holding ring pressure, corrugation pressure, edge pressure, conditioner rotation speed, wafer rotation speed, polishing table rotation speed, and A-type slurry Flow rate, Type B slurry flow rate, Type C slurry flow rate, Consumption of polishing table backing film, Consumption of polishing pad, Consumption of wafer carrier flex, Consumption of partition film, Consumption of dresser, Dresser station consumption, dressing fluid status, chambers used for wafer processing, process stages, wafer identifiers, time cuts, wafer ring position identifiers, and polishing machine identifiers. The first 18 main process variables were selected for statistical distribution analysis. Other identifier variables had less effect on the target output and were therefore not analyzed as predictors.

In step (1), the method of removing outliers is as follows: using Grubbs to detect outliers, the purpose is to improve the prediction accuracy, outliers are generated by sensor measurement failure and random errors of process parameters, and are maximum or minimum values.

A kind of GMDH neural network wafer CMP material removal rate prediction method as described above, in step (2), the effective process variable is a variable with a statistical width ranging from 0.12 to 11 (the width is the difference between the maximum value and the minimum value in the variable). Difference). Narrowly distributed variables do not increase the accuracy of the MRR value because the rotational speed, pressure, and flow rate variable data are distributed over a narrow range throughout the CMP process, and pressure, spin speed, and slurry flow rate are tightly controlled in actual wafer CMP . These process parameters are basically fixed values to ensure wafer material removal accuracy and removal uniformity. From a physical point of view, pressure and rotational speed are key factors affecting MRR, but from a computational point of view, including pressure and rotational speed in the GMDH neural network model does not increase the MRR prediction accuracy.

A GMDH neural network method for predicting the removal rate of wafer CMP material as described above, when the polishing sample data set refers to the rough polishing sample data set, the effective process variables are: backing film consumption, polishing pad consumption, partition Film consumption and flexible board consumption; the distribution of other invalid variables is relatively discrete and basically a constant; therefore, these variables cannot be used as predictors of the model;

Alternatively, when the polishing sample data set refers to the fine polishing sample data set, the effective process variables are: backing film consumption, polishing pad consumption and partition film consumption.

The above-mentioned method for predicting the removal rate of wafer CMP material by GMDH neural network, in step (4), when the polishing sample data set refers to the rough polishing sample data set, m=8, and the input process corresponding to the input feature vector The variable features are: the mean of the consumption of the backing film, the skewness of the consumption of the backing film, the mean of the consumption of the polishing pad, the standard deviation of the consumption of the polishing pad, the skewness of the consumption of the polishing pad, the deviation of the consumption of the partitioned film. Average value, skewness of partition film consumption and average value of flexible board consumption;

Or, when the polishing sample data set refers to the precise polishing sample data set, m=8, and the input process variable characteristics corresponding to the input feature vector are respectively: the skewness of the consumption of the backing film, the average consumption of the polishing pad, the polishing pad Standard deviation of consumption, skewness of pad consumption, kurtosis of pad consumption, mean of zoned film consumption, standard deviation of zoned film consumption and skewness of zoned film consumption.

The acquisition methods of the eigenvalues are well known.

Wafer CMP material removal rate prediction method of a kind of GMDH neural network as above, in step (5),

The dataset formed by m eigenvectors is A, as follows:

Among them, (x _1,b ,x _2,b ,…,x _a,b ,…,x _n,b ) ^T is the b-th eigenvector in data set A, and x _a,b is in data set A The corresponding eigenvalue in the b-th eigenvector in the a-th sample, m=8, a∈{1,2,…,n},b∈{1,2,…,m};

The normalization process refers to the normalization of the feature vectors in the data set A one by _{one to} obtain a normalized data set. x _a,b ,…,x _n,b ) ^T , a∈{1,2,…,n},b∈{1,2,…,m}, the normalization formula is:

Among them, x _normalized is the normalized eigenvalue in the b-th eigenvector, x _actual is the eigenvalue in the b-th eigenvector, x _max is the largest eigenvalue in the b-th eigenvector, and x _min is The smallest eigenvalue in the bth eigenvector, b∈{1,2,…,m};

个样本作为训练特征集A′，记为：In the normalized dataset, randomly selected

The samples are taken as the training feature set A', denoted as:

为训练特征集A′中的第b个特征向量，x′_a,b为训练特征集A′中的第a个样本中第b个特征向量中对应的特征值，n₁为训练样本量，m＝8， a∈{1,2,…,n₁},b∈{1,2,…,m}。in,

is the b-th feature vector in the training feature set A', x' _{a, b} are the corresponding eigenvalues in the b-th feature vector in the a-th sample in the training feature set A', n ₁ is the training sample size, m=8, a∈{1,2,...,n ₁ },b∈{1,2,...,m}.

The wafer CMP material removal rate prediction method of a kind of GMDH neural network as above, in step (6), the concrete steps of training GMDH neural network model are:

(61) Establish the first hidden layer:

其中，m＝8， P为每层隐层中最大神经元总数阈值；(611) Take two eigenvectors X _i and X _j arbitrarily from the 8 eigenvectors in the training feature set A' to create _G1 quadratic polynomial equations, and use them as basic neurons, that is, the total number of basic neurons in the first hidden layer

Among them, m=8, P is the threshold of the maximum number of neurons in each hidden layer;

(612) Calculate the model corresponding to each basic neuron in the first hidden layer according to Volterra quadratic polynomial regression

为二次多项方程式的目标输出向量预测值，

指第1隐层中第r个基本神经元模型中第a个样本的目标输出预测值，x′_a,j指从输入中选择第a个样本的第j个输入特征值，且作为连接形成第1隐层第r个基本神经元模型的元素，a∈{1,2,…,n₁},b∈{1,2,…,m}；in,

is the predicted value for the target output vector of the quadratic polynomial equation,

refers to the target output prediction value of the a-th sample in the r-th basic neuron model in the first hidden layer, x′ _a,j refers to the j-th input feature value of the a-th sample selected from the input, and is formed as a connection The element of the rth basic neuron model of the 1st hidden layer, a∈{1,2,…,n ₁ },b∈{1,2,…,m};

与Y_r ¹的差异最小为目标，采用最小二乘法计算得到；其中，Y_r ¹为训练特征集A′中n₁个训练样本的实际MRR值构成的向量；{w ₀ ,w ₂ ,w ₃ ,w ₄ ,w ₅ } is the coefficient of the quadratic polynomial equation, the coefficient is

The minimum difference with Y _r ¹ is the target, which is calculated by the least squares method; wherein, Y _r ¹ is the vector formed by the actual MRR values of n ₁ training samples in the training feature set A';

值；即(613) Calculate the output root mean square error of each neuron in the first hidden layer respectively

value; that is

为第1隐层中第r个基本神经元模型中第a个样本的目标输出预测值，

为为第1隐层中第r个基本神经元模型中第a个样本的目标输出真实值；in,

is the target output prediction value of the a-th sample in the r-th basic neuron model in the first hidden layer,

Output the true value for the target of the a-th sample in the r-th basic neuron model in the first hidden layer;

(614) Rank the output root mean square errors of all neurons in the first hidden layer from small to large, and take the top P neurons as effective neurons to form the first hidden layer;

G₂＞P，重复步骤(611)～(614)，得到含有P个神经元的第2隐层，其中，第1隐层中参与组合连接形成第2隐层的有U₁个有效神经元；(615) Use the outputs of the P neurons in the first hidden layer as the input feature vector of the second hidden layer; then the second hidden layer forms G ₂ basic neurons, and

G ₂ >P, repeat steps (611) to (614) to obtain the second hidden layer containing P neurons, wherein, in the first hidden layer, there are U ₁ effective neurons participating in the combined connection to form the second hidden layer ;

的均值E₁，即(616) Calculate the output of U ₁ effective neurons in the first hidden layer participating in the combined connection to form the second hidden layer

The mean E ₁ of , namely

(62) Establish an intermediate hidden layer: the output of the P neurons in the k-1th hidden layer (equivalent to the 1st hidden layer) is used as the input feature vector of the kth hidden layer (equivalent to the 2nd hidden layer) , repeat steps (611) to (616) to obtain an intermediate hidden layer;

k≥2；Among them, the total number of basic neurons in the kth hidden layer

k≥2;

的均值E_k，即The output of U _k effective neurons in the k-1 hidden layer participating in the combined connection to form the k hidden layer

The mean E _k of , namely

(63) Establish the output layer: when E _k-1 -E _k ≤ 0.3 (that is, when the E _k of the k-th hidden layer does not decrease significantly with the increase of the number of hidden layers), the training stops; and the k-th hidden layer The two smaller output RMSE neurons are used as new input vectors and their corresponding target output MRR vectors to construct a quadratic polynomial equation, and the output of this equation is used as the final output prediction value of the GMDH neural network model.

A method for predicting the removal rate of wafer CMP material based on a GMDH neural network as described above, P=12.

beneficial effect

(1) The virtual prediction method of wafer CMP material removal rate of a kind of GMDH neural network of the present invention, the use of GMDH network has the advantages of single-cycle prediction ability and short running time, self-organization selects the optimal feature set to establish a wafer MRR prediction model . The combination of comprehensive consideration of physics knowledge and statistics overcomes the defects of traditional prediction methods that only consider fewer variables and ignore the impact of important consumption variables on MRR. It solves the problem that the grinding removal rate during the wafer CMP process cannot be obtained quickly and accurately.

(2) The virtual prediction method of wafer CMP material removal rate of a kind of GMDH neural network of the present invention comprehensively considers error sources such as polishing process drift and difference between different batches of wafer products, in order to improve the accuracy of the prediction model, respectively Two modes of wafer rough polishing and fine polishing are modeled separately.

(3) The virtual prediction method of the wafer CMP material removal rate of a GMDH neural network of the present invention, from the network structure of rough polishing training, it can be seen that the average value of the consumption variables of the polishing pad, the backing film and the flexible plate is selected as the most effective prediction factor. The most efficient variable used extensively in the input layer polynomial equation at this time is the pad consumption mean.

(4) The virtual prediction method of the wafer CMP material removal rate of a GMDH neural network of the present invention, from the structure of the fine polishing training, it can be seen that the average value, standard deviation and skewness of the polishing pad consumption, the skewness and partition of the backing film The film consumption variable skew was chosen as the most effective predictor, and the most effective variable widely used in the input layer polynomial equation at this time was the pad consumption standard deviation.

(5) The virtual prediction method of the wafer CMP material removal rate of a GMDH neural network of the present invention, the accurate prediction of the MRR value is quickly obtained through the network model, whether it is a fine polishing mode or a rough polishing mode, it is the polishing pad wear consumption It has the greatest impact on the target output MRR. Therefore, if the predicted value is not within the range of the MRR value, the process parameters should be adjusted in time, for example, the wearable materials such as new polishing pads and dressers should be replaced in time. According to the 2016PHM data, combined with the calculation results of the experimental prediction error evaluation index, it is proved that the MRR prediction method proposed in this paper is better than the physical model and the traditional neural network prediction effect. Suitable for nonlinear complex CMP process modeling.

Description of drawings

1 and 2 are flowcharts of wafer removal rate prediction of the present invention;

Fig. 3 (a) is 4 MRR abnormal value detection results of the present invention;

Fig. 3 (b) is the MRR value distribution figure of two working modes in the CMP process of the present invention;

4 is a schematic diagram of a trained GMDH network structure in the rough wafer throwing stage of the present invention;

Fig. 5 and Fig. 6 are respectively the prediction result of rough throwing stage and fine throwing stage of the present invention;

FIG. 7 is a statistical analysis diagram of process variables in the rough throwing mode of the present invention.

Detailed ways

The present invention will be further described below in conjunction with specific embodiments. It should be understood that these examples are only used to illustrate the present invention and not to limit the scope of the present invention. In addition, it should be understood that after reading the content taught by the present invention, those skilled in the art can make various changes or modifications to the present invention, and these equivalent forms also fall within the scope defined by the appended claims of the present application.

A method for predicting the removal rate of wafer CMP materials based on GMDH neural network, the schematic flowchart of which is shown in Figures 1-2, and specifically includes the following steps:

(1) Obtain a polishing sample data set after removing outliers; the number of samples is n, and each sample contains 25 process variables and corresponding MRR values (ie, material removal rate);

Process variables include chamber pressure, main external pressure, center pressure, holding ring pressure, corrugation pressure, edge pressure, dresser rotation speed, wafer rotation speed, polishing table rotation speed, type A slurry flow rate, type B slurry flow rate, type C Slurry flow rate, polishing table backing film consumption, polishing pad consumption, wafer carrier flex board consumption, partitioned film consumption, dresser consumption, dresser table consumption, conditioning fluid status , chamber used for wafer processing, process stage, wafer identifier, time cut, wafer ring position identifier and polishing machine identifier. The first 18 main process variables were selected for statistical distribution analysis. Other identifier variables had less effect on the target output and were therefore not analyzed as predictors.

The method of removing outliers is: using Grubbs to detect outliers, the purpose is to improve the prediction accuracy, outliers are caused by sensor measurement failure and random errors of process parameters, which are maximum or minimum values.

(2) Statistically analyze the main process variables generated by several wafer polishing in the polishing sample data set, and determine b effective processes with a statistical width ranging from 0.12 to 11 (the width is the difference between the maximum value and the minimum value of the variables). variable; where, b<a;

(3) Extract the mean, standard deviation, skewness and kurtosis of each effective process variable, and obtain 4*b eigenvectors;

(4) The regression correlation analysis method is used to screen the 4*b eigenvectors and the corresponding MRR values, and after setting the correlation coefficient threshold, m eigenvectors can be determined as the input eigenvectors of the GMDH neural network model; wherein, m =8, m<(4*b);

(5) Normalize the data set A formed by m feature vectors to obtain a training feature set A' and a test feature set, wherein the sample size of the training feature set is n ₁ , and the sample size of the test feature set is n ₂ , n=n ₁ +n ₂ ; the specific process is as follows:

The dataset formed by m eigenvectors is A, as follows:

Among them, (x _1,b ,x _2,b ,…,x _a,b ,…,x _n,b ) ^T is the b-th eigenvector in data set A, and x _a,b is in data set A The corresponding eigenvalue in the b-th eigenvector in the a-th sample, m=8, a∈{1,2,…,n},b∈{1,2,…,m};

The normalization process refers to the normalization of the feature vectors in the data set A one by _{one to} obtain a normalized data set. x _a,b ,…,x _n,b ) ^T , a∈{1,2,…,n},b∈{1,2,…,m}, the normalization formula is:

Among them, x _normalized is the normalized eigenvalue in the b-th eigenvector, x _actual is the eigenvalue in the b-th eigenvector, x _max is the largest eigenvalue in the b-th eigenvector, and x _min is The smallest eigenvalue in the bth eigenvector, b∈{1,2,…,m};

个样本作为训练特征集A′，记为：In the normalized dataset, randomly selected

The samples are taken as the training feature set A', denoted as:

为训练特征集A′中的第b个特征向量，x′_a,b为训练特征集 A′中的第a个样本中第b个特征向量中对应的特征值，n₁为训练样本量，m＝8， a∈{1,2,…,n₁},b∈{1,2,…,m}；in,

is the b-th feature vector in the training feature set A', x' _{a, b} are the corresponding eigenvalues in the b-th feature vector in the a-th sample in the training feature set A', n ₁ is the training sample size, m=8, a∈{1,2,...,n ₁ },b∈{1,2,...,m};

(6) Using the binary quadratic Volterra polynomial regression model, the m feature vectors in the training feature set A' with a sample size of n ₁ are used as the input layer, the corresponding MRR value in the training feature set is the output layer, and the GMDH neural network model is trained. ;which is:

为训练特征集A′中的第b个特征向量，x′_a,b为训练特征集 A′中的第a个样本中第b个特征向量中对应的特征值，y_a为训练特征集A′中第a个样本对应的实际MRR值，n₁为训练样本量，a∈{1,2,…,n₁},b∈{1,2,…,m}；in,

is the b-th feature vector in the training feature set A', x' _{a, b} are the corresponding eigenvalues in the b-th feature vector in the a-th sample in the training feature set A', y _a is the training feature set A The actual MRR value corresponding to the a-th sample in ', n ₁ is the training sample size, a∈{1,2,...,n ₁ },b∈{1,2,...,m};

The specific steps for training the GMDH neural network model are:

(61) Establish the first hidden layer:

其中，m＝8， P为每层隐层中最大神经元总数阈值；P＝12；(611) Take two eigenvectors X _i and X _j arbitrarily from the 8 eigenvectors in the training feature set A' to create _G1 quadratic polynomial equations, and use them as basic neurons, that is, the total number of basic neurons in the first hidden layer

Among them, m=8, P is the threshold of the maximum number of neurons in the hidden layer of each layer; P=12;

(612) Calculate the model corresponding to each basic neuron in the first hidden layer according to Volterra quadratic polynomial regression

为二次多项方程式的目标输出向量预测值，

指第1隐层中第r个基本神经元模型中第a个样本的目标输出预测值，r为第1隐层中基本神经元的序号，x′_a,j指从输入中选择第a个样本的第j个输入特征值，且作为连接形成第1隐层第r个基本神经元模型的元素，a∈{1,2,…,n₁},b∈{1,2,…,m}；P＝12。in,

is the predicted value for the target output vector of the quadratic polynomial equation,

Refers to the target output prediction value of the a-th sample in the r-th basic neuron model in the first hidden layer, r is the serial number of the basic neuron in the first hidden layer, x' _{a, j} refers to selecting the a-th sample from the input The jth input feature value of the sample, and as the element connected to form the rth basic neuron model of the first hidden layer, a∈{1,2,…,n ₁ },b∈{1,2,…,m }; P=12.

与Y_r ¹的差异最小为目标，采用最小二乘法计算得到；其中，Y_r ¹为训练特征集A′中n₁个训练样本的实际MRR值构成的向量；{w ₀ ,w ₂ ,w ₃ ,w ₄ ,w ₅ } is the coefficient of the quadratic polynomial equation, the coefficient is

The minimum difference with Y _r ¹ is the target, which is calculated by the least squares method; wherein, Y _r ¹ is the vector formed by the actual MRR values of n ₁ training samples in the training feature set A';

值；即(613) Calculate the output root mean square error of each neuron in the first hidden layer respectively

value; that is

为第1隐层中第r个基本神经元模型中第a个样本的目标输出预测值，

为为第1隐层中第r个基本神经元模型中第a个样本的目标输出真实值，r为第1隐层中基本神经元的序号；in,

is the target output prediction value of the a-th sample in the r-th basic neuron model in the first hidden layer,

is the target output real value of the a-th sample in the r-th basic neuron model in the first hidden layer, and r is the serial number of the basic neuron in the first hidden layer;

(614) Rank the output root mean square errors of all neurons in the first hidden layer from small to large, and take the top P neurons as effective neurons to form the first hidden layer;

G₂＞P，重复步骤(611)～(614)，得到含有P个神经元的第2隐层，P＝12，其中，第1隐层中参与组合连接形成第2隐层的有U₁个有效神经元；(615) Take the outputs of the P neurons in the first hidden layer as the input feature vector of the second hidden layer, P=12; then the second hidden layer forms G ₂ basic neurons, and

G ₂ >P, repeat steps (611) to (614) to obtain the second hidden layer containing P neurons, P=12, wherein U ₁ participates in the combined connection to form the second hidden layer in the first hidden layer effective neurons;

的均值E₁，即(616) Calculate the output of U ₁ effective neurons in the first hidden layer participating in the combined connection to form the second hidden layer

The mean E ₁ of , namely

Among them, r is the serial number of U ₁ effective neurons in the first hidden layer;

(62) establishing an intermediate hidden layer: the outputs of the P neurons in the k-1 hidden layer are used as the input feature vector of the k hidden layer, and steps (611) to (616) are repeated to obtain the intermediate hidden layer;

k≥2；Among them, the total number of basic neurons in the kth hidden layer

k≥2;

的均值E_k，即The output of U _k effective neurons in the k-1 hidden layer participating in the combined connection to form the k hidden layer

The mean E _k of , namely

(63) Establish the output layer: when E _k-1 -E _k ≤ 0.3 (that is, when the E _k of the k-th hidden layer does not decrease significantly with the increase of the number of hidden layers), the training stops; and the k-th hidden layer The two smaller output RMSE neurons are used as new input vectors and their corresponding target output MRR vectors to construct a quadratic polynomial equation, and the output of this equation is used as the final output prediction value of the GMDH neural network model.

(7) input the m eigenvalues as input in the test feature set (sample set to be tested) into the trained GMDH network model, then output the predicted MRR value;

(8) Compare the predicted MRR value with the MRR value corresponding to the input m eigenvalues in the test feature set, and obtain the prediction accuracy of the model.

Using the above-mentioned method for predicting the removal rate of wafer CMP materials using a GMDH neural network, the data set of rough samples with an MRR value of 140-170 nm/min collected by sensors on the CMP equipment (the MRR value distribution diagram is shown in Figure 3 (Fig. 3). b)) to predict, the data comes from the 2016 PHM Challenge, which uses Grubbs to detect outliers, and found that 4 MRR values are much larger than 170nm/min outliers (outlier detection results are shown in Figure 3(a)), Obtain the rough-throwing sample data set after removing outliers; the number of samples in the rough-throwing sample data set is n=102, and each sample contains 25 process variables and corresponding MRR values (that is, material removal rate);

In the data set of rough polishing samples after removing outliers, five samples of wafer polishing were randomly selected for statistical analysis of process variables (as shown in Figure 7), and 4 effective process variables were determined (variables with a data width of 0.12 to 11, Namely backing film consumption, polishing pad consumption, partitioned film consumption and flexible board consumption); wherein, the distribution range of backing film consumption is 10.83, the distribution range of polishing pad consumption is 9.63, and the consumption of partitioned film is 10.83. The distribution range is 3.25, and the distribution range of flexible board consumption is 0.12; the distribution of other invalid variables is relatively discrete and basically a constant; therefore, these variables cannot be used as predictors of the model;

Extract the mean, standard deviation, skewness and kurtosis of each effective process variable in the rough throw sample data set, and obtain 16 eigenvectors;

The regression correlation analysis method is used to screen the 16 eigenvectors and the corresponding MRR values in the coarse throwing sample data set, and after setting the correlation coefficient threshold (valued at 0.65), 8 eigenvectors with strong correlation can be determined as the GMDH neural network. The input feature vector of the network model, see Table 1, as follows:

Table 1

serial number feature variable name X₁ Average backing film consumption X₂ Backing film consumption skewness X₃ Average pad consumption X₄ Standard deviation of polishing pad consumption X₅ Pad consumption skewness X₆ Mean value of partitioned membrane consumption X₇ Partition film consumption skewness X₈ Average consumption of flexible boards

是被筛选为剔除的神经元，根据模型评价准则这些神经元组合形成的下一层新神经元输出 RMSE较大，说明这些神经元与输出MRR相关性弱，不参与下一层的网络连接。则

是第一隐层的有效神经元。当构筑到第4隐层时，所有有效神经元输出RMSE的均值不再随着隐层数的增加有明显的下降趋势，训练停止，得到含有4个隐层的GMDH神经网络拓扑结构，即得到GMDH网络模型。The schematic diagram of the trained GMDH network structure is shown in Figure 4. From the input layer, it can be seen that the most widely used input vector of the network is _X3 (that is, the average polishing pad consumption in Table 1), which is the most effective MRR predictor. In the first hidden layer,

is the neuron that was screened out. According to the model evaluation criteria, the output RMSE of the new neurons in the next layer formed by the combination of these neurons is larger, indicating that these neurons are weakly correlated with the output MRR and do not participate in the network connection of the next layer. but

is the effective neuron of the first hidden layer. When the fourth hidden layer is constructed, the mean value of the output RMSE of all effective neurons no longer has a significant downward trend with the increase of the number of hidden layers, the training stops, and the topology of the GMDH neural network with 4 hidden layers is obtained, that is, GMDH network model.

Input the 8 eigenvalues of the corresponding test feature set as the input into the trained GMDH network model, then output the predicted MRR value;

The predicted MRR value and the test feature set are compared with the MRR values corresponding to the input 8 eigenvalues, and the accuracy of the model prediction is obtained. The schematic diagram of the prediction result is shown in Figure 5. In the rough throwing mode, the prediction result is accurate. Rate: mean square error MSE is 3.95, root mean square error RMSE is 1.99.

Using the above-mentioned method for predicting the removal rate of wafer CMP materials using a GMDH neural network, the precision polishing sample data set with an MRR value of 50 to 110 nm/min collected by the sensor on the CMP equipment (the MRR value distribution diagram is shown in Figure 3 ( b) shown) to make predictions, the data is taken from the 2016PHM challenge data, Grubbs is used to detect outliers, and the refined sample data set after removing outliers is obtained (outlier detection results are shown in Figure 3(a)); The number is n=105, and each sample contains 25 process variables and corresponding MRR values (ie, material removal rate);

The samples generated from a single wafer in the refined polishing sample dataset after removing outliers were analyzed to determine 3 valid process variables (variables with a data width of 0.12 to 11, namely backing film consumption, polishing pad consumption and partitioning) membrane consumption);

Extract the mean, standard deviation, skewness and kurtosis of each effective process variable to obtain 12 eigenvectors;

The 12 eigenvectors and the corresponding MRR values are screened by the regression correlation analysis method, and after setting the correlation coefficient threshold (valued at 0.7), 8 eigenvectors can be determined as the input eigenvectors of the GMDH neural network model, see table 2, as follows:

Table 2

serial number feature variable name X₁ Backing film consumption skewness X₂ Average pad consumption X₃ Standard deviation of polishing pad consumption X₄ Pad consumption skewness X₅ Pad consumption kurtosis X₆ Mean consumption of zonal film X₇ Standard deviation of zonal film consumption X₈ Partition film consumption skewness

Input the 8 feature vector samples from the test feature set as input into the trained GMDH network model, then output the predicted MRR value;

Compare the predicted MRR value and the test feature set with the MRR values corresponding to the input 8 eigenvalues to obtain the accuracy of the model prediction. The schematic diagram of the prediction result is shown in Figure 6. In the fine throwing working mode, the prediction result is accurate. Rate: mean square error MSE is 9.82, root mean square error RMSE is 3.13.

Table 1 shows the detailed prediction results of training samples and test samples under two different working modes

The training model obtained from the training samples in Table 1 will also perform error analysis with the real value, which is called training error.

The prediction results show that the predicted MRR values obtained by the GMDH network are in good agreement with the real measured values. When establishing the network topology, a balance point is found between the fitting accuracy of the training samples and the prediction accuracy of the test set to ensure that the network model is even in small When the sample or noise is large, the algorithm can still reflect the real internal relationship of the system to the greatest extent (the nonlinear relationship between each consumption feature and the MRR value), thereby ensuring the optimality and generalization of the built model. The model can effectively monitor the real-time variation of MRR of wafer CMP process. The mean square error (MSE) and root mean square error (RMSE) were used as model performance evaluation metrics. The smaller the RMSE, the higher the model prediction accuracy.

Claims (4)

1. a wafer CMP material removal rate prediction method of GMDH neural network, is characterized in that: comprise the steps: (1) Obtain a polishing sample data set after removing outliers; the number of samples is n, and each sample contains a process variable and a corresponding MRR value; The polishing sample data set is collected by the sensor on the CMP equipment. When the MRR value is 140-170 nm/min, the polishing sample data set refers to the rough polishing sample data set; when the MRR value is 50-110 nm/min, the polishing sample data set is The data set refers to the precise sample data set; (2) Statistical analysis is performed on the main process variables generated by several wafer polishing in the polishing sample data set, and b effective process variables are determined; wherein, b<a; Valid process variables are variables with a statistical width ranging from 0.12 to 11; when the polishing sample data set refers to the rough polishing sample data set, the valid process variables are: backing film consumption, polishing pad consumption, partition film consumption and flexibility plate consumption; or, when the polishing sample data set refers to the fine polishing sample data set, the valid process variables are: backing film consumption, polishing pad consumption and partition film consumption; (3) Extract the mean, standard deviation, skewness and kurtosis of each effective process variable, and obtain 4*b eigenvectors; (4) Use regression correlation analysis method to screen 4*b eigenvectors and corresponding MRR values, and after setting the correlation coefficient threshold, m eigenvectors can be determined as the input eigenvectors of the GMDH neural network model; When the polishing sample data set refers to the rough polishing sample data set, m=8, and the input process variable characteristics corresponding to the input feature vector are: the mean value of the consumption of the backing film, the skewness of the consumption of the backing film, and the consumption of the polishing pad. The mean value of the amount, the standard deviation of the polishing pad consumption, the skewness of the polishing pad consumption, the mean value of the partition film consumption, the skewness of the partition membrane consumption and the mean value of the flexible board consumption; Or, when the polishing sample data set refers to the fine polishing sample data set, m=8, and the input process variable features corresponding to the input feature vector are respectively: the skewness of the consumption of the backing film, the average consumption of the polishing pad, the polishing pad Standard deviation of consumption, skewness of polishing pad consumption, kurtosis of polishing pad consumption, mean value of partitioned film consumption, standard deviation of partitioned film consumption and skewness of partitioned film consumption; (5) Normalize the data set A formed by the m feature vectors to obtain a training feature set A', wherein the sample size of the training feature set A' is n ₁ , and n ₁ <n; (6) Using the binary quadratic Volterra polynomial regression model, the m feature vectors in the training feature set A' with a sample size of n ₁ are used as the input layer, the corresponding MRR value in the training feature set is the output layer, and the GMDH is trained and obtained. Neural network model, namely:

in,

is the b-th feature vector in the training feature set A', x' _{a, b} are the corresponding eigenvalues in the b-th feature vector in the a-th sample in the training feature set A', y _a is the training feature set A The actual MRR value corresponding to the a-th sample in ', n ₁ is the training sample size, a∈{1,2,...,n ₁ },b∈{1,2,...,m}; (7) Input the m eigenvalues in the sample to be tested as input into the trained GMDH network model, and output the predicted MRR value. 2. the wafer CMP material removal rate prediction method of a kind of GMDH neural network according to claim 1, is characterized in that, in step (5), The data set formed by m eigenvectors is A, as follows:

Among them, (x _1,b ,x _2,b ,…,x _a,b ,…,x _n,b ) ^T is the b-th eigenvector in data set A, and x _a,b is in data set A The corresponding eigenvalue in the b-th eigenvector in the a-th sample, m=8, a∈{1,2,…,n},b∈{1,2,…,m}; The normalization process refers to the normalization of the feature vectors in the data set A one by _{one to} obtain a normalized data set. x _a,b ,…,x _n,b ) ^T , a∈{1,2,…,n},b∈{1,2,…,m}, the normalization formula is:

Among them, x _normalized is the normalized eigenvalue in the b-th eigenvector, x _actual is the eigenvalue in the b-th eigenvector, x _max is the largest eigenvalue in the b-th eigenvector, and x _min is The smallest eigenvalue in the bth eigenvector, b∈{1,2,…,m}; In the normalized dataset, randomly selected

The samples are taken as the training feature set A', denoted as:

in,

is the b-th feature vector in the training feature set A', x' _{a, b} are the corresponding eigenvalues in the b-th feature vector in the a-th sample in the training feature set A', n ₁ is the training sample size, m=8, a∈{1,2,...,n ₁ },b∈{1,2,...,m}. 3. the wafer CMP material removal rate prediction method of a kind of GMDH neural network according to claim 2, is characterized in that, in step (6), the concrete steps of training GMDH neural network model are: (61) Establish the first hidden layer: (611) Take two eigenvectors X _i and X _j arbitrarily from the 8 eigenvectors in the training feature set A' to create _G1 quadratic polynomial equations, and use them as basic neurons, that is, the total number of basic neurons in the first hidden layer

Among them, m=8, P is the threshold of the maximum number of neurons in each hidden layer; (612) Calculate the model corresponding to each basic neuron in the first hidden layer according to Volterra quadratic polynomial regression

in,

is the predicted value for the target output vector of the quadratic polynomial equation,

refers to the target output predicted value of the a-th sample in the r-th basic neuron model in the first hidden layer, x′ _a,j refers to the j-th input feature value of the a-th sample selected from the input, and is formed as a connection The element of the rth basic neuron model of the 1st hidden layer, a∈{1,2,…,n ₁ },b∈{1,2,…,m}; {w ₀ ,w ₂ ,w ₃ ,w ₄ ,w ₅ } is the coefficient of the quadratic polynomial equation, the coefficient is

and

The minimum difference is the target, which is calculated by the least square method; among them,

is a vector formed by the actual MRR values of n ₁ training samples in the training feature set A'; (613) Calculate the output root mean square error of each neuron in the first hidden layer respectively

value; that is

in,

is the target output prediction value of the a-th sample in the r-th basic neuron model in the first hidden layer,

Output the true value for the target of the a-th sample in the r-th basic neuron model in the first hidden layer; (614) Sort the output root mean square errors of all neurons in the first hidden layer from small to large, and take the top P neurons as effective neurons to form the first hidden layer; (615) Use the outputs of the P neurons in the first hidden layer as the input feature vector of the second hidden layer; then the second hidden layer forms G ₂ basic neurons, and

Steps (611) to (614) are repeated to obtain a second hidden layer containing P neurons, wherein, in the first hidden layer, there are U ₁ effective neurons participating in the combined connection to form the second hidden layer; (616) Calculate the output of U ₁ effective neurons in the first hidden layer participating in the combined connection to form the second hidden layer

The mean E ₁ of , namely

(62) Establishing an intermediate hidden layer: each output of the P neurons in the k-1 hidden layer is used as the input feature vector of the k hidden layer, and steps (611) to (616) are repeated to obtain the intermediate hidden layer; Among them, the total number of basic neurons in the kth hidden layer

The output of U _k effective neurons in the k-1 hidden layer participating in the combined connection to form the k hidden layer

The mean E _k of , that is

(63) Establish the output layer: when E _k-1 -E _k ≤ 0.3, the training stops; and the 2 neurons with smaller output RMSE in the kth hidden layer are used as the new input vector and the corresponding target output MRR vector to construct If the quadratic polynomial equation is used, the output of the equation is used as the final output prediction value of the GMDH neural network model. 4 . The method for predicting the removal rate of wafer CMP material by a GMDH neural network according to claim 3 , wherein P=12. 5 .

Images