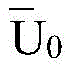CN108345753B - Crosstalk noise prediction method for non-parallel cable - Google Patents
Crosstalk noise prediction method for non-parallel cable Download PDFInfo
- Publication number
- CN108345753B CN108345753B CN201810179567.8A CN201810179567A CN108345753B CN 108345753 B CN108345753 B CN 108345753B CN 201810179567 A CN201810179567 A CN 201810179567A CN 108345753 B CN108345753 B CN 108345753B
- Authority
- CN
- China
- Prior art keywords
- matrix
- cable
- crosstalk
- electromagnetic
- parallel
- Prior art date
- Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
- Active
Links
- 238000000034 method Methods 0.000 title claims abstract description 31
- 239000011159 matrix material Substances 0.000 claims abstract description 131
- 239000004020 conductor Substances 0.000 claims abstract description 18
- 230000014509 gene expression Effects 0.000 claims description 15
- 239000007787 solid Substances 0.000 claims description 7
- 230000005540 biological transmission Effects 0.000 claims description 6
- 238000004364 calculation method Methods 0.000 claims description 6
- NAWXUBYGYWOOIX-SFHVURJKSA-N (2s)-2-[[4-[2-(2,4-diaminoquinazolin-6-yl)ethyl]benzoyl]amino]-4-methylidenepentanedioic acid Chemical compound C1=CC2=NC(N)=NC(N)=C2C=C1CCC1=CC=C(C(=O)N[C@@H](CC(=C)C(O)=O)C(O)=O)C=C1 NAWXUBYGYWOOIX-SFHVURJKSA-N 0.000 claims description 3
- 230000035699 permeability Effects 0.000 claims description 3
- 239000013598 vector Substances 0.000 claims description 3
- 230000001629 suppression Effects 0.000 abstract description 4
- 230000008878 coupling Effects 0.000 abstract description 3
- 238000010168 coupling process Methods 0.000 abstract description 3
- 238000005859 coupling reaction Methods 0.000 abstract description 3
- 230000009286 beneficial effect Effects 0.000 abstract description 2
- 238000013461 design Methods 0.000 abstract description 2
- 230000000246 remedial effect Effects 0.000 abstract description 2
- 238000012360 testing method Methods 0.000 abstract description 2
- 238000010586 diagram Methods 0.000 description 4
- 238000011160 research Methods 0.000 description 4
- 238000004458 analytical method Methods 0.000 description 3
- 230000008569 process Effects 0.000 description 3
- 230000005674 electromagnetic induction Effects 0.000 description 2
- 230000008859 change Effects 0.000 description 1
- 238000011161 development Methods 0.000 description 1
- 238000005516 engineering process Methods 0.000 description 1
- 230000010354 integration Effects 0.000 description 1
- 230000007246 mechanism Effects 0.000 description 1
- 230000009897 systematic effect Effects 0.000 description 1
Images
Classifications
-
- G—PHYSICS
- G06—COMPUTING; CALCULATING OR COUNTING
- G06F—ELECTRIC DIGITAL DATA PROCESSING
- G06F30/00—Computer-aided design [CAD]
- G06F30/20—Design optimisation, verification or simulation
Landscapes
- Engineering & Computer Science (AREA)
- Physics & Mathematics (AREA)
- Theoretical Computer Science (AREA)
- Computer Hardware Design (AREA)
- Evolutionary Computation (AREA)
- Geometry (AREA)
- General Engineering & Computer Science (AREA)
- General Physics & Mathematics (AREA)
- Communication Cables (AREA)
- Measurement Of Resistance Or Impedance (AREA)
Abstract
The invention discloses a crosstalk noise prediction method aiming at a non-parallel cable, which comprises the steps of establishing a wire-wound crosstalk model according to actual cable parameters, analyzing the non-parallel cable by using a segmented cascade method, and comparing a multi-conductor cable under a straight condition in a segmented mode to establish a non-parallel multi-conductor electromagnetic coupling model; according to a common solution of the cable crosstalk, a non-parallel cable equation is established, an equivalent electromagnetic parameter matrix is provided, and the near-end and far-end electromagnetic crosstalk of the non-parallel cable is predicted. By predicting the size and the actual harm degree of the electromagnetic crosstalk, the method has important theoretical and engineering significance on the efficient operation of the electrical equipment, accurately predicts the crosstalk, is beneficial to quickly predicting and finding potential crosstalk problems in the early stage of design, and prevents the problems in the prior art; meanwhile, as a basis for designing crosstalk suppression measures, a theoretical basis is provided for implementing the remedial measures of crosstalk suppression in the testing stage after the electrical equipment is manufactured, so that the stability of the equipment system is improved.
Description
Technical Field
The invention relates to the technical field of electromagnetic compatibility, in particular to a crosstalk noise prediction method for a non-parallel cable.
Background
In electromagnetic compatibility, the interference of an electronic device on itself is generally referred to as crosstalk. The crosstalk between cables means that energy is converted through coupling between electromagnetism between the cables to form a kind of interference on the original signal. In engineering use, a large number of cables exist, and in recent years, industrial development requires that electric power devices have the characteristics of high efficiency, high reliability, high performance and the like. There is a need for "high integration" and "high frequency" of electrical equipment, where the cable as a connector must be placed in a small space and still transmit extremely fast electrical energy or signals, and cable crosstalk within the device is often not negligible.
The existing method for solving the crosstalk generated by coupling of the field lines comprises directly solving maxwell equations or equivalent second-order equations thereof, and specific mainstream methods comprise a time domain finite difference method, a finite element method, a moment method and the like. The finite difference method of time domain is to approximate the central difference quotient of field quantity to the first order partial derivative quotient of time and space, and to obtain the field distribution by recursion to simulate the time domain propagation process of wave. The finite element method is to convert the solution problem of the given Laplace equation into an extremum problem for solving the functional. The moment method is a method for solving linear differential equations, and discretizes a continuous equation into an algebraic equation set, and takes the matrix change solution as the mathematical basis.
At present, the research on the cable crosstalk is systematic, and the electromagnetic mechanism and the worst state of the cable crosstalk are deeply researched. However, most of the researches take cable bundles with ideal spatial layout (straight arrangement) as research objects, and the cable bundles with unconventional layout of real engineering exist in large quantity, and in summary, the researches on non-parallel cables are lacked. In addition, chinese invention patent (CN104007326A) discloses a method for rapidly predicting frequency domain dynamic characteristics of crosstalk of a wire harness for a vehicle, which can achieve rapid prediction of frequency domain dynamic characteristics of crosstalk of a cable for a vehicle, but the technology of the patent cannot predict crosstalk of a non-parallel cable.
Disclosure of Invention
The purpose of the invention is as follows: the invention aims to provide a method for predicting crosstalk noise between non-parallel cables.
The technical scheme is as follows: the invention relates to a crosstalk noise prediction method for a non-parallel cable, which comprises the following steps:
the first step is as follows: acquiring space position parameters between non-parallel cables;
the second step is that: establishing a multi-conductor model of unit length, paralleling analytical formulas of an impedance matrix Z and an admittance matrix Y of the cable corresponding to the unit length with respect to a basic electromagnetic matrix of the cable, and deriving a basic electromagnetic matrix element analytical formula of the cable by combining a multi-conductor transmission line theory and acting space parameters;
the third step: the method for predicting the non-parallel multi-conductor crosstalk based on the segmented cascade is characterized in that an analog method is used for differentiating a non-parallel cable, namely the segmented cascade, a non-parallel electromagnetic parameter matrix is equivalent to a parallel electromagnetic parameter matrix, and an electromagnetic equivalent matrix is solved;
the fourth step: and solving the non-parallel cable crosstalk by combining the boundary condition matrix.
Wherein, the spatial position parameters in the first step comprise an inclination angle, a near-end distance, a far-end distance, a cable length and a ground clearance.
In the second step, the analytic expressions of the impedance matrix Z and the admittance matrix Y are:
wherein, R is a resistance matrix, L is an inductance matrix, G is a conductance matrix, C is a capacitance matrix, ω is 2 pi f, f is a frequency, R, L, G, C is a basic parameter matrix of the cable, since the G matrix representing electromagnetic induction is very small, it is generally directly ignored, when the R, L, C matrix is solved, then the Z, Y matrix can also be solved.
The element calculation formula of the resistance matrix R is as follows:
(2) the formula is divided into two parts according to the relation between the radius of the solid core wire and the skin depth, wherein sigma is the conductivity of the wire core conductor, rw is the radius of the solid core round conductor, and delta is the skin depth; for a stranded wire, one can consider the parallel connection of multiple solid wires with radius rws (rws is the radius of one wire core).
The element calculation formula of the inductance matrix L is as follows:
wherein h isiAnd hjFor the height of the cable above the ground, sijIs the actual distance between the two cables;
sij＝b+z·tan(a)
wherein, a is the intersection angle of the cables, b is the minimum distance between the cables, and z is the transverse distance.
And the third step is to substitute the electromagnetic matrix elements obtained in the second step into analytical expressions of a resistance matrix R and an inductance matrix L, wherein the analytical expressions of the resistance matrix R and the inductance matrix L are as follows:
after the inductance matrix L is obtained, substituting into the analytic expression of the capacitance matrix C:
C＝μεL-1 (6)
wherein epsilon is a dielectric constant, and mu is a magnetic permeability coefficient;
substituting the obtained resistance matrix R, inductance matrix L and capacitance matrix C into the analytic formulas of the impedance matrix Z and the admittance matrix Y in the second step to obtain Z and Y, and obtaining the electromagnetic equivalent matrix Z by first integrating the distance Z and then dividing the integrated distance by the total length ddAnd YdThe following are:
where z is the lateral distance and d is the cable length.
The fourth step is specifically as follows:
solving a first order differential equation set by the equation (1) to obtain:
solving an electromagnetic matrix equivalent to the parallel cable according to the formula (8);
the boundary condition equations are listed:
wherein,
and
is a thevenin equivalent voltage source with z-0 and z-d at two ends of the transmission line, and simultaneously
A far-end crosstalk matrix of a non-parallel cable; the equation shows thevenin equivalence of the ports, and various circuits connected with the ports at the two ends of the cable can be equivalent to the forms of a power supply and an internal resistor, thereby simplifying the analysis process,
combining the equivalent electromagnetic parameter matrix with a second-order moment solving method of the crosstalk of the parallel cable, and obtaining the equivalent electromagnetic parameter matrix through the formulas (8) and (9):
wherein d is the cable length, e is a natural constant, gamma is a diagonal matrix, the diagonal elements of the diagonal matrix are characteristic roots of a matrix (YZ), and P is a matrix formed by characteristic vectors corresponding to the characteristic roots of the matrix (YZ);
solving the crosstalk matrix in turn according to the formula (10), (11), (12) and (13)
Has the advantages that: compared with the prior art, the invention has the advantages that: firstly, establishing a segmented cascade-based non-parallel cable model, providing an equivalent electromagnetic parameter matrix, and enabling the non-parallel electromagnetic parameter matrix to be equivalent by using parallel cable parameters, so that the problem of predicting the non-parallel wiring harness crosstalk is solved; secondly, by predicting the size and the actual hazard degree of the electromagnetic crosstalk, the method has important theoretical and engineering significance on the efficient operation of the electrical equipment, accurately predicts the crosstalk, is beneficial to rapidly predicting and finding potential crosstalk problems in the early stage of design, and prevents the problems in the bud; meanwhile, as a basis for designing crosstalk suppression measures, a theoretical basis is provided for implementing the remedial measures of crosstalk suppression in the testing stage after the electrical equipment is manufactured, so that the stability of the equipment system is improved.
Drawings
FIG. 1 is a schematic diagram of spatial position parameter acquisition between non-parallel cables;
FIG. 2 is a schematic diagram of a parallel cable crosstalk analysis model;
FIG. 3 is a schematic diagram of a non-parallel cable segment cascade model;
fig. 4 is a schematic diagram of the crosstalk boundary condition of the cable.
Detailed Description
The technical scheme of the invention is further explained by combining the attached drawings.
A crosstalk noise prediction method for non-parallel cables, comprising the steps of:
the first step is as follows: as shown in fig. 1, spatial position information between the cables, including a tilt angle, a proximal end distance, a distal end distance, a cable length, a ground clearance height, and the like, is obtained by using the position sensor. The specific sensor model is determined according to the predicted cable type, and detailed description is not provided in the invention, but only relevant space parameters can be measured;
the second step is that: establishing a multi-conductor model of unit length, paralleling analytical formulas of an impedance matrix Z and an admittance matrix Y of the cable corresponding to the unit length with respect to a basic electromagnetic matrix of the cable, and deriving a basic electromagnetic matrix element analytical formula of the cable by combining a multi-conductor transmission line theory and acting space parameters; on the basis of meeting the engineering precision, the electromagnetic matrix of each section can be solved by using an analytical expression. R in the parallel cable crosstalk model shown in FIG. 2iiAnd rjjResistance per unit length of cable,/iiAnd ljjRepresenting the self-inductance of the cable per unit length,/ijThen represents the mutual inductance per unit length between the cables; c. Cii、cjjAnd gii、gjjRespectively representing the self-capacitance and self-conductance of the cable per unit length, cijAnd gijThen the corresponding mutual capacitance and mutual conductance are represented. Z represents the total length of the cable across, dz represents the differential length of the MTLs, and the corresponding voltage and current phasors of each cable are also obtained.
The analytic expressions of the impedance matrix Z and the admittance matrix Y are as follows:
wherein, R is a resistance matrix, L is an inductance matrix, G is a conductance matrix, C is a capacitance matrix, ω is 2 pi f, f is a frequency, R, L, G, C is a basic parameter matrix of the cable, since the G matrix representing electromagnetic induction is very small, it is generally directly ignored, when the R, L, C matrix is solved, then the Z, Y matrix can also be solved.
The element calculation formula of the resistance matrix R is as follows:
(2) the formula is divided into two parts according to the relation between the radius of the solid core wire and the skin depth, wherein sigma is the conductivity of the wire core conductor, rw is the radius of the solid core round conductor, and delta is the skin depth; for a stranded wire, one can consider the parallel connection of multiple solid wires with radius rws (rws is the radius of one wire core).
The element calculation formula of the inductance matrix L is as follows:
wherein h isiAnd hjFor the height of the cable above the ground, sijIs the actual distance between the two cables;
sij＝b+z·tan(a)
wherein a is the intersection angle of the cables, b is the minimum distance between the cables, and z is the transverse distance
The third step: the method for predicting the non-parallel multi-conductor crosstalk based on the segmented cascade is characterized in that an analog method is used for differentiating a non-parallel cable, namely the segmented cascade, a non-parallel electromagnetic parameter matrix is equivalent to a parallel electromagnetic parameter matrix, and an electromagnetic equivalent matrix is solved; as shown in fig. 3, the cable is cut into m parts. If the value of m is infinite, each of the conductors between the conductors may be parallel to each other. It follows that the parallel multi-conductor transmission line equation for each segment still holds.
Substituting the electromagnetic matrix elements obtained in the second step into analytical expressions of a resistance matrix R and an inductance matrix L, wherein the analytical expressions of the resistance matrix R and the inductance matrix L are as follows:
after the inductance matrix L is obtained, substituting into the analytic expression of the capacitance matrix C:
C＝μεL-1 (6)
wherein epsilon is a dielectric constant, and mu is a magnetic permeability coefficient;
substituting the obtained resistance matrix R, inductance matrix L and capacitance matrix C into the analytic formulas of the impedance matrix Z and the admittance matrix Y in the second step to obtain Z and Y, and obtaining the electromagnetic equivalent matrix Z by first integrating the distance Z and then dividing the integrated distance by the total length ddAnd YdThe following are:
wherein z is the lateral distance and d is the cable length
The fourth step: and solving the non-parallel cable crosstalk by combining the boundary condition matrix.
Solving a first order differential equation set by the equation (1) to obtain:
solving an electromagnetic matrix equivalent to the parallel cable according to the formula (8);
from the boundary condition matrix shown in FIG. 4, the boundary condition equations are listed:
wherein,
and
thevenin with z-0 and z-d at two ends of transmission lineEquivalent voltage source, while
A far-end crosstalk matrix of a non-parallel cable; the equation shows thevenin equivalence of the ports, and various circuits connected with the ports at the two ends of the cable can be equivalent to the forms of a power supply and an internal resistor, thereby simplifying the analysis process,
combining the equivalent electromagnetic parameter matrix with a second-order moment solving method of the crosstalk of the parallel cable, and obtaining the equivalent electromagnetic parameter matrix through the formulas (8) and (9):
wherein d is the cable length, e is a natural constant, gamma is a diagonal matrix, the diagonal elements of the diagonal matrix are characteristic roots of a matrix (YZ), and P is a matrix formed by characteristic vectors corresponding to the characteristic roots of the matrix (YZ);
solving the crosstalk matrix in turn according to the formula (10), (11), (12) and (13)
Claims (1)
1. A crosstalk noise prediction method for a non-parallel cable, comprising the steps of:
the first step is as follows: acquiring space position parameters between non-parallel cables;
the second step is that: establishing a multi-conductor model of unit length, paralleling analytical expressions of an impedance matrix Z and an admittance matrix Y of the cable corresponding to the unit length with respect to a basic electromagnetic matrix of the cable, and deriving an element analytical expression of the basic electromagnetic matrix of the cable;
the third step: the non-parallel electromagnetic parameter matrix is equivalent by using a parallel electromagnetic parameter matrix, and an electromagnetic equivalent matrix is solved;
the fourth step: solving the non-parallel cable crosstalk by combining the boundary condition matrix;
in the first step, the spatial position parameters comprise an inclination angle, a near-end distance, a far-end distance, a cable length and a ground clearance;
in the second step, the analytic expressions of the impedance matrix Z and the admittance matrix Y are:
wherein, R is a resistance matrix, L is an inductance matrix, G is a conductance matrix, C is a capacitance matrix, ω is 2 pi f, and f is frequency;
the element calculation formula of the resistance matrix R is as follows:
wherein σ is the electrical conductivity of the core conductor, rwIs the radius of the solid core round conductor, δ is the skin depth;
the element calculation formula of the inductance matrix L is as follows:
wherein h isiAnd hjFor the height of the cable above the ground, sijIs the actual distance between the two cables;
sij＝b+z·tan(a)
wherein a is the intersection angle of the cables, b is the minimum distance between the cables, and z is the transverse distance;
and the third step is to substitute the electromagnetic matrix elements obtained in the second step into analytical expressions of a resistance matrix R and an inductance matrix L, wherein the analytical expressions of the resistance matrix R and the inductance matrix L are as follows:
after the inductance matrix L is obtained, substituting into the analytic expression of the capacitance matrix C:
C＝μεL-1 (6)
wherein epsilon is a dielectric constant, and mu is a magnetic permeability coefficient;
substituting the obtained resistance matrix R, inductance matrix L and capacitance matrix C into the analytic formulas of the impedance matrix Z and the admittance matrix Y in the second step to obtain Z and Y, and then obtaining the electromagnetic equivalent matrix ZdAnd YdThe following are:
wherein z is the transverse distance and d is the cable length;
the fourth step is specifically as follows:
solving a first order differential equation set by the equation (1) to obtain:
solving an electromagnetic matrix equivalent to the parallel cable according to the formula (8);
the boundary condition equations are listed:
wherein,
and
is a thevenin equivalent voltage source with z-0 and z-d at two ends of the transmission line, and simultaneously
A far-end crosstalk matrix of a non-parallel cable;
combining the equivalent electromagnetic parameter matrix with a second-order moment solving method of the crosstalk of the parallel cable, and obtaining the equivalent electromagnetic parameter matrix through the formulas (8) and (9):
wherein d is the cable length, e is a natural constant, gamma is a diagonal matrix, the diagonal elements of the diagonal matrix are characteristic roots of a matrix (YZ), and P is a matrix formed by characteristic vectors corresponding to the characteristic roots of the matrix (YZ);
solving the crosstalk matrix in turn according to the formula (10), (11), (12) and (13)
Priority Applications (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| CN201810179567.8A CN108345753B (en) | 2018-03-05 | 2018-03-05 | Crosstalk noise prediction method for non-parallel cable |
Applications Claiming Priority (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| CN201810179567.8A CN108345753B (en) | 2018-03-05 | 2018-03-05 | Crosstalk noise prediction method for non-parallel cable |
Publications (2)
| Publication Number | Publication Date |
|---|---|
| CN108345753A CN108345753A (en) | 2018-07-31 |
| CN108345753B true CN108345753B (en) | 2021-09-07 |
Family
ID=62957840
Family Applications (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| CN201810179567.8A Active CN108345753B (en) | 2018-03-05 | 2018-03-05 | Crosstalk noise prediction method for non-parallel cable |
Country Status (1)
| Country | Link |
|---|---|
| CN (1) | CN108345753B (en) |
Families Citing this family (8)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN109710995A (en) * | 2018-12-07 | 2019-05-03 | 江苏益邦电力科技有限公司 | A kind of crosstalk noise prediction technique for random arrangement cable |
| CN109992819A (en) * | 2019-01-25 | 2019-07-09 | 南京师范大学镇江创新发展研究院 | A kind of cable cross-talk processing method based on adaptive intersection approximate algorithm |
| CN110516362A (en) * | 2019-08-28 | 2019-11-29 | 哈尔滨工程大学 | A kind of FDTD method for solving of multi-conductor transmission lines magnetic distribution |
| CN110531171B (en) * | 2019-08-28 | 2021-04-06 | 湖南大学 | Calculation method for determining cable crosstalk critical wiring distance |
| CN110554247A (en) * | 2019-08-28 | 2019-12-10 | 广州广电计量检测股份有限公司 | crosstalk simulation modeling method and simulation model of non-parallel cable |
| CN110909481B (en) * | 2019-11-29 | 2023-05-23 | 北京应用物理与计算数学研究所 | Complex cable bundle distribution parameter modeling method based on moment method |
| CN111368436B (en) * | 2020-03-06 | 2023-07-21 | 重庆邮电大学 | Time domain modeling analysis method for electromagnetic coupling effect of bending line on conducting plate |
| CN114722552B (en) * | 2022-06-09 | 2022-11-08 | 深圳荣耀智能机器有限公司 | Cable length verification method and electronic equipment |
Family Cites Families (5)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US7733198B1 (en) * | 2007-05-15 | 2010-06-08 | Sandia Corporation | Microfabricated bulk wave acoustic bandgap device |
| CN103048563B (en) * | 2012-12-19 | 2016-02-10 | 南京航空航天大学 | The method for quick predicting of a kind of right angle above the ground cable bundle terminal crosstalk |
| CN104007327B (en) * | 2014-06-18 | 2017-03-15 | 吉林大学 | A kind of method of fast prediction vehicle harness time-domain radiation susceptibility |
| CN104849572B (en) * | 2015-05-24 | 2017-11-03 | 浙江大学 | A kind of HW High Way cross talk restraining method decomposed based on electromagnetic field mode |
| CN105956309B (en) * | 2016-05-13 | 2019-05-14 | 南京航空航天大学 | A kind of " encoder " design method for eliminating the stable state crosstalk of transmission line distal end |
-
2018
- 2018-03-05 CN CN201810179567.8A patent/CN108345753B/en active Active
Also Published As
| Publication number | Publication date |
|---|---|
| CN108345753A (en) | 2018-07-31 |
Similar Documents
| Publication | Publication Date | Title |
|---|---|---|
| CN108345753B (en) | Crosstalk noise prediction method for non-parallel cable | |
| Gustavsen et al. | Parameter determination for modeling system transients-Part II: Insulated cables | |
| CN110531171B (en) | Calculation method for determining cable crosstalk critical wiring distance | |
| Li et al. | Measurement-based modeling and worst-case estimation of crosstalk inside an aircraft cable connector | |
| Tatematsu | A technique for representing coaxial cables for FDTD-based surge simulations | |
| Kurokawa et al. | Behavior of overhead transmission line parameters on the presence of ground wires | |
| CN110110497A (en) | A kind of nondestructive evaluation method of power transmission cable and attachment high frequency electrical parameter | |
| JP2004030598A (en) | System for predicting electrical action of multi-port device having balanced device port | |
| CN104865441B (en) | A kind of crosstalk frequency spectrum computational methods | |
| CN109710995A (en) | A kind of crosstalk noise prediction technique for random arrangement cable | |
| Maier et al. | A high-frequency simulation model of a MV cable joint | |
| Ardon et al. | MoM and PEEC method to reach a complete equivalent circuit of a static converter | |
| Radja et al. | Improved rlmc-circuit hf-dependent parameters using fe-em computation dedicated to predict fast transient voltage along insulated windings | |
| CN102979512B (en) | Black box analyzing method and device for acquiring transmission characteristic of logging cable | |
| Ma et al. | Predicting Radiated Emissions from a Complex Transportation System Wiring Harness | |
| Stevanović et al. | Multiconductor cable modeling for EMI simulations in power electronics | |
| McGahay | Conformal mapping solution for interdigital comb capacitors between ground planes | |
| Lu et al. | Calculation of Capacitance Matrix of Non-uniform Multi-conductor Transmission Lines based on S-parameters | |
| Almas et al. | Modeling of a power transformer winding for deformation detection based on frequency response analysis | |
| CN110909481A (en) | Complex cable bundle distribution parameter modeling method based on moment method | |
| Skibin et al. | High frequency cable models for system level simulations in power electronics applications | |
| Negri et al. | Inductively Coupled In-Circuit Measurement of Multiport Admittance Parameters | |
| Patel et al. | MoM-SO: A fast and fully-automated method for resistance and inductance computation in high-speed cables | |
| Petersen et al. | Comparison of experimental measurements of current distribution in a flat conductor with simulated results from the partial inductance method | |
| Franchet et al. | Modelling the effect of a defect on crosstalk signals under the weak coupling assumption |
Legal Events
| Date | Code | Title | Description |
|---|---|---|---|
| PB01 | Publication | ||
| PB01 | Publication | ||
| SE01 | Entry into force of request for substantive examination | ||
| SE01 | Entry into force of request for substantive examination | ||
| GR01 | Patent grant | ||
| GR01 | Patent grant |