KR20180098395A - 이미지 품질을 최적화하는 디스플레이 디바이스 및 방법 - Google Patents

Abstract

본 발명은 2차원 및/또는 3차원 물체의 홀로그램 재구성을 위한 디스플레이 디바이스에 관한 것이다. 물체는 복수의 물체 점을 포함한다. 디스플레이 디바이스는 조명 유닛, 공간 광 변조기 디바이스 및 분리기를 포함한다. 조명 디바이스는 충분히 코히어런트한 광을 방출한다. 디스플레이될 물체 점들의 서브-홀로그램은 공간 광 변조기 디바이스의 픽셀들로 인코딩된다. 분리기는 인접한 물체 점들의 서브-홀로그램들에 의해 생성된 관찰자의 눈에서 인접한 점 확산 함수들을, 인접한 점 확산 함수들이 서로에게 상호 인코히어런트가 되도록 분리하기 위해 제공된다.

Description

이미지 품질을 최적화하는 디스플레이 디바이스 및 방법

본 발명은 망막의 물체 간 점 크로스토크(retinal inter object point crosstalk)를 억제할 수 있는 재구성 장면의 화질을 최적화 및 향상시키는 디스플레이 디바이스 및 방법에 관한 것이다.

본 디스플레이 디바이스는 2차원(2D) 및/또는 3차원(3D) 이미지를 디스플레이하도록 적응되어 있다. 2차원 이미지 또는 3차원 이미지는 또한 2차원 또는 3차원 콘텐츠 또는 영화를 포함한다는 것을 이해해야 한다.

본 발명의 적용 분야는 바람직하게는 홀로그램 이미지의 3차원 표시(presentation)를 위한 디스플레이 디바이스를 포함한다.

2차원 이미지 또는 영화/비디오의 표시를 위한 상업적으로 이용 가능한 디스플레이 디바이스에서, 고분해능로 전체 표면의 밝고 균일한 조명을 실현하는 것이 필요하다. 디스플레이 패널의 역할을 하는 공간 광 변조기 디바이스는 넓은 각도 범위의 광을 방출해야 한다. 표시될 정보는 디스플레이 디바이스의 공간 광 변조기 디바이스에 기록된다. 광원 유닛을 포함하는 조명 유닛에 의해 방출된 광은 공간 광 변조기 디바이스에 기록되는 정보로 변조되고, 공간 광 변조기 디바이스는 종종 동시에 스크린 또는 디스플레이 패널로서 작용한다. 그러므로, 공간 광 변조기 디바이스 상에 광 빔의 평행한 입사를 엄격하게 보장하고 공간 광 변조기 디바이스의 높은 재생률(refresh rate)을 달성할 필요가 있다. 공간 광 변조기 디바이스에 기록된 정보의 3차원 표시의 고품질을 달성하기 위해, 공간 광 변조기 디바이스의 전체 표면의 균일한 조명 이외에, 적어도 조명 유닛 외부에서 결합된 파면(wave front)의 정의된 콜리메이션이 필요하다. 이는 생성될 재구성의 형태로의 홀로그램 표시를 위해 매우 중요하다. 예를 들어, 3차원 장면의 물체 점들로 구성된 물체일 수 있는 홀로그램 정보는 공간 광 변조기 디바이스의 픽셀에서 진폭 및 위상 값의 형태로 인코딩된다. 인코딩된 물체 점들은 공간 광 변조기 디바이스에 의해 방출되는 웨이브 필드(wave field)에 의해 재구성된다.

파면의 위상 및 진폭 모두를 변조시키는 역할을 하는 복소 홀로그램 값은 종래의 공간 광 변조기 디바이스의 단일 픽셀에서 만족스럽게 직접 디스플레이될 수 없다. 그러나, 픽셀 당 단지 하나의 값의 변조, 즉 위상 전용 변조 또는 진폭 전용 변조는 바람직하게 움직이는 3차원 장면의 불충분한 홀로그램 재구성을 야기한다. 복소수 홀로그램 값의 직접적이고 따라서 (일반화된 파라미터의 의미에서) 최적인 표시는 바람직하게는 공간 광 변조기 디바이스에서 동시에 동일한 평면에서 복소수 값 변조에 의해서만 달성될 수 있다.

그러나, 바람직하게는 개개의 물체 점 또는 물체 점 구름으로 구성된 3차원 물체의 홀로그램 재구성은 재구성된 물체를 바라 보는 관찰자의 눈의 망막에서 물체 점 간 크로스토크를 유발하여, 설계된 망막 이미지에 추가된 입자성(graininess)을 도입함으로써 표시의 화질을 감소시킨다. 여기서, "망막 물체 점 간 크로스토크(retinal inter object point crosstalk)"라는 용어는 "스페클(speckle)"이라는 용어와 동일한 것을 기술하지 않는다는 것을 지적해야 한다. 언뜻 보기에는 이것이 가능할 수 있지만 면밀한 조사에서 근본적인 차이가 있다.

스페클은 실제 랜덤 3차원(3D) 간섭 효과이다. 다시 말해, 스페클 효과는 동일 주파수의 코히어런트(coherent) 파면의 간섭을 야기하며, 이는 합쳐져서 진폭이 랜덤하게 변하는 결과적인 파면을 얻는다. 예를 들어, 거친 표면에 레이저 광을 비추어 스페클을 생성할 수 있다. 두 종류의 스페클, 객관적인(objective) 스페클 및 주관적인(subjective) 스페클이 있다. 객관적인 스페클은 3D 공간에서 생성된 3D 간섭 패턴으로서, 즉 거친 표면으로부터 산란된 코히어런트 광이 다른 표면 또는 평면 상에 있을 때 정의된다. 주관적인 스페클은 개개 물체에 의해 인식되는 간섭 패턴으로서, 즉 코히어런트 광으로 조명된 거친 표면이 이미징된 다음 스페클 패턴이 이미지 평면에서 관찰될 때 정의된다. 이미징 수단이 사용된다. 스페클이라는 용어는 예를 들어, Goodman, J. W.(1976), "스페클의 근본적인 성질(Some fundamental properties of speckle)", JOSA, 66(11), 1145-1150에 기술되어 있다.

용어 "망막 물체 점 간 크로스토크"는 인접한 점 확산 함수(point spread function, PSF)의 코히어런트 중첩 때문이다. 공간에서 생성된 인접한 물체 점들은 물체 점들을 바라 보는 사용자/관찰자의 눈의 망막에 존재하는 인접한 점 확산 함수로 변환된다. 관찰자의 눈의 망막에서 생성된 간섭 패턴은 WO 2004/044659 A1에 기재된 서브-홀로그램 인코딩 기술을 사용함으로써 공간에서 생성된 2개의 인접한 3D 물체 점을 나타내는 인접한 점 확산 함수의 복소수 값 분포에 의존한다. 예를 들어, 약간의 위상 변화조차도 관찰자의 눈의 망막에서 얻어진 강도 분포(intensity distribution)를 현저하게 변화시킬 수 있으며, 따라서 관찰자에 의해 검출될 수 있다. 상호 코히어런스 및 상호 위상차에 의존하는 인접한 점 확산 함수의 이러한 중첩을 설명하는 예는 G. Futterer의 문서 "UV-Shearing Interferometrie zur Vermessung lithographischer "Phase Shift" Masken und VUV-Strukturierung", Progress in modern optics, Vol. 4, IOIP, MPF, Universitat ErlangenNurnberg, 2005, ISBN: 3-932393-61-2의 섹션 4.1.1에서 찾을 수 있다.

망막 물체 점 간 크로스토크의 이러한 효과는 분석적으로 고려될 수 있으며 가시적인 입자성이 없는 3D 물체 점 또는 3D 물체 점 클라우드의 설계된 강도 분포를 달성하기 위해 망막 점 확산 함수를 조정(tailor)할 수 있다. 예를 들어 망막과 같은 검출기 평면으로 전달되는 물체의 위상 및 강도 분포를 조정함으로써 타겟 강도 프로파일을 생성할 수 있는 방법을 설명하는 예는 G. Futterer의 문서 "UV-Shearing Interferometrie zur Vermessung lithographischer "Phase Shift" Masken und VUV-Strukturierung", Progress in modern optics, Vol. 4, IOIP, MPF, Universitat ErlangenNurnberg, 2005, ISBN: 3-932393-61-2의 섹션 1.1.1에서 찾을 수 있다.

스페클이라는 용어는 망막 물체 점 간 크로스토크로 인한 영향을 설명하기 위해 여전히 종종 오해의 소지가 있게 사용된다. 내부 물체 점 간 크로스토크에 추가하여 나타날 수 있는 스페클은 망막 물체 점 간 크로스토크라는 용어와 명확하게 구분되어야 한다. 이 2개의 서로 다른 용어는 위에서 언급한 것처럼 물리학적인 의미에서 기본적으로 상이한 두 가지 현상을 기술한다.

공지된 선행 기술 문서는 컬러 필터(들) 및 하나의 RGB(적색, 녹색, 청색) 컬러 필터 그룹을 갖는 홀로그램의 약 1/20도 내에서의 1차원(1D) 인코딩 또는 약 1/20도에서 약간 작게까지 수평 각도 범위에 걸쳐 있는 수직 서브-홀로그램을 가진 컬러 순차 1D 인코딩된 RGB를 기술하며, 약 1/20도는 1/40도 각도 범위보다 훨씬 큰 것을 의미한다.

문서 WO 2010/052331 A1은 컬러 필터를 갖는 디스플레이를 기술한다. RGB 베이스 컬러의 평행 수직 컬러 스트라이프(stripe)를 갖는 컬러 필터가 이미지 분리 수단(image separating means)에 할당된다. 컬러 스트라이프는 컬러 필터 내에서 주기적으로 수평으로 반복된다. 광 변조기는 관찰자의 좌안 및 우안에 대해 수 개의 픽셀 열로 인터레이스된 각 컬러에 대한 2개의 홀로그램의 시퀀스를 포함한다. 컬러 필터와 홀로그램의 주기는 동일한 확장 정도로 서로에 대해 배열되며, 컬러 스트라이프 및 상기 컬러 스트라이프의 컬러의 홀로그램을 갖는 적어도 2개의 픽셀 열이 분리 요소(separating element)에 할당된다.

종래 기술의 다른 문서에서, 직교 편광된 편광 필터가 공간 광 변조기 디바이스에 제공되어 공간 광 변조기 디바이스의 이웃하는 픽셀들 사이의 크로스토크를 감소시키는 디스플레이 디바이스가 개시되어 있다. 그러나 크로스토크가 망막 물체 점 간 크로스토크와 혼동되어서는 안된다는 것을 여기서 주목해야 한다.

문서 US 8,441,703 B2는 재구성된 점 확산 함수의 오버랩을 나타내지 않기 위해 서로 적당히 큰 거리로 배치되는 공간적으로 얇은(thinned) 물체 점을 재구성하는 방법을 설명한다.

따라서, 본 발명의 목적은 홀로그램으로 재구성된 2차원 및/또는 3차원 물체의 화질을 최적화 및 향상시키는 디스플레이 디바이스 및 방법을 제공하는 것이다. 특히, 본 발명의 목적은, 점 확산 함수의 사이드 로브(side lobe)를 억제할 수 있고, 망막 물체 점 간 크로스토크를 저감하여, 향상된 또는 최적의 화질을 얻을 수 있는 디스플레이 디바이스 및 방법을 제공하는 것이다.

이러한 이유로, 본 발명에 따른 목적은 청구항 1의 특징에 의해 달성된다.

2차원 및/또는 3차원 물체의 홀로그램 재구성을 위한 디스플레이 디바이스는 복수의 물체 점들을 포함한다. 디스플레이 디바이스는 조명 유닛, 공간 광 변조기 디바이스 및 분리기(separator)를 포함한다. 조명 유닛은 공간 광 변조기 디바이스에 입사하는 충분한 코히어런트한 광을 방출한다. 공간 광 변조기 디바이스 상에 디스플레이될 물체 점들의 서브-홀로그램은 픽셀로 인코딩된다. 향상된 화질을 달성하기 위하여 인접한 점 확산 함수들이 서로에게 상호 인코히어런트되도록, 분리기는 인접한 물체 점들의 서브-홀로그램에 의해 발생된 관찰자의 눈에서 인접한 점 확산 함수들을 분리하기 위해 제공된다.

망막상의 설계된 강도 분포의 최적화는 예를 들어 위상 및 진폭 적응을 포함하는 상호 코히어런트한 물체 점 최적화에 의해, 그리고 최종 설계/타겟 강도 분포를 얻기 위해 물체 점들의 상호 인코히어런트 서브 세트를 그들의 강도 분포에서 적응시킴으로써 달성될 수 있다. 이는 상호 코히어런트한 점 확산 함수의 합 강도 분포, 예를 들어, 1/30도로 각도 이격된 것들이 이상적인 3D 콘텐츠의 일부를 나타내는 타겟 강도 분포를 얻기 위해 점 확산 함수의 복소수 값 분포를 수정함으로써 최적화될 수 있다는 것을 의미한다. 이제 최적화된 물체 점의 코히어런트 서브 세트는 인코히어런트한 다른 서브 세트와 중첩된다. 따라서, 물체 점들의 상이한 서브-세트는 서로에 대해 인코히어런트하다.

복소수 값 공간 광 변조기 디바이스(SLM(C-SLM))를 사용할 수 있다. 공간 광 변조기 디바이스는 예를 들어, 샌드위치 형 공간 광 변조기 디바이스일 수 있으며, 이는 예를 들어, 진폭을 변조하는 제1 공간 광 변조기(A-SLM) 및 위상을 변조하는 제2 공간 광 변조기(P-SLM)를 포함하거나, 그 반대를 포함한다.

따라서, 본 발명에 따른 주요 아이디어는 최상의 상황에서 1/60도인 인간의 눈의 각도 분해능 한도 내에서 각으로 배치되는 이미징된 3차원(3D) 물체 점들과 동등한 재구성된 점 확산 함수의 상호 인코히어런트 서브 세트를 사용하는 것이다.

본 발명의 더욱 바람직한 실시 예 및 개선점은 종속항에 정의된다.

본 발명의 바람직한 제1 실시 예에서, 디스플레이 디바이스는 물체가 적어도 2개의 물체 평면으로 분할되고, 각각의 물체 평면은 서로에 대해 각 변위(angularly displaced) 또는 시프트되는, 적어도 2개, 바람직하게는 3개의 수직 서브 세트 및 적어도 2개, 바람직하게는 3개의 수평 서브 세트로 분할된다.

공간적으로 얇은 물체 점들을 재구성하는 것이 제공된다. 그것은 예를 들어, 인간의 눈의 각도 분해능인 1/60도보다 큰 1/30도 범위의 물체 점 격자의 각도 분해능으로 재구성하는 것을 의미한다. 또한, 관찰자의 눈의 망막 상에 일어나는, 물체 점 간 크로스토크를 겪는, 이미지 품질을 향상시키기 위해 서로에 대해 각 변위 또는 시프트되는 2개 또는 바람직하게는 3개의 수직 서브 세트 및 2개 또는 바람직하게는 3개의 수평 서브 세트를 사용하는 것이 제공된다.

도 2에는 망막 물체 점 간 크로스토크의 원인인 점 확산 함수의 사이드 로브(side lobe) 간섭의 도면이 도시되어 있다. 상세히, 도 2는 에어(Airy)-함수를 사용하여 기술된 인접한 점 확산 함수의 중첩을 도시한다. 실선은 광학 시스템의 분해능 한계에서 인코히어런트 중첩을 나타내며, 이는 인간의 눈의 경우 1/60도 각도 간격과 동등하다. 도 2의 파선은 분해능 한계에서 2개의 점 확산 함수의 코히어런트 중첩을 나타낸다. 이 2개의 코히어런트 점 확산 함수 간의 상대적인 위상차는 제로이다. 두 점 사이의 중심에 존재하는 강도 감소의 백분율은 인코히어런트 경우와 동일하며, 이는 강도 분포의 중심의 좌측 및 우측 편에 존재하는 피크 강도의 약 75%이다. 점선은 분해능 한계에서 2개의 점 확산 함수의 코히어런트 중첩을 보여준다. 이 2개의 코히어런트 점 확산 함수 간의 상대적인 위상차는 π(Pi)이다. 이 경우 2개의 점 확산 함수 사이에 제로의 강도 값이 있다. 도 2는 코히어런트 경우에 상호 코히어런스 및 상호 위상 차가 인간의 눈의 망막에서 얻은 강도 분포의 정의에 있어 중요하다는 것을 보여준다.

3차원 물체 점을 나타내는 인접한 망막 점 확산 함수는 서로 간섭한다. 인접한 망막 점 확산 함수의 간섭을 방지 또는 제거하는 한 가지 방법은 생성된 회절 패턴의 사이드 로브를 감소시키거나(reduce) 약화시켜(diminish), 점 확산 함수의 외부 중첩 구역에서의 간섭을 감소시키는 것이다. 그러나, 일반적으로 망막 물체 점 간 크로스토크의 문제는 그러한 동작에 의해 해결되지 않는다. 시작으로서, 회절 패턴의 사이드 로브가 감소되어 물체 강도 분포를 달성한다. 코히어런트 점 확산 함수들이 함께 더 가깝게 이동하고 따라서 오버랩 영역을 확대하는 경우, 도입된 위상 시프트는 획득된 강도 분포를 정의한다. 예를 들어, 위상 시프팅 마스크에 사용되는 π(Pi)의 상대적 위상 시프트는 2개의 인접한 물체 점들 사이에 어두운 선을 생성하고 서로에게 인식된 상호 거리를 증가시킬 것이다. 이것은 도 2에 도시되어 있다. 2개의 인접 물체 점 사이의 어두운 선을 피하기 위해 π/2의 상호 위상차를 사용하는 것이 바람직하다. 이것은 최적화를 위한 시작 값으로만 사용될 수 있다는 것을 유의해야 한다. 이것은 또한 재구성된 물체 점 사이에 존재하는 무작위 위상 분포가 바람직하지 않음을 지적한다. π에 근접한 인접 위상차의 값은 재구성된 물체를 바라 보는 관찰자의 눈의 망막에 존재하는 화질을 감소시킨다.

본 발명에 따르면, 관찰자 평면 내의 가상 시야 윈도우(viewing window) 내의 상이한 위치들로부터 볼 수 있는 3차원 물체의 적당한 일정한 강도 분포를 가능하게 하기 위해, 망막 점 확산 함수 PSF의 임의 현저한 오버랩을 회피하여 회절 패턴의 사이드 로브의 형상을 최적화하고, 사이드 로브를 감소시켜 인접한 망막 점 확산 함수 PSF_ij의 상대적 위상차를 최적화하기 위해 상이한 접근법이 제공된다. 인접한 물체 점들 사이의 무작위 상대적 위상 시프트가 인코딩되는 경우, 사용된 위상 범위를 ±π/4 미만으로 제한하는 것이 바람직하다. 이는 또한 3x 또는 4x 1/60도의 상대적 각도 거리에 배치되는 물체 점에 대해서도 사용될 수 있으며, 이는 HD(high definition) 시야라고 불린다.

본 발명의 또 다른 바람직한 실시 예에서, 공간 광 변조기 디바이스에서 1차원 인코딩된 홀로그램 또는 2차원 인코딩된 홀로그램의 경우, 분리기는 컬러 필터 스트라이프 배열(arrangement), 바람직하게는 원색 필터 스트라이프 배열로서 설계될 수 있다는 것이 제공된다.

예를 들어 VPO(vertical parallax only)를 의미하는 1차원(1D) 인코딩을 사용하는 경우, 3차원 장면 또는 3차원 물체의 물체 점을 생성하기 위해 공간 광 변조기 디바이스의 상호 인코히어런트 열이 사용되어야 한다. 이것은 컬러 필터 스트라이프 배열을 사용하고, 또한 시간-순차적(time-sequential) 컬러 생성을 사용하여 실현될 수 있다.

예를 들어 미세 추적을 위해 LC(liquid crystal)-편광 격자가 사용되는 경우, 상이한 컬러가 시간-순차적으로 디스플레이될 수 있다. 이는 또한 본 발명이 일반적으로 컬러 필터 스트라이프 또는 컬러 필터의 사용에 명시적으로 제한되지 않는다는 것을 의미한다.

1/60도 각도 분해능 또는 각 도마다 60개의 물체 점과 동등한 HD(high definition) 분해능에 필요한 수보다 더 많은 공간 광 변조기 디바이스(SLM)의 1차원(1D) 인코딩된 스트라이프를 사용하는 것이 바람직하다. 이는 컬러 필터를 사용하여 실현할 수 있다. 그러나 어떤 경우에는 컬러 필터가 올바른 방법이 아닐 것이다. 컬러 필터를 사용하는 경우, 적어도 2개의 RGB(적색, 녹색, 청색) 필터 스트라이프 세트를 1/60 °의 수평 각도 범위 내에 배치해야 한다. 물체 점은 인터레이스 방식으로 재구성될 수 있다. 따라서, 복수의 물체 점들로 구성된 재구성된 장면을 관찰하는 관찰자의 눈의 망막상에서 재구성된 인접한 물체 점들은 서로 인코히어런트이다.

바람직하게는, 공간 광 변조기 디바이스의 각각의 주요(primary) 서브-홀로그램 또는 초기 픽셀은 적어도 2개의 서브 세트를 나타내고 적어도 두개의 웨이브 필드를 생성하는 적어도 2개의 정의된 부분으로 세분될 수 있다. 다시 말해서, 주요 서브-홀로그램을 포함하는 공간 광 변조기 디바이스 상의 구역(zone) 또는 영역은 적어도 2개의 서브 세트 또는 정의된 부분으로 세분될 수 있다. 컬러 필터 스트라이프의 삼중선(triplet)(RGB)을 각 서브 세트에 지정할 수 있다. 보다 바람직하게는 광 변조기 디바이스의 주요 서브-홀로그램 또는 단일 초기 픽셀에 할당된 컬러 스트라이프의 밀도를 예를 들어, 픽셀 당 3개의 컬러 스트라이프의 원래 밀도의 3배(3x) 또는 4배(4x)로 증가시키는 것이다. 이것은 각각의 주요 서브-홀로그램 또는 각각의 초기 픽셀이 3개 또는 4개의 정의된 부분, 소위 3개 또는 4개의 서브 세트로 세분화되는 것을 의미하고, 컬러 필터 스트라이프의 삼중선(RGB)이 각 정의된 부분 또는 서브 세트로 할당된다.

본 발명의 또 다른 바람직한 실시 예에서, 컬러 필터 스트라이프 배열은 흡수형 염료 기반 필터 배열 또는 유전체 필터 배열인데, 이는 초기 픽셀 또는 주요 서브-홀로그램의 서브 세트에 할당되도록 구조화되는 것이 제공될 수 있다.

컬러 필터 스트라이프 배열 또는 일반적으로 컬러 필터는 복소 변조 웨이브 필드를 제공하는 SLM에 필수인 프레임 속도를 줄이기 위해 사용될 수 있다. 바람직하게는 SLM 픽셀에 정렬된 구조의 흡수형 염료 기반 필터 어레이를 사용하는 것이 가능하다. 현대 코팅 기술은 또한 노치 필터를 스트라이프 배열로 적용하는 것을 가능하게 한다. 이것은 컬러 스트라이프가 원색 RGB(적색, 녹색, 청색) 중 1개만을 투과하면서 2개를 반사할 수 있다는 것을 의미한다. 이는 0.9보다 큰 투과율로 행해질 수 있지만, 이러한 특정 컬러 스트라이프의 다른 2개의 요구되지 않는 파장은 1에 가까운 계수로 반사된다.

유리하게는, 인코딩될 2차원(2D) 홀로그램의 경우, 주요 서브-홀로그램 또는 초기 픽셀의 적어도 2개의 정의된 부분은 픽셀이 수평 또는 수직으로 분리되는 2개의 절반을 형성한다는 것이 제공될 수 있다.

공간 광 변조기 디바이스(SLM)는 변조 요소로서 픽셀을 갖는다. 픽셀은 직사각형, 정사각형 또는 원형 또는 육각형 또는 임의 다른 형상을 가질 수 있다. 이러한 SLM의 픽셀은 적어도 2개의 정의된 부분으로 분할될 수 있다. 픽셀의 이러한 2개의 정의된 부분은 2개의 절반을 형성할 수 있다. 이것은 우측 및 좌측 부분/절반/서브 세트 또는 상부 및 하부 부분/절반/서브 세트를 형성하기 위하여 픽셀을 수평으로 또는 수직으로 분리할 수 있음을 의미한다. 본질적으로, 픽셀의 두 부분 또는 서브 세트가 SLM 외부에서 생성된다. SLM의 우측 서브 세트 및 SLM의 좌측 서브 세트 또는 하부 서브 세트 및 상부 서브 세트는 SLM의 푸리에 평면에서 등가 강도 분포를 생성한다. 다시 말해서, 우측/상부 서브 세트에 대한 진폭 분포의 푸리에 평면에서의 강도 분포 및 좌측/하부 서브 세트에 대한 진폭 분포는 SLM에서 일정 위상이 사용되는 경우 동일하다. 두 가지 푸리에 변환의 위상 값은 이 설명과 관련이 없다. 따라서, SLM의 2개의 서브 세트의 인코히어런트 중첩이 진폭 분포로서 사용된다.

또한, 분리기는 바람직하게는 정의된 편광 상태를 갖는 광을 2개의 패턴화된 광 서브 세트로 변환시키기 위해 패턴화된 리타더(patterned retarder)의 배열로서 설계된다는 것이 유리하게 제공될 수 있다.

패턴화된 리타더의 배열은 예를 들어 선형 편광 상태일 수 있는 초기 편광 상태를 2개의 패턴화된 서브 세트로 변환하기 위해 제공된다. 2개의 패턴화된 서브 세트는 직교 편광 상태를 갖는다. 예를 들어, SLM의 픽셀의 주요 애퍼처, 예를 들어, 정사각형 형상의 픽셀 애퍼처 또는 임의 다른 적합한 형상은 2개의 부분으로 분할된다. 이것은 SLM의 초기 픽셀 카운트가 두 배로 증가하므로 SLM의 초기 픽셀 밀도도 두 배가 됨을 의미한다. 초기 픽셀 또는 주요 서브-홀로그램의 2개의 서브 세트에는 정의된 패턴화된 리타더가 제공된다. 제1 서브 세트에는 a + π/4 패턴화된 리타더가 제공될 수 있으며, 제2 서브 세트에는 a - π/4 패턴화된 리타더가 제공될 수 있다. 각각의 픽셀의 이들 2개의 서브 세트를 포함하는 SLM이 선형 편광된 광으로 조명되면, SLM의 출사 평면에서, 상이한 패턴화된 리타더를 운반하는 SLM의 각각의 픽셀의 2개의 서브 세트와 관련된 2개의 직교 편광된 웨이브 필드가 존재할 것이다. 다시 말해서, 패턴화된 리타더의 배열은 픽셀의 평면 내에 제공될 수 있고, 공간 광 변조기 디바이스의 픽셀에 할당될 수 있으며, 여기서 픽셀의 각 정의된 부분 또는 픽셀의 각 서브 세트에는 패턴화된 리타더의 배열의 정의된 패턴화된 리타더가 제공된다. 픽셀의 적어도 2개의 정의된 부분은 직교 편광을 제공하는 상이한 패턴화된 리타더를 갖는다. 유리하게는, 수평 방향으로만 또는 수직 방향으로만 보여지는 인접한 패턴화된 리타더의 편광 방향은 서로 직교한다.

본 발명의 다른 실시 예에서, 패턴화된 리타더의 배열은 픽셀의 적어도 2개의 정의된 부분에 할당된 패턴화된 편광 필터의 배열로서 설계된다는 것이 제공될 수 있다. 이것은 픽셀의 하나의 서브 세트에 대한 수평으로 배향된 전기장의 투과 및 픽셀의 다른 서브 세트에 대한 수직으로 배향된 전기장의 투과를 허용한다. 따라서 패턴화된 편광 필터들의 배열은 스트라이프 패턴을 제공하며, 스트라이프 패턴은 투과된 편광 상태의 교대하는 방향을 갖는다.

본 발명에 따라, 패턴화된 편광 필터들의 배열은 수직 방향(y 방향) 및 수평 방향(x 방향)을 따라 고정된 패턴인 직교 편광 상태들의 패턴을 제공할 수 있고, 깊이 방향(z 방향)을 따라 패턴은 반전되어 교대로 사용된다는 것이 제공될 수 있다.

물체 점은 공간의 상이한 그리드에서 생성될 수 있다. 3차원 공간에서 물체의 깊이 평면은 교대하는 할당 패턴을 가질 수 있다. 이것은 동일한 x 좌표 및 동일한 y 좌표를 갖지만 인접한 깊이 평면에 배치되는 물체 점이 바람직하게는 직교 편광 상태를 가질 수 있다는 것을 의미한다. 즉, 편광 상태를 나타내는 물체의 깊이 평면에 대한 할당 패턴은 교대로 z 좌표를 따라 사용될 수 있다. 따라서, 편광 상태는 인접한 z 평면에 대해 반전된다. 그러나 가장 간단한 방법은 수직 방향과 수평 방향을 따라 고정 패턴을 사용하고, 관찰자와의 거리 또는 물체가 분할되는 상이한 z 평면들의 거리인 z 좌표(깊이 좌표)를 따라 교대로 반전시키는 것일 수 있다.

본 발명의 또 다른 유리한 실시 예에서, 디스플레이 디바이스는 광의 전파 방향에서 보았을 때, 공간 광 변조기 디바이스 뒤에 배치되어, 2개의 상호 인코히어런트 웨이브 필드를 포함하는 단일 출사(exit) 편광 상태를 갖는 광을 제공하는 비-패턴화된 리타더를 포함하는 것이 제공될 수 있다.

바람직하게는 편광 필터로서 설계될 수 있는 SLM 뒤에 배치된 비-패턴화된 리타더를 추가하는 것은, 2개의 상호 인코히어런트 웨이브 필드를 포함하는 광의 단일 출사 편광 상태를 제공한다. 이 2개의 상호 인코히어런트 웨이브 필드는 3차원(3D) 물체 또는 장면의 일부를 포함하거나 운반한다.

또한, 본 발명에 따른 디스플레이 디바이스는 물체 점을 나타내는 서브-홀로그램의 계산에서 정의된 각도 범위 내에서 물체 점을 측 방향으로 시프트하기 위해 쐐기 함수(wedge function)가 사용되는 방식으로 제공될 수 있다.

2개의 직교 편광을 실현하기 위해, 서브-홀로그램에서 쐐기 함수를 인코딩할 수 있는데, 이는 관찰자 평면에서 시야 윈도우에 걸치는 각도 범위 내에서 물체 점을 측 방향으로 시프트할 수 있다. 홀로그램을 SLM으로 2차원(2D) 인코딩하기 위해, 쐐기 함수의 인코딩은 수평 방향뿐만 아니라 수직 방향을 따라 수행될 수 있다. 다시 말해서, 예를 들어, 픽셀의 정방형(quadratic)/정사각형(square) 영역의 좌측 및 우측 분리는 인접한 직교 편광된 망막 점 확산 함수의 좌측 및 우측 분리인 수평 분리를 생성할 수 있다. 픽셀 영역의 상부 및 하부 분리는 인접한 직교 편광된 망막 점 확산 함수의 상부 및 하부 분리인 수직 분리를 생성할 수 있다. 이는 또한 픽셀의 직사각형 형상 또는 임의 다른 적절한 픽셀 형상에 적용될 수 있다.

홀로그램의 1차원(1D) 인코딩과는 대조적으로, 홀로그램의 2차원(2D) 인코딩은 임의 모양의 2차원 위상 쐐기 함수의 실현 가능성을 제공한다. 잠재적인 2차원 쐐기 분포의 서브 세트만 필요하다. 즉, 쐐기 함수는 임의 형상의 2차원 위상 쐐기 함수일 수 있다.

본 발명의 또 다른 실시 예에서, 개별 물체 점에 대한 파면의 복소수 값의 상대적 위상은, 물체의 인접한 물체 점을 나타내는 점 확산 함수에 의해 생성되는 관찰자의 눈에서의 총 강도 분포와 타겟 강도 분포 사이의 차이가 최소화되는 방식으로 정의된다. 망막 상의 물체 점의 계산을 통해 이를 수행할 수 있다. 너무 많은 강도가 있는 영역에서는 망막 상의 강도가 감소되고 강도가 너무 낮은 영역에서는 강도가 증가된다. 다시 말해서, 강도의 실제 분포는 강도의 타겟 분포에 적응된다.

물체 또는 장면의 개별 물체 점의 상대적 위상, 즉 상호 위상차는 "관찰자의 눈의 망막의 평면에서 타겟 강도 분포(should be/target intensity distribution in the plane of the retina of the eye of the observer) I(X, Y)_retina" 및 "눈의 망막의 평면에서 총 강도 분포(is/total intensity distribution in the plane of the retina of the eye) I(X, Y)_retina"의 차이를 최소화하는 방식으로 선택될 수 있다. 분석 모델을 사용하여 최적의 위상과 강도를 직접 계산할 수 있다. 이러한 분석 모델을 사용할 수 없는 경우 다음 절차를 사용할 수 있다. 망막 물체 점 간 크로스토크가 아직 고려되지 않은 최적화된 이미지는 예를 들어, WPM(wave propagation method)을 사용하거나 프레넬 변환(Fresnel transformation)을 사용함으로써 모델에서 망막으로 전파될 수 있다. 다음으로, 타겟 강도 분포와 총 강도 분포 사이의 편차가 결정된다. 다음 단계에서, 개별 물체 점들의 위상은 편차가 감소되는 방식으로 수정되거나 달라질 수 있다. 절차는 반복적일 수 있다. 이것은 공간 광 변조기의 최적 복소수 값을 계산하는 동안 추가 반복에 관한 것이다.

개개의 물체 점에 대한 파면의 복소수 값의 진폭은, 물체의 인접한 물체 점을 나타내는 점 확산 함수에 의해 생성된 관찰자의 눈에서의 총 강도 분포와 타겟 강도 분포의 차이가 최소화되는 식으로 유리하게 정의될 수 있다. 망막 상의 물체 점의 계산을 통해 이를 수행할 수 있다. 너무 많은 강도가 있는 곳에서는 망막 상의 강도가 감소되고 강도가 너무 낮은 곳에서는 강도가 증가된다. 다시 말해서, 강도의 실제 분포는 강도의 타겟 분포에 적응된다.

각 물체 점의 파면의 복소수 값의 강도, 즉 진폭은 관찰자의 눈의 망막 평면에서 "관찰자의 눈의 망막의 평면에서 타겟 강도 분포 I(X, Y)_retina" 및 "눈의 망막의 평면에서 총 강도 분포 I(X, Y)_retina"의 차이를 최소화하는 방식으로 선택될 수 있다. 분석 모델을 사용하여 최적의 위상과 강도를 직접 계산할 수 있다. 이러한 분석 모델을 사용할 수 없는 경우 다음 절차를 사용할 수 있다. 망막 물체 점 간 크로스토크가 아직 고려되지 않은 최적화된 이미지는 예를 들어, WPM(wave propagation method)을 사용하거나 프레넬 변환(Fresnel transformation)을 사용함으로써 모델에서 망막으로 전파될 수 있다. 다음으로, 타겟 강도 분포와 총 강도 분포 사이의 편차가 결정된다. 다음 단계에서, 개별 물체 점들의 진폭은 편차가 감소되는 방식으로 수정될 수 있다. 절차는 반복적일 수 있다. 이것은 공간 광 변조기의 최적 복소수 값을 계산하는 동안 추가 반복에 관한 것이다.

다시 말해서, 반복 최적화를 선택할 수 있다. 2개의 물체 점들 사이의 상대적인 페이징(phasing)이 타겟 강도 분포에 더 가깝게 도달하기 위하여 어느 방향으로 시프트되어야 하는지는 인코딩될 이미지 콘텐츠에 의존한다. 중첩은 분석적이다. 이 방법으로 한 점과 다른 점들도 수학적으로 생성될 수 있다. 한 점에 이웃하는 점을 분석적으로 배치할 수 있다. 즉, 이미지는 상기 이미지의 에지를 따라 생성될 수 있다.

대안적으로 초기 인코딩을 사용할 수도 있고, 이 초기 인코딩은 그 후 반복적으로 최적화된다. 이 과정에서 타겟 강도 분포 또는 타겟 이미지와의 편차 또는 차이를 확인해야 한다. 임계 값이 반복을 중지시키기 위해 제공된다.

또한, 이는 아포다이제이션 프로파일 또는 아포다이제이션 함수를 제공하는 것이 유리하다. 아포다이제이션 프로파일은 공간 광 변조기 디바이스의 픽셀의 평면에 제공되어 물체의 개개의 물체 점들의 아포다이즈된 서브-홀로그램을 달성할 수 있다.

적당히 큰(예를 들어, ≤ HD/2(최대 분해능의 절반)) 물체 점의 경우, 물체 점은 "타겟 강도 분포(should be/target intensity distribution) I(X, Y)_retina" 및 "총 강도 분포(is/total intensity distribution) I(X, Y)_retina"의 차이를 최소화하는 방식으로 수정될 수 있다. 이것은 눈의 점 확산 함수에 의해 픽업될 평면 내에 형성되는 물체 점들을 나타내는 아포다이즈된 서브-홀로그램에 의해 수행될 수 있다. 관찰자가 보고 있는 모든 물체 점이 SLM에 의해 생성된다. 따라서, SLM의 서브-홀로그램에 존재하는 복소수 값 강도 분포는 감소된 사이드 로브를 갖는 점 확산 함수를 생성하기 위해 사용될 수 있다. 이것은 예를 들어. 관찰자의 눈의 망막에 점 확산 함수를 생성할 수 있는 아포다이즈된 서브-홀로그램을 사용하는 것을 의미한다. 이러한 점 확산 함수는 에어리(Airy) 분포이면 안 되고, 사이드 로브가 없는 가우스(Gauss) 분포여야 한다. 물체 점들의 강도 분포에서의 사이드 로브는 "타겟 강도 분포 I(X, Y)_retina" 및 "총 강도 분포 I(X, Y)_retina"의 차이를 최소화하는 방식으로 억제되거나 형상화에서 심지어 영향을 받을 수 있다. 그러나, 중첩시에 망막 상의 타겟 강도 분포에 대한 더 낮은 편차가 달성될 수 있다면, 사이드 로브는 또한 증가될 수 있다.

이 방법은 적당히 큰 물체 점에 더 잘 적용될 수 있다. 그러나, 해당 애플리케이션에만 국한되지는 않는다. 사이드 로브의 강도의 변화는 매우 작은 물체 점 및 그에 따른 큰 서브-홀로그램에 대해 그다지 효율적이지 못하다.

서브-홀로그램에 대한 아포다이제이션 함수는 a(x, y)_SLM(SLM 평면에서의 아포다이제이션 함수) 및 phase(x, y)_SLM(SLM 평면에서의 아포다이제이션 함수)일 수 있고, 이는 c(x, y)_SLM(SLM 평면에서의 아포다이제이션 함수)을 의미한다. 따라서 SLM 평면 내에서 사용되는 아포다이제이션 함수는 복소수 값을 가질 수 있다.

본 발명의 다른 실시 예에서, SLM의 서브-홀로그램은 그 형상이 수정 가능하다는 것이 제공될 수 있다.

SLM의 서브-홀로그램은 임의 형상을 가질 수 있다. 서브-홀로그램의 외형은 다양할 수 있다. 이러한 파라미터의 변화는 개개의 물체 점들의 망막 점 확산 함수의 모양을 변화시킨다. 예를 들어, 원형 또는 정방형/정사각형 모양이 사용될 수 있고 다른 모든 실용적인 형태도 사용될 수 있다. 특히, 2차원(2D) 인코딩의 경우, 서브-홀로그램의 수정된 형상을 사용함으로써 물체 점들의 형상화가 사용될 수 있다. 서브-홀로그램의 형상은 물체 점에 따라 적응될 수 있다. 적응된 형태는 고정된 원형 또는 정방형 모양에만 사용할 수 있는 c(x, y)_SLM과 관련된다. 문자 "c"는 그것이 복소수 값과 관련이 있음을 의미한다.

바람직하게는, 관찰자의 눈에 제공된 점 확산 함수의 고정된 미리 정의된 그리드가 사용되는 것이 제공될 수 있다.

점 확산 함수 PSF_ij의 고정 그리드는 물체 점에 의해 생성된 강도 분포에서 사이드 로브를 최적화하기 위해 사용될 수 있다. 점 확산 함수의 이러한 고정된 그리드는 점 확산 함수 PSF_ij의 상대적 위상차 및 강도를 최적화하는 데에도 사용될 수 있다. 이러한 최적화로, 재구성된 망막 이미지가 획득될 수 있는데, 이는 3차원(3D) 장면의 타겟 망막 이미지에 매우 가깝다. 점 확산 함수 PSF_ij에 관한 접미사 ij는 2차원 그리드의 점를 나타내는 인덱스이며, 바람직하게는 망막 수용체의 2차원 구형 곡선에 배치된 점이다.

바람직하게는 와이어 그리드 편광자 구조를 사용함으로써 조명 유닛이 2개의 직교 편광된 웨이브 필드를 방출하는 방식으로 적응될 수 있다는 것이 추가로 제공될 수 있다.

조명 유닛은 2개의 직교 편광된 웨이브 필드를 방출하기 위한 수단을 포함할 수 있거나 이를 위해 적응될 수 있다. 바람직하게는, 그러한 수단은 예를 들어, 와이어 그리드 편광자 구조 또는 와이어 그리드 편광자, 바람직하게는 2차원 와이어 그리드 편광자 구조일 수 있다. 와이어 그리드 편광자 구조는 조명 유닛에 제공된 2개의 미러로 된 미러로서 구현될 수 있으며, 이들은 조명 유닛의 적어도 하나의 광원의 공진기의 단부에서 사용된다. 적어도 하나의 광원은 예를 들어, 레이저 또는 레이저 다이오드일 수 있다. 이 특별한 와이어 그리드 편광자 구조의 주기는 일반적으로 π/2n보다 작고, 여기서 π는 레이저(레이저는 사용된 광원에 대해 이 맥락에서 사용됨. 즉, 그것은 또한 레이저 다이오드 또는 LED일 수도 있음) 파장이고, n은 와이어 그리드 편광자의 기판/구조의 상응하는 굴절률이다. 2개의 선형 직교 편광 상태는 와이어 그리드 편광자 구조를 사용하여 최대 반사율을 가지며, 반사율은 1(100 %)에 가깝다. 금속의 2차원 스트라이프 와이어 그리드 편광자 구조는 유전체 층 스택을 추가함으로써 그 반사율을 향상시킬 수 있다. 이러한 2차원 와이어 그리드 편광자 구조는 또한 조명 유닛에서 사용될 수 있다. 예를 들어, 와이어 그리드 편광자 구조 또는 다른 종류의 미러가 2개의 직교 선형 출사 편광 상태를 제공하기 위하여 조명 유닛의 광원 캐비티의 단부에서 사용될 수 있다.

조명 유닛은 웨이브 필드를 생성하도록 제공된 적어도 하나의 광원, 바람직하게는 레이저 또는 레이저 다이오드를 포함할 수 있다. 조명 유닛은 원색 당 적어도 하나의 광원을 포함할 수 있다. 조명 유닛이 스트라이프와 같은 광원 배열을 포함하는 것이 또한 제공될 수 있다.

바람직하게는, 원색 RGB(적색, 녹색, 청색)마다 적어도 2개의 상호 인코히어런트 광원이 제공될 수 있다.

본 발명에 따르면, 공간 광 변조기 디바이스는 코히어런트 방향을 따라 ≤1/60도이고 인코히어런트 방향을 따라 0.5 내지 1도인 평면파(plane wave)들의 각 스펙트럼으로 조명될 수 있다.

공간 광 변조기 디바이스는, 인코히어런트 방향인 수평으로 예를 들어 0.5도 내지 1도의 평면파의 각 스펙트럼으로 조명될 수 있다. 이는 관찰자 평면에서 수평 스윗 스팟(sweet spot)에 걸쳐 있기에 충분하다. 평면파의 각 스펙트럼은 1/60도보다 상당히 작은 것이 바람직하며, 이는 예를 들어, 코히어런트 방향인 수직 방향을 따라, 또는 다시 말해서 1차원(1D) 인코딩된 홀로그램 3차원(3D) 디스플레이 디바이스의 서브-홀로그램 인코딩의 방향을 따라 1/120도만인 것을 의미한다. 요구되는 경우에 따라, 코히어런트 방향은 또한 수평 방향일 수 있고 인코히어런트 방향은 수직 방향일 수 있다.

유리하게는, 상호 코히어런스 필드가 최대 확장으로 제한되고, 최대 확장은 공간 광 변조기 디바이스에서 가장 큰 서브-홀로그램의 크기라는 것이 제공될 수 있다.

사용된 광원과 관련하여, 광원에 의해 방출되는 광의 코히어런스는 가능한 한 낮아야 하지만 물체 점들의 공간 광 변조기 디바이스로의 홀로그램 인코딩을 위해 요구되는 만큼 높아야 한다. 관찰자 평면의 관찰자 윈도우는 관찰자가 다른 위치로 이동하면 추적 디바이스에 의해 추적될 수 있다. 본 발명에 따른 디스플레이 디바이스의 광 경로에서 관찰자 윈도우 및 추가의 회절 광학 요소를 추적하는데 요구되는 추적 각도는 공간 광 변조기 상의 서브-홀로그램의 확장에 관련된 영역 내에서 광로차(optical path difference)를 도입한다. 이것은 ≤ 0.1nm의 조명 유닛의 광원의 선폭에 대한 이유이다. 도입된 광로차뿐만 아니라 선폭이 증가하면 재구성시 물체 또는 장면이 번질 수도 있다. 그런 번짐(smearing)은 디스플레이 디바이스에 사용되는 회절 광학 요소에 의해 생성되는 회절 분산에 의해 초래된다.

광원의 선폭은 바람직하게는 ≤ 0.1nm이어야 하며, 요구되는 코히어런스 특성의 한 측면일 뿐이다. 또 다른 측면은 공간 코히어런스의 확장 또는 더 정확하게는 상호 코히어런스의 절대 값이다. 공간 광 변조기 디바이스의 픽셀들의 평면에 제공된 인접한 컬러 필터 스트라이프들 사이의 상호 코히어런스는 예를 들어 > 0.8인 광의 충분한 코히어런스가 컬러 필터 스트라이프의 방향을 따라 제공되는 동안 제거될 수 있다. 또한, 예를 들어 1차원 라인형 세그먼트로 맞추어진 컬러 필터 스트라이프와 평행하게 배향될 수 있는 상호 코히어런스 필드는 최대 확장으로 제한된다. 최대 확장은 가장 큰 서브-홀로그램의 크기를 가질 수 있다.

예를 들어, 광로차의 최대치, 따라서 사용된 광원의 선폭 또는 상호 코히어런스의 최대 확장을 특정하기 위해, 시야 윈도우의 크기 및 공간 광 변조기 디바이스로의 그 투영은 고려되어서는 안 되며, 그러한 절차는 공간 광 변조기 디바이스 상의 서브-홀로그램의 크기를 정의하는데 사용될 수 있다. 그러나, 인간의 눈의 입사 동공(entrance pupil)은 이를 특정하고 광의 가장 낮은 가능한 코히어런스를 위한 충분한 파라미터를 얻기 위해 사용되거나 고려되어야 한다.

공간 광 변조기 디바이스는 복소수 값 공간 광 변조기 디바이스로서 유리하게 설계될 수 있다. 이러한 복소수 값 공간 광 변조기 디바이스는 상이한 원색(RGB)에 관한 상이한 인코히어런트 물체 점 서브 세트를 재구성할 수 있어야 한다.

본 발명은 상이한 원색에 관한 상이한 인코히어런트 물체 점 서브 세트를 한번에 재구성할 수 있게 하는 단일 공간 광 변조기 디바이스(SLM)만을 사용하는 디스플레이 디바이스를 설명한다.

본 발명의 목적은 또한 청구항 제31항에 따른 방법에 의해 달성된다.

본 발명은 재구성된 2차원 및/또는 3차원 물체의 화질을 최적화하고 향상시키는 방법에 관한 것으로, 각각의 물체는 복수의 물체 점을 포함한다. 각각의 물체 점에 대해, 서브-홀로그램이 계산되고, 이는 공간 광 변조기 디바이스의 픽셀로 인코딩된다. 재구성된 인접한 물체 점들은 관찰자의 눈에서 인접한 물체 확산 함수를 생성한다. 점 확산 함수는 분리기(separator)에 의해 분리되어, 인접한 점 확산 함수는 유리하게는 망막 물체 점 간 크로스토크를 제거하기 위해 관찰자의 눈에 단지 코히어런트하게 중첩된다.

유리하게는, 관찰자에게 디스플레이될 물체 점을 나타내는 웨이브 필드의 인코히어런트 서브 세트가 생성되어 인코히어런트하게 중첩되는 것이 제공될 수 있다.

이제, 본 발명의 교시를 유리하게 구성 및 개선(refine)하고 및/또는 상기 기술된 실시 예들을 서로 가능한 한 조합하는 다양한 가능성이 존재한다. 이와 관련하여, 한편으로는 특허 청구항 1에 종속하는 특허 청구항이 참조되고, 다른 한편으로는 도면의 도움으로 본 발명의 바람직한 예시적인 실시 예에 대한 다음 설명이 참조된다. 도면의 도움으로 본 발명의 바람직한 예시적인 실시 예의 설명과 관련하여, 교시의 바람직한 구성 및 개선이 일반적으로 또한 설명된다.

도 1은 컴퓨터-생성된 홀로그램을 갖는 3차원 물체의 재구성을 위한 방법과 관련된 디스플레이 디바이스의 개략도를 도시한다.
도 2는 종래 기술에 따라 인접한 점 확산 함수가 중첩된 점 확산 함수의 강도 분포를 도시한다.
도 3은 본 발명에 따른 컬러 필터 스트라이프 배열로서 설계된 분리기를 도시하한다.
도 4는 도 1에 도시된 공간 광 변조기 디바이스의 일부분에 의해 재구성된 7 개의 백색 물체 점의 단일 선들을 도시한다.
도 5는 물체 점들을 포함하는 장면을 바라 보는 관찰자에 의한 포커싱된 및 비-포커싱된 물체 점들의 망막 배치의 예를 도시한다.
도 6은 이진 진폭 전송이 제공되는 픽셀 애퍼처 및 0.9의 필 팩터(fill factor)을 갖는 10개의 픽셀의 10배를 의미하는 공간 광 변조기 디바이스의 부분을 도시한다.
도 7은 공간 광 변조기 디바이스의 평면의 진폭 분포를 나타내는 도 6 내에 도시된 강도 분포의 푸리에 변환의 강도 분포를 도시한다.
도 8은 이진 진폭 전송이 제공되는 픽셀 애퍼처의 우측 절반 및 약 0.5의 필 팩터만을 사용하는 공간 광 변조기 디바이스의 부분을 도시한다.
도 9는 공간 광 변조 디바이스의 평면의 진폭 분포를 나타내는 도 8 내에 도시된 강도 분포의 푸리에 변환의 강도 분포를 도시한다.
도 10은 이진 진폭 전송이 제공되는 픽셀 애퍼처의 좌측 절반 및 약 0.5의 필 팩터만을 사용하는 공간 광 변조기 디바이스의 부분을 도시한다.
도 11은 본 발명에 따른 디스플레이 디바이스의 조명 유닛에 사용되는 2차원 와이어 그리드 편광자 구조의 예를 도시한다.
도 12는 이진 진폭 전송이 제공되고, 수평 배향된 전기장의 투과를 위한 패턴화된 편광 필터가 사용되는, 픽셀 애퍼처 및 0.5의 필 팩터를 갖는 공간 광 변조기 디바이스의 부분을 도시한다.
도 13은 이진 진폭 전송이 제공되고, 수직 배향된 전기장의 투과를 위한 패턴화된 편광 필터가 사용되는, 픽셀 애퍼처 및 0.5의 필 팩터를 갖는 공간 광 변조기 디바이스의 부분을 도시한다.
도 14는 공간 광 변조기 디바이스의 픽셀의 2개의 서브 세트가 네스트(nest)되고, 2개의 서브 세트가 직교 출사 편광 상태를 갖는 패턴화된 리타더의 배열이 제공된 공간 광 변조기 디바이스의 부분을 도시한다.
도 15는 이진 진폭 전송이 제공되는 픽셀 애퍼처 및 약 0.25의 필 팩터를 갖는 공간 광 변조기 디바이스의 부분을 도시한다.
도 16은 도 15 내에 도시된 강도 분포의 푸리에 변환의 강도 분포를 도시한다.
도 17은 공간 광 변조기 디바이스의 픽셀의 2개의 서브 세트들은 도 14의 것과 직교하여 네스트되고, 2개의 서브 세트들은 직교 출사 편광 상태를 가지는, 패턴화된 리타더들의 배열이 제공된 공간 광 변조기 디바이스의 부분을 도시한다.
도 18은 공간에서 또는 관찰자의 눈의 망막에서 재구성된 3차원 물체 점을 지칭하는, 직교 편광 상태의 바둑판 형태의 할당 패턴을 도시한다.

유사한 도면 부호는 개별적인 도면에서 및 제공된다면 수반되는 설명에서 유사한 컴포넌트를 나타낸다. 다음에서, 공간 광 변조기 디바이스의 앞에서와 같이, "앞에서(in front of)" 및 "뒤에서(behind)"라는 명칭은 광의 전파 방향과 관련하여 보이는 광을 의미한다.

2차원 및/또는 3차원 장면 또는 물체의 홀로그램 재구성을 위한 디스플레이 디바이스는 공간 광 변조기 디바이스(4) 및 조명 유닛(5)을 포함한다. 장면 또는 물체는 도 1에 도시된 바와 같이 복수의 물체 점을 포함한다. 도 1은 장면 또는 물체의 공간 광 변조기 디바이스(4)로의 인코딩을 개략적으로 나타낸다. 3차원 물체(1)는 복수의 물체 점들로 구성되고, 그 중 4개의 물체 점(1a, 1b, 1c 및 1d)만이 여기서 인코딩을 설명하기 위해 표시된다. 가상 관찰자 윈도우(2)가 또한 도시되어 있으며, 이를 통해 관찰자(여기서 눈으로 표시됨)는 재구성된 장면을 관찰할 수 있다. 정의된 시야 영역 또는 가시 영역으로서의 가상 관찰자 윈도우(2) 및 4개의 선택된 물체 점(1a, 1b, 1c 및 1d)에 의해, 피라미드 몸체가 이들 물체 점(1a, 1b, 1c 및 1d)을 통해 각각 투영되어 공간 광 변조기 디바이스(4)(여기서 부분적으로만 나타남)의 변조 표면(3)상에 연속된다. 변조 표면(3)에서, 이것은 인코딩 영역의 형상이 시야 윈도우(2)의 형상과 일치하지 않아야 하는 공간 광 변조기 디바이스(4)의 인코딩 영역을 초래한다. 즉, 공간 광 변조기 디바이스(4) 상의 인코딩 영역은 또한 시야 윈도우(2)가 물체 점을 통하여 변조 표면(3) 상으로 투영되는 것에 의해 규정된 바와 같이 더 크거나 더 작을 수 있다. 인코딩 영역은 물체의 각각의 물체 점(1a, 1b, 1c 및 1d)에 할당되며, 물체 점(1a, 1b, 1c 및 1d)은 서브-홀로그램(3a, 3b, 3c 및 3d)에 홀로그램으로 인코딩된다. 따라서, 각각의 서브-홀로그램(3a, 3b, 3c 및 3d)은 공간 광 변조기 디바이스의 변조 표면(3)의 단지 하나의 영역에만 기입되거나 인코딩된다. 도 1로부터 알 수 있는 바와 같이, 물체 점(1a, 1b, 1c, 1d)의 위치에 의존하여, 개별 서브-홀로그램(3a, 3b, 3c 및 3d)은 변조 표면(3) 상에서 완전히 또는 부분적으로만(즉, 특정 영역에서만) 오버랩될 수 있다. 이러한 방식으로 재구성될 물체(1)에 대한 홀로그램을 변조 표면(3)에 인코딩 또는 기입하기 위해서는, 물체(1)의 모든 물체 점들로 상기한 바와 같은 잘차를 수행해야 한다. 따라서, 홀로그램은 다수의 개별 서브-홀로그램(3a, 3b, 3c, 3d, ... 3n)으로 구성된다. 공간 광 변조기 디바이스에서 이러한 방식으로 컴퓨터-생성된 홀로그램은 광학 시스템과 관련하여 조명 유닛(5)(개략적으로만 도시됨)에 의한 재구성을 위해 조명된다.

도 1을 참조하면, 인코딩 영역들에 의해 정의된 홀로그램의 섹션 내의 개별 서브-홀로그램(3a, 3b, 3c 및 3d)은 본질적으로 일정한 진폭을 가지며, 그 값은 물체 점들의 밝기 및 거리, 렌즈 함수에 상응하는 위상, 렌즈의 초점 길이 및 물체 점의 깊이 좌표에 따라 변화하는 인코딩 영역의 크기의 함수로서 결정된다. 인코딩 영역에 의해 정의된 섹션 외부에서, 개별 서브-홀로그램의 진폭은 값 0을 갖는다. 홀로그램은 모든 서브-홀로그램(3a, 3b, 3c, 3d ... 3n)의 복소수 값 합에 의해 얻어진다.

조명 유닛(5)은 바람직하게 홀로그램 디스플레이 디바이스 내에서 사용되는 몇몇 특정 수정을 포함할 수 있다. 조명 유닛은 코히어런트 광 및 감소된 공간 및/또는 시간 코히어런스만을 도시하는 광에 사용될 수 있다. 진폭 아포다이제이션 및 위상 아포다이제이션은 조명 유닛(5)의 입구 평면 뒤에 전파되는 강도 프로파일을 최적화하는 데 사용될 수 있다. 컬러 필터는 이를 상이한 컬러들에 대해 개별적으로 최적화할 수 있는 기회를 제공한다. 사양은 별개의 실시 예에 따라 다르다.

이하에서는, 재구성된 장면 또는 물체 점의 이미지 품질을 감소시키는 망막 물체 점 간 크로스토크의 억제에 대해 기술하고 설명할 것이다. 이러한 망막 물체 점 간 크로스토크는 3차원 장면 또는 물체의 홀로그램 재구성 중에 초래된다.

요구되는 화질을 얻기 위해서는 디스플레이 디바이스에 최적화해야 할 복수 개의 파라미터가 존재한다. 고려해야 할 하나의 파라미터는 인간 눈의 입사 동공의 직경이다. 이를 위해 점 확산 함수에 대한 선험적 지식이 사용되며, 이는 홀로그램 3차원 장면을 관찰하는 관찰자에게 적용되는 실제 상황에 가깝다. 디스플레이 디바이스와 관련된 정의된 위치에서 관찰자의 눈의 위치를 검출하는 눈 추적 및 눈 검출 시스템을 사용하여 얻어진 데이터가 사용될 수 있다. 관찰자의 눈의 입사 동공의 직경은 관찰자가 보고 있는 장면 또는 물체의 휘도에 의존한다. 따라서, 장면이나 물체의 현재 휘도를 참조하는 값이 사용될 수 있다. 또한, 관찰자의 위치를 기록(record)하고, 특히 관찰자의 눈의 입사 동공을 기록하기 위한 적어도 하나의 카메라를 포함하는 눈 추적 및 눈 검출 시스템에 의해 제공되는 화상(pictures)이 또한 관찰자의 눈의 입사 동공의 직경의 더 정확한 값을 추출하는데 사용될 수 있다.

원칙적으로 관찰자의 눈은 물체에서 나오는 3차원 필드를 "픽업(pick up)"하는 데 사용되는 에어리 모양의 점 확산 함수를 가질 수 있다. 관찰자의 눈이 예를 들어, 1m에 놓인 물체 점에 촛점을 맞추는 경우. 상기 1m에 놓이고 눈의 망막 상에 결상되는 물체 점의 점 확산 함수는 예를 들어, 0.8m에 놓인 물체 점의 점 확산 함수보다 작고, 1.5m에 배치된 물체 점의 점 확산 함수보다 작다. 다시 말해서, 관찰자가 초점을 맞추고 있는 물체 점이 가장 작은 점 확산 함수를 가진 눈의 망막으로 전달(transfer)된다. 그러나, 초점이 맞지 않거나(out-of-focus) 심지어 약간 초점이 맞지 않은 물체 점은 초점을 맞춘(in-focus) 물체 점의 점 확산 함수로서 더 큰 점 확산 함수를 가진다. 디포커싱(defocusing)은 해당 디포커스된 물체 평면의 점 확산 함수를 넓히는 것을 의미한다.

물체의 모든 물체 점의 웨이브 필드의 이러한 "픽업 및 웨이브 전달(pick up and wave transfer)" 함수, 즉 초점이 맞추어진 평면의 점 확산 함수는 관찰자의 눈의 동일한 입사 동공을 통과해야 한다. 관찰자가 보고 있는 물체의 인접한 물체 점이 서로 매우 가깝다는 사실로 인해, 이들 물체 점들로부터 나오는 전달 웨이브 필드는 동일한 위치 또는 장소에서 거의 동일한 각도로 관찰자의 눈의 입사 동공과 충돌한다. 따라서, 고려되어야 하는 눈의 입사 동공의 위상 함수는 동일하다. 다시 말해서, 여기에 공통 경로 배열이 있다. 픽업되어 망막으로 전달되는 인접한 물체 점의 복소수 값 점 확산 함수는 동일하다. 그렇지 않으면 매우 멀리 떨어져 있는 물체 점에 대해 약간 상이한 점 확산 함수가 고려되어야 한다. 예를 들어, 디스플레이 디바이스의 광축에 가까운 물체 점의 전달을 위해, 약간 더 넓은 점 확산 함수로 전달되는 이미지의 에지에서의 물체 점에 대하여 더 좁은 점 확산 함수가 사용될 수 있다.

물체의 인접한 물체 점들 사이의 망막 물체 점 간 크로스토크를 최소화하기 위해 다음 파라미터가 수정되어야 한다:

I) 물체 점으로부터 나오는 상대적 위상,

II) 물체 점으로부터 나오는 상대적 진폭, 및

III) 2개의 인접한 회절 차수의 각도 범위 내에서 약간 시프트될 수 있는, 서로 인접한 물체 점들의 횡 방향 위치 또는 거리. 즉, ±1/60도 또는 ±1/40도의 범위에서 물체 점이 시프트될 수 있는 작은 위상 쇄기가 사용된다. 따라서, 그것은 등거리(equidistant) 도트 매트릭스와 약간 상이하다.

재구성된 물체 또는 장면의 이미지 품질을 최적화하기 위해, 홀로그램 재구성을 수행하기 전에 물체 또는 장면은 개별 깊이 평면으로 분할된다. 상대적 위상, 상대적 진폭 및 측 방향 위치에 대한 이들 값은 예를 들어, 각 원색 RGB(적색, 녹색, 청색)에 대해 눈에 제시된 휘도와 상관 관계가 있는 2mm, 2.2mm, 2.4mm, .... 3.6mm로서의 입사 동공 직경들의 세트에 대해 각각의 단일 이산 깊이 평면에 대해 예를 들어, 128개의 깊이 평면들에 대해 최적화되어야 한다. 따라서, 상대적 위상, 상대적 진폭, 및 측 방향 위치에 대해 최적화된 값을 포함하는 생성된 데이터 세트는 룩업 테이블(look-up table, LUT)에 저장될 수 있다. 이러한 생성된 데이터 세트는 공간 광 변조기 디바이스에서 인코딩될 서브-홀로그램의 계산에 포함될 수 있다.

관찰자의 눈의 동공의 추정 가능한 애퍼처를 결정하기 위한 제1 접근법은 평균 휘도를 사용하여 적어도 우측 범위(right range) 내에 있을 수 있는 입사 동공 직경을 선택할 수 있으며, 우측 범위는 예를 들어 텔레비전의 경우 50-250 cd/m², 데스크탑 모니터의 경우 100-300 cd/m²이다. 휘도 강도는 이미지 콘텐츠로부터 계산될 수 있다. 제2 접근법은 눈 추적 시스템의 데이터를 사용하여 입사 동공 직경을 측정하고 룩업 테이블의 우측 데이터 서브 세트를 선택할 수 있다.

상기 파라미터를 최적화하기 위한 하나의 가능성으로서 물체 점에 대응하는 서브-홀로그램을 계산하는 동안, 예를 들어 25 cd/m² 내지 1000 cd/m²인 요구되는 범위 내에 실질적으로 있을 수 있는 눈의 입사 동공 직경을 선택하는데 평균 휘도가 사용될 수 있다. 또 다른 가능성은 눈 추적 및 검출 시스템의 획득된 데이터를 이용하는 것일 수 있다. 이러한 데이터로 입사 동공 직경이 측정될 수 있고 룩업 테이블의 필요한 데이터 서브 세트가 선택될 수 있다. 다시 말하면, 거리 측정과 관련하여 눈 추적 및 검출 시스템의 카메라에 의해 기록된 이미지는 동공의 직경을 결정하는 데 사용될 수 있다.

또 다른 가능성은 눈의 2개의 광축의 회전 각을 정의하기 위해 관찰자의 눈의 입사 동공의 거리를 사용하는 것일 수 있다. 이 방식으로 눈의 초점 거리에 있는 2개의 광축의 교차점을 결정할 수 있다. 이를 위해 각 관찰자에 대한 개별 교정(calibration)이 필요할 수 있다. 이는 각 관찰자가 한 번 처리하는 교정 루틴을 구현하여 수행할 수 있다.

그러나 제한된 파라미터 세트만 수정되거나 적응되거나 변경될 수 있다.

예는 실제일 수 있고 따라서 디스플레이 디바이스의 전방에 있을 수 있는 복수의 물체 점이다. 관찰자의 눈은 물체 점의 이러한 평면(들)에 집중될 수 있다. 관찰자의 눈의 점 확산 함수는 이러한 물체 점들을 픽업하여, 이들을 관찰자의 눈의 망막으로 전달한다.

진행할 여러 옵션이 있으며, 옵션들은 필요하거나 요구되거나 적합한 경우 결합될 수 있다.

1)

단일 물체 점은 "관찰자의 눈의 망막에서 타겟 강도 분포(should be/target intensity distribution on the retina of the eye of the observer) I(X, Y)_retina" 및 "눈의 망막에서 총 강도 분포(is/total intensity distribution on the retina of the eye of the observer) I(X, Y)_retina"의 차이가 최소화되는 방식으로 깊이 평면에서 가상으로 시프트될 수 있고, 여기서 I는 눈의 망막의 평면에서의 강도 분포이고, x 및 y는 눈의 망막 내의 좌표이고, x 축 및 y 축의 값으로 지칭된다. 이것은 이하 SLM이라고도 지칭되는 공간 광 변조기 디바이스로 인코딩될 서브-홀로그램의 계산에 작은 오프셋 위상 함수를 도입함으로써 수행될 수 있다. 관찰자 평면에 제공된 1차원 또는 2차원 시야 윈도우의 각도 범위 내의 물체 점들의 시프트는 본 발명과 무관하다.

2)

상대적 위상 또는 더 정확하게는 개별 물체 점들의 상호 위상 차는 "관찰자의 눈의 망막에서 타겟 강도 분포 I(X, Y)_retina" 및 "눈의 망막에서 총 강도 분포 I(X, Y)_retina"의 차이가 최소화되는 방식으로 선택될 수 있다. 이를 위해 관찰자의 눈이 계산 과정에 포함된다. 이미지의 생성은 망막에서 계산된다. 따라서, 망막은 기준 평면이다. 시작 점은 인코딩될 장면이다. 망막에서 이미지의 반복 최적화가 수행될 수 있다. 제1 단계에서 모든 서브-홀로그램을 추가하여 망막으로 전파할 수 있다. 그런 다음, 망막 상의 총 강도 분포의 망막 상의 타겟 강도 분포로의 편차가 결정될 수 있다. 위상, 진폭 및 위치를 변경할 수 있다. 편차는 재결정될 수 있다. 이것은 반복 루프를 사용하여 수행할 수 있다. 편차 임계 값은 종료 조건으로서 예를 들어, 편차가 5%보다 작으면, 선택될 수 있다. 또한, 반복 횟수를 제한하는 것도 가능하다.

3)

개개의 물체 점들의 강도 또는 진폭은 "관찰자의 눈의 망막에서 타겟 강도 분포 I(X, Y)_retina" 및 "눈의 망막에서 총 강도 분포 I(X, Y)_retina"의 차이가 최소화되는 방식으로 선택될 수 있다. 이를 위해 관찰자의 눈이 계산 과정에 포함된다. 이미지의 생성은 망막에서 계산된다. 따라서, 망막은 기준 평면이다. 시작 점은 인코딩될 장면이다. 망막에서 이미지의 반복 최적화가 수행될 수 있다. 제1 단계에서 모든 서브-홀로그램을 추가하여 망막으로 전파할 수 있다. 그런 다음, 망막 상의 총 강도 분포의 망막 상의 타겟 강도 분포로의 편차가 결정될 수 있다. 위상, 진폭 및 위치를 변경할 수 있다. 편차는 재결정될 수 있다. 이것은 반복 루프를 사용하여 수행할 수 있다. 편차 임계 값은 종료 조건으로서 예를 들어, 편차가 5%보다 작으면, 선택될 수 있다. 또한, 반복 횟수를 제한하는 것도 가능하다.

4)

예를 들어 물체 점을 픽업하여 관찰자의 눈의 망막으로 전달하는 점 확산 함수의 50%만큼 클 수 있는 적당한 큰 물체 점의 경우, "관찰자의 눈의 망막에서 타겟 강도 분포 I(X, Y)_retina" 및 "눈의 망막에서 총 강도 분포 I(X, Y)_retina"의 차이가 최소화되는 방식으로 물체 점이 수정될 수 있다. 이것은 예를 들어, 눈의 점 확산 함수에 의해 픽업되는 평면 내에 제공되는 물체 점들을 나타내는 아포다이즈된 서브-홀로그램을 사용함으로써 행해질 수 있다. 관찰자가 보고 있는 모든 물체 점이 SLM에 의해 생성된다. 따라서, SLM의 서브-홀로그램에 존재하는 복소수 값 분포는 감소된 사이드 로브를 갖는 점 확산 함수를 생성하기 위해 사용될 수 있다. 이는 관찰자의 눈의 망막에서 점 확산 함수를 생성할 수 있는 아포다이즈된 서브-홀로그램을 사용하여 수행될 수 있다. 점 확산 함수는 에어리 분포가 없어야 하지만, 예를 들어 사이드 로브가 전혀 없는 가우스 분포는 있어야 한다.

물체 점에 의해 생성된 강도 분포의 사이드 로브는 "관찰자의 눈의 망막에서 타겟 강도 분포 I(X, Y)_retina" 및 "눈의 망막에서 총 강도 분포 I(X, Y)_retina"의 차이를 최소화하는 방식으로 억제되거나 심지어 형성될 수 있다. 사이드 로브는 또한 그렇게 하도록 증가될 수 있다. 사이드 로브 형상 변화는 추가 파라미터 변화로서 사용되어, 관찰자의 눈의 망막 상의 타겟 강도 분포 I(X, Y)_retina에 대한 총 강도 분포의 차이를 감소시킬 수 있다.

이러한 절차는 물체 또는 장면의 적당한 큰 물체 점에 대해 보다 효율적으로 작동할 수 있다. 매우 작은 물체 점 및 따라서 큰 서브-홀로그램이 사용된다면, "관찰자의 눈의 망막에서 타겟 강도 분포 I(X, Y)_retina"와 "눈의 망막에서 총 강도 분포 I(X, Y)_retina"의 차이의 변화가 그다지 효율적이지 않을 수 있다.

서브-홀로그램 아포다이제이션은 a(x, y)_SLM(진폭-SLM) 및 phase(x, y) _SLM(위상-SLM)일 수 있고, 이는 c(x, y)_SLM(복소수 값 SLM)을 초래할 수 있다. 따라서, SLM 평면 내에서 사용되는 아포다이제이션은 복소수 값을 가질 수 있다.

5)

2차원(2D) 인코딩의 경우, 사용된 서브-홀로그램의 수정된 형상을 사용하여 물체 점을 형상화할 수 있다. 서브-홀로그램의 적응된 형상은 복소수-값 SLM c(x, y)_SLM과 관련되고, 이는 예를 들어 고정된 원형 또는 정방형/정사각형 형상만 사용한다. 예를 들어, 육각형 서브-홀로그램 또는 종횡비가 약간 변경된 서브-홀로그램을 사용할 수도 있다. 일반적으로 복소수 값 분포는 다양할 수 있다. 사용된 파라미터는 3차원 장면의 콘텐츠에 따라 달라질 수 있다. 이것은 서브-홀로그램의 아포다이제이션의 복소수 값 분포가 콘텐츠의 변화에 따라 변경될 수 있음을 의미한다. 다시 말해서, 개별 서브-홀로그램의 위상 및 진폭의 분포는 다양할 수 있다.

6)

예를 들어, 모든 z-평면을 포함하는 재구성된 물체 또는 장면의 전체 최적화를 실현하는 것이 불가능하다면(여기서 z는 디스플레이 디바이스의 광축에 평행한 종방향 거리임), 수렴(시선) 추적을 사용하여 관심 있는 깊이 평면을 정의할 수 있다. 이를 위해 관찰자는 무엇을 보거나 시선을 주는지 결정된다. 눈 추적 및 검출 시스템은 관찰자의 눈길(look)이 정의될 수 있도록 눈길 또는 시선을 결정할 수 있다. 따라서, SLM으로의 서브-홀로그램의 인코딩에 대한 결과는 z-평면 또는 관찰자가 보고 있는 z-평면의 범위와 관련하여 최적화될 수 있다.

1) ~ 6)에 설명된 옵션을 서로 결합하여 양호하거나 필요한 고품질을 얻을 수 있다.

앞에서 언급한 이러한 옵션을 결합할 수 있지만 가장 직접적인 방법 또는 보다 실제적인 방법은 점 확산 함수 PSF_ij의 고정된 그리드를 사용하고, 3차원 물체 또는 장면의 설계된 망막 이미지에 적당히 가까운 재구성된 망막 이미지를 얻기 위해서 사이드 로브, 상대적 위상 차 및 점 확산 함수 PSF_ij의 강도를 최적화하는 것이다. 점 확산 함수 PSF_ij에 관한 접미사 ij는 2차원 그리드의 점, 바람직하게는 2차원 구형 곡선 검출기 평면 또는 망막 표면에 배치된 가상 그리드의 점을 나타내는 인덱스이다.

이하, 본 발명은 SLM에서 1차원(1D) 인코딩된 홀로그램에 대해 기술된다:

일반적으로, 상술한 옵션 1) 내지 6)은 1차원 인코딩된 홀로그램에 대한 다음 옵션에 부가적으로 사용될 수 있다. 따라서, 사이드 로브 억제, 망막 물체 점 간 크로스토크 감소 및 화질에 대한 최적화가 더욱 향상될 수 있다. 다음 설명은 1차원만을 언급한다. 1차원에서만의 망막 이미지의 최적화는 단지 1차원에서 점 확산 함수 PSF_ij의 가장 가까운 이웃을 분석하고 최적화하는 것을 의미하며, 2차원에서 이웃하는 점 확산 함수 PSF_ij를 최적화하는 것보다 빠르게 실현될 수 있다. 이 때문에, 예를 들면, 반복 최적화 또는 분석 최적화가 실시간으로 수행될 수 있다. 이것은 또한 게임에서와 마찬가지로 적극적인 사용자 상호 작용을 위해 충분히 빠르고 효율적이다.

사람의 눈 즉, 관찰자의 눈의 제한된 각도 분해능을 사용하는 것은 SLM에서 1차원 인코딩된 홀로그램에 사용될 수 있는 하나의 옵션이다. 이를 위해, 서로에 대해 인코히어런트하고, 하나의 인코딩된 선으로 보이는, 물체 점들의 여러 1차원 인코딩된 선이 제공된다. 따라서, SLM 상의 인코히어런트 방향의 픽셀 밀도가 증가된다. 각각의 1차원 인코딩된 선은 예를 들어, 1/60도에서 관찰자에게 표시되는 물체 점의 1/3을 생성한다. 예를 들어, 관찰자가 볼 수 있는 인접한 물체 점 들간의 크로스토크를 감소시키기 위해 도(degree) 당 180 픽셀까지의 픽셀 밀도 또는 그 이하가 인코히어런트 방향 내에서 사용된다.

예를 들어, 최상의 경우 조건에서 1/60 도인 인간의 눈의 각도 분해능은 분해될 수 있는 물체 점의 측 방향 확장과 동등하다. 텔레비전(TV)에 대해 일반적으로 가정될 수 있는 디스플레이 디바이스까지 3.5m의 평균 시야 거리에서, 1/60도는 2개의 물체 점들의 서로까지의 1.02mm 측 방향 확장과 동등하다. 실제 분해능이 현저히 더 적지만, 예를 들어 1.2mm의 주기적인 간격이 텔레비전 애플리케이션의 분해능 한계로서 사용될 수 있다. 실제 분해능는 이 상황에서 최상의 경우 상황에 대해 휘도가 제공되지 않음을 의미하거나, 관찰자 눈의 개별 수차가 얻어진 유효 분해능을 감소시킬 수 있음을 의미한다. 예를 가능한 한 간단히 하기 위해 이 값을 1.2mm로 선택하였다. VPO(vertical parallax only)을 의미하는 수직 홀로그램 인코딩이 사용된다면, 서브-홀로그램은 SLM 상에서 수직 스트라이프로서 배열된다.

복소 변조 웨이브 필드를 제공하는 SLM에 대해 필수적인 프레임 속도를 줄이기 위해 컬러 필터를 사용할 수 있다. 그를 위해 SLM 픽셀에 정렬된 구조로 되어 있는 일반적으로 알려진 흡수형 염료 기반 필터 어레이가 사용될 수 있다. 현대 코팅 기술은 예를 들어 스트라이프 배열에서 노치 필터를 적용하는 것을 가능하게 한다. 이것은 컬러 스트라이프가 원색인 RGB 중 두 가지를 반사하면서 나머지 원색을 투과할 수 있음을 의미한다. 이는 1에 가까운 계수를 갖는 이러한 특정 스트라이프의 2개의 불필요한 파장을 반사하면서 0.9보다 큰 투과 계수로 행해질 수 있다.

예를 들어, 위에서 설명된 3.5m 시야 거리에서 인간의 눈의 최상의 경우 분해능 한계(1/60도)에 적당히 가까운 1.2mm의 수평 폭 내에서 3개의 컬러 필터 스트라이프를 제공하는 것으로 가정할 수 있다.

종래 기술에서 1.2mm의 이러한 폭 내에서 3개의 컬러 필터 스트라이프를 사용하는 것이 알려져 있다. 따라서, 폭이 각각 400μm인 3개의 RGB 컬러 필터 스트라이프가 있다. 따라서, 적색, 녹색 및 청색 컬러 필터 스트라이프는 각각 400㎛의 폭을 갖는다.

도 3에 따르면, 수직 스트라이프의 밀도는 훨씬 더 증가한다. 수직 스트라이프의 밀도는 종래 기술에 따른 밀도보다 예를 들어 2배, 3배(3X) 또는 4배(4X) 높다. 이제, 1.2㎜의 이러한 예시적인 폭 내에 2쌍, 3쌍 또는 4쌍 또는 RGB 컬러 필터 스트라이프가 있다. 이것은 133.3μm 또는 100μm만의 폭을 가진 컬러 스트라이프가 있음을 의미한다.

예를 들어, 총 40도의 누적된 회절 각을 갖는 회절 컴포넌트를 사용하는 홀로그램 디스플레이 디바이스에 대한 조건은 조명 유닛의 광원의 <0.1nm의 선폭이다. 또한, 예를 들어, 조명 유닛의 백라이트의 투명한 표면에 적용될 수 있는 반사 방지 코팅은 디스플레이 디바이스에 사용되는 브래그 회절-기반의 볼륨 격자의 광의 스쳐가는 입사(grazing incidence) 및 스펙트럼 선택성에서, 광원의 0.1nm의 중심 파장 길이의 안정성을 제공한다. 이는 예를 들어 각각 > 500mW인 광학 출력에서 447nm, 457nm, 532nm, 638nm 및 650nm에서 이용 가능한 DPSS(diode pumped solid state) 레이저를 광원으로서 사용하여 달성될 수 있다. 또한, 활성 매체 내에 또는 그 매체에 적당히 가깝게 브래그 공진기 격자를 갖는 DFB(distributed feedback) 레이저 다이오드로서, 또는 외부 브래그 공진기를 이용하는 파장 안정화된 레이저 다이오드로서의 광원도 또한 이러한 요건을 충족할 수 있다.

광원, 예를 들면, 레이저 다이오드의 스위칭 시간이 어떤 이유로든 예를 들어 1ms로 감소되어야 한다면, 프로젝터로부터 알려진 추가 기계식 셔터 또는 시간 동기화된 컬러 필터 휠이 조명 유닛에서 사용될 수 있다. DFB 레이저 다이오드는 적당히 빠른 스위칭을 보여 주며, 상이한 설계 파장으로 만들어질 수 있다. 또한, 소위 Q-스위치 레이저 장치는 파장 안정화 브래그 공진기 접근법과 함께 사용될 수 있다. 이는 실질적으로 이용 가능한 레이저 광원이 본 발명에 따른 디스플레이 디바이스에 사용될 수 있음을 나타낸다.

관찰자 평면의 시야 윈도우로부터 디스플레이 디바이스까지의 3.5m 거리에서, 8mm의 수직 시야 윈도우는 SLM 상에서 195.6㎛의 픽셀 크기를 요구할 것이다. 이것은 약 200μm의 픽셀 크기를 의미한다. 따라서, 수직 픽셀 피치는 수평 픽셀 피치보다 크다.

관찰자 평면 내의 시야 윈도우로부터 디스플레이 디바이스까지의 3.5m 대신에 단지 1.5m의 평균 시야 거리가 사용된다면, 주어진 픽셀 치수의 수는 2.3의 계수로 나누어져야 한다. 필요한 경우에 따라 이러한 경우가 있을 수 있다. 그러나, 홀로그램 1D 인코딩된 3D 텔레비전 애플리케이션의 경우, 3.5m 거리가 더 적당하다.

도 3은 SLM의 일부를 정면도로 도시한다. SLM은 인접한 물체 점들의 서브-홀로그램에 의해 생성된 관찰자의 눈에서 인접한 점 확산 함수들을 분리하여, 인접한 점 확산 함수들이 서로에 대해 상호 인코히어런트가 되도록 하는 분리기를 구비한다. 분리기는 여기에서 컬러 필터 배열, 바람직하게는 원색(RGB) 필터 배열로서 설계된다. 이러한 컬러 필터 배열은 주로 HD의 3배로 오버샘플링된 1D 인코딩된 홀로그램 3D 텔레비전 디스플레이 디바이스에 제공되지만, 2차원(2D) 인코딩된 홀로그램 3D 텔레비전 디스플레이 디바이스에 제공될 수도 있다. 이러한 디스플레이 디바이스는 디스플레이 디바이스까지의 평균 관찰자 시야 거리 Zmean = 3.5m를 위해 설계된다. 이 시야 거리에서, 도 3에 도시된 바와 같은 1.2 ㎜의 컬러 필터 배열의 수평 확장은 인간 눈의 각 분해능인 1/60도와 동등하다. 분리기 또는 각각의 원색 RGB(적색, 녹색, 청색)에 대한 컬러 필터 배열의 이러한 실시 예에서, 3개의 스트라이프 컬러 필터(r1, g1, b1, r2, g2, b2, r3, g3, b3)가 제공되고, SLM의 1.2mm의 수평 치수를 가진 부분에 할당된다. 다시 말해서, SLM의 수평 치수가 1.2mm인 각 부분에는 각 원색 RGB에 대해 3개의 스트라이프 컬러 필터(r1, g1, b1, r2, g2, b2, r3, g3, b3)를 포함하는 컬러 필터 배열이 제공된다. 이것은 9개의 스트라이프 컬러 필터가 1/60도의 수평 각도 범위 내에 제공된다는 것을 의미한다. 참조 부호(r1, r2 및 r3)는 적색 컬러 필터 스트라이프를 나타내고, 참조 부호(g1, g2 및 g3)는 녹색 컬러 스트라이프를 나타내고, 참조 부호(b1, b2 및 b3)는 청색 컬러 스트라이프를 나타낸다. 도 3에서, 상이한 필링(filling) 패턴은 3개의 상이한 원색 RGB의 컬러 필터 스트라이프를 표시한다.

물론, 인코딩 방향이 수평 방향인 경우, 수평 방향으로 컬러 필터 배열을 배열하는 것도 가능하다.

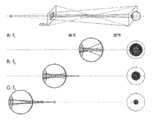
도 3에 도시된 SLM의 일부에 의해 재구성된 물체 점들의 개략도가 도 4에 도시되어 있다. 설명을 위해 7개의 물체 점들이 사용된다.

도 4a는 수직 각도 거리 1/60도에서의 물체의 7개의 백색 물체 점(object point, OP)의 재구성을 도시한다. 도시된 원은 각각 관찰자의 눈의 망막 상에 존재하는 점 확산 함수의 회절 패턴의 강도 분포의 최초의 최소값을 표시한다. 단순화를 위해, 물체 점(OP)의 원형 형상이 여기에서 가정된다. 이는 이러한 측면을 설명하기 위한 것일 뿐이다. 그러나, 물체 점(OP)의 그러한 원형 형상은 용어 VPO를 사용하여 식별되는 1차원 인코딩된 홀로그램에 대해 꽤 정확하지는 않을 수 있다.

도 4b는 수직 각도 거리 1/60도에서 7개의 적색 물체 점들의 재구성을 도시한다. 이들 7개의 적색 물체 점들은 도 4a에 따른 백색 물체 점들의 적색 서브 세트를 형성한다. 도시된 바와 같이, 적색 서브 세트는 컬러 필터 스트라이프(r1, r2 및 r3)에 의해 생성된 모든 부분을 포함한다.

도 4c는 컬러 필터 스트라이프(r1)에 의해서만 생성되는 적색 서브 세트의 부분의 재구성을 도시한다. 즉, 컬러 필터 스트라이프(r1)는 도 4a에 따라 첫 번째, 네 번째, 일곱 번째, 열 번째, ...물체 점(OP)에 대한 백색 물체 점(OP)의 적색 서브 세트를 생성한다. 여기서는 컬러 필터 스트라이프(r1)가 적색 물체 점을 생성하는 것을 볼 수 있고, 여기서 적색 물체 점은 중첩되지 않는다.

도 4d는 컬러 필터 스트라이프(r2)에 의해서만 생성되는 적색 서브 세트의 부분의 재구성을 도시한다. 다시 말해서, 컬러 필터 스트라이프(r2)는 도 4a에 따라 두 번째, 다섯 번째, 여덟 번째, 열한 번째 ... 물체 점(OP)에 대한 백색 물체 점(OP)의 적색 서브 세트를 생성한다. 또한 컬러 필터 스트라이프(r2)는 중첩되지 않는 적색 물체 점, 여기서는 2개의 물체 점을 생성한다. 컬러 필터 스트라이프(r2)에 의해 생성된 물체 점은 컬러 필터 스트라이프(r1)에 의해 생성된 물체 점까지 원의 반의 오프셋으로 재구성된다.

도 4e는 컬러 필터 스트라이프(r3)에 의해서만 생성되는 적색 서브 세트의 부분의 재구성을 도시한다. 다시 말해서, 컬러 필터 스트라이프(r3)는 도 4a에 따라 세 번째, 여섯 번째, 아홉 번째, 열두 번째,... 물체 점(OP)에 대한 백색 물체 점(OP)의 적색 서브 세트를 생성한다. 또한, 컬러 필터 스트라이프(r3)는 중첩되지 않는 적색 물체 점, 여기서는 2개의 물체 점을 생성한다. 컬러 필터 스트라이프(r3)에 의해 생성된 물체 점은 컬러 필터 스트라이프(r2)에 의해 생성된 물체 점까지 원의 반의 오프셋으로 재구성된다.

컬러 적색에 따른 절차는 다른 원색인 녹색과 청색에 그에 맞게 적용된다.

결과적으로, 7개의 백색 물체 점들이 3개의 원색 RGB를 사용하여 재구성되며, 3개의 측 방향으로 변위된 컬러 필터 스트라이프는 각각의 원색 RGB에 할당된다. 1/60도의 수평 각도 범위 내에서, 도 3에서 볼 수 있는 바와 같이, r1, g1, b1, r2, g2, b2, r3, g3 및 b3으로 표시된 수직 컬러 필터 스트라이프가 제공된다. 여기서 컬러 필터 스트라이프 배열로서 설계된 분리기를 갖는 SLM을 조명하기 위해, 조정된(tailored) 수평으로 인코히어런트 광이 사용된다. 사용된 광의 공간 코히어런스는 예를 들어, 수직 방향을 따라 > 0.9이며, 이는 서브-홀로그램의 인코딩 방향이다. 1에 가깝다는 것을 의미하는 적당히 높은 코히어런스의 종방향 확장은 예를 들어, 5mm 또는 5mm ~ 10mm일 수 있다.

서로 인접한 열이 서로에 대해 상호 인코히어런트한 방식으로 1D 인코딩에 사용되는 SLM의 상호 열의 상호 코히어런스를 준비하는 것이 중요하다. 이것은 조명 유닛에 스트라이프 모양의 광원 배열을 사용하여 수행될 수 있다.

도 4에서 알 수 있는 바와 같이, 1차원(1D) 인코딩된 홀로그램 디스플레이 디바이스의 단일 라인 또는 일부는 3개의 상이한 컬러로 그리고 단일 원색 RGB를 참조하는 추가적인 서브 세트들로 분할된다.

도 4로부터 더 알 수 있는 바와 같이, 코히어런트 서브 세트로부터 재구성된 물체 점들 사이에는 오버랩(overlap) 또는 중첩(superposition)이 없다. 원은 각각 재구성된 물체 점의 회절 패턴의 첫 번째 최소값을 나타내며 이는 망막 점 확산 함수의 첫 번째 최소값을 의미한다. 정확하게, 점 확산 함수의 외부 사이드 로브를 보여주는 추가 원들이 도시되거나 제공되어야 한다. 그러나, 명확성을 위해서, 첫번 째 최소값 또는 첫번 째 사이드 로브만이 도 4에 도시되어 있다.

일반적으로, 개별 원의 중첩이 없음은 관찰자의 눈의 망막에 인접한 점 확산 함수의 충분한 분리가 제공됨을 의미한다. 그러나 광의 작은 부분이 있을 수 있으며, 재구성된 2개의 인접한 코히어런트 물체 점들과 여전히 중첩된다. 그러나 재구성된 장면이나 물체의 품질에는 큰 영향을 미치지 않는다. 또한, 관찰자의 눈의 망막에서 얻어지는 타겟 강도 분포의 잔여 오류의 이러한 작은 값은 최적화 프로세스의 최적화 알고리즘에서 고려되어 사용될 수 있으며, 최적화 프로세스는 인식 가능한 망막 물체 점 간 크로스토크 없음을 의미하는 타겟 망막 이미지로 검출된 망막 이미지를 근사시킨다. 이 알고리즘은 타겟/실제 비교 및 파라미터의 반복 변형을 참조한다. 망막 물체 점 간 크로스토크를 회피하기 위한 망막 이미지의 추가 최적화는 예를 들어, 항목 1) ~ 6)에서 위에서 기술되고 설명된 개별적인 또는 모든 옵션을 적용함으로써 제공될 수 있다.

컬러 필터 스트라이프 배열로서 설계된 분리기를 포함하는 기술된 SLM은, 예를 들어, 수평 방향으로 0.5도 내지 1도인 평면파의 각 스펙트럼을 방출하는 적어도 하나의 광원을 갖는 조명 유닛에 의해 조명된다. 이러한 평면파의 각 스펙트럼은 코히어런트 방향이 수직 방향이고 반대 방향인 경우 관찰자 평면에서 수평 스윗 스팟에 걸치기에 충분하다. 평면파의 각 스펙트럼은 수직 방향으로 1/60도보다 상당히 작은 것, 예를 들어 단지 1/120도인 것이 바람직하며, 수직 방향은 3차원 장면 또는 물체의 재구성을 위한 1차원(1D) 인코딩된 홀로그램 디스플레이 디바이스의 서브-홀로그램의 인코딩의 방향이다.

디스플레이 디바이스에 제공된 인코딩 유닛 또는 계산 유닛은 물체 점의 고화질(HD) 콘텐츠를 도 4에 따라 서브 세트들로 분리(split)하는 것이 바람직하다. 따라서, 도 4는 또한 인코딩될 콘텐츠의 재어셈블리을 위한 명령어를 도시한다. SLM 상의 1차원(1D) 수직 라인의 ≤ 1/60도의 평면파의 각 스펙트럼 내의 4개의 컬러 필터 스트라이프 배열에 대한 각각의 제3 점 또는 심지어 각각의 제4 점이 도 3에 도시된 SLM의 일부분의 또 다른 서브-컬러 필터 라인에 할당된다. 이것은 3차원(3D) 공간에서 정의된 물체 점들에 의해 생성되는 개별 서브-홀로그램의 신속한 재할당을 제공하는 전자 회로의 블록도로 간단히 전송될 수 있다.

도 4에 개략적으로 도시된 실시 예는 관찰자가 물체 점들에 초점을 맞추고 있는 경우 상호 코히어런트한 물체 점들의 공간적 배치의 상황을 설명한다.

도 5는 관찰자의 눈에서 물체 또는 장면의 초점이 포커싱된(focussed) 및 비-포커싱된(non-focussed) 물체 점들의 망막 위치를 나타낸다. 볼 수 있는 바와 같이, 비-포커싱된 물체 점의 에너지가 퍼져서 망막의 배경을 생성할 것이다. 관찰자가 3차원(3D) 장면의 전경(foreground)을 보면 가장 높은 상대적 흐림이 발생한다. 관찰자가 3차원(3D) 장면의 배경(background)을 보면 가장 낮은 상대적 흐림이 발생하며, 배경은 예를 들어, 서브-홀로그램의 컴퓨터 생성 홀로그램(computer-generated hologram, CGH)이 위치되는 평면인 홀로그램 디스플레이 평면 뒤에 예를 들어, 수 미터 멀리 떨어져 있는 홀로그램 재구성된 물체 점들을 의미한다.

도 5의 A는 가장 완화된 상황을 도시한다. 물체 점의 초점 거리의 가장 큰 음의 값을 가진 서브-홀로그램에서 발생하는 망막의 배경이 널리 퍼진다. 그러나, 이 배경은 관찰자가 보고 있거나 집중하고 있는 물체 점에 코히어런트하게 중첩될 수 있다. 다시 말해서, 관찰자는 대략 눈과 CGH 사이의 작은 원을 보고 있다. 따라서, 원의 이미지는 정확히 눈의 망막에 이미징된다. 여기에 직사각형과 별로서 도시된 비-포커싱된 물체 점도 눈으로 이미징되지만 눈의 망막에 초점을 맞추지는 못한다. 직사각형으로서 도시된 물체 점은 CGH로서 도시낸 디스플레이 디바이스보다 훨씬 뒤에 있으므로, 도 5의 우측에서 볼 수 있는 것처럼 널리 확산된 배경만을 초래할 것이다.

도 5의 B는 관찰자가 CGH의 평면에 제공되는 별을 보고있는 상황을 도시한다. 직사각형과 별로서 도시된 비-포커싱된 물체 점도 눈 안과 눈 뒤에서 이미징되지만 눈의 망막에 초점을 맞추지는 못한다.

도 5의 C는 관찰자가 CGH의 평면 뒤에 제공된 직사각형을 보고 있는 상황을 도시한다. 원과 별으로서 도시된 비-포커싱된 물체 점은 눈의 망막 뒤에 이미징되므로 눈의 망막에 초점을 맞추지 못한다.

컬러 필터 스트라이프 배열을 SLM 상에 분리기로서 제공함으로써, 컬러 필터 스트라이프 배열의 인접한 컬러 필터 스트라이프들 사이의 상호 코히어런스가 제거될 수 있다. 이를 위해 조명 유닛에는 공간 확장 광원을 사용할 수 있다. 콜리메이트(collimate)될 광원의 종횡비는 예를 들어 1:60일 수 있다. 이러한 방식으로, 수평 방향(인코딩 방향이 아님)에 코히어런스가 없다. 따라서, 인접한 컬러 필터 스트라이프의 코히어런트 중첩 및 이러한 방식으로 야기된 화질의 방해가 방지될 수 있다.

본 발명에 따르면, 한 세트의 컬러 필터 스트라이프(단지 하나의 적색 스트라이프, 하나의 녹색 스트라이프 및 하나의 청색 스트라이프를 포함함)에 더하여 추가적인 컬러 필터 스트라이프를 사용함으로써 도입된 추가적인 수직 분리 및 그에 따른 더 높은 픽셀 카운트는 수직 방향을 따라 이웃인 물체 점들 간의 상호 코히어런스를 제거한다. 이것은 상호 코히어런스의 추가적인 감소의 효과를 가져오고 따라서 망막 물체 점 간 크로스토크의 추가 감소를 초래한다.

그러나, 내부 축 물체 점의 코히어런스는 여전히 존재한다. "내부 축 물체 점의 코히어런스(coherence of inner axial object points)"라는 표현은 1차원(1D) 렌즈 라인 세그먼트으로서 인코딩된 서브-홀로그램의 공통 오버랩 영역을 공유하는 물체 점의 코히어런스를 지칭한다. 이것은 단일 컬러 필터를 참조하는 물체 점들에 의해 생성된 크로스토크에도 불구하고 더 이상 다른 모든 물체 점 크로스토크를 다루지 않아야 한다는 것을 의미하며, 물체 점들이 서로의 뒤에 위치되고(디스플레이 디바이스의 광축에 평행한 z-방향을 따르는 것을 의미함), 촛점 밖(out-of-focus) 상황에서 서로 인접하여 위치된다(z-축에 수직인 평면에 있음을 의미함). 이것은 관찰자가 상이한 평면을 보고 있는 상황에서 여기에 고려된 평면에 초점이 맞지 않는다는 것을 의미한다.

위에서 설명한 최적화는 정의된 물체 점의 수를 줄인 경우에만 적용해야 한다. 이는 컬러 필터 스트라이프 배열 및 홀로그램의 1차원 인코딩의 경우, 최적화는 1차원에서만 수행되며, 예를 들어 3 ~ 4개의 이웃하는 물체 점들에 대해서만 수행된다는 것을 의미한다.

도 5는 또한 가중치 행렬(weighting matrix)을 생성하는 개념을 포함한다. 이러한 가중치 행렬은 예를 들어, 상이한 물체 점에 주어진 위상 값의 최적화에 대해 사용될 수 있다. 도 5의 A의 경우에, 디스플레이 디바이스의 뒤쪽에 있고 직사각형으로만 도시된 물체 점은 망막 상의 넓게 퍼지는 배경을 초래하고 따라서 1차(first order) 접근법에서는 무시될 수 있다.

도 5의 C의 경우에, 모든 인라인(inline) 및 예를 들어, 수직으로 5mm인 공간 코히어런스의 확장을 따라 동일한 컬러 필터 스트라이프에 관련된 인라인 물체 점에 근접한 상대적 위상 값은 서로에 대해 그에 따라 최적화되어야 하는데, 3개의 축 물체 점이 서로 가깝기 때문이다. 인라인이란 여기에서 예를 들어, 1/60도 내에서 3개의 엇갈린(staggered) 선이 단 하나의 선으로 보이는 것을 의미한다. 한 가지 옵션은 단일 컬러 필터 스트라이프의 동일한 코히어런트 영역과 관련된 인라인 물체 점의 오버랩되는 서브-홀로그램을 동일한 위상 값으로 설정하는 것이다. 그러나, 일반적으로 단지 하나의 파라미터로서의 위상 값은 디스플레이된 이미지 콘텐츠에 관해서 최적화되어야 한다. 이것은 오버랩된 선명하거나 흐린 코히어런트 물체 점의 상대적인 강도를 포함한다.

이하의 설명은 홀로그램의 1차원 인코딩을 위해 사용될 수 있는 적어도 하나의 광원을 포함하는 조명 유닛을 참조한다. 적어도 하나의 광원에 의해 방출되는 광의 코히어런스는 가능한 한 낮아야 하지만 홀로그램 인코딩을 위해 요구되는 만큼 높아야 한다. 관찰자의 이동 및 디스플레이 디바이스에 제공되는 추가적인 회절 광학 요소들에 따라 관찰자 평면에서 시야 윈도우를 추적하기 위해 도입될 추적 각은 서브-홀로그램의 확장에 기반한 영역 내에 광로차를 도입한다. 따라서, 예를 들어, 사용되는 레이저 광원으로서 설계된 광원의 선폭은 ≤ 0.1nm 이어야 한다. 도입된 광로차뿐만 아니라, 증가된 선폭은 또한 재구성에서 번짐(smearing)을 유발할 것이다. 번짐은 디스플레이 디바이스에 사용된 회절 광학 요소에 의해 도입된 회절 분산으로 인한 것일 수 있다. 이 과정에서 모든 효과가 합산된다.

조명 유닛의 광원의 선폭은 ≤ 0.1nm 이어야 하며, 코히어런스의 한 측면에 지나지 않는다. 또 다른 측면은 공간 코히어런스의 확장이거나 상호 코히어런스의 절대 값을 보다 분명하게 표현한 것이다. 인접한 컬러 필터 스트라이프들 사이의 상호 코히어런스는 전술한 바와 같이 제거될 수 있는 반면, 광의 충분한 코히어런스(예를 들어 > 0.8)는 컬러 필터 스트라이프의 방향을 따라, 즉 인코딩 방향을 따라 제공될 수 있다. 또한, 컬러 필터 스트라이프(들)에 평행하게 배향된 1차원 라인형 세그먼트로 맞추어진 상호 코히어런스 영역은 가장 큰 서브-홀로그램의 크기에 따라 최대 확장으로 제한된다.

광로차의 최대 값 및 따라서 사용된 광원의 선폭 또는 상호 코히어런스의 최대 범위를 지정하기 위해, 서브-홀로그램의 크기를 정의하는데 사용될 수 있는 시야 윈도우의 전체 크기 및 SLM으로의 투영이 고려되지 않아야 한다. 인간 눈의 입사 동공이나 관찰자의 눈만 고려하는 것이 더 낫다. 눈의 입사 동공은 가장 낮은 코히어런스를 특성을 갖는 요구되는 코히어런스 파라미터를 얻기 위해 광로차의 최대 값 및 따라서 사용된 광원의 선폭 또는 상호 코히어런스의 최대 범위를 특정하는데 사용될 수 있다.

사용된 광의 코히어런스를 감소시키는 것은 교란 효과 없이 높은 이미지 콘트라스트 및 의도된 망막 이미지를 제공하기 위한 기본적인 요건이다. 즉, 의도하지 않은 코히어런트 크로스토크를 방지하기 위해 필요에 따라 적당히 높은 코히어런스를 제공하는 방식으로 광의 코히어런스를 감소시키는 것이 중요하다. 또한, 조명 유닛, 관찰자의 눈의 망막 및 SLM을 포함하는 전체 시스템, 즉 관찰자의 눈과 관련된 전체 디스플레이 디바이스의 복소수 값 점 확산 함수는 또한 최적화되어야 한다.

이하에서, 본 발명은 SLM에서 2차원(2D) 인코딩된 홀로그램에 대해 기술되며, 이는 망막 물체 점 간 크로스토크의 감소를 위한 절차를 상세하게 사용한다:

홀로그램의 2차원(2D) 인코딩과의 관계에는 여러 측면이 있다. 관찰자의 눈의 망막에 의해 검출된 완벽한 이미지의 타겟 강도 분포 또는 최종 설계 강도 분포와 관련하여 점 확산 함수를 최적화하는 일반적인 요건은 1차원 인코딩된 홀로그램에 대해 이미 기술되고 설명되었다.

1차원(1D) 인코딩된 홀로그램에 대해 이미 기술된 웨이브 필드를 나타내는 3차원(3D) 물체의 독립적이고 상호 코히어런트한 서브 세트의 생성은 또한 2차원(2D) 인코딩된 홀로그램에도 적용될 수 있다. 다시 말해서, 컬러 필터 배열로서 설계된 분리기는 2차원 인코딩된 홀로그램에도 적용될 수 있다. 컬러 필터 배열은 홀로그램이 2개의 코히어런트 방향으로 인코딩되는, 사용되는 SLM에 적응되어야 한다. 예를 들어, 바이엘(Bayer) 컬러 필터 어레이 또는 바이엘 패턴을 컬러 필터 배열로서 사용할 수 있다.

예를 들어, 관찰자의 눈의 망막 상의 인접한 점 확산 함수들 사이의 크로스토크를 감소시키기 위해, SLM의 픽셀의 표준 픽셀 애퍼처가 사용될 수 있으며, 이는 예를 들어, 600 mm의 시야 거리에서 사용되는 2차원 인코딩된 3차원 홀로그램 디스플레이 디바이스에 대해 33 ㎛ × 33 ㎛이다. 간략화를 위해, 픽셀의 직사각형 모양의 픽셀 애퍼처가 가정될 수 있다. 또한, 예를 들어, 가우스 형 진폭 아포다이제이션 또는 소위 카이저-베셀-윈도우(Kaiser-Bessel-Window)로서 아포다이제이션 프로파일이 적용될 수 있다.

예로서, 직사각형 모양의 픽셀 애퍼처를 갖는 SLM을 사용하는 것으로 가정한다. 이것은 도 6에 도시되어 있는데, 여기서 10 × 10 픽셀이 도시된다. SLM의 필 팩터(fill factorm FF)는 대략 FF = 0.9이며 이상적인 값이다. 이러한 필 팩터는 33 ㎛의 픽셀 피치를 갖는 투과형 SLM에 의해서가 아니라 예를 들어, LCoS(liquid crystal on silicon)로서 예를 들어, 반사 형 SLM에 의해 실현될 수 있다.

도 7은 SLM 평면의 진폭 분포를 나타내는 도 6에 도시된 강도 분포의 푸리에 변환의 강도 분포를 도시한다. 중심 스폿은 푸리에 변환 평면 내에서 SLM의 회절 패턴의 0차 회절 차수와 동등하며, 이것은 시야 윈도우의 평면 또는 관찰자 평면이다. SLM에 대해 가정된 FF = 0.9의 매우 높은 필 팩터로 인해, 중심 0차 회절 차수 스폿보다 눈에 보이는 더 높은 회절 차수는 아마 없을 것이다. 이 계산을 위해 SLM의 일정 위상이 가정된다. 다시 말해서, 인코딩에 의해 도입된 위상 변화는 관찰자의 눈의 평면 내에 존재하는 더 높은 회절 차수의 강도 값을 분명히 상당히 증가시킬 것이다. FF = 1의 필 팩터는 더 높은 회절 차수의 강도, 즉 0보다 큰 회절 차수 인덱스 m, 또는 두 방향으로 m_x 및 m_y > 1을 갖는 회절 차수의 강도를 완전히 제거하지는 않을 것이다. 더 높은 회절 차수는 일정한 위상 분포가 SLM에 기록되지 않으면 존재할 것이다. 그러나 일반적으로 더 높은 회절 차수 피크의 값은 SLM에 디스플레이된 인코딩된 콘텐츠에 따라 변경되지만 더 높은 필 팩터는 더 작은 필 팩터보다 더 높은 회절 차수에서 더 적은 강도를 초래할 것이다. 그러나, 여기에 설명된 SLM의 일반적인 레이아웃에 대해서는 일정한 위상으로 가정된다.

상기 개시된 바와 같이, 픽셀의 직사각형 형태의 애퍼처를 갖는 SLM이 가정된다. 그러나, 픽셀은 예를 들어 이제 정방형이 아니고 1 : 2의 폭 대 높이의 비율을 갖는다. 이러한 SLM은 도 8에 도시되며, 여기서 10 × 10 픽셀이 도시된다. SLM의 필 팩터(FF)는 대략 FF = 0.5이고, 즉 0.5보다 약간 작을 수 있고 예를 들어 단지 0.45일 수 있다. 그러나 상기 실시 예를 간단하고 이해하기 쉽게 유지하기 위해 여기서 0.5의 필 팩터를 가정할 수 있다. 픽셀 피치는 예를 들어 양방향, 즉 수평 및 수직으로 33 ㎛이다. SLM의 픽셀 높이는 33 μm에 가깝지만, 상기 픽셀의 폭은 16 μm에 가까울 뿐이다. SLM의 픽셀 애퍼처의 좌측 절반만이 이 실시 예에서 사용된다.

도 9는 관찰자의 눈의 평면 내에서 도 8에 도시된 강도 분포의 푸리에 변환의 강도 분포를 도시한다. 중심 피크는 0차 회절 차수의 강도이다. y-방향, 즉 수평 방향으로의 SLM의 더 큰 필 팩터는 시야 윈도우의 평면 또는 관찰자의 평면인 관찰자의 눈의 평면에서 y-방향을 따라 감소된 사이드 로브를 초래한다. 따라서, SLM의 수평 방향을 따라 더 큰 필 팩터를 사용하는 것이 바람직하다. 도 8에 도시된 강도 분포는 빈 홀로그램을 인코딩하는 경우, 즉 SLM 평면에서 일정한 위상 값을 사용하고 SLM의 모든 픽셀에 대해 동일한 진폭을 사용하는 경우의 시야 윈도우 평면의 강도 분포와 동일하다. 도 6 및 도 7에 도시된 푸리에 변환과 비교하면, 픽셀의 감소된 수평 폭은 그 푸리에 변환 평면, 즉 관찰자의 눈이 제공되는 시야 윈도우의 평면에서 SLM의 ± 1차 수평 회절 차수를 증가시킨다. 도 8 및 도 9에 도시된 이 실시 예에서, m = ± 3보다 큰 수평 회절 차수는 이웃하는 눈에서 관찰 경험을 방해하지 않을 정도로 충분히 작은 강도를 나타낸다. 여기서, 현저한 수평 ± 4차 회절 차수는 존재하지 않는다.

예를 들어, 청색 원색에 대한 파장 λ = 450 nm이고, 데스크탑 형 홀로그램 3차원(3D) 디스플레이 디바이스 내에서 사용되는 체적 격자 기반 필드 렌즈의 초점 길이 f = 600 ㎜이고 픽셀 피치가 33 μm라고 가정하면, 청색 광에 의해 형성된 관찰자 평면 내의 시야 윈도우는 약 8 mm × 8 mm의 확장을 갖는다. 3차 회절 차수는 0차 회절 차수 스폿으로부터 약 24 mm에 제공된다. 판독(read) 원색에 대해 가정된 λ = 650 nm의 파장에 대해, 3차 회절 차수는 제로 회절 차수 스폿으로부터 약 35 mm에 제공된다. 이것은 65 mm의 관찰자의 두 눈의 평균 거리의 경우, 35 mm의 거리가 충분하다는 것을 의미한다.

도 10은 픽셀의 직사각형 형상의 애퍼처 및 대략 0.5의 필 팩터를 갖는 SLM의 이진 진폭 투과를 도시한다. 여기서 10 × 10 픽셀이 다시 도시된다. 도 10에 도시된 실시 예는 도 6에 도시된 픽셀 애퍼처의 좌측 절반만을 사용하거나 도 8에 도시된 분포에서 사용되지 않는 영역을 사용하는 것과 동일하다. 즉, 도 10에 따르면, 픽셀 애퍼처의 좌측 절반만이 사용된다. 중요한 것은 여기서 도 6에 도시된 픽셀의 초기 상황이 사용되고 이러한 초기 SLM 중 2개의 서브 세트가 생성된다는 사실이다. 우측 서브 세트는 도 8의 SLM에 의해 도시되고, 좌측 서브 세트는 도 10의 SLM에 의해 도시된다.

도 8에 도시된, 도 6에 도시된 초기 SLM의 우측 서브 세트 및 도 10에 도시된 SLM에 의해 예시된 초기 SLM의 좌측 서브 세트는 SLM의 푸리에 평면에서 등가 강도 분포를 생성한다. 다시 말해서, 도 8에 도시된 진폭 분포의 푸리에 평면의 강도 분포와 도 10에 도시된 진폭 분포는 일정한 위상이 SLM에서 사용된다면 동일하고 도 9에 도시된 바와 같을 것이다. 이 시점에서 두 푸리에 변환의 위상이 상이하다는 것은 서로 관련성이 없다. 이것은 도 7 및 도 9의 SLM의 2개의 서브 세트가 코히어런트하게 중첩되는 경우에 고려되어야만 한다. 그러나, 본 발명에 따르면, 도 7 및 도 9에 도시된 SLM의 2개의 서브 세트의 인코히어런트 중첩이 진폭 분포로서 사용된다.

관찰자에게 디스플레이될 3차원(3D) 홀로그램 물체를 나타내는 웨이브 필드의 인코히어런트 서브 세트를 생성하기 위해 SLM의 상이한 유형의 서브 세트가 사용될 수 있다. 웨이브 필드의 인코히어런트 서브 세트를 생성하기 위해 분리기가 사용될 수 있다. 분리기로서, 공간 분리 컬러를 제공하는 컬러 필터 스트라이프 배열, 공간 분리 직교 편광 상태를 제공하는 패턴화된 리타더의 배열, 또는 SLM을 조명하는 웨이브 필드의 공간 분리된 할당을 제공하는 조명 유닛 내의 광원 배열이 사용될 수 있다.

SLM의 물리적 50 % 어드레싱이 사용된다. 단순화 및 본 발명의 간단한 설명을 위해, 본 발명의 단순한 실시 예에만 집중된다. 단순한 실시 예는 SLM의 간단한 서브 세트만을, 즉 도 6에 도시된 SLM의 2개의 간단한 서브 세트를 사용하는 것을 의미하는데, 도 8 및 도 10에 도시되어 있다.

필 팩터(FF)가 도 10에 도시된 것보다 훨씬 더 작으면, 예를 들어, 33 ㎛ × 33 ㎛의 주요 정사각형 형상의 픽셀을 2개의 서브 세트로 세분화하는 것이 바람직하며, 이 서브 세트는 픽셀의 우측 및 좌측 부분을 사용하는 대신에 픽셀의 상부 및 하부 부분을 사용함으로써 얻어진다. 따라서, 2 : 1의 픽셀의 폭 대 높이의 비율을 구현하는 것이 바람직할 수 있다. SLM의 더 높은 회절 차수는 수평 방향이 아니라 수직 방향을 따라 지배적일 것이고, 이로 인해 관찰자의 좌측 눈과 우측 눈에 디스플레이되는 콘텐츠 간의 잠재적 크로스토크를 감소시킨다. 이 실시 예를 사용할 확률은, SLM의 구현된 레이아웃의 가장 작은 구조적 치수인 SLM의 제조 프로세스의 임계 치수가 예를 들어 단지 5 ㎛인 경우 증가된다. 3 ㎛의 임계 치수는 더 큰 필 팩터로 이어질 것이다. 따라서, 예를 들어, 단지 5 ㎛의 임계 치수를 사용하는 것이 바람직하다.

다음은 패턴화된 리타더의 배열로서 설계된, 분리기가 제공된 SLM의 실시 예를 기술한다. 패턴화된 리타더의 배열은 예를 들어 선형 편광 상태일 수 있는 초기 편광 상태를 갖는 SLM 상에 입사하는 광을 2개의 패턴화된 광의 서브 세트로 변환하는데 사용된다. 2개의 패턴화된 광의 서브 세트는 직교 편광 상태를 갖는다. 예를 들어, 도 6에서 볼 수 있는 바와 같이, 주요 정방형/정사각형 모양의 픽셀 애퍼처가 두 부분으로 분할된다. 이것은 초기 픽셀 카운트 및 따라서 초기 픽셀 밀도가 두 배가 된다는 것을 의미한다. 예를 들어 도 8 및 도 10에서 볼 수 있는 바와 같이, SLM의 모든 픽셀의 2개의 픽셀 서브 세트에 패턴화된 리타더의 배열이 제공된다. 픽셀의 제1 서브 세트에는 예를 들어, a + π/4 패턴화된 리타더가 제공되고 픽셀의 제2 서브 세트에는 예를 들어, a - π/4 패턴화된 리타더가 제공된다. 이러한 2개의 픽셀의 서브 세트를 포함하는 SLM이 SLM의 출사 평면에서 선형 편광된 광으로 조명되면, 상이한 패턴화된 리타더를 갖는 2개의 SLM 서브 세트를 참조하는 2개의 직교 편광된 웨이브 필드가 존재할 것이다.

다음 섹션에서는 컬러 당 하나, 2개 또는 여러 개의 광원이 제공되는지 설명한다. 고전 광학 또는 일반적으로 비-편광-선택 광학이 시야 윈도우의 평면을 형성하는데 사용될 수 있다면, 관찰자에게 표시될 3차원 물체를 나타내는 웨이브 필드의 2개의 공간 인터레이스된 서브 세트를 생성하기 위하여 설명된 실시 예가 사용될 수 있다. 관찰자의 눈의 망막에 이미징된 인접한 물체 점들은 직교 편광 상태를 나타내며 따라서 상호 코히어런트 점과 동일한 방식으로 또는 더 자세히 망막 점 확산 함수와 동일한 방식으로 간섭한다. 다시 말해서, 한 방향으로는 코히어런스가 없다. 따라서, 한 방향을 따라 관찰자의 눈의 망막 상의 인접한 점 확산 함수인 인접한 물체 점들 사이의 코히어런트 망막 물체 점 간 크로스토크가 없다.

그러나, 빔 경로 내의 SLM을 따르는 광학 요소가 편광 선택성이거나 단일 편광 상태만을 필요로 하는 경우, 2개의 상호 인코히어런트 웨이브 필드를 구현하기 위해 상이한 방식이 사용되어야 한다. 이 경우 공통 출사 편광 상태를 사용해야 한다. 이것은 단일 주요 광원이 사용되는 경우 상호 인코히어런스가 존재하지 않을 것이라는 것을 의미한다.

원색별로 SLM을 조명하는 적어도 2개의 상호 인코히어런트 광원을 사용해야 한다. SLM은 예를 들어, 패턴화된 리타더의 배열로서 설계된 분리기를 포함한다. 패턴화된 리타더의 배열은 SLM의 픽셀에 할당된다. 바람직하게는, 패턴화된 리타더의 배열은 픽셀의 적어도 2개의 정의된 부분, 특히 SLM의 픽셀 애퍼처의 2개의 서브 세트에 할당된 패턴화된 편광 필터의 배열로서 설계된다.

예를 들어, 2개의 직교 편광된 웨이브 필드를 수용하기 위해 최적화된 쐐기 형 조명 유닛을 사용할 수 있다. 하나의 웨이브 필드는 조명 유닛의 제1 광원으로부터 나온다. 이 광은 예를 들어 TE(transverse electric) 극성일 수 있다. 다른 웨이브 필드는 조명 유닛의 제2 광원으로부터 나온다. 이 광은 예를 들어 TM(transverse magnetic) 극성일 수 있다. 마지막으로, SLM은 2개의 웨이브 필드로 조명된다.

도 11은 광원으로서 레이저 다이오드의 공진기의 단부에서 사용되는 2개의 미러 중 하나로서 구현될 수 있는 2차원 와이어 그리드 편광자의 실시 예를 도시한다. 도시된 패턴은 2개의 교차된 고 반사 1차원(1D) 와이어 그리드 구조를 생성함으로써 실현될 수 있다. 이 특별한 와이어 그리드 형 편광자의 주기는 π/2n보다 작으며, 여기서 π는 광원, 예를 들어 레이저 다이오드의 파장이고, n은 편광자의 기판/구조의 굴절률이다. 2개의 선형 직교 편광 상태는 1에 가까운 최대 반사율을 갖는다. 금속 2차원 스트라이프 와이어 그리드 편광자 구조는 유전체층 스택을 추가함으로써 그 반사율을 향상시킬 수 있다. 예를 들어, 도 11에서 와이어 그리드 편광자 구조 또는 상이한 미러 버전이 예를 들어, 2개의 직교 선형 출사 편광 상태를 SLM로부터 제공하기 위하여 광원 캐비티의 단부에서 사용될 수 있다. 예를 들면. 조명 유닛에 브래그 형 공진기 미러를 추가함으로써 파장 안정화가 구현될 수 있다. 따라서, 예를 들어, 0.1 nm인 광원의 선폭은 안정된 파장과 결합될 수 있으며, 이는 디스플레이 디바이스의 동작 동안 예를 들어 약 0.1nm 미만으로 시프트된다. 이 구조는 상호 인코히어런트한 SLM으로부터 2개의 직교 편광된 출사 빔을 얻기 위해 더 결합될 수 있거나, 추가로 전개될 수 있다. 이것은 비용 효율적인 단일 광원, 예를 들어, 본 발명에 따른 디스플레이 디바이스에 사용될 수 있는 레이저 다이오드 형 광원을 실현할 수 있다는 것을 의미한다.

다른 애플리케이션의 경우 예를 들어. SLM 외부의 3개 이상의 상호 인코히어런트 출사 빔이 생성될 수 있다. 이 출사 빔은 선형 편광된다.

도 12에는 SLM의 이진 진폭 투과가 도시되어 있다. SLM은 직사각형 모양의 픽셀 애퍼처와 약 FF = 0.5의 필 팩터를 포함한다. 여기서, 10 × 10 픽셀이 예로서 다시 표시된다. 필 팩터는 도 8에 도시된 SLM의 필 팩터와 동일하다. 패턴화된 리타더, 바람직하게는 패턴화된 편광 필터의 배열로서 설계된 분리기는 SLM의 픽셀, 특히 SLM의 픽셀의 애퍼처에 할당된다. 패턴화된 편광 필터는 수평 배향 전기장의 투과를 허용한다. 여기서는 SLM의 모든 픽셀에 할당될 수 있는 단 하나의 패턴화된 편광 필터만 필요하다.

도 13은 직사각형 형상의 픽셀 애퍼처 및 대략 FF = 0.5의 필 팩터를 갖는 SLM의 이진 진폭 투과를 도시한다. 여기서 10 × 10 픽셀이 예로서 다시 도시된다. 필 팩터는 도 10에 도시된 SLM의 필 팩터와 동일하다. 패턴화된 리타더, 바람직하게는 패턴화된 편광 필터의 배열로서 설계된 분리기는 SLM의 픽셀, 특히 SLM의 픽셀의 애퍼처에 할당된다. 패턴화된 편광 필터는 수직 배향 전기장의 투과를 허용한다. 여기서는 SLM의 모든 픽셀에 할당될 수 있는 단 하나의 패턴화된 편광 필터만 필요하다.

SLM의 픽셀의 2개의 서브 세트의 네스트된 배열이 도 14에 도시되어 있다. SLM의 행(row)에서 2개의 인접한 서브 세트는 각각 SLM으로부터의 광의 직교하는 출사 편광을 생성한다. 이것은 SLM의 2개의 인접한 열이 SLM로부터의 광의 직각 출사 편광을 생성함을 의미한다. 도 14에 도시된 이 실시 예는 도 12 및 도 13에 도시된 실시 예들의 조합이다. 도 12 및 도 13에 도시된 패턴화된 필터에 따른 단 하나의 패턴화된 편광 필터만이 SLM의 실시 예에 사용될 수 없다. 따라서, 개별 픽셀 또는 SLM의 개별 열에 할당된 네스트된 편광 세그먼트를 포함하는 패턴화된 편광 필터가 사용되어야 한다. 또는, 픽셀의 2개의 인접한 서브 세트가 SLM으로부터의 광의 직교 출사 편광을 생성하는 방식으로 서로 배열되는 2개의 패턴화된 편광 필터가 사용되어야 한다.

광의 전파 방향에서 볼 때, SLM 뒤에 추가적인 단일 편광 필터를 추가하면, 3차원 물체 장면의 일부를 운반하는 2개의 상호 인코히어런트 웨이브 필드를 포함하는 단일 광 출사 편광 상태가 제공된다. 이 웨이브 필드는 이제 디스플레이 디바이스의 모든 광학 요소를 통해 전파될 수 있고, 이는 이러한 요소들의 편광 선택도에 관계없이 빔 경로 내에서 이어진다. 예를 들어, 빔 경로에서 SLM을 따르는 편광 유형 LC 격자는 원형 편광된 광으로 조명되어야 한다; 그런 다음 그것을 조명하는 웨이브 필드의 필요한 편광 상태를 제공하기 위해 리타더가 사용되어야 한다.

또한, 홀로그램의 2차원(2D) 인코딩에서, 컬러 필터 스트라이프의 배열이 SLM 평면에서 사용될 수 있다. 이를 위해 홀로그램 3차원 데스크탑 디스플레이 디바이스의 경우 33 ㎛ × 33 ㎛일 수 있는 SLM의 픽셀의 초기 픽셀 애퍼처가 적어도 3개의 서브-픽셀 또는 3개의 서브 세트 또는 일반적으로 픽셀의 3개의 정의된 부분으로 분할되어야 한다. 도 15는 직사각형 형상의 픽셀 애퍼처 및 대략 FF = 0.25만의 필 팩터를 갖는 SLM의 이진 진폭 투과를 도시한다. 여기서 10 × 10 픽셀이 예로 다시 도시된다. 이것은 도 6에 도시된 픽셀 애퍼처의 우측 하부 1/4, 즉 최대 애퍼처의 1/4만 사용하는 것과 동일하다. 물론, 픽셀의 상이한 정의된 부분들, 예를 들어 픽셀의 좌측 상부 1/4에도 사용될 수 있다.

도 16은 도 15에 도시된 강도 분포의 푸리에 변환의 강도 분포를 도시한다.이 강도 분포는 관찰자의 눈의 평면에서 생성된다. 도면의 중앙 피크는 0차 회절 차수의 강도를 도시한다. SLM의 FF = 0.25의 작은 필 팩터는 더 높은 회절 차수의 강도를 증가시킨다. 예를 들면 더 높은 회절 차수를 유지하면서, 허용된 한도 내에서 관찰자 평면에서 시야 윈도우의 평면 내에 존재하는 초기 33 ㎛ × 33 ㎛ 픽셀 크기 내에 3개의 서브 픽셀을 구현하는 것이 가능하다는 것을 알 수 있다.

원색 RGB 중 하나와 관련된 컬러 필터 스트라이프의 배열의 컬러 필터 세그먼트를 포함하는 서브-픽셀 또는 픽셀의 서브 세트는 예를 들어, 16 ㎛ × 16 ㎛만의 확장을 가진다. 이처럼 작은 픽셀을 구현하는 것은 아마 비용이 많이 든다. 그러나, 고도의 기술적 노력 없이도 수년 내에 가능할 수 있다. 또한, 필 팩터를 가능한 한 높게 유지하기 위해 픽셀의 제조 내에서 작은 임계 치수가 요구된다. 따라서, 예를 들어, 2차원 인코딩된 복소수 값의 SLM 내에서 컬러 필터를 구현하기 위해서는 3 ㎛의 임계 치수가 필요할 수 있다.

또한, 2차원 컬러 필터 스트라이프의 배열은 유리하게는 예를 들어 직교 편광 필터로서 설계된 패턴화된 리타더의 배열과 결합될 수 있다. 그러나, 이는 SLM의 제조에서 실용적인 임계 치수를 단지 2 ㎛까지 감소시킬 수 있다. 예를 들어 33 ㎛ × 33 ㎛의 초기 픽셀 크기는 예를 들어 픽셀 또는 서브 픽셀의 6개의 정의된 부분 또는 서브 세트로 분할되어야 한다. 이는 컬러 필터 스트라이프 및 2개의 추가적인 패턴화된 편광 필터와 관련하여 세 가지 컬러를 의미한다. 각 편광 필터는 컬러 필터 스트라이프의 삼중선(triplet)에 할당된다. 따라서, 각 원색 RGB는 픽셀의 2개의 작은 서브 세트로 표현된다. 픽셀의 두 서브 세트는 직교 편광된 광을 방출한다.

예를 들어, 도 14에 도시된 각각의 픽셀 애퍼처는 예를 들어, 픽셀의 세 가지 컬러 서브 세트로 세분될 수 있다. 그러나, 이를 위해서는 상당한 기술적 노력이 필요하며 따라서 초기 제품에 대한 가장 빠른 방법이 아닐 수도 있다.

SLM의 픽셀들의 애퍼처들의 직사각형 배열들에 추가하여, 예를 들어, 픽셀들의 애퍼처들의 육각형 배열이 사용될 수 있다. 이들 배열에는 또한 패턴화된 리타더, 바람직하게는 패턴화된 편광 필터 및/또는 패턴화된 컬러 필터 스트라이프의 배열이 제공될 수 있다.

SLM에 의해 방출된 광의 2개의 직교 편광의 아마 보다 실제적인 구현은 일반적으로 쐐기 함수를 SLM의 서브-홀로그램으로 인코딩하는 것일 수 있다. 이러한 방식으로, 시야 윈도우에 걸친 각도 범위 내의 물체 점은 측 방향으로 시프트될 수 있다. 홀로그램의 2차원 인코딩을 위해, 이것은 수직 방향뿐만 아니라 수평 방향을 따라 행해질 수 있다. 다시 말해서, 도 14에서 볼 수 있는 바와 같이, 픽셀의 정방형/정사각형 영역의 좌측 분리 및 우측 분리가 수평 분리를 생성할 수 있고, 이는 인접한 직교 편광된 망막 점 확산 함수의 좌측 분리 및 우측 분리이다. 픽셀의 정사각형 영역의 상부 분리 및 하부 분리는 수직 분리를 생성할 수 있는데, 이것은 인접한 직교 편광된 망막 점 확산 함수의 상부 분리 및 하부 분리이다. 이것은 또한 SLM 평면 내의 픽셀 모양의 초기 정방형 영역이 상부 직사각형과 하부 직사각형 부분 또는 서브 세트으로 분할되는 경우에도 적용된다. 이러한 SLM은 도 14에 도시된 SLM이 시계 방향 또는 반 시계 방향으로 약 90도 회전되는 것일 것이다. 이것은도 17에 도시되어 있으며, 도 17에서는 SLM 평면에서 편광 필터들의 배열이 도시되고, 편광 필터의 배열이 도 14중 하나와 직교하도록 배열된다.

요약하면, 본 발명에 따르면, 예를 들어, 디스플레이 디바이스의 SLM에 의해 생성된 웨이브 필드의 2개 이상의 서브 세트가 존재하며, 이들은 상호 인코히어런트하다. 1차원 인코딩의 경우, 컬러 필터 스트라이프의 배열, 패턴화된 리타더의 배열, 특히 직교 편광을 갖는 편광 필터의 배열, 또는 이들의 조합이 3차원 물체 또는 장면을 부분적으로 표현하는 웨이브 필드의 상호 인코히어런트 서브 세트를 제공하기 위해 사용될 수 있다. 2차원 인코딩의 경우, 1차원 인코딩에서 2개의 직교 편광 상태를 가지며 조명 유닛 내의 상이한 광원들로부터 방출되는 광으로 SLM을 조명하는 것이 또한 가능하다. 이 광은 투과된 편광 상태의 교대하는 방향을 갖는 편광 필터의 스트라이프 패턴을 조명할 수 있다. 또한, 2차원 인코딩의 경우, 편광 필터 다음에는 추가의 비-패턴화된 리타더, 특히 단일 편광 상태만을 투과하는 편광 필터가 뒤따른다. 광이 여기 분실될 수도 있다. 그러나, 이제 디스플레이 디바이스의 빔 경로에서 SLM 다음의 광학 요소를 조명하는 2개의 상호 인코히어런트 인코딩된 웨이브 필드가 존재한다. 또한 한 방향을 따라 서브-홀로그램에서 추가 위상 쐐기로 인코딩될 수 있다. 1차원 인코딩의 경우와 대조적으로, 2차원 인코딩은 SLM의 서브-홀로그램에 인코딩된 임의의 모양의 2차원 위상 쐐기 함수의 실현을 제공한다. 잠재적인 2차원 쐐기 분포의 하나의 서브 세트만이 그를 위해 필요하다.

인접한 물체 점들의 유리한 편광 인코딩 패턴은 재구성된 물체 점들에 적용되는 바둑판 같은 분포에 의해 주어진다. 또한, 허니 콤 모양의 분포가 또한 사용될 수 있으며, 이는 또한 2개의 직교 편광을 제공한다. 이것은 관찰자가 물체 점에 초점을 맞춘 경우에 물체 점의 평면 또는 관찰자의 눈의 망막 평면에 제공된다. 또한, 예를 들면, 상호 인코히어런트 패턴의 다른 무작위 분포를 사용할 수도 있다.

도 18에는 관찰자가 이들 물체 점에 초점을 맞춘 경우에 관찰자의 눈의 망막에서 또는 공간에서 재구성된 3차원 물체 점을 나타내는 직교 편광 상태의 바둑판 모양의 할당 패턴이 도시되어 있다. 물체 점은 공간의 상이한 그리드에서 생성될 수 있다. 도 18에서, 공간에서 재구성된 98 픽셀 × 98 픽셀의 편광 상태가 보여질 수 있다. 이것은 예를 들어, 물체의 한 평면일 뿐이다. 3차원 공간에서, 인접한 깊이 평면은 교번하는 할당 패턴을 포함할 수 있다. 이것은 동일한 x-좌표(수평 방향) 및 y-좌표(수직 방향)를 갖지만 인접한 깊이 평면에 배치되는 물체 점이 바람직하게는 직교 편광 상태를 가질 수 있음을 의미한다. 다시 말해서, 도 18에 도시된 편광 상태 할당 패턴은 교대로 z-방향(깊이 방향, 즉 디스플레이 디바이스의 광축에 평행)으로 사용될 수 있으며, 즉, 편광 상태는 인접한 z-평면에 대해 반전(invert)된다.

도 18의 이러한 간단한 그리드는 또한 육각형 허니콤 형 그리드로 변경될 수 있다. 장면의 콘텐츠와 관련된 초기 패턴을 임의로 변경할 수도 있다. 그러나 이것은 아마도 인코딩 프로세스의 최적화의 복잡성을 더욱 증가시킬 것이다. 또한, 편광 상태 할당 패턴은 2차원(x 및 y 방향)뿐만 아니라 z-좌표를 따라 변경될 수 있다. 그러나 가장 간단한 방법은 수직 방향(y-방향)과 수평 방향(x-방향)을 따라 고정 패턴을 사용하여 깊이 방향(z-방향)을 따라 교대로 반전시킬 수 있고 이는 관찰자와의 거리 또는 서로 상이한 z-평면 간의 거리이다.

다음 설명은 헤드 마운티드 디스플레이와 관련된 망막 물체 점 간 크로스토크 감소를 위한 점 확산 함수 PSF_ij의 계산을 참조한다. 그러나, 이전에 볼 수 있듯이 망막 점 확산 함수 최적화는 1차원 인코딩 및 2차원 인코딩을 위한 모든 유형의 서브-홀로그램 기반 홀로그램 디스플레이 디바이스에도 사용될 수 있다. 결과적으로, 본 발명은 직접 뷰 디스플레이 디바이스, 예를 들어, 1차원 VPO 인코딩된 홀로그램을 사용하여 텔레비전 디스플레이 디바이스의 2차원 인코딩을 사용하는 데스크탑 디스플레이 디바이스 용으로 사용될 수 있다.

가장 간단한 경우는 수직 배향 서브-홀로그램을 사용하는 1차원 인코딩된 VPO(vertical parallax only) 홀로그래피이다. 조명 유닛의 광원이 코히어런스의 복잡도의 최적화된 절대 값을 제공하기 위하여 적응되면, 즉 단순한 점 광원이 아닌 경우, 가장 큰 서브-홀로그램의 크기와 같거나 그보다 작은 상호 거리를 갖는 하나의 수직 선의 픽셀만이 상호 코히어런트하도록 보장될 수 있다.

조명 유닛의 일차원 VPO 인코딩 및 맞춤 조명을 가정하고, 인접한 점 확산 함수의 최적화가 SLM의 한 방향을 따라 각 열에 대해 개별적으로 수행될 수 있다. 더욱이, 최적화될 이산 점 확산 함수의 가까운 이웃들만이 고려되어야 한다.

SLM의 좌측 상부 모서리의 서브-홀로그램을 예로 들면, 각 컬러를 개별적으로 제공할 수 있으며 망막 점 확산 기능 PSF_ij를 계산할 수 있다. 인덱스 i는 SLM의 열을 표시하는 데 사용될 수 있고 인덱스 j는 계산 프로세스에 사용된 SLM의 행을 표시하는 데 사용될 수 있다. 이것들은 공간에서 생성된 물체 점들의 망막 그리드의 인덱스이다. 이 인덱스는 또한 망막 물체 점과 관련된 이산 서브-홀로그램을 나타내는 데 사용될 수 있다. 인간 눈의 입사 동공의 정의된 직경은 장면의 밝기와 관련하여 가정될 수 있으며, 100 cd/m²의 경우 2.9 mm이다. 최적화되지 않은 모든 서브-홀로그램은 이미 생성되었거나 서로 후에 막 생성될 것이다. 예를 들어, 최적화되지 않은 모든 서브-홀로그램이 이미 생성되었다고 가정한다. 그 다음, 제1 점 확산 함수 PSF₁₁가 계산된다.

최적화 프로세스의 계산 부하는 고화질(HD) 콘(cone)에 집중될 수 있다. 이는 고화질 1/60도 분해능이 약 10도 각도로 중앙 콘에서만 볼 수 있다는 것을 의미한다. 최적화 동안에 주로 중심 콘에 집중할 수 있다. 따라서, 고화질(HD) 콘에서보다 많은 전력이 다른 영역들, 예를 들면, 망막의 가장자리에 대해 사용될 수 있다. 관찰자 평면에 있는 단일 관찰자에게는 눈과 색마다 하나의 고화질 콘이 제공된다. 콘의 수는 관찰자의 수에 따라 다르다. 시선 추적은 고화질 콘을 정확하게 제공하는 데 필요하다. 이것은 디스플레이 디바이스에서 시선 추적을 통합하는 것이 바람직하다는 것을 의미한다.

더욱이, 비-고화질 콘 영역의 얇은(thinned) 물체가 사용될 수 있다. 예를 들어, 시야의 테두리에서 16배 큰 밝기로 물체 점이 재구성되는 한, 4 × 4 시닝(thinning)을 2차원 인코딩에 사용할 수 있다. 이는 영역 당 광 에너지가 일정하게 유지되기 때문에 문제가 되지 않는다. 2차원 인코딩의 경우, 수직 방향 및 수평 방향을 따라서만 매 4번째 물체 점마다 사용될 수 있다. VPO 인코딩된 홀로그램의 경우 SLM의 열을 따라 4번 시닝만을 수행할 수 있다.

또한 눈과 컬러별로 하나의 고화질 콘을 낮은 분해능의 프러스텀(frustum)으로 투영하는 것이 가능하다. 이는 직접 뷰 디스플레이 디바이스와 프로젝션 디스플레이 디바이스의 조합일 수 있다. 또는, 시선 추적 데이터에 의해 정의되는 대형 저 분해능 프러스텀 생성 디스플레이 디바이스 및 고화질 콘 생성 디스플레이 디바이스의 조합일 수 있다. 그러나, 이것은 아마 상당한 기술적 노력을 추가할 수 있다.

관찰자의 눈의 망막에 점 확산 함수 PSF₁₂를 생성하는 VPO 인코딩된 홀로그램 예제의 제2 서브-홀로그램으로 돌아간다. 이제 제2 서브-홀로그램만이 변경된다. 즉, 점 확산 함수 PSF₁₁의 타겟 강도 및 설계 강도인 점 확산 함수 PSF₁₂를 획득하기 위해, 점 확산 함수 PSF₁₁에 대한 위상 오프셋 및 점 확산 함수 PSF₁₂의 강도 값이 변경된다. 즉, 예를 들어 그것은 위상 오프셋 및 강도 변경에 사용된다. 그 다음, 코히어런트하게 더해진 2개의 점 확산 함수 PSF₁₁ 및 PSF₁₂에 인접하여, 점 확산 함수 PSF₁₃가 배치된다. 이제, 점 확산 함수 PSF₁₁ + PSF₁₂ + PSF₁₃의 코히어런트 합의 설계 강도 분포를 얻기 위해 초기 점 확산 함수 PSF₁₃를 변경하기 위한 위상 오프셋 및 강도 변화가 한번 더 사용된다. 그런데, 이것은 j에서 j + 1에서 j + 2 ... j + N까지, 즉 SLM의 이산 열, 여기서는 열 1에 의해 형성된 마지막 점 확산 함수 PSF_ij에 의해 설명될 수 있다. 그런 다음 SLM의 다음 열이 수행된다. VPO 인코딩된 홀로그램의 경우 SLM의 열을 따라 행해진 최적화 프로세스가 병렬로 수행될 수 있다. 이것은 맞춤 조명을 사용하는 경우 SLM의 열이 상호 인코히어런트하다는 사실에 기인한다. 계산 및 최적화 알고리즘을 빠르고 간단하게 유지하기 위해, 망막에 국부적으로 제공된 점 확산 함수의 피크 강도 값을 최적화 프로세스의 기준으로 사용할 수 있다. 예를 들어. 단일 피크 강도 값 대신 1/60도 각도 범위의 적분(integral) 강도 값을 사용하는 것이 여전히 의미 있을 수 있다. 그러나 그 차이는 작다. 예를 들어, 최적화를 위한 단일 점 확산 함수의 3개 이상의 샘플링 점을 사용하는 것은 더 많은 노력, 즉 더 많은 계산 부하를 추가할 수 있다.

홀로그램의 2차원 인코딩을 위해, 최적화는 홀로그램의 1차원 인코딩에 대해 아날로그 방식으로 수행될 수 있다. 예를 들어, 그것은 서브-홀로그램의 상부 좌측 모서리 또는 물체 점들의 망막 점 확산 함수 PSF_ij에서 시작될 수 있다. 제1 점 확산 함수 PSF₁₁가 형성되고 제2 점 확산 함수 PSF₁₂가 더해진다. 이러한 합해진 점 확산 함수는 필요하다면 위상 오프셋과 강도의 변화를 사용하여 최적화된다. 그러면, 예를 들어, 점 확산 함수 PSF₂₁이 더해지고 위상 및 강도를 사용하여 또한 최적화된다. 이제 점 확산 함수 PSF₂₂가 더해지고 필요에 따라 위상 오프셋과 강도 값이 변경된다. 그러면, 예를 들어 점 확산 함수 PSF₁₃이 더해지고 위상 오프셋 및 강도 값이 최적화된다. 점 확산 함수 PSF_ij의 다음 인덱스들은 예를 들어, 23 및 31이 될 수 있고, 그 뒤에 14가 될 수 있다. 예를 들어, 이는 서브-홀로그램의 좌측 상단 모서리에서 시작하여 우측 하단 모서리에 도달할 때까지 단계별로 장면을 채우고 최적화할 수 있음을 의미한다.

이 최적화 프로세스에 대한 상이한 경로가 사용될 수 있다. 예를 들어 점 확산 함수 PSF₁₁로 시작한 다음 점 확산 함수 PSF₁₂, PSF₁₃, PSF₁₄, ..내지 PSF_1N으로 갈 수 있고, 여기서 N은 생성될 수직 물체 점들의 수, 예를 들어 1000개의 물체 점 또는 심지어 2000개의 물체 점이다. M에서 수평적으로 생성되는 물체 점들의 수는 예를 들면 2000 내지 4000일 수 있다. 상세하게, 이것은 처음에 서브-홀로그램의 첫 번째 열이 채워지고 완료된 다음 단계별로 두 번째 열의 요소들, 즉 점 확산 함수 PSF₂₁, PSF₂₂, PSF₂₃, PSF₂₄ , ..내지 PSF_2N가 더해짐을 의미할 수 있다. 여기에서는 단계별 채우기 및 최적화가 서브-홀로그램의 좌측에서 우측으로 수행된다. 이 방식으로 M, N의 2차원 행렬을 생성할 수 있다.

SLM에 대한 미리 정의 가능한 방향을 따라 계속되는 이러한 최적화는 또한 멀티 코어 집적 회로가 사용되는 경우 병렬 방식으로 수행될 수 있다. 따라서, 서브-홀로그램 내의 시작점은 임의 방식으로 선택될 수 있거나 적어도 몇몇 시작점이 선택될 수 있다. 서브-홀로그램의 국부적으로 최적화된 영역(최적화 중에 채워지는 영역)이 서로 충돌하면, 천이 영역을 최적화할 수 있다. 상호 갭이 예를 들어. 5개의 점 확산 함수 PSF_ij만이라면. 이것은 이미 행해질 수 있다. 이것은 점 확산 함수가 하나의 구역의 테두리(rim)에 추가될 수 있고 이웃하는 구역의 테두리의 작은 부분이 2개의 인접한 구역 사이에 존재하는 갭의 채우기 중에 이미 고려될 수 있음을 의미한다.

인위적이고 혼란스러운 낮은 공간 주파수 변조의 출현을 피하기 위해 다수의 랜덤화된 시작점을 사용하는 랜덤화된 로컬 최적화가 사용될 수 있다. 최적화 프로세스는 단일 점 확산 함수 PSF_ij의 위상 오프셋 및 강도 오프셋만을 사용하여 간단하게 만들 수 있다.

실시간 애플리케이션에 필요할 수 있는 계산 속도를 증가시키기 위해, 예를 들어, 이미 미리 최적화될 수 있는 예를 들어 선, 표면, 삼각형 및 작은 분리된 물체로서의 이미지 세그먼트에 대해 룩업 테이블(look-up-table, LUT)이 사용될 수 있다.

시선 추적 데이터가 이미 사용된 경우 직접 뷰 디스플레이에서 예를 들어, 10도의 고화질 콘 접근법을 사용하기 위해서, 시선 추적 데이터를 이용하여 관찰자의 눈의 입사 동공의 직경을 구하면, 공간 상의 물체 점을 픽업하는 눈의 점 확산 함수가 모니터링될 수 있다. 이는 실제 상황에 더 가까운 점 확산 함수 데이터를 사용할 수 있음을 의미한다. 따라서 더 나은 최적화 결과를 얻을 수 있다. 룩업 테이블은 또한 인간 눈의 상이한 점 확산 함수, 즉 눈의 입사 동공의 상이한 직경 및 상이한 초점 길이 f_eye를 나타내기 위해 사용될 수 있다.

물론, 헤드-마운티드 디스플레이에 대해 설명된 최적화 프로세스는 예를 들어, 다른 디스플레이 디바이스, 직접 뷰 디스플레이 디바이스, 프로젝션 디스플레이 디바이스에 사용될 수 있다.

마지막으로, 본 발명에 따라 설명된 디스플레이 디바이스에 대한 실시 예는 청구된 교시(claimed teaching)를 설명하기 위해서만 이해되어야 하지만 청구된 교시는 이들 실시 예에 한정되지 않는다는 것을 명시적으로 밝혀야 한다. 실시 예의 조합이 또한 가능하다.

Claims (33)

1. 복수의 물체 점들을 포함하는 2차원 및/또는 3차원 물체들의 홀로그램 재구성을 위한 디스플레이 디바이스에 있어서,
   - 충분한 코히어런트한 광을 방출하는 조명 유닛;
   - 디스플레이될 물체 점들의 서브-홀로그램들이 픽셀들로 인코딩되는 공간 광 변조기 디바이스; 및
   - 인접한 물체 점들의 서브-홀로그램들에 의해 생성된 관찰자의 눈에서의 인접한 점 확산 함수(point spread function)들을, 상기 인접한 점 확산 함수들이 서로에게 상호 인코히어런트하도록 분리시키는 분리기를 포함하는 것인 디스플레이 디바이스.
2. 제1항에 있어서, 상기 물체는 적어도 2개의 물체 평면으로 분할되고, 각각의 물체 평면은 서로에 대해 각 변위 또는 시프트되는 적어도 2개의 수직 서브 세트 및 적어도 2개의 수평 서브 세트로 분할되는 것인, 디스플레이 디바이스.
3. 제1항 또는 제2항에 있어서, 상기 공간 광 변조기 디바이스에서 1차원 인코딩된 홀로그램들 또는 2차원 인코딩된 홀로그램들의 경우, 상기 분리기는 컬러 필터 스트라이프 배열, 바람직하게는 원색 필터 스트라이프 배열로서 설계되는 것인, 디스플레이 디바이스.
4. 제1항 내지 제3항 중 어느 한 항에 있어서, 상기 공간 광 변조기 디바이스의 각각의 초기 픽셀은 적어도 2개의 서브 세트를 나타내고 적어도 2개의 웨이브 필드를 생성하는 적어도 2개의 정의된 부분으로 세분되는 것인 디스플레이 디바이스.
5. 제4항에 있어서, 컬러 필터 스트라이프의 삼중선(triplet)이 각각의 서브 세트에 할당되는 것인 디스플레이 디바이스.
6. 제3항, 제4항, 또는 제5항 중 어느 한 항에 있어서, 상기 컬러 필터 스트라이프 배열은 흡수형 염료 기반 필터 배열 또는 상기 서브 세트에 할당된 구조로 되어 있는 유전체 필터 배열인 것인 디스플레이 디바이스.
7. 제4항에 있어서, 인코딩될 2차원 홀로그램의 경우, 상기 초기 픽셀의 적어도 2개의 정의된 부분은 픽셀이 수평 또는 수직으로 분리되는 2개의 절반을 형성하는 것인, 디스플레이 디바이스.
8. 제1항 또는 제2항에 있어서, 상기 분리기는 패턴화된 리타더(patterned retarder)들의 배열로서 설계되는 것인 디스플레이 디바이스.
9. 제8항에 있어서, 상기 패턴화된 리타더들의 배열은 정의된 편광 상태를 갖는 광을 2개의 패턴화된 광 서브 세트로 변환하기 위해 제공되는 것인 디스플레이 디바이스.
10. 제8항 또는 제9항에 있어서, 상기 패턴화된 리타더들의 배열은 상기 픽셀들의 평면 내에 제공되고 상기 공간 광 변조기 디바이스의 상기 픽셀들에 할당되고, 상기 초기 픽셀의 각각의 정의된 부분에 패턴화된 리타더들의 배열의 정의된 패턴화된 리타더가 제공되는 것인 디스플레이 디바이스.
11. 제10항에 있어서, 상기 초기 픽셀의 적어도 2개의 정의된 부분은 직교 편광을 제공하는 상이한 패턴화된 리타더들을를 갖는 것인 디스플레이 디바이스.
12. 제8항 내지 제11항 중 어느 한 항에 있어서, 수평 방향으로만 또는 수직 방향으로만 보여지는 인접한 패턴화된 리타더들의 편광 방향이 서로에 대해 직교하는 것인 디스플레이 디바이스.
13. 제8항 내지 제11항 중 어느 한 항에 있어서, 상기 패턴화된 리타더들의 배열은 상기 초기 픽셀들의 적어도 2개의 정의된 부분들에 할당된 패턴화된 편광 필터들의 배열로서 설계되는 것인 디스플레이 디바이스.
14. 제13항에 있어서, 상기 패턴화된 편광 필터들의 배열은 투과된 편광 상태의 교대하는 방향을 갖는 스트라이프 패턴을 제공하는 것인 디스플레이 디바이스.
15. 제13항 또는 제14항에 있어서, 상기 패턴화된 편광 필터들의 배열은 수직 방향(y 방향) 및 수평 방향(x 방향)을 따라 고정된 패턴인 직교 편광 상태들의 패턴을 제공하고, 깊이 방향(z 방향)을 따라 상기 패턴이 반전되어 교대하는 방식으로 사용되는 것인 디스플레이 디바이스.
16. 제1항 내지 제15항 중 어느 한 항에 있어서, 2개의 상호 인코히어런트 웨이브 필드를 포함하는 단일 출사 편광 상태를 갖는 광을 제공하기 위해, 광의 전파 방향으로 보았을 때, 상기 공간 광 변조기 디바이스 뒤에 배열된 비-패턴화된 리타더를 더 포함하는 것인 디스플레이 디바이스.
17. 제1항 내지 제16항 중 어느 한 항에 있어서, 상기 물체 점을 나타내는 서브-홀로그램의 계산에 있어서, 정의된 각도 범위 내에서 물체 점들을 측 방향으로 시프트하기 위해 쐐기 함수(wedge function)가 사용되는 것인 디스플레이 디바이스.
18. 제17항에 있어서, 상기 쐐기 함수는 임의의 모양의 2차원 위상 쐐기 함수 인 것인 디스플레이 디바이스.
19. 제1항 내지 제18항 중 어느 한 항에 있어서, 상기 물체의 인접하는 물체 점들을 나타내는 점 확산 함수에 의해 생성된 관찰자의 눈에서의 총 강도 분포와 타겟 강도 분포 사이의 차이가 최소화되는 식으로, 상기 개별적인 물체 점들에 대한 파면들의 복소수 값들의 상대적인 위상이 정의되는 것인 디스플레이 디바이스.
20. 제1항 내지 제18항 중 어느 한 항에 있어서, 상기 물체의 인접하는 물체 점들을 나타내는 점 확산 함수에 의해 생성된 관찰자의 눈에서의 총 강도 분포와 타겟 강도 분포 사이의 차이가 최소화되는 식으로, 상기 개별적인 물체 점들에 대한 파면들의 복소수 값들의 진폭이 정의되는 것인 디스플레이 디바이스.
21. 제1항 내지 제20항 중 어느 한 항에 있어서, 물체의 개별적인 물체 점들의 아포다이즈된 서브-홀로그램들을 달성하기 위해, 아포다이제이션 프로파일이 상기 공간 광 변조기 디바이스의 픽셀들의 평면에 제공되는 것인 디스플레이 디바이스.
22. 제1항 내지 제21항 중 어느 한 항에 있어서, 상기 서브-홀로그램들은 그 모양이 수정 가능한 것인 디스플레이 디바이스.
23. 제1항 내지 제22항 중 어느 한 항에 있어서, 상기 관찰자의 눈에 제공된 물체 점 확산 함수의 고정된 미리 정의된 그리드가 사용되는 것인 디스플레이 디바이스.
24. 제1항 내지 제23항 중 어느 한 항에 있어서, 상기 조명 유닛은 바람직하게는 와이어 그리드 편광자 구조를 사용하여 2개의 직교 편광된 웨이브 필드를 방출하는 방식으로 적응되는(adapted) 것인 디스플레이 디바이스.
25. 제1항 내지 제24항 중 어느 한 항에 있어서, 상기 조명 유닛은 웨이브 필드를 생성하도록 제공된 적어도 하나의 광원, 바람직하게는 레이저 또는 레이저 다이오드를 포함하는 것인 디스플레이 디바이스.
26. 제1항 내지 제25항 중 어느 한 항에 있어서, 상기 조명 유닛은 원색 당 적어도 하나의 광원을 포함하는 것인 디스플레이 디바이스.
27. 제1항 내지 제26항 중 어느 한 항에 있어서, 상기 조명 유닛은 스트라이프 형 광원 배열을 포함하는 것인 디스플레이 디바이스.
28. 제1항 내지 제27항 중 어느 한 항에 있어서, 원색 당 적어도 2개의 상호 인코히어런트 광원이 제공되는 것인 디스플레이 디바이스.
29. 제1항 내지 제28항 중 어느 한 항에 있어서, 상기 공간 광 변조기 디바이스는 코히어런트 방향을 따라 ≤ 1/60도이고, 인코히어런트 방향을 따라 0.5도 내지 1도인 평면파의 각 스펙트럼으로 조명되는 것인 디스플레이 디바이스.
30. 제1항 내지 제29항 중 어느 한 항에 있어서, 상기 상호 코히어런스 필드는 최대 확장으로 제한되고, 상기 최대 확장은 상기 공간 광 변조기 디바이스에서 가장 큰 서브-홀로그램의 크기인 것인, 디스플레이 디바이스.
31. 제1항 내지 제30항 중 어느 한 항에 있어서, 상기 공간 광 변조기 디바이스는 상이한 원색에 관련된 상이한 인코히어런트 물체 점 서브 세트를 재구성할 수 있는 복소수 값 공간 광 변조기 디바이스로서 설계된 것인 디스플레이 디바이스.
32. 재구성된 2차원 및/또는 3차원 물체의 이미지 품질을 최적화하는 방법에 있어서,
    각각의 물체는 복수의 물체 점을 포함하고, 각각의 물체 점에 대해 공간 광 변조기 디바이스의 픽셀들로 인코딩되는 서브-홀로그램이 계산되고, 재구성된 인접한 물체 점들은 관찰자의 눈에서 인접한 점 확산 함수들을 생성하고, 상기 점 확산 함수들은 상기 인접한 점 확산 함수들이 상기 관찰자의 눈에서 단지 인코히어런트하게 중첩되도록 분리기에 의해 분리되는 것인 2차원 및/또는 3차원 물체의 이미지 품질 최적화 방법.
33. 제32항에 있어서, 상기 관찰자에게 디스플레이될 상기 물체 점을 나타내는 웨이브 필드의 인코히어런트 서브 세트가 생성되고 인코히어런트하게 중첩되는 것인 2차원 및/또는 3차원 물체의 이미지 품질 최적화 방법.

Images