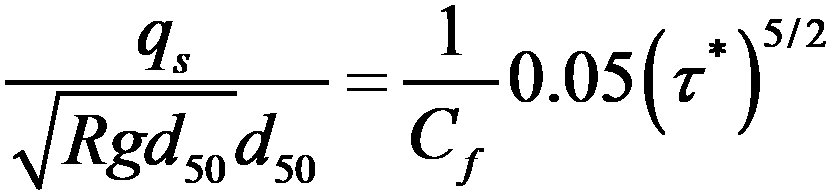KR101497993B1 - Method and apparatus for analyzing river sedimentation and flushing using quasi-2-dimensional quasi-steady model - Google Patents

Method and apparatus for analyzing river sedimentation and flushing using quasi-2-dimensional quasi-steady model Download PDF

Info

Publication number
KR101497993B1
KR101497993B1 KR20140114507A KR20140114507A KR101497993B1 KR 101497993 B1 KR101497993 B1 KR 101497993B1 KR 20140114507 A KR20140114507 A KR 20140114507A KR 20140114507 A KR20140114507 A KR 20140114507A KR 101497993 B1 KR101497993 B1 KR 101497993B1
Authority
KR
South Korea
Prior art keywords
quasi
distribution
calculating
sediment
lateral
Prior art date
Application number
KR20140114507A
Other languages
Korean (ko)
Inventor
최성욱
Original Assignee
연세대학교 산학협력단
Priority date (The priority date is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the date listed.)
Filing date
Publication date
Application filed by 연세대학교 산학협력단 filed Critical 연세대학교 산학협력단
Priority to KR20140114507A priority Critical patent/KR101497993B1/en
Application granted granted Critical
Publication of KR101497993B1 publication Critical patent/KR101497993B1/en

Links

Images

Classifications

    • G—PHYSICS
    • G01—MEASURING; TESTING
    • G01C—MEASURING DISTANCES, LEVELS OR BEARINGS; SURVEYING; NAVIGATION; GYROSCOPIC INSTRUMENTS; PHOTOGRAMMETRY OR VIDEOGRAMMETRY
    • G01C13/00—Surveying specially adapted to open water, e.g. sea, lake, river or canal
    • G01C13/008—Surveying specially adapted to open water, e.g. sea, lake, river or canal measuring depth of open water
    • G—PHYSICS
    • G06—COMPUTING; CALCULATING OR COUNTING
    • G06F—ELECTRIC DIGITAL DATA PROCESSING
    • G06F17/00—Digital computing or data processing equipment or methods, specially adapted for specific functions
    • G06F17/10—Complex mathematical operations

Landscapes

  • Engineering & Computer Science (AREA)
  • Physics & Mathematics (AREA)
  • General Physics & Mathematics (AREA)
  • Mathematical Physics (AREA)
  • Data Mining & Analysis (AREA)
  • Theoretical Computer Science (AREA)
  • Mathematical Optimization (AREA)
  • Mathematical Analysis (AREA)
  • Algebra (AREA)
  • Pure & Applied Mathematics (AREA)
  • Databases & Information Systems (AREA)
  • Software Systems (AREA)
  • General Engineering & Computer Science (AREA)
  • Computational Mathematics (AREA)
  • Life Sciences & Earth Sciences (AREA)
  • Hydrology & Water Resources (AREA)
  • Radar, Positioning & Navigation (AREA)
  • Remote Sensing (AREA)
  • Management, Administration, Business Operations System, And Electronic Commerce (AREA)

Abstract

The present invention provides a method for analyzing river sedimentation and flushing to which a quasi-two-dimensional quasi-steady model is applied using a computer, including the steps of: calculating a cross section longitudinal depth average flow velocity and a longitudinal cross section depth in overall section of interest based on one dimensional quasi-steady model with respect to given morphological data including initial river topography, flow rate, sediment particle sizes, sediment inflow amounts, branches, etc.; a total sediment load per unit width on the longitudinal cross section using the calculated depth average flow speed and cross section depth; calculating a longitudinal bed elevation according to the one dimensional quasi-steady model using the total sediment load per unit width on the longitudinal cross section; calculating a traverse flow velocity distribution according to a lateral distribution method using the calculated average flow velocity, depth and bed elevation on the longitudinal cross section; calculating a traverse sediment load distribution based on the traverse flow velocity distribution; and calculating a traverse morphological change based on the traverse sediment load distribution.

Description

준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 방법 및 장치{METHOD AND APPARATUS FOR ANALYZING RIVER SEDIMENTATION AND FLUSHING USING QUASI-2-DIMENSIONAL QUASI-STEADY MODEL}BACKGROUND OF THE INVENTION Field of the Invention The present invention relates to a quasi-two-dimensional quasi-rectification model, and more particularly, to a method and apparatus for analyzing a stream,

본 발명은 하천 퇴적 해석 기술에 관한 것으로, 더욱 상세하게는, 준정류 모형을 이용한 하천 퇴적 해석 기술에 관한 것이다.The present invention relates to a river sedimentation analysis technique, and more particularly, to a river sedimentation analysis technique using a quasi-rectification model.

20세기에 수자원의 확보를 위해 댐을 건설하는 것이 중요했다면, 21세기에는 동일 목적으로 댐의 기능 즉 저수용량을 유지시키는 것이 화두라고 하겠다. 이는 댐을 개발할 만한 적지는 이미 개발이 완료되었으며 여러 가지 환경문제로 말미암아 추가로 댐을 건설할 수 있는 나라가 많지 않기 때문이다.If it was important to build a dam to secure water resources in the 20th century, maintaining the function of dams for the same purpose, the low capacity, will be the topic of discussion in the 21st century. This is because some of the dams have already been developed and there are not many countries that can build additional dams due to various environmental problems.

Morris et al. (2007)에 의하면 전 세계적으로 각국의 댐은 저수지 퇴사에 의해 매년 1% 정도 저수용량이 줄어든다고 보고하고 있다. 우리나라도 류태상 등(2010)에 따르면 담수 후 20년 이상된 9개 댐의 경우, 지난 10년간의 퇴사량이 346백만㎥으로 부항댐과 화북댐 저수량의 6~7배에 해당된다고 한다. 또한, 대청댐의 경우 비사량이 91년 114㎥/㎢/yr에서 06년에는 616㎥/㎢/yr으로 5.4배나 증가한 것으로 보고되고 있다. 이와 같은 자료는 우리나라의 댐도 이제 저수지 퇴사 문제에서 자유롭지 못할 것을 예견하게 해준다.Morris et al. (2007) report that dams around the world are reducing capacity by 1% per year due to reservoir retirement. According to Ryu Tae Sang et al. (2010) in Korea, 9 dams over 20 years after the freshwater eruption have reached 346 million ㎥ in the last 10 years, which is 6 to 7 times of the reservoirs of Hwabang Dam and Hwabuk Dam. In addition, it is reported that Daecheong Dam increased by 5.4 times from 114m3 / ㎢ / yr in 1991 to 616m3 / ㎢ / yr in 2006. These data suggest that Korea's dams are no longer free from reservoir retirement problems.

일반적으로 하류에 댐이 있는 하도에서 하류방향으로 갈수록 배수효과에 의해 수심이 증가하게 되며 이에 따라 유속은 감소하게 된다. 이때 하상의 전단응력은 대략 유속의 제곱에 비례하므로 댐에 가까워질수록 소류력이 줄어든다. 또한, 하류로 갈수록 정수압이 증가하여 하상토의 이동이 어려워진다. 따라서 상류에서 이동한 유사는 댐체 부근에 퇴적되는데, 이것이 저수지 퇴사현상의 핵심 메카니즘이다.Generally, the water depth is increased by the drainage effect in the downstream direction from the lower stream where the dam is located downstream, and the flow rate is decreased accordingly. At this time, the shear stress of the bed is proportional to the square of the flow velocity. Further, the hydrostatic pressure increases toward the downstream, making it difficult to move the bed soil. Therefore, the similarity moved upstream is deposited near the dam, which is a key mechanism of the reservoir retirement phenomenon.

하천에서 일어나는 하상변동에 관한 수치해석의 역사는 짧지 않다. 최초의 연구들은 유동과 하상의 파속이 크게 다르다는 사실에 기초하여 유동과 하상토 보존 방정식을 분리해석하였다. 이후에는, 급변류 또는 천이류에 의한 하상변동을 모의하기 위해 부정류 방정식을 직접 해석하는 모형도 제시되었다. 하지만 이들 모형들은 유동에 대해 정상류 가정을 하지 않기 때문에 계산량이 매우 많아 장기적인 하도 변형 예측 문제에는 적용하기 어렵다.The history of numerical analysis on river bed fluctuations in rivers is not short. The first studies have segregated the flow and bed soil conservation equations based on the fact that the velocities of the bed and the bed are very different. Thereafter, a model for direct analysis of the unsteady flow equations was also presented to simulate the fluctuation of the bed due to rapid or transient flow. However, since these models do not have a steady flow assumption for the flow, the computational complexity is so large that it is difficult to apply to long-term deformation prediction problems.

본 발명이 해결하고자 하는 과제는 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 방법 및 장치를 제공하는 데에 있다.SUMMARY OF THE INVENTION The present invention is directed to a method and apparatus for analyzing and dropping streams using quasi-two-dimensional quasi-rectification models.

본 발명이 해결하고자 하는 과제는 부정류 방정식보다 훨씬 적은 연산량으로 부정류 방정식 모형에 비해 크게 떨어지지 않는 정확도를 제공할 수 있는 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 방법 및 장치를 제공하는 데에 있다.A problem to be solved by the present invention is to provide a method and an apparatus for analyzing a stream leaving and breaking by applying a quasi-two-dimensional quasi-rectifying model capable of providing an accuracy that does not fall far below that of an unsteady flow equation model with much less computational complexity than an unsteady flow equation There is.

본 발명이 해결하고자 하는 과제는 장시간에 걸친 예측 결과를 제공할 수 있는 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 방법 및 장치를 제공하는 데에 있다.SUMMARY OF THE INVENTION It is an object of the present invention to provide a method and an apparatus for analyzing river discharge and distribution using a quasi-two-dimensional quasi-rectification model capable of providing a long-term prediction result.

본 발명이 해결하고자 하는 과제는 수심 평균 유속(depth-averaged velocity), 하상 전단 응력(bed shear stress), 횡방향 전단(lateral shear) 및 하천 지형(channel geometry)의 횡방향 분포를 제공할 수 있는 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 방법 및 장치를 제공하는 데에 있다.The problem to be solved by the present invention is to provide a method and apparatus for providing a lateral distribution of depth-averaged velocity, bed shear stress, lateral shear and channel geometry, A quasi-two-dimensional quasi-rectifying model is applied to a method of and apparatus for analyzing a stream leaving and discharging.

본 발명의 해결과제는 이상에서 언급된 것들에 한정되지 않으며, 언급되지 아니한 다른 해결과제들은 아래의 기재로부터 당업자에게 명확히 이해될 수 있을 것이다.The solution to the problem of the present invention is not limited to those mentioned above, and other solutions not mentioned can be clearly understood by those skilled in the art from the following description.

본 발명의 일 측면에 따른 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 방법은 컴퓨터를 이용한 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 방법으로서,The quasi-two-dimensional quasi-rectification model according to one aspect of the present invention is applied to a river sedimentation and distribution analysis method using a quasi-two-dimensional quasi-rectification model using a computer.

상기 컴퓨터가,The computer comprising:

(a) 최초 하천 지형, 유량, 퇴적 입자 크기, 퇴적물 유입량, 지류 등을 포함하는 주어진 하상 데이터에 관하여 1차원 준정류 모형에 기초하여 전체 관심 구간의 수직 단면의 종방향 수심 평균 유속과 종방향 단면 수심을 산출하는 단계;(a) Based on a one-dimensional quasi-rectification model for given bedside data including initial stream topography, flow, sediment particle size, sediment flow, tributaries, etc., Calculating a depth of water;

(b) 산출된 수심 평균 유속과 단면 수심을 이용하여 종방향 단면의 단위폭당 총 유사량을 산출하는 단계;(b) calculating a total amount of similarity per unit width of the longitudinal section by using the calculated water depth average velocity and the depth of the section;

(c) 산출한 종방향 단위폭당 총 유사량을 이용하여 1차원 준정류 모형에 따라 종방향 하상고를 산출하는 단계;(c) calculating the longitudinal undersurface height in accordance with the one-dimensional quasi-rectification model using the calculated total amount per longitudinal unit width;

(d) 산출된 종방향 수직 단면의 평균 유속, 수심 및 하상고를 이용하여 횡분배법에 따라 횡방향 유속 분포를 산출하는 단계;(d) calculating the lateral flow velocity distribution according to the lateral distribution method using the average flow velocity, water depth, and bottom height of the vertical longitudinal section;

(e) 횡방향 유속 분포에 기초하여 횡방향 유사량 분포를 산출하는 단계; 및(e) calculating a lateral similarity distribution based on the lateral flow velocity distribution; And

(f) 횡방향 유사량 분포에 기초하여 횡방향 하상 변동을 산출하는 단계를 포함할 수 있다.(f) calculating the lateral river bed variation based on the lateral similarity distribution.

일 실시예에 따라, (b) 상기 종방향 단면의 단위폭당 총 유사량을 산출하는 단계는, 다음 수학식According to an embodiment, (b) calculating a total similarity amount per unit width of the longitudinal cross section may be calculated by the following equation

Figure 112014082966392-pat00001
Figure 112014082966392-pat00001

의 해를 산출하는 단계를 포함하고,And calculating a solution of the solution,

여기서, qs는 산출되어야 하는 단위폭당 총 유사량, R은 수중 비중(submerged specific gravity), d50은 유사 입자들(sediment particles)의 중간 크기(median size),

Figure 112014082966392-pat00002
는 무차원 전단 응력(Shields stress), Cf는 하상 저항 계수, g는 중력 가속도일 수 있다.Where q s is the total amount of sediment per unit width to be calculated, R is the submerged specific gravity, d 50 is the median size of the sediment particles,
Figure 112014082966392-pat00002
Is the dimensionless shear stress, C f is the bed resistance coefficient, and g is the gravitational acceleration.

일 실시예에 따라, (b) 상기 종방향 단면의 단위폭당 총 유사량을 산출하는 단계는, 다음 수학식According to an embodiment, (b) calculating a total similarity amount per unit width of the longitudinal cross section may be calculated by the following equation

Figure 112014082966392-pat00003
Figure 112014082966392-pat00003

의 해를 산출하는 단계를 포함하고,And calculating a solution of the solution,

여기서, Cs는 유속 기반 중량 농도(flux-based mass concentration)이고, a1 및 a2는 경험적 파라미터들(empirical parameters)이며,

Figure 112014082966392-pat00004
은 유사 내의 퇴적물의 비중량(specific weight of sediment in sediment-laden flow),
Figure 112014082966392-pat00005
는 퇴적물의 비중량(specific weight of sediment),
Figure 112014082966392-pat00006
는 퇴적물의 하강 속도일 수 있다.Where C s is the flux-based mass concentration, a 1 and a 2 are the empirical parameters,
Figure 112014082966392-pat00004
Is the specific weight of sediment in sediment-laden flow,
Figure 112014082966392-pat00005
Is the specific weight of sediment,
Figure 112014082966392-pat00006
May be the descent rate of the sediment.

일 실시예에 따라, (c) 상기 종방향 하상고를 산출하는 단계는,According to one embodiment, (c) the step of calculating the longitudinal undersurface comprises:

다음 수학식The following equation

Figure 112014082966392-pat00007
Figure 112014082966392-pat00007

의 해를 산출하는 단계를 포함하고,And calculating a solution of the solution,

여기서,

Figure 112014082966392-pat00008
는 종방향 하상고(bed elevation), t는 시간,
Figure 112014082966392-pat00009
는 하상 물질의 공극률(porosity of bed material),
Figure 112014082966392-pat00010
는 단위폭당 총 유사량(sediment load per unit width), x는 상류로부터 해당 지점까지 종방향 거리일 수 있다.here,
Figure 112014082966392-pat00008
Is bed elevation, t is time,
Figure 112014082966392-pat00009
Is the porosity of the bed material,
Figure 112014082966392-pat00010
Is the sediment load per unit width, and x may be the longitudinal distance from the upstream to the corresponding point.

일 실시예에 따라, (d) 상기 횡분배법에 따라 횡방향 유속 분포를 산출하는 단계는According to one embodiment, (d) calculating the lateral flow velocity distribution according to the lateral distribution method comprises

다음 수학식The following equation

Figure 112014082966392-pat00011
Figure 112014082966392-pat00011

의 해를 산출하는 단계를 포함하고,And calculating a solution of the solution,

여기서, x는 종방향 거리, y는 횡방향 거리이며,

Figure 112014082966392-pat00012
는 물의 밀도, g는 중력 가속도, H는 수심, Sx는 x 방향의 하상 경사(bed slope),
Figure 112014082966392-pat00013
는 하상 전단 응력(bed shear stress), Bg는
Figure 112014082966392-pat00014
로 정의되는 기하학적 인자(geometric factor), Sy는 y 방향의 하상 경사,
Figure 112014082966392-pat00015
는 수심 평균 횡방향 전단 응력(depth-averaged lateral shear stress)이며,
Figure 112014082966392-pat00016
는 이차류 영향을 나타내는 항(term due to secondary currents)일 수 있다.Where x is the longitudinal distance, y is the lateral distance,
Figure 112014082966392-pat00012
G is the gravitational acceleration, H is the depth of water, S x is the bed slope in the x direction,
Figure 112014082966392-pat00013
Is the bed shear stress, B g is the shear stress
Figure 112014082966392-pat00014
S y is the y-direction slope of the bed,
Figure 112014082966392-pat00015
Is the depth-averaged lateral shear stress,
Figure 112014082966392-pat00016
May be term due to secondary currents.

일 실시예에 따라, 상기 수심 평균 횡방향 전단 응력

Figure 112014082966392-pat00017
은 다음 수학식According to one embodiment, the depth-averaged transverse shear stress
Figure 112014082966392-pat00017
Is expressed by the following equation

Figure 112014082966392-pat00018
Figure 112014082966392-pat00018

에 의해 산출되고,Lt; / RTI >

여기서

Figure 112014082966392-pat00019
는 와류 점성(eddy viscosity)으로서, 유속의 차이로 인해 발생하는 수주(water column) 사이의 전단 응력을 결정하고,
Figure 112014082966392-pat00020
는 물의 밀도이며 Ud는 x 방향의 수심 평균 유속일 수 있다.here
Figure 112014082966392-pat00019
Is the eddy viscosity, which determines the shear stress between water columns due to the difference in flow velocity,
Figure 112014082966392-pat00020
Is the density of water and U d is the depth-averaged velocity in the x direction.

일 실시예에 따라, 상기 이차류 항

Figure 112014082966392-pat00021
은 다음 수학식According to one embodiment, the secondary flow term
Figure 112014082966392-pat00021
Is expressed by the following equation

Figure 112014082966392-pat00022
Figure 112014082966392-pat00022

에 의해 산출되고,Lt; / RTI >

여기서,

Figure 112014082966392-pat00023
및
Figure 112014082966392-pat00024
는 각각 유속의 시간 평균된 x 방향 및 y 방향 성분들이고, z는 수직 방향 거리이며 H는 수심이며,
Figure 112014082966392-pat00025
는 물의 밀도일 수 있다.here,
Figure 112014082966392-pat00023
And
Figure 112014082966392-pat00024
Are the time-averaged x-direction and y-direction components of the flow velocity, z is the vertical distance and H is the water depth,
Figure 112014082966392-pat00025
Can be the density of water.

일 실시예에 따라, 상기 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 방법은, 장기간 시뮬레이션을 위해, 매 시간 단위마다 단계 (a) 내지 단계 (f)를 반복하는 단계를 더 포함할 수 있다.According to one embodiment, the method of analyzing stream leaving and distributing using the quasi-two-dimensional quasi-rectifier model may further include repeating steps (a) to (f) for each time unit for long-term simulation have.

일 실시예에 따라, 상기 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 방법은, 상기 (f) 단계 이후에, (g) 활동 알고리즘을 이용하여 하상 경사의 변형을 산출하는 단계를 더 포함할 수 있다.According to one embodiment, the method of analyzing a stream leaving and breaking by applying the quasi-two-dimensional quasi-rectification model further comprises: (g) calculating a deformation of a bed slope using an activity algorithm after the step (f) can do.

본 발명의 다른 측면에 따른 컴퓨터프로그램은, 컴퓨터에서 본 발명의 실시예들에 따른 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 방법의 각 단계들을 실행시키기 위해 기록매체에 저장될 수 있다.A computer program according to another aspect of the present invention may be stored in a recording medium for executing each step of a stream leaving and breaking analysis method in which a quasi-two-dimensional quasi-rectifying model according to embodiments of the present invention is applied to a computer.

본 발명의 또 다른 측면에 따른 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 장치는,According to another aspect of the present invention, there is provided an apparatus for analyzing a stream withdrawal and a distribution using a quasi-two-dimensional quasi-rectification model,

하상 데이터에 관하여 1차원 준정류 모형에 기초하여 전체 관심 구간의 수직 단면의 수심 평균 유속과 단면 수심을 산출하고, 산출된 수심 평균 유속과 단면 수심을 이용하여 종방향 단면의 단위폭당 총 유사량을 산출하며, 산출한 종방향 단위폭당 총 유사량을 이용하여 1차원 준정류 모형에 따라 종방향 하상고를 산출하는 1차원 준정류 모형 계산부;Based on the one-dimensional quasi-rectification model for the river data, the water depth average velocity and the water depth of the vertical section of the whole section of interest are calculated, and the total amount of sediment per unit width of the longitudinal section is calculated using the calculated water depth average velocity and the water depth A one-dimensional quasi-rectified model calculation unit for calculating the vertical lower elevation according to the one-dimensional quasi-rectification model using the calculated total similar amount per longitudinal unit width;

산출된 종방향 수직 단면의 평균 유속, 수심 및 하상고를 이용하여 횡분배법(LDM)에 따라, 복수의 횡방향 단위폭 구역들의 각각에 대해 횡방향 유속 분포를 산출하는 횡방향 유속 분포 계산부;A lateral flow velocity distribution calculation section for calculating a lateral flow velocity distribution for each of a plurality of transverse unit width zones in accordance with a transverse distribution method (LDM) using an average flow velocity, a depth of water, ;

상기 횡방향 유속 분포에 기초하여, 모든 단위폭 구역들의 각각마다 횡방향 유사량의 분포를 산출하는 횡방향 유사량 분포 계산부; 및 A lateral similarity distribution calculation unit for calculating a distribution of the lateral direction similarity amount for each of all the unit width zones based on the lateral flow velocity distribution; And

횡방향 유사량 분포에 기초하여 횡방향 하상 변동을 산출하는 횡방향 하상 변동 계산부를 포함할 수 있다.And a lateral river bed variation calculation unit for calculating the lateral river bed fluctuation based on the lateral direction similarity distribution.

상기 횡방향 하상 변동 계산부는,The transverse river bed variation calculation unit may calculate,

활동 알고리즘을 이용하여 하상 경사의 변형을 산출하도록 동작할 수 있다.May be operable to calculate deformation of the bed slope using an activity algorithm.

본 발명의 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 방법 및 장치에 따르면, 부정류 방정식보다 훨씬 적은 연산량으로 부정류 방정식 모형에 비해 크게 떨어지지 않는 정확도를 제공할 수 있다.According to the method and apparatus for stream leaving and dumping analysis using the quasi-two-dimensional quasi-rectification model of the present invention, it is possible to provide accuracy that does not fall far below that of the unsteady flow equation model with much less computational complexity than the unsteady flow equation.

본 발명의 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 방법 및 장치에 따르면, 장시간에 걸친 예측 결과를 제공할 수 있다.According to the method and apparatus for stream leaving and distribution analysis using the quasi-two-dimensional quasi-rectification model of the present invention, prediction results over a long period of time can be provided.

본 발명의 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 방법 및 장치에 따르면, 수심 평균 유속, 하상 전단 응력, 횡방향 전단 및 하천 지형의 횡방향 분포를 제공할 수 있다.According to the method and apparatus for stream leaving and dumping analysis using the quasi-two-dimensional quasi-rectification model of the present invention, it is possible to provide the lateral distribution of the depth-of-the-stream mean velocity, the bed shear stress, the lateral shear and the river terrain.

본 발명의 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 방법 및 장치에 따르면, 동일한 연산 능력을 가진 시뮬레이션 시스템을 가지고 훨씬 긴 기간 동안 하상 변동을 예측할 수 있거나, 동일한 예측 기간의 하상 변동의 예측에 들어가는 비용을 절감할 수 있으며, 동일한 비용과 시간 내에서 좀더 다양한 조건에서 하상 변동을 시뮬레이션할 수 있다.According to the method and apparatus for stream leaving and distribution analysis using the quasi-two-dimensional quasi-rectification model of the present invention, it is possible to predict a river bed variation over a much longer period with a simulation system having the same calculation capability, And it is possible to simulate river bed variations under more varied conditions within the same cost and time.

본 발명의 효과는 이상에서 언급된 것들에 한정되지 않으며, 언급되지 아니한 다른 효과들은 아래의 기재로부터 당업자에게 명확하게 이해될 수 있을 것이다.The effects of the present invention are not limited to those mentioned above, and other effects not mentioned can be clearly understood by those skilled in the art from the following description.

도 1은 본 발명의 일 실시예에 따른 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 방법을 예시한 순서도이다.
도 2는 본 발명의 일 실시예에 따른 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 방법에 따라 중국 황하강 유역의 샤오량디 댐에 관하여 2003년, 2004년 및 2006년에 각각 얻은 횡방향 하천 지형의 예측 결과와 실측 결과를 비교한 그래프들이다.
도 3은 본 발명의 일 실시예에 따른 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 장치를 예시한 블록도이다.FIG. 1 is a flowchart illustrating a method of analyzing a stream leaving and applying a quasi-two-dimensional quasi-rectification model according to an embodiment of the present invention.
FIG. 2 is a graph showing the result of a river quenching and dumping analysis using a quasi-two-dimensional quasi-rectification model according to an embodiment of the present invention. As shown in FIG. 2, These are graphs comparing predicted and measured results.
FIG. 3 is a block diagram illustrating an apparatus for analyzing a stream leaving and applying a quasi-two-dimensional quasi-rectifier model according to an embodiment of the present invention.

본문에 개시되어 있는 본 발명의 실시예들에 대해서, 특정한 구조적 내지 기능적 설명들은 단지 본 발명의 실시예를 설명하기 위한 목적으로 예시된 것으로, 본 발명의 실시예들은 다양한 형태로 실시될 수 있으며 본문에 설명된 실시예들에 한정되는 것으로 해석되어서는 아니 된다.For the embodiments of the invention disclosed herein, specific structural and functional descriptions are set forth for the purpose of describing an embodiment of the invention only, and it is to be understood that the embodiments of the invention may be practiced in various forms, The present invention should not be construed as limited to the embodiments described in Figs.

이하, 첨부한 도면들을 참조하여, 본 발명의 바람직한 실시예를 보다 상세하게 설명하고자 한다. 도면상의 동일한 구성요소에 대해서는 동일한 참조부호를 사용하고 동일한 구성요소에 대해서 중복된 설명은 생략한다.Hereinafter, preferred embodiments of the present invention will be described in detail with reference to the accompanying drawings. The same reference numerals are used for the same constituent elements in the drawings and redundant explanations for the same constituent elements are omitted.

도 1은 본 발명의 일 실시예에 따른 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 방법을 예시한 순서도이다.FIG. 1 is a flowchart illustrating a method of analyzing a stream leaving and applying a quasi-two-dimensional quasi-rectification model according to an embodiment of the present invention.

도 1을 참조하면, 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 방법은 단계(S11)에서, 최초 하천 지형, 유량, 퇴적 입자 크기, 퇴적물 유입량, 지류 등을 포함하는 주어진 하상 데이터에 관하여 1차원 준정류 모형(1D Quasi-steady Model)에 기초하여 전체 관심 구간의 수직 단면의 종방향 수심 평균 유속(cross section depth averaged velocity)과 종방향 단면 수심(hydraulic depth)을 산출한다.Referring to FIG. 1, in the step S11, a method of analyzing a stream leaving and distributing with a quasi-two-dimensional quasi-rectification model will be described with respect to a given river bed data including an initial river terrain, a flow rate, a sediment particle size, a sediment inflow amount, Based on the 1D quasi-steady model, the cross section depth averaged velocity and the longitudinal hydraulic depth of the vertical section of the entire area of interest are calculated.

1차원 준정류 모형은 하천의 장기간 하상 변동(long-term morphological change)을 산출하는 데에 흔히 사용된다. 1차원 준정류 모형은, 유수에 의한 하도 형태의 변화를 모의하는 데에 있어서, 유동(flow change)에 비하여 하도 변화(bed elevation)의 특성 시간이 매우 길기 때문에 유동 방정식에서 시간에 따른 변화를 무시할 수 있다(quasi-steady)는 가정에 기반한다. One-dimensional semi-rectification models are commonly used to produce long-term morphological changes in streams. The one-dimensional quasi-rectification model neglects the time-dependent change in the flow equation because the characteristic time of the bed elevation is very long compared to the flow change in simulating the change of the bed shape by the water flow. Quasi-steady is based on assumptions.

구체적으로, 단계(S11)에서 연산되는 1차원 준정류 모형은 다음 수학식 1의 유동에 관한 1차원 연속 방정식(1D continuity equation)과 수학식 2의 운동량 방정식(momentum equation)을 포함할 수 있다.Specifically, the one-dimensional quasi-rectification model computed in step S11 may include a 1D continuity equation for the flow of equation (1) and a momentum equation of equation (2).

Figure 112014082966392-pat00026
Figure 112014082966392-pat00026

Figure 112014082966392-pat00027
Figure 112014082966392-pat00027

수학식 1 및 2에서, x는 종방향 거리(longitudinal direction), t는 시간, q는 단위폭당 유량(unit discharge), UA는 수심 평균 유속, HA는 단면 수심, g는 중력 가속도,

Figure 112014082966392-pat00028
는 하상고(bed elevation), Cf는 하상 저항 계수(flow resistance coefficient)이다.In the equations (1) and (2), x is the longitudinal direction, t is the time, q is the unit discharge, U A is the depth average velocity, H A is the depth of the section, g is the gravitational acceleration,
Figure 112014082966392-pat00028
Is the bed elevation, and C f is the flow resistance coefficient.

위와 같은 준정류 모형은 하상고의 특성 시간이 유동의 특성 시간에 비해 훨씬 크다는 가정 하에 1차원 천수 방정식(shallow water equation)으로부터 도출될 수 있으므로, 급변류 또는 한계류에 의한 하상 변동에는, 예를 들어 댐의 붕괴나 둑의 범람과 같은 경우에는 적용하기 어렵다.Since the quasi-rectified model can be derived from the one-dimensional shallow water equation, assuming that the characteristic time of the lower elevation is much larger than the characteristic time of the flow, It is difficult to apply it in cases such as the collapse of a dam or the flooding of a dam.

한편, 위의 1차원 준정류 모형은 예를 들어 엑스너(Exner) 방정식과 같은 하상토 보존 방정식(bed sediment conservation equation)을 더 가지는데, 이를 계산하기 위해서는 먼저 단위폭당 총 유사량(sediment load per unit width)을 알아야 한다.On the other hand, the above one-dimensional quasi-rectified model has more bed sediment conservation equations like the Exner equation. In order to calculate this, the total sediment load per unit width.

이어서, 단계(S12)에서, 산출된 수심 평균 유속과 단면 수심을 이용하여 종방향 단면의 단위폭당 총 유사량을 산출한다.Subsequently, in step S12, the total similarity amount per unit width of the longitudinal section is calculated using the calculated depth-average flow velocity and the section depth.

구체적으로, 단위폭당 총 유사량은 예를 들어 다음 수학식 3과 같은 Engelund-Hansen 방정식 또는 수학식 4와 같은 Yang 방정식을 이용하여 산출될 수 있다.Specifically, the total amount of similarity per unit width can be calculated using, for example, the Engelund-Hansen equation as shown in Equation (3) or the Yang equation as shown in Equation (4).

Figure 112014082966392-pat00029
Figure 112014082966392-pat00029

여기서, qs는 산출되어야 하는 단위폭당 총 유사량, R은 수중 비중(submerged specific gravity), d50은 유사 입자들(sediment particles)의 중간 크기(median size),

Figure 112014082966392-pat00030
는 무차원 전단 응력(Shields stress), Cf는 하상 저항 계수, g는 중력 가속도이다.Where q s is the total amount of sediment per unit width to be calculated, R is the submerged specific gravity, d 50 is the median size of the sediment particles,
Figure 112014082966392-pat00030
Is shear stress, C f is bed resistance and g is gravitational acceleration.

다만, 수학식 3의 Engelund-Hansen 방정식은 입자 직경이 0.15 mm 이사인 경우에는 바람직하지 않을 수 있다. However, the Engelund-Hansen equation of Equation (3) may not be desirable when the particle diameter is 0.15 mm.

대부분의 유사량 산출 방정식들은 세류사(wash load)를 고려하지 않은데, 세류사의 존재는 유체의 점성(fluid viscosity), 유사 침강 속도(sediment fall velocity) 및 유사의 비중량(specific weight of sediment)에 영향을 미치기 때문에 무시할 수 없는 경우도 많다. 그러한 경우에는 수학식 4의 Yang 방정식을 이용할 수 있다. 아래의 Yang 방정식은 높은 농도의 세류사를 가진, 퇴적물이 많은(sediment-laden) 유체 흐름을 위한 방정식이다.Most of the similarity calculation equations do not take the wash load into consideration, and the existence of trilys affects the fluid viscosity, sediment fall velocity and specific weight of sediment There are many cases where it can not be ignored. In such a case, the Yang equation of Equation (4) can be used. The Yang equation below is an equation for sediment-laden fluid flow with a high concentration of trichloride.

Figure 112014082966392-pat00031
Figure 112014082966392-pat00031

여기서, Cs는 유속 기반 중량 농도(flux-based mass concentration)이고, a1 및 a2는 경험적 파라미터들(empirical parameters)이며,

Figure 112014082966392-pat00032
은 유체 내의 퇴적물의 비중량(specific weight of sediment in sediment-laden flow),
Figure 112014082966392-pat00033
는 퇴적물의 비중량(specific weight of sediment),
Figure 112014082966392-pat00034
는 퇴적물의 하강 속도이다.Where C s is the flux-based mass concentration, a 1 and a 2 are the empirical parameters,
Figure 112014082966392-pat00032
Is the specific weight of sediment in sediment-laden flow,
Figure 112014082966392-pat00033
Is the specific weight of sediment,
Figure 112014082966392-pat00034
Is the descent rate of sediment.

단계(S13)에서, 산출한 종방향 단위폭당 총 유사량을 이용하여 1차원 준정류 모형에 따라 종방향 하상고(longitudinal bed elevation)를 산출한다.In step S13, the longitudinal bed elevation is calculated according to the one-dimensional quasi-rectification model using the calculated total amount per longitudinal unit width.

구체적으로, 수학식 5와 같은 하상토 보존 방정식을 이용하여 종방향 하상고를 산출할 수 있다.Specifically, the longitudinal lower elevation can be calculated using Equation (5).

Figure 112014082966392-pat00035
Figure 112014082966392-pat00035

여기서,

Figure 112014082966392-pat00036
는 종방향 하상고(bed elevation), t는 시간,
Figure 112014082966392-pat00037
는 하상 물질의 공극률(porosity of bed material),
Figure 112014082966392-pat00038
는 단위폭당 총 유사량(sediment load per unit width), x는 상류로부터 해당 지점까지 종방향 거리이다.here,
Figure 112014082966392-pat00036
Is bed elevation, t is time,
Figure 112014082966392-pat00037
Is the porosity of the bed material,
Figure 112014082966392-pat00038
Is the sediment load per unit width, and x is the longitudinal distance from the upstream to the corresponding point.

상술한 단계들(S11 내지 S13)을 통해, 종방향의 1차원 준정류 모형을 통한 종방향 수직 단면의 평균 유속, 수심 및 하상고가 산출된다.Through the above-described steps S11 to S13, the average flow velocity, depth, and bed elevation of the longitudinal vertical section through the longitudinal one-dimensional quasi-rectification model are calculated.

이어서, 단계(S14)에서, 산출된 종방향 수직 단면의 평균 유속, 수심 및 하상고를 이용하여 횡분배법(Lateral Distribution Method, LDM)에 따라, 복수의 횡방향 단위폭 구역들의 각각에 대해 횡방향 유속 분포를 산출한다.Next, in step S14, the average lateral velocity of the vertical vertical section, the depth of the vertical section, and the height of the vertical section are used to calculate the transverse distribution width Direction flow velocity distribution.

유량의 횡분배법은 Shiono and Knight와 Walker et al에 의해 각각 독립적으로 도출된 기법으로서, 하천의 한 측점에서 유량 및 수위가 결정된 경우에, 지배 방정식(Governing equation)의 해석을 통해 횡방향의 단위폭당 유량을 구하는 기법이다. The lateral distribution method of flow rate is derived independently from each other by Shiono and Knight and Walker et al. In the case where the flow rate and the water level are determined at one point of a river, the lateral unit It is a technique to obtain the flow rate per square meter.

본 발명에 적합하도록 변형된 유속 횡분배법은 다음 수학식 6과 같이 표현된다.The modified transverse velocity distribution method suitable for the present invention is expressed by the following Equation (6).

Figure 112014082966392-pat00039
Figure 112014082966392-pat00039

여기서, x는 종방향 거리, y는 횡방향 거리이며,

Figure 112014082966392-pat00040
는 물의 밀도, g는 중력 가속도, H는 수심, Sx는 x 방향의 하상 경사(bed slope),
Figure 112014082966392-pat00041
는 하상 전단 응력(bed shear stress), Bg는
Figure 112014082966392-pat00042
로 정의되는 기하학적 인자(geometric factor), Sy는 y 방향의 하상 경사,
Figure 112014082966392-pat00043
는 수심 평균 횡방향 전단 응력(depth-averaged lateral shear stress)이며,
Figure 112014082966392-pat00044
는 이차류 영향을 나타내는 항(term due to secondary currents)이다.Where x is the longitudinal distance, y is the lateral distance,
Figure 112014082966392-pat00040
G is the gravitational acceleration, H is the depth of water, S x is the bed slope in the x direction,
Figure 112014082966392-pat00041
Is the bed shear stress, B g is the shear stress
Figure 112014082966392-pat00042
S y is the y-direction slope of the bed,
Figure 112014082966392-pat00043
Is the depth-averaged lateral shear stress,
Figure 112014082966392-pat00044
Is the term due to secondary currents.

수학식 6은 총 유량(total discharge)을 하천 지형과 유체 역학에 따라 횡방향으로 분포시키는 지배 방정식이다. 수학식 6은 각각의 단위폭 구역마다 양 측면에서 미끄럼 경계 조건(free-slip boundary conditions)을 가지는 중앙 유한 차분법(centered finite difference scheme)을 적용함으로써 이산화(discretized)될 수 있다. 그 결과로 얻는 비선형 방정식의 해는 뉴턴-랩슨(Newton-Raphson) 법을 이용하여 계산될 수 있다.Equation (6) is a governing equation that distributes the total discharge in the lateral direction according to the stream topography and the hydrodynamics. Equation (6) can be discretized by applying a centered finite difference scheme with free-slip boundary conditions on each side for each unit width region. The resulting solution of the nonlinear equations can be calculated using the Newton-Raphson method.

한편, 하상 전단 응력

Figure 112014082966392-pat00045
은 다음의 수학식 7과 같이 주어질 수 있다.On the other hand,
Figure 112014082966392-pat00045
Can be given by the following Equation (7).

Figure 112014082966392-pat00046
Figure 112014082966392-pat00046

여기서

Figure 112014082966392-pat00047
는 물의 밀도, f는 Darcy-Weisbach의 마찰 계수(friction factor)이고, Ud는 x 방향의 수심 평균 유속(depth-averaged velocity)이다. here
Figure 112014082966392-pat00047
Is the density of water, f is the friction factor of Darcy-Weisbach, and U d is the depth-averaged velocity in the x direction.

또한, 각각의 횡방향 수주(water column) 간에 발생하는 수심 평균 횡방향 전단 응력

Figure 112014082966392-pat00048
은 다음 수학식 8과 같이 주어질 수 있다.Also, the depth-averaged transverse shear stresses occurring between each transverse water column
Figure 112014082966392-pat00048
Can be given by the following equation (8).

Figure 112014082966392-pat00049
Figure 112014082966392-pat00049

여기서,

Figure 112014082966392-pat00050
는 변동 유속(fluctuating velocities)에 의한 레이놀즈 응력(Reynolds stress)이다. 와류 점성 이론(Eddy Viscosity Concept)에 따라, 횡방향 전단 응력
Figure 112014082966392-pat00051
은 다음 수학식 9와 같이 다시 쓸 수 있다.here,
Figure 112014082966392-pat00050
Is the Reynolds stress due to fluctuating velocities. According to the Eddy Viscosity Concept, transverse shear stress
Figure 112014082966392-pat00051
Can be rewritten as Equation (9).

Figure 112014082966392-pat00052
Figure 112014082966392-pat00052

여기서

Figure 112014082966392-pat00053
는 와류 점성(eddy viscosity)으로서 유속의 차이로 인해 발생하는 수주 사이의 전단 응력을 결정하고,
Figure 112014082966392-pat00054
는 물의 밀도이며 Ud는 x 방향의 수심 평균 유속이다. here
Figure 112014082966392-pat00053
Is the eddy viscosity, which determines the shear stress between several weeks due to the difference in flow velocity,
Figure 112014082966392-pat00054
Is the density of water and U d is the depth average velocity in the x direction.

마지막으로, 수학식 6의 이차류 항

Figure 112014082966392-pat00055
은 다음 수학식 10과 같이 정의된다.Finally, the secondary term of equation (6)
Figure 112014082966392-pat00055
Is defined as < EMI ID = 10.0 >

Figure 112014082966392-pat00056
Figure 112014082966392-pat00056

여기서,

Figure 112014082966392-pat00057
및
Figure 112014082966392-pat00058
는 각각 유속의 시간 평균된 x 방향 및 y 방향 성분들이고, z는 수직 방향 거리이며 H는 수심이며,
Figure 112014082966392-pat00059
는 물의 밀도이다.here,
Figure 112014082966392-pat00057
And
Figure 112014082966392-pat00058
Are the time-averaged x-direction and y-direction components of the flow velocity, z is the vertical distance and H is the water depth,
Figure 112014082966392-pat00059
Is the density of water.

이어서, 단계(S15)에서, 횡방향 유속 분포에 기초하여, 모든 단위폭 구역들의 각각마다 횡방향 유사량의 분포를 산출한다.Subsequently, in step S15, the distribution of the transverse similar amount is calculated for each of all the unit width zones based on the lateral flow velocity distribution.

하상 경사에 퇴적되는 유사 입자들은 항력(drag), 중력, 쿨롱 저항력(Coulomb resistive force)와 같은 힘들 사이의 균형 또는 불균형에 의해 형태가 유지되거나 붕괴될 수 있다. 이러한 하상 유사의 이송(transport of bedload)은 다음 수학식 11에 따른 Kovacs and Parker의 벡터 공식(vectorial formula)에 의해 산출될 수 있다.Similar particles deposited in the slope of the bed can be retained or collapsed by a balance or imbalance between forces such as drag, gravity, Coulomb resistive force. This transport of bedload can be calculated by the vectorial formula of Kovacs and Parker according to the following equation (11).

Figure 112014082966392-pat00060
Figure 112014082966392-pat00060

여기서,

Figure 112014082966392-pat00061
는 단위폭당 하상 유사량의 벡터 부피 하상 유사 이송율(vectorial volume bedload transport rate of bed sediment per unit width)이고,
Figure 112014082966392-pat00062
는 평균 입자 유속(mean particle velocity)이며,
Figure 112014082966392-pat00063
로 정의되는데,
Figure 112014082966392-pat00064
는 전체 부피 중 퇴적물(sediment)의 부피 비율(volume fraction of sediment)이고
Figure 112014082966392-pat00065
는 하상으로부터 퇴적층(bedload layer)의 높이이다.here,
Figure 112014082966392-pat00061
Is the vectorial volume bedload transport rate of bed sediment per unit width per unit width,
Figure 112014082966392-pat00062
Is the mean particle velocity,
Figure 112014082966392-pat00063
Lt; / RTI >
Figure 112014082966392-pat00064
Is the volume fraction of sediment in the total volume
Figure 112014082966392-pat00065
Is the height of the bedload layer from the bed.

한편, 단계(S16)에서, 횡방향 유사량 분포에 기초하여 횡방향 하상 변동을 산출한다.On the other hand, in step S16, the lateral river bed variation is calculated based on the lateral direction similarity distribution.

구체적으로, 다음 수학식 12와 같이 횡방향 하상고를 산출함으로써 횡방향 하상 변동을 얻을 수 있다.Specifically, the lateral river bed fluctuation can be obtained by calculating the lateral lower elevation as shown in the following equation (12).

Figure 112014082966392-pat00066
Figure 112014082966392-pat00066

여기서,

Figure 112014082966392-pat00067
는 횡방향 하상고, t는 시간,
Figure 112014082966392-pat00068
는 하상 물질의 공극률,
Figure 112014082966392-pat00069
는 횡방향 단위폭당 총 유사량, y는 횡방향 거리이다.here,
Figure 112014082966392-pat00067
T is the time,
Figure 112014082966392-pat00068
The porosity of the bed material,
Figure 112014082966392-pat00069
Is the total amount of similarity per lateral unit width, and y is the lateral distance.

다음으로 단계(S17)에서, 활동 알고리즘(sliding algorithm)을 이용하여 하상 경사의 변형을 산출한다. Next, in step S17, a deformation of the bed slope is calculated using a sliding algorithm.

구체적으로 활동 알고리즘은 Menendez, A.N., Laciana, C.E., Garcia, P.E. (2008) "An integrated hydrodynamic-sedimentologic-morphologic model for the evolution of alluvial channels cross sections", Engineering Applications of Computational Fluid Mechanics, Vol. 2, No. 4, pp. 411-426을 참조할 수 있다.Specifically, the activity algorithm is Menendez, A.N., Laciana, C.E., Garcia, P.E. (2008) "An integrated hydrodynamic-sedimentologic-morphologic model for the evolution of alluvial channels cross sections ", Engineering Applications of Computational Fluid Mechanics, Vol. 2, No. 4, pp. 411-426.

시간의 흐름에 따라 단계(S11)부터 단계(S17)은 반복할 수 있다.Steps S11 to S17 may be repeated according to the flow of time.

본 발명의 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 방법은 수치 데이터와 수리 모형에 기초한 다수의 방정식들의 계산으로 구성되므로, 컴퓨터에서 구현될 수 있다.The quasi-two-dimensional quasi-rectification model of the present invention can be implemented in a computer because it consists of calculation of a number of equations based on numerical data and mathematical models.

본 발명의 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 방법을 컴퓨터 상에서 구현할 때의 연산 절차를 간단히 설명하면, 먼저 특정 시점에 수학식 1 및 2와 같은 배수 방정식들(backwater equations)과 수학식 5와 같은 하상토 보존 방정식을 계산하여 종방향의 각 측정점마다 수면 상승(water surface elevation), 단면 평균 유속(section-averaged velocity) 및 하상고 변동(bed elevation change)을 산출한다.The operation procedure of implementing the method of analyzing the stream leaving and breaking by applying the quasi-two-dimensional quasi-rectifying model of the present invention will be briefly described. First, at a specific point in time, backwater equations such as Equations 1 and 2, The water surface elevation, section-averaged velocity, and bed elevation change are calculated for each longitudinal measurement point by calculating the equation of bed reservoir as shown in Equation (5).

이어서, 각 측정점마다, 수학식 2가 배수 방정식의 해로부터 얻은 수면 상승을 가지고 해가 산출된다. 통상적으로, 횡방향 분배법을 통해 계산된 단위폭당 유사량들을 합산하여 얻는 총 유량(total discharge)는 실제 총 유량과 같지 않다. 각각의 수직 횡단면에서 단위폭당 유량은, 단면에 걸친 유속 배분이 균일 흐름 조건(uniform flow condition) 하에서의 배분과 유사할 것이라는 가정 하에, 실제 유량을 배분하여 얻어진다.Then, for each measurement point, the solution is calculated by the equation (2) with the surface elevation obtained from the solution of the multiple equation. Typically, the total discharge obtained by summing the similar amounts per unit volume calculated through the lateral distribution method is not equal to the actual total flow. The flow rate per unit width in each vertical cross section is obtained by distributing the actual flow rate, assuming that the flow rate distribution across the cross section will be similar to the distribution under a uniform flow condition.

각 측정점의 폭 방향을 따라 하상 유사를 배분할 수 있도록, 위의 연산 절차가 반복된다. 즉, 총 하상 유사는 단면의 주변에서 평균화된 전단 유속을 이용하여 추정된다. 이어서 단위 하상 유사가 횡분배법에 의해 예측된다. 일반적으로 폭 방향의 단위 하상 유사들의 합은 총 하상 유사와 같지 않을 수 있다. 총 하상유사가 위와 같은 가정 하에 각각의 수직 단면에서 배분된다.The above calculation procedure is repeated so that the bed similarity can be distributed along the width direction of each measurement point. That is, the total bed profile is estimated using the shear flow rate averaged around the cross section. The unit bed similarity is then predicted by the transverse distribution method. In general, the sum of the unit bed weights in the width direction may not be equal to the total bed variation. The total bed profile is distributed in each vertical section under the above assumptions.

마지막으로, 하천 형태의 변화가, 물의 흐름이 각 연산 범위 내에서 균일하다는 가정 하에, 하상 유사 이송(bedload transport) 및 활동(sliding)을 고려하여 산출된다.Finally, changes in stream shape are calculated taking into account bedload transport and sliding, assuming that the water flow is uniform within each operating range.

도 2는 본 발명의 일 실시예에 따른 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 방법에 따라 중국 황하강 유역의 샤오량디 댐에 관하여 2003년, 2004년 및 2006년에 각각 얻은 횡방향 하천 지형의 예측 결과와 실측 결과를 비교한 그래프이다.FIG. 2 is a graph showing the result of a river quenching and dumping analysis using a quasi-two-dimensional quasi-rectification model according to an embodiment of the present invention. As shown in FIG. 2, This is a graph comparing predicted and measured results of the terrain.

샤오랑디 댐은 황하의 본류 상에 건설된 댐으로서, 중국 허난성 싼먼시아 댐으로부터 하류로 128.42 km 떨어져 있고, 연평균 유량은 400x106㎥, 연평균 하상 유사는 13.47x109 톤이며, 12 개의 주요 지류들이 있다.Xiao Lang Dam is a dam constructed in the main stream of the Yellow River, 128.42 km downstream from the Henan Province of China, and has an average annual flow of 400 × 10 6 ㎥, 13.47 × 10 9 tons per year, and 12 major tributaries .

도 2를 참조하면, 도 2의 (a), (b) 및 (c)는 각각 2003년, 2004년 및 2006년에 각각 얻은 횡방향 하천 지형의 예측 결과와 실측 결과를 비교한 그래프들로서, 최초의 하상 경사(initial bed라고 표시)가 굵은 흑색 실선으로 표시되고 실측 조사 결과(surveyed라고 표시)가 얇은 흑색 실선, 기존의 GSTARS4 시뮬레이션 방식에 따른 예측 결과(Ahn(2011)로 표시)는 얇은 청색 실선으로 표시되고, 본 발명의 준2차원 준정류 모형에 따른 예측 결과(present study로 표시)는 얇은 적색 실선으로 표시된다.2, (a), (b) and (c) of FIG. 2 are graphs comparing predicted results of lateral river terrain obtained in 2003, 2004 and 2006, respectively, (Denoted as initial bed) is indicated by a thick black solid line, and a black solid line with a measured result (indicated as surveyed) and a predicted result according to the existing GSTARS4 simulation method (indicated by Ahn (2011) And the prediction result (represented by the present study) according to the quasi-two-dimensional quasi-rectification model of the present invention is indicated by a thin red solid line.

2003년 10월의 하천 지형은 그해 8월에 홍수로 인해 실제로 댐 상류에 엄청난 양의 퇴적이 발생하였는데, 본 발명의 준2차원 준정류 모형도 실측 결과에 충분히 근접한 예측 결과를 나타냈으며, 이는 기존에 널리 이용되는 GSTARS4 시뮬레이션 방식의 예측 결과에 비해 손색이 없다.The river topography of October, 2003, due to the flood in August of that year, actually produced a huge amount of sediment upstream of the dam. The quasi-two-dimensional quasi-rectification model of the present invention also showed a prediction result sufficiently close to the actual measurement result, Compared to the widely used GSTARS4 simulation method prediction results.

2004년 10월의 하천 지형은 전년도에 퇴적된 퇴적토가 침식되면서 댐이 있는 방향으로 이동되었는데, 본 발명의 준2차원 준정류 모형은 실측 결과에 대해 일부 구간에서는 근접한 예측 결과를 나타냈다. 본 발명의 모형이 큰 오차를 가지는 구간에서는 기존의 GSTARS4 시뮬레이션 방식의 예측 결과도 오차가 크게 존재하는 점을 감안할 필요가 있다.The river topography of October 2004 was moved to the direction of the dam due to the erosion of sediment deposited in the previous year. The quasi - two - dimensional quasi - rectification model of the present invention showed close prediction results in some sections of the experimental results. It is necessary to consider that there is a large error in the prediction result of the existing GSTARS4 simulation method in the section where the model of the present invention has a large error.

2006년 10월의 하천 지형은 전반적으로 퇴적토가 긴 구간에 걸쳐 퇴적되는 모습을 보였는데, 본 발명의 준2차원 준정류 모형도 실측 결과에 충분히 근접한 예측 결과를 나타냈으며, 이는 기존에 널리 이용되는 GSTARS4 시뮬레이션 방식의 예측 결과에 비해 손색이 없다.The stream topography of October 2006 showed a sedimentation over a long section as a whole, and the quasi-two-dimensional quasi-rectification model of the present invention also showed a prediction result close enough to the actual measurement results, There is no difference compared to the simulation results.

도 3은 본 발명의 일 실시예에 따른 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 장치를 예시한 블록도이다.FIG. 3 is a block diagram illustrating an apparatus for analyzing a stream leaving and applying a quasi-two-dimensional quasi-rectifier model according to an embodiment of the present invention.

도 3을 참조하면, 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 장치(30)는 1차원 준정류 모형 계산부(31), 횡방향 유속 분포 계산부(32), 횡방향 유사량 분포 계산부(33), 횡방향 하상 변동 계산부(34) 및 데이터베이스(35)를 포함할 수 있다.Referring to FIG. 3, the stream withdrawal and distribution analyzer 30 applying the quasi-two-dimensional quasi-rectification model includes a one-dimensional quasi-rectification model calculation unit 31, a lateral flow velocity distribution calculation unit 32, Section 33, a lateral river bed variation calculation section 34 and a database 35. [

데이터베이스(35)는 최초 하천 지형, 유량, 퇴적 입자 크기, 퇴적물 유입량, 지류 등을 포함하는 주어진 하상 데이터를 저장하며, 1차원 준정류 모형 계산부(31), 횡방향 유속 분포 계산부(32), 횡방향 유사량 분포 계산부(33), 횡방향 하상 변동 계산부(34)의 각각에 필요한 하상 데이터를 제공한다.The database 35 stores the given bedside data including the initial river terrain, the flow rate, the sediment particle size, the sediment inflow amount, the tributary flow, etc. and includes a one-dimensional quasi-rectified model calculation unit 31, a lateral flow velocity distribution calculation unit 32, The lateral similarity distribution calculating section 33, and the lateral river bed variation calculating section 34, respectively.

1차원 준정류 모형 계산부(31)는 하상 데이터에 관하여 1차원 준정류 모형에 기초하여 전체 관심 구간의 수직 단면의 수심 평균 유속과 단면 수심을 산출하고, 산출된 수심 평균 유속과 단면 수심을 이용하여 종방향 단면의 단위폭당 총 유사량을 산출하며, 산출한 종방향 단위폭당 총 유사량을 이용하여 1차원 준정류 모형에 따라 종방향 하상고를 산출한다.The one-dimensional quasi-rectification model calculator 31 calculates the depth-averaged flow velocity and the cross-sectional water depth of the vertical section of the entire interest area based on the one-dimensional quasi-rectification model with respect to the bedside data, and uses the calculated depth- , And the vertical bottom height is calculated according to the one-dimensional quasi-rectification model using the calculated total amount per unit width of the longitudinal direction calculated.

구체적으로, 1차원 준정류 모형 계산부(31)가 계산하는 1차원 준정류 모형은 상술한 수학식 1의 유동에 관한 1차원 연속 방정식과 수학식 2의 운동량 방정식을 포함할 수 있다.Specifically, the one-dimensional quasi-rectification model calculated by the one-dimensional quasi-rectification model calculation unit 31 may include a one-dimensional continuity equation related to the flow of the equation (1) and a momentum equation of the equation (2).

구체적으로, 단위폭당 총 유사량은 상술한 수학식 3과 같은 Engelund-Hansen 방정식 또는 수학식 4와 같은 Yang 방정식을 이용하여 산출될 수 있다.Specifically, the total amount of similarity per unit width can be calculated using the Engelund-Hansen equation as shown in Equation (3) or the Yang equation as shown in Equation (4).

구체적으로, 종방향 하상고는 상술한 수학식 5와 같은 하상토 보존 방정식을 이용하여 산출될 수 있다.Specifically, the longitudinal lower elevation can be calculated by using the bed soil storage equation as shown in Equation (5).

횡방향 유속 분포 계산부(32)는 산출된 종방향 수직 단면의 평균 유속, 수심 및 하상고를 이용하여 횡분배법(LDM)에 따라, 복수의 횡방향 단위폭 구역들의 각각에 대해 횡방향 유속 분포를 얻는다.The transverse flow velocity distribution calculation section 32 calculates the transverse flow velocity distribution for each of the plurality of transverse unit width zones according to the transverse distribution method (LDM) using the average flow velocity, depth and lower elevation of the calculated vertical vertical cross- Obtain the distribution.

본 발명에 적합하도록 변형된 유속 횡분배법은 상술한 수학식 6 내지 수학식 10에 의해 설명된다.The flow velocity distribution method modified to be suitable for the present invention is explained by the above-described Equations (6) to (10).

횡방향 유사량 분포 계산부(33)는 횡방향 유속 분포에 기초하여, 모든 단위폭 구역들의 각각마다 횡방향 유사량의 분포를 산출한다.The lateral similarity amount distribution calculation unit 33 calculates the distribution of the lateral direction similarity amount for each of all unit width regions based on the lateral direction flow velocity distribution.

하상 유사의 이송은 상술한 수학식 11에 따른 Kovacs and Parker의 벡터 공식에 의해 산출될 수 있다.The transfer of bed similarity can be calculated by the vector formula of Kovacs and Parker according to the above-mentioned Equation (11).

횡방향 하상 변동 계산부(34)는 횡방향 유사량 분포에 기초하여 횡방향 하상 변동을 산출한다.The lateral river-bed variation calculation unit 34 calculates the lateral river-bed variation based on the lateral-direction similarity distribution.

구체적으로, 상술한 수학식 12와 같이 횡방향 하상고를 산출함으로써 횡방향 하상 변동을 얻을 수 있고, Menendez 등의 활동 알고리즘을 이용하여 하상 경사의 변형을 산출할 수 있다.More specifically, lateral lateral bed fluctuation can be obtained by calculating lateral lateral elevation as shown in Equation (12) above, and deformation of bed slope can be calculated using an activity algorithm such as Menendez et al.

이렇게 하여, 본 발명에 따르면, 하천의 중심선(thalweg)을 따라 종방향으로 산출된 하상 변동에 기초하여 각 측정점마다 횡방향의 하상 변동도 함께 산출됨으로써, 하천을 따라 실제로 2차원적 시뮬레이션을 수행하는 대신에, 2차원적 시뮬레이션에 가깝게 준2차원적으로, 하상의 퇴적을 시뮬레이션할 수 있다.In this manner, according to the present invention, the river level fluctuation in the lateral direction is also calculated for each measurement point together with the river level variation calculated in the longitudinal direction along the center line of the river, thereby realizing a two-dimensional simulation Instead, it is possible to simulate bed deposition two-dimensionally close to a two-dimensional simulation.

본 발명에 따른 이러한 준2차원적 방식을 이용하면, 동일한 연산 능력을 가진 시뮬레이션 시스템을 가지고 훨씬 긴 기간 동안의 하상 변동을 예측할 수 있거나, 동일한 예측 기간이라면 하상 변동의 예측에 들어가는 비용을 절감할 수 있으며, 또는 동일한 비용과 처리 시간 내에서라면 좀더 다양하고 정밀한 조건에서 하상 변동을 시뮬레이션할 수 있다.Using this quasi-two-dimensional method according to the present invention, a simulation system with the same computation capability can be used to predict river changes over a much longer period of time, or the cost of predicting river changes can be reduced if the same prediction period is used , Or simulate river changes under more varied and precise conditions within the same cost and processing time.

본 실시예 및 본 명세서에 첨부된 도면은 본 발명에 포함되는 기술적 사상의 일부를 명확하게 나타내고 있는 것에 불과하며, 본 발명의 명세서 및 도면에 포함된 기술적 사상의 범위 내에서 당업자가 용이하게 유추할 수 있는 변형예와 구체적인 실시예는 모두 본 발명의 권리범위에 포함되는 것이 자명하다고 할 것이다.It is to be understood that both the foregoing general description and the following detailed description of the present invention are exemplary and explanatory and are intended to provide further explanation of the invention as claimed. It will be understood that variations and specific embodiments which may occur to those skilled in the art are included within the scope of the present invention.

또한, 본 발명에 따른 장치는 컴퓨터로 읽을 수 있는 기록매체에 컴퓨터가 읽을 수 있는 코드로서 구현하는 것이 가능하다. 컴퓨터가 읽을 수 있는 기록매체는 컴퓨터 시스템에 의하여 읽힐 수 있는 데이터가 저장되는 모든 종류의 기록장치를 포함한다. 기록매체의 예로는 ROM, RAM, 광학 디스크, 자기 테이프, 플로피 디스크, 하드 디스크, 비휘발성 메모리 등을 포함한다. 또한 컴퓨터가 읽을 수 있는 기록매체는 네트워크로 연결된 컴퓨터 시스템에 분산되어 분산방식으로 컴퓨터가 읽을 수 있는 코드가 저장되고 실행될 수 있다.Further, the apparatus according to the present invention can be implemented as a computer-readable code on a computer-readable recording medium. A computer-readable recording medium includes all kinds of recording apparatuses in which data that can be read by a computer system is stored. Examples of the recording medium include ROM, RAM, optical disk, magnetic tape, floppy disk, hard disk, nonvolatile memory and the like. The computer-readable recording medium may also be distributed over a networked computer system so that computer readable code can be stored and executed in a distributed manner.

30 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 장치
31 1차원 준정류 모형 계산부
32 횡방향 유속 분포 계산부
33 횡방향 유사량 분포 계산부
34 횡방향 하상 변동 계산부
35 데이터베이스30 A quasi-two-dimensional quasi-rectification model is applied to river discharge and discharge analysis
31 One-dimensional semi-rectification model calculation unit
32 lateral flow velocity distribution calculation section
33 Transverse direction similarity distribution calculation unit
34 transverse direction bed variation calculation unit
35 databases

Claims (18)

컴퓨터를 이용한 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 방법으로서,
상기 컴퓨터가,
(a) 최초 하천 지형, 유량, 퇴적 입자 크기, 퇴적물 유입량, 지류 등을 포함하는 주어진 하상 데이터에 관하여 1차원 준정류 모형에 기초하여 전체 관심 구간의 수직 단면의 종방향 수심 평균 유속과 종방향 단면 수심을 산출하는 단계;
(b) 산출된 수심 평균 유속과 단면 수심을 이용하여 종방향 단면의 단위폭당 총 유사량을 산출하는 단계;
(c) 산출한 종방향 단위폭당 총 유사량을 이용하여 1차원 준정류 모형에 따라 종방향 하상고를 산출하는 단계;
(d) 산출된 종방향 수직 단면의 평균 유속, 수심 및 하상고를 이용하여 횡분배법에 따라 횡방향 유속 분포를 산출하는 단계;
(e) 횡방향 유속 분포에 기초하여 횡방향 유사량 분포를 산출하는 단계; 및
(f) 횡방향 유사량 분포에 기초하여 횡방향 하상 변동을 산출하는 단계를 포함하는 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 방법.A computerized quasi - two - dimensional quasi -
The computer comprising:
(a) Based on a one-dimensional quasi-rectification model for given bedside data including initial stream topography, flow, sediment particle size, sediment flow, tributaries, etc., Calculating a depth of water;
(b) calculating a total amount of similarity per unit width of the longitudinal section by using the calculated water depth average velocity and the depth of the section;
(c) calculating the longitudinal undersurface height in accordance with the one-dimensional quasi-rectification model using the calculated total amount per longitudinal unit width;
(d) calculating the lateral flow velocity distribution according to the lateral distribution method using the average flow velocity, water depth, and bottom height of the vertical longitudinal section;
(e) calculating a lateral similarity distribution based on the lateral flow velocity distribution; And
(f) calculating the transverse river bed variation based on the lateral direction similarity distribution, wherein the quasi-two-dimensional quasi-rectification model is applied to the river sedimentation and distribution analysis. 청구항 1에 있어서, (b) 상기 종방향 단면의 단위폭당 총 유사량을 산출하는 단계는, 다음 수학식
Figure 112014082966392-pat00070

의 해를 산출하는 단계를 포함하고,
여기서, qs는 산출되어야 하는 단위폭당 총 유사량, R은 수중 비중(submerged specific gravity), d50은 유사 입자들(sediment particles)의 중간 크기(median size),
Figure 112014082966392-pat00071
는 무차원 전단 응력(Shields stress), Cf는 하상 저항 계수, g는 중력 가속도인 것을 특징으로 하는 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 방법.2. The method according to claim 1, wherein (b) calculating a total similarity amount per unit width of the longitudinal cross-
Figure 112014082966392-pat00070

And calculating a solution of the solution,
Where q s is the total amount of sediment per unit width to be calculated, R is the submerged specific gravity, d 50 is the median size of the sediment particles,
Figure 112014082966392-pat00071
Is a non-dimensional shear stress, C f is a bed resistance coefficient, and g is a gravitational acceleration. 청구항 1에 있어서, (b) 상기 종방향 단면의 단위폭당 총 유사량을 산출하는 단계는, 다음 수학식
Figure 112014082966392-pat00072

의 해를 산출하는 단계를 포함하고,
여기서, Cs는 유속 기반 중량 농도(flux-based mass concentration)이고, a1 및 a2는 경험적 파라미터들(empirical parameters)이며,
Figure 112014082966392-pat00073
은 유사 내의 퇴적물의 비중량(specific weight of sediment in sediment-laden flow),
Figure 112014082966392-pat00074
는 퇴적물의 비중량(specific weight of sediment),
Figure 112014082966392-pat00075
는 퇴적물의 하강 속도인 것을 특징으로 하는 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 방법.2. The method according to claim 1, wherein (b) calculating a total similarity amount per unit width of the longitudinal cross-
Figure 112014082966392-pat00072

And calculating a solution of the solution,
Where C s is the flux-based mass concentration, a 1 and a 2 are the empirical parameters,
Figure 112014082966392-pat00073
Is the specific weight of sediment in sediment-laden flow,
Figure 112014082966392-pat00074
Is the specific weight of sediment,
Figure 112014082966392-pat00075
Is a descending rate of the sediment. The method of analyzing the stream sedimentation and distribution using the quasi-two-dimensional semi-rectification model. 청구항 1에 있어서, (c) 상기 종방향 하상고를 산출하는 단계는,
다음 수학식
Figure 112014082966392-pat00076

의 해를 산출하는 단계를 포함하고,
여기서,
Figure 112014082966392-pat00077
는 종방향 하상고(bed elevation), t는 시간,
Figure 112014082966392-pat00078
는 하상 물질의 공극률(porosity of bed material),
Figure 112014082966392-pat00079
는 단위폭당 총 유사량(sediment load per unit width), x는 상류로부터 해당 지점까지 종방향 거리인 것을 특징으로 하는 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 방법.The method of claim 1, wherein (c)
The following equation
Figure 112014082966392-pat00076

And calculating a solution of the solution,
here,
Figure 112014082966392-pat00077
Is bed elevation, t is time,
Figure 112014082966392-pat00078
Is the porosity of the bed material,
Figure 112014082966392-pat00079
Is the sediment load per unit width, and x is the longitudinal distance from the upstream to the corresponding point. The quasi-two-dimensional quasi-rectification model is applied to the river sedimentation and distribution analysis. 청구항 1에 있어서, (d) 상기 횡분배법에 따라 횡방향 유속 분포를 산출하는 단계는
다음 수학식
Figure 112014082966392-pat00080

의 해를 산출하는 단계를 포함하고,
여기서, x는 종방향 거리, y는 횡방향 거리이며,
Figure 112014082966392-pat00081
는 물의 밀도, g는 중력 가속도, H는 수심, Sx는 x 방향의 하상 경사(bed slope),
Figure 112014082966392-pat00082
는 하상 전단 응력(bed shear stress), Bg는
Figure 112014082966392-pat00083
로 정의되는 기하학적 인자(geometric factor), Sy는 y 방향의 하상 경사,
Figure 112014082966392-pat00084
는 수심 평균 횡방향 전단 응력(depth-averaged lateral shear stress)이며,
Figure 112014082966392-pat00085
는 이차류 영향을 나타내는 항(term due to secondary currents)인 것을 특징으로 하는 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 방법.The method of claim 1, further comprising: (d) calculating a lateral flow velocity distribution in accordance with the lateral distribution method
The following equation
Figure 112014082966392-pat00080

And calculating a solution of the solution,
Where x is the longitudinal distance, y is the lateral distance,
Figure 112014082966392-pat00081
G is the gravitational acceleration, H is the depth of water, S x is the bed slope in the x direction,
Figure 112014082966392-pat00082
Is the bed shear stress, B g is the shear stress
Figure 112014082966392-pat00083
S y is the y-direction slope of the bed,
Figure 112014082966392-pat00084
Is the depth-averaged lateral shear stress,
Figure 112014082966392-pat00085
Is a term due to secondary currents. The quasi-two-dimensional quasi-rectification model is applied to the river sedimentation and distribution analysis. 청구항 5에 있어서, 상기 수심 평균 횡방향 전단 응력
Figure 112014082966392-pat00086
은 다음 수학식
Figure 112014082966392-pat00087

에 의해 산출되고,
여기서
Figure 112014082966392-pat00088
는 와류 점성(eddy viscosity)으로서, 유속의 차이로 인해 발생하는 수주(water column) 사이의 전단 응력을 결정하고,
Figure 112014082966392-pat00089
는 물의 밀도이며 Ud는 x 방향의 수심 평균 유속인 것을 특징으로 하는 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 방법.The method of claim 5, wherein the depth-averaged transverse shear stress
Figure 112014082966392-pat00086
Is expressed by the following equation
Figure 112014082966392-pat00087

Lt; / RTI >
here
Figure 112014082966392-pat00088
Is the eddy viscosity, which determines the shear stress between water columns due to the difference in flow velocity,
Figure 112014082966392-pat00089
Is the density of water and U d is the depth average velocity in the x direction. 청구항 5에 있어서, 상기 이차류 항
Figure 112014082966392-pat00090
은 다음 수학식
Figure 112014082966392-pat00091

에 의해 산출되고,
여기서,
Figure 112014082966392-pat00092
및
Figure 112014082966392-pat00093
는 각각 유속의 시간 평균된 x 방향 및 y 방향 성분들이고, z는 수직 방향 거리이며 H는 수심이며,
Figure 112014082966392-pat00094
는 물의 밀도인 것을 특징으로 하는 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 방법.The method according to claim 5,
Figure 112014082966392-pat00090
Is expressed by the following equation
Figure 112014082966392-pat00091

Lt; / RTI >
here,
Figure 112014082966392-pat00092
And
Figure 112014082966392-pat00093
Are the time-averaged x-direction and y-direction components of the flow velocity, z is the vertical distance and H is the water depth,
Figure 112014082966392-pat00094
Is a density of water. The method of analyzing the drainage and distribution of streams by applying the quasi-two-dimensional quasi-rectification model. 청구항 1에 있어서, 장기간 시뮬레이션을 위해, 매 시간 단위마다 단계 (a) 내지 단계 (f)를 반복하는 단계를 더 포함하는 것을 특징으로 하는 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 방법.The method according to claim 1, further comprising repeating steps (a) through (f) for each time unit for a long-term simulation, wherein the quasi-two-dimensional quasi-rectification model is applied. 청구항 1에 있어서,
상기 (f) 단계 이후에, (g) 활동 알고리즘을 이용하여 하상 경사의 변형을 산출하는 단계를 더 포함하는 것을 특징으로 하는 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 방법.The method according to claim 1,
The method of claim 1, further comprising: (g) calculating a deformation of the bed slope using the activity algorithm after the step (f). 컴퓨터에서 청구항 1 내지 청구항 9 중 어느 한 청구항에 따른 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 방법의 각 단계들을 실행시키기 위해 기록매체에 저장된 컴퓨터 프로그램.A computer program stored on a recording medium for executing each step of a stream leaving and breaking analysis method applying a quasi-two-dimensional quasi-rectifying model according to any one of claims 1 to 9 to a computer. 하상 데이터에 관하여 1차원 준정류 모형에 기초하여 전체 관심 구간의 수직 단면의 수심 평균 유속과 단면 수심을 산출하고, 산출된 수심 평균 유속과 단면 수심을 이용하여 종방향 단면의 단위폭당 총 유사량을 산출하며, 산출한 종방향 단위폭당 총 유사량을 이용하여 1차원 준정류 모형에 따라 종방향 하상고를 산출하는 1차원 준정류 모형 계산부;
산출된 종방향 수직 단면의 평균 유속, 수심 및 하상고를 이용하여 횡분배법(LDM)에 따라, 복수의 횡방향 단위폭 구역들의 각각에 대해 횡방향 유속 분포를 산출하는 횡방향 유속 분포 계산부;
상기 횡방향 유속 분포에 기초하여, 모든 단위폭 구역들의 각각마다 횡방향 유사량의 분포를 산출하는 횡방향 유사량 분포 계산부; 및
횡방향 유사량 분포에 기초하여 횡방향 하상 변동을 산출하는 횡방향 하상 변동 계산부를 포함하는 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 장치.Based on the one-dimensional quasi-rectification model for the river data, the water depth average velocity and the water depth of the vertical section of the whole section of interest are calculated, and the total amount of sediment per unit width of the longitudinal section is calculated using the calculated water depth average velocity and the water depth A one-dimensional quasi-rectified model calculation unit for calculating the vertical lower elevation according to the one-dimensional quasi-rectification model using the calculated total similarity per unit length in the longitudinal direction;
A lateral flow velocity distribution calculation section for calculating a lateral flow velocity distribution for each of a plurality of transverse unit width zones in accordance with a transverse distribution method (LDM) using an average flow velocity, a depth of water, ;
A lateral similarity distribution calculation unit for calculating a distribution of the lateral direction similarity amount for each of all the unit width zones based on the lateral flow velocity distribution; And
An apparatus for analyzing river sedimentation and distribution using a quasi - two - dimensional quasi - rectification model including a lateral river bed variation calculation unit for calculating a lateral river bed variation based on a lateral direction similarity distribution. 청구항 11에 있어서, 상기 1차원 준정류 모형 계산부는 상기 종방향 단면의 단위폭당 총 유사량을 산출하기 위해 다음 수학식
Figure 112014082966392-pat00095

의 해를 산출하도록 동작하고,
여기서, qs는 산출되어야 하는 단위폭당 총 유사량, R은 수중 비중(submerged specific gravity), d50은 유사 입자들(sediment particles)의 중간 크기(median size),
Figure 112014082966392-pat00096
는 무차원 전단 응력(Shields stress), Cf는 하상 저항 계수, g는 중력 가속도인 것을 특징으로 하는 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 장치.[Claim 12] The method of claim 11, wherein the one-dimensional quasi-rectification model calculator calculates a total amount of similarity per unit width of the longitudinal cross-
Figure 112014082966392-pat00095

Lt; RTI ID = 0.0 >
Where q s is the total amount of sediment per unit width to be calculated, R is the submerged specific gravity, d 50 is the median size of the sediment particles,
Figure 112014082966392-pat00096
Is a non-dimensional shear stress, C f is a bed resistance coefficient, and g is a gravitational acceleration. 청구항 11에 있어서, 상기 1차원 준정류 모형 계산부는 상기 종방향 단면의 단위폭당 총 유사량을 산출하기 위해 다음 수학식
Figure 112014082966392-pat00097

의 해를 산출하도록 동작하고,
여기서, Cs는 유속 기반 중량 농도(flux-based mass concentration)이고, a1 및 a2는 경험적 파라미터들(empirical parameters)이며,
Figure 112014082966392-pat00098
은 유사 내의 퇴적물의 비중량(specific weight of sediment in sediment-laden flow),
Figure 112014082966392-pat00099
는 퇴적물의 비중량(specific weight of sediment),
Figure 112014082966392-pat00100
는 퇴적물의 하강 속도인 것을 특징으로 하는 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 장치.[Claim 12] The method of claim 11, wherein the one-dimensional quasi-rectification model calculator calculates a total amount of similarity per unit width of the longitudinal cross-
Figure 112014082966392-pat00097

Lt; RTI ID = 0.0 >
Where C s is the flux-based mass concentration, a 1 and a 2 are the empirical parameters,
Figure 112014082966392-pat00098
Is the specific weight of sediment in sediment-laden flow,
Figure 112014082966392-pat00099
Is the specific weight of sediment,
Figure 112014082966392-pat00100
Is a descending rate of the sediment, and a quasi-two-dimensional quasi-rectification model is applied to the river sedimentation and distribution analysis apparatus. 청구항 11에 있어서, 상기 1차원 준정류 모형 계산부는 상기 종방향 하상고를 산출하기 위해 다음 수학식
Figure 112014082966392-pat00101

의 해를 산출하도록 동작하고,
여기서,
Figure 112014082966392-pat00102
는 종방향 하상고(bed elevation), t는 시간,
Figure 112014082966392-pat00103
는 하상 물질의 공극률(porosity of bed material),
Figure 112014082966392-pat00104
는 단위폭당 총 유사량(sediment load per unit width), x는 상류로부터 해당 지점까지 종방향 거리인 것을 특징으로 하는 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 장치.[12] The method of claim 11, wherein the one-dimensional quasi-rectification model calculator calculates the vertical low-
Figure 112014082966392-pat00101

Lt; RTI ID = 0.0 >
here,
Figure 112014082966392-pat00102
Is bed elevation, t is time,
Figure 112014082966392-pat00103
Is the porosity of the bed material,
Figure 112014082966392-pat00104
Is a sediment load per unit width, and x is a longitudinal distance from the upstream to the corresponding point. A quasi-two-dimensional quasi-rectification model is applied to the river sedimentation and distribution analysis. 청구항 11에 있어서, 상기 횡방향 유속 분포 계산부는 상기 횡분배법에 따라 횡방향 유속 분포를 산출하기 위해 다음 수학식
Figure 112014082966392-pat00105

의 해를 산출하도록 동작하고,
여기서, x는 종방향 거리, y는 횡방향 거리이며,
Figure 112014082966392-pat00106
는 물의 밀도, g는 중력 가속도, H는 수심, Sx는 x 방향의 하상 경사(bed slope),
Figure 112014082966392-pat00107
는 하상 전단 응력(bed shear stress), Bg는
Figure 112014082966392-pat00108
로 정의되는 기하학적 인자(geometric factor), Sy는 y 방향의 하상 경사,
Figure 112014082966392-pat00109
는 수심 평균 횡방향 전단 응력(depth-averaged lateral shear stress)이며,
Figure 112014082966392-pat00110
는 이차류 영향을 나타내는 항(term due to secondary currents)인 것을 특징으로 하는 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 장치.[12] The method of claim 11, wherein the transverse flow velocity distribution calculation unit calculates a transverse flow velocity distribution according to the transverse distribution method,
Figure 112014082966392-pat00105

Lt; RTI ID = 0.0 >
Where x is the longitudinal distance, y is the lateral distance,
Figure 112014082966392-pat00106
G is the gravitational acceleration, H is the depth of water, S x is the bed slope in the x direction,
Figure 112014082966392-pat00107
Is the bed shear stress, B g is the shear stress
Figure 112014082966392-pat00108
S y is the y-direction slope of the bed,
Figure 112014082966392-pat00109
Is the depth-averaged lateral shear stress,
Figure 112014082966392-pat00110
Is a term due to secondary currents. The quasi-two-dimensional quasi-rectification model is applied to the river discharge and discharge analysis. 청구항 15에 있어서, 상기 수심 평균 횡방향 전단 응력
Figure 112015001139969-pat00111
은 다음 수학식
Figure 112015001139969-pat00112

에 의해 산출되고,
여기서
Figure 112015001139969-pat00113
는 와류 점성(eddy viscosity)으로서, 유속의 차이로 인해 발생하는 수주(water column) 사이의 전단 응력을 결정하고,
Figure 112015001139969-pat00114
는 물의 밀도이며 Ud는 x 방향의 수심 평균 유속인 것을 특징으로 하는 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 장치.16. The method of claim 15, wherein the depth-averaged transverse shear stress
Figure 112015001139969-pat00111
Is expressed by the following equation
Figure 112015001139969-pat00112

Lt; / RTI >
here
Figure 112015001139969-pat00113
Is the eddy viscosity, which determines the shear stress between water columns due to the difference in flow velocity,
Figure 112015001139969-pat00114
Is the density of water and U d is the depth-averaged velocity in the x direction. 청구항 15에 있어서, 상기 이차류 항
Figure 112014082966392-pat00115
은 다음 수학식
Figure 112014082966392-pat00116

에 의해 산출되고,
여기서,
Figure 112014082966392-pat00117
및
Figure 112014082966392-pat00118
는 각각 유속의 시간 평균된 x 방향 및 y 방향 성분들이고, z는 수직 방향 거리이며 H는 수심이며,
Figure 112014082966392-pat00119
는 물의 밀도인 것을 특징으로 하는 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 장치.16. The method of claim 15,
Figure 112014082966392-pat00115
Is expressed by the following equation
Figure 112014082966392-pat00116

Lt; / RTI >
here,
Figure 112014082966392-pat00117
And
Figure 112014082966392-pat00118
Are the time-averaged x-direction and y-direction components of the flow velocity, z is the vertical distance and H is the water depth,
Figure 112014082966392-pat00119
Is a density of water. A quasi-two-dimensional quasi-rectification model is applied to the river sedimentation and distribution analysis. 청구항 11에 있어서, 상기 횡방향 하상 변동 계산부는,
활동 알고리즘을 이용하여 하상 경사의 변형을 산출하도록 동작하는 것을 특징으로 하는 준2차원 준정류 모형을 적용한 하천 퇴사 및 배사 해석 장치.12. The apparatus according to claim 11, wherein the lateral river-
And the operation algorithm is used to calculate the deformation of the slope of the river bed.
KR20140114507A 2014-08-29 2014-08-29 Method and apparatus for analyzing river sedimentation and flushing using quasi-2-dimensional quasi-steady model KR101497993B1 (en)

Priority Applications (1)

Application Number Priority Date Filing Date Title
KR20140114507A KR101497993B1 (en) 2014-08-29 2014-08-29 Method and apparatus for analyzing river sedimentation and flushing using quasi-2-dimensional quasi-steady model

Applications Claiming Priority (1)

Application Number Priority Date Filing Date Title
KR20140114507A KR101497993B1 (en) 2014-08-29 2014-08-29 Method and apparatus for analyzing river sedimentation and flushing using quasi-2-dimensional quasi-steady model

Publications (1)

Publication Number Publication Date
KR101497993B1 true KR101497993B1 (en) 2015-03-05

Family

ID=53026049

Family Applications (1)

Application Number Title Priority Date Filing Date
KR20140114507A KR101497993B1 (en) 2014-08-29 2014-08-29 Method and apparatus for analyzing river sedimentation and flushing using quasi-2-dimensional quasi-steady model

Country Status (1)

Country Link
KR (1) KR101497993B1 (en)

Cited By (8)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
CN106846475A (en) * 2017-02-08 2017-06-13 长江水利委员会长江科学院 A kind of river historical Appearance digital restoration method
CN107703741A (en) * 2017-08-31 2018-02-16 上海电力学院 Robot motion's system identifying method based on quasi-mode type calibration Kalman filtering
CN108595726A (en) * 2017-12-29 2018-09-28 河海大学 A kind of river bed adjusting method based on silt underwater information warfare
CN111539153A (en) * 2020-04-07 2020-08-14 长江水利委员会长江科学院 Water and sand combined optimization scheduling method based on pre-constructed sediment information base
CN113569408A (en) * 2021-07-28 2021-10-29 黄河水利委员会黄河水利科学研究院 Representative characterization method for mechanical property of river ice
CN116049699A (en) * 2023-04-03 2023-05-02 武汉大学 Method, device, equipment and storage medium for identifying flushing gravity center of alluvial river
CN117074718A (en) * 2023-08-18 2023-11-17 长江水利委员会水文局 Method for real-time fitting of ADCP data to layering flow rate of hydrologic test
CN118052169A (en) * 2024-04-16 2024-05-17 长江水利委员会长江科学院 Method and system for calculating scouring stability duration of downstream sandy pebble river course of reservoir

Non-Patent Citations (1)

* Cited by examiner, † Cited by third party
Title
assessment of reservoir sedimentation using quasi two dimensional model(advances in river sediment research, 2013) *

Cited By (13)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
CN106846475A (en) * 2017-02-08 2017-06-13 长江水利委员会长江科学院 A kind of river historical Appearance digital restoration method
CN107703741A (en) * 2017-08-31 2018-02-16 上海电力学院 Robot motion's system identifying method based on quasi-mode type calibration Kalman filtering
CN108595726A (en) * 2017-12-29 2018-09-28 河海大学 A kind of river bed adjusting method based on silt underwater information warfare
CN108595726B (en) * 2017-12-29 2021-06-11 河海大学 Riverbed adjusting method based on underwater repose angle of sediment
CN111539153B (en) * 2020-04-07 2023-12-08 长江水利委员会长江科学院 Water-sand joint optimization scheduling method based on preconfigured sediment information base
CN111539153A (en) * 2020-04-07 2020-08-14 长江水利委员会长江科学院 Water and sand combined optimization scheduling method based on pre-constructed sediment information base
CN113569408B (en) * 2021-07-28 2024-02-20 黄河水利委员会黄河水利科学研究院 Representative characterization method of river ice mechanical property
CN113569408A (en) * 2021-07-28 2021-10-29 黄河水利委员会黄河水利科学研究院 Representative characterization method for mechanical property of river ice
CN116049699A (en) * 2023-04-03 2023-05-02 武汉大学 Method, device, equipment and storage medium for identifying flushing gravity center of alluvial river
CN117074718A (en) * 2023-08-18 2023-11-17 长江水利委员会水文局 Method for real-time fitting of ADCP data to layering flow rate of hydrologic test
CN117074718B (en) * 2023-08-18 2024-05-14 长江水利委员会水文局 Method for real-time fitting of ADCP data to layering flow rate of hydrologic test
CN118052169A (en) * 2024-04-16 2024-05-17 长江水利委员会长江科学院 Method and system for calculating scouring stability duration of downstream sandy pebble river course of reservoir
CN118052169B (en) * 2024-04-16 2024-06-11 长江水利委员会长江科学院 Method and system for calculating scouring stability duration of downstream sandy pebble river course of reservoir

Similar Documents

Publication Publication Date Title
KR101497993B1 (en) Method and apparatus for analyzing river sedimentation and flushing using quasi-2-dimensional quasi-steady model
Simons et al. Flume studies using medium sand (0.45 mm)
Lajeunesse et al. Bed load transport in turbulent flow at the grain scale: Experiments and modeling
Haun et al. Three-dimensional measurements and numerical modelling of suspended sediments in a hydropower reservoir
Jia et al. Three-dimensional modeling of bank erosion and morphological changes in the Shishou bend of the middle Yangtze River
Bai et al. Simulating unsteady flow and sediment transport in vegetated channel network
Nardi et al. Quantification of riverbank erosion and application in risk analysis
Goel et al. Application of support vector machines in scour prediction on grade-control structures
Juez et al. Numerical assessment of bed-load discharge formulations for transient flow in 1D and 2D situations
Qian et al. Well-balanced numerical modelling of non-uniform sediment transport in alluvial rivers
Zhang et al. An experimental study of fluvial processes at asymmetrical river confluences with hyperconcentrated tributary flows
Moussa Predicting the deposition in the Aswan High Dam Reservoir using a 2-D model
Samma et al. Numerical simulation of scour and flow field over movable bed induced by a submerged wall jet
Lee et al. Turbid density current venting through reservoir outlets
Chen et al. Case study: Two-dimensional model simulation of channel migration processes in West Jordan River, Utah
Uotani et al. Experimental and numerical study on hydrodynamics of riparian vegetation
Xia et al. Modelling of hyperconcentrated flood and channel evolution in a braided reach using a dynamically coupled one-dimensional approach
Guguloth et al. Accuracy evaluation of scour depth equations under the submerged vertical jet
Luo et al. The effect of stress history on fluctuation of bedload transport rate and bed topography in gravel-bed streams
Zheng et al. A novel explicit-implicit coupled solution method of SWE for long-term river meandering process induced by dambreak
Kadia et al. Discharge characteristics of triangular weir with upstream ramp and its CFD modelling using ANSYS CFX module
Olsen et al. Numerical modelling of bank failures during reservoir draw-down
Huang et al. Modelling of meander migration in an incised channel
Dehghani et al. 3D numerical simulation of local scouring under hydrographs
CN107090798A (en) Restoration ＆ saturation coefficient computational methods under a kind of reservoir over-saturation sediment transport state

Legal Events

Date Code Title Description
E701 Decision to grant or registration of patent right
GRNT Written decision to grant
LAPS Lapse due to unpaid annual fee