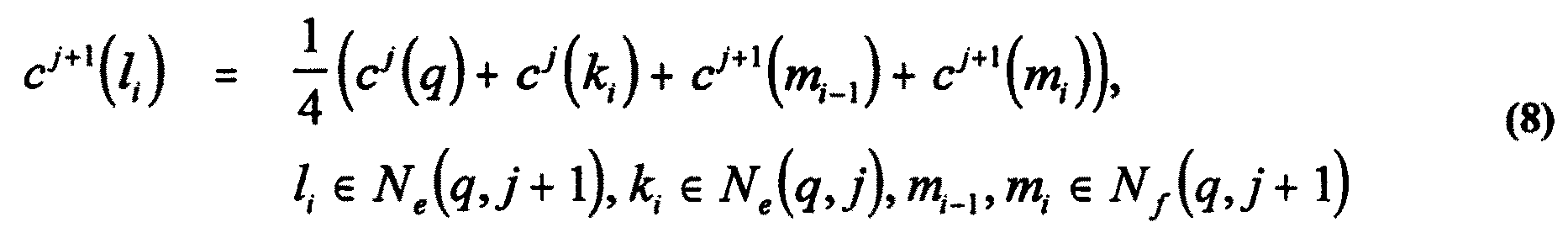JP4885196B2 - 細分表面における滑らかな特徴線の生成 - Google Patents

Description

本発明は、全般的にコンピュータ・グラフィックスの分野に関し、特に、物体の表面を
表現する細分表面上の滑らかな特徴線の生成に関する。

一般に、コンピュータ・グラフィックスでは、物体は、特定のレベルのメッシュによっ
て表現される表面として表現される。特定のレベルのメッシュは、辺により連結されてい
る、三次元空間の１組の頂点または点からなる。辺は、三角形、四辺形などの形をとる多
角形面を定める。あるコンピュータ・グラフィックスの操作では、現在の表現よりも高い
解像度で表面の表現を生成することが望まれる。四辺形のメッシュによって定められる表
面と関連して用いられるＣａｔｍｕｌｌ−Ｃｌａｒｋ表面細分法と、三角形のメッシュに
よって定められる表面と関連して用いられるＬｏｏｐ表面細分法を含め、現在の表現より
も高い解像度で表面の表現を生成するいくつかの一般的な方法が存在する。一般に、双方
の方法は、次のより高い細分度のメッシュを生成するために、メッシュの特定のレベルで
表面を定めるそれぞれの頂点において、それぞれの細分則を用いる。「細分表面」または
「極限表面」と呼ばれるそれぞれの物体の表面は、細分度が無限大になったときに、メッ
シュによって定められるものとして理解される。

ある細分表面の特徴は、それぞれの表面を定めるメッシュ内の特徴線によって、定める
ことができる。特徴線は、鋭い折り目または滑らかな曲りの形をとりうる。滑らかな特徴
線の場合、表面に接する平面に垂直なベクトルである法線ベクトルは、滑らかな特徴線を
横切って連続的に変化する。他方、鋭い折り目の場合、法線ベクトルは、折り目を横切っ
て不連続に変化し、実際、その折り目のところでは定義されない。しかしながら、滑らか
な曲りの定義は、特定の細分度におけるメッシュ内の頂点を横切る曲りの鋭さを定めるた
めに用いられる１つまたは複数のパラメータを用いて、鋭い折り目の定義から得ることが
できる。カリフォルニア州パサデナのカリフォルニア工科大学における１９９８年のＤ．
Ｚｏｒｉｎによる博士論文「静的細分および多重解像度表面表現（Ｓｔａｔｉｏｎａｒｙ
Ｓｕｂｄｉｖｉｓｉｏｎ Ａｎｄ Ｍｕｌｔｉ−Ｒｅｓｏｌｕｔｉｏｎ Ｓｕｒｆａｃｅ
Ｒｅｐｒｅｓｅｎｔａｔｉｏｎ）」は、パラメータを用いて、滑らかな特徴線を生成する
方法を説明しているが、そこで説明されている方法では、表面のトポロジーのいくつかの
頂点において滑らかでない表面でさえ、比較的質の低い表面になってしまう。ＡＣＭ Ｓ
ＩＧＧＲＡＰＨ １９９８におけるＳＩＧＧＲＡＰＨ９８会議議事録、会議年報集、８５
から９４ページのＴ．ＤｅＲｏｓｅらの「キャラクタ・アニメーションにおける細分表面
（Ｓｕｂｄｉｖｉｓｉｏｎ ｓｕｒｆａｃｅｓ ｉｎ ｃｈａｒａｃｔｏｒ ａｎｉｍａｔｉ
ｏｎ）」は、ＡＣＭ ＳＩＧＧＲＡＰＨ １９９４におけるＳＩＧＧＲＡＰＨ ９４ 会議議
事録、会議年報集のＨ．Ｈｏｐｐｅらの「小片円滑表面再構成（Ｐｉｅｃｅｗｉｓｅ Ｓ
ｍｏｏｔｈ Ｓｕｒｆａｃｅ ｒｅｃｏｎｓｔｒｕｃｔｉｏｎ）」で説明されているように
、鋭い折り目に対応する細分則を、選択された緻密度に至るまで適用し、その後、滑らか
な内部点に対応する規則を適用することによって、滑らかな特徴線を生ずる方法を説明し
ている。明確に異なる２つの種類の規則を適用することによって、その結果として得られ
る表面の効率的な評価が困難になる。

本発明は、細分表面内に滑らかな特徴線を生成する新規かつ改良されたシステムと方法
を提供する。

簡単に要約すれば、本発明は、選択されたレベルにおいて、それぞれの辺によって複数
の隣接点に連結された少なくとも１つの点を含む複数の点を有するメッシュ表現によって
定められた表面内に、メッシュ表現内の頂点と、少なくとも１つの隣接点と、この頂点と
この少なくとも１つの隣接点を相互接続する辺と関連して定められる特徴の表現を生成す
るシステムを提供する。この特徴生成システムは、重みベクトル生成モジュールと、特徴
表現生成モジュールを有する。重みベクトル生成モジュールは、複数のレベルで定められ
、少なくとも１つのパラメータの値が、メッシュの少なくとも２つのレベルにおいて異な
る値をとるパラメータ化された細分則にもとづいて、少なくとも１つの重みベクトルを生
成するように構成される。特徴表現生成モジュールは、特徴の表現を生成するために、少
なくとも１つの重みベクトルと、頂点およびその隣接点の位置を用いるように構成されて
いる。

本発明の一実施態様は、細分表面内に滑らかな特徴線を生成するシステムを有する。

本発明は、添付されている特許請求の範囲において、特徴が指摘される。本発明の上記
の利点およびその他の利点は、添付の図面と関連して行われる以下の説明を参照すること
によって、より良く理解できるであろう。

図１は、本発明にしたがって構成された、細分表面と関連して滑らかな特徴線を生成す
るシステムを含むコンピュータ・グラフィックス・システム１０を示す。図１を参照する
と、コンピュータ・グラフィックス・システムは、プロセッサ・モジュール１１と、１つ
または複数のオペレータ入力装置１２と、１つまたは複数の表示装置１３を含む。表示装
置１３は、オペレータに対して、テキストおよび／または画像の形で表示スクリーン上に
情報を表示するフレーム・バッファとビデオ表示端末のようなものを通常有する。コンピ
ュータ・グラフィックス・システム１０のオペレータ入力装置１２は、ディジタル化タブ
レット１５とともに通常用いられるペン１４と、トラックボールまたはマウス装置１６を
通常含む。一般に、ペン１４とディジタル化タブレットは、オペレータによって、いくつ
かのモードで用いられる。１つのモードでは、ペン１４とディジタル化タブレットは、コ
ンピュータ・グラフィック・システムに、更新された明暗情報を出力するために用いられ
る。他のモードでは、ペンとディジタル化タブレットは、例えば、表面トリミングや他の
情報のための線引きのような通常のコンピュータ・グラフィックス情報を、コンピュータ
・グラフィックス・システム１０に入力し、これにより、システム１０が通常のコンピュ
ータ・グラフィックス操作を行えるようにするために、オペレータによって用いられる。
トラックボールまたはマウス装置１６は、オペレータが、ペンとディジタル化タブレット
で入力できる、画面上の特定の点まで、スクリーンの上でカーソルまたはポインタを動か
すために用いることができる。コンピュータ・グラフィックス・システム１０は、オペレ
ータがシステム１０にテキスト入力を行うために用いることができるキーボード（不図示
）もまた含めてもよい。

プロセッサ・モジュール１１は、１つまたは複数のマイクロプロセッサの形をとるプロ
セッサと、主メモリを一般に含み、１つまたは複数のディスク記憶装置を含む大容量記憶
サブシステムを一般に含むだろう。メモリとディスク記憶装置は、プロセッサによって処
理されるデータとプログラム（まとめて「情報」とする）を一般に保存し、プロセッサに
よって生成された処理データを保存する。プロセッサ・モジュールは、オペレータ入力装
置１２と表示装置１３への接続を含み、オペレータ入力装置１２を介してオペレータによ
って入力された情報を受け取り、その入力情報を処理し、処理された情報をメモリおよび
／または大容量記憶サブシステムに保存する。さらに、プロセッサ・モジュールは、メモ
リとディスク記憶装置から得た情報と、それによって生成された処理データの一部を形成
するビデオ表示情報を、オペレータへの表示を行う表示装置に出力できる。プロセッサ・
モジュール１１は、ハードコピー出力の生成を容易にするプリンタのようなハードコピー
出力装置への接続（不図示）と、システム１０を、情報の転送を容易にする公衆電話シス
テムおよび／またはコンピュータネットワークのようなものに接続するモデムおよび／ま
たはネットワーク・インタフェース（これも不図示）もまた含んでいてもよい。

本発明は、三次元の細分表面内に滑らかな特徴線を生成するシステムを提供する。細分
表面は、三次元のメッシュを形成するために、辺によって相互接続された制御点によって
定められる。一般に、細分表面は、まず、特定の粗さまたは細かさのメッシュによって定
められる。いくつかの方法のうちの１つを用いて、メッシュは、細分度が向上する一連の
レベルを通して緻密にされ、細分表面は、細分度が無限に達すると極限になる。以下では
、各メッシュレベルはインデックスで特定され、あるメッシュレベルがインデックス「ｊ
」によって特定されると、次のより高い細分度のメッシュはインデックス「ｊ＋１」で特
定される。細分表面は、細分度が無限大になるにつれてほぼ制御点になる、表面の「極限
点」の位置と、関連する法線ベクトルの向きによってほぼ定められる。各法線ベクトルは
、細分表面上のそれぞれの点における接面の向きを定め、それぞれの点において細分表面
に接するベクトルの交差積によって定めることができる。

滑らかな特徴線生成システムによって行われる動作を説明する前に、このシステムで用
いられる２つの表面細分法、すなわち、前記Ｌｏｏｐ表面細分法とＣａｔｍｕｌｌ‐Ｃｌ
ａｒｋ表面細分法を説明するのは有益であろう。

Ｌｏｏｐ表面細分法を、図２および図３と関連して説明する。図２は、メッシュによっ
た定められた表面の例と、それから得られた細分表面の一部を示し、図３は、この表面細
分法を理解するのに有用なステンシルを示す。一般に、Ｌｏｏｐの表面細分法では、元の
メッシュ中の各三角形の面は、次のより高い細分度のメッシュを定める複数の副面に分割
される。次のより高い細分度のメッシュの頂点は、元のメッシュ内の頂点の位置の重み平
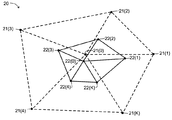
均を用いて配置される。さらに詳しくいえば、図２を参照すると、位置ｃ^j（ｑ）に配置
されている頂点ｖ_q（頂点ｖ_q＝ｖ_q（０））と、それぞれの位置ｃ^j（１）からｃ^j（Ｋ）
における位置に配置されている複数すなわち「Ｋ」個の周囲の点ｖ_q（１）からｖ_q（Ｋ）
（一般に、ｖ_q（ｋ））２１（１）から２１（Ｋ）（一般に参照番号２１（ｋ）によって
特定されている）を含む、「ｊ」細分度におけるメッシュ２０が示されている。点ｖ_q（
ｋ）２１（ｋ）は、辺によって頂点ｖ_qに接続されている、メッシュ２０内の点である。
（頂点ｖ_qに接続されている点の数「Ｋ」のことをときどき頂点の「価数」と呼ぶことが
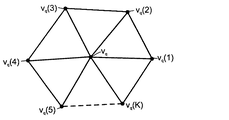
ある。）図３に示されているステンシルは、それぞれの頂点ｖ_qを囲んでいる点について
のインデックス「ｋ」の順序付けを理解するのに有用である。頂点ｖ_qに接続されている
、メッシュ内の点ｖ_q（ｋ）のインデックスのセットをＮ（ｑ，ｊ）で示すと、次のより
高い細分度「ｊ＋１」におけるメッシュは、位置ｃ^j+1（ｑ）に配置されている頂点ｖ′_q
２２（０）と、位置ｃ^j+1（ｌ）に配置され、頂点ｖ′_q２２（０）に接続されている一群
の周囲の点ｖ′_q（ｌ）２２（ｌ）に対応する。より高い細分度のメッシュは、

によって求められる位置ｃ^j+1（ｑ）における頂点ｖ′_q２２（０）と、

によって求められる位置ｃ^j+1（ｌ）における点ｖ′_q（ｌ）２２（ｌ）を生成することに
よって構成される。ここで、重み付け因子ａ（Ｋ）は、

によって与えられる。式（１）と（２）は、次のように、細分行列Ｓ_T,K（ここで、イン
デックス「Ｔ」は「三角形」を指す）を用いて、細分則を定める単一の式にまとめること
ができる。

これは成分ごとに、

として書くことができる。ここで、

であり、ここで、インデックス「ｌ」と「ｍ」は「０」から「Ｋ」までの範囲にあり、「
Ｋ」を含む。

式（１）と（２）、または、同等な式（４）から（６）は、細分度「ｊ＋１」における
メッシュに点を生成するために、細分度「ｊ」におけるメッシュ内の各点を頂点として選
択することによって適用される。Ｌｏｏｐの表面細分法は、所望の細分度のメッシュを生
成するために繰り返し適用される。式（２）は、この方法が頂点として点ｖ_q２１（０）
に適用されたときに形成される点ｖ′_q（ｌ）２２（ｌ）が、この方法が頂点として点ｖ_q
（ｋ）２１（ｋ）に適用されたときに同じ位置になることを定めることが分かるであろう
。

Ｌｏｏｐ表面細分法は、「ｊ＋１」レベルのメッシュを形成するために相互接続された
、
（ｉ）レベル「ｊ」のメッシュ内の各点対に対する、および、一般に各点対の間のどこ
かの、次のより高い（「ｊ＋１」）細分度のメッシュ内の位置ｃ^j+1（ｌ）における１つ
の新しい点（上で説明した点ｖ′_q（ｌ）を参照）と、
（ｉｉ）「ｊ」レベルのメッシュ内の各点に対する、および、一般に各点にいくらか近
くの、「ｊ＋１」レベルのメッシュ内の位置ｃ^j+1（ｑ）における再配置された点（上で
説明した頂点ｖ′_qを参照）を生成することがわかるだろう。

Ｃａｔｍｕｌｌ‐Ｃｌａｒｋ細分法は、少数の隣接頂点を用いて滑らかな表面を生成す
る。Ｃａｔｍｕｌｌ‐Ｃｌａｒｋ表面細分法を、図４Ａから図４Ｅおよび図５と関連して
説明する。図４Ａは、メッシュによって定められた表面の一例を示し、図４Ｂから図４Ｅ
は、図４Ａに示されている表面から得られる細分表面を生成するのに行われる操作を理解
するのに有用である。図５は、表面細分法を理解するのに有用なステンシルを示しており
、特に、この表面細分法が実行される頂点ｖ_q（頂点ｖ_q＝ｖ_q（０））を囲む点に対する
インデックス「ｋ」の順序付けを理解するのに有用である。図４Ａを参照すると、この図
は、４つの四辺形３１（１）から３１（４）からなるメッシュ３０を示している。各四辺
形を面と呼ぶ。四辺形は、四辺形３１（１）から３１（４）のすべてに共通である点３２
（０）と、他の点３２（１）から３２（８）によって定められている。一般に、Ｃａｔｍ
ｕｌｌ‐Ｃｌａｒｋ表面細分法は、
（ｉ）各面に対して、面点３３（１）から３３（４）が、それぞれの面を定める点３２
（ｐ）の平均として生成される面点生成ルーチン（図４Ｂを参照）と、
（ｉｉ）各辺に対して、新しい辺点３４（１）から３４（４）が、面の２つの新しい面
点が隣接している元の辺の中間点の平均として生成される辺点生成ルーチン（図４Ｃを参
照。面点生成ルーチンの間に生成された面点が白抜きの円として示されている）と、
（ｉｉｉ）頂点点３５が、元の頂点点に隣接する面に対してルーチン（ｉ）で生成され
た新しい面点の位置と、元の頂点点に入射する元の辺の中間点の位置と、元の頂点点の位
置と、元の頂点点の価数に関連して生成される頂点点ルーチン（図４Ｄを参照。面点と辺
点生成ルーチンの間に生成された面点および辺点が白抜きの円として示されている）と、
（ｉｖ）
（ａ）各新しい面点は、元の面を定める辺の辺点に接続され、
（ｂ）各新しい頂点点は、元の頂点点に入射する全ての元の辺の新しい辺点に接続され
るメッシュ接続ステップ（図４Ｅを参照）を含めた一連のルーチンで実行される。

さらに詳しくいえば、Ｃａｔｍｕｌｌ‐Ｃｌａｒｋ細分法では、場所ｃ^j（ｑ）におけ
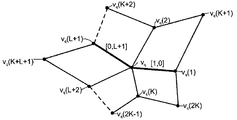
る頂点ｖ_qに対して、
（ｉ）Ｎ_e（ｑ，ｊ）によって、それに接続されている１次の隣接点ｃ^j（ｌ）（たとえ
ば、点３２（０）に対して、点３２（２）と点３２（８））のインデックスのセットと、
（ｉｉ）Ｎ_f（ｑ，ｊ）によって、頂点ｃ^j（ｑ）と関連するレベル「ｊ」の面に関して
、頂点ｃ^j（ｑ）の向かい側にある２次の隣接点（たとえば、点３２（０）に対して、点
３２（１））のインデックスのセットを示して、次のより高い細分度「ｊ＋１」における
メッシュが次のようにして形成される。面点生成ルーチンでは、面点は、次のようにして
求められた位置ｃ^j+1（ｍ_i）において生成され、配置される。

辺点生成ルーチンでは、辺点は、次のようにして求められた位置ｃ^j+1（ｌ_i）において生
成され、配置される。

頂点点生成ルーチンでは、新しい頂点点は、次のようにして求められた位置において生成
され、配置される。

点ｃ^jのみで表わすという観点から、式（９）の最後の項を置換すると、

一般に、四辺形のメッシュに対しては、このシステムは、式（９）のＫ＝３の場合を除
いて、Ｃａｔｍｕｌｌ‐Ｃｌａｒｋ細分法を用いる。この場合、このシステムは、

を用いる。ここで、γ＝３／３８である。式（１１）は、Ｋ＝３に対して、γ＝１／１２
のかわりにγ＝３／３８であることを除き、γ＝１／４ＫであるＣａｔｍｕｌｌ‐Ｃｌａ
ｒｋ細分法（式（９））に対応する。点ｃ^jのみで表わすという観点から（式（１０）と
比較されたい）、

である。これらの式は、細分行列Ｓ_Q,K（ここで、インデックス「Ｑ」は「四辺形」を示
す）を用いて細分則を定める単一の式によって、次のようにまとめることができる。

これは、

として成分で書くことができる。ここで、

であり、ここで、インデックス「ｌ」と「ｍ」は「０」から「２Ｋ」までの範囲をとり、
「２Ｋ」を含む。

上の説明から明らかなように、１つの「ｊ」番目の細分度における四辺形メッシュに適
用されるＣａｔｍｕｌｌ‐Ｃｌａｒｋ表面細分法は、「ｊ」番目の細分度におけるメッシ
ュと同数の点を有する、次に高い「ｊ＋１」番目の細分度における四辺形メッシュを生成
するが、より高い（「ｊ＋１」）細分度における点は、「ｊ」番目のレベルにおける位置
とは異なる位置にある。式（７）から（１２）、または、等価的な式（１３）から（１５
）は、細分度「ｊ＋１」におけるメッシュに対する点を生成するために、細分度「ｊ」に
おけるメッシュ内の各点を頂点として選択することにより適用される。所望の任意の細分
度のメッシュを生成するために、Ｃａｔｍｕｌｌ‐Ｃｌａｒｋ表面細分法を繰り返し適用
できる。

細分表面内の鋭い折り目は、上で説明した表面細分式（三角形メッシュの場合には式（
６）から（８）、四辺形メッシュの場合には式（１３）から（１５））を部分的に修正す
ることによって生成される。これを、折り目が生じるそれぞれの頂点ｖ_q（ｖ_q＝ｖ_q（０
））の両側における点についてのインデックス「ｋ」の順序付けを理解するのに有用なス
テンシルを示す図６と関連して説明する。折り目が生じるメッシュの辺に印をつけること
によって、細分表面上の折り目の位置を定める一連の辺を定めることができる。三角形メ
ッシュと四辺形メッシュの双方の場合のように、より高い「ｊ＋１」番目の細分度の頂点
および点の位置ｃ^j+1を、「ｊ」番目のレベルの頂点および点の位置ｃ^jから、次のように
細分行列Ｓ_C（ここで、インデックス「Ｃ」は「折り目」を示す）を有する細分則を定め
る単一の式を用いて求めることできる。

これは成分で、

として書くことができる。ここで、

であり、ここで、インデックス「ｌ」と「ｍ」は「０」から「２」までの範囲をとり、「
２」を含む。この細分則は、細分表面が三角形メッシュと四辺形メッシュの双方によって
定められる場合の折り目に対して用いることができる。

本発明は、細分表面内に滑らかな特徴線を生成するシステムと方法を提供する。鋭い折
り目におけるように、滑らかな特徴線は、特徴線を定めることになる、所与のレベルの一
連の辺を印すことによって定められる。滑らかな特徴線と関連づけられる辺が印される最
低細分度は、滑らかな特徴線に対する設定レベル「ｊ_D」と呼ばれる。さらに、鋭さパラ
メータが、滑らかな特徴線に対する設定レベルｊ_D内に印されている各辺と関連づけられ
る。一実施形態では、鋭さパラメータの値は、区間［０，１］、すなわち、端の点を含め
て「０」と「１」の間の実数の形をとる。辺が値「０」を有する鋭さパラメータを有する
ならば、その辺に沿う折り目は存在しない。他方、辺が値「１」を有する鋭さパラメータ
を有するならば、その辺は上述のように鋭い折り目の一部をなす。

一般に、滑らかな特徴線は、上述した細分則（三角形メッシュの場合には式（４）から
（６）、四辺形メッシュの場合には式（１３）から（１５）を参照）を一般化した細分則
を用いることによって得られる。細分則は、生成される滑らかな特徴線が交差する頂点の
２つの側における鋭さパラメータのそれぞれの値である２つのパラメータｓ₁とｓ₂を用い
る。細分表面の極限表面、すなわち、細分表面の極限点によって定められる表面は、滑ら
かな特徴線の近くでは滑らかである。すなわち、滑らかな特徴線と関連づけられた極限表
面上の各点に対して、すなわち、点のそれぞれの側における鋭さパラメータの値が「１」
以外である各点に対して、極限表面に垂直なベクトルの向きは絶えず変化する。しかしな
がら、鋭い折り目の場合にあたる、鋭さパラメータが値「１」を有するような点における
極限表面に対しては、点のそれぞれの側に対する法線ベクトルの向きが異なるから、法線
ベクトルは定められない。

コンピュータ・グラフィックス・システム１０が滑らかな特徴線の生成に関連して行う
動作を、三角形メッシュを定める細分表面の場合、図７から１０と関連して、四辺形メッ
シュを定める細分表面の場合、図１１から１４と関連して説明する。双方の場合、滑らか
な特徴線は、印されている辺に対応する線に近い細分表面の領域で、極限点の位置と、そ
れぞれの極限点における法線ベクトルによって定められる。上記のように、法線ベクトル
は、それぞれの極限点における２つの接線ベクトル、すなわち、それぞれの極限点におい
て滑らかな特徴線に沿う接線ベクトルと、それぞれの極限点において滑らかな特徴線と交
差する接線ベクトルの交差積に対応する。

図７を参照すると、この図は、インデックスが図に示されているようにつけられた頂点
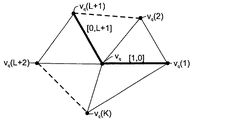
ｖ_q（頂点ｖ_q＝ｖ_q（０））と点ｖ_q（１）からｖ_q（Ｋ）を有する三角形メッシュによっ
て定められた細分表面の一部を示している。滑らかな特徴線の一部を定める折り目が、辺
ｖ_q（１）、ｖ_q（辺（１，０）として参照される）およびｖ_q、ｖ_q（Ｌ＋１）（辺（０，
Ｌ＋１）として参照される）に沿って、点ｖ_q（１）、頂点ｖ_q、点ｖ_q（Ｌ＋１）を通る
ように、頂点がラベル付けされている。辺（１，０）と関連づけられた鋭さパラメータの
値はｓ₁として参照され、辺（０，Ｌ＋１）と関連づけられた鋭さパラメータの値はｓ₂と
して参照される。辺（１，０）と（０，Ｌ＋１）は折り目を定める辺であると示されてい
るので、鋭さパラメータの値はゼロではない。頂点ｖ_qにある他の辺と関連づけられた鋭
さパラメータの値は「ゼロ」のこともあれば、ゼロでないこともある。一般に、式（４）
（または、等価的な式（５））で記述されている細分則は、細分行列を用いて、それぞれ
の頂点の位置を求めるために用いることができる。

ここで、式（６）におけるように、インデックス「１」と「ｍ］は「ゼロ」から「Ｋ」ま
での範囲にあり、かつ、「Ｋ」を含み、ｓ₃＝（ｓ₁＋ｓ₂）／２、すなわち、辺（１，０
）および（０，Ｌ＋１）と関連づけられたパラメータｓ₁とｓ₂の値の平均である。

接線ベクトルの向きが、不規則な頂点およびその近傍において、絶えず変化するように
するために、鋭さパラメータの値は、メッシュのレベルが高くなるにつれて徐々に小さく
する。滑らかな特徴線の場合、メッシュのレベルが高くなるにつれて、鋭さパラメータの
値を繰り返し更新すると、ゼロに近い値が得られる。そうすると、接線ベクトルの向きが
、極限表面内で絶えず変化することになる。一実施形態では、鋭さパラメータｓ₁とｓ₂が
、頂点の両側で同じ値「ｓ」を有する（すなわち、ｓ₁＝ｓ₂）ような頂点ｖ_qに対しては
、鋭さパラメータ更新関数は、

となる。すなわち、より高い「ｊ＋１」番目の細分度のメッシュにおける鋭さパラメータ
ｓ₁とｓ₂の値ｓ（ｊ＋１）は、より低い（「ｊ番目」）レベルのメッシュにおける鋭さパ
ラメータｓ₁とｓ₂の値ｓ（ｊ）の２乗である。他方、鋭さパラメータｓ₁とｓ₂の値が頂点
の両側で一定ではない（すなわち、ｓ₁≠ｓ₂）ような頂点ｖ_qに対しては、鋭さパラメー
タ更新関数は、双方の鋭さパラメータｓ₁とｓ₂の値の関数である。一実施形態では、関数
は、

と、

となるように選択され、二次スプラインに対応する線形組み合わせをほぼ提供する。

鋭さパラメータｓ₁とｓ₂の値はレベルごとに変わるので、滑らかな曲線の細分行列（Ｓ
_sc,T,K,L（ｓ₁，ｓ₂））_lm（式（１９））も細分度ごとに一定ではない。したがって、細
分表面に対する極限点の位置と接線ベクトルの向きを求めるために従来用いられている固
有値解析はここでは用いない。上で示唆したように、細分表面は、極限点および法線ベク
トルの集合（または、等価的に、各法線ベクトルに対しての２つの接線ベクトル）によっ
て定められ、これらは、式（４）をそのメッシュに対する設定レベル「ｊ_D」からレベル
ｊ＝∞まで繰り返し適用することによって生成される。設定レベルｊ_Dは、細分表面内で
それぞれの滑らかな特徴線が定められる最低の細分度「ｊ」である。したがって、極限点
の位置を求めるために、無限の細分行列

が計算される。ここで、Ｓ_sc,T,K、_L（ｓ₁（ｊ），ｓ₂（ｊ））は、式（２３）の右辺の
行列積における「ｊ」番目のレベルに対応する鋭さパラメータに対して、式（１９）と関
連して上で説明した細分行列である。式（２３）の左辺のＳ_sc,T,K、_L,LP（ｓ₁，ｓ₂）に
対して、独立変数ｓ₁とｓ₂は、滑らかな特徴線の設定レベルにおける鋭さパラメータ、す
なわち、ｓ₁＝ｓ₁（ｊ_D）およびｓ₂＝ｓ₂（ｊ_D）を示し、下付き文字「ＬＰ」は「極限点
」を示す。行列の乗算は交換則が成り立たないので、式（２３）における行列積中の因子
の順序は重要である。式（２３）で、積中の因子の左から右への順序は、式（４）によっ
て示唆されているように、左のｊ＝∞から右のｊ＝ｊ_Dまで広がる。

行列積（式（２３））は、「Ｋ＋１」行を有する「Ｋ＋１」×「Ｋ＋１」の行列に収束
し、各行を有する成分は、他の行の成分と同一で、同じ順序である。極限点の位置σ（ｑ
）を求めるための重み値ｌ_LPのベクトルは、次のようにして得られる。

ここで、ベクトルｖ_LPは、滑らかな特徴線が無い場合にはＬｏｏｐ細分法を用いて細分表
面の極限点の位置を求めるのに用いられる重みのベクトルである。すなわち、

である。ここで、

であり、ここで、ａ（Ｋ）は式（３）で定められる。頂点ｖ_q（０）と関連づけられた極
限点の位置σ（ｑ）は、細分表面内の滑らかな特徴線の設定レベルｊ_Dに、または、その
設定レベルより高い任意の細分度に対応するメッシュ中において、頂点ｖ_q（０）の位置
ｃ^jD（ｑ）と、頂点ｖ_q（０）の周囲の隣接点ｖ_q（ｋ）の位置ｃ^jD（ｋ）（ｋ＝１，．．
．，Ｋ）から、ｌ_LPの成分を重み値として用いることによって計算される。極限点重みベ
クトルｌ_LP（ｓ₁，ｓ₂）の成分は、成分ごとおよび価数ごとに６つの値を用いて、ｓ₁と
ｓ₂の２次多項式によって満足に近似できる。

Ｌ＝Ｋ／２ならば、対称性を考慮することにより、成分ごとの値の数を減らすことがで
きる。この場合、極限点重みベクトルｌ_LPの成分は次の対称関係を満たす。

１．極限点重みベクトルｌ_LPの「ｉ」番目の成分は、ｌ_LPの「Ｋ＋２−ｉ」番目の成分
に等しい。すなわち、ｉ＝Ｋ／２＋２，．．．，Ｋに対して、（ｌ_LP）_i＝（ｌ_LP）_K+2-i
である。これは、細分行列（式（１９））が折り目線に関して折り返しても不変であると
いうことの結果である。その結果、近似は、成分ｉ＝０，１，．．．，Ｋ／２＋１につい
て生成する必要があるだけである。

２．さらに、細分行列（式（１９））はｓ₁とｓ₂において対称的であるので、（ｌ_LP（
ｓ₁，ｓ₂））_i＝（ｌ_LP（ｓ₂，ｓ₁））_K/2+2-iであり、近似は、ｉ＝０，１，．．．，［
Ｋ／４＋１］について生成する必要があるだけである。ここで、「［ｘ／ｙ］」は商「ｘ
／ｙ；」中の最大整数を示す。

３．さらに、パラメータｓ₁とｓ₂の特定の値が相互交換されるならば、頂点ｖ_qは同じ
ように振る舞うので、（ｌ_LP（ｓ₁，ｓ₂））₀＝（ｌ_LP（ｓ₂，ｓ₁））₀であり、近似は、
ｓ₁とｓ₂中の対称的な２次多項式のみを用いて、すなわち、４つの係数を用いて行うこと
ができる。

４．さらに、「Ｋ」が「４」の倍数ならば、上の点（１）および（２）から、（ｌ_LP（
ｓ₁，ｓ₂））_K/4+1＝（ｌ_LP（ｓ₂，ｓ₁））_K/4+1である。したがって、これらの成分は、
４つの係数を用いて対称的な２次の多項式を用いて近似できる。
一実施形態では、Ｌ＝Ｋ／２であるかどうかとは無関係に、多項式の近似は、最小二乗チ
ェビシェフ近似法を用いて計算される。行列積（式（２３））はチェビシェフ多項式

の根からなる、領域（ｓ₁，ｓ₂）内の格子の点において計算される。ここで、ｉ，ｊ＝０
，．．．，Ｎ−１である。一実施形態では、「Ｎ」が「８」としてとられるので、式（２
７）には「６４」個の標本点がある。対称的な場合（ｉ＝０またはＫ／４＋１）には、多
項式

非対称な場合（その他の「ｉ」）には、多項式

に対する係数ｂ_ij（対称的な場合にはｊ＝０，．．．，３、非対称的な場合にはｊ＝０，
．．．，５）は、最小二乗法によって求められる。この演算では、コンピュータ・グラフ
ィックス・システム１０は、行列積（式（２７）で定められているように、点（ｓ₁，ｓ₂
）で計算された式（２３））を計算する。その後、Ｎ²個の多項式（式（２８）および／
または（２９））のセットが、（ｓ₁，ｓ₂）領域内のそれぞれの点（式（２７））におけ
るｓ₁とｓ₂の値を用いて生成される。各多項式は、行列積の行のそれぞれの「ｉ」番目の
成分に等しい。その後、コンピュータ・グラフィックス・システム１０は、最小二乗近似
法を用いて、多項式中の係数ｂ_ijの値を求める。係数ｂ_ijの値が求められた後、これらは
、式（２８）と（２９）を用いて、極限点重みベクトルｌ_LPの成分の値を生成するために
用いられる。

最小２乗近似における誤差は、領域（ｓ₁，ｓ₂）にわたって振動的ふるまいを有し、こ
の振動の振幅がこの領域にわたって一様に分布されているならば最小化される。これは、
良く近似されている点に対して重み付けられた最小二乗法により課される制約を緩め、良
く近似されていない点に対する制約をきつくすることにより行うことができる。重み付け
られた最小二乗法では、上で説明した最小二乗法を用いて係数ｂ_ijの値が計算された後、
多項式（式（２８）および／または式（２９））が（ｓ₁，ｓ₂）領域内の各点で計算され
、その値は、行列積（式（２３））のそれぞれの要素について生成された値と比較され、
これらの間の差を反映する重み値が決定される。その後、この重み値は、係数ｂ_ijの値の
近似を不均一に制限するのに用いることができる。

図８は、Ｃプログラミング言語の形で、ｂ［Ｋ／２−２］［ｉ］［ｊ］のインデックス
付けをした、Ｋ＝４，６，．．．，１６についての係数ｂ_ijの表を示している。ここで、
「ｉ」は、ｉ＝０，．．．，［Ｋ／４＋１］の範囲内の値をとる、極限点重みベクトルｌ
_LPの成分のインデックスであり、「ｊ」は近似多項式の係数ｂ_ijのインデックスである。

頂点ｖ_q（０）と関連づけられた極限点重みベクトルｌ_LPが上で説明したように生成さ
れた後、極限点重みベクトルｌ_LPは、頂点ｖ_q（０）と関連づけられた極限点の位置σ（
ｑ）を次のように求めるために、頂点ｖ_q（０）の位置ｃ^j（ｑ）と、頂点ｖ_q（０）の近
傍の点ｖ_q（ｋ）の位置ｃ^j（ｋ）（ｋ＝１，．．．，Ｋ）と一緒に次のように用いること
できる。

（ｌ_LP（ｓ₁，ｓ₂））_iは、ｌ_LP（ｓ₁，ｓ₂）の「ｉ」番目の成分を示す。これは、滑ら
かな特徴線に対する設定レベルｊ＝ｊ_Dと、設定レベルｊ_Dより高い細分度における鋭さパ
ラメータ値ｓ₁とｓ₂についての極限点重みベクトルｌ_LPに対応する。

一実施形態は、接線ベクトルを生成するのに用いる重み値のベクトルｌ_Cとｌ_Sについて
の良い近似を得るために、類似の多項式近似法を用いる。接線ベクトル重みベクトルｌ_C
は、接線ベクトルを滑らかな特徴線に沿って生成するのに用いられ、接線ベクトル重みベ
クトルｌ_Sは、それぞれの接線ベクトル重みベクトルが関連づけられている頂点ｖ_q（０）
と関連づけられている極限点において滑らかな特徴線を横切って接線ベクトルを生成する
のに用いられる。この方法では、ベクトルｌ_C（Ｊ）が次のようにして生成される。

ここで、右辺の行ベクトルの２つのゼロでない成分は、行ベクトル中の位置「１」におい
て「１」であり、位置Ｋ／２＋１において「負の１」であり、「・」はドット積を示す。
式（３１）に従ってベクトルｌ_C（Ｊ）を生成した後、値は正規化され、極限がＪ→∞と
してとられる。

ベクトルｌ_C（式（３２））の成分は、図７に示すように、頂点ｖ_q（０）のそれぞれの位
置と、頂点ｖ_q（０）の周囲の点ｖ_q（ｋ）（ｋ＝１，．．．，Ｋ）を乗ずるのに用いられ
る一連の重み値を形成する。これらの和が、頂点ｖ_q（０）と関連づけられた細分表面上
の点における滑らかな特徴線に沿う接線ベクトルを定める。

極限点重みベクトルｌ_LPの成分の場合のように、接線ベクトル重みベクトルｌ_Cの成分
は、ｓ₁とｓ₂における多項式、この場合には三次の多項式により近似できる。したがって
、接線ベクトル重みベクトルｌ_Cの成分の近似は、成分当りおよび価数当り１０個までの
数を用いることによって効率的に生成できる。Ｌ＝Ｋ／２ならば、対称性を考慮すること
によって、接線ベクトル重みベクトルｌ_Cの成分を生成するのに用いられる多項式係数の
数を減らすことができる。この場合、接線ベクトル重みベクトルｌ_Cの成分は次の対称関
係を満たす。

１．接線ベクトル重みベクトルｌ_Cの「ｉ」番目の成分と、「ｋ＋２−ｉ」番目の成分
が、ｉ＝Ｋ／２＋２，．．．，Ｋに対して等しい。すなわち、（ｌ_C）_i＝（ｌ_C）_K+2-iで
ある。これは、折り目線に関して折り返されたときに細分行列（式（１９））が不変であ
ることの結果である。結果として、近似は、成分ｉ＝０，１，．．．，Ｋ／２＋１につい
て生成する必要があるのみである。

２．さらに、（ｌ_C（ｓ₁，ｓ₂））_i＝−（ｌ_C（ｓ₂，ｓ₁））_K/2+2-iであるので、近似
は、成分ｉ＝０，１，．．．，［Ｋ／４＋１］について生成する必要があるのみである。

３．さらに、ｓ₁とｓ₂の特定の値が相互交換されるならば、頂点ｖ_qは、接線ベクトル
の向きが逆であることを除き、同じようにふるまうので、（ｌ_C（ｓ₁，ｓ₂））₀＝−（ｌ
_C（ｓ₂，ｓ₁））₀となる。この場合、近似は、４つの係数を用いる、ｓ₁とｓ₂における反
対称３次多項式のみを用いて生成できる。

４．さらに、「Ｋ」が「４」の倍数ならば、すぐ上の点（１）と（２）から、（ｌ_C（
ｓ₁，ｓ₂））_K/4+1＝−（ｌ_C（ｓ₂，ｓ₁））_K/4+1である。したがって、４つの係数を用
いる反対称多項式を用いて、これらの成分を近似できる。
一実施形態では、近似多項式もまた、上で説明した極限点近似と関連して用いたものに類
似する最小二乗チェビシェフ近似法を用いて計算できる。式（３１）の行列積は、チェビ
シェフ多項式（式（２７））の根からなる、（ｓ₁，ｓ₂）領域内の格子の点において計算
される。反対称（ｉ＝０またはＫ／４＋１）の場合には、多項式

非対称（「ｉ」はそれ以外）の場合には、多項式

の係数ｂ_ij（反対称の場合にはｊ＝０，．．．，３、非対称の場合にはｊ＝０，．．．，
９）は、上述したように最小二乗法を用いて求められる。

滑らかな特徴線に沿って接線ベクトルを生成するのと類似するやり方（上の式（３１）
から（３４）を参照）で、重み値のベクトルｌ_Sが、滑らかな特徴線を交差する接線ベク
トルを生成するのに用いられる。接線ベクトル重みベクトルｌ_Sの成分は、頂点ｖ_q（０）
と、頂点ｖ_q（０）の周囲の点ｖ_q（１）からｖ_q（Ｋ）の位置を乗ずるために用いられる
一連の重み値を有する（図７を参照）。これらの和は、滑らかな特徴線を横切る接線ベク
トルを有する。この方法では、ベクトルｌ_S（Ｊ）は次のようにして生成される。

ベクトルｌ_S（Ｊ）は、接線ベクトル重みベクトルｌ_Sを生成するために、式（３２）と関
連して上で説明したのと類似のやり方で正規化され、極限がＪ→∞のように取られる。

Ｌ＝Ｋ／２のとき、接線ベクトル重みベクトルｌ_Sは、

である。これは、ゼロである鋭さパラメータと関連づけられた滑らかな特徴線の場合にお
けるのと同じである。

接線ベクトル重みベクトルｌ_Sの成分は、鋭さパラメータｓ₁とｓ₂の三次多項式を用い
てｌ_S（ｓ₁，ｓ₂）として近似できる。多項式の係数を生成するのに行われる演算は、滑
らかな特徴線に沿って接線ベクトルを生成するのに用いられる接線ベクトル重みベクトル
ｌ_Cについて上で説明した多項式の係数を生成するのに行われる演算に対応する（式（３
１）から（３４））。

図９は、Ｃプログラミング言語の形で、ｂ［Ｋ／２−２］［ｉ］［ｊ］をインデックス
付けする、Ｋ＝４，６，．．．，１６に対する係数ｂ_ijの表を示している。ここで、「ｉ
」は、ｉ＝０，．．．，［Ｋ／４＋１］の範囲内の値をとる、ｌ_Cの成分のインデックス
であり、「ｊ」は、近似多項式の係数ｂ_ijのインデックスである。

上記のように、接線ベクトル重みベクトルｌ_C（＝ｌ_C（ｓ₁，ｓ₂））とｌ_S（＝ｌ_S（ｓ
₁，ｓ₂））（ここで、ｓ₁，ｓ₂は、滑らかな特徴線に対する設定レベルｊ＝ｊ_Dにおける
鋭さパラメータ値である）が、頂点ｖ_q（０）の位置ｃ^j（ｑ）および隣接点ｖ_q（ｋ）の
位置ｃ^j（ｋ）（ｋ＝１，．．．，Ｋ）と一緒に用いられる。特に、それぞれの接線ベク
トル重みベクトルの成分が、頂点と隣接点の位置に重みをつけるために用いられ、その和
は接線ベクトルを含む。すなわち、滑らかな特徴線に沿う接線ベクトルｅ_C（ｑ）と、滑
らかな特徴線を交差する接線ベクトルｅ_S（ｑ）は、

として生成される。ここで、ｌ_C（ｓ₁，ｓ₂）＝ｌ_Cおよびｌ_S（ｓ₁，ｓ₂）＝ｌ_S（ここで
、ｓ₁とｓ₂は、滑らかな特徴線についての設定レベルｊ＝ｊ_Dにおける鋭さパラメータ値
である）であり、インデックス０，．．．，Ｋが図７に示されている。

ある場合には、極限点重みベクトルｌ_LPと接線ベクトル重みベクトルｌ_C、ｌ_Sについて
の近似を生成するために多項式を用いることは実際的でない。たとえば、滑らかな特徴線
の構成の数がある数を超えるならば、おのおのは異なる多項式の集合を要するので、多項
式の数は、この方法を用いるのが実際的でない程度まで増加する。極限点重みベクトルｌ
_LPと接線ベクトル重みベクトルｌ_C、ｌ_Sについての近似を生成するかわりの方法は外挿を
用いる。

極限点重みベクトルｌ_LP（ｓ₁，ｓ₂）の近似を生成する外挿法は、インデックス「ｊ」
の有限値に対する式（２３）の初めのいくつかの係数で始まる。以下では、滑らかな特徴
線に対する設定レベルｊ_Dがレベル「ゼロ」であると仮定するが、これは説明の一般性を
制限するものではないことがわかるであろう。因子ｊ＝Ｊ，Ｊ−１，．．．，０ととるこ
とによって生成された行列積は、

と、

によって与えられる。ここで、極限Ｊ＝０の場合（この場合には、行列積を生成するのに
因子はない）には、行列積Ｓ_sc,T,K,L,LP（０）（ｓ₁，ｓ₂）は大きさが「Ｋ＋１」×「
Ｋ＋１」の単位行列である。極限点の位置σ（ｑ）を求めるための重み値ｌ_LPのベクトル
が次のようにして得られる。

ここで、ν_LPは、式（２８）および（２９）と関連して、上で定められている。

によって行われる。ここで、ｌ_LP（Ｊ）は式（４０）で定められ、係数ｂ_jは、

によって与えられる。この外挿法は、頂点が一定であろうが不定であろうが、任意の頂点
について用いることができる。さらに、この方法は、それぞれの頂点を通る任意の形状の
折り目と、それぞれの頂点についての価数「Ｋ」の任意の値について用いることができる
。

ある外挿法も、接線ベクトル重みベクトルｌ_Cとｌ_Sを生成するために用いることができ
る。一般に、この方法では、上述した行列積Ｓ_sc,T,K,L,LP（Ｊ）（ｓ₁，ｓ₂）（式（３
８）と（３９））は、その後、
（１）接線ベクトル重みベクトルｌ_Cが生成されるならば、ベクトルｖ_Cによって乗ぜら
れ、接線ベクトル重みベクトルｌ_Sが生成されるならば、ベクトルｖ_Sによって乗ぜられ、
（２）（１）からの結果が、その後、それぞれの接線ベクトル重みベクトルを正規化さ
れた形で維持する拡張係数によって乗ぜられる。
接線ベクトル重みベクトルｌ_Cとｌ_Sの近似は、

から生成される。ここで、ｄ（Ｋ）は拡張係数を表す。ベクトルｖ_Cとｖ_Sは、

によって与えられ、拡張係数ｄ（Ｋ）は、滑らかな場合についての細分行列の固有値の１
つの逆数、すなわち、

である。接線ベクトル重みベクトルｌ_Cとｌ_Sの近似は、

によって与えられる。ここで、係数ｂ_Jは、式（４２）に与えられている形をとる。この
外挿法は、あらゆる構成と関連して用いることができる。重みベクトルｌ_Cを用いて生成
された接線ベクトルは、ほぼ、頂点ｖ_q（０）と点ｖ_q（１）の間の辺［１，０］の方向に
向けられ、重みベクトルｌ_Sを用いて生成された接線ベクトルは、ほぼ、辺［１，０］に
垂直に向けられる。細分表面内の所与のレベル「ｊ」に対する辺［１，０］と［０，Ｌ＋
１］の間の角度は通常１８０度ではないが、レベル「ｊ」が無限に近づくと、その角度は
１８０度に近づく。したがって、極限において、すなわち、「ｊ」が無限に近づくと、頂
点ｖ_q（０）と関連づけられた極限点の一方の側の辺に沿う接線ベクトルは、同じ頂点と
関連づけられた極限点の他方の側における辺に沿う接線ベクトルとは反対方向に近づく。
同様に、頂点ｖ_q（０）と関連づけられた極限点の一方の側の辺と交差する接線ベクトル
は、同じ頂点と関連づけられた極限点の他方の側における辺と交差する接線ベクトルとは
反対方向に近づく。

この背景で、三角形メッシュについての細分表面に対する極限点と接線ベクトルを生成
するのに有用な重みベクトルｌ_LP、ｌ_C、ｌ_Sの生成における、コンピュータ・グラフィッ
クス・システム１０によって行われる動作を、図１０に示されているフローチャートと関
連して説明する。この図を参照すると、コンピュータ・グラフィックス・システム１０は
、式（１９）に関連して上で説明したように、細分行列Ｓ_sc,T,K,L（ｓ₁（ｊ），ｓ₂（ｊ
））（ｊ＝０，１，２）をまず初期化する（ステップ１００）。その後、コンピュータ・
グラフィックス・システム１０は、Ｊ＝２，３に対して、行列積Ｓ_sc,T,K,L,LP（Ｊ）（
ｓ₁，ｓ₂）を生成する（ステップ１０１）。Ｊ＝１に対して、Ｓ_sc,T,K,L,LP（１）（ｓ₁
，ｓ₂）＝Ｓ_sc,T,K,L（ｓ₁，ｓ₂）であり、上で示唆したように、Ｊ＝０に対して、Ｓ_sc,
T,K,L,LP（０）（ｓ₁，ｓ₂）は「Ｋ＋１」×「Ｋ＋１」の単位行列である。

コンピュータ・グラフィックス・システム１０が、行列積Ｓ_sc,T,K,L,LPを生成した後
、それは、各行列積Ｓ_sc,T,K,L,LP（Ｊ）（ｓ₁，ｓ₂）（Ｊ＝０，１，２，３）の最初の
行をとり、式（４１）の外挿式にしたがって、極限点重みベクトルｌ_LPについての成分ご
との近似を生成する（ステップ１０２）。さらに、コンピュータ・グラフィックス・シス
テム１０は、式（４３）と関連して上で説明したように、ベクトルｌ_C（Ｊ）とｌ_S（Ｊ）
（Ｊ＝０，１，２，３）を生成するために、行列積Ｓ_sc,T,K,L,LP（Ｊ）（ｓ₁，ｓ₂）、
拡張係数ｄ（Ｋ）、ベクトルｖ_Cとｖ_Sを用いる（ステップ１０３）。Ｊ＝０に対して、そ
れぞれの重みベクトルは、ｌ_C（０）＝ｖ_Cおよびｌ_S（０）＝ｖ_Sである。ステップ１０３
に続いて、コンピュータ・グラフィックス・システム１０は、式（４６）にしたがって、
接線ベクトル重みベクトルｌ_Cとｌ_Sについての近似を生成するために、ｌ_C（Ｊ）とｌ_S（
Ｊ）を用いる（ステップ１０４）。極限点重みベクトルｌ_LPと接線ベクトル重みベクトル
ｌ_Cとｌ_Sが生成された後、極限点および接線ベクトルを上述のようにして生成でき（それ
ぞれ、式（３０）と（３７）を参照）、法線ベクトルが、接線ベクトルの間の交差積とし
て生成される（ステップ１０５）。

四辺形メッシュによって定められる細分表面の場合に滑らかな特徴線を生成することと
関連して、コンピュータ・グラフィックス・システム１０によって行われる動作を、図１
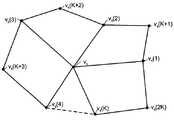
１から１３および図１０のフローチャートと関連して説明する。図１１を参照すると、こ
の図は、インデックスがこの図に示されているように付けられている頂点ｖ_q（頂点ｖ_q＝
ｖ_q（０））および点ｖ_q（１）からｖ_q（２Ｋ）を有する三角形メッシュによって定めら
れた細分表面の一部を示している。点ｖ_q（１）からｖ_q（Ｋ）は、頂点ｖ_qの１次の隣接
点であり、点ｖ_q（Ｋ＋１）からｖ_q（２Ｋ）は、頂点ｖ_qの２次の隣接点であることがわ
かるであろう。頂点は、折り目が辺ｖ_q（１）、ｖ_q（これらは辺（１，０）として参照さ
れる）とｖ_q、ｖ_q（Ｌ＋１）（これらは辺（０，Ｌ＋１）として参照される）に沿って、
点ｖ_q（１）、頂点ｖ_q（０）、点ｖ_q（Ｌ＋１）を通るように、ラベル付けされる。辺（
１，０）と関連づけられた鋭さパラメータの値はｓ₁として参照され、辺（０，Ｌ＋１）
と関連づけられた鋭さパラメータの値はｓ₂として参照される。一般に、式（１３）と（
１４）に記述されている細分則は、式（１５）と関連して上で説明した細分行列のかわり
に、細分行列

を用いて、それぞれの頂点の位置を求めるために用いることができる。ここで、式（１９
）のように、ｓ₃＝（ｓ₁＋ｓ₂）／２であり、辺（１，０）と（０，Ｌ＋１）と関連づけ
られたパラメータｓ₁とｓ₂の値の平均である。

三角形メッシュによって形成された細分表面の場合のように、それぞれの接線ベクトル
の向きを種々の細分度における不規則な頂点およびその近傍において絶えず変化させるた
めに、鋭さパラメータの値はメッシュの細分度が高くなるにつれて徐々に減らす。一実施
形態では、コンピュータ・グラフィックス・システムは、四辺形メッシュによって定めら
れている細分表面の場合に、三角形メッシュによって定められている細分表面の場合にお
けるのと同じように、鋭さパラメータの値を変化させる（上の式（２０）から（２２）を
参照）。

三角形メッシュによって定められる細分表面の場合のように、四辺形メッシュによって
定められる細分表面の場合に頂点ｖ_q（０）と関連づけられた極限点の位置を求めるため
に、無限細分行列積

が計算される。ここで、Ｓ_sc,Q,K,L（ｓ₁（ｊ），ｓ₂（ｊ））は、ｊ番目のレベルと関連
づけられた鋭さパラメータ値ｓ₁とｓ₂についての式（４７）からの細分行列であり、イン
デックスｊ_Dは滑らかな折り目の設定レベルを示す。式（４８）の左辺において、独立変
数ｓ₁とｓ₂に対して、ｓ₁＝ｓ₁（ｊ_D）およびｓ₂＝ｓ₂（ｊ_D）である。三角形メッシュに
よって定められる細分表面の場合のように、式（４８）における行列積は、同一の行を有
する行列に収束し、この場合に、各行はサイズが２Ｋ＋１である。頂点ｖ_q（０）と関連
づけられた極限点の位置σ（ｑ）を求めるための重み値_LPのベクトルが次のように得られ
る。

ここで、ベクトルｖ_LPは、滑らかな特徴線が無い場合に、四辺形メッシュによって定めら
れる細分表面の極限点の位置を求めるのに用いられる重みベクトルである。すなわち、

ここで、式（５０）において、値「４」を有する「Ｋ」個の成分と、値「１」を有する「
Ｋ」個の成分がある。

行ベクトルｌ_LP（ｓ₁，ｓ₂）の成分ｌ_LP（ｓ₁，ｓ₂）_i（ｉ＝０，．．．，２Ｋ）と、
頂点ｖ_q（０）の位置ｃ^j（０）と、隣接点ｖ_q（ｉ）のｃ^j（ｉ）（ｉ＝１，．．．，２Ｋ
）が、頂点ｖ_q（０）に関連する極限点の位置σ（ｑ）を決定するために次のように用い
られる。

三角形メッシュによって定められている細分表面の場合のように、極限点重みベクトル
ｌ_LP（ｓ₁，ｓ₂）の成分を、多項式展開を用いて近似できる。極限点重みベクトルｌ_LP（
ｓ₁，ｓ₂）の成分を、成分ごとおよび価数ごとに６つの値を用いて、ｓ₁とｓ₂の二次多項
式によって満足に近似できる。「Ｋ」の値が偶数であり、Ｌ＝Ｋ／２ならば、対称性を考
慮することにより、成分ごとの値の数を減らすことができる。この場合、極限点重みベク
トルｌ_LPの成分は次の対称関係を満たす。

１．極限点重みベクトルｌ_LP（ｓ₁，ｓ₂）の「ｉ番目」の成分は、極限点重みベクトル
ｌ_LP（ｓ₁，ｓ₂）の「Ｋ＋２−ｉ」番目の成分に等しい。すなわち、ｉ＝２，．．．，Ｋ
／２に対して、（ｌ_LP（ｓ₁，ｓ₂））_i＝（ｌ_LP（ｓ₁，ｓ₂））_K+2-1であり、極限点重み
ベクトルｌ_LP（ｓ₁，ｓ₂）の「ｉ」番目の成分は、極限点重みベクトルｌ_LP（ｓ₁，ｓ₂）
の「３Ｋ＋１−ｉ」番目の成分に等しい。すなわち、ｉ＝Ｋ＋１，．．．，Ｋ＋Ｋ／２に
対して、（ｌ_LP（ｓ₁，ｓ₂））_i＝（ｌ_LP（ｓ₁，ｓ₂））_3K+1-iである。

２．ｉ＝１，．．．，Ｋ／２＋１に対して、（ｌ_LP（ｓ₁，ｓ₂））_i＝（ｌ_LP（ｓ₁，ｓ
₂））_K/2+2-iであり、ｉ＝Ｋ＋１，．．．，Ｋ＋Ｋ／２＋１に対して、（ｌ_LP（ｓ₁，ｓ₂
））_i＝（ｌ_LP（ｓ₁，ｓ₂））_2K+K/2+1-iである。

３．（ｌ_LP（ｓ₁，ｓ₂））₀＝（ｌ_LP（ｓ₂，ｓ₁））₀である。

４．「Ｋ」が「４」の倍数ならば、（ｌ_LP（ｓ₁，ｓ₂））_K/4+1＝（ｌ_LP（ｓ₂，ｓ₁）
）_K/4+1であり、「Ｋ」が「４」の倍数でないならば、（ｌ_LP（ｓ₁，ｓ₂））_K+[K/4]+1＝
（ｌ_LP（ｓ₂，ｓ₁））_K+[K/4]+1である。
すぐ上で説明した対称関係が与えられると、ｉ＝０，．．．，［Ｋ／４］＋１およびｉ＝
Ｋ＋１，．．．，Ｋ＋［Ｋ／４］＋１についての極限点重みベクトルｌ_LPに対する近似を
生成することだけが必要であり、さらに、「Ｋ」の任意の偶数値に対してはｉ＝０につい
て、「Ｋ」が「４」の倍数ならばｉ＝Ｋ／４＋１について、「Ｋ」が偶数であるが、「４
」の倍数でなければｉ＝Ｋ＋［Ｋ／４］＋１について、対称的な多項式を用いることがで
きる。

三角形メッシュによって定められる細分表面の場合のように、一実施形態では、四辺形
メッシュによって定められる細分表面の場合、Ｌ＝Ｋ／２かどうかとは無関係に、近似多
項式が最小二乗チェビシェフ近似法を用いて計算される（上の式（２７）を参照）。この
場合、対称的な場合には、多項式

非対称的な場合には、多項式

の係数ｂ_ij（対称的な場合にはｊ＝０，．．．，３、非対称的な場合にはｊ＝０，．．．
，５）が最小二乗法によって求められる。図１２は、Ｋ＝４、Ｌ＝２に対して、「ｉ」の
値がｉ＝０；１；２；５の場合の係数ｂ_ijの表を示している。係数ｂ_ijが生成された後（
式（５２）と（５３））、これらは、式（５１）と関連して上で説明したように、極限点
σ（ｑ）の位置を生成するために用いられる極限点重みベクトルｌ_LPを、三角形メッシュ
によって定められる細分表面の場合とおなじように生成するために用いられる。

四辺形メッシュによって定められている細分表面の場合の接線ベクトルは、三角形メッ
シュによって定められる細分表面の場合に接線ベクトルを生成するために用いられるのと
同様な方法で生成される。一般に、この方法では、上述した行列積Ｓ_sc,Q,K,L,LP（Ｊ）
（ｓ₁，ｓ₂）（式（４８））が生成され、その後、三角形メッシュの場合における接線ベ
クトル重みベクトルの場合のように、
（１）接線ベクトル重みベクトルｌ_Cが生成されているならば、ベクトルｖ_Cによって乗
ぜられ、接線ベクトル重みベクトルｌ_Sが生成されているならば、ベクトルｖ_Sによって乗
ぜられ、
（２）（１）からの結果が、その後、それぞれの接線ベクトルを正規化された形に維持
する拡張係数によって乗ぜられる。
まず、ベクトルｌ_C（Ｊ）（ｓ₁，ｓ₂）とｌ_S（Ｊ）（ｓ₁，ｓ₂）が、

として生成される。四辺形メッシュによって定められる細分表面の場合には、それぞれの
ベクトルｖ_Cとｖ_Sは、

によって与えられ、拡張係数は、滑らかな内部頂点についての細分行列（式４７）の部分
支配的な固有値の逆数として与えられる。

ここで、Ａ_Kは、

によって定められる。

接線ベクトル重みベクトルｌ_Cとｌ_Sは、接線ベクトルを次のように生成するために用い
られる。

ここで、インデックス付けは、図１１に示されている。

三角形メッシュによって定められる細分表面の場合のように、四辺形メッシュによって
定められる細分表面の場合には、接線ベクトル重みベクトルｌ_Cを用いて生成され、頂点
ｖ_q（０）について生成された接線ベクトルｅ_C（ｑ）は、頂点ｖ_q（０）と関連づけられ
た極限点を通る滑らかな特徴線にほぼ沿うように向けられ、接線ベクトル重みベクトルｌ
_Sを用いて生成された接線ベクトルｅ_S（ｑ）は、頂点ｖ_q（０）と関連づけられた極限点
を通る滑らかな特徴線にほぼ垂直に向けられる。

また、三角形メッシュによって定められる細分表面の場合のように、四辺形メッシュに
よって定められる細分表面の場合の接線ベクトル重みベクトルは、多項式近似を用いて近
似できる。接線ベクトル重みベクトルｌ_C（ｓ₁，ｓ₂）とｌ_S（ｓ₁，ｓ₂）の成分は、一般
に、成分ごとおよび価数ごとに１０個の値を用いて、ｓ₁とｓ₂における三次多項式により
満足に近似できる。「Ｋ」の値が偶数であり、Ｌ＝Ｋ／２ならば、対称性を考慮すること
によって、成分ごとの値の数を減らすことができる。この場合、接線ベクトル重みベクト
ルｌ_Cの成分は次の対称関係を満たす。

１．接線ベクトル重みベクトルｌ_C（ｓ₁，ｓ₂）の「ｉ」番目の成分が、接線ベクトル
重みベクトルｌ_C（ｓ₁，ｓ₂）の「Ｋ＋２−ｉ」番目の成分に等しい。すなわち、ｉ＝２
，．．．，Ｋ／２に対して、（ｌ_C（ｓ₁，ｓ₂））_i＝（ｌｃ（ｓ₁，ｓ₂））_K+2-iであり
、接線ベクトル重みベクトルｌ_C（ｓ₁，ｓ₂）の「ｉ」番目の成分が、接線ベクトル重み
ベクトルｌ_C（ｓ₁，ｓ₂）の「３Ｋ＋１−ｉ」番目の成分に等しい。すなわち、ｉ＝Ｋ＋
１，．．．，Ｋ＋Ｋ／２に対して、（ｌ_C（ｓ₁，ｓ₂））_i＝（ｌ_C（ｓ₁，ｓ₂））_3K+1-i
である。

２．ｉ＝１，．．．，Ｋ／２＋１に対して、（ｌ_C（ｓ₁，ｓ₂））_i＝−（ｌ_C（ｓ₁，ｓ
₂））_K/2+2-iであり、ｉ＝Ｋ＋１，．．．，Ｋ＋Ｋ／２＋１に対して、（ｌ_C（ｓ₁，ｓ₂
））_i＝−（ｌ_C（ｓ₁，ｓ₂））_2K+K/2+1-iである。

３．（ｌ_C（ｓ₁，ｓ₂））₀＝−（ｌ_C（ｓ₂，ｓ₁））₀である。

４．「Ｋ」が「４」の倍数ならば、（ｌ_C（ｓ₁，ｓ₂））_K/4+1＝−（ｌ_C（ｓ₂，ｓ₁）
）_K/4+1であり、「Ｋ」が「４」の倍数でないならば、（ｌ_C（ｓ₁，ｓ₂））_K+[K/4]+1＝
−（ｌ_C（ｓ₂，ｓ₁））_K+[K/4]+1である。
すぐ上で説明した対称関係が与えられると、ｉ＝０，．．．，［Ｋ／４］＋１およびｉ＝
Ｋ＋１，．．．，Ｋ＋［Ｋ／４］＋１に対して近似を生成することだけが必要であり、さ
らに、「Ｋ」の任意の偶数値に対しｉ＝０について、「Ｋ」が「４」の倍数ならばｉ＝Ｋ
／４＋１について、「Ｋ」が偶数であるが、「４」の倍数でなければｉ＝Ｋ＋［Ｋ／４］
＋１について、反対称的な多項式も用いることができる。

三角形メッシュによって定められる細分表面の場合のように、一実施形態では、近似多
項式もまた、上述した極限点近似と関連して用いられたのと同じ最小二乗チェビシェフ近
似法を用いて計算される。式（４８）行列積は、チェビシェフ多項式（式（２７））の根
からなる、（ｓ₁，ｓ₂）領域内の格子の点において計算される。この場合、反対称的な場
合には、多項式

非対称的な場合には、多項式

の係数ｂ_ij（反対称的な場合にはｊ＝０，．．．，３、非対称的な場合にはｊ＝０，．．
．，９）は、最小二乗法を用いて求められる。最小二乗法と関連して行われる演算は、三
角形メッシュによって定められる細分表面の場合に上で説明したものに対応する。接線ベ
クトル重みベクトルｌ_Sの成分は、鋭さパラメータｓ₁とｓ₂における三次多項式を用いて
、ｌ_S（ｓ₁，ｓ₂）として近似できる。多項式の係数を生成するのに行われる演算は、滑
らかな特徴線に沿って接線ベクトルを生成するのに用いられる接線ベクトル重みベクトル
ｌ_Cについて上で説明した、多項式の係数を生成するのに行われる演算に対応する。図１
３は、ｉ＝０；１；２；５に対応する、Ｋ＝４およびＬ＝２に対する係数ｂ_ijの表を示し
ている。

接線ベクトル重みベクトルｌ_Cとｌ_Sが生成された後、これらは、式（５８）と関連して
上で説明したように、接線ベクトルｅ_Cとｅ_Sを生成するために用いられる。

三角形メッシュによって定められる細分表面の場合のように、ある場合には、極限点重
みベクトルｌ_LPおよび接線ベクトル重みベクトルｌ_Cとｌ_Sについての近似を生成するため
に、多項式を用いることは実際的ではない。極限点重みベクトルｌ_LPおよび接線ベクトル
重みベクトルｌ_Cとｌ_Sについての近似を生成するかわりの方法は、多項式外挿を用いる。
この外挿法は，式３８から４６と関連して上で説明した方法と似ている。

多項式外挿法を用いて、四辺形メッシュによって定められる細分表面についての極限点
重みベクトルｌ_LPおよび接線ベクトル重みベクトルｌ_Cとｌ_Sを生成することと関連して、
コンピュータ・グラフィックス・システム１０によって行われる動作は、三角形メッシュ
によって定められる細分表面について、図１０と関連して上で説明したものと似ており、
その説明は、図１０を参照すべきである。

このシステムは、多くの利点を有する。特に、本発明は、パラメータの値が、少なくと
もいくつかのレベルで変化する、同じくパラメータ化された細分則を各レベルで適用する
ことによって、選択されたレベルにおける制御メッシュによって定められる表現から細分
表面を生成するシステムを提供する。本発明は、滑らかな特徴線を定めるパラメータの値
が少なくともいくつかのレベルで変化する、同じくパラメータ化された細分則を各レベル
で用いて、細分表面内に滑らかな特徴線を生成することを特に提供する。結果として得ら
れる細分表面は、比較的質が高く、効率的に計算できる。

多くの変更と修正を、本明細書で説明したようなシステムに施してもよいことが理解で
きるだろう。たとえば、このシステムを三角形面と四辺形面のメッシュと関連して説明し
てきたが、このシステムは、種々の多角形構造の面を有するメッシュと関連して有用性を
見出してもよいことが理解できるだろう。

さらに、特定の細分則（式（１９）と（４６））について説明してきたが、他の細分則
も有用性を見出すことができることが理解できるであろう。

さらに、鋭さパラメータｓ₁とｓ₂を更新する方法を説明し、重みベクトルｌ_LP、ｌ_C、
ｌ_Sを近似する種々の方法を説明してきたが、他のパラメータ更新方法および近似方法に
も有用性を見出だすことができることが理解できるであろう。

さらに、本明細書で説明した外挿法と関連して、係数ｂ_Jの数と、式（４１）と（４６
）における総和についての上限（「３」）は、「３」次以外の多項式が外挿で用いられる
ならば、異なることがありうることが理解できるであろう。

本発明によるシステムは、専用ハードウェア、汎用コンピュータ・システム、または、
これらの組み合わせから全体または一部が構成され、その任意の部分を適切なプログラム
によって制御してもよいことが理解できるであろう。任意のプログラムは、全体または一
部において、従来の方法で、システムの一部を含み、または、システム上に保持され、ま
たは、全体としてまたは部分的に、従来の方法で情報を転送するネットワークまたはその
他の機構を介してシステムへ提供してもよい。さらに、このシステムは、情報を従来の方
法で転送するネットワークまたはその他の機構を介して、システムに直結でき、あるいは
、システムへ情報を転送できるオペレータ入力要素（不図示）を用いて、オペレータによ
って入力された情報によって動作および／またはさもなければ制御するようにしてもよい
ことが理解できるであろう。

以上の説明は、本発明の特定の実施形態に限定されている。しかしながら、本発明の利
点のいくつかまたは全てを維持しながら、本発明に種々の変更と修正を行うことができる
ことは明らかである。これらおよび他の変更および修正を、本発明の要旨および範囲内に
含めることが、添付した特許請求の範囲の目的である。

本発明にしたがって構成された、細分表面内に滑らかな特徴線を生成するシステムを含むコンピュータ・グラフィックス・システムを示す。 Ｌｏｏｐ表面細分法が適用されている表面を表現するメッシュを示す。 Ｌｏｏｐ表面細分法を理解するのに有用なステンシルを示す。 Ｃａｔｍｕｌｌ‐Ｃｌａｒｋ表面細分法が適用されている表面を表現するメッシュを示す。 Ｃａｔｍｕｌｌ‐Ｃｌａｒｋ表面細分法を理解するのに有用なステンシルを示す。 細分表面上に鋭い折り目を生成する方法を理解するのに有用なステンシルを示す。 三角形のメッシュによって定められた細分表面と関連して用いられる、滑らかな特徴線を生成する方法を理解するのに有用なステンシルを示す。 図７と関連して説明した、三角形のメッシュによって定められた表面と関連して用いられる方法で用いられる係数の表を示す。 図７と関連して説明した、三角形のメッシュによって定められた表面と関連して用いられる方法で用いられる係数の表を示す。 図７と関連して説明した、三角形のメッシュによって定められた表面と関連して用いられる方法と関連して、コンピュータ・グラフィックス・システムによって行われる動作を説明するフローチャートを示す。 四辺形のメッシュによって定められた細分表面と関連して用いられる、滑らかな特徴線を生成する方法を理解するのに有用なステンシルを示す。 図１１と関連して説明した、四辺形のメッシュによって定められた表面と関連して用いられる方法で用いられる係数の表を示す。 図１１と関連して説明した、四辺形のメッシュによって定められた表面と関連して用いられる方法で用いられる係数の表を示す。

Claims (18)

1. 選択されたレベルで、それぞれの辺によって複数の隣接点に連結された少なくとも１つの点を含む複数の点を有するメッシュによる表現での特徴線によって定められた表面内に、前記メッシュによる表現の頂点と、少なくとも１つの隣接点と、該頂点と該少なくとも１つの隣接点を相互接続する辺に関連して定められた特徴の表現を生成するシステムであって、
   Ａ． 複数のレベルで定められ、少なくとも１つのパラメータの値が前記メッシュの少なくとも２つのレベルで異なる値をとる、パラメータ化された細分則にもとづいて、第１の重みベクトルと第２の重みベクトルを生成するために前記パラメータ化された細分則が前記頂点の両側での鋭さパラメータのそれぞれの値であるパラメータを使用するようにして、重み値の第１の並びからなる前記第１の重みベクトルと重み値の第２の並びからなる前記第２の重みベクトルとを生成するように構成された重みベクトル生成モジュールと、
   Ｂ． 前記重みベクトルの少なくとも１つと、前記頂点と前記隣接点の位置を用い、
   前記第１の並びを用いて前記頂点と前記頂点の周りの前記隣接点とのそれぞれの位置に乗算し、複数の第１の乗算結果を得ることと、
   前記第１の乗算結果の和を求めて、前記頂点に関連する前記表面の上の点での特徴を規定する滑らかな特徴線に沿った第１の接線ベクトルを求めることと、
   前記第２の並びを用いて前記頂点と前記頂点の周りの前記隣接点とのそれぞれの位置に乗算し、複数の第２の乗算結果を得ることと、
   前記第２の乗算結果の和を求めて、前記頂点に関連する前記表面の上の点での特徴を規定する滑らかな特徴線を横切る第２の接線ベクトルを求めることと、
   前記滑らかな特徴線に沿った前記第１の接線ベクトルと前記滑らかな特徴線を横切る前記第２の接線ベクトルとの交差積をとることにより、前記表面に接する面に垂直な法線ベクトルを生成することと、
   によって、前記特徴の表現を生成するように構成された特徴表現生成モジュールと、
   を有し、
   前記重みベクトル生成モジュールは、選択された数学関数によって関連づけられた少なくとも２つのレベルにおいて異なる値をとる、前記少なくとも１つのパラメータの値を用いるように構成され、
   前記滑らかな特徴線は、それを横切って前記法線ベクトルが連続的に変化する特徴線である、
   システム。
2. 前記滑らかな特徴線は、頂点と、２つの隣接点と、該頂点とそれぞれの該隣接点を相互
   接続する辺に関連して定められ、前記重みベクトル生成モジュールは、前記滑らかな特徴
   線がそれに沿うように定められる各前記辺と関連づけられたパラメータ値を有するパラメ
   ータ化された細分則を用いるように構成されている、請求項１に記載のシステム。
3. 前記重みベクトル生成モジュールは、値が同じである、前記滑らかな特徴線がそれに沿
   うように定められる前記辺と関連づけられたパラメータを用いるように構成されている、
   請求項２に記載のシステム。
4. 前記重みベクトル生成モジュールは、前記滑らかな特徴線がそれに沿うように定められ
   る前記辺に沿う鋭い折り目を反映する細分則に関連する前記パラメータを用いるように構
   成され、前記パラメータの値は、区間［０，１］において定められ、ここで、より大きい
   値がより鋭い折り目を定め、より低いレベルにおける前記パラメータの値は、
   

   

   によって関連づけられた、より高いレベルにおける前記パラメータの値に関連づけられ、
   ここで、ｓ(ｊ)はレベル「ｊ」における前記パラメータの値を表し、ｓ(ｊ＋１)は前記よ
   り高いレベル「ｊ＋１」における前記パラメータの値を表す、請求項３に記載のシステム
   。
5. 前記重みベクトル生成モジュールは、値が異なる、前記滑らかな特徴線がそれに沿うよ
   うに定められる前記辺と関連づけられたパラメータを用いるように構成されている、請求
   項２に記載のシステム。
6. 前記重みベクトル生成モジュールは、前記滑らかな特徴線がそれに沿うように定められ
   る前記辺に沿う鋭い折り目を反映する細分則に関連する前記パラメータを用いるように構
   成され、前記パラメータの値は、区間［０，１］において定められ、ここで、より大きい
   値がより鋭い折り目を定め、より低いレベルにおける前記パラメータの値は、
   

   

   と、
   

   

   によって関連づけられた、より高いレベルにおける前記パラメータの値に関連づけられ、
   ここで、ｓ₁(ｊ)とｓ₂(ｊ)は、レベル「ｊ」におけるそれぞれの辺と関連づけられた前記
   パラメータの値を表し、ｓ₁(ｊ＋１)とｓ₂(ｊ＋１)は、前記より高いレベル「ｊ＋１」に
   おけるそれぞれの辺と関連づけられた前記パラメータの値を表す、請求項５に記載のシス
   テム。
7. 選択されたレベルで、それぞれの辺によって複数の隣接点に連結された少なくとも１つの点を含む複数の点を有するメッシュによる表現での特徴線によって定められた表面内に、前記メッシュによる表現の頂点と、少なくとも１つの隣接点と、該頂点と該少なくとも１つの隣接点を相互接続する辺と関連して定められた特徴の表現を生成するシステムを提供するコンピュータと関連づけて用いられるコンピュータプログラムであって、
   Ａ． 前記コンピュータを、複数のレベルで定められ、少なくとも１つのパラメータの値が前記メッシュの少なくとも２つのレベルで異なる値をとる、パラメータ化された細分則にもとづいて、前第１の重みベクトルと第２の重みベクトルを生成するために前記パラメータ化された細分則が前記頂点の両側での鋭さパラメータのそれぞれの値であるパラメータを使用するようにして、重み値の第１の並びからなる前記第１の重みベクトルと重み値の第２の並びからなる前記第２の重みベクトルとを生成するように構成された重みベクトル生成モジュールと、
   Ｂ． 前記コンピュータを、前記重みベクトルの少なくとも１つと、前記頂点と前記隣接点の位置を用い、
   前記第１の並びを用いて前記頂点と前記頂点の周りの前記隣接点とのそれぞれの位置に乗算し、複数の第１の乗算結果を得ることと、
   前記第１の乗算結果の和を求めて、前記頂点に関連する前記表面の上の点での特徴を規定する滑らかな特徴線に沿った第１の接線ベクトルを求めることと、
   前記第２の並びを用いて前記頂点と前記頂点の周りの前記隣接点とのそれぞれの位置に乗算し、複数の第２の乗算結果を得ることと、
   前記第２の乗算結果の和を求めて、前記頂点に関連する前記表面の上の点での特徴を規定する滑らかな特徴線を横切る第２の接線ベクトルを求めることと、
   前記滑らかな特徴線に沿った前記第１の接線ベクトルと前記滑らかな特徴線を横切る前記第２の接線ベクトルとの交差積をとることにより、前記表面に接する面に垂直な法線ベクトルを生成することと、
   によって、前記特徴の表現を生成するように構成された特徴表現生成モジュールと、
   として機能させ、
   前記重みベクトル生成モジュールは、選択された数学関数によって関連づけられた少なくとも２つのレベルにおいて異なる値をとる、前記少なくとも１つのパラメータの値を用いることができるように構成され、
   前記滑らかな特徴線は、それを横切って前記法線ベクトルが連続的に変化する特徴線である、コンピュータプログラム。
8. 前記滑らかな特徴線は、頂点と、２つの隣接点と、該頂点とそれぞれの該隣接点を相互
   接続する辺と関連して定められ、前記重みベクトル生成モジュールは、前記滑らかな特徴
   線がそれに沿うように定められる各前記辺と関連づけられたパラメータ値を有するパラメ
   ータ化された細分則を用いることができるように構成されている、請求項７に記載のコン
   ピュータプログラム。
9. 前記重みベクトル生成モジュールは、値が同じである、前記滑らかな特徴線がそれに沿
   うように定められる前記辺と関連づけられたパラメータを用いることができるように構成
   されている、請求項８に記載のコンピュータプログラム。
10. 前記重みベクトル生成モジュールは、前記滑らかな特徴線がそれに沿うように定められ
    る前記辺に沿う鋭い折り目を反映する細分則に関連する前記パラメータを用いることがで
    きるように構成され、前記パラメータの値は、区間［０，１］において定められ、ここで
    、より大きい値がより鋭い折り目を定め、より低いレベルにおける前記パラメータの値は
    、
    

    

    によって関連づけられた、より高いレベルにおける前記パラメータの値に関連づけられ、
    ここで、ｓ(ｊ)はレベル「ｊ」における前記パラメータの値を表し、ｓ(ｊ＋１)は前記よ
    り高いレベル「ｊ＋１」における前記パラメータの値を表す、請求項９に記載のコンピュ
    ータプログラム。
11. 前記重みベクトル生成モジュールは、値が異なる、前記滑らかな特徴線がそれに沿うよ
    うに定められる前記辺と関連づけられたパラメータを用いることができるように構成され
    ている、請求項８に記載のコンピュータプログラム。
12. 前記重みベクトル生成モジュールは、前記滑らかな特徴線がそれに沿うように定められ
    る前記辺に沿う鋭い折り目を反映する細分則に関連する前記パラメータを用いることがで
    きるように構成され、前記パラメータの値は、区間［０，１］において定められ、ここで
    、より大きい値がより鋭い折り目を定め、より低いレベルにおける前記パラメータの値は
    、
    

    

    と、
    

    

    によって関連づけられた、より高いレベルにおける前記パラメータの値に関連づけられ、
    ここで、ｓ₁(ｊ)とｓ₂(ｊ)は、レベル「ｊ」におけるそれぞれの辺と関連づけられた前記
    パラメータの値を表し、ｓ₁(ｊ＋１)とｓ₂(ｊ＋１)は、前記より高いレベル「ｊ＋１」に
    おけるそれぞれの辺と関連づけられた前記パラメータの値を表す、請求項１１に記載のコ
    ンピュータプログラム。
13. 選択されたレベルで、それぞれの辺によって複数の隣接点に連結された少なくとも１つの点を含む複数の点を有するメッシュによる表現での特徴線によって定められた表面内に、前記メッシュによる表現の頂点と、少なくとも１つの隣接点と、該頂点と該少なくとも１つの隣接点を相互接続する辺に関連して定められた特徴の表現を生成する方法であって、
    Ａ． 複数のレベルで定められ、少なくとも１つのパラメータの値が前記メッシュの少なくとも２つのレベルで異なる値をとる、パラメータ化された細分則にもとづいて、第１の重みベクトルと第２の重みベクトルを生成するために前記パラメータ化された細分則が前記頂点の両側での鋭さパラメータのそれぞれの値であるパラメータを使用するようにして、重みベクトル生成モジュールが、重み値の第１の並びからなる前記第１の重みベクトルと重み値の第２の並びからなる前記第２の重みベクトルとを生成する重みベクトル生成ステップと、
    Ｂ． 特徴表現生成モジュールが前記特徴の表現を生成する特徴表現生成ステップであって、前記重みベクトルの少なくとも１つと、前記頂点と前記隣接点の位置を用い、
    前記第１の並びを用いて前記頂点と前記頂点の周りの前記隣接点とのそれぞれの位置に乗算し、複数の第１の乗算結果を得ることと、
    前記第１の乗算結果の和を求めて、前記頂点に関連する前記表面の上の点での特徴を規定する滑らかな特徴線に沿った第１の接線ベクトルを求めることと、
    前記第２の並びを用いて前記頂点と前記頂点の周りの前記隣接点とのそれぞれの位置に乗算し、複数の第２の乗算結果を得ることと、
    前記第２の乗算結果の和を求めて、前記頂点に関連する前記表面の上の点での特徴を規定する滑らかな特徴線を横切る第２の接線ベクトルを求めることと、
    前記滑らかな特徴線に沿った前記第１の接線ベクトルと前記滑らかな特徴線を横切る前記第２の接線ベクトルとの交差積をとることにより、前記表面に接する面に垂直な法線ベクトルを生成することと、
    によって前記特徴の表現を生成する特徴表現生成ステップと、
    を有し、
    前記重みベクトル生成ステップは、選択された数学関数によって関連づけられた少なくとも２つのレベルにおいて異なる値をとる、前記少なくとも１つのパラメータの値を用いるステップを含み、
    前記滑らかな特徴線は、それを横切って前記法線ベクトルが連続的に変化する特徴線である、方法。
14. 前記滑らかな特徴線は、頂点と、２つの隣接点と、該頂点とそれぞれの該隣接点を相互
    接続する辺に関連して定められ、前記重みベクトル生成ステップは、前記滑らかな特徴線
    がそれに沿うように定められる各前記辺と関連づけられたパラメータ値を有するパラメー
    タ化された細分則を用いるステップを含む、請求項１３に記載の方法。
15. 前記重みベクトル生成ステップは、値が同じである、前記滑らかな特徴線がそれに沿う
    ように定められる前記辺と関連づけられたパラメータを用いるステップを含む、請求項１
    ４に記載の方法。
16. 前記重みベクトル生成ステップは、前記滑らかな特徴線がそれに沿うように定められる
    前記辺に沿う鋭い折り目を反映する細分則に関連する前記パラメータを用いるステップを
    含み、前記パラメータの値は、区間［０，１］において定められ、ここで、より大きい値
    がより鋭い折り目を定め、より低いレベルにおける前記パラメータの値は、
    

    

    によって関連づけられた、より高いレベルにおける前記パラメータの値に関連づけられ、
    ここで、ｓ(ｊ)はレベル「ｊ」における前記パラメータの値を表し、ｓ(ｊ＋１)は前記よ
    り高いレベル「ｊ＋１」における前記パラメータの値を表す、請求項１５に記載の方法。
17. 前記重みベクトル生成ステップは、値が異なる、前記滑らかな特徴線がそれに沿うよう
    に定められる前記辺と関連づけられたパラメータを用いるステップを含む、請求項１４に
    記載の方法。
18. 前記重みベクトル生成ステップは、前記滑らかな特徴線がそれに沿うように定められる
    前記辺に沿う鋭い折り目を反映する細分則に関連する前記パラメータを用いるステップを
    含み、前記パラメータの値は、区間［０，１］において定められ、ここで、より大きい値
    がより鋭い折り目を定め、より低いレベルにおける前記パラメータの値は、
    

    

    と、
    

    

    によって関連づけられた、より高いレベルにおける前記パラメータの値に関連づけら、こ
    こで、ｓ₁(ｊ)とｓ₂(ｊ)は、レベル「ｊ」におけるそれぞれの辺と関連づけられた前記パ
    ラメータの値を表し、ｓ₁(ｊ＋１)とｓ₂(ｊ＋１)は、前記より高いレベル「ｊ＋１」にお
    けるそれぞれの辺と関連づけられた前記パラメータの値を表す、請求項１７に記載の方法
    。

Images