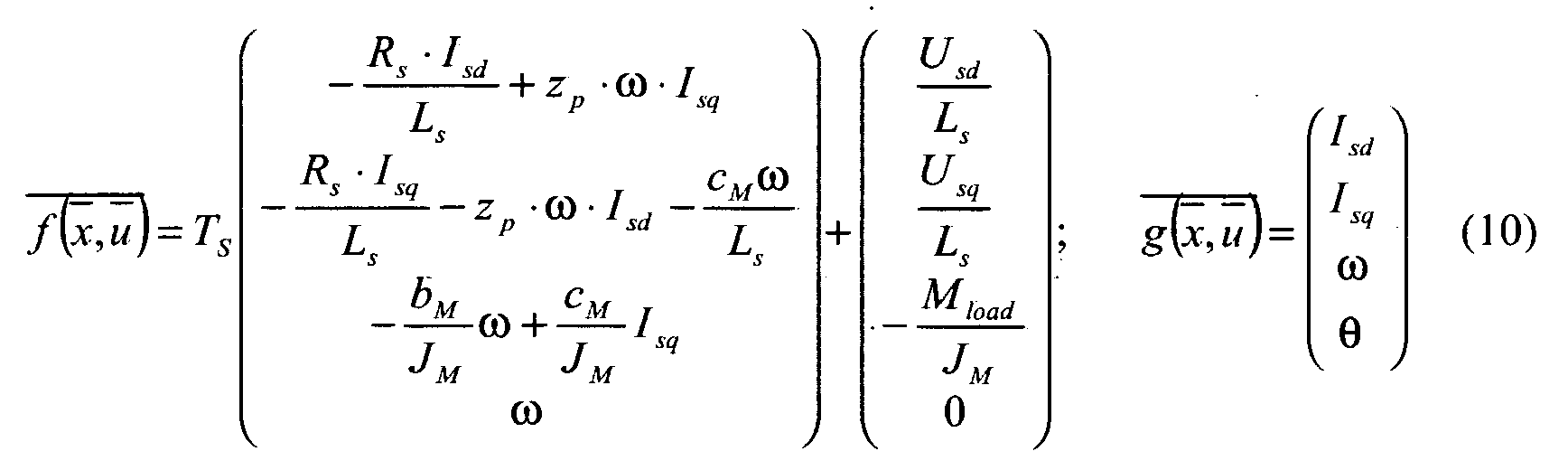EP1885054B1 - Method of estimating the state of a system and related device for estimating position and speed of the rotor of a brushless motor - Google Patents
Method of estimating the state of a system and related device for estimating position and speed of the rotor of a brushless motor Download PDFInfo
- Publication number
- EP1885054B1 EP1885054B1 EP06425561A EP06425561A EP1885054B1 EP 1885054 B1 EP1885054 B1 EP 1885054B1 EP 06425561 A EP06425561 A EP 06425561A EP 06425561 A EP06425561 A EP 06425561A EP 1885054 B1 EP1885054 B1 EP 1885054B1
- Authority
- EP
- European Patent Office
- Prior art keywords
- ref
- motor
- function
- state
- rotor
- Prior art date
- Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
- Not-in-force
Links
- 238000000034 method Methods 0.000 title claims description 75
- 230000006870 function Effects 0.000 claims description 61
- 230000008569 process Effects 0.000 claims description 19
- 238000004422 calculation algorithm Methods 0.000 claims description 16
- 238000005259 measurement Methods 0.000 claims description 13
- 238000013178 mathematical model Methods 0.000 claims description 10
- 238000004804 winding Methods 0.000 claims description 6
- 238000012549 training Methods 0.000 claims description 3
- 238000005070 sampling Methods 0.000 claims description 2
- 239000011159 matrix material Substances 0.000 description 26
- 238000013459 approach Methods 0.000 description 14
- 238000004088 simulation Methods 0.000 description 9
- 238000010586 diagram Methods 0.000 description 7
- 238000012360 testing method Methods 0.000 description 6
- 230000009471 action Effects 0.000 description 5
- 230000009467 reduction Effects 0.000 description 5
- 239000005557 antagonist Substances 0.000 description 3
- 230000008878 coupling Effects 0.000 description 3
- 238000010168 coupling process Methods 0.000 description 3
- 238000005859 coupling reaction Methods 0.000 description 3
- 230000004044 response Effects 0.000 description 3
- 238000013528 artificial neural network Methods 0.000 description 2
- 230000005540 biological transmission Effects 0.000 description 2
- 238000011217 control strategy Methods 0.000 description 2
- 239000000446 fuel Substances 0.000 description 2
- 230000006872 improvement Effects 0.000 description 2
- 230000006698 induction Effects 0.000 description 2
- 238000012544 monitoring process Methods 0.000 description 2
- 238000005312 nonlinear dynamic Methods 0.000 description 2
- 241000196324 Embryophyta Species 0.000 description 1
- 230000002159 abnormal effect Effects 0.000 description 1
- 230000032683 aging Effects 0.000 description 1
- 230000004075 alteration Effects 0.000 description 1
- 230000008901 benefit Effects 0.000 description 1
- 238000004364 calculation method Methods 0.000 description 1
- 239000003638 chemical reducing agent Substances 0.000 description 1
- 238000001514 detection method Methods 0.000 description 1
- 238000006073 displacement reaction Methods 0.000 description 1
- 230000008571 general function Effects 0.000 description 1
- 230000002068 genetic effect Effects 0.000 description 1
- 230000010354 integration Effects 0.000 description 1
- 238000011835 investigation Methods 0.000 description 1
- 230000001537 neural effect Effects 0.000 description 1
- 230000003287 optical effect Effects 0.000 description 1
- 238000005457 optimization Methods 0.000 description 1
- 230000010355 oscillation Effects 0.000 description 1
- 239000002245 particle Substances 0.000 description 1
- 238000012545 processing Methods 0.000 description 1
- 230000000306 recurrent effect Effects 0.000 description 1
- 230000011664 signaling Effects 0.000 description 1
- 238000012546 transfer Methods 0.000 description 1
Images
Classifications
-
- G—PHYSICS
- G05—CONTROLLING; REGULATING
- G05B—CONTROL OR REGULATING SYSTEMS IN GENERAL; FUNCTIONAL ELEMENTS OF SUCH SYSTEMS; MONITORING OR TESTING ARRANGEMENTS FOR SUCH SYSTEMS OR ELEMENTS
- G05B13/00—Adaptive control systems, i.e. systems automatically adjusting themselves to have a performance which is optimum according to some preassigned criterion
- G05B13/02—Adaptive control systems, i.e. systems automatically adjusting themselves to have a performance which is optimum according to some preassigned criterion electric
- G05B13/04—Adaptive control systems, i.e. systems automatically adjusting themselves to have a performance which is optimum according to some preassigned criterion electric involving the use of models or simulators
-
- H—ELECTRICITY
- H02—GENERATION; CONVERSION OR DISTRIBUTION OF ELECTRIC POWER
- H02P—CONTROL OR REGULATION OF ELECTRIC MOTORS, ELECTRIC GENERATORS OR DYNAMO-ELECTRIC CONVERTERS; CONTROLLING TRANSFORMERS, REACTORS OR CHOKE COILS
- H02P21/00—Arrangements or methods for the control of electric machines by vector control, e.g. by control of field orientation
- H02P21/13—Observer control, e.g. using Luenberger observers or Kalman filters
-
- H—ELECTRICITY
- H02—GENERATION; CONVERSION OR DISTRIBUTION OF ELECTRIC POWER
- H02P—CONTROL OR REGULATION OF ELECTRIC MOTORS, ELECTRIC GENERATORS OR DYNAMO-ELECTRIC CONVERTERS; CONTROLLING TRANSFORMERS, REACTORS OR CHOKE COILS
- H02P21/00—Arrangements or methods for the control of electric machines by vector control, e.g. by control of field orientation
- H02P21/14—Estimation or adaptation of machine parameters, e.g. flux, current or voltage
- H02P21/18—Estimation of position or speed
-
- H—ELECTRICITY
- H02—GENERATION; CONVERSION OR DISTRIBUTION OF ELECTRIC POWER
- H02P—CONTROL OR REGULATION OF ELECTRIC MOTORS, ELECTRIC GENERATORS OR DYNAMO-ELECTRIC CONVERTERS; CONTROLLING TRANSFORMERS, REACTORS OR CHOKE COILS
- H02P21/00—Arrangements or methods for the control of electric machines by vector control, e.g. by control of field orientation
- H02P21/24—Vector control not involving the use of rotor position or rotor speed sensors
Definitions
- This invention relates the techniques for estimating the evolution of a system and more particularly to a method for estimating the state of a system.
- the method of this invention may be used for estimating position and speed of a brushless motor without employing speed and position sensors and may be implemented in a hardware form.
- the invention further relates to a device for generating estimation signals of position and speed of the rotor of a brushless motor, to a feedback control device of a brushless motor and to a power steering system that implement the method of this invention.
- Electric motors are used in the automotive field not only in electrically powered cars but also as actuators in servo-systems for driving pumps, compressors and the like.
- Permanent magnet brushless motors are often preferred in these automotive applications.
- the characteristics of permanent magnet brushless motors are particularly suitable for automotive applications: they are relatively lightweight, have a high power density, a small size and are very reliable, though they are relatively expensive (due to the costs of the magnets used for fabricating the rotor), more difficult to control than a traditional DC electrical machine, and require more or less precise angular position sensors (depending on the brushless motor and the control strategy).
- a second angular position sensor is commonly installed for controlling that the first sensor be working correctly.
- a sensorless estimation algorithm could compensate errors due to aging or to alterations of the main sensor, making superfluous the second sensor and thus solving the drawback of its encumbrance.
- estimators of the angular position of the rotor of a permanent magnet brushless machine may be found in literature [4].
- one of the most used techniques is based on the so-called "state observers" for monitoring the state of the system. In this case it is necessary to know at least roughly a mathematical model of the electric machine.
- Figure 1 illustrates the block diagram of a typical field oriented control of a permanent magnet brushless machine (BLDC).
- the feedback signals, I sd (direct current) and I sq (quadrature current), that the PI controllers compare with the reference currents I sd ref and I sq ref , are obtained with a double transform of the phase currents of the motor I U , I V and I W .
- the dynamics of the brushless motor may be studied both in the system of coordinates (d,q) as well as in the system ( ⁇ , ⁇ ).
- z p indicates the number of polar pairs
- c M the constant of the electric machine (that is the ratio between the generated torque and the current I sq circulating when the rotor is blocked)
- the values of state variables of the brushless motor that in equation (5) are the current I sq and the speed ⁇ , may be estimated with the so-called “state estimators”, that are algorithms for calculating the values of state variables of a system, if a mathematical model thereof defined in function of the detected inputs and outputs variables is known.
- a state observer that is largely used for controlling brushless motors is the so-called Luenberg state observer [4].
- the optimal state observer is the Kalman filter.
- the gain of the filter is calculated considering also the statistical properties of the noise of the process (uncertainty relative to the knowledge of the dynamics of the system) and of the measurement error.
- the extended Kalman filter (EKF) is an improvement of the Kalman filter suitable for systems having a nonlinear dynamics and may be used for estimating speed and position of the rotor. Therefore, it is possible to use equations (4) as a mathematical model of the brushless motor.
- the system of nonlinear equations is linearized and discretized around sampling instants taken at constant intervals, thus the standard Kalman filter is applied to the linearized system of discrete-time equations.
- k) of the system at the step k +1 is a function of the a priori estimation x(k
- k ⁇ f x ⁇ k
- k ⁇ x ⁇ ⁇ k
- the values of the matrix of gains K(k) are adjusted such that the estimated values of the outputs g(x ⁇ (k
- the EKF may be used when the covariance matrices of the process noise Q and of the measurement noise R are known. If these matrices are known, it is possible to calculate at each step the gain of the EKF and thus to estimate the state of the system.
- different model-based approaches are compared for estimating the angular position of the rotor of a permanent magnet brushless machine, a Luenberger state observer, a reduced Luenberger state observer, an EKF and so on. The best performances in terms of accuracy in tracking the kinematics of the rotor are provided by the EKF.
- the computational loads that is scalar multiplications, integrations, trigonometric functions
- 0) are estimated during an off-line training phase by means of an evolutionary algorithm for minimizing a pre-established cost function defined in function of the estimated outputs of the system, of the detected outputs, of the estimated values of at least a state of the system and of the corresponding detected values in response to a pre-established input pattern. This allows even to obtain accurate estimations of data of state of a system without knowing all initial conditions.
- the cost function is the mean square error of the difference between the estimated and the measured outputs and between the estimated values of at least a state variable of the system and the corresponding detected values, in response to a pre-established input pattern.
- 0) are known and it is possible to estimate data of state starting from the inputs and the outputs of the system.
- the just described technique to a brushless motor, it is possible to estimate position and speed of the rotor of the motor without installing dedicated sensors thereon, but simply by detecting the currents that flows through the windings (that are the outputs of the brushless motor) and the driving voltages of the motor (that are the inputs of the motor).
- the method of this invention for estimating position and speed of a brushless motor may be implemented in a relative device.
- a device may be used for controlling a brushless motor, or it may be introduced in the control loop of a brushless motor of a power steering system, in order to make the driver feel an antagonist torque on the steering wheel determined, according to a pre-established waveform, in function of the speed of the vehicle and of the steering angle.
- the methods of this invention may even be implemented via software by a program executed by a computer or a microprocessor.
- This invention discloses a method based on a so-called free-derivative state observer for estimating data of state variables of a system that may be used, in particular, for estimating, in a sensorless fashion, speed and position of the rotor of a brushless motor without installing dedicated sensors.
- the method of this invention is advantageous both from the point of view of the computational load required for its implementation and from the point of view of the rapidity of its response and the accuracy of its estimations.
- the method of this invention uses a soft computing procedure based on the use of evolutionary algorithms.
- the method has been tested on an EPS application (Electric Power Steering), that is on specific application patterns of an EPS system wherein the brushless motor is used for providing a torque for helping the driver while steering.
- EPS application Electric Power Steering
- f x f x ⁇ + f ⁇ ⁇ x ⁇ ⁇ x - x ⁇ + f 2 x ⁇ 2 ⁇ x - x ⁇ 2 + f 3 x ⁇ 6 ⁇ x - x ⁇ 3 + ...
- f DD ⁇ x ⁇ f ⁇ x ⁇ + h - f ⁇ x ⁇ - h 2 ⁇ h
- f DD ⁇ x ⁇ f ⁇ x ⁇ + h + f ⁇ x ⁇ - h - 2 ⁇ f x ⁇ h 2
- Equation (14) may be interpreted as a Taylor approximation in which the derivatives are substituted by central finite differences such as equations (15). In order to evaluate the accuracy of the approximation it is sufficient to substitute in equation (14) the Taylor series expansion (equation (11)) in place of f ( x ⁇ + h ) and f ( x ⁇ - h ).
- f x ⁇ + f DD ⁇ x ⁇ ⁇ x - x ⁇ + f DD ⁇ x ⁇ 2 ⁇ x - x ⁇ 2 f x ⁇ + f ⁇ ⁇ x ⁇ ⁇ x - x ⁇ + f ⁇ ⁇ x ⁇ 2 ⁇ x - x ⁇ 2 + f 3 x ⁇ ⁇ h 2 2 ⁇ 3 + f 5 x ⁇ ⁇ h 4 2 ⁇ 3 ⁇ 4 ⁇ 5 + ... ⁇ x - x ⁇ + f 4 x ⁇ ⁇ h 2 2 ⁇ 3 ⁇ 4 + f 6 x ⁇ ⁇ h 4 2 ⁇ 3 ⁇ 4 ⁇ 5 ⁇ 6 + ... ⁇ x - x ⁇ 2
- Figure 2 compares the polynomial approximation to the second order of a function f in the neighborhood of a point x ⁇ carried out respectively with the Stirling approximation formula and the Taylor series expansion. It is possible to infer that the approximation obtained with the Taylor series expansion worsen significantly the more we get far from point x ⁇ .
- the Stirling interpolation formula of the second order, with the parameter h equal to 3.5 fairly approximates the function even relatively far from the point of interest.
- ⁇ p and ⁇ p represent the average and difference operators, respectively.
- EKF is one of the most known state observers used for tracking the functioning state of a nonlinear system. It is based on the Taylor series approximation formula, that depends only upon the current estimation of the state variables of the system and not upon the uncertainty/variance associated to this estimation.
- DD1 and DD2 filters are among the most known state observer, they are used for tracking nonlinear systems and they are based on the Stirling approximation formula. These filters are based to the first and second order approximations, respectively, described by equations (27), (29), (31) and (32).
- the filter to be used is a DD1 filter, but the same considerations apply, mutatis mutandis, also if a filter DD2 or any other filter based on the Stirling approximation formula of any order, even larger than the second order, is used.
- f represent the nonlinear function that ties the state variables of the system, the inputs and the process noise at step k -th to the a priori estimation of the state variables at step ( k +1)-th.
- This difficulty is overcome, according to an aspect of this invention, by carrying out a preliminary off-line tuning.
- This preliminary operation is carried out by driving the system according to a pre-established input pattern, sensing the values of output variables and of at least a state variable instant by instant through sensors and updating the covariance matrices of the measurement noise and the process noise and the initial values of the covariance matrix of the state with and evolutionary algorithm such to minimize a pre-established cost function.
- this cost function is the root mean square of the difference between the estimated values and the respective sensed values.
- the state observer is trained for estimating data of state variables of the system without using the sensor of the state variable.
- a state observer may be used in particular (but not only) for controlling a brushless motor without using any position and/or speed sensor.
- FIG. 3 depicts the block diagram of a state observer of this invention OPTIMIZED STATE OBSERVER for controlling in a field oriented mode the brushless motor BLDC motor.
- the inputs of the state observer of this invention are the voltages U sq ref and U sd ref generated by the controllers PI that implement a proportional-integral function, that control the electric machine through the PWM stage and the currents I sq and I sd in the rotoric reference system.
- the values of these currents are obtained by measuring the currents I U , I V and I W and by applying the above mentioned Clarke and Park transforms.
- a characteristic of the state observer of this invention consists in that it is capable of estimating speed and position of a brushless motor without using a dedicated sensor (such as resolvers, Hall sensors, encoders and the like).
- the estimation of the rotor position is used for carrying out the direct and inverse Park transforms.
- the initial values of the covariance matrix of the state variables and the covariance matrices associated to the process noise and measurement noise are determined in an off-line tuning phase.
- Figure 4 shows how the initial value of the covariance matrix of the state variables and how the covariance matrix relative to the process noise are adjusted because of the automatic tuning guided by evolutionary algorithms.
- the state observer of this invention may be used for estimating position and speed of the rotor of a brushless motor even without knowing the initial position of the rotor, but by knowing exclusively its initial speed. This is not a limitation when the initial speed is known (e. g. it is null), for example it the control of the motor starts when it is still.
- a column type EPS system [1] and [2] has been considered.
- the brushless motor contained therein is connected to the steering column through torque reducers.
- Figure 5 describes the experimental set-up of the EPS system in HILS configuration (Hardware-In-the-Loop Simulation).
- a further brushless motor is used for providing to the rack-pinion system different profiles of load torques.
- both brushless motors the motor that powers the steering by supplying a supplementary steering torque through the torque reduction gears and the motor that supplies an antagonist torque to the rack-pinion system, are controlled by a PC.
- the torque and the steering angle are measured by a torque sensor mounted on the top of the steering column.
- Figure 8 depicts the sensor.
- the sensor is a torsion bar in which two optical encoders measure respectively the angular position of the steering-wheel ⁇ SW (steering angle) and the angular position ⁇ SS in respect to the steering column (that is the angular position in respect to the steering shaft).
- the described EPS system in Figures 5 and 6 may be subdivided into two parts, a steering column and an assisting electric motor.
- T s , T l , T m be the steering torque, the load torque transmitted from the rack-pinion system to the steering column and the torque generated by the assisting electric motor, respectively.
- the load torque T l it takes into account the friction between the wheels and the road and the efficiency of the mechanic gears for transmitting torques (rack-pinion, steering shaft and the like).
- J m ⁇ ⁇ ⁇ m + b M ⁇ ⁇ ⁇ m T m - T l N
- J m and b M are the inertia momentum and the dampening coefficient of the electric motor
- N is the ratio reduction/transmission relative to the reduction gear that couples the assisting electric motor to the steering column.
- the equations used for describing the functioning of the brushless motor of this application are equations (4).
- the factor n considers how, in function of the geometric-mechanical characteristics of the EPS system, the steering angle ⁇ SW imposed by the driver is transmitted to the wheels.
- T road The antagonist torque T road due to the coupling of the wheels with the road is simply obtained by the vector product of the force F R to which the rack is subjected during the motion of the vehicle and the radius r of the pinion:
- Figure 8 depicts the graph of the load torque due to friction between the road and the wheels of the vehicle for certain established values of the slipping angle and of the slipping ratio ( s, ⁇ ) .
- an EPS system The main functions of an EPS system are the reduction of the steering torque and the improvement of the return of the steering wheel to its start position after a cornering (a displacement describing a J).
- a cornering a displacement describing a J
- an assisting torque is initially provided to the steering column for reducing the torque that a driver feels while steering.
- the EPS system rotates the steering-wheel to its initial position without oscillations and overshoots, that otherwise would be present if the power steering system was not present.
- time intervals in which the control logic circuitry of the EPS is enabled for reducing the steering torque and for rotating the steering wheel in its initial position are distinct.
- Figure 9 depicts a block diagram of the control logic for reducing the steering torque in an EPS system.
- the idea of this control consists in encoding in the block TORQUE MAP the driving style of a driver, that is a function of the speed V of the vehicle and of the steering angle ⁇ SW established by the driver.
- the objective of the control is to make that the torque felt by the driver while steering, that is T S , be as close as possible to the reference torque, that is T rs , stored in the look-up table of the block TORQUE MAP.
- the function that gives the steering torque upon the vehicle speed and the steering angle ⁇ SW may be illustrated as follows:
- FIG 10 the graphs of the reference steering torque in function of the speed of the vehicle and of the steering angle are depicted.
- a sample 3-D representation of a look-up table of the reference steering torques is depicted in Figure 11 .
- Figures 12 , 13 , 14 , 15, 16 illustrate the results of a simulation of the EPS system in which the kinematics (position and speed) of the rotor of the brushless motor has been estimated on a test pattern by means of the method of this invention and compared with that measured through dedicated sensors.
- Figure 14 is a detail view of the graph of Figure 12 . It is evident how fast the values estimated with the method of this invention are corrected for tracking the waveform that describes the measured position of the rotor by a dedicated sensor.
- the method of this invention is effective even when both speed and initial position of the rotor are unknown.
- Figure 18 depicts the result of a simulation in which also the initial speed of the rotor has been supposed unknown. This situation could occur for example in an EPS application when, because of the fact that the vehicle is running fast in a highway, the electric motor is disabled, or in an e-brake application when, because of an abrupt brake after having brought a piston in its rest position, the rotor of an electric motor is disconnected from the servo-system that couples it to the piston. In both cases, the method of this invention is capable of resuming in a short time an efficient tracking of the kinematics of the rotor even using an inaccurate determination of the initial conditions.
- parameters of the filter DD1 are optimized through evolutionary (genetic) algorithms, such as the PSOA (Particle Swarm Optimization Algorithm) or ES (Evolution Strategies).
- the optimized tuning procedure of this invention not only simplifies the set-up phase of the considered model of the state observer but, which is of paramount importance, allows to enhance the tracking performances.
- Figure 18 shows the results that have been obtained, after having spent a very long time for searching the optimal values of parameters of the filter in the estimation of the angular position of the rotor of the brushless machine on the same specific patterns of the same application considered in Figures 12 , 13 and 14 .
- an optimized tuning of the parameters of the filter it is possible to compensate immediately the fact that the initial angular position of the rotor is unknown and it is possible to have a negligible error in steady-state conditions.
- the method for estimating data of state variables can be used for tracking the kinematics of the rotor of a brushless motor.
- a device of this invention for estimating speed and position of a rotor of a motor could replace a dedicated sensor used for monitoring the rotor position.
- the method of this invention could be used in a diagnostic device for sensing, possibly in advance, abnormal functioning of certain parts of the system, such as for example possible faults of sensors, of actuators, or even variations of intrinsic structural parameters of the system. Depending on the cases, these faults could be simply diagnosed for signaling the driver that parts/subsystems of the vehicle need to be checked, or could be balanced/compensated by adjusting internal parameters of the control system.
Landscapes
- Engineering & Computer Science (AREA)
- Power Engineering (AREA)
- Health & Medical Sciences (AREA)
- Artificial Intelligence (AREA)
- Computer Vision & Pattern Recognition (AREA)
- Evolutionary Computation (AREA)
- Medical Informatics (AREA)
- Software Systems (AREA)
- Physics & Mathematics (AREA)
- General Physics & Mathematics (AREA)
- Automation & Control Theory (AREA)
- Control Of Motors That Do Not Use Commutators (AREA)
Description
- This invention relates the techniques for estimating the evolution of a system and more particularly to a method for estimating the state of a system. The method of this invention may be used for estimating position and speed of a brushless motor without employing speed and position sensors and may be implemented in a hardware form. The invention further relates to a device for generating estimation signals of position and speed of the rotor of a brushless motor, to a feedback control device of a brushless motor and to a power steering system that implement the method of this invention.
- Electric motors are used in the automotive field not only in electrically powered cars but also as actuators in servo-systems for driving pumps, compressors and the like.
- Many functional devices of a car are motorized, such as the fuel pump, the over-modulation compressor, the transmission gears, the power steering, and so forth.
- Traditionally, these functional devices were servo-assisted by exploiting the motor torque available on the shaft of the thermal engine of the car. This implied inefficiencies in using part of the mechanical energy obtained by burning fuel for powering these devices. Lately the use of electric motors, that notoriously convert electric energy into mechanical energy, has become more and more the preferred choice. Permanent magnet brushless motors are often preferred in these automotive applications. The characteristics of permanent magnet brushless motors are particularly suitable for automotive applications: they are relatively lightweight, have a high power density, a small size and are very reliable, though they are relatively expensive (due to the costs of the magnets used for fabricating the rotor), more difficult to control than a traditional DC electrical machine, and require more or less precise angular position sensors (depending on the brushless motor and the control strategy).
- In particular, when implementing control strategies that contemplate a sinusoidal modulation of the PWM (Pulse Width Modulation), whether DC (trapezoidal induced back electromotive force) or AC (sinusoidal induced back electromotive force), it is necessary to use sensors of the angular position, such as (incremental or absolute) encoders and resolvers that are relatively expensive (encoders) or require complicated sensing techniques (resolvers).
- For these reasons, the use of sensorless control algorithms that, based upon the detection of quantities the value of which is measurable and/or available in a simple and economic way, provide a more or less approximated estimation of the angular position of the rotor. Many applications do not allow to use sensorless techniques because, particularly model-based techniques (that is the techniques based on a mathematic model of the physical system) do not allow an accurate estimation of the angular position at low speeds and do not provide any estimation at practically null speed.
- In certain applications this problem is eliminated by implementing alignment procedures and by using start-up ramps destined to initialize the sensorless algorithm. It is evident that certain applications, such as for example electrically assisted power steering systems, do not allow pauses between the instant of application of the reference signal and its effective actuation. For these applications, that are safety-critical applications, sensorless algorithms may be a reliable alternative.
- Often in traditional control systems, a second angular position sensor is commonly installed for controlling that the first sensor be working correctly. Indeed, a sensorless estimation algorithm could compensate errors due to aging or to alterations of the main sensor, making superfluous the second sensor and thus solving the drawback of its encumbrance.
- Many examples of use of estimators of the angular position of the rotor of a permanent magnet brushless machine may be found in literature [4]. In particular, as far as the model-based approaches are concerned, one of the most used techniques is based on the so-called "state observers" for monitoring the state of the system. In this case it is necessary to know at least roughly a mathematical model of the electric machine.
-
Figure 1 illustrates the block diagram of a typical field oriented control of a permanent magnet brushless machine (BLDC). The feedback signals, Isd (direct current) and Isq (quadrature current), that the PI controllers compare with the reference currents -
- The PI controllers (that is the controllers with a proportional-integral action), generate reference voltages
are supplied to the PWM generator. - The dynamics of the brushless motor may be studied both in the system of coordinates (d,q) as well as in the system (α,β). In the system (d,q), the dynamics of the system is expressed by the following equations:
wherein zp indicates the number of polar pairs, cM the constant of the electric machine (that is the ratio between the generated torque and the current Isq circulating when the rotor is blocked), Rs and Ls the resistance and the inductance of the windings, Usd and Usq the reference voltages. As far as the equation of mechanical equilibrium is concerned, JM, bM and Mload indicate the momentum of inertia, a dampening coefficient and the load moved by the electric machine, respectively. -
- The values of state variables of the brushless motor, that in equation (5) are the current Isq and the speed θ̇, may be estimated with the so-called "state estimators", that are algorithms for calculating the values of state variables of a system, if a mathematical model thereof defined in function of the detected inputs and outputs variables is known.
- A state observer that is largely used for controlling brushless motors is the so-called Luenberg state observer [4].
- This state observer, even if it is relatively simple, applies only for systems the dynamics of which is described by linear equations. In practice, it may be applied for tracking the kinematics of the rotor of a brushless electric machine if the approximation of equations (5) is reasonable.
- In case it is not possible to estimate the angular position by using the linear equations (5), the parameters of the observer must be estimated by introducing a Lyapunov function to be minimized.
- This technique is rather complicated because it presumes that an exact model of the motor be known and an appropriate choice of the Lyapunov function to be minimized. Moreover, it is necessary to estimate at least two of the three phase currents of the motor and the supply voltages.
- A state observer that considers also the noise that disturbs the measurement of the values of state variables is the extended Kalman filter. In order to better understand the field of application of this invention, the functioning of an extended Kalman filter is briefly explained.
- From a statistical point of view, the optimal state observer is the Kalman filter. The gain of the filter is calculated considering also the statistical properties of the noise of the process (uncertainty relative to the knowledge of the dynamics of the system) and of the measurement error.
- The extended Kalman filter (EKF) is an improvement of the Kalman filter suitable for systems having a nonlinear dynamics and may be used for estimating speed and position of the rotor. Therefore, it is possible to use equations (4) as a mathematical model of the brushless motor.
- The advantage in respect to other "model-based" approaches (such as the Luenberger state observer) consists in not needing to use a linear approximation of the nonlinear mathematical model that describes the dynamics of the motor.
-
-
x(k) the state of the system, -
u(k) the input of the system, -
y(k) the output of the system, -
v(k) the process noise, -
w(k) the measurement noise - In order to apply the EKF to a system of continuous-time nonlinear system of equation, the system of nonlinear equations is linearized and discretized around sampling instants taken at constant intervals, thus the standard Kalman filter is applied to the linearized system of discrete-time equations.
-
-
- In order to make the Kalman filter provides accurate estimations of the outputs of the system, the values of the matrix of gains
K(k) are adjusted such that the estimated values of the outputsg(x̂(k|k-1) ,u(k)) by the Kalman filter be as close as possible to the effectively measured outputsy(k) . - By linearizing and discretizing a system of input-state-output equations, the result is that the variation of the state of the system from step k to step k+1, that is
may be described as follows:
and the gainK(k) of the EKF filter is:
with
beingP(k+1|k) andP(k|k) covariance matrices associated to the estimations of the state a priori and a posteriori, respectively. The latter express the uncertainties that affect the a priori and a posteriori estimations of the state, respectively. For the system of equations that describe a brushless motor, choosing as state, input and output variables the following quantities:
being ω = θ̇, it is:
having supposed, for sake of simplicity, Lsd = Lsq = Ls. As a consequence: - In practice, the EKF may be used when the covariance matrices of the process noise
Q and of the measurement noiseR are known. If these matrices are known, it is possible to calculate at each step the gain of the EKF and thus to estimate the state of the system. In [4] different model-based approaches are compared for estimating the angular position of the rotor of a permanent magnet brushless machine, a Luenberger state observer, a reduced Luenberger state observer, an EKF and so on. The best performances in terms of accuracy in tracking the kinematics of the rotor are provided by the EKF. In the cited article the computational loads (that is scalar multiplications, integrations, trigonometric functions) of the various approaches are compared among them, and it results that the EKF is very burdensome form a computational point of view. - As for other model-based approaches, there is no a deterministic and objective method for determining the covariance matrices of the measurement and process noise, and they must be fixed for using the extended Kalman filter. An imprecise estimation of the matrices
Q andR may cause an imprecise control of the system to be controlled. - Moreover, an inappropriate choice of the values of the components of the covariance matrix
P(0|0) associated to the estimation a posteriori of the initial state may worsen sensibly the precision of the control. - The published patent application
US 2005/0007044 discloses a method and an apparatus for realizing a state observer control system for a motor that uses an extended Kalman filter to predict rotor positions and/or speed under variable loading conditions. - The article by Alma Y. Alanis et al., "Discrete-time recurrent neural induction motor control using Kalman learning", IJCNN 2006, International Joint Conference on Neural Networks, July 2006, pages 1993-2000, XP002410493, discloses a technique for tracking evolutions of discrete-time induction motors in presence of bounded disturbances, using a high order neural network structure to identify the plant model and a discrete-time control law that combines discrete time and sliding control modes.
- These drawbacks are obviated with the method of this invention for estimating data of the state of a system. The method of this invention, as well as the EKF filters, allows to use nonlinear mathematical models that describe the systems, but ensures a more accurate precision.
- This outstanding result is due to the fact that the method of this invention is based on the EKF technique, but it differs from it for adapting it to work with a filter that implements a first degree Stirling approximation formula.
- Moreover, the matrices
Q ,R andP(0|0) are estimated during an off-line training phase by means of an evolutionary algorithm for minimizing a pre-established cost function defined in function of the estimated outputs of the system, of the detected outputs, of the estimated values of at least a state of the system and of the corresponding detected values in response to a pre-established input pattern. This allows even to obtain accurate estimations of data of state of a system without knowing all initial conditions. - Preferably, the cost function is the mean square error of the difference between the estimated and the measured outputs and between the estimated values of at least a state variable of the system and the corresponding detected values, in response to a pre-established input pattern.
- Once the off-line training phase is finished, the matrices
Q ,R andP(0|0) are known and it is possible to estimate data of state starting from the inputs and the outputs of the system. In practice, by applying the just described technique to a brushless motor, it is possible to estimate position and speed of the rotor of the motor without installing dedicated sensors thereon, but simply by detecting the currents that flows through the windings (that are the outputs of the brushless motor) and the driving voltages of the motor (that are the inputs of the motor). - The method of this invention for estimating position and speed of a brushless motor may be implemented in a relative device. Such a device may be used for controlling a brushless motor, or it may be introduced in the control loop of a brushless motor of a power steering system, in order to make the driver feel an antagonist torque on the steering wheel determined, according to a pre-established waveform, in function of the speed of the vehicle and of the steering angle.
- Alternatively, the methods of this invention may even be implemented via software by a program executed by a computer or a microprocessor.
- The invention is defined in the annexed claims.
-
-
Figure 1 depicts a block diagram of a typical field oriented control of a permanent magnet brushless machine. -
Figure 2 compares the second order polynomial approximations of a function f (solid line) obtained respectively with the Stirling interpolation formula (dot-dashed line) and with the series of Taylor (dashed line). -
Figure 3 is a block diagram of the model of state observer of this invention used for tracking the kinematics of the rotor of a permanent magnet brushless machine (i.e. BLDC motor). -
Figure 4 schematically depicts the operation carried out by the evolutionary algorithms on the covariance matrices of the state variables and on the covariance matrix of the process noise. -
Figure 5 depicts a block diagram of a column EPS system in HILS (Hardware-In-The-Loop Simulation) configuration. -
Figure 6 depicts a torque sensor used for measuring the steering torque TS felt by a driver while steering. -
Figure 7 depicts schematically the rack-pinion system associated to the considered EPS system. -
Figure 8 depicts a typical waveform of the load torque (solid line) due to friction between the road and the wheels in function of the steering angle (dashed line) determined by a driver during the motion of a vehicle. -
Figure 9 depicts a block diagram of the control logic for reducing the steering torque in an EPS system of this invention. -
Figure 10 depicts a possible waveform of the reference steering torque in function of the speed of the vehicle and of the steering angle. -
Figure 11 is a sample 3-D representation of a typical look-up table used for describing how the reference steering torque depends on the vehicle speed and on the steering angle. -
Figure 12 compares the waveform of the estimated position of the rotor in function of the time with that measured by an ad hoc sensor and with that estimated using only an input-state-output mathematical model of the system, using a specific test pattern and ignoring the initial position of the rotor. -
Figure 13 is a magnified view of a portion of the graph ofFigure 12 between about 0.8 and 1.15 seconds. -
Figure 14 is a magnified view of a portion of the graph ofFigure 12 between about 0.2 and 0.225 seconds. -
Figure 15 compares the estimated speed of the rotor according to the method of this invention with that measured by an ad hoc sensor and with that estimated using only an input-state-output mathematical model of the system. -
Figure 16 is a magnified view of a portion of the graph ofFigure 12 between about 1.7 and about 1.95 seconds. -
Figure 17 compares the speed of the rotor estimated according to the method of this invention with that measured by an ad hoc sensor and with that estimated using only an input-state-output mathematical model of the system, ignoring the initial speed of the rotor. -
Figure 18 compares the rotor position estimated by the non optimized state observer DD1 with the position of the rotor measured by an ad hoc sensor and with the angular position of the rotor estimated using only an input-state-output mathematical model of the system, ignoring both the initial speed and the initial position of the rotor. - This invention discloses a method based on a so-called free-derivative state observer for estimating data of state variables of a system that may be used, in particular, for estimating, in a sensorless fashion, speed and position of the rotor of a brushless motor without installing dedicated sensors.
- Compared with other model-based approaches used for tracking the kinematics of the rotor (such as the Extended Kalman Filter), the method of this invention is advantageous both from the point of view of the computational load required for its implementation and from the point of view of the rapidity of its response and the accuracy of its estimations.
- As far as the tuning of parameters of the "free derivative" filter is concerned, the method of this invention uses a soft computing procedure based on the use of evolutionary algorithms.
- The method has been tested on an EPS application (Electric Power Steering), that is on specific application patterns of an EPS system wherein the brushless motor is used for providing a torque for helping the driver while steering.
- In order to better understand the method of this invention, a brief introduction to "free derivative" observers is provided hereinbelow.
- Numerous articles available in literature show how in different applications concerning systems with nonlinear dynamics the use of free-derivative state observers for estimating the state variables of the systems provides more accurate results than traditional approaches such as EKF [3].
- Before showing how a free-derivative state observer can be used for carrying out an accurate tracking of the kinematics of the rotor of a permanent magnet brushless machine, a brief introduction to the techniques used for developing this state observer is provided. In particular, a different way of approximating locally an arbitrary function without using the classic Taylor expansion of the function will be shown.
-
- In general, with the Taylor series expansion, the more elements of the series are considered, the more accurate is the approximation of the function.
- There are various formulas for interpolating functions that do not require the calculation of derivatives but simply need evaluating the function in a finite number of points. Implementation of these interpolating formulas is simpler than traditional interpolating formulas.
-
- Equation (14) may be interpreted as a Taylor approximation in which the derivatives are substituted by central finite differences such as equations (15). In order to evaluate the accuracy of the approximation it is sufficient to substitute in equation (14) the Taylor series expansion (equation (11)) in place of f(x̅ + h) and f(x̅ - h). Therefore,
- From equation (16) it is possible to infer that the polynomial approximation to the second order based on the Stirling formula coincides with the Taylor approximation of the function to the second order but for a remainder (that is of the two last terms at the right side of equation (16)) the value of which may be controlled through the parameter h.
- This is one of the characteristics that characterize the Stirling interpolation formula and thus makes the approximation of functions with this formula more flexible in than with traditional approaches.
-
Figure 2 compares the polynomial approximation to the second order of a function f in the neighborhood of a point x̅ carried out respectively with the Stirling approximation formula and the Taylor series expansion. It is possible to infer that the approximation obtained with the Taylor series expansion worsen significantly the more we get far from point x̅. The Stirling interpolation formula of the second order, with the parameter h equal to 3.5 fairly approximates the function even relatively far from the point of interest. -
- In equations (18) µ p and δ p represent the average and difference operators, respectively.
-
- While the Taylor series expansions of f and f̃ in a neighborhood of points x̅ and z̅, respectively, is the same, the Stirling approximation formula does not provide the same result:
wherein ep is the unity vector with p components, that is:
and sp indicates the p-th column of matrix S. It is possible to show that with an appropriate choice of the linear transform S and of the parameter h it is possible to optimize the approximation of a function f of a stochastic variable. -
- Let us calculate the above mentioned mean values using an approximation of the function based on the Stirling approximation formula. In this context it is particularly useful a linear transform such as
where the matrix S is the Cholesky factor of the covariance matrix Px, that is it is a upper triangular matrix for which the following equation: -
-
-
-
-
- EKF is one of the most known state observers used for tracking the functioning state of a nonlinear system. It is based on the Taylor series approximation formula, that depends only upon the current estimation of the state variables of the system and not upon the uncertainty/variance associated to this estimation.
- The so-called DD1 and DD2 filters, described in the document [3], are among the most known state observer, they are used for tracking nonlinear systems and they are based on the Stirling approximation formula. These filters are based to the first and second order approximations, respectively, described by equations (27), (29), (31) and (32).
- Deep investigations carried out by the present applicant indicated that one of the characteristics that distinguish the latter approach compared with traditional approaches (such as the EKF), is an approximation of the dynamics of the system that considers not only the current estimation of the state variables but also uncertainties relating to these estimations.
- In order to further enhance precision, it has been devised a technique for using filters DD1 and DD2 in an algorithm similar to EKF in which inner parameters of the filters DD1 and DD2 are established through evolutionary algorithms.
- Hereinafter, reference will be made exclusively to the case in which the filter to be used is a DD1 filter, but the same considerations apply, mutatis mutandis, also if a filter DD2 or any other filter based on the Stirling approximation formula of any order, even larger than the second order, is used.
- Compared to the EKF, the Jacobian matrix of equation (10) is substituted by the finite differences. While the formulas for updating the state are the same of that used in an EKF, formulas for updating covariance matrices are sensibly different.
- Given the Cholesky factorizations of the covariance matrices Q, R, of process noise and of measurement noise, that corrupts measures of the outputs of the process, and the Cholesky factorizations of the covariance matrices P̅, P̂ associated to the estimation of the state a priori and a posteriori, respectively,
for equation (29) it is:
wherein ŝx,j, s̅x,j, sw,j, sv,j is the j-th column of the matrix Ŝx , S̅x , Sw, Sv, respectively. -
-
-
- For the a priori update of the state equation (27) is used. In this case f represent the nonlinear function that ties the state variables of the system, the inputs and the process noise at step k-th to the a priori estimation of the state variables at step (k+1)-th. Therefore, by applying equation (27), the following equation is obtained:
while, for the a priori update of the covariance matrix of the state, equations (29) and (35) are obtained, -
-
-
-
-
-
- Even for using a DD1 or DD2 filter it is necessary to know the covariance matrices of the process noise, of the measurement noise and of the initial value of the covariance matrix relative to the estimation of the state variables.
- This difficulty is overcome, according to an aspect of this invention, by carrying out a preliminary off-line tuning. This preliminary operation is carried out by driving the system according to a pre-established input pattern, sensing the values of output variables and of at least a state variable instant by instant through sensors and updating the covariance matrices of the measurement noise and the process noise and the initial values of the covariance matrix of the state with and evolutionary algorithm such to minimize a pre-established cost function.
- Preferably, this cost function is the root mean square of the difference between the estimated values and the respective sensed values.
- Once the covariance matrices Q̅, R̅ and the initial values of the covariance matrix of the state are determined off-line, the state observer is trained for estimating data of state variables of the system without using the sensor of the state variable. Such a state observer may be used in particular (but not only) for controlling a brushless motor without using any position and/or speed sensor.
- In order to better understand how the control method of this invention works, let us refer to the case of a brushless motor, but the same considerations hold mutatis mutandis for any other physical system the functioning of which is to be controlled, such as DC or AC electric motors.
- The free-derivative state observer shown above is used for estimating position and speed of a permanent magnet brushless motor.
Figure 3 depicts the block diagram of a state observer of this invention OPTIMIZED STATE OBSERVER for controlling in a field oriented mode the brushless motor BLDC motor. - The inputs of the state observer of this invention are the voltages
- A characteristic of the state observer of this invention consists in that it is capable of estimating speed and position of a brushless motor without using a dedicated sensor (such as resolvers, Hall sensors, encoders and the like). The estimation of the rotor position is used for carrying out the direct and inverse Park transforms.
- The initial values of the covariance matrix of the state variables and the covariance matrices associated to the process noise and measurement noise are determined in an off-line tuning phase.
Figure 4 shows how the initial value of the covariance matrix of the state variables and how the covariance matrix relative to the process noise are adjusted because of the automatic tuning guided by evolutionary algorithms. - The performances of the state observer are excellent thanks to the tuning procedure of the parameters of the filter.
- Compared with other known approaches available in literature, such as the approaches described in the introduction (Luenberger observer, EKF), the state observer of this invention may be used for estimating position and speed of the rotor of a brushless motor even without knowing the initial position of the rotor, but by knowing exclusively its initial speed. This is not a limitation when the initial speed is known (e. g. it is null), for example it the control of the motor starts when it is still.
- Also this characteristic distinguishes the method of this invention from other approaches, making it implementable in real-time applications that involve electric machines such as the EPS systems [7].
- As an application of a system on which to test the method of this invention for controlling a brushless motor, a column type EPS system [1] and [2] has been considered. The brushless motor contained therein is connected to the steering column through torque reducers.
Figure 5 describes the experimental set-up of the EPS system in HILS configuration (Hardware-In-the-Loop Simulation). A further brushless motor is used for providing to the rack-pinion system different profiles of load torques. - Through these profiles it is possible to simulate the torque that opposes the steering action of the driver due to the coupling of the wheels of the vehicle with the road during the running of the vehicle. In HILS configuration both brushless motors, the motor that powers the steering by supplying a supplementary steering torque through the torque reduction gears and the motor that supplies an antagonist torque to the rack-pinion system, are controlled by a PC. The torque and the steering angle are measured by a torque sensor mounted on the top of the steering column.
-
Figure 8 depicts the sensor. The sensor is a torsion bar in which two optical encoders measure respectively the angular position of the steering-wheel θ SW (steering angle) and the angular position θ SS in respect to the steering column (that is the angular position in respect to the steering shaft). The steering torque applied by the driver during the motion of the vehicle is given by the following relation,
wherein ktorsion is the torsion rigidity of the torsion bar. - From a mechanic point of view the described EPS system in
Figures 5 and 6 may be subdivided into two parts, a steering column and an assisting electric motor. Let Ts, Tl, Tm be the steering torque, the load torque transmitted from the rack-pinion system to the steering column and the torque generated by the assisting electric motor, respectively. As far as the load torque Tl is concerned, it takes into account the friction between the wheels and the road and the efficiency of the mechanic gears for transmitting torques (rack-pinion, steering shaft and the like). From the equation that describes the mechanical equilibrium of the electric motor,
wherein Jm and bM are the inertia momentum and the dampening coefficient of the electric motor, N is the ratio reduction/transmission relative to the reduction gear that couples the assisting electric motor to the steering column. - In practice, the position θ m of the rotor of the electric motor (the rotor is connected to a servo-system that, through a reduction gear allows the motor to transfer the generated torque to the steering torque) and the angle θ SS sensed by the torque sensor to the steering shaft are tied to the ratio N, indeed θm = NθSS. The equations used for describing the functioning of the brushless motor of this application are equations (4).
- In order to complete the model of the EPS system, an estimation of the load torque Tl is required. In order to estimate the resisting torque due to the coupling of the wheels with the road the Dugoff model [5] has been used. Referring to
Figure 7 , transversal friction Fy and longitudinal friction Fx that act on the wheel during the motion of the vehicle are expressed through the following equations:
wherein Kx and Ky represent the longitudinal and the lateral rigidity of the wheel, while A, s, α are respectively the area of contact of the wheel with the road surface, the slipping ratio and the slipping angle. The force FR transmitted to the rack by friction that acts on the wheels is
wherein δ is the real steering angle transmitted to the wheel from the steering system. It is tied to the steering angle fixed by the driver through a simple linear equation, θSW = nδ. The factor n considers how, in function of the geometric-mechanical characteristics of the EPS system, the steering angle θSW imposed by the driver is transmitted to the wheels. -
-
Figure 8 depicts the graph of the load torque due to friction between the road and the wheels of the vehicle for certain established values of the slipping angle and of the slipping ratio (s, α). - For sake of ease, in the simulation of the EPS system it has been assumed that the load torque T1 coincides with the torque Troad, that is contributions to Tl due to the efficiency of the steering system have been neglected.
- The main functions of an EPS system are the reduction of the steering torque and the improvement of the return of the steering wheel to its start position after a cornering (a displacement describing a J). In a typical cornering, an assisting torque is initially provided to the steering column for reducing the torque that a driver feels while steering. Immediately after the steering action, the EPS system rotates the steering-wheel to its initial position without oscillations and overshoots, that otherwise would be present if the power steering system was not present.
- In other words, time intervals in which the control logic circuitry of the EPS is enabled for reducing the steering torque and for rotating the steering wheel in its initial position are distinct.
- In the ECU that manage EPS systems two distinct control logics are implemented for these two distinct control/servo-assistance actions. In simulations carried out it has been considered only the first of these two distinct aspects of the action of an EPS system.
-
Figure 9 depicts a block diagram of the control logic for reducing the steering torque in an EPS system. - The idea of this control consists in encoding in the block TORQUE MAP the driving style of a driver, that is a function of the speed V of the vehicle and of the steering angle θ SW established by the driver. The objective of the control is to make that the torque felt by the driver while steering, that is TS, be as close as possible to the reference torque, that is Trs, stored in the look-up table of the block TORQUE MAP. The function that gives the steering torque upon the vehicle speed and the steering angle θ SW may be illustrated as follows:
- it is well known that at low speeds, for example during parking maneuvers or in traffic jams, drivers desire a relevant assisting torque Ta be supplied by the electric motor for driving with a little effort, while at high speeds drivers desire a stronger steering torque, in order to feel more secure while steering, that is a weaker assisting torque Ta is required from the EPS system;
- the assisting torque increases with the steering angle, for example proportionally to it.
- In
Figure 10 the graphs of the reference steering torque in function of the speed of the vehicle and of the steering angle are depicted. A sample 3-D representation of a look-up table of the reference steering torques is depicted inFigure 11 . - All the mechanical part of the column EPS system described in this chapter have been modeled using the MATLAB/SIMULINK™ tool.
- In the architecture of EPS system described in the previous section a model of a permanent magnet brushless machine controlled with a field oriented control technique has been used. The free derivative state observer uses this model for estimating at each simulation step angular position and speed of the rotor of the electric machine. The testing of the model has been carried out on typical pattern of the application of EPS system, that is for sinusoidal waveforms of the steering angle and increasing profiles of the vehicle speed. The results obtained with the simulation demonstrate the effectiveness of this invention.
-
Figures 12 ,13 ,14 ,15, 16 illustrate the results of a simulation of the EPS system in which the kinematics (position and speed) of the rotor of the brushless motor has been estimated on a test pattern by means of the method of this invention and compared with that measured through dedicated sensors. - Comparing the results it is evident that only with the method of this invention it is possible to obtain accurate estimations even if the initial position of the rotor is not known. Indeed, in the graph of
Figure 12 , the curve, that represent the graph of the position of the rotor obtained by using solely the equations of the dynamics of the system, do not track the sensed values because it is not possible to compensate the fact that the initial position of the rotor is unknown. The waveform is sinusoidal, but it is translated in respect to the sensed waveform by a certain amount. - This result shows that the method of this invention is capable of estimating correctly the position of the rotor even when the assumed initial state of the system is not accurately determined. Such a situation could occur when the electric motor is started-up, because the initial speed of the rotor is known (it is null) but it could not be possible to determine precisely its initial position.
-
Figure 14 is a detail view of the graph ofFigure 12 . It is evident how fast the values estimated with the method of this invention are corrected for tracking the waveform that describes the measured position of the rotor by a dedicated sensor. - Moreover, the method of this invention is effective even when both speed and initial position of the rotor are unknown.
-
Figure 18 depicts the result of a simulation in which also the initial speed of the rotor has been supposed unknown. This situation could occur for example in an EPS application when, because of the fact that the vehicle is running fast in a highway, the electric motor is disabled, or in an e-brake application when, because of an abrupt brake after having brought a piston in its rest position, the rotor of an electric motor is disconnected from the servo-system that couples it to the piston. In both cases, the method of this invention is capable of resuming in a short time an efficient tracking of the kinematics of the rotor even using an inaccurate determination of the initial conditions. - It is worth remarking an important aspect of this invention: parameters of the filter DD1 are optimized through evolutionary (genetic) algorithms, such as the PSOA (Particle Swarm Optimization Algorithm) or ES (Evolution Strategies). The optimized tuning procedure of this invention not only simplifies the set-up phase of the considered model of the state observer but, which is of paramount importance, allows to enhance the tracking performances.
-
Figure 18 shows the results that have been obtained, after having spent a very long time for searching the optimal values of parameters of the filter in the estimation of the angular position of the rotor of the brushless machine on the same specific patterns of the same application considered inFigures 12 ,13 and 14 . With an optimized tuning of the parameters of the filter, it is possible to compensate immediately the fact that the initial angular position of the rotor is unknown and it is possible to have a negligible error in steady-state conditions. - From the test of the described model in a simulation of an EPS application, it is evident that the method for estimating data of state variables can be used for tracking the kinematics of the rotor of a brushless motor. A device of this invention for estimating speed and position of a rotor of a motor could replace a dedicated sensor used for monitoring the rotor position.
- In safety critical applications (for example the e-brake) in which two or more sensors of different kind are used, such a device could be used instead of one of these sensors. For non safety-critical applications, it could be used for a sensorless control of the brushless electric machine.
- Finally, independently from the type of application, the method of this invention could be used in a diagnostic device for sensing, possibly in advance, abnormal functioning of certain parts of the system, such as for example possible faults of sensors, of actuators, or even variations of intrinsic structural parameters of the system. Depending on the cases, these faults could be simply diagnosed for signaling the driver that parts/subsystems of the vehicle need to be checked, or could be balanced/compensated by adjusting internal parameters of the control system.
-
- [1] J. H. Kim, J. B. Song, Control Logic for an Electric Power Steering System using Assist Motor, .
- [2] A. Badawy, J. Zuraski, F. Bolourchi and A. Chandy, Modeling and Analysis of an Electric Power Steering System, SAE paper 1999-01-0399, 1999.
- [3] M. Norgaard, N. K. Poulsen, O. Ravn, Advances in Derivative-Free State Estimation for Nonlinear Systems, Department of Mathematical Modelling and Department of Automation Technical University of Denmark, technical report: IMM-REP-1998-15.
- [4] W. Reinelt, C. Lundquist, and H. Johansson, On-Line Sensor Monitoring in an Active Front Steering System using Extended Kalman Filter, SAE paper 2005-01-1271.
- [5] H. Dugoff, P.S. Fancher, An Analysis of the tyre Traction Properties and their Influenceon Vehicle Dynamic Performance, SAE paper 700377, 1970.
- [6] H.G. Beyer, The Theory of Evolution Strategies, Natural Computing Series, Springer, 2001.
- [7] P. Vas, Sensorless Vector and Direct Torque Control, Oxford Science Pubblications, Springer, 1998.
Claims (11)
- A method for estimating data of state variables of a system, whereby an input-state-output mathematical model of the system is known, comprising the following steps:installing a circuit for estimating data of state variables of the system, comprising at least a filter implementing an estimation according to a Stirling approximation formula of any order, in function of input data, output data of the system and of parameters of the filter representing values of components of covariance matrices of process noise and of measurement noise of the system;training said estimator by carrying out off-line the steps of:supplying the system with pre-established input patterns and detecting corresponding output data and a datum of at least a state variable of the system,estimating said a datum of said at least one state variable of the system for said input pre-established patterns,adjusting said parameters of the filter with an evolutionary algorithm for minimizing a pre-established cost function defined in function of the estimated output data of the system, of the sensed output data, of said at least one estimated datum of state of the system and of the corresponding sensed datum of state;estimating said data of state of the system during the normal functioning using said off-line trained estimator.
- The method of claim 1, wherein said pre-established cost function is the root means square of the difference between the estimated output data of the system and the sensed output data and between said at least one estimated datum of state of the system and the corresponding sensed datum of state.
- The method of claim 1, wherein said evolutionary algorithm is a PSOA or a ES.
- The method of claim 1, wherein said filter is a DD1 or a DD2 filter.
- A method for estimating position and speed of the rotor of a brushless motor controlled in a feedback loop that includes circuit means for generating feedback signals representing the currents (Isq , Isd ) circulating in the motor in respect to a rotoric reference system in function of the currents sensed in the windings of the motor, a controller input with said representative signals
- The method of claim 5, wherein the values of said currents (Isq, Isd ) circulating in the motor referred to the rotoric reference system are obtained from sensed samples of the current flowing through the windings of the motor by carrying out a Clarke transform followed by a Park transform defined in function of the estimated position of the rotor at the current PWM cycle.
- A device for generating signals representative of the speed and of the position of the rotor of a brushless motor controlled in a feedback loop that includes circuit means adapted to generate feedback signals representing the currents (Isq, Isd ) circulating in the motor in respect to a rotoric reference system in function of the currents sensed in the windings of the motor, a controller input with said representative signals
- A device for feedback controlling a brushless motor, comprising:circuit means adapted to generate feedback signals representing the currents (Isq, Isd ) circulating in the motor in respect to a rotoric reference system in function of the currents sensed in the windings of the motor and in function of the position of the rotor at the current PWM;a controller input with said representative signals
- A power steering system adapted to generate an auxiliary steering torque (Ta ) while steering, comprising:a brushless motor adapted to generate said auxiliary torque (Ta ) in function of control signals input thereto;a sensor adapted to generate a signal representing a total torque (TS ) that driver must balance;a control circuitry of the motor comprising:the device of claim 8 adapted to control said motor in function of reference signals
- The power steering system of claim 9, further comprising circuit means adapted to establish said reference value (Trs ) in function of the vehicle speed on which the power steering system is installed and of the steering angle of the vehicle.
- Program for computer loadable in the internal memory of a computer, comprising a software code adapted to carry out the steps of the method according to one of claims from 1 to 6 when said code is executed by said computer.
Priority Applications (3)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| DE602006009643T DE602006009643D1 (en) | 2006-08-03 | 2006-08-03 | A system for estimating the state of a system and associated apparatus for determining the position and speed of a brushless motor |
| EP06425561A EP1885054B1 (en) | 2006-08-03 | 2006-08-03 | Method of estimating the state of a system and related device for estimating position and speed of the rotor of a brushless motor |
| US11/833,053 US7659685B2 (en) | 2006-08-03 | 2007-08-02 | Method of estimating the state of a system and relative device for estimating position and speed of the rotor of a brushless motor |
Applications Claiming Priority (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| EP06425561A EP1885054B1 (en) | 2006-08-03 | 2006-08-03 | Method of estimating the state of a system and related device for estimating position and speed of the rotor of a brushless motor |
Publications (2)
| Publication Number | Publication Date |
|---|---|
| EP1885054A1 EP1885054A1 (en) | 2008-02-06 |
| EP1885054B1 true EP1885054B1 (en) | 2009-10-07 |
Family
ID=37460189
Family Applications (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| EP06425561A Not-in-force EP1885054B1 (en) | 2006-08-03 | 2006-08-03 | Method of estimating the state of a system and related device for estimating position and speed of the rotor of a brushless motor |
Country Status (3)
| Country | Link |
|---|---|
| US (1) | US7659685B2 (en) |
| EP (1) | EP1885054B1 (en) |
| DE (1) | DE602006009643D1 (en) |
Cited By (3)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| DE102013009518A1 (en) | 2013-06-06 | 2014-12-11 | Audi Ag | Motor vehicle with a fuel heater |
| CN104993765A (en) * | 2015-08-04 | 2015-10-21 | 重庆大学 | Method for estimating rotating speed of brushless direct current motor |
| RU2617586C1 (en) * | 2015-10-13 | 2017-04-25 | Борис Александрович Челдышов | Non-contact torque drive |
Families Citing this family (61)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| DE102006061929A1 (en) * | 2006-12-20 | 2008-06-26 | Takata-Petri Ag | Optical steering angle sensor for determining the absolute value of the steering angle |
| US8700686B1 (en) * | 2007-11-13 | 2014-04-15 | The Mathworks, Inc. | Robust estimation of time varying parameters |
| CN101355337B (en) * | 2008-08-19 | 2010-06-02 | 华南理工大学 | Control method for driving permanent magnet synchronous motor base on magnetic field orthotropic control |
| JP2010095075A (en) | 2008-10-15 | 2010-04-30 | Jtekt Corp | Vehicle steering apparatus |
| DE102008064001A1 (en) * | 2008-12-19 | 2010-06-24 | Abb Technology Ag | Method for diagnosing actuators |
| US20120019217A1 (en) * | 2009-03-04 | 2012-01-26 | Paul Scherrer Institut | Control concept for a digitally controlled magnetic supply device |
| DE102010004658A1 (en) * | 2009-11-25 | 2011-05-26 | Continental Automotive Gmbh | Method for operating a fuel pump in a motor vehicle and fuel pump |
| FR2959030B1 (en) * | 2010-04-14 | 2012-07-06 | Commissariat Energie Atomique | DEVICE AND METHOD FOR OBSERVING OR CONTROLLING A NON-LINEAR SYSTEM |
| US8190307B2 (en) * | 2010-08-23 | 2012-05-29 | King Fahd University Of Petroleum & Minerals | Control optimization method for helicopters carrying suspended loads |
| US8473147B2 (en) * | 2011-03-23 | 2013-06-25 | GM Global Technology Operations LLC | State of health indicator for a vehicle fuel delivery system |
| DE102011076734A1 (en) * | 2011-05-30 | 2012-12-06 | Robert Bosch Gmbh | Method and device for angle estimation in a synchronous machine |
| US20130043815A1 (en) * | 2011-08-15 | 2013-02-21 | Hsia-Yuan Hsu | Protection circuit for a d.c. brushless motor pump |
| US20130320894A1 (en) * | 2011-08-15 | 2013-12-05 | Hsia-Yuan Hsu | Protection circuit for a d.c. brushless motor pump |
| US9097767B2 (en) * | 2012-01-09 | 2015-08-04 | GM Global Technology Operations LLC | DC-motor and fuel pump faults and brush-wear prognosis |
| US8593088B2 (en) * | 2012-01-13 | 2013-11-26 | Chrysler Group Llc | Method and system for controlling an electric motor for a vehicle |
| JP6324323B2 (en) * | 2012-03-15 | 2018-05-16 | ボルグワーナー スウェーデン エービー | Electrical drive shaft device for road vehicles |
| KR101349464B1 (en) * | 2012-07-05 | 2014-01-09 | 현대자동차주식회사 | Commercial vehicle's hybrid power steering system and performance and fuel ratio improving method thereof |
| US9219432B2 (en) * | 2012-07-25 | 2015-12-22 | System General Corporation | Control systems and methods for angle estimation of permanent magnet motors |
| CN102843089B (en) * | 2012-08-23 | 2014-11-05 | 四川长虹电器股份有限公司 | Control method of permanent magnet synchronous motor (PMSM) for frequency conversion refrigerator |
| EP2725706A1 (en) * | 2012-10-23 | 2014-04-30 | ABB Technology AG | Model predictive control with reference tracking |
| CN103840725B (en) * | 2012-11-26 | 2016-05-18 | 台达电子工业股份有限公司 | Permanent-magnet synchronous motor rotor position deviation measurement device and method |
| TWI475238B (en) * | 2012-11-29 | 2015-03-01 | Ind Tech Res Inst | Method for estimating power of motor and apparatus using the same |
| US9444382B2 (en) * | 2013-01-30 | 2016-09-13 | Infineon Technologies Ag | Optimized field oriented control strategies for permanent magnet synchronous motors |
| US9479099B2 (en) * | 2013-01-30 | 2016-10-25 | Infineon Technologies Ag | Stator flux magnitude and direction control strategies for permanent magnet synchronous motors |
| US8981702B2 (en) * | 2013-03-15 | 2015-03-17 | Texas Instruments Incorporated | Automated motor control |
| US20140327379A1 (en) * | 2013-05-03 | 2014-11-06 | Texas Instruments Incorporated | Position sensorless drive system and method for permanent magnet motors |
| US9024569B2 (en) * | 2013-06-28 | 2015-05-05 | Eaton Corporation | System and method of rotor time constant online identification in an AC induction machine |
| CN103414416A (en) * | 2013-07-11 | 2013-11-27 | 中国大唐集团科学技术研究院有限公司 | Permanent magnet synchronous motor sensorless vector control system based on EKF |
| JP6130275B2 (en) * | 2013-09-05 | 2017-05-17 | カルソニックカンセイ株式会社 | Estimation apparatus and estimation method |
| US9146557B1 (en) * | 2014-04-23 | 2015-09-29 | King Fahd University Of Petroleum And Minerals | Adaptive control method for unmanned vehicle with slung load |
| EP2940857B1 (en) * | 2014-04-28 | 2018-11-28 | dSPACE digital signal processing and control engineering GmbH | Method for emulating a three-phase brushless DC motor with a load emulator |
| FR3028362B1 (en) * | 2014-11-10 | 2016-12-23 | Renault Sas | METHOD AND SYSTEM FOR CONTROLLING A SYNCHRONOUS ELECTRIC MACHINE WITH PERMANENT MAGNETS. |
| TWI551874B (en) | 2015-03-13 | 2016-10-01 | 財團法人工業技術研究院 | Motor efficiency analysis method for motor inverter |
| CN104811117B (en) * | 2015-05-08 | 2017-11-21 | 张家港智电柔性输配电技术研究所有限公司 | A kind of method of permanent-magnetic synchronous motor rotor speed estimate |
| DE102015108617A1 (en) * | 2015-06-01 | 2016-12-01 | Brose Fahrzeugteile GmbH & Co. Kommanditgesellschaft, Würzburg | Brushless DC motor |
| CN105024613A (en) * | 2015-06-26 | 2015-11-04 | 广东美的制冷设备有限公司 | Obtaining method of motor off-line resistance value, controller and air conditioner |
| US9995119B2 (en) * | 2015-11-16 | 2018-06-12 | Ge Oil & Gas Esp, Inc. | Electric submersible pumping system with permanent magnet motor |
| US10846596B2 (en) * | 2015-11-23 | 2020-11-24 | Daniel Chonghwan LEE | Filtering, smoothing, memetic algorithms, and feasible direction methods for estimating system state and unknown parameters of electromechanical motion devices |
| US10459472B2 (en) * | 2015-12-07 | 2019-10-29 | Hamilton Sundstrand Corporation | Model predictive control optimization for power electronics |
| CN106130426B (en) * | 2016-07-18 | 2018-09-25 | 南京理工大学 | Based on EKF without sensor ultrahigh speed permanent magnet synchronous motor method for controlling number of revolution |
| DE102016225253A1 (en) * | 2016-12-16 | 2018-06-21 | Robert Bosch Gmbh | Method for detecting the rack position in a steering system with electric servomotor |
| CN106998160A (en) * | 2017-04-18 | 2017-08-01 | 广东浪潮大数据研究有限公司 | A kind of condition control method of brshless DC motor, device and brshless DC motor |
| US10333444B2 (en) * | 2017-08-31 | 2019-06-25 | Eaton Intelligent Power Limited | System and method for stability control in adjustable speed drive with DC link thin film capacitor |
| DE102017121952A1 (en) * | 2017-09-21 | 2019-03-21 | Trw Automotive Gmbh | Method for detecting disturbances in a steering system and steering system for a motor vehicle |
| US10520728B2 (en) * | 2017-10-17 | 2019-12-31 | Visteon Global Technologies, Inc. | Embedded optimization algorithm of parameters to drive deployment mechanism for displays |
| CN108177652A (en) * | 2017-12-27 | 2018-06-19 | 广州大学 | The track keeping method and system of a kind of four-wheel steering delivery vehicle |
| FR3076331B1 (en) | 2018-01-02 | 2020-02-14 | Foundation Brakes France | BRAKE ACTUATOR AND METHOD OF CONTROLLING THE SAME |
| CN108306567A (en) * | 2018-01-20 | 2018-07-20 | 江南大学 | It is a kind of based on IGSO optimize EKF without sensor permanent magnet synchronous motor speed estimation method |
| CN108717266B (en) * | 2018-05-30 | 2021-03-12 | 迪比(重庆)智能科技研究院有限公司 | Neural self-adaptive tracking control method for wind field fan power based on disturbance observer |
| CN109062052B (en) * | 2018-08-31 | 2021-05-18 | 湖北工业大学 | Quad-rotor unmanned aerial vehicle integral sliding mode control method based on extended state observer |
| FR3086473B1 (en) * | 2018-09-20 | 2020-10-02 | Ifp Energies Now | METHOD OF DETERMINING THE MAGNETIC FLOW OF AN ELECTRIC MACHINE |
| CN109149923B (en) * | 2018-10-08 | 2020-05-26 | 淮阴工学院 | APFC control system for estimating control rate on line |
| CN109270455B (en) * | 2018-10-24 | 2021-02-02 | 郑州轻工业学院 | Induction motor state monitoring method based on weak-sensitivity ensemble Kalman filtering |
| US11159112B2 (en) * | 2018-11-30 | 2021-10-26 | The Trustees Of Columbia University In The City Of New York | Systems and methods for high performance filtering techniques for sensorless direct position and speed estimation |
| CN109713971B (en) * | 2019-03-01 | 2020-05-12 | 北京理工大学 | Disturbance suppression method for permanent magnet synchronous motor |
| DE102019211800B4 (en) | 2019-08-06 | 2022-12-15 | Conti Temic Microelectronic Gmbh | Method and device for determining the speed and the angle of rotation of a motor shaft of a mechanically commutated DC motor |
| TWI717001B (en) * | 2019-09-05 | 2021-01-21 | 登騰電子股份有限公司 | Motor controller and motor control method |
| CN112947648B (en) * | 2021-03-04 | 2021-11-23 | 江西理工大学 | Agricultural greenhouse environment prediction method and system |
| CN113114076A (en) * | 2021-04-15 | 2021-07-13 | 哈尔滨理工大学 | Motor rotor position estimation method based on exponential fitting volume Kalman filtering |
| CN113708690A (en) * | 2021-09-01 | 2021-11-26 | 上海节卡机器人科技有限公司 | Load inertia identification method and device, electronic equipment and system |
| CN113821893B (en) * | 2021-09-30 | 2023-09-05 | 中国航发控制系统研究所 | Self-adaptive state estimation method for aero-engine servo actuation system |
Family Cites Families (5)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US6316904B1 (en) * | 2000-06-27 | 2001-11-13 | Ford Global Technologies, Inc. | Speed and rotor time constant estimation for torque control of an induction motor |
| US6832119B2 (en) * | 2001-09-20 | 2004-12-14 | Ge Fanuc Automation North America, Inc. | Methods and systems for torque ripple compensation |
| US6768284B2 (en) * | 2002-09-30 | 2004-07-27 | Eaton Corporation | Method and compensation modulator for dynamically controlling induction machine regenerating energy flow and direct current bus voltage for an adjustable frequency drive system |
| US7276877B2 (en) | 2003-07-10 | 2007-10-02 | Honeywell International Inc. | Sensorless control method and apparatus for a motor drive system |
| JP4589093B2 (en) * | 2004-12-10 | 2010-12-01 | 日立オートモティブシステムズ株式会社 | Synchronous motor driving apparatus and method |
-
2006
- 2006-08-03 EP EP06425561A patent/EP1885054B1/en not_active Not-in-force
- 2006-08-03 DE DE602006009643T patent/DE602006009643D1/en active Active
-
2007
- 2007-08-02 US US11/833,053 patent/US7659685B2/en not_active Expired - Fee Related
Cited By (3)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| DE102013009518A1 (en) | 2013-06-06 | 2014-12-11 | Audi Ag | Motor vehicle with a fuel heater |
| CN104993765A (en) * | 2015-08-04 | 2015-10-21 | 重庆大学 | Method for estimating rotating speed of brushless direct current motor |
| RU2617586C1 (en) * | 2015-10-13 | 2017-04-25 | Борис Александрович Челдышов | Non-contact torque drive |
Also Published As
| Publication number | Publication date |
|---|---|
| US20090033259A1 (en) | 2009-02-05 |
| US7659685B2 (en) | 2010-02-09 |
| EP1885054A1 (en) | 2008-02-06 |
| DE602006009643D1 (en) | 2009-11-19 |
Similar Documents
| Publication | Publication Date | Title |
|---|---|---|
| EP1885054B1 (en) | Method of estimating the state of a system and related device for estimating position and speed of the rotor of a brushless motor | |
| US11046359B2 (en) | Steer-by-wire system and control method thereof | |
| Hoseinnezhad et al. | Calibration of resolver sensors in electromechanical braking systems: A modified recursive weighted least-squares approach | |
| CN109756169B (en) | Current sensor fault mitigation for permanent magnet DC-driven steering systems | |
| KR102558215B1 (en) | Steer by Wire System and Controlling Method Thereof | |
| CN110182253B (en) | Quadrant-type friction compensation for tire load estimation for steering systems | |
| JP5124483B2 (en) | Method and apparatus for driving a synchronous machine | |
| US20070085414A1 (en) | Estimating torque/force exerted by a load against a motor-driven actuator | |
| EP2234266A1 (en) | Motor control device and electric power steering device | |
| JP2002320398A (en) | Rotor angle detector of dc brushless motor | |
| CN110620540B (en) | Parameter learning for permanent magnet synchronous motor drives | |
| CN111656676B (en) | Control device for power conversion device and motor drive system | |
| CN111656674B (en) | Control device, control method, and motor drive system for power conversion device | |
| EP2830211A1 (en) | Control device for three-phase ac induction motor and control method for three-phase ac induction motor | |
| US9540044B2 (en) | Hand wheel angle from vehicle dynamic sensors or wheel speeds | |
| Klier et al. | Active front steering (part 1): Mathematical modeling and parameter estimation | |
| JP4655677B2 (en) | Power transmission system test apparatus and control method thereof | |
| CN114389504A (en) | Optimal torque control for multiphase synchronous motors with open circuit conditions | |
| JP2020535059A (en) | A method for driving and controlling a steering system having an electric steering assist unit | |
| Weiskircher et al. | Rack force estimation for electric power steering | |
| KR101987703B1 (en) | Steer by Wire System and Controlling Method Thereof | |
| KR101888518B1 (en) | Motor control apparatus and active roll stabilizer having the same and motor control method | |
| CN113104096A (en) | Observer design for estimating motor speed of brushed electric power steering system | |
| CN110001764B (en) | High bandwidth universal electric power steering system controller | |
| KR101962647B1 (en) | Steer by Wire System and Controlling Method Thereof |
Legal Events
| Date | Code | Title | Description |
|---|---|---|---|
| PUAI | Public reference made under article 153(3) epc to a published international application that has entered the european phase |
Free format text: ORIGINAL CODE: 0009012 |
|
| AK | Designated contracting states |
Kind code of ref document: A1 Designated state(s): AT BE BG CH CY CZ DE DK EE ES FI FR GB GR HU IE IS IT LI LT LU LV MC NL PL PT RO SE SI SK TR |
|
| AX | Request for extension of the european patent |
Extension state: AL BA HR MK YU |
|
| 17P | Request for examination filed |
Effective date: 20080729 |
|
| 17Q | First examination report despatched |
Effective date: 20080826 |
|
| AKX | Designation fees paid |
Designated state(s): DE FR GB IT |
|
| GRAP | Despatch of communication of intention to grant a patent |
Free format text: ORIGINAL CODE: EPIDOSNIGR1 |
|
| GRAS | Grant fee paid |
Free format text: ORIGINAL CODE: EPIDOSNIGR3 |
|
| GRAA | (expected) grant |
Free format text: ORIGINAL CODE: 0009210 |
|
| AK | Designated contracting states |
Kind code of ref document: B1 Designated state(s): DE FR GB IT |
|
| REG | Reference to a national code |
Ref country code: GB Ref legal event code: FG4D |
|
| REF | Corresponds to: |
Ref document number: 602006009643 Country of ref document: DE Date of ref document: 20091119 Kind code of ref document: P |
|
| RAP2 | Party data changed (patent owner data changed or rights of a patent transferred) |
Owner name: STMICROELECTRONICS SRL |
|
| PLBE | No opposition filed within time limit |
Free format text: ORIGINAL CODE: 0009261 |
|
| STAA | Information on the status of an ep patent application or granted ep patent |
Free format text: STATUS: NO OPPOSITION FILED WITHIN TIME LIMIT |
|
| 26N | No opposition filed |
Effective date: 20100708 |
|
| PG25 | Lapsed in a contracting state [announced via postgrant information from national office to epo] |
Ref country code: IT Free format text: LAPSE BECAUSE OF FAILURE TO SUBMIT A TRANSLATION OF THE DESCRIPTION OR TO PAY THE FEE WITHIN THE PRESCRIBED TIME-LIMIT Effective date: 20091007 |
|
| REG | Reference to a national code |
Ref country code: FR Ref legal event code: ST Effective date: 20110502 |
|
| PG25 | Lapsed in a contracting state [announced via postgrant information from national office to epo] |
Ref country code: FR Free format text: LAPSE BECAUSE OF NON-PAYMENT OF DUE FEES Effective date: 20100831 |
|
| PGFP | Annual fee paid to national office [announced via postgrant information from national office to epo] |
Ref country code: GB Payment date: 20110728 Year of fee payment: 6 |
|
| GBPC | Gb: european patent ceased through non-payment of renewal fee |
Effective date: 20120803 |
|
| PG25 | Lapsed in a contracting state [announced via postgrant information from national office to epo] |
Ref country code: GB Free format text: LAPSE BECAUSE OF NON-PAYMENT OF DUE FEES Effective date: 20120803 |
|
| PGFP | Annual fee paid to national office [announced via postgrant information from national office to epo] |
Ref country code: DE Payment date: 20130722 Year of fee payment: 8 |
|
| REG | Reference to a national code |
Ref country code: DE Ref legal event code: R119 Ref document number: 602006009643 Country of ref document: DE |
|
| REG | Reference to a national code |
Ref country code: DE Ref legal event code: R119 Ref document number: 602006009643 Country of ref document: DE Effective date: 20150303 |
|
| PG25 | Lapsed in a contracting state [announced via postgrant information from national office to epo] |
Ref country code: DE Free format text: LAPSE BECAUSE OF NON-PAYMENT OF DUE FEES Effective date: 20150303 |