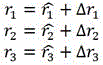CN113768541A - 一种复杂曲面超声阵列换能器阵元位置误差校正方法 - Google Patents
一种复杂曲面超声阵列换能器阵元位置误差校正方法 Download PDFInfo
- Publication number
- CN113768541A CN113768541A CN202111251637.4A CN202111251637A CN113768541A CN 113768541 A CN113768541 A CN 113768541A CN 202111251637 A CN202111251637 A CN 202111251637A CN 113768541 A CN113768541 A CN 113768541A
- Authority
- CN
- China
- Prior art keywords
- array
- error
- array element
- coordinates
- corrected
- Prior art date
- Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
- Granted
Links
- 238000000034 method Methods 0.000 title claims abstract description 33
- 238000012937 correction Methods 0.000 title claims description 29
- 238000003384 imaging method Methods 0.000 abstract description 9
- 239000013307 optical fiber Substances 0.000 description 5
- 238000003491 array Methods 0.000 description 3
- 238000003325 tomography Methods 0.000 description 3
- 238000013461 design Methods 0.000 description 2
- 238000010586 diagram Methods 0.000 description 2
- 230000009286 beneficial effect Effects 0.000 description 1
- 230000007547 defect Effects 0.000 description 1
- 230000001788 irregular Effects 0.000 description 1
- 238000005259 measurement Methods 0.000 description 1
- 238000012986 modification Methods 0.000 description 1
- 230000004048 modification Effects 0.000 description 1
- 238000012634 optical imaging Methods 0.000 description 1
- 238000010895 photoacoustic effect Methods 0.000 description 1
- 238000011160 research Methods 0.000 description 1
- 238000006467 substitution reaction Methods 0.000 description 1
- 238000002604 ultrasonography Methods 0.000 description 1
- 238000012285 ultrasound imaging Methods 0.000 description 1
Images
Classifications
-
- A—HUMAN NECESSITIES
- A61—MEDICAL OR VETERINARY SCIENCE; HYGIENE
- A61B—DIAGNOSIS; SURGERY; IDENTIFICATION
- A61B8/00—Diagnosis using ultrasonic, sonic or infrasonic waves
- A61B8/58—Testing, adjusting or calibrating the diagnostic device
-
- A—HUMAN NECESSITIES
- A61—MEDICAL OR VETERINARY SCIENCE; HYGIENE
- A61B—DIAGNOSIS; SURGERY; IDENTIFICATION
- A61B5/00—Measuring for diagnostic purposes; Identification of persons
- A61B5/0093—Detecting, measuring or recording by applying one single type of energy and measuring its conversion into another type of energy
- A61B5/0095—Detecting, measuring or recording by applying one single type of energy and measuring its conversion into another type of energy by applying light and detecting acoustic waves, i.e. photoacoustic measurements
Landscapes
- Health & Medical Sciences (AREA)
- Life Sciences & Earth Sciences (AREA)
- Physics & Mathematics (AREA)
- Surgery (AREA)
- Medical Informatics (AREA)
- Pathology (AREA)
- Veterinary Medicine (AREA)
- Engineering & Computer Science (AREA)
- Biomedical Technology (AREA)
- Heart & Thoracic Surgery (AREA)
- Public Health (AREA)
- Molecular Biology (AREA)
- Biophysics (AREA)
- Animal Behavior & Ethology (AREA)
- General Health & Medical Sciences (AREA)
- Nuclear Medicine, Radiotherapy & Molecular Imaging (AREA)
- Radiology & Medical Imaging (AREA)
- Acoustics & Sound (AREA)
- Ultra Sonic Daignosis Equipment (AREA)
Abstract
本发明公开了一种复杂曲面超声阵列换能器阵元位置误差校正方法,该方法首先将待校正位置阵元坐标作为初始值;设定误差平方和比较阈值;然后获取点声源坐标及其到待校正位置阵元的距离;最后将非线性方程组线性化;根据最小二乘法解算坐标;将误差平方和预设门限比较。本发明以最小二乘法为基础,通过迭代解算出阵列换能器中各阵元的位置坐标,利用校正后的阵元位置坐标进行超声和光声成像,可以有效解决复杂曲面超声阵列换能器因阵元位置误差导致的图像发散和伪影问题,从而得到物体高精度的重构图像。
Description
技术领域
本发明涉及超声和光声成像领域,尤其涉及一种复杂曲面超声阵列换能器阵元位置误差校正方法。
背景技术
超声层析成像(Ultrasound Computed Tomography,简称UCT)是指通过从物体外部检测到的超声波信号数据重建物体内部(横断面)信息的技术。该技术依据声波在不同介质中传播速度的差异,将多条通过介质的声波射线走时提取出来,反演出介质的声波速度空间分布图像,来精确地描述目标体的集合形态和物理特征。
光声断层成像(Photoacoustic computed tomography, 简称PACT)是指利用光声效应获取物体二维断层图像或者三维立体图像的一种新兴成像技术。该技术结合了光学成像和超声成像的优点,能够实现分辨率和对比度都较高的生物组织成像。尤其是其非入侵式和非电离式的成像特点,在生物医学领域具有重要应用价值。
超声成像和光声成像都要用到包含多个阵元的超声阵列换能器。在层析图像重建中,只有得到各个阵元的精确位置,才能得到精准的图像。但由于现有工艺条件的限制,在诸如碗型阵列、环形阵列以及柔性阵列等复杂曲面超声阵列换能器中,各阵元的实际位置与理论设计位置会存在一定的误差,阵元的位置误差会对重建图像产生严重影响,导致图像出现发散或伪影等现象。因此,研究一种阵列阵元位置误差校正方法对超声成像和光声成像具有重要的应用价值。
发明内容
本发明的目的是针对现有技术不足,提供一种复杂曲面超声阵列换能器阵元位置误差校正方法,以得到各阵元的实际位置,从而准确重构出图像。
为达到上述目的,本发明采用的技术方案是:一种复杂曲面超声阵列换能器阵元位置误差校正方法,包括以下步骤:
S1,通过圆环阵列的半径和超声阵列换能器阵元个数计算得到超声阵列换能器待校正位置阵元坐标,将该坐标作为该阵元坐标初始值;
S2,设定误差平方和比较阈值;
S3,获取外部引入的点声源坐标,并分别计算点声源坐标到步骤S1得到的超声阵列换能器待校正位置阵元的距离,得到非线性距离方程组;
S4,将步骤S3得到的非线性距离方程组线性化;
S5,根据最小二乘法解算步骤S4线性化的距离方程组,计算坐标值估计误差,得到待校正位置阵元的准确阵元坐标;
S6,将误差平方和与步骤S2设定的比较阈值进行比较:若误差平方和小于比较阈值,则停止迭代;若误差平方和大于比较阈值,则重复步骤S3~ S5进行迭代,直至误差平方和小于比较阈值。
进一步地,所述步骤S2具体为:根据阵元位置校正系统中空间坐标测量设备精度的平方和,并结合迭代收敛速度,设定误差平方和比较阈值。
进一步地,所述步骤S3具体为:获取用于阵元位置校正的三个点声源空间坐标,并通过采集到的光声信号的时延信息分别计算得到点声源到步骤S1中超声阵列换能器待校正位置阵元的距离;设待校正位置阵元的坐标为;所述三个点声源空间坐标分别到待校正位置阵元的距离可表示为如下方程组:
进一步地,所述步骤S4具体为:
因此可得到:
进一步地,所述步骤S5具体为:
可计算得到坐标值的估计误差为:
进一步地,所述步骤S6具体为:
本发明的有益效果为:本发明所提出的利用光纤诱导的光声点声源来对超声阵列换能器阵元位置误差进行校正的方法,能够准确地解算出各阵元的实际位置,将各阵元位置坐标信息带入到图像重建中,可以获得体模清晰准确的重构图像。解决复杂曲面超声阵列换能器因阵元位置误差导致的图像发散和伪影的问题。
附图说明
图1是本发明实施例中的阵元坐标解算流程;
图2是本发明实施例中的环形阵列阵元位置校正示意图;
图3是本发明实施例中的阵列校正前后各阵元到阵列圆心的距离;
图4是本发明实施例中的阵列校正前点光源重建图像;
图5是本发明实施例中的阵列校正后点光源重建图像;
图6是本发明实施例中的阵列校正前交叉发丝重建图像;
图7是本发明实施例中的阵列校正后交叉发丝重建图像。
具体实施方式
为使本申请的上述目的、特征和优点能够更加明显易懂,下面结合附图对本申请的具体实施方式做详细的说明。在下面的描述中阐述了很多具体细节以便于充分理解本申请。但是本申请能够以很多不同于在此描述的其它方式来实施,本领域技术人员可以在不违背本申请内涵的情况下做类似改进,因此本申请不受下面公开的具体实施的限制。
下面结合附图来具体描述本发明的优选实施例,其中,附图构成本申请一部分,并与本发明的实施例一起用于阐释本发明的原理,并非用于限定本发明的范围。
定位三维空间中的某一未知点,需要在空间中选取至少三个不同位置点作为已知点,分别以它们为圆心,以未知点与它们的距离作为半径画出球面,三个球面会有两个相交点。根据未知点和三个球面的几何关系,可以排除其中一个点,剩下的那个点即是需要被定位的未知点。如果考虑测量误差,可用多次迭代的最小二乘法解算未知点的坐标值,那么该模型利用多个已知点可以得到更加准确的结果。本发明基于三点定位的模型作以介绍,多点情况下的步骤与之相似,故不再赘述。
S1,通过圆环阵列的半径和超声阵列换能器阵元个数计算得到超声阵列换能器待校正位置阵元坐标,将该坐标作为该阵元坐标初始值。
S2,根据阵元位置校正系统中空间坐标测量设备精度的平方和,并结合迭代收敛速度,设定误差平方和比较阈值。
S3,获取外部引入的点声源坐标,并分别计算点声源坐标到步骤S1得到的超声阵列换能器待校正位置阵元的距离,得到非线性距离方程组;具体为:
获取用于阵元位置校正的三个点声源空间坐标,并通过采集到的光声信号的时延信息分别计算得到点声源到步骤S1中超声阵列换能器待校正位置阵元的距离;设待校正位置阵元的坐标为;所述三个点声源空间坐标分别到待校正位置阵元的距离可表示为如下方程组:
S4,将步骤S3得到的非线性距离方程组线性化;具体为:
因此可得到:
S5,根据最小二乘法解算步骤S4线性化的距离方程组,计算坐标值估计误差,得到待校正位置阵元的准确阵元坐标;具体为:
可计算得到坐标值的估计误差为:
S6,将误差平方和与步骤S2设定的比较阈值进行比较:若误差平方和小于比较阈值,即,则停止迭代;若误差平方和大于比较阈值,则重复步骤S3~S5,将步骤S5得到的坐标值估计误差用来修正和,直至误差平方和小于比较阈值。
实施例1
本发明实例1描述的是通过光纤诱导的光声点声源来校正包含512阵元的环形超声阵列换能器阵元位置误差,如图2所示。该实例1可简化为二维平面定位问题,即在平面中选取三个不同位置点作为已知点,分别以它们为圆心,以未知点与它们的距离作为半径画圆,则三个圆会相交于一点。该点即是需要被定位的未知点。如果三圆未相交于一点,因采用最小二乘法迭代计算,可求得最接近未知点的坐标估值。
针对超声阵列换能器阵元位置误差进行校正,需解算出每个阵元的实际空间位置。在其测量区域内放置一个光纤光声点声源,通过数据采集系统得到阵列各通道接收到的光声信号。上述操作至少进行三次,其中光纤光声点声源的位置各不相同。
本发明实施例1中的阵元坐标解算流程图如图1所示,包括如下步骤:
S1,通过圆环阵列的半径和超声阵列换能器阵元个数计算得到超声阵列换能器待校正位置阵元坐标,将该坐标作为该阵元坐标初始值。
S2,根据阵元位置校正系统中空间坐标测量设备精度的平方和,并结合迭代收敛速度,设定误差平方和比较阈值。
S3,获取点声源坐标及其到待校正位置阵元的距离。
根据前文叙述获取用于阵元位置校正的三个点声源空间坐标,并通过采集光声信号的时延信息计算得到点声源到待校正位置阵元的距离。设待校正位置阵元的坐标为。将三个点声源分别到待校正位置阵元的距离可表示为如下方程组:
S4,将非线性方程组线性化。
则可得到
S5,根据最小二乘法解算坐标。
可计算得到坐标值为:
S6,将误差平方和预设门限比较。
用最小二乘法计算阵元坐标需要通过多次迭代收敛后最终计算出各阵元准确的的空间坐标。若误差平方和小于比较阈值,即,则停止迭代;若误差平方和大于比较阈值,则首先将各阵元根据阵列形状计算的坐标作为初始值,重复步骤S3~S5,将步骤S5迭代得到的坐标值估计误差用来修正和,直至误差平方和小于比较阈值,即才停止迭代。
根据上述步骤不光可以校正规则的线列阵、圆环阵和平面阵中各个阵元的平面位置,还可以校正诸如碗型阵列、环形阵列以及柔性阵列等空间几何分布不规则的复杂曲面超声阵列换能器系统中各个阵元的平面位置。
阵列校正前后各阵元到阵列圆心的距离参见图3。原本设计的阵列为半径50毫米,512个阵元沿圆环均匀分布。校正后可以看出各阵元的实际位置与设计存在一定的误差。
阵列校正前后对点光源和凝胶中交叉发丝两种体模的重建图像结果参见图4至图7。其中,图4、图5分别是本发明实施例中的阵列校正前后的点光源重建图像;图6、图7是是本发明实施例中的阵列校正前后的交叉发丝重建图像。通过比较上述四幅图可以看出,在对阵列进行校正前,系统对体模的重建图像有发散和伪影现象,对阵列进行校正后,能够清晰准确地呈现体模重建图像。
综上所述,本发明所提出的利用光纤诱导的光声点声源来对超声阵列换能器阵元位置误差进行校正的方法,能够准确地解算出各阵元的实际位置,将各阵元位置坐标信息带入到图像重建中,可以获得体模清晰准确的重构图像。
以上所述,仅为本发明较佳的具体实施方式,但本发明的保护范围并不局限于此,任何熟悉本技术领域的技术人员在本发明揭露的技术范围内,可轻易想到的变化或替换,都应涵盖在本发明的保护范围之内。
Claims (6)
1.一种复杂曲面超声阵列换能器阵元位置误差校正方法,其特征在于,包括以下步骤:
S1,通过圆环阵列的半径和超声阵列换能器阵元个数计算得到超声阵列换能器待校正位置阵元坐标,将该坐标作为该阵元坐标初始值;
S2,设定误差平方和比较阈值;
S3,获取外部引入的点声源坐标,并分别计算点声源坐标到步骤S1得到的超声阵列换能器待校正位置阵元的距离,得到非线性距离方程组;
S4,将步骤S3得到的非线性距离方程组线性化;
S5,根据最小二乘法解算步骤S4线性化的距离方程组,计算坐标值估计误差,得到待校正位置阵元的准确阵元坐标;
S6,将误差平方和与步骤S2设定的比较阈值进行比较:若误差平方和小于比较阈值,则停止迭代;若误差平方和大于比较阈值,则重复步骤S3~ S5进行迭代,直至误差平方和小于比较阈值。
2.根据权利要求1所述的复杂曲面超声阵列换能器阵元位置误差校正方法,其特征在于,所述步骤S2具体为:根据阵元位置校正系统中空间坐标测量设备精度的平方和,并结合迭代收敛速度,设定误差平方和比较阈值。
Priority Applications (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| CN202111251637.4A CN113768541B (zh) | 2021-10-27 | 2021-10-27 | 一种复杂曲面超声阵列换能器阵元位置误差校正方法 |
Applications Claiming Priority (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| CN202111251637.4A CN113768541B (zh) | 2021-10-27 | 2021-10-27 | 一种复杂曲面超声阵列换能器阵元位置误差校正方法 |
Publications (2)
| Publication Number | Publication Date |
|---|---|
| CN113768541A true CN113768541A (zh) | 2021-12-10 |
| CN113768541B CN113768541B (zh) | 2024-02-13 |
Family
ID=78956707
Family Applications (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| CN202111251637.4A Active CN113768541B (zh) | 2021-10-27 | 2021-10-27 | 一种复杂曲面超声阵列换能器阵元位置误差校正方法 |
Country Status (1)
| Country | Link |
|---|---|
| CN (1) | CN113768541B (zh) |
Cited By (1)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN116482035A (zh) * | 2023-06-21 | 2023-07-25 | 之江实验室 | 一种基于柔性超声探头的光声断层成像方法及装置 |
Citations (12)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN101097256A (zh) * | 2006-06-28 | 2008-01-02 | 深圳迈瑞生物医疗电子股份有限公司 | 超声波束合成聚焦参数实时计算方法及装置 |
| CN101770022A (zh) * | 2009-12-30 | 2010-07-07 | 南京航空航天大学 | 基于遗传算法的mimo雷达阵列位置误差自校正方法 |
| CN104007413A (zh) * | 2014-04-28 | 2014-08-27 | 电子科技大学 | 考虑信源方位误差的阵列位置误差校正方法 |
| JP2015116256A (ja) * | 2013-12-17 | 2015-06-25 | 株式会社東芝 | 超音波診断装置及び超音波プローブ |
| CN105242236A (zh) * | 2015-09-28 | 2016-01-13 | 黑龙江大学 | 宽带信号超分辨测向中的阵元位置误差校正方法 |
| US20160066792A1 (en) * | 2014-09-05 | 2016-03-10 | Canon Kabushiki Kaisha | Object information acquiring apparatus |
| CN105403814A (zh) * | 2014-08-11 | 2016-03-16 | 国家电网公司 | 用于变压器局部放电源的定位方法和装置 |
| CN106501367A (zh) * | 2016-10-10 | 2017-03-15 | 清华大学 | 基于椭圆弧扫描转换的相控阵超声回波成像方法 |
| WO2017098641A1 (ja) * | 2015-12-10 | 2017-06-15 | 株式会社日立製作所 | 超音波送受信装置、および、超音波送受信方法 |
| CN106889973A (zh) * | 2015-12-17 | 2017-06-27 | 佳能株式会社 | 被检体信息获取装置及其控制方法 |
| CN107966694A (zh) * | 2017-10-24 | 2018-04-27 | 苏州佳世达电通有限公司 | 一种超声波探头的校正方法和系统 |
| CN112023283A (zh) * | 2020-08-03 | 2020-12-04 | 西安交通大学 | 基于高阶孔径自相关的环形多阵列超声被动成像方法及系统 |
-
2021
- 2021-10-27 CN CN202111251637.4A patent/CN113768541B/zh active Active
Patent Citations (12)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN101097256A (zh) * | 2006-06-28 | 2008-01-02 | 深圳迈瑞生物医疗电子股份有限公司 | 超声波束合成聚焦参数实时计算方法及装置 |
| CN101770022A (zh) * | 2009-12-30 | 2010-07-07 | 南京航空航天大学 | 基于遗传算法的mimo雷达阵列位置误差自校正方法 |
| JP2015116256A (ja) * | 2013-12-17 | 2015-06-25 | 株式会社東芝 | 超音波診断装置及び超音波プローブ |
| CN104007413A (zh) * | 2014-04-28 | 2014-08-27 | 电子科技大学 | 考虑信源方位误差的阵列位置误差校正方法 |
| CN105403814A (zh) * | 2014-08-11 | 2016-03-16 | 国家电网公司 | 用于变压器局部放电源的定位方法和装置 |
| US20160066792A1 (en) * | 2014-09-05 | 2016-03-10 | Canon Kabushiki Kaisha | Object information acquiring apparatus |
| CN105242236A (zh) * | 2015-09-28 | 2016-01-13 | 黑龙江大学 | 宽带信号超分辨测向中的阵元位置误差校正方法 |
| WO2017098641A1 (ja) * | 2015-12-10 | 2017-06-15 | 株式会社日立製作所 | 超音波送受信装置、および、超音波送受信方法 |
| CN106889973A (zh) * | 2015-12-17 | 2017-06-27 | 佳能株式会社 | 被检体信息获取装置及其控制方法 |
| CN106501367A (zh) * | 2016-10-10 | 2017-03-15 | 清华大学 | 基于椭圆弧扫描转换的相控阵超声回波成像方法 |
| CN107966694A (zh) * | 2017-10-24 | 2018-04-27 | 苏州佳世达电通有限公司 | 一种超声波探头的校正方法和系统 |
| CN112023283A (zh) * | 2020-08-03 | 2020-12-04 | 西安交通大学 | 基于高阶孔径自相关的环形多阵列超声被动成像方法及系统 |
Non-Patent Citations (2)
| Title |
|---|
| 任翠霞;王珍;段翔;刘红明;何子述;: "考虑信源方位误差的阵元位置误差校正", 雷达科学与技术, no. 04 * |
| 王鼎;林四川;李长胜;: "一种新的阵元位置误差有源校正算法", 雷达科学与技术, no. 03 * |
Cited By (2)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN116482035A (zh) * | 2023-06-21 | 2023-07-25 | 之江实验室 | 一种基于柔性超声探头的光声断层成像方法及装置 |
| CN116482035B (zh) * | 2023-06-21 | 2023-11-17 | 之江实验室 | 一种基于柔性超声探头的光声断层成像方法及装置 |
Also Published As
| Publication number | Publication date |
|---|---|
| CN113768541B (zh) | 2024-02-13 |
Similar Documents
| Publication | Publication Date | Title |
|---|---|---|
| King et al. | Evaluation of in vitro measurement accuracy of a three‐dimensional ultrasound scanner. | |
| CN107367229B (zh) | 自由双目立体视觉转轴参数标定方法 | |
| Hsu et al. | Real-time freehand 3D ultrasound calibration | |
| Noda et al. | Shape estimation algorithm for ultrasound imaging by flexible array transducer | |
| CN105023282A (zh) | 一种基于压缩感知的稀疏投影超声ct图像重建方法 | |
| CN113768541B (zh) | 一种复杂曲面超声阵列换能器阵元位置误差校正方法 | |
| Noda et al. | Ultrasound imaging with a flexible probe based on element array geometry estimation using deep neural network | |
| Koch et al. | An ultrasound tomography system with polyvinyl alcohol (PVA) moldings for coupling: In vivo results for 3-D pulse-echo imaging of the female breast | |
| Merdes et al. | Locating a catheter transducer in a three-dimensional ultrasound imaging field | |
| Bergmeir et al. | Comparing calibration approaches for 3D ultrasound probes | |
| Omidvar et al. | An intrinsic shape estimation algorithm for flexible ultrasound probes intended for clinical applications | |
| Omidvar et al. | Shape estimation of flexible ultrasound arrays using spatial coherence: A preliminary study | |
| Harris et al. | Performance of ultrasound based measurement of 3D displacement using a curvilinear probe for organ motion tracking | |
| Bald et al. | Automatic localization of an ultrasound probe with the help of magnetic sensors | |
| BrendelP et al. | A simple and accurate calibration method for 3D freehand ultrasound | |
| China et al. | FLEX: FLexible transducer with EXternal tracking for ultrasound imaging with patient-specific geometry estimation | |
| CN109946388B (zh) | 基于统计逆的电学/超声双模态内含物边界重建方法 | |
| CN104899902B (zh) | 一种血管内光声二维图像的重建方法 | |
| Wein et al. | Image-based method for in-vivo freehand ultrasound calibration | |
| Meza et al. | A low-cost multi-modal medical imaging system with fringe projection profilometry and 3D freehand ultrasound | |
| Abeysekera et al. | Calibration for position tracking of swept motor 3-d ultrasound | |
| Filipik et al. | Time-of-flight based calibration of an ultrasonic computed tomography system | |
| CN106645396A (zh) | 一种气液两相流含气率测量方法 | |
| Jintamethasawat et al. | Error analysis of speed of sound reconstruction in ultrasound limited angle transmission tomography | |
| Bezek et al. | Global speed-of-sound prediction using transmission geometry |
Legal Events
| Date | Code | Title | Description |
|---|---|---|---|
| PB01 | Publication | ||
| PB01 | Publication | ||
| SE01 | Entry into force of request for substantive examination | ||
| SE01 | Entry into force of request for substantive examination | ||
| GR01 | Patent grant | ||
| GR01 | Patent grant |