CN111199124A - Method for calculating no-load electromagnetic excitation force wave of surface-mounted permanent magnet synchronous motor - Google Patents
Method for calculating no-load electromagnetic excitation force wave of surface-mounted permanent magnet synchronous motor Download PDFInfo
- Publication number
- CN111199124A CN111199124A CN202010044043.5A CN202010044043A CN111199124A CN 111199124 A CN111199124 A CN 111199124A CN 202010044043 A CN202010044043 A CN 202010044043A CN 111199124 A CN111199124 A CN 111199124A
- Authority
- CN
- China
- Prior art keywords
- air gap
- permanent magnet
- force
- magnetic conductance
- magnetomotive force
- Prior art date
- Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
- Pending
Links
Images
Classifications
-
- H—ELECTRICITY
- H02—GENERATION; CONVERSION OR DISTRIBUTION OF ELECTRIC POWER
- H02K—DYNAMO-ELECTRIC MACHINES
- H02K21/00—Synchronous motors having permanent magnets; Synchronous generators having permanent magnets
- H02K21/02—Details
- H02K21/021—Means for mechanical adjustment of the excitation flux
- H02K21/022—Means for mechanical adjustment of the excitation flux by modifying the relative position between field and armature, e.g. between rotor and stator
- H02K21/025—Means for mechanical adjustment of the excitation flux by modifying the relative position between field and armature, e.g. between rotor and stator by varying the thickness of the air gap between field and armature
-
- H—ELECTRICITY
- H02—GENERATION; CONVERSION OR DISTRIBUTION OF ELECTRIC POWER
- H02K—DYNAMO-ELECTRIC MACHINES
- H02K21/00—Synchronous motors having permanent magnets; Synchronous generators having permanent magnets
- H02K21/12—Synchronous motors having permanent magnets; Synchronous generators having permanent magnets with stationary armatures and rotating magnets
- H02K21/14—Synchronous motors having permanent magnets; Synchronous generators having permanent magnets with stationary armatures and rotating magnets with magnets rotating within the armatures
Landscapes
- Engineering & Computer Science (AREA)
- Power Engineering (AREA)
- Iron Core Of Rotating Electric Machines (AREA)
- Permanent Field Magnets Of Synchronous Machinery (AREA)
Abstract
The invention provides a method for calculating a surface-mounted permanent magnet synchronous motor no-load electromagnetic excitation force wave, which starts from permanent magnet magnetomotive force and air gap magnetic conductance, respectively simulates finite elements of a structure model with or without tooth grooves of a motor based on a two-dimensional static field to obtain the permanent magnet magnetomotive force and air gap magnetic conductance distribution, performs Fourier decomposition on the permanent magnet magnetomotive force and air gap magnetic conductance distribution, and calculates to obtain an no-load magnetomotive force and air gap magnetic conductance expression including amplitude, frequency and phase; according to the Maxwell tensor method, the magnetomotive force and the air gap magnetic conductance are substituted into the electromagnetic force density expression to obtain all force wave amplitudes under different frequencies and different orders, so that the calculation time is greatly shortened; meanwhile, the influence of the slot size and the iron core saturation degree on the air gap magnetic conductance and the permanent magnet magnetomotive force can be accurately considered, and the amplitude of each force wave under different frequencies and different orders can be accurately obtained.
Description
Technical Field
The invention belongs to the field of calculation of a no-load electromagnetic excitation force wave of a permanent magnet synchronous motor, and relates to a method for calculating a no-load electromagnetic excitation force wave of a surface-mounted permanent magnet synchronous motor.
Background
The statements in this section merely provide background information related to the present disclosure and may not necessarily constitute prior art.
In recent years, the permanent magnet synchronous motor has the advantages of simple structure, high efficiency, high power density and the like, and has wide application prospect in various fields. With the increasing of the power grade of the motor and the increasing of the performance of the motor, the low-noise and high-performance permanent magnet synchronous motor is more and more favored by people, the vibration and noise level of the motor becomes an important index for measuring the performance of the motor, especially in high-speed and high-power occasions with high requirements on the performance of the motor, the vibration and noise problems of the motor directly affect the operation stability and the working reliability of the whole system, and the weakening of the electromagnetic vibration and the noise of the motor becomes one of the problems to be solved urgently.
As a main source of motor vibration and noise, the electromagnetic vibration of the motor is excited by an electromagnetic excitation force wave which is generated by the action of a motor air gap magnetic field on a motor stator core and changes along with time and space, so that the accurate analysis and calculation of the electromagnetic excitation force wave become the key of the motor electromagnetic vibration analysis.
At present, the following three methods are mainly adopted for calculating and analyzing the electromagnetic excitation force wave: magnetomotive force-magnetic conductance method, magnetic field analysis method, and finite element method. The magnetomotive force-magnetic conductance method can conveniently give the frequency, the rotating speed and the phase of electromagnetic excitation force waves, but the accurate value of the air gap magnetic conductance is difficult to obtain, and the application of the air gap magnetic conductance is limited to a certain extent, so that the method can conveniently carry out qualitative analysis, but cannot carry out quantitative accurate calculation; although the magnetic field analysis method can conveniently calculate the air gap magnetic field and the vibration force wave, when the saturation of the iron core and the complex shape of the tooth socket are considered, the calculation period is prolonged and the calculation precision is reduced; the finite element method can consider the influence of various factors such as saturation and the like, can accurately calculate the air gap magnetic field and the electromagnetic force density, but is difficult to distinguish excitation force waves with different sources, cannot obtain detailed relation between each order of force waves and structural parameters, and is not beneficial to weakening of electromagnetic vibration.
The three methods for calculating the electromagnetic force have advantages and disadvantages, can not accurately determine a complete expression of each electromagnetic force wave including amplitude, rotating speed, frequency and phase, can not accurately evaluate the influence of a single electromagnetic force wave on vibration, can not accurately evaluate the overall effect of each electromagnetic force wave on vibration, and is not beneficial to analysis and attenuation of electromagnetic vibration.
Disclosure of Invention
The invention provides a method for calculating a no-load electromagnetic excitation force wave of a surface-mounted permanent magnet synchronous motor, which considers the influence of a complex structure and iron core saturation of the motor, accurately determines a complete expression of radial electromagnetic force waves of each order including amplitude, rotating speed, frequency and phase, and lays a theoretical foundation for calculation, analysis, evaluation and weakening of subsequent electromagnetic vibration.
According to some embodiments, the following technical scheme is adopted in the disclosure:
a method for calculating a surface-mounted permanent magnet synchronous motor no-load electromagnetic excitation force wave comprises the following steps:
starting from the magnetomotive force of the permanent magnet and the air gap magnetic conductance, respectively carrying out finite element simulation on a structural model with or without a tooth groove of the motor based on a two-dimensional static field to obtain the magnetomotive force of the permanent magnet and the air gap magnetic conductance distribution, carrying out Fourier decomposition on the magnetomotive force and the air gap magnetic conductance distribution, and calculating to obtain an expression of the air gap magnetic conductance and the no-load magnetomotive force including the amplitude, the frequency and the phase;
according to the Maxwell tensor method, the results of all components of the magnetomotive force and the air gap permeance are substituted into an electromagnetic force density expression to obtain all force wave amplitudes under different frequencies and different orders.
As an alternative embodiment, the influence of core saturation and the complex shape of the slot is taken into account when determining the air gap permeance.
As an alternative embodiment, the permanent magnet magnetomotive force and the air gap permeance are solved by a Maxwell 2D static field solver.
As an alternative embodiment, by determining the sources of excitation force waves with different orders and different frequencies, detailed relationships between the force waves of each order and the structural parameters are obtained.
As an alternative embodiment, higher harmonic components of the magnetomotive force and the air gap permeance are ignored in the calculation.
As an alternative embodiment, in the calculation process, the frequency included in the unloaded electromagnetic excitation force wave is an even multiple of the fundamental frequency, the minimum frequency is 2f, the order is an integer multiple of the number of poles, and the minimum order is 2 p.
The method is suitable for any surface-mounted permanent magnet synchronous motor and is not limited by factors such as the shape, the material and the magnetizing direction of a permanent magnet.
The electromagnetic excitation force wave content in the surface-mounted permanent magnet synchronous motor is accurately, systematically and completely analyzed and calculated, the generation mechanism and the change rule are summarized, the mapping relation between the structural parameters of the motor and the electromagnetic excitation force waves of each order is obtained, and a solid theoretical foundation is laid for weakening the electromagnetic excitation force waves and improving the vibration and noise performance of the motor.
A computing system for a surface-mounted permanent magnet synchronous motor no-load electromagnetic excitation force wave comprises:
the finite element simulation module is configured to start from the permanent magnet magnetomotive force and the air gap magnetic conductance, respectively perform finite element simulation on a structure model with or without tooth grooves of the motor based on a two-dimensional static field to obtain the permanent magnet magnetomotive force and the air gap magnetic conductance distribution, perform Fourier decomposition on the permanent magnet magnetomotive force and the air gap magnetic conductance distribution, and calculate to obtain an no-load magnetomotive force and air gap magnetic conductance expression including the amplitude, the frequency and the phase;
and the calculation module is configured to substitute the results of the magnetomotive force and the magnetic conductance of the air gap into an electromagnetic force density expression according to a Maxwell tensor method to obtain all the force wave amplitudes under different frequencies and different orders.
A computer readable storage medium stores a plurality of instructions, wherein the instructions are suitable for being loaded by a processor of a terminal device and executing the calculation method of the no-load electromagnetic excitation force wave of the surface-mounted permanent magnet synchronous motor.
A terminal device comprising a processor and a computer readable storage medium, the processor being configured to implement instructions; the computer-readable storage medium is used for storing a plurality of instructions, and the instructions are suitable for being loaded by a processor and executing the calculation method of the no-load electromagnetic excitation force wave of the surface-mounted permanent magnet synchronous motor.
Compared with the prior art, the beneficial effect of this disclosure is:
the solution of the magnetomotive force of the permanent magnet and the magnetic conductance of the air gap can be completed only by using a two-dimensional static field solver, so that the calculation time is greatly shortened; meanwhile, the influence of the slot size and the iron core saturation degree on the air gap magnetic conductance and the permanent magnet magnetomotive force can be accurately considered, and the amplitude of each force wave under different frequencies and different orders can be accurately obtained. The method provides convenience for the rapid and accurate calculation of each order of electromagnetic excitation force wave and the weakening of the subsequent specific order of electromagnetic excitation force wave, and lays a foundation for the weakening of the electromagnetic vibration of the permanent magnet synchronous motor.
Drawings
The accompanying drawings, which are included to provide a further understanding of the disclosure, illustrate embodiments of the disclosure and together with the description serve to explain the disclosure and are not to limit the disclosure.
FIG. 1 is a diagram illustrating the calculation results of the present embodiment;
FIG. 2 is a schematic diagram of the relative positions of the permanent magnet and the armature;
FIG. 3 is a schematic view of a gearless slot configuration of the motor;
FIG. 4 is a schematic view of a cogging configuration of the motor;
FIG. 5 is a schematic diagram of a finite element simulation model of a 6-pole 36-slot SPMSM;
FIG. 6 is a model schematic of a toothless slot structure of the motor;
FIG. 7 is a schematic view of the distribution of air gap flux density under one magnetic pole along the circumference;
FIG. 8(a) (b) is a schematic diagram of the distribution of the magnetomotive force of the permanent magnet in the circumferential direction and its harmonic content for one period;
FIG. 9 is a model schematic of a cogging configuration of an electric machine;
FIG. 10(a) and (b) are schematic diagrams showing the air gap flux density and the air gap effective length along the circumference under one pitch.
The specific implementation mode is as follows:
the present disclosure is further described with reference to the following drawings and examples.
It should be noted that the following detailed description is exemplary and is intended to provide further explanation of the disclosure. Unless defined otherwise, all technical and scientific terms used herein have the same meaning as commonly understood by one of ordinary skill in the art to which this disclosure belongs.
It is noted that the terminology used herein is for the purpose of describing particular embodiments only and is not intended to be limiting of example embodiments according to the present disclosure. As used herein, the singular forms "a", "an" and "the" are intended to include the plural forms as well, and it should be understood that when the terms "comprises" and/or "comprising" are used in this specification, they specify the presence of stated features, steps, operations, devices, components, and/or combinations thereof, unless the context clearly indicates otherwise.
As mentioned in the background art, with the increasing of the power level of the motor and the increasing of the performance of the motor, the low-noise and high-performance permanent magnet synchronous motor is more and more favored by people, the vibration and noise level of the motor becomes an important index for measuring the performance of the motor, especially in high-speed and high-power occasions with high requirements on the performance of the motor, the vibration and noise problems of the motor will directly affect the operation stability and the working reliability of the whole system, and weakening the electromagnetic vibration and noise of the motor becomes one of the problems to be solved urgently.
As a main source of motor vibration and noise, the electromagnetic vibration of the motor is excited by an electromagnetic excitation force wave which is generated by the action of a motor air gap magnetic field on a motor stator core and changes along with time and space, so that the accurate calculation of the electromagnetic excitation force wave becomes the key of the electromagnetic vibration analysis of the motor. Aiming at the defects of a finite element method and a magnetomotive force-magnetic conductance method in electromagnetic excitation force wave calculation, the invention provides a quick and accurate calculation method of a surface-mounted permanent magnet synchronous motor no-load electromagnetic excitation force wave, which comprises the following steps:
(1) simulating a tooth-groove-free structure model of the motor based on a two-dimensional static field to obtain the magnetomotive force distribution of the permanent magnet;
(2) simulating a toothed groove structure model of the motor based on a two-dimensional static field, and processing air gap flux density distribution in one tooth pitch to obtain air gap flux guide distribution;
(3) fourier decomposition is carried out on the obtained permanent magnet magnetomotive force and the air gap magnetic conductance to obtain no-load magnetomotive force and air gap magnetic conductance expressions including amplitude, frequency and phase.
(4) According to the Maxwell tensile method, the results of all components of the magnetomotive force and the air gap permeance are substituted into an electromagnetic force density expression, and all force wave amplitudes under different frequencies and different orders are accurately obtained.
(5) The accuracy of the rapid and accurate calculation method is verified by a finite element method.
For the sake of analysis, it is specified that the relative position angle α between the permanent magnet and the armature in the motor is the angle between the center line of a given tooth and the center line of the permanent magnet pole, and θ is 0 ° and is set on the center line of the pole, as shown in fig. 2.
In the formula, mu0For air permeability, δ (θ, α) is the distribution of the effective air gap length along the circumference when the relative position of the stator and the rotor changes, and is related to the stator tooth slot distribution and the structural parameters thereof, and F (θ) is the air gap equivalent magnetomotive force.
Fig. 3 is a schematic view of a toothless slot structure of the motor, in which both the inner surface of the stator and the outer surface of the rotor are smooth planes. In the figure F1(theta) is the distribution of the magnetic pressure drop of the whole air gap along the circumferential direction, namely the magnetomotive force of the permanent magnet; fδ(theta) distribution of magnetomotive force in a uniform air gap excluding the permanent magnet in the circumferential direction, B0(theta) is the distribution of air gap flux density along the circumferential direction, delta is the air gap length, hm (theta) is the thickness of the permanent magnet in the magnetizing direction, and for the surface-mounted permanent magnet synchronous motor, [ delta + hm (theta)]Is a constant.
When the stator has no tooth space, the air gap is uniform, and delta is a constant, and the air gap magnetic voltage drop can be calculated by the following formula:
then Fδ(θ) can be expressed as:
therefore, the air gap flux density B in the motor model with the tooth-free groove structure is obtained0(theta) is distributed along the circumferential direction and substituted into formula (2) to obtain permanent magnet magnetomotive force F1(theta). Meanwhile, the permanent magnet magnetomotive force can be expressed as:
where ω is the electrical angular velocity of the rotor rotation, p is the motor pole pair number, FμThe amplitude of the mu-order harmonic of the rotary magnetomotive force can be obtained by calculating the permanent magnet magnetomotive force F1(θ) is obtained by performing fourier decomposition.
FIG. 4 is a schematic view of a cogging configuration of the motor, where (- π/z, π/z) is a pitch within the permanent magnet polar arc range, z is the number of stator slots, and F is the constant magnetomotive force generated by the permanent magnet acting across the air gap; fδtAir gap magnetic voltage drop at the motor tooth part just facing the permanent magnet, BδtThe magnetic density of the air gap on the surface of the motor tooth opposite to the permanent magnet.
The air gap corresponding to the motor tooth part is a uniform air gap, namely delta is a constant, so BδtAnd keeping the magnetic voltage drop of the air gap corresponding to the motor tooth part at the moment basically unchanged, wherein the magnetic voltage drop of the air gap corresponding to the motor tooth part can be expressed as follows:
in the whole tooth pitch range, the outer surface of the rotor is approximately equal magnetic potential surface, and the air gap magnetomotive force of each air gap is considered to be Fδt。
Due to tooth groovesThe air gap is not uniform in the whole circumference, and the effective length delta of the air gap at one pitch is determined according to the formula (1)r(θ, α) can be expressed as:
in the formula, Bδt(theta, α) is the distribution of the air gap flux density along the circumference in a pitch range, when the unit area of the no-load air gap flux guide lambdar(θ, α) can be obtained according to the following equation:
for a surface-mounted permanent magnet synchronous motor, the stator armature has a slot on its inner surface to embed a winding, and the air-gap flux guide can be expressed as
In the formula, Λr0Being a constant component of the permeance of the air gap, ΛrmThe amplitude of m-th harmonic of the air gap permeance can be obtained by the determined air gap permeance Lambdar(θ, α) is obtained by performing fourier decomposition.
In order to verify the calculation accuracy of the permanent magnet magnetomotive force and the no-load air gap permeance, a 6-pole 36-slot SPMSM motor is taken as an example in the section for analysis, the main structural dimension parameters are shown in Table 1, and a finite element simulation model is shown in FIG. 5.
Table 16 pole 36 slot SPMSM major structure dimension parameters
Fig. 6 shows a tooth-groove-free structure model of a motor under one magnetic pole, which is subjected to simulation analysis by a Maxwell 2D static field solver to obtain an air gap flux density B under one magnetic pole0The distribution in the circumferential direction of (θ) is shown in fig. 7. Substituting the calculation result of the air gap flux density into the formula (2) according to the period of the motor magnetic fieldAnd (5) obtaining the magnetomotive force of the permanent magnet through the characteristics and the symmetry. Distribution F of permanent magnet magnetomotive force in circumferential direction under one period1And (theta) and the harmonic content thereof are shown in FIG. 8, so that a complete permanent magnet magnetomotive force expression including amplitude and frequency can be quickly and accurately obtained.
FIG. 9 shows a cogging structure model of a motor under one magnetic pole, which is subjected to simulation analysis by a Maxwell 2D static field solver to obtain an air gap flux density B at an air gap midpoint Mδt0.849T, is substituted into the formula (5), and the air gap magnetomotive force F in the whole tooth pitch range is obtainedδtIs 3041.332A. Meanwhile, the air gap magnetic density B under one tooth pitch which is opposite to the magnetic poleδt(θ, α) distribution along the circumference as shown in FIG. 10(a), the effective air gap length δ at one pitch can be obtained according to equation (6)r(θ, α) As shown in FIG. 10(b), the unloaded air gap permeance Λ can be obtainedr(theta, α) Fourier decomposition is carried out on the magnetic flux, so that the constant component of the air gap magnetic conductance and the amplitude of the harmonic component of the air gap magnetic conductance are obtained as shown in the table 2, and the complete air gap magnetic conductance expression including the amplitude and the frequency can be accurately obtained.
TABLE 2 amplitude of the constant component of the air gap permeance and its harmonic component
According to maxwell's tensor, the radial electromagnetic force density acting on the inner surface of the stator core of the motor can be expressed as:
in the formula, Bn(theta, α) is the radial component of the air gap flux density, the expression of the permanent magnet magnetomotive force and the no-load air gap permeance is substituted into formula (9), and the expression of the obtained no-load electromagnetic excitation force wave is as follows:
the above formula was collated to obtain the no-load electromagnetic wave content shown in table 3. According to different sources of each component of the no-load electromagnetic excitation force wave, the method can be divided into three categories: the first type is generated by the square of the airgap flux density of the time-based wave without considering the tooth harmonic component caused by slotting; the second type results from the tooth harmonic air gap flux density squared when considering the tooth harmonic components caused by slotting; the third type is generated by the interaction of the fundamental and tooth harmonic air gap flux densities. As can be seen from the table, the frequency included in the no-load electromagnetic excitation force wave is an even number of times of the fundamental frequency, the minimum frequency is 2f, the order is an integer multiple of the number of poles, and the minimum order is 2 p.
TABLE 3 No-load electromagnetic wave content
The generation mechanisms of the force waves of all orders are arranged to obtain main low-order unloaded electromagnetic force wave sources as shown in the table 4 (the data in the table are in an a/b form, wherein a represents the force wave order, and b represents the multiple of the force wave frequency relative to the fundamental frequency). Because the high-order harmonic component of the air gap magnetic conductance and the higher-order magnetomotive force harmonic component act to generate the low-order electromagnetic excitation force wave, and the amplitude of the low-order electromagnetic excitation force wave is small, the table only lists the action results of the low-order magnetomotive force harmonic wave with the higher amplitude and the constant component and the low-order harmonic component of the air gap magnetic conductance. The parenthesized item is the action result of low-order magnetomotive force harmonic and low-order harmonic component of air gap magnetic conductance, and the negative sign indicates that the turning direction of the parenthesized item is opposite to that of the permanent magnet fundamental wave magnetic field; the unbracketed phase is the result of the interaction of the low order magnetomotive force harmonics with the constant component of the air gap permeance.
TABLE 4 Main Low-order No-load electromagnetic force wave sources
According to the results summarized in tables 3 and 4, the amplitude of the fundamental frequency wave of 6 th order and 2 times can be expressed as:
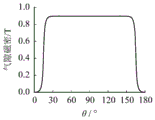
substituting the calculation results of the permanent magnet magnetomotive force and each component of the no-load air gap permeance into the formula to obtain the 6 th order/2 times fundamental frequency force wave with the amplitude of 93.18kN/m2. Meanwhile, finite element software is used for solving the motor no-load electromagnetic excitation force wave to obtain a 6-order/2-time fundamental frequency force wave with the amplitude of 95.42kN/m2. As can be seen from the calculation results, neglecting higher harmonic components of magnetomotive force and air gap permeance makes the calculation results smaller, but still has quite high accuracy. Finally, the radial force density amplitudes at different frequencies and different orders are obtained as shown in fig. 1.
As will be appreciated by one skilled in the art, embodiments of the present disclosure may be provided as a method, system, or computer program product. Accordingly, the present disclosure may take the form of an entirely hardware embodiment, an entirely software embodiment or an embodiment combining software and hardware aspects. Furthermore, the present disclosure may take the form of a computer program product embodied on one or more computer-usable storage media (including, but not limited to, disk storage, CD-ROM, optical storage, and so forth) having computer-usable program code embodied therein.
The present disclosure is described with reference to flowchart illustrations and/or block diagrams of methods, apparatus (systems), and computer program products according to embodiments of the disclosure. It will be understood that each flow and/or block of the flow diagrams and/or block diagrams, and combinations of flows and/or blocks in the flow diagrams and/or block diagrams, can be implemented by computer program instructions. These computer program instructions may be provided to a processor of a general purpose computer, special purpose computer, embedded processor, or other programmable data processing apparatus to produce a machine, such that the instructions, which execute via the processor of the computer or other programmable data processing apparatus, create means for implementing the functions specified in the flowchart flow or flows and/or block diagram block or blocks.
These computer program instructions may also be stored in a computer-readable memory that can direct a computer or other programmable data processing apparatus to function in a particular manner, such that the instructions stored in the computer-readable memory produce an article of manufacture including instruction means which implement the function specified in the flowchart flow or flows and/or block diagram block or blocks.
These computer program instructions may also be loaded onto a computer or other programmable data processing apparatus to cause a series of operational steps to be performed on the computer or other programmable apparatus to produce a computer implemented process such that the instructions which execute on the computer or other programmable apparatus provide steps for implementing the functions specified in the flowchart flow or flows and/or block diagram block or blocks.
The above description is only a preferred embodiment of the present disclosure and is not intended to limit the present disclosure, and various modifications and changes may be made to the present disclosure by those skilled in the art. Any modification, equivalent replacement, improvement and the like made within the spirit and principle of the present disclosure should be included in the protection scope of the present disclosure.
Although the present disclosure has been described with reference to specific embodiments, it should be understood that the scope of the present disclosure is not limited thereto, and those skilled in the art will appreciate that various modifications and changes can be made without departing from the spirit and scope of the present disclosure.
Claims (9)
1. A method for calculating a surface-mounted permanent magnet synchronous motor no-load electromagnetic excitation force wave is characterized by comprising the following steps: the method comprises the following steps:
starting from the magnetomotive force of the permanent magnet and the air gap magnetic conductance, respectively carrying out finite element simulation on a structural model with or without a tooth groove of the motor based on a two-dimensional static field to obtain the magnetomotive force of the permanent magnet and the air gap magnetic conductance distribution, carrying out Fourier decomposition on the magnetomotive force and the air gap magnetic conductance distribution, and calculating to obtain an expression of the air gap magnetic conductance and the no-load magnetomotive force including the amplitude, the frequency and the phase;
according to the Maxwell tensor method, the results of all components of the magnetomotive force and the air gap permeance are substituted into an electromagnetic force density expression to obtain all force wave amplitudes under different frequencies and different orders.
2. The method for calculating the no-load electromagnetic excitation force wave of the surface-mounted permanent magnet synchronous motor as claimed in claim 1, wherein the method comprises the following steps: the effect of core saturation and the complex shape of the tooth slots are taken into account when determining the air gap permeance.
3. The method for calculating the no-load electromagnetic excitation force wave of the surface-mounted permanent magnet synchronous motor as claimed in claim 1, wherein the method comprises the following steps: and solving the magnetomotive force of the permanent magnet and the magnetic conductance of the air gap by a Maxwell 2D static field solver.
4. The method for calculating the no-load electromagnetic excitation force wave of the surface-mounted permanent magnet synchronous motor as claimed in claim 1, wherein the method comprises the following steps: and obtaining detailed relations between the force waves of all orders and the structural parameters by determining the sources of the excitation force waves of different orders and different frequencies.
5. The method for calculating the no-load electromagnetic excitation force wave of the surface-mounted permanent magnet synchronous motor as claimed in claim 1, wherein the method comprises the following steps: higher harmonic components of the magnetomotive force and the air gap permeance are ignored in the calculation process.
6. The method for calculating the no-load electromagnetic excitation force wave of the surface-mounted permanent magnet synchronous motor as claimed in claim 1, wherein the method comprises the following steps: in the calculation process, the frequency contained in the no-load electromagnetic excitation force wave is even multiple of the fundamental frequency, the minimum frequency is 2f, the order is integral multiple of the pole number, and the minimum order is 2 p.
7. A computing system of surface-mounted permanent magnet synchronous motor no-load electromagnetic excitation force waves is characterized in that: the method comprises the following steps:
the finite element simulation module is configured to start from the permanent magnet magnetomotive force and the air gap magnetic conductance, respectively perform finite element simulation on a structure model with or without tooth grooves of the motor based on a two-dimensional static field to obtain the permanent magnet magnetomotive force and the air gap magnetic conductance distribution, perform Fourier decomposition on the permanent magnet magnetomotive force and the air gap magnetic conductance distribution, and calculate to obtain an no-load magnetomotive force and air gap magnetic conductance expression including the amplitude, the frequency and the phase;
and the calculation module is configured to substitute the results of the magnetomotive force and the magnetic conductance of the air gap into an electromagnetic force density expression according to a Maxwell tensor method to obtain all the force wave amplitudes under different frequencies and different orders.
8. A computer-readable storage medium characterized by: the method comprises the steps of storing a plurality of instructions, wherein the instructions are suitable for being loaded by a processor of a terminal device and executing the method for calculating the no-load electromagnetic excitation force wave of the surface-mounted permanent magnet synchronous motor according to any one of claims 1-6.
9. A terminal device is characterized in that: the system comprises a processor and a computer readable storage medium, wherein the processor is used for realizing instructions; the computer readable storage medium is used for storing a plurality of instructions, and the instructions are suitable for being loaded by a processor and executing the method for calculating the no-load electromagnetic excitation force wave of the surface-mounted permanent magnet synchronous motor according to any one of claims 1-6.
Priority Applications (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| CN202010044043.5A CN111199124A (en) | 2020-01-15 | 2020-01-15 | Method for calculating no-load electromagnetic excitation force wave of surface-mounted permanent magnet synchronous motor |
Applications Claiming Priority (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| CN202010044043.5A CN111199124A (en) | 2020-01-15 | 2020-01-15 | Method for calculating no-load electromagnetic excitation force wave of surface-mounted permanent magnet synchronous motor |
Publications (1)
| Publication Number | Publication Date |
|---|---|
| CN111199124A true CN111199124A (en) | 2020-05-26 |
Family
ID=70747593
Family Applications (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| CN202010044043.5A Pending CN111199124A (en) | 2020-01-15 | 2020-01-15 | Method for calculating no-load electromagnetic excitation force wave of surface-mounted permanent magnet synchronous motor |
Country Status (1)
| Country | Link |
|---|---|
| CN (1) | CN111199124A (en) |
Cited By (4)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN112069709A (en) * | 2020-09-04 | 2020-12-11 | 天津大学 | Motor electromagnetic vibration rapid calculation method considering stator tooth modulation effect |
| CN112468051A (en) * | 2020-11-13 | 2021-03-09 | 中国人民解放军海军工程大学 | Multiphase permanent magnet motor high-frequency vibration rapid analysis method and suppression strategy thereof |
| CN112531941A (en) * | 2020-12-25 | 2021-03-19 | 合肥工业大学 | Method for optimizing Halbach array surface plug-in permanent magnet motor |
| CN114157198A (en) * | 2021-11-02 | 2022-03-08 | 河海大学 | Rapid calculation method for electromagnetic excitation force of permanent magnet synchronous motor stator under power supply of PWM inverter |
Citations (4)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN108563912A (en) * | 2018-05-11 | 2018-09-21 | 北京理工大学 | A kind of analytic method of durface mounted permanent magnet synchronous motor air-gap field |
| CN109508480A (en) * | 2018-10-23 | 2019-03-22 | 华中科技大学 | A kind of construction low-frequency harmonics electric current calculates the semi-analytic method of motor high frequency electromagnetic force |
| US20190222160A1 (en) * | 2016-09-05 | 2019-07-18 | Hitachi Automotive Systems, Ltd. | Control Method and Control Device for Rotary Electric Motor, and Rotary Electric Motor Drive System |
| CN110233590A (en) * | 2019-06-18 | 2019-09-13 | 北京理工大学 | A kind of new-energy automobile permanent magnet synchronous motor noise control method based on harmonic injection |
-
2020
- 2020-01-15 CN CN202010044043.5A patent/CN111199124A/en active Pending
Patent Citations (4)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US20190222160A1 (en) * | 2016-09-05 | 2019-07-18 | Hitachi Automotive Systems, Ltd. | Control Method and Control Device for Rotary Electric Motor, and Rotary Electric Motor Drive System |
| CN108563912A (en) * | 2018-05-11 | 2018-09-21 | 北京理工大学 | A kind of analytic method of durface mounted permanent magnet synchronous motor air-gap field |
| CN109508480A (en) * | 2018-10-23 | 2019-03-22 | 华中科技大学 | A kind of construction low-frequency harmonics electric current calculates the semi-analytic method of motor high frequency electromagnetic force |
| CN110233590A (en) * | 2019-06-18 | 2019-09-13 | 北京理工大学 | A kind of new-energy automobile permanent magnet synchronous motor noise control method based on harmonic injection |
Non-Patent Citations (1)
| Title |
|---|
| 邢泽智: "表贴式永磁同步电机电磁激振力波的快速准确计算与分析", 《中国优秀博硕士学位论文全文数据库(硕士)工程科技Ⅱ辑》 * |
Cited By (8)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN112069709A (en) * | 2020-09-04 | 2020-12-11 | 天津大学 | Motor electromagnetic vibration rapid calculation method considering stator tooth modulation effect |
| CN112069709B (en) * | 2020-09-04 | 2022-05-17 | 天津大学 | Motor electromagnetic vibration rapid calculation method considering stator tooth modulation effect |
| CN112468051A (en) * | 2020-11-13 | 2021-03-09 | 中国人民解放军海军工程大学 | Multiphase permanent magnet motor high-frequency vibration rapid analysis method and suppression strategy thereof |
| CN112468051B (en) * | 2020-11-13 | 2022-06-03 | 中国人民解放军海军工程大学 | Multiphase permanent magnet motor high-frequency vibration rapid analysis method and suppression strategy thereof |
| CN112531941A (en) * | 2020-12-25 | 2021-03-19 | 合肥工业大学 | Method for optimizing Halbach array surface plug-in permanent magnet motor |
| CN112531941B (en) * | 2020-12-25 | 2022-01-25 | 合肥工业大学 | Method for optimizing Halbach array surface plug-in permanent magnet motor |
| CN114157198A (en) * | 2021-11-02 | 2022-03-08 | 河海大学 | Rapid calculation method for electromagnetic excitation force of permanent magnet synchronous motor stator under power supply of PWM inverter |
| CN114157198B (en) * | 2021-11-02 | 2023-09-22 | 河海大学 | Method for calculating electromagnetic exciting force of permanent magnet synchronous motor stator under power supply of PWM inverter |
Similar Documents
| Publication | Publication Date | Title |
|---|---|---|
| CN111199124A (en) | Method for calculating no-load electromagnetic excitation force wave of surface-mounted permanent magnet synchronous motor | |
| Hur et al. | Vibration reduction of IPM-type BLDC motor using negative third harmonic elimination method of air-gap flux density | |
| CN105005692B (en) | A kind of Magnetic Field for Permanent Magnet Electrical Machines analysis and torque calculation method based on analytic method | |
| CN111241735B (en) | Method for calculating load electromagnetic excitation force wave of built-in permanent magnet synchronous motor | |
| CN112906145B (en) | Method and system for analyzing electromagnetic force and electromagnetic vibration noise of motor | |
| Xing et al. | Reduction of radial electromagnetic force waves based on PM segmentation in SPMSMs | |
| CN113765251B (en) | Method for determining rotor segmentation mode for weakening vibration of integer slot permanent magnet motor | |
| Kim et al. | Characteristics analysis method of axial flux permanent magnet motor based on 2-D finite element analysis | |
| CN108206660B (en) | Torque analysis method of novel five-phase meter-embedded permanent magnet synchronous motor | |
| Hong et al. | Piecewise stagger poles with continuous skew edge for vibration reduction in surface-mounted PM synchronous machines | |
| CN109508480B (en) | Semi-analytic method for calculating high-frequency electromagnetic force of motor by constructing low-frequency harmonic current | |
| Ishibashi et al. | Numerical simulation of electromagnetic vibration of small induction motors | |
| CN108319768B (en) | Permanent magnet motor armature reaction magnetic field prediction method based on computer | |
| Krykowski et al. | Computer analysis of high‐speed PM BLDC motor properties | |
| Gotovac et al. | Analytical model of permeance variation losses in permanent magnets of the multipole synchronous machine | |
| CN113765324B (en) | Asymmetric modular permanent magnet auxiliary synchronous reluctance motor and vibration noise optimization method thereof | |
| Faiz et al. | Analytical calculation of magnetic field in surface-mounted permanent-magnet machines with air-gap eccentricity | |
| Dai et al. | A hybrid calculation method of radial electromagnetic force based on finite element method and analytic method in a permanent magnet synchronous machine | |
| Van Der Giet et al. | Fast-and-easy acoustic optimization of PMSM by means of hybrid modeling and FEM-to-measurement transfer functions | |
| Huang et al. | Analytical modeling of axial flux PM machines with eccentricities | |
| Abbaszadeh et al. | Analytical quasi 3D modeling of an axial flux PM motor with static eccentricity fault | |
| Hu et al. | Analysis of radial electromagnetic force in permanent magnet machine with manufacturing tolerance | |
| Podhajecki et al. | Numerical and experimental vibration analysis of BLDC motor | |
| Jiang | Analysis of cogging torque of permanent magnet synchronous motor with different pole slots | |
| CN113281567B (en) | Virtual winding-based permanent magnet motor air gap field harmonic separation method |
Legal Events
| Date | Code | Title | Description |
|---|---|---|---|
| PB01 | Publication | ||
| PB01 | Publication | ||
| SE01 | Entry into force of request for substantive examination | ||
| SE01 | Entry into force of request for substantive examination | ||
| RJ01 | Rejection of invention patent application after publication | ||
| RJ01 | Rejection of invention patent application after publication |
Application publication date: 20200526 |