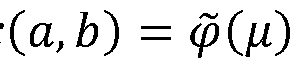WO2024261250A1 - Method for extracting a homomorphic encrypted element from a homomorphic encrypted list and method for inserting a homomorphic encrypted element into a homomorphic encrypted list - Google Patents

Method for extracting a homomorphic encrypted element from a homomorphic encrypted list and method for inserting a homomorphic encrypted element into a homomorphic encrypted list Download PDF

Info

Publication number
WO2024261250A1
WO2024261250A1 PCT/EP2024/067453 EP2024067453W WO2024261250A1 WO 2024261250 A1 WO2024261250 A1 WO 2024261250A1 EP 2024067453 W EP2024067453 W EP 2024067453W WO 2024261250 A1 WO2024261250 A1 WO 2024261250A1
Authority
WO
WIPO (PCT)
Prior art keywords
homomorphic
encrypted
list
homomorphic encrypted
polynomial
Prior art date
Application number
PCT/EP2024/067453
Other languages
French (fr)
Inventor
Philippe CHARTIER
Michel Koskas
Mohammed LEMOU
Florian MÉHATS
Original Assignee
Ravel Technologies
Priority date (The priority date is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the date listed.)
Filing date
Publication date
Application filed by Ravel Technologies filed Critical Ravel Technologies
Publication of WO2024261250A1 publication Critical patent/WO2024261250A1/en

Links

Classifications

    • H—ELECTRICITY
    • H04—ELECTRIC COMMUNICATION TECHNIQUE
    • H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
    • H04L9/00—Cryptographic mechanisms or cryptographic arrangements for secret or secure communications; Network security protocols
    • H04L9/008—Cryptographic mechanisms or cryptographic arrangements for secret or secure communications; Network security protocols involving homomorphic encryption
    • H—ELECTRICITY
    • H04—ELECTRIC COMMUNICATION TECHNIQUE
    • H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
    • H04L9/00—Cryptographic mechanisms or cryptographic arrangements for secret or secure communications; Network security protocols
    • H04L9/30—Public key, i.e. encryption algorithm being computationally infeasible to invert or user's encryption keys not requiring secrecy
    • H04L9/3093—Public key, i.e. encryption algorithm being computationally infeasible to invert or user's encryption keys not requiring secrecy involving Lattices or polynomial equations, e.g. NTRU scheme

Definitions

  • DESCRIPTION TITLE Method for extracting a homomorphic encrypted element from a homomorphic encrypted list and method for inserting a homomorphic encrypted element into a homomorphic encrypted list
  • TECHNICAL FIELD The technical field is that of homomorphic cryptography methods, devices and systems. More particularly, the field of the invention is that of the manipulation of homomorphic encrypted lists.
  • TECHNOLOGICAL BACKGROUND Homomorphic cryptography which allows calculations or data processing to be performed on encrypted data, without first decrypting them, has attracted a lot of attention recently. Indeed, the digital processing of personal data has become omnipresent in our daily lives.
  • LWE learning with errors
  • Homomorphic cryptography methods therefore respond, among other things, to the technical challenge of allowing: - an external, generally remote, service and processing server to perform "blind" operations on encrypted data, without decrypting it, this server not having the key necessary to decrypt the data, - the encrypted data being provided by another, distinct entity (a client, in the IT sense), which has the encryption key.
  • These data processing operations can consist of performing individual operations, data by data, to format or filter them for example. They can also involve data comparison, sorting or grouping operations. Handling homomorphic encrypted elements can be complex and requires the development of methods to perform mathematical operations in the space of ciphers.
  • the known methods also called cryptographic primitives, we can cite the following techniques (the symbols bra and ket ⁇ ...
  • a first aspect of the invention relates to a method for extracting a homomorphic encrypted element ⁇ $ % ⁇ , from a homomorphic encrypted list ⁇ $ ⁇ , the homomorphic encrypted element ⁇ $ % ⁇ being associated with an index &, & being between 0 and N-1, the elements of the list $ belonging to a torus T, the list $ and the index & being encrypted using the same key, said method comprising the following steps: - Obtaining a homomorphic cipher ⁇ Q ⁇ X ⁇ ⁇ of a polynomial Q(X), Q(X) being an aggregation of the elements $ ) of the list $ , j being between 0 and N- 1, each coefficient of the polynomial Q ⁇ X ⁇ being a linear combination of elements of the list $, Q ⁇ X ⁇ belonging to a quotient space ⁇ /* + ⁇ , ⁇ being a space of polynomials of degree N-1
  • the symbols bra and ket ⁇ ... ⁇ indicate a homomorphic encrypted element of a quantity.
  • the symbol ⁇ & ⁇ indicates a homomorphic encrypted element of an integer &.
  • homomorphic modular product ⁇ reproduces, in the space of ciphers, the result of a product of two plaintext elements.
  • homomorphic cipher of ⁇ - is meant a homomorphic cipher of the quantity ⁇ ⁇ - 234 + ⁇ , . ⁇ 567 being between 0 and M-1.
  • cyclotomic polynomial of order M is meant, in a known manner, the unitary polynomial whose complex roots are exactly the M-th primitive roots of unity.
  • aggregation, or "packing" is meant a representation of the list L in the form of a polynomial.
  • each coefficient of the polynomial Q(X) representing the list L comprises a linear combination of elements of the list L.
  • Each linear combination may comprise one or more elements of the list L.
  • the method according to the first aspect of the invention is a general method for extracting a homomorphic encrypted element from a homomorphic encrypted list from the homomorphic cipher ⁇ 8 ⁇ ⁇ of the index & corresponding to the element of interest ⁇ $ % ⁇ .
  • the extraction of the homomorphic encrypted element is carried out in a completely homomorphic manner, namely without the need to decrypt the elements of the list or the index.
  • the method according to the first aspect of the invention performs a function of the homomorphic extractor type, or "homomorphic getter” according to the English terminology.
  • the method according to the first aspect of the invention is a general method that can be implemented for any list of elements belonging to the torus T and indexed according to an integer &.
  • the extraction method according to one aspect of the invention therefore makes it possible to extract a homomorphic encrypted element from a homomorphic encrypted list without the need to decrypt the element or the list. This is possible thanks to the prior preparation of the polynomial Q(x) as an aggregation of elements of the list L and of the monomial P(X) representing the index i corresponding to the element to be extracted.
  • the encrypted polynomial ⁇ 9 ⁇ ⁇ is an encrypted representation of the list L and the encrypted monomial ⁇ 8 ⁇ ⁇ is an encrypted representation of the index i. It is important to note that ⁇ 9 ⁇ ⁇ and ⁇ 8 ⁇ ⁇ can be obtained homomorphically from the encrypted elements of the list ⁇ $ ⁇ and the encrypted index ⁇ & ⁇ without the need for prior decryption. Indeed, one of the advantages of the method according to the first aspect of the invention is to be able to extract an encrypted element from the encrypted list without the need for decryption of the list or the index associated with the element to be extracted.
  • the product polynomial ⁇ C ⁇ X ⁇ ⁇ then contains the encrypted element to be extracted in the form of its k-th coefficient.
  • the coefficient k is determined from the aggregation used to obtain the polynomial Q and the function ⁇ used in the monomial P(X). In other words, the prior construction of P(X) and Q(X) uniquely identifies the coefficient k of ⁇ C ⁇ X ⁇ ⁇ containing the element of the homomorphic encrypted list to be extracted.
  • the extraction method according to the first aspect of the invention may further comprise a step of receiving the index ⁇ & ⁇ and the list ⁇ $ ⁇ , ⁇ 9 ⁇ ⁇ and ⁇ 8 ⁇ ⁇ being obtained from the ciphers ⁇ & ⁇ and ⁇ $ ⁇ .
  • the elements of the list are encrypted as coefficients of a polynomial of degree N-1, the list being a ciphertext homomorphic of ⁇ N ) A O ⁇ B $ ) ⁇ M ⁇ ) ⁇ .
  • the coefficients of the polynomial Q(X) are simply the elements of the list L (the linear combinations each include a single element).
  • the function P ⁇ K ⁇ is a function of the integer j with values in the integers between 0 and N-1.
  • the function P is for example a function of type P ⁇ K ⁇ ⁇ ⁇ K ⁇ T ⁇ ⁇ 56 L, with T an integer.
  • Another example of a function is P ⁇ K ⁇ ⁇ ⁇ T ⁇ K ⁇ ⁇ 56 L with T odd.
  • the index i is the homomorphic cipher of
  • the function R ⁇ & ⁇ is a function from the integer i to values in the integers between 0 and N- 1.
  • the function is for example a function of type R ⁇ & ⁇ ⁇ ⁇ K ⁇ T ⁇ ⁇ 56 L, with T an integer.
  • Another example of a function is R ⁇ ⁇ K ⁇ ⁇ ⁇ T ⁇ K ⁇ ⁇ 56 L with T odd.
  • the coefficient of interest namely the element of the list to be extracted, then becomes the coefficient of order P ⁇ & ⁇ ⁇ R ⁇ & ⁇ of the polynomial determined using the homomorphic modular product. It is therefore possible to extract the element of the homomorphic encrypted list by calculating the coefficient of order P ⁇ & ⁇ ⁇ R ⁇ & ⁇ of the polynomial ⁇ B .
  • the functions P ⁇ & ⁇ and R ⁇ & ⁇ are chosen as being the identity function, namely P ⁇ & ⁇ ⁇ & and R ⁇ & ⁇ ⁇ &.
  • the coefficient to be extracted is then simply the coefficient of order zero of the polynomial ⁇ ! ⁇ ⁇ .
  • the extraction of a coefficient of given order from an encrypted polynomial is a primitive known in homomorphic cryptography.
  • extracting the zero coefficient from a homomorphic cipher of a polynomial is particularly simple to implement. Having associated on the one hand the encryption of the elements of the list as coefficients of a polynomial of degree N-1 and on the other hand the encryption of the exponent i as an exponent of a monomial is far from obvious. The combination of these features has never been used in homomorphic cryptography and allows to obtain a general method for extracting a homomorphic encrypted element from a homomorphic encrypted list.
  • the use of these two different homomorphic encryptions for the elements of the list and the index makes it possible to simplify the extraction of the sought element, which can be carried out as a calculation of the zero coefficient of a polynomial obtained by homomorphic modular product.
  • the extraction of an element from a homomorphic encrypted list using the method according to the first aspect of the invention is therefore general, reliable and fast.
  • the homomorphic encrypted polynomial ⁇ 9 ⁇ ⁇ is obtained according to the following formula -
  • the homomorphic encrypted monomial ⁇ 8 ⁇ is determined according to the following formula Definition of TLWE encryption
  • TLWE encryption "Torus Learning with Errors" according to English terminology, we mean a known method of homomorphic encryption of an element t belonging to the torus T.
  • the ciphertext V$XY ⁇ F ⁇ is determined according to the following formula: V$XY ⁇ F ⁇ ⁇ ⁇ ⁇ , ⁇ ⁇ ...
  • TRLWE encryption "Torus Ring Learning With Errors" according to English terminology, we mean a known method of homomorphic encryption of a polynomial ⁇ belonging to the polynomial ring V _ ⁇ ⁇ V ⁇ /! ⁇ , where C is a cyclotomic polynomial and for example ! ⁇ ⁇ ⁇ N ⁇ 1 with N being a power of 2.
  • C is a cyclotomic polynomial and for example ! ⁇ ⁇ ⁇ N ⁇ 1 with N being a power of 2.
  • polynomial ring the space of polynomials of degree N to coefficients in the torus T..
  • the encryption key s and its projection vector a are vectors belonging to the set ⁇ [ N ⁇ ⁇ .
  • the ciphertext VW$XY ⁇ is determined according to the following formula: VW$XY ⁇ ⁇ ⁇ ⁇ ⁇ ⁇ , ⁇ ⁇ ⁇ ... ⁇ ⁇ ⁇ , ⁇ ⁇
  • the polynomial ] ⁇ is a polynomial of the same degree as ⁇ ⁇ whose coefficients represent the random noise added to the ciphertext of the message ⁇ ⁇ .
  • the coefficients of e(X) can have a Gaussian distribution centered around zero with a variance ⁇ 2 .
  • TRGSW encryption or “Gentry, Sahai, Waters Torus Ring encryption” in English, means a known method of homomorphic encryption of a polynomial m(X) belonging to the polynomial ring ⁇ / ⁇ + ⁇ with a key s, s being a vector belonging to the set ⁇ ⁇ ⁇ b .
  • the homomorphic modular product ⁇ reproduces, in the cipher space, the result of a product between plaintext elements.
  • the method of calculating the homomorphic modular product ⁇ depends on the properties of the ciphertext elements to be multiplied. For example, in the case of a product between C ⁇ VWZ[X ⁇ and c ⁇ VW$XY ⁇ we obtain: !
  • a second aspect of the invention relates to a method for inserting a homomorphic encrypted element ⁇ ⁇ ⁇ into a homomorphic encrypted list ⁇ $ ⁇ so as to obtain a modified homomorphic encrypted list ⁇ $′ ⁇ , in which: - The homomorphic encrypted element ⁇ ⁇ ⁇ is obtained by homomorphic encryption of a plaintext element ⁇ belonging to a torus T; - The homomorphic encrypted list ⁇ $ ⁇ is obtained from a plaintext list $ comprising the elements $ ) , K being an integer between 0 and L ⁇ 1, N being an integer greater than or equal to 1, the elements $ ) belonging to the torus T, the homomorphic encrypted list ⁇ $ ⁇ being in the form of a homomorphic cipher - The modified homomorphic ciphertext ⁇ $′ ⁇ is a homomorphic ciphertext of a plaintext list $' comprising the elements $ ) p ⁇ $ ) for K ⁇ &, & being an integer between 0 and
  • the symbol ⁇ indicates the difference between two elements belonging to the torus T.
  • the symbol ⁇ indicates the sum between two polynomials whose coefficients have a value in the torus T or in the space ⁇ /* + ⁇ .
  • the method according to the second aspect of the invention makes it possible to introduce a homomorphic cipher ⁇ ⁇ ⁇ into a homomorphic cipher list ⁇ $ ⁇ .
  • This method in combination with the method according to the first aspect of the invention, provides a complete technique for manipulating homomorphic cipher lists.
  • the reading of a list namely the extraction of one of its elements, as well as its modification, namely the replacement of one of its elements, are possible.
  • the step of extracting the element 6 B ⁇ ⁇ $ % ⁇ from the cipher list homomorphic ⁇ $ ⁇ is performed using the method according to the first aspect of the invention.
  • the homomorphic encrypted list is a homomorphic cipher calculated according to the formula -
  • the homomorphic cipher element ⁇ ⁇ ⁇ is calculated according to the formula V$XY ⁇ ;
  • the homomorphic cipher ⁇ & ⁇ is calculated according to the formula VWZ
  • the step of obtaining a homomorphic cipher of the quantity ⁇ ⁇ includes: - Compute a homomorphic cipher of the quantity ⁇ ⁇ $ % as the homomorphic difference between a homomorphic cipher element ⁇ ⁇ ⁇ of ⁇ and a homomorphic cipher element ⁇ $ % ⁇ of the element $ % of the list $ so as to determine the quantity -
  • the step of obtaining the quantity VW$XY ⁇ ⁇ $ % ⁇ M ⁇ % ⁇ ⁇ is carried out by applying an automorphism.
  • the functions P ⁇ & ⁇ and R ⁇ & ⁇ are the identity function so as to have P ⁇ & ⁇ ⁇ & and R ⁇ & ⁇ ⁇ &.
  • Another aspect of the invention relates to a computer program comprising instructions executable by a processor and designed to implement a method according to the second aspect of the invention when these instructions are executed by said processor.
  • a third aspect of the invention comprises a cryptographic processing server for processing a homomorphic encrypted list comprising a communication module and a calculation module: - The communication module being configured to receive, from an entity external to the server, a homomorphic encrypted index ⁇ & ⁇ or ⁇ 8 ⁇ ; - The calculation module being configured to extract, from a homomorphic encrypted list ⁇ $ ⁇ , a homomorphic encrypted element ⁇ $ % ⁇ associated with the homomorphic encrypted index ⁇ & ⁇ or ⁇ 8 ⁇ , in accordance with the method according to the first aspect of the invention.
  • the calculation module of the processing server determines the homomorphic modular product ⁇ & ⁇ ⁇ $ ⁇ ⁇ ⁇ ⁇ OQ ⁇ % ⁇ $ ⁇ and extracts it from it opportunely chosen so as to obtain an encrypted version of the element of the list sought.
  • the communication module is further configured to receive, from an entity external to the server, a homomorphic encrypted element ⁇ ⁇ ⁇ .
  • the calculation module is programmed to introduce the homomorphic encrypted element ⁇ ⁇ ⁇ into a homomorphic encrypted list ⁇ $ ⁇ in accordance with the method according to the second aspect of the invention.
  • a fourth aspect of the invention relates to a client configured to encrypt the index & in the form of a homomorphic encrypted index ⁇ & ⁇ or ⁇ 8 ⁇ and/or the message ⁇ in the form of a homomorphic encrypted message ⁇ ⁇ ⁇ and to communicate the homomorphic encrypted index ⁇ & ⁇ or ⁇ 8 ⁇ and/or the homomorphic encrypted message ⁇ ⁇ ⁇ to the server according to the third aspect of the invention via a communication channel.
  • the encrypted index ⁇ & ⁇ is for example in the form of an encrypted monomial ⁇ 9 ⁇ ⁇ .
  • a fifth aspect of the invention relates to a cryptographic system comprising: - A cryptographic processing server according to the third aspect of the invention; - A client according to the fourth aspect of the invention.
  • the cryptographic processing server receives only homomorphic encrypted quantities and extracts an element from the list without the need to perform decryption.
  • Figure 2a schematically illustrates the aggregation of a list according to an embodiment of the first aspect of the invention.
  • Figure 2b schematically illustrates the extraction of a homomorphic encrypted element from a homomorphic encrypted list according to an embodiment of the first aspect of the invention.
  • Figure 3 illustrates a flowchart of an embodiment of the method for inserting a homomorphic encrypted element into a homomorphic encrypted list according to the second aspect of the invention.
  • Figure 4a schematically illustrates certain steps of an embodiment of the method according to the second aspect of the invention.
  • Figure 4b schematically illustrates the insertion of a homomorphic encrypted element into a homomorphic encrypted list according to an embodiment of the method according to the second aspect of the invention.
  • Figure 5 illustrates an embodiment of a cryptographic system for processing a homomorphic encrypted list according to an aspect of the invention.
  • DETAILED DESCRIPTION Figure 1 [Fig.1] schematically represents an embodiment of the method 100 for extracting a homomorphic encrypted element ⁇ $ % ⁇ from a homomorphic encrypted list ⁇ $ ⁇ .
  • the method 100 according to the embodiment illustrated in Figure 1 comprises a step 101 of obtaining a homomorphic encrypted element ⁇ Q ⁇ X ⁇ ⁇ of a polynomial Q(X).
  • the polynomial Q(X) belongs to the set ⁇ ⁇ ⁇ ⁇ /* + ⁇ ⁇ ⁇ .
  • the method 100 as illustrated in FIG. 1 further comprises a step 102 of obtaining a homomorphic cipher ⁇ P ⁇ X ⁇ ⁇ of a monomial P ⁇ X ⁇ ⁇ ⁇ -, . being a function of the index & associated with the element ⁇ $ % ⁇ to be obtained.
  • the monomial P(X) belongs to / ⁇ /* + ⁇ , / ⁇ being a set of polynomials with coefficients in the integers.
  • the homomorphic cipher polynomial ⁇ C ⁇ X ⁇ ⁇ is determined as a homomorphic modular product between ⁇ P ⁇ X ⁇ ⁇ and ⁇ Q ⁇ X ⁇ ⁇ .
  • the extraction step 104 of the coefficient k of ⁇ C ⁇ X ⁇ ⁇ makes it possible to obtain the element ⁇ $ % ⁇ to be extracted from the list ⁇ $ ⁇ .
  • the homomorphic encrypted monomial ⁇ 8 ⁇ ⁇ is obtained from a plaintext index &, & being an integer between 0 and L ⁇ 1.
  • the homomorphic encrypted monomial ⁇ 8 ⁇ ⁇ is obtained as a homomorphic ciphertext of the quantity ⁇ OQ ⁇ % ⁇ .
  • the homomorphic encrypted polynomial ⁇ 9 ⁇ is obtained from the plaintext list $ comprising the elements $ ) , K being an integer between 0 and L ⁇ 1.
  • the elements $ ) belong to the torus T.
  • the homomorphic encrypted polynomial ⁇ 9 ⁇ is obtained as a homomorphic ciphertext of the quantity ⁇ N ) A O ⁇ B $ ) ⁇ M ⁇ ) ⁇ .
  • the elements of the plaintext list are encoded as coefficients of a polynomial which is then homomorphically encrypted.
  • the homomorphic modular product calculated during step 103 is calculated according to the following formula ! ⁇ ⁇ ⁇ 8 ⁇ ⁇ 9 ⁇ .
  • the quantity ! ⁇ is a polynomial of degree N with coefficients with values in the torus T. It is therefore possible to obtain a homomorphic cipher of the element $ % , namely ⁇ $ % ⁇ , during a step 104 of extracting the coefficient of order P ⁇ & ⁇ ⁇ of the polynomial ! ⁇ .
  • Figures 2a and 2b illustrate in more detail certain steps of an embodiment of the method 100 according to the first aspect of the invention.
  • the plaintext list $ is a sorted set of elements $ ) , j being between 0 and N-1.
  • the framed element $ % corresponds to the element that we want to extract from the list.
  • the homomorphic encrypted polynomial ⁇ 9 ⁇ is obtained as:
  • the homomorphic cipher of the index ⁇ & ⁇ is obtained according to the formula ⁇ & ⁇ ⁇ VWZ[X ⁇ O% ⁇ .
  • the function P ⁇ & ⁇ is the identity function, P ⁇ & ⁇ ⁇ &.
  • the function R ⁇ & ⁇ is also chosen to be equal to the identity function, R ⁇ & ⁇ ⁇ &.
  • the term of interest x y becomes, in the product polynomial C, the zero coefficient.
  • FIG. 3 illustrates a flowchart of an embodiment of the method 400 for inserting a homomorphic ciphertext element ⁇ ⁇ ⁇ into a homomorphic ciphertext list ⁇ $ ⁇ so as to obtain a modified homomorphic ciphertext list ⁇ $′ ⁇ .
  • the homomorphic ciphertext element ⁇ ⁇ ⁇ is obtained by homomorphic encryption of a plaintext element ⁇ belonging to a torus T.
  • the ciphertext list homomorphic ⁇ $ ⁇ is obtained from a plaintext list $ comprising the elements $ ) , K being an integer between 0 and L ⁇ 1, N being an integer greater than or equal to 1.
  • the elements $ ) belong to the torus T and the homomorphic encrypted list ⁇ $ ⁇ is in the form of a homomorphic ciphertext of ⁇ N ) A O ⁇ B $ ) ⁇ M ⁇ ) ⁇ .
  • the objective of the insertion method 400 is to obtain a new homomorphic encrypted list ⁇ $′ ⁇ which is the homomorphic ciphertext of a plaintext list $′.
  • the plaintext list $′ is identical to the starting list $ except for the element $ p % which has been replaced by the element ⁇ .
  • the embodiment of the method 400 according to the second aspect of the invention comprises: - Receiving 401 the homomorphic encrypted element ⁇ ⁇ ⁇ , the homomorphic encrypted list ⁇ $ ⁇ and a homomorphic cipher ⁇ & ⁇ in the form of a homomorphic cipher of ⁇ ⁇ ⁇ , ⁇ $ ⁇ and ⁇ & ⁇ being encrypted using the same key s; - Extract, using the method 100 according to the first aspect of the invention, the element 6 B ⁇ ⁇ $ % ⁇ 402 from the homomorphic encrypted list ⁇ $ ⁇ ; - Calculate 403 homomorphically the difference 6 ⁇ ⁇ ⁇ ⁇ ⁇ 6 B ⁇ ⁇ ⁇ $ % ⁇ ; - Obtain 404 a homomorphic cipher of the quantity ⁇ ⁇ ; - Obtain the modified homomorphic encrypted list
  • Step 402 of extracting the element 6 B ⁇ ⁇ $ % ⁇ from the homomorphic encrypted list ⁇ $ ⁇ therefore comprises the implementation of the method 100 according to the first aspect of the invention.
  • FIG. 4a illustrates in detail certain steps of an embodiment of the method 400 according to the fourth aspect of the invention, the functions P ⁇ & ⁇ ]FR ⁇ & ⁇ being in this case the identity functions.
  • the starting list ⁇ $ ⁇ is obtained from the plaintext list $ by computing a homomorphic ciphertext of type
  • the homomorphic encrypted element is calculated according to the formula V$XY ⁇ and the homomorphic encrypted index according to the formula VWZ[X ⁇ O% ⁇ . These last two elements are not shown in Figure 4a.
  • the function P ⁇ & ⁇ is chosen to be equal to P ⁇ & ⁇ ⁇ &.
  • the element x y to be replaced in the list L can for example be extracted as the zero coefficient of the homomorphic encrypted polynomial obtained by calculating the homomorphic modular product ⁇ & ⁇ $ ⁇ .
  • Step 405 of obtaining the homomorphic encrypted list ⁇ $′ ⁇ is carried out, according to the embodiment illustrated in FIG. 4b, by calculating the homomorphic encrypted list VW$XY $ ⁇ which can be expressed as follows: The last equation shows that the element $ % has been replaced in the new homomorphic cipher by the element ⁇ .
  • step 405 comprises the conversion of V$XY ⁇ ⁇ $ % ⁇ into VW$XY ⁇ ⁇ $ % ⁇ .
  • ⁇ and $ % belonging to the torus T the homomorphic cipher of their difference is a TLWE type cipher.
  • the conversion of a TLWE type cipher into TRLWE is carried out using primitives known in homomorphic cryptography.
  • step 405 of the method 400 according to the second aspect of the invention the quantity VW$XY ⁇ ⁇ ⁇ ⁇ $ % ⁇ ⁇ M ⁇ % ⁇ ⁇ must be evaluated, whereas the homomorphic cipher of the index is in the form of a homomorphic cipher of ⁇ OQ ⁇ % ⁇ , VWZ[X ⁇ OQ ⁇ % ⁇ ⁇ .
  • the quantity VW$XY ⁇ ⁇ can then be obtained in the following way: - Compute a homomorphic cipher of the quantity ⁇ ⁇ $ % as the homomorphic difference between a homomorphic cipher element ⁇ ⁇ ⁇ of ⁇ and a homomorphic cipher element ⁇ $ % ⁇ of the element $ % of the list $ so as to determine the quantity VW$XY ⁇ ⁇ $ % ⁇ ; - Compute the homomorphic modular product ⁇ & ⁇ ⁇ ⁇ ⁇ $ % ⁇ to determine the quantity - Obtain, from the quantity VW$XY ⁇ ⁇ $ % ⁇ OQ ⁇ % ⁇ ⁇ , the quantity ⁇ ⁇ $ % ⁇ M ⁇ % ⁇ ⁇ in the form of VW$XY ⁇ ⁇ ⁇ $ % ⁇ M ⁇ % ⁇ ⁇ .
  • the step of obtaining the quantity VW$XY ⁇ ⁇ $ % ⁇ M ⁇ % ⁇ ⁇ is carried out by applying an automorphism.
  • Figure 5 illustrates an embodiment of a cryptographic system 500 for manipulating a homomorphic encrypted list according to one aspect of the invention.
  • the cryptographic system 500 comprises a cryptographic processing server for extracting a homomorphic encrypted element from a homomorphic encrypted list 501.
  • the cryptographic server 501 comprises a communication module 502 and a calculation module 503.
  • the calculation module 502 is configured to receive, from an entity external to the server, a homomorphic encrypted index ⁇ & ⁇ .
  • the calculation module 503 is configured to extract, from a homomorphic encrypted list, a homomorphic encrypted element ⁇ $ % ⁇ associated with the encrypted index homomorphic ⁇ & ⁇ in accordance with the method 100 according to the first aspect of the invention.
  • the cryptographic system 500 further comprises a client 504 configured to encrypt the index & in the form of a homomorphic encrypted index ⁇ & ⁇ , for example in the form of a homomorphic encrypted monomial ⁇ 8 ⁇ and to communicate the homomorphic encrypted index ⁇ & ⁇ to the server via a communication channel 504c.
  • the client 504 is configured to calculate the ciphertext of the index ⁇ & ⁇ in the form VWZ[X ⁇ OM ⁇ % ⁇ ⁇ .
  • the server 501 is configured to implement the method 400 of inserting a homomorphic encrypted element into a homomorphic encrypted list.
  • the client 504 is then configured to encrypt the element ⁇ so as to obtain a homomorphic encrypted element ⁇ ⁇ ⁇ .
  • the client 504 is further configured to transmit the homomorphic encrypted element ⁇ ⁇ ⁇ to the server 501 via a communication channel 504c.
  • Description of the procedure for refreshing a homomorphic cipher When two encrypted messages are added together, an encrypted message is obtained, which is an encrypted version of the sum of the two initial unencrypted messages, the noise component of which is higher than for the two initial encrypted messages.
  • a refresh procedure generally called "bootstrapping" is performed repeatedly. This procedure produces a refreshed version of c, i.e.
  • the bootstrapping procedure usually involves a homomorphic evaluation of the quantity ⁇ M .
  • ⁇ is a functional refresh polynomial of degree less than or equal to N-1 whose coefficients are chosen according to the characteristics of the message space and a target function; and ⁇ is the integer closest to 2N(ba.s): ⁇ 2L ⁇ ⁇ ⁇ .
  • homomorphic evaluation means a calculation performed using encrypted quantities, without prior decryption (without knowing the key s).
  • target function means a mathematical function applied to the encrypted message at the same time as the refresh.
  • the target function is the identity function.
  • the constant term of ⁇ M . ⁇ 56 ⁇ N ⁇ 1 ⁇ is a refreshed version of c, that is, an encrypted version of ⁇ with a limited noise component e' (usually smaller than the noise component of c, when c comes from previous – homomorphic – data processing operations; in any case, e' is small enough to allow a decryption of c', with a low error rate).
  • e' usually smaller than the noise component of c, when c comes from previous – homomorphic – data processing operations; in any case, e' is small enough to allow a decryption of c', with a low error rate.
  • ⁇ 1 ⁇ can be decomposed into a calculation of a sequence of modular products given by: Where the sk are the n components of the vector s.
  • each product “.” is a modular product: the term on the left, for example ⁇ O ⁇ or , belongs to Z ⁇ ⁇ X ⁇ ⁇ Z ⁇ X ⁇ / ⁇ X N ⁇ 1 ⁇ , the term on the right, for example ⁇ or belongs to TN[X].
  • TN[X] T[X]/(X N +1).
  • Such a product is similar to the product y. ⁇ i, y being an integer and ⁇ belonging to T (except that we work on polynomial fields, instead of number fields).
  • the homomorphic computation of ⁇ 5] ⁇ B u ⁇ M . ⁇ v is not immediate because of the presence of the secret key s, which is not known.
  • a modular product such as y. ⁇ i or X j .v(X) can be computed homomorphically by defining the exterior product ⁇ ⁇ ⁇ ⁇ ⁇ ⁇ ⁇ ⁇ ⁇ ⁇ % ⁇ .
  • the quantity ⁇ ⁇ ⁇ ⁇ % ⁇ ⁇ % is the encrypted version of the message ⁇ i.
  • TRGSW cipher of z
  • the acronym TRGSW comes from the English “Gentry, Sahai, Waters Torus Ring encryption”, adapted from an encryption method that was proposed in the article “Homomorphic encryption from learning with errors: Conceptually-simpler, asymptotically-faster, attribute-based”, by C. Gentry, A. Sahai, and B. Waters, InCrypto'13, 2013).
  • it is possible to calculate the product ⁇ ⁇ ⁇ without knowing the components sk, k 1...n of the secret key and therefore without knowing the secret key s.
  • Bootstrap keys (usually public) are encrypted versions of the components sk of the secret key s encrypted using another key s'.
  • the encrypted version ! ⁇ ⁇ ⁇ ⁇ ⁇ ⁇ of a polynomial with integer coefficients y, ! ⁇ is calculated using the method detailed below.

Landscapes

  • Engineering & Computer Science (AREA)
  • Signal Processing (AREA)
  • Computer Networks & Wireless Communication (AREA)
  • Computer Security & Cryptography (AREA)
  • Pure & Applied Mathematics (AREA)
  • Mathematical Physics (AREA)
  • Physics & Mathematics (AREA)
  • Mathematical Optimization (AREA)
  • Computing Systems (AREA)
  • Theoretical Computer Science (AREA)
  • Mathematical Analysis (AREA)
  • General Physics & Mathematics (AREA)
  • Algebra (AREA)
  • Storage Device Security (AREA)
  • Information Retrieval, Db Structures And Fs Structures Therefor (AREA)

Abstract

The invention relates to a method (100) for obtaining a homomorphic encrypted element < L i > from a homomorphic encrypted list < L >, the elements of the list L belonging to a torus T, the method comprising the following steps: obtaining a homomorphic encryption < Q(X) > (101) of a polynomial Q(X), wherein Q(X) is an aggregation of the elements L j of the list L; obtaining a homomorphic encryption < P(X) > (102) of a monomial P(X) = X y , wherein y is a function of the index i associated with the element < L i > to be obtained; determining a homomorphic encrypted polynomial < C(X) > (103) as a homomorphic modular product between < P(X) > and < Q(X) >; extracting the coefficient k (104) of the homomorphic encrypted polynomial < C(X) >, wherein k is determined on the basis of the polynomial Q(X) and the function y used in the monomial P(X), the coefficient k of the homomorphic encrypted polynomial < C(X) > corresponding to the homomorphic encrypted element < L i > to be obtained.

Description

DESCRIPTION TITRE : Procédé d’extraction d’un élément chiffré homomorphe d’une liste chiffrée homomorphe et procédé d’insertion d’un élément chiffré homomorphe dans une liste chiffré homomorphe DOMAINE TECHNIQUE Le domaine technique est celui des méthodes, dispositifs et systèmes de cryptographie homomorphe. Plus particulièrement, le domaine de l’invention est celui de la manipulation de listes chiffrées homomorphes. ARRIERE-PLAN TECHNOLOGIQUE La cryptographie homomorphe, qui permet d'effectuer des calculs ou des traitements de données sur des données chiffrées, sans les déchiffrer au préalable, a suscité beaucoup d'attention dernièrement. En effet, le traitement numérique de données personnelles est devenu omniprésent dans notre vie quotidienne. La protection de la confidentialité de ces données, et de la vie privée des individus concernés est donc devenue critique, car ces données personnelles ont tendance à circuler de plus en plus dans les environnements en systèmes digitaux que nous utilisons au quotidien. Dans ce contexte, les techniques de chiffrement et traitement homomorphe apparaissent comme une solution très prometteuse, car elles permettent de traiter des données tout en préservant de manière particulièrement sûre l'anonymat et le caractère privé de ces données, ces dernières n'étant pas déchiffrées pendant leur traitement. La cryptographie homomorphe peut être basée sur le schéma de cryptage dit "apprentissage avec erreur" (« learning with errors » ou LWE, en anglais), dans lequel le message crypté

Figure imgf000003_0001
est dérivé du message non crypté µ selon la formule suivante : b=µ+e+a.s, où : s est une clé secrète, a est un vecteur choisi au hasard, pour projeter la clé secrète s, et e est une composante de bruit aléatoire, ajoutée à µ+a.s. Pour décrypter le message, une personne possédant la clé secrète s peut calculer la quantité b-a.s (égale à µ+e), puis arrondir le résultat pour supprimer la composante de bruit e et retrouver le message µ. Bien entendu, le terme de bruit e doit être et rester suffisamment petit si l'on veut pouvoir récupérer le message µ. Les méthodes de cryptographie homomorphe répondent donc, entre autres, à l’enjeu technique qui consiste à permettre : - à un serveur de services et traitements, externe, généralement distant, d’effectuer des opérations « en aveugle » sur des données chiffrées, sans les déchiffrer, ce serveur ne disposant d’ailleurs pas de la clef nécessaire pour déchiffrer les données, - les données, chiffrées, étant fournies par une autre entité, distincte (un client, au sens informatique), qui, elle, dispose de la clef de chiffrement. Ces opérations de traitement de données peuvent consister à effectuer des opérations individuelles, donnée par donnée, pour les mettre en forme ou les filtrer par exemple. Elles peuvent aussi concerner des opérations de comparaison entre données, de tri ou de regroupement. La manipulation d’éléments chiffrés homomorphes peut être complexe et requiert le développement de méthodes permettant de réaliser les opérations mathématiques dans l’espace des chiffrés. Parmi les méthodes connues, également appelées primitives cryptographiques, nous pouvons citer les techniques suivantes (les symboles bra et ket ^... ^ indiquent un chiffré homomorphe de la quantité entre les symboles) : Addition homomorphe : si ^^ ^ ^ ^^ ^ et ^^ ^ ^ ^^ ^ sont deux chiffrés homomorphes de deux éléments
Figure imgf000004_0001
et ^^ appartenant au tore T, il est possible d’obtenir la somme des chiffrés en utilisant l’addition homomorphe ^^ ⊕ ^^ = ^ ^^ ^ ^^ ^ Soustraction homomorphe : si ^^ ^ ^ ^^ ^ et ^^ ^ ^ ^^ ^ sont deux chiffrés homomorphes de deux éléments
Figure imgf000004_0002
et ^^ appartenant au tore T, il est possible d’obtenir la différence des chiffrés en utilisant la soustraction homomorphe ^^ ⊖ ^^ = ^ ^^ ^ ^^ ^ Addition homomorphe de polynômes : si ^^ ^ ^ ^^^^^ ^ et ^^ ^ ^ ^^^^^ ^ sont deux chiffrés homomorphes de deux éléments
Figure imgf000005_0001
et ^^ appartenant à l’anneau de polynômes de degré N, ^^^^^ ^ ^^^^/^^^ ^ ^^, il est possible d’obtenir le polynôme somme dans l’espace des chiffrés en utilisant l’addition homomorphe des polynômes ^^ ⊕ ^^ = ^ ^^^^^ ^ ^^^^^ ^ Soustraction homomorphe de polynômes : si ^^ ^ ^
Figure imgf000005_0002
^ et ^^ ^ ^ ^^^^^ ^ sont deux chiffrés homomorphes de deux éléments
Figure imgf000005_0003
et ^^ appartenant à l’anneau de polynômes de degré N, ^^^^^ ^ ^^^^/^^^ ^ ^^, avec par exemple N une puissance de 2, il est possible d’obtenir le polynôme différence dans l’espace des chiffrés en utilisant la soustraction homomorphe des polynômes : ^^ ⊝ ^^ = ^ ^^^^^ ^ ^^^^^ ^ Produit modulaire homomorphe : Si C ^ ^ ^^^^ ^ et c ^ ^ ^^^^ ^ sont deux chiffrés homomorphes de deux éléments ^^^^ et ^^^^ appartenant à l’anneau de polynômes de degré N, ^^^^^ ^ ^^^^/^^^ ^ ^^, il est possible d’obtenir le polynôme produit dans l’espace des chiffrés en utilisant le produit modulaire homomorphe : ! ⊡ ^ ^ ^ ^^^^ ⋅ ^^^^ ^ Ces primitives cryptographiques permettent donc de réaliser plusieurs opérations mathématiques dans l’espace des chiffrés homomorphes, en reproduisant les opérations mathématiques standard effectuées dans l’espace en clair. Cependant, la cryptographie homomorphe a été très peu appliquée à la manipulation de listes ou ensembles chiffrées. Certaines méthodes de chiffrement homomorphe des éléments d’une liste ont été récemment proposées, par exemple dans l’article « Faster Amortized FHEW bootstrapping using Ring » de G. De Micheli et al., https://eprint.iacr.org/2023/112, 2023). Toutefois, ces techniques portent sur le chiffrement homomorphe d’éléments individuels d’une liste, sans donner des indications concernant par exemple des manipulations complètes de listes homomorphes. Il existe donc un besoin de développer des techniques permettant de réaliser des opérations complexes sur les listes chiffrée homomorphe, par exemple en extrayant un élément chiffré homomorphe d’une liste chiffrée homomorphe ou encore en modifiant une liste chiffrée homomorphe par suppression ou ajout d’un élément chiffré homomorphe. Par ailleurs, il est nécessaire de développer des méthodes de manipulations de listes chiffrées homomorphes qui soient fiables, rapides et peu coûteuses en termes de ressources de calcul. RESUME DE L’INVENTION Pour résoudre au moins partiellement les problèmes évoqués précédemment, un premier aspect de l’invention concerne un procédé d’extraction d’un élément chiffré homomorphe ^ $% ^, d’une liste chiffrée homomorphe ^ $ ^, l’élément chiffré homomorphe ^ $% ^ étant associé à un indice &, & étant compris entre 0 et N-1, les éléments de la liste $ appartenant à un tore T, la liste $ et l’indice & étant chiffrés à l’aide d’une même clé, ledit procédé comprenant les étapes suivantes : - Obtenir un chiffré homomorphe ^ Q^X^ ^ d’un polynôme Q(X), Q(X) étant une agrégation des éléments $) de la liste $ , j étant compris entre 0 et N- 1, chaque coefficient du polynôme Q^X^ étant une combinaison linéaire d’éléments de la liste $, Q^X^ appartenant à un espace quotient ^^^^/*+^^^, ^^^^ étant un espace des polynômes de degré N-1 avec coefficients à valeurs dans le tore T et *+^^^ étant un polynôme cyclotomique d’ordre M ; - Obtenir un chiffré homomorphe ^ P^X^ ^ d’un monôme P^X^ ^ ^-, . étant une fonction de l’indice & associé à l’élément ^ $% ^ à obtenir, P^X^ appartenant à un espace quotient /^^^/*+^^^, /^^^ étant un ensemble de polynômes à coefficients dans les nombres entiers ; - Déterminer un polynôme chiffré homomorphe ^ C^X^ ^ en tant que produit modulaire homomorphe entre ^ P^X^ ^ et ^ Q^X^ ^ ; - Extraire le coefficient k du polynôme chiffré homomorphe ^ C^X^ ^ , k étant déterminé sur la base du polynôme Q(X) et de la fonction . utilisée dans le monôme P(X), le coefficient k du polynôme chiffré homomorphe ^ C^X^ ^ correspondant à l’élément chiffré homomorphe ^ $% ^ à obtenir. Les symboles bra et ket ^... ^ indiquent un chiffré homomorphe d’une quantité. Par exemple, le symbole ^ & ^ indique un chiffré homomorphe d’un entier &. Par produit modulaire homomorphe, également indiqué par le symbole ⊡, il est entendu une opération entre deux chiffrés homomorphes, ^ A ^ et ^ B ^ , telle que ^ A ^ ⊡ ^ B ^ = ^ A B ^ . En d’autres termes, le produit modulaire homomorphe ⊡ reproduit, dans l’espace des chiffrés, le résultat d’un produit de deux éléments en clair. Par chiffré homomorphe de ^- , il est entendu un chiffré homomorphe de la quantité ^^- 234 +^, . ^567 étant compris entre 0 et M-1. Par polynôme cyclotomique d’ordre M, il est entendu, de façon connue, le polynôme unitaire dont les racines complexes sont exactement les racines primitives M-ièmes de l’unité. L’ordre M est défini par M = tα avec t premier quelconque et α un nombre entier quelconque. Par agrégation, ou « packing » selon la terminologie anglaise, il est entendu une représentation de la liste L sous la forme d’un polynôme. Dans le cas du procédé selon un aspect de l’invention chaque coefficient du polynôme Q(X) représentant la liste L comprend une combinaison linéaire d’éléments de la liste L. Chaque combinaison linéaire peut comprendre un ou plusieurs éléments de la liste L. Le procédé selon le premier aspect de l’invention est une méthode générale pour extraire un élément chiffré homomorphe d’une liste chiffré homomorphe à partir du chiffré homomorphe ^ 8 ^^^ ^ de l’indice & correspondant à l’élément d’intérêt ^ $% ^. L’extraction de l’élément chiffré homomorphe est réalisée de façon complétement homomorphe, à savoir sans besoin de déchiffrer les éléments de la liste ou l’indice. En d’autres termes, le procédé selon le premier aspect de l’invention réalise une fonction de type extracteur homomorphe, ou « homomorphic getter » selon la terminologie anglaise. Il est important de noter que le procédé selon le premier aspect de l’invention est une méthode générale qui peut être mise en œuvre pour n’importe quelle liste d’éléments appartenant au tore T et indexés selon un entier &. Le procédé d’extraction selon un aspect de l’invention permet donc d’extraire un élément chiffré homomorphe d’une liste chiffrée homomorphe sans besoins de déchiffrer l’élément ou la liste. Cela est possible grâce à la préparation préalable du polynôme Q(x) en tant qu’agrégation d’éléments de la liste L et du monôme P(X) représentant l’indice i correspondant à l’élément à extraire. En d’autres termes, le polynôme chiffré ^ 9 ^^^ ^ est une représentation chiffrée de la liste L et le monôme chiffré ^ 8 ^^^ ^ est une représentation chiffrée de l’indice i. Il est important de noter que ^ 9 ^^^ ^ et ^ 8 ^^^ ^ peuvent être obtenus de façon homomorphe à partir des éléments chiffrés de la liste ^ $ ^ et de l’indice chiffré ^ & ^ sans besoin de déchiffrement préalable. En effet, un des avantages du procédé selon le premier aspect de l’invention est de pouvoir extraire un élément chiffré de la liste chiffrée sans besoin de déchiffrement de la liste ou de l’indice associé à l’élément à extraire. Le polynôme produit ^ C^X^ ^ contient alors l’élément chiffré à extraire sous la forme de son k-ième coefficient. Le coefficient k est déterminé à partir de l’agrégation utilisée pour obtenir le polynôme Q et de la fonction γ utilisée dans le monôme P(X). En d’autres termes, la construction préalable de P(X) et Q(X) identifie univoquement le coefficient k de ^ C^X^ ^ contenant l’élément de la liste chiffrée homomorphe à extraire. Les inventeurs ont donc mis au point une technique pour l’extraction d’un élément d’une liste chiffré homomorphe qui est à la fois simple et rapide à mettre en œuvre et qui repose sur la préparation préalable de l’agrégation Q(X) et du monôme P(X) représentant respectivement la liste L et l’indice i associé à l’élément chiffré homomorphe à extraire de la liste. Dans un ou plusieurs modes de réalisation : - chaque coefficient du polynôme Q(X) est une combinaison linéaire obtenue selon la formule suivante $: ; < ^ $ < = >?
Figure imgf000008_0001
) = >? avec 0 D E D F ^ 2, 0 D H D + I ^ 1, et - le coefficient du polynôme ^ C^X^ ^ correspondant à l’élément chiffré homomorphe ^ $% ^ à extraire est le coefficient k = 0, γ étant égale à 7 ^ &. Cette construction du polynôme Q(X) permet de positionner l’élément de la liste à extraire en correspondance du coefficient k = 0 du polynôme produit ^ C^X^ ^ . Par ailleurs, ce choix pour les coefficients du polynôme Q(X) permet d’extraire efficacement le chiffré homomorphe de l’élément de la liste souhaité pour une large gamme de valeurs des paramètres t, M et γ. En effet, les inventeurs ont réussi à trouver des constructions du polynôme Q(X) et du monôme P(X) qui sont particulièrement adaptées pour l’extraction de l’élément ^ $% ^. Des telles constructions sont non évidentes pour l’homme du métier, d’autant plus que si l’agrégation Q(X) et le polynôme P(X) ne sont pas opportunément choisis, il y a une forte probabilité de tomber sur une combinaison linéaire d’éléments de la liste ^ $ ^ et non pas sur l’élément d’intérêt ^ $% ^. Dans un ou plusieurs modes de réalisation, le procédé d’extraction selon le premier aspect de l’invention peut en outre comprendre une étape de recevoir l’indice ^ & ^ et la liste ^ $ ^, ^ 9^^^ ^ et ^ 8^^^ ^ étant obtenus à partir des chiffrés ^ & ^ et ^ $ ^. Dans un ou plusieurs modes de réalisation : - Le polynôme chiffré homomorphe ^ 9 ^ est obtenu à partir de la liste $ comprenant les éléments $), K étant un entier compris entre 0 et L ^ 1, le polynôme chiffré homomorphe ^ 9 ^ étant sous la forme d’un chiffré homomorphe de
Figure imgf000009_0001
, P^K^ étant une fonction à valeurs dans l’ensemble des nombres entiers compris entre 0 et N-1 et M = 2α ; - Le monôme chiffré homomorphe ^ 8 ^ est obtenu à partir de l’indice &, ^ 8 ^ étant sous la forme d’un chiffré homomorphe de ^OQ^%^ , R^&^ étant une fonction à valeurs dans l’ensemble des nombres entiers compris entre 0 et N-1 ; - Le polynôme chiffré homomorphe ^ !^^^ ^ est obtenu selon la formule ^
Figure imgf000009_0002
- Le coefficient k du polynôme ^ !^^^ ^ à extraire est donné par S ^ P^&^ ^ Par chiffré homomorphe de
Figure imgf000009_0003
, il est entendu un chiffré homomorphe de la quantité
Figure imgf000009_0004
Ce mode de réalisation illustre un exemple de coopération entre l’agrégation d’éléments de la liste sous forme de polynôme Q(X) et le chiffrement du monôme P(X). Cela est possible grâce au fait que les éléments de la liste sont chiffrés en tant que coefficients d’un polynôme de degré N-1, la liste étant un chiffré homomorphe de ∑N ) A O^ B $)^M^)^ . Dans ce cas les coefficients du polynôme Q(X) sont simplement les éléments de la liste L (les combinaisons linéaires comprennent chacune un seul élément). La fonction P^K^ est une fonction de l’entier j à valeurs dans les nombres entiers compris entre 0 et N-1. La fonction P est par exemple une fonction de type P^K^ ^ ^ K ^ T^ ^56 L, avec T un entier. Un autre exemple de fonction est P^K^ ^ ^T ∗ K^ ^56 L avec T impair. Par ailleurs, l’indice i est le chiffré homomorphe de
Figure imgf000010_0001
La fonction R^&^ est une fonction de l’entier i à valeurs dans les nombres entiers compris entre 0 et N- 1. La fonction
Figure imgf000010_0002
est par exemple une fonction de type R^&^ ^ ^ K ^ T^ ^56 L, avec T un entier. Un autre exemple de fonction est R ^ ^K^ ^ ^T ∗ K^ ^56 L avec T impair. En combinant ces deux techniques de chiffrement homomorphe, les inventeurs ont découvert qu’il est possible d’extraire l’élément recherché en calculant le produit modulaire homomorphe
Figure imgf000010_0003
Avantageusement, ce produit modulaire homomorphe résulte en une rotation des coefficients du polynôme Q(X) de départ. Le coefficient d’intérêt, à savoir l’élément de la liste à extraire, devient alors le coefficient d’ordre P^&^ ^ R^&^ du polynôme déterminé à l’aide du produit modulaire homomorphe. Il est donc possible d’extraire l’élément de la liste chiffrée homomorphe en calculant le coefficient d’ordre P^&^ ^ R^&^ du polynôme ^B. Selon un ou plusieurs modes de réalisation, les fonctions P^&^ et R^&^ sont choisies comme étant la fonction identité, à savoir P^&^ ^ & et R^&^ ^ &. Le coefficient à extraire est alors simplement le coefficient d’ordre zéro du polynôme ^ !^^^ ^. L’extraction d’un coefficient d’ordre donné d’un polynôme chiffré est une primitive connue en cryptographie homomorphe. De plus, l’extraction du coefficient zéro d’un chiffré homomorphe d’un polynôme est particulièrement simple à mettre en œuvre. L’avoir associé d’une part le chiffrement des éléments de la liste en tant que coefficients d’un polynôme de degré N-1 et d’autre part le chiffrement de l’exposant i en tant qu’exposant d’un monôme est loin d’être évident. La combinaison de ces caractéristiques n’a jamais été utilisée en cryptographie homomorphe et permet d’obtenir une méthode générale pour l’extraction d’un élément chiffré homomorphe d’une liste chiffrée homomorphe. Avantageusement, l’utilisation de ces deux chiffrements homomorphes différents pour les éléments de la liste et l’indice permet de simplifier l’extraction de l’élément recherché, qui peut être effectuée en tant que calcul du coefficient zéro d’un polynôme obtenu par produit modulaire homomorphe. L’extraction d’un élément d’une liste chiffrée homomorphe grâce au procédé selon le premier aspect de l’invention est donc générale, fiable et rapide. Selon un mode de réalisation du procédé selon le premier aspect de l’invention : - La polynôme chiffré homomorphe ^ 9^^^ ^ est obtenu selon la formule suivante
Figure imgf000011_0001
- Le monôme chiffré homomorphe ^ 8 ^ est déterminé selon la formule suivante
Figure imgf000011_0002
Définition de chiffrement TLWE Par chiffrement TLWE, « Torus Learning with Errors » selon la terminologie anglaise, on entend une méthode connue de chiffrement homomorphe d’un élément t appartenant au tore T. Le chiffré V$XY^F^ est déterminé selon la formule suivante : V$XY^F^ ^ ^^^, ^^... ^\, ^ ^
Figure imgf000011_0003
Le vecteur s est la clé de chiffrement, le vecteur a est un vecteur de projection de la clé s, ou masque, et la quantité e est un bruit aléatoire. Définition de chiffrement TRLWE Par chiffrement TRLWE, « Torus Ring Learning With Errors » selon la terminologie anglaise, on entend une méthode connue de chiffrement homomorphe d’un polynôme ^ appartenant à l’anneau de polynômes V_^^^ ^ V^^^/!^^^, où C est un polynôme cyclotomique et par exemple !^^^ ^ ^N ^ 1 avec N étant une puissance de 2. On entend ici par anneau de polynômes l’espace des polynômes de degré N à coefficients dans le tore T.. La clé de chiffrement s et son vecteur de projection a sont des vecteurs appartenant à l’ensemble ^[N^^^^\. Le chiffré VW$XY^^^ est déterminé selon la formule suivante : VW$XY^^^ ^ ^^^^^^, ^^^^^... ^\^^^, ^^^^ ^
Figure imgf000012_0001
Le polynôme ]^^^ est un polynôme du même degré que ^ ^^^ dont les coefficients représentent le bruit aléatoire ajouté au chiffré du message ^ ^^^. Par exemple les coefficients de e(X) peuvent avoir une distribution gaussienne centrée autour de zéro avec une variance σ2. Définition de chiffrement TRGSW Par chiffrement TRGSW, “Gentry, Sahai, Waters Torus Ring encryption” selon la terminologie anglaise, on entend une méthode connue de chiffrement homomorphe d’un polynôme m(X) appartenant à l’anneau de polynômes `^^^/Φ+^^^ avec une clé s, s étant un vecteur appartenant à l’ensemble ^`^^^^b. Le chiffré TRGSW de m est alors déterminé de la façon suivante : VWZ[X^^^ ^ ` ^ ^c avec f^ Z ^ e ⋮ h, où zj, j=1…l(K+1), sont l(K+1) version chiffrées de 0, la valeur f?^b>^^ nulle 0 étant chiffrée avec s’, l étant un nombre entier positif donné; et ci est une matrice dont la dimension est ^j ^ 1^ k ^j ^ 1^ k H et dont les coefficients appartiennent au tore T, Hi ? étant égale à :
Figure imgf000012_0002
B étant un nombre entier supérieur ou égal à 2. Définition de produit modulaire homomorphe ⊡ entre un TRGSW et un TRLWE On entend par produit modulaire homomorphe ⊡ une opération entre deux chiffrés homomorphes, ^ A ^ et ^ B ^ , telle que ^ A ^ ⊡ ^ B ^ = ^ A B ^ . En d’autres termes, le produit modulaire homomorphe ⊡ reproduit, dans l’espace des chiffré, le résultat d’un produit entre éléments en clair. La méthode de calcul du produit modulaire homomorphe ⊡ dépend des propriétés des éléments chiffrés à multiplier. Par exemple dans le cas d’un produit entre C ^ VWZ[X^^^ et c ^ VW$XY^^^ on obtient : ! ⊡ ^ ^ VW$XY ^^ ⋅ ^^ L’avantage de ce mode de réalisation et que le calcul du produit modulaire homomorphe ^B ^ ^ & ^ ⊡^ $ ^ ^ ^ ^OQ^%^$ ^ peut être réalisé de façon connue, en utilisant la technique pour le produit d’une quantité chiffrée TRLWE et d’une quantité chiffrée TRGSW. Le polynôme produit est alors un chiffré TRLWE dont le coefficient d’ordre zéro est l’élément de la liste à extraire. Un autre aspect de l’invention porte sur un programme d’ordinateur comprenant des instructions exécutables par un processeur et conçues pour mettre en œuvre un procédé selon le premier aspect de l’invention lorsque ces instructions sont exécutées par ledit processeur. Un deuxième aspect de l’invention porte sur un procédé d’insertion d’un élément chiffré homomorphe ^ µ ^ dans une liste chiffrée homomorphe ^ $ ^ de sorte à obtenir une liste chiffrée homomorphe modifiée ^ $′ ^, dans lequel : - L’élément chiffré homomorphe ^ µ ^ est obtenu par chiffrement homomorphe d’un élément en clair µ appartenant à un tore T ; - La liste chiffrée homomorphe ^ $ ^ est obtenue à partir d’une liste en clair $ comprenant les éléments $), K étant un entier compris entre 0 et L ^ 1, N étant un nombre entier supérieur ou égal à 1, les éléments $) appartenant au tore T, la liste chiffrée homomorphe ^ $ ^ étant sous la forme d’un chiffré homomorphe
Figure imgf000013_0001
- La liste chiffrée homomorphe modifiée ^ $′ ^ est un chiffré homomorphe d’une liste en clair $’ comprenant les éléments $) p ^ $)
Figure imgf000013_0002
pour K ^ &, & étant un entier compris entre 0 et N-1 ; Ledit procédé comprenant les étapes suivantes : - Recevoir l’élément chiffré homomorphe ^ µ ^, la liste chiffrée homomorphe ^ $ ^ et un chiffré homomorphe ^ & ^ sous la forme d’un chiffré homomorphe de
Figure imgf000014_0001
^ µ ^, ^ $ ^ et ^ & ^ étant chiffrés à l’aide d’une même clé s ; - Extraire, conformément au procédé selon le premier aspect de l’invention, l’élément 6B ^ ^ $% ^ de la liste chiffrée homomorphe ^ $ ^ ; - Calculer de façon homomorphe la différence 6^ ^^ µ ^ ⊝ 6B ^ ^ µ ^ $% ^ ; - Obtenir un chiffré homomorphe de la quantité ^^µ ^
Figure imgf000014_0002
; - Obtenir la liste chiffrée homomorphe modifiée ^ $′ ^ en calculant de façon homomorphe
Figure imgf000014_0003
Les opérations soustraction homomorphe, notée par le symbole ⊝, et addition homomorphe, notée par le symbole ⊕, sont des primitives cryptographiques connues. Dans le cas de la différence ^ µ ^ ⊝ 6B ^ ^ µ ^ $% ^, le symbole ⊝ indique la différence entre deux éléments appartenant au tore T. Dans le cas de la somme
Figure imgf000014_0004
le symbole ⊕ indique la somme entre deux polynômes dont les coefficients sont à valeur dans le tore T ou à l’espace ^^^^/*+^^^. Le procédé selon le deuxième aspect de l’invention permet d’introduire un chiffré homomorphe ^ µ ^ dans une liste chiffrée homomorphe ^ $ ^. Ce procédé, en combinaison avec le procédé selon le premier aspect de l’invention, fournit une technique complète de manipulation de listes chiffrées homomorphes. En d’autres termes grâce aux procédés selon le premier et le deuxième aspect de l’invention, la lecture d’une liste, à savoir l’extraction d’un des ses éléments, ainsi que sa modification, à savoir le remplacement d’un de ses éléments, sont possibles. Dans un ou plusieurs modes de réalisation du procédé selon le deuxième aspect de l’invention, l’étape d’extraire l’élément 6B ^ ^ $% ^ de la liste chiffrée homomorphe ^ $ ^ est réalisée à l’aide du procédé selon le premier aspect de l’invention. Dans un ou plusieurs modes de réalisation du procédé selon le deuxième aspect de l’invention : - La liste chiffrée homomorphe est un chiffré homomorphe calculé selon la formule
Figure imgf000015_0001
- L’élément chiffré homomorphe ^ µ ^ est calculé selon la formule V$XY^µ^ ; - Le chiffré homomorphe ^ & ^ est calculé selon la formule VWZ
Figure imgf000015_0002
Dans un ou plusieurs modes de réalisation du procédé selon le quatrième aspect de l’invention, l’étape d’obtenir un chiffré homomorphe de la quantité ^^µ ^
Figure imgf000015_0003
comprend : - Calculer un chiffré homomorphe de la quantité µ ^ $% en tant que différence homomorphe entre un élément chiffré homomorphe ^ µ ^ de µ et un élément chiffré homomorphe ^ $% ^ de l’élément $% de la liste $ de manière à déterminer la quantité
Figure imgf000015_0004
- Calculer le produit modulaire homomorphe ^ & ^ ⊡ ^ µ ^ $% ^ pour déterminer la quantité
Figure imgf000015_0005
- Obtenir, à partir de la quantité VW$XY^^µ ^ $%^^OQ^%^^, un chiffré homomorphe de la quantité ^^µ ^
Figure imgf000015_0006
sous la forme de VW$XY^^µ ^ $%^^M^%^^. Si la fonction R^&^ est du type R^&^ ^ r ∗ & et R^&^ ^ r′ ∗ & , r et r′ étant premiers avec M, l’étape d’obtenir la quantité VW$XY^^µ ^ $%^^M^%^^ est réalisée en appliquant un automorphisme. Dans un ou plusieurs modes de réalisation du procédé d’insertion selon le deuxième aspect de l’invention, les fonctions P^&^ et R^&^ sont la fonction identité de sorte à avoir P^&^ ^ & et R^&^ ^ &. Un autre aspect de l’invention porte sur un programme d’ordinateur comprenant des instructions exécutables par un processeur et conçues pour mettre en œuvre un procédé selon le deuxième aspect de l’invention lorsque ces instructions sont exécutées par ledit processeur. Un troisième aspect de l’invention comprend un serveur de traitement cryptographique pour le traitement d’une liste chiffrée homomorphe comprenant un module de communication et un module de calcul : - Le module de communication étant configuré pour recevoir, de la part d’une entité externe au serveur, un indice chiffré homomorphe ^ & ^ ou ^ 8 ^; - Le module de calcul étant configuré pour extraire, d’une liste chiffrée homomorphe ^ $ ^, un élément chiffré homomorphe ^ $% ^ associé à l’indice chiffré homomorphe ^ & ^ ou ^ 8 ^, conformément au procédé selon le premier aspect de l’invention. Selon un mode de réalisation, le module de calcul du serveur de traitement selon le premier aspect de l’invention détermine le produit modulaire homomorphe ^ & ^ ⊡^ $ ^ ^ ^ ^OQ^%^$ ^ et en extrait opportunément choisi de sorte à obtenir un chiffré de l’élément de la liste recherché. Selon un mode de réalisation, le module de communication est en outre configuré pour recevoir, de la part d’une entité externe au serveur, un élément chiffré homomorphe ^ µ ^. Selon un mode de réalisation, le module de calcul est programmé pour introduire l’élément chiffré homomorphe ^ µ ^ dans une liste chiffrée homomorphe ^ $ ^ conformément au procédé selon le deuxième aspect de l’invention. Un quatrième aspect de l’invention porte sur un client configuré pour chiffrer l’indice & sous la forme d’indice chiffré homomorphe ^ & ^ ou ^ 8 ^ et/ou le message µ sous la forme d’un message chiffré homomorphe ^ µ ^ et pour communiquer l’indice chiffré homomorphe ^ & ^ ou ^ 8 ^ et/ou le message chiffré homomorphe ^ µ ^ au serveur selon le troisième aspect de l’invention via un canal de communication. L’indice chiffré ^ & ^ est par exemple sous la forme d’un monôme chiffré ^ 9^^^ ^. Un cinquième aspect de l’invention porte sur un système cryptographique comprenant : - Un serveur de traitement cryptographique selon le troisième aspect de l’invention ; - Un client selon le quatrième aspect de l’invention. Grâce au système cryptographique selon le cinquième aspect de l’invention le serveur de traitement cryptographique ne reçoit que des quantités chiffrées homomorphes et réalise l’extraction d’un élément de la liste sans besoin d’effectuer un déchiffrement. La présente technologie et ses différentes applications seront mieux comprises à la lecture de la description qui suit et à l’examen des figures qui l’accompagnent. BREVE DESCRIPTION DES FIGURES Les figures sont présentées à titre indicatif et nullement limitatif. La figure 1 illustre un ordinogramme d’un mode de réalisation du procédé d’extraction d’un élément chiffré homomorphe d’une liste chiffrée homomorphe selon le premier aspect de l’invention. La figure 2a illustre schématiquement l’agrégation d’une liste selon un mode de réalisation le premier aspect de l’invention. La figure 2b illustre schématiquement l’extraction d’un élément chiffré homomorphe d’une liste chiffrée homomorphe selon un mode de réalisation du premier aspect de l’invention. La figure 3 illustre un ordinogramme d’un mode de réalisation du procédé d’insertion d’un élément chiffré homomorphe dans une liste chiffrée homomorphe selon le deuxième aspect de l’invention. La figure 4a illustre schématiquement certaines étapes d’un mode de réalisation du procédé selon le deuxième aspect de l’invention. La figure 4b illustre schématiquement l’insertion d’un élément chiffré homomorphe dans une liste chiffrée homomorphe selon un mode de réalisation du procédé selon le deuxième aspect de l’invention. La figure 5 illustre un mode de réalisation d’un système cryptographique pour le traitement d’une liste chiffrée homomorphe selon un aspect de l’invention. DESCRIPTION DETAILLEE La figure 1 [Fig.1] représente schématiquement un mode de réalisation du procédé 100 d’extraction d’un élément chiffré homomorphe ^ $% ^ d’une liste chiffré homomorphe ^ $ ^. Le procédé 100 selon le mode de réalisation illustré à la figure 1 comprend une étape 101 d’obtenir un chiffré homomorphe ^ Q^X^ ^ d’un polynôme Q(X). Le polynôme Q(X) appartient à l’ensemble ^^^^/*+ ^^^. ^^^^ est un espace des polynômes de degré N-1 avec coefficients à valeurs dans le tore T. *+^^^ est un polynôme cyclotomique d’ordre M et degré N. Chaque coefficient du polynôme Q(X) est une combinaison linéaire d’éléments de la liste L. Le procédé 100 tel qu’illustré à la figure 1 comprend en outre une étape 102 d’obtenir un chiffré homomorphe ^ P^X^ ^ d’un monôme P^X^ ^ ^-, . étant une fonction de l’indice & associé à l’élément ^ $% ^ à obtenir. Le monôme P(X) appartient à /^^^/*+^^^, /^^^ étant un ensemble de polynômes à coefficients dans les nombres entiers. Lors de l’étape 103, le polynôme chiffré homomorphe ^ C^X^ ^ est déterminé en tant que produit modulaire homomorphe entre ^ P^X^ ^ et ^ Q^X^ ^. L’étape d’extraction 104 du coefficient k de ^ C^X^ ^ permet d’obtenir l’élément ^ $% ^ à extraire de la liste ^ $ ^. Le monôme chiffré homomorphe ^ 8^^^ ^ est obtenu à partir d’un indice en clair &, & étant un entier compris entre 0 et L ^ 1. Selon un mode de réalisation, le monôme chiffré homomorphe ^ 8^^^ ^ est obtenu en tant que chiffré homomorphe de la quantité ^OQ^%^ . Selon un mode de réalisation, le polynôme chiffré homomorphe ^ 9 ^ est obtenue à partir de la liste en clair $ comprenant les éléments $), K étant un entier compris entre 0 et L ^ 1. Les éléments $) appartiennent au tore T. Dans ce mode de réalisation le polynôme chiffré homomorphe ^ 9 ^ est obtenu en tant que chiffré homomorphe de la quantité ∑N ) A O^ B $)^M^)^ . En d’autres termes, les éléments de la liste en clair sont encodés en tant que coefficients d’un polynôme qui est ensuite chiffré de façon homomorphe. Dans ce mode de réalisation, le produit modulaire homomorphe calculé lors de l’étape 103 est calculé selon la formule suivante !^^^ ^ ^ 8 ^ ⊡^ 9 ^. La quantité !^^^ est un polynôme de degré N avec coefficients à valeur dans le tore T. Il est donc possible d’obtenir un chiffré homomorphe de l’élément $%, à savoir ^ $% ^ , lors d’une étape 104 d’extraction du coefficient d’ordre P^&^ ^
Figure imgf000019_0001
du polynôme !^^^. Les figures 2a et 2b illustrent plus en détail certaines étapes d’un mode de réalisation du procédé 100 selon le premier aspect de l’invention. Selon le mode de réalisation illustré à la figure 2a, la liste en clair $ est un ensemble trié d’éléments $), j étant compris entre 0 et N-1. Dans ce cas, l’élément $% encadré correspond à l’élément que l’on veut extraire de la liste. Le polynôme chiffré homomorphe ^ 9 ^ est obtenu en tant que :
Figure imgf000019_0002
Le chiffré homomorphe de l’indice ^ & ^ est obtenu selon la formule ^ & ^ ^ VWZ[X^^O%^. Dans ce cas la fonction P^&^ est la fonction identité, P^&^ ^ &. La fonction R^&^ est elle aussi choisie comme étant égale à la fonction identité, R^&^ ^ &. Le choix d’un chiffrement TRLWE pour le polynôme Q encodant les éléments de la liste et d’un chiffrement TRGSW pour le monôme P encodant l’indice permet de calculer le produit modulaire homomorphe ^ P ^⊡^ Q ^ en tant que : TRLWEuXO^ ∑^ ^ A O^ B L^X^ v ^ TRLWE (LBXO^+ L^ XO^>^ ^ … ^ ^^XO^>^+ …
Figure imgf000019_0003
Comme il est illustré à la figure 2b, le terme d’intérêt xy devient, dans le polynôme produit C, le coefficient zéro. Il est donc possible d’extraire un chiffré homomorphe de l’élément d’intérêt en tant que coefficient zéro du polynôme résultant du produit modulaire homomorphe. La figure 3 illustre un ordinogramme d’un mode de réalisation du procédé 400 d’insertion d’un élément chiffré homomorphe ^ µ ^ dans une liste chiffrée homomorphe ^ $ ^ de sorte à obtenir une liste chiffrée homomorphe modifiée ^ $′ ^. L’élément chiffré homomorphe ^ µ ^ est obtenu par chiffrement homomorphe d’un élément en clair µ appartenant à un tore T. La liste chiffrée homomorphe ^ $ ^ est obtenue à partir d’une liste en clair $ comprenant les éléments $), K étant un entier compris entre 0 et L ^ 1, N étant un nombre entier supérieur ou égal à 1. Selon l’exemple illustré à la figure 3, les éléments $) appartiennent au tore T et la liste chiffrée homomorphe ^ $ ^ est sous la forme d’un chiffré homomorphe de ∑N ) A O^ B $)^M^)^ . L’objectif du procédé d’insertion 400 est d’obtenir une nouvelle liste chiffrée homomorphe ^ $′ ^ qui est le chiffré homomorphe d’une liste en clair $′. La liste en clair $′ est identique à la liste de départ $ à l’exception de l’élément $p % qui a été remplacé par l’élément µ. Pour ce faire, le mode de réalisation du procédé 400 selon le deuxième aspect de l’invention comprend : - Recevoir 401 l’élément chiffré homomorphe ^ µ ^, la liste chiffrée homomorphe ^ $ ^ et un chiffré homomorphe ^ & ^ sous la forme d’un chiffré homomorphe de
Figure imgf000020_0001
^ µ ^, ^ $ ^ et ^ & ^ étant chiffrés à l’aide d’une même clé s ; - Extraire, à l’aide du procédé 100 selon le premier aspect de l’invention, l’élément 6B ^ ^ $% ^ 402 de la liste chiffrée homomorphe ^ $ ^ ; - Calculer 403 de façon homomorphe la différence 6^ ^^ µ ^ ⊝ 6B ^ ^ µ ^ $% ^ ; - Obtenir 404 un chiffré homomorphe de la quantité ^^µ ^
Figure imgf000020_0002
; - Obtenir la liste chiffrée homomorphe modifiée ^ $′ ^ 405 en calculant de façon homomorphe la somme ^ ^µ ^ $%^^M^%^ ^ ⊕ ^ $ ^ . L’étape 402 d’extraire l’élément 6B ^ ^ $% ^ de la liste chiffrée homomorphe ^ $ ^ comprend donc la mise en œuvre du procédé 100 selon le premier aspect de l’invention. La figure 4a illustre en détail certaines étapes d’un mode de réalisation du procédé 400 selon le quatrième aspect de l’invention, les fonctions P^&^ ]F R^&^étant dans ce cas les fonctions identité. Selon le mode de réalisation illustré à la figure 4a, la liste de départ ^ $ ^ est obtenue à partir de la liste en clair $ en calculant un chiffré homomorphe de type
Figure imgf000021_0001
L’élément chiffré homomorphe est calculé selon la formule V$XY^µ^ et l’indice chiffré homomorphe selon la formule VWZ[X^^O%^. Ces deux derniers éléments ne sont pas représentés à la figure 4a. Dans le cas illustré à la figure 4a, la fonction P^&^ est choisie comme étant égale à P^&^ ^ &. Ce choix de techniques de chiffrement permet de calculer le produit modulaire homomorphe ^ & ^⊡^ $ ^ en tant que chiffré d’un polynôme : TRLWEuXO^ ∑^ ^ A O^ B L^X^ v = TRLWE (LBXO^+ L^ XO^>^ ^ … ^ ^^XO^>^+ …
Figure imgf000021_0002
L’élément xy à remplacer dans la liste L peut par exemple être extrait en tant que coefficient zéro du polynôme chiffré homomorphe obtenu en calculant le produit modulaire homomorphe ^ & ^⊡^ $ ^. L’étape 405 d’obtenir la liste chiffrée homomorphe ^ $′ ^ est realisée, selon le mode de réalisation illustré à la figure 4b, en calculant le chiffré homomorphe VW$XY
Figure imgf000021_0003
$ ^ qui peut être exprimé de la façon suivante :
Figure imgf000021_0004
La dernière équation montre que l’élément $% a été remplacé dans le nouveau chiffré homomorphe par l’élément µ. Selon ce mode de réalisation, l’étape 405 comprend la conversion de V$XY^µ ^ $%^ en VW$XY^µ ^ $%^. En effet µ et $% appartenant au tore T, le chiffré homomorphe de leur différence est un chiffré de type TLWE. La conversion d’un chiffré de type TLWE en TRLWE est réalisé à l’aide de primitives connues en cryptographie homomorphe. Il est important de noter que lors de l’étape 405 du procédé 400 selon le deuxième aspect de l’invention, la quantité VW$XY ^^µ ^ $% ^^M^%^^ doit être évaluée, alors que le chiffré homomorphe de l’indice est sous la forme d’un chiffré homomorphe de ^OQ^%^, VWZ[X^^OQ^%^^. Selon un mode de réalisation du procédé 400, la quantité VW$XY ^^µ ^
Figure imgf000022_0001
peut alors être obtenue da la façon suivante : - Calculer un chiffré homomorphe de la quantité µ ^ $% en tant que différence homomorphe entre un élément chiffré homomorphe ^ µ ^ de µ et un élément chiffré homomorphe ^ $% ^ de l’élément $% de la liste $ manière à déterminer la quantité VW$XY^µ ^ $%^ ; - Calculer le produit modulaire homomorphe ^ & ^ ⊡ ^ µ ^ $% ^ pour déterminer la quantité
Figure imgf000022_0002
- Obtenir, à partir de la quantité VW$XY^^^µ ^ $%^^OQ^%^^, la quantité ^^µ ^ $%^^M^%^^ sous la forme de VW$XY^^^µ ^ $%^^M^%^^. Si la fonction R^&^ est du type R^&^ ^ r &, r étant premier avec M, M étant l’ordre du polynôme cyclotomique, l’étape d’obtenir la quantité VW$XY^^µ ^ $%^^M^%^^ est réalisée en appliquant un automorphisme. On entend ici par automorphisme une primitive connue en cryptographie homomorphe dont la définition est la suivante : Si ^ ^ VW$XY^^^^^^ et u est un entier premier avec N, l’automorphisme ^^F effectue l’opération suivante ^^F^^, ^) = VW$XY^^^^^^^. La figure 5 illustre un mode de réalisation d’un système cryptographique 500 pour la manipulation d’une liste chiffrée homomorphe selon un aspect de l’invention. Le système cryptographique 500 comprend un serveur de traitement cryptographique pour l’extraction d’un élément chiffré homomorphe d’une liste chiffrée homomorphe 501. Le serveur cryptographique 501 comprend un module de communication 502 et un module de calcul 503. Le module de calcul 502 est configuré pour recevoir, de la part d’une entité externe au serveur, un indice chiffré homomorphe ^ & ^. Le module de calcul 503 est configuré pour extraire, d’une liste chiffrée homomorphe, un élément chiffré homomorphe ^ $% ^ associé à l’indice chiffré homomorphe ^ & ^ conformément au procédé 100 selon le premier aspect de l’invention. Le système cryptographique 500 comprend en outre un client 504 configuré pour chiffrer l’indice & sous la forme d’indice chiffré homomorphe ^ & ^, par exemple sous forme d’un monôme chiffré homomorphe ^ 8 ^ et pour communiquer l’indice chiffré homomorphe ^ & ^ au serveur via un canal de communication 504c. Selon un mode de réalisation du système cryptographique 500, le client 504 est configuré pour calculer le chiffré de l’indice ^ & ^ sous la forme VWZ[X^^OM^%^^ . Selon un mode de réalisation du système cryptographique 500, le serveur 501 est configuré pour mettre un œuvre le procédé 400 d’insertion d’un élément chiffré homomorphe dans une liste chiffrée homomorphe. Le client 504 est alors configuré pour chiffrer l’élément µ de sorte à obtenir un élément chiffré homomorphe ^ µ ^. Le client 504 est en outre configuré pour transmettre l’élément chiffré homomorphe ^ µ ^ au serveur 501 via un canal de communication 504c. Description de la procédure de rafraichissement d’un chiffré homomorphe Lorsque l'on additionne deux messages cryptés, on obtient un message crypté, qui est une version cryptée de la somme des deux messages initiaux non cryptés, dont la composante de bruit est plus élevée que pour les deux messages cryptés initiaux. Ainsi, pour empêcher le terme de bruit d'augmenter et de croître au cours du traitement des données, une procédure de rafraîchissement, généralement appelée "bootstrapping", est exécutée de manière répétée. Cette procédure produit une version rafraîchie de c, c'est-à-dire un message crypté c' qui est décrypté lui aussi en tant µ (lorsqu'il est décrypté en utilisant s), mais dont la composante de bruit est plus petite que celle de c. La procédure de "bootstrapping" comprend habituellement une évaluation homomorphe de la quantité ^M . ^^^^ avec : ^^^^ est un polynôme de rafraîchissement fonctionnel de degré inférieur ou égal à N-1 dont les coefficients sont choisis en fonction des caractéristiques de l’espace des messages et d’une fonction cible ; et α est l’entier le plus proche de 2N(b-a.s) : ⌊2L^^ ^ ^. ^^⌉ On entend ici par évaluation homomorphe, un calcul réalisé en utilisant des quantités chiffrées, sans déchiffrement préalable (sans connaitre la clef s). On entend ici par fonction cible une fonction mathématique appliquée au message chiffré en même temps que le rafraîchissement. Dans le cas d’un simple rafraîchissement, la fonction cible est la fonction identité. Pour un polynôme ^^^^ opportunément choisi, le terme constant de ^M . ^^^^^56^^N ^ 1^, à savoir coefBuXM . v^X^v, est une version rafraichie de c, c’est- à-dire une version chiffrée de µ avec une composante de bruit e’ limitée (généralement plus petite que la composante de bruit de c, lorsque c est issu d’opérations de traitement de données – homomorphe – précédentes ; quoiqu’il en soit, e’ est suffisamment petit pour permettre un déchiffrement de c’, avec un taux d’erreur faible). De façon connue, le calcul homomorphique de la quantité ^5]^Bu^M .
Figure imgf000024_0001
^ 1^ peut être décomposé en un calcul d’une séquence de produits modulaires donnés par :
Figure imgf000024_0002
Où les sk sont les n composantes du vecteur s. Dans l’équation ci-dessus, lorsque calculée de manière homomorphe, chaque produit “.” est un produit modulaire : le terme à gauche, par exemple ^O^^ ou
Figure imgf000024_0003
, appartient à ℤ^^X^ ^ ℤ^X^/^XN ^ 1^, le terme à droite, par exemple ^^^^ ou
Figure imgf000024_0004
appartient à TN[X]. Ici on définit TN[X] = T[X]/(XN+1). Un tel produit est similaire au produit y.µi, y étant un entier et µ appartenant à T (si ce n’est que l’on travaille sur des corps de polynômes, au lieu de corps de nombres). Le calcul homomorphique de ^5]^Bu^M. ^^^^v est non immédiat à cause de la présence de la clé secrète s, qui n’est pas connue. Toutefois, il est connu qu’un produit modulaire tel que y.µi ou Xj.v(X) peut être calculé de façon homomorphe en définissant le produit extérieur χ^ ^^^^ ⊡ ^^^ ^^^% ^. La quantité ^^^ ^^^% ^ ^ ^% est la version chiffrée du message µi. La quantité est le chiffrement “TRGSW“ de z (l’acronyme TRGSW vient de l’anglais “Gentry, Sahai, Waters Torus Ring encryption”, adaptée d’une méthode de chiffrement qui a été proposée dans l’article “Homomorphic encryption from learning with errors: Conceptually-simpler, asymptotically-faster, attribute-based”, by C. Gentry, A. Sahai, and B. Waters, InCrypto’13, 2013). En outre, de façon connue, il est possible de calculer le produit
Figure imgf000025_0001
^^^^µ^ sans connaître les composantes sk, k = 1…n de la clé secrète et donc sans connaître la clé secrète s. En effet, comme les composantes sk, k = 1…n appartiennent chacune à B={0,1} (i.e. : sont chacune binaire), la quantité ^O^^ ^  est égale à ^^O^^  ^ 1^^\ ^ 1 qui est chiffré comme
Figure imgf000025_0002
Il s’ensuit qu’une version chiffrée de ^M . ^^^^^56^^N ^ 1^peut être calculée sans avoir accès à la clé secrète s en utilisant la version chiffrée χ^ ^^^\ ^ des composants sk. Ces versions chiffrées des composantes de s sont parfois appelées clés de Boostsrap BK\ ^ χ^ ^^^\^ (« Bootstrap key » en anglais). Les clés de Bootstrap (généralement publiques) sont des versions chiffrées des composantes sk de la clé secrète s chiffrées en utilisant une autre clé s’. χ^ ^^^^ est définie comme étant égale à Z ^ yHi ^ avec : f^ Z ^ e ⋮ h, où zj, j=1…l(K+1), sont l(K+1) version chiffrées de 0, la valeur f?^b>^^ nulle 0 étant chiffrée avec s’, l étant un nombre entier positif donné; et Hi ^ est une matrice dont la dimension est ^j ^ 1^ k ^j ^ 1^ k H et dont les coefficients appartiennent au tore T, Hi ? étant égale à :
Figure imgf000025_0003
B étant un nombre entier supérieur ou égal à 2. Le produit extérieur ! ⊡ ^, entre : - Un message chiffré c ^ ^^^ ^^µ^, ^ ∈ ¥¦>^, correspondant à un message µ appartenant au tore TN[X] et - La version chiffrée ! ^ χ^ ^^^^ d’un polynôme à coefficients entiers y, ! ∈
Figure imgf000025_0004
est calculée selon la méthode détaillée ci-après. Les K+1 composantes cj, j=1..K+1 du message chiffré c ^
Figure imgf000026_0001
sont en quelque sorte décomposées en utilisant un système en base B (comme celui utilisé pour calculer les χ^ ^)
Figure imgf000026_0002
Ensuite, il est possible de calculer
Figure imgf000026_0003
dans laquelle ∑i,? ^^^! est le produit matriciel ligne-colonne et
Figure imgf000026_0004
est une matrice de dimension (n+1)×l dont la forme est la suivante :
Figure imgf000026_0005
Figure imgf000026_0006
Avec Le résultat ! ⊡ ^ appartient à ¥¦>^ et est une version chiffrée de y.µ. En d’autres termes, en décryptant cette quantité avec la clé s’ on retrouve y.µ. Cette méthode de calcul peut être appliquée à tout message appartenant au tore T. En utilisant les clés BKi introduite ci-dessus, on obtient pour le calcul homomorphe de coef0(Xα.v(X)),à savoir
Figure imgf000026_0007
l’équation suivante :
Figure imgf000026_0008
Figure imgf000026_0009
L’équation ci-dessus permet donc d’effectuer le rafraîchissement ou bootstrapping du message chiffré sans besoin de connaître la clé de chiffrement. DESCRIPTION TITLE: Method for extracting a homomorphic encrypted element from a homomorphic encrypted list and method for inserting a homomorphic encrypted element into a homomorphic encrypted list TECHNICAL FIELD The technical field is that of homomorphic cryptography methods, devices and systems. More particularly, the field of the invention is that of the manipulation of homomorphic encrypted lists. TECHNOLOGICAL BACKGROUND Homomorphic cryptography, which allows calculations or data processing to be performed on encrypted data, without first decrypting them, has attracted a lot of attention recently. Indeed, the digital processing of personal data has become omnipresent in our daily lives. The protection of the confidentiality of this data, and of the privacy of the individuals concerned has therefore become critical, because this personal data tends to circulate more and more in the digital system environments that we use on a daily basis. In this context, homomorphic encryption and processing techniques appear to be a very promising solution, because they allow data to be processed while preserving the anonymity and privacy of these data in a particularly secure manner, since the latter are not decrypted during their processing. Homomorphic cryptography can be based on the so-called "learning with errors" (LWE) encryption scheme, in which the encrypted message
Figure imgf000003_0001
is derived from the unencrypted message µ according to the following formula: b=µ+e+as, where: s is a secret key, a is a randomly chosen vector, to project the secret key s, and e is a random noise component, added to µ+as To decrypt the message, a person with the secret key s can calculate the quantity ba.s (equal to µ+e), then round the result to remove the noise component e and recover the message µ. Of course, the noise term e must be and remain sufficiently small if we want to be able to recover the message µ. Homomorphic cryptography methods therefore respond, among other things, to the technical challenge of allowing: - an external, generally remote, service and processing server to perform "blind" operations on encrypted data, without decrypting it, this server not having the key necessary to decrypt the data, - the encrypted data being provided by another, distinct entity (a client, in the IT sense), which has the encryption key. These data processing operations can consist of performing individual operations, data by data, to format or filter them for example. They can also involve data comparison, sorting or grouping operations. Handling homomorphic encrypted elements can be complex and requires the development of methods to perform mathematical operations in the space of ciphers. Among the known methods, also called cryptographic primitives, we can cite the following techniques (the symbols bra and ket ^... ^ indicate a homomorphic cipher of the quantity between the symbols): Homomorphic addition: if ^ ^ ^ ^ ^ ^ ^ and ^ ^ ^ ^ ^ ^ ^ are two homomorphic ciphers of two elements
Figure imgf000004_0001
and ^ ^ belonging to the torus T, it is possible to obtain the sum of the ciphers using the homomorphic addition ^ ^ ⊕ ^ ^ = ^ ^ ^ ^ ^ ^ ^ Homomorphic subtraction: if ^ ^ ^ ^ ^ ^ ^ and ^ ^ ^ ^ ^ ^ ^ are two homomorphic ciphers of two elements
Figure imgf000004_0002
and ^ ^ belonging to the torus T, it is possible to obtain the difference of the ciphertexts using the homomorphic subtraction ^ ^ ⊖ ^ ^ = ^ ^ ^ ^ ^ ^ ^ Homomorphic addition of polynomials: if ^ ^ ^ ^ ^ ^ ^^^ ^ and ^ ^ ^ ^ ^ ^ ^^^ ^ are two homomorphic numbers of two elements
Figure imgf000005_0001
and ^ ^ belonging to the ring of polynomials of degree N, ^ ^ ^^^ ^ ^^^^/^^ ^ ^ ^^, it is possible to obtain the polynomial sum in the space of ciphers using the homomorphic addition of the polynomials ^ ^ ⊕ ^ ^ = ^ ^ ^ ^^^ ^ ^ ^ ^^^ ^ Homomorphic subtraction of polynomials: if ^ ^ ^ ^
Figure imgf000005_0002
^ and ^ ^ ^ ^ ^ ^ ^^^ ^ are two homomorphic ciphers of two elements
Figure imgf000005_0003
and ^ ^ belonging to the ring of polynomials of degree N, ^ ^ ^^^ ^ ^^^^/^^ ^ ^ ^^, with for example N a power of 2, it is possible to obtain the difference polynomial in the space of ciphers using the homomorphic subtraction of polynomials: ^ ^ ⊝ ^ ^ = ^ ^ ^ ^^^ ^ ^ ^ ^^^ ^ Homomorphic modular product: If C ^ ^ ^^^^ ^ and c ^ ^ ^^^^ ^ are two homomorphic ciphers of two elements ^^^^ and ^^^^ belonging to the ring of polynomials of degree N, ^ ^ ^^^ ^ ^^^^/^^ ^ ^ ^^, it is possible to obtain the product polynomial in the space of ciphers using the homomorphic modular product: ! ⊡ ^ ^ ^ ^^^^ ⋅ ^^^^ ^ These cryptographic primitives therefore allow to perform several mathematical operations in the space of homomorphic ciphertexts, by reproducing the standard mathematical operations performed in the plaintext space. However, homomorphic cryptography has been very little applied to the manipulation of encrypted lists or sets. Some methods for homomorphic encryption of the elements of a list have recently been proposed, for example in the article "Faster Amortized FHEW bootstrapping using Ring" by G. De Micheli et al., https://eprint.iacr.org/2023/112, 2023). However, these techniques concern the homomorphic encryption of individual elements of a list, without giving indications concerning for example complete manipulations of homomorphic lists. There is therefore a need to develop techniques for performing complex operations on homomorphic encrypted lists, for example by extracting a homomorphic encrypted element from a homomorphic encrypted list or by modifying a homomorphic encrypted list by deleting or adding a homomorphic encrypted element. Furthermore, it is necessary to develop methods for manipulating homomorphic encrypted lists that are reliable, fast and inexpensive in terms of computing resources. SUMMARY OF THE INVENTION To at least partially solve the problems mentioned above, a first aspect of the invention relates to a method for extracting a homomorphic encrypted element ^ $ % ^, from a homomorphic encrypted list ^ $ ^, the homomorphic encrypted element ^ $ % ^ being associated with an index &, & being between 0 and N-1, the elements of the list $ belonging to a torus T, the list $ and the index & being encrypted using the same key, said method comprising the following steps: - Obtaining a homomorphic cipher ^ Q^X^ ^ of a polynomial Q(X), Q(X) being an aggregation of the elements $ ) of the list $ , j being between 0 and N- 1, each coefficient of the polynomial Q^X^ being a linear combination of elements of the list $, Q^X^ belonging to a quotient space ^^^^/* + ^^^, ^^^^ being a space of polynomials of degree N-1 with coefficients with values in the torus T and * + ^^^ being a cyclotomic polynomial of order M; - Obtain a homomorphic cipher ^ P^X^ ^ of a monomial P^X^ ^ ^-, . being a function of the index & associated with the element ^ $ % ^ to be obtained, P^X^ belonging to a quotient space /^^^/* + ^^^, /^^^ being a set of polynomials with coefficients in the integers; - Determine a homomorphic cipher polynomial ^ C^X^ ^ as a homomorphic modular product between ^ P^X^ ^ and ^ Q^X^ ^; - Extract the coefficient k from the homomorphic cipher polynomial ^ C^X^ ^ , k being determined on the basis of the polynomial Q(X) and the function . used in the monomial P(X), the coefficient k of the homomorphic encrypted polynomial ^ C^X^ ^ corresponding to the homomorphic encrypted element ^ $ % ^ to be obtained. The symbols bra and ket ^... ^ indicate a homomorphic encrypted element of a quantity. For example, the symbol ^ & ^ indicates a homomorphic encrypted element of an integer &. By homomorphic modular product, also indicated by the symbol ⊡, is meant an operation between two homomorphic ciphers, ^ A ^ and ^ B ^ , such that ^ A ^ ⊡ ^ B ^ = ^ AB ^ . In other words, the homomorphic modular product ⊡ reproduces, in the space of ciphers, the result of a product of two plaintext elements. By homomorphic cipher of ^- , is meant a homomorphic cipher of the quantity ^ ^- 234 +^ , . ^567 being between 0 and M-1. By cyclotomic polynomial of order M, is meant, in a known manner, the unitary polynomial whose complex roots are exactly the M-th primitive roots of unity. The order M is defined by M = t α with t any prime and α any integer. By aggregation, or "packing" according to the English terminology, is meant a representation of the list L in the form of a polynomial. In the case of the method according to one aspect of the invention, each coefficient of the polynomial Q(X) representing the list L comprises a linear combination of elements of the list L. Each linear combination may comprise one or more elements of the list L. The method according to the first aspect of the invention is a general method for extracting a homomorphic encrypted element from a homomorphic encrypted list from the homomorphic cipher ^ 8 ^^^ ^ of the index & corresponding to the element of interest ^ $ % ^. The extraction of the homomorphic encrypted element is carried out in a completely homomorphic manner, namely without the need to decrypt the elements of the list or the index. In other words, the method according to the first aspect of the invention performs a function of the homomorphic extractor type, or "homomorphic getter" according to the English terminology. It is important to note that the method according to the first aspect of the invention is a general method that can be implemented for any list of elements belonging to the torus T and indexed according to an integer &. The extraction method according to one aspect of the invention therefore makes it possible to extract a homomorphic encrypted element from a homomorphic encrypted list without the need to decrypt the element or the list. This is possible thanks to the prior preparation of the polynomial Q(x) as an aggregation of elements of the list L and of the monomial P(X) representing the index i corresponding to the element to be extracted. In other words, the encrypted polynomial ^ 9 ^^^ ^ is an encrypted representation of the list L and the encrypted monomial ^ 8 ^^^ ^ is an encrypted representation of the index i. It is important to note that ^ 9 ^^^ ^ and ^ 8 ^^^ ^ can be obtained homomorphically from the encrypted elements of the list ^ $ ^ and the encrypted index ^ & ^ without the need for prior decryption. Indeed, one of the advantages of the method according to the first aspect of the invention is to be able to extract an encrypted element from the encrypted list without the need for decryption of the list or the index associated with the element to be extracted. The product polynomial ^ C^X^ ^ then contains the encrypted element to be extracted in the form of its k-th coefficient. The coefficient k is determined from the aggregation used to obtain the polynomial Q and the function γ used in the monomial P(X). In other words, the prior construction of P(X) and Q(X) uniquely identifies the coefficient k of ^ C^X^ ^ containing the element of the homomorphic encrypted list to be extracted. The inventors have therefore developed a technique for extracting an element of a homomorphic encrypted list that is both simple and quick to implement and which is based on the prior preparation of the aggregation Q(X) and the monomial P(X) respectively representing the list L and the index i associated with the homomorphic encrypted element to be extracted from the list. In one or more embodiments: - each coefficient of the polynomial Q(X) is a linear combination obtained according to the following formula $ : ; < ^ $ < = >?
Figure imgf000008_0001
) = >? with 0 DEDF ^ 2, 0 DHD + I ^ 1, and - the coefficient of the polynomial ^ C^X^ ^ corresponding to the homomorphic cipher element ^ $ % ^ to be extracted is the coefficient k = 0, γ being equal to 7 ^ &. This construction of the polynomial Q(X) makes it possible to position the element of the list to be extracted in correspondence with the coefficient k = 0 of the product polynomial ^ C^X^ ^ . Furthermore, this choice for the coefficients of the polynomial Q(X) makes it possible to efficiently extract the homomorphic cipher of the desired element of the list for a wide range of values of the parameters t, M and γ. Indeed, the inventors have succeeded in finding constructions of the polynomial Q(X) and the monomial P(X) which are particularly suitable for extracting the element ^ $ % ^. Such constructions are not obvious to those skilled in the art, especially since if the aggregation Q(X) and the polynomial P(X) are not appropriately chosen, there is a high probability of coming across a linear combination of elements of the list ^ $ ^ and not the element of interest ^ $ % ^. In one or more embodiments, the extraction method according to the first aspect of the invention may further comprise a step of receiving the index ^ & ^ and the list ^ $ ^, ^ 9^^^ ^ and ^ 8^^^ ^ being obtained from the ciphers ^ & ^ and ^ $ ^. In one or more embodiments: - The homomorphic encrypted polynomial ^ 9 ^ is obtained from the list $ comprising the elements $ ) , K being an integer between 0 and L ^ 1, the homomorphic encrypted polynomial ^ 9 ^ being in the form of a homomorphic cipher of
Figure imgf000009_0001
, P^K^ being a function with values in the set of integers between 0 and N-1 and M = 2 α ; - The homomorphic encrypted monomial ^ 8 ^ is obtained from the index &, ^ 8 ^ being in the form of a homomorphic cipher of ^ OQ^%^ , R^&^ being a function with values in the set of integers between 0 and N-1 ; - The homomorphic encrypted polynomial ^ !^^^ ^ is obtained according to the formula ^
Figure imgf000009_0002
- The coefficient k of the polynomial ^ !^^^ ^ to be extracted is given by S ^ P^&^ ^ By homomorphic cipher of
Figure imgf000009_0003
, it is understood as a homomorphic number of the quantity
Figure imgf000009_0004
This embodiment illustrates an example of cooperation between the aggregation of elements of the list in the form of a polynomial Q(X) and the encryption of the monomial P(X). This is possible due to the fact that the elements of the list are encrypted as coefficients of a polynomial of degree N-1, the list being a ciphertext homomorphic of ∑ N ) A O^ B $ ) ^ M^)^ . In this case the coefficients of the polynomial Q(X) are simply the elements of the list L (the linear combinations each include a single element). The function P^K^ is a function of the integer j with values in the integers between 0 and N-1. The function P is for example a function of type P^K^ ^ ^ K ^ T^ ^56 L, with T an integer. Another example of a function is P^K^ ^ ^T ∗ K^ ^56 L with T odd. Furthermore, the index i is the homomorphic cipher of
Figure imgf000010_0001
The function R^&^ is a function from the integer i to values in the integers between 0 and N- 1. The function
Figure imgf000010_0002
is for example a function of type R^&^ ^ ^ K ^ T^ ^56 L, with T an integer. Another example of a function is R ^ ^K^ ^ ^T ∗ K^ ^56 L with T odd. By combining these two homomorphic encryption techniques, the inventors discovered that it is possible to extract the sought element by computing the homomorphic modular product
Figure imgf000010_0003
Advantageously, this homomorphic modular product results in a rotation of the coefficients of the starting polynomial Q(X). The coefficient of interest, namely the element of the list to be extracted, then becomes the coefficient of order P^&^ ^ R^&^ of the polynomial determined using the homomorphic modular product. It is therefore possible to extract the element of the homomorphic encrypted list by calculating the coefficient of order P^&^ ^ R^&^ of the polynomial ^ B . According to one or more embodiments, the functions P^&^ and R^&^ are chosen as being the identity function, namely P^&^ ^ & and R^&^ ^ &. The coefficient to be extracted is then simply the coefficient of order zero of the polynomial ^ !^^^ ^. The extraction of a coefficient of given order from an encrypted polynomial is a primitive known in homomorphic cryptography. Moreover, extracting the zero coefficient from a homomorphic cipher of a polynomial is particularly simple to implement. Having associated on the one hand the encryption of the elements of the list as coefficients of a polynomial of degree N-1 and on the other hand the encryption of the exponent i as an exponent of a monomial is far from obvious. The combination of these features has never been used in homomorphic cryptography and allows to obtain a general method for extracting a homomorphic encrypted element from a homomorphic encrypted list. Advantageously, the use of these two different homomorphic encryptions for the elements of the list and the index makes it possible to simplify the extraction of the sought element, which can be carried out as a calculation of the zero coefficient of a polynomial obtained by homomorphic modular product. The extraction of an element from a homomorphic encrypted list using the method according to the first aspect of the invention is therefore general, reliable and fast. According to an embodiment of the method according to the first aspect of the invention: - The homomorphic encrypted polynomial ^ 9^^^ ^ is obtained according to the following formula
Figure imgf000011_0001
- The homomorphic encrypted monomial ^ 8 ^ is determined according to the following formula
Figure imgf000011_0002
Definition of TLWE encryption By TLWE encryption, "Torus Learning with Errors" according to English terminology, we mean a known method of homomorphic encryption of an element t belonging to the torus T. The ciphertext V$XY^F^ is determined according to the following formula: V$XY^F^ ^ ^^ ^ , ^ ^ ... ^ \ , ^ ^
Figure imgf000011_0003
The vector s is the encryption key, the vector a is a projection vector of the key s, or mask, and the quantity e is random noise. Definition of TRLWE encryption By TRLWE encryption, "Torus Ring Learning With Errors" according to English terminology, we mean a known method of homomorphic encryption of a polynomial ^ belonging to the polynomial ring V _ ^^^ ^ V^^^/!^^^, where C is a cyclotomic polynomial and for example !^^^ ^ ^ N ^ 1 with N being a power of 2. Here, we mean by polynomial ring the space of polynomials of degree N to coefficients in the torus T.. The encryption key s and its projection vector a are vectors belonging to the set ^[ N ^^^^ \ . The ciphertext VW$XY^^^ is determined according to the following formula: VW$XY^^^ ^ ^^ ^ ^^^, ^ ^ ^^^... ^ \ ^^^, ^^^^ ^
Figure imgf000012_0001
The polynomial ]^^^ is a polynomial of the same degree as ^ ^^^ whose coefficients represent the random noise added to the ciphertext of the message ^ ^^^. For example, the coefficients of e(X) can have a Gaussian distribution centered around zero with a variance σ 2 . Definition of TRGSW encryption TRGSW encryption, or “Gentry, Sahai, Waters Torus Ring encryption” in English, means a known method of homomorphic encryption of a polynomial m(X) belonging to the polynomial ring `^^^/Φ + ^^^ with a key s, s being a vector belonging to the set ^ `^^^ ^b . The TRGSW ciphertext of m is then determined as follows: VWZ[X^^^ ^ ` ^ ^c with f ^ Z ^ e ⋮ h, where zj, j=1…l(K+1), are l(K+1) ciphertext versions of 0, the value f ?^b>^^ zero 0 being ciphertext with s', l being a given positive integer; and c i is a matrix whose dimension is ^j ^ 1^ k ^j ^ 1^ k H and whose coefficients belong to the torus T, H i ? being equal to:
Figure imgf000012_0002
B being an integer greater than or equal to 2. Definition of homomorphic modular product ⊡ between a TRGSW and a TRLWE We understand by homomorphic modular product ⊡ an operation between two homomorphic ciphertexts, ^ A ^ and ^ B ^ , such that ^ A ^ ⊡ ^ B ^ = ^ AB ^ . In in other words, the homomorphic modular product ⊡ reproduces, in the cipher space, the result of a product between plaintext elements. The method of calculating the homomorphic modular product ⊡ depends on the properties of the ciphertext elements to be multiplied. For example, in the case of a product between C ^ VWZ[X^^^ and c ^ VW$XY^^^ we obtain: ! ⊡ ^ ^ VW$XY ^^ ⋅ ^^ The advantage of this embodiment is that the calculation of the homomorphic modular product ^ B ^ ^ & ^ ⊡^ $ ^ ^ ^ ^ OQ^%^ $ ^ can be carried out in a known manner, using the technique for the product of a ciphertext quantity TRLWE and a ciphertext quantity TRGSW. The polynomial produced is then a ciphertext TRLWE whose zeroth order coefficient is the element of the list to be extracted. Another aspect of the invention relates to a computer program comprising instructions executable by a processor and designed to implement a method according to the first aspect of the invention when these instructions are executed by said processor. A second aspect of the invention relates to a method for inserting a homomorphic encrypted element ^ µ ^ into a homomorphic encrypted list ^ $ ^ so as to obtain a modified homomorphic encrypted list ^ $′ ^, in which: - The homomorphic encrypted element ^ µ ^ is obtained by homomorphic encryption of a plaintext element µ belonging to a torus T; - The homomorphic encrypted list ^ $ ^ is obtained from a plaintext list $ comprising the elements $ ) , K being an integer between 0 and L ^ 1, N being an integer greater than or equal to 1, the elements $ ) belonging to the torus T, the homomorphic encrypted list ^ $ ^ being in the form of a homomorphic cipher
Figure imgf000013_0001
- The modified homomorphic ciphertext ^ $′ ^ is a homomorphic ciphertext of a plaintext list $' comprising the elements $ ) p ^ $ )
Figure imgf000013_0002
for K ^ &, & being an integer between 0 and N-1; Said method comprising the following steps: - Receive the homomorphic cipher element ^ µ ^, the homomorphic cipher list ^ $ ^ and a homomorphic cipher ^ & ^ in the form of a homomorphic cipher of
Figure imgf000014_0001
^ µ ^, ^ $ ^ and ^ & ^ being encrypted using the same key s; - Extract, in accordance with the method according to the first aspect of the invention, the element 6 B ^ ^ $ % ^ from the homomorphic encrypted list ^ $ ^; - Homomorphically calculate the difference 6 ^ ^^ µ ^ ⊝ 6 B ^ ^ µ ^ $ % ^; - Obtain a homomorphic cipher of the quantity ^^µ ^
Figure imgf000014_0002
; - Obtain the modified homomorphic encrypted list ^ $′ ^ by computing homomorphically
Figure imgf000014_0003
The operations homomorphic subtraction, denoted by the symbol ⊝, and homomorphic addition, denoted by the symbol ⊕, are known cryptographic primitives. In the case of the difference ^ µ ^ ⊝ 6 B ^ ^ µ ^ $ % ^, the symbol ⊝ indicates the difference between two elements belonging to the torus T. In the case of the sum
Figure imgf000014_0004
the symbol ⊕ indicates the sum between two polynomials whose coefficients have a value in the torus T or in the space ^^^^/* + ^^^. The method according to the second aspect of the invention makes it possible to introduce a homomorphic cipher ^ µ ^ into a homomorphic cipher list ^ $ ^. This method, in combination with the method according to the first aspect of the invention, provides a complete technique for manipulating homomorphic cipher lists. In other words, thanks to the methods according to the first and second aspects of the invention, the reading of a list, namely the extraction of one of its elements, as well as its modification, namely the replacement of one of its elements, are possible. In one or more embodiments of the method according to the second aspect of the invention, the step of extracting the element 6 B ^ ^ $ % ^ from the cipher list homomorphic ^ $ ^ is performed using the method according to the first aspect of the invention. In one or more embodiments of the method according to the second aspect of the invention: - The homomorphic encrypted list is a homomorphic cipher calculated according to the formula
Figure imgf000015_0001
- The homomorphic cipher element ^ µ ^ is calculated according to the formula V$XY^µ^; - The homomorphic cipher ^ & ^ is calculated according to the formula VWZ
Figure imgf000015_0002
In one or more embodiments of the method according to the fourth aspect of the invention, the step of obtaining a homomorphic cipher of the quantity ^^µ ^
Figure imgf000015_0003
includes: - Compute a homomorphic cipher of the quantity µ ^ $ % as the homomorphic difference between a homomorphic cipher element ^ µ ^ of µ and a homomorphic cipher element ^ $ % ^ of the element $ % of the list $ so as to determine the quantity
Figure imgf000015_0004
- Calculate the homomorphic modular product ^ & ^ ⊡ ^ µ ^ $ % ^ to determine the quantity
Figure imgf000015_0005
- Obtain, from the quantity VW$XY^^µ ^ $ % ^^ OQ^%^ ^, a homomorphic number of the quantity ^^µ ^
Figure imgf000015_0006
in the form of VW$XY^^µ ^ $ % ^^ M^%^ ^. If the function R^&^ is of the type R^&^ ^ r ∗ & and R^&^ ^ r′ ∗ & , r and r′ being prime with M, the step of obtaining the quantity VW$XY^^µ ^ $ % ^^ M^%^ ^ is carried out by applying an automorphism. In one or more embodiments of the insertion method according to the second aspect of the invention, the functions P^&^ and R^&^ are the identity function so as to have P^&^ ^ & and R^&^ ^ &. Another aspect of the invention relates to a computer program comprising instructions executable by a processor and designed to implement a method according to the second aspect of the invention when these instructions are executed by said processor. A third aspect of the invention comprises a cryptographic processing server for processing a homomorphic encrypted list comprising a communication module and a calculation module: - The communication module being configured to receive, from an entity external to the server, a homomorphic encrypted index ^ & ^ or ^ 8 ^; - The calculation module being configured to extract, from a homomorphic encrypted list ^ $ ^, a homomorphic encrypted element ^ $ % ^ associated with the homomorphic encrypted index ^ & ^ or ^ 8 ^, in accordance with the method according to the first aspect of the invention. According to one embodiment, the calculation module of the processing server according to the first aspect of the invention determines the homomorphic modular product ^ & ^ ⊡^ $ ^ ^ ^ ^ OQ^%^ $ ^ and extracts it from it opportunely chosen so as to obtain an encrypted version of the element of the list sought. According to one embodiment, the communication module is further configured to receive, from an entity external to the server, a homomorphic encrypted element ^ µ ^. According to one embodiment, the calculation module is programmed to introduce the homomorphic encrypted element ^ µ ^ into a homomorphic encrypted list ^ $ ^ in accordance with the method according to the second aspect of the invention. A fourth aspect of the invention relates to a client configured to encrypt the index & in the form of a homomorphic encrypted index ^ & ^ or ^ 8 ^ and/or the message µ in the form of a homomorphic encrypted message ^ µ ^ and to communicate the homomorphic encrypted index ^ & ^ or ^ 8 ^ and/or the homomorphic encrypted message ^ µ ^ to the server according to the third aspect of the invention via a communication channel. The encrypted index ^ & ^ is for example in the form of an encrypted monomial ^ 9^^^ ^. A fifth aspect of the invention relates to a cryptographic system comprising: - A cryptographic processing server according to the third aspect of the invention; - A client according to the fourth aspect of the invention. By means of the cryptographic system according to the fifth aspect of the invention, the cryptographic processing server receives only homomorphic encrypted quantities and extracts an element from the list without the need to perform decryption. The present technology and its various applications will be better understood upon reading the following description and examining the accompanying figures. BRIEF DESCRIPTION OF THE FIGURES The figures are presented for information purposes only and are not limiting. Figure 1 illustrates a flowchart of an embodiment of the method for extracting a homomorphic encrypted element from a homomorphic encrypted list according to the first aspect of the invention. Figure 2a schematically illustrates the aggregation of a list according to an embodiment of the first aspect of the invention. Figure 2b schematically illustrates the extraction of a homomorphic encrypted element from a homomorphic encrypted list according to an embodiment of the first aspect of the invention. Figure 3 illustrates a flowchart of an embodiment of the method for inserting a homomorphic encrypted element into a homomorphic encrypted list according to the second aspect of the invention. Figure 4a schematically illustrates certain steps of an embodiment of the method according to the second aspect of the invention. Figure 4b schematically illustrates the insertion of a homomorphic encrypted element into a homomorphic encrypted list according to an embodiment of the method according to the second aspect of the invention. Figure 5 illustrates an embodiment of a cryptographic system for processing a homomorphic encrypted list according to an aspect of the invention. DETAILED DESCRIPTION Figure 1 [Fig.1] schematically represents an embodiment of the method 100 for extracting a homomorphic encrypted element ^ $ % ^ from a homomorphic encrypted list ^ $ ^. The method 100 according to the embodiment illustrated in Figure 1 comprises a step 101 of obtaining a homomorphic encrypted element ^ Q^X^ ^ of a polynomial Q(X). The polynomial Q(X) belongs to the set ^ ^ ^ ^ /* + ^ ^ ^ . ^ ^ ^ ^ is a space of polynomials of degree N-1 with coefficients with values in the torus T. * + ^^^ is a cyclotomic polynomial of order M and degree N. Each coefficient of the polynomial Q(X) is a linear combination of elements of the list L. The method 100 as illustrated in FIG. 1 further comprises a step 102 of obtaining a homomorphic cipher ^ P^X^ ^ of a monomial P^X^ ^ ^-, . being a function of the index & associated with the element ^ $ % ^ to be obtained. The monomial P(X) belongs to /^^^/* + ^^^, /^^^ being a set of polynomials with coefficients in the integers. In step 103, the homomorphic cipher polynomial ^ C^X^ ^ is determined as a homomorphic modular product between ^ P^X^ ^ and ^ Q^X^ ^. The extraction step 104 of the coefficient k of ^ C^X^ ^ makes it possible to obtain the element ^ $ % ^ to be extracted from the list ^ $ ^. The homomorphic encrypted monomial ^ 8^^^ ^ is obtained from a plaintext index &, & being an integer between 0 and L ^ 1. According to one embodiment, the homomorphic encrypted monomial ^ 8^^^ ^ is obtained as a homomorphic ciphertext of the quantity ^ OQ^%^ . According to one embodiment, the homomorphic encrypted polynomial ^ 9 ^ is obtained from the plaintext list $ comprising the elements $ ) , K being an integer between 0 and L ^ 1. The elements $ ) belong to the torus T. In this embodiment, the homomorphic encrypted polynomial ^ 9 ^ is obtained as a homomorphic ciphertext of the quantity ∑ N ) A O^ B $ ) ^ M^)^ . In other words, the elements of the plaintext list are encoded as coefficients of a polynomial which is then homomorphically encrypted. In this embodiment, the homomorphic modular product calculated during step 103 is calculated according to the following formula !^^^ ^ ^ 8 ^ ⊡^ 9 ^. The quantity !^^^ is a polynomial of degree N with coefficients with values in the torus T. It is therefore possible to obtain a homomorphic cipher of the element $ % , namely ^ $ % ^ , during a step 104 of extracting the coefficient of order P^&^ ^
Figure imgf000019_0001
of the polynomial !^^^. Figures 2a and 2b illustrate in more detail certain steps of an embodiment of the method 100 according to the first aspect of the invention. According to the embodiment illustrated in Figure 2a, the plaintext list $ is a sorted set of elements $ ) , j being between 0 and N-1. In this case, the framed element $ % corresponds to the element that we want to extract from the list. The homomorphic encrypted polynomial ^ 9 ^ is obtained as:
Figure imgf000019_0002
The homomorphic cipher of the index ^ & ^ is obtained according to the formula ^ & ^ ^ VWZ[X^^ O% ^. In this case the function P^&^ is the identity function, P^&^ ^ &. The function R^&^ is also chosen to be equal to the identity function, R^&^ ^ &. The choice of a TRLWE cipher for the polynomial Q encoding the elements of the list and a TRGSW cipher for the monomial P encoding the index allows us to calculate the homomorphic modular product ^ P ^⊡^ Q ^ as: TRLWEuX O^ ∑ ^ ^ A O^ BL ^ X ^ v ^ TRLWE (L B X O^ + L ^ X O^>^ ^ … ^ ^ ^ X O^>^ + …
Figure imgf000019_0003
As illustrated in Figure 2b, the term of interest x y becomes, in the product polynomial C, the zero coefficient. It is therefore possible to extract a homomorphic ciphertext of the element of interest as the zero coefficient of the polynomial resulting from the homomorphic modular product. Figure 3 illustrates a flowchart of an embodiment of the method 400 for inserting a homomorphic ciphertext element ^ µ ^ into a homomorphic ciphertext list ^ $ ^ so as to obtain a modified homomorphic ciphertext list ^ $′ ^. The homomorphic ciphertext element ^ µ ^ is obtained by homomorphic encryption of a plaintext element µ belonging to a torus T. The ciphertext list homomorphic ^ $ ^ is obtained from a plaintext list $ comprising the elements $ ) , K being an integer between 0 and L ^ 1, N being an integer greater than or equal to 1. According to the example illustrated in FIG. 3, the elements $ ) belong to the torus T and the homomorphic encrypted list ^ $ ^ is in the form of a homomorphic ciphertext of ∑ N ) A O^ B $ ) ^ M^)^ . The objective of the insertion method 400 is to obtain a new homomorphic encrypted list ^ $′ ^ which is the homomorphic ciphertext of a plaintext list $′. The plaintext list $′ is identical to the starting list $ except for the element $ p % which has been replaced by the element µ. To do this, the embodiment of the method 400 according to the second aspect of the invention comprises: - Receiving 401 the homomorphic encrypted element ^ µ ^, the homomorphic encrypted list ^ $ ^ and a homomorphic cipher ^ & ^ in the form of a homomorphic cipher of
Figure imgf000020_0001
^ µ ^, ^ $ ^ and ^ & ^ being encrypted using the same key s; - Extract, using the method 100 according to the first aspect of the invention, the element 6 B ^ ^ $ % ^ 402 from the homomorphic encrypted list ^ $ ^; - Calculate 403 homomorphically the difference 6 ^ ^^ µ ^ ⊝ 6 B ^ ^ µ ^ $ % ^; - Obtain 404 a homomorphic cipher of the quantity ^^µ ^
Figure imgf000020_0002
; - Obtain the modified homomorphic encrypted list ^ $′ ^ 405 by homomorphically calculating the sum ^ ^µ ^ $ % ^^ M^%^ ^ ⊕ ^ $ ^ . Step 402 of extracting the element 6 B ^ ^ $ % ^ from the homomorphic encrypted list ^ $ ^ therefore comprises the implementation of the method 100 according to the first aspect of the invention. FIG. 4a illustrates in detail certain steps of an embodiment of the method 400 according to the fourth aspect of the invention, the functions P^&^ ]FR^&^ being in this case the identity functions. According to the embodiment illustrated in Figure 4a, the starting list ^ $ ^ is obtained from the plaintext list $ by computing a homomorphic ciphertext of type
Figure imgf000021_0001
The homomorphic encrypted element is calculated according to the formula V$XY^µ^ and the homomorphic encrypted index according to the formula VWZ[X^^ O% ^. These last two elements are not shown in Figure 4a. In the case illustrated in Figure 4a, the function P^&^ is chosen to be equal to P^&^ ^ &. This choice of encryption techniques makes it possible to calculate the homomorphic modular product ^ & ^⊡^ $ ^ as an encrypted polynomial: TRLWEuX O^ ∑ ^ ^ A O^ BL ^ X ^ v = TRLWE (L B X O^ + L ^ X O^>^ ^ … ^ ^ ^ X O^>^ + …
Figure imgf000021_0002
The element x y to be replaced in the list L can for example be extracted as the zero coefficient of the homomorphic encrypted polynomial obtained by calculating the homomorphic modular product ^ & ^⊡^ $ ^. Step 405 of obtaining the homomorphic encrypted list ^ $′ ^ is carried out, according to the embodiment illustrated in FIG. 4b, by calculating the homomorphic encrypted list VW$XY
Figure imgf000021_0003
$ ^ which can be expressed as follows:
Figure imgf000021_0004
The last equation shows that the element $ % has been replaced in the new homomorphic cipher by the element µ. According to this embodiment, step 405 comprises the conversion of V$XY^µ ^ $ % ^ into VW$XY^µ ^ $ % ^. Indeed, µ and $ % belonging to the torus T, the homomorphic cipher of their difference is a TLWE type cipher. The conversion of a TLWE type cipher into TRLWE is carried out using primitives known in homomorphic cryptography. It is important to note that during step 405 of the method 400 according to the second aspect of the invention, the quantity VW$XY ^ ^ µ ^ $ % ^ ^ M^%^ ^ must be evaluated, whereas the homomorphic cipher of the index is in the form of a homomorphic cipher of ^ OQ^%^ , VWZ[X^^ OQ^%^ ^. According to one embodiment of the method 400, the quantity VW$XY ^^µ ^
Figure imgf000022_0001
can then be obtained in the following way: - Compute a homomorphic cipher of the quantity µ ^ $ % as the homomorphic difference between a homomorphic cipher element ^ µ ^ of µ and a homomorphic cipher element ^ $ % ^ of the element $ % of the list $ so as to determine the quantity VW$XY^µ ^ $ % ^; - Compute the homomorphic modular product ^ & ^ ⊡ ^ µ ^ $ % ^ to determine the quantity
Figure imgf000022_0002
- Obtain, from the quantity VW$XY ^ ^^µ ^ $ % ^^ OQ^%^ ^, the quantity ^^µ ^ $ % ^^ M^%^ ^ in the form of VW$XY ^ ^^µ ^ $ % ^^ M^%^ ^. If the function R^&^ is of the type R^&^ ^ r &, r being prime to M, M being the order of the cyclotomic polynomial, the step of obtaining the quantity VW$XY^^µ ^ $ % ^^ M^%^ ^ is carried out by applying an automorphism. Here, we mean by automorphism a primitive known in homomorphic cryptography whose definition is as follows: If ^ ^ VW$XY^^^^^^ and u is a prime integer to N, the automorphism ^^F performs the following operation ^^F^^, ^) = VW$XY^^^^ ^ ^^. Figure 5 illustrates an embodiment of a cryptographic system 500 for manipulating a homomorphic encrypted list according to one aspect of the invention. The cryptographic system 500 comprises a cryptographic processing server for extracting a homomorphic encrypted element from a homomorphic encrypted list 501. The cryptographic server 501 comprises a communication module 502 and a calculation module 503. The calculation module 502 is configured to receive, from an entity external to the server, a homomorphic encrypted index ^ & ^. The calculation module 503 is configured to extract, from a homomorphic encrypted list, a homomorphic encrypted element ^ $ % ^ associated with the encrypted index homomorphic ^ & ^ in accordance with the method 100 according to the first aspect of the invention. The cryptographic system 500 further comprises a client 504 configured to encrypt the index & in the form of a homomorphic encrypted index ^ & ^, for example in the form of a homomorphic encrypted monomial ^ 8 ^ and to communicate the homomorphic encrypted index ^ & ^ to the server via a communication channel 504c. According to one embodiment of the cryptographic system 500, the client 504 is configured to calculate the ciphertext of the index ^ & ^ in the form VWZ[X^^ OM^%^ ^ . According to one embodiment of the cryptographic system 500, the server 501 is configured to implement the method 400 of inserting a homomorphic encrypted element into a homomorphic encrypted list. The client 504 is then configured to encrypt the element µ so as to obtain a homomorphic encrypted element ^ µ ^. The client 504 is further configured to transmit the homomorphic encrypted element ^ µ ^ to the server 501 via a communication channel 504c. Description of the procedure for refreshing a homomorphic cipher When two encrypted messages are added together, an encrypted message is obtained, which is an encrypted version of the sum of the two initial unencrypted messages, the noise component of which is higher than for the two initial encrypted messages. Thus, to prevent the noise term from increasing and growing during data processing, a refresh procedure, generally called "bootstrapping", is performed repeatedly. This procedure produces a refreshed version of c, i.e. an encrypted message c' which is also decrypted as µ (when decrypted using s), but whose noise component is smaller than that of c. The bootstrapping procedure usually involves a homomorphic evaluation of the quantity ^ M . ^^^^ with: ^^^^ is a functional refresh polynomial of degree less than or equal to N-1 whose coefficients are chosen according to the characteristics of the message space and a target function; and α is the integer closest to 2N(ba.s): ⌊2L^^ ^ ^. ^^⌉ Here, homomorphic evaluation means a calculation performed using encrypted quantities, without prior decryption (without knowing the key s). Here, target function means a mathematical function applied to the encrypted message at the same time as the refresh. In the case of a simple refresh, the target function is the identity function. For a polynomial ^ ^ ^ ^ conveniently chosen, the constant term of ^ M . ^^^^^56^^ N ^ 1^, namely coef B uX M . v^X^v, is a refreshed version of c, that is, an encrypted version of µ with a limited noise component e' (usually smaller than the noise component of c, when c comes from previous – homomorphic – data processing operations; in any case, e' is small enough to allow a decryption of c', with a low error rate). As is known, the homomorphic calculation of the quantity ^5]^ B u^ M .
Figure imgf000024_0001
^1 ^ can be decomposed into a calculation of a sequence of modular products given by:
Figure imgf000024_0002
Where the sk are the n components of the vector s. In the above equation, when calculated homomorphically, each product “.” is a modular product: the term on the left, for example ^ O^^ or
Figure imgf000024_0003
, belongs to ℤ ^ ^X^ ^ ℤ^X^/^X N ^ 1^, the term on the right, for example ^^^^ or
Figure imgf000024_0004
belongs to TN[X]. Here we define TN[X] = T[X]/(X N +1). Such a product is similar to the product y.µi, y being an integer and µ belonging to T (except that we work on polynomial fields, instead of number fields). The homomorphic computation of ^5]^ B u^ M . ^^^^v is not immediate because of the presence of the secret key s, which is not known. However, it is known that a modular product such as y.µi or X j .v(X) can be computed homomorphically by defining the exterior product χ ^ ^^ ^ ^ ⊡ ^^ ^ ^^ ^ % ^ . The quantity ^^ ^ ^^ ^ % ^ ^ ^ % is the encrypted version of the message µi. The quantity is the “TRGSW” cipher of z (the acronym TRGSW comes from the English “Gentry, Sahai, Waters Torus Ring encryption”, adapted from an encryption method that was proposed in the article “Homomorphic encryption from learning with errors: Conceptually-simpler, asymptotically-faster, attribute-based”, by C. Gentry, A. Sahai, and B. Waters, InCrypto'13, 2013). Furthermore, as is known, it is possible to calculate the product
Figure imgf000025_0001
^^ ^ ^µ^ without knowing the components sk, k = 1…n of the secret key and therefore without knowing the secret key s. Indeed, as the components sk, k = 1…n each belong to B={0,1} (ie: are each binary), the quantity ^ O^^ ^ is equal to ^ ^ O^^ ^ 1 ^ ^ \ ^ 1 which is encrypted as
Figure imgf000025_0002
It follows that an encrypted version of ^ M . ^ ^ ^ ^ ^56 ^ ^ N ^ 1 ^ can be computed without having access to the secret key s by using the encrypted version χ ^ ^^ ^ \ ^ of the components sk. These encrypted versions of the components of s are sometimes called Bootstrap keys BK \ ^ χ ^ ^ ^^ \ ^ ('Bootstrap keys' in English). Bootstrap keys (usually public) are encrypted versions of the components sk of the secret key s encrypted using another key s'. χ ^ ^ ^^^ is defined to be equal to Z ^ yH i ^ with: f ^ Z ^ e ⋮ h, where zj, j=1…l(K+1), are l(K+1) encrypted versions of 0, the value f ?^b>^^ zero 0 being encrypted with s', l being a given positive integer; and H i ^ is a matrix whose dimension is ^j ^ 1^ k ^j ^ 1^ k H and whose coefficients belong to the torus T, H i ? being equal to:
Figure imgf000025_0003
B being an integer greater than or equal to 2. The exterior product ! ⊡ ^, between: - An encrypted message c ^ ^^ ^ ^^ µ ^ , ^ ∈ ¥ ¦>^ , corresponding to a message µ belonging to the torus TN[X] and - The encrypted version ! ^ χ ^ ^^ ^ ^ of a polynomial with integer coefficients y, ! ∈
Figure imgf000025_0004
is calculated using the method detailed below. The K+1 components cj, j=1..K+1 of the encrypted message c ^
Figure imgf000026_0001
are somehow decomposed using a base B system (like the one used to calculate χ ^ ^ )
Figure imgf000026_0002
Then it is possible to calculate
Figure imgf000026_0003
in which ∑ i,? ^^^! is the row-column matrix product and
Figure imgf000026_0004
is a matrix of dimension (n+1)×l whose form is as follows:
Figure imgf000026_0005
Figure imgf000026_0006
With The result ! ⊡ ^ belongs to ¥ ¦>^ and is an encrypted version of y.µ. In other words, by decrypting this quantity with the key s' we find y.µ. This method of calculation can be applied to any message belonging to the torus T. Using the keys BKi introduced above, we obtain for the homomorphic calculation of coef0(X α .v(X)), namely
Figure imgf000026_0007
the following equation:
Figure imgf000026_0008
Figure imgf000026_0009
The above equation therefore allows refreshing or bootstrapping the encrypted message without needing to know the encryption key.

Claims

REVENDICATIONS [Revendication 1] Procédé d’obtention (100) d’un élément chiffré homomorphe ^ $% ^ d’une liste chiffrée homomorphe ^ $ ^, l’élément chiffré homomorphe ^ $% ^ étant associé à un indice &, & étant compris entre 0 et N-1, les éléments de la liste $ appartenant à un tore T, la liste $ et l’indice & étant chiffrés à l’aide d’une même clé, ledit procédé comprenant les étapes suivantes : - Obtenir un chiffré homomorphe ^ Q^X^ ^ (101) d’un polynôme Q(X), Q(X) étant une agrégation des éléments $) de la liste $ , j étant compris entre 0 et N-1, chaque coefficient du polynôme Q^X^ étant une combinaison linéaire d’éléments de la liste $, Q^X^ appartenant à un espace quotient ^^^^/*+^^^, ^^^^ étant un espace des polynômes de degré N-1 avec coefficients à valeurs dans le tore T et *+^^^ étant un polynôme cyclotomique d’ordre M ; - Obtenir un chiffré homomorphe ^ P^X^ ^ (102) d’un monôme P^X^ ^ ^-, . étant une fonction de l’indice & associé à l’élément ^ $% ^ à obtenir, P^X^ appartenant à un espace quotient /^^^/*+^^^, /^^^ étant un ensemble de polynômes à coefficients dans les nombres entiers ; - Déterminer un polynôme chiffré homomorphe ^ C^X^ ^ (103) en tant que produit modulaire homomorphe entre ^ P^X^ ^ et ^ Q^X^ ^ ; - Extraire le coefficient k (104) du polynôme chiffré homomorphe ^ C^X^ ^, k étant déterminé sur la base du polynôme Q(X) et de la fonction . utilisée dans le monôme P(X), le coefficient k du polynôme chiffré homomorphe ^ C^X^ ^ correspondant à l’élément chiffré homomorphe ^ $% ^ à obtenir. [Revendication 2] Procédé d’obtention (100) d’un élément chiffré homomorphe ^ $% ^ d’une liste chiffrée homomorphe ^ $ ^ selon la revendication précédente dans lequel - chaque coefficient du polynôme Q(X) est une combinaison linéaire obtenue selon la formule suivante $: ; ;< = >? ^ ∑ ) A B $) < = >? avec 0 D E D F ^ 2, 0 D H D + I ^ 1, et - le coefficient du polynôme ^ C^X^ ^ correspondant à l’élément chiffré homomorphe ^ $% ^ à extraire est le coefficient k = 0, γ étant égale à 7 ^ &. [Revendication 3] Procédé d’obtention (100) d’un élément chiffré homomorphe ^ $% ^ d’une liste chiffrée homomorphe ^ $ ^ selon la revendication 1 dans lequel : • Le polynôme chiffré homomorphe ^ 9 ^ est obtenu à partir de la liste $ comprenant les éléments $), K étant un entier compris entre 0 et L ^ 1, le polynôme chiffré homomorphe ^ 9 ^ étant sous la forme d’un chiffré homomorphe de
Figure imgf000028_0001
, P^K^ étant une fonction à valeurs dans l’ensemble des nombres entiers compris entre 0 et N-1 et et M = 2α ; • Le monôme chiffré homomorphe ^ 8 ^ est obtenu à partir de l’indice &, ^ 8 ^ étant sous la forme d’un chiffré homomorphe de ^OQ^%^ , R^&^ étant une fonction à valeurs dans l’ensemble des nombres entiers compris entre 0 et N-1 ; • Le polynôme chiffré homomorphe ^ !^^^ ^ est obtenu selon la formule
Figure imgf000028_0002
• Le coefficient k du polynôme ^ !^^^ ^ à extraire est donné par S ^ P^&^ ^ R^&^. [Revendication 4] Procédé selon la revendication précédente dans lequel : • Le polynôme chiffré homomorphe ^ 9 ^ est déterminé selon la formule suivante ^ 9 ^ ^ VW$XY^∑N ) A O^ B $)^M^)^ ^ ; • Le monôme chiffré homomorphe ^ 8 ^ est déterminé selon la formule suivante
Figure imgf000028_0003
[Revendication 5] Procédé selon la revendication 3 ou la revendication 4 dans lequel les fonctions P^&^ et R^&^ sont la fonction identité de sorte à avoir P^&^ ^ & et R^&^ ^ & et le coefficient k du polynôme ^ ! ^ à extraire est le coefficient k = 0. [Revendication 6] Programme d’ordinateur comprenant des instructions exécutables par un processeur et conçues pour mettre en œuvre un procédé selon l’une quelconque des revendications 1 à 5 lorsque ces instructions sont exécutées par ledit processeur. [Revendication 7] Procédé d’insertion (400) d’un élément chiffré homomorphe ^ µ ^ dans une liste chiffrée homomorphe ^ $ ^ de sorte à obtenir une liste chiffrée homomorphe modifiée ^ $′ ^, dans lequel : - L’élément chiffré homomorphe ^ µ ^ est obtenu par chiffrement homomorphe d’un élément en clair µ appartenant à un tore T ; - La liste chiffrée homomorphe ^ $ ^ est obtenue à partir d’une liste en clair $ comprenant les éléments $), K étant un entier compris entre 0 et L ^ 1, N étant un nombre entier supérieur ou égal à 1, les éléments $) appartenant au tore T, la liste chiffrée homomorphe ^ $ ^ étant sous la forme d’un chiffré homomorphe de
Figure imgf000029_0001
; - La liste chiffrée homomorphe modifiée ^ $′ ^ est un chiffré homomorphe d’une liste en clair $’ comprenant les éléments $) p ^ $) pour K
Figure imgf000029_0002
pour K ^ &, & étant un entier compris entre 0 et N-1 ; Ledit procédé comprenant les étapes suivantes : • Recevoir (401) l’élément chiffré homomorphe ^ µ ^, la liste chiffrée homomorphe ^ $ ^ et un indice chiffré homomorphe ^ & ^ sous la forme d’un chiffré homomorphe de
Figure imgf000029_0003
^ µ ^, ^ $ ^ et ^ & ^ étant chiffrés à l’aide d’une même clé s ; • Extraire, conformément au procédé selon l’une quelconque des revendications 1 à 5, l’élément 6B ^ ^ $% ^ (402) de la liste chiffrée homomorphe ^ $ ^ ; • Calculer de façon homomorphe la différence 6^ ^^ µ ^ ⊝ 6B ^ ^ µ ^
Figure imgf000030_0001
• Obtenir (404) un chiffré homomorphe de la quantité ^^µ ^ $%^^M^%^^ ; • Obtenir la liste chiffrée homomorphe modifiée ^ $′ ^ (405) en calculant de façon homomorphe la somme ^ ^µ ^ $%^^M^%^ ^ ⊕ ^ $ ^ . [Revendication 8] Procédé d’insertion (400) d’un élément chiffré homomorphe ^ µ ^ dans une liste chiffrée homomorphe ^ $ ^ selon la revendication précédente dans lequel : • La liste chiffrée homomorphe est un chiffré homomorphe calculé selon la formule
Figure imgf000030_0002
• L’élément chiffré homomorphe ^ µ ^ est calculé selon la formule V$XY^µ^ ; • Le chiffré homomorphe ^ & ^ est calculé selon la formule VWZ[X^^OQ^%^^. [Revendication 9] Procédé d’insertion (400) d’un élément chiffré homomorphe ^ µ ^ dans une liste chiffrée homomorphe ^ $ ^ selon la revendication précédente dans lequel l’étape (404) d’obtenir un chiffré homomorphe de la quantité ^^µ ^ comprend : • Calculer un chiffré homomorphe de la quantité µ ^ $% en tant que différence homomorphe entre un élément chiffré homomorphe ^ µ ^ de µ et un élément chiffré homomorphe ^ $% ^ de l’élément $% de la liste $ de manière à déterminer la quantité formule VW$XY^µ ^ $%^ ; • Calculer le produit modulaire homomorphe ^ & ^ ⊡ ^ µ ^ $% ^ pour déterminer la quantité VW$XY^^µ ^ $%^^OQ^%^^ ; • Obtenir, à partir de la quantité VW$XY^^µ ^ $%^^OQ^%^^, un chiffré homomorphe de la quantité
Figure imgf000031_0001
sous la forme de VW$XY^^µ ^ $%^^M^%^^. [Revendication 10] Procédé d’insertion (400) d’un élément chiffré homomorphe ^ µ ^ dans une liste chiffrée homomorphe ^ $ ^ selon l’une des revendications 7 à 9 dans lequel les fonctions P^&^ et R^&^ sont la fonction identité de sorte à avoir P^&^ ^ & et R^&^ ^ &. [Revendication 11] Programme d’ordinateur comprenant des instructions exécutables par un processeur et conçues pour mettre en œuvre un procédé selon l’une quelconque des revendications 7 à 10 lorsque que ces instructions sont exécutées par ledit processeur. [Revendication 12] Serveur (501) de traitement cryptographique pour le traitement d’une liste chiffrée homomorphe comprenant un module de communication (502) et un module de calcul (503) : • Le module de communication (502) étant configuré pour recevoir, de la part d’une entité externe au serveur, un indice chiffré homomorphe ; • Le module de calcul (503) étant configuré pour extraire, d’une liste chiffrée homomorphe ^ $ ^, un élément chiffré homomorphe ^ $% ^ associé à l’indice chiffré homomorphe, conformément au procédé selon l’une des revendications 1 à 5. [Revendication 13] Serveur (501) de traitement cryptographique pour le traitement d’une liste chiffrée homomorphe selon la revendication précédente dans lequel : - Le module de communication (502) est en outre configuré pour recevoir un élément chiffré homomorphe ^ µ ^ ; - le module de calcul (503) est en outre configuré pour introduire l’élément chiffré homomorphe ^ µ ^ dans une liste chiffrée homomorphe ^ $ ^ conformément au procédé selon l’une des revendications 7 à 10. [Revendication 14] Client (504) configuré pour chiffrer l’indice & sous la forme d’indice chiffré homomorphe ^ & ^ et/ou un élément µ sous la forme d’élément chiffré homomorphe ^ µ ^ et pour communiquer l’indice chiffré homomorphe ^ & ^ et/ou l’élément chiffré homomorphe ^ µ ^ à un serveur (501) selon la revendication 7 ou 8 via un canal de communication (504c). [Revendication 15] Système cryptographique (500) pour le traitement d’une liste chiffrée homomorphe comprenant : - Un serveur (501) de traitement cryptographique pour le traitement d’une liste chiffrée homomorphe selon la revendication 7 ou la revendication 8; - Un client (504) selon la revendication 9. CLAIMS [Claim 1] Method for obtaining (100) a homomorphic encrypted element ^ $ % ^ of a homomorphic encrypted list ^ $ ^, the homomorphic encrypted element ^ $ % ^ being associated with an index &, & being between 0 and N-1, the elements of the list $ belonging to a torus T, the list $ and the index & being encrypted using the same key, said method comprising the following steps: - Obtaining a homomorphic cipher ^ Q^X^ ^ (101) of a polynomial Q(X), Q(X) being an aggregation of the elements $ ) of the list $ , j being between 0 and N-1, each coefficient of the polynomial Q^X^ being a linear combination of elements of the list $, Q^X^ belonging to a quotient space ^^^^/* + ^^^, ^^^^ being a space of polynomials of degree N-1 with coefficients with values in the torus T and * + ^^^ being a cyclotomic polynomial of order M; - Obtain a homomorphic cipher ^ P^X^ ^ (102) of a monomial P^X^ ^ ^-, . being a function of the index & associated with the element ^ $ % ^ to be obtained, P^X^ belonging to a quotient space /^^^/* + ^^^, /^^^ being a set of polynomials with coefficients in the integers; - Determine a homomorphic cipher polynomial ^ C^X^ ^ (103) as a homomorphic modular product between ^ P^X^ ^ and ^ Q^X^ ^; - Extract the coefficient k (104) from the homomorphic cipher polynomial ^ C^X^ ^, k being determined on the basis of the polynomial Q(X) and the function . used in the monomial P(X), the coefficient k of the homomorphic encrypted polynomial ^ C^X^ ^ corresponding to the homomorphic encrypted element ^ $ % ^ to be obtained. [Claim 2] Method for obtaining (100) a homomorphic encrypted element ^ $ % ^ of a homomorphic encrypted list ^ $ ^ according to the preceding claim in which - each coefficient of the polynomial Q(X) is a linear combination obtained according to the following formula $ : ; ; < = >? ^ ∑ ) AB $ ) < = >? with 0 DEDF ^ 2, 0 DHD + I ^ 1, and - the coefficient of the polynomial ^ C^X^ ^ corresponding to the homomorphic encrypted element ^ $ % ^ to be extracted is the coefficient k = 0, γ being equal to 7 ^ &. [Claim 3] Method for obtaining (100) a homomorphic encrypted element ^ $ % ^ of a homomorphic encrypted list ^ $ ^ according to claim 1 in which: • The homomorphic encrypted polynomial ^ 9 ^ is obtained from the list $ comprising the elements $ ) , K being an integer between 0 and L ^ 1, the homomorphic encrypted polynomial ^ 9 ^ being in the form of a homomorphic cipher of
Figure imgf000028_0001
, P^K^ being a function with values in the set of integers between 0 and N-1 and and M = 2 α ; • The homomorphic encrypted monomial ^ 8 ^ is obtained from the index &, ^ 8 ^ being in the form of a homomorphic cipher of ^ OQ^%^ , R^&^ being a function with values in the set of integers between 0 and N-1 ; • The homomorphic encrypted polynomial ^ !^^^ ^ is obtained according to the formula
Figure imgf000028_0002
• The coefficient k of the polynomial ^ !^^^ ^ to be extracted is given by S ^ P^&^ ^ R^&^. [Claim 4] Method according to the preceding claim in which: • The homomorphic encrypted polynomial ^ 9 ^ is determined according to the following formula ^ 9 ^ ^ VW$XY^∑ N ) A O^ B $ ) ^ M^)^ ^ ; • The homomorphic encrypted monomial ^ 8 ^ is determined according to the following formula
Figure imgf000028_0003
[Claim 5] Method according to claim 3 or claim 4 in which the functions P^&^ and R^&^ are the identity function so as to have P^&^ ^ & and R^&^ ^ & and the coefficient k of the polynomial ^ ! ^ to be extracted is the coefficient k = 0. [Claim 6] Computer program comprising instructions executable by a processor and designed to implement a method according to any one of claims 1 to 5 when these instructions are executed by said processor. [Claim 7] Method of inserting (400) a homomorphic encrypted element ^ µ ^ into a homomorphic encrypted list ^ $ ^ so as to obtain a modified homomorphic encrypted list ^ $′ ^, in which: - The homomorphic encrypted element ^ µ ^ is obtained by homomorphic encryption of a plaintext element µ belonging to a torus T; - The homomorphic encrypted list ^ $ ^ is obtained from a plaintext list $ comprising the elements $ ) , K being an integer between 0 and L ^ 1, N being an integer greater than or equal to 1, the elements $ ) belonging to the torus T, the homomorphic encrypted list ^ $ ^ being in the form of a homomorphic cipher of
Figure imgf000029_0001
; - The modified homomorphic ciphertext ^ $′ ^ is a homomorphic ciphertext of a plaintext list $' comprising the elements $ ) p ^ $ ) for K
Figure imgf000029_0002
for K ^ &, & being an integer between 0 and N-1; Said method comprising the following steps: • Receiving (401) the homomorphic encrypted element ^ µ ^, the homomorphic encrypted list ^ $ ^ and a homomorphic encrypted index ^ & ^ in the form of a homomorphic cipher of
Figure imgf000029_0003
^ µ ^, ^ $ ^ and ^ & ^ being encrypted using the same key s ; • Extract, in accordance with the method according to any one of claims 1 to 5, the element 6 B ^ ^ $ % ^ (402) from the homomorphic encrypted list ^ $ ^; • Homomorphically calculate the difference 6 ^ ^^ µ ^ ⊝ 6 B ^ ^ µ ^
Figure imgf000030_0001
• Obtain (404) a homomorphic cipher of the quantity ^^µ ^ $ % ^^ M^%^ ^ ; • Obtain the modified homomorphic cipher list ^ $′ ^ (405) by homomorphically calculating the sum ^ ^µ ^ $ % ^^ M^%^ ^ ⊕ ^ $ ^ . [Claim 8] Method for inserting (400) a homomorphic cipher element ^ µ ^ into a homomorphic cipher list ^ $ ^ according to the preceding claim in which: • The homomorphic cipher list is a homomorphic cipher calculated according to the formula
Figure imgf000030_0002
• The homomorphic encrypted element ^ µ ^ is calculated according to the formula V$XY^µ^; • The homomorphic encrypted element ^ & ^ is calculated according to the formula VWZ[X^^ OQ^%^ ^. [Claim 9] A method of inserting (400) a homomorphic encrypted element ^ µ ^ into a homomorphic encrypted list ^ $ ^ according to the preceding claim, in which the step (404) of obtaining a homomorphic encrypted element of the quantity ^^µ ^ comprises: • Calculating a homomorphic encrypted element of the quantity µ ^ $ % as a homomorphic difference between a homomorphic encrypted element ^ µ ^ of µ and a homomorphic encrypted element ^ $ % ^ of the element $ % of the list $ so as to determine the quantity formula VW$XY^µ ^ $ % ^; • Calculate the homomorphic modular product ^ & ^ ⊡ ^ µ ^ $ % ^ to determine the quantity VW$XY^^µ ^ $ % ^^ OQ^%^ ^ ; • Obtain, from the quantity VW$XY^^µ ^ $ % ^^ OQ^%^ ^, a homomorphic number of the quantity
Figure imgf000031_0001
in the form of VW$XY^^µ ^ $ % ^^ M^%^ ^. [Claim 10] Method for inserting (400) a homomorphic encrypted element ^ µ ^ into a homomorphic encrypted list ^ $ ^ according to one of claims 7 to 9 in which the functions P^&^ and R^&^ are the identity function so as to have P^&^ ^ & and R^&^ ^ &. [Claim 11] Computer program comprising instructions executable by a processor and designed to implement a method according to any one of claims 7 to 10 when these instructions are executed by said processor. [Claim 12] Cryptographic processing server (501) for processing a homomorphic encrypted list comprising a communication module (502) and a calculation module (503): The communication module (502) being configured to receive, from an entity external to the server, a homomorphic encrypted index; The calculation module (503) being configured to extract, from a homomorphic encrypted list ^ $ ^, a homomorphic encrypted element ^ $ % ^ associated with the homomorphic encrypted index, in accordance with the method according to one of claims 1 to 5. [Claim 13] Cryptographic processing server (501) for processing a homomorphic encrypted list according to the preceding claim, in which: - The communication module (502) is further configured to receive a homomorphic encrypted element ^ µ ^; - the calculation module (503) is further configured to introduce the homomorphic encrypted element ^ µ ^ into an encrypted list homomorphic ^ $ ^ according to the method according to one of claims 7 to 10. [Claim 14] Client (504) configured to encrypt the index & in the form of homomorphic encrypted index ^ & ^ and/or an element µ in the form of homomorphic encrypted element ^ µ ^ and to communicate the homomorphic encrypted index ^ & ^ and/or the homomorphic encrypted element ^ µ ^ to a server (501) according to claim 7 or 8 via a communication channel (504c). [Claim 15] Cryptographic system (500) for processing a homomorphic encrypted list comprising: - A cryptographic processing server (501) for processing a homomorphic encrypted list according to claim 7 or claim 8; - A client (504) according to claim 9.
PCT/EP2024/067453 2023-06-21 2024-06-21 Method for extracting a homomorphic encrypted element from a homomorphic encrypted list and method for inserting a homomorphic encrypted element into a homomorphic encrypted list WO2024261250A1 (en)

Applications Claiming Priority (2)

Application Number Priority Date Filing Date Title
FR2306359A FR3150381A1 (en) 2023-06-21 2023-06-21 Method for extracting a homomorphic encrypted element from a homomorphic encrypted list and method for inserting a homomorphic encrypted element into a homomorphic encrypted list
FRFR2306359 2023-06-21

Publications (1)

Publication Number Publication Date
WO2024261250A1 true WO2024261250A1 (en) 2024-12-26

Family

ID=88838806

Family Applications (1)

Application Number Title Priority Date Filing Date
PCT/EP2024/067453 WO2024261250A1 (en) 2023-06-21 2024-06-21 Method for extracting a homomorphic encrypted element from a homomorphic encrypted list and method for inserting a homomorphic encrypted element into a homomorphic encrypted list

Country Status (2)

Country Link
FR (1) FR3150381A1 (en)
WO (1) WO2024261250A1 (en)

Non-Patent Citations (3)

* Cited by examiner, † Cited by third party
Title
CHILLOTTI ILARIA ET AL: "TFHE: Fast Fully Homomorphic Encryption Over the Torus", JOURNAL OF CRYPTOLOGY, SPRINGER US, NEW YORK, vol. 33, no. 1, 25 April 2019 (2019-04-25), pages 34 - 91, XP036987049, ISSN: 0933-2790, [retrieved on 20190425], DOI: 10.1007/S00145-019-09319-X *
G. DE MICHELI ET AL., FASTER AMORTIZED FHEW BOOTSTRAPPING USING RING, 2023, Retrieved from the Internet <URL:https://eprint.iacr.org/2023/112>
LIN CHENGYU ET AL: "XSPIR: Efficient Symmetrically Private Information Retrieval from Ring-LWE", 25 September 2022, 20220925, PAGE(S) 217 - 236, XP047634693 *

Also Published As

Publication number Publication date
FR3150381A1 (en) 2024-12-27

Similar Documents

Publication Publication Date Title
EP3535923B1 (en) Method for secure classification using a transcryption operation
FR3097353A1 (en) COLLABORATIVE LEARNING METHOD OF AN ARTIFICIAL NEURON NETWORK WITHOUT DISCLOSURE OF LEARNING DATA
EP3078155B1 (en) Method of updating a file tree stored on a storage server
EP3211823B1 (en) Method for confidential execution of a program operating on data encrypted by means of homomorphic encryption
EP3861670A1 (en) Low latency calculation transcryption method applied to homomorphic encryption
FR2788650A1 (en) PUBLIC AND PRIVATE KEY CRYPTOGRAPHIC PROCESS
WO2012152607A1 (en) Device and method for generating keys with enhanced security for fully homomorphic encryption algorithm
FR2856539A1 (en) Broadcasted information encryption and/or decryption tracing method, involves implementing secret cryptographic function by multiple decoders, each including memory storing mathematical description of function
FR3095537A1 (en) CONFIDENTIAL DATA CLASSIFICATION METHOD AND SYSTEM
EP4262141B1 (en) Confidential multi-user interrogation method for the presence of a record in a database
EP2391052A1 (en) Method for computing a function and corresponding device
EP2391051B1 (en) Method for determining a representation of a multiplication of elements of a finite field
WO2024261250A1 (en) Method for extracting a homomorphic encrypted element from a homomorphic encrypted list and method for inserting a homomorphic encrypted element into a homomorphic encrypted list
FR2922393A1 (en) TRACABLE SYSTEM FOR THE ENCRYPTION / ENCRYPTION OF DIFFUSED DIGITAL DATA
WO2013024230A2 (en) Device and method for compressing public keys for a fully homomorphic encryption algorithm
WO2024261249A1 (en) Method for detecting the presence of a homomorphic encrypted element in a homomorphic encrypted set
WO2024184144A1 (en) Method for refreshing an encrypted message for homomorphic cryptography, and homomorphic cryptography method
EP2274869B1 (en) White-box protection of cryptographical algorithms comprising a calculation in quadratic form
EP3008851B1 (en) System and method for delegating bilinear pairing computations to a server
FR3150380A1 (en) Method for determining an encrypted message, associated refreshing, extraction and aggregation method
WO1998037662A1 (en) Cryptographic system comprising a ciphering and deciphering system and a key escrow system and associated appliances and devices
FR3105684A1 (en) CRYPTOGRAPHIC PROCESSING PROCESS, ELECTRONIC DEVICE AND ASSOCIATED COMPUTER PROGRAM
EP2294750B1 (en) Traceable method and system for broadcasting digital data
EP4576650A1 (en) Method of data processing
FR3136920A1 (en) Method for homomorphic determination of the sign of a message by dilation, associated methods and devices

Legal Events

Date Code Title Description
121 Ep: the epo has been informed by wipo that ep was designated in this application

Ref document number: 24733231

Country of ref document: EP

Kind code of ref document: A1