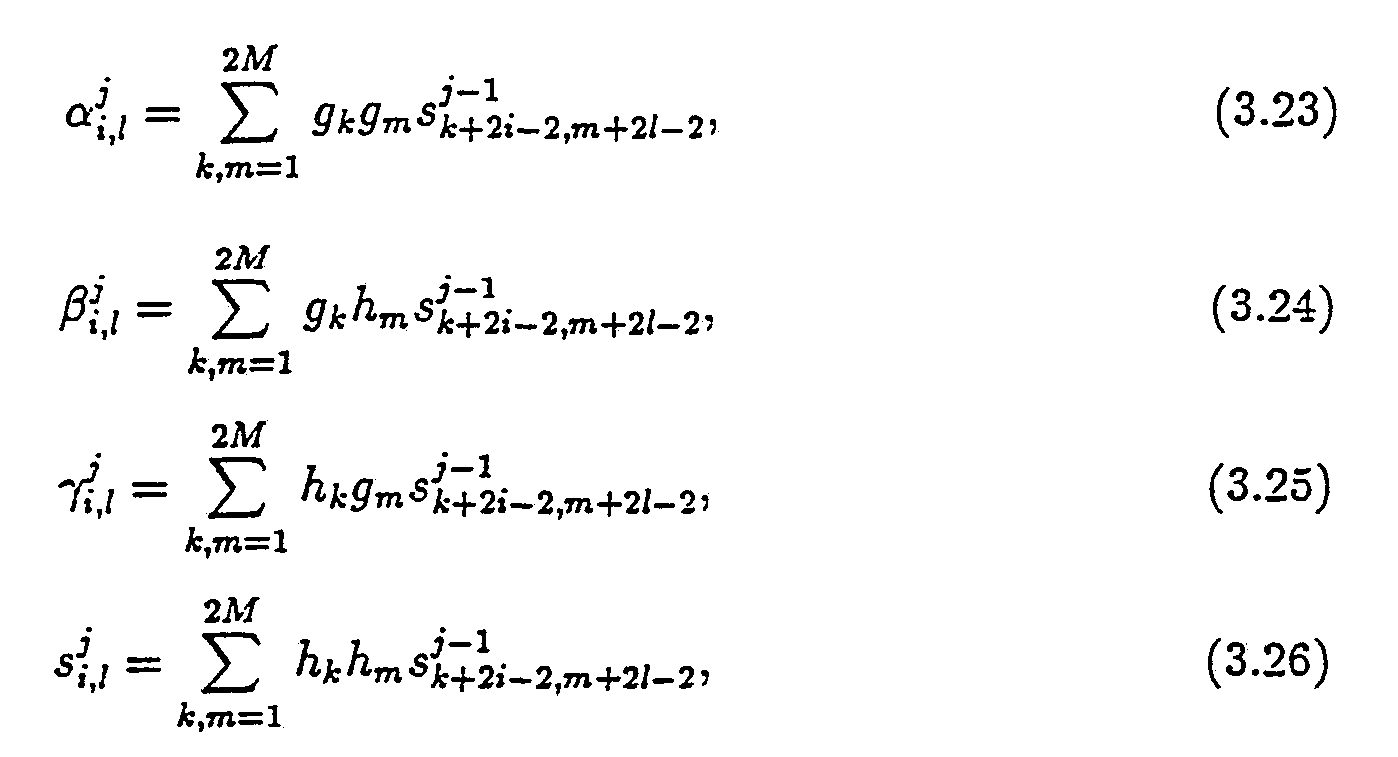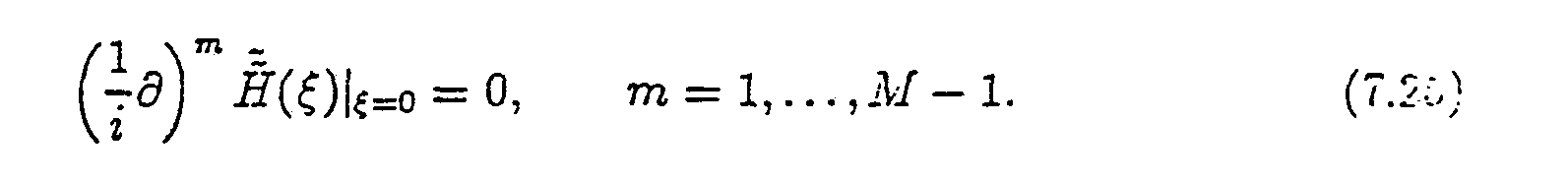Description
METHOD AND APPARATUS FOR MACHINE PROCESSING USING WAVELET/WAVELET-PACKET BASES
FIELD OF THE INVENTION
This invention relates to apparatus and techniques for machine processing of values representative of physical
quantities. The invention was made with Government support under grant numbers N00014-88-K0020, N00014-89-J1527 and
N00014-86-K0310 awarded by the Office of Navel Research of the Department of Defense. The U.S. Government has certain rights in the invention.
BACKGROUND OF THE INVENTION
There are many practical situations where it is necessary or desirable to apply an operator, representable by a matrix of two or more dimensions, to a set of values, representable by a vector (or by another matrix, which can be visualized as a group of vectors). As one example, consider the situation in weather prediction when one has input readings of wind velocities and needs to compute a map of pressure distributions from which subsequent weather patterns can be forcasted. The wind
velocities can be represented as a vector, and an operator, which may be a matrix in the form of a generalized Hubert transform, can be applied to the vector to obtain the desired pressure distributions. For a typical weather prediction problem, the matrix will be large, and multiplying the vector by the matrix will require an enormous number of computations. For example, for a vector with N elements and an NxN matrix, the
multiplication will require order O(N2) computations. If the input vector is group of vectors viewed as another NxN matrix, the multiplication of the two matrices will require order O(N3) operations. When it is considered that the input vector may be of a dynamic nature (e.g., the input data concerning wind
velocities constantly changing), the computational task can be overwhelming.
It is among the objects of the present invention to provide a technique and apparatus to ease the computational burden in the machine processing of values representative of physical
quantities. It is among the further objects of the invention to provide a technique and apparatus which achieves a saving of storage space and/or bandwidth when information is stored and/or transmitted.
SUMMARY OF THE INVENTION
The present invention is based, in part, on the fact that many vectors and matrices encountered in practical numerical computation of physical problems are in some sense smooth; i.e., their elements are smooth functions of their indices. As will become understood, an aspect of the invention involves, inter alia, transforming vectors and matrices and converting to a sparse form.
The invention is applicable for use in a machine processing system such as a digital computer. A received first set of values is representative of any physical quantities and a second received set of values is representative of an operator. The first set of values may represent, for example, a measured or generated signal as a function of time, position, temperature, pressure, intensity, or any other index or parameter. The values may also represent, for example, coordinate positions, size, shape, or any other numerically representable physical
quantities. These examples are not intended to be limiting, and others could be set forth. The first set of values can be representable as a one dimensional vector or, for example, any number or combination of vectors that can be visualized or treated (e.g. sequentially or otherwise) as a matrix of two or more dimensions. The second set of values may represent any operator to be applied to the first set of values. Examples, again not limiting, would be a function or, like the first set of values, an arrangement representative of physical quantities. For most advantageous use of the present invention, the operator values should preferably be substantially smoothly varying; that is, with no more than a small fraction of sharp discontinuities
in the variation between adjacent values. An embodiment of the invention is a method for applying said operator to said first set of values, and comprises the following steps: transforming the first set of values, on a wavelet/wavelet-packet basis, into a transformed vector; transforming the second set of values, on a wavelet/wavelet-packet basis, into a transformed matrix;
performing a thresholding operation on the transformed matrix to obtain a processed transformed matrix; multiplying the
transformed vector by the processed transformed matrix to obtain a product vector; and back-transforming, on a
wavelet/wavelet-packet basis, the product vector. The
thresholding operation may also be performed on the transformed vector. As used herein, wavelets are zero mean value orthogonal basis functions which are non-zero over a limited extent and are used to transform an operator by their application to the
operator in a finite number of scales (dilations) and positions (translations) to obtain transform coefficients. [In the computational context, very small non-zero values may be treated as zero if they are known not to affect the desired accuracy of the solution to a problem.] Reference can be made, for example, to: A. Haar, Zur Theorie der Orthogonalen Functionsysteme, Math Annal. 69 (1910); K.G. Beauchamp, Walsh Functions And Their
Applications, Academic Press (1975); I. Daubechies, Orthonormal Bases of Compactly Supported Wavelets, Comm. Pure Appl. Math XL1 (1988). Wavelet-packets, which are described in U.S. Patent Application Serial No. 525,973, are obtained from combinations of wavelets. Back-transforming, or reverse transforming, is an operation of a type opposite to that of obtaining transform coefficients; namely, one wherein transform coefficients are utilized to reconstruct a set of values. As used herein, a wavelet/wavelet-packet basis means that either wavelets or
wavelet-packets or both are used to obtain the transform or back-transform, as the case may be.
In a described embodiment of the invention, the step of transforming the first set of values, on a wavelet/wavelet-packet basis, comprises generating difference values and at least one sum value, the difference values being obtained by taking
successively coarser differences among the first set of values. In this embodiment, the step of transforming the second set of values, on a wavelet/wavelet-packet basis, also comprises
generating difference values and at least one sum value, the difference values being obtained by taking successively coarser differences among the second set of values.
In a first form of the described embodiment (also referred to as the "non-standard" form), the transformed vector has a number of sum values that is substantially equal to the number of difference values generated from the first set of values, the sum values being generated by taking successively coarser sums among said first set of values. In this first form, said at least one sum value of the transformed matrix consists of a single sum value for the second set of values, the single sum value being an average of substantially all the second set of values.
In a second form of the described embodiment (also referred to as the "standard form"), said at least one sum value of the transformed vector consists of a single sum value, the single sum value being an average of substantially all the first set of values. In this second form, the at least one sum value of the transformed matrix consists of a single row of sum values.
In the described embodiments, the difference and sum values may be weighted sum and difference values.
A typical output as obtained using the techniques hereof is close to the vector that would have been obtained by
conventionally multiplying the original vector by the operator matrix. The closeness of the approximation will depend on the thresholding performed on the transformed matrix. As the threshold is raised (which tends to remove more non-zero values from the transformed matrix) the approximation becomes less accurate. However, as will be demonstrated, for reasonable threshold values that strikingly sparsify the transformed matrix and permit commensurate reduction in computational requirements, the approximation is quite good. Indeed, as will also be demonstrated, the reduction in overall error which results from the reduced number of computations (and, therefore, reduced accumulation of rounding error from individual computations)
tends to offset somewhat the approximation errors that result from thresholding. As will become better understood, for applications where the operator is to be utilized repetitively, so that computation of the transformed matrix need only be performed once, there is a striking saving of computational cost when processing each input vector.
The practical applications of the invention are many and varied, and the following summarizes a few exemplary fields wherein the techniques and apparatus of the invention can be employed: processing and enhancement of audio and video
information; processing of seismic and well logging information to obtain measurements and models of earth formations; medical imaging processing; optical processing; calculation of potentials and fluid flow; and computation of optimum design of structural parts. Substantial saving of storage space and/or bandwidth can also be achieved when the thresholded matrix and/or vector is stored and/or transmitted.
Further features and advantages of the invention will become more readily apparent from the following detailed description when taken in conjunction with the accompanying drawings.
BRIEF DESCRIPTION OF THE DRAWINGS
Fig. 1 is a block diagram of a system which can be used to implement an embodiment of the invention and to practice an embodiment of the method of the invention.
Fig. 2 is a diagram of positions in a concert hall which is useful in gaining initial understanding of an application of the invention.
Fig. 3 illustrates a vector transformed on a wavelet basis and a matrix transformed on a wavelet basis in accordance with a first form of an embodiment of the invention.
Fig. 4 shows groupings of matrix component values utilized in an illustration of the first form of an embodiment of the invention.
Fig. 5 shows the polarities of the group members used to obtain the different types of matrix component values for the first form of matrix transformation in the disclosed embodiment.
Fig. 6A, 6B and 6C illustrate the matrix and vector
transformations, on a wavelet basis, for a second form of an embodiment of the invention.
Fig. 7 is a flow diagram of a routine for programming a processor to implement an embodiment of the invention.
Fig. 8 is a flow diagram of the routine for transforming a vector on a wavelet basis.
Fig. 9 is a flow diagram of the routine for transforming a matrix on a wavelet basis using the first form of an embodiment of the invention.
Fig. 10 is a flow diagram of the routine for transforming a matrix on a wavelet basis using the second form of an embodiment of the invention.
Fig. 11 is a flow diagram of the routine for threshold processing a transformed matrix or vector.
Fig. 12 is a flow diagram of a routine for applying a matrix operator to a vector.
Fig. 13 is a flow diagram of a routine for reconstructing a vector, on a wavelet basis, for a first form of an embodiment of the invention.
Fig. 14 is a flow diagram of a routine for reconstructing a vector, on a wavelet basis, for a second form of an embodiment of the invention.
Fig. 15 is an illustration of a type of wavelet that can be utilized in an embodiment of the invention.
Fig. 16 is an illustration of a transformed threshold- processed matrix, of the first form, for the operator of
Example 1.
Fig. 17 is an illustration of a transformed
threshold-processed matrix, of the second form, for the operator of Example 1.
Fig. 18 is an illustration of a transformed threshold- processed matrix, of the first form, for the operator of
Example 2.
Fig. 19 is an illustration of a transformed
threshold-processed matrix, of the second form, for the operator of Example 2.
Fig. 20 is a diagram of positions in a concert hall which is useful in understanding another application of the invention.
Fig.s 20-24 are diagrams illustrating further applications of the invention.
Fig.s 25A and 25B are diagrams illustrating conversion from the first form to the second form.
DESCRIPTION OF THE PREFERRED EMBODIMENTS
Referring to Fig. 1, there is shown a block diagram of a system 100 which can be used to implement an embodiment of the invention and to practice an embodiment of the method of the invention when a processor 110 of the system is programmed in the manner to be described. The processor 110 may be any suitable processor, for example an electronic digital or analog processor or microprocessor. It will be understood that any general purpose or special purpose processor, or other machine that can perform the computations described herein, electronically, optically, or by other means, can be utilized. The processor 110, which for purposes of the particular described embodiments hereof can be considered as the processor or CPU of a general purpose electronic digital computer, such as a SUN-3/50 Computer, sold by Sun Microsystems, will typically include memories 125 clock and timing circuitry 130, input/output functions 135 and display functions 140, which may all be of conventional types. Data 150, which is either already in digital form, or is
converted to digital form by suitable sampling and
analog-to-digital converter 145, is input to the processor 110. The data 150 is illustrated as a first set of values f1, f2, f3..., which can be considered as a vector f. The set of values can represent any physical quantity. For example, the values may represent a measured or generated signal, as a function of time, position, temperature, pressure, intensity, or any other index or parameter. The values may also represent coordinate positions, size, shape, or any other numerically representable physical quantities. Specific examples will be treated later. The values 150 can be representable as a one dimensional vector or, for example, any number or combination of vectors that can be
visualized or treated (e.g. sequentially) as a matrix of two or more dimensions.
Also input to the processor 110 is data 160 representative of a second set of values, depicted in Fig. 1 by a matrix K, that represents an operator to be applied to the vector f. For most advantageous use of the present invention, the operator values should preferably be substantially smoothly varying; that is, with no more than a small fraction of sharp discontinuities in the variation between adjacent values. The data 160 may comprise the actual operator to be applied to the data 150 or, for example, data from which an appropriate operator can be computed by processor 110.
After processing in accordance with the invention, an output set of values F1, F2, F3..., illustrated in Fig. 1 as a vector F, is produced, the vector F being a useful approximation of the operator K applied to the input vector f . In accordance with a feature of the invention, and as will be described further, the number of computations needed for effective application of the operator to the input vector is reduced, thereby saving time, memory requriements, bandwidth, cost, or a combination of these.
Various examples of applications of the present invention will be described hereinbelow, but for purposes of initially understanding an application of the invention a simplified example will be set forth. Consider the arrangement of Fig. 2 which shows a sound source 210 that may be, for example a musical instrument. An acoustic transducer, such a microphone 220, is located at a first position (1) within a concert hall 200. The acoustic signal received by the transducer 220 is a signal
A1(t), represented by the sketch in Fig. 2. The signal A1(t) can be sampled over a particular time interval, and at a suitable rate, to obtain digital samples representable as a vector f, having values f1, f2, f3... . Assume that one wants to generate, from the signal A1(t), an acoustic signal that represents the sound as heard at another position (2) in the hall. The task is fairly complex in that the sound waves have many reflective paths (in addition to the direct paths) of travel in the hall, with different characteristic arrival times and phases. The
relationship of the signal at location 2 with respect to the signal at location 1 will be determined by the positions of 1 and 2 with respect to the source 210, and by the shape of the hall 200. It is known that the relationship is approximated by an operator which can be represented by a matrix in two or more dimensions. The vector can be multiplied by the operator matrix to obtain an output vector which, after digital-to-analog conversion, will approximately represent the sound segment heard at location 2. For a matrix of substantial size, multiplying each input vector (representative of a segment of sampled acoustic signal) by the operator matrix will require a
relatively large number of computations. For example, assume that the acoustic signal vector has N elements, and that the operator matrix has NxN elements. In such case, each time the vector is multiplied by the matrix, N individual multiplications and N additions are required. The desirability of substantially reducing this computational burden, without unduly compromising the accuracy of the result, is evident. The advantage can be thought of in terms of increased speed for a given computational capability, or reduction in required computing power for a given allotted time, or both.
The foregoing is a simplified example of the type of machine processing task for which the system and technique of the present invention will be advantageous. The invention substantially reduces the computational burden without undue compromise in the accuracy of the result. There are various types of machine processing applications wherein operators to be applied are represented by very large matrices in two or more dimensions, and, as will become understood, the benefits of the invention become more pronounced as the magnitude of the original
computational task is increased. The example set forth above, for the purpose of initial explanation, is but one of many situations in which the system and technique of the invention can be employed, and a number of examples and applications are described hereinbelow after the following description of
different forms of the invented technique. Reference can also be made to Appendices I and II, appended hereto.
In accordance with an embodiment of the invention, the vector f is transformed, on a wavelet basis (as previously defined), to obtain a transformed vector designated fwp. The present illustrative embodiment uses the well known Haar
functions, as defined by the relationship (2.1) of Appendix I. Haar coefficients dk j and averages Sk j are computed in accordance with relationships (2.7) through (2.12) of Appendix I. Omitting the normalizing weights (which are 1//2 for Haar wavelets), the first level coefficients (differences) dk 1 are obtained as
d1 1 = f1 - f2
d2 1 = f3 - f4
d3 1 = f5 - f6
.
.
.
The first level averages (sums) s 1 are obtained as
s11 = f1 + f2
s21 = f3 + f4
s31 = f5 + f6
.
.
.
The second level coefficients dk 2 are obtained as
d1 2 = s1 1 - s2 1
d2 2 = s3 1 - s4 1
d3 2 = s5 1 - s6 1
.
.
.
The second level averages sk 2 are obtained as
s1 2 = s1 1 + s2 1
s2 2 = s3 1 + s4 1
s3 2 = s5 1 - s6 1
.
.
.
Thus, the pyramid scheme illustrated in (2.12) of Appendix I can
be used to develop all dk j and sk j in accordance with the
relationships (2.10) and (2.11). For N Samples, evaluating a complete set of coefficients and averages will require 2(N-1) additions and 2N multiplications. There will be (N-1)
coefficients and (N-1) averages. As an example, if there are 256 samples, there will be 255 coefficients and 255 averages
obtained. In such case, it is known that the original samples could be completely recovered from the 255 [(i.e., (N-1)]
coefficients dk j and the single highest level average, s. [The recovery formulas are given in (3.15) of Appendix I.] The other 254 averages, sk j, are not needed for this purpose, but are utilized to advantage in the present embodiment, as described further hereinbelow. The component values for the transformed vector fw are illustrated in the strip on the right side of
Fig. 3.
A matrix K(x,y), represents an operator that is to be applied to the vector f. The matrix has a first row of values designated K11, K12, K13, ..., a second row of values designated K21, K22, K23, ... , and so on. The present illustration uses Haar functions to obtain transformed sets of values designated αj, βj, and γj, in accordance with the relationships (2.13) through
(2.26) of Appendix I. The values α1, β1 and γ1 (the first level values) contain the most detailed difference information, with successively higher level values of αj, βj and γj successively containing less detailed (coarser) difference information. Sums are developed at each level, and used only for obtaining the difference information at the next level. Only the last sum is saved. In the present embodiment, the values can be visualized as being stored in a transformed matrix arrangement as
illustrated in Fig. 3; i.e., in regions starting (for first level designations) in the upper left-hand corner of the
transformed matrix and descending, for successively higher level designations, toward the lower right-hand corner. The procedure is as follows. Again, omitting normalizing weights, the first level coefficients and sums are:
First row of α1, β1 , γ1 and S1 α1 1 1 = + K11 - K12 - K21 + K22
β1 1 1 = + K11 + K12 - K21 - K22
γ111 = + K11 - K12 + K21 - K22
S111 = + K11 + K12 + K21 + K22 α1 1 2 = + K13 - K14 - K23 + K24
β1 1 2 = + K13 + K14 - K23 - K24
γ1 1 2 = + K13 - K14 + K23 - K24
S1 1 2 = + K13 + K14 + K23 + K24 α1 1 3 = + K15 - K16 - K25 + K26
β1 1 3 = + K15 + K16 - K25 - K26
γ1 1 3 = + K15 - K16 + K25 - K26
S1 1 3 = + K15 + K16 + K25 + K26
and so on, for the first row of α1, the first row of β1 the first row of γ1, and the first row of S1. Second row of α1, β1, γ1 and S1
α2 1 1 = + K31 - K32 - K41 + K42
β2 1 1 = + K31 + K32 - K41 - K42
γ2 1 1 = + K31 - K32 + K41 - K42
S2 1 1 = + K31 + K32 + K41 + K42 α2 1 2 = + K33 - K34 - K43 + K44
β2 1 2 = + K33 + K34 - K43 - K44
γ2 1 2 = + K33 - K34 + K43 - K44
S2 1 2 = + K33 + K34 + K43 + K44 α2 1 3 = + K35 - K36 - K45 + K46
β2 1 3 = + K35 + K36 - K45 - K46
γ2 1 3 = + K35 - K36 + K45 - K46
S2 1 3 = + K35 + K36 + K45 + K46
and so on, for the second row of α1, the second row of β1, the second row of γ1, and the second row of S1. The subsequent rows of α1, β1, γ1 and S1 are developed in similar manner. The
procedure is illustrated in Fig.s 4 and 5, with Fig. 4 showing the groups of four values (circled) used for the first and second rows of the first level computations, and Fig. 5 showing the
polarities for the differences α, β and γ, and the sum S. The second level coefficients and sums can then be developed from the first level sums, as follows:
First row of α2, β2, γ2 and S2 α1 2 1 = + S1 1 1 - S1 1 2 - S2 1 1 + S2 1 2
β1 2 1 = + S1 1 1 + S1 1 2 - S2 1 1 - S2 1 2
γ1 2 1 = + S1 1 1 - S1 1 2 + S2 1 1 - S2 1 2
S1 2 1 = + S1 1 1 + S1 1 2 + S2 1 1 + S2 1 2 α1 2 2 = + S1 1 3 - S1 1 4 - S2 1 3 + S2 1 4
β1 2 2 = + S1 1 3 + S1 1 4 - S2 1 3 - S2 1 4
γ1 2 2 = + S1 1 3 - S1 1 4 + S2 1 3 - S2 1 4
S1 2 2 = + S1 1 3 + S1 1 4 + S2 1 3 + S2 1 4 α1 2 3 = + S1 1 5 - S1 1 6 - S2 1 5 + S2 1 6
β1 2 3 = + S1 1 5 + S1 1 6 - S2 1 5 - S2 1 6
γ1 2 3 = + S1 1 5 - S1 1 6 + S2 1 5 - S2 1 6
S1 2 3 = + S1 1 5 + S1 1 6 + S2 1 5 + S2 1 6
and so on, for the first row of each.
Second row of α2, β2, γ2 and S2 α2 2 1 = + S3 1 1 - S3 1 2 - S4 1 1 + S4 1 2
β2 2 1 = + S3 1 1 + S3 1 2 - S4 1 1 - S4 1 2
γ2 2 1 = + S3 1 1 - S3 1 2 + S4 1 1 - S4 1 2
S2 2 1 = + S3 1 1 + S3 1 2 + S4 1 1 + S4 1 2 α2 2 2 = + S3 1 3 - S3 1 4 - S4 1 3 + S4 1 4
β2 2 2 = + S3 1 3 + S3 1 4 - S4 1 3 - S4 1 4
γ2 2 2 = + S3 1 3 - S3 1 4 + S4 1 3 - S4 1 4
S2 2 2 = + S3 1 3 + S3 1 4 + S4 1 3 + S4 1 4 α2 2 3 = + S3 1 5 - S3 1 6 - S4 1 5 + S4 1 6
β2 2 3 = + S3 1 5 + S3 1 6 - S4 1 5 - S4 1 6
γ2 2 3 = + S3 1 5 - S3 1 6 + S4 1 5 - S4 1 6
S2 2 3 = + S3 1 5 + S3 1 6 + S4 1 5 + S4 1 6
and so on, for the second row of each.
Subsequent levels of αk, βk, γk and Sk can be computed, in similar manner, and positioned in diagonally descending order toward the lower right-hand corner of the transformed matrix of Fig. 3. The final sum is stored in the lower rightmost corner of the transformed matrix. From the above, and the illustration of Fig. 3, it can be seen that for an original matrix size NxN, the transformed matrix of Fig. 3 will have dimensions 2(N-1)x2(N-1), and there will be up to log2N levels or "groups" of αk, βk and γk, with the final sum being associated with the highest level group. To facilitate understanding, it is assumed in this example that there are log2N levels. The transformed matrix is designated Kw. Thus, for example, a 256x256 matrix will
transform, in this format, to 510x510, with eight "groups" of α, β and γ. Of course, only 2562 members of the transformed matrix will have values (even before the thresholding, to be described) the rest of the matrix in this format being empty. The final sum will be placed in the lower right-hand quadrant of the final "group" (the corresponding quadrants of all other groups being empty), as illustrated in the Figure. The transformed matrix is designated Kw.
The next step in the present embodiment is to set to zero (i.e., effectively remove from the transformed matrix) the matrix members that have values less than a predetermined magnitude;
i.e. remove all matrix members (other than the final S) whose absolute values are less than a predetermined threshold. This can be routinely done by scanning the completed matrix, or by performing the thresholding operation as each level of the matrix is constructed (all values of S being retained, of course, for computation of the next level) .
The next step in the present embodiment involves multiplying the vector which has been transformed on a wavelet basis (and is designated fw), by the matrix which has been transformed on a wavelet basis and threshold-modified (and is then designated Kwp) . This can be achieved, in known fashion, by multiplying the vector fw, a row at a time, by the rows of K^ to obtain the individual members of a product vector fwp. Techniques for multiplying a
vector by a matrix are well known in the art, as are techniques for efficiently achieving this end when the matrix is sparse and has a large percentage of zero (or empty) values. These zero values, or strings of them, can be flagged beforehand, so that only those matrix positions, or strings of positions which have non-zero values will be considered in the multiplication process. It will be understood that for this form of the invention the transformed matrix, Kw, and/or the threshold-modified version thereof, Kwp, can be stored in other formats than that used for illustration in the Fig. 3 (such as a continuous string of values), so long as the transformed values are in known positions to achieve the appropriate multiplication of values of vector and matrix rows, in accordance with the scheme of the Fig. 3
illustration.
The product vector fwp that results from the described multiplication will have individual component values in the same arrangement as illustrated in the transformed vector of Fig. 3; namely differences now designated d1 1p, d2 1p . . . . , d1 2p ,
d
2 2p......
/ ' a nd so on, and sums now designated s
1 1p, s
2 1p.....
S / s
1 2p, s
2 2p . ...
/ / and so on, but where the p in the
superscript indicates that these transformed vector values have been processed, in this case as a result of having been
multiplied by the transformed matrix Kw.
The transformed and processed vector fwp can then be
back-transformed, on a wavelet basis, to obtain an output vector, F, that is close to the vector that would have been obtained by conventionally multiplying the original vector f by the matrix K. This can be done, for example, in accordance with the
relationships (2.27) through (2.30) and (3.15) of Appendix I. In particular, the highest level sp and the highest level dp are combined to obtain the next lower level difference and sum information. [The sum information is accumulated at each step.] The sum and difference information can then be used to obtain the next lower level information, and so on, until the lowest level information values, which are the components of F, are obtained.
As stated, the output vector F is close to the vector that would have been obtained by conventionally multiplying the
original vector f by the matrix K. The closeness of the
approximation will depend on the thresholding performed on the transformed matrix Kw. As the threshold is raised (which tends to remove more non-zero values from the transformed matrix Kw) the approximation becomes less accurate. However, as will be demonstrated, for reasonable threshold values that strikingly sparsify the transformed matrix and permit commensurate reduction in computational requirements, the approximation is quite good. Indeed, as will also be demonstrated, the reduction in overall error which results from the reduced number of computations (and, therefore, reduced accumulation of rounding error from individual computations) tends to offset somewhat the approximation errors that result from thresholding. As will become better understood, for applications where the operator [matrix K(x,y), for the above example] is to be utilized repetitively, so that computation of the transformed matrix need only be performed once, there is a striking saving of computational cost when processing each input vector.
A feature of the described first form of the invention is the "decoupling" among the different levels (or coarseness scales) which are a measure of difference between adjacent elements (at the lowest processing level) or adjacent groups of elements (at successively higher levels, as the groups get larger) when the transformed matrix and vector are multiplied. [See, for example, (4.32) - (4.58), and accompanying text, in Appendix I]. In other words, and as can be seen by visualizing the vector fw in a horizontal configuration for successive multiplication by the matrix rows, the lowest level α, β and γ of the transformed matrix Kw are combined only with the lowest level difference and sum information of the transformed vector fw.
Similarly, the second lowest levels of Kw and fw are combined, and so on. There are no "cross-terms" between levels. It is seen that the difference terms of fw interact with the α and γ terms of Kw at each level, and the sum terms of fw interact with the β terms.
A further embodiment hereof is referred to as a second form or "standard form". In this embodiment, the Haar (or other
wavelet or wave packet) coefficients and sum that are stored are those that could be used to recover the original vector or matrix (as the case may be), and they are generated and arranged in a symmetrical fashion that permits inversion. Assume, again, that one has a vector f with values f1, f2, f3,..., and that Haar functions are then used as representative wavelet or wave packet transform vehicles. In this embodiment, however, the transformed vector, fw, contains only the difference information (i.e., coefficients designated d1 1, d2 1, d3 1,...
/ d1 2, d2 2, d3,...
and so on), and the final sum (s), as illustrated in the
right-hand strip of Fig. 6C. Assume, again, that a matrix K(x,y) represents an operator that is to be applied to the vector f (see Fig. 6A). The matrix again has a first row of values designated K11, K12, K13..., a second row of values designated K21, K22, K23..., and so on. This illustration again uses Haar
functions to obtain transformed values; in this case, in
accordance with the relationships (2.10) through (2.12) of
Appendix I. First, each row of the matrix is processed to obtain coefficients (differences) and a final sum, in the same manner as used to transform the vector f to fw as just described and as shown in the strip at the right-hand side of Fig. 6C. In
particular, the first matrix row K11, K12, K13... K1N is converted to D1 1 1 , D1 1 2 , D1 1 3....D1 1, N- 1 , S1N , where
D1 1 1 = K11 - K12
D1 1 2 = K13 - K14
.
.
.
D1 1 ( N/2 ) = K1 ( N- 1 ) - K1N
D1 1 ( N/2+ 1 ) = S1 1 1 - S1 1 2
.
.
.
D1 1 ( 3N/4 ) = S1 1 ( N/2- 1 ) - S1 1 (N/2 )
D1 1 ( 3N/4+1 ) = S1 1 (N/2+1) - S1 1 (N/2+2 )
.
S1 1 N = K11 + K12 + .. .K1N where
S1 1 1 = K11 + K12
S1 1 1 = K13 + K14
.
.
.
S1 1 (N/2) = K1(N-1) + K1N
S1 1 (N/2+1) = S1 1 1 + S1 1 2
.
.
.
S1 1 (3N/4) = S1 1 (N/2-1) + S1 1 (N/2)
S1 1 (3N/4+1) = S1 1 (N/2+1) + S1 1 (N/2+2)
.
.
.
Similarly, the second row K21, K22, K23...K2N is converted to D211, D2 1 2, D2 1 3...D2,N-1 S2,N , and each subsequent row is converted in similar manner. The result is shown in Fig. 6B. Next, the same procedure is applied, by column, to the individual columns of the Fig. 6B arrangement. In particular, the column D1 1 1, D2 1 1, D3 1 1... , is converted to D1 2 1, D2 2 1, D3 2 1..., where
D1 2 1 = S1 1 1 - S2 1 1
D2 2 1 = S3 1 1 - S4 1 1
.
.
.
D( 2 N/2)1 = S( 1 N-1)1 - SN 1 1
D( 2 N/2+1)1 = S1 2 1 - S2 2 1
.
.
.
D( 2 3N/4)1 = S( 2 N/2+1)1 - S( 2 N/2+2)1
.
.
.
SN 2 1 = S1 1 1 + S2 1 1..... SN 1 1
where
S1 2 1 = S1 1 1 + S2 1 1
S 2 2 1 = S 3 1 1 + S 4 1 1
.
.
.
S( 2 N/2 ) 1 = S( 1 N-1) 1 + SN 1 1
S(N 2 /2+1)1 = S 1 2 1 + S 2 2 1
.
.
.
S( 2 3N/4)1 = S( 2 N/2+1)1 + S( 2 N/2+2)1
.
.
.
Similarly, the column D1 1 2, D2 1 2, D3 1 2...DN 1 2 is converted to D1 2 2 , D2 2 2, D3 2 2...SN 2 2, and each subsequent column is converted in similar manner with the resultant transformed matrix, Kw, being illustrated in Fig. 6C.
A thresholding procedure can then be applied to the
transformed matrix, as previously described. An advantage of the resultant sparse matrix (which is obtained when a matrix is transformed using the just-described second form, and then processed with a thresholding operation) is that its product after multiplication by another similarly transformed matrix, will remain in said second form.
After multiplication of Kw by fw, and other suitable
manipulation, the resultant vector fwp can be back-transformed, using the reverse of the procedure described to obtain fw, to obtain the output vector F. This can be done, for example, in accordance with relationships (3.15) of Appendix I. [Also see observation 3.1 of Appendix I.] In particular, the sum sp and the highest level dp difference are combined to obtain the next lower level sum information, which is then combined with the
difference information at that level to obtain the next lower level sum information, and so on, until the components of output vector F are obtained.
Referring to Fig. 7, there is shown an overview flow diagram of the routine for programming the processor 110 (Fig. 1) to implement the technique of the first or second forms of the disclosed embodiment of the invention. The block 710 represents the routine, described further in conjunction with Fig. 8, for transforming the vector f on a wavelet basis to obtain a
transformed vector fw, in either the first or second form. The block 720 represents the routine for transforming the matrix K, on a wavelet basis, to obtain a transformed matrix, Kw. The first form matrix transformation is further described in
conjunction with Fig. 9, and the second form matrix
transformation is further described in conjunction with Fig. 10. The block 730 represents the routine, described further in conjunction with Fig. 11, for threshold processing of the transformed matrix Kw to obtain the transformed processed matrix Kwp. The block 740 represents the routine, described further in conjunction with Fig. 12, for applying the transformed and processed operator matrix Kwp to the transformed vector fw to obtain a product vector fwp. The block 750 represents the routine for back-transforming from fwp, on a wavelet basis, to obtain the output vector F.
Fig. 8 is a flow diagram of a routine for transforming the vector f, on a wavelet basis, into a transformed vector fw; that is, for the first form, a vector having coefficients
(differences) and sums as indicated for the transformed vector components illustrated in the strip on the right-hand side of Fig. 3 and, for the second form, the coefficients and the single final sum illustrated in the strip on the right-hand side of Fig. 6C. The block 810 represents the inputting of the vector component values f1, f2, ... fN of the vector to be transformed. The first level coefficients (differences) can then be computed and stored, as represented by the block 820. These differences are in accordance with the relationships set forth above for the d values, each being computed as a difference of adjacent
component values of the vector being transformed. The first level sums are then also computed and stored from the vector component values, as described hereinabove, to obtain the s1 values, and as represented by the block 830. [For the first form (Fig. 3), all the sums will be retained for fw, whereas for the second form (Fig. 6), only the final sum is part of fw.] The block 840 is then entered, this block representing the computing and storing of the next higher level differences (for example, the d2 values) from the previous level sums. Also computed and stored, from the previous level sums, are the next higher level sums, as represented by the block 850. Inquiry is then made (diamond 860) as to whether the last level has been processed. [There will be at most log2N levels for a vector having N components.] If not, the level index is incremented (block 870) and the block 840 is re-entered. The loop 875 continues until all differences and sums of the transformed vector have been computed and stored, whereupon the inquiry of diamond 860 is answered in the negative and the vector transformation is
complete.
Fig. 9 shows the routine for transforming the matrix K
(which, in the present example, is an NxN matrix, where N is a power of 2), on a wavelet basis, to obtain a transformed matrix Kw of the first form and as illustrated in Fig. 3. In the
routine of Fig. 9, the block 910 represents the reading in of the matrix values for the matrix K. The block 920 represents the computation and storage of the first level α, β, γ, and S values in accordance with relationships first set forth above. In the present embodiment, the values of α, β and γ are stored at positions (or, if desired, with index numbers, or in a sequence) that correspond to the indicated positions of Fig. 3, and which will result in suitable multiplication of each transformed vector element by the appropriate transformed matrix value in accordance with the routine of Fig. 12. The sums, S, need only be stored until used for obtaining the next level of transform values, with only the final sum being retained in the transformed matrix of the first form of the present embodiment. Next, the block 930 represents computation and storage, from the previous level
values of S, of the next higher level values of α, β, γ and S, in accordance with the above relationships. Again each computed value is stored at a matrix position (or, as previously
indicated, with an appropriate index or sequence) in accordance with the diagram of Fig. 3. Inquiry is then made (diamond 940) as to whether the highest level has been processed. For an NxN matrix, there will be at most log2N levels, as previously noted. If not, the level index is incremented (block 950), and the block 930 is re-entered. The loop 955 then continues until the
transform values have been computed and stored for all levels.
Fig. 10 shows the routine for transforming the matrix K, on a wavelet basis, to obtain a transformed matrix Kw of the second form and as illustrated in Fig. 6C. The block 1010 represents the reading in of the matrix values for the matrix K. The block 1020 represents the computation and storage of the row
transformation coefficient values D1 and sums S1 in accordance with the relationships described in conjunction with Fig. 6B. Next, the block 1030 represents the computation and storage of the column transformation coefficient values D2 and S2 in
accordance with the relationships described in conjunction with Fig. 6C.
Fig. 11 is a flow diagram illustrating a routine for
processing the transformed matrix to remove members thereof that have an absolute magnitude smaller than a predetermined
threshold. It will be understood that, if desired, at least some of the thresholding can be performed as the transformed matrix is being computed and stored, but the thresholding of the present embodiment is shown as a subsequent operation for ease of
illustration. The block 1110 represents initiation of the scanning process, by initializing an index used to sequence through the transformed matrix members. Inquiry is made (diamond 1115) as to whether the absolute value of the currently indexed matrix element is greater than the predetermined threshold. If the answer is yes, the diamond 1120 is entered, and inquiry is made as to whether a flag is set. The flag is used to mark strings of below threshold element values, so that they can effectively be considered as zeros during subsequent processing.
If a flag is not currently set, the block 1125 is entered, this block representing the setting of a flag for the address of the current matrix component. Diamond 1160 is then entered, and is also directly entered from the "yes" output of diamond 1120. If the threshold is exceeded, the diamond 1130 is entered, and inquiry is made as to whether the flag is currently set. If it is, the flag is turned off (block 1135) and diamond 1160 is entered. If not, diamond 1160 is entered directly. Diamond 1160 represents the inquiry as to whether the last element of the matrix has been reached. If not, the index is incremented to the next element (block 1150), and the loop 1155 is continued until the entire transformed matrix has been processed so that flags are set to cover those elements, or sequences of elements, that are to be considered as zero during subsequent processing.
Referring to Fig. 12, there is shown a flow diagram of a routine for multiplying the transformed vector fw by the
transformed and threshold-processed matrix Kwp. In the present illustrative embodiment, the previously described flags are used to keep track of strings of zeros in the matrix, and each element of the vector and matrix is considered for ease of illustration. It will be understood, however, that various techniques are known in the art for multiplying matrices,
including sparse matrices, in efficient fashion [see, for example, S. Pissanetsky, Sparse Matrix Technology, Academic
Press, 1984]. Such techniques can also be used for multiplying matrices having bands of information in approximately known positions, as will occur in certain cases hereof. In the
illustrative routine of Fig. 12, indices used to keep track of the matrix row (block 1210) and the vector element and
corresponding matrix column (block 1220) are initialized.
Inquiry is made (diamond 1225) as to whether the flag is set for the current matrix element. If so, the element index can skip to the end of the string of elements on the row at which the flag is still set, this function being represented by the block 1230. If the flag is not set at this element of the matrix, the block 1235 is entered, this block representing the multiplying of the
current vector and matrix elements . The product is then added to
the current row accumulator, as represented by the block 1240. Inquiry is then made (diamond 1245, which is also entered from the output of block 1230) as to whether the last element of the row has been reached. If not, the matrix and vector element index is incremented (block 1250), and the loop 1255 is continued until the row is complete. When this occurs, the block 1260 is entered, this block representing the storing of the accumulator contents (which is the total for the current matrix row times the vector) at the component of the output vector that
corresponds to the current row. Inquiry is then made (diamond 1265) as to whether the last row has been reached. If not, the row index is incremented (block 1280) and the block 1220 is re-entered. The loop 1285 then continues as the vector fw is multiplied by each row of the matrix Kwp, and the individual components of the output vector fwp are computed and stored.
It will be understood that alternative techniques can be utilized for multiplying a sparse matrix by a vector. For example, a simplified sparse matrix format, which provides fast processing, can employ one-dimensional arrays (vectors)
designated a , ia, and ja. Vector a would contain only the non-zero elements of the matrix, and integer vectors ia and ja would respectively contain the row and column locations of the element. The total number of elements in each of the vectors a, ia, ja, is equal to the total number of nonzero elements in the original matrix. The vector a, with its associated integer vectors used as indices, can then be applied to a desired vector or matrix (which may also be in a similar sparse format) to obtain a product.
Referring to Fig. 13, there is shown a flow diagram of the routine for back-transforming to obtain an output vector F from the transformed and processed vector fwp of the first form. The block 1310 represents initializing to first consider the highest level sum and difference components of fwp. The next lower level sum information is then computed from the previous level sum and difference information, this operation being represented by the block 1320. For example, and as previously described at the last level using Haar wavelets, the sum and difference would be added
and subtracted to respectively obtain the two next lower level sums. The block 1330 is then entered, this block representing the adding of the sum information to the existing sum information at the next lower level. Inquiry is then made (diamond 1340) as to whether the lowest level has been reached. If not, the level index is decremented (block 1350), and the the block 1320 is re-entered. The next lower level sum information is then
computed, as before, and the loop 1355 continues until the lowest level has been reached. The lowest level sum and difference information is then combined (block 1370) to obtain the
components of an output vector F, and the result is read out (block 1380).
Fig. 14 is a flow diagram of the routine for back- transforming to obtain the output vector F from the transformed and processed vector f^ of the second form. The routine is similar to that of the Fig. 13 routine (for the first form), except that there is no extra sum information to be accumulated at each succeeding lower level. Accordingly, all blocks of like reference numerals to those of Fig. 13 represent similar
functions, but there is no counterpart of block 1330.
The Haar wavelet system, used for ease of explanation herein, often does not lead to transformed and thresholded matrices that decay away from the diagonals (i.e., for example, the diagonals between the upper left corner and the lower right corner of the square regions of Fig. 3) as fast as can be
achieved with other wavelet bases. To obtain faster decay in these cases, one can employ a wavelet/wavelet-packet basis in which the wavelet elements (or wavelet-packets) have several vanishing moments. These are described for example in (3.1) - (3.26) of Appendix I. Reference can also be made to I.
Daubechies, Orthonormal Bases of Compactly Supported Wavelets, Comm. Pure, Applied Math, XL1, 1988; Y. Meyer Principe
d' Incertitude, Bases Hilbertiennes et Algebres d'Operateurs, Seminaire Bourbaki, 1985-86, 662, Astέrisque (Societe'
Mathematique de France); S. Mallat, Review of Multifrequency
Channel Decomposition of Images and Wavelet Models, Technical Report 412, Robotics Report 178, NYU (1988), and thee
aboverefrenced U.S. Patent Application Serial No. 525,973.
The wavelet illustrated in Fig. 15 has two vanishing
moments. As used herein, the number of vanishing moments, for a wavelet Ψ(x) is determined by the highest integer n for which
∫ψ(x) xkdx = 0
where 0≤k<n-l, and this is known as the vanishing moments
condition. Using this convention, the Haar wavelet has 1
vanishing moment, and the wavelet of Fig. 15 has 2 vanishing moments. To obtain faster decay away from the diagonal, it is preferable that the wavelet (and/or wavelet-packet obtained from combining wavelets) has a plurality of vanishing moments, with several vanishing moments being most preferred. The wavelet of Fig. 15 has defining coefficients as follows: (See Daubechies, supra) :
h2 = (1 + / /
h2 = (3 + / /
h3 = (3 - /
g 1 = h4
g2 = -h3
g3 = h2
g4 = -h1
The vanishing moments condition, written in terms of defining coefficients, would be the following:
and L is the number of coefficients.
Referring again to the wavelet of Fig. 15, the procedure for applying this wavelet would be similar to that described above for the Haar wavelet, but groups of 4 elements would be utilized, and would be multiplied by the h coefficients and the g
coefficients to obtain the respective averages and differences.
It is generally advantageous to utilize wavelets (and/or wavelet-packets) having as many vanishing moments as is
practical, it being understood that the computational burden of computing the transformed vectors and/or matrices increases as the number of vanishing moments (and coefficients) increases. Accordingly, a trade-off exists which will generally lead to use of a moderate number of vanishing moments, as in the illustrative examples below.
EXAMPLES
Properties of various types of matrices, including the extent to which they are rendered sparse using the techniques hereof, are illustrated in conjunction with the following
examples. The numerical experiments of these examples were performed on a SUN-3/50 computer equipped with an MC68881
floating-point accelerator. The algorithms were applied to a number of different operators, using a FORTRAN program, as described in the examples to follow. Column 1 of the Table accompanying each example shows the number of nodes N in the discretization of the operator. An N-component random vector is multiplied by each NxN matrix for each example, for N = 64, 128, 256, 512, and 1024. Calculations were performed, in both single precision (7 digit precision) and double precision (15 digit precision). Ts is the CPU time, in seconds, that is required for performing the multiplication using conventional technique; that is, an order O(N2) operation. Tw is the CPU time that is required for performing the multiplication on a wavelet basis. The wavelet used for these examples was of the type described by Daubechies [see I. Daubechies Orthonormal Bases of Compactly Supported Wavelets, Comm. Pure, Applied Math, XL1, 1988], with the number of vanishing moments and defining coefficients as indicated for each example. [It will be understood that the higher the number of vanishing moments, the more defining
coefficients a wavelet will have, and accuracy can, to some degree, be traded off against processing time.] Td is the CPU time used to obtain the first form of the operator (e.g. Fig. 3).
The L2 (normalized) and L∞ (normalized) errors are taken with respect to double precision calculations for the conventional matrix multiplication technique [order O(N2)]. L2 is the square root of the sum of the squares of the difference at each matrix point. L∞ is the largest single difference. The last column of each Table indicates the compression coefficient, Ccomp, which is the ratio of the number of elements in the matrix, N2, to the number of non-zero elements in the threshold-processed matrix, using the first form of the invention. In all Figures 16 to 23, the matrices are depicted for N = 256.
Example 1
were processed using wavelets with six first moments set equal to zero, and setting to zero all resultant matrix entries whose absolute values were smaller than 10-7 , with results shown in Table 1 and Fig. 16. The second form (so-called "standard form") threshold-processed matrix is shown in Fig. 17.
The operator represented by the matrix of this example has the familiar Hubert transform characteristic which can be used in various practical applications. For example, consider the problem in weather prediction, first noted in the Background section hereof, when one has input readings of wind velocities and wishes to compute a map of pressure distributions from which subsequent weather patterns can be forecasted. The operator used in computing the pressure distributions may be of the type set forth in this example.
The Table 1 shows the striking advantage of the processing hereof as the matrix size increases. For example, for N = 1024, Ts is 30.72 seconds, whereas Tw is only a small fraction as much (3.72 seconds). Although Td is quite high (605.74 seconds, without optimized software) in this example, it will be
understood that for most applications Td will only have to be computed once, or infrequently. Another advantage of the sparse matrix is illustrated by comparing the normalized errors L and
L∞ for single precision multiplication with the normalized erro L2 and L∞ for the processing hereof (designated "FWT" for "fast wavelet transform"). [As indicated above, for all such
measurements, the normalizing factor is the double precision measurements using conventional matrix multiplication technique. It is seen that FWT error values are less than the single precision error values in all cases, with the contrast greatest for largest N. It is thus seen that computational rounding erro tends to accumulate less when there are many fewer non-zero members in the matrix.
Example 2
In this example the matrices considered are of the form -l
where i, j = 1, . . . , N and N = 2n.
This matrix is not a function of i-j and is therefore not a convolution type matrix, and its singularities are more
complicated, and not known a priori. Wavelets of six vanishing moments and a threshold of 10
-7 were used The results are shown in Fig. 18 and are tabulated in Table 2. The second form matrix is shown in Fig. 19. The cost of constructing the second form of the operator is proportional to Ν
2.
Fig. 20 illustrates a simplified example of how an
embodiment of the invention can be used to advantage for
efficient inverting of a matrix. Consider, again, the concert hall 200, sound source 210, and acoustic transducer 200, as in the Fig. 2 example. In the present illustration, however, it is assumed that one wishes to use the received acoustic signal
(which results from a direct signal and many reflected signals of different characteristic path lengths - and accordingly differen arrival times and phases) in order to compute the original signal at the source 210. Again, assume that a segment of the signal A1(t) is sampled and digitized to obtain the vector f. A matrix, designated K, can be determined, in known fashion, from the shap of the hall and the respective positions of the sound source 210 and the receiving transducer 220. If a segment of the original sound (sampled and digitized) is representable in this example by the vector F, and F were known, one could obtain the vector f from the vector F and the matrix K. In the present example, however, it is assumed that one has the vector f from the
measurements at the receiving transducer, and that F is the unknown to be determined. In such instance, it is necessary to invert K to obtain an inverted matrix K-1, and then use this inverted matrix in conjunction with the vector f in order to obtain the vector F. The procedure, in conventional fashion, is illustrated in Fig. 20. Techniques for inversion of a matrix are well known in the art. For a matrix of substantial size,
however, the inversion process involves a large number of
computations (for example, of the order of N2 computations for an NxN matrix). However, if the matrix being inverted is sparse, the computational task is drastically reduced, as illustrated for similar situations above.
The improved procedure, in accordance with an embodiment of the invention, is illustrated in Fig. 21. The matrix f is transformed, on a wavelet/wavelet-packet basis, using the above second form (or "standard form") to obtain fw. This can be done in accordance with the procedure described in conjunction with Fig. 6 (flow diagram of Fig. 8). Also, as before, the matrix K is transformed, using the second form, as also illustrated in conjunction with Fig. 6 (and the flow diagram with Fig. 10), to obtain Kw. The matrix is then threshold processed (e.g. flow diagram of Fig. 11) to obtain Kwp, and the matrix is inverted to obtain [Kwp]-1 (see Appendix II). The inverted matrix can then be multiplied by the vector fw (e.g. flow diagram of Fig. 12) to obtain the product vector fwp, and the output vector, F, can be recovered by back-transforming (e.g. flow diagram of Fig. 14).
As first noted above, substantially smooth vectors can, if desired, also be compressed by threshold processing prior to multiplication by a transformed and threshold processed matrix. The procedure is similar to that set forth in the flow diagram of Fig. 11, except that a step of threshold processing the
transformed vector fw is performed before the vector is
multiplied by the matrix. This is illustrated in Fig. 22, which shows the vector fw processed to obtain fwp. In this case, the product vector is designated fwpp.
Fig. 23 illustrates the procedure for matrix multiplication (see also Appendix II), for example, where one matrix L
represents a first set of values representative of physical quantities, and a second matrix K represents an operator to be applied. [It will be understood that the matrix L, in any number of dimensions, can be visualized as a set of vectors f.] In the Fig. 23 illustration, only one of the matrices (K) is compressed by threshold processing. In the similar example illustrated in Fig. 24, both matrices are threshold processed before
multiplication of the matrices. In both Fig. 23 and Fig. 24, the
product matrix is designated Mw, and the back-transformed output matrix is designated M. In both cases, the second form (or so-called standard form) is utilized. The back-transform
technique is as described in conjunction with the flow diagram of Fig. 14, but with the columns and than rows being processed (in the manner of individual vectors processed as illustrated in Fig. 6), in the reverse of the order described in conjunction with Fig. 6.
As described in Appendix I, e.g. at relationships (4.27) through (4.29), one can convert between the above-described first and second forms, or vice versa, as desired. For example, if the first (non-standard) form has been utilized and a sparse matrix is obtained, the conversion to the second (standard) form will not require undue computation, and the second form may be
advantageous for an operation such as inverting the matrix. A simplified illustration of the procedure is shown in Fig.s 25A and 25B. Fig. 25A illustrates the first form (as in Fig. 3 above), with three levels. Fig. 25B shows how the information in Fig . 25A can be converted to the second form using the
above-referenced relationships of Appendix I. In particular, the α1, α2 and α3 and S3 information is placed, without change, in the matrix positions illustrated in Fig. 25B. The β information is placed as shown in Fig. 25B, but after conversion by
considering each row of β1, β2 and β3 as a vector and converting the vectors, in the manner of conversion of the vector of Fig. 6A - 6C above, to obtain β1, β2 and β3. Similarly, the γ
information is placed as shown in Fig. 25B, but after conversion by considering each column of γ , γ and γ as a vector and converting the vectors, in the manner of conversion of the vector of Fig. 6A - 6C above, to obtain Conversion can
also be effected from the second form to the first form, if desired.
The invention has been described with reference to
particular preferred embodiments, but variations within the spirit and scope of the invention will occur to those skilled in the art. For example, it will be understood that after
sparsifying a matrix as taught herein, the matrix information
could be incorporated in a special purpose chip or integrated circuit, e.g. for repetitive use, or could be the basis for a very fast special purpose computational logic circuit.
Appendix I
I Introduction
The purpose of this paper is to introduce a class of numerical algorithms designed for rapid application of dense matrices (or integral operators) to vectors. As is well-known, applying directly a dense NxN- matrix to a vector requires roughly N2 operations, and this simple fact is a cause of serious difficulties encountered in large-scale computations. For example, the main reason for the limited use of integral equations as a numerical tool in large-scale computations is that they normally lead to dense systems of linear algebraic equations, and the latter have to be solved, either directly or iteratively. Most iterative methods for the solution of systems of linear equations involve the application of the matrix of the system to a sequence of recursively generated vectors, which tends to be prohibitively expensive for large-scale problems. The situation is even worse if a direct solver for the linear system is used, since such solvers normally require O(N3) operations. As a result, in most areas of computational mathematics dense matrices axe simply avoided whenever possible. For example, finite difference and finite element methods can be viewed as devices for reducing a partial differential equation to a sparse linear system. In this case, the cost of sparsity is the inherently high condition number of the resulting matrices.
For translation invariant operators, the problem of excessive cost of applying (or inverting) the dense matrices has been met by the Fast Fourier Transform (FFT) and related algorithms (fast convolution schemes, etc.). These methods use algebraic properties of a matrix to apply it to a vector in order N log(N) operations. Such schemes are exact in exact arithmetic, and are fragile in the sense that they depend on the exact algebraic properties of the operator for their applicabilitv. A more recent group of fast
algorithms [1,2,5,9] uses explicit analytical properties of specific operators to rapidly apply them to arbitrary vectors. The algorithms in this group are approximate in exact arithmetic (though they are capable of producing any prescribed accuracy), do not require that the operators in question be translation invariant, and are considerably more adaptable than the algorithms based on the FFT and its variants.
In this paper, we introduce a radical generalization of the algorithms of [1,2,5,9]. We describe a method for the fast numerical application to arbitrary vectors of a wide variety of operators. The method normally requires order O(N) operations, and is directly applicable to all Calderon-Zygmund and pseudo- differential operators. While each of the algorithms of [1,2,5,9] addresses a particular operator and uses an analytical technique specifically tailored to it, we introduce several numerical tools applicable in all of these (and many other) situations. The algorithms presented here are meant to be a general tool similar to FFT. However, they do not require that the operator be translation invariant, and are approximate in exact arithmetic, though they achieve any prescribed finite accuracy. In addition, the techniques of this paper generalize to certain classes of multi-linear transformations (see Section 4.6 below).
We use a class of orthonormal "wavelet" bases generalizing the Haar functions and originally introduced by Stromberg [10] and Meyer [7]. The specific wavelet basis functions used in this paper were constructed by I. Daubechies [4], and are remarkably well adapted to numerical calculations. In these bases (for a given accuracy) integral operators satisfying certain analytical estimates have a band-diagonal form, and can be applied to arbitrary functions in a 'fast' manner. In particular, Dirichlet and Neumann boundary value problems for certain elliptic partial differential equations can be solved in order N calculations, where N is the number of nodes in the discretization of the boundary of the region. Other applications include an O(N log(N)) algorithm for the evaluation of Legendre series, and similar schemes (comparable in speed to FFT in the same dimensions) for other special function expansions. In general, the scheme of this paper can be viewed as a method for the conversion (whenever regularity permits) of dense matrices to a sparse form.
Once the sparse form of the matrix is obtained, applying it to an arbitrary vector is an order O(N) procedure, while the construction of the sparse form in general requires O(N2) operations. On the other hand, if the structure of the singularities of the matrix is known a priori (as for Green's functions of elliptic operators or for Calderon-Zygmund operators) the compression of the operator to a banded form is an order O(N) procedure. The non-zero entries of the resulting compressed matrix mimic the structure of the singularities of the original kernel.
Effectively, this paper provides two schemes for the numerical evaluation of integral operators. The first is a straightforward realization ("standard form") of the matrix of the operator in the wavelet basis. This scheme is an order Nlog(N) procedure (even for such simple operators as multiplication by a function). While this straightforward realization of the matrix is a useful numerical tool in itself, its range of applicability is significantly extended by the second scheme, which we describe in this paper in more detail. This realization ("non-standard form") leads to an order N scheme. The estimates for the latter follow from the more subtle analysis of the proof of the "T(1) theorem" of David and Journe (see [3]). We also present two numerical examples showing that our algorithms can be useful for certain operators which are outside the class for which we provide proofs. The paper is organized as follows. In Section II we use the well-known Haar basis to describe a simplified version of the algorithm. In Section III we summarize the relevant facts from the theory of wavelets. Section IV contains an analysis of a class of integral operators for which we obtain an order N algorithm, and a description of a version of the algorithm for bilinear operators. Section V contains a detailed description and a complexity analysis of the scheme. Finally, in Section VI we present several numerical applications.
Generalizations to higher dimensions and numerical operator calculus containing O(Nlog(N)) implementations of pseudodifferential operators and their inverses will appear in a sequel to this paper.
II The algorithm in the Haar system
The Haar functions h
j,k with integer indices j and k are defined by
1
Clearly, the Haar function hj,k(x) is supported in the dyadic interval Ij,k
Ij,k = [2i(k - l), ^k}. (2.2)
1We define the basis so that the dyadic scale with the index j is finer than the scale with index j + 1. This choice of indexing is convenient for numerical applications.
We will use the notation hj,k(x) = h Ij,k(x) = hl(x) = 2-j/2h(2-jx - k + 1), where h(x) = h0 ,1 (x). We index the Haar functions by dyadic intervals Ij,k and observe that the system hIj,k(x) forms an orthonormal basis of L2(R) (see, for example, [8]).
We also introduce the normalized characteristic function X I
j,k(x)
where lIj,kl denotes the length of Ij,k, and will use the notation Xj,k = XIj,k.
Given a function f ∈ L2(R) and an interval l C R, we define its Haar coefficient di oi f
and " average" s
l of f on I as
and observe that
where I' and I" are the left and the right halves of I.
To obtain a numerical method for calculating the Haar coefficients of a function we proceed as follows. Suppose we are given N = 2
n "samples" of a function, which can for simplicity be thought of as values of scaled averages
of f on intervals of length 2-n. We then get the Haar coefficients for the intervals of length 2- n+1 via (2.6), and obtain the coefficients
4
We also compute the 'averages' fy J
on the intervals of length 2
-n+1. Repeating this procedure, we obtain the Haar coefficients and averages
4 ^ 4 4
for j = 0, ... , n - 1 and k = 1, . .. , 2n-j-1. This is illustrated by the pyramid scheme
K
It is easy to see that evaluating the whole set of coefficients dl, sl in (2.12) requires 2(N - 1) additions and 2N multiplications.
In two dimensions, there are two natural ways to construct Haar systems. The first is simply the tensor product hlxJ = hi <g> hJ, so that each basis function hlxJ is supported on the rectangle I x J. The second basis is defined by associating three basis functions: hl(x)hl,(y), hl(x)Xl' (y), and Xl(x)hl' (y) to each square I x I', where I and I' are two dyadic intervals of the same length.
We consider an integral operator
T(f)(x) =∫κ(x,y)f(y)dy, (2.13) and expand its kernel (formally) as a function of two variables in the two-dimensional Haar series h r
where the sum extends over all dyadic squares I x I' with lIl = lI'l, and where α
ll' =∫∫ K(x, y)h
l(x)h
l'(y)dxdy, (2.15) β
ll' =∫∫ K (x , y)h
l(x)X
l' (y)dxdy, (2.16) and
γll' =∫∫ K(x, y)Xl(x)hl' (y)dxdy. (2.17)
When I = Ij,k, I' = lj,k, (see (2.2)), we will also use the notation
( ) defining the matrices α
j = {
Substituting (2.14) into (2.13), we obtain
(recall that in each of the sums in (2.21) I and I' always have the same length).
To discretize (2.21), we define projection operators >
and approximate T by
(2.23) where Po is the projection operator on the finest scale. An alternative derivation of (2.21) consists of expanding T0 in a 'telescopic' series
T0 = P0TP0 =∑(Pj-1TPj-1 - PjTPj) + PnTPn
[(P
j-1 - P
j)T(P
j-1 - P
j) + (P
j-1 - P
j)TP
j + P
jT(P
j-1 - P
j)] + P
nTP
n.
(2.24) Defining the operators Qj with j = 1, 2, . . . , n, by the formula
Qj = Pj-1 - Pj, (2.25) we can rewrite (2.24) in the form
T
0 = (Q
jTQ
j + Q
jTP
j + P
jTQ
j) + P
nTP
n . (2.26)
The latter can be viewed as a decomposition of the operator T into a sum of contributions from different scales. Comparing (2.14) and (2.26), we observe that while the term P
nTP
n (or its equivalent) is absent in (2.14), it appears in (2.26) to compensate for the finite number of scales.
Observation 2.1. Clearly, expression (2.21) can be viewed as a scheme for the numerical application of the operator T to arbitrary functions. To be more specific, given a function f, we start with discretizing it into samples
k = 1, 2, . .. ,N, which are then converted into a vector ∈ R
2N-2 consisting of all coefficients
J and ordered as
Then, we construct the matrices α
j, β
j , γ
j for j = 1, 2, . . . , n (see (2.15) - (2.20) and Observation 3.2) corresponding to the operator T, and evaluate the vectors
{
k},
via the formulae
where d
3' =
k = 1, 2, .. . , 2
n-j , with j = 1, . .. ,n. Finally, we define an approximation T
^ to T
0 by the formula 2 M 2
Clearly,
T /) is a restriction of the operator T
0 in (2.23) on a finite-dimensional subspace of i
2(R). A rapid procedure for the numerical evaluation of the operator is
described (in a more general situation) is Section III below.
It is convenient to organize the matrices αj, βj, γj with j = 1, 2. . . , n into a single matrix, depicted in Figure 1, and for reasons that will become clear in Section IV, the matrix in Figure 1 will be referred to as the non-standard form of the operator T, while (2.14) will be referred to as the "non-standard" representation of T (note that the (2.14) is not the matrix realization of the operator T0 in the Haar basis).
III Wavelets with vanishing moments and associated quadratures
3.1. Wavelets with vanishing moments. Though the Haar system leads to simple algorithms, it is not very useful in actual calculations, since the decay of αll', βll', γll' away from diagonal is not sufficiently fast (see below). To have a faster decay, it is necessary to use a basis in which the elements have several vanishing moments. In our algorithms, we use the orthonormal bases of compactly supported wavelets constructed by I. Daubechies [4] following the work of Y. Meyer [7] and S. Mallat [6]. We now describe these orthonormal bases.
Consider functions ψ and φ (corresponding to h and X in Section II), which satisfy the following relations:
where
9k = (-1)k-1h2M-k+1, k = 1, . . . , 2M (3.3) and
∫φ(x)dx = 1. (3.4)
The coefficients h are chosen so that the functions
ψ j,k(x) = 2-j/2ψ(2-j x - k + 1), (3.5) where j and k are integers, form an orthonormal basis and, in addition, the function ψ has M vanishing moments
∫ψ(x)xmdx = 0, m = 0, . . . , M - 1. (3.6)
We will also need the notation φ
j,k(x) = 2
-j/ 2φ (2
-jx - k + 1). (3.7)
Note that the Haar system is a particular case of (3.1)-(3.6) with M = 1 and h
1 = h
2 =
φ = X and ψ = h, and that the expansion (2.14)-(2.17) and the nonstandard form in (2.26) in Section II can be rewritten in any wavelet basis by simply replacing functions X and h by φ and ψ respectively.
Remark 3.1. Several classes of functions φ, ψ have been constructed in recent years, and we refer the reader to [4] for a detailed description of some of those.
Remark 3.2. Unlike the Haar basis, the functions φl, φJ can have overlapping supports for As a result, the pyramid structure (2.12) 'spills out' of the interval [1, N] on which the structure is originally defined. Therefore, it is technically convenient to replace the original structure with a periodic one with period N. This is equivalent to replacing the original wavelet basis with its periodized version (see [8]).
3.2. Wavelet-based quadratures. In the preceeding subsection, we introduce a procedure for calculating the coefficients
for all j≥ 1, k = 1, 2, . . . , N, given the coefficients for k = 1, 2, ... ,N. In this subsection, we introduce a set of quadrature
formulae for the efficient evaluation of the coefficients
corresponding to smooth functions f. The simplest class of procedures of this kind is obtained under the assumption that there exists a real constant T
M such that the function φ satisfies the condition
∫φ(x + TM)xm dx = 0, for m = 1,2, . . . , M - 1, (3.8)
∫φ(x) dx = 1, (3.9) i.e. that the first M - 1 'shifted' moments of φ are equal to zero, while its integral is equal to 1. Recalling the definition of
∫ f(x) φ(2
n x - k + 1) dx = ∫ f(x + 2
-n(k - 1)) φ(2
nx) dx, (3.10)
expanding f into a Taylor series around 2
-n(k - 1 + T
M ), and using (3.8), we obtain ∫ f(x + 2
-n(k - 1)) φ (2
nx) dx = f(2
-n(k - 1 + T
M)) + O(2-^ (3.11)
In effect, (3.11), is a one-point quadrature formula for the evaluation of Applying the same calculation to with j≥ 1, we easily obtain
f(2
-n+j(k - 1 + T
M)) + O(2
-( n-jW * (3.12)
which turns out to be extremely useful for the rapid evaluation of the coefficients of compressed forms of matrices (see Section IV below).
Though the compactly supported wavelets found in [4] do not satisfy the condition (3.8), a slight variation of the procedure described there produces a basis satisfying (3.8), in addition to (3.1) - (3.6).
It turns out that the filters in Table 1 are 50% longer that those in the original wavelets found in [4], given the same order M. Therefore, it might be desirable to adapt the numerical scheme so that the 'shorter' wavelets could be used. Such an adaptation (by means of appropriately designed quadrature formulae for the evaluation of the integrals (3.10)) is presented at pages 1-24 to 1-28.
Remark 3.3. We do not discuss in this paper wavelet-based quadrature formulae for the evaluation of singular integrals, since such schemes tend to be problem-specific. Note, however, that for all integrable kernels quadrature formulae of the type developed in this paper are adequate with minor modifications.
3.3. Fast wavelet transform. For the rest of this section, we treat the procedures being discussed as linear transformations in RN, viewed as the Euclidean space of all periodic sequences with the period N.
Replacing the Haar basis with a basis of wavelets with vanishing moments, and assuming that the coefficients
= 1, 2, . . . ,N axe given, we replace the expressions (2.8) - (2.11) with the formulae and
where are viewed as periodic sequences with the period 2
n-j (see also Remark
3.2 above). As is shown in [4], the formulae (3.13) and (3.14) define an orthogonal mapping O
j : R
2n-j+1 → R
2n-j-1, converting the coefficients
3 with k = 1, 2, . . . ,2
n-j+1 into the coefficients £ with k = 1,2, . . . ,2
n-3, and the inverse of O
j is given by the
formulae
H
Obviously, given a f
unction f of the form
it can be expressed in the form /
with 5 J = 1,2, .. .2n-j+1 given by (3.15).
Observation 3.1. Given the coefficients
1, 2, . .. , N, recursive application of the formulae (3.13), (3.14) yields a numerical procedure for evaluating the coefficients
for all j = 1, 2, . . . , n, k = 1, 2, . . . , 2
n-j, with a cost proportional to N. Similarly, given the values
for all j = 1,2, . .. , n, k = 1,2, . .. , 2
n-J, and s" (note that the vector s
n contains only one element) we can reconstruct the coefficients
for all k = 1, 2, . . . , N by using (3.15) recursively for j = n, n - 1, . .. , 0. The cost of the latter procedure is also O(N). Finally, given an expansion of the form i
/ it costs O(N) to evaluate all coefficients
fc = 1, 2, . . . , N by the recursive application of the formula (3.17) with j = n, n - 1, . . . , 0.
Observation 3.2. It is easy to see that the entries of the matrices α
j , β
j , γ
j with j -= 1,2. . . ,n, are the coefficients of the two-dimensional wavelet expansion of the function K(x, y), and can be obtained by a two-dimensional version of the pyramid scheme (2.12), (3.13), (3.14). Indeed, the definitions (2.15)- (2.17) of these coefficients can be rewritten in the form
2
and we will define an additional set of coefficients
by the formula
4
Now, given a set of coefficients with i, I = 1,2,...,N, repeated application of the
formulae (3.13), (3.14) produces
with i,l = 1,2,...,2n-j, j = 1,2,...,n. Clearly, formulae (3.23) - (3.26) are a two- dimensional version of the pyramid scheme (2.12), and provide an order N2 scheme for the evaluation of the elements of all matrices αj,βj,γj with j = 1,2...,n.
IV Integral operators and accuracy estimates
4.1. Non-standard form of integral operators. In order to describe methods for 'compression' of integral operators, we restrict our attention to several specific classes of operators frequently encountered in analysis. In particular, we give exact estimates for pseudo- differential and Calderon-Zygmund operators.
We start with several simple observations. The non-standard form of a kernel K(x, y) is obtained by evaluating the expressions αll' =∫∫ K (x,y) ψl(x) ψl'(y) dxdy, (4.1) βll' =∫∫ K (x, y) ψι(x) φl' (y) dxdy, (4.2) and
γll' =∫∫ K (x,y) φl(x) Ψl'(y) dxdy. (4.3)
(see Figure 1). Suppose now that K is smooth on the square I x I'∈ [0, N] x [0, N ]. Expanding K into a Taylor series around the center of I x I', combining (3.6) with (4.1) - (4.3) and remembering that the functions ψ
l, ψ
l' are supported on the intervals I, I' respectively, we obtain the estimate
Obviously, the right-hand side of (4.4) is small whenever either | l | or the derivatives involved are small, and we use this fact to 'compress' matrices of integral operators by converting them to the non-standard form, and discarding the coefficients that are smaller than a chosen threshold.
To be more specific, consider pseudo-differential operators and Calderon-Zygmund operators. These classes of operators are given by integral or distributional kernels that are smooth away from the diagonal, and the case of Calderon-Zygmund operators is particularly simple. These operators have kernels K(x, y) which satisfy the estimates f
for some M≥ 1. To illustrate the use of the estimates (4.6) for the compression of operators, consider the simplest case of M = 1, so that
βll' =∫∫ K(x, y)hι(x)Xl'(y)dxdy, (4.7) where we assume that the distance between I and I' is greater than than | l |. Since
∫hl' dy = 0, (4.8)
we have
where x
l denotes the center of the interval I. In other words, the coefficient β
ll , decays quadratically as a function of the distance between the intervals I, I', and for sufficiently large N and finite precision of calculations, most of the matrix can be discarded, leaving only a band around the diagonal. Howev
er, algorithms using the above estimates (with M = 1) tend to be quite inefficient, due to the slow decay of the matrix elements with their distance from the diagonal. The following simple proposition generalizes the estimate (4.9) for the case of larger M, and provides an analytical tool for efficient numerical compression of a wide class of operators.
Proposition 4.1. Suppose that in the expansion (2.14), the wavelets φ, ψ satisfy the conditions (3.1) - (3.3), and (3.6). Then for any kernel K satisfying the conditions (4.6), the coefficients
in the non-standard form (see (2.18) - (2.20) and Figure 1 ) satisfy the estimate for all
Remark 4.1. For most numerical applications, the estimate (4.10) is quite adequate, as long as the singularity of K is integrable across each row and each column (see the following section). To obtain a more subtle analysis of the operator T0 (see (2.23) above) and correspondingly tighter estimates, some of the ideas arising in the proof of the "T(1)" theorem of David and Journe are required. We discuss these issues in more detail in Section 4.5 below.
Similar considerations apply in the case of pseudo-differential operators. Let T be a pseudo-differential operator with symbol σ(x, ξ) defined by the formula
where K is the distributional kernel of T. Assuming that the symbols σ of T and σ* of T* satisfy the standard conditions
we easily obtain the inequality h p
for all integer i, l.
Remark 4.2. A simple case of the estimate (4.15) is provided by the operator T =
in which case it is obvious that
where the sequence {β
i} is defined by the formula
provided a sufficiently smooth wavelet φ(x) is used.
4.2. Numerical calculations and compression of operators. Suppose now that we approximate the operator
by the operator
obtained from
by setting to zero all coefficients of matrices α = {a
ll, }, β = {β
ll, }, γ = {7
ll,} outside of bands of width B≥ 2M around their diagonals. It is easy to see that
where C is a constant determined by the kernel K. In other words, the matrices α,β, γ can be approximated by banded matrices α
B, β
B, γ
B respectively, and the accuracy of the approximation is
In most numerical applications, the accuracy ε of calculations is fixed, and the parameters of the algorithm (in our case, the band width B and order M) have to be chosen
in such a manner that the desired precision of calculations is achieved. If M is fixed, then B has to be such that
In other words,
* has been approximated to precision ε with its truncated version, which can be applied to arbitrary vectors for a cost proportional to N log
2(log
2(N)), which for all practical purposes does not differ from N. A considerably more detailed investigation (see Remark 4.1 above and Section 4.5 below) permits the estimate (4.21) to be replaced with the estimate
making the application of the operator
to an arbitrary vector with arbitrary fixed accuracy into a procedure of order exactly O(N).
Whenever sufficient analytical information about the operator T is available, the evaluation of those entries in the matrices a,β, γ that are smaller than a given threshold can be avoided altogether, resulting in an O(N) algorithm (see Section V below for a more detailed description of this procedure).
Remark 4.3. Both Proposition 4.1 and the subsequent discussion assume that the kernel K is non-singulax everywhere outside the diagonal, on which it is permitted to have integrable singularities. Clearly, it can be generalized to the case when the singularities of K are distributed along a finite number of bands, columns, rows, etc. While the analysis is not considerably complicated by this generalization, the implementation of such a procedure on the computer is significantly more involved (see Section V below).
4.3. Rapid evaluation of the non-standard form of an operator. In this subsection, w e construct an efficient procedure for the evaluation of the elements of the non-standard form of an operator T lying within a band of width B around the diagonal. The procedure assumes that T satisfies conditions (4.5). (4.6), of Section IV, and has an operation count proportional to NB (as opposed to the O(N
2) estimate for the general procedure described in Observation 3.2).
To be specific, consider the evaluation of the coefficients \ for all j = 1, 2, , ... , n, and I i - 1 |≤ B. According to (3.24),
which involves the coefficients in a band of size 3B defined by the condition
ZB. Clearly, (3.26), could be used recursively to obtain the required coefficients ) and
the resulting procedure would require order N
2 operations. We therefore compute the coefficients
directly by using appropriate quadratures. In particular, the application of the one-point quadrature (3.12) to K (x, y), combined with the estimate (4.6), gives *
If the wavelets used do not satisfy the moment condition (3.8), more complicated quadratures have to be used (see Appendix B to this paper).
4.4. The standard matrix realization in the wavelet basis. While the evaluation of the operator T via the non-standard form (i.e., via the matrices aj, βj, γj) is an efficient tool for applying it to arbitrary functions, it is not a representation of T in any basis. There are obvious advantages to obtaining a mechanism for the compression of operators that is simply a representation of the operator in a suitably chosen basis, even at the cost of certain sacrifices in the speed of calculations (provided that the cost stays O(N) or O(Nlog(N)) ). It turns out that simply representing the operator T in the basis of wavelets satisfying the conditions (3.6) results (to any fixed accuracy) in a matrix containing no more than 0(N log(N)) non-zero elements. Indeed, the elements of the matrix representing T in this basis are of the form.
T
lJ = (Tψι, ψ J). (4.25) with I, J all possible pairs of diadic intervals in R, not necessarily such that | l |=| J | . Combining estimates (4.5), (4.6) with (3.6), we easily see that
where CM is a constant depending on M, K, and the choice of the wavelets, d (I, J) denotes the distance between I, J, and it is assumed that | I |≤ | J |. It is easy to see
that for large N and fixed ε≥ 0, only O(Nlog(N)) elements of the matrix (4.25) will be greater than ε, and by discarding all elements that are smaller than a predetermined threshold, we compress it to O(Nlog(N)) elements.
Remark 4.4. A considerably more detailed investigation (see [8] ) shows that in fact the number of elements in the compressed matrix is asymptotically proportional to N, as long as the images of the constant function under the mappings T and T* are smooth. Fortunately, the latter is always the case for pseudo-differential and many other operators.
Numerically, evaluation of the compressed form of the matrix {TlJ} starts with the calculation of the coefficients so (see (2.7) ) via an appropriately chosen quadrature formula. For example, if the wavelets used satisfy the conditions (3.8), (3.9), the one- point formula (3.10) is quite adequate. Other quadrature formulae for this purpose can be found in Appendix B to this paper. Once the coefficients so have been obtained, the subsequent calculations can be carried out in one of three ways.
1. The naive approach is to construct the full matrix of the operator T in the basis associated with wavelets by following the pyramid (2.12). After that, the elements of the resulting matrix that are smaller than a predetermined threshold, axe discarded. Clearly, this scheme requires O(N2) operations, and does not require any prior knowledge of the structure of T.
2. When the structure of singularities of the kernel K is known, the locations of the coefficients of the matrix {TlJ} exceeding the threshold ε can be determined a priori. After that, these can be evaluated by simply using appropriate quadrature formulae on each of the supports of the corresponding basis functions. The resulting procedure requires order 0(N log(N)) operations when the operator in question is either Calderon-Zygmund or pseudo-differential, and is easily adaptable to other distributions of singularities of the kernel.
3. The third approach is to start with the non-standard form of the operator T. compress it, and convert the compressed version into the standard form. This simplifies the error analysis of the scheme, enabling one to use the one-point quadratures (3.10). The conversion procedure starts with the formula
K(x, y) ψ(2
-jx - (k - 1)) dx ) φ(2
-jy - (I - 1)) dy, (4.27)
which is an immediate consequence of (2.16), (2.19). Combining (4.27) with (3.14), we
immediately obtain y
where I = I
j,k and J = I
j+ 1 ,i. Similarly, we define the set of coefficients {S
ι,j} via the formula
and observe that these are the coefficients
in the pyramid scheme (2.12). In general, given the coefficients S
lJ on step m (that is, for all pairs (l, J) such that | J |= 2
m | l |), we move to the next step by applying the formula (4.28) recursively.
Remark 4.5. Clearly, the above procedure amounts to simply applying the pyramid scheme (2.12) each column of the matrix βj.
4.5. Uniform estimates for discretizations of Calderon-Zygmund operators.
As has been observed in Remark 4.1, the estimates (4.10) are adequate for most numerical purposes. However, they can be strengthened in two important respects.
1. The condition (4.11) can be eliminated under a weak cancellation condition (4.30).
2. The condition (4.10) does not by itself guarantee either the boundedness of the operator T, or the uniform (in N) boundedness of its discretizations T0. In this section, we provide the necessary and sufficient conditions for the boundedness of T, or, equivalently, for the uniform boundedness of its discretizations T0. This condition is, in fact, a reformulation of the 'T(1) ' theorem of David and Journe.
Uniform boundedness of the matrices a, β, γ. We start by observing that estimates (4.5), (4.6) are not sufficient to conclude that
are bounded for |i -ℓ|≤ 2M (for example, consider K(x, y) = We therefore need to assume that
T defines a bounded operator on L
2 or a substantially weaker condition
for all dyadic intervals I (this is the "weak cancellation condition", see [8]). Under this condition and the conditions (4.5), (4.6) Proposition 4.1 can be extended to
for all i, l (see [8]).
Uniform boundedness of the operators T
0. We have seen in (2.26) a decomposition of the operator T
0 into a sum of contributions from the different "scales j" . More precisely, the matrices α
j, β
j,γ
3 act on the vector {
where d
j are coordinates of the function with respect to the orthogonal set of functions 2
-3 /2ψ(2
-3x - k), and the s
j are auxiliary quantities needed to calculate the
The remarkable feature of the nonstandard form is the decoupling achieved among the scales j followed by a simple coupling performed in the reconstruction formulas (3.17). (The standard form, by contrast, contains matrix entries reflecting "interactions" between all pairs of scales). In this subsection, we analyze this coupling mechanism in the simple case of the Haar wavelets, in effect reproducing the proof of the 'T(1)' theorem (see [3]).
For simplicity, we will restrict our attention to the case where α = γ = 0, and β satisfies conditions (4.31) (which axe essentially equivalent to (4.5), (4.6), (4.31)). In this case, for the Haar wavelets we have
which can be rewritten in the form
where
3 and
It is easy to see (by expressing si in terms of d
l) that the operator
is bounded on L
2 whenever (4.31) is satisfied with M = 1. We are left with the "diagonal" operator
with
Clearly
If we choose f = X
J where J is a dyadic interval we find s
l = |I|
1 /2 for I C J from which we deduce that a necessary condition for B
2 to define a bounded operator on L
2(R) is given as
but since the hi for I C J are orthogonal in L2(J),
Combining (4.41) with (4.42), we obtain ^
Expression (4.44) is usually called bounded dyadic mean oscillation condition (BMO) on β. and is necessary for the boundedness of B2 on L2. It has been proved by Carleson (see, for example, [8]) that the condition (4.41) is necessary and sufficient for the following inequality to hold
Combining these remarks we obtain
Theorem 4.1 (G. David, J.L. Journé) Suppose that the operator
T(f) =∫K(x,y) f(y) dy (4.46) satisfies the conditions (4.5), (4.6), (4.30). Then the necessary and sufficient condition for T to be bounded on L2 is that
β(x) -= T(1)(x), (4.47) γ(x) = T*(1)(x) (4.48) belong to dyadic B.M.O. i.e. satisfy condition (4.44).
We have shown that the operator T in Theorem 4.1 can be decomposed as a sum of three terms
T = B1 + B2 + B3, (4.49)
B2(f) = ∑hιβιsl, (4.50)
B3(f) =∑XιγιdI, (4.51) with |I| 1 /2βl = (hl, β), γl = (Xl, γ), β = T(1), and γ = T*(1).
The principal term B1, when converted to the standard form, has a band structure with decay rate independent of N . The terms B2, B3 are bounded in the standard form only when β, γ are in B.M.O. (see [8]).
4.6. Algorithms for bilinear functionals The terms B2, B3 are bilinear transformations in (β, f), (γ, f) respectively. Such "pseudo products" occur frequently as differentials (in the direction β ) of non-linear functionals of f (see [3]). In this section, we show that pseudo-products can be implemented in order N operation (or for the same cost as ordinary multiplication). To be specific, we have the following proposition (see [3]).
Proposition 4.2. Let K(x, y, z) satisfy the conditions
and the bilinear functional B(f,g) be defined by the formula
B(f, g)(x) =∫ K(x, y, z) /(y) g(z) dydz (4.54)
Then the bilinear functional B(f, g) can be applied to a pair of arbitrary functions f,g for a cost proportinal to N, with the proportionality coefficient depending on M and the desired accuracy, and independent of the kernel K.
Following is an outline of an algorithm implementing such a procedure. As in the linear case, we write
where Q = J x J', |I| = |J| = |J'| and ψ
Q(y, z) is a wavelet basis in two variables (i.e.
Substituting in (4.55) into (4.54) we obtain f U
where
denote the coefficients of the function K(x,y, z) in the three-dimensional wavelet basis. Therefore, combining (4.57) with Observation 3.1, we obtain an order O(N) algorithm for the evaluation of (4.54) on an arbitrary pair of vectors.
It easily follows from the estimates (4.52), (4.53) that
resulting in banded matrices and a "compressed" version having O(N) entries (also, compare (4.58) with (4.10) ).
Similar results can be obtained for many classes of non-linear functionals whose differentials satisfy the conditions analogous to (4.52), (4.53).
In this Appendix we construct quadrature formulae using the compactly supported wavelets of [4] which do not satisfy condition (3.8). These quadrature formulae are similar to the quadrature formula (3.12) in that they do not require explicit evaluation of the function φ{x) and are completely determined by the filter coefficients {
Our interest in these quadrature formulae stems from the fact that for a given number M of vanishing moments of the basis functions, the wavelets of [4] have the support of length 2M compared with 3M for the wavelets satisfying condition (3.8). Since our algoritms depend linearly on the size of the support, using wavelets of [4] and quadrature formulae of this appendix makes these algorithms
50% faster.
We use these quadrature formulae to evaluate the coefficients
of smooth functions without the pyramid scheme (2.12), where
are computed via (3.13) for j =- 1, . . . ,n.
First, we explain how to compute Recalling the definition of
we look for the coefficients { /}{^/ 1 such that
for polynomials of degree less than M. Using (7.2), we arrive at the linear algebraic svstem for the coefficients
,
where the moments of the function φ(x) are computed in terms of the filter coefficients
Given the coefficients c
1. we obtain the quadrature formula for computing
The moments of the function φ are obtained by differentiating (an appropriate number of times) its Fourier transform φ,
and setting ξ = 0. The expressions for the moments / x
m φ(x) dx in terms of the filter coefficients
2 f are found using formula for φ [4],
The moments∫ xm φ(x) dx are obtained numerically (within the desired accuracy) by recursively generating a sequence of vectors,
Each vector {M^ 1 1 represents M moments of the product in (7.6) with r terms.
We now derive formulae to compute the coefficients of smooth functions without the pyramid scheme (2.12). Let us formulate the follo
wing
Proposition B1. Let the coefficients be those of a smooth function at some scale j. Then
is a formula to compute the coefficients
at the scale j + 1 from those at the scale j. The coefficients in (7.10) are solutions of the linear algebraic system
and where M
m are the moments of the coefficients h
k scaled for convenience bv 1/H(0) = 2
-1/2 ,
Using Proposition B1 we prove the following
Lemma B1. Let the coefficients
be those of a smooth function at some scale j. Then
2 / 4
is a formula to compute the coefficients at the scale j + r from those at the scale j, with r > 1. The coefficients in (7.13) are obtained by recursively generating the sequence of vectors {
fY { } as solutions of the linear algebraic system
where the sequence of the moments } is computed via
; where
We note that for r = 1 (7.13) reduces to (7.10).
Proof of Proposition B1.
Let H(ξ) denote the Fourier transform of the filter with the coefficients
Clearly, the moments M
m in (7.12) can be written as
Also, the trigonometric polynomial H(ξ) can always be written as the product,
where we choose Q to be of the form
and H to have zero moments
By differentiating (7.19) appropriate number of times, setting ξ = 0 and using (7.21) we arrive at (7.11). Solving (7.11), we find the coefficients
Since moments of
vanish, the convolution with the coefficients of the filter
H reduces to the one-point quadrature formula of the type in (3.12). Thus applying H reduces to applying Q and scaling the result by 1/H(0) = 2
-1/2. Clearly, there are only M coefficients of Q compared to 2M of if, and the particular form of the filter 0 (7.20) w as chosen so that only even- second entry of starting with k = 1, is multiplied by
a coefficient of the filter Q.
Proof of Lemma B1.
Lemma B1 is proved by induction. Since for r = 1 (7.13) reduces to (7.10), we have to show that given (7.13), it also holds if r is increased by one.
Let
be the subsequence consisting of every 2
T entry of
starting with ifc— j Applying filter in (7.13) is equivalent to applying filter P
r to where
To obtain (7.13), where r is increased by one, we use the quadrature formula (7.10) of Proposition B1. Therefore, the result is obtained by convolving
with the coefficients of the filter Q(ξ)P
r(ξ), where Q(ξ) is defined in (7.20).
Let us construct a new filter Q
r+1 by factoring Q(ξ)P
r(ξ) similar to (7.19),
where we chose Q
r+1 to be of the form
Again, since moments of
vanish, the convolution with the coefficients of the filter reduces to scaling the result by 2
-1/
2.
To compute moments
of Q(ξ)P
r(ξ) we differentiate Q(ξ)P
r(ξ) appropriaic number of times, set ξ = 0 and arrive at (7.15) and (7.16). To obtain the linear algebraie system (7.14) for the coefficients
we differentiate (7.23) appropriate number of times, set ξ = 0 and use (7.25).
Recalling that the filter P
r is applied to the subsequence
we arrive at (7.13). where r is increased by one.
References
[1] B. Alpert and V. Rokhlin, A Fast Algorithm for the Evaluation of Legendre Expansions, Yale University Technical Report, YALEU/DCS/RR-671 (1989).
[2] J. Carrier, L. Greengard and V. Rokhlin A Fast Adaptive Multipole Algorithm for Particle Simulations, Yale University Technical Report, YALEU/DCS/RR-496 (1986), SIAM Journal of Scientific and Statistical Computing, 9 (4), 1988.
[3] R. Coifman and Yves Meyer, Non-linear Harmonic Analysis, Operator Theory and P.D.E., Annals of Math Studies, Princeton, 1986, ed. E. Stein.
[4] I. Daubechies, Orthonormal Bases of Compactly Supported Wavelets, Comm. Pure, Applied Math, XLI, 1988.
[5] L. Greengard and V. Rokhlin, A Fast Algorithm for Particle Simulations, Journal of Computational Physics, 73(1), 325, 1987.
[6] S. Mallat, Review of Multifrequency Channel Decomposition of Images and Wavelet Models, Technical Report 412, Robotics Report 17S, NYU (1988).
[7] Y. Meyer Principe d .ncertitude, bases hilbertiennes et algέbres d'operateurs, Seminaire Bourbaki, 1985-86, 662, Asterisque (Socie te Mathematique de France).
[8] Y. Meyer, Wavelets and Operators, Analysis at Urbana, vol.1, edited by E.Berkson, N.T.Peck and J.Uhl, London Math. Society, Lecture Notes Series 137, 1989.
[9] S.T. O'Donnel and V. Rokhlin, A Fast Algorithm for the Numerical Evaluation of Conformal Mappings, Yale University Technical Report, YALEU/DCS/RR-554 (1987), SIAM Journal of Scientific and Statistical Computing, 1989.
[10] J.O. Stromberg, A Modified Haar System and Higher Order Spline Systems, Conference in harmonic analysis in honor of Antoni Zygmund, Wadworth math, series, edited by W. Beckner and al., II, 475-493.
APPENDIX II
FAST WAVELET TRANSFORMS AND NUMERICAL
ALGORITHMS.
I Introduction
In this paper we continue the description of numerical algorithms based on Fast Wavelet Transforms [l] and introduce Fast Numerical Calculus of Operators.
Historically the operator calculus has been a theoretical tool nearly useless for co mputational purposes. The reason for this is the fact that the multiplication of two dense matrices is O(N3) procedure, and is more time consuming than, for example, inversion of a matrix. On the other hand, for sparse matrices (banded, for example) the product normally has a wider band than each of the multiplicants. Therefore, there is no point in constructing a calculus of sparse matrices.
In wavelet bases a wide class of operators for fixed but arbitrary accuracy has a sparse representation in the standard and non-standard forms described in [1]. We observe that if the product of two operators satisfies the same conditions as the multiplicants [1] then the sparsity of the product is no worse than that of the multiplicants. Using this observation we introduce in this paper Fast Numerical Calculus of Operators. The key ingredient in our approach is O(N) (or, possibly, O(N log N), or. at most O(N log2 N)) algorithm to multiply two operators which ordinarily are represented by dense matrices.
Performance of a great number of algorithms requiring matrix multiplication has been limited by O(N3) operations. In this paper we consider several important examples of such algorithms, namely, power of an operator, construction of the generalized inverse and the scaling and squaring method for computing the exponential of an operator and similar algorithms for sine and cosine of an operator. For computing the generalized inverse we use the iterative algorithm [2,3.4] with some modifications. Provided that the operator and its generalized inverse are both compressible, we obtain O (N log R ) (or at most O( N l og2 N log R)) algorithm, where R is the condition number of the matrix. Computing the power of an operator is done by the direct application of the mutiplication algorithm. By replacing the ordinary matrix multiplication in the scaling and squaring method and, provided that the operator and its exponential are both compressible, we obtain a fast algorithm. We note that the compressibility of the resulting operator in these algorithms can be verined analytically or through a small scale numerical experiment.
Finally, we note that our algorithms are also applicabie to operators with singularities not only on the diagonal. In such cases one needs to verify that matrices involved are compressible at all stages of computations.
II Interpretation of the non-standard and standard forms
Let us briefly review the non-standard and standard forms described in [1] and give inter- pretation to the banded structures that appear in these forms. The wavelet basis induces a multiresolution analysis on L2(R), i.e. a decomposition of the Hubert space L2(R) into a chain of subspaces
...CV
2CV
1 CV
0CV
-1CV
-2C... (2.1) such that
By defining W
j as an orthogonal complement of V
j in V
j-i,
the space L
2(R) is represented as a direct sum
On each fixed scale j the wavelets {ψj,k(x)}k∈Z form an orthonormal basis of Wj and the functions {ψj,k{x)}k∈Z form an orthonormal basis of Vj.
Let T be an operator
T : L2(R)→ L2(R). (2.5)
The non-standard form is a representation (see [1]) of the operator T as a chain of triples
T={Aj,Bj,Tj}j∈Z (2.6) acting on the subspaces Vj and Wj,
Aj.'Wj→Wj, (2.7)
B- : Vj→ Wj, (2.8)
Tj : Wj→ Vj. (2.9)
The operators {Aj,Bj,Tj}j∈Z are defined (see [1]) as Aj = QjTQj, Bj = QjTPj and Tj = PjTQj, where Pj is the projection operator on the subspace Vj and Qj = Pj-1 - Pj is the projection operator on the subspace Wj.
The operators {A
j,B
j,T
j}
j∈Z admit a recursive definition (see [1]) via the relation
where operators Tj = PjTPj,
Tj : Vj→ Vj. (2.11)
If there is the coarsest scale n then the chain of the subspaces (2.1) is replaced by Vn C . . . C V2 C V1 C V0 C V-1 C V-2 C . . ,
and the representation of the operator T by
τ = {{Aj, Bj, Fj}j∈Z:j≥n, Tn}, (2. 13) where Tn = PnTPn.
In numerical realizations the operator T is represented by (2.6) only over the finite number of scales; without loss of generality we set the scale j = 0 to be the finest scale. We then have (instead of (2.12))
Vn C . . . C V2 C V1 C V0, V0 C L2(R). (2.14)
In numerical realizations the subspace V0 is finite dimensional (see [1]).
We will now make the foUowing observations:
1). The map (2.7) implies that the operator Aj describes interaction only on the scale j since the subspace Wj is an element of the direct sum in (2.4)
2). The operators Bj, Pj (2.8) and (2.9) describe the interacion between the scale j and the coarser scales . Indeed, the subspace Vj contains all the subspaces Vj, with j' > j (see (2.1)).
3). The operator Tj is an "averaged" version of the operator Tj-1.
Using the wavelet basis with M vanishing moments we force operators {Aj, Bj, Tj}j∈Z to decay roughly as 1/dM , where d is a distance from the diagonal (provided that the operator T is a Calderon-Zygmund or Pseudodifferential operator). For any given accuracy we consider banded approximations to {Aj, B j, Tj}j∈Z and show in [1] that it is a uniform approximation to the operator T.
Therefore, for any given accuracy the banded structure illustrated, for example, i n Figure 2 of [1] is the result of spatial locality of interaction in the non-standard representation.
The standard form is obtained by representing
and considering for each scale j the operators
If there is the coarsest scale n then instead of (2.15) we have
In this case the operators
= j + 1, . . . , n are as in (2.16) and (2.17). ln addition, for each scale j there axe operators
(In this notation
f
n £
n)
If there is a finite number of scales and V
o is finite dimensional then the standard form is a representation of T
o = P
oTP
o as
The operators (2.21) are organized as blocks of the matrix depicted in Figure 1.
If the operator T has a singularity only on the diagonal then for a fixed accuracy all the operators in (2.21) (except T
n) are banded. Due to periodization (see [1]) there might be additional horizontal bands in the operators
P and vertical in
of width not exceeding I
H - 2, where I
H is the number of the filter coefficients {h
k} of the filter E (see [ 1]).
As a result, the standard form has several "finger" bands which correspond to the interaction between different scales, i.e. operators
j j as depicted in Figure 2. For a large class of operators (pseudodifferential, for example) the interaction between different scales as characterized by the size of the coefficients of "finger" bands, decays as the distance j' -j between the scales increases. Therefore, if the scales j and j' axe well separated then for a given accuracy the operators can be neglected.
Ill Multiplication of two matrices in the standard form
The standard form of an operator leads to at most 0(N log N) algorithm for multiplication of an arbitrary vector by a matrix. For example, to multiply a vector by a diagonal matrix with random entries would require O(N log N) operations using the standard form. Alternatively, we describe in [1] an O(N) algorithm which uses the non-standard form.
However, the advantages of the standard form become evident when we multiply two operators. In this case the direct use of the non-standard form would require O(N2) operations while multiplying operators in the standard form requires at most Of.V log" N) operations.
and
Since the standard form is a representation in an orthonomal basis (which is the tensor product of one-dimensional bases), when two standard form axe multiplied the result is also
a standard form in the same basis. Thus, the product T must have a representation
Due to the block structure of the corresponding matrix (see Figure 1), each element of (3.3) is obtained as a sum of products of the corresponding blocks of T and T. For example, 2
If the operators
have a singularity only on the diagonal then it is clear that
is banded with possible additional horizontal and vertical bands due to the contribution from the term This example is generic for all operators in (3.3) except for J ]
j = 1, , . . , n and T
n. The latter are dense due to the terms involving
It is easy now to estimate the number of operations necessary to compute T. Let C
o x C
o, where C = be the size of
Let C be either C
o or the maximum width of bands in T
whichever is greater. To compute T we need to compute 2(n - jo) + 1 blocks with at most 2 x C x 2
n-1 non-zero elements from n - j
0 + 1 terms, 2(n - j
o - 1) + 1 blocks with at most 2 x C x 2
n-2 non-zero elements from n - j
0 + 1 terms, etc. Thus, we need to perform at most
operations. Therefore, it takes no more than 0(N log2 N) operations to obtain T, where N = 2n.
If, in addition, for a given accuracy when the scales j and
are well separated the operators B
can be neglected, then the number of oϋerations reduces asvmptotically to O(N).
However, the most important point in the algorithm is the fact that, unlike in the case of the ordinary sparse matrices, we are allowed to set all the entries in the product that are below the threshold of accuracy to zero.
Let be approximations to obtained by setting all entries that are
less than e to zero. Without loss of generality let us assume that
||T|| ||T|| 1. Using the
The right hand side of (3.6) is dominated by 3ε.
Thus, if we square an operator twice (i.e. compute T4) we might be loosing one significant digit. One the other hand, such computation is fast since for a wide class of operators the "finger " band structure is maintained by the thresholding after multiplication.
IV Fast iterative construction of the generalized in - verse
For constructing the generalized inverse A+ of the matrix A we use the following result [2,3,4]:
Let σ1 be the largest singular value of the m x n matrix A and consider the sequence of matrices Xk
Xk+1 = 2Xk - XkAXk (4.1 ) with
Xo = C.A-, (4.2 ) where A* is the adjoint matrix and 0 < α < 2/σ1. Then the sequence Xk converges to th e generalized inverse A+ .
When this result is combined with the fast multiplication algorithm of Section III we obtain an algorithm for constructing the generalized inverse in at most O(N(logN)2 log R) operations, where R is the condition number of the matrix. By the condition number we understand the ratio of the largest singulax value to the smallest singular value above the threshold of accuracy.
First we present two simple but important modifications of the algorithm (4.1)-(4.2) compared to the description in [4]. We then proceed to describe conditions under which this algorithm is fast.
Our analysis of the iteration (4.1)-(4.2) follows that of [4] except for the error control and the criterion to terminate the iteration. For square fuli rank matrices the iteration (4.1)-(4.2) is self-correcting. In [4] it is stated that "an arbitrary small perturbation in A+ will be reduced by the iteration only if A is square and nonsingular". The criterion for th e termination of the iteration is a consequence of this conclusion.
We found a simple procedure to reduce the error of the iteration (4.1)-(4.2) if A is not of full rank and this allows us to use a different and more simple criterion to terminate the iteration than that used in [4].
Analysis of the iteration (4.1)-(4.2) is carried out by using the singular value decom- position of matrix A,
where U and V axe unitary matrices and Σ is a diagonal matrix with entries σ
1≥ σ
2≥ . ..≥ σ
r > ε where e is the accuracy threshold. Our goal is to construct
where∑
-1 is the diagonal matrix with entries
One can easily verify (see [4]) that where T
k are diagonal, and
In (4.5) V and U axe unitary matrices from (4.3) and Xk axe matrices in (4.1)-(4.2).
FoUowing [4], let us perturb the matrix V*XkU in (4.5) by an error matrix E so that instead of the right hand side of (4.5) we have
Iterating once, we obtain
Let us drop the quadratic terms O(|| E ||2) in E, so that we obtain
From this point on our analysis differs from that of [4], where by examining the term
the authors conclude that "if A is not of full rank, so that E
22 is nonvoid, the error will tend to increase" .
Assuming that the iteration has converged, i.e. Tk = Tk+1 =∑-1 , let us consider the error for the combination
Using (4.9) and (4.10) we have
where we drop the quadratic terms in and set E1 1 = 0. The combination (4.11) does not show a tendency to increase the error. To obtain this combination we just need to compute XkAXk after we know that the iteration had converged. This, in turn, can be detected using the criterion
|Trace(Xk+1A) - Trace(Xk A)| < ε. (4.13 )
One can verify that step to step change of Trace(XkA) is greater than e unless the iteration had converged. Also, after the iteration had converged Trace(XkA) = Rank(A) = r, which is an integer (up to accuracy ε).
To summarize, we iterate using (4.1) and check condition (4.13) after each iterati on. After condition (4.13) is satisfied, we compute A+ = XkAXk. In the process, we also have computed the rank of the matrix A.
Let us now explain conditions under which this algorithm is fast. Throughout the iteration it is necessary to maintain the "finger" band structure of the operators. We note that such structure is an attribute of a class of operators. To clarify this last point let us identify a class of operators for which we know a priori that their products axe from the sa me class. We consider pseudodifferential operators from L
o(X). These operators form an algebra, and the inverse of an operator from L
o(X) is also in L
o( X). The kernels of operators from this class may have a singularity only on the diagonal. Thus, we know a priori that T has the same structure of bans as the multiplicants, provided T, T∈ L
o(X). (It is also clear that a pseudodifferential operator from L
j(X), where
φ can be modified by preconditioning by a standard operator so that the product will be in L
o(X). For example, if T∈ L
-2(X) then ΔT∈ L
o(X), where Δ is the Laplacian. Such preconditioning is a fast operation because of the fast multiplication algorithm). Therefore, at least for the pseudodifferential operators we know that the structure of the band will be maintained automatically. In addition, due to self-correcting property of the iteration (4.1)-(4.2), the accuracy of the final answer does not depend on the number of iterations.
We note that the number of iterations in (4.1) is proportional to log(P) (it is roughly equal to 2log(P)). In fact, to reduce the amount of time spend per iteration one may comp ute with low-accuracy threshold and after iteration converges use high-accuracy threshold a nd iterate again. In such case the latter iteration will converge in just a few steps, since the low-accuracy generalized inverse acts as a preconditioner.
Observation 1. We note that it is easy to envision situations in which matrices arising from more general operators than the pseudodifferential operators will also be amenable to our treatment.
Observation 2. The condition number of most matrices that arize in applications grows (at worst) as a Np as a function of size N and, therefore, the total number of operati ons to compute the generalized inverse is O(N log3 N). When the condition number does not grow with size, we need only O( N log2 N) operations. This estimate drops further to O(N) if the operator is pseudodifferential.
Remark 1 on the problem of inversion of the Generalized Radon Transform
There is an important application of the iteration (4.1)-(4.2) to the inversion of the Generalized Radon Transform (GRT). The GRT of a function u is the function Ru defined on a family of hypersurfaces: the value of the Ru on a given hypersurface is the integral of u with some weight over that hypersurface [5],
For (s,ω)∈ R
1 x S
n-1 we write the GRT as v(s,ω)≡ (Ru)(s,ω) = / a(x,ω)δ(s - Φ(x,ω))u(x)dx, (4.14) where the real valued function Φ(x,θ)∈ C
∞ (X x (R
n\{0})) is homogeneous with respect to θ of degree one, d
xΦ does not vanish anywhere in X x (R
n\{0}) and the function h defined as is positive in X x (R
n\{0}).
Together with the generalized Radon transform, one is lead to consider a dual operator
(R*v)(y)= b(y,ω)υ(s,ω)l
s-Φ{y,ω)dw, (4.16)
which is often called the generalized backprojection in applications. The operator R* is the adjoint operator in an appropriate space.
In (4.14) and (4.16) the (positive) weights a(x,θ),b(y,θ)∈ C∞ (X x (Rn\{0})) are homogeneous functions with respect to θ of degree zero.
To solve the problem of inversion of the GRT a pseudodifferential operator F is con- structed [5] such that F = R*KR, where the operator K is a one-dimensional convolution with the kernel K(s - s'), where
By choosing b(y,θ) = h(y,θ)/a(y,θ), it is shown in [5] that
F = I + T, (4.18) where T∈ L-1(X) a smoothing operator.
Let us denote A =
and by A" = (the operator can be constructed
easily). We have from (4.18)
A*A-=I + T (4.19)
We now proceed to construct a sequence of operators using the iteration (4.1)-(4.2)
Xk+1 = 2Xk - XkAXk (4.20) starting with X0 = A*. It is easy to verify that
XkA = I + T2k (4.21)
Alternatively, to avoid using
by setting Y
k = X
k-
the iteration (4.20)-(4.21) is written as follows
Yk +1 = 2Yk - YkKRYk, (4.22)
starting with Yo = R*. We then have
YkKR = I + T2k. (4.2 3)
Since T∈ L-1(X) is a pseudodifferential operator, the operator T2 k in (4.21) or (4.23) rapidly becomes a regularizing operator as k→∞ .
Let us point out a remarkable cancellation that is hidden in the iteration (4.1)-(4.2). Given (4.18) one can improve smoothing property of the discrepancy T by the standard methods, namely, by expanding T further T = T
1 + T
2 + . .. h T,∈ L
-1(X), 1 = 1,2, . .. (see [5]) and constructing operators to cancel this series t term. In such approach symbols of operators contain the increasing number of deriv
atives. On the other hand, (4.2 1 ) shows that the disrepancy T
2k does not have any derivatives in its symbol and T
2k∈ L
-2 k ( X).
We will address the problem of inversion of the GRT in greater detail elsewhere.
Remark 2 on iterative computation of the Projection Operator on the Null Space.
It is often necessary to compute a projection operator Pnull on the null space of a giv en operator A. For example, in Kaxmarkax's algorithm [6] this is the most expensive step of the computation. We note that a modification of iteration (4.1)-(4.2) yields an iterative algorithm for computing Pnull and it is a fast algorithm for a wide class of operators represented in the wavelet bases.
Let us consider instead of (4.1)-(4.2) the foUowing iteration
with
Xo = a(A'A)
2, (4.25) where A* is the adjoint matrix and 0 < α < 2/σ
1. It is easy to show either directly or by, for example, combining an invariant representation for P
null = I - A*( AA*
)A with the iteration (4.1)-(4.2) to compute the generalized inverse (AA*)
that I-X
k converges to P
null. The fast multiplication algorithm makes (4.24)-(4.25) a fast algoritm for a wide class of operators wi th the same complexity as the algorithm for the generalized inverse. The important difference is, however, that (4.24)-(4.25) does not require compressibility of the inverse operator but only of the powers of the operator.
References
[1] Appendix I.
[2] G.Schulz, Iterative Berechnung der reziproken Matrix, Z. Angew. Math. Mech. 13, 57-59, 1933.
[3] A. Ben-Israel and D. Cohen On iterative computation of generalized inverses and asso- ciate projections, J. SIAM Numer. Anal., v.3, 3, 410-419, 1966.
[4] T. Söderström and G.W.Stewart On the numerical properties of an iterative method for computing the Moore-Penrose generalized inverse, J. SIAM Numer. Anal., v.ll, 1, 61-74, 1974.
[5] G. Beylkin, The inversion problem and applications of the generalized Radon transfo rm, Comm. Pure Appl. Math, v.37, 5, 579-599, 1984.
[6] N. Karmaxkax, A new polynomial-time algorithm for linear programming Combinatorica, v.4, 4, 373-395, 1984.