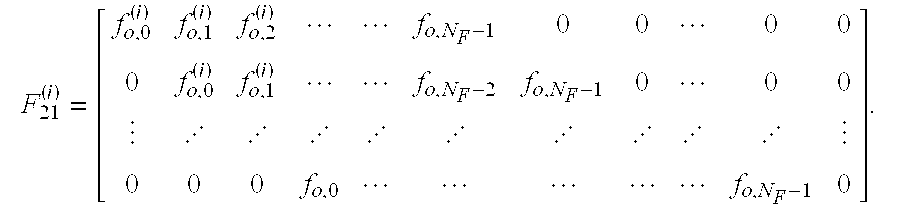US20030202612A1 - Method and system for rate enhanced SHDSL - Google Patents
Method and system for rate enhanced SHDSL Download PDFInfo
- Publication number
- US20030202612A1 US20030202612A1 US10/321,601 US32160102A US2003202612A1 US 20030202612 A1 US20030202612 A1 US 20030202612A1 US 32160102 A US32160102 A US 32160102A US 2003202612 A1 US2003202612 A1 US 2003202612A1
- Authority
- US
- United States
- Prior art keywords
- shdsl
- bits
- bit
- present
- data rate
- Prior art date
- Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
- Abandoned
Links
- 238000000034 method Methods 0.000 title claims description 35
- 230000005540 biological transmission Effects 0.000 claims abstract description 16
- 230000004044 response Effects 0.000 claims description 18
- 239000011159 matrix material Substances 0.000 description 33
- 238000005516 engineering process Methods 0.000 description 17
- 230000001965 increasing effect Effects 0.000 description 16
- 238000012360 testing method Methods 0.000 description 16
- 238000004891 communication Methods 0.000 description 15
- 238000010586 diagram Methods 0.000 description 15
- 230000006870 function Effects 0.000 description 15
- 238000005070 sampling Methods 0.000 description 11
- 230000003595 spectral effect Effects 0.000 description 10
- 238000013461 design Methods 0.000 description 9
- 230000003044 adaptive effect Effects 0.000 description 8
- 238000013459 approach Methods 0.000 description 7
- 230000008901 benefit Effects 0.000 description 6
- 238000011161 development Methods 0.000 description 6
- 238000012986 modification Methods 0.000 description 6
- 230000004048 modification Effects 0.000 description 6
- 230000008569 process Effects 0.000 description 6
- 238000012545 processing Methods 0.000 description 6
- RYGMFSIKBFXOCR-UHFFFAOYSA-N Copper Chemical compound [Cu] RYGMFSIKBFXOCR-UHFFFAOYSA-N 0.000 description 5
- 238000007493 shaping process Methods 0.000 description 5
- 230000008859 change Effects 0.000 description 4
- 238000006243 chemical reaction Methods 0.000 description 4
- 229910052802 copper Inorganic materials 0.000 description 4
- 239000010949 copper Substances 0.000 description 4
- 230000000694 effects Effects 0.000 description 4
- 238000005457 optimization Methods 0.000 description 3
- 238000012546 transfer Methods 0.000 description 3
- BKCJZNIZRWYHBN-UHFFFAOYSA-N Isophosphamide mustard Chemical compound ClCCNP(=O)(O)NCCCl BKCJZNIZRWYHBN-UHFFFAOYSA-N 0.000 description 2
- 230000002708 enhancing effect Effects 0.000 description 2
- 238000001914 filtration Methods 0.000 description 2
- 238000010348 incorporation Methods 0.000 description 2
- 230000002452 interceptive effect Effects 0.000 description 2
- 230000003287 optical effect Effects 0.000 description 2
- 238000013139 quantization Methods 0.000 description 2
- 230000009467 reduction Effects 0.000 description 2
- 230000000630 rising effect Effects 0.000 description 2
- 230000001360 synchronised effect Effects 0.000 description 2
- 208000001613 Gambling Diseases 0.000 description 1
- 239000006057 Non-nutritive feed additive Substances 0.000 description 1
- 101100476979 Rhodobacter capsulatus sdsA gene Proteins 0.000 description 1
- AZDRQVAHHNSJOQ-UHFFFAOYSA-N alumane Chemical class [AlH3] AZDRQVAHHNSJOQ-UHFFFAOYSA-N 0.000 description 1
- 230000001174 ascending effect Effects 0.000 description 1
- 230000009286 beneficial effect Effects 0.000 description 1
- 239000011230 binding agent Substances 0.000 description 1
- 239000000969 carrier Substances 0.000 description 1
- 230000002860 competitive effect Effects 0.000 description 1
- 230000000295 complement effect Effects 0.000 description 1
- 238000012937 correction Methods 0.000 description 1
- 238000009432 framing Methods 0.000 description 1
- 230000006872 improvement Effects 0.000 description 1
- 238000003780 insertion Methods 0.000 description 1
- 230000037431 insertion Effects 0.000 description 1
- 238000009434 installation Methods 0.000 description 1
- 238000013507 mapping Methods 0.000 description 1
- 230000007246 mechanism Effects 0.000 description 1
- 230000006855 networking Effects 0.000 description 1
- 230000008520 organization Effects 0.000 description 1
- 238000007781 pre-processing Methods 0.000 description 1
- 238000011084 recovery Methods 0.000 description 1
- 230000009131 signaling function Effects 0.000 description 1
- 238000001228 spectrum Methods 0.000 description 1
- 230000003068 static effect Effects 0.000 description 1
- 238000012549 training Methods 0.000 description 1
- 230000002087 whitening effect Effects 0.000 description 1
Images
Classifications
-
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L1/00—Arrangements for detecting or preventing errors in the information received
- H04L1/004—Arrangements for detecting or preventing errors in the information received by using forward error control
- H04L1/0056—Systems characterized by the type of code used
- H04L1/0057—Block codes
-
- H—ELECTRICITY
- H03—ELECTRONIC CIRCUITRY
- H03H—IMPEDANCE NETWORKS, e.g. RESONANT CIRCUITS; RESONATORS
- H03H17/00—Networks using digital techniques
- H03H17/02—Frequency selective networks
- H03H17/0283—Filters characterised by the filter structure
- H03H17/0286—Combinations of filter structures
- H03H17/0288—Recursive, non-recursive, ladder, lattice structures
-
- H—ELECTRICITY
- H03—ELECTRONIC CIRCUITRY
- H03M—CODING; DECODING; CODE CONVERSION IN GENERAL
- H03M13/00—Coding, decoding or code conversion, for error detection or error correction; Coding theory basic assumptions; Coding bounds; Error probability evaluation methods; Channel models; Simulation or testing of codes
- H03M13/03—Error detection or forward error correction by redundancy in data representation, i.e. code words containing more digits than the source words
- H03M13/23—Error detection or forward error correction by redundancy in data representation, i.e. code words containing more digits than the source words using convolutional codes, e.g. unit memory codes
- H03M13/235—Encoding of convolutional codes, e.g. methods or arrangements for parallel or block-wise encoding
-
- H—ELECTRICITY
- H03—ELECTRONIC CIRCUITRY
- H03M—CODING; DECODING; CODE CONVERSION IN GENERAL
- H03M13/00—Coding, decoding or code conversion, for error detection or error correction; Coding theory basic assumptions; Coding bounds; Error probability evaluation methods; Channel models; Simulation or testing of codes
- H03M13/25—Error detection or forward error correction by signal space coding, i.e. adding redundancy in the signal constellation, e.g. Trellis Coded Modulation [TCM]
- H03M13/253—Error detection or forward error correction by signal space coding, i.e. adding redundancy in the signal constellation, e.g. Trellis Coded Modulation [TCM] with concatenated codes
-
- H—ELECTRICITY
- H03—ELECTRONIC CIRCUITRY
- H03M—CODING; DECODING; CODE CONVERSION IN GENERAL
- H03M13/00—Coding, decoding or code conversion, for error detection or error correction; Coding theory basic assumptions; Coding bounds; Error probability evaluation methods; Channel models; Simulation or testing of codes
- H03M13/25—Error detection or forward error correction by signal space coding, i.e. adding redundancy in the signal constellation, e.g. Trellis Coded Modulation [TCM]
- H03M13/256—Error detection or forward error correction by signal space coding, i.e. adding redundancy in the signal constellation, e.g. Trellis Coded Modulation [TCM] with trellis coding, e.g. with convolutional codes and TCM
-
- H—ELECTRICITY
- H03—ELECTRONIC CIRCUITRY
- H03M—CODING; DECODING; CODE CONVERSION IN GENERAL
- H03M13/00—Coding, decoding or code conversion, for error detection or error correction; Coding theory basic assumptions; Coding bounds; Error probability evaluation methods; Channel models; Simulation or testing of codes
- H03M13/29—Coding, decoding or code conversion, for error detection or error correction; Coding theory basic assumptions; Coding bounds; Error probability evaluation methods; Channel models; Simulation or testing of codes combining two or more codes or code structures, e.g. product codes, generalised product codes, concatenated codes, inner and outer codes
- H03M13/2933—Coding, decoding or code conversion, for error detection or error correction; Coding theory basic assumptions; Coding bounds; Error probability evaluation methods; Channel models; Simulation or testing of codes combining two or more codes or code structures, e.g. product codes, generalised product codes, concatenated codes, inner and outer codes using a block and a convolutional code
- H03M13/2936—Coding, decoding or code conversion, for error detection or error correction; Coding theory basic assumptions; Coding bounds; Error probability evaluation methods; Channel models; Simulation or testing of codes combining two or more codes or code structures, e.g. product codes, generalised product codes, concatenated codes, inner and outer codes using a block and a convolutional code comprising an outer Reed-Solomon code and an inner convolutional code
-
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L1/00—Arrangements for detecting or preventing errors in the information received
- H04L1/004—Arrangements for detecting or preventing errors in the information received by using forward error control
- H04L1/0041—Arrangements at the transmitter end
-
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L1/00—Arrangements for detecting or preventing errors in the information received
- H04L1/004—Arrangements for detecting or preventing errors in the information received by using forward error control
- H04L1/0041—Arrangements at the transmitter end
- H04L1/0042—Encoding specially adapted to other signal generation operation, e.g. in order to reduce transmit distortions, jitter, or to improve signal shape
-
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L1/00—Arrangements for detecting or preventing errors in the information received
- H04L1/004—Arrangements for detecting or preventing errors in the information received by using forward error control
- H04L1/0045—Arrangements at the receiver end
-
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L1/00—Arrangements for detecting or preventing errors in the information received
- H04L1/004—Arrangements for detecting or preventing errors in the information received by using forward error control
- H04L1/0045—Arrangements at the receiver end
- H04L1/0047—Decoding adapted to other signal detection operation
-
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L1/00—Arrangements for detecting or preventing errors in the information received
- H04L1/004—Arrangements for detecting or preventing errors in the information received by using forward error control
- H04L1/0056—Systems characterized by the type of code used
- H04L1/0059—Convolutional codes
-
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L1/00—Arrangements for detecting or preventing errors in the information received
- H04L1/004—Arrangements for detecting or preventing errors in the information received by using forward error control
- H04L1/0056—Systems characterized by the type of code used
- H04L1/0059—Convolutional codes
- H04L1/006—Trellis-coded modulation
-
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L25/00—Baseband systems
- H04L25/02—Details ; arrangements for supplying electrical power along data transmission lines
- H04L25/03—Shaping networks in transmitter or receiver, e.g. adaptive shaping networks
- H04L25/03006—Arrangements for removing intersymbol interference
- H04L25/03012—Arrangements for removing intersymbol interference operating in the time domain
- H04L25/03019—Arrangements for removing intersymbol interference operating in the time domain adaptive, i.e. capable of adjustment during data reception
- H04L25/03057—Arrangements for removing intersymbol interference operating in the time domain adaptive, i.e. capable of adjustment during data reception with a recursive structure
- H04L25/03063—Arrangements for removing intersymbol interference operating in the time domain adaptive, i.e. capable of adjustment during data reception with a recursive structure using fractionally spaced delay lines or combinations of fractionally and integrally spaced taps
-
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L27/00—Modulated-carrier systems
- H04L27/02—Amplitude-modulated carrier systems, e.g. using on-off keying; Single sideband or vestigial sideband modulation
-
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L27/00—Modulated-carrier systems
- H04L27/32—Carrier systems characterised by combinations of two or more of the types covered by groups H04L27/02, H04L27/10, H04L27/18 or H04L27/26
- H04L27/34—Amplitude- and phase-modulated carrier systems, e.g. quadrature-amplitude modulated carrier systems
- H04L27/3405—Modifications of the signal space to increase the efficiency of transmission, e.g. reduction of the bit error rate, bandwidth, or average power
-
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L27/00—Modulated-carrier systems
- H04L27/32—Carrier systems characterised by combinations of two or more of the types covered by groups H04L27/02, H04L27/10, H04L27/18 or H04L27/26
- H04L27/34—Amplitude- and phase-modulated carrier systems, e.g. quadrature-amplitude modulated carrier systems
- H04L27/3405—Modifications of the signal space to increase the efficiency of transmission, e.g. reduction of the bit error rate, bandwidth, or average power
- H04L27/3416—Modifications of the signal space to increase the efficiency of transmission, e.g. reduction of the bit error rate, bandwidth, or average power in which the information is carried by both the individual signal points and the subset to which the individual points belong, e.g. using coset coding, lattice coding, or related schemes
- H04L27/3427—Modifications of the signal space to increase the efficiency of transmission, e.g. reduction of the bit error rate, bandwidth, or average power in which the information is carried by both the individual signal points and the subset to which the individual points belong, e.g. using coset coding, lattice coding, or related schemes in which the constellation is the n - fold Cartesian product of a single underlying two-dimensional constellation
- H04L27/3433—Modifications of the signal space to increase the efficiency of transmission, e.g. reduction of the bit error rate, bandwidth, or average power in which the information is carried by both the individual signal points and the subset to which the individual points belong, e.g. using coset coding, lattice coding, or related schemes in which the constellation is the n - fold Cartesian product of a single underlying two-dimensional constellation using an underlying square constellation
-
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L5/00—Arrangements affording multiple use of the transmission path
- H04L5/003—Arrangements for allocating sub-channels of the transmission path
- H04L5/0044—Arrangements for allocating sub-channels of the transmission path allocation of payload
-
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L25/00—Baseband systems
- H04L25/02—Details ; arrangements for supplying electrical power along data transmission lines
- H04L25/03—Shaping networks in transmitter or receiver, e.g. adaptive shaping networks
- H04L25/03006—Arrangements for removing intersymbol interference
- H04L2025/0335—Arrangements for removing intersymbol interference characterised by the type of transmission
- H04L2025/03375—Passband transmission
- H04L2025/03414—Multicarrier
-
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L25/00—Baseband systems
- H04L25/02—Details ; arrangements for supplying electrical power along data transmission lines
- H04L25/03—Shaping networks in transmitter or receiver, e.g. adaptive shaping networks
- H04L25/03006—Arrangements for removing intersymbol interference
- H04L2025/03433—Arrangements for removing intersymbol interference characterised by equaliser structure
- H04L2025/03439—Fixed structures
- H04L2025/03445—Time domain
- H04L2025/03471—Tapped delay lines
- H04L2025/03484—Tapped delay lines time-recursive
- H04L2025/03503—Tapped delay lines time-recursive as a combination of feedback and prediction filters
-
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L25/00—Baseband systems
- H04L25/02—Details ; arrangements for supplying electrical power along data transmission lines
- H04L25/03—Shaping networks in transmitter or receiver, e.g. adaptive shaping networks
- H04L25/03006—Arrangements for removing intersymbol interference
- H04L2025/03433—Arrangements for removing intersymbol interference characterised by equaliser structure
- H04L2025/03439—Fixed structures
- H04L2025/03445—Time domain
- H04L2025/03471—Tapped delay lines
- H04L2025/03509—Tapped delay lines fractionally spaced
-
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L25/00—Baseband systems
- H04L25/02—Details ; arrangements for supplying electrical power along data transmission lines
- H04L25/03—Shaping networks in transmitter or receiver, e.g. adaptive shaping networks
- H04L25/03006—Arrangements for removing intersymbol interference
- H04L2025/03592—Adaptation methods
- H04L2025/03598—Algorithms
- H04L2025/03611—Iterative algorithms
Definitions
- the present invention relates generally to rate enhanced SHDSL, more particularly, to a spectrally compliant and transparent method and system for rate enhanced SHDSL.
- DSL Digital Subscriber Line
- coaxial cables are capable of providing always-on connections, however, its presence is insignificant compared to millions and millions of wired telephone customers who are connected by a twisted pair of copper wires.
- Other technologies such as satellite, wireless, and optical, either provide limited coverage, limited bandwidth, or are too expensive for deployment to individual customers.
- DSL technology is uniquely positioned to provide the broadband link between individual customer premise and the central office, the so-called last-mile of the high-bandwidth communication network.
- DSL is the fastest growing among emerging broadband technologies for very good reasons.
- DSL utilizes the existing copper wire network infrastructure.
- voice modems such as V.34 and V.90, used in most personal computers that provide up to 56 kbps dial-up connection
- DSL provides a high bandwidth always-on connection with typical connection speeds from 384 kbps to 6 Mbps.
- DSL is affordable with easy installation, simple turn-up, and high service reliability.
- the successful deployment of DSL is capable of providing digital broadband connection to anyone with an analog telephone line.
- DSL services have been standardized over time by regional organizations such as, American National Standard Institute (ANSI), European Telecommunication Standard Institute (ETSI), and by world telecommunication organization International Telecommunication Union (ITU). These DSL standards define data communication protocols to connect customer premise equipment (CPE) to the central office (CO) and to provide connections to various networks, such as DSL service providers, virtual private networks (VPN), or the Internet.
- CPE customer premise equipment
- VPN virtual private networks
- Various forms of digital data e.g., voice, video, and data
- DSL equipment is connected to the public switched telephone network (PSTN).
- PSTN public switched telephone network
- ISP Internet service provider
- Voice over DSL is capable of providing computer-to-computer, computer-to-telephone, and telephone-to-telephone voice services using an integrated access device (IAD).
- Video over DSL includes transport of MPEG-1 or MPEG-2 files, video conferencing using Internet Protocol (IP) standard such as ITU H.323, WebCam, and video mail.
- IP Internet Protocol
- DSL supports simple data transport, e.g., bearer services, for virtual private network (VPN), leased data line such as T1 and E1, Point-to-Point Protocol (PPP), Asynchronous transfer mode (ATM), and Internet Protocol (IP).
- VPN virtual private network
- PPP Point-to-Point Protocol
- ATM Asynchronous transfer mode
- IP Internet Protocol
- DSL has gone though a major evolution over the last decade and a collection of technologies, commonly referred to as xDSL, are developed under the umbrella of DSL.
- xDSL subscriber loop digital transmission technology
- ISDN integrated services digital network
- IDL integrated digital loop carrier
- HDSL high-speed asymmetric service
- SDSL Secure Digital
- ADSL high-speed asymmetric service
- HDSL2 high-speed asymmetric service
- VDSL very high-speed asymmetric service
- SHDSL is a wire line Digital Subscriber Line (DSL) transmission technology that is designed to accommodate the need for higher data rates in telecommunication access networks.
- DSL Digital Subscriber Line
- SHDSL supports duplex transmission of symmetric data rates over mixed gauge two-wire twisted metallic pairs, as described in the International Telecommunication Union (ITU) standard G.992.1—“Asymmetric Digital Subscriber Line (ADSL) Transceivers”, the body of which is incorporated herein by reference.
- One feature of the SHDSL includes the ability to support a wide range of data rates from 192 kbps to 2.312 Mbps which may include existing T1 and E1 rate services. Though such a range of data rates is adequate to accommodate a large number of real world applications, there are applications, such as MDU/MTU, Ethernet and others, that require or at least prefer a data rate beyond 2.312 Mbps.
- Traditional methods for attempting to achieve a data rate over 2.312 Mbps generally involve an optional four wire mode as specified in the ITU standard. However, as the name suggests the four wire operation requires an additional pair of wires. Availability of such extra pairs of wire is not guaranteed and even if they are available, the four wire solution is not an efficient utilization of the infrastructure.
- a Rate-Enhanced (RE)-SHDSL of an embodiment of the present invention provides enhancement of the SHDSL transceiver to support a data rate beyond 2.312 Mbps as specified in ITU standard; development of a method that is efficient, easy to implement, and flexible to design; achievement of the enhanced data rate without additional transmit bandwidth, transmit power, or cross-talk to other applications; and enhanced transceivers that comply with spectral management and/or other requirements.
- RE Rate-Enhanced
- a rate enhanced system for supporting duplex transmission of symmetric data rates comprises an encoder comprising a serial to parallel converter for receiving a serial data bit, and for generating a parallel word having M bits; a convolutional encoder for receiving a first bit of the M bits of the parallel word, and for generating two encoded bits; and a mapper for receiving the two encoded bits and the remaining M ⁇ 1 bits of the parallel word, and for generating a symbol; wherein M is greater than three.
- R d represents an original data rate for SHDSL; constellation size associated with the mapper is greater than 16-PAM; a single pair of wires is implemented; the system is compatible with four wire operations for doubling of data rate; the transmit masks correspond to that of SHDSL standard; the mapper is a 2 M+1 PAM constellation, wherein M is greater than 3; a receiver comprises a deframer for supporting enhanced data rates greater than 2.312 Mbps; and a decoder for supporting a constellation size greater than 16-PAM; the decoder is a Trellis decoder.
- a method for supporting duplex transmission of symmetric data rates comprises the steps of receiving a serial data bit; generating a parallel word having M bits in response to the serial data bit; receiving a first bit of the M bits of the parallel word; generating two encoded bits in response to the first bit; receiving the two encoded bits and the remaining M ⁇ 1 bits of the parallel word; and generating a symbol in response to the two encoded bits and the remaining M ⁇ 1 bits of the parallel word wherein M is greater than three.
- FIG. 1 a is a table illustrating enhanced data rates of RE-SHDSL as a function of number of data bits per symbol, according to an embodiment of the present invention.
- FIG. 1 b is a table illustrating a mapper definition, according to an embodiment of an aspect of the present invention.
- FIG. 1 c is a table illustrating a mapper definition, according to an embodiment of an aspect of the present invention.
- FIG. 2 illustrates a block diagram of TCM encoder for RE-G.SHDSL, according to an embodiment of an aspect of the present invention.
- FIG. 3 illustrates a setup for fractionally spaced DFE with pre-equalizer, according to an embodiment of the present invention.
- FIG. 4 illustrates a pre-equalizer design test case, according to an embodiment of the present invention.
- FIG. 5 is a flowchart illustrating of an algorithm for determining pre-equalizer coefficients, according to an embodiment of the present invention.
- FIG. 6 is a diagram of a receiver sigma-delta block, according to an embodiment of the present invention.
- FIG. 7 is a diagram of a digital sigma-delta block, according to an embodiment of the present invention.
- FIG. 8 is a diagram of a combiner structure, according to an embodiment of the present invention.
- FIG. 9 is a diagram of a digital sigma-delta block with multiple decimation stages, according to an embodiment of the present invention.
- FIG. 10 is a diagram of a first decimator stage with a sinc filter, according to an embodiment of the present invention.
- FIG. 11 is a diagram of a combiner-sinc filter, according to an embodiment of the present invention.
- FIG. 12 is a diagram of a polyphase combiner-sinc filter, according to an embodiment of the present invention.
- FIG. 13 is the flowchart of an efficient bit loading algorithm, according to an embodiment of the present invention.
- FIG. 14 illustrates a table of number of bits and required power levels for incorporation into the bit loading algorithm, according to an embodiment of the present invention.
- FIG. 15 is a flowchart illustrating PC-WPAM, according to an embodiment of the present invention.
- FIG. 16 illustrates an example of an output of PC-IPAM, according to an embodiment of the present invention.
- FIG. 17 is a flowchart illustrating WF-IPAM, according to an embodiment of the present invention.
- FIG. 18 is a flowchart illustrating PC-GSM, according to an embodiment of the present invention.
- FIG. 19 illustrates an example of an output of GSM, according to an embodiment of the present invention.
- FIG. 20 is a schematic diagram of a hardware architecture in which the inventive aspects of the present invention may be incorporated.
- FIG. 21 is a block diagram illustrating details of SNR margin, according to an embodiment of the present invention.
- FIG. 22 illustrates a flowchart describing hardware algorithm for SNR margin, according to an embodiment of the present invention.
- FIG. 23 is a schematic diagram of a hardware architecture in which the inventive aspects of the present invention may be incorporated.
- the International Telecommunications Union has adopted a standard for Single-pair High-speed Digital Subscriber Line (SHDSL) technology to address the need for higher data rates in telecommunication access networks.
- SHDSL Single-pair High-speed Digital Subscriber Line
- the ITU recommendations for SHDSL e.g., G.992.1
- applications such as MDU/MTU, Ethernet and others, that may require or at least prefer a data rate beyond 2.312 Mbps.
- an efficient, easy to implement, and flexible method and system for increasing the data rate of the existing SHDSL transceivers is provided.
- the Rate-Enhanced (RE)-SHDSL of an embodiment of the present invention satisfies spectral compatibility requirements and is further transparent to other applications.
- the RE-SHDSL of an embodiment of the present invention supports a variety of functions.
- RE-SHDSL is an efficient and easy to implement approach to increase the data rate of an existing SHDSL transceiver. Rate enhancement may be achieved by increasing the number of data bits per symbol thereby increasing signal constellations. The effective use of larger constellations is one difference between RE-SHDSL and SHDSL.
- the RE-SHDSL achieves a higher data rate without requiring additional transmit bandwidth or transmit power.
- the rate enhancement achieved by RE-SHDSL of an embodiment of the present invention is flexible compared to a four wire approach specified in the standard. As in SHDSL, RE-SHDSL may support a single pair wires.
- RE-SHDSL uses the same (or substantially similar) set of transmit masks as specified in SHDSL standard. As a result, there is no need for additional transmit masks.
- RE-SHDSL is compatible with four wire operations and may be used in a four wire mode (or other mode) to achieve an additional doubling of data rate.
- RE-SHDSL may be used for both region specific Annexes A and B of the ITU standard G.992.1 for SHDSL as well as other standards.
- the RE-SHDSL system of an embodiment of the present invention does not require an additional pair of wires and provides a more flexible rate enhancement.
- Features of RE-SHDSL system include spectral compliance and transparency for successful deployment of any DSL as well as other technology.
- RE-SHDSL is fully compliant to spectral management requirements where the enhancements are transparent to other services deployed in the same binder, e.g., to any other service RE-SHDSL appears substantially the same as SHDSL.
- deployment of RE-SHDSL does not create additional crosstalk for other applications.
- SHDSL transceivers may include a precoded system with Trellis Coded Pulse Amplitude Modulation (TC-PAM) line code.
- TC-PAM Trellis Coded Pulse Amplitude Modulation
- an encoder may be used to convert 3 data bits into 4 coded bits.
- the coded 4 bits may be converted into a symbol using a 16-PAM constellation mapper.
- the symbol rate is a system parameter that dictates the transmission bandwidth. Generally, the higher the symbol rate, the larger the required bandwidth. Hence, if the constellation size is fixed, a larger bandwidth may be used to support higher data rates. However, such an approach would violate spectral compatibility and would not be transparent to other applications.
- RE-SHDSL of an embodiment of the present invention uses more then 3 data bits per symbol.
- the data rate may be increased by increasing a constellation size and allocating more bits per symbol while keeping the symbol rate fixed.
- the encoding scheme as described in SHDSL may be used with the exception that the number of uncoded bits are increased.
- the transmit filter and the transmit Power Spectral Density (PSD) remain identical (or substantially similar) to that of SHDSL.
- R d represents the original data rate for SHDSL. Since M is larger than 3, the enhanced date rate R ed is larger than the original data rate R d .
- the SHDSL system is capable of supporting data rates from 192 kbps up to 2.312 Mbps with an 8 kbps increment. For every supported data rate, there is a specific transmit mask defined in the standard G.992.1.
- the RE-SHDSL of an embodiment of the present invention uses the transmit mask corresponding to the particular SHDSL data rate from the specifications. As a result, RE-SHDSL is automatically spectrally compliant and transparent to other applications.
- FIG. 1 a is a table illustrating enhanced data rates of RE-SHDSL as a function of number of data bits per symbol according to an embodiment of the present invention.
- Column 110 provides a system type;
- column 112 provides data bits per symbol;
- column 114 provides coded bits per symbol;
- column 116 provides constellation size;
- column 118 provides data rate with 1.5 Mb PSD;
- column 120 provides data rate with 2.0 Mb PSD;
- column 122 provides data rate with 2.312 Mb PSD.
- the RE-SHDSL approach of an embodiment of the present invention is applicable to region specific Annexes A and B of the ITU standard G.992.1 for SHDSL, as well as other standards.
- the frame structure of RE-SHDSL incorporates a payload size that is larger than that of SHDSL.
- the value of n is larger than 36.
- FIG. 2 is a diagram of a Trellis Coded Modulation (TCM) Encoder, according to an embodiment of the present invention.
- TCM Trellis Coded Modulation
- the first bit s 1 (m) may be encoded using a convolutional encoder 220 , such as a half rate convolutional encoder, to generate two encoded bits x 1 (m) and x 2 (m).
- the other M ⁇ 1bits s 2 (m), S 3 (m), . . . , s M (m) may be essentially untouched and renamed x 3 (m), x 4 (m), . . .
- x M+1 (m) as follows: s 2 ⁇ ( m ) ⁇ x 3 ⁇ ( m ) s 3 ⁇ ( m ) ⁇ x 4 ⁇ ( m ) ⁇ ⁇ s M ⁇ ( m ) ⁇ x M + 1 ⁇ ( m ) .
- the M+1 bits ⁇ x 1 (m), x 2 (m), x 3 (m), x 4 (m) . . . x M+1 (m) ⁇ may then be used to form a symbol using a 2 M+1 -PAM constellation 230 .
- Symbol to bit error may be minimized (e.g., by a Gray Code or other code) to simplify the decoder design where the bit labeled x 1 (m) represents a Least Significant Bit (LSB) and x M+1 (m) represents a Most Significant Bit (MSB).
- LSB Least Significant Bit
- MSB Most Significant Bit
- [0054] represents a decimal representation of the M+1 bits, where x 1 is the LSB.
- the normalized constellation points may be represented using B binary bits in 2's complement form.
- the number of bits B may be larger than M+1 where the extra bits B ⁇ M ⁇ 1 may determine the precision available for soft decision on the decoder and the overall performance of the Trellis Coded Modulation (TCM) scheme.
- TCM Trellis Coded Modulation
- at least 8 extra bits may be provided for soft decision, e.g., B ⁇ M+9.
- FIGS. 1 b and 1 c An exemplary listing of 128-PAM points are shown in FIGS. 1 b and 1 c .
- Column 130 indicates mapper-in, column 132 indicates output level;
- column 134 indicates output (HEX),
- column 136 indicates mapper-in;
- column 138 indicates output level and
- column 140 indicates output (HEX).
- Column 150 indicates mapper-in, column 152 indicates output level;
- column 154 indicates output (HEX),
- column 156 indicates mapper-in;
- column 158 indicates output level and
- column 160 indicates output (HEX).
- the ITU standard for SHDSL specifies transmit power spectral densities, e.g., transmit masks, for every supported rate from 192 kbps to 2.312 Mbps with 8 kbps increment.
- the RE-SHDSL transmit signal uses one of the masks defined in SHDSL standard.
- the selection process for a transmit mask involves using an appropriate transmit mask corresponding to the SHDSL rate R d .
- the enhanced data rate R ed is defined as (M/3)R d where R d is the original SHDSL rate and M is number of data bits per symbol. For each M, every enhanced data rate R ed corresponds to a SHDSL data rate R d and hence, a specific transmit mask.
- an embodiment of the present invention uses a transmit mask corresponding to the SHDSL rate R d , thereby eliminating a need for any new transmit masks and guarantees spectral compatibility and transparency to other users.
- the RE-SHDSL receiver may include a deframer and a Trellis decoder.
- the deframer may provide added capacity for handling enhanced data rates.
- the Trellis decoder may be redesigned to handle a constellation size higher than 16-PAM. Additional bits added to the RE-SHDSL may be uncoded bits, which do not effect the convolutional coding. As a result, it is possible to design the Trellis decoder to accommodate higher constellations with minimal change.
- the Gray code used in the mapper definition may simplify the decoder design for higher constellations.
- One such implementation may include a situation where the major blocks of the decoder remain substantially same with minor changes to the input and output stages. Using such an implementation of the Trellis decoder, a SHDSL receiver may be modified to handle RE-SHDSL with minimal redesign effort.
- the constellation size cannot be increased without limit, e.g., the value of M cannot be too larger.
- the signal to noise ratio (SNR) required at the receiver may increase by approximately 6 dB.
- SNR signal to noise ratio
- RE-SHDSL frame structure has the ability to handle a higher payload rate or larger payload blocks.
- the maximum allowed value for the parameter n, that determines the payload rate and the payload block size is 12M instead of 36 as specified in SHDSL. Note that M (>3) is the number of bits per symbol for the RE-SHDSL system.
- the TCM-encoder may accommodate a larger number of uncoded bits as shown in FIG. 2. This effects the serial to parallel converter 210 and the mapper block 230 within the TCM-encoder.
- Convolutional encoder 220 may receive first bit s 1 (m) and generate two bits x 1 (m) and x 2 (m).
- the 16-PAM mapper 230 may receive x 1 (m), x 2 (m), x 3 (m), x 4 (m) and x 5 (m) to generate y(m).
- RE-SHDSL of an embodiment of the present invention is an efficient and easy to implement approach for increasing the data rate of existing SHDSL transceivers.
- the rate enhancement may be achieved by increasing the number of data bits per symbol (M >3).
- M data bits per symbol
- the SHDSL standard specifies the use of 3 bits per symbol and 16-PAM constellation.
- 4 or more bits per symbol and constellation size larger than 16-PAM are used in RE-SHDSL of an embodiment of the present invention.
- an embodiment of the present invention provides a method for effective use of larger constellations.
- the RE-SHDSL of an embodiment of the present invention achieves a higher data rate without requiring any additional transmit bandwidth or transmit power.
- the rate enhancement achieved by RE-SHDSL of an embodiment of the present invention is flexible compared to the standard specified four wire approach.
- the rate enhancement may depend in part on the number of bits per symbol M.
- RE-SHDSL of an embodiment of the present invention may use a single pair of wire, at a minimum.
- RE-SHDSL uses the same (or substantially similar) set of transmit masks as specified in SHDSL standard. As a result, there is no need for additional transmit masks.
- RE-SHDSL satisfies spectral compatibility requirements and is transparent to other applications.
- RE-SHDSL is further compatible with four wire operations as well as other modes.
- RE-SHDSL may be used in a four wire mode to achieve an additional doubling of data rate.
- RE-SHDSL may be used for both region specific Annexes A and B of the ITU standard G.992.1 for SHDSL, as well as other standards.
- an efficient iterative algorithm for the computation of pre-equalizer coefficients is provided.
- a pre-equalizer is a non-adaptive filter that precedes the adaptive equalizer filter.
- the pre-equalizer serves to counteract against fixed components of a communication channel.
- An algorithm of an embodiment of the present invention may be used to compute pre-equalizer coefficients in an optimal manner based on a worst case mean square error minimization.
- a pre-equalizer may be considered a non-adaptive component of an overall equalizer structure.
- Linear distortion to be corrected by the equalization process may be partly caused by known transmit filter characteristics. This results in a common component for different channel scenarios where the use of a pre-equalizer block basically targets to exploit this fact.
- Viewing the functioning of a feedforward filter as a combination of signal to noise ratio (SNR) improvement through matched filtering and post-cursor inter symbol interference (ISI) correction motivates the use of a pre-equalizer to match the stationary component of the channel. This provides a greater degree of freedom for the feedforward equalizer to handle ISI.
- SNR signal to noise ratio
- ISI post-cursor inter symbol interference
- a pre-equalizer block increases an effective equalizer length without increasing the number of taps to be trained. This provides potentially longer loops as the need for a longer equalizer increases with the increasing impulse response length of longer loops.
- An increased equalizer length also improves SNR performance in noise cases by enhancing the ability to increase noise rejection and ISI compensation. This property is especially beneficial for cases where the SNR gap between an infinite length Decision Feedback Equalizer (DFE) and a finite impulse response (FIR) DFE equalizer is considerably large. Even in the cases where this gap is small, use of a pre-equalizer may provide enhanced whitening of an error spectrum and therefore an improved Bit Error Rate (BER) performance.
- DFE Decision Feedback Equalizer
- FIR finite impulse response
- the use of a pre-equalizer may also increase the speed and performance of equalizer training, in particular, a blind section, by providing a pre-processing of the signal input to the equalizer.
- FIG. 3 illustrates an overall equalization model for a fractionally spaced Decision Feedback Equalizer (DFE) with an oversampling factor M that employs a pre-equalizer filter, according to an embodiment of the present invention.
- DFE Decision Feedback Equalizer
- Signal xk represents a transmitted digital input sequence that is received by upsampling block 310 .
- Signal x k is upsampled by a factor M at 310 , where upsampling may involve the insertion of M ⁇ 1 zeros in between the samples of signal x k .
- Other methods of upsampling may also be implemented.
- the upsampled signal is received by channel 312 .
- Channel 312 models an overall linear distortion caused by a combination of a transmit filter, communication medium and/or a receive filter.
- Channel 312 may be modeled by a linear time invariant filter with coefficients h l .
- An output of channel 312 may be corrupted by a noise sequence n k where n k is formed by passing a white noise sequence v k through a noise shaping filter 314 with an impulse response g k .
- Signal y k is an input sequence received by pre-equalizer 316 which may include a combination of an output of channel 312 and noise sequence n k .
- the pre-equalizer 316 and decision feedback equalizer which may include components such as feed-forward equalizer 318 and feedback equalizer 322 , process signal y k to counteract against the effects of channel and noise.
- Signal y k is first processed by a pre-equalizer filter 316 with impulse response ⁇ p k ; k ⁇ ⁇ 0, . . . , 2N P ⁇ 1 ⁇ where the pre-equalizer filter may be non-adaptive.
- the output of the pre-equalizer filter 316 is further filtered by a feed-forward equalizer 318 with coefficients ⁇ f k ; k ⁇ ⁇ 0, . . . , 2N F ⁇ 1 ⁇ where the feed-forward equalizer may be adaptive and then downsampled by a factor M by downsampling block 320 . Downsampling may involve selecting one sample out of M consecutive samples.
- the output of the downsampling unit 320 may be combined with an output of a feedback equalizer 322 to produce output sequence z k where the feedback equalizer 322 may be adaptive.
- the feedback equalizer processes the previous decisions where the feedback equalizer has coefficients ⁇ b k ; k ⁇ ⁇ 0, . . . , N B ⁇ 1 ⁇ .
- the decision unit 324 uses z k to produce final decisions d k .
- N T test cases with corresponding channel impulse responses 412 ( ⁇ h l (i) ; l ⁇ ⁇ 0, . . . , N C ⁇ 1 ⁇ , i ⁇ ⁇ 0, . . . , N T ⁇ ) and noise shaping filters 414 ( ⁇ g k (i) ; k ⁇ ⁇ 0, . . . , N G ⁇ 1 ⁇ , i ⁇ ⁇ 0, . . .
- pre-equalizer coefficients 416 ⁇ p k ⁇ are kept fixed while the adaptive feedforward filter coefficients 418 ⁇ f k (i) ⁇ and the adaptive feedback equalizer coefficients 422 ⁇ b k (i) ⁇ may be different for each test case.
- An embodiment of the present invention provides an algorithm for computing static pre-equalizer coefficients and minimizing the maximum value of the mean square of the error between z k and x k over a range of possible test cases.
- Algorithm parameters may include predetermined constants independent of the data to be used in the algorithm. The following values may be adjusted to achieve different levels of performance.
- N p Half Pre-equalizer Length.
- N F Half Feedforward Equalizer Length.
- N B Feedback Equalizer Length.
- N I Number of algorithm iterations.
- N C Half Channel Length.
- N T Number of test cases.
- ⁇ 2 x Transmit signal power.
- N G The length of noise shaping filter.
- h e,l (i) h 2l (i) l ⁇ ⁇ 0, . . . , N C ⁇ 1 ⁇
- h o,l (i) h 2l+1 (i) l ⁇ ⁇ 0, . . . , N C ⁇ 1 ⁇
- ⁇ P l , l ⁇ ⁇ 0, . . . , 2N P ⁇ 1 ⁇ The pre-equalizer filter coefficients.
- p e,l p 2l l ⁇ ⁇ 0, . . . , N P ⁇ 1 ⁇ .
- p o,l p 2l+1 l ⁇ ⁇ 0, . . . , N P ⁇ 1 ⁇ .
- f e,k (i) f 2k (i) k ⁇ ⁇ 0, . . . , N F ⁇ 1 ⁇
- f o,k (i) f 2k+1 (i) k ⁇ ⁇ 0, . . . , N F ⁇ 1 ⁇
- L 1 (i) scalar, length variable.
- L 2 (i) scalar, length variable.
- L 3 (i) scalar, length variable.
- t scalar, intermediate search variable used in optimization algorithm.
- G (i) (N P +N F ⁇ 1 ⁇ N P +N F +N G ⁇ 2)
- Matrix convolution matrix for the noise shaping filter.
- H o (i) (N F +N P ⁇ 1) ⁇ N F +N P +N C ⁇ 2) Matrix, odd channel convolution matrix.
- H e (i) (N F +N P ⁇ 1) ⁇ N F +N P +N C ⁇ 2) Matrix, even channel convolution matrix.
- FIG. 5 illustrates a flowchart of an algorithm for determining pre-equalizer coefficients, according to an embodiment of the present invention.
- iteration may be initialized to a predetermined value, such as 0.
- Algorithm-II described below may be applied to obtain p.
- iteration may be incremented by a predetermined value, such as 1. For example, iteration may be set to iteration+1.
- it may be determined whether iteration N I . If so, then stop at step 520 else go to step 512 .
- Step 1 Set L 1 (i) as the maximum of the following 2 quantities:
- M (i) [0 N B ⁇ d (i) +1 IN B 0 N B ⁇ L 1 (i) ⁇ d (i) ⁇ 1 N B ].
- Step 10 Form the matrix P 1 using the formula
- P 1 [P e 0 N F ⁇ 1 P o ].
- Step 11 Form the matrix P 2 using the formula
- Step 1 Set L 3 (i) as the maximum of the below 2 quantities:
- a (i) may be computed using any matrix square root algorithm.
- Step 16 Solve the following semidefinite programming optimization problem (using any SDP solver or optimization tool with SDP capability)
- ADC Analog to Digital Conversion
- ADC refers to discretization of an input analog signal in both time and magnitude.
- Sigma Delta converters provide high resolution analog to digital conversion. The high resolution may be achieved through over-sampling of an input signal at a rate higher than its bandwidth.
- a Sigma Delta Analog to Digital (AD) Converter may include at least two stages, such as an Analog Quantizer block and a Digital Combiner-Downsampling block.
- the Analog Quantizer block oversamples an input analog signal and produces a high-rate digital signal with typically two levels (e.g., 1 bit) or four levels (e.g., 2-bits), for example.
- This low magnitude resolution over-sampled signal may be converted to a higher magnitude resolution (e.g. 16 bits) and a lower rate signal by the Digital Combiner-Downsampling block.
- An embodiment of the present invention is directed to a polyphase combiner and sigma-delta decimator block structure.
- An embodiment of the present invention provides an efficient implementation of a sigma-delta decimator block which may be enabled by an effective decoupling of a polyphase IIR structure into a cascade of a polyphase FIR bank and a single phase IIR filter.
- a reduction in hardware implementation may be achieved by reducing timing requirements for filtering and high rate clock generation.
- a reduction in power consumption may be achieved by the use of a lower rate clock.
- an embodiment of the present invention provides a low complexity, low power consumption implementation of a sigma delta combiner and decimator blocks through the use of a polyphase structure.
- FIG. 6 illustrates an analog to digital converter, according to an embodiment of the present invention.
- Analog signals are converted into digital signals by A/D Converters by various methods, which may include Sigma-Delta A/D conversion.
- Sigma-Delta A/D conversion an input analog signal may be sampled into a 2-bit (in some cases one bit or other number of bits) high-rate digital signal by Analog Sigma-Delta block 610 .
- the digital signal is then down-sampled and converted into a high resolution (e.g., 16-bit) and lower rate digital signal by a Digital Sigma-Delta Decimator block 620 . As shown in FIG.
- Analog Sigma-Delta block 610 generates a two-bit digital output, D 1 and D 2 .
- D 1 and D 2 are binary signals with rate R.
- D 1 carries a sampled signal with quantization noise and D 2 carries quantization noise cancellation information.
- the Digital Sigma-Delta Decimator 620 combines D 1 and D 2 and then decimates the combination by a factor M.
- FIG. 7 illustrates components of a Digital Sigma-Delta Decimator, according to an embodiment of the present invention.
- a Digital Sigma-Delta Decimator 620 may include a Combine 710 and a decimation filter stage which may include a Multistage Decimator 720 .
- Combiner 710 receives D 1 and D 2 from the Analog Sigma-Delta block 610 and generates a combined signal.
- the Multistage Decimator 720 receives the combined signal and generates a digital sigma-delta output.
- FIG. 8 illustrates components of a combiner, according to an embodiment of the present invention.
- Combiner may include two filters, C 1 and C 2 one for each input branch and a summing junction.
- D 1 may be filtered by filter C 1
- D 2 may be filtered by filter C 2 wherein the filtered signals are combined by a summing junction.
- Additional filters may be implemented for additional inputs.
- FIG. 9 illustrates components of a multistage decimator, according to an embodiment of the present invention.
- the decimation factor M is not a prime number and therefore may be factored into multiple integer factors, e.g.,
- M M 1 M 2 . . . M L .
- the decimator may be implemented as a L-stage decimator, as shown in FIG. 9.
- the combined signal of D 1 and D 2 may be received by a first decimation stage having a sub-sampling factor of M 1 .
- the output of the first decimation stage may be received by a second decimation stage having a sub-sampling factor of M 2 .
- a Lth decimation stage having a sub-sampling factor of M L may generate a digital sigma-delta output.
- the first stage may operate with a highest clock rate.
- the first stage may be implemented with a simple filter such as a Finite Impulse Response (FIR) sinc filter of order K.
- FIR Finite Impulse Response
- the combination of the sinc filter and a down-sampling function may be efficiently implemented as shown in FIG. 10.
- S 1 represents a Kth order integrator filter implemented as a cascade of K integrators and
- S 2 represents a Kth order differentiator which may be implemented as a cascade of K differentiators.
- FIG. 11 illustrates components of a decimator, according to an embodiment of the present invention.
- FIG. 11 shows a combiner 1110 and a first stage decimator 1120 with a sinc filter structure.
- the combiner 1110 may operate at a high clock with frequency R MHz.
- Combiner 1110 includes a filter C 1 , a filter C 2 and a summer.
- a polyphase structure for the combiner 1110 and sinc filter integrator combination may be implemented such that a lower rate clock may be implemented. This may be accomplished by merging the combiner 1110 and sinc integrator filter operations with a decimation operation as shown by 1120 in FIG. 11.
- decimator 1120 includes S 1 , a downsampling block M and S 2 .
- An embodiment of the present invention proposes a low complexity solution for the polyphase structure.
- FIG. 12 illustrates a low complexity, efficient polyphase structure, according to an embodiment of the present invention.
- a first portion of the polyphase structure includes filters C 11 , C 12 , C 13 and C 14 for receiving inputs D 11 , D 12 , D 21 , and D 22 respectively. The outputs of filters C 11 , C 12 , C 13 and C 14 are then combined by a first summer and received by filter F 1 .
- a second portion of the polyphase structure includes filters C 21 , C 22 , C 23 and C 24 for receiving inputs D 11 , D 12 , D 21 , and D 22 respectively. The outputs of filters C 21 , C 22 , C 23 and C 24 are then combined by a second summer and received by filter F 2 .
- the outputs of filters F 1 and F 2 are combined by a third summer and received by a decimator structure.
- the decimator structure may include a Kth order integrator filter S 1 , a down-sampling function block N and a Kth order differentiator S 2 .
- the decimator structure generates a digital sigma-delta output.
- Combiner Filter C 1 of FIG. 11 has filter coefficients given as ⁇ c1 k ; k ⁇ ⁇ 0, . . . , (2N 1 ⁇ 1) ⁇ where 2N 1 is the filter length which is an even value.
- Combiner Filter C 2 of FIG. 11 Combiner Filter 2 has filter coefficients given as ⁇ c2 k ; k ⁇ ⁇ 0, . . . , (2N 2 ⁇ 1) ⁇ where 2N 2 is the filter length which is an even value.
- Filter C11 has coefficients ⁇ c11 k ; k ⁇ ⁇ 0, . . . , N 1 ⁇ 1 ⁇ where
- c 11 k c 1 2k k ⁇ ⁇ 0, . . . , N 1 ⁇ 1 ⁇ .
- c 12 k+1 c 1 2k+1 k ⁇ ⁇ 0, . . . , N 1 ⁇ 1 ⁇ .
- Filter C13 has coefficients ⁇ c13 k ; k ⁇ ⁇ 0, . . . , N 2 ⁇ 1 ⁇ where
- c 13 k c 2 2k k ⁇ ⁇ 0, . . . , N 2 ⁇ 1 ⁇ .
- c 14 k+1 c 2 2k+1 k ⁇ ⁇ 0, . . . , N 2 ⁇ 1 ⁇ .
- Filter C21 has coefficients ⁇ c21 k ; k ⁇ ⁇ 0, . . . , N 1 ⁇ 1 ⁇ where
- c 21 k c 1 2k+1 k ⁇ ⁇ 0, . . . , N 1 ⁇ 1 ⁇ .
- Filter C22 has coefficients ⁇ c22 k ; k ⁇ ⁇ 0, . . . , N 1 ⁇ 1 ⁇ where
- c 22 k c (1) 2k k ⁇ ⁇ 0, . . . , N 1 ⁇ 1 ⁇ .
- Filter C23 has coefficients ⁇ c23 k ; k ⁇ ⁇ 0, . . . , N 2 ⁇ 1 ⁇ where
- c 23 k c 2 2k+1 k ⁇ ⁇ 0, . . . , N 2 ⁇ 1 ⁇ .
- Filter C24 has coefficients ⁇ c24 k ; k ⁇ ⁇ 0, . . . , N 2 ⁇ 1 ⁇ where
- c 24 k c 2 2k k ⁇ ⁇ 0, . . . , N 2 ⁇ 1 ⁇ .
- D 11 and D 12 For input data sequences D 11 and D 12 , even sub-samples of D 1 may be represented by D 11 and odd sub-samples of the D 1 may be represented by D 12 .
- An analog sigma delta may provide two outputs, for example, for D 1 with one output for (D 11 ) and one output for (D 12 ) where each line has a rate of R/2.
- an analog sigma delta may provide a single output with clock of R/2 with even samples (D 11 ) sent at a rising edge and odd samples (D 12 ) sent at a falling edge. In the latter case, D 11 and D 12 may be obtained as separate lines with rate of R/2 by appropriately sampling the single line output for D 1 .
- D 21 and D 22 For input data Sequences D 21 and D 22 , even sub-samples of D 2 may be represented by D 21 and odd sub-samples of the D 2 may be represented by D 22 .
- An analog sigma delta may provide two outputs, for example, for D 2 with one output for (D 21 ) and one output for (D 22 ) where each line has a rate of R/2.
- an analog sigma delta may provide a single output with clock of R/2 but even samples (D 21 ) sent at a rising edge and odd samples (D 22 ) sent at a falling edge. In the latter case, D 21 and D 22 may be obtained as separate lines with rate of R2 by appropriately sampling the single line output for D 1 .
- a data stream is partitioned and modulated to be transmitted on several independent sub-channels (also called sub-carriers or tones).
- Each sub-channel may have a different data rate, depending on transmission conditions and/or other factors.
- the total data rate of the system may be defined as a summation of the data rates of individual sub-channels.
- the data rate of each sub-channel may be determined with the consideration of various factors, including the Signal-to-Noise Ratio (SNR) at each tone, the PSD constraint, and/or other considerations.
- SNR Signal-to-Noise Ratio
- bit loading algorithms Algorithms that attempt to operate with these often conflicting requirements and further attempt to optimize the data rate allocation among the tones are referenced as bit loading algorithms.
- an efficient bit loading algorithm (EBLA) is provided.
- EBLA may be optimized for DMT systems with a QAM (Quadrature-Amplitude Modulation) scheme and constraints on the transmitting PSD.
- QAM Quadrature-Amplitude Modulation
- the bit loading algorithm of an embodiment of the present invention may be applied in any DMT communication systems.
- EBLA may automatically decide whether an optimal solution can be obtained efficiently. If so, an optimal solution is generated. If not, a sub-optimal solution with a performance close to an optimal solution is calculated.
- EBLA may be optimized for QAM-based systems with PSD constraints where optimal solutions may be obtained efficiently when possible.
- An adjustment mechanism may be incorporated into the bit loading algorithm of an embodiment of the present invention to minimize the amount of processing of a Greedy Search Module (GSM). As a result, total computational time may be reduced. When a sub-optimal solution is desired, a water-filling procedure may be implemented to expedite solutions.
- EBLA may accommodate different modulation and coding methods used in various communication systems.
- An embodiment of the present invention provides a reliable and efficient bit loading algorithm for generating an optimal solution when conditions permit, or a sub-optimal solution when computational costs associated with obtaining optimal solutions is daunting.
- e n (b n ) represents power allocated at nth tone in order to transmit b n data bits.
- ⁇ e n (b n ) represents an increment in power required at the nth tone to load one more bit, from b n ⁇ 1 bits to b n bits, e.g.,
- c n represents a PSD constraint at the nth tone.
- the power level allocated for the nth tone may not exceed this constraint, e.g., e n (b n ) is less than or equal to c n .
- P represents an aggregate power budget. This parameter restricts how much power is allocated for the system, e.g., E is less than or equal to P.
- ⁇ n represents a tone condition indicator at the nth tone. This parameter may be proportional to the noise power and depend on the choice of coding scheme.
- a first scenario involves a Bit-Rate Maximization (BRM) problem.
- BRM Bit-Rate Maximization
- the aggregate data rate B is maximized under certain constraints. These constraints may involve the total power being less or equal to P and the power at each tone being less or equal to the PSD constraint, e.g., e n (b n ) ⁇ c n .
- a second scenario involves a Margin Maximization (MM) problem. In this scenario, an aggregate data rate B is given and the total power required by the system is maximized to support that data rate, with or without the PSD and/or other constraints. Other scenarios may be implemented.
- the BRM problem generally occurs more frequently.
- a total power constraint is closely related to the PSD constraint.
- an optimal solution may be obtained easily for the BRM problem.
- the MM problem is inherently a more complicated scenario. Therefore, an optimal solution may be determined with a much higher computational cost.
- EBLA of an embodiment of the present invention exploits advantages of the first scenario (the BRM problem) and generates one or more optimal solutions.
- the BRM problem the BRM problem
- an embodiment of the present invention provides one or more acceptable sub-optimal solutions with a moderate or reasonable computational cost.
- FIG. 13 is the flowchart of an efficient bit loading algorithm, according to an embodiment of the present invention.
- FIG. 13 incorporates functional modules, which may include Scenario Selection Module (SSM) 1310 , PSD-Constrained Initial Power/bit Allocation Module (PC-IPAM) 1312 , Water-Filling Initial Power/bit Allocation Module (WF-EPAM) 1314 , PSD-Constrained Greedy Search Module (PC-GSM) 1316 , and Water-Filling Greedy Search Module (WF-GSM) 1318 .
- SSM Scenario Selection Module
- PC-IPAM PSD-Constrained Initial Power/bit Allocation Module
- WF-EPAM Water-Filling Initial Power/bit Allocation Module
- PC-GSM PSD-Constrained Greedy Search Module
- WF-GSM Water-Filling Greedy Search Module
- SSM 1310 determines which path to implement based on various conditions and factors. Based on an output of SSM 1310 , PC-IPAM 1312 and PC-GSM 1316 may be used to generate optimal bit loading solutions. If an optimal solution is not deemed feasible at SSM 1310 , WF-IPAM 1314 and WF-GSM 1318 may be used to generate sub-optimal solutions in an efficient manner.
- SSM 1310 decides whether a BRM or MM problem applies and invokes PC-IPAM 1312 or WF-IPAM 1314 accordingly. In addition, SSM 1310 may distinguish among other problems or scenarios as well. SSM 1310 also obtains information on the transmission condition and calculates the tone condition indicator ⁇ n , which reflects the condition on the nth tone.
- IPAM generates an initial power and/or bit allocation efficiently.
- the initial power or bit allocation should be close to an optimal bit loading solution so that a small number of adjustments may be made by GSM for obtaining optimal or sub-optimal solutions.
- PC-IPAM 1312 or WF-IPAM 1314 may be invoked.
- PC-IPAM 1312 efficiently obtains an initial power and/or bit allocation close to an optimal bit loading solution.
- the procedure takes advantage of the fact that the scenario (or condition) is essentially PSD-constrained.
- a total power constraint may include the power transmitted by a “nominal” PSD, which refers to the PSD constraint lowered by the amount of approximately 2.5 dB.
- FIG. 14 illustrates a table of number of bits and power levels for incorporation into the bit loading algorithm, according to an embodiment of the present invention. Other variations or types of references may be used. In particular, the table of FIG.
- FPAM may determine an initial bit and power allocation.
- FIG. 15 is a flowchart illustrating PC-IPAM, according to an embodiment of the present invention.
- the steps of FIG. 15 may be designed for ADSL modems.
- a value of b n may be determined.
- the value of b n may be selected such that e n (b n ) ⁇ c n ⁇ q ⁇ e n (b n +1) for each tone, where c n is the PSD constraint, b n is the bit allocation, e n (b n ) is the power allocation, and q is an adjustment factor, as determined at step 1512 .
- bit number at some tones may be set to 0, at step 1516 and the allocated power may be set to 0, at step 1518 because G.992.1 does not allow 1 bit to be loaded.
- the resulting bit and power allocation may be referred to as an initial bit and power allocation.
- other values may be assigned to the variables.
- the adjustment factor q if chosen properly, is highly effective in enabling the initial power and bit allocation to represent an optimal solution, thereby reducing computational costs at GSM. For example, a value corresponding to 1.5 dB decrease is a reasonable choice. However, for additional effectiveness, the value for the adjustment factor should be chosen based on conditions, such as a transmission condition. For example, if the transmission condition is such that many tones are usable on the condition that they are allocated with a power level greater the nominal PSD, then q may be reduced.
- FIG. 16 illustrates an example of an output of PC-IPAM 1312 , according to an embodiment of the present invention.
- the thick solid line 1610 represents PSD constraint c n .
- the dotted line 1616 represents a power level c n ⁇ q.
- the thin solid line 1614 represents an initial power allocation e n (b n ) and the dashed line 1612 represents a power level to support one more bit, e.g., e n (b n +1).
- tone 1 and 2 are examples of such tones.
- Tone 3 and 5 are examples of such tones. Whether to load more bits may depend on the amount of the total power budget remaining. This decision as well as choosing which tones to load more bits may be handled in the next procedure, GSM, as discussed in detail below.
- the bit loading algorithm of an embodiment of the present invention incorporates a combination of WF-IPAM 1314 and WF-GSM 1318 to provide sub-optimal solutions which are close to the optimal solutions at low costs and effort.
- the name “Water-Filling” refers to a procedure of calculating optimal transmitting PSDs for general communication systems.
- WF-IPAM 1314 generates water-filling solutions and then truncates the solutions to meet various requirements and/or conditions associated with DMT systems, e.g., ADSL modems.
- the resulting solutions of an embodiment of the present invention are close to optimal solutions, also known as sub-optimal solutions.
- FIG. 17 is a flowchart illustrating WF-IPAM, according to an embodiment of the present invention.
- the procedure of FIG. 17 may be designed for ADSL modems, for example.
- the values of ⁇ log 2 ( ⁇ 1 ), log 2 ( ⁇ 2 ), . . . , log 2 ( ⁇ N ) ⁇ may be calculated.
- these calculated values may be sorted in an order, such as in ascending order.
- the sorted values may be renamed as ⁇ log 2 ( ⁇ 1 ), log 2 ( ⁇ 2 ), . . . , log 2 ( ⁇ nN ) ⁇ .
- the initial bit number b n may be determined by truncating the value of ⁇ k ⁇ log 2 ( ⁇ n ) to an integer. If it is determined that the value of the bit number is 1, at step 1726 , then b n is set to a predetermined value, such as 0, at step 1728 .
- the initial power allocation may be calculated as e n (b n ), at step 1730 .
- WF-GSM provides a fine tuning function for the truncated water-filling solution. The details of WF-GSM are discussed below.
- GSM functionality fine tunes the initial power and bit allocation.
- PC-GSM 1316 or WF-GSM 1318 may be implemented. Other options may also be available.
- PC-GSM 1316 produces optimal bit loading solutions, while WF-GSM 1318 produces sub-optimal solutions, in response to the particular conditions and/or other factors.
- FIG. 18 is a flowchart illustrating PC-GSM, according to an embodiment of the present invention.
- FIG. 18 illustrates the steps involved in PC-GSM 1316 .
- an efficient tone may be determined. This may involve determining which tone has the smallest (or a small enough) ⁇ e n (b n +1) and whether the tone is permissible as determined by an increased power level not exceeding the PSD constraint c n and the number of bits not exceeding a predetermined value. Other constraints may be taken into consideration.
- whether enough power budget is left for the tone may be determined. If so, the power at that tone may be increased to e n (b n +1) at step 1816 .
- the bit number may be updated to (b n +1). These steps may be repeated until no other bits can be added without exceeding the aggregate power budget or until permissible tones are unavailable, at which point the process is terminated at step 1814 .
- the procedure as used in ADSL modems may be further optimized by taking into account special requirements and/or conditions associated with ADSL.
- FIG. 19 illustrates an example of an output of PC-GSM 1316 , according to an embodiment of the present invention.
- PC-GSM 1316 may choose tones 1, 2, 4, and 6 to increase the allocated power and bit number, as shown in FIG. 19.
- tone 8 may be loaded one more bit without violating the PSD constraint, it is not chosen because the remaining power budget is not enough to support an additional bit.
- WF-GSM 1318 follows the steps as illustrated in FIG. 18, according to an embodiment of the present invention. The steps discussed above in connection with FIG. 18 may be repeated until the aggregate data rate requirement is met, the remained power budget is not enough, or permissible tones are unavailable.
- WF-GSM 1318 may be modified in a similar manner as PC-GSM 1316 may be optimized for ADSL. Other modifications may be made for other types of modems and/or systems.
- GlobespanVirata Corporation's AluminumTM DSL PHY is designed for full duplex symmetric transmission over ordinary single twisted copper pair when used, for instance, with the Aluminum Analog Front End (AFE).
- AFE Aluminum Analog Front End
- This chipset supports programmable data rates ranging from 192 Kbps to 4.6 Mbps on a single pair, and provides reach greater than 18,000 feet at 1.5 Mbps. Loop-lengths of up to 26,000 ft are supported at lower data rates.
- the AluminumTM chipset includes digital communications subsystems, which may include a combination of echo canceller, pre-coder, feed forward equalizer and decision feedback equalizer. GlobespanVirata also offers its customers a comprehensive suite of technology solutions available to aid in the design, development and deployment of symmetric DSL products. This includes the BD3801 development reference platform for the AluminumTM chipset.
- AluminumTM and the AluminumTM AFE are HDSL2/G.shdsl/2B1Q Synchronous Digital Subscriber Line (SDSL) compliant.
- the AluminumTM chipset provides customers with a data throughput increase of up to 100 percent over competitive G.shdsl solutions and enables the development of symmetric DSL products with lower power consumption, greater reach and higher performance than was previously possible.
- AluminumTM and AluminumTM AFE may be purchased as a bundle with GlobespanVirata's HeliumTM communications processor and comprehensive network protocol stack, creating a complete customer premises equipment solution for symmetric DSL gateways, routers, and integrated access devices (IAD).
- IAD integrated access devices
- GlobespanVirata is also delivering a symmetric DSL to Ethernet router reference design.
- HeliumTM is a low-cost, Physical Layer Device (PHY)-neutral communications processor that enables high-speed Internet access capability for single- and multiple-user endpoint devices such as Universal Serial Bus (USB) modems, home gateway devices and small office/home office (SOHO) routers.
- the HeliumTM chip may be fully integrated with a networking and protocol software suite that handles Asynchronous Transfer Mode (ATM), frame, routing, bridging and signaling functions, as well as Simple Network Management Protocol (SNMP) management.
- ATM Asynchronous Transfer Mode
- SNMP Simple Network Management Protocol
- FIG. 20 is a schematic diagram of a hardware architecture in which the inventive aspects of the present invention may be incorporated.
- the inventive concepts discussed above may be achieved with the processing aid of Million Instructions per Second (MIPS) 2010 shown in FIG. 20.
- MIPS Million Instructions per Second
- the functionality related to rate enhanced SHDSL and efficient polyphase implementation of sigma delta analog to digital converter may be implemented in the AluminumTM 200 and/or 204 DSL Processor, as detailed below.
- the inventive concepts discussed above may be incorporated into chip sets, such as GlobespanVirata Corporation's AluminumTM 200 or 204 DSL Processor, which is also known as GlobespanVirata's second generation symmetric high-speed DSL processor.
- AluminumTM 200 or 204 may support several modes of operation including: International Telecommunications Union (ITU) G.991.2 (G.shdsl), American National Standard Institute (ANSI) T1E1.4 (High Speed Digital Subscriber Line (HDSL) 2) and single-pair 2B1Q SDSL.
- ITU International Telecommunications Union
- G.991.2 G.shdsl
- ANSI American National Standard Institute
- HDSL High Speed Digital Subscriber Line
- AluminumTM 200 or 204 provides compliance with the ITU G.991.2 standard, as well as other standards. Data rates from 192 Kbps to 2.3 Mbps are supported on 8 Kbps boundaries.
- AluminumTM 200 or 204 provides at least three additional base data rates above 2.3 Mbps: 3.096 Mbps, 4.104 Mbps and 4.616 Mbps.
- PSD power spectral density
- the AluminumTM 200 or 204 DSL Processor may support Transmission Protocol Specific—Transmission Convergence (TPS-TC) defined in G.991.2 including dual-bearer mode.
- TPS-TC Transmission Protocol Specific—Transmission Convergence
- the AluminumTM 200 or 204 may provide services such as simultaneous Synchronous Transfer Mode (STM) voice and ATM data transport.
- STM Synchronous Transfer Mode
- Support for analog voice and G.shdsl on the same copper pair is provided through the AluminumTM 200's or 204's G.shdsl-over-POTS mode.
- vendors and other entities may deliver the reach and symmetric performance of G.shdsl without giving up POTS service.
- G.shdsl-over-POTS further works with current ADSL splitters and microfilters, as well as other devices and components.
- the AluminumTM 200 or 204 DSL Processor may work in conjunction with GlobespanVirata's AluminumTM 200 Smart Analog Front End/Line Driver device, for example.
- the AluminumTM 200 or 204 may control the AluminumTM 200 AFE through a digital serial bus and may further provide for parameter calibration, power cutback and other functions. This configurability of the present invention allows the AFE to better match line conditions for higher performance and greater reach.
- the BD3802 is a development platform for AluminumTM 200 or 204 DSL Chipset, providing a comprehensive set of hardware and firmware tools to assist users in rapid development and deployment of products and services.
- Product applications may include Symmetric DSL routers and Integrated Access Devices (IAD); DSL Access Multiplexers (DSLAMs); Multi-tenant and Multi-dwelling unit networks; T1/E1 distribution products; and T1/E1 pairgain systems (using 3 Mbps and higher data rates).
- IAD Integrated Access Devices
- DSL Access Multiplexers DSL Access Multiplexers
- Multi-tenant and Multi-dwelling unit networks T1/E1 distribution products
- T1/E1 pairgain systems using 3 Mbps and higher data rates.
- Specification details may include ITU G.991.2 (G.shdsl) compliant; T1E1.4 HDSL2 compliant; ETSL ETR-152 compliant (single pair); support for data rates, presently, from 192 Kbps to 4616 Kbps on 8 Kbps increments; programmable framer supports G.shdsl, HDSL2, European Telecommunications Standard Institute (ETSI) SDSL, HDSL and transparent framing; UTOPIA Level 2 interface for ATM data and two independent serial interfaces for STM data; and 8-bit multiplexed or non-multiplexed host bus to connect to a variety of host Central Processing Units (CPUs).
- CPUs Central Processing Units
- MIPS Reduced Instruction Set Computing (RISC) engine and control registers 2010 may be coupled to a host interface 2022 , which may in turn be coupled to a 8-bit host interface.
- a serial data input may be coupled to an input of Tx Framer TPS-TC 2012 , which is further coupled to a Trellis Encoder/Mapper 2014 .
- Trellis Encoder/Mapper 2014 may provide an input to Precoder 2016 where Precoder 2016 may be coupled to a Tx Filter 2018 .
- Tx Filter 2018 may be coupled to (sigma-delta) S-D interpolating filter 2020 which is coupled to an output, Tx out.
- Utopia-2 Interface 2024 may be coupled to an input of Tx Framer TPS-TC 2012 and may further receive data from a Rx Framer TPS-TC 2026 .
- S-D Decimation filter 2038 receives an input from Rx In and is coupled to an adder 2040 .
- Adder 2030 sums outputs from filter 2038 and echo canceller 2032 and generates an output to Feed Forward (FF) equalizer 2030 .
- FF equalizer 2030 may be coupled to a Timing Recovery Phase Locked Loop (PLL) 2036 at an input.
- PLL Timing Recovery Phase Locked Loop
- Timing Recover PLL 2036 may be coupled to Volt Controlled Oscillator Digital Analog Converter (VCXO DAC), which in the case of the STUR is used to adjust the sampling phase to match that of the transmitting modem.
- FF equalizer 2030 may be coupled to a Trellis Decoder 2028 , which may be in turn coupled to Rx Framer TPS-TC 2026 .
- a SNR margin 2042 may be coupled to FF equalizer 2030 and Rx Framer TPS-TC 2026 , which may be further coupled to a Serial Data output.
- AluminumTM 204 may include SNR margin 2042 , as discussed above and as shown in FIG. 20. Details of SNR margin 2042 are shown in FIG. 21.
- a purpose of a SNR-margin estimator may include determining SNR for a given constellation and input signal. The output of the estimator may include the SNR margin value in dB.
- the SNR-margin estimator may include a hardware module that performs the SNR computation. Software may select certain parameters based on the constellation type.
- FIG. 21 illustrates a block diagram showing the basic operation of a SNR-margin estimator.
- a hardware module may perform a SNR-margin estimate that operates on a continuous stream of input samples and produces a SNR value. The margin may be found by comparing SNR to a minimum value.
- the software may perform a function of specifying the number of samples to average over as well as the signal power for a particular constellation.
- the error signal may be computed by subtracting an input sample from a decoder or slicer output as shown in equation below.
- slicer or decoder 2110 may receive an input signal x(n) to generate an output of d(n).
- input signal x(n) may be an input to function 2112 (e.g., z ⁇ K ) for generating an output to be subtracted from d(n) by adder 2114 .
- the output of adder 2114 may include an error signal as defined in the equation above.
- K may be defined as the delay through the decoder or slicer and d(n) may be a soft-decision output of Trellis decoder or an output of a slicer 2110 .
- This error signal may be equal to the noise in the signal if the assumption is made that the decision, d(n), is correct. This leads to a mean-squared-error (MSE) being approximately equal to the noise power as shown in equation below.
- MSE mean-squared-error
- Function 2116 may receive error signal e(n) and generate a square of the error signal e 2 (n).
- Function 2118 may receive squared error signal and generate MSE. In particular, function 2118 may accumulate N values and right shift by log2(N).
- Function 2120 may receive MSE and generate 10log 10 (MSE).
- MSE 10log 10
- the estimate of the fraction, k f may then be improved by estimating the logarithms nonlinear fractional component using equation below.
- Adder 2122 may be used to calculate SNR margin by subtracting the result of function 2120 from 10log 10 (P s ) ⁇ SNR min .
- the following precisions may be assumed, such as Polynomial coefficients are 10-bits ⁇ 0x002, 0x152, 0x3aa ⁇ ; power samples are 16-bits; the rough estimate of the log fraction, ⁇ circumflex over (k) ⁇ f , is minimum 8-bits; the resulting log is 16 bits, 6 integer and 10 fractional bits.
- An example may include the following log estimation where log 2 (00000000101010b) may be calculated.
- N The number of samples to average over, may be input by software. This is input as log 2 (N) and hardware will set the appropriate bit in a counter and then use the input value for the final shift.
- Another parameter may include the logarithm of the signal power. This value may be constellation specific and may be a parameter input by software even if the module works with one constellation.
- Yet another parameter may include the minimum SNR acceptable, SNR min .
- FIG. 22 illustrates a flowchart describing a hardware algorithm for SNR margin, according to an embodiment of the present invention.
- a start of a hardware algorithm for SNR margin may be initiated.
- Variables such as n and sum may be initialized.
- an error signal, the square of the error signal and an accumulated result may be determined.
- the margin may be determined by subtracting a signal. Step 2220 indicates the end of the algorithm.
- the output may include SNR margin, which may include five integer bits. This means that a maximum value this output may have is approximately 31 dB. This may be compared to a threshold of 0-15 dB to determine if the margin is too small.
- the 16-bit SNR value may be subtracted from the reference, which may also be 16 bits. The value may then be rounded and the lower 5 integer bits compared to the threshold.
- FIG. 23 is a schematic diagram of a hardware architecture which may function with devices supporting certain inventive aspects of the present invention.
- AFE such as the AluminumTM 200 AFE
- AFE is a G.SHDSL/HDSL2/2B1Q SDS1 compliant Analog Front End (AFE) with integrated line driver designed to be used with GlobespanVirata's AluminumTM 200 or 204 Symmetric DSL Processor to an external 2/4 wire hybrid.
- AFE Analog Front End
- AluminumTM 200 AFE conforms to G.shdsl PSD masks for every rate when interfaced to the AluminumTM 200 or 204 DSL Processor, AluminumTM 200 AFE also conforms to the HDSL2 OPTIS PSD mask at 1.544 Mbps. AluminumTM 200 AFE may be used in a central office or remote application mode, selectable by configuring the programmable filters in the AluminumTM 200 or 204 DSL Processor.
- the AluminumTM 200 AFE may include a high resolution 16-bit TX Digital Analog Converter (DAC) in the transmit path and one high resolution 16-bit RX Analog Digital Converter (ADC) in the receive path.
- a 10-bit DAC for the VCXO control is also integrated in the AluminumTM 200 AFE to reduce the number of required external components.
- the transmitter programmable attenuation control (PAC) and the receiver programmable gain amplifier (PGA) may be programmed via the AluminumTM 200 or 204 processor through a two-wire serial bus.
- AluminumTM 200 AFE has a low total power consumption of less than 800 mWatt (including the line drive) in full operation mode.
- An external line driver may also be used for HDSL2 and asymmetric PSD applications.
- AluminumTM 200 AFE may also provide a power down mode for stand-by operation.
- Product applications may include symmetric DSL routers and integrated access devices; DSL access multiplexers (DSLAMs); multi-tenant and multi-dwelling unit networks; T1/E1 distribution products; and T1/E1 pairgain systems (using proprietary 3 Mbps and higher data rates).
- Specification details may include ITU G.991.2 (G.shdsl) compliant; T1E1.4 HDSL2 compliant; ETSI ETR-152 compliant (single pair); and support for data rates from 192 Kbps to 2.312 Mbps and 8 Kbps increments, plus three additional rates of 3.096 Mbps, 4.104 Mbps and 4.616 Mbps.
- a transmission line may include a Tx Digital Audio Video (DAV) 2310 coupled to a Tx Filter 2312 , further coupled to a Programmable Attenuation Control (PAC) 2314 .
- PAC 2314 is coupled to a Line Driver 2316 , which is coupled to a Tx Tip & Ring.
- PAC 2314 may be further coupled to a HDSL2 bypass.
- a receiving line includes Automatic Gain Control (AGC) 2318 coupled to Rx Tip & Ring at an input and Rx Filter 2320 at an output.
- Rx Filter 2320 is coupled to Rx ADC 2322 .
- a control/testing interface 2326 may be provided on a serial line.
- a clocking subsystem 2324 may receive a plurality of inputs.
- the hardware architecture of FIG. 23 may further include a Current and Voltage Reference Generator (IV-REF) Subsystem 2328 .
- IV-REF Current and Voltage Reference Generator
Landscapes
- Engineering & Computer Science (AREA)
- Signal Processing (AREA)
- Computer Networks & Wireless Communication (AREA)
- Physics & Mathematics (AREA)
- Probability & Statistics with Applications (AREA)
- Theoretical Computer Science (AREA)
- Power Engineering (AREA)
- Computer Hardware Design (AREA)
- Mathematical Physics (AREA)
- Digital Transmission Methods That Use Modulated Carrier Waves (AREA)
- Communication Control (AREA)
- Dc Digital Transmission (AREA)
Abstract
Description
- This application claims priority from provisional application Serial No. 60/340,246, filed Dec. 18, 2001, which is incorporated by reference.
- The present invention relates generally to rate enhanced SHDSL, more particularly, to a spectrally compliant and transparent method and system for rate enhanced SHDSL.
- The advent of the Internet and the widespread popularity of personal computers have created an unprecedented demand for high bandwidth networks. Generally, Internet applications, from simple email to real time video conferencing, from web surfing to interactive movies, from interactive games to virtual TV stations, from online trading to online gambling, demand a higher bandwidth communication network. A fundamental challenge for the communication industry is to provide a reliable and affordable high bandwidth communication link to all types of Internet users. Various competing wire-line, wireless, and optical broadband technologies are deployed to partially meet the ever-increasing demand for higher bandwidth. The fastest growing broadband technology is the Digital Subscriber Line (DSL) technology, which provides a high bandwidth always-on connection over standard twisted pair copper media of the conventional telephone network. Among other wire-line media, coaxial cables are capable of providing always-on connections, however, its presence is insignificant compared to millions and millions of wired telephone customers who are connected by a twisted pair of copper wires. Other technologies, such as satellite, wireless, and optical, either provide limited coverage, limited bandwidth, or are too expensive for deployment to individual customers. As a result, DSL technology is uniquely positioned to provide the broadband link between individual customer premise and the central office, the so-called last-mile of the high-bandwidth communication network.
- DSL is the fastest growing among emerging broadband technologies for very good reasons. First of all, DSL utilizes the existing copper wire network infrastructure. Secondly, compared to the voice modems, such as V.34 and V.90, used in most personal computers that provide up to 56 kbps dial-up connection, DSL provides a high bandwidth always-on connection with typical connection speeds from 384 kbps to 6 Mbps. Moreover, DSL is affordable with easy installation, simple turn-up, and high service reliability. The successful deployment of DSL is capable of providing digital broadband connection to anyone with an analog telephone line.
- DSL services have been standardized over time by regional organizations such as, American National Standard Institute (ANSI), European Telecommunication Standard Institute (ETSI), and by world telecommunication organization International Telecommunication Union (ITU). These DSL standards define data communication protocols to connect customer premise equipment (CPE) to the central office (CO) and to provide connections to various networks, such as DSL service providers, virtual private networks (VPN), or the Internet. Various forms of digital data (e.g., voice, video, and data) can be transported using DSL technology. For transport of voice, DSL equipment is connected to the public switched telephone network (PSTN). For transport of video and data, DSL equipment uses the Internet via an Internet service provider (ISP). Voice over DSL (VoDSL) is capable of providing computer-to-computer, computer-to-telephone, and telephone-to-telephone voice services using an integrated access device (IAD). Video over DSL includes transport of MPEG-1 or MPEG-2 files, video conferencing using Internet Protocol (IP) standard such as ITU H.323, WebCam, and video mail. In addition, DSL supports simple data transport, e.g., bearer services, for virtual private network (VPN), leased data line such as T1 and E1, Point-to-Point Protocol (PPP), Asynchronous transfer mode (ATM), and Internet Protocol (IP).
- Like other communication technologies, DSL has gone though a major evolution over the last decade and a collection of technologies, commonly referred to as xDSL, are developed under the umbrella of DSL. One type of subscriber loop digital transmission technology involves an integrated services digital network (ISDN), which has replaced a significant portion of the analog phone lines in Europe and Japan. ISDN offers integrated voice and data services and connection speed up to 144 kbps. Due to the high cost of deployment, an alternative solution called integrated digital loop carrier (IDLC) has been deployed in United States. However, resulting data rates were considered inadequate for individual customers. As a result, advanced DSL technologies were developed, which include HDSL, SDSL, ADSL, HDSL2, SHDSL, and VDSL, all of which are capable of connection speed in excess of 1 Mbps. These advanced DSL technologies were developed to address different needs and application demands, while serving different market segments. For example, SHDSL is a symmetric service designed for long reach office applications with connection speed of 1.5 Mbps, whereas, VDSL is designed to provide a very high-speed asymmetric service for a short-range applications.
- SHDSL is a wire line Digital Subscriber Line (DSL) transmission technology that is designed to accommodate the need for higher data rates in telecommunication access networks. In particular, SHDSL supports duplex transmission of symmetric data rates over mixed gauge two-wire twisted metallic pairs, as described in the International Telecommunication Union (ITU) standard G.992.1—“Asymmetric Digital Subscriber Line (ADSL) Transceivers”, the body of which is incorporated herein by reference.
- One feature of the SHDSL includes the ability to support a wide range of data rates from 192 kbps to 2.312 Mbps which may include existing T1 and E1 rate services. Though such a range of data rates is adequate to accommodate a large number of real world applications, there are applications, such as MDU/MTU, Ethernet and others, that require or at least prefer a data rate beyond 2.312 Mbps. Traditional methods for attempting to achieve a data rate over 2.312 Mbps generally involve an optional four wire mode as specified in the ITU standard. However, as the name suggests the four wire operation requires an additional pair of wires. Availability of such extra pairs of wire is not guaranteed and even if they are available, the four wire solution is not an efficient utilization of the infrastructure.
- These and other drawbacks exist with current technologies.
- Aspects of the present invention overcome the problems noted above, and realize additional advantages.
- According to an aspect of an embodiment of the present invention, a Rate-Enhanced (RE)-SHDSL of an embodiment of the present invention provides enhancement of the SHDSL transceiver to support a data rate beyond 2.312 Mbps as specified in ITU standard; development of a method that is efficient, easy to implement, and flexible to design; achievement of the enhanced data rate without additional transmit bandwidth, transmit power, or cross-talk to other applications; and enhanced transceivers that comply with spectral management and/or other requirements.
- According to one embodiment of the present invention, a rate enhanced system for supporting duplex transmission of symmetric data rates, comprises an encoder comprising a serial to parallel converter for receiving a serial data bit, and for generating a parallel word having M bits; a convolutional encoder for receiving a first bit of the M bits of the parallel word, and for generating two encoded bits; and a mapper for receiving the two encoded bits and the remaining M−1 bits of the parallel word, and for generating a symbol; wherein M is greater than three.
- In accordance with other aspects of this exemplary embodiment of the present invention, the encoder is a Trellis coded modulation encoder; a receiver comprises a Trellis decoder for accommodating a constellation size greater than 16-PAM; the system supports an enhanced data rate which is greater than 2.312 Mbps; the enhanced data rate is defined as
- wherein M>3 wherein R d represents an original data rate for SHDSL; constellation size associated with the mapper is greater than 16-PAM; a single pair of wires is implemented; the system is compatible with four wire operations for doubling of data rate; the transmit masks correspond to that of SHDSL standard; the mapper is a 2M+1 PAM constellation, wherein M is greater than 3; a receiver comprises a deframer for supporting enhanced data rates greater than 2.312 Mbps; and a decoder for supporting a constellation size greater than 16-PAM; the decoder is a Trellis decoder.
- In accordance with another embodiment of the present invention, a method for supporting duplex transmission of symmetric data rates, comprises the steps of receiving a serial data bit; generating a parallel word having M bits in response to the serial data bit; receiving a first bit of the M bits of the parallel word; generating two encoded bits in response to the first bit; receiving the two encoded bits and the remaining M−1 bits of the parallel word; and generating a symbol in response to the two encoded bits and the remaining M−1 bits of the parallel word wherein M is greater than three.
- The accompanying drawings, which are incorporated in and constitute a part of this specification, illustrate various embodiments of the invention and, together with the description, serve to explain the principles of the invention.
- The present invention can be understood more completely by reading the following Detailed Description of the Invention, in conjunction with the accompanying drawings, in which:
- FIG. 1 a is a table illustrating enhanced data rates of RE-SHDSL as a function of number of data bits per symbol, according to an embodiment of the present invention.
- FIG. 1 b is a table illustrating a mapper definition, according to an embodiment of an aspect of the present invention.
- FIG. 1 c is a table illustrating a mapper definition, according to an embodiment of an aspect of the present invention.
- FIG. 2 illustrates a block diagram of TCM encoder for RE-G.SHDSL, according to an embodiment of an aspect of the present invention.
- FIG. 3 illustrates a setup for fractionally spaced DFE with pre-equalizer, according to an embodiment of the present invention.
- FIG. 4 illustrates a pre-equalizer design test case, according to an embodiment of the present invention.
- FIG. 5 is a flowchart illustrating of an algorithm for determining pre-equalizer coefficients, according to an embodiment of the present invention.
- FIG. 6 is a diagram of a receiver sigma-delta block, according to an embodiment of the present invention.
- FIG. 7 is a diagram of a digital sigma-delta block, according to an embodiment of the present invention.
- FIG. 8 is a diagram of a combiner structure, according to an embodiment of the present invention.
- FIG. 9 is a diagram of a digital sigma-delta block with multiple decimation stages, according to an embodiment of the present invention.
- FIG. 10 is a diagram of a first decimator stage with a sinc filter, according to an embodiment of the present invention.
- FIG. 11 is a diagram of a combiner-sinc filter, according to an embodiment of the present invention.
- FIG. 12 is a diagram of a polyphase combiner-sinc filter, according to an embodiment of the present invention.
- FIG. 13 is the flowchart of an efficient bit loading algorithm, according to an embodiment of the present invention.
- FIG. 14 illustrates a table of number of bits and required power levels for incorporation into the bit loading algorithm, according to an embodiment of the present invention.
- FIG. 15 is a flowchart illustrating PC-WPAM, according to an embodiment of the present invention.
- FIG. 16 illustrates an example of an output of PC-IPAM, according to an embodiment of the present invention.
- FIG. 17 is a flowchart illustrating WF-IPAM, according to an embodiment of the present invention.
- FIG. 18 is a flowchart illustrating PC-GSM, according to an embodiment of the present invention.
- FIG. 19 illustrates an example of an output of GSM, according to an embodiment of the present invention.
- FIG. 20 is a schematic diagram of a hardware architecture in which the inventive aspects of the present invention may be incorporated.
- FIG. 21 is a block diagram illustrating details of SNR margin, according to an embodiment of the present invention.
- FIG. 22 illustrates a flowchart describing hardware algorithm for SNR margin, according to an embodiment of the present invention.
- FIG. 23 is a schematic diagram of a hardware architecture in which the inventive aspects of the present invention may be incorporated.
- The following description is intended to convey a thorough understanding of the invention by providing a number of specific embodiments and details involving compliancy testing applications. It is understood, however, that the invention is not limited to these specific embodiments and details, which are exemplary only. It is further understood that one possessing ordinary skill in the art, in light of known systems and methods, would appreciate the use of the invention for its intended purposes and benefits in any number of alternative embodiments, depending upon specific design and other needs.
- The International Telecommunications Union (ITU) has adopted a standard for Single-pair High-speed Digital Subscriber Line (SHDSL) technology to address the need for higher data rates in telecommunication access networks. The ITU recommendations for SHDSL (e.g., G.992.1) mandate the support of a wide range of data rates from 192 kilo bits per second (kbps) to 2.312 mega bits per second (Mbps). There are applications, such as MDU/MTU, Ethernet and others, that may require or at least prefer a data rate beyond 2.312 Mbps. According to an aspect of an embodiment of the present invention, an efficient, easy to implement, and flexible method and system for increasing the data rate of the existing SHDSL transceivers is provided. The Rate-Enhanced (RE)-SHDSL of an embodiment of the present invention satisfies spectral compatibility requirements and is further transparent to other applications.
- The RE-SHDSL of an embodiment of the present invention supports a variety of functions. RE-SHDSL is an efficient and easy to implement approach to increase the data rate of an existing SHDSL transceiver. Rate enhancement may be achieved by increasing the number of data bits per symbol thereby increasing signal constellations. The effective use of larger constellations is one difference between RE-SHDSL and SHDSL. The RE-SHDSL achieves a higher data rate without requiring additional transmit bandwidth or transmit power. The rate enhancement achieved by RE-SHDSL of an embodiment of the present invention is flexible compared to a four wire approach specified in the standard. As in SHDSL, RE-SHDSL may support a single pair wires. RE-SHDSL uses the same (or substantially similar) set of transmit masks as specified in SHDSL standard. As a result, there is no need for additional transmit masks. RE-SHDSL is compatible with four wire operations and may be used in a four wire mode (or other mode) to achieve an additional doubling of data rate. RE-SHDSL may be used for both region specific Annexes A and B of the ITU standard G.992.1 for SHDSL as well as other standards.
- The RE-SHDSL system of an embodiment of the present invention does not require an additional pair of wires and provides a more flexible rate enhancement. Features of RE-SHDSL system include spectral compliance and transparency for successful deployment of any DSL as well as other technology. In other words, RE-SHDSL is fully compliant to spectral management requirements where the enhancements are transparent to other services deployed in the same binder, e.g., to any other service RE-SHDSL appears substantially the same as SHDSL. As a result, deployment of RE-SHDSL does not create additional crosstalk for other applications.
- As specified in the ITU standard G.991.2, SHDSL transceivers may include a precoded system with Trellis Coded Pulse Amplitude Modulation (TC-PAM) line code. In particular, an encoder may be used to convert 3 data bits into 4 coded bits. The coded 4 bits may be converted into a symbol using a 16-PAM constellation mapper. For every 3 data bits, the SHDSL transceiver generates one symbol with a symbol rate R s, which is one-third of the data rate Rd, e.g., Rs=Rdd/3. The symbol rate is a system parameter that dictates the transmission bandwidth. Generally, the higher the symbol rate, the larger the required bandwidth. Hence, if the constellation size is fixed, a larger bandwidth may be used to support higher data rates. However, such an approach would violate spectral compatibility and would not be transparent to other applications.
- In contrast to the SHDSL system where 3 data bits are used to form a symbol, RE-SHDSL of an embodiment of the present invention uses more then 3 data bits per symbol. The data rate may be increased by increasing a constellation size and allocating more bits per symbol while keeping the symbol rate fixed. Moreover, to simplify the transceiver design, the encoding scheme as described in SHDSL may be used with the exception that the number of uncoded bits are increased. An advantage of this approach is that there is no need to change signal processing blocks following the mapper. In other words, the change in number of bits per symbol and the consequent change in constellation size do not effect the signal processing operations that follow the mapper. In particular, the transmit filter and the transmit Power Spectral Density (PSD) remain identical (or substantially similar) to that of SHDSL. With that in mind, M (>3) may represent the number of data bits used per symbol for RE-SHDSL, where the enhanced data rate R ed is given by
- where R drepresents the original data rate for SHDSL. Since M is larger than 3, the enhanced date rate Red is larger than the original data rate Rd. The SHDSL system is capable of supporting data rates from 192 kbps up to 2.312 Mbps with an 8 kbps increment. For every supported data rate, there is a specific transmit mask defined in the standard G.992.1. The RE-SHDSL of an embodiment of the present invention uses the transmit mask corresponding to the particular SHDSL data rate from the specifications. As a result, RE-SHDSL is automatically spectrally compliant and transparent to other applications.
- Typical exemplary values of M along with the corresponding enhanced date rates are shown in FIG. 1 a. FIG. 1a is a table illustrating enhanced data rates of RE-SHDSL as a function of number of data bits per symbol according to an embodiment of the present invention.
Column 110 provides a system type;column 112 provides data bits per symbol;column 114 provides coded bits per symbol;column 116 provides constellation size;column 118 provides data rate with 1.5 Mb PSD;column 120 provides data rate with 2.0 Mb PSD; andcolumn 122 provides data rate with 2.312 Mb PSD. As shown in FIG. 1a, when M=4, a data rate of 3.08 Mbps may be achieved by implementing a constellation size of 32-PAM. The RE-SHDSL approach of an embodiment of the present invention is applicable to region specific Annexes A and B of the ITU standard G.992.1 for SHDSL, as well as other standards. - The frame structure of RE-SHDSL incorporates a payload size that is larger than that of SHDSL. In SHDSL standard, each payload block is defined as k bits long, where k=12(i+8n) bits, and the corresponding payload rate is given by 64n+8i kbps. The parameters n and i are two integer defined by 3≦n≦36 and 0≦i≦7. For example, for n =36 and i=1, a payload rate is equal to 2.312 Mbps. For RE-SHDSL, the value of n is larger than 36. The exact range of n depends on the vale of M and is given by 3≦n≦12M. For M=6 or double rate applications, the range of values for n is 3≦n≦72.
- FIG. 2 is a diagram of a Trellis Coded Modulation (TCM) Encoder, according to an embodiment of the present invention. For RE-SHDSL, more than 3 data bits are used to form a symbol y(m), as shown in FIG. 2. In this case, each M (>3) serial data bits, {d(n), d(n+1), d(n +2), . . . , d(n+M−1)} may be converted by
converter 210 to an M bit parallel word {s1(m), s2(m), s3(m), . . . , sM(m)}. The first bit s1(m) may be encoded using aconvolutional encoder 220, such as a half rate convolutional encoder, to generate two encoded bits x1(m) and x2(m). The other M−1bits s2(m), S3(m), . . . , sM(m) may be essentially untouched and renamed x3(m), x4(m), . . . , xM+1(m), as follows: - The M+1 bits {x 1(m), x2(m), x3(m), x4(m) . . . xM+1(m)} may then be used to form a symbol using a 2M+1-
PAM constellation 230. Symbol to bit error may be minimized (e.g., by a Gray Code or other code) to simplify the decoder design where the bit labeled x1(m) represents a Least Significant Bit (LSB) and xM+1(m) represents a Most Significant Bit (MSB). Using the Gray (or other) code, the M+1 output bits may be mapped to 2M+1-PAM as described below. As K=2M+1, the K normalized constellation points may be defined as -
-
- For a fixed point implementation, the normalized constellation points may be represented using B binary bits in 2's complement form. The number of bits B may be larger than M+1 where the extra bits B−M−1 may determine the precision available for soft decision on the decoder and the overall performance of the Trellis Coded Modulation (TCM) scheme. For example, at least 8 extra bits may be provided for soft decision, e.g., B≧M+9.
- An exemplary listing of 128-PAM points are shown in FIGS. 1 b and 1 c. FIG. 1b illustrates mapper definition for M=6 and a 128 PAM scenario. Column 130 indicates mapper-in, column 132 indicates output level; column 134 indicates output (HEX), column 136 indicates mapper-in; column 138 indicates output level and column 140 indicates output (HEX). FIG. 1c illustrates additional information for the M=6 and a 128 PAM scenario. Column 150 indicates mapper-in, column 152 indicates output level; column 154 indicates output (HEX), column 156 indicates mapper-in; column 158 indicates output level and column 160 indicates output (HEX). The binary representation of the output of the mapper may be given with B=16.
- As mentioned above, there is generally no other signal processing requirement to support the larger constellation for RE-SHDSL of an embodiment of the present invention. In other words, following the mapper of FIG. 2 the signal processing for the RE-SHDSL is identical (or substantially similar) to that of the SHDSL. Hence, most or all the blocks that follow the TCM-mapper remain unchanged. In particular, the precoder, transmit filter, and analog front end do not require modification.
- The ITU standard for SHDSL specifies transmit power spectral densities, e.g., transmit masks, for every supported rate from 192 kbps to 2.312 Mbps with 8 kbps increment. According to an embodiment of the present invention, the RE-SHDSL transmit signal uses one of the masks defined in SHDSL standard. The selection process for a transmit mask involves using an appropriate transmit mask corresponding to the SHDSL rate R d. The enhanced data rate Red is defined as (M/3)Rd where Rd is the original SHDSL rate and M is number of data bits per symbol. For each M, every enhanced data rate Red corresponds to a SHDSL data rate Rd and hence, a specific transmit mask. For an enhanced data rate Red, an embodiment of the present invention uses a transmit mask corresponding to the SHDSL rate Rd, thereby eliminating a need for any new transmit masks and guarantees spectral compatibility and transparency to other users.
- According to another embodiment of the present invention, the RE-SHDSL receiver may include a deframer and a Trellis decoder. The deframer may provide added capacity for handling enhanced data rates. The Trellis decoder may be redesigned to handle a constellation size higher than 16-PAM. Additional bits added to the RE-SHDSL may be uncoded bits, which do not effect the convolutional coding. As a result, it is possible to design the Trellis decoder to accommodate higher constellations with minimal change. In addition, the Gray code used in the mapper definition may simplify the decoder design for higher constellations. One such implementation may include a situation where the major blocks of the decoder remain substantially same with minor changes to the input and output stages. Using such an implementation of the Trellis decoder, a SHDSL receiver may be modified to handle RE-SHDSL with minimal redesign effort.
- For practical implementations, the constellation size cannot be increased without limit, e.g., the value of M cannot be too larger. Generally, for every additional bit, the signal to noise ratio (SNR) required at the receiver may increase by approximately 6 dB. For example, with M=6 the required SNR is about 43.5 dB as opposed to the 27.5 dB required for SHDSL.
- Various modifications may be implemented for a standard SHDSL transceiver to incorporate RE-SHDSL functionality. RE-SHDSL frame structure has the ability to handle a higher payload rate or larger payload blocks. In particular, the maximum allowed value for the parameter n, that determines the payload rate and the payload block size, is 12M instead of 36 as specified in SHDSL. Note that M (>3) is the number of bits per symbol for the RE-SHDSL system.
- The TCM-encoder may accommodate a larger number of uncoded bits as shown in FIG. 2. This effects the serial to
parallel converter 210 and themapper block 230 within the TCM-encoder. The Trellis decoder block in the receiver may accommodate higher size constellations. As pointed out, there are efficient implementations available that require minimal changes to the decoder block. In the exemplary case where M=4, a 4-bit serial to parallel converter and a 16-PAM mapper may be implemented where d(n) may be converted into a 4 bit word, which may include si(m), s2(m), s3(m) and s4(m).Convolutional encoder 220 may receive first bit s1(m) and generate two bits x1(m) and x2(m). The 16-PAM mapper 230 may receive x1(m), x2(m), x3(m), x4(m) and x5(m) to generate y(m). - RE-SHDSL of an embodiment of the present invention is an efficient and easy to implement approach for increasing the data rate of existing SHDSL transceivers. The rate enhancement may be achieved by increasing the number of data bits per symbol (M >3). Generally, the SHDSL standard specifies the use of 3 bits per symbol and 16-PAM constellation. In contrast, 4 or more bits per symbol and constellation size larger than 16-PAM are used in RE-SHDSL of an embodiment of the present invention. In addition, an embodiment of the present invention provides a method for effective use of larger constellations.
- The RE-SHDSL of an embodiment of the present invention achieves a higher data rate without requiring any additional transmit bandwidth or transmit power. The rate enhancement achieved by RE-SHDSL of an embodiment of the present invention is flexible compared to the standard specified four wire approach. The rate enhancement may depend in part on the number of bits per symbol M. As in SHDSL, RE-SHDSL of an embodiment of the present invention may use a single pair of wire, at a minimum. RE-SHDSL uses the same (or substantially similar) set of transmit masks as specified in SHDSL standard. As a result, there is no need for additional transmit masks. RE-SHDSL satisfies spectral compatibility requirements and is transparent to other applications. Deployment of RE-SHDSL does not create additional crosstalk to other services. RE-SHDSL is further compatible with four wire operations as well as other modes. For example, RE-SHDSL may be used in a four wire mode to achieve an additional doubling of data rate. RE-SHDSL may be used for both region specific Annexes A and B of the ITU standard G.992.1 for SHDSL, as well as other standards.
- According to another aspect of the present invention, an efficient iterative algorithm for the computation of pre-equalizer coefficients is provided. A pre-equalizer is a non-adaptive filter that precedes the adaptive equalizer filter. The pre-equalizer serves to counteract against fixed components of a communication channel. An algorithm of an embodiment of the present invention may be used to compute pre-equalizer coefficients in an optimal manner based on a worst case mean square error minimization.
- A pre-equalizer may be considered a non-adaptive component of an overall equalizer structure. Linear distortion to be corrected by the equalization process may be partly caused by known transmit filter characteristics. This results in a common component for different channel scenarios where the use of a pre-equalizer block basically targets to exploit this fact. Viewing the functioning of a feedforward filter as a combination of signal to noise ratio (SNR) improvement through matched filtering and post-cursor inter symbol interference (ISI) correction motivates the use of a pre-equalizer to match the stationary component of the channel. This provides a greater degree of freedom for the feedforward equalizer to handle ISI.
- A pre-equalizer block increases an effective equalizer length without increasing the number of taps to be trained. This provides potentially longer loops as the need for a longer equalizer increases with the increasing impulse response length of longer loops.
- An increased equalizer length also improves SNR performance in noise cases by enhancing the ability to increase noise rejection and ISI compensation. This property is especially beneficial for cases where the SNR gap between an infinite length Decision Feedback Equalizer (DFE) and a finite impulse response (FIR) DFE equalizer is considerably large. Even in the cases where this gap is small, use of a pre-equalizer may provide enhanced whitening of an error spectrum and therefore an improved Bit Error Rate (BER) performance.
- The use of a pre-equalizer may also increase the speed and performance of equalizer training, in particular, a blind section, by providing a pre-processing of the signal input to the equalizer.
- An embodiment of the present invention is directed to providing an algorithm for computing pre-equalizer coefficients. FIG. 3 illustrates an overall equalization model for a fractionally spaced Decision Feedback Equalizer (DFE) with an oversampling factor M that employs a pre-equalizer filter, according to an embodiment of the present invention.
- Signal xk represents a transmitted digital input sequence that is received by upsampling block 310. Signal xk is upsampled by a factor M at 310, where upsampling may involve the insertion of M−1 zeros in between the samples of signal xk. Other methods of upsampling may also be implemented. The upsampled signal is received by
channel 312.Channel 312 models an overall linear distortion caused by a combination of a transmit filter, communication medium and/or a receive filter.Channel 312 may be modeled by a linear time invariant filter with coefficients hl. An output ofchannel 312 may be corrupted by a noise sequence nk where nk is formed by passing a white noise sequence vk through a noise shaping filter 314 with an impulse response gk. - Signal y k is an input sequence received by
pre-equalizer 316 which may include a combination of an output ofchannel 312 and noise sequence nk. The pre-equalizer 316 and decision feedback equalizer, which may include components such as feed-forward equalizer 318 and feedback equalizer 322, process signal yk to counteract against the effects of channel and noise. - Signal y k is first processed by a
pre-equalizer filter 316 with impulse response{pk; k ∈ {0, . . . , 2NP−1}} where the pre-equalizer filter may be non-adaptive. The output of thepre-equalizer filter 316 is further filtered by a feed-forward equalizer 318 with coefficients {fk; k ∈ {0, . . . , 2NF−1}} where the feed-forward equalizer may be adaptive and then downsampled by a factor M by downsampling block 320. Downsampling may involve selecting one sample out of M consecutive samples. - The output of the downsampling unit 320 may be combined with an output of a feedback equalizer 322 to produce output sequence zk where the feedback equalizer 322 may be adaptive. The feedback equalizer processes the previous decisions where the feedback equalizer has coefficients {bk; k ∈ {0, . . . , NB−1}}. Finally, the decision unit 324 uses zk to produce final decisions dk.
- According to an embodiment of the present invention, the algorithm performs the computation of the pre-equalizer coefficients for the structure, such as one illustrated in FIG. 3 where M=2. As shown in FIG. 4, there may exist N T test cases with corresponding channel impulse responses 412 ({hl (i); l ∈ {0, . . . , NC−1}, i ∈ {0, . . . , NT}}) and noise shaping filters 414 ({gk (i); k ∈ {0, . . . , NG−1}, i ∈ {0, . . . , NG−1}}) that may be targeted to optimize the pre-equalizer coefficients. As shown in FIG. 4, pre-equalizer coefficients 416 {pk} are kept fixed while the adaptive feedforward filter coefficients 418 {fk (i)} and the adaptive feedback equalizer coefficients 422 {bk (i)} may be different for each test case.
- An embodiment of the present invention provides an algorithm for computing static pre-equalizer coefficients and minimizing the maximum value of the mean square of the error between z k and xk over a range of possible test cases.
- Algorithm parameters may include predetermined constants independent of the data to be used in the algorithm. The following values may be adjusted to achieve different levels of performance.
Np: Half Pre-equalizer Length. NF: Half Feedforward Equalizer Length. NB: Feedback Equalizer Length. NI: Number of algorithm iterations. NC: Half Channel Length. NT: Number of test cases. σ2x: Transmit signal power. NG: The length of noise shaping filter. - {g l (i), l ∈ {0, . . . , NG−1}}: The impulse response of a noise shaping filter for the ith test case.
- {h l (i), l ∈ {0, . . . , 2NC−1}}: The channel impulse response for the ith test case.
- {h e,l (i), l ∈ {0, . . . , NC−1}}: The even-indexed samples of a channel impulse response for the ith test case, where
- h e,l (i) =h 2l (i) l ∈ {0, . . . , N C−1}
- {h o,l (i), l ∈ {0, . . . , NC−1}}: The odd-indexed samples of a channel impulse response for the ith test case, where
- h o,l (i) =h 2l+1 (i) l ∈ {0, . . . , N C−1}
- The following provides descriptions of variables that may be used in an algorithm of an embodiment of the present invention.
- {P l, l ∈ {0, . . . , 2NP−1}}: The pre-equalizer filter coefficients.
- {P e,l, l ∈ {0, . . . , NP−1}}: The even-indexed pre-equalizer filter coefficients, where
- p e,l =p 2l l ∈ {0, . . . , N P−1}.
- {p o,l, l ∈ {0, . . . , NP−1}}: The odd-indexed pre-equalizer filter coefficients, where
- p o,l =p 2l+1 l ∈ {0, . . . , N P−1}.
-
- {f k (i), k ∈ {0, . . . , 2NF−1}}: Feedforward filter coefficients in the ith test case.
- {f e,k (i), k ∈ {0, . . . , NF−1}}: Even feedforward filter coefficients in the ith test case,
- where
- f e,k (i) =f 2k (i) k ∈ {0, . . . , N F−1}
- {f o,k (i), k ∈ {0, . . . , NF−1}}: Odd feedforward filter coefficients in the ith test case.
- f o,k (i) =f 2k+1 (i) k ∈ {0, . . . , NF−1}
-
- {b k (i), k ∈ {0, . . . , NB−1}}: Feedback coefficients in the ith test case.
-
- L 1 (i): scalar, length variable.
- L 2 (i): scalar, length variable.
- L 3 (i): scalar, length variable.
- L d (i): (d(i)+L3 (i)+1×1) Vector, intermediate variable.
- Q (i): (NB+L3 (i)−d(i)×NT×NB) Matrix, intermediate variable.
- C o (i): (NF+NP×NF+NP+NC−1) Matrix, odd channel convolution matrix.
- C e (i): (NF+NP−1×NF+NP+NC−2) Matrix, even channel convolution matrix.
- C (i): (2NF+2NP−1×L3 (i)) Matrix, intermediate variable.
- q (i): (1×2NP+NBNT) Vector, intermediate variable.
- Z (i): (2NP+NBNT×2NP+NBNT) Matrix, intermediate variable.
- A (i): ((NTNB+2NP)×(NTNB+2NP)) Matrix, intermediate variable.
- t: scalar, intermediate search variable used in optimization algorithm.
- G (i): (NP+NF−1×NP+NF+NG−2) Matrix, convolution matrix for the noise shaping filter.
- M (i): (NB×L1 (i)) Matrix, intermediate variable.
- H o (i): (NF+NP−1)×NF+NP+NC−2) Matrix, odd channel convolution matrix.
- H e (i): (NF+NP−1)×NF+NP+NC−2) Matrix, even channel convolution matrix.
- H (i): (NF+NP−1×L1 (i)) Matrix, intermediate variable.
- P o: (NF×NF+NP−1) Matrix, odd pre-equalizer convolution matrix.
- P e: (NF×NF+NP−1) Matrix, even pre-equalizer convolution matrix.
- P 1: (NF×2NF+2NP−1) Matrix, intermediate variable.
- P 2: (NF×2NF+2NP−1) Matrix, intermediate variable.
- P: (2N F×2NF+2NP−1) Matrix, intermediate variable.
- Rs n 1xn−d i: (2NF+NB×1) Matrix, cross correlation vector.
- Rs n 1: (2NF+NB×2NF+NB) Matrix, covariance matrix.
- FIG. 5 illustrates a flowchart of an algorithm for determining pre-equalizer coefficients, according to an embodiment of the present invention. At
step 510, iteration may be initialized to a predetermined value, such as 0. At step 512, Algorithm-I described below may be applied to obtain f(i) for all i=1, . . . , NT. At step 514, Algorithm-II described below may be applied to obtain p. Atstep 516, iteration may be incremented by a predetermined value, such as 1. For example, iteration may be set to iteration+1. Atstep 518, it may be determined whether iteration=NI. If so, then stop atstep 520 else go to step 512. - Algorithm-I
-
Step 1. Set L1 (i) as the maximum of the following 2 quantities: - NP+NC+NF−2,
- d(i)+1+NB
-
Step 2. Set L2 (i) using the formula - L 2 (i) =L 1 (i) −N C −N F −N P+1,
-
-
Step 4. Form the NB×L1 (i) matrices M(i) for all i=1, . . . , NT, using the formula - M (i)=[0N B ×d (i)+1 IN B 0N B ×L 1 (i) −d (i)−1N B].
-
-
-
-
-
-
Step 10. Form the matrix P1 using the formula - P 1 =[P e 0N F×1 P o].
- Step 11. Form the matrix P 2 using the formula
- P 2 =[P o P e 0N F×1].
-
- Step 13. Finally compute f (i) for all i=1, . . . , NT, using the formula
- f (i)=(P(H (i)(I−M (i) M (i)T)H (i)T +G (i) G (i)T)(i) P T)−1 PH (i)
- Algorithm II
-
Step 1. Set L3 (i) as the maximum of the below 2 quantities: - d(i)+NB
- NP+NF+NC−1
-
-
-
-
-
-
-
-
-
-
- Step 12. Form the matrices q (i) for all i=1, . . . , NT, using formula
- q (i) =L d (i)T [C (i)T F (i)T Q (i)T]T.
-
- Step 14. Form the matrices A (i) by taking square root of matrices Z(i) e.g., Z(i)=A(i) A(i)*, where the operation * refers to taking transpose of matrix and taking the complex conjugate of its entries. Here A(i) may be computed using any matrix square root algorithm.
-
-
Step 16. Solve the following semidefinite programming optimization problem (using any SDP solver or optimization tool with SDP capability) -
- Step 17. Set p=x 1:(Np)
- Another aspect of the present invention relates to Analog to Digital Conversion (ADC), which is a process of sampling a continuous-time analog signal in time and mapping these time samples into a digital sequence with finite levels. ADC refers to discretization of an input analog signal in both time and magnitude. For example, Sigma Delta converters provide high resolution analog to digital conversion. The high resolution may be achieved through over-sampling of an input signal at a rate higher than its bandwidth.
- A Sigma Delta Analog to Digital (AD) Converter may include at least two stages, such as an Analog Quantizer block and a Digital Combiner-Downsampling block. The Analog Quantizer block oversamples an input analog signal and produces a high-rate digital signal with typically two levels (e.g., 1 bit) or four levels (e.g., 2-bits), for example. This low magnitude resolution over-sampled signal may be converted to a higher magnitude resolution (e.g. 16 bits) and a lower rate signal by the Digital Combiner-Downsampling block.
- An embodiment of the present invention is directed to a polyphase combiner and sigma-delta decimator block structure. An embodiment of the present invention provides an efficient implementation of a sigma-delta decimator block which may be enabled by an effective decoupling of a polyphase IIR structure into a cascade of a polyphase FIR bank and a single phase IIR filter. As a result, a reduction in hardware implementation may be achieved by reducing timing requirements for filtering and high rate clock generation. In addition, a reduction in power consumption may be achieved by the use of a lower rate clock. Thus, an embodiment of the present invention provides a low complexity, low power consumption implementation of a sigma delta combiner and decimator blocks through the use of a polyphase structure.
- FIG. 6 illustrates an analog to digital converter, according to an embodiment of the present invention. Analog signals are converted into digital signals by A/D Converters by various methods, which may include Sigma-Delta A/D conversion. For high performance Sigma-Delta A/D conversion, an input analog signal may be sampled into a 2-bit (in some cases one bit or other number of bits) high-rate digital signal by Analog Sigma-
Delta block 610. The digital signal is then down-sampled and converted into a high resolution (e.g., 16-bit) and lower rate digital signal by a Digital Sigma-Delta Decimator block 620. As shown in FIG. 6, Analog Sigma-Delta block 610 generates a two-bit digital output, D1 and D2. Both D1 and D2 are binary signals with rate R. For example, D1 carries a sampled signal with quantization noise and D2 carries quantization noise cancellation information. The Digital Sigma-Delta Decimator 620 combines D1 and D2 and then decimates the combination by a factor M. - FIG. 7 illustrates components of a Digital Sigma-Delta Decimator, according to an embodiment of the present invention. A Digital Sigma-
Delta Decimator 620 may include aCombine 710 and a decimation filter stage which may include aMultistage Decimator 720.Combiner 710 receives D1 and D2 from the Analog Sigma-Delta block 610 and generates a combined signal. TheMultistage Decimator 720 receives the combined signal and generates a digital sigma-delta output. - FIG. 8 illustrates components of a combiner, according to an embodiment of the present invention. Combiner may include two filters, C 1 and C2 one for each input branch and a summing junction. For example, D1 may be filtered by filter C1 and D2 may be filtered by filter C2 wherein the filtered signals are combined by a summing junction. Additional filters may be implemented for additional inputs.
- FIG. 9 illustrates components of a multistage decimator, according to an embodiment of the present invention. As far as the structure of the decimator is concerned, it may be assumed for an exemplary application that the decimation factor M is not a prime number and therefore may be factored into multiple integer factors, e.g.,
- M=M1M2 . . . ML.
- As a result, the decimator, as shown by 720, may be implemented as a L-stage decimator, as shown in FIG. 9. A sub-sampling factor for the first stage, M1, may be an even number, e.g., M1=2*N where N is an integer. The combined signal of D1 and D2 may be received by a first decimation stage having a sub-sampling factor of M1. The output of the first decimation stage may be received by a second decimation stage having a sub-sampling factor of M2. Finally, a Lth decimation stage having a sub-sampling factor of ML may generate a digital sigma-delta output.
- According to one example of an embodiment of the present invention, the first stage may operate with a highest clock rate. The first stage may be implemented with a simple filter such as a Finite Impulse Response (FIR) sinc filter of order K. The combination of the sinc filter and a down-sampling function may be efficiently implemented as shown in FIG. 10. S 1 represents a Kth order integrator filter implemented as a cascade of K integrators and S2 represents a Kth order differentiator which may be implemented as a cascade of K differentiators. An advantage of this implementation is that mathematical operations are limited to addition thereby enhancing the simplicity of the method and system.
- FIG. 11 illustrates components of a decimator, according to an embodiment of the present invention. FIG. 11 shows a combiner 1110 and a first stage decimator 1120 with a sinc filter structure. According to an example, the combiner 1110 may operate at a high clock with frequency R MHz. Combiner 1110 includes a filter C1, a filter C2 and a summer. A polyphase structure for the combiner 1110 and sinc filter integrator combination may be implemented such that a lower rate clock may be implemented. This may be accomplished by merging the combiner 1110 and sinc integrator filter operations with a decimation operation as shown by 1120 in FIG. 11. In particular, decimator 1120 includes S1, a downsampling block M and S2. An embodiment of the present invention proposes a low complexity solution for the polyphase structure.
- FIG. 12 illustrates a low complexity, efficient polyphase structure, according to an embodiment of the present invention. A first portion of the polyphase structure includes filters C 11, C12, C13 and C14 for receiving inputs D11, D12, D21, and D22 respectively. The outputs of filters C11, C12, C13 and C14 are then combined by a first summer and received by filter F1. A second portion of the polyphase structure includes filters C21, C22, C23 and C24 for receiving inputs D11, D12, D21, and D22 respectively. The outputs of filters C21, C22, C23 and C24 are then combined by a second summer and received by filter F2. The outputs of filters F1 and F2 are combined by a third summer and received by a decimator structure. The decimator structure may include a Kth order integrator filter S1, a down-sampling function block N and a Kth order differentiator S2. The decimator structure generates a digital sigma-delta output.
- The parameter descriptions used in the structures discussed above may include the following:
- Combiner Filter C 1 of FIG. 11:
Combiner Filter 1 has filter coefficients given as {c1k; k ∈ {0, . . . , (2N1−1)}} where 2N1 is the filter length which is an even value. - Combiner Filter C 2 of FIG. 11:
Combiner Filter 2 has filter coefficients given as {c2k; k ∈ {0, . . . , (2N2−1)}} where 2N2 is the filter length which is an even value. - According to an embodiment of the present invention as shown in FIG. 12, the following may apply:
- Subsampling factor N: N=M 1/2.
- Filter C11 has coefficients {c11 k; k ∈ {0, . . . , N1−1}} where
- c11k =c12k k ∈ {0, . . . , N 1−1}.
- Filter C12 has coefficients {c12 k; k ∈ {0, . . . , N1}} where c120=0 and
- c12k+1 =c12k+1 k ∈ {0, . . . , N 1−1}.
- Filter C13 has coefficients {c13 k; k ∈ {0, . . . , N2−1}} where
- c13k =c22k k ∈ {0, . . . , N 2−1}.
- Filter C14 has coefficients {c14 k; k ∈ {0, . . . , N2}} where c140=0
- c14k+1 =c22k+1 k ∈ {0, . . . , N 2−1}.
- Filter C21 has coefficients {c21 k; k ∈ {0, . . . , N1−1}} where
- c21k =c12k+1 k ∈ {0, . . . , N 1−1}.
- Filter C22 has coefficients {c22 k; k ∈ {0, . . . , N1−1}} where
- c22k =c (1) 2k k ∈ {0, . . . , N1−1}.
- Filter C23 has coefficients {c23 k; k ∈ {0, . . . , N2−1}} where
- c23k =c22k+1 k ∈ {0, . . . , N 2−1}.
- Filter C24 has coefficients {c24 k; k ∈ {0, . . . , N2−1}} where
- c24k =c22k k ∈ {0, . . . , N 2−1}.
-
-
- For input data sequences D 11 and D12, even sub-samples of D1 may be represented by D11 and odd sub-samples of the D1 may be represented by D12. An analog sigma delta may provide two outputs, for example, for D1 with one output for (D11) and one output for (D12) where each line has a rate of R/2. In addition, an analog sigma delta may provide a single output with clock of R/2 with even samples (D11) sent at a rising edge and odd samples (D12) sent at a falling edge. In the latter case, D11 and D12 may be obtained as separate lines with rate of R/2 by appropriately sampling the single line output for D1.
- For input data Sequences D 21 and D22, even sub-samples of D2 may be represented by D21 and odd sub-samples of the D2 may be represented by D22. An analog sigma delta may provide two outputs, for example, for D2 with one output for (D21) and one output for (D22) where each line has a rate of R/2. In addition, an analog sigma delta may provide a single output with clock of R/2 but even samples (D21) sent at a rising edge and odd samples (D22) sent at a falling edge. In the latter case, D21 and D22 may be obtained as separate lines with rate of R2 by appropriately sampling the single line output for D1.
- In a Discrete MultiTone (DMT) based communication system (e.g., for supporting ADSL modems), a data stream is partitioned and modulated to be transmitted on several independent sub-channels (also called sub-carriers or tones). Each sub-channel may have a different data rate, depending on transmission conditions and/or other factors. The total data rate of the system may be defined as a summation of the data rates of individual sub-channels. The data rate of each sub-channel may be determined with the consideration of various factors, including the Signal-to-Noise Ratio (SNR) at each tone, the PSD constraint, and/or other considerations. Algorithms that attempt to operate with these often conflicting requirements and further attempt to optimize the data rate allocation among the tones are referenced as bit loading algorithms. According to an embodiment of the present invention, an efficient bit loading algorithm (EBLA) is provided. EBLA may be optimized for DMT systems with a QAM (Quadrature-Amplitude Modulation) scheme and constraints on the transmitting PSD. The bit loading algorithm of an embodiment of the present invention may be applied in any DMT communication systems.
- According to an embodiment of the present invention, EBLA may automatically decide whether an optimal solution can be obtained efficiently. If so, an optimal solution is generated. If not, a sub-optimal solution with a performance close to an optimal solution is calculated. For example, EBLA may be optimized for QAM-based systems with PSD constraints where optimal solutions may be obtained efficiently when possible.
- An adjustment mechanism may be incorporated into the bit loading algorithm of an embodiment of the present invention to minimize the amount of processing of a Greedy Search Module (GSM). As a result, total computational time may be reduced. When a sub-optimal solution is desired, a water-filling procedure may be implemented to expedite solutions. EBLA may accommodate different modulation and coding methods used in various communication systems.
- An embodiment of the present invention provides a reliable and efficient bit loading algorithm for generating an optimal solution when conditions permit, or a sub-optimal solution when computational costs associated with obtaining optimal solutions is formidable.
- The following variables may be implemented in the bit loading algorithm of an embodiment of the present invention.
- b n represents the number of data bits allocated to the nth tone, where n represents the tone index. According to an embodiment of the present invention, a total of N tones may be used, e.g., n=1, . . . , N. In ADSL systems, bn may be an integer ranging from 2 to 15, or may be set to 0, for example.
- e n(bn) represents power allocated at nth tone in order to transmit bn data bits.
- Δe n(bn) represents an increment in power required at the nth tone to load one more bit, from bn−1 bits to bn bits, e.g.,
- Δe n(b n)=e n(b n)−e n(b n−1).
-
-
- c n represents a PSD constraint at the nth tone. According to an example, the power level allocated for the nth tone may not exceed this constraint, e.g., en(bn) is less than or equal to cn.
- P represents an aggregate power budget. This parameter restricts how much power is allocated for the system, e.g., E is less than or equal to P.
- α n represents a tone condition indicator at the nth tone. This parameter may be proportional to the noise power and depend on the choice of coding scheme.
- At least two different bit loading scenarios are recognized. A first scenario involves a Bit-Rate Maximization (BRM) problem. In this scenario, the aggregate data rate B is maximized under certain constraints. These constraints may involve the total power being less or equal to P and the power at each tone being less or equal to the PSD constraint, e.g., e n(bn)≦cn. A second scenario involves a Margin Maximization (MM) problem. In this scenario, an aggregate data rate B is given and the total power required by the system is maximized to support that data rate, with or without the PSD and/or other constraints. Other scenarios may be implemented.
- For example, in a DMT system, such as a system for supporting ADSL modems, the BRM problem generally occurs more frequently. In this scenario, a total power constraint is closely related to the PSD constraint. As a result, an optimal solution may be obtained easily for the BRM problem. On the other hand, the MM problem is inherently a more complicated scenario. Therefore, an optimal solution may be determined with a much higher computational cost.
- EBLA of an embodiment of the present invention exploits advantages of the first scenario (the BRM problem) and generates one or more optimal solutions. For the MM problem, an embodiment of the present invention provides one or more acceptable sub-optimal solutions with a moderate or reasonable computational cost.
- FIG. 13 is the flowchart of an efficient bit loading algorithm, according to an embodiment of the present invention. FIG. 13 incorporates functional modules, which may include Scenario Selection Module (SSM) 1310, PSD-Constrained Initial Power/bit Allocation Module (PC-IPAM) 1312, Water-Filling Initial Power/bit Allocation Module (WF-EPAM) 1314, PSD-Constrained Greedy Search Module (PC-GSM) 1316, and Water-Filling Greedy Search Module (WF-GSM) 1318. Other functional modules may also be incorporated in accordance with an embodiment of the present invention.
- According to an embodiment of the present invention, there are at least two paths in the execution of the bit loading algorithm.
SSM 1310 determines which path to implement based on various conditions and factors. Based on an output ofSSM 1310, PC-IPAM 1312 and PC-GSM 1316 may be used to generate optimal bit loading solutions. If an optimal solution is not deemed feasible atSSM 1310, WF-IPAM 1314 and WF-GSM 1318 may be used to generate sub-optimal solutions in an efficient manner. -
SSM 1310 decides whether a BRM or MM problem applies and invokes PC-IPAM 1312 or WF-IPAM 1314 accordingly. In addition,SSM 1310 may distinguish among other problems or scenarios as well.SSM 1310 also obtains information on the transmission condition and calculates the tone condition indicator αn, which reflects the condition on the nth tone. - IPAM generates an initial power and/or bit allocation efficiently. In particular, the initial power or bit allocation should be close to an optimal bit loading solution so that a small number of adjustments may be made by GSM for obtaining optimal or sub-optimal solutions. Depending on the output of
SSM 1310, either PC-IPAM 1312 or WF-IPAM 1314 may be invoked. - For a BRM problem, PC-
IPAM 1312 efficiently obtains an initial power and/or bit allocation close to an optimal bit loading solution. The procedure takes advantage of the fact that the scenario (or condition) is essentially PSD-constrained. In ADSL systems, a total power constraint may include the power transmitted by a “nominal” PSD, which refers to the PSD constraint lowered by the amount of approximately 2.5 dB. - To devise an efficient PC-
IPAM 1312, information related to a system's modulation may be incorporated into the bit loading algorithm of an embodiment of the present invention. For example, in ADSL systems, the QAM scheme may be adopted for modulation (or other purpose). IPAM may incorporate a built-in table (or other reference) of power en(bn) based on QAM (or other schemes). FIG. 14 illustrates a table of number of bits and power levels for incorporation into the bit loading algorithm, according to an embodiment of the present invention. Other variations or types of references may be used. In particular, the table of FIG. 14 illustrates the relation between the number of data bits and the power level for supporting the number of data bits in an ADSL modem compliant to ITU G.992.1 standard (or other standard). Based on this table (or other similar reference), FPAM may determine an initial bit and power allocation. - FIG. 15 is a flowchart illustrating PC-IPAM, according to an embodiment of the present invention. The steps of FIG. 15 may be designed for ADSL modems. At
step 1510, a value of bn may be determined. The value of bn may be selected such that en(bn) ≦cn−q<en(bn+1) for each tone, where cn is the PSD constraint, bn is the bit allocation, en(bn) is the power allocation, and q is an adjustment factor, as determined atstep 1512. Atstep 1514, if a bit number at some tones equals 1, then the bit number at that tone may be set to 0, atstep 1516 and the allocated power may be set to 0, atstep 1518 because G.992.1 does not allow 1 bit to be loaded. The resulting bit and power allocation may be referred to as an initial bit and power allocation. Depending on other conditions and constraints, other values may be assigned to the variables. - The adjustment factor q, if chosen properly, is highly effective in enabling the initial power and bit allocation to represent an optimal solution, thereby reducing computational costs at GSM. For example, a value corresponding to 1.5 dB decrease is a reasonable choice. However, for additional effectiveness, the value for the adjustment factor should be chosen based on conditions, such as a transmission condition. For example, if the transmission condition is such that many tones are usable on the condition that they are allocated with a power level greater the nominal PSD, then q may be reduced.
- FIG. 16 illustrates an example of an output of PC-
IPAM 1312, according to an embodiment of the present invention. There are 10 tones in this example. The thicksolid line 1610 represents PSD constraint cn. The dotted line 1616 represents a power level cn−q. The thinsolid line 1614 represents an initial power allocation en(bn) and the dashedline 1612 represents a power level to support one more bit, e.g., en(bn+1). The inequality - e n(b n)≦cn −q<e n(b n+1)
- holds for all n=1 to 10. As shown in FIG. 16, several tones may be loaded with one more bit without violating the PSD constraint. For example,
tone Tone - For a MM scenario, the computational cost to obtain optimal solutions may be considered formidable. The bit loading algorithm of an embodiment of the present invention incorporates a combination of WF-
IPAM 1314 and WF-GSM 1318 to provide sub-optimal solutions which are close to the optimal solutions at low costs and effort. The name “Water-Filling” refers to a procedure of calculating optimal transmitting PSDs for general communication systems. WF-IPAM 1314 generates water-filling solutions and then truncates the solutions to meet various requirements and/or conditions associated with DMT systems, e.g., ADSL modems. The resulting solutions of an embodiment of the present invention are close to optimal solutions, also known as sub-optimal solutions. - FIG. 17 is a flowchart illustrating WF-IPAM, according to an embodiment of the present invention. The procedure of FIG. 17 may be designed for ADSL modems, for example. At
step 1710, the values of {log2(α1), log2(α2), . . . , log2(αN)} may be calculated. Atstep 1712, these calculated values may be sorted in an order, such as in ascending order. Atstep 1714, the sorted values may be renamed as {log2(α1), log2(α2), . . . , log2(αnN)}. Atstep 1716, a water-filling procedure may be initiated by setting an iteration index k=1 and λ1=B+log2(αn1). At step 1718, it may be determined whether λk>log2(αnk+1) and k<N are satisfied. If so, atstep 1720, the equation λk+1=(1/(k+1))(kλk+log2(αnk+1)) is set where k is increased by a predetermined value, such as 1.Step 1716 is then repeated. Otherwise, the value of λk is recorded atstep 1722. Atstep 1724, the initial bit number bn may be determined by truncating the value of λk−log2(αn) to an integer. If it is determined that the value of the bit number is 1, atstep 1726, then bn is set to a predetermined value, such as 0, atstep 1728. The initial power allocation may be calculated as en(bn), atstep 1730. - There may be instances where the initial bit allocation does not achieve the aggregate data rate. In other words, the summation of b n may be less than B. Therefore, WF-GSM provides a fine tuning function for the truncated water-filling solution. The details of WF-GSM are discussed below.
- GSM functionality fine tunes the initial power and bit allocation. Depending on the output of
SSM 1310, PC-GSM 1316 or WF-GSM 1318 may be implemented. Other options may also be available. PC-GSM 1316 produces optimal bit loading solutions, while WF-GSM 1318 produces sub-optimal solutions, in response to the particular conditions and/or other factors. - FIG. 18 is a flowchart illustrating PC-GSM, according to an embodiment of the present invention. In particular, FIG. 18 illustrates the steps involved in PC-
GSM 1316. Atstep 1810, an efficient tone may be determined. This may involve determining which tone has the smallest (or a small enough) Δen(bn+1) and whether the tone is permissible as determined by an increased power level not exceeding the PSD constraint cn and the number of bits not exceeding a predetermined value. Other constraints may be taken into consideration. Atstep 1812, whether enough power budget is left for the tone may be determined. If so, the power at that tone may be increased to en(bn+1) atstep 1816. Atstep 1818, the bit number may be updated to (bn+1). These steps may be repeated until no other bits can be added without exceeding the aggregate power budget or until permissible tones are unavailable, at which point the process is terminated atstep 1814. - The procedure as used in ADSL modems, for example, may be further optimized by taking into account special requirements and/or conditions associated with ADSL. When choosing an efficient and permissible tone, Δe n(bn+1) may be used for tones whose initial bn is larger than 1, and (½)Δen(2) for tones whose initial bn is 0. If a tone with initial bn=0 is chosen, power allocation for that tone may be increased from 0 to en(2) and the bit number from 0 to 2.
- FIG. 19 illustrates an example of an output of PC-
GSM 1316, according to an embodiment of the present invention. In response to an input received from PC-IPAM 1312, PC-GSM 1316 may choosetones tone 8 may be loaded one more bit without violating the PSD constraint, it is not chosen because the remaining power budget is not enough to support an additional bit. - WF-
GSM 1318 follows the steps as illustrated in FIG. 18, according to an embodiment of the present invention. The steps discussed above in connection with FIG. 18 may be repeated until the aggregate data rate requirement is met, the remained power budget is not enough, or permissible tones are unavailable. For ADSL modems, WF-GSM 1318 may be modified in a similar manner as PC-GSM 1316 may be optimized for ADSL. Other modifications may be made for other types of modems and/or systems. - The computational complexity of the PC-
IPAM 1312 and PC-GSM 1316 is approximately kN where N represents a number of tones involved and k represents an integer, usually around 20 to 30 when N=256, for example. - GlobespanVirata Corporation's Aluminum™ DSL PHY is designed for full duplex symmetric transmission over ordinary single twisted copper pair when used, for instance, with the Aluminum Analog Front End (AFE). This chipset supports programmable data rates ranging from 192 Kbps to 4.6 Mbps on a single pair, and provides reach greater than 18,000 feet at 1.5 Mbps. Loop-lengths of up to 26,000 ft are supported at lower data rates.
- The Aluminum™ chipset includes digital communications subsystems, which may include a combination of echo canceller, pre-coder, feed forward equalizer and decision feedback equalizer. GlobespanVirata also offers its customers a comprehensive suite of technology solutions available to aid in the design, development and deployment of symmetric DSL products. This includes the BD3801 development reference platform for the Aluminum™ chipset. Aluminum™ and the Aluminum™ AFE are HDSL2/G.shdsl/2B1Q Synchronous Digital Subscriber Line (SDSL) compliant.
- The Aluminum™ chipset provides customers with a data throughput increase of up to 100 percent over competitive G.shdsl solutions and enables the development of symmetric DSL products with lower power consumption, greater reach and higher performance than was previously possible. Aluminum™ and Aluminum™ AFE may be purchased as a bundle with GlobespanVirata's Helium™ communications processor and comprehensive network protocol stack, creating a complete customer premises equipment solution for symmetric DSL gateways, routers, and integrated access devices (IAD). In support of this symmetric DSL chipset and software solution, GlobespanVirata is also delivering a symmetric DSL to Ethernet router reference design.
- Helium™ is a low-cost, Physical Layer Device (PHY)-neutral communications processor that enables high-speed Internet access capability for single- and multiple-user endpoint devices such as Universal Serial Bus (USB) modems, home gateway devices and small office/home office (SOHO) routers. The Helium™ chip may be fully integrated with a networking and protocol software suite that handles Asynchronous Transfer Mode (ATM), frame, routing, bridging and signaling functions, as well as Simple Network Management Protocol (SNMP) management.
- FIG. 20 is a schematic diagram of a hardware architecture in which the inventive aspects of the present invention may be incorporated. The inventive concepts discussed above may be achieved with the processing aid of Million Instructions per Second (MIPS) 2010 shown in FIG. 20. For example, the functionality related to rate enhanced SHDSL and efficient polyphase implementation of sigma delta analog to digital converter may be implemented in the Aluminum™ 200 and/or 204 DSL Processor, as detailed below. The inventive concepts discussed above may be incorporated into chip sets, such as GlobespanVirata Corporation's Aluminum™ 200 or 204 DSL Processor, which is also known as GlobespanVirata's second generation symmetric high-speed DSL processor. Aluminum™ 200 or 204 may support several modes of operation including: International Telecommunications Union (ITU) G.991.2 (G.shdsl), American National Standard Institute (ANSI) T1E1.4 (High Speed Digital Subscriber Line (HDSL) 2) and single-pair 2B1Q SDSL. A solution for customer premises G.shdsl equipment, Aluminum™ 200 or 204 provides compliance with the ITU G.991.2 standard, as well as other standards. Data rates from 192 Kbps to 2.3 Mbps are supported on 8 Kbps boundaries. In addition, Aluminum™ 200 or 204 provides at least three additional base data rates above 2.3 Mbps: 3.096 Mbps, 4.104 Mbps and 4.616 Mbps.
- The power spectral density (PSD) of the transmitted signal is programmable and supports defined symmetric and asymmetric PSDs. In addition, the adaptability of the PSD shaper may allow support of new PSDs that may be defined in the future.
- The Aluminum™ 200 or 204 DSL Processor may support Transmission Protocol Specific—Transmission Convergence (TPS-TC) defined in G.991.2 including dual-bearer mode. By providing at least two independent serial channels, in addition to a
UTOPIA Level 2 port, the Aluminum™ 200 or 204 may provide services such as simultaneous Synchronous Transfer Mode (STM) voice and ATM data transport. - Support for analog voice and G.shdsl on the same copper pair is provided through the Aluminum™ 200's or 204's G.shdsl-over-POTS mode. By using this capability, vendors and other entities may deliver the reach and symmetric performance of G.shdsl without giving up POTS service. G.shdsl-over-POTS further works with current ADSL splitters and microfilters, as well as other devices and components.
- The Aluminum™ 200 or 204 DSL Processor may work in conjunction with GlobespanVirata's Aluminum™ 200 Smart Analog Front End/Line Driver device, for example. The Aluminum™ 200 or 204 may control the Aluminum™ 200 AFE through a digital serial bus and may further provide for parameter calibration, power cutback and other functions. This configurability of the present invention allows the AFE to better match line conditions for higher performance and greater reach.
- The BD3802 is a development platform for Aluminum™ 200 or 204 DSL Chipset, providing a comprehensive set of hardware and firmware tools to assist users in rapid development and deployment of products and services.
- Product applications may include Symmetric DSL routers and Integrated Access Devices (IAD); DSL Access Multiplexers (DSLAMs); Multi-tenant and Multi-dwelling unit networks; T1/E1 distribution products; and T1/E1 pairgain systems (using 3 Mbps and higher data rates).
- Specification details may include ITU G.991.2 (G.shdsl) compliant; T1E1.4 HDSL2 compliant; ETSL ETR-152 compliant (single pair); support for data rates, presently, from 192 Kbps to 4616 Kbps on 8 Kbps increments; programmable framer supports G.shdsl, HDSL2, European Telecommunications Standard Institute (ETSI) SDSL, HDSL and transparent framing;
UTOPIA Level 2 interface for ATM data and two independent serial interfaces for STM data; and 8-bit multiplexed or non-multiplexed host bus to connect to a variety of host Central Processing Units (CPUs). - As shown in FIG. 20, MIPS Reduced Instruction Set Computing (RISC) engine and
control registers 2010 may be coupled to ahost interface 2022, which may in turn be coupled to a 8-bit host interface. A serial data input may be coupled to an input of Tx Framer TPS-TC 2012, which is further coupled to a Trellis Encoder/Mapper 2014. Trellis Encoder/Mapper 2014 may provide an input toPrecoder 2016 wherePrecoder 2016 may be coupled to aTx Filter 2018.Tx Filter 2018 may be coupled to (sigma-delta) S-D interpolatingfilter 2020 which is coupled to an output, Tx out. Utopia-2Interface 2024 may be coupled to an input of Tx Framer TPS-TC 2012 and may further receive data from a Rx Framer TPS-TC 2026.S-D Decimation filter 2038 receives an input from Rx In and is coupled to anadder 2040.Adder 2030 sums outputs fromfilter 2038 and echo canceller 2032 and generates an output to Feed Forward (FF)equalizer 2030.FF equalizer 2030 may be coupled to a Timing Recovery Phase Locked Loop (PLL) 2036 at an input. At an output, Timing RecoverPLL 2036 may be coupled to Volt Controlled Oscillator Digital Analog Converter (VCXO DAC), which in the case of the STUR is used to adjust the sampling phase to match that of the transmitting modem.FF equalizer 2030 may be coupled to aTrellis Decoder 2028, which may be in turn coupled to Rx Framer TPS-TC 2026. In addition, in the case of the Aluminum™ 204, aSNR margin 2042 may be coupled toFF equalizer 2030 and Rx Framer TPS-TC 2026, which may be further coupled to a Serial Data output. - In particular, Aluminum™ 204 may include
SNR margin 2042, as discussed above and as shown in FIG. 20. Details ofSNR margin 2042 are shown in FIG. 21. A purpose of a SNR-margin estimator may include determining SNR for a given constellation and input signal. The output of the estimator may include the SNR margin value in dB. The SNR-margin estimator may include a hardware module that performs the SNR computation. Software may select certain parameters based on the constellation type. FIG. 21 illustrates a block diagram showing the basic operation of a SNR-margin estimator. - A hardware module may perform a SNR-margin estimate that operates on a continuous stream of input samples and produces a SNR value. The margin may be found by comparing SNR to a minimum value. The software may perform a function of specifying the number of samples to average over as well as the signal power for a particular constellation.
- The error signal may be computed by subtracting an input sample from a decoder or slicer output as shown in equation below.
- e(n)=d(n)−x(n−K)
- For example, slicer or
decoder 2110 may receive an input signal x(n) to generate an output of d(n). In addition, input signal x(n) may be an input to function 2112 (e.g., z−K) for generating an output to be subtracted from d(n) byadder 2114. The output ofadder 2114 may include an error signal as defined in the equation above. - K may be defined as the delay through the decoder or slicer and d(n) may be a soft-decision output of Trellis decoder or an output of a
slicer 2110. This error signal may be equal to the noise in the signal if the assumption is made that the decision, d(n), is correct. This leads to a mean-squared-error (MSE) being approximately equal to the noise power as shown in equation below. -
Function 2116 may receive error signal e(n) and generate a square of the error signal e2(n). Function 2118 may receive squared error signal and generate MSE. In particular, function 2118 may accumulate N values and right shift by log2(N). - The signal power for a given constellation is known, so the first term on the right of equation above is a constant and the MSE dB value may be computed. For the log estimation, the following may be used. The desire is to estimate log 2(MSE),
- MSE=2k=2(k i +k f )=2k i 2k f
- where the exponent k is the sum of an integer part, k i, and a fractional part (less than 1), kf, as shown below.
- k=k i +k f
-
- Where k i is found by noting the position of the most significant bit (MSB).
Function 2120 may receive MSE and generate 10log10(MSE). In particular, the estimate of the fraction, kf, may then be improved by estimating the logarithms nonlinear fractional component using equation below. - k f≅0.0090+1.3211{circumflex over (k)} f−0.3369k f 2
- The result is the approximate log 2(MSE) of an integer number. To find 10log10(MSE), the scaling operation in equation below may be performed.
- 10log 10(MSE)=10log 10(2)log 2(MSE)
- Finally, the SNR margin may be computed using equation below.
- SNR margin =SNR−SNR min
-
Adder 2122 may be used to calculate SNR margin by subtracting the result offunction 2120 from 10log10(Ps)−SNRmin. The following precisions may be assumed, such as Polynomial coefficients are 10-bits {0x002, 0x152, 0x3aa}; power samples are 16-bits; the rough estimate of the log fraction, {circumflex over (k)}f, is minimum 8-bits; the resulting log is 16 bits, 6 integer and 10 fractional bits. - An example may include the following log estimation where log 2(0000000010101010b) may be calculated.
- The bit location of the first 1 is 7 so this means k i=7=111. To estimate {circumflex over (k)}f, the MSB is removed leaving 0101010b, which is the rough estimate of the fractional part of the log. The rough estimate of log2 is then 111.0101010, which is 7.328125. kf≅(0.0090)+(1.3211)(0.328125)+(0.3369)(0.328125)2. Therefore, k≅7.4062 To find 10log10(0000000010101010b), 10log10(2)*k=22.2949. The actual result calculated with a calculator is 22.304.
- Several parameters may be implemented by software for the proper operation of the SNR-margin estimator. The number of samples to average over, N, may be input by software. This is input as log 2(N) and hardware will set the appropriate bit in a counter and then use the input value for the final shift. Another parameter may include the logarithm of the signal power. This value may be constellation specific and may be a parameter input by software even if the module works with one constellation. Yet another parameter may include the minimum SNR acceptable, SNRmin.
- FIG. 22 illustrates a flowchart describing a hardware algorithm for SNR margin, according to an embodiment of the present invention. At
step 2210, a start of a hardware algorithm for SNR margin may be initiated. Variables, such as n and sum may be initialized. Atstep 2212, an error signal, the square of the error signal and an accumulated result may be determined. Atstep 2214, it may be determined whether n=N−1 wherein N may be a summation length. If not, variable n may be adjusted by a predetermined value (as shown by n++) wherestep 2212 may be invoked. Otherwise, a logarithm may be determined and further scaled, at step 2216. At step 2218, the margin may be determined by subtracting a signal.Step 2220 indicates the end of the algorithm. - An input to the hardware algorithm may include summation length, N. This number may be a power of 2 and may range from approximately 64 to approximately 32768. Summation length may be input as log 2(N). Other inputs may include constellation type, 10log10(Ps) and SNRmin, which represents a minimum SNR to obtain a specific BER, for example. Storage factors may include log2(Nmax)+22=15+22=37 bit accumulator to store the power sum. This accumulator may be cleared to zero every time a new average is started. Other storage factors may include K+1, where K represents the delay from a Trellis decoder input to output, samples of the input signal, 12-bits each, for example. The output may include SNR margin, which may include five integer bits. This means that a maximum value this output may have is approximately 31 dB. This may be compared to a threshold of 0-15 dB to determine if the margin is too small. The 16-bit SNR value may be subtracted from the reference, which may also be 16 bits. The value may then be rounded and the lower 5 integer bits compared to the threshold.
- FIG. 23 is a schematic diagram of a hardware architecture which may function with devices supporting certain inventive aspects of the present invention. AFE, such as the Aluminum™ 200 AFE, is a G.SHDSL/HDSL2/2B1Q SDS1 compliant Analog Front End (AFE) with integrated line driver designed to be used with GlobespanVirata's Aluminum™ 200 or 204 Symmetric DSL Processor to an external 2/4 wire hybrid.
- The Aluminum™ 200 AFE conforms to G.shdsl PSD masks for every rate when interfaced to the Aluminum™ 200 or 204 DSL Processor, Aluminum™ 200 AFE also conforms to the HDSL2 OPTIS PSD mask at 1.544 Mbps. Aluminum™ 200 AFE may be used in a central office or remote application mode, selectable by configuring the programmable filters in the Aluminum™ 200 or 204 DSL Processor.
- The Aluminum™ 200 AFE may include a high resolution 16-bit TX Digital Analog Converter (DAC) in the transmit path and one high resolution 16-bit RX Analog Digital Converter (ADC) in the receive path. A 10-bit DAC for the VCXO control is also integrated in the Aluminum™ 200 AFE to reduce the number of required external components. The transmitter programmable attenuation control (PAC) and the receiver programmable gain amplifier (PGA) may be programmed via the Aluminum™ 200 or 204 processor through a two-wire serial bus.
- Aluminum™ 200 AFE has a low total power consumption of less than 800 mWatt (including the line drive) in full operation mode. An external line driver may also be used for HDSL2 and asymmetric PSD applications. Aluminum™ 200 AFE may also provide a power down mode for stand-by operation.
- Product applications may include symmetric DSL routers and integrated access devices; DSL access multiplexers (DSLAMs); multi-tenant and multi-dwelling unit networks; T1/E1 distribution products; and T1/E1 pairgain systems (using proprietary 3 Mbps and higher data rates). Specification details may include ITU G.991.2 (G.shdsl) compliant; T1E1.4 HDSL2 compliant; ETSI ETR-152 compliant (single pair); and support for data rates from 192 Kbps to 2.312 Mbps and 8 Kbps increments, plus three additional rates of 3.096 Mbps, 4.104 Mbps and 4.616 Mbps.
- As shown in FIG. 23, a transmission line may include a Tx Digital Audio Video (DAV) 2310 coupled to a
Tx Filter 2312, further coupled to a Programmable Attenuation Control (PAC) 2314.PAC 2314 is coupled to aLine Driver 2316, which is coupled to a Tx Tip & Ring.PAC 2314 may be further coupled to a HDSL2 bypass. A receiving line includes Automatic Gain Control (AGC) 2318 coupled to Rx Tip & Ring at an input andRx Filter 2320 at an output.Rx Filter 2320 is coupled toRx ADC 2322. A control/testing interface 2326 may be provided on a serial line. Aclocking subsystem 2324 may receive a plurality of inputs. The hardware architecture of FIG. 23 may further include a Current and Voltage Reference Generator (IV-REF)Subsystem 2328. - While the foregoing description includes many details and specificities, it is to be understood that these have been included for purposes of explanation only, and are not to be interpreted as limitations of the present invention. Many modifications to the embodiments described above can be made without departing from the spirit and scope of the invention.
- The present invention is not to be limited in scope by the specific embodiments described herein. Indeed, various modifications of the present invention, in addition to those described herein, will be apparent to those of ordinary skill in the art from the foregoing description and accompanying drawings. Thus, such modifications are intended to fall within the scope of the following appended claims. Further, although the present invention has been described herein in the context of a particular implementation in a particular environment for a particular purpose, those of ordinary skill in the art will recognize that its usefulness is not limited thereto and that the present invention can be beneficially implemented in any number of environments for any number of purposes. Accordingly, the claims set forth below should be construed in view of the full breath and spirit of the present invention as disclosed herein.
Claims (21)
Priority Applications (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| US10/321,601 US20030202612A1 (en) | 2001-12-18 | 2002-12-18 | Method and system for rate enhanced SHDSL |
Applications Claiming Priority (2)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| US34024601P | 2001-12-18 | 2001-12-18 | |
| US10/321,601 US20030202612A1 (en) | 2001-12-18 | 2002-12-18 | Method and system for rate enhanced SHDSL |
Publications (1)
| Publication Number | Publication Date |
|---|---|
| US20030202612A1 true US20030202612A1 (en) | 2003-10-30 |
Family
ID=23332502
Family Applications (3)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| US10/321,509 Expired - Lifetime US6788236B2 (en) | 2001-12-18 | 2002-12-18 | Method and system for implementing a sigma delta analog-to-digital converter |
| US10/321,508 Active 2024-12-13 US7076514B2 (en) | 2001-12-18 | 2002-12-18 | Method and system for computing pre-equalizer coefficients |
| US10/321,601 Abandoned US20030202612A1 (en) | 2001-12-18 | 2002-12-18 | Method and system for rate enhanced SHDSL |
Family Applications Before (2)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| US10/321,509 Expired - Lifetime US6788236B2 (en) | 2001-12-18 | 2002-12-18 | Method and system for implementing a sigma delta analog-to-digital converter |
| US10/321,508 Active 2024-12-13 US7076514B2 (en) | 2001-12-18 | 2002-12-18 | Method and system for computing pre-equalizer coefficients |
Country Status (3)
| Country | Link |
|---|---|
| US (3) | US6788236B2 (en) |
| AU (1) | AU2002364572A1 (en) |
| WO (1) | WO2003055195A2 (en) |
Cited By (25)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US20050243941A1 (en) * | 2004-04-29 | 2005-11-03 | Texas Instruments Incorporated | M-dimension M-PAM trellis code system and associated trellis encoder and decoder |
| US20050249246A1 (en) * | 2002-07-12 | 2005-11-10 | Reidar Schumann-Olsen | Method of transporting data streams through an sdh switched network |
| WO2006088566A2 (en) * | 2005-02-19 | 2006-08-24 | Rlh Industries, Inc. | Hdsl optical fiber transmission system and method |
| US20070206625A1 (en) * | 2006-03-01 | 2007-09-06 | Junichi Maeda | Communication device, communication system, and communication method performing communication using a plurality of signals having different frequencies |
| US20090028268A1 (en) * | 2007-07-24 | 2009-01-29 | Texas Instruments Inc. | Variable power communications including rapid switching between coding constellations of various sizes |
| US20100135469A1 (en) * | 2004-02-11 | 2010-06-03 | Aware, Inc. | Communication channel capacity estimation |
| US7986742B2 (en) | 2002-10-25 | 2011-07-26 | Qualcomm Incorporated | Pilots for MIMO communication system |
| US8134976B2 (en) | 2002-10-25 | 2012-03-13 | Qualcomm Incorporated | Channel calibration for a time division duplexed communication system |
| US8145179B2 (en) | 2002-10-25 | 2012-03-27 | Qualcomm Incorporated | Data detection and demodulation for wireless communication systems |
| US8169944B2 (en) | 2002-10-25 | 2012-05-01 | Qualcomm Incorporated | Random access for wireless multiple-access communication systems |
| US8194770B2 (en) | 2002-08-27 | 2012-06-05 | Qualcomm Incorporated | Coded MIMO systems with selective channel inversion applied per eigenmode |
| US8203978B2 (en) | 2002-10-25 | 2012-06-19 | Qualcomm Incorporated | Multi-mode terminal in a wireless MIMO system |
| US8208364B2 (en) | 2002-10-25 | 2012-06-26 | Qualcomm Incorporated | MIMO system with multiple spatial multiplexing modes |
| US8218609B2 (en) | 2002-10-25 | 2012-07-10 | Qualcomm Incorporated | Closed-loop rate control for a multi-channel communication system |
| US8320301B2 (en) | 2002-10-25 | 2012-11-27 | Qualcomm Incorporated | MIMO WLAN system |
| US8358714B2 (en) | 2005-06-16 | 2013-01-22 | Qualcomm Incorporated | Coding and modulation for multiple data streams in a communication system |
| US8570988B2 (en) | 2002-10-25 | 2013-10-29 | Qualcomm Incorporated | Channel calibration for a time division duplexed communication system |
| US20140169501A1 (en) * | 2011-06-10 | 2014-06-19 | Moshe Nazarathy | Receiver, transmitter and a method for digital multiple sub-band processing |
| US8855226B2 (en) | 2005-05-12 | 2014-10-07 | Qualcomm Incorporated | Rate selection with margin sharing |
| US8873365B2 (en) | 2002-10-25 | 2014-10-28 | Qualcomm Incorporated | Transmit diversity processing for a multi-antenna communication system |
| US9154274B2 (en) | 2002-10-25 | 2015-10-06 | Qualcomm Incorporated | OFDM communication system with multiple OFDM symbol sizes |
| US9473269B2 (en) | 2003-12-01 | 2016-10-18 | Qualcomm Incorporated | Method and apparatus for providing an efficient control channel structure in a wireless communication system |
| WO2019225311A1 (en) * | 2018-05-22 | 2019-11-28 | 日本電信電話株式会社 | Optical communication system, optical transmitter and optical receiver |
| US10972319B2 (en) * | 2018-09-12 | 2021-04-06 | Texas Instruments Incorporated | Clockless decision feedback equalization (DFE) for multi-level signals |
| CN112787630A (en) * | 2019-11-06 | 2021-05-11 | 意法半导体国际有限公司 | High throughput digital filter architecture for processing unary coded data |
Families Citing this family (69)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US6922407B2 (en) * | 2000-02-14 | 2005-07-26 | Texas Instruments Incorporated | HomePNA 10M8 compliant transceiver |
| AU2001292819A1 (en) * | 2000-09-20 | 2002-04-02 | Lockheed Martin Corporation | Object oriented framework architecture for sensing and/or control environments |
| US20020184348A1 (en) * | 2000-09-20 | 2002-12-05 | Lockheed Martin Corporation | Object oriented framework architecture for sensing and/or control environments |
| JP2005519521A (en) * | 2002-03-05 | 2005-06-30 | コーニンクレッカ フィリップス エレクトロニクス エヌ ヴィ | Mobile terminal with downlink synchronization via iterative correlation system |
| US7385913B2 (en) * | 2002-04-24 | 2008-06-10 | Motorola, Inc. | Method and apparatus for compensating for variations in a receive portion of a wireless communication device |
| JP2004080210A (en) * | 2002-08-13 | 2004-03-11 | Fujitsu Ltd | Digital filter |
| US7339990B2 (en) * | 2003-02-07 | 2008-03-04 | Fujitsu Limited | Processing a received signal at a detection circuit |
| US6968296B2 (en) * | 2003-04-04 | 2005-11-22 | Radiodetection Limited | Cable detector with decimating filter and filtering method |
| US7586982B2 (en) * | 2003-05-06 | 2009-09-08 | Nokia Corporation | Kalman filter based method and apparatus for linear equalization of CDMA downlink channels |
| JP2006526916A (en) * | 2003-05-09 | 2006-11-24 | コーニンクレッカ フィリップス エレクトロニクス エヌ ヴィ | Method and apparatus for setting transmission power of a mobile communication device |
| WO2004105336A2 (en) * | 2003-05-20 | 2004-12-02 | Globespanvirata Incorporated | Method and system for mitigating fourier transform side lobes |
| US7272193B2 (en) * | 2003-06-30 | 2007-09-18 | Intel Corporation | Re-mapping trellis encoded data associated with a 2-bit constellation tone to data associated with a pair of 1-bit constellation tones |
| US20080059551A1 (en) * | 2003-07-23 | 2008-03-06 | Koninklijke Philips Electronics N.V. | Device and Method for Composing Codes |
| US7254165B2 (en) * | 2003-08-07 | 2007-08-07 | Intel Corporation | Re-configurable decoding in modem receivers |
| US7084800B2 (en) * | 2003-08-19 | 2006-08-01 | Broadcom Corporation | System and method for shuffling mapping sequences |
| US7428669B2 (en) * | 2003-12-07 | 2008-09-23 | Adaptive Spectrum And Signal Alignment, Inc. | Adaptive FEC codeword management |
| EP1653721A1 (en) * | 2004-11-02 | 2006-05-03 | Alcatel | Modem with selectable power spectral density masks |
| US7577203B2 (en) * | 2005-03-24 | 2009-08-18 | Dell Products L.P. | Minimizing non-deterministic noise by using wavelet transform |
| US8073135B2 (en) * | 2005-05-10 | 2011-12-06 | Adaptive Spectrum And Signal Alignment, Inc. | Binder identification |
| US7991122B2 (en) | 2005-06-02 | 2011-08-02 | Adaptive Spectrum And Signal Alignment, Inc. | DSL system training |
| US7813420B2 (en) * | 2005-06-02 | 2010-10-12 | Adaptive Spectrum And Signal Alignment, Inc. | Adaptive GDFE |
| US7817745B2 (en) * | 2005-06-02 | 2010-10-19 | Adaptive Spectrum And Signal Alignment, Inc. | Tonal precoding |
| US7688884B2 (en) * | 2005-06-10 | 2010-03-30 | Adaptive Spectrum And Signal Alignment, Inc. | Vectored DSL nesting |
| US7852952B2 (en) * | 2005-06-10 | 2010-12-14 | Adaptive Spectrum And Signal Alignment, Inc. | DSL system loading and ordering |
| US7199739B2 (en) * | 2005-06-15 | 2007-04-03 | Sigmatel, Inc. | Programmable sample rate analog to digital converter and method for use therewith |
| US7782852B2 (en) * | 2005-10-11 | 2010-08-24 | Teranetics, Inc. | Multiple modulation rate 10Gbase-T transmission |
| US7205914B1 (en) * | 2005-10-28 | 2007-04-17 | Motorola, Inc. | System and method for efficient upsampled signal processing |
| US7196648B1 (en) * | 2005-12-23 | 2007-03-27 | Cirrus Logic, Inc. | Non-integer decimation using cascaded intergrator-comb filter |
| US8130871B2 (en) * | 2006-01-09 | 2012-03-06 | Sigmatel, Inc. | Integrated circuit having radio receiver and methods for use therewith |
| US8228795B2 (en) * | 2006-04-19 | 2012-07-24 | Broadcom Corporation | Method and system for extended reach copper transceiver |
| US7839955B2 (en) * | 2006-05-30 | 2010-11-23 | Fujitsu Limited | System and method for the non-linear adjustment of compensation applied to a signal |
| US7817757B2 (en) * | 2006-05-30 | 2010-10-19 | Fujitsu Limited | System and method for independently adjusting multiple offset compensations applied to a signal |
| US7764757B2 (en) * | 2006-05-30 | 2010-07-27 | Fujitsu Limited | System and method for the adjustment of offset compensation applied to a signal |
| US7787534B2 (en) * | 2006-05-30 | 2010-08-31 | Fujitsu Limited | System and method for adjusting offset compensation applied to a signal |
| US7804894B2 (en) | 2006-05-30 | 2010-09-28 | Fujitsu Limited | System and method for the adjustment of compensation applied to a signal using filter patterns |
| US7839958B2 (en) * | 2006-05-30 | 2010-11-23 | Fujitsu Limited | System and method for the adjustment of compensation applied to a signal |
| US7801208B2 (en) * | 2006-05-30 | 2010-09-21 | Fujitsu Limited | System and method for adjusting compensation applied to a signal using filter patterns |
| US7804921B2 (en) | 2006-05-30 | 2010-09-28 | Fujitsu Limited | System and method for decoupling multiple control loops |
| US7848470B2 (en) * | 2006-05-30 | 2010-12-07 | Fujitsu Limited | System and method for asymmetrically adjusting compensation applied to a signal |
| US7760798B2 (en) | 2006-05-30 | 2010-07-20 | Fujitsu Limited | System and method for adjusting compensation applied to a signal |
| US7817712B2 (en) * | 2006-05-30 | 2010-10-19 | Fujitsu Limited | System and method for independently adjusting multiple compensations applied to a signal |
| EP2337371B8 (en) * | 2006-06-06 | 2018-05-23 | Assia Spe, Llc | DSL system |
| US20140369480A1 (en) | 2013-06-12 | 2014-12-18 | Adaptive Spectrum And Signal Alignment, Inc. | Systems, methods, and apparatuses for implementing a dsl system |
| US7941091B1 (en) * | 2006-06-19 | 2011-05-10 | Rf Magic, Inc. | Signal distribution system employing a multi-stage signal combiner network |
| US8355404B2 (en) * | 2006-09-06 | 2013-01-15 | Broadcom Corporation | Method and system for an asymmetric PHY in extended range ethernet LANs |
| HUE052068T2 (en) * | 2006-08-31 | 2021-04-28 | Ericsson Ab | Method and arrangement in a digital subscriber line system |
| US7564388B2 (en) * | 2006-12-12 | 2009-07-21 | Seagate Technology Llc | Power efficient equalizer design |
| US8064510B1 (en) | 2007-03-15 | 2011-11-22 | Netlogic Microsystems, Inc. | Analog encoder based slicer |
| US8040943B1 (en) * | 2007-03-15 | 2011-10-18 | Netlogic Microsystems, Inc. | Least mean square (LMS) engine for multilevel signal |
| US8054873B2 (en) * | 2007-03-15 | 2011-11-08 | Netlogic Microsystems, Inc. | Joint phased training of equalizer and echo canceller |
| US7852915B2 (en) * | 2007-03-21 | 2010-12-14 | Freescale Semiconductor, Inc. | Adaptive equalizer for communication channels |
| CN101617490B (en) * | 2007-06-26 | 2013-09-04 | 美国博通公司 | Method and system for adaptation between different closed-loop, open-loop and hybrid techniques for multiple antenna systems |
| WO2009125322A1 (en) * | 2008-04-08 | 2009-10-15 | Nxp B.V. | Radio receiver gain control |
| US8879643B2 (en) | 2008-04-15 | 2014-11-04 | Qualcomm Incorporated | Data substitution scheme for oversampled data |
| US8625539B2 (en) * | 2008-10-08 | 2014-01-07 | Blackberry Limited | Method and system for supplemental channel request messages in a wireless network |
| US8619897B2 (en) * | 2008-12-09 | 2013-12-31 | Netlogic Microsystems, Inc. | Method and apparatus of frequency domain echo canceller |
| US20110206118A1 (en) * | 2010-02-19 | 2011-08-25 | Lazar Bivolarsky | Data Compression for Video |
| EP2501089B1 (en) * | 2011-03-18 | 2016-12-14 | Imec | Frequency-domain adaptive feedback equalizer |
| US9341676B2 (en) * | 2011-10-07 | 2016-05-17 | Alcatel Lucent | Packet-based propagation of testing information |
| US8915646B2 (en) * | 2012-03-30 | 2014-12-23 | Integrated Device Technology, Inc. | High accuracy temperature sensor |
| US9363039B1 (en) * | 2012-11-07 | 2016-06-07 | Aquantia Corp. | Flexible data transmission scheme adaptive to communication channel quality |
| US20140341265A1 (en) * | 2013-03-11 | 2014-11-20 | Nikola Alic | Method for subrate detection in bandwidth constrained communication systems |
| GB2541260B (en) | 2015-04-29 | 2020-02-19 | Carrier Corp | System and method of data communication that compensates for wire characteristics |
| US10069666B2 (en) * | 2015-07-20 | 2018-09-04 | Telefonaktiebolaget Lm Ericsson (Publ) | Transceiver architecture that maintains legacy timing by inserting and removing cyclic prefix at legacy sampling rate |
| US9729170B1 (en) * | 2016-06-27 | 2017-08-08 | Xilinx, Inc. | Encoding scheme for processing pulse-amplitude modulated (PAM) signals |
| US10554335B2 (en) * | 2016-09-29 | 2020-02-04 | Futurewei Technologies, Inc. | ADC bit allocation under bit constrained MU-massive MIMO systems |
| CN115299016B (en) * | 2020-02-14 | 2024-06-25 | 华为技术有限公司 | Multi-rate crest factor reduction |
| CN112929030A (en) * | 2021-01-25 | 2021-06-08 | 中山大学 | Noise shaping method for direct alignment detection DMT system |
| DE102021202832A1 (en) | 2021-03-23 | 2022-09-29 | Baumüller Nürnberg GmbH | Method for determining a cumulative value from a number of individual values that change over time |
Citations (59)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US2632058A (en) * | 1946-03-22 | 1953-03-17 | Bell Telephone Labor Inc | Pulse code communication |
| US4245345A (en) * | 1979-09-14 | 1981-01-13 | Bell Telephone Laboratories, Incorporated | Timing acquisition in voiceband data sets |
| US4285061A (en) * | 1979-09-14 | 1981-08-18 | Bell Telephone Laboratories, Incorporated | Equalizer sample loading in voiceband data sets |
| US4347615A (en) * | 1979-09-19 | 1982-08-31 | Plessey Overseas Limited | Transversal equalizers |
| US4416015A (en) * | 1981-12-30 | 1983-11-15 | Bell Telephone Laboratories, Incorporated | Timing acquisition in voiceband data sets |
| US4606027A (en) * | 1983-10-12 | 1986-08-12 | Nec Corporation | Error correction apparatus using a Viterbi decoder |
| US4890298A (en) * | 1986-12-11 | 1989-12-26 | Plessey Overseas Limited | Troposcatter modem receiver |
| US5220570A (en) * | 1990-11-30 | 1993-06-15 | The Board Of Trustees Of The Leland Stanford Junior University | Programmable viterbi signal processor |
| US5226060A (en) * | 1992-01-08 | 1993-07-06 | Universal Data Systems, Inc. | Modem receiver with nonlinear equalization |
| US5333149A (en) * | 1991-08-19 | 1994-07-26 | Sgs-Thomson Microelectronics S.A. | Process and a circuit for adapting coefficients in a modem equalizer |
| US5457705A (en) * | 1992-09-22 | 1995-10-10 | Nec Corporation | Method of and system for data transmission employing trellis coded modulation |
| US5479447A (en) * | 1993-05-03 | 1995-12-26 | The Board Of Trustees Of The Leland Stanford, Junior University | Method and apparatus for adaptive, variable bandwidth, high-speed data transmission of a multicarrier signal over digital subscriber lines |
| US5502736A (en) * | 1992-05-26 | 1996-03-26 | Nec Corporation | Viterbi decoder for decoding error-correcting encoded information symbol string |
| US5509021A (en) * | 1992-05-27 | 1996-04-16 | Nec Corporation | Viterbi decoder for decoding error-correcting encoded information symbol string |
| US5598434A (en) * | 1994-12-20 | 1997-01-28 | Fujitsu Limited | Automatic equalizer with a branched input for improved accuracy |
| US5636244A (en) * | 1995-07-26 | 1997-06-03 | Motorola, Inc. | Method and apparatus for initializing equalizer coefficents using peridioc training sequences |
| US5751734A (en) * | 1996-11-04 | 1998-05-12 | Samsung Electronics Co., Ltd. | Decoding method and apparatus using trace deletion for Viterbi algorithm |
| US5796756A (en) * | 1996-02-28 | 1998-08-18 | Samsung Electronics Co., Ltd. | Survivor memory device in viterbi decoder using trace deletion method |
| US5838729A (en) * | 1996-04-09 | 1998-11-17 | Thomson Multimedia, S.A. | Multiple mode trellis decoder for a digital signal processing system |
| US5896372A (en) * | 1997-02-20 | 1999-04-20 | International Business Machines Corporation | Method and apparatus for creating virtual high bandwidth data channels |
| US5928378A (en) * | 1996-08-23 | 1999-07-27 | Daewoo Electronics Co., Ltd. | Add-compare-select processor in Viterbi decoder |
| US5946361A (en) * | 1994-06-23 | 1999-08-31 | Oki Electric Industry Co., Ltd. | Viterbi decoding method and circuit with accelerated back-tracing and efficient path metric calculation |
| US5953376A (en) * | 1996-09-26 | 1999-09-14 | Lucent Technologies Inc. | Probabilistic trellis coded modulation with PCM-derived constellations |
| US5970104A (en) * | 1997-03-19 | 1999-10-19 | Cadence Design Systems, Inc. | Method and apparatus for generating branch metrics and branch indices for convolutional code Viterbi decoders |
| US5986598A (en) * | 1997-12-19 | 1999-11-16 | Motorola, Inc. | Sigma delta data converter with feed-forward path to stabilize integrator signal swing |
| US5995562A (en) * | 1995-10-25 | 1999-11-30 | Nec Corporation | Maximum-likelihood decoding |
| US6038251A (en) * | 1996-05-09 | 2000-03-14 | Texas Instruments Incorporated | Direct equalization method |
| US6055268A (en) * | 1996-05-09 | 2000-04-25 | Texas Instruments Incorporated | Multimode digital modem |
| US6057793A (en) * | 1998-06-12 | 2000-05-02 | Oak Technology, Inc. | Digital decimation filter and method for achieving fractional data rate reduction with minimal hardware or software overhead |
| US6069879A (en) * | 1996-11-14 | 2000-05-30 | Chatter; Mukesh | Method of and system architecture for high speed dual symmetric full duplex operation of asymmetric digital subscriber lines |
| US6084917A (en) * | 1997-12-16 | 2000-07-04 | Integrated Telecom Express | Circuit for configuring and dynamically adapting data and energy parameters in a multi-channel communications system |
| US6112232A (en) * | 1998-01-27 | 2000-08-29 | Phasecom Ltd. | Data communication device for CATV networks |
| US6154161A (en) * | 1998-10-07 | 2000-11-28 | Atmel Corporation | Integrated audio mixer |
| US6166666A (en) * | 1998-10-19 | 2000-12-26 | Microsoft Corporation | Method and apparatus for compression and encoding of unicode strings |
| US6212654B1 (en) * | 1997-07-22 | 2001-04-03 | Lucent Technologies Inc. | Coded modulation for digital storage in analog memory devices |
| US6232901B1 (en) * | 1999-08-26 | 2001-05-15 | Rockwell Collins, Inc. | High performance sigma-delta-sigma low-pass/band-pass modulator based analog-to-digital and digital-to-analog converter |
| US6232902B1 (en) * | 1998-09-22 | 2001-05-15 | Yokogawa Electric Corporation | Sigma-delta analog-to-digital converter |
| US6292124B1 (en) * | 1999-02-05 | 2001-09-18 | Nippon Precision Circuits, Inc. | Delta-sigma D/A converter |
| US20010036232A1 (en) * | 2000-02-11 | 2001-11-01 | Paradyne Corporation | Interleaved generalized convolutional encoder |
| US6344812B1 (en) * | 1999-06-07 | 2002-02-05 | Nippon Precision Circuits, Inc. | Delta sigma digital-to-analog converter |
| US6369730B1 (en) * | 1999-04-21 | 2002-04-09 | U.S. Philips Corporation | Sigma-delta analog-to-digital converter |
| US6388601B1 (en) * | 1998-10-23 | 2002-05-14 | Thomson-Csf | Delay compensation for analog-to-digital converter in sigma-delta modulators |
| US6424280B2 (en) * | 2000-01-21 | 2002-07-23 | Texas Instruments Incorporated | Signal clipping circuit for switched capacitor sigma delta analog to digital converters |
| US6424279B1 (en) * | 1999-06-26 | 2002-07-23 | Korea Advanced Institute Of Science And Technology | Sigma-delta analog-to-digital converter using mixed-mode integrator |
| US6441761B1 (en) * | 1999-12-08 | 2002-08-27 | Texas Instruments Incorporated | High speed, high resolution digital-to-analog converter with off-line sigma delta conversion and storage |
| US6445734B1 (en) * | 1999-06-30 | 2002-09-03 | Conexant Systems, Inc. | System and method of validating equalizer training |
| US6452521B1 (en) * | 2001-03-14 | 2002-09-17 | Rosemount Inc. | Mapping a delta-sigma converter range to a sensor range |
| US6456219B1 (en) * | 2000-02-22 | 2002-09-24 | Texas Instruments Incorporated | Analog-to-digital converter including two-wire interface circuit |
| US6456217B1 (en) * | 1999-09-02 | 2002-09-24 | Nec Corporation | Digital/analog converter having delta-sigma type pulse modulation circuit |
| US6483449B2 (en) * | 2000-07-11 | 2002-11-19 | Stmicroelectronics S.R.L. | Digital-analog converter comprising a third order sigma delta modulator |
| US6489913B1 (en) * | 2001-09-24 | 2002-12-03 | Tektronix, Inc. | Sub-ranging analog-to-digital converter using a sigma delta converter |
| US6496128B2 (en) * | 1999-05-05 | 2002-12-17 | Infineon Technologies Ag | Sigma-delta analog-to-digital converter array |
| US6498819B1 (en) * | 1998-10-19 | 2002-12-24 | Motorola, Inc. | Integrated multi-mode bandpass sigma-delta receiver subsystem with interference mitigation and method of using same |
| US6498573B2 (en) * | 1999-08-04 | 2002-12-24 | Infineon Technologies Ag | Sigma-delta A/D converter |
| US6515607B2 (en) * | 2001-05-25 | 2003-02-04 | Archic Tech, Corp. | Delta-sigma modulator |
| US6515605B2 (en) * | 2001-04-30 | 2003-02-04 | Texas Instruments Incorporated | Base station having high speed, high resolution, digital-to-analog converter with off-line sigma delta conversion and storage |
| US6625116B1 (en) * | 1999-05-07 | 2003-09-23 | Adtran, Inc. | System, methods and apparatus for increasing the data rate on an existing repeatered telecommunication channel structure |
| US6956872B1 (en) * | 2000-05-22 | 2005-10-18 | Globespanvirata, Inc. | System and method for encoding DSL information streams having differing latencies |
| US6993067B1 (en) * | 2000-02-11 | 2006-01-31 | Paradyne Corporation | Fractional bit rate encoding in a pulse amplitude modulation communication system |
Family Cites Families (10)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US669730A (en) * | 1898-11-03 | 1901-03-12 | Edward E Kilbourn | Knitting-machine. |
| ATE172052T1 (en) * | 1992-08-06 | 1998-10-15 | Koninkl Philips Electronics Nv | RECEIVING ARRANGEMENT FOR RECEIVING A DIGITAL SIGNAL FROM A TRANSMISSION MEDIUM WITH VARIABLE EQUALIZATION MEANS |
| US5963160A (en) * | 1993-09-13 | 1999-10-05 | Analog Devices, Inc. | Analog to digital conversion using nonuniform sample rates |
| US5590065A (en) * | 1994-08-10 | 1996-12-31 | Crystal Semiconductor Corporation | Digital decimation filter for delta sigma analog-to-digital conversion with reduced hardware compelexity |
| US5751615A (en) * | 1995-11-14 | 1998-05-12 | Advanced Micro Devices, Inc. | Implementation of a digital decimation filter and method |
| US6292121B1 (en) * | 1998-01-09 | 2001-09-18 | Lecroy Corporation | Delta sigma-analog-to-digital converter |
| US6470365B1 (en) * | 1999-08-23 | 2002-10-22 | Motorola, Inc. | Method and architecture for complex datapath decimation and channel filtering |
| US6393052B2 (en) * | 2000-02-17 | 2002-05-21 | At&T Corporation | Method and apparatus for minimizing near end cross talk due to discrete multi-tone transmission in cable binders |
| US6628707B2 (en) * | 2001-05-04 | 2003-09-30 | Radiant Networks Plc | Adaptive equalizer system for short burst modems and link hopping radio networks |
| US6697003B1 (en) * | 2003-04-17 | 2004-02-24 | Texas Instruments Incorporated | System and method for dynamic element matching |
-
2002
- 2002-12-18 WO PCT/US2002/040344 patent/WO2003055195A2/en not_active Application Discontinuation
- 2002-12-18 AU AU2002364572A patent/AU2002364572A1/en not_active Abandoned
- 2002-12-18 US US10/321,509 patent/US6788236B2/en not_active Expired - Lifetime
- 2002-12-18 US US10/321,508 patent/US7076514B2/en active Active
- 2002-12-18 US US10/321,601 patent/US20030202612A1/en not_active Abandoned
Patent Citations (59)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US2632058A (en) * | 1946-03-22 | 1953-03-17 | Bell Telephone Labor Inc | Pulse code communication |
| US4245345A (en) * | 1979-09-14 | 1981-01-13 | Bell Telephone Laboratories, Incorporated | Timing acquisition in voiceband data sets |
| US4285061A (en) * | 1979-09-14 | 1981-08-18 | Bell Telephone Laboratories, Incorporated | Equalizer sample loading in voiceband data sets |
| US4347615A (en) * | 1979-09-19 | 1982-08-31 | Plessey Overseas Limited | Transversal equalizers |
| US4416015A (en) * | 1981-12-30 | 1983-11-15 | Bell Telephone Laboratories, Incorporated | Timing acquisition in voiceband data sets |
| US4606027A (en) * | 1983-10-12 | 1986-08-12 | Nec Corporation | Error correction apparatus using a Viterbi decoder |
| US4890298A (en) * | 1986-12-11 | 1989-12-26 | Plessey Overseas Limited | Troposcatter modem receiver |
| US5220570A (en) * | 1990-11-30 | 1993-06-15 | The Board Of Trustees Of The Leland Stanford Junior University | Programmable viterbi signal processor |
| US5333149A (en) * | 1991-08-19 | 1994-07-26 | Sgs-Thomson Microelectronics S.A. | Process and a circuit for adapting coefficients in a modem equalizer |
| US5226060A (en) * | 1992-01-08 | 1993-07-06 | Universal Data Systems, Inc. | Modem receiver with nonlinear equalization |
| US5502736A (en) * | 1992-05-26 | 1996-03-26 | Nec Corporation | Viterbi decoder for decoding error-correcting encoded information symbol string |
| US5509021A (en) * | 1992-05-27 | 1996-04-16 | Nec Corporation | Viterbi decoder for decoding error-correcting encoded information symbol string |
| US5457705A (en) * | 1992-09-22 | 1995-10-10 | Nec Corporation | Method of and system for data transmission employing trellis coded modulation |
| US5479447A (en) * | 1993-05-03 | 1995-12-26 | The Board Of Trustees Of The Leland Stanford, Junior University | Method and apparatus for adaptive, variable bandwidth, high-speed data transmission of a multicarrier signal over digital subscriber lines |
| US5946361A (en) * | 1994-06-23 | 1999-08-31 | Oki Electric Industry Co., Ltd. | Viterbi decoding method and circuit with accelerated back-tracing and efficient path metric calculation |
| US5598434A (en) * | 1994-12-20 | 1997-01-28 | Fujitsu Limited | Automatic equalizer with a branched input for improved accuracy |
| US5636244A (en) * | 1995-07-26 | 1997-06-03 | Motorola, Inc. | Method and apparatus for initializing equalizer coefficents using peridioc training sequences |
| US5995562A (en) * | 1995-10-25 | 1999-11-30 | Nec Corporation | Maximum-likelihood decoding |
| US5796756A (en) * | 1996-02-28 | 1998-08-18 | Samsung Electronics Co., Ltd. | Survivor memory device in viterbi decoder using trace deletion method |
| US5838729A (en) * | 1996-04-09 | 1998-11-17 | Thomson Multimedia, S.A. | Multiple mode trellis decoder for a digital signal processing system |
| US6055268A (en) * | 1996-05-09 | 2000-04-25 | Texas Instruments Incorporated | Multimode digital modem |
| US6038251A (en) * | 1996-05-09 | 2000-03-14 | Texas Instruments Incorporated | Direct equalization method |
| US5928378A (en) * | 1996-08-23 | 1999-07-27 | Daewoo Electronics Co., Ltd. | Add-compare-select processor in Viterbi decoder |
| US5953376A (en) * | 1996-09-26 | 1999-09-14 | Lucent Technologies Inc. | Probabilistic trellis coded modulation with PCM-derived constellations |
| US5751734A (en) * | 1996-11-04 | 1998-05-12 | Samsung Electronics Co., Ltd. | Decoding method and apparatus using trace deletion for Viterbi algorithm |
| US6069879A (en) * | 1996-11-14 | 2000-05-30 | Chatter; Mukesh | Method of and system architecture for high speed dual symmetric full duplex operation of asymmetric digital subscriber lines |
| US5896372A (en) * | 1997-02-20 | 1999-04-20 | International Business Machines Corporation | Method and apparatus for creating virtual high bandwidth data channels |
| US5970104A (en) * | 1997-03-19 | 1999-10-19 | Cadence Design Systems, Inc. | Method and apparatus for generating branch metrics and branch indices for convolutional code Viterbi decoders |
| US6212654B1 (en) * | 1997-07-22 | 2001-04-03 | Lucent Technologies Inc. | Coded modulation for digital storage in analog memory devices |
| US6084917A (en) * | 1997-12-16 | 2000-07-04 | Integrated Telecom Express | Circuit for configuring and dynamically adapting data and energy parameters in a multi-channel communications system |
| US5986598A (en) * | 1997-12-19 | 1999-11-16 | Motorola, Inc. | Sigma delta data converter with feed-forward path to stabilize integrator signal swing |
| US6112232A (en) * | 1998-01-27 | 2000-08-29 | Phasecom Ltd. | Data communication device for CATV networks |
| US6057793A (en) * | 1998-06-12 | 2000-05-02 | Oak Technology, Inc. | Digital decimation filter and method for achieving fractional data rate reduction with minimal hardware or software overhead |
| US6232902B1 (en) * | 1998-09-22 | 2001-05-15 | Yokogawa Electric Corporation | Sigma-delta analog-to-digital converter |
| US6154161A (en) * | 1998-10-07 | 2000-11-28 | Atmel Corporation | Integrated audio mixer |
| US6166666A (en) * | 1998-10-19 | 2000-12-26 | Microsoft Corporation | Method and apparatus for compression and encoding of unicode strings |
| US6498819B1 (en) * | 1998-10-19 | 2002-12-24 | Motorola, Inc. | Integrated multi-mode bandpass sigma-delta receiver subsystem with interference mitigation and method of using same |
| US6388601B1 (en) * | 1998-10-23 | 2002-05-14 | Thomson-Csf | Delay compensation for analog-to-digital converter in sigma-delta modulators |
| US6292124B1 (en) * | 1999-02-05 | 2001-09-18 | Nippon Precision Circuits, Inc. | Delta-sigma D/A converter |
| US6369730B1 (en) * | 1999-04-21 | 2002-04-09 | U.S. Philips Corporation | Sigma-delta analog-to-digital converter |
| US6496128B2 (en) * | 1999-05-05 | 2002-12-17 | Infineon Technologies Ag | Sigma-delta analog-to-digital converter array |
| US6625116B1 (en) * | 1999-05-07 | 2003-09-23 | Adtran, Inc. | System, methods and apparatus for increasing the data rate on an existing repeatered telecommunication channel structure |
| US6344812B1 (en) * | 1999-06-07 | 2002-02-05 | Nippon Precision Circuits, Inc. | Delta sigma digital-to-analog converter |
| US6424279B1 (en) * | 1999-06-26 | 2002-07-23 | Korea Advanced Institute Of Science And Technology | Sigma-delta analog-to-digital converter using mixed-mode integrator |
| US6445734B1 (en) * | 1999-06-30 | 2002-09-03 | Conexant Systems, Inc. | System and method of validating equalizer training |
| US6498573B2 (en) * | 1999-08-04 | 2002-12-24 | Infineon Technologies Ag | Sigma-delta A/D converter |
| US6232901B1 (en) * | 1999-08-26 | 2001-05-15 | Rockwell Collins, Inc. | High performance sigma-delta-sigma low-pass/band-pass modulator based analog-to-digital and digital-to-analog converter |
| US6456217B1 (en) * | 1999-09-02 | 2002-09-24 | Nec Corporation | Digital/analog converter having delta-sigma type pulse modulation circuit |
| US6441761B1 (en) * | 1999-12-08 | 2002-08-27 | Texas Instruments Incorporated | High speed, high resolution digital-to-analog converter with off-line sigma delta conversion and storage |
| US6424280B2 (en) * | 2000-01-21 | 2002-07-23 | Texas Instruments Incorporated | Signal clipping circuit for switched capacitor sigma delta analog to digital converters |
| US20010036232A1 (en) * | 2000-02-11 | 2001-11-01 | Paradyne Corporation | Interleaved generalized convolutional encoder |
| US6993067B1 (en) * | 2000-02-11 | 2006-01-31 | Paradyne Corporation | Fractional bit rate encoding in a pulse amplitude modulation communication system |
| US6456219B1 (en) * | 2000-02-22 | 2002-09-24 | Texas Instruments Incorporated | Analog-to-digital converter including two-wire interface circuit |
| US6956872B1 (en) * | 2000-05-22 | 2005-10-18 | Globespanvirata, Inc. | System and method for encoding DSL information streams having differing latencies |
| US6483449B2 (en) * | 2000-07-11 | 2002-11-19 | Stmicroelectronics S.R.L. | Digital-analog converter comprising a third order sigma delta modulator |
| US6452521B1 (en) * | 2001-03-14 | 2002-09-17 | Rosemount Inc. | Mapping a delta-sigma converter range to a sensor range |
| US6515605B2 (en) * | 2001-04-30 | 2003-02-04 | Texas Instruments Incorporated | Base station having high speed, high resolution, digital-to-analog converter with off-line sigma delta conversion and storage |
| US6515607B2 (en) * | 2001-05-25 | 2003-02-04 | Archic Tech, Corp. | Delta-sigma modulator |
| US6489913B1 (en) * | 2001-09-24 | 2002-12-03 | Tektronix, Inc. | Sub-ranging analog-to-digital converter using a sigma delta converter |
Cited By (53)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US20050249246A1 (en) * | 2002-07-12 | 2005-11-10 | Reidar Schumann-Olsen | Method of transporting data streams through an sdh switched network |
| US8194770B2 (en) | 2002-08-27 | 2012-06-05 | Qualcomm Incorporated | Coded MIMO systems with selective channel inversion applied per eigenmode |
| US8711763B2 (en) | 2002-10-25 | 2014-04-29 | Qualcomm Incorporated | Random access for wireless multiple-access communication systems |
| US9240871B2 (en) | 2002-10-25 | 2016-01-19 | Qualcomm Incorporated | MIMO WLAN system |
| US8750151B2 (en) | 2002-10-25 | 2014-06-10 | Qualcomm Incorporated | Channel calibration for a time division duplexed communication system |
| US10382106B2 (en) | 2002-10-25 | 2019-08-13 | Qualcomm Incorporated | Pilots for MIMO communication systems |
| US9967005B2 (en) | 2002-10-25 | 2018-05-08 | Qualcomm Incorporated | Pilots for MIMO communication systems |
| US9312935B2 (en) | 2002-10-25 | 2016-04-12 | Qualcomm Incorporated | Pilots for MIMO communication systems |
| US9154274B2 (en) | 2002-10-25 | 2015-10-06 | Qualcomm Incorporated | OFDM communication system with multiple OFDM symbol sizes |
| US9048892B2 (en) | 2002-10-25 | 2015-06-02 | Qualcomm Incorporated | MIMO system with multiple spatial multiplexing modes |
| US7986742B2 (en) | 2002-10-25 | 2011-07-26 | Qualcomm Incorporated | Pilots for MIMO communication system |
| US8134976B2 (en) | 2002-10-25 | 2012-03-13 | Qualcomm Incorporated | Channel calibration for a time division duplexed communication system |
| US8145179B2 (en) | 2002-10-25 | 2012-03-27 | Qualcomm Incorporated | Data detection and demodulation for wireless communication systems |
| US8170513B2 (en) | 2002-10-25 | 2012-05-01 | Qualcomm Incorporated | Data detection and demodulation for wireless communication systems |
| US8169944B2 (en) | 2002-10-25 | 2012-05-01 | Qualcomm Incorporated | Random access for wireless multiple-access communication systems |
| US9031097B2 (en) | 2002-10-25 | 2015-05-12 | Qualcomm Incorporated | MIMO system with multiple spatial multiplexing modes |
| US8203978B2 (en) | 2002-10-25 | 2012-06-19 | Qualcomm Incorporated | Multi-mode terminal in a wireless MIMO system |
| US8208364B2 (en) | 2002-10-25 | 2012-06-26 | Qualcomm Incorporated | MIMO system with multiple spatial multiplexing modes |
| US8218609B2 (en) | 2002-10-25 | 2012-07-10 | Qualcomm Incorporated | Closed-loop rate control for a multi-channel communication system |
| US9013974B2 (en) | 2002-10-25 | 2015-04-21 | Qualcomm Incorporated | MIMO WLAN system |
| US8934329B2 (en) | 2002-10-25 | 2015-01-13 | Qualcomm Incorporated | Transmit diversity processing for a multi-antenna communication system |
| US8355313B2 (en) | 2002-10-25 | 2013-01-15 | Qualcomm Incorporated | MIMO system with multiple spatial multiplexing modes |
| US8913529B2 (en) | 2002-10-25 | 2014-12-16 | Qualcomm Incorporated | MIMO WLAN system |
| US8462643B2 (en) | 2002-10-25 | 2013-06-11 | Qualcomm Incorporated | MIMO WLAN system |
| US8483188B2 (en) | 2002-10-25 | 2013-07-09 | Qualcomm Incorporated | MIMO system with multiple spatial multiplexing modes |
| US8570988B2 (en) | 2002-10-25 | 2013-10-29 | Qualcomm Incorporated | Channel calibration for a time division duplexed communication system |
| US8320301B2 (en) | 2002-10-25 | 2012-11-27 | Qualcomm Incorporated | MIMO WLAN system |
| US8873365B2 (en) | 2002-10-25 | 2014-10-28 | Qualcomm Incorporated | Transmit diversity processing for a multi-antenna communication system |
| US9473269B2 (en) | 2003-12-01 | 2016-10-18 | Qualcomm Incorporated | Method and apparatus for providing an efficient control channel structure in a wireless communication system |
| US9876609B2 (en) | 2003-12-01 | 2018-01-23 | Qualcomm Incorporated | Method and apparatus for providing an efficient control channel structure in a wireless communication system |
| US10742358B2 (en) | 2003-12-01 | 2020-08-11 | Qualcomm Incorporated | Method and apparatus for providing an efficient control channel structure in a wireless communication system |
| US20100135469A1 (en) * | 2004-02-11 | 2010-06-03 | Aware, Inc. | Communication channel capacity estimation |
| US8654931B2 (en) * | 2004-02-11 | 2014-02-18 | Aware, Inc. | Communication channel capacity estimation |
| US8971500B2 (en) | 2004-02-11 | 2015-03-03 | Broadcom Corporation | Communication channel capacity estimation |
| US7356088B2 (en) * | 2004-04-29 | 2008-04-08 | Texas Instruments Incorporated | M-dimension M-PAM trellis code system and associated trellis encoder and decoder |
| US20050243941A1 (en) * | 2004-04-29 | 2005-11-03 | Texas Instruments Incorporated | M-dimension M-PAM trellis code system and associated trellis encoder and decoder |
| WO2006088566A3 (en) * | 2005-02-19 | 2007-11-15 | Rlh Ind Inc | Hdsl optical fiber transmission system and method |
| WO2006088566A2 (en) * | 2005-02-19 | 2006-08-24 | Rlh Industries, Inc. | Hdsl optical fiber transmission system and method |
| US20060188259A1 (en) * | 2005-02-19 | 2006-08-24 | James Furey | HDSL optical fiber transmission system and method |
| US8855226B2 (en) | 2005-05-12 | 2014-10-07 | Qualcomm Incorporated | Rate selection with margin sharing |
| US8358714B2 (en) | 2005-06-16 | 2013-01-22 | Qualcomm Incorporated | Coding and modulation for multiple data streams in a communication system |
| US20070206625A1 (en) * | 2006-03-01 | 2007-09-06 | Junichi Maeda | Communication device, communication system, and communication method performing communication using a plurality of signals having different frequencies |
| US8249092B2 (en) * | 2006-03-01 | 2012-08-21 | Sumitomo Electric Networks, Inc. | Communication device, communication system, and communication method performing communication using a plurality of signals having different frequencies |
| US7929626B2 (en) * | 2007-07-24 | 2011-04-19 | Texas Instruments Incorporated | Variable power communications including rapid switching between coding constellations of various sizes |
| US20090028268A1 (en) * | 2007-07-24 | 2009-01-29 | Texas Instruments Inc. | Variable power communications including rapid switching between coding constellations of various sizes |
| US20140169501A1 (en) * | 2011-06-10 | 2014-06-19 | Moshe Nazarathy | Receiver, transmitter and a method for digital multiple sub-band processing |
| US9503284B2 (en) * | 2011-06-10 | 2016-11-22 | Technion Research And Development Foundation Ltd. | Receiver, transmitter and a method for digital multiple sub-band processing |
| US10931486B2 (en) | 2011-06-10 | 2021-02-23 | Technion Research And Development Foundation Ltd. | Transmitter, receiver and a method for digital multiple sub-band processing |
| WO2019225311A1 (en) * | 2018-05-22 | 2019-11-28 | 日本電信電話株式会社 | Optical communication system, optical transmitter and optical receiver |
| JP2019205045A (en) * | 2018-05-22 | 2019-11-28 | 日本電信電話株式会社 | Optical communication system, optical transmitter, and optical receiver |
| US11349572B2 (en) * | 2018-05-22 | 2022-05-31 | Nippon Telegraph And Telephone Corporation | Optical transmission system, optical transmitting apparatus, and optical receiving apparatus |
| US10972319B2 (en) * | 2018-09-12 | 2021-04-06 | Texas Instruments Incorporated | Clockless decision feedback equalization (DFE) for multi-level signals |
| CN112787630A (en) * | 2019-11-06 | 2021-05-11 | 意法半导体国际有限公司 | High throughput digital filter architecture for processing unary coded data |
Also Published As
| Publication number | Publication date |
|---|---|
| US7076514B2 (en) | 2006-07-11 |
| WO2003055195A2 (en) | 2003-07-03 |
| US20030235245A1 (en) | 2003-12-25 |
| AU2002364572A8 (en) | 2003-07-09 |
| AU2002364572A1 (en) | 2003-07-09 |
| US20040021595A1 (en) | 2004-02-05 |
| US6788236B2 (en) | 2004-09-07 |
| WO2003055195A3 (en) | 2003-11-13 |
Similar Documents
| Publication | Publication Date | Title |
|---|---|---|
| US7076514B2 (en) | Method and system for computing pre-equalizer coefficients | |
| US5987061A (en) | Modem initialization process for line code and rate selection in DSL data communication | |
| US6597746B1 (en) | System and method for peak to average power ratio reduction | |
| US6044107A (en) | Method for interoperability of a T1E1.4 compliant ADSL modem and a simpler modem | |
| US6021158A (en) | Hybrid wireless wire-line network integration and management | |
| US6002722A (en) | Multimode digital modem | |
| US6038251A (en) | Direct equalization method | |
| US5809033A (en) | Use of modified line encoding and low signal-to-noise ratio based signal processing to extend range of digital data transmission over repeaterless two-wire telephone link | |
| US6055268A (en) | Multimode digital modem | |
| US6292515B1 (en) | Dual mode bit and gain loading circuit and process | |
| US7113491B2 (en) | Method and system for varying an echo canceller filter length based on data rate | |
| US6370191B1 (en) | Efficient implementation of error approximation in blind equalization of data communications | |
| EP0831624A2 (en) | A modem | |
| EP0828363A2 (en) | Multicode modem with a plurality of analogue front ends | |
| US6084906A (en) | ADSL transceiver implemented with associated bit and energy loading integrated circuit | |
| US6128348A (en) | Method for configuring data and energy parameters in a multi-channel communications system | |
| US20030099285A1 (en) | Method and system for determining data rate using sub-band capacity | |
| US20030101206A1 (en) | Method and system for estimating a base-2 logarithm of a number | |
| US20030086486A1 (en) | Method and system for determining maximum power backoff using frequency domain geometric signal to noise ratio | |
| EP1701498B1 (en) | High speed communications system for analog subscriber connections | |
| US6233275B1 (en) | High speed communications system for analog subscriber connections | |
| WO2003013048A2 (en) | Power backoff method and system for g.shdsl modem using frequency domain geometric signal to noise ratio | |
| US20030053533A1 (en) | Non-iterative time-domain equalizer | |
| KR100349987B1 (en) | High speed communications system for analog subscriber connections | |
| JP2000059456A (en) | Method for adjusting adaptive filter for filter pair for qam/cap receiver and adaptive cap receiver |
Legal Events
| Date | Code | Title | Description |
|---|---|---|---|
| AS | Assignment |
Owner name: GLOBESPAN VIRATA INC., NEW JERSEY Free format text: ASSIGNMENT OF ASSIGNORS INTEREST;ASSIGNORS:HALDER, BIJIT;PAL, DEBAJYOTI;ERDOGAN,ALPER TUNGA;REEL/FRAME:014190/0962;SIGNING DATES FROM 20030506 TO 20030608 |
|
| STCB | Information on status: application discontinuation |
Free format text: ABANDONED -- FAILURE TO RESPOND TO AN OFFICE ACTION |
|
| AS | Assignment |
Owner name: BROOKTREE BROADBAND HOLDING, INC., CALIFORNIA Free format text: ASSIGNMENT OF ASSIGNORS INTEREST;ASSIGNOR:GLOBESPANVIRATA, INC.;REEL/FRAME:038803/0606 Effective date: 20040228 Owner name: IKANOS COMMUNICATIONS, INC., CALIFORNIA Free format text: ASSIGNMENT OF ASSIGNORS INTEREST;ASSIGNORS:CONEXANT SYSTEMS, INC.;CONEXANT, INC.;BROOKTREE BROADBAND HOLDING, INC.;REEL/FRAME:038874/0270 Effective date: 20090824 |