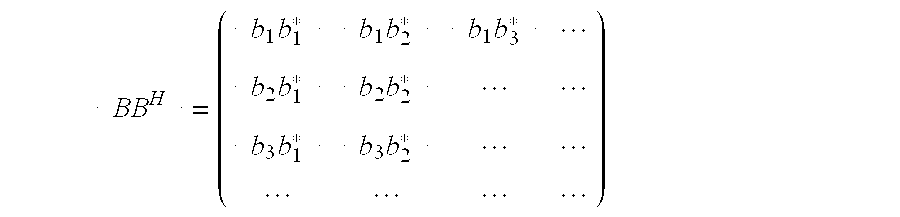US20020176485A1 - Multi-cast communication system and method of estimating channel impulse responses therein - Google Patents
Multi-cast communication system and method of estimating channel impulse responses therein Download PDFInfo
- Publication number
- US20020176485A1 US20020176485A1 US09/825,058 US82505801A US2002176485A1 US 20020176485 A1 US20020176485 A1 US 20020176485A1 US 82505801 A US82505801 A US 82505801A US 2002176485 A1 US2002176485 A1 US 2002176485A1
- Authority
- US
- United States
- Prior art keywords
- channel
- training
- communication device
- sequence
- bursts
- Prior art date
- Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
- Abandoned
Links
- 230000004044 response Effects 0.000 title claims abstract description 126
- 238000004891 communication Methods 0.000 title claims description 81
- 238000000034 method Methods 0.000 title claims description 73
- 238000012549 training Methods 0.000 claims abstract description 159
- 108010076504 Protein Sorting Signals Proteins 0.000 claims description 46
- 239000011159 matrix material Substances 0.000 claims description 39
- 239000013598 vector Substances 0.000 claims description 31
- 125000004122 cyclic group Chemical group 0.000 claims description 27
- 238000012545 processing Methods 0.000 claims description 26
- 239000002131 composite material Substances 0.000 claims description 21
- 238000001914 filtration Methods 0.000 claims description 14
- 230000007246 mechanism Effects 0.000 claims description 9
- 238000011084 recovery Methods 0.000 claims description 8
- 238000004590 computer program Methods 0.000 claims description 7
- 230000036961 partial effect Effects 0.000 claims description 6
- HPNSNYBUADCFDR-UHFFFAOYSA-N chromafenozide Chemical compound CC1=CC(C)=CC(C(=O)N(NC(=O)C=2C(=C3CCCOC3=CC=2)C)C(C)(C)C)=C1 HPNSNYBUADCFDR-UHFFFAOYSA-N 0.000 claims description 4
- 230000008878 coupling Effects 0.000 claims description 4
- 238000010168 coupling process Methods 0.000 claims description 4
- 238000005859 coupling reaction Methods 0.000 claims description 4
- 239000013589 supplement Substances 0.000 abstract description 3
- 108091006146 Channels Proteins 0.000 description 251
- 230000005540 biological transmission Effects 0.000 description 27
- 238000003775 Density Functional Theory Methods 0.000 description 22
- 238000001228 spectrum Methods 0.000 description 20
- 230000000875 corresponding effect Effects 0.000 description 12
- 230000006870 function Effects 0.000 description 12
- 230000008569 process Effects 0.000 description 8
- 230000001413 cellular effect Effects 0.000 description 7
- 239000006185 dispersion Substances 0.000 description 6
- 230000001427 coherent effect Effects 0.000 description 5
- 239000000047 product Substances 0.000 description 5
- 238000001514 detection method Methods 0.000 description 4
- 238000010586 diagram Methods 0.000 description 4
- 230000002829 reductive effect Effects 0.000 description 4
- 230000010267 cellular communication Effects 0.000 description 3
- 230000000694 effects Effects 0.000 description 3
- PCHJSUWPFVWCPO-UHFFFAOYSA-N gold Chemical compound [Au] PCHJSUWPFVWCPO-UHFFFAOYSA-N 0.000 description 3
- 239000010931 gold Substances 0.000 description 3
- 229910052737 gold Inorganic materials 0.000 description 3
- 238000002955 isolation Methods 0.000 description 3
- 230000002441 reversible effect Effects 0.000 description 3
- 230000001360 synchronised effect Effects 0.000 description 3
- 108091081062 Repeated sequence (DNA) Proteins 0.000 description 2
- 239000000969 carrier Substances 0.000 description 2
- 230000001143 conditioned effect Effects 0.000 description 2
- 238000011109 contamination Methods 0.000 description 2
- 230000002596 correlated effect Effects 0.000 description 2
- 238000013461 design Methods 0.000 description 2
- 230000000670 limiting effect Effects 0.000 description 2
- 230000002411 adverse Effects 0.000 description 1
- 230000003321 amplification Effects 0.000 description 1
- 238000013459 approach Methods 0.000 description 1
- 238000003491 array Methods 0.000 description 1
- 230000008901 benefit Effects 0.000 description 1
- 230000003139 buffering effect Effects 0.000 description 1
- 230000008859 change Effects 0.000 description 1
- 230000000295 complement effect Effects 0.000 description 1
- 238000013329 compounding Methods 0.000 description 1
- 238000012937 correction Methods 0.000 description 1
- 238000005314 correlation function Methods 0.000 description 1
- 230000001351 cycling effect Effects 0.000 description 1
- 230000007547 defect Effects 0.000 description 1
- 230000001419 dependent effect Effects 0.000 description 1
- 230000001627 detrimental effect Effects 0.000 description 1
- 238000006073 displacement reaction Methods 0.000 description 1
- 230000009977 dual effect Effects 0.000 description 1
- 230000006872 improvement Effects 0.000 description 1
- 230000003993 interaction Effects 0.000 description 1
- 229940050561 matrix product Drugs 0.000 description 1
- 238000012986 modification Methods 0.000 description 1
- 230000004048 modification Effects 0.000 description 1
- 238000003199 nucleic acid amplification method Methods 0.000 description 1
- 238000011017 operating method Methods 0.000 description 1
- 230000003287 optical effect Effects 0.000 description 1
- 230000000737 periodic effect Effects 0.000 description 1
- 230000009467 reduction Effects 0.000 description 1
- 230000001105 regulatory effect Effects 0.000 description 1
- 238000005070 sampling Methods 0.000 description 1
- 230000011664 signaling Effects 0.000 description 1
- 230000007480 spreading Effects 0.000 description 1
- 238000012360 testing method Methods 0.000 description 1
- 230000009466 transformation Effects 0.000 description 1
- 238000009966 trimming Methods 0.000 description 1
Images
Classifications
-
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L25/00—Baseband systems
- H04L25/02—Details ; arrangements for supplying electrical power along data transmission lines
- H04L25/0202—Channel estimation
- H04L25/0224—Channel estimation using sounding signals
-
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L1/00—Arrangements for detecting or preventing errors in the information received
- H04L1/02—Arrangements for detecting or preventing errors in the information received by diversity reception
- H04L1/06—Arrangements for detecting or preventing errors in the information received by diversity reception using space diversity
- H04L1/0618—Space-time coding
-
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L25/00—Baseband systems
- H04L25/02—Details ; arrangements for supplying electrical power along data transmission lines
- H04L25/0202—Channel estimation
- H04L25/0212—Channel estimation of impulse response
-
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L25/00—Baseband systems
- H04L25/02—Details ; arrangements for supplying electrical power along data transmission lines
- H04L25/0202—Channel estimation
- H04L25/024—Channel estimation channel estimation algorithms
- H04L25/025—Channel estimation channel estimation algorithms using least-mean-square [LMS] method
-
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L25/00—Baseband systems
- H04L25/02—Details ; arrangements for supplying electrical power along data transmission lines
- H04L25/03—Shaping networks in transmitter or receiver, e.g. adaptive shaping networks
- H04L25/03006—Arrangements for removing intersymbol interference
- H04L25/03159—Arrangements for removing intersymbol interference operating in the frequency domain
-
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L25/00—Baseband systems
- H04L25/02—Details ; arrangements for supplying electrical power along data transmission lines
- H04L25/03—Shaping networks in transmitter or receiver, e.g. adaptive shaping networks
- H04L25/03006—Arrangements for removing intersymbol interference
- H04L2025/0335—Arrangements for removing intersymbol interference characterised by the type of transmission
- H04L2025/03375—Passband transmission
- H04L2025/03414—Multicarrier
Definitions
- This invention relates, in general, to a multi-cast communication system and a method of estimating channel impulse response (IR) therein, and is particularly, but not exclusively, applicable to communication environments employing space-time coding.
- the present invention is also applicable, without imposing limitation, to code division multiple access (CDMA) schemes, orthogonal frequency division multiplexing (OFDM) or the global system for mobile (GSM) communication, and also to systems having base stations configured to transmit on either a time-aligned or unsynchronised basis.
- CDMA code division multiple access
- OFDM orthogonal frequency division multiplexing
- GSM global system for mobile
- GSM, CDMA, and OFDM systems and those systems using space-time coding usually require estimation of impulse responses (IR's) between a terminal antenna and several base antennas, especially in instances when the relative signal strengths of the base stations are similar.
- IR impulse responses
- the physical channel through which propagation occurs can have a severely detrimental effect on the ability to recover data accurately, especially with increasing data rates. Consequently, by knowing the IR, compensation for channel-induced defects can be applied to improve accuracy in data recovery, e.g. through interference cancellation techniques. More especially, with multiple transmit elements at a base station, irrespective of whether there is more than one serving base station, multipath interference results in an inability to resolve individual channels.
- IR determination is particularly taxing at a handoff point at cell boundaries of, potentially, two or three serving base stations (or Node Bs in the context of CDMA and the Universal Mobile Telecommunications System (UMTS)).
- UMTS Universal Mobile Telecommunications System
- impulse responses can also be used to assist in downlink softhandover.
- interference cancellation coherent soft hand-off or space-time coding generally requires a more accurate estimate of channel propagation conditions (than that required with RAKE filtering or matched filtering).
- a long history of interference cancelling base station algorithms that yield indifferent null-steering performance lends support to this view.
- cyclic Steiner codes are found in the pilot tones for the time division duplex (TDD) component of European UMTS, as presented in the ETSI 3GPP Document TS25.211 “Transport channels and physical channels” v.3.2.0, 1999.
- TDD time division duplex
- random data sectors sandwich an observation window that is preceded by a cyclic prefix of a latter portion of the observation window.
- data in the observation window is a function purely of the pilot sequence (comprised from the combination of the cyclic prefix and data in the observation window) and is not corrupted by spurious unknown data in any way.
- the 3G Partnership Project (3GPP) have defined training sequences for TDD (time division duplex) having overall chip lengths of 256 and 512 chips; the overall lengths are derived from 192 chips and 464 chips of basic pseudo-random number sequence codes with, respectively, an additional cyclic prefix of either 64 chips and 114 chips.
- Each training sequences is designed to allow channel impulse response estimation for differing numbers of users, namely three users in the case of the 256-chip training sequence and eight users in the case of the 512-chip training sequence.
- the training sequences are utilised in the receiving unit to estimate the channel impulse response based on a complex cross-correlation (in real and imaginary phase and amplitude components) between received chips and a local replica of the training sequence.
- a complex cross-correlation in real and imaginary phase and amplitude components
- cyclic offsetting of Steiner codes allows utilisation of a fast Fourier transform (FFT) technique to solve individual channel impulse responses.
- FFT fast Fourier transform
- Steiner cyclic pilot codes can therefore be used in estimating, with a single correlator, channel impulse responses of multiple users that do not mutually interfere.
- Steiner codes may be Gold codes.
- cyclic redundancy may be avoided if a training sequence contains a sufficient number of chips, with the overall length of the training sequence determined by the prevailing dispersion conditions associated with the channel. Additionally, for estimating CIR, it is also necessary to consider the physical state of the receiving unit, since the channel for a slow moving or stationary receiving unit (e.g. a handheld device) is ostensibly stable, i.e. constant.
- ⁇ y ⁇ ⁇ s 1 , s 2 ⁇ circle over (x) ⁇ h 1 ⁇ + ⁇ s 2 , s 1 ⁇ circle over (x) ⁇ h 2 ⁇
- ⁇ circle over (x) ⁇ means a discrete-time convolution operation.
- the receiver output is correlated with the PN sequence of the first antenna, the impulse responses of the two distinct channels are recovered in superposed form with a relative time shift of half a block. If the maximum probable duration of the impulse responses is finite and known and less than half the PN code length, the two channel estimates are non-overlapping and orthogonal and can be recovered by slicing into two halves an output of a correlator block.
- the process extends easily to estimating M channels by splitting the generic PN sequence into M segments ⁇ s 1 , s 2 , . . .
- ⁇ s M ⁇ means a short symbol sequence
- transmissions from the base antenna transmit elements follow the sequences ⁇ S 1 , S 2 , . . . S M ⁇ , ⁇ S M , S 1 , . . . S 1 , . . . S M ⁇ 1 ⁇ , . . . ⁇ S M ⁇ 1 , S M , S M ⁇ 2 ⁇ .
- the processing block is correlated with only the first copy, ⁇ S 1 , S 2 , . . . S M ⁇ of the PN sequence whereupon, at the correlator output, the M different channel impulse responses separate out in time and appear in sequence.
- the cyclic head is different for each downlink path, but this is purely a transmitter burden, whereas the receiver samples the waveform and continues to see the same rotated training sequence. In this way, a common discrete Fourier Transform operation can be used to resolve multiple downlink channel impulse responses.
- a cyclic copy of the end of each rotated sequence may be prefixed at the start of the pilot block.
- the total extent of the transmitted pilot burst is 512+K samples of which the first K contaminated samples are discarded at the receiver.
- the maximum number M of channel impulse responses that can be estimated by the Steiner method is: M ⁇ N K
- N is the length of the training sequence (samples) and K is the maximum likely number of samples in the channel impulse response.
- a time domain channel estimation ⁇ circumflex over (n) ⁇ 1 (t) for pilot sequence s 1 (t) convolved through channel h(t) that is subject to noise n(t) may be obtained through a time-reversed correlation of the received sequence with a matched filter having the form s 1 * ( ⁇ t).
- the channel estimation takes the form ⁇ 1 ( ⁇ k).
- matched filtering of the PN sequence in the receiver can be performed through fast Fourier Transform (FFT) techniques. If the received data block of N samples is ⁇ y 1 , y 2 , . . . y N ⁇ (which could be a sequence like ⁇ S 1 , S 2 . . . S M ⁇ ), then FFT operation yields: ⁇ s 0 , s 1 ⁇ ⁇ ... ⁇ ⁇ s N - 1 ⁇ ⁇ ⁇ FFT ⁇ S ⁇ y 0 , y 1 ⁇ ⁇ ...y N - 1 ⁇ ⁇ ⁇ FFT ⁇ Y
- matched filtering operation in the time domain is equivalent to a point-by-point multiplication in the discrete Fourier domain, namely:
- ⁇ 1 ⁇ 0 , ⁇ 1 . . . ⁇ N/2 ⁇ 1 ⁇
- ⁇ 2 ⁇ N/2 . . . ⁇ N ⁇ 1 ⁇
- the Wiener least squares filter provides an equalisation technique that utilises a modified inverse filter that controls the white noise response of the filter, i.e. the undesired enhancement of thermal noise from the antenna.
- a modified inverse filter that controls the white noise response of the filter, i.e. the undesired enhancement of thermal noise from the antenna.
- STTD Space-time transmit diversity
- UTRA European UMTS Terrestrial Radio Access
- UTRA European UMTS Terrestrial Radio Access
- Utilization of the Wiener filter in a communication system environment is further discussed in the Applicant's co-pending European Patent application 01300520.2 (Applicant's reference 118721D-Hudson) having both a priority claim to U.S. patent application Ser. No. 09/488,721 and corresponding to the continuation-in-part application (Applicant's reference 11872IDUS041-Hudson) filed in respect thereof, all incorporated herein by reference.
- Equalisers and channel whiteners are generally not well conditioned, especially if the channel has zeros or deep minima in its frequency response.
- ⁇ 2 is the variance of the thermal noise level in the frequency domain. If the DFT is orthogonal, i.e. a unitary matrix operation, then this ⁇ 2 value is the same as the time domain noise variance per sample, but most FFT algorithms apply some form of scaling for which allowance must be made.
- PN training sequences sent from multiple base stations (or Node Bs) employing one or more transmit elements are subject to multipath that results in code cross-correlation and an inability at a receiver to resolve the individual channels and establish the individual channel-specific impulse responses. More specifically, whilst time alignment of base station transmissions may produce a summation of signals at the receiver (when employing appropriate windowing on a chip-by-chip basis with respect to identifiable correlation spikes), the receiver is only able to detect a composite channel impulse response that is unlikely to reflect accurately any of the actual transmission paths.
- the composite channel impulse response may be sufficient in the context of soft handover (in IS-95, for example), the composite channel impulse response is generally insufficient in third generation systems, including systems offering space-time coding.
- third generation systems including systems offering space-time coding.
- service providers to provide synchronicity between base station transmissions since synchronised transmissions increase infrastructure costs, such as through the necessary provision of an accurate timing reference.
- a method of determining channel impulse responses of a plurality of channels to a communication device comprising: performing transform operations on both a replica of a signal sequence s n and a received training sequence y n by the communication device in at least one burst, the received training sequence y n being the signal sequence as received through a channel, the transform operations arranged to generate a multiplicity of signal sequence frequency bins and a multiplicity of training sequence frequency bins; performing point-by-point operations between corresponding signal sequence frequency bins and training sequence frequency bins; and concatenating the point-by-point operations associated with the channel to provide a composite frequency response for the channel, the composite frequency response allowing, in the time domain, generation of the channel impulse response for the channel.
- MMSE minimum mean square error
- the MMSE estimation technique preferably employs a Weiner filtering operation providing:
- Cov(B) is a covariance matrix of thermal noise
- S H Y is a matched filter operation arranged to minimize the signal to noise ratio but not to remove mutual interference between channel estimates
- (S H S+Cov(B)) ⁇ 1 is a decoupling matric that removes the coupling between different channels caused by any non-ideal nature of the training sequences.
- the number of bursts sent to the communication device from each transmitting unit in communication contact therewith is calculated as a multiplication of: a number of transmitting elements in a transmit array of a transmitting unit; and a number of transmitting units in communication contact with the communication device.
- a method of determining channel impulse responses of channels incident to a communication device comprising: and transmitting multiple quasi-orthogonal pseudo-noise sequences as bursts from multiple base stations each having at least one transmit element, successive bursts providing an extended training sequence for use in channel estimation at the communication device; applying a Wiener frequency domain MMSE deconvolution with frequency domain spatial decoupling matrices to generate channel impulse response estimates for the channels.
- a further aspect of the present invention provides a computer program product for a processor within a receiver device, the computer program product comprising: code that performs transform operations on both a replica of a signal sequence s n and a received training sequence y n received by the communication device in at least one burst, the received training sequence y n being the signal sequence as received through a channel, the transform operations arranged to generate a multiplicity of signal sequence frequency bins and a multiplicity of training sequence frequency bins; code that performs point-by-point operations between corresponding signal sequence frequency bins and training sequence frequency bins; and code that concatenates the point-by-point operations associated with the channel to provide a composite frequency response for the channel, the composite frequency response allowing, in the time domain, generation of the channel impulse response for the channel; wherein the codes reside in a computer readable medium.
- a communication device having a receiver coupled, in use, to receive a plurality of channels supporting a signal sequence y n and training sequence bursts, the communication device having: a signal processing platform to perform transform operations on both a replica of a signal sequence s n and a received training sequence y n received by the communication device in at least one burst, the received training sequence y n being the signal sequence as received through a channel, the transform operations arranged to generate a multiplicity of signal sequence frequency bins and a multiplicity of training sequence frequency bins; the signal processing platform arranged to perform point-by-point operations between corresponding signal sequence frequency bins and training sequence frequency bins; and the signal processing platform further arranged to concatenate the point-by-point operations associated with the channel to provide a composite frequency response for the channel, the composite frequency response allowing, in the time domain, generation of the channel impulse response for the channel.
- Yet another aspect of the present invention provides a communication receiver comprising: means for receiving, in use, multiple quasi-orthogonal pseudo-noise sequences as bursts from multiple base stations each having at least one transmit element, successive bursts providing an extended training sequence for use in channel estimation at the communication receiver; and means for applying a Wiener frequency domain MMSE deconvolution with frequency domain spatial decoupling matrices to generate channel impulse response estimates for the channels.
- the present invention provides a mechanism for resolving a composite channel into a plurality of sub-channels with which specific individual channel impulse responses can be associated with and calculated using a numerically efficient fast transform technique.
- individual channels can be resolved to generate channel impulse responses to aid in data recovery.
- the present invention is particularly applicable in the estimation of the channel impulse responses between multi-element base stations (in different cells) and the receive antenna array of a subscriber unit located at a 2-way or 3-way handoff point where interference is generally very high.
- the present invention provides increased accuracy in channel estimation, with smaller errors experienced than in an uncoupled case. Indeed, tests have shown that normalised mobile station errors in channel estimation for the present invention can achieve results of 14.8 decibels (compared with 6.1 dB and 7.1 dB for techniques solely employing a matched filter and Weiner filter, respectively, in channel impulse response estimation).
- the present invention even in conditions of varying base station transmit power, provides an improved accuracy in channel impulse response estimation, which accuracy is reflected in a general measured improvement of about 7 dB over a range of transmit signal strengths of ⁇ 20 dB for second base station (relative to a carrier signal from a first base station being set at +3 dB above thermal noise at the clip level).
- the present invention is therefore able to operate in interference and soft handover environments where interference becomes a problem.
- a solution for estimating several downlink channels from different base antennas to a single terminal antenna by the use of multiple training bursts has been described.
- the method involves the use of N ⁇ N decoupling matrices in the Fourier domain to solve for N channels and gives superior results compared with attempts to use matched filters designed for added white Gaussian noise (AWGN) channels.
- AWGN white Gaussian noise
- FIG. 1 is a schematic block diagram of a basic transmitter and receiver architecture 10 in which processing circuitry may be adapted to support the underlying principles of the present invention
- FIG. 2 is a diagrammatic illustration of a typical cellular communication system
- FIG. 3 shows a mechanism and schematic block diagram for channel impulse response estimation that may be adapted to support the principles of the preferred embodiments of the present invention
- FIG. 4 is a transmission regime for a training sequence according to a preferred embodiment of the present invention.
- FIG. 5 a schematic block diagram of the channel estimation process and architecture according to a preferred embodiment of the present invention.
- FIG. 6 is a Steiner code variant of FIG. 4.
- Steiner codes may also be used in OFDM systems though, in this case, it may be preferred to use the intrinsic OFDM symbol for training sequences.
- the same basic pilot sequence can be time shifted and re-used (with properly determined cyclic headers) to function for a number of different downlink channels, and only one FFT correlation process is needed to solve for all the channels simultaneously.
- the technique is ideal for wideband fat pipe systems where the same user signal is radiated from different antennas of a transmit diversity antenna or a space-time coded antenna system.
- Channel estimation by this method is accurate enough to allow adequate interference cancellation of intercell interference, which is usually quite difficult to achieve in CDMA systems due to low grade estimates of the interference parameters.
- Transmit and receive chains 100 , 101 may be combined in a transceiver arrangement of a station, such as a base station/Node B or a mobile device of a cellular radio system or the like.
- a station such as a base station/Node B or a mobile device of a cellular radio system or the like.
- Individual transmit and receive chains could, of course, be implemented in isolation, whereby unidirectional (as opposed to bi-directional) communication is supported across, for example, an air-interface, such as a CDMA or 3G radio environment (although the present invention is more widely applicable to multi-point transmission systems).
- signal source 102 generates signals 104 which are encoded by encoder 106 , such as a half rate turbo coder.
- Encoded signals 107 are modulated and subjected to CDMA spreading by modulator/spreader 108 and then filtered by pulse shaper digital filter 110 .
- a digital to analog (D/A) converter is arranged to produce analog signals 114 which are generally filtered in a second filter 116 to limit any aliasing effect at transmission.
- a mixer 118 up-converts baseband signals 120 to transmission frequencies prior to amplification in power amplifier 122 and transmission from antenna 124 .
- some of the functional blocks in the transmit chain can be realised as discrete or collocated into a single chip or processing block.
- Transmitted signals 126 are received by receive antenna 128 of an addressed station.
- Received signals 130 are communicated to a down-converting mixer 132 via an amplifier 134 , which down-converting mixer typically produces an intermediate frequency signal for initial signal processing.
- a filter 134 isolates a desired frequency spectrum 136 for signal processing, which frequency spectrum is converted to a digital domain representation 137 by analog to digital (A-D) converter 138 .
- the digital domain representation 137 is digitally filtered in digital channel pulse shaper filter 140 and then applied in series to a combined demodulator/equaliser slicer and RAKE despreader 142 and then a channel decoder 144 .
- Recovered information 145 is ultimately received by terminal receiving equipment (TRE) 146 . It will be understood that channel filtering generally distorts the channel impulse response and the channel filter becomes part of the unknown channel.
- the transmit and receive chains 100 , 101 are invariably micro-processor ( ⁇ P) controlled operations.
- a controller 150 and associated memory 152 (which may be a combination of random access (RAM) and read only (ROM)) is shown as being common to both the transmit and receive chains 100 , 101 .
- the memory 152 stores control algorithms, such as equalisation and modulation algorithms, and also operands and incident data is subject to signal processing requirements.
- common circuitry between the transmit and receive chains can be shared to reduce component count, subject to the inclusion of suitable switching and regulating circuitry.
- at least some of the functions within one or both of the transmit and receive chains 100 , 101 can be implemented either entirely or partially as code, e.g. equalisation and demodulation. It is these code blocks, application specific integrated circuits or memory modules that can be adapted or up-graded to support the present invention.
- Wideband CDMA-specific components can be replaced or substituted to support an arbitrarily selected communication protocol, e.g. an FDD environment employing TDM techniques or a multicarrier environment.
- FIG. 2 is a diagrammatic illustration of a typical cellular communication system 170 showing a subscriber unit 172 (preferably having multiple receive elements 174 - 180 ) at cell boundaries between three potentially serving base stations 182 - 186 .
- a subscriber unit 172 preferably having multiple receive elements 174 - 180
- transmit signal strengths For an equidistant displacement of the subscriber unit from the base stations, one could expect that transmit signal strengths to be roughly equal, subject to the respective paths and the associated physical environments.
- the general purpose of FIG. 2 is to illustrate a physical environment in which the present invention finds exemplary application.
- the cellular communication system 170 is shown with three cells 188 - 192 and a single subscriber unit 172 , but clearly cellular systems may include many cells in multiple layers, with each cell servicing a multiplicity of subscriber units.
- Incoming signals 126 to the subscriber unit 172 are received from the antenna 128 at a transmission rate of I /T ch of the system.
- an entire slot of a frame is sampled (A/D converted) at the Nyquist rate and read into memory 152 (of FIG. 1) prior to commencement of information recovery.
- the incoming signals 126 can be received from any digital source of signals and are not restricted to wireless communications, with the base stations utilising single or multiple radiating elements in each transmit antenna array.
- Signal processing of incoming signals 126 for optimised data recovery is clearly subject to knowledge of the channel impulse response (i.e. the “channel spectrum”), with this determined from training sequences sent from the base stations according to a predetermined regime, e.g. once per slot, once per frame or on any other appropriate basis.
- An exemplary mechanism for data recovery is described in the aforementioned European and U.S. patent applications (e.g. EP 01300520.2).
- FIG. 3 shows a mechanism for channel impulse response estimation that is adapted to support the principles of the preferred embodiment of the present invention.
- a training sequence 250 preferably located in and extractable from each slot of a frame, falls incident on receive antenna 128 , which training sequence is demodulated in the receive chain (as will be readily appreciated) to recover the random sequence y k , e.g. a generated pseudo-random number sequence.
- the form and structure of the training sequence will be described in detail later, since the structure is inexorably associated with an ability to resolve individual channels for channel impulse response estimation according to the present invention.
- the recovered random sequence y k is subjected to a DFT function 252 to produce a channel sequence spectrum y k 254 .
- a DFT function 252 Within the memory 152 associated with the receive chain there is stored a replica of the original training sequence s k 260 , which original training sequence s k 260 has a corresponding known sequence spectrum s k 262 obtained by subjecting the original training sequence s k 260 to an FFT function.
- the known sequence spectrum s k 262 may simply be stored in the memory since it is this sequence spectrum s k 262 that is used to assess the channel impulse response.
- the DFT function 252 may be performed by a specific digital signal processor (DSP) or the processor 150 of FIG. 1.
- DSP digital signal processor
- the channel spectrum therefore assumes the form of an x-point, e.g. 512-point, DFT sample stored temporarily in, for example, RAM.
- an impulse response spectrum H k 268 that can be stored in memory for the duration of at least the related slot and longer if desired.
- processing overhead is reduced at the expense of accuracy in any correction of the variations in the channel due to Doppler.
- time alignment of the received and transmitted training sequences is required prior to cross-correlation.
- the impulse response spectrum H k 268 may be further refined and so it is subjected to an IFFT function 270 to generate an estimated time domain representation h k thereof having an arbitrary number of taps/channels that can be used as a matched filter, if desired.
- each tap is representative of a weight for the channel impulse response.
- trimming of the number of taps reduces the channel impulse response to manageable processing levels, with the reduction reflecting the greatest expected channel impulse response (CIR) duration (presently understood to be seventy-one chips in length in 3GPP, although this number is an arbitrarily selected cut-off).
- CIR channel impulse response
- a control processor 272 From the reduced number of taps in the channel impulse response, most values will approximate to zero and so a control processor 272 , based on a level or number threshold, selects only those N significant taps that most noticeably reflect the channel to produce a best estimate channel impulse response h′ k 274 . Selection of the N most significant taps may simply force lesser taps to be forced to zero. By limiting the channel impulse response to the most significant taps, processing is reduced and a final error in the channel limited. In the latter respect, it will be understood that all tap values will have an associated error from thermal noise, channel interference and other adverse channel and processing artefacts, so the compounding of errors is mitigated.
- FIG. 4 Concerning transmission of a training sequence according to a preferred embodiment of the present invention, reference is made to FIG. 4.
- the structuring of base station transmissions (in the timing frame of FIG. 4) is assumed to reflect a three site system in which each of three base stations includes a single transmit element.
- the basic principle employed in the specific embodiment of FIG. 4 can be developed for multi-element transmit arrays from two or more base stations.
- FIG. 4 is representative of successive training sequence transmission bursts from each of three base stations (Base TX 1 , Base TX 2 and Base TX 3 ).
- the number of training sequences transmitted from all transmit elements follow a squared law, i.e.
- bursts from the various base stations are preferably time aligned at transmission, although a windowing function at the receiver (that steps through a chip-wise time correlation) may be employed to time align the transmitted sequences snk. Since channel delay is generally no greater than about 20 ⁇ s, then the receiver need only step through a chip count commensurate with the maximum channel delay. For example, at an operating frequency (chipping rate) of one megahertz (1 MHz), 20 ⁇ s correspond to twenty chips.
- each base station transmits a finite (predetermined) length of training sequence s, which training sequence may vary from 1-chip or more.
- training sequence may vary from 1-chip or more.
- each burst will be tens of chips in length and preferably at least about sixty chips in length and most preferably in excess of about one hundred chips.
- the length of the training sequence is restricted to manageable levels to avoid inefficient use of communication resource for more important data transmissions.
- the nomenclature adopted in FIG. 4 with respect to the bursts follows the convention that the first subscript (n) represents an identity of the transmitting base station whereas the second subscript (k) represents the sequence number. In the context of Base TX 1 , FIG.
- a channel sequence spectrum y k is formed (for each burst (t 1 -t 3 )) from the summation of the individual sequences s 11 , S 21 , S 31 from the base stations transmitting in that burst.
- the length of the PN code must be at least M times the maximum channel dispersion.
- the PN code length must be at least MN times the channel impulse response duration and each element of each base station would transmit an end-around rotated version of the code with a different unique offset.
- the differing round-trip propagation times to the subscriber unit must also be taken into account in the channel model so codes becomes increasingly extended.
- a more flexible option for allowing expansion of the number of serving base stations is to use an alternating sequence of different Steiner codes, each of which on its own is only just long enough for the number of elements in a single base station to be resolved.
- each base station having a single transmitting element. If the N base stations each with a single element are received by a single element antenna of a subscriber unit, such as cellphone or terminal, then if the N bases simultaneously send N strings of N different pseudorandom bursts and such that there are N 2 different sequences altogether, then the individual channel impulse responses can be resolved at the terminal.
- the present invention is particularly interested in a three-base station situation which, statistically, occurs most frequently.
- the base stations are preferably synchronised to a time accuracy much less than the duration of any cyclic prefix (which is typically of the order of about 10 ⁇ s to 20 ⁇ s for urban microwave propagation).
- the m th received burst is now the convolution:
- the present invention applies a DFT operation to both the received sequence y n and the various local replicas of the training sequences S mn , and then does a multiplication together of the corresponding frequency bins of the received signal sequence Y n (being the signal sequence s n as received through a channel) with the corresponding frequency bins of the replica of the training sequence S mn . Summation (i.e.
- the process of the present invention generally involves periodic buffering, for example, of frequency bin data and vector results pertaining to channel impulse responses, as will be appreciated by the skilled addressee.
- the channel is assumed constant for the duration of the burst events with respect to slow moving subscriber units, e.g. mobile units having a velocity of less than about ten kilometres per hour (10 kph).
- the k th frequency bin received for the first burst can be expressed as the sum of components from the base stations and their channels:
- the k th frequency bin for the second burst can be expressed as:
- the kth frequency bin for the third burst is:
- MMSE minimum mean square error
- Cov(B) is the covariance matrix of the thermal noise, which is often approximated by an identity matrix ⁇ 2 I.
- the equation immediately above can be considered as two entities, namely as a matched filter SHY arranged to minimize the signal to noise ratio but not to remove mutual interference between channel estimates, followed a decoupling matric (S H S+Cov(B)) ⁇ 1 that removes the coupling between different channels caused by the non-ideal nature of the PN sequences.
- the inverse DFTs for each radio channel are therefore of the form: ( H 1 ( 0 ) H 1 ( 1 ) H 1 ( 2 ) ⁇ H 1 ( z ) ) ⁇ ⁇ iDFT ⁇ ( h 1 ( 0 ) h 1 ( 1 ) h 1 ( 2 ) ⁇ h 1 ( z ) ) , ( H 2 ( 0 ) H 2 ( 1 ) H 2 ( 2 ) ⁇ H 2 ( z ) ) ⁇ ⁇ iDFT ⁇ ( h 2 ( 0 ) h 2 ( 1 ) h 2 ( 2 ) ⁇ h 2 ( z ) ) ,
- the decoupling matrix term S H S is a matrix product, where S H is the conjugate transpose of the sequence, i.e. the transposed matrix with all elements complex conjugated.
- each channel concatenation of the numerous frequency bins allows generation of a time domain vectors of the channel impulse response for a channel, the time domain vectors generated from an inverse DFT process within a suitable processing block, such as an ASIC or control processor 150 (of FIG.
- STC space time coding
- FIG. 5 which is generally complementary to FIGS. 1, 3 and 4 , there is shown a schematic block diagram of the channel estimation process and architecture 500 of a preferred embodiment of the present invention, the process based on a two base station (BS 1 and BS 2 ) transmission environment having two training bursts.
- the training sequences s x ( ⁇ ) are, in this exemplary case, Gold codes, with individual first 502 and second 504 training sequences transmitted in a first burst 506 .
- the first training sequence 502 is subjected to first channel 508
- the second training sequence is subjected to a second channel 510 .
- Both channels are combined at the receiver 512 and are further subject to a first noise component (N 1 ( ⁇ )) 513 .
- first and second matched filters 514 and 516 provide a time reversed conjugated inversion of the respective first and second training sequences 502 and 504 , with outputs from the first and second matched filters 514 and 516 provided to a frequency domain coupler 518 supporting the frequency domain decoupling matrix (S H S+Conv(B)) ⁇ 1 .
- Third 520 and fourth 522 training sequences transmitted in a second burst 524 are respectively subjected to first channel 508 and second channel 510 . Both channels are combined at the receiver 512 and are further subject to a second noise component 526 (typically different to the first noise component).
- third 528 and fourth 530 matched filters provide a time reversed conjugated inversion of the respective third and fourth training sequences 520 and 522 , with outputs from the third and fourth matched filters 528 and 530 provided to the frequency domain coupler 518 .
- the frequency domain coupler then provides channel impulse response vectors ⁇ circle over (H) ⁇ 1 ( ⁇ ) and ⁇ circle over (H) ⁇ 1 ( ⁇ ) (reference numerals 532 and 534 ) for the first and second channels, respectively, based on the foregoing point-by-point manipulation of individual (frequency domain) frequency bins.
- the preferred embodiment of the present invention therefore shows how accurate channel estimation is possible through the use of Wiener frequency domain MMSE deconvolution combined with frequency domain spatial decoupling matrices, with quasi-orthogonal Gold codes allocated to base stations and their antenna elements.
- the principles of the present invention can also be applied to resolve multiple channels by a single training burst; this has particular application in OFDM systems where it may not be possible to transmit Steiner codes because of hardware constraints.
- the present invention can be modified, in the fashion now shown, to operate with a single arbitrary training sequence yet still resolve multiple channels in a least squares sense.
- a single training burst situation is algebraically undetermined in the two channel case. If the burst is of length L, there are 2L unknowns in the two channels which cannot be determined from L observations at one antenna. However, if there are also 1 ⁇ 2 L linear constraints associated with each channel impulse response the equations become solvable again.
- the simplest constraints are that the channel impulse responses ⁇ h 0 . . .
- the training sequence transmissions of FIG. 4 are implemented as Steiner cyclic training sequence variant; this is shown in FIG. 6 in which successive bursts 602 and 604 from different base stations BS 1 and BS 2 contain repeated sequence portions of an entire training sequence.
- This particular embodiment of the present invention offers an optimum combination of frequency domain Wiener filtering and MMSE spatial decoupling for the estimation process.
- the high accuracy of channel estimation that the combination of techniques offers is a desirable if not essential for coherent null steering and soft hand off in CDMA and OFDM.
- the sequences ⁇ s 11 ⁇ , ⁇ s 21 ⁇ , ⁇ s 12 ⁇ , ⁇ s 22 ⁇ are four linearly independent random sequences transmitted in pairs from the two antennas as shown. These sequences transform into the DFT domain as s 11 , S 21 , S 12 , S 11 . Similarly the channel impulse responses are H 1 , H 2 in the DFT domain (for the two channels in the exemplary case of a two base station system having single transmit elements).
- the receiver e.g. receiver chain samples the two received blocks and, via a DFT function, transforms to the Frequency domain as Y 1 and Y 2 .
- the required guard intervals, which prevent dispersion contamination by unknown data, are already provided in the Steiner sequences and additional, i.e.
- Cyclic shifting of channel impulse responses h 2 , h 4 and h 6 takes into account the reverse shift as detailed immediately above with the effect that the six sequences received at the antenna of the subscriber (or other addressed unit) are Y 1 , Y 2 , Y 3 , Y 4 , ⁇ Y 5 and ⁇ Y 6 . Moreover, the six sequences are obtained from a repetition of only three Steiner codes that are individually and uniquely assigned to each base station, i.e. both transmit elements send identical sequences in the same burst, with the subscriber unit generating a cyclically shifted channel impulse response h x for one of the two radiating elements of the base station's transmit array.
- This reverse shift manipulation results in only three different PN sequences being utilised in this particular embodiment, with the channel impulse responses of FIG. 7 taking the form ( h 1 +h 2 ), ( h 3 + h 4 ) and ( h 5 + h 6 ) to provide the received sequence Y 1 , Y 2 , Y 3 , Y 4 , Y ⁇ 5 and ⁇ Y 6 .
- the preferred embodiment that uses Steiner codes for m base antenna elements can be used in multiple cells and MMSE channel estimation is obtainable for a number n of bases giving a total of nm downlink channels.
- Different cells will use a different basic PN code, whereas the elements within a single cell will use the Steiner cyclic offsets of a single PN code.
- the extra workload (processing overhead) involved is the inversion of an n ⁇ n matrix in each frequency bin.
- Embodiments of the invention may be implemented as computer program code encoded on a computer program product for use with a computer system. It is expected that such a computer program product may be distributed as a removable medium with accompanying printed or electronic documentation (e.g. shrink-wrapped software), preloaded with a computer system or distributed from a server or electronic bulletin board over a network (e.g. the Internet or World Wide Web).
- a series of computer instructions can therefore either be fixed on a tangible medium or fixed in a computer data signal embodied in a carrier wave that is transmittable to a computer system using wireline or wireless transmission techniques.
- the present invention can find application as downloadable code in a software radio.
- the removable i.e.
- tangible) medium may be a computer readable media, such as a diskette, CD-ROM, DVD-ROM or RAM, fixed disk, magneto-optical disks, ROMs, flash memory or magnetic or optical cards.
- the series of computer instructions embodies all or part of the functionality previously described herein with respect to the system.
- Software embodiments of the invention may be implemented in any conventional computer programming language.
- preferred embodiments may be implemented in a procedural programming language (e.g. “C”) or an object oriented programming language (e.g. “C++”).
- the duration of the OFDM training burst is N S sub-carrier symbols and there are N F sub-carriers then the burst effectively has N S *N F samples or chips which is quite a substantial number. In practice, this means that multiple channel estimation in OFDM might not be too difficult.
- the lower limit for the duration of the training sequences would be that it must be capable of supporting an orthogonal, or at least a linearly independent, set of codes for say m base station antennas seen from the terminal (in one or more cells). Superficially, this would require m full sub-carrier slots and for HSD with 150 ⁇ s slots we need a duration of 150 ⁇ s.
- cyclic prefixes could be replaced by blank (zero) carriers to provide isolation between burst sequences.
- base station refers to serving infrastructure irrespective of the form of air-interface adopted by the exemplary CDMA-based architecture of the preferred embodiment.
- base station should be construed broadly and, where necessary, to include references to communication relay devices. While the main applications are in channel estimation on a downlink for CDMA and OFDM in order to apply coherent soft hand-off and interference cancellation in locations where two or more base stations are at similar ranges and the weaker base stations, if ignored, cause mutual interference, the preferred embodiments are not intended to be limiting to these specific arrangements.
Abstract
Multiple Steiner codes are transmitted as bursts (s11, S12, . . . S33 , 560, 524) from multiple base stations (182, 184, 186) having one or more transmit elements (174, 176, 178, 180), with successive bursts providing an extended training sequence for use in channel estimation at an addressed unit (172), such as a mobile handset. Accurate channel estimation is possible through the use of Wiener frequency domain MMSE deconvolution (518) combined with frequency domain spatial decoupling matrices, with quasi-orthogonal pseudo-noise sequences (502, 504, 520, 522) allocated to base stations and their antenna elements. The use of Steiner codes to supplement Wiener frequency domain MMSE deconvolution and frequency domain spatial decoupling results in the possibility of allocating only a single training sequence to each base station provided that the training sequence is of sufficient length to encompass all multiple time-translated channel impulse responses (H).
Description
- This invention relates, in general, to a multi-cast communication system and a method of estimating channel impulse response (IR) therein, and is particularly, but not exclusively, applicable to communication environments employing space-time coding. The present invention is also applicable, without imposing limitation, to code division multiple access (CDMA) schemes, orthogonal frequency division multiplexing (OFDM) or the global system for mobile (GSM) communication, and also to systems having base stations configured to transmit on either a time-aligned or unsynchronised basis.
- GSM, CDMA, and OFDM systems and those systems using space-time coding usually require estimation of impulse responses (IR's) between a terminal antenna and several base antennas, especially in instances when the relative signal strengths of the base stations are similar. As will be understood, the physical channel through which propagation occurs can have a severely detrimental effect on the ability to recover data accurately, especially with increasing data rates. Consequently, by knowing the IR, compensation for channel-induced defects can be applied to improve accuracy in data recovery, e.g. through interference cancellation techniques. More especially, with multiple transmit elements at a base station, irrespective of whether there is more than one serving base station, multipath interference results in an inability to resolve individual channels. Indeed, even orthogonally structured data (such as different and time dispersed training sequences) can become cross-correlated (in the face of multipath interference) and hence unusable to resolve individual channels/paths in the context of a deterministic IR approach. Furthermore, it will be appreciated that IR determination is particularly taxing at a handoff point at cell boundaries of, potentially, two or three serving base stations (or Node Bs in the context of CDMA and the Universal Mobile Telecommunications System (UMTS)). At cell-boundary handover, the issue of IR is complicated by that fact that downlink carrier to interference ratios (CIRs) can be zero or negative.
- When available, impulse responses can also be used to assist in downlink softhandover.
- The use of matched filtering of standard training sequences to determine channel IR's is considered adequate to drive fingers of a RAKE filter in CDMA applications, such as IS-95 and CDMA2000, given that incoherent soft handoff is also allowed. However, more recent cellular system proposals will stretch matched filtering techniques to their limits and beyond due to the use of higher data throughputs (with more bits per symbol, e.g. higher quadrature amplitude modulation QAM levels) requiring higher energy per bit/noise floor (E b/No) than existing systems, such as IS-95. Such higher data rate cellular systems include the Enhanced Data-rate for GSM Evolution (EDGE) system.
- In any event, interference cancellation, coherent soft hand-off or space-time coding generally requires a more accurate estimate of channel propagation conditions (than that required with RAKE filtering or matched filtering). In this respect, a long history of interference cancelling base station algorithms (that yield indifferent null-steering performance) lends support to this view.
- In terms of proposed 3G (third generation) cellular systems, it is known to use training sequences with a cyclic prefix for pilot tones in orthogonal frequency division multiplexing (OFDM) and CDMA. When a channel has an impulse response of known maximum duration, the use of Steiner codes allows re-use of the same training sequence with a time-offset method to measure simultaneously the channel impulse responses of several users or several antenna with a single fast Fourier transform (FFT) operation Steiner codes are discussed in the paper “A comparison of uplink channel estimation techniques for MC/JD-CDMA transmission systems” by B. Steiner and R. Valentin, Proceedings IEEE 5th International Symposium on Spread Spectrum Techniques and Applications 1998, Volume: 2, pp. 640-646. Indeed, cyclic Steiner codes are found in the pilot tones for the time division duplex (TDD) component of European UMTS, as presented in the ETSI 3GPP Document TS25.211 “Transport channels and physical channels” v.3.2.0, 1999. In terms of a frame structure for a pilot tone, random data sectors sandwich an observation window that is preceded by a cyclic prefix of a latter portion of the observation window. Provided that the duration of the cyclic prefix exceeds the channel impulse response, then data in the observation window is a function purely of the pilot sequence (comprised from the combination of the cyclic prefix and data in the observation window) and is not corrupted by spurious unknown data in any way.
- The 3G Partnership Project (3GPP) have defined training sequences for TDD (time division duplex) having overall chip lengths of 256 and 512 chips; the overall lengths are derived from 192 chips and 464 chips of basic pseudo-random number sequence codes with, respectively, an additional cyclic prefix of either 64 chips and 114 chips. Each training sequences is designed to allow channel impulse response estimation for differing numbers of users, namely three users in the case of the 256-chip training sequence and eight users in the case of the 512-chip training sequence.
- The training sequences are utilised in the receiving unit to estimate the channel impulse response based on a complex cross-correlation (in real and imaginary phase and amplitude components) between received chips and a local replica of the training sequence. In this regard, it is usual, on a per channel basis, to take a correlation of the channel impulse response (h) with the sequence (s) from the transmitter. More particularly, from a single base station having multiple transmit elements, cyclic offsetting of Steiner codes allows utilisation of a fast Fourier transform (FFT) technique to solve individual channel impulse responses. Steiner cyclic pilot codes can therefore be used in estimating, with a single correlator, channel impulse responses of multiple users that do not mutually interfere. Steiner codes may be Gold codes.
- As will be understood, the requirement for cyclic redundancy to mitigate data corruption caused by multipath may be obviated provided that the length of the transmitted training sequence (or pilot tone) is sufficiently long. In generality, cyclic redundancy may be avoided if a training sequence contains a sufficient number of chips, with the overall length of the training sequence determined by the prevailing dispersion conditions associated with the channel. Additionally, for estimating CIR, it is also necessary to consider the physical state of the receiving unit, since the channel for a slow moving or stationary receiving unit (e.g. a handheld device) is ostensibly stable, i.e. constant.
- By way of practical explanation of Steiner code operation from a dual element array of a base station transmitter, it will be appreciated that, in estimating the two channels from the two radiating elements to a single receive antenna, the two radiating elements use a common generic pseudorandom number (PN) training sequence {s 1, s2} which is end-around shifted (in this case by half a block) to {s2, S1} for the second element. The two channel impulse responses are {h1}, {h2} and the receiver antenna sees the superposition of the two convolved sequences:
- {y}={s 1 , s 2 }{circle over (x)}{h 1 }+{s 2 , s 1 }{circle over (x)}{h 2}
- where {circle over (x)} means a discrete-time convolution operation. When the receiver output is correlated with the PN sequence of the first antenna, the impulse responses of the two distinct channels are recovered in superposed form with a relative time shift of half a block. If the maximum probable duration of the impulse responses is finite and known and less than half the PN code length, the two channel estimates are non-overlapping and orthogonal and can be recovered by slicing into two halves an output of a correlator block. Clearly the process extends easily to estimating M channels by splitting the generic PN sequence into M segments { s 1, s 2, . . . s M}, where {s} means a short symbol sequence, and wherein transmissions from the base antenna transmit elements follow the sequences {S 1, S 2, . . . S M}, {S M, S 1, . . . S 1, . . . S M−1}, . . . {S M−1, S M, S M−2}.
- At the receive antenna, the processing block is correlated with only the first copy, {S 1, S2, . . . SM} of the PN sequence whereupon, at the correlator output, the M different channel impulse responses separate out in time and appear in sequence. Clearly, the cyclic head is different for each downlink path, but this is purely a transmitter burden, whereas the receiver samples the waveform and continues to see the same rotated training sequence. In this way, a common discrete Fourier Transform operation can be used to resolve multiple downlink channel impulse responses.
- As previously indicated, in order to avoid contamination with unknown data which usually immediately precedes the training sequence, a cyclic copy of the end of each rotated sequence may be prefixed at the start of the pilot block. In other words, when working with, say, 512-point processing blocks and when the duration of the channel impulse response is K samples, the total extent of the transmitted pilot burst is 512+K samples of which the first K contaminated samples are discarded at the receiver.
-
- where N is the length of the training sequence (samples) and K is the maximum likely number of samples in the channel impulse response.
- Unfortunately, with Steiner codes, the resolution of base stations in different cells is much less attractive. Specifically, whilst it would be possible to continue to expand the Steiner method with ever increasing numbers of built in channels M (e.g. perhaps twice or three times the number needed for one base station), estimating more channels needs longer training sequences and synchronisation of the relevant base stations. Increasing training sequence length, however, is not the main difficulty; a bigger problem is that this Steiner solution would effectively constrain all the bases to use one and the same fundamental PN sequence and this would not allow addressed units to discriminate between bases by different codes when they are searching for hand-off possibilities. Steiner is also inflexible since there is contention over the order in which the bases should cycle their training sequences. This contention will appear at all six interfaces of the base's cell with other cells in a hexagonal layout and so sequence cycling must be set up to be compatible with all adjacent sites that could be affected.
- As will now be appreciated, communication systems demand the resolution of multiple channels that combine to provide a composite channel impulse response C from observed training sequences S transmitted by several base stations each with multiple antenna elements. In this regard, a time domain channel estimation {circumflex over (n)} 1(t) for pilot sequence s1(t) convolved through channel h(t) that is subject to noise n(t) may be obtained through a time-reversed correlation of the received sequence with a matched filter having the form s1* (−t). In the frequency domain, the channel estimation takes the form Ĥ1(ωk).
- For the purposes of channel estimation, matched filtering of the PN sequence in the receiver can be performed through fast Fourier Transform (FFT) techniques. If the received data block of N samples is {y 1, y2, . . . yN} (which could be a sequence like {S 1, S 2. . . S M}), then FFT operation yields:
- In other words, matched filtering operation in the time domain is equivalent to a point-by-point multiplication in the discrete Fourier domain, namely:
- Ĥ k (MF) =Y k ·S k * k=0 . . . 2n−1
-
- with two different channel estimates contained in the semi-sequences of { h}, namely:
- {ĥ} 1 ={ĥ 0 , ĥ 1 . . . ĥ N/2−1}
- {ĥ} 2 ={ĥ N/2 . . . ĥ N−1}
- Of course, once in the frequency domain, sidelobes present in the frequency spectrum in a channel estimation circuit containing a matched filter may be minimised through the use of a Wiener (least squares) filter technique.
- The Wiener least squares filter provides an equalisation technique that utilises a modified inverse filter that controls the white noise response of the filter, i.e. the undesired enhancement of thermal noise from the antenna. The paper “Smart Antennas for Third Generation Mobile Radio Systems” by Martin Haardt (Siemens), Stanford Colloquium on Smart Antennas”, July 1999, describes channel equalisation in terms of the Wiener filtering response, and explores how two or more receiving antennas can be included in the description of the received data. A further paper by H Sari et al titled “Transmission Techniques for Digital TV Broadcasting”, IEEE communications magazine 33(2) February 1995, discusses channel equalisation in the context of the Wiener filter mechanism. Space-time transmit diversity (STTD) is included in the standards for 3G cellular systems in the European UMTS Terrestrial Radio Access (UTRA) system and similar systems in the American CDMA2000 proposals. Consequently, it is important for these STTD systems to implement efficiently data recovery and equalisation algorithms. Utilisation of the Wiener filter in a communication system environment is further discussed in the Applicant's co-pending European Patent application 01300520.2 (Applicant's reference 118721D-Hudson) having both a priority claim to U.S. patent application Ser. No. 09/488,721 and corresponding to the continuation-in-part application (Applicant's reference 11872IDUS041-Hudson) filed in respect thereof, all incorporated herein by reference. Equalisers and channel whiteners are generally not well conditioned, especially if the channel has zeros or deep minima in its frequency response. The stable minimum mean square error (MMSE) Wiener filter solution for the channel is therefore:
- where σ 2 is the variance of the thermal noise level in the frequency domain. If the DFT is orthogonal, i.e. a unitary matrix operation, then this σ2 value is the same as the time domain noise variance per sample, but most FFT algorithms apply some form of scaling for which allowance must be made.
- Use of the Wiener filter solution results in residual errors caused mainly mainly by thermal noise in the sidelobes (and not error due to imperfections in the code sequence); this can be contrasted with PN sequence autocorrelation sidelobes experienced in a matched filter environment.
- The paper by J. Blantz et al on the “Performance of a cellular hybrid C/TDMA mobile radio system applying joint detection and coherent receiver antenna diversity”, IEEE J. Selected Areas in Comms. 12(4), May 1994, pp.568-579, describes a multi-user detection algorithm. A second paper by A. Klein et al on “Zero forcing and minimum mean square error equalisation for multiuser detection in code-division multiple access channels”, IEEE Trans. Veh. Tech. 45(2), May 1996, pp.276-287, provides further context to the present invention.
- In overview, therefore, PN training sequences sent from multiple base stations (or Node Bs) employing one or more transmit elements are subject to multipath that results in code cross-correlation and an inability at a receiver to resolve the individual channels and establish the individual channel-specific impulse responses. More specifically, whilst time alignment of base station transmissions may produce a summation of signals at the receiver (when employing appropriate windowing on a chip-by-chip basis with respect to identifiable correlation spikes), the receiver is only able to detect a composite channel impulse response that is unlikely to reflect accurately any of the actual transmission paths. Moreover, whilst the composite channel impulse response may be sufficient in the context of soft handover (in IS-95, for example), the composite channel impulse response is generally insufficient in third generation systems, including systems offering space-time coding. Furthermore, there is a reticence shown by service providers to provide synchronicity between base station transmissions since synchronised transmissions increase infrastructure costs, such as through the necessary provision of an accurate timing reference.
- According to a first aspect of the invention there is provided a method of determining channel impulse responses of a plurality of channels to a communication device, the method comprising: performing transform operations on both a replica of a signal sequence s n and a received training sequence yn by the communication device in at least one burst, the received training sequence yn being the signal sequence as received through a channel, the transform operations arranged to generate a multiplicity of signal sequence frequency bins and a multiplicity of training sequence frequency bins; performing point-by-point operations between corresponding signal sequence frequency bins and training sequence frequency bins; and concatenating the point-by-point operations associated with the channel to provide a composite frequency response for the channel, the composite frequency response allowing, in the time domain, generation of the channel impulse response for the channel.
- It is preferred to use a set of matrix operations in the frequency domain to resolve channels to the communication device from multiple transmitting stations, the matrix operations providing solvable linear equations for the channel impulse response H and the signal sequence S expressible in a matrix-vector form at each frequency bin.
- A minimum mean square error (MMSE) estimation technique is preferable to solve the linear equations, although other mathematical techniques are possible (as will be appreciated).
- The MMSE estimation technique preferably employs a Weiner filtering operation providing:
- Ĥ=( S H S=Cov(B))−1 S H Y
- where: Cov(B) is a covariance matrix of thermal noise; S HY is a matched filter operation arranged to minimize the signal to noise ratio but not to remove mutual interference between channel estimates; and (SHS+Cov(B))−1 is a decoupling matric that removes the coupling between different channels caused by any non-ideal nature of the training sequences.
- In a preferred embodiment, the number of bursts sent to the communication device from each transmitting unit in communication contact therewith is calculated as a multiplication of: a number of transmitting elements in a transmit array of a transmitting unit; and a number of transmitting units in communication contact with the communication device.
- In a second aspect of the present invention there is provided a method of determining channel impulse responses of channels incident to a communication device, the method comprising: and transmitting multiple quasi-orthogonal pseudo-noise sequences as bursts from multiple base stations each having at least one transmit element, successive bursts providing an extended training sequence for use in channel estimation at the communication device; applying a Wiener frequency domain MMSE deconvolution with frequency domain spatial decoupling matrices to generate channel impulse response estimates for the channels.
- In another aspect of the present invention there is provided a method of determining channel impulse responses of a plurality of channels established between a plurality of transmitting elements and a communication device in a communication system, the method comprising: substantially simultaneously transmitting different training bursts from, each of the plurality of transmitting elements, each burst having a length at least as long as a maximum channel duration in the communication system multiplied by a number corresponding to the plurality of transmitting elements; recovering at the communication device a signal sequence y n from the different training bursts sn; and resolving the plurality of channels to recover associated channel impulse responses H for each channel by solving an algebraic matrix operation expressed in matrix-vector form as Y=SH, where: S is a matrix of partial training bursts for each channel, each training burst segmented into N pieces in the time domain; Y is a vector of a received signal sequence; and H is a concatenation of different channel impulse response vectors.
- A further aspect of the present invention provides a computer program product for a processor within a receiver device, the computer program product comprising: code that performs transform operations on both a replica of a signal sequence s n and a received training sequence yn received by the communication device in at least one burst, the received training sequence yn being the signal sequence as received through a channel, the transform operations arranged to generate a multiplicity of signal sequence frequency bins and a multiplicity of training sequence frequency bins; code that performs point-by-point operations between corresponding signal sequence frequency bins and training sequence frequency bins; and code that concatenates the point-by-point operations associated with the channel to provide a composite frequency response for the channel, the composite frequency response allowing, in the time domain, generation of the channel impulse response for the channel; wherein the codes reside in a computer readable medium.
- According to another aspect of the present invention there is provided a communication device having a receiver coupled, in use, to receive a plurality of channels supporting a signal sequence y n and training sequence bursts, the communication device having: a signal processing platform to perform transform operations on both a replica of a signal sequence sn and a received training sequence yn received by the communication device in at least one burst, the received training sequence yn being the signal sequence as received through a channel, the transform operations arranged to generate a multiplicity of signal sequence frequency bins and a multiplicity of training sequence frequency bins; the signal processing platform arranged to perform point-by-point operations between corresponding signal sequence frequency bins and training sequence frequency bins; and the signal processing platform further arranged to concatenate the point-by-point operations associated with the channel to provide a composite frequency response for the channel, the composite frequency response allowing, in the time domain, generation of the channel impulse response for the channel.
- Yet another aspect of the present invention provides a communication receiver comprising: means for receiving, in use, multiple quasi-orthogonal pseudo-noise sequences as bursts from multiple base stations each having at least one transmit element, successive bursts providing an extended training sequence for use in channel estimation at the communication receiver; and means for applying a Wiener frequency domain MMSE deconvolution with frequency domain spatial decoupling matrices to generate channel impulse response estimates for the channels.
- In one aspect of the present invention there is provided a communication device operational to receive a plurality of training sequences on a plurality of channels and a signal sequence y n, the communication device comprising: a receiver for substantially simultaneously receiving, in use, different training bursts from each of the plurality of channels emanating from a plurality of transmit elements, each burst having a length at least as long as a maximum channel duration multiplied by a number corresponding to the plurality of transmit elements; recovery circuitry for recovering, in use, the signal sequence yn and the different training bursts sn; and a processor arranged to resolve the plurality of channels to recover associated channel impulse responses H for each channel by solving an algebraic matrix operation expressed in matrix-vector form as Y=SH, where: S is a matrix of partial training bursts for each channel, each training burst segmented into N pieces in the time domain; Y is a vector of a received signal sequence; and H is a concatenation of different channel impulse response vectors.
- According to the present invention, a base station of a communication system may be provided in which base station a transmitter chain is arranged to transmit multiple quasi-orthogonal pseudo-noise sequences as training bursts s n from at least one transmit element and further arranged to transmit a signal sequence yn, successive training bursts providing an extended training sequence for use in channel estimation at a communication device of the communication system, the transmitter chain substantially simultaneously transmitting, in use, different training bursts from each of the at least one transmit element, each training burst having a length at least as long as a maximum channel duration in the communication system multiplied by a number corresponding to a plurality of channels to the communication device, the extended training sequence and the signal sequence yn providing a resolution mechanism to the communication device allowing the communication device to resolving the plurality of channels to recover associated channel impulse responses H for each channel by solving an algebraic matrix operation expressed in matrix-vector form as Y=SH, where: S is a matrix of partial training bursts for each channel, each training burst segmented into N pieces in the time domain; Y is a vector of a received signal sequence; and H is a concatenation of different channel impulse response vectors.
- Advantageously, the present invention provides a mechanism for resolving a composite channel into a plurality of sub-channels with which specific individual channel impulse responses can be associated with and calculated using a numerically efficient fast transform technique. In other words, irrespective of whether or not there are synchronized base station transmission to an addressed unit from multiple base stations having one or more radiating element, individual channels can be resolved to generate channel impulse responses to aid in data recovery. Beneficially, the present invention is particularly applicable in the estimation of the channel impulse responses between multi-element base stations (in different cells) and the receive antenna array of a subscriber unit located at a 2-way or 3-way handoff point where interference is generally very high.
- It can be shown that for a dispersive channel having two transmitting base stations, the present invention provides increased accuracy in channel estimation, with smaller errors experienced than in an uncoupled case. Indeed, tests have shown that normalised mobile station errors in channel estimation for the present invention can achieve results of 14.8 decibels (compared with 6.1 dB and 7.1 dB for techniques solely employing a matched filter and Weiner filter, respectively, in channel impulse response estimation). The present invention, even in conditions of varying base station transmit power, provides an improved accuracy in channel impulse response estimation, which accuracy is reflected in a general measured improvement of about 7 dB over a range of transmit signal strengths of ±20 dB for second base station (relative to a carrier signal from a first base station being set at +3 dB above thermal noise at the clip level). The present invention is therefore able to operate in interference and soft handover environments where interference becomes a problem.
- A solution for estimating several downlink channels from different base antennas to a single terminal antenna by the use of multiple training bursts has been described. The method involves the use of N×N decoupling matrices in the Fourier domain to solve for N channels and gives superior results compared with attempts to use matched filters designed for added white Gaussian noise (AWGN) channels. Interference cancellation, space-time coding, and coherent soft hand-off can be enhanced by the use of the present invention.
- At least one exemplary embodiment of the present invention will now be described with reference to the following drawings, in which:
- FIG. 1 is a schematic block diagram of a basic transmitter and
receiver architecture 10 in which processing circuitry may be adapted to support the underlying principles of the present invention; - FIG. 2 is a diagrammatic illustration of a typical cellular communication system;
- FIG. 3 shows a mechanism and schematic block diagram for channel impulse response estimation that may be adapted to support the principles of the preferred embodiments of the present invention;
- FIG. 4 is a transmission regime for a training sequence according to a preferred embodiment of the present invention;
- FIG. 5 a schematic block diagram of the channel estimation process and architecture according to a preferred embodiment of the present invention; and
- FIG. 6 is a Steiner code variant of FIG. 4.
- Before discussing the preferred embodiment of the present invention, it should be noted that consideration has been given to employing Steiner codes in combination with Wiener MMSE estimation in the Fourier domain to obtain a low cost multi-user channel estimation method that is highly efficient for simultaneously estimating a number of channels on the downlink for CDMA systems. Steiner codes may also be used in OFDM systems though, in this case, it may be preferred to use the intrinsic OFDM symbol for training sequences. Given only prior knowledge of the maximum extent of the channel impulse response, the same basic pilot sequence can be time shifted and re-used (with properly determined cyclic headers) to function for a number of different downlink channels, and only one FFT correlation process is needed to solve for all the channels simultaneously. The technique is ideal for wideband fat pipe systems where the same user signal is radiated from different antennas of a transmit diversity antenna or a space-time coded antenna system. Channel estimation by this method is accurate enough to allow adequate interference cancellation of intercell interference, which is usually quite difficult to achieve in CDMA systems due to low grade estimates of the interference parameters.
- Referring now to FIG. 1, there is shown a basic transmitter and
receiver architecture 10 in which processing logic or circuitry may be adapted to support the underlying principles of the present invention. Transmit and receivechains - For the sake of explanation only, the following description of the preferred embodiment will be based on a wideband CDMA system and so references to “CDMA” should be construed broadly and without specific limitation.
- In transmit
chain 100, signalsource 102 generatessignals 104 which are encoded byencoder 106, such as a half rate turbo coder. Encoded signals 107 are modulated and subjected to CDMA spreading by modulator/spreader 108 and then filtered by pulse shaperdigital filter 110. Following filtering, a digital to analog (D/A) converter is arranged to produceanalog signals 114 which are generally filtered in asecond filter 116 to limit any aliasing effect at transmission. Amixer 118 up-converts baseband signals 120 to transmission frequencies prior to amplification inpower amplifier 122 and transmission fromantenna 124. Of course, as will be appreciated, some of the functional blocks in the transmit chain can be realised as discrete or collocated into a single chip or processing block. - Transmitted
signals 126 are received by receiveantenna 128 of an addressed station.Received signals 130 are communicated to a down-convertingmixer 132 via anamplifier 134, which down-converting mixer typically produces an intermediate frequency signal for initial signal processing. Afilter 134 isolates a desiredfrequency spectrum 136 for signal processing, which frequency spectrum is converted to adigital domain representation 137 by analog to digital (A-D)converter 138. Thedigital domain representation 137 is digitally filtered in digital channelpulse shaper filter 140 and then applied in series to a combined demodulator/equaliser slicer and RAKE despreader 142 and then a channel decoder 144.Recovered information 145 is ultimately received by terminal receiving equipment (TRE) 146. It will be understood that channel filtering generally distorts the channel impulse response and the channel filter becomes part of the unknown channel. - The transmit and receive
chains controller 150 and associated memory 152 (which may be a combination of random access (RAM) and read only (ROM)) is shown as being common to both the transmit and receivechains memory 152 stores control algorithms, such as equalisation and modulation algorithms, and also operands and incident data is subject to signal processing requirements. Moreover, common circuitry between the transmit and receive chains can be shared to reduce component count, subject to the inclusion of suitable switching and regulating circuitry. Additionally, as will be understood, at least some of the functions within one or both of the transmit and receivechains - Wideband CDMA-specific components can be replaced or substituted to support an arbitrarily selected communication protocol, e.g. an FDD environment employing TDM techniques or a multicarrier environment.
- FIG. 2 is a diagrammatic illustration of a typical
cellular communication system 170 showing a subscriber unit 172 (preferably having multiple receive elements 174-180) at cell boundaries between three potentially serving base stations 182-186. For an equidistant displacement of the subscriber unit from the base stations, one could expect that transmit signal strengths to be roughly equal, subject to the respective paths and the associated physical environments. The general purpose of FIG. 2 is to illustrate a physical environment in which the present invention finds exemplary application. For purposes of clarity, thecellular communication system 170 is shown with three cells 188-192 and asingle subscriber unit 172, but clearly cellular systems may include many cells in multiple layers, with each cell servicing a multiplicity of subscriber units. At the hand-off point midway between two or three base stations, it is necessary to distinguish the channel impulse responses for a doubled or tripled number of channels from multiple base antenna elements. If the CIRs are not estimated jointly, the carrier to interference (C:I) ratio is very low within the training sequences and the channel estimates will be correspondingly poor. Given that each base station always has several TX element channels to estimate it is reasonable to use the Steiner method in the intracell mode, allocating one PN sequence per base station with cyclic rotation to distinguish between the bases' antenna elements, as described previously. -
Incoming signals 126 to thesubscriber unit 172 are received from theantenna 128 at a transmission rate of I/Tch of the system. By way of practical implementation, an entire slot of a frame is sampled (A/D converted) at the Nyquist rate and read into memory 152 (of FIG. 1) prior to commencement of information recovery. Theincoming signals 126 can be received from any digital source of signals and are not restricted to wireless communications, with the base stations utilising single or multiple radiating elements in each transmit antenna array. Signal processing ofincoming signals 126 for optimised data recovery is clearly subject to knowledge of the channel impulse response (i.e. the “channel spectrum”), with this determined from training sequences sent from the base stations according to a predetermined regime, e.g. once per slot, once per frame or on any other appropriate basis. An exemplary mechanism for data recovery is described in the aforementioned European and U.S. patent applications (e.g. EP 01300520.2). - As regards the channel spectrum, reference is made to FIG. 3 that shows a mechanism for channel impulse response estimation that is adapted to support the principles of the preferred embodiment of the present invention. A
training sequence 250, preferably located in and extractable from each slot of a frame, falls incident on receiveantenna 128, which training sequence is demodulated in the receive chain (as will be readily appreciated) to recover the random sequence yk, e.g. a generated pseudo-random number sequence. The form and structure of the training sequence will be described in detail later, since the structure is inexorably associated with an ability to resolve individual channels for channel impulse response estimation according to the present invention. - In overview and without initially discussing the preferred embodiment, the recovered random sequence y k is subjected to a DFT function 252 to produce a channel
sequence spectrum y k 254. Within thememory 152 associated with the receive chain there is stored a replica of the original training sequence sk 260, which original training sequence sk 260 has a corresponding known sequence spectrum sk 262 obtained by subjecting the original training sequence sk 260 to an FFT function. The known sequence spectrum sk 262 may simply be stored in the memory since it is this sequence spectrum sk 262 that is used to assess the channel impulse response. - The DFT function 252 may be performed by a specific digital signal processor (DSP) or the
processor 150 of FIG. 1. The channel spectrum therefore assumes the form of an x-point, e.g. 512-point, DFT sample stored temporarily in, for example, RAM. - It will be noted that the frequency domain sequence spectrum s k 262 is essentially flat with slight perturbations about a nominally constant magnitude.
-
- to produce an impulse
response spectrum H k 268 that can be stored in memory for the duration of at least the related slot and longer if desired. Clearly, by storing the impulseresponse spectrum H k 268 for an extended period, processing overhead is reduced at the expense of accuracy in any correction of the variations in the channel due to Doppler. As will be understood, time alignment of the received and transmitted training sequences is required prior to cross-correlation. - Optionally, the impulse
response spectrum H k 268 may be further refined and so it is subjected to an IFFT function 270 to generate an estimated time domain representation hk thereof having an arbitrary number of taps/channels that can be used as a matched filter, if desired. In other words, each tap is representative of a weight for the channel impulse response. Within the time domain, trimming of the number of taps reduces the channel impulse response to manageable processing levels, with the reduction reflecting the greatest expected channel impulse response (CIR) duration (presently understood to be seventy-one chips in length in 3GPP, although this number is an arbitrarily selected cut-off). From the reduced number of taps in the channel impulse response, most values will approximate to zero and so acontrol processor 272, based on a level or number threshold, selects only those N significant taps that most noticeably reflect the channel to produce a best estimate channel impulse response h′k 274. Selection of the N most significant taps may simply force lesser taps to be forced to zero. By limiting the channel impulse response to the most significant taps, processing is reduced and a final error in the channel limited. In the latter respect, it will be understood that all tap values will have an associated error from thermal noise, channel interference and other adverse channel and processing artefacts, so the compounding of errors is mitigated. - A complete understanding of the principles of the present invention will now be gleaned from the following description of specific signal processing interactions and transmission techniques.
- Concerning transmission of a training sequence according to a preferred embodiment of the present invention, reference is made to FIG. 4. For the sake of explanation, the structuring of base station transmissions (in the timing frame of FIG. 4) is assumed to reflect a three site system in which each of three base stations includes a single transmit element. Of course, the basic principle employed in the specific embodiment of FIG. 4 can be developed for multi-element transmit arrays from two or more base stations. Essentially, FIG. 4 is representative of successive training sequence transmission bursts from each of three base stations (Base TX 1, Base TX2 and Base TX3). In generality, the number of training sequences transmitted from all transmit elements follow a squared law, i.e. for three base stations each having single radiating elements then there would be three successive bursts (t1-t3) separated, preferably, by guard periods (g1 and g2) or cyclic prefixes. Bursts from the various base stations are preferably time aligned at transmission, although a windowing function at the receiver (that steps through a chip-wise time correlation) may be employed to time align the transmitted sequences snk. Since channel delay is generally no greater than about 20 μs, then the receiver need only step through a chip count commensurate with the maximum channel delay. For example, at an operating frequency (chipping rate) of one megahertz (1 MHz), 20 μs correspond to twenty chips.
- During each burst (t 1-t3), each base station transmits a finite (predetermined) length of training sequence s, which training sequence may vary from 1-chip or more. Typically, each burst will be tens of chips in length and preferably at least about sixty chips in length and most preferably in excess of about one hundred chips. Clearly, the length of the training sequence is restricted to manageable levels to avoid inefficient use of communication resource for more important data transmissions. The nomenclature adopted in FIG. 4 with respect to the bursts follows the convention that the first subscript (n) represents an identity of the transmitting base station whereas the second subscript (k) represents the sequence number. In the context of Base TX1, FIG. 4 is illustrative of three sequences s11, S12 and S13 during bursts t1, t2 and t3, respectively. A channel sequence spectrum yk is formed (for each burst (t1-t3)) from the summation of the individual sequences s11, S21, S31 from the base stations transmitting in that burst.
- For channel estimation, it will be appreciated that the number of samples required is dependent upon bandwidth, e.g. with a symbol rate of 284 kbps (kilo bits per second), GSM systems require about five samples of the channel.
- It is well known that DFT's have a wrap-round effect that is equivalent to the data being cyclic. Consequently, in (contiguous) observation windows each encoded with the same PN sequence, DFT's can be used to perform a discrete convolution operation. Circulant matrices are equivalent to these DFT operations, which circulant matrices can be defined as follows. In a system in which the training sequence is S={s 0, s2, s2, s3, s4}, the cyclic extension is the channel impulse response is H={h0, h1, h2, h3, h4} and the observation window arranged to hold data Y={y0, y1, y2, y3, y4}, then Y is the cyclic convolution of S with H:
- with N=4. If the associated DFT's are the sequence spectrum S k, the channel impulse response H and the channel sequence spectrum Yk is then:
- Y k =S k {circle over (x)}H k
- where {circle over (x)} is a point-by point-product.
- In developing a solution to the problem of channel estimation in the presence of interference or multi-user channel estimation (in either non-dispersive or highly dispersive channels), the inventor has appreciated that the fundamental problems associated with channel isolation/resolution can be expressed algebraically in similar terms to multi-user detection algorithms, as referenced above by J. Blantz et al and A. Klein et al.
- In the Steiner code method described above, to estimate M channels the length of the PN code must be at least M times the maximum channel dispersion. In an N base station situation, each base station with M elements, while the Steiner method can continue to be used, the PN code length must be at least MN times the channel impulse response duration and each element of each base station would transmit an end-around rotated version of the code with a different unique offset. In the multiple base station situation, the differing round-trip propagation times to the subscriber unit must also be taken into account in the channel model so codes becomes increasingly extended. A more flexible option for allowing expansion of the number of serving base stations is to use an alternating sequence of different Steiner codes, each of which on its own is only just long enough for the number of elements in a single base station to be resolved.
- To appreciate the present invention, it is preferable to consider a communication system having N active/serving base stations for a call, with each base station having a single transmitting element. If the N base stations each with a single element are received by a single element antenna of a subscriber unit, such as cellphone or terminal, then if the N bases simultaneously send N strings of N different pseudorandom bursts and such that there are N 2 different sequences altogether, then the individual channel impulse responses can be resolved at the terminal. In practice, the present invention is particularly interested in a three-base station situation which, statistically, occurs most frequently.
- The base stations are preferably synchronised to a time accuracy much less than the duration of any cyclic prefix (which is typically of the order of about 10 μs to 20 μs for urban microwave propagation). The m th received burst is now the convolution:
-
-
- Thus, rather than performing a convolution of the channel impulse response h n with the mth sequence smn from the nth base transmitter element, the present invention applies a DFT operation to both the received sequence yn and the various local replicas of the training sequences Smn, and then does a multiplication together of the corresponding frequency bins of the received signal sequence Yn (being the signal sequence sn as received through a channel) with the corresponding frequency bins of the replica of the training sequence Smn. Summation (i.e. concatenation) of the individual multiplication products associated with each channel provide a composite frequency response for the channel, the composite frequency response allowing, in the time domain, generation of the channel impulse response for the channel. The process of the present invention generally involves periodic buffering, for example, of frequency bin data and vector results pertaining to channel impulse responses, as will be appreciated by the skilled addressee.
- In other words, taking an exemplary 128-point Fourier transform of both the received sequence y with the training sequence s yields one hundred and twenty-eight corresponding frequency bins in the frequency domain. Multiplication together of corresponding frequency bins of the received sequence with the same frequency bin of the signal (training) sequence s generates a matrix containing solvable linear equations in H and S. Summation (i.e. concatenation) of the individual multiplication products associated with each channel then provides a composite frequency response for that channel, which composite frequency response can be used in the time domain (through an inverse FFT) to provide a channel impulse response.
- It will be appreciated that the channel is assumed constant for the duration of the burst events with respect to slow moving subscriber units, e.g. mobile units having a velocity of less than about ten kilometres per hour (10 kph).
- In the DFT domain, the k th frequency bin received for the first burst can be expressed as the sum of components from the base stations and their channels:
- Y 1 (k) =S 11 (k) +S 12 (k) H 2 (k) +S 13 (k) H 3 (k) +B 1 (k)
- Similarly, the k th frequency bin for the second burst can be expressed as:
- Y 2 (2) =S 21 (k) H 1 (k) +S 22 (k) H 2 (k) +S 23 (k) H 3 (k) +B 2 (k)
- And, finally, the kth frequency bin for the third burst is:
- Y 3 (k) =S 31 (k) H 1 (k) +S 32 (k) H 2 (k) +S 33 (k) H 3 (k) +B 3 (k)
-
- which can be written in the matrix vector form at each frequency k bin (which for clarity is omitted):
- Y=SH+B
-
- These equations are solved using a minimum mean square error (MMSE), e.g. Weiner filter, method providing:
- Ĥ=(S H S+Cov(B))−1 S H Y
- Here Cov(B) is the covariance matrix of the thermal noise, which is often approximated by an identity matrix σ 2I. The equation immediately above can be considered as two entities, namely as a matched filter SHY arranged to minimize the signal to noise ratio but not to remove mutual interference between channel estimates, followed a decoupling matric (SHS+Cov(B))−1 that removes the coupling between different channels caused by the non-ideal nature of the PN sequences. The inverse DFTs for each radio channel are therefore of the form:
- where z is the frequency bin (or its time domain equivalent).
-
- In terms of each channel concatenation of the numerous frequency bins allows generation of a time domain vectors of the channel impulse response for a channel, the time domain vectors generated from an inverse DFT process within a suitable processing block, such as an ASIC or control processor 150 (of FIG.
- It is now possible to extend the basic concept of multiple channel estimation to a situation in which each base station has a plurality of transmit element; this scenario arises in, for example, systems employing space time coding (STC). It will be appreciated that STC is a collection of techniques for transmitting a number of parallel data streams from multiple transmit antennas with the aim of increasing bit rate for a given total transmitter power. In STC, it will be appreciated that the 2×2 frame structure is expanded to an N-element array, usually having at least four transmit elements. For example, in a four element STC transmitting antenna we might organise the user data in blocks of four symbols and transmit them in different order from the four elements via 16 channels to 4 receiving elements. This is a natural extension of the two element STTD procedure, the main difference from STTD being that multiple receiving elements are essential to get a bandwidth expansion in STC whereas STTD is aimed purely at improving the reliability of the received data and is not concerned with bit rate expansion. Thus STTD will function with a single receive antenna, while STC requires a minimum of two. The principle difference between an STTD arrangement (that is discussed in detail below) and STC is that each component of the block vectors and block matrices (for STTD given below) contains an increasing number of elements (i.e. CIR samples, transmitted data samples and received data samples) consistent with the adopted coding method in each STC derivative.
- Referring briefly to FIG. 5, which is generally complementary to FIGS. 1, 3 and 4, there is shown a schematic block diagram of the channel estimation process and
architecture 500 of a preferred embodiment of the present invention, the process based on a two base station (BS1 and BS2) transmission environment having two training bursts. The training sequences sx(ω) are, in this exemplary case, Gold codes, with individual first 502 and second 504 training sequences transmitted in afirst burst 506. Thefirst training sequence 502 is subjected tofirst channel 508, whereas the second training sequence is subjected to asecond channel 510. Both channels are combined at thereceiver 512 and are further subject to a first noise component (N1(ω)) 513. In this exemplary case, first and second matchedfilters 514 and 516 provide a time reversed conjugated inversion of the respective first andsecond training sequences filters 514 and 516 provided to afrequency domain coupler 518 supporting the frequency domain decoupling matrix (SHS+Conv(B))−1. Third 520 and fourth 522 training sequences transmitted in asecond burst 524 are respectively subjected tofirst channel 508 andsecond channel 510. Both channels are combined at thereceiver 512 and are further subject to a second noise component 526 (typically different to the first noise component). In this exemplary case, third 528 and fourth 530 matched filters provide a time reversed conjugated inversion of the respective third andfourth training sequences filters frequency domain coupler 518. The frequency domain coupler then provides channel impulse response vectors {circle over (H)}1(ω) and {circle over (H)}1(ω) (reference numerals 532 and 534) for the first and second channels, respectively, based on the foregoing point-by-point manipulation of individual (frequency domain) frequency bins. - The preferred embodiment of the present invention therefore shows how accurate channel estimation is possible through the use of Wiener frequency domain MMSE deconvolution combined with frequency domain spatial decoupling matrices, with quasi-orthogonal Gold codes allocated to base stations and their antenna elements.
- The principles of the present invention can also be applied to resolve multiple channels by a single training burst; this has particular application in OFDM systems where it may not be possible to transmit Steiner codes because of hardware constraints. The present invention can be modified, in the fashion now shown, to operate with a single arbitrary training sequence yet still resolve multiple channels in a least squares sense. A single training burst situation is algebraically undetermined in the two channel case. If the burst is of length L, there are 2L unknowns in the two channels which cannot be determined from L observations at one antenna. However, if there are also ½ L linear constraints associated with each channel impulse response the equations become solvable again. The simplest constraints are that the channel impulse responses {h 0 . . . hk} are of finite duration. If K<½ L then we write the equations as follows. Let Sm be the circulant matrices representing the training bursts and Hm be the IR vectors for
channels # 1 and #2. However, with a matrix solution not be circulant, the ability to use FFT to solve the following equation is lost, but resolution of the channels is still possible with use of a matrix of the form: - In generality, with respect to two parallel channels using a single training burst, if there are a large number of linear constraints C attached to the channel impulse responses (such as finite durations) then a number of channels can be solved with a single training burst. Algebraically, if the there are N c constraints on each channel vector of L elements and C channels, the sum of the number of independent degrees of freedom is C(L−Nc). If the length of the training sequence is NT>C(L−Nc), then all of the independent degrees of freedom can be solved; this method is used in Steiner codes to estimate multiple channels using a single training sequence
- Whilst benefits are attained through use of the channel impulse response estimation scheme described so far (in which the number of processing blocks is equal to the total number of channels to avoid code contention problems), some processing efficiency (i.e. DSP load) associated with Steiner codes is lost since there is a requirement to invert a matrix in each frequency bin whose dimension is equal to the number of channels, i.e. the number of transmitting cells times the number of base antenna elements per cell.
- In a further preferred embodiment of the present invention, therefore, the training sequence transmissions of FIG. 4 are implemented as Steiner cyclic training sequence variant; this is shown in FIG. 6 in which
successive bursts - Since the S matrix has no particular orthogonality properties, matched filtering is not advisable. Instead, if the following MMSE matrix operation is performed at each frequency; the result combines spatial decoupling with a Wiener frequency weighting function and overall gives an MMSE solution. It requires a 2×2 matrix inversion in each frequency bin for two cell operation (with each base station having a single transmit element):
- By combining Steiner cyclic pilot rotation for transmissions from the transmit elements of each base station according to the present invention, interference-free mobiles near a centre of the cell are allowed to resolve their channels in the usual (conventional) way. At the cell periphery where interference becomes significant, the training sequences need to be expanded to provide enough degrees of freedom such that the simultaneous equations for all of the channels become algebraically determinate; a repeating pattern of the Steiner PN sequences allows this to occur.
- In the exemplary case where a receiver observes six sequences, as shown in FIG. 7, the result in the Fourier domain is that there are sufficient degrees of freedom to solve for six channels {h 1} to {h6}. It should be note that, in FIG. 7, the introduction of sign reversals allows for distinction to be drawn between codes in successive bursts, with the mechanism of sign reversal therefore reducing the overall number of Steiner codes required to implement a system according to the present invention. The equations relating the received signal Y to the sequences U, V, Wand the channels H in the frequency domain are:
-
-
- Cyclic shifting of channel impulse responses h 2, h4 and h6 (of FIG. 7) takes into account the reverse shift as detailed immediately above with the effect that the six sequences received at the antenna of the subscriber (or other addressed unit) are Y 1, Y 2, Y 3, Y 4, −Y 5and −Y 6. Moreover, the six sequences are obtained from a repetition of only three Steiner codes that are individually and uniquely assigned to each base station, i.e. both transmit elements send identical sequences in the same burst, with the subscriber unit generating a cyclically shifted channel impulse response h x for one of the two radiating elements of the base station's transmit array. This reverse shift manipulation results in only three different PN sequences being utilised in this particular embodiment, with the channel impulse responses of FIG. 7 taking the form (h 1+h2), (h 3+h 4) and (h 5 +h 6) to provide the received sequence Y 1, Y 2, Y 3, Y 4, Y−5 and −Y 6. The determinant of the sign change matrix of this solution is 4, as shown below:
- with Fourier transforms:
- y 1→:Y1 y2→Y2 Y3→Y3
- h 1→H1 h2→H2 h3→H3
-
- Provided a resultant matrix in this set of equations is well conditioned and invertible, then the set of channel impulse responses can be solved. A sampling design for the repetitions that offers near-orthogonality between repeated sequences is, however, required, such that different bases can be resolved without ill-conditioning of the equations. Such designs, as used for space-time codes, are readily available in statistics literature.
- By employing the preferred embodiment of the present invention where Steiner codes supplement to point-by-point DFT multiplication mechanism, accuracy in estimated channel impulse responses is limited by channel noise rather than imperfection in the codes.
- The preferred embodiment that uses Steiner codes for m base antenna elements can be used in multiple cells and MMSE channel estimation is obtainable for a number n of bases giving a total of nm downlink channels. Different cells will use a different basic PN code, whereas the elements within a single cell will use the Steiner cyclic offsets of a single PN code. The extra workload (processing overhead) involved is the inversion of an n×n matrix in each frequency bin. The inclusion of the use of Steiner codes to supplement the basic inventive concept of Wiener frequency domain MMSE deconvolution combined with frequency domain spatial decoupling matrices results in the possibility of allocating only a single training sequence to each base station provided that the training sequence is of sufficient length to encompass all the multiple time-translated channel impulse responses.
- Embodiments of the invention may be implemented as computer program code encoded on a computer program product for use with a computer system. It is expected that such a computer program product may be distributed as a removable medium with accompanying printed or electronic documentation (e.g. shrink-wrapped software), preloaded with a computer system or distributed from a server or electronic bulletin board over a network (e.g. the Internet or World Wide Web). A series of computer instructions can therefore either be fixed on a tangible medium or fixed in a computer data signal embodied in a carrier wave that is transmittable to a computer system using wireline or wireless transmission techniques. For example, the present invention can find application as downloadable code in a software radio. The removable (i.e. tangible) medium may be a computer readable media, such as a diskette, CD-ROM, DVD-ROM or RAM, fixed disk, magneto-optical disks, ROMs, flash memory or magnetic or optical cards. The series of computer instructions embodies all or part of the functionality previously described herein with respect to the system.
- Software embodiments of the invention may be implemented in any conventional computer programming language. For example, preferred embodiments may be implemented in a procedural programming language (e.g. “C”) or an object oriented programming language (e.g. “C++”).
- Although the preferred operating method is realised by general or specific-purpose processor or logic circuits programmed with suitable machine-executable instructions, hardware components may possibly be used to implement certain features of the present invention. Of course, the present invention may be performed by a combination of hardware and software.
- It will, of course, be appreciated that the above description has been given by way of example only and that modifications in detail may be made within the scope of the present invention. For example, while the preferred embodiment is has been described in relation to a multi-cast system in which each base station has a single transmit element, the present invention is clearly applicable to multi-element transmitters and to single isolated cells supporting transmissions from a single base station having a transmit array. Furthermore, while the preferred embodiment has been described in the context of a CDMA system, the present invention is generally applicable to any dispersive or imperfect channel that acts to corrupt symbols, including systems employing TDD and FDM techniques and other types of links, such as digital subscriber lines (DSL) and all digital transmission systems.
- Indeed, although the technique of the preferred embodiment of the present invention has been described for a CDMA application where the number of chips in the training burst is easily identified, the principles of the present invention apply to OFDM, wavelets (e.g. Daubechies's wavelets) and any similar orthogonal or near-orthogonal signaling waveforms. With specific regard to an OFDM signal, such an OFDM signal is treated as a single wide-band modulated carrier in the time domain and an estimate of the time domain channel impulse response is made in an identical way to that described in the preferred embodiment. If a constraint is made that the duration of the impulse responses is small, the equations become algebraically soluble (or “observable” in the context of control theory jargon) and in this way a large number of parallel channels can be estimated using a single training burst.
- If the duration of the OFDM training burst is N S sub-carrier symbols and there are NF sub-carriers then the burst effectively has NS*NF samples or chips which is quite a substantial number. In practice, this means that multiple channel estimation in OFDM might not be too difficult. The lower limit for the duration of the training sequences would be that it must be capable of supporting an orthogonal, or at least a linearly independent, set of codes for say m base station antennas seen from the terminal (in one or more cells). Superficially, this would require m full sub-carrier slots and for HSD with 150 μs slots we need a duration of 150 μs. However the wideband methods described here only require that the duration of the training sequence is ≧m times the duration of the channel impulse response so, for a channel with τ μs dispersion and signal bandwidth B MHz, the duration of the training sequence need only be τBm samples. For example, if the signal bandwidth is 6 MHz, the channel dispersion is 5 μs and there are seven base station antennas with channels to be determined, the minimum duration of the training sequence is 210 samples or 6×5×7/6 =35 μs, i.e. only ⅕ of a nominal sub-carrier symbol. In practice, however, this duration would need to be increased significantly (and preferably about ten-fold or so) to improve estimation accuracy.
- In transmission bursts from base stations having single transmit elements, cyclic prefixes could be replaced by blank (zero) carriers to provide isolation between burst sequences.
- It should be understood that reference to a base station refers to serving infrastructure irrespective of the form of air-interface adopted by the exemplary CDMA-based architecture of the preferred embodiment. In other words, the term base station should be construed broadly and, where necessary, to include references to communication relay devices. While the main applications are in channel estimation on a downlink for CDMA and OFDM in order to apply coherent soft hand-off and interference cancellation in locations where two or more base stations are at similar ranges and the weaker base stations, if ignored, cause mutual interference, the preferred embodiments are not intended to be limiting to these specific arrangements.
Claims (27)
1. A method of determining channel impulse responses of a plurality of channels to a communication device, the method comprising:
performing transform operations on both a replica of a signal sequence sn and a received training sequence yn received by the communication device in at least one burst, the received training sequence yn being the signal sequence as received through a channel, the transform operations arranged to generate a multiplicity of signal sequence frequency bins and a multiplicity of training sequence frequency bins;
performing point-by-point operations between corresponding signal sequence frequency bins and training sequence frequency bins; and
concatenating the point-by-point operations associated with the channel to provide a composite frequency response for the channel, the composite frequency response allowing, in the time domain, generation of the channel impulse response for the channel.
2. The method according to claim 1 , further comprising:
separating training sequence bursts emanating from a single element transmitter by one of a cyclic prefix and a blank (zero) carrier.
3. The method according to claim 1 , wherein multiple Steiner codes are transmitted as training sequences, the multiple Steiner codes sent from multiple transmit elements in multiple training bursts.
4. The method according to claim 3 , wherein the multiple Steiner codes are transmitted from multiple elements of a base station transmit antenna.
5. The method according to claim 1 , further comprising using a set of matrix operations in the frequency domain to resolve channels to the communication device from multiple transmitting stations, the matrix operations providing solvable linear equations for the channel impulse response H and the signal sequence S expressible in a matrix-vector form at each frequency bin in terms of the received training sequence Y.
6. The method according to claim 5 , further comprising solving the linear equations using a minimum mean square error (MMSE) estimation technique.
7. The method according to claim 6 , wherein the MMSE estimation technique employs a Weiner filtering operation providing:
Ĥ=(S H S+Cov(B))−1 S H Y
where
Cov(B) is a covariance matrix of thermal noise;
SHY is a matched filter operation arranged to minimize the signal to noise ratio but not to remove mutual interference between channel estimates; and
(SHS+Cov(B))−1 is a decoupling matric that removes the coupling between different channels caused by any non-ideal nature of the training sequences.
8. The method according to claim 2 , wherein the number of bursts sent to the communication device from each transmitting unit in communication contact therewith is calculated as a multiplication of:
a number of transmitting elements in a transmit array of a transmitting unit; and
a number of transmitting units in communication contact with the communication device.
9. The method according to claim 8 , wherein training sequence burst between transmitting units are time-aligned.
10. A method of determining channel impulse responses of channels incident to a communication device, the method comprising: and
transmitting multiple quasi-orthogonal pseudo-noise sequences as bursts from multiple base stations each having at least one transmit element, successive bursts providing an extended training sequence for use in channel estimation at the communication device;
applying a Wiener frequency domain MMSE deconvolution with frequency domain spatial decoupling matrices to generate channel impulse response estimates for the channels.
11. The method according to claim 10 , wherein the quasi-orthogonal pseudo-noise sequences are Steiner codes.
12. The method according to claim 11 , further comprising allocating only a single training sequence to each base station, the single training sequence being of sufficient length to encompass all multiple time-translated channel impulse responses.
13. A communication device operational to receive a plurality of training sequences on a plurality of channels, the communication device comprising:
14. A method of determining channel impulse responses of a plurality of channels established between a plurality of transmitting elements and a communication device in a communication system, the method comprising:
substantially simultaneously transmitting different training bursts from each of the plurality of transmitting elements, each burst having a length at least as long as a maximum channel duration in the communication system multiplied by a number corresponding to the plurality of transmitting elements;
recovering at the communication device a signal sequence yn from the different training bursts sn; and
resolving the plurality of channels to recover associated channel impulse responses H for each channel by solving an algebraic matrix operation expressed in matrix-vector form as Y=SH, where: S is a matrix of partial training bursts for each channel, each training burst segmented into N pieces in the time domain; Y is a vector of a received signal sequence; and H is a concatenation of different channel impulse response vectors.
15. A computer program product for a processor within a receiver device, the computer program product comprising:
code that performs transform operations on both a replica of a signal sequence sn and a received training sequence yn received by the communication device in at least one burst, the received training sequence yn being the signal sequence as received through a channel, the transform operations arranged to generate a multiplicity of signal sequence frequency bins and a multiplicity of training sequence frequency bins;
code that performs point-by-point operations between corresponding signal sequence frequency bins and training sequence frequency bins; and
code that concatenates the point-by-point operations associated with the channel to provide a composite frequency response for the channel, the composite frequency response allowing, in the time domain, generation of the channel impulse response for the channel;
wherein the codes reside in a computer readable medium.
16. A communication device having a receiver coupled, in use, to receive a plurality of channels supporting a signal sequence yn and training sequence bursts, the communication device having:
a signal processing platform to perform transform operations on both a replica of a signal sequence sn and a received training sequence yn received by the communication device in at least one burst, the received training sequence yn being the signal sequence as received through a channel, the transform operations arranged to generate a multiplicity of signal sequence frequency bins and a multiplicity of training sequence frequency bins;
the signal processing platform arranged to perform point-by-point operations between corresponding signal sequence frequency bins and training sequence frequency bins; and
the signal processing platform further arranged to concatenate the point-by-point operations associated with the channel to provide a composite frequency response for the channel, the composite frequency response allowing, in the time domain, generation of the channel impulse response for the channel.
17. The communication device according to claim 16 , wherein multiple Steiner codes are transmitted as the training sequences, the multiple Steiner codes sent to the receiver through multiple channels in multiple training bursts.
18. The communication device according to claim 16 , wherein the signal processing platform operates to establish a set of matrix operations in the frequency domain to resolve channels to the communication device from multiple transmitting stations, the matrix operations providing solvable linear equations for the channel impulse response H and the training sequence S expressible in a matrix-vector form at each frequency bin.
19. The communication device according to claim 18 , wherein the signal processing platform solves the linear equations using a minimum mean square error (MMSE) estimation technique.
20. The communication device according to claim 19 , wherein the MMSE estimation technique employs a Weiner filtering operation providing:
{circle over (H)}=(S H S+Cov(B))−1 S H Y
where:
Cov(B) is a covariance matrix of thermal noise;
SHY is a matched filter operation arranged to minimize the signal to noise ratio but not to remove mutual interference between channel estimates; and
(SHS+Cov(B))−1 is a decoupling matric that removes the coupling between different channels caused by any non-ideal nature of the training sequences.
21. A communication receiver comprising:
means for receiving, in use, multiple quasi-orthogonal pseudo-noise sequences as bursts from multiple base stations each having at least one transmit element, successive bursts providing an extended training sequence for use in channel estimation at the communication receiver; and
means for applying a Wiener frequency domain MMSE deconvolution with frequency domain spatial decoupling matrices to generate channel impulse response estimates for the channels.
22. The communication receiver of claim 21 , wherein the quasi-orthogonal pseudo-noise sequences are Steiner codes.
23. A communication device operational to receive a plurality of training sequences on a plurality of channels and a signal sequence yn, the communication device comprising:
a receiver for substantially simultaneously receiving, in use, different training bursts from each of the plurality of channels emanating from a plurality of transmit elements, each burst having a length at least as long as a maximum channel duration multiplied by a number corresponding to the plurality of transmit elements;
recovery circuitry for recovering, in use, the signal sequence yn from the different training bursts sn; and
a processor arranged to resolve the plurality of channels to recover associated channel impulse responses H for each channel by solving an algebraic matrix operation expressed in matrix-vector form as Y=SH, where: S is a matrix of partial training bursts for each channel, each training burst segmented into N pieces in the time domain; Y is a vector of a received signal sequence; and H is a concatenation of different channel impulse response vectors.
24. A base station of a communication system, the base station comprising:
a transmitter chain arranged to transmit multiple quasi-orthogonal pseudo-noise sequences as training bursts sn from at least one transmit element and further arranged to transmit a signal sequence yn, successive training bursts providing an extended training sequence for use in channel estimation at a communication device of the communication system, the transmitter chain substantially simultaneously transmitting, in use, different training bursts from each of the at least one transmit element, each training burst having a length at least as long as a maximum channel duration in the communication system multiplied by a number corresponding to a plurality of channels to the communication device, the extended training sequence and the signal sequence yn providing a resolution mechanism to the communication device allowing the communication device to resolving the plurality of channels to recover associated channel impulse responses H for each channel by solving an algebraic matrix operation expressed in matrix-vector form as Y=SH, where: S is a matrix of partial training bursts for each channel, each training burst segmented into N pieces in the time domain; Y is a vector of a received signal sequence; and H is a concatenation of different channel impulse response vectors.
25. The base station of claim 24 , wherein the transmit chain is further arranged to separate training bursts emanating from the at least one transmit element by one of a cyclic prefix and a blank (zero) carrier.
26. The base station of claim 24 , wherein multiple Steiner codes are transmitted as training bursts, the multiple Steiner codes sent from multiple transmit elements in multiple training bursts.
27. The base station of claim 24 , wherein the number of training bursts sent to the communication device from each base station in communication contact therewith is calculated as a multiplication of:
a number of transmitting elements in a transmit array of a base station; and
a number of base stations in communication contact with the communication device.
Priority Applications (6)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| US09/825,058 US20020176485A1 (en) | 2001-04-03 | 2001-04-03 | Multi-cast communication system and method of estimating channel impulse responses therein |
| US10/109,915 US7149239B2 (en) | 2001-04-03 | 2002-03-29 | Communication system and methods of estimating channel impulse responses therein |
| PCT/GB2002/001336 WO2002082683A2 (en) | 2001-04-03 | 2002-04-03 | Frequency domain channel estimation for multiple channels using wiener minimum mean squared error (mmse) filtering |
| EP02720111A EP1378072A2 (en) | 2001-04-03 | 2002-04-03 | Communication system and methods of estimating channel impulse responses therein |
| AU2002251181A AU2002251181A1 (en) | 2001-04-03 | 2002-04-03 | Frequency domain channel estimation for multiple channels using wiener minimum mean squared error (mmse) filtering |
| CA002443414A CA2443414A1 (en) | 2001-04-03 | 2002-04-03 | Frequency domain channel estimation for multiple channels using wiener minimum mean squared error (mmse) filtering |
Applications Claiming Priority (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| US09/825,058 US20020176485A1 (en) | 2001-04-03 | 2001-04-03 | Multi-cast communication system and method of estimating channel impulse responses therein |
Related Child Applications (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| US10/109,915 Continuation-In-Part US7149239B2 (en) | 2001-04-03 | 2002-03-29 | Communication system and methods of estimating channel impulse responses therein |
Publications (1)
| Publication Number | Publication Date |
|---|---|
| US20020176485A1 true US20020176485A1 (en) | 2002-11-28 |
Family
ID=25243018
Family Applications (2)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| US09/825,058 Abandoned US20020176485A1 (en) | 2001-04-03 | 2001-04-03 | Multi-cast communication system and method of estimating channel impulse responses therein |
| US10/109,915 Expired - Lifetime US7149239B2 (en) | 2001-04-03 | 2002-03-29 | Communication system and methods of estimating channel impulse responses therein |
Family Applications After (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| US10/109,915 Expired - Lifetime US7149239B2 (en) | 2001-04-03 | 2002-03-29 | Communication system and methods of estimating channel impulse responses therein |
Country Status (2)
| Country | Link |
|---|---|
| US (2) | US20020176485A1 (en) |
| AU (1) | AU2002251181A1 (en) |
Cited By (39)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US20030138053A1 (en) * | 2001-11-15 | 2003-07-24 | The Regents Of The University Of California | Time reversal communication system |
| US20030223514A1 (en) * | 2002-05-31 | 2003-12-04 | Pladdy Christopher J. | Channel estimator using one or more correlation reference vectors to eliminate data related noise |
| US20030231728A1 (en) * | 2002-06-17 | 2003-12-18 | Oki Techno Centre (Singapore) Pte Ltd. | Frequency estimation in a burst radio receiver |
| US20040116122A1 (en) * | 2002-09-20 | 2004-06-17 | Interdigital Technology Corporation | Enhancing reception using intercellular interference cancellation |
| US20040125743A1 (en) * | 2000-09-29 | 2004-07-01 | Hashem Bassam M. | Dynamic sub-carrier assignment in OFDM systems |
| US20040184399A1 (en) * | 2003-03-20 | 2004-09-23 | Rong-Liang Chiou | Channel estimation in OFDM systems |
| US20040208255A1 (en) * | 2003-04-15 | 2004-10-21 | Shikio Yoshida | Wireless communication apparatus and wireless communication system |
| WO2004105335A1 (en) * | 2003-05-22 | 2004-12-02 | Ntt Docomo, Inc. | Apparatus and method for processing an impulse response of a channel |
| EP1627475A2 (en) * | 2003-05-13 | 2006-02-22 | Interdigital Technology Corporation | Method for soft and softer handover in time division duplex code division multiple access (tdd-cdma) networks |
| US20060058061A1 (en) * | 2002-09-19 | 2006-03-16 | Matsushita Electric Industrial Co., Ltd. | Transmitting apparatus receiving apparatus radio communication method and radio communication system |
| US20060067437A1 (en) * | 2004-09-30 | 2006-03-30 | Silicon Laboratories Inc. | Wireless communication system and method with frequency burst acquisition feature using autocorrelation |
| US20060072685A1 (en) * | 2004-09-30 | 2006-04-06 | Silicon Laboratories Inc. | Wireless communication system with hardware-based frequency burst detection |
| US20060159187A1 (en) * | 2005-01-14 | 2006-07-20 | Haifeng Wang | System and method for utilizing different known guard intervals in single/multiple carrier communication systems |
| US7082159B2 (en) * | 2000-11-29 | 2006-07-25 | Telefonaktiebolaget Lm Ericsson (Publ) | Methods and arrangements in a telecommunications system |
| US20060227748A1 (en) * | 2005-02-11 | 2006-10-12 | Anastasios Stamoulis | Selection of a thresholding parameter for channel estimation |
| US20060250939A1 (en) * | 2005-03-28 | 2006-11-09 | Wang Michael M | Optimal timing and frequency acquisition for OFDM systems |
| US20070202919A1 (en) * | 2003-04-22 | 2007-08-30 | Shu David B | Separating Mixed Signals In A Cellular Environment |
| WO2007119135A2 (en) * | 2006-04-19 | 2007-10-25 | Nokia Corporation | Modified dual symbol rate for uplink mobile communications |
| US20070263752A1 (en) * | 2006-05-11 | 2007-11-15 | Telefonaktiebolaget Lm Ericsson (Publ) | Delay-doppler channel response demodulation method and apparatus |
| US20070286862A1 (en) * | 2004-04-02 | 2007-12-13 | Rees Robert C | Cancer Associated Antigens |
| US20080310372A1 (en) * | 2005-05-12 | 2008-12-18 | Feng Li | Method for Estimating Direction-of-Arrival of Terminal in Multiple Co-Frequency Cells |
| US7489719B1 (en) * | 2005-05-11 | 2009-02-10 | Bae Systems Information And Electronic Systems Integration Inc. | Training sequences, methods and wireless communication systems providing security-enhanced initialization |
| US20090129442A1 (en) * | 2007-10-11 | 2009-05-21 | Mohebbi Behzad B | Cdma unii link |
| US7567637B2 (en) | 2004-09-30 | 2009-07-28 | St-Ericsson Sa | Wireless communication system and method with frequency burst acquisition feature using autocorrelation and narrowband interference detection |
| US20090252251A1 (en) * | 2006-08-21 | 2009-10-08 | Koninklijke Philips Electronics N.V. | Transform-domain feedback signaling for mimo communication |
| WO2009124568A1 (en) * | 2008-04-11 | 2009-10-15 | Trident Microsystems (Far East) Ltd. | Method and circuit device for correlation and reshaping based channel estimation in a dtmb receiver |
| US20090285327A1 (en) * | 2006-06-23 | 2009-11-19 | Panasonic Corporation | Radio transmitting apparatus, radio receiving apparatus, and pilot generating method |
| US20090288121A1 (en) * | 2007-07-05 | 2009-11-19 | Shelby Kevin A | Transmission of Multimedia Streams to Mobile Devices With Variable Training Information |
| US20100316145A1 (en) * | 2007-09-13 | 2010-12-16 | Samsung Electronics Co., Ltd. | Method for channel estimation and feedback in wireless communication system |
| US20120087406A1 (en) * | 2010-10-11 | 2012-04-12 | Samsung Electronics Co., Ltd. | Device and method for receiving downlink signal in wireless communication system |
| US8913582B1 (en) * | 2009-03-05 | 2014-12-16 | Marvell International Ltd. | Systems and methods for selecting a modulation and coding scheme for wireless communication between wireless devices in a wireless network |
| US8982803B1 (en) | 2009-03-05 | 2015-03-17 | Marvell International Ltd. | Systems and methods for link adaption in wireless communication systems |
| US9014621B2 (en) * | 2009-04-10 | 2015-04-21 | Nextivity, Inc. | Short-range cellular booster |
| US20150381259A1 (en) * | 2007-11-21 | 2015-12-31 | The Directv Group, Inc. | Wireless Communications Systems and Methods |
| US9414279B2 (en) | 2002-03-22 | 2016-08-09 | Microsoft Technology Licensing, Llc | Simultaneous communication with multiple base stations |
| CN107979547A (en) * | 2016-10-24 | 2018-05-01 | 深圳超级数据链技术有限公司 | Channel estimation methods and device |
| CN107979548A (en) * | 2016-10-24 | 2018-05-01 | 深圳超级数据链技术有限公司 | Signal processing method and device |
| US10027428B2 (en) * | 2016-01-25 | 2018-07-17 | Innowireless Co., Ltd. | Method of calibrating power for MIMO-OFDM transmitter |
| US10700800B2 (en) | 2003-05-21 | 2020-06-30 | Regents Of The University Of Minnesota | Estimating frequency-offsets and multi-antenna channels in MIMO OFDM systems |
Families Citing this family (134)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| DE10006520A1 (en) * | 2000-02-15 | 2001-09-06 | Infineon Technologies Ag | Method for estimating channel parameters of radio channels of a W-CDMA mobile radio system |
| US8363744B2 (en) | 2001-06-10 | 2013-01-29 | Aloft Media, Llc | Method and system for robust, secure, and high-efficiency voice and packet transmission over ad-hoc, mesh, and MIMO communication networks |
| US6759743B2 (en) * | 2000-09-11 | 2004-07-06 | Xytrans, Inc. | Thick film millimeter wave transceiver module |
| US7142595B1 (en) * | 2001-04-12 | 2006-11-28 | Conexant, Inc. | System and method for decreasing cross-talk effects in time-domain-modulation (TDM) digital subscriber line (DSL) systems |
| US7269127B2 (en) * | 2001-10-04 | 2007-09-11 | Bae Systems Information And Electronic Systems Integration Inc. | Preamble structures for single-input, single-output (SISO) and multi-input, multi-output (MIMO) communication systems |
| GB2384660B (en) * | 2002-01-25 | 2004-11-17 | Toshiba Res Europ Ltd | Reciever processing systems |
| US6714769B2 (en) * | 2002-03-08 | 2004-03-30 | Interdigital Technology Corporation | Method and system for implementing smart antennas and diversity techniques |
| US7397870B2 (en) * | 2002-06-07 | 2008-07-08 | Texas Instruments Incorporated | Ultra-wideband (UWB) receiver |
| WO2004004172A1 (en) * | 2002-07-01 | 2004-01-08 | Nokia Corporation | Method and apparatus to establish constellations for imperfect channel state information at a receiver |
| US7118877B2 (en) * | 2002-07-08 | 2006-10-10 | Wyeth | Caspase 9 activation and uses therefor |
| US6987797B2 (en) * | 2002-07-26 | 2006-01-17 | Qualcomm Incorporated | Non-parametric matched filter receiver for wireless communication systems |
| US8194770B2 (en) | 2002-08-27 | 2012-06-05 | Qualcomm Incorporated | Coded MIMO systems with selective channel inversion applied per eigenmode |
| US7529177B2 (en) * | 2002-08-28 | 2009-05-05 | Agere Systems Inc. | Dithering scheme using multiple antennas for OFDM systems |
| KR100450849B1 (en) * | 2002-09-03 | 2004-10-01 | 한국전자통신연구원 | Adaptive Interference Suppression Apparatus for Space-Time Block Coded Direct Sequence/Code Division Multiple Access Communication System |
| US7889819B2 (en) * | 2002-10-04 | 2011-02-15 | Apurva Mody | Methods and systems for sampling frequency offset detection, correction and control for MIMO OFDM systems |
| US8170513B2 (en) * | 2002-10-25 | 2012-05-01 | Qualcomm Incorporated | Data detection and demodulation for wireless communication systems |
| US8169944B2 (en) | 2002-10-25 | 2012-05-01 | Qualcomm Incorporated | Random access for wireless multiple-access communication systems |
| US8570988B2 (en) | 2002-10-25 | 2013-10-29 | Qualcomm Incorporated | Channel calibration for a time division duplexed communication system |
| US20040081131A1 (en) | 2002-10-25 | 2004-04-29 | Walton Jay Rod | OFDM communication system with multiple OFDM symbol sizes |
| US8218609B2 (en) * | 2002-10-25 | 2012-07-10 | Qualcomm Incorporated | Closed-loop rate control for a multi-channel communication system |
| US8134976B2 (en) | 2002-10-25 | 2012-03-13 | Qualcomm Incorporated | Channel calibration for a time division duplexed communication system |
| US8208364B2 (en) | 2002-10-25 | 2012-06-26 | Qualcomm Incorporated | MIMO system with multiple spatial multiplexing modes |
| US8320301B2 (en) * | 2002-10-25 | 2012-11-27 | Qualcomm Incorporated | MIMO WLAN system |
| US7002900B2 (en) * | 2002-10-25 | 2006-02-21 | Qualcomm Incorporated | Transmit diversity processing for a multi-antenna communication system |
| US7986742B2 (en) | 2002-10-25 | 2011-07-26 | Qualcomm Incorporated | Pilots for MIMO communication system |
| US7324429B2 (en) | 2002-10-25 | 2008-01-29 | Qualcomm, Incorporated | Multi-mode terminal in a wireless MIMO system |
| US7421029B2 (en) * | 2002-12-20 | 2008-09-02 | Unique Broadband Systems, Inc. | Impulse response shortening and symbol synchronization in OFDM communication systems |
| US7826342B2 (en) * | 2003-01-15 | 2010-11-02 | Telefonaktiebolaget Lm Ericsson | Correlation method for channel estimation for OFDM |
| US7042967B2 (en) * | 2003-03-03 | 2006-05-09 | Interdigital Technology Corporation | Reduced complexity sliding window based equalizer |
| CN100479338C (en) * | 2003-03-03 | 2009-04-15 | 美商内数位科技公司 | Reduced complexity sliding window based equalizer |
| US7418067B1 (en) * | 2003-04-14 | 2008-08-26 | Magnolia Broadband Inc. | Processing diversity signals at a mobile device using phase adjustments |
| CN100566204C (en) * | 2003-04-21 | 2009-12-02 | 三菱电机株式会社 | Radio communication device, dispensing device, receiving system and wireless communication system |
| IL155828A0 (en) * | 2003-05-09 | 2003-12-23 | Zion Hadad | Handoff system and method |
| US8149960B2 (en) * | 2003-05-23 | 2012-04-03 | Zenith Electronics Llc | Channel estimation for frequency selective multipath channels with long delay spreads based on an assumed physical channel |
| US7889804B2 (en) * | 2003-05-30 | 2011-02-15 | Mohammad Jaber Borran | Partially coherent constellations for multiple-antenna systems |
| US7394865B2 (en) * | 2003-06-25 | 2008-07-01 | Nokia Corporation | Signal constellations for multi-carrier systems |
| US7433382B1 (en) * | 2003-07-07 | 2008-10-07 | Miao George J | Spread spectrum based multichannel modulation for ultra wideband communications |
| WO2005015791A1 (en) * | 2003-08-08 | 2005-02-17 | Nortel Networks Limited | Communication signal equalization systems and methods |
| CN1581740B (en) * | 2003-08-15 | 2012-10-17 | 上海贝尔阿尔卡特股份有限公司 | Feedback type channel estimating method and device based on PN sequence and pilot frequency in OFDM system |
| KR100950646B1 (en) * | 2003-10-16 | 2010-04-01 | 삼성전자주식회사 | Method for transmitting preamble in order to synchronous mimo ofdm communication system |
| DE10348818B4 (en) * | 2003-10-21 | 2005-11-10 | Universität Hannover | Method for controlling a guard interval of data streams in digital radio transmission devices and radio receiver device for this purpose |
| US7660275B2 (en) * | 2003-10-24 | 2010-02-09 | Qualcomm Incorporated | Local and wide-area transmissions in a wireless broadcast network |
| US7616698B2 (en) | 2003-11-04 | 2009-11-10 | Atheros Communications, Inc. | Multiple-input multiple output system and method |
| US20050113142A1 (en) * | 2003-11-20 | 2005-05-26 | Telefonaktiebolaget Lm Ericsson (Publ) | Temporal joint searcher and channel estimators |
| US20050113141A1 (en) * | 2003-11-20 | 2005-05-26 | Telefonaktiebolaget Lm Ericsson (Publ) | Spatial joint searcher and channel estimators |
| US7308286B2 (en) * | 2003-11-20 | 2007-12-11 | Telefonaktiebolaget Lm Ericsson (Publ) | Multi-dimensional joint searcher and channel estimators |
| US9473269B2 (en) | 2003-12-01 | 2016-10-18 | Qualcomm Incorporated | Method and apparatus for providing an efficient control channel structure in a wireless communication system |
| US7609786B2 (en) * | 2004-01-28 | 2009-10-27 | Qualcomm Incorporated | Channel estimation for a communication system using spectral estimation |
| CN1879426B (en) | 2004-01-29 | 2010-06-23 | 桥扬科技有限公司 | Methods and apparatus for multi-carrier, multi-cell wireless communication networks |
| EP1712019B1 (en) | 2004-01-29 | 2014-01-15 | Neocific, Inc. | Methods and apparatus for overlaying multi-carrier and direct sequence spread spectrum signals in a broadband wireless communication system |
| WO2005078949A1 (en) * | 2004-02-12 | 2005-08-25 | Nec Corporation | Mobile communication system and wireless apparatus used therein |
| JP4388077B2 (en) * | 2004-02-19 | 2009-12-24 | 株式会社エヌ・ティ・ティ・ドコモ | Apparatus and method for effective channel estimation and apparatus and method for providing a pilot sequence |
| US8077691B2 (en) * | 2004-03-05 | 2011-12-13 | Qualcomm Incorporated | Pilot transmission and channel estimation for MISO and MIMO receivers in a multi-antenna system |
| JP4652846B2 (en) | 2004-03-11 | 2011-03-16 | パナソニック株式会社 | Communication terminal device and communication relay method |
| US11309943B2 (en) | 2004-04-02 | 2022-04-19 | Rearden, Llc | System and methods for planned evolution and obsolescence of multiuser spectrum |
| US10985811B2 (en) | 2004-04-02 | 2021-04-20 | Rearden, Llc | System and method for distributed antenna wireless communications |
| US11394436B2 (en) | 2004-04-02 | 2022-07-19 | Rearden, Llc | System and method for distributed antenna wireless communications |
| US8542763B2 (en) | 2004-04-02 | 2013-09-24 | Rearden, Llc | Systems and methods to coordinate transmissions in distributed wireless systems via user clustering |
| US8654815B1 (en) * | 2004-04-02 | 2014-02-18 | Rearden, Llc | System and method for distributed antenna wireless communications |
| US10200094B2 (en) | 2004-04-02 | 2019-02-05 | Rearden, Llc | Interference management, handoff, power control and link adaptation in distributed-input distributed-output (DIDO) communication systems |
| US10886979B2 (en) | 2004-04-02 | 2021-01-05 | Rearden, Llc | System and method for link adaptation in DIDO multicarrier systems |
| US10277290B2 (en) | 2004-04-02 | 2019-04-30 | Rearden, Llc | Systems and methods to exploit areas of coherence in wireless systems |
| US11451275B2 (en) | 2004-04-02 | 2022-09-20 | Rearden, Llc | System and method for distributed antenna wireless communications |
| US10749582B2 (en) | 2004-04-02 | 2020-08-18 | Rearden, Llc | Systems and methods to coordinate transmissions in distributed wireless systems via user clustering |
| US7720042B2 (en) * | 2004-04-02 | 2010-05-18 | Lg Electronics Inc. | Method for transmitting and receiving data signal in MIMO system |
| US10187133B2 (en) | 2004-04-02 | 2019-01-22 | Rearden, Llc | System and method for power control and antenna grouping in a distributed-input-distributed-output (DIDO) network |
| US10425134B2 (en) | 2004-04-02 | 2019-09-24 | Rearden, Llc | System and methods for planned evolution and obsolescence of multiuser spectrum |
| US9312929B2 (en) | 2004-04-02 | 2016-04-12 | Rearden, Llc | System and methods to compensate for Doppler effects in multi-user (MU) multiple antenna systems (MAS) |
| US7684372B2 (en) * | 2004-05-04 | 2010-03-23 | Ipwireless, Inc. | Signaling MIMO allocations |
| EP1784930B1 (en) * | 2004-05-04 | 2016-03-23 | Sony Corporation | Training sequence allocations for MIMO transmissions |
| US7418046B2 (en) * | 2004-07-22 | 2008-08-26 | Qualcomm Inc. | Pilot transmission and channel estimation for multiple transmitters |
| US7646703B2 (en) | 2004-07-27 | 2010-01-12 | Broadcom Corporation | Backward-compatible long training sequences for wireless communication networks |
| US9685997B2 (en) | 2007-08-20 | 2017-06-20 | Rearden, Llc | Systems and methods to enhance spatial diversity in distributed-input distributed-output wireless systems |
| TWI256219B (en) * | 2004-08-09 | 2006-06-01 | Realtek Semiconductor Corp | Interference alleviation equalizer of multi-carrier communication system and method thereof |
| US20060045170A1 (en) * | 2004-08-30 | 2006-03-02 | Samsung Electronics Co., Ltd. | Apparatus and method for canceling interference in a single antenna 1xEV-DV mobile station |
| KR100899749B1 (en) * | 2005-01-13 | 2009-05-27 | 삼성전자주식회사 | Method for transmitting and receiving preamble sequences in an orthogonal frequency division multiplexing communication system using multiple input multiple output scheme |
| US7466749B2 (en) | 2005-05-12 | 2008-12-16 | Qualcomm Incorporated | Rate selection with margin sharing |
| US7894818B2 (en) * | 2005-06-15 | 2011-02-22 | Samsung Electronics Co., Ltd. | Apparatus and method for multiplexing broadcast and unicast traffic in a multi-carrier wireless network |
| US20070002724A1 (en) * | 2005-06-15 | 2007-01-04 | Samsung Electronics Co., Ltd. | Apparatus and method for broadcast superposition and cancellation in a multi-carrier wireless network |
| US8358714B2 (en) | 2005-06-16 | 2013-01-22 | Qualcomm Incorporated | Coding and modulation for multiple data streams in a communication system |
| US20080198836A1 (en) * | 2005-06-24 | 2008-08-21 | Koninklijke Philips Electronics N.V. | Method and Apparatus For Synchronization in Wireless Communication System |
| US20070002939A1 (en) * | 2005-06-29 | 2007-01-04 | Tellabs Operations, Inc. | Method and apparatus for testing a data path |
| EP1955509A4 (en) | 2005-11-28 | 2011-07-06 | Lg Electronics Inc | Method and apparatus for generating and transmitting code sequence in a wireless communication system |
| US7817735B2 (en) * | 2006-01-11 | 2010-10-19 | Amicus Wireless Technology Ltd. | Device and method of performing channel estimation for OFDM-based wireless communication system |
| EP2456088A1 (en) | 2006-02-28 | 2012-05-23 | Rotani Inc. | Methods and apparatus for overlapping mimo antenna physical sectors |
| US7742770B2 (en) | 2006-03-24 | 2010-06-22 | Agere Systems Inc. | Method and apparatus for improved antenna isolation for per-antenna training using variable scaling |
| US7672412B2 (en) | 2006-04-05 | 2010-03-02 | Research In Motion Limited | Method and receiver for estimating the channel impulse response using a constant modulus interference removal iteration |
| US7860128B2 (en) * | 2006-06-28 | 2010-12-28 | Samsung Electronics Co., Ltd. | System and method for wireless communication of uncompressed video having a preamble design |
| EP2119064A4 (en) * | 2007-01-10 | 2012-09-19 | Ericsson Telefon Ab L M | Method for classifying radio channels |
| US8068407B2 (en) * | 2007-03-13 | 2011-11-29 | Nec Laboratories America, Inc. | Group MMSE-DFD with order and filter computation for reception on a cellular downlink |
| US20080225688A1 (en) * | 2007-03-14 | 2008-09-18 | Kowalski John M | Systems and methods for improving reference signals for spatially multiplexed cellular systems |
| US8526524B2 (en) * | 2007-03-27 | 2013-09-03 | Qualcomm Incorporation | Orthogonal reference signal permutation |
| US7881392B2 (en) * | 2007-03-30 | 2011-02-01 | Hong Kong Applied Science And Technology Research Institute Co., Ltd. | OFDM/OFDMA timing synchronization using non-consecutive pilot subcarrier assignment |
| EP2141822B1 (en) * | 2007-04-20 | 2016-05-04 | Fujitsu Limited | Equalizer control apparatus, equalizer control method, and wireless terminal having that control apparatus |
| TW200919993A (en) * | 2007-10-26 | 2009-05-01 | Univ Nat Chiao Tung | Method and apparatus for determining a channel impulse response |
| US9432080B2 (en) * | 2008-01-11 | 2016-08-30 | Lantiq Deutschland Gmbh | Probing and estimation of cross-coupling |
| CN101227439B (en) * | 2008-02-01 | 2010-06-09 | 北京航空航天大学 | Method for determining uplink exploration field based on iteration search channel estimation |
| WO2009123598A1 (en) * | 2008-04-04 | 2009-10-08 | Beceem Communications Inc. | Managing handoffs between overlaid networks |
| US8711981B2 (en) * | 2008-07-17 | 2014-04-29 | Freescale Semiconductor, Inc. | Integrated testing circuitry for high-frequency receiver integrated circuits |
| KR20100025869A (en) * | 2008-08-28 | 2010-03-10 | 한국전자통신연구원 | Apparatus and method of channel equalization using channel estimation |
| US9942078B2 (en) * | 2009-05-29 | 2018-04-10 | Avago Technologies General Ip (Singapore) Pte. Ltd. | Methods and apparatus for simultaneous estimation of frequency offset and channel response for MU-MIMO OFDMA |
| US8259830B1 (en) * | 2009-10-14 | 2012-09-04 | Google Inc. | Simultaneous use of multiple radio frequency channels |
| US8817687B2 (en) * | 2009-11-06 | 2014-08-26 | Futurewei Technologies, Inc. | System and method for channel estimation in wireless communications systems |
| KR101574191B1 (en) * | 2010-01-07 | 2015-12-03 | 삼성전자주식회사 | Apparatus and method for estimating channel in broadband wireless communication system |
| US9231836B2 (en) * | 2010-06-11 | 2016-01-05 | Centre Of Excellence In Wireless Technology | Robust channel estimation of OFDM systems |
| CN103222204B (en) * | 2010-11-17 | 2016-11-02 | 诺基亚技术有限公司 | For reducing in communication system the apparatus and method of the interference between frequency division duplex signaling and time-division duplex signal |
| US20120250533A1 (en) * | 2011-03-29 | 2012-10-04 | Tom Harel | Symmetrization of channel impulse response |
| US8750363B2 (en) * | 2011-04-08 | 2014-06-10 | Broadcom Corporation | Methods and apparatus for weighted equalization |
| US8891710B2 (en) * | 2011-08-11 | 2014-11-18 | Texas Instruments Incorporated | Frequency-domain filtering for channel estimation in communications systems |
| JP2013046131A (en) * | 2011-08-23 | 2013-03-04 | Mitsubishi Electric Research Laboratories Inc | Method for estimating time-varying and frequency-selective channels |
| CN102664850B (en) * | 2012-04-13 | 2014-10-22 | 豪威科技(上海)有限公司 | Multi-carrier mode low-complexity channel noise-reducing method and device thereof in wireless local area network (WLAN) |
| US11189917B2 (en) | 2014-04-16 | 2021-11-30 | Rearden, Llc | Systems and methods for distributing radioheads |
| US11050468B2 (en) | 2014-04-16 | 2021-06-29 | Rearden, Llc | Systems and methods for mitigating interference within actively used spectrum |
| US11190947B2 (en) | 2014-04-16 | 2021-11-30 | Rearden, Llc | Systems and methods for concurrent spectrum usage within actively used spectrum |
| US10194346B2 (en) | 2012-11-26 | 2019-01-29 | Rearden, Llc | Systems and methods for exploiting inter-cell multiplexing gain in wireless cellular systems via distributed input distributed output technology |
| US9973246B2 (en) | 2013-03-12 | 2018-05-15 | Rearden, Llc | Systems and methods for exploiting inter-cell multiplexing gain in wireless cellular systems via distributed input distributed output technology |
| US10164698B2 (en) | 2013-03-12 | 2018-12-25 | Rearden, Llc | Systems and methods for exploiting inter-cell multiplexing gain in wireless cellular systems via distributed input distributed output technology |
| US8923364B1 (en) | 2013-03-13 | 2014-12-30 | Google Inc. | Transmitting data over discontiguous portions of radio frequency spectrum |
| US10547358B2 (en) | 2013-03-15 | 2020-01-28 | Rearden, Llc | Systems and methods for radio frequency calibration exploiting channel reciprocity in distributed input distributed output wireless communications |
| US9166837B2 (en) | 2013-06-11 | 2015-10-20 | Qualcomm Incorporated | Base station assisted frequency domain equalization |
| JP2015073260A (en) * | 2013-09-04 | 2015-04-16 | 富士通株式会社 | Radio communication system and radio communication method |
| RU2014104571A (en) * | 2014-02-10 | 2015-08-20 | ЭлЭсАй Корпорейшн | SYSTEMS AND METHODS FOR AN EFFECTIVE PERFORMANCE AREA FOR DATA ENCODING |
| US11290162B2 (en) | 2014-04-16 | 2022-03-29 | Rearden, Llc | Systems and methods for mitigating interference within actively used spectrum |
| CN106454922B (en) * | 2015-08-10 | 2018-11-02 | 电信科学技术研究院 | A kind of uplink detection method and device in non-orthogonal multiple access system |
| EP3255851B1 (en) | 2016-06-08 | 2019-08-07 | Nxp B.V. | Processing module for a communication device and method therefor |
| EP3321712A1 (en) * | 2016-11-11 | 2018-05-16 | Nxp B.V. | Processing module and associated method |
| EP3370464B1 (en) | 2017-03-02 | 2020-02-26 | Nxp B.V. | Processing module and associated method |
| EP3370082B1 (en) | 2017-03-02 | 2020-12-09 | Nxp B.V. | Processing module and associated method |
| EP3370365B1 (en) | 2017-03-02 | 2020-07-01 | Nxp B.V. | Processing module and associated method |
| EP3370083B1 (en) | 2017-03-02 | 2020-08-26 | Nxp B.V. | Processing module and associated method |
| EP3386218B1 (en) | 2017-04-03 | 2021-03-10 | Nxp B.V. | Range determining module |
| CN112688889B (en) * | 2020-12-11 | 2022-03-29 | 北京邮电大学 | Channel estimation method and device of unmanned aerial vehicle measurement and control system |
| US11792056B2 (en) | 2020-12-18 | 2023-10-17 | Samsung Electronics Co., Ltd. | Method of performing synchronization and frequency offset estimation based on simultaneous phase compensation of single training sequence and receiver performing the same |
| US11824603B1 (en) * | 2022-09-26 | 2023-11-21 | Qualcomm Incorporated | Superimposed pilots signaling for dense MU-MIMO |
Citations (5)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US5623511A (en) * | 1994-08-30 | 1997-04-22 | Lucent Technologies Inc. | Spread spectrum code pulse position modulated receiver having delay spread compensation |
| US6141393A (en) * | 1999-03-03 | 2000-10-31 | Motorola, Inc. | Method and device for channel estimation, equalization, and interference suppression |
| US6515978B1 (en) * | 1999-04-19 | 2003-02-04 | Lucent Technologies Inc. | Methods and apparatus for downlink diversity in CDMA using Walsh codes |
| US6680967B1 (en) * | 1998-08-21 | 2004-01-20 | Nokia Mobile Phones, Ltd. | Receiver |
| US6765969B1 (en) * | 1999-09-01 | 2004-07-20 | Motorola, Inc. | Method and device for multi-user channel estimation |
Family Cites Families (18)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US5517122A (en) * | 1993-11-04 | 1996-05-14 | The Regents Of University Of California | T2 restoration and noise suppression of hybrid MR images using Wiener and linear prediction techniques |
| US5745484A (en) * | 1995-06-05 | 1998-04-28 | Omnipoint Corporation | Efficient communication system using time division multiplexing and timing adjustment control |
| US6121927A (en) * | 1996-10-29 | 2000-09-19 | Nokia Telecommunications Oy | Determination of terminal location in a radio system |
| US6421334B1 (en) * | 1998-05-13 | 2002-07-16 | Nortel Networks Limited | Technique for time alignment of uplink CDMA signals |
| US6618452B1 (en) * | 1998-06-08 | 2003-09-09 | Telefonaktiebolaget Lm Ericsson (Publ) | Burst carrier frequency synchronization and iterative frequency-domain frame synchronization for OFDM |
| US6229842B1 (en) * | 1998-07-16 | 2001-05-08 | Telefonaktiebolaget Lm Ericsson (Publ) | Adaptive path selection threshold setting for DS-CDMA receivers |
| US6370183B1 (en) * | 1998-10-26 | 2002-04-09 | Nortel Networks Limited | Predictive rake receiver for CDMA mobile radio systems |
| US6289062B1 (en) * | 1998-12-11 | 2001-09-11 | Nortel Networks Limited | Method and apparatus for high rate data communication utilizing an adaptive antenna array |
| JP2000261412A (en) * | 1999-03-06 | 2000-09-22 | Matsushita Electric Ind Co Ltd | Interference signal eliminating device |
| US6233273B1 (en) * | 1999-06-29 | 2001-05-15 | Intersil Americas Inc. | Rake receiver with embedded decision feedback equalizer |
| US6765894B1 (en) * | 1999-07-05 | 2004-07-20 | Matsushita Electric Industrial Co, Ltd. | Communication terminal apparatus and base station apparatus |
| US6850505B1 (en) * | 1999-09-01 | 2005-02-01 | Telefonaktiebolaget L M Ericsson (Publ) | Method and apparatus for Doppler frequency estimation |
| US6614836B1 (en) * | 2000-01-28 | 2003-09-02 | Intersil Americas Inc. | Biased-corrected rake receiver for direct sequence spread spectrum waveform |
| JP3387471B2 (en) * | 2000-02-14 | 2003-03-17 | 日本電気株式会社 | Spread spectrum communication system receiver and path search method for spread spectrum communication |
| US6661857B1 (en) * | 2000-07-10 | 2003-12-09 | Intersil Americas Inc. | Rapid estimation of wireless channel impulse response |
| US7233625B2 (en) * | 2000-09-01 | 2007-06-19 | Nortel Networks Limited | Preamble design for multiple input—multiple output (MIMO), orthogonal frequency division multiplexing (OFDM) system |
| FR2821502A1 (en) * | 2001-02-27 | 2002-08-30 | Thomson Csf | METHOD AND DEVICE FOR ESTIMATING A PROPAGATION CHANNEL FROM ITS STATISTICS |
| JP3969275B2 (en) * | 2002-10-15 | 2007-09-05 | 株式会社日立製作所 | Wireless position measuring method and apparatus |
-
2001
- 2001-04-03 US US09/825,058 patent/US20020176485A1/en not_active Abandoned
-
2002
- 2002-03-29 US US10/109,915 patent/US7149239B2/en not_active Expired - Lifetime
- 2002-04-03 AU AU2002251181A patent/AU2002251181A1/en not_active Abandoned
Patent Citations (5)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US5623511A (en) * | 1994-08-30 | 1997-04-22 | Lucent Technologies Inc. | Spread spectrum code pulse position modulated receiver having delay spread compensation |
| US6680967B1 (en) * | 1998-08-21 | 2004-01-20 | Nokia Mobile Phones, Ltd. | Receiver |
| US6141393A (en) * | 1999-03-03 | 2000-10-31 | Motorola, Inc. | Method and device for channel estimation, equalization, and interference suppression |
| US6515978B1 (en) * | 1999-04-19 | 2003-02-04 | Lucent Technologies Inc. | Methods and apparatus for downlink diversity in CDMA using Walsh codes |
| US6765969B1 (en) * | 1999-09-01 | 2004-07-20 | Motorola, Inc. | Method and device for multi-user channel estimation |
Cited By (73)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US20040125743A1 (en) * | 2000-09-29 | 2004-07-01 | Hashem Bassam M. | Dynamic sub-carrier assignment in OFDM systems |
| US7031753B2 (en) * | 2000-09-29 | 2006-04-18 | Nortel Networks Limited | Dynamic sub-carrier assignment in OFDM systems |
| US7082159B2 (en) * | 2000-11-29 | 2006-07-25 | Telefonaktiebolaget Lm Ericsson (Publ) | Methods and arrangements in a telecommunications system |
| US7460605B2 (en) * | 2001-11-15 | 2008-12-02 | Lawrence Livermore National Security, Llc | Time reversal communication system |
| US20030138053A1 (en) * | 2001-11-15 | 2003-07-24 | The Regents Of The University Of California | Time reversal communication system |
| US9414279B2 (en) | 2002-03-22 | 2016-08-09 | Microsoft Technology Licensing, Llc | Simultaneous communication with multiple base stations |
| US20030223514A1 (en) * | 2002-05-31 | 2003-12-04 | Pladdy Christopher J. | Channel estimator using one or more correlation reference vectors to eliminate data related noise |
| US7289580B2 (en) * | 2002-05-31 | 2007-10-30 | Zenith Electronics Corporation | Channel estimator using one or more correlation reference vectors to eliminate data related noise |
| US20030231728A1 (en) * | 2002-06-17 | 2003-12-18 | Oki Techno Centre (Singapore) Pte Ltd. | Frequency estimation in a burst radio receiver |
| US7720172B2 (en) * | 2002-09-19 | 2010-05-18 | Panasonic Corp. | Transmitting apparatus receiving apparatus, radio communication method and radio communication system |
| US20060058061A1 (en) * | 2002-09-19 | 2006-03-16 | Matsushita Electric Industrial Co., Ltd. | Transmitting apparatus receiving apparatus radio communication method and radio communication system |
| US20040116122A1 (en) * | 2002-09-20 | 2004-06-17 | Interdigital Technology Corporation | Enhancing reception using intercellular interference cancellation |
| US7342974B2 (en) * | 2003-03-20 | 2008-03-11 | Silicon Integrated Systems Corp. | Channel estimation in OFDM systems |
| US20040184399A1 (en) * | 2003-03-20 | 2004-09-23 | Rong-Liang Chiou | Channel estimation in OFDM systems |
| US20040208255A1 (en) * | 2003-04-15 | 2004-10-21 | Shikio Yoshida | Wireless communication apparatus and wireless communication system |
| US7406129B2 (en) * | 2003-04-15 | 2008-07-29 | Sharp Kabushiki Kaisha | Wireless communication apparatus and wireless communication system |
| US7826870B2 (en) | 2003-04-22 | 2010-11-02 | Raytheon Company | Separating mixed signals in a cellular environment |
| US20070202919A1 (en) * | 2003-04-22 | 2007-08-30 | Shu David B | Separating Mixed Signals In A Cellular Environment |
| EP1627475A2 (en) * | 2003-05-13 | 2006-02-22 | Interdigital Technology Corporation | Method for soft and softer handover in time division duplex code division multiple access (tdd-cdma) networks |
| EP1627475A4 (en) * | 2003-05-13 | 2011-06-15 | Interdigital Tech Corp | Method for soft and softer handover in time division duplex code division multiple access (tdd-cdma) networks |
| US10700800B2 (en) | 2003-05-21 | 2020-06-30 | Regents Of The University Of Minnesota | Estimating frequency-offsets and multi-antenna channels in MIMO OFDM systems |
| US11303377B2 (en) | 2003-05-21 | 2022-04-12 | Regents Of The University Of Minnesota | Estimating frequency-offsets and multi-antenna channels in MIMO OFDM systems |
| WO2004105335A1 (en) * | 2003-05-22 | 2004-12-02 | Ntt Docomo, Inc. | Apparatus and method for processing an impulse response of a channel |
| US20070286862A1 (en) * | 2004-04-02 | 2007-12-13 | Rees Robert C | Cancer Associated Antigens |
| US7593482B2 (en) | 2004-09-30 | 2009-09-22 | St-Ericsson Sa | Wireless communication system with hardware-based frequency burst detection |
| US20060067437A1 (en) * | 2004-09-30 | 2006-03-30 | Silicon Laboratories Inc. | Wireless communication system and method with frequency burst acquisition feature using autocorrelation |
| US8054918B2 (en) * | 2004-09-30 | 2011-11-08 | ST-Ericsson S.A. | Wireless communication system and method with frequency burst acquisition feature using autocorrelation |
| US20060072685A1 (en) * | 2004-09-30 | 2006-04-06 | Silicon Laboratories Inc. | Wireless communication system with hardware-based frequency burst detection |
| US7567637B2 (en) | 2004-09-30 | 2009-07-28 | St-Ericsson Sa | Wireless communication system and method with frequency burst acquisition feature using autocorrelation and narrowband interference detection |
| US20060159187A1 (en) * | 2005-01-14 | 2006-07-20 | Haifeng Wang | System and method for utilizing different known guard intervals in single/multiple carrier communication systems |
| US8761312B2 (en) * | 2005-02-11 | 2014-06-24 | Qualcomm Incorporated | Selection of a thresholding parameter for channel estimation |
| US20060227748A1 (en) * | 2005-02-11 | 2006-10-12 | Anastasios Stamoulis | Selection of a thresholding parameter for channel estimation |
| US20060250939A1 (en) * | 2005-03-28 | 2006-11-09 | Wang Michael M | Optimal timing and frequency acquisition for OFDM systems |
| US7489719B1 (en) * | 2005-05-11 | 2009-02-10 | Bae Systems Information And Electronic Systems Integration Inc. | Training sequences, methods and wireless communication systems providing security-enhanced initialization |
| US20080310372A1 (en) * | 2005-05-12 | 2008-12-18 | Feng Li | Method for Estimating Direction-of-Arrival of Terminal in Multiple Co-Frequency Cells |
| US8054785B2 (en) * | 2005-05-12 | 2011-11-08 | Shanghai Ultimate Power Communications Technology Co., Ltd. | Method for estimating direction-of-arrival of terminal in multiple co-frequency cells |
| WO2007119135A2 (en) * | 2006-04-19 | 2007-10-25 | Nokia Corporation | Modified dual symbol rate for uplink mobile communications |
| US20070286300A1 (en) * | 2006-04-19 | 2007-12-13 | Nokia Corporation | Modified dual symbol rate for uplink mobile communications |
| WO2007119135A3 (en) * | 2006-04-19 | 2008-01-31 | Nokia Corp | Modified dual symbol rate for uplink mobile communications |
| US7808964B2 (en) * | 2006-04-19 | 2010-10-05 | Nokia Corporation | Modified dual symbol rate for uplink mobile communications |
| WO2007130397A2 (en) * | 2006-05-03 | 2007-11-15 | Raytheon Company | Separating mixed signals in a cellular environment |
| WO2007130397A3 (en) * | 2006-05-03 | 2008-03-20 | Raytheon Co | Separating mixed signals in a cellular environment |
| US7970081B2 (en) * | 2006-05-11 | 2011-06-28 | Telefonaktiebolaget Lm Ericsson (Publ) | Delay-doppler channel response demodulation method and apparatus |
| US20070263752A1 (en) * | 2006-05-11 | 2007-11-15 | Telefonaktiebolaget Lm Ericsson (Publ) | Delay-doppler channel response demodulation method and apparatus |
| US20090285327A1 (en) * | 2006-06-23 | 2009-11-19 | Panasonic Corporation | Radio transmitting apparatus, radio receiving apparatus, and pilot generating method |
| US9155024B2 (en) * | 2006-06-23 | 2015-10-06 | Panasonic Intellectual Property Corporation Of America | Radio transmitting apparatus, radio receiving apparatus, and pilot generating method |
| US10097246B2 (en) * | 2006-08-21 | 2018-10-09 | Koninklijke Philips N.V. | Transform-domain feedback signaling for MIMO communication |
| US20090252251A1 (en) * | 2006-08-21 | 2009-10-08 | Koninklijke Philips Electronics N.V. | Transform-domain feedback signaling for mimo communication |
| US20160105225A1 (en) * | 2006-08-21 | 2016-04-14 | Koninklijke Philips N.V. | Transform-domain feedback signaling for mimo communication |
| US9231683B2 (en) * | 2006-08-21 | 2016-01-05 | Koninklijke Philips N.V. | Transform-domain feedback signaling for MIMO communication |
| US20090288121A1 (en) * | 2007-07-05 | 2009-11-19 | Shelby Kevin A | Transmission of Multimedia Streams to Mobile Devices With Variable Training Information |
| US9009761B2 (en) * | 2007-07-05 | 2015-04-14 | Coherent Logix, Incorporated | Wireless transport framework with variable frequency domain training |
| US9363543B2 (en) * | 2007-07-05 | 2016-06-07 | Coherent Logix, Incorporated | Wireless system with variable training information based on device type |
| US8347339B2 (en) * | 2007-07-05 | 2013-01-01 | Coherent Logix, Incorporated | Transmission of multimedia streams to mobile devices with variable training information |
| US8650598B2 (en) * | 2007-07-05 | 2014-02-11 | Coherent Logix, Incorporated | Wireless transport framework with variable equalizer training |
| US20130089131A1 (en) * | 2007-07-05 | 2013-04-11 | Coherent Logix Incorporated | Wireless Transport Framework with Variable Equalizer Training |
| US20140075489A1 (en) * | 2007-07-05 | 2014-03-13 | Coherent Logix, Incorporated | Wireless Transport Framework with Variable Frequency Domain Training |
| US20150181264A1 (en) * | 2007-07-05 | 2015-06-25 | Coherent Logix, Incorporated | Wireless System with Variable Training Information Based on Device Type |
| US20100316145A1 (en) * | 2007-09-13 | 2010-12-16 | Samsung Electronics Co., Ltd. | Method for channel estimation and feedback in wireless communication system |
| US8718167B2 (en) * | 2007-09-13 | 2014-05-06 | Samsung Electronics Co., Ltd. | Method for channel estimation and feedback in wireless communication system |
| US8351366B2 (en) * | 2007-10-11 | 2013-01-08 | Nextivity, Inc. | CDMA UNII link |
| US20090129442A1 (en) * | 2007-10-11 | 2009-05-21 | Mohebbi Behzad B | Cdma unii link |
| US10003394B2 (en) * | 2007-11-21 | 2018-06-19 | The Directv Group, Inc. | Wireless communications systems and methods |
| US20150381259A1 (en) * | 2007-11-21 | 2015-12-31 | The Directv Group, Inc. | Wireless Communications Systems and Methods |
| WO2009124568A1 (en) * | 2008-04-11 | 2009-10-15 | Trident Microsystems (Far East) Ltd. | Method and circuit device for correlation and reshaping based channel estimation in a dtmb receiver |
| US8982803B1 (en) | 2009-03-05 | 2015-03-17 | Marvell International Ltd. | Systems and methods for link adaption in wireless communication systems |
| US8913582B1 (en) * | 2009-03-05 | 2014-12-16 | Marvell International Ltd. | Systems and methods for selecting a modulation and coding scheme for wireless communication between wireless devices in a wireless network |
| US9014621B2 (en) * | 2009-04-10 | 2015-04-21 | Nextivity, Inc. | Short-range cellular booster |
| US20120087406A1 (en) * | 2010-10-11 | 2012-04-12 | Samsung Electronics Co., Ltd. | Device and method for receiving downlink signal in wireless communication system |
| US8750361B2 (en) * | 2010-10-11 | 2014-06-10 | Samsung Electronics Co., Ltd | Device and method for receiving downlink signal in wireless communication system |
| US10027428B2 (en) * | 2016-01-25 | 2018-07-17 | Innowireless Co., Ltd. | Method of calibrating power for MIMO-OFDM transmitter |
| CN107979547A (en) * | 2016-10-24 | 2018-05-01 | 深圳超级数据链技术有限公司 | Channel estimation methods and device |
| CN107979548A (en) * | 2016-10-24 | 2018-05-01 | 深圳超级数据链技术有限公司 | Signal processing method and device |
Also Published As
| Publication number | Publication date |
|---|---|
| US7149239B2 (en) | 2006-12-12 |
| AU2002251181A1 (en) | 2002-10-21 |
| US20030043887A1 (en) | 2003-03-06 |
Similar Documents
| Publication | Publication Date | Title |
|---|---|---|
| US20020176485A1 (en) | Multi-cast communication system and method of estimating channel impulse responses therein | |
| EP3295578B1 (en) | Orthogonal time frequency space modulation system | |
| AU2002360451B2 (en) | Efficient multiple input multiple output system for multi-path fading channels | |
| US20200145273A1 (en) | Orthogonal time frequency space communication system compatible with ofdm | |
| KR100557102B1 (en) | Device and method for joint detection receiver which use orthogonal codes with a variable in communication system | |
| JP4362504B2 (en) | Single user detection | |
| US7254171B2 (en) | Equaliser for digital communications systems and method of equalisation | |
| US7590169B2 (en) | Multipath interference reduction on pilot estimation with legacy system interoperability | |
| EP1617611B1 (en) | Propagation path estimation method and apparatus | |
| US8619920B2 (en) | Two-dimensional code spreading for interleaved FDMA system | |
| US20130083778A1 (en) | Wideband Analog Channel Information Feedback | |
| EP1552405B1 (en) | Efficient joint detection | |
| WO2002082683A2 (en) | Frequency domain channel estimation for multiple channels using wiener minimum mean squared error (mmse) filtering | |
| JP4105157B2 (en) | Data estimation based on segmental channel equalization | |
| EP1119146A2 (en) | Frequency-domain equalisation | |
| Farhang-Boroujeny et al. | Multicode Signaling in a Filter Bank Multicarrier Spread Spectrum System and Its Application to HF Communications |
Legal Events
| Date | Code | Title | Description |
|---|---|---|---|
| AS | Assignment |
Owner name: NORTEL NETWORKS LIMITED, CANADA Free format text: ASSIGNMENT OF ASSIGNORS INTEREST;ASSIGNOR:HUDSON, JOHN E.;REEL/FRAME:012057/0328 Effective date: 20010409 |
|
| STCB | Information on status: application discontinuation |
Free format text: ABANDONED -- FAILURE TO RESPOND TO AN OFFICE ACTION |
|
| AS | Assignment |
Owner name: MALIKIE INNOVATIONS LIMITED, IRELAND Free format text: ASSIGNMENT OF ASSIGNORS INTEREST;ASSIGNOR:BLACKBERRY LIMITED;REEL/FRAME:064104/0103 Effective date: 20230511 |