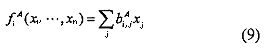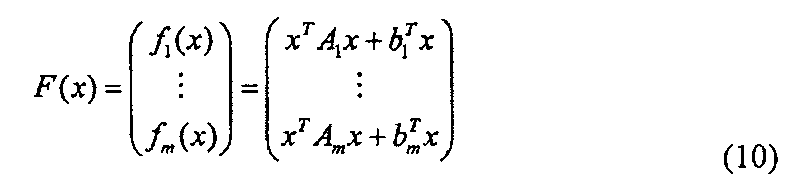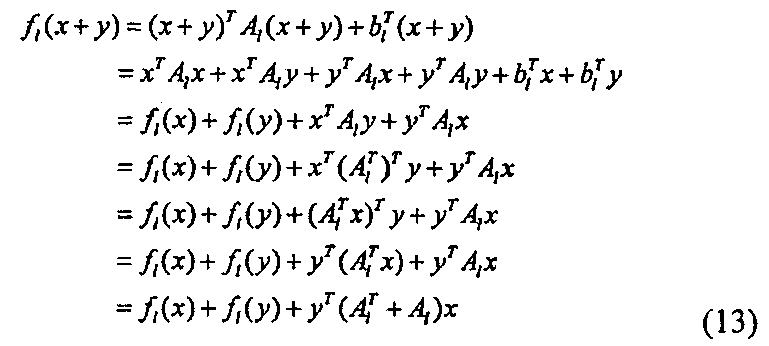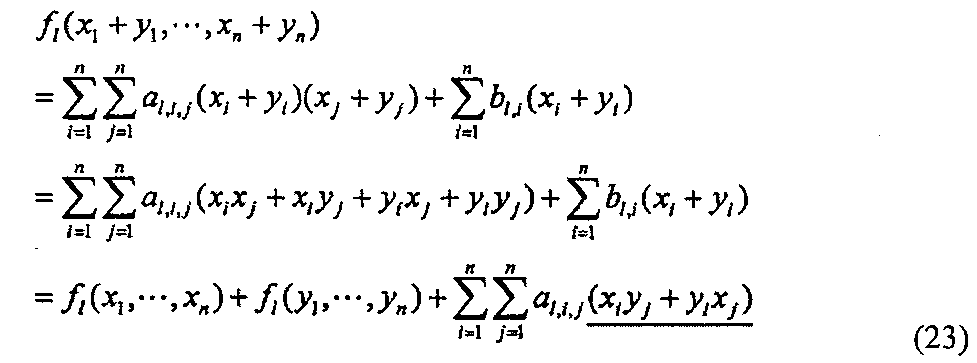RU2600103C2 - Устройство обработки информации, способ обработки информации, программа и носитель записи - Google Patents
Устройство обработки информации, способ обработки информации, программа и носитель записи Download PDFInfo
- Publication number
- RU2600103C2 RU2600103C2 RU2014104078/08A RU2014104078A RU2600103C2 RU 2600103 C2 RU2600103 C2 RU 2600103C2 RU 2014104078/08 A RU2014104078/08 A RU 2014104078/08A RU 2014104078 A RU2014104078 A RU 2014104078A RU 2600103 C2 RU2600103 C2 RU 2600103C2
- Authority
- RU
- Russia
- Prior art keywords
- algorithm
- information
- prover
- verifier
- messages
- Prior art date
Links
- 230000010365 information processing Effects 0.000 title claims abstract description 50
- 238000003672 processing method Methods 0.000 title description 5
- 230000004044 response Effects 0.000 claims abstract description 202
- 239000013598 vector Substances 0.000 claims abstract description 187
- 238000000034 method Methods 0.000 claims description 307
- 238000012795 verification Methods 0.000 claims description 230
- 230000006870 function Effects 0.000 claims description 198
- 238000012545 processing Methods 0.000 claims description 9
- 238000004364 calculation method Methods 0.000 abstract description 54
- 230000000694 effects Effects 0.000 abstract description 8
- 239000000126 substance Substances 0.000 abstract 1
- 238000004422 calculation algorithm Methods 0.000 description 1007
- 230000008569 process Effects 0.000 description 140
- 230000002452 interceptive effect Effects 0.000 description 94
- 238000012546 transfer Methods 0.000 description 75
- 238000010586 diagram Methods 0.000 description 50
- 238000005516 engineering process Methods 0.000 description 43
- 230000014509 gene expression Effects 0.000 description 31
- 230000003993 interaction Effects 0.000 description 29
- 230000007704 transition Effects 0.000 description 29
- 230000000873 masking effect Effects 0.000 description 23
- 238000012986 modification Methods 0.000 description 21
- 230000004048 modification Effects 0.000 description 21
- 230000005540 biological transmission Effects 0.000 description 16
- 238000004891 communication Methods 0.000 description 16
- 230000007246 mechanism Effects 0.000 description 9
- 238000006243 chemical reaction Methods 0.000 description 8
- 230000003287 optical effect Effects 0.000 description 6
- 238000000354 decomposition reaction Methods 0.000 description 4
- 230000007423 decrease Effects 0.000 description 4
- 230000009466 transformation Effects 0.000 description 4
- 239000003795 chemical substances by application Substances 0.000 description 3
- 239000000284 extract Substances 0.000 description 3
- 238000013507 mapping Methods 0.000 description 3
- 238000005316 response function Methods 0.000 description 3
- 239000004065 semiconductor Substances 0.000 description 3
- 238000000844 transformation Methods 0.000 description 3
- 101150012579 ADSL gene Proteins 0.000 description 2
- 102100020775 Adenylosuccinate lyase Human genes 0.000 description 2
- 108700040193 Adenylosuccinate lyases Proteins 0.000 description 2
- 230000009286 beneficial effect Effects 0.000 description 2
- 230000008859 change Effects 0.000 description 2
- 238000013478 data encryption standard Methods 0.000 description 2
- 239000004973 liquid crystal related substance Substances 0.000 description 2
- 239000010453 quartz Substances 0.000 description 2
- 238000012552 review Methods 0.000 description 2
- VYPSYNLAJGMNEJ-UHFFFAOYSA-N silicon dioxide Inorganic materials O=[Si]=O VYPSYNLAJGMNEJ-UHFFFAOYSA-N 0.000 description 2
- 238000001228 spectrum Methods 0.000 description 2
- NAWXUBYGYWOOIX-SFHVURJKSA-N (2s)-2-[[4-[2-(2,4-diaminoquinazolin-6-yl)ethyl]benzoyl]amino]-4-methylidenepentanedioic acid Chemical compound C1=CC2=NC(N)=NC(N)=C2C=C1CCC1=CC=C(C(=O)N[C@@H](CC(=C)C(O)=O)C(O)=O)C=C1 NAWXUBYGYWOOIX-SFHVURJKSA-N 0.000 description 1
- 230000015572 biosynthetic process Effects 0.000 description 1
- 239000002131 composite material Substances 0.000 description 1
- 238000004590 computer program Methods 0.000 description 1
- 238000013500 data storage Methods 0.000 description 1
- 238000011161 development Methods 0.000 description 1
- 238000007689 inspection Methods 0.000 description 1
- 239000011159 matrix material Substances 0.000 description 1
- 230000003252 repetitive effect Effects 0.000 description 1
- 238000012360 testing method Methods 0.000 description 1
- 235000021419 vinegar Nutrition 0.000 description 1
- 239000000052 vinegar Substances 0.000 description 1
Images
Classifications
-
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L9/00—Cryptographic mechanisms or cryptographic arrangements for secret or secure communications; Network security protocols
- H04L9/30—Public key, i.e. encryption algorithm being computationally infeasible to invert or user's encryption keys not requiring secrecy
-
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L9/00—Cryptographic mechanisms or cryptographic arrangements for secret or secure communications; Network security protocols
- H04L9/08—Key distribution or management, e.g. generation, sharing or updating, of cryptographic keys or passwords
- H04L9/0861—Generation of secret information including derivation or calculation of cryptographic keys or passwords
- H04L9/0869—Generation of secret information including derivation or calculation of cryptographic keys or passwords involving random numbers or seeds
-
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L9/00—Cryptographic mechanisms or cryptographic arrangements for secret or secure communications; Network security protocols
- H04L9/32—Cryptographic mechanisms or cryptographic arrangements for secret or secure communications; Network security protocols including means for verifying the identity or authority of a user of the system or for message authentication, e.g. authorization, entity authentication, data integrity or data verification, non-repudiation, key authentication or verification of credentials
- H04L9/3218—Cryptographic mechanisms or cryptographic arrangements for secret or secure communications; Network security protocols including means for verifying the identity or authority of a user of the system or for message authentication, e.g. authorization, entity authentication, data integrity or data verification, non-repudiation, key authentication or verification of credentials using proof of knowledge, e.g. Fiat-Shamir, GQ, Schnorr, ornon-interactive zero-knowledge proofs
-
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L9/00—Cryptographic mechanisms or cryptographic arrangements for secret or secure communications; Network security protocols
- H04L9/32—Cryptographic mechanisms or cryptographic arrangements for secret or secure communications; Network security protocols including means for verifying the identity or authority of a user of the system or for message authentication, e.g. authorization, entity authentication, data integrity or data verification, non-repudiation, key authentication or verification of credentials
- H04L9/3218—Cryptographic mechanisms or cryptographic arrangements for secret or secure communications; Network security protocols including means for verifying the identity or authority of a user of the system or for message authentication, e.g. authorization, entity authentication, data integrity or data verification, non-repudiation, key authentication or verification of credentials using proof of knowledge, e.g. Fiat-Shamir, GQ, Schnorr, ornon-interactive zero-knowledge proofs
- H04L9/3221—Cryptographic mechanisms or cryptographic arrangements for secret or secure communications; Network security protocols including means for verifying the identity or authority of a user of the system or for message authentication, e.g. authorization, entity authentication, data integrity or data verification, non-repudiation, key authentication or verification of credentials using proof of knowledge, e.g. Fiat-Shamir, GQ, Schnorr, ornon-interactive zero-knowledge proofs interactive zero-knowledge proofs
-
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L9/00—Cryptographic mechanisms or cryptographic arrangements for secret or secure communications; Network security protocols
- H04L9/32—Cryptographic mechanisms or cryptographic arrangements for secret or secure communications; Network security protocols including means for verifying the identity or authority of a user of the system or for message authentication, e.g. authorization, entity authentication, data integrity or data verification, non-repudiation, key authentication or verification of credentials
- H04L9/3236—Cryptographic mechanisms or cryptographic arrangements for secret or secure communications; Network security protocols including means for verifying the identity or authority of a user of the system or for message authentication, e.g. authorization, entity authentication, data integrity or data verification, non-repudiation, key authentication or verification of credentials using cryptographic hash functions
-
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L9/00—Cryptographic mechanisms or cryptographic arrangements for secret or secure communications; Network security protocols
- H04L9/32—Cryptographic mechanisms or cryptographic arrangements for secret or secure communications; Network security protocols including means for verifying the identity or authority of a user of the system or for message authentication, e.g. authorization, entity authentication, data integrity or data verification, non-repudiation, key authentication or verification of credentials
- H04L9/3271—Cryptographic mechanisms or cryptographic arrangements for secret or secure communications; Network security protocols including means for verifying the identity or authority of a user of the system or for message authentication, e.g. authorization, entity authentication, data integrity or data verification, non-repudiation, key authentication or verification of credentials using challenge-response
Landscapes
- Engineering & Computer Science (AREA)
- Computer Security & Cryptography (AREA)
- Computer Networks & Wireless Communication (AREA)
- Signal Processing (AREA)
- Computing Systems (AREA)
- Theoretical Computer Science (AREA)
- Storage Device Security (AREA)
- Information Retrieval, Db Structures And Fs Structures Therefor (AREA)
Abstract
Изобретение относится к области криптографической обработки данных. Технический результат - эффективная схема аутентификации с открытым ключом с высоким уровнем безопасности. Устройство обработки информации содержит: модуль генерирования сообщений для генерирования сообщения N раз (где N≥2), на основе набора F=(f1, …, fm) многопорядковых многочленов с многими переменными, определенного на кольце K, и вектора s, являющегося элементом множества Kn, и вычисления первого значения хеш-функции, на основе указанных сообщений N раз; модуль предоставления сообщений для предоставления проверяющему первого значения хеш-функции; модуль генерирования промежуточной информации для генерирования третьей информации N раз, с использованием первой информации, выбранной произвольно проверяющим, и второй информации N раз, и генерирования второго значения хеш-функции, на основе третьей информации N раз; модуль предоставления промежуточной информации для предоставления проверяющему второго значения хеш-функции; и модуль предоставления ответов для предоставления проверяющему информации ответов N раз. 4 н. и 6 з.п. ф-лы, 40 ил.
Description
Область техники, к которой относится изобретение
Предлагаемая технология относится к устройству обработки информации, способу обработки информации, программе и носителю записи.
Уровень техники
В условиях быстрого развития технологий обработки информации и технологий связи, документы, независимо от того, официальные это документы или частные документы, были быстро преобразованы в цифровую форму. При преобразовании таких документов в цифровую форму многие индивидуумы и компании проявляют значительный интерес к управлению безопасностью электронных документов. В ответ на повышение этого интереса, в различных областях активно исследовалась безопасность от действий по вмешательству в электронные документы, таких как перехват или подделка электронных документов. Что касается перехвата электронных документов, то безопасность обеспечивается, например, посредством шифрования электронных документов. Кроме того, что касается подделки электронных документов, то безопасность обеспечивается, например, посредством использования цифровых подписей. Однако, в случае, когда используемые шифрование и цифровые подписи не имеют высокой стойкости по отношению к вмешательству, достаточная безопасность не обеспечивается.
Цифровая подпись используется для указания автора электронного документа. Соответственно, цифровая подпись должна быть сделана такой, чтобы генерировать ее мог только автор электронного документа. Если бы имеющее злой умысел третье лицо было бы в состоянии сгенерировать ту же самую цифровую подпись, то такое третье лицо могло бы выдавать себя за автора этого электронного документа. Таким образом, электронный документ был бы подделан имеющим злой умысел третьим лицом. Для предотвращения такой подделки были высказаны различные соображения, касающиеся безопасности цифровой подписи. В качестве схем цифровой подписи, которые широко используются в настоящее время, известны, например, схема (RSA) цифровой подписи (схема цифровой подписи, основанная на криптографическом алгоритме "Rivest, Shamir & Adleman", названном по фамилиям разработчиков) или схема (DSA) цифровой подписи (схема цифровой подписи, основанная на "Алгоритме цифровой подписи").
В схеме RSA цифровой подписи в качестве основы ее безопасности принимается "трудность разложения на простые сомножители большого составного числа (в дальнейшем, именуемая как задача разложения на простые сомножители)". Кроме того, в схеме (DSA) цифровой подписи в качестве основы ее безопасности принимается "трудность решения дискретной логарифмической задачи". Эти основания основываются на том, что алгоритма, который эффективно решает задачу разложения на простые сомножители или задачу дискретного логарифмирования, используя классический компьютер, не существует. Таким образом, вышеупомянутые трудности предполагают вычислительную сложность для классического компьютера. Однако говорят, что решения задачи разложения на простые сомножители или дискретной логарифмической задачи можно эффективно вычислять при использовании квантового компьютера.
Аналогично схеме RSA цифровой подписи и схеме DSA цифровой подписи во многих из схем цифровой подписи и схем аутентификации с открытым ключом, которые используются в настоящее время, также, в качестве основы безопасности, принимается трудность задачи разложения на простые сомножители или дискретной логарифмической задачи. Таким образом, если квантовый компьютер внедрен в практическое использование, то безопасность таких схем цифровой подписи и схем аутентификации с открытым ключом не будет обеспечена. Соответственно, желательна реализация новых схем цифровой подписи и схем аутентификации с открытым ключом, в которых в качестве основы безопасности принимается задача, отличная от таких задач, как задача разложения на простые сомножители или дискретная логарифмическая задача, которые могут быть с легкостью решены квантовым компьютером. В качестве задачи, которая не решается с легкостью квантовым компьютером, существует, например, задача, относящаяся к многочлену с многими переменными.
Например, в качестве схем цифровой подписи, в которых в качестве основы безопасности принимается задача многочлена с многими переменными, известны схемы, основанные на криптографии Matsumoto-Imai (Мацумото-Имаи) (MI - криптографии), криптографии с использованием скрытого уравнения поля (HFE - криптографии), схеме цифровой подписи "Масло - уксус" (OV - схеме) и криптографии по способу сглаженного преобразования (ТТМ - криптографии). Например, схема цифровой подписи, основанная на HFE - криптографии раскрыта в нижеследующих документах 1 и 2 из списка непатентной литературы.
Список упоминаемых документов
Непатентная литература
Документ 1 непатентной литературы: Jacques Patarin Asymmetric Cryptography with a Hidden Monomial. CRYPTO 1996 (Жак Патарен Асимметричная криптография со скрытым одночленом, CRYPTO, 1996 г.), стр. 45-60.
Документ 2 непатентной литературы: Patarin, J., Courtois, N., and Goubin, L. QUARTZ, 128-Bit Long Digital Signatures. In Naccache, D., Ed. Topics in Cryptology - CT-RSA 2001 (San Francisco, CA, USA, April 2001), vol. 2020 of Lecture Notes in Computer Science, Springer-Verlag (Патарен Ж., Кортоис H., и Гоубин Л., КВАРЦ, Цифровые подписи длиной в 128 битов. В Вопросах криптологии под редакций Нэккэш Д., СТ-RSA 2001 г. (Сан-Франциско, Калифорния, США, апрель 2001 г.), том 2020 Записей лекции по информатике, Springer-Verlag.) стр. 282-297.
Раскрытие изобретения
Техническая задача
Как было описано выше, задача многочлена с многими переменными представляет собой пример задачи, именуемой NP - трудный задачей, которую трудно решить даже при использовании квантового компьютера. Обычно, схема аутентификации с открытым ключом, которая использует задачу многочлена с многими переменными, типизированную в способе HFE или ему подобном, использует систему многопорядковых уравнений с многими переменными, имеющую специальную "лазейку". Например, предусматривается система многопорядковых уравнений с многими переменными: F (x1, …, xn)=y относительно x1, …, xn, и линейные преобразования A и B, и линейные преобразования A и B сохраняются в тайне. В этом случае, система F многопорядковых уравнений с многими переменными и линейные преобразования A и B являются лазейками.
Сторона, которая знает лазейки F, A и B, может решить уравнение B(F(A(x1, …, xn)))=y′ относительно x1, …, xn. С другой стороны, уравнение B(F(A(x1, …, xn)))=y′ относительно x1, …, xn не решается стороной, которая не знает лазеек F, A и B. С использованием этого механизма можно реализовать схему аутентификации с открытым ключом и схему цифровой подписи, в которых за основу безопасности принята трудность решения системы многопорядковых уравнений с многими переменными.
Как было упомянуто выше, для того, чтобы реализовать схему аутентификации с открытым ключом или схему цифровой подписи, необходимо подготовить специальную систему многопорядковых уравнений с многими переменными, удовлетворяющую выражению B(F(A(x1, …, xn)))=y. Кроме того, во время генерирования цифровой подписи, необходимо решить F систему многопорядковых уравнений с многими переменными. По этой причине, располагаемая система F многопорядковых уравнений с многими переменными была ограничена относительно легко разрешимыми уравнениями. То есть в предшествующих схемах использовалась только система многопорядковых уравнений с многими переменными B(F(A(x1, …, xn)))=y комбинированной формы для трех функций ("лазеек") B, F, и A, которая могла быть относительно легко решена, и, таким образом, трудно было гарантировать достаточную безопасность.
Желательно предложить устройство обработки информации, способ обработки информации, программу и носитель записи, которые являются новыми и усовершенствованными и способными реализовать эффективную схему аутентификации с открытым ключом с высоким уровнем безопасности, использующую систему многопорядковых уравнений с многими переменными, для которой эффективное средство решения ("лазейка") не известно.
Решение задачи
В соответствии с одним аспектом предлагаемой технологии, предусматривается устройство обработки информации, содержащее модуль генерирования сообщений для генерирования сообщения N раз (где N≥2), основываясь на наборе F=(f1, …, fm) многопорядковых многочленов с многими переменными, определенном на кольце K, и векторе s, являющемся элементом множества Kn, и вычисления первого значения хеш-функции, основанного на этих сообщениях N раз, модуль предоставления сообщений для предоставления проверяющему, хранящей указанный набор F многопорядковых многочленов с многими переменными и вектор y=(y1, …, ym)=(f1(s), …, fm(s)), первого значения хеш-функции, модуль генерирования промежуточной информации для генерирования третьей информации N раз, используя первую информацию, случайным образом выбранную проверяющей стороной по соответствующим сообщениям N раз, и второй информации N раз, полученной при генерировании этих сообщений, и генерирования второго значение хеш-функции, основанного на третьей информации N раз, модуль предоставления промежуточной информации для предоставления проверяющему второго значения хеш-функции, и модуль предоставления ответов для предоставления проверяющему информации ответов N раз, соответствующей моделям проверки, выбранным проверяющей стороной из k (где k≥2) моделей проверки по соответствующим сообщениям N раз, части сообщений и части третьей информации, причем указанная часть сообщений и указанная часть третьей информации не подлежат получению даже при выполнении с использованием набора F многопорядковых многочленов с многими переменными, вектора y и информации ответа, операции, заранее подготовленной для модели проверки, соответствующей, информации ответа, при этом вектор s представляет собой секретный ключ. Набор F многопорядковых многочленов с многими переменными и вектор y представляют собой открытые ключи. Сообщения и третья информация представляют собой информацию, получаемую при выполнении указанной операции, заранее подготовленной для модели проверки, соответствующей информации ответа, с использованием открытых ключей, первой информации и информации ответа или информации, полученной на основе информации ответа.
В соответствии с другим аспектом предлагаемой технологии, предусматривается устройство обработки информации, содержащее модуль хранения информации, который хранит набор F=(f1, …, fm) многопорядковых многочленов с многими переменными, определенный на кольце K, и вектор y=(y1, …, ym)=(f1(s), …, fm(s)), модуль получения сообщений для получения первого значения хеш-функции, вычисленного на основе сообщений для N раз (где N≥2), сгенерированных на основе набора F многопорядковых многочленов с многими переменными и вектора s, являющегося элементом множества Kn, модуль предоставления информации для предоставления доказывающей стороне, предоставившей эти сообщения, первой информации, выбранной случайным образом по соответствующим сообщениям N раз, модуль получения промежуточной информации для получения второго значения хеш-функции, вычисленной на основе третьей информации N раз, сгенерированной доказывающим с использованием первой информации N раз и второй информации N раз, полученной при генерировании указанных сообщений, модуль предоставления информации о модели для предоставления доказывающему информации о моделях проверки, выбираемых случайным образом из k (где k≥3) моделей проверки по соответствующим сообщениям N раз, модуль получения ответов для получения от доказывающего информации ответов, соответствующей моделям проверки, выбранным по соответствующим сообщениям N раз, и проверяющий модуль для проверки, на основании набора F многопорядковых многочленов с многими переменивши, вектора y, первой информации, информации ответа, первом значении хеш-функции и втором значение хеш-функции, хранит ли доказывающий вектор s. Вектор s представляет собой секретный ключ. Набор F многопорядковых многочленов с многими переменными и вектор y представляют собой открытые ключи. Сообщения и третья информация представляют собой информацию, получаемую при выполнении операции, заранее подготовленной для модели проверки, соответствующей информации ответа, с использованием открытых ключей, первой информации и информации ответа или информации, полученной на основе информации ответа.
В соответствии с другим аспектом предлагаемой технологии, предусматривается способ обработки информации, содержащий: этап, на котором генерируют сообщения N раз (где N≥2), основываясь на наборе F=(f1, …, fm) многопорядковых многочленов с многими переменными, определенном на кольце K, и векторе s, являющемся элементом множества Kn, и вычисляют первое значение хеш-функции, основанное на указанных сообщениях N раз, этап, на котором предоставляют проверяющему, обладающему указанным набором F многопорядковых многочленов с многими переменными и вектором y=(y1, …, ym)=(f1(s), …, fm(s)), первое значение хеш-функции, этап, на котором генерируют третью информацию N раз, используя первую информацию, случайным образом выбранную проверяющей стороной по соответствующим сообщениям N раз, и вторую информацию N раз, полученную при генерировании указанных сообщений, и генерируют второе значение хеш-функции, основанное на третьей информации N раз, этап, на котором предоставляют проверяющему второе значение хеш-функции, и этап, на котором предоставляют проверяющему информацию ответов N раз, соответствующую моделям проверки, выбранным проверяющим из k (где k≥2) моделей проверки по соответствующим сообщениям N раз, части сообщений и части третьей информации, причем указанная часть сообщений и указанная часть третьей информации не подлежит получению даже при выполнении операции с использованием набора F многопорядковых многочленов с многими переменными, вектора y и информации ответа, заранее подготовленной для модели проверки, соответствующей информации ответа. Вектор s представляет собой секретный ключ. Набор F многопорядковых многочленов с многими переменными и вектор у представляют собой открытые ключи. Сообщения и третья информация представляют собой информацию, получаемую при выполнении указанной операции, заранее подготовленной для модели проверки, соответствующей информации ответа, с использованием открытых ключей, первой информации и информации ответа или информации, полученной на основе информации ответа.
В соответствии с другим аспектом предлагаемой технологии, предусматривается способ обработки информации, содержащий: этап, на котором хранят набор F=(f1, …, fm) многопорядковых многочленов с многими переменными, определенный на кольце K, и вектор y=(y1, …, ym)=(f1(s), …, fm(s)), модуль получения сообщений для получения первого значения хеш-функции, вычисленного на основе сообщений N раз (где N≥2), сгенерированных на основе набора F многопорядковых многочленов с многими переменными и вектора s, являющегося элементом множества Kn, этап, на котором предоставляют доказывающей стороне, предоставившей указанные сообщения, первой информации, выбранной случайным образом по соответствующим сообщениям N раз, этап, на котором получают второе значение хеш-функции, вычисленное на основе третьей информации N раз, сгенерированной доказывающим с использованием первой информации N раз и второй информации N раз, полученной при генерировании указанных сообщений, модуль предоставления информации о модели для предоставления доказывающему информации о моделях проверки, выбираемых случайным образом из k (где k≥3) моделей проверки по соответствующим сообщениям N раз, этап, на котором получают от доказывающей стороне информации ответов, соответствующей моделям проверки, выбранным по соответствующим сообщениям N раз, и этап, на котором проверяют на основании набора F многопорядковых многочленов с многими переменными, вектора y, первой информации, информации ответа, первом значении хеш-функции и втором значение хеш-функции, хранит ли доказывающий вектор s. Вектор s представляет собой секретный ключ. Набор F многопорядковых многочленов с многими переменными и вектор y представляют собой открытые ключи. Сообщения и третья информация представляют собой информацию, получаемую при выполнении операции, заранее подготовленной для модели проверки, соответствующей информации ответа, с использованием открытых ключей, первой информации и информации ответа или информации, полученной на основе информации ответа.
В соответствии с другим аспектом предлагаемой технологии, предусматривается программа, вызывающая выполнение компьютером: функции генерирования сообщений, выполненной с возможностью генерирования сообщения N раз (где N≥2), основываясь на наборе F=(f1, …, fm) многопорядковых многочленов с многими переменными, определенном на кольце K, и векторе s, который является элементом множества Kn, и вычисления первого значения хеш-функции, на основании указанных сообщений N раз; функции предоставления сообщений, выполненной с возможностью предоставления проверяющему, хранящей указанный набор F многопорядковых многочленов с многими переменными и вектор y=(y1, …, ym)=(f1(s), …, fm(s)), первого значения хеш-функции; функции генерирования промежуточной информации, выполненной с возможностью генерирования третьей информации N раз, с использованием первой информации, выбранной случайным образом проверяющей стороной по соответствующим сообщениям N раз, и второй информации N раз, полученной при генерировании указанных сообщений, и генерирования второго значения хеш-функции, основанного на третьей информации N раз; функции предоставления промежуточной информации, выполненной с возможностью предоставления проверяющему второго значения хеш-функции; и функции предоставления ответов, выполненной с возможностью предоставления проверяющему информации ответов N раз, соответствующей моделям проверки, выбранным проверяющей стороной из k (где k≥2) моделей проверки по соответствующим сообщениям N раз, части сообщений и части третьей информации, причем указанная часть сообщений и указанная часть третьей информации не подлежат получению даже при выполнении операции, с использованием набора F многопорядковых многочленов с многими переменными, вектора y и информации ответа, заранее подготовленной для модели проверки, соответствующей информации ответа. Вектор s представляет собой секретный ключ. Набор F многопорядковых многочленов с многими переменными и вектор y представляют собой открытые ключи. Сообщения и третья информация представляют собой информацию, получаемую при выполнении этой операции, заранее подготовленной для модели проверки, соответствующей информации ответа, с использованием открытых ключей, первой информации и информации ответа или информации, полученной на основе информации ответа.
В соответствии с другим аспектом предлагаемой технологии, предусматривается программа, вызывающая выполнение компьютером: функции хранения информации, выполненной с возможностью хранения набора F=(f1, …, fm) многопорядковых многочленов с многими переменными, определенного на кольце K, и вектора y=(y1, …, ym)=(f1(s), …, fm(s)); модуля получения получаемых сообщений для получения первого значения хеш-функции, вычисленного на основе сообщений N раз (где N≥2), сгенерированных на основе набора F многопорядковых многочленов с многими переменными и вектора s, являющегося элементом множества Kn; функции предоставления информации, выполненной с возможностью предоставления доказывающей стороне, предоставившей указанные сообщения, первой информации, выбранной случайным образом по соответствующим сообщениям N раз; функции получения промежуточной информации, выполненной с возможностью получения второго значения хеш-функции, вычисленного на основе третьей информации N раз, сгенерированной доказывающим с использованием первой информации N раз и второй информации N раз, полученной при генерировании указанных сообщений; модуля предоставления информации о модели для предоставления доказывающей стороне информации о моделях проверки, выбираемых случайным образом из k (где k≥3) моделей проверки по соответствующим сообщениям N раз, функции получения ответов, выполненной с возможностью получения от доказывающего информации ответов, соответствующей моделям проверки, выбранным по соответствующим сообщениям N раз, и функции проверки, выполненной с возможностью проверки на основании набора F многопорядковых многочленов с многими переменными, вектора y, первой информации, информации ответа, первом значении хеш-функции и втором значение хеш-функции, хранит ли доказывающий вектор s. Вектор s представляет собой секретный ключ. Набор F многопорядковых многочленов с многими переменными и вектор y представляют собой открытые ключи. Сообщения и третья информация представляют собой информацию, получаемую при выполнении операции, заранее подготовленной для модели проверки, соответствующей информации ответа, с использованием открытых ключей, первой информации и информации ответа или информации, полученной на основе информации ответа.
В соответствии с другим аспектом предлагаемой технологии, предусматривается машиночитаемый носитель записи, хранящий записанную на нем программу, вызывающую выполнение компьютером: функции генерирования сообщений, выполненной с возможностью генерирования сообщения N раз (где N≥2), на основании набора F=(f1, …, fm) многопорядковых многочленов с многими переменными, определенного на кольце K, и вектора s, являющегося элементом множества Kn, и вычисления первого значения хеш-функции, на основе указанных сообщений N раз; функции предоставления сообщений, выполненной с возможностью предоставления проверяющему, хранящей указанный набор F многопорядковых многочленов с многими переменными и вектором y=(y1, …, ym)=(f1(s), …, fm(s)), первого значения хеш-функции; функции генерирования промежуточной информации, выполненной с возможностью генерирования третьей информации N раз, с использованием первой информации, случайным образом выбранной проверяющей стороной по соответствующим сообщениям N раз, и второй информации N раз, полученной при генерировании указанных сообщений, и генерирования второго значения хеш-функции, основанного на третьей информации N раз; функции предоставления промежуточной информации, выполненной с возможностью предоставления проверяющему второго значения хеш-функции; и функции предоставления ответов, выполненной с возможностью предоставления проверяющему информации ответов N раз, соответствующей моделям проверки, выбранным проверяющей стороной из k (где k≥2) моделей проверки по соответствующим сообщениям N раз, части сообщений и части третьей информации, причем указанная часть сообщений и указанная часть третьей информации не подлежат получению даже при выполнении операции, с использованием набора F многопорядковых многочленов с многими переменными, вектора y и информации ответа, заранее подготовленной для модели проверки, соответствующей информации ответа. Вектор s представляет собой секретный ключ. Набор F многопорядковых многочленов с многими переменными и вектор y представляют собой открытые ключи. Сообщения и третья информация представляют собой информацию, получаемую при выполнении указанной операции, заранее подготовленной для модели проверки, соответствующей информации ответа, с использованием открытых ключей, первой информации и информации ответа или информации, полученной на основе информации ответа.
В соответствии с другим аспектом предлагаемой технологии, предусматривается машиночитаемый носитель записи, хранящий записанную на нем программу, вызывающую выполнение компьютером: функции хранения информации, выполненной с возможностью хранения набора F=(f1, …, fm) многопорядковых многочленов с многими переменными, определенного на кольце K, и вектора y=(y1, …, ym)=(f1(s), …, fm(s)); модуля получения получаемых сообщений для получения первого значения хеш-функции, вычисленного на основе сообщений N раз (где N≥2), сгенерированных на основе набора F многопорядковых многочленов с многими переменными и вектора s, являющегося элементом множества Kn; функции предоставления информации, выполненной с возможностью предоставления доказывающей стороне, предоставившей указанные сообщения, первой информации, выбранной случайным образом по соответствующим сообщениям N раз; функции получения промежуточной информации, выполненной с возможностью получения второго значения хеш-функции, вычисленного на основе третьей информации N раз, сгенерированной доказывающим с использованием первой информации N раз и второй информации N раз, полученной при генерировании указанных сообщений; модуль предоставления информации о модели для предоставления доказывающей стороне информации о моделях проверки, выбираемых случайным образом из k (где k≥3) моделей проверки по соответствующим сообщениям N раз, функции получения ответов, выполненную с возможностью получения от доказывающего информации ответов, соответствующей моделям проверки, выбранным по соответствующим сообщениям N раз, и функции проверки, выполненной с возможностью проверки, на основании набора F многопорядковых многочленов с многими переменными, вектора y, первой информации, информации ответа, первого значения хеш-функции и второго значения хеш-функции, хранит ли доказывающий вектор s. Вектор s представляет собой секретный ключ. Набор F многопорядковых многочленов с многими переменными и вектор y представляют собой открытые ключи. Сообщения и третья информация представляют собой информацию, получаемую при выполнении операции, заранее подготовленной для модели проверки, соответствующей информации ответа, с использованием открытых ключей, первой информации и информации ответа или информации, полученной на основе информации ответа.
В соответствии с другим аспектом предлагаемой технологии, предусматривается программа, вызывающая выполнение компьютером функции каждого модуля, включенного в состав указанного устройства обработки информации. Кроме того, предусматривается машиночитаемый носитель записи, хранящий указанную программу, записанную на нем.
Полезные эффекты изобретения
В соответствии с предлагаемой технологией, описанной выше, имеется возможность реализовать эффективную схему аутентификации с открытым ключом, имеющую высокий уровень безопасности, с использованием системы многопорядковых уравнений с многими переменными, для которой не известно эффективное средство решения ("лазейка").
Краткое описание чертежей
Фиг. 1 представляет собой пояснительное схематическое изображение для описания структуры алгоритма схемы аутентификации с открытым ключом;
фиг. 2 представляет собой пояснительное схематическое изображение для описания структуры алгоритма схемы цифровой подписи;
фиг. 3 представляет собой пояснительное схематическое изображение для описания схемы аутентификации с открытым ключом, имеющей n переходов;
фиг. 4 представляет собой пояснительное схематическое изображение для описания алгоритма схемы аутентификации с открытым ключом, соответствующей первому варианту реализации (с 3 переходами) предлагаемой технологии;
фиг. 5 представляет собой пояснительное схематическое изображение для описания расширенного алгоритма схемы аутентификации с открытым ключом, соответствующей тому же самому варианту реализации изобретения;
фиг. 6 представляет собой пояснительное схематическое изображение для описания, преобразованного в параллельную форму алгоритма схемы аутентификации с открытым ключом, соответствующей тому же самому варианту реализации изобретения;
фиг. 7 представляет собой пояснительное схематическое изображение для описания конкретного алгоритма схемы аутентификации с открытым ключом, соответствующей тому же самому варианту реализации изобретения;
фиг. 8 представляет собой пояснительное схематическое изображение для описания эффективного алгоритма схемы аутентификации с открытым ключом, соответствующей тому же самому варианту реализации изобретения;
фиг. 9 представляет собой пояснительное схематическое изображение для описания эффективного алгоритма схемы аутентификации с открытым ключом, соответствующей тому же самому варианту реализации изобретения;
фиг. 10 представляет собой пояснительное схематическое изображение для описания эффективного алгоритма схемы аутентификации с открытым ключом, соответствующей тому же самому варианту реализации изобретения;
фиг. 11 представляет собой пояснительное схематическое изображение для описания преобразования схемы аутентификации с открытым ключом, соответствующей тому же самому варианту реализации изобретения, в параллельную форму;
фиг. 12 представляет собой пояснительное схематическое изображение для описания способа преобразования эффективного алгоритма схемы аутентификации с открытым ключом, соответствующей тому же самому варианту реализации изобретения, в алгоритм схемы цифровой подписи;
фиг. 13 представляет собой пояснительное схематическое изображение для описания способа преобразования эффективного алгоритма схемы аутентификации с открытым ключом, соответствующей тому же самому варианту реализации изобретения, в алгоритм эффективной схемы цифровой подписи;
фиг. 14 представляет собой пояснительное схематическое изображение для описания параллельно - последовательной структуры эффективного алгоритма схемы аутентификации с открытым ключом, соответствующей тому же самому варианту реализации изобретения;
фиг. 15 представляет собой пояснительное схематическое изображение для описания последовательно-параллельной структуры эффективного алгоритма схемы аутентификации с открытым ключом, соответствующей тому же самому варианту реализации изобретения;
фиг. 16 представляет собой пояснительное схематическое изображение для описания алгоритма схемы аутентификации с открытым ключом, соответствующей второму варианту реализации (с 5 переходами) предлагаемой технологии;
фиг. 17 представляет собой пояснительное схематическое изображение для описания расширенного алгоритма схемы аутентификации с открытым ключом, соответствующей тому же самому варианту реализации изобретения;
фиг. 18 представляет собой пояснительное схематическое изображение для описания преобразованного в параллельную форму алгоритма схемы аутентификации с открытым ключом, соответствующей тому же самому варианту реализации изобретения.
фиг. 19 представляет собой пояснительное схематическое изображение для описания преобразования расширенного алгоритма схемы аутентификации с открытым ключом, соответствующей тому же самому варианту реализации изобретения, в параллельную форму;
фиг. 20 представляет собой пояснительное схематическое изображение для описания конкретного алгоритма схемы аутентификации с открытым ключом, соответствующей тому же самому варианту реализации изобретения;
фиг. 21 представляет собой пояснительное схематическое изображение для описания эффективного алгоритма схемы аутентификации с открытым ключом, соответствующей тому же самому варианту реализации изобретения;
фиг. 22 представляет собой пояснительное схематическое изображение для описания эффективного алгоритма схемы аутентификации с открытым ключом, соответствующей тому же самому варианту реализации изобретения;
фиг. 23 представляет собой пояснительное схематическое изображение для описания эффективного алгоритма схемы аутентификации с открытым ключом, соответствующей тому же самому варианту реализации изобретения;
фиг. 24 представляет собой пояснительное схематическое изображение для описания эффективного алгоритма схемы аутентификации с открытым ключом, соответствующей тому же самому варианту реализации изобретения;
фиг. 25 представляет собой пояснительное схематическое изображение для описания эффективного алгоритма схемы аутентификации с открытым ключом, соответствующей тому же самому варианту реализации изобретения;
фиг. 26 представляет собой пояснительное схематическое изображение для описания эффективного алгоритма схемы аутентификации с открытым ключом, соответствующей тому же самому варианту реализации изобретения;
фиг. 27 представляет собой пояснительное схематическое изображение для описания эффективного алгоритма схемы аутентификации с открытым ключом, соответствующей тому же самому варианту реализации изобретения;
фиг. 28 представляет собой пояснительное схематическое изображение для описания преобразования эффективного алгоритма схемы аутентификации с открытым ключом, соответствующей тому же самому варианту реализации изобретения, в параллельную форму;
фиг. 29 представляет собой пояснительное схематическое изображение для описания преобразования эффективного алгоритма схемы аутентификации с открытым ключом, соответствующей тому же самому варианту реализации изобретения, в параллельную форму;
фиг. 30 представляет собой пояснительное схематическое изображение для описания дополнительного упрощения эффективного алгоритма схемы аутентификации с открытым ключом, соответствующей тому же самому варианту реализации изобретения;
фиг. 31 представляет собой пояснительное схематическое изображение для описания дополнительного упрощения эффективного алгоритма схемы аутентификации с открытым ключом, соответствующей тому же самому варианту реализации изобретения;
фиг. 32 представляет собой пояснительное схематическое изображение для описания параллельно-последовательной структуры эффективного алгоритма схемы аутентификации с открытым ключом, соответствующей тому же самому варианту реализации изобретения;
фиг. 33 представляет собой пояснительное схематическое изображение для описания параллельно - последовательной структуры эффективного алгоритма схемы аутентификации с открытым ключом, соответствующей тому же самому варианту реализации изобретения;
фиг. 34 представляет собой пояснительное схематическое изображение для описания последовательно-параллельной структуры эффективного алгоритма схемы аутентификации с открытым ключом, соответствующей тому же самому варианту реализации изобретения;
фиг. 35 представляет собой пояснительное схематическое изображение для описания последовательно-параллельной структуры эффективного алгоритма схемы аутентификации с открытым ключом, соответствующей тому же самому варианту реализации изобретения;
фиг. 36 представляет собой пояснительное схематическое изображение для описания способа повышения надежности интерактивного протокола, соответствующего первому и второму вариантам реализации изобретения;
фиг. 37 представляет собой пояснительное схематическое изображение для описания способа повышения надежности интерактивного протокола, соответствующего первому и второму вариантам реализации изобретения;
фиг. 38 представляет собой пояснительное схематическое изображение для описания примера конфигурации аппаратных средств устройства обработки информации, способного исполнять алгоритм, соответствующий каждому варианту реализации предлагаемой технологии;
фиг. 39 представляет собой таблицу, в которой проиллюстрировано сравнение эффективности схем аутентификации с открытым ключом, соответствующим первому и второму вариантам реализации предлагаемой технологии; и
фиг. 40 представляет собой пояснительное схематическое изображение для описания весьма подходящего способа задания параметра, используемого в схеме аутентификации с открытым ключом, соответствующей первому и второму вариантам реализации предлагаемой технологии, и его полезных эффектах.
Осуществление изобретения
Далее, со ссылкой на прилагаемые чертежи будут подробно описаны предпочтительные варианты реализации предлагаемого изобретения. Отметим, что в этом описании и чертежах, элементы, которые имеют, по существу, одинаковую функцию и структуру, обозначены одинаковыми ссылочными позициями, и их повторное объяснение не приводится.
Последовательность описания
Далее, кратко опишем последовательность описания вариантов реализации предлагаемой технологии, приводимого ниже. Сначала, со ссылкой на фиг. 1, будет кратко описана структура алгоритма схемы аутентификации с открытым ключом. После этого, со ссылкой на фиг. 2, будет описана структура алгоритма схемы цифровой подписи. После этого, со ссылкой на фиг. 3, будет описана схема аутентификации с открытым ключом, имеющая n переходов.
После этого, со ссылкой на фиг. 4 будет описан алгоритм схемы аутентификации с открытым ключом, соответствующей первому варианту реализации (с 3 переходами) предлагаемой технологии. После этого, со ссылкой на фиг. 5 будет описан расширенный алгоритм схемы аутентификации с открытым ключом, соответствующей тому же самому варианту реализации изобретения. После этого, со ссылкой на фиг. 6 будет описан преобразованный в параллельную форму алгоритм схемы аутентификации с открытым ключом, соответствующей тому же самому варианту реализации изобретения. После этого, со ссылкой на фиг. 7 будет описан конкретный алгоритм схемы аутентификации с открытым ключом, соответствующей тому же самому варианту реализации изобретения. После этого, со ссылкой на фиг. 8-15, будет описан эффективный алгоритм схемы аутентификации с открытым ключом, соответствующей тому же самому варианту реализации изобретения.
После этого, со ссылкой на фиг. 16 будет описан алгоритм схемы аутентификации с открытым ключом, соответствующей второму варианту реализации (с 5 переходами) предлагаемой технологии. После этого, со ссылкой на фиг. 17 будет описан расширенный алгоритм схемы аутентификации с открытым ключом, соответствующей тому же самому варианту реализации изобретения. После этого, со ссылкой на фиг. 18 и 19 будет описан преобразованный в параллельную форму алгоритм схемы аутентификации с открытым ключом, соответствующей тому же самому варианту реализации изобретения. После этого, со ссылкой на фиг. 20 будет описан конкретный алгоритм схемы аутентификации с открытым ключом, соответствующей тому же самому варианту реализации изобретения. После этого, со ссылкой на фиг. 21-35, будет описан эффективный алгоритм схемы аутентификации с открытым ключом, соответствующей тому же самому варианту реализации изобретения.
После этого, будет описан расширенный способ для применения эффективных алгоритмов, соответствующих первому и второму вариантам реализации предлагаемой технологии к многочлену с многими переменными, имеющему второй или более высокий порядок. После этого, будет описан механизм повышения надежности интерактивного протокола, соответствующего первому и второму вариантам реализации предлагаемой технологии. Вслед за этим, со ссылкой на фиг. 36 и 37 будет описан механизм предотвращения разглашения секретного ключа, вызванного неправильным запросом, и механизм устранения риска подделки. После этого, со ссылкой на фиг. 38 будет описан пример конфигурации аппаратных средств устройства обработки информации, способного реализовать алгоритмы, соответствующие первому и второму вариантам реализации предлагаемой технологии.
В заключение, будут кратко изложены резюме технической сущности предлагаемых вариантов реализации изобретения и полезных функциональных результатов, получаемых от этой технической сущности изобретения.
Детализированное описание параграфов
1: Введение
1-1: Алгоритм схемы аутентификации с открытым ключом
1-2: Алгоритмы для схемы цифровой подписи
1-3: Схема аутентификации с открытым ключом, имеющая N переходов
2: Первый вариант реализации изобретения
2-1: Алгоритм схемы аутентификации с открытым ключом
2-2: Расширенный алгоритм
2-3: Алгоритм, преобразованный в параллельную форму
2-4: Конкретный пример (в случае, когда используется многочлен второго порядка)
2-5: Эффективный алгоритм
2-6: Модификация, превращающая в схему цифровой подписи
2-6-1: Способ преобразования
2-6-2: Упрощение алгоритма цифровой подписи
2-7: Форма системы многопорядковых уравнений с многими переменными
2-7-1: Форма, относящаяся к блочному шифру с общим ключом
2-7-2: Форма, относящаяся к хеш-функции
2-7-3: Форма, относящаяся к поточному шифру
2-8: Последовательно-параллельный гибридный алгоритм
3: Второй вариант реализации изобретения
3-1: Алгоритм схемы аутентификации с открытым ключом
3-2: Расширенный алгоритм
3-3: Алгоритм, преобразованный в параллельную форму
3-4: Конкретный пример (в случае, когда используется многочлен второго порядка)
3-5: Эффективный алгоритм
3-6: Последовательно-параллельный гибридный алгоритм
4: Расширение эффективного алгоритма
4-1: Многочлен с многими переменными, имеющий высокий порядок
4-2: Схема расширения (добавление члена высокого порядка
5: Механизм повышения надежности
5-1: Способ задания параметров системы
5-2: Способ реагирования на неправильный запрос
5-2-1: Способ реагирования доказывающего
5-2-2: Способ реагирования проверяющего
6: Конфигурация аппаратных средств
7: Заключение
1: Введение
Сначала, прежде чем варианты реализации предлагаемой технологии будут описаны подробно, сделаем краткие обзоры алгоритма схемы аутентификации с открытым ключом, алгоритма схемы цифровой подписи и схемы аутентификации с открытым ключом имеющей n переходов.
1-1: Алгоритм схемы аутентификации с открытым ключом
Сначала, со ссылкой на фиг. 1, сделаем краткий обзор алгоритма схемы аутентификации с открытым ключом. Фиг. 1 представляет собой пояснительное схематическое изображение для описания структуры алгоритма схемы аутентификации с открытым ключом.
Аутентификация с открытым ключом используется тогда, когда некоторая сторона (доказывающий) убеждает другую сторону (проверяющий) в том, что оно является этой самой доказывающим, используя при этом открытый ключ pk и секретный ключ sk. Например, открытый ключ pkA доказывающего A доводится до сведения проверяющего B. С другой стороны, секретной ключ skA доказывающего A, сохраняется доказывающим A в тайне. В соответствии со схемой аутентификации с открытым ключом, сторона, которая знает секретный ключ skA, соответствующий открытому ключу pkA, рассматривается как сама доказывающий.
Для того, чтобы доказывающий A, используя схему аутентификации с открытым ключом, доказала проверяющему B то, что она A является самой доказывающим A, доказывающий A, посредством интерактивного протокола (протокола диалогового взаимодействия), представляет проверяющему B доказательство, свидетельствующее о том, что оно знает секретный ключ skA, соответствующей открытому ключу pkA. Доказательство, свидетельствующее о том, что доказывающий A знает секретный ключ skA, в таком случае представляется проверяющему B, и в случае, при котором проверяющий B может одобрить это доказательство, подлинность доказывающего A (того факта, что это и есть собственно доказывающий A) подтверждена.
Однако для обеспечения безопасности схема аутентификации с открытым ключом требует соблюдение нижеследующих условий.
Первое условие заключается в том, чтобы "снизить в максимально возможной степени вероятность совершения фальсификации, в тот момент времени, когда выполняется интерактивный протокол, фальсификатором, не имеющим секретного ключа sk". Тот факт, что удовлетворено это первое условие, именуется как "прочность". Другими словами, "прочность" означает, что "фальсификация не совершена во время исполнения интерактивного протокола фальсификатором, не имеющим секретный ключ sk, с вероятностью, отличной от пренебрежимо малой". Второе условие заключается в том, что "даже если выполнен интерактивный протокол, информация о секретном ключе skA доказывающего A ни в коей мере не разглашалась проверяющему В". Тот факт, что удовлетворено это второе условие, именуется как "нулевое знание".
Безопасное проведение аутентификации с открытым ключом включает в себя использование интерактивного протокола, демонстрирующего как "прочность", так и "нулевое знание". Если бы процесс аутентификации был гипотетически проведен с использованием интерактивного протокола, лишенного "прочности" и "нулевого знания", то имелась бы вполне определенная возможность ложной верификации и вполне определенная возможность раскрытия информации о секретном ключе, и, таким образом, подлинность доказывающего не будет доказана даже в том случае, если сам процесс будет завершен успешно. Следовательно, вопрос о том, каким образом обеспечивать "прочность" и "нулевое знание" в отношении протокола сеанса связи является важным.
Модель
Как показано на фиг. 1, в модели схемы аутентификации с открытым ключом присутствуют две стороны, а именно, доказывающий и проверяющий. Доказывающий генерирует пару, состоящую из открытого ключа pk и секретного ключа sk, уникальную для этой доказывающего, с использованием алгоритма Gen генерирования ключей. После этого, доказывающий выполняет интерактивный протокол с проверяющей стороной, используя при этом пару, состоящую из секретного ключа sk и открытого ключа pk, сгенерированных с использованием алгоритма Gen генерирования ключей. В это время, доказывающий выполняет интерактивный протокол, используя при этом алгоритм P доказывающего. Как было описано выше, в этом интерактивном протоколе доказывающий доказывает проверяющему, используя при этом алгоритм P доказывающего, то, что оно обладает секретным ключом sk.
С другой стороны, проверяющий выполняет интерактивный протокол, используя при этом алгоритм V проверяющего, и проверяет то, действительно ли доказывающий обладает секретным ключом, соответствующим открытому ключу, который опубликовало доказывающий. Таким образом, проверяющий представляет собой сторону, которая проверяет то, действительно ли доказывающий обладает секретным ключом, соответствующим открытому ключу. Как было описано, модель схемы аутентификации с открытым ключом образована двумя сторонами, а именно, доказывающим и проверяющей стороной, и тремя алгоритмами, а именно, алгоритмом Gen генерирования ключей, алгоритмом P доказывающего и алгоритмом V проверяющего.
В дополнение к этому отметим, что в нижеследующем описании используются выражения "доказывающий" и "проверяющий", но эти выражения, строго говоря, означают стороны. Следовательно, объект, который выполняет алгоритм Gen генерирования ключей и алгоритм P доказывающего, представляет собой устройство обработки информации, соответствующий стороне "доказывающий". Аналогичным образом, объект, который выполняет алгоритм V проверяющего, представляет собой устройство обработки информации. Конфигурация аппаратных средств этих устройств обработки информации является такой, как, например, показана на фиг. 38. Таким образом, алгоритм Gen генерирования ключей, алгоритм P доказывающего и алгоритм V проверяющего выполняются центральным процессором 902 на основе программы, записанной в постоянном запоминающем устройстве 904, оперативном запоминающем устройстве 906, запоминающем модуле 920, на съемном носителе записи 928 или тому подобном.
Алгоритм Gen генерирования ключей
Алгоритм Gen генерирования ключей используется доказывающим. Алгоритм Gen генерирования ключей представляет собой алгоритм для генерирования пары, состоящей из открытого ключа pk и секретного ключа sk уникальных для этого доказывающего. Открытый ключ pk, сгенерированный алгоритмом Gen генерирования ключей, опубликовывается. Кроме того, опубликованный открытый ключ pk используется проверяющим. С другой стороны, секретный ключ sk, сгенерированный алгоритмом Gen генерирования ключа сохраняется доказывающим в тайне. Секретный ключ sk, который доказывающий сохраняет в тайне, используется для того, чтобы доказывать проверяющему обладание доказывающим секретным ключом sk, соответствующим открытому ключу pk. Формально, алгоритм Gen генерирования ключа представляется как формула (1), приведенная ниже, как алгоритм, который берет в качестве входных данных параметр (1λ) безопасности (где λ представляет собой целое число, составляющее 0 или более), и выдает на выходе секретный ключ sk и открытый ключ pk.
Математическое выражение 1
Алгоритм P доказывающего
Алгоритм P доказывающего используется доказывающим. Алгоритм P доказывающего представляет собой алгоритм для доказывания проверяющему того, что доказывающий обладает секретным ключом sk, соответствующим открытому ключу pk. Другими словами, алгоритм P доказывающего представляет собой алгоритм, который берет в качестве входных данных открытый ключ pk и секретный ключ sk и выполняет интерактивный протокол.
Алгоритм V проверяющего
Алгоритм V проверяющего используется проверяющим. Алгоритм V проверяющего представляет собой алгоритм, который в ходе исполнения протокола сеанса связи проверяет то, действительно ли доказывающий хранит секретный ключ sk, соответствующим открытому ключу pk. Алгоритм V проверяющего представляет собой алгоритм, который принимает в качестве входных данных открытый ключ pk, и выдает на выходе 0 или 1 (1 бит) в соответствии с результатами выполнения протокола сеанса связи. При этом проверяющий решает, что доказывающий неподлинно в случае, при котором алгоритм V проверяющего выводит 0, и решает, что доказывающий подлинно в случае, при котором алгоритм V проверяющего выдает 1. Формально, алгоритм V проверяющего выражается согласно нижеследующей формуле (2).
Математическое выражение 2
Как было сказано выше, реализация значимой аутентификации с открытым ключом включает в себя удовлетворение интерактивным протоколом двум условиям: "прочности" и "нулевого знания". Однако, доказывание того, что доказывающий обладает секретным ключом sk, включает в себя исполнение доказывающим процедуры, зависящей от секретного ключа sk, и, после уведомления проверяющего о результате, побуждение проверяющего к выполнению проверки, основанной на содержании этого уведомления. Процедура, зависящая от секретного ключа sk исполняется для обеспечения "прочности". В то же время, никакая информация о секретном ключе sk не должна быть открыта проверяющему. По этой причине, вышеупомянутые алгоритм Gen генерирования ключей, алгоритм P доказывающего и алгоритм V проверяющего разрабатываются с большим мастерством для того, чтобы удовлетворить эти требования.
Таким образом, вышеприведенное объяснение резюмирует алгоритмы в схеме аутентификации с открытым ключом.
1-2: Алгоритмы для схемы цифровой подписи
Далее, со ссылкой на фиг. 2, будут резюмированы алгоритмы для схемы цифровой подписи. Фиг. 2 представляет собой пояснительное схематическое изображение, резюмирующее алгоритмы для схемы цифровой подписи.
В отличие от бумажных документов, нет возможности физически подписать или приложить печать к цифровым данным. По этой причине, доказывание того, кто является создателем цифровых данных, включает в себя электронную систему, дающую результаты, аналогичные физическому подписанию или приложению печати к бумажному документу. Эта система представляет собой цифровые подписи. Термин "цифровая подпись" относится к системе, которая ассоциативно связывает заданные данные с данными подписи, известными только создателю данных, осуществляет предоставление данных подписи получателю, и осуществляет проверку этих данных подписи на стороне получателя.
Модель
Как проиллюстрировано на фиг. 2, в модели схемы цифровой подписи существуют две стороны: подписывающая сторона и проверяющий. Кроме того, модель схемы цифровой подписи составлена из трех алгоритмов: алгоритма Gen генерирования ключей, алгоритма Sig генерирования цифровой подписи и алгоритма Ver проверки цифровой подписи.
Подписывающий использует алгоритм Gen генерирования ключей для того, чтобы сгенерировать парные ключ sk цифровой подписи и ключ pk проверки, уникальные для подписывающего. Подписывающий также использует алгоритм Sig генерирования цифровой подписи для того, чтобы сгенерировать цифровую подпись q для прикрепления ее к сообщению M. Другими словами, подписывающий представляет собой сторону, которая прикрепляет цифровую подпись к сообщению M. Между тем, проверяющий использует алгоритм Ver проверки цифровой подписи для того, чтобы проверить цифровую подпись, прикрепленную к сообщению M. Другими словами, проверяющий представляет собой сторону, которая проверяет цифровую подпись q для того, чтобы подтвердить то, действительно ли создателем сообщения M является подписывающий.
Отметим, что, хотя в дальнейшем в описании используются термины "подписывающий" и "проверяющий", эти термины, в конечном счете, означают стороны. Следовательно, агент, который исполняет алгоритм Gen генерирования ключей и алгоритм Sig генерирования цифровой подписи, представляет собой устройство обработки информации, соответствующее стороне "подписывающего". Аналогичным образом агент, который исполняет алгоритм Ver проверки цифровой подписи, представляет собой устройство обработки информации. Конфигурация аппаратных средств этих устройств обработки информации является такой, как, например, проиллюстрирована на фиг. 38. Другими словами, алгоритм Gen генерирования ключей, алгоритм Sig генерирования цифровой подписи и алгоритм Ver проверки цифровой подписи выполняются устройством, таким как центральный процессор 902 на основе программы, записанной в устройство, такое как постоянное запоминающее устройство 904, оперативное запоминающее устройство 906, запоминающий модуль 920 или на съемный носитель 928 записи.
Алгоритм Gen генерирования ключей
Алгоритм Gen генерирования ключей используется подписывающим. Алгоритм Gen генерирования ключей представляет собой алгоритм, который генерирует парные ключ sk цифровой подписи и ключ pk проверки, уникальные для подписывающего. Ключ pk проверки, сгенерированный алгоритмом Gen генерирования ключей опубликовывается. Между тем, подписывающий держит ключ sk цифровой подписи, сгенерированный алгоритмом Gen генерирования ключей, в тайне. Затем ключ sk цифровой подписи используется для того, чтобы сгенерировать цифровую подпись q для того, чтобы прикрепить ее к сообщению М. Например, алгоритм Gen генерирования ключей принимает в качестве входных данных некоторый параметр 1p безопасности (где p представляет собой целое число, равное или большее чем 0), и выдает на выходе ключ sk цифровой подписи и ключ pk проверки. В этом случае, алгоритм Gen генерирования ключа может быть формально выражен так, как в нижеследующей формуле (3).
Математическое выражение 3
Алгоритм Sig генерирования цифровой подписи
Алгоритм Sig генерирования цифровой подписи используется подписывающим. Алгоритм Sig генерирования цифровой подписи представляет собой алгоритм, который генерирует цифровую подпись, подлежащую присоединению к сообщению M. Алгоритм Sig генерирования цифровой подписи представляет собой алгоритм, который принимает в качестве входных данных ключ sk цифровой подписи и сообщение M, и выдает на выходе цифровую подпись (q. Алгоритм Sig генерирования цифровой подписи может быть выражен формально так, как в нижеследующей формуле (4).
Математическое выражение 4
Алгоритм Ver проверки цифровой подписи
Алгоритма Ver проверки цифровой подписи используется проверяющим. Алгоритм Ver проверки цифровой подписи представляет собой алгоритм, который проверяет то, действительно ли цифровая подпись q является подлинной цифровой подписью для сообщения M. Алгоритм Ver проверки цифровой подписи представляет собой алгоритм, который в качестве входных данных принимает ключ pk проверки подписывающего, сообщение M, и цифровую подпись q, и выдает 0 или 1 (1 бит). Алгоритм Ver проверки цифровой подписи может быть выражен формально так, как в нижеследующей формуле (5). При этом, проверяющий решает, что цифровая подпись q является неподлинной в случае, при котором алгоритм Ver проверки цифровой подписи выдает 0 (случай, при котором ключ pk проверки отвергает сообщение М и цифровую подпись q), и решает, что цифровая подпись Ver является неподлинной в случае, при котором алгоритм Ver проверки цифровой подписи выдает 1 (случай, при котором ключ pk проверки признает сообщение М и цифровую подпись q.
Математическое выражение 5
Таким образом, вышеприведенное объяснение резюмирует алгоритмы в схеме цифровой подписи.
1-3: Схема аутентификации с открытым ключом, имеющая N переходов
Далее, со ссылкой на фиг. 3 будет описана схема аутентификации с открытым ключом, имеющая n переходов. Фиг. 3 представляет собой пояснительное схематическое изображение, на котором проиллюстрирована схема аутентификации с открытым ключом, имеющая n переходов.
Как было сказано выше, схема аутентификации с открытым ключом представляет собой схему аутентификации, которая в ходе исполнения интерактивного протокола доказывает проверяющему то, что доказывающий обладает секретным ключом sk, соответствующим открытому ключу pk. Кроме того, интерактивный протокол должен удовлетворить двум условиям: "прочности" и "нулевого знания". По этой причине, в ходе исполнения интерактивного протокола как доказывающий, так и проверяющий обмениваются информацией n раз, исполняя при этом соответствующие процессы, как это проиллюстрировано на фиг. 3.
В случае схемы аутентификации с открытым ключом, имеющей n переходов, доказывающий выполняет процесс, используя алгоритм P доказывающего (операция #1), и передает информацию T1 проверяющему. Вслед за этим, проверяющий исполняет процесс, использующий алгоритм V проверяющего (операция #2), и передает информацию T2 доказывающему. Это исполнение и процессы и передача информации Tk последовательно проводятся для k=3 по n (операция #k), и, в конце концов, процесс (операция #n+1) исполнен. Передача и прием информации n раз, выполняемая таким образом, соответственно, именуется схемой аутентификации с открытым ключом, имеющая "n переходов".
Таким образом, вышеприведенное объяснение описывает схему аутентификации с открытым ключом, имеющую n переходов.
2: Первый вариант реализации изобретения
Далее, будет дано описание первого варианта реализации предлагаемой технологии. Варианты реализации здесь относятся к схеме аутентификации с открытым ключом и схеме цифровой подписи, безопасность которых основывается на трудности решения системы многопорядковых уравнений с многими переменными. Однако, варианты реализации при этом отличаются от технологий предшествующего уровня техники, таких как схемы HFE цифровой подписи (схемы цифровой подписи на основе HFE-криптографии), и относятся к схемам аутентификации с открытым ключом и схемам цифровой подписи, которые используют систему многопорядковых уравнений с многими переменными, в которой отсутствует средство эффективного решения ("лазейки").
2-1: Алгоритм схемы аутентификации с открытым ключом
Прежде всего, со ссылкой на фиг. 4 будет описан алгоритм схемы аутентификации с открытым ключом (в дальнейшем именуемый как, "предлагаемый способ"), соответствующий предлагаемому варианту реализации изобретения. Фиг. 4 представляет собой пояснительное схематическое изображение для описания алгоритма, соответствующего предлагаемому способу. Предлагаемый способ имеет конфигурацию с алгоритмом Gen генерирования ключей, алгоритмом P доказывающего и алгоритмом V проверяющего. Ниже будут описаны структуры соответствующих алгоритмов.
Алгоритм Gen генерирования ключей
Алгоритм Gen генерирования ключей генерирует m многочленов f1(x1, …, xn), …, fm(x1, …, xn) с многими переменными определенных в кольце k и вектор s=(s1, …, sn), который является элементом множества Kn. После этого, алгоритм Gen генерирования вычисляет y=(y1, …, ym)<-(f1(s), …, fm(s)). Кроме того, алгоритм Gen генерирования задает (f1(x1, …, xn), …, fm(x1, …, xn), y) в открытом ключе pk и задает s в качестве секретного ключа. Далее, вектор (x1, …, xn) представлен как x, а пара многочленов (f1(x), …, fm(x)) с многими переменными представлена как F(х).
Алгоритм P доказывающего, алгоритм V проверяющего
Далее, со ссылкой на фиг. 4 будет описан процесс, выполняемый согласно алгоритму P доказывающего, и процесс, выполняемый согласно алгоритму V проверяющего в ходе исполнения интерактивного протокола.
В ходе исполнения вышеназванного интерактивного протокола, доказывающий ни в коей мере не разглашает проверяющему информацию о секретном ключе s и показывает проверяющему, что "сам он знает s, удовлетворяющий y=F(s)". С другой стороны, проверяющий проверяет то, действительно ли доказывающий знает s, удовлетворяющий y=F(s). Открытый ключ pk предполагается сообщенным проверяющему. Кроме того, секретный ключ s предполагается сохраняемым доказывающим в тайне. Далее, описание будет дано со ссылкой на блок-схему алгоритма, проиллюстрированную на фиг. 4.
Операция #1:
Сначала, алгоритм P доказывающего выбирает какое-либо число w. Вслед за этим, алгоритм P доказывающего генерирует вектор r, который является элементом множества Kn, и некоторое число wA, применяя это число w к генератору G1 псевдослучайных чисел. Таким образом, алгоритм P доказывающего вычисляет (r, wA)<-G1(w). Вслед за этим, алгоритм P доказывающего генерирует многочлен
с многими переменными, применяя число wA к генератору G2 псевдослучайных чисел. Таким образом, алгоритм P доказывающего вычисляет FA<-G2(wA).
Операция #1 (продолжение):
Вслед за этим, алгоритм P доказывающего вычисляет z<-s-r. Это вычисление эквивалентно маскированию секретного ключа s вектором r. В дополнение к этому, алгоритм P доказывающего вычисляет FB(x)<-F(x+r)+FA(x). Это вычисление эквивалентно маскированию многочлена F(x+r) с многими переменными, для x, посредством многочлена FA(x) с многими переменными.
Операция #1 (продолжение):
Вслед за этим, алгоритм P доказывающего генерирует значение c1 хеш-функции для z и FA(z). Таким образом, алгоритм P доказывающего вычисляет c1<-H1(FA(z), z). Кроме того, алгоритм P доказывающего генерирует значение c2 хеш-функции для числа wA. Таким образом, алгоритм P доказывающего вычисляет c2<-H2(wA). Кроме того, алгоритм P доказывающего генерирует значение c3 хеш-функции для многочлена FB с многими переменными. Таким образом, алгоритм P доказывающего вычисляет c3<-H3(FB(x)). Отметим, что вышеупомянутые H1(…), Н2(…), Н3(…) представляют собой хеш-функции. Значения (c1, c2, c3) хеш-функции отправляются, в качестве сообщения, алгоритму V проверяющего. При этом следует отметить, что информация об s, информация об r и информация огнив коей мере не разглашается проверяющему.
Операция #2:
После приема сообщения (c1, c2, c3), алгоритм V проверяющего выбирает то, какую модель проверки, из числа трех моделей проверки, использовать. Например, алгоритм V проверяющего может выбрать некоторое численное значение из числа трех численных значений {0, 1, 2}, представляющих модели проверки, и задать это выбранное численное значение в запросе d. Этот запрос d отправляется алгоритму P доказывающего.
Операция #3:
После приема запроса d, алгоритм P доказывающего генерирует ответ Rsp для того, чтобы отправить его алгоритму V проверяющего в ответ на принятый запрос d. В случае, при котором d=0, алгоритм P доказывающего генерирует ответ σ=w. В случае, при котором d=1, алгоритм P доказывающего генерирует ответ σ=(wA, z). В случае, при котором d=2, алгоритм P доказывающего генерирует ответ
. Ответ σ, сгенерированный в ходе операции #3, отправляется алгоритму V проверяющего. При этом следует отметить, что в случае, при котором d=0, проверяющему ни в коей мере не разглашается информация о z, а в случае, при котором d=1 или 2, проверяющему ни в коей мере не разглашается информация об r.
Операция #4:
Алгоритм V проверяющего, который принял ответ σ, выполняет, используя принятый ответ σ, нижеследующий процесс проверки.
В случае, при котором d=0, алгоритм V проверяющего вычисляет (rA, wB)<-G1(σ). Кроме того, алгоритм V проверяющего вычисляет FC<-G2(wB). После этого, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство c2=H2(wB). В дополнение к этому, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство c3=H3(F(x+rA)+Fc(x)). Алгоритм V проверяющего, в случае, при котором все эти проверки являются успешными, выдает на выходе значение 1, указывающее на успешную аутентификацию, а в случае, при котором проверка терпит неудачу, выдает на выходе значение 0, указывающее на неудачную аутентификацию.
В случае, при котором d=1, алгоритм V проверяющего задает (wB, zA)<-σ. Кроме того, алгоритм V проверяющего вычисляет FC<-G2(wB). После этого, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство c1=H1(FC(zA), zA). В дополнение к этому, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство c2=Н2(wB). Алгоритм V проверяющего, в случае, при котором все эти проверки являются успешными, выдает на выходе значение 1, указывающее на успешную аутентификацию, а в случае, при котором проверка терпит неудачу, выдает на выходе значение 0, указывающее на неудачную аутентификацию.
В случае, при котором d=2, алгоритм V проверяющего задает (FD, zA)<-σ. После этого, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство c1=H1(FD(zA)-y, zA). В дополнение к этому, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство c3=H3(FD). Алгоритм V проверяющего, в случае, при котором все эти проверки являются успешными, выдает на выходе значение 1, указывающее на успешную аутентификацию, а в случае, при котором проверка терпит неудачу, выдает на выходе значение 0, указывающее на неудачную аутентификацию.
Выше был описан пример структуры каждого алгоритма, относящегося к предлагаемому способу.
"Прочность" предлагаемого способа
Далее, будет дополнительно представлено описание "прочности" предлагаемого способа. "Прочность" предлагаемого способа обеспечивается на основе той логики, что, когда алгоритм P доказывающего возвращает соответствующий ответ о для всех запросов d=0, 1 и 2, выбираемых алгоритмом V проверяющего, можно вычислить FD, FC, zA,и r1, удовлетворяющие следующим формуле (6) и формуле (7), приведенным ниже.
Математическое выражение 6
При обеспечении вышеупомянутой "прочности", тот факт, что успешная подделка с вероятностью выше, чем 2/3 не возможна, гарантирован до тех пор, пока не будет решена задача решения мультипорядковой системы уравнений с многими переменными. Таким образом, для того, чтобы надлежащим образом дать ответы на все запросы d=0, 1, 2 от проверяющего, фальсификатор должен вычислить FD, FC, rA и zA, удовлетворяющие приведенным выше формуле (6) и формуле (7). Другими словами, фальсификатор должен вычислить s, удовлетворяющее F(s)=y. Однако, сохраняется вероятность того, что фальсификатор даст надлежащие ответы для двух более высоких запросов из числа запросов d=0, 1, 2 от проверяющего. Следовательно, вероятность успеха ложной проверки становится 2/3. Далее, при неоднократном выполнении вышеописанного интерактивного протокола достаточно большое количество раз, вероятность успешной подделки становится пренебрежимо малой.
Выше была описана "прочность" предлагаемого способа.
Модифицированный пример
Представим теперь модифицированный пример вышеописанного алгоритма. Алгоритм Gen генерирования ключей вычисляет y<-F(s) и задает (F, y) в качестве открытого ключа. Однако, в предлагаемом модифицированном примере, алгоритм Gen генерирования ключей вычисляет (y1, …, ym)<-F(s) и
, и задает, в качестве открытого ключа,
. В случае этой модификации, имеется возможность выполнять интерактивный протокол при y=0.
Кроме того, алгоритм P доказывающего генерирует сообщение c1, основываясь на FB(z) и z. Однако, вследствие соотношения FB(z)=FA(z), даже в том случае, когда произведено та модификация, что сообщение c1 генерируется на основе FA(z) и z, реализуется аналогичный интерактивный протокол. Кроме того, структура алгоритма P доказывающего может быть модифицирована таким образом, чтобы значение хеш-функции для FB(z) и значение хеш-функции для z вычислялись отдельно и затем отправлялись, в качестве сообщения, алгоритму V проверяющего.
Кроме того, алгоритм P доказывающего генерирует вектор r и число wA применяя число w к генератору G1 псевдослучайных чисел. Кроме того, алгоритм P доказывающего генерирует многочлен FA(x) с многими переменными, применяя число wA к генератору G2 псевдослучайных чисел. Однако, структура алгоритма P доказывающего может быть модифицирована таким образом, чтобы с самого начала вычислялось w=(r, FA), используя тождественное отображение как G1. В этом случае, нет необходимости применять число w к G1. То же самое имеет место и для G2.
Кроме того, в интерактивном протоколе в качестве открытого ключа используется (F, y). Многочлен F с многими переменными, включенный в состав открытого ключа представляет собой параметр, который не зависит от секретного ключа sk. По этой причине, во всей системе можно использовать общий многочлен F с многими переменными, не задавая многочлен F с многими переменными для каждого доказывающего. В этом случае, у достаточен в качестве открытого ключа, задаваемого для каждого доказывающего, и, таким образом, имеется возможность уменьшить размер открытого ключа. Однако, с точки зрения безопасности, желательно задавать многочлен F с многими переменными для каждого доказывающего. Способ задания многочлена F с многими переменными в этом случае будет описан позже подробно.
Кроме того, в интерактивном протоколе в качестве открытого ключа используется (f1, …, fm, y), и F=(f1, …, fm) представляет собой параметр, который может быть надлежащим образом выбран. По этой причине, например, доказывающий и проверяющий могут подготовить некоторое начальное значение wpk для случайных чисел вычислять F<-G*(wpk) с использованием генератора G* псевдо случайных чисел. В этом случае, даже тогда, когда открытый ключ представляет собой (wpk, y), а в качестве открытого ключа делают известным (F, y), имеется возможность уменьшить размер открытого ключа.
В алгоритме, c1, c2 и c3 вычисляются c, использованием хеш-функций H1, H2 и H3, но вместо хеш-функции может быть использована функция СОМ связывания. Функция СОМ связывания представляет собой функцию, в которой сомножителями являются символьная строка S и случайное число ρ. Пример функции связывания включает в себя схему, которую опубликовали на международной конференции CRYPTO в 1996 г. Shai Halevi (Шэй Хейлви) и Silvio Micali (Сильвио Микали).
В случае, когда используется функция связывания, перед вычислением c1, c2 и c3 подготавливаются случайные числа ρ1, ρ2 и ρ3, и c1, c2 и c3 генерируются посредством применения функций СОМ(·, ρ1), СОМ(·, ρ2) и СОМ(·, ρ2) связывания вместо применения хеш-функций H1(·), Н2(·) и Н3(·). Здесь, ρi, необходимое для того, чтобы проверяющий сгенерировал ci, задается для включения в ответ σ и отправки. Эта модификация может быть применена к полному алгоритму, который будет описан позже.
Выше был описан модифицированный пример предлагаемого способа.
2-2: Расширенный алгоритм
Далее, со ссылкой на фиг. 5 будет описан алгоритм схемы аутентификации с открытым ключом (в дальнейшем именуемый как "расширенный способ"), расширенный по отношению к предлагаемому способу. Фиг. 5 представляет собой пояснительное схематическое изображение для описания последовательности операций интерактивного протокола, основанного на расширенной технологии.
В описываемом здесь расширенном способе, сообщение (c1, c2, c3), передаваемое при первой пересылке, преобразуется в одно значение с хеш-функции и отправляется проверяющему. Здесь, проверяющему вместе с ответом σ отправляется сообщение, которое почти не восстанавливается с использованием ответа σ, отправляемого при третьей пересылке. При применении расширенного способа можно уменьшить количество информации, отправляемой проверяющему в ходе исполнения интерактивного протокола. Далее будет подробно описана структура каждого алгоритма, относящегося к расширенному способу.
Алгоритм Gen генерирования ключей
Алгоритм Gen генерирования ключей генерирует m многочленов f1(x1, …, xn), …, fm(x1, …, xn) с многими переменными, определенных в кольце k, и вектор s=(s1, …, sn), который является элементом множества Kn. После этого, алгоритм Gen генерирования вычисляет y=(y1, …, ym)<-(f1(s), …, fm(s)). Кроме того, алгоритм Gen генерирования задает (f1(x1, …, xn), …, fm(x1, …, xn), y) в открытом ключе pk и задает s в качестве секретного ключа. Далее, вектор (x1, …, xn) представлен как x, а пара многочленов (f1(x), …, fm(x)) с многими переменными представлена как F(х).
Алгоритм P доказывающего, алгоритм V проверяющего
Далее, со ссылкой на фиг. 5 будет описан процесс, выполняемый согласно алгоритму P доказывающего, и процесс, выполняемый согласно алгоритму V проверяющего в ходе исполнения интерактивного протокола.
В ходе исполнения вышеназванного интерактивного протокола, доказывающий ни в коей мере не разглашает проверяющему информацию о секретном ключе s и показывает проверяющему, что "сам он знает s, удовлетворяющий y=F(s)". С другой стороны, проверяющий проверяет то, действительно ли доказывающий знает s, удовлетворяющий y=F(s). Открытый ключ pk предполагается сообщенным проверяющему. Кроме того, секретный ключ s предполагается сохраняемым доказывающим в тайне. Далее, описание будет дано со ссылкой на блок-схему алгоритма, проиллюстрированную на фиг. 5.
Операция #1:
Сначала, алгоритм P доказывающего выбирает какое-либо число w. Вслед за этим, алгоритм P доказывающего генерирует вектор r, который является элементом множества Kn, и некоторое число wA, применяя это число w к генератору G1 псевдослучайных чисел. Таким образом, алгоритм P доказывающего вычисляет (r, wA)<-G1(w). Вслед за этим, алгоритм P доказывающего генерирует многочлен
с многими переменными, применяя число wA к генератору G2 псевдослучайных чисел. Таким образом, алгоритм P доказывающего вычисляет FA<-G2(wA).
Операция #1 (продолжение):
Вслед за этим, алгоритм P доказывающего вычисляет z<-s-r. Это вычисление эквивалентно маскированию секретного ключа s вектором r. В дополнение к этому, алгоритм P доказывающего вычисляет FB(x)<-F(x+r)+FA(x). Это вычисление эквивалентно маскированию набора F(x+r) многочленов по x посредством набора FA(x) многочленов.
Операция #1 (продолжение):
Далее, алгоритм P доказывающего генерирует значение c1 хеш-функции для FB(z) и z. Другими словами, алгоритм P доказывающего вычисляет c1<-H1(F(z), z). Кроме того, алгоритм P доказывающего генерирует значение c2 хеш-функции для числа wA. Таким образом, алгоритм P доказывающего вычисляет c2<-Н2(wA). Кроме того, алгоритм P доказывающего генерирует значение c3 хеш-функции для набора (FB) многочленов. Другими словами, алгоритм P доказывающего вычисляет c3<-Н3(FB)). H1(…), Н2(…), Н3(…) представляют собой хеш-функции. В случае расширенной схемы, алгоритм P доказывающего применяет набор (c1, c2, c3) значений хеш-функции к хеш-функции Н для того, чтобы сгенерировать значение с хеш-функции и отправляет это значение с хеш-функции алгоритму V проверяющего.
Операция #2:
После приема значения с хеш-функции, алгоритм V проверяющего выбирает то, какую модель проверки, из числа трех моделей проверки, использовать. Например, алгоритм V проверяющего может выбрать некоторое численное значение из числа трех численных значений {0, 1, 2}, представляющих модели проверки, и задать это выбранное численное значение в запросе d. Этот запрос d отправляется алгоритму P доказывающего.
Операция #3:
После приема запроса d, алгоритм P доказывающего генерирует ответ σ для того, чтобы отправить его алгоритму V проверяющего в ответ на принятый запрос d. В случае, при котором d=0, алгоритм P доказывающего генерирует ответ (σ, с*)=(w, c1). В случае, при котором d=1, алгоритм P доказывающего генерирует ответ (σ, с*)=(wA, z), c3). В случае, при котором d=2, алгоритм P доказывающего генерирует ответ (σ, с*)=(FB, z), c2). Ответ (σ, с*), сгенерированный в ходе операции #3, отправляется алгоритму V проверяющего.
Операция #4:
После приема ответа σ, алгоритм V проверяющего исполняет, используя принятый ответ (σ, с*), нижеследующий процесс проверки.
В случае, когда d=0, алгоритм V проверяющего вычисляет (rA,wB)<-G1(σ). После этого, алгоритм V проверяющего вычисляет FC<-G2(wB). После этого, алгоритм V проверяющего вычисляет
. После этого, алгоритм V проверяющего вычисляет
. Затем, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство
. После этого, алгоритм V проверяющего, в случае, когда эта проверка является успешной, выдает на выходе значение 1, представляющее успешную аутентификацию, а в случае, когда проверка терпит неудачу, выдает на выходе значение 0, представляющее неудачную аутентификацию.
В случае, когда d=1, алгоритм V проверяющего задает (wB,zA)<-σ. После этого, алгоритм V проверяющего вычисляет FC<-G2(wB). После этого, алгоритм V проверяющего вычисляет
. После этого, алгоритм V проверяющего вычисляет
. Затем, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство
. После этого, алгоритм V проверяющего, в случае, когда эта проверка является успешной, выдает на выходе значение 1, представляющее успешную аутентификацию, а в случае, когда проверка терпит неудачу, выдает на выходе значение 0, представляющее неудачную аутентификацию.
В случае, когда d=2, алгоритм V проверяющего задает (FD,zA)<-σ. После этого, алгоритм V проверяющего вычисляет
. После этого, алгоритм V проверяющего вычисляет
. Затем, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство
. После этого, алгоритм V проверяющего, в случае, когда эта проверка является успешной, выдает на выходе значение 1, представляющее успешную аутентификацию, а в случае, когда проверка терпит неудачу, выдает на выходе значение 0, представляющее неудачную аутентификацию.
Выше была описана структура каждого алгоритма, относящегося к расширенному способу. Применяя расширенный способ, можно уменьшить количество информации, передаваемой и принимаемой во время исполнения интерактивного протокола.
2-3: Алгоритм, преобразованный в параллельную форму
Как было описано выше, применение протокола сеанса связи, соответствующего предлагаемому способу и расширенному способу, делает возможным удерживать вероятность успешной подделки на уровне 2/3 или меньше. Следовательно, исполнение протокола сеанса связи дважды дает возможность удерживать вероятность успешной подделки на уровне (2/3)2 или меньше. Более того, если протокол сеанса связи выполняется N раз, то вероятность успешной подделки становится (2/3)N, и если N задается как достаточно большое число (например, N=140), то вероятность успешной подделки становится пренебрежимо малой.
Потенциально возможные способы исполнения интерактивного протокола множество раз включают в себя, например, последовательный способ, в котором обмен сообщением, запросом и ответом последовательно повторяется множество раз, и параллельный способ, в котором обмен множественными сообщениями, запросами и ответами осуществляется в ходе однократного обмена. Далее будет описан способ распространения интерактивного протокола, соответствующего предлагаемому способу, на интерактивный протокол (в дальнейшем именуемый как "алгоритм, преобразованный в параллельную форму"), относящийся к параллельному способу. Например, алгоритм, преобразованный в параллельную форму, проиллюстрирован на фиг. 6. Далее, со ссылкой на фиг. 6, будут описаны подробности алгоритма, преобразованного в параллельную форму.
Алгоритма Gen генерирования ключей
Алгоритм Gen генерирования ключей генерирует m многочленов f1(x1, …, xn), …, fm(x1, …, xn) с многими переменными, определенных в кольце k, и вектор s=(s1, …, sn), который является элементом множества Kn. После этого, алгоритм Gen генерирования вычисляет y=(y1, …, ym)<-(f1(s), …, fm(s)). Кроме того, алгоритм Gen генерирования задает (f1(x1, …, xn), …, fm(x1, …, xn), y) в открытом ключе pk и задает s в качестве секретного ключа. Далее, вектор (x1, …, xn) представлен как x, а пара многочленов (f1(x), …, fm(x)) с многими переменными представлена как F(x).
Алгоритм P доказывающего, алгоритм V проверяющего
Далее, со ссылкой на фиг. 5 будет описан процесс, выполняемый согласно алгоритму P доказывающего, и процесс, выполняемый согласно алгоритму V проверяющего в ходе исполнения интерактивного протокола.
В ходе исполнения вышеназванного интерактивного протокола, доказывающий ни в коей мере не разглашает проверяющему информацию о секретном ключе s и показывает проверяющему, что "сам он знает s, удовлетворяющий y=F(s)". С другой стороны, проверяющий проверяет то, действительно ли доказывающий знает s, удовлетворяющий y=F(s). Открытый ключ pk предполагается сообщенным проверяющему. Кроме того, секретный ключ s предполагается сохраняемым доказывающим в тайне. Далее, описание будет дано со ссылкой на блок-схему алгоритма, проиллюстрированную на фиг. 6.
Операция #1:
Прежде всего, алгоритм P доказывающего выполняет нижеследующие процессы: с (1) по (8), для i=1 по N.
Процесс (1): Алгоритм P доказывающего выбирает произвольным образом некоторое число wi.
Процесс (2): Алгоритм P доказывающего применяет число wi к генератору G1 псевдослучайных чисел и генерирует вектор ri, который является элементом множества Kn, и некоторое число
. Другими словами, алгоритм P доказывающего вычисляет
.
Процесс (3): Алгоритм P доказывающего применяет число
к генератору G2 псевдослучайных чисел и генерирует набор
многочленов с многими переменными. Другими словами, алгоритм P доказывающего вычисляет
.
Процесс (4): Алгоритм P доказывающего вычисляет zi<-si-ri. Это вычисление соответствует операции маскирования секретного ключа si с использованием вектора ri.
Процесс (5): Алгоритм P доказывающего вычисляет
. Это вычисление соответствует операции маскирования, набора F(x+ri) многочленов для x с использованием набора
многочленов.
Процесс (6): Алгоритм P доказывающего генерирует значение c1,I хеш-функции для
и zi. Другими словами, алгоритм P доказывающего вычисляет
.
Процесс (7): Алгоритм P доказывающего генерирует значение c2,i хеш-функции для числа
. Другими словами, алгоритм P доказывающего вычисляет
.
Процесс (8): Алгоритм P доказывающего генерирует значение c3,I хеш-функции для
. Другими словами, алгоритм P доказывающего вычисляет
.
H1(…), H2(…) и H3(…) представляют собой хеш-функции. Кроме того, значения (c1,i, c2,i, c3,i) хеш-функций являются сообщениями.
Для i=1 по N, после выполнения процессов: с (1) по (8), сообщение (c1,i, c2,i, c3,i) (i=1 по N), сгенерированное в ходе операции #1, отправляется алгоритму V проверяющего.
Операция #2:
После приема сообщения (c1, i, c2, i, c3, i) (i=1 по N), алгоритм V проверяющего выбирает то, какую модель проверки, из числа трех моделей проверки, использовать, для каждого из i=1 по N. Например, алгоритм V проверяющего, для каждого из i=1 по N, может выбрать некоторое численное значение из числа трех численных значений {0, 1, 2}, представляющих модели проверки, и задать это выбранное численное значение в запросе di. Запросы di отправляются алгоритму P доказывающего.
Операция #3:
Алгоритм P доказывающего, который принял запрос di (i=1 по N), генерирует ответ σi, подлежащий отправке алгоритму V проверяющего в ответ на запрос di. При этом, алгоритм P доказывающего выполняет нижеследующие процессы: с (1) по (3), для i=1 по N.
Процесс (1): В случае, когда di составляет 0, алгоритм P доказывающего генерирует ответ σi=wi.
После того, как процессы; с (1) по (3) выполнены, ответ σi (i=1 по N) отправляются алгоритму V проверяющего.
Операция #4:
Алгоритм V проверяющего, который принял ответ σi (i=1 по N), выполняет, используя принятый ответ σi (i=1 по N), нижеследующий процесс проверки.
В случае, при котором d=0, алгоритм V проверяющего вычисляет
. Кроме того, алгоритм V проверяющего вычисляет
. После этого, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство
. В дополнение к этому, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство
. Алгоритм V проверяющего, в случае, при котором все эти проверки являются успешными, выдает на выходе значение 1, указывающее на успешную аутентификацию, а в случае, при котором проверка терпит неудачу, выдает на выходе значение 0, указывающее на неудачную аутентификацию.
В случае, при котором d=1, алгоритм V проверяющего задает
. Кроме того, алгоритм V проверяющего вычисляет
. После этого, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство
. В дополнение к этому, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство
. Алгоритм V проверяющего, в случае, при котором все эти проверки являются успешными, выдает на выходе значение 1, указывающее на успешную аутентификацию, а в случае, при котором проверка терпит неудачу, выдает на выходе значение 0, указывающее на неудачную аутентификацию.
В случае, при котором d=2, алгоритм V проверяющего задает
. После этого, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство
. В дополнение к этому, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство
. Алгоритм V проверяющего, в случае, при котором все эти проверки являются успешными, выдает на выходе значение 1, указывающее на успешную аутентификацию, а в случае, при котором проверка терпит неудачу, выдает на выходе значение 0, указывающее на неудачную аутентификацию.
Выше был описан способ параллельного выполнения интерактивного протокола предлагаемого способа. Как было описано выше, поскольку этот интерактивный протокол предлагаемого способа выполняется повторяющимся образом, вероятность успешной подделки становится пренебрежимо малой.
Кроме того, может быть сделана такая модификация, что после операции #1 вместо отправки проверяющему (c1,1, c1,2, c1,3, …, CN,1, cN,2, cN,3) может быть отправлено значение c=H(c1,1, c1,2, c1,3, …, CN,1, cN,2, cN,3) хеш-функции. Здесь, ввиду присутствия сообщения, которое с трудом восстанавливается по ответу, интерактивный протокол необходимо модифицировать таким образом, чтобы это сообщение отправлялось от доказывающего проверяющему вместе с ответом. При применении этой модификации сообщение, отправляемое при первой пересылке представляет собой единственное значение с хеш-функции, и, следовательно, трафик передачи информации значительно уменьшается. Например, в случае N-кратной параллельной повторяющейся структуры, количество порций информации, подлежащих отправке, может быть уменьшено на 2N-1.
Подходящий способ задания параметров
Интерактивный протокол, соответствующий предлагаемому варианту реализации изобретения, гарантирует безопасность от пассивной атаки. Однако, в случае, когда применяется вышеописанный способ повторяющегося параллельного выполнения интерактивного протокола, для доказательства того, что надежно обеспечена безопасность от активной атаки, необходимо чтобы соблюдалось условие, которое будет описано ниже.
Вышеописанный интерактивный протокол представляет собой алгоритм для подтверждения проверяющему того факта, что "доказывающий знает s, удовлетворяющий y=F(s), для y", посредством использования пары ключей (открытый ключ y и секретный ключ s). По этой причине, при выполнении взаимодействия, принятого при проверке, нельзя отрицать вероятность того, что информация, которая указывает на то, что "доказывающий использует s во время взаимодействия", известна проверяющему. Кроме того, для многочлена F с многими переменными не обеспечена стойкость к коллизии. По этой причине, в случае, когда вышеописанный интерактивный протокол выполняется параллельно повторяющимся образом, трудно без какого - либо условия доказать, что безопасность от активной атаки обеспечена надежно.
Соответственно, изобретатели предлагаемой технологии исследовали способ сделать так, чтобы информация, указывающая на то, что "доказывающий использует s во время взаимодействия", не была известна проверяющему, даже тогда, когда выполняется взаимодействие, принятое при этой проверке. В дополнение к этому, изобретатели предлагаемой технологии разработали способ, делающий возможным обеспечение безопасности от активной атаки, даже тогда, когда вышеописанный интерактивный протокол выполняется повторяющимся образом параллельно. Этот способ представляет собой способ, заключающийся в задании количества m многочленов f1, …, fm, используемых в качестве открытых ключей, имеющим значение, в достаточной мере более низкое, чем количество n переменных. Например, m и n задаются таким образом, чтобы 2m-n<<1 (например, в случае, когда n=160, а m=80,2-80<<1).
В схемах, безопасность которых основывается на трудности решения системы многопорядковых уравнений с многими переменными, трудно сгенерировать другой секретный ключ s2, соответствующий открытому ключу pk, даже в том случае, когда секретный ключ s1 и открытый ключ pk, ему соответствующий, заданы. По этой причине, в случае, когда обеспечено, что для открытого ключа pk существует два или больше секретных ключей s, можно сделать так, чтобы информация, указывающая на то, что "доказывающий использует s во время взаимодействия", не была известна проверяющему, даже тогда, когда выполняется взаимодействие, принятое при проверке. Таким образом, в случае, когда обеспечение этого достигнуто, безопасность от активной атаки может быть обеспечена даже тогда, когда интерактивный протокол выполняется повторяющимся образом параллельно.
В случае, когда, со ссылкой на фиг. 40, рассматривается функция F: Kn->Km, включающая в себя количество m многопорядковых многочленов с n переменными (где n>m), количество элементов области определения, не имеющих второго прообраза, составляет, самое большее,
|. По этой причине, в случае, когда
задано достаточно малым, вероятность выбора элементов области определения, не имеющих второго прообраза, может быть сделана пренебрежимо малой. Таким образом, в случае, когда количество m многопорядковых многочленов f1, …, fm с n переменными задается имеющим значение, в достаточной мере более низкое, чем количество n переменных, можно обеспечить то, чтобы для открытого ключа pk существовало два или более секретных ключа s. Следовательно, даже тогда, когда выполняется взаимодействие, принятое при проверке, можно сделать так, чтобы информация, указывающая на то, что "доказывающий использует s во время взаимодействия", была не известна проверяющему. Таким образом, безопасность от активной атаки обеспечивается даже тогда, когда интерактивный протокол выполняется повторяющимся образом параллельно.
Как было описано выше, налагая это задаваемое условие, при котором количество m многопорядковых многочленов f1, …, fm с n переменными задается имеющим значение, в достаточной мере более низкое, чем количество n переменных (где n>m и предпочтительно, чтобы 2m-n<<1), можно обеспечить безопасность в случае, когда интерактивный протокол выполняется параллельно повторяющимся образом.
2-4: Конкретный пример (в случае, когда используется многочлен второго порядка
Далее, со ссылкой на фиг. 7, будет описан пример, в котором в качестве многочлена F с многими переменными используется многочлен второго порядка с n переменными. Фиг. 7 представляет собой пояснительное схематическое изображение для описания конкретного примера предлагаемого способа.
Алгоритм Gen генерирования ключей
Алгоритм Gen генерирования ключей генерирует m многочленов f1(x1, …, xn), …, fm(x1, …, xn) с многими переменными, определенных в кольце k, и вектор s=(s1, …, sn), который является элементом множества Kn. После этого, алгоритм Gen генерирования вычисляет y=(y1, …, ym)<-(f1(s), …, fm(s)). Кроме того, алгоритм Gen генерирования задает (f1, …, fm, y) в качестве открытого ключа pk и задает s в качестве секретного ключа. Далее, вектор (x1, …, xn) представлен обозначением x, а набор многочленов (f1(x), …, fm(x)) с многими переменными представлен обозначением F(x). Здесь, многочлен fi(x) второго порядка выражается так, как в нижеследующей Формуле (8).
Математическое выражение 7
Алгоритм P доказывающего, алгоритм V проверяющего
Далее, со ссылкой на фиг. 7 будут описаны процессы, выполняемые согласно алгоритму P доказывающего алгоритму V проверяющего, в ходе исполнения интерактивного протокола.
Операция #1:
Прежде всего, алгоритм P доказывающего произвольным образом выбирает некоторое число w. После этого, алгоритм P доказывающего применяет число w к генератору G1 псевдослучайных чисел и генерирует вектор r, который является элементом множества Kn, и число wA. Другими словами, алгоритм P доказывающего вычисляет (r, wA)<-G1(w). После этого, алгоритм P доказывающего применяет число wA к генератору G2 псевдослучайных чисел и генерирует набор линейных многочленов
. Другими словами, алгоритм P доказывающего вычисляет
. Здесь, линейный многочлен
выражен так, как в нижеприведенной формуле (9). Кроме того, набор линейных многочленов
представлен обозначением FA(x).
Математическое выражение 8
Операция #1 (продолжение):
После этого, алгоритм P доказывающего вычисляет z<-s-r. Это вычисление соответствует операции маскирования секретного ключа s с использованием вектора r. Кроме того, алгоритм P доказывающего вычисляет FB(x)<-F(x+r)+FA(x). Это вычисление соответствует операции маскирования многочлена F(x+r), имеющего второй порядок, для x с использованием линейного многочлена FA(x), В F(х+r) информация, связанная с r, представлена только слагаемым x первого порядка. Таким образом, вся информация связанная с r, маскирована посредством FA(x).
Операция #1 (продолжение):
После этого, алгоритм P доказывающего вычисляет значение c1 хеш-функции для FA(z) и z. Другими словами, алгоритм P доказывающего вычисляет c1<-H1(FA(z), z). Кроме того, алгоритм P доказывающего генерирует значение с2 хеш-функции для числа wA. Другими словами, алгоритм P доказывающего вычисляет c2<-Н2(wA). Кроме того, алгоритм P доказывающего генерирует значение c3 хеш-функции для многочлена FB с многими переменными. Другими словами, алгоритм P доказывающего вычисляет c3<-H3(FB). H1(…), H2(…) и H3(…) представляют собой хеш-функции. Сообщение (c1, c2, c3), сгенерированное в ходе операции #1, отправляется алгоритму V проверяющего.
Операция #2:
После приема сообщения (c1, c2, c3), алгоритм V проверяющего выбирает то, какую модель проверки, из числа трех моделей проверки, использовать. Например, алгоритм V проверяющего может выбрать некоторое численное значение из числа трех численных значений {0, 1, 2}, представляющих модели проверки, и задать это выбранное численное значение в запросе d. Этот запрос d отправляется алгоритму P доказывающего.
Операция #3:
После приема запроса d, алгоритм P доказывающего генерирует ответ а подлежащий отправке алгоритму V проверяющего в ответ на принятый запрос d. В случае, при котором d=0, алгоритм P доказывающего генерирует ответ σ=w. В случае, при котором e=1, алгоритм P доказывающего генерирует ответ σ=(wA, z). В случае, при котором d=2, алгоритм P доказывающего генерирует ответ σ=(FB(z), z). Ответ σ, сгенерированный в ходе операции #3, отправляется алгоритму V проверяющего.
Операция #6:
После приема ответа σ, алгоритм V проверяющего исполняет, используя принятый ответ σ, нижеследующий процесс проверки.
В случае, при котором d=0, алгоритм V проверяющего вычисляет (rA, wB)<-G1(σ). Кроме того, алгоритм V проверяющего вычисляет FC<-G2(wB). После этого, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство c2=Н2(wB). В дополнение к этому, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство c3=H3(F(x+rA)+FC(x)). Алгоритм V проверяющего, в случае, при котором все эти проверки являются успешными, выдает на выходе значение 1, указывающее на успешную аутентификацию, а в случае, при котором проверка терпит неудачу, выдает на выходе значение 0, указывающее на неудачную аутентификацию.
В случае, при котором d=1, алгоритм V проверяющего задает (wB, zA)<-σ. Кроме того, алгоритм V проверяющего вычисляет FC<-G2(wB). После этого, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство c1=H1(FC(zA), zA). В дополнение к этому, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство c2=H2(wB). Алгоритм V проверяющего, в случае, при котором все эти проверки являются успешными, выдает на выходе значение 1, указывающее на успешную аутентификацию, а в случае, при котором проверка терпит неудачу, выдает на выходе значение 0, указывающее на неудачную аутентификацию.
В случае, при котором d=2, алгоритм V проверяющего задает (FD, zA)<-σ. После этого, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство c1=H1(FD(zA)-y, zA). В дополнение к этому, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство c3=H3(FD). Алгоритм V проверяющего, в случае, при котором все эти проверки являются успешными, выдает на выходе значение 1, указывающее на успешную аутентификацию, а в случае, при котором проверка терпит неудачу, выдает на выходе значение 0, указывающее на неудачную аутентификацию.
Выше был описан конкретный пример предлагаемого способа.
2-5: Эффективный алгоритм
Далее, будет описан способ упрощения алгоритма, соответствующего предлагаемому способу. Набор многочленов (f1(x), …, fm(x)) второго порядка может быть выражен в нижеследующей Формуле (10). Здесь, x представляет собой x1, …, xn. Кроме того, A1, …, Am представляют собой матрицу n×n. Кроме того, каждое из b1, …, bm представляет собой вектор n×1.
Математическое выражение 9
При использовании этого выражения многочлен F с многими переменными может быть выражен так, как в нижеследующих формуле (11) и формуле (12). Из нижеследующей формулы (13) с легкостью можно подтвердить, что удовлетворяется это выражение.
Математическое выражение 10
При делении, таким образом, F (x+y) на первую часть, зависящую от x, вторую часть, зависящую от у, и третью часть, зависящую, как от x, так и от y, слагаемое Fb(x, y), соответствующее третьей части, становится билинейным относительно x и y. Использование этого свойства делает возможным создание эффективного алгоритма.
Например, используем вектор t0, который является элементом множества Kn, и вектор e0, который является элементом множества Km, для того, чтобы выразить многочлен FA(x), который используется для маскирования многочлена F(х+r) с многими переменными, как FA(x)=Fb(x, t)+e. В этом случае, сумма многочлена F(х+r) с многими переменными и FA(x) выражается так, как в формуле (14), приведенной ниже.
При этом, в случае, когда tA=r+t, eA=F(r)+е, многочлен FB(x)=F(x+r)+FA(x) с многими переменными может быть выражен посредством вектора t1, который является элементом множества Kn, и вектора e1, который является элементом множества Km. По этой причине, при задании "FA(х)=Fb(х, t)+е", FA и FB могут быть выражены с использованием вектора в Kn и вектора в Km, и таким образом размер данных, необходимых для передачи, может быть значительно уменьшен. В частности, эффективность передачи информации может быть повышена в степени от тысяч до десятков тысяч раз.
Математическое выражение 11
В соответствии с этой модификацией, из FB (или FA) ни в коей мере не происходит утечки информации, относящейся к r. Например, в случае, когда заданы еА и tA (или e и t), трудно узнать информацию об r, если не известны е и t (или еА и tA). Соответственно, даже в том случае, когда эта модификация применяется в предлагаемом способе, нулевое знание гарантируется. Далее, со ссылкой на фигуры: с 8 по 10 будет описан эффективный алгоритм, относящийся к предлагаемому способу. Поскольку структура алгоритма Gen генерирования ключей не изменяется, то ее детализированное описание здесь приведено не будет.
Пример 1 структуры эффективного алгоритма: фиг. 8
Прежде всего, будет описана структура эффективного алгоритма, проиллюстрированного на фиг. 8. Операция #1:
Алгоритм P доказывающего произвольным образом выбирает некоторое число w. После этого, алгоритм P доказывающего применяет число w к генератору G1 псевдослучайных чисел и генерирует вектор r, который является элементом множества Kn, и число wA. Другими словами, алгоритм P доказывающего вычисляет (r, wA)<-G1(w). После этого, алгоритм P доказывающего применяет число wA к генератору G2 псевдослучайных чисел и генерирует два вектора: вектор t, который является элементом множества Kn, и вектор e, который является элементом множества Km. Другими словами, алгоритм P доказывающего вычисляет (t, e)<-G2(wA). После этого, алгоритм P доказывающего вычисляет z<-s-r. Это вычисление соответствует операции маскирования секретного ключа s с использованием вектора r. Кроме того, алгоритм P доказывающего вычисляет tA<-r+t. После этого, алгоритм P доказывающего вычисляет еА<-F(r)+e.
Операция #1 (продолжение):
После этого, алгоритм P доказывающего вычисляет Fb(z, t), основываясь на Формуле (14), и вычисляет c1<-H1(Fb(z, t)+e, z). Кроме того, алгоритм P доказывающего генерирует значение c2 хеш-функции для числа wA. Другими словами, алгоритм P доказывающего вычисляет c2<-H2(wA). Кроме того, алгоритм P доказывающего генерирует значение c3 хеш-функции для двух векторов: tA и eA. Другими словами, алгоритм P доказывающего вычисляет c3<-H3(tA, eA). H1(…), Н2(…) и Н3(…) представляют собой хеш-функции. Сообщение (c1, c2, c3), сгенерированное в ходе операции #1, отправляется алгоритму V проверяющего.
Операция #2:
После приема сообщения (c1, c2, c3), алгоритм V проверяющего выбирает то, какую модель проверки, из числа трех моделей проверки, использовать. Например, алгоритм V проверяющего может выбрать некоторое численное значение из числа трех численных значений {0, 1, 2}, представляющих модели проверки, и задать это выбранное численное значение в запросе d Этот запрос d отправляется алгоритму P доказывающего.
Операция #3:
После приема запроса d, алгоритм P доказывающего генерирует ответ σ, подлежащий отправке алгоритму V проверяющего в ответ на принятый запрос d. В случае, при котором d=0, алгоритм P доказывающего генерирует ответ σ=w. В случае, при котором d=1, алгоритм P доказывающего генерирует ответ σ=(wA, z). В случае, при котором d=2, алгоритм P доказывающего генерирует ответ σ=(tA, tA, z). Ответ σ, сгенерированный в ходе операции #3, отправляется алгоритму V проверяющего.
Операция #6:
После приема ответа σ, алгоритм V проверяющего исполняет, используя принятый ответ σ нижеследующий процесс проверки.
В случае, при котором d=0, алгоритм V проверяющего вычисляет (rA, rB)<-G1(σ). Кроме того, алгоритм V проверяющего вычисляет (tB, eB<-G2(wB). После этого, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство c2=H2(wB). В дополнение к этому, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство c3=H3(rA+tB, F(rA)+eB). Алгоритм V проверяющего, в случае, при котором все эти проверки являются успешными, выдает на выходе значение 1, указывающее на успешную аутентификацию, а в случае, при котором проверка терпит неудачу, выдает на выходе значение 0, указывающее на неудачную аутентификацию.
В случае, при котором d=1, алгоритм V проверяющего задает (wB, zA)<-σ. Кроме того, алгоритм V проверяющего вычисляет (tB, eB)<-G2(wB). После этого, алгоритм V а в проверяющего проверяет то, действительно ли соблюдается равенство c1=H1(Fb(zA, tB)+eB, zA). В дополнение к этому, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство c2=H2(wB). Алгоритм V проверяющего, в случае, при котором все эти проверки являются успешными, выдает на выходе значение 1, указывающее на успешную аутентификацию, а в случае, при котором проверка терпит неудачу, выдает на выходе значение 0, указывающее на неудачную аутентификацию.
В случае, при котором d=2, алгоритм V проверяющего задает (tC, eC, zA)<-σ. После этого, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство c1=H1(F(zA)+Fb(zA, tC)+eC-y, zA). В дополнение к этому, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство С3=H3(tC, eC). Алгоритм V проверяющего, в случае, при котором все эти проверки являются успешными, выдает на выходе значение 1, указывающее на успешную аутентификацию, а в случае, при котором проверка терпит неудачу, выдает на выходе значение 0, указывающее на неудачную аутентификацию.
Выше был описан пример 1 структуры эффективного алгоритма. При использовании эффективного алгоритма, размер данных, необходимых для передачи, может быть значительно уменьшен. Кроме того, поскольку нет необходимости вычислять F(x+r), то также повышается эффективность вычисления.
Пример 2 структуры эффективного алгоритма: фиг. 9
Далее, будет описана структура эффективного алгоритма, проиллюстрированного на фиг. 9. Даже в том случае, когда применяется структура, проиллюстрированная на фиг. 9, аналогично случаю, когда применяется структура, проиллюстрированная на фиг. 8, достигается тот эффект, что повышаются эффективность передачи информации и эффективность вычисления. Здесь, будет описано отличие от структуры, проиллюстрированной на фиг. 8.
В ходе операции #3 алгоритма, проиллюстрированного на фиг. 8, в случае, когда d=0, σ задается равным w, но в качестве σ, в случае, когда d=0, может использоваться информация, которая может быть восстановлена по (r, t, e). Например, как проиллюстрировано на фиг. 9, в ходе операции #3, в качестве σ, в случае, когда d=0, может быть использовано (wA, tA). При этом, в случае, когда выполняется эта модификация, необходимо модифицировать часть содержания проверки, выполняемой согласно алгоритму V проверяющего в ходе операции #4. В частности, в ходе операции #4 в случае, когда d=0, в содержании проверки, выполняемой согласно алгоритму V проверяющего, проверка равенства c3=H3(rA+tB, F(rA)+eB) заменяется проверкой равенства c3=H3(tA, F(tA-tB)+eB).
Выше был описан пример 2 структуры эффективного алгоритма.
Пример 3 структуры эффективного алгоритма: фиг. 10
Далее, будет описана структура эффективного алгоритма, проиллюстрированного на фиг. 10.
Операция #1:
Алгоритм P доказывающего произвольным образом генерирует вектор r, t, который является элементом множества Kn, и вектор e0, который является элементом множества Km. Вслед за этим, алгоритм P доказывающего вычисляет rA<-s-r. Это вычисление эквивалентно маскированию секретного ключа s посредством вектора r. В дополнение к этому, алгоритм P доказывающего вычисляет tA<-r-t. Вслед за этим, алгоритм P доказывающего вычисляет eA<-F(r)-e.
Операция #1 (продолжение):
Вслед за этим, алгоритм P доказывающего вычисляет c1<-H1(Fb(rA, t)+e, rA. Вслед за этим, алгоритм P доказывающего вычисляет c2<-H2(t, e). Вслед за этим, алгоритм P доказывающего вычисляет c3<-Н3(tA, eA). H1(…), Н2(…) и H3(…) представляют собой хеш-функции. Сообщение (c1, c2, c3), сгенерированное в ходе операции #1, отправляется алгоритму V проверяющего.
Операция #2:
После приема сообщения (c1, c2, c3), алгоритм V проверяющего выбирает то, какую модель проверки, из числа трех моделей проверки, использовать. Например, алгоритм V проверяющего может выбрать некоторое численное значение из числа трех численных значений {0, 1, 2}, представляющих модели проверки, и задать это выбранное численное значение в запросе d Этот запрос d отправляется алгоритму P доказывающего.
Операция #3:
После приема запроса d, алгоритм P доказывающего генерирует ответ о, подлежащий отправке алгоритму V проверяющего в ответ на запрос d. В случае, при котором d=0, алгоритм P доказывающего генерирует ответ σ=(r, tA, eA). В случае, при котором d=1, алгоритм P доказывающего генерирует ответ σ=(rA, t, e). В случае, при котором d=2, алгоритм P доказывающего генерирует ответ σ=(rA, tA, eA). Ответ σ, сгенерированный в ходе операции #3, отправляется алгоритму V проверяющего.
Операция #4:
После приема ответа σ, алгоритм V проверяющего исполняет, используя принятый ответ σ, нижеследующий процесс проверки.
В случае, при котором d=0, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство c2=Н2(r-tA, F(r)-еА). В дополнение к этому, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство c3=H3(tA, еА). Алгоритм V проверяющего, в случае, при котором все эти проверки являются успешными, выдает на выходе значение 1, указывающее на успешную аутентификацию, а в случае, при котором проверка терпит неудачу, выдает на выходе значение 0, указывающее на неудачную аутентификацию.
В случае, при котором d=1, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство c1=H1(Fb,(rA, t)+e, rA). В дополнение к этому, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство с2=Н2(t, e). Алгоритм V проверяющего, в случае, при котором все эти проверки являются успешными, выдает на выходе значение 1, указывающее на успешную аутентификацию, а в случае, при котором проверка терпит неудачу, выдает на выходе значение 0, указывающее на неудачную аутентификацию.
В случае, при котором d=2, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство c1=H1(y-F(rA)-Fb(tA, rA)-eA, rA). В дополнение к этому, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство c3=H3(tA, еА). Алгоритм V проверяющего, в случае, при котором все эти проверки являются успешными, выдает на выходе значение 1, указывающее на успешную аутентификацию, а в случае, при котором проверка терпит неудачу, выдает на выходе значение 0, указывающее на неудачную аутентификацию.
Выше был описан пример 3 структуры эффективного алгоритма. При использовании эффективного алгоритма, размер данных, необходимых для передачи, может быть значительно уменьшен. Кроме того, поскольку нет необходимости вычислять F(x+r), то также повышается эффективность вычисления.
Преобразование эффективного алгоритма в параллельную форму: фиг. 11
Далее, со ссылкой на фиг. 11, будет описан способ преобразования эффективного алгоритма в параллельную форму. Структура (в дальнейшем именуемая как "алгоритм, преобразованный в параллельную форму"), проиллюстрированная на фиг. 11, представляет собой структуру, в которой в параллельную форму преобразован эффективный алгоритм, относящийся к примеру 3 структуры.
Операция #1:
Алгоритм P доказывающего выполняет процессы: с (1) по (6), для i=1 по N.
Процесс (1): Алгоритм P доказывающего произвольным образом генерирует векторы ri, ti, которые являются элементами множества Kn, и вектор ei, который является элементом множества Km.
Процесс (2): Алгоритм P доказывающего вычисляет
. Это вычисление эквивалентно маскированию секретного ключа s посредством вектора ri. В дополнение к этому, алгоритм P доказывающего вычисляет
.
Процесс (5): Алгоритм P доказывающего вычисляет c2,i<-H2(ti, ei).
Операция #1 (продолжение):
После исполнения вышеупомянутых процессов: с (1) по (6), для i=1 по N, алгоритм P доказывающего вычисляет Cmt<-H(c1,1, c2,1, c3,1, …, c1,N, c2,N, c3,N). H1(…), Н2(…) и H3(…) представляют собой хеш-функции. Значение Cmt хеш-функции, сгенерированное в ходе операции #1, отправляется алгоритму V проверяющего. Таким образом, сообщение (c1,1, c2 1, c3 1, …, c1,N, c2,N, c3,N) прежде, чем быть отправленным алгоритму V проверяющего преобразуется в значение хеш-функцию, предоставляя таким образом возможность снизить объем передачи информации.
Операция #2:
После приема значения Cmt хеш-функции, алгоритм V проверяющего выбирает то, какую модель проверки, из числа трех моделей проверки, использовать для каждого i=1 по N. Например, алгоритм V проверяющего может, для каждого i=1 по N, выбрать некоторое численное значение из числа трех численных значений {0, 1, 2}, представляющих модели проверки, и задать это выбранное численное значение в запросе di. Запросы d1, …, dN отправляются алгоритму P доказывающего.
Операция #3:
После приема запросов: d1, …, dN, алгоритм P доказывающего генерирует ответы: Rsp1, …, RspN, для отправки алгоритму V проверяющего в ответ на каждый из принятых запросов: d1, …, dN. В случае, при котором di=0, алгоритм P доказывающего генерирует
. Далее, алгоритм P доказывающего генерирует Rspi=(σi, с1, i). В случае, при котором di=1, алгоритм P доказывающего генерирует ответ
. Далее, алгоритм P доказывающего генерирует Rspi=(σi, c3, i). В случае, при котором Chi=2, алгоритм P доказывающего генерирует ответ
. Далее, алгоритм P доказывающего генерирует Rspi=(σi, c2, i).
Ответы: Rsp1, …, RspN, сгенерированные в ходе операции #3, отправляются алгоритму V проверяющего.
Операция #4:
После приема ответов: Rsp1, …, RspN, алгоритм V проверяющего исполняет, используя принятые ответы Rsp1, …, RspN, нижеследующие процессы: с (1) по (3), для i=1 по N. При этом, алгоритм V проверяющего исполняет процесс (1) для случая, при котором di=0, процесс (2) в случае, при котором Chi=1, и процесс (3) в случае при котором di=2.
Процесс (1): В случае, при котором di=0, алгоритм V проверяющего извлекает
из Rspi. Вслед за этим, алгоритм V проверяющего вычисляет
. В дополнение к этому, алгоритм V проверяющего вычисляет
. После этого алгоритм V проверяющего сохраняет (c1,i, с2,1, c3,i).
Процесс (2): В случае, при котором di=1, алгоритм V проверяющего извлекает
из Rspi. Вслед за этим, алгоритм V проверяющего вычисляет
. В дополнение к этому, алгоритм V проверяющего вычисляет
. После этого алгоритм V проверяющего сохраняет (c1,i, с2,i, С3,i).
Процесс (3): В случае, при котором di=2, алгоритм V проверяющего извлекает
из Rspi. Вслед за этим, алгоритм V проверяющего вычисляет
. В дополнение к этому, алгоритм V проверяющего вычисляет
. После этого алгоритм V проверяющего сохраняет (c1,i, с2,i, С3,i).
После выполнения вышеупомянутых процессов: с (1) по (3), для i=1 по N, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство Cmt=H(c1,1, с2,1, c3,1, …, с1,N, с2,N, c3,N). Алгоритм V проверяющего, в случае, при котором все проверка является успешной, выдает на выходе значение 1, указывающее на успешную аутентификацию, а в случае, при котором проверка терпит неудачу, выдает на выходе значение 0, указывающее на неудачную аутентификацию.
Выше было описано преобразование эффективного алгоритма в параллельную форму. Преобразованный в параллельную форму алгоритм, проиллюстрированный на фиг. 11, включает в себя механизм, при котором сообщение, прежде чем быть отправленным, преобразуется в значение хеш-функции. Этот механизм повышает эффективность передачи информации.
2-6: Модификация, превращающая в схему цифровой подписи
Далее будет представлен способ модификации схемы аутентификации с открытым ключом, соответствующей предлагаемому способу, превращающий ее в схему цифровой подписи. В случае, когда доказывающий в модели схемы аутентификации с открытым ключом соответствует подписывающему в схеме цифровой подписи, аппроксимация модели схемы цифровой подписи может быть легко истолкована в том смысле, что только доказывающий может убедить проверяющий. Опишем, основанный на этой идее способ модификации схемы аутентификации с открытым ключом, соответствующей предлагаемого способа, превращающий ее в схему цифровой подписи.
2-6-1: Способ преобразования
Опишем здесь, в качестве примера, способ преобразования примера 3 структуры эффективного алгоритма в алгоритм схемы цифровой подписи. Алгоритм примера 3 структуры в общих чертах выражен следующими четырьмя операциями: с #1 по #4, которые проиллюстрированы на фиг. 12.
Операция #1 включает в себя процесс (1) генерирования
и процесс (2) вычисления Cmt<-H(c1,1, с2,1, с3,1, …, с1,N, с2,N, с3,N). Cmt, сгенерированный в ходе операции #1 алгоритмом P доказывающего, отправляется алгоритму V проверяющего.
Операция #2 включает в себя процесс выбора d1, …, dN. d1, …, dN, выбранные в ходе операции #2 алгоритмом V проверяющего, отправляются алгоритму P доказывающего.
Операция #3 включает в себя процесс генерирования Rsp1, …, RspN с использованием d1, …, dN и a1, …, aN. Этот процесс выражен как Rspi<-Select(di, ai)(Rspi<-Выбор (di, ai)). Rsp1, …, RspN, сгенерированные в ходе операции #3 алгоритмом P доказывающего, отправляются алгоритму V проверяющего.
Операция #4 включает в себя процесс (1) воспроизведения c1,1, с2,1, с3,1, …, с1,N, с2,N, с3,N, использующий d1, …, dN и Rsp1, …, RspN, и процесс (2) проверки Cmt=H(c1,1, с2,2, с3,3, …, c1,N, с2,N, с3,N) с использованием воспроизведенных c1,1, с2,1, с3,1, …, c1,N, с2,N, c3,N.
Этот алгоритм схемы аутентификации с открытым ключом, выраженный посредством вышеописанных операций: с операции #1 по операцию #4, модифицирован, будучи превращен в алгоритм Sig генерирования цифровой подписи и алгоритм Ver проверки цифровой подписи, проиллюстрированные на фиг. 12.
Алгоритм Sig генерирования цифровой подписи
Сначала, будет описана структура алгоритма Sig генерирования цифровой подписи. Алгоритм Sig генерирования цифровой подписи включает в себя нижеследующие процессы: с (1) по (5).
Процесс (2): Алгоритм Sig генерирования цифровой подписи вычисляет Cmt<-H(c1,1, с2,1, с3,1, …, с1,N, с2,N, с3,N). Здесь, M представляет собой документ, на который ставится подпись.
Процесс (3): Алгоритм Sig генерирования цифровой подписи вычисляет (d1, …, dN)<-Н(М, Cmt). Здесь, M представляет собой документ, на который ставится подпись.
Процесс (4): Алгоритм Sig генерирования цифровой подписи вычисляет Rspi<-Select (di, ai) (Rspi<-Выбор (di, ai)).
Процесс (5): Алгоритм Sig генерирования цифровой подписи задает (Cmt, Rsp1, …, RspN) в качестве подписи.
Алгоритм Ver проверки цифровой подписи
Далее, будет описана структура алгоритма Ver проверки цифровой подписи. Алгоритм Ver проверки цифровой подписи включает в себя нижеследующие процессы: с (1)по (3).
Процесс (1): Алгоритм Ver проверки цифровой подписи вычисляет (d1, …, dN)<-Н(M, Cmt).
Процесс (2): Алгоритм Ver проверки цифровой подписи генерирует c1,1, с2,1, с3,1, …, с1,N, с2,N, с3,N, используя d1, …, dN и Rsp1, …, RspN.
Процесс (3): Алгоритм Ver проверки цифровой подписи проверяет Cmt=H(c1,1, с2,1, с3,1, …, с1,N, с2,N, с3,N), используя воспроизведенные c1,1, с2,1, с3,1, …, с1,N, с2,N, с3,N.
Как было описано выше, установив соответствие доказывающего в модели схемы аутентификации с открытым ключом с подписывающим в схеме цифровой подписи, можно модифицировать алгоритм схемы аутентификации с открытым ключом, превратив его в алгоритм схемы цифровой подписи.
2-6-2: Упрощение алгоритма цифровой подписи
При этом, сосредоточившись на структуре алгоритма Sig генерирования цифровой подписи, проиллюстрированной на фиг. 13, сосредотачиваются, можно понять, что в ходе процессов (2) и (3) выполнялось вычисление значения хеш-функции. Кроме того, сосредоточившись на структуре алгоритма Ver проверки цифровой подписи, можно понять, что в ходе процесса (1) выполнялось то же самое вычисление значения хеш-функции, что и в ходе процесса (3) алгоритма Sig генерирования цифровой подписи. Усовершенствовав конфигурации алгоритма Sig генерирования цифровой подписи и алгоритма Ver проверки цифровой подписи, сосредоточившись на этих процессах, как это проиллюстрировано на фиг. 13, можно дополнительно повысить эффективность вычисления.
Алгоритм Sig генерирования цифровой подписи
Сначала будет описана усовершенствованная структура алгоритма Sig генерирования цифровой подписи. Алгоритм Sig генерирования цифровой подписи включает в себя нижеследующие процессы: с (1) по (4).
Процесс (2): Алгоритм Sig генерирования цифровой подписи вычисляет (d1, …, dN)<-Н (М, c1,1, с2,2, с3,3, …, с1,N, с2,N, с3,N). Здесь, М представляет собой документ, на который ставится подпись.
Процесс (3): Алгоритм Sig генерирования цифровой подписи вычисляет Rspi<-Select (di, ai) (Rspi<-Выбор (di, ai)).
Процесс (4): Алгоритм Sig генерирования цифровой подписи задает (d1, …, dN, Rsp1, …, RspN) в качестве подписи.
Алгоритм Ver проверки цифровой подписи
Далее, будет описана структура усовершенствованного алгоритма Ver проверки цифровой подписи. Алгоритм Ver проверки цифровой подписи включает в себя нижеследующие процессы (1) и (2).
Процесс (1): Алгоритм Ver проверки цифровой подписи генерирует c1,1, с2,1, с3,1, …, с1,N, с2,N, с3,N, используя d1, …, dN и Rsp1, …, Rsp1, …, RspN.
Процесс (3): Алгоритм Ver проверки цифровой подписи проверяет (d1, …, dN)=Н(М, c1,1, с2,1, с3,1, …, с1,N, с2,N, с3,N), используя воспроизведенные c1,1, с2,1, с3,1, …, с1,N, с2,N, с3,N
Усовершенствовав структуру алгоритма Sig генерирования цифровой подписи и алгоритма Ve проверки цифровой подписи так, как это описано выше, вычисление значения хеш-функции в каждом алгоритме уменьшается на один раз. В результате этого, может быть дополнительно повышена эффективность вычисления.
2-7: Форма системы многопорядковых уравнений с многими переменными
Как было описано выше, предлагаемый способ представляет собой схему, в которой безопасность основывается на трудности решения системы многопорядковых уравнений с многими переменными. Кроме того, признак предлагаемого способа заключается в том, что может быть использована сложная система многопорядковых уравнений с многими переменными. В вышеприведенном описании, нет никакого специального ограничения по форме системы многопорядковых уравнений с многими переменными, но желательно использовать систему многопорядковых уравнений с многими переменивши, включающую в себя технологию элемента шифрования, в которой трудность в достаточной мере компенсируется в выражении. Далее, будет представлен конкретный пример системы многопорядковых уравнений с многими переменными, к которой может быть применена предлагаемый способ.
2-7-1: Форма, относящаяся к блочному шифру с общим ключом
Технология блочного шифра с общим ключом, такая как ES, DES (Стандарт шифрования данных) или KATAN, представляет собой элементную технологию, которая часто анализируется и имеет высокую безопасность и надежность. Блочный шифр с общим ключом может быть выражен системой многопорядковых уравнений с многими переменными, имеющей в качестве переменных ключ, незашифрованный текст и зашифрованный текст блочного шифра с общим ключом. В системе многопорядковых уравнений с многими переменными, когда переменным, представляющим незашифрованный текст и зашифрованный текст задаются значения, система многопорядковых уравнений с многими переменными становится уравнением, имеющим в качестве переменной только переменную, представляющую ключ.
Решение системы многопорядковых уравнений с многими переменными, выражающей блочный шифр с общим ключом, соответствует восстановлению ключа блочного шифра с общим ключом исходя из незашифрованного текста и зашифрованного текста. Другими словами, пока сохраняется безопасность блочного шифра с общим ключом, обеспечивается трудность нахождения решения системы многопорядковых уравнений с многими переменными, выражающей блочный шифр с общим ключом. По этой причине, в случае, когда в предлагаемом способе применяется система многопорядковых уравнений с многими переменными, выражающая некоторый блочный шифр с общим ключом, реализуется схема аутентификации с открытым ключом, имеющая безопасность, эквивалентную безопасности этого блочного шифра с общим ключом.
При этом, в случае, когда блочный шифр с общим ключом выражен системой многопорядковых уравнений с многими переменными, имеющими такие переменные, как ключ, незашифрованный текст и зашифрованный текст, поскольку порядок многочлена увеличивается, размер данных для выражения системы уравнений увеличивается. В связи с этим, в дополнение к ключу, незашифрованному тексту и зашифрованному тексту вводится переменная, представляющая внутреннее состояние в каждом цикле. Благодаря введению этой переменной можно понизить порядок системы многопорядковых уравнений с многими переменными, выражающей блочный шифр с общим ключом. Например, вместо переменных, представляющих незашифрованный текст и зашифрованный текст, подставляются надлежащие значения, и вводится система уравнений, относящаяся к ключу, и переменной, представляющей внутреннее состояние. В случае, когда используется этот способ, количество переменных увеличивается, но порядок уменьшается, и, соответственно, выражение системы уравнений становится компактным.
2-7-2: Форма, относящаяся к хеш-функции
Аналогичным образом, в предлагаемом способе может быть применена система многопорядковых уравнений с многими переменными, относящаяся к хеш-функциям, таким как SHA - 1 или SHA - 256. Хеш-функция может быть выражена системой многопорядковых уравнений с многими переменными, имеющей в качестве переменных сообщение, которое является входными данными хеш-функции, и значение хеш-функции, которое является ее выходными данными. В системе многопорядковых уравнений с многими переменными, в случае, когда переменной, представляющей значение хеш-функции, задается надлежащее значение, получается система многопорядковых уравнений с многими переменными, относящаяся к переменной, представляющей соответствующие входные данные.
Решение этой системы многопорядковых уравнений с многими переменными соответствует восстановлению значения сообщения, служащего базисом, исходя из значения хеш-функции. Другими словами, пока сохраняется безопасность (однонаправленная характеристика) хеш-функции, гарантируется трудность решения системы многопорядковых уравнений с многими переменными, выражающей эту хеш-функцию. По этой причине, в случае, когда в предлагаемом способе применяется система многопорядковых уравнений с многими переменными, выражающая некоторую хеш-функцию, реализуется схема аутентификации с открытым ключом, основанная на безопасности этой хеш-функции.
При этом, в случае, когда хеш-функция выражена системой многопорядковых уравнений с многими переменными, имеющей в качестве переменных входное сообщение и значение хеш-функции, поскольку порядок многочлена увеличивается, размер данных, выражающих систему уравнений, увеличивается. В связи с этим, в дополнение входному сообщению и значению хеш-функции вводится переменная, представляющая внутреннее состояние. Благодаря введению этой переменной можно понизить порядок системы многопорядковых уравнений с многими переменными, выражающей хеш-функцию. Например, вместо переменной, представляющей значение хеш-функции, подставляется надлежащее значение, и вводится система уравнений, относящаяся к входному сообщению, и переменной, представляющей внутреннее состояние. В случае, когда используется этот способ, количество переменных увеличивается, но порядок уменьшается, и, соответственно, выражение системы уравнений становится компактным.
2-7-3: Форма, относящаяся к поточному шифру
Аналогичным образом, в предлагаемом способе может быть применена система многопорядковых уравнений с многими переменными, относящаяся к поточному шифру, такому как Trivium. Поточный шифр может быть выражен системой многопорядковых уравнений с многими переменными, относящихся к переменной, представляющей первоначальное внутреннее состояние поточного шифра, и переменной, представляющей выводимый поток данных. В этом случае, когда переменной, представляющей выводимый поток данных, задается надлежащее значение, получается система многопорядковых уравнений с многими переменными, относящаяся к переменной, представляющей соответствующее первоначальное внутреннее состояние.
Решение этой системы многопорядковых уравнений с многими переменными соответствует восстановлению, значения сообщения, служащего базисом, исходя из значения выводимого потока данных. Другими словами, пока гарантируется безопасность поточного шифра, гарантируется трудность решения системы многопорядковых уравнений с многими переменными, выражающей этот поточный шифр. По этой причине, в случае, когда в предлагаемом способе применяется система многопорядковых уравнений с многими переменными, выражающая некоторый поточный шифр, реализуется схема аутентификации с открытым ключом, основанная на безопасности этого поточного шифра.
При этом, в случае, когда поточный шифр выражен системой многопорядковых уравнений с многими переменными, имеющей в качестве переменных первоначальное входное состояние и выходной поток данных, порядок многочлена увеличивается, и, соответственно, размер (данных) для выражения системы уравнений, увеличивается. В связи с этим, в дополнение первоначальному входному состоянию и выходному потоку данных вводится переменная, представляющая внутреннее состояние в каждом цикле. Благодаря введению этой переменной можно понизить порядок системы многопорядковых уравнений с многими переменными, выражающей поточный шифр. Например, в случае, когда вместо переменной, представляющей выходной поток данных, подставляется надлежащее значение, вводится система уравнений, относящаяся к первоначальному внутреннему состоянию и переменной, представляющей внутреннее состояние в цикле. В случае, когда используется этот способ, количество переменных увеличивается, но порядок уменьшается, и, соответственно, выражение системы уравнений становится компактным.
Выше были описаны конкретные примеры системы многопорядковых уравнений с многими переменными, применимых в предлагаемом способе.
2-8: Последовательно-параллельный гибридный алгоритм
Для того чтобы сделать вероятность успешной подделки пренебрежимо малой, необходимо, чтобы интерактивный протокол, как было описано выше, выполнялся множество раз. Кроме того, в качестве способов выполнения интерактивного протокола множество раз, были представлены последовательный способ и параллельный способ. В частности, параллельный способ был описан в связи с конкретным преобразованным в параллельную форму алгоритмом. Далее, будет представлен алгоритм гибридного типа, в котором последовательный способ объединен с параллельным способом.
Гибридная структура 1
Алгоритм гибридного типа (в дальнейшем именуемый как "параллельно-последовательный алгоритм") будет описан со ссылкой на фиг. 14. На фиг. 14 проиллюстрирована базовая структура предлагаемого способа, преобразованный в последовательную форму алгоритм, в котором эта базовая структура преобразована в последовательную форму, преобразованный в параллельную форму алгоритм, в котором эта базовая структура преобразована в параллельную форму, и параллельно-последовательный алгоритм.
В базовой структуре, при первой пересылке, от доказывающего проверяющему отправляется сообщение (c1, c2, c3). При второй пересылке, от проверяющего доказывающему отправляется запрос d. При третьей пересылке, от доказывающего проверяющему отправляется ответ σ.
В случае, когда базовая структура преобразована в параллельную форму, при первой пересылке, от доказывающего проверяющему отправляются сообщения (c1,1, с2,1, с3,1, …, с1,N, с2,N, с3,N) для N раз. При второй пересылке, от проверяющего доказывающему отправляются запросы (d1, …, dN) для N раз. При третьей пересылке, от доказывающего проверяющему отправляются ответы (σ1, …, σN) для N раз. Преобразованный в параллельную форму алгоритм, относящийся к предлагаемому способу, гарантирует безопасность от пассивной атаки. Кроме того, количество взаимодействий составляет просто три раза. Кроме того, поскольку сообщения для N раз, отправляемые при первой пересылке, собираются посредством одного значения хеш-функции, то эффективность передачи информации может быть повышена.
Между тем, в случае, когда базовая структура преобразована в последовательную форму, при первой пересылке, от доказывающего проверяющему отправляется сообщение (c1,1, c2,1, с3,1) для одного раза. При второй пересылке, от проверяющего доказывающему отправляется запрос d1 для одного раза. При третьей пересылке, от доказывающего проверяющему отправляется ответ σ1 для одного раза. В ходе четвертой перехода, от доказывающего проверяющему отправляется сообщение (c1,2, c2,2, c3,2) для одного раза. При пятой пересылке, от проверяющего доказывающему отправляется запрос d2 для одного раза. При шестой пересылке, от доказывающего проверяющему отправляется ответ σ2 для одного раза. Аналогичным образом, взаимодействие повторяющимся образом выполняется до тех пор, пока от доказывающего проверяющему не будет отправлен ответ σN. Преобразованный в последовательную форму алгоритм гарантирует безопасность от активной атаки. Кроме того, можно доказать, что возможность подделки наверняка уменьшается.
Далее, параллельно-последовательный алгоритм представляет собой алгоритм, имеющий характеристики алгоритма, преобразованного в параллельную форму, и характеристики алгоритма, преобразованного в последовательную форму. В параллельно-последовательном алгоритме, проиллюстрированном на фиг. 14, при первой пересылке, от доказывающего проверяющему отправляются сообщения (c1,1, с2,1, с3,1, …, с1,N, с2,N, с3,N) для N раз. При второй пересылке, от проверяющего доказывающему отправляется запрос d1 для одного раза. При третьей пересылке, от доказывающего проверяющему отправляется ответ σ1 для одного раза. Соответственно, осуществляется обмен запросом d2, …, dN и ответом σ2, …, σN между доказывающим и проверяющим.
Параллельно-последовательный алгоритм, основанный на предлагаемом способе, гарантирует безопасность от пассивной атаки. Кроме того, количество взаимодействий составляет просто 2N+1. Кроме того, поскольку сообщения для N раз, подлежащие отправке при первой пересылке преобразуются в одно значение хеш-функции, то эффективность передачи информации может быть повышена.
Гибридная структура 2
Другой алгоритм гибридного типа (в дальнейшем именуемый как "последовательно-параллельный алгоритм") будет описан со ссылкой на фиг. 15. На фиг. 15 проиллюстрирована базовая структура, относящаяся к предлагаемому способу, преобразованный в последовательную форму алгоритм, в котором эта базовая структура преобразована в последовательную форму, преобразованный в параллельную форму алгоритм, в котором эта базовая структура преобразована в параллельную форму, и последовательно-параллельный алгоритм. Структуры и характеристики базовой структуры, алгоритма преобразованного в последовательную форму, и алгоритма, преобразованного в параллельную форму, являются одинаковыми с теми, которые описаны выше.
Последовательно-параллельный алгоритм, проиллюстрированный на фиг. 15, представляет собой алгоритм, имеющий как характеристики алгоритма, преобразованного в параллельную форму, так и характеристики алгоритма, преобразованного в последовательную форму. В последовательно-параллельном алгоритме, проиллюстрированном на фиг. 15, при первой пересылке, от доказывающего проверяющему отправляются сообщения (c1,1, c2,1, c3,1) для одного раза. При второй пересылке, от проверяющего доказывающему отправляется запрос d1 для одного раза. После этого, между доказывающим и проверяющим осуществляется обмен сообщениями: (c1,2, c2,2, c3,1), …, (c1,N, c2,N, c3,N), и запросами: d2, …, dN. После того, как от проверяющего доказывающему отправлен запрос dN, от доказывающего проверяющему отправляются ответы: σ1, …, σN, для N раз.
Последовательно-параллельный алгоритм, основанный на предлагаемом способе, гарантирует безопасность от активной атаки. Кроме того, количество взаимодействий составляет просто 2N+1.
Выше был описан алгоритм гибридного типа, основанный на предлагаемом способе.
Выше был описан первый вариант реализации предлагаемой технологии.
3: Второй вариант реализации изобретения
Далее, будет описан второй вариант реализации предлагаемой технологии. До сих пор описывалась схема аутентификации с открытым ключом, имеющая 3 перехода. В предлагаемом варианте реализации изобретения, будет описана схема аутентификации с открытым ключом, имеющая 5 переходов (в дальнейшем именуемая как "предлагаемый способ"). Предлагаемый способ представляет собой схему обеспечения "прочности" схемы аутентификации с открытым ключом за счет задания 2q моделей проверки проверяющим.
В схеме аутентификации с открытым ключом, имеющей 3 перехода, соответствующей первому варианту реализации изобретения, вероятность ложной проверки, приходящаяся на одно исполнение интерактивного протокола, составляет 2/3, но в предлагаемом способе вероятность ложной проверки, приходящаяся на одно исполнение интерактивного протокола, составляет 1/2+1/q, как это будет описано позже. Здесь, q представляет собой порядок кольца, которое используется. Таким образом, когда порядок кольца является достаточно большим, как это проиллюстрировано на фиг. 39, в соответствии с предлагаемым способом, вероятность ложной проверки, каждый раз можно уменьшить, и вероятность ложной проверки может быть в достаточной мере уменьшена при исполнении интерактивного протокола малое количество раз.
Интерактивный протокол, относящийся к схеме аутентификации с открытым ключом, имеющей 5 переходов, может рассматриваться как обладающий более низкой эффективностью, чем интерактивный протокол, относящийся к схеме аутентификации с открытым ключом, имеющей 3 перехода. Однако, в схеме аутентификации с открытым ключом, имеющей 5 переходов, в случае, когда порядок кольца является достаточно большим, вероятность ложной проверки, приходящаяся на одно исполнение интерактивного протокола, близка к 1/2, и, соответственно, для достижения того же самого уровня безопасности необходимо небольшое количество исполнений интерактивного протокола.
Например, в случае, когда желательно, чтобы эта вероятность ложной проверки была равна или меньше чем 1/2n, интерактивный протокол в схеме аутентификации с открытым ключом, имеющей 3 перехода, должен быть исполнен n/(log3-1)=1,701n раз или больше. С другой стороны, интерактивный протокол в схеме аутентификации с открытым ключом, имеющей 5 переходов, должен быть исполнен n/(1-log(1+1/q)) раз или больше. Соответственно, как проиллюстрировано на фиг. 39, в случае, когда q=24, трафик передачи информации, необходимый для того, чтобы реализовать тот же самый уровень безопасности, меньше в схеме аутентификации с открытым ключом, имеющей 5 переходов, чем в схеме аутентификации с открытым ключом, имеющей 3 перехода.
3-1: Алгоритм схемы аутентификации с открытым ключом
Далее, со ссылкой на фиг. 16 будет описана структура алгоритма, относящегося к схеме аутентификации с открытым ключом, имеющей 5 переходов, (в дальнейшем именуемой как предлагаемый способ). Фиг. 16 представляет собой пояснительное схематическое изображение для описания алгоритма, соответствующего предлагаемому способу.
Алгоритм Gen генерирования ключей
Алгоритм Gen генерирования ключей генерирует m многочленов f1(x1, …, xn), …, fm(x1, …, xn) с многими переменными, определенных в кольце k и вектор s=(s1, …, sn), который является элементом множества Kn. После этого, алгоритм Gen генерирования вычисляет y=(y1, …, ym)<-(f1(s), …, fm(s)). Кроме того, алгоритм Gen генерирования задает (f1, …, fm, y) в качестве открытого ключа pk и задает s в качестве секретного ключа. Далее, вектор (x1, …, xn) представлен обозначением x, а набор многочленов (f1(x), …, fm(x)) с многими переменными представлен обозначением F(х).
Алгоритм P доказывающего, алгоритм V проверяющего
Далее, со ссылкой на фиг. 16 будут описаны процессы, выполняемые согласно алгоритму P доказывающего и алгоритму V проверяющего в ходе исполнения интерактивного протокола. В ходе исполнения вышеназванного интерактивного протокола, доказывающий ни в коей мере не разглашает проверяющему информацию о секретном ключе s и показывает проверяющему, что "сам он (доказывающий) знает s, удовлетворяющий y=F(s)". С другой стороны, проверяющий проверяет то, действительно ли доказывающий знает s, удовлетворяющий y=F(s). Открытый ключ pk предполагается сообщенным проверяющему. Кроме того, секретный ключ s предполагается сохраняемым доказывающим в тайне. Далее, описание будет дано со ссылкой на блок - схему алгоритма, проиллюстрированную на фиг. 16.
Операция #1:
Прежде всего, алгоритм P доказывающего выбирает произвольным образом некоторое число w. После этого, алгоритм P доказывающего генерирует вектор r, который является элементом множества Kn, и пару многочленов
с n переменными, применяя это число w к генератору G псевдослучайных чисел. Таким образом, алгоритм P доказывающего вычисляет (r, FA)<-G1(w). Вслед за этим, алгоритм P доказывающего вычисляет z<-s-r. Это вычисление эквивалентно маскированию секретного ключа s посредством вектора r.
Операция #1 (продолжение):
После этого, алгоритм P доказывающего генерирует значение c1 хеш-функции для FA(z) и z. Другими словами, алгоритм P доказывающего вычисляет c1<-H1(FA(z), z). Кроме того, алгоритм P доказывающего генерирует значение с2 хеш-функции для числа w. Другими словами, алгоритм P доказывающего вычисляет c1<-H2(w). H1(…), H2(…) и H3(…) представляют собой хеш-функции. Сообщение (c1, c2), сгенерированное в ходе операции #1, отправляется проверяющему. При этом следует отметить, что информация, относящаяся к s, информация, относящаяся к r, и информация, относящаяся к z, ни в коей мере не разглашается проверяющему.
Операция #2:
Алгоритм V проверяющего случайным образом выбирает одно число α из исходных данных для q колец K и отправляет выбранное число α алгоритму P доказывающего.
Операция #3:
После приема числа α, алгоритм P доказывающего вычисляет FB(x)<-αF(x+r)+FA(x). Это вычисление эквивалентно маскированию многочлена F(x+r0) с многими переменными, для x, посредством многочлена FA(x) с многими переменными. Многочлен FB с многими переменными, сгенерированный в ходе операции #3, отправляется алгоритму V проверяющего. При этом следует отметить, что в случае, при котором d=0, проверяющему ни в коей мере не разглашается информация о z, а в случае, при котором d=1, проверяющему ни в коей мере не разглашается информация об r.
Операция #4:
После приема многочлена FB с многими переменными, алгоритм V проверяющего выбирает то, какую модель проверки, из числа двух моделей проверки, использовать. Например, алгоритм V проверяющего может выбрать некоторое численное значение из числа двух численных значений {0, 1}, представляющих модели проверки, и задать выбранное численное значение в запросе d. Этот запрос d отправляется алгоритму P доказывающего.
Операция #5:
После приема запроса d, алгоритм P доказывающего генерирует ответ а для того, чтобы отправить его алгоритму V проверяющего в ответ на принятый запрос d. В случае, при котором d=0, алгоритм P доказывающего генерирует ответ σ=w. В случае, при котором d=1, алгоритм P доказывающего генерирует ответ σ=z. Ответ σ, сгенерированный в ходе операции #5, отправляется алгоритму V проверяющего.
Операция #6:
После приема ответа σ, алгоритм V проверяющего исполняет, используя принятый ответ σ, нижеследующий процесс проверки.
В случае, при котором d=0, алгоритм V проверяющего вычисляет (rA, FC)<-G(σ). После этого, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство с2=Н2(σ). В дополнение к этому, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство FB(x)=αF(x+rA)+FC(x). Алгоритм V проверяющего, в случае, при котором все эти проверки являются успешными, выдает на выходе значение 1, указывающее на успешную аутентификацию, а в случае, при котором проверка терпит неудачу, выдает на выходе значение 0, указывающее на неудачную аутентификацию.
В случае, при котором d=1, алгоритм V проверяющего задает zA<-σ. Кроме того, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство c1=H1(FC(zA)-αy, zA). Алгоритм V проверяющего, в случае, при котором все эти проверки являются успешными, выдает на выходе значение 1, указывающее на успешную аутентификацию, а в случае, при котором проверка терпит неудачу, выдает на выходе значение 0, указывающее на неудачную аутентификацию.
Выше был описан пример структуры каждого алгоритма, относящегося к предлагаемому способу.
"Прочность" в соответствии с предлагаемым способом
"Прочность" предлагаемого способа обеспечивается исходя из того факта, что исходя из содержания ответа, когда алгоритм P доказывающего надлежащим образом дает ответ на запрос d=0 и 1 в отношении (c1, c2) и двух (α1, α2), выбранных алгоритмом V проверяющего, могут быть вычислены
,
, FC, rA и zA, удовлетворяющие нижеследующим формулам: с формулы (15) по формулу (17).
Математическое выражение 12
При обеспечении вышеупомянутой "прочности" предлагаемого способа, тот факт, что подделка с вероятностью выше, чем 1/2+1/q не возможна, обеспечивается до тех пор, пока не решена задача решения систем многопорядковых уравнений с многими переменными. Таким образом, для того, чтобы надлежащим образом дать ответы на все запросы d=0 и 1, поступающие от проверяющего, фальсификатор должен вычислить
,
, FC, rA и zA, удовлетворяющие вышеприведенным формуле (15) и формуле (17). Другими словами, фальсификатор должен вычислить s, удовлетворяющий F (s)=y. Соответственно, фальсификатор не сможет преуспеть с подделкой с вероятностью выше, чем 1/2+1/q, до тех пор, пока не решена задача решения систем многопорядковых уравнений с многими переменными. Кроме того, при повторяющемся исполнении вышеописанного интерактивного протокола достаточно большое количество раз вероятность успешной подделки становится пренебрежимо малой.
Модифицированный пример
Алгоритм Gen генерирования ключа вычисляет y<-F(s) и задает (F, y) в качестве открытого ключа. Однако, алгоритм Gen генерирования ключа может быть сконфигурирован таким образом, чтобы задавать (y1, …, ym)<-F(s), вычислять
и задавать
в качестве открытого ключа. В случае этой модификации, интерактивный протокол может быть выполнен между алгоритмом P доказывающего и алгоритмом V проверяющего при y=0.
Кроме того, алгоритм P доказывающего может отдельно вычислять значение хеш-функции для FB(z) и значение хеш-функции для z и отправлять каждое значение хеш-функции проверяющему как сообщение.
Кроме того, алгоритм P доказывающего применяет число w к генератору G1 псевдослучайных чисел и генерирует вектор r и число wA. Кроме того, алгоритм P доказывающего применяет число wA к генератору псевдослучайных чисел G2 и генерирует многочлен FA(x) с многими переменными. Однако, алгоритм P доказывающего может быть сконфигурирован таким образом, чтобы выполнять тождественное отображение на G1 и вычислять w=(r, FA) с начала. В этом случае, нет необходимости применять число w к G1. Это, аналогичным образом, относится к G2.
Выше был описан модифицированный пример предлагаемого способа.
3-2: Расширенный алгоритм
Далее, со ссылкой на фиг. 17 будет описан алгоритм схемы аутентификации с открытым ключом (в дальнейшем именуемый как "расширенный способ"), расширенный по отношению к предлагаемому способу. Фиг. 17 представляет собой пояснительное схематическое изображение для описания последовательности операций интерактивного протокола, основанного на расширенном способе.
Описываемый здесь расширенный способ представляет собой схему преобразования многочлена FB с многими переменными, подлежащего отправке при третьей пересылке, в единственное значение (c3) хеш-функции и отправки значения (c3) хеш-функции проверяющему. Посредством этого расширения можно наполовину уменьшить трафик передачи информации в случае, когда в ходе исполнения интерактивного протокола проверяющему отправляется многочлен FB с многими переменными, имеющий большой размер выражения, и можно уменьшить средний размер данных, подлежащих обмену. Далее будет подробно описана структура каждого алгоритма в расширенном способе.
Алгоритм Gen генерирования ключей
Алгоритм Gen генерирования ключей генерирует многочлены f1(x1, …, xn), …, fm(x1, …, xn) с многими переменными, определенные в кольце k, и вектор s=(s1, …, sn), который является элементом множества Kn. После этого, алгоритм Gen генерирования вычисляет y=(y1, …, ym)<-(f1(s), …, fm(s)). Кроме того, алгоритм Gen генерирования задает (f1, …, fm, y) в качестве открытого ключа pk и задает s в качестве секретного ключа. Далее, вектор (x1, …, xn) представлен обозначением x, а набор многочленов (f1(x), …, fm(x)) с многими переменными представлен обозначением F(х).
Алгоритм P доказывающего, алгоритм V проверяющего
Далее, со ссылкой на фиг. 17 будут описаны процессы, выполняемые согласно алгоритму P доказывающего и алгоритму V проверяющего в ходе исполнения интерактивного протокола. В ходе исполнения вышеназванного интерактивного протокола, доказывающий ни в коей мере не разглашает проверяющему информацию о секретном ключе s и показывает проверяющему, что "сам он знает s, удовлетворяющий y=F(s)". С другой стороны, проверяющий проверяет то, действительно ли доказывающий знает s, удовлетворяющий y=F(s). Открытый ключ pk предполагается сообщенным проверяющему. Кроме того, секретный ключ s предполагается сохраняемым доказывающим в тайне. Далее, описание будет дано со ссылкой на блок - схему алгоритма, проиллюстрированную на фиг. 4. Операция #1:
Сначала, алгоритм P доказывающего выбирает произвольным образом некоторое число w. Вслед за этим, алгоритм P доказывающего генерирует вектор r, который является элементом множества Kn, и многочлен FA(x) с многими переменными, применяя это число w к генератору G псевдослучайных чисел. Таким образом, алгоритм P доказывающего вычисляет (r, FA)<-G1(w). Вслед за этим, алгоритм P доказывающего вычисляет z<-s-r. Это вычисление эквивалентно маскированию секретного ключа s посредством вектора r.
Операция #1 (продолжение):
Вслед за этим, алгоритм P доказывающего генерирует FA(z) и значение (c1) хеш-функции для z. То есть, алгоритм P доказывающего вычисляет c1<-H1(FA(z), z). Кроме того, алгоритм P доказывающего вычисляет значение (с2) хеш-функции для числа w. То есть, алгоритм P доказывающего вычисляет с2<-Н2(w). H1(…), Н2(…) и H3(…), описанные выше, представляют собой хеш-функции. Сообщения (c1, с2), сгенерированные в ходе операции #1, отправляются проверяющему.
Операция #2:
После приема сообщений (c1, с2), алгоритм V проверяющего случайным образом выбирает одно число а из исходных данных для q колец K и отправляет выбранное число а алгоритму P доказывающего.
Операция #3:
Алгоритм P доказывающего, который принял число а, вычисляет FB(x)<-αF(x+r)+FA(x). Это вычисление соответствует операции маскирования многочлена F(x+r) с многими переменными, для x, с использованием многочлена FA(x) с многими переменными. Кроме того, алгоритм P доказывающего генерирует значение (c3) хеш-функции для многочлена FB с многими переменными. Другими словами, алгоритм P доказывающего вычисляет c3<-H3(FB(x)). H3(…) представляет собой хеш-функцию. Сообщение c3, сгенерированное в ходе операции #3, отправляется проверяющему.
Операция #4:
После приема многочлена F2 с многими переменными, алгоритм V проверяющего выбирает то, какую модель проверки, из числа двух моделей проверки, использовать. Например, алгоритм V проверяющего может выбрать некоторое численное значение из числа двух численных значений {0, 1}, представляющих модели проверки, и задать выбранное численное значение в запросе d. Этот запрос d отправляется алгоритму P доказывающего.
Операция #5:
После приема запроса d, алгоритм P доказывающего генерирует ответ а для того, чтобы отправить его алгоритму V проверяющего в ответ на принятый запрос d. В случае, при котором d=0, алгоритм P доказывающего генерирует ответ σ=w. В случае, при котором d=1, алгоритм P доказывающего генерирует ответ σ=(z, FB). Ответ σ, сгенерированный в ходе операции #5, отправляется алгоритму V проверяющего.
Операция #6:
После приема ответа σ, алгоритм V проверяющего исполняет, используя принятый ответ σ, нижеследующий процесс проверки.
В случае, при котором d=0, алгоритм V проверяющего вычисляет (rA, Fc)<-G(σ). После этого, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство с2=Н2(σ). В дополнение к этому, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство c3=H3(αF(x+rA)+FC(x)). Алгоритм V проверяющего, в случае, при котором все эти проверки являются успешными, выдает на выходе значение 1, указывающее на успешную аутентификацию, а в случае, при котором проверка терпит неудачу, выдает на выходе значение 0, указывающее на неудачную аутентификацию.
В случае, при котором d=1, алгоритм V проверяющего вычисляет (zA, FC)<-σ. После этого, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство c1=H1(FC(zA)-αy, zA). Алгоритм V проверяющего, в случае, при котором все эти проверки являются успешными, выдает на выходе значение 1, указывающее на успешную аутентификацию, а в случае, при котором проверка терпит неудачу, выдает на выходе значение 0, указывающее на неудачную аутентификацию.
Выше был описан процесс, выполняемый согласно каждому алгоритму во время исполнения интерактивного протокола расширенной схемы. Посредством этого расширения можно наполовину уменьшить трафик передачи информации в случае, когда в ходе исполнения интерактивного протокола проверяющему отправляется многочлен FB с многими переменными, имеющий большой размер выражения, и можно уменьшить средний размер данных, подлежащих обмену.
3-3: Алгоритм, преобразованный в параллельную форму
Как было описано выше, применение интерактивного протокола, относящегося к предлагаемому способу и расширенному способу, делает возможным удерживать вероятность успешной подделки на уровне (1/2+1/q) или меньше. Следовательно, исполнение интерактивного протокола дважды дает возможность удерживать вероятность успешной подделки на уровне(1/2+1/q)2 или меньше. Более того, если интерактивный протокол выполняется N раз, вероятность успешной подделки становится (1/2+1/q)N, и если N задается как достаточно большое число (например, N=80), то вероятность успешной подделки становится пренебрежимо малой.
Потенциально возможные способы исполнения интерактивного протокола множество раз включают в себя последовательный способ, в котором обмен сообщением, запросом и ответом последовательно повторяется множество раз, и параллельный способ, в котором, например, обмен множественными сообщениями, запросами и ответами осуществляется в ходе однократного обмена. Далее будет описан способ распространения интерактивного протокола, соответствующего предлагаемому способу, на интерактивный протокол (в дальнейшем именуемый как "алгоритм, преобразованный в параллельную форму"), относящийся к параллельному способу. Например, алгоритм, преобразованный в параллельную форму, проиллюстрирован на фиг. 18. Далее, со ссылкой на фиг. 18, будут описаны подробности алгоритма, преобразованного в параллельную форму.
Алгоритма Gen генерирования ключей
Алгоритм Gen генерирования ключей генерирует многочлены f1(x1, …, xn), …, fm(x1, …, xn) с многими переменными, определенные в кольце k, и вектор s=(s1, …, sn), который является элементом множества Kn. После этого, алгоритм Gen генерирования ключей вычисляет y=(y1, …, ym)<-(f1(s), …, fm(s)). Кроме того, алгоритм Gen генерирования ключей задает (f1, …, fm, y) в качестве открытого ключа pk и задает s в качестве секретного ключа. Далее, вектор (x1, …, xn) представлен обозначением x, а набор многочленов (f1(х), …, fm(x)) с многими переменными представлен обозначением F(х).
Алгоритм P доказывающего, алгоритм V проверяющего
Далее, со ссылкой на фиг. 18 будет описан процесс, выполняемый согласно алгоритму P доказывающего, и процесс, выполняемый согласно алгоритму V проверяющего в ходе исполнения интерактивного протокола.
В ходе исполнения вышеназванного интерактивного протокола, доказывающий ни в коей мере не разглашает проверяющему информацию о секретном ключе s и показывает проверяющему, что "сам он знает s, удовлетворяющий y=F(s)". С другой стороны, проверяющий проверяет то, действительно ли доказывающий знает s, удовлетворяющий y=F(s). Открытый ключ pk предполагается сообщенным проверяющему. Кроме того, секретный ключ s предполагается сохраняемым доказывающим в тайне. Далее, описание будет дано со ссылкой на блок-схему алгоритма, проиллюстрированную на фиг. 18.
Операция #1:
Прежде всего, алгоритм P доказывающего выполняет нижеследующие процессы: с (1) по (5), для i=1 по N.
Процесс (1): Алгоритм P доказывающего выбирает произвольным образом некоторое число wi.
Процесс (2): Алгоритм P доказывающего применяет число wi к генератору G псевдослучайных чисел и генерирует вектор ri, который является элементом множества Kn, и набор
многочленов. Другими словами, алгоритм P доказывающего вычисляет
.
Процесс (3): Алгоритм P доказывающего вычисляет zi<-s-ri. Это вычисление соответствует операции маскирования секретного ключа s с использованием вектора ri.
Процесс (4): Алгоритм P доказывающего вычисляет значение (c1,i) хеш-функции для
и zi. Другими словами, алгоритм P доказывающего вычисляет
.
Процесс (5): Алгоритм P доказывающего генерирует значение (c2,i) хеш-функции для числа
. Другими словами, алгоритм P доказывающего вычисляет
.
После того, как процессы: с (1) по (5), выполнены для i=1 по N, сообщение (c1,i, c2,i) (i=1 по N), сгенерированное в ходе операции #1, отправляется алгоритму V проверяющего.
Операция #2:
Алгоритм V проверяющего, который принял сообщение (c1,i, c2,i) (i=1 по N), выбирает случайным образом N чисел α1, …, αN из исходных данных для q колец K. После этого, алгоритм V проверяющего отправляет выбранные числа α1, …, αN алгоритму P доказывающего.
Операция #3:
Алгоритм P доказывающего, который принял числа α1, …, αN, вычисляет
для i=1 по N. Это вычисление соответствует операции маскирования многочлена F(x+ri) с многими переменными, для x, с использованием многочлена
с многими переменными. После этого, алгоритм P доказывающего отправляет многочлен
с многими переменными алгоритму V проверяющего.
Операция #4:
После приема многочлена
с многими переменными, алгоритм V проверяющего выбирает то, какую модель проверки, из числа двух моделей проверки, использовать для i=1 по N. Например, алгоритм V проверяющего может выбрать некоторое численное значение из числа двух численных значений {0, 1}, представляющих модели проверки для i=1 по N, и задать выбранное численное значение в запросе di. Эти запросы di отправляются алгоритму P доказывающего.
Операция #5:
Алгоритм P доказывающего, который принял запрос di (i=1 по N) генерирует ответ σi, подлежащий отправке алгоритму V проверяющего в ответ на запрос di. При этом, алгоритм P доказывающего выполняет нижеследующие процессы (1) и (2) для i=1 по N.
Процесс (1): В случае, когда di=0, алгоритм P доказывающего генерирует ответ σi=wi.
Процесс (2): В случае, когда di=1, алгоритм P доказывающего генерирует ответ σi=zi.
После того, как процессы (1) и (2) выполнены, ответ σi (i=1 по N) отправляется алгоритму V проверяющего.
Операция #6:
После приема ответа σi (i=1 по N), алгоритм V проверяющего, используя принятый ответ σi, исполняет процесс проверки. Отметим, что нижеследующие процессы исполняются для i=1 по N.
В случае, при котором di=0, алгоритм V проверяющего вычисляет
. После этого, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство с2, i=Н2(σi). В дополнение к этому, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство
. Алгоритм V проверяющего, в случае, при котором все эти проверки являются успешными, выдает на выходе значение 1, указывающее на успешную аутентификацию, а в случае, при котором проверка терпит неудачу, выдает на выходе значение 0, указывающее на неудачную аутентификацию.
В случае, при котором di=1, алгоритм V проверяющего вычисляет
. Кроме того, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство
. Алгоритм V проверяющего, в случае, при котором все эти проверки являются успешными, выдает на выходе значение 1, указывающее на успешную аутентификацию, а в случае, при котором проверка терпит неудачу, выдает на выходе значение 0, указывающее на неудачную аутентификацию.
Выше был описан способ параллельного выполнения интерактивного протокола предлагаемого способа. Как было описано выше, поскольку этот интерактивный протокол предлагаемого способа выполняется повторяющимся образом, вероятность успешной подделки становится пренебрежимо малой. Кроме того, имеется возможность аналогичным образом преобразовать в параллельную форму расширенную схему.
Модифицированный пример
Кроме того, структура интерактивного протокола может быть модифицирована таким образом, что после операции #1 вместо отправки проверяющему (c1,1, c1,2, …, cN,1, CN,2) может быть отправлено значение Н (c1,1, c1,2, …, cN,1, cN,2) хеш-функции. В случае этой модификации в качестве сообщения при первой пересылке отправляется единственное значение хеш-функции, и, следовательно, имеется возможность существенно уменьшить трафик передачи информации. Однако, поскольку имеется сообщение, которое почти не восстанавливается алгоритмом V проверяющего, даже с использованием информации, присланной от алгоритма P доказывающего, необходимо отправлять соответствующее сообщение вместе с отправкой ответа. Посредством этой структуры, в случае структуры с n-кратным параллельным повторением, можно уменьшить количество порций информации, подлежащих отправке, на N-1.
Преобразованный в параллельную форму алгоритм, относящийся к расширенной схеме
Далее, со ссылкой на фиг. 19 будет описана структура преобразованного в параллельную форму алгоритма, относящегося к расширенной схеме. Структура алгоритма Gen генерирования ключей является той же самой, что и в преобразованном в параллельную форму алгоритме, относящемся к предлагаемому способу, и, соответственно, ее детализированное описание приводиться не будет.
Операция #1:
Прежде всего, алгоритм P доказывающего выполняет нижеследующие процессы: с (1) по (5), для i=1 по N.
Процесс (1): Алгоритм P доказывающего выбирает произвольным образом некоторое число wi.
Процесс (2): Алгоритм P доказывающего применяет число wi к генератору G псевдослучайных чисел и генерирует вектор ri, который является элементом множества Kn, и набор
многочленов с многими переменными. Другими словами, алгоритм P доказывающего вычисляет
.
Процесс (3): Алгоритм P доказывающего вычисляет zi<-s-ri. Это вычисление соответствует операции маскирования секретного ключа s с использованием вектора ri.
Процесс (4): Алгоритм P доказывающего вычисляет значение (c1,i) хеш-функции для
и zi. Другими словами, алгоритм P доказывающего вычисляет
.
Процесс (5): Алгоритм P доказывающего генерирует значение (c2,i) хеш-функции для числа wi. Другими словами, алгоритм P доказывающего вычисляет c2,i<-H2(wi).
После того, как процессы: с (1) по (5), выполнены для i=1 по N, сообщение (c1,i, c2,i) (i=1 по N), сгенерированное в ходе операции #1, отправляется алгоритму V проверяющего.
Операция #2:
Алгоритм V проверяющего, который принял сообщение (c1,i, c2,i) (i=1 по N), выбирает случайным образом n чисел α1, …, αN из исходных данных для q колец K. После этого, алгоритм V проверяющего отправляет выбранные числа α1, …, αN доказывающему.
Операция #3:
Алгоритм P доказывающего, который принял числа α1, …, αN, вычисляет
для i=1 по N. Это вычисление соответствует операции маскирования многочлена F(x+ri) с многими переменными, для x, с использованием многочлена
с многими переменными. После этого, алгоритм P доказывающего генерирует значение (с3) хеш-функции для многочленов
с многими переменивши. Другими словами, алгоритм P доказывающего вычисляет
. H3(…) представляет собой хеш-функцию. Сообщение c3, сгенерированное в ходе операции #3, отправляется алгоритму V проверяющего.
Операция #4:
После приема сообщения c3, алгоритм V проверяющего выбирает то, какую модель проверки, из числа двух моделей проверки, использовать для каждого из i=1 по N. Например, алгоритм V проверяющего может, для каждого из i=1 по N, выбрать некоторое численное значение из числа двух численных значений {0, 1}, представляющих модели проверки, и задать выбранное численное значение в запросе di. Этот запрос di отправляется алгоритму P доказывающего.
Операция #5:
Алгоритм P доказывающего, который принял запрос di (i=1 по N) генерирует ответ σi, подлежащий отправке алгоритму V проверяющего в ответ на запрос di. При этом, алгоритм P доказывающего выполняет нижеследующие процессы (1) и (2) для i=1 по N.
Процесс (1): В случае, когда di=0, алгоритм P доказывающего генерирует ответ σi=wi.
После того, как процессы (1) и (2) выполнены, ответ σi (i=1 по N) отправляется алгоритму V проверяющего.
Операция #6:
После приема ответа σi (i=1 по N), алгоритм V проверяющего, используя принятый ответ σi, исполняет процесс проверки. Отметим, что нижеследующие процессы исполняются для i=1 по N.
В случае, при котором di=0, алгоритм V проверяющего вычисляет
. Кроме того, алгоритм V проверяющего вычисляет
. После этого, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство c2,i=H2(σi). В дополнение к этому, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство
. Алгоритм V проверяющего, в случае, при котором все эти проверки являются успешными, выдает на выходе значение 1, указывающее на успешную аутентификацию, а в случае, при котором проверка терпит неудачу, выдает на выходе значение 0, указывающее на неудачную аутентификацию.
В случае, при котором di=1, алгоритм V проверяющего задает
. После этого, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство
. Алгоритм V проверяющего, в случае, при котором все эти проверки являются успешными, выдает на выходе значение 1, указывающее на успешную аутентификацию, а в случае, при котором проверка терпит неудачу, выдает на выходе значение 0, указывающее на неудачную аутентификацию.
Выше была описана структура преобразованного в параллельную форму алгоритма, относящегося к расширенной схеме.
Подходящий способ задания параметров
Аналогично интерактивному протоколу, соответствующему первому варианту реализации изобретения, интерактивный протокол, соответствующий предлагаемому варианту реализации изобретения, гарантирует уровень безопасности от пассивной атаки. Однако, в случае, когда применяется этот способ повторяющегося параллельного выполнения интерактивного протокола, для доказательства того, что гарантируется уровень безопасности от активной атаки, необходимо чтобы соблюдалось условие, которое будет описано ниже.
Этот интерактивный протокол представляет собой протокол, в котором доказывающий доказывает проверяющему, посредством их взаимодействия с использованием некоторого набора, состоящего из пары ключей (открытого ключа y и секретного ключа s), тот факт, что "доказывающий знает s, заставляющий выполняться y=F(s)", не выдавая при этом проверяющему информацию о секретном ключе s. По этой причине, при выполнении взаимодействия, принятого при проверке, трудно отрицать вероятность того, что информация, означающая то, что "доказывающий использовал s во время взаимодействия", известна проверяющему. В дополнение к этому, для многочлена F с многими переменными не гарантирована стойкость к коллизии. По этой причине, в случае, когда вышеописанный интерактивный протокол выполняется параллельно повторяющимся образом, трудно безусловно доказать, что безопасность от активной атаки надежно гарантирована.
В этой связи, изобретатели предлагаемой технологии проанализировали способ предотвращения того, чтобы информация, означающая то, что "доказывающий использовал s во время взаимодействия", была известна проверяющему, даже тогда, когда выполняется взаимодействие, принятое при проверке. Кроме того, изобретатели предлагаемой технологии разработали способ подтверждения того, что безопасность от активной атаки гарантирована, даже тогда, когда вышеописанный интерактивный протокол повторяющимся образом выполняется параллельно. Этот способ представляет собой способ обеспечения задания условия, при котором количество m многочленов f1, …, fm, используемых в качестве открытого ключа, задается имеющим значение, в достаточной мере более низкое, чем количество n переменных. Например, тип задаются таким образом, чтобы 2m-n<<1 (например, в случае, когда n=160, а m=80, 2-80<<1).
В вышеописанной схеме, в которой основой безопасности является трудность решения системы многопорядковых уравнений с многими переменными, трудно сгенерировать другой секретный ключ s2, соответствующий открытому ключу pk, даже в том случае, когда секретный ключ s1 и соответствующий ему открытый ключ pk заданы. По этой причине, в случае, когда гарантировано, что для открытого ключа pk существует два или больше секретных ключей s, имеется возможность предотвращения того, чтобы информация, означающая то, что "доказывающий использует s во время взаимодействия", не была известна проверяющему, даже тогда, когда выполняется взаимодействие, принятое при проверке. Другими словами, в случае, когда такая гарантия может быть дана, безопасность от активной атаки может быть гарантирована даже тогда, когда интерактивный протокол повторяющимся образом выполняется параллельно.
В случае, когда, со ссылкой на фиг. 40, рассматривается функция F: Kn->Km, сконфигурированная из m многопорядковых многочленов с n переменными (где n>m), количество элементов в области определения, не имеющих второго прообраза, составляет, самое большее,
. По этой причине, в случае, когда
задано достаточно малым, вероятность того, что будет выбран элемент в области определения, не имеющий второго прообраза, может быть сделана пренебрежимо малой. Другими словами, в случае, когда количество m многопорядковых многочленов f1, …, fm с n переменными задается имеющим значение, в достаточной мере более низкое чем количество n переменных, можно гарантировать то, что для открытого ключа pk существует два или более секретных ключа s. Следовательно, даже тогда, когда выполняется взаимодействие, принятое при проверке, имеется возможность предотвращения того, чтобы информация, означающая то, что "доказывающий использует s во время взаимодействия", была известна проверяющему, и безопасность от активной атаки гарантируется даже тогда, когда интерактивный протокол повторяющимся образом выполняется параллельно.
Как было описано выше, при этом задании условия для задания количества m многопорядковых многочленов f1, …, fm с n переменными имеющим значение, в достаточной мере более низкое, чем количество n переменных (где n>m и предпочтительно, чтобы 2m-n<<1), можно гарантировать безопасность в случае, когда интерактивный протокол повторяющимся образом выполняется параллельно.
3-4: Конкретный пример (в случае, когда используется многочлен второго порядка
Далее, со ссылкой на фиг. 20, будет описан пример, в котором в качестве многочлена F с многими переменными используется многочлен второго порядка с n переменными. Фиг. 20 представляет собой пояснительное схематическое изображение для описания конкретного примера предлагаемого способа.
Алгоритма Gen генерирования ключей
Алгоритм Gen генерирования ключей генерирует m многочленов f1(x1, …, xn), …, fm(x1, …, xn) второго порядка, определенных в кольце k, и вектор s=(s1, …, sn), который является элементом множества Kn. После этого, алгоритм Gen генерирования ключей вычисляет y=(y1, …, ym)<-(f1(s), …, fm(s)). Кроме того, алгоритм Gen генерирования ключей задает (f1, …, fm, y) в качестве открытого ключа pk и задает s в качестве секретного ключа. Далее, вектор (x1, …, xn) представлен обозначением x, а набор многочленов (f1(x), …, fm(x)) с второго порядка представлен обозначением F(х).
Алгоритм P доказывающего, алгоритм V проверяющего
Далее, со ссылкой на фиг. 20 будет описан процесс, выполняемый согласно алгоритму P доказывающего, и процесс, выполняемый согласно алгоритму V проверяющего, в ходе исполнения интерактивного протокола.
Операция #1:
Прежде всего, алгоритм P доказывающего произвольным образом выбирает некоторое число w. После этого, алгоритм P доказывающего применяет число w к генератору G псевдослучайных чисел и генерирует вектор r, который является элементом множества Kn, и набор многочленов
с многими переменными. Другими словами, алгоритм P доказывающего вычисляет (r, FA)<-G(w). После этого, алгоритм P доказывающего вычисляет z<-s-r. Это вычисление соответствует операции маскирования секретного ключа s с использованием вектора r. Здесь, многочлен
второго порядка выражен так, как в нижеприведенной формуле (18).
Математическое выражение 13
Операция #1 (продолжение):
После этого, алгоритм P доказывающего генерирует значение c1 хеш-функции для FA(z) и z. Другими словами, алгоритм P доказывающего вычисляет c1<-H1(FA(z), z). Кроме того, алгоритм P доказывающего генерирует значение с2 хеш-функции для числа w. Другими словами, алгоритм P доказывающего вычисляет c2<-Н2(w). H1(…) и Н2(…) представляют собой хеш-функции. Сообщение (c1, с2), сгенерированное в ходе операции #1, отправляется алгоритму V проверяющего.
Операция #2:
Алгоритм V проверяющего, который принял сообщение (c1, с2) выбирает случайным образом некоторое число а из q колец K и отправляет выбранное число а алгоритму P доказывающего.
Операция #3:
Алгоритм P доказывающего, который принял число а, вычисляет FB(x)<-αF(x+r)+FA(x). Это вычисление соответствует операции маскирования многочлена F(x+r) с многими переменными, для x, с использованием многочлена FA(x) с многими переменными. Многочлен FB с многими переменными, сгенерированный в ходе операции #3, отправляется алгоритму V проверяющего.
Операция #4:
Алгоритм V проверяющего, который принял многочлен FB с многими переменными, выбирает из числа двух моделей проверки модель проверки, подлежащую использованию. Например, алгоритм V проверяющего выбирает некоторое численное значение из числа двух численных значений {0, 1}, представляющих типы моделей проверки, и выбирает это выбираемое численное значение в запрос d Этот запрос d отправляется алгоритму P доказывающего.
Операция #5:
Алгоритм P доказывающего, который принял запрос d, генерирует ответ σ подлежащий отправке алгоритму V проверяющего в ответ на принятый запрос d. В случае, когда d=0, алгоритм P доказывающего генерирует ответ σ=w. В случае, при котором d=1, алгоритм P доказывающего генерирует ответ σ=z. Ответ σ, сгенерированный в ходе операции #5, отправляется алгоритму V проверяющего.
Операция #6:
Алгоритм V проверяющего, который принял ответ σ, выполняет, используя принятый ответ σ, нижеследующий процесс проверки.
В случае, когда d=0, алгоритм V проверяющего вычисляет (rA, FC)<-G(σ). После этого, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство c2=H2(σ). Кроме того, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство FB(x)=αF(x+rA)+FC(x). Алгоритм V проверяющего, в случае, когда эти проверки являются успешными, выдает на выходе значение 1, представляющее успешную аутентификацию, а в случае, когда эти проверки терпят неудачу, выдает на выходе значение 0, представляющее неудачную аутентификацию.
В случае, при котором d=1, алгоритм V проверяющего выполняет zA<-s. После этого, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство c1=H1(FB(zA)-αy, zA). Алгоритм V проверяющего, в случае, когда эта проверка является успешной, выдает на выходе значение 1, представляющее успешную аутентификацию, а в случае, когда эта проверка терпит неудачу, выдает на выходе значение 0, представляющее неудачную аутентификацию.
Выше был описан конкретный пример предлагаемого способа.
3-5: Эффективный алгоритм
Далее, будет описан способ упрощения алгоритма, соответствующего предлагаемому способу. Аналогично способу упрощения, описанному в первом варианте реализации изобретения, многочлен FA(x) с многими переменными, используемый для маскирования многочлена F(x+r) с многими переменными выражается как FA(x)=Fb(x, t)+e с использованием двух векторов: вектора t, который является элементом множества Kn, и вектора е, который является элементом множества Km. При использовании этого выражения, для многочлена F(x+r) с многими переменными получается соотношение, выражаемое нижеследующей формулой (19).
Математическое выражение 14
Таким образом, в случае, когда tA=αr+t и eA=αF(r)+e, маскированный многочлен FB(x)=αF(x+r)+FA(x) с многими переменными может быть выражен посредством двух векторов: вектора tA, который является элементом множества Kn, и вектора eA, который является элементом множества Km. По этой причине, при задании FA(x)=Fb(x, t), FA и FB могут быть выражены с использованием вектора, принадлежащего Kn, и вектора, принадлежащего Km, и, соответственно, размер данных, необходимых для связи можно значительно уменьшить. В частности, затраты связи можно уменьшить приблизительно в несколько тысяч или десятков тысяч раз.
Посредством этой модификацией, из F2 (или F1) ни в коей мере не происходит утечки информации, относящейся к r0. Например, даже в том случае, когда заданы еА и tA (или e и t), информация об r ни в коей мере не известна до тех пор, пока не известны е и t (или eA и tA). Соответственно, даже в том случае, когда выполняется эта модификация, нулевое знание гарантируется. Далее, со ссылкой на фиг. 21-27, будет описан эффективный алгоритм, относящийся к предлагаемому способу. Поскольку структура алгоритма Gen генерирования ключей не изменяется, то ее детализированное описание приведено не будет.
Пример 1 структуры эффективного алгоритма: фиг. 21
Прежде всего, будет описана структура эффективного алгоритма, проиллюстрированного на фиг. 21.
Операция #1:
Прежде всего, алгоритм P доказывающего произвольным образом выбирает некоторое число w. После этого, алгоритм P доказывающего применяет число w к генератору G псевдослучайных чисел и генерирует векторы r и t, которые являются элементами множества Kn, и вектор e, который является элементом множества Km. Другими словами, алгоритм P доказывающего вычисляет (r, t, e)<-G(w). После этого, алгоритм P доказывающего вычисляет z<-s-r. Это вычисление соответствует операции маскирования секретного ключа s с использованием вектора r.
Операция #1 (продолжение):
После этого, алгоритм P доказывающего генерирует значение c1 хеш-функции для Fb(z, t)+e и z. Другими словами, алгоритм P доказывающего вычисляет c1<-H1(Fb(z, t)+e, z). Кроме того, алгоритм P доказывающего генерирует значение с2 хеш-функции для числа w. Другими словами, алгоритм P доказывающего вычисляет c2<-Н2(w). H1(…) и Н2(…) представляют собой хеш-функции. Сообщение (c1, с2), сгенерированное в ходе операции #1, отправляется алгоритму V проверяющего.
Операция #2:
Алгоритм V проверяющего, который принял сообщение (c1, c2), выбирает случайным образом некоторое число а из q колец K, и отправляет выбранное число а алгоритму P доказывающего.
Операция #3:
Алгоритм P доказывающего, который принял число а, вычисляет tA<-αr+t. Кроме того, алгоритм P доказывающего вычисляет еА<-αF(r)+е. После этого, алгоритм P доказывающего отправляет tA и еА алгоритму V проверяющего.
Операция #4:
Алгоритм V проверяющего, который принял tA и еА, выбирает из двух моделей проверки модель проверки, подлежащую использованию. Например, алгоритм V проверяющего выбирает некоторое численное значение из числа двух численных значений {0, 1}, представляющих типы моделей проверки, и выбирает это выбираемое численное значение в запрос d Этот запрос d отправляется алгоритму P доказывающего.
Операция #5:
Алгоритм P доказывающего, который принял запрос d, генерирует ответ σ, подлежащий отправке алгоритму V проверяющего в ответ на принятый запрос d. В случае, когда d=0, алгоритм P доказывающего генерирует ответ σ=w. В случае, когда d=1, алгоритм P доказывающего генерирует ответ σ=z. Ответ σ, сгенерированный в ходе операции #5, отправляется алгоритму V проверяющего.
Операция #6:
Алгоритм V проверяющего, который принял ответ σ, выполняет, используя принятый ответ σ, нижеследующий процесс проверки.
В случае, когда d=0, алгоритм V проверяющего вычисляет (rA, tB, eB)<-G(σ). После этого, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство с2=Н2(σ). Кроме того, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство tA=αrA+tB. Кроме того, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство еА=αF(rA)+eB. Алгоритм V проверяющего, в случае, когда эти проверки являются успешными, выдает на выходе значение 1, представляющее успешную аутентификацию, а в случае, когда эти проверки терпят неудачу, выдает на выходе значение 0, представляющее неудачную аутентификацию.
В случае, когда d=1, алгоритм V проверяющего выполняет zA<-s. После этого, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство c1=H1(α(F(zA)-y)+Fb(zA, tA)+eA, zA). Алгоритм V проверяющего, в случае, когда эта проверка является успешной, выдает на выходе значение 1, представляющее успешную аутентификацию, а в случае, когда эта проверка терпит неудачу, выдает на выходе значение 0, представляющее неудачную аутентификацию.
Выше был описан пример (1) структуры эффективного алгоритма. При использовании этого эффективного алгоритма, размер данных, необходимых для передачи, может быть значительно уменьшен. Кроме того, поскольку нет необходимости вычислять F(x+r), то также повышается эффективность вычисления.
Пример 2 структуры эффективного алгоритма: фиг. 22
Далее, будет описана структура эффективного алгоритма, проиллюстрированного на фиг. 22. В случае, когда применяется структура, проиллюстрированная на фиг. 22, аналогично случаю, когда применяется структура, проиллюстрированная на фиг. 20, достигается тот эффект, что повышаются эффективность передачи информации и эффективность вычисления. Здесь, будет описано отличие от структуры, проиллюстрированной на фиг. 20.
В ходе операции #5 алгоритма, проиллюстрированного на фиг. 20, в случае, когда d=0, σ задается равным w, но в качестве σ, задаваемого в случае, когда d=0, может использоваться информация, которая может быть восстановлена по (r, t, e). Например, как проиллюстрировано на фиг. 22, в ходе операции #5, в качестве σ, задаваемого в случае, когда d=0, может быть использовано r. При этом, в случае, когда выполняется эта модификация, необходимо заменить вычисление с2<-Н2(w) в ходе операции #1 на с2<-Н2 (r, t, e). В частности, в ходе операции #6 в случае, когда d=0, содержание проверки, выполняемой согласно алгоритму V проверяющего, заменяется на проверку с2=Н2(r, tA-αr, еА-αF(r)).
Выше был описан пример 2 структуры эффективного алгоритма.
Пример 3 структуры эффективного алгоритма: фиг. 23
Далее, будет описана структура эффективного алгоритма, проиллюстрированного на фиг. 23. В случае, когда применяется структура, проиллюстрированная на фиг. 23, аналогично случаю, когда применяется структура, проиллюстрированная на фиг. 20, достигается тот эффект, что повышаются эффективность передачи информации и эффективность вычисления. Здесь, будет описано отличие от структуры, проиллюстрированной на фиг. 22.
В ходе операции #3 алгоритма, проиллюстрированного на фиг. 22, выполняется вычисление tA<-αr+t, но это вычисление может быть заменено на вычисление tA<-α(r+t), как это проиллюстрировано на фиг. 23. Например, как проиллюстрировано на фиг. 22, в ходе операции #5, r может быть использовано в качестве σ, задаваемого в случае, когда d=0. В случае, когда выполняется эта модификация, в ходе операции #6, когда d=0, содержание проверки, выполняемой согласно алгоритму V проверяющего, заменяется на проверку с2=Н2(r, α-1tA-r, еА-αF(r)).
Выше был описан пример 3 структуры эффективного алгоритма.
Пример 4 структуры эффективного алгоритма: фиг. 24
Далее, будет описана структура эффективного алгоритма, проиллюстрированного на фиг. 24. В случае, когда применяется структура, проиллюстрированная на фиг. 24, аналогично случаю, когда применяется структура, проиллюстрированная на фиг. 20, достигается тот эффект, что повышаются эффективность передачи информации и эффективность вычисления. Здесь, будет описано отличие от структуры, проиллюстрированной на фиг. 22.
В ходе операции #3 алгоритма, проиллюстрированного на фиг. 22, выполняется вычисление eA<-αF(r)+e, но это вычисление может быть заменено на вычисление еА<-α(F(r)+е), как это проиллюстрировано на фиг. 24. В случае, когда выполняется эта модификация, в ходе операции #6, когда d=0, содержание проверки, выполняемой согласно алгоритму V проверяющего, заменяется на проверку с2=Н2(e, tA-αr, еА-α-1eA-F(r)).
Выше был описан пример 4 структуры эффективного алгоритма.
Пример 5 структуры эффективного алгоритма: фиг. 25
Далее, будет описана структура эффективного алгоритма, проиллюстрированного на фиг. 25. В случае, когда применяется структура, проиллюстрированная на фиг. 25, аналогично случаю, когда применяется структура, проиллюстрированная на фиг. 20, достигается тот эффект, что повышаются эффективность передачи информации и эффективность вычисления. Здесь, будет описано отличие от структуры, проиллюстрированной на фиг. 22.
В ходе операции #5 алгоритма, проиллюстрированного на фиг. 22, в случае, когда d=0, σ задается равным r, но в качестве σ, задаваемого в случае, когда d=0, может использоваться информация, которая может быть восстановлена по (r, t, e) с использованием (tA, eB). Например, как проиллюстрировано на фиг. 25, в ходе операции #5, в качестве σ, задаваемого в случае, когда d=0, может быть использовано t. При этом, в случае, когда выполняется эта модификация, α, в ходе операции #2, выбирается из α, которое является элементом множества RK\{0}. В частности, в ходе операции #6 в случае, когда d=0, содержание проверки, выполняемой согласно алгоритму V проверяющего, заменяется на проверку с2=Н2(α-1(tA-1), t, еА-αF(α-1(tA-t))).
Структурный пример 5 из эффективного алгоритма был описан выше.
Пример 6 структуры эффективного алгоритма: фиг. 26
Далее, будет описана структура эффективного алгоритма, проиллюстрированного на фиг. 26. В случае, когда применяется структура, проиллюстрированная на фиг. 26, аналогично случаю, когда применяется структура, проиллюстрированная на фиг. 20, достигаются те эффекты, что повышаются эффективность передачи информации и эффективность вычисления. Здесь, будет описано отличие от структуры, проиллюстрированной на фиг. 25.
В ходе операции #3 алгоритма, проиллюстрированного на фиг. 25, выполняется вычисление tA<-αr+t, но это вычисление может быть заменено на вычисление tA<-α(r+t), как это проиллюстрировано на фиг. 26. В случае, когда выполняется эта модификация, в ходе операции #6, когда d=0, содержание проверки, выполняемой согласно алгоритму V проверяющего, заменяется на проверку с2=Н2(α-1tA-t, t, еА-αF(α-1tA-1)).
Выше был описан пример 6 структуры эффективного алгоритма.
Пример 7 структуры эффективного алгоритма: фиг. 27
Далее, будет описана структура эффективного алгоритма, проиллюстрированного на фиг. 27. В случае, когда применяется структура, проиллюстрированная на фиг. 27, аналогично случаю, когда применяется структура, проиллюстрированная на фиг. 20, достигается тот эффект, что повышаются эффективность передачи информации и эффективность вычисления. Здесь, будет описано отличие от структуры, проиллюстрированной на фиг. 25.
В ходе операции #3 алгоритма, проиллюстрированного на фиг. 25, выполняется вычисление eA<-αF(r)+е, но это вычисление может быть заменено на вычисление eA<-α(F(r)+е), как это проиллюстрировано на фиг. 27. В случае, когда выполняется эта модификация, в ходе операции #6, когда d=0, содержание проверки, выполняемой согласно алгоритму V проверяющего, заменяется на проверку с2=Н2(α-1(tA-t), t, α-1eA-αF(α-1(tA-t))).
Выше был описан пример 7 структуры эффективного алгоритма.
Преобразование эффективного алгоритма в параллельную форму: фиг. 29
Далее, со ссылкой на фиг. 29, будет описан способ преобразования эффективного алгоритма в параллельную форму. Структура (в дальнейшем именуемая как "алгоритм, преобразованный в параллельную форму"), проиллюстрированная на фиг. 29, представляет собой структуру, в которой в параллельную форму преобразован эффективный алгоритм, проиллюстрированный на фиг. 28. Эффективный алгоритм, проиллюстрированный на фиг. 28, имеет, по существу, ту же самую структуру, что и эффективный алгоритм, проиллюстрированный на фиг. 22. Описание будет продолжено с блок-схемой алгоритма, проиллюстрированной на фиг. 29.
Операция #1:
Алгоритм P доказывающего выполняет нижеследующие процессы: с (1) по (4), для i=1 по N.
Процесс (1): Алгоритм P доказывающего произвольным образом выбирает векторы ri, ti, которые являются элементами множества Kn, и вектор ei, который является элементом множества Km.
Процесс (2): Алгоритм P доказывающего вычисляет
. Это вычисление соответствует операции маскирования секретного ключа s с ипользованием вектора ri.
Процесс (3): Алгоритм P доказывающего вычисляет ci,1<-H1(ri,ti,ei).
Сообщение (c1,1, c2,1, …, c1,N, c2,N), сгенерированное в ходе операции #1, отправляется алгоритму V проверяющего.
Операция #2:
После приема сообщений (c1,1, с2,1, …, c1,N, с2,N), алгоритм V проверяющего выбирает случайным образом одно число αi из исходных данных для q колец K, для каждого из i=1 по N, и отправляет выбранное число αi алгоритму P доказывающего.
Операция #3:
После приема числа αi (i=1 по N), алгоритм P доказывающего вычисляет
для i=1 по N. В дополнение к этому, алгоритм P доказывающего вычисляет
для i=1 по N. После этого, алгоритм P доказывающего отправляет
и
алгоритму V проверяющего.
Операция #4:
После приема
и
, алгоритм V проверяющего выбирает то, какую модель проверки, из числа двух моделей проверки, использовать для i=1 по N. Например, алгоритм V проверяющего может выбрать некоторое численное значение из числа двух численных значений {0, 1}, представляющих модели проверки, и задать это выбранное численное значение в запросе di. Этот запрос d1 (i=1 по N) отправляются алгоритму P доказывающего.
Операция #5:
После приема запроса di (где i=1 по N), алгоритм P доказывающего генерирует ответ di для отправки алгоритму V проверяющего в ответ на принятый запрос di для i=1 по N. В случае, при котором di=0, алгоритм P доказывающего генерирует ответ σi=ri. В случае, при котором di=1, алгоритм P доказывающего генерирует ответ
. Ответ σi, сгенерированный в ходе операции #5, отправляется алгоритму V проверяющего.
Операция #4:
Алгоритм V проверяющего, который принял ответ σi (i=1 по N), выполняет, используя принятый ответ σi (i=1 по N), нижеследующий процесс проверки. Нижеследующий процесс выполняется для i=1 по N.
В случае, при котором di=0, алгоритм V проверяющего исполняет ri<-σi. После этого, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство
. Алгоритм V проверяющего, в случае, при котором все эти проверки являются успешными, выдает на выходе значение 1, указывающее на успешную аутентификацию, а в случае, при котором проверка терпит неудачу, выдает на выходе значение 0, указывающее на неудачную аутентификацию.
В случае, при котором di=1, алгоритм V проверяющего исполняет
. После этого, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство
. Алгоритм V проверяющего, в случае, при котором все эти проверки являются успешными, выдает на выходе значение 1, указывающее на успешную аутентификацию, а в случае, при котором проверка терпит неудачу, выдает на выходе значение 0, указывающее на неудачную аутентификацию.
Выше было описано преобразование эффективного алгоритма в параллельную форму.
Упрощение алгоритма, преобразованного в параллельную форму: фиг. 30 Преобразованный в параллельную форму алгоритм, проиллюстрированный на фиг. 29, может быть упрощен так, как это проиллюстрировано на фиг. 30. Как проиллюстрировано на фиг. 30, этот преобразованный в параллельную форму алгоритм сконфигурирован таким образом, чтобы преобразовывать сообщение (c1,1, c2,1, …, c1,N, c2,N) в значение с хеш-функции и отправлять значение с хеш-функции от алгоритма P доказывающего алгоритму V проверяющего при первой пересылке в ходе операции #1. Кроме того, этот преобразованный в параллельную форму алгоритм сконфигурирован таким образом, чтобы в ходе операции #5, в случае, когда di=0, генерировать ответ σi=(ri, c2,i), а в случае, когда di=1, генерировать ответ
. Кроме того, этот преобразованный в параллельную форму алгоритм сконфигурирован таким образом, чтобы в ходе операции #6 выполнять нижеследующий процесс.
Операция #6:
Прежде всего, алгоритм V проверяющего выполняет процессы (1) и (2) для i=1 по N. На практике, в случае, когда di=0, выполняется процесс (1), а в случае, когда di=1, выполняется процесс (2).
Процесс (1): В случае, когда di=0, алгоритм V проверяющего выполняет (ri, с2,i)<-σi. Кроме того, алгоритм V проверяющего вычисляет
. После этого, алгоритм V проверяющего сохраняет (с1,i, c2,i).
Процесс (2): В случае, когда di=1, алгоритм V проверяющего выполняет
. Кроме того, алгоритм V проверяющего вычисляет
. После этого, алгоритм V проверяющего сохраняет (c1,i, c2,i).
После того, как процессы (1) и (2) выполнены для i=1 по N, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство c=H(c1,1, c2,1, …, c1,N, c2,N). Алгоритм V проверяющего, в случае, когда эта проверка является успешной, выдает на выходе значение 1, представляющее успешную аутентификацию, а в случае, когда эта проверка терпит неудачу, выдает на выходе значение 0, представляющее неудачную аутентификацию.
Выше было описано упрощение алгоритма, преобразованного в параллельную форму.
Дополнительное упрощение алгоритма, преобразованного в параллельную форму: фиг. 31
Преобразованный в параллельную форму алгоритм, проиллюстрированный на фиг. 30, может быть дополнительно упрощен так, как это проиллюстрировано на фиг. 31. Как проиллюстрировано на фиг. 30, этот преобразованный в параллельную форму алгоритм сконфигурирован таким образом, чтобы преобразовывать сообщение
в значение V хеш-функции и отправлять значение V хеш-функции от алгоритма P доказывающего алгоритму V проверяющего при третьей пересылке в ходе операции #3. Кроме того, этот преобразованный в параллельную форму алгоритм сконфигурирован таким образом, чтобы в ходе операции #5, в случае, когда di=0, генерировать ответ σi=(ri, ti, ei, c2,i), а в случае, когда di=1, генерировать ответ
. Кроме того, этот преобразованный в параллельную форму алгоритм сконфигурирован таким образом, чтобы в ходе операции #6 выполнять нижеследующий процесс.
Операция #6:
Прежде всего, алгоритм V проверяющего выполняет процессы (1) и (2) для i=1 по N. На практике, в случае, когда di=0, выполняется процесс (1), а в случае, когда di=1, выполняется процесс (2).
Процесс (1): В случае, когда di=0, алгоритм V проверяющего выполняет (ri, ti, ei, c2,i)<-σi. После этого, алгоритм V проверяющего вычисляет c1,i=H1(ri, ti, ei). После этого, алгоритм V проверяющего сохраняет (с1,i, с2,i) и
.
Процесс (2): В случае, когда di=1, алгоритм V проверяющего выполняет
. После этого, алгоритм V проверяющего вычисляет
. После этого, алгоритм V проверяющего сохраняет (c1,i, c2,i) и (
,
).
После того, как процессы (1) и (2) выполнены для i=1 по N, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство с=H(c1,1, c2,1, …, c1,N, c2,N). Кроме того, алгоритм V проверяющего проверяет то, действительно ли соблюдается равенство
. Алгоритм V проверяющего, в случае, когда эти проверки являются успешными, выдает на выходе значение 1, представляющее успешную аутентификацию, а в случае, когда эти проверки терпят неудачу, выдает на выходе значение 0, представляющее неудачную аутентификацию.
Выше была описана структура дополнительного упрощения алгоритма, преобразованного в параллельную форму. Как было описано выше, поскольку множество порций информации, обмен которыми осуществляется между алгоритмом P доказывающего и алгоритмом V проверяющего, преобразуются в значение хеш-функции, то имеется возможность уменьшить размер передаваемых данных при третьей пересылке. Кроме того, поскольку структура алгоритма модифицирована таким образом, чтобы генерировать ri, ti и ei из единственного начального значения для случайных чисел в алгоритме, то ожидаемое значение размера передаваемых данных можно уменьшить. Кроме того, в случае, когда установлено такое ограничение, чтобы количество нулей, выбранных в качестве запроса di было равным количеству выбранных единиц, размер передаваемых данных наверняка уменьшится.
Например, в случае, когда (q, n, m, N) заданы как (24, 45, 30, 88), в алгоритме, проиллюстрированном на фиг. 30, открытый ключ занимает 120 битов, секретный ключ занимает 180 битов, и размер передаваемых данных составляет 42840 битов. Между тем, в алгоритме, проиллюстрированном на фиг. 31, в случае, когда (q, n, m, N) заданы как (24, 45, 30, 88), открытый ключ доступа занимает 120 битов, секретный ключ занимает 180 битов, а размер передаваемых данных составляет 27512 битов. Когда упрощение алгоритма, преобразованного в параллельную форму, дополнительно выполнено так, как это было описано выше, имеется возможность замечательным образом уменьшить размер передаваемых данных.
3-6: Последовательно-параллельный гибридный алгоритм
Для того чтобы сделать вероятность успешной подделки пренебрежимо малой, необходимо, чтобы интерактивный протокол, как было описано выше, выполнялся множество раз. Кроме того, в качестве способов выполнения интерактивного протокола множество раз, были представлены последовательный способ и параллельный способ. В частности, параллельный способ был описан в связи с конкретным преобразованным в параллельную форму алгоритмом. Далее, будет представлен алгоритм гибридного типа, в котором последовательный способ объединен с параллельным способом.
Гибридная структура 1
Алгоритм гибридного типа (в дальнейшем именуемый как "параллельно-последовательный алгоритм") будет описан со ссылкой на фиг. 32. На фиг. 32 проиллюстрирована базовая структура, относящаяся к предлагаемому способу, преобразованный в последовательную форму алгоритм, в котором эта базовая структура преобразована в последовательную форму, преобразованный в параллельную форму алгоритм, в котором эта базовая структура преобразована в параллельную форму, и параллельно-последовательный алгоритм.
В базовой структуре, при первой пересылке, от доказывающего проверяющему отправляется сообщение (с1, с2). При второй пересылке, от проверяющего доказывающему отправляется число α. При третьей пересылке, от доказывающего проверяющему отправляются векторы tA и еА. При четвертой пересылке, от проверяющего доказывающему отправляется запрос d. При пятой пересылке, от доказывающего проверяющему отправляется ответ σ.
В случае, когда базовая структура преобразована в параллельную форму, при первой пересылке, от доказывающего проверяющему отправляются сообщения (c1,1, c2,1, …, c1,N, c2,N) для N раз. При второй пересылке, от проверяющего доказывающему отправляются числа (α1, …, αN) для N раз. При третьей пересылке, от доказывающего проверяющему отправляются векторы
для N раз. При четвертой пересылке, от проверяющего доказывающему отправляются запросы (d1, …, dn) для N раз. При пятой пересылке, от доказывающего проверяющему отправляются ответы (σ1, …, σN) для N раз.
Преобразованный в параллельную форму алгоритм, относящийся к предлагаемому способу, гарантирует безопасность от пассивной атаки. Кроме того, количество взаимодействий составляет просто пять раз. Кроме того, поскольку сообщения для N раз, отправляемые при первой пересылке, или векторы для N раз, отправляемые при третьей пересылке, преобразовываются в одно значение хеш-функции, то эффективность передачи информации может быть повышена.
Между тем, в случае, когда базовая структура преобразована в последовательную форму, при первой пересылке, от доказывающего проверяющему отправляется сообщение (c1,1, c2,1) для одного раза. При второй пересылке, от проверяющего доказывающему отправляется число α1 для одного раза. При третьей пересылке, от доказывающего проверяющему отправляется вектор (
,
) для одного раза. При четвертой пересылке, от проверяющего доказывающему отправляется запрос d1 для одного раза. При пятой пересылке, от доказывающего проверяющему отправляется ответ σ1 для одного раза. Аналогичным образом, взаимодействие выполняется повторяющимся образом до тех пор, пока от доказывающего проверяющему не будет отправлен ответ σN. Преобразованный в последовательную форму алгоритм гарантирует безопасность от активной атаки. Кроме того, можно доказать, что возможность ложной проверки наверняка уменьшается.
Параллельно-последовательный алгоритм представляет собой алгоритм, имеющий как характеристики алгоритма, преобразованного в параллельную форму, так и характеристики алгоритма, преобразованного в последовательную форму. В параллельно-последовательном алгоритме, проиллюстрированном на фиг. 32, при первой пересылке, от доказывающего проверяющему отправляются сообщения (c1,1, c2,1, …, c1,N, c2,N) для N раз. При второй пересылке, от проверяющего доказывающему отправляется число он для одного раза. При третьей пересылке, от доказывающего проверяющему отправляется вектор (
,
) для одного раза. При четвертой пересылке, от проверяющего доказывающему отправляется запрос d1 для одного раза. При пятой пересылке, от доказывающего проверяющему отправляется ответ σ1 для одного раза. После этого, между доказывающим и проверяющим осуществляется обмен данными: α2, …, αN,
,
, …,
,
, d2, …, dN, и σ2, …, σN.
Параллельно-последовательный алгоритм, основанный на предлагаемом способе, гарантирует безопасность от пассивной атаки. Кроме того, количество взаимодействий составляет просто 4N+1. Кроме того, в случае, когда сообщения для N раз, отправляемые при первой пересылке, собираются одним значением хеш-функции, эффективность передачи информации может быть повышена.
Гибридная структура 2
Другой параллельно-последовательный алгоритм будет описан со ссылкой на фиг. 33. На фиг. 32 проиллюстрирована базовая структура, относящаяся к предлагаемому способу, преобразованный в последовательную форму алгоритм, в котором эта базовая структура преобразована в последовательную форму, преобразованный в параллельную форму алгоритм, в котором эта базовая структура преобразована в параллельную форму, и параллельно-последовательный алгоритм. Структура и характеристики базовой структуры, алгоритма, преобразованного в последовательную форму, и алгоритма преобразованного в параллельную форму, являются одинаковыми с теми, которые описаны выше.
Параллельно-последовательный алгоритм, проиллюстрированный на фиг. 33, представляет собой алгоритм, имеющий как характеристики алгоритма, преобразованного в параллельную форму, так и характеристики алгоритма, преобразованного в последовательную форму. В этом параллельно - последовательном алгоритме, при первой пересылке, от доказывающего проверяющему отправляются сообщения (c1,1, c2,1, …, c1,N, c2,N) для N раз. При второй пересылке, от проверяющего доказывающему отправляются числа (α1, …, αN) для N раз. При третьей пересылке, от доказывающего проверяющему отправляются векторы (
,
, …,
,
) для N раз. При четвертой пересылке, от проверяющего доказывающему отправляется запрос d1 для одного раза. При пятой пересылке, от доказывающего проверяющему отправляется ответ σ1 для одного раза. После этого, между доказывающим и проверяющим осуществляется обмен данными: d2, …, dN, и σ2, …, σN.
Параллельно-последовательный алгоритм, основанный на предлагаемом способе, гарантирует безопасность от пассивной атаки. Кроме того, количество взаимодействий составляет просто 3N+3. Кроме того, поскольку сообщения для N раз, подлежащие отправке при первой пересылке, преобразуются в одно значение хеш-функции, эффективность передачи информации может быть повышена.
Гибридная структура 3
Другой алгоритм гибридного типа (в дальнейшем именуемый как "последовательно-параллельный алгоритм") будет описан со ссылкой на фиг. 34. На фиг. 34 проиллюстрирована базовая структура, относящаяся к предлагаемому способу, преобразованный в последовательную форму алгоритм, в котором эта базовая структура преобразована в последовательную форму, преобразованный в параллельную форму алгоритм, в котором эта базовая структура преобразована в параллельную форму, и последовательно-параллельный алгоритм. Структуры и характеристики базовой структуры, алгоритма преобразованного в последовательную форму, и алгоритма, преобразованного в параллельную форму, являются одинаковыми с теми, которые описаны выше.
Последовательно-параллельный алгоритм, проиллюстрированный на фиг. 34, представляет собой алгоритм, имеющий как характеристики алгоритма, преобразованного в параллельную форму, так и характеристики алгоритма, преобразованного в последовательную форму. В этом последовательно-параллельном алгоритме, при первой пересылке, от доказывающего проверяющему отправляются сообщения (c1,1, c2,1) для одного раза. При второй пересылке, от проверяющего доказывающему отправляется число α1 для одного раза. При третьей пересылке, от доказывающего проверяющему отправляется вектор (
,
) для одного раза. При четвертой пересылке, от проверяющего доказывающему отправляется запрос d1 для (одного раза). После этого, между доказывающим и проверяющим осуществляется обмен данными: c1,2, c2,2, …, c1,N, c2,N, α2, …, αN,
,
, …,
,
, и d2, …, dN. В конце концов, от доказывающего проверяющему отправляются ответы (σ1, …, σN).
Последовательно-параллельный алгоритм, основанный на предлагаемой технологии, гарантирует безопасность от активной атаки. Кроме того, количество взаимодействий составляет просто 4N+1 раз.
Гибридная структура 4
Другой последовательно-параллельный алгоритм будет описан со ссылкой на фиг. 35. На фиг. 35 проиллюстрирована базовая структура, относящаяся к предлагаемому способу, преобразованный в последовательную форму алгоритм, в котором эта базовая структура преобразована в последовательную форму, преобразованный в параллельную форму алгоритм, в котором эта базовая структура преобразована в параллельную форму, и последовательно-параллельный алгоритм. Структуры и характеристики базовой структуры, алгоритма преобразованного в последовательную форму, и алгоритма, преобразованного в параллельную форму, являются одинаковыми с теми, которые описаны выше.
Последовательно-параллельный алгоритм, проиллюстрированный на фиг. 35, представляет собой алгоритм, имеющий как характеристики алгоритма, преобразованного в параллельную форму, так и характеристики алгоритма, преобразованного в последовательную форму. В этом последовательно - параллельном алгоритме, при первой пересылке, от доказывающего проверяющему отправляются сообщения (c1,1, c2,1) для одного раза. При второй пересылке, от проверяющего доказывающему отправляется число α1 для одного раза. После этого, между доказывающим и проверяющим осуществляется обмен данными: c1,2, c2,2, …, c1,N, c2,N и α2, …, αN. После передачи αN от доказывающего проверяющему отправляются векторы (
,
, …,
,
) для N раз. Далее, от проверяющего доказывающему отправляются запросы (d1, …, d1) для N раз. В конце концов, от доказывающего проверяющему отправляются ответы (σ1, …, σN).
Последовательно-параллельный алгоритм, основанный на предлагаемом способе, гарантирует безопасность от пассивной атаки. Кроме того, количество взаимодействий составляет просто 2N+3 раз.
Выше был описан алгоритм гибридного типа, основанный на предлагаемом способе.
Выше был описан второй вариант реализации предлагаемой технологии. Форма многомерной системы уравнений с многими переменными является той же самой, что и в первом варианте ее реализации.
4: Расширение эффективного алгоритма
Между тем, эффективные алгоритмы, соответствующие первому и второму вариантам реализации изобретения, имеют структуру, при которой в качестве открытого ключа (или параметра системы) используется многочлен с многими переменными, имеющий второй порядок, выраженный нижеследующей Формулой (20). Однако, эти эффективные алгоритмы могут быть расширены таким образом, чтобы иметь структуру, при которой в качестве открытого ключа (или параметра системы) используется многочлен с многими переменными, имеющий третий или более высокий порядок.
4-1: Многочлен с многими переменными, имеющий высокий порядок
Например, рассмотрим структуру, при которой в качестве открытого ключа (или параметра системы) используется многочлен с многими переменными, имеющий третий или более высокий порядок (смотри, нижеследующую Формулу (21)), и определенный на поле с порядком q=pk.
Математическое выражение 15
В эффективных алгоритмах, соответствующих первому и второму вариантам реализации изобретения, многочлен f1 с многими переменными применим в качестве открытого ключа в случае, когда нижеследующая Формула (22) является билинейной для (x1, …, xn) и (y1, …, yn). В многочлене с многими переменными, выраженном Формулой (20), билинейность может быть легко обнаружена (подчеркнутые части являются линейными по каждому из xi и yi, согласно тому, что выражено в нижеследующей Формуле (23). Кроме того, в многочлене с многими переменными, выраженном Формулой (21), билинейность может быть аналогичным образом обнаружена, согласно тому, что выражено в нижеследующей Формуле (24). Подчеркнутая часть в нижеследующей Формуле (24) представляет билинейность в поле GFP порядка р. Таким образом, в случае, когда многочлене с многими переменными, выраженный Формулой (21), используется в качестве открытого ключа эффективного алгоритма, соответствующего второму варианту реализации изобретения, число α, подлежащее отправке проверяющему после операции #2 этого алгоритма, должно быть ограничено элементом GFP.
Математическое выражение 16
По вышеупомянутой причине, имеется возможность составить алгоритм, в котором в качестве открытого ключа используется многочлен с многими переменными, имеющий третий или более высокий порядок, и выраженный Формулой (21), расширив эффективные алгоритмы, соответствующие первому и второму вариантам реализации изобретения.
Далее, дадим обзор соотношения между многочленом с многими переменными, выраженным Формулой (20), (в дальнейшем, именуемым как "многочлен второго порядка") и многочленом с многими переменными, выраженным Формулой (20), (в дальнейшем именуемым как "многопорядковый многочлен"). При этом, рассматриваются многочлен второго порядка с nk переменными, определенный на поле порядка q=р и многопорядковый многочлен с n переменными, определенный на поле порядка q=pk. В этом случае, трудность решения системы уравнений, сконфигурированной из mk многочленов второго порядка, эквивалентна трудности решения системы уравнений, сконфигурированной из m многопорядковых многочленов. Например, система уравнений, сконфигурированная из 80 многочленов второго порядка, имеющих 80 переменных, определенных на поле порядка 2, является эквивалентной по трудности решения 10 многопорядковым многочленам с 10 переменными, определенным на поле порядка 28.
Другими словами, в случае, когда элемент поля GFpk и элемент поля GFPk рассматриваются при изоморфном отображении как одинаковые, существует функция, выраженная m наборами многопорядковых многочленов, имеющих n - переменных, определенными на поле порядка q=pk, которая эквивалентна функции, выраженной mk наборами многочленов второго порядка, имеющих nk переменными, определенными на поле порядка q=р. Например, в случае, когда элемент поля GF(28) и элемент поля GF(2)8 рассматриваются при изоморфном отображении как одинаковые, существует функция, выраженная 10 наборами многопорядковых многочленов, имеющих 10 переменных, определенными на поле порядка 28, которая эквивалентна функции, выраженной 80 наборами многочленов второго порядка, имеющих 80 переменных, определенными на поле порядка 2. Таким образом, имеется возможность произвольным образом выбирать то, использовать ли многочлен второго порядка или многопорядковый многочлен.
Теперь, дадим обзор эффективности вычисления в случае, когда используется многочлен второго порядка по сравнению с эффективностью вычисления в случае, когда используется многопорядковый многочлен.
В случае, когда используется многочлен второго порядка, имеющий nk переменных, определенный на поле порядка 2, операция, входящая в состав этого алгоритма, выполняется над nk 1 - битовыми переменными. Другими словами, операционной единицей является 1 бит. Между тем, в случае, когда (используется) многопорядковый многочлен с n - переменными, определенный на поле порядка 2k, операция, входящая в состав этого алгоритма, выполняется над nk - битовыми переменными. Другими словами, операционной единицей является к битов, k (k=2, 3, 4, …) может быть задано произвольным образом. Таким образом, при реализации алгоритма, задавая к надлежащее значение, можно повысить эффективность вычисления. Например, в случае, когда алгоритм реализуется на 32 - разрядной архитектуре, структура алгоритма, при которой операция выполняется в единицах, состоящих из 32 битов, имеет более высокую эффективность вычисления, чем структура, при которой операция выполняется в единицах, состоящих из одного бита.
При расширении эффективных алгоритмов, соответствующих первому и второму вариантам реализации изобретения, таким образом, чтобы в качестве открытого ключа мог быть использован многопорядковый многочлен, как описано выше, имеется возможность настраивать операционную единицу в соответствии с архитектурой, на которой это реализуется. В результате эффективность вычисления может быть повышена.
4-2: Схема расширения (добавление члена высокого порядка)
Между тем, в качестве способа использования многопорядкового многочлена, имеющего третий или более высокий порядок, рассматривается также способ добавления члена третьего или более высокого порядка к многочлену второго порядка. Например, согласно тому, что выражено в нижеследующей Формуле (25), рассматривается способ добавления члена четвертого порядка к многочлену второго порядка, выраженному Формулой (20). Когда многопорядковый многочлен f1 определен так, как в нижеследующей Формуле (25), член g1 (x, y), определенный нижеследующей Формулой (26), выражается так, как в нижеследующей Формуле (27). Далее, член g1 (x, y) упоминается как "полярная форма".
Математическое выражение 17
Как выражено в Формуле (27), член g1 (x, y) не является билинейным. В связи с этим, 6 членов xixj, имеющих две переменные из числа четырех переменных x1, x2, x3 и x4, и 3 члена xixjxk, имеющих три переменные из числа четырех переменных x1, x2, x3 и x4, выражаются посредством четырех переменных: tij,
, tijk и
, так, как в нижеследующих Формулах (28) и (29). В случае, когда используется это выражение, эффективный алгоритм может быть реализован с использованием многочлена с многими переменными, имеющего третий или более высокий порядок. В примере, выраженном в Формуле (25), к многочлену второго порядка добавляется член четвертого порядка, но вместо члена четвертого порядка может быть добавлен член третьего порядка (например, x1x2x3) или пятого или более высокого порядка (например, x1x2x3x4x5). Добавляя член третьего или более высокого порядка, можно повысить надежность уравнения.
Математическое выражение 18
5: Механизм для повышения надежности
Далее, будет представлен механизм для дополнительного повышения надежности алгоритмов, соответствующих первому и второму вариантам реализации изобретения.
5-1: Способ задания параметров системы
Выше не было описано то, каким образом задавать коэффициенты многочленов с многими переменными и начальное значение для случайных чисел, используемое для генерирования этих коэффициентов, (в дальнейшем, именуемые как коэффициенты и тому подобное для многочленов с многими переменивши). Коэффициенты и тому подобное для многочленов с многими переменными могут быть параметрами, общими для системы, или могут быть параметрами, различающимися для каждого пользователя.
Однако, в случае, когда коэффициенты и тому подобное для многочленов с многими переменными задаются как параметры, общие для системы, может быть необходимо обновлять настроечные параметры всей системы, если обнаружена слабость этих многочленов с многими переменными. Кроме того, для многочленов с многими переменными, имеющими случайно выбираемые коэффициенты, анализируется средняя надежность (трудность решения), но трудно гарантировать достаточную надежность для многочленов с многими переменными, имеющих некоторые конкретные коэффициенты.
Соответственно, изобретатели предлагаемой технологии разработали структуру, в которой коэффициенты многочленов с многими переменными генерируются путем использования строки символов или тому подобного, выбираемой каждым пользователем в качестве начального значения для генератора псевдослучайного чисел и генерирования коэффициентов этих многочленов с многими переменными. Например, потенциально возможные способы включают в себя способ использования, в этом начальном значении, адреса электронной почты пользователя и способ использования, в этом начальном значении, строки символов, в которой объединены адрес электронной почты, дата обновления и тому подобное. В случае, когда используются такие способы, даже если обнаружена слабость многочленов с многими переменными, имеющих коэффициенты, сгенерированные из данной строки символов, то влияние (этой слабости) ограничено только пользователем, использующим эти многочлены с многими переменными, имеющие эти коэффициенты. Кроме того, поскольку эти многочлены с многими переменными изменяются просто путем изменения строки символов, слабость может легко быть устранена.
Выше был описан способ задания параметров системы. В вышеприведенном описании, в качестве примера была приведена строка символов, но для каждого пользователя может использоваться различная последовательность чисел или различная последовательность знаков.
5-2: Способ реагирования на неправильный запрос
Далее будет описан способ реагирования на неправильный запрос.
5-2-1: Способ реагирования доказывающего
Как проиллюстрировано на фиг. 36, существует возможность того, что проверяющий во время исполнения интерактивного протокола подаст ложный запрос. В примере, показанном на фиг. 36, доказьшающий отправляет проверяющему сообщение (c1, с2, с3), проверяющий отправляет доказывающему запрос d=0, и после этого от доказывающего проверяющему отправляется ответ σ, соответствующий запросу d=0. Этот процесс является нормальным взаимодействием.
Однако, в примере, показанном на фиг. 36, проверяющий далее требует, чтобы доказывающий отправило ответ σ, соответствующий запросу d=1. Если доказывающий в ответ на это требование отправляет проверяющему ответ а, соответствующий запросу d=1, то секретный ключ разглашается проверяющему. На практике вероятно разглашение секретного ключа. Например, проверяющий может сделать вид, что при второй пересылке, вместо запроса d=1 был отправлен запрос d=0, и может дополнительно запросить ответ Rsp, отвечающий на запрос d=1. С другой стороны, доказывающий может неправильно понять, что биты запроса d, отправленного при второй пересылке, превратились в другие биты вследствие ошибки при передаче данных.
В связи с этим, изобретатели предлагаемой технологии разработали способ, как избежать этого разглашения секретного ключа. В частности, изобретатели предлагаемой технологии разработали способ, заключающийся в том, что в случае, когда доказывающий запрашивает ответы, соответствующие двум или более запросам d по единственному сообщению, принимается решение о том, должно ли взаимодействие быть прекращено или оно должно быть возобновлено с первой перехода с использованием нового случайного числа. В случае, когда применяется этот способ, секретный ключ не разглашается, даже тогда, когда проверяющий ложно запрашивает ответы, соответствующие двум или более запросам d.
Был описан способ предотвращения разглашения секретного ключа при неправильном запросе. При этом, в качестве примера была описана базовая структура с 3 переходами, но тот же самый способ может быть применен к последовательному способу, параллельному способу или алгоритму гибридного типа, и в этом случае, безопасность может быть повышена. Конечно, этот способ аналогичным образом применяется даже к алгоритму с 5 переходами.
5-2-2: Способ реагирования проверяющего
Кроме того, как проиллюстрировано на фиг. 37, доказывающий может ложно запросить повторную передачу запроса d. В примере, показанном на фиг. 37, доказывающий отправляет проверяющему сообщение (c1, c2, c3), проверяющий отправляет доказывающему запрос d=0, и после этого доказывающий требует повторную передачу запроса d. В ответ на это требование, когда проверяющий вновь случайным образом выбирает запрос d, возможно, будет выбран запрос d=1 отличный от запроса d=0, который был отправлен. В этом случае, от проверяющего доказывающему отправляется запрос d=1. В примере, показанном на фиг. 37, доказывающий отправляет проверяющему ответ σ, соответствующий запросу d=1.
Однако, существует возможность того, что это доказывающий в состоянии ответить на запрос d=1, но не на запросу d=0. Другими словами, трудно исключить риск совершения доказывающим подделки. Например, доказывающий может потребовать, чтобы проверяющий повторно передал запрос d, поскольку запрос d был утерян. Однако, проверяющий может подумать, что отправленный перед этим запрос был потерян вследствие ошибки при передаче данных и повторно передать запрос d в ответ на требование доказывающего. После этого, в случае, когда повторно переданный запрос d отличается от запроса d, переданного перед этим, подделка является успешной.
Как можно понять из примера, показанного на фиг. 37, в случае, когда этот запрос d выбирается случайным образом, доказывающий подвергается риску подделки. В связи с этим, изобретатели предлагаемой технологии разработали способ предотвращения риска подделки. В этом способе, интерактивный протокол усовершенствован таким образом, чтобы в случае, когда доказывающий требует повторную передачу запроса d по единственному сообщению, проверяющий прекращает взаимодействие или снова посылает тот же самый запрос d, что и предшествующий запрос, не генерируя новое случайное число. В случае, когда применяется этот способ, имеется возможность предотвратить риск подделки, использующей требование повторной передачи запроса d.
Выше был описан способ предотвращения успешной подделки при неправильном запросе. При этом, в качестве примера была описана базовая структура с 3 переходами, но тот же самый способ может быть применен к последовательному способу, параллельному способу или алгоритму гибридного типа, и в этом случае, безопасность может быть повышена. Этот способ аналогичным образом применяется к алгоритму с 5 переходами.
6: Конфигурация аппаратных средств
Каждый алгоритм, описанный выше, может быть выполнен с использованием, например, конфигурации аппаратных средств устройства обработки информации, показанного на фиг. 38. Таким образом, обработка данных согласно каждому алгоритму может быть реализована путем управления аппаратными средствами, показанными на фиг. 38, с использованием компьютерной программы. В дополнение к этому, тип этих аппаратных средств является произвольным, и может представлять собой персональный компьютер, мобильное информационное оконечное устройство, такое как мобильный телефон, PHS или PDA, игровой машины, контактной или бесконтактной интегральной микросхемы, контактной или бесконтактной карты с интегральной схемой, или различные типы информационных бытовых приборов. Помимо этого, PHS представляет собой сокращение для персональной портативной телефонной системы. Кроме того, PDA представляет собой сокращение для персонального цифрового секретаря.
Как показано на фиг. 38, эти аппаратные средства главным образом включают: в себя центральный процессор (CPU) 902, постоянное запоминающее устройство (ROM) 904, оперативное запоминающее устройство (RAM) 906, шину 908 центрального процессора и мост 910. Кроме того, эти аппаратные средства включают в себя внешнюю шину 912, интерфейс 914, модуль 916 ввода, модуль 918 вывода, запоминающий модуль 920, привод 922, соединительный порт 924 и модуль 926 связи. Помимо этого, CPU - сокращение для центрального процессора. Кроме того, ROM представляет собой сокращение для постоянного запоминающего устройства. Кроме того, RAM представляет собой сокращение для оперативного запоминающее устройства.
Центральный процессор 902, например, функционирует как арифметический процессор или управляющий модуль и управляет всей работой или частью работы каждого структурного элемента, основываясь на различных программах, записанных в постоянном запоминающем устройстве 904, оперативном запоминающем устройстве 906, запоминающем модуле 920 или на съемном носителе 928 записи. Постоянное запоминающее устройство 904 представляет собой средство для хранения, например, программы, подлежащей загрузке в центральный процессор 902, или данных или тому подобного, используемых в арифметической операции. Оперативное запоминающее устройство 906 временно или постоянно хранит, например, программу, подлежащую загрузке в центральный процессор 902, или различные параметры или тому подобное, произвольным образом изменяющиеся в ходе исполнения программы.
Эти структурные элементы соединены друг с другом посредством, например, шины 908 центрального процессора, способной выполнять высокоскоростную передачу данных. Для ее части, шина 908 центрального процессора соединена через мост 910 с внешней шиной 912, у которой, например, скорость передачи данных является относительно низкой. Помимо этого, модуль 916 ввода представляет собой, например, "мышь", клавиатуру, сенсорную панель, кнопку, переключатель или рычаг. Кроме того, модуль 916 ввода может представлять собой пульт дистанционного управления, который может передавать управляющий сигнал с использованием инфракрасного луча или других радиоволн, (в дальнейшем, именуемый как пульт дистанционного управления).
Модуль 918 вывода представляет собой, например, устройство отображения, такое как электронно-лучевая трубка (CRT), жидкокристаллический дисплей (LCD), плазменная панель отображения (PDP) или электролюминесцентный дисплей (ELD), устройство вывода звука, такое как громкоговоритель или головные телефоны, принтер, мобильный телефон, или факсимильный аппарат, которые могут визуально или в звуковой форме сообщать пользователю полученную информацию. Помимо этого, CRT представляет собой сокращение для электронно-лучевой трубки. LCD представляет собой сокращение для жидкокристаллического дисплея. PDP представляет собой сокращение для плазменной панели отображения. Кроме того, ELD представляет собой сокращение для электролюминесцентного дисплея.
Запоминающий модуль 920 представляет собой устройство для хранения различных данных. Запоминающий модуль 920 представляет собой, например, магнитное запоминающее устройство, такое как накопитель на жестком магнитном диске (HDD), полупроводниковое запоминающее устройство, оптическое запоминающее устройство или магнитооптическое запоминающее устройство. HDD представляет собой сокращение для накопителя на жестком магнитном диске.
Привод 922 представляет собой устройство, которое считывает информацию, записанную на съемном носителе 928 записи, таком как магнитный диск, оптический диск, магнитооптический диск, или полупроводниковое запоминающее устройство, или записывает информацию на съемный носитель 928 записи. Съемный носитель 928 записи представляет собой, например, носитель на DVD (цифровом универсальном диске), носитель "Blu-ray", носитель на HD-DVD, различные типы носителей на полупроводниковых запоминающего устройствах или тому подобное. Конечно, съемный носитель 928 записи может представлять собой, например, электронное устройство или карту с интегральной схемой (1С), на которой установлена бесконтактная интегральная микросхема. 1С представляет собой сокращение для интегральной схемы.
Соединительный порт 924 представляет собой такой порт, как порт USB, порт ШЕЕ 1394 (стандарта 1394 Института инженеров по электротехнике и электронике (США)), SCSI, порт RS - 232 С (Рекомендованного стандарта 232 С), или порт для подсоединения подсоединяемого извне устройства 930, такого как оптический акустический терминал. Подсоединяемое извне устройство 930 представляет собой, например, принтер, мобильный музыкальный проигрыватель, цифровую фотокамеру, цифровую видеокамеру или записывающее устройство на интегральной схеме. Помимо этого, USB представляет собой сокращение для универсальной последовательной шины. Кроме того, SCSI представляет собой сокращение для интерфейса малых компьютерных систем.
Модуль 926 связи является устройством связи, соединяемым с сетью 932, и представляет собой, например, плату связи для проводной или беспроводной локальной сети (LAN), Bluetooth (зарегистрированный товарный знак) или WUSB, маршрутизатор системы оптической связи, маршрутизатор ADSL или устройство для контактной или бесконтактной связи. Сеть 932, соединенная с модулем 926 связи состоит из сети, соединенной посредством проводов или беспроводным образом, и представляет собой, например, сеть "Интернет", локальную сеть бытового применения, оптическую связь в инфракрасной части спектра, оптическую связь в видимой части спектра, радиовещание или спутниковую связь. Помимо этого, LAN представляет собой сокращение для локальной сети. Кроме того, WUSB представляет собой сокращение для беспроводной USB (универсальной последовательной шины). Кроме того, ADSL представляет собой сокращение для асимметричной цифровой абонентской линии.
7: Резюме
В заключение, будет кратко описано техническое содержание, соответствующее варианту реализации предлагаемой технологии. Сформулированное здесь техническое содержание может быть применено к различным устройствам обработки информации, таким как персональный компьютер, мобильный телефон, игровая машина, информационное оконечное устройство, информационный бытовой прибор, автомобильная навигационная система и тому подобное. Кроме того, функция устройства обработки информации, описываемого ниже, может быть реализована с использованием одного устройства обработки информации или с использованием множества устройств обработки информации. Помимо этого, средства хранения данных и средства арифметической обработки данных, которые используются для выполнения процесса устройством обработки информации, описываемым ниже, могут быть установлены на этом устройстве обработки информации или могут быть установлены на устройстве, соединенном с ним через сеть.
Элементы устройства обработки информации реализованы следующим образом. Например, аппарат обработки информации, описанный в нижеследующем пункте (1), может показать проверяющему, что знает о секретном ключе s, не разглашая ни в коей мере информацию о секретном ключе s проверяющему, посредством выполнения интерактивного протокола с проверяющим, использующего в качестве открытого ключа набор F многопорядковых многочленов с многими переменными. Другими словами, устройство обработки информации, описываемое в нижеследующем пункте (1), имеет аутентификационную функцию, относящуюся к схеме аутентификации с открытым ключом, в которой безопасность основывается на трудности решения системы многопорядковых уравнений с многими переменными. Кроме того, устройство обработки информации, описываемое в нижеследующем пункте (1), перед отправкой преобразует сообщение, подлежащее отправке проверяющему при первой пересылке, и третью информацию, подлежащую отправке проверяющему при третьей пересылке, в значение хеш-функции. Таким образом, размер передаваемых данных значительно уменьшается, и эффективность передачи информации повышается.
(1) Устройство обработки информации, содержащее:
модуль генерирования сообщений для генерирования сообщения N раз (где N≥2), основываясь на наборе F=(f1, …, fm) многопорядковых многочленов с многими переменными, определенном на кольце K, и векторе s, являющемся элементом множества Kn, и вычисления первого значения хеш-функции, основанного на указанных сообщениях N раз;
модуль предоставления сообщений для предоставления проверяющему, хранящему указанный набор F многопорядковых многочленов с многими переменивши и вектор y=(y1, …, ym)=(f1(s), …, fm(s)), первого значения хеш-функции;
модуль генерирования промежуточной информации для генерирования третьей информации N раз, с использованием первой информации, произвольно выбранной проверяющим по соответствующим сообщениям N раз, и второй информации N раз, полученной при генерировании указанных сообщений, и генерирования второго значения хеш-функции, на основании третьей информации N раз;
модуль предоставления промежуточной информации для предоставления проверяющему второго значения хеш-функции; и
модуль предоставления ответа для предоставления проверяющему информации ответа N раз, соответствующей моделям проверки, выбранным проверяющим из k (где k≥2) моделей проверки по соответствующим сообщениям N раз, части сообщений и части третьей информации, причем указанная часть сообщений и указанная часть третьей информации не подлежат получению даже при выполнении операции, с использованием набора F многопорядковых многочленов с многими переменными, вектора y и информации ответа, заранее подготовленной для модели проверки, соответствующей информации ответа, при этом
вектор s представляет собой секретный ключ, а
набор F многопорядковых многочленов с многими переменными и вектор у представляют собой открытые ключи, причем
сообщения и третья информация представляют собой информацию, получаемую при выполнении указанной операции, заранее подготовленной для модели проверки, соответствующей информации ответа, с использованием открытых ключей, первой информации и информации ответа или информации, полученной на основе информации ответа.
(2) Устройство обработки информации по п. (1), в котором
набор F многопорядковых многочленов с многими переменными задается так, что Fb (x, y), определенный как Fb (x, y)=F(х+y)-F(x)-F(y), является билинейным для x и y.
(3) Устройство обработки информации по п. (1) или (2), в котором набор F многопорядковых многочленов с многими переменными генерируется с использованием информации, отличающейся в зависимости от пользователя, генерирующего открытые ключи.
(4) Устройство обработки информации по п. (1), в котором
набор F многопорядковых многочленов с многими переменными выражается суммой набора
многочленов с многими переменными, имеющих второй порядок, так, что Fb (x, y), определенный как Fb (х, y)=F(x+y)-F(x)-F(y), является билинейным для x и y, и набора
члена третьего или более высокого порядка.
(5) Устройство обработки информации, содержащее:
модуль хранения информации для хранения набора F=(f1, …, fm) многопорядковых многочленов с многими переменными, определенного на кольце K, и вектора y=(y1, …, ym)=(f1(s), …, fm(s));
модуль получения сообщений для получения первого значения хеш-функции, вычисленного на основе сообщений N раз (где N≥2), сгенерированных на основе набора F многопорядковых многочленов с многими переменными и вектора s, являющегося элементом множества Kn;
модуль предоставления информации для предоставления доказывающему, предоставившему указанные сообщения, первой информации, выбранной случайным образом по соответствующим сообщениям N раз;
модуль получения промежуточной информации для получения второго значения хеш-функции, вычисленного на основе третьей информации N раз, сгенерированной доказывающим с использованием первой информации N раз и второй информации N раз, полученной при генерировании указанных сообщений;
модуль предоставления информации о модели для предоставления доказывающему информации о моделях проверки, выбираемых случайным образом из k (где k≥3) моделей проверки по соответствующим сообщениям N раз;
модуль получения ответов для получения от доказывающего информации ответов, соответствующей моделям проверки, выбранным по соответствующим сообщениям N раз; и
проверяющий модуль для проверки, хранит ли доказывающий вектор s, основываясь на наборе F многопорядковых многочленов с многими переменными, векторе y, первой информации, информации ответа, первом значении хеш-функции и втором значение хеш-функции, при этом
вектор s представляет собой секретный ключ, а
набор F многопорядковых многочленов с многими переменными и вектор у представляют собой открытые ключи, причем
сообщения и третья информация представляют собой информацию, получаемую при выполнении операции, заранее подготовленной для модели проверки, соответствующей информации ответа, с использованием открытых ключей, первой информации и информации ответа или информации, полученной на основе информации ответа.
(6) Устройство обработки информации по п. (5), в котором
набор F многопорядковых многочленов с многими переменными задается так, что Fb(x, y), определенный как Fb (x, y)=F(x+y)-F(x)-F(y), является билинейным для x и y.
(7) Устройство обработки информации по п. (5) или (6), в котором
набор F многопорядковых многочленов с многими переменными сгенерирован с использованием информации, отличающейся в зависимости от пользователя, генерирующего открытые ключи.
(8) Устройство обработки информации по п. (5), в котором
набор F многопорядковых многочленов с многими переменными выражается суммой набора
многочленов с многими переменными, имеющих второй порядок, так, что Fb (x, y), определенный как Fb(x, y)=F(x+y)-F(x)-F(y), является билинейным для x и y, и набора
члена третьего или более высокого порядка.
(9) Способ обработки информации, содержащий:
этап, на котором генерируют сообщения N раз (где N≥2), основываясь на наборе F=(f1, …, fm) многопорядковых многочленов с многими переменными, определенном на кольце K, и векторе s, являющемся элементом множества Kn, и вычисляют первое значение хеш-функции, основанное на указанных сообщениях N раз;
этап, на котором предоставляют проверяющему, хранящему указанный набор F многопорядковых многочленов с многими переменными и вектор y=(y1, …, ym)=(f1(s), …, fm(s)), первое значение хеш-функции;
этап, на котором генерируют третью информацию N раз, используя первую информацию, произвольно выбранную проверяющим по соответствующим сообщениям N раз, и второй информации N раз, полученной при генерировании указанных сообщений, и генерируют второе значение хеш-функции, основанное на третьей информации N раз;
этап, на котором предоставляют проверяющему второе значение хеш-функции; и
этап, на котором предоставляют проверяющему информацию ответов N раз, соответствующую моделям проверки, выбранным проверяющим из к (где k≥2) моделей проверки по соответствующим сообщениям N раз, части сообщений и части третьей информации, причем указанная часть сообщений и указанная часть третьей информации не подлежат получению даже при выполнении операции, с использованием набора F многопорядковых многочленов с многими переменными, вектора y и информации ответа, заранее подготовленной для модели проверки, соответствующей информации ответа, при этом
вектор s представляет собой секретный ключ, а
набор F многопорядковых многочленов с многими переменными и вектор y представляют собой открытые ключи, причем
сообщения и третья информация представляют собой информацию, получаемую при выполнении указанной операции, заранее подготовленной для модели проверки, соответствующей информации ответа, с использованием открытых ключей, первой информации и информации ответа или информации, полученной на основе информации ответа.
(10) Способ обработки информации, содержащий:
этап, на котором хранят набор F=(f1, …, fm) многопорядковых многочленов с многими переменными, определенный на кольце K, и вектор y=(y1, …, ym)=(f1(s), …, fm(s));
модуль получения сообщений для получения первого значения хеш-функции, вычисленного на основе сообщений N раз (где N≥2), сгенерированных на основе набора F многопорядковых многочленов с многими переменными и вектора s, являющегося элементом множества Kn;
этап, на котором предоставляют доказывающему, предоставившему указанные сообщения, первую информацию, произвольно выбранную по соответствующим сообщениям N раз;
этап, на котором получают второе значение хеш-функции, вычисленное на основе третьей информации N раз, сгенерированной доказывающим с использованием первой информации N раз и второй информации N раз, полученной при генерировании указанных сообщений;
модуль предоставления информации о модели для предоставления доказывающему информации о моделях проверки, выбираемых случайным образом из k (где k≥3) моделей проверки по соответствующим сообщениям N раз;
этап, на котором получают от доказывающего информацию ответов, соответствующую моделям проверки, выбранным по соответствующим сообщениям N раз; и
этап, на котором проверяют, хранит ли доказывающий вектор S, основываясь на наборе F многопорядковых многочленов с многими переменными, векторе y, первой информации, информации ответа, первом значении хеш-функции и втором значение хеш-функции, при этом
вектор s представляет собой секретный ключ, а
набор F многопорядковых многочленов с многими переменными и вектор у представляют собой открытые ключи, причем
сообщения и третья информация представляют собой информацию, получаемую при выполнении операции, заранее подготовленной для модели проверки, соответствующей информации ответа, с использованием открытых ключей, первой информации и информации ответа или информации, полученной на основе информации ответа.
(11) Программа, вызывающая выполнение компьютером:
функции генерирования сообщений, выполненной с возможностью генерирования сообщения N раз (где N≥2), основываясь на наборе F=(f1, …, fm) многопорядковых многочленов с многими переменными, определенном на кольце K, и векторе s, являющемся элементом множества Kn, и вычисления первого значения хеш-функции, основанное на указанных сообщениях N раз;
функции предоставления сообщений, выполненной с возможностью предоставления проверяющему, обладающему указанным набором F многопорядковых многочленов с многими переменными и вектором y=(y1, …, ym)=(f1(s), …, fm(s)), первого значения хеш-функции;
функции генерирования промежуточной информации, выполненной с возможностью генерирования третьей информации N раз, с использованием первой информации, произвольно выбранной проверяющим по соответствующим сообщениям N раз, и второй информации N раз, полученной при генерировании указанных сообщений, и генерирования второго значения хеш-функции, основанное на третьей информации N раз;
функции предоставления промежуточной информации, выполненной с возможностью предоставления проверяющему второго значения хеш-функции; и
функции предоставления ответов, выполненной с возможностью предоставления проверяющему информации ответов N раз, соответствующей моделям проверки, выбранным проверяющим из k (где k≥2) моделей проверки по соответствующим сообщениям N раз, части сообщений и части третьей информации, причем указанная часть сообщений и эта часть третьей информации не подлежат получению даже при выполнении операции с использованием набора F многопорядковых многочленов с многими переменными, вектора y и информации ответа, заранее подготовленной для модели проверки, соответствующей информации ответа, при этом
вектор s представляет собой секретный ключ, а
набор F многопорядковых многочленов с многими переменными и вектор у представляют собой открытые ключи, причем
сообщения и третья информация представляют собой информацию, получаемую при выполнении указанной операции, заранее подготовленной для модели проверки, соответствующей информации ответа, с использованием открытых ключей, первой информации и информации ответа или информации, полученной на основе информации ответа.
(12) Программа, вызывающая выполнение компьютером:
функции хранения информации, выполненной с возможностью хранения набора F=(f1, …, fm) многопорядковых многочленов с многими переменными, определенного на кольце K, и вектора y=(y1, …, ym)=(f1(s), …, fm(s));
модуля получения получаемых сообщений для получения первого значения хеш-функции, вычисленного на основе сообщений N раз (где N≥2), сгенерированных на основе набора F многопорядковых многочленов с многими переменными и вектора s, являющегося элементом множества Kn;
функции предоставления информации, выполненной с возможностью предоставления доказывающему, предоставившему указанные сообщения, первую информацию, произвольно выбранную по соответствующим сообщениям N раз;
функции получения промежуточной информации, выполненной с возможностью получения второго значения хеш-функции, вычисленного на основе третьей информации N раз, сгенерированной доказывающим с использованием первой информации N раз и второй информации N раз, полученной при генерировании указанных сообщений;
модуля предоставления информации о модели для предоставления доказывающему информации о моделях проверки, выбираемых произвольно из k (где k≥3) моделей проверки по соответствующим сообщениям N раз;
функции получения ответа, выполненной с возможностью получения от доказывающего информации ответа, соответствующей моделям проверки, выбранным по соответствующим сообщениям N раз; и
функции проверки, выполненной с возможностью проверки, хранит ли доказывающий вектор s, основываясь на наборе F многопорядковых многочленов с многими переменными, векторе y, первой информации, информации ответа, первом значении хеш-функции и втором значение хеш-функции, при этом
вектор s представляет собой секретный ключ, а
набор F многопорядковых многочленов с многими переменными и вектор у представляют собой открытые ключи, причем
сообщения и третья информация представляют собой информацию, получаемую при выполнении операции, заранее подготовленной для модели проверки, соответствующей информации ответа, с использованием открытых ключей, первой информации и информации ответа или информации, полученной на основе информации ответа.
(13) Машиночитаемый носитель записи, хранящий записанную на нем программу, вызывающую выполнение компьютером:
функции генерирования сообщений, выполненной с возможностью генерирования сообщения N раз (где N≥2), основываясь на наборе F=(f1, …, fm) многопорядковых многочленов с многими переменными, определенном на кольце K, и векторе s, являющемся элементом множества Kn, и вычисления первого значения хеш-функции, основанного на указанных сообщениях N раз;
функции предоставления сообщений, выполненной с возможностью предоставления проверяющему, хранящему указанный набор F многопорядковых многочленов с многими переменными и вектор y=(y1, …, ym)=(f1(s), …, fm(s)), первого значения хеш-функции;
функции генерирования промежуточной информации, выполненной с возможностью генерирования третьей информации N раз, с использованием первой информации, выбранной произвольно проверяющим по соответствующим сообщениям N раз, и второй информации N раз, полученной при генерировании указанных сообщений, и генерирования второго значения хеш-функции, основанного на третьей информации N раз;
функции предоставления промежуточной информации, выполненной с возможностью предоставления проверяющему второго значения хеш-функции; и
функции предоставления ответов, выполненной с возможностью предоставления проверяющему информации ответов N раз, соответствующей моделям проверки, выбранным проверяющим из k (где k≥2) моделей проверки по соответствующим сообщениям N раз, части сообщений и части третьей информации, причем указанная часть сообщений и указанная часть третьей информации не подлежат получению даже при выполнении операции, с использованием набора F многопорядковых многочленов с многими переменными, вектора y и информации ответа, заранее подготовленной для модели проверки, соответствующей информации ответа, при этом
вектор s представляет собой секретный ключ, а
набор F многопорядковых многочленов с многими переменными и вектор у представляют собой открытые ключи, причем
сообщения и третья информация представляют собой информацию, получаемую при выполнении указанной операции, заранее подготовленной для модели проверки, соответствующей информации ответа, с использованием открытых ключей, первой информации и информации ответа или информации, полученной на основе информации ответа.
(14) Машиночитаемый носитель записи, хранящий записанную на нем программу, вызывающую выполнение компьютером:
функции хранения информации, выполненной с возможностью хранения набора F=(f1, …, fm) многопорядковых многочленов с многими переменными, определенного на кольце K, и вектора y=(y1, …, ym)=(f1(s), …, fm(s));
модуля получения получаемых сообщений для получения первого значения хеш-функции, вычисленного на основе сообщений N раз (где N≥2), сгенерированных на основе набора F многопорядковых многочленов с многими переменными и вектора s, являющегося элементом множества Kn;
функции предоставления информации, выполненной с возможностью предоставления доказывающему, предоставившему указанные сообщения, первой информации, выбранной случайным образом по соответствующим сообщениям N раз;
функции получения промежуточной информации, выполненной с возможностью получения второго значения хеш-функции, вычисленного на основе третьей информации N раз, сгенерированной доказывающим с использованием первой информации N раз и второй информации N раз, полученной При генерировании указанных сообщений;
модуля предоставления информации о модели для предоставления доказывающему информации о моделях проверки, выбираемых произвольно из k (где k≥3) моделей проверки по соответствующим сообщениям N раз;
функции получения ответов, выполненной с возможностью получения от доказывающего информации ответов, соответствующей моделям проверки, выбранным по соответствующим сообщениям N раз; и
функции проверки, выполненной с возможностью проверки, хранит ли доказьшающий вектор s, основываясь на наборе F многопорядковых многочленов с многими переменными, векторе y, первой информации, информации ответа, первом значении хеш-функции и втором значение хеш-функции, при этом
вектор s представляет собой секретный ключ, а
набор F многопорядковых многочленов с многими переменными и вектор у представляют собой открытые ключи, причем
сообщения и третья информация представляют собой информацию, получаемую при выполнении операции, заранее подготовленной для модели проверки, соответствующей информации ответа, с использованием открытых ключей, первой информации и информации ответа или информации, полученной на основе информации ответа.
(15) Устройство обработки информации по любому из пп. (1)-(8),
в котором тип имеют соотношение: m<n.
(16) Устройство обработки информации по п. (15),
в котором тип имеют соотношение: 2m-n<<1.
Замечания
Алгоритм P доказывающего представляет собой пример модуля генерирования сообщений, модуля предоставления сообщений, модуля предоставления ответов, модуля генерирования промежуточной информации и модуля предоставления промежуточной информации. Кроме того, алгоритм V проверяющего представляет собой пример модуля хранения информации, модуля получения информации, модуля предоставления информации о модели, модуля получения ответов, проверяющего модуля и модуля получения промежуточной информации.
Выше, со ссылкой на прилагаемые чертежи, были описаны предпочтительные варианты реализации предлагаемого изобретения, хотя, конечно же, предлагаемое изобретение не ограничено вышеупомянутыми примерами. Специалист, имеющий квалификацию в данной области техники, может в рамках объема прилагаемой формулы изобретения найти различные изменения и модификации, и следует понимать, что они естественным образом будут подпадать под технический объем предлагаемого изобретения.
Перечень ссылочных позиций
Gen алгоритм генерирования ключей
Р алгоритм доказывающего
V алгоритм проверяющего
Sig алгоритм генерирования цифровой подписи
Ver алгоритм проверки цифровой подписи
Claims (10)
1. Устройство обработки информации, содержащее:
модуль генерирования сообщений для генерирования сообщения N раз (где N≥2), на основе набора F=(f1, …, fm) многопорядковых многочленов с многими переменными, определенного на кольце K, и вектора s, являющегося элементом множества Kn, и вычисления первого значения хеш-функции, на основе указанных сообщений N раз;
модуль предоставления сообщений для предоставления проверяющему, хранящему указанный набор F многопорядковых многочленов с многими переменными и вектор y=(y1, …, ym)=(f1(s), …, fm(s)), первого значения хеш-функции;
модуль генерирования промежуточной информации для генерирования третьей информации N раз, с использованием первой информации, выбранной произвольно проверяющим по соответствующим сообщениям N раз, и второй информации N раз, полученной при генерировании указанных сообщений, и генерирования второго значения хеш-функции, на основе третьей информации N раз;
модуль предоставления промежуточной информации для предоставления проверяющему второго значения хеш-функции; и
модуль предоставления ответов для предоставления проверяющему информации ответов N раз, соответствующей моделям проверки, выбранным проверяющим из k (где k≥2) моделей проверки по соответствующим сообщениям N раз, части сообщений и части третьей информации, при этом
вектор s представляет собой секретный ключ, а
набор F многопорядковых многочленов с многими переменными представляет собой открытый ключ или настроечные параметры системы, причем
вектор y представляет собой открытый ключ, а
сообщения и третья информация представляют собой информацию, получаемую при выполнении операции, заранее подготовленной для модели проверки, соответствующей информации ответа, с использованием открытых ключей, первой информации и информации ответа или информации, полученной на основе информации ответа, при этом
указанная часть сообщений и указанная часть третьей информации представляют собой информацию, не подлежащую получению даже при выполнении операции, с использованием набора F многопорядковых многочленов с многими переменными, вектора y и информации ответа, заранее подготовленной для модели проверки, соответствующей информации ответа.
модуль генерирования сообщений для генерирования сообщения N раз (где N≥2), на основе набора F=(f1, …, fm) многопорядковых многочленов с многими переменными, определенного на кольце K, и вектора s, являющегося элементом множества Kn, и вычисления первого значения хеш-функции, на основе указанных сообщений N раз;
модуль предоставления сообщений для предоставления проверяющему, хранящему указанный набор F многопорядковых многочленов с многими переменными и вектор y=(y1, …, ym)=(f1(s), …, fm(s)), первого значения хеш-функции;
модуль генерирования промежуточной информации для генерирования третьей информации N раз, с использованием первой информации, выбранной произвольно проверяющим по соответствующим сообщениям N раз, и второй информации N раз, полученной при генерировании указанных сообщений, и генерирования второго значения хеш-функции, на основе третьей информации N раз;
модуль предоставления промежуточной информации для предоставления проверяющему второго значения хеш-функции; и
модуль предоставления ответов для предоставления проверяющему информации ответов N раз, соответствующей моделям проверки, выбранным проверяющим из k (где k≥2) моделей проверки по соответствующим сообщениям N раз, части сообщений и части третьей информации, при этом
вектор s представляет собой секретный ключ, а
набор F многопорядковых многочленов с многими переменными представляет собой открытый ключ или настроечные параметры системы, причем
вектор y представляет собой открытый ключ, а
сообщения и третья информация представляют собой информацию, получаемую при выполнении операции, заранее подготовленной для модели проверки, соответствующей информации ответа, с использованием открытых ключей, первой информации и информации ответа или информации, полученной на основе информации ответа, при этом
указанная часть сообщений и указанная часть третьей информации представляют собой информацию, не подлежащую получению даже при выполнении операции, с использованием набора F многопорядковых многочленов с многими переменными, вектора y и информации ответа, заранее подготовленной для модели проверки, соответствующей информации ответа.
2. Устройство обработки информации по п. 1, в котором
набор F многопорядковых многочленов с многими переменными задан так, что Fb(x, y), определенный как Fb(x, y)=F(х+y)-F(x)-F(y), является билинейным для x и y.
набор F многопорядковых многочленов с многими переменными задан так, что Fb(x, y), определенный как Fb(x, y)=F(х+y)-F(x)-F(y), является билинейным для x и y.
3. Устройство обработки информации по п. 1, в котором
набор F многопорядковых многочленов с многими переменными сгенерирован с использованием информации, отличающейся в зависимости от пользователя, генерирующего открытые ключи.
набор F многопорядковых многочленов с многими переменными сгенерирован с использованием информации, отличающейся в зависимости от пользователя, генерирующего открытые ключи.
4. Устройство обработки информации по п. 1, в котором
набор F многопорядковых многочленов с многими переменными выражен суммой набора FA=(f1 A, …, fm A) многочленов с многими переменными, имеющих второй порядок, так, что Fb(x, y), определенный как Fb(х, y)=F(x+y)-F(x)-F(y), является билинейным для х и y, и набора GA=(g1 A, …, gm A) члена третьего или более высокого порядка.
набор F многопорядковых многочленов с многими переменными выражен суммой набора FA=(f1 A, …, fm A) многочленов с многими переменными, имеющих второй порядок, так, что Fb(x, y), определенный как Fb(х, y)=F(x+y)-F(x)-F(y), является билинейным для х и y, и набора GA=(g1 A, …, gm A) члена третьего или более высокого порядка.
5. Устройство обработки информации, содержащее:
модуль хранения информации для сохранения набора F=(f1, …, fm) многопорядковых многочленов с многими переменными, определенного на кольце K, и вектора y=(y1, …, ym)=(f1(s), …, fm(s));
модуль получения сообщений для получения первого значения хеш-функции, вычисленного на основе сообщений N раз (где N≥2), сгенерированных на основе набора F многопорядковых многочленов с многими переменными и вектора s, являющегося элементом множества Kn;
модуль предоставления информации для предоставления доказывающему, предоставившему указанные сообщения, первой информации, выбранной произвольно по соответствующим сообщениям N раз;
модуль получения промежуточной информации для получения второго значения хеш-функции, вычисленного на основе третьей информации N раз, сгенерированной доказывающим с использованием первой информации N раз и второй информации N раз, полученной при генерировании указанных сообщений;
модуль предоставления информации о модели для предоставления доказывающему информации о моделях проверки, выбираемых произвольно из k (где k≥2) моделей проверки по соответствующим сообщениям N раз;
модуль получения ответов для получения от доказывающего информации ответов, соответствующей моделям проверки, выбранным по соответствующим сообщениям N раз; и
проверяющий модуль для проверки, хранит ли доказывающий вектор s, на основе набора F многопорядковых многочленов с многими переменными, вектора y, первой информации, информации ответа, первого значения хеш-функции и второго значения хеш-функции, при этом
вектор s представляет собой секретный ключ, а
набор F многопорядковых многочленов с многими переменными представляет собой открытый ключ или настроечные параметры системы, причем
вектор y представляет собой открытый ключ, а
сообщения и третья информация представляют собой информацию, получаемую при выполнении операции, заранее подготовленной для модели проверки, соответствующей информации ответа, с использованием открытых ключей, первой информации и информации ответа или информации, полученной на основе информации ответа.
модуль хранения информации для сохранения набора F=(f1, …, fm) многопорядковых многочленов с многими переменными, определенного на кольце K, и вектора y=(y1, …, ym)=(f1(s), …, fm(s));
модуль получения сообщений для получения первого значения хеш-функции, вычисленного на основе сообщений N раз (где N≥2), сгенерированных на основе набора F многопорядковых многочленов с многими переменными и вектора s, являющегося элементом множества Kn;
модуль предоставления информации для предоставления доказывающему, предоставившему указанные сообщения, первой информации, выбранной произвольно по соответствующим сообщениям N раз;
модуль получения промежуточной информации для получения второго значения хеш-функции, вычисленного на основе третьей информации N раз, сгенерированной доказывающим с использованием первой информации N раз и второй информации N раз, полученной при генерировании указанных сообщений;
модуль предоставления информации о модели для предоставления доказывающему информации о моделях проверки, выбираемых произвольно из k (где k≥2) моделей проверки по соответствующим сообщениям N раз;
модуль получения ответов для получения от доказывающего информации ответов, соответствующей моделям проверки, выбранным по соответствующим сообщениям N раз; и
проверяющий модуль для проверки, хранит ли доказывающий вектор s, на основе набора F многопорядковых многочленов с многими переменными, вектора y, первой информации, информации ответа, первого значения хеш-функции и второго значения хеш-функции, при этом
вектор s представляет собой секретный ключ, а
набор F многопорядковых многочленов с многими переменными представляет собой открытый ключ или настроечные параметры системы, причем
вектор y представляет собой открытый ключ, а
сообщения и третья информация представляют собой информацию, получаемую при выполнении операции, заранее подготовленной для модели проверки, соответствующей информации ответа, с использованием открытых ключей, первой информации и информации ответа или информации, полученной на основе информации ответа.
6. Устройство обработки информации по п. 5, в котором
набор F многопорядковых многочленов с многими переменными задан так, что Fb(х, y), определенный как Fb(х, y)=F(х+y)-F(x)-F(y), является билинейным для х и y.
набор F многопорядковых многочленов с многими переменными задан так, что Fb(х, y), определенный как Fb(х, y)=F(х+y)-F(x)-F(y), является билинейным для х и y.
7. Устройство обработки информации по п. 5, в котором
набор F многопорядковых многочленов с многими переменными сгенерирован с использованием информации, отличающейся в зависимости от пользователя, генерирующего открытые ключи.
набор F многопорядковых многочленов с многими переменными сгенерирован с использованием информации, отличающейся в зависимости от пользователя, генерирующего открытые ключи.
8. Устройство обработки информации по п. 5, в котором
набор F многопорядковых многочленов с многими переменными выражен суммой набора FA=(f1 A, …, fm A) многочленов с многими переменными, имеющих второй порядок, так, что Fb(х, y), определенный как Fb(х, y)=F(x+y)-F(x)-F(y), является билинейным для х и y, и набора GA=(g1 A, …, gm A) члена третьего или более высокого порядка.
набор F многопорядковых многочленов с многими переменными выражен суммой набора FA=(f1 A, …, fm A) многочленов с многими переменными, имеющих второй порядок, так, что Fb(х, y), определенный как Fb(х, y)=F(x+y)-F(x)-F(y), является билинейным для х и y, и набора GA=(g1 A, …, gm A) члена третьего или более высокого порядка.
9. Способ обработки информации, содержащий:
этап, на котором генерируют сообщения N раз (где N≥2), на основе набора F=(f1, …, fm) многопорядковых многочленов с многими переменными, определенного на кольце K, и вектора s, являющегося элементом множества Kn, и вычисляют первое значение хеш-функции, на основе указанных сообщений N раз;
этап, на котором предоставляют проверяющему, хранящему указанный набор F многопорядковых многочленов с многими переменными и вектор y=(y1, …, ym)=(f1(s), …, fm(s)), первое значение хеш-функции;
этап, на котором генерируют третью информацию N раз, с использованием первой информации, произвольно выбранной проверяющим по соответствующим сообщениям N раз, и второй информации N раз, полученной при генерировании указанных сообщений, и генерируют второе значение хеш-функции, на основе третьей информации N раз;
этап, на котором предоставляют проверяющему второе значение хеш-функции; и
этап, на котором предоставляют проверяющему информацию ответов N раз, соответствующую моделям проверки, выбранным проверяющим из k (где k≥2) моделей проверки по соответствующим сообщениям N раз, части сообщений и части третьей информации, при этом
вектор s представляет собой секретный ключ, а
набор F многопорядковых многочленов с многими переменными представляет собой открытый ключ или настроечные параметры системы, причем
вектор y представляет собой открытый ключ, а
сообщения и третья информация представляют собой информацию, получаемую при выполнении операции, заранее подготовленной для модели проверки, соответствующей информации ответа, с использованием открытых ключей, первой информации и информации ответа или информации, полученной на основе информации ответа, при этом
указанная часть сообщений и указанная часть третьей информации представляют собой информацию, не подлежащую получению даже при выполнении указанной операции, с использованием набора F многопорядковых многочленов с многими переменными, вектора y и информации ответа, заранее подготовленной для модели проверки, соответствующей информации ответа.
этап, на котором генерируют сообщения N раз (где N≥2), на основе набора F=(f1, …, fm) многопорядковых многочленов с многими переменными, определенного на кольце K, и вектора s, являющегося элементом множества Kn, и вычисляют первое значение хеш-функции, на основе указанных сообщений N раз;
этап, на котором предоставляют проверяющему, хранящему указанный набор F многопорядковых многочленов с многими переменными и вектор y=(y1, …, ym)=(f1(s), …, fm(s)), первое значение хеш-функции;
этап, на котором генерируют третью информацию N раз, с использованием первой информации, произвольно выбранной проверяющим по соответствующим сообщениям N раз, и второй информации N раз, полученной при генерировании указанных сообщений, и генерируют второе значение хеш-функции, на основе третьей информации N раз;
этап, на котором предоставляют проверяющему второе значение хеш-функции; и
этап, на котором предоставляют проверяющему информацию ответов N раз, соответствующую моделям проверки, выбранным проверяющим из k (где k≥2) моделей проверки по соответствующим сообщениям N раз, части сообщений и части третьей информации, при этом
вектор s представляет собой секретный ключ, а
набор F многопорядковых многочленов с многими переменными представляет собой открытый ключ или настроечные параметры системы, причем
вектор y представляет собой открытый ключ, а
сообщения и третья информация представляют собой информацию, получаемую при выполнении операции, заранее подготовленной для модели проверки, соответствующей информации ответа, с использованием открытых ключей, первой информации и информации ответа или информации, полученной на основе информации ответа, при этом
указанная часть сообщений и указанная часть третьей информации представляют собой информацию, не подлежащую получению даже при выполнении указанной операции, с использованием набора F многопорядковых многочленов с многими переменными, вектора y и информации ответа, заранее подготовленной для модели проверки, соответствующей информации ответа.
10. Способ обработки информации, содержащий:
этап, на котором сохраняют набор F=(f1, …, fm) многопорядковых многочленов с многими переменными, определенный на кольце K, и вектор y=(y1, …, ym)=(f1(s), …, fm(s)); при этом
модуль получения сообщений выполнен с возможностью получения первого значения хеш-функции, вычисленного на основе сообщений N раз (где N≥2), сгенерированных на основе набора F многопорядковых многочленов с многими переменными и вектора s, являющегося элементом множества Kn;
этап, на котором предоставляют доказывающему, предоставившему указанные сообщения, первую информацию, произвольно выбранную по соответствующим сообщениям N раз;
этап, на котором получают второе значение хеш-функции, вычисленное на основе третьей информации N раз, сгенерированной доказывающим с использованием первой информации N раз и второй информации N раз, полученной при генерировании указанных сообщений; при этом
модуль предоставления информации о модели выполнен с возможностью предоставления доказывающему информации о моделях проверки, выбираемых произвольно из k (где k≥2) моделей проверки по соответствующим сообщениям N раз;
этап, на котором получают от доказывающего информацию ответа, соответствующую моделям проверки, выбранным по соответствующим сообщениям N раз; и
этап, на котором проверяют, хранит ли доказывающий вектор s, на основе набора F многопорядковых многочленов с многими переменными, вектора y, первой информации, информации ответа, первого значения хеш-функции и второго значения хеш-функции, при этом
вектор s представляет собой секретный ключ, а
набор F многопорядковых многочленов с многими переменными представляет собой открытый ключ или настроечные параметры системы, причем
вектор y представляет собой открытый ключ, а
сообщения и третья информация представляют собой информацию, получаемую при выполнении операции, заранее подготовленной для модели проверки, соответствующей информации ответа, с использованием открытых ключей, первой информации и информации ответа или информации, полученной на основе информации ответа.
этап, на котором сохраняют набор F=(f1, …, fm) многопорядковых многочленов с многими переменными, определенный на кольце K, и вектор y=(y1, …, ym)=(f1(s), …, fm(s)); при этом
модуль получения сообщений выполнен с возможностью получения первого значения хеш-функции, вычисленного на основе сообщений N раз (где N≥2), сгенерированных на основе набора F многопорядковых многочленов с многими переменными и вектора s, являющегося элементом множества Kn;
этап, на котором предоставляют доказывающему, предоставившему указанные сообщения, первую информацию, произвольно выбранную по соответствующим сообщениям N раз;
этап, на котором получают второе значение хеш-функции, вычисленное на основе третьей информации N раз, сгенерированной доказывающим с использованием первой информации N раз и второй информации N раз, полученной при генерировании указанных сообщений; при этом
модуль предоставления информации о модели выполнен с возможностью предоставления доказывающему информации о моделях проверки, выбираемых произвольно из k (где k≥2) моделей проверки по соответствующим сообщениям N раз;
этап, на котором получают от доказывающего информацию ответа, соответствующую моделям проверки, выбранным по соответствующим сообщениям N раз; и
этап, на котором проверяют, хранит ли доказывающий вектор s, на основе набора F многопорядковых многочленов с многими переменными, вектора y, первой информации, информации ответа, первого значения хеш-функции и второго значения хеш-функции, при этом
вектор s представляет собой секретный ключ, а
набор F многопорядковых многочленов с многими переменными представляет собой открытый ключ или настроечные параметры системы, причем
вектор y представляет собой открытый ключ, а
сообщения и третья информация представляют собой информацию, получаемую при выполнении операции, заранее подготовленной для модели проверки, соответствующей информации ответа, с использованием открытых ключей, первой информации и информации ответа или информации, полученной на основе информации ответа.
Applications Claiming Priority (3)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| JP2011-177334 | 2011-08-12 | ||
| JP2011177334A JP5790289B2 (ja) | 2011-08-12 | 2011-08-12 | 情報処理装置、情報処理方法、プログラム、及び記録媒体 |
| PCT/JP2012/069452 WO2013024699A1 (ja) | 2011-08-12 | 2012-07-31 | 情報処理装置、情報処理方法、プログラム、及び記録媒体 |
Publications (2)
| Publication Number | Publication Date |
|---|---|
| RU2014104078A RU2014104078A (ru) | 2015-08-10 |
| RU2600103C2 true RU2600103C2 (ru) | 2016-10-20 |
Family
ID=47715021
Family Applications (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| RU2014104078/08A RU2600103C2 (ru) | 2011-08-12 | 2012-07-31 | Устройство обработки информации, способ обработки информации, программа и носитель записи |
Country Status (8)
| Country | Link |
|---|---|
| US (1) | US10122531B2 (ru) |
| EP (1) | EP2744147B1 (ru) |
| JP (1) | JP5790289B2 (ru) |
| CN (1) | CN103718501B (ru) |
| BR (1) | BR112014002850A2 (ru) |
| CA (1) | CA2839094C (ru) |
| RU (1) | RU2600103C2 (ru) |
| WO (1) | WO2013024699A1 (ru) |
Families Citing this family (7)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| FR3006782A1 (fr) * | 2013-06-11 | 2014-12-12 | France Telecom | Procede et systeme de delegation d'un calcul d'une valeur de couplage bilineaire a un serveur de calcul |
| EP2824480A1 (en) | 2013-07-09 | 2015-01-14 | The European Union, represented by the European Commission | Digitally-signed satellite radio-navigation signals |
| CN103490897B (zh) * | 2013-09-17 | 2017-04-05 | 华南理工大学 | 一种多变量公钥签名/验证系统及签名/验证方法 |
| US10091000B2 (en) * | 2014-09-24 | 2018-10-02 | Intel Corporation | Techniques for distributing secret shares |
| US9819495B2 (en) * | 2014-10-02 | 2017-11-14 | Qualcomm Incorporated | Systems and methods of dynamically adapting security certificate-key pair generation |
| CN104486078A (zh) * | 2014-12-01 | 2015-04-01 | 北京成众志科技有限公司 | 一种信息多阶防伪编码与认证方法 |
| CN115225278B (zh) * | 2022-06-07 | 2024-06-04 | 西安电子科技大学 | 基于数据感知哈希的数据持有性证明方法 |
Family Cites Families (7)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US7961876B2 (en) * | 2005-01-11 | 2011-06-14 | Jintai Ding | Method to produce new multivariate public key cryptosystems |
| CN1870499B (zh) * | 2005-01-11 | 2012-01-04 | 丁津泰 | 产生新的多变量公钥密码系统的方法 |
| US8019079B2 (en) * | 2007-07-08 | 2011-09-13 | Georgia Tech Research Corporation | Asymmetric cryptosystem employing paraunitary matrices |
| JP4764447B2 (ja) * | 2008-03-19 | 2011-09-07 | 株式会社東芝 | グループ署名システム、装置及びプログラム |
| JP5532048B2 (ja) * | 2009-07-13 | 2014-06-25 | 日本電気株式会社 | 匿名認証署名システム、ユーザ装置、検証装置、署名方法、検証方法およびそれらのプログラム |
| IL206139A0 (en) * | 2010-06-02 | 2010-12-30 | Yaron Sella | Efficient multivariate signature generation |
| JP5594034B2 (ja) * | 2010-07-30 | 2014-09-24 | ソニー株式会社 | 認証装置、認証方法、及びプログラム |
-
2011
- 2011-08-12 JP JP2011177334A patent/JP5790289B2/ja not_active Expired - Fee Related
-
2012
- 2012-07-31 EP EP12824052.0A patent/EP2744147B1/en not_active Not-in-force
- 2012-07-31 BR BR112014002850A patent/BR112014002850A2/pt not_active Application Discontinuation
- 2012-07-31 WO PCT/JP2012/069452 patent/WO2013024699A1/ja not_active Ceased
- 2012-07-31 RU RU2014104078/08A patent/RU2600103C2/ru not_active IP Right Cessation
- 2012-07-31 US US14/237,010 patent/US10122531B2/en active Active
- 2012-07-31 CN CN201280037655.5A patent/CN103718501B/zh not_active Expired - Fee Related
- 2012-07-31 CA CA2839094A patent/CA2839094C/en not_active Expired - Fee Related
Also Published As
| Publication number | Publication date |
|---|---|
| CA2839094C (en) | 2020-05-12 |
| EP2744147A4 (en) | 2015-09-09 |
| EP2744147B1 (en) | 2018-09-26 |
| US10122531B2 (en) | 2018-11-06 |
| CN103718501B (zh) | 2017-04-19 |
| WO2013024699A1 (ja) | 2013-02-21 |
| CA2839094A1 (en) | 2013-02-21 |
| US20140205087A1 (en) | 2014-07-24 |
| EP2744147A1 (en) | 2014-06-18 |
| RU2014104078A (ru) | 2015-08-10 |
| JP2013042316A (ja) | 2013-02-28 |
| BR112014002850A2 (pt) | 2017-03-01 |
| CN103718501A (zh) | 2014-04-09 |
| JP5790289B2 (ja) | 2015-10-07 |
Similar Documents
| Publication | Publication Date | Title |
|---|---|---|
| JP5736816B2 (ja) | 認証装置、認証方法、プログラム、及び署名生成装置 | |
| RU2600103C2 (ru) | Устройство обработки информации, способ обработки информации, программа и носитель записи | |
| CN102957538A (zh) | 信息处理设备和信息处理方法 | |
| RU2603551C2 (ru) | Устройство обработки информации, способ обработки информации, программа и носитель информации | |
| US10075299B2 (en) | Information processing apparatus, signature providing method, signature verifying method, program, and recording medium | |
| WO2013024627A1 (ja) | 情報処理装置、署名生成装置、情報処理方法、署名生成方法、及びプログラム | |
| US9184914B2 (en) | Information processing apparatus and information processing method | |
| US9490978B2 (en) | Information processing apparatus and information processing method | |
| JP2013042317A (ja) | 情報処理装置、及び情報処理方法 | |
| HK1193232A (en) | Information processing device and information processing method |
Legal Events
| Date | Code | Title | Description |
|---|---|---|---|
| MM4A | The patent is invalid due to non-payment of fees |
Effective date: 20200801 |