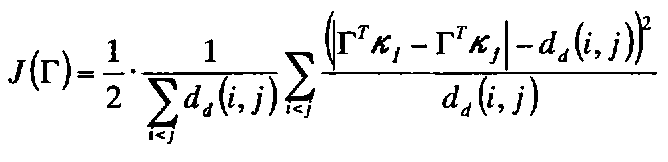JP5284530B2 - Information processing method and information processing apparatus - Google Patents
Information processing method and information processing apparatus Download PDFInfo
- Publication number
- JP5284530B2 JP5284530B2 JP2012256706A JP2012256706A JP5284530B2 JP 5284530 B2 JP5284530 B2 JP 5284530B2 JP 2012256706 A JP2012256706 A JP 2012256706A JP 2012256706 A JP2012256706 A JP 2012256706A JP 5284530 B2 JP5284530 B2 JP 5284530B2
- Authority
- JP
- Japan
- Prior art keywords
- distance
- data
- mapping
- processing data
- classes
- Prior art date
- Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
- Active
Links
Images
Landscapes
- Image Analysis (AREA)
Description
本発明は、冗長性を削減した高効率なデータの表現技術、このデータを用いた処理技術に関するものである。 The present invention relates to a highly efficient data representation technique with reduced redundancy and a processing technique using this data.
近年、非特許文献1のIsomapや、非特許文献2のLocally Linear Enbedding(LLE)に代表される、非線形の次元圧縮手法が提案されている。これらは、高次元空間内で、より低次元の超曲面(Manifold)上にあると考えられるデータを、Manifold固有の表面形状が許容できる程度に保存された、新たな低次元の空間に写像する手法を提供する。
In recent years, nonlinear dimensional compression techniques represented by Isomap of
係る手法は、より低次元の空間でデータを表現できるという意味で、高効率なパターン表現には成功している。しかし、データが何れのクラスに属するかという情報は用いておらず、データの分類を効率的に表すという点では、最適であるとは言えない。 Such a technique has succeeded in highly efficient pattern expression in the sense that data can be expressed in a lower dimensional space. However, information about which class the data belongs to is not used, and it is not optimal in terms of efficiently representing the data classification.
これに対し、特許文献1に開示されている手法では、カーネルフィッシャー線形識別関数、またはフィッシャー線形判別関数を用いて、従来のIsomap法を拡張することにより、パターン分類のための画像を表す方法を提供している。
On the other hand, in the method disclosed in
また、非特許文献3においては、従来のIsomap法の改良として、他クラスに属するデータ間の測地線距離を強制的に増加させることにより、クラス間の分離度を高める写像を構築する手法が提案されている。 Non-Patent Document 3 proposes a method for constructing a map that increases the degree of separation between classes by forcibly increasing the geodesic distance between data belonging to other classes as an improvement of the conventional Isomap method. Has been.
このように、Manifold固有の表面形状を許容できる程度に保存し、且つパターン分類のためのデータを表現できる方法が望まれている。
本発明は以上の問題に鑑みてなされたものであり、Manifold固有の表面形状を、許容できる程度に保存し、且つパターン分類に適した、データ表現方法、及びその表現方法を利用した、パターン識別方法に係る技術を提供することを目的とする。 The present invention has been made in view of the above problems. A data representation method that preserves the unique surface shape of Manifold to an acceptable level and is suitable for pattern classification, and pattern identification using the representation method. It aims at providing the technique concerning a method.
より具体的には、あるクラスにラベル付けされた複数のデータにおいて、同一のクラスのデータ集合が1つのクラスタとして表現され、且つ各クラスタ間の距離を所望の距離に設定可能なデータ表現方法、及びその表現方法を利用したパターン識別方法である。 More specifically, in a plurality of data labeled with a certain class, a data representation method in which a data set of the same class is represented as one cluster, and the distance between each cluster can be set to a desired distance, And a pattern identification method using the expression method.
本発明の目的を達成するために、例えば、本発明の情報処理方法は以下の構成を備える。 In order to achieve the object of the present invention, for example, an information processing method of the present invention comprises the following arrangement.
即ち、情報処理装置が行う情報処理方法であって、
入力手段が、それぞれ異なるクラスに属する処理データを入力する入力工程と、
第1の計算手段が、前記入力工程で入力したそれぞれの処理データ間の測地線距離関係を求める第1の計算工程と、
設定手段が、前記クラス間の距離を求め、前記クラス間の距離が所定の値よりも小さい場合に、前記クラス間の距離が大きくなるように、クラス間分離度を設定する設定工程と、
更新手段が、前記処理データのそれぞれが属するクラスの前記設定されたクラス間分離度に基づいて、同じクラスに属する処理データ間の測地線距離が、他クラスに属する処理データとの測地線距離よりも小さくなるように、前記処理データ間の測地線距離関係を更新する更新工程と、
第2の計算手段が、前記更新工程で更新された測地線距離関係を用いて、ユークリッド距離関係を近似するデータ写像関係を示す情報を求める第2の計算工程と
を備えることを特徴とする。
That is, an information processing method performed by the information processing apparatus,
An input process in which input means inputs process data belonging to different classes;
A first calculation step in which a first calculation means obtains a geodesic distance relationship between the respective processing data input in the input step;
A setting step for obtaining a distance between the classes, and setting a degree of separation between classes so that the distance between the classes is increased when the distance between the classes is smaller than a predetermined value;
The updating means determines that the geodesic distance between the processing data belonging to the same class is based on the geodesic distance with the processing data belonging to another class based on the set inter-class separation degree of the class to which each of the processing data belongs. Updating step of updating the geodesic distance relationship between the processing data,
The second calculation means includes a second calculation step for obtaining information indicating a data mapping relationship that approximates the Euclidean distance relationship using the geodesic distance relationship updated in the updating step.
本発明の構成によれば、Manifold固有の表面形状を、許容できる程度に保存し、且つパターン分類に適した、データ表現方法、及びその表現方法を利用した、パターン識別方法に係る技術を提供することができる。 According to the configuration of the present invention, there is provided a data expression method that preserves the unique surface shape of Manifold to an acceptable level and is suitable for pattern classification, and a technique related to a pattern identification method using the expression method. be able to.
先ず、本実施形態の概要について説明する。 First, an outline of the present embodiment will be described.
本実施形態は、それぞれ異なるクラスに属する処理データと共に、処理データが属するクラスを示すラベルデータを入力すると、入力したそれぞれの処理データ間の距離関係を求める(第1の計算)。そして、クラス間のクラス間分離度を設定し、距離関係を示す情報を、ラベルデータと、クラス間分離度を示す情報と、に基づいて更新すると、更新された情報が示す距離関係を近似するデータ写像関係を示す情報を求める(第2の計算)。 In this embodiment, when the label data indicating the class to which the process data belongs are input together with the process data belonging to different classes, the distance relationship between the input process data is obtained (first calculation). Then, the inter-class separation degree between the classes is set, and when the information indicating the distance relationship is updated based on the label data and the information indicating the inter-class separation degree, the distance relationship indicated by the updated information is approximated. Information indicating the data mapping relationship is obtained (second calculation).
ここで、求める距離関係とは測地線距離関係であり、データ写像関係を示す情報を用いて近似される距離関係はユークリッド距離関係である。 Here, the distance relationship to be obtained is the geodesic distance relationship, and the distance relationship approximated using information indicating the data mapping relationship is the Euclidean distance relationship.
2つの処理データx1、x2間のグラフ距離dG(x1、x2)が、x1、x2が近傍で無い場合は∞であるとする。この時、2つの処理データξ、ζ間の測地線距離dM(ξ、ζ)は、dG(ξ、ζ)か、処理データとは異なる処理データaを経由するdG(ξ、a)+dG(a、ζ)の、何れか小さい方である。 It is assumed that the graph distance dG (x 1 , x 2 ) between the two processing data x 1 and x 2 is ∞ when x 1 and x 2 are not in the vicinity. At this time, the geodesic distance dM (ξ, ζ) between the two processing data ξ and ζ is dG (ξ, ζ) or dG (ξ, a) + dG () passing through the processing data a different from the processing data. a, ζ), whichever is smaller.
ここで、グラフ距離とは、2つの処理データx1、x2間のグラフ距離dG(x1、x2)が、x1、x2が近傍である場合、ユークリッド距離や、マンハッタン距離といった、いわゆるミンコフスキー距離である。または、マハラノビス距離といった統計的な距離である。 Here, the graph distance is a graph distance dG (x 1 , x 2 ) between the two processing data x 1 and x 2 , such as Euclidean distance and Manhattan distance when x 1 and x 2 are nearby. This is the so-called Minkowski distance. Or a statistical distance such as Mahalanobis distance.
クラス間分離度は、予め定義されたクラス間の分離度に応じて設定すればよい。このクラス間分離度は、分離度が大きい場合、つまり、ある2つのクラスの差異を強調したいなど、クラスの関係を大きく分離して表現したい場合には、その2つのクラス間におけるクラス間分離度を大きくする。逆に、分離度が小さい場合、例えば、ある2つのクラスを明確に区別しなくてもよいような、クラスの関係を大きく分離して表現しなくてもよい場合には、その2つのクラス間におけるクラス間分離度を小さくする。 What is necessary is just to set the isolation degree between classes according to the isolation degree between the classes defined beforehand. When the degree of separation between the two classes is large, that is, when the relationship between the classes is to be expressed largely separated, for example, to emphasize the difference between two classes, the degree of separation between the two classes. Increase On the other hand, when the degree of separation is small, for example, when it is not necessary to express the relationship between classes so much that the two classes do not need to be clearly distinguished, Reduce the degree of separation between classes.
また、このクラス間分離度は、クラス間の距離を求め、このクラス間の距離に基づいて、クラス間分離度を設定するようにしてもよい。この場合は、クラス間の距離が小さい時に、クラス間分離度を大きく設定するのが好適である。このようにすることにより、分離表現が比較的困難な2つのクラスを、効率よく分離表現することが可能になる。クラス間の距離を求める手法としては、クラスタ分析において一般的な、最短距離法や、最長距離法、群平均法、重心法、メジアン法、ウォード法、可変法等を用いて、クラス間の距離を求めるようにすればよい。 The interclass separation degree may be obtained by obtaining a distance between classes and setting the interclass separation degree based on the distance between the classes. In this case, when the distance between classes is small, it is preferable to set the degree of separation between classes large. By doing so, it is possible to efficiently separate and express two classes that are relatively difficult to separate. Distances between classes can be obtained by using the shortest distance method, longest distance method, group average method, centroid method, median method, Ward method, variable method, etc., which are common in cluster analysis. Should be requested.
また、2つの処理データx1、x2が近傍であるか否かは、処理データx1から距離の近いものから順番に予め設定された個数までの処理データに処理データx2が存在する場合に、2つのデータx1、x2が近傍であると判定することを特徴とする。または、2つの処理データx1、x2間の距離が予め設定された距離以内である場合に、2つの処理データx1、x2が近傍であると判定するようにしてもよい。 Whether or not the two processing data x 1 and x 2 are in the vicinity is determined when the processing data x 2 exists in the processing data up to a preset number in order from the closest to the processing data x 1. Further, it is characterized in that it is determined that the two data x 1 and x 2 are in the vicinity. Alternatively, when the distance between the two processing data x 1 and x 2 is within a preset distance, it may be determined that the two processing data x 1 and x 2 are in the vicinity.
また、距離関係の更新では、2つの処理データのそれぞれが属するクラスのクラス間分離度に比例して処理データ間の距離を更新するとともに、同クラスに属する処理データとの距離が、他クラスに属する処理データとの距離よりも小さくなるように更新する。 Also, in updating the distance relationship, the distance between the processing data is updated in proportion to the class separation of the class to which each of the two processing data belongs, and the distance from the processing data belonging to the same class is changed to the other class. Update to be smaller than the distance to the processing data to which it belongs.
同クラスに属する処理データとの距離が、他クラスに属する処理データとの距離よりも小さくなるように更新する方法としては、同クラスに属する処理データとの距離に1より小さい正の数を乗じる手法が挙げられる。また、同クラスに属する処理データとの距離を、他クラスに属する処理データとの距離よりも小さくなるような正の数とするようにしてもよい。 As a method of updating so that the distance to the processing data belonging to the same class becomes smaller than the distance to the processing data belonging to the other class, the distance to the processing data belonging to the same class is multiplied by a positive number smaller than 1. A method is mentioned. Further, the distance from the processing data belonging to the same class may be a positive number that is smaller than the distance from the processing data belonging to another class.
データ写像関係を求める手法は、写像後の空間における距離関係と更新後の距離関係の誤差を最小にする写像を求める手法である。このような手法として、多次元尺度法を用いて処理データの写像後の対応関係を求める手法が挙げられる。また、多次元尺度法を用いて処理データの写像後の対応関係を求め、その後、求めた対応関係を教師データとしてトレーニングしたニューラルネットワークを構築するような手法でもよい。このニューラルネットワークとしては、多層フィードフォワード型ニューラルネットワークを用いることができる。 The method for obtaining the data mapping relationship is a method for obtaining a mapping that minimizes an error between the distance relationship in the post-mapping space and the updated distance relationship. As such a method, there is a method for obtaining a correspondence relationship after processing data is mapped using a multidimensional scaling method. Alternatively, a method may be used in which a correspondence relationship after processing data is mapped using a multidimensional scaling method and then a neural network in which the obtained correspondence relationship is trained as teacher data is constructed. As this neural network, a multilayer feedforward type neural network can be used.
また、データ写像関係を求める手法としては、写像後の空間における距離関係と更新後の距離関係の誤差を最小にする線形写像を求めるような手法でも構わない。このような手法としては次のようなものが挙げられる。即ち、i番目、j番目の処理データをxi、xjとし、i番目、及びj番目の処理データ間の更新後の距離関係をdd(i、j)とした時、
なる誤差関数J(A)を最小化する線形写像行列Aを求める手法が挙げられる。
As a method for obtaining the data mapping relationship, a method for obtaining a linear mapping that minimizes the error between the distance relationship in the mapped space and the updated distance relationship may be used. Examples of such methods include the following. That is, when the i-th and j-th processing data are x i and x j and the updated distance relationship between the i-th and j-th processing data is d d (i, j),
A method for obtaining a linear mapping matrix A that minimizes the error function J (A) is given.
また、データ写像関係を求める手法としては、写像後の空間における距離関係と更新後の距離関係の誤差を最小にする非線形写像φ(x)を求める手法が挙げられる。ここで非線形写像φ(x)は、半正定値性を満たす実対称関数であるカーネル関数K(ξ、ζ)と、処理データxi(i=1、2、・・・)用いて、φ(x)=Σαi・K(x、xi)と表される。 As a method for obtaining the data mapping relationship, there is a method for obtaining a nonlinear mapping φ (x) that minimizes an error between the distance relationship in the post-mapping space and the updated distance relationship. Here, the nonlinear mapping φ (x) is obtained by using the kernel function K (ξ, ζ) that is a real symmetric function satisfying the semi-definite value and the processing data x i (i = 1, 2,...) (X) = Σα i · K (x, x i )
この非線形写像φ(x)は、ベクトルκiを、処理データxiに対する処理データxjとのカーネル関数値K(xi、xj)をj番目の要素とするベクトルとし、処理データxiと処理データyiと間の更新後の距離関係をdd(i、j)とした時、
なる誤差関数J(Γ)を最小化する行列Γを求め、求めた行列Γのi行目の行ベクトルを、αiとすることにより求められる。または、更に、λを正の定数、|γk|L1を行列Γのk番目の列ベクトルのL1ノルムとした時、
なる誤差関数J(Γ)を最小化する行列Γを求め、求めた行列Γのi行目の行ベクトルを、αiとするようにして求めてもよい。これらの写像を求める際に、少なくとも、写像後の距離関係の順序が、更新後の距離関係の順序を満たすようにしてもよい。
The non-linear mapping phi (x) is a vector kappa i, kernel function value K (x i, x j) of the process data x j for processing data x i and a vector whose j-th element, processing the data x i And d d (i, j) is the updated distance relationship between the processing data y i and the processing data y i
The matrix Γ that minimizes the error function J (Γ) is obtained, and the row vector of the i-th row of the obtained matrix Γ is obtained as α i . Or, further, when λ is a positive constant and | γ k | L1 is the L1 norm of the k-th column vector of the matrix Γ,
The matrix Γ that minimizes the error function J (Γ) is obtained, and the row vector of the i-th row of the obtained matrix Γ may be obtained as α i . When obtaining these mappings, at least the order of the distance relations after mapping may satisfy the order of the updated distance relations.
更に、パターン識別に適用するには、データ写像関係により写像される空間において定義可能なそれぞれ異なるクラスを識別する識別規則を示す情報を生成し、識別対象データを入力(第2の入力)して、生成した情報が示すデータ写像規則を用いて写像する。そして、写像されたデータと、生成した情報が示すデータ写像規則を用いて、識別対象データのラベルを識別する。 Furthermore, to apply to pattern identification, information indicating identification rules for identifying different classes that can be defined in the space mapped by the data mapping relationship is generated, and identification target data is input (second input). The data is mapped using the data mapping rule indicated by the generated information. And the label of identification object data is identified using the mapped data and the data mapping rule which the produced | generated information shows.
以下では、このような本発明の幾つかの実施形態について、添付図面を参照しながら詳細に説明する。なお、以下に説明する技術事項のうち幾つかを適宜選択し、適宜組み合わせて用いても良い。 Hereinafter, several embodiments of the present invention will be described in detail with reference to the accompanying drawings. Note that some of the technical matters described below may be selected as appropriate and used in appropriate combination.
[第1の実施形態]
本実施形態で取り扱う画像は、人物の顔を含む原画像からこの顔の領域を切り出すことで得られる、縦20画素、横20画素のサイズの抽出画像(パターン画像)であって、グレースケール画像であるとする。もちろん、複数の人物の顔が原画像中に含まれている場合には、パターン画像(データ)は複数存在する。また、それぞれのパターン画像中の顔領域(パターン)には、誰の顔であるのかを示すラベルが付けられている(ラベリング処理済み)。即ち、本実施形態で取り扱うこのパターン画像には、このラベルのデータも含まれているものとして説明する。
[First Embodiment]
The image handled in the present embodiment is an extracted image (pattern image) having a size of 20 pixels in length and 20 pixels in width obtained by cutting out an area of this face from an original image including a human face, and is a grayscale image. Suppose that Of course, when a plurality of human faces are included in the original image, there are a plurality of pattern images (data). In addition, a label indicating who the face is is attached to the face area (pattern) in each pattern image (labeling processing is completed). That is, the description will be made on the assumption that the pattern image handled in the present embodiment includes the data of the label.
本実施形態では、係るパターンを新たな空間上にマッピングするデータ表現方法(技術)について説明する。 In the present embodiment, a data expression method (technology) for mapping such a pattern onto a new space will be described.
縦横20画素のサイズの抽出画像は、各画素値をラスタスキャン的に要素として並べた20×20=400次元のベクトルと見なせる。この場合、1つのパターンは、400次元空間内の1つの点となる。一般に、”人物の顔”といった特定のカテゴリであるパターンの集合は、400次元の空間に比べて、より低次元の超曲面(Manifold)を形成する。つまり、“人物の顔”を表現するには、400次元は冗長であり、より低い次元の空間で表現可能である。 An extracted image having a size of 20 pixels in length and width can be regarded as a 20 × 20 = 400-dimensional vector in which pixel values are arranged as elements in a raster scan. In this case, one pattern is one point in the 400-dimensional space. In general, a set of patterns of a specific category such as “person's face” forms a lower-dimensional hypersurface than a 400-dimensional space. That is, in order to express “a person's face”, the 400th dimension is redundant and can be expressed in a lower-dimensional space.
この冗長性を削減するための、最も一般的な手法として、主成分分析(PCA)を用いた手法がある。しかし、“人物の顔”のように、例えば顔の向きの変動等、本質的に非線形な変動を含むパターンの集合に対して、パターン分布が正規分布であることを仮定しているPCAでは、充分な冗長性削減を期待できない。 As a most general method for reducing this redundancy, there is a method using principal component analysis (PCA). However, in PCA that assumes that the pattern distribution is a normal distribution for a set of patterns that include essentially non-linear variations such as “face of a person”, such as variations in face orientation, Cannot expect sufficient redundancy reduction.
そこで、非特許文献1で提案されているIsomapでは、先ず、上記非線形な超曲面上にある任意の2点のデータについて、超曲面に沿った、この2点のデータの最短距離である測地線距離を近似的に推定する。そして、多次元尺度法(Multidimensinal Scaling:MDS)を用いて、すべてのデータの組み合わせについて推定した測地線距離関係を、ユークリッド距離として近似する写像を求める。これにより、本質的に非線形な分布の集合を、冗長性を削減した、よりコンパクトな空間で表現することが可能になる。
Therefore, in Isomap proposed in
しかし、PCAも同様であるが、Isomapでは、”人物の顔”というカテゴリをコンパクトな空間で表現することを目的としているため、必ずしも、例えば、その画像が誰であるかといった分類を表現するのに適した空間になるとは限らない。そこで本実施形態では、1つのカテゴリ内を細分化する、例えば人物の種別のような分類に適した空間での表現を、データに予め付加されたラベルを用いて行う。 However, PCA is the same, but Isomap aims to express the category of “person's face” in a compact space, and therefore, for example, it always expresses a classification such as who the image is. It may not be a suitable space. Therefore, in the present embodiment, an expression in a space suitable for classification such as the type of person, for example, is performed using a label added in advance to data.
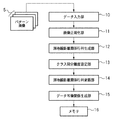
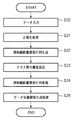
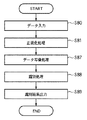
図1は、人物の顔の領域についてラベル付け(ラベリング)がなされたパターン画像を用いたデータ表現処理を行う情報処理装置の機能構成例を示すブロック図である。また、係る情報処理装置が係るパターン画像を用いて行うデータ表現処理のフローチャートを図2に示す。以下では、図1,2を用いて、係るデータ表現処理について説明する。なお、以下の説明は、パターン画像のサイズが他のサイズであっても、ラベリング対象が人物の顔以外であっても、実質的には同じである。 FIG. 1 is a block diagram illustrating an example of a functional configuration of an information processing apparatus that performs data expression processing using a pattern image that is labeled (labeled) with respect to a human face area. FIG. 2 shows a flowchart of data expression processing performed by the information processing apparatus using the pattern image. Hereinafter, the data expression process will be described with reference to FIGS. Note that the following description is substantially the same even if the size of the pattern image is another size or the labeling target is other than a human face.
ステップS20では、データ入力部10は、以上説明したような1以上のパターン画像5を入力し、後段の画像正規化部11に転送する。データ入力部10によるパターン画像の入力は、インターネットなどのネットワークを介して外部から送信されたパターン画像を受信することで行うようにしても良い。また、ハードディスクドライブ装置などの大容量情報記憶装置に保存されているパターン画像を読み出すことで行うようにしても良い。何れにせよ、本情報処理装置にパターン画像を入力する形態については特に限定するものではない。
In step S <b> 20, the
ここで、i番目にデータ入力部10に入力されたパターン画像を構成する各画素をラスタスキャン的に並べた400次元のベクトルを~xiとし、そのラベルをyiとする。従って、「N個のパターン画像をデータ入力部10に入力する」とは、~xiとyiのセットをNセットデータ入力部10に入力することに等価である(i=1、2、・・・、N)。
Here, the 400-dimensional vectors each pixel arranged in a raster scan manner constituting the i th input to the
ラベルの値は、同一人物で同じ値になるように設定するのであれば、如何なる値であっても良い。ここでは説明を簡単にするために、m人(m>1)の種別が存在するデータセットを用いる場合、yi∈{1、2、・・・、m}と、m個のクラスラベルを用いて表現するようにすればよい。 The label value may be any value as long as the same value is set for the same person. Here, for the sake of simplicity, when using a data set in which m types (m> 1) exist, y i ∈ {1, 2,..., M} and m class labels are set. It should be expressed using.
ここで、データ入力部10に入力されたデータの内、このラベルが同一であるデータの集合を、1つのクラスと定義する。また以下では、ラベルがcであるデータの集合をクラスcとする。
Here, among the data input to the
次にステップS21では、画像正規化部11は、データ入力部10から転送されたデータのうち、パターン画像に対応する~xiを正規化したxi=(~xi−ui・1)/σiを、全てのパターン画像(i)について求める。そして、求めたそれぞれのxiを保持しておく。
Next, in step S21, the
ここで、uiは、~xiベクトルの、各要素の平均値である。また、1は、全ての要素が1である、~xiと同次元、つまり400次元のベクトルである。またσiは、~xiベクトルの、各要素の標準偏差である。ここでの正規化処理は必須では無いが、一般に、本実施形態のように、データ入力部10に入力するデータが画像等の場合は、全体的な信号(ここでは各画素値)の強弱の変動による要因を排除する必要があるため、上記のような正規化を行うと良い。
Here, u i is the average value of each element of the ˜xi vector. Also, 1, all elements are 1, ~ x i and the same dimension, i.e. a 400-dimensional vector. Σ i is the standard deviation of each element of the ˜xi vector. The normalization process here is not essential, but generally, when the data input to the
ここまでの処理で、N組の、正規化後のパターン画像xiと、そのラベルyiの組が、画像正規化部11等が有するメモリに格納される。
Through the processing so far, N sets of normalized pattern images x i and their labels y i are stored in a memory included in the
次にステップS22では、測地線距離関係行列生成部12は先ず、画像正規化部11が正規化したN個のパターン画像から2つのパターン画像を取り出す。N個のパターン画像から2つのパターン画像を選択する組み合わせ数はN!/2!(N−2)!(=M)通りあるので、2つのパターン画像によるセットがMセット得られる。そして、Mセットのそれぞれのセットについて、前述のIsomapと同様に、2つのパターン画像間の測地線距離dM(i、j)(ここで、dM(i、j)は、i番目のパターン画像xiと、j番目のパターン画像xjとの間の測地線距離)を算出する。そして、M個の測地線距離dM(i、j)が得られると、測地線距離関係行列DMを求める。
In step S22, the geodesic distance relationship
測地線距離関係行列DMは、i行j列の成分が、dM(i、j)の行列であり、入力されたパターン画像数がN個であるため、N次正方行列となる。また、成分である測地線距離dM(i、j)は、dM(i、j)=dM(j、i)なので、測地線距離関係行列DMは対称行列となり、且つdM(i、i)=0なので、対角成分は全て0となる。 The geodesic distance relationship matrix DM is an N-th order square matrix because the component of i rows and j columns is a matrix of dM (i, j) and the number of input pattern images is N. Further, since the geodesic distance dM (i, j) as a component is dM (i, j) = dM (j, i), the geodesic distance relation matrix DM is a symmetric matrix and dM (i, i) = Since it is 0, all diagonal components are 0.
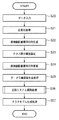
測地線距離は、前述のように、入力された多数のデータが構成するManifoldの表面に沿った、データ間の最短距離である。ここで、ステップS22において行われる、本実施形態における測地線距離の近似的な算出方法を、図3に示したフローチャートを用いて説明する。図3は、近似的な測地線距離算出の処理を示すフローチャートである。なお、図3のフローチャートに従った処理は、測地線距離関係行列生成部12が行うものとする。
As described above, the geodesic distance is the shortest distance between data along the surface of the manifold formed by a large number of input data. Here, the approximate calculation method of the geodesic distance in this embodiment performed in step S22 is demonstrated using the flowchart shown in FIG. FIG. 3 is a flowchart showing an approximate geodesic distance calculation process. Note that the processing according to the flowchart of FIG. 3 is performed by the geodesic distance relationship
先ず、ステップS320では、N個のパターン画像のうち、任意の2点間のユークリッド距離dx(i、j)を、全ての組み合わせについて算出し、ユークリッド距離関係行列Dxを求める。ここで、dx(i、j)は、i番目のパターン画像xiと、j番目のパターン画像xjとの間のユークリッド距離である。 First, in step S320, the Euclidean distance dx (i, j) between any two points of the N pattern images is calculated for all combinations to obtain the Euclidean distance relation matrix Dx. Here, dx (i, j) is the Euclidean distance between the i-th pattern image x i and the j-th pattern image x j .
ユークリッド距離関係行列Dxは、i行j列の成分が、dx(i、j)の行列であり、測地線距離関係行列DMと同様に、N次正方の対角成分が0である対称行列である。本実施形態では、ステップS320においてユークリッド距離を用いた。しかし、これに限るものではなく、例えばマンハッタン距離等のミンコフスキー距離や、マハラノビス距離といった統計的な距離等、対称性や、非負性といった、一般的な距離の公理を満たすものであれば、その他の指標を用いても構わない。 The Euclidean distance relationship matrix Dx is a symmetric matrix in which the component of i rows and j columns is a matrix of dx (i, j), and the diagonal component of the Nth order square is 0, like the geodesic distance relationship matrix DM. is there. In this embodiment, the Euclidean distance is used in step S320. However, the present invention is not limited to this. For example, a Minkowski distance such as a Manhattan distance, a statistical distance such as a Mahalanobis distance, and other general distance axioms such as symmetry and non-negativeity are satisfied. An indicator may be used.
続いて、ステップS321において、今度は、入力されたN個のパターン画像のうち、任意の2点間のグラフ距離dG(i、j)を、全ての組み合わせについて算出し、グラフ距離関係行列DGを求める。ここで、dG(i、j)は、i番目のパターン画像xiと、j番目のパターン画像xjとの間のグラフ距離である。 Subsequently, in step S321, the graph distance dG (i, j) between any two points of the input N pattern images is calculated for all combinations, and the graph distance relationship matrix DG is calculated. Ask. Here, dG (i, j) is a graph distance between the i-th pattern image x i and the j-th pattern image x j .
ここで、グラフ距離とは、例えば、i番目のパターン画像xiと、j番目のパターン画像xjと2点が近傍である場合は、dG(i、j)=dx(i、j)であり、この2点が近傍でない場合は、dG(i、j)=∞となる距離である。現実的な演算においては、∞という数値は利用できないので、∞の代わりに、任意の2つのパターン画像間のユークリッド距離に比べ、充分に大きい定数を利用すればよい。グラフ距離関係行列DGは、i行j列の成分がdG(i、j)の行列であり、やはり同様に、N次正方の対角成分が0である対称行列である。 Here, the graph distance is, for example, dG (i, j) = dx (i, j) when the i-th pattern image x i and the j-th pattern image x j are close to each other. If the two points are not in the vicinity, the distance is dG (i, j) = ∞. In a realistic calculation, since the numerical value ∞ cannot be used, a sufficiently large constant may be used instead of ∞, compared to the Euclidean distance between any two pattern images. The graph distance relationship matrix DG is a matrix whose component of i rows and j columns is dG (i, j), and is also a symmetric matrix whose N-order square diagonal component is 0 as well.
2点が近傍であるか否かは、本実施形態では、それぞれのパターン画像自身から、ステップS320において求めた距離が近いものから順に、自身を除いたk個(k≧1)のパターン画像(自身を含めると、(k+1)個のデータ)を近傍であると判定する。そして、ある2点のパターン画像で、どちらの点においても近傍であると判定されなかった場合、その2点は近傍ではないと判定する。このように本実施形態では、自身以外で、距離の近い順にk個のパターン画像を近傍としているが、例えば、距離が正の値ε以内である関係のパターン画像を近傍とするようにしても良い。この場合、εは、全てのパターン画像のそれぞれにおいて、少なくとも、自身を除く1つのパターン画像が近傍とみなされる程度に大きい値にする必要がある。しかしεが大きすぎると、本来近傍とみなすべきでないパターン画像までが、近傍とされてしまうため、あまり大きな値にすることは好ましくない。入力されたパターン画像の数等にも依存するが、通常このεは、数個程度のパターン画像が近傍とみなされる程度の大きさにしておくと良い。 In the present embodiment, whether or not two points are in the vicinity is determined in accordance with k pattern images (k ≧ 1) from which each of the pattern images itself is removed in order from the closest distance obtained in step S320 ( Including itself, it is determined that (k + 1) pieces of data) are in the vicinity. If it is determined that neither of the two points is adjacent in the pattern image of two points, it is determined that the two points are not close. As described above, in the present embodiment, the k pattern images are arranged in the order of the shortest distance except for itself. For example, a pattern image having a relationship whose distance is within the positive value ε may be set as the vicinity. good. In this case, ε needs to be set to a value that is large enough that at least one pattern image other than itself is regarded as a neighborhood in each of all pattern images. However, if ε is too large, even a pattern image that should not be regarded as a neighborhood is regarded as a neighborhood, so it is not preferable to make the value too large. Although it depends on the number of input pattern images and the like, it is usually preferable to set ε to a size that allows several pattern images to be regarded as neighboring.
ステップS322では、ステップS321で求めたグラフ距離関係行列DGに対してFloyd−Warshall法を用い、入力されたN個のパターン画像のうち任意の2点間の前述の測地線距離dM(i、j)を、全ての組み合わせについて算出する。これにより、測地線距離関係行列DMを求める。Floyd−Warshall法によりi番目のパターン画像xiと、j番目のパターン画像xjの2点間の測地線距離dM(i、j)は、dM(i、j)=min{dG(i、j)、dG(i、k)+dG(k、j)}、k≠i、jのように計算される。 In step S322, the above-mentioned geodesic distance dM (i, j between any two points of the input N pattern images is used by using the Floyd-Warshall method for the graph distance relation matrix DG obtained in step S321. ) Is calculated for all combinations. Thereby, a geodesic distance relationship matrix DM is obtained. The geodesic distance dM (i, j) between two points of the i-th pattern image x i and the j-th pattern image x j by the Floyd-Warshall method is dM (i, j) = min {dG (i, j), dG (i, k) + dG (k, j)}, k ≠ i, j.
以上のステップS320〜ステップS322までの処理により、測地線距離関係行列DMを求めることができる。 The geodesic distance relationship matrix DM can be obtained by the processing from step S320 to step S322.
次に、ステップS23では、クラス間分離度設定部13がクラス間分離度設定処理を行う。以下に、クラス間分離度設定部13が行う処理について詳細に説明する。
Next, in step S23, the interclass separation
クラス間分離度設定部13は、クラス間分離度ν(cp、cq)を設定する。ここで、cp、及びcqは、クラスラベルであり、本実施形態では、m人の種別が存在するパターン画像セットを用いるので、cp、cq∈{1、2、・・・、m}となり、クラス間分離度ν(cp、cq)には、m×mの組み合わせが存在する。このクラス分離度ν(cp、cq)は、クラスcpと、クラスcq間の分離表現度合いを表しており、そのクラス間の所望の分離度合いに応じて設定する。具体的には、分離度合いを高めたい場合は、このクラス分離度を1より大きく設定し、分離度合いを下げたい場合は1より小さく設定する。また、特に分離度合いを変更する必要がない場合は、このクラス分離度は1に設定する。ここでの分離度合いとは、前述のように、クラス間の差異の強調度合いであり、例えばクラスcpと、クラスcqの差異を強調して表現したい場合には、この2つのクラス間のクラス間分離度ν(cp、cq)を1より大きく設定するようにすればよい。
The interclass separation
この定義のように、クラス間分離度は、可換な2クラス間の関係により設定するものであるため、対称性ν(cp、cq)=ν(cq、cp)を満たす。また、同クラス間のクラス間分離度ν(cp、cp)は、実際には用いないため任意であり、単純に1に設定しておけばよい。 As in this definition, the degree of separation between classes is set by the relationship between two commutative classes, and therefore satisfies the symmetry ν (cp, cq) = ν (cq, cp). Further, the inter-class separation degree ν (cp, cp) between the same classes is arbitrary because it is not actually used, and may be simply set to 1.
次に、本実施形態におけるクラス分離度の設定方法について説明する。本実施形態では、各クラスの分離表現を促進するために、以下の手法により、類似したクラス間のクラス間分離度を1より大きく設定し、類似していないクラス間のクラス間分離度は1に設定する。 Next, a method for setting the class separation degree according to this embodiment will be described. In this embodiment, in order to promote the separated expression of each class, the class separation degree between similar classes is set to be larger than 1 by the following method, and the class separation degree between dissimilar classes is 1. Set to.
まず、全クラスから2クラスを選択する全ての組み合わせにおいて、その2クラスが類似しているか否かの判定を行う。2クラスが類似しているか否かの判定方法としては様々な方法が考えられるが、本実施形態では、クラスタ分析で一般的な最短距離法を用いてクラス間の距離を算出し、そのクラス間の距離が閾値より小さい場合に、その2クラスが類似していると判定する。そして、類似していると判定された2クラス間のクラス間分離度を1より大きく設定する。本実施形態では、具体的には、上記閾値を、求めたクラス間の距離で除算した値を、クラス間分離度として設定する。類似していると判定されるクラス間の距離は、上記閾値より小さいので、この値は必ず1より大きい値となる。また、類似していると判定されなかった2クラス間のクラス間分離度は1に設定する。 First, in all combinations in which two classes are selected from all classes, it is determined whether or not the two classes are similar. Various methods can be considered as a method for determining whether two classes are similar. In this embodiment, the distance between classes is calculated using a general shortest distance method in cluster analysis, and between the classes. If the distance is smaller than the threshold, it is determined that the two classes are similar. Then, the degree of class separation between two classes determined to be similar is set to be greater than one. In the present embodiment, specifically, a value obtained by dividing the threshold value by the obtained distance between classes is set as the degree of class separation. Since the distance between classes determined to be similar is smaller than the above threshold, this value is always greater than 1. Further, the degree of class separation between two classes that are not determined to be similar is set to 1.
上記閾値は、例えば兄弟等の類似している人物の顔が類似していると判定されるような値を実験的に予め求めておき、それを用いるようにすればよい。また、本実施形態では、最短距離法を用いてクラス間の距離を算出するが、最長距離法や、群平均法、重心法、メジアン法、ウォード法、可変法等、その他のクラス間の距離を算出する手法を用いても構わない。更に、類似したクラス間のクラス間分離度として、上記閾値を、求めたクラス間の距離で除算した値を設定するが、例えば1以上の値を設定する等、1より大きくなるような設定方法であれば、その他の方法であっても構わない。 For the threshold value, for example, a value that is determined to be similar for faces of similar persons such as siblings may be experimentally obtained in advance and used. In this embodiment, the distance between classes is calculated using the shortest distance method, but the distance between other classes such as the longest distance method, group average method, centroid method, median method, Ward method, variable method, etc. You may use the method of calculating. Further, as a degree of class separation between similar classes, a value obtained by dividing the above threshold value by the obtained distance between classes is set. Any other method may be used.
以上のように、本実施形態では、クラス間の距離に基づいてクラス間分離度を設定するが、これに限るものではなく、予めクラスラベルに与えられた情報に基づいて、クラス間分離度を設定するようにしても構わない。例えば、予めA氏とB氏が双子であるという情報が与えられていれば、A氏とB氏という2つのクラス間のクラス間分離度を1より大きい適当な値に設定するようにしてもよい。 As described above, in the present embodiment, the degree of class separation is set based on the distance between classes. However, the present invention is not limited to this, and the degree of class separation is determined based on information given to class labels in advance. You may make it set. For example, if information that Mr. A and Mr. B are twins is given in advance, the degree of class separation between two classes, Mr. A and Mr. B, may be set to an appropriate value greater than 1. Good.
また、クラス間分離度の設定は、類似するクラス間のクラス間分離度を高めるという設定方法に限るものではなく、その他の設定方法を用いることも可能である。例えば、所定のクラスcpを、その他のクラスcq(q≠p)と明確に分離表現したいような場合は、ν(cp、cq)[∀q、q≠p]を全て1より大きい値に設定し、その他を全て1に設定するというような設定方法が挙げられる。また、クラスcpとcqを、明確に区別する必要がないような場合は、ν(cp、cq)のみを1より小さい値に設定し、その他は全て1に設定するというような設定方法でも構わない。このように、本実施形態で説明するデータ表現方法では、各クラス間の所望の分離度合いに応じて、任意にクラス間分離度を設定することが可能である。 Further, the setting of the degree of class separation is not limited to the setting method of increasing the degree of class separation between similar classes, and other setting methods can be used. For example, if a predetermined class cp is to be clearly expressed separately from other classes cq (q ≠ p), ν (cp, cq) [、 q, q ≠ p] are all set to a value greater than 1. However, there is a setting method in which all others are set to 1. Further, when there is no need to clearly distinguish between classes cp and cq, a setting method may be used in which only ν (cp, cq) is set to a value smaller than 1 and all others are set to 1. Absent. As described above, in the data expression method described in the present embodiment, it is possible to arbitrarily set the degree of separation between classes according to the desired degree of separation between classes.
次にステップS24では、測地線距離関係行列更新部14は、歪曲測地線距離dd(i、j)を算出し、歪曲測地線距離関係行列Ddを算出する。ここで、dd(i、j)は、測地線距離関係行列生成部12において求めたi番目のパターン画像xiと、j番目のパターン画像xjとの間の歪曲測地線距離を示す。また、歪曲測地線距離dd(i、j)は、i番目のパターン画像xiと、j番目のパターン画像xjとの間の測地線距離dM(i、j)を、ラベルyi及びyjと、クラス間分離度ν(yi、yj)に基づき更新したものである。
Next, in step S24, the geodesic distance relationship
本実施形態では、この歪曲測地線距離dd(i、j)を、dd(i、j)=dM(i、j)・[ν(yi、yj)−{ν(yi、yj)−β}・δyi、yj]のように求める。ここで、δi、jは、クロネッカーのδ記号で、i=jの時、δi、j=1、i≠jの時、δi、j=0である。また、係数βは、1より小さい正の数である。即ち、歪曲測地線距離dd(i、j)は、i番目のデータxiと、j番目のデータxjが、同一のラベル、つまり、同一のクラスに属する場合は、dd(i、j)=β・dM(i、j)となり、測地線距離dM(i、j)より小さくなる。 In the present embodiment, this distorted geodesic distance dd (i, j) is expressed as dd (i, j) = dM (i, j). [Ν (y i , y j ) − {ν (y i , y j )-[Beta]}. Delta.yi, yj ]. Here, δ i, j is the Kronecker δ symbol. When i = j, δ i, j = 1, and when i ≠ j, δ i, j = 0. The coefficient β is a positive number smaller than 1. That is, the distorted geodesic distance dd (i, j) is dd (i, j) when the i-th data x i and the j-th data x j belong to the same label, that is, the same class. = Β · dM (i, j), which is smaller than the geodesic distance dM (i, j).
一方、同一のラベルでない、つまり異なるクラスに属する場合は、dd(i、j)=dM(i、j)・ν(yi、yj)となる。従って、歪曲測地線距離dd(i、j)は、測地線距離dM(i、j)に、クラス間分離度ν(yi、yj)を乗じたものになる。 On the other hand, when they are not the same label, that is, belong to different classes, dd (i, j) = dM (i, j) · ν (y i , y j ). Accordingly, the distorted geodesic distance dd (i, j) is obtained by multiplying the geodesic distance dM (i, j) by the interclass separation ν (y i , y j ).
また、2つのデータが同一クラスである場合に乗じる係数βは、以下の条件を満たす値を求め、それを設定する。この条件は、同一クラスである任意の2つのパターン画像xi、xjと、この2つのパターン画像とは異なるクラスの任意のパターン画像xcにおいて、dd(i、j)=β・dM(i、j)<dd(i、c)=dM(i、c)・ν(yi、yc)を満たすことである。つまり、同クラスである2つのパターン画像間の歪曲測地線距離は、異なるクラスの任意のパターン画像との距離より小さくなるようにすれば良い。究極的には、β=0とすることで、必ず上記関係を満たすことができるが、後述のデータ写像関係生成部15における処理において不都合を生じさせる可能性が高くなるため、β>0である値を設定するようにする。
Further, the coefficient β to be multiplied when the two data are of the same class is obtained by setting a value satisfying the following condition. This condition is that dd (i, j) = β · dM () in any two pattern images x i and x j of the same class and in any pattern image x c of a class different from the two pattern images. i, j) <dd (i, c) = dM (i, c) · ν (y i , y c ). That is, the distorted geodesic distance between two pattern images of the same class may be made smaller than the distance from any pattern image of a different class. Ultimately, by setting β = 0, the above relationship can be satisfied, but β> 0 because there is a high possibility of causing inconvenience in processing in the data mapping
本実施形態に係るデータ表現方法では、上記のように、同一のクラスであるパターン画像間の距離が、異なるクラスであるパターン画像との距離よりも小さくなるように、パターン画像間の距離関係を更新する。また、その上記条件において、異なるクラスのパターン画像間の距離は、設定したクラス間分離度に基づいて更新される。これにより、パターン画像のクラス内での連続的な変動、例えばパターン画像が“人物の顔”の画像であれば、正面向きから横向きに変化するような、原特徴空間における非線形で連続的な変動を変動の軸方向に凝集させた距離関係を構築することになる。また、各クラス間の関係については、所望のクラスの分離度合いに基づいた距離関係を構築することになる。本実施形態では、上記同一のクラスであるパターン画像間における距離関係の更新を、同一クラスであるパターン画像間距離に、係数βを乗じて更新することによって行う。 In the data expression method according to the present embodiment, as described above, the distance relationship between pattern images is set so that the distance between pattern images that are the same class is smaller than the distance between pattern images that are different classes. Update. Further, under the above conditions, the distance between pattern images of different classes is updated based on the set degree of separation between classes. As a result, continuous fluctuations within the class of pattern images, for example, if the pattern image is a “person's face” image, non-linear and continuous fluctuations in the original feature space that change from front to side A distance relationship is constructed by agglomerating in the axial direction of fluctuation. As for the relationship between the classes, a distance relationship based on the desired degree of class separation is constructed. In the present embodiment, the distance relationship between pattern images of the same class is updated by multiplying the distance between pattern images of the same class by a coefficient β.
しかし、パターン画像間における距離関係の更新は、これに限るものではなく、同一のクラスであるパターン画像間の距離が、異なるクラスであるパターン画像との距離よりも小さくなるような更新手法であれば、その他の方法を用いても構わない。例えば、同一クラスである全てのパターン画像間の距離を、異なるクラスのパターン画像との距離より小さい、定数ρに更新するようにしても構わない。 However, the updating of the distance relationship between pattern images is not limited to this, and any updating method in which the distance between pattern images of the same class is smaller than the distance between pattern images of different classes. For example, other methods may be used. For example, the distance between all pattern images of the same class may be updated to a constant ρ that is smaller than the distance from pattern images of different classes.
次にステップS25では、データ写像関係生成部15は、測地線距離関係行列更新部14が算出した歪曲測地線距離関係行列Ddを用い、全てのパターン画像xiそれぞれに対応する写像先である、出力ベクトルziを求める。
Next, in step S25, the data mapping
以下では、測地線距離関係行列更新部14が算出したi番目のパターン画像xiに対応する出力ベクトルziを、i番目の出力ベクトルziと表記する。ここで出力ベクトルは、i番目の出力ベクトルziと、j番目の出力ベクトルzjのユークリッド距離dz(i、j)が、i番目のパターン画像xiと、j番目のパターン画像xjの歪曲測地線距離dd(i、j)の近似となるように求められる。本実施形態では、前述のIsomapと同様に、多次元尺度法(MDS)を用いて、このような出力ベクトルを求める(MDSを用いた出力ベクトルの算出法については、非特許文献1を参照)。
Hereinafter, the output vector z i corresponding to the i-th pattern image x i calculated by the geodesic distance relationship
通常、可視化を目的としてMDSを用いる場合、出力ベクトルを3次元以下とするが、本実施形態に係るデータ表現方法は、特に可視化を目的としているわけではないため、出力ベクトルは、4次元以上であっても構わない。この出力ベクトルの次元を非常に高くすれば、上記距離の近似を比較的厳密に行うことができる。しかし、データの冗長性を削減するという目的では、入力データ(パターン画像)の次元(本実施形態では、400次元)より小さくなるように、可能な限り出力ベクトルの次元を小さくする方が良い。 Usually, when MDS is used for the purpose of visualization, the output vector is three dimensions or less. However, since the data representation method according to the present embodiment is not particularly intended for visualization, the output vector is four dimensions or more. It does not matter. If the dimension of this output vector is made very high, the distance can be approximated relatively accurately. However, for the purpose of reducing data redundancy, it is better to make the dimension of the output vector as small as possible so as to be smaller than the dimension of the input data (pattern image) (400 dimensions in this embodiment).
そこで本実施形態では、入力された全パターン画像のペアの、それぞれの距離誤差率のうち、最大の距離誤差率が所定値以下である最小の次元で出力ベクトルを求めるようにする。ここで、i番目のデータと、j番目のデータの距離誤差率は、|dd(i、j)−dz(i、j)|/dd(i、j)である。ここで用いる最大の距離誤差率の許容範囲は、入力されたパターン画像のカテゴリ等に依存するが、例えば10%以下というようにすれば良い。また、本実施形態では、最大の距離誤差率が、予め設定された値以下になるような最小の次元を出力ベクトルの次元として用いた。しかしながら、これに限るものではなく、例えば距離誤差率の総和が予め設定された値以下になるような最小の次元を、出力ベクトルの次元としても良い。 Therefore, in the present embodiment, an output vector is obtained with a minimum dimension in which the maximum distance error rate is equal to or less than a predetermined value among the distance error rates of all pairs of input pattern images. Here, the distance error rate between the i-th data and the j-th data is | dd (i, j) −dz (i, j) | / dd (i, j). The allowable range of the maximum distance error rate used here depends on the category or the like of the input pattern image, but may be set to 10% or less, for example. In the present embodiment, the minimum dimension such that the maximum distance error rate is equal to or less than a preset value is used as the dimension of the output vector. However, the present invention is not limited to this. For example, the minimum dimension such that the sum of the distance error rates is not more than a preset value may be set as the dimension of the output vector.
以上説明したデータ入力部10からデータ写像関係生成部15までの各部における処理により、ラベル付きの各パターン画像について、~xi→xi→ziという対応関係を得ることができる。これにより、全パターン画像について、冗長性を削減した出力ベクトルziの次元の空間において、出力ベクトルziが、同クラスであるパターン画像間で近づく。つまり、1つのクラスタとして表現され、尚且つ、各クラスに対応するクラスタを、所望の分離度合いで表現することが可能になる。
By the processing in each unit from the
そしてデータ写像関係生成部15はその後、ラベル付きの各パターン画像について求めた~xi→xi→ziという対応関係を示す情報をメモリ16に格納する。係る情報の表現方法については特に限定するものではないが、例えば、~xiのファイル名、xiのファイル名、ziのファイル名をこの順番で関連付けたファイルを作成しても良い。
The data mapping
本実施形態では、パターン画像として、人物の顔を切り出したグレースケール画像と、それが何れの人物であるのかのラベルを用いたが、これに限るものではない。例えば、パターン画像の代わりに、予め設定された単語を発話した音声データと、その単語をラベルとするデータを用いても良い。更には、HTMLで記述されたWebページと、そのコンテンツカテゴリをラベルとしたものであっても良い。即ち、ラベル付けされた元のデータ間で、類似度を反映する何らか距離を定義できるものであれば、どのようなデータであっても、本実施形態は適用可能である。 In the present embodiment, as the pattern image, a grayscale image obtained by cutting out a person's face and a label indicating which person it is are used. However, the present invention is not limited to this. For example, instead of the pattern image, voice data that utters a preset word and data with the word as a label may be used. Furthermore, a web page described in HTML and its content category may be used as a label. That is, the present embodiment can be applied to any data as long as it can define some distance that reflects the similarity between the labeled original data.
[第2の実施形態]
本実施形態では、第1の実施形態で示したデータ表現方法を応用する。本実施形態では、人物の顔を含む原画像からこの顔の領域を切り出すことで得られる縦20画素、横20画素のサイズの抽出画像(パターン画像)であって、グレースケール画像であるパターン画像を入力し、それが何れの人物を含むものであるのかを識別する。もちろん、この入力するパターン画像には、第1の実施形態で説明したようなラベリング処理は行っていない。
[Second Embodiment]
In the present embodiment, the data expression method shown in the first embodiment is applied. In the present embodiment, a pattern image which is an extracted image (pattern image) having a size of 20 pixels in the vertical direction and 20 pixels in the horizontal direction obtained by cutting out the face area from the original image including the face of the person, and is a grayscale image. To identify which person it contains. Of course, the input pattern image is not subjected to the labeling process as described in the first embodiment.
本実施形態は、学習モードと識別モードの2つモードから構成される。 This embodiment includes two modes, a learning mode and an identification mode.
学習モードでは、第1の実施形態で取り扱ったパターン画像、即ち、ラベリング処理済みのパターン画像を用いてデータ写像関係を近似的に構築し、その写像先の空間で、各ラベルに対応するクラスのモデルを生成する。 In the learning mode, the data mapping relationship is approximately constructed using the pattern images handled in the first embodiment, that is, the pattern images that have been labeled, and the class corresponding to each label is mapped in the mapping destination space. Generate a model.
識別モードでは先ず、学習モードで構築したデータ写像関係を用いて、ラベリング処理がなされていないパターン画像を写像する。そして写像先の空間で、学習モードで生成した、各ラベルに対応するクラスのモデルを用い、その画像が、何れの人物の顔画像であるかを識別する。 In the identification mode, first, a pattern image that has not been labeled is mapped using the data mapping relationship constructed in the learning mode. In the mapping destination space, a model of a class corresponding to each label generated in the learning mode is used to identify which person's face image the image is.
<学習モード>
図4は、本実施形態に係る情報処理装置を構成する各部のうち、学習モード時において動作する各部についてのみ、その機能構成を示したブロック図である。なお、図4において、図1に示した構成と共通の部分については、同じ番号を付けており、その説明は省略する。
<Learning mode>
FIG. 4 is a block diagram illustrating the functional configuration of only the units that operate in the learning mode among the units that configure the information processing apparatus according to the present embodiment. In FIG. 4, the same reference numerals are given to portions common to the configuration shown in FIG. 1, and description thereof is omitted.
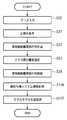
図5は、本実施形態に係る情報処理装置が学習モード時に行う処理のフローチャートである。なお、図5において、図2に示した構成と共通の部分については、同じ番号を付けており、その説明は省略する。 FIG. 5 is a flowchart of processing performed by the information processing apparatus according to the present embodiment in the learning mode. In FIG. 5, the same reference numerals are given to portions common to the configuration shown in FIG. 2, and description thereof is omitted.
以下、図4,5を用いて、学習モード時における処理について説明する。 Hereinafter, the processing in the learning mode will be described with reference to FIGS.
本実施形態では、N個のパターン画像(第1の実施形態で取り扱ったパターン画像と同じで、ラベリング処理済みのパターン画像)を入力し、入力したそれぞれのパターン画像について第1の実施形態と同様の処理を行う。これにより、各パターン画像に対する出力ベクトル(本実施形態ではこの出力ベクトルの次元数がhであったとする)を求める。ここまでの処理については、第1の実施形態での処理と同様であるので、説明を省略する。 In the present embodiment, N pattern images (the same as the pattern images handled in the first embodiment, which have been subjected to labeling processing) are input, and each input pattern image is the same as in the first embodiment. Perform the process. Thereby, an output vector for each pattern image (in this embodiment, the number of dimensions of the output vector is h) is obtained. Since the processing so far is the same as the processing in the first embodiment, the description thereof is omitted.
データ写像関係生成部15までの処理により、i=1、2、・・・、Nまでの任意のiにおけるラベルyi、正規化後ベクトルxi、出力ベクトルziの、3つから構成されるデータセット(トレーニングデータセット)が得られる。このトレーニングデータセットを用いて、近似システム構築処理部46は、xi→ziという写像を近似するシステムを構築する。本実施形態では、この写像を近似するシステムとして、3層のフィードフォワードニューラルネットワーク(3層NN)を用いる。
By the processing up to the data mapping
この3層NNは、入力層、中間層、出力層の3層構造になっており、それぞれの層が複数のニューロンを有する。 The three-layer NN has a three-layer structure of an input layer, an intermediate layer, and an output layer, and each layer has a plurality of neurons.
入力層のニューロン数は、正規化後ベクトルの次元数400次元と同一の400個であり、これらの入力層のニューロンは、3層NNへの入力データである400次元のベクトルの各要素値を、それぞれの状態値とする。 The number of neurons in the input layer is 400, which is the same as the 400-dimensional dimension of the normalized vector, and these input layer neurons have each element value of the 400-dimensional vector as input data to the 3-layer NN. , Each state value.
中間層のニューロン数は、データ写像関係生成部15での処理において決まり、これらの中間層のニューロンは、入力層の全ニューロンと結合する。
The number of neurons in the intermediate layer is determined by the processing in the data mapping
ここで結合とは、ある重みを持っており、結合先ニューロン(中間層のニューロンであれば、入力層のニューロン)の状態値に、その重みを乗じたものを入力として受け取るものである。中間層のニューロンは、受け取った全ての入力の総和を取り、そこから予め設定された値(閾値)を差し引いた値に、予め設定された非線形変換を行った値を状態値とする。これらの重みの値や閾値は、初期の状態ではランダムな値を設定しておき、後述する近似システム構築処理部46での処理において値が確定する。また、上記非線形変換は、いわゆるシグモイド関数を用いた変換が一般的であり、本実施形態では、この非線形変換として、双曲線正接関数(f(u)=tanh(u))を用いる。
Here, the connection has a certain weight and receives as input the state value of the connection destination neuron (in the case of an intermediate layer, the neuron of the input layer) multiplied by the weight. The neurons in the intermediate layer take the sum of all received inputs, and use a value obtained by performing a preset nonlinear transformation as a value obtained by subtracting a preset value (threshold value) from the sum. Random values are set for these weight values and threshold values in the initial state, and the values are determined in the processing in the approximate system
出力層のニューロン数は、出力ベクトルの次元数と同一の個数であり、これらの出力層のニューロンは、中間層の全ニューロンと結合する。出力ベクトルの次元数は前述のように、データ写像関係生成部15における処理により決まり、ここでは上述のように、出力ベクトルの次元数がhであったとしたので、出力層のニューロン数はh個となる。
The number of neurons in the output layer is the same as the number of dimensions of the output vector, and these output layer neurons are connected to all the neurons in the intermediate layer. As described above, the number of dimensions of the output vector is determined by the processing in the data mapping
出力層のニューロンは、中間層のニューロンと同様に、結合先のニューロン(ここでは中間層のニューロン)の状態値に、結合ごとの重みを乗じた値を入力として受け取る。そして、受け取った全ての入力の総和を取り、そこから閾値を差し引いた値を状態値、つまり出力値とする。このように、出力層のニューロンは、中間層のニューロンとは異なり、非線形変換を行わない。 Similarly to the intermediate layer neuron, the output layer neuron receives, as an input, a value obtained by multiplying the state value of the connection destination neuron (here, the intermediate layer neuron) by the weight for each connection. Then, the sum of all received inputs is taken, and a value obtained by subtracting the threshold value from the sum is used as a state value, that is, an output value. Thus, unlike the neurons in the intermediate layer, the neurons in the output layer do not perform nonlinear conversion.
中間層のニューロンからの結合の重みの値や閾値に関しても、中間層のニューロンと同様に、初期の状態ではランダムな値を設定しておき、この近似システム構築処理部46での処理において値が確定する。
As for the connection weight value and threshold value from the neurons in the intermediate layer, as in the case of the neurons in the intermediate layer, a random value is set in the initial state, and the value is set in the processing by the approximate system
上記3層構造の演算システムを用い、400次元のベクトルの各要素値を、入力層の400個のニューロンのそれぞれの状態値として設定する(以下では単に、3層NNへ入力すると記す)ことで、出力層の、h個のニューロンの状態値が得られる。このh個のニューロンの状態値を、h次元のベクトルの各要素値と考えると、この3層NNを用いた演算により、400次元ベクトルから、h次元ベクトルへの写像が行われるとみなせる。 Using the above three-layer arithmetic system, each element value of a 400-dimensional vector is set as the state value of each of the 400 neurons in the input layer (hereinafter simply described as being input to the three-layer NN). The state values of h neurons in the output layer are obtained. If the state values of the h neurons are considered as the element values of the h-dimensional vector, it can be regarded that the mapping from the 400-dimensional vector to the h-dimensional vector is performed by the calculation using the three-layer NN.
ここで、上述したように、結合の重みの値や閾値を様々に変更することで、中間層のニューロンの数にも依存するが、任意の写像を、任意の精度で近似できることが知られている。そこで本実施形態では、この3層NNを用い、結合の重みの値や閾値を調整することで、上記トレーニングデータセットの、任意のiにおけるxi→ziという写像、つまり、正規化後ベクトルから出力ベクトルへの写像を近似する。 Here, as described above, it is known that an arbitrary mapping can be approximated with an arbitrary accuracy, depending on the number of neurons in the intermediate layer, by variously changing the value of the connection weight and the threshold. Yes. Therefore, in the present embodiment, by using the three-layer NN and adjusting the value of the connection weight and the threshold value, the mapping of the training data set x i → z i at an arbitrary i, that is, the normalized vector Approximate the mapping from to the output vector.
図5において、ステップS56では、近似システム構築処理部46が写像を近似するシステムを構築する処理を行う。
In FIG. 5, in step S56, the approximate system
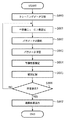
以下では、ステップS56において近似システム構築処理部46が行う処理、即ち、3層NNの結合の重みの値や閾値の調整、及び中間層のニューロン数の決定について、同処理のフローチャートを示す図6を用いて説明する。
In the following, the processing performed by the approximate system
先ず、ステップS660では、データ写像関係生成部15までの処理により得られた前述のトレーニングデータセット(ラベル、正規化後ベクトル、出力ベクトルの3つを1組とするN組のデータセット)を、2つのセットに分割する。この2つのセットのうち、1つは、結合の重みの値や閾値の調整に用い、以下では、このセットを、調整用セットとする。もう1つのセットは、後述のステップS664における検定に用い、以下では、このセットを検定用セットとする。
First, in step S660, the above-described training data set (N sets of data including three of the label, the normalized vector, and the output vector) obtained by the processing up to the data mapping
分割の際には、N組のトレーニングデータから、M組(0<M<N)をランダムに選択し、それらを検定用セットとする。そして、残りの(N−M)組が、調整用セットとなる。Mの値は、任意であるが、本実施形態では、Nの30%とする。ここで、この2つのセットの両方において、全てのラベルそれぞれのデータが、少なくとも1つ存在することが好ましい。そこで本実施形態では、もし、どちらかのセットにおいて、あるラベルのデータが1つも存在しない場合は、もう一度ランダムに選択をやり直すようにする。 At the time of division, M sets (0 <M <N) are randomly selected from N sets of training data, and these are set as a test set. The remaining (N−M) pairs are adjustment sets. Although the value of M is arbitrary, in this embodiment, it is 30% of N. Here, in both of these two sets, it is preferable that there is at least one data of each label. Therefore, in this embodiment, if there is no data of a certain label in either set, the selection is performed again at random.
続いてステップS661では、中間層のニューロンの数を設定する。最初は中間層のニューロンの数を予め定めた数に設定する。そして、後述するステップS666における判定により、再度ステップS661に戻ってきた場合に、中間層のニューロンの数を1つ増加させる。最初に設定する中間層のニューロンの数は任意であるが、初めはできるだけ少ない数にしておくことが好ましい。そこで、本実施形態では、初期の中間層のニューロンの数を2とする。 In step S661, the number of intermediate layer neurons is set. Initially, the number of neurons in the intermediate layer is set to a predetermined number. Then, when the process returns to step S661 again by the determination in step S666 described later, the number of neurons in the intermediate layer is increased by one. The number of neurons in the intermediate layer to be initially set is arbitrary, but it is preferable to initially set the number as small as possible. Therefore, in the present embodiment, the number of neurons in the initial intermediate layer is two.
次に、ステップS662では、全ての結合の重みの値と閾値をランダムな値に初期化する。ここでは、後のステップS663での処理における初期値依存性を低減するために、全ての値をほぼ0とみなせる程度に小さな値にすることが好ましい。 In step S662, the weight values and threshold values of all the connections are initialized to random values. Here, in order to reduce the dependency on the initial value in the subsequent processing in step S663, it is preferable to set all values to a value that can be regarded as almost zero.
ステップS663では、ステップS662で初期化した結合の重みの値と閾値からスタートし、調整用セットを用いた結合の重みの値と閾値の調整を行い、調整用セット内の、正規化後ベクトルから出力ベクトルという写像を近似した3層NNを構築する。ここでは、調整用セットの中の全ての正規化後ベクトルそれぞれを3層NNに入力した時に、出力層のh個のニューロンのそれぞれの状態値が、それぞれに対応する出力ベクトルの各要素値に近づくように、結合の重みの値と閾値の調整を行う。この調整では、多層フィードフォワードニューラルネットワークの学習手法として一般的な、誤差逆伝播法を用いる。誤差逆伝播法を用いた、結合の重みの値と閾値の調整手法の詳細は、S. Haykin, “Neural Networks A Comprehensive Foundation 2nd Edition”, Prentice Hall, pp. 156-255, July 1998を参照されたい。 In step S663, the value of the connection weight and the threshold value initialized in step S662 are started, the value of the connection weight and the threshold value are adjusted using the adjustment set, and the normalized vector in the adjustment set is used. A three-layer NN approximating the mapping of output vectors is constructed. Here, when all the normalized vectors in the adjustment set are input to the third layer NN, the state values of the h neurons in the output layer are changed to the element values of the corresponding output vectors. The values of the connection weight and the threshold are adjusted so as to approach each other. In this adjustment, a general error back-propagation method is used as a learning method for the multilayer feedforward neural network. See S. Haykin, “Neural Networks A Comprehensive Foundation 2nd Edition”, Prentice Hall, pp. 156-255, July 1998, for details on how to adjust the value of the connection weight and threshold using the backpropagation method. I want.
そしてこの調整を、調整用セットの中の全ての正規化後ベクトルそれぞれを3層NNに入力した時に得られる出力層のh個のニューロンの状態値と、それぞれに対応する出力ベクトルの各要素値との誤差が収束した段階で終了する。本実施形態では、この誤差として、出力層のh個のニューロンの状態値と、対応する出力ベクトルの各要素値の2乗誤差総和を用いる。また、誤差が収束したか否かの判定は、誤差逆伝播法を用いた、予め設定されたステップ数の調整において、ほぼ誤差が減少しなくなった時(例えば、誤差の減少率が1%以下であった時など)に、誤差が収束したと判定する。判定に用いる「予め設定されたステップ数」は任意に設定すればよいが、これが小さすぎると、本来は収束していないのに、誤って収束したと判定してしまう可能性が高くなる。しかし、これが大きすぎると、収束判定がなされない可能性が高くなるので、確実に収束判定がなされるような値を実験的に決めて設定するようにすれば良い。 Then, this adjustment is performed with the state values of the h neurons in the output layer obtained when all the normalized vectors in the adjustment set are input to the third layer NN, and the element values of the corresponding output vectors. The process ends when the error between and has converged. In the present embodiment, as this error, the sum of square errors of the state values of h neurons in the output layer and each element value of the corresponding output vector is used. Further, whether or not the error has converged is determined when the error is almost not reduced in the adjustment of the preset number of steps using the error back propagation method (for example, the error reduction rate is 1% or less). It is determined that the error has converged. The “preset number of steps” used for the determination may be arbitrarily set. However, if the number is too small, there is a high possibility that it is determined that the convergence has been erroneously performed although it has not originally converged. However, if this is too large, there is a high possibility that the convergence determination will not be made. Therefore, it is only necessary to experimentally determine and set a value that ensures the convergence determination.
以上説明したステップS663における処理により、中間層のニューロン数が、ステップS661で設定した数の場合の3層NNを用いた、調整用セット内の正規化後ベクトルから出力ベクトルという写像を近似する3層NNの構築が完了する。 By the processing in step S663 described above, the mapping of the output vector from the normalized vector in the adjustment set using the three-layer NN when the number of neurons in the intermediate layer is the number set in step S661 is approximated 3 The construction of the layer NN is completed.
ステップS664では、検定用セットを用いて、ステップS663において構築した3層NNの写像性能を評価する。ここではまず、ステップS663において構築した3層NNに、検定用セット内の全ての正規化後ベクトルをそれぞれ入力し、それぞれの入力に対応する出力層のh個のニューロンの状態値を得る。そして、得られた各h個の状態値と、入力した正規化後ベクトルに対応する、検定用セット内の出力ベクトルの各要素値との2乗誤差総和を求める。この2乗誤差が小さい程、未知の正規化後データに対して所望の写像を行う性能が高いと言える。そこで、この2乗誤差総和を、ステップS663において構築した3層NNの写像性能の評価値として用いる。つまり、この評価値が小さいほど、写像性能が高いと判断できる。 In step S664, the mapping performance of the three-layer NN constructed in step S663 is evaluated using the test set. Here, first, all normalized vectors in the test set are input to the three-layer NN constructed in step S663, and the state values of h neurons in the output layer corresponding to the respective inputs are obtained. Then, the sum of square errors between the obtained h state values and each element value of the output vector in the test set corresponding to the input normalized vector is obtained. It can be said that the smaller this square error is, the higher the performance of performing a desired mapping on unknown post-normalization data. Therefore, this sum of square errors is used as an evaluation value of the mapping performance of the three-layer NN constructed in step S663. That is, it can be determined that the smaller the evaluation value, the higher the mapping performance.
ステップS665では、ステップS663にて構築した3層NNの中間層のニューロン数、全ての結合の重みの値、閾値、及びステップS664で求めた写像性能の評価値を、それぞれデータとして近似システム構築処理部46が有するメモリに記録する。
In step S665, the number of neurons in the intermediate layer of the three-layer NN constructed in step S663, the values of all connection weights, the threshold value, and the evaluation value of the mapping performance obtained in step S664 are respectively used as approximate system construction processing. It records in the memory which the
ステップS666では、これまでにメモリ内に記録した評価値を用いて、3層NNの写像性能が悪化しているか否かを判定する。係る判定の結果、悪化したと判定した場合は、処理をステップS667に進める。一方、悪化していないと判定した場合は、処理をステップS661に戻し、上述のように、中間層のニューロンの数を1つ増加させ、ステップS662以降の処理を行う。 In step S666, it is determined whether or not the mapping performance of the three-layer NN is deteriorated using the evaluation values recorded in the memory so far. As a result of such determination, if it is determined that the condition has deteriorated, the process proceeds to step S667. On the other hand, if it is determined that the condition has not deteriorated, the process returns to step S661, and as described above, the number of neurons in the intermediate layer is increased by one, and the processes after step S662 are performed.
ここで、ステップS666では、予め設定されたステップ数分前にステップS665で記録された3層NNの評価値に比べ、それ以降の3層NNの評価値が全て悪化、つまり2乗誤差総和が大きい場合に、写像性能が悪化していると判定する。「予め設定されたステップ数」は小さすぎると、悪化したか否かの判定を誤る可能性が高くなるので、現実的な程度に大きい値を設定しておけば良い。初期の段階では、「予め設定されたステップ数」分前の評価値が無いため、悪化の判断はできない。その場合は、必ずステップS661に戻るようにする。 Here, in step S666, the evaluation values of the three layers NN thereafter are all deteriorated compared to the evaluation values of the three layers NN recorded in step S665 a number of steps set in advance, that is, the sum of square errors is reduced. When it is larger, it is determined that the mapping performance is deteriorated. If the “preset number of steps” is too small, there is a high possibility of erroneous determination as to whether or not it has deteriorated, so a large value may be set to a practical level. In the initial stage, since there is no evaluation value before “the preset number of steps”, it is not possible to determine the deterioration. In that case, the process always returns to step S661.
ステップS667では、これまでにステップS665で記録された写像性能の評価値のうち最も評価値が小さいものを選択する。そして選択した評価値と共にステップS665で記録された中間層のニューロン数、全ての結合の重みの値、閾値を、後述するクラスモデル生成部47に出力する。
In step S667, the evaluation value with the smallest evaluation value is selected from the evaluation values of the mapping performance recorded so far in step S665. Then, together with the selected evaluation value, the number of neurons in the intermediate layer, the values of all connection weights, and threshold values recorded in step S665 are output to the class
以上説明したステップS660からステップS667までの処理により、汎化性能の高い、正規化後ベクトルから出力ベクトルへの写像を近似するシステムとして、適切な中間層のニューロン数を有する3層NNが構築される。 By the processing from step S660 to step S667 described above, a three-layer NN having an appropriate number of neurons in the intermediate layer is constructed as a system that approximates the mapping from the normalized vector to the output vector with high generalization performance. The
本実施形態では、上記手法を用いて、正規化後ベクトルから出力ベクトルへの写像を近似する3層NNを構築した。しかし、本実施形態はこれに限るものではなく、その他、一般的な3層NNの構築方法を用いても構わない。更に、本実施形態では、正規化後ベクトルから出力ベクトルへの写像を近似するシステムとして、3層NNを用いたが、これに限るものではない。例えば、3層以上のフィードフォワードニューラルネットワークや、カーネル法を用いたサポートベクター回帰法等の非線形な写像システムにより、上記非線形な写像を近似するようにしても構わない。 In the present embodiment, a three-layer NN that approximates the mapping from the normalized vector to the output vector is constructed using the above method. However, the present embodiment is not limited to this, and a general three-layer NN construction method may be used. Furthermore, in the present embodiment, the three-layer NN is used as a system for approximating the mapping from the normalized vector to the output vector, but the present invention is not limited to this. For example, the nonlinear mapping may be approximated by a nonlinear mapping system such as a feedforward neural network having three or more layers or a support vector regression method using a kernel method.
次にステップS57では、クラスモデル生成部47が、近似システム構築処理部46での処理において構築した3層NNと、トレーニングデータセットを用いて、各ラベルに対応するクラスモデルを生成する。ここで生成するクラスモデルとは、後述の識別モードにおいて用いるものであり、3層NNにより写像される先の空間において、クラスの識別を行うための識別器のパラメータ生成に対応する。例えば、識別モードにおいて、線形識別関数を用いたクラス識別を行う場合、線形識別関数の係数ベクトルwcと、バイアス値bc(cはクラスラベル)を生成すればよい。
Next, in step S57, the class
本実施形態では、識別モードでのクラス識別において最近傍法を用いるため、各クラスについて少なくとも1つのプロトタイプデータを生成する。具体的には先ず、構築した3層NNにトレーニングデータセット内の正規化後ベクトルを入力し、その時の3層NNの出力層のh個のニューロンの状態値を算出する。そして、その状態値を各要素値とするh次元の写像後ベクトルと、対応するラベルのセット、つまり3層NNにより写像された後のデータとそのラベルを、プロトタイプデータとして、メモリ48に記録する処理を行う。このプロトタイプデータの記録は、トレーニングデータセット内からランダムに選択したデータに対して行ってもよいが、本実施形態では、全てのデータに対して行うようにする。
In this embodiment, since the nearest neighbor method is used in class identification in the identification mode, at least one prototype data is generated for each class. Specifically, first, the normalized vector in the training data set is input to the constructed three-layer NN, and the state values of h neurons in the output layer of the three-layer NN at that time are calculated. Then, the h-dimensional post-mapping vector having the state value as each element value and the corresponding label set, that is, the data after mapping by the three-layer NN and the label are recorded in the
以上の処理により、近似システム構築処理部46での処理において構築した3層NNと、クラスモデル生成部47において記録した複数のプロトタイプデータが得られ、これをもって、学習モードでの処理が終了する。つまり学習モードでは、入力されたデータが冗長性が削減された同一クラスのデータであれば近づき、クラス間の分離度度合いが所望の分離度合いとなるような空間に写像され、その写像を近似するシステムを構築する。そして、その写像先で、各クラスのモデルを生成する。
With the above processing, the three-layer NN constructed in the processing in the approximate system
<識別モード>
図7は、本実施形態に係る情報処理装置を構成する各部のうち、識別モード時において動作する各部についてのみ、その機能構成を示したブロック図である。
<Identification mode>
FIG. 7 is a block diagram illustrating the functional configuration of only the units that operate in the identification mode among the units that configure the information processing apparatus according to the present embodiment.
図8は、本実施形態に係る情報処理装置が識別モード時に行う処理のフローチャートである。 FIG. 8 is a flowchart of processing performed by the information processing apparatus according to the present embodiment in the identification mode.
以下、図7,8を用いて、識別モード時における処理について説明する。 Hereinafter, processing in the identification mode will be described with reference to FIGS.
先ずステップS80では、データ入力部70によって、誰の画像であるのかを識別する対象であるパターン画像75(ラベリング処理がなされていないパターン画像)を入力する。
First, in step S80, the
次にステップS81では、画像正規化部71がパターン画像75に対して、第1の実施形態において説明した画像正規化部11と同様の画像正規化処理を行い、正規化後の画像の各画素値をラスタスキャン的に並べた400次元のベクトルを生成する。ここで得られたこのベクトルを、正規化後ベクトルxとする。
Next, in step S81, the
ステップS87では、データ写像処理部77が、学習モードにおいて得られた3層NNを用いて、写像後ベクトルzを算出する。写像後ベクトルzは、学習モードにおいて得られた3層NNに、正規化後ベクトルxを入力し、その時の3層NNの出力層のh個のニューロンの状態値を各要素値としたh次元のベクトルである。
In step S87, the data
次にステップS88では、識別処理部78が、最近傍法を用いたクラス識別を行うため、先ず、データ写像処理部77が算出した写像後ベクトルzと、学習モードで記録した全プロトタイプデータの写像後ベクトルとのユークリッド距離を算出する。そして、算出した距離が、最も小さかった写像後ベクトルを選択し、それに対応して記録されているラベルを求める。
In step S88, since the
次にステップS89では、識別結果出力部79は、識別処理部78が求めたラベルに対応する人物の種別を示す情報を出力する。ラベルに対応する人物の種別は、予めテーブルとして識別結果出力部79が有するメモリ内に保持しておけばよい。係る情報については特に限定するものではないが、例えば、人物名など、人物に関する情報を記したテキスト文章データでも良い。また、本情報処理装置に人物名を発声させるための音声データであっても良い。この場合、情報処理装置には、この音声データに基づいて音声信号を生成する為の構成と、この音声信号に従った音声を出力する音声スピーカとを設ける必要がある。
In step S89, the identification
以上説明した処理により、識別対象のパターン画像から、それが誰の顔画像であるのかを識別する処理が可能になる。本実施形態では、入力されるパターン画像(顔の画像)は、予め学習モードで用いたデータ内に含まれる人物である場合を想定しているため、識別結果は、必ず学習モードで用いたデータ内に含まれる人物の何れかとなる。もし、学習モードで用いたデータ内に含まれない人物の画像が入力されるような場合は、識別処理部78において求めた最も小さい距離が予め設定された値以上であった場合、それは不明な人物の画像であるという識別結果にすればよい。ここで用いる「予め設定された値」は、データ内に含まれない人物の画像を入力し、それが不明な人物の画像であると判定されるように、実験的に求めてやればよい。
With the processing described above, it is possible to identify who the face image is from the pattern image to be identified. In the present embodiment, since the input pattern image (face image) is assumed to be a person included in the data used in the learning mode in advance, the identification result is always the data used in the learning mode. One of the persons included in the inside. If an image of a person not included in the data used in the learning mode is input, if the smallest distance obtained by the
以上説明した、学習モード、及び識別モードの処理により、ラベルの付与されていないパターン画像を入力し、それが何れの人物であるかを識別する処理が可能になる。本実施形態では、識別モードにおける識別処理部78による識別処理に最近傍法を用いたが、これに限るものではなく、k−最近傍法や、サポートベクターマシン等、その他の一般的な識別方法を用いても実現できることは明らかである。その場合、学習モードのクラスモデル生成部47における、各クラスのモデル化の処理も、用いる識別処理において必要な、いわゆるパラメータの学習や、データの収集といった処理に変更すればよい。
By the processing in the learning mode and the identification mode described above, it is possible to input a pattern image to which no label is attached and to identify which person it is. In the present embodiment, the nearest neighbor method is used for the identification processing by the
このように、本実施形態に係るパターン識別方法では先ず、同クラスのデータ同士ならば、そのデータ間の距離が他のクラスのデータとの距離よりも近づけ、クラス間の関係が所望の分離度合いで表現されるようなデータ写像システムが構築される。そして、この構築されたデータ写像システムにより写像される写像先の空間において、クラス識別を行う識別器を生成しておく。このデータ写像システムを用いて新たに入力されたデータを写像し、写像後のデータを、生成した識別器を用いて識別することで、所望のクラス分離度合いに応じた識別特性を有し、データの本質的に非線形な変動に対して頑健なパターン識別を行うことができる。 As described above, in the pattern identification method according to the present embodiment, first, if data of the same class are used, the distance between the data is closer than the distance between the data of other classes, and the relationship between the classes is a desired degree of separation. A data mapping system represented by Then, a classifier for class identification is generated in the mapping destination space mapped by the constructed data mapping system. Newly input data is mapped using this data mapping system, and the data after mapping is identified using the generated classifier. It is possible to perform pattern identification that is robust against essentially non-linear fluctuations.
第1の実施形態と同様の手法で、クラス間分離度を設定した場合、類似したクラス間の分離度合いが高まるようになるため、類似したクラスの分離度が高まるような識別特性を得ることができる。これは、類似したクラス間の差異が強調されるような空間への写像システムを構築したことにより実現される特性である。これにより、識別が比較的困難な対象であっても、良好な識別結果を得ることが可能になる。 When the class separation degree is set in the same manner as in the first embodiment, the degree of separation between similar classes is increased, so that it is possible to obtain an identification characteristic that increases the degree of separation of similar classes. it can. This is a characteristic realized by constructing a mapping system to a space in which differences between similar classes are emphasized. This makes it possible to obtain a good identification result even for an object that is relatively difficult to identify.
また、第1の実施形態における説明で述べた、クラス間分離度の設定方法により、様々な識別特性を得ることが可能になる。例えば、クラスcpと、その他のクラスcq(q≠p)のクラス間分離度を全て1より大きい値に設定し、その他を全て1に設定したような場合、新しく入力したクラスcq(q≠p)のデータを、クラスcpであると誤って判定する確率を低くすることができる。 In addition, various identification characteristics can be obtained by the method for setting the degree of class separation described in the description of the first embodiment. For example, a class c p, is set to all 1 value greater than the interclass separation degree of other classes c q (q ≠ p), when, as set all other 1, newly entered class c q ( The probability of erroneously determining that data of q ≠ p) is class c p can be reduced.
以上のような特性は、例えば、顔画像を用いた強固なセキュリティーシステムの構築等において有用である。具体的には、上位の権限を有する人物のクラスを、上記クラスcpのように扱うことで、一般の人物が誤って上位の権限を有する人物であると判定される可能性を低くすることができ、信頼性の高いセキュリティーシステムを構築することができる。また、同様のセキュリティーシステムを考えた場合、同程度の権限を有する人物同士であれば、誤ってそれらの人物を取り違えて判定したとしても実害は少ない。そのため、そのような人物のクラスは、明確に区別する必要がないため、それらのクラス間分離度を1より小さい値に設定してもよい。このようにすることにより、相対的に、権限が異なるクラス間での分離度合いを高めることができ、権限の異なる人物を取り違えて判定する確率を低くできる。このように、本実施形態に係るパターン識別方法では、クラス間分離度の設定により、所望の識別特性を有したパターン識別方法を実現することができる。 The above characteristics are useful, for example, in the construction of a strong security system using face images. Specifically, the class of persons having elevated privileges, by treating as described above class c p, to reduce the possibility of being determined to be a person with a higher authority incorrectly ordinary person It is possible to build a highly reliable security system. Further, when considering a similar security system, even if persons having the same level of authority are mistakenly determined by mistaken those persons, there is little actual harm. For this reason, such classes of persons do not need to be clearly distinguished, and thus the degree of separation between classes may be set to a value smaller than 1. By doing so, it is possible to relatively increase the degree of separation between classes with different authorities, and to reduce the probability of misidentifying persons with different authorities. Thus, in the pattern identification method according to the present embodiment, a pattern identification method having desired identification characteristics can be realized by setting the degree of separation between classes.
[第3の実施形態]
本実施形態では、第2の実施形態で示したパターン識別方法の変形として、第2の実施形態と同様に、ラベリング処理がなされていないパターン画像を入力し、それが何れの人物であるかを識別する、パターン識別方法の例を示す。
[Third Embodiment]
In this embodiment, as a modification of the pattern identification method shown in the second embodiment, as in the second embodiment, a pattern image that has not been subjected to labeling processing is input, and which person it is is determined. An example of a pattern identification method for identifying is shown.
本実施形態も第2の実施形態と同様に、学習モードと識別モードの2つモードから構成される。本実施形態において各モードで行う処理は、第2の実施形態とほぼ同様であるが、データ写像関係生成部15、近似システム構築処理部46、クラスモデル生成部47での処理に対応する部分、及びデータ写像処理部77での処理に対応する部分のみが異なる。そのため、以下ではこの異なる部分のみについて説明し、処理が同様の部分は、説明を割愛する。
Similar to the second embodiment, the present embodiment also includes two modes, a learning mode and an identification mode. The processing performed in each mode in this embodiment is almost the same as in the second embodiment, but the portions corresponding to the processing in the data mapping
<学習モード>
図9は、本実施形態に係る情報処理装置を構成する各部のうち、学習モード時において動作する各部についてのみ、その機能構成を示したブロック図である。なお、図9において、図1に示した構成と共通の部分については、同じ番号を付けており、その説明は省略する。
<Learning mode>
FIG. 9 is a block diagram illustrating the functional configuration of only the units that operate in the learning mode among the units that configure the information processing apparatus according to the present embodiment. In FIG. 9, the same reference numerals are given to portions common to the configuration shown in FIG. 1, and description thereof is omitted.
図10は、本実施形態に係る情報処理装置が学習モード時に行う処理のフローチャートである。なお、図10において、図2に示した構成と共通の部分については、同じ番号を付けており、その説明は省略する。 FIG. 10 is a flowchart of processing performed by the information processing apparatus according to the present embodiment in the learning mode. In FIG. 10, parts common to those shown in FIG. 2 are given the same reference numerals, and descriptions thereof are omitted.
以下、図9,10を用いて、学習モード時における処理について説明する。 Hereinafter, the processing in the learning mode will be described with reference to FIGS.
本実施形態でも、N個のパターン画像(第1の実施形態で取り扱ったパターン画像と同じで、ラベリング処理済みのパターン画像)を入力し、入力したそれぞれのパターン画像について第1の実施形態と同様の処理を行う。これにより、各パターン画像に対する出力ベクトル(本実施形態ではこの出力ベクトルの次元数がhであったとする)を求める。ここまでの処理については、第1の実施形態での処理と同様であるので、説明を省略する。 Also in this embodiment, N pattern images (the same as the pattern images handled in the first embodiment, which have been labeled) are input, and each input pattern image is the same as in the first embodiment. Perform the process. Thereby, an output vector for each pattern image (in this embodiment, the number of dimensions of the output vector is h) is obtained. Since the processing so far is the same as the processing in the first embodiment, the description thereof is omitted.
第2の実施形態では、この求めた歪曲測地線距離関係を近似的に保存する、新たな空間への写像システムを、MDSと3層NNの構築の、2段階のステップにより構築した。 In the second embodiment, a mapping system to a new space that approximately stores the obtained distorted geodesic distance relationship is constructed by two steps of construction of MDS and three-layer NN.
本実施形態では、この写像システムとして線形写像システムを用い、線形写像システム構築処理部96において、歪曲測地線距離関係行列と、画像正規化部11において正規化した正規化後ベクトルのセットから、この線形写像システムを構築する。ここでの処理は、図10のステップS106に対応する。
In the present embodiment, a linear mapping system is used as the mapping system, and the linear mapping system
先ず、ステップS106において線形写像システム構築処理部96が行う処理について説明する。ここで、構築すべき線形システムを、行列表記としてAとする。Aは、入力が正規化後ベクトルの次元、つまり、ここでは400次元であるので、写像後の空間の次元をhとすると、400×hの行列となる。このシステムに、400次元のベクトルxを入力した時に、出力として得られるベクトルzは、z=ATxと表せ、これはh次元のベクトルとなる。ここで、ATは、Aの転置行列である。この時、任意のi、j番目の、それぞれの正規化後ベクトルxi、xjを写像した出力ベクトルzi、zj(=ATxi、ATxj)間のユークリッド距離が、歪曲測地線距離dd(i、j)を近似するような線形写像システムを構築する。そこで、本実施形態では、以下の式1に示す誤差関数J(A)の最小化問題として、この線形写像Aを求める。
First, the process performed by the linear mapping system
本実施形態では、これを最小化するAを、最急降下法により求める。ここで、Aのk列目の列ベクトルをak(akは400次元のベクトルで、k=1、2、・・・、h)とする。最急降下法では、まずAの全成分をランダムに初期化する。そして、式2に基づき、Aの成分を逐次更新していく。 In the present embodiment, A that minimizes this is obtained by the steepest descent method. Here, the column vector of the k-th column of A is a k (a k is a 400-dimensional vector, k = 1, 2,..., H). In the steepest descent method, first, all components of A are initialized at random. And based on Formula 2, the component of A is updated sequentially.
ここでa’kは、1回更新した後の、Aのk列目の列ベクトルであり、ηは、1回更新における更新量を決める正の比例定数である。また、∇akは、ベクトルakでの偏微分であり、∇akJ(A)は、式3により求められる。 Here, a ′ k is a column vector of the k-th column of A after being updated once, and η is a positive proportionality constant that determines the update amount in the one-time update. Also, ∇ ak is a partial differentiation with respect to the vector ak , and ∇ ak J (A) is obtained by Equation 3.
本実施形態では、式2に示した更新を、式1の誤差関数J(A)の値が収束するまで逐次行い、収束後の行列Aを得る。ここでの収束は、第2の実施形態における、3層NNの誤差収束判定と同様に、予め設定されたステップ数分の更新において、ほぼ誤差が減少しなくなった時に、誤差が収束したと判定すればよい。ηの値はこの収束と関わっており、これが大きすぎると、誤差がうまく収束しない可能性が高くなるが、小さすぎると、収束までに多くの更新を要する。そこでこのηは、現実的に許される程度の更新回数で収束する程度に小さい値に設定しておくことが好ましい。
In the present embodiment, the update shown in Expression 2 is sequentially performed until the value of the error function J (A) in
上記手法により、誤差関数J(A)の最小化問題として、線形写像行列Aを求めることができる。上記説明ではこのAの列数をhとして一般化したが、このhの値を定める必要がある。一般に、このhが大きい方が近似性能が高い、即ち、誤差関数J(A)の値を小さくすることができる。しかし、hが小さい方が冗長性を削減した空間に写像できる。そこで本実施形態では、様々な値のhにおいて上記手法によりAを求め、その中で予め設定された条件を満たすもののうち、hが最も小さい値であるAを選択するようにする。具体的には先ず、hの値の初期値を1とし、Aを求めるごとにhの値を1ずつ増加させる。そして、各hの値で求めたAにおいて、次の式4に示す条件を満たすかどうかを検証する。 By the above method, the linear mapping matrix A can be obtained as a minimization problem of the error function J (A). In the above description, the number of columns of A is generalized as h, but it is necessary to determine the value of h. In general, the larger h is, the higher the approximation performance is, that is, the value of the error function J (A) can be reduced. However, a smaller h can be mapped to a space with reduced redundancy. Therefore, in the present embodiment, A is obtained by the above method for various values of h, and A having the smallest value of h is selected from among those satisfying preset conditions. Specifically, first, the initial value of h is set to 1, and the value of h is increased by 1 each time A is obtained. Then, it is verified whether or not the condition shown in the following Expression 4 is satisfied in A obtained by the value of each h.
式4は、写像後の空間における任意の3点の距離関係が、少なくとも歪曲測地線距離関係の順序を満たすか否かの条件を意味する。hを1つずつ増加させてAを求め、上記式4の関係を満たすAが求められた場合、そこで演算を終了し、その時のAを、この線形写像システム構築処理部96において求めるべき線形写像システムとして自身が有するメモリ内に記録し、保持しておく。本実施形態では、上記式1のような誤差関数を定義し、それを最小化する線形写像Aを、最急降下法により求めた。しかし、これに限るものではなく、歪曲測地線距離関係をできるだけ保存、特に順序を保存するような線形写像を求める方法であれば、その他の誤差関数を利用したり、解析的にAを求めたりしても構わない。
Equation 4 means a condition as to whether or not the distance relationship between any three points in the mapped space satisfies at least the order of the distorted geodesic distance relationship. h is incremented by 1 to obtain A, and when A satisfying the relationship of the above equation 4 is obtained, the operation is terminated, and the linear mapping to be obtained in this linear mapping system
次にステップS107では、クラスモデル生成部97により、線形写像システム構築処理部96の処理において構築した線形写像システムと、画像正規化部11により正規化された全正規化後ベクトルとを用い、各ラベルに対応するクラスモデルを生成する。
In step S107, the class
ここでは、第2の実施形態と同様に、先ず、構築した線形写像システムAに、正規化後ベクトルを入力し、その時の線形写像システムの出力ベクトルを算出する。そして、そのh次元の出力ベクトルを写像後ベクトルとし、対応するラベルと共に、後述の識別モード時に用いるプロトタイプデータとして、メモリ98に記録する処理を行う。このプロトタイプデータの記録についても第2の実施形態と同様に、トレーニングデータセット内からランダムに選択したデータに対して行ってもよいが、本実施形態でも全てのデータに対して行うようにする。
Here, as in the second embodiment, first, a normalized vector is input to the constructed linear mapping system A, and an output vector of the linear mapping system at that time is calculated. Then, the h-dimensional output vector is used as a post-mapping vector, and is recorded in the
以上の処理により、線形写像システム構築処理部96での処理において構築した線形写像システムAと、クラスモデル生成部97において記録した複数のプロトタイプデータが得られ、これをもって、学習モードでの処理が終了する。つまり学習モードでは、入力されたデータが、冗長性が削減された同一クラスのデータであれば近づき、クラス間の分離度合いが所望の分離度合いとなるような空間に写像する線形写像システムAを構築し、その写像先で各クラスのモデルを生成することになる。
With the above processing, the linear mapping system A constructed in the processing in the linear mapping system
<識別モード>
本実施形態に係る識別モードは、処理部の基本的な構成は、第2の実施形態における識別モードの構成と同様であり、図7のデータ写像処理部77に対応する処理部における処理の内容のみが異なる。そのため、ここでは特に処理部の構成を図示せず、データ写像処理部77に対応する処理部における処理の内容のみ説明し、その他の処理については、説明を省略する。
<Identification mode>
In the identification mode according to the present embodiment, the basic configuration of the processing unit is the same as the configuration of the identification mode in the second embodiment, and the processing contents in the processing unit corresponding to the data
本実施形態も第2の実施形態と同様に、データを入力し、画像の正規化を行う。そして、本実施形態のデータ写像処理部では、学習モードにおいて得られた線形写像システムAを用いて写像後ベクトルzを算出する。写像後ベクトルzは、学習モードにおいて得られた線形写像システムAに、正規化後ベクトルxを入力した時に得られるh次元のベクトルである。つまり、第2の実施形態においては、3層NNを用いて写像後ベクトルを求めたところを、線形写像システムを用いて求めるという部分が異なるのみである。この後の第2の実施形態における識別処理部78、識別結果出力部79に対応する処理は、第2の実施形態と同様に、最近傍のプロトタイプを検索し、その結果を出力する。
Similar to the second embodiment, this embodiment also inputs data and normalizes the image. Then, the data mapping processing unit of the present embodiment calculates a post-mapping vector z using the linear mapping system A obtained in the learning mode. The post-mapping vector z is an h-dimensional vector obtained when the normalized vector x is input to the linear mapping system A obtained in the learning mode. That is, in the second embodiment, the difference is that a post-mapping vector obtained using a three-layer NN is obtained using a linear mapping system. Subsequent processing corresponding to the
以上、第3の実施形態における処理の、第2の実施形態における処理との差異について説明した。識別処理において用いる手法に関しては第2の実施形態と同様に様々な手法が適用可能であり、また、想定外の入力パターンに対する対応も、第2の実施形態において説明した方法と同様にすればよい。 In the above, the difference of the process in 3rd Embodiment from the process in 2nd Embodiment was demonstrated. As for the method used in the identification processing, various methods can be applied as in the second embodiment, and the correspondence to an unexpected input pattern may be the same as the method described in the second embodiment. .
[第4の実施形態]
本実施形態では、第3の実施形態で示したパターン識別方法の変形として、第3の実施形態における線形写像を、カーネル関数を用いて非線形写像に拡張した場合のパターン識別方法の例を示す。
[Fourth Embodiment]
In this embodiment, as a modification of the pattern identification method shown in the third embodiment, an example of a pattern identification method when the linear mapping in the third embodiment is expanded to a nonlinear mapping using a kernel function is shown.
第3の実施形態では、線形写像を用いてデータ間の歪曲測地線距離関係をできるだけ保存(特に距離の順序において)し、且つ冗長性を削減できる写像を構築した。線形写像を用いた場合、データの分布が比較的単純な形状(非線形であっても)であれば、上記目的を達成できる。しかし、データの分布が非常に複雑な形状である場合は、目標となる写像を構築できない可能性が高くなる。 In the third embodiment, a linear map is used to store a distorted geodesic distance relationship between data as much as possible (particularly in the order of distances), and a map that can reduce redundancy is constructed. When the linear mapping is used, the above object can be achieved if the data distribution is relatively simple (even non-linear). However, if the data distribution has a very complicated shape, there is a high possibility that a target mapping cannot be constructed.
そこで、本実施形態では、第3の実施形態における線形写像部分、つまり線形写像行列Aを用いて入力データを写像する部分を、カーネル関数を用いた非線形な写像に変更する。ここでカーネル関数とは、ある集合χを対象とした時に、χ×χを定義域とする実対称関数で、半正定値性を満たす関数である。このようなカーネル関数の例として、多項式カーネルK(x、x’)=(x・x’+1)pや、ガウシアンカーネルK(x、x’)=exp(−|x−x’|2/σ2)が一般的である。 Therefore, in this embodiment, the linear mapping portion in the third embodiment, that is, the portion mapping input data using the linear mapping matrix A is changed to a non-linear mapping using a kernel function. Here, the kernel function is a real symmetric function having a domain of χ × χ when a certain set χ is targeted, and a function satisfying the semi-definite property. Examples of such kernel functions include polynomial kernel K (x, x ′) = (x · x ′ + 1) p and Gaussian kernel K (x, x ′) = exp (− | x−x ′ | 2 / σ 2 ) is common.
本実施形態では、このようなカーネル関数を用い、入力データxから出力データzへの非線形写像システムを構築する。このように本実施形態は、第3の実施形態とは、写像システムの部分が線形写像であるのかカーネル関数を用いた非線形写像であるのかが異なるのみである。そこで、本実施形態の説明では、カーネル関数を用いた非線形線形写像の構築と、それを用いた非線形写像のみを説明し、その他の部分に関しては説明を省略する。 In this embodiment, such a kernel function is used to construct a nonlinear mapping system from input data x to output data z. As described above, this embodiment differs from the third embodiment only in whether the mapping system portion is a linear mapping or a nonlinear mapping using a kernel function. Therefore, in the description of the present embodiment, only the construction of the nonlinear linear mapping using the kernel function and the nonlinear mapping using the kernel function will be described, and description of other portions will be omitted.
第3の実施形態では、入力データxから出力データzへの写像システムとして、z=ATxという線形写像を用いた。これに対し、本実施形態の非線形写像は、入力されたデータ数N個のh次元ベクトルαn(n=1、2、・・・、N)と、それぞれに対応する入力ベクトルxn、及びカーネル関数K(x、x’)用い、z=Σαn・K(x、xn)と表される。ここで、Σは、n=1からn=Nまでの総和を意味する。 In the third embodiment, a linear mapping z = A T x is used as a mapping system from input data x to output data z. On the other hand, the non-linear mapping of the present embodiment is based on the input N number of h-dimensional vectors α n (n = 1, 2,..., N) and the corresponding input vectors x n , and Using the kernel function K (x, x ′), z = Σα n · K (x, x n ). Here, Σ means the sum from n = 1 to n = N.
この写像は、どのようなカーネル関数を用いるか(関数自体の選択や、上記カーネル関数例でのpやσ等のパラメータ)にも依存するが、それを固定して考えると、N個のh次元ベクトルαnのみにより決まる。そこで本実施形態ではカーネル関数として上記ガウシアンカーネルを用い、データ間の歪曲測地線距離関係をできるだけ保存し、且つ冗長性を削減できる写像の構築を、N個のh次元ベクトルαnを最適化することにより行う。ガウシアンカーネルのパラメータσは任意の定数で構わないが、凡そ入力データ間のユークリッド距離オーダーの定数にしておくことが好ましい。 This mapping depends on what kernel function is used (selection of the function itself and parameters such as p and σ in the above kernel function example). It is determined only by the dimension vector α n . Therefore, in the present embodiment, the Gaussian kernel is used as a kernel function, and the mapping of geodesic distance between data as much as possible is preserved as much as possible, and the construction of a map that can reduce redundancy is optimized for N h-dimensional vectors α n. By doing. The parameter σ of the Gaussian kernel may be an arbitrary constant, but is preferably a constant in the order of the Euclidean distance between the input data.
このN個のh次元ベクトルαnの最適化は、式5に示す誤差関数J(Γ)の最小化問題の解として得られる。 The optimization of the N h-dimensional vectors α n is obtained as a solution to the minimization problem of the error function J (Γ) shown in Equation 5.
ここでΓはk列目の列ベクトルがN次元ベクトルγk(k=1、2、・・・、h)のN行h列の行列である。また式中のκiは、K(xi、xk)をk番目の要素とするN次元のベクトルであり、κi={K(xi、x1)、K(xi、x2)、・・・、K(xi、xN)}Tである。本実施形態においてもこの誤差関数を最小化するΓを、最急降下法により求める。そこでまず、Γの全成分をランダムに初期化する。そして、式6に基づき、Γの成分を逐次更新していく。 Here, Γ is a matrix of N rows and h columns where the column vector of the kth column is an N-dimensional vector γ k (k = 1, 2,..., H). Also, κ i in the equation is an N-dimensional vector having K (x i , x k ) as the k-th element, and κ i = {K (x i , x 1 ), K (x i , x 2). ),..., K (x i , x N )} T. Also in this embodiment, Γ that minimizes this error function is obtained by the steepest descent method. First, all components of Γ are initialized at random. Then, based on Expression 6, the component of Γ is sequentially updated.
ここでγ’kは、1回更新した後のΓのk列目の列ベクトルであり、ηは第3の実施形態と同様に、1回更新における更新量を決める正の比例定数である。また、∇γkは、ベクトルγkでの偏微分であり、∇γkJ(Γ)は第3の実施形態と同様に、式7により求められる。 Here, γ ′ k is a column vector of the kth column of Γ after being updated once, and η is a positive proportionality constant that determines the update amount in the one-time update, as in the third embodiment. Further, γ γk is a partial differentiation with respect to the vector γ k , and ∇ γk J (Γ) is obtained by Expression 7 as in the third embodiment.
本実施形態でも、第3の実施形態と同様に、式6に示した更新を、式5の誤差関数J(Γ)の値が収束するまで逐次行い、収束後の行列Γを得る。この収束後の行列Γのn行目の行ベクトルが、求めるh次元ベクトルαnとなる。収束の判定や、ηの設定も、第3の実施形態と同様にすればよいので、説明を省略する。 Also in this embodiment, as in the third embodiment, the update shown in Expression 6 is sequentially performed until the value of the error function J (Γ) in Expression 5 converges to obtain a converged matrix Γ. The row vector of the nth row of the converged matrix Γ is the h-dimensional vector α n to be obtained. The determination of convergence and the setting of η may be performed in the same manner as in the third embodiment, and thus description thereof is omitted.
Γの列数hは、第3の実施形態と同様の手法で求めてもよいが、第2の実施形態において用いた3層NNの中間層のニューロン数決定手法と同様の交差検定法を用いる方が好適である。この場合、まずデータを調整用セットと、検定用セットに分割し、調整用セットを用いて、第3の実施形態と同様に、様々なhの値において上記手法によりΓを求める。そして、各hの値で得られたΓで決まる写像z=Σαk・K(x、xk)を、検定用セットに対して適用し、それらが予め設定された条件を満たすもののうち、hが最も小さい値であるΓを選択するようにすればよい。ここで用いる条件としては、第3の実施形態において示した式4の条件や、第1の実施形態において用いた入力された全データのペアの、それぞれの距離誤差率の内、最大の距離誤差率が、予め設定された値以下であるといった条件を用いればよい。 The number h of columns of Γ may be obtained by the same method as in the third embodiment, but the cross-validation method similar to the method for determining the number of neurons in the intermediate layer of the three-layer NN used in the second embodiment is used. Is preferred. In this case, first, the data is divided into an adjustment set and a test set, and Γ is obtained by the above method at various values of h using the adjustment set as in the third embodiment. Then, the mapping z = Σα k · K (x, x k ) determined by Γ obtained by the value of each h is applied to the test set, and among those satisfying a preset condition, h Γ having the smallest value may be selected. The conditions used here include the condition of Equation 4 shown in the third embodiment and the maximum distance error among the respective distance error rates of all input data pairs used in the first embodiment. A condition that the rate is equal to or less than a preset value may be used.
本実施形態も、上記式5のような誤差関数を定義し、それを最小化する行列Γを、最急降下法により求めた。しかし、これに限るものではなく、歪曲測地線距離関係を、特に順序を保存するように、写像する非線形変換を決定する行列Γを求める方法であれば、その他の誤差関数を利用したり、解析的に行列Γを求めたりしても構わない。特に、式5に示した誤差関数に関しては、よりスパースな解を得るため、Γに関するL1ノルムを正則化項として付加し、式8のようにしてもよい。 Also in the present embodiment, an error function such as Equation 5 is defined, and a matrix Γ that minimizes the error function is obtained by the steepest descent method. However, the present invention is not limited to this, and any other error function can be used or analyzed as long as it is a method for obtaining a matrix Γ that determines a nonlinear transformation to be mapped so as to preserve the order of the distorted geodesic distance. Alternatively, the matrix Γ may be obtained. In particular, with respect to the error function shown in Equation 5, in order to obtain a sparse solution, the L1 norm for Γ may be added as a regularization term, and Equation 8 may be used.
ここで、|γk|L1はγkのL1ノルムであり、第2項のΣkは、k=1からk=hまでの総和を意味する。また、λは正則化の効果を決める正のパラメータであり、正則化の効果を決める定数である。このλの値を大きくすることで正則化の効果が強まるが、実際に用いる値としては、求めるスパースネスと、最終的な写像性能に応じて実験的に決めてやればよい。誤差関数を式8とした場合には、式7に示した、∇γkJ(Γ)は、式9のようになる。 Here, | γ k | L1 is the L1 norm of γ k , and Σ k in the second term means the sum from k = 1 to k = h. Λ is a positive parameter that determines the effect of regularization, and is a constant that determines the effect of regularization. Increasing the value of λ increases the effect of regularization, but the actual value to be used may be determined experimentally according to the required sparseness and the final mapping performance. When the error function is represented by Expression 8, ∇ γk J (Γ) illustrated in Expression 7 is represented by Expression 9.
ここでΛkは、γkのn番目の要素をγknとした場合、この行列Λkの、n行n列目の対角成分がλ/|γkn|で、それ以外の成分は全て0となる、N次の対角行列である。よって、よりスパースな解を得るためには、この式9を用い、式6に示した更新を、式8の誤差関数J(Γ)の値が収束するまで逐次行い、収束後の行列Γを得るようにすればよい。 Here, Λ k is a case where the n-th element of γ k is γ kn , the diagonal component of the n th row and the n th column of this matrix Λ k is λ / | γ kn |, and all other components are It is an Nth-order diagonal matrix that becomes zero. Therefore, in order to obtain a more sparse solution, using Equation 9, the update shown in Equation 6 is sequentially performed until the value of the error function J (Γ) in Equation 8 converges, and the converged matrix Γ is obtained. You can get it.
第3の実施形態におけるクラスモデル生成部97や、データ写像処理部77に対応する本実施形態での処理では、第3の実施形態における線形写像z=ATxを、学習モード時のカーネル関数Kを用いて、z=Σαk・K(x、xk)と置き換えるだけでよい。
In the processing in this embodiment corresponding to the class
上記手法により、第3の実施形態における線形写像を、カーネル関数を用いた非線形な写像に置き換えることができ、より複雑なパターンの分布に対応可能となる。本実施形態では、カーネル関数を固定として説明したが、様々なカーネル関数(関数自体の選択や、上記カーネル関数例でのpやσ等のパラメータも含めて)を用いて上記写像を構築し、その中で、交差検定における誤差関数の値が最小のものを選ぶようにしてもよい。 By the above method, the linear mapping in the third embodiment can be replaced with a non-linear mapping using a kernel function, and it is possible to deal with a more complicated pattern distribution. In the present embodiment, the kernel function is described as fixed. However, the mapping is constructed using various kernel functions (including selection of the function itself and parameters such as p and σ in the kernel function example) Among them, the one with the smallest error function value in cross-validation may be selected.
上記説明した、第2から第4の実施形態のパターン識別方法の例では、人物の顔を切り出したグレースケール画像を入力データとして用いた。しかし、これに限るものではなく、その他のカテゴリの画像データや、音声データに対しても適用可能であることは明らかである。また、例えばWebコンテンツ等の一般的なデータであっても、各データの距離、及びいくつかのパラメータによって定まるそのデータに対する多次元空間への写像が定義できれば、第2から第4の実施形態における入力データとして用いることができる。この場合、式1、5、又は式8に示したような誤差関数を用い、写像を決めるパラメータを、この誤差関数が最小になるように定めてやればよい。
In the example of the pattern identification method of the second to fourth embodiments described above, a grayscale image obtained by cutting out a person's face is used as input data. However, the present invention is not limited to this, and it is obvious that the present invention can be applied to other categories of image data and audio data. For example, even in the case of general data such as Web contents, the mapping of the data to the multidimensional space determined by the distance of each data and some parameters can be defined in the second to fourth embodiments. It can be used as input data. In this case, an error function as shown in
[第5の実施形態]
図1,4,7,9に示した各部(メモリを除く)は、上記実施形態では全てハードウェアでもって構成されているものとして説明した。しかしこれら各部をソフトウェアでもって実装しても良い。即ち、各部に対応する処理をコンピュータに実行させるためのコンピュータプログラムとして実装しても良い。
[Fifth Embodiment]
1, 4, 7, and 9 have been described as being configured by hardware in the above embodiment. However, these parts may be implemented by software. That is, you may implement as a computer program for making a computer perform the process corresponding to each part.
図11は、図1,4,7,9に示した各部をコンピュータプログラムでもって実装した場合に、このコンピュータプログラムを実行するコンピュータのハードウェア構成例を示すブロック図である。 FIG. 11 is a block diagram showing a hardware configuration example of a computer that executes a computer program when the units shown in FIGS. 1, 4, 7, and 9 are implemented by the computer program.
CPU1101は、RAM1102やROM1103に格納されているプログラムやデータを用いて本コンピュータ全体の制御を行うと共に、図1,4,7,9に示した各部が行う各処理を実行する。
The
RAM1102は、外部記憶装置1106からロードされたプログラムやデータ、I/F1107を介して外部から受信したプログラムやデータを一時的に記憶するためのエリアを有する。また、RAM1102は、CPU1101が各種の処理を実行する際に用いるワークエリアを有する。即ち、RAM1102は、各種のエリアを適宜提供することができる。また、RAM1102は、メモリ16,48,98としても機能する。
The
ROM1103には、本コンピュータの設定データやブートプログラムなどが格納されている。
The
操作部1104は、キーボードやマウスなどにより構成されており、本コンピュータのユーザが操作することで、各種の指示やデータを入力することができる。例えば、上記各説明における「設定する処理」では、ユーザが操作部1104を用いて入力したものを受け付ける、というようにしても良い。
The
表示部1105は、CRTや液晶画面などにより構成されており、CPU1101による処理結果を画像や文字などでもって表示することができる。例えば、上記識別モードにおける処理結果としての識別結果を画像や文字などでもって表示することができる。また、パターン画像の一覧をこの表示部1105の表示画面上に表示させ、本コンピュータにおいて処理すべき対象としてのパターン画像をこの一覧表示されたパターン画像群から操作部1104でもって選択させるようにしても良い。
The
外部記憶装置1106は、ハードディスクドライブ装置に代表される大容量情報記憶装置である。ここには、OS(オペレーティングシステム)や、図1,4,7,9に示した各部の機能をCPU1101に実行させるためのプログラムやデータ、また、予め設定されているものとして説明した関数プログラムやデータなども保存されている。また、パターン画像など、処理対象のデータについてもこの外部記憶装置1106に保存されている。なお、外部記憶装置1106は、メモリ16,48,98の機能をも兼ねても良い。
The
外部記憶装置1106に保存されているプログラムやデータはCPU1101による制御に従って適宜RAM1102にロードされる。そしてCPU1101はこのロードされたプログラムやデータを用いて処理を実行する。これにより本コンピュータは、図1,4,7,9に示した各部による処理を実行することができる。
Programs and data stored in the
I/F1107は、本コンピュータを外部の機器と接続するためのものである。例えば、このI/F1107をLANやインターネット等のネットワークに接続することで、例えば、ネットワーク上の機器からパターン画像などをこのI/F1107を介してダウンロードすることができる。また、本コンピュータによる処理結果をこのI/F1107を介してネットワーク上の機器に対して送信することもできる。
The I /
1108は上述の各部を繋ぐバスである。なお、図11に示した構成は一例であり、以上説明したコンピュータプログラムを実行可能な構成であれば、コンピュータは如何なる構成を有していても良い。
A
[その他の実施形態]
また、本発明の目的は、以下のようにすることによって達成されることはいうまでもない。即ち、前述した実施形態の機能を実現するソフトウェアのプログラムコードを記録したコンピュータ読み取り可能な記録媒体(または記憶媒体)を、システムあるいは装置に供給する。そして、そのシステムあるいは装置のコンピュータ(またはCPUやMPU)が記録媒体に格納されたプログラムコードを読み出し実行する。この場合、記録媒体から読み出されたプログラムコード自体が前述した実施形態の機能を実現することになり、そのプログラムコードを記録した記録媒体は本発明を構成することになる。
[Other Embodiments]
Needless to say, the object of the present invention can be achieved as follows. That is, a computer-readable recording medium (or storage medium) that records software program codes for realizing the functions of the above-described embodiments is supplied to the system or apparatus. Then, the computer (or CPU or MPU) of the system or apparatus reads and executes the program code stored in the recording medium. In this case, the program code itself read from the recording medium realizes the functions of the above-described embodiment, and the recording medium on which the program code is recorded constitutes the present invention.
また、コンピュータが読み出したプログラムコードを実行することにより、そのプログラムコードの指示に基づき、コンピュータ上で稼働しているオペレーティングシステム(OS)などが実際の処理の一部または全部を行う。その処理によって前述した実施形態の機能が実現される場合も含まれることは言うまでもない。 Further, by executing the program code read by the computer, an operating system (OS) or the like running on the computer performs part or all of the actual processing based on the instruction of the program code. Needless to say, the process includes the case where the functions of the above-described embodiments are realized.
さらに、記録媒体から読み出されたプログラムコードが、コンピュータに挿入された機能拡張カードやコンピュータに接続された機能拡張ユニットに備わるメモリに書込まれたとする。その後、そのプログラムコードの指示に基づき、その機能拡張カードや機能拡張ユニットに備わるCPUなどが実際の処理の一部または全部を行い、その処理によって前述した実施形態の機能が実現される場合も含まれることは言うまでもない。 Furthermore, it is assumed that the program code read from the recording medium is written in a memory provided in a function expansion card inserted into the computer or a function expansion unit connected to the computer. After that, based on the instruction of the program code, the CPU included in the function expansion card or function expansion unit performs part or all of the actual processing, and the function of the above-described embodiment is realized by the processing. Needless to say.
本発明を上記記録媒体に適用する場合、その記録媒体には、先に説明したフローチャートに対応するプログラムコードが格納されることになる。 When the present invention is applied to the recording medium, program code corresponding to the flowchart described above is stored in the recording medium.
Claims (25)
入力手段が、それぞれ異なるクラスに属する処理データを入力する入力工程と、
第1の計算手段が、前記入力工程で入力したそれぞれの処理データ間の測地線距離関係を求める第1の計算工程と、
設定手段が、前記クラス間の距離を求め、前記クラス間の距離が所定の値よりも小さい場合に、前記クラス間の距離が大きくなるように、クラス間分離度を設定する設定工程と、
更新手段が、前記処理データのそれぞれが属するクラスの前記設定されたクラス間分離度に基づいて、同じクラスに属する処理データ間の測地線距離が、他クラスに属する処理データとの測地線距離よりも小さくなるように、前記処理データ間の測地線距離関係を更新する更新工程と、
第2の計算手段が、前記更新工程で更新された測地線距離関係を用いて、ユークリッド距離関係を近似するデータ写像関係を示す情報を求める第2の計算工程と
を備えることを特徴とする情報処理方法。 An information processing method performed by an information processing apparatus,
An input process in which input means inputs process data belonging to different classes;
A first calculation step in which a first calculation means obtains a geodesic distance relationship between the respective processing data input in the input step;
A setting step for obtaining a distance between the classes, and setting a degree of separation between classes so that the distance between the classes is increased when the distance between the classes is smaller than a predetermined value;
The updating means determines that the geodesic distance between the processing data belonging to the same class is based on the geodesic distance with the processing data belonging to another class based on the set inter-class separation degree of the class to which each of the processing data belongs. Updating step of updating the geodesic distance relationship between the processing data,
The second calculation means comprises a second calculation step for obtaining information indicating a data mapping relationship that approximates the Euclidean distance relationship using the geodesic distance relationship updated in the updating step. Processing method.
2つの処理データξ、ζ間の測地線距離dM(ξ、ζ)は、dG(ξ、ζ)か、当該処理データとは異なる処理データaを経由するdG(ξ、a)+dG(a、ζ)の、何れか小さい方であることを特徴とする請求項1に記載の情報処理方法。 When the graph distance dG (x 1 , x 2 ) between the two processing data x 1 and x 2 is ∞ when x 1 and x 2 are not nearby,
The geodesic distance dM (ξ, ζ) between the two processing data ξ and ζ is dG (ξ, ζ) or dG (ξ, a) + dG (a, passing through the processing data a different from the processing data. The information processing method according to claim 1, which is smaller of ζ).
なる誤差関数J(A)を最小化する線形写像行列Aを求めることを特徴とする請求項15に記載の情報処理方法。 In the second calculation step, the i-th and j-th processing data are x i and x j , and the updated distance relationship between the i-th and j-th processing data is d d (i, j). Time,
The information processing method according to claim 15, wherein a linear mapping matrix A that minimizes the error function J (A) is calculated.
なる誤差関数J(Γ)を最小化する行列Γを求め、求めた行列Γのi行目の行ベクトルを、前記αiとすることを特徴とする請求項17に記載の情報処理方法。 Wherein in the second calculation step, the vector kappa i, wherein the processing data x j for processing data x i kernel function value K (x i, x j) to a vector whose j-th element, processing the data x i And d d (i, j) is the updated distance relationship between the processing data y i and the processing data y i
18. The information processing method according to claim 17, wherein a matrix Γ that minimizes the error function J (Γ) is obtained, and a row vector of the i-th row of the obtained matrix Γ is set to the α i .
なる誤差関数J(Γ)を最小化する行列Γを求め、求めた行列Γのi行目の行ベクトルを、前記αiとすることを特徴とする請求項17に記載の情報処理方法。 Wherein in the second calculation step, the vector kappa i, wherein the processing data x j for processing data x i kernel function value K (x i, x j) to a vector whose j-th element, processing the data x i And the processed data y i is the updated distance relationship d d (i, j), λ is a positive constant, | γ k | L1 is the L1 norm of the k-th column vector of the matrix Γ,
18. The information processing method according to claim 17, wherein a matrix Γ that minimizes the error function J (Γ) is obtained, and a row vector of the i-th row of the obtained matrix Γ is set to the α i .
入力手段が、それぞれ異なるクラスに属する処理データを入力する入力工程と、
第1の計算手段が、前記入力工程で入力したそれぞれの処理データ間の測地線距離関係を求める第1の計算工程と、
設定手段が、前記クラス間の距離を求め、前記クラス間の距離が所定の値よりも小さい場合に、前記クラス間の距離が大きくなるように、クラス間分離度を設定する設定工程と、
更新手段が、前記処理データのそれぞれが属するクラスの前記設定されたクラス間分離度に基づいて、同じクラスに属する処理データ間の測地線距離が、他クラスに属する処理データとの測地線距離よりも小さくなるように、前記処理データ間の測地線距離関係を更新する更新工程と、
第2の計算手段が、前記更新工程で更新された測地線距離関係を用いて、ユークリッド距離関係を近似するデータ写像関係を示す情報を求める第2の計算工程と、
生成手段が、前記データ写像関係により写像される空間において定義可能な前記それぞれ異なるクラスを識別する識別規則を示す情報を生成する生成工程と、
第2の入力手段が、識別対象データを入力する第2の入力工程と、
写像手段が、前記識別対象データを、前記第2の計算工程で求めた情報が示すデータ写像関係を用いて写像する写像工程と、
識別手段が、前記写像工程で写像されたデータと、前記生成工程で生成した情報が示す前記識別規則を用いて、前記識別対象データのラベルを識別する識別工程と
を備えることを特徴とする情報処理方法。 An information processing method performed by an information processing apparatus,
An input process in which input means inputs process data belonging to different classes;
A first calculation step in which a first calculation means obtains a geodesic distance relationship between the respective processing data input in the input step;
A setting step for obtaining a distance between the classes, and setting a degree of separation between classes so that the distance between the classes is increased when the distance between the classes is smaller than a predetermined value;
The updating means determines that the geodesic distance between the processing data belonging to the same class is based on the geodesic distance with the processing data belonging to another class based on the set inter-class separation degree of the class to which each of the processing data belongs. Updating step of updating the geodesic distance relationship between the processing data,
A second calculation step in which a second calculation means obtains information indicating a data mapping relationship that approximates the Euclidean distance relationship using the geodesic distance relationship updated in the updating step;
A generating step for generating information indicating identification rules for identifying the different classes definable in a space mapped by the data mapping relationship;
A second input step in which the second input means inputs identification target data;
A mapping step in which mapping means maps the identification target data using a data mapping relationship indicated by information obtained in the second calculation step;
The identification means comprises: an identification step of identifying a label of the identification target data using the data mapped in the mapping step and the identification rule indicated by the information generated in the generation step. Processing method.
それぞれ異なるクラスに属する処理データを入力する入力手段と、
前記入力手段が入力したそれぞれの処理データ間の測地線距離関係を求める第1の計算手段と、
前記クラス間の距離を求め、前記クラス間の距離が所定の値よりも小さい場合に、前記クラス間の距離が大きくなるように、クラス間分離度を設定する設定手段と、
前記処理データのそれぞれが属するクラスの前記設定されたクラス間分離度に基づいて、同じクラスに属する処理データ間の測地線距離が、他クラスに属する処理データとの測地線距離よりも小さくなるように、前記処理データ間の測地線距離関係を更新する更新手段と、
前記更新手段によって更新された測地線距離関係を用いて、ユークリッド距離関係を近似するデータ写像関係を示す情報を求める第2の計算手段と
を備えることを特徴とする情報処理装置。 An information processing apparatus,
Input means for inputting processing data belonging to different classes,
First calculation means for obtaining a geodesic distance relationship between processing data input by the input means;
A setting means for obtaining a distance between the classes, and setting a degree of separation between classes so that the distance between the classes is increased when the distance between the classes is smaller than a predetermined value;
Based on the set class separation degree of the class to which each of the processing data belongs, the geodesic distance between the processing data belonging to the same class is smaller than the geodesic distance with the processing data belonging to another class. Updating means for updating a geodesic distance relationship between the processing data;
An information processing apparatus comprising: second calculation means for obtaining information indicating a data mapping relation that approximates the Euclidean distance relation using the geodesic distance relation updated by the updating means.
それぞれ異なるクラスに属する処理データを入力する入力手段と、
前記入力手段が入力したそれぞれの処理データ間の測地線距離関係を求める第1の計算手段と、
前記クラス間の距離を求め、前記クラス間の距離が所定の値よりも小さい場合に、前記クラス間の距離が大きくなるように、クラス間分離度を設定する設定手段と、
前記処理データのそれぞれが属するクラスの前記設定されたクラス間分離度に基づいて、同じクラスに属する処理データ間の測地線距離が、他クラスに属する処理データとの測地線距離よりも小さくなるように、前記処理データ間の測地線距離関係を更新する更新手段と、
前記更新手段によって更新された測地線距離関係を用いて、ユークリッド距離関係を近似するデータ写像関係を示す情報を求める第2の計算手段と、
前記データ写像関係により写像される空間において定義可能な前記それぞれ異なるクラスを識別する識別規則を示す情報を生成する生成手段と、
識別対象データを入力する第2の入力手段と、
前記識別対象データを、前記第2の計算手段で求めた情報が示すデータ写像関係を用いて写像する写像手段と、
前記写像手段によって写像されたデータと、前記生成手段が生成した情報が示す識別規則を用いて、前記識別対象データのラベルを識別する識別手段と
を備えることを特徴とする情報処理装置。 An information processing apparatus,
Input means for inputting processing data belonging to different classes,
First calculation means for obtaining a geodesic distance relationship between processing data input by the input means;
A setting means for obtaining a distance between the classes, and setting a degree of separation between classes so that the distance between the classes is increased when the distance between the classes is smaller than a predetermined value;
Based on the set class separation degree of the class to which each of the processing data belongs, the geodesic distance between the processing data belonging to the same class is smaller than the geodesic distance with the processing data belonging to another class. Updating means for updating a geodesic distance relationship between the processing data;
Second calculation means for obtaining information indicating a data mapping relation approximating the Euclidean distance relation using the geodesic distance relation updated by the updating means;
Generating means for generating information indicating identification rules for identifying the different classes definable in a space mapped by the data mapping relationship;
A second input means for inputting identification target data;
Mapping means for mapping the identification target data using a data mapping relationship indicated by information obtained by the second calculation means;
An information processing apparatus comprising: data mapped by the mapping unit; and an identification unit that identifies a label of the identification target data using an identification rule indicated by information generated by the generation unit.
Priority Applications (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| JP2012256706A JP5284530B2 (en) | 2012-11-22 | 2012-11-22 | Information processing method and information processing apparatus |
Applications Claiming Priority (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| JP2012256706A JP5284530B2 (en) | 2012-11-22 | 2012-11-22 | Information processing method and information processing apparatus |
Related Parent Applications (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| JP2007130898A Division JP5144123B2 (en) | 2007-05-16 | 2007-05-16 | Information processing method and information processing apparatus |
Publications (2)
| Publication Number | Publication Date |
|---|---|
| JP2013065336A JP2013065336A (en) | 2013-04-11 |
| JP5284530B2 true JP5284530B2 (en) | 2013-09-11 |
Family
ID=48188713
Family Applications (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| JP2012256706A Active JP5284530B2 (en) | 2012-11-22 | 2012-11-22 | Information processing method and information processing apparatus |
Country Status (1)
| Country | Link |
|---|---|
| JP (1) | JP5284530B2 (en) |
Families Citing this family (3)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN107609461A (en) | 2017-07-19 | 2018-01-19 | 阿里巴巴集团控股有限公司 | The training method of model, the determination method, apparatus of data similarity and equipment |
| US20220230051A1 (en) * | 2018-11-18 | 2022-07-21 | Innatera Nanosystems B.V. | Spiking Neural Network |
| CN113159080A (en) * | 2020-01-22 | 2021-07-23 | 株式会社东芝 | Information processing apparatus, information processing method, and storage medium |
Family Cites Families (2)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US7379602B2 (en) * | 2002-07-29 | 2008-05-27 | Honda Giken Kogyo Kabushiki Kaisha | Extended Isomap using Fisher Linear Discriminant and Kernel Fisher Linear Discriminant |
| JP3996470B2 (en) * | 2002-08-23 | 2007-10-24 | 日本電信電話株式会社 | Visual information classification method, visual information classification apparatus, visual information classification program, and recording medium recording the program |
-
2012
- 2012-11-22 JP JP2012256706A patent/JP5284530B2/en active Active
Also Published As
| Publication number | Publication date |
|---|---|
| JP2013065336A (en) | 2013-04-11 |
Similar Documents
| Publication | Publication Date | Title |
|---|---|---|
| JP5144123B2 (en) | Information processing method and information processing apparatus | |
| CN109117864B (en) | Coronary heart disease risk prediction method, model and system based on heterogeneous feature fusion | |
| CN112836672A (en) | A Dimensionality Reduction Method for Unsupervised Data Based on Adaptive Neighbor Graph Embedding | |
| CN110929029A (en) | Text classification method and system based on graph convolution neural network | |
| JP4618098B2 (en) | Image processing system | |
| Zhang et al. | Flexible auto-weighted local-coordinate concept factorization: A robust framework for unsupervised clustering | |
| US11775851B2 (en) | User verification method and apparatus using generalized user model | |
| US11625612B2 (en) | Systems and methods for domain adaptation | |
| WO2019102984A1 (en) | Learning device and learning method, identification device and identification method, program, and recording medium | |
| CN112164002A (en) | Training method, device, electronic device and storage medium for face correction model | |
| JP5284530B2 (en) | Information processing method and information processing apparatus | |
| CA3068891C (en) | Method and system for generating a vector representation of an image | |
| CN115910382A (en) | Method for predicting side effects of drugs by using restricted Boltzmann machine based on penalty regular term | |
| CN116662834B (en) | Fuzzy hyperplane clustering method and device based on sample style characteristics | |
| WO2021059527A1 (en) | Learning device, learning method, and recording medium | |
| CN116778339A (en) | Method and system for selecting hyperspectral wave bands by aid of local view auxiliary discrimination | |
| CN116503320A (en) | Hyperspectral image anomaly detection method, device, equipment and readable storage medium | |
| JP7347750B2 (en) | Verification device, learning device, method, and program | |
| Atukorale et al. | Hierarchical overlapped neural gas network with application to pattern classification | |
| Perwej et al. | The State-of-the-Art Handwritten Recognition of Arabic Script Using Simplified Fuzzy ARTMAP and Hidden Markov Models | |
| Doaud et al. | Using swarm optimization to enhance autoencoders images | |
| Pr | Improving performance of deep learning models using input propagation | |
| CN104363981B (en) | Face verification method and system | |
| Li et al. | Laplacian sparse dictionary learning for image classification based on sparse representation | |
| JP7544254B2 (en) | Learning device, learning method, and program |
Legal Events
| Date | Code | Title | Description |
|---|---|---|---|
| TRDD | Decision of grant or rejection written | ||
| A01 | Written decision to grant a patent or to grant a registration (utility model) |
Free format text: JAPANESE INTERMEDIATE CODE: A01 Effective date: 20130430 |
|
| A61 | First payment of annual fees (during grant procedure) |
Free format text: JAPANESE INTERMEDIATE CODE: A61 Effective date: 20130529 |
|
| R151 | Written notification of patent or utility model registration |
Ref document number: 5284530 Country of ref document: JP Free format text: JAPANESE INTERMEDIATE CODE: R151 |