JP2022185568A - 粘度測定方法及び装置 - Google Patents

Abstract

【課題】広い粘度範囲の流体に対応できる粘度測定方法及びそのための装置を提供する。【解決手段】一定の粘性のある流体を粘性に抗って流路中に流すためには、圧力を印加する必要がある。この圧力の印加により流路には内圧が生じる。この内圧により流路が変形するのを流路内壁のひずみなどとして検出することで、この流体の粘性を求めることができる。粘度測定装置としては、粘度を測定すべき流体が流れる流路と、流体を流すことにより流路の内壁に生じた変形の量を測定する手段と、測定された変形の量に基づいて流体の粘度を求める手段とを設ける。【選択図】図１

Description

本発明は粘度測定方法及びそのための装置に関し、特に広い粘度範囲の流体に対応可能な粘度測定方法及び装置に関する。

流体の粘度を測定することはその特性を判定する点で非常に重要であり、例えば流体が何であるかを同定するためにも使用できる。気体と液体の一方の粘度を測定するための技術は多数存在するが、気体と液体との性質に著しい差があって両者の粘度の値には大幅な差異が存在するために、単一の方法で気体と液体の両方の粘度を調べるのは非常に困難である。

日常生活やその他の面で最もありふれた流体の特性は粘性である。例えば、水は粘度が比較的小さい流体である一方、蜂蜜は粘度がかなり大きい。気体も粘性を有するが、その値は液体のものよりもはるかに低い。従って、異なる気体の間の粘度の違いを液体と同じように簡単に識別することはできない。粘度の値は気体については１０^－６～１０^－５Ｐａ・ｓ、また液体については１０^－４～１０^８Ｐａ・ｓという極めて広い範囲で変化する。その結果、粘度の大きさを求めるためには多数の異なる解析技法が使用される。例えば、液体の粘度は回転式粘度計を使用して試料を撹拌することで測定できる。この測定装置は典型的には１０^－３～１０^６Ｐａ・ｓという広い範囲で動作し、したがって多くの異なる液体の粘度を測定できる。これとは対照的に、気体の粘度の測定はもっと困難であり、多くの異なる方法が使用されている。このような方法としては、毛細管中の圧力の差分を測定すること、落下する物体の粘性抵抗を測定すること、円盤の振動の減衰を測定すること、光の散乱を測定すること、回転する浮遊円盤の速度の変化を測定すること、光の吸収を測定すること、ＱＣＭ（quartz crystal microbalance）や微小カンチレバーのような振動する物体の共振周波数のシフトを測定すること、及び管に流体を流すことでその粘性により管の内壁に印加される流れ方向の力やこの力による管の伸びを測定すること（特許文献１）などがある。

しかしながら、同じ装置を使用して気体と液体の両方の粘度を測定するために適用できる手法はわずかしかない。両方のタイプの流体の粘度を測定することの一つの例は、微小カンチレバーを使用してこれを波動伝搬解析（wave propagation analysis）と組み合わせることである。それでもなお、気体測定のためにはナノスケールの厚さの微小カンチレバー、また液体測定のためにはマイクロメートルスケールの厚さの微小カンチレバーという、寸法の大きく異なる複数の微小カンチレバーが必要とされる。その結果、液体用と気体用とに別々の装置を使用しなければならない。他の例は、ガラス毛細管を使用して異なる相、すなわち液体及び蒸気という相、の水の粘度を観測するというものがある。これらの測定は数１０ＭＰａという高い最大圧力に加え、数１００ｋＰａから始まる広い圧力範囲をも必要とするので、高圧ポンプ及び高性能の圧力トランスデューサを使用することが必須となる。気泡流、スラグ流（slug flow）、また環状流（annular flow）のような気体及び液体という２つの相を含む流れは、粘度測定のための標準的な技術を使用して解析することができるが、これらの流れの性質は流れ中の連続相によって支配され、流れ全体の粘度は液体の粘度の方に類似したものとなる。非常に困難なことは、粘度の範囲の両極端を単一の装置を使用して測定することである。気体は、回転式粘度計のような既存の技術で測定するには拡散性が大きすぎる。他方、液体は、ガス用の既存の手法によって粘性依存のパラメータの変化の大きさを測定するには、構成の設計を大きく変更したり複雑化したりすることなしには、通常は粘度が大きすぎる。気体と液体の両方の粘度を測定できる単一の装置は、非常に小さな気体の粘度からそれらよりも大幅に大きな液体の粘度までの広大な範囲の粘度を調べることができなければならない。このような装置があれば、気体、液体またこれらの混合物等のいかなる流体の測定を、構成の変更なしで可能とし、これにより例えば粘度に基づいた流体の同定を実現することができる。

本発明の一側面によれば、粘度を測定すべき流体を流路に流し、前記流体を流すことにより前記流路の内壁に生じた変形の量を測定し、前記測定された変形の量に基づいて前記流体の粘度を求める粘度測定方法が与えられる。
ここで、前記変形の量をひずみとして測定してよい。
また、前記ひずみは前記内壁上または前記内壁中に生じるひずみであってよい。
また、前記ひずみは前記内壁表面であって前記ひずみを測定する位置における前記内壁表面に沿った方向のひずみであってよい。
また、前記ひずみは前記流路に交差する面による前記流路の断面内のひずみであってよい。
また、前記内壁の変形は前記流路に交差する面による前記流路の断面の形状の変形であり、前記ひずみは前記変形によって前記断面形状の辺が変位することにより前記辺の長さが変化して生じるひずみであってよい。
また、前記ひずみの大きさは前記変位の量の２乗に比例するものであってよい。
また、粘度が既知の流体を前記流路に流したときの前記変形の量を測定することにより前記変形の量と粘度の絶対値との関係を較正してよい。
また、前記既知の流体が前記流路を流れる際の流量は、前記粘度を測定すべき流体が前記流路を流れる流量と同じであってよい。
本発明の他の側面によれば、粘度を測定すべき流体が流れる流路と、前記流体を流すことにより前記流路の内壁に生じた変形の量を測定する手段と、前記測定された変形の量に基づいて前記流体の粘度を求める手段とを設け、上記何れかの粘度測定方法により前記流体の粘度を測定する粘度測定装置が与えられる。
ここで、前記変形の量を測定する手段は前記流路の内壁上または内壁中に設けられたひずみゲージであってよい。
また、前記粘度測定装置は気体と液体の両方の粘度を測定してよい。

本発明の粘度測定方法及び装置によれば、非常に広い粘度範囲の流体の粘度を測定することが可能になる。従って、例えば、必要な場合には液体と気体の両者などの広範な粘度の流体の粘度を測定する装置を提供することができる。もちろん、測定対象として想定している流体が気体のみあるいは液体のみという場合であっても本発明を適用できることは言うまでもない。また、本発明によれば流路壁等は固定されていてよいなど、測定原理上微小な変形を起こす部分以外の可動部材は不要であり、また測定対象の流体の流路内に何らかの部材を突出させたり、また流路中の流体そのものを取り出すなどの構造等も原理上不要であるため、構造が単純で堅牢な粘度測定装置を提供できる。

（ａ）実施例で使用したひずみゲージの光学顕微鏡像。（ｂ）ＰＤＭＳで作製された微小流体装置の写真、及びその部分拡大写真。右側部分に示す部分拡大写真は装置に埋め込まれたひずみゲージを示す。（ｃ）微小流路装置（（ｂ）に示す）の３Ｄ構造図。（ｄ、ｅ）微小流路のすぐ上にあって微小流路に交差するように配置されたひずみゲージの断面構造図。なお、ここで使用されているひずみゲージは、エポキシ膜（Epoxy film）の片面先端にひずみを検知する部材（具体的には合金）（図中ではGaugeと表記）が配され、同一面上の反対側先端に銅電極（Cu electrode）が配される構造となっている。（ｅ）に示す部分拡大断面構造図は、流れがない場合（左側、[Without flow]）及び流れがある場合（右側、[With flow]）の微小流路の変形の状況を示す（寸法の記載は省略）。 （ａ）５種類の気体、すなわちＣＯ_２、Ｎ_２、空気（Ａｉｒ）、Ｈｅ及びＡｒについての流量１０ｍＬ／分の流れを断続した場合における実施例の微小流体装置の出力電圧（Output Voltage）の時間変化を示す図。（ｂ）５種類の気体、すなわちＣＯ_２、Ｎ_２、空気（Ａｉｒ）、Ｈｅ及びＡｒについての流量１０ｍＬ／分の場合における実施例の微小流体装置の出力電圧を粘度（Viscosity）の関数として示す図。この図においてはその右側縦軸に出力電圧に対応するひずみ（Strain）の大きさも示す（出力電圧とひずみとは比例関係にある）。これら５つのデータ点をべき乗則関数でフィッティングして図中に破線で示す。また、フィッティング結果の式を図中の左下寄り領域中に示す。 （ａ）粘度が互いに異なる１０種類の気体、すなわちＣ_３Ｈ_８、Ｈ_２、Ｃ_２Ｈ_６、ＣＨ_４、ＳＯ_２、ＣＯ_２、Ｎ_２、空気（Ａｉｒ）、Ｈｅ及びＡｒを流量１０ｍＬ／分で流した場合（Under flow）の実施例の微小流体装置中のひずみゲージの断面プロファイルについてのＦＥＡ結果を示す図。ひずみゲージの変形（Deformation）は微小流路の幅に沿った位置（Position along channel width）の関数としてプロットされている。淡灰色で網掛けした２．８ｍｍ～４．３ｍｍの位置は、ひずみゲージの１μｍ下に微小流路が存在している領域である。図には、比較のため、気体を流していない状態（No flow）での断面プロファイル（変形の大きさが０．０００ｍｍの直線）も示している。（ｂ）上記１０種類の気体について、変形を粘度（Viscosity）の関数としてプロットした図。これら１０個のデータ点をべき乗則関数でフィッティングした結果を破線として示す。また、フィッティング結果の式を図中の左下寄り領域中に示す。 （ａ）、（ｂ）ひずみゲージ上のひずみ（流路壁の壁面に沿った方向のひずみ）εをΔｈと関連付けるための概念図。 流量１０ｍＬ／分の場合の１０種類の気体、すなわちＣ_３Ｈ_８、Ｈ_２、Ｃ_２Ｈ_６、ＣＨ_４、ＳＯ_２、ＣＯ_２、Ｎ_２、空気（Ａｉｒ）、Ｈｅ及びＡｒについてのＦＥＡによる出力電圧（Expected output voltage）を粘度（Viscosity）の関数として中抜き正方形でプロットした図。これらのデータ点をべき乗則にフィッティングして破線で示し、このフィッティング結果の式を図中の左下寄りの領域に示す。さらに、５種類の気体、すなわちＣＯ_２、Ｎ_２、空気（Ａｉｒ）、Ｈｅ及びＡｒについての実験結果の実測データを中実の正方形で示す。 粘度が既知の各種の気体について、本発明の実施例により求められた粘度（Predicted viscosity）を既知の粘度（Known viscosity）の関数として示す図（中実の下向き三角形のプロット：Present Invention）。この図には、比較対照として従来の文献に示された同様なデータもプロットしてある（中実の正方形：Igarashi et al.、中実の上向き三角形：Zhang et al.、中実の円形：Meijer et al.）。 流量（Flow rate）が０．１ｍＬ／分～１５０ｍＬ／分の範囲における１０種類の気体、すなわちＣ_３Ｈ_８、Ｈ_２、Ｃ_２Ｈ_６、ＣＨ_４、ＳＯ_２、ＣＯ_２、Ｎ_２、空気（Ａｉｒ）、Ｈｅ及びＡｒについてのＦＥＡによる変形（Deformation）を粘度（Viscosity）の関数として示す図。図中のプロットは、下から上の順で流量０．１、０．５、１．０、２．５、５、６、７、８、９、１０、１５、２０、２５、５０、１００及び１５０ｍＬ／分にそれぞれ対応する。すべてのデータ点を流量毎にべき乗則にフィッティングし、その結果を図中の実線で示す。 流量（Flow rate）の関数としての指数部（Exponent）ｎを示す図。ｎの値は図７に示されるΔｈ－μのプロットへのべき乗則フィッティングにより得られるものである。 流量（Flow rate）が１０ｍＬ／分でＡｒを流した場合の微小流路（Microchannel）の変形（Deformation）の分布を示すカラーマップをモノクローム化した図。 流量が左から右へ向かってそれぞれ６、７、８及び９ｍＬ／分の場合の５種類の気体、すなわちＣＯ_２、Ｎ_２、空気（Ａｉｒ）、Ｈｅ及びＡｒについての実施例の微小流体装置のひずみゲージの測定された出力電圧（Output Voltage）の時間関数を示す図。 流量が６、７、８、９及び１０ｍＬ／分の５種類の気体、すなわちＣＯ_２、Ｎ_２、空気（Ａｉｒ）、Ｈｅ、及びＡｒの粘度（Viscosity）の関数として実施例の微小流体装置のひずみゲージの出力電圧（Output voltage）を示す図。流量１０ｍＬ／分の場合に得られたデータ点は図２（ｂ）に示すものと同じである。 実施例の微小流体装置中のひずみゲージからの出力電圧（Output voltage）の時間変化を、７種類の液体、すなわち左から右へそれぞれ水、ＭｅＯＨ水溶液（ＭｅＯＨ濃度がそれぞれ２０、４０、６０及び８０ｖｏｌ％）、メタノール、及びＩＰＡについて示す図（各図中の左上の表記（例えば「Ｈ_２Ｏ（Ｍ０Ｈ１０）など」）は、これらの液体を識別するためのものである）。ここで、各液体は流量０．２５ｍＬ／分で約４秒間流した後、流れを止めた。 （ａ）流量０．２５ｍＬ／分で７種類の液体、すなわちＭｅＯＨ、水、ＩＰＡ及び４通りの異なる濃度のＭｅＯＨ水溶液（上記図１２の説明を参照）についての実施例の微小流体装置中のひずみゲージからの出力電圧（Output voltage）を粘度（Viscosity）の関数として示す図。（ｂ）ＭｅＯＨの水溶液中での体積割合（Volume fraction of MeOH in H₂O）に対するｅ_ｏｕｔ ^１／ｍの変化（■）及び報告された粘度（Reported Viscosity）の値（淡灰色の●）をプロットした図。両者はよく一致していることが判る。

本願では流体が気体であってもまた液体であっても、その粘度の測定を容易に実現する方法及びそのための粘度測定方法及び装置が与えられる。この目的に向け、まずは流体を変形可能な流路に流す。この流路の変形は流体の流れを引き起こすために必要とされる圧力に依存するが、この圧力は流体の粘度に依存する。例えば微小流路のすぐ上にあってこの微小流路に交差するように埋め込まれたひずみゲージにより、流体の流れによって引き起こされた流路の変形をひずみとして測定できる。なお、ひずみを測定する具体的な手段としては実施例に記載した通常のひずみゲージ以外にも、光の干渉などで非接触にひずみを測定する手段などもあるが、必要に応じて適宜選択することができる。このひずみは流体の流れによって引き起こされた流路の変形の二乗に比例する。これにより同一の装置を使用して、例えば流体の粘度に基づいて気体だけではなく液体を精密に判別することが可能となる。

本発明によれば、１台で広いダイナミックレンジにわたって流体の粘度を測定する方法及び装置が与えられる。このような装置は、例えば微小流体装置（microfluidic device）により実現できる。この微小流体装置は変形可能な微小流路（microchannel）を使用する。ここで当該変形は流体の流れを駆動する圧力に比例するが、圧力は流体の粘度に比例する。微小流路は例えばpolydimethylsiloxane（PDMS）で作られ、ここに微小流路上にあってこの流路を横切る態様でひずみゲージが埋め込まれており、流体の流れによって引き起こされるひずみを微小流路の変形として効率的に測定する。後述する実施例では、測定対象の流体の流れによって引き起こされたひずみを二酸化炭素（ＣＯ_２）、窒素、空気、ヘリウム（Ｈｅ）及びアルゴン（Ａｒ）の気体の粘度並びにメタノール（ＭｅＯＨ），水、イソプロピルアルコール（ＩＰＡ）及び４通りの異なる濃度のメタノール水溶液の液体の粘度の粘性であって気体と比べて少なくとも２桁大きな値の粘度と関連付けるという非限定的な例を挙げる。

なお、上では「微小流体装置」、「微小流路」なる用語を使用したが、本発明の原理から明らかなように、ここで使用する装置や流路が微小であることは必須の要件ではない。流路が微小である場合には粘度測定の際に必要とされる測定対象の流体の量が少なくて済む点で有利である。しかし、流路が細い場合には、流体中に微小な異物が混入したり、流体中の成分が流路内に付着・沈積等しやすかったりする場合には、流路の閉塞が起こりやすくなる。あるいは、閉塞しなくとも流体が流路を流れる際の各種のパラメータが変化することで測定結果に誤差が導入される可能性があるなど、不利な面もある。従って、粘度測定の際の各種の条件も考慮の上で装置・流路等のサイズを定めるのが良い。

流体の粘度を判定する標準的な方法は、流体を既知の形状の流路に通して、このときに流体を流すために必要とされる圧力降下ｐを測定することである。流体の粘度μは圧力降下ｐに比例する。この方法は流路が変形可能である場合にも適用可能である。上記関係は非線形、すなわちｐ∝μ^ｎ（ｎ＝０．２５以下）（非特許文献１）である。しかしながら、ここでｎの値が小さいので粘度μの微妙な変化が圧力降下ｐに与える影響はあまり大きくない。すなわち、この方法では粘度の違いに対する感度は限定されたものとなる。

そこで、本発明ではこれとは別の測定原理を採用した。具体的には、本発明では変形可能な流路を使用し、圧力降下ｐではなく流路内の流体の圧力による流路の変形それ自体を測定する。この流路の変形を求めるには、例えば流路の内壁のひずみをひずみゲージ等を用いて測定すればよい。例えばこの測定の具体例を示す本願実施例の装置（図１、詳細は後述）では、polydimethylsiloxane（ＰＤＭＳ）で作製された断面が矩形の流路を使用し、この流路のすぐ上にあって流路に交差する形で埋め込まれ、また薄いＰＤＭＳの層で流体から分離されたひずみゲージ（Strain gauge）を使用して、測定対象の流体の流れにより引き起こされた流路の変形（Deformation）Δｈを測定する。図１では当該ＰＤＭＳ層が非常に薄いために図示は省略してある。ひずみε（ここではひずみゲージ中の検知部の長さの変化、すなわち図１（ａ）の上半分にあるループ状の線路の上下方向の伸び）はΔｈ^２に比例し、変形Δｈは流体の流量にかかわりなく圧力降下ｐに比例する。これにより、気体から液体までの範囲に及ぶ非常に広い範囲にわたって高精度で流体の粘度を測定することができる。なお、図１に示す構成ではひずみゲージが流路の内壁表面上に設置されており、そのひずみ検知部は図１（ａ）の上半分にあるループ状の線路になっていることからわかるように、測定されるひずみεは流路内壁表面に沿った方向のひずみである。また、ひずみゲージ等のひずみを測定する手段（センサ等）が流路内壁表面ではなく内壁内部に埋め込まれている場合でも、ひずみ検知部のループ状の線路が流路内壁表面に沿った方向に延びている場合には、実質的に流路内壁表面に沿った方向のひずみが測定される。ここで、流路の内壁面が波打っていたり流路の内径が場所によって異なっていたりするなど、流路がその内部の流体の流れの方向に沿って一様でない場合には、流路内の内壁表面であってひずみゲージ等のひずみを測定する手段（センサ等）の設置位置における内壁表面に沿った方向（この設置位置における内壁表面の接平面に沿った方向）のひずみが測定される。また、ひずみを測定する手段が内壁内部の比較的浅い位置に埋め込まれているのであれば、内壁表面であって当該埋め込み位置の真上に位置する内壁表面に沿った方向のひずみが実質的に測定される。

なお、本願明細書、また図１に示す装置の形状を見ると、流路の断面（正確には流路内を流体が流れる方向に直交する面による流路断面、以下単に断面と呼ぶ）が矩形であるとして説明を行っている。しかし、これは説明をわかりやすくするための単なる例示であって、本発明の原理上は断面は任意の形状としてよい。また、以下の説明では、流路の断面を、流路内を流体が流れる方向に直交する面による断面としているが、流路の断面はこれに限定されるものではない。より一般的には、流路の断面とは、流路内を流体が流れる方向に直交するかあるいは斜めに横切る面（流路に交差する面と呼ぶ）によって流路を切断した断面であることに注意されたい。従って、流路の断面内のひずみも、一般的にはこのような流路に交差する面による断面内のひずみである。

ただし、図１（ｅ）に示すように流路の変形（ここでは流路内壁に生じるひずみ）の測定を流路内壁の全周ではなくその一部分でしか行わない構成とする場合には、流路内壁の周のうちでこのような変形の検出対象に入っていない部分の変形が変形の検出対象となっている部分の変形を吸収することで変形の検出感度を低下させるという悪影響を小さくするように、流路の形状その他を決めるのが望ましい。例えば、図１（ｄ）、（ｅ）等から判るように、本実施例では流路の断面は矩形形状であり、当該矩形の上側長辺に沿ってひずみゲージが設置されている。ここで流路中に流体を流すことによる流路内の圧力上昇により引き起こされる流路の変形において上側長辺以外の変形も無視できないものであった場合、たとえば当該圧力上昇によって図１（ｅ）右側に示すように流路断面の上側長辺がせり上がるような変形が起こり、この時に上側長辺内に発生する引っ張り応力で断面の側壁（左右の短辺）が引っ張られて流路の中心部に向かって倒れ込むような変形を起こした場合には、上記引っ張り応力が一部緩和されることにより上側長辺のひずみも減少する。このような場合には変形の検出感度が低下する。このような感度低下を抑えるためには、例えば、長辺の長さと短辺の長さとの比の値（アスペクト比）を大きくすることで側壁の倒れ込みを小さくする、流路壁の肉厚が均一ではなく上側長辺部分の肉厚を他の部分よりも薄くしておく、上側長辺部分の材料として他の部分の材料よりも剛性の小さいものを使用する、あるいは内壁表面に近い部分は同じ材料を使用しても上側長辺部分以外の壁を剛性の高い材料でできた部材に強固に張り付ける、などの構成を採用すればよい。

また、上の説明では流路を形成するための材料として特定の材料であるＰＤＭＳを挙げたが、これは単なる例示であって、実際には任意の材料を使用できる。このような材料としては流路を形成するための加工性が良好であり、また流路中に無理のない流量で流体を流した場合に、そこで生じる圧力の変化が流路内壁に引き起こす変形の量がひずみゲージ等で充分に測定可能であって、またそのような変形が可逆的な変形であることが望ましい。

また、図１（ｄ）では、流路の内壁面のうちの上面側に、流路の変形の量を測定するためのひずみゲージ中のひずみ検知部（図中ではGaugeと表記）を上述の図示しない極薄のＰＤＭＳ層及びひずみゲージの基板である３０μｍ厚のエポキシ膜（Epoxy film）を介して設置するように図示されている。しかし、この検知部が直接流体に接触するように配置してもよいし、逆に内壁材料の中の内壁面に近い位置に検知部が埋め込まれた配置などでもよい。検知部（対象の変形の量を検出する部材）は流路の内壁に発生する変形の量（ひずみであれば内壁面に沿って発生するひずみ）を充分な感度で測定できる位置であればその配置位置は問わない。なお、図１（ｄ）では、エポキシ膜の同一表面上にはひずみ検知部の他に銅電極も固定されており、これはひずみ検知部が固定されている先端部とは反対側に配置されている。

また、図１（ｃ）等に示す装置中の流路の構成例では流路は直線状であり、またその断面の形状・サイズも流体の流れの方向に沿って一様である。もちろん、必要に応じて流体の流れの方向に沿った断面形状・サイズを変化させてもよい。

また、本発明の粘度測定を行う際には、上述した測定方法から判るように測定対象の流体を流す流路の変形を知ることができればよいのであるから、当該流路の内部には特定の形状を有する構造の類は何ら必要とされない。このような流路内の構造は測定装置の脆弱性を引き起こす原因となり得るが、本発明ではそのような流路の内部構造が必要とされないことから、堅牢な測定装置を実現することが可能となる。さらには、上で言及した従来技術においては流路上の圧力降下を測定していたが、本発明におけるような流路の変形の量の測定は、流路内を流れる流体の圧力を何らかの形で取り出す必要はなく、流路周囲部分（流路の内壁等）のひずみを既存のひずみゲージなどの簡単な構造の手段で検知することで実現できるため、粘度測定装置の構造が単純化されるという点でも本発明は従来技術に比べて有利である。さらに、本発明は流路中に流体を流し、その際の流路内の圧力変化による流路の変形に基づいて流体の粘度を求めるという原理によるものであるため、流路が設けられている器具の形状・サイズ・材料にもよるが、このような変形は短時間のうちに定常状態に到達するため、粘度測定に要する時間も短時間となる。実際、図１に示す装置を使用した実験では、流体の流速を適切に設定することにより、流体を流路に流し始めてから数秒以内に流路の変形量が定常状態に到達した。これにより、流体の粘度の実時間測定や連続測定が可能となる。

また、本発明に係る装置はその構造が単純であり、また可動部分がほとんどないため、通常使用されている製造技術を使用することで再現性良く製造できる。そのため、煩雑な設定、調整なしで高精度の粘度測定が可能となる。

ここで、上述した流路の変形の量と流路を流れる流体の粘度とはべき乗則に従い、また上に述べたひずみと流路の変形の量との関係はひずみεが流路の変形Δｈ^２に比例する関係にあることを説明する。

流路中に流れる流体とこの流体により流路内壁に印加される圧力による流路の変形との関係は、図１に示す具体的な装置の流路構成で考えても一般性を失うものではないので、以下では図１の装置を使用した実験及び当該装置の有限要素解析（ＦＥＡ）の結果を参照する。まず、図２に示す実験では、各種の気体流を図１の装置に与えて、それぞれの気体流についてのひずみゲージの出力電圧ｅ_ｏｕｔの時間変化を測定した（図２（ａ））。これらの気体の粘度が既知であるので、これらの出力電圧ｅ_ｏｕｔと粘度μとの関係を求めることができる。この関係は図２（ｂ）に示すようにべき乗則ｅ_ｏｕｔ∝μ^ｍ（ここでｍ＝０．８５９）に従う関係であることが判る。ここで、ひずみゲージの出力電圧ｅ_ｏｕｔは測定した流路内壁のひずみ（より具体的には流路内壁の気体流に直交する方向の内壁の長さの伸び率）を直接反映するものであることに注意されたい。

更に、図１に示す具体的な装置の流路に上記実験で使用した気体及び他のガスを流した場合についての有限要素解析（ＦＥＡ）を行い、この際の当該流路の変形の量（流路の上側内壁の上方への変位）Δｈとこれらの気体の粘度との関係を調べた。図３（ｂ）に示すように、この関係はべき乗則Δｈ∝μ^ｎ（ここでｎ＝０．４３４）に従う関係であることが判る。

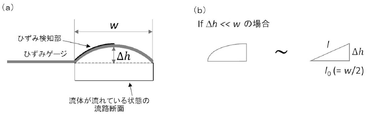
図４は、粘度測定対象の流体を流す流路を流路内の流れに垂直な平面で切断した場合の断面を示す概念図である。流路の断面形状は長辺の長さがｗである矩形であり、流体は断面図に垂直な方向に流れる。ひずみゲージは流路の長辺に沿って設置されており、流路内の流体の圧力による流路内壁の長辺方向のひずみ、すなわち長辺方向の壁面の伸びを測定する。ここにおいて、図４（ａ）に流路の断面形状を示す。この流路に流体を流していない状態、すなわち流体の流れによって流路にこれによる圧力が発生していない状態では、流路の上側の内壁面は図中で横方向の破線で示す位置にあり、断面全体は矩形形状になっている。流路に流体が流れている（図では流体は紙面に垂直な方向に流れる）と、これにより流路内の圧力が上昇するため、流路が膨張して、流路の内壁面が半円筒（断面がほぼ円形である筒状物（以下、単に円筒と呼ぶ）をその中心軸を含む平面に沿って縦割りにした形状）を伏せたような形状（以下、半円筒形状と称する）に変形する。これを流路の中心軸に垂直な平面で切断した断面図で見れば、図４（ａ）に示すような上向きに凸な曲線形状となる。この半円筒形状（断面図で見れば上に凸な曲線形状）の頂上部分が元の位置から上側内壁面に垂直な方向に移動した距離を流路の変形Δｈとする。また、流路の幅（矩形の長辺の長さ）をｗとする。図４（ａ）に示したモデルにおいては、解析を単純化するために、流路内壁面のうちで断面が上側の長辺である上面のみが外側へ向かって凸状に変形し、他の面（矩形の短辺及び下側の長辺に対応）は全く変形しないように描かれている。もちろん、流路内の圧力は内壁面全体にわたって印加されるが、例えば上面側の壁厚が他の部分に比べて極めて薄くなるように作製されているなどの場合には内壁面の変形（膨張）には図示したような傾向が現れる。また、すべての内壁面の変形を考慮して解析しても得られる結果は図のように単純化したモデルによる場合と同等であることは明らかであろう。

図４（ａ）では、流路断面の上側の長辺上にひずみゲージのひずみ検知部が設けられている。このひずみ検知部は長辺全体ではなく、上に凸な円弧状部分の上側にやや細い黒い曲線で示すように、その左半分に設置されている。従って、流路に液体を流しておらず、これによる圧力が流路内に発生していない場合には、ひずみ検知部は直線状となり、その長さはｗ／２である。ここではｌ_０≡ｗ／２とおく。長辺左端から流路内壁上面が圧力の上昇によって上に凸な曲線状に変形すると、よく知られているようにひずみゲージのひずみ検知部も同じように変形して引き延ばされる。この長さの変化（正確には長さの変化と元の長さの比の値）がひずみεとして求められる。

ここで、通常の材料を使用して流路を形成した場合には、そこに流体を流すことによる圧力が引き起こす流路の形状・サイズ変化は、流路断面のサイズ（幅など）に比べると非常に小さい。特に、流路の上面が圧力により変形することでひずみゲージのひずみ検知部が曲線形状に変形した場合を考えると、この変形によるひずみ検知部の伸びは、図４（ｂ）に示すように、底辺の長さがｌ_０、高さがΔｈである直角三角形の斜辺の長さｌと底辺の長さｌ_０との差で充分に高い精度で近似することができる。すなわち、下式を得る。

ここで、上記近似は１／２乗のテイラー展開結果の高次の項が十分小さいとして無視することにより行った。また、ひずみεは以下のように表される。

式（Ｓ１）と式（Ｓ２）より下式を導くことができる。

これより、ひずみεはΔｈ^２にほぼ比例することが判る。上述のべき乗則に関して言えば、上述の２つのべき乗則関数ｅ_ｏｕｔ∝μ^ｍ（左辺のひずみゲージの出力電圧ｅ_ｏｕｔはひずみεとほぼ比例関係にあるとしてよい）とΔｈ∝μ^ｎとを比較した場合に、ひずみは粘性の指数の２倍の指数のべき乗関数に従って変化するので、粘性のわずかな違いがひずみの違いへと鋭敏に反映されることがわかる。

ここで注意しておくが、流路に流す流体の流量が上述したべき乗則の関数の指数に影響を与えるなどの理由により、上述の測定原理だけでは相対的な粘度、すなわち２つの流体の粘度が同じであるか、また違う場合にはこれら粘度の大小関係、粘度の比などはわかるが、絶対的な粘度はまだわからない。なお、粘度の比の値は、上述のべき乗関数ｅ_ｏｕｔ∝μ^ｍ指数で示される出力電圧と粘度の関係から、出力電圧ｅ_ｏｕｔを１／ｍ乗した値の比が粘度μの比に等しいことにより求めることができる。絶対的な粘度を求めるには、ここで検討しなかった測定系の流体力学的なまたその他のパラメータを含めてさらに精密な解析を行ってもよいし、あるいは粘度が既知である１種類または複数種類の標準流体を同じ測定系に与えて得られた結果を使って検量線を作成することにより測定装置を較正すればよい。

上で述べた測定装置の較正においては、流体の流量がべき乗則の関数の指数に影響することから、検量線を引くための測定と粘度を求める対象である流体の測定とで流量を揃える必要がある。両測定における流速を精密に一致させるのは手間がかかることがあり、また測定対象の流体の流量が常に同じであることが保証されていない場合には複数通りの流量についての較正用の測定を行う必要がある。そこで、複数通りの（あるいは連続変化する）流量についての較正用の測定結果を簡単な手順で得ることが望ましい。そのためには、例えば流路上でその内壁に生じた変形の量が測定される箇所よりも下流に別の流路を接続し、当該別の流路から、測定している流体とは別の相の流体（例えば、前段で気体を測定しているなら液体、液体を測定しているなら気体）を流路中に混入させる。これにより、これより下流では気体ドメインと液体ドメインが流路中を交互に流れる気液二相流が形成される。この場合、流路の断面積は既知なので、気体および液体、各々のドメイン長と、それらドメインが流路におけるある一点を通過するのに要する時間を計測することで流量が計算できる。ここで気体ドメインと液体ドメインが切り替わったことは例えば流路中に光を照射して透過光を検出することで光学的に検出することができる。それ以外にも例えば流路中の流体の振動を検出したり、上述の光学的な検出と同じく流路に機械的な振動を与えてその伝搬や気体－液体界面による反射を検出することで両ドメインの切り替わりを検出することも可能である。これにより、流量を多段階であるいは連続的に変化させながら流路内壁の変形量を測定することができる。

なお、上の説明では解析を簡単にするために流路の断面が矩形であるとしたが、これは一般性を失う仮定ではない。具体的には、断面形状が通常の流路として採用するとは考えられないような極端に複雑な形状でない限りは、流路内壁の接平面に垂直な方向の変位であると定義できる流路の変形Δｈと、流路内壁面上であってひずみを測定する領域の流れに直交する方向のひずみεとの関係を考えることにより、このことを確認できる。ここで、流路の変形Δｈは流路を構成する材料として通常のものを使用する限り流路の幅に比べてかなり小さいということを考えれば、上記解析の過程で使用したところのひずみの測定対象である部分の形状を図４（ｂ）に示すように三角形で近似しても、当該部分の長さについては充分良好な近似が与えられる。従って、上記解析と同様な計算を行うことで、このような一般的な場合であっても、ひずみεの大きさについての支配的な項はΔｈ^２であるということができる。

また、上に述べた本発明の粘度測定方法は、厳密にはニュートン流体、すなわち流れの剪断応力（接線応力）と流れの速度勾配（ずり速度、せん断速度）とが比例する流体に適用できるものであり、以下に示す実施例においてもニュートン流体について測定を行った。しかしながら、流れの剪断応力と流れの速度勾配との関係が比例関係からわずかにずれる程度の場合には、本発明の粘度測定方法を使用して測定された粘度は実用上充分に高い精度を有する。従って、測定対象の流体がどの程度の非ニュートン性を有するかがわかれば、本発明の粘度測定方法により得られる粘度の精度を知ることができる。更には、通常必要とされる粘度の値は流れの速度がある限定された範囲についてのものであるため、このような場合には非ニュートン性がかなり大きくても本発明により得られた粘度の値はそのような使用状況の場合に粘度の値として使用できるものになる。あるいは、粘度を定数として取り扱うのが不都合である場合でも、例えば複数通りの流速について本発明の方法で粘度を求め、これにより流速と粘度との関数関係を所望の精度で定めることもできる。従って、本発明が適用可能な流体はニュートン流体に限定されるものではないことをここに注意しておく。

以下、実施例に基づいて本発明をさらに詳細に説明する。なお、以下の実施例は発明の理解を助けるための例示であって、本発明をこれに限定する意図はないことに注意されたい。また、以下では図１に示す微小流路装置を使用するものとして説明を行っているが、ここで「微小」と呼んでいるのは図１（ｃ）、（ｄ）等に示すようにここに例示した具体的な装置の寸法が微小であることを反映するだけであり、本発明自体はこのような装置が微小であることを必須とするものではなく、測定に支障のない限り任意の寸法としてよいことに重ねて注意しておく。

＜気体測定＞
先ず一組の気体、具体的にはＣＯ_２、Ｎ_２、空気（Ａｉｒ）、Ｈｅ及びＡｒについて、微小流路装置を用いて、流量１０ｍＬ／分で測定した結果を図２に示す。ひずみゲージの出力電圧は、図２（ａ）に示すように、気体の流れの有無（図中では「Gas on」及び「off」として表記）及びその気体の種類に依存する。各気体についての出力はそのピーク電圧により特徴付けられる（図２（ｂ）に示すグラフではピーク電圧を出力電圧としてプロットした）。このピーク電圧は下式に示すようにひずみに比例する：

ここでｅ_Ｂはブリッジ電圧（２．５Ｖ）、またＫ_ｓはひずみゲージのゲージ率（２．１１）である。測定されたひずみは、図２（ｂ）に示すように、粘度μに比例する。このデータはべき乗則関数ｅ_ｏｕｔ∝μ^ｍ（ここでｍ＝０．８５９、図２（ｂ）のグラフ中の左下寄りの領域に記載されたフィッティング結果の式を参照）で良好に記述される。従って、この変形可能な微小流路は、気体粘度の高感度な測定を実現する。

この装置のこのような応答の原因を調べるため、図１に示す本願実施例の微小流路装置についての有限要素解析（ＦＥＡ）を行った。この解析により、気体の流れがひずみゲージの変形にどのように影響するかを詳細に調べることができる。ここで、気体の流量を１０ｍＬ／分に設定し、粘度を変更して微小流路の変形及びその結果としての流路内壁の変形量である流路内壁（ここでは矩形の流路断面の上側の長辺に対応する内壁）の上方（この内壁の表面に垂直な方向）への変位Δｈを調べた。ＦＥＡを行うにあたっては、実際の測定に使用した５種類の気体に加えて、他の一般的な気体であるプロパン（Ｃ_３Ｈ_８），エタン（Ｃ_２Ｈ_６）、水素（Ｈ_２）、メタン（ＣＨ_４）及び二酸化硫黄（ＳＯ_２）についての粘度も追加した。これらの気体により、一般的な気体の大部分に相当する広い範囲の粘度がカバーされる。ＦＥＡシミュレーションにより、微小流路の変形の程度は、図３（ａ）からわかるように、気体の粘度に依存する。従って、変位Δｈを測定することにより、気体の粘度を判定することができる。この依存性は、図３（ｂ）に示すように、べき乗則Δｈ∝μ^ｎ（ここでｎ＝０．４３４）によって良好に記述される。

ＦＥＡの結果を測定結果と比較するため、微小流路のシミュレートされた変形に従ってひずみゲージから得られる出力電圧を求める。このひずみゲージ中でのひずみ検知部、すなわち図１（ａ）中に示されたループ状の線路、は図１（ｅ）に概略的に示すように微小流路上でその幅ｗのほぼ半分まで伸びている。もちろん、ひずみ検知部が覆う範囲はこれに限定されるものでなく、必要に応じて適宜定めることができることは言うまでもない。以下ではこのひずみ検知部が流路幅ｗのちょうど１／２の長さであるとして解析を進める。流路幅に比べて内壁の変位が小さい場合、すなわちΔｈ＜＜ｗが成立する場合には、すでに図４（ａ）、（ｂ）を参照して説明したように、テイラー展開を使用してひずみゲージ上のひずみεを下式のように表すことができる。

Δｈ∝μ^ｎであるので、出力電圧も粘度への依存性を示す。すなわち、ｅ_ｏｕｔ∝μ^２ｎとなり、したがってｍ＝２ｎとなる。シミュレートした結果は測定データと非常によく一致し、両者は図５に示すように、指数ｍ＝０．８５９である、粘度についてのべき乗則を示す。

ここで、本実施例で得られた実験データを同じ温度（２０℃）で得られたものとして先行文献で報告されているデータと比較したグラフを図６に示す。同図において、Igarashi et al.、Meijer et al.及びZhang et al.はそれぞれ非特許文献２、３及び４である。本発明に基づいて求められた粘度は既知の粘度の値とよく一致している。他方、非特許文献２～４で報告された粘度の値は場合により多少のずれが見られる。これにより本発明の方法の信頼性が示唆される。

各種の流れの条件についての挙動を調べるため、流量を変化させてＦＥＡシミュレーションを行った。その結果、図７に示すように、すべての場合で、変形と粘度との間にべき乗則関係が見られた。しかしながら、興味深いことに、この関係における指数部は流量に従って変化する。具体的には、図８に示すように、最小流量（０．１ｍＬ／分）においてはｎ≒１であり、流量を増加させるとｎは単調に減少し、約６０ｍＬ／分以降、ｎ=０．２５に漸近する。流量が非常に少ない場合には、微小流路はごくわずかしか変形しないはずであり、その結果ｎ≒１となる。流量が大きい場合のｎの漸近的な値は約０．２５であるが、この値は、ＰＤＭＳ製の微小流路の底面が固いガラス基板に接着されていて流体の流れの下でその上面（接着されている面（底面）の反対側の面）だけが変形する状況において流体を流した場合について解析的に計算された結果（非特許文献１）とほとんど等価である。本願での形状については、ＦＥＡシミュレーションの結果により、流体の流れによって引き起こされるひずみは、装置全体がＰＤＭＳで作製されているにもかかわらず、主にその上面側で起こることを示唆している。これは、図９に示すように微小流路の底面が相対的にかなり深い位置にあることによるものである。すべての場合において、流体圧変化による流路断面の変形に従って上側内壁面が引き延ばされる長さ（長さの変化分ｌ－ｌ_０）を、元の長さｌ_０で割った値として定義されるひずみ（上述の式（Ｓ２）参照）は変形の二乗に比例し、したがって出力電圧も指数部が２ｎである粘度のべき乗則依存性を示す。

ＦＥＡによって予測される挙動を実験結果と比較するため、５種類の気体の流量を６ｍＬ／分から９ｍＬ／分の間で変化させた場合のひずみゲージの出力電圧を測定した。その結果を図１０に示す。ここで、指数部は流量に強く依存した。この実験の形態では、流量変化のきざみが１ｍＬ／分という小さいものであるにもかかわらず、出力電圧の粘度依存性は、図１１に示すように、異なるものとなった。それにもかかわらず、各々の気体についての結果は互いに明確に区別できる。図１１に示されるように、各々の場合、データはべき乗則依存性により良好に記述され、また測定結果から得られた指数部（上述のひずみゲージの出力電圧ｅ_ｏｕｔが従うべき乗則関数ｅ_ｏｕｔ∝μ^ｍの指数部ｍ）はＦＥＡシミュレーションによって予測されたもの（流路の変形の量Δｈが従うべき乗関数則関数Δｈ∝μ^ｎの指数部ｎ）の２倍となる。

ここで、流量が６ｍＬ／分の場合に得られた応答では、出力電圧は気体の注入開始後数秒以内に最大値に到達し、その後は時間が経過しても変化しなかった。これに対して、流量を１０ｍＬ／分とした場合には出力電圧の時間波形にはややオーバーシュートが見られ、前述のような短時間での飽和特性は見られなかった。この事実は、粘度測定対象流体の流路への導入の際の流量等の測定条件を適宜設定することにより、粘度の実時間での測定や流路を流れている流体の変化を実時間でまた連続的に検出することが可能となることを示している。

ここでの測定は窒素を空気から区別するのに十分なだけ正確である。実際、両者の粘度の違いはわずか０．０５×１０^－５Ｐａ・ｓである。測定のノイズレベルは１μＶ未満であるので、粘度の違いがわずかに０．０１×１０^－５Ｐａ・ｓ程度であるｎ－ブタンとイソブタン（粘度はそれぞれ７．３９×１０^－６Ｐａ・ｓ及び７．４８×１０^－６Ｐａ・ｓ）のような構造異性体同士でさえも識別することができる測定精度を有する。しかしながら、指数部ｎは流量の関数として変化するので、本発明の測定装置は使用前に較正を行う必要がある。

＜液体測定＞
気体の粘度は１０^－６Ｐａ・ｓ～１０^－５Ｐａ・ｓの範囲で変化する。他方、液体の粘度はほぼ１０^－３Ｐａ・ｓから、多くの場合これよりも非常に大きな値まで変化する。それにもかかわらず、本発明に係る装置は微小流路を流れる液体に対して気体と同じような態様で応答し、したがって液体の粘性を測定するためにも使用できる。

これを示すために、ＭｅＯＨ、水及びＩＰＡ等のいくつかの液体について測定を行った結果を示す。これらの液体の２０℃における粘度はそれぞれ０．６０×１０^－３Ｐａ・ｓ、１．０×１０^－３Ｐａ・ｓ及び２．４×１０^－３Ｐａ・ｓである。各測定における流量を０．２５ｍＬ／分に設定した。各々の液体について、その流れをオン／オフした時のそれぞれの時間依存性のひずみゲージ出力電圧を測定し、図１２に示す結果を得た。これからわかるように、信号出力と粘度との間に明確な相関性がある。図１３（ａ）に示すように、これらのデータはｍ（＝２ｎ）＝０．８２０としたべき乗則によく一致する。粘度の範囲を更に広げるため、ＭｅＯＨ濃度を２０、４０、６０及び８０ｖｏｌ％に設定したＭｅＯＨ水溶液についても測定を行った。アルコール－水二元系の粘度は混合比に対して単純な線形依存性を示さず、その代わりに単調ではない態様で変化する。アルコール分子と水分子との間の水素結合が当該混合物の粘度を決めるにあたって重要な役割を演じ、その効果は特定の比率で最大となる。これにより、そこで粘度が最大となる。それにもかかわらず、その測定データは、図１３（ａ）に示すように、べき乗則に直接的に従う。さらには、ｅ_ｏｕｔ ^１／ｍをＭｅＯＨ体積割合の関数としてプロットすることにより、図１３（ｂ）に示すように、報告された粘度値によく一致する単調でない傾向があることが判る。ここで用いた液体の粘度は気体測定に用いた気体の粘度よりもほぼ５０倍大きいが、液体についての流量は気体の場合のほぼ１／４０であり、粘度と流量との積の値が同じ態様での測定を行うことになる。しかしながら、液体について得られたｍの値は気体についてのＦＥＡシミュレーションから予測された値と直接的に比較することはできない。従って、微小流体装置は事前に気体と液体とで別個に較正する必要がある。それにもかかわらず、本装置は気体及と液体との両者を含む任意の流体の粘度を定めるために使用することができる。

＜結論＞
polydimethylsiloxane製の微小流体装置を作製し、変形可能な微小流路を通して装置中に流体、すなわち気体及び液体、を流すことで当該流体の粘度を測定した。ここで、微小流路の変形は流体の流れを引き起こすために必要な圧力に依存するが、この圧力は流体の粘度に依存する。この目的のために、微小流路装置中にひずみゲージを埋め込んだが、その位置は微小流路のすぐ上であってこれと交差する、つまりこれを跨ぐように定めた。この構成により、流体の流れによって引き起こされる変形を効率的に測定してこの変形をひずみに変換することができるようになる。このひずみは変形の二乗に比例する。この装置によれば、単一の装置を使用して気体と液体の何れの粘度でも測定することができる。また、これにより、粘度だけでいくつかの気体を精密に識別するに十分な分解能を達成できるが、ここでの当該粘度の範囲は１，４７×１０^－５Ｐａ・ｓから２．２２×１０^－５Ｐａ・ｓまでである。また、本発明に係る同一の微小流体装置を使用して、メタノール、水、イソプロピルアルコール及び４種類の異なるアルコール濃度を有するメタノール水溶液等のいくつかの液体の粘性を測定できる。これらの液体の粘度は０．６０×１０^－３Ｐａ・ｓから２．４×１０^－３Ｐａ・ｓの範囲であり、上述の気体に比べてほぼ２桁大きな粘度になっている。「可搬性」、「ポイントオブケア検査」、「装着可能」及び「現場」装置への要求が高まりつつある状況では、非常に広いダイナミックレンジ、作製の容易さ及び高い精度を有する本発明のような装置は、検体間の差異を判別するために粘度を用いることのできる多くの応用に有用であろう。

［実験の細部］
＜ＰＤＭＳ装置の作製＞
以下では実施例で使用したＰＤＭＳ製の装置の作製手順を具体的に説明する。ネガフォトレジストSU-8 3035を清浄な３インチ片面研磨済みシリコンウエハー上にスピンコーティング手順（３０００ｒｐｍで３０秒間）によりスピンコートして、２５μｍ厚のフォトレジスト層を形成した。９５℃で１５分間ベーキングした後、フォトレジスト層にフォトマスクをプリントして紫外線で露光した。これに続いて、フォトマスクをウエハーから除去し、ウエハーを再度ベーキングした。このベーキングは６５℃で１分間、次いで９５℃で５分間行った。硬化していないレジストをpropylene glycol methyl ether acetate（ＰＧＭＥＡ）で８分間洗い流すことにより、微小流路構造が形成されたマスター型を得た。

微小流路モールド手順を適用して、マスター型から微小流路を複製した。主剤と硬化剤（重量比１０：１、Sylgard 182）とからなる液体ＰＤＭＳ混合物をSU-8マスター型に注ぎ、次いでガス除去を行った。６５℃で数時間硬化させた後、ＰＤＭＳをマスター型から剥離させた。生検パンチを使用して、流入口（図１（ｃ）に示す「Inlet」）及び流出口（図１（ｃ）に示す「Outlet」）用の貫通孔（それぞれ内径０．７５ｍｍ、外径１．５ｍｍ）を形成した。このＰＤＭＳブロック（図１（ｃ）に示す「Bottom PDMS layer」）を、ひずみゲージ（図１（ｃ）に示す「Strain gauge」）が埋め込まれた１ｍｍ厚の別個のＰＤＭＳ薄層（図１（ｃ）に示す「Top PDMS layer」）に不可逆的に接着した。この際、安定した接着を形成するため、７０Ｗで２０秒間のプラズマ処理を行った。９５℃で数１０分間加熱して接着強度を高めることで、ＰＤＭＳ微小流路装置の製造が完了した。このＰＤＭＳ微小流路装置の写真を図１（ｂ）に示す。

＜ＰＤＭＳ微小流路装置での気体／液体流測定＞
このＰＤＭＳ微小流路装置を使用して、各種の気体及び液体の流れにより引き起こされたひずみを測定した。すべての測定において、株式会社東京測器研究所（Tokyo Measuring instruments Laboratory Co., Ltd.）から購入したひずみゲージ（ゲージパターン：FLKB-1-11、長さ：４．３ｍｍ、幅：１．４ｍｍ、厚さ：３０μｍ、ゲージ率：２．１１、ゲージ抵抗：１２０Ω）を使用した。このひずみゲージの正確な寸法を示す顕微鏡像を図１（ａ）に示す。ひずみゲージからの全ての出力電圧はNI 9237 simultaneous bridge module（National Instruments Corporation）を使用して、ブリッジ電圧２．５Ｖを印加して測定し、サンプリングレート２０Ｈｚで記録した。データ収集プログラムはLabVIEW（National Instruments Corporation）を使用して設計した。ガス流はマスフローコントローラ（MFC；株式会社堀場製作所SEC-N112MGM）を使って調節した。この流れは流入口から流量１０ｍＬ／分で２０秒間注入し、次いで２０秒間の気体流のない時間間隔を置いた。同様な気体流サイクルを流量６、７、８及び９ｍＬ／分としたものにも与えた。漏れがないことを確認するため、体積流量計（volumetric flow meter）（ProFLOW 6000 Electronic Flowmeter, Restek Corporation）を使って流出口で流量を測定した。実験はＣＯ_２、Ｎ_２、空気、Ｈｅ及びＡｒを使用して行った。

液体流の測定については、シリンジポンプ（PHD 2000 Dual Syringe Pump, Harvard Apparatus）を使用して流量を０．２５ｍＬ／分に設定した。ＭｅＯＨ、水、ＩＰＡ及び４通りの異なった濃度のＭｅＯＨ水溶液を使用した。ＭｅＯＨ水溶液については、濃度を２０、４０、６０及び８０ｖｏｌ％に設定した。これらの水溶液試料を、図１２及び図１３中ではそれぞれＭ２Ｈ８、Ｍ４Ｈ６、Ｍ６Ｈ４及びＭ８Ｈ２の記号で示す。また、同様な記法として、水をＭ０Ｈ１０、またＭｅＯＨをＭ１０Ｈ０という記号で示すこともある。

＜ＦＥＡシミュレーション＞
ＦＥＡシミュレーション用構造力学モジュール（Structural Mechanics Module for the FEA simulation）を備えたCOMSOL Multiphysics 5.6を使用した。図１（ａ）～（ｄ）に示す寸法を有するＰＤＭＳ製の装置をモデル化した。シミュレーションに使用したすべてのパラメータを下表に示す。この装置の構造全体を約６００００個の要素のメッシュに分割した。実験に使用したＣＯ_２、Ｎ_２、空気、Ｈｅ及びＡｒに加えて、５種類の気体、すなわちＣ_３Ｈ_８、Ｈ_２、Ｃ_２Ｈ_６、ＣＨ_４及びＳＯ_２もまた追加でシミュレートして、それぞれのフィッティングカーブをできるだけ正確に求めた。なお、表１に示すパラメータのうち、「微小流路の高さ」に関しては、図１（ｄ）では「Channel」の高さを２５μｍと示しているが、装置の製造時に生じ得る不可避的な誤差（±数μｍ程度）を考慮して、シミュレーションでは２７μｍの値を設定した。

以上詳細に説明したように、本発明によれば広い粘度範囲の流体（気体、液体、その他、気体－液体二相流体などの特殊な流体）の粘度を簡単にまた高精度で測定することができる。また、本発明は単に粘度を測定するだけではなく、粘度測定に基づく他の分野への応用も可能である。一例を挙げれば、本発明は粘度の違いにより分子を識別することへも応用できる。この分子識別に当たって、本発明が提供する高い測定精度により、例えば粘度の違いがわずかに０．０１×１０^－５Ｐａ・ｓ程度であるｎ－ブタンとイソブタンの識別も可能となる。

特開昭６３－１５３４４７号公報

T. Gervais, J. El-Ali, A. Gunther and K. F. Jensen, Lab Chip, 2006, 6, 500-507. K. Igarashi, K. Kawashima and T. Kagawa, Sens. Actuator A-Phys., 2007, 140, 1-7. A. S. Meijer, A. S. de Wijn, M. F. E. Peters, N. J. Dam and W. van de Water, J. Chem. Phys., 2010, 133, 164315. J. T. Zhang, H. Lin and J. Che, Metrologia, 2013, 50, 377-384. Ogasawara, T. et al., Compos. Sci. Technol. 71, 1826-1833 (2011).

Claims (12)

1. 粘度を測定すべき流体を流路に流し、
   前記流体を流すことにより前記流路の内壁に生じた変形の量を測定し、
   前記測定された変形の量に基づいて前記流体の粘度を求める
   粘度測定方法。
2. 前記変形の量をひずみとして測定する、請求項１に記載の粘度測定方法。
3. 前記ひずみは前記内壁上または前記内壁中に生じるひずみである、請求項２に記載の粘度測定方法。
4. 前記ひずみは前記内壁表面であって前記ひずみを測定する位置における前記内壁表面に沿った方向のひずみである、請求項３に記載の粘度測定方法。
5. 前記ひずみは前記流路に交差する面による前記流路の断面内のひずみである、請求項３または４に記載の粘度測定方法。
6. 前記内壁の変形は前記流路に交差する面による前記流路の断面の形状の変形であり、
   前記ひずみは前記変形によって前記断面形状の辺が変位することにより前記辺の長さが変化して生じるひずみである、請求項２から５の何れかに記載の粘度測定方法。
7. 前記ひずみの大きさは前記変位の量の２乗に比例する、請求項６に記載の粘度測定方法。
8. さらに、粘度が既知の流体を前記流路に流したときの前記変形の量を測定することにより前記変形の量と粘度の絶対値との関係を較正する、請求項１から７の何れかに記載の粘度測定方法。
9. 前記既知の流体が前記流路を流れる際の流量は、前記粘度を測定すべき流体が前記流路を流れる流量と同じである、請求項８に記載の粘度測定方法。
10. 粘度を測定すべき流体が流れる流路と、
    前記流体を流すことにより前記流路の内壁に生じた変形の量を測定する手段と、
    前記測定された変形の量に基づいて前記流体の粘度を求める手段と
    を設け、
    請求項１から９の何れかに記載の粘度測定方法により前記流体の粘度を測定する粘度測定装置。
11. 前記変形の量を測定する手段は前記流路の内壁上または内壁中に設けられたひずみゲージである、請求項１０に記載の粘度測定装置。
12. 前記粘度測定装置は気体と液体の両方の粘度を測定する、請求項１１に記載の粘度測定装置。

Images