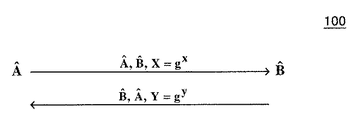JP2009526411A - 装置またはネットワークによって相互接続された2当事者間の交換の方法、信号伝送媒体、および装置(チャレンジ・レスポンス署名および高性能で安全なDiffie−Hellmanプロトコルに関する方法および構造) - Google Patents
装置またはネットワークによって相互接続された2当事者間の交換の方法、信号伝送媒体、および装置(チャレンジ・レスポンス署名および高性能で安全なDiffie−Hellmanプロトコルに関する方法および構造) Download PDFInfo
- Publication number
- JP2009526411A JP2009526411A JP2007554563A JP2007554563A JP2009526411A JP 2009526411 A JP2009526411 A JP 2009526411A JP 2007554563 A JP2007554563 A JP 2007554563A JP 2007554563 A JP2007554563 A JP 2007554563A JP 2009526411 A JP2009526411 A JP 2009526411A
- Authority
- JP
- Japan
- Prior art keywords
- value
- key
- hat
- function
- party
- Prior art date
- Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
- Withdrawn
Links
- 238000000034 method Methods 0.000 title claims abstract description 72
- 230000008054 signal transmission Effects 0.000 title claims description 9
- 230000004044 response Effects 0.000 title description 19
- 230000006870 function Effects 0.000 claims description 75
- 238000004364 calculation method Methods 0.000 claims description 24
- 230000002452 interceptive effect Effects 0.000 claims description 14
- 238000009795 derivation Methods 0.000 claims description 10
- 238000012545 processing Methods 0.000 claims description 6
- 238000007620 mathematical function Methods 0.000 claims 3
- 230000008901 benefit Effects 0.000 description 15
- 238000004458 analytical method Methods 0.000 description 14
- 238000004891 communication Methods 0.000 description 13
- 238000013461 design Methods 0.000 description 11
- 238000012360 testing method Methods 0.000 description 11
- 238000012795 verification Methods 0.000 description 10
- 230000007774 longterm Effects 0.000 description 9
- 230000007246 mechanism Effects 0.000 description 7
- 230000004913 activation Effects 0.000 description 4
- 238000013459 approach Methods 0.000 description 4
- 238000012790 confirmation Methods 0.000 description 4
- 230000003993 interaction Effects 0.000 description 4
- 230000008569 process Effects 0.000 description 4
- 230000009466 transformation Effects 0.000 description 4
- 238000004422 calculation algorithm Methods 0.000 description 3
- 230000009977 dual effect Effects 0.000 description 3
- 230000010365 information processing Effects 0.000 description 3
- 238000013500 data storage Methods 0.000 description 2
- 238000010586 diagram Methods 0.000 description 2
- 230000001965 increasing effect Effects 0.000 description 2
- 239000003999 initiator Substances 0.000 description 2
- 230000008450 motivation Effects 0.000 description 2
- 230000003287 optical effect Effects 0.000 description 2
- TVZRAEYQIKYCPH-UHFFFAOYSA-N 3-(trimethylsilyl)propane-1-sulfonic acid Chemical compound C[Si](C)(C)CCCS(O)(=O)=O TVZRAEYQIKYCPH-UHFFFAOYSA-N 0.000 description 1
- 230000009471 action Effects 0.000 description 1
- 239000000654 additive Substances 0.000 description 1
- 230000000996 additive effect Effects 0.000 description 1
- 230000003190 augmentative effect Effects 0.000 description 1
- 230000006399 behavior Effects 0.000 description 1
- 230000005540 biological transmission Effects 0.000 description 1
- 230000008859 change Effects 0.000 description 1
- 239000002131 composite material Substances 0.000 description 1
- 125000004122 cyclic group Chemical group 0.000 description 1
- 238000011161 development Methods 0.000 description 1
- 238000005516 engineering process Methods 0.000 description 1
- 230000002708 enhancing effect Effects 0.000 description 1
- 230000002427 irreversible effect Effects 0.000 description 1
- 230000001343 mnemonic effect Effects 0.000 description 1
- 230000008520 organization Effects 0.000 description 1
- 230000002093 peripheral effect Effects 0.000 description 1
- 238000011160 research Methods 0.000 description 1
- 238000004088 simulation Methods 0.000 description 1
- 230000003068 static effect Effects 0.000 description 1
- 238000012546 transfer Methods 0.000 description 1
- 238000000844 transformation Methods 0.000 description 1
- 238000010200 validation analysis Methods 0.000 description 1
Images
Classifications
-
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L9/00—Cryptographic mechanisms or cryptographic arrangements for secret or secure communications; Network security protocols
- H04L9/08—Key distribution or management, e.g. generation, sharing or updating, of cryptographic keys or passwords
- H04L9/0816—Key establishment, i.e. cryptographic processes or cryptographic protocols whereby a shared secret becomes available to two or more parties, for subsequent use
- H04L9/0838—Key agreement, i.e. key establishment technique in which a shared key is derived by parties as a function of information contributed by, or associated with, each of these
- H04L9/0841—Key agreement, i.e. key establishment technique in which a shared key is derived by parties as a function of information contributed by, or associated with, each of these involving Diffie-Hellman or related key agreement protocols
- H04L9/0844—Key agreement, i.e. key establishment technique in which a shared key is derived by parties as a function of information contributed by, or associated with, each of these involving Diffie-Hellman or related key agreement protocols with user authentication or key authentication, e.g. ElGamal, MTI, MQV-Menezes-Qu-Vanstone protocol or Diffie-Hellman protocols using implicitly-certified keys
-
- G—PHYSICS
- G06—COMPUTING; CALCULATING OR COUNTING
- G06Q—INFORMATION AND COMMUNICATION TECHNOLOGY [ICT] SPECIALLY ADAPTED FOR ADMINISTRATIVE, COMMERCIAL, FINANCIAL, MANAGERIAL OR SUPERVISORY PURPOSES; SYSTEMS OR METHODS SPECIALLY ADAPTED FOR ADMINISTRATIVE, COMMERCIAL, FINANCIAL, MANAGERIAL OR SUPERVISORY PURPOSES, NOT OTHERWISE PROVIDED FOR
- G06Q20/00—Payment architectures, schemes or protocols
- G06Q20/30—Payment architectures, schemes or protocols characterised by the use of specific devices or networks
- G06Q20/36—Payment architectures, schemes or protocols characterised by the use of specific devices or networks using electronic wallets or electronic money safes
- G06Q20/367—Payment architectures, schemes or protocols characterised by the use of specific devices or networks using electronic wallets or electronic money safes involving electronic purses or money safes
- G06Q20/3678—Payment architectures, schemes or protocols characterised by the use of specific devices or networks using electronic wallets or electronic money safes involving electronic purses or money safes e-cash details, e.g. blinded, divisible or detecting double spending
-
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L9/00—Cryptographic mechanisms or cryptographic arrangements for secret or secure communications; Network security protocols
- H04L9/06—Cryptographic mechanisms or cryptographic arrangements for secret or secure communications; Network security protocols the encryption apparatus using shift registers or memories for block-wise or stream coding, e.g. DES systems or RC4; Hash functions; Pseudorandom sequence generators
- H04L9/0643—Hash functions, e.g. MD5, SHA, HMAC or f9 MAC
-
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L9/00—Cryptographic mechanisms or cryptographic arrangements for secret or secure communications; Network security protocols
- H04L9/08—Key distribution or management, e.g. generation, sharing or updating, of cryptographic keys or passwords
- H04L9/0816—Key establishment, i.e. cryptographic processes or cryptographic protocols whereby a shared secret becomes available to two or more parties, for subsequent use
- H04L9/0819—Key transport or distribution, i.e. key establishment techniques where one party creates or otherwise obtains a secret value, and securely transfers it to the other(s)
- H04L9/083—Key transport or distribution, i.e. key establishment techniques where one party creates or otherwise obtains a secret value, and securely transfers it to the other(s) involving central third party, e.g. key distribution center [KDC] or trusted third party [TTP]
- H04L9/0833—Key transport or distribution, i.e. key establishment techniques where one party creates or otherwise obtains a secret value, and securely transfers it to the other(s) involving central third party, e.g. key distribution center [KDC] or trusted third party [TTP] involving conference or group key
-
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L9/00—Cryptographic mechanisms or cryptographic arrangements for secret or secure communications; Network security protocols
- H04L9/30—Public key, i.e. encryption algorithm being computationally infeasible to invert or user's encryption keys not requiring secrecy
- H04L9/3066—Public key, i.e. encryption algorithm being computationally infeasible to invert or user's encryption keys not requiring secrecy involving algebraic varieties, e.g. elliptic or hyper-elliptic curves
-
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L9/00—Cryptographic mechanisms or cryptographic arrangements for secret or secure communications; Network security protocols
- H04L9/32—Cryptographic mechanisms or cryptographic arrangements for secret or secure communications; Network security protocols including means for verifying the identity or authority of a user of the system or for message authentication, e.g. authorization, entity authentication, data integrity or data verification, non-repudiation, key authentication or verification of credentials
- H04L9/321—Cryptographic mechanisms or cryptographic arrangements for secret or secure communications; Network security protocols including means for verifying the identity or authority of a user of the system or for message authentication, e.g. authorization, entity authentication, data integrity or data verification, non-repudiation, key authentication or verification of credentials involving a third party or a trusted authority
-
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L9/00—Cryptographic mechanisms or cryptographic arrangements for secret or secure communications; Network security protocols
- H04L9/32—Cryptographic mechanisms or cryptographic arrangements for secret or secure communications; Network security protocols including means for verifying the identity or authority of a user of the system or for message authentication, e.g. authorization, entity authentication, data integrity or data verification, non-repudiation, key authentication or verification of credentials
- H04L9/3218—Cryptographic mechanisms or cryptographic arrangements for secret or secure communications; Network security protocols including means for verifying the identity or authority of a user of the system or for message authentication, e.g. authorization, entity authentication, data integrity or data verification, non-repudiation, key authentication or verification of credentials using proof of knowledge, e.g. Fiat-Shamir, GQ, Schnorr, ornon-interactive zero-knowledge proofs
-
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L9/00—Cryptographic mechanisms or cryptographic arrangements for secret or secure communications; Network security protocols
- H04L9/32—Cryptographic mechanisms or cryptographic arrangements for secret or secure communications; Network security protocols including means for verifying the identity or authority of a user of the system or for message authentication, e.g. authorization, entity authentication, data integrity or data verification, non-repudiation, key authentication or verification of credentials
- H04L9/3247—Cryptographic mechanisms or cryptographic arrangements for secret or secure communications; Network security protocols including means for verifying the identity or authority of a user of the system or for message authentication, e.g. authorization, entity authentication, data integrity or data verification, non-repudiation, key authentication or verification of credentials involving digital signatures
-
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L9/00—Cryptographic mechanisms or cryptographic arrangements for secret or secure communications; Network security protocols
- H04L9/32—Cryptographic mechanisms or cryptographic arrangements for secret or secure communications; Network security protocols including means for verifying the identity or authority of a user of the system or for message authentication, e.g. authorization, entity authentication, data integrity or data verification, non-repudiation, key authentication or verification of credentials
- H04L9/3271—Cryptographic mechanisms or cryptographic arrangements for secret or secure communications; Network security protocols including means for verifying the identity or authority of a user of the system or for message authentication, e.g. authorization, entity authentication, data integrity or data verification, non-repudiation, key authentication or verification of credentials using challenge-response
Landscapes
- Engineering & Computer Science (AREA)
- Computer Security & Cryptography (AREA)
- Computer Networks & Wireless Communication (AREA)
- Signal Processing (AREA)
- Business, Economics & Management (AREA)
- Accounting & Taxation (AREA)
- Finance (AREA)
- Theoretical Computer Science (AREA)
- General Physics & Mathematics (AREA)
- Physics & Mathematics (AREA)
- Mathematical Optimization (AREA)
- Strategic Management (AREA)
- Power Engineering (AREA)
- Algebra (AREA)
- Mathematical Analysis (AREA)
- General Business, Economics & Management (AREA)
- Mathematical Physics (AREA)
- Pure & Applied Mathematics (AREA)
- Computing Systems (AREA)
- Storage Device Security (AREA)
- Mobile Radio Communication Systems (AREA)
- Data Exchanges In Wide-Area Networks (AREA)
- Medicines Containing Antibodies Or Antigens For Use As Internal Diagnostic Agents (AREA)
Abstract
【解決手段】 受信側当事者(検証者)は、値X=F1(x)を計算するために秘密の値xを選択し、ここでF1は少なくとも1つの引数を有する第1の所定の関数を含み、値xはF1の少なくとも1つの引数のうちの1つである。署名側当事者(署名者)は、値Y=F2(y)を計算するために秘密の値yを選択し、ここでF2は少なくとも1つの引数を有する第2の所定の関数を含み、値yはF2の少なくとも1つの引数のうちの1つである。署名者は値Xを入手し、署名者は秘密鍵bと公開鍵Bとを有する。署名者は値s=F3(y,b,X)を計算し、ここでF3は少なくとも3つの引数を有する第3の所定の関数を含み、値y、秘密鍵b、および値XはF3の少なくとも3つの引数のうちの3つの引数である。
【選択図】 図10
Description
によって表され、伝統的には「アリス(Alice)」と見なされることになる(第2の当事者
は伝統的には「ボブ(Bob)」と見なされる)。一般に、「ハット表記法(hatnotation)」は、名前、電子メール・アドレス、役割など、プロトコル内の当事者の論理IDまたは「識別(distinguishing)」IDを表すために使用される。場合によっては、これらのIDはデジタル証明書で増強することができる。本明細書では繰り返さないが、仮出願で提供されるより完全な数理解析のために、攻撃者を含むプロトコル内のすべての当事者は、確率的多項式タイム・マシンを介して実現されるものと見なされる。また、攻撃者はMによっても表され、ここでMは「悪意のある(malicious)」ことを意味する可能性がある。
Aハット、BハットというIDが公開鍵証明書などの追加の情報を含む可能性があるかまたはこれらのIDがすべてまとめて省略される可能性があることを除いて、MQVプロトコルでの通信は、図1に描写されている基本非認証DHプロトコル100と同一である。
およびe=
である。
HMQVプロトコル(「H」は「ハッシュ」を意味するものと見なすことができる)は、いくつかの模範的な実施形態では、比較のためにステップ302に示されている従来のMQVプロトコルへの追加であり、図3のステップ303に示されているようなハッシュを含むことができる、MQVの単純だが強力な変種である。しかし、ハッシュを行わず、ハッシュ以外の技法を使用しない代替諸実施形態が本明細書で論じられ、本発明の概念にも含まれるので、最初の問題として、これらの模範的な実施形態の1つまたは複数のハッシュ・ステップが本発明にとって前提条件ではないことも留意すべきである。本発明のより基本的な概念は、MQVプロトコルの模範的なハッシュ・バージョンを含む、いくつかの適用例および実施形態がそこから進化したチャレンジ・レスポンス署名方式に関するものである。
で表される場合が多く、kビットの出力を有し、σ値に適用されるハッシュ関数はHで表される。実際には、異なる出力長を有する同じハッシュ関数を使用することができ、このため、Hバーの代わりに記号Hが使用されることもある。ニーモニックとして、Hバー内のバーは、この関数の出力が指数として使用されることを示している。
HMQVプロトコルがMQVプロトコルとはどのように異なるかは明らかでなければならないが、ある意味でより基本的な本発明のもう1つの態様が存在する。すなわち、HMQVの背後にある中心的設計および分析要素として存在する主なテクニカル・ツールは、「チャレンジ・レスポンス署名」と呼ばれ、Fiat−Shamir方法を使用するSchnorrの識別方式の新しい変種を基礎として実現される、新しい形の対話式署名である。その結果として、本発明の「指数チャレンジ・レスポンス」(XCR)署名が得られる。SchnorrおよびFiat−Shamir方法とXCR署名との関係については以下に論じる。
図4に例示されている指数チャレンジ・レスポンス(XCR)署名方式500は以下のように定義される。すなわち、Bハットで表されるXCR方式内の署名者は、秘密鍵b∈RZqと公開鍵B=gbとを所有する。Aハットで表される検証者(またはチャレンジャ)は、x∈RZqの場合にAハットがX=gxとして計算する最初のチャレンジXを提供し、ここでxはAハットによって選択され、秘密に保持される。チャレンジXを使用する所与のメッセージm上のBハットの署名は、
(i)Bハットはy∈RZqを選択し、Y=gyをAハットに送信する。
(ii)Aハットはランダム値e∈RZqで応答する。
(iii)Bハットは値s=y+ebをAハットに送信する。Aハットは、gs=YBeが有効である場合のみ、受け入れる。
lはHバー(Y,m)内のビット数とする。明らかなことに、lが小さくなるほど署名方式の効率が高くなることを示す。これに対して、指数Hバー(Y,m)が予測可能であると、署名方式が不安定になるので、lが小さすぎる場合、セキュリティ・バウンド(security bound)が不良であることを示す。しかし、セキュリティのためにどの程度の大きさのlが必要であるかが問題である。
とりわけ、HMQVプロトコルの分析に適用されるXCR署名のいくつかの適用例では、チャレンジャAハットと署名者Bハットとの対話の順序を変更することができる。
(i)AハットはBハットにメッセージmを提示し、BハットはYを出力し、その後の何らかの時点で
(ii)AハットはBハットに(Y,m,X)を提供し、Bハットは
XCR署名(Y,σ)のペアをペア(Y,H(σ))で置き換えることが可能であり、ここでHはハッシュ関数であり、このような「ハッシュXCR」署名は「HCR」と略記される。XCR特性によって検証者がYのついてσを再計算できるので、Yが与えられると、H(σ)も計算することができ、このため、変更済みHCR署名を検証できることに留意されたい。
XCR(およびHCR)署名は、X=Aを書き込むことにより、非対話式だが検証者固有のものにすることができ、ここでAは、図6に図示されている通り、検証者の公開鍵である。これは、非常に効率的な非対話式で検証者固有の否認可能認証メカニズムを提供する。ある変形では、当事者Aハットの固有の公開鍵Aを使用するのではなく、後者は署名者が使用するために1つまたは複数のチャレンジを公表する(たとえば、Webサイトでポストする)ことができ、したがって、Aハット自体が署名時に使用可能ではない場合でも、これらのチャレンジが使用可能になる。
XCR署名の顕著な特性(とりわけ、共有秘密および公開鍵暗号化に基づくものを含み、他の「否認可能」チャレンジ・レスポンス・メカニズムからそれを区別するもの)は、これらの署名を正規の否認不能な署名に「変換」する能力である。変換可能署名は、否認可能認証の特性を有し、すなわち、意図された受信側のみによって検証することができるが、署名者も自分の秘密署名鍵を明かさずに自分が所与の署名の作成者であることを最終的に証明することができる。
XCR署名の重要な特性の1つは、チャレンジを選択したチャレンジャが独力で署名を計算できることである。ここで、任意の2当事者Aハット、Bハットがチャレンジャと署名者という二重の役割で互いに対話でき、それぞれがいかなる第三者も捏造できない署名を生成するという特性を備えた関連チャレンジ・レスポンス署名方式(本明細書では「二重XCR方式」または略してDCRという)を導出するためにこの特性を利用する方法が示される。その上、これは、この方式をHMQVプロトコルにとって重要なものにするものであり、結果として得られるAハットおよびBハットによる署名は同じ値を有する。より正確には、それらはXCR署名ペア内に同じXSIG成分を有する。
HMQVプロトコルは、その基本的2メッセージ交換において、そこから両当事者AハットおよびBハットが
1.Initiate(Aハット,Bハット): Aハットは、値X=gx、x∈RZqを生成し、(不完全な)セッション(Aハット,Bハット,X)として識別するHMQVのローカル・セッションを作成し、その発信メッセージとして値Xを出力する。
この起動の意味は、AハットがBハットとのセッションの起動側(initiator)として起動されていることであり、Xはこのセッションの一部としてピアBハットに配信する予定のメッセージである。当事者Aハットはセッションの「保有者(holder)」(または「所有者(owner)」)と呼ばれ、Bハットはセッションに対する「ピア」と呼ばれ、Xは発信(DH)値と呼ばれる。
2.Respond(Aハット,Bハット,Y): AハットはY≠0であることをチェックする。そうである場合、Aハットは、値X=gx、x∈RZqを生成し、Xを出力し、ID(Aハット,Bハット,X,Y)およびセッション鍵H(π((Aハット,Bハット,X,Y))を有するセッションを完了する。ここで、Aハットは、ピアBハットおよび着信値Yを有するセッションにおいて応答側として起動されている。この場合、Aハットは直ちにそのセッションを完了する(それ以上の着信メッセージはまったく存在しない)。着信値Yがゼロである場合、Aハットが起動を無視することに留意されたい。
3.Complete(Aハット,Bハット,X,Y): Aハットは、Y≠0であることと、ID(Aハット,Bハット,X)を有する公開セッションを有することをチェックする。これらの条件のいずれかが適合しない場合、Aハットは起動を無視し、適合する場合、AハットはセッションID(Aハット,Bハット,X,Y)およびセッション鍵K=H(π((Aハット,Bハット,X,Y))を有するセッションを完了する。これは、(申し立てによると)ピアBハットからの応答である着信値Yによる、このプロトコルにおける第2のメッセージの配信を表している。
3メッセージHMQV−C(Cは「鍵確認(key Confirmation)」を意味する)プロトコルは図8に描写されている。このプロトコルは、HMQVのすべてのセキュリティ特性、特に同じ計算コストを享受する。しかし、これは、第3のメッセージをプロトコルに追加し、プロトコル・メッセージの長さをわずかに増加させるものである。
HMQVプロトコルは、ピアBハットおよびセッション鍵Kを有するセッションを完了する当事者Aハットに基本的な保証を提供し、Bハットが破壊されていない場合、BハットのみがおそらくKを把握することができる。このプロトコルが提供しないものは、Bハットがセッションを完了したかまたはセッション鍵を計算したというAハットに対する保証である。その上、Bハットは、セッションの実行中に「活動中」ではなかった可能性がある。
完全転送秘密は、それにより長期秘密鍵が漏洩しても古いセッション鍵のセキュリティを危険にさらさない、鍵交換プロトコルの非常に望ましい特性である。より形式的には、破壊されていない当事者Aハットが破壊されていないピアBハットとの鍵交換セッションを確立する場合、AハットでKが満了した後で攻撃者がAハットを破壊するかまたはBハットでKが満了した後で攻撃者がBハットを破壊しても、セッション鍵Kは引き続き安全である。HMQVを含む、暗黙認証を伴う2メッセージ・プロトコルはいずれも、活発な攻撃者に対する完全な完全転送秘密を提供することができない。その代わりに、望むことができる最良のものは、HMQVによって提供される弱い形のPFSである。基本的な2メッセージHMQVに対するHMQV−Cの主な利点は、仮出願にさらに説明されている通り、それがHMQVの固有の制限を引き上げ、完全なPFSを提供することである。
鍵交換に関するCanetti/Krawczykのモデルは、仮出願におけるMQVおよびHMQVの分析の基礎であり、実社会環境の場合のように、他のアプリケーションと同時に実行されたときに鍵交換プロトコルのセキュリティを保証することを目標とする、より意欲的なモデルに拡張されている。このモデルは、鍵交換の汎用構成可能性(UC:Universal-Composability)モデルとして知られている。
図9に示されている1パス鍵交換プロトコルは、送信側Aハットから受信側Bハットに送信された単一メッセージから構成され、両当事者およびセッションが以下に定義するように破壊されていない限り、そこから両当事者はそれぞれの秘密鍵と公開鍵を使用して、AハットおよびBハットのみがおそらく把握できる固有の鍵を導出する。
(i)(Aハット,Bハット)は2つのID AハットおよびBハットを含むメッセージを表すものとし、d=Hバー(X,(Aハット,Bハット))の結果になるようにdを設定する。
(ii)
(iii)K=H(σ,Aハット)を設定し、ここでHは必要な鍵の長さに等しいビット数を出力する。同じ鍵Kは、X≠0であることをチェックした後、BハットによってK=H((XAd)b)として計算される。変形では、K=H(σ,Aハット,Bハット)である。
従来のMQVプロトコルに比較して、HMQVプロトコルは、以下のものを含む、いくつかのパフォーマンス上の利点を提供する。HMQVは、このプロトコルで伝送されるDH値に関する高価な素数次数テストの必要性を立証可能に省くものである。仮出願で実証されている通り、攻撃者がローグ(rogue)DH値の選択の恩恵を受けうる唯一の方法は、ゼロになるようにそれらを選択することであり、したがって、単純な非ゼロ・チェックがHMQVで必要なすべてである。このため、素数次数テストの必要性またはMQVプロトコルで同時に使用される余因数hの必要性はまったくない。
(1)HMQVは、CanettiおよびKrawczykの強い形式的鍵交換モデルで安全なものである。
(2)HMQVは、両当事者の秘密鍵にアクセスできない攻撃者による詐称に耐えるものである。
(3)HMQVは、交換の当事者のIDにXCR署名を適用し、その結果、UKSおよびその他の認証攻撃を回避することにより、これらの当事者のIDと鍵との間に固有の結合を確立する。
(4)HMQVは、セッション鍵およびその他のセッション情報の部分漏洩が存在しても安全であり、換言すれば、HMQVはいわゆる「既知の鍵(known key)」の攻撃に対する抵抗力がある。とりわけ、異なるセッション鍵は、互いに「計算上独立」するように保証される。
(5)このプロトコルは、「鍵漏洩詐称(KCI:key-compromise impersonation)」攻撃に対する抵抗力として知られる追加レベルの保護を提供し、すなわち、これは、Aに対して他の当事者を詐称できるように当事者Aの秘密鍵を学習する攻撃者を阻止する。
(6)鍵確認を有する3メッセージHMQVプロトコルは、立証可能な完全転送秘密(PFS)を提供し、すなわち、2当事者の長期秘密鍵が最終的に開示された場合でも、漏洩前にこれらの当事者によって作成されたセッション鍵は引き続き安全である。
(7)鍵確認を有する3メッセージ・プロトコルは、いわゆる「汎用構成可能」鍵交換プロトコルの追加のセキュリティ上の利点を享受し、すなわち、他のプロトコルによって安全に構成することができる。
(8)HMQVのセキュリティは、静的公開鍵の形式および構造に関する特別なテストに依存せず、対応する秘密鍵のいわゆる「所有証明(proof of possession)」を必要としない。MQVを含む、同様のプロトコルを上回るHMQVのこのような利点により、認証局(CA:certificationauthority)は、登録公開鍵についてこのような特別なチェックを実行する負担から解放され、その結果、より現実的で実用的なセキュリティの保証が得られるが、とりわけ、多くのローカルCAがこのようなチェックを実行できないかまたは実行するように構成されていないためである。その上、CAによるこのようなテスト(たとえば、所有証明)の正当な実行により、追加のセキュリティ上の脆弱性に対してプロトコルを開放することは、留意する価値がある。
(9)2メッセージおよび3メッセージHMQVプロトコルは、一時公開鍵(すなわち、値XおよびY)の次数のテストを必要とせず、その結果、場合によっては高価なものになりうるテストを回避する。しかし、両当事者の一時秘密鍵を学習する可能性のある攻撃者に耐えることがプロトコルのセキュリティである場合、このようなテストは必要である。また、1パスHMQVプロトコルのセキュリティについても、このテストは必要である。MQVのように、これらのテストは、プロトコル内のσ値の「余因数べき乗」で置き換えることができる。基礎となる代数群に応じて、所定の群内の帰属関係など、群の元に関する追加のテストが必要になる場合もある。
比較のやり方として、特許および学術論文に記載されているMQVはプロトコルの設計および説明でも署名の概念を使用することは、留意する価値がある。これは、MQVに関連して「暗黙署名」と呼ばれ、秘密署名鍵の所有者のみが署名値を生成できるデジタル署名のより伝統的な概念に従うものである(具体的には、MQVは、秘密署名鍵と、一時秘密鍵および公開鍵との1次結合によって形成されるElGamalのような署名を指す)。しかし、プロトコルは、これらの署名の特性を完全に使用するまでには至らない。とりわけ、MQVプロトコルは、そのプロトコルの当事者のIDを明示的に認証する方法として署名を使用せず、これにより、Kaliskiによって発見された有名な「未知の鍵の共有(UKS:unknown key share)」などの重大な認証障害が発生する。
(1)Vは、秘密の値xを選択し、値X=F1(x)を計算し、ここでF1は所与の関数であり、次にXをSに送信する。
(2)Sは、秘密の値yを選択し、値Y=F2(y)を計算し、ここでF2は所与の関数であり、次にYをVに送信する。
(3)Sは、値s=F3(y,b,X,m)を計算し、ここでF3は所与の関数であり、次にsをVに送信する。
(4)Vは、値s′=F4(x,Y,B,m)を計算し、値s′と受信した値sに対するその関連とを基礎として、mの確実性を決定する。
(a)F1、F2は一方向関数である。XCRでは、これらの一方向関数はX=gxおよびY=gyである。
(b)XCR署名では、この関数は
(c)s′=sである場合のみ、mを認証として受け入れる。この最後の変種は、それにより、チャレンジXの背後にある秘密を把握することによって検証者が署名を再計算できる、典型的なXCR署名の特性を利用する。
(d)
図10は、本発明による情報処理/コンピュータ・システムの典型的なハードウェア構成を例示しており、このシステムは好ましくは少なくとも1つのプロセッサまたは中央演算処理装置(CPU:central processing unit)1011を有する。
Claims (38)
- 装置またはネットワークによって相互接続された2当事者間の交換の方法において、
受信側当事者(検証者)が値X=F1(x)を計算するために秘密の値xを選択し、ここでF1は少なくとも1つの引数を有する第1の所定の関数を含み、前記値xはF1の前記少なくとも1つの引数のうちの1つであり、
署名側当事者(署名者)が値Y=F2(y)を計算するために秘密の値yを選択し、ここでF2は少なくとも1つの引数を有する第2の所定の関数を含み、前記値yはF2の前記少なくとも1つの引数のうちの1つであり、
前記署名者が前記値Xを入手し、前記署名者が秘密鍵bと公開鍵Bとを有し、
前記署名者が値s=F3(y,b,X)を計算し、ここでF3は少なくとも3つの引数を有する第3の所定の関数を含み、前記値y、前記秘密鍵b、および前記値XはF3の前記少なくとも3つの引数のうちの3つの引数であり、
値s′を計算するために第4の所定の関数F4(x,Y,B)が存在し、F4は少なくとも3つの引数を有し、前記値x、前記値Y、および前記公開鍵BはF4の前記少なくとも3つの引数のうちの3つの引数であるが、値sはF4の引数ではなく、
前記検証者と前記署名者との間で共有され、前記F1、F2、F3、およびF4のいずれかにおいて任意の引数の基礎として働くような秘密が存在せず、
前記値s′が所定の方法で前記値sに関連するものと判断された場合に前記検証者が前記値sおよびs′を有効な認証子と見なすことができる、方法。 - F1およびF2のうちの少なくとも1つが一方向関数を含む、請求項1に記載の方法。
- 前記値sおよびs′が、s=s′である場合に有効な認証子であると判断される、請求項1に記載の方法。
- s′の計算ならびに前記値sおよびs′が関連するものであると判断されるかどうかの判断のうちの少なくとも一方が、前記検証者および前記署名者以外の当事者によって実行される、請求項1に記載の方法。
- 2当事者間で共有される秘密を導出するために前記値sおよび前記値s′が使用される、請求項1に記載の方法。
- 前記検証者が前記値Yを入手し、sおよびs′が前記所定の方法で関連するかどうかを判断するために前記値s′を計算するためにこれを使用すること
をさらに含む、請求項1に記載の方法。 - メッセージmが、認証対象であり、F3の引数およびF4の引数を含み、それにより、前記値sおよび前記値s′が前記メッセージm内の情報を含むことができ、
前記値sおよびs′が前記所定の方法で関連するものであると判断された場合に前記メッセージが認証される、請求項1に記載の方法。 - 2当事者間で共有される秘密を導出するために前記値sおよび前記値s′が使用される、請求項7に記載の方法。
- 前記メッセージmが、少なくとも前記交換の前記当事者の一方のIDを含む、請求項8に記載の方法。
- 前記署名者が前記値sを前記検証者に送信すること
をさらに含む、請求項7に記載の方法。 - 前記s=s′である場合に前記メッセージが認証される、請求項7に記載の方法。
- 前記公開鍵B=gbであり、gが次数qの有限群の生成元であり、前記秘密鍵bが0<b<q−1になるような整数であり、
前記値X=gxであり、xが0<x<q−1になるような整数であり、前記値Y=gyであり、yが0<y<q−1になるような整数であり、
前記署名者が前記値s=f1(X)f2(m,Y,y,b)を計算し、f1が第1の数学関数を含み、f2が第2の数学関数を含み、引数mがメッセージを含む、請求項1に記載の方法。 - qが素数である、請求項12に記載の方法。
- 前記値sが所定の方法で前記値s′に関連するものと判断された場合に前記メッセージmが認証済みと見なされる、請求項12に記載の方法。
- 前記値sが前記値s′に等しいと判断された場合に前記メッセージmが認証済みと見なされる、請求項14に記載の方法。
- f1が恒等関数から構成される、請求項12に記載の方法。
- f2が、f2の前記引数の少なくとも1つがハッシュされるようなハッシュ関数を含む、請求項12に記載の方法。
- ハッシュされた前記引数の1つが非ヌル・メッセージmである、請求項17に記載の方法。
- 前記メッセージmが、コンピュータまたはシステムあるいはネットワーク内の当事者のIDを含む、請求項12に記載の方法。
- f2(m,Y,y,b)=y+H(Y,m)b mod qであり、ここでHは一方向関数、暗号化関数、および暗号ハッシュ関数のうちの1つである暗号関数を含む、請求項17に記載の方法。
- 前記値s′=(YB{H(Y,m)})f3(x)であり、ここでf3(x)は少なくとも1つの引数を有する数学関数を含み、前記値xはf3(x)の前記少なくとも1つの引数のうちの1つの引数である、請求項20に記載の方法。
- f3(x)=xである、請求項21に記載の方法。
- s=s′である場合のみ、前記メッセージmを認証すること
をさらに含む、請求項21に記載の方法。 - 前記検証者が、秘密鍵a、公開鍵A=ga、およびメッセージm′を有し、前記値s′がm上の前記署名者の署名を含むと同時に、前記値sがm′上の前記検証者の署名を含む、請求項21に記載の方法。
- 前記関数f3(x)=x+H(X,m′)a mod qである、請求項24に記載の方法。
- xが前記検証者によってランダムに選択され、yが前記署名者によってランダムに選択される、請求項1に記載の方法。
- 前記第1の値X=gxが、前記証明者により検索可能になるように前記検証者によって公開された値を含み、それにより、前記認証の非対話式バージョンを可能にする、請求項1に記載の方法。
- 前記値sおよびs′がさらにハッシュされる、請求項21に記載の方法。
- 請求項1に記載の前記方法の諸ステップの少なくとも1つを実行するためにデジタル処理装置によって実行可能な複数の機械可読命令からなるプログラムを具体的に実施する信号伝送媒体。
- 前記署名者について請求項1に記載した前記関数F2およびF3を計算するための計算機
を含む装置。 - 装置またはネットワークによって相互接続された2当事者間で認証鍵を確立するための方法において、
第1の当事者が秘密鍵aと公開鍵Aとを有する場合に、前記秘密鍵aが0<a<q−1になるような整数であり、qが正整数であり、gが次数qの有限群の生成元であり、Aが前記値gによって生成され、A=gaとして計算された前記群内の元であり、
第2の当事者が秘密鍵bと公開鍵B=gbとを有し、前記秘密鍵bが0<b<q−1になるような整数であり、
前記第1の当事者が値X=gxを計算するために秘密の値xを選択し、xが0<x<q−1になるような整数であり、前記値Xが前記第2の当事者に伝達され、
前記第2の当事者が値Y=gyを計算するために秘密の値yを選択し、yが0<y<q−1になるような整数であり、前記値Yが前記第1の当事者に伝達され、
前記第1の当事者が値s=f1(Y,B,m){f2(x,a,m’)}を計算し、ここでm、m′は前記当事者間で既知であるかまたは交換されたメッセージを含み、前記第2の当事者が値s′=f3(X,A,m′){f4(y,b,m)}を計算し、
前記関数f2およびf4のうちの少なくとも1つが少なくとも1つの引数を有する関数Hを含み、このような1つの引数が前記メッセージmおよびm′のうちの少なくとも1つであり、ここでHは一方向関数、暗号化関数、および暗号ハッシュ関数のうちの1つである暗号関数を含み、
前記第1および第2の当事者がそれぞれ前記値sおよびs′から共有鍵を導出する、方法。 - (i)前記値xおよびXの計算が、前記第1の当事者の前記秘密鍵と、前記当事者のうちの一方または複数の前記公開鍵とを含むことと、
(ii)前記値yおよびYの計算が、前記第2の当事者の前記秘密鍵と、前記当事者のうちの一方または複数の前記公開鍵とを含むこと
のうちの少なくとも一方が該当する、請求項31に記載の方法。 - sおよびs′からの共有鍵の前記導出が、一方向関数、暗号化関数、および暗号ハッシュ関数のうちの1つである暗号関数を含む、請求項31に記載の方法。
- 前記メッセージmおよびm′のうちの少なくとも1つが前記第1および第2の当事者のうちの一方のIDを含む、請求項31に記載の方法。
- f1(Y,B,m)=YBH(Y,m)であり、
f2(x,a,m′)=(x+H(X,m′)a) mod qであり、
f3(X,A,m′)=XAH(X,m’)であり、
f4(y,b,m)=(y+H(Y,m)b) mod qであり、
Hが一方向関数、暗号化関数、および暗号ハッシュ関数のうちの1つである暗号関数を含む、少なくとも2つの引数からなる関数である、請求項31に記載の方法。 - 前記メッセージmおよびm′のうちの少なくとも1つが前記第1および第2の当事者のうちの少なくとも一方のIDを含む、請求項35に記載の方法。
- (i)前記値xおよびXの計算が、前記第1の当事者の前記秘密鍵と、前記当事者のうちの一方または複数の前記公開鍵とを含むことと、
(ii)前記値yおよびYの計算が、前記第2の当事者の前記秘密鍵と、前記当事者のうちの一方または複数の前記公開鍵とを含むこと
のうちの少なくとも一方が該当する、請求項36に記載の方法。 - sおよびs′からの共有鍵の前記導出が、一方向関数、暗号化関数、および暗号ハッシュ関数のうちの1つである暗号関数を含む、請求項36に記載の方法。
Applications Claiming Priority (3)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| US65179805P | 2005-02-10 | 2005-02-10 | |
| US11/348,304 US7747865B2 (en) | 2005-02-10 | 2006-02-07 | Method and structure for challenge-response signatures and high-performance secure Diffie-Hellman protocols |
| PCT/EP2006/050841 WO2006084896A1 (en) | 2005-02-10 | 2006-02-10 | Challenge-response signatures and secure diffie-hellman protocols |
Publications (2)
| Publication Number | Publication Date |
|---|---|
| JP2009526411A true JP2009526411A (ja) | 2009-07-16 |
| JP2009526411A5 JP2009526411A5 (ja) | 2010-09-02 |
Family
ID=36781288
Family Applications (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| JP2007554563A Withdrawn JP2009526411A (ja) | 2005-02-10 | 2006-02-10 | 装置またはネットワークによって相互接続された2当事者間の交換の方法、信号伝送媒体、および装置(チャレンジ・レスポンス署名および高性能で安全なDiffie−Hellmanプロトコルに関する方法および構造) |
Country Status (8)
| Country | Link |
|---|---|
| US (1) | US7747865B2 (ja) |
| EP (1) | EP1847062B1 (ja) |
| JP (1) | JP2009526411A (ja) |
| AT (1) | ATE403297T1 (ja) |
| CA (1) | CA2596500C (ja) |
| DE (1) | DE602006002025D1 (ja) |
| ES (1) | ES2308725T3 (ja) |
| WO (1) | WO2006084896A1 (ja) |
Cited By (20)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| JP2009130872A (ja) * | 2007-11-28 | 2009-06-11 | Nippon Telegr & Teleph Corp <Ntt> | 鍵共有方法、第1装置、第2装置、及び、それらのプログラム |
| JP2011061306A (ja) * | 2009-09-07 | 2011-03-24 | Nippon Telegr & Teleph Corp <Ntt> | 情報共有システム、方法及びプログラム |
| JP2012151648A (ja) * | 2011-01-19 | 2012-08-09 | Nippon Telegr & Teleph Corp <Ntt> | 情報共有方法、情報共有システム、情報共有装置、及びプログラム |
| JP2014050084A (ja) * | 2012-09-04 | 2014-03-17 | Nippon Telegr & Teleph Corp <Ntt> | 鍵交換システム、要求装置、応答装置、鍵交換方法、およびプログラム |
| JP2017501637A (ja) * | 2014-01-02 | 2017-01-12 | テンセント・テクノロジー・(シェンジェン)・カンパニー・リミテッド | 署名検証方法、装置、およびシステム |
| JP2019507510A (ja) * | 2016-02-23 | 2019-03-14 | エヌチェーン ホールディングス リミテッドNchain Holdings Limited | 情報及び階層的で決定性の暗号化鍵のセキュアな交換のための共通秘密の決定 |
| JP2019511035A (ja) * | 2016-02-23 | 2019-04-18 | エヌチェーン ホールディングス リミテッドNchain Holdings Limited | スマートコントラクトに基づく自動給与支払方法及びシステムをもたらす、ブロックチェーン上の給与支払に関連付けられた暗号通貨の効率的な転送のための方法及びシステム |
| US10659223B2 (en) | 2016-02-23 | 2020-05-19 | nChain Holdings Limited | Secure multiparty loss resistant storage and transfer of cryptographic keys for blockchain based systems in conjunction with a wallet management system |
| US10715336B2 (en) | 2016-02-23 | 2020-07-14 | nChain Holdings Limited | Personal device security using elliptic curve cryptography for secret sharing |
| US11120437B2 (en) | 2016-02-23 | 2021-09-14 | nChain Holdings Limited | Registry and automated management method for blockchain-enforced smart contracts |
| US11182782B2 (en) | 2016-02-23 | 2021-11-23 | nChain Holdings Limited | Tokenisation method and system for implementing exchanges on a blockchain |
| US11194898B2 (en) | 2016-02-23 | 2021-12-07 | nChain Holdings Limited | Agent-based turing complete transactions integrating feedback within a blockchain system |
| JP2022037089A (ja) * | 2016-02-23 | 2022-03-08 | エヌチェーン ホールディングス リミテッド | ブロックチェーンからのデータのセキュアな抽出のための暗号方法及びシステム |
| US11308486B2 (en) | 2016-02-23 | 2022-04-19 | nChain Holdings Limited | Method and system for the secure transfer of entities on a blockchain |
| US11373152B2 (en) | 2016-02-23 | 2022-06-28 | nChain Holdings Limited | Universal tokenisation system for blockchain-based cryptocurrencies |
| US11410145B2 (en) | 2016-02-23 | 2022-08-09 | nChain Holdings Limited | Blockchain-implemented method for control and distribution of digital content |
| US11455378B2 (en) | 2016-02-23 | 2022-09-27 | nChain Holdings Limited | Method and system for securing computer software using a distributed hash table and a blockchain |
| US11606219B2 (en) | 2016-02-23 | 2023-03-14 | Nchain Licensing Ag | System and method for controlling asset-related actions via a block chain |
| US11625694B2 (en) | 2016-02-23 | 2023-04-11 | Nchain Licensing Ag | Blockchain-based exchange with tokenisation |
| US12107952B2 (en) | 2016-02-23 | 2024-10-01 | Nchain Licensing Ag | Methods and systems for efficient transfer of entities on a peer-to-peer distributed ledger using the blockchain |
Families Citing this family (38)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US9054861B2 (en) * | 2005-06-14 | 2015-06-09 | Certicom Corp. | Enhanced key agreement and transport protocol |
| DE102007001070B3 (de) * | 2006-09-29 | 2008-04-30 | Siemens Ag | Verfahren zum verschlüsselten Datenausgleich eines Systems mit mindestens einem Datenträger und einem Lesegerät |
| KR100753843B1 (ko) | 2006-09-29 | 2007-08-31 | 한국전자통신연구원 | 양 방향 채널 환경에서의 키 교환 프로토콜을 단 방향 채널환경에서의 키 교환 프로토콜로 변환하는 방법 |
| KR101356736B1 (ko) * | 2007-01-19 | 2014-02-06 | 삼성전자주식회사 | 콘텐츠의 무결성을 확인하기 위한 콘텐츠 제공 장치 및방법 및 콘텐츠 사용 장치 및 방법, 및 콘텐츠 사용 장치를폐지하는 콘텐츠 제공 장치 및 방법 |
| US20090006202A1 (en) * | 2007-02-26 | 2009-01-01 | Picup, Llc | System and method for providing identity-based services |
| CN101175076B (zh) * | 2007-10-23 | 2012-01-11 | 赵运磊 | 在线计算高效、可抵赖、不可锻造安全的密钥交换方法 |
| US8533474B2 (en) * | 2008-02-27 | 2013-09-10 | Red Hat, Inc. | Generating session keys |
| EP2124382A1 (de) * | 2008-05-20 | 2009-11-25 | Siemens Aktiengesellschaft | Verfahren zum verschlüsselten Datenaustausch und Kommunikationssystem |
| CN102318260B (zh) | 2008-12-16 | 2016-04-20 | 塞尔蒂卡姆公司 | 密钥协商协议的加速 |
| US10068282B2 (en) * | 2009-06-24 | 2018-09-04 | Uniloc 2017 Llc | System and method for preventing multiple online purchases |
| EP2334008A1 (en) * | 2009-12-10 | 2011-06-15 | Tata Consultancy Services Limited | A system and method for designing secure client-server communication protocols based on certificateless public key infrastructure |
| US8837741B2 (en) | 2011-09-12 | 2014-09-16 | Qualcomm Incorporated | Systems and methods for encoding exchanges with a set of shared ephemeral key data |
| US9143937B2 (en) | 2011-09-12 | 2015-09-22 | Qualcomm Incorporated | Wireless communication using concurrent re-authentication and connection setup |
| US9439067B2 (en) | 2011-09-12 | 2016-09-06 | George Cherian | Systems and methods of performing link setup and authentication |
| US9503259B2 (en) * | 2012-02-09 | 2016-11-22 | Irdeto B.V. | System and method for generating and protecting cryptographic keys |
| EP2677681A1 (de) * | 2012-06-19 | 2013-12-25 | Bundesrepublik Deutschland, vertreten durch das Bundesministerium des Innern, vertreten durch das Bundesamt für Sicherheit | Verfahren zur zumindest einseitig authentisierten, sicheren Kommunikation zwischen zwei Kommunikationspartnern |
| WO2014181189A2 (en) * | 2013-03-15 | 2014-11-13 | Assa Abloy Ab | Non-repudiation of electronic transactions |
| US9294503B2 (en) | 2013-08-26 | 2016-03-22 | A10 Networks, Inc. | Health monitor based distributed denial of service attack mitigation |
| US10574633B2 (en) * | 2014-06-18 | 2020-02-25 | Visa International Service Association | Efficient methods for authenticated communication |
| US9756071B1 (en) | 2014-09-16 | 2017-09-05 | A10 Networks, Inc. | DNS denial of service attack protection |
| US9537886B1 (en) | 2014-10-23 | 2017-01-03 | A10 Networks, Inc. | Flagging security threats in web service requests |
| US9584318B1 (en) | 2014-12-30 | 2017-02-28 | A10 Networks, Inc. | Perfect forward secrecy distributed denial of service attack defense |
| US9900343B1 (en) | 2015-01-05 | 2018-02-20 | A10 Networks, Inc. | Distributed denial of service cellular signaling |
| US9848013B1 (en) * | 2015-02-05 | 2017-12-19 | A10 Networks, Inc. | Perfect forward secrecy distributed denial of service attack detection |
| US10063591B1 (en) | 2015-02-14 | 2018-08-28 | A10 Networks, Inc. | Implementing and optimizing secure socket layer intercept |
| RU2663972C1 (ru) | 2015-02-27 | 2018-08-14 | Телефонактиеболагет Лм Эрикссон (Пабл) | Обеспечение безопасности при связи между устройством связи и сетевым устройством |
| US20170063853A1 (en) * | 2015-07-10 | 2017-03-02 | Infineon Technologies Ag | Data cipher and decipher based on device and data authentication |
| US10505984B2 (en) | 2015-12-08 | 2019-12-10 | A10 Networks, Inc. | Exchange of control information between secure socket layer gateways |
| US10469594B2 (en) | 2015-12-08 | 2019-11-05 | A10 Networks, Inc. | Implementation of secure socket layer intercept |
| US11184168B2 (en) * | 2016-02-19 | 2021-11-23 | Nec Corporation | Method for storing data on a storage entity |
| US10116634B2 (en) | 2016-06-28 | 2018-10-30 | A10 Networks, Inc. | Intercepting secure session upon receipt of untrusted certificate |
| SG10201606164TA (en) * | 2016-07-26 | 2018-02-27 | Huawei Int Pte Ltd | System and method for obtaining a common session key between devices |
| US10158666B2 (en) | 2016-07-26 | 2018-12-18 | A10 Networks, Inc. | Mitigating TCP SYN DDoS attacks using TCP reset |
| US11012435B2 (en) | 2017-12-19 | 2021-05-18 | International Business Machines Corporation | Multi factor authentication |
| US11122033B2 (en) * | 2017-12-19 | 2021-09-14 | International Business Machines Corporation | Multi factor authentication |
| CN109995509B (zh) * | 2019-05-08 | 2021-07-06 | 西安电子科技大学 | 基于消息恢复签名的认证密钥交换方法 |
| CN114154200B (zh) * | 2021-12-09 | 2024-05-24 | 山东大学 | 基于可交换弱伪随机函数的隐私集合求并方法及系统 |
| US11973861B2 (en) * | 2022-02-09 | 2024-04-30 | Northrop Grumman Systems Corporation | Secure key generation |
Family Cites Families (8)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US4200770A (en) * | 1977-09-06 | 1980-04-29 | Stanford University | Cryptographic apparatus and method |
| US5491750A (en) * | 1993-12-30 | 1996-02-13 | International Business Machines Corporation | Method and apparatus for three-party entity authentication and key distribution using message authentication codes |
| US6487661B2 (en) * | 1995-04-21 | 2002-11-26 | Certicom Corp. | Key agreement and transport protocol |
| US5761305A (en) | 1995-04-21 | 1998-06-02 | Certicom Corporation | Key agreement and transport protocol with implicit signatures |
| US6226383B1 (en) * | 1996-04-17 | 2001-05-01 | Integrity Sciences, Inc. | Cryptographic methods for remote authentication |
| GB9621274D0 (en) * | 1996-10-11 | 1996-11-27 | Certicom Corp | Signature protocol for mail delivery |
| CA2369540C (en) * | 2001-12-31 | 2013-10-01 | Certicom Corp. | Method and apparatus for computing a shared secret key |
| US7073068B2 (en) * | 2002-05-24 | 2006-07-04 | Lucent Technologies Inc. | Method and apparatus for distributing shares of a password for use in multi-server password authentication |
-
2006
- 2006-02-07 US US11/348,304 patent/US7747865B2/en not_active Expired - Fee Related
- 2006-02-10 CA CA2596500A patent/CA2596500C/en active Active
- 2006-02-10 ES ES06708184T patent/ES2308725T3/es active Active
- 2006-02-10 DE DE602006002025T patent/DE602006002025D1/de active Active
- 2006-02-10 EP EP06708184A patent/EP1847062B1/en active Active
- 2006-02-10 JP JP2007554563A patent/JP2009526411A/ja not_active Withdrawn
- 2006-02-10 WO PCT/EP2006/050841 patent/WO2006084896A1/en active IP Right Grant
- 2006-02-10 AT AT06708184T patent/ATE403297T1/de not_active IP Right Cessation
Non-Patent Citations (1)
| Title |
|---|
| JPN6010044353, Hugo Krawczyk, "HMQV:A High−Performance Secure Diffie−Hellman Protocol", Cryptology ePrint Archive, 20050706, Report 2005/176, p.1−62 * |
Cited By (38)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| JP2009130872A (ja) * | 2007-11-28 | 2009-06-11 | Nippon Telegr & Teleph Corp <Ntt> | 鍵共有方法、第1装置、第2装置、及び、それらのプログラム |
| JP2011061306A (ja) * | 2009-09-07 | 2011-03-24 | Nippon Telegr & Teleph Corp <Ntt> | 情報共有システム、方法及びプログラム |
| JP2012151648A (ja) * | 2011-01-19 | 2012-08-09 | Nippon Telegr & Teleph Corp <Ntt> | 情報共有方法、情報共有システム、情報共有装置、及びプログラム |
| JP2014050084A (ja) * | 2012-09-04 | 2014-03-17 | Nippon Telegr & Teleph Corp <Ntt> | 鍵交換システム、要求装置、応答装置、鍵交換方法、およびプログラム |
| US10915896B2 (en) | 2014-01-02 | 2021-02-09 | Tencent Technology (Shenzhen) Company Limited | Signature verification method, apparatus, and system |
| JP2017501637A (ja) * | 2014-01-02 | 2017-01-12 | テンセント・テクノロジー・(シェンジェン)・カンパニー・リミテッド | 署名検証方法、装置、およびシステム |
| US11854003B2 (en) | 2014-01-02 | 2023-12-26 | Tencent Technology (Shenzhen) Company Limited | Signature verification method, apparatus, and system |
| US11347838B2 (en) | 2016-02-23 | 2022-05-31 | Nchain Holdings Ltd. | Blockchain implemented counting system and method for use in secure voting and distribution |
| US11373152B2 (en) | 2016-02-23 | 2022-06-28 | nChain Holdings Limited | Universal tokenisation system for blockchain-based cryptocurrencies |
| US10715336B2 (en) | 2016-02-23 | 2020-07-14 | nChain Holdings Limited | Personal device security using elliptic curve cryptography for secret sharing |
| US10652014B2 (en) | 2016-02-23 | 2020-05-12 | nChain Holdings Limited | Determining a common secret for the secure exchange of information and hierarchical, deterministic cryptographic keys |
| JP2021044828A (ja) * | 2016-02-23 | 2021-03-18 | エヌチェーン ホールディングス リミテッドNchain Holdings Limited | ウォレット管理システムと併せたブロックチェーンベースのシステムのための暗号鍵のセキュアなマルチパーティ損失耐性のある記憶及び転送 |
| US11120437B2 (en) | 2016-02-23 | 2021-09-14 | nChain Holdings Limited | Registry and automated management method for blockchain-enforced smart contracts |
| US11126976B2 (en) | 2016-02-23 | 2021-09-21 | nChain Holdings Limited | Method and system for efficient transfer of cryptocurrency associated with a payroll on a blockchain that leads to an automated payroll method and system based on smart contracts |
| US11182782B2 (en) | 2016-02-23 | 2021-11-23 | nChain Holdings Limited | Tokenisation method and system for implementing exchanges on a blockchain |
| US11194898B2 (en) | 2016-02-23 | 2021-12-07 | nChain Holdings Limited | Agent-based turing complete transactions integrating feedback within a blockchain system |
| JP2022037089A (ja) * | 2016-02-23 | 2022-03-08 | エヌチェーン ホールディングス リミテッド | ブロックチェーンからのデータのセキュアな抽出のための暗号方法及びシステム |
| US11308486B2 (en) | 2016-02-23 | 2022-04-19 | nChain Holdings Limited | Method and system for the secure transfer of entities on a blockchain |
| JP2019511035A (ja) * | 2016-02-23 | 2019-04-18 | エヌチェーン ホールディングス リミテッドNchain Holdings Limited | スマートコントラクトに基づく自動給与支払方法及びシステムをもたらす、ブロックチェーン上の給与支払に関連付けられた暗号通貨の効率的な転送のための方法及びシステム |
| US11349645B2 (en) | 2016-02-23 | 2022-05-31 | Nchain Holdings Ltd. | Determining a common secret for the secure exchange of information and hierarchical, deterministic cryptographic keys |
| US11356280B2 (en) | 2016-02-23 | 2022-06-07 | Nchain Holdings Ltd | Personal device security using cryptocurrency wallets |
| JP7083754B2 (ja) | 2016-02-23 | 2022-06-13 | エヌチェーン ホールディングス リミテッド | スマートコントラクトに基づく自動給与支払方法及びシステムをもたらす、ブロックチェーン上の給与支払に関連付けられた暗号通貨の効率的な転送のための方法及びシステム |
| US10659223B2 (en) | 2016-02-23 | 2020-05-19 | nChain Holdings Limited | Secure multiparty loss resistant storage and transfer of cryptographic keys for blockchain based systems in conjunction with a wallet management system |
| US11410145B2 (en) | 2016-02-23 | 2022-08-09 | nChain Holdings Limited | Blockchain-implemented method for control and distribution of digital content |
| US11455378B2 (en) | 2016-02-23 | 2022-09-27 | nChain Holdings Limited | Method and system for securing computer software using a distributed hash table and a blockchain |
| JP7164580B2 (ja) | 2016-02-23 | 2022-11-01 | エヌチェーン ホールディングス リミテッド | ウォレット管理システムと併せたブロックチェーンベースのシステムのための暗号鍵のセキュアなマルチパーティ損失耐性のある記憶及び転送 |
| JP7164580B6 (ja) | 2016-02-23 | 2022-11-28 | エヌチェーン ライセンシング アーゲー | ウォレット管理システムと併せたブロックチェーンベースのシステムのための暗号鍵のセキュアなマルチパーティ損失耐性のある記憶及び転送 |
| US11606219B2 (en) | 2016-02-23 | 2023-03-14 | Nchain Licensing Ag | System and method for controlling asset-related actions via a block chain |
| US11621833B2 (en) | 2016-02-23 | 2023-04-04 | Nchain Licensing Ag | Secure multiparty loss resistant storage and transfer of cryptographic keys for blockchain based systems in conjunction with a wallet management system |
| US11625694B2 (en) | 2016-02-23 | 2023-04-11 | Nchain Licensing Ag | Blockchain-based exchange with tokenisation |
| JP7292365B2 (ja) | 2016-02-23 | 2023-06-16 | エヌチェーン ライセンシング アーゲー | ブロックチェーンからのデータのセキュアな抽出のための暗号方法及びシステム |
| US11727501B2 (en) | 2016-02-23 | 2023-08-15 | Nchain Licensing Ag | Cryptographic method and system for secure extraction of data from a blockchain |
| US11755718B2 (en) | 2016-02-23 | 2023-09-12 | Nchain Licensing Ag | Blockchain implemented counting system and method for use in secure voting and distribution |
| JP2019507510A (ja) * | 2016-02-23 | 2019-03-14 | エヌチェーン ホールディングス リミテッドNchain Holdings Limited | 情報及び階層的で決定性の暗号化鍵のセキュアな交換のための共通秘密の決定 |
| US11936774B2 (en) | 2016-02-23 | 2024-03-19 | Nchain Licensing Ag | Determining a common secret for the secure exchange of information and hierarchical, deterministic cryptographic keys |
| US11972422B2 (en) | 2016-02-23 | 2024-04-30 | Nchain Licensing Ag | Registry and automated management method for blockchain-enforced smart contracts |
| US12032677B2 (en) | 2016-02-23 | 2024-07-09 | Nchain Licensing Ag | Agent-based turing complete transactions integrating feedback within a blockchain system |
| US12107952B2 (en) | 2016-02-23 | 2024-10-01 | Nchain Licensing Ag | Methods and systems for efficient transfer of entities on a peer-to-peer distributed ledger using the blockchain |
Also Published As
| Publication number | Publication date |
|---|---|
| DE602006002025D1 (de) | 2008-09-11 |
| EP1847062B1 (en) | 2008-07-30 |
| ES2308725T3 (es) | 2008-12-01 |
| US7747865B2 (en) | 2010-06-29 |
| CA2596500C (en) | 2014-03-25 |
| CA2596500A1 (en) | 2006-08-17 |
| ATE403297T1 (de) | 2008-08-15 |
| WO2006084896A1 (en) | 2006-08-17 |
| US20060179319A1 (en) | 2006-08-10 |
| EP1847062A1 (en) | 2007-10-24 |
Similar Documents
| Publication | Publication Date | Title |
|---|---|---|
| JP2009526411A (ja) | 装置またはネットワークによって相互接続された2当事者間の交換の方法、信号伝送媒体、および装置(チャレンジ・レスポンス署名および高性能で安全なDiffie−Hellmanプロトコルに関する方法および構造) | |
| Krawczyk | HMQV: A high-performance secure Diffie-Hellman protocol | |
| JP4384728B2 (ja) | 内在的署名を用いた鍵一致及び輸送プロトコル | |
| US7139917B2 (en) | Systems, methods and software for remote password authentication using multiple servers | |
| US9571274B2 (en) | Key agreement protocol | |
| Cremers et al. | One-round Strongly Secure Key Exchange with Perfect Forward Secrecy and Deniability. | |
| JP2001313634A (ja) | 通信方法 | |
| US20100169658A1 (en) | Elliptic curve-based message authentication code | |
| Daniel et al. | An efficient eCK secure certificateless authenticated key agreement scheme with security against public key replacement attacks | |
| CN101116281A (zh) | 询问-应答签名和安全迪菲-海尔曼协议 | |
| US20160352689A1 (en) | Key agreement protocol | |
| Abusukhon et al. | An authenticated, secure, and mutable multiple‐session‐keys protocol based on elliptic curve cryptography and text‐to‐image encryption algorithm | |
| Yoon et al. | A new authentication scheme for session initiation protocol | |
| Farash et al. | A provably secure and efficient two‐party password‐based explicit authenticated key exchange protocol resistance to password guessing attacks | |
| Zhao et al. | sHMQV: An efficient key exchange protocol for power-limited devices | |
| Krzywiecki et al. | Deniable key establishment resistance against eKCI attacks | |
| Yeun | Design, analysis and applications of cryptographic techniques | |
| Vesterås | Analysis of key agreement protocols | |
| Asbullah et al. | A proposed CCA-secure encryption on an ElGamal variant | |
| Shim | The risks of compromising secret information | |
| Farash et al. | Security of multiple-key agreement protocols and propose an enhanced protocol | |
| Tan | Identity-based authenticated multiple key agreement protocol with PKG forward security | |
| Glushachenko | Public key cryptosystems and their application in digital signature algorithms | |
| Flores | On Provable Security of Entity Authentication Schemes | |
| Luo et al. | Secure authentication protocols resistant to guessing attacks |
Legal Events
| Date | Code | Title | Description |
|---|---|---|---|
| A521 | Request for written amendment filed |
Free format text: JAPANESE INTERMEDIATE CODE: A523 Effective date: 20100712 |
|
| A871 | Explanation of circumstances concerning accelerated examination |
Free format text: JAPANESE INTERMEDIATE CODE: A871 Effective date: 20100712 |
|
| A975 | Report on accelerated examination |
Free format text: JAPANESE INTERMEDIATE CODE: A971005 Effective date: 20100727 |
|
| A131 | Notification of reasons for refusal |
Free format text: JAPANESE INTERMEDIATE CODE: A131 Effective date: 20100803 |
|
| A761 | Written withdrawal of application |
Free format text: JAPANESE INTERMEDIATE CODE: A761 Effective date: 20100902 |