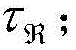CN116331256A - Track changing planning method, track changing planning equipment and track changing planning storage medium for distributed driving electric automobile - Google Patents

Abstract

The invention discloses a lane change track planning method, equipment and storage medium for a distributed driving electric automobile, wherein the lane change track planning method comprises the following steps: generating an unconstrained generalized lane change track cluster according to the vehicle track planning curve fitting function; selecting a lane change track cluster meeting the stability domain of the distributed driving electric automobile from the generalized lane change track clusters; in a lane change track cluster meeting the stable domain of the distributed driving electric automobile, calculating the feasible domain of the automobile according to the geometric constraint of the environment and the road boundary; based on an improved algorithm combining an analytic hierarchy process and a technology approaching to ideal, an optimal lane change track is selected by evaluating a stability index, a track tracking accuracy index, a comfort index and a lane change efficiency index. The path planning algorithm fully utilizes the advantage of independent and controllable four wheels of the distributed driving electric vehicle, integrates new dynamic characteristics of the vehicle into the path planning algorithm, and improves the running efficiency and safety of the electric vehicle.

Description

Distributed drive electric vehicle lane change trajectory planning method, device and storage medium

Technical Field

The present invention relates to a distributed drive intelligent electric vehicle lane change trajectory planning method, relates to a distributed drive intelligent electric vehicle path planning technology, and belongs to the field of new energy vehicle design and manufacturing.

Background Art

Distributed drive electric vehicles, compared with traditional centralized electric vehicles that are converted from oil to electricity, are a new chassis drive configuration. The drive motor is directly installed in or near the drive wheel. The chassis of this new power configuration has the advantage of all-round mobility and is gradually developing towards a digital chassis. Therefore, it is evaluated by experts in the automotive field as a special chassis for smart electric vehicles and the best carrier for achieving safe and efficient unmanned driving. It has become the mainstream trend of the development of future smart electric vehicles. In recent years, the number of cars has continued to grow, which has led to some problems becoming increasingly prominent, such as frequent traffic accidents and increased traffic congestion. The electrification, networking and intelligence of automobiles have become the trend of future development, so the high intelligence of distributed drive electric vehicles has become an inevitable trend of future development. Autonomous driving technology is divided into levels 0 to 5. With the increase in the level of automobile driving automation, the vehicle system is less dependent on the driver. At this stage, the autonomous driving level of mass-produced smart electric vehicles is in the range of levels 2 to 3. In other words, the more mature autonomous driving technology can only achieve conditional autonomous driving functions. Therefore, the autonomous driving technology of smart electric vehicles should improve its adaptability to different traffic scenarios and maintain vehicle stability in scenarios such as high-speed collision avoidance and emergency obstacle avoidance. Distributed drive electric vehicles have a higher degree of control freedom, and the difficulty of developing automotive intelligent technology will also be higher. The intelligence of distributed drive electric vehicles is challenging.

Vehicle trajectory planning technology is one of the important links in the realization of autonomous driving technology. Since vehicles generally travel in complex traffic environments or at high speeds, the requirements for vehicle trajectory planning algorithms are generally higher than those for indoor robots, and more kinematic and dynamic factors need to be considered. Commonly used trajectory planning algorithm classifications include algorithms based on graph search, algorithms based on curve fitting, algorithms based on numerical optimization, algorithms based on artificial potential fields, algorithms based on sampling, and algorithms based on intelligent methods. Vehicle lane change trajectory planning is one of the common traffic scenarios. When a vehicle is driving on the road and encounters scenarios such as overtaking and obstacle avoidance, it is necessary to plan a driving trajectory in advance that conforms to human driving habits, while satisfying the vehicle stability constraints, environmental geometry constraints, and road boundary constraints. The planned path has high lane change efficiency and is easy to track and control, so as to achieve multi-objective optimization of the trajectory. At present, the trajectory planning algorithm of centralized intelligent electric vehicles is generally conservative, and kinematic factors are relatively more considered while dynamic factors are ignored. The study of the stability domain mechanism of distributed drive electric vehicles greatly affects the final result of path planning. How to closely combine kinematics and dynamics for vehicle planning has become one of the key issues in trajectory planning of distributed drive intelligent electric vehicles, and is one of the necessary paths for highly intelligent vehicles. In the context of vehicle intelligence, it is crucial to make full use of the stability domain of distributed drive electric vehicles for upper-level path planning. The relationship between the intelligent driving layer and the chassis control layer of distributed drive electric vehicles is inseparable.

Summary of the invention

The technical problem to be solved by the present invention is the key problem of the trajectory planning of lane change of distributed drive intelligent electric vehicles. A method, device and storage medium for the trajectory planning of lane change of distributed drive intelligent electric vehicles are proposed. The proposed trajectory planning algorithm can complete traffic scenes such as lane change, overtaking, emergency obstacle avoidance, etc. in complex traffic environments, and is also applicable to high-speed or low-speed driving conditions. The path planning algorithm fully utilizes the advantages of the four wheels of distributed drive electric vehicles being independently controllable, and its dynamic performance is improved compared to the centralized type. The kinematic and dynamic characteristics of the vehicle are integrated into the trajectory planning algorithm, and the efficiency and safety of electric vehicle driving are improved.

The technical solution adopted by the present invention to solve the technical problem comprises the following steps:

A distributed drive electric vehicle lane change trajectory planning method, characterized by comprising the following steps:

Generate unconstrained generalized lane-changing trajectory clusters based on the vehicle trajectory planning curve fitting function;

Among the generated unconstrained generalized lane-changing trajectory clusters, the lane-changing trajectory clusters that meet the stability domain of distributed drive electric vehicles are selected;

In the selected lane-changing trajectory cluster that satisfies the stability domain of the distributed drive electric vehicle, the feasible domain of the vehicle is calculated according to the environmental geometric constraints and the road boundary;

In the calculated vehicle feasible domain, an improved algorithm based on the combination of hierarchical analysis method and approximation to ideal technology is used to select the optimal lane changing trajectory by evaluating the stability index, trajectory tracking accuracy index, comfort index and lane changing efficiency index.

Designing an unconstrained generalized lane-changing trajectory cluster consists of the following parts:

(I) The optimal longitudinal displacement, velocity, acceleration, and jerk expressions are determined.

a). It is necessary to minimize the longitudinal fluctuation and construct a performance indicator to minimize the longitudinal fluctuation:

The following constraints need to be met:

为换道过程的终止时刻，设初始时刻τ₀＝0，因此换道过程的时间为

x(t)为车辆换道过程中纵向位移函数，

和v_x(t)表示车辆换道过程中的纵向车速；

和a_x(t)表示车辆换道过程中的纵向加速度；

和j_x(t)表示车辆换道过程中的纵向急动度；L为车辆换道的纵向距离，v_x0为换道过程中纵向速度的初始值，

为换道过程中纵向速度的终值；Among them, η _x is the cost function of longitudinal fluctuation, minη _x is the minimum value of the performance index for minimizing longitudinal fluctuation; τ ₀ is the initial time of the lane change trajectory,

is the end time of the lane changing process, and the initial time τ ₀ = 0, so the lane changing process time is

x(t) is the longitudinal displacement function of the vehicle during lane changing,

and v _x (t) represents the longitudinal speed of the vehicle during the lane change process;

and a _x (t) represents the longitudinal acceleration of the vehicle during the lane change process;

and j _x (t) represent the longitudinal jerk of the vehicle during lane change; L is the longitudinal distance of the vehicle during lane change, v _x0 is the initial value of the longitudinal velocity during lane change,

is the final value of the longitudinal speed during the lane changing process;

b). To solve the above performance indicators, construct the Hamiltonian function H _x as

Among them, κ _x1 is the Lagrangian operator corresponding to v _x , κ _x2 is the Lagrangian operator corresponding to a _x , and κ _x3 is the Lagrangian operator corresponding to j _x .

c) According to the Pontryagin maximum principle, the co-state equation is expressed as:

解得：κ_x1＝m₀

The solution is: κ _x1 = m ₀

解得：κ_x2＝m₁-m₀t

The solution is: κ _x2 = m ₁ - m ₀ t

解得：

The solution is:

Among them, m ₀ , m ₁ and m ₂ are unknown constants.

The extreme value condition is:

解得：

The solution is:

in,

d). In the geodetic coordinate system, according to the above steps, the expressions of the optimal longitudinal displacement, velocity, acceleration and jerk during lane change are:

为换道时间，L为车辆换道的纵向距离，v_x0为纵向速度的初始值。Where j _x (t), a _x (t), v _x (t) and x (t) represent the functions of the vehicle longitudinal jerk, acceleration, velocity and displacement, respectively, and t is the time as the independent variable of the function.

is the lane changing time, L is the longitudinal distance of the vehicle changing lanes, and _vx0 is the initial value of the longitudinal speed.

(II) The optimal lateral displacement, velocity, acceleration, and jerk expressions are determined.

a). It is necessary to minimize lateral fluctuations and construct performance indicators that minimize lateral fluctuations:

The following constraints need to be met:

为换道过程的终止时刻，设初始时刻τ₀＝0，因此换道过程的时间为

y(t)表示车辆换道过程中的侧向位移函数，

和v_y(t)表示车辆换道过程中的侧向车速；

和a_y(t)表示车辆换道过程中的侧向加速度；

和j_y(t)表示车辆换道过程中的侧向急动度；D为车辆换道的侧向距离；v_y0为换道过程中侧向速度的初始值，

为换道过程中侧向速度的终值；Among them, η _y is the cost function of lateral fluctuation, minη _y is the minimum value of the performance index for minimizing lateral fluctuation; τ ₀ is the initial time of the lane change trajectory,

is the end time of the lane changing process, and the initial time τ ₀ = 0, so the lane changing process time is

y(t) represents the lateral displacement function of the vehicle during lane changing.

and _vy (t) represents the lateral speed of the vehicle during the lane change process;

and a _y (t) represents the lateral acceleration of the vehicle during lane change;

and j _y (t) represent the lateral jerk of the vehicle during lane change; D is the lateral distance of the vehicle during lane change; v _y0 is the initial value of the lateral velocity during lane change,

is the final value of the lateral speed during the lane changing process;

b). To solve the above performance indicators, the Hamiltonian function _Hy is constructed as

Among them, κ _y1 is the Lagrangian operator corresponding to v _y , κ _y2 is the Lagrangian operator corresponding to a _y , and κ _y3 is the Lagrangian operator corresponding to j _y .

c) According to the Pontryagin maximum principle, the co-state equation is expressed as:

解得：κ_y1＝n₀

The solution is: κ _y1 = n ₀

解得：κ_y2＝n₁-n₀t

The solution is: κ _y2 = n ₁ -n ₀ t

解得：

The solution is:

Among them, n ₀ , n ₁ and n ₂ are unknown constants.

The extreme value condition is:

解得：

The solution is:

in,

d). In the geodetic coordinate system, according to the above steps, the expressions of the optimal lateral jerk, acceleration, velocity and displacement during the lane change process are obtained as follows:

为换道时间，D为车辆换道的侧向距离，v_y0为侧向速度的初始值。Where j _y (t), a _y (t), _vy (t) and y (t) represent the functions of the vehicle's lateral jerk, acceleration, velocity and displacement, respectively, and t is the time as the independent variable of the function.

is the lane changing time, D is the lateral distance of the vehicle changing lanes, and v _y0 is the initial value of the lateral speed.

(III) Determination of the lane-changing trajectory expression of a distributed drive intelligent electric vehicle based on a quintic polynomial.

During the lane changing process, the longitudinal speed of the vehicle is kept constant, and the longitudinal acceleration is unchanged to minimize the longitudinal fluctuation of the vehicle. Therefore, it can be obtained:

v _x (t) = v _x0

Wherein, v _x (t) represents the longitudinal vehicle speed function during the lane changing process, and v _x0 is the initial value of the longitudinal vehicle speed.

The lane-changing trajectory of a distributed drive smart electric vehicle based on a quintic polynomial is expressed as:

从而得到一系列无约束的广义换道轨迹簇。Among them, x(t) is the longitudinal displacement of the lane changing process, y(t) is the lateral displacement of the lane changing process, and t is the independent variable of the function. Under a certain initial vehicle speed v _x0 , different lane changing times

Thus, a series of unconstrained generalized lane-changing trajectory clusters are obtained.

The selection of lane-changing trajectory clusters that meet the stability domain of distributed drive electric vehicles includes the following parts:

(I) Analysis of stability domain mechanism.

a). To analyze the influence mechanism of the stability domain of distributed drive electric vehicles, it is necessary to establish a four-wheel vehicle model of distributed drive electric vehicles, and its dynamic equation is:

为横摆角速度的一阶导数；β表示质心侧偏角，

为质心侧偏角的一阶导数；v_x为纵向车速；δ_f为车辆前轮转角；a为车辆重心到前轴的距离，b为车辆重心到后轴的距离；l_f为车辆前轴轴距，l_r为车辆后轴轴距；m为整车质量；I_z为绕z轴的转动惯量。Where F _yij is the tire lateral force, its subscripts ij = fl, fr, rl, rr represent the left front wheel, right front wheel, left rear wheel and right rear wheel of the tire respectively, r represents the yaw angular velocity,

is the first-order derivative of the yaw rate; β represents the sideslip angle of the center of mass,

is the first-order derivative of the sideslip angle at the center of mass; _vx is the longitudinal vehicle speed; _δf is the front wheel turning angle of the vehicle; a is the distance from the center of gravity of the vehicle to the front axle, b is the distance from the center of gravity of the vehicle to the rear axle; _lf is the wheelbase of the front axle of the vehicle, _lr is the wheelbase of the rear axle of the vehicle; m is the mass of the vehicle; _Iz is the moment of inertia about the z-axis.

b). The tire side slip angle α _ij is calculated as follows:

Among them, α _ij is the tire side slip angle, and its subscripts ij=fl, fr, rl, rr represent the left front wheel, right front wheel, left rear wheel and right rear wheel of the tire respectively.

c). The calculation formula of tire vertical load F _zij is:

Wherein, F _zij is the vertical load on the tire, and its subscripts ij = fl, fr, rl, rr represent the left front wheel, right front wheel, left rear wheel and right rear wheel of the tire respectively; a _x is the longitudinal acceleration of the vehicle, a _y is the lateral acceleration of the vehicle; and h is the height of the center of mass of the vehicle.

d). Calculate the tire lateral force equation based on the Fiala tire model:

Among them, F _yij is the tire lateral force, and its subscripts ij = fl, fr, rl, rr represent the left front wheel, right front wheel, left rear wheel and right rear wheel of the tire respectively; C _α is the tire cornering stiffness; α _slij is the sideslip angle corresponding to the tire entering the saturation area, and its subscripts ij = fl, fr, rl, rr represent the left front wheel, right front wheel, left rear wheel and right rear wheel of the tire respectively; μ is the road adhesion coefficient.

(II) Analysis of vehicle stability domain mechanism based on phase plane method.

a). List the differential equations according to the system state equation:

From the above formula, we can get:

Wherein, x ₁ and x ₂ are state parameters of the vehicle system, and f ₁ (x ₁ ,x ₂ ) and f ₂ (x ₁ ,x ₂ ) are differential equations of the vehicle system.

b) In the vehicle system, assume that the state trajectory x(t) starting from the initial state x ₀ =(x ₁ (0), x ₂ (0)) remains within the local range and meets the following conditions:

是确定常数，满足条件则系统在局部范围内渐进稳定，所以此时系统稳定。相平面分析中，稳定轨迹最后收敛到平衡点，不稳定轨迹将无法收敛最后发散。Where x(t) is the function of the vehicle state parameter changing with time,

is a constant. If the condition is met, the system is asymptotically stable in the local range, so the system is stable at this time. In phase plane analysis, the stable trajectory finally converges to the equilibrium point, and the unstable trajectory will not converge and finally diverge.

(III) Based on the phase plane analysis method, the stability domain analysis of different vehicle states is performed.

Select the influence of different absolute vehicle speeds, road adhesion coefficients, and front wheel steering angles on the vehicle stability domain. The specific steps include the following:

a). According to the phase plane analysis method, the function equation of the vehicle's center of mass sideslip angle β and yaw rate r can be obtained. β is the independent variable of the function, r is the dependent variable of the function, and the function expression of the stable domain is:

In the above function expression, b ₀ , b ₁ , b ₂ , and b ₃ are respectively:

b ₀ =b/v _x , b ₁ =tan(α _slrl +α _slrl ), b ₂ =(r ₂ -r ₁ )/(β ₂ -β ₁ ), b ₃ =r ₁ -β ₁ (r ₂ -r ₁ )/(β ₂ -β ₁ )

r ₁ =ug/v _x , r ₂ =v _x /(a+b)(tan((α _slfl +α _slfr )/2+δ _max )-tan((α _slrl +α _slrr )/2)),

β ₂ =b/(a+b)(tan((α _slfl +α _slfr )/2+δ _max )-tan((α _slrl +α _slrr )/2))+tan((α _slrl +α _slrr ) /2).

The expression of δ _max in the above formula is:

Among them, _b0 , _b1 , _b2 , and _b3 are the unknown coefficients of the stable domain function expression respectively; _r1 , r2, _β1 , _β2 , and _δmax are intermediate variables; _αslfl , _αslfr , _αslrl , _{and αslrr are} the sideslip angles corresponding to the left front, right front, left rear, and right rear tires entering the saturation area respectively; a is the distance from the center of gravity of the vehicle to the front axle, and b is the distance from the center of gravity of the vehicle to the rear axle; _vx is the longitudinal velocity of the vehicle, μ is the road adhesion coefficient, and g is the acceleration of gravity.

b). According to the division range of the stability domain, different absolute vehicle speeds, road adhesion coefficients, and front wheel turning angles are selected to analyze different stability domains. The specific steps are as follows:

When the road adhesion coefficient and the front wheel steering angle remain unchanged, different vehicle absolute speeds of 5, 10, 15, 20, 25, 30, 35, and 40 m/s are selected for stability domain analysis;

When the absolute vehicle speed and the front wheel steering angle remain unchanged, different road adhesion coefficients of 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, and 1.0 are selected for stability domain analysis;

When the absolute vehicle speed and road adhesion coefficient remain unchanged, different front wheel steering angles of -30, -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, and 30 degrees are selected for stability domain analysis.

c). Based on the stability domain set obtained from the above analysis, the formula for calculating the vehicle's real-time center of mass sideslip angle and yaw rate is:

Among them, _vx is the longitudinal speed of the vehicle, _vy is the lateral speed of the vehicle, _ay is the lateral acceleration of the vehicle, r is the yaw rate of the vehicle, and β is the sideslip angle of the center of mass of the vehicle.

Whether the vehicle state exceeds the stable domain is determined based on the sideslip angle of the center of mass and the yaw angular velocity. The lane-changing trajectory that exceeds the stable domain will be eliminated, and finally the lane-changing trajectory that satisfies the vehicle's stable domain will be retained.

Considering surrounding vehicles and pedestrians as environmental geometric constraints, lane lines, traffic rules, etc. as road boundaries, the global feasible domain of the vehicle is calculated to include the following parts:

(I) Take the geometric center of the vehicle and the front vehicle, and take the maximum length from the geometric center to the vehicle body as the radius of the geometric circle, denoted as R _l and R _f respectively, and draw a geometric circle. Therefore, the tangent point of the geometric circle of the vehicle and the front vehicle becomes the critical point of collision, so a boundary line of the global feasible domain can be obtained.

(II) Considering the constraints of lane lines, traffic rules or rear vehicles, the tangent point of the geometric circle or lane line between the vehicle and the rear vehicle becomes the critical point of collision. Combining the above steps, a closed global feasible domain of the vehicle can be obtained. Among the lane change trajectory clusters that meet the stability of distributed drive electric vehicles, trajectory clusters that meet the constraints of environmental geometry, lane lines and traffic rules are further screened out.

Based on the improved algorithm combining the analytic hierarchy process (AHP) and the technique to approach the ideal (TOPSIS), the optimal lane-changing trajectory is selected by evaluating the stability index, trajectory tracking accuracy index, comfort index and lane-changing efficiency index. The algorithm includes the following parts:

(I) Establishment of evaluation indicators.

a). Establish evaluation indicators such as stability index, trajectory tracking accuracy index, comfort index and lane changing efficiency of lane changing trajectory planning respectively:

Constructing vehicle stability index:

为换道时间，F_yi(t)为前轴或后轴的侧向力关于时间的函数表达式，F_zi(t)为前轴或后轴的垂向载荷关于时间的函数表达式，

为路面附着系数的门限值。Among them, _Js is the vehicle stability evaluation index,

is the lane changing time, F _yi (t) is the function expression of the lateral force of the front axle or rear axle with respect to time, F _zi (t) is the function expression of the vertical load of the front axle or rear axle with respect to time,

is the threshold value of the road adhesion coefficient.

b). Construct vehicle trajectory tracking accuracy indicators:

为换道时间，v_x为车辆纵向车速，

为车辆质心侧偏角角速度函数表达式，

为质心侧偏角门限值；h(t)为车辆的理想规划轨迹；y(t)为车辆的实际行驶轨迹；

为理想规划轨迹与实际行驶轨迹误差的门限值。Among them, _Jt is the vehicle trajectory tracking accuracy evaluation index,

is the lane changing time, _vx is the longitudinal speed of the vehicle,

is the angular velocity function expression of the vehicle's center of mass sideslip angle,

is the center of mass sideslip angle threshold; h(t) is the ideal planned trajectory of the vehicle; y(t) is the actual driving trajectory of the vehicle;

is the threshold value of the error between the ideal planned trajectory and the actual driving trajectory.

c). Construct vehicle comfort index:

为换道时间，a_y(t)为车辆的纵向加速度，

为车辆侧向加速度门限值，θ(t)为侧倾角，

为侧倾角门限值。Among them, J _c is the vehicle comfort evaluation index,

is the lane changing time, a _y (t) is the longitudinal acceleration of the vehicle,

is the vehicle lateral acceleration threshold, θ(t) is the roll angle,

is the roll angle threshold.

d). Constructing lane-changing efficiency index:

为换道时间。Among them, _Je is the vehicle lane-changing efficiency evaluation index,

The lane change time.

(II) An improved algorithm based on the combination of the analytic hierarchy process (AHP) and the technique of approaching the ideal (TOPSIS).

a). Construction of judgment matrix. The optimal lane-changing trajectory cluster is calculated from the trajectory clusters that meet the constraints. This can overcome the tediousness of using the TOPSIS algorithm alone in the multi-objective calculation process and the subjectivity of using the AHP algorithm alone in the calculation process. The target layer A includes m evaluation indicators A ₁ , A ₂ , A ₃ , …, A _m . The target layer A corresponds to the determination of the influencing indicators J ₁ , J ₂ , J ₃ , J ₄ , …, J _n of the matrix B. The judgment matrix B is constructed with an order of n×n. The matrix B is shown as follows:

Among them, the element _bij in the matrix is the importance of the lane-changing trajectory planning evaluation index _Ji to the lane-changing trajectory planning evaluation index _Jj , _bji = 1/ _bij . When the element _bij = 1, the two lane-changing trajectory planning evaluation indicators are equally important; when the element _bij = 3, the lane-changing trajectory planning evaluation index _Ji is slightly more important than the lane-changing trajectory planning evaluation index _Jj ; when the element _bij = 5, the lane-changing trajectory planning evaluation index _Ji is significantly more important than the lane-changing trajectory planning evaluation index _Jj ; when the element _bij = 7, the lane-changing trajectory planning evaluation index _Ji is strongly more important than the lane-changing trajectory planning evaluation index Jj; when the element _bij = 9, the lane-changing trajectory planning evaluation index _Ji is absolutely more important than the lane-changing trajectory planning evaluation index _{Jj ;} when the value of the element is 2, 4, 6, 8, it means that it is in the middle state of the element value of 1, 3, 5, 7, 9.

b). Determine the indicator weight. According to the above judgment matrix, calculate the sum of each column, normalize the elements of each column, and further add the normalized results by row to calculate the square root vector. Finally, the normalized square root vector is used to obtain the ranking weight vector. The calculation formula is:

为对每列元素规范化的结果，b_ij为判断矩阵中的元素，W_i为归一化处理结果按照行相加的结果，W_i为排序权向量。in,

is the result of normalizing the elements in each column, _bij is the element in the judgment matrix, _Wi is the result of adding the normalized results in rows, and _Wi is the sorting weight vector.

c). Consistency test. First calculate the maximum eigenvalue of the judgment matrix B, then perform a consistency test on it to obtain the consistency ratio. When the consistency ratio is less than 0.1, the consistency of the judgment matrix meets the conditions.

Among them, λ _max is the maximum eigenvalue of the judgment matrix, matrix B is the judgment matrix, _Wi is the sorting weight vector, w is the element in the sorting weight vector, CI is the consistency test standard, CR is the consistency ratio, RI is the average random consistency index, and n is the order of rows or columns of the judgment matrix.

d). Total hierarchical sorting. Based on the results of hierarchical single sorting, calculate the composite weight of the best solution of the indicator layer relative to the target layer. Assume that the target layer A includes m evaluation indicators A ₁ , A ₂ , A ₃ , …, A _m , and the weights corresponding to the evaluation indicators of the target layer are a ₁ , a ₂ , a ₃ , …, a _m , and the indicator layer J includes n evaluation indicators J ₁ , J ₂ , J ₃ , J ₄ , …, J _n , and the weight corresponding to a certain target layer A _i is c _1i , c _2i , c _3i , …, c _ni . Therefore, the weights corresponding to each indicator of the indicator layer are c ₁ , c ₂ , c ₃ , …, c _n .

Among them, _cj is the weight corresponding to each indicator of the indicator layer, _cij is the weight corresponding to a certain target layer _Ai , and _ai is the weight corresponding to the evaluation indicator of the target layer.

e). Initial evaluation index establishment. Assuming that n evaluation indexes are J = {J ₁ , J ₂ , J ₃ , ..., J _n }, each of which has m characteristic indexes R = {r ₁ , r ₂ , r ₃ , ..., r _m }, the initial evaluation matrix is:

Among them, _rij is the jth indicator of the i-th evaluation target in the target layer.

f). Matrix standardization. Because each evaluation index has different dimensions, each evaluation index is normalized and the calculation formula is:

The calculation process of the weighted normalization matrix is:

H=(v _ij ) _n×m = (ω _j r _ij ) _n×m

Among them, _rij is the jth evaluation index of the i-th evaluation target in the target layer, _vij represents the weighted element of the i-th row and j-th column, and _ωj represents the weight of the j-th evaluation index.

g). Calculation of positive ideal solution, negative ideal solution and the distance between them. The positive ideal solution means that each evaluation index takes the most ideal value solution, and the negative ideal solution means that each evaluation index takes the worst value solution. The expression is:

The positive ideal solution is:

The negative ideal solution is:

Among them, V ⁺ is the positive ideal solution, ^V- is the negative ideal solution, _J1 is the benefit-type indicator set, _J2 is the cost-type indicator set, and _vij represents the weighted element in the i-th row and j-th column.

The distance between each evaluation index and the positive ideal solution and the negative ideal solution is:

为各个评价指标与正理想值的距离，

为各个评价指标与负理想值的距离，v_ij表示加权之后的第i行、j列元素，

和

分别对应正理想解V⁺和负理想解V^-中的元素。in,

is the distance between each evaluation index and the positive ideal value,

is the distance between each evaluation index and the negative ideal value, _vij represents the weighted element in the i-th row and j-th column,

and

They correspond to the elements in the positive ideal solution V ⁺ and the negative ideal solution ^V- respectively.

h). Closeness calculation: calculate the relative closeness between the evaluation index and the ideal solution. The greater the closeness, the better the lane change trajectory.

Closeness:

为各个评价指标与正理想值的距离，

为各个评价指标与负理想值的距离，当贴近度C_i越大，即越接近于1的时候，说明该换道轨迹最优，因此最终获得最优的换道轨迹。Among them, _Ci is the closeness,

is the distance between each evaluation index and the positive ideal value,

is the distance between each evaluation index and the negative ideal value. When the closeness _Ci is larger, that is, closer to 1, it means that the lane changing trajectory is optimal, so the optimal lane changing trajectory is finally obtained.

The present invention also provides a device, characterized in that it comprises:

one or more processors;

A memory for storing one or more programs;

When the one or more programs are executed by the one or more processors, the one or more processors implement the above-mentioned distributed drive electric vehicle lane change trajectory planning method.

The present invention also provides a storage medium having a computer program stored thereon, wherein the program, when executed by a processor, implements the above-mentioned distributed drive electric vehicle lane change trajectory planning method.

Compared with the prior art, the present invention has the following beneficial effects:

1. Reveal the mechanical constraints and stability domain mechanisms between the functional subsystems of distributed drive electric vehicles, integrate the kinematic and dynamic characteristics of the vehicle into the trajectory planning algorithm, and achieve efficient calculation of the optimal trajectory in the upper-level vehicle planning;

2. Based on constraints such as vehicle stability domain, environmental geometry, and road boundaries, the global feasible domain of the vehicle is divided to improve the efficiency of optimal lane change trajectory calculation;

3. An improved algorithm based on the combination of the analytic hierarchy process (AHP) and the technique to approach the ideal (TOPSIS) is used to evaluate the stability index, trajectory tracking accuracy index, comfort index and lane changing efficiency index to select the optimal lane changing trajectory. It can overcome the tediousness of using the TOPSIS algorithm alone in the multi-objective calculation process and overcome the subjectivity of the AHP algorithm alone in the calculation process.

BRIEF DESCRIPTION OF THE DRAWINGS

FIG1 is a block diagram of a lane-changing trajectory planning system for a distributed drive intelligent electric vehicle in an example of the present invention.

Figure 2 is the dynamic model of a distributed drive intelligent electric vehicle.

FIG3 is a diagram showing the stability domain analysis results of a distributed drive intelligent electric vehicle regarding vehicle speed.

FIG4 is a diagram showing the stability domain analysis results of the distributed drive intelligent electric vehicle regarding the adhesion coefficient.

FIG5 is a diagram showing the stability domain analysis results of a distributed drive smart electric vehicle regarding the front wheel turning angle.

DETAILED DESCRIPTION

The present invention will now be described in further detail with reference to the accompanying drawings. These drawings are simplified schematic diagrams, which only illustrate the basic structure of the present invention in a schematic manner, and therefore only show the components related to the present invention.

The present invention proposes a distributed drive intelligent electric vehicle lane change trajectory planning method, as shown in Figures 1-5, the method of the present invention specifically includes the following steps:

The technical solution adopted by the present invention to solve the technical problem comprises the following steps:

Step 1: According to the curve interpolation method, the vehicle performs curve fitting of the trajectory under certain specific conditions, selects a quintic polynomial function as the trajectory planning curve fitting function, and generates an unconstrained generalized lane change trajectory cluster;

Step 2: Analyze and summarize the influence mechanism of the stability domain of distributed drive electric vehicles, and select lane changing trajectory clusters that meet the stability domain of distributed drive electric vehicles according to the above series of lane changing trajectory clusters;

Step 3: Consider surrounding vehicles and pedestrians as environmental geometric constraints, lane lines, traffic rules, etc. as road boundaries, and calculate the feasible domain of the vehicle;

Step 4: Based on an improved algorithm that combines the analytic hierarchy process (AHP) and the technique for order preference for similarity to ideal solution (TOPSIS), the optimal lane changing trajectory is selected by evaluating the stability index, trajectory tracking accuracy index, comfort index and lane changing efficiency index.

As a further optimization of the above solution, the unconstrained generalized lane-changing trajectory cluster designed in step 1 includes the following parts:

(I) The optimal longitudinal displacement, velocity, acceleration, and jerk expressions are determined.

a). It is necessary to minimize the longitudinal fluctuation and construct a performance indicator to minimize the longitudinal fluctuation:

The following constraints need to be met:

为换道过程的终止时刻，设初始时刻τ₀＝0，因此换道过程的时间为

x(t)为车辆换道过程中纵向位移函数，

和v_x(t)表示车辆换道过程中的纵向车速；

和a_x(t)表示车辆换道过程中的纵向加速度；

和j_x(t)表示车辆换道过程中的纵向急动度；L为车辆换道的纵向距离，v_x0为换道过程中纵向速度的初始值，

为换道过程中纵向速度的终值；Among them, η _x is the cost function of longitudinal fluctuation, minη _x is the minimum value of the performance index for minimizing longitudinal fluctuation; τ ₀ is the initial time of the lane change trajectory,

is the end time of the lane changing process, and the initial time τ ₀ = 0, so the time of the lane changing process is

x(t) is the longitudinal displacement function of the vehicle during lane changing,

and v _x (t) represents the longitudinal speed of the vehicle during the lane change process;

and a _x (t) represents the longitudinal acceleration of the vehicle during lane change;

and j _x (t) represent the longitudinal jerk of the vehicle during lane change; L is the longitudinal distance of the vehicle during lane change, v _x0 is the initial value of the longitudinal velocity during lane change,

is the final value of the longitudinal speed during the lane changing process;

b). To solve the above performance indicators, construct the Hamiltonian function H _x as

Among them, κ _x1 is the Lagrangian operator corresponding to v _x , κ _x2 is the Lagrangian operator corresponding to a _x , and κ _x3 is the Lagrangian operator corresponding to j _x .

c) According to the Pontryagin maximum principle, the co-state equation is expressed as:

解得：κ_x1＝m₀

The solution is: κ _x1 = m ₀

解得：κ_x2＝m₁-m₀t

The solution is: κ _x2 = m ₁ - m ₀ t

解得：

The solution is:

Among them, m ₀ , m ₁ and m ₂ are unknown constants.

The extreme value condition is:

解得：

The solution is:

in,

d). In the geodetic coordinate system, according to the above steps, the expressions of the optimal longitudinal displacement, velocity, acceleration and jerk during the lane change process are:

为换道时间，L为车辆换道的纵向距离，v_x0为纵向速度的初始值。Where j _x (t), a _x (t), v _x (t) and x (t) represent the functions of the vehicle longitudinal jerk, acceleration, velocity and displacement, respectively, and t is the time as the independent variable of the function.

is the lane changing time, L is the longitudinal distance of the vehicle changing lanes, and _vx0 is the initial value of the longitudinal speed.

(II) The optimal lateral displacement, velocity, acceleration, and jerk expressions are determined.

a). It is necessary to minimize lateral fluctuations and construct performance indicators that minimize lateral fluctuations:

The following constraints need to be met:

为换道过程的终止时刻，设初始时刻τ₀＝0，因此换道过程的时间为

y(t)表示车辆换道过程中的侧向位移函数，

和v_y(t)表示车辆换道过程中的侧向车速；

和a_y(t)表示车辆换道过程中的侧向加速度；

和j_y(t)表示车辆换道过程中的侧向急动度；D为车辆换道的侧向距离；v_y0为换道过程中侧向速度的初始值，

为换道过程中侧向速度的终值；Among them, η _y is the cost function of lateral fluctuation, minη _y is the minimum value of the performance index for minimizing lateral fluctuation; τ ₀ is the initial time of the lane change trajectory,

is the end time of the lane changing process, and the initial time τ ₀ = 0, so the lane changing process time is

y(t) represents the lateral displacement function of the vehicle during lane changing.

and _vy (t) represents the lateral speed of the vehicle during the lane change process;

and a _y (t) represents the lateral acceleration of the vehicle during lane change;

and j _y (t) represent the lateral jerk of the vehicle during lane change; D is the lateral distance of the vehicle during lane change; v _y0 is the initial value of the lateral velocity during lane change,

is the final value of the lateral speed during the lane changing process;

b). To solve the above performance indicators, the Hamiltonian function _Hy is constructed as

Among them, κ _y1 is the Lagrangian operator corresponding to v _y , κ _y2 is the Lagrangian operator corresponding to a _y , and κ _y3 is the Lagrangian operator corresponding to j _y .

c) According to the Pontryagin maximum principle, the co-state equation is expressed as:

解得：κ_y1＝n₀

The solution is: κ _y1 = n ₀

解得：κ_y2＝n₁-n₀t

The solution is: κ _y2 = n ₁ -n ₀ t

解得：

The solution is:

Among them, n ₀ , n ₁ and n ₂ are unknown constants.

The extreme value condition is:

解得：

The solution is:

in,

d). In the geodetic coordinate system, according to the above steps, the expressions of the optimal lateral jerk, acceleration, velocity and displacement during the lane change process are obtained as follows:

为换道时间，D为车辆换道的侧向距离，v_y0为侧向速度的初始值。Where j _y (t), a _y (t), _vy (t) and y (t) represent the functions of the vehicle's lateral jerk, acceleration, velocity and displacement, respectively, and t is the time as the independent variable of the function.

is the lane changing time, D is the lateral distance of the vehicle changing lanes, and v _y0 is the initial value of the lateral speed.

(III) Determination of the lane-changing trajectory expression of a distributed drive intelligent electric vehicle based on a quintic polynomial.

During the lane changing process, the longitudinal speed of the vehicle is kept constant, and the longitudinal acceleration is unchanged to minimize the longitudinal fluctuation of the vehicle. Therefore, it can be obtained:

v _x (t) = v _x0

Wherein, v _x (t) represents the longitudinal vehicle speed function during the lane changing process, and v _x0 is the initial value of the longitudinal vehicle speed.

The lane-changing trajectory of a distributed-drive smart electric vehicle based on a quintic polynomial is expressed as:

从而得到一系列无约束的广义换道轨迹簇。Among them, x(t) is the longitudinal displacement of the lane changing process, y(t) is the lateral displacement of the lane changing process, and t is the independent variable of the function. Under a certain initial vehicle speed v _x0 , different lane changing times

Thus, a series of unconstrained generalized lane-changing trajectory clusters are obtained.

As a further optimization of the above solution, step 2 of screening lane change trajectory clusters that meet the stability domain of the distributed drive electric vehicle includes the following parts:

(I) Analysis of stability domain mechanism.

a). To analyze the influence mechanism of the stability domain of distributed drive electric vehicles, it is necessary to establish a four-wheel vehicle model of distributed drive electric vehicles, as shown in Figure 2, and its dynamic equation is:

为横摆角速度的一阶导数；β表示质心侧偏角，

为质心侧偏角的一阶导数；v_x为纵向车速；δ_f为车辆前轮转角；a为车辆重心到前轴的距离，b为车辆重心到后轴的距离；l_f为车辆前轴轴距，l_r为车辆后轴轴距；m为整车质量；I_z为绕z轴的转动惯量。Where F _yij is the tire lateral force, its subscripts ij = fl, fr, rl, rr represent the left front wheel, right front wheel, left rear wheel and right rear wheel of the tire respectively, r represents the yaw angular velocity,

is the first-order derivative of the yaw rate; β represents the sideslip angle of the center of mass,

is the first-order derivative of the sideslip angle at the center of mass; _vx is the longitudinal vehicle speed; _δf is the front wheel turning angle of the vehicle; a is the distance from the center of gravity of the vehicle to the front axle, b is the distance from the center of gravity of the vehicle to the rear axle; _lf is the wheelbase of the front axle of the vehicle, _lr is the wheelbase of the rear axle of the vehicle; m is the mass of the vehicle; _Iz is the moment of inertia about the z-axis.

b). The tire side slip angle α _ij is calculated as follows:

Among them, α _ij is the tire side slip angle, and its subscripts ij=fl, fr, rl, rr represent the left front wheel, right front wheel, left rear wheel and right rear wheel of the tire respectively.

c). The calculation formula of tire vertical load F _zij is:

Wherein, F _zij is the vertical load on the tire, and its subscripts ij = fl, fr, rl, rr represent the left front wheel, right front wheel, left rear wheel and right rear wheel of the tire respectively; a _x is the longitudinal acceleration of the vehicle, a _y is the lateral acceleration of the vehicle; and h is the height of the center of mass of the vehicle.

d). Calculate the tire lateral force equation based on the Fiala tire model:

Among them, F _yij is the tire lateral force, and its subscripts ij = fl, fr, rl, rr represent the left front wheel, right front wheel, left rear wheel and right rear wheel of the tire respectively; C _α is the tire cornering stiffness; α _slij is the sideslip angle corresponding to the tire entering the saturation area, and its subscripts ij = fl, fr, rl, rr represent the left front wheel, right front wheel, left rear wheel and right rear wheel of the tire respectively; μ is the road adhesion coefficient.

(II) Analysis of vehicle stability domain mechanism based on phase plane method.

a). List the differential equations according to the system state equation:

From the above formula, we can get:

Wherein, x ₁ and x ₂ are state parameters of the vehicle system, and f ₁ (x ₁ ,x ₂ ) and f ₂ (x ₁ ,x ₂ ) are differential equations of the vehicle system.

b) In the vehicle system, assume that the state trajectory x(t) starting from the initial state x ₀ =(x ₁ (0), x ₂ (0)) remains within the local range and meets the following conditions:

是确定常数，满足条件则系统在局部范围内渐进稳定，所以此时系统稳定。相平面分析中，稳定轨迹最后收敛到平衡点，不稳定轨迹将无法收敛最后发散。Among them, x(t) is the function of the vehicle state parameter changing with time,

is a constant. If the condition is met, the system is asymptotically stable in the local range, so the system is stable at this time. In phase plane analysis, the stable trajectory finally converges to the equilibrium point, and the unstable trajectory will not converge and finally diverge.

(III) Based on the phase plane analysis method, the stability domain analysis of different vehicle states is performed.

Select the influence of different absolute vehicle speeds, road adhesion coefficients, and front wheel steering angles on the vehicle stability domain. The specific steps include the following:

a). According to the phase plane analysis method, the function equation of the vehicle's center of mass sideslip angle β and yaw rate r can be obtained. β is the independent variable of the function, r is the dependent variable of the function, and the function expression of the stable domain is:

In the above function expression, b ₀ , b ₁ , b ₂ , and b ₃ are respectively:

b ₀ =b/v _x , b ₁ =tan(α _slrl +α _slrl ), b ₂ =(r ₂ -r ₁ )/(β ₂ -β ₁ ), b ₃ =r ₁ -β ₁ (r ₂ -r ₁ )/(β ₂ -β ₁ )

r ₁ =ug/v _x , r ₂ =v _x /(a+b)(tan((α _slfl +α _slfr )/2+δ _max )-tan((α _slrl +α _slrr )/2)),

β ₂ =b/(a+b)(tan((α _slfl +α _slfr )/2+δ _max )-tan((α _slrl +α _slrr )/2))+tan((α _slrl +α _slrr ) /2).

The expression of δ _max in the above formula is:

Among them, _b0 , _b1 , _b2 , and _b3 are the unknown coefficients of the stable domain function expression respectively; _r1 , r2, _β1 , _β2 , and _δmax are intermediate variables; _αslfl , _αslfr , _αslrl , _{and αslrr are} the sideslip angles corresponding to the left front, right front, left rear, and right rear tires entering the saturation area respectively; a is the distance from the center of gravity of the vehicle to the front axle, and b is the distance from the center of gravity of the vehicle to the rear axle; _vx is the longitudinal velocity of the vehicle, μ is the road adhesion coefficient, and g is the acceleration of gravity.

b). According to the division range of the stability domain, as shown in Figure 3-5, different absolute vehicle speeds, road adhesion coefficients, and front wheel angles are selected to analyze different stability domains. The specific steps are as follows:

When the road adhesion coefficient and the front wheel steering angle remain unchanged, different vehicle absolute speeds of 10, 15, 20, and 25 m/s are selected for stability domain analysis;

When the absolute vehicle speed and the front wheel steering angle remain unchanged, different road adhesion coefficients of 0.2, 0.4, 0.6, and 0.8 are selected to perform stability domain analysis;

When the absolute vehicle speed and road adhesion coefficient remain unchanged, different front wheel steering angles of 0, 5, 10, and 15 degrees are selected for stability domain analysis.

c). Based on the stability domain set obtained from the above analysis, the formula for calculating the vehicle's real-time center of mass sideslip angle and yaw rate is:

Among them, _vx is the longitudinal speed of the vehicle, _vy is the lateral speed of the vehicle, _ay is the lateral acceleration of the vehicle, r is the yaw rate of the vehicle, and β is the sideslip angle of the center of mass of the vehicle.

Whether the vehicle state exceeds the stable domain is determined based on the sideslip angle of the center of mass and the yaw angular velocity. The lane-changing trajectory that exceeds the stable domain will be eliminated, and finally the lane-changing trajectory that satisfies the vehicle's stable domain will be retained.

As a further optimization of the above scheme, step 3 considers surrounding vehicles and pedestrians as environmental geometric constraints, lane lines, traffic rules, etc. as road boundaries, and calculates the global feasible domain of the vehicle to include the following parts:

(I) Take the geometric center of the vehicle and the front vehicle, and take the maximum length from the geometric center to the vehicle body as the radius of the geometric circle, denoted as R _l and R _f respectively, and draw a geometric circle. Therefore, the tangent point of the geometric circle of the vehicle and the front vehicle becomes the critical point of collision, so a boundary line of the global feasible domain can be obtained.

(II) Considering the constraints of lane lines, traffic rules or rear vehicles, the tangent point of the geometric circle or lane line between the vehicle and the rear vehicle becomes the critical point of collision. Combining the above steps, a closed global feasible domain of the vehicle can be obtained. Among the lane change trajectory clusters that meet the stability of distributed drive electric vehicles, trajectory clusters that meet the constraints of environmental geometry, lane lines and traffic rules are further screened out.

As a further optimization of the above scheme, step 4 is based on an improved algorithm combining the analytic hierarchy process (AHP) and the technique to approach the ideal (TOPSIS), and selects the optimal lane-changing trajectory by evaluating the stability index, trajectory tracking accuracy index, comfort index and lane-changing efficiency index, which includes the following parts:

(I) Establishment of evaluation indicators.

a). Establish evaluation indicators such as stability index, trajectory tracking accuracy index, comfort index and lane changing efficiency of lane changing trajectory planning respectively:

Constructing vehicle stability index:

为换道时间，F_yi(t)为前轴或后轴的侧向力关于时间的函数表达式，F_zi(t)为前轴或后轴的垂向载荷关于时间的函数表达式，

为路面附着系数的门限值。Among them, _Js is the vehicle stability evaluation index,

is the lane changing time, F _yi (t) is the function expression of the lateral force of the front axle or rear axle with respect to time, F _zi (t) is the function expression of the vertical load of the front axle or rear axle with respect to time,

is the threshold value of the road adhesion coefficient.

b). Construct vehicle trajectory tracking accuracy indicators:

为换道时间，v_x为车辆纵向车速，

为车辆质心侧偏角角速度函数表达式，

为质心侧偏角门限值；h(t)为车辆的理想规划轨迹；y(t)为车辆的实际行驶轨迹；

为理想规划轨迹与实际行驶轨迹误差的门限值。Among them, _Jt is the vehicle trajectory tracking accuracy evaluation index,

is the lane changing time, _vx is the longitudinal speed of the vehicle,

is the angular velocity function expression of the vehicle's center of mass sideslip angle,

is the center of mass sideslip angle threshold; h(t) is the ideal planned trajectory of the vehicle; y(t) is the actual driving trajectory of the vehicle;

is the threshold value of the error between the ideal planned trajectory and the actual driving trajectory.

c). Construct vehicle comfort index:

为换道时间，a_y(t)为车辆的纵向加速度，

为车辆侧向加速度门限值，θ(t)为侧倾角，

为侧倾角门限值。Among them, J _c is the vehicle comfort evaluation index,

is the lane changing time, a _y (t) is the longitudinal acceleration of the vehicle,

is the vehicle lateral acceleration threshold, θ(t) is the roll angle,

is the roll angle threshold.

d). Constructing lane-changing efficiency index:

为换道时间。Among them, _Je is the vehicle lane-changing efficiency evaluation index,

The lane change time.

(II) An improved algorithm based on the combination of the analytic hierarchy process (AHP) and the technique of approaching the ideal (TOPSIS).

a). Construction of judgment matrix. The optimal lane-changing trajectory cluster is calculated from the trajectory clusters that meet the constraints. This can overcome the tediousness of using the TOPSIS algorithm alone in the multi-objective calculation process and the subjectivity of using the AHP algorithm alone in the calculation process. The target layer A includes m evaluation indicators A ₁ , A ₂ , A ₃ , …, A _m . The target layer A corresponds to the determination of the influencing indicators J ₁ , J ₂ , J ₃ , J ₄ , …, J _n of the matrix B. The judgment matrix B is constructed with an order of n×n. The matrix B is shown as follows:

Among them, the element _bij in the matrix is the importance of the lane-changing trajectory planning evaluation index _Ji to the lane-changing trajectory planning evaluation index _Jj , _bji = 1/ _bij . When the element _bij = 1, the two lane-changing trajectory planning evaluation indicators are equally important; when the element _bij = 3, the lane-changing trajectory planning evaluation index _Ji is slightly more important than the lane-changing trajectory planning evaluation index _Jj ; when the element _bij = 5, the lane-changing trajectory planning evaluation index _Ji is significantly more important than the lane-changing trajectory planning evaluation index _Jj ; when the element _bij = 7, the lane-changing trajectory planning evaluation index _Ji is strongly more important than the lane-changing trajectory planning evaluation index Jj; when the element _bij = 9, the lane-changing trajectory planning evaluation index _Ji is absolutely more important than the lane-changing trajectory planning evaluation index _{Jj ;} when the value of the element is 2, 4, 6, 8, it means that it is in the middle state of the element value of 1, 3, 5, 7, 9.

b). Determine the indicator weight. According to the above judgment matrix, calculate the sum of each column, normalize the elements of each column, and further add the normalized results by row to calculate the square root vector. Finally, normalize the square root vector to get the ranking weight vector. The calculation formula is:

为对每列元素规范化的结果，b_ij为判断矩阵中的元素，

为归一化处理结果按照行相加的结果，W_i为排序权向量。in,

is the result of normalizing each column element, _bij is the element in the judgment matrix,

is the result of adding the normalized results in rows, and _Wi is the sorting weight vector.

c). Consistency test. First calculate the maximum eigenvalue of the judgment matrix B, then perform a consistency test on it to obtain the consistency ratio. When the consistency ratio is less than 0.1, the consistency of the judgment matrix meets the conditions.

Among them, λ _max is the maximum eigenvalue of the judgment matrix, matrix B is the judgment matrix, _Wi is the sorting weight vector, w is the element in the sorting weight vector, CI is the consistency test standard, CR is the consistency ratio, RI is the average random consistency index, and n is the order of rows or columns of the judgment matrix.

d). Total hierarchical sorting. Based on the results of hierarchical single sorting, calculate the composite weight of the best solution of the indicator layer relative to the target layer. Assume that the target layer A includes m evaluation indicators A ₁ , A ₂ , A ₃ , …, A _m , and the weights corresponding to the evaluation indicators of the target layer are a ₁ , a ₂ , a ₃ , …, a _m , and the indicator layer J includes n evaluation indicators J ₁ , J ₂ , J ₃ , J ₄ , …, J _n , and the weight corresponding to a certain target layer A _i is c _1i , c _2i , c _3i , …, c _ni . Therefore, the weights corresponding to each indicator of the indicator layer are c ₁ , c ₂ , c ₃ , …, c _n .

Among them, _cj is the weight corresponding to each indicator of the indicator layer, _cij is the weight corresponding to a certain target layer _Ai , and _ai is the weight corresponding to the evaluation indicator of the target layer.

e). Initial evaluation index establishment. Assuming that n evaluation indexes are J = {J ₁ , J ₂ , J ₃ , ..., J _n }, each of which has m characteristic indexes R = {r ₁ , r ₂ , r ₃ , ..., r _m }, the initial evaluation matrix is:

Among them, _rij is the jth indicator of the i-th evaluation target in the target layer.

f). Matrix standardization. Because each evaluation index has different dimensions, each evaluation index is normalized and the calculation formula is:

The calculation process of the weighted normalization matrix is:

H=(v _ij ) _n×m = (ω _j r _ij ) _n×m

Among them, _rij is the jth evaluation index of the i-th evaluation target in the target layer, _vij represents the weighted element of the i-th row and j-th column, and _ωj represents the weight of the j-th evaluation index.

g). Calculation of positive ideal solution, negative ideal solution and the distance between them. The positive ideal solution means that each evaluation index takes the most ideal value solution, and the negative ideal solution means that each evaluation index takes the worst value solution. The expression is:

The positive ideal solution is:

The negative ideal solution is:

Among them, V ⁺ is the positive ideal solution, ^V- is the negative ideal solution, _J1 is the benefit-type indicator set, _J2 is the cost-type indicator set, and _vij represents the weighted element in the i-th row and j-th column.

The distance between each evaluation index and the positive ideal solution and the negative ideal solution is:

为各个评价指标与正理想值的距离，

为各个评价指标与负理想值的距离，v_ij表示加权之后的第i行、j列元素，

和

分别对应正理想解V⁺和负理想解V^-中的元素。in,

is the distance between each evaluation index and the positive ideal value,

is the distance between each evaluation index and the negative ideal value, _vij represents the weighted element in the i-th row and j-th column,

and

They correspond to the elements in the positive ideal solution V ⁺ and the negative ideal solution ^V- respectively.

h). Closeness calculation: calculate the relative closeness between the evaluation index and the ideal solution. The greater the closeness, the better the lane change trajectory.

Closeness:

为各个评价指标与正理想值的距离，

为各个评价指标与负理想值的距离，当贴近度C_i越大，即越接近于1的时候，说明该换道轨迹最优，因此最终获得最优的换道轨迹。Among them, _Ci is the closeness,

is the distance between each evaluation index and the positive ideal value,

is the distance between each evaluation index and the negative ideal value. When the closeness _Ci is larger, that is, closer to 1, it means that the lane changing trajectory is optimal, so the optimal lane changing trajectory is finally obtained.

An embodiment of the present invention further provides an electronic device, including:

one or more processors;

A memory for storing one or more programs;

When the one or more programs are executed by the one or more processors, the one or more processors implement the above-mentioned distributed drive electric vehicle lane change trajectory planning method.

Through the device, a lane-changing trajectory planning method for a distributed drive electric vehicle can be obtained, and the obtained optimal trajectory can be sent to the distributed drive intelligent electric vehicle.

An embodiment of the present invention further provides a storage medium on which a computer program is stored. When the program is executed by a processor, the distributed drive electric vehicle lane change trajectory planning method as described above is implemented.

It will be understood by those skilled in the art that, unless otherwise defined, all terms (including technical and scientific terms) used herein have the same meaning as those generally understood by those skilled in the art to which this application belongs. It should also be understood that terms such as those defined in common dictionaries should be understood to have meanings consistent with the meanings in the context of the prior art, and will not be interpreted with idealized or overly formal meanings unless defined as herein.

The meaning of "and/or" described in this application means that the situations where each exists alone or both exist at the same time are included.

The term “connection” as used in this application may mean a direct connection between components or an indirect connection between components via other components.

Based on the above ideal embodiments of the present invention, the relevant staff can make various changes and modifications without departing from the technical concept of the present invention through the above description. The technical scope of the present invention is not limited to the content in the specification, and its technical scope must be determined according to the scope of the claims.

Claims (10)

1. A distributed drive electric vehicle lane change trajectory planning method, characterized in that it comprises the following steps: Generate unconstrained generalized lane-changing trajectory clusters based on the vehicle trajectory planning curve fitting function; Among the generated unconstrained generalized lane-changing trajectory clusters, the lane-changing trajectory clusters that meet the stability domain of distributed drive electric vehicles are selected; In the selected lane-changing trajectory cluster that satisfies the stability domain of the distributed drive electric vehicle, the feasible domain of the vehicle is calculated according to the environmental geometric constraints and the road boundary; In the calculated vehicle feasible domain, an improved algorithm based on the combination of hierarchical analysis method and approximation to ideal technology is used to select the optimal lane changing trajectory by evaluating the stability index, trajectory tracking accuracy index, comfort index and lane changing efficiency index. 2. A distributed drive electric vehicle lane change trajectory planning method according to claim 1, characterized in that, according to the vehicle trajectory planning curve fitting function, an unconstrained generalized lane change trajectory cluster expression is generated as follows:

Among them, x(t) is the longitudinal displacement of the lane changing process, y(t) is the lateral displacement of the lane changing process, t is the independent variable of the function, v _x0 is the initial vehicle speed,

is the lane changing time, and D is the lateral distance of the vehicle changing lanes. 3. A distributed drive electric vehicle lane change trajectory planning method according to claim 2, characterized in that generating an unconstrained generalized lane change trajectory cluster comprises: Constructing performance indicators that minimize longitudinal fluctuations:

The constraints that need to be met are:

Among them, η _x is the cost function of longitudinal fluctuation, minη _x is the minimum value of the performance index for minimizing longitudinal fluctuation; τ ₀ is the initial time of the lane change trajectory,

is the end time of the lane changing process, and the initial time τ ₀ = 0, so the lane changing process time is

x(t) is the longitudinal displacement function of the vehicle during lane changing,

and v _x (t) represents the longitudinal speed of the vehicle during the lane change process;

and a _x (t) represents the longitudinal acceleration of the vehicle during lane change;

and j _x (t) represent the longitudinal jerk of the vehicle during lane change; L is the longitudinal distance of the vehicle during lane change, v _x0 is the initial value of the longitudinal velocity during lane change,

is the final value of the longitudinal speed during the lane changing process; The constructed Hamiltonian function H _x is:

Among them, κ _x1 is the Lagrangian operator corresponding to v _x , κ _x1 = m ₀ ; κ _x2 is the Lagrangian operator corresponding to a _x , κ _x2 = m ₁ -m ₀ t; κ _x3 is the Lagrangian operator corresponding to j _x ;

in,

According to the Hamiltonian function H _x , solve the performance index:

In the geodetic coordinate system, the expressions of the optimal longitudinal displacement, velocity, acceleration, and jerk during lane change are obtained as follows:

Where j _x (t), a _x (t), v _x (t) and x (t) represent the functions of the vehicle longitudinal jerk, acceleration, velocity and displacement, respectively, and t is the time as the independent variable of the function.

is the lane changing time, L is the longitudinal distance of the vehicle changing lanes, and v _x0 is the initial value of the longitudinal speed; It is necessary to minimize lateral fluctuations and construct performance indicators that minimize lateral fluctuations:

The following constraints need to be met:

Among them, η _y is the cost function of lateral fluctuation, minη _y is the minimum value of the performance index for minimizing lateral fluctuation; τ ₀ is the initial time of the lane change trajectory,

is the end time of the lane changing process, and the initial time τ ₀ = 0, so the lane changing process time is

y(t) represents the lateral displacement function of the vehicle during lane changing.

and _vy (t) represents the lateral speed of the vehicle during the lane change process;

and a _y (t) represents the lateral acceleration of the vehicle during lane change;

and j _y (t) represent the lateral jerk of the vehicle during lane change; D is the lateral distance of the vehicle during lane change; v _y0 is the initial value of the lateral velocity during lane change,

is the final value of the lateral speed during the lane changing process; Construct the Hamiltonian function _Hy :

Among them, κ _y1 is the Lagrangian operator corresponding to v _y , κ _y1 =n ₀ ; κ _y2 is the Lagrangian operator corresponding to a _y , κ _y2 =n ₁ -n ₀ t; κ _y3 is the Lagrangian operator corresponding to j _y ,

in,

According to the Hamiltonian function _Hy , solve the performance index:

In the geodetic coordinate system, the expressions for the optimal lateral jerk, acceleration, velocity, and displacement during lane change are obtained as follows:

Wherein, j _y (t), a _y (t), _vy (t) and y(t) represent the functions of the vehicle's lateral jerk, acceleration, velocity and displacement, respectively, D is the lateral distance of the vehicle's lane change, and _vy0 is the initial value of the lateral velocity; During the lane changing process, the longitudinal speed of the vehicle is kept constant, and the longitudinal acceleration is unchanged to minimize the longitudinal fluctuation of the vehicle. Therefore, it can be obtained: v _x (t) = v _x0 Where v _x (t) represents the longitudinal vehicle speed function during the lane change process, v _x0 is the initial value of the longitudinal vehicle speed; At a certain initial speed v _x0 , different lane changing times

Thus, a series of unconstrained generalized lane-changing trajectory clusters are obtained:

4. The method for planning lane change trajectories of a distributed drive intelligent electric vehicle according to claim 1, characterized in that, from the generated unconstrained generalized lane change trajectory clusters, a lane change trajectory cluster satisfying the stability domain of the distributed drive electric vehicle is selected, comprising: Build a four-wheel vehicle model of a distributed drive electric vehicle:

Where F _yij is the tire lateral force, its subscripts ij = fl, fr, rl, rr represent the left front wheel, right front wheel, left rear wheel and right rear wheel of the tire respectively, r represents the yaw angular velocity,

is the first-order derivative of the yaw rate; β represents the sideslip angle of the center of mass,

is the first-order derivative of the sideslip angle of the center of mass; _vx is the longitudinal speed; _δf is the front wheel turning angle of the vehicle; a is the distance from the center of gravity of the vehicle to the front axle, b is the distance from the center of gravity of the vehicle to the rear axle; _lf is the wheelbase of the front axle of the vehicle, _lr is the wheelbase of the rear axle of the vehicle; m is the mass of the vehicle; _Iz is the moment of inertia about the z-axis; Calculate the slip angles of the four tires:

Wherein, α _ij is the tire slip angle, and its subscripts ij = fl, fr, rl, rr represent the left front wheel, right front wheel, left rear wheel and right rear wheel of the tire respectively; Calculate the vertical loads on the four tires:

Where, F _zij is the vertical load on the tire, and its subscripts ij = fl, fr, rl, rr represent the left front wheel, right front wheel, left rear wheel and right rear wheel of the tire respectively; a _x is the longitudinal acceleration of the vehicle, a _y is the lateral acceleration of the vehicle; h is the height of the center of mass of the vehicle; Calculate the tire lateral force equation based on the Fiala tire model:

Wherein, F _yij is the tire lateral force, and its subscripts ij = fl, fr, rl, rr represent the left front wheel, right front wheel, left rear wheel and right rear wheel of the tire respectively; C _α is the tire cornering stiffness; α _slij is the side slip angle corresponding to the tire entering the saturation area, and its subscripts ij = fl, fr, rl, rr represent the left front wheel, right front wheel, left rear wheel and right rear wheel of the tire respectively; μ is the road adhesion coefficient; The vehicle stability domain mechanism analysis is carried out based on the phase plane method, and the differential equation group is listed according to the system state equation:

From the above formula, we can get:

Among them, x ₁ and x ₂ are state parameters of the vehicle system, f ₁ (x ₁ ,x ₂ ) and f ₂ (x ₁ ,x ₂ ) are differential equations of the vehicle system; In the vehicle system, it is assumed that the state trajectory x(t) starting from the initial state x ₀ =(x ₁ (0), x ₂ (0)) remains within the local range and meets the following conditions:

Among them, x(t) is the function of the vehicle state parameters changing with time, x _l ∈R is a certain constant; Based on the phase plane analysis method, the stability domain of different vehicle states is analyzed, and the influence of different absolute vehicle speeds, road adhesion coefficients, and front wheel steering angles on the vehicle stability domain are selected respectively. The specific steps include the following: According to the phase plane analysis method, the function equation of the vehicle's center of mass sideslip angle β and yaw rate r can be obtained. β is the independent variable of the function, r is the dependent variable of the function, and the function expression of the stable domain is:

In the above function expression, b ₀ , b ₁ , b ₂ , and b ₃ are respectively: b ₀ =b/v _x , b ₁ =tan(α _slrl +α _slrl ), b ₂ =(r ₂ -r ₁ )/(β ₂ -β ₁ ), b ₃ =r ₁ -β ₁ (r ₂ -r ₁ )/(β ₂ -β ₁ ) r ₁ =ug/v _x , r ₂ =v _x /(a+b)(tan((α _slfl +α _slfr )/2+δ _max )-tan((α _slrl +α _slrr )/2)),

β ₂ =b/(a+b)(tan((α _slfl +α _slfr )/2+δ _max )-tan((α _slrl +α _slrr )/2))+tan((α _slrl +α _slrr ) /2). The expression of δ _max in the above formula is:

Wherein, b ₀ , b ₁ , b ₂ , b ₃ are the unknown coefficients of the stable domain function expression, r ₁ , r ₂ , β ₁ , β ₂ , δ _max are the intermediate variables; α _slfl , α _slfr , α _slrl , α _slrr are the sideslip angles corresponding to the left front, right front, left rear, and right rear tires entering the saturation region, respectively; a is the distance from the center of gravity of the vehicle to the front axle, and b is the distance from the center of gravity of the vehicle to the rear axle; v _x is the longitudinal speed of the vehicle, μ is the road adhesion coefficient, and g is the acceleration of gravity; According to the division range of the stability domain, different absolute vehicle speeds, road adhesion coefficients, and front wheel turning angles are selected to analyze different stability domains; According to the stable domain set obtained by the above analysis, combined with the vehicle's real-time center of mass sideslip angle and yaw rate calculation formula:

Wherein, _vx is the longitudinal speed of the vehicle, _vy is the lateral speed of the vehicle, _ay is the lateral acceleration of the vehicle, r is the yaw rate of the vehicle, and β is the sideslip angle of the center of mass of the vehicle; Whether the vehicle state exceeds the stable domain is determined based on the sideslip angle of the center of mass and the yaw angular velocity. The lane-changing trajectory that exceeds the stable domain will be eliminated, and finally the lane-changing trajectory that satisfies the vehicle's stable domain will be retained. 5. A method for planning lane change trajectories of a distributed drive electric vehicle according to claim 1, characterized in that, in the selected lane change trajectory cluster that satisfies the stability domain of the distributed drive electric vehicle, a feasible domain of the vehicle is calculated according to the environmental geometric constraints and the road boundary, comprising: Take the geometric center of the vehicle and the front vehicle, and take the maximum length from the geometric center to the vehicle body as the radius of the geometric circle, denoted as R _l and R _f respectively, and draw the geometric circle; Considering the lane lines, traffic rules or constraints of the rear vehicle, the tangent point of the geometric circle or lane line between the vehicle and the rear vehicle becomes the critical point of collision; Combined with the final retained lane-changing trajectory that satisfies the vehicle's stability domain, a closed global feasible domain of the vehicle is obtained. 6. A distributed drive electric vehicle lane change trajectory planning method according to claim 1, characterized in that, in the calculated vehicle feasible domain, an improved algorithm based on a combination of a hierarchical analysis method and a technology close to the ideal is used to select the optimal lane change trajectory by evaluating a stability index, a trajectory tracking accuracy index, a comfort index, and a lane change efficiency index, including: Establish the stability index, trajectory tracking accuracy index, comfort index and lane changing efficiency index of lane changing trajectory planning respectively; Based on an improved algorithm combining the analytic hierarchy process and the ideal approximation technique, the optimal lane-changing trajectory cluster is calculated from the trajectory clusters that meet the constraints. 7. A distributed drive electric vehicle lane change trajectory planning method according to claim 6, characterized in that: Constructed vehicle stability index:

Among them, _Js is the vehicle stability evaluation index,

is the lane changing time, F _yi (t) is the function expression of the lateral force of the front axle or rear axle with respect to time, F _zi (t) is the function expression of the vertical load of the front axle or rear axle with respect to time,

is the threshold value of the road adhesion coefficient; The constructed vehicle trajectory tracking accuracy index is:

Among them, _Jt is the vehicle trajectory tracking accuracy evaluation index,

is the lane changing time, _vx is the longitudinal speed of the vehicle,

is the angular velocity function expression of the vehicle's center of mass sideslip angle,

is the center of mass sideslip angle threshold; h(t) is the ideal planned trajectory of the vehicle; y(t) is the actual driving trajectory of the vehicle;

is the threshold value of the error between the ideal planned trajectory and the actual driving trajectory; The constructed vehicle comfort index is:

Among them, J _c is the vehicle comfort evaluation index,

is the lane changing time, a _y (t) is the longitudinal acceleration of the vehicle,

is the vehicle lateral acceleration threshold, θ(t) is the roll angle,

is the roll angle threshold. Constructed lane-changing efficiency index:

Among them, _Je is the vehicle lane-changing efficiency evaluation index,

is the lane change time; Based on an improved algorithm combining the analytic hierarchy process and the ideal approximation technique, the optimal lane-changing trajectory cluster is calculated from the trajectory clusters that meet the constraints. 8. A distributed drive electric vehicle lane change trajectory planning method according to claim 7, characterized in that the improved algorithm steps are as follows: The target layer A includes m evaluation indicators A ₁ , A ₂ , A ₃ , …, A _m . The target layer A corresponds to the determination influencing indicators J ₁ , J ₂ , J ₃ , J ₄ , …, J _n of the judgment matrix B. The judgment matrix B is constructed with an order of n×n. The judgment matrix B is shown as follows:

Among them, the element _bij in the matrix is the importance of the lane-changing trajectory planning evaluation index _Ji to the lane-changing trajectory evaluation index _Jj , _bji = 1/ _bij ; Determine the indicator weights. According to the above judgment matrix, calculate the sum of each column, normalize the elements of each column, and further add the normalized results by row to calculate the square root vector. Finally, normalize the square root vector to get the ranking weight vector. The calculation formula is:

in,

is the result of normalizing each column element, _bij is the element in the judgment matrix,

is the result of adding the normalized results in rows, and _Wi is the sorting weight vector; Consistency test: first calculate the maximum eigenvalue of the judgment matrix B, then perform a consistency test on it to obtain the consistency ratio. When the consistency ratio is less than 0.1, the consistency of the judgment matrix meets the conditions.

Among them, λ _max is the maximum eigenvalue of the judgment matrix, matrix B is the judgment matrix, _Wi is the sorting weight vector, w is the element in the sorting weight vector, CI is the consistency test standard, CR is the consistency ratio, RI is the average random consistency index, and n is the order of the rows or columns of the judgment matrix; The total hierarchical sorting calculates the composite weight of the best solution of the indicator layer relative to the target layer based on the single hierarchical sorting results. Assume that the target layer A includes m evaluation indicators A ₁ , A ₂ , A ₃ , …, A _m , and the weights corresponding to the evaluation indicators of the target layer are a ₁ , a ₂ , a ₃ , …, a _m ; the indicator layer J includes n evaluation indicators J ₁ , J ₂ , J ₃ , J ₄ , …, J _n , and the weight corresponding to a certain target layer A _i is c _1i , c _2i , c _3i , …, c _ni ; therefore, the weights corresponding to each indicator of the indicator layer are c ₁ , c ₂ , c ₃ , …, c _n respectively:

Among them, _cj is the weight corresponding to each indicator of the indicator layer, _cij is the weight corresponding to a certain target layer _Ai , and _ai is the weight corresponding to the evaluation indicator of the target layer; Initial evaluation index establishment, assuming that n evaluation indexes are J = {J ₁ ,J ₂ ,J ₃ ,...,J _n }, each of which has m characteristic indexes R = {r ₁ ,r ₂ ,r ₃ ,…,r _m }, then the initial evaluation matrix is:

Among them, _rij is the jth indicator of the i-th evaluation target in the target layer; Matrix standardization, normalize each evaluation index, the calculation formula is:

The calculation process of the weighted normalization matrix is: H=(v _ij ) _n×m = (ω _j r _ij ) _n×m Among them, _rij is the jth evaluation index of the i-th evaluation target in the target layer, _vij represents the weighted i-th row and j-th column element, and _ωj represents the weight of the j-th evaluation index; The calculation of positive ideal solution, negative ideal solution and the distance between them. The positive ideal solution means that each evaluation index takes the most ideal value solution, and the negative ideal solution means that each evaluation index takes the worst value solution. The expression is: The positive ideal solution is:

The negative ideal solution is:

Among them, V ⁺ is the positive ideal solution, V ^- is the negative ideal solution, J ₁ is the benefit-type indicator set, J ₂ is the cost-type indicator set, and _vij represents the weighted element in the i-th row and j-th column; The distance between each evaluation index and the positive ideal solution and the negative ideal solution is:

in,

is the distance between each evaluation index and the positive ideal value,

is the distance between each evaluation index and the negative ideal value, _vij represents the weighted element in the i-th row and j-th column,

and

They correspond to the elements in the positive ideal solution V ⁺ and the negative ideal solution V ^- respectively; Closeness calculation, calculate the relative closeness between the evaluation index and the ideal solution: Closeness:

Among them, _Ci is the closeness,

is the distance between each evaluation index and the positive ideal value,

is the distance between each evaluation index and the negative ideal value. When the closeness _Ci is larger, that is, closer to 1, it means that the lane changing trajectory is optimal, so the optimal lane changing trajectory is finally obtained. 9. A device, comprising: one or more processors; A memory for storing one or more programs; When the one or more programs are executed by the one or more processors, the one or more processors implement the lane change trajectory planning method for a distributed drive electric vehicle as described in any one of claims 1-8. 10. A storage medium having a computer program stored thereon, wherein when the program is executed by a processor, the distributed drive electric vehicle lane change trajectory planning method as described in any one of claims 1 to 8 is implemented.

Images