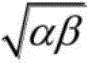CN116170601B - Image compression method based on four-column vector block singular value decomposition - Google Patents

Image compression method based on four-column vector block singular value decomposition Download PDF

Info

Publication number
CN116170601B
CN116170601B CN202310451246.XA CN202310451246A CN116170601B CN 116170601 B CN116170601 B CN 116170601B CN 202310451246 A CN202310451246 A CN 202310451246A CN 116170601 B CN116170601 B CN 116170601B
Authority
CN
China
Prior art keywords
column
column vector
block
vector
image
Prior art date
Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
Active
Application number
CN202310451246.XA
Other languages
Chinese (zh)
Other versions
CN116170601A (en
Inventor
胡塘
玉虓
王锡尔
刘志威
Current Assignee (The listed assignees may be inaccurate. Google has not performed a legal analysis and makes no representation or warranty as to the accuracy of the list.)
Zhejiang Lab
Original Assignee
Zhejiang Lab
Priority date (The priority date is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the date listed.)
Filing date
Publication date
Application filed by Zhejiang Lab filed Critical Zhejiang Lab
Priority to CN202310451246.XA priority Critical patent/CN116170601B/en
Publication of CN116170601A publication Critical patent/CN116170601A/en
Application granted granted Critical
Publication of CN116170601B publication Critical patent/CN116170601B/en
Active legal-status Critical Current
Anticipated expiration legal-status Critical

Links

Images

Classifications

    • H—ELECTRICITY
    • H04—ELECTRIC COMMUNICATION TECHNIQUE
    • H04N—PICTORIAL COMMUNICATION, e.g. TELEVISION
    • H04N19/00—Methods or arrangements for coding, decoding, compressing or decompressing digital video signals
    • H04N19/42—Methods or arrangements for coding, decoding, compressing or decompressing digital video signals characterised by implementation details or hardware specially adapted for video compression or decompression, e.g. dedicated software implementation
    • H04N19/423—Methods or arrangements for coding, decoding, compressing or decompressing digital video signals characterised by implementation details or hardware specially adapted for video compression or decompression, e.g. dedicated software implementation characterised by memory arrangements
    • H—ELECTRICITY
    • H04—ELECTRIC COMMUNICATION TECHNIQUE
    • H04N—PICTORIAL COMMUNICATION, e.g. TELEVISION
    • H04N19/00—Methods or arrangements for coding, decoding, compressing or decompressing digital video signals
    • H04N19/10—Methods or arrangements for coding, decoding, compressing or decompressing digital video signals using adaptive coding
    • H04N19/169—Methods or arrangements for coding, decoding, compressing or decompressing digital video signals using adaptive coding characterised by the coding unit, i.e. the structural portion or semantic portion of the video signal being the object or the subject of the adaptive coding
    • H04N19/17—Methods or arrangements for coding, decoding, compressing or decompressing digital video signals using adaptive coding characterised by the coding unit, i.e. the structural portion or semantic portion of the video signal being the object or the subject of the adaptive coding the unit being an image region, e.g. an object
    • H04N19/176—Methods or arrangements for coding, decoding, compressing or decompressing digital video signals using adaptive coding characterised by the coding unit, i.e. the structural portion or semantic portion of the video signal being the object or the subject of the adaptive coding the unit being an image region, e.g. an object the region being a block, e.g. a macroblock
    • H—ELECTRICITY
    • H04—ELECTRIC COMMUNICATION TECHNIQUE
    • H04N—PICTORIAL COMMUNICATION, e.g. TELEVISION
    • H04N19/00—Methods or arrangements for coding, decoding, compressing or decompressing digital video signals
    • H04N19/42—Methods or arrangements for coding, decoding, compressing or decompressing digital video signals characterised by implementation details or hardware specially adapted for video compression or decompression, e.g. dedicated software implementation
    • H04N19/436—Methods or arrangements for coding, decoding, compressing or decompressing digital video signals characterised by implementation details or hardware specially adapted for video compression or decompression, e.g. dedicated software implementation using parallelised computational arrangements
    • Y—GENERAL TAGGING OF NEW TECHNOLOGICAL DEVELOPMENTS; GENERAL TAGGING OF CROSS-SECTIONAL TECHNOLOGIES SPANNING OVER SEVERAL SECTIONS OF THE IPC; TECHNICAL SUBJECTS COVERED BY FORMER USPC CROSS-REFERENCE ART COLLECTIONS [XRACs] AND DIGESTS
    • Y02—TECHNOLOGIES OR APPLICATIONS FOR MITIGATION OR ADAPTATION AGAINST CLIMATE CHANGE
    • Y02D—CLIMATE CHANGE MITIGATION TECHNOLOGIES IN INFORMATION AND COMMUNICATION TECHNOLOGIES [ICT], I.E. INFORMATION AND COMMUNICATION TECHNOLOGIES AIMING AT THE REDUCTION OF THEIR OWN ENERGY USE
    • Y02D10/00—Energy efficient computing, e.g. low power processors, power management or thermal management

Landscapes

  • Engineering & Computer Science (AREA)
  • Multimedia (AREA)
  • Signal Processing (AREA)
  • Computing Systems (AREA)
  • Theoretical Computer Science (AREA)
  • Image Processing (AREA)

Abstract

本发明公开一种基于四列列向量分块奇异值分解的图像压缩方法，该方法中待压缩图像以矩阵形式输入，每四列图像元素为一组进行平均分块，一列图像元素对应一列列向量，对每一块内的四列列向量进行两两组合，并分别计算各种组合对应的二阶范数以及单位向量内积，根据单位列向量内积大小，决定最终组合方式以及数据源头交换规则；并执行单边雅克比旋转计算操作；与列向量输入数据源头交换规则相一致，单边雅克比计算更新的结果输出也按照相应规则写回并覆盖原有的列向量数据。本发明可实现矩阵奇异值分解的图像压缩过程低效计算行为减少、收敛速度加快以及并行计算效率提升。

Figure 202310451246

The invention discloses an image compression method based on block singular value decomposition of four-column vectors. In the method, the image to be compressed is input in the form of a matrix, and every four-column image element is divided into groups on average, and one column of image elements corresponds to one column. Vector, combine the four-column vectors in each block in pairs, and calculate the second-order norm and unit vector inner product corresponding to each combination, and determine the final combination method and data source exchange according to the size of the unit column vector inner product rules; and perform unilateral Jacobian rotation calculation operations; consistent with the column vector input data source exchange rules, the updated result output of unilateral Jacobian calculations is also written back and overwrites the original column vector data according to the corresponding rules. The invention can realize the reduction of inefficient calculation behavior in the image compression process of matrix singular value decomposition, the acceleration of convergence speed and the improvement of parallel calculation efficiency.

Figure 202310451246

Description

Image compression method based on four-column vector block singular value decomposition
Technical Field
The invention relates to the field of image compression processing, in particular to an image compression method based on four-column vector block singular value decomposition.
Background
Matrix singular value decomposition plays an important role in the field of signal processing, and is widely used in scenes such as image compression, data mining, signal processing, recommendation algorithm and the like. Especially in the field of image compression, an image compression technology based on singular value decomposition obtains singular values and corresponding singular vectors by carrying out matrix singular value decomposition on an original input image, then only the most important singular values and the corresponding singular vectors are reserved in the front for reverse construction, and the pressure of image compression, storage capacity and transmission bandwidth is reduced under the condition that important visual information is not lost. In addition, the image compression method based on singular value decomposition can determine the singular value of the reverse construction original image and the number of the singular vectors corresponding to the singular value according to the compression quality requirement, has a good elastic adjustment function, and therefore becomes one of research hotspots in the current image compression field.
However, the image compression technology based on singular value decomposition has computationally intensive and memory intensive lifting points due to singular value decomposition, and the computational complexity is presented
Figure SMS_1
Exponentially growing, lengthy iterative operations result in exceptionally slow convergence rates. The unilateral Jacobian algorithm is suitable for realizing singular value decomposition function based on very large scale integrated circuits (Very Large Scale Integration Circuit, VLSI) including FPGA due to the simplicity and high parallelism property, and further realizes high-performance real-time image compression technology. At present, a two-by-two traversal combination mode is adopted in the sequence cyclic scheduling process of the unilateral Jacobian algorithm, and when the column dimension n is large, column vectors are combined pairwise>
Figure SMS_2
Significantly increasing, each "sweep" requires n-1 cycles of loop traversal, and each cycle corresponds to n/2 Jacobian rotation computation of the column vector, such that frequent data accesses and computations in the convergence iteration process, plus an increase in row dimension m, result in a proportional increase in the number of clock beats of data accesses and computations. Because the single-sided Jacobian algorithm does not satisfy the exchange law, each iteration process can only calculate between respective column vector pairs according to a determined sequence scheduling rule, even if the column vector pairs are orthogonal or nearly orthogonal to each other, the second-order norm, inner product and Givens matrix included in the single-sided Jacobian rotation calculation process are still executed
Figure SMS_3
Operations such as generation and Givens rotation update, and the like, thereby causing a large amount of inefficient convergence calculation behaviors to occur.
Disclosure of Invention
To reduce inefficient computational behavior in singular value decomposition based image compressionThe invention provides an image compression method based on four-column vector block singular value decomposition, which is characterized in that a base 4 strategy with 4 column pixels as a block replaces the traditional base 2 strategy with 2 column pixels as a block for an input image to be compressed, an average block is carried out on an input image matrix, 4 column pixels in each block, namely 4 column vectors, can be combined in pairs, 3 combinations can be provided, each combination comprises 2 pairs of column vectors, and the method is characterized in that the unit vector inner product gamma is calculated by
Figure SMS_4
Is determined by gamma/as a decision condition for inefficient convergence behaviour>
Figure SMS_5
The ordering rules determine the final column vector pair combination mode of each block in the loop iteration process. In addition, aiming at the fact that the row dimension m in the image size is overlarge, an s-segment type data structure is adopted, pixel elements of the image are uniformly distributed in s-block SRAM (static random access memory) for storage, so that synchronous access and calculation are carried out among the s-block SRAM, and according to an on-chip distributed SRAM storage architecture formed by the s-segment data structure, a calculation circuit is embedded among all SRAM macro units, and a near-memory calculation hardware circuit architecture is realized.
The aim of the invention is achieved by the following technical scheme:
on the one hand, the image compression method based on four-column vector block singular value decomposition is characterized in that the pixels of an input image are m rows and n columns, the pixels are taken as the input of a singular value decomposition compression circuit in a matrix form, every 4 columns of image elements are a group, the 4 columns of image elements correspond to the 4 columns of column vectors, the input image is divided evenly, if n/4 can not be divided evenly, the tail of the image to be compressed is supplemented with 1 column of all 0 elements in advance, so that the operation is divided evenly and shared
Figure SMS_6
Column vector block->
Figure SMS_7
Representing an upward rounding; each column vector block is composed of a 2 x 2 structure of 4 columns of column vectors, each columnThe column vector in the lower left corner of the vector block is denoted as A i The column vector in the upper left corner is denoted as A j The column vector in the lower right corner is denoted as A p The column vector in the upper right corner is denoted as A q ；
The intra-block calculation steps for each column vector partition are as follows:
s1: calculation A i 、A j 、A p 、A q Respective second order norms alpha i 、α j 、α p 、α q Combining four column vectors two by two, and calculating the inner product gamma between two column vectors in each combination ij And gamma is equal to pq ，γ ip And gamma is equal to jq ，γ iq And gamma is equal to jp And corresponding unit vector inner product
Figure SMS_8
And->
Figure SMS_9
，/>
Figure SMS_10
And->
Figure SMS_11
，/>
Figure SMS_12
And->
Figure SMS_13
；
S2: sorting 6 unit vector inner products in the column vector block, and taking the rest candidate combinations as final combinations if the two unit vector inner products with the minimum absolute value are distributed in 2 candidate combinations; if the two unit vector inner products with the minimum absolute value and the second smallest are distributed in the same candidate combination, the candidate group with the absolute value of the second smallest unit vector inner product is eliminated, and the last remaining candidate combination is selected as a final combination;
s3: if the final combination is A i And A is a j ，A p And A is a q Then there is no need to sourceInput execution exchanges data operations; if final combination A i And A is a q ，A p And A is a j At this time, the ith column is exchanged with the p column vector data source; if final combination A i And A is a p ，A q And A is a j At this time, the p-th column is exchanged with the j-th column vector data source;
s4: executing Givens rotation calculation operation of 2 pairs of column vectors in column vector block according to classical unilateral Jacobi algorithm;
s5: according to the source exchange rule of the column vector input data in the step S3, the output of the updated result of the Givens rotary calculation is written back and covers the original column vector data according to the corresponding rule;
s6: and repeatedly executing S1-S4 until a convergence condition is reached, sorting the obtained singular values in a descending order, selecting the first k singular values, thereby converting the storage of the pixel matrix of the original m rows and n columns into a left singular matrix of the m rows and k columns and a right singular matrix of the k rows and n columns, and compressing the storage of the input image to the original (m+n+1) k/(m n).
On the other hand, a column vector storage circuit based on an image compression method of four column vector block singular value decomposition, for each column vector, a data structure of s segments is customized, s segments correspond to s-block SRAMs, and taking the ith column vector as an example, column vector elements, namely a (1, i), a (2, i), a (3,i), …, a (m, i), are sequentially stored in the s-block SRAMs in a row-first mode.
In yet another aspect, a computer readable storage medium has stored thereon a program which, when executed by a processor, implements an image compression method based on four-column vector block singular value decomposition.
The beneficial effects of the invention are as follows:
(1) The invention replaces the traditional base 2 strategy by the base 4 strategy, increases the combination options of column vector pairs under the condition of the same access times, and passes the unit vector inner product gamma ∈
Figure SMS_14
Sequencing and serving as a judging condition of the low-efficiency convergence behavior, reducing the low-efficiency convergence calculation behavior, and furtherAnd the reduction of the total calculated amount of singular value decomposition is realized.
(2) Aiming at 3 possible column vector pair combination modes, a nominal column index method is adopted, only input sources and output results participating in Givens rotation calculation are exchanged, and the simplicity and the easy realization of a round-robin sequence strategy are maintained.
(3) The invention can obviously reduce the low-efficiency convergence calculation amount of singular value decomposition of a large dense matrix, reduce the clock cycle number required by data access and calculation, and improve the time sequence of the whole circuit, thereby obviously improving the convergence speed.
(4) The invention can adjust and extract the ratio of the first k singular values and the corresponding singular vectors according to the compression ratio to realize elastic compression.
Drawings
FIG. 1 is a schematic diagram of an s-staged SRAM memory and its near memory computing circuit architecture.
Fig. 2 is a schematic diagram of a data structure of a 1 st column image element of an image to be compressed and an SRAM memory thereof when s=4.
Fig. 3 is a schematic diagram of a method for compressing a block singular value decomposition image based on four columns and vectors.
FIG. 4 is a circuit diagram of the second order norm, inner product, unit vector inner product calculation based on four rows of vector partitions.
Fig. 5 is a column vector pair combination scheme based on four column vector blocks and a data exchange diagram thereof.
Fig. 6 is a detailed circuit schematic of Givens rotation calculation.
Fig. 7 is a schematic diagram of image compression based on four-column vector singular value decomposition.
Fig. 8 is a comparison of 224 row by 224 size images before and after compression based on a four column vector method.
Detailed Description
Reference will now be made in detail to exemplary embodiments, examples of which are illustrated in the accompanying drawings. When the following description refers to the accompanying drawings, the same numbers in different drawings refer to the same or similar elements, unless otherwise indicated. The implementations described in the following exemplary examples are not representative of all implementations consistent with the present application. Rather, they are merely examples of apparatus and methods consistent with some aspects of the present application as detailed in the accompanying claims.
The terminology used in the present application is for the purpose of describing particular embodiments only and is not intended to be limiting of the present application. As used in this application and the appended claims, the singular forms "a," "an," and "the" are intended to include the plural forms as well, unless the context clearly indicates otherwise. It should also be understood that the term "and/or" as used herein refers to and encompasses any or all possible combinations of one or more of the associated listed items.
It should be understood that although the terms first, second, third, etc. may be used herein to describe various information, these information should not be limited by these terms. These terms are only used to distinguish one type of information from another. For example, a first message may also be referred to as a second message, and similarly, a second message may also be referred to as a first message, without departing from the scope of the present application. The word "if" as used herein may be interpreted as "at … …" or "at … …" or "responsive to a determination", depending on the context.
As shown in fig. 1, in the image compression method based on four-column vector block singular value decomposition of the present embodiment, the pixels of the input image are m rows×n columns, and are used as the input of the singular value decomposition compression circuit in matrix form, each 4 columns of image elements are a group, the 4 columns of image elements correspond to the 4 columns of column vectors, the input image is divided into average groups, if n/4 cannot be divided, the end of the image to be compressed is supplemented with 1 column of all 0 elements in advance, so that the operation is divided and shared
Figure SMS_15
Column vector block->
Figure SMS_16
Representing an upward rounding; each column vector block is composed of a 2 x 2 structure of 4 column vectors, with the column vector in the lower left corner of each column vector block denoted as a i The column vector in the upper left corner is denoted as A j The column vector in the lower right corner is denoted asA p The column vector in the upper right corner is denoted as A q ；
The intra-block calculation steps for each column vector partition are as follows:
s1: calculation A i 、A j 、A p 、A q Respective second order norms alpha i 、α j 、α p 、α q And combining four column vectors two by two, namely A i ~A j And A is a p ~A q ，A i ~A p And A is a j ~A q ，A i ~A q And A is a j ~A p The method comprises the steps of carrying out a first treatment on the surface of the Calculating the inner product gamma between two column vectors in each combination ij And gamma is equal to pq ，γ ip And gamma is equal to jq ，γ iq And gamma is equal to jp And corresponding unit vector inner product
Figure SMS_17
And (3) with
Figure SMS_18
，/>
Figure SMS_19
And->
Figure SMS_20
，/>
Figure SMS_21
And->
Figure SMS_22
。
S2: sorting 6 unit vector inner products in the column vector block, and taking the rest candidate combinations as final combinations if the two unit vector inner products with the minimum absolute value are distributed in 2 candidate combinations; if the two unit vector inner products with the smallest absolute value are distributed in the same candidate combination, the candidate group with the absolute value being the unit vector inner product with the next smallest absolute value is excluded, and the last remaining candidate combination is selected as the final combination.
As one of the embodiments, assume that
Figure SMS_25
Is the unit vector inner product with the smallest amplitude, < ->
Figure SMS_28
Is the unit vector inner product with the smallest amplitude, at this time, due to +.>
Figure SMS_31
And->
Figure SMS_24
Distributed among 2 candidate combinations, thus, directly selecting the remaining A i ~A q And A is a j ~A p As a final combination; let->
Figure SMS_27
Is the unit vector inner product with the smallest amplitude,
Figure SMS_30
is the unit vector inner product of the amplitude of the sub-small, < >>
Figure SMS_32
Is the unit vector inner product with the next smallest amplitude, at this time, due to
Figure SMS_23
、/>
Figure SMS_26
Distributed over the same candidate combination, thus excluding the next smallest +.>
Figure SMS_29
The combination is selected to be the rest A i ~A j And A is a p ~A q As a final combination.
S3: according to the final combination mode of 4 column vectors in S2, determining the column vector data input source in the Givens rotation calculation: if the final combination is A i And A is a j ，A p And A is a q The data exchange operation is not required to be executed for the source input; if final combination A i And A is a q ，A p And A is a j At this time, the ith column is exchanged with the p column vector data source; if final combination A i And A is a p Or A q And A is a j At this time, the p-th column is exchanged with the j-th column for vector data source.
Each time a round of Givens rotation calculation is executed, a column switching rule in a column vector block is as follows:
column vector 1 block: the lower left is exchanged for lower right, the upper left is exchanged for lower left, and the upper right is exchanged for upper left;
first, the
Figure SMS_33
The column vectors are partitioned: the lower left is exchanged for lower right, and the upper right is exchanged for upper left;
first, the
Figure SMS_34
Column vector partitioning: the column vector in the upper right corner is kept stationary, the lower right is swapped to the upper left, and the lower left is swapped to the lower right.
Each time a round of Givens rotation computation is performed, the inter-block column exchange rule of column vector partitioning is: the lower right of the previous column vector block is swapped to the lower left of the current column vector block and the upper left of the current column vector block is swapped to the upper right of the previous column vector block.
S4: executing Givens rotation calculation operation of 2 pairs of column vectors in column vector block according to classical unilateral Jacobi algorithm; the formula for the Givens rotation calculation is as follows:
Figure SMS_35
，
wherein cos θ and sin θ take the following values:
Figure SMS_36
wherein,,
Figure SMS_37
and->
Figure SMS_38
Column vector inputs representing the ith and jth columns prior to the r-th round of Givens transform, are>
Figure SMS_39
And
Figure SMS_40
column vector outputs representing the ith and jth columns after the r-th round of Givens transform update, if gamma ij Not less than 0 and alpha i -α j Not less than 0, or gamma ij < 0 and alpha i -α j If the value is less than 0, sin theta takes positive sign, otherwise takes negative sign, and cos theta and sin theta form a Givens rotation matrix; another pair of column vectors in the partition->
Figure SMS_41
And->
Figure SMS_42
The same operation is performed.
S5: and (3) according to the source exchange rule of the column vector input data in the step (S3), writing back and covering the original column vector data according to the corresponding rule by the output of the updated result of the Givens rotation calculation.
The write-back rule is:
if the current combination is A i And A is a j ，A p And A is a q Outputting the result without executing exchange processing;
if the current combination is A p And A is a j ，A i And A is a q Outputting the result
Figure SMS_43
Write back and cover the corresponding SRAM memory of the p-th column vector,/in the SRAM memory>
Figure SMS_44
Writing back and covering the SRAM storage corresponding to the ith column vector;
if the current combination is A i And A is a p ，A q And A is a j Outputting the result
Figure SMS_45
Write back and cover the corresponding SRAM memory of the jth column vector,/in the column vector>
Figure SMS_46
Writing back and covering the SRAM storage corresponding to the p-th column vector.
In the whole column vector calculation process, as shown in fig. 3, a round-robin scheduling mechanism is used to perform counterclockwise cyclic scheduling on the column vector after Givens rotation calculation, namely, according to a nominal column vector index, column vector 1 is transmitted to column vector 3, column vector 3 is transmitted to column vector 5, column vector 5 is transmitted to column vectors 7 and …, column vector n-3 is transmitted to column vector n-1, column vector n-1 is transmitted to n-2, column vector n-2 is transmitted to n-4 and …, column vector 4 is transmitted to 2, and column vector 2 is transmitted to column vector 1. And repeatedly executing the operation until the absolute convergence or the custom convergence condition is reached.
And S3, inputting a switching rule by a data source and outputting a switching rule by a calculation result in S5, wherein the q-th column vector in the upper right corner is kept fixed, and the rest column vector data are switched. The nominal column vector index is kept unchanged, namely is consistent with the classical unilateral Jacobi algorithm, and real data corresponding to the nominal column vector index is processed according to an S5 exchange rule;
in S4
Figure SMS_47
And->
Figure SMS_48
、/>
Figure SMS_49
And->
Figure SMS_50
The source data is input into the column vector which is processed by the switching rule according to the finally determined combination mode in the step S3, and the second-order norm and the vector inner product are correspondingly calculated based on the processing of the switching rule.
S6: and repeatedly executing S1-S4 until convergence conditions are reached, sorting the obtained singular values in a descending order, selecting the first k singular values, and accordingly converting the storage of the pixel matrix of m rows and n columns of the input image into only k singular values, and the left singular matrix of m rows and k columns and the right singular matrix of k rows and n columns, so that the compression ratio of the image is (m+n+1) k/(m n).
After reaching the preset convergence condition, obtaining a right singular matrix V, wherein each column vector is the right singular vector V i Calculating square root of second order norm of n columns of vectors of the input matrix to obtain n singular values, dividing each column of vectors by the corresponding singular value to obtain left singular vector U i I=1, 2, …, n; extracting the first k singular values and the corresponding singular vectors in descending order to perform image reverse construction to obtain
Figure SMS_51
And k is less than or equal to n, so that image compression is realized.
In addition, the singular value decomposition acceleration method of the embodiment of the invention has better effect on large dense matrixes with n more than or equal to 100 and m more than or equal to n.
On the other hand, the embodiment of the invention provides a column vector storage circuit of a singular value decomposition accelerating method based on single-side Jacobian of four column vector blocks, wherein for each column vector, a data structure of s segments is customized, the s segments correspond to s-block SRAMs, and the i-th column vector is taken as an example, and column vector elements, namely A (1, i), A (2, i), A (3,i), … and A (m, i), are sequentially stored in the s-block SRAMs according to a row priority mode.
For on-chip distributed SRAM storage formed by a customized s-segment data structure, a calculation logic circuit comprising a column vector second-order norm, a column vector inner product, a unit vector inner product and Givens transformation is embedded among all SRAM macro units, so that near-memory calculation is realized.
The s-sectional data structure improves the data access and calculation efficiency by s times, and the clock beat is reduced to 1/s; according to the abundant distributed SRAM formed by the s-sectional data structure, computational logic resources are embedded among SRAM macro cells, so that the delay of a data channel is reduced, the time sequence of a circuit is improved, the problem of a storage wall of singular value decomposition of a large dense matrix is effectively relieved, and the effect of near-memory computation is achieved.
Taking the image to be compressed with 224 rows by 224 columns as an example, which is common in the deep learning field, each pixel bit width is 8 bits, the s segmentation method adopts 4 segments, and the specification bit depth of the SRAM is 64 depths by 8 bits, which belongs to the small-scale memory macro unit which is common in the integrated circuit design field. Therefore, 224 data in total of each 1 column of pixels of the image to be compressed is averagely distributed to 4 SRAMs for storage, and each block of SRAMs is enough for storing 224/4=56 pixel data, and provides a certain redundancy, and the 224 row×224 column size of the image to be compressed occupies 896 small SRAMs in total, so as to form a distributed SRAM hardware storage circuit architecture. By embedding the calculation logic circuit between the distributed SRAM macro units, as shown in fig. 1, the column vector can carry out access and operation of singular value decomposition with s=4 times of parallel efficiency, meanwhile, the routing delay of a data channel is reduced, the time sequence quality of the circuit is improved, the problem of a storage wall is relieved, the effect of a near-memory calculation hardware circuit architecture is realized, and the image compression performance is improved. The 4-segment data of the 1 st column element of the image to be compressed is shown in fig. 2 according to the row priority storage sequence.
According to the classical unilateral Jacobi algorithm, 224 columns of image pixels are divided into 112 pairs of column vectors and calculated in parallel, if a traditional base 2 strategy singular value decomposition method is adopted, each sweep needs to execute 223 rounds of 112 pairs of column vector Givens rotation update calculation, and at least 8 times of sweep can meet the convergence condition, namely at least 224× (224-1) ×8= 399616 clock beats are needed. By adopting the image compression method based on the four-column vector block singular value decomposition, the convergence condition can be met only by 6 times of sweep, the clock beat number is close to (224/4+4-1) x (224-1) x 6= 78942, and only about 19.75% of the original clock beat number is needed, so that the calculated amount is obviously reduced, the convergence progress is improved, and the real-time performance of image compression is improved. And for the 224 singular values and the corresponding singular vectors, the first 22 largest singular values and singular vectors are extracted according to the first 10%, compression transmission and reverse image construction are carried out, the compression ratio is close to 5:1, the image main body information is reserved, and the subsequent transmission bandwidth and storage capacity are reduced.
The specific implementation process of this embodiment is as follows:
step 1: the image to be compressed in 224 rows by 224 columns is divided into blocks averagely by adopting a base 4 strategy, the 1 st block is the 1 st image element in the 1 st to 4 th columns, the 2 nd block is the 5 th to 8 th image elements in the … th columns, and the 56 th block is the 221 st to 224 th image elements, as shown in fig. 3, wherein n=224. Calculating the second order norm alpha inside the 1 st partition 1 、α 2 、α 3 And alpha 4 According to the combination of two by two, there are 3 alternative modes, namely A 1 ~A 2 And A is a 3 ~A 4 ，A 1 ~A 3 And A is a 2 ~A 4 ，A 1 ~A 4 And A is a 2 ~A 3 Thus respectively calculating the corresponding inner products gamma 12 And gamma is equal to 34 ，γ 13 And gamma is equal to 24 ，γ 14 And gamma is equal to 23 And unit vector inner product thereof
Figure SMS_52
And->
Figure SMS_53
，/>
Figure SMS_54
And->
Figure SMS_55
，
Figure SMS_56
And->
Figure SMS_57
A block second order norm, vector inner product and unit vector inner product calculation circuit is shown in fig. 4; the remaining 49 blocks are concurrently synchronized to perform similar calculations.
Step 2: taking the 1 st partition as an example, for
Figure SMS_60
、/>
Figure SMS_62
，/>
Figure SMS_65
、/>
Figure SMS_59
，/>
Figure SMS_63
And
Figure SMS_66
the 6 unit vector inner products are sequenced, the unit vector inner products are important indexes for representing the mutual orthogonality degree among the column vectors, and the 6 unit vector inner products are sequenced to select from 3 optional combinations; still taking the 1 st block as an example, assume +.>
Figure SMS_68
Is the unit vector inner product in which the absolute value is the smallest, < >>
Figure SMS_58
Is the unit vector inner product with the absolute value being the next smallest, at this time, A is selected 1 ~A 4 And A is a 2 ~A 3 As a final combination; however, it is assumed that the two unit vector inner products with the smallest absolute values are simultaneously distributed in one candidate combination, e.g. +.>
Figure SMS_61
And->
Figure SMS_64
If the absolute value is the least and the next least unit vector inner products, then the candidate group of the absolute value next least unit vector inner products needs to be further confirmed, and the assumption is that
Figure SMS_67
Is the unit vector inner product with the absolute value of the next smallest, at this time, A is selected 1 ~A 3 And A is a 2 ~A 4 As a final column vector pair combination; through the optimization selection of the combination of the step of column vectors, the obvious reduction of the low-efficiency convergence calculation behavior can be realized. Correspondingly, the rest 55 blocksAnd similar operations are performed concurrently and synchronously.
Step 3: according to the final combination of 4 column vectors, i.e. 4 column image elements in step 2, the switching of the column vector data input sources in the subsequent Givens rotation calculation is determined, and here, taking the 2 nd block as an example, for the 5 th to 8 th column image elements, as shown in fig. 5, the switching rule of the column vector data input sources is shown. As in (a) of fig. 5, assuming that the final combination is a pair of 5 th and 6 th column image elements and a pair of 7 th and 8 th column image elements, no exchange of data input sources is required. As in (b) of fig. 5, assuming that the final combination is a pair of 5 th and 7 th column image elements, and a pair of 6 th and 8 th column image elements, the nominal column index is unchanged for the 6 th and 7 th column image elements, but the data actually involved in Givens calculation is exchanged at the output of the SRAM read port, i.e., for the 6 th column image element, the nominal column index is 6, but the real data is from the column index 7; for the 7 th column image element, it is nominally column indexed 7, but the real data comes from column index 6. Similarly, as in (c) of fig. 5, assuming that the final combination is a pair of 5 th and 8 th column image elements and a pair of 6 th and 7 th column image elements, the nominal column index is unchanged for the 5 th and 7 th column image elements, but the data actually involved in Givens calculation is exchanged at the output of the SRAM read port, i.e., for the 5 th column image pixel, its nominal column index is 5, but the real data comes from the column index of 7; for the 7 th column image element, it is nominally column indexed 7, but the real data comes from column index 5. During this process, the 8 th column of picture element column index in the upper right corner remains unchanged. Accordingly, the remaining 55 blocks concurrently perform similar operations in synchronization.
Step 4: according to the unilateral Jacobi algorithm, performing Givens transformation calculation operation on 2 pairs of column vectors in each block, and calculating a Givens matrix by a second-order norm and a vector inner product according to the combination mode finally determined in the step 2
Figure SMS_69
According to the data exchange rule of step 3, givens rotation is performed on elements from 1 st row to m=224 th row of each column vector respectivelyTurning to a computing update, and s=4, so that the rotating computing update operation is also improved by 4 times of parallel computing efficiency; the Givens rotation calculation detailed circuit is shown in fig. 6.
Step 5: according to the column vector input data source exchange rule in the step 3, the output of the updated result of the Givens rotation calculation is written back and covers the original column vector data according to the corresponding rule. Taking the 2 nd block as an example, if the combination in the step 3 is that the 5 th and the 6 th column image elements are in a pair, the 7 th and the 8 th column image elements are in a pair, the nominal column index is consistent with the real data source, and the output result does not need to be exchanged; if the 5 th and 7 th column image pixels are paired in step 3, the 6 th and 8 th column image pixels are paired, and the 6 th and 7 th column image elements participate in Givens rotation calculation to exchange the input source, the result is written back and covers the original data, namely the nominal data
Figure SMS_70
Calculating the output of the updated result and writing back the SRAM storage input port where the 7 th column of image elements are actually located, and nominally +.>
Figure SMS_71
Calculating an updating result, outputting and writing back to an SRAM storage input port where the 6 th column of image elements are truly positioned; if the 5 th and 8 th column image elements are in a pair and the 6 th and 7 th column image elements are in a pair in the step 3, the result is written back and covers the original data in the original direction, namely, the nominal->
Figure SMS_72
Calculating the output of the updated result and writing back the SRAM storage input port where the 7 th column of image elements are actually located, and nominally +.>
Figure SMS_73
And outputting and writing the calculated and updated result back to the SRAM storage input port where the 5 th column image pixel is actually positioned. The remaining 55 blocks are concurrently synchronized with similar processing.
Step 6: column vectors of the 224 th column are fixed, and counterclockwise cyclic scheduling is carried out on the column vectors after Givens rotation calculation by a round-robin scheduling mechanism, namely according to a nominal column vector index, the 1 st column image element is transmitted to the 3 rd column image element, the 3 rd column image element is transmitted to the 5 th column image element, the 5 th column image element is transmitted to the 7 th column image element, …, the 197 th column image element is transmitted to the 199 th column image element, the 199 th column image element is transmitted to the 198 th column image element, the 198 th column image element is transmitted to the 196 th column image element, the …, the 4 th column image element is transmitted to the 2 nd column image element, and the 2 nd column image element is transmitted to the 1 st column image element.
Step 7: and (3) repeatedly executing the steps 1-6, wherein the preset convergence judgment condition can be met through 6 times of sweep.
Step 8: according to step 7, 224 singular values are obtained, S 1 ，S 2 ，S 3 ，…，S 224 And 224 rows by 224 columns of left singular matrix U and right singular matrix V, the 224 columns of column vectors being divided by the respective corresponding singular values to obtain left singular vector U i I=1, 2,3, …,224, each column of right singular matrix V has a column vector V i Namely right singular vectors. Fig. 7 is a compression schematic diagram based on four-column vector singular value decomposition, and when the value of k is far smaller than n, the compression ratio can be large, and the magnitude of k can be adjusted to realize elastic compression. As shown in fig. 8, the present invention is used to compare before and after compression, where (a) in fig. 8 is original image, and (b) in fig. 8 is k=22, i.e. the maximum first 10% singular value and the corresponding singular vector are extracted, and the method uses
Figure SMS_74
Reverse construction is carried out, and the compression ratio is close to 5:1; in fig. 8 (c) k=34, i.e. the first 15% of maximum singular values and corresponding singular vectors are extracted, using +.>
Figure SMS_75
Reverse construction was performed with a compression ratio approaching 10:3.
Compared with the classical unilateral Jacobian algorithm for realizing singular value decomposition image compression, the embodiment of the invention can realize singular value decomposition image compression, and the invention has the same access and storageThe column vector pair combining option is increased under the condition of times, by the unit vector inner product gamma-
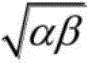
Figure SMS_76
Sequencing and serving as a judging condition of the low-efficiency convergence behavior, reducing the number of the low-efficiency convergence calculation behaviors, further reducing the total calculated amount of singular value decomposition, and further improving the real-time performance of image compression; aiming at a possible 3 column vector pair combination mode, a nominal column index sequence is adopted, only input sources and output results which participate in Givens rotation calculation are exchanged, and the simplicity and the easy realization of a round-robin sequence strategy are maintained; the s-sectional data structure improves the data access and calculation efficiency by s times, and the clock beat is 1/s of the original clock; according to the abundant distributed SRAM formed by the s-sectional data structure, computational logic resources are embedded among SRAM macro cells, so that the delay of a data channel is reduced, the time sequence of a circuit is improved, the problem of a storage wall of singular value decomposition of a large dense matrix is effectively relieved, and the effect of near-memory computation is achieved. Therefore, the invention can realize the reduction of the low-efficiency convergence calculation amount in the matrix singular value decomposition process, the improvement of the parallel access and calculation efficiency and the remarkable acceleration of the convergence speed.
The embodiment of the invention also provides a computer readable storage medium, on which a program is stored, which when executed by a processor, implements the image compression method based on the four-column vector block singular value decomposition in the above embodiment.
Other embodiments of the present application will be apparent to those skilled in the art from consideration of the specification and practice of the disclosure herein. This application is intended to cover any variations, uses, or adaptations of the application following, in general, the principles of the application and including such departures from the present disclosure as come within known or customary practice within the art to which the application pertains. It is intended that the specification and examples be considered as exemplary only, with a true scope and spirit of the application being indicated by the following claims.
It is to be understood that the present application is not limited to the precise arrangements and instrumentalities shown in the drawings, which have been described above, and that various modifications and changes may be effected without departing from the scope thereof. The scope of the application is limited only by the appended claims.

Claims (10)

1.一种基于四列列向量分块奇异值分解的图像压缩方法，其特征在于，输入图像的像元为m行×n列，以矩阵形式作为奇异值分解压缩电路的输入，每4列图像元素为一组，4列图像元素对应4列列向量，对输入图像进行平均分组，若n/4不能整除，则预先对待压缩图像的末尾增补1列全0元素的操作，使其整除且共有
Figure QLYQS_1
个列向量分块，/>
Figure QLYQS_2
表示向上取整；每个列向量分块由4列列向量组成2×2的结构，每个列向量分块的左下角的列向量表示为Ai，左上角的列向量表示为Aj，右下角的列向量表示为Ap，右上角的列向量表示为Aq；1. An image compression method based on four-column column vector block singular value decomposition, characterized in that, the pixel of the input image is m rows × n columns, and is used as the input of the singular value decomposition compression circuit in matrix form, and every 4 columns The image elements are a group, and the 4 columns of image elements correspond to 4 columns of vectors, and the input image is grouped evenly. If n/4 cannot be divisible, the operation of adding 1 column of all 0 elements to the end of the compressed image is to be performed in advance to make it divisible and in total
Figure QLYQS_1
column vector blocks, />
Figure QLYQS_2
Represents rounding up; each column vector block is composed of 4 column vectors to form a 2×2 structure, the column vector in the lower left corner of each column vector block is denoted as A i , and the column vector in the upper left corner is denoted as A j , The column vector in the lower right corner is denoted as A p , and the column vector in the upper right corner is denoted as A q ; 每个列向量分块的块内计算步骤如下：The intra-block calculation steps of each column vector block are as follows: S1：计算Ai、Aj、Ap、Aq各自的二阶范数αi、αj、αp、αq，并将四个列向量两两组合，计算每种组合内的两个列向量间的内积γij与γpq，γip与γjq，γiq与γjp，以及对应的单位向量内积与
Figure QLYQS_3
，/>
Figure QLYQS_4
与/>
Figure QLYQS_5
，/>
Figure QLYQS_6
与/>
Figure QLYQS_7
；S1: Calculate the second-order norms α i , α j , α p , α q of A i , A j , A p , and A q respectively, and combine the four column vectors in pairs, and calculate two The inner product between column vectors γ ij and γ pq , γ ip and γ jq , γ iq and γ jp , and the corresponding unit vector inner product and
Figure QLYQS_3
, />
Figure QLYQS_4
with />
Figure QLYQS_5
, />
Figure QLYQS_6
with />
Figure QLYQS_7
; S2：对列向量分块内的6个单位向量内积进行排序，若绝对值最小的两个单位向量内积分布在其中的2个候选组合中，则以剩下候选组合作为最终组合；若绝对值最小和次小的两个单位向量内积分布在同一个候选组合中，则排除绝对值为次次小的单位向量内积所在的候选组，选择最后剩下的那一个候选组合作为最终组合；S2: Sort the inner products of the six unit vectors in the column vector block, if the inner products of the two unit vectors with the smallest absolute value are distributed in two of the candidate combinations, then use the remaining candidate combinations as the final combination; if If the two unit vector inner products with the smallest and second smallest absolute values are distributed in the same candidate combination, then exclude the candidate group whose absolute value is the second smallest unit vector inner product, and select the last remaining candidate combination as the final combination; S3：若最终组合是Ai与Aj，Ap与Aq，则不需要对源头输入执行交换数据操作；若最终组合Ai与Aq，Ap与Aj，此时第i列与第p列列向量数据源头交换；若最终组合Ai与Ap，Aq与Aj，此时第p列与第j列列向量数据源头交换；S3: If the final combination is A i and A j , A p and A q , there is no need to perform an exchange data operation on the source input; if the final combination is A i and A q , A p and A j , then column i and The source of the column vector data of the p-th column is exchanged; if the final combination of A i and A p , A q and A j , the source of the column vector data of the p-th column and the j-th column is exchanged; S4：根据经典单边雅克比算法执行列向量分块内部2对列向量的Givens旋转计算操作；S4: According to the classic unilateral Jacobian algorithm, perform the Givens rotation calculation operation of two pairs of column vectors inside the column vector block; S5：根据S3中列向量输入数据源头交换规则，Givens旋转计算更新的结果输出也按照相应规则写回并覆盖原有的列向量数据；S5: According to the source exchange rules of the column vector input data in S3, the updated result output of Givens rotation calculation is also written back and overwrites the original column vector data according to the corresponding rules; S6：反复执行S1~S4，直至达到收敛条件，对获得的奇异值降序排序，选取前k个奇异值，从而将原始m行n列的像元矩阵的存储变换为仅存储k个奇异值，以及m行k列的左奇异矩阵和k行n列的右奇异矩阵，将输入图像的存储压缩将至原来的（m+n+1）*k /（m*n）。S6: Execute S1~S4 repeatedly until the convergence condition is reached, sort the obtained singular values in descending order, select the first k singular values, and transform the storage of the original pixel matrix with m rows and n columns into only k singular values, And the left singular matrix with m rows and k columns and the right singular matrix with k rows and n columns compress the storage of the input image to the original (m+n+1)*k/(m*n). 2.根据权利要求1所述的基于四列列向量分块奇异值分解的图像压缩方法，其特征在于，每执行完一轮Givens旋转计算，列向量分块内的列交换规则为：2. the image compression method based on four-column column vector block singular value decomposition according to claim 1, is characterized in that, every round of Givens rotation calculation is performed, the column exchange rule in the column vector block is: 第1个列向量分块：左下交换成右下，左上交换成左下，右上交换成左上；The first column vector is divided into blocks: the lower left is replaced by the lower right, the upper left is replaced by the lower left, and the upper right is replaced by the upper left; 第
Figure QLYQS_8
个列向量分块：左下交换成右下，右上交换成左上；No.
Figure QLYQS_8
A column vector is divided into blocks: the lower left is replaced by the lower right, and the upper right is replaced by the upper left; 第
Figure QLYQS_9
列向量分块：保持右上角的列向量不动，右下交换成左上，左下交换成右下。No.
Figure QLYQS_9
Column vector block: Keep the column vector in the upper right corner unchanged, replace the lower right with upper left, and replace the lower left with lower right. 3.根据权利要求1所述的基于四列列向量分块奇异值分解的图像压缩方法，其特征在于，每执行完一轮Givens旋转计算，列向量分块的块间列交换规则为：前一个列向量分块的右下交换成当前列向量分块的左下，当前列向量分块的左上交换成前一个列向量分块的右上。3. the image compression method based on the singular value decomposition of four-column column vector blocks according to claim 1, is characterized in that, every round of Givens rotation calculation is performed, the row exchange rule between the blocks of column vector blocks is: before The lower right of a column vector block is replaced with the lower left of the current column vector block, and the upper left of the current column vector block is replaced with the upper right of the previous column vector block. 4.根据权利要求1所述的基于四列列向量分块奇异值分解的图像压缩方法，其特征在于，所述S4中的Givens旋转计算的公式如下：4. the image compression method based on four columns column vector block singular value decomposition according to claim 1, is characterized in that, the formula that the Givens rotation in described S4 calculates is as follows:
Figure QLYQS_10
，
Figure QLYQS_10
, 其中cosθ和sinθ取值如下：The values of cosθ and sinθ are as follows:
Figure QLYQS_11
；
Figure QLYQS_11
; 其中，
Figure QLYQS_12
和/>
Figure QLYQS_13
表示第r轮Givens变换前的第i和第j列的列向量输入，/>
Figure QLYQS_14
和/>
Figure QLYQS_15
表示第r轮Givens变换更新后的第i和第j列的列向量输出，若γij≥0且αi-αj≥0，或者γij＜0且αi-αj＜0，则sinθ取正号，反之则取负号，cosθ和sinθ构成Givens旋转矩阵；分块内另一对列向量/>
Figure QLYQS_16
和/>
Figure QLYQS_17
执行相同操作。in,
Figure QLYQS_12
and />
Figure QLYQS_13
Represents the column vector input of the i-th and j-th columns before the r-th round of Givens transformation, />
Figure QLYQS_14
and />
Figure QLYQS_15
Indicates the column vector output of the i-th and j-th columns after the r-th round of Givens transformation update, if γ ij ≥ 0 and α i -α j ≥ 0, or γ ij <0 and α i -α j <0, then sinθ Take the positive sign, otherwise take the negative sign, cosθ and sinθ constitute the Givens rotation matrix; another pair of column vectors in the block />
Figure QLYQS_16
and />
Figure QLYQS_17
Do the same. 5.根据权利要求1所述的基于四列列向量分块奇异值分解的图像压缩方法，其特征在于，所述S5的写回规则为：5. the image compression method based on four-column column vector block singular value decomposition according to claim 1, is characterized in that, the write-back rule of described S5 is: 若当前组合是Ai与Aj，Ap与Aq，则输出结果不需要执行交换处理；If the current combination is A i and A j , A p and A q , the output result does not need to be exchanged; 若当前组合是Ap与Aj，Ai与Aq，则结果输出
Figure QLYQS_18
写回且覆盖第p列列向量对应的SRAM存储中，/>
Figure QLYQS_19
写回且覆盖第i列列向量对应的SRAM存储中；If the current combination is A p and A j , A i and A q , the result output
Figure QLYQS_18
Write back and overwrite the SRAM storage corresponding to the p-th column vector, />
Figure QLYQS_19
Write back and overwrite the SRAM storage corresponding to the i-th column column vector; 若当前组合是Ai与Ap，Aq与Aj，则输出结果
Figure QLYQS_20
写回且覆盖第j列列向量对应的SRAM存储中，/>
Figure QLYQS_21
写回且覆盖第p列列向量对应的SRAM存储中。If the current combination is A i and A p , A q and A j , then output the result
Figure QLYQS_20
Write back and overwrite the SRAM storage corresponding to the jth column vector, />
Figure QLYQS_21
Write back and overwrite the p-th column corresponding to the SRAM storage. 6.根据权利要求1所述的基于四列列向量分块奇异值分解的图像压缩方法，其特征在于，待压缩图像的列像元数量n≥100。6 . The image compression method based on block singular value decomposition of four columns of column vectors according to claim 1 , wherein the number of columns of pixels of the image to be compressed is n≥100. 7 . 7.根据权利要求6所述的基于四列列向量分块奇异值分解的图像压缩方法，其特征在于，待压缩图像的行像元数量大于等于列像元数量，即m≥n。7. The image compression method based on four-column vector block singular value decomposition according to claim 6, wherein the number of row pixels of the image to be compressed is greater than or equal to the number of column pixels, ie m≥n. 8.一种如权利要求1~7中任意一项所述的基于四列列向量分块奇异值分解的图像压缩方法的列向量存储电路，其特征在于，8. a column vector storage circuit based on the image compression method of four-column column vector block singular value decomposition as described in any one of claims 1～7, it is characterized in that, 对于每一列列向量，定制s分段的数据结构，s分段对应s块SRAM，以第i列列向量为例，该列列向量元素即A(1,i)，A(2,i)，A(3,i)，…，A(m,i)按行优先方式依次存储到s块SRAM中。For each column vector, customize the data structure of s segment, s segment corresponds to s block SRAM, take the i-th column vector as an example, the column vector elements are A(1,i), A(2,i) , A(3,i),..., A(m,i) are sequentially stored in the s-block SRAM in a row-first manner. 9.根据权利要求8所述的列向量存储电路，其特征在于，对于定制的s分段数据结构形成的片内分布式SRAM存储，在各SRAM宏单元间嵌入包括列向量二阶范数、各列列向量内积、单位向量内积以及Givens旋转变换在内的计算逻辑电路，实现近存计算硬件电路架构。9. column vector storage circuit according to claim 8, is characterized in that, for the on-chip distributed SRAM storage that the customized s segmentation data structure forms, between each SRAM macrocell, embedding comprises column vector second-order norm, Computational logic circuits including the inner product of column-column vectors, unit vector inner product, and Givens rotation transformation realize near-memory computing hardware circuit architecture. 10.一种计算机可读存储介质，其上存储有程序，该程序被处理器执行时，实现权利要求1~7中任意一项所述的基于四列列向量分块奇异值分解的图像压缩方法。10. A computer-readable storage medium, on which a program is stored, and when the program is executed by a processor, the image compression based on the singular value decomposition of four-column vector blocks described in any one of claims 1 to 7 is realized method.
CN202310451246.XA 2023-04-25 2023-04-25 Image compression method based on four-column vector block singular value decomposition Active CN116170601B (en)

Priority Applications (1)

Application Number Priority Date Filing Date Title
CN202310451246.XA CN116170601B (en) 2023-04-25 2023-04-25 Image compression method based on four-column vector block singular value decomposition

Applications Claiming Priority (1)

Application Number Priority Date Filing Date Title
CN202310451246.XA CN116170601B (en) 2023-04-25 2023-04-25 Image compression method based on four-column vector block singular value decomposition

Publications (2)

Publication Number Publication Date
CN116170601A CN116170601A (en) 2023-05-26
CN116170601B true CN116170601B (en) 2023-07-11

Family

ID=86418601

Family Applications (1)

Application Number Title Priority Date Filing Date
CN202310451246.XA Active CN116170601B (en) 2023-04-25 2023-04-25 Image compression method based on four-column vector block singular value decomposition

Country Status (1)

Country Link
CN (1) CN116170601B (en)

Families Citing this family (4)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
CN116382617B (en) * 2023-06-07 2023-08-29 之江实验室 FPGA-based Singular Value Decomposition Accelerator with Parallel Sorting Function
CN117997351A (en) * 2024-02-01 2024-05-07 自然资源部第二海洋研究所 Ocean observation data self-adaptive compression method, device and system and storage medium
CN119537381A (en) * 2025-01-22 2025-02-28 山东浪潮科学研究院有限公司 A singular value decomposition acceleration method and device based on GPGPU
CN119884023B (en) * 2025-03-31 2025-06-10 山东浪潮科学研究院有限公司 Parallel computing core caching method, device and medium based on multi-compression scheme

Citations (5)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
CN111680028A (en) * 2020-06-09 2020-09-18 天津大学 Synchrophasor measurement data compression method for distribution network based on improved singular value decomposition
CN111814792A (en) * 2020-09-04 2020-10-23 之江实验室 A Feature Point Extraction and Matching Method Based on RGB-D Image
CN112596701A (en) * 2021-03-05 2021-04-02 之江实验室 FPGA acceleration realization method based on unilateral Jacobian singular value decomposition
CN113536228A (en) * 2021-09-16 2021-10-22 之江实验室 A FPGA Acceleration Implementation Method of Matrix Singular Value Decomposition
WO2022110867A1 (en) * 2020-11-27 2022-06-02 苏州浪潮智能科技有限公司 Image compression sampling method and assembly

Patent Citations (5)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
CN111680028A (en) * 2020-06-09 2020-09-18 天津大学 Synchrophasor measurement data compression method for distribution network based on improved singular value decomposition
CN111814792A (en) * 2020-09-04 2020-10-23 之江实验室 A Feature Point Extraction and Matching Method Based on RGB-D Image
WO2022110867A1 (en) * 2020-11-27 2022-06-02 苏州浪潮智能科技有限公司 Image compression sampling method and assembly
CN112596701A (en) * 2021-03-05 2021-04-02 之江实验室 FPGA acceleration realization method based on unilateral Jacobian singular value decomposition
CN113536228A (en) * 2021-09-16 2021-10-22 之江实验室 A FPGA Acceleration Implementation Method of Matrix Singular Value Decomposition

Non-Patent Citations (2)

* Cited by examiner, † Cited by third party
Title
Image compression with multiresolution singular value decomposition and other methods;R.Ashin等;《Mathematical and computer modelling》;全文 *
基于奇异值分解的图像质量评价;骞森;朱剑英;;东南大学学报(自然科学版)(04);全文 *

Also Published As

Publication number Publication date
CN116170601A (en) 2023-05-26

Similar Documents

Publication Publication Date Title
CN116170601B (en) Image compression method based on four-column vector block singular value decomposition
CN109886400B (en) Convolutional Neural Network Hardware Accelerator System Based on Convolution Kernel Splitting and Its Computing Method
CN108241890B (en) Reconfigurable neural network acceleration method and architecture
CN111738433B (en) Reconfigurable convolution hardware accelerator
WO2018139177A1 (en) Processor, information processing device, and processor operation method
US20060002471A1 (en) Motion estimation unit
WO2019170049A1 (en) Convolutional neural network acceleration device and method
CN110163354A (en) A kind of computing device and method
CN110796236B (en) Vectorization implementation method for pooling of multi-sample multi-channel convolutional neural network
WO2022007265A1 (en) Dilated convolution acceleration calculation method and apparatus
CN111242268A (en) Method for searching convolutional neural network
KR20240035999A (en) Hybrid machine learning architecture using neural processing units and compute-in-memory processing elements
CN117237190B (en) Lightweight image super-resolution reconstruction system and method for edge mobile devices
CN115221102A (en) Method for optimizing convolution operation of system on chip and related product
CN112419455A (en) Human action video generation method, system and storage medium based on human skeleton sequence information
CN113191935B (en) Reconfigurable hardware acceleration method and system for Gaussian pyramid construction
CN111767994A (en) A neuron computing module
CN115238863A (en) A hardware acceleration method, system and application for convolutional layer of convolutional neural network
CN116309059A (en) A video super-resolution method and system based on deformable 3D convolutional network
US20210173590A1 (en) Data processing method, electronic apparatus, and computer-readable storage medium
Jiang et al. MCA: Moment channel attention networks
CN115880149A (en) Video frame interpolation method and system based on lightweight driver and three-scale coding
CN112837212B (en) Image arbitrary style migration method based on manifold alignment
CN114219699A (en) Matching cost processing method and circuit and cost aggregation processing method
CN117218031B (en) Image reconstruction method, device and medium based on DeqNLNet algorithm

Legal Events

Date Code Title Description
PB01 Publication
PB01 Publication
SE01 Entry into force of request for substantive examination
SE01 Entry into force of request for substantive examination
GR01 Patent grant
GR01 Patent grant