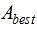CN113312712A - Recursive permutation evolution experimental design method for aircraft optimization design - Google Patents
Recursive permutation evolution experimental design method for aircraft optimization design Download PDFInfo
- Publication number
- CN113312712A CN113312712A CN202110856433.7A CN202110856433A CN113312712A CN 113312712 A CN113312712 A CN 113312712A CN 202110856433 A CN202110856433 A CN 202110856433A CN 113312712 A CN113312712 A CN 113312712A
- Authority
- CN
- China
- Prior art keywords
- sample
- design
- matrix
- evolution
- sample matrix
- Prior art date
- Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
- Granted
Links
- 238000013461 design Methods 0.000 title claims abstract description 105
- 238000005457 optimization Methods 0.000 title claims abstract description 27
- 238000003050 experimental design method Methods 0.000 title abstract description 13
- 238000000034 method Methods 0.000 claims abstract description 47
- 238000004364 calculation method Methods 0.000 claims abstract description 12
- 239000011159 matrix material Substances 0.000 claims description 95
- 150000001875 compounds Chemical class 0.000 claims description 11
- 238000012217 deletion Methods 0.000 claims description 9
- 230000037430 deletion Effects 0.000 claims description 9
- 230000009466 transformation Effects 0.000 claims description 9
- 238000002474 experimental method Methods 0.000 claims description 8
- 238000004088 simulation Methods 0.000 claims description 8
- 241001611138 Isma Species 0.000 claims description 3
- 102000002274 Matrix Metalloproteinases Human genes 0.000 claims description 3
- 108010000684 Matrix Metalloproteinases Proteins 0.000 claims description 3
- 235000006629 Prosopis spicigera Nutrition 0.000 claims description 3
- 240000000037 Prosopis spicigera Species 0.000 claims description 3
- 125000004122 cyclic group Chemical group 0.000 claims description 3
- 238000013401 experimental design Methods 0.000 abstract description 24
- 230000001603 reducing effect Effects 0.000 abstract description 8
- 238000004422 calculation algorithm Methods 0.000 description 14
- 238000012360 testing method Methods 0.000 description 13
- 230000009467 reduction Effects 0.000 description 12
- 238000012549 training Methods 0.000 description 3
- 238000013519 translation Methods 0.000 description 3
- 239000003795 chemical substances by application Substances 0.000 description 2
- 238000010276 construction Methods 0.000 description 2
- 230000007547 defect Effects 0.000 description 2
- 238000010586 diagram Methods 0.000 description 2
- 230000008859 change Effects 0.000 description 1
- 238000004891 communication Methods 0.000 description 1
- 230000008094 contradictory effect Effects 0.000 description 1
- 230000000694 effects Effects 0.000 description 1
- 230000008030 elimination Effects 0.000 description 1
- 238000003379 elimination reaction Methods 0.000 description 1
- 238000005516 engineering process Methods 0.000 description 1
- 230000002708 enhancing effect Effects 0.000 description 1
- 238000011156 evaluation Methods 0.000 description 1
- 238000009413 insulation Methods 0.000 description 1
- 238000013507 mapping Methods 0.000 description 1
- 238000012986 modification Methods 0.000 description 1
- 230000004048 modification Effects 0.000 description 1
- 238000012803 optimization experiment Methods 0.000 description 1
- 230000035939 shock Effects 0.000 description 1
- 238000002922 simulated annealing Methods 0.000 description 1
- XLYOFNOQVPJJNP-UHFFFAOYSA-N water Substances O XLYOFNOQVPJJNP-UHFFFAOYSA-N 0.000 description 1
Images
Classifications
-
- G—PHYSICS
- G06—COMPUTING; CALCULATING OR COUNTING
- G06F—ELECTRIC DIGITAL DATA PROCESSING
- G06F30/00—Computer-aided design [CAD]
- G06F30/10—Geometric CAD
- G06F30/15—Vehicle, aircraft or watercraft design
-
- G—PHYSICS
- G06—COMPUTING; CALCULATING OR COUNTING
- G06F—ELECTRIC DIGITAL DATA PROCESSING
- G06F30/00—Computer-aided design [CAD]
- G06F30/20—Design optimisation, verification or simulation
- G06F30/27—Design optimisation, verification or simulation using machine learning, e.g. artificial intelligence, neural networks, support vector machines [SVM] or training a model
Landscapes
- Engineering & Computer Science (AREA)
- Physics & Mathematics (AREA)
- Geometry (AREA)
- Theoretical Computer Science (AREA)
- General Physics & Mathematics (AREA)
- Evolutionary Computation (AREA)
- General Engineering & Computer Science (AREA)
- Computer Hardware Design (AREA)
- Medical Informatics (AREA)
- Software Systems (AREA)
- Computer Vision & Pattern Recognition (AREA)
- Artificial Intelligence (AREA)
- Automation & Control Theory (AREA)
- Aviation & Aerospace Engineering (AREA)
- Computational Mathematics (AREA)
- Mathematical Analysis (AREA)
- Mathematical Optimization (AREA)
- Pure & Applied Mathematics (AREA)
- Management, Administration, Business Operations System, And Electronic Commerce (AREA)
Abstract
The invention discloses a recursive evolution experimental design method for aircraft optimization design. And inserting the evolution design into the interval of the original sample and optimizing, thereby realizing the expansion of the sample and obtaining the expansion design with good performance. Because the recursive evolution sequence expansion method is adopted for the large sample experimental design, the sample amount of the optimized object expanded each time is small, thereby improving the efficiency of the experimental design and greatly reducing the optimization time of the experimental design. On the basis of ensuring the uniformity of the sample, the calculation efficiency is obviously improved, and an efficient and feasible method is provided for improving the experimental design of aircraft optimization. The method is applied to the technical field of optimization design of aircrafts.
Description
Technical Field
The invention relates to the technical field of aircraft optimization design, in particular to a recursive permutation evolution experimental design method for aircraft optimization design.
Background
In the design optimization of the aircraft, due to the limitation of calculation time and calculation resources, a large number of physical experiments are not feasible in many times, and numerical simulation and solution are required to be carried out through a high-precision simulation model. As design parameters and constraints increase, simulation models for the system become very complex, a large amount of time is consumed for a single simulation, and the computational cost for evaluating all design solutions is unacceptable. In order to solve the problem, researchers provide that sample points with good uniformity in a design space are obtained through an experimental design method, the consumption of computing resources is reduced, and meanwhile, the mutual relation of all experimental factors and the influence of the mutual relation on results are fully revealed, so that subsequent design optimization is guided.
The current common experimental design has a continuous local enumeration method and a translation propagation algorithm, optimizes the Latin hypercube and the like:
sequential local enumeration method: the method is a method for generating sample points in sequence, and can generate maximum and minimum samples which are uniformly distributed, so that the minimum distance between the samples is maximized;
the translation propagation algorithm: the small-size basic sample with superior space filling performance and mapping performance is translated to quickly obtain an experimental sample with larger size and good uniformity;
optimizing Latin hypercube experimental design: and (3) optimizing the random Latin hypercube by using a minimum distance maximization uniformity criterion as a target function through an arrangement optimization algorithm to obtain an experimental design with excellent uniformity performance. Commonly used permutation optimization algorithms include an enhanced random evolution algorithm, a simulated annealing algorithm, and the like.
The current commonly used experimental design method has the defects that:
the principle of a continuous local enumeration algorithm and a translation propagation algorithm is simple, but the uniformity of a sample point which is usually designed under the condition of a high-dimensional large sample is poor, so that the uniformity requirement in the design optimization experiment design of an aircraft is difficult to meet;
the space filling performance of the sample points obtained by the common optimized Latin hypercube algorithm is excellent, but the calculation efficiency is not good under the conditions of high dimensionality and large sample number.
Disclosure of Invention
Aiming at the defects in the prior art, the invention provides the experimental design method for the recursive evolution of the aircraft optimization design, which can be used for simply, efficiently and quickly designing the experimental design method for the recursive evolution.
In order to achieve the aim, the invention provides a recursive evolution experimental design method facing to aircraft optimization design, which comprises the following steps:
step 5, uniformly inserting the evolution design into the interval of the initial sample matrix one by one based on the row interval of the sample matrix to obtain an updated sample matrix;
step 6, judging whether the number of samples in the sample matrix is greater than or equal to the number of samples in the sample matrixmIf yes, entering step 7, otherwise, returning to step 5;
step 7, generating a sample set based on the samples in the sample matrix, and deleting (the sample set is farthest from the center of the design space) ((K·p+1-m) Obtaining all required sample points and outputting the sample points;
and 8, simulating the high-precision sample obtained by design, and guiding subsequent modeling by using an output result obtained by simulation.
In one embodiment, step 3, the method comprisesp+1 piecesThe sample matrix of sample points is:
in the formula (I), the compound is shown in the specification,A 1representing a sample matrix generated by the optimal latin hypercube,x p d(+1)is shown aspThe first of +1 samplesdThe number of the design variables is one,drepresenting the dimensions of the design variables.
In one embodiment, in step 4, the sample points in the sample matrix are cyclically deleted, and the sample point with the best uniformity after deletion is selectedpEach sample point is used as an evolution design, and specifically comprises the following steps:
arbitrarily deleted sample matrixA 1A sample point ofTo obtain a matrixThe method comprises the following steps:
according toiDifference in value, matrixIn common withp+1 manifestation form, hereinp+1 matricesTo select the one with the best uniformityAs an evolutionary designThe method comprises the following steps:
in one embodiment, when the sample matrix isA 1When the current is over;
the steps 5-6 specifically comprise:
sample matrixA 1Includedp+1 samples, i.e. sample matrixA 1Is uniformly divided intopA matrix of intervals, samplesA 1All the intervals of (A) form (a)p×d) Experimental space (2)B 1The method comprises the following steps:
in the formula (I), the compound is shown in the specification,b pd representing a sample matrixA 1To middledThe design variables arepExperimental space elements formed at intervals;
inserting the superposition relation of the evolution design based on the formula into the sample matrixA 1In (b), an overall matrix is obtainedA 1 B 1) The method comprises the following steps:
keeping the transformation relation between each column of the evolution design and the first column unchanged to integrateVolume matrix (A 1 B 1) Is/are as followsOptimizing the first row of the evolution design after the superposition by taking the criterion value as the objective function to obtain a sample matrix with excellent integral sample uniformity (A 1 A 2) The method comprises the following steps:
wherein the sample matrix isA 1 A 2) The newly added sample is the second folded sample setA 2;
Judging the sample matrix (A 1 A 2) Whether the number of samples in (1) is greater than or equal tomIf yes, go to step 7, otherwise return to step 5.
In one embodiment, when the sample matrix is: (A)A 1···A j-1) In the above-mentioned order, wherein,A j-1is shown asj-1-fold of the sample,j=3,4,…,K;
the steps 5-6 are specifically as follows:
for the firstjSample folding setA j By making inequality calculationsMinimum of establishmenttIs the current sample matrix (A 1···A j-1) The number of times each dimension of the design variable is evolved to be equally dividedtRepresenting the current sample matrix: (A 1···A j-1) Is divided intot×p) An interval, a sample matrix: (A 1···A j-1) All spaces will be formedtA (a)p×d) Open end of experimental spaceB 1,B 2,···,B t Is that:
order parameterThe evolution design of the next step is inserted intoAn experimental spaceB o The method comprises the following steps:
maintaining the transformation relationship between each row of the evolution design and the first row unchanged, and optimizing the first row of the evolution design after the superposition to obtain a new sample matrix (A 1···A j );
Judging the sample matrix (A 1···A j ) Whether the number of samples in (1) is greater than or equal tomIf yes, go to step 7, otherwise, makej=jAnd after +1, returning to the step 5.
According to the recursive permutation evolution experimental design method for the aircraft optimization design, rapid sample expansion is realized by performing permutation evolution on the optimal Latin hypercube of the small sample, the experimental design under any sample is obtained, the space filling performance is good, the design speed is high, the optimization time of the experimental design is greatly reduced, the calculation efficiency is obviously improved on the basis of ensuring the sample uniformity, and an efficient and feasible method is provided for improving the experimental design of the aircraft optimization.
Drawings
In order to more clearly illustrate the embodiments of the present invention or the technical solutions in the prior art, the drawings used in the description of the embodiments or the prior art will be briefly described below, it is obvious that the drawings in the following description are only some embodiments of the present invention, and for those skilled in the art, other drawings can be obtained according to the structures shown in the drawings without creative efforts.
FIG. 1 is a flowchart of a design method of a recursive evolution experiment in an embodiment of the present invention;
FIG. 2 is a geometric profile of a drag reducing rod in an embodiment of the present invention;
FIG. 3 is a schematic view of the geometric parameters of a drag reducing rod in an embodiment of the present invention;
FIG. 4 shows an embodiment of the present inventionKrigingThe model is a schematic diagram of the test result of the successively trained agent model by the method of the embodiment;
FIG. 5 is a schematic diagram comparing the runtime of the enhanced random evolution algorithm under the same conditions and the space filling performance of the generated experimental design in the embodiment of the present invention.
The implementation, functional features and advantages of the objects of the present invention will be further explained with reference to the accompanying drawings.
Detailed Description
The technical solutions in the embodiments of the present invention will be clearly and completely described below with reference to the drawings in the embodiments of the present invention, and it is obvious that the described embodiments are only a part of the embodiments of the present invention, and not all of the embodiments. All other embodiments, which can be derived by a person skilled in the art from the embodiments given herein without making any creative effort, shall fall within the protection scope of the present invention.
It should be noted that all the directional indicators (such as up, down, left, right, front, and rear … …) in the embodiment of the present invention are only used to explain the relative position relationship between the components, the movement situation, etc. in a specific posture (as shown in the drawing), and if the specific posture is changed, the directional indicator is changed accordingly.
In addition, the descriptions related to "first", "second", etc. in the present invention are only for descriptive purposes and are not to be construed as indicating or implying relative importance or implicitly indicating the number of technical features indicated. Thus, a feature defined as "first" or "second" may explicitly or implicitly include at least one such feature. In the description of the present invention, "a plurality" means at least two, e.g., two, three, etc., unless specifically limited otherwise.
In the present invention, unless otherwise expressly stated or limited, the terms "connected," "secured," and the like are to be construed broadly, and for example, "secured" may be a fixed connection, a removable connection, or an integral part; the connection can be mechanical connection, electrical connection, physical connection or wireless communication connection; they may be directly connected or indirectly connected through intervening media, or they may be connected internally or in any other suitable relationship, unless expressly stated otherwise. The specific meanings of the above terms in the present invention can be understood by those skilled in the art according to specific situations.
In addition, the technical solutions in the embodiments of the present invention may be combined with each other, but it must be based on the realization of those skilled in the art, and when the technical solutions are contradictory or cannot be realized, such a combination of technical solutions should not be considered to exist, and is not within the protection scope of the present invention.
The embodiment discloses a recursive evolution experimental design method for aircraft optimization design. And inserting the experimental design into the interval of the original sample and optimizing, thereby realizing the expansion of the sample and obtaining the expansion design with good performance. Because the recursive evolution sequence expansion method is adopted for the large sample experimental design, the sample amount of the optimized object expanded each time is small, and therefore the efficiency of the experimental design is improved.
Consider a typical aircraft design optimization problem whose objective function and constraint conditions are shown below:
in the formula (I), the compound is shown in the specification,for designing variables, the upper and lower bounds of the variable areAndwherein,,To design the dimensions of the variables.
And carrying out experimental design in the normalized design space to obtain uniformly distributed initial sample points for subsequent experiments or modeling, and fully revealing the influence of each experimental factor on an experimental result and the mutual relation among the factors while reducing experimental resources so as to guide the optimal design of the aircraft. The embodiment provides a recursive evolution experimental design method, which can obtain an initial sample matrix with better uniform performance with less calculation consumption, and with reference to fig. 1, the method specifically includes the following steps:
by randomLHDMaximum minimum distance for design variablesCriterion (Criterion) is an objective function, and an enhanced random evolution algorithm is adopted (ESEAlgorithm) to maximize the minimum distance between samples, resulting inUniformly distributed samples in a design space are used as first folding samplesSample matrixThe method comprises the following steps:
in the formula (I), the compound is shown in the specification,A 1representing a sample matrix generated by the optimal latin hypercube,x p d(+1)is shown aspThe first of +1 samplesdThe number of the design variables is one,ddimension, sample matrix, representing design variablesNumber of lines ofI.e. comprisep+ 1 sample points, thus naturally dividing the design domain of each dimension intoAnd (4) a plurality of intervals.
arbitrarily deleted sample matrixA 1A sample point ofTo obtain a matrixThe method comprises the following steps:
according toiDifference in value, matrixIn common withp+1 manifestation, evaluation of sample homogeneity after deletion, wherep+1 matricesTo select the one with the best uniformityAs an evolutionary designThe method comprises the following steps:
evolution designFor each column ofTo express, each column of the evolution design can pass through the corresponding transformation matrixAnd the first columnMultiplication results in:
in the formula (I), the compound is shown in the specification,designed for evolutionTo middleiTransformation matrices corresponding to columns, all transformation matricesOnce determined, the entire evolution designIs only related to the arrangement of the first column, and therefore only the first column of the evolutionary design is optimized, maintaining the transformation matrixAnd the whole evolution design can be optimized without change.
Step 5, designing evolution one by one based on row interval of sample matrixpUniformly inserting the sample points into the interval of the initial sample matrix to obtain an updated sample matrix;
step 6, judging whether the number of samples in the sample matrix is greater than or equal to the number of samples in the sample matrixmIf yes, entering step 7, otherwise, returning to step 5;
when the sample matrix isA 1Then, the steps 5-6 specifically include:
sample matrixA 1Includedp+1 samples, i.e. sample matrixA 1Is uniformly divided intopA matrix of intervals, samplesA 1All the intervals of (A) form (a)p×d) OfTest spaceB 1The method comprises the following steps:
in the formula (I), the compound is shown in the specification,b pd representing a sample matrixA 1To middledThe design variables arepExperimental space elements formed at intervals;
inserting the superposition relation of the evolution design based on the formula into the sample matrixA 1In (b), an overall matrix is obtainedA 1 B 1) The method comprises the following steps:
keeping the transformation relationship between each column of the evolutionary design and the first column unchanged with the overall matrix (A 1 B 1) Is/are as followsOptimizing the first row of the evolution design after the superposition by taking the criterion value as the objective function to obtain a sample matrix with excellent integral sample uniformity (A 1 A 2) The method comprises the following steps:
wherein the sample matrix isA 1 A 2) The newly added sample is the second folded sample setA 2;
Judging the sample matrix (A 1 A 2) Whether the number of samples in (1) is greater than or equal tomIf yes, go to step 7, otherwise return to step 5.
When the sample matrix is (A 1···A j-1) In the above-mentioned order, wherein,A j-1is shown asj-1-fold of the sample,j=3,4,…,K(ii) a For example, when the sample matrix is the above matrix (A 1 A 2) When the temperature of the water is higher than the set temperature,j=3;
for the firstjSample folding setA j By making inequality calculationsMinimum of establishmenttIs the current sample matrix (A 1···A j-1) The number of times each dimension of the design variable is evolved to be equally dividedtRepresenting the current sample matrix: (A 1···A j-1) Is divided intot×p) An interval, a sample matrix: (A 1···A j-1) All spaces will be formedtA (a)p×d) Open end of experimental spaceB 1,B 2,···,B t Is that:
order parameterThe evolution design of the next step is inserted intoAn experimental spaceB o The method comprises the following steps:
maintaining the transformation relationship between each row of the evolution design and the first row unchanged, and optimizing the first row of the evolution design after the superposition to obtain a new sample matrix (A 1···A j );
Judging the sample matrix (A 1···A j ) Whether the number of samples in (1) is greater than or equal tomIf yes, go to step 7, otherwise, makej=jAnd after +1, returning to the step 5.
Step 7, generating a sample set based on the samples in the sample matrix, and deleting (the sample set is farthest from the center of the design space) ((K·p+1-m) Obtaining all required sample points and outputting the sample points;
and 8, simulating the high-precision sample obtained by design, and guiding subsequent modeling by using an output result obtained by simulation.
The present embodiment will be further described with reference to specific examples.
Taking the design of the drag reduction rod of the aircraft as an example, an example is given. Referring to fig. 2-3, the drag reduction rod, as one of the passive drag reduction technologies, has the advantages of simple structure, good drag reduction effect and the like, and is widely applied to shock wave drag reduction of an aircraft in an actual engineering system. The resistance reducing effect of the resistance reducing rod is influenced by the physical dimension parameters including the top end radius of the resistance reducing rod, the rod length of the resistance reducing rod and the like.
First of all useOLHDGenerating an experimental design of 15 sample points, modeling 14 samples with the highest density points removed, testing the model by using the 14 samples obtained by the evolution of the initial experimental design, merging the samples used for testing into the initial samples to continue modeling under the condition that the prediction precision does not meet the requirement, evolving to obtain new 14 samples and continuing testing, and repeating the expansion of the samples and the testing of the model until the prediction precision of the model meets the design standard. The method comprises the following specific steps:
applications ofOLHDExperimental design for generating 15 sample pointsA 1;
For experimental designA 1Applications ofRELHDEvolution design for obtaining 14 sample points by using method;
Elimination of experimental design by krigingA 1Constructing a drag reduction rod resistance coefficient model by 14 sample points behind the highest density point, and testing the model by using an evolution design;
and judging whether the prediction precision of the model reaches the standard or not. If the resistance coefficient performance prediction model does not reach the standard, expanding the sample obtained by evolution into an experimental design, modeling again by using the expanded sample, continuously evolving to obtain 14 new sample points for retesting, judging program convergence if the resistance coefficient performance prediction model reaches the standard, and adding the test sample into the training sample to complete the final resistance coefficient performance prediction model construction of the drag reduction rod;
because the geometric shape of the drag reduction rod is an axisymmetric shape, the calculation efficiency can be improved by adopting the axisymmetric condition for calculation, and the axisymmetric condition is selected for numerical simulation.
Selected as the radius of the top end of the drag reduction rodRAnd drag reduction rod lengthLAs design input, resistance coefficient as output, boundary condition as pressure far field condition and wall surface no-slip heat insulation wall condition, gas model as complete gas model, airflow parameter as standard sea level atmospheric parameter, turbulence model as selectionThe model is simulated, and the value range of the design variable and other specific parameters are shown in table 1:
TABLE 1 resistance-reducing structural parameter table
The method of the embodiment is adopted to establish a drag reduction rod performance prediction model, and is firstly appliedOLHDGenerating an experimental design of 15 sample points, modeling 14 samples with the highest density points removed, testing the model by using 14 samples obtained by the evolution of the initial experimental design, merging the samples used for testing into the initial samples to continue modeling under the condition that the prediction precision does not meet the requirement, evolving to obtain new 14 samples and continuing testing, and repeating the expansion of the samples and the modelingAnd (4) checking the model until the prediction precision of the model meets the design standard. When a fifth group of test samples are obtained through evolution, the model precision is lower than 0.01, and the expected standard is achieved. By usingKrigingThe test results of the proxy models successively trained by the method are shown in fig. 4. With the gradual increase of training samples, the agent model reflects the real information of the model more and more, and the prediction precision of new samples is gradually improved. When the fifth group of evolution samples are applied for testing, the model error is lower than 0.01, and the model construction of drag reduction rod resistance coefficient prediction is completed.
The results of comparing the 70 sample points generated by the experimental design method with the running time of the enhanced random evolution algorithm under the same conditions and the filling performance of the generated experimental design space are shown in fig. 5. It can be seen from the figure that the spatial uniformity of the method is better than that of the method under the condition of generating two-dimensional 70 sample pointsESEThe method has far higher calculation efficiency and only needs 252msThe training can be completed, and 2141 is needed for enhancing the random evolution algorithmmsThe high efficiency and effectiveness of the method are shown.
The above description is only a preferred embodiment of the present invention, and is not intended to limit the scope of the present invention, and all modifications and equivalents of the present invention, which are made by the contents of the present specification and the accompanying drawings, or directly/indirectly applied to other related technical fields, are included in the scope of the present invention.
Claims (5)
1. A recursive arrangement evolution experiment design method for aircraft optimization design is characterized by comprising the following steps:
step 1, determining optimized design variables of the aircraft, and normalizing the design variables to [0,1 ]]Within a span, wherein the number of samples of the aircraft optimization demand ismA plurality of;
step 2, mixingmNumber of samples is evenly divided intoKIs folded intoA 1、A 2、···、A K Wherein each fold comprisespThe number of the samples is one,pis prepared from (a)m/K) Rounding upwards;
step 3, generating an initial sample through the optimal Latin hypercube to obtain the sample withpA sample matrix of +1 uniform sample points;
step 4, carrying out cyclic deletion operation on the sample points in the sample matrix, and selecting the sample points with optimal uniformity after the deletion operationpTaking each sample point as an evolution design;
step 5, uniformly inserting the evolution design into the interval of the initial sample matrix one by one based on the row interval of the sample matrix to obtain an updated sample matrix;
step 6, judging whether the number of samples in the sample matrix is greater than or equal to the number of samples in the sample matrixmIf yes, entering step 7, otherwise, returning to step 5;
step 7, generating a sample set based on the samples in the sample matrix, and deleting (the sample set is farthest from the center of the design space) ((K·p+1-m) Obtaining all required sample points and outputting the sample points;
and 8, simulating the high-precision sample obtained by design, and guiding subsequent modeling by using an output result obtained by simulation.
2. The design method for the recursive evolution experiment of the aircraft-oriented optimization design according to claim 1, wherein in step 3, the design method haspA sample matrix of +1 sample points, which is:
in the formula (I), the compound is shown in the specification,A 1representing a sample matrix generated by the optimal latin hypercube,x p d(+1)is shown aspThe first of +1 samplesdThe number of the design variables is one,drepresenting the dimensions of the design variables.
3. The design method of the recursive evolution experiment for the aircraft optimization design according to claim 2, wherein in step 4, the sample points in the sample matrix are cyclically deleted to selectWith optimum homogeneity after the deletion operationpEach sample point is used as an evolution design, and specifically comprises the following steps:
arbitrarily deleted sample matrixA 1A sample point ofTo obtain a matrixThe method comprises the following steps:
according toiDifference in value, matrixIn common withp+1 manifestation form, hereinp+1 matricesTo select the one with the best uniformityAs an evolutionary designThe method comprises the following steps:
4. the design method of recursive evolution experiment for aircraft optimization design according to claim 3, wherein the design method comprisesCharacterized in that when the sample matrix isA 1When the current is over;
the steps 5-6 specifically comprise:
sample matrixA 1Includedp+1 samples, i.e. sample matrixA 1Is uniformly divided intopA matrix of intervals, samplesA 1All the intervals of (A) form (a)p×d) Experimental space (2)B 1The method comprises the following steps:
in the formula (I), the compound is shown in the specification,b pd representing a sample matrixA 1To middledThe design variables arepExperimental space elements formed at intervals;
inserting the superposition relation of the evolution design based on the formula into the sample matrixA 1In (b), an overall matrix is obtainedA 1 B 1) The method comprises the following steps:
keeping the transformation relationship between each column of the evolutionary design and the first column unchanged with the overall matrix (A 1 B 1) Is/are as followsThe criterion value optimizes the first column of the post-stack evolution design for the objective function,obtaining a sample matrix having excellent uniformity of the entire sample: (A 1 A 2) The method comprises the following steps:
wherein the sample matrix isA 1 A 2) The newly added sample is the second folded sample setA 2;
Judging the sample matrix (A 1 A 2) Whether the number of samples in (1) is greater than or equal tomIf yes, go to step 7, otherwise return to step 5.
5. The design method of the recursive evolution experiment oriented to the optimization design of the aircraft according to claim 4, wherein when the sample matrix is (A)A 1···A j-1) In the above-mentioned order, wherein,A j-1is shown asj-1-fold of the sample,j=3,4,…,K;
the steps 5-6 are specifically as follows:
for the firstjSample folding setBy making inequality calculationsMinimum of establishmenttI.e. the current sample matrixThe number of times each dimension of the design variable is evolved to be equally dividedtRepresents the current sample matrixIs divided intot×p) An interval, a sample matrix: (A 1···A j-1) All the spacing blocksBecome intotA (a)p×d) Open end of experimental spaceB 1,B 2,···,B t Is that:
order parameterThe evolution design of the next step is inserted intoAn experimental spaceB o The method comprises the following steps:
maintaining the transformation relationship between each row of the evolution design and the first row unchanged, and optimizing the first row of the evolution design after the superposition to obtain a new sample matrix (A 1···A j );
Judging the sample matrix (A 1···A j ) Whether the number of samples in (1) is greater than or equal tomIf yes, go to step 7, otherwise, makej=jAnd after +1, returning to the step 5.
Priority Applications (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| CN202110856433.7A CN113312712B (en) | 2021-07-28 | 2021-07-28 | Recursive permutation evolution experimental design method for aircraft optimization design |
Applications Claiming Priority (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| CN202110856433.7A CN113312712B (en) | 2021-07-28 | 2021-07-28 | Recursive permutation evolution experimental design method for aircraft optimization design |
Publications (2)
| Publication Number | Publication Date |
|---|---|
| CN113312712A true CN113312712A (en) | 2021-08-27 |
| CN113312712B CN113312712B (en) | 2021-09-21 |
Family
ID=77381774
Family Applications (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| CN202110856433.7A Active CN113312712B (en) | 2021-07-28 | 2021-07-28 | Recursive permutation evolution experimental design method for aircraft optimization design |
Country Status (1)
| Country | Link |
|---|---|
| CN (1) | CN113312712B (en) |
Cited By (1)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN113823359A (en) * | 2021-09-18 | 2021-12-21 | 南京工业大学 | Method for optimizing casting cooling process parameters of aluminum alloy steering gear valve shell |
Citations (4)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US20060290696A1 (en) * | 2001-07-03 | 2006-12-28 | Pasternak Solutions Llc | Method and apparatus for implementing level of detail with ray tracing |
| CN103792850A (en) * | 2014-01-22 | 2014-05-14 | 中国电子科技集团公司第二十九研究所 | Method for establishing equivalent model of radar servo system |
| US20140372091A1 (en) * | 2013-06-14 | 2014-12-18 | Wallace LARIMORE | Method and system of dynamic model identification for monitoring and control of dynamic machines with variable structure or variable operation conditions |
| CN105653827A (en) * | 2016-03-17 | 2016-06-08 | 北京工业大学 | Method for designing Terminal sliding mode controller of hypersonic vehicle |
-
2021
- 2021-07-28 CN CN202110856433.7A patent/CN113312712B/en active Active
Patent Citations (4)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US20060290696A1 (en) * | 2001-07-03 | 2006-12-28 | Pasternak Solutions Llc | Method and apparatus for implementing level of detail with ray tracing |
| US20140372091A1 (en) * | 2013-06-14 | 2014-12-18 | Wallace LARIMORE | Method and system of dynamic model identification for monitoring and control of dynamic machines with variable structure or variable operation conditions |
| CN103792850A (en) * | 2014-01-22 | 2014-05-14 | 中国电子科技集团公司第二十九研究所 | Method for establishing equivalent model of radar servo system |
| CN105653827A (en) * | 2016-03-17 | 2016-06-08 | 北京工业大学 | Method for designing Terminal sliding mode controller of hypersonic vehicle |
Non-Patent Citations (2)
| Title |
|---|
| ZI-PENG WANG 等: "On Designing Sampled-Data Observer for Linear Time-Delay Distributed Parameter Systems", 《2018 37TH CHINESE CONTROL CONFERENCE (CCC)》 * |
| 杨希祥 等: "智能优化算法及其在飞行器优化设计领域的应用综述", 《宇航学报》 * |
Cited By (1)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN113823359A (en) * | 2021-09-18 | 2021-12-21 | 南京工业大学 | Method for optimizing casting cooling process parameters of aluminum alloy steering gear valve shell |
Also Published As
| Publication number | Publication date |
|---|---|
| CN113312712B (en) | 2021-09-21 |
Similar Documents
| Publication | Publication Date | Title |
|---|---|---|
| Tamayo et al. | Multilevel adaptive cross approximation (MLACA) | |
| Khatouri et al. | Metamodeling techniques for CPU-intensive simulation-based design optimization: a survey | |
| CN108121856A (en) | A kind of full flight domain aerocraft dynamic stability analysis method | |
| CN114036805B (en) | Forward modeling method, device, equipment and medium for three-dimensional steady-state heat conduction geothermal field | |
| CN115374673A (en) | Time domain heat conduction simulation method and storage medium | |
| CN107092710A (en) | A kind of method of the determination optimum structure size based on hypervolume iteration global optimization approach | |
| CN113806991A (en) | Engine combustion noise optimization prediction method and device and storage medium | |
| Hu | An adaptive finite volume method for 2D steady Euler equations with WENO reconstruction | |
| Klemetsdal et al. | Efficient reordered nonlinear Gauss–Seidel solvers with higher order for black-oil models | |
| CN114171127A (en) | Method for simulating supersonic combustion flow by constructing self-adaptive reaction mechanism | |
| Baranger et al. | Locally refined discrete velocity grids for deterministic rarefied flow simulations | |
| CN113312712A (en) | Recursive permutation evolution experimental design method for aircraft optimization design | |
| KR100957066B1 (en) | Method of nuclear reactor core analysis using characteristic of porous media | |
| Bonfiglioli et al. | The role of mesh generation, adaptation, and refinement on the computation of flows featuring strong shocks | |
| CN116049977A (en) | Parameter multi-objective optimization method for aero-engine combustion chamber | |
| Blonigan et al. | Multigrid‐in‐time for sensitivity analysis of chaotic dynamical systems | |
| CN107526869B (en) | Numerical method for reducing order of input/output window model of adaptive three-dimensional microwave tube based on function approximation | |
| Srinivasan et al. | An upwinded state approximate Riemann solver | |
| Amsallem et al. | Real-time solution of computational problems using databases of parametric linear reduced-order models with arbitrary underlying meshes | |
| CN114036806B (en) | Three-dimensional ground temperature field numerical simulation method based on heat conductivity anisotropic medium | |
| Wu et al. | Adaptive training of local reduced bases for unsteady incompressible Navier–Stokes flows | |
| Padovan et al. | Multi objective robust design optimization of airfoils in transonic field (MORDO) | |
| CN115935131A (en) | Pressure loss distortion multi-parameter optimization method for air intake system | |
| CN119989545B (en) | Parameter design method, system, medium and equipment of aircraft | |
| Choudhary et al. | Implementation and Assessment of a Residual-Based r-Adaptation Technique on Structured Meshes |
Legal Events
| Date | Code | Title | Description |
|---|---|---|---|
| PB01 | Publication | ||
| PB01 | Publication | ||
| SE01 | Entry into force of request for substantive examination | ||
| SE01 | Entry into force of request for substantive examination | ||
| GR01 | Patent grant | ||
| GR01 | Patent grant |