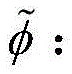CN110848166A - Axial flow compressor surge frequency prediction method - Google Patents
Axial flow compressor surge frequency prediction method Download PDFInfo
- Publication number
- CN110848166A CN110848166A CN201911106649.0A CN201911106649A CN110848166A CN 110848166 A CN110848166 A CN 110848166A CN 201911106649 A CN201911106649 A CN 201911106649A CN 110848166 A CN110848166 A CN 110848166A
- Authority
- CN
- China
- Prior art keywords
- compressor
- coefficient
- axial flow
- representing
- flow
- Prior art date
- Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
- Granted
Links
Images
Classifications
-
- F—MECHANICAL ENGINEERING; LIGHTING; HEATING; WEAPONS; BLASTING
- F04—POSITIVE - DISPLACEMENT MACHINES FOR LIQUIDS; PUMPS FOR LIQUIDS OR ELASTIC FLUIDS
- F04D—NON-POSITIVE-DISPLACEMENT PUMPS
- F04D27/00—Control, e.g. regulation, of pumps, pumping installations or pumping systems specially adapted for elastic fluids
- F04D27/001—Testing thereof; Determination or simulation of flow characteristics; Stall or surge detection, e.g. condition monitoring
-
- F—MECHANICAL ENGINEERING; LIGHTING; HEATING; WEAPONS; BLASTING
- F05—INDEXING SCHEMES RELATING TO ENGINES OR PUMPS IN VARIOUS SUBCLASSES OF CLASSES F01-F04
- F05D—INDEXING SCHEME FOR ASPECTS RELATING TO NON-POSITIVE-DISPLACEMENT MACHINES OR ENGINES, GAS-TURBINES OR JET-PROPULSION PLANTS
- F05D2260/00—Function
- F05D2260/81—Modelling or simulation
-
- F—MECHANICAL ENGINEERING; LIGHTING; HEATING; WEAPONS; BLASTING
- F05—INDEXING SCHEMES RELATING TO ENGINES OR PUMPS IN VARIOUS SUBCLASSES OF CLASSES F01-F04
- F05D—INDEXING SCHEME FOR ASPECTS RELATING TO NON-POSITIVE-DISPLACEMENT MACHINES OR ENGINES, GAS-TURBINES OR JET-PROPULSION PLANTS
- F05D2260/00—Function
- F05D2260/82—Forecasts
Landscapes
- Engineering & Computer Science (AREA)
- Mechanical Engineering (AREA)
- General Engineering & Computer Science (AREA)
- Control Of Positive-Displacement Air Blowers (AREA)
Abstract
The invention discloses a method for predicting the surge frequency of an axial flow compressor, which is used for solving the technical problem of poor practicability of the conventional method for measuring the surge frequency of the axial flow compressor. The technical scheme includes that physical and geometric modeling is firstly carried out on an experiment table of the axial flow compressor to obtain a conservation control equation of a corresponding model, a numerical method is used for solving, and a Fourier is used for analyzing a numerical result under a stall passing working condition, so that the surge frequency of the axial flow compressor is obtained. The simulation model of the axial flow compressor system is established, so that the construction of an experiment platform and a data acquisition system is avoided, the experiment data measurement process is converted into the process of obtaining parameter values through a numerical solution, then the numerical results are directly used for data analysis and processing, the surge frequency of the compressor is analyzed by Fourier transform, a large amount of labor and material cost is saved, and the practicability is good.
Description
Technical Field
The invention belongs to the field of gas turbine engines, and particularly relates to a method for predicting the surge frequency of an axial flow compressor.
Background
The document "fast fourier transform and wavelet transform analysis of compressor surge sound signals, energy technology, 2010, Vol31, No.3, p 125-128" discloses a method for analyzing and processing surge signal data obtained by experiments by using fast fourier transform and wavelet transform. The method is characterized in that on the basis of obtaining compressor surge data through experiments, after the frequency spectrum analysis is carried out on the test data through fast Fourier transform, the frequency of the compressor surge is proved to be below 50 hz. Then, the data is further processed by utilizing wavelet transformation, and a sound characteristic signal for representing that the compressor enters surge is obtained. The surge frequency obtained by the method is accurate and reliable, and a good theoretical basis and basis are provided for monitoring the state of the compressor and diagnosing faults by using sound signals in actual production. However, the method for obtaining the surge frequency in the document needs to design experiments in advance, a large number of sensors and equipment for acquiring signals, and depends on the experimental environment, and more importantly, the method has high cost of manpower and material resources and poor practicability.
Disclosure of Invention
In order to overcome the defect that the existing axial flow compressor surge frequency measuring method is poor in practicability, the invention provides a method for predicting the surge frequency of an axial flow compressor. The method comprises the steps of firstly, carrying out physical and geometric modeling on an experiment table of the axial flow compressor to obtain a conservation control equation of a corresponding model, solving by using a numerical method, and then analyzing a numerical result under a stall passing working condition by using Fourier, so as to obtain the surge frequency of the axial flow compressor. The simulation model of the axial flow compressor system is established, so that the construction of an experiment platform and a data acquisition system is avoided, the experiment data measurement process is converted into the process of obtaining parameter values through a numerical solution, then the numerical results are directly used for data analysis and processing, the surge frequency of the compressor is analyzed by Fourier transform, a large amount of labor and material cost is saved, and the practicability is good.
The technical scheme adopted by the invention for solving the technical problems is as follows: the method for predicting the surge frequency of the axial flow compressor is characterized by comprising the following steps of:
step one, establishing a physical and geometric model of an axial flow compressor;
measuring the geometric dimension of the actual axial flow compressor, replacing the compressor with a swash plate to generate pressure rise, replacing an inlet pipeline and an outlet pipeline of the compressor with a pipeline with a uniform section, simulating a backpressure environment by a gas collection cavity, controlling the flow by a throttle valve, and setting the Mach number of an inlet to obtain an axial flow compressor simulation model.
Step two, writing a control equation according to the established axial flow compressed air simulation model:
a. flow disturbances in the compressor;
pressure rise of a single blade row by unsteady flow:obtaining the pressure rise of the N-stage compressor as follows:then define the circumferential average of φ:here, the circumferential flow coefficient Φ and the tangential velocity coefficient h are represented as Φ (ξ) + g (ξ, θ), h ═ h (ξ, θ), where θ represents the circumferential angle, ξ represents the rotor rotation radian, Φ represents the axial flow coefficient, Φ represents the circumferential average of the axial flow coefficient, F (Φ) represents the axisymmetric steady-state performance of the blade row, τ represents the hysteresis constant, a ≡ R/(N τ U) represents the reciprocal of the blade passage time hysteresis parameter, U represents the rotation speed at the average radius, Δ P represents the outlet pressure minus the inlet pressure, h represents the circumferential velocity coefficient, and t represents time.
b. Flow disturbances in the inlet duct and the guide vanes;
introducing a velocity potentialAnd disturbance velocity potentialThen velocity potentialExpressed as:the pressure rise far upstream to the guide vane inlet at this time is expressed as:wherein P isTThe total pressure at the inlet is shown,the potential of the speed is represented by,representing the disturbance velocity potential, η axial position coordinates, ξ rotor radian, phi axial flow coefficient, phi circumferential average value of the axial flow coefficient, l1The inlet duct length is indicated.
c. Flow disturbances in the outlet duct and the outlet guide vanes;
definition of pressure coefficientThen at the downstream pipe outlet (η ═ l)E) Comprises the following steps:then introducing a parameter m to obtain the static pressure change in the outlet pipeline:wherein p issRepresenting the static pressure in the collecting chamber, p representing the static pressure in the outlet duct, lERepresenting the dimensionless length, l, of the downstream pipeTThe outlet duct length is indicated and m is the compressor duct flow parameter.
d. Static pressure rise to the tail end of the outlet of the compressor;
the static pressure rise from the inlet to the end of the outlet pipe is:
defining the effective length l of compressor and its upstream and downstream pipelinesCAnd a:due to the disturbance velocity potential at the upstream of the compressorSatisfies the laplace equation:then, when it is expanded into a fourier series and only the first order term is considered, there are:and introducing a variable Y:the total pressure rise was obtained as:
wherein p issRepresenting the static pressure in the gas-collecting chamber, pTRepresenting total inlet pressure, N representing compressor stage number, phi representing axial flow coefficient, phi representing circumferential average value of axial flow coefficient, lERepresenting the dimensionless length, l, of the downstream pipe1Inlet duct length, m representing a compressor duct flow parameter, a ≡ R/(Ntau U) representing the inverse of a vane passage time lag parameter, Y representing compressor inlet disturbance potential, KGThe inlet guide vane loss coefficient is expressed.
e. Flow in the gas collection cavity and the exhaust valve pipeline;
the flow equation in the gas collection cavity and the exhaust pipeline is as follows:
and using parabolic equationsTo represent the pressure drop characteristic of the throttle valve. The axial flow coefficient phi of the downstream pipeTExpressed as:then, integrating in the circumferential direction:wherein FTRepresenting a function of the throttle characteristic, [ phi ]TRepresents the flow coefficient of the throttle pipe,/cThe effective length of the pipeline upstream and downstream of the compressor is shown, and psi represents the total static pressure rise coefficient.
f. A total set of governing equations;
and (3) the equations are arranged to obtain a complete control equation set of the compression system model:
and (3) carrying out order reduction processing on the equation set by using a Galerkin method, namely carrying out Fourier expansion on the variable Y, and replacing the variable Y by using a first order term to obtain a 1-order differential equation set related to time:
where Ψ represents the total static pressure rise coefficient, ΦTExpressing the flow coefficient of the throttling pipeline, Y expressing the disturbance potential of the inlet of the compressor, H and W expressing the relevant parameters of the axisymmetric characteristic line, FTTo representA throttling characteristic function, phi represents the axial flow coefficient of the compressor, J represents the square of the circumferential amplitude of the axial flow coefficient, lcIndicating the effective length of the upstream and downstream conduits of the compressor, psic0The total static pressure rise coefficient under zero flow conditions is shown.
Solving a control equation set by utilizing a four-order Runge Kutta method;
selecting a three-dimensional axisymmetric characteristic line as an initial characteristic line of the compressor, and then solving a control equation set of a simulation model of the compression system by using a four-order R-K numerical method, wherein the formula is as follows:
after solving the control equation set, the B parameter is continuously changed until the critical B parameter is found. And then selecting a plurality of different parameters B on the side larger than the critical parameter B, and calculating the change condition of the flow coefficient or the total static pressure rise coefficient of the compressor along with time under the surge working condition.
Step four, calculating surge frequency;
and D, processing the change data of the compressor flow coefficient or the total static pressure rise coefficient along with time under the surge working conditions corresponding to the different B parameters obtained in the step three by utilizing discrete Fourier transform to obtain the surge frequency under the different B parameters.
The invention has the beneficial effects that: the method comprises the steps of firstly, carrying out physical and geometric modeling on an experiment table of the axial flow compressor to obtain a conservation control equation of a corresponding model, solving by using a numerical method, and then analyzing a numerical result under a stall passing condition by using Fourier, so as to obtain the surge frequency of the axial flow compressor. The simulation model of the axial flow compressor system is established, so that the construction of an experiment platform and a data acquisition system is avoided, the experiment data measurement process is converted into the process of obtaining parameter values through a numerical solution, then the numerical results are directly used for data analysis and processing, the surge frequency of the compressor is analyzed by Fourier transform, a large amount of labor and material cost is saved, and the practicability is good.
The present invention will be described in detail below with reference to the accompanying drawings and specific embodiments.
Drawings
FIG. 1 is a schematic view of an axial flow compressor experimental bench for the method of the present invention.
Fig. 2 is a schematic diagram of a physical and geometric model of the axial flow compression system constructed according to fig. 1.
Fig. 3 is a graph of the total static coefficient of the compressor over time for different B parameters calculated according to the simulation model of the compression system shown in fig. 2.
Fig. 4 is a graphical representation of frequency results after discrete fourier transformation from the data of fig. 3.
Detailed Description
Reference is made to fig. 1-4. The method for predicting the surge frequency of the axial flow compressor comprises the following specific steps:
1. establishing a physical and geometric model of the axial flow compressor;
the geometric dimensions of an actual axial flow compressor are measured firstly, and comprise the length of an inlet and outlet pipeline, the section area, the length-diameter ratio of the compressor, the volume of a gas collection cavity and the like, and then the geometric dimensions are simplified into a compression system model, namely a swash plate is used for replacing the compressor to generate pressure rise, the uniform-section pipeline is used for replacing the inlet and outlet pipeline of the compressor, a large gas collection cavity is used for simulating a backpressure environment, and a throttle valve is used for controlling the flow. Then, assuming that the mach number at the inlet is low and the gas in the compressor duct is incompressible, the process can be summarized as a simulation model from the actual compression system of fig. 1 to the compression system of fig. 2.
b) Column writing a model control equation set;
after a compression system model is established, a control equation set is established according to the Moore-Greitzer theory. The main process is as follows:
① flow disturbances in the compressor;
first, all parameters are dimensionless to obtain a tangential coordinate θ, an axial coordinate η, and a dimensionless time coordinate ξ.
In which there is also a non-stationarity between the individual rotor and stator, it can be expressed as:
then, the pressure rise of the N-stage compressor under the unsteady condition can be obtained as follows:
next, the circumferential average of φ is defined as:
the circumferential flow coefficient phi and the tangential velocity coefficient h can be expressed as phi (ξ) + g (ξ, theta), h (ξ, theta), where theta represents the circumferential angle, η represents the axial coordinate value, ξ represents the rotor turning camber, phi represents the axial flow coefficient, phi represents the circumferential average of the axial flow coefficient, F (phi) represents the axisymmetric steady-state performance of the blade row, tau represents the hysteresis constant, a ≡ R/(N tau U) represents the inverse of the blade passage time lag parameter, U represents the rotational speed at the mean radius, deltap represents the port pressure minus the inlet pressure, and h represents the circumferential velocity coefficient.
② flow disturbances within the inlet duct and vanes;
the pressure difference between the inlet and the outlet of the guide vane can be expressed as:because the upstream pipeline of the inlet guide vane is in non-rotational flow, the velocity potential is introducedFrom the far upstream integration to the director inlet, one then obtains, according to bernoulli's equation:
introducing disturbance velocity potentialThe original velocity potential may then be expressed as The pressure rise far upstream to the guide vane inlet at this time can be expressed as:
wherein P isTThe total pressure at the inlet is shown,the potential of the speed is represented by,representing the disturbance velocity potential,/1Inlet duct length.
③ flow disturbances within the outlet duct and outlet guide vanes;
definition of pressure coefficientThen at the downstream pipe outlet (η ═ l)E) Comprises the following steps:then introducing a parameter m to obtain the static pressure change in the outlet pipeline:wherein p issRepresenting the static pressure in the collecting chamber, p representing the static pressure in the outlet duct, lERepresenting the dimensionless length, l, of the downstream pipeTThe outlet duct length is indicated and m is the compressor duct flow parameter.
④ static pressure rise to the compressor outlet end;
far forward atmospheric conditions p from the system inletTTo the end of the outlet duct there may be a variation in static pressure in the circumferential direction, while the flow in the collecting volume and the downstream exhaust throttle valve duct contains only axial disturbances. At this time, the static pressure rise from the inlet to the end of the outlet pipe can be expressed as:
defining the effective length l of compressor and its upstream and downstream pipelinesC:If the flow dynamic response in the compressor is considered to be lagged to be pure inertia, then:wherein L isRIs the blade row axial length, k is the coefficient that accounts for the blade row clearance effect, and γ is the effective stagger angle of the blade row. At this point, the total pressure rise can be written as:
disturbance velocity potential upstream of compressorSatisfies the laplace equation:and then expanded into a fourier series. When only the first order term is considered, there are:introducing a variable Y:then there are:
the variable Y satisfies at this time: h is Yθ;g=-YθθY (ξ, θ +2 pi) ═ Y (ξ, θ) andwherein N represents the compressor stage number, Y represents the compressor inlet disturbance potential, KGThe inlet guide vane loss coefficient is expressed.
⑤ flow in the plenum and exhaust valve conduit;
the flow in the gas collection cavity and the exhaust pipeline is one-dimensional unsteady flow, and the control equation is as follows:
wherein, FT(ΦT) For the pressure drop characteristic of the throttle valve, a parabolic equation is used for expression, namely:at this time, the axial flow coefficient phi of the downstream pipelineTCan be expressed as:integration in the circumferential direction using the properties of Y yields:wherein FTRepresenting a function of the throttle characteristic, [ phi ]TRepresents the flow coefficient of the throttle pipe,/cThe effective length of the pipeline upstream and downstream of the compressor is shown, and psi represents the total static pressure rise coefficient.
⑥ general control equations;
to this end, the complete control equation set for the compression system model described above may be written:
the system of equations is of order 3 for angle and 1 for time and is not easily solved. Then, using a galileo method to perform order reduction processing on the equation set (performing fourier expansion on the variable Y and using a first-order term for substitution), obtaining (phi represents a circumferential average flow coefficient, psi represents a total static pressure rise coefficient, and J represents the square of circumferential disturbance amplitude):
wherein H and W represent parameters related to axisymmetric characteristic line, J represents square of circumferential amplitude of axial flow coefficient, ψc0Representing the total static pressure rise coefficient at zero flow.
c) Solving a control equation set by utilizing a four-order Runge Kutta method;
in order to solve the control equation system, an initial value and an initial characteristic line of the compressor are required to be given. From Koff's studies, it is known that the three-fold axisymmetric characteristic line can be used to better describe the pressure rise characteristics of the compressor over the entire flow range. Therefore, the model selects the cubic axisymmetric characteristic line as the initial characteristic line.
After part of initial values and initial characteristic lines of the compressor are given, solving a control equation set of a simulation model of the compression system by adopting a four-order R-K numerical method, wherein the formula is as follows:
after solving the control equation set, the critical B parameter can be found by continuously changing the B parameter. And then, the B parameter is larger than the critical B parameter, and the flow coefficient, the total static pressure rise coefficient and the change situation of the working point along with the time of the compressor under the surge working condition under different B parameters are calculated (see figure 3).
d) Calculating the surge frequency;
and analyzing the change process of the flow coefficient of the compressor or the total static pressure rise coefficient of the compressor along with time under the different B parameters obtained in the fourth step by utilizing Fourier analysis, obtaining the corresponding surge frequency under the B parameters, and providing a surge frequency range. Here, it is necessary to use a fourier method to analyze discrete data points, and the specific method is as follows:i.e. transforming the discrete points in the time domain to the frequency domain, thereby obtaining the frequency, which is the surge frequency.
e) Error analysis
The calculated surge frequency is compared with the surge frequency obtained from the actual compressor experimental data and a prediction error is given (see fig. 4).
Claims (1)
1. The method for predicting the surge frequency of the axial flow compressor is characterized by comprising the following steps of:
step one, establishing a physical and geometric model of an axial flow compressor;
measuring the geometric dimension of an actual axial flow compressor, replacing the compressor with a swash plate to generate pressure rise, replacing an inlet pipeline and an outlet pipeline of the compressor with a pipeline with a uniform section, simulating a backpressure environment by a gas collection cavity, controlling the flow by a throttle valve, and setting the Mach number of an inlet to obtain an axial flow compressor simulation model;
step two, writing a control equation according to the established axial flow compressed air simulation model:
a. flow disturbances in the compressor;
pressure rise of a single blade row by unsteady flow:obtaining the pressure rise of the N-stage compressor as follows:then define the circumferential average of φ:at this time, the circumferential flow coefficient phi and the tangential velocity coefficient h are expressed as phi (ξ) + g (ξ, theta), h as h (ξ, theta), where theta represents the circumferential angle, ξ represents the rotor turning radian, phi represents the axial flow coefficient, phi represents the circumferential average of the axial flow coefficient, F (phi) represents the axisymmetric steady-state performance of the blade row, tau represents the hysteresis constant, a ≡ R/(Ntau U) represents the reciprocal of the blade passage time hysteresis parameter, U represents the rotation speed at the average radius, deltaP represents the outlet pressure minus the inlet pressure, h represents the circumferential velocity coefficient, and t represents the time;
b. flow disturbances in the inlet duct and the guide vanes;
introducing a velocity potentialAnd disturbance velocity potentialThen velocity potentialExpressed as:the pressure rise far upstream to the guide vane inlet at this time is expressed as:wherein P isTThe total pressure at the inlet is shown,the potential of the speed is represented by,representing the disturbance velocity potential, η axial position coordinates, ξ rotor radian, phi axial flow coefficient, phi circumferential average value of the axial flow coefficient, l1Represents the inlet duct length;
c. flow disturbances in the outlet duct and the outlet guide vanes;
definition of pressure coefficientThen at the downstream pipe outlet (η ═ l)E) Comprises the following steps:then introducing a parameter m to obtain the static pressure change in the outlet pipeline:wherein p issRepresenting the static pressure in the collecting chamber, p representing the static pressure in the outlet duct, lERepresenting the dimensionless length, l, of the downstream pipeTRepresenting the length of an outlet pipeline, and m represents a compressor pipeline flow parameter;
d. static pressure rise to the tail end of the outlet of the compressor;
the static pressure rise from the inlet to the end of the outlet pipe is:
defining the effective length l of compressor and its upstream and downstream pipelinesCAnd a:due to the disturbance velocity potential at the upstream of the compressorSatisfies the laplace equation:then, when it is expanded into a fourier series and only the first order term is considered, there are:and introducing a variable Y:the total pressure rise was obtained as:
wherein p issRepresenting the static pressure in the gas-collecting chamber, pTRepresenting total inlet pressure, N representing compressor stage number, phi representing axial flow coefficient, phi representing circumferential average value of axial flow coefficient, lERepresenting the dimensionless length, l, of the downstream pipe1Inlet duct length, m representing a compressor duct flow parameter, a ≡ R/(Ntau U) representing the inverse of a vane passage time lag parameter, Y representing compressor inlet disturbance potential, KGRepresenting the inlet guide vane loss coefficient;
e. flow in the gas collection cavity and the exhaust valve pipeline;
the flow equation in the gas collection cavity and the exhaust pipeline is as follows:
and isUsing parabolic equationsTo represent the pressure drop characteristic of the throttle valve; the axial flow coefficient phi of the downstream pipeTExpressed as:then, integrating in the circumferential direction:wherein FTRepresenting a function of the throttle characteristic, [ phi ]TRepresents the flow coefficient of the throttle pipe,/cRepresenting the effective length of an upstream pipeline and a downstream pipeline of the compressor, and psi represents a total static pressure rise coefficient;
f. a total set of governing equations;
and (3) the equations are arranged to obtain a complete control equation set of the compression system model:
and (3) carrying out order reduction processing on the equation set by using a Galerkin method, namely carrying out Fourier expansion on the variable Y, and replacing the variable Y by using a first order term to obtain a 1-order differential equation set related to time:
where Ψ represents the total static pressure rise coefficient, ΦTExpressing the flow coefficient of the throttling pipeline, Y expressing the disturbance potential of the inlet of the compressor, H and W expressing the relevant parameters of the axisymmetric characteristic line, FTExpressing a throttling characteristic function, phi expressing an axial flow coefficient of the compressor, J expressing the square of the circumferential amplitude of the axial flow coefficient, lcIndicating the effective length of the upstream and downstream conduits of the compressor, psic0Represents the total static pressure rise coefficient under the condition of zero flow;
solving a control equation set by utilizing a four-order Runge Kutta method;
selecting a three-dimensional axisymmetric characteristic line as an initial characteristic line of the compressor, and then solving a control equation set of a simulation model of the compression system by using a four-order R-K numerical method, wherein the formula is as follows:
continuously changing the B parameter until finding out a critical B parameter after solving the control equation set; then selecting a plurality of different parameters B on one side larger than the critical parameter B, and calculating the change condition of the flow coefficient or the total static pressure rise coefficient of the compressor along with time under the surge working condition;
step four, calculating surge frequency;
and D, processing the change data of the compressor flow coefficient or the total static pressure rise coefficient along with time under the surge working conditions corresponding to the different B parameters obtained in the step three by utilizing discrete Fourier transform to obtain the surge frequency under the different B parameters.
Priority Applications (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| CN201911106649.0A CN110848166B (en) | 2019-11-13 | 2019-11-13 | Axial flow compressor surge frequency prediction method |
Applications Claiming Priority (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| CN201911106649.0A CN110848166B (en) | 2019-11-13 | 2019-11-13 | Axial flow compressor surge frequency prediction method |
Publications (2)
| Publication Number | Publication Date |
|---|---|
| CN110848166A true CN110848166A (en) | 2020-02-28 |
| CN110848166B CN110848166B (en) | 2021-05-07 |
Family
ID=69600121
Family Applications (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| CN201911106649.0A Active CN110848166B (en) | 2019-11-13 | 2019-11-13 | Axial flow compressor surge frequency prediction method |
Country Status (1)
| Country | Link |
|---|---|
| CN (1) | CN110848166B (en) |
Cited By (7)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN111473002A (en) * | 2020-04-30 | 2020-07-31 | 山东恒洋风机有限公司 | Air-cooled mining axial fan of low noise device |
| CN112001128A (en) * | 2020-06-10 | 2020-11-27 | 大连理工大学 | Axial flow compressor stall surge prediction method based on deep learning |
| CN113591223A (en) * | 2021-08-09 | 2021-11-02 | 同济大学 | Surging boundary prediction method of centrifugal compression system for fuel cell vehicle |
| CN113688510A (en) * | 2021-08-09 | 2021-11-23 | 同济大学 | Surging prediction method of centrifugal compression system for fuel cell vehicle |
| CN114112176A (en) * | 2021-11-10 | 2022-03-01 | 中国航发沈阳发动机研究所 | External pipeline design method for connecting surge differential pressure or pressure sensor |
| CN114962318A (en) * | 2022-05-26 | 2022-08-30 | 东北大学 | Compressor surge control method and device, storage medium and computer equipment |
| CN118466210A (en) * | 2024-05-28 | 2024-08-09 | 大连理工大学 | Active stable control method for aviation compressor based on disturbance observation and compensation |
Citations (7)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| JPS57129297A (en) * | 1981-02-02 | 1982-08-11 | Hitachi Ltd | Stall predicting and controlling apparatus for axial- flow compressor |
| US6098010A (en) * | 1997-11-20 | 2000-08-01 | The Regents Of The University Of California | Method and apparatus for predicting and stabilizing compressor stall |
| CN104239614A (en) * | 2014-09-01 | 2014-12-24 | 西北工业大学 | Method for simulating aerodynamic instability signal of compressor |
| CN105298889A (en) * | 2015-09-24 | 2016-02-03 | 西北工业大学 | Gas compressor surge detection method |
| CN107165850A (en) * | 2017-06-27 | 2017-09-15 | 西北工业大学 | A kind of rotating stall of axial flow compressor method for early warning recognized based on frequency domain hump |
| CN107202028A (en) * | 2017-05-31 | 2017-09-26 | 北京理工大学 | A kind of turbocharger centrifugal compressor surge recognition methods |
| CN110162858A (en) * | 2019-05-14 | 2019-08-23 | 中国科学院工程热物理研究所 | Compressor Stability prediction technique |
-
2019
- 2019-11-13 CN CN201911106649.0A patent/CN110848166B/en active Active
Patent Citations (7)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| JPS57129297A (en) * | 1981-02-02 | 1982-08-11 | Hitachi Ltd | Stall predicting and controlling apparatus for axial- flow compressor |
| US6098010A (en) * | 1997-11-20 | 2000-08-01 | The Regents Of The University Of California | Method and apparatus for predicting and stabilizing compressor stall |
| CN104239614A (en) * | 2014-09-01 | 2014-12-24 | 西北工业大学 | Method for simulating aerodynamic instability signal of compressor |
| CN105298889A (en) * | 2015-09-24 | 2016-02-03 | 西北工业大学 | Gas compressor surge detection method |
| CN107202028A (en) * | 2017-05-31 | 2017-09-26 | 北京理工大学 | A kind of turbocharger centrifugal compressor surge recognition methods |
| CN107165850A (en) * | 2017-06-27 | 2017-09-15 | 西北工业大学 | A kind of rotating stall of axial flow compressor method for early warning recognized based on frequency domain hump |
| CN110162858A (en) * | 2019-05-14 | 2019-08-23 | 中国科学院工程热物理研究所 | Compressor Stability prediction technique |
Cited By (13)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN111473002A (en) * | 2020-04-30 | 2020-07-31 | 山东恒洋风机有限公司 | Air-cooled mining axial fan of low noise device |
| WO2021248746A1 (en) * | 2020-06-10 | 2021-12-16 | 大连理工大学 | Axial flow compressor stall and surge prediction method based on deep learning |
| CN112001128A (en) * | 2020-06-10 | 2020-11-27 | 大连理工大学 | Axial flow compressor stall surge prediction method based on deep learning |
| CN112001128B (en) * | 2020-06-10 | 2022-05-10 | 大连理工大学 | Axial flow compressor stall surge prediction method based on deep learning |
| CN113688510A (en) * | 2021-08-09 | 2021-11-23 | 同济大学 | Surging prediction method of centrifugal compression system for fuel cell vehicle |
| CN113591223A (en) * | 2021-08-09 | 2021-11-02 | 同济大学 | Surging boundary prediction method of centrifugal compression system for fuel cell vehicle |
| CN113591223B (en) * | 2021-08-09 | 2024-01-23 | 同济大学 | Surge boundary prediction method of centrifugal compression system for fuel cell vehicle |
| CN113688510B (en) * | 2021-08-09 | 2024-02-27 | 同济大学 | Surge prediction method of centrifugal compression system for fuel cell vehicle |
| CN114112176A (en) * | 2021-11-10 | 2022-03-01 | 中国航发沈阳发动机研究所 | External pipeline design method for connecting surge differential pressure or pressure sensor |
| CN114112176B (en) * | 2021-11-10 | 2023-09-22 | 中国航发沈阳发动机研究所 | Design method of external pipeline connected with surge pressure difference or pressure sensor |
| CN114962318A (en) * | 2022-05-26 | 2022-08-30 | 东北大学 | Compressor surge control method and device, storage medium and computer equipment |
| CN118466210A (en) * | 2024-05-28 | 2024-08-09 | 大连理工大学 | Active stable control method for aviation compressor based on disturbance observation and compensation |
| CN118466210B (en) * | 2024-05-28 | 2024-10-25 | 大连理工大学 | Active stable control method for aviation compressor based on disturbance observation and compensation |
Also Published As
| Publication number | Publication date |
|---|---|
| CN110848166B (en) | 2021-05-07 |
Similar Documents
| Publication | Publication Date | Title |
|---|---|---|
| CN110848166B (en) | Axial flow compressor surge frequency prediction method | |
| CN101375293A (en) | Apparatus and method for compressor and turbine performance simulation | |
| CN111503025B (en) | Low-pressure-ratio axial flow compressor model level performance calculation method | |
| CN109409016B (en) | Visualization method for unsteady flow of aero-engine compressor | |
| CN115014690B (en) | Wind tunnel test method for transient aerodynamic characteristics of continuous variable flow of air inlet channel | |
| CN113915156B (en) | Compressor surge fault detection method based on diesel engine supercharger transient model | |
| CN112149233B (en) | Echo state network-based aeroengine dynamic thrust estimation method | |
| CN111079920B (en) | Prediction method for flow non-uniformity coefficient of turbine gas collection cavity outlet | |
| Kulkarni et al. | Vibratory response characterization of a radial turbine wheel for automotive turbocharger application | |
| Cravero et al. | Numerical prediction of tonal noise in centrifugal blowers | |
| Poensgen et al. | Three-Dimensional Wake Decay Inside of a Compressor Cascade and Its Influence on the Downstream Unsteady Flow Field: Part I—Wake Decay Characteristics in the Flow Passage | |
| CN113188805A (en) | Noise simulation test device and test analysis method for supercharger | |
| CN206270056U (en) | A kind of silencer transmission loss test system for aerodynamic noise | |
| Yang et al. | Effect of different geometrical inlet pipes on a high speed centrifugal compressor | |
| CN110146267B (en) | Method for detecting flutter of valve plate of totally-enclosed refrigeration compressor | |
| CN113158592A (en) | Method for calculating air flow pulsation of pipeline of screw compressor | |
| CN114645858A (en) | Centrifugal compressor performance test bench device under variable working condition of engine | |
| CN114077775B (en) | Dynamic pressure intelligent measurement method for aeroengine | |
| Montenegro et al. | A quasi 3D approach for the modelling of an automotive turbocharger’s compressor | |
| CN116384010B (en) | Engine bench fan rotor axial force evaluation method capable of being corrected in real time | |
| CN112503018A (en) | One-dimensional over-stall performance analysis method for axial flow compression system | |
| Berdanier et al. | Quantifying Blockage in a Multistage Compressor for Different Tip Clearances Using Steady and Unsteady Pressure Measurements | |
| CN214277396U (en) | Noise simulation testing device for supercharger | |
| CN211144878U (en) | End face nozzle for axial flow compressor model level flow measurement | |
| Methling et al. | The Pre‐Stall Behavior of a 4‐Stage Transonic Compressor and Stall Monitoring Based on Artificial Neural Networks |
Legal Events
| Date | Code | Title | Description |
|---|---|---|---|
| PB01 | Publication | ||
| PB01 | Publication | ||
| SE01 | Entry into force of request for substantive examination | ||
| SE01 | Entry into force of request for substantive examination | ||
| GR01 | Patent grant | ||
| GR01 | Patent grant |