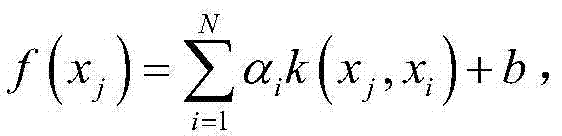CN103577690A - Sparse nonparametric body area channel probability representation method - Google Patents

Abstract

A sparse non-parametric body domain channel probability characterization method, comprising the following steps: S1 adopts the electromagnetic wave transceiver in the body area network to collect data; S2 constructs an empirical distribution function, and solves the empirical distribution function through a step function; S3 uses the empirical distribution function Myopia density function, and construct regression function; S4 solve regression coefficient by linear programming; S5 obtain corresponding probability function by deriving regression function; S6 evaluate and analyze the obtained sparse non-parametric probability model. The characterization model proposed by the present invention is not restricted by specific propagation situations, and is more suitable for wireless communication in the body area network due to its non-parametric characteristics. It overcomes the problem that previous models have strict requirements on sample size. By controlling the number of support vectors in the regression process, the coefficients of a large number of linear combinations are zero, and the "sparseness" of regression coefficients is realized.

Description

A kind of sparse nonparametric body area channel probability characterizing method

Technical field

The invention belongs to radio wave propagation technical field, relate to the probability characterizing method based on finite sample of Fdtd Method technology and channel characterization method, particularly body area channel.

Background technology

Statistical model for radio wave propagation, its important component part is exactly the sign of probability, in many communication environments, probability is all used as the important means that characterizes radio wave propagation, if terrestrial environment is (referring to Matthias Patzold, Ulrich Killat, and Frank Laue, " A Deterministic Digital Simulation Model for Suzuki Processes with Application to a Shadowed Rayleigh Land Mobile Radio Channel, " IEEE Transactions on Vehicular Technology, Vol.45, No.2.pp.318-331, 1996.), mobile satellite communication (referring to: Chun Loo, " A Statistical Model for a Land Mobile Satellite Link, " IEEE Transactions on Vehicular Technology, Vol.34, No.3.pp.122-127, 1985.), indoor environment (referring to: Adel A.M.Saleh, and Reinaldo A.Valenzuela, " A Statistical Model for Indoor Multipath Propagation, " IEEE Journal on Selected Areas in Communications, Vol.5, No.2, pp.128-137, 1987.), outdoor communication environments (referring to: Klaus Ingemann Pedersen, Preben E.Mogensen, and Bernard H.Fleury, " A Stochastic Model of the Temporal and Azimuthal Dispersion Seen at the Base Station in Outdoor Propagation Environments, " IEEE Transactions on Vehicular Technology, Vol.49, No.2.pp.437-447, 2000.), digital mobile communication environments (referring to: Tor Aulin, " Characteristics of a Digital Mobile Radio Channel, " IEEE Transactions on Vehicular Technology, Vol.30, No.2.pp.45-53, 1981.), multi-user's mobile circumstances (referring to: Jean-Paul M.G.Linnartz, " Exact Analysis of the Outage Probability in Multiple-User Mobile Radio, " IEEE Transactions on Communications, Vol.40, No.1, pp.20-23, 1992.), Nakagami decline communication environments etc. (referring to: Valentine A.Aalo, " Performance of Maximal-Ratio Diversity Systems in a Correlated Nakagami-Fading Environment, " IEEE Transactions on Communications, Vol.43, No.8, pp.2360-2369, 1995.).In recent years, body centre's radio communication has worldwide caused widely to be paid close attention to, and wherein the sign of body centre's radio wave propagation is important core content.In body centre's communication, probability function can be used to characterize communication mode (referring to Simon L.Cotton, Gareth A.Conway, and William G.Scanlon, " A Time-Domain Approach to the Analysis and Modeling of On-Body Propagation Characteristics Using Synchronized Measurements at2.45GHz, " IEEE Transactions on Antennas and Propagation, Vol.57, No.4, pp.943-955,2009.), simultaneously, also there is scholar to characterize the ultra-wideband channel of body surface, and reach a conclusion: Nakagami distributes and can simulate well root mean square and postpone (referring to Andrea Sani, Akram Alomainy, George Palikaras, Yuriy Nechayev, Yang Hao, Clive Parini, and Peter S.Hall, " Experimental Characterization of UWB On-Body Radio Channel in Indoor Environment Considering Different Antennas, " IEEE Transactions on Antennas and Propagation, Vol.58, No.1, pp.238-241, 2010.).It should be noted that for other communication environments, parameter probabilistic approximation is to propagate the core methed characterizing, but, for the situation of body centre, due to the existence of human body, the rationality of this propagation representation pattern is to be worth discussion, and this problem is seldom concerned.Previously in document, mentioning supervision parameter estimation and semi-supervised parameter estimation is the main method that characterizes other environment, even for the situation on body surface, also used parameter estimation (referring to Andrea Sani, Akram Alomainy, George Palikaras, Yuriy Nechayev, Yang Hao, Clive Parini, and Peter S.Hall, " Experimental Characterization of UWB On-Body Radio Channel in Indoor Environment Considering Different Antennas, " IEEE Transactions on Antennas and Propagation, Vol.58, No.1, pp.238-241, 2010.).In parameter estimation, first suppose a special probability model, then, by optimizing a large amount of parameters, carry out this model of matching.But when radio wave propagation occurs in health around time, not having ripe parameter probability model can reference, therefore, need to introduce nonparametric probability model.In non-parametric estmation, do not suppose special functional form, probability is determined by data itself completely.From above definition, we can see, nonparametric probability model is the actual conditions that meet body centre's radio communication, and reason is that the channel in this communication environments is often subject to posture, the impact of individual difference etc.The basis of nonparametric probability is proposed (referring to E.Fix by the people such as Fix, and J.L.Hodges, " Discriminatory analysis; nonparametric discrimination, " U.S.Air Force School of Aviation Medicine, Randolph Field, Contract, AF-41-(128)-31,1951.), their result based on concept be continuity point density function around can by this point around among a small circle interior discrete point estimate.Although nonparametric probability estimate has made some progress at present, if Density Estimator is (referring to Rosenblatt.M, " Remarks on Some Nonparametric Estimates of a Density Function, " The Annals of Mathematical Statistics, Vol.27, No.3, pp.832-837, 1956.) and K nearest-neighbors method (referring to D.O.Loftsgaarden, and C.P.Quesenberry, " nonparametric estimate of a multivariate density function, " Annals of Mathematical Statistics, Vol.36, No.3, pp.1049-1051, 1965.) etc.But these two kinds of methods need a large amount of samples to maintain the needs of precision, and in fact in body centre's situation, only can obtain limited sample.Under this background, Weston etc. (referring to: J.Weston, A.Gammerman, M.Stitson, V.Vapnik, V.Vovk, and C.Watkins, " Support vector density estimation, " Advances in Kernel Methods-Support Vector Learning, B.

c.Burges, and A.Smola, Eds.Cambridge, MA:MIT Press, 1999.) propose support vector technology and can solve linear programming equation, and can be applied in probability problem, like this, required sample size can greatly reduce.

Summary of the invention

The object of the invention is to overcome the deficiency that in existing body area network, channel probability model relies on existing parameter model and is difficult to promote, in conjunction with the radio wave propagation theory of representation in body area network, utilize kernel function combination to approach the cumulative distribution function of empirical distribution function, utilize on this basis linear programming for solution regression coefficient, finally by differentiate, obtain having the nonparametric probability model of coefficient feature.

Concrete, propose the present invention and propose a kind of sparse nonparametric body area channel probability characterizing method, comprise the following steps:

S1 data acquisition step: adopt the electromagnetic wave transceiver image data in body area network;

S2 builds empirical distribution function, and solves empirical distribution function by step function;

S3 use experience distribution function approximate densities function, and build regression function;

S4 is by linear programming for solution regression coefficient;

S5 is by regression function, differentiate obtains corresponding probability function;

S6 assesses and analyzes the sparse nonparametric probability model obtaining.

On the basis of technique scheme, described S2 comprises,

Definition density function is:

$F\left(x\right)=P(X\≤x)={\∫}_{-\∞}^{x}p\left(t\right)\mathrm{dt},---\left(1\right)$

Wherein F (x) is corresponding distribution function, passes through solve equation

obtain corresponding density function, wherein and introducing and the approximate empirical distribution function F of F (x) _l(x) calculate F (x),

$F_l\left(x\right)=\frac{1}{l}\underset{i=1}{\overset{l}{\mathrm{\Σ}}}\mathrm{\θ}(x^1-{x_i}^1)...\mathrm{\θ}(x^d-{x_i}^d),---\left(2\right)$

Wherein θ (u) is step function, x ₁..., x _lit is d dimensional vector; When formula (2) is applied to body area network, dimension becomes one, empirical distribution function writing:

$F_l\left(x\right)=\frac{1}{l}\underset{i=1}{\overset{l}{\mathrm{\Σ}}}\mathrm{\θ}(x-x_i),---\left(3\right)$

Wherein θ (u) is step function.

On the basis of technique scheme, described S3 comprises,

The selection of substrate: from the bottom of orthogonal basis to regression function, regression problem can be expressed as to the linear combination of substrate:

$f\left(x_j\right)=\underset{i=1}{\overset{N}{\mathrm{\Σ}}}{\mathrm{\α}}_{i}k(x_j,x_i)+b,---\left(4\right)$

Wherein k is substrate, and f is the linear combination of substrate;

On the basis of technique scheme, described S4 comprises,

Minimize

the standard returning as assessment, wherein || α || ₁1 norm of α, ξ _ibe regression error, be restricted to accordingly:

$\left\{\begin{array}{c}{d}_j-\underset{i=1}{\overset{N}{\mathrm{\Σ}}}{\mathrm{\α}}_{i}k(x_j,x_i)-b\≤\mathrm{\ϵ}+{\mathrm{\ξ}}_j\\ \underset{i=1}{\overset{N}{\mathrm{\Σ}}}{\mathrm{\α}}_{i}k(x_j,x_i)+b-d_j\≤\mathrm{\ϵ}+{\mathrm{\ξ}}_j.\\ \mathrm{\ξ}\≥0\\ j=\mathrm{1,2},...,N\end{array}\right.---\left(5\right)$

Variable α and b are split into two parts;

$\left\{\begin{array}{c}\mathrm{\α}={\mathrm{\α}}^{+}-{\mathrm{\α}}^{-}\\ b=b^{+}-b^{-}\end{array}\right..---\left(6\right)$

Objective function is $\min \underset{i=1}{\overset{N}{\mathrm{\Σ}}}({\mathrm{\α}}_i^{+}-{\mathrm{\α}}_i^{-}+2C{\mathrm{\ξ}}_i),$ Be restricted to accordingly:

$\left\{\begin{array}{c}-\underset{i=1}{\overset{N}{\mathrm{\Σ}}}({\mathrm{\α}}_i^{+}-{\mathrm{\α}}_i^{-})k(x_j,x_i)-b^{+}+b^{-}-{\mathrm{\ξ}}_j+u_j=\mathrm{\ϵ}-d_j\\ \underset{i=1}{\overset{N}{\mathrm{\Σ}}}({\mathrm{\α}}_i^{+}-{\mathrm{\α}}_i^{-})k(x_j,x_i)+b^{+}-b^{-}-{\mathrm{\ξ}}_j+u_j=\mathrm{\ϵ}+d_j.\\ {\mathrm{\α}}_j^{+},{\mathrm{\α}}_j^{-},b^{+},b^{-},{\mathrm{\ξ}}_j,u_j\≥0\\ j=\mathrm{1,2},...,N\end{array}\right.---\left(7\right)$

Solve equation: z=(α ⁺α ^-b ⁺b ^-ξ u), $A=\left(\begin{array}{cc}-K& K-11-\mathrm{II}\\ K& -K1-1-\mathrm{II}\end{array}\right),b=\left(\begin{array}{c}\mathrm{\ϵ}-d\\ \mathrm{\ϵ}+d\end{array}\right),$ C=(11002C0) ^T

Force definition:

$f\left(0\right)=\underset{i=1}{\overset{N}{\mathrm{\Σ}}}{\mathrm{\α}}_{i}k(0,x_i)+b=0,f\left(1\right)=\underset{i=1}{\overset{N}{\mathrm{\Σ}}}{\mathrm{\α}}_{i}k(1,x_i)+b=1.---\left(8\right)$

And restrictive condition becomes:

$\left\{\begin{array}{c}-\underset{i=1}{\overset{N}{\mathrm{\Σ}}}{\mathrm{\α}}_{i}k(x_j,x_i)-b-{\mathrm{\ξ}}_j+u_j=\mathrm{\ϵ}-d_j\\ \underset{i=1}{\overset{N}{\mathrm{\Σ}}}{\mathrm{\α}}_{i}k(x_j,x_i)+b-{\mathrm{\ξ}}_j+u_j=\mathrm{\ϵ}+d_j\\ \underset{i=1}{\overset{N}{\mathrm{\Σ}}}{\mathrm{\α}}_{i}k(0,x_i)+b=0.\\ \underset{i=1}{\overset{N}{\mathrm{\Σ}}}{\mathrm{\α}}_{i}k(1,x_i)+b=1\\ \underset{i=1}{\overset{N}{\mathrm{\Σ}}}{\mathrm{\α}}_i=1\\ \mathrm{\α},b,{\mathrm{\ξ}}_j,u_j\≥0j=\mathrm{1,2},...N\end{array}\right.---\left(9\right)$

By building matrix, can obtain: z=(ab ξ u), $A=\left(\begin{array}{ccc}-K& -1& -\mathrm{II}\\ K& 1& -\mathrm{II}\\ K& (0,x)& 100\\ K& (1,x)& 100\end{array}\right),b=\left(\begin{array}{c}\mathrm{\&epsiv;}-d\\ \mathrm{\&epsiv;}+\mathrm{<figure-callout\; id="0"\; label="d"\; filenames="HDA0000403772020000011.png,HDA0000403772020000021.png"\; state="\{\{state\}\}">d</figure-callout>}\\ 0\\ 1\end{array}\right),$ c=(102C0) ^T。

On the basis of technique scheme, described S5 comprises,

Build $k(x_i,x_j)=\tanh ({\mathrm{ax}}_i^T{x}_j+r)$ As kernel function, wherein

$k=\frac{1}{1+e^{-t(x_i-x_j)}}.---\left(10\right)$

The present invention compares tool with art methods and has the following advantages:

What traditional probability radio wave propagation characterizing method was used is typical nonparametric model, i.e. logarithm-normal model, and the characterization model that the present invention proposes is not subject to specifically to propagate the restriction of situation, due to its nonparametric characteristic, is more suitable for the radio communication in body area network.

Finite sample (10 ²rank) be the key character of body centre communication, existing technology is that conventional model is transplanted to during body centre's radio wave propagation characterizes, but these models have suitable requirement to sample size, only has when sample size acquires a certain degree its precision just secure.The present invention has overcome model in the past has the harsh problem requiring to sample size, and by control the quantity of support vector in regression process, the coefficient that makes a large amount of linear combinations is zero, has realized " rarefaction " of regression coefficient.

Accompanying drawing explanation

Fig. 1 is basis transformation schematic diagram of the present invention;

Fig. 2 is algorithm flow chart of the present invention;

Fig. 3 is the Sigmoid kernel function schematic diagram under special parameter;

Fig. 4 is the parameter model approximate diagram of path loss;

Fig. 5 be path loss nonparametric model approximate diagram and with the comparison diagram of parameter model;

Fig. 6 is the parameter model approximate diagram of RMS decay;

Fig. 7 be RMS decay nonparametric model approximate diagram and with the comparison diagram of parameter model.

Embodiment

Below in conjunction with accompanying drawing, describe the sparse nonparametric probability characterizing method in the present invention in detail.

The first step, the solving of empirical distribution function.Density function can be defined as:

$F\left(x\right)=P(X\&le;x)={\&Integral;}_{-\&infin;}^{x}p\left(t\right)\mathrm{dt},---\left(1\right)$

Wherein F (x) is corresponding distribution function.Pass through solve equation

can obtain corresponding density function, wherein

problem is that, in actual body centre's situation, F (x) is unknown, therefore can not directly from F (x), calculate p (t), is therefore faced with the problem of inferring F (x) from unknown data.The radio wave propagation parameter of body centre is independently, conventionally can and measure by Fdtd Method and obtain, and therefore, from radio wave propagation parameter, calculating F (x) becomes the key problem that solves probability sign.By introducing empirical distribution function Fl (x), can be similar to F (x):

$F_l\left(x\right)=\frac{1}{l}\underset{i=1}{\overset{l}{\mathrm{\&Sigma;}}}\mathrm{\&theta;}(x^1-{x_i}^1)...\mathrm{\&theta;}(x^d-{x_i}^d),---\left(2\right)$

Wherein θ (u) is step function, x ₁..., x _lit is d dimensional vector; Notice that dimension becomes one when this model is applied to body area network, like this, empirical distribution function can be write:

$F_l\left(x\right)=\frac{1}{l}\underset{i=1}{\overset{l}{\mathrm{\&Sigma;}}}\mathrm{\&theta;}(x-x_i),---\left(3\right)$

Wherein θ (u) is step function.

Second step, the selection of substrate: from the bottom of orthogonal basis to regression function.As a rule, for two-dimentional Euclidean space, at the bottom of orthogonal basis, be defined and do: { i=(1,0), j=(0,1) }, and it has just formed and has told somebody what one's real intentions are

.From accompanying drawing 1, can find out, in the time of at the bottom of using orthogonal basis, the coefficient of orthogonal vector is evident as plural number.For the complexity of reduction ratio, need to carry out basis transformation.In accompanying drawing 1, new substrate (i', j') the straight line l that is used to fit, wherein the starting point of basis vector has been moved to the terminal of straight line, and like this, the complexity of coefficient has been greatly diminished.This basis transformation method has also been used in regression function, and wherein corresponding coefficient is used to represent probability.The essence of this idea comes from Parzen window method, and in Parzen window method, the linear combination of kernel function has formed probability function p _n(x):

Wherein be called as kernel function

can be counted as substrate.Yet in using the process of Parzen window method, the quantity of independent variable, much larger than the needs of normal matching, in order to reduce the quantity of variable, need to build new substrate, this is similar with the basis transformation of mentioning before.The proposition regression problems such as Vapnic can be expressed as:

$f\left(x_j\right)=\underset{i=1}{\overset{N}{\mathrm{\&Sigma;}}}{\mathrm{\&alpha;}}_{i}k(x_j,x_i)+b,---\left(5\right)$

Wherein k is substrate, and f is the linear combination of substrate.By applying suitable substrate, some coefficient a _iequal zero, so just obtained the characteristic of " sparse ", this is the huge advantage with respect to Parzen window method.

The 3rd step, solves regression coefficient.Formula (5) can be used to solve empirical distribution function, but problem is how to solve corresponding regression coefficient.Vapnic proposes to minimize

can be used as the standard that assessment returns, wherein || α || ₁1 norm of α, ξ _iit is regression error.Be restricted to accordingly:

$\left\{\begin{array}{c}{d}_j-\underset{i=1}{\overset{N}{\mathrm{\&Sigma;}}}{\mathrm{\&alpha;}}_{i}k(x_j,x_i)-b\&le;\mathrm{\&epsiv;}+{\mathrm{\&xi;}}_j\\ \underset{i=1}{\overset{N}{\mathrm{\&Sigma;}}}{\mathrm{\&alpha;}}_{i}k(x_j,x_i)+b-d_j\&le;\mathrm{\&epsiv;}+{\mathrm{\&xi;}}_j.\\ \mathrm{\&xi;}\&GreaterEqual;0\\ j=\mathrm{1,2},...,N\end{array}\right.---\left(6\right)$

Due to the needs of linear programming, the number of unknown number should be more than zero, so we can split into two parts variable; Meanwhile, introducing variable u makes inequality problem become equation problem.

$\left\{\begin{array}{c}\mathrm{\&alpha;}={\mathrm{\&alpha;}}^{+}-{\mathrm{\&alpha;}}^{-}\\ b=b^{+}-b^{-}\end{array}\right..---\left(7\right)$

Objective function is $\min \underset{i=1}{\overset{N}{\mathrm{\&Sigma;}}}({\mathrm{\&alpha;}}_i^{+}-{\mathrm{\&alpha;}}_i^{-}+2C{\mathrm{\&xi;}}_i),$ Be restricted to accordingly:

$\left\{\begin{array}{c}-\underset{i=1}{\overset{N}{\mathrm{\&Sigma;}}}({\mathrm{\&alpha;}}_i^{+}-{\mathrm{\&alpha;}}_i^{-})k(x_j,x_i)-b^{+}+b^{-}-{\mathrm{\&xi;}}_j+u_j=\mathrm{\&epsiv;}-d_j\\ \underset{i=1}{\overset{N}{\mathrm{\&Sigma;}}}({\mathrm{\&alpha;}}_i^{+}-{\mathrm{\&alpha;}}_i^{-})k(x_j,x_i)+b^{+}-b^{-}-{\mathrm{\&xi;}}_j+u_j=\mathrm{\&epsiv;}+d_j.\\ {\mathrm{\&alpha;}}_j^{+},{\mathrm{\&alpha;}}_j^{-},b^{+},b^{-},{\mathrm{\&xi;}}_j,u_j\&GreaterEqual;0\\ j=\mathrm{1,2},...,N\end{array}\right.---\left(8\right)$

Then can carry out solve equation by structural matrix: z=(α+α-b+b-ξ u), $A=\left(\begin{array}{cc}-K& K-11-\mathrm{II}\\ K& -K1-1-\mathrm{II}\end{array}\right)$ $b=\left(\begin{array}{c}\mathrm{\&epsiv;}-d\\ \mathrm{\&epsiv;}+d\end{array}\right),$ C=(11002C0) ^T。This problem is from being to ask 4N+2 the optimal problem variable in essence.But these restrictions are only to return for the support vector of standard, when using recurrence to approach empirical distribution function, these restrictions need to be corrected.First, factor alpha _ishould be a positive number, therefore be necessary variable to resolve into two parts; Secondly, force definition regression function in the value at 0 and 1 place, this is similar to probability is very crucial:

$f\left(0\right)=\underset{i=1}{\overset{N}{\mathrm{\&Sigma;}}}{\mathrm{\&alpha;}}_{i}k(0,x_i)+b=0,f\left(1\right)=\underset{i=1}{\overset{N}{\mathrm{\&Sigma;}}}{\mathrm{\&alpha;}}_{i}k(1,x_i)+b=1.---\left(9\right)$

These two additional conditions have guaranteed that the separate regression steps of standard can be used as the approximate of probability, so restrictive condition becomes:

$\left\{\begin{array}{c}-\underset{i=1}{\overset{N}{\mathrm{\&Sigma;}}}{\mathrm{\&alpha;}}_{i}k(x_j,x_i)-b-{\mathrm{\&xi;}}_j+u_j=\mathrm{\&epsiv;}-d_j\\ \underset{i=1}{\overset{N}{\mathrm{\&Sigma;}}}{\mathrm{\&alpha;}}_{i}k(x_j,x_i)+b-{\mathrm{\&xi;}}_j+u_j=\mathrm{\&epsiv;}+d_j\\ \underset{i=1}{\overset{N}{\mathrm{\&Sigma;}}}{\mathrm{\&alpha;}}_{i}k(0,x_i)+b=0.\\ \underset{i=1}{\overset{N}{\mathrm{\&Sigma;}}}{\mathrm{\&alpha;}}_{i}k(1,x_i)+b=1\\ \underset{i=1}{\overset{N}{\mathrm{\&Sigma;}}}{\mathrm{\&alpha;}}_i=1\\ \mathrm{\&alpha;},b,{\mathrm{\&xi;}}_j,u_j\&GreaterEqual;0j=\mathrm{1,2},...N\end{array}\right.---\left(10\right)$

By building matrix, can obtain: z=(ab ξ u), $A=\left(\begin{array}{ccc}-K& -1& -\mathrm{II}\\ K& 1& -\mathrm{II}\\ K& (0,x)& 100\\ K& (1,x)& 100\end{array}\right),b=\left(\begin{array}{c}\mathrm{\&epsiv;}-d\\ \mathrm{\&epsiv;}+\mathrm{<figure-callout\; id="0"\; label="d"\; filenames="HDA0000403772020000011.png,HDA0000403772020000021.png"\; state="\{\{state\}\}">d</figure-callout>}\\ 0\\ 1\end{array}\right),$ c=(102C0) ^T。Corresponding problem becomes the optimal value that solves 3N+1 variable under 2N+2 restriction.Up to the present, by application linear programming, can image space obtain data ( _x1, y ₁), (x ₂, y ₂) ..., (x _n, y _n) empirical distribution function.

The 4th step, builds kernel function.

In the method, intend building

as kernel function.Notice some combination for kernel functional parameter, nuclear matrix Q is positive semi-definite, and this is necessary for function very.The propositions such as Hsuan-Tien for the situation of a>0 and r<0, when r hour, the nuclear matrix of sigmoid function is positive semi-definite, so we consider the sigmoid function (accompanying drawing 3) of following form.

$k=\frac{1}{1+e^{-t(x_i-x_j)}}.---\left(11\right)$

The 5th step, application and assessment.

1. about static body surface arrowband path loss model.

Printed monopole antenna in 2.4GHz impedance matching is used as electromagnetic wave transceiver.HP8720ES vector network analyzer is used to carry out the measurement of frequency domain, and object is to obtain the transmission coefficient between dual-mode antenna, and the impact of cable can be eliminated by calibrating.The impact producing for antenna in order to reduce health, the distance between monopole antenna and health is set to 4mm; In the process of measuring, the tested stance of taking all the time.The environment of experiment measuring is darkroom, and object is in order to eliminate environment for the impact of probability model, to make it more targeted.

As known in us, lognormal model is often used to characterize indoor environment:

$\mathrm{PL}={\mathrm{<figure-callout\; id="0"\; label="PL"\; filenames="HDA0000403772020000011.png,HDA0000403772020000021.png"\; state="\{\{state\}\}">PL</figure-callout>}}_0+{10}_{\mathrm{\&gamma;}}{\log }_{10}\frac{\mathrm{<figure-callout\; id="0"\; label="d\; d"\; filenames="HDA0000403772020000011.png,HDA0000403772020000021.png"\; state="\{\{state\}\}">d</figure-callout>}}{d_{}}+X_g,---\left(12\right)$

The path loss of PL Shi YidBWei unit wherein, PL ₀reference distance d ₀the path loss at place, γ is path loss index, d is distance, X _git is any gaussian variable of zero-mean.Fort etc. make hypothesis, and for body area network, path loss model can represent by (12).Clearly, this is a parametric assumption, and parameter is loss γ.But, the prerequisite that it should be noted that this lognormal model of application is that sample size is very large, make this judgement according to being in this model, conventionally with the straight line under least square rule, predict loss γ, and least square method itself needs a large amount of samples to guarantee its precision.For body centre's situation, only can collect limited sample, like this, should use and not need the nonparametric of priori probability model.Main cause is that body area channel can be affected by a lot of other factors, and it is obvious that the directive significance of priori is not so good as other communication environments.As shown in Figure 4, these parameter models are all used to the empirical distribution function of approximate path loss in relevant parameter model comparison, and the parameter model using has: lognormal model, Weibull model and normal model.Notice that these models are all for the concrete situation in wireless body area network, so we have introduced nonparametric model.Accompanying drawing 5 has provided the nonparametric model after coefficient adjustment.The mathematical form of regression function is

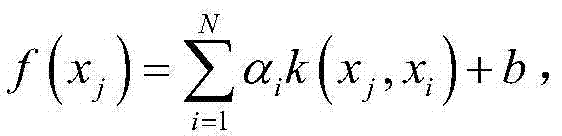
only have a small amount of coefficient to be not equal to 0, this is the basic reason that realizes sparse representation.Accompanying drawing 5 has provided the core procedure of setting up the sparse probability model of body area network, wherein factor alpha _ithereby be assigned to new kernel function K and obtain nonparametric probability function.Notice that ε is independent of other coefficients, so the ε that we can define in body area network is:

$\mathrm{\&epsiv;}=\frac{3\mathrm{\&sigma;}\sqrt{\frac{1\mathrm{nl}}{l}}}{l},---\left(13\right)$

The standard deviation that wherein σ is noise, l is data length.Another coefficient C can define by following equation:

$C=\frac{\max \left(\right|\stackrel{\&OverBar;}{y}+3{\mathrm{\&sigma;}}_y|,|\stackrel{\&OverBar;}{y}-3{\mathrm{\&sigma;}}_y\left|\right)}{l},---\left(14\right)$

Wherein

the mean value of training output, σ _ybe the standard deviation of output, l is the length of data.5 pairs of nonparametric models of accompanying drawing and several parameter model contrast, and regression coefficient is all optimized in advance.In non-parametric Model Selection, the sparse sexual needs of error of fitting and sign consider simultaneously, and in the situation of health of standing, we have selected ε=0.1 as coefficient.

2. the nonparametric probability model of decaying about ultra-wideband channel RMS in the non-sight line of static body surface.

In this test, co-planar waveguide antenna is used as transmitter and receiver.The frequency range of transmission response is 3-10GHz, same, measures to be arranged in darkroom and carries out.The position of emitting antenna is in left lumbar region, and receiving antenna is along the back-moving of health.The shock response of channel can obtain by application inverse Fourier transform, and the sampling time is 50ps, has 1601 frequencies.In research in the past, Nakagami distribution, Gaussian distribution and lognormal distribution are often used as reference model (accompanying drawing 6).Equally, by coefficient, optimize, chosen $(C=\frac{\max \left(\right|\stackrel{-}{y}+3{\mathrm{\&sigma;}}_y|,|\stackrel{-}{y}-3{\mathrm{\&sigma;}}_y\left|\right)}{l},\mathrm{\&epsiv;}=0.01)$ As regression coefficient, and carried out contrasting (accompanying drawing 7) with several parameter models.

The above; it is only the embodiment in the present invention; but protection scope of the present invention is not limited to this; any people who is familiar with the method is in the disclosed technical scope of the present invention; can understand conversion or the replacement expected; all should be encompassed in of the present invention comprise scope within, therefore, protection scope of the present invention should be as the criterion with the protection domain of claims.

Claims (5)

1. a sparse nonparametric body area channel probability characterizing method, is characterized in that: comprise the following steps:

S1 adopts vector network analyzer image data;

S2 builds empirical distribution function, and solves empirical distribution function by step function;

S3 use experience distribution function approximate densities function, and build regression function;

S4 is by linear programming for solution regression coefficient;

S5 is by regression function, differentiate obtains corresponding probability function;

S6 assesses and analyzes the sparse nonparametric probability model obtaining.

2. a kind of sparse nonparametric body area channel probability characterizing method as claimed in claim 1, is characterized in that: described S2 comprises,

Definition density function is:

wherein F (x) is corresponding distribution function, passes through solve equation

obtain corresponding density function, wherein

and introducing and the approximate empirical distribution function F of F (x) _l(x) calculate F (x),

wherein θ (u) is step function, x ₁..., x _lit is d dimensional vector; When formula (2) is applied to body area network, dimension becomes one, empirical distribution function writing:

wherein θ (u) is step function.

3. a kind of sparse nonparametric body area channel probability characterizing method as claimed in claim 2, is characterized in that: described S3 comprises,

The selection of substrate: from the bottom of orthogonal basis to regression function, regression problem can be expressed as to the linear combination of substrate:

wherein k is substrate, and f is the linear combination of substrate.

4. a kind of sparse nonparametric body area channel probability characterizing method as claimed in claim 3, is characterized in that: described S4 comprises,

Minimize

the standard returning as assessment, wherein || α || ₁1 norm of α, ξ _ibe regression error, be restricted to accordingly:

Variable α and b are split into two parts;

objective function is

be restricted to accordingly:

solve equation: z=(α+α ^-b ⁺b ^-ξ u), c=(11002C0) ^t

Force definition:

and restrictive condition becomes:

by building matrix, can obtain: z=(ab ξ u),

c=(102C0) ^t.

5. a kind of sparse nonparametric body area channel probability characterizing method as claimed in claim 4, is characterized in that: described S5 comprises,

Build

as kernel function, wherein

。

Images