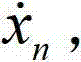CN102736628B - Legged robot stability control method and system with environmental adaptation - Google Patents

Abstract

A method and system for controlling the stability of a legged robot with environmental adaptability. The control method compares the relevant parameter information of the previous ground-touching process with the expected control target, and implements the horizontal motion speed of the flight phase and the total energy of the system. Feedback control, predictive control of ground contact angle and system energy compensation control, finally realize the expected stable periodic motion of the SLIP equivalent model of the legged robot in different ground environments. The system includes a system state detection module and a stability control module. The present invention does not need to establish a specific robot dynamics model, does not need to calculate the precise fixed point contact angle, and realizes control convergence through feedback control. The control method is simple and the calculation is fast, which solves the problem of real-time control in existing methods. , Insufficient adaptability and other issues. And it has better adaptability to unknown environment, which provides a better solution for the stability control of legged robots.

Description

A kind of legged type robot stability control method and system with environmental suitability

Technical field

The invention belongs to Robotics field, be specifically related to a kind of legged type robot stability control method and system with environmental suitability.

Background technology

Earth top has over more than 50% being the complex-terrains such as massif or marsh, and with respect to wheeled robot and caterpillar robot, legged type robot has better adaptability and exercise performance on these complex-terrains.People wish that legged type robot can be stablized as the various sufficient formula animals of occurring in nature on the complex-terrain of land, motion fast, thereby the auxiliary mankind complete various tasks.Therefore, increasing researchist is incorporated into bionics method among robot research, by the bionics method of studying, learn, imitating, copies and reproduce biological structure, function and controlling mechanism.

The biology of occurring in nature is a complicated nonlinearity system often, and many legs, multi-joint and muscle redundancy are serious, therefore biosome is not added the imitation of simplification and reappears quite difficulty and unrealistic.In order to address this problem, researchist scientific and reasonable by the various relatively uniform model representations for animal with different skeletal structures, leg number and attitude, obtain corresponding equivalent parameters simultaneously, make every effort to by the rationally effectively motion of the next equivalent sufficient formula animal of simplified model.

For the equivalent model that the behavioral trait of investigation entire system is set up should be simplified the most, a kind of effective trial is spring inverted pendulum model (SLIP, Spring Loaded Inverted Pendulum), be about to biosome and be reduced to simple substance amount---spring system, by different quality, rigidity, damping and relevant morphological parameters, characterize concrete biosome motion.SLIP model is the valid model of the research legged type robot that grown up since the eighties in 20th century, researchist is by the careful research of mammiferous shank and muscle is shown to elastic mechanism is present in the motion of animal really, and the performance of animal is had a great impact.The parameters such as this model can effectively be explained the buffering of shank to ground shock, angle, the shank equivalent stiffness of landing by adjustment System can reach the object of control system tangential movement speed and jumping height.And the concept of the virtual leg of equivalence proposing by relevant scholar, legged type robot (as biped robot, quadruped robot, six biped robots etc.) all can be equivalent to simplify most simple substance amount---spring system is that single SLIP equivalent model carries out research and analysis.

Existing legged type robot mostly rests on the laboratory model machine stage, rarely can really realize the motion control under complex environment, and its difficult point is just that the Dynamic Stability Control method under legged type robot complex environment is still immature.Legged type robot is the system of a kind of multiple degrees of freedom, strong nonlinearity, many redundancies, and its Holonomic Dynamics specificity analysis is very complicated, and the dynamic stability control of directly it being carried out under complex environment often can not meet the requirement of realtime control.Therefore increasing researchist starts to start with from SLIP equivalent model, the dynamic stability control method of research and analysis SLIP equivalent model under complex environment, thereby take this equivalent model as basis, again extend and extend to whole legged type robot, by letter, entered numerously, finally reach the object that whole legged type robot system stability is controlled.

Prior art one discloses a kind of cycle stability motion control method for undamped SLIP model, it is the kinetics equation in flight phase and the phase that lands by derivation undamped SLIP model, approximate obtain in the whole process that lands SLIP model land angle and the relation of liftoff angle and time, and the relation of whole land process medi-spring length and time etc.And then by the value iteration to different variable elements, emulation obtains the state before and after once landing of SLIP model under different condition, thereby finds the suitable initial parameter that meets the periodic motion of SLIP fixed point, realizes its stable motion and controls.

Prior art two discloses a kind of cycle stability motion control method for there being damping SLIP model, it has increased damping term in SLIP kinetic model is derived, considered the energy loss in whole motion process, be similar to and obtain the energy loss equation that SLIP model lands in process, by changing the methods such as spring rate, the energy of loss is compensated, continue by the value iteration to different variable elements, emulation obtains SLIP model after the energy compensating state before and after landing, thereby find the suitable initial parameter that meets the periodic motion of SLIP fixed point, realizing its stable motion controls.

After prior art is studied, the inventor finds: what in prior art one, consider is a kind of very good equivalent model, it has ignored the damping factor existing in legged type robot motion process, in reflection robot actual motion process, has model error; And although prior art two has been considered the damping factor of equivalent model, and the energy losing in its motion process is compensated, but this technology realizes fixed point and stablizes control and need to just can find suitable initial condition by a large amount of assignment iteration, the requirement that discontented biped robot system real time is controlled, is difficult for being used in actual robot stabilized control.And prior art has all only been considered the control of SLIP model in plane landform, complex environment landform comparatively is not had to adaptability.

Summary of the invention

The object of the present invention is to provide a kind of legged type robot stability control method and system that can overcome above-mentioned defect, take SLIP equivalent model as research object, not only consider the damping loss in legged type robot motion process, and make the SLIP model after control no longer only be adapted to plane landform, the comparatively complicated landform such as step, hollow is also had and stablizes adaptability preferably, to the starting condition of model, require lower in addition, do not need repeatedly iteration, solved the unappeasable problem of realtime control.

A kind of legged type robot stability control method with environmental suitability provided by the invention, the method comprises the steps:

The 1st step systematic parameter initialization, comprises the proportional gain factor k that system essential information, corner PID control _p, integration time constant k _iwith derivative time constant k _d; Make n=1; The energy that order is contacted to earth for the first time and compensated mutually

be zero; Target is controlled in initialization, and calculates motion stable period desirable system gross energy E _d; Described system essential information comprises quality m, equivalent spring rigidity k, equivalent damping c and the long r of initial equivalent leg ₀; Described control target comprises motion expectation stable period horizontal velocity

with the vertical height of expectation peak

The 2nd step detects the initial level speed before contacting to earth for the first time

The 3rd step calculated the angle θ that contacts to earth for the n time before contacting to earth for the n time _tD;

The 4th step real-time detecting system state, obtains the status information of current time SLIP model, comprises the horizontal velocity of barycenter A

vertical direction speed

the pivot angle θ of leg, leg length r, vertical direction strength of one's legs F _cwith current system time t;

The 5th step judges whether SLIP model contacts to earth, and the decision condition constantly that contacts to earth is foot end strength of one's legs F _cgeneration is greater than zero sudden change by equalling zero to, and the vertical speed of system

if contacted to earth, carry out the 7th step, if contacted to earth, do not carry out the 6th step;

The 6th step is controlled by PID, before contacting to earth for the n time, SLIP model is controlled to the predetermined angle of contacting to earth, the angle θ even if the pivot angle of leg equals to contact to earth _tD;

The 7th step reads etching system correlation behavior parameter while contacting to earth, and comprises the horizontal velocity constantly of contacting to earth

vertical speed the long r of equivalence leg _tD, and the actual angle θ that contacts to earth _tD, and calculate etching system gross energy E while contacting to earth _n, be the system gross energy before that contacts to earth for the n time;

The 8th step judges whether SLIP model is compressed to bottom, if be compressed to bottom, carries out the 9th step, otherwise carries out the 4th step;

The 9th step is carried out system capacity compensation, makes system reach desirable system gross energy E _d:

The 10th step judges that whether SLIP model is liftoff, if liftoff execution the 11st step, otherwise would carry out the 9th step;

The 11st step reads etching system correlation behavior parameter when liftoff, comprises the horizontal velocity in the liftoff moment vertical speed

the long r of equivalence leg _lO, and the actual angle θ that contacts to earth _lO, and calculate etching system gross energy E when liftoff _n+1, be the system gross energy afterwards that contacts to earth for the n time;

The 12nd step is calculated the energy of system loss in the process of contacting to earth for the n time

its computing formula is:

${\mathrm{\ΔE}}_n^{-}=E_n+{\mathrm{\ΔE}}_n^{+}-E_{n+1}$

Wherein,

be the energy that should compensate in the process of contacting to earth for the n time,

initial value be 0;

The 13rd step is calculated the energy that should compensate in the process of contacting to earth for the n+1 time ${\mathrm{\ΔE}}_{n+1}^{+}=E_d+{\mathrm{\ΔE}}_n^{-}-E_{n+1};$

The 14th step judges whether SLIP system moves and arrives destination, if do not arrive destination, carries out the 3rd step, otherwise finish.

The present invention compared with prior art has following advantage: 1) do not need that equivalent SLIP model is carried out to complicated kinetics equation and derive, the mathematical expression formula that does not need to obtain energy loss and the angle that lands in the whole process that lands, has reduced model equivalent error when having simplified control algolithm; 2) have real-time, do not need to carry out repeatedly initial value iteration, the real-time that can meet actual legged type robot is controlled requirement; 3) there is good landform adaptive faculty, have certain autonomous adaptability, can apply to stable control of legged type robot under landform circumstances not known.

Accompanying drawing explanation

Fig. 1 is example control object equivalence SLIP model structure schematic diagram of the present invention;

Fig. 2 is equivalent SLIP model sport process schematic diagram;

The stability control method controller architecture figure that Fig. 3 provides for example of the present invention;

The stability control method process flow diagram that Fig. 4 provides for example of the present invention;

Fig. 5 402 calculates the Angle Method schematic diagram that contacts to earth in Fig. 4;

Fig. 6 408 carries out system capacity compensation method schematic diagram in Fig. 4;

Fig. 7 is the vertical height analogous diagram under equivalent SLIP model no stability is controlled;

Fig. 8 is that equivalent SLIP model is applied the vertical height analogous diagram under stability control method provided by the invention;

Fig. 9 is the motion schematic diagram of equivalent SLIP model under kame-and-kettle topography;

Figure 10 is that equivalent SLIP model is applied the vertical height analogous diagram that stability control method provided by the invention moves under kame-and-kettle topography;

Figure 11 is that equivalent SLIP model is applied the horizontal velocity analogous diagram that stability control method provided by the invention moves under kame-and-kettle topography;

Figure 12 is the motion schematic diagram of equivalent SLIP model under terrace relief;

Figure 13 is that equivalent SLIP model is applied the vertical height analogous diagram that stability control method provided by the invention moves under terrace relief;

Figure 14 is that equivalent SLIP model is applied the horizontal velocity analogous diagram that stability control method provided by the invention moves under terrace relief.

Embodiment

For making the object, technical solutions and advantages of the present invention clearer, below in conjunction with accompanying drawing, embodiment of the present invention is described in further detail.Obviously, described embodiment is only the present invention's part embodiment, rather than whole embodiment.Embodiment based in the present invention, those of ordinary skills, at the every other embodiment that does not have to obtain under creative work prerequisite, belong to protection domain of the present invention.

As Fig. 1 (a) is depicted as example control object equivalence SLIP model structure schematic diagram of the present invention.Quality-spring inverted pendulum SLIP model of legged type robot equivalence is by equivalent mass piece 101, equivalent leg bar 102, and equivalent spring damping system 103 and equivalent sufficient bar 104 form.Equivalent mass piece 101 is whole legged type robot system equivalent mass place, and its barycenter is A point, and equivalent mass represents with m.Equivalence leg bar 102 is with equivalent mass piece 101 for revolute pair is connected, and tie point is some A; One end of equivalent spring damping system 103 and equivalent leg bar 102 are affixed, the other end and equivalent sufficient bar 104 are affixed, equivalence leg bar 102, equivalent sufficient bar 104 and equivalent spring damping system 103 three's coaxial cables form legged type robot equivalence leg system jointly, and equivalent leg length represents with r.The spring that equivalent spring damping system 103 is k by rigidity and damping are that the damper of c forms, and characterize respectively equivalent leg rigidity and the equivalent damping of legged type robot.When whole equivalent SLIP model contacts to earth and the contact point P of ground _tDrepresent, the angle of contacting to earth is equivalent leg axis A-P _tDangle with y direction, represents with θ.Because the whole equivalences of quality are concentrated to equivalent mass piece 101, therefore equivalent leg bar 102, equivalent spring damping system 103 and equivalent sufficient bar 104 quality are ignored.

As shown in Fig. 1 (b), equivalent SLIP model has two freedoms of motion, is respectively equivalent leg bar 102 with respect to the rotational freedom of equivalent mass piece 101 and equivalent spring damping system 103 along equivalent leg axis A-P _tDone-movement-freedom-degree.Rotational freedom is driven by corner driver 105, and driving moment represents with T, and one-movement-freedom-degree is driven by equivalent force driver 106, and driving force represents with F.The multiple sensors of detection system state is installed on legged type robot, in equivalent SLIP model, be respectively angular transducer 107, speed pickup 108, spring linear transducer 109 and foot end foot sensor 110 form, sensor-based system detects SLIP model sport state constantly, and the stability control method providing for example of the present invention provides heat transfer agent.

As shown in Figure 2, SLIP motion process can regard as two different motion stages alternately, the phase of flying stage and contacting to earth the phase stage.The flight phase stage is SLIP model motion stage aloft, and this stage system is only subject to the effect of gravity, the flight phase 203 as the flight phase 201 before the n time contact to earth (n is since 1) and before contacting to earth for the n+1 time.The phase of the contacting to earth stage is that SLIP model foot end contacted to earth to the stage that built on stilts soars again, and this stage system can affect its dynamics because spring-compressed discharges, as after contacting to earth for the n time contact to earth mutually 202 and contact to earth for the n+1 time before the phase 204 of contacting to earth.Flight has a special state mutually, and vertically y direction movement velocity is zero flight phase peak state constantly, as before contacting to earth for the n time, fly phase peak 205 and contact to earth for the n+1 time before the phase peak 206 that flies.Because only have Action of Gravity Field in flight mutually, whole system is the loss of Conservative Systems noenergy, and the representative information of the phase peak 205 that flies before can contacting to earth with the n time characterizes the system state before contacting to earth for the n time, the horizontal velocity of the phase peak that flies before contacting to earth for the n time

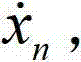
equivalence barycenter is to the vertical height on ground

system gross energy E now _n.The representative information of phase peak 206 of in like manner flying before available contacting to earth for the n+1 time characterizes the system state before contacting to earth for the n+1 time, the horizontal velocity of the phase peak that flies before contacting to earth for the n+1 time

equivalence barycenter is to the vertical height on ground

system gross energy E now _n+1.The stage that the phase of flying before contacting to earth for the n time peak 205 flies between phase peak 206 before contacting to earth to the n+1 time is a spring cycle.The target that SLIP stability is controlled makes after the n time is contacted to earth by control exactly, and system all can reach the setting expectation state before motion starts, and expects horizontal velocity

with the vertical height of expectation peak

thereby realize motion stable period.Contact to earth and there are mutually three special states, just contacted to earth constantly, spring-compressed is zero moment and liftoff moment again to minimum vertical y direction movement velocity, as contacted to earth constantly 207 and contact to earth for the n+1 time the moment 210 for the n time, be compressed to the bottom moment 208 for the n time and be compressed to 211, the n the liftoff moment 209 and the n+1 time liftoff moment 212 of the bottom moment for the n+1 time.Energy loss and compensation all occur in the phase stage of contacting to earth, and the energy of the loss of wherein contacting to earth for the n time is used

represent, the energy of the compensation of contacting to earth for the n time is used represent, the energy of the loss of contacting to earth for the n+1 time is used

represent, the energy of the compensation of contacting to earth for the n+1 time is used

represent.

As shown in Figure 4, the stability control method that example of the present invention provides is realized motion convergence stable period by the angle prediction of contacting to earth, system capacity compensation and FEEDBACK CONTROL, and concrete steps are as follows:

Step 401: systematic parameter initialization, comprises that initialization system essential information is as quality m, equivalent spring rigidity k, equivalent damping c, the long r of initial equivalent leg ₀.System herein refers to the organic whole consisting of equivalent mass piece, equivalent leg, revolute pair and corresponding control method, and the structural parameters that systematic parameter is control object can directly obtain after control object is determined; The proportional gain factor k that corner PID controls _p, integration time constant k _i, derivative time constant k _d, the definite of above three parameters need be according to concrete system, by test or emulation, determine, with lead leg can fast and stable the predetermined angle that controls to, and there is not overshoot and be as the criterion; Make n=1; The energy that order is contacted to earth for the first time and compensated mutually

be zero; Initialization is controlled target as motion expectation stable period horizontal velocity

the vertical height of expectation peak these two parameters are the motion state that desirable system reaches; And calculation stability periodic motion desirable system gross energy E _d, its computing formula is:

$E_d=m{\stackrel{\·}{x}}_d^2/2+{\mathrm{mgy}}_{{\mathrm{apex}}_d}---\left(1\right)$

Wherein, g is acceleration of gravity.

Step 402: detect the initial level speed before contacting to earth for the first time for the angle calculation of contacting to earth of step 403 provides data.

Step 403: calculated the angle θ that contacts to earth constantly that contacts to earth for the n time before contacting to earth for the n time _tD.

As shown in Figure 5, concrete computation process is:

By controlling after the different angles of contacting to earth completes the process of contacting to earth for the n time, have three kinds of different results, $\left(a\right){\stackrel{\&CenterDot;}{x}}_n={\stackrel{\&CenterDot;}{x}}_{n+1},$ $\left(b\right){\stackrel{\&CenterDot;}{x}}_n<{\stackrel{\&CenterDot;}{x}}_{n+1},$ $\left(c\right){\stackrel{\&CenterDot;}{x}}_n>{\stackrel{\&CenterDot;}{x}}_{n+1},$ Wherein

be the previous horizontal velocity of contacting to earth for the n time, it is the horizontal velocity afterwards of contacting to earth for the n time.When

time, we claim the P of touchdown point now _tDjust be neutral point P _n, the identical touchdown point of state before and after can guaranteeing to contact to earth.Before SLIP model contacts to earth at every turn, its horizontal velocity is judged and is more also had three kinds of different situations, $\left(a\right){\stackrel{\&CenterDot;}{x}}_n={\stackrel{\&CenterDot;}{x}}_d,$ $\left(b\right){\stackrel{\&CenterDot;}{x}}_n<{\stackrel{\&CenterDot;}{x}}_d,$ $\left(c\right){\stackrel{\&CenterDot;}{x}}_n>{\stackrel{\&CenterDot;}{x}}_d,$ If situation (a), we wish to control the SLIP angle of contacting to earth and continue to drop on neutral point, and the state after contacting to earth is like this still the horizontal velocity of our expectation; If situation (b), controls the angle of contacting to earth and makes touchdown point P _tDin advance in neutral point P _n, the horizontal velocity after contacting to earth like this

can increase the horizontal velocity with convergence expectation

Δ S is actual touchdown point P _tDwith neutral point P _nbetween adjustment distance; If in like manner situation (c), controls the angle of contacting to earth and makes touchdown point P _tDlag behind neutral point P _n, the horizontal velocity after contacting to earth like this

can reduce the horizontal velocity with convergence expectation

Δ S is actual touchdown point P _tDwith neutral point P _nbetween adjustment distance.By S ₀be defined as half of the process sports level distance of contacting to earth when touchdown point is neutral point.Wherein Δ S, S ₀computing formula is:

${\mathrm{<figure-callout\; id="0"\; label="S"\; filenames="HDA00001755806500043.png,HDA00001755806500051.png"\; state="\{\{state\}\}">S</figure-callout>}}_0={\stackrel{\&CenterDot;}{x}}_{{\mathrm{avg}}_n}\&CenterDot;t_s/2---\left(2\right)$

$\mathrm{\&Delta;S}=\mathrm{\&mu;}\&CenterDot;({\stackrel{\&CenterDot;}{x}}_n-{\stackrel{\&CenterDot;}{x}}_d)/r_0---\left(3\right)$

The whole PREDICTIVE CONTROL angle θ that contacts to earth _tDcomputing formula is:

${\mathrm{\&theta;}}_{\mathrm{TD}}=\arcsin (({\mathrm{<figure-callout\; id="0"\; label="S"\; filenames="HDA00001755806500043.png,HDA00001755806500051.png"\; state="\{\{state\}\}">S</figure-callout>}}_0+\mathrm{\&Delta;S})/r_0)=\arcsin (({\stackrel{\&CenterDot;}{x}}_{{\mathrm{avg}}_n}\&CenterDot;t_s/2+\mathrm{\&mu;}({\stackrel{\&CenterDot;}{x}}_n-{\stackrel{\&CenterDot;}{x}}_d))/r_0)---\left(4\right)$

T wherein _sbe the process T.T. of contacting to earth for the n time, can contact to earth constantly and the liftoff moment calculates by detection;

be the process average horizontal velocity of contacting to earth for the n time, adopt average velocity to calculate here more accurate; μ is that touchdown point and neutral point are adjusted distance proportion coefficient, and the definite of this parameter need be according to concrete robot system, and the method by test or emulation obtains, can make robot stabilized walking be as the criterion.

Step 404: real-time detecting system state, comprises the horizontal velocity of barycenter A

vertical direction speed

the pivot angle θ of leg, leg length r, vertical direction strength of one's legs F _c, current system time t, obtains the status information of current time SLIP model, is convenient to carry out correlated judgment.

Step 405: hold foot sensor and fuselage speed pickup to judge whether SLIP model contacts to earth by foot, the decision condition constantly that contacts to earth is foot end strength of one's legs F _cgeneration is greater than zero sudden change by equalling zero to, and the vertical speed of system

the execution step 407 if contacted to earth, if do not contact to earth execution step 406.

Step 406: control by PID, before contacting to earth for the n time, SLIP model is controlled to the predetermined angle of contacting to earth.Its control inputs is current pivot angle, is output as joint moment.

Step 407: read etching system correlation behavior parameter while contacting to earth, comprise the horizontal velocity constantly of contacting to earth

vertical speed

the long r of equivalence leg _tD, the actual angle θ that contacts to earth _tD, and calculate etching system gross energy E while contacting to earth _n, being the system gross energy before that contacts to earth for the n time, its computing formula is:

$E_n=m{\stackrel{\&CenterDot;}{x}}_{\mathrm{TD}}^2/2+m{\stackrel{\&CenterDot;}{y}}_{\mathrm{TD}}^2/2+{\mathrm{mgr}}_{\mathrm{TD}}{\cos \mathrm{\&theta;}}_{\mathrm{TD}}+k{(r_0-r_{\mathrm{TD}})}^2/2---\left(6\right)$

Step 408: hold foot sensor and fuselage speed pickup to judge whether SLIP model is compressed to bottom by foot, be compressed to bottom moment decision condition for foot end strength of one's legs F _c>0, and the vertical speed of system if be compressed to bottom execution step 409, if be not compressed to bottom execution step 404.

Step 409: carry out system capacity compensation:

As shown in Figure 6, example of the present invention is enumerated the method for three kinds of different compensation energy, and detailed process is as follows:

Method (a), is being compressed to bottom increase constantly along the momentum F of spring direction _ndt, can calculate wish compensation energy by theorem of momentum and be

time driving force F _n, its computing formula is:

$F_n=(-{\mathrm{mv}}_B+\sqrt{{\left({\mathrm{mv}}_B\right)}^2+2m\&CenterDot;{\mathrm{\&Delta;E}}_n^{+}})/\mathrm{dt}---\left(7\right)$

Wherein, Δ E _n ⁺be the energy that contacts to earth for the n time and compensate, here, when n=1, Δ E _n ⁺=0, when n>1, Δ E _n ⁺in a upper flight phase process, calculate the Δ E calculating while being flight phase n-1 _n+1 ⁺, its computing method are shown in step 413, v _bwhile compensating for momentum, etching system is along the resultant velocity of spring direction, and dt is the time interval that momentum increases, and the computing method of resultant velocity size are as follows:

$v_B=\stackrel{\&CenterDot;}{x}\&CenterDot;\cos \mathrm{\&theta;}+\stackrel{\&CenterDot;}{y}\&CenterDot;\sin \mathrm{\&theta;}---\left(8\right)$

θ,

with

the detected value obtaining for step 404.

Method (b) starts until the liftoff moment of system continues to increase the compensation constant force F along spring direction constantly bottom being compressed to _n, can calculate wish compensation energy and be time driving force F _n, its computing formula is:

$F_n={\mathrm{\&Delta;E}}_n^{+}/(r_0-r_B)---\left(9\right)$

R wherein ₀equivalent leg during for nothing compression is long, r _blong for being compressed to bottom equivalent leg constantly.

Method (c) starts until the liftoff time changing system of system equivalent stiffness increases compensate for stiffness Δ k on the basis of former equivalent stiffness k constantly bottom being compressed to, and can calculate wish compensation energy to be

time compensate for stiffness Δ k, its computing formula is:

$\mathrm{\&Delta;k}={2\mathrm{\&Delta;E}}_n^{+}/{(r_0-r_B)}^2---\left(10\right)$

R wherein ₀equivalent leg during for nothing compression is long, r _blong for being compressed to bottom equivalent leg constantly.

Compensate for stiffness Δ k is by controlling driving force F _nrealize F _nin whole process, conversion constantly, can calculate by Hooke theorem, and its computing formula is:

F _n=Δk·(r ₀-r) (11)

R wherein ₀equivalent leg during for nothing compression is long, and the equivalent leg that r is any current time is long, F _nin whole process along with spring discharges length variations and changes.

Step 4lO: hold foot sensor and fuselage speed pickup to judge that whether SLIP model is liftoff by foot, liftoff moment decision condition is foot end strength of one's legs F _cgeneration is by being greater than zero to null sudden change, and the vertical speed of system

if liftoff execution step 411, if do not have liftoff execution step 409.

Step 411: read etching system correlation behavior parameter when liftoff, as the horizontal velocity in the liftoff moment

vertical speed

the long r of equivalence leg _lO, the actual angle θ that contacts to earth _lO, and calculate etching system gross energy E when liftoff _n+l, being the system gross energy afterwards that contacts to earth for the n time, its computing formula is:

$E_{n+1}=m{\stackrel{\&CenterDot;}{x}}_{\mathrm{LO}}^2/2+m{\stackrel{\&CenterDot;}{y}}_{\mathrm{LO}}^2/2+{\mathrm{mgr}}_{\mathrm{LO}}{\cos \mathrm{\&theta;}}_{\mathrm{LO}}+k{(r_0-r_{\mathrm{LO}})}^2/2---\left(12\right)$

Step 412: the energy that calculates system loss in the process of contacting to earth for the n time its computing formula is:

${\mathrm{\&Delta;E}}_n^{-}=E_n+{\mathrm{\&Delta;E}}_n^{+}-E_{n+1}---\left(13\right)$

Wherein,

be the energy that should compensate in the process of contacting to earth for the n time,

initial value be 0.

Step 413: calculate the energy that should compensate in the process of contacting to earth for the n+1 time of next time contacting to earth

not only consider the difference of current system energy and motion stable period desirable system gross energy, and the extra energy that increases the last process loss of contacting to earth is as energy precompensation, its computing formula is:

${\mathrm{\&Delta;E}}_{n+1}^{+}=E_d+{\mathrm{\&Delta;E}}_n^{-}-E_{n+1}---\left(14\right)$

E wherein _dfor motion stable period desirable system gross energy.

Step 414: judging whether SLIP system moves arrives destination, if do not arrive destination, carry out step 403, if arrive destination, control flow finishes.

In example of the present invention; energy compensation process is to consider in system compresses, to bottom, constantly to start until the liftoff moment ending phase of system; in other stages, also can similarly carry out energy compensating; as system, contact to earth and constantly start to the liftoff moment ending phase of system; system is contacted to earth and is constantly started to system compresses to bottom stage etc. constantly; in this not explanation one by one, all among protection domain of the present invention.

As shown in Figure 3, the stabilitrak that example of the present invention provides adopts FEEDBACK CONTROL, and it comprises system state detection module 301 and stable control module 302.

Stablize control module 302 by the angle control module 305 of contacting to earth, PID controller 306, energy compensating module 307 and balancing force controller 308 form.

Contact to earth when the angle control module of contacting to earth 305 the realizes flight calculating at angle, computing method are shown in formula (4).

PID controller 306 is controlled and is realized the control signal θ that module 305 transmits by PID _tD.Energy compensating module 307 computing systems are from spring-compressed to minimum point to the energy that needs compensation during taking off, and computing method are suc as formula shown in (14).

Balancing force controller 308, by changing spring rate, changes the compensation that the acting force acting in equivalent mass is realized system capacity, and computing method are shown in formula (10), (11).

System state detection module 301, this module detects in real time to the system state amount of using in controlling, if some quantity of state controlled device can detect itself, control system directly reads, otherwise, need to install corresponding sensor and detect.

During system works, input U _dfor SLIP model stability post exercise expectation state, comprise aspiration level speed

with the vertical height of expectation peak

can calculate expectation peak gross energy E _d.By system state detection module 301, current system state and desirable system state are carried out to feedback ratio, the horizontal velocity that obtains differing

with the system gross energy Δ E differing _n.The horizontal velocity differing by contacting to earth, angle control module 305 calculates the angle θ that contacts to earth _tD, continue to obtain driving moment T by PID controller 306 _n+1, by servo-driver 303, act in controlled device 304 it controlled; The system gross energy Δ E differing _nby energy compensating control module 307, calculate to contact to earth for the n+1 time and need mutually the energy of compensation

continuation is compensated driving force F by balancing force controller 308 _n+1, by servo-driver 303, act in controlled device 304 it controlled.Instantiation:

With instantiation emulation, control effect explanation below, basic parameter arranges as follows:

SLIP model equivalent mass m=0.54kg, equivalent spring rigidity k=6N/mm, equivalent damping c=0.00035Ns/mm, the long r of initial equivalent leg ₀=120mm, initial vertically height H ₀=170mm.

PID controls is input as current pivot angle, is output as joint moment.The rule that this example adopts is as follows:

$F=k_P(\mathrm{\&theta;}-{\mathrm{\&theta;}}_{\mathrm{TD}})+k_d(\stackrel{\&CenterDot;}{\mathrm{\&theta;}}-{\stackrel{\&CenterDot;}{\mathrm{\&theta;}}}_{\mathrm{TD}})+\&Integral;(\mathrm{\&theta;}-{\mathrm{\&theta;}}_{\mathrm{TD}})\mathrm{dt}$

Wherein F is joint drive moment, k _p, k _i, k _dfor the gain parameter that PID controls, θ is the current pivot angle of the leg that detects of the 4th step, θ _tDbe that the angle of contacting to earth of calculating in the 3rd step is pivot angle,

be respectively θ, θ _tDderivative, i.e. the rate of change of the pivot angle of current pivot angle and expectation.

Fig. 7 is the vertical height analogous diagram under equivalent SLIP model no stability is controlled.This emulation is in order to verify the situation of the vertical jump process of SLIP model while controlling without motion stabilization.SLIP model initial level speed now

control target for expectation horizontal velocity the vertical height of expectation peak

from simulation curve, SLIP model is along with the number of times that contacts to earth increases, not having the peak under energy compensating vertically to decline highly gradually, from the vertical height of peak of expectation

more and more far away, system does not reach the control target of expectation motion stable period.

Vertical height analogous diagram under the stability control method that Fig. 8 provides for equivalent SLIP model application example of the present invention.Starting condition is all identical with Fig. 7 with control target, from simulation curve, can see, except contacting to earth for the first time, because landform is unknown, cause surmounting the vertical height of expectation peak, the jump of contacting to earth afterwards controls convergence very soon, has substantially reached the vertical height of peak of expectation

thereby realized the control target of system expectation motion stable period.

Fig. 9 is the motion schematic diagram of equivalent SLIP model under kame-and-kettle topography.SLIP model initial level speed now

control target for expectation horizontal velocity

the vertical height of expectation peak this emulation is in order to verify that stability control method that example of the present invention provides and system are in the adaptive faculty under complex-terrain comparatively such as non-level land landform.Figure 9 shows that kame-and-kettle topography, cup depth is h ₁=30mm.Peak vertically height emulated data be all SLIP model barycenter relatively and Fig. 9 midplane CD measure.

The vertical height analogous diagram that the stability control method that Figure 10 provides for equivalent SLIP model application example of the present invention moves under kame-and-kettle topography.By simulation curve, can see that reality vertically highly vertically highly can better realize and overlapping with expectation peak, realize the vertically highly control requirement of fast and stable of SLIP model peak under kame-and-kettle topography.

The horizontal velocity analogous diagram that the stability control method that Figure 11 provides for equivalent SLIP model application example of the present invention moves under kame-and-kettle topography.Can seeing that by simulation curve flight phase horizontal velocity differs greatly because landform is unknown except contacting to earth for the first time, later horizontal velocity is all in aspiration level speed upper and lower fluctuation within a narrow range, realistic robot motion's situation, can realize the control requirement of SLIP model flight phase horizontal velocity fast and stable under kame-and-kettle topography.

Figure 12 is the motion schematic diagram of equivalent SLIP model under terrace relief.SLIP model initial level speed now control target for expectation horizontal velocity

the vertical height of expectation peak

this emulation is in order to verify that stability control method that example of the present invention provides and system are in the adaptive faculty under complex-terrain comparatively such as non-level land landform.Figure 12 shows that terrace relief, ladder height is h ₂=30mm.Peak vertically height emulated data be all SLIP model barycenter relatively and Figure 12 midplane CD measure.

The vertical height analogous diagram that the stability control method that Figure 13 provides for equivalent SLIP model application example of the present invention moves under terrace relief.By simulation curve, can see that reality vertically highly vertically highly can better realize and overlapping with expectation peak, realize the vertically highly control requirement of fast and stable of SLIP model peak under terrace relief.

The horizontal velocity analogous diagram that the stability control method that Figure 14 provides for equivalent SLIP model application example of the present invention moves under terrace relief.Can seeing that by simulation curve flight phase horizontal velocity differs greatly because landform is unknown except contacting to earth for the first time, later horizontal velocity is all in aspiration level speed

upper and lower fluctuation within a narrow range, realistic robot motion's situation, can realize the control requirement of SLIP model flight phase horizontal velocity fast and stable under kame-and-kettle topography.

The stability control method that example of the present invention proposes and system are without setting up concrete Dynamic Models of Robot Manipulators, the accurate fixed point that do not need the to derive angle of contacting to earth, but by constantly and expectation state relatively feed back and finally realize stability and restrain, control method is simple, calculate rapidly, well solved the problems such as existing method real-time is not enough, adaptability is inadequate.And there is good circumstances not known adaptability, for legged type robot stability, control a kind of good solution is provided.

Claims (7)

1. A footed robot stability control method with environmental adaptability, the method may further comprise the steps: Step 1 System parameter initialization, including basic system information, proportional gain coefficient k _P of corner PID control, integral time constant k _I and differential time constant k _D ; set n=1; set the energy of the first ground contact phase compensation

is zero; initialize the control target, and calculate the total energy E _d of the expected system of stable periodic motion; the basic information of the system includes mass m, equivalent spring stiffness k, equivalent damping c and initial equivalent leg length r ₀ ; the Control objectives include stable periodic motion desired horizontal velocity

and the desired vertical height y _apexd of the highest point; Step 2 Detect initial horizontal velocity before first touchdown Step 3 Calculate the nth touchdown angle θ _TD before the nth touchdown; Step 4 Real-time detection of the system status to obtain the status information of the SLIP model at the current moment, including the horizontal velocity of the center of mass A

vertical speed

Leg swing angle θ, leg length r, vertical foot force F _c and current system time t; Step 5. Determine whether the SLIP model touches the ground. The condition for judging the moment of touchdown is that the force F _C at the end of the foot changes suddenly from zero to greater than zero, and the vertical velocity of the system

If it touches the ground, go to step 7, if not, go to step 6; Step 6 Control the SLIP model to the predetermined touchdown angle before the nth touchdown through PID control, even if the swing angle of the leg is equal to θ _TD ; Step 7 Read the relevant state parameters of the system at the moment of touchdown, including the horizontal speed at the moment of touchdown vertical speed

The equivalent leg length r _TD , and the actual ground contact angle θ _TD , and calculate the total system energy E _n at the time of ground contact, which is the total energy of the system before the nth ground contact; Step 8 Determine whether the SLIP model is compressed to the bottom; if it is compressed to the bottom, perform step 9, otherwise perform step 4; Step 9 Perform system energy compensation to make the system reach the desired total system energy E _d : Step 10 Determine whether the SLIP model is off the ground, if it is off the ground, go to step 11, otherwise go to step 9; Step 11 Read the relevant state parameters of the system at the moment of departure, including the horizontal speed at the moment of departure

vertical speed Equivalent leg length r _LO , and actual ground contact angle θ _LO , and calculate the total system energy E _n+1 at the time of liftoff, which is the total system energy after the nth ground contact; Step 12 Calculate the energy lost by the system during the nth touchdown

Its calculation formula is: in,

is the energy that should be compensated during the nth touchdown process,

The initial value of is 0; Step 13 Calculate the energy that should be compensated during the n+1th touchdown

Step 14 Determine whether the SLIP system has reached the destination, if not, go to step 3, otherwise end. the 2. the footed robot stability control method with environmental adaptability according to claim 1, is characterized in that, in the 3rd step, The calculation process of the nth touchdown angle θ _TD is: Let ΔS be the adjusted distance between the actual touchdown point P _TD and the neutral point P _N ; _S0 is half of the horizontal distance of the touchdown process when the touchdown point is the neutral point,

but where t _s is the total time of the nth touchdown process,

is the average horizontal speed of the nth touchdown process, and μ is the proportional coefficient of the adjusted distance between the touchdown point and the neutral point. 3. The environmental adaptability footed robot stability control method according to claim 1 or 2, characterized in that the total energy of the system E _n at the moment of touching the ground is the calculation of the total energy of the system before the nth touch of the ground The formula is:

. 4. The method for controlling the stability of a legged robot with environmental adaptability according to claim 1 or 2, wherein in the 9th step, the method for compensating energy is as follows: Increase the impulse F _n dt along the spring direction at the moment of compression to the bottom, and calculate the energy to be compensated as When the driving force F _n , its calculation formula is:

Among them, v _B is the total velocity of the system along the direction of the spring at the moment of impulse compensation, dt is the time interval of impulse increase,

. 5. The method for controlling the stability of a legged robot with environmental adaptability according to claim 1 or 2, wherein in the 9th step, the method for compensating energy is as follows: From the moment of compression to the bottom until the moment when the system lifts off the ground, the compensation constant force F _n along the direction of the spring is continuously increased, and the energy to be compensated is calculated as

When the driving force F _n , its calculation formula is:

Where r ₀ is the equivalent leg length without compression, and r _B is the equivalent leg length at the moment of compression to the bottom. 6. The method for controlling the stability of a legged robot with environmental adaptability according to claim 1 or 2, wherein in the 9th step, the method for compensating energy is as follows: Change the equivalent stiffness of the system from the moment of compression to the bottom until the moment when the system lifts off the ground, and increase the compensation stiffness Δk on the basis of the original equivalent stiffness k. The calculation formula is:

Where r ₀ is the equivalent leg length without compression, r _B is the equivalent leg length at the moment of compression to the bottom; The compensation stiffness Δk is realized by controlling the driving force F _n , and F _n changes all the time during the whole process, and its calculation formula is: F _n =Δk·(r ₀ -r) Where r ₀ is the equivalent leg length without compression, and r is the equivalent leg length at any current moment. 7. The environmental adaptability footed robot stability control method according to claim 1 or 2, characterized in that in the sixth step, the input of the PID control is the current swing angle, and the output is the joint torque. the

Images