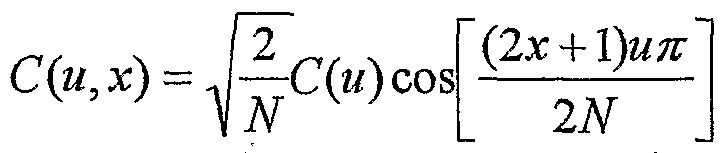WO2002003710A1

WO2002003710A1 - Fast efficient computation of the discrete cosine transform (dct) of digital video data

Info

Publication number: WO2002003710A1
Application number: PCT/US2001/040999
Authority: WO
Inventors: Kim Jongil
Original assignee: Media Excel, Inc.
Priority date: 2001-06-15
Filing date: 2001-06-15
Publication date: 2002-01-10
Also published as: AU2001273587A1

Abstract

A method for selectively computing and quantizing the components of the Discrete Cosine Transform of image data is presented. The method employs decomposition of the image data to successively obtain functions possessing even or odd symmetry about axes of the data. Threshold conditions may be applied to these auxiliary functions to determine which transform components may be deemed to be zero without further computation. Considerable reduction in the number of computations and memory required to compress video data is achived.

Description

FAST EFFICIENT COMPUTATION OF THE DISCRETE COSINE TRANSFORM (DCT) OF DIGITAL VIDEO DATA

Technical Field of the Invention

This invention relates to compression of digitally sampled video data.

Background of the Invention

Compression of video data is frequently employed to increase the number of video images that can be transmitted through a transmission channel per unit time and to increase the number of video images that can be stored in a storage medium of a given capacity. Several video compression standards, such as MPEG and H.263, have been developed to enable interoperability between different video systems made by different manufacturers. The major video compression standards require that the video encoder that compresses the video data implement a Discrete Cosine Transform (DCT) of the data. The standards also require that the video decoder that decompresses compressed video data implement an Inverse Discrete Cosine Transform (IDCT) of the compressed data. A block diagram of a standard video encoder is shown in Figure 1. Each video frame is divided into 16 x 16 pixel macro blocks. Motion Estimation 10 and Motion Compensated Prediction 15 may be implemented for each macro-block as shown. After the motion-compensated prediction process is performed for a macro-block, a Discrete Cosine Transformation 100 is performed upon each of four 8 x 8 pixel blocks of uncompressed video data comprising the macro-block.

The two dimensional Discrete Cosine Transform (DCT), F(u,v), of an N x N digitally sampled video image, f(x,y), is given by: F(u,v) =

for u = 0,1, ..., N-l, v = 0,1, ..., N-l and where C(u), C(v) = 2 /2 for u, v = 0 and C(u), C(v) = 1 otherwise. Thus, the 8 x 8 DCT, F(u,v) , of an 8 x 8 digitally sampled video image, f(x, v) , is given by:

7 7 (2x + ϊ)uπ (2y + ϊ)vπ

F(u,v) = C(u)C(v)∑ ∑f(x,y)cos\ cos x=0 y=0 Ϊ6 16

for u = 0,1,..., 7, v = 0,1,..., 7 and where C(M), C(V) = /2 / 2 for u, v = 0 and C(#),C(v) = l otherwise. Here, the integer index, x, is the vertical coordinate of the image and the integer index, y, is the horizontal coordinate of the image. The integer index, u, is the vertical coordinate of the image transform and the integer index, v, is the horizontal coordinate of the image transform. Thus, the image, f(x, y) , is transformed into a function of the vertical and horizontal spatial frequency indices, u and v. After computation of the DCT of the 8 x 8 video image, the transform components, F(u,v), are quantized 150. Inverse quantization 250 is employed and an Inverse Discrete Cosine Transformation 200 is implemented for use in the motion compensated prediction process 15.

The two dimensional Inverse Discrete Cosine Transform (IDCT), f(x,y), from the N x NDCT, F(u, v) , is given by:

(2x + l)uπ (2y + l)vπ

/(*» ') = ^ ∑ ∑C(u)C(v)F(u,v)cos cos

«=0 v=0 2ΪV 2N

for x = 0, 1, ... ,N-1 and y = 0,1, ... ,N-1. Thus, the 8 x 8 IDCT is given by:

for x = 0,l,...,7 and^ = 0,l,...,7

The quantized transform components are zigzag scanned 20, as shown in Figure 2, to create a one-dimensional sequence of spatial frequency components in approximately descending order. Due to the "energy compaction property" of an orthogonal transform, the DCT of a video image generally produces a two-dimensional energy spectrum with most of the energy concentrated about the low frequency components, especially, the "DC" term, ^(0,0) . Therefore, the one-dimensional sequence of quantized frequency components can be expected to approach zero after some number of terms, and the sequence will contain a long trail of zeros at the end. An End of Block (EOB) symbol is inserted after the last non-zero component to indicate where the non-trivial portion of the sequence ends.

Variable Length Coding 25 is employed to use shorter sequences to encode the more frequently occurring symbols and longer sequences to encode the less frequently occurring symbols to achieve a higher compression ratio. Finally, a buffer 30 is employed to enable adaptive adjustment of the quantization parameter to control the bit rate of the compressed video output by the encoder. By increasing the quantization step size, more DCT components will be quantized to zero. By decreasing the quantization step size less DCT components will be quantized to zero. In the configuration of Figure 1, all of the DCT components are computed even though many will be quantized to zero. In particular, much of the energy in the transformed image can be expected to be concentrated in the low frequency components of F(u,v)wit the probability of a transform component quantizing to zero generally increasing with higher frequency. Therefore, computation of many of the transform components, F(u,v) , will prove to be a waste of computational resources since they will , ultimately quantize to zero. A need exists for methods and systems to eliminate the computation of DCT components that would probably quantize to zero. Summary of the Invention

The present invention increases the speed and efficiency of video image compression by providing efficient methods and systems for computing the Discrete Cosine Transform (DCT) and for selective application of thresholds to preclude computation and quantization of DCT components that have a high probability of quantizing to zero or that otherwise may be set to zero while maintaining image quality above a desired level.

The present invention provides methods for selectively determining transform components of the discrete cosine transform and omitting computation and quantization of transform components that may be deemed to be zero without substantial reduction in the quality of the image when reconstructed at an encoder. The present invention also provides methods for selectively determining transform components while minimizing the number of multiplications needed to compute transform components that are deemed necessary for adequate representation of the image. The present invention further provides for the efficient use of memory by reusing memory storage during the process of selectively computing transform components. The present invention further provides for the merger of quantization arithmetic with the multiplication of coefficients of the discrete cosine transform to obtain yet a further reduction in computations needed to compute the discrete cosine transform.

According to the present invention a selective computational approach is employed that exploits the symmetry and energy compaction properties of the Discrete Cosine Transform. This is accomplished by expressing the transform components in terms of a first set of symmetrical functions of the pixel coordinates of the image. The first set of symmetrical functions is computed without multiplication to achieve a considerable reduction in the complexity of computing the components of the DCT. The values of the first set of symmetrical functions can replace in memory the pixel values of the image to achieve a reduction in memory required to compute the DCT. Threshold conditions are then applied to one or more of the first set of symmetrical functions to determine whether further computation of the transform components corresponding to these functions is required. In many cases, further computation is not required and additional reduction in computational burden is therefore achieved. In cases where further computation is required, the first set of symmetrical functions are themselves expressed in terms of a second set of symmetrical functions of the pixel coordinates of the image. This second set of symmetrical functions can also be computed without multiplication to achieve yet a further reduction in the complexity of computing the components of the DCT. The values of the second set of symmetrical functions can replace in memory the values of the first set of symmetrical functions to achieve yet a further reduction in memory required to compute the DCT. Threshold conditions are then applied to one or more of the second set of functions to determine whether further computation of the transform components corresponding to these functions is required. In many cases, further computation is not required and a further reduction in the amount of computation to determine the DCT is thereby achieved. The process of decomposing the DCT into successive sets of symmetrical functions may continue until no further symmetry decomposition can be achieved. In these cases, successive application of threshold conditions to the remaining DCT components can be employed to further reduce the amount of computation required.

Thus, according to the methods of the present invention considerable efficiency is achieved by computing only those transform components that would not quantize to zero for a given quantization parameter. This results in a considerable reduction in the number of multiplications required to compute the discrete cosine transform of the image. This also results in reduction of the quantization computations that must be employed in the image encoder. Further, the inverse quantization and inverse discrete cosine transformation performed in a video encoder as part of the motion estimation process can be applied only to the transform components that are not deemed to be zero, resulting in yet a further reduction in the computations to be performed by the encoder. Yet further, the entire array of transform components need not be scanned since the non-zero components have been identified in the process of determining which transform components may be deemed to be zero.

These and other features and aspects of the present invention may be better understood by reference to the attached drawings and the following written description ofpreferred embodiments. Brief Description of the Drawings

1. Figure 1 is a block diagram of a standard video encoder.

2. Figure 2 is a block diagram of a matrix of transform components illustrating an order of zigzag scanning.

3. Figure 3 is a digital computation structure for implementing computations according to the methods of the present invention.

4. Figure 4 is a flow chart of a threshold process applied according to the methods of the present invention. 5. Figure 5 is a block diagram of a system for implementing the methods of the present invention.

6. Figure 6 is an illustration of a two dimensional array of image pixels.

7. Figure 7 is a digital computation structure for implementing computations according to the methods of the present invention. 8. Figure 8 is an illustration of a two dimensional array of symmetrical function values.

9. Figure 9 is a digital computation structure for implementing computations according to the methods of the present invention.

10. Figure 10 is an illustration of a two dimensional array of symmetrical function values.

11. Figure 11 is a digital computation structure for implementing computations according to the methods of the present invention.

12. Figure 12 is an illustration of a two dimensional array of symmetrical function values.

13. Figure 13 is a digital computation structure for implementing computations according to the methods of the present invention.

14. Figure 14 is a digital computation structure for implementing computations according to the methods of the present invention.

15. Figure 15 is a digital computation structure for implementing computations according to the methods of the present invention.

16. Figure 16 is a digital computation structure for implementing computations according to the methods of the present invention. Description of Preferred Embodiments

The N x NDCT, F(u,v), of an N x N digitally sampled video image, f(x,y), is given by:

for u = 0,1,..., N-l, v = 0,1,..., N-l and where C(w),C(v) = V2 /2for u, v = 0 and C(u),C(v) = 1 otherwise.

A significant reduction in the number of additions and multiplications to compute the transform components, F(u,v) , can be achieved by exploiting the symmetry properties of the cosine functions. The symmetry properties of the two dimensional DCT cosine functions can be described by reference to the one dimensional Ν-point DCT, F(u) , given by:

for u = 0,1, ...,N-1 and where C(u) = V2 /2 for u = 0 and C(u) = 1 otherwise. The cosine function possesses even symmetry about the line x = (N-l)/2 when u is an even integer and possesses odd symmetry about the line x = (N~l)/2 when u is an odd integer. If we define C(u,x) as:

for x = 0,1,, .. N-l, and u = 0,1,..., N-l, then C(u,x') = (-\)^uC(u,x) , where x = (N~V) - x for x = 0, 1, ... , (N/2-1) . Using this notation, the equation for F(u) may be rewritten as follows: F(u) = ∑f(x)C(u,x)

= ∑imC(u,x)+f(x')C(u,x')] x=0

= ∑C(«,x)[/(x)+(-l)"/( ')] x= m 2

= ∑C(u,x)fi(x) x=0 for u = 0,1,..., N-l. The function, ₀"(x) = (x) + (-l)"/(x')_> possesses even symmetry about the axis, (N-1J/2, i is an even integer and possesses odd symmetry about the axis, (N-1J/2, ifu is an odd integer.

Thus, using the symmetry properties of the cosine function, the N-point DCT of f(x) can been decomposed into an (N/2)-point DCT of /₀" (x) . This process can be repeated forN > 4 and u an even integer as follows:

2

F(u) = ∑f₀ ^«(x)C(u,x) x=0

= ∑[/_o" (*) C(u, x) +/₀" (x') C(u, x'y x=0

= ∑c(_M) ^χ)[/₀"(^χ)+(-i)^H/Vo^M(^χ')] x=0

∑C(«,x)/₁"(x)

for u equal to an even integer, and x

for x = 0,1,..., (N/4-1) . The function, f"(x)= /₀"(x)+ (-l)"^/2/₀"(x'), possesses even symmetry about the axis,

[(N/2)-l]/2, if u/2 is an even integer and possesses odd symmetry about the axis, [(N/2)- l]/2, if u/2 is an odd integer. Thus, the N-point DCT of fix) can be decomposed into an

(N/4)-point DCT of /," (x) for u an even integer. This process of decomposition can be continued as long as is an integer for n = 0, 1, ... , log₂ (N) - 1. The decomposition process just described can be applied to the two dimensional DCT as follows:

N-l N-\ ^v) = ∑∑ C(u,v, x,y)f(x,y) χ=0 y=0

= ∑ ∑ C(u, v, x, y)[f(x, v) + (-D^v f(x, /)] x=0 y=0

= ∑ ∑ C(u, v, x, y)[f(x, y) + (-l)^v/(x, v') + (-1)" /(*', y) + (-l)"^+v/(x', /)]

= ∑ ∑ C(u, v, x,y)f (x,y) x=0 y=0 where x = (N- l) - x for x = 0, 1, 2, 3,...(Ν/2-l), y = (N- \) -yi x y = 0, 1, 2, 3,... (N/2-1), and

(2x + \)uπ 2y + l)vπ

0,v,x,.yj = — C(u)C(v) cos cos

N 2ΪV 2N for u,v = 0,1,2,3, ...N-l. The function, ./_Oo ^V( ,. , possesses even symmetry about the axis x = (N-l)/2 if w is an even integer and possesses odd symmetry about the axis x = (N- l)/2 if u is an odd integer. Similarly, the function, f^(x,y) , possesses even symmetry about the axis v = (N-l)/2 if v is an even integer and possesses odd symmetry about the axis.y = (N-l)/2 if v is an odd integer.

Therefore, by exploiting the symmetry properties of the cosine functions, the NxN DCT of /(x,j has been decomposed into an (N/2) x (N/2) DCT of f£(x,y) .

This process of decomposition can be continued as long as or y is an integer for

n,m = 0,l„..., log₂(N) - l . For example, if Ν > A, the DCT can be further decomposed for v equal to an even integer as follows:

F(u,v) C(u,v,x,y)[f (x,y) + (-iγf (x,y')]

for x'= [(N-l)] - x for x = 0,1,2,...(N/2)-l,/ = [(N/2)-l] - for v = 0,l,2,...(N/4)-l, «

= 0,1,2,3... N-l, and v = 2,4,6,. ,.N-2. The function /₀"^v(x, v) possesses even symmetry about the axis y - [(N/2)-l]/2 for v/2 an even integer and possesses odd symmetry about the axis y - [(N/2)-l]/2 for v/2 an odd integer. For u equal to an even integer, the DCT can be decomposed yet further as follows:

*"(«,v) = ∑ ∑ C(u,v,x,y)[f (x,y) + (-\γ f^» (x',y)} x=0 y=

for x'= [(N/2)-l] - x for x = 0,l,2,...(N/4)-l, y' = [(N/2)-l] - v for y = 0,l,2,...(N/4)-l, ω = 0,2,4,6... N-2, and v = 0,2,4,6,... N-2. The function f™ (x, y) possesses even symmetry about the axis x = [(N/2)-l]/2 for u/2 an even integer and possesses odd symmetry about the axis x = [(N/2)-l]/2 for u/2 an odd integer.

In general, therefore, the Discrete Cosine Transform may be successively decomposed and expressed in terms of a set of functions, f^(x,y) that possess even or odd symmetry about the x x y axis according to whether or y is an even or odd

integer, respectively, for n, m = 0, 1 , ... , log₂ (N) - 1. In terms of the functions, f (^χ, y) , the DCT can be expressed as:

where L„ = N ^ f _N

U

> «+! -1, L„. = ra+1 2"l_x for /,= 0,l,...,(N/2" -1), and v =

2^ml_y for l_y = 0,l,...,(N/2^m -1). A function, fZ(^χ,y), possesses even symmetry about

the axis x = when is an even integer and possesses odd symmetry

2" about the axis x is an odd integer. Similarly, a function,

N fZ(^x _>y)_> possesses even symmetry about the axis = — -1 when is an

2.

even integer and possesses odd symmetry about the axis y 1 when ^v/ _m is

an odd integer. Given the initial functio /^( , y) = f χ_} y) , the functions, fZ(.^x _>y)_> ^can be derived successively from preceding functions as follows:

fZ(*,y) = fnlm-v>(^χ,y) + (^{~ m} Λ?»-i) (*,/), when ^ is an integer;

fZ (^χ, y) = /(»-i_)m (x, y) + (^~ 1) ^2" "-ι_)m (*', y) , when ^/„ is an integer; and

when %_m is an integer and %„ is an integer, for χ'= [(N/2" )-l] - x for x =

/ 2 / 2

0,l,...,(N/2"⁺¹ )-l, y = [(N/2^M )-l] - v for = 0,l,...,(N/2^m+1 )-l, and where τ? or m takes on non-negative integer values less than or equal to log₂(N) - l , respectively. In particular, when y is an integer and y _n is an integer, then we have the following : _m are both even we have:

fZ (x, y) = fZ (*> y) - /("/-ix,-!) (*> y) + f" ^ (*> /) + / IX-D (*'. y) + cϊ (*'. ')

When y is odd and y is even we have:

fnm \^X> y ⁼ fnm (^XJ ⁼ /(n-iχm-1) (^X» J ⁺ J(n-l)(»ι-l) ^X> ^V ) ^_ /(n-iχm-1) (^X > J') ^~~ /(n-iχ»ι-l) ^X > J' )

When „ is even and /_m is odd we have: / . / 2 fnm (^X> ) ^~ fnm (^X> ^~ /(n-iχm-1) (^X> ^~ /("-lXm-1) (^X> ^ ) ⁺ /(n-iχro-1) (^X'> ^) ^~ /(n-iχm-1) (^X ' )

When and %_m are both odd we have:

Λm (^X? >7

(^X> ^~

(^X> .V ) ^_ f(n-iχm-l) (^X > *) + /(«-iχm-l) (^X > .V )

These functions may be computed efficiently using the digital computation structure shown in Figure 3, where the arrows indicate multiplication by minus 1, and the dots imply two-input integer adders. The structure of Figure 3 shows that the functions, fZ(^x _>y) _> require 8 additions and no multiplications for each coordinate pair (x,v) for a total of 8 x(N 2"⁺¹ ) x (N/2"'⁺¹ ) additions. As is customary, multiplication by minus one is not included when determining the computational burden of a digital implementation, since multiplication by minus one can be accomplished by negation of a ^■ sign bit.

According to the methods of the present invention, a threshold condition can be applied to functions, fZ(^x _>y)_> that are obtained by successive decomposition of the DCT to selectively omit the computation of corresponding transform components, F(u, v) , that would be quantized to zero. This is illustrated in Figure 4. First, a function, f (^x,y)_> is computed 400 as described above. Then a threshold condition is applied to the function 420. If the function passes the threshold condition then further decomposition may be implemented 425. If not, then the transform components, F(u,v) , corresponding to the function „„ (x, ^;)may be computed 440 and quantized 450. If the function fails the threshold condition then the corresponding transform components, F(u,v) , are deemed to be zero 430.

Thus, selective computation of transform components is achieved by successive application of threshold conditions to the functions, fZ(^x _>y) _> that are obtained by successive decomposition of the DCT. Significant improvement in speed and efficiency is achieved by eliminating the computation of transform components that may be deemed to be zero and also eliminating the quantization arithmetic for these components. In conventional video encoding systems, quantization is applied to a transform component after it is computed. Thus, after a transform component is computed it may be quantized

F(u v) as follows: — ' is computed and truncated or rounded to a nearest integer, where q is 2qw"^v the quantization parameter, which is typically an integer between 1 and 31, and w^uv is a human visual weighting parameter that accounts for the spatial frequency dependence of human visual perception. The visual weighting factor, w"^v, is a non-decreasing function of frequency because the frequency sensitivity of human visual perception decreases as spatial frequency increases. Thus, elimination of the transform components corresponding to higher spatial frequencies is less likely to result in a degradation of the image that can be perceived by a human being. It will be understood that in some implementations, the visual weighting factor is assumed to be equal to one for all u and v. In many cases, the transform components, F(u,v) , will be quantized to zero for all but the very lowest values of u and v, because the energy in the frequency spectrum of an image is typically concentrated about .F(0,0) . Thus, computation and quantization of many of the transform components is a waste of time. According to the methods of the present invention, threshold conditions are applied prior to and during the process of computing the transform components to selectively eliminate computation and quantization of those transform components that are likely to be quantized to zero. This results in a substantial reduction in the number of computations that are performed to encode the image and substantially increases the speed of the encoder. Therefore, after computing a set of symmetry functions, fZ(^χ,y), we apply threshold conditions to one or more of these functions to make an initial determination whether the computation of any transform components may be eliminated. The threshold conditions may be applied to the functions as follows: First, we compute:

which requires (L_n + 1) x (L_m + 1) additions for each term, f , and no multiplications. The magnitude operation involves the mere setting of a sign bit. Then, we apply a threshold test: If f < Q"^V , then the corresponding transform components, F(u, v) , are deemed to be zero. In other words, for a function, fZ(^x _>y)_> ^we compute the sum of the absolute values of its data components. If the sum does not exceed a threshold level, Q"^v , we deem the corresponding transform components, F(u,v) , to be zero. If that sum does exceed the threshold, then we retain the data components for use in further computations. Thus, a transform component will be deemed zero if its corresponding symmetry function, f (^x _>y)_> fώte the threshold condition, and further computations will be performed upon fZ (x, y) otherwise.

The threshold level, Q^m , is preferably a composite of the following factors: q, the quantization parameter; w^uv, the visual weighting parameter for F(u,v) ; and k^ω , as pre- determined from C(u, v, x, y) ; and where

Q^uv = 2qw^uvk^m

F(u v) Clearly, if — ^-^ quantizes to zero then the sum of absolute values of the coefficients,

f^uv(x,y), of the cosine functions in the equation for F(u,v) will not exceed Q^uv .

Therefore, deeming these values of F(u, v)to be zero is justified. In practice, since the DC component is visually more important than high frequency components, w"^v can be set equal to l/(2q) for u and v both zero, so that F(0,0) is finely quantized regardless of the value of the quantization parameter q.

The value of k^m may be selected according to the desired degree of correlation between the transform components that are deemed to be zero and the transform components that would quantize to zero if actually computed and quantized. Thus, in one embodiment £"^vmay be chosen as the maximum, over (x,y), of the magnitude of

C^} (u,v,x, y) , where the superscript, -1, indicates the reciprocal. Alternatively, k"^vmay be chosen as the average, over (x,.y),of the values of the magnitude of C^_1 (u, v, x, ) . Yet another alternative is to choose k^uv as a weighted average, over (x, v), of the values of the magnitude of C^~ (u,v,x, y) . The corresponding values of Q^uv = 2qw"^vk"^v may be computed in advance, stored in Read-Only-Memory (ROM) and retrieved as needed. Figure 5 illustrates a system for implementing the methods of the present invention described above. The system 500 comprises Random Access Memory (RAM) 510 for storing values of the image pixels and the values of the functions fZ, (.^χ _>y) ■ The threshold levels Q^uvaxe stored in ROM 520. The computations and logical operations

described above, including computation of the functions, f (^x _>y)_> ^andf _> ^an<i implementation of the threshold conditions, are performed by processor 530. Processor 530 may be implemented as a microprocessor, digital signal processor or other processing device with suitable functionality operating under the directions of software. Alternatively, system 500 may be implemented in an Application Specific Integrated Circuit (ASIC) or in other suitably designed hardware. Configuration of system 500 is within the skill of persona of ordinary skill in the art given the disclosure provided herein.

Thus, a selective computation of an NxN image is accomplished by decomposing the image into a set of auxiliary functions that possess even or odd symmetry about axes of the image. Threshold conditions may then be applied to these functions to exclude computation and quantization of transform components that would quantize to zero for a given quantization parameter. For the transform components that are not deemed to be zero as a result of the application of these threshold conditions, the auxiliary functions possessing even symmetry may be further decomposed to obtain a second set of auxiliary functions that possess even or odd symmetry about an x or y axis. Threshold conditions may then be applied to this second set of auxiliary functions to further exclude computation and quantization for transform components that would quantize to zero. This process is repeated until no further decomposition can be obtained. Successive application of threshold conditions for the remaining DCT components may be applied to obtain further computational reductions. The method of the present invention described above for selectively computing transform components for an NxN image block may be specifically applied to the 8x 8 DCT as will now be described. Figure 6 shows an 8x 8 block of image pixels, obtained by digitally sampling a video image, which may be represented by a function, f(x,y), for x = 0,1,..., 7 and y = 0,1,..., 7. As shown, is the vertical coordinate and y is the horizontal coordinate. To compress a digitally sampled video image, the Discrete Cosine Transform is employed to obtain a set of 8 x 8 transform components, F(u,v), where u is the vertical frequency index and v is the horizontal frequency index.

(2x + \)uπ

For the 8 x 8 DCT we have the following results: the function cos

16 possesses even symmetry about the axis, x_c = 112, when u is an even integer, and possesses odd symmetry about the axis, x_c =7/2, when u is an odd integer. Therefore,

(2x + ϊ)uπ (2(l-x) + ϊ)uπ cos (-1)" cos

16 16 for x = 0,1,2,3.

(2y + l)vπ

Similarly, the function cos possesses even symmetry about the axis, 16 v_c=7/2,when v is an even integer, and possesses odd symmetry about the axis, y_c-71 when v is an odd integer. Therefore,

for y = 0,1,2,3.

By application of these symmetry properties, the equation for the transform components, F(u, v) , can be written as follows:

where, f (x, y) is given by:

fS (^χ,y) = f(^χ,y) + (-i)V(^χ,7 - y) + (-1) "f⁽7 - ^χ, y) + H)"⁺V(7 - ^χ,7 - v) for x = 0,1,2,3 and y = 0,1,2,3. Henceforth, f^uv denotes f , and thus, f^uv(x,y) indicates foo(^χ,y). When u and v are both even we have:

/"^v(x^) = /o?(x^) = /^∞(x^) = /(x^) + /(^7-v) + /(7-x,v) + /(7-x,7-v) When u is odd and v is even we have: f"^v(^χ,y) = f^oe(^χ,y) = f(^χ,y) + f(^χ,^'7 -y) - f(7 - ,y) - fC> - ^χ,7 -y)

When u is even and v is odd we have:

/"^v(x^) = /^e°(x₃ ) = /(x^) - /(x,7 -^) + /(7 - x,3 ) - /(7 - x,7 - v) When u and v are both odd we have: f^m i^χ,y) = f°° ( ,y) = f( ,y) - fW - y - fO - ^χ,y) + f(i - ^χ,ι - y)

The values of f^uv (x, y) are now the intermediate coefficients of the cosine functions in the equation for computing F(u,v) . Each of the functions, f^uv(x,y), are the algebraic sum of image pixel values that have coordinates equidistant from an axis of symmetry. These functions possess even symmetry about a vertical axis of the image if v is even or odd symmetry about a vertical axis of the image if v is odd, and possess even symmetry about a horizontal axis of the image if u is even or odd symmetry about a horizontal axis of the image if u is odd.

The symmetry functions, f^uv(x,y), can be computed efficiently using the digital computation structure shown in Figure 7, where the arrows indicate multiplication by minus 1 and dots imply adders. The structure in Figure 7 shows that the computation of the functions, f^uv(x,y) , require 8 x 16 additions and no multiplications.

The data of /"^v(x, )may replace in memory the data of /(x_3ιy) as the computations depicted in Figure 7 are performed, thereby allowing for a reduction in the memory required to compute the Discrete Cosine Transform (DCT). The organization of the data of f"^v(x, v)in memory may be visualized in matrix form as shown in Figure 8, wherein each of the four quadrants of the 8 x 8 matrix contain a 4 x 4. sub-matrix of the data of one of the four functions f^ee °^e,f^eo, and f°°.

We now apply threshold conditions to the functions, f"^v(x,y), to selectively eliminate the computation and quantization of transform components that are likely to be quantized to zero.

As previously noted, in many cases, the transform components, F(u,v) , will be quantized to zero for all but the very lowest values of u and v, because the energy in the frequency spectrum of an image is typically concentrated about . (0,0) . Thus, computation of many of the transform components is a waste of time. According to the methods of the present invention, threshold conditions are applied prior to and during the process of computing the transform components to selectively eliminate computation and quantization of those transform components that are likely to be quantized to zero. This results in a substantial reduction in the number of computations that are performed to encode the image and substantially increases the speed of the encoder. Also, as previously noted, the Inverse Discrete Cosine Transform implemented by the encoder in the motion estimation process is only applied to the transform components that are not deemed to be zero, thereby achieving further reduction in computations performed by the encoder.

Therefore, after computing each of the first set of symmetry functions, f^uv(x, y), we apply threshold conditions to one or more of these functions to make an initial determination whether the computation of any transform components may be eliminated. The threshold conditions may be applied to the functions as follows: First, we compute:

which requires 16 additions for each term, /'"^' , and no multiplications. The magnitude operation involves the mere setting of a sign bit. Then, we apply a threshold test: If f^uv < Q^m , then the corresponding transform components, F(u,v) , are deemed to be zero. In other words, for a function, f^uv(x,y), we compute the sum of the absolute values of its data components. If the sum does not exceed a threshold level, Q "^v , the function, f"^v(x, ) , fails the threshold test, and we deem the corresponding transform components, F(u,v) , to be zero. If that sum does exceed the threshold, the function, f"^v(x,y) , passes the threshold test, and we retain the data components for use in further computations. Thus, a transform component will be deemed zero if its corresponding symmetry function, f"^v(x,y), fails to satisfy the threshold condition, and further computations will be performed upon f^v(x,y) otherwise. For a certain quantization parameter q, the threshold function, Q^uv , is regarded as a non-decreasing function of frequency, because w"^v is an increasing function of frequency and &"^v does not vary as much over frequency as w"^v does. Therefore, the minimum threshold value, Q^uv , over the all frequencies is deemed to be Q⁰⁰. Accordingly, we proceed to apply a threshold condition to the function, f^ee(x, y) , as follows. First, we compute:

y)

Then, we apply a threshold test: If f^ee < Q^ee , then the corresponding transform components, F(u,v) , are deemed to be zero. In other words, for the function f^ee(x, y) we compute the sum of the absolute values of its data components. If the sum does not exceed the threshold level, Q^ee , we deem the corresponding transform components, F(u, v) , to be zero. If that sum does exceed the threshold, then we retain the data components for use in further computations. Thus, the transform components of all even frequencies of u and even frequencies of v will be deemed zero if its corresponding symmetry function, f^ee(x,y) , fails the threshold condition, and further computations will be performed upon f^ee(x,y) otherwise.

In one embodiment of the invention, the value of Q^ee may be different for each frequency pair (u, v) according to the value of the visual weighting parameter, w^ee .However, in a preferred embodiment, Q" is chosen as Q" = β⁰⁰ = 2 Λ⁰⁰ . That is, Q^ee is chosen to be the threshold level corresponding to (u,v) = (0,0) because it is the

minimum threshold value among all even-even frequencies. If f^ee fails the threshold condition for this choice of Q^ee , then (0,0) would quantize to zero. And further, the

inequality f^ee < Q^ee holds for all other even-even frequencies of u and v, since β⁰⁰ is the

minimum value of Q^ee . Thus, if f^ee <2qw°°k⁰⁰ , then all transform components of even- even frequencies may be deemed to be zero. In most cases, however, f^ee can be expected to exceed the threshold level, Q^m , because a large portion of the energy in an image, f(x, y) , is concentrated in the DC component, F(0,0). Therefore, in most cases, further computation using the symmetry functions, fZ(^χ, y) , ^are required. If f^ee exceeds the threshold level, Q⁰⁰ , then further decomposition is performed for/,^,'(x, v) , as long as symmetry exists,and in turn, threshold conditions are applied. When further symmetry does not exist and f exceeds the threshold level, then the transform components are computed using:

^n L_m

F(u,v) = ∑∑C(u,v,x,y)fZ(x,y) x=0 7=0 A threshold condition is next applied to f^oe(x,y) , or alternatively, f^e°(x,y) , as follows. First, we compute:

Then, we apply a threshold test: If f^oe < Q^oe , then the corresponding transform components, F(u, v) , are deemed to be zero. In other words, for the function f^oe(x, )we compute the sum of the absolute values of its data components. If the sum does not exceed the threshold level, Q^oe , we deem the corresponding odd-even transform components, F(u,v) , to be zero. If that sum does exceed the threshold, then we retain the data components for use in further computations. Thus, a transform component will be deemed zero if its corresponding symmetry function, f^oe(x,y) , fails the threshold condition, and further computations will be performed upon f^oe (x, y) otherwise.

In one embodiment of the invention, the value of Q°^e may be different for each frequency pair (u,v) according to the value of the visual weighting parameter, w^oe .

However, in a preferred embodiment, Q^oe is chosen as Q^oe= Q^w = 2qw^wk^m . That is,

Q^oeis chosen to be the threshold level corresponding to (u,v)= (1,0) because it is the minimum threshold value among all odd-even frequencies. If f^oe fails the threshold condition for this choice of Q^oe , then F(l,0) would quantize to zero. And further, the inequality f^oe < Q°^e holds for all other odd-even frequencies of u and v, since β¹⁰ is the

minimum value of Q^oe . Thus, if f^oe <2qw^wk^w, then all transform components, F(u,v) , for u odd and v even may be deemed to be zero.

Threshold conditions are also applied to the functions, f^eo(x,y) and f°°( ,y) -

Thus, if f^eo < <2⁰¹then all transform components for (w-even, v-odd) would be deemed to be zero, and further computations would be performed using f^eo(x,y) otherwise.

Similarly, if f°° < Qⁿ , then all transform components for (w-odd, v-odd) would be deemed to be zero, and further computations would be performed using f°°(^x,y) otherwise. As yet another alternative, certain transform components may automatically be deemed to be zero, without regard to the threshold conditions discussed above. For example, an implementation that automatically deems to be zero values of F(u, v) for u and v both odd would reduce the computational burden of video encoding and yet may yield, at least in some applications, acceptable image quality when the compressed video is reconstructed after transmission

It will also be noted that deeming a transform component to be zero would entail setting to zero the memory location where that component is to be stored, unless the memory locations where the transform components are stored are initialized to zero. Thus, if the location in memory where F(u,v)is to be stored is initialized to zero, then it is not necessary to again set to zero those memory locations where a value F(u,v) deemed to be zero is stored. Alternatively, values of F(u,v)may occupy the same memory locations as were stored the original image pixels, and then the memory locations wherein values of F(u, v) that are deemed to be zero are stored will be set to zero. For those transform components that are not deemed to be zero at this stage of the implementation, further computations are performed, as will now be described. Decomposition for Even u and Even v: Further analysis of the symmetry properties of

(2x + X)uπ the cosine functions yields the following results. The function cos possesses

16 even symmetry about the horizontal axis, x_c =3/2, when u is 0 or 4, and possesses odd symmetry about the horizontal axis, x_c =3/2, when u is 2 or 6. Therefore,

(2x + ϊ)uπ (2(3-x) + l /r^" cos (-1)"" cos 16 16 for u = 0,2,4,6 and x = 0,1.

(2v + l)v^r

Similarly, the function cos possesses even symmetry about the 16 vertical axis, v_c = 3 / 2, when v is 0 or 4, and possesses odd symmetry about the vertical axis, y_c = 3 / 2, when v is 2 or 6. Therefore,

(2y + ϊ)vπ (2(3-y) + l)vπ cos = (-l)^v/2cos| 16 16 for v = 0,2,4,6 and = 0,1.

By application of these symmetry properties we can write the equation for F(u, v) when both u and v are even as follows:

for v = 0,2,4,6, x = 0,1, v = 0,2,4,6, y = 0,1, and where

gT^χ,y) = r^e(^χ, y) + (-i)^v/2/^ee(^χ,3 -y)+ (-ιγⁿr -^χ,y)+ (-!)<^•" v<3 - ^χ,3 - y)

wherer^e(x, ) = /(x,v) + (x,7- ) + /(7-x,v) + (7-x,7- ). When u is 0 or 4 and v is 0 or 4 we have: gTΛ^χ,y) = g:Λ^{e χ},y) = f^ee(,y)+r^e( -y)+f^eeQ- ,y)+f^ee - -y)

When u is 2 or 6 and v is 0 or 4 we have:

When u is 0 or 4 and v is 2 or 6 we have: g:(^χ,y) = g (^χ,y) = f^ee(^χ,y)-f^βe( ,3-y)+ θ-^χ,y)-r ^~χ -y)

When u is 2 or 6 and v is 2 or 6 we have: g::(^χ,y) = g:(^χ,y) = f^ee(^χ>y)-r( -y)-f^ee -^χ,y)+f^eeQ-^χβ-y)

Finally, we have: r(^χ,y) = HgTΛ,y)+gΛ^χ,y)+gTΛ^χ,y)+g:(^χ,y)]

The functions, "(x, ), are the algebraic sum of values of f^e(x,y) that have coordinates equidistant from an axis of symmetry. The functions g (^x _>y) can be computed efficiently using the digital computation structure of Figure 9. The structure in Figure 9 shows that the computation of the functions, g^' (x,y), require 4x8 additions and no multiplications.

The data of g"ζ(x,y) may replace in memory the data of f^ee(x,y) as the computations depicted in Figure 9 are performed, thereby allowing for a further reduction in the memory required to compute the Discrete Cosine Transform (DCT). The organization of the data of g"(x, )in memory may be visualized in matrix form as shown in Figure 10, wherein each of the four quadrants of the 4x4 matrix contain a 2 x 2 sub-matrix of the data of one of the four functions gZ, Z_{> e}°_> ^arK* gZ-

The values of gZ(^χ, y), are now the intermediate coefficients of the cosine functions in the equation for computing F(u,v) for u and v both even. These functions possess even symmetry about the vertical axis, = 3/2, if v/2 is even or odd symmetry about the vertical axis, y = 3/2, if v/2 is odd, and possess even symmetry about the horizontal axis, x - 3/2, if u/2 is even or odd symmetry about the horizontal axis, x = 3/2, if u/2 is odd.

We may now apply a threshold condition to each of the functions, g"_e ^v(x, v), as follows. First we compute:

which requires 4 x 4 additions for all integer values of % , % • Then we apply a

threshold test: If " < Q^uv , then the corresponding transform components, F(u, v) , are deemed to be zero. In other words, for a function, g i^x _>y) , we compute the sum of the absolute values of its data components. If the sum does not exceed a threshold level, Q^m , we deem the corresponding transform components, F(u, v) , for all integer values of

o ' Vi ' ' ^t0 ^^e zeroes. If the sum does exceed the threshold, then we retain the data components for use in further computations. Thus, a transform component will be deemed zero if its corresponding symmetry function, gZ(^χ,y), fails the threshold condition, and further computations will be performed upon g^u _e ( ,y) otherwise.

Accordingly, for ^UΔ and ^vyi both even integers, we proceed to apply a threshold

condition to the function, g (x, y) as follows. First we compute:

Then we apply a threshold test: If g_e ^e _e ^e < Q^es , then the corresponding transform components, F(u,v) , are deemed to be zero. Otherwise, the values of gZ(^χ,y) are used in further computations. In one embodiment of the invention, the value of Q^ee may be different for each frequency pair (u,v). However, in a preferred embodiment, Q^ee is chosen as Q^ee = Q⁰⁰ = 2qw⁰⁰k⁰⁰ . That is, Q^eeis chosen as the threshold level

corresponding to (u,v) = (0,0). If gZ fails the threshold test for this choice of Q ^β, then

for all even integer values of % and % , F(u,v) would quantize to zero.

In most cases, however, g can be expected to exceed the threshold level, Q⁰⁰ , because a large portion of the energy in an image is concentrated in the DC term, ^(0,0). Therefore, in most cases, further computation using the symmetry functions, g"_e ^v(x, ) , are required.

A threshold condition is next applied to gZ(^χ,y) , ^or alternatively, g^e _e°(^χ,y), as follows. First, we compute:

Then, we apply a threshold test: If g < Q° then the corresponding transform components, for all ^uyi - odd and y. - even , F(u,v) , are deemed to be zero. Otherwise,

the values of g (^χ,y) ^Αre used in further computations. In one embodiment of the invention, the value of Q^oe may be different for each frequency pair (u,v). However, in a preferred embodiment, β^oeis chosen as Q°^e= Q²⁰ = 2qw²⁹k²⁰ . That is, Q^oeis chosen as

the threshold level corresponding to (u,v) = (2,0). If g fails the threshold test for this choice of Q^oe , then for all % - odd and % ~ even , F(u, v) would quantize to zero.

Threshold conditions are also applied to the functions gZ(x,y) and gZ(^x,y) -

Thus, if gZ < Q°², then all transform components for (u/2-even, v/2-odd), would be deemed to be zero, and further computations would be performed using gZ(x,y) otherwise. Similarly, if g°° < Q²² , then all transform components for (u/2-odd, v/2-odd), would be deemed to be zero, and further computations would be performed using gZ(^x,y) otherwise.

As previously noted, in most cases we may anticipate that g_ee ^e > Q⁰⁰ . To continue the decomposition process, we note that the components of g_e ^e _e ^e(x,y) aτe intermediate coefficients for the computation of F(u,v) for u = 0,4 and v = 0,4 only, which are the transform components for % - even and ^VΔ - even . Further analysis of the symmetry properties of the cosine functions yields the following results. The function

cos (2x + ϊ)uπ possesses even symmetry a ιbou Jt. J t.1he _t hori ■zonta ,l axis, x_c - .1, / / „2, w ιhen u is

16 0, and possesses odd symmetry about the horizontal axis, x_c - 1/2, when t/is 4. Therefore,

(2x + \)uπ (2(l-x) + l cos (-1)" cos 16 16 for « = 0,4and = 0.

(2 + l)v?r

Similarly, the function cos possesses even symmetry about the 16 vertical axis, y_c = 1/2, when v is 0, and possesses odd symmetry about the vertical axis, y_c = 1/2, hen is 4. Therefore:

for v = 0,4 and y = 0.

By application of these symmetry properties we can write the equation for F(u, v) when u = 0,4 and v = 0,4 as follows:

uπ vπ

F(u,v) = ±C(u)C(v)K cos cos 16 ^~\6 where

K = gZ (0=0) + H)^v/4 gZ (,i) + (-i)"^/4 gZ C >) + (-i)"^+v)/4 gZ ( D

When u and v are both zero we have:

A- =K =gZ(,o)+gZ(o,r)+gZi, )+_g i,ϊ)

When u is 4 and v is 0 we have:

A^* = * - rf (o,o) + ₈z (o,i) - gz ,o) - : (1,1)

When u is 0 and v is 4 we have:

When both w and v are 4 we have:

The values of h™ are now the intermediate coefficients of the cosine functions in the equation for computing F(u, v) for u/2 and v/2 both even. The functions, h™ , are the algebraic sum of the values of g_e ^e _e ^e(x,y)t at have coordinates equidistant from an axis of symmetry. We may utilize the digital computation structure depicted in Figure 11 to compute the functions /z"_e ^v . Computation of h"* requires 8 additions and no multiplications. The data of h^may replace in memory the data of gZ( ,y)as the computations depicted in Figure 11 are performed, thereby allowing for yet a further reduction in the memory required to compute the Discrete Cosine Transform (DCT). The organization of the data of ?"_e ^v in memory may be visualized in matrix form as shown in Figure 12, wherein each of the four quadrants of the 2x2 matrix contain one of the four functions Λ∞,Λ*,λ ,andλ .

We may now apply a threshold condition to each of the terms λ*_e ^v as follows. First we compute:

JT = h"

Then, we apply a threshold test: if hZ <Q"^V, the corresponding transform component, F(u,v) is deemed to be zero. If the absolute value of a term, lr_e , exceeds the predetermined threshold, Q^uv , then we use the term to compute F(u,v) as follows:

F(0,0) = ±f

F( ) =

where it will be recognized that division by eight can be implemented digitally by a binary shift operation.

We now continue the description by addressing the computation of F(u,v) fox the remaining values of u and v. When u is 2 or 6 and v is 0 or 4, we have:

^;(,^ = ^( , ) = ^e( , ) + /-(,3- )- -(3- ,v)- ^e(3- ,3-3,) where, f^ee (x, y) = f(x, y) + f(x,l - v) + f(l - x, y) + f(l - x,l - y) , and application of the symmetry properties of the cosine function yields the following equation:

for u = 2,6 and v = 0,4 and where:

K (*) = g (*,0) + g (*,1) for u = 2 or 6 and v = 0; (x) = ^;( ,0) - ^;;( ,l) for _W = 2 or 6 and = 4.

The functions, A" , are the algebraic sum of values of the symmetry function g°_e ^e(x,y)th.at have coordinates equidistant from an axis of symmetry. The functions h™_e can be computed efficiently using the digital computation structure depicted in Figure 13, which requires 2 x 4 additions and no multiplications. The data of h™ can replace the data of g (^χ,y)^m memory to conserve memory resources.

The values of A (x) are now the intermediate coefficients of the cosine functions for computing F(u, v) . These functions possess even symmetry about the vertical axis, v = V2, if v = 0 and odd symmetry about the vertical axis, v = ^lA, if v = 4.

We may now apply a threshold condition to each of the functions h as follows. First we compute:

= ∑|/ (^χ)| x=0 for u - 2,6 and v = 0,4 , which requires 2 x 4 additions and no multiplications. We then apply a threshold test: If h < Q"^v , then the corresponding transform component is deemed to be zero. In other words, for each function, h^u _e , we determine if the sum of the absolute values of its terms exceeds the predetermined threshold, Q^uv . If the absolute value of a term, h" , exceeds the predetermined threshold, Q^uv , then we use the term to compute F(u,v) as follows:

We now continue the description by addressing the computation of F(u,v) fox the remaining values of u and v. When u is 0 or 4 and v is 2 or 6, we have: gZ(^χ,y) = g (^χ,y) = r(^χ,y)-f^ee(^χ,3-y)+f^ee0-^χ,y)-f^ee - -y) where, /^« (x, y) = f(x, y) + f(x,l -y) + f(l -x,y) + f(l - x,7 - ) , and application of the symmetry properties of the cosine function yields the following equation:

F(u,v) = iC(«)C(v)∑/ (v)cos uπ ^~(2y + V)vπ cos

7=0 16^~ 16 for u = 0,4 and v = 2,6 and where: ( ) = (0, ) + (l, )for_M = 0and -2or6; ::(y) = g^e(0,y)-g (l,y)foxu = Aandv = 2or6.

The functions, h , are the algebraic sum of values of the symmetry function gZ(^χ, j that have coordinates equidistant from an axis of symmetry. The functions K"₀ can be computed efficiently using the digital computation structure depicted in Figure 14 as shown, which requires 2 x 4 additions and no multiplications. The data of h^%™ can replace the data of g_e ^e°(x,y)m^' memory to conserve memory resources.

The values of h™(y) axe now the coefficients of the cosine functions for computing F(u,v) . These functions possess even symmetry about the horizontal axis, x = V, if u = 0 and odd symmetry about the horizontal axis, x = V₂, if u = A. We may now apply a threshold condition to each of the functions h™ as follows. First we compute:

for u = 0,4 and v = 2,6 , which requires 2 x 4 additions and no multiplications. We then apply a threshold test: If h" < Q^uv , then the corresponding transform component is deemed to be zero. In other words, for each function, h™₀ , we determine if the sum of the absolute values of its terms exceeds the predetermined threshold, Q^m .

If the absolute value of a term, h" , exceeds the predetermined threshold, Q"^v , then we use the term to compute F(u, v) as follows:

1 (4,6) = fJ (v)cos ^'(2v + l)6 ^"

7=0 16

The remaining values of (w,v)for both w and even are F(2,2), F(2,6), F(6,2), and F(6,6) . For these values of u and v F(u,v) is determined according to:

for u ~ 2,6, x = 0,1, v = 2,6, y = 0,1, and where gZ( ,y) = r(^χ,^y)-f^{e χ ~}y)-r⁽?-^χ,y)+ro~^χβ-y)

Further reduction in computations may be achieved as follows. First, a scale of F (2,2) is computed and its magnitude is subtracted from g as computed above:

where α is a scale factor that may be adjusted to achieve a desired level of correlation between the transform components that are deemed to be zero and the transform components that would actually quantized to zero if computed and quantized. Decreasing α increases that level of correlation, whereas increasing α decreases that level of correlation. As α is decreased to zero, the correlation approaches 100%. For α equal to 8, the correlation is about 75%. Setting α equal to 4 yields about 95% correlation. It will be recognized that division and multiplication by a power of two may be implemented as a binary shift operation rather than as an actual division or multiplication operation. Therefore, α may preferably be set equal to 4. Now, if the remaining value of g°° is less than the threshold Q°° , then

F(2,6),F(6,2), ndF(6,6) axe deemed to be zero. Otherwise, a scale of (2,6)is computed and its magmtude is subtracted from the current value of g '■

Then if the remaining value of g is less than the threshold QZ en (6,2), and F(6,6) are deemed to be zero. Otherwise, a scale of (6,2) is computed and its magnitude is subtracted from the current value of g '■

Then if the remaining value of gZ is less than the threshold QZ F(6,6) is deemed to be zero. Otherwise, -F(6,6) is computed. Thus, selective computation of the transform components, F(u,v) , when u/2 and v/2 are both odd, is accomplished by computing the scaled magnitude of each value of F(u, v) when u/2 and v/2 axe both odd, in a sequential order until the scaled magnitude of F(u,v)in the sequence falls below a threshold level to which it is compared; wherein for each scaled magnitude of F(u,v) computed, the threshold level to which it is compared is computed as the threshold level to which the previous value of the scaled magnitude ofF(«,v)was compared minus the scaled magnitude of the previous value of F(u,v) computed; and deeming a value of F(u,v) to be zero if its scaled magnitude falls below the threshold to which it is compared and deeming to be zero all subsequent values of F(u,v) in the sequence.

This completes the process for computing all values of F(u,v) for both u and v even. Decomposition for Odd u and Even v : When u is odd and v is even, we have:

F(u,v) = ∑∑f°^eC(u,v,x,y) x=07=0 where:

with: /^MV(x,v) = /^oe(x,v) = (x,;) + /(x,7- )- (7-x, )-/(7-x,7- ) for u = 1,3,5,7 and v = 0,2,4,6.

To facilitate selective computation of F(u,v) for these frequency pairs we compute the following functions: gz (*,o) = g ( =r^e (*,o) + r (^χ,i) + r (,2) + r w) ; gz (^χ,i) = go°i () = (^χ,o) + r (^χ,i) - r M - r (^χ ) ; gzχ,2) = git (x) = r (χ,o) - r (χ,i) - ^oe (χ,2) + r (^χ ) ;

^(x,3) = _e ⁶(x) = /^O2(x,0)-/^oe(x₅l) + /^oe(x,2)-/^oe(x,3). for u = 1,3,5,7, x = 0,1, 2,3 and v = 0,2,4,6.

The functions, gZ(^χ,y), ^are the algebraic sum of values of f^oe(x,y)that have coordinates equidistant from an axis of symmetry. The functions gζ can be computed efficiently using the digital computation structure of Figure 15. The structure of Figure

15 shows that the computation of the functions g requires 4 x 8 additions and no multiplications. The data of g^may replace in memory the data of ^oe(x,_,y)as the computations depicted in Figure 15 are performed, thereby allowing for yet a further reduction in the amount of memory required to compute the Discrete Cosine Transform. To compute the transform components for u odd and v = 0 we proceed as follows.

We first apply a threshold condition by computing:

This requires 4 additions and no multiplications. If g „Zo0 < _^ Q _/-v_oiO_e , then the transform components for u odd and v even are deemed to be zero. Otherwise, we compute as follows:

(l,0) = ∑^°(x)C(l,0,x,0) x=0

If gZ° < Q _e , then the transform components for u = 3,5,7 and v = 0 are deemed to be zero. Otherwise, we compute as follows:

i^?(3,0) = ∑ _e°(x)C(3,0,x,0) x=0

If g _e < Q _β° , then the transform components for u = 5,7 and v = 0 are deemed to be zero. Otherwise, we compute as follows:

^(5,0) = ∑ ;_e°(x)C(5,0,x,0) x=0

If g°° < Ql , then the transform component for u = 1 and v = 0 is deemed to be zero. Otherwise, we compute as follows:

^(7,0) = ∑g _e°(x)C(7,0,x,0) x=ϋ This completes the computations for the transform components for u odd and v = 0.

To compute the transform components for u odd and v = 4 we proceed as follows. We first apply a threshold condition by computing:

This requires 4 additions and no multiplications. If g₀°_s < Q , then the transform components for u = 1,3,5,7 and v = 4 are deemed to be zero. Otherwise, we compute as follows:

If gZ° < Qlt, then the transform components for u = 3,5,7 and v = 4 are deemed to be zero. Otherwise, we compute as follows:

If gZ° < QZ⁵ , then the transform components for u = 5,7 and v - A axe deemed to be zero. Otherwise, we compute as follows:

F(5,A) = ∑gZ° (x)C(5,A,x,0) x=0

If gZ° < Ql , then the transform component for u — 1 and v = 4 is deemed to be zero. Otherwise, we compute as follows:

i⁷(7,4) = tg_o ^o4(x)C(7,4,x,0) x=0 This completes the computations for the transform components for u odd and v = 4.

To compute the transform components for u odd and v = 2 we proceed as follows. We first apply a threshold condition by computing:

goe

This requires 4 additions and no multiplications. If g°² < Q^l _e ² , then F(l,2) , F(3,2) F(5,2) andF(l,2) axe deemed to be zero. Otherwise, we compute as follows:

Ke (*) = u" (*, ) - r (^χ,3)] + *, ir (^χ,i) - r { M for x=0, 1,2,3, and where k = 0.41421 is the ratio of C(ιι,2,x,l) to C(u,2,x,0). This requires 4 x 4 additions and 4 multiplications. Note, that the quantities in the square brackets are obtained from nodes A and B of the digital computation structure of Figure 15. Then we apply the following threshold condition:

If

< Ql , then, (l,2) , (l,2) , F(3,2) , F(5,2) and

F(l,2) axe deemed to be zero. Otherwise, we compute:

(l,2) = ∑/2_oe(x)C(l,2,x,0) x=0

Then we apply the following threshold condition: If

, then F(3,2) , F(5,2) and F(l,2) axe deemed to be zero. Otherwise, we compute:

F(3,2) = ∑h_oe(x)C(3,2,x,0) x=0

Then we apply the following threshold condition: If

< Q _e , then, F(5,2) and (7,2) are deemed to be zero. Otherwise, we compute:

F(5,2) = ∑h_Oe( )C(5,2, x,0) x=0

Then we apply the following threshold condition:

If

F (1 ,2) is deemed to be zero. Otherwise, we compute:

F(l,2) = ∑K_e( )C(l,2,^χ,0) x=0

This completes the decomposition for when u is odd and v equal to 2. We note that additional reduction in computations can be achieved by computing, storing and reusing the partial sums, h_oe (²) + (³) , K (°) ~ K_e (1) » K_e (²) - Ke (³) ^as required for the application of the threshold conditions just given.

To compute the transform components for u odd and v = 6 we proceed as follows. We first apply a threshold condition by computing:

goe

This requires 4 additions and no multiplications. If g₀°_e ⁶ < Q _e , then (l,6) , F(3,6) , F(5,6) and F (1,6) axe deemed to be zero. Otherwise, we compute as follows:

Ke (^χ) = *_ u^oe (^χ,o) - r (^χ,3)3 - vr (^χ,i) - r (^χM for x=0,l,2,3, and where k_x= 0.41421 is the ratio of C(u,6,x,0) to C(u,6,x,l). This requires 4 x 4 additions and 4 multiplications. Then we apply the following threshold condition: If \K_e ) + K_e(D + K_e(2) + K_e )\ < Q_oe ⁶ , thenF(l,6) , F(3,6) ,F(5,6) andF(l,6) axe deemed to be zero. Otherwise, we compute:

F(l,6) = ∑h_oe(x)C(\,6,x,\) x=0

Then we apply the following threshold condition:

If ) -Ke O-) -K_e(2) -

< Q_o ³!, thenF(3,6) , F(5,6) dF(l,6) axe deemed to be zero. Otherwise, we compute:

F(3,6) = ∑h_oe(x)C(3,6, x,ϊ) x=0

Then we apply the following threshold condition:

If - eQ) + K_e(2) +

< Q_o ⁵e⁶ , the F (5, 6) and F (1,6) are deemed to be zero. Otherwise, we compute:

F(5,6) = ∑h_oe(x)C(5,6,x,V) x=0

Then we apply the following threshold condition:

If

< Q , then, F(l,6) is deemed to be zero. ' Otherwise, we compute:

(7,6) = ∑/2_oe(x)C(7,6, x,l) x=0

This completes the decomposition for when u is odd and v equal to 6. We note that additional reduction in computations can be achieved by computing, storing and reusing the partial sums, h_oe (2) + h_oe (3) , K_e (°) ~ K_e (1) , K_e (²) - K_e (³) as required for the application of the threshold conditions just given. This completes the process of determining F(u, v) for u odd and v even. Next, the decomposition of the Discrete Cosine Transform for n even and v odd will be described.

Decomposition for Even u and Odd v : When u is even and v is odd, we have:

F(u,v) = ∑∑rC(u,v,x,y) . x=0 7=0 where:

(2x + \)uπ (2 + l)v7r^'

C(u, v, x, v) = _jC(u)C(v) cos cos 16 16 with: f^uv(^χ,y) = f^e°(^χ,y) = f(^χ,y)-f(^χ,i-y)+f(i- ^χ,y)-f(i-^χ,ι-y) for v = 1,3,5,7 and u = 0,2,4,6.

To facilitate selective computation of F(u, v) for these frequency pairs we compute the following functions: g (0,y) = g_e ⁰ _o°(y) = r°(0,y) + r°(l,y) + r°(2,y) + r°(3,y) ; gZ(Xy) = g_e (y) = r^o(0, ) + l,y) -r(2,y) -r(3,y);

g y) = ge⁴o°(y) = r^o ,^y)-f^eo&y)-r⁽2,^y)+r° ,y) ,- g i y) = g?_o (y) = f^eo(0,y)- f^e°(l,y) + r°(2,y)-r°(3,y) . for v = 1,3,5,7, = 0,1, 2,3 and u = 0,2,4,6.

The functions, g^u ₀°(x,y) , are the algebraic sum of values of f^eo(x, )that have coordinates equidistant from an axis of symmetry. The functions g"°can be computed efficiently using the digital computation structure of Figure 16. The structure of Figure 16 shows that the computation of the functions g"° requires 4x8 additions and no multiplications. The data of g"°may replace in memory the data of f ^o(x,y) as the computations depicted in Figure 16 are performed, thereby allowing for yet a further reduction in the amount of memory required to compute the Discrete Cosine Transform. To compute the transform components for v odd and u = 0 we proceed as follows. We first apply a threshold condition by computing:

o eo / eo s

7=0

This requires 4 additions and no multiplications. If g°° < Q _α , then the transform components for v odd and u even are deemed to be zero. Otherwise, we compute as follows:

F(0,l) = ∑gZ° (y)C(0,l,0,y)

7=0 If Z < Qf_o , then the transform components for v = 3,5,7 and u = 0 are deemed to be zero. Otherwise, we compute as follows:

^(0,3) = ∑g_e°_o°( )C(0,3,0, )

7=0

If g_eo < QZ , then the transform components for v = 5,7 and u = 0 are deemed to be zero. Otherwise, we compute as follows:

F( ,5) = ∑g_e°_o ^o(y)C(0,5,0,y)

7=0

If g_e°° < QZ , then the transform component for v = 7 and u = 0 is deemed to be zero. Otherwise, we compute as follows:

(0,7) = ∑g°;( )C(0,7,0, v)

7=0 This completes the computations for the transform components for v odd and u =

0. To compute the transform components for v odd and a = 4 we proceed as follows. We first apply a threshold condition by computing:

G eo / i eo )

7=0

This requires 4 additions and no multiplications. If g_e° < Q ₀ , then the transform components for v = 1,3,5,7 and u = A axe deemed to be zero. Otherwise, we , compute as follows:

F(A,l) = ∑gt:(y)C(A,l,0,y)

7=0

If g⁴° < Q ₀ , then the transform components for v = 3,5,7 and ιι = A are deemed to be zero. Otherwise, we compute as follows:

If g _o < Qf_o , then the transform components for v = 5,7 and u = A are deemed to be zero. Otherwise, we compute as follows: F(A,5) = ∑gZ⁴ (y)C(A,5,0,y)

7=0

If g _o ^< Q l , then the transform component for v = 7 and u = A is deemed to be zero. Otherwise, we compute as follows:

F(A,l) = ∑g_eo ^o(y)C(A,l,0,y)

7=0 This completes the computations for the transform components for u odd and v =

4.

To compute the transform components for v odd and u = 2 we proceed as follows. We first apply a threshold condition by computing:

ό eo i eo J

7=0 This requires 4 additions and no multiplications. If g_e ²° < Qf₀ , then -F(2,l) ,

F(2,3) F(2,5) and/⁷ (2, 7) are deemed to be zero. Otherwise, we compute as follows: K_o(y) - ir°(0,y)-r^o(3,y)] + k_l[ (l,y)- (2,y)] for .v=0, 1,2,3, and where k_λ= 0.41421 is the ratio of C(2,v,l j ) to C(2,v,0j/). This requires 4x4 additions and 4 multiplications. Note that the quantities in the square brackets can be obtained from nodes A and B of the digital computation structure of Figure 16. Then we apply the following threshold condition:

If K (0) + K_o (1) + K_o (2) + K_o (3)1 < Q , then i^?(2,l) , (2,3) , F(2,S) and F(2,l) are deemed to be zero. Otherwise, we compute:

(2,l) = ∑/*_eo(j)C(2,l,0, )

7=0 Then we apply the following threshold condition:

If

< Q?_{o >} thenF(2,3), F(2,5) andF(2,l) axe deemed to be zero. Otherwise, we compute:

(2,3) = ∑/7_eoO,)C(2,3,0, )

7=0

Then we apply the following threshold condition: If _o(0) -KAD + K_o ) + K ) < Q_eo , then,F(2,5) andF(2,l) are deemed to be zero. Otherwise, we compute:

(2,5) = ∑/2_eo(v)C(2,5,0, v)

7=0

Then we apply the following threshold condition:

If KoΦ)-KoQ-) + K_o(Z) -K_o ) \ < Qeό , then, F(2,l)is deemed to be zero.

Otherwise, we compute:

F(2,7) = ∑/*_eo( )C(2,7,0, v)

7=0

This completes the decomposition for when v is odd and u equal to 2. We note that additional reduction in computations can be achieved by computing, storing and reusing the partial sums, h_eo (²) + K_o (³) , K_o (°) ^~ K_o CO > (²) - K_o (³) as required for the application of the threshold conditions just given.

^=0

This requires 4 additions and no multiplications. If gl < Q_e ⁶° , then F(6,l) , _Jp(6,3),i⁷(6,5)and_JF(6,7) are deemed to be zero. Otherwise, we compute as follows: K_o(y) = k_l[r^o(0,y) - (3,y)]-[r^o(l,y) -r°(2,y)] for v-0,1,2,3, and where k_λ= 0.41421 is the ratio of C(6,v,0j/) to C(6,v,lj/). This requires 4 x 4 additions and 4 multiplications. Then we apply the following threshold condition: If K (0) + K_o (1) + K_o (2) + K_o (3) < Q , then (6,l) , F(6,3) , F(6,5) and F(6,l) axe deemed to be zero. Otherwise, we compute:

^(6,l) = ∑A_eoωC(6,l,l, v)

7=0

Then we apply the following threshold condition: If

- K_o (3)| < Q , then (6,3) , F(6,5) andF(6,l) axe deemed to be zero. Otherwise, we compute:

F(6,3) = ∑K_o(y)C(6,3,l,y)

7=0 ^■

Then we apply the following threshold condition:

If K_o )-K_o( ) + K_o(2) + K₀(3)\ < Q ₀ , then,F(6,5) andF(6,l) are deemed to be zero. Otherwise, we compute:

(6,5) = ∑/*_eoCvX7(6,5,l, v)

7=0

Then we apply the following threshold condition:

If K_o (0) - K_o (1) + K_o (2) - K_o (3) < QZ , then, (6,7) is deemed to be zero.

Otherwise, we compute:

F(6,l) = ∑K₀(y)C(6,l,l,y)

7=0

This completes the decomposition for when v is odd and u equal to 6. We note that additional reduction in computations can be achieved by computing, storing and reusing the partial sums, h_eo (²) + K_o (³) , K_o (°) ^~ K_o ( , K_o (²) - (³) as required for the application of the threshold conditions just given.

This completes the process of determining F(u,v) for v odd and u even. Next, the decomposition of the Discrete Cosine Transform for u odd and v odd will be described.

Decomposition for Odd u and Odd v : When u and v are both odd, F(u,v) is determined according to:

F(u,v) = ∑∑f°°(x,y)C(ιι,v, x,y) x-0 7=0 where:

(2x + \)uπ (2y + \)vπ

C(u, v, x, y) = )rC(u)C(v) cos cos Ϊ6 16 for u and v both odd and: f⁰⁰(^χ,y) = f(^χ,y) -f(^χ,'7 -y)-fσ -^χ,y)+f(7^{~ χ},7-y)

Further reduction in computations can be achieved as follows. First, the order of computing F(u,v) is as shown in Figure 2, so that successive values of F(u,v) can be expected to be less in magnitude than a preceding value. For each transform component, F(u, v) , computed, its magnitude is subtracted from f°° as computed above so that f⁰⁰ is reduced according to:

where α is a scale factor that may be adjusted to achieve a desired level of correlation between the transform components that are deemed to be zero and the transform components that would actually quantized to zero if computed and quantized. Decreasing α increases that level of correlation, whereas increasing α decreases that level of correlation. As α is decreased to zero, the correlation approaches 100%. For α equal to 8, the correlation is about 75%. Setting α equal to 4 yields about 95% correlation.

Then, if the remaining value of f°° is less than the given threshold Q°° , then the remaining values of F(u,v) axe deemed to be zero. Otherwise, the next descending value of F(u,v)is computed, f°° is again reduced according to:

and f°° is again compared to the threshold. This process is continued until f°° <

Q°° . Thus, selective computation of the transform components, F(u,v) , when u and v are both odd, is accomplished by computing the scaled magnitude of each value of F(u, v) when u and v are both odd, in a sequential order until the scaled magnitude of a value of F(u,v) in the sequence falls below a threshold level to which it is compared; wherein for each scaled magnitude of F(u,v) computed, the threshold level to which it is compared is computed as the threshold level to which the previous value of the scaled magnitude of («,v)was compared minus the scaled magnitude of the previous value of F(u,v) computed; and deeming a value of F(u,v) to be zero if its scaled magnitude falls below the threshold to which it is compared and deeming to be zero all subsequent values of F(u, v) in the sequence.

This completes the process of selectively determining the transform components, F(u,v) , of the discrete cosine transform. To summarize, according to the present invention, the DCT of NxN pixel image is successively decomposed into sets of intermediate functions which possess even or odd symmetry according to whether a scale of the frequency variables, (u,v), axe even or odd integers. Specifically, the DCT can be decomposed in terms of functions that possess even or odd symmetry according to whether y and ^v/_n , n=0,l,2... log₂(N) -l, are even or odd integers. A threshold

condition is then applied to one or more of these functions. If the function fails the threshold condition, the corresponding one or more transform components are deemed to be zero. Otherwise, the transform component is computed and quantized. All quantization factors, as well as the cosine functions, can be computed in advance, stored in memory tables, and retrieved as needed. Finally, when further decomposition of the DCT is not possible, successive threshold conditions are applied to the remaining transform components to further reduce the computations required to compute the DCT.

The methods of the invention described above may be implemented in a microprocessor, digital signal processor or other processing device operating under the directions of software in conjunction with sufficient memory. Alternatively, the invention may be implemented in an applications specific integrated circuit or other suitably designed hardware.

The foregoing written description of preferred embodiments illustrate that the present invention is well suited to achieve a substantial increase in the speed and efficiency of video compression while minimizing computational complexity and memory usage. Persons of ordinary skill in the art will readily recognize variations of these embodiments, given the disclosure herein, and, therefore, the invention is not limited by the foregoing written description. Rather, the invention is defined by the appended claims.

What is claimed is:

Claims

1. A method for selectively determining components, F(u,v), of a discrete cosine transform of a two-dimensional image, f(x, v), comprising the steps of: computing a set of functions, f"^v(x,y), possessing even or odd symmetry about an axis of the image; and deeming a transform component, F(u,v), to be zero if a function, f^uv(x,y), fails to satisfy a threshold condition applied to the function, f^uv(x, v) .

2. The method of claim 1, wherein the step of computing a function, f^uv(x,y), possessing symmetry about an axis comprises the step of determining an algebraic sum of image pixels that have coordinates equidistant from the axis of symmetry.

3. The method of claim 1, wherein values of the image are replaced in memory by values of a function f^uv (x, y).

A. The method of claim 1, wherein the step of applying a threshold condition to a function, f"^v(x, y), comprises determining if the sum of the magnitudes of the values of the function exceeds a threshold value.

5. The method of claim 1, further comprising the steps of: determining a sequential order of transform components; deeming a transform component to be zero if a scaled magnitude of the transform component fails a threshold condition; and deeming to be zero all transform components in the sequence that succeed a transform component deemed to be zero.

6. The method of claim 1, further comprising the steps of: computing a set of functions, g"^v(x,y), derived from a function, f"^v(x,y), possessing even or odd symmetry about an axis of the image: and deeming a transform component, F(u, v), to be zero if a function, g^uv(x, y), fails to satisfy a threshold condition applied to the function, f"^v(x, y) .

7. The method of claim 6, wherein the step of computing a function, g"^v(x, ), possessing symmetry about an axis comprises the step of determining an algebraic sum of values of a function, f"^v(x,y), that have coordinates that are equidistant from the axis of symmetry.

8. The method of claim 6, wherein values of a function, f^uv(x,y), axe replaced in memory by values of a function g"^v(x,y).

9. The method of claim 6, wherein the step of applying a threshold condition to a function, g^uv(x,y) , comprises determining if the sum of the magnitudes of the values of the function exceeds a threshold value.

10. The method of claim 1, further comprising the steps of: determining a sequential order of transform components; deeming a transform component to be zero if a scaled magnitude of the transform component fails a threshold condition; and deeming to be zero all transform components in the sequence that succeed a transform component deemed to be zero.

11. A video compression system for selectively determining components, F(u,v), of a discrete cosine transform of a two-dimensional image, f(x,y), comprising: a processor for: computing a set of one or more functions, f^uv(x,y), possessing even or odd symmetry about an axis of the image; and deeming a transform component, F(u, v), to be zero if a function, /^uv(x, v), fails to satisfy a threshold condition applied to the function,

/^<"'(x, v) ; and memory for: storing values of F(u, v) and f^uv (x, v) .

12. The system of claim 11, wherein the process of computing a function, f"^v(x,y), possessing symmetry about an axis comprises the step of determining an algebraic sum of image pixels that have coordinates equidistant from the axis of symmetry.

13. The system of claim 11, wherein values of the image are replaced in memory by values of a function f"^v (x, y).

14. The system of claim 11, wherein the process of applying a threshold condition to a function, f"^v(x, y), comprises determining if the sum of the magnitudes of the values of the function exceeds a threshold value.

15. The system of claim 11, further comprising the process of: determining a sequential order of transform components; deeming a transform component to be zero if a scaled magnitude of the transform component fails a threshold condition; and deeming to be zero all transform components in the sequence that succeed a transform component deemed to be zero.

16. The system of claim 11, further comprising the process of: computing a set of functions, g^uv(x,y), derived from a function, f"^v(x,y), possessing even or odd symmetry about an axis of the image: and deeming a transform component, F(u, v), to be zero if a function, g^uv(x,y), fails to satisfy a threshold condition applied to the function, f"^v(x, y) .

17. The system of claim 16, wherein the process of computing a function, g"^v(x, ), possessing symmetry about an axis comprises the step of determining an algebraic sum of values of a function, f^uv(x,y), that have coordinates that are equidistant from the axis of symmetry.

18. The system of claim 16, wherein values of a function, f^v(^χ,y), are replaced in memory by values of a function g"^v(x, y).

19. The system of claim 11, further comprising the steps of: determining a sequential order of transform components; deeming a transform component to be zero if a scaled magnitude of the transform component fails a threshold condition; and deeming to be zero all transform components in the sequence that succeed a transform component deemed to be zero.

20. A method for selectively determining components, F(u, v), of a discrete cosine transform of a two-dimensional image, f(x, y), comprising the steps of: (a) decomposing the discrete cosine transform to obtain a set of functions, f"^v(x,y), possessing even or odd symmetry about an axis of the image; and

(b) deeming a transform component, F(u, v), to be zero if a function, /"" (x, v), fails to satisfy a threshold condition applied to the function, f"^v (x, y) ; and

(c) repeating steps (a) and (b) until no further decomposition can be achieved.