DE102015211055A1

DE102015211055A1 - Kapazitiver Füllstandsgrenzschalter für wässrige Lösungen in einem Tank

Info

Publication number: DE102015211055A1
Application number: DE102015211055.9A
Authority: DE
Inventors: Markus Tahedl; Christian Weber
Original assignee: IFM Electronic GmbH
Current assignee: IFM Electronic GmbH
Priority date: 2014-06-18
Filing date: 2015-06-16
Publication date: 2015-12-24

Abstract

Bei einem kapazitiven Füllstandsgrenzschalter für wässrige Lösungen in einem Tank aus einem nichtleitenden Material, der folgende Voraussetzungen erfüllt, müssen für die Generierung eines Schaltsignals zwei eindeutige Bedingungen erfüllt sein. Die Voraussetzungen sind: der Füllstandsgrenzschalter ist an der Außenseite des Tanks montierbar, die Wandstärke des Tanks ist unbekannt, die Messelektrode hat einen Durchmesser von weniger al 30 mm. Die Bedingungen für die Generierung des Schaltsignals sind: der Betrag der Admittanz muss größer als ein einen vorgegebenen Grenzwert sein und der Phasenwinkel muss größer als ein vorgegebener Grenzwinkel sein, wobei die Messfrequenz typischerweise zwischen 1 und 20 MHz liegt.

Description

Kapazitive Füllstandssensoren werden in vielen Bereichen der Prozessmesstechnik eingesetzt.
In der Regel handelt es sich um Tauchsonden, wie sie in der DE 10 2011 003 158 A1 beschrieben sind.
Viele Anwender setzen Füllstandssensoren weniger zur Füllstandbestimmung sondern hauptsächlich zur Überwachung von Grenzständen in Behältern ein.
Die Überwachung von Grenzständen ist mit einfachen kapazitiven Füllstandsgrenzschaltern möglich, die außen am Tank in der Höhe des zu überwachenden Grenzstandes angebracht werden. Übersteigt die Füllhöhe im Tank den Grenzstand, so gibt der Füllstandsgrenzschalter ein Schaltsignal aus, das z. B. an eine Steuerung SPS weitergeleitet wird und zum Abschalten einer Pumpe führt.
Mit kapazitiven Füllstandssensoren können z. B. leitfähige wässrige Lösungen erfasst werden.
Problematisch beim Einsatz von kapazitiven Füllstandsgrenzschalter sind leitfähige Anhaftungen auf der Innenseite des Tanks, die zu Fehlauslösungen des Schalters führen können.
Weiterhin ist es für eine sichere Messung notwendig, das Wandmaterial (nichtleitend) und die Wandstärke des Tanks zu berücksichtigen. In der Regel sind diese Größen nicht bekannt.
Kapazitive Füllstandsgrenzschalter wie z. B. der KI5082 der Fa. ifm electronic, weisen eine Messelektrode auf, die einen Durchmesser von weniger als 30 mm aufweist.
Auf der Basis der beigefügten Modellrechnungen ist es möglich, einen kapazitiven Füllstandsgrenzschalter anzugeben, der ein sicheres Schalten auch bei unbekannter Wandstärke und unbekanntem Wandmaterial des Tanks und trotz leitfähiger Anhaftungen auf der Tankinnenseite ermöglicht.
Es sind Anhaftungen mit einer sehr geringen Leitfähigkeit (destilliertes Wasser) oder aber Anhaftungen mit einer sehr hohen Leitfähigkeit wie z. B. bei einer 2-molaren Kaliumchloridlösung 212 mS/cm denkbar.
Um Anhaftungen noch sicherer zu detektieren kann die Messung auch bei mehreren Messfrequenzen, die typischerweise höher als 1 MHz liegen, durchgeführt werden.
Bei bekannter Geometrie des Tanks ist es möglich die Leitfähigkeit und die Dicke der Anhaftungsschicht ebenfalls durch Messung mit mehreren Frequenzen zu ermitteln.
Nachfolgend ist die Erfindung anhand eines in der Zeichnung dargestellten Ausführungsbeispiels näher erläutert.
Es zeigen:
1 Verlauf des Betrages der elektrischen Admittanz als Funktion der Messfrequenz für einen ersten Fall (best case)
In 2 Verlauf der Phase der Admittanz. gemäß 1
3 Verlauf des Betrages der elektrischen Admittanz als Funktion der Messfrequenz für einen zweiten Fall (worst case)
In 4 Verlauf der Phase der Admittanz gemäß 3.
In 1 ist der Verlauf der Admittanz für zwei Schichtdicken 0.1 mm und 100 mm als Funktion der Frequenz bei einem ersten Fall („best case“) dargestellt. Die Wanddicke ist mit 1 mm relativ klein, wodurch die elektrische Kopplung mit dem Medium sehr gut wird. Der Elektrodendurchmesser beträgt 24 mm. Bei diesem ersten Fall können auch Medien mit einer hohen Leitfähigkeit von 800 mS/cm noch sicher detektiert werden. Im Verlauf der Admittanz lässt sich quasi kein Unterschied zwischen Anhaftung und voll (Schichtdicke 100 mm) erkennen.
Dagegen sieht man im Verlauf des Phasenwinkels 2 ab 2 MHz, dass sich die beiden Kurven aufspalten. Wählt man hier den Wert 10 MHz, so unterschieden sich die beiden Verlustwinkel so signifikant, dass hier ein Schwellwert sinnvoll wählbar ist. Der Schwellwert könnte z. B. bei 89° liegen.
In 3 ist der Verlauf der Admittanz für zwei Schichtdicken 0.1 mm und 100 mm als Funktion der Frequenz bei einem zweiten Fall („worst case“) dargestellt. Die Wanddicke ist mit 10 mm relativ groß, wodurch die elektrische Kopplung mit dem Medium relativ schlecht ist. Der Elektrodendurchmesser beträgt ebenfalls 24 mm. Bei diesem zweiten Fall können nur Medien mit einer geringen Leitfähigkeit 30 mS/cm noch sicher detektiert werden. Im Verlauf der Admittanz lässt sich quasi kein Unterschied zwischen Anhaftung und voll (Schichtdicke 100 mm) erkennen.
Dagegen sieht man im Verlauf des Phasenwinkels ab 2 MHz, dass sich die beiden Kurven aufspalten. Wählt man hier den Wert 10 MHz, so unterschieden sich die beiden Verlustwinkel so signifikant, dass hier ein Schwellwert sinnvoll wählbar ist. Der Schwellwert könnte z. B. bei 89° liegen.
Durch die Auswertung des Phasenwinkels ist es möglich zwischen Anhaftungen im Bereich der Elektrode und einem vollen Tank sicher zu unterscheiden.
Die Wand des Tanks kann auch nur aus einem nichtleitenden Fenster bestehen. Der übrige Tank kann auch metallisch sein.
Unter wässrigen Lösungen werden auch andere flüssige leitfähige Medien verstanden. Die Modelrechnungen sehen wie folgt aus.
In der industriellen Anwendung kapazitiver Sensoren ist die kontaktlose Detektion leitfähiger Schichten flüssiger Medien von Bedeutung. Dabei ist die Sensorimpedanz abhängig von der Frequenz und Eigenschaften des Mediums. Um den Einfluss dieser Parameter zu ermitteln, wurde ein zweidimensionales, rotationssymmetrisches Modell erstellt, mit dem sich eine gute Übereinstimmung mit einer FEM-Simulation erzielen lässt. Aus den durchgeführten Untersuchungen geht hervor, dass sich aus den Parametern eines geeigneten Ersatzschaltbildes ein Maß für Leitfähigkeit und Schichtdicke des Mediums ableiten lässt.
Kapazitive Sensoren bieten interessante Möglichkeiten zur kontaktlosen Detektion flüssiger, leitfähiger Medien. Zur Auslegung solcher Systeme ist es notwendig, den Einfluss unterschiedlicher Parameter auf die Sensorimpedanz ermitteln zu können. Häufig wird dies durch FEM-Simulationen erreicht, wobei bei dieser Methode zunächst alle Feldgrößen berechnet werden müssen, bevor die Sensorimpedanz ermittelt werden kann. Das kann sehr zeitaufwendig sein, besonders dann, wenn viele Kombinationen aus Schichtdicke und Leitfähigkeit untersucht werden sollen, zumal feine Strukturen durch entsprechend kleine finite Elemente abgebildet werden müssen. Eine Übersicht zu diversen kapazitiven Messverfahren für Flüssigkeiten findet sich in [14]. In [1] wird unter anderem die Modellierung von Elektrodenarrays zur medienberührenden Füllstandsmessung behandelt. Hier befinden sich die Elektroden jedoch im Kontakt mit dem zu untersuchenden Medium. Im Gegensatz dazu wird in [4] eine Tauchsonde modelliert, deren Elektroden von einer dünnen, isolierenden Schicht vom Medium getrennt sind. Die Beschreibung der Sonde erfolgt hier mittels der FEM-Methode. Ebenso ist es möglich, mittels Kapazitätstomographie, die Permittivitätsverteilung eines Wasser-Öl-Gas-Gemisches in einer kreisrunden Zuleitung anhand von FEM-Methoden und komplexen Bildrekonstruktionsalgorithmen zu ermitteln [10]. Dafür ist jedoch die Verwendung von Mehrelektrodensystemen erforderlich.
In dieser Arbeit wird zur Lösung des Vorwärtsproblems sein analytisches Modell erstellt, mit dem sich der Einfluss einer dünnen, leitfähigen Schicht hinter einer nicht-leitenden Barriere auf die Sensorimpedanz einer einzelnen Elektrode untersuchen lässt. Für die Bestimmung von Leitfähigkeit und Schichtdicke aus der berechneten Impedanz ist das Rückwärtsproblem zu lösen. Dazu werden mittels nichtlinearer Regression die Parameter eines geeigneten Ersatzschaltbildes ermittelt. Mit Hilfe dieses modellbasierten Ansatzes werden Rückschlusse auf Leitfähigkeit und Dicke der zu untersuchenden Schicht gezogen.
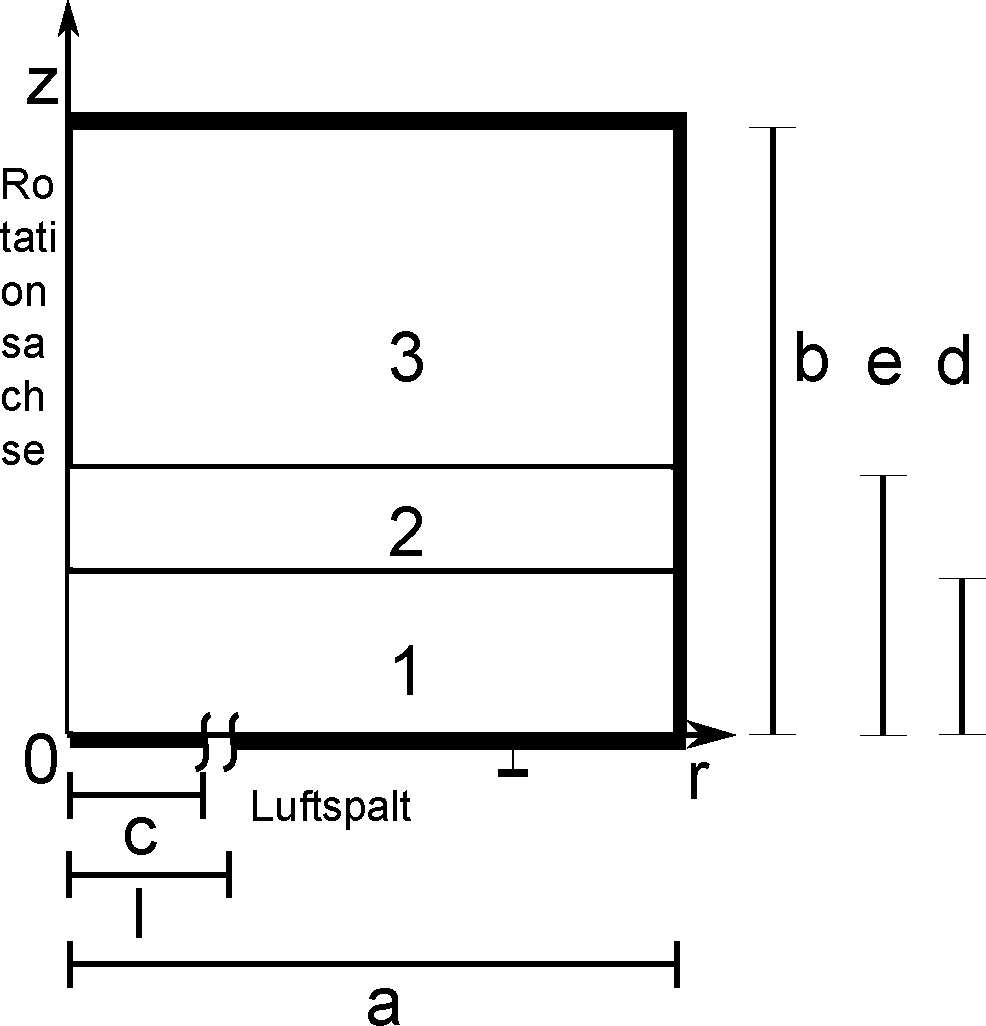
Um den Einfluss leitfähiger Medien untersuchen zu können, wurde ein rotationssymmetrisches Modell erstellt, das in drei Bereiche mit unterschiedlicher Leitfähigkeit und Permittivitat aufgeteilt ist. Der Sensor wird in Abbildung 1 durch eine Elektrode mit dem Radius c repräsentiert, die durch einen Luftspalt der Länge l – c von der Masse des Aufbaus getrennt ist. Bereich 1 ist hier eine isolierende Barriere, durch die die Elektrode vom zu untersuchenden Medium in Bereich 2 getrennt ist. Bereich 3 repräsentiert den Raum hinter der leitfähigen Schicht, der typischerweise Luft ist. Ausgangspunkt für die Modellierung ist die Kontinuitätsgleichung der elektrischen Stromdichte j → [6]:
Mit der Leitfähigkeit σ, der elektrischen Feldkonstante ε₀, der relativen Permittivität ε_r, der imaginären Einheit j, dem Flächenelement dA und der elektrischen Feldstärke E →. Vereinfachend erfolgt eine Beschränkung auf zeitharmonische Vorgänge mit der Kreisfrequenz ω. Der linke Summand ist die leitungsgebundene Stromdichte σE →, der rechte Summand die dielektrische Verschiebungsstromdichte jωε₀ε_rE →. Aus Gleichung 1 ist erkennbar, dass die Summe aller Ströme, die in den betrachteten Bereich herein- oder herausfließen gleich Null sein muss, sofern sich die Ladungsmenge darin nicht zeitlich ändert [6]. Mit dem Satz von Gauß wird aus Gleichung 1:
Mit dV: Volumenelement
Vereinfachend wird angenommen, dass die Materialeigenschaften in den einzelnen Teilgebieten konstant bezüglich der Ortskoordinaten sind. Des Weiteren kann die elektrische Feldstärke als Gradient eines elektrischen Skalarpotenzials φ dargestellt werden [6]. Man substituiert also E → = –gradφ in Gleichung 2 und erhält: (σ + jωε₀ε_r)Δφ = 0 mit Δφ = divgradφ
Der Ansatz führt auf eine Laplace-Gleichung. Da es sich um ein rotationssymmetrisches Modell handelt, muss der Laplace-Operator ∆ in Zylinderkoordinaten definiert werden. Mit [5] ergibt sich die zu lösende Differenzialgleichung:
Mit den Ortskoordinaten r und z (s. Abbildung 1).
Die Lösung von Gleichung 3 erfolgt mittels des Ansatzes der Separation der Variablen [12] und wird in [2] wie folgt angegeben:
Mit den Koeffizienten q_i,n, A_i,n und B_i,n. J₀(r) ist die Besselfunktion erster Art und nullter Ordnung. Der Index n repräsentiert die Regionen in Abbildung 1. Es müssen insgesamt neun Koeffizienten bestimmt werden. Zunächst werden die Randbedingungen für das Modell festgelegt. Um die Elektrode abbilden zu können, werden Dirichlet-Randbedingungen [7] verwendet, wobei am unteren Rand des Modells mit konstantem Potenzial u₀ auf der Elektrode der folgende Zusammenhang angenommen wird:
Auf den beiden anderen Rändern in Abbildung 1 wird vereinfachend das Potenzial auf 0V festgelegt: φ(a, z) = 0 φ(r, b) = 0 (6)(7)
Man setzt Gleichung 6 in Gleichung 4 ein und erhält:
Dieser Ausdruck wird nur dann zu Null, wenn der folgende Zusammenhang gilt [2]:
α_0,m ist die m-te Nullstelle der Besselfunktion erster Art und nullter Ordnung. Dieser Zusammenhang gilt fur alle q_i,n, weil der Rand aus Gleichung 6 alle drei Gebiete durchläuft. Daher ist es ausreichend, statt q_i,n nur noch q_i zu schreiben. Als nächstes wird Gleichung 5 in Gleichung 4 eingesetzt:
Um B_i,1 bestimmen zu können, muss die Funktion ϕ(r, 0) in Form einer Fourier-Bessel-Reihe dargestellt werden. Die Berechnung wird dann wie folgt durchgeführt [8]:
Mit Hilfe von [11] ergibt sich die folgende Lösung:
H₀ und H₁ sind die Struve-Funktionen [11]. Die fehlenden 5 Konstanten, für Gleichung 4 für die 3 Gebiete aus Abbildung 1, können nun mit Hilfe eines linearen Gleichungssystems ermittelt werden. Unter der Annahme, dass auf den beiden Grenzflachen zwischen den Gebieten 1 und 2 bzw. 2 und 3 die Ladungsmenge zeitlich konstant ist, werden mit [7] für das Potenzial auf den Grenzflächen die folgenden Zusammenhänge angenommen: φ₁(r, d) = φ₂(r, d) φ₂(r, e) = φ₃(r, e) (13)(14)
Ebenso sind dann die Normalkomponenten der Stromdichte J →_n stetig. Das führt mit [7] zu folgenden Bedingungen: J₁,norm(r, d) = J₂,norm(r, d) (15) J₂,norm(r, e) = J₃,norm(r, e) (16)
Zusammen mit der Randbedingung aus Gleichung 7 ergeben sich die fünf benötigten Gleichungen. Für die Stromdichte gilt außerdem der Zusammenhang: J →_n = jωε * / nε₀gradφ (17)
Mit der komplexen Permittivitat [7]:
Zunächst setzt man die Gleichungen 13, 14 und 7 in Gleichung 4 ein. Anschließend wird zuerst Gleichung 4 in Gleichung 17 eingesetzt. In diesen Zusammenhang können dann die Bedingungen aus Gleichung 15 und 16 eingesetzt werden. Man erhalt ein lineares Gleichungssystem Mx = b_v (s. Gleichungen 19 und 20), dessen Lösung die fehlenden Koeffizienten liefert.
Im vorherigen Abschnitt wurde ein analytischer Zusammenhang für das elektrische Potenzial für die Geometrie in Abbildung 1 hergeleitet. Nun wird mit Hilfe des Potenzials ein Ausdruck für die Sensorimpedanz in Abhängigkeit von der Geometrie, der Arbeitsfrequenz und den Materialeigenschaften hergeleitet. Hier bezeichnet der Begriff Sensorimpedanz die Impedanz zwischen der Elektrode und der Masse am Rand des Modells. Um diese bestimmen zu können, muss zunächst der Strom I durch die Elektrode ermittelt werden. Das erfolgt durch Integration der Normalkomponente der Stromdichte J →₁, die in der Elektrodenebene in positive z-Richtung in den betrachteten Bereich hinein fließt. Um Gleichung 17 zur Berechnung der Stromdichte heranziehen zu können, muss zunächst die Lösung für das elektrische Potenzial (Gleichung 4) in den Zusammenhang E → = –gradφ eingesetzt werden. So ergibt sich das folgende Integral: I = ∫_Sjωε₀ε * / 1gradφ₁dA → = jωε₀ε * / 1∫_Sgradφ₁dA → (21)
Für die Berechnung des Stroms ist nur der Anteil der Stromdichte relevant, der durch die Elektrode fließt, also senkrecht darauf steht. Die Elektrodenfläche ist ein Kreis in der r-Ebene für z = 0, also ist nur die Normalkomponente ∂φ1/∂z des elektrischen Feldes relevant. Das Flächenelement für eine solche Ebene ist dA = rdrdβ mit dem Winkel β [5]. Man leitet also φ₁(r, z) nach z ab und setzt das Ergebnis für z = 0 in Gleichung 21 ein:
Die Lösung des äußeren Integrals ist 2π, weil der Integrand eine Konstante in Bezug auf β ist. q_i und A_i,1 sind Konstanten und können vor das Integral gezogen werden. Das so übrig bleibende Integral
wird mit [12] gelöst. Damit lautet die Lösung für den Strom wie folgt:
Die komplexe Impedanz Z wird dann mit dem in den Randbedingungen vorgegebenen Potenzial u₀ über Z = u₀/I berechnet:
Die Informationen über Materialeigenschaften und Geometrie sind im Parameter A_i,1 enthalten.
In Abschnitt 2 wurden analytische Ausdrücke für das elektrische Potenzial in Gleichung 4 und die Sensorimpedanz in Gleichung 24 hergeleitet. Jetzt soll mit Hilfe eines FEM-Modells mit identischer Geometrie das Ergebnis der Berechnungen überprüft werden. Da es sich beim analytischen Ergebnis um eine unendliche Reihe handelt, muss auch der Einfluss des Reihenabbruchs untersucht werden. Die Implementierung des analytischen Modells wurde mit Hilfe von [13] und [9] durchgeführt. Zur Untersuchung des Einflusses des Reihenabbruchs nach einer Anzahl N von Reihensummanden wurde eine Berechnung mit den Abmessungen und Materialeigenschaften aus Tabelle 1 und 2 bei einer Leitfähigkeit von σ = 212 mS / cm, einer Schichtdicke e – d = 0,5 mm und einer Frequenz von 110 MHz durchgeführt, um eine ausreichend hohe Stromdichte im betrachteten Gebiet zu erreichen. Für N > 1000 liegt die relative Änderung der berechneten Werte unter 1 / 100‰.
Für die FEM-Simulation wurden ebenfalls die Parameter aus Tabelle 1 und 2 verwendet. Abbildung 2 zeigt den Betrag der komplexen Sensorimpedanz Z für eine konstante Schichtdicke e – d = 0,5 mm und drei verschiedene Leitfähigkeiten in einem Frequenzbereich von 10 kHz bis 110 MHz mit N = 10000. Im Betrag ergibt sich aufgrund des nichtleitenden Bereichs 1 der zu erwartende 1 / ω-Verlauf. Für niedrige Frequenzen bewegt sich auch die Phase bei nahezu –90°, da sich die leitfähige Schicht wie eine Elektrode verhält. Steigt die Frequenz, verbessert sich die kapazitive Kopplung in das Medium (Bereich 2 in Abbildung 1), sodass ein leitungsgebundener Strom zu fließen beginnt, welcher sich in einer steigenden Phase äußert. Da der Imaginärteil der Impedanz für hohe Frequenzen gegen Null strebt, ihr Realteil jedoch durch die Leitfähigkeit des Mediums begrenzt ist, strebt die Phase nach Erreichen ihres Maximums wieder auf ihren Ausgangspunkt zurück. Der Minimalwert des Realteils fällt für höhere Leitfähigkeiten, was zu einer Verschiebung des Phasenmaximums zu höheren Frequenzen führt. Abbildung 3 zeigt die relative Abweichung des Betrags und der Phase der Sensorimpedanz zwischen FEM-Simulation und analytischer Berechnung. Diese bewegt sich für den Betrag bei maximal 0,4‰ und für die Phase bei maximal 0,08‰.
Jetzt sollen anhand der berechneten Daten des analytischen Modells Rückschlüsse auf die Dicke und die Leitfähigkeit der dünnen leitenden Schicht in Bereich 2 von Abbildung 1 gezogen werden. Um die grundsätzlichen Zusammenhänge ermitteln zu können, erfolgt hier eine Beschränkung auf wässrige Medien mit einer Permittivität ε₂ = 78 und über die Frequenz konstante Materialeigenschaften. Grundsätzlich erlaubt das erstellte Modell jedoch auch die Verwendung von frequenzabhängigen Materialeigenschaften.
Zur Charakterisierung dünner leitfähiger Schichten wird dann mit Hilfe der von [3] zur Verfügung gestellten Software eine nichtlineare Regression der simulierten Daten an das Ersatzschaltbild aus Abbildung 6 [4] durchgeführt. Im Schaltbild repräsentiert R₁ die Kontaktimpedanz einer gedachten kapazitiv angetriebenen Elektrode. Das RC-Glied R₂∥C₂ stellt den resistiven bzw. kapazitiven Pfad der Stromdichte durch das zu untersuchende Medium dar. In C₁ gehen alle kapazitiven Anteile der Stromdichte ein, die direkt von der Elektrode zum Rand des Modells fließen. Die für die Regression benötigten Daten werden mit den Parametern aus den Tabellen 1 bis 3 in einem Frequenzbereich von 10 kHz bis 110 MHz errechnet.
Da es sich um ein kapazitiv gekoppeltes System handelt, ist die Reihenkapazität C_k von Bereich 1 bei kleinen Frequenzen dominant. Sie kann mit
approximiert und vom Impedanzspektrum subtrahiert werden. So ergibt sich in den Abbildung 4 und Abbildung 5 ein aussagekräftigeres Bild über die Eigenschaften der zu untersuchenden Schicht.
Insbesondere bei dünnen Schichten ist zu erkennen, dass der betreffende Nyquist Plot aus zumindest zwei gegeneinander verschobenen Halbkreisen besteht. Das deutet auf das Vorhandensein von zumindest zwei Zeitkonstanten, also zumindest zwei relevanten Strompfade, hin. Bei der Wahl der Modellabmessungen ist jedoch darauf zu achten, dass die empirisch ermittelte Bedingung e – d / a ≳ 0,01 erfüllt ist. Eine Empfangselektrode mit zu großem Radius am unteren Rand des Modells würde sonst zur Ausbildung weiterer dominanter Zeitkonstanten führen. Diese können dann mit einem Modell zweiter Ordnung nicht mehr approximiert werden. Ebenso liegt im betrachteten Frequenzbereich die maximal modellierbare Leitfähigkeit bei ca. 20 mS / cm. Sollen höhere Leitfähigkeiten modelliert werden, muss auch die Maximalfrequenz entsprechend steigen. Für die nachfolgend betrachteten Fälle wurde das mit dem Betrag der Impedanz gewichtete Residuum r_e ²[3] zwischen der simulierten Impedanz und der modellierten Impedanzkennlinie berechnet. Es liegt bei maximal 6,39·10^–5.
Tabelle 4 zeigt die errechneten Parameter und die von [3] berechneten relativen Abweichungen der Parameter in Abhängigkeit von der Leitfähigkeit der Schicht. Wie erwartet führt eine Änderung der Leitfähigkeit in guter Näherung nur zu einer Änderung von R₁ und R₂. Auch ist das Produkt (R₁ + R₂)·σ näherungsweise konstant, sodass bei bekannter Geometrie des Aufbaus die Leitfähigkeit der Schicht aus R₁ und R₂ berechnet werden kann.
Die Schichtdicke hat Einfluss auf mehrere Parameter der Ersatzschaltbildes (s. Tabelle 5). Steigt die Dicke der leitfähigen Schicht, so reduzieren sich entsprechend die beiden ohmschen Widerstände. Eine höhere Schichtdicke führt auch zu einer Erhöhung der mittleren Permittivität, sodass alle Kapazitäten des Ersatzschaltbildes ebenfalls steigen. Interessant ist das Verhältnis R₂/R₁ der beiden Widerstände. Für steigende Schichtdicken wird R₂ klein gegenüber dem Kontaktwiderstand R₁. Wie Tabelle 6 zeigt, ist dieses Verhältnis in guter Näherung unabhängig von der Leitfähigkeit der Schicht. Es kann also als Maß für die Schichtdicke herangezogen werden.
Es sollte der Einfluss von dünnen, leitfähigen Schichten auf die Elektrodenimpedanz eines kapazitiven Sensors untersucht werden. Hierfür wurde zunächst ein rotationssymmetrisches analytisches Modell auf Basis der Laplace-Gleichung erstellt. Aus den mit dem Modell berechneten Impedanzdaten wurden mittels nichtlinearer Regression die Parameter eines geeigneten Ersatzschaltbildes bestimmt. Es zeigt sich eine gute Übereinstimmung zwischen dem analytischen Modell und der FEM-Simulation. Aus den durchgeführten Untersuchungen geht hervor, dass sich aus den Parametern des Ersatzschaltbildes ein Maß für die Leitfähigkeit und die Schichtdicke des zu untersuchenden Mediums ableiten lässt.
Die vorgeschlagene Approximation unterliegt jedoch der empirisch ermittelten Bedingung e – d / a > 0,01. Ist diese nicht erfüllt, muss die Ordnung des Ersatzschaltbildes erhöht werden. Für den gewählten Frequenzbereich liegt die modellierbare Leitfähigkeit bei ca. 20 mS / cm. Wird dieser Wert überschritten, ist eine Anpassung des betrachteten Frequenzbereichs erforderlich.

[1] Alonso, Ramon C.: Liquid Interface Level Sensing using Electrode Arrays, UPC BarcelonaTech, Diss., 2007
[2] Asano, K.: Electrostatic potential and field in a cylindrical tank containing charged liquid. In: Electrical Engineers, Proceedings of the Institution of 124 (1977), Nr. 12, S. 1277–1281. http://dx.doi.org/10.1049/piee.1977.0269. – DOI 10.1049/piee.1977.0269. – ISSN 0020–3270
[3] Bondarenko, A. S.; Ragoisha, G.A.; Pomerantsev, A. L. (Hrsg.): Potentiodynamic electrochemical impedance spectroscopy. Nova Science Publ., 2005. – 89–102 S. http://www.abc. chemistry.bsu.by/vi/analyser/
[4] Biswas, Karabi; Sen, Siddhartha; Dutta, Pranab K.: Modeling of a capacitive probe in a polarizable medium. In: Sensors and Actuators A: Physical 120 (2005), Nr. 1, 115–122. http://dx.doi.org/http://dx.doi.org/10.1016/j.sna.2004.11.025. – DOI http://dx.doi.org/10.1016/j.sna.2004.11.025. – ISSN 0924–4247
[5] Bronstein; Semendjajew; Musiol; Mühlig: Taschenbuch der Mathematik. Verlag Harri Deutsch, 1995
[6] Henke, H.; Henke, H. (Hrsg.): Elektromagnetische Felder. Springer, 2007
[7] Küpfmüller, K.; Mathis, W.; Reibiger, A.: Theoretische Elektrotechnik: eine Einfuhrung 16¨.
Springer-Verlag GmbH, 2005 (Springer-Lehrbuch Series). http://books.google.de/books?id=oZufPwAACAAJ. – ISBN 9783540207924
[8] Lehner, G.: Elektromagnetische Feldtheorie. Springer-Verlag GmbH, 2010
[9] Lundgren, J.: ZEROBESS Zeros of Bessel functions/derivatives of 1st and 2nd kind. [Zugriff am: 12.11.2013]
[10] Li, Yi; Yang, Wuqiang; Wu, Zhipeng; Tsamakis, D.; Xie, Chenggang; Huang, Songming; Lenn, C.: Gas/oil/water flow measurement by electrical capacitance tomography. In: Imaging Systems and Techniques (IST), 2012 IEEE International Conference on, 2012, S. 83–88
[11] Rosenheinrich, Werner: Tables of some indefinite Integrals of Bessel functions. Online. http://www.fh-jena.de/~rsh/Forschung/Stoer/besint.pdf. [Zugriffam: 9.11.2013]
[12] Smythe, William R.; Harnwell, G. P. (Hrsg.): Static and Dynamic Electricity. McGraw-Hill, 1950
[13] Theodoulidis, T.: Struve Functions. Online. http://www.mathworks.de/matlabcentral/fileexchange/37302-struve-functions. [Zugriff am: 15.11.2013]
[14] Zangl, H.; Fuchs, A.; Bretterklieber, Th.: Non-invasive measurements of fluids by means of capacitive sensors. In: Elektrotechnik und Informationstechnik 126 (2009), Nr. 1–2, 8–12. http://www.scopus.com/inward/record.url? eid=2-s2.064249124635&partnerID=40&md5=af77a81f159e7fa7ba1fcce9f0589759. –

Bereich	σ [mS/cm]	r	Material
1	0	3,4	z.B. POM
2	Sweep-Parameter	78	z.B. Wässrige Lösung¨
3	0	1	z.B. Luft

Abmessung	Länge [m]
a	0,035
b	0,1
c	0,0095
d	0,002
e	Sweep-Parameter
l	0,011

σ [mS/cm]	Schichtdicke [mm]
0,5	0,25
1	0,5
1,5	0,75

	Leitfähigkeit [mS/cm]¨
	0,5	1	1,5
C₁[F]	4,59E–12	4,59E–12	4,60E–12
C₂[F]	2,64E–11	2,65E–11	2,66E–11
R₁[Ω]	5809,4	2907,8	1940,6
R₂[Ω]	3492	1743,6	1160,6
r² _e	1,06E–5	8,8E–6	8,8E–6

	Schichtdicke [mm]
	0,25	0,5	0,75
C₁[F]	3,31E–12	4,59E–12	5,72E–12
C₂[F]	2,09E–11	2,65E–11	3,26E–11
R₁[Ω]	5140,9	2907,8	2109,6
R₂[Ω]	4144,8	1743,6	996,18
r² _e	5,75E–5	8,8E–6	2,19E–6

	Leitfähigkeit [mS/cm]¨
Schichtdicke [mm]		0,5	1
		1,5
0,25	0,8084	0,8062	0,8038
0,5		0,601	0,5996
		0,5980
0,75	0,4731	0,4722	0,4712

ZITATE ENTHALTEN IN DER BESCHREIBUNG
Diese Liste der vom Anmelder aufgeführten Dokumente wurde automatisiert erzeugt und ist ausschließlich zur besseren Information des Lesers aufgenommen. Die Liste ist nicht Bestandteil der deutschen Patent- bzw. Gebrauchsmusteranmeldung. Das DPMA übernimmt keinerlei Haftung für etwaige Fehler oder Auslassungen.
Zitierte Patentliteratur

DE 102011003158 A1 [0002]

Zitierte Nicht-Patentliteratur

Alonso, Ramon C.: Liquid Interface Level Sensing using Electrode Arrays, UPC BarcelonaTech, Diss., 2007 [0062]
Asano, K.: Electrostatic potential and field in a cylindrical tank containing charged liquid. In: Electrical Engineers, Proceedings of the Institution of 124 (1977), Nr. 12, S. 1277–1281. http://dx.doi.org/10.1049/piee.1977.0269. – DOI 10.1049/piee.1977.0269. – ISSN 0020–3270 [0062]
Bondarenko, A. S.; Ragoisha, G.A.; Pomerantsev, A. L. (Hrsg.): Potentiodynamic electrochemical impedance spectroscopy. Nova Science Publ., 2005. – 89–102 S. http://www.abc. chemistry.bsu.by/vi/analyser/ [0062]
Biswas, Karabi; Sen, Siddhartha; Dutta, Pranab K.: Modeling of a capacitive probe in a polarizable medium. In: Sensors and Actuators A: Physical 120 (2005), Nr. 1, 115–122. http://dx.doi.org/http://dx.doi.org/10.1016/j.sna.2004.11.025. – DOI http://dx.doi.org/10.1016/j.sna.2004.11.025. – ISSN 0924–4247 [0062]
Bronstein; Semendjajew; Musiol; Mühlig: Taschenbuch der Mathematik. Verlag Harri Deutsch, 1995 [0062]
Henke, H.; Henke, H. (Hrsg.): Elektromagnetische Felder. Springer, 2007 [0062]
Küpfmüller, K.; Mathis, W.; Reibiger, A.: Theoretische Elektrotechnik: eine Einfuhrung 16¨ [0062]
Springer-Verlag GmbH, 2005 (Springer-Lehrbuch Series). http://books.google.de/books?id=oZufPwAACAAJ. – ISBN 9783540207924 [0062]
Lehner, G.: Elektromagnetische Feldtheorie. Springer-Verlag GmbH, 2010 [0062]
Lundgren, J.: ZEROBESS Zeros of Bessel functions/derivatives of 1st and 2nd kind. [Zugriff am: 12.11.2013] [0062]
Li, Yi; Yang, Wuqiang; Wu, Zhipeng; Tsamakis, D.; Xie, Chenggang; Huang, Songming; Lenn, C.: Gas/oil/water flow measurement by electrical capacitance tomography. In: Imaging Systems and Techniques (IST), 2012 IEEE International Conference on, 2012, S. 83–88 [0062]
Rosenheinrich, Werner: Tables of some indefinite Integrals of Bessel functions. Online. http://www.fh-jena.de/~rsh/Forschung/Stoer/besint.pdf. [Zugriffam: 9.11.2013] [0062]
Smythe, William R.; Harnwell, G. P. (Hrsg.): Static and Dynamic Electricity. McGraw-Hill, 1950 [0062]
Theodoulidis, T.: Struve Functions. Online. http://www.mathworks.de/matlabcentral/fileexchange/37302-struve-functions. [Zugriff am: 15.11.2013] [0062]
Zangl, H.; Fuchs, A.; Bretterklieber, Th.: Non-invasive measurements of fluids by means of capacitive sensors. In: Elektrotechnik und Informationstechnik 126 (2009), Nr. 1–2, 8–12. http://www.scopus.com/inward/record.url? eid=2-s2.064249124635&partnerID=40&md5=af77a81f159e7fa7ba1fcce9f0589759. – [0062]

Claims

Verfahren zum Betreiben eines kapazitiven Füllstandsgrenzschalters für wässrige Lösungen in einem aus einem nichtleitenden Material bestehenden Tank, der an der Außenwand des Tanks montierbar ist, mit einer Messelektrode die einen Durchmesser von weniger als 30 mm aufweist, und einer mit der Elektrode verbundenen Messschaltung, die den Betrag und die Phase der elektrischen Admittanz zwischen der Messelektrode und der Umgebung ermittelt, und die ein Schaltsignal ausgibt, wenn folgende zwei Bedingungen erfüllt sind: der Betrag der Admittanz muss größer als ein vorgegebener Grenzwert sein und der Phasenwinkel muss größer als ein vorgegebener Grenzwinkel sein.
Verfahren nach Anspruch 1, dadurch gekennzeichnet, dass die Messfrequenz größer als 1 MHz ist.
Verfahren nach einem der vorhergehenden Ansprüchen, dadurch gekennzeichnet, dass die Messfrequenz in einem Bereich zwischen 1–20 MHz liegt.
Verfahren nach nach einem der vorhergehenden Ansprüchen, dadurch gekennzeichnet, dass die Frequenz so gewählt wird, dass der Phasenwinkel bei einer Anhaftung des Mediums und der Phasenwinkel bei vollem Tank einen merklichen Unterschied zeigen.
Verfahren zum Betreiben eines kapazitiven Füllstandsgrenzschalters nach nach einem der vorhergehenden Ansprüchen, dadurch gekennzeichnet, dass bei einer Wandstärke des Tanks von 1 mm und einer Leitfähigkeit des Mediums von 800 mS/cm die Messfrequenz bei 10 MHz und, die Admittanz größer als 5 10^–4S und der Phasenwinkel größer als 89° ist.
Verfahren zum Betreiben eines kapazitiven Füllstandsgrenzschalters nach nach einem der vorhergehenden Ansprüchen 1–4, dadurch gekennzeichnet, dass bei einer Wandstärke des Tanks von 10 mm und einer Leitfähigkeit des Mediums von 30 mS/cm die Messfrequenz bei 10 MHz und, die Admittanz größer als 1 10^–4 S und der Phasenwinkel größer als 89° ist.
Verfahren zum Betreiben eines kapazitiven Füllstandsgrenzschalters nach einem der vorhergehenden Ansprüche, dadurch gekennzeichnet, dass ein auf die Verschmutzung der Tankinnenwand im Bereich der Elektrode hinweisendes Warnsignal ausgegeben wird, wenn der Phasenwinkel kleiner als ein vorgegebener Grenzwinkel ist.